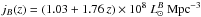| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526712 | |
| Published online | 20 November 2015 | |
Supernova rates from the SUDARE VST-OmegaCAM search
I. Rates per unit volume⋆,⋆⋆
1 INAF, Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: enrico.cappellaro@oapd.inaf.it
2 INAF, Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
3 Departemento de Ciencias Fisicas, Universidad Andres Bello, 037-0134 Santiago, Chile
4 Millennium Institute of Astrophysics, Santiago, Chile
5 Astrophysics Group, Physics Department, University of the Western Cape, Private Bag X17, 7535 Bellville, Cape Town, South Africa
6 INAF–Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
7 INAF, Osservatorio Astronomico di Catania, via S. Sofia 78, 95123 Catania, Italy
8 Dipartimento di Fisica, Universitá Federico II, 80126 Napoli, Italy
9 Astrophysics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
10 Department of Physical Sciences, The Open University, Milton Keynes, MK7 6AA, UK
11 ASI Science Data Center, via del Politecnico snc, 00133 Roma, Italy
Received: 9 June 2015
Accepted: 14 September 2015
Aims. We describe the observing strategy, data reduction tools, and early results of a supernova (SN) search project, named SUDARE, conducted with the ESO VST telescope, which is aimed at measuring the rate of the different types of SNe in the redshift range 0.2 < z < 0.8.
Methods. The search was performed in two of the best studied extragalactic fields, CDFS and COSMOS, for which a wealth of ancillary data are available in the literature or in public archives. We developed a pipeline for the data reduction and rapid identification of transients. As a result of the frequent monitoring of the two selected fields, we obtained light curve and colour information for the transients sources that were used to select and classify SNe by means of an especially developed tool. To accurately characterise the surveyed stellar population, we exploit public data and our own observations to measure the galaxy photometric redshifts and rest frame colours.
Results. We obtained a final sample of 117 SNe, most of which are SN Ia (57%) with the remaining ones being core collapse events, of which 44% are type II, 22% type IIn and 34% type Ib/c. To link the transients, we built a catalogue of ~1.3 × 105 galaxies in the redshift range 0 < z ≤ 1, with a limiting magnitude KAB = 23.5 mag. We measured the SN rate per unit volume for SN Ia and core collapse SNe in different bins of redshifts. The values are consistent with other measurements from the literature.
Conclusions. The dispersion of the rate measurements for SNe-Ia is comparable to the scatter of the theoretical tracks for single degenerate (SD) and double degenerate (DD) binary systems models, therefore it is not possible to disentangle among the two different progenitor scenarios. However, among the three tested models (SD and the two flavours of DD that either have a steep DDC or a wide DDW delay time distribution), the SD appears to give a better fit across the whole redshift range, whereas the DDC better matches the steep rise up to redshift ~1.2. The DDW instead appears to be less favoured. Unlike recent claims, the core collapse SN rate is fully consistent with the prediction that is based on recent estimates of star formation history and standard progenitor mass range.
Key words: supernovae: general / galaxies: star formation / Galaxy: stellar content / surveys
Based on observations made with ESO telescopes at the Paranal Observatory under programme ID 088.D-4006, 088.D-4007, 089.D-0244, 089.D-0248, 090.D-0078, 090.D-0079, 088.D-4013, 089.D-0250, 090.D-0081.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The evolution of the supernova (SN) rate with redshift provides the observational link between the cosmic star formation history (SFH), the initial mass function, and the stellar evolutionary scenarios leading to the explosions. Until recently, the available measurements were limited to the local Universe and to sparse, sometimes conflicting, high redshift measurements (e.g. Dahlen et al. 2012; Maoz et al. 2014,and references therein). The new generation of panoramic detectors, now available in many observatories, has substantially improved the survey capabilities and, as a consequence, the number of SN searches and rate measurements. Most of the searches were devoted to type Ia SNe whose progenitor scenario is still strongly debated but the interest in core collapse SNe (CC SN) is also growing.
The notion that measuring the evolution of the type Ia SN rate with redshifts, in combination with measuring the SFH, can be used to constrain the SN Ia progenitor scenarios was first illustrated by Madau et al. (1998; see also Sadat et al. 1998; Ruiz-Lapuente & Canal 1998). Early measurements were puzzling, showing a very rapid raise of the SN Ia rate up to redshift ~1 and then a decline at higher redshift (Dahlen et al. 2004, 2008; Barris & Tonry 2006). This implied a long delay from star formation to explosion for the SN Ia progenitors, which appears to conflict with the indications derived from measuring rates in the galaxies of the local Universe (Mannucci et al. 2005). Subsequent measurements did not confirm the early results but the issue is still being debated (e.g. Kuznetsova et al. 2008; Rodney & Tonry 2010; Smith et al. 2012; Perrett et al. 2012; Graur et al. 2014, and reference therein).
Early measurements of CC SNe show that, as expected, the rates track the cosmic star history (Botticella et al. 2008), though the scaling factor seems to be a factor two smaller than expected from the SFH. A possible explanation is that many dim CC SNe are missed by SN searches (Horiuchi et al. 2011) and/or part of the missing SNe may be hidden in the dusty nuclear regions of star-burst galaxies (Dahlen et al. 2012, and reference therein). However, it is fair to say that the significance of the claimed discrepancy is still doubtful.
In addition, we note that, in most cases, the cosmic SN rates were derived from surveys designed to identify un-reddened SN Ia for the cosmological distance ladder. In these cases, the specific observing strategy and/or candidate selection criteria may introduce biases in the event statistics, which can be difficult to account for adequately. As a consequence, the SN rates derived from these surveys may be inaccurate.
Knowledge of the properties of the parent stellar population is fundamentally important when using the SN rate evolution to constrain the SN progenitor scenarios. This means that the volume of Universe searched for SNe needs to be characterized in terms of the galaxy distribution as a function of redshift, mass, and star formation history.
Based on these considerations, we conceived a new SN search (Supernova Diversity and Rate Evolution, SUDARE, Botticella et al. 2013), with a primary goal of measuring SN rates at medium redshift, that is 0.2 <z< 0.8. To combine the requirements of good statistics (>200 events) and the availability of ancillary data for the surveyed fields, we planned a four-year project to monitor two very well known extragalactic fields, the Chandra Deep Field South (CDFS) and the Cosmic Evolution Survey (COSMOS) fields. As a result of the long term commitment of many different observing programmes, extended multi-band photometry is available for these fields. These data allow an accurate characterization of the galaxy sample, which is crucial to inferring general properties of the SN progenitors.
The present paper describes the SUDARE survey strategy, the procedures for the identification of transients, and the SN candidate selection and classification after the first two years of observations. Then, we discuss the definition of the galaxy sample and the procedure to derive photometric redshifts. Finally, we estimate the SN rates per unit volume at different redshifts and compare them to published estimates. A detailed study of SN rates as a function of different galaxy parameters will be presented in a companion paper (Botticella et al., in prep., hereafter PII).
Throughout the paper, we adopt H0 = 70kms-1Mpc-1, ΩM = 0.3, and ΩΛ = 0.7. Magnitudes are in the AB system.
Field coordinates and compact log of observations.
2. The survey
The SUDARE SN survey was performed using the VLT Survey Telescope (VST, Capaccioli & Schipani 2011) equipped with the OmegaCAM camera (Kuijken 2011), that started regular operations in October 2011 at ESO Paranal (Chile). The VST has a primary mirror of 2.6 m and a f/5.5 modified Ritchey-Chretien optical layout that is designed to deliver a large, uniform focal plane. The camera is equipped with a mosaic of 8 × 4 CCDs, each with 4k × 2k pixels. These cover one square degree with a pixel scale of 0.214″ pix-1, which allows for an optimal sampling of the PSF, even in good seeing conditions. The thinned CD44-82 devices from E2V have the advantage of an excellent quantum efficiency in the blue bands, with the only drawback being that the i and z bands suffer from significant fringing contamination.
Most of the observing time at this facility is committed to ESO public surveys1 but a fraction of the time is dedicated to guaranteed time observations (GTO) that were made available to the telescope and instrument teams in reward for their investments in the construction and installation of the instruments.
SUDARE is a four-year programme and this paper is devoted to analysing the first two observing seasons for VOICE-CDFS and one season for COSMOS. We are currently completing the monitoring of both fields for the two subsequent seasons.
The time allocated to our project to monitor VOICE-CDFS was from the VST and OMEGAcam GTO. The observing strategy is to span 4 deg2 in four pointings, with one pointing for each observing season (August to January). Here we present data from two of these pointings.
To extend the photometric coverage, we implemented a synergy with the VOICE (VST Optical Imaging of the CDFS and ES1 Fields) project (Covone et al. in preparation). VOICE is a GTO program that aims to secure deep optical counterparts to existing multi-band photometry of selected fields. The multiband catalogue will be used to study the mass assembly and star formation history in galaxies by combining accurate photometric redshifts, stellar masses, and weak lensing maps.
The monitoring of the COSMOS field instead relies on a proposal submitted for ESO VST open time (P.I. Pignata). For this field we maintained the same pointing coordinates from one season to the next. This allows us to detect transients with very long time evolution. However, the data may be prone to cosmic variance because of the limited area that was probed. The survey strategy consists of monitoring the selected fields every three days in the r band, excluding only ~5 days around full moon. The exposure time is 30 min with the aim of reaching a magnitude limit of 25 in average sky conditions. Each observation is split into five × 6 min exposures with a dithering pattern designed to fill the gaps between the detector chips (that range from 25 to 85 arcsec). Because of the dithering, the effective area covered, by combining the exposures of a given field, is 1.15 deg2, although there is a reduced S/N ratio at the edge.
With a more relaxed cadence (3–4 times per month), we also planned for g- and i-band exposures. With these observations we can measure the colour of the transients that are essential for their photometric classification and obtain an estimate of the extinction along the line of sight. Adapting to the rules for the observing blocks in service mode at ESO, the planned observing sequence is g−r, r, r−i with a three-day interval between each block. To ensure good quality images, we required a maximum seeing of 1.2″ (FWHM) at the beginning of the exposure. This, along with the obvious requirement of clear sky, implied that the actual epochs of observations often deviate from the ideal scenario, mainly because of unsuitable sky conditions.
Table 1 lists the pointing coordinates for each field, along with the field size, the observing season, the number of available epochs in the different bands, and the range and median value of the seeing measured for the r-band exposures. The full log of observations is given in Table A.1 where, for each epoch, we list the seeing (in arcsec) and m50, the magnitude corresponding to a transient detection efficiency of 50% (cf. Sect. 3).
The SN search was complemented by three runs of one night each at the ESO-VLT for the spectroscopic classification of a dozen candidates. These observations, described in Sect. 4.3, were intended as spot checks of the SN photometric classification tool (Sect. 4). We note that, as a by-product, the SUDARE data archive was also used to explore the performance and completeness of AGN detection via variability (De Cicco et al. 2015; Falocco et al. 2015).
2.1. Image calibration
The raw data were retrieved from the ESO archive and transferred to the VST data-reduction node in OAC-Naples. Here the first part of the data reduction was performed using the VST-Tube pipeline (Grado et al. 2012). A description of the VST-Tube data reduction process is reported in De Cicco et al. (2015). In short, the pipeline first performs flat fielding, gain harmonisation, and illumination correction and all images for a given field are registered to the same spatial grid and photometric scale. Finally, the dithered images for one epoch are median averaged to produce one stacked image. The pipeline also delivers weight pixel masks that track each pixel, with the number of dithered exposures contributing to the combined image, after accounting for CCD gaps, bad pixels and cosmic rays being rejected.
The pipeline was also used to produce deep stacked images by combining all the exposures in a given filter with the best image quality, i.e. those with a seeing ≤0.8″. These stacked images, which reach a limiting magnitude ~1 mag fainter than good single epoch exposures (the 3σ mag limits are 26.2, 25.6, 24.9 mag for r, g, and i bands, respectively) were used to extract galaxy photometry to complement the public multiband catalogues. (Section 6).
2.2. Transient detection
To detect transient sources and the selection of SN candidates, the mosaic images were processed with an ad hoc pipeline. This was made up of a collection of python scripts that makes use of pyraf and pyfits2 tasks and incorporates other publicly available software for specific tasks, in particular SExtractor (Bertin & Arnouts 1996) for source detection and characterisation, hotpants3 for PSF match and image difference, daophot (Stetson 1987) for accurate point spread function (PSF) fit photometry, stilts4 for catalogue handling, and mysql for the transient database. The flowchart of the SUDARE pipeline is as follows:
-
1.
We produced a mask for saturated stars that is combined with theweight map produced by VST-Tube to build a bad pixel mask foreach mosaic image. Those pixels flagged as “bad” were excludedfrom further analysis.
-
2.
For each image we computed the difference from a selected template image. This required deriving the convolution kernel that matches the PSF of the two images. The method is described in Alard (2000) though we used the hotpants implementation. For the first observing season, we note that we did not have earlier templates and we therefore used images acquired on purpose a few months after completion of the transient survey campaign as templates.
-
3.
Using SExtractor, the transient candidates were identified as positive sources in the difference image. Depending on the image quality and detection threshold, the candidate list starts with several thousands objects for each epoch. Most detections are artefacts that result from poorly masked CCD defects, poorly removed cosmic rays, residual from the subtraction of bright sources, reflection ghosts from bright sources, etc.
-
4.
The transient candidates were ranked by means of a custom algorithm that uses a number of measured SExtractor metrics for the detected sources. The most informative parameters and the ranking scores were selected and calibrated through extensive artificial star experiments. In these experiments, a number of fake stars were placed in the search image, which is then processed through the detection and ranking pipeline. The success rate of artificial star recovery was compared to the number of residual spurious sources. We found that the most informative parameters were the source FWHM, flux_ratio, isoarea and magnitudes, which had been measured at different apertures. By properly selecting these parameters, we can drastically reduce the number of spurious events while limiting the number of good candidates that were improperly rejected. The performance of the ranking algorithm depends on image quality. On average, we found that we can eliminate ~95% of the spurious transients at the cost of losing ~5% of good candidates. Correction for the lost SNe is incorporated in the detection efficiency (cf. Sect. 3), since we used the same algorithm to select real and fake SNe. After this selection, 100 candidates per field and epoch are typically left for the next steps of human inspection and validation.
-
5.
To associate each transient with its possible host galaxy, we cross-correlated the transient list with the galaxy catalogues derived from the deep r-band-stacked image (cf. Sect. 6). A galaxy is adopted as the host for a given transient when the latter appears engulfed in the galaxy’s boundaries. The boundaries are those of the ellipse defined by the SExtractor parameters CXX, CYY, and CXY through the equation
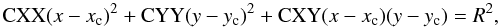 where xc, yc is the galaxy centre and, following the SExtractor’s manual, we assume that the isophotal limit corresponds to R = 3. In four cases the transient/host galaxy-pairing was ambiguous because of the overlap of the ellipses of different galaxies. In these cases, we also compared the consistency of the host galaxy redshift with the indication of SN photometric classification (cf. Sect. 4). For only two transients were no counterparts detected in the deep-stacked image (cf. Table A.2).
where xc, yc is the galaxy centre and, following the SExtractor’s manual, we assume that the isophotal limit corresponds to R = 3. In four cases the transient/host galaxy-pairing was ambiguous because of the overlap of the ellipses of different galaxies. In these cases, we also compared the consistency of the host galaxy redshift with the indication of SN photometric classification (cf. Sect. 4). For only two transients were no counterparts detected in the deep-stacked image (cf. Table A.2). -
6.
The information available for the best ranked candidates was posted on web pages where the user can inspect the images and the candidate metrics for the search and template epochs. They can then select the good candidates, assigning each of them a preliminary classification according to different classes (SN, AGN, variable star, moving object etc.). The selected candidates are then archived in a mysql database.
-
7.
For all selected candidates, we derived accurate light curves by measuring the source magnitude at all available epochs. We measured both aperture and PSF-fit photometry in the original search images and in the difference images. We verified that the PSF-fit gives more reliable measurements than plain aperture integration, mainly because PSF photometry is less sensitive to background noise.
The transient search process was performed in the r band for each epoch. In general good SN candidates will have multiple detections in the database because of the dense temporal sampling. In principle, we can easily implement a candidate selection, based on multiple occurrences of a given source in the database, which would further reduce spurious candidates. However, at the present stage of the project, we have adopted a conservative approach, accepting the burden of the visual examination of many candidates to maximise the proportion of completeness.
3. Detection efficiency
To derive the SN rates, we need to obtain an accurate estimate of the completeness of our search. This is done by extensive artificial star experiments that explore a range of magnitudes and positions in the images.
For every search image, we first obtain the PSF from the analysis of isolated field stars. Then, a number of fake stars of a given magnitude, which are generated by scaling the PSF and adding the proper Poisson noise, are injected onto the search image. To mimic the range of properties of real sources, three different criteria are adopted to position the fake stars, with roughly the same number of stars for each class. The three classes are:
-
events associated with galaxies. From the source catalogue on thefield (cf. Sect. 6) we picked a random sample ofgalaxies, and one fake star was placed in each of them. Theposition inside the galaxy was chosen randomly, following thedistribution of r-band flux intensity.
-
events that coincide with persistent, point-like sources. Fake stars were added to the same position of existing sources in the field. This mimics SNe in the nucleus of compact host galaxies, variable AGNs, and variable stars.
-
events with no counterpart in the template image. These were placed at random positions across the field of view, irrespective of existing sources or of the possible coincidence with CCD defects or gaps.
The images with fake stars were processed with the search pipeline and the number of detected events surviving after the ranking procedure were counted. The percentage of detected over injected events gives the detection efficiency for the given magnitude. The experiment is repeated, sampling the magnitude range of interest (18 <r< 26) to derive the detection efficiency as a function of magnitude.
We inject 500 fake stars per experiment per image and repeat the experiment five times for a given magnitude. In fact, adding a large number of fake stars could bias the computation of the convolution kernel, hence the image subtraction process that makes the experiments less reliable.
An example of the derived detection efficiencies as a function of magnitude for one epoch and field is shown in Fig. 1, where the error bars show the dispersions from the three experiments. As can be seen in Fig. 1, the detection efficiency as a function of magnitude can be represented by the following analytical function: 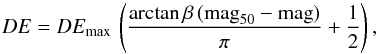 (1)where DEmax is the maximum value of the detection efficiency, mag50 is the magnitude corresponding to the 50% drop in the detection efficiency, and β measures the decline rate of the DE. The best-fit parameters are determined through least squares minimisation of the residuals (e.g. Fig. 1). Note that the maximum detection efficiency is ~95%, even at the bright magnitude end. This is because not all the pixels of the image are useful, and indeed the bad pixel mask (cf. step 1 of the SUDARE pipeline) flags 5−10% of the image area.
(1)where DEmax is the maximum value of the detection efficiency, mag50 is the magnitude corresponding to the 50% drop in the detection efficiency, and β measures the decline rate of the DE. The best-fit parameters are determined through least squares minimisation of the residuals (e.g. Fig. 1). Note that the maximum detection efficiency is ~95%, even at the bright magnitude end. This is because not all the pixels of the image are useful, and indeed the bad pixel mask (cf. step 1 of the SUDARE pipeline) flags 5−10% of the image area.
 |
Fig. 1 Transient detection efficiency as a function of magnitude for the r-band observation of COSMOS on 2012 March 15. The dots are the averages of 3 artificial star experiments with the errorbar being the dispersion whereas the line is the adopted efficiency curve after the fit with the Eq. (1) (DEmax = 93%, mag50 = 23.0 mag, and β = 6.1). |
We verified that the detection efficiencies measured independently for each of the three classes of fake stars, as described above, are similar to a dispersion of mag50 values of ~0.3 mag. and hereafter we will use these average values. We also found that the values of DEmax and β are very similar for each epoch and field with a mean value of 95% ± 3 and 4 ± 2, respectively. The artificial star experiment described above was repeated for all epochs and fields of the search, and the resulting detection efficiencies are used in the rate calculation.
List of templates SNe used for the SUDARE’s SN photometric classification tool.
4. Transient classification
The result of the transient search was a list of ~350 SN candidates. A percentage of these transients are coincident with persistent sources and can, therefore, be SNe in the nucleus of the host galaxies, as well as variable stars or AGNs. In fact, after the analysis of Falocco et al. (2015) and De Cicco et al. (2015), three candidates with slow evolving light curves were found to coincide with X-ray sources. These were classified as AGN and removed from the SN candidate sample. We also removed all transients with spectroscopic or photometric redshift z> 1 (~25%) from the SN candidate list.
We used the measured light curve and colour evolution to constrain the nature of the transients and to classify SNe in their different types. Taking a conservative approach, we only considered candidates with at least five photometric measurements at different epochs (even in different filters) were considered. Because of the frequent monitoring of our survey, this criterion excludes four candidates with a negligible effect on the SN counts.
The photometric classification is more reliable if the redshift of the host galaxy is available. When the transient is not associated with a host galaxy or when the host redshift is not available, the redshift is left as a free parameter in the transient light curve fitting (see next section).
4.1. Photometric classification of SNe
For the photometric classification we used a tool developed for the SUDARE project. This tool compares the SN candidate multi-colour light curves with those of SN templates and identifies the best-matching template, redshift, extinction, and luminosity class. The tool was developed following the strategy of the SN classification tool PSNID (Sako et al. 2011). We developed our own tool because we wanted to explore different priors for the fitting parameters and a different classification scheme.
We collected a sample of templates for different SN types, for which both multicolour light curves and sequence of spectra are available (Table 2). The spectra were needed to estimate the K-correction. The templates were retrieved from a database of SN light curves and spectra that we collected in the study of SNe at ESO and the ASIAGO Observatory (the template spectra can also be downloaded from WISEREP6, the SN spectra database; Yaron & Gal-Yam 2012).
The templates were selected to represent well-established SN types, namely Ia, Ib, Ic, IIb, II Plateau and Linear, and IIn, with the addition of representative peculiar events (see individual references for details). In particular, we included SN 2008es as representative of the recently discovered class of very luminous SNe (SLSN, Quimby et al. 2007, 2013; Gal-Yam 2012) which, although intrinsically very rare, may be detected in high redshift searches because of their large volume sampling. The steps for the photometric typing were:
-
for each template, we derived K-correction tables as a function of phase from maximum and redshift (in the range 0 <z< 1). K-corrections were obtained as the difference of the synthetic photometry measured on the rest frame spectra and on the same spectra once properly redshifted. The redshift range, for which we could derive accurate K-correction, is limited by the lack of UV coverage from most templates. This is a particular problem for the g band, where we were forced to accept uncertain extrapolations;
-
the K-corrected light curves of template SNe were used to predict the observer frame light curves in the gri bands, exploring the 0 <z< 1 redshifts range and the −0.3 <EB−V< 1 mag extinction range (the negative lower limit for the EB−V range allows for uncertainties in the correction of the template extinction and for variance in the intrinsic SN colour). With the goal to minimise the uncertainties in the K-correction, the template input band was taken to best match the observer frame band for the given redshift, e.g. we use the template V,B,U bands to predict the observer frame r-band light curve of SNe at redshift z ~ 0.1, 0.4, and 0.7, respectively;
-
we estimated the goodness of the fit of the template to the observed light curve, by computing the sum of the square of flux residuals weighted by the photometric errors (χ2) for each simulated light curve of the grid. As well as the redshift and extinction ranges, we explored a range of epochs of maximum, Tmax (the initial guess is the epoch of the observed r band’s brightest point) and of intrinsic luminosities, and Δ(μ) (allowing for a ±0.3 mag flux scaling of the template). The residuals for all bands were summed up together and, therefore, each band contributes to the overall χ2 with a weight proportional to the number of measurements;

Fig. 2 Example of the output of the SN-typing procedure. The top panel shows the observed r-band light curve that, in this case, is compared to the template K-corrected B-band light curve. The bottom panels show the observed light curve and template fit for the g band (left) and i band (right). Blue dots represent the SN candidate observed magnitudes (arrows indicate upper limits) while red open circles represent the template photometry. The legend identifies the best fitting template and parameters.
-
for the selection of the best-fitting template, we used Bayesian model selection (e.g. Poznanski et al. 2007a; Kuznetsova & Connolly 2007; Rodney & Tonry 2009). In particular, following Sako et al. (2011), we computed the Bayesian evidence for each SN type:
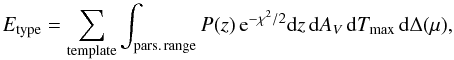 where the fitting parameters are the redshift
z,
with P(z) its probability
distribution, the extinction AV, the time of
maximum Tmax, and the flux-scaling factor
Δ(μ).
The spectroscopic redshift was used as a prior if available and in this case for
P(z) we adopted a normal
distribution centered at the spectroscopic redshift and with σ = 0.005. Otherwise,
if a photometric redshift estimate was available, we used as redshift prior the
P(z) provided by the
photometric redshift code (cf. Sect. 6.3.1).
In the worst case, either when the host galaxy was not detected, or when the
photometric redshift was poorly constrained, we adopted a flat prior in the range
0 <z<
1. In all cases we adopted flat prior for the extinction
distribution and for the flux scaling. More critical was the choice of templates. As
emphasised by Rodney & Tonry (2009), the
Bayesian approach relies on an appropriate template list that should be as complete
as possible but, at the same time, should avoid duplicates. When the template list
includes rare, peculiar events, especially if they mimic the properties of a more
frequent SN type, it is appropriate to use frequency priors. Alternatively, for
specific applications one may exclude ambiguous cases or rare, peculiar SN types
(cf. Sako et al. 2011) from the template
list. Our template list, given in Table 2, is
intended to represent the full range of the most frequent SN type with a number of
templates for each class that is broadly consistent with their frequency in a volume
limited SN sample (Li et al. 2011b). After
that, we adopted flat priors for the relative rate of each template within a given
class and for the relative rates of the different SN types. We computed the Bayesian
probability for each of the main SN types as
where the fitting parameters are the redshift
z,
with P(z) its probability
distribution, the extinction AV, the time of
maximum Tmax, and the flux-scaling factor
Δ(μ).
The spectroscopic redshift was used as a prior if available and in this case for
P(z) we adopted a normal
distribution centered at the spectroscopic redshift and with σ = 0.005. Otherwise,
if a photometric redshift estimate was available, we used as redshift prior the
P(z) provided by the
photometric redshift code (cf. Sect. 6.3.1).
In the worst case, either when the host galaxy was not detected, or when the
photometric redshift was poorly constrained, we adopted a flat prior in the range
0 <z<
1. In all cases we adopted flat prior for the extinction
distribution and for the flux scaling. More critical was the choice of templates. As
emphasised by Rodney & Tonry (2009), the
Bayesian approach relies on an appropriate template list that should be as complete
as possible but, at the same time, should avoid duplicates. When the template list
includes rare, peculiar events, especially if they mimic the properties of a more
frequent SN type, it is appropriate to use frequency priors. Alternatively, for
specific applications one may exclude ambiguous cases or rare, peculiar SN types
(cf. Sako et al. 2011) from the template
list. Our template list, given in Table 2, is
intended to represent the full range of the most frequent SN type with a number of
templates for each class that is broadly consistent with their frequency in a volume
limited SN sample (Li et al. 2011b). After
that, we adopted flat priors for the relative rate of each template within a given
class and for the relative rates of the different SN types. We computed the Bayesian
probability for each of the main SN types as 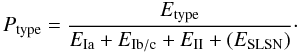 We note that for the purpose of assigning
probability, we merged regular type II and type IIn templates. However, in the
subsequent analysis, we indicated when the best-fitting template (the one with the
highest probability) is a type IIn. Also, after verifying that none of our candidate
has a significant probability of matching an SLSN, the corresponding template was
dropped from the fitting list and the ESLSN term in Eq. (4.1) cancelled. This was done to allow a direct
comparison with SNANA (see next section);
We note that for the purpose of assigning
probability, we merged regular type II and type IIn templates. However, in the
subsequent analysis, we indicated when the best-fitting template (the one with the
highest probability) is a type IIn. Also, after verifying that none of our candidate
has a significant probability of matching an SLSN, the corresponding template was
dropped from the fitting list and the ESLSN term in Eq. (4.1) cancelled. This was done to allow a direct
comparison with SNANA (see next section); -
for the most probable SN type, we record the best fitting template along with the fit parameters corresponding to the χ2 minimum. Of about 250 transients, 117 were classified as SNe. Most of the remaining ones have erratic light curves that are consistent with those of AGNs. An example of the output of the SN-typing procedure is shown in Fig. 2.
 (Col. 14), the number of photometric measurements with, in parenthesis, the number of measurements with S/N ratio >2 (Col. 15) and the integrated right tail probability of the χ2 distribution (Pχ2, Col. 16).
(Col. 14), the number of photometric measurements with, in parenthesis, the number of measurements with S/N ratio >2 (Col. 15) and the integrated right tail probability of the χ2 distribution (Pχ2, Col. 16).
In some cases, the Pχ2 probability is fairly low (15 SNe have Pχ2< 10-4). Sometimes this is because of one or two deviant measurements, while sometimes there is evidence of some variance in the light curve, which is not fully represented by the adopted template selection. We have to consider the possibility that these events are not SNe.
Also, for some candidates with a small χ2, the number of actual detections (photometric measurements with S/N ratio >2) is so small that it is not possible to assess the SN nature of the transient source definitely (for 12 candidates the number of detection is Ndet< = 7).
To these probable SNe (indicated with PSN in the last column of Table A.2), we attribute a weight 0.5 in the rate calculation. The impact of the arbitrary thresholds for Pχ2 and the Ndet and the adopted PSN weight will be estimated in Sect. 7.3.
To evaluate the uncertainties of our classification tool, in the next two sections we compare our derived SN types with a) photometric classifications that were obtained using the public software package SNANA (Kessler et al. 2009) and b) with the spectroscopic observations of a small sample of “live” transients, which were observed while still in a bright state.
4.2. Comparison with the photometric classifications by PSNID in SNANA
To check our procedure and evaluate the related uncertainties, we performed the photometric classification of our SN candidates using the public code PSNID in the SNANA7 implementation (Sako et al. 2011; Kessler et al. 2009). Overall, the approach of PSNID is similar to the one adopted here; besides the implementation of the computation algorithm, the main difference is in the template list. In particular, for SN Ia we adopted the fitting set-up of Sako et al. (2011), while for CC SNe we used the extended list of 24 templates available in the SNANA distribution8.
For the fit with PSNID, we also set the host-galaxy redshift as a prior with the same range of uncertainty as in our procedure. In this case, however, for photometric redshift we also assume a normal distribution for P(z) with the σ provided by the photometric redshift code.
A comparison of the classifications obtained with the two tools is illustrated in Fig. 3. The pie chart shows the SN classifications in the four main types using the SUDARE tool, and the sectors with different colours within a given wedge show the PSNID classifications. For two events, marked in grey, the fit with PSNID fails.
The figure shows that the identification of SN Ia is quite consistent (92% of the type Ia classified by our tool are confirmed by PSNID) and there is a good agreement also for the normal type II (77% of the classifications are matched). The agreement is poor for type Ib/c and for type IIn (only 40% are matched in both cases). The latter result is not surprising, considering the wide range of luminosity evolution: the choice of input templates is crucial for these classes of SNe.
However, we note that, despite the discrepancy in the classification of individual events of specific sub-types, there is an excellent agreement of the event counts in each class, except for type IIn, as shown in Table 3. This implies that, as far as the SN rates are concerned, using either classification tools makes a little difference, with the exception the exception of type IIn where the difference is ~40%.
In Table 3, we also report the SN count for the different classes using the Bayesian probability. It appears that, with respect to the count of the most probable type, the number of SN Ia is slightly reduced, whereas the number of Ib/c increases. This is not unexpected, given the similarity of the light curves of type Ia and Ib/c (in many cases an event can have a significant probability of being either a type Ia or a type Ib/c) and the fact that type Ia are intrinsically more frequent than Ib/c. The effect however is small, <5% in both cases.
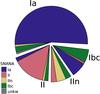 |
Fig. 3 Comparison of the SN classifications obtained with the different tools. The exploded wedges are the SN type fractions obtained with our SUDARE tool and the coloured sectors are the SNANA classification. |
Comparison of photometric classification with the different tools. In parenthesis we report the events labelled as probable SNe.
4.3. Comparison with spectroscopic classification
For a small sample of the SN candidates we obtained immediate spectroscopic classification. Observations were scheduled at the ESO VLT telescope equipped with FORS2 at three epochs for a total allocation of two nights. The telescope time allocation, which was fixed several months in advance of the actual observations, dictated the choice of the candidates. We selected transients that were “live” (above the detection threshold) at the time of observations, and among these, we gave a higher priority to the brightest candidates with the aim of securing a higher S/N for the spectra.
For the instrument set-up, we used two different grisms, GRIS_300V and GRIS_300I, covering the wavelength range 400–900 nm and 600–1000 nm, respectively, with similar resolution of about 1 nm. The choice of the grism for a particular target was based on the estimated redshift of the host galaxy, with the GRISM_300I used for redshift z> 0.4.
We were able to take the spectrum of 17 candidates. Spectra were reduced using standard recipes in IRAF. In three cases, the S/N was too low for a conclusive transient classification and we were only able to obtain the host galaxy redshifts. Four of the candidates turned out to be variable AGNs, in particular Seyfert galaxies at redshifts between 0.25 <z< 0.5. We stress that, to maximise the chance of obtaining useful spectra, we tried to observe the candidate shortly after discovery. This means that, at the time of observations, we did not yet have a full light curve and, hence, a reliable photometric classification. Eventually, all the four AGN exhibit an erratic luminosity evolution that, if known at the time of spectroscopic observations, would have allowed us to reject them as SN candidates.
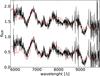 |
Fig. 4 Observed spectrum of SN 2012gs obtained with FORS2 on MJD 56 252.0 (black line) is compared to that of the SN Ic 2007gr at phase −9d (top) and of the type Ia SN 1991T at phase + 14d (bottom). In both cases it is adopted for SN 2012gs at redshift z = 0.5, as measured from the narrow emission lines of the host galaxy. |
Ten transients were confirmed as SNe, and their spectral type were assigned through cross-correlation with libraries of SN template spectra using GEneric cLAssification TOol (GELATO, Harutyunyan et al. 2008) and the Supernova Identification code (SNID, Blondin & Tonry 2007). The spectroscopically classified SNe, identified with a label in Table A.2, turned out to be six type Ia, two type Ic, one type II and one type IIn. In all cases, the SN type was coincident with the independent photometric classification, with one exception (SN 2012gs) that was classified Ic from spectroscopy and Ia from photometry.
As shown in Fig. 4, the spectrum of SN 2012gs can be fitted both by a template of type Ic SN well before maximum or by a type Ia SN two weeks after maximum, in both cases the redshift was z ~ 0.5. On the other hand, when we consider the light curve (Fig. 5), it turns out that the spectrum was obtained two weeks after maximum, and therefore the first alternative can now be rejected. Therefore, revising the original spectroscopic classification, SN 2012gs is classified as type Ia.
 |
Fig. 5 SN 2012gs light-curve fit, obtained using our tool. The best match is obtained with SN 1991T and the maximum is estimated to occur on MJD 56 235.1. |
4.4. Classification uncertainties
The comparison of the photometric and spectroscopic classifications, even if for a very small sample, confirms that photometric typing is reliable, in particular when the redshift of the host galaxy is known. For our photometric tools, we have not yet performed as detailed a testing as has been performed for PSNID. In particular, Sako et al. (2011) show that PSIND can identify SN Ia with a success rate of 90%. This appears consistent with the results obtained from the comparison of PSNID and SUDARE tools. The performances of photometric classification for CC SN are more difficult to quantify, because of both the lack of suitable spectroscopic samples (Sako et al. 2011), and the limitation of simulated samples (Kessler et al. 2010). From the comparison of the CC SN classification of the PSNID and SUDARE tools, we found differences in the individual classifications of 25% for type II events and 40% for type Ib/c events. These should be considered as the lower limit of the uncertainty because the two codes adopt similar approaches, the main difference being the choice of templates. On the other hand, the discrepancy on the overall SN counts of a given type is much lower, typically a few percent, although for type IIn it is about 40%. Based on these considerations and while waiting for a more detailed testing, we adopt the following uncertainties for SN classification: 10% for Ia, 25% for II, 40% for Ib/c, and IIn.
5. The SN sample
 |
Fig. 6 Histogram of the r-band SN magnitudes at discovery. The dotted line shows the distribution of m50 (the magnitude where the detection efficiency is 0.5) for the r-band observations (as reported in Table 2). |
As a result of the selection and classification process, we obtained a sample of 117 SNe, 27 of which are marked as probable SNe (PSNe). The distribution of the SN apparent magnitude at discovery, plotted in Fig. 6, shows a peak at mag r = 23.5−24 that is consistent with expectations, given the detection efficiencies (see Sect. 3).
We found that 57% of the SNe are of type Ia, 19% of type II, 9% of type IIn, and 15% of type Ib/c. We notice that the percentage in different subtypes is quite close to the fraction of SN types in magnitude-limited samples. For instance, the updated Asiago SN Catalog9 includes 56% Ia, 27% II, 4% IIn, and 10% Ib/c (counting only SNe discovered since 2000), with only some differences for the most uncertain events classified as type IIn in our sample. The result is encouraging when we consider that we did not make any assumptions on the percentage of the different SN types in our typing procedure. This also implies that the relative rates of the different SN types are similar in the local Universe and at z ~ 0.5.
At the same time, the SN = type distribution in our sample is very different from that derived in a volume-limited sample, such as that derived for the LOSS survey (Li et al. 2011b), which gives the following SN-type percentages: Ia 24%, Ib/c 19%, II 52%, and IIn 5%. The much higher number of SN Ia in our sample is a natural consequence of the high luminosity of SN Ia in comparison to other types, which makes it possible to discover SN Ia in a much higher volume. This also explains the SN redshift distribution shown in Fig. 7. While SN Ia are found at z ~ 0.8, the redshift limit for the discovered SN II is only z ~ 0.4. The relatively rare but bright type IIn are, on average, discovered at higher redshifts.
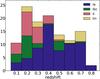 |
Fig. 7 Redshift distribution of the discovered SNe for the different types. |
6. The galaxy sample
To relate the occurrence of SN events to their parent stellar population, we need to characterise the galaxy population in the survey fields and in the redshift range that was explored by the SN search. For this purpose, the extensive multi-wavelength coverage of both COSMOS and CDFS provides a unique opportunity. In particular, the analysis of deep multi-band surveys of the COSMOS field has already been published (Muzzin et al. 2013), and we could retrieve the required information, such as photometric redshifts, galaxy masses, and star formation rates directly from public catalogues. For the CDFS fields, we instead performed our own analysis, but closely followed the method described by Muzzin et al. (2013). In the following, we describe the detection and characterisation of the galaxies in our search field.
6.1. COSMOS field
A photometric catalogue of the sources in the COSMOS field has been produced by Muzzin et al. (2013), and is available through the UltraVISTA survey website10. The catalogue covers an area of 1.62 deg2 and encompasses the entire 1.15 deg2 area monitored by SUDARE. The catalogue also includes photometry in 30 bands obtained from: i) optical imaging from Subaru/SuprimeCam (grizBV plus 12 medium/narrow bands IA427 – IA827) and CFHT/MegaCam (u∗) (Taniguchi et al. 2007; Capak et al. 2007); ii) NIR data from VISTA/VIRCAM (YJHK bands, McCracken et al. 2012); iii) UV imaging from GALEX (FUV and NUV channels, Martin et al. 2005); and iv) MIR/FIR data from Spitzer’s IRAC+MIPS cameras (3.6, 4.5, 5.8, 8.0, 24, and 70, 160 μm channels from Sanders et al. 2007; and Frayer et al. 2009).
The optical and NIR imaging for COSMOS have comparable though not identical PSF widths (FWHMs are in the range 0.5″−1.2″). For an accurate measurement of galaxy colours, Muzzin et al. (2013) performed the PSF homogenisation by degrading the image quality of all bands to the same image quality as the band with the worst seeing (with a seeing of 1′′–1.2′′). Source detection and photometric measurements were performed using the SExtractor package in dual image mode with the non-degraded K image adopted as the reference for source detection. The flux_auto in all bands was measured with an aperture of 2.5 times the Kron radius, which includes >96% of the total flux of the galaxy (Kron 1980). Hereafter, the K-band magnitude was corrected to the total flux by measuring the growth curve of bright stars out to a radius of 8′′ (depending on the magnitude this correction ranges between 2–4%).
The space-based imaging from GALEX, IRAC and MIPS have more complicated PSF shapes and larger FWHM, therefore photometry for these bands was performed separately (see Sects. 3.5 and 3.6 in Muzzin et al. 2013).
The photometry in all bands is corrected for Galactic dust attenuation, using dust maps from Schlegel et al. (1998) and using the Galactic Extinction Curve of Cardelli et al. (1989). The corrections were of the order of 15% in the GALEX bands, 5% in the optical band, and <1% in the NIR and MIR bands.
Star- vs. galaxy-separation was performed in the J−K versus u−J colour space, where there is a clear segregation between the two components (Fig. 3 of Muzzin et al. 2013). Sources were classified as galaxies if they match the following criteria: ![\begin{eqnarray} {ll}\label{colorselect} J - K > 0.18 \times (u - J) - 0.75 & \mbox{~~~~~~for}\,\, u - J < 3.0 \nonumber \\[3mm] J - K > 0.08 \times (u - J) - 0.45 & \mbox{otherwise}. \end{eqnarray}](/articles/aa/full_html/2015/12/aa26712-15/aa26712-15-eq104.png) (2)The photometric redshifts for the galaxy sample were obtained with the EAZY11 code (Brammer et al. 2008). EAZY fits the galaxy SEDs with a linear combination of templates and includes optional flux- and redshift-based priors. In addition, EAZY introduces a rest frame template error function to account for wavelength dependent template mismatch. This function gives different weights to different wavelength regions and ensures that the formal redshift uncertainties are realistic.
(2)The photometric redshifts for the galaxy sample were obtained with the EAZY11 code (Brammer et al. 2008). EAZY fits the galaxy SEDs with a linear combination of templates and includes optional flux- and redshift-based priors. In addition, EAZY introduces a rest frame template error function to account for wavelength dependent template mismatch. This function gives different weights to different wavelength regions and ensures that the formal redshift uncertainties are realistic.
The set of templates adopted by Muzzin et al. (2013) includes: i) six templates derived from the PEGASE models (Fioc & Rocca-Volmerange 1999); ii) a red template from the models of Maraston (2005); iii) a 1 Gyr old single-burst (Bruzual & Charlot 2003) model to improve the fits for galaxies with post-starburst-like SEDs; and iv) a slightly dust-reddened young population to improve the fits for a population of UV-bright galaxies. Muzzin et al. (2013) chose to use the v1.0 template error function and the K magnitude prior, and allowed photometric redshift solutions in the range 0 <z< 6.
Photometric redshifts are extremely sensitive to errors in photometric zeropoints. A common procedure to address this problem is to refine the zeropoints using a subsample of galaxies with spectroscopic redshifts (e.g. Ilbert et al. 2006; Brammer et al. 2011). Muzzin et al. (2013) used an iterative code developed for the NMBS survey (see Whitaker et al. 2011) and found zeropoint offsets of the order of ~0.05 mag for the optical bands and of 0.1–0.2 mag for the NIR bands.
To remain above the 90% completeness limit and guarantee the consistency with the CDFS catalogue (see next section), we selected all galaxies with K band magnitude ≤23.5 from the full COSMOS catalogue. We further restrict the catalogue to the sky area coverage of our field of view (1.15 deg2) and redshift range 0 <z< 1 of interest for the SN search, obtaining a final count of 67 417 galaxies.
6.2. VOICE-CDFS
Areas of different sizes around the original CDFS field have been variously observed at different depths from the X-ray through the UV, Optical, IR to the Radio. The 0.5 deg2 Extended CDFS (ECDFS) multi-wavelength data set has been carefully reduced and band-merged over the years (e.g. Cardamone et al. 2010; Hsu et al. 2014, and references therein). Conversely, most public multi-wavelength data over the VOICE-CDFS 4 deg2 area have been collected recently and are not available as a homogeneous database for our study. For our purposes we thus collected, merged, and analysed most existing data ourselves.
Available data over the VOICE-CDFS area include the following:
-
GALEX UV deep imaging (Martinet al. 2005). The GALEXphotometry is from the GALEX GR6Plus7 datarelease12.
-
SUDARE/VOICE u,g,r,i deep imaging (this work, Vaccari et al., in prep.)
-
VISTA Deep Extragalactic Observations (VIDEO, Jarvis et al. 2013) Z, Y, J, H, K deep imaging
-
SERVS Spitzer Warm 3.6 and 4.5 micron deep imaging (Mauduit et al. 2012)
-
SWIRE Spitzer IRAC and MIPS 7-band (3.6, 4.5, 5.8, 8.0, 24, 70, 160 micron) imaging (Lonsdale et al. 2003).
While data products are available as public catalogues for most of the multi-wavelength surveys listed above, SERVS and SWIRE data were re-extracted and band-merged with all other data sets as part of the Spitzer Data Fusion project (Vaccari et al. 2010)13.
Because the VIDEO survey is still in progress, the sky areas covered by SUDARE and VIDEO do not fully overlap at the moment. This restricts our analysis to the overlapping region, while for galaxy detection, we lack a small portion of our VOICE-CDFS1 and VOICE-CDFS2 (0.14 and 0.05 deg2, respectively). However, for the estimate of SN rates in the cosmic volume surveyed by SUDARE, we use the full area covered by the two fields.
Deep image stacks have been obtained from SUDARE and VOICE data as described in Sect. 2.1. The VIDEO exposures were processed at the Cambridge Astronomical Survey Unit (CASU) using the pipeline developed specifically for reducing VIRCAM data, as part of the VISTA Data Flow System (VDFS)14 (Irwin et al. 2004). The stacks produced by CASU were combined by taking the weighted mean with SWarp.
CDFS stacks in optical and NIR filters show a very small variation in seeing (ranging from 0.8′′ to 0.9′′) and we do not need to perform PSF homogenisation to measure colours, but only resample both VST and VISTA images to the same pixel scale of 0.21′′ pixel-1 (for this we used SWarp).
Source detection and photometry for VOICE-CDFS were performed with SExtractor in dual image mode, with the K-band image used as a reference for the source detection.
The photometry was corrected for Galactic extinction, which corresponded to a flux correction of 3% in the optical and <1% in the NIR. Then, we separated galaxies from stars using Eq. (2).
For all galaxies in the catalogue we obtained photometric redshift using the EAZY code, adopting the same parameters and templates described in Sect. 6.1. The main difference between the two fields is the number of filters available for the analysis: 12 filters for CDFS and 30 for COSMOS. To reduce catastrophic failures, we do not compute photometric redshifts for the sources that were detected in less than 6 filters (<5%).
Similar to Muzzin et al. (2013), the magnitude zero-points were verified using the iterative procedure developed by Brammer (p.c.). The procedure is based on the comparison of photometric to spectroscopic redshifts: systematic deviations are translated into zero-point offset corrections using K as the “anchor” filter, then the photometric scale is adjusted and EAZY re-run. We did not calculate offsets for GALEX and Spitzer bands. We found that the g,r,i bands require small offsets (≤0.05 mag) while the u band requires an offset of 0.14 mag and the NIR bands, about 0.1 mag.
Also for VOICE-CDFS, we selected all the galaxies with K-band magnitude <23.5 and redshift 0 <z ≤ 1, which results in a final catalogue of 92 324 galaxies for VOICE-CDFS. Considering a small overlap of the two pointings the total area covered is 2.05 deg2.
The distribution of K-band magnitudes and photometric redshifts for the COSMOS and VOICE-CDFS galaxy samples are shown in Figs. 8 and 9, respectively.
 |
Fig. 8 Distribution of K magnitude for galaxies in CDFS (solid line) and COSMOS (dashed line) catalogues. |
 |
Fig. 9 Redshift distribution (zpeak) for galaxies in CDFS (solid line) and COSMOS (dashed line) catalogues. |
 |
Fig. 10 Width of the 68% confidence intervals computed from the redshift-probability distribution as a function of galaxy magnitude (top panel) and redshift (bottom panel). |
6.3. Accuracy of photometric redshifts
We explored different methods to assess the quality of photometric redshifts: i) analysing the width of confidence intervals and quality measurements provided by EAZY; ii) comparing different redshift estimators; iii) comparing the photometric redshifts with available spectroscopic redshifts; and iv) comparing our estimates with photometric redshifts from other groups.
6.3.1. Internal error estimates
EAZY provides multiple estimators of the photometric redshifts amongst which we choose zpeak, which corresponds to the peak of the redshift probability distribution P(z). As a measure of the uncertainty, the code provides 68, 95, and 99% confidence intervals that are calculated by integrating the P(z). The confidence intervals are a strong function of the galaxy’s apparent magnitude and redshift, as shown in Fig.10 for the 68% level. The narrower confidence intervals for the COSMOS field, with respect to the VOICE-CDFS field, are the result of the better sampling of the SED for the galaxies of the former field.
EAZY also provides a redshift quality parameter, Qz15 that is intended as a robust estimate of the reliability of the photometric redshift (Brammer et al. 2008). Poor fits (Qz> 1) may be caused by uncertainties in the photometry, poor match of the intrinsic SED from the adopted templates, or degeneracies and nonlinear mapping in the colour-z space. We found good quality photometric redshifts (Qz ≤ 1) for 75% and 93% of the galaxies in CDFS and COSMOS field, respectively.
In several cases the P(z) function is multimodal, so that zpeak, which corresponds to the peak of P(z), does not properly reflect the probability distribution. Wittman (2009) introduced a very simple alternative estimator that represents the redshift probability distribution, incorporating the redshift uncertainties. This redshift estimator is drawn randomly from the P(z) and denoted with zMC because it results from a Monte Carlo sampling of the full P(z). The difference between zpeak and zMC can be used as an indication of the internal uncertainties of photometric redshifts. The difference in the redshift distribution that was obtained with different redshift estimators can be seen in Fig. 11.
 |
Fig. 11 Distribution of zpeak (solid line) and zMC (dashed line) of the galaxies in COSMOS (top panel) and in CDFS catalogues (bottom panel). |
6.3.2. Comparison with spectroscopic redshifts
Spectroscopic redshifts are available for a fairly large number of galaxies for both our fields. The spectroscopic redshifts for 4733 galaxies in the COSMOS field were taken from Muzzin et al. (2013) while for the CDFS field, the data for 3362 galaxies were collected from the literature, from different sources and with flags for different quality. A comparison of photometric and spectroscopic redshifts for these subsamples is shown in Fig. 12.
We calculated the normalized, median absolute deviation16, (NMAD) which is less sensitive to outliers compared to the standard deviation (Brammer et al. 2008). For CDFS we found σNMAD = 0.02, which is comparable to that found in other surveys with a similar number of filters, whereas for COSMOS, σNMAD = 0.005.
Another useful indication of the photometric redshift quality is the fraction of “catastrophic” redshifts defined as the fraction of galaxies for which |zphot−zspec|/(1 + zspec) > 5σNMAD. For the CDFS field, we found a fairly large fraction of catastrophic redshifts (~14%). After removing these outliers, the rms dispersion Δz/ (1 + z) = 0.02. The same analysis for the COSMOS field (see Muzzin et al. 2013, for details) gives a fraction of fiveσ outliers as low as 4% and a very small rms dispersion for the rest of the sample (0.005).
 |
Fig. 12 Comparison of photometric vs. spectroscopic redshifts from COSMOS (top panel) and CDFS (bottom panel). |
6.3.3. Comparison with zphot from other surveys
The comparison between photometric and spectroscopic redshifts is biased towards brighter galaxies for which it is easier to observe the spectrum. To analyse the accuracy of our photometric redshifts in a wider luminosity range, we compare our estimates to those obtained by the Multiwavelength Survey by Yale-Chile (MUSYC, Cardamone et al. 2010), which covers the ~30′ × 30′ ‘Extended’ Chandra Deep Field-South (that is included in CDFS1) with 18 medium-band filter optical imaging from the Subaru telescope, ten broadband optical and NIR imaging from the ESO MPG 2.2 m (Garching-Bonn Deep Survey), ESO NTT and the CTIO Blanco telescopes along with four MIR bands IRAC imaging from the Spitzer SIMPLE project. The MUSYC catalogue lists BVR-selected sources with photometric redshifts derived with the EAZY program. Therefore the main difference is that the MUSYC catalogue makes use of a much larger number of filters compared with SUDARE, which significantly improves the photometric redshift accuracy.
By cross-correlating the two catalogues with a search radius of 2″, we found 1830 common galaxies. In Fig. 13, we plot the differences between the zphot estimates as a function of the  . We find evidence of a some systematic differences at low redshifts z< 0.3, with the zphot from SUDARE being higher but, overall, the two catalogues show a fair agreement with a scatter Δz/ (1 + z) = 0.05 and a five σ outlier fraction of 10%.
. We find evidence of a some systematic differences at low redshifts z< 0.3, with the zphot from SUDARE being higher but, overall, the two catalogues show a fair agreement with a scatter Δz/ (1 + z) = 0.05 and a five σ outlier fraction of 10%.
 |
Fig. 13 Comparison of our photometric redshift for CDFS and MUSYC photometric redshifts. |
7. Computing SN rates
To compute the SN rate, we need to introduce the method of the control time (CT, Zwicky 1942). The CT of one observation is defined as the interval of time during which an SN occurring at a given redshift is expected to remain above the detection limit of the image. The total CT of an observing campaign is properly computed by adding the CT of the individual observations (Cappellaro et al. 1997). Then, the SN rate is computed as the number of events detected in the survey divided by the total CT.
The CT depends on the SN luminosity and light curve evolution and , therefore, varies for different SN types. We considered the following main SN types separately: Ia, Ib/c, II (including IIP and IIL), and IIn and SLSN.
7.1. The control time
To compute the CT we select a template light curve that is representative of a given SN subtype (SNi), a redshift (z, in the range 0 <z< 1), and an extinction value in the range AV = 0−2 mag (in the host galaxy rest frame). To take into account the diversity of the photometric evolution for SNe of different types, we used a wide collection of light curve templates (listed in Table 2). We considered four representative subtypes for thermonuclear SNe (normal, bright, faint and peculiar), six subtypes for hydrogen rich SNe (IIP, IIP faint, IIL, IIb, IIn, plus peculiars), three subtypes for stripped envelope SNe (Ib, Ic, Ic broad line), along with a template for SLSN. In some cases, we use a few templates for the same SN subtype to take into account the photometric variance within the class.
Then:
-
we define a useful range for the epochs of explosion. To be de-tectable in our search, a SN needs to explode in the interval[t0−365d,tK], where t0 and tK are the epochs of the first and last observations of the given field, respectively. In fact, for the redshift range of interest of our survey, an SN that exploded one year earlier than the first observation is far too faint to be detected;
-
we compute the expected magnitude, mi, at each epoch of observations, ti (with i = 1,2,...K, where K is the number of observations), for an SN that explodes at an epoch xj that is included in the time interval defined above. To derive these estimates, we use the SN template light curve, the proper K-corrections, the distance modulus for the selected redshift, and the adopted extinction;
-
the detection probability pi(xj) of the simulated event at each observing epoch is given by the detection efficiency for the expected magnitude, ϵi(mi), which is estimated as described in Sect.3. The detection probability for the whole observing campaign is derived as the complement of the probability of non-detection at any of the epochs, that is
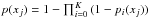 ;
; -
we simulate a number N of events that explore the possible epochs of explosion, in the interval [t0−365d,tK]. We can then compute
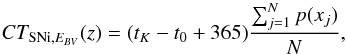 (3)where t is expressed in Julian Day. The accuracy of
the CT computation above depends on the sampling for the explosion epoch in the
defined interval. After some experiments, we found that a sampling of 1 d is more
than adequate, considering the contribution of other error sources as well;
(3)where t is expressed in Julian Day. The accuracy of
the CT computation above depends on the sampling for the explosion epoch in the
defined interval. After some experiments, we found that a sampling of 1 d is more
than adequate, considering the contribution of other error sources as well; -
for the extinction distribution, following Neill et al. (2006), we adopted a half-normal distribution, with σE(B−V) = 0.2. We adopt the same distribution for all SN subtypes, although we may expect different SN types, exploding in different environments, to suffer different amounts of extinction. In particular, the distribution of Neill et al. (2006) was derived for SN Ia and is likely to underestimate the effect for CC SNe. In Sect. 7.3, we verify (a posteriori) the consistency of our assumptions about the extinction distribution and estimate how its uncertainty propagates in the systematic uncertainty of SN rates;
-
finally, the CT for each of the main SN types was computed by accounting for the subtype distribution and for the adopted extinction distribution (details below):
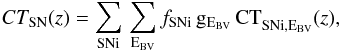 (4)where fSNi is the SN subtype fraction and gEBV the
distribution of colour excess E(B−V)
(multiple templates for a given subtype are given equal weight).
(4)where fSNi is the SN subtype fraction and gEBV the
distribution of colour excess E(B−V)
(multiple templates for a given subtype are given equal weight).
-
type Ia: 70% normal, 10% bright 1991T-like, 15% faint1991bg-like, and 5% 2002cx-like;
-
type II: 60% IIP, 10% 2005cs-like, 10% 1987A-like, 10% IIL , and 10% IIb;
-
type Ib/c: 27% Ib, 68% Ic, and 5% 1998bw-like;
-
type IIn: 45% 1998S-like, 45% 2010jl-like, 10% 2005gj-like.
We stress that these subtype distributions are obtained from a local sample and it is possible, or even expected, that they will evolve with cosmic time. In Sect. 7.3 we estimate the uncertainty implied by this assumption.
 |
Fig. 14 Control time as a function of redshift for different SN types (in days per deg2) averaged across the three survey fields. |
7.2. SN rate per unit volume
The volumetric SN rates per redshift bins in the range 0 <z< 1 is calculated as: 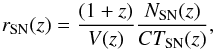 (5)where NSN(z) is the number of SNe of the given type in the specific redshift bin, CTSN(z) is the control time, and the factor (1 + z) corrects for time dilation. V(z) is the comoving volume for the given redshift bin, which is computed as
(5)where NSN(z) is the number of SNe of the given type in the specific redshift bin, CTSN(z) is the control time, and the factor (1 + z) corrects for time dilation. V(z) is the comoving volume for the given redshift bin, which is computed as ![\begin{equation} \label{eq:volume} V(z)=\frac{4\pi}{3} \frac{\Theta}{41\,253}\left[ \frac{c}{H_0}\int_{z_1}^{z_2}\frac{{\rm d}z^\prime}{\sqrt{\Omega_{\rm M}(1+z^\prime)^3+\Omega_\Lambda}} \right]^3~\mathrm{Mpc}^3, \end{equation}](/articles/aa/full_html/2015/12/aa26712-15/aa26712-15-eq156.png) (6)where Θ is the search area in deg2 and z is the mid-point of the redshift bin with extremes z1,z2.
(6)where Θ is the search area in deg2 and z is the mid-point of the redshift bin with extremes z1,z2.
Relative systematic errors.
7.3. Statistical and systematic errors
We derive the oneσ lower and upper confidence limits from the event statistics as in Gehrels (1986). Afterwards, these values are converted into confidence limits of SN rates through error propagation of Eq. (5).
There are many sources of systematic errors. To estimate each specific contribution we performed a number of experiments that calculate SN rates under different assumptions.
Transient misclassification
As described in Sect. 4.1, for a percentage of SN candidates (23%) the SN confirmation remains uncertain. These PSNe are attributed a weight of 0.5 in the rate calculation. To obtain an estimate of the impact of this assumption, we compute the rate in the extreme cases assuming a weight of 0 and 1, respectively, for these events. As an error estimate, we take the deviation from the reference value of the rates obtained in the two extreme cases. It turns out the error is of the order of 10−15% (Table 4). One concern is that we set arbitrary thresholds for Pχ2 and Npt to attribute the flag of PSN. To test the impact of this assumption, we computed the SN rate by adopting different thresholds: 10-3 or 10-6 for Pχ2 and 5 or 9 for Npt. In all cases, we found that the deviations for the reference value are <10% (typically ~5%).
SN photometric typing
For the errors of SN typing, we adopt the values discussed in Sect. 4, that is, 10% for type Ia, 25% for type II and 40% for type Ib/c and IIn, independently on redshift. It appears that the error in SN typing has, in general, a moderate impact for type Ia, whilst it is one of the dominant sources for SN CC in general.
Subtype distribution
The adopted SN subtype distribution affects the estimate of SN rates because the subtypes have different light curves and, hence, different control times. We consider an error of 50% for the number of the subclasses and, as an estimate of the contribution to the systematic error, we take the range of values of the SN rates obtained with the extreme subtype distribution. This is a significant source of error, typically 10–20%, but with a peak of 40% for type IIn SNe.
Detection efficiencies
We performed Monte Carlo simulations, assuming that the value of the detection-magnitude limit of each observation has normal error distribution with σ = 1.0 mag. We found that the frequent monitoring of our survey means that the large uncertainty in the detection efficiency for each single epoch does not have a strong impact on the overall uncertainty. The propagated error on the rates is ≤10%.
Host galaxy extinction In our computation, we adopt a half-normal distribution of E(B−V) with σ = 0.2 mag for both type Ia and CC SNe. To estimate the effect of this assumption, the SN rates have been recalculated, assuming a distribution with σ = 0.1 mag and σ = 0.3 mag. We evaluate that the error on the rates is of the order of 5−10%. The uncertainty is more critical for CC SNe (11%) and for the highest redshift bin of type Ia SNe (14%).
The consistency of the adopted extinction distribution was verified a posteriori. We computed estimates of the SN rates for a range of σE(B−V) values ranging from 0 to 0.5 mag. For each adopted σE(B−V), we computed the expected distribution of extinction of the detected SNe. This is different from the intrinsic distribution because of the bias against the detection of SNe with high extinction, which have a shorter control time. The expected extinction distribution is compared with the observed distribution (Fig. 15), and the best matching σ is determined using a Kolmogorov-Smirnov two-sided test. We found a best match for σE(B−V) = 0.25 mag, using the full SN sample or σE(B−V) = 0.28 mag, including only type Ia events and excluding probable SNe (PSN). Given the uncertainties, we consider that these values are consistent with the adopted distribution from Neill et al. (2006). We note that the adopted E(B−V) distribution was only used for the CT calculation and not for the SN photometric classifier.
 |
Fig. 15 Predicted (line) vs. observed (bars) cumulative extinction distribution. |
Photometric redshifts
We compare the results obtained using the two alternative photo-z estimatator zpeak and zmc (cf. Sect. 6.3.1). It turns out that this is the most significant source of error, especially for type Ia SNe. A detailed analysis shows that the most important effect is for the redshift of SN host galaxies, while the effect on the control time of the galaxy population has a smaller impact.
Cosmic variance
The possible under/over-density of galaxies in the field of view that are the result of cosmic variance impacts on the SN rate measurements. Using the cosmic variance calculator of Trenti & Stiavelli (2008), we found that cosmic variance can add an uncertainty of the SN rate of 5–10% but for the low redshift bin the variance can be as large as 15–20%. We note that the cosmic variance bias is averaged out when rate measurements from different sky fields are analysed together as for SUDARE.
In Table 4 we report the individual systematic errors along with the overall error obtained by their sum in quadrature. We do not include the effect of cosmic variance in the error budget, since this is not a measurement error. Rather, this is an uncertainty related to the particular galaxy sampling in our survey. The overall systematic error is typically of the order of 30−40%, and is larger than the statistical error.
8. SN rates as a function of cosmic time
Our SN rates per unit volume are reported in Table 5. Columns 1 and 2 report the SN type and redshift bin, Col. 3 gives the number of SNe (the number of PSNe is in parenthesis), Col. 4 the rate measurements, and Cols. 5 and 6, the statistical and systematic errors, respectively. The redshift bins were chosen to include a significant number of SNe (a minimum number of ten SNe) with the exception of the nearest redshift bin (0.05 <z< 0.15) , where we only collected a few SNe.
SN rates per unit volume [10-4 yr-1 Mpc-3].
 |
Fig. 16 CC SN rate per unit volume. All measurements do not account for the correction for hidden SNe. To obtain the predicted SN rate from the measured SFR, we adopt 8, 40 M⊙ as the lower and upper mass limits for SN CC progenitors and the proper IMF, Salpeter for Madau & Dickinson (2014) and SalA for Hopkins & Beacom (2006). The dashed lines show the predicted SN rate, assuming the fraction of hidden SNe given in (Mattila et al. 2012). |
8.1. Core collapse SNe
Figure 16 shows a comparison of our estimate for the rate of CC SNe with all measurements available in the literature. To obtain the CC SN rate, we cumulated type II, Ib/c, and IIn events.
Our results are in good agreement with other measurements. We note that in Fig. 16 we report the value of Melinder et al. (2012) and Dahlen et al. (2012) with no correction for the fraction of hidden SNe (Mattila et al. 2012). We will return to this point later.
Given the short lifetime of their progenitors (<30 Myr), there is a simple, direct relation between the CC SN and the current SF rate: 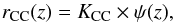 (7)where ψ(z) is the SFR and KCC is the number of stars per unit mass that produce CC SNe, or:
(7)where ψ(z) is the SFR and KCC is the number of stars per unit mass that produce CC SNe, or: 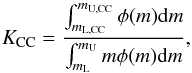 (8)where φ(m) is the initial mass function (IMF), mL and mU are the extreme limits of the stellar mass range and mL,CC and mU,CC, the mass range of CC SN progenitors.
(8)where φ(m) is the initial mass function (IMF), mL and mU are the extreme limits of the stellar mass range and mL,CC and mU,CC, the mass range of CC SN progenitors.
Assuming that KCC does not evolve significantly in the redshift range of interest, the evolution of the CC SN rates with redshift is a direct tracer of the cosmic SF history (SFH). Conversely, we can use existing estimates of the SFH to compute the expected CC SN rate, assuming a mass range for their progenitors. To do this consistently one has to use the same IMF (or KCC) adopted to derive the SFR. Indeed, although Kcc depends on the IMF in Eq. (8), the ratio between the cosmic SFR and CC rate does not give a real indication on the IMF, since both quantities actually trace the number of massive stars that produce both UV photons and CC SN events. The formal dependence on the IMF of this ratio is introduced by the extrapolation factor used to derive the SFH from luminosity measurement to convert the number of massive stars formed at the various redshifts into the total stellar mass that has been formed.
The CC progenitor mass range is still uncertain, both for the low and upper limit. Stellar evolution models suggest a typical range of 9−40 M⊙ (Heger et al. 2003) for CC SNe, though the upper limit strongly depends on metallicity and other factors, e.g. rotation or binarity. In recent years, it was feasible to search for the progenitor star for a number of nearby CC SN in archival pre-explosion images (Smartt 2009, 2015, and references therein). This allows an estimate of the masses of their progenitor stars to be obtained, or, if not detected, an estimate of upper limits. By comparing the observed mass distribution with the IMF, it was argued that the minimum initial mass is 8 ± 1 M⊙. The same analysis also suggests a paucity of progenitors of SN II with mass greater than 20 M⊙, which would indicate that these stars collapse directly in to a black hole, without producing a bright optical transient (Smartt 2009). However this result needs to be confirmed so hereafter, following the trend of the literature in the field, we adopt an upper limit of 40 M⊙.
With a mass range 8−40 M⊙ for the SN CC progenitors we obtain a scale factor 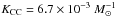 for a standard Salpeter IMF or
for a standard Salpeter IMF or 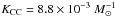 for a modified Salpeter IMF (SalA), with a slope of −1.3 below 0.5 M⊙ (similar to what adopted in Hopkins & Beacom 2006).
for a modified Salpeter IMF (SalA), with a slope of −1.3 below 0.5 M⊙ (similar to what adopted in Hopkins & Beacom 2006).
Assuming the 8−40 M⊙ mass range, it has been claimed that the comparisons between the SFH from Hopkins & Beacom (2006; hereafter HB06) and the published measurements of CC SN rates showed a discrepancy of a factor two at all redshifts (Botticella et al. 2008; Bazin et al. 2009).Horiuchi et al. (2011) argue that this indicates a “supernova rate problem” for which they propose some possible explanations: either many CC SNe are missed in the optical searches because of heavy dust-obscuration, or there is a significant fraction of intrinsically very faint (or dark) SNe at which point, after the core has collapsed, the whole ejecta falls back onto the black hole.
On the other hand, Botticella et al. (2012) found that the CC SN rate in a sample of galaxies within 11 Mpc is consistent with that expected from the SFR derived from FUV luminosities. Taylor et al. (2014), based on the SDSS-II SN sample, estimated that the fraction of missing events is about 20%. Gerke et al. (2015) performed a search for failed SNe by monitoring a sample of nearby galaxies (<10 Mpc). After four yr they found only one candidate, which suggests an upper limit of 40% for the fraction of dark events among CC SNe that, unfortunately, is not yet a strong constraint. To detect the CC SNe hidden by strong extinction, several infrared SN searches have been performed in local starburst galaxies (Maiolino et al. 2002; Mannucci et al. 2003; Mattila & Meikle 2001; Miluzio et al. 2013), in some cases exploiting adaptive optics (Cresci et al. 2007; Mattila et al. 2007; Kankare et al. 2008, 2012) to improve the spatial resolution. However, despite the efforts, it has not been possible to unveil the hidden SNe.
An alternative approach to estimating the fraction of hidden SNe was made with the conservative assumption that all SNe in the nucleus of luminous and ultra-luminous infrared galaxies (LIRGs and ULIRGs) are lost by optical survey (Mannucci et al. 2007). Using this approach, Mattila et al. (2012) suggest that the fraction of missed SNe increases from the average local value of ~19% to ~38% at z ~ 1.2.
The CC SN rate predicted using two different SFH from HB06 and the recent results of Madau & Dickinson (2014; hereafter MD14) are shown in Fig. 16. The two SFH lead to different predictions with a discrepancy of about a factor 2. Indeed, the cosmic SFR derived by MD14 at virtually all redshifts is lower than the HB06’s. In addition, the MD14 SF rates assume a straight Salpeter IMF, so that the number of massive stars formed in the Universe at all epochs is further diminished when compared to predictions obtained with HB06’s SFH. Both factors concur in producing the final result shown in Fig. 16. The predictions based on the MD14 SFH are in good agreement with the data. We note that applying the Mattila et al. correction for hidden SNe (dashed green lines in the figure) improves the fit at low redshift but gives a worse comparison at high redshift.
The HB06 SFH instead over-predicts the CC rate, if the progenitors come from the mass range 8 to 40 M⊙. In this case, correcting for hidden SN improves the agreement at high redshift, but still overestimates the CC SN rates at z< 0.4 (dashed blue line).
On the other hand, as mentioned above, the uncertainty in the CC progenitor mass range is still significant. Indeed, most recent data collection seems too indicate a lower mass limit as high as 9−10 M⊙ (Smartt 2015). If we use this in combination with the upper mass limits for CC SN progenitors of ~20 M⊙ (e.g. Smartt 2009; Gerke et al. 2015), and also include the correction for hidden SNe, this results in the SFR severely under-predicting the CC rate (by over a factor of three if we refer to the MD14 SFR).
All together, it is fair to say that the both statistic and systematics errors on SN rate and SFR measurements and the uncertainties on the progenitor mass range are too large to invoke an “SN rate problem” and hence to speculate on possible explanations. One of the goals we aim to achieve with our survey is to obtain measurements of the evolution of specific SN subtype. While the statistics of the present sample is still small, we can however obtain some preliminary measurements.
8.1.1. SN Ib/c
We found that at the mean redshift z = 0.25, type Ib/c are 40 ± 13% of CC SNe. This compares very well with the estimates of Li et al. (2011a) for the local Universe, who measure a fraction of Ib/c that ranges from 46 ± 17% in early spiral galaxies to 20 ± 5% in late spirals, with an average value of 33 ± 9%. The physical reason of the difference in CC SN population in early and late spirals is not understood, although it is possibly related to a metallicity effect (Li et al. 2011a).
Given the limited statistics of our sample, we can only conclude that there is no evidence for evolution with redshift of the Ib/c fraction.
8.2. SN IIn
Our estimate of the rate of type IIn SNe is uncertain for two reasons: SNe IIn are rare and the event statistics are very poor. In addition, the variety in luminosity and light curve evolution that, in some cases, mimic those of other SNe (e.g. SN IIL or SLSN) makes the photometric classification very uncertain (cf. Sect. 7.3). However, because of the intrinsically bright and slowly evolving luminosity, we could detect type IIn SNe in a redshfit range comparable to that of SN Ia.
In the 0.15–0.35 redshift bin, we estimate that type IIn are 4 ± 3% of all CC SNe. This number is consistent with the 6 ± 2% value measured in the local Universe (Li et al. 2011a).
On the other hand, the apparent decrease in the rate at higher redshift (a factor ~2.5 in the redshift bin 0.35–0.75, compared with the nearest bin) appears at odds, considering that the overall CC SN rate in the same redshift interval increases by about the same factor.
Either there is a strong evolution of the type IIn rate with redshift or, in our search, we are missing (or mis-classifying) over two-thirds of the distant type IIn. Both explanations are difficult to accept: we will need to verify this result at the end of our survey with better statistics and, possibly, an improved template list.
8.3. Superluminous SNe
Super-luminous supernovae (SLSNe) that radiate more than 1044 erg s-1 at their peak luminosity (about 100 times more luminous than usual Type Ia and CC SNe) have recently been discovered in faint galaxies, typically at high redshifts. The origin of these events is still unclear: the host environment and energetics suggest massive stellar explosions but their power source is still a matter of debate. In fact, several subclasses have been introduced that are possibly related to different explosion scenarios (Gal-Yam 2012).
We did not detect any SLSN in our surveyed volume up to z = 0.75. However the null result for SLSN can provide interesting constraints for the rates of these objects. From simple Poisson statistics, we find that the probability of obtaining a null result is 5% when the expected values is 3.0. Therefore one should expect that the rate of SLSNe is no higher than 9 × 10-7 yr-1 Mpc-3 at a mean redshift z ~ 0.5. This firm upper limit is consistent with the rate estimated by Quimby et al. (2013) of 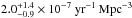 at a mean redshift z = 0.16 that is 1 SLSN for each 500 CC SNe.
at a mean redshift z = 0.16 that is 1 SLSN for each 500 CC SNe.
We note that between z = 0.15 and z = 0.5 the CC rate measurements increase by almost a factor of three. Our upper limit does not preclude a similar increase for the SLSN rate; clearly we need to obtain a more significative result that will become feasible once our survey has been completed.
 |
Fig. 17 Our estimates of the SN Ia rate at z = 0.25,0.45,0.65 are compared with the other values from literature. The rate of Cappellaro et al. (1999), Hardin et al. (2000), Madgwick et al. (2003), Blanc et al. (2004) were given per unit luminosity. They are converted in rate per unit volume using the following relation of the luminosity density as a function of redshift: |
8.4. SNe Ia
Our measurements of the rate of SN Ia are shown in Fig. 17 along with all those available from the literature17. Our results appear in agreement with other measurements within the statistical errors. We note, however, that our estimates seem to be on the high side compared with the bulk of published measurements.
 |
Fig. 18 Histogram of published estimates of the SN Ia rate in the three redshift bins of our measurements. All values are scaled to the mean redshift of the bin, assuming a linear evolution of the rate with redshift (see text). In red we show our measurements. The black lines are the Gaussian curve whose mean and variance are computed from the data and reported in each panel’s legend. The averages and dispersions were computed by weighting the individual measurements with the inverse of their statistical errors. |
In Fig. 18 we plot the histogram of the measurements for the three bins of redshift that correspond to our measurements. The effect of the rate evolution within each of these redshift bins has been removed by scaling the measurements to the mean redshift of the bin, assuming that the rate scales as rIa ∝ 0.6 × z, that, as a first order approximation, fits the rate evolution up to redshift ~1 (the exact slope of the relation may be slightly different but it is not crucial for the comparison we are performing here).
It appears from Fig. 18 that for each bin the distribution of measurements (our own included) are consistent with a normal distribution, and the dispersion is well understood considering the statistical and systematic errors affecting the measurements. As a consequence, we will use average values as the best estimates of the SN Ia rate for the comparison with models in the following. The average rates per redshift bin are reported in Table 6, where Col. 1 gives the redshift bin, Col. 2 the average redshift, Cols. 3 and 4 the average rate and dispersion, and Col. 5 the number of measurements per bin. We note that, for redshift z> 0.75 in the computation of the average rate, we did not correct the individual measurements for the possible rate evolution inside the bin.
Average of SN Ia rate measurements per redshift bin (units 10-4 yr-1 Mpc-3).
In Fig. 20 we compare the average SN Ia rate measurements with the expected evolution for different progenitor scenarios predicted by Greggio (2005). Models in Greggio (2005) assume that SNIa progenitors are close binary systems that attain explosion upon reaching the Chandrasekhar mass either because of mass accretion from a companion star (single degenerate, SD) or by merging with another WD (double degenerate, DD). The delay between the birth of the binary system and its final explosion ranges from ~40 Myr to the Hubble time so that, at each epoch, the SN events in a galaxy are the result of the contributions of all past stellar generations. Following Greggio (2005), the expected SN Ia rate at the time t is 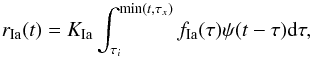 (9)where KIa is the number of SN Ia progenitors per unit mass of the stellar generation, fIa(τ) is the distribution function of the delay times, and ψ(t−τ) is the star formation rate at the epoch t−τ. The integration is extended over the full range of the delay time τ in the range τi and min(t,τx), with τi and τx being the minimum and maximum possible delay times for a given progenitor scenario. According to stellar evolution, fIa(τ) is a decreasing function of the delay time, with a slope that depends on details of the scenario leading to the SN explosion. One can then use Eq. (9) to constrain the progenitor’s model using the trend of the SNIa rate with cosmic time, after specifying the cosmic SFH. In the following, we adopt the MD14 SFH and assume that KIa does not vary with cosmic time.
(9)where KIa is the number of SN Ia progenitors per unit mass of the stellar generation, fIa(τ) is the distribution function of the delay times, and ψ(t−τ) is the star formation rate at the epoch t−τ. The integration is extended over the full range of the delay time τ in the range τi and min(t,τx), with τi and τx being the minimum and maximum possible delay times for a given progenitor scenario. According to stellar evolution, fIa(τ) is a decreasing function of the delay time, with a slope that depends on details of the scenario leading to the SN explosion. One can then use Eq. (9) to constrain the progenitor’s model using the trend of the SNIa rate with cosmic time, after specifying the cosmic SFH. In the following, we adopt the MD14 SFH and assume that KIa does not vary with cosmic time.
 |
Fig. 19 Distribution functions of the delay times that were selected for our theoretical predictions for the single degenerate (green), and double degenerate models (blue and red, see text for more details). The thin lines show the cumulative fraction of events as a function of time. |
We select three DTD models, plotted in Fig. 19, and test their predictions for the cosmic SNIa rate. The models include a single SD, and two flavours of the double degenerates, either with a close binary separation (DDC), or wide (DDW), which predict a steep and a mildly decreasing distribution of the delay times, respectively (see Greggio 2005, 2010, for more details). The selected models correspond to a very different time evolution following a burst of star formation. For the DDC, SD, and DDW models, 50% of the explosions occur within the first 0.45, 1, and 1.6 Gyr, respectively, while the fraction of events within 500 Myr is 0.55, 0.3, and 0.18 of the total. The late epoch declines are also different, the rate scaling by t-1.3 and t-0.8 for the DDC and DDW models, respectively.
Figure 20 shows the predicted rates as a function of redshift for each of the three models, having assumed the Madau and Dickinson cosmic SFH. The best fit of the models with observations was derived by least square minimisation weighting the measurement by their σ and gives 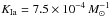 for SD and DDW and
for SD and DDW and 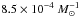 for DDC.
for DDC.
The smallest residuals in the whole redshift range is obtained for the SD model (rms = 0.0028). The DDC model (rms = 0.0088) gives an excellent fit of up to redshift z ~ 1.2, but predicts a relatively mild decline at higher redshift (still not in conflict with the observations). Instead, the DDW model (rms = 0.012) shows an overall shallow evolution with respect to the observations. Our conclusion is that, since the dispersion of the rate measurements is comparable to the scatter of theoretical tracks, we cannot discriminate between SD and DD models, although the DD scenarios model with close binary separation seems favoured.
We note that, while the impact of adopting different cosmic SFHs, whether MD14 or HB06, on the predicted rate is negligible, it is more relevant for the estimate of constant KIa, i.e the number of stars which end up as a SNIa per unit mass of the parent stellar population. In particular, fitting the observations with HB06 SFH requires KIa = 5.9, 5.7, 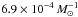 for SD, DDW, and DDC respectively, values which are ~20% smaller than those obtained when using the MD14 SFH. The number of potential progenitors per stellar mass unit depends on the IMF and, assuming 3−8 M⊙ for the range of SN Ia progenitors, it is 0.021 for a plain Salpeter IMF and 0.028 for a SalA. Stars that should end up as SN Ia t account for the observed rates in the selected mass range are 4% and 2% using the MD14 and HB06 SFH, respectively. These fractions are close to the lower edge of the range, as reported in Maoz and Mannucci (2012). While they remain large with respect to most theoretical predictions from binary population synthesis codes, they still represent a minor fraction of all potential progenitors.
for SD, DDW, and DDC respectively, values which are ~20% smaller than those obtained when using the MD14 SFH. The number of potential progenitors per stellar mass unit depends on the IMF and, assuming 3−8 M⊙ for the range of SN Ia progenitors, it is 0.021 for a plain Salpeter IMF and 0.028 for a SalA. Stars that should end up as SN Ia t account for the observed rates in the selected mass range are 4% and 2% using the MD14 and HB06 SFH, respectively. These fractions are close to the lower edge of the range, as reported in Maoz and Mannucci (2012). While they remain large with respect to most theoretical predictions from binary population synthesis codes, they still represent a minor fraction of all potential progenitors.
In any case, we conclude that there is no need to invoke adhoc delay time distributions that are unrelated to the standard expectations from stellar evolution theory. This confirms earlier conclusions (e.g. Förster et al. 2006; Blanc & Greggio 2008; Greggio et al. 2008).
 |
Fig. 20 Average values of the SN Ia rates per unit volume as a function of redshift. The still unique measurement at z> 2 of Rodney et al. (2014) is also plotted. For the derivation of the SNIa rate model evolution, we adopted the SFH from Madau & Dickinson (2014). |
In a forthcoming paper (PII), we will use a detailed characterisation of the properties of the galaxy sample in order to investigate the dependence of SN rates on galaxy parameters and to obtain additional constraints on the SN progenitor scenarios.
9. Conclusions
We presented the preliminary results of a new SN search, SUDARE, that was designed to measure SN rates in the redshift range 0 <z< 1. This paper describes the survey strategy, the selection and confirmation of candidates, the construction of the galaxy catalogue and the rate estimates based on the first two years of the survey.
We selected two of the best studied extragalactic fields as search fields, CDFS and COSMOS, for which a wealth of multiband coverage is available. Our own data, the synergy with the VOICE project, the complementary data from the VIDEO survey, along with public data from the literature, allowed us to obtain a multiband photometric catalogue for galaxies with magnitudes K ≤ 23.5 that we exploited to estimate the photometric redshift using the EAZY code (Brammer et al. 2008).
We discovered 117 SNe, of which 27 were assigned a weight =0.5 because of a poor template match or a low number of detections. Most of the SNe are classified as type Ia (57%). For the core collapse, 44% are type II, 22% type IIn, and 34% type Ib/c.
With this SN sample and an accurate measurement of the detection efficiency of our search, we computed the rate of SNe per unit volume. For the CC SNe, our measurements are in excellent agreement with previous results and fully consistent with the predictions from the cosmic SFH of Madau & Dickinson (2014), assuming a standard mass range for the progenitors (8 <M< 40 M⊙). Therefore, previous claims of a significant disagreement between SFH and CC SN rates are not confirmed. This conclusion relies on the revision of the cosmic SFH because our rate estimates are consistent with other measurements from literature.
For the SN Ia, our measurements are consistent with literature values within the errors. We conclude that the dispersion of SN Ia rate estimates and the marginal differences for the evolution with cosmic time of the volumetric SN rate does not allow us to discriminate between SD and DD progenitor scenarios. However, with respect to the three tested models (SD, DDC and DDW from Greggio 2010), the SD gives a better fit on the whole redshift range, whereas the DDC appears to perfectly match the steep rise of the rate up to redshift 1.2. The DDW model that corresponds to a wide binary separation and a relatively flat delay time distribution does not seem favourable.
As a first attempt at searching for the evolution of SN diversity, we found no evidence of the evolution of the SN Ib/c fraction. The fraction of type IIn SNe, as detected in the 0.15 <z<.35 redshift bin, is consistent with the measurements for the local Universe. The rate in the higher redshift bin is formally significantly lower. Whether this is evidence of some evolution or a bias in our survey needs to be verified with more data.
Online material
Appendix A: Additional tables
Log of observations.
List of supernovae.
A package provided by A. Becker (http://www.astro.washington.edu/users/becker/v2.0/hotpants.html).
http://das.sdss2.org/ge/sample/sdsssn/SNANA-PUBLIC. We used SNANA version 10_39k.
We used the Nugent SED templates updated by D.Scolnic as illustrated in http://kicp-workshops.uchicago.edu/SNphotID_2012/depot/talk-scolnic-daniel.pdf
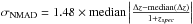 as in Brammer et al. (2008), where Δz = (zphot−zspec). The normalization factor of 1.48 ensures that NMAD of a Gaussian distribution is equal to its standard deviation, and the subtraction of median(Δz) removes possible systematic offsets
as in Brammer et al. (2008), where Δz = (zphot−zspec). The normalization factor of 1.48 ensures that NMAD of a Gaussian distribution is equal to its standard deviation, and the subtraction of median(Δz) removes possible systematic offsets
We do not plot original measurements that have later been revised or superseded as follows: Madgwick et al. (2003) by Graur & Maoz (2013), Poznanski et al. (2007b) by Graur et al. (2011), Dahlen et al. (2004, 2008), Kuznetsova et al. (2008) by (Barris & Tonry 2006) by Rodney & Tonry (2010), Neill et al. (2006, 2007) by Perrett et al. (2012).
Acknowledgments
We thank the referee, Steve Rodney, for useful comments and suggestions. We also thank G. Brammer for helping with galaxy photometric redshifts. We acknowledge the support of grant ASI n.I/023/12/0 “Attivitá relative alla fase B2/C per la missione Euclid”, MIUR PRIN 2010-2011, “The dark Universe and the cosmic evolution of baryons: from current surveys to Euclid” and PRIN-INAF “Galaxy Evolution With The VLT Survey Telescope (VST)” (PI A. Grado). G.P. acknowledge the support of Proyecto Regular FONDECYT 1140352 and of the Ministry of Economy, Development, and Tourism’s Millennium Science Initiative through grant IC 12009, awarded to The Millennium Institute of Astrophysics, MAS. M.V. acknowledges support from the Square Kilometre Array South Africa project, the South African National Research Foundation and Department of Science and Technology (DST/CON 0134/2014), the European Commission Research Executive Agency (FP7-SPACE-2013-1 GA 607254) and the Italian Ministry for Foreign Affairs and International Cooperation (PGR GA ZA14GR02).
References
- Alard, C. 2000, A&AS, 144, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aldering, G., Antilogus, P., Bailey, S., et al. 2006, ApJ, 650, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Altavilla, G., Fiorentino, G., Marconi, M., et al. 2004, MNRAS, 349, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Barbary, K., Aldering, G., Amanullah, R., et al. 2012, ApJ, 745, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Barbon, R., Benetti, S., Cappellaro, E., et al. 1995, A&AS, 110, 513 [NASA ADS] [Google Scholar]
- Barris, B. J., & Tonry, J. L. 2006, ApJ, 637, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Bazin, G., Palanque-Delabrouille, N., Rich, J., et al. 2009, A&A, 499, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benetti, S., Meikle, P., Stehle, M., et al. 2004, MNRAS, 348, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanc, G., & Greggio, L. 2008, New A, 13, 606 [Google Scholar]
- Blanc, G., Afonso, C., Alard, C., et al. 2004, A&A, 423, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blondin, S., & Tonry, J. L. 2007, ApJ, 666, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Botticella, M. T., Riello, M., Cappellaro, E., et al. 2008, A&A, 479, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botticella, M. T., Smartt, S. J., Kennicutt, R. C., et al. 2012, A&A, 537, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botticella, M. T., Cappellaro, E., Pignata, G., et al. 2013, The Messenger, 151, 29 [NASA ADS] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., Whitaker, K. E., van Dokkum, P. G., et al. 2011, ApJ, 739, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Candia, P., Krisciunas, K., Suntzeff, N. B., et al. 2003, PASP, 115, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioli, M., & Schipani, P. 2011, The Messenger, 146, 2 [NASA ADS] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., Turatto, M., Tsvetkov, D. Y., et al. 1997, A&A, 322, 431 [NASA ADS] [Google Scholar]
- Cappellaro, E., Evans, R., & Turatto, M. 1999, A&A, 351, 459 [NASA ADS] [Google Scholar]
- Cardamone, C. N., van Dokkum, P. G., Urry, C. M., et al. 2010, ApJS, 189, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Catchpole, R. M., Whitelock, P. A., Menzies, J. W., et al. 1989, MNRAS, 237, 55P [NASA ADS] [CrossRef] [Google Scholar]
- Clocchiatti, A., Benetti, S., Wheeler, J. C., et al. 1996a, AJ, 111, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Clocchiatti, A., Wheeler, J. C., Brotherton, M. S., et al. 1996b, ApJ, 462, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Mannucci, F., Della Valle, M., & Maiolino, R. 2007, A&A, 462, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dahlen, T., Strolger, L.-G., Riess, A. G., et al. 2004, ApJ, 613, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Strolger, L.-G., & Riess, A. G. 2008, ApJ, 681, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Strolger, L.-G., Riess, A. G., et al. 2012, ApJ, 757, 70 [NASA ADS] [CrossRef] [Google Scholar]
- De Cicco, D., Paolillo, M., Covone, G., et al. 2015, A&A, 574, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dilday, B., Smith, M., Bassett, B., et al. 2010, ApJ, 713, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Elmhamdi, A., Danziger, I. J., Chugai, N., et al. 2003, MNRAS, 338, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Falocco, S., Paolillo, M., Covone, G., et al. 2015, A&A, 579, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fassia, A., Meikle, W. P. S., Vacca, W. D., et al. 2000, MNRAS, 318, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Richmond, M. W., Branch, D., et al. 1992, AJ, 104, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1999, ArXiv eprints [arXiv:astro-ph/9912179] [Google Scholar]
- Förster, F., Wolf, C., Podsiadlowski, P., & Han, Z. 2006, MNRAS, 368, 1893 [NASA ADS] [CrossRef] [Google Scholar]
- Frayer, D. T., Sanders, D. B., Surace, J. A., et al. 2009, AJ, 138, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A. 2012, Science, 337, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, J. R., Kochanek, C. S., & Stanek, K. Z. 2015, MNRAS, 450, 3289 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, S., Halpern, J. P., Grupe, D., et al. 2009, ApJ, 690, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Grado, A., Capaccioli, M., Limatola, L., & Getman, F. 2012, Mem. Soc. Astron. Ital. Suppl., 19, 362 [Google Scholar]
- Graur, O., & Maoz, D. 2013, MNRAS, 430, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., Poznanski, D., Maoz, D., et al. 2011, MNRAS, 417, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., Rodney, S. A., Maoz, D., et al. 2014, ApJ, 783, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., Bianco, F. B., & Modjaz, M. 2015, MNRAS, 450, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greggio, L. 2010, MNRAS, 406, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Greggio, L., Renzini, A., & Daddi, E. 2008, MNRAS, 388, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Suntzeff, N. B., Bravo, J., & Phillips, M. M. 1990, PASP, 102, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Pinto, P. A., Maza, J., et al. 2001, ApJ, 558, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Maza, J., Pinto, P. A., et al. 2002, AJ, 124, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Hardin, D., Afonso, C., Alard, C., et al. 2000, A&A, 362, 419 [NASA ADS] [Google Scholar]
- Harutyunyan, A. H., Pfahler, P., Pastorello, A., et al. 2008, A&A, 488, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Horesh, A., Poznanski, D., Ofek, E. O., & Maoz, D. 2008, MNRAS, 389, 1871 [NASA ADS] [CrossRef] [Google Scholar]
- Horiuchi, S., Beacom, J. F., Kochanek, C. S., et al. 2011, ApJ, 738, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, L.-T., Salvato, M., Nandra, K., et al. 2014, ApJ, 796, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. J., Valenti, S., Kotak, R., et al. 2009, A&A, 508, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inserra, C., Turatto, M., Pastorello, A., et al. 2012, MNRAS, 422, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M. J., Lewis, J., Hodgkin, S., et al. 2004, in Optimizing Scientific Return for Astronomy through Information Technologies, eds. P. J. Quinn, & A. Bridger, SPIE Conf. Ser., 5493, 411 [Google Scholar]
- Jarvis, M. J., Bonfield, D. G., Bruce, V. A., et al. 2013, MNRAS, 428, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Kankare, E., Mattila, S., Ryder, S., et al. 2008, ApJ, 689, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Kankare, E., Mattila, S., Ryder, S., et al. 2012, ApJ, 744, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Bernstein, J. P., Cinabro, D., et al. 2009, PASP, 121, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Bassett, B., Belov, P., et al. 2010, PASP, 122, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Kirshner, R. P., Jeffery, D. J., Leibundgut, B., et al. 1993, ApJ, 415, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K. 2011, The Messenger, 146, 8 [NASA ADS] [Google Scholar]
- Kuznetsova, N. V., & Connolly, B. M. 2007, ApJ, 659, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsova, N., Barbary, K., Connolly, B., et al. 2008, ApJ, 673, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B., Kirshner, R. P., Phillips, M. M., et al. 1993, AJ, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Gates, E. L., et al. 2002a, PASP, 114, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Li, W., et al. 2002b, AJ, 124, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Filippenko, A. V., Chornock, R., et al. 2003, PASP, 115, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Chornock, R., Leaman, J., et al. 2011a, MNRAS, 412, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Leaman, J., Chornock, R., et al. 2011b, MNRAS, 412, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Lira, P., Suntzeff, N. B., Phillips, M. M., et al. 1998, AJ, 115, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., della Valle, M., & Panagia, N. 1998, MNRAS, 297, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Madgwick, D. S., Hewett, P. C., Mortlock, D. J., & Wang, L. 2003, ApJ, 599, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Maguire, K., Di Carlo, E., Smartt, S. J., et al. 2010, MNRAS, 404, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Vanzi, L., Mannucci, F., et al. 2002, A&A, 389, 84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Maiolino, R., Cresci, G., et al. 2003, A&A, 401, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Della Valle, M., & Panagia, N. 2007, MNRAS, 377, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Matheson, T., Kirshner, R. P., Challis, P., et al. 2008, AJ, 135, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., & Meikle, W. P. S. 2001, MNRAS, 324, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Väisänen, P., Farrah, D., et al. 2007, ApJ, 659, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Dahlen, T., Efstathiou, A., et al. 2012, ApJ, 756, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Mauduit, J.-C., Lacy, M., Farrah, D., et al. 2012, PASP, 124, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Lucy, L. B., Danziger, I. J., et al. 1993, A&A, 269, 423 [NASA ADS] [Google Scholar]
- Mazzali, P. A., Valenti, S., Della Valle, M., et al. 2008, Science, 321, 1185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melinder, J., Dahlen, T., Mencía Trinchant, L., et al. 2012, A&A, 545, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miluzio, M., Cappellaro, E., Botticella, M. T., et al. 2013, A&A, 554, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJS, 206, 8 [Google Scholar]
- Neill, J. D., Sullivan, M., Balam, D., et al. 2006, AJ, 132, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. D., Sullivan, M., Balam, D., et al. 2007, in The Multicolored Landscape of Compact Objects and Their Explosive Origins, eds. T. di Salvo, G. L. Israel, L. Piersant, et al., AIP Conf. Ser., 924, 421 [Google Scholar]
- Okumura, J. E., Ihara, Y., Doi, M., et al. 2014, PASJ, 66, 49 [NASA ADS] [Google Scholar]
- Pain, R., Fabbro, S., Sullivan, M., et al. 2002, ApJ, 577, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Pastorello, A., Zampieri, L., Turatto, M., et al. 2004, MNRAS, 347, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Pastorello, A., Sauer, D., Taubenberger, S., et al. 2006, MNRAS, 370, 1752 [NASA ADS] [CrossRef] [Google Scholar]
- Pastorello, A., Kasliwal, M. M., Crockett, R. M., et al. 2008, MNRAS, 389, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Pastorello, A., Valenti, S., Zampieri, L., et al. 2009, MNRAS, 394, 2266 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Benetti, S., Cappellaro, E., et al. 1996, MNRAS, 278, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Cappellaro, E., Danziger, J., et al. 2001, ApJ, 555, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K., Sullivan, M., Conley, A., et al. 2012, AJ, 144, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Mazzali, P. A., Nomoto, K., Lazzati, D., & Cappellaro, E. 2004, ApJ, 607, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Maoz, D., & Gal-Yam, A. 2007a, AJ, 134, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Maoz, D., Yasuda, N., et al. 2007b, MNRAS, 382, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzo, M., Meikle, W. P. S., Fassia, A., et al. 2004, MNRAS, 352, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Quimby, R. M., Aldering, G., Wheeler, J. C., et al. 2007, ApJ, 668, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Quimby, R. M., Yuan, F., Akerlof, C., & Wheeler, J. C. 2013, MNRAS, 431, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Richmond, M. W., Treffers, R. R., Filippenko, A. V., et al. 1994, AJ, 107, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Richmond, M. W., Treffers, R. R., Filippenko, A. V., et al. 1995, AJ, 109, 2121 [NASA ADS] [CrossRef] [Google Scholar]
- Rodney, S. A., & Tonry, J. L. 2009, ApJ, 707, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Rodney, S. A., & Tonry, J. L. 2010, ApJ, 723, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Rodney, S. A., Riess, A. G., Strolger, L.-G., et al. 2014, AJ, 148, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lapuente, P., & Canal, R. 1998, ApJ, 497, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lapuente, P., Cappellaro, E., Turatto, M., et al. 1992, ApJ, 387, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Sadat, R., Blanchard, A., Guiderdoni, B., & Silk, J. 1998, A&A, 331, L69 [NASA ADS] [Google Scholar]
- Sako, M., Bassett, B., Connolly, B., et al. 2011, ApJ, 738, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2015, PASA, 32, 16 [Google Scholar]
- Smith, M., Nichol, R. C., Dilday, B., et al. 2012, ApJ, 755, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Scoville, N., Murayama, T., et al. 2007, ApJS, 172, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S., Pastorello, A., Mazzali, P. A., et al. 2006, MNRAS, 371, 1459 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S., Navasardyan, H., Maurer, J. I., et al. 2011, MNRAS, 413, 2140 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M., Cinabro, D., Dilday, B., et al. 2014, ApJ, 792, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [Google Scholar]
- Turatto, M., Benetti, S., Cappellaro, E., et al. 1996, MNRAS, 283, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Turatto, M., Suzuki, T., Mazzali, P. A., et al. 2000, ApJ, 534, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Vaccari, M., Marchetti, L., Franceschini, A., et al. 2010, A&A, 518, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, S., Elias-Rosa, N., Taubenberger, S., et al. 2008, ApJ, 673, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, S., Fraser, M., Benetti, S., et al. 2011, MNRAS, 416, 3138 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C., Harkness, R. P., Clocchiatti, A., et al. 1994, ApJ, 436, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Labbé, I., van Dokkum, P. G., et al. 2011, ApJ, 735, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Wittman, D. 2009, ApJ, 700, L174 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1942, ApJ, 96, 28 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of photometric classification with the different tools. In parenthesis we report the events labelled as probable SNe.
All Figures
 |
Fig. 1 Transient detection efficiency as a function of magnitude for the r-band observation of COSMOS on 2012 March 15. The dots are the averages of 3 artificial star experiments with the errorbar being the dispersion whereas the line is the adopted efficiency curve after the fit with the Eq. (1) (DEmax = 93%, mag50 = 23.0 mag, and β = 6.1). |
| In the text | |
 |
Fig. 2 Example of the output of the SN-typing procedure. The top panel shows the observed r-band light curve that, in this case, is compared to the template K-corrected B-band light curve. The bottom panels show the observed light curve and template fit for the g band (left) and i band (right). Blue dots represent the SN candidate observed magnitudes (arrows indicate upper limits) while red open circles represent the template photometry. The legend identifies the best fitting template and parameters. |
| In the text | |
 |
Fig. 3 Comparison of the SN classifications obtained with the different tools. The exploded wedges are the SN type fractions obtained with our SUDARE tool and the coloured sectors are the SNANA classification. |
| In the text | |
 |
Fig. 4 Observed spectrum of SN 2012gs obtained with FORS2 on MJD 56 252.0 (black line) is compared to that of the SN Ic 2007gr at phase −9d (top) and of the type Ia SN 1991T at phase + 14d (bottom). In both cases it is adopted for SN 2012gs at redshift z = 0.5, as measured from the narrow emission lines of the host galaxy. |
| In the text | |
 |
Fig. 5 SN 2012gs light-curve fit, obtained using our tool. The best match is obtained with SN 1991T and the maximum is estimated to occur on MJD 56 235.1. |
| In the text | |
 |
Fig. 6 Histogram of the r-band SN magnitudes at discovery. The dotted line shows the distribution of m50 (the magnitude where the detection efficiency is 0.5) for the r-band observations (as reported in Table 2). |
| In the text | |
 |
Fig. 7 Redshift distribution of the discovered SNe for the different types. |
| In the text | |
 |
Fig. 8 Distribution of K magnitude for galaxies in CDFS (solid line) and COSMOS (dashed line) catalogues. |
| In the text | |
 |
Fig. 9 Redshift distribution (zpeak) for galaxies in CDFS (solid line) and COSMOS (dashed line) catalogues. |
| In the text | |
 |
Fig. 10 Width of the 68% confidence intervals computed from the redshift-probability distribution as a function of galaxy magnitude (top panel) and redshift (bottom panel). |
| In the text | |
 |
Fig. 11 Distribution of zpeak (solid line) and zMC (dashed line) of the galaxies in COSMOS (top panel) and in CDFS catalogues (bottom panel). |
| In the text | |
 |
Fig. 12 Comparison of photometric vs. spectroscopic redshifts from COSMOS (top panel) and CDFS (bottom panel). |
| In the text | |
 |
Fig. 13 Comparison of our photometric redshift for CDFS and MUSYC photometric redshifts. |
| In the text | |
 |
Fig. 14 Control time as a function of redshift for different SN types (in days per deg2) averaged across the three survey fields. |
| In the text | |
 |
Fig. 15 Predicted (line) vs. observed (bars) cumulative extinction distribution. |
| In the text | |
 |
Fig. 16 CC SN rate per unit volume. All measurements do not account for the correction for hidden SNe. To obtain the predicted SN rate from the measured SFR, we adopt 8, 40 M⊙ as the lower and upper mass limits for SN CC progenitors and the proper IMF, Salpeter for Madau & Dickinson (2014) and SalA for Hopkins & Beacom (2006). The dashed lines show the predicted SN rate, assuming the fraction of hidden SNe given in (Mattila et al. 2012). |
| In the text | |
 |
Fig. 17 Our estimates of the SN Ia rate at z = 0.25,0.45,0.65 are compared with the other values from literature. The rate of Cappellaro et al. (1999), Hardin et al. (2000), Madgwick et al. (2003), Blanc et al. (2004) were given per unit luminosity. They are converted in rate per unit volume using the following relation of the luminosity density as a function of redshift: |
| In the text | |
 |
Fig. 18 Histogram of published estimates of the SN Ia rate in the three redshift bins of our measurements. All values are scaled to the mean redshift of the bin, assuming a linear evolution of the rate with redshift (see text). In red we show our measurements. The black lines are the Gaussian curve whose mean and variance are computed from the data and reported in each panel’s legend. The averages and dispersions were computed by weighting the individual measurements with the inverse of their statistical errors. |
| In the text | |
 |
Fig. 19 Distribution functions of the delay times that were selected for our theoretical predictions for the single degenerate (green), and double degenerate models (blue and red, see text for more details). The thin lines show the cumulative fraction of events as a function of time. |
| In the text | |
 |
Fig. 20 Average values of the SN Ia rates per unit volume as a function of redshift. The still unique measurement at z> 2 of Rodney et al. (2014) is also plotted. For the derivation of the SNIa rate model evolution, we adopted the SFH from Madau & Dickinson (2014). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.