| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526368 | |
| Published online | 04 December 2015 | |
Vacuum ultraviolet of hydrogenated amorphous carbons
II. Small hydrocarbons production in Photon Dominated Regions⋆
1
CNRS-INSU, Institut d’Astrophysique Spatiale, UMR
8617, 91405
Orsay,
France
e-mail:
emmanuel.dartois@u-psud.fr
2
Université Paris Sud, Institut d’Astrophysique Spatiale, UMR
8617, Bâtiment 121,
91405
Orsay,
France
3
CNRS-IN2P3, Institut de Physique Nucléaire d’Orsay, UMR
8608, 91406
Orsay,
France
4
Université Paris Sud, Institut de Physique Nucléaire d’Orsay, UMR
8608, IN2P3-CNRS, Bâtiment
103, 91406
Orsay,
France
5
Centro de Astrobiología, INTA-CSIC, Carretera de Ajalvir, km 4,
Torrejón de Ardoz, 28850
Madrid,
Spain
6
Sackler Laboratory for Astrophysics, Leiden Observatory,
University of Leiden, PO Box
9513, 2300 RA
Leiden, The
Netherlands
7
CNRS-INP, Institut des Sciences Moléculaires d’Orsay, UMR
8214, 91405
Orsay,
France
8
Université Paris-Sud, Institut des Sciences Moléculaires d’Orsay,
UMR 8214, Bâtiment
210, 91405
Orsay,
France
Received: 21 April 2015
Accepted: 16 October 2015
Context. Hydrogenated amorphous carbons (a–C:H) are a major component of the carbonaceous solids present in the interstellar medium. The production and existence of these grains is connected in particular with the balance between their photolysis, radiolysis, and hydrogenation. During grain processing, H2 and other small organic molecules, radicals, and fragments are released into the gas phase.
Aims. We perform photolytic experiments on laboratory produced interstellar a–C:H analogues to monitor and quantify the release of species and compare to relevant observations in the interstellar medium.
Methods. Hydrogenated amorphous carbon analogues at low temperature are exposed to ultraviolet (UV) photons, under ultra-high vacuum conditions. The species produced are monitored using mass spectrometry and post irradiation temperature-programmed desorption. Additional experiments are performed using deuterated analogues and the species produced are unambiguously separated from background contributions. We implement the laboratory measured yields for the released species in a time dependent model to investigate the effect of the UV photon irradiation of hydrogenated amorphous carbons in a photon dominated region, and estimate the associated time scale.
Results. The UV photolysis of hydrogenated amorphous carbons leads to the production of H2 molecules and small hydrocarbons. The model shows that the photolytic evolution of a–C:Hs in photon dominated regions, such as the Horsehead Nebula, can raise the abundance of carbonaceous molecules by several orders of magnitude at intermediate visual extinctions, i.e., after the C+ maximum and before the dense cloud conditions prevail where models generally show a minimum abundance for such carbonaceous species. The injection time peak ranges from a thousand to ten thousand years in the models, considering only the destruction of such grains and no re-hydrogenation. This time scale is consistent with the estimated advection front of a photon dominated region, which replenishes it with freshly exposed material.
Key words: astrochemistry / molecular processes / ISM: abundances / ultraviolet: ISM / methods: laboratory: solid state / photon-dominated region (PDR)
Appendices are available in electronic form at http://www.aanda.org
This work was supported by the ANR COSMISME project, grant ANR-2010-BLAN-0502 of the French Agence Nationale de la Recherche. Part of the equipment used in this work, as well as missions, have been financed by the ANR and French INSU-CNRS program “Physique et Chimie du Milieu Interstellaire” (PCMI).
© ESO, 2015
1. Introduction
Carbonaceous molecules occupy a significant position in interstellar chemistry networks. In the gas phase most of the ionized or neutral molecules detected in the interstellar and circumstellar media contain at least one carbon atom. Carbon chemistry thus plays a dominant role in the understanding of the structure and evolution of the interstellar medium (ISM). Small hydrocarbons have been observed in circumstellar shells for a long time (e.g., C4H, C5H; Guelin et al. 1978; Cernicharo et al. 1986) and in the external-UV-shielded molecular dark clouds (e.g., C3H2, C2H, C4H, C6H; Thaddeus et al. 1985; Gottlieb et al. 1983; Gupta et al. 2009). The diffuse interstellar medium is no exception to the rule, and these small hydrocarbons are also detected in abundance (Lucas & Liszt 2000; Gerin et al. 2011; Liszt et al. 2012). One particular zone of interest where small carbonaceous radicals, molecules, and their fragments can be observed are sharp molecular clouds edges exposed to energetic photons. These photon dominated regions (PDRs; Fuente et al. 2003; Gerin et al. 2005; Teyssier et al. 2005; Pety et al. 2005; Guzmán et al. 2015) are rich in these hydrocarbons (like CCH, c-C3H2, C4H), and provide tests for the chemistry models in the diffuse to molecular transition.
Only recently have pure gas phase models been able to approach the observed column densities abundance of many of the observed species (e.g., Pety et al. 2012; Cuadrado et al. 2015; Guzmán et al. 2015), although they still underpredict abundances at some PDR positions. Several authors suggest that such abundances may arise instead from the products of the UV photodissociation of carbonaceous grains or polycyclic aromatic hydrocarbons (PAHs, Teyssier et al. 2004; Pety et al. 2005). In addition to gas phase reactions, exchanges between gas and solid phases must thus be established for a comprehensive carbon chemistry network description. Some laboratory experiments and theoretical calculations suggest that PAHs may fragment into small carbon clusters and molecules under photon impact (C2, C3, C2H2, etc.) (Joblin 2003; Le Page et al. 2003; Allain et al. 1996b,a; Leger et al. 1989; Scott et al. 1997), feeding the interstellar medium with small carbon clusters and molecules. Hydrogenated amorphous carbons (known in the literature as a–C:H or HAC) are abundantly observed in the ISM, and their interaction with UV photons could also participate in the origin of many of these small hydrocarbons (e.g., Alata et al. 2014; Duley et al. 2015).
In this article, we experimentally investigate the production and release of hydrocarbons from the UV photolysis of a–C:H interstellar analogues under ultra-high vacuum conditions. In Sects. 2 and 3 we present the experiments and the results. In Sect. 4 the experimental results are included in a PDR model of the Horsehead Nebula to constrain the impact of this release on the observed gas phase species. Finally, in Sect. 5 we present the conclusions and perspectives.
2. Experiments description
The ultra-high vacuum (UHV) experiments were performed in the interstellar astrochemistry chamber (ISAC). We give here a short description of the setup. For more details we refer the reader to Muñoz Caro et al. (2010). The ISAC chamber reaches UHV by using a combination of a series of turbo pumps and a Titanium sublimation pump. The attained pressure is typically on the order of P ≃ 2.5−4 × 10-11 mbar. Cooling is done by means of a closed-cycle helium cryostat. The temperature achieved is about 8 K at the cooled holder where our interstellar dust analogue is placed. A quadrupole mass spectrometer (QMS) is located behind the substrate. It can measure masses between 1 (u) and 200 (u) with a mass resolution of m/ Δm ≃ 50. Molecules are ionized by electron impact (set at 70 eV electron energy) and accelerated into the QMS mass filter. The electron impact ionization induces the fragmentation of species. The parent molecules are thus detected via their ion and fragments. The fragmentation pattern combined to the ionization cross section of each species must be taken into account to retrieve the parent abundance. The UV photons are generated by a hydrogen flow discharge lamp by using an Evenson cavity coupled to a 2.45 GHz RF microwave generator, and enter the vacuum chamber through a MgF2 window. Hydrogenated (and deuterated) amorphous carbon dust analogues (a–C:H and a–C:D, respectively) are prepared using the SICAL-P experiment, consisting of a low pressure (0.5−0.6 mbar), high power (100W) plasma enhanced chemical vapor deposition method (PECVD) using CH4 (or CD4) gas precursors (see Alata et al. 2014, for details). The deposition is made on an IR transparent ZnSe substrate and the resulting analogue thickness is about 2 microns. Two irradiation experiments have been performed for a–C:H and a–C:D films under similar conditions at the same irradiation dose (≃4.7 × 1018 photon cm-2). The UV photon energies are distributed between 6.8 and 10.5 eV, and the average energy per emitted photon is about 8.6 eV (Chen et al. 2014; Cruz-Diaz et al. 2014). A typical experimental sequence consists in cooling the dust analogue to 8 K and then irradiating the dust with UV photons, followed by a post irradiation temperature programmed desorption (TPD, 5 K/min) allowing for the release and QMS detection of the trapped photolytically produced species. Before irradiation, we record a blank experiment without irradiation: the cold finger is placed at 8 K for 1 h followed by a TPD at 5 K/min. This allows us to identify eventual pollutions at given masses. The main masses affected are those dominated by cryopumped H2O, N2, and CO2 contributions. After the blank experiment, the film was cooled down again and then irradiated for 5 h and heated at a rate of 5 K/min (TPD). During the irradiation and TPD, all QMS mass signals are recorded.
3. Results
The photolytic production of H2 and CH4 from a–C:H were first reported in Alata et al. (2014). These experimental results encouraged us to explore the higher mass photolysis products requiring the use of a UHV chamber. Most produced species are released from the film during the TPD. The desorption peak temperature depends on the nature of each species. The species are detected after electron impact ionization in the QMS, which produces fragments. The relative quantity of the species are related to the QMS signal by taking into account both the ionization cross sections for different species, and the fragmentation branching ratios after electron impact ionization (e.g., CH4 is detected via CH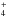 , CH
, CH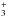 , CH
, CH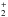 , CH+, C+, and 13C contributions). These ionization cross sections and fragmentation patterns are found for many stable species in the NIST database1.
, CH+, C+, and 13C contributions). These ionization cross sections and fragmentation patterns are found for many stable species in the NIST database1.
To perform the analysis, the TPD signals are integrated over time to produce the integrated mass spectra for each experiment. These integrated TPD signals, which give an overview of the mass spectra, are shown in Figs. 1 and 2 for the a–C:H and a–C:D experiments, respectively. The parent species contribution are obtained by a matrix analysis. A cracking pattern matrix M (n × m) is built where the rows are the n measured masses and the m columns are the normalized cracking pattern of the m considered species. The species contribution are retrieved by minimizing the linear least-squares problem,
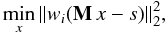 where s is the vector of n QMS measured intensities; x is the species cracking pattern contributions, which have to be divided by their ionization cross sections to obtain their relative contributions; and wi is a weighting factor (equal to 1 or 0) that includes only the measured m/z where the cracking patterns of the considered species contribute significantly or are known with a sufficient accuracy. The results of these minimizations relative to CH4 and CD4 are given in Tables 1 and 2. The calculated synthetic spectra are shown by the filled bar graphs in Figs. 1 and 2. The main contaminant species (H2O, N2, CO2, CO, O2) contributing to the signal are included in these minimizations and are shown by filled bar graphs with a distinct color. The reported error bars include only the statistical errors computed when adjusting the model to the measurements. However, these error bars miss the systematic error bars that do exist, including species that would not be included in the minimization, branching ratios uncertainties (they are taken as equal for hydrogenated and deuterated species in the absence of specific measurements), differences in ionization efficiencies, and also eventual slight differences in the film produced with hydrogenated and deuterated precursors. In addition, the N2 pollution peak affects the minimizations unevenly, falling mostly on the retrieval of the intensity for the main peak of C2H4 and C2D2 for the species produced with the H and D films, respectively. Taking this into account, Tables 1 and 2 show that both target films, which are two independent measurements, provide very similar results.
where s is the vector of n QMS measured intensities; x is the species cracking pattern contributions, which have to be divided by their ionization cross sections to obtain their relative contributions; and wi is a weighting factor (equal to 1 or 0) that includes only the measured m/z where the cracking patterns of the considered species contribute significantly or are known with a sufficient accuracy. The results of these minimizations relative to CH4 and CD4 are given in Tables 1 and 2. The calculated synthetic spectra are shown by the filled bar graphs in Figs. 1 and 2. The main contaminant species (H2O, N2, CO2, CO, O2) contributing to the signal are included in these minimizations and are shown by filled bar graphs with a distinct color. The reported error bars include only the statistical errors computed when adjusting the model to the measurements. However, these error bars miss the systematic error bars that do exist, including species that would not be included in the minimization, branching ratios uncertainties (they are taken as equal for hydrogenated and deuterated species in the absence of specific measurements), differences in ionization efficiencies, and also eventual slight differences in the film produced with hydrogenated and deuterated precursors. In addition, the N2 pollution peak affects the minimizations unevenly, falling mostly on the retrieval of the intensity for the main peak of C2H4 and C2D2 for the species produced with the H and D films, respectively. Taking this into account, Tables 1 and 2 show that both target films, which are two independent measurements, provide very similar results.
 |
Fig. 1 Top: QMS integrated signal recorded during the TPD of an irradiated a–C:H film (blue histogram). The synthetic mass spectrum obtained by a matrix analysis is shown with filled bar graphs; the associated error bars come from the minimization procedure. Bottom: ratio of the fitted versus measured individual mass spectra for the main peaks (left axis, squares), and peak temperature associated with the TPD for the considered mass (right axis, circles). |
 |
Fig. 2 Same as Fig. 1 for an irradiated a–C:D film with the expected mass separation peak pattern every two m/z due to the deuterium substitution. The data peaks at uneven m/z are due to eventual pollution and hydrogen contamination in the film. |
Photoproduced species relative to CH4 (%, ± 2σ).
Photoproduced species relative to CD4 (%, ± 2σ).
Selected m/z TPD spectra recorded post irradiation are shown in Fig. 3. The chosen masses are relatively pure, i.e., filled by a small number of parents, and are indicated in parentheses. The desorption maximum occurs at temperatures increasing with the parent species molecular weight, from about 150 K for CH4 to 220 K for C4Hy species.
 |
Fig. 3 TPD spectra recorded for selected m/z for the a–C:H experiment. The chosen masses are dominated by a small amount of fragments contributing to the signal. The corresponding parent species are given in brackets, as obtained from the minimization. The desorption temperature peaks are indicated by vertical dashed lines. |
4. PDR model of the Horsehead Nebula
To investigate the effect of the UV photon irradiation of hydrogenated amorphous carbons in a photon dominated region, we implement the laboratory measured yields for the released species in a model.
4.1. Calculation method
Our purpose is to describe the effects of a–C:H photolysis as a function of time in a photon dominated region. We chose the Horsehead Nebula template, which is exposed to the UV flux from the O9.5V star σ ori, estimated at 60 times the standard interstellar radiation field in Draine units. We use a combination of two codes to achieve our goals. The Meudon PDR code2 (Le Petit et al. 2006) is used to model in detail the stationary gas phase chemistry at the border of the cloud illuminated by a high UV flux. The Nahoon code3 (Wakelam 2006) is then used to follow the time dependence of the perturbation induced by the injection of the species released by a–C:H photolysis.
The Meudon PDR code considers a plane-parallel slab of gas and dust illuminated by a UV radiation field coming from one or both sides of the cloud. It is a stationary model solving for the radiative transfer, species chemistry and thermal balance. The density and thermal structures are determined in a consistent way using a constant pressure P = 1.6 × 106 K cm-3 to reach a dense cloud hydrogen density of nH ≈ 2 × 105 cm-3 as in recent previous models. The intensity of the incident UV flux χ is set to 60 times the interstellar radiation field in Draine units (see Draine 1978; Habart et al. 2005), and the cosmic-ray ionization rate is set to ζ = 5 × 10-17 s-1 (Goicoechea et al. 2009). The initial gas phase abundances are those corresponding to the Horsehead Nebula (see Goicoechea et al. 2006, Table 6); the sulfur abundance is set accordingly to S / H = 3.5 × 10-6. The Meudon code is run with the chemistry network of Chabot et al. (2013), which can be found in the Kida database (Wakelam et al. 2012). We retrieve the following outputs from the Meudon PDR code to be used at the input in the time dependent code: the density of H (nH), the temperature, the equilibrium chemical abundances, and the photodissociation rates. The Meudon PDR code runs with its own photodissociation rates for several species, including those governing the opacity (H2 and CO). Details of this calculation are presented in Appendix A.
Sulfur is known to be an element of importance for the degree of ionization, via charge exchange with C+, which may strongly affect the hydrocarbon abundances. In addition, sulfur has been thoroughly discussed in previous articles on the Horsehead Nebula. Therefore, we found it useful in this context to keep track of its influence in the modeling, in the absence of a S absolute abundance measurement. The influence of setting a lower sulfur abundance in the model output is presented in Appendix B. The net effect of low S abundance is to increase the overall CnHy abundances by about an order of magnitude, still much lower than the hydrocarbons brought by a–C:H photodestruction at intermediate AV.
The second code used is a modified version of the Nahoon4 chemical model developed by V. Wakelam (Wakelam 2006). The Nahoon code follows the time-dependent chemistry of gas-phase species for a single spatial point (zero dimension), with fixed temperature, density, UV, and cosmic ray fluxes. Before solving the system, it checks at each iteration for the correct stoechiometric balance (numerical check sum) for each reaction. In other words, it verifies that the reactants and the products have the same number of chemical elements.
Such a gas phase check sum makes it difficult to add desorption reactions involving exchange and modifications of the chemical nature of the bulk solid phase to the existing codes. The inclusion of reactions involving an a–C:H grain made of a thousand to a billion carbon and hydrogen atoms, as well as all the possible produced species, becomes intractable under such a check sum scheme. As a matter of computing time, it is not possible to treat all the intermediate species between large a–C:H grains and small hydrocarbons. The huge number of differential equations would be impossible to handle. As a consequence, to take into account the decrease in the hydrocarbon photo-production of a–C:H grains with time, associated with their photolytic destruction, we introduce a specific numerical scheme. The reaction rate is proportional to the product of grain number density times the photodestruction rate. To run the models it is numerically simpler to reduce the photodestruction rate instead of the grain number density, thus accounting for the grain destruction but avoiding the checksum issue. Specifically, at the end of each time step, the overall abundance of a–C:Hs is kept constant, but we multiply the a–C:H photo-destruction rate by a factor F which depends on the abundance of a–C:H destroyed by UV photon at the previous time steps. Therefore, the abundance of grains stays constant, equal to the initial abundance, but the rate of the reaction evolves as a function of the history of the a–C:H grains. The initial number density [ a−C:H ] 0 is set to ![\hbox{$f_{\rm a{-}C:H}^C \times \frac{\rm [C]}{\rm [H]} \times n_{\rm H}$}](/articles/aa/full_html/2015/12/aa26368-15/aa26368-15-eq51.png) , where
, where 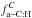 is the fraction of interstellar carbon abundance locked into a–C:H,
is the fraction of interstellar carbon abundance locked into a–C:H, ![\hbox{$\rm \frac{[C]}{[H]}$}](/articles/aa/full_html/2015/12/aa26368-15/aa26368-15-eq53.png) the cosmic carbon abundance (taken as 3 × 10-4), and nH the total hydrogen number density. At iteration i, Fi is equal to
the cosmic carbon abundance (taken as 3 × 10-4), and nH the total hydrogen number density. At iteration i, Fi is equal to ![\begin{equation} F_{i} = \dfrac{{\rm [a {-}C{:}H}]_{0} - \sum\limits_{n\,=\,1}^{i\,-\,1} [{\rm a{-}C:H}]_{n}}{\rm [a{-}C{:}H]_{0}} \cdot \label{F} \end{equation}](/articles/aa/full_html/2015/12/aa26368-15/aa26368-15-eq57.png) (1)The rate of the photo-destruction reactions is defined by the product of the rate coefficient ki in s-1 and the densities of the reactants. The rate coefficient represents the intrinsic velocity of the photo-destruction reaction. It is calculated as
(1)The rate of the photo-destruction reactions is defined by the product of the rate coefficient ki in s-1 and the densities of the reactants. The rate coefficient represents the intrinsic velocity of the photo-destruction reaction. It is calculated as 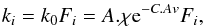 (2)where A is the unattenuated photo-destruction rate in a reference interstellar radiation field multiplied by the intensity factor of the incident UV flux χ in Draine units, as described previously, and e− C.Av represents the continuum attenuation by the dust. We adopt a typical value of C = 2 (e.g., Wakelam et al. 2012).
(2)where A is the unattenuated photo-destruction rate in a reference interstellar radiation field multiplied by the intensity factor of the incident UV flux χ in Draine units, as described previously, and e− C.Av represents the continuum attenuation by the dust. We adopt a typical value of C = 2 (e.g., Wakelam et al. 2012).
 |
Fig. 4 Output of the Horsehead Nebula photon dominated region time dependent model for observed selected hydrocarbons (CCH, c-C3H, c-C3H2, C4H). The abundances are shown as a function of visual extinction in the cloud illuminated by the σOri star (see Appendix A for details) and time. For each species the upper panel shows the abundance at time 103 yr (close to the maximum injection by dust grains, for clarity): initial model without hydrogenated amorphous carbon photolysis (lower curve), with model I including reactions up to CH4 (dotted line), model II reactions up to C2Hy (dashed line), model III reactions up to C3Hy (upper curve). For each species, in the lower panel, the corresponding abundance ratio with the addition of photolytic reactions over the abundance without the addition of the photolytic reactions is shown for all times. |
To include the a–C:H UV photolysis products, we add the following reactions: 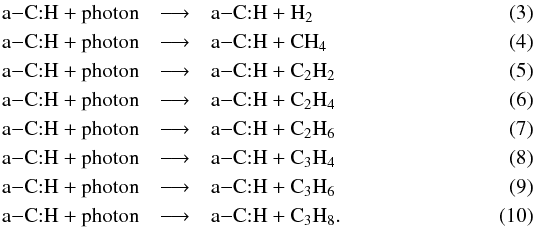 The unattenuated photo-destruction rate A can be obtained from the measured a–C:H photo destruction cross section multiplied by the species photo-production yield (
The unattenuated photo-destruction rate A can be obtained from the measured a–C:H photo destruction cross section multiplied by the species photo-production yield (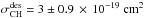 ,
, 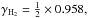 and γCH4 = 0.031 × γH2; Alata et al. 2014), and the standard FUV (6 < hν< 13.6 eV) interstellar radiation field adopted from Draine (1978), corresponding to
and γCH4 = 0.031 × γH2; Alata et al. 2014), and the standard FUV (6 < hν< 13.6 eV) interstellar radiation field adopted from Draine (1978), corresponding to 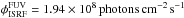 .
.
Using the measurements from this work, the corresponding photo-destruction rates A are AH2 = 2.79 × 10-11 s-1, ACH4 = 8.6 × 10-13 s-1, AC2H2 = 2.3 × 10-14 s-1, AC2H4 = 5.6 × 10-14 s-1, AC2H6 = 7.1 × 10-14 s-1, AC3H4 = 1.2 × 10-14 s-1, AC3H6 = 3.3 × 10-14 s-1, and AC3H8 = 2.2 × 10-14 s-1. On the basis of these reactions we define three models of increasing complexity to follow the effect of the a–C:H photodestruction: Model I includes reactions up to CH4 (3 to 4), model II reactions up to C2Hy, and model III reactions up to C3Hy. The compounds C2H6 and C3H8 are not available in the used KIDA version of the code, and so we decided to add the C2H6 rate to the C2H4 value. The situation is similar for C3H8, which was added to C3H6.
These models are compared to the initial model without a–C:H photolysis reactions. For each model we compute the time evolution of the chemistry induced by the incorporation of a–C:H photolysis with the modified version of the Nahoon model for several slabs in the PDR. Each slab is defined by a temperature, a density, a set of photolytic rates, and a set of chemical abundances. We use the same chemistry network (Chabot et al. 2013) as the one used in the Meudon PDR code. For each slab we check that without injecting the a–C:H grains photo-products, the chemical abundances do not evolve with time, i.e., that the equilibrium is reached. We note that in our procedure we implicitly assume that the opacity is relatively unaffected by the molecular species released from a–C:H grains. This is a reasonable assumption (see Fig. A.3).
4.2. Results and discussions
The results of these calculations, assuming conservatively that about 5% of the cosmic carbon is locked in a–C:H (i.e., 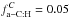 ), are presented in Fig. 4 for selected species (CCH, c-C3H,c-C3H2, C4H) that have been observed in the Horsehead PDR. The temperature, density, and ionization degree as a function of the visual extinction (Av) for the constant pressure model for the Horsehead Nebula are given in the Appendix. In Fig. 4 the abundances are presented as a function of visual extinction and time in the upper panels. The abundance ratios obtained by including the a–C:H photolysis divided by the initial model (≡
), are presented in Fig. 4 for selected species (CCH, c-C3H,c-C3H2, C4H) that have been observed in the Horsehead PDR. The temperature, density, and ionization degree as a function of the visual extinction (Av) for the constant pressure model for the Horsehead Nebula are given in the Appendix. In Fig. 4 the abundances are presented as a function of visual extinction and time in the upper panels. The abundance ratios obtained by including the a–C:H photolysis divided by the initial model (≡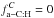 ) are given in the lower panel; this ratio gives insights into the chemical seeding of the gas by a–C:H photoproducts and the subsequent spread over the chemical gas phase network.
) are given in the lower panel; this ratio gives insights into the chemical seeding of the gas by a–C:H photoproducts and the subsequent spread over the chemical gas phase network.
When adding the C2Hy reactions, the abundances increase especially as the considered species are closely in the reaction scheme (CnHy species with n close to 2). Adding the C3Hy reactions, the large hydrocarbons increase, but rather moderately. However, the networks considered are incomplete for such large species; only 24 reactions involving C3H4 and 2 reactions involving C3H6 in the actual version. The small species abundances increase by two (e.g., CCH) to more than three (e.g., C4H) orders of magnitude.
Recent models including the condensation and surface chemistry are able to increase the amount of small hydrocarbons in the dense cloud ultraviolet shielded region (e.g., Pety et al. 2012; Cuadrado et al. 2015; Guzmán et al. 2015), in particular as the hydrocarbon scavenger species are frozen onto grains and thus the chemical equilibrium is displaced, producing higher hydrocarbons abundances. Our models show that a–C:H photolysis brings additional small molecules in the intermediate region where 2 ≲ Av ≲ 4, where there is a deficit in small hydrocarbons in many models. This Av window corresponds to a region where C+ chemistry is no longer dominant anymore and photons are still abundant. The column density differences observed in the Horsehead PDR at visual extinctions Av ~ 1 (IR peak) and the one observed at Av ~ 4 (Cloud) for CCH, c-C3H2, and C4H are between about a factor of 5 and 30 (Pety et al. 2005, 2012). In the absence of hydrocarbons/radicals released by the photolysis of hydrogenated amorphous carbons dust grains, the corresponding differences in the model output lie between 3 and more than 5 orders of magnitude. As seen for each species in the lower panels of Fig. 4, at times between 103 and 104 yr, the injection of hydrocarbons from carbonaceous dust grains may help in reconciling models with observations in the Horsehead Nebula as suggested earlier (e.g., Pety et al. 2005) as these differences are therefore reduced by 2 to 4 orders of magnitude.
In this time dependent model, the species abundances increase at the highest rate for time scales on the order of 103 to 104 yr, and then decrease as the a–C:H are progressively destroyed. As an interesting outcome of the time evolution, these results must be compared to the advection time scale of molecular material from the shielded regions into the surface zones in PDRs because of the advance of the ionization and dissociation fronts. Hollenbach & Tielens (1997) estimate a value on the order of 0.5−1 km s-1. At a distance of 400 pc to the Horsehead Nebula (cloud distance: Lada et al. 1991; σOri distance: 352 ± 113 pc Perryman et al. 1997), an arc second corresponds to about 6 × 1015 cm, or less than 2 × 103 yr advection time. Equivalently, the physical distance between AV = 0.5 and AV = 1 in the constant pressure model corresponds to about 7.8 × 1015 cm, equivalent to 2.5−5 × 103 yr. Thus if a–C:H grains are present at the diffuse to dense interface, they are constantly renewed within time scales on the same order as the advection front, replenishing the photoproducts reservoir.
5. Conclusion
Hydrogenated amorphous carbon interstellar analogues were produced in the laboratory and were exposed to UV photons to explore the FUV interstellar radiation processing at low temperature in a ultra-high vacuum system.
Even if the main photolysis product is H2, hydrocarbons with up to four carbon atoms are detected by post irradiation temperature programmed desorption coupled to mass spectrometry. The experimentally measured a–C:H photo destruction cross section multiplied by the species photo-production yield are implemented in a time dependent astrophysical model of a photon dominated region corresponding to the Horsehead Nebula.
According to the results of this time dependent model, the abundance of small hydrocarbons (such as CCH, c-C3H2, C4H) can temporarily rise by several orders of magnitude and can provide an additional source of hydrocarbons to solve the mismatch between observations and models at intermediate visual extinctions. The corresponding hydrocarbons injection time scale at these visual extinctions in the cloud is in the range of a thousand to ten thousand years. Estimations of typical PDR advection front velocities, on the order of km s-1, ensures that with such destruction time scales, the medium is constantly refilled with unprocessed, freshly exposed grains, considering only the photolytic destruction processes for such grains and no re-hydrogenation.
Thus, the irradiation and evolution of interstellar grains must be implemented in models to constrain observations and to renew the interest in further development of time dependent chemical models to follow observed abundances. The reference networks should also be completed in order to include highly hydrogenated hydrocarbon species.
Online material
Appendix A: PDR calculation details
In this appendix, the general outputs of the PDR model used in the article are presented. The model is run, as detailed in the article, with a constant pressure P = 1.6 × 106 K cm-3 (corresponding to a dense cloud hydrogen density of nH ≈ 2 × 105 cm-3), an incident UV flux χ set to 60 times the interstellar radiation field in Draine units (see Draine 1978; Habart et al. 2005), and a cosmic ray ionization rate set to ζ = 5 × 10-17 s-1 (Goicoechea et al. 2009). The initial gas phase abundances are those used for the Horsehead Nebula (see Goicoechea et al. 2006, Table 6) with the sulfur abundance set to S / H = 3.5 × 10-6.
Figure A.1 presents the temperature, density, and ionization degree as a function of the visual extinction (Av) at the output of the PDR code.
 |
Fig. A.1 Temperature (purple dotted line), total hydrogen density (blue dashed line), and ionization degree (green solid line) as a function of visual extinction. |
 |
Fig. A.2 Photodissociation rates of CO (blue dashed dotted lines) and H2 (red dashed lines) and photoionization rates of C (green dotted lines) and S (purple solid lines) as a function of the visual extinction in the Meudon code (no symbols) and in Nahoon (diamond lines). |
 |
Fig. A.3 Abundance of H (brown long dashed line), electrons (red solid line), CO (yellow dotted lines), C (green dash-dotted line), C+ (blue short dotted line), and H+ (purple short and long dashed line) for times of 300 yr (circle), 1000 yr (triangle), 104 yr (pentagon), and 108 yr (diamond) as a function of the visual extinction. |
 |
Fig. A.4 Coefficient Fi as a function of time for Av = 0.5 (blue solid line), Av = 1 (purple dashed line), Av = 3 (green dotted lines), Av = 5 (orange dashed dotted line), and Av = 7 (brown dashed line). |
 |
Fig. A.5 Ratio of the abundance of CCH with or without the inclusion of photo-desorption reactions as a function of the percent of carbon in a–C:H for Av = 3 at 1000 yr (blue dash-dotted line) and for Av = 4 at 10 000 yr (purple solid line). |
Figure A.2 shows the photodissociation rates of H2, CO, and the photoionization rates of C and S in the Meudon and in the Nahoon codes before our modifications. We have modified the photodissociation rates in the Nahoon code in order to make them equal to those in the Meudon code. In particular, the photo-dissociation rates of H2 and CO were very different (by several orders of magnitude) in the Meudon code and in Nahoon.
As shown in Fig. A.3, the abundance of key species at different times is not affected by the addition of the a–C:H photolysis reactions. This implies that the added photolytic reactions do not perturb the initial opacity of the cloud model.
The rate coefficient factor Fi, discussed in the article, was checked for all visual extinctions in the model. As shown in Fig. A.4, the higher the visual extinction, the longer it takes for Fi to decrease. It takes approximately 200 yr, 5000 yr, and 2 × 107 yr to reduce Fi by about a factor of two at visual extinctions equal to 1, 3, and 7 mag, respectively.
In Fig. A.5 the influence of the adopted fraction of interstellar carbon abundance locked into a–C:H grains is shown. The abundance of gas phase carbonaceous molecules in the model increases linearly with the percent fraction of carbon contained in the a–C:H. The case of CCH is presented in Fig. A.5. With 5% of carbon locked in a–C:Hs, the abundance of CCH increases by a factor of 40 at Av = 4 and 10 000 yr, and by a factor 60 at Av = 3 and 1000 yr.
Appendix B: Influence of the sulfur abundance
 |
Fig. B.1 Output of the Horsehead Nebula photon dominated region model III with a low sulfur abundance in the initial conditions (S / H = 5.8 × 10-8) for the CCH hydrocarbon abundance as a function of visual extinction in the cloud illuminated by the σOri star (see Appendix A for details). The abundance of CCH is shown in the top panel at different times after injection of the a–C:H grain photolysis in the model. The corresponding abundance ratio of CCH with the addition of photolytic reactions divided by the abundance without the addition of the photolytic reactions is shown in the bottom panel for the same times. |
In the modeling we initally used the sulfur abundance as derived by Goicoechea et al. (2006) for the Horsehead Nebula. Because the sulfur abundance to be adopted is generally highly debated, we show the influence of setting the sulfur abundance to a lower abundance value S / H = 5.8 × 10-8 on our results.
 |
Fig. B.2 Same as Fig. B.1 with a low sulfur abundance in the initial conditions for C3H2: abundance of C3H2 (top) and abundance ratio of C3H2 with the addition of photolytic reactions divided by the abundances without the addition of photolytic reactions (bottom) for different times. |
 |
Fig. B.3 Same as Fig. B.1 with a low sulfur abundance in the initial conditions for C4H: abundance of C4H (top) and abundance ratio of C4H with the addition of photolytic reactions divided by the abundances without the addition of photolytic reactions (bottom) for different times. |
Acknowledgments
This work was supported by the ANR COSMISME project, grant ANR-2010-BLAN-0502 of the French Agence Nationale de la Recherche. Part of the equipment used in this work has been financed by the ANR and French INSU-CNRS program “Physique et Chimie du Milieu Interstellaire” (PCMI). G.A.C.D. and G.M.M.C. were financed by Spanish MINECO projects AYA2011-29375. We also wish to thank the anonymous referee for the comments and suggestions, as well as the language editor, that helped to improve the manuscript.
References
- Alata, I., Cruz-Diaz, G. A., Muñoz Caro, G. M., & Dartois, E. 2014, A&A, 569, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Kahane, C., Gomez-Gonzalez, J., & Guelin, M. 1986, A&A, 164, L1 [NASA ADS] [Google Scholar]
- Chabot, M., Béroff, K., Gratier, P., Jallat, A., & Wakelam, V. 2013, ApJ, 771, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-J., Chuang, K.-J., Muñoz Caro, G. M., et al. 2014, ApJ, 781, 15 [Google Scholar]
- Cruz-Diaz, G. A., Muñoz Caro, G. M., Chen, Y.-J., & Yih, T.-S. 2014, A&A, 562, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuadrado, S., Goicoechea, J. R., Pilleri, P., et al. 2015, A&A, 575, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duley, W. W., A. Zaidi, A., Wesolowski, M. J., & Kuzmin, S. 2015, MNRAS, 447, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Rodríguez-Franco, A., García-Burillo, S., Martín-Pintado, J., & Black, J. H. 2003, A&A, 406, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Roueff, E., Le Bourlot, J., et al. 2005, Astrochemistry: Recent Successes and Current Challenges, 231, 153 [Google Scholar]
- Gerin, M., Kaźmierczak, M., Jastrzebska, M., et al. 2011, A&A, 525, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., Hily-Blant, P., & Le Bourlot, J. 2009, A&A, 498, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gottlieb, C. A., Gottlieb, E. W., Thaddeus, P., & Kawamura, H. 1983, ApJ, 275, 916 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guelin, M., Green, S., & Thaddeus, P. 1978, ApJ, 224, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, H., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2009, ApJ, 691, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, V. V., Pety, J., Goicoechea, J. R., et al. 2015, ApJ, 800, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Habart, E., Abergel, A., Walmsley, C. M., Teyssier, D., & Pety, J. 2005, A&A, 437, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, E. A., Bally, J., & Stark, A. A. 1991, ApJ, 368, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H., Sonnentrucker, P., Cordiner, M., & Gerin, M. 2012, ApJ, 753, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. S. 2000, A&A, 358, 1069 [NASA ADS] [Google Scholar]
- Muñoz Caro, G. M., Jiménez-Escobar, A., Martín-Gago, J. Á., et al. 2010, A&A, 522, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Pety, J., Teyssier, D., Fossé, D., et al. 2005, A&A, 435, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, D., Fossé, D., Gerin, M., et al. 2004, A&A, 417, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, D., Hily-Blant, P., Gerin, M., et al. 2005, ESA SP, 577, 423 [NASA ADS] [Google Scholar]
- Thaddeus, P., Vrtilek, J. M., & Gottlieb, C. A. 1985, ApJ, 299, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V. 2006, Astrophysics Software Database, 28 [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: QMS integrated signal recorded during the TPD of an irradiated a–C:H film (blue histogram). The synthetic mass spectrum obtained by a matrix analysis is shown with filled bar graphs; the associated error bars come from the minimization procedure. Bottom: ratio of the fitted versus measured individual mass spectra for the main peaks (left axis, squares), and peak temperature associated with the TPD for the considered mass (right axis, circles). |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for an irradiated a–C:D film with the expected mass separation peak pattern every two m/z due to the deuterium substitution. The data peaks at uneven m/z are due to eventual pollution and hydrogen contamination in the film. |
| In the text | |
 |
Fig. 3 TPD spectra recorded for selected m/z for the a–C:H experiment. The chosen masses are dominated by a small amount of fragments contributing to the signal. The corresponding parent species are given in brackets, as obtained from the minimization. The desorption temperature peaks are indicated by vertical dashed lines. |
| In the text | |
 |
Fig. 4 Output of the Horsehead Nebula photon dominated region time dependent model for observed selected hydrocarbons (CCH, c-C3H, c-C3H2, C4H). The abundances are shown as a function of visual extinction in the cloud illuminated by the σOri star (see Appendix A for details) and time. For each species the upper panel shows the abundance at time 103 yr (close to the maximum injection by dust grains, for clarity): initial model without hydrogenated amorphous carbon photolysis (lower curve), with model I including reactions up to CH4 (dotted line), model II reactions up to C2Hy (dashed line), model III reactions up to C3Hy (upper curve). For each species, in the lower panel, the corresponding abundance ratio with the addition of photolytic reactions over the abundance without the addition of the photolytic reactions is shown for all times. |
| In the text | |
 |
Fig. A.1 Temperature (purple dotted line), total hydrogen density (blue dashed line), and ionization degree (green solid line) as a function of visual extinction. |
| In the text | |
 |
Fig. A.2 Photodissociation rates of CO (blue dashed dotted lines) and H2 (red dashed lines) and photoionization rates of C (green dotted lines) and S (purple solid lines) as a function of the visual extinction in the Meudon code (no symbols) and in Nahoon (diamond lines). |
| In the text | |
 |
Fig. A.3 Abundance of H (brown long dashed line), electrons (red solid line), CO (yellow dotted lines), C (green dash-dotted line), C+ (blue short dotted line), and H+ (purple short and long dashed line) for times of 300 yr (circle), 1000 yr (triangle), 104 yr (pentagon), and 108 yr (diamond) as a function of the visual extinction. |
| In the text | |
 |
Fig. A.4 Coefficient Fi as a function of time for Av = 0.5 (blue solid line), Av = 1 (purple dashed line), Av = 3 (green dotted lines), Av = 5 (orange dashed dotted line), and Av = 7 (brown dashed line). |
| In the text | |
 |
Fig. A.5 Ratio of the abundance of CCH with or without the inclusion of photo-desorption reactions as a function of the percent of carbon in a–C:H for Av = 3 at 1000 yr (blue dash-dotted line) and for Av = 4 at 10 000 yr (purple solid line). |
| In the text | |
 |
Fig. B.1 Output of the Horsehead Nebula photon dominated region model III with a low sulfur abundance in the initial conditions (S / H = 5.8 × 10-8) for the CCH hydrocarbon abundance as a function of visual extinction in the cloud illuminated by the σOri star (see Appendix A for details). The abundance of CCH is shown in the top panel at different times after injection of the a–C:H grain photolysis in the model. The corresponding abundance ratio of CCH with the addition of photolytic reactions divided by the abundance without the addition of the photolytic reactions is shown in the bottom panel for the same times. |
| In the text | |
 |
Fig. B.2 Same as Fig. B.1 with a low sulfur abundance in the initial conditions for C3H2: abundance of C3H2 (top) and abundance ratio of C3H2 with the addition of photolytic reactions divided by the abundances without the addition of photolytic reactions (bottom) for different times. |
| In the text | |
 |
Fig. B.3 Same as Fig. B.1 with a low sulfur abundance in the initial conditions for C4H: abundance of C4H (top) and abundance ratio of C4H with the addition of photolytic reactions divided by the abundances without the addition of photolytic reactions (bottom) for different times. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


