| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526553 | |
| Published online | 03 November 2015 | |
Molecular depletion times and the CO-to-H2 conversion factor in metal-poor galaxies⋆
1 INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi, 5, 50125 Firenze, Italy
e-mail: hunt@arcetri.astro.it
2 Observatorio Astronómico Nacional (OAN) – Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
3 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
4 Observatoire de Paris, LERMA, Collège de France, CNRS, PSL, Sorbonne University UPMC, 75014 Paris, France
5 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6 Astronomy Department, King Abdulaziz University, PO Box 80203 Jeddah, Saudia Arabia
7 ALMA JAO, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago, Chile
8 Cavendish Laboratory, University of Cambridge, 19 J.J. Thomson Avenue, Cambridge CB3 0HE, UK
9 ESO, Karl Schwarzschild str. 2, 85748 Garching bei München, Germany
Received: 18 May 2015
Accepted: 14 September 2015
Tracing molecular hydrogen content with carbon monoxide in low-metallicity galaxies has been exceedingly difficult. Here we present a new effort, with IRAM 30-m observations of 12CO(1–0) of a sample of 8 dwarf galaxies having oxygen abundances ranging from 12 + log(O/H) ~ 7.7 to 8.4. CO emission is detected in all galaxies, including the most metal-poor galaxy of our sample (0.1 Z⊙); to our knowledge this is the largest number of 12CO(1–0) detections ever reported for galaxies with 12 + log(O/H) ≲ 8 (0.2 Z⊙) outside the Local Group. We calculate stellar masses, Mstar, and star-formation rates (SFRs), and analyze our results in conjunction with galaxy samples from the literature. Extending previous results for a correlation of the molecular gas depletion time, τdep, with Mstar and specific SFR (sSFR), we find a variation in τdep of a factor of 200 or more (from ≲50 Myr to ~10 Gyr) over a spread of ~103 in sSFR and Mstar. We exploit the variation of τdep to constrain the CO-to-H2 mass conversion factor αCO at low metallicity, and assuming a power-law variation find αCO∝Z/Z⊙-2, similar to results based on dust continuum measurements compared with gas mass. By including Hi measurements, we show that the fraction of total gas mass relative to the baryonic mass is higher in galaxies that are metal poor, of low mass, and with high sSFR. Finally, comparisons of the data with star-formation models of the molecular gas phases show that the models are generally quite successful, but at metallicities Z/Z⊙≲ 0.2, there are some discrepancies.
Key words: galaxies: dwarf / galaxies: starburst / galaxies: star formation / galaxies: ISM / ISM: general
© ESO, 2015
1. Introduction
Dense clumps in cool molecular clouds are thought to be the “cradles” of star formation, but finding molecules at low metallicities has been exceedingly difficult. In dwarf galaxies with nebular oxygen abundances ≲0.3 Z⊙ (12 + log(O/H) ≲ 8.2)1, despite vigorous on-going star formation, there seems to be very little CO (Sage et al. 1992; Taylor et al. 1998; Gondhalekar et al. 1998; Barone et al. 2000; Leroy et al. 2005, 2007; Buyle et al. 2006; Schruba et al. 2012; Cormier et al. 2014). Intriguingly, this is the same metallicity “threshold” below which little or no polycyclic aromatic hydrocarbon (PAH) emission is detected in metal-poor galaxies (Engelbracht et al. 2005; Wu et al. 2006; Madden et al. 2006; Hunt et al. 2010).
The reason for this deficit in CO at low metallicities is not yet completely understood, although there is strong evidence for “CO-dark” molecular gas in the interstellar medium (ISM; e.g., Wolfire et al. 2010; Leroy et al. 2011; Planck Collaboration XIX 2011; Paradis et al. 2012; Lebouteiller et al. 2012; Pineda et al. 2014). Such a component would result from a diffuse or metal-poor ISM in which CO suffers from enhanced photodissociation relative to H2 (e.g., Maloney & Black 1988; Bolatto et al. 1999; Glover & Mac Low 2011; Narayanan et al. 2012). H2 can effectively avoid the photodissociation effects of UV radiation through self-shielding, even at relatively low gas surface densities, ΣISM. On the other hand, CO needs higher ΣISM to self-shield, thus implying that the CO-to-H2 ratio should vary even within an individual molecular cloud (e.g., Röllig et al. 2006; Leroy et al. 2013a; Hughes et al. 2013). Under conditions of low ΣISM and low dust extinction AV, most of the carbon would be in other forms such as Ci or Cii, rather than in CO.
Observing targets.
Nevertheless, even under extreme conditions in a metal-poor ISM, it is likely that stars form in cool, dense molecular clouds (e.g., Krumholz et al. 2011). However, H2, the dominant molecular component of giant molecular clouds, is not directly observable, but rather inferred from line emission of rotational transitions of 12CO(1–0), unfortunately deficient at low metallicity. Constraining the properties of metal-poor molecular clouds observationally is difficult because the factor, αCO, relating CO luminosity 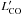 to H2 mass MH2 can vary dramatically, through the presence of CO-dark gas. αCO can be more than 50 times higher than the Galactic value in metal-poor environments and in regions of low AV and low ΣISM (Israel 1997; Leroy et al. 2009b, 2011; Pineda et al. 2010; Bolatto et al. 2011; Schruba et al. 2012; Sandstrom et al. 2013). Although the relation between CO and H2 has been the subject of much debate (see Bolatto et al. 2013, for a recent review), it is clear that at some low metallicity, probably ≲0.05–0.1 Z⊙, CO ceases to become a useful tracer of total H2 mass.
to H2 mass MH2 can vary dramatically, through the presence of CO-dark gas. αCO can be more than 50 times higher than the Galactic value in metal-poor environments and in regions of low AV and low ΣISM (Israel 1997; Leroy et al. 2009b, 2011; Pineda et al. 2010; Bolatto et al. 2011; Schruba et al. 2012; Sandstrom et al. 2013). Although the relation between CO and H2 has been the subject of much debate (see Bolatto et al. 2013, for a recent review), it is clear that at some low metallicity, probably ≲0.05–0.1 Z⊙, CO ceases to become a useful tracer of total H2 mass.
In this paper, we begin to explore the limits to which CO can trace H2 in metal-poor star-forming galaxies. We first describe the targets and ancillary data in Sect. 2, and the 12CO(1–0) observations and data analysis in Sect. 3. In Sect. 4, we compare our results with previous work, and assess the dependence of CO luminosity on star-formation rate (SFR). Section 5 describes constraints on αCO and τdep, the molecular gas depletion time, i.e., the time required to consume the H2 gas reservoir. We adopt a variation of the method proposed by Saintonge et al. (2011b), extending it to low metallicity in order to separate the effects of τdep variations from variations of αCO. In Sect. 6, we analyze the H2 content of our sample and compare it with Hi for a compilation of galaxies taken from the literature. We discuss the implications of our results in Sect. 7, and, in Sect. 8, summarize our results and present our conclusions.
2. The targets and the ancillary data
The observing sample was defined mainly on the basis of detected H2 emission, either in the ro-vibrational transitions at 2 μm, or the purely rotational transitions in the mid-infrared (e.g., Spitzer/IRS); however, we also targeted some galaxies that had already been observed in CO (see Sect. 3.4). Table 1 lists the sample galaxies (ordered alphabetically by name), together with relevant observational parameters; Figs. 1 and 2 show thumbprint images.
 |
Fig. 1 Top row, from left to right in alphabetical order of name: SDSS composite (ugriz) images of CGCG 007−025, Haro 3 (NGC 3353), II Zw 40, Mrk 996. Bottom row, leftmost panel: NGC 1156 (image taken from DSS2, reprocessed); then from left to right SDSS images of NGC 7077, UM 448, UM 462. Images are oriented with North up, East left, and are 50′′ on a side, except for NGC 1156 which is ~10′. The color of II Zw 40 is reddened by >2 mag AV from the Galaxy. NGC 1140 and SBS 0335−052E, both of which harbor SSCs and whose images are not from SDSS, are shown in Fig. 2. |
2.1. Individual source description
The targets have several characteristics in common, in addition to their low metallicities. All of them, with the exception of NGC 7077 and SBS 0335−052E, are sufficiently bright in the infrared (IR) to have been identified in the (faint) IRAS point-source catalogue. In fact, II Zw 40 was identified as a 60-μm peaker source by Vader et al. (1993). Except for NGC 7077, all galaxies host conspicuous Wolf-Rayet populations (Schaerer et al. 1999; Guseva et al. 2000; Zhang et al. 2007); they are all also rich in atomic gas (see Sect. 6). This section describes particular features of the individual sources (in alphabetical order by name as in Table 1).
⋆ CGCG 007−025
This galaxy is the most metal-poor (12 + log(O/H) = 7.7, ~0.1 Z⊙) 12CO(1–0) detection of our sample (see Sect. 4). Although it appears in an isolated galaxy catalogue (van Zee 2001), it has a companion, a dwarf irregular galaxy at 8.3 kpc projected separation (84 km s-1 velocity separation) which may have triggered the current star-formation episode (van Zee 2001). It is also found to be a member of a compact group by Focardi & Kelm (2002). CGCG 007−025 has the bluest U−B color of any dwarf galaxy in the van Zee (2001) sample, with a very clumpy morphology as seen in Fig. 1. The radiation field is sufficiently hard to excite [Fev], a line that requires ionizing radiation with photon energies exceeding 4 Ryd (54.4 eV) (Thuan & Izotov 2005). Although a population of Wolf-Rayet stars has been detected in this galaxy (Zhang et al. 2007), these are insufficient to power the high-excitation emission lines, thought instead to be due to fast radiative shocks (Thuan & Izotov 2005). Hunt et al. (2010) found evidence for rotational H2 emission, and despite the low metallicity of CGCG 007−025, also 7.7 μm and 11.3 μm emission from PAHs. Judging from the relatively high density of its ionized gas (~300 cm-3, Izotov et al. 2007), CGCG 007−025 is an example of an “active” starburst, forming stars in compact dense regions (Hirashita & Hunt 2004).
 |
Fig. 2 NGC 1140 and SBS 0335−052E taken from composite HST images; both galaxies host super-star clusters (Hunter et al. 1994b; Reines et al. 2008). The image of NGC 1140 is ~90′′ on a side, and SBS 0335−052E ~5′′, and orientation is North up, East left. |
⋆ II Zw 40 (UGCA 116)
Although we did not observe this source in 12CO(1–0), it is included in our CO survey of higher-J lines (Hunt et al., in prep.); thus we consider it in our sample here. From its discovery, together with I Zw 18, as an extragalactic Hii region (Sargent & Searle 1970), II Zw 40 has been the subject of much scrutiny. Its two-tailed optical morphology and kinematics suggest that it is the result of a collision between two gas-rich dwarf galaxies which triggered the current starburst (Baldwin et al. 1982; van Zee et al. 1998). Near-infrared recombination lines show that more than half the 2 μm flux comes from free-free emission, and warm dust contributes at least ~25% to the 3–4 μm fluxes (Joy & Lester 1988). Emission from the ro-vibrational transitions of H2 at 2 μm was discovered by Vanzi et al. (1996), and later found to be in a cloud distinct from the primary Hii region (Vanzi et al. 2008). Visual extinction AV is spatially variable in II Zw 40 and can be as high as ≳10 mag in the nucleus (Vanzi et al. 2008). This galaxy is undergoing a massive starburst in a region of ~150 pc in diameter powered by ~5000–10 000 OV stars (Beck et al. 2002; Kepley et al. 2014). These massive stars are driving copious stellar winds which alter the observed kinematics (Bordalo et al. 2009), and also produce high-ionization [Fev] (Thuan & Izotov 2005). Like CGCG 007−025, the high density derived from optical spectra (~500–1400 cm-3, Bordalo et al. 2009) and the small dimensions of the star-formation episode imply that it is an “active” starburst.
⋆ Mrk 996
Mrk 996 is an unusual blue compact dwarf galaxy, with smooth early-type morphology and a system of globular clusters (Thuan et al. 1996). Virtually all its star formation occurs in the central region of the galaxy (~315 pc in radius). Because of its high central density (~106 cm-3) and broad emission lines (~900 km s-1, Thuan et al. 1996), it was thought that there could be an accreting intermediate-mass black hole; however X-ray observations revealed no compact point source (Georgakakis et al. 2011). A high ionization [Oiv] line is detected in Mrk 996 (Thuan et al. 2008), that, like [Fev], needs ~4 Ryd to excite it. Thus, fast radiative shocks are also present in this galaxy, as its emission-line properties are inconsistent with any other source of ionization (Georgakakis et al. 2011). The lowest rotational transition of H2 (~28 μm) is found in Mrk 996, the only one in the sample of Hunt et al. (2010) in which it was detected.
⋆ NGC 1140 (Mrk 1063)
NGC 1140 is a barred dwarf irregular galaxy with peculiar morphology and a central starburst. The Hα luminosity of its central Hii complex is 40 times higher than that of the giant Hii region 30 Doradus in the Large Magellanic Cloud. Within this complex, roughly 500 pc in diameter, there are 6–7 blue super-star clusters (SSCs; Hunter et al. 1994b; de Grijs et al. 2004), the most luminous of these containing almost 6000 O stars (Moll et al. 2007). Although there is no galactic-scale outflow in this galaxy, powerful shocks from the massive SSCs are disrupting the ISM on scales up to 1–2 kpc radius (Westmoquette et al. 2010). Kinematic and other evidence suggests that the formation of the SSCs and the larger-scale starburst have been triggered by an interaction or merger event with a low-luminosity late-type spiral about 1 Gyr ago (Hunter et al. 1994a,b; Westmoquette et al. 2010).
⋆ NGC 1156
A typical barred Magellanic irregular about 25% brighter in the B band than the Large Magellanic Cloud, NGC 1156 is the most quiescent galaxy in our sample. It has been described as the least disturbed galaxy in the Local Universe, with no significant galaxy within 700 kpc (Karachentsev et al. 1996). More recent Hi observations revealed a single dwarf galaxy at a distance of 80 kpc (Minchin et al. 2010) which however is too faint to provide any measurable perturbation. The star formation in NGC 1156 is spread out in Hii regions spanning the entire bar+disk, and the kinematics of the ionized (and atomic) gas and stars is consistent with circular rotation about a common axis (Hunter et al. 2002).
⋆ NGC 3353 (Haro 3, Mrk 35)
NGC 3353, the most metal-rich galaxy in our sample (12 + log(O/H) ~ 8.4, see Table 1), is a dwarf irregular hosting a galaxy-wide starburst. However, high-resolution radio images show that most of the starburst activity is concentrated within a single knot to the northwest of the galaxy nucleus (Johnson et al. 2004). The star clusters in this knot are quite young (1–4 Myr) and massive (~106 M⊙) and reside in a region with AV~ 2–8 mag, implying that much of the current star formation is currently enshrouded in dust (Johnson et al. 2004). In fact, optical measures of the extinction are smaller than those measured with the radio and near-infrared observations (Steel et al. 1996; Cairós et al. 2007). Detailed photoionization models of the infrared fine-structure lines suggest that there are at least two emission zones in this galaxy: one with low extinction, visible in the optical, and another, optically invisible with much higher extinction (Hunt et al. 2006). Rotational H2 has been detected in NGC 3353, and the detection of the high-excitation [Oiv] line (≳4 Ryd) implies that radiative shocks are also present (Hunt et al. 2010). Like other galaxies in this sample, kinematic evidence suggests that a merger is responsible for triggering the starburst in NGC 3353 (Cairós et al. 2007).
⋆ NGC 7077 (Mrk 900)
NGC 7077 is classified as an early-type galaxy, E/S0, but with peculiar morphology, and relatively blue colors (Gil de Paz et al. 2003; Micheva et al. 2013). It is an isolated galaxy, part of the van Zee (2000) sample, with red colors in its outer regions (see also Fig. 1). These red colors are in contrast with the strong (blue) nuclear starburst which has an intensity comparable to that of 30 Doradus (van Zee 2000). Perhaps the most salient feature of NGC 7077 is its extended ultraviolet disk, suggesting that the disk of this galaxy is in an active growth phase (Moffett et al. 2012).
⋆ SBS 0335−052E
Like, II Zw 40, we did not observe this source in 12CO(1–0), but it is included in our CO survey of higher-J lines (Hunt et al., in prep.); thus we consider it here. This is the most metal-poor galaxy of our sample (12 + log(O/H) ~ 7.2), with a neighbor at ~22 kpc distance (SBS 0335−052W, Pustilnik et al. 2001). This companion, embedded in a common Hi cloud, is the most metal-poor star-forming galaxy known in the Local Universe (12 + log(O/H) ~ 7.1, Lipovetsky et al. 1999; Izotov et al. 2005). High-resolution optical and near-infrared imaging shows that the star formation activity in SBS 0335−052E is confined to six massive SSCs, with the two youngest ones (≲3 Myr) each comprising ~5000 O7.5 V stars (Reines et al. 2008). Despite its extremely low abundance, SBS 0335−052E is known to have extremely high extinction (AV≳ 15 mag, Plante & Sauvage 2002; Houck et al. 2004), and ≳104 M⊙ of dust surrounding only the two youngest SSCs (Hunt et al. 2001, 2014). Warm H2 is clearly present in this galaxy, with strong emission from ro-vibrational transitions at 2 μm (Vanzi et al. 2000, 2011). The cm-regime radio spectrum is highly self-absorbed, implying ionized-gas densities of ≳3000 cm-3 (Hunt et al. 2004; Johnson et al. 2009). SBS 0335−052E is the proto-typical “active” starburst with its star-formation activity occurring in compact (unresolved at HST resolution), dense regions (Hirashita & Hunt 2004).
⋆ UM 448 (Arp 161, UGC 6665)
UM 448 is a merger remnant with residual tidal tails, and so IR luminous (LIR = 6.3 × 1010 L⊙) that it would almost be classified as a Luminous IR Galaxy (LIRG, Dopita et al. 2002). Despite its low metal abundance (12 + log(O/H) ~ 8.0, 0.2 Z⊙, see Table 1), this galaxy shows clear PAH emission (Galliano et al. 2008). This is perhaps because of a metallicity gradient which reaches a peak value of 12 + log(O/H) ~ 8.4 toward the northwest, a region of lower temperature (James et al. 2013). There is evidence for age gradients in the stellar populations and complex ionized emission-line kinematics, both of which probably reflect the merger nature of UM 448 (James et al. 2013).
⋆ UM 462 (Mrk 1307, UGC 6850)
Like many of the galaxies in our sample, UM 462 is possibly tidally interacting with a relatively close neighbor, UM 461 (Taylor et al. 1995), although van Zee et al. (1998) concluded that the Hi kinematics are inconsistent with this. Most of the star formation in UM 462 occurs in two main knots of star formation, although high-resolution observations resolve at least four starbursting regions with disrupted kinematics (Vanzi et al. 2002; James et al. 2010). The Wolf-Rayet content of this galaxy has been disputed by James et al. (2010) who do not find evidence to support a significant Wolf-Rayet classification. Vanzi et al. (2002) found ro-vibrational H2 emission in this galaxy, but no evidence for [Feii], implying that the star-formation episodes must be younger than ~10 Myr. The knots of star formation are so compact and luminous as to be classified as SSCs (Vanzi 2003).
2.2. An additional source, I Zw 18
Although I Zw 18 was not included in our sample, it was observed, although not detected, in the 12CO(1–0) transition by Leroy et al. (2007). Because of its extreme low metallicity, similar to SBS 0335−052E, we have incorporated this galaxy in our analysis (see also Schruba et al. 2012). We have adopted the SFR from Hunt et al. (2005), and calculated the stellar mass, Mstar, as described below (see also Fumagalli et al. 2010).
Like II Zw 40, I Zw 18 was discovered as an extragalactic Hii region by Sargent & Searle (1970). Together with the SBS 0335−052E and SBS 0035−052W pair, it is the most metal-poor star-forming galaxy in the Local Universe with 12 + log(O/H) = 7.17–7.22 (Thuan & Izotov 2005). Most, if not all, of the current star formation occurs in two main clusters, although the “C component” (or Zwicky’s flare) is also forming stars (Izotov et al. 2001). However, the two clusters are not as extreme as those in SBS 0335−052E (and other galaxies in our sample), being somewhat less luminous than 30 Doradus (Hunter & Thronson 1995). Like SBS 0335−052E, around the main star clusters there is a complex structure of filaments and arcs from ionized gas, and the complex Hi morphology and kinematics suggest that the current star-formation episode was triggered by an interaction with the C component (Lelli et al. 2012). Unlike SBS 0335−052E, however, there is no evidence for a dense gas component in I Zw 18; the radio continuum spectrum follows the trend expected for optically thin free-free emission (Hunt et al. 2005) with an ionized-gas density of ≲100 cm-3, similar to that found from optical spectra (Izotov et al. 2001). Despite their similarly low metal abundance, the dust masses, dust-to-gas, and dust-to-stars mass ratios in I Zw 18 are more than 100 times lower than in SBS 0335−052E (Hunt et al. 2014), implying that the density of the cool gas in the ISM may play an important role in dust formation (Schneider et al. 2015).
2.3. SFRs and stellar masses
We have calculated the SFRs for our targets according to Calzetti et al. (2010) using Hα and 24 μm luminosities (their Eq. (17)). This approach obviates the need for uncertain extinction corrections, and has the added advantage of accounting for the general behavior of dust opacity in galaxies. Many of the Hα total fluxes come from Gil de Paz et al. (2003, Haro 3, II Zw 40, Mrk 996, NGC 7077), but others come from van Zee (2000, CGCG 007−, Kennicutt et al. (2009, NGC 1140, NGC 1156), Dopita et al. (2002, UM 448), and James et al. (2010, UM 462). The 24 μm fluxes are taken from Engelbracht et al. (2008), Temi et al. (2009, NGC 7077), or Hunt et al. (in prep.). For SBS 0335−052E and I Zw 18, we take the SFR measured by high-frequency radio free-free emission (Johnson et al. 2009; Hunt et al. 2005).
Following Grossi et al. (2015), stellar masses, Mstar, were estimated according to the recipe given by Wen et al. (2013) based on WISE W1 (3.4 μm) luminosities. This approach exploits the relatively constant mass-to-light ratios of stellar populations, independently of metallicity and age, at near-infrared wavelengths (Norris et al. 2014; McGaugh & Schombert 2014). However, when W1 photometry was not available, we used IRAC 3.6 μm photometry instead. In fact, the two bands are very similar; using data from Brown et al. (2014), Grossi et al. (2015) find for spirals a mean flux ratio F3.4/F3.6 = 1.02 ± 0.035. Including also the data for dwarf irregulars from Brown et al. (2014) gives a mean flux ratio F3.4/F3.6 = 0.98 ± 0.061. Thus, we conclude that the ratio of the W1 and IRAC 3.6 μm bands is unity, with 5–6% scatter for galaxies like our targets.
We used the Hii-galaxy formulation by Wen et al. (2013), rather than what they found for their full sample; the Hii galaxies have the lowest mass-to-light ratios in their compilation, corresponding roughly to the bluest regions of the galaxies studied by Zibetti et al. (2009). To better take into account the weak trends with abundance found by Wen et al. (2013), we also applied an approximate correction for low metallicity (by multiplying the mass-to-light ratio by 0.8: Wen et al. 2013, see their Fig. 17).
However, before applying the Hii-galaxy relation by Wen et al. (2013), we first subtracted nebular emission and emission from hot dust. Such contamination can be very important in the near-infrared and can contribute 50% or more to the observed flux at these wavelengths (Hunt et al. 2001, 2002, 2012; Smith & Hancock 2009). The ionized gas continuum contribution to the 3.4–3.6 μm flux was estimated from the SFR using the emission coefficients from Osterbrock & Ferland (2006). The subtraction of hot dust is based on the assumption that H-band emission is entirely stellar. Because H-band photometry is available for most of our sample, we used the data from Brown et al. (2014) to estimate the maximum possible IRAC 3.6 μm/ H-band ratio in galaxies similar to our targets; 95% of the spiral/dwarf irregular galaxies have a flux ratio ≤2.4. This corresponds to a (Vega-based) [H-3.6] color of ~0.8, consistent with what is found for the pure stellar component in star-forming galaxies (Hunt et al. 2002). After subtraction of the nebular component, any excess over this ratio was attributed to hot dust and subtracted. We found that hot dust can contribute between 10% and 50% in the 3.4–3.6 μm bands (most significantly for II Zw 40, SBS 0335−052E).
We compared the stellar masses obtained with the formulation of Wen et al. (2013) to those calculated according to Lee et al. (2006) based on IRAC 4.5 μm luminosities (used by Hunt et al. 2012), and find they are consistent to within 0.2 dex. Moreover, for the galaxies having both W1 and IRAC data, the stellar masses obtained from 3.6 μm luminosities are within ~5% of those from W1 as expected. The Kroupa-like broken power-law initial mass function (IMF) used by Calzetti et al. (2010) and consequently for our calculation of SFRs is consistent with the IMF for Mstar by Wen et al. (2013).
2.4. Hi measurements
All the sample galaxies have been observed in Hi, half of them with interferometric maps. For the galaxies with resolved observations, for comparison with CO, we have attempted to compute the Hi mass, MHI, by integrating the mean Hi surface density within only the optical radius. Because virtually all metal-poor dwarf galaxies show Hi emission well outside their optical radius (e.g., Hunter et al. 1994a; van Zee et al. 1998; van Zee 2000; Ekta et al. 2009; Lelli et al. 2012, 2014), these values of MHI are typically a factor of 2–10 lower than the total Hi mass, integrated over the entire Hi extent. Table 1 reports both values of MHI when resolved Hi maps are available.
2.5. Comparison samples
To expand the parameter space for our analysis, we also considered another dwarf sample with CO detections (Schruba et al. 2012), as well as normal star-forming galaxies, LIRGs, and Ultra-LIRGs (ULIRGs, Gao & Solomon 2004; Graciá-Carpio et al. 2008; García-Burillo et al. 2012). For the latter galaxies, we converted their published IR luminosity to SFR according to Kennicutt (1998), after applying the correction to a Kroupa (2001) IMF for consistency with our SFRs and those of Schruba et al. (2012). For the Schruba et al. CO(2–1) observations, we applied the factor they recommend to convert 12CO(2–1) to 12CO(1–0): ICO2−1/ICO1−0 = 0.7. Stellar masses for the Gao & Solomon (2004) and García-Burillo et al. (2012) samples were taken from Skibba et al. (2011), and for the galaxies from Schruba et al. (2012), masses were adopted either from Hunt et al. (2012) or Lee et al. (2006). These latter estimates are based on IRAC photometry similar to the method used here, as described in Sect. 2.3.
We incorporated also the galaxies from the CO(2–1) APEX Low-redshift Legacy Survey of MOlecular Gas (ALLSMOG, Bothwell et al. 2014). This sample is essentially an extension to lower stellar masses (8.5 < log(Mstar/M⊙) ≤ 10) of the COLDGASS galaxies studied by Saintonge et al. (2011a,b). For consistency with Schruba et al. (2012), to convert 12CO(2–1) to 12CO(1–0), we again use ICO2−1/ICO1−0 = 0.7, rather than ICO2−1/ICO1−0 = 1 as in Bothwell et al. (2014). Because of the ~0.4 dex offset between the ALLSMOG metallicity calibration and the mainly direct-temperature2 determinations used here (e.g., Hunt et al. 2012; Andrews & Martini 2013), the oxygen metallicities given by Bothwell et al. (2014) were converted to the Pettini & Pagel (2004) calibration according to Kewley & Ellison (2008)3. Finally, to extend the metallicity range to extremely metal-poor galaxies (XMPs), we incorporate the sample from Filho et al. (2013) which, however, have no CO measurements; we include them to better investigate gas content at low metallicities.
Both the ALLSMOG and the Filho et al. (2013) galaxies have stellar masses and SFRs taken from the MPA-JHU catalogue (Kauffmann et al. 2003; Brinchmann et al. 2004), the same basis for calibration used by Wen et al. (2013). However, the automatic algorithm used by the SDSS does not always provide the correct global photometry for galaxies whose surface brightness is not uniformly distributed (e.g., in clumps or knots). This should not be a problem for the ALLSMOG galaxies, which tend to be extended spirals, but could be a problem for the comparison with the XMP sample by Filho et al. (2013). In fact, Filho et al. (2013) found that comparing mass-to-light ratios based on optical colors gave as much as an order of magnitude Mstar excess over the SDSS estimates; the discrepancies tend to be largest for galaxies with either cometary or two-/multiple-knot morphology. To check for systematic differences between the near-infrared method used here (IRAC, WISE) and in Hunt et al. (2012; see also Madden et al. 2013) and the optically-determined (MPA-JHU) SDSS values, we searched the MPA-JHU database and found 17 low-metallicity galaxies for which we had calculated stellar masses in Hunt et al. (2012) using 4.5 μm luminosities. Although the contributions of the nebular continuum and hot dust emission have been subtracted, the values of Mstar using IRAC/WISE photometry are, on average, 17 times larger than those with SDSS with a scatter of ~0.4 dex. We investigated the morphology of the galaxies in this comparison and find that they tend to be very clumpy, with either multiple knots or cometary features. Comparing the SDSS photometry with the broad-band JHK photometry for these galaxies gives NIR-optical colors that are extremely red, unrealistically so for these blue galaxies; the implication is that the optical fluxes are being underestimated. We thus ascribe this difference to the difficulty of the SDSS automated photometric algorithms when confronted with multiple clumps. As a consequence, in our comparisons with the XMP sample, these uncertainties should be kept in mind.
3. The CO observations
We have observed 12CO(1–0) in our sample galaxies over a three-year period from 2008 to 2010 with the IRAM 30-m telescope (Pico Veleta, Spain).
3.1. IRAM observations
In September, 2009, and September, 2010, we observed six galaxies4 in 12CO(1–0) with the Eight Mixer Receiver (EMIR) using the Wideband Line Multiple Autocorrelator (WILMA) backend. Observations of 12CO(1–0) for NGC 1140 and NGC 1156 were performed with the AB receivers in November, 2008, using the 1 and 4 MHz backends at 3 and 1.3 mm (88–115 GHz, 219–229 GHz, respectively). The precipitable water vapor was ≲4 mm during the 2008 run, giving system temperatures of Tsys of ≲370 K at 3 mm. In 2009, the conditions were worse (≲11 mm), but the EMIR receivers had comparable Tsys, ~335 K at 3 mm; in 2010, our most extensive run, Tsys varied from ~230 K to ≳400 K, with precipitable water vapor ranging from ~4 mm to 10 mm. In all runs, we used wobbler switching with a throw of 90′′. Intensity calibration was performed with two absorbers at different temperatures.
Pointing was checked at regular intervals (every 1.5 h) on nearby planets or bright quasars (e.g., 0234+285), and focus tests were carried out every 4 h during the night and every 3 h during the day. Pointing errors never exceeded ~3′′, and were usually ≲2′′. Given the beam size (half-power beam width) of ~22 ′′, this was more than sufficient.
12CO(1–0) emission line parameters.
 |
Fig. 3 12CO(1–0) average spectra for the observed galaxies. Top row, from left to right in alphabetical order of name: CGCG 007−025, Mrk 996, and NGC 1140. Second row: NGC 1156, NGC 3353 (Haro 3) two pointings ([0, 0], [0, +10′′]. Third row: NGC 3353 third pointing [–6′′, –9′′]), NGC 7077 (Mrk 900), UM 448. Bottom row: UM 462. The baselines are shown as a horizontal solid line, together with the multiple-component Gaussian fits as described in Sect. 3.2. The vertical axes are in |
3.2. Data reduction
We adopted the GILDAS/CLASS data reduction package to obtain mean spectra5. To remove the continuum from each spectrum, a polynomial baseline was fitted to the line-free regions of each scan (defined a priori) and subtracted; the scans were thereafter smoothed and averaged, and a constant baseline subtracted. We measured the peak intensities, central velocities, full width half-maximum (FWHM) and velocity-integrated fluxes of the detected lines by fitting Gaussian profiles to the data. In most cases, there is significant velocity structure in the emission, so we fit the line profiles to multiple Gaussians. In these cases we use the sum of the integrated line intensities from the multiple Gaussian fits in the analysis (see Table 2).
Antenna temperatures (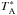 ) have been converted to main-beam temperatures (Tmb) by dividing the antenna temperatures by η ≡ Beff/Feff, where Beff (=0.78) and Feff (=0.94) are the beam and forward hemisphere efficiencies, respectively (i.e., Tmb =
) have been converted to main-beam temperatures (Tmb) by dividing the antenna temperatures by η ≡ Beff/Feff, where Beff (=0.78) and Feff (=0.94) are the beam and forward hemisphere efficiencies, respectively (i.e., Tmb = 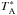 /η). To convert the measured 12CO(1–0) brightness temperatures, [Tmb (K)] to fluxes [S (Jy)], we used the standard IRAM 30-m conversion factor of 3.906 Jy K-1. The 12CO(1–0) line profiles are shown in Fig. 3, together with the Gaussian fits obtained using the GILDAS/CLASS package as described above and reported in Table 2. Although a few of the individual velocity components are too narrow to be significant (e.g., NGC 1140, NGC 1156), we have checked that the total intensities are robust to the details of the fitting.
/η). To convert the measured 12CO(1–0) brightness temperatures, [Tmb (K)] to fluxes [S (Jy)], we used the standard IRAM 30-m conversion factor of 3.906 Jy K-1. The 12CO(1–0) line profiles are shown in Fig. 3, together with the Gaussian fits obtained using the GILDAS/CLASS package as described above and reported in Table 2. Although a few of the individual velocity components are too narrow to be significant (e.g., NGC 1140, NGC 1156), we have checked that the total intensities are robust to the details of the fitting.
3.3. Aperture corrections
The IRAM 30 m has a beam with an FWHM of ~22 ′′ at 3 mm. Consequently, the largest galaxies in our sample (NGC 1140, NGC 1156, NGC 3353, see Table 1) may be missing flux. We have attempted to correct for this by adopting the approach of Saintonge et al. (2011a) who calibrated aperture corrections using the set of nearby galaxies observed by Kuno et al. (2007). We applied Eq. (2) by Saintonge et al. (2011a) based on optical size, but used the geometric means of the major and minor axes given in Table 1. These corrections amount to an increase in line intensities by a factor of 1.64 for NGC 1140 and 3.23 for NGC 1156.
For NGC 3353 (Haro 3), we have additional pointings spaced by roughly 0.5 beams, hence not independent. Where necessary, Saintonge et al. (2011a) used spacings of 0.75 beams along the major axis, and found a mean ratio between the offset flux and the central flux of 0.33. The corresponding ratio for the [−6′′, −9′′] pointing of NGC 3353 (along the southern major axis) is 0.53, larger than the offset corresponding to the wider spacing by Saintonge et al. (2011a), but consistent with what could be expected for the closer spacing of our offset. Hence, for NGC 3353, we adopted Eq. (3) of Saintonge et al. (2011a) with their mean ratio between offset and central intensities (0.33); this correction gives a multiplicative factor of 1.41. Table 2 also reports the 12CO(1–0) intensities corresponding to the aperture corrections for these galaxies which we will adopt throughout the paper.
3.4. Comparison with previous CO observations
Because some of the galaxies in our sample have previous CO observations, here we compare our results with those. Sage et al. (1992) observed NGC 3353, NGC 7077, UM 448, and UM 462, and securely detected only the former two. The results for NGC 3353, obtained with the IRAM 30-m, are in good agreement with our central pointing (they find an integrated CO intensity of 1.98 ± 0.28 K km s-1), although we find ~70% of their CO emission for NGC 7077 (they find 0.68 ± 0.1 K km s-1). Our detections of UM 448 and UM 462 are consistent with their marginal detections obtained with the NRAO 12-m.
UM 462 was also observed by Brinks & Taylor (1997) and Gondhalekar et al. (1998), neither of whom detected the galaxy; their upper limits (<0.28 K km s-1 and <0.5 K km s-1, respectively) are somewhat discrepant with our detection (0.7–0.8 K km s-1), as well as with the marginal detection of Sage et al. (1992, ~0.7 K km s-1.
NGC 1140 was observed previously by Albrecht et al. (2004) and NGC 1156 by Leroy et al. (2005). The two previous observations are reasonably consistent with our results.
4. CO luminosity and SFR
Our new IRAM observations have successfully detected 12CO(1–0) down to a metallicity of 12 + log(O/H) = 7.74 (CGCG 007−025, signal-to-noise ratio 3.0, see Table 2), which is the lowest metallicity at which CO has been (tentatively) detected (see WLM: 12 + log(O/H) = 7.8, Elmegreen et al. 2013). To our knowledge, Table 2 gives the largest number of 12CO(1–0) detections ever reported for 12 + log(O/H) ≲ 8 (0.2 Z⊙) outside the Local Group.
In the following, we compare the integrated CO luminosity, 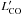 , with SFR as calculated in Sect. 2.3.
, with SFR as calculated in Sect. 2.3. 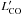 was derived according to the formulation of Solomon & Vanden Bout (2005), using the appropriate Jy-to-K conversion (see Sect. 3 for the IRAM value). The result is shown in Fig. 4.
was derived according to the formulation of Solomon & Vanden Bout (2005), using the appropriate Jy-to-K conversion (see Sect. 3 for the IRAM value). The result is shown in Fig. 4.
 |
Fig. 4 SFR vs. |
Not surprisingly, most of the metal-rich star-forming galaxies in the comparison samples follow the linear correlation between SFR and 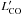 , as formulated by Gao & Solomon (2004), shown as the rightmost dashed line (corrected to the Kroupa IMF used here for SFR, see Sect. 2); the horizontal dotted line in Fig. 4 gives the IR luminosity limit above which the linear LIR-
, as formulated by Gao & Solomon (2004), shown as the rightmost dashed line (corrected to the Kroupa IMF used here for SFR, see Sect. 2); the horizontal dotted line in Fig. 4 gives the IR luminosity limit above which the linear LIR-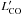 correlation of Gao & Solomon (2004) no longer holds. The metal-poor dwarf galaxies in our sample show a similar correlation but offset to lower
correlation of Gao & Solomon (2004) no longer holds. The metal-poor dwarf galaxies in our sample show a similar correlation but offset to lower 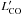 by a factor of ~30:
by a factor of ~30: 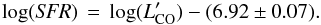 The best-fitting slope obtained with a robust fitting technique (Li 1985; Fox 1997) is unity within the errors (1.05 ± 0.15); thus, for consistency with Gao & Solomon (2004), we fixed a unit slope and derived the corresponding intercept as given above and shown in Fig. 4. Although we did not use the data of Schruba et al. (2012) to establish the best-fit regression, most of those galaxies also follow the trend for our sample (see Fig. 4). The exceptions are the two most metal-poor galaxies, SBS 0335−052E and I Zw 18.
The best-fitting slope obtained with a robust fitting technique (Li 1985; Fox 1997) is unity within the errors (1.05 ± 0.15); thus, for consistency with Gao & Solomon (2004), we fixed a unit slope and derived the corresponding intercept as given above and shown in Fig. 4. Although we did not use the data of Schruba et al. (2012) to establish the best-fit regression, most of those galaxies also follow the trend for our sample (see Fig. 4). The exceptions are the two most metal-poor galaxies, SBS 0335−052E and I Zw 18.
Judging from our sample alone, the offset between SFRs and high 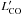 and low
and low 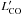 is apparently independent of metallicity, at least to the lowest oxygen abundance of our sample, 12 + log(O/H) ~ 7.7. However, CGCG 007−025 at this metallicity is only tentatively detected, and our other detected galaxies have a relatively narrow spread in metallicities, 12 + log(O/H) ~ 8. If we include in the regression the Schruba et al. (2012) compilation and their five 12CO(2–1) detections (converted to 12CO(1–0) as described above), we find a significant correlation between the SFR/
is apparently independent of metallicity, at least to the lowest oxygen abundance of our sample, 12 + log(O/H) ~ 7.7. However, CGCG 007−025 at this metallicity is only tentatively detected, and our other detected galaxies have a relatively narrow spread in metallicities, 12 + log(O/H) ~ 8. If we include in the regression the Schruba et al. (2012) compilation and their five 12CO(2–1) detections (converted to 12CO(1–0) as described above), we find a significant correlation between the SFR/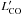 ratio and 12 + log(O/H), as shown in Fig. 5 (Pearson parametric correlation coefficient, −0.88, >99.999% significance level). Two galaxies are discrepant with this metallicity trend, CGCG 007−025 and SBS 0335−052E. SBS 0335−052E was not directly observed in 12CO(1–0), so there may be some problems with the multiplicative factor relating CO(3–2) to CO(1–0) (see Hunt et al. 2014). CGCG 007−025, on the other hand, is directly observed in 12CO(1–0) but the detection is only tentative. More CO(1–0) observations at metallicities below 12 + log(O/H) = 8 are needed to verify this inconsistency, especially because of the expectation that for Z/Z⊙≲ 0.1, CO may cease to be a viable tracer of H2 (Bolatto et al. 2013). We discuss the implications of the relation between SFR/
ratio and 12 + log(O/H), as shown in Fig. 5 (Pearson parametric correlation coefficient, −0.88, >99.999% significance level). Two galaxies are discrepant with this metallicity trend, CGCG 007−025 and SBS 0335−052E. SBS 0335−052E was not directly observed in 12CO(1–0), so there may be some problems with the multiplicative factor relating CO(3–2) to CO(1–0) (see Hunt et al. 2014). CGCG 007−025, on the other hand, is directly observed in 12CO(1–0) but the detection is only tentative. More CO(1–0) observations at metallicities below 12 + log(O/H) = 8 are needed to verify this inconsistency, especially because of the expectation that for Z/Z⊙≲ 0.1, CO may cease to be a viable tracer of H2 (Bolatto et al. 2013). We discuss the implications of the relation between SFR/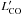 and abundance in the following section.
and abundance in the following section.
 |
Fig. 5 SFR/ |
5. Molecular depletion times, the CO-to-H2 conversion factor, and specific SFR
Although we have shown that 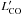 is correlated with SFR even at low metallicity, the main parameter of interest is H2 mass, MH2. In fact, the study of low-metallicity star formation and H2 content is hampered by the unknown factor, αCO, used to convert observed CO intensities to MH2. Observationally, MH2, αCO, and the time required to consume the molecular gas reservoir, τdep, are intimately related and difficult to disentangle. By definition, τdep depends inversely on the star-formation rate τdep≡MH2/SFR =
is correlated with SFR even at low metallicity, the main parameter of interest is H2 mass, MH2. In fact, the study of low-metallicity star formation and H2 content is hampered by the unknown factor, αCO, used to convert observed CO intensities to MH2. Observationally, MH2, αCO, and the time required to consume the molecular gas reservoir, τdep, are intimately related and difficult to disentangle. By definition, τdep depends inversely on the star-formation rate τdep≡MH2/SFR = 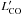 αCO/SFR, but the potential simplicity of predicting MH2 from SFR (or vice versa) through τdep is compromised by the necessary CO-to-H2 factor. The observed (or directly derivable) quantities are
αCO/SFR, but the potential simplicity of predicting MH2 from SFR (or vice versa) through τdep is compromised by the necessary CO-to-H2 factor. The observed (or directly derivable) quantities are 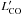 and SFR; thus only the ratio, τdep/αCO, is constrained.
and SFR; thus only the ratio, τdep/αCO, is constrained.
Much effort has been devoted to finding the dependence of αCO on metal abundance (e.g., Wilson 1995; Israel 1997; Rosolowsky et al. 2003; Bolatto et al. 2008, 2013; Leroy et al. 2009b, 2011; Genzel et al. 2012; Schruba et al. 2012). High-resolution cloud virial mass measurements tend to find little or no dependence on metallicity (Wilson 1995; Rosolowsky et al. 2003; Bolatto et al. 2008). However, because CO is found only in dense regions, rather than in diffuse gas, αCO depends on the physical scales probed by the observations, especially at low metallicity (Rubio et al. 1993). Given the relatively constant τdep in nearby star-forming spirals (e.g., Bigiel et al. 2008, 2011; Leroy et al. 2008), some groups have assumed a constant τdep to infer αCO in metal-poor galaxies. Such an assumption tends to give a steep dependence of αCO on O/H: αCO-1∝ (Z/Z⊙)~2−3 (Genzel et al. 2012; Schruba et al. 2012). An alternative approach relies on IR observations to derive MH2 and infer αCO by estimating the dust-to-gas ratio and assuming it is the same in adjacent regions with/without H2. This method has the considerable advantage of being independent of CO observations altogether, but requires comparable quantities of both Hi and H2, and relies on the assumption that emissivity properties of dust grains are the same in dense and diffuse environments. Recent work using this method, introduced by Israel (1997), also gives super-linear slopes, although somewhat shallower (and with large scatter) than those obtained with the assumption of constant τdep: αCO-1∝ (Z/Z⊙)~1.6−2 (Gratier et al. 2010; Leroy et al. 2011; Bolatto et al. 2011).
Here we present a different approach to constrain αCO at low metallicity. We exploit the results by Saintonge et al. (2011b; see also Huang & Kauffmann 2014) who find a significant inverse correlation of τdep with sSFR: galaxies with higher sSFR also have shorter molecular gas depletion times. However, sSFR tends to also be inversely correlated with metallicity (e.g., Salim et al. 2014), as shown in Fig. 6 (adapted from Hunt et al. 2012). Thus, we must find a way to disentangle the effects of sSFR on τdep from those of metallicity.
 |
Fig. 6 Specific SFR vs. 12 + log(O/H) for our sample and including data from the literature (Hunt et al. 2012; Schruba et al. 2012; Filho et al. 2013; Bothwell et al. 2014). The metallicities for the ALLSMOG (Bothwell et al. 2014) sample have been modified as discussed in the text. As in Fig. 4, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The regression line is a robust best-fit of the Local Volume Legacy (LVL, Lee et al. 2009) and the dwarf irregulars from Lee et al. (2006). The various colors for the LVL give the Hubble type (early types red, magenta; late types blue, cyan). |
5.1. The CO-to-H2 conversion factor
Saintonge et al. (2011b) found that star-forming galaxies of lower mass have much shorter τdep than more massive ones, while the depletion time for atomic gas remains relatively constant. They also found that τdep is strongly correlated with sSFR, with a single relation being able to fit both “normal” (“main-sequence”, e.g., Salim et al. 2007) galaxies and more extreme starbursts including LIRGs and ULIRGs. Their relation is based on a single value of αCO, appropriate for the properties of their sample, selected by stellar mass.
 |
Fig. 7
|
 |
Fig. 8 Residuals from the regression shown in Fig. 7 vs. sSFR (left panel) and vs. 12 + log(O/H) (right). We include here data for our sample and literature data (COLDGASS: Huang & Kauffmann 2014; Gao & Solomon 2004; García-Burillo et al. 2012; Schruba et al. 2012; Bothwell et al. 2014). The horizontal dashed line in the left panel shows 0 to aid the eye, while the regression in the right panel is the robust fit to the significant trend of the residuals of the |
 |
Fig. 9 τdep vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (COLDGASS: Huang & Kauffmann 2014; Gao & Solomon 2004; García-Burillo et al. 2012; Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The regression line is our fit to the Schruba et al. (2012) and our sample as described in the text. |
Here we explore the hypothesis that the Saintonge et al. correlation between τdep and sSFR extends to the lower-mass (and higher sSFR) galaxies in our sample. However, for a better comparison with our SFR estimates, we use the COLDGASS data by Huang & Kauffmann (2014) who re-evaluated the SFRs within the IRAM beam using additional mid-infrared and UV data for COLDGASS galaxies. Because there is some evidence that the SFRs from fitting of spectral-energy distributions such as done by Saintonge et al. (2011b) are overestimated relative to those from Hα+24 μm or FUV+24 μm (e.g., Leroy et al. 2013a; Huang & Kauffmann 2014), the comparison with the COLDGASS sample should be more consistent using the SFRs by Huang & Kauffmann (2014)6. In addition to the COLDGASS data, we also consider other data from the literature where both CO measurements and stellar masses are available (see Sect. 2.5). The dashed line in Fig. 7 indicates our fit with a robust linear regression to COLDGASS data (using the SFRs and Mstar within a 22′′ aperture by Huang & Kauffmann 2014), together with the samples of Gao & Solomon (2004) and García-Burillo et al. (2012): log(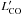 /SFR) = (−0.38 ± 0.03) log(sSFR) + ( 4.75 ± 0.31). The new fit is consistent with that found by Huang & Kauffmann (2014) for only the COLDGASS galaxies. However, both the dwarf galaxies in our sample and those in Schruba et al. (2012) show large residuals relative to the general trend.
/SFR) = (−0.38 ± 0.03) log(sSFR) + ( 4.75 ± 0.31). The new fit is consistent with that found by Huang & Kauffmann (2014) for only the COLDGASS galaxies. However, both the dwarf galaxies in our sample and those in Schruba et al. (2012) show large residuals relative to the general trend.
The residuals to this fit are plotted vs. sSFR and O/H in Fig. 8. Because τdep = αCO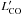 /SFR, the residuals from the correlation of
/SFR, the residuals from the correlation of 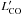 /SFR on sSFR should eliminate the dependence on τdep: [
/SFR on sSFR should eliminate the dependence on τdep: [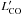 /SFR](observed)/τdep(fit) = [αCO(Z)/αCO(Z⊙)] -1. Thus, these residuals should correspond directly to the inverse of αCO, relative to Z⊙. The left panel of Fig. 8 demonstrates that there is no additional correlation with sSFR not accounted for by the COLDGASS relation; however, the right panel shows that there is a clear correlation with O/H. The correlation of the residuals with metallicity is able to almost completely rectify the deviation of the low-metallicity galaxies by almost two orders of magnitude from the COLDGASS galaxies. We find a robust fitted slope of αCO-1∝ (Z/Z⊙)1.96±0.16, more shallow than found with the assumption of constant τdep (Schruba et al. 2012; Genzel et al. 2012), but consistent with the αCO metallicity dependence found by using dust continuum measurements (Leroy et al. 2011; Bolatto et al. 2011).
/SFR](observed)/τdep(fit) = [αCO(Z)/αCO(Z⊙)] -1. Thus, these residuals should correspond directly to the inverse of αCO, relative to Z⊙. The left panel of Fig. 8 demonstrates that there is no additional correlation with sSFR not accounted for by the COLDGASS relation; however, the right panel shows that there is a clear correlation with O/H. The correlation of the residuals with metallicity is able to almost completely rectify the deviation of the low-metallicity galaxies by almost two orders of magnitude from the COLDGASS galaxies. We find a robust fitted slope of αCO-1∝ (Z/Z⊙)1.96±0.16, more shallow than found with the assumption of constant τdep (Schruba et al. 2012; Genzel et al. 2012), but consistent with the αCO metallicity dependence found by using dust continuum measurements (Leroy et al. 2011; Bolatto et al. 2011).
For the calculation of MH2, we adopt a solar value αCO = 3.2 M⊙ (K km s-1 pc2)-1, not including a factor of 1.36 for helium (see also Saintonge et al. 2011b). For our galaxies and those from Schruba et al. (2012) and Bothwell et al. (2014) having metallicities Z/Z⊙< 1 (12 + log(O/H) < 8.69), we applied αCO∝ (Z/Z⊙)-1.96; for metallicities Z/Z⊙≥ 1, we used the constant αCO as given above. Figure 9 shows the result of converting our 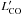 observations to MH2. Although there is some scatter, the trend of τdep with sSFR established by Saintonge et al. (2011b), Huang & Kauffmann (2014) seems to extend to the higher sSFRs and shorter τdep of these dwarf galaxies. A steeper dependence of αCO on metallicity would be inconsistent with this trend, but more data at 12 + log(O/H) ≲ 8 are needed to better assess any systematics.
observations to MH2. Although there is some scatter, the trend of τdep with sSFR established by Saintonge et al. (2011b), Huang & Kauffmann (2014) seems to extend to the higher sSFRs and shorter τdep of these dwarf galaxies. A steeper dependence of αCO on metallicity would be inconsistent with this trend, but more data at 12 + log(O/H) ≲ 8 are needed to better assess any systematics.
In any case, in agreement with previous work (e.g., Saintonge et al. 2011b; Bothwell et al. 2014; Huang & Kauffmann 2014), our analysis shows a strong variation of the molecular gas depletion times, with values ranging from ~10 Gyr for the COLDGASS galaxies to ~70 Myr for II Zw 40 and even smaller, ≲10 Myr for SBS 0335−052E, NGC 5253 and NGC 1569 (from Schruba et al. 2012). This variation is correlated with a range in sSFRs of almost three orders of magnitude.
The right panel of Fig. 9 suggests that τdep depends weakly on metallicity, even after the αCO dependence has been accounted for. The regression line is the robust fit to our galaxies and those from Schruba et al. (2012); the correlation is significant (Pearson coefficient of 0.38, significance >99.9%), with a slope of 0.64 ± 0.11. A similar (weak) effect was also found by Leroy et al. (2013a), but over a narrower range in metallicities and τdep. Because τdep and sSFR are correlated, and sSFR and O/H are also correlated (see Fig. 6), such a result is perhaps not surprising; it could be the result of the secondary dependence on sSFR or on Mstar. In Sect. 7, we discuss forms of αCO and its metallicity dependence (e.g., Wolfire et al. 2010; Krumholz et al. 2011).
 |
Fig. 10 τdep vs. Mstar for our sample and including data from the literature (Huang & Kauffmann 2014; Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. Our robust best-fit regression for these samples is shown as a dashed line; the dotted line corresponds to the slope for the COLDGASS galaxies alone (Huang & Kauffmann 2014). |
Because O/H and Mstar are correlated through the mass-metallicity relation, in Fig. 10, we have investigated the possibility that τdep depends on Mstar. This correlation is also formally significant, even more so than the one with O/H (Pearson coefficient of 0.56, significance >99.999%). The slope of 0.46 ± 0.03 (shown by a dashed line in Fig. 10) is similar to that (0.41 ± 0.05) found for the COLDGASS galaxies alone. Our results suggest that low-mass metal-poor galaxies tend to have high sSFR (Fig. 6) and shorter H2 depletion times (Figs. 9, 10), and the two properties are correlated. This result is not altogether new, although we have shown that it extends to much lower stellar masses and higher sSFRs than the COLDGASS sample.
6. Atomic and molecular gas content
The implication is that for low-mass, metal-poor galaxies, with high sSFR, τdep is systematically shorter than for more massive, metal-rich systems. Because our sample combined with the Schruba et al. (2012) and the Filho et al. (2013) compilation spans a wide range of O/H and sSFR, with 12CO(1–0) detections down to Z/Z⊙~ 0.1, it is well suited to assess the dependence on these parameters of molecular and total gas (Hi+H2) content, relative to stellar mass and total baryonic mass. The Hi masses, MHI, for our sample are given in Table 1 (see also Sect. 2.4) and we have taken MHI for the Schruba et al. (2012) galaxies from Walter et al. (THINGS, 2008) when available, or otherwise from Kennicutt et al. (2003).
We first investigate any trends of MH2-to-total gas mass fraction in Fig. 11, both as a function of sSFR (left panel) and 12 + log(O/H) (right). We use total Hi mass for this comparison, although it is almost certainly more extended than the H2 (see Table 1), which usually resides within the optical confines of the galaxy (Regan et al. 2001; Leroy et al. 2009a). The combined samples suggest a weak trend for H2 fractions to decrease at low sSFR, but there is no trend with O/H. A better assessment of both trends would require more CO data from high-sSFR and metal-poor galaxies (and resolved Hi measurements).
 |
Fig. 11 MH2/Mgas = MH2/(MHI+MH2) vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (Schruba et al. 2012; Bothwell et al. 2014); the left panel gives also the COLDGASS data (Huang & Kauffmann 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. |
Figure 12 shows the total gas Mgas (≡ MH2+MHI) fraction relative to the total baryonic mass Mbaryonic (≡Mgas+Mstar) as a function of stellar mass. As in Fig. 11, we use the total Hi mass for our targets (Col. 12 in Table 1). By including also the data from Schruba et al. (2012), Filho et al. (2013), Bothwell et al. (2014), Huang & Kauffmann (2014), we find there is a significant correlation between gas mass fraction and Mstar, as shown by the robust regression line. This is mainly due to the spread in Mstar of the two most extreme samples, COLDGASS and Filho et al. (2013). At low gas-mass fractions, this may also be partially induced by the co-dependence of the two axes, because of the presence of Mstar. Nevertheless, the trend is roughly continuous over a factor of 105 of Mstar, from ~106 to ~1011 M⊙.
Two of our sample galaxies are clear outliers, Mrk 996 and NGC 7077, both of which have a smooth elliptical-type morphology despite their low metallicity. Thus they may have already exhausted much of their Hi, since the H2-to-total gas mass fractions are relatively high, ~40%. These two galaxies could be in the process of quenching their star formation, unless more gas is accreted from the outside.
We examine in Fig. 13 the trend of total gas mass relative to Mbaryonic vs. sSFR (left panel) and 12 + log(O/H) (right). Here also the total gas fraction is significantly correlated with both sSFR and 12 + log(O/H) (see the robust regression lines), although there are significant outliers in our sample for the metallicity trend, which is mainly dominated by the XMP galaxies. However, as in Fig. 12, there may be a co-dependence of the two axes because of the presence of Mstar (left panel) and because of the stellar mass-metallicity correlation (right).
The Hi depletion times, τdep(Hi), for our combined sample are shown in Fig. 14. There is more than an order-of-magnitude scatter, but no systematic trend relative to sSFR. This result is similar to that found for more massive galaxies, and the horizontal dashed line in Fig. 14 corresponds to the roughly constant τdep(Hi) of 3.4 Gyr found for the GASS galaxies by Schiminovich et al. (2010). Figure 14 shows a possible weak trend with O/H, which starts to affect τdep(Hi) at 12 + log(O/H) ≲ 8. This could be a consequence of the large fraction of Hi-dominated galaxies at these metallicities (e.g., Krumholz 2013).
In general, we find that galaxies are more gas rich at low stellar masses, at high sSFRs, and at low metallicities, although the metallicity trends tend to have more scatter. Similar conclusions have been reached by Bothwell et al. (2014) and by Filho et al. (2013), although for a more limited range in parameter space. Our combined samples span five orders of magnitude in Mstar, a factor of ~103 in sSFR, and a factor of ~100 in oxygen abundance. The trends for total gas fraction are similar to those we find for the molecular gas depletion time τdep: low-mass, metal-poor, and high sSFR galaxies tend to have shorter τdep. τdep decreases by a factor of ~100 over a variation of ~1000 in sSFR and a factor of ~10 in O/H. However, Hi depletion times are roughly constant, although with large scatter, across this entire range of sSFR and O/H.
 |
Fig. 12 Mgas = (MHI+MH2)/Mbaryonic vs. Mstar, including data from the literature (COLDGASS: Huang & Kauffmann 2014; Schruba et al. 2012; Filho et al. 2013; Bothwell et al. 2014). Our robust best-fit regression for these samples is shown as a dashed line. |
 |
Fig. 13 Mgas = (MHI+MH2)/Mbaryonic vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (Schruba et al. 2012; Filho et al. 2013; Bothwell et al. 2014); the left panel gives also the COLDGASS detections (Saintonge et al. 2011b). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The regression lines shown in both panels correspond to our fit of the galaxies from Schruba et al. (2012), Filho et al. (2013), ALLSMOG, and our sample as described in the text (with all the uncertainties alluded to in Sect. 2.5). |
 |
Fig. 14 τdep(Hi) vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The constant τdep(Hi), shown by a horizontal dashed line, corresponds to 3.4 Gyr as found for the GASS sample (Schiminovich et al. 2010). |
7. Discussion
The short molecular gas depletion times, τdep≲ 100 Myr, we find at the highest sSFRs (≳0.1 Gyr-1) are comparable to starbursts at z ≳ 1; they are smaller than those found for “main-sequence” galaxies at similar redshifts (Genzel et al. 2015). Thus, the low-metallicity galaxies studied here may be low-mass analogues of starbursts observed at cosmological distances. This is not unlikely since most of them are likely merging or interacting systems (see Sect. 2.1). A starburst could enhance star-formation efficiency, namely the quantity of H2 converted into stars over a free-fall time (e.g., Krumholz et al. 2009); mergers or interactions would be expected to drive gas into the central regions, causing higher gas densities which could, at least partly, compensate for the low metallicity through increased self shielding.
Independently of the origin of the short molecular gas depletion times, the secondary dependence of τdep on Mstar and/or metallicity is not straightforward to interpret. Because of the way we have derived the molecular gas depletion times, the determination of a power-law dependence of αCO on metallicity is intimately related to τdep. To better understand whether short τdep and its dependence on Mstar and O/H are artefacts of our derivation of αCO, here we investigate an alternative formulation of αCO, and its potential relation with τdep. What we have defined as τdep is the inverse of what Krumholz et al. (2011) call specific gas SFRs, SSFRgas(CO, H2, total), the ratio of SFR surface densities to the various gas components of the ISM: Σgas, ΣH2, and ΣHI. Given a total gas mass surface density, Σgas, Krumholz et al. give precise predictions for the fraction of molecular gas mass in the form of H2, fH2, as well as the fraction of molecular gas where CO dominates over other forms of carbon, fCO.
In their models (see also Krumholz et al. 2009; McKee & Krumholz 2010), fH2 is a function of the ratio of the interstellar radiation field (ISRF) at the surface of the gas cloud, 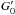 , and the hydrogen number volume density, nH, as well as the dust optical depth to UV photons, τdust. fH2 depends on metallicity through τdust which is assumed to be linearly proportional to Z/Z⊙. The transition in a cloud of atomic and ionized carbon to CO is driven mainly by dust extinction, thus cloud optical depth. The fraction of gas mass where the carbon is in CO form, fCO, depends on fH2, modified by an exponential function which depends only weakly on
, and the hydrogen number volume density, nH, as well as the dust optical depth to UV photons, τdust. fH2 depends on metallicity through τdust which is assumed to be linearly proportional to Z/Z⊙. The transition in a cloud of atomic and ionized carbon to CO is driven mainly by dust extinction, thus cloud optical depth. The fraction of gas mass where the carbon is in CO form, fCO, depends on fH2, modified by an exponential function which depends only weakly on 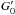 , and nH, but strongly on metallicity through AV (i.e., τdust), assumed to vary linearly with Z/Z⊙ (for more details see Wolfire et al. 2010). In these models, SFR surface density depends on fH2 and Σgas, and is defined by a roughly constant timescale, 2.6 Gyr. Thus, by assuming a characteristic value for
, and nH, but strongly on metallicity through AV (i.e., τdust), assumed to vary linearly with Z/Z⊙ (for more details see Wolfire et al. 2010). In these models, SFR surface density depends on fH2 and Σgas, and is defined by a roughly constant timescale, 2.6 Gyr. Thus, by assuming a characteristic value for 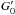 /nH, Krumholz et al. (2011) derive the dependence of the gas SSFRs on gas mass surface density, Σgas, and metallicity, Z/Z⊙.
/nH, Krumholz et al. (2011) derive the dependence of the gas SSFRs on gas mass surface density, Σgas, and metallicity, Z/Z⊙.
Figure 15 shows their predictions together with the data we have analyzed here. Although the models are formulated in terms of surface densities, to better compare with global values Krumholz et al. (2011) include a resolution correction factor (c), which we have adopted according to their prescription. Following Krumholz et al. (2011), the data points correspond to molecular gas masses, MH2(CO), inferred from CO luminosities using a constant conversion factor, αCO = 4.4 M⊙ (K km s-1 pc2)-1; this is the same αCO as used up to now (see Saintonge et al. 2011b) but here with the inclusion of helium. The CO-inferred molecular mass has been derived assuming a total gas surface density Σgas = 20 M⊙ pc-2; as shown by the blue curves in Fig. 15, the exact value of Σgas is not critical. As emphasized by Krumholz et al. (2011), this inferred mass MH2(CO) should not be interpreted as the total mass of molecular gas, but rather the mass of the molecular gas where the predominant form of carbon is CO. Also shown in Fig. 15 are the Krumholz et al. (2011) model predictions7 as a function of metallicity, Z/Z⊙, for three values of total gas column density (for more details see Krumholz et al. 2011). The models of CO-inferred H2 mass differ from the true H2 mass by a multiplicative factor that varies exponentially with Z/Z⊙ (because of the form of fCO described above, see also Wolfire et al. 2010; Bolatto et al. 2013). As in Krumholz et al. (2011), the SSFRgas(H2, CO) curves are shown only for metallicities and total gas surface densities that are sufficiently high that the H2 and CO mass fractions are non-zero. Like the data compilation presented by Krumholz et al. (2011), our data are also qualitatively consistent with the trends predicted by the models.
 |
Fig. 15 Ratio of SFR and CO-inferred H2 mass vs. relative metallicity as described in the text, including our data and data from the literature (COLDGASS: Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. Following Krumholz et al. (2011), here MH2 is inferred with a constant αCO = 4.4 M⊙ (K km s-1 pc2)-1, as described in the text. Also shown are the predictions by Krumholz et al. (2011), showing three values for total gas surface density, Σgas: 5 M⊙ pc-2, 20 M⊙ pc-2, and 80 M⊙ pc-2 indicated by dashed, dotted, and solid lines, respectively. Total gas corresponds to red, purple to H2, and blue to CO. |
 |
Fig. 16 Ratio of SFR and CO-inferred H2 mass vs. relative metallicity as described in the text, including our data and data from the literature (COLDGASS: Huang & Kauffmann 2014; Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. In the left panel, MH2 is inferred with our formulation of αCO as a power-law dependence on O/H as described in the text; in the right panel, we use the exponentially-dependent αCO as found by Wolfire et al. (2010), Krumholz et al. (2011). Also shown are the predictions by Krumholz et al. (2011), showing three values for total gas surface density, Σgas: 5 M⊙ pc-2, 20 M⊙ pc-2, and 80 M⊙ pc-2 indicated by dashed, dotted, and solid lines, respectively. Red color shows total gas, purple H2, and blue CO. |
Figure 15 shows that the data and the models agree extremely well for the prediction of CO luminosity; however at significantly sub-solar metallicities, Z/Z⊙≲ 0.2, there are some discrepancies relative to the H2 prediction, with some data exceeding by a factor of 3 or more the expected variation of the αCO factor. This is shown in Fig. 16 where we compare the power-law dependence of αCO derived previously with the exponential variation predicted by the models. Unlike in Fig. 15 where MH2(CO) depended on a constant αCO, here we derive MH2 from a metallicity-dependent αCO; the left panel shows the power-law dependency αCO∝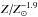 as shown in previous figures, and the right panel the exponential dependency found by Wolfire et al. (2010) and Krumholz et al. (2011), αCO∝exp( −Z/Z⊙). As discussed above, such a dependence arises through the assumption that αCO depends exponentially on the visual extinction within the clouds, AV, and that AV is proportional to Z/Z⊙.
as shown in previous figures, and the right panel the exponential dependency found by Wolfire et al. (2010) and Krumholz et al. (2011), αCO∝exp( −Z/Z⊙). As discussed above, such a dependence arises through the assumption that αCO depends exponentially on the visual extinction within the clouds, AV, and that AV is proportional to Z/Z⊙.
Because both MH2 and SFR predicted by the Krumholz et al. (2011) models depend on fH2, the expectation is that SSFR(H2) should be constant, independently of metallicity. Figure 16 shows that the data do not quantitatively follow this trend, but rather show a residual increase of SSFR(H2) toward low metallicities. Neither formulation (power-law or exponential) of αCO gives a horizontal trend of SSFR(H2) as a function of Z/Z⊙. The exponential αCO seems to better approximate the models around solar metallicity, but overestimates αCO at Z/Z⊙~ 0.1. On the other hand, the power-law αCO reproduces well the lowest metallicity SSFR(H2) (perhaps by construction, given that our αCO was heavily influenced by the lowest metallicity galaxy in our sample). In any case, it seems that the short depletion times, corresponding to high SSFR(gas) are not a result of our approach, nor is our power-law formulation of αCO significantly inferior to the exponential one.
As shown in Fig. 16, galaxies with Z/Z⊙≲ 0.2 are not always consistent with the model predictions for SSFR(H2). Because of the large span of τdep [inverse of SSFR(H2)] in our sample, it could be that the roughly constant timescale in the models is an oversimplification; indeed the Krumholz models are not designed for starbursts with potentially short depletion times and a high-density ISM. Moreover, there is strong evidence that clumping factors are different for molecular and atomic phases (Leroy et al. 2013b), implying that the use of a single correction factor to compare the predictions by Krumholz et al. (2011) with observations is almost certainly an oversimplification.
There could also be other problems with the applicability of the model predictions to these metal-poor starbursts, since αCO could have additional parameter dependencies beyond metallicity. The assumption of constant 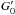 /nH may not be valid at low metallicities; the Krumholz et al. (2011) models assume
/nH may not be valid at low metallicities; the Krumholz et al. (2011) models assume 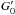 = 1, but the average UV flux
= 1, but the average UV flux 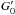 at low metallicities is expected to be harder and, at a given total stellar mass, more intense because of the warmer stellar temperatures. There could also be some problem with the assumption that dust opacities and the capacity of the gas to self-shield from UV radiation vary linearly with metallicity. As mentioned in Sect. 2, even at a similar low metallicity, galaxies can have dramatically different dust-to-gas and dust-to-stars mass ratios (Hunt et al. 2014). Schneider et al. (2015) suggest that this difference is due to the differences in the density of the cool gas in the ISM, because of the increased efficiency of grain formation in high-density environments. Thus, in addition to metallicity, ISM volume density could also be an important parameter for governing both the Hi-to-H2 and the H2-to-CO transitions in galaxies. However, the incidence of high ISM densities at low metallicities is not yet well established. More observations of the molecular ISM are needed for metal-poor galaxies, especially at Z/Z⊙≲0.1−0.2 where the validity of CO as a tracer of H2 begins to be called into question.
at low metallicities is expected to be harder and, at a given total stellar mass, more intense because of the warmer stellar temperatures. There could also be some problem with the assumption that dust opacities and the capacity of the gas to self-shield from UV radiation vary linearly with metallicity. As mentioned in Sect. 2, even at a similar low metallicity, galaxies can have dramatically different dust-to-gas and dust-to-stars mass ratios (Hunt et al. 2014). Schneider et al. (2015) suggest that this difference is due to the differences in the density of the cool gas in the ISM, because of the increased efficiency of grain formation in high-density environments. Thus, in addition to metallicity, ISM volume density could also be an important parameter for governing both the Hi-to-H2 and the H2-to-CO transitions in galaxies. However, the incidence of high ISM densities at low metallicities is not yet well established. More observations of the molecular ISM are needed for metal-poor galaxies, especially at Z/Z⊙≲0.1−0.2 where the validity of CO as a tracer of H2 begins to be called into question.
8. Summary and conclusions
We have detected 12CO(1–0) with IRAM 30-m observations of a sample of 8 metal-poor dwarf galaxies, including a tentative detection at a metallicity of 12 + log(O/H) = 7.7, ~0.1 Z/Z⊙. By calculating stellar masses and SFRs for our sample, and comparing our observations with a compilation of data from the literature, we have extended the trend for molecular τdep with stellar specific SFR by Saintonge et al. (2011b) to lower metallicities, lower stellar masses, and higher sSFRs. In agreement with Saintonge et al. (2011b) and Huang & Kauffmann (2014), we conclude that τdep is not constant in galaxies; in our combined sample τdep varies by a factor of 200 or more (from ≲50 Myr to ~10 Gyr) over a range of 103 in stellar sSFR and Mstar.
By exploiting the correlation of τdep with sSFR, we were able to constrain αCO as a function of metallicity, and found a dependence of αCO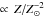 , similar to that found by work based on dust-continuum measurements compared with gas mass (Leroy et al. 2011; Bolatto et al. 2011). In conjunction with atomic gas measurements taken from the literature, we used our formulation for αCO to infer total gas masses, and total baryonic masses. The gas mass relative to the total baryonic mass depends on Mstar, stellar sSFR, and O/H; we found significant correlations for all three parameters in the sense that gas-mass fractions are higher for galaxies of lower stellar mass, lower metallicity and higher sSFR. However, despite large scatter, the Hi SFR depletion time is roughly constant for our combined sample, ~3.4 Gyr (see also Schiminovich et al. 2010).
, similar to that found by work based on dust-continuum measurements compared with gas mass (Leroy et al. 2011; Bolatto et al. 2011). In conjunction with atomic gas measurements taken from the literature, we used our formulation for αCO to infer total gas masses, and total baryonic masses. The gas mass relative to the total baryonic mass depends on Mstar, stellar sSFR, and O/H; we found significant correlations for all three parameters in the sense that gas-mass fractions are higher for galaxies of lower stellar mass, lower metallicity and higher sSFR. However, despite large scatter, the Hi SFR depletion time is roughly constant for our combined sample, ~3.4 Gyr (see also Schiminovich et al. 2010).
We have examined our data in the context of the star-formation models by Krumholz et al. (2011), and compared the power-law formulation of αCO with the theoretically motivated exponential formulation. The predicted ratios of SFR and gas mass compare extremely well for the CO data, but the SSFR(H2) inferred from either form of αCO are inconsistent for Z/Z⊙≲ 0.2. A residual trend of SSFR(H2) remains even when it should be invariant with metallicity according to the models. The cause of the disagreement is not clear but could arise from the starburst nature of our metal-poor sample; more observations of molecular tracers at low metallicity are needed to perform a more extended comparison with model predictions.
Throughout this work, we will rely on the Asplund et al. (2009) solar abundance calibration of 12 + log(O/H) = 8.69.
The electron temperature derived from the ratio of the [Oiii] λ4363 auroral line to lower-excitation lines ([Oiii] λ4959, 5007) is converted to a metallicity after correcting for unseen phases of ionization (e.g., Osterbrock & Ferland 2006).
We have performed the entire analysis with both datasets and confirm an overestimate of ~0.2 dex in the SFRs measured by Saintonge et al. (2011b) relative to Huang & Kauffmann (2014). This change affects only slightly the metallicity dependence of αCO, steepening the power-law index by 0.08 with respect to the Huang & Kauffmann (2014) data.
Here we continue to use the 8.69 solar calibration of Asplund et al. (2009) rather than the value of 12 + log(O/H) = 8.79 used by Krumholz et al. (2011).
Acknowledgments
We are grateful to the IRAM staff, both in Granada and at Pico Veleta, for ably managing the logistics and the telescope/receiver operations. The referee’s comments were timely and insightful, and improved the manuscript. We thank the International Space Science Institute (Bern) for hospitality during the conception of this paper, and Amelie Saintonge and Mei-Ling Huang who kindly gave us their COLDGASS data in digital form. L.K.H. acknowledges support from PRIN-INAF 2012/13. We made use of the NASA/IPAC Extragalactic Database (NED).
References
- Albrecht, M., Chini, R., Krügel, E., Müller, S. A. H., & Lemke, R. 2004, A&A, 414, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Spinrad, H., & Terlevich, R. 1982, MNRAS, 198, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Barone, L. T., Heithausen, A., Hüttemeister, S., Fritz, T., & Klein, U. 2000, MNRAS, 317, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, S. C., Turner, J. L., Langland-Shula, L. E., et al. 2002, AJ, 124, 2516 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Walter, F., et al. 2011, ApJ, 730, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Jackson, J. M., & Ingalls, J. G. 1999, ApJ, 513, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Rosolowsky, E., Walter, F., & Blitz, L. 2008, ApJ, 686, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Jameson, K., et al. 2011, ApJ, 741, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bordalo, V., Plana, H., & Telles, E. 2009, ApJ, 696, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Wagg, J., Cicone, C., et al. 2014, MNRAS, 445, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Brinks, E., & Taylor, C. L. 1997, IAU Symp., 170, 406 [NASA ADS] [Google Scholar]
- Brown, M. J. I., Moustakas, J., Smith, J.-D. T., et al. 2014, ApJS, 212, 18 [Google Scholar]
- Buyle, P., Michielsen, D., de Rijcke, S., Ott, J., & Dejonghe, H. 2006, MNRAS, 373, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Cairós, L. M., Caon, N., García-Lorenzo, B., et al. 2007, ApJ, 669, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Wu, S.-Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2014, A&A, 564, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Grijs, R., Smith, L. J., Bunker, A., et al. 2004, MNRAS, 352, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Pereira, M., Kewley, L. J., & Capaccioli, M. 2002, ApJS, 143, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Ekta, B., Pustilnik, S. A., & Chengalur, J. N. 2009, MNRAS, 397, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Rubio, M., Hunter, D. A., et al. 2013, Nature, 495, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Gordon, K. D., Rieke, G. H., et al. 2005, ApJ, 628, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Filho, M. E., Winkel, B., Sánchez Almeida, J., et al. 2013, A&A, 558, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Focardi, P., & Kelm, B. 2002, A&A, 391, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fox, J. 1997, Applied regression analysis, linear models, and related models (Thou- sand Oaks, CA: Sage publications) [Google Scholar]
- Fumagalli, M., Krumholz, M. R., & Hunt, L. K. 2010, ApJ, 722, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- García-Burillo, S., Usero, A., Alonso-Herrero, A., et al. 2012, A&A, 539, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Tacconi, L. J., Combes, F., et al. 2012, ApJ, 746, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Tsamis, Y. G., James, B. L., & Aloisi, A. 2011, MNRAS, 413, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Mac Low, M.-M. 2011, MNRAS, 412, 337 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gondhalekar, P. M., Johansson, L. E. B., Brosch, N., Glass, I. S., & Brinks, E. 1998, A&A, 335, 152 [NASA ADS] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., Fuente, A., & Usero, A. 2008, A&A, 479, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 522, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossi, M., Hunt, L. K., Madden, S. C., et al. 2015, A&A, 574, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guseva, N. G., Izotov, Y. I., & Thuan, T. X. 2000, ApJ, 531, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., & Hunt, L. K. 2004, A&A, 421, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houck, J. R., Charmandaris, V., Brandl, B. R., et al. 2004, ApJS, 154, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huang, M.-L., & Kauffmann, G. 2014, MNRAS, 443, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, A., Meidt, S. E., Colombo, D., et al. 2013, ApJ, 779, 46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Vanzi, L., & Thuan, T. X. 2001, A&A, 377, 66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Giovanardi, C., & Helou, G. 2002, A&A, 394, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Dyer, K. K., Thuan, T. X., & Ulvestad, J. S. 2004, ApJ, 606, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Dyer, K. K., & Thuan, T. X. 2005, A&A, 436, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Thuan, T. X., Sauvage, M., & Izotov, Y. I. 2006, ApJ, 653, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Thuan, T. X., Izotov, Y. I., & Sauvage, M. 2010, ApJ, 712, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L., Magrini, L., Galli, D., et al. 2012, MNRAS, 427, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Testi, L., Casasola, V., et al. 2014, A&A, 561, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, D. A., & Thronson, H. A., Jr. 1995, ApJ, 452, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Gallagher, J. S., & Rautenkranz, D. 1982, ApJS, 49, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., van Woerden, H., & Gallagher, J. S., III 1994a, ApJS, 91, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., O’Connell, R. W., & Gallagher, J. S., III 1994b, AJ, 108, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Rubin, V. C., Swaters, R. A., Sparke, L. S., & Levine, S. E. 2002, ApJ, 580, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, F. P. 1997, A&A, 328, 471 [NASA ADS] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2004, ApJ, 602, 200 [CrossRef] [Google Scholar]
- Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 2001, ApJ, 560, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Guseva, N. G. 2005, ApJ, 632, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- James, B. L., Tsamis, Y. G., & Barlow, M. J. 2010, MNRAS, 401, 759 [NASA ADS] [CrossRef] [Google Scholar]
- James, B. L., Tsamis, Y. G., Barlow, M. J., Walsh, J. R., & Westmoquette, M. S. 2013, MNRAS, 428, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, K. E., Indebetouw, R., Watson, C., & Kobulnicky, H. A. 2004, AJ, 128, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, K. E., Hunt, L. K., & Reines, A. E. 2009, AJ, 137, 3788 [NASA ADS] [CrossRef] [Google Scholar]
- Joy, M., & Lester, D. F. 1988, ApJ, 331, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I., Musella, I., & Grimaldi, A. 1996, A&A, 310, 722 [NASA ADS] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Jr., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kepley, A. A., Reines, A. E., Johnson, K. E., & Walker, L. M. 2014, AJ, 147, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2013, MNRAS, 436, 2747 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 699, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Leroy, A. K., & McKee, C. F. 2011, ApJ, 731, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Kuno, N., Sato, N., Nakanishi, H., et al. 2007, PASJ, 59, 117 [NASA ADS] [Google Scholar]
- Lebouteiller, V., Cormier, D., Madden, S. C., et al. 2012, A&A, 548, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, H., Skillman, E. D., Cannon, J. M., et al. 2006, ApJ, 647, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., Fraternali, F., & Sancisi, R. 2012, A&A, 537, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014, MNRAS, 445, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A., Bolatto, A. D., Simon, J. D., & Blitz, L. 2005, ApJ, 625, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A., Cannon, J., Walter, F., Bolatto, A., & Weiss, A. 2007, ApJ, 663, 990 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009a, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Bot, C., et al. 2009b, ApJ, 702, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013a, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Lee, C., Schruba, A., et al. 2013b, ApJ, 769, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G. K. 1985, Robust regression. In Exploring Data Tables, Trends, and Shapes, eds. D. C. Hoaglin, F. Mosteller, & J. W. Tukey (Wiley) [Google Scholar]
- Lipovetsky, V. A., Chaffee, F. H., Izotov, Y. I., et al. 1999, ApJ, 519, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Galliano, F., Jones, A. P., & Sauvage, M. 2006, A&A, 446, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Maloney, P., & Black, J. H. 1988, ApJ, 325, 389 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Krumholz, M. R. 2010, ApJ, 709, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Micheva, G., Östlin, G., Bergvall, N., et al. 2013, MNRAS, 431, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Minchin, R. F., Momjian, E., Auld, R., et al. 2010, AJ, 140, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Moffett, A. J., Kannappan, S. J., Baker, A. J., & Laine, S. 2012, ApJ, 745, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Moll, S. L., Mengel, S., de Grijs, R., Smith, L. J., & Crowther, P. A. 2007, MNRAS, 382, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Krumholz, M. R., Ostriker, E. C., & Hernquist, L. 2012, MNRAS, 421, 3127 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, M. A., Meidt, S., Van de Ven, G., et al. 2014, ApJ, 797, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd, eds. D. E. Osterbrock, & G. J. Ferland (Sausalito, CA: University Science Books) [Google Scholar]
- Paradis, D., Dobashi, K., Shimoikura, T., et al. 2012, A&A, 543, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paturel, G., Theureau, G., Bottinelli, L., et al. 2003, A&A, 412, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. L., Velusamy, T., Langer, W. D., et al. 2010, A&A, 521, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. L., Langer, W. D., & Goldsmith, P. F. 2014, A&A, 570, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIX. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plante, S., & Sauvage, M. 2002, AJ, 124, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Pustilnik, S. A., Brinks, E., Thuan, T. X., Lipovetsky, V. A., & Izotov, Y. I. 2001, AJ, 121, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, M. W., Thornley, M. D., Helfer, T. T., et al. 2001, ApJ, 561, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Reines, A. E., Johnson, K. E., & Hunt, L. K. 2008, AJ, 136, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A&A, 451, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosolowsky, E., Engargiola, G., Plambeck, R., & Blitz, L. 2003, ApJ, 599, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Rubio, M., Lequeux, J., & Boulanger, F. 1993, A&A, 271, 9 [NASA ADS] [Google Scholar]
- Sage, L. J., Salzer, J. J., Loose, H.-H., & Henkel, C. 1992, A&A, 265, 19 [NASA ADS] [Google Scholar]
- Saintonge, A., Kauffmann, G., Kramer, C., et al. 2011a, MNRAS, 415, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Kauffmann, G., Wang, J., et al. 2011b, MNRAS, 415, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Ly, C., et al. 2014, ApJ, 797, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Sandstrom, K. M., Leroy, A. K., Walter, F., et al. 2013, ApJ, 777, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, W. L. W., & Searle, L. 1970, ApJ, 162, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., Contini, T., & Pindao, M. 1999, A&AS, 136, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schiminovich, D., Catinella, B., Kauffmann, G., et al. 2010, MNRAS, 408, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Hunt, L. K., & Valiante, R. 2015, MNRAS, submitted [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2012, AJ, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Dale, D., et al. 2011, ApJ, 738, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. J., & Hancock, M. 2009, AJ, 138, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Van den Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Steel, S. J., Smith, N., Metcalfe, L., Rabbette, M., & McBreen, B. 1996, A&A, 311, 721 [Google Scholar]
- Swaters, R. A., van Albada, T. S., van der Hulst, J. M., & Sancisi, R. 2002, A&A, 390, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, C. L., Brinks, E., Grashuis, R. M., & Skillman, E. D. 1995, ApJS, 99, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, C. L., Kobulnicky, H. A., & Skillman, E. D. 1998, AJ, 116, 2746 [NASA ADS] [CrossRef] [Google Scholar]
- Temi, P., Brighenti, F., & Mathews, W. G. 2009, ApJ, 707, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., & Izotov, Y. I. 2005, ApJS, 161, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1996, ApJ, 463, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Lipovetsky, V. A., Martin, J.-M., & Pustilnik, S. A. 1999, A&AS, 139, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thuan, T. X., Hunt, L. K., & Izotov, Y. I. 2008, ApJ, 689, 897 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L. 2000, AJ, 119, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L. 2001, AJ, 121, 2003 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L., & Haynes, M. P. 2006, ApJ, 636, 214 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L., Skillman, E. D., & Salzer, J. J. 1998, AJ, 116, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Vader, J. P., Frogel, J. A., Terndrup, D. M., & Heisler, C. A. 1993, AJ, 106, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L. 2003, A&A, 408, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzi, L., Rieke, G. H., Martin, C. L., & Shields, J. C. 1996, ApJ, 466, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Hunt, L. K., Thuan, T. X., & Izotov, Y. I. 2000, A&A, 363, 493 [NASA ADS] [Google Scholar]
- Vanzi, L., Hunt, L. K., & Thuan, T. X. 2002, A&A, 390, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzi, L., Cresci, G., Telles, E., & Melnick, J. 2008, A&A, 486, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanzi, L., Cresci, G., Sauvage, M., & Thompson, R. 2011, A&A, 534, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigroux, L., Stasińska, G., & Comte, G. 1987, A&A, 172, 15 [NASA ADS] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, X.-Q., Wu, H., Zhu, Y.-N., et al. 2013, MNRAS, 433, 2946 [NASA ADS] [CrossRef] [Google Scholar]
- Westmoquette, M. S., Gallagher, J. S., & de Poitiers, L. 2010, MNRAS, 403, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D. 1995, ApJ, 448, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Hao, L., Brandl, B. R., et al. 2006, ApJ, 639, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, W., Kong, X., Li, C., Zhou, H.-Y., & Cheng, F.-Z. 2007, ApJ, 655, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H.-W. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top row, from left to right in alphabetical order of name: SDSS composite (ugriz) images of CGCG 007−025, Haro 3 (NGC 3353), II Zw 40, Mrk 996. Bottom row, leftmost panel: NGC 1156 (image taken from DSS2, reprocessed); then from left to right SDSS images of NGC 7077, UM 448, UM 462. Images are oriented with North up, East left, and are 50′′ on a side, except for NGC 1156 which is ~10′. The color of II Zw 40 is reddened by >2 mag AV from the Galaxy. NGC 1140 and SBS 0335−052E, both of which harbor SSCs and whose images are not from SDSS, are shown in Fig. 2. |
| In the text | |
 |
Fig. 2 NGC 1140 and SBS 0335−052E taken from composite HST images; both galaxies host super-star clusters (Hunter et al. 1994b; Reines et al. 2008). The image of NGC 1140 is ~90′′ on a side, and SBS 0335−052E ~5′′, and orientation is North up, East left. |
| In the text | |
 |
Fig. 3 12CO(1–0) average spectra for the observed galaxies. Top row, from left to right in alphabetical order of name: CGCG 007−025, Mrk 996, and NGC 1140. Second row: NGC 1156, NGC 3353 (Haro 3) two pointings ([0, 0], [0, +10′′]. Third row: NGC 3353 third pointing [–6′′, –9′′]), NGC 7077 (Mrk 900), UM 448. Bottom row: UM 462. The baselines are shown as a horizontal solid line, together with the multiple-component Gaussian fits as described in Sect. 3.2. The vertical axes are in |
| In the text | |
 |
Fig. 4 SFR vs. |
| In the text | |
 |
Fig. 5 SFR/ |
| In the text | |
 |
Fig. 6 Specific SFR vs. 12 + log(O/H) for our sample and including data from the literature (Hunt et al. 2012; Schruba et al. 2012; Filho et al. 2013; Bothwell et al. 2014). The metallicities for the ALLSMOG (Bothwell et al. 2014) sample have been modified as discussed in the text. As in Fig. 4, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The regression line is a robust best-fit of the Local Volume Legacy (LVL, Lee et al. 2009) and the dwarf irregulars from Lee et al. (2006). The various colors for the LVL give the Hubble type (early types red, magenta; late types blue, cyan). |
| In the text | |
 |
Fig. 7
|
| In the text | |
 |
Fig. 8 Residuals from the regression shown in Fig. 7 vs. sSFR (left panel) and vs. 12 + log(O/H) (right). We include here data for our sample and literature data (COLDGASS: Huang & Kauffmann 2014; Gao & Solomon 2004; García-Burillo et al. 2012; Schruba et al. 2012; Bothwell et al. 2014). The horizontal dashed line in the left panel shows 0 to aid the eye, while the regression in the right panel is the robust fit to the significant trend of the residuals of the |
| In the text | |
 |
Fig. 9 τdep vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (COLDGASS: Huang & Kauffmann 2014; Gao & Solomon 2004; García-Burillo et al. 2012; Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The regression line is our fit to the Schruba et al. (2012) and our sample as described in the text. |
| In the text | |
 |
Fig. 10 τdep vs. Mstar for our sample and including data from the literature (Huang & Kauffmann 2014; Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. Our robust best-fit regression for these samples is shown as a dashed line; the dotted line corresponds to the slope for the COLDGASS galaxies alone (Huang & Kauffmann 2014). |
| In the text | |
 |
Fig. 11 MH2/Mgas = MH2/(MHI+MH2) vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (Schruba et al. 2012; Bothwell et al. 2014); the left panel gives also the COLDGASS data (Huang & Kauffmann 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. |
| In the text | |
 |
Fig. 12 Mgas = (MHI+MH2)/Mbaryonic vs. Mstar, including data from the literature (COLDGASS: Huang & Kauffmann 2014; Schruba et al. 2012; Filho et al. 2013; Bothwell et al. 2014). Our robust best-fit regression for these samples is shown as a dashed line. |
| In the text | |
 |
Fig. 13 Mgas = (MHI+MH2)/Mbaryonic vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (Schruba et al. 2012; Filho et al. 2013; Bothwell et al. 2014); the left panel gives also the COLDGASS detections (Saintonge et al. 2011b). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The regression lines shown in both panels correspond to our fit of the galaxies from Schruba et al. (2012), Filho et al. (2013), ALLSMOG, and our sample as described in the text (with all the uncertainties alluded to in Sect. 2.5). |
| In the text | |
 |
Fig. 14 τdep(Hi) vs. sSFR (left panel) and vs. 12 + log(O/H) (right) for our sample and including data from the literature (Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. The constant τdep(Hi), shown by a horizontal dashed line, corresponds to 3.4 Gyr as found for the GASS sample (Schiminovich et al. 2010). |
| In the text | |
 |
Fig. 15 Ratio of SFR and CO-inferred H2 mass vs. relative metallicity as described in the text, including our data and data from the literature (COLDGASS: Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. Following Krumholz et al. (2011), here MH2 is inferred with a constant αCO = 4.4 M⊙ (K km s-1 pc2)-1, as described in the text. Also shown are the predictions by Krumholz et al. (2011), showing three values for total gas surface density, Σgas: 5 M⊙ pc-2, 20 M⊙ pc-2, and 80 M⊙ pc-2 indicated by dashed, dotted, and solid lines, respectively. Total gas corresponds to red, purple to H2, and blue to CO. |
| In the text | |
 |
Fig. 16 Ratio of SFR and CO-inferred H2 mass vs. relative metallicity as described in the text, including our data and data from the literature (COLDGASS: Huang & Kauffmann 2014; Schruba et al. 2012; Bothwell et al. 2014). As in previous figures, the open triangles for Schruba et al. (2012) correspond to their compilation of data from the literature and the filled ones to their metal-poor dwarf observations. In the left panel, MH2 is inferred with our formulation of αCO as a power-law dependence on O/H as described in the text; in the right panel, we use the exponentially-dependent αCO as found by Wolfire et al. (2010), Krumholz et al. (2011). Also shown are the predictions by Krumholz et al. (2011), showing three values for total gas surface density, Σgas: 5 M⊙ pc-2, 20 M⊙ pc-2, and 80 M⊙ pc-2 indicated by dashed, dotted, and solid lines, respectively. Red color shows total gas, purple H2, and blue CO. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


