| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 14 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526418 | |
| Published online | 02 November 2015 | |
Modelling the atmosphere of the carbon-rich Mira RU Virginis⋆,⋆⋆
1
University of ViennaDepartment of Astrophysics,
Türkenschanzstrasse 17,
180
Vienna,
Austria
e-mail:
gioia.rau@univie.ac.at
2
Institut d’Astronomie et d’Astrophysique, Université libre de
Bruxelles, Boulevard du Triomphe CP 226, ,
1050
Bruxelles,
Belgium
3
Department of Physics and Astronomy G. Galilei,
Vicolo dell’Osservatorio 3,
35122
Padova,
Italy
4
Royal Observatory of Belgium, Ringlaan 3, 1180
Brussels,
Belgium
Received: 27 April 2015
Accepted: 29 August 2015
Context. We study the atmosphere of the carbon-rich Mira RU Vir using the mid-infrared high spatial resolution interferometric observations from VLTI/MIDI.
Aims. The aim of this work is to analyse the atmosphere of the carbon-rich Mira RU Vir with hydrostatic and dynamic models, in this way deepening the knowledge of the dynamic processes at work in carbon-rich Miras.
Methods. We compare spectro-photometric and interferometric measurements of this carbon-rich Mira AGB star with the predictions of different kinds of modelling approaches (hydrostatic model atmospheres plus MOD-More Of Dusty, self-consistent dynamic model atmospheres). A geometric model fitting tool is used for a first interpretation of the interferometric data.
Results. The results show that a joint use of different kinds of observations (photometry, spectroscopy, interferometry) is essential for shedding light on the structure of the atmosphere of a carbon-rich Mira. The dynamic model atmospheres fit the ISO spectrum well in the wavelength range λ = [2.9,25.0] μm. Nevertheless, a discrepancy is noticeable both in the SED (visible) and in the interferometric visibilities (shape and level), which is a possible explanation are intra-/inter-cycle variations in the dynamic model atmospheres, as well as in the observations. The presence of a companion star and/or a disk or a decrease in mass loss within the past few hundred years cannot be excluded, but these explanations are considered unlikely.
Key words: techniques: interferometric / instrumentation: high angular resolution / circumstellar matter / stars: atmospheres / stars: AGB and post-AGB / stars: fundamental parameters
Based on observations made with ESO telescopes at La Silla Paranal Observatory under programme IDs: 085.D-0756 and 093. D-0708.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The asymptotic giant branch (AGB) is the late evolutionary stage of low-to-intermediate mass stars (typically ~0.8 to ~8M⊙). These objects are characterized by a C–O core and He/H-burning shells, surrounded by a convective envelope, while the atmosphere consists of atomic and molecular gas, including dust grains. Stellar pulsation can generate shock waves that run through the atmosphere. These shocks can propagate outwards, causing a levitation of the outer atmosphere layers and improving the conditions for the formation of dust, which may then lead to a dust-driven wind.
At the early stages of their life, AGB stars have a carbon-to-oxygen-ratio below one. The third dredge-up can turn the chemistry of these objects from oxygen- into carbon-rich (Iben & Renzini 1983). Carbon-rich AGB stars are important contributors to the enrichment of the interstellar medium, and in their spectra there are signs of carbon-bearing molecules such as C2, C3, C2H2, CN, or HCN, while the dust is mainly dominated by amorphous carbon dust grains and SiC (Loidl et al. 2001; Yamamura & de Jong 2000).
By studying the stellar atmospheres of AGB stars, we hope to better understand many processes that can occur, such as the dust formation and mass loss via strong stellar winds or the connection between pulsation and atmospheric structure. In the case of C-rich AGB stars with no pronounced pulsation, most of the observables derived from hydrostatic models agree fairly well with the observations (Aringer et al. 2009). However, as the star evolves, time-dependent processes become more important, and the atmosphere expands, causing a decrease in the effective temperature. As a result, model atmospheres that take those dynamic processes into account (pulsation, dust formation, mass loss) are necessary (e.g. Bowen 1988; Fleischer et al. 1992; Höfner & Dorfi 1997; Höfner et al. 2003; see also the excellent reviews from Woitke 2003 and Höfner 2007).
RU Vir photometry in different filters adopted from Nowotny et al. (2011), in units of mag.
In recent years there has been an increase in the number of works that investigate the atmosphere of AGB stars by combining various techniques (Wittkowski et al. 2001, 2008, 2011; Neilson & Lester 2008; Martí-Vidal et al. 2011). On the other hand, to date only a few interferometric observations of carbon stars have been compared with model atmospheres (Sacuto et al. 2011; Paladini et al. 2011; Cruzalèbes et al. 2013; Klotz et al. 2013; van Belle et al. 2013).
In this paper we intend to study the atmosphere of the carbon-rich Mira RU Vir, by means of photometry, spectroscopy, interferometry, and model atmospheres (Mattsson et al. 2010; Aringer et al. 2009), using the most recent grid of dynamic atmosphere models and synthetic spectra (Eriksson et al. 2014). RU Vir is a C-rich AGB Variable Star of Mira type. It has a period of 433.2 days in the V-band (Samus et al. 2009). Its distance is 910 pc (based on the period-luminosity relation from Whitelock et al. 2006), the amplitude of the variability in the V-band is 5.2 mag, and the average value of the magnitude in V is ⟨ V ⟩ = 11.6 mag. RU Vir is surrounded by a carbon-rich dusty shell made of amorphous carbon (AmC) and silicon carbide (SiC). The latter shows its presence through the strong emission feature around ~11 μm.
We present MIDI (MID-infrared Interferometric instrument) observations (P.I. G. Rau: ID 093.D-0708(A)) that probe regions of dust formation in the circumstellar envelope (Nowotny et al. 2011; Danchi et al. 1994). In a forthcoming paper, we will also consider a larger sample of carbon-rich AGB stars.
In Sect. 2 we present the photometry, the spectroscopy, and the interferometric observations of RU Vir and describe the data reduction performed. Section 3 explores the geometry of the environment and the fit of the geometrical models to the interferometric visibilities to constrain the morphology and the brightness distribution of the object. In general, the visibility V as a function of spatial frequencies u and v, as described, for example, in Winters et al. (1995), is the two-dimensional Fourier transform of the intensity distribution I(η,ζ), where η and ζ are the corresponding coordinates on the celestial sphere. In the special case of a circular symmetric intensity distribution, which is produced by spherical symmetric models, the visibility is given by the Hankel transform of the intensity profile: 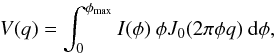 where
where 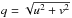 is the spatial frequency, φ the angular separation from the centre of the star (φ = r/d) with d the distance of the star, r the radius, and J0 the zeroth-order Bessel function. Therefore, the term interferometric visibilities will from now on be referred to as visibilities V, used to denote the normalized quantity V(q) /V(0). In Sects. 4 and 5 we investigate the modelling of the atmosphere of RU Vir from the hydrostatic and hydrodynamic point of view. In Sect. 6 we propose some of the possible scenarios that could justify the optical excess (Sect. 6.2) and the discrepancy in the visibilities (Sect. 6.3). Moreover, a discussion of the stellar parameters can be found in Sect. 6.1. Finally, we present the conclusions and perspectives for future works in Sect. 7.
is the spatial frequency, φ the angular separation from the centre of the star (φ = r/d) with d the distance of the star, r the radius, and J0 the zeroth-order Bessel function. Therefore, the term interferometric visibilities will from now on be referred to as visibilities V, used to denote the normalized quantity V(q) /V(0). In Sects. 4 and 5 we investigate the modelling of the atmosphere of RU Vir from the hydrostatic and hydrodynamic point of view. In Sect. 6 we propose some of the possible scenarios that could justify the optical excess (Sect. 6.2) and the discrepancy in the visibilities (Sect. 6.3). Moreover, a discussion of the stellar parameters can be found in Sect. 6.1. Finally, we present the conclusions and perspectives for future works in Sect. 7.
2. Observational data for RU Vir
2.1. ISO spectrum
RU Vir was observed with the Short Wavelength Spectrometer on board the ISO satellite (SWS, de Graauw et al. 1996) once on 20 July 1996 (Sloan et al. 2003). This ISO/SWS spectrum covers the wavelength range form 2.36 to 45.35 μm with a spectral resolution of R ≈ 200. For the purpose of our investigations, an error of ± 10% is assumed for wavelength < 4.05 μm and ± 5% towards red wavelengths (Sloan et al. 2003). The ISO spectrum can be seen in black in Fig. 4.
2.2. Photometry
RU Vir photometry in the filters B, V, R, I, J, H, and K is given in Table 1. For our study, following Nowotny et al. (2011), we picked the B, V, R, I observations from Eggen (1975) and J, H, K observations from Whitelock et al. (2006). The photometry is taken at the same phase φ as the ISO/SWS spectrum, which can be calculated in the following way: 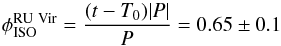 (1)where t is the time of the observation in Julian date, T0 the selected phase-zero point, corresponding to the nearest visual light maximum of the star. The light curves were interpolated to this phase (Nowotny et al. 2011, Fig. 8 there). The uncertainties of the different photometric measurements are estimated from the uncertainty in the phase and the scatter of the phased light curve data.
(1)where t is the time of the observation in Julian date, T0 the selected phase-zero point, corresponding to the nearest visual light maximum of the star. The light curves were interpolated to this phase (Nowotny et al. 2011, Fig. 8 there). The uncertainties of the different photometric measurements are estimated from the uncertainty in the phase and the scatter of the phased light curve data.
The visual light curve of RU Vir from AAVSO observations is shown in Fig. 1. The time of the observation of the ISO spectrum and the time interval of Eggen (1975) photometry (covers more than one pulsation cycle) are shown. The light curves favour the presence of a secondary period on a timescale of ~30 yr (Percy & Bagby 1999).
 |
Fig. 1 AAVSO light curve of RU Vir in black. The grey shadow shows the time range of the BVRI photometry observed by Eggen (1975). The vertical green, blue, and violet lines denote the epoch of the ISO spectrum, JHK photometry, MIDI observation, respectively. |
2.3. MIDI data
RU Vir was observed in 2010 (ID: 085.D-0756(C)) and 2014 (ID: 093.D-0708(A)) with the 1.8 m Auxiliary Telescopes (ATs) of the Very Large Telescope Interferometer MIDI (Leinert et al. 2003). MIDI provides wavelength-dependent visibilities, photometry, and differential phases in the N-band (λrange = [8,13]μm).
The journal of the observations is available in Table A.1. The calibrators used are listed below the corresponding science, and the second-to-last column identifies whether the observations are carried out in SCI-PHOT or HIGH-SENS mode. All the observations are in low spectral resolution (R = 30). The uv-coverage is shown in Fig. 2. The main characteristics of the calibrators are listed in Table 2. The choice of the calibrators follows the selection criteria described in Klotz et al. (2012a).
Data were reduced with the latest data reduction software package MIA+EWS (Jaffe 2004). The calibrated visibilities at different baselines are plotted in Fig. 3. The wavelength-dependent visibility exhibits the typical shape of the visibilities for carbon stars with dust shells containing SiC grains (Paladini et al., in prep.). There is a drop between 8−9 μm caused by C2 H2 + HCN opacities and another decline in the visibility shape at ~11.3 μm due to SiC.
The difference in position angle between the two sets of the observations (in 2010 and 2014) does not allow us to perform a check for interferometric variability because they do not probe the same spatial frequencies. So far, interferometric variability was observed only for one star (V Oph, Ohnaka et al. 2007); therefore, we decided to analyse the data all at the same time. When it comes to studying the geometry below (Sect. 3) we keep in mind that if these two points push for an asymmetric solution, then variability could still be an explanation.
The MIDI differential phase is zero, and the MIDI spectra are shown in Fig. 4. The shape of the MIDI spectra agree within the errors with the ISO spectrum. The difference in flux level between the two sets of MIDI observations is typical for C-rich Miras (Hron et al. 1997).
Parameters of the calibrator targets.
 |
Fig. 3 RU Vir calibrated visibilities at different baselines and projected angles. |
 |
Fig. 4 Comparison of observational data with modelling results. The black line shows the ISO/SWS spectrum of RU Vir, the green line the SED corrected from dust emission. The orange and violet shadows indicate the MIDI spectra, while the grey one denotes the hydrostatic models grid. The best-fitting model is shown in cyan. |
3. Geometrical models
3.1. Geometry of the environment
Before comparing the model atmospheres and the data, we studied the morphology of the circumstellar environment, interpreting the MIDI interferometric data with geometric models. This has been done by using the geometrical model-fitting tool GEM-FIND (GEometrical Model Fitting for INterferometric Data) of Klotz et al. (2012b). The program fits geometrical models to wavelength-dependent visibilities in the N-band, to constrain the morphology and brightness distribution of an object. A detailed description of the fitting strategy and of the χ2 minimization procedure can be found in Klotz et al. (2012a).
Different models with optically thick (models with one component) or thin (models with two components) circumstellar envelopes were tested. In Table 3 we list the corresponding reduced χ2 values and the parameters fitting best. In the case of elliptic models, the ratio of major and minor axes is shown. The brightness ratio is indicated for the two-component models with a circular uniform disc (UD) and a circular Gaussian. In the latter case, the fit was performed with a fixed value of the angular diameter, to avoid having too many free parameters in the fit. We started the fit of the composite model by imposing that the diameter is equal to the one derived from the θ/ (V − K) relation of van Belle et al. (2013): θ = 2.18 mas. Then we increased the diameter by steps of 2 mas until a θmax = 20 mas.
One-component spherically symmetric and elliptical models have large reduced χ2 and are not able to reproduce the data. A better fit to the data is obtained by a two-component model, including a circular UD plus a Gaussian distribution of the circular dusty envelope. This yields a reduced 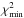 of 0.96 for a central star simulated by a UD with angular diameter at 11 μm of 18 mas (see Table 3), probably because of molecular opacities. In Fig. 3 we show the the visibilities vs. wavelength, while in Fig. 5 the fit of the visibility vs. baseline is shown at different wavelengths.
of 0.96 for a central star simulated by a UD with angular diameter at 11 μm of 18 mas (see Table 3), probably because of molecular opacities. In Fig. 3 we show the the visibilities vs. wavelength, while in Fig. 5 the fit of the visibility vs. baseline is shown at different wavelengths.
In general, the geometric models show that, for the u-v covered by our RU Vir observations, there is no major asymmetry detected.
 |
Fig. 5 Comparison of observational data with the best-fitting geometrical model. The calibrated visibilities are shown versus baseline length for two different wavelengths (left: 8.5 μm; right: 11.5 μm). The symbols represent MIDI observations at three different baseline configurations. The lines show the best-fitting model that consists of a circular UD and a circular Gaussian. |
GEM-FIND results. For each fit (one or two components), the full width at half maximum and angular diameter at 11 μm are given.
4. Hydrostatic model atmospheres + MOD models of dusty envelopes
Following Sacuto et al. (2011), we perform the first step of our study first by fitting the ISO spectrum with hydrostatic model atmospheres (COMARCS models, Aringer et al. 2009). Each hydrostatic model is identified by the following initial parameters: mass, effective temperature, C/O, log(g), metallicity. Details about these model atmospheres and the computed spectra are described in Aringer et al. (2009). The resolution of each synthetic spectrum1 is R = 200 to match the resolution of ISO and the spectral range [0.4,45.0] μm.
Since RU Vir is a dust-enshrouded carbon-Mira, we included dust by using the radiative transfer code MOD-More Of Dusty (Groenewegen 2012). This code is based on DUSTY, which is a publicly available 1D dust radiative transfer code (Ivezić & Elitzur 1995), whose mathematical formulation is described in detail in Ivezić et al. (1997). MOD tries to optimize a set of parameters (e.g. luminosity, dust optical depth, dust condensation temperature, and slope of the density law) with some constraints as spectro- photometric-data, 1D intensity profiles and visibility curves. A quantitative measure of the quality of the fit is obtained through performing a χ2 minimization, where the χ2 are computed separately for all the four types of observations. We note at this point that the dust condensation temperature in this context actually is the dust temperature at the inner boundary of the dust shell. Following previous work (e.g. Groenewegen 2012) we call it the dust condensation temperature.
Following Sacuto et al. (2011), we use a mixture of 90% AmC and 10% SiC for the dust composition. This ratio gave the best results for the ISO/SWS spectrum of the carbon star R Scl. Fits for RU Vir with a lower SiC fraction were not as good. The optical constants for the opacities of silicon carbide are taken from Pitman et al. (2008) and amorphous carbon from Rouleau & Martin (1991). Since the standard grain size distribution of DUSTY produced SiC features that were much too peaked, we used the distribution of hollow spheres (DHS, Groenewegen 2012, and references therein) with a mean grain size of the dust mixture of 0.2 μm. This grain size is similar to the typical sizes found from models for dust-driven mass loss (Mattsson & Höfner 2011). However, we note that these models only include amorphous carbon grains. On the other hand, the SiC grains found in presolar meteorites have sizes of the order of 1 μm (e.g. Gail & Sedlmayr 2013), indicating that our mean size is consistent with laboratory data. The chosen grain size distribution then gave a good fit of the SiC feature.
4.1. Fitting procedure
The hydrostatic models alone are not able to reproduce the ISO spectrum. This is because the hydrostatic models do not include dust, while the dust content in the atmosphere of RU Vir is quite prominent, as the spectral energy distribution from ISO/SWS shows (see Fig. 4, black line). In the following, we use the hydrostatic model atmosphere as the inner radiation source for MOD. The model parameters are selected as described below. Considering that RU Vir is located in the vicinity of the Sun, a first selection of the hydrostatic models was made by choosing only those models with solar metallicity. With the aim of being independent of the distance, each hydrostatic model spectrum was normalized to the ISO flux at 2.9 μm. We chose this wavelength because the local minimum of the molecular absorption resides here (Aringer et al. 2009).
We constrained the effective temperature of RU Vir by fitting the ISO spectrum with the synthetic spectra and by performing a χ2 minimization in the range [2.9,3.6] μm. The molecular features in this wavelength range are good temperature indicators for hydrostatic C stars (Jørgensen et al. 2000), and they provide a first approximation for our case. The result obtained in this way is T = 3100 ± 100 K. The C/O is set to C/O = 2.0, because this value is the one corresponding to the lowest χ2 in the wavelength region above. Figure 6 illustrates the χ2 vs. Teff in the wavelength range chosen as the best for the parameter determination; the best-fitting value is located at the minimum of the χ2.
 |
Fig. 6 Results of the χ2 fitting for the effective temperature and of the synthetic spectra based on COMARCS models with the ISO spectrum. The fit is done in the range of [2.9,3.6] μm. |
Output values of MOD fitting for three different cases.
We proceed by including the dust component with MOD a posteriori, as described below. With MOD we fit the photometry (see Sect. 2.2), spectroscopy (see Sect. 2.1), and interferometry (see Sect. 2.3) of the star. The input parameters of MOD are effective temperature (determined with the hydrostatic model atmosphere fit), distance, and the dust properties. The optical depth τ, the parameter that governs the shape of the density law p, and the dust condensation temperature Tc can be fitted or set to a fixed value.
An iterative procedure was used to assess how much the spectrum used for the inner radiation source is affected by dust emission. We determined a “corrected” ISO spectrum by performing a MOD fit using the 3100 K spectrum (see Fig. 4) derived above. We then subtracted the contribution of the dust emission at each wavelength from the total flux, in this way obtaining a stellar photospheric contribution. Repeating the effective temperature determination results in a best-fit model atmosphere with an effective temperature of 3000 K, i.e. only slightly cooler than the first estimate. This model spectrum was then used for the remaining calculations. We note that the corrected ISO spectrum has its maximum flux at a longer wavelength than the hydrostatic model, but the depth of the 3 μm feature is very similar to the model. This indicates that any difference between the corrected and the original ISO spectrum is caused by residual dust emission and not an incorrect model temperature.
As there is no generally agreed value of the dust condensation temperature in the literature, we performed the fit using three different Tc values: (i) Tc = 1000 K, based on the theoretical equilibrium condensation temperature from Gail & Sedlmayr (2013); and (ii) Tc = 1300 K (an average of the dust condensation temperature values from Nowotny et al. 2011 and from Lobel et al. 1999); (iii) finally we allowed all the input parameters to vary freely to verify the behaviour of the models. The results are shown in Table 4.
To check the importance of the ISO spectrum for the final result of the MOD fit, we made some experiments using a coarser sampled ISO spectrum and artificially increasing the error associated with the ISO spectrum. These tests show that the full ISO spectrum is essential for constraining the parameters of the dust envelope. Nevertheless, the real uncertainties of the dust parameters are considerably higher than their formal errors.
In Fig. 7 we present the comparison between the photometry (violet circles), the spectroscopy (blue line), and the SED of the best-fitting model. We note that the photometry shortwards of 1 μm cannot be well reproduced even if a maximum of free parameters is allowed. A hotter effective temperature cannot solve this discrepancy because it would be incompatible with the strength of the molecular features in the ISO spectrum. Figure 8 shows the comparison between MOD visibilities (lines) and observed visibilities (circles). Because the observed visibilities do not depend strongly on the wavelength, we selected only the two wavelengths corresponding to the maximum and minimum visibility (Fig. 3). Comparing the spatial frequencies at a given visibility level, one can conclude that the model is roughly a factor 2 too small. The visibilities could be brought to agreement by assuming a distance of ~300 pc, but this is unrealistically small. Therefore we have to conclude that the model is not extended enough or is missing a component. Another possibility is a difference between the observed and synthetic brightness contrast of multiple shells.
We now compare the observations with the dynamic model atmospheres (DMAs), which in principle would provide a more complete and physically consistent description of RU Vir.
 |
Fig. 7 Comparison of observed photometry (Table 2.2) and spectroscopy with the best-fitting synthetic spectrum based on hydrostatic model atmospheres and a dusty envelope (see Table 4 + Sect. 5.1). |
 |
Fig. 8 Comparison of MOD visibilities (lines) compared with the VLTI/MIDI observations of RU Vir (circles) at 9.8 μm (blue) and 11.4 μm (violet). |
5. Dynamic model atmospheres
In this section we present the analysis made by using the DMAs from Mattsson et al. (2010) and model spectra from Eriksson et al. (2014). For a detailed description of the modelling approach see Höfner & Dorfi (1997), Höfner (1999), Höfner et al. (2003), Mattsson et al. (2010), and Eriksson et al. (2014). For applications to observations we refer the reader to Loidl et al. (1999), Gautschy-Loidl et al. (2004), Nowotny et al. (2010, 2011). Those models are the result of solving the system of equations for hydrodynamics, frequency-dependent, and spherically symmetric radiative transfer, plus a set of equations that describe the time-dependent dust grains formation, growth, and evaporation. The dynamic model starts from an initial hydrostatic structure. The stellar pulsation is introduced by a “piston”, i.e. a variable inner boundary below the stellar photosphere, while the dust formation (only amorphous carbon) is evaluated by the “method of moments” (Gauger et al. 1990; Gail & Sedlmayr 1988).
The main parameters that characterise the DMA are luminosity L, effective temperature Teff (corresponding Rosseland radius, defined by the distance from the centre of the star to the layer at which the Rosseland optical depth equals unity), [Fe/H], C/O, as well as for the dynamical aspects period P, piston velocity amplitude Δu, and the parameter fl used to adjust the luminosity amplitude of the model. The resulting proprieties of the hydrodynamic calculations are the mean degree of condensation, wind velocity, and the mass-loss rate. Each model provides a set of “time steps”, representing the different phases of the stellar pulsation.
We computed synthetic spectra using the COMA code and the associated radiative transfer (Aringer 2000; Aringer et al. 2009). The abundances of all the relevant atomic, molecular, and dust species were computed, starting from temperature-density structure and considering the equilibrium for ionization and molecule formation. Both the continuous gas opacity and the intensities of atomic and molecular spectral lines, are subsequently calculated assuming LTE. The corresponding data are consistent with the ones used for constructing the models and are listed in Cristallo et al. (2007) and Aringer et al. (2009). SiC is added a posteriori with COMA by dividing the condensed material from the model into 90% amorphous carbon using data from (Rouleau & Martin 1991) and 10% silicon carbide based on (Pegourie 1988).
To be consistent with the model spectra from Eriksson et al. (2014), we have treated all grain opacities in small particle limit2 (SPL). The temperature of the SiC particles was assumed to be equal to the one of amorphous carbon. This is justified, since the overall distribution of the absorption is quite similar for both species, except for the SiC feature around 11.4 μm. As a consequence, the addition of SiC would also not cause significant changes in the thermal model structure. It should be noted that the effects of scattering are not included, since the SPL is adopted.
 |
Fig. 9 Reduced |
5.1. The DMA fitting procedure
Given the difficulties of MOD to reproduce the photometry, and the fact that the ISO/SWS spectrum provides the strongest constraints for gas and dust, we decided to first base the comparison with DMA only on the ISO/SWS spectrum. Thus we performed a χ2 minimization in the wavelength range: 2.9−25 μm between spectroscopic observation (ISO/SWS spectrum) and each of the 540 models of the grid (with a total of ~140 000 time steps). Based on the χ2 we obtain a best-fitting time step for each model.
In Fig. 9, the χ2 vs. average outflow velocity at the outer boundary and vs. mass loss are shown. In Table 5 we list the parameters of the best three time steps of the whole grid and the corresponding χ2. These time steps cover the 68% confidence region of χ2. The relevant SEDs, without SiC added, are shown in the left-hand panel of Fig. 10. The right-hand panel shows in grey all the time steps of the model that belong to the best-fitting time step (χ2 = 9.79). This best fitting time-step is marked in pink, now with the artificial inclusion of SiC (see also inset in Fig. 10).
There is good agreement between models and observations in the spectral range of the ISO spectrum. Even based on this broad range of ~140 000 time steps, it is not possible to reproduce the photometry shortwards of 1 μm. Possible explanations for this disagreement are discussed in Sect. 6.
 |
Fig. 10 Left: observational data (ISO spectrum in black line and photometry in violet circles) compared with synthetic spectra of the three best-fitting time steps (belonging to different DMA). Right: best-fitting time step (pink) compared with ISO (black). The grey lines are the various other phases (time steps) of the same model. |
Three best-fitting time-step dynamic models from the whole grid from Eriksson et al. (2014) resulting from comparison in Sect. 5.2.
5.2. MIDI data vs. dynamic models
Following Paladini et al. (2009), we calculated the intensity and visibility profiles for all the time steps of the best-fitting DMA derived in Sect. 5.1. We combined all the interferometric data (even though they are taken at different epochs, see Sect. 2.3), and we performed a χ2 test to obtain the best-fitting visibility profile. We obtained a new best-fitting time step for the visibilities observations of RU Vir, different from the one fitting the ISO spectrum best.
The time step best fitting the visibility is shown in Fig. 11. The upper panels illustrate the behaviour of the intensity profiles at two wavelengths (8.5 and 11.4μm), while the lower panels show the visibility vs. spatial frequencies. The phase of the best-fitting time step is 0.24, i.e. slightly different from that one best fitting the SED (see Sect. 6). The best-fitting time step has a Rosseland radius of 2.561 mas (500.9 R⊙) and a luminosity of 3982.8 L⊙.
The intensities are characterized by a first lobe (the photosphere with the hotter molecular gas) followed by two shells. The first shell is brighter at 11.4μm, where SiC contributes. While at short wavelengths (lower left panel) the visibility can reproduce the data, at long wavelengths (lower right panel) the model is off. The size of the model stays the same (~20 AU), but the flux ratio between the different components is changing.
The discrepancy between the model and the data is also observed when plotting the wavelengthdependent visibility for the three baseline configurations (Fig. 12). While at short wavelengths (8−9μm), the synthetic visibilities match the level of the observations, at longer wavelengths there is a slope in the model that is not observed in the data. The differences between model and observations are more pronounced when the baselines are shorter.
 |
Fig. 11 Comparison of interferometric observational data for RU Vir with the modelling results based on the DMA that best-fit the visibilities. Top: intensity profile at two different wavelengths: 8.5 μm and 11.4 μm. Bottom: visibility vs. baseline; the black line shows the dynamic model, and the coloured symbols illustrate the MIDI measurements at different baselines configurations. |
 |
Fig. 12 Wavelength-dependent visibilities in the MIDI range. The different panels show the three different baseline configurations of our observations. Models are plotted in full line and observations in dashed lines at different projected baselines (see colour legend). |
6. Discussion
While all our attempts to reproduce the SED (ISO spectrum + photometry) and interferometric MIDI data by different models showed some agreement, three major discrepancies remain: (1) no model can describe both the optical part and the infrared part of the SED. This may be interpreted either as an excess in the optical or beyond 2 μm. (2) The model visibilities show higher values and/or a different behaviour as a function of wavelength than the MIDI data. (3) The DMA predict fluxes that are too low beyond 14 μm.
Since (1) and (2) apply to all model approaches, we believe that this is mostly caused by properties of the object that can be described neither by the rather flexible MOD approach nor by the physically consistent DMA (see Sects. 6.2 and 6.3). In the following, we compare our results with previous work and discuss possible reasons for the discrepancies.
6.1. Stellar parameters vs. values from the literature
As described in Sects. 4 and 5, stellar parameters were derived from the fit of synthetic spectra based on COMARCS hydrostatic models + MOD to the observations (see Fig. 7) and from the study of the SED and MIDI data with the DMAs. The best-fitting optical depth value resulting from this work is τ0.55 = 7.96 ± 0.10 at λ = 0.55 μm. Lorenz-Martins et al. (2001) find τ = 2.5 at 1 μm. Ivezić & Elitzur (1995) indicate an optical depth value at the wavelength λ = 2.2 μm of τ2.2 = 0.47. Assuming τλ ∝ 1 /λ and scaling the above literature results to 0.55 μ, we arrive at 4.5 and 1.9, respectively. Our value is significantly higher, but our result is based on a broader and much better sampled SED, which should explain the differences.
The Rosseland radius of the best-fitting time step(s) of ~2.6 mas is close to the ones derived from the diameter (V − K) relations of van Belle (1999) and van Belle et al. (2013): 2.7 mas and 2.81 mas, respectively. The intensity distribution of the DMA (Fig. 11) has a radius of ~20 mas, which is comparable to the half width half maximum (HWHM) resulting from the GEM-FIND fit. If we adopt these numbers for the photospheric (stellar) and outer envelope radius, we can conclude that we are observing the stratification of the star out to ~6−7R⋆. Moreover, the agreement of the GEM-FIND radius with the DMA radius supports the fact that the discrepancy between the MIDI data and the DMA are due to different flux ratios between the various shells in the photosphere and envelope, rather than a global difference in size.
The effective temperature is a parameter that distinguishes the different DMAs. Literature values for RU Vir are in the range: [1945−2200] K (Bergeat & Chevallier 2005; Lorenz-Martins et al. 2001). These values agree with the one derived from the Rosseland radius of the time step that fits the SED (Teff = 2050 K), while the value obtained for the MIDI fit is slightly higher (Teff = 2545 K). Both temperatures are lower than the ones derived from fitting a static model to the C2H2 feature in the [2.9,3.6] μm region (3000 K) and than the static initial model of the best-fitting DMAs (2800 K). As elaborated in Nowotny et al. (2005), dynamic effects can cause the atmospheric structure of DMAs to be fundamentally different from any static model, including the static initial model of the DMAs. Therefore, a Teff derived from fitting a static model atmosphere to observations is only very indirectly linked to the Teff of the static initial model of the best-fitting DMA, so a comparison between the two is somewhat misleading in general. In the case of the strongly pulsating atmosphere of RU Vir and especially for the [2.9,3.6] μm region we are fitting, this is particularly relevant (Loidl et al. 1999). We also note that DMAs with Teff = 3000 K often do not produce the outflow required to reproduce the SED of RU Vir (e.g. Eriksson et al. 2014). Given the highly non-static atmospheric structure of the DMA, there is no straightforward relation between these different temperatures, but the results indicate that the [2.9,3.6] μm region is a reasonable indicator for the (static) effective temperature.
Finally, the mass of the best-fitting dynamic model is 1.5 M⊙. This value agrees with the 1.48 M⊙ obtained from the period-mass-radius relation of Vassiliadis & Wood (1993).
6.2. The shape of the SED
Given the success of both models in reproducing the IR part of the SED, we consider an optical excess flux to be more likely than an IR excess and will discuss this option first. The flux difference between observed photometry and the models (spectroscopy) in the V-band is at least a factor of ~10 in the SED. The quality of those used BVRI data appears to be high as judged from later measurements, such as Alfonso-Garzón et al. (2012). This author shows a lightcurve that, at the phase of the ISO spectrum, has V ≈ 11.6. This value is even brighter than the one used in the SED (see Table 1); moreover, the amplitude in the same band is ~2 mag, and this can still not justify our excess in V.
A much hotter temperature of the Mira photosphere can be ruled out as the origin of the excess on the basis of the strength of the molecular features around 3μm. Assuming a contribution from a companion would thus be the most obvious possibility. However, the optical spectrum (e.g. Barnbaum 1992) shows no signatures from another star and no emission lines as is typical of a symbiotic system (Welty & Wade 1995). RU Vir has a GALEX NUV-flux but no FUV-flux (Bianchi et al. 2014). Based on this flux and the predictions for white dwarf models (Bianchi et al. 2011), one can exclude the presence of a white dwarf. One may also use the V and I magnitudes to assess the properties of a possible companion. However, after correcting V and I for the contribution from the dusty envelope as fitted with MOD, the resulting (V − I) and MV cannot be reconciled with any main sequence companion. Therefore a stellar companion cannot explain the SED shape.
The presence of a sub-stellar companion that is not seen in the optical spectrum may, however, imply the presence of a dusty disk that would produce excess emission in the IR. A star like V Hya would be a possible template (Sahai et al. 2008). The above-mentioned GALEX flux is, however, a few orders of magnitude lower than what is expected for such an evolved star with an accretion disk. As is evident from the MOD fit, the optical and near-IR parts of the SED do not show the amount of reddening as expected from the dust emission seen at longer wavelengths. Therefore any disk must not obscure the stellar photosphere, meaning it should be seen almost face on. This would also be the only disk orientation compatible with the lack of evidence for asymmetries from the MIDI data. We thus consider a disk as a very unlikely explanation.
One aspect that has not been discussed so far is that the optical photometry and the ISO spectrum were obtained many different pulsation cycles apart. While we have interpolated the optical and IR photometry to the pulsation phase of the ISO spectrum, this cannot correct for any cycle-to-cycle differences. As mentioned in Sect. 2.2, RU Vir has a long secondary period in the optical, which could be an indication for such inter-cycle variations. Interestingly, our best-fitting DMA also has notable inter-cycle variations. However, the optical and ISO data were obtained at similar phases of the long-term optical changes. Therefore, to explain the full SED with our best-fitting DMA model, inter-cycle variations and a rather large phase uncertainty within a cycle have to be combined.
It is known that there are differences between visual phases and DMA model phases and that these differences, as well as the effects of cycle-to-cycle variations, increase towards shorter wavelengths (Nowotny et al. 2011). Therefore intra-cycle variations, together with phase assignment uncertainties, might improve the agreement between the observed and the DMA SEDs but are probably not enough. Obtaining a broad SED within one pulsation cycle would be the only way to verify this.
6.3. The visibilities
While the shape of the MOD visibilities are similar to the observations, the systematically lower observed level cannot be achieved by assuming a reasonable smaller distance (Sect. 4). Reducing the dust condensation temperature can lower the visibilities but produces the wrong shape. Therefore we believe that a simple two-component MOD model (star plus envelope with a single power law for the density) cannot reproduce the visibilities.
With regard to the slope of the DMA visibilities, we identify two possible explanations for the discrepancies observed.
-
(i)
The first one is related to the model. The models with highmass-loss rates produce a shell-like gas (and dust) componentthat is not observed in the data, i.e. the actualdensity distribution is smoother. This explanation is supported bythe fact that models that do not produce a wind also do not exhibitthe kind of slope seen in the best-fit DMA. An example of thevisibility of this kind of model is shown in Sacutoet al. (2011). A comprehensivecomparison of the dynamic model grid with interferometricobservations of dusty and dust-free objects will be able to excludeor confirm this hypothesis.
-
(ii)
Besides this explanation, another possibility is that the environment around the star is clumpy. This might also explain the lack of reddening mentioned in Sect. 6.2. Because of the presence of clumps, the shells appear fainter than what is predicted by the model. On the other hand, we do not observe any signal of clumps (i.e. departure from asymmetries) in the differential phases. Future observations with the second-generation VLTI instrument MATISSE will provide differential phases but also closure phases that will be more sensitive to small asymmetries. This kind of observation will be able to confirm the presence of clumps.
The differences between synthetic visibilities based on the DMA and MIDI visibilities around the SiC feature are most pronounced for the longest baselines, i.e. closest to the star. Since the formation process of SiC is not really known, the calculations assume that the SiC abundance scales with the amorphous carbon abundance as provided by the DMA. The above differences indicate that SiC could form farther in and/or in a smaller amount, but this has to be confirmed by comparisons based on a larger sample of stars.
That the model phases best fitting the SED and the visibilities are different is probably caused by the above-mentioned cycle-to-cycle variations of the best DMA model. In the MIDI-range these variations are comparable to the intra-cycle variations, meaning that a certain pulsation phase within one cycle may give similar visibility profiles as a different phase in another cycle.
6.4. The flux beyond 14 μm
The long-wavelength region of the SED can be reproduced well with MOD, while the DMA always predicts too steep a decline in flux towards the longest wavelengths. Tests have shown that an extension of the DMA farther out cannot account for this difference. Assuming a smoother density distribution of the DMA, as already argued from the visibilities and as present in the MOD model, should increase the dust emission at longer wavelengths. A more extensive comparison between DMA and a larger sample of C-rich Miras (Rau et al., in prep.) is needed to check whether the difference beyond 14 μm is found only in RU Vir or is a general characteristic of DMAs.
A higher mass loss in the past might be an explanation for this, although the shell parameters from MOD are close to a stationary wind solution. If the mass loss has even stopped in the recent past, this might also account for the overall differences in the shape of the SED because a very small mass loss now should shift the emission from circumstellar dust to longer wavelengths. However, besides the good fit with a stationary wind, a higher mass loss in the past would affect the visual light curve. But the average visual magnitude and the period have been stable over the past ~100 yr, and therefore such a scenario is also not very likely.
7. Conclusions
As demonstrated in this study, the joint use of photometry, spectroscopy, and interferometry and a comparison with models is essential to achieving a full understanding of the atmospheres of AGB stars. In this work we presented a study of the atmosphere of the Mira C-rich star RU Vir. We combined spectroscopic photometric and interferometric observations and hydrostatic and dynamic model atmospheres, as well as simple geometrical models. Until now, the only studies with a similar approach to the one in the present study are those by Sacuto et al. (2011) on R Scl and RT Vir Sacuto et al. (2013) on RT Vir. While R Scl is a semi-regular pulsating star and RT Vir an M-type star, RU Vir is the first carbon-rich Mira variable for which photometry, spectroscopy, and interferometry are compared to DMAs. Studying C-rich stars is particularly important since DMAs are more advanced for the C-rich stars than for the O-rich stars, because the dust formation process is considered to be simpler and better understood in the C-rich case (Nowotny et al. 2010, 2011).
The HWHM derived by the GEM-FIND fitting shows overall agreement with the DMA size in the N-band (see Sect. 6.1). Furthermore, the Rosseland radius corresponding to the time step that best fits the interferometric data is in agreement with the diameter derived via the (V − K) relation by van Belle (1999) and van Belle et al. (2013). The fitted effective temperature of the best-fitting DMA time steps is in the range of previous observational estimates but much lower than the temperature of the hydrostatic model of Sect. 4.1 and of the initial model of the best-fitting DMA.
The shape of the SED in the ISO range can be reproduced well with both MOD and DMA, and some discrepancies remain shortwards of 2μm and longwards of 14μm. A similar situation exists with regard to the interferometric data, both in the shape and in the visibility level. Some of the differences might be explained by a combination of intra- and inter-cycle differences since the observations are spread over many pulsation cycles and both the star and the best-fitting DMA show inter-cycle variations. Other possible reasons could be a decrease in mass loss over the last few hundred years or a sub-stellar companion associated with a dusty disk. However, these scenarios are not considered to be very likely, and to check them, further observations and modelling are both necessary. Based on the current work, we suspect that RU Vir is a somewhat peculiar object. Extending the comparison between models and observations to a larger sample of C-rich Mira variables (Rau et al., in prep.) will be necessary to clarify this, and will provide the general characteristics of the atmospheres of these stars and further constraints for the models.
Online material
Appendix A: Observing log
Journal of the MIDI observations of RU Vir.
 |
Fig. A.1 Comparison of the observational MIDI data with the best-fitting geometrical model (see Table 3). Shown are visibilities vs. wavelength at different position angles and baseline lengths (see Fig. 3 for the complete set of visibilities). Black lines represent the MIDI observations of RU Vir. Light blue lines represent the fit of the best-fitting UD+Gaussian model. |
Available at http://stev.oapd.inaf.it/synphot/Cstars/
Acknowledgments
The authors thank the anonymous referee for his constructive comments that helped us to improve the paper. This work is supported by the Austrian Science Fund FWF under project numbers AP23006, P23586, and P2198-N16. We are grateful to K. Eriksson for his continuous help and valuable comments. M. Mecina and T. Lebzelter are thanked for many helpful discussions. This research made use of SIMBAD database, operated at the CDS, Strasbourg, France, and NASA/IPAC Infrared Science Archive. B.A. acknowledges the support from the project STARKEY funded by the ERC Consolidator Grant, G.A. n. 615604, and C.P. acknowledges financial support from the FNRS Research Fellowship – Chargé de Recherche.
References
- Alfonso-Garzón, J., Domingo, A., Mas-Hesse, J. M., & Giménez, A. 2012, A&A, 548, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aringer, B. 2000, in The Carbon Star Phenomenon, ed. R. F. Wing, IAU Symp., 177, 519 [Google Scholar]
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnbaum, C. 1992, ApJ, 385, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeat, J., & Chevallier, L. 2005, A&A, 429, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, L., Efremova, B., Herald, J., et al. 2011, MNRAS, 411, 2770 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, L., Conti, A., & Shiao, B. 2014, VizieR Online Data Catalog: II/335 [Google Scholar]
- Bowen, G. H. 1988, ApJ, 329, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Lederer, M. T., & Aringer, B. 2007, ApJ, 667, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Cruzalèbes, P., Jorissen, A., Rabbia, Y., et al. 2013, MNRAS, 434, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Danchi, W. C., Bester, M., Degiacomi, C. G., Greenhill, L. J., & Townes, C. H. 1994, AJ, 107, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- de Graauw, T., Haser, L. N., Beintema, D. A., et al. 1996, A&A, 315, L49 [NASA ADS] [Google Scholar]
- Eggen, O. J. 1975, ApJS, 29, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksson, K., Nowotny, W., Höfner, S., Aringer, B., & Wachter, A. 2014, A&A, 566, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fleischer, A. J., Gauger, A., & Sedlmayr, E. 1992, A&A, 266, 321 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 1988, A&A, 206, 153 [NASA ADS] [Google Scholar]
- Gail, H.-P., & Sedlmayr, E. 2013, Physics and Chemistry of Circumstellar Dust Shells (Cambridge: Cambridge University Press) [Google Scholar]
- Gauger, A., Sedlmayr, E., & Gail, H.-P. 1990, A&A, 235, 345 [NASA ADS] [Google Scholar]
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2012, A&A, 543, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höfner, S. 1999, A&A, 346, L9 [NASA ADS] [Google Scholar]
- Höfner, S. 2007, in Why Galaxies Care About AGB Stars: Their Importance as Actors and Probes, eds. F. Kerschbaum, C. Charbonnel, & R. F. Wing, ASP Conf. Ser., 378, 145 [Google Scholar]
- Höfner, S., & Dorfi, E. A. 1997, A&A, 319, 648 [NASA ADS] [Google Scholar]
- Höfner, S., Gautschy-Loidl, R., Aringer, B., & Jørgensen, U. G. 2003, A&A, 399, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hron, J., Loidl, R., & Kerschbaum, F. 1997, Ap&SS, 251, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Z., & Elitzur, M. 1995, ApJ, 445, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Z., Groenewegen, M. A. T., Men’shchikov, A., & Szczerba, R. 1997, MNRAS, 291, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. J. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, SPIE Conf. Ser., 5491, 715 [Google Scholar]
- Jørgensen, U. G., Hron, J., & Loidl, R. 2000, A&A, 356, 253 [NASA ADS] [Google Scholar]
- Klotz, D., Sacuto, S., Kerschbaum, F., et al. 2012a, A&A, 541, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klotz, D., Sacuto, S., Paladini, C., Hron, J., & Wachter, G. 2012b, in SPIE Conf. Ser., 8445, 1 [Google Scholar]
- Klotz, D., Paladini, C., Hron, J., et al. 2013, A&A, 550, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leinert, C., Graser, U., Richichi, A., et al. 2003, The Messenger, 112, 13 [NASA ADS] [Google Scholar]
- Lobel, A., Doyle, J. G., & Bagnulo, S. 1999, A&A, 343, 466 [NASA ADS] [Google Scholar]
- Loidl, R., Höfner, S., Jørgensen, U. G., & Aringer, B. 1999, A&A, 342, 531 [NASA ADS] [Google Scholar]
- Loidl, R., Lançon, A., & Jørgensen, U. G. 2001, A&A, 371, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorenz-Martins, S., de Araújo, F. X., Codina Landaberry, S. J., de Almeida, W. G., & de Nader, R. V. 2001, A&A, 367, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martí-Vidal, I., Marcaide, J. M., Quirrenbach, A., et al. 2011, A&A, 529, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., & Höfner, S. 2011, A&A, 533, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2010, A&A, 509, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2008, A&A, 490, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Lebzelter, T., Hron, J., & Höfner, S. 2005, A&A, 437, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Höfner, S., & Aringer, B. 2010, A&A, 514, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Aringer, B., Höfner, S., & Lederer, M. T. 2011, A&A, 529, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohnaka, K., Driebe, T., Weigelt, G., & Wittkowski, M. 2007, A&A, 466, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladini, C., Aringer, B., Hron, J., et al. 2009, A&A, 501, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paladini, C., van Belle, G. T., Aringer, B., et al. 2011, A&A, 533, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pegourie, B. 1988, A&A, 194, 335 [NASA ADS] [Google Scholar]
- Percy, J. R., & Bagby, D. H. 1999, PASP, 111, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Pitman, K. M., Hofmeister, A. M., Corman, A. B., & Speck, A. K. 2008, A&A, 483, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Sacuto, S., Aringer, B., Hron, J., et al. 2011, A&A, 525, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacuto, S., Ramstedt, S., Höfner, S., et al. 2013, A&A, 551, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahai, R., Findeisen, K., Gil de Paz, A., & Sánchez Contreras, C. 2008, ApJ, 689, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Samus, N. N., Kazarovets, E. V., Pastukhova, E. N., Tsvetkova, T. M., & Durlevich, O. V. 2009, PASP, 121, 1378 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G. C., Kraemer, K. E., & Price, S. D. 2003, in The Calibration Legacy of the ISO Mission, eds. L. Metcalfe, A. Salama, S. B. Peschke, & M. F. Kessler, ESA SP, 481, 447 [Google Scholar]
- van Belle, G. T. 1999, PASP, 111, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- van Belle, G. T., Paladini, C., Aringer, B., Hron, J., & Ciardi, D. 2013, ApJ, 775, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Welty, A. D., & Wade, R. A. 1995, AJ, 109, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Whitelock, P. A., Feast, M. W., Marang, F., & Groenewegen, M. A. T. 2006, MNRAS, 369, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winters, J. M., Fleischer, A. J., Gauger, A., & Sedlmayr, E. 1995, A&A, 302, 483 [NASA ADS] [Google Scholar]
- Wittkowski, M., Hummel, C. A., Johnston, K. J., et al. 2001, A&A, 377, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Driebe, T., et al. 2008, A&A, 479, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Ireland, M., et al. 2011, A&A, 532, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, 387 [Google Scholar]
- Yamamura, I., & de Jong, T. 2000, in ISO Beyond the Peaks: The 2nd ISO Workshop on Analytical Spectroscopy, eds. A. Salama, M. F. Kessler, K. Leech, & B. Schulz, ESA SP, 456, 155 [Google Scholar]
All Tables
RU Vir photometry in different filters adopted from Nowotny et al. (2011), in units of mag.
GEM-FIND results. For each fit (one or two components), the full width at half maximum and angular diameter at 11 μm are given.
Three best-fitting time-step dynamic models from the whole grid from Eriksson et al. (2014) resulting from comparison in Sect. 5.2.
All Figures
 |
Fig. 1 AAVSO light curve of RU Vir in black. The grey shadow shows the time range of the BVRI photometry observed by Eggen (1975). The vertical green, blue, and violet lines denote the epoch of the ISO spectrum, JHK photometry, MIDI observation, respectively. |
| In the text | |
 |
Fig. 2 uv-coverage of the MIDI RU Vir observations listed in Table A.1, dispersed in wavelengths. |
| In the text | |
 |
Fig. 3 RU Vir calibrated visibilities at different baselines and projected angles. |
| In the text | |
 |
Fig. 4 Comparison of observational data with modelling results. The black line shows the ISO/SWS spectrum of RU Vir, the green line the SED corrected from dust emission. The orange and violet shadows indicate the MIDI spectra, while the grey one denotes the hydrostatic models grid. The best-fitting model is shown in cyan. |
| In the text | |
 |
Fig. 5 Comparison of observational data with the best-fitting geometrical model. The calibrated visibilities are shown versus baseline length for two different wavelengths (left: 8.5 μm; right: 11.5 μm). The symbols represent MIDI observations at three different baseline configurations. The lines show the best-fitting model that consists of a circular UD and a circular Gaussian. |
| In the text | |
 |
Fig. 6 Results of the χ2 fitting for the effective temperature and of the synthetic spectra based on COMARCS models with the ISO spectrum. The fit is done in the range of [2.9,3.6] μm. |
| In the text | |
 |
Fig. 7 Comparison of observed photometry (Table 2.2) and spectroscopy with the best-fitting synthetic spectrum based on hydrostatic model atmospheres and a dusty envelope (see Table 4 + Sect. 5.1). |
| In the text | |
 |
Fig. 8 Comparison of MOD visibilities (lines) compared with the VLTI/MIDI observations of RU Vir (circles) at 9.8 μm (blue) and 11.4 μm (violet). |
| In the text | |
 |
Fig. 9 Reduced |
| In the text | |
 |
Fig. 10 Left: observational data (ISO spectrum in black line and photometry in violet circles) compared with synthetic spectra of the three best-fitting time steps (belonging to different DMA). Right: best-fitting time step (pink) compared with ISO (black). The grey lines are the various other phases (time steps) of the same model. |
| In the text | |
 |
Fig. 11 Comparison of interferometric observational data for RU Vir with the modelling results based on the DMA that best-fit the visibilities. Top: intensity profile at two different wavelengths: 8.5 μm and 11.4 μm. Bottom: visibility vs. baseline; the black line shows the dynamic model, and the coloured symbols illustrate the MIDI measurements at different baselines configurations. |
| In the text | |
 |
Fig. 12 Wavelength-dependent visibilities in the MIDI range. The different panels show the three different baseline configurations of our observations. Models are plotted in full line and observations in dashed lines at different projected baselines (see colour legend). |
| In the text | |
 |
Fig. A.1 Comparison of the observational MIDI data with the best-fitting geometrical model (see Table 3). Shown are visibilities vs. wavelength at different position angles and baseline lengths (see Fig. 3 for the complete set of visibilities). Black lines represent the MIDI observations of RU Vir. Light blue lines represent the fit of the best-fitting UD+Gaussian model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.