| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525661 | |
| Published online | 28 October 2015 | |
The early days of the Sculptor dwarf spheroidal galaxy⋆
1 Laboratoire d’astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire, 1290 Versoix, Switzerland
e-mail: pascale.jablonka@epfl.ch
2 GEPI, Observatoire de Paris, CNRS, Université de Paris Diderot, 92195 Meudon Cedex, France
3 Institute of Astronomy, Russian Academy of Sciences, 119017 Moscow, Russia
4 Department Cassiopee, University of Nice Sophia-Antipolis, Observatoire de Côte d’Azur, CNRS, 06304 Nice Cedex 4, France
5 McDonald Observatory, University of Texas, Fort Davis, TX 79734, USA
6 Department of Physics and Astronomy, University of Victoria, PO Box 3055 STN CSC, Victoria, BC V8W 3P6, Canada
7 Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
8 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
9 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700AV Groningen, The Netherlands
10 Instituto de Astrofisica de Canarias, calle via Lactea s/n, 38205 San Cristobal de La Laguna, Tenerife, Spain
11 Universidad de La Laguna, Dpto. Astrofísica, 38206 La Laguna, Tenerife, Spain
12 Department of Physics and Astronomy, University of Victoria, 3800 Finnerty Road, Victoria, BC, V8P 1A1, Canada
13 European Southern Observatory, Karl-Schwarzschild-str. 2, 85748 Garching bei München, Germany
Received: 14 January 2015
Accepted: 24 June 2015
We present the high-resolution spectroscopic study of five −3.9 ≤ [Fe/H] ≤ −2.5 stars in the Local Group dwarf spheroidal, Sculptor, thereby doubling the number of stars with comparable observations in this metallicity range. We carry out a detailed analysis of the chemical abundances of α, iron peak, and light and heavy elements, and draw comparisons with the Milky Way halo and the ultra-faint dwarf stellar populations. We show that the bulk of the Sculptor metal-poor stars follow the same trends in abundance ratios versus metallicity as the Milky Way stars. This suggests similar early conditions of star formation and a high degree of homogeneity of the interstellar medium. We find an outlier to this main regime, which seems to miss the products of the most massive of the Type II supernovae. In addition to its help in refining galaxy formation models, this star provides clues to the production of cobalt and zinc. Two of our sample stars have low odd-to-even barium isotope abundance ratios, suggestive of a fair proportion of s-process. We discuss the implication for the nucleosynthetic origin of the neutron capture elements.
Key words: stars: abundances / Local Group / galaxies: dwarf / galaxies: formation
© ESO, 2015
1. Introduction
Star formation in dwarf galaxies has been the focus of many recent galaxy formation simulations. An extremely wide variety of topics are affected by the processes at play, from the evolutionary core/cusp-shape of the dark matter density profiles (e.g. Teyssier et al. 2013); to the “too big to fail problem”, which raises questions about the matching between dark matter halos and their stellar masses (e.g. Boylan-Kolchin et al. 2011, Sawala et al. 2013); to the nature of dark matter (e.g. Governato et al. 2015); and to the identification of the sources that were able to reionize the universe (e.g. Wise et al. 2014). Understanding such processes is then fundamentally necessary in order to accurately simulate these processes.
Although still limited, spectroscopic surveys of dwarf spheroidal galaxies (dSphs) have already shed substantial light on their evolution. It follows that their star formation efficiency is much lower than that of the Milky Way (MW), as revealed by the comparisons between the chemical imprints of dSphs and the MW. Indeed, the metallicity ([Fe/H]) at which Type Ia supernovae (SNeIa) dominate the chemical evolution of these small systems is at least a dex smaller than in the MW (Koch et al. 2008a; Tolstoy et al. 2009; Letarte et al. 2010; Kirby et al. 2011; Lemasle, in prep., Hendricks et al. 2014). Detailed abundances therefore allow us to place restrictions on the mass range and the period during which small galactic systems could have merged to form larger ones, as they need to share similar chemical patterns. Another merit of investigating the elemental abundances of individual stars inside dSphs resides in their power to help in the identification of stellar nucleosynthesis sites. The very different evolutionary paths of dSphs result in very distinct chemical signatures providing a series of constraints to the models. For instance, this is the case of the neutron-capture elements. The gradual enrichment in r-process elements may well depend on the galactic baryonic mass. Below [Fe/H] ~−3.5 all galaxies seem to have similar, very low, levels of barium and strontium. At higher metallicities, the smallest dwarfs stay at this low level, whereas more massive galaxies such as Sextans dSph eventually reach the solar value observed in the MW (Tafelmeyer et al. 2010).This type of evidence is crucial to helping distinguish among various possible origins such as a specific type of core collapse supernovae (e.g. Winteler et al. 2012), neutron star mergers (e.g. Wanajo et al. 2014), or spinstars (e.g. Cescutti et al. 2013). Another example is provided by the carbon. Very few carbon-rich extremely metal-poor stars have been found in dSphs, in contrast with the Galactic halo (Skúladóttir et al. 2015). This differential signature provides pieces of evidence to be interpreted on the type of stars whose nucleosynthetic production can be retained or accumulated in galaxies.
Dwarf spheroidal galaxies, located at the faint and challenging end of the galaxy luminosity function, have essentially only been targeted in their centres where the most recent star formation is concentrated, hence probing the end of their star formation history and chemical evolution (e.g. Tolstoy et al. 2009). The first evolutionary steps of these systems remain mostly unexplored, yet focusing on the extremely metal-poor regime ([Fe/H] ≤ −3) adds two major dimensions to chemical evolution studies. One is related to the initial mass function (IMF) in the early stages of galaxy formation. Whether or not the IMF is universal is of critical importance, and provides deep insights into star formation processes. How many massive (20–100 M⊙) stars can a dwarf system of final stellar mass 105–107 M⊙ form is a puzzle. Only the analysis of [α/Fe] at very low metallicity, i.e. the Type II supernovae (SNeII)-dominated regime, is discriminant. The second dimension addresses the mixing of the SNe ejecta in the interstellar medium (ISM). The binding energy of dwarf systems is low, and the turbulence induced by the supernova explosions can generate pockets of ISM with very different levels of chemical enrichment, which would reveal themselves as large, observable dispersions in stellar abundance ratios.
Unfortunately, we know of at most five [Fe/H] < −3 stars per galaxy for which we have high-resolution spectroscopy, for example in Sextans, Sculptor, Fornax, Ursa Minor and Draco (Aoki et al. 2009; Cohen & Huang 2009, 2010; Tafelmeyer et al. 2010; Frebel et al. 2010a; Simon et al. 2015), as well as in the ultra-faint dwarfs, Boötes (Norris et al. 2010b; Feltzing et al. 2009; Ishigaki et al. 2014), Segue I (Norris et al. 2010a; Frebel et al. 2014), Leo IV (Simon et al. 2010), and Ursa Major II (Frebel et al. 2010b). This dearth of data spans a factor of 100 in mass-to-light ratio, preventing any global analysis of how star formation starts up and is sustained in these systems.
This paper presents the high-resolution spectroscopic analysis of five new metal-poor stars in the Local Group dwarf spheroidal galaxy Sculptor. Combining this new dataset with earlier work, there are now ten stars that have been observed at high spectroscopic resolution, and fourteen in total accounting for the medium-resolution analysis of Starkenburg et al. (2013), making Sculptor the first dwarf spheroidal galaxy in which trends and dispersion in the very metal-poor regime can start being established in some detail. These trends reveal the nature of the first generations of stars (e.g. mass, numbers, spatial distribution), and the level of homogeneity of the primitive ISM (e.g. size/mass of star forming regions, nature and energy of the explosion of supernovae).
This paper is structured as follows: Sect. 2 introduces the selection of our sample and its general properties. Section 3 presents the determination of the stellar atmospheric parameters and the calculations of the abundances. Section 4 describes the specific treatment required by some of the elements. Section 5 presents our results and discusses their implications. We end this paper with a short summary of our findings in Sect. 6.
2. Sample
2.1. Selection, observations, and data reduction
Our sample was drawn from the medium-resolution CaT survey of Battaglia et al. (2008a). Starkenburg et al. (2010) provided the community with a new CaT calibration, which enables stellar metallicity to be estimated down to [Fe/H] =−4. We selected the probable extremely metal-poor stars (EMPS), which were bright enough to be observed at high resolution. Figure 1 gives their spatial distribution and Fig. 2 their location on the red giant branch (RGB) of the Sculptor dSph. Three stars, scl002_06, scl031_11, and scl074_02 had been observed previously at medium resolution with Xshooter by Starkenburg et al. (2013). The high-resolution spectroscopy brings a number of new and crucial elements, such as Co, Al, Si, Sc, and Mn. We conduct a brief comparison between the results of the two studies in Sect. 5.2.
 |
Fig. 1 Spatial distribution of the EMPS analyzed in this paper. The grey circles show the Sculptor member stars from the CaT analysis from Battaglia et al. (2008a). The orange circles indicate our new sample of stars with chemical abundances derived from high-resolution spectroscopy. The star symbols identify the EMPS of Frebel et al. (2010a) and Simon et al. (2015), while the upright triangles points to the sample of Tafelmeyer et al. (2010) and inverted triangles the EMPS of Starkenburg et al. (2013), which have not been reanalyzed at high resolution. |
 |
Fig. 2 V−I versus I colour–magnitude diagram of Sculptor on which we superimpose the positions of the EMPS discussed in this paper. The photometry is taken from de Boer et al. (2011). The orange circles indicate our new sample of stars with chemical abundances derived from high-resolution spectroscopy. The star symbols identify the EMPS of Frebel et al. (2010a) and Simon et al. (2015), while the upright triangles show the sample of Tafelmeyer et al. (2010) and inverted triangles the EMPS of Starkenburg et al. (2013), which have not been reanalyzed at high resolution. |
The observations were conducted in service mode with the UVES spectrograph attached to the VLT second unit, Kueyen. The slit width was set to 1′′, ensuring a resolving power R = 45000 between ~3500 Å and ~6850 Å. The journal of the observations, including target names, coordinates, the useable wavelength range for each star, signal-to-noise ratios per wavelength range, and exposure times is given in Table 1.
Journal of the observations.
The reduction was done with the ESO UVES pipeline (release 5.09) with optimal extraction. The 1D spectra resulting from order merging were then visually examined and the remaining obvious cosmic rays were removed by hand, using the IRAF1 splot subroutine.
2.2. Radial velocities and equivalent widths
Each of the three UVES wavelength ranges was normalized using DAOSPEC2 (Stetson & Pancino 2008, 2010), and subsequently 4DAO3. This code allows some spectral regions (e.g. telluric lines, residuals of sky lines) to be masked and displays the Gaussian fit to each individual line (Mucciarelli 2013). For the two red spectral ranges, the order merging resulted in a flux modulation requiring a high-order polynomial fit of the continuum. In the few cases where large amplitude wiggles still remained, the continuum was then placed manually and the equivalent widths (EQWs) were recalculated with Gaussian fits or direct integration with the iraf splot routine.
The DAOSPEC and 4DAO codes actually fit saturated Gaussians to the strong lines, not simple Gaussians. Nevertheless, they can not fit the wide, Lorentz-like wings of the profile of very strong lines, in particular beyond 200 mÅ. This is especially the case at very high resolution (Kirby & Cohen 2012). Therefore, we systematically measured all strong lines manually, using Gaussian fits as well as direct integration. When the DAOSPEC estimates agreed with these manual measurements within the DAOSPEC error bars, they were kept. This happened in the majority of the cases. Otherwise, we adopted the manual value closest to the DAOSPEC measurement. Direct integration was preferred when the wings of strong lines were too poorly fitted by a Gaussian.
In all cases we adopted the error δEQW computed by DAOSPEC. It is given by Stetson & Pancino (2008)
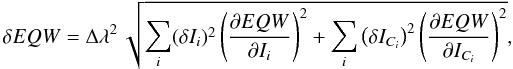 where Ii and δIi are the intensity of the observed line profile at pixel i and its uncertainty, while ICi and δICi are the intensity and uncertainty of the corresponding continuum. The uncertainties on the intensities are estimated from the scatter of the residuals that remain after subtraction of the fitted line (or lines, in the case of blends). This is a lower limit to the real EQW error because systematic errors like the continuum placement are not accounted for. The EQWs are provided in Table 2.
where Ii and δIi are the intensity of the observed line profile at pixel i and its uncertainty, while ICi and δICi are the intensity and uncertainty of the corresponding continuum. The uncertainties on the intensities are estimated from the scatter of the residuals that remain after subtraction of the fitted line (or lines, in the case of blends). This is a lower limit to the real EQW error because systematic errors like the continuum placement are not accounted for. The EQWs are provided in Table 2.
Line parameters, observed equivalent widths, and elemental abundances.
The radial velocities (RV) were calculated with 4DAO in each spectral range on the normalized spectra in which the telluric features were masked. For a given star, the RVs obtained from the three spectral ranges agree to within ± 0.7 km s-1 (Table 1). The average RV of each star coincides with that of the Sculptor dSph galaxy (110.6 ± 0.5 km s-1) within three times the velocity dispersion, σ = 10.1 ± 0.3 km s-1 measured by Battaglia et al. (2008a), meaning that our stars are highly probable members.
3. Stellar parameters
3.1. Models, codes, and ingredients
We adopted the MARCS 1D spherical atmosphere models with standard abundances. They were downloaded from the MARCS web site4 (Gustafsson et al. 2008), and interpolated using Thomas Masseron’s interpol_modeles code available on the same web site. The models are all computed for [α/ Fe] = + 0.4, which is perfectly suited for all our stars except ET0381. We were able to verify for this star that a model with [α/ Fe] = + 0.0 gives an FeI abundance larger by 0.03 dex and a microturbulence velocity larger by 0.05 km s-1. Unfortunately, models with [α/ Fe] = −0.4 are not available, but we can expect a systematic shift well within the uncertainties based on the differences between the enhanced and solar alpha models.
The star scl002_06 has the lowest surface gravity in our sample and unfortunately there is no available MARCS model at [Fe/H] < −3.0, log g< 1.0 and Teff< 4500 K. At these extremely low metallicities models suffer numerical instabilities and it is exceedingly difficult to make them converge (B. Plez, priv. comm.). In order to minimize systematic errors, we therefore chose to extrapolate the model grid for [Fe/H] = −4.0 along the log g axis for Teff= 4000, 4250, and 4500 K. The extrapolation was a linear one, applied to the logarithmic quantities ([Fe/H], log g, and log Teff) and based on the models with log g= 1.5 and 1.0. Three more models were defined in this way, with log g= 0.5, [Fe/H] = −4.0, [α/ Fe] = + 0.4, and Teff= 4000, 4250, and 4500 K. The Teff versus τ5000 relation of an example of extrapolation is displayed in Fig. 3, showing a smooth variation from one model to the other. Extrapolations along the [Fe/H] and the Teff axis were also tested, but were less convincing. Then the Masseron’s interpolating code was used with the extended grid.
 |
Fig. 3 Teff – log(τ) relation for the extrapolated model of scl002_06 (blue), compared with grid models for [Fe/H] = −3.0 (black) and −4.0 (red), and log g= 0.5,1.0,1.5, for Teff = 4300 K. All these models are interpolated in Teff between 4250 and 4500 K, but those with log g< 1.0 and [Fe/H] = −4.0 are interpolated between eight models (4250,4500;0.5,1.0;−4.0,−3.0), two of which are extrapolated (4250,4500;0.5;−4.0) from the MARCS grid. By chance, the model interpolated for scl002_06 (full blue curve) almost exactly coincides with the (4300;0.5;−4.0) model (full red curve), except in the range −0.5 < log(τ5000< + 0.4. |
Magnitudes, CaT metallicities, and corresponding photometric effective temperatures and surface gravities of our stars.
The abundance analysis and the spectral synthesis calculation were performed with the turbospectrum code (Alvarez & Plez 1998; Plez 2012), which assumes local thermodynamic equilibrium (LTE), but treats continuum scattering in the source function. We used a plane parallel transfer for the line computation to be consistent with our previous work on EMPS Tafelmeyer et al. (2010). The same code was used to produce synthetic spectra of short spectral intervals with various abundances and to estimate the C abundance by visual interpolation in the G-band of the CH molecule.
The adopted solar abundances in Table 7 are from Anders & Grevesse (1989) and Grevesse & Sauval (1998). Our line list combines those of Tafelmeyer et al. (2010) and Van der Swaelmen et al. (2013), with the exception of the CH molecule for which we used the list published by Masseron et al. (2014). The turbospectrum code was fed with information on the spectral lines taken from the VALD database (Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999, 2000). However, we kept the log (gf) values from the original list. The central wavelengths and oscillator strengths are given in Table 2.
3.2. First photometric approximations to the effective temperature and surface gravity
The first approximation of the stellar effective temperature was based on the V- and I-band magnitudes measured in de Boer et al. (2011, 2012) and based on J and Ks photometry taken from the VISTA commissioning data, which was also calibrated onto the 2MASS photometric system.
We assumed Av = 3.24·EB−V (Cardelli et al. 1989) and EB−V = 0.018 (Schlegel et al. 1998). The final photometric Teff for each star indicated in Table 3 corresponds to the simple average of the three-colour temperatures derived from V−I, V−J, and V−K with the calibration of Ramírez & Meléndez (2005).
Because of the very small number of detectable Fe ii lines, we determined log g from its relation with Teff using the calibration for the bolometric correction of Alonso et al. (1999), 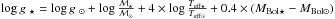 , where log g⊙ = 4.44, Teff ⊙ = 5790 K, Mbol ⊙ = 4.75, and ℳ = 0.8 ℳ⊙. The distance of Pietrzyński et al. (2008)d = 85.9 kpc, was adopted to calculate Mbol.
, where log g⊙ = 4.44, Teff ⊙ = 5790 K, Mbol ⊙ = 4.75, and ℳ = 0.8 ℳ⊙. The distance of Pietrzyński et al. (2008)d = 85.9 kpc, was adopted to calculate Mbol.
3.3. Final stellar parameters
The convergence to our final effective temperatures and microturbulence velocities (vt) presented in Table 4 was achieved iteratively as a trade off between minimizing the trends of metallicity derived from the Fe i lines with excitation potentials (χexc) and reduced equivalent widths, log(EQW/λ), and minimizing the difference between Fe ii and Fe i abundances on the other hand. Starting from the initial photometric parameters we adjusted Teff and vt by minimizing the slopes of the diagnostic plots, allowing the slope to deviate from zero by no more than 2σ, the uncertainties on the slopes. New values of log g were then computed from the equation above.
Final spectroscopic stellar parameters.
Following Tafelmeyer et al. (2010), we only considered the Fe lines with χexc > 1.4 eV in order to avoid 3D effects as much as possible. We also discarded lines that were too weak (defined as EQW < 20 mÅ in the red and EQW < 30−40 mÅ in the blue) because their measurements were noisier than the rest. We rejected all iron lines with EQW > 200 Å to minimize biases on the stellar parameters because such lines differ too much from a Gaussian shape. However, we did keep a few such strong lines for interesting elements such as Mg, but checked the corresponding abundances through synthetic spectra, because as discussed in Sect. 2.2, their non-Gaussian shape may induce a bias in the EQW determination. Finally we used the predicted EQWs in the Fe i abundance versus log(EQW/λ) diagram, following Magain (1984). Although this does not change the results in a very significant way, it does reduce vt by 0.1−0.3 km s-1 and increase [Fe/H] by a few hundredths of a dex in a systematic way, compared to using the observed equivalent widths.
The final stellar parameters are given in Table 4. The typical errors are ~ 100 K on Teff, ~ 0.1 dex on log g, assuming a ± 0.1 M⊙ error on ℳ⋆ and a 0.2 mag error on Mbol, and about 0.2 km s-1 on vt.
3.4. Hyperfine structure
The hyperfine structure (HFS) broadens the line profile and tends to increase its EQW for a given abundance because it tends to de-saturate the line. Therefore, the abundances of elements with a significant HFS broadening, such as Sc, Mn, Co, and Ba are biased when they are determined from the line EQWs, if HFS is neglected.
We determined the HFS correction to the abundance related to each line of the elements concerned, by running Chris Sneden’s MOOG code5 with the blend driver on a line list including the HFS components, as in North et al. (2012). The HFS components with their oscillator strengths were taken from Prochaska & McWilliam (2000) for Sc and Mn, and from the Kurucz web site6 for Co and Ba. The HFS correction is small for weak lines (e.g. for the Ba ii subordinate lines), but may reach −0.5 dex for Mn i.
3.5. Final abundances
The final abundances are calculated as the weighted mean of the abundances obtained from the individual lines, where the weights are the inverse variances of the single line abundances. These variances were propagated by turbospectrum from the estimated errors on the corresponding equivalent widths. The average abundances based on EQWs and the C abundances are given in Table 7.
The upper limits to the Eu, Ba, Y, or Zn abundances are also provided. They are based on visual inspection of the observed spectrum, on which seven synthetic spectra were overplotted, with abundance varying by steps of 0.1 dex. The adopted upper limit corresponds to a synthetic line lying at the level of about −1σ, where σ is the rms scatter of the continuum.
3.5.1. Errors
In order to make the errors on EQW more realistic, we added quadratically a 5% error to the EQW error estimated by DAOSPEC, so that no EQW has an error smaller than 5%. The errors estimated in this way were found to be generally larger than those obtained from the Cayrel (1988) formula revised by Battaglia et al. (2008b). They are given in Table 2.
The σEQW errors listed in Table 7 are defined in the same way as in Tafelmeyer et al. (2010) and Starkenburg et al. (2013). The average abundance error due to the EQW error alone for one average line is σEQW. Here, it is computed as 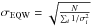 , where N is the number of lines. The σX errors correspond to the rms scatter of the individual line abundances, divided by the square root of the number of lines, N:
, where N is the number of lines. The σX errors correspond to the rms scatter of the individual line abundances, divided by the square root of the number of lines, N: 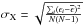 . The final error on the average abundances is defined as σfin = max(σEQW,σX,σFe). As a consequence, no element X can have σX<σFe; this is particularly important for species with a very small number of lines.
. The final error on the average abundances is defined as σfin = max(σEQW,σX,σFe). As a consequence, no element X can have σX<σFe; this is particularly important for species with a very small number of lines.
The errors provided in Table 2 do not include the propagation of the errors on the stellar parameters, especially Teff. For this purpose, we give the effect of a 100 K Teff increase on mean abundances in Table 5. Since log g and vt change according to Teff, we do not consider them to be independent. Therefore, the impact of a variation in Teff on the abundances is given after log g was adapted to the new Teff value and vt was optimized on the basis of the Fe i abundance versus log(EQW/λ) diagram.
4. Comments on specific abundances
Table 2 presents the measurement of the equivalent widths of the lines that have been considered in the analysis and their corresponding elemental abundances. In the next few subsections, we address a few distinctive points. Elements and stars that did not require any specific treatment or that gave consistent results for all lines and are not prone to any possible biases such as the non-local thermodynamic equilibrium (NLTE) effect do not appear in this section and we refer the reader to Table 2 and Sect. 5.
4.1. Carbon
The C abundance is based on the intensity of the CH molecular feature at 4323−4324 Å in the G band. To compute a synthesis in this region, the oxygen and nitrogen abundances have to be known or assumed, since part of the carbon is locked in the CO and CN molecules. As do Tafelmeyer et al. (2010) and Starkenburg et al. (2013), we assume that the [O/Fe] ratio is the same as [Mg/Fe] and that [N/Fe] is solar, because we are unable to measure the oxygen and nitrogen abundance. We also adopt 12C /13C = 6, an appropriate value to the tip of the RGB (Spite et al. 2006). Figure 5 shows a comparison between five synthetic spectra with increasing C abundance and the observed spectrum of the star ET0381.
Barium LTE and NLTE abundances, NLTE abundance corrections, and the effect of uncertainties in stellar parameters on abundances (in dex) derived from individual lines of Ba ii in ET0381 and scl_03_059.
4.2. α elements
-
Magnesium. The Mg abundance is based on 4 or 6 lines distributed from the violet to the yellow part of the spectrum. Four of them are strong, with EQW > 100 mÅ, while the other two are much weaker, nevertheless they all provide consistent abundances. We avoided the Mg i λ3829 Å line because it is strongly blended.
-
Titanium. The Ti i abundances rely on 4 to 11 faint lines giving consistent values, while the Ti ii abundances are based on 17 to 28 lines, many of them stronger, and giving more scattered results. We adopt the Ti ii abundances as representative of titanium because they are less sensitive to NLTE effects.
4.3. Iron peak elements
-
Manganese. The abundance is based on 3 to 5 lines. They are corrected for HFS. The strong, blue resonance lines at λ4030 Å, 4033 Å, and 4034 Å suffer from NLTE effects and from some blends, but they are the only ones available in the most metal poor stars. To minimize the effects of blends, we did not consider the λ4033, 4034 Å lines for ET0381. In the three stars where the blue resonance lines (λ4030 Å, 4033 Å, and 4034 Å) and subordinate ones (λ4041 Å, 4823 Å) could be measured, the abundances resulting from the former are 0.2−0.3 dex lower than those resulting from the latter. This is qualitatively consistent with, but less pronounced than, the 0.5 dex difference seen by Venn et al. (2012) for their own stars.
-
Nickel. The abundances are based on 2 to 3 lines, avoiding the blended λ4231 Å line.
-
Zinc. The only usable line is the very faint Zn i at λ4810 Å, and only an upper limit to the abundance could be determined.
4.4. Neutron capture elements
-
Strontium. The Sr abundance is based on two resonance lines, Sr ii λ4077 Å and λ4215 Å. The latter is blended primarily with the Fe i λ4215.423 Å line, and also, to a much lesser extent, by faint molecular CN lines. Because that iron line is relatively strong for ET0381, according to its spectral synthesis, we did not consider Sr ii λ4215 Å in that star.
-
Europium. Only one line, Eu ii λ4129 Å can be used in our spectral range, though in all cases it was too faint to be detected. Thus we are only able to give upper limits to the Eu abundances.
-
Barium. Barium is represented by at least five isotopes with significant contributions from the odd atomic mass (A) nuclei. Indeed the ratio between the even-A and the odd isotopes n(134Ba+136Ba+138Ba):n(135Ba+137Ba) is 82:18, or in other words the fraction of odd-A isotopes, fodd, is 0.18 in the solar system (Lodders et al. 2009). While for the odd-A isotopes the nucleon-electron spin interactions lead to hyper-fine splitting of the energy levels, the even isotopes are unaffected by HFS. The level splitting of Ba ii reaches its maximum at ground state, and the components of the resonance line 4934 Å are separated by 78 mÅ (Brix & Kopfermann 1952; Becker & Werth 1983; Blatt & Werth 1982; Silverans et al. 1980), and the Ba abundance derived from this line depends on the isotope mixture adopted in the calculations. Consequently, the barium abundances of ET0381 and scl_03_059 were determined from the Ba ii subordinate lines Ba ii 5853, 6141, and 6497 Å, which are hardly affected by HFS (Table 2), while the Ba ii 4934 Å line was used to determine the Ba even-to-odd isotope abundance ratios, by requiring that all lines return the same abundance. The Ba ii 4934 and 6141 Å lines were corrected for their blend with Fe i lines by synthesis.
It is commonly accepted that the elements heavier than Ba have a pure r-process origin in the metal-poor MW halo stars (Truran 1981). The r-process model of Kratz et al. (2007) predicts fodd = 0.438 in the classical waiting-point (WP) approximation. Another estimate of fodd is provided by the analysis of the contribution of the r-process to the solar system (SS) Ba abundance and subtraction of the s-process contribution from the solar total abundance, with a range of possible fractions, fodd = 0.46 (Travaglio et al. 1999), 0.522 (Sneden et al. 1996), 0.601 (Bisterzo et al. 2014), and 0.72 (McWilliam 1998).
We first considered fodd = 0.46 and 0.72 to derive the Ba ii abundance from the λ4934 Å line. In both cases and for both ET0381 and scl_03_059, we found significant discrepancies between the abundances derived from the subordinate lines and from the resonance line (Table 6). Further investigation shows that these differences are removed for fodd = 0.18, i.e. the solar Ba isotope mixture (Lodders et al. 2009) or even fodd = 0.11, which is predicted by Bisterzo et al. (2014) for pure s-process production.
Abundances.
We performed a series of tests to estimate how much of the differences between the subordinate and the Ba ii 4934 Å lines found for the r-process Ba isotope mixtures could simply arise from uncertainties in our analysis:
-
i)
We tested the exact same methodology on HE1219-0312, a well-known r-process enhanced star with[Eu/Fe] = + 1.4 (Hayek et al. 2009). Using the spectrum reduced by Norbert Christlieb, we find a mean abundance of the Ba ii 5853 Å, 6141 Å, and 6496 Å, lines to be
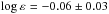 in LTE calculation, and −0.16 ± 0.11 in NLTE. The λ4934 Å line leads to an NLTE abundance of −0.09 for fodd = 0.46 and 0.21 for fodd = 0.18. This rules out a low fodd. Our analysis is also in agreement with the results of Hayek et al. (2009), who determined logϵ(Ba) =−0.14.
in LTE calculation, and −0.16 ± 0.11 in NLTE. The λ4934 Å line leads to an NLTE abundance of −0.09 for fodd = 0.46 and 0.21 for fodd = 0.18. This rules out a low fodd. Our analysis is also in agreement with the results of Hayek et al. (2009), who determined logϵ(Ba) =−0.14. -
ii)
Since the atmosphere of very metal-poor stars can be subject to deviation from LTE, we performed NLTE calculations, following the procedure of Mashonkina et al. (1999). It turns out that the departure from LTE is very small for the Ba ii 4934 Å line, with a NLTE abundance correction of ΔNLTE = log εNLTE−log εLTE = 0.00 for ET0381 and −0.01 dex for scl_03_059 (Table 6). As to the subordinate lines, the NLTE calculation leads to higher abundances by 0.05 dex to 0.1 dex, resulting in even larger discrepancies with the Ba ii 4934 Å line.
-
iii)
Another source of uncertainty arises from the atmospheric parameters. The consequence of a variation of each of Teff, log g, or vt has been estimated (Table 6). The “total” quantities correspond to the total impact of varying stellar parameters, computed as the quadratic sum of the three sources of uncertainties. For ET0381, these uncertainties produce very similar abundance shifts for the Ba ii 4934 Å and the subordinate lines, and, therefore cannot explain the difference between them. For scl_03_059, the abundance derived from the Ba ii 4934 Å line is slightly more affected than the subordinate lines, however, not large enough yet to explain the observed discrepancy.
-
We did not use any 3D hydrodynamical model atmospheres to derive the abundances of barium. This element is only detected in the Ba ii majority species, and the detected lines arise either from the ground or low-excitation levels. Dobrovolskas et al. (2013) predicted that the (3D−1D) abundance corrections for metal-poor giant stars are small for the Ba ii Eexc = 0 and 2 eV lines: (3D−1D) = −0.05 dex and 0.0 dex, respectively, in the 5020/2.5/−2 model and (3D−1D) = −0.10 dex and −0.02 dex in the 5020/2.5/−3 model. The Ba ii 5853, 6141, 6496 Å lines arise from the Eexc = 0.6−0.7 eV level. Interpolating between Eexc = 0 and 2 eV in Dobrovolskas et al. (2013), one sees that the difference between the Ba ii 4934 Å and the Ba ii subordinate lines would not be reduced since the (3D–1D) abundance correction is more negative for the Ba ii 4934 Å than for the other lines. It turns out that none of the above plausible sources of errors is sufficient to explain the difference between the subordinate and the Ba ii 4934 Å lines. Figure 4 displays the result of our NLTE synthesis assuming fodd = 0.18 for the Ba II 4934 Å line. All Ba lines, which have very different strengths, are well reproduced whether they are blended with Fe i lines or not. In conclusion, one can assert that, for ET0381 and scl_03_059, consistency between the different lines of Ba ii can only be achieved by applying a low fraction of the odd-A Ba isotopes, fodd between 0.18 and 0.11. At first glance this result would imply a dominant contribution of the s-process to barium. The implications and alternative scenarios are discussed further in Sect. 5.7.
 |
Fig. 4 Synthesis of the Ba lines for ET0381 (upper panel) and scl_03_059 (lower panel). A value of fodd = 0.18 is taken for the Ba ii 4934 Å. The observed spectra are shown in black. The red continuous, green dashed, and green dotted curves correspond to the theoretical spectra of the full blend, pure Ba ii lines, and Fe i blending lines, respectively. |
5. Discussion
5.1. Comparison samples: references, symbols, and colour codes in figures
In all figures, the grey points show the location of RGB stars in the Milky Way halo (Honda et al. 2004; Cayrel et al. 2004; Spite et al. 2005, 2006; Aoki et al. 2005, 2007; Cohen et al. 2013, 2006, 2004; Lai et al. 2008; Yong et al. 2013; Ishigaki et al. 2013).
The Sculptor stars are shown in orange. We distinguish the new sample presented in this paper by large circles with error bars. These error bars add in quadrature the random and systematic uncertainties listed in Tables 2 and 5. The sample of Tafelmeyer et al. (2010) is shown by upright triangles, while the Starkenburg et al. (2013) stars, which were not re−observed at high resolution, are shown by inverted triangles. The sample of Simon et al. (2015) including the Frebel et al. (2010a) star are indicated by a star. For part of the elements smaller orange circles, at slightly higher metallicities than the stars discussed here, are from Tolstoy et al. (2009) and Hill et al. (in prep.).
Figures 14 and 7 show the dataset of Tafelmeyer et al. (2010) with green triangles for Sextans and blue triangles for Fornax. The Ursa Minor population is shown by purple stars (Cohen & Huang 2010), while the two Carina stars from Venn et al. (2012) are seen in pink circles. We indicate in Fig. 7 the Draco stars with cyan circles (Cohen & Huang 2009; Shetrone et al. 2013; Kirby et al. 2015).
 |
Fig. 5 Observed spectrum of ET0381 in a short spectral region of the molecular CH band. Synthetic spectra with [C/Fe]=−2.0 to + 0.5 are shown as well. The numbers indicated on the left are the corresponding [C/Fe] values. |
The ultra−faint dwarf spheroidal galaxies are displayed with black symbols. Ursa Major II from Frebel et al. (2010b) is identified with upright triangles, Coma Berenices from Frebel et al. (2010b) with stars, Leo IV from Simon et al. (2010) with squares, Hercules from Koch et al. (2008b), Adén et al. (2011) with pointing down triangles, Segue I from Norris et al. (2010a), Frebel et al. (2014) with right-pointing triangles, Boötes from Norris et al. (2010b,a), Lai et al. (2011), Feltzing et al. (2009), Ishigaki et al. (2014) with diamonds.
5.2. Comparison of medium- and high-resolution analyses
The left panel of Fig. 6 compares the abundances obtained at medium resolution by Starkenburg et al. (2013) and those of our high-resolution analysis for the chemical elements in common.
Overall the agreement is very good, it is even excellent for scl002_06. The largest difference in [Fe/H] is found for scl031_11 with δ[Fe i/H] = 0.41, the present analysis having a lower metallicity. This is a 2.5σ shift considering the error quoted in Starkenburg et al. (2013) in particular due to the uncertainties on the atmospheric parameters (0.16 dex total). We have better constraints with 38 Fe i lines instead of 23, and were able to get a spectroscopic temperature that is 100 K lower than the photometric initial value. This could partly explain the differences between the two studies. The difference in iron abundance for scl074_02 is less straightforward to explain given that Teff and log g are identical within 5 K and 0.02, respectively. This led us to compare the equivalent widths of the lines of Fe i, which are common to both studies. The right panel of Fig. 6 reveals that there is a small but systematic shift towards higher EQWs in Starkenburg et al. (2013), for lines with EQW > 50 mÅ. These lines are located in the blue noisiest part of the spectra. In the present work, we find scl074_02 and scl002_06 at very similar metallicities, while Starkenburg et al. determine a 0.4 dex higher metallicity for scl074_02 than for scl002_06. The Xshooter spectrum of scl002_06 had a mean signal-to-noise ratio of 70 against 48 for scl074_02 in the range 4000 Å to 7000 Å where the Fe i lines are compared, leading to slightly overestimated EQWs – as far as we can tell from the lines we have in common – probably responsible for the higher [Fe/H] in Starkenburg et al. (2013).
This comparison confirms the ability of medium resolution to get good accurate abundances when it is conducted over a larger wavelength range. Potential biases can be removed by reaching high signal-to-noise ratios.
 |
Fig. 6 Comparison between Starkenburg et al. (2013) and the present analysis, obtained from medium-resolution (Xshooter) and high-resolution (UVES) spectra, respectively. For the three stars in common, the left panel compares the elemental abundances, whereas the right panel displays the equivalent widths of the Fe i lines that were used in both analyses. |
 |
Fig. 7 Relation between [C/Fe] and the luminosity of the very metal-poor RGB stars selected as Teff< 5300 Å and [Fe/H] < −2.5. The dotted line corresponds to the limits of Aoki et al. (2007) distinguishing between carbon-rich and normal population. The green colour identifies the EMPS in Sextans with a stellar symbol for the analysis of Honda et al. (2011), and with upright triangles for the Tafelmeyer et al. (2010) sample. The blue triangle identifies Fornax (Tafelmeyer et al. 2010). The cyan circles show the observations in Draco by Shetrone et al. (2013) and Kirby et al. (2015), while the point above the dotted line is the carbon-rich RGB found by Cohen & Huang (2009) in this galaxy. The observations of Kirby et al. (2015) in Ursa Minor are shown in purple. The references of the other comparisons samples are given in Sect. 5.1. The Milky Way halo stars are shown in grey. The Sculptor stars are seen in orange. The errors on their luminosities are calculated for a 100 K uncertainty in Teff . The ultra−faint dwarf spheroidal galaxies are indicated with black symbols. Ursa Major II is identified with upright triangles, Coma Berenices with stars, Leo IV with squares, Hercules with pointing down triangles, Segue I with pointing right triangles, and Boötes with diamonds. |
5.3. Carbon
Figure 7 shows how the carbon-to-iron ratio of the EMPS in Sculptor varies with stellar luminosity. The comparison sample is built from stars with Teff≤ 5300 K and [Fe/H] < −2.5.
It has been predicted that the onset position along the RGB of an extra mixing between the bottom of the stellar convective envelope and the outermost layers of the advancing hydrogen-shell is located at 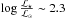 for a metal-poor 0.8 M⊙ star (Charbonnel 1994; Gratton et al. 2000; Spite et al. 2005; Eggleton et al. 2008). Our sample of EMPS in Sculptor falls above this limit and therefore is expected to have converted C into N by the CNO cycle. This is indeed the most likely origin of their low [C/Fe] ratios seen in Fig. 7.
for a metal-poor 0.8 M⊙ star (Charbonnel 1994; Gratton et al. 2000; Spite et al. 2005; Eggleton et al. 2008). Our sample of EMPS in Sculptor falls above this limit and therefore is expected to have converted C into N by the CNO cycle. This is indeed the most likely origin of their low [C/Fe] ratios seen in Fig. 7.
To date only one carbon-enhanced metal-poor star ([Fe/H] ≤ −2.) with no enhancement of the main r- or s -process elements (CEMP-no star) has been identified in Sculptor (Skúladóttir et al. 2015). The existence of this star would in principle suggest that one should find many more remnants of the initial enrichment in carbon at lower metallicity, but none has been found so far at [Fe/H] ≤−2.5. Skúladóttir et al. (2015) notice that the fraction of CEMP-no stars in Sculptor starts deviating from the expected number derived from the statistics in the Milky Way halo below [Fe/H] ≤−3. With a ~30% fraction of CEMP stars among the Milky Way halo EMPS (see also Yong et al. 2013; Lee et al. 2013; Placco et al. 2014), they argue that we should have observed three CEMP stars in Sculptor in this metallicity range. Among the classical dwarfs, only in Sextans and Draco have such stars been detected. One star in Sextans is a CEMP-s star with [C/Fe] = 1 (Honda et al. 2011). The other ones are CEMP-no stars; they do not have a particularly high value of [C/Fe] in absolute terms, but it is higher than expected at these stellar luminosities (Tafelmeyer et al. 2010; Cohen & Huang 2009). Meanwhile, as seen in Fig. 7, a larger population may have been identified in lower mass systems such as Ursa Major II, Segue I, and Boötes. However they have lower metallicities, with [Fe/H] between −3 and −2.5 and they have in the vast majority larger gravities than the RGBs in the classical dSphs studied so far with log g between 1.4 and 2 (Frebel et al. 2010b; Norris et al. 2010a; Lai et al. 2011).
When it comes to small numbers, the sample selection criteria may seriously enter into play. It is no secret that the detection of CEMPs in classical dwarfs is random, i.e. not particularly focused on C-abundances and the search for extremely metal-poor stars in those systems is notoriously difficult; only nine known [Fe/H] ≤−3 stars have been discovered in Sculptor, one of the best studied classical dSph. In comparison, dedicated works on the properties of EMPS and the fraction of carbon stars in the Milky Way halo have been going on for many years with targeted selections, allowing for example the creation of databases such as SAGA (Suda et al. 2008) with 100 [Fe/H] ≤−3 stars.
Restricting the comparison to the same stellar evolutionary range in Sculptor and in the Milky Way halo, namely [Fe/H] ≤ −3, log g≤ 1.6, and Teff≤ 4800 K, out of the compilation of Placco et al. (2014), there are three major contributing samples: Hollek et al. (2011) with 10 stars out of which 9 CEMP stars defined as falling above the phenomenological line of Aoki et al. (2007), separating normal and carbon-rich stars (7 carbon rich stars with the Placco et al. definition); Yong et al. (2013) with 10 stars in total and 3 CEMP stars, and Barklem et al. (2005) with 13 stars out of which 2 CEMP stars (none with the Placco et al. definition). This illustrates how sensitive the statistics are to the selection of the sample, varying from 90% to 15% of stars with high carbonicity ([C/Fe] ratios, Carollo et al. 2012) in individual samples to 46% when combining them all.
Another feature in calculating the statistics of carbonicity in different galaxies is related to the spatial distribution. Carollo et al. (2012) find that the fraction of CEMP stars is larger by a factor of ~1.5 between the inner and the outer halo for −3 ≤ [Fe/H] ≤ −2.5, rising from ~20% to 30%. Lee et al. (2013) further notice that by restricting stars to within a <5 kpc distance from the Galactic mid-plane, the fraction of CEMP stars does not increase with decreasing metallicity. What part of the Milky Way halo should the samples in dSphs, which are spatially randomly distributed, be compared with?
In conclusion, the comparison of the CEMP star fraction in dSphs and the Milky Way is promising to unveil both the origin of carbon and the conditions of formation of the different systems. However, it seems to require further investigation at least along the RGBs in classical dwarfs, reaching larger gravities.
5.4. The α elements
Figures 8 and 9 display [Mg/Fe], [Si/Fe], [Ca/Fe], and [Ti/Fe] as a function of [Fe/H]. For these elements as for the others, we present the results of our analysis together with earlier works on Sculptor Tafelmeyer et al. (2010), Frebel et al. (2010a), Starkenburg et al. (2013).
5.4.1. Global features
The bulk (80%) of the metal-poor and extremely metal-poor stars observed so far in Sculptor follow the main trend of the Milky Way halo stars for the four α-elements presented here, i.e. they mostly have supersolar abundance ratios. The scatter of this plateau is also very similar in the two galaxies. There are three outliers with subsolar ratios, ET0381, scl051_05, and scl_11_1_4296. The star ET0381 at [Fe/H] ~ −2.5 is the only one with consistent low ratios for the four elements and which can robustly be attributed to an ISM inhomogeneity, although it is likely also the case of scl051_05. Indeed Starkenburg et al. (2013) could not measure Si, but Ti, Mg, and Ca were securely derived from 2 to 5 lines. The star scl_11_1_4296 from Simon et al. (2015) exhibits low [α/Fe] in three of the four elements, but a normal, Milky Way-like [Ti ii/Fe]. Interestingly, the uncertainty on [Fe/H] for this star is similar to the underabundance in Mg, Si, and Ca. Moreover, its abundance of Ti ii is derived from 11 lines as opposed to a single line in Si and Ca, and two lines for Mg. This all calls for confirmation of these first determinations. Finally, scl07-50 (Tafelmeyer et al. 2010) has a subsolar [Ca/Fe] ratio, but here again the Ca abundance is derived from a single resonance line. A forthcoming paper dedicated to accurate NLTE corrections will provide a better view, with a higher value, on the intrinsic Ca abundance of this star (Mashonkina et al., in prep.).
 |
Fig. 8 Magnesium- and silicon-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey (Honda et al. 2004; Cayrel et al. 2004; Spite et al. 2005, 2006; Aoki et al. 2005, 2007; Cohen et al. 2013, 2006, 2004; Lai et al. 2008; Yong et al. 2013; Ishigaki et al. 2013). We distinguish the new Sculptor sample presented in this paper by large circles with error bars. These error bars add in quadrature the random and systematic uncertainties listed in Tables 2 and 5. The sample of Tafelmeyer et al. (2010) is shown with upright triangles, while the Starkenburg et al. (2013) stars, which were not re−observed at high resolution, are displayed with inverted triangles. The Frebel et al. (2010a) and Simon et al. (2015) stars are indicated by a star. |
 |
Fig. 9 Calcium- and titanium-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
In conclusion, so far robust evidence for the existence of pockets of chemical inhomogeneity in the early days of Sculptor comes from two stars out of 14, scl051_05 and ET0381; the rest of the metal-poor population appears as homogeneous as the Milky Way halo within the observational uncertainties. Indeed, a supersolar plateau in [α/Fe] is expected when stars form out of an ISM in which the ejecta of the massive stars, in numbers following a classical IMF, are sufficiently well mixed (Pagel 2009). This means that whatever the process that led to this homogeneity, it was the same in Sculptor and in the Milky Way halo, or at least, the processes at play were scalable to the different sizes/masses of the systems.
5.4.2. The origin of the outsiders
There are two ways to produce the low [α/Fe] ratios observed for ET0381 and scl051_05. One is to increase [Fe/H] at a given α-element abundance by the ejecta of SNeIa and the second is to lower the abundance of α-elements at a fixed iron abundance, by varying the ratio between faint and massive SNeII. In the following we investigate the two possibilities, concentrating on ET0381 for which we have the most detailed chemical information:
-
If ET0381 were polluted by the ejecta of SNeIa, the secondnucleosynthetic signature of such an event would be a largeproduction of nickel. We can assume that before being pollutedthe ISM from which ET0381 arose was of classical composition,i.e. on the [α/Fe] plateau formed by the SNeII products. Its initialmetallicity [Fe/H]i would then be −3.31 ± 0.2 (for [Mg/H] = −2.91 ± 0.2, i.e. [Mg/Fe] ~ 0.4), corresponding to [Ni/H]i = −3.31 ± 0.2. The W7 model of SNeIa nucleosynthesis, which is widely used in galactic chemical evolution models (Nomoto et al. 1984; Iwamoto et al. 1999) and also in the work of Travaglio et al. (2005) varying the metallicity, predicts 58Ni (a stable isotope of Ni) to be overproduced by a factor of 1 to ~3 relative to iron, compared to the solar abundances. If Ni were produced just as much as Fe, the corresponding final abundance [Ni/H] = −2.44 would already exceed the observations. Chromium is also largely produced by SNeIa. Following the same line of reasoning as for Ni, from an initial [Cr/H]i = −3.61 ± 0.2, corresponding to the classical Milky Way halo level of a [Fe/H] = −3.31 ± 0.2 star, with a SNeI producing at least twice as much Cr than Fe compared to the solar abundances, the final [Cr/H] should be −2.44 ± 0.2 instead of −2.75 ± 0.1. Additionally, the knee of the [α/Fe] versus [Fe/H] relation in Sculptor is found at [Fe/H] > −2 (Tolstoy et al. 2009), hence at higher metallicity than the two outliers shown here. This means that we are not witnessing a major onset of the SNeIa explosions. Therefore, ET0381 would need to form from an unusual type of SNeIa, since the rest of the chemical evolution of Sculptor looks very chemically homogeneous. The last piece of evidence comes from the existing observations of stars with metallicity larger than −2, i.e. past the metallicity at which the SNeIa are the major contributors to the chemical evolution of Sculptor (Tolstoy et al. 2009). Shetrone et al. (2003) measured the abundance of cobalt in four such stars, and they have [Co/Fe] close to or above solar, far above the present value for ET0381. In summary, although there are no models of metal-poor SNeI that can definitely infer the amount of iron peak elements they would release, for now there is a body of corroborating evidence that a pollution by their sole ejecta is unlikely to explain the chemical features of ET0381.
-
The more massive the SNeII, the larger their yield of α-elements. Therefore, ET0381 (and possibly scl051_05) could probably arise from a pocket of ISM that had not been polluted (or at least that was under-polluted) by the most massive of the SNeII. A quick calculation with the yields of Tsujimoto et al. (1995) shows that missing the ejecta of the stars more massive than 20 M⊙ leads to subsolar [α/Fe]. With such a truncated IMF, it takes only 30 Myr for a single stellar population born from a gas clump 50 times more massive to reach [Fe/H] = −2.5 and [Mg/Fe] = −0.5. Although it is beyond the scope of the present paper to run full and detailed simulations to understand how pockets of ISM can have discordant abundance ratios in an otherwise homogeneous galaxy, we ran a few tests with the chemo-dynamical tree-SPH code GEAR (Revaz & Jablonka 2012). We followed at very high spatial resolution (30 pc), the evolution of a 8 × 108 M⊙ total mass system, forming stellar particles of 125 M⊙ out of 500 M⊙ gas particles. For the purpose of our test, we switched off the explosions of the SNeIa and only considered the SNeII. We fixed the star formation parameter c⋆ to 0.01 and the feedback efficiency to ϵ = 0.5, allowing us to reproduce as closely as possible the properties of the Local Group dSphs (Revaz et al., in prep.). Very low [α/Fe] stars are indeed created. They form in a dense gas shell expanding around the centre of the galaxy, which is created by the explosion energy release from a strong star formation burst at the origin of the first stars. In this simulation, a 14 M⊙ SNeII polluted a gas particle with initial [Fe/H] = −4.2. This region receiving 0.6% of the ejected metals was then shifted to [Fe/H] = −2.64 and [Mg/Fe] = −0.44. The rarity of this event (5% of the stellar population) and the fact that it falls naturally in the rest of the evolution of the galaxy that we know lead us to favour this scenario for ET0381, i.e. a lack of ejecta of the most massive SNeII.
5.5. One odd-Z element: scandium
The NLTE corrections for scandium derived from Sc ii are small, a few hundredths of a dex (Zhang et al. 2008, 2014), hence negligible, while the corrections for Na and Al are much larger, of the order of a few tenths of a dex (Andrievsky et al. 2007, 2008), and will be published in Mashonkina, et al., (in prep.).
Scandium can be produced by a number of different channels in massive stars, but it is not synthesized in SNeIa (Woosley et al. 2002). Figure 11 shows how below [Fe/H] ~ −3, the Sculptor EMPS beautifully follows the MW halo solar trend. The only exception is ET0381, with [Sc/Fe] = −0.43, corroborating the hypothesis that this star is lacking products from SNeII ejecta.
5.6. Iron peak-elements
Figures 10−12 present the elements produced by explosive nucleosynthesis, and specifically the behaviour of the elemental abundance ratios relative to iron of nickel, cobalt, chromium, and manganese as a function of metallicity.
 |
Fig. 10 Cobalt- and zinc-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
 |
Fig. 11 Scandium- and nickel-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
 |
Fig. 12 Chromium- and manganese-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
In the Milky Way, the [Ni/Fe] abundance ratio is roughly constant in stars of very different metallicities. This is generally understood as the fact that Ni is produced abundantly by both complete and incomplete Si burning (Umeda & Nomoto 2002), and the present dataset is no exception to this rule.
The other elements are likely more informative, because they are produced in two distinct regions characterized by the peak temperature of the shock material. Above 5 × 109 K material undergoes complete Si burning and its products include Co and Zn, while at lower temperature incomplete Si burning takes place and after decay produces Cr and Mn (e.g. Umeda & Nomoto 2002, and references therein). The mass cut, which divides the ejecta and the compact remnant, is located close to the border of complete and incomplete Si-burning regions. The large [Zn/Fe] and [Co/Fe] values at low metallicity in the Milky Way halo stars are a challenge to nucleosynthesis models and the exact relations between the explosion energy, the mass of the stars and the fallback/mixing processes are still much discussed by the experts (Nakamura et al. 1999; Umeda & Nomoto 2005; Limongi & Chieffi 2012). Milky Way halo stars do not seem discriminant enough to distinguish between the different scenarii. Our new sample of EMPs may help shed light on these questions, in particular by constraining the role of the progenitor mass.
With its low [Co/Fe] and [Zn/Fe], ET0381 stands out clearly from the Galactic trends, while it follows perfectly the Milky Way halo stars in [Cr/Fe] and [Mn/Fe]. This is again consistent with the assumption that this star is missing the product of the high-mass tail of the SNeII, i.e. the major producers of Co and Zn, and confirms that the depth of the mass cut or the explosion energy does vary with the SNeII progenitor mass, the most massive ones having deeper mass cuts or more energetic explosions. It is not possible at this stage to distinguish between the depth of the mass cut and energy: the complete Si-burning region is enlarged in both cases; increasing the energy produces effects similar to making the mass cut deeper without changing the mass coordinate of the mass cut (Umeda & Nomoto 2005). Meanwhile the outer Si-incomplete burning regions are most insensitive to the cut or energy, explaining why there is no signature of the specificity of ET0381 in Mn and Cr. The fact that one can estimate which stellar mass range is missing in the composition of ET0381 from the α-elements makes this star a unique calibrator for the models of nucleosynthesis.
Two other stars, scl002_06 and scl074_02, lie slightly below the Galactic halo star trends in Co. However, their case is different from that of ET0381; they are not simultaneously depleted in Zn. As will be discussed in Mashonkina, et al., (in prep.) the magnitude of the NLTE correction for Co in these two stars is ~0.2 dex, reducing significantly the gap between them and the Milky Way halo, without fully withdrawing their difference (1σ). These stars would have a solar [Co/Fe] at [Fe/H] = −3.5, while this level is reached at [Fe/H] = −3 in the Milky Way halo. We could be witnessing a consequence of the difference in star formation history between the two galaxies. In a similar way to the knee in [α/Fe], which appears at lower metallicity in galaxies forming stars less efficiently, the decline in [Co/Fe] is seen at lower metallicity in Sculptor than in the Milky Way. This hypothesis needs further support from additional observations in the [Fe/H] = −3.5 to −2.5 range.
5.7. Neutron capture elements
5.7.1. General trends
Figure 13 characterizes the two neutron capture elements that we could measure in our stars, barium and strontium, as a function of the iron abundance, while Fig.14 indicates the positions of the two dominating productions of Ba and Sr at different stages of the galaxy chemical evolution, the weak and main r-process, following the observations and definitions of François et al. (2007). All Sculptor stars at [Fe/H] > −3.5 with Sr and Ba measurements fall in the weak r-process regime and so would the rest of stars with upper limits only in Ba. Below [Fe/H] ~ −3.5, the stars in Sculptor follow the Milky Way halo trend in [Ba/Fe] and [Sr/Fe], with [Sr/Ba] ratios which can be low even at [Ba/H ~ −4, again similar to the value measured in our Galaxy.
 |
Fig. 13 Barium- and strontium-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The open circles correspond to HE 1219-0312, HD 140283, HD 122563, HD 88609, and HE 2327-5642, five Milky Way halo stars for which the odd-A fraction could be estimated. The ultra−faint dwarf spheroidal galaxies are displayed with black symbols. Ursa Major II is identified with triangles, Coma Berenices with stars, Leo IV with squares, Hercules with pointing down triangles, Segue I with pointing right triangles, and Boötes with diamonds. The full references are given in Sect. 5.1. |
 |
Fig. 14 Barium-to-strontium ratio as a function of [Ba/H] in Sculptor seen in orange, compared to the Milky Way halo stars presented in grey. The open circles correspond to HE 1219-0312, HD 140283, HD 122563, HD 88609, and HE 2327-5642, five Milky Way halo stars for which the odd-A fraction could be estimated. Sextans is shown with green triangles, Fornax with a blue triangle. The Ursa Minor population is shown with purple stars while the two Carina stars are seen in pink circles. The full references are given in Sect. 5.1. |
Figure 13 suggests that the first channel for the production of Ba and Sr is in place early (−4 ≤ [Fe/H] ≤ −3.5) and in all galaxies whatever their stellar masses. Core collapse supernovae would therefore make a natural channel of production, as we know from the other class of chemical elements that they do explode (Woosley et al. 1994; Qian & Wasserburg 2007). However, this channel would only be applicable to the abundance floor in heavy (Ba) and light (Sr) elements. It is interesting to note that ET0381, which is most likely missing some of highest mass SNeII ejecta, is not particularly low in [Sr/H] and [Ba/H]. Its level of enrichment is comparable to the other Sculptor stars in the weak-process regime. This is a clear sign that medium-mass SNeII contribute to the production of neutron capture elements and particularly to nucleosynthesis of the light elements. Along this line Draco119, a [Fe/H] = −2.9 star in Draco which is shown by Fulbright et al. (2004) to be very depleted both in Ba and Sr, is also suspected of having missed the ejecta of the low-mass tail of the SNeII.
As mentioned above, excluding ET0381 and scl051_05 given their global peculiar chemical patterns, both the effective measurements and the upper limits in Sculptor indicate that [Ba/Fe] and [Sr/Fe] increase from [Fe/H] = −3.5 with increasing [Fe/H], just as the Galactic halo does. This is in sharp contrast with the behaviour of the neutron-capture elements in the UFDs. With the exception of three stars in Hercules (François et al. 2012), the abundance of the neutron-capture elements does not rise in the UFDs. Instead it scatters around a mean floor level of ~−1.3 in [Sr/Fe] and −0.9 in [Ba/Fe]. The mass of Hercules is highly uncertain; given that it is considerably elongated (Coleman et al. 2007) hence potentially stripped, it was likely more massive in the past than is measured today.
5.7.2. The role of galaxy mass
Mass is the major structural difference between Sculptor (or classical dSphs) and the UFDs: while Sculptor has a V-magnitude MV ~ −11.2, and a velocity dispersion σ ~ 9−10 km s-1 (Battaglia et al. 2008a; Walker et al. 2009), the UFDs have much smaller masses with σ between ~3 and 6 km s-1 and have a sparse stellar population, MV< −4 mag (Simon & Geha 2007; Geha et al. 2009). The probability of producing Sr and Ba seems to correlate with the number of massive stars formed in the systems. Tafelmeyer et al. (2010) also reported normal [Sr/Fe] and [Ba/Fe] ratios in Sextans, supporting this idea. In Fig. 14 galaxies more massive than Carina (i.e. known to have an efficient early period of star formation), follow the trend defined by the MW halo stars. This suggests that the main nucleosynthesis source of both the light and the heavy r-process elements is linked to the galaxy stellar mass, in the sense that there is elemental enrichment only above a given mass threshold. Independently, Tsujimoto & Shigeyama (2014a,b) recently promoted the neutron star mergers as low-probability events satisfying the above constrains. This is a very promising hypothesis also because it seems that the SNeII do not synthesize the heavy r-process elements (Wanajo 2013), while the neutron star mergers are successful in producing both the heavy and light r-process elements (Wanajo et al. 2014; Just et al. 2015).
5.7.3. Coupling different channels of production?
Our dataset provides an additional piece of information, which should help the identification of the nucleoynthesis site of Ba and Sr. We indicate in Figs. 13 and 14 the position of five [Fe/H] < −2.5 Milky Way halo stars for which the Ba odd-A isotope fraction has been derived so far. They all have [Eu/Ba] between 0.48 and 0.79, classically interpreted as the signature of an r-process. Three stars have measured low or moderate fodd: HD 88609 (fodd = −0.02 ± 0.09, Gallagher et al. 2012), HD 122563 (fodd = 0.22 ± 0.15, Mashonkina et al. 2008), and HD 140283 (Collet et al. 2009; Gallagher et al. 2012, with fodd = 0.15 ± 0.12 and fodd = 0.02 ± 0.06, respectively). The exact value of fodd of HD 140283 continues to foster discussion in the literature. Noticeably, the various determinations are all based on the shape of the Ba ii 4554 Å line, but the results oscillate between a minimum value of fodd at 0.02 and a maximum at 0.38 (Magain 1995; Lambert & Allende Prieto 2002; Gallagher et al. 2015), still below the pure r-process threshold. Two other stars, HE2327-5642 (fodd = 0.5, Mashonkina et al. 2010) and now HE1219-0312 from this study (fodd ≥ 0.46), have high fodd signature of a pure r-process. They also have the largest Ba abundances. The other three stars have low [Ba/Fe], corresponding to the [Ba/Fe] floor level as defined by the [Fe/H] ∈ [−4, −3] stars. In Fig. 14, HD 122563, HD 140283, and HD 88609 fall in the so-called weak r-process regime and so do ET0381 and scl_03_059, while HE 1219-0312 and HE 2327-5642 are clearly in the main regime. Hence, the value of fodd could be linked to the nucleosynthetic origin of the neutron capture elements, which may be different in the two regimes.
Adopting the nucleosynthesis prescriptions of Frischknecht et al. (2012), Cescutti et al. (2013) proposed that stars with high [Sr/Ba] abundances are polluted by the s-process in massive (10−40 M⊙) rapidly rotating stars, and predicted that they should have low values of the odd/even isotopes of Ba. This matches our results well. There is one caveat, however (also seen in Cescutti & Chiappini 2014): the stars with low fodd also have very low model [Ba/Fe] and [Sr/Fe], while in the Sculptor and Milky Way halos stars, if [Ba/Fe] can be low, [Sr/Fe] is already close to solar. Leaving room for future improvement and refinement of the nucleosynthesis spinstar models, one can still seriously consider the hypothesis that part of the neutron capture elements are produced through the s-process channel in massive stars. This would even ease the understanding of the low [Ba/Fe] and [Sr/Fe] in UFDs. Indeed, these stars exhibit a normal [α/Fe] plateau, hence they do not miss the high-mass part of the IMF; moreover, most of them have high [Sr/Ba]. This early channel of production of the neutron capture elements could be coupled with rarer events such as neutron star mergers as suggested above, which would only be able to enrich massive galaxies. Models of pure r-process should probably also be investigated in order to see whether they can produce low fodd. To our knowledge this has not yet been done, or published.
5.8. To be or not to be pair-instable
The low [α/Fe] ratio and large contrasts between the abundances of odd and even element pairs of the Milky Way halo star, SDSS J001820.5-093939.2, a cool main-sequence star, led Aoki et al. (2014) to consider the hypothesis that this star was holding the pattern records of a pair-instability supernova (PISN). Figure 15 compares the abundances of SDSS J001820.5-093939.2 and ET0381 in logϵ units. The similarity in all measured elements between the two stars is striking and raises the possibility of a common origin. There are a number of low [α/Fe] stars known (Ivans et al. 2003; Venn et al. 2012), but none shares so many identical features.
 |
Fig. 15 Comparison of the elemental abundances of ET0381 in the Sculptor dSph and SDSS J001820.5-093939.2 in the Milky Way halo. The upper limits are identified by triangles. |
Aoki et al. (2014) rightly pointed out that very low carbon abundances are found in highly evolved red giants and are often interpreted as the result of internal extra-mixing. According to Placco et al. (2014), the original carbon abundance of ET0381 should be about 0.7 dex higher than measured. The rest of the chemical elements on which we can base the comparison with SDSS J001820.5-093939.2 are not prone to modifications due to mixing.
There is a major obstacle to ET0381 tracing the ejecta of a PISN. A simple calculation shows that the explosion of a ~ 200 × 1051 erg event would exceed the binding energy of the gas in a virialized ~ 5 × 108 M⊙ dwarf system, such as Sculptor, assuming a Plummer sphere profile, in agreement with the more sophisticated simulations of Wada & Venkatesan (2003). Of course, the exact feedback energy that a system can sustain depends on the galaxy mass and profile: the more concentrated the profile, the stronger the resistance of the galaxy. However, even before considering the extreme feedback limit when the gas is ejected to infinity, one faces the fact that the huge amount of feedback energy heats the gas to a temperature above 106 K, and makes it expand, strongly decreasing its density. The gas cooling time becomes very long, moving from the Myr to Gyr scale. Therefore, the time necessary for the galaxy to be able to form stars again is clearly not negligible, whereas there is no sign in the Sculptor star formation history of any quiescent period. Along a similar line of argument, Revaz et al. (2009) demonstrated that the chemical homogeneity of the Sculptor and Fornax dSphs strongly constrains the supernova effective feedback energy, setting it up to a low value.
In conclusion, if the peculiar chemical abundance pattern of SDSS J001820.5-093939.2 has the same origin as that of ET0381, it could be due to a depletion in massive SNeII ejecta rather than to the signature of a PISN. This could also alleviate the much larger Na, Al, V, and Mn in SDSS J001820.5-093939.2 than in the PISN synthesis models Aoki et al. (2014).
6. Summary
We presented the high-resolution spectroscopic analysis of five very metal-poor stars in the Milky Way dSph satellite, Sculptor. This doubles the number of stars in this metallicity range with comparable observations. The abundances of 16 elements could be derived: Fe i, Fe ii, C, Na i, Mg i, Al i, Si i, Ca i, Sc ii, Ti i, Ti ii, Cr i, Mn i, Co i, Ni i, Sr i, and Ba ii. Upper limits could be estimated for three more elements: Zn i, Y ii, and Eu ii.
In combination with previous works the low-metallicity tail of the early generation of stars in Sculptor could be better characterized, with consequences for our understanding of galaxy evolution and stellar nucleosynthesis. Our main results can be summarized as follows:
-
The bulk (80%) of the metal-poor and extremely metal-poor stars observed so far in Sculptor unambiguously follow the main trend of the Milky Way halo stars for the α-elements presented here. Both populations are also similar in iron-peak and neutron capture elements. This is expected when stars form out of an ISM in which the ejecta of the massive stars, in numbers following a classical IMF, are sufficiently well mixed. This implies that the early conditions of star formation were the same in Sculptor and in the Milky Way halo, or at least, that the processes at play were scalable to the different sizes/masses of the systems.
-
Despite overall chemical homogeneity, our dataset reveals one new star, ET0381, at [Fe/H] =−2.5 which is remarkably poor in α- and iron-peak elements for its metallicity. From nucleosynthesis arguments and with the help of a few simple chemo-dynamical simulation, we conjecture that ET0381 arose from a pocket of ISM missing the ejecta of the most massive Type II supernovae.
-
The analysis of the iron-peak element abundances of ET0381 supports the theoretical predictions that the depth of the mass cut and/or the explosion energy vary with the SNeII progenitor mass, and that Co and Zn are largely produced by the high-mass tail of the massive stars. The fact that one can estimate from the α-elements which SNII mass range is missing in the composition of ET0381 makes this star a unique calibrator for the models of nucleosynthesis.
-
Our analysis brings important clues on the nucleosynthetic site of the neutron capture elements:
i): We find that the gradual enrichment in barium andstrontium of the Sculptor metal-poor stars closely followsthe evolution of the MW halo, contrary to the stellarpopulation in ultra-faint dwarfs. This provides furtherevidence that the mass of a galaxy is an important driver of itschemical evolution and more specifically of its ability toproduce neutron capture elements.
ii): The Sculptor −3.5 < [Fe/H] < −2.5 stars for which both Sr and Ba have been measured so far, fall in the so-called weak r-process regime, like stars in the other massive classical dwarfs.
iii): The comparison of the abundances derived from the Ba ii subordinate and 4934 Å lines reveals that their agreement can only be achieved for a solar Ba isotope mixture, meaning a low odd-to-even isotope abundance ratios. Further comparison with a set of Milky Way halo stars suggests that fodd is linked to the origin of the neutron capture elements. Low fodd are predicted by the models of spinstar producing Ba and Sr through the s-process, but some of their predictions are not corroborated by our observations. We call for refined models and investigation on whether pure r-process could generates low fodd as well.
iv): We find evidence that the medium-mass SNeII play a role in the production of the light neutron capture elements, as represented by Sr.
v): We postulate a double (at least) origin of the neutron capture elements. One is most probably linked to the massive stars that generate the abundance floor; the other could be related to rare events correlating with the stellar mass of the galaxies, such as the neutron star mergers.
A comparison between ET0381 and the Milky Way halo star SDSS J001820.5-093939.2 reveals striking similarities and suggests a common origin. It is highly improbable that ET0381 could hold the pattern records of a pair-instability supernova, as was proposed for SDSS J001820.5-093939.2, because the Sculptor dSph would be disrupted by the enormous energy release at the time of the SNeII explosions. Even without disruption, a long period of quiescence in its star formation, imposed by the long gas cooling time, should be observed, but it is not. We suggest that SDSS J001820.5-093939.2, like ET0381, is missing the ejecta of the most massive SNeII and that the signature of a PISN has yet to be found.
Acknowledgments
Pascale Jablonka and Pierre North gratefully acknowledge financial support from the Swiss National Science Foundation. Lyudmila Mashonkina is supported by the Russian Foundation for Basic Research (grant 14-02-91153). Else Starkenburg gratefully acknowledges funding through the CIFAR Global Scholar network. This work also benefited from the International Space Science Institute (ISSI) in Bern, thanks to the funding of the team “The first stars in dwarf galaxies”. We thank the VISTA commissioning team for providing J, Ks photometry which was observed during the commissioning process. We thank Prof. Bertrand Plez for his help in the use of turbospectrum We enjoyed lively and fruitful discussions with M. Limongi, G. Meynet, and S. Wanajo.
References
- Adén, D., Eriksson, K., Feltzing, S., et al. 2011, A&A, 525, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A, 481, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Honda, S., Beers, T. C., et al. 2005, ApJ, 632, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Arimoto, N., Sadakane, K., et al. 2009, A&A, 502, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Tominaga, N., Beers, T. C., Honda, S., & Lee, Y. S. 2014, Science, 345, 912 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, G., Helmi, A., Tolstoy, E., et al. 2008a, ApJ, 681, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008b, MNRAS, 383, 183 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Becker, W., & Werth, G. 1983, Z. Phys. A Hadrons and Nuclei, 311, 41 [Google Scholar]
- Bisterzo, S., Travaglio, C., Gallino, R., Wiescher, M., & Käppeler, F. 2014, ApJ, 787, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Blatt, R., & Werth, G. 1982, Phys. Rev. A, 25, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2011, MNRAS, 415, L40 [CrossRef] [Google Scholar]
- Brix, P., & Kopfermann, H. 1952, Landolt-Börnstein, I/5 (Berlin: Springer) [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., & Chiappini, C. 2014, A&A, 565, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Chiappini, C., Hirschi, R., Meynet, G., & Frischknecht, U. 2013, A&A, 553, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C. 1994, A&A, 282, 811 [NASA ADS] [Google Scholar]
- Cohen, J. G., & Huang, W. 2009, ApJ, 701, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., & Huang, W. 2010, ApJ, 719, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Christlieb, N., McWilliam, A., et al. 2004, ApJ, 612, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., McWilliam, A., Shectman, S., et al. 2006, AJ, 132, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Christlieb, N., Thompson, I., et al. 2013, ApJ, 778, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, M. G., de Jong, J. T. A., Martin, N. F., et al. 2007, ApJ, 668, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Collet, R., Asplund, M., & Nissen, P. E. 2009, PASA, 26, 330 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, T. J. L., Tolstoy, E., Saha, A., et al. 2011, A&A, 528, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Boer, T. J. L., Tolstoy, E., Hill, V., et al. 2012, A&A, 539, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobrovolskas, V., Kučinskas, A., Steffen, M., et al. 2013, A&A, 559, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P., Dearborn, D. S. P., & Lattanzio, J. C. 2008, ApJ, 677, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Feltzing, S., Eriksson, K., Kleyna, J., & Wilkinson, M. I. 2009, A&A, 508, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- François, P., Depagne, E., Hill, V., et al. 2007, A&A, 476, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- François, P., Monaco, L., Villanova, S., et al. 2012, in AIP Conf. Ser. 1484, eds. S. Kubono, T. Hayakawa, T. Kajino, H. Miyatake, T. Motobayashi, & K. Nomoto, 460 [Google Scholar]
- Frebel, A., Kirby, E. N., & Simon, J. D. 2010a, Nature, 464, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Simon, J. D., Geha, M., & Willman, B. 2010b, ApJ, 708, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Simon, J. D., & Kirby, E. N. 2014, ApJ, 786, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulbright, J. P., Rich, R. M., & Castro, S. 2004, ApJ, 612, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, A. J., Ryan, S. G., Hosford, A., et al. 2012, A&A, 538, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, A. J., Ludwig, H.-G., Ryan, S. G., & Aoki, W. 2015, A&A, 579, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geha, M., Willman, B., Simon, J. D., et al. 2009, ApJ, 692, 1464 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Weisz, D., Pontzen, A., et al. 2015, MNRAS, 448, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayek, W., Wiesendahl, U., Christlieb, N., et al. 2009, A&A, 504, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hendricks, B., Koch, A., Walker, M., et al. 2014, A&A, 572, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollek, J. K., Frebel, A., Roederer, I. U., et al. 2011, ApJ, 742, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Honda, S., Aoki, W., Kajino, T., et al. 2004, ApJ, 607, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Honda, S., Aoki, W., Arimoto, N., & Sadakane, K. 2011, PASJ, 63, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Ishigaki, M. N., Aoki, W., & Chiba, M. 2013, ApJ, 771, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Ishigaki, M. N., Aoki, W., Arimoto, N., & Okamoto, S. 2014, A&A, 562, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivans, I. I., Sneden, C., James, C. R., et al. 2003, ApJ, 592, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Just, O., Bauswein, A., Pulpillo, R. A., Goriely, S., & Janka, H.-T. 2015, MNRAS, 448, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., & Cohen, J. G. 2012, AJ, 144, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Cohen, J. G., Smith, G. H., et al. 2011, ApJ, 727, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Guo, M., Zhang, A. J., et al. 2015, ApJ, 801, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Grebel, E. K., Gilmore, G. F., et al. 2008a, AJ, 135, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., McWilliam, A., Grebel, E. K., Zucker, D. B., & Belokurov, V. 2008b, ApJ, 688, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kratz, K.-L., Farouqi, K., Pfeiffer, B., et al. 2007, ApJ, 662, 39 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D. K., Lee, Y. S., Bolte, M., et al. 2011, ApJ, 738, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., & Allen de Prieto, C. 2002, MNRAS, 335, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Masseron, T., et al. 2013, AJ, 146, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Letarte, B., Hill, V., Tolstoy, E., et al. 2010, A&A, 523, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limongi, M., & Chieffi, A. 2012, ApJS, 199, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Plame, H., & Gail, H.-P. 2009, in Landolt-Börnstein – Group VI Astronomy and Astrophysics Numerical Data and Functional Relationships in Science and Technology Vol. 4B: Solar System. ed. J. E. Trümper, 4.4. (Berlin: Springer), 44 [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Magain, P. 1995, A&A, 297, 686 [NASA ADS] [Google Scholar]
- Mashonkina, L., Gehren, T., & Bikmaev, I. 1999, A&A, 343, 519 [NASA ADS] [Google Scholar]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Christlieb, N., Barklem, P. S., et al. 2010, A&A, 516, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Plez, B., Van Eck, S., et al. 2014, A&A, 571, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A. 2013, ArXiv e-prints [arXiv:1311.1403] [Google Scholar]
- Nakamura, T., Umeda, H., Nomoto, K., Thielemann, F.-K., & Burrows, A. 1999, ApJ, 517, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Wheeler, J. C. 1984, ApJ, 279, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Wyse, R. F. G., Gilmore, G., et al. 2010a, ApJ, 723, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Yong, D., Gilmore, G., & Wyse, R. F. G. 2010b, ApJ, 711, 350 [NASA ADS] [CrossRef] [Google Scholar]
- North, P., Cescutti, G., Jablonka, P., et al. 2012, A&A, 541, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagel, B. E. J. 2009, Nucleosynthesis and Chemical Evolution of Galaxies (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Pietrzyński, G., Gieren, W., Szewczyk, O., et al. 2008, AJ, 135, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 2012, Turbospectrum: Code for spectral synthesis, astrophysics Source Code Library [ascl:1205.004] [Google Scholar]
- Prochaska, J. X., & McWilliam, A. 2000, ApJ, 537, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z., & Wasserburg, G. J. 2007, Phys. Rep., 442, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Revaz, Y., & Jablonka, P. 2012, A&A, 538, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Revaz, Y., Jablonka, P., Sawala, T., et al. 2009, A&A, 501, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Baltic Astron., 6, 244 [Google Scholar]
- Sawala, T., Frenk, C. S., Crain, R. A., et al. 2013, MNRAS, 431, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M., Venn, K. A., Tolstoy, E., et al. 2003, AJ, 125, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Shetrone, M. D., Smith, G. H., Stanford, L. M., Siegel, M. H., & Bond, H. E. 2013, AJ, 145, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Silverans, R. E., Borghs, G., Dumont, G., & van den Cruyce, J. M. 1980, Z. Phys. A Hadrons and Nuclei, 295, 311 [Google Scholar]
- Simon, J. D., & Geha, M. 2007, ApJ, 670, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Frebel, A., McWilliam, A., Kirby, E. N., & Thompson, I. B. 2010, ApJ, 716, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Jacobson, H. R., Frebel, A., et al. 2015, ApJ, 802, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Skúladóttir, Á., Tolstoy, E., Salvadori, S., et al. 2015, A&A, 574, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C., McWilliam, A., Preston, G. W., et al. 1996, ApJ, 467, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Cayrel, R., Hill, V., et al. 2006, A&A, 455, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starkenburg, E., Hill, V., Tolstoy, E., et al. 2010, A&A, 513, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starkenburg, E., Hill, V., Tolstoy, E., et al. 2013, A&A, 549, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Stetson, P. B., & Pancino, E. 2010, DAOSPEC: An Automatic Code for Measuring Equivalent Widths in High-resolution Stellar Spectra, astrophysics Source Code Library [Google Scholar]
- Suda, T., Katsuta, Y., Yamada, S., et al. 2008, PASJ, 60, 1159 [NASA ADS] [Google Scholar]
- Tafelmeyer, M., Jablonka, P., Hill, V., et al. 2010, A&A, 524, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, R., Pontzen, A., Dubois, Y., & Read, J. I. 2013, MNRAS, 429, 3068 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Galli, D., Gallino, R., et al. 1999, ApJ, 521, 691 (T99) [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Hillebrandt, W., & Reinecke, M. 2005, A&A, 443, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Truran, J. W. 1981, A&A, 97, 391 [NASA ADS] [Google Scholar]
- Tsujimoto, T., & Shigeyama, T. 2014a, A&A, 565, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsujimoto, T., & Shigeyama, T. 2014b, ApJ, 795, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2002, ApJ, 565, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Swaelmen, M., Hill, V., Primas, F., & Cole, A. A. 2013, A&A, 560, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venn, K. A., Shetrone, M. D., Irwin, M. J., et al. 2012, ApJ, 751, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., & Venkatesan, A. 2003, ApJ, 591, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., Sen, B., & Woodroofe, M. 2009, AJ, 137, 3109 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S. 2013, ApJ, 770, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Wanajo, S., Sekiguchi, Y., Nishimura, N., et al. 2014, ApJ, 789, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Winteler, C., Käppeli, R., Perego, A., et al. 2012, ApJ, 750, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Demchenko, V. G., Halicek, M. T., et al. 2014, MNRAS, 442, 2560 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Wilson, J. R., Mathews, G. J., Hoffman, R. D., & Meyer, B. S. 1994, ApJ, 433, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Norris, J. E., Bessell, M. S., et al. 2013, ApJ, 762, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H. W., Gehren, T., & Zhao, G. 2008, A&A, 481, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, H. W., Gehren, T., & Zhao, G. 2014, in IAU Symp. 298, eds. S. Feltzing, G. Zhao, N. A. Walton, & P. Whitelock, 453 [Google Scholar]
All Tables
Magnitudes, CaT metallicities, and corresponding photometric effective temperatures and surface gravities of our stars.
Barium LTE and NLTE abundances, NLTE abundance corrections, and the effect of uncertainties in stellar parameters on abundances (in dex) derived from individual lines of Ba ii in ET0381 and scl_03_059.
All Figures
 |
Fig. 1 Spatial distribution of the EMPS analyzed in this paper. The grey circles show the Sculptor member stars from the CaT analysis from Battaglia et al. (2008a). The orange circles indicate our new sample of stars with chemical abundances derived from high-resolution spectroscopy. The star symbols identify the EMPS of Frebel et al. (2010a) and Simon et al. (2015), while the upright triangles points to the sample of Tafelmeyer et al. (2010) and inverted triangles the EMPS of Starkenburg et al. (2013), which have not been reanalyzed at high resolution. |
| In the text | |
 |
Fig. 2 V−I versus I colour–magnitude diagram of Sculptor on which we superimpose the positions of the EMPS discussed in this paper. The photometry is taken from de Boer et al. (2011). The orange circles indicate our new sample of stars with chemical abundances derived from high-resolution spectroscopy. The star symbols identify the EMPS of Frebel et al. (2010a) and Simon et al. (2015), while the upright triangles show the sample of Tafelmeyer et al. (2010) and inverted triangles the EMPS of Starkenburg et al. (2013), which have not been reanalyzed at high resolution. |
| In the text | |
 |
Fig. 3 Teff – log(τ) relation for the extrapolated model of scl002_06 (blue), compared with grid models for [Fe/H] = −3.0 (black) and −4.0 (red), and log g= 0.5,1.0,1.5, for Teff = 4300 K. All these models are interpolated in Teff between 4250 and 4500 K, but those with log g< 1.0 and [Fe/H] = −4.0 are interpolated between eight models (4250,4500;0.5,1.0;−4.0,−3.0), two of which are extrapolated (4250,4500;0.5;−4.0) from the MARCS grid. By chance, the model interpolated for scl002_06 (full blue curve) almost exactly coincides with the (4300;0.5;−4.0) model (full red curve), except in the range −0.5 < log(τ5000< + 0.4. |
| In the text | |
 |
Fig. 4 Synthesis of the Ba lines for ET0381 (upper panel) and scl_03_059 (lower panel). A value of fodd = 0.18 is taken for the Ba ii 4934 Å. The observed spectra are shown in black. The red continuous, green dashed, and green dotted curves correspond to the theoretical spectra of the full blend, pure Ba ii lines, and Fe i blending lines, respectively. |
| In the text | |
 |
Fig. 5 Observed spectrum of ET0381 in a short spectral region of the molecular CH band. Synthetic spectra with [C/Fe]=−2.0 to + 0.5 are shown as well. The numbers indicated on the left are the corresponding [C/Fe] values. |
| In the text | |
 |
Fig. 6 Comparison between Starkenburg et al. (2013) and the present analysis, obtained from medium-resolution (Xshooter) and high-resolution (UVES) spectra, respectively. For the three stars in common, the left panel compares the elemental abundances, whereas the right panel displays the equivalent widths of the Fe i lines that were used in both analyses. |
| In the text | |
 |
Fig. 7 Relation between [C/Fe] and the luminosity of the very metal-poor RGB stars selected as Teff< 5300 Å and [Fe/H] < −2.5. The dotted line corresponds to the limits of Aoki et al. (2007) distinguishing between carbon-rich and normal population. The green colour identifies the EMPS in Sextans with a stellar symbol for the analysis of Honda et al. (2011), and with upright triangles for the Tafelmeyer et al. (2010) sample. The blue triangle identifies Fornax (Tafelmeyer et al. 2010). The cyan circles show the observations in Draco by Shetrone et al. (2013) and Kirby et al. (2015), while the point above the dotted line is the carbon-rich RGB found by Cohen & Huang (2009) in this galaxy. The observations of Kirby et al. (2015) in Ursa Minor are shown in purple. The references of the other comparisons samples are given in Sect. 5.1. The Milky Way halo stars are shown in grey. The Sculptor stars are seen in orange. The errors on their luminosities are calculated for a 100 K uncertainty in Teff . The ultra−faint dwarf spheroidal galaxies are indicated with black symbols. Ursa Major II is identified with upright triangles, Coma Berenices with stars, Leo IV with squares, Hercules with pointing down triangles, Segue I with pointing right triangles, and Boötes with diamonds. |
| In the text | |
 |
Fig. 8 Magnesium- and silicon-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey (Honda et al. 2004; Cayrel et al. 2004; Spite et al. 2005, 2006; Aoki et al. 2005, 2007; Cohen et al. 2013, 2006, 2004; Lai et al. 2008; Yong et al. 2013; Ishigaki et al. 2013). We distinguish the new Sculptor sample presented in this paper by large circles with error bars. These error bars add in quadrature the random and systematic uncertainties listed in Tables 2 and 5. The sample of Tafelmeyer et al. (2010) is shown with upright triangles, while the Starkenburg et al. (2013) stars, which were not re−observed at high resolution, are displayed with inverted triangles. The Frebel et al. (2010a) and Simon et al. (2015) stars are indicated by a star. |
| In the text | |
 |
Fig. 9 Calcium- and titanium-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
| In the text | |
 |
Fig. 10 Cobalt- and zinc-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
| In the text | |
 |
Fig. 11 Scandium- and nickel-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
| In the text | |
 |
Fig. 12 Chromium- and manganese-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The new Sculptor sample presented in this paper are shown by large circles. |
| In the text | |
 |
Fig. 13 Barium- and strontium-to-iron ratios as a function of [Fe/H] in Sculptor seen in orange, compared to the Milky Way halo stars in grey. The open circles correspond to HE 1219-0312, HD 140283, HD 122563, HD 88609, and HE 2327-5642, five Milky Way halo stars for which the odd-A fraction could be estimated. The ultra−faint dwarf spheroidal galaxies are displayed with black symbols. Ursa Major II is identified with triangles, Coma Berenices with stars, Leo IV with squares, Hercules with pointing down triangles, Segue I with pointing right triangles, and Boötes with diamonds. The full references are given in Sect. 5.1. |
| In the text | |
 |
Fig. 14 Barium-to-strontium ratio as a function of [Ba/H] in Sculptor seen in orange, compared to the Milky Way halo stars presented in grey. The open circles correspond to HE 1219-0312, HD 140283, HD 122563, HD 88609, and HE 2327-5642, five Milky Way halo stars for which the odd-A fraction could be estimated. Sextans is shown with green triangles, Fornax with a blue triangle. The Ursa Minor population is shown with purple stars while the two Carina stars are seen in pink circles. The full references are given in Sect. 5.1. |
| In the text | |
 |
Fig. 15 Comparison of the elemental abundances of ET0381 in the Sculptor dSph and SDSS J001820.5-093939.2 in the Milky Way halo. The upper limits are identified by triangles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


