EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 582 (October 2015) A&A, 582 (2015) A25 Full HTML
Free Access
Issue
A&A
Volume 582, October 2015
Article Number A25
Number of page(s) 19
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201526610
Published online 30 September 2015

© ESO, 2015

1. Introduction

Stellar physics is undergoing a revolution thanks to the wealth of asteroseismic data that have been made available by space missions, such as CoRoT (Baglin 2006) and Kepler (Gilliland et al. 2010). With the seismic analyses of these stars providing the frequencies of the stellar eigenmodes, asteroseismology has become an essential tool for understanding stellar physics.

Solar-type stars have been observed over periods exceeding six months using CoRoT and Kepler, thus providing many lists of mode frequencies required for seismic analysis (See Appourchaux et al. 2012, and references therein). Additional invaluable information about the evolution of stars is provided by the study of the internal structure of red giants (Bedding et al. 2011; Beck et al. 2011, 2012; Mosser et al. 2012a,b) and of sub-giants (Deheuvels et al. 2012; Benomar et al. 2013). The large asteroseismic database of Kepler allowed us to estimate the properties of an ensemble of solar-type stars that is large enough to perform statistical studies (Chaplin et al. 2014).

The availability of several mode-frequency sets provided by Appourchaux et al. (2012) allowed Metcalfe et al. (2014) to infer the radius, mass, and the age of 42 stars: model-dependent stellar parameters that all require a proper calibration. Knowing the effective temperature, the measurements of the frequency of maximum mode power and of the large frequency separation provide a proxy of the stellar radius and masses using scaling relations (Chaplin et al. 2014). These scaling relations also require independent calibration for being applied to other stars.

The proper calibration of stellar radii can be performed by using stellar radii derived using interferometric measurements (Creevey et al. 2007; Bigot et al. 2011; Bazot et al. 2011; Huber et al. 2012; White et al. 2013). With these interferometric stellar radii, one can also derive a proxy of the stellar masses using scaling relations as in Huber et al. (2012), stellar masses that also need an independent calibration. The best way to measure stellar masses is to use binary systems for which the orbital motion can be observed either by spectroscopy or by imagery. Many eclipsing binaries having an oscillating red giant component have been discovered by Hekker et al. (2010) and Gaulme et al. (2013). These eclipsing binaries have a rather short orbital period that allows an efficient measurement of radial velocity, thereby providing an orbital solution of the system (Beck et al. 2014).

If the binary system can be imaged, we can then derive the mass of the binary system from the semi-major axis and the period of the system from Kepler’s third law (Kepler 1619). The seismic detection of such binaries would then provide an independent determination of the total mass of the system, as well as calibrating their common stellar age. Miglio et al. (2014) predicts that about a handful of solar-like stars are detectable as seismic binaries in the Kepler data set. There have been three pairs of binary stars that were observed by Kepler. The pair 16 Cyg A and 16 Cyg B is a pair for which solar-like p modes were observed (Metcalfe et al. 2012). Although these two stars are gravitationally bound, the orbital period is unfortunately estimated to be longer than 30 000 years (Hauser & Marcy 1999); in this case, the seismic determination of the system mass would constrain the orbit. KIC9139151 and KIC9139163 stars also provided seismic radii, masses, and ages (Metcalfe et al. 2014). This pair appears to also be gravitationally bound since they have the same parallax and proper motion (van Leeuwen 2007), but their relative motion observed between 1850 and 2007 does not allow one to derive a meaningful orbit. These binary systems are clearly resolved such that the time series of each component can be separately observed. When the two components are too close to be separated, the fluctuations of each star is merged into a single time series. Such seismic binaries have been discovered with Kepler data such as HD 176465 discovered by White in 2011 (priv. comm.). This binary system has been observed from 1975 until today (Heintz 1975; Scardia et al. 2008). Unfortunately given the separation angles measured, the orbital period is likely to be longer than 600 years which makes the determination of the orbit rather unlikely in the near term.

Fortunately, another seismic binary, HIP 93511, was discovered in the Kepler data at the beginning of 2012, which happened to be a binary system already observed with speckle interferometry providing an estimate of the orbital period of the system (Horch et al. 2012). This paper details the analysis of the seismic signals of the two stars of HIP 93511 together with a new determination of the orbital system. The first section details the fundamental parameters of the stars. The second section provides the seismic analysis leading to the inference of the oscillation mode parameters. The third section provides the orbital analysis which is detailed in several appendices. The fourth section provides the stellar modelling of the two stars, and then we conclude with a discussion of the stellar parameters of the system.

Table 1

Main stellar and seismic parameters of HIP 93511.

2. Fundamental parameters of the binary

2.1. From the literature

HIP 93511 (or HD 177412) is a Main Sequence F8 V star which the main stellar parameters are given in Table 1. The effective temperature and metallicity constraints used in the modelling were chosen according to the values obtained from colour calibrations by Casagrande et al. (2011). All values in the table are derived from photometry and spectroscopy but not from asteroseismology. The effective temperature is consistent with that of Pinsonneault et al. (2012) but higher than that of Bruntt et al. (2012) by 1-σ.

We derived the apparent, global, Johnson magnitude, VJ of the system from the Tycho VT and BT magnitudes, VT = 7.938 ± 0.009 and BT = 8.482 ± 0.011 mag, using the transformation from Mamajek et al. (2002) and taking interstellar extinction from Bruntt et al. (2012) into account as E(B − V) = 0.01 ± 0.02. It yields VJ = 7.880 ± 0.013 mag consistent with that of Table 1.

The absolute visual magnitude is related to the luminosity of a binary system which was discovered by the Yale-Southern Connecticut speckle program at the WIYN1 3.5-m Telescope (named YSC 13). This binary was then first observed in speckle interferometry by (Horch et al. 2008) and many times after that; Table A.5 provides the astrometric observation as well as the magnitude difference between the two components which is ΔmV = 0.88 ± 0.05. This difference corresponds to a visual brightness ratio EB/EA = 0.4446 ± 0.0205. We calculated the apparent visual magnitude of the A component VA,J from 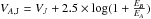VA,J=VJ+2.5×log(1+EBEA)\hbox{$V_{A, \mathrm{J}}=V_J+2.5\times \log(1+\frac{E_B}{E_A})$}. For the B component, VB,J reads VB,J = VA,J + ΔmV. We derived the bolometric correction of the A component BCV,A = − 0.04 ± 0.01 from its Teff, log g, and [ Fe / H ] using the tools developed by VandenBerg & Clem (2003) and updated in 2008. Then we derived the luminosity of the A component, LA/L⊙ = 4.15 ± 0.47 from VA, BCV,A, and the Hipparcos parallax. The bolometric correction of the B component was obtained iteratively starting from the A-component parameters log g and Teff and then adjusting to log g and Teff of the best model of the B star. The corresponding luminosity is LB/L⊙ = 1.85 ± 0.222.

thumbnail Fig. 1

Power spectrum of the intensity fluctuations as a function of frequency smoothed with a 1-μHz boxcar, showing the mode power peak at 1200 μHz for Star A and at 2200 μHz for Star B (left), and a zoom in on that secondary spectrum (right).

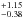Casagrande et al. (2011) provided an age of 3.19+0.64-1.10\hbox{$^{+0.64}_{-1.10}$} Gyr and a primary mass of 1.35+0.13-0.07M⊙\hbox{$^{+0.13}_{-0.07}~M_{\sun}$} using the BaSTI3 stellar models. They also gave an age of 2.93+1.15-0.38\hbox{$^{+1.15}_{-0.38}$} Gyr and a primary mass of 1.41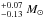+0.07-0.13M⊙\hbox{$^{+0.07}_{-0.13}~M_{\sun}$} using the PADOVA4 stellar models. These values should be taken with caution since the analysis did not take the binarity of HIP 93511 into account.

2.2. From observations

We retrieved from the Canada-France-Hawaii Telescope (CFHT) archive5 the spectrum of HIP 93511, obtained with the ESPaDOnS spectrograph on 2010, May 28 in spectroscopic mode. The spectrum, reduced with the Libre-ESpRIT package6 (Donati et al. 1997), covers the 3700–10 400 Å spectral range with a resolving power of about 80 000.

We looked for the presence of the secondary star in the ESPaDOnS spectrum by comparing the least-squared deconvolution (LSD) profile (Fig. 2, bottom panel Donati et al. 1997; Kochukhov et al. 2010) with that of a Gaussian concluding that the LSD profile is symmetric with no visible presence of the secondary star, therefore HIP 93511 is a single-line spectroscopic binary (SB1). The line bisector as well did not show the presence of the secondary star.

From the stellar parameters of the two stars (in particular temperature, gravity, and radius) recovered by photometric means, we were able to conclude that the lines of the secondary star should be present in the spectrum and therefore they blend completely with the spectral lines of the primary star. To estimate the metallicity of the two stars, we computed synthetic spectra with the atmospheric parameters of the two stars, combined them according to their luminosity ratio and compared to the observed spectrum. We calculated synthetic spectra with SYNTH3 (Kochukhov 2007) on the basis of line lists extracted from the Vienna Atomic Line Database (VALD) archive (Piskunov et al. 1995; Ryabchikova et al. 1999; Kupka et al. 1999) and of the model atmospheres calculated with the LLmodels stellar model atmosphere code (Shulyak et al. 2004). For all calculations we assumed a microturbulence velocity of 0.85 km s-1 (Valenti & Fischer 2005).

As the spectral lines of the two stars blend completely, we had to assume that the two stars share the same chemical composition, which is likely to some extent, given the common origin. The projected rotational velocity (υsini) of the two stars cannot be directly measured from the spectral lines, but the Gaussian shape of the LSD profile allows us to conclude that the two stars should have a similar (υsini) between 5 and 6 km s-1, depending whether a macroturbulence velocity component of the order of 4 km s-1 is taken into account or not.

Under these assumptions, we compared the profile of single unblended spectral lines in the observed spectrum with synthetic spectral lines, combined in such a way to simulate the spectrum of the binary system as a whole. We derived an iron abundance, relative to the Sun (Asplund et al. 2009), of − 0.20 ± 0.15 dex. Given the uncertainties on the stellar parameters and the large degeneracy in the line fitting, the uncertainty has to be taken more as an abundance range, rather than an actual error bar. The top panel of Fig. 2 shows the observed spectrum in comparison to the synthetic ones calculated for each of the two components and for the binary as a whole.

In the same way, we derived the abundances of a further 14 elements: C, Na, Mg, Si, Ca, Sc, Ti, Cr, Mn, Co, Ni, Cu, Y, Ba. Their abundances follow the same trend as iron, with the exception of an overabundance of C and Ba (+0.3 dex), although the carbon overabundance is likely to be due to non-LTE effects. These effects are supposed to be positive for Ba (Mashonkina & Zhao 2006), therefore the overabundance is likely to be real.

3. Seismic data analysis

3.1. Time series and power spectra

Kepler observations were obtained in two different operating modes: long cadence (LC) and short cadence (SC; Gilliland et al. 2010; Jenkins et al. 2010). This work is based on SC data. For the brightest stars (down to Kepler magnitude Kp ≈ 12), SC observations could be obtained for a limited number of stars (up to 512 at any given time) with sampling cadence of 58.84876 s (Nyquist frequency of ~8.5 mHz), which permits a more precise exoplanet transit timing and improves the performance of asteroseismology for main sequence and sub-giants stars. Kepler observations are divided into three-month-long quarters (Q). The binary system was observed during quarters Q7 to Q15. Therefore, the length of data gives a frequency resolution of about 14.3 nHz. The light curves were concatenated and high-pass filtered using a triangular smoothing with full-width-at-half-maximum of one day, to minimise the effects of long-period instrumental drifts. The amount of data missing from the time series is about 5%. The single-sided power spectrum was produced using the Lomb-Scargle periodogram (Scargle 1982), properly calibrated to comply with Parseval’s theorem (see Appourchaux 2014). Figure 1 shows the power spectrum of the binary with a zoom-in on the envelope of mode power at 2200 μHz. With a Point Spread Function of about 7 pixels (95% encircled energy), the two stars are not separated and the flux of the two stars is measured, hence providing a truly seismic binary.

thumbnail Fig. 2

Top panel: comparison between the observed spectrum (black solid line) and best fitting synthetic spectrum (red dashed line) calculated by combining the spectra of the two components (blue dash-dotted lines). The elements corresponding to the main spectral features are given on the top of the panel. For visualisation purposes, the legend has been put in the bottom panel. Bottom panel: LSD profile obtained from the observed ESPaDOnS spectrum.

3.2. Mode parameter extraction

3.2.1. Power spectrum model

The power spectrum was fitted in two steps: one for each group of mode power.

Step 1. The power spectrum was modelled over a frequency range covering 20 large frequency separations (Δν) between successive radial orders in the range 580–1620 μHz. The stellar background was modelled using a single component Harvey model (Harvey 1985) with two parameters and a white noise component. The stellar background was fitted prior to the extraction of the mode parameters and then held at a fixed value. For each radial order, the model parameters were mode frequencies (one for each degree, l = 0,1,2,3), a single mode height (with assumed ratios between degrees as 1.00, 1.50, 0.50, 0.03), and a single mode linewidth for all degrees; a total of 6 parameters per order. The relative heights h(l,m) (where m is the azimuthal order) of the rotationally split components of the modes depend on the stellar inclination angle, as given by Gizon & Solanki (2003). The rotational splitting and stellar inclination angle were chosen to be common for all of the modes; it adds 2 additional free parameters. The mode profile was assumed to be Lorentzian. In total, the number of free parameters for 20 orders was 6 × 20 + 2 = 122. The model was used to fit the power spectrum using maximum likelihood estimators (MLE). For the MLE, formal uncertainties in each parameter were derived from the inverse of the Hessian matrix (for more details on MLE, significance, and formal errors, see Appourchaux 2014).

Step 2. The corrected power spectrum from the previous fit was then used for fitting the mode power around 2200 μHz in the range 1700–3050 μHz. The power spectrum was modelled over a frequency range covering 13 large frequency separations. The background was modelled using a single white noise component, fitted prior to the extraction of the mode parameters and then held at a fixed value. For each radial order, the model parameters were the same as for Step 1 resulting in a total of 6 parameters per order, and with the rotational splitting and the stellar inclination angle common for all the modes.

In total, the number of free parameters for 13 orders was 6 × 13 + 2 = 80. The model was used to fit the power spectrum using maximum likelihood estimators (MLE).

thumbnail Fig. 3

Large frequency separation as a function of frequency for both stars (left Star A, right Star B): (plus) l = 0 modes, (black star) l = 1 modes, (green star) l = 2 modes.

thumbnail Fig. 4

Left: mode amplitude as a function of the order of the maximum mode power for Star A (black open diamond) and Star B (green open diamond). Right: mode linewidth as a function of the order of the maximum mode power for Star A (black open diamond) and Star B (green open diamond).

3.2.2. Guess parameter, fitting procedures, and quality assurance

The procedure for the initial guess of the parameters is described in Appourchaux et al. (2012), in which the steps of the fitting procedure are also described. These steps are repeated here for completeness:

  • 1.

    We fit the power spectrum as the sum of a stellar backgroundmade up of a combination of a Lorentzian profile and white noise,as well as a Gaussian oscillation mode envelope with threeparameters (the frequency of the maximum mode power, themaximum power, and the width of the mode power).

  • 2.

    We fit the power spectrum with n orders using the mode profile model described above, with no rotational splitting and the stellar background fixed as determined in step 1.

  • 3.

    We repeat step 2 but leave the rotational splitting and the stellar inclination angle as free parameters, and then apply a likelihood ratio test to assess the significance of the fitted splitting and inclination angle.

The steps above were used for the main mode power at 1200 μHz, and repeated for the mode power at 2200 μHz but with no Lorentzian profile for the stellar background. The procedure for the quality assurance of the frequencies obtained for both stars is described in Appourchaux et al. (2012) with a slight modification. In Appourchaux et al. (2012) when an order is not accepted by the statistical test, then each degree within an order is tested for rejection resulting in the acceptance of the full order when at least one degree is accepted, which leads to the inclusion of spurious modes at very low signal-to-noise ratio. We modified the procedure by testing all degrees for any order, resulting in a systematic search for spurious modes. The new procedure excluded several l = 2 modes at either end of the mode envelope spectrum.

3.2.3. Results

The tables of frequencies are given in Appendix A, while the tables of mode height, linewidth, and amplitude are given in Appendix B. Note that the frequencies need to be corrected taking the radial velocity of the binary system into account, that is needed to convert the observed frequencies at the heliocentric location to those of the source. The correction is −10-4ν as derived by Davies et al. (2014) which is about 1-σ for the best modes. Figure 3 shows the large and small frequency separations obtained for both stars. For Star A, one can clearly see the seismic signature of the second Helium ionisation zone being an oscillatory variation of the large separation with a periodicity of νHeII = 300μHz or τHeII = 1600 s, similar to what has already been detected in other solar-like stars (Mazumdar et al. 2014). Figure 4 gives the comparison of the mode amplitude and linewidth for both stars.

thumbnail Fig. 5

Correlation maps of the posterior probability following the Bayesian analysis of the orbit of HIP 93511: (top, left) The argument of the periastron (ω) vs. the longitude of the ascending nodes (Ω), (top, right) the semi-major axis a vs. the eccentricity e, (bottom, left) the orbital period T0 vs. the semi-major axis a, (bottom, right) the orbital period T0 vs. the periastron passage T1.

3.2.4. Masses and radii from scaling relations

We can derive the mass and the radius of the two stars from scaling relations using the large frequency separation (Δν) and the frequency of maximum power (νmax). For this we used the definition of the large frequency separation as the asymptotic large frequency separation (Δνas) as given by Eq. (6) of Mosser et al. (2013). For finding νmax, we fitted a parabola over 5 monopole modes around the maximum of mode height.

Since we do not have independent measurements of the effective temperature of either star, we derived a scaling relation using the luminosity of the two stars determined from the Hipparcos distance and the ratio of luminosities derived from speckle interferometry. These scaling relations were independently found from Miglio et al. (2012). The scaling relations are then written as: RR⊙=(νmaxνref)4/5 (ΔνasΔνref)−8/5(LL⊙)1/10\begin{equation} \frac{R}{R_\sun}=\left(\frac{\nu_{\rm max}}{\nu_{\rm ref}}\right)^{4/5} \, \left(\frac{\Delta\nu_{\rm as}}{\Delta\nu_{\rm ref}}\right)^{-8/5} \left(\frac{L}{L_\sun}\right)^{1/10} \end{equation}(1)and MM⊙=(νmaxνref)12/5 (ΔνasΔνref)−14/5(LL⊙)3/10\begin{equation} \frac{M}{M_\sun}=\left(\frac{\nu_{\rm max}}{\nu_{\rm ref}}\right)^{12/5} \, \left(\frac{\Delta\nu_{\rm as}}{\Delta\nu_{\rm ref}}\right)^{-14/5} \left(\frac{L}{L_\sun}\right)^{3/10} \end{equation}(2)where the reference values are taken from Mosser et al. (2013) as νref = 3104μHz and Δνref = 138.8μHz. Using these two relations, for Star A, having Δνas = 63.80 ± 0.06 μHz and νmax = 1157 ± 9 μHz, we derive MA = 1.27 ± 0.04 M⊙ and RA = 1.82 ± 0.02 R⊙; for Star B, having Δνas = 104.2 ± 0.7 μHz and νmax = 2223 ± 30 μHz, we derive MB = 1.20 ± 0.06 M⊙ and RB = 1.29 ± 0.02 R⊙. The total seismic mass of the system is then 2.43 ± 0.07 M⊙. We point out that the error bars result from the straight propagation from the seismic and luminosity observations; any additional errors due to physics are not taken into account.

We can also deduce the effective temperature of the two stars from the luminosities and seismic radii as Teff,A = 6080 ± 155 K and Teff,B = 5900 ± 159 K. This value for Star A is in agreement with the measurements of Casagrande et al. (2011).

3.2.5. Stellar ages from a proxy

Using large frequency separation. Lundkvist et al. (2014) showed that a stellar age can be derived from the measurement of Δν and of the stellar mass: this is asteroseismology made easy or AME. The relation they derived is based upon a grid of stellar evolutionary models that cover masses ranging from 0.7 M⊙ to 1.6 M⊙, and metallicities from −0.3 dex to +0.3 dex. For deriving the stellar age for our two stars, we used the data made available on the AME web site7. Using data from Fig. A.10 and Fig. A.11 of Lundkvist et al. (2014), we derived the age of the stars from the measured large frequency separations and the seismic masses: AgeA = 4.0 ± 0.7 Gyr and AgeB = 2.2 ± 0.9 Gyr. The error bars were derived from a Monte-Carlo simulation taking the errors quoted above into account for Δν and the seismic mass for a fixed metallicity of −0.1 dex and a mass for each star of 1.3 M⊙ and 1.2 M⊙. By taking the weighted mean, the age of the binary is then 3.3 ± 0.6 Gyr.

Using small frequency separation. Lebreton & Montalbán (2009) showed that the ratio r02 (the ratio of the small frequency separation δ02 to the large frequency separation Δν) was very sensitive to the age of the star. Using the data corresponding to the right hand side of their Fig. 5, we derived a simple relation between the age of a star and the small frequency separation as: 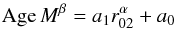Age Mβ=a1r02α+a0\begin{equation} {\rm Age}\,M^{\beta}=a_1 r_{02}^{\alpha} + a_0 \end{equation}(3)where the Age is expressed in Gyr, M is the mass of the star in solar mass, r02 is the ratio, a1 is the linear coefficient and a0 the offset. For a model without overshoot, we have from a fit of the relation for stellar masses ranging from 1.10 M⊙ to 1.25 M⊙: α = 0.54, β = 2.37, a1 = − 97.7 Gyr, a0 = 29.6 Gyr. Using the measured ratio r02,A = 0.072 ± 0.001 and r02,B = 0.0714 ± 0.0025 and the seismic masses, we derived the ages of the stars: AgeA = 3.4 ± 0.3 Gyr and AgeB = 4.0 ± 0.6 Gyr. The error bars were derived from Monte-Carlo simulations taking the errors for r02 and the seismic mass into account. The mean age of the binary is then 3.7 ± 0.3 Gyr. One can see that this method provides more consistent and more precise stellar ages for the two stars than the one using the large frequency separation.

Of course values derived above are sensitive to other physical parameters such as overshoot and chemical composition. The goal of these proxies are to provide an estimate of the stellar age without having to do more advanced stellar modelling, thereby also providing an input guess for the stellar modelling. The use of these proxies as guess will be validated by the stellar modelling.

4. Orbit data analysis

4.1. Observations

Speckle interferometry for getting the relative position of close binaries has been in use since the 1970’s (Labeyrie et al. 1974). This technique has been widely used in recent years for observing binary stars at a variety of telescopes such as SOAR (e.g. Tokovinin et al. 2014), the US Naval Observatory (Mason et al. 2013), Gemini North (Horch et al. 2012), WIYN (e.g. Horch et al. 2011) and the Brera Astronomical Observatory in Merate (Prieur et al. 2014). This binary was already observed in speckle interferometry and its orbital elements were published by (Horch et al. 2012) and references therein. The observations were performed from 2006 to 2014 using different instruments allowing the authors to get the position of the two stars to better than a few mas. Table A.5 provides the result of the observations.

Table 2

Parameters of the orbit using speckle interferometric observations of HIP 93511.

4.2. Orbit parameter extraction

The methodology for the derivation of the orbit is provided in Appendices B and C. The results of the procedure give the correlation between the different orbital parameters as in Fig. 5. The result of the Bayesian analysis is provided in Table 2. The total mass of the system in unit of the solar mass is derived from the following equation: 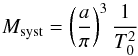Msyst=(aπ)31T02\begin{equation} M_{\rm syst}=\left(\frac{a}{\pi}\right)^3 \frac{1}{T_0^2} \end{equation}(4)where a is the semi-major axis in mas, T0 is the orbital period in years and π is the parallax. The mass of the system is then 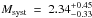Msyst=2.34-0.33+0.45\hbox{$M_{\rm syst}~=~2.34^{+0.45}_{-0.33}$} M⊙. The error bars were derived using Monte Carlo simulation as described in Appendix D. About 50% of the uncertainty is due to the uncertainty in the parallax. With new data from the Gaia ESA8 mission available in 2017, we can expect to reduce the parallax error by a factor 10. Within 4 years, new orbital measurements will provide error bars on the semi-major axis and the orbital period of the system about twice smaller. With more time and more data points, the error bar on the mass of the system will be brought to about 0.17 M⊙.

thumbnail Fig. 6

Orbit calculated with data shown with open diamonds. All points are drawn with line segments from the data point to the location of the ephemeris prediction on the orbital path. North is down and east is to the right.

Table 3

Characteristics of each model set used for inferring the stellar parameters of the two stars.

5. Stellar model comparisons

Detailed modelling using stellar structure evolution models was performed to determine more precise but model-dependent stellar quantities for each component. Table 3 shows the main characteristics of the 4 set of models used for inferring the stellar parameters of the binary system. Other details departing from this table are added in the corresponding sections.

All of the approaches used rely on a merit function for finding the optimal stellar parameters. The best model is obtained by minimising the merit function χ2 where χ2=((ymod−yobs)T C-1(ymod−yobs))+(∑i=1N(Yi−Yi,modσYi)2)\begin{eqnarray} \chi^2 = \left(\left ( y_{\rm mod} - y_{\rm obs} \right )^{\rm T} \, {\rm C^{-1}} \! \left ( y_{\rm mod} - y_{\rm obs} \right )\right) +\left(\sum_{i=1}^N \left(\frac{Y_{i}\!-\!Y_{i, {\rm mod}}}{\sigma_{Y_i}}\right)^2\right) \label{chi2} \end{eqnarray}(5)yobs denote the observations (e.g. frequency ratios, frequencies, luminosity, etc.) and ymod denote the predicted values from the model, T denotes the transposed matrix, and C is the covariance matrix associated with the observations; and Yi denotes a stellar parameter having regularisation parameters Yi,mod with some weight factor as σYi. The first term in parenthesis is the regular least squares taking the potential correlation between the observations into account. If there is no correlation, this classically reduces to the sum of squares. The second term in parenthesis is a regularisation term used to constraint the merit function, it is similar to an optimisation with Maximum A Priori (or MAP).

Table 4

Stellar parameters of the two stars for all the models.

5.1. Grid model, mode frequencies, and empirical surface correction (Verma)

In addition to the NACRE reaction rates, we used those of Imbriani et al. (2005) for 14N(p,γ)15O.

We constructed models independently for each star on a grid of stellar parameters – the mass M, initial helium abundance Yi, initial metallicity [Fe/H]i, mixing-length αMLT, and the overshoot parameter αOV. We generate 1500 random grid points for each star in a reasonable subspace of the parameter space (M: [ 1.15,1.40 ] M⊙, Yi: [ 0.22,0.32 ], [Fe/H]i: [ − 0.15,0.15 ], αMLT: [ 1.5,2.0 ], αOV: [ 0.00,0.05 ] for Star A; and M: [ 1.00,1.20 ] M⊙, Yi: [ 0.22,0.32 ], [Fe/H]i: [ − 0.15,0.15 ], αMLT: [ 1.5,2.0 ], αOV = 0.00 for Star B). The initial metallicity range was shifted to higher value to compensate for diffusion.

We corrected the model frequencies using the prescription of Kjeldsen et al. (2008), and fitted it to the observed frequencies to get the representative models for the stars. We accepted only those models that had a χ2 per mode less than 200 and the luminosity, effective temperature, and metallicity within 5σ of the observation. In this way, we got two ensembles of models, one for each star, with different mass, helium abundance, metallicity, mixing-length, and age (and overshoot parameter in case of Star A).

To test the consistency of some of the unreliable observables and determine the mass and radius of the stars, we defined a χ2 as in Eq. (5) with the regularisation term. To test the consistency of the observed effective temperature and luminosity with the models, we estimated them independently using 5 observables y; the metallicity, average separations (⟨ Δ0 ⟩ n and ⟨ δ02 ⟩ n), and average ratios (⟨ r02 ⟩ n and ⟨ r01 ⟩ n), and the regularisation terms Y included Teff and L. The covariance matrix C is assumed to be diagonal. The effective temperature and luminosity determined in this manner are consistent with the observation for both stars (see Col. 2 of Table 4).

To determine the mass and radius of the two stars, we repeated the exercise we did for effective temperature and luminosity but the regularisation terms Y included were M and R. We used two additional constraints in this case, the effective temperature and the luminosity. The values obtained of mass and radius are listed in Col. 2 of Table 4 for both the stars.

We found the individual ages for Star A and Star B to be 3.5 ± 0.6 Gyr and 4.1 ± 0.6 Gyr, respectively. The common age of the binary system was found to be 3.8 ± 0.4 Gyr. They are all consistent within the error bars. The full results are given in Table 4.

5.2. Free model, mode frequencies, and empirical surface correction (Lebreton)

To model the stars we proceeded as explained in Lebreton & Goupil (2014).

A Levenberg-Marquardt minimisation was used to adjust the free parameters in the modelling in order to minimise the merit functions per Eq. (5) (see Miglio & Montalbán 2005), with no regularisation term and assuming that the covariance matrix C is diagonal. For the optimisation of the model of Star A, we chose as observables y, the surface metallicity ([ Fe / H ] s = − 0.08 ± 0.10), the luminosity (L = 4.15 ± 0.47 L⊙) and the individual seismic frequencies. For Star B, we chose as constraints the luminosity (L = 1.85 ± 0.22 L⊙), the surface metallicity assumed to be similar to that of Star A, and the individual seismic frequencies. We corrected for near-surface effects on the theoretical frequencies taking the mode inertia into account as in Kjeldsen et al. (2008). In the modelling, the free model parameters are the age of the star, the mass, the initial helium content and initial (Z/X)0 ratio, and the free parameter αCGM entering the description of convection. For Star A, we also considered overshooting of the convective core.

The results obtained are listed in Table 4. The sum of the masses of the two components is MA + MB = 2.34 ± 0.05 M⊙ which agrees very well with the determination from the orbit. The luminosities LA and LB, surface metallicity [ Fe / H ] s, and effective temperature Teff,A are in agreement with observed values. The optimisation provides an effective temperature of Star B slightly warmer than that of Star A. We point out that the optimised model of Star A includes a moderate overshooting of the convective core, while for Star B, the optimised model is less massive and has no convective core.

5.3. Free model, mode frequencies and analytical surface correction (Ball)

For Star A, we used the frequency data, photometric observations from Casagrande et al. (2011) and luminosity derived in Sect. 2.1. For Star B, we used the frequencies and just the same metallicity as Star A, plus luminosity derived in Sect. 2.1.

Best fit models are determined by first computing an initial fit to the stellar parameters from a grid of models. The merit function used as per Eq. (5) includes observables y as Teff (when available), log L, [Fe/H], average Δν, and νmax, with no regularisation term and assuming the covariance matrix is diagonal. The models cover the mass range 0.60 M⊙ to 1.60 M⊙ in steps of 0.02 M⊙, and initial metal abundances Z in the range 0.001 to 0.040 in steps of 0.001. The helium abundance is presumed to follow the enrichment law Y = 0.245 + 1.450Z (Pietrinferni et al. 2004). The mixing length parameter was fixed at its solar-calibrated value of 1.908, with the same physics. Initial ranges for the mass and metallicity of the star were estimated using the SEEK method (Quirion et al. 2010), assuming that all the observables are normally-distributed and all priors on the parameters are uniform. We then generated 10 random, uniformly-distributed realisations of the parameters, with mass and metallicity in the ranges above, α between 1.2 and 2.4, and Yi between 0.20 and 0.36. To this sample, we also added an initial guess at the median values reported by the initial grid-based fit (with α = 1.8 and Y = 0.28). These 11 initial guesses were then optimised using a downhill simplex optimisation (Nelder & Mead 1965), with all models with a χ2< 1000 being recorded. In this latter case, we optimised the merit function without Δν and νmax, instead using the individual oscillation frequencies, corrected according to the cubic correction given by Ball & Gizon (2014).

We estimated the best-fit parameters and uncertainties for the underlying stellar model parameters computing the ellipses that bound specific values of the 2 samples determined during the optimisation. Rather than just using the 1-σ boundary, we used larger regions because they were better sampled, and divided the parameters by the appropriate fraction to provide 1-σ uncertainties. For the derived parameters (e.g. luminosity and radius) we linearised about the best-fit model parameters and propagated the uncertainties derived from the 2 contours, above. The full results are given in Table 4.

5.4. Grid model and frequency ratios (Creevey)

To determine the fundamental parameters for Stars A and B using stellar evolution models, we compared the observed asteroseismic data along with the luminosity ratio (LA/LB) or the individual luminosities (L) to the theoretical values predicted by stellar evolution models.

We adopted three different approaches for determining the parameters for both stars. The first approach consisted in studying the stars individually to obtain an estimate of the parameters of the stars independent of the results given in Sect. 3 and the second approach used the combined information from both stars. In the final approach we began with the best results from the second approach and proceeded with a local minimisation algorithm to refine the parameters. In this last stage there were no grid points, models were evaluated on the fly and thus there is no resolution issue associated with a grid. The advantage of the latter two approaches is that we assume that the age and initial composition is identical for both stars.

First approach. We constructed grids of stellar models and evaluated the χ2 function at each point in the grid. The merit function as per Eq. (5) includes the r01 and r02 frequency ratios and the luminosity for each star. The merit function does not include any regularisation terms but includes the covariance matrix which is not diagonal in this case since we use the ratios for the optimisation. When a grid has many dimensions, the number of models to evaluate becomes very large. Thus we created several grids with some fixed parameters. The reference grid fixed the initial composition and αov at values of (Zi,Yi,αov) = (0.014,0.271,0.200). Subsequent grids adopted different Zi = 0.011 and 0.018, thus the three values of the metallicity are [M/H] = –0.25, –0.10, and +0.02 approximately. The choice for Yi = 0.271 is somewhat arbitrary but motivated to adopt a value consistent with that for the Sun as given by Serenelli & Basu (2010) of 0.273 ± 0.007 (when extra mixing is considered). We did also explore the impact of changing this value to Yi = 0.281. For each grid of models we adopted two values of αCONV = 1.75 and 2.10, and the range of masses explored varied from M = 1.00 to 1.38 M⊙ in steps ranging between 0.01 and 0.02 M⊙. Pulsation frequencies were calculated for a range of ages for each stellar model between 1 Gyr and 6 Gyr, only for those models that haven’t begun climbing the red giant branch. The metallicity is not well constrained and for this reason we do not include it as a constraint, but restrict our models to grids with a large range of surface metallicity. This approach was used to narrow the search range for the optimal model.

Second approach. It consisted in specifying two masses, two values of αCONV, along with a common value of Yi,Zi. For each of the two models, the age of the corresponding model is optimised along the model track by direct comparison just with the frequency data. For those models whose optimised age is within 0.10 Gyr for the two models, we selected the optimal parameters by calculating their χ2 values.

Final approach. From the second approach we selected the models with the lowest χ2 values and then performed a local minimisation to refine the final optimal parameters. We did this for each of the chemical composition combinations Zi,Yi = (0.011,0.271),(0.014,0.271),(0.014,0.281). We ignore the results from the solar-metallicity models as their χ2 values are much larger than those from the other grids. In this last step, the merit function as per Eq. (5) includes the r01 and r02 frequency ratios, the lowest l = 0 radial order mode with a tolerance level of 2 μHz, one large frequency spacing for Star A; we included the same for Star B. The merit function does not include any regularisation terms but includes the covariance matrix which is again not diagonal.

The optimal stellar parameters are given in Table 4. The error bars were calculated by performing Monte Carlo simulations on the best-fit parameters. By assuming that these parameters exactly describe the real stars, the observations can be described by the model observables (e.g. the frequencies and luminosity from the model). We created simulated data by adding errors to the (model) observations. These errors were given by scaling the real observational error by a random number drawn from a Gaussian distribution, such as yi,sim = yi,true + N(0,ϵi,real), where ϵi,real are the real observational errors for the observed data (frequencies, luminosity ratio etc.), and yi,true are what the real observables are from our best model. The yi,sim are thus the simulated set of observed data.

We assume that the model behaves linearly locally, and so we can use a simple inversion method to calculate the parameter changes (dP) to make to an initial guess of the parameters P0 in order to bring the model observables into line with the simulated observations, see Creevey et al. (2011). (This involves calculating the Jacobian matrix dF/dP evaluated at the solution, where F are the observables, such as luminosity ratio and frequency ratios.) This was repeated 10 000 times. To calculate the uncertainties we fitted Gaussian functions to the distributions of dP + P0 (=fitted parameters) for each parameter, and the uncertainty is given as the 1-σ width. The covariance matrix of the stellar parameters can be easily calculated using the distributions of stellar parameters (dP+P0), and thus we can compute the 1-σ models at the edge of the error ellipses in order to evaluate the model observables (radius, luminosity etc.) and their uncertainties.

5.5. Inversion for the hydrostatic structure of Star A

The p-mode spectrum of Star A is rich and accurate enough to yield the hydrostatic structure of the stellar core with direct inversion of the oscillation frequencies. Here, we implement the technique described in Roxburgh & Vorontsov (2003a) and references therein.

A distinctive feature of this approach is that a proxy model (the initial guess) is truncated well below the upper turning points of the acoustic modes, to eliminate from the analysis the uncertain effects operating in the near-surface layers. The phases of partial waves (which are solutions to the linear adiabatic oscillation equations, which satisfy regularity conditions at the stellar centre) at the truncation boundary are calculated with the measured oscillation frequencies. The proxy model is then adjusted for these phases, which are calculated with modes of different degree, to fall on a single slowly varying function of frequency alone.

The proxy model, which may differ significantly from the target, is improved iteratively in linearised steps using an appropriate form of the variational principle, described in detail in Vorontsov et al. (2013). In this iterative process, we address “seismic” models – the models which can be represented by two functions of radial coordinate, the representation which is sufficient for the normal-mode analysis. Explicitly, we describe the model by a cubic B-spline for the running mean density m(r) /r3; we discard the effects of a small uncertainty in the adiabatic exponent in the deep stellar interior (i.e. we make no attempt of inverting for two functions of radial coordinate). After the linearised descent is completed, we end up with a new seismic model to be used in the next iteration.

Each linearised descent in the parameter-space (the coefficients of the B-spline representation) is performed with conjugate gradients; a limited number of the inner descents (amount of conjugate gradients in use) plays a role of the regularisation parameter (i.e. the regularisation which we implement is the so-called iterative regularisation).

To make use of the well-known degeneracy of the seismic models with respect to their oscillation frequencies, we implement a homology re-scaling of both the model and the input frequencies. When represented in dimensionless variables, one particular seismic model describes a two-parameter family of physical models, where the density profile ρ(r) scales as M/R3, squared sound speed c2(r) scales as M/R, squared buoyancy frequency N2 and squared oscillation frequencies ω2 both scale as M/R3. We bring an initial proxy model to its dimensionless representation: the resulted dimensionless model now describes a two-parametric family of physical models which differ in M and R. We bring the measured frequencies to their dimensionless values without imposing any à priori constraints on the stellar mass and radius: instead, we adjust M/R3 in this scaling such as to achieve the best performance of the inversion (the best likelihood of the result obtained when iterations converge). In this way, the inversion provides a best-fit value for M/R3 (i.e. for the mean density). The inverted dimensionless model now describes a one-parameter family of physical models, all the models in the family satisfy the input data. Each model in this family can be rescaled to different values of M and R, but with keeping M/R3 unchanged. In this re-scaling, which does not change the oscillation frequencies, ρ(r) and N2(r) remain unchanged, but c2(r) re-scales in proportion to M2 / 3.

The results obtained with an evolved model of a 1.1 M⊙ star (central hydrogen abundance Xc = 0.05) taken as an initial guess are shown in Fig. 7. The steep decrease in the sound-speed towards the centre (Fig. 7a), together with big density contrast (Fig. 7b) indicate that the star is at a very late stage of the main-sequence evolution. The resulting steep gradient in the molecular weight is responsible for the sharp variation of the buoyancy frequency (Fig. 7c). Note that the prominent wiggles in the N2-curves below 0.1R are due to model discretisation (the cubic spline for m(r) /r3 is continuous together with two derivatives, but provides N2(r) with discontinuities in its first derivative).

thumbnail Fig. 7

Structural inversion for Star A: the sound speed a), density b), and buoyancy frequency c). Dashed green lines show a (re-scaled) model taken as an initial guess; solid green lines display the inverted result. Thin blue lines result from adding the measured frequencies with Gaussian noise, of variance corresponding to the reported uncertainties, in 10 realisations, to address the sensitivity of the inversion to random errors in the input data.

We do not see any signature of a convective core in the results of this inversion. It does not mean, however, that the star does not have a convective core. The inversion starts with a smooth initial guess, and any rapid variations in the solution are only developed during iterative descents to fit the data. The signatures of a convective core can thus be smeared away by the inversion when the data quality is not high enough to resolve the core boundary. Resolving the core is especially hard, and needs data of exceptionally high accuracy, when the spatial variation of seismic parameters occurs on a scale short compared with the radial wavelength of observable p modes.

6. Discussion

Figures 8 and 9 show the comparison of the best-model ratios r01 / 10 and r02 with the observations. We chose to show only these ratios because they are nearly insensitive to the impact of surface effect frequency corrections. From Table 4 we can see the commonalities and differences of the models of the binary system.

For Star A, the models provide two masses: 1.25–1.27 M⊙ and 1.34–1.39 M⊙, two radii of 1.82 R⊙  and 1.86 R⊙; for the age all the models but that of Ball give a value consistent with 3.4 Gyr. For Star B, all models provide a mass close to 1.10 M⊙, a median radius of 1.23 R⊙; for the age all the models gives a value consistent with 4.1 Gyr (Creevey providing a common age). The total mass of the system is in the range 2.34–2.53 M⊙  consistent with that derived by astrometry. For 3 models, the age of the binary system is in the range 3.4–3.9 Gyr while for Ball the age is about 2.7 Gyr. All models return a very consistent log g for either star; this is the result of the very tight correlation between M and R as shown by (Gai et al. 2011).

The models of Verma/Ball, of Lebreton and of Creevey are all based on 3 different evolution codes. The models with MESA return consistent mass and radius for either star, while the age is different for Star A. The model of Ball provides a higher effective temperature and a higher luminosity for Star A compared with the other models. Verma and Lebreton use a different evolution code but still return the same age for Star A and B while Creevey with a different evolution code returns a different age.

All models require an overshoot for Star A, while no model needs overshoot for Star B on the main sequence stage. The models of Verma/Ball also have an overshoot which is coded differently compared to that of Lebreton and Creevey. While the mass and age for Star A may differ depending on the model, the presence of a convective core is indeed required by all models to explain the measured ratio r01. The convective core is not detected by inversion because the method presented here is not sensitive enough for such purpose. The mass boundary between stars having a convective core or not depends upon the metallicity (see for instance Bressan et al. 2012). For a metallicity of Z ≈ 0.02, the limit is about 1.125 M⊙. The presence of a convective core has already been found by seismic analysis in other stars such as HD 49933 (Benomar et al. 2010; Roxburgh 2015), HD 203608 (Deheuvels et al. 2010), and KIC12009504 (Silva Aguirre et al. 2013) while ruled out for KIC 6106415 (Silva Aguirre et al. 2013) and α Cen A (de Meulenaer et al. 2010), both with mass around 1.1 M⊙. In the case of our binary with a common metallicity of about Z = 0.02, we then have two stars lying on either side of the limit which may be then in the range [1.14–1.25] M⊙. We also outline that the value of the overshoot for Star A given by the models of Lebreton and Creevey is also consistent with the correlation with the stellar mass as found by Deheuvels (2015).

thumbnail Fig. 8

Seismic properties of the optimised models of Star A. Left panel: comparison of the observed frequency separation ratios r01 / 10(n) (models are the coloured lines). Right panel: comparison of the observed frequency separation ratios r02(n) (models are the coloured lines).

thumbnail Fig. 9

Seismic properties of the optimised model of Star B. Left panel: comparison of the observed frequency separation ratios r01 / 10(n) (models are the coloured lines). Right panel: comparison of the observed frequency separation ratios r02(n) (models are the coloured lines).

6.1. Analysis of model differences

The major discrepancies are related to the mass and radius of Star A and the common age of the stars. It is not easy to understand and disentangle the differences because, aside from the fact that teams used different stellar codes, methods and input physics, there are many degeneracies in the parameters governing stellar evolution.

There are several possible causes for the discrepancy of the mass and radius of Star A as given by Verma/Ball compared to the other models. First, MESA, used by Verma and Ball, is a recent evolution code. Some results of the MESA code have been compared with those of another code in Paxton et al. (2011). However the comparisons of the MESA interior structures have not been shown with many details. On the other hand, the results of the ASTEC and CESAM codes have been validated by thorough comparisons performed in the framework of the ESTA/CoRoT stellar model comparison project9 in the collaborative work of Lebreton et al. (2008) and of Monteiro et al. (2006). Second, the surface frequency correction is a known source of discrepancy between the models and the observations as originally shown for the Sun by Christensen-Dalsgaard & Thompson (1997); this could be an explanation since the methodology used by Lebreton is different from that of Ball. Third, the optimisation parameters used by Verma is different to that of Lebreton and Ball which could explain together with the use of regularisation terms the difference for the mass of Star A. Fourth, the different assumptions on the physics (opacities, convection, nuclear rates, atmospheric boundary conditions, etc.) could also explain the different results.

The age provided by Ball is clearly different from the other models. In light of the previous discrepancy list, could there be a common source of discrepancy? First, since the MESA code is used both by Verma and Ball, that code should not be the source of the difference. Second, the surface frequency correction used by Ball is different from that of Verma/Lebreton. Third, the optimisation parameters differ between Ball/Lebreton and the other modellers.

We also note that the higher mass of Star A derived by Ball is correlated with a lower age for Star A since main-sequence lifetime roughly scales as M-2.5. A higher mass of 10% corresponds to a lower age by –25%, which is consistent when comparing the age of Ball with that of Lebreton. This is not consistent when comparing Ball and Verma. For models having similar helium and [Fe/H] (Ball/Creevey), a higher mass is also related to a higher luminosity, hence resulting in a higher effective temperature. It seems that a better fit to frequencies provided by Ball results in a difficulty to reproduce the observed luminosity.

What are the likely reasons for the discrepancies? From the above, since the MESA code has not been thoroughly tested with respect to the other evolution codes, we might not exclude that code from the list of culprit. Since Ball and Lebreton both use model frequencies for the optimisation parameters, the resulting χ2 is very sensitive to the surface frequency correction. On the other hand Creevey and to some extent Verma are less sensitive to the surface frequency correction because of the use of frequency separations and ratios. For these latter, the lack of sensitivity was explained by Roxburgh & Vorontsov (2003b). The additional regularisation parameters of Verma may also contribute to a different χ2. Finally, the assumption regarding the physics of the stars may be related to initial helium abundance, the convective parameter α or the overshoot prescription. Metcalfe et al. (2009, their Fig. 5) performed a sensitivity analysis considering seismic data for the Sun and showed the theoretical correlations that exist between initial helium abundance and mass. Baudin et al. (2012) found a similar result in a red giant star observed by CoRoT. Lebreton & Goupil (2014) examined in detail the correlation between model input parameters of the CoRoT target HD 52265. 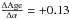They quantified the anti-correlation of the mass with the initial helium abundance to be ΔY0ΔM=−0.58\hbox{$\frac{\Delta Y_{0}}{\Delta M}=-0.58$} and also suggested a correlation of the age with the mixing length parameter of ΔAgeΔα=+0.13\hbox{$\frac{\Delta {\rm Age}}{\Delta \alpha}=+0.13$}. The ΔY0ΔM\hbox{$\frac{\Delta Y_{0}}{\Delta M}$} anti-correlation can account for the mass difference between Verma and Lebreton but not for the mass difference between Ball and Creevey since their initial helium abundance is the same. 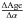The ΔAgeΔα\hbox{$\frac{\Delta {\rm Age}}{\Delta \alpha}$} correlation cannot account for the lower age obtained by Ball since the mixing length parameter is higher.

6.2. What is needed for progress?

Clearly, the use of existing surface frequency corrections, especially for stars that are significantly different from the Sun, need to be properly compared such as in Schmitt & Basu (2015). In their stellar-age dating, Otí Floranes et al. (2005) and Miglio & Montalbán (2005) showed that the frequency difference ratios where very powerful age indicators (See also the pioneering works of Ulrich 1986; Christensen-Dalsgaard 1988). In the case of HD 52265, Lebreton & Goupil (2014) examined different sets of seismic constraints and showed that the use of frequency ratios provide the best accuracy and precision for the age of the star. Therefore the use of method not based upon surface frequency correction should also be tested using the MESA evolution code (Verma and Ball). One can also notice that despite the lack of use of the frequency ratios for optimisation, Ball provides lower values for r01 of Star A. In order to go further, it would be best if all modellers used the same optimisation parameters including the frequency ratios.

The optimisation approach also needs to be assessed. The raw χ2 contribution of the seismic parameters is roughly proportional to the number of modes, i.e. greater than typically 50. On the other hand, the raw χ2 contribution of the classical parameters is about 2 to 3 depending on the number of parameters. It is quite clear that while being correct from a statistical point of view, it slants the optimisation towards the seismic parameters. A Bayesian approach to this optimisation problem will take the classical parameters into account in a more realistic way such as in Bazot et al. (2012).

The differences in physics cannot be ruled out. A comparison of the MESA evolution code and its associated physics is also required. There are several differences with CESAM2K and ASTEC such as atomic diffusion, convection, and overshoot prescription that need to be assessed. In addition the modulation in r01 observed in Fig. 9 can be explained by the impact of penetrative convection on mode frequencies (Monteiro et al. 1994). Similar results have been obtained by Lebreton & Goupil (2012) for HD 52265. Therefore by reducing the differences with r01, the inclusion of penetrative convection in the model may improve the physical description of the stars.

A deeper analysis of the impact of all the input and optimisation parameters in a similar fashion as done by Lebreton & Goupil (2014) is indeed required and is beyond the scope of this article.

7. Conclusions

We use Kepler data for measuring the seismic mode parameters of two spatially unresolved stars in a single time series. We provide the seismic mode frequencies, mode linewidths, and mode heights of the two stars and derived using scaling relations the mass, the radius, and the age of the two stars in a binary system. We also derive the orbit characteristics using speckle interferometry which gives an independent measurement of the total mass of the system. We also model the stars using the mode frequencies and four different stellar model pipelines. The seismic mass of the binary system derived with the models is consistent with that determined with astrometry. For 3 models, the age of the binary system is in the range 3.4–3.9 Gyr while for another model the age is about 2.7 Gyr. There is a clear detection of a convective core in Star A, while Star B does not have any. The mass of Star B provided by the models is consistent with a value of [1.08–1.14] M⊙. On the other hand, the models provide two sets of values for Star A: [1.25–1.27] M⊙ and [1.34–1.39] M⊙. There are still differences between the models that are related either to the physics used, or the surface frequency correction, or to the optimisation strategy.

The seismic and modelling analysis mimics what will be done for the PLATO mission (Rauer et al. 2014). In particular, the seismic calibration of absolute stellar age is in principle possible using binary stars or cluster systems which requires a detailed study of systematic errors due to the physics used in the different models. This kind of data will be extensively used for validation of the PLATO pipeline.

Online material

Appendix A: Seismic and orbital data

Table A.1

Frequencies for Star A.

Table A.2

Frequencies for Star B.

Table A.3

Mode linewidths, mode heights and mode amplitude for Star A.

Table A.4

Mode linewidths, mode heights and mode amplitude for Star B.

Table A.5

Speckle interferometric data of the orbital position of the binary.

Appendix B: Astrometric orbit

The coordinates of the orbit on the plane of the sky (x,y) are derived as follows: x=AX+FYy=BX+GY\appendix \setcounter{section}{2} \begin{eqnarray} &&x= A X + F Y \\[1mm] &&y= B X + G Y \end{eqnarray}where A,B,F,G are the Thiele-Innes elements, and (X,Y) are the position of the object in the plane of the orbit. The Thieles-Innes elements are related to the semi-major axis a, to the inclination of the orbit i on the plane of sky and to the argument of the periastron (ω) and the longitude of the ascending nodes (Ω) as: A=a(cosΩcosω−sinΩsinωcosi)B=a(sinΩcosω+cosΩsinωcosi)F=−a(cosΩsinω+sinΩcosωcosi)G=−a(sinΩsinω−cosΩcosωcosi).\appendix \setcounter{section}{2} \begin{eqnarray} &&A=a(\cos \Omega \cos \omega - \sin \Omega \sin \omega \cos i) \\[1mm] &&B=a(\sin \Omega \cos \omega + \cos \Omega \sin \omega \cos i) \\[1mm] &&F=-a(\cos \Omega \sin \omega + \sin \Omega \cos \omega \cos i) \\[1mm] &&G=-a(\sin \Omega \sin \omega - \cos \Omega \cos \omega \cos i). \end{eqnarray}The position of the orbit in the plane of the orbit is given by: X=acosE−eY=a(1−e2sinE)\appendix \setcounter{section}{2} \begin{eqnarray} &&X=a \cos E - e \\ &&Y=a(\sqrt{1-e^2}\sin E) \end{eqnarray}where E is the eccentric anomaly and e is the orbit eccentricity. The eccentric anomaly can be found by solving the following equation: 2πT0(t−T1)=E−esinE\appendix \setcounter{section}{2} \begin{equation} \frac{2 \pi}{T_0}(t-T_{1})=E-e \sin E \end{equation}(B.9)where T0 is the orbit periodicity and T1 is the time of passage at periastron.

Appendix C: Derivation of the orbit

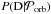For the derivation of the orbit, we computed the log  likelihood of the data D given the orbital parameters (\hbox{${\cal P}_{\rm orb}$}=(Ω,ω,i,a,e,T1,T0)), \hbox{$P({\rm D} | {\cal P}_{\rm orb})$} as: logP(D|𝒫orb)=∑i=1i=N−((xi(𝒫orb)−xiobs)2+(yi(𝒫orb)−yiobs)22σi2)\appendix \setcounter{section}{3} \begin{equation} \log P({\rm D} | {\cal P}_{\rm orb}) = \sum_{i=1}^{i=N} -\left(\frac{(x_i({\cal P}_{\rm orb})-x_i^{\rm obs})^2+(y_i({\cal P}_{\rm orb})-y_i^{\rm obs})^2}{2 \sigma_i^2}\right) \end{equation}(C.1)where D are the data, \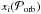hbox{$x_i({\cal P}_{\rm orb})$} and \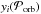hbox{$y_i({\cal P}_{\rm orb})$} are the output of the astrometric model of Appendix A at time ti, and xiobs\hbox{$x_i^{\rm obs}$} and yiobs\hbox{$y_i^{\rm obs}$} are the observations at time ti, and the σi are the estimated errors of the observations. There are two approaches used for deriving the orbital parameters:

  • Frequentist: minimisation of the log  likelihood

  • Bayesian: Monte Carlo Markov Chain using the Metropolis Hasting algorithm.

The first approach is equivalent to the use of a non-linear least square fit. The error bars are derived using the inverse of the Hessian matrix. This is the classical way of estimating parameters from a model and observation. The error bars were also verified using a Monte-Carlo simulation of the orbit. When the estimated parameters are close to a minimum, the error bars from the Hessian and the Monte-Carlo simulations are similar (See Appourchaux 2014).

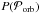Unfortunately, the error bars returned by the two methods gave inconsistent results which is why we implemented the second approach which is based upon a Bayesian framework. In that case, we derived the posterior probability (\hbox{$P({\cal P}_{\rm orb} | D)$}) of the parameters using Bayes’ theorem as: P(𝒫orb|D)=P(𝒫orb)P(D|𝒫orb)P(D)\appendix \setcounter{section}{3} \begin{equation} P({\cal P}_{\rm orb} | {\rm D}) = \frac{ P({\cal P}_{\rm orb}) P({\rm D} | {\cal P}_{\rm orb})}{P({\rm D})} \end{equation}(C.2)where \hbox{$P({\cal P}_{\rm orb})$} is the a priori probability of the orbital parameters, and P(D) is the global normalisation likelihood. The derivation of the posterior probabilities can be done using the Metropolis Hasting algorithm (See as a starting point, Appourchaux 2014). We use a Markov Chain for exploring the space to go from a set 𝒫orbt\hbox{${\cal P}_{\rm orb}^{t}$} to another set 𝒫orbt′\hbox{${\cal P}_{\rm orb}^{t'}$}, assuming that either set have the same probabilities, i.e. 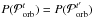P(𝒫orbt)=P(𝒫orbt′)\hbox{$P({\cal P}_{\rm orb}^{t})=P({\cal P}_{\rm orb}^{t'})$}. The Metropolis-Hasting algorithm then requires that we accept the new set 𝒫orbt′\hbox{${\cal P}_{\rm orb}^{t'}$} using the following ratio: r=P(𝒫orbt′|D)P(𝒫orbt|D)=P(D|𝒫orbt′)P(D|𝒫orbt)·\appendix \setcounter{section}{3} \begin{equation} r=\frac{P({\cal P}_{\rm orb}^{t'} | {\rm D})}{P({\cal P}_{\rm orb}^{t} | {\rm D})}=\frac{P({\rm D} | {\cal P}_{\rm orb}^{t'})}{P({\rm D} | {\cal P}_{\rm orb}^{t})}\cdot \end{equation}(C.3)This is simply the ratio of the likelihood given in Eq. (B.1). The new value is accepted if r<α with probability α (drawn from a uniform distribution) otherwise it is rejected.

We set 10 chains of 10 million points each, with the following starting points taken randomly: Ω(degrees)≈U(0,180)ω(degrees)≈U(0,180)i(degrees)≈U(0,60)a(mas)≈N(0.075,0.003)e≈U(0.4,0.8)T1(years)≈U(1995,2005)T0(years)≈N(14,20).\appendix \setcounter{section}{3} \begin{eqnarray} \Omega({\rm degrees}) &\approx& U(0,180) \nonumber\\ \omega ({\rm degrees}) &\approx& U(0,180)\nonumber\\ i ({\rm degrees}) &\approx& U(0,60)\nonumber\\ a ({\rm mas}) &\approx& N(0.075,0.003)\nonumber\\ e &\approx& U(0.4,0.8)\nonumber\\ T_1({\rm years}) &\approx& U(1995,2005)\nonumber\\ T_0({\rm years}) &\approx& N(14, 20). 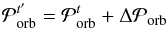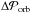\end{eqnarray}(C.4)The new set of parameters is computed from a random walk from the previous value as: 𝒫orbt′=𝒫orbt+Δ𝒫orb\appendix \setcounter{section}{3} \begin{equation} {\cal P}_{\rm orb}^{t'}={\cal P}_{\rm orb}^{t}+\Delta {\cal P}_{\rm orb} \end{equation}(C.5)where \hbox{$\Delta {\cal P}_{\rm orb}$} is given by a multinomial normal distribution with independent parameters: Δ𝒫orb≈N(0;11.5,11.5,5.75,0.001,0.01,1,1)αrate\appendix \setcounter{section}{3} \begin{equation} \Delta {\cal P}_{\rm orb} \approx N(0;11.5, 11.5, 5.75, 0.001, 0.01, 1, 1) \alpha_{\rm rate} \end{equation}(C.6)where αrate is an adjustable parameter that is reduced by a factor 2 until the rate of acceptance of the new value t′ is above 25%. The proper convergence of the chains was verified using the Gelman-Rubin \hbox{$\hat{R}$} test (Gelman & Rubin 1992) as implemented by Ford (2006). After rejecting the initial burn-in phase (10% of the chain), all values of the \hbox{$\hat{R}$} test of the 7 sets of parameters were below 1.1. Then the chains provide the posterior probability for each parameter. For all chains of each parameter, we computed the median and the credible intervals at 16% and 84%, corresponding to a 1-σ interval for a normal distribution. The advantage of this

percentile definition over the mode (maximum of the posterior distribution) or the mean (average of the distribution) is that it is conservative with respect to any change of variable over these parameters.

Appendix D: Derivation of the mass of the binary system and the associated errors

Knowing the distance (via the parallax π), the semi-major axis a and the period of the system T0, we can deduce from the Kepler’s third law the total mass of the binary system in units of the solar mass as 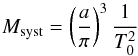Msyst=(aπ)31T02\appendix \setcounter{section}{4} \begin{equation} M_{\rm syst}=\left(\frac{a}{\pi}\right)^3 \frac{1}{T_0^2} \end{equation}(D.1)where π is in mas. The error bars can be computed assuming that the semi-major axis, the orbital period, and parallax are independent of each other as: 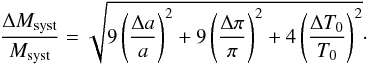ΔMsystMsyst=9(Δaa)2+9(Δππ)2+4(ΔT0T0)2·\appendix \setcounter{section}{4} \begin{equation} \frac{\Delta M_{\rm syst}}{M_{\rm syst}}=\sqrt{9 \left(\frac{\Delta a}{a}\right)^2+9 \left(\frac{\Delta \pi}{\pi}\right)^2+4 \left(\frac{\Delta T_0}{T_0}\right)^2}\cdot \end{equation}(D.2)In order to derive the corresponding credible intervals for the mass of the system, we use a Monte-Carlo simulation using the chains for the semi-major axis and the period from our Bayesian analysis, and use a randomised parallax as inferred from van Leeuwen (2007) for HIP 93511. The use of the MCMC chains explicitly includes the correlation between the orbital period and the semi-major axis for the final error propagation. The three values were then injected in Eq. (D.1) for getting the median and the credible intervals.

1

The WIYN Observatory is a joint facility of the University of Wisconsin-Madison, Indiana University, the National Optical Astronomy Observatory and the University of Missouri.

2

Both luminosity values are lower by 0.2σ compared to the values computed using (B − V) as a constraint (Roxburgh, priv. comm.).

8

European Space Agency.

Acknowledgments

T.A. gratefully acknowledges the financial support of the Centre National d’Etudes Spatiales (CNES) under a PLATO grant. T.L.C., W.J.C., and G.R.D. acknowledge financial support from the UK Science and Technology Facilities Council (STFC). W.B. and L.G. acknowledge support from the Deutsche Forschungsgemeinschaft SFB 963 “Astrophysical Flow Instabilities and Turbulence” (Project A18). L.G. acknowledges research funding from the Center for Space Science, NYU Abu Dhabi Institute, UAE. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation. We are indebted to Ian Roxburgh for extensively commenting on the paper and for his timely contribution. We are grateful to Sébastien Salmon for commenting on an earlier version of the paper. We are also indebted to Georges Herriman for silently accepting to use the name Krazy and Ignatz for these two stars. We are grateful to the anonymous referee for the constructive and useful comments.

References

  1. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
  2. Appourchaux, T. 2014, in Asteroseismology, 22nd Canary Islands Winter School of Astrophysics (Cambridge, UK: Cambridge University Press), eds. P. L. Pallé, & C. Esteban, 123 [Google Scholar]
  3. Appourchaux, T., Chaplin, W. J., García, R. A., et al. 2012, A&A, 543, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baglin, A. 2006, The CoRoT mission, pre-launch status, stellar seismology and planet finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA SP-1306 (Noordwijk, The Netherlands: ESA Publication Division) [Google Scholar]
  7. Ball, W. H., & Gizon, L. 2014, A&A, 568, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Baudin, F., Barban, C., Goupil, M. J., et al. 2012, A&A, 538, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bazot, M., Ireland, M. J., Huber, D., et al. 2011, A&A, 526, L4 [Google Scholar]
  10. Bazot, M., Bourguignon, S., & Christensen-Dalsgaard, J. 2012, MNRAS, 427, 1847 [NASA ADS] [CrossRef] [Google Scholar]
  11. Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  12. Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
  13. Beck, P. G., Hambleton, K., Vos, J., et al. 2014, A&A, 564, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Benomar, O., Baudin, F., Marques, J. P., et al. 2010, Astron. Nachr., 331, 956 [NASA ADS] [CrossRef] [Google Scholar]
  16. Benomar, O., Bedding, T. R., Mosser, B., et al. 2013, ApJ, 767, 158 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Bigot, L., Mourard, D., Berio, P., et al. 2011, A&A, 534, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
  20. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [NASA ADS] [CrossRef] [Google Scholar]
  22. Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] [Google Scholar]
  23. Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Chaplin, W. J., Basu, S., Huber, D., et al. 2014, ApJS, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
  25. Christensen-Dalsgaard, J. 1988, in Advances in Helio- and Asteroseismology, eds. J. Christensen-Dalsgaard, & S. Frandsen, IAU Symp., 123, 295 [Google Scholar]
  26. Christensen-Dalsgaard, J. 2008a, Ap&SS, 316, 113 [NASA ADS] [CrossRef] [Google Scholar]
  27. Christensen-Dalsgaard, J. 2008b, Ap&SS, 316, 13 [NASA ADS] [CrossRef] [Google Scholar]
  28. Christensen-Dalsgaard, J., & Thompson, M. J. 1997, MNRAS, 284, 527 [NASA ADS] [Google Scholar]
  29. Cox, J. P., & Giuli, R. T. 1968, Principles of stellar evolution and nucleosynthesis (New-York: MacGraw-Hill) [Google Scholar]
  30. Creevey, O. L., Monteiro, M. J. P. F. G., Metcalfe, T. S., et al. 2007, ApJ, 659, 616 [NASA ADS] [CrossRef] [Google Scholar]
  31. Creevey, O. L., Metcalfe, T. S., Brown, T. M., Jiménez-Reyes, S., & Belmonte, J. A. 2011, ApJ, 733, 38 [NASA ADS] [CrossRef] [Google Scholar]
  32. Davies, G. R., Handberg, R., Miglio, A., et al. 2014, MNRAS, 445, L94 [NASA ADS] [CrossRef] [Google Scholar]
  33. de Meulenaer, P., Carrier, F., Miglio, A., et al. 2010, A&A, 523, A54 [Google Scholar]
  34. Deheuvels, S. 2015, in Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. G. T. van Belle, & H. C. Harris, 18, 489 [Google Scholar]
  35. Deheuvels, S., Michel, E., Goupil, M. J., et al. 2010, A&A, 514, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
  37. Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  38. Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
  40. Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
  41. Gai, N., Basu, S., Chaplin, W. J., & Elsworth, Y. 2011, ApJ, 730, 63 [NASA ADS] [CrossRef] [Google Scholar]
  42. Gaulme, P., McKeever, J., Rawls, M. L., et al. 2013, ApJ, 767, 82 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gelman, A., & Rubin, D. B. 1992, Statistical Science, 7, 457 [Google Scholar]
  44. Gilliland, R. L., Jenkins, J. M., Borucki, W. J., et al. 2010, ApJ, 713, L160 [NASA ADS] [CrossRef] [Google Scholar]
  45. Gizon, L., & Solanki, S. K. 2003, ApJ, 589, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  46. Gontcharov, G. A. 2006, Astron. Lett., 32, 759 [NASA ADS] [CrossRef] [Google Scholar]
  47. Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse (Springer Verlag), 15 [Google Scholar]
  48. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  49. Harvey, J. 1985, in Future missions in solar, heliospheric and space plasma physics, eds. E. Rolfe, & B. Battrick (Noordwijk, The Netherlands: ESA Publications Division), ESA SP-235, 199 [Google Scholar]
  50. Hauser, H. M., & Marcy, G. W. 1999, PASP, 111, 321 [NASA ADS] [CrossRef] [Google Scholar]
  51. Heintz, W. D. 1975, ApJS, 29, 315 [NASA ADS] [CrossRef] [Google Scholar]
  52. Hekker, S., Debosscher, J., Huber, D., et al. 2010, ApJ, 713, L187 [NASA ADS] [CrossRef] [Google Scholar]
  53. Henyey, L., Vardya, M. S., & Bodenheimer, P. 1965, ApJ, 142, 841 [NASA ADS] [CrossRef] [Google Scholar]
  54. Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
  55. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
  56. Horch, E. P., van Altena, W. F., Cyr, Jr., W. M., et al. 2008, AJ, 136, 312 [NASA ADS] [CrossRef] [Google Scholar]
  57. Horch, E. P., Falta, D., Anderson, L. M., et al. 2010, AJ, 139, 205 [NASA ADS] [CrossRef] [Google Scholar]
  58. Horch, E. P., Gomez, S. C., Sherry, W. H., et al. 2011, AJ, 141, 45 [NASA ADS] [CrossRef] [Google Scholar]
  59. Horch, E. P., Howell, S. B., Everett, M. E., & Ciardi, D. R. 2012, AJ, 144, 165 [NASA ADS] [CrossRef] [Google Scholar]
  60. Horch, E. P., van Altena, W. F., Demarque, P., et al. 2015, AJ, 149, 151 [NASA ADS] [CrossRef] [Google Scholar]
  61. Huber, D., Ireland, M. J., Bedding, T. R., et al. 2012, ApJ, 760, 32 [NASA ADS] [CrossRef] [Google Scholar]
  62. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  63. Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010, ApJ, 713, L87 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kepler, J. 1619, Harmonices Mundi (Linz, Austria: Johann Planck), 189 [Google Scholar]
  66. Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kochukhov, O. P. 2007, in Physics of Magnetic Stars, eds. I. I. Romanyuk, D. O. Kudryavtsev, O. M. Neizvestnaya, & V. M. Shapoval, 109 [Google Scholar]
  68. Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  70. Labeyrie, A., Bonneau, D., Stachnik, R. V., & Gezari, D. Y. 1974, ApJ, 194, L147 [NASA ADS] [CrossRef] [Google Scholar]
  71. Lebreton, Y., & Goupil, M. J. 2012, A&A, 544, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Lebreton, Y., & Goupil, M. J. 2014, A&A, 569, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Lebreton, Y., & Montalbán, J. 2009, in IAU Symp. 258, eds. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, 419 [Google Scholar]
  74. Lebreton, Y., Montalbán, J., Christensen-Dalsgaard, J., Roxburgh, I. W., & Weiss, A. 2008, Ap&SS, 316, 187 [NASA ADS] [CrossRef] [Google Scholar]
  75. Lundkvist, M., Kjeldsen, H., & Silva Aguirre, V. 2014, A&A, 566, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Maeder, A. 1975, A&A, 40, 303 [NASA ADS] [Google Scholar]
  77. Mamajek, E. E., Meyer, M. R., & Liebert, J. 2002, AJ, 124, 1670 [NASA ADS] [CrossRef] [Google Scholar]
  78. Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Mashonkina, L., & Zhao, G. 2006, A&A, 456, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Mason, B. D., Hartkopf, W. I., & Hurowitz, H. M. 2013, AJ, 146, 56 [NASA ADS] [CrossRef] [Google Scholar]
  81. Mazumdar, A., Monteiro, M. J. P. F. G., Ballot, J., et al. 2014, ApJ, 782, 18 [NASA ADS] [CrossRef] [Google Scholar]
  82. Metcalfe, T. S., Creevey, O. L., & Christensen-Dalsgaard, J. 2009, ApJ, 699, 373 [NASA ADS] [CrossRef] [Google Scholar]
  83. Metcalfe, T. S., Chaplin, W. J., Appourchaux, T., et al. 2012, ApJ, 748, L10 [NASA ADS] [CrossRef] [Google Scholar]
  84. Metcalfe, T. S., Creevey, O. L., Doğan, G., et al. 2014, ApJS, 214, 27 [NASA ADS] [CrossRef] [Google Scholar]
  85. Michaud, G., & Proffitt, C. R. 1993, in IAU Colloq. 137: Inside the Stars, eds. W. W. Weiss, & A. Baglin, ASP Conf. Ser., 40, 246 [Google Scholar]
  86. Miglio, A., & Montalbán, J. 2005, A&A, 441, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [NASA ADS] [CrossRef] [Google Scholar]
  88. Miglio, A., Chaplin, W. J., Farmer, R., et al. 2014, ApJ, 784, L3 [NASA ADS] [CrossRef] [Google Scholar]
  89. Monteiro, M. J. P. F. G., Christensen-Dalsgaard, J., & Thompson, M. J. 1994, A&A, 283, 247 [NASA ADS] [Google Scholar]
  90. Monteiro, M. J. P. F. G., Lebreton, Y., Montalban, J., et al. 2006, in ESA SP 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 363 [Google Scholar]
  91. Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  92. Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012a, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012b, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Mosser, B., Michel, E., Belkacem, K., et al. 2013, A&A, 550, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Nelder, J., & Mead, R. 1965, Comput. J., 7, 308 [Google Scholar]
  96. OtíFloranes, H., Christensen-Dalsgaard, J., & Thompson, M. J. 2005, MNRAS, 356, 671 [NASA ADS] [CrossRef] [Google Scholar]
  97. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  98. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
  99. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  100. Pinsonneault, M. H., An, D., Molenda-Żakowicz, J., et al. 2012, ApJS, 199, 30 [NASA ADS] [CrossRef] [Google Scholar]
  101. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
  102. Prieur, J.-L., Scardia, M., Pansecchi, L., et al. 2014, Astron. Nachr., 335, 817 [NASA ADS] [CrossRef] [Google Scholar]
  103. Quirion, P.-O., Christensen-Dalsgaard, J., & Arentoft, T. 2010, ApJ, 725, 2176 [NASA ADS] [CrossRef] [Google Scholar]
  104. Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
  105. Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
  106. Roxburgh, I. W. 2015, A&A, 574, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Roxburgh, I., & Vorontsov, S. 2003a, Ap&SS, 284, 187 [NASA ADS] [CrossRef] [Google Scholar]
  108. Roxburgh, I. W., & Vorontsov, S. V. 2003b, A&A, 411, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., Kupka, F., & Weiss, W. W. 1999, Phys. Scr. T, 83, 162 [NASA ADS] [CrossRef] [Google Scholar]
  110. Scardia, M., Prieur, J.-L., Pansecchi, L., et al. 2008, Astron. Nachr., 329, 54 [NASA ADS] [CrossRef] [Google Scholar]
  111. Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
  112. Schmitt, J. R., & Basu, S. 2015, ApJ, 808, 123 [NASA ADS] [CrossRef] [Google Scholar]
  113. Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
  114. Seaton, M. J. 2005, MNRAS, 362, L1 [NASA ADS] [CrossRef] [Google Scholar]
  115. Serenelli, A. M., & Basu, S. 2010, ApJ, 719, 865 [NASA ADS] [CrossRef] [Google Scholar]
  116. Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Silva Aguirre, V., Basu, S., Brandão, I. M., et al. 2013, ApJ, 769, 141 [NASA ADS] [CrossRef] [Google Scholar]
  118. Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
  119. Tokovinin, A., Mason, B. D., & Hartkopf, W. I. 2014, AJ, 147, 123 [NASA ADS] [CrossRef] [Google Scholar]
  120. Ulrich, R. K. 1986, ApJ, 306, L37 [NASA ADS] [CrossRef] [Google Scholar]
  121. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  122. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. VandenBerg, D. A., & Clem, J. L. 2003, AJ, 126, 778 [NASA ADS] [CrossRef] [Google Scholar]
  124. Vorontsov, S. V., Baturin, V. A., Ayukov, S. V., & Gryaznov, V. K. 2013, MNRAS, 430, 1636 [NASA ADS] [CrossRef] [Google Scholar]
  125. White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Main stellar and seismic parameters of HIP 93511.

In the text
Table 2

Parameters of the orbit using speckle interferometric observations of HIP 93511.

In the text
Table 3

Characteristics of each model set used for inferring the stellar parameters of the two stars.

In the text
Table 4

Stellar parameters of the two stars for all the models.

In the text
Table A.1

Frequencies for Star A.

In the text
Table A.2

Frequencies for Star B.

In the text
Table A.3

Mode linewidths, mode heights and mode amplitude for Star A.

In the text
Table A.4

Mode linewidths, mode heights and mode amplitude for Star B.

In the text
Table A.5

Speckle interferometric data of the orbital position of the binary.

In the text

All Figures

thumbnail Fig. 1

Power spectrum of the intensity fluctuations as a function of frequency smoothed with a 1-μHz boxcar, showing the mode power peak at 1200 μHz for Star A and at 2200 μHz for Star B (left), and a zoom in on that secondary spectrum (right).
In the text
thumbnail Fig. 2

Top panel: comparison between the observed spectrum (black solid line) and best fitting synthetic spectrum (red dashed line) calculated by combining the spectra of the two components (blue dash-dotted lines). The elements corresponding to the main spectral features are given on the top of the panel. For visualisation purposes, the legend has been put in the bottom panel. Bottom panel: LSD profile obtained from the observed ESPaDOnS spectrum.
In the text
thumbnail Fig. 3

Large frequency separation as a function of frequency for both stars (left Star A, right Star B): (plus) l = 0 modes, (black star) l = 1 modes, (green star) l = 2 modes.
In the text
thumbnail Fig. 4

Left: mode amplitude as a function of the order of the maximum mode power for Star A (black open diamond) and Star B (green open diamond). Right: mode linewidth as a function of the order of the maximum mode power for Star A (black open diamond) and Star B (green open diamond).
In the text
thumbnail Fig. 5

Correlation maps of the posterior probability following the Bayesian analysis of the orbit of HIP 93511: (top, left) The argument of the periastron (ω) vs. the longitude of the ascending nodes (Ω), (top, right) the semi-major axis a vs. the eccentricity e, (bottom, left) the orbital period T0 vs. the semi-major axis a, (bottom, right) the orbital period T0 vs. the periastron passage T1.
In the text
thumbnail Fig. 6

Orbit calculated with data shown with open diamonds. All points are drawn with line segments from the data point to the location of the ephemeris prediction on the orbital path. North is down and east is to the right.
In the text
thumbnail Fig. 7

Structural inversion for Star A: the sound speed a), density b), and buoyancy frequency c). Dashed green lines show a (re-scaled) model taken as an initial guess; solid green lines display the inverted result. Thin blue lines result from adding the measured frequencies with Gaussian noise, of variance corresponding to the reported uncertainties, in 10 realisations, to address the sensitivity of the inversion to random errors in the input data.
In the text
thumbnail Fig. 8

Seismic properties of the optimised models of Star A. Left panel: comparison of the observed frequency separation ratios r01 / 10(n) (models are the coloured lines). Right panel: comparison of the observed frequency separation ratios r02(n) (models are the coloured lines).
In the text
thumbnail Fig. 9

Seismic properties of the optimised model of Star B. Left panel: comparison of the observed frequency separation ratios r01 / 10(n) (models are the coloured lines). Right panel: comparison of the observed frequency separation ratios r02(n) (models are the coloured lines).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.