| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526298 | |
| Published online | 15 October 2015 | |
Solar-cycle variations of the internetwork magnetic field
UMR 7293 Lagrange, Université de Nice Sophia Antipolis, CNRS, Observatoire
de la Côte d’Azur,
Campus Valrose,
06108
Nice,
France
e-mail: marianne.faurobert; gilbert.ricort]@unice.fr
Received: 11 April 2015
Accepted: 28 July 2015
Context. The quiet Sun exhibits a rich and complex magnetic structuring that is still not fully resolved or understood.
Aims. We intend to contribute to the debate about the origin of the internetwork magnetic fields and whether or not they are related to the global solar dynamo.
Methods. We analyzed center-to-limb polarization measurements obtained with the SOT/SP spectropolarimeter onboard the Hinode satellite outside active regions in 2007 and 2013, that is, at a minimum and a maximum of the solar cycle, respectively. We examined 10′′ × 10′′ maps of the unsigned circular and linear polarization in the FeI 630.25 nm line in regions located away from network elements. The maps were corrected for bias and focus variations between the two data sets. Then we applied a Fourier spectral analysis to examine wether the spatial structuring of the internetwork magnetic fields shows significant differences between the minimum and maximum of the cycle.
Results. Neither the mean values of the unsigned circular and linear polarizations in the selected 10′′ × 10′′ maps nor their spatial fluctuation power spectra show significant center-to-limb variations. For the unsigned circular polarization the power of the spatial fluctuations is lower in 2013 than in 2007, but the spectral slope is unchanged. The linear polarization spectra show no significant differences in 2013 and 2007, but the spectrum of 2013 is more strongly affected by noise.
Conclusions. The small-scale magnetic structuring in the internetwork is different in our 2013 and 2007 data. Surprisingly, we find a lower spatial fluctuation power at the solar maximum in the internetwork magnetic structuring. This indicates some complex interactions between the small-scale magnetic structures in the quiet Sun and the global dynamo, as predicted by recent numerical simulations. This result has to be confirmed by further statistical studies with larger data sets.
Key words: techniques: high angular resolution / Sun: atmosphere / Sun: magnetic fields / Sun: photosphere / Sun: granulation
© ESO, 2015
1. Introduction
The quiet-Sun (QS) magnetic fields consist of network and internetwork (IN) elements. The network elements show strong fields of the order of kG and are located at the borders of the supergranular cells, while the IN elements, in the cell interior, show a distribution of field strengths with much weaker fields and mixed polarities at small scale (Sánchez Almeida & Martínez González 2011, for a review). A recent study by Gošić et al. (2014) from Hinode deep magnetograms at 0.3′′ spatial resolution estimated that 14% of the QS magnetic flux is in the form of internetwork elements.
The origin of the network and IN elements is unclear. Numerical simulations by Vögler & Schüssler (2007) and Steiner et al. (2008) have shown that the vigorous convective motions in the solar photosphere, where the dynamic pressure of the flows exceeds the magnetic pressure, can efficiently amplify the magnetic energy at small scales from a magnetic seed. In these simulations the dynamo action operates at the granular scale and the magnetic amplification mainly takes place in the turbulent flows of the intergranular lanes. However, it is unclear whether such a mechanism is really observed in the Sun because the magnetic strength derived from numerical simulations, for instance, seems to be significantly smaller than what is measured in the QS (Danilovic et al. 2010). We refer to Martínez Pillet (2013) for a critical review of numerical simulations as compared to QS magnetic field observations. Other possible sources of magnetic fields in the QS might be the turbulent dissipation of active regions present at large scale that is associated with the global solar dynamo, or different types of dynamo processes acting at larger scales (Solanki 2009; Rieutord & Rincon 2010; Stein 2012; Martínez Pillet 2013).
An interesting test to distinguish between a local or a global dynamo is to see whether the QS magnetic fields vary with the solar cycle, in relation with the global solar dynamo. However, such investigations on IN magnetic elements require very high spatial resolution and high polarimetric sensitivity measurements by a long-term stable instrument. The SOT/SP instrument (Lites et al. 2013) of the Solar Optical Telescope (SOT; Tsuneta et al. 2008) onboard the Hinode mission (Kosugi et al. 2007), which has been in operation since 2006, now provides the required facilities. Recently, Buehler et al. (2013) have analyzed linear and circular polarization maps obtained in very quiet regions of the internetwork at disk center from 2007 to 2013 with the Hinode/SP instrument. They neither found significant variations in polarization level nor in size distribution of the polarization patches with the solar cycle. Lites et al. (2014) investigated the center-to-limb variations of the circular and linear polarization signals measured in the very weakly polarized regions of the internetwork between 2008 and 2013 using the Hinode/SP irradiance program. They found no evidence for systematic changes as a function of time and solar latitude in either the weak unsigned line-of-sight flux or in the measures of the transverse flux. On the other hand, using the MDI data set of the entire solar cycle 23, Jin et al. (2011) have shown that the cyclic variation of both number and total flux of small-scale magnetic elements in the range ≃(3–30) ×1018 Mx are anticorrelated with sunspot number.
In this paper we also address the question of solar cycle variations of the QS magnetic fields, but we use a different approach. We use center-to-limb observations performed with Hinode/SP in December 2007 and 2013, that is, at a minimum and a maximum of the solar cycle, respectively. The observations on December 19, 2007 are part of the original irradiance survey program HOP 79 (later modified in 2008 for lower data rates, then continued in that mode to the present), where pole-to-pole scans with full spatial resolution (0.16′′/pixel) were performed. The data from December 7, 2013 are taken from a dedicated HOP where the same strategy was carried out with the full 0.16′′/pixel resolution. However, due to the limited data transfer rate, the polar regions were not observed in 2013. Maps of line-integrated unsigned circular and linear polarization in the FeI 630 nm lines were derived from these two observing runs, and we analyzed the Fourier power spectra of their spatial fluctuations.
One advantage of using Fourier spectra is that it is quite easy to implement procedures for correcting them for the noise affecting the signal and for the effect of possible focus variations of the instrument. A defocus modifies the modulation transfer function (MTF) of the instrument, which affects the Fourier spectra through a multiplicative function that can be quite easily modeled (it is a varying phase term over the entrance pupil of the telescope). If the noise is not correlated to the signal, the Fourier spectrum of the observed signal is the sum of the “true” signal spectrum and of the noise spectrum. The noise spectrum may be estimated from the polarization spectrum that is obtained in the continuum band. We remark that the effect of noise on the probability distribution function (PDF) of a signal is more difficult to deal with because the PDF of the observed signal is the convolution of the noise PDF with the true signal PDF.
The data analysis procedures we carried out are detailed in the second section of the paper. In the third part we extract two sets of 10′′ × 10′′ polarization maps from the observations made in 2007 and 2013, avoiding the network elements, and we apply a spatial Fourier analysis to explore their magnetic structuring. We first compare the average power of the polarization fluctuations in three spatial frequency bands corresponding to meso-granular, granular, and subgranular scales. Then we compute the ensemble average of the spectra and compare the results for the 2013 an 2007 data sets. We also compare the IN spectra with those obtained for the full original 130′′ × 30′′ maps of the data sets containing both network and IN elements.
2. Data analysis
2.1. Polarization maps
Starting with the level-1 SOT/SP spectra, we computed images of the unsigned circular and linear polarizations in the FeI 630.25 nm line. The wavelength-integrated unsigned circular polarization in the line is computed following Lites et al. (2014) as 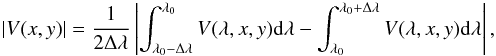 (1)and the linear polarization as
(1)and the linear polarization as 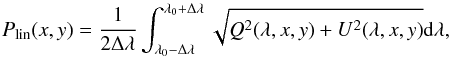 (2)where the wavelength λ0 is the line center position and 2Δλ is the spectral range where the line absorption is detected, that is, between [λ0−0.027 nm, λ0 + 0.027 nm] for the FeI 630.25 nm line. At each pixel along the spectrograph slit, we determine λ0 from the location of the minimum of the line intensity profile.
(2)where the wavelength λ0 is the line center position and 2Δλ is the spectral range where the line absorption is detected, that is, between [λ0−0.027 nm, λ0 + 0.027 nm] for the FeI 630.25 nm line. At each pixel along the spectrograph slit, we determine λ0 from the location of the minimum of the line intensity profile.
The wavelength-integrated linear polarization computed following Eq. (2) is affected by a bias because we accumulate the noise contribution when adding positive quantities. We estimated this bias by computing the linear polarization in the continuum band, where we assume that it is only due to the accumulation of noise.
Comparing the average continuum intensity of 2007 and 2013, we noticed that the efficiency of the detector has decreased by a factor 0.78 over this period of time. In the following, the polarization is normalized by the continuum intensity so that this loss of efficiency does not affect the results.
2.2. Polarization spatial power spectra
We compared the Fourier spectra of the polarization spatial fluctuations for the 2007 and 2013 data. The use of Fourier spectra instead of direct image investigations and PDF estimates allows addressing two important effects of the signal processing, namely the effect of noise and the effect of a possible variable defocus of the instrument. The Fourier transform of a 2D signal S(x,y) is defined by 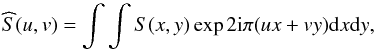 (3)and its spatial power spectrum by
(3)and its spatial power spectrum by 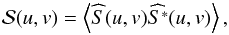 (4)where the symbol ⟨⟩ denotes an ensemble average and
(4)where the symbol ⟨⟩ denotes an ensemble average and 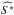 is the complex conjugate of
is the complex conjugate of 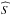 .
.
The spatial fluctuations of the signal are then most of the time studied by considering the radial average of the 2D Fourier spectrum, which is obtained through 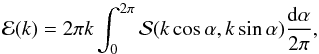 (5)where the spatial wavenumber
(5)where the spatial wavenumber 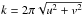 is related to the spatial wavelength λs of the fluctuations by k = 2π/λs.
is related to the spatial wavelength λs of the fluctuations by k = 2π/λs.
We remark here that the radial average of the 2D power spectrum provides meaningful information about the spatial structuring only when the signal is isotropic on average (in the sense of the ensemble average). For solar images observed away from disk center, the projection effect leading to foreshortening of the images in the radial direction has to be accounted for. We took this effect into account by averaging the 2D power spectra over elliptical bands instead of circular ones. A second effect, of instrumental origin, leads to anisotropy in the 2D power spectra when the discretization of the images by the CCD camera does not obey the Shannon criteria. This effect, referred to as spectral aliasing, is likely to take place in SOT/SP image spatial power spectra because the pixel size of the camera (0.16′′) is larger than half the spatial resolution of the SOT telescope (λ/D = 0.26′′ with λ = 630 nm and D = 0.5 m). This effect is imprinted on the MTF of the instrument, as illustrated in Fig. 1. This figure shows a 3D view of the MTF of the instrument, computed on a grid of 64 × 64 pixels. The MTF is given by the autocorrelation of the entrance pupil of the instrument. We considered a 0.5-m circular pupil with the SOT central obscuration. In Fig. 1 we show the MTF for the case where the pixel size obeys the Shannon criteria (0.13′′/pixel) and the effective MTF of SOT/SP with a spatial sampling of 0.16′′/pixel. In the spectral domain, the pixel sizes are 1/(64 × 0.13) arcsec-1 and 1/(64 × 0.16) arcsec-1, respectively. We note that the undersampling leads to anisotropy of the MTF and that it does not reach zero at the highest spatial frequency on the u and v axis. This will lead to an overestimate of the spatial power spectra at high spatial frequencies. We now address this problem.
 |
Fig. 1 MTF of the SOT/SP instrument. The (u,v) unit is given in pixels. The upper panel shows the data with image sampling of 0.13′′/pixel according to Shannon criteria, in spatial frequency units one pixel is 1/(64 × 0.13) arcsec-1. The lower panel shows the data with undersampling of the images (0.16′′/pixel), the pixel size in spatial frequency units is 1/(64 × 0.16) arcsec-1. |
2.3. Modified radial averaging for undersampled power spectra
A careful inspection of Fig. 1 shows that the alteration of the MTF due to undersampling appears at high spatial frequencies in some parts on the (u,v) plane, but that it is unchanged in the corners of the plane, namely for values of the integration angle α of Eq. (5) close to ± π/ 4 and ± 3π/ 4. We propose to restrict the angle integration of 2D power spectra to the domains were the MTF is not affected by the undersampling distortion. We checked that integrating on four intervals π/ 6-wide around the four corners of the (u,v) plane gives much better results for the radial spectra than integrating over the full angular domain. This is illustrated in Fig. 2, where we show the radial spectrum of the continuum intensity at disk center derived with both methods. We clearly see the aliasing effect when the standard method is used; in that case, the intensity spectrum saturates at high spatial frequencies, whereas it continues to decrease when we use the modified radial averaging method.
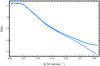 |
Fig. 2 Radial power spectrum of the continuum intensity at disk center in Log-Lin scales. The full line represents the standard averaging method, the dashed line the modified averaging. |
2.4. Defocus
Buehler et al. (2013) pointed out that the focusing of the SOT telescope varies slightly with time and that this can affect the polarization measurements at small scales. The effect of a defocus of the instrument is equivalent to multiplying the entrance pupil with the phase term exp [(2iπ/λ)(x2 + y2) /F] , which would be produced by a lens of focal length F. We computed the MTF for various values of the defocus, also taking into account the undersampling of the camera.
To check for focus variation between the observation runs in 2007 and 2013, we computed the power spectra of the continuum intensity in both data sets for images at the center of the solar disk. Assuming that the continuum intensity patterns do not vary significantly with the solar cycle, we may ascribe the difference of the power spectra to instrumental effects, in particular to focus variations, writing 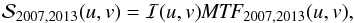 (6)we obtain
(6)we obtain 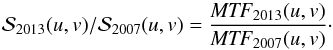 (7)In Fig. 3 we show the radial averages (standard and modified) of both the ratio MTF2013/MTF2007 (for different values of the phase term) and the ratio of the continuum intensity power spectra in 2013 and 2007 data. We see that the shape of the continuum intensity spectrum has changed between 2007 and 2013 (the ratio varies with the spatial frequency), and that the change is quite well explained in the low- and mid-spatial frequency ranges if we account for a defocus of the instrument between the two observing runs. The comparison shown in Fig. 3 indicates a relative phase between 1.2π and 1.4π, corresponding to a relative defocus of 0.58 mm to 0.67 mm (about three to four steps of the focus mechanism within the SOT focal plane package). At high spatial frequencies we note a significant increase of the radial average of the power spectrum in 2013 that cannot be explained by a defocus effect. This may be due to an increase of the noise level in 2013 data with respect to those in 2007 or to a real increase of the continuum intensity fluctuations at small scales.
(7)In Fig. 3 we show the radial averages (standard and modified) of both the ratio MTF2013/MTF2007 (for different values of the phase term) and the ratio of the continuum intensity power spectra in 2013 and 2007 data. We see that the shape of the continuum intensity spectrum has changed between 2007 and 2013 (the ratio varies with the spatial frequency), and that the change is quite well explained in the low- and mid-spatial frequency ranges if we account for a defocus of the instrument between the two observing runs. The comparison shown in Fig. 3 indicates a relative phase between 1.2π and 1.4π, corresponding to a relative defocus of 0.58 mm to 0.67 mm (about three to four steps of the focus mechanism within the SOT focal plane package). At high spatial frequencies we note a significant increase of the radial average of the power spectrum in 2013 that cannot be explained by a defocus effect. This may be due to an increase of the noise level in 2013 data with respect to those in 2007 or to a real increase of the continuum intensity fluctuations at small scales.
 |
Fig. 3 The thick full curve represents the standard radial average of the ratio of the continuum intensity power spectra at disk center in 2013 and 2007 data, the thick dashed curve the modified radial average. The thin curves indicate the modified radial average of MTF ratio for various defocus. The dashed line plots the relative phase default of 1.4π, the full line the relative phase default of 1.2π, and the dotted line the relative phase default of π. |
2.5. Noise
If the noise is not correlated with the signal, the power spectrum of the observed signal is the sum of the true signal spectrum and of the noise spectrum. As the continuum band should not show any polarization, we estimate that the noise spectra are well represented by the polarization spectra recorded in the continuum band. In the following we therefore eliminate the noise from the line polarization spectrum by subtracting the continuum polarization spectrum. However, this procedure is only valid when the signal-to-noise ratio is significantly higher than one; in the opposite situation, when signal and noise are on the same order of magnitude, the errors on the noise estimate become on the same order of magnitude as the signal, and it is not possible to apply this simple correction procedure. We encountered this problem when treating the linear polarization spectrum of the FeI 630.15 nm line where the signal-to-noise ratio is on the order of unity at high spatial frequencies. As this line is less sensitive to magnetic fields than the FeI 630.25 nm line, we chose in this study to concentrate on the 630.25 nm data alone.
We also remark that the noise on the integrated | V | is smaller than the noise per pixel of wavelength because we added the V signal over each line wing (see Eq. (1)), that is, typically on 14 wavelength pixels. This means that the noise level on the line-wing integral is lower by a factor 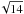 than the noise/pixel. When subtracting the two line-wing integrals, the noise is multiplied by a factor
than the noise/pixel. When subtracting the two line-wing integrals, the noise is multiplied by a factor 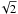 . We therefore estimate that the noise on the integrated unsigned circular polarization is on the order of the noise per wavelength pixel divided by
. We therefore estimate that the noise on the integrated unsigned circular polarization is on the order of the noise per wavelength pixel divided by 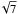 . For the linear polarization we integrated on positive quantities (see Eq. (2)), which means that the noise is not averaged out, the noise level on the integral is on the order of the noise per wavelength pixel.
. For the linear polarization we integrated on positive quantities (see Eq. (2)), which means that the noise is not averaged out, the noise level on the integral is on the order of the noise per wavelength pixel.
 |
Fig. 4 Mean value of the polarization in our 98 IN images. Triangles represent 2013 data, black circles the 2007 data. The upper panel shows the unsigned circular polarization, the lower panel the linear polarization after bias correction. |
3. Internetwork magnetic structuring
To isolate the weak IN from the network fields, we extracted two sets of 10′′ × 10′′ images from the data of 2007 and 2013. They were selected by locating in the unsigned circular polarization maps of the QS the areas that showed the weakest average signal over 10′′ × 10′′ surfaces. This was achieved by computing the sliding averages over 10′′ × 10′′ regions in the 130′′ × 30′′ maps of our two data sets and by selecting the regions with the lowest mean values in each map. We chose to retain seven regions in each QS map. This procedure allowed us to select 98 regions with low unsigned circular polarization signals that were evenly distributed along the south-north polar axis.
Figure 4 shows the values of the mean unsigned circular and linear polarization (after bias subtraction) in the 98 images of these two sets as functions of the heliocentric angle. Because in December the solar B angle is close to zero, the heliocentric angle is equal to the solar latitude. We did not observe any significant center-to-limb variations for either our 2007 or our 2013 data sets, but did detect some fluctuations around a mean value from one image to another, neither did we detect any significant differences between the distributions of the values at the two dates. However, we notice that the lowest values of the unsigned circular polarization in 2007 are somewhat lower than the lowest values in 2013. We did not observe any enhancements of the unsigned circular polarization close to the activity belts in the 2013 data, but the linear polarization of some IN maps in 2013 may be affected by the effects of active region remnants, giving rise to some enhancement of their mean linear polarization at | sinθ | ≃ 0.6.
Lites et al. (2013) reported synoptic maps of the weak IN that showed a center-to-limb increase of the unsigned circular polarization in the weak IN elements (their Fig. 4d) together with a center-to-limb decrease of the linear polarization (their Fig. 7b). The results shown in Fig. 4 do not allow us to confirm or to contradict these findings because our selection criteria are quite different. We here consider mean values of the polarization signals over 10′′ × 10′′ areas, whereas in Lites et al. (2013), the selected IN elements form a collection of isolated patches with much smaller sizes.
In our sets of images we did not detect any significant center-to-limb variations of the average unsigned circular or linear polarizations. This indicates that the average vertical and horizontal magnetic components on scales on the order of 10 arcsec are statistically identical in the IN.
Then we computed the polarization Fourier spectra of the 10′′ × 10′′ selected images to obtain their spectrum at spatial scales between 10′′ and 0.3′′. To easily compare the center-to-limb behavior of the spectra, we considered the average fluctuation power over three spatial frequency bands, namely the low-frequency (LF) band (spatial frequencies lower than 0.5 arcsec-1), the mid-frequency (MF) band (spatial frequencies between 0.5 and 2 arcsec-1), and the high-frequency (HF) band (spatial frequencies higher than 2 arcsec-1). This corresponds to meso-granular, granular, and subgranular scales, respectively.
We estimated the noise spectrum from the spectrum computed in the continuum and removed it from the FeI 630.25 nm line polarization spectrum. We also corrected the spectra for the focus variation between the 2007 and 2013 observations.
 |
Fig. 5 Average power of the unsigned circular polarization fluctuations in the 98 IN images for three spatial frequency bands on a Log scale. Circles represent the 2007 data set, triangles that of 2013. The dashed line indicates the average value in 2007, the dotted lines the average value in 2013. The upper panel shows the meso-granular scales, the middle panel the granular scales, and the lower panel the subgranular scales. |
The results are shown in Figs. 5 and 6 for the unsigned circular polarization and the linear polarization, respectively. In the three spatial frequency bands the power of the polarization fluctuations shows variations from one image to another with a random-like dispersion around a mean value and no significant center-to-limb variations. The mean values in 2007 are stronger than in 2013, but the difference is on the same order as the dispersion of the values. We note that for the linear polarization the fluctuation power in some of the selected images is very close to the noise level (resulting in very low mean fluctuation levels after noise correction in the three bands for some of the IN maps in our selections). We return to this point below.
Since the polarization fluctuation power in the three spatial scale bands does not vary significantly with the location of the IN image, we performed an ensemble averaging of the 98 spectra that probably is representative of the spatial structuring of the polarization in the IN. Figure 7 shows the spectra in the FeI 630.25 nm line before noise subtraction together with the noise spectra derived from the continuum band, as explained in Sect. 2. We also show the effect of the defocus correction on the 2007 spectra. We observe that the rms noise has increased by a factor 2.5 in 2013 with respect to 2007.
The signal-to-noise ratio for the unsigned circular polarization spectrum is on the order of 100 to 1000 at large scales and decreases at small scales, where it is on the order of 10 to 20. The signal-to-noise ratio of the linear polarization power spectrum was on the order of 10 in 2007 and 2 in 2013. The noise-correction procedure is thus barely valid for the linear polarization in 2013 data, and the noise-corrected spectra are still affected by the inaccuracy of the noise fluctuation estimate.
We note that the relative defocus of the 2007 observations only has a weak effect on the polarization spectra. At spatial scales smaller than one arcsecond, it decreases the measured polarization fluctuation power by a factor 0.88.
The spectra obtained after noise subtraction are shown in Fig. 8, where we also show the standard deviations over the 98 IN regions of our data sets. For the linear polarization, the radial spectra show a constant power at all resolved scales, suggesting a noise-like behavior without a characteristic spatial scale, and the difference between the 2007 and 2013 spectra in our data sets is not significant. We note that the strong rms-fluctuations of the 2013 spectrum are due to a poor signal-to-noise ratio.
The situation is different for the unsigned circular polarization, where the signal-to-noise ratio is good. We observe that the power of the fluctuations is weaker in 2013, but the spectral slope has not changed. The difference between the averaged spectra is marginally significant, it is on the same order of magnitude as the dispersion of the individual spectra of the different IN images in our data sets.
 |
Fig. 7 Power spectra of the polarization spatial fluctuations averaged over the 98 IN images in our data sets. The thick full line represents the 2007 data corrected for defocus, the thick dashed linethe 2013 data corrected for defocus, and the dark dotted line the 2007 data without defocus correction. The thin full line indicates the 2007 continuum corrected for defocus, the thin dashed line the 2013 continuum corrected for defocus, and the thin dotted line the 2007 continuum without defocus correction. The upper panel shows the unsigned circular polarization, the lower panel the linear polarization. |
 |
Fig. 8 Power spectra of the polarization spatial fluctuations in the IN corrected for noise and defocus (see text) shown on log-lin scales. The errors bars show the standard deviations over the 98 IN images in our data sets. The full line represents the 2007 data, the dashed lines the 2013 data. The upper panel shows the unsigned circular polarization, the lower panel the linear polarization. |
 |
Fig. 9 Comparison of the unsigned circular-polarization-reduced spectra in the IN and in the QS maps. The thick full line represents 2007 IN data, the thick dashed lines the 2013 IN data, the thin full line the 2007 QS maps, and the thin dashed line the 2013 QS maps. The curves are shown on log-lin scales. |
We also computed reduced spectra for the unsigned circular polarization by dividing the spectrum of each image by the square of the mean polarization over the image. Reduced spectra are related to the contrast of the structures. It is interesting to compare the IN reduced spectra with the reduced spectra of the full QS maps obtained from the original 130′′ × 30′′ scans. We verified that the reduced spectra of the unsigned circular polarization maps in the QS show very little center-to-limb variations, therefore we averaged the spectra that were obtained from 14 scans along the south-north polar axis. Each spectrum was obtained from an ensemble average of 12 spectra over 20′′ × 20′′ regions covering the full 130′′ × 30′′ map. Using 20′′ × 20′′ surfaces in the QS instead of 10′′ × 10′′ as in the IN allowed us to explore the spatial structuring of the QS up to larger spatial scales and to increase the spectral resolution of the Fourier spectrum. This is clear in Fig. 9, where the spatial frequency grid for the QS spectra is twice as fine as the IN grid. This does not change the behavior of the spectrum, however. The IN and QS reduced spectra are compared in Fig. 9, where we also show their standard deviations. The QS maps contain both network and IN elements, but their polarization spectrum is mainly affected by network elements that contribute to more than 80 percent of the magnetic flux (Gošić et al. 2014). First, we observe that the difference between the reduced IN spectra in 2013 and in 2007 now appears clearly; the difference is significantly larger than the standard deviation in both data sets. We find that the contrast fluctuations of the IN structures in 2013 are lower than in 2007 by a factor 1.7, but the slopes of the two spectra are identical. We also note that the spectra do not show a maximum at granular scales, but continue to increase at meso-granular scales.
For the full QS the reduced spectra are identical in 2007 and 2013, except at large scales (typically at scales larger than 2 arcsec), where the power of the fluctuations is greater in 2013. The power of the reduced fluctuations at large scale is on the same order of magnitude in the IN and in the QS, but the spectral slope is larger in the QS, where we observe a stronger decrease of the fluctuation power at granular and subgranular scales.
The recent paper by Gošić et al. (2014), based on high-resolution and high-sensitivity Hinode magnetograms, shows how the IN magnetic elements move toward the network boundaries and interact with the network elements by either cancellation or merging. The authors found that merging is the dominant mechanism and that the IN continuously supplies flux to the network. According to their estimate, the total magnetic flux contained in the network can be completely refreshed by the contribution of the IN in less than 24 h, and IN elements are the main contributors to the network flux. The merging processes can lead to different spectral shapes in IN and network magnetic structures. However, the increase of the magnetic fluctuations at large scales in the network in our 2013 data is probably due to the additional contribution of active region remnants that would add magnetic flux at meso-granular scales in the network, but not in the IN.
4. Conclusion
It is not straightforward to compare our results with the findings of Lites et al. (2014) and Buehler et al. (2013) because the methods we used are very different. The spectral analysis uses a whole image to analyze its polarization structures at various scales, it also allows performing ensemble averages on similar images. The effect of noise can be corrected for more easily if the signal-to-noise ratio is high enough than on PDF estimates from polarization maps. As the solar-cycle variation that we found is a weak effect on the polarization spatial fluctuation power spectrum, it is probably hardly seen on the PDF of the IN magnetic flux, which is affected by some noise convolution.
Both Lites et al. (2014) and Buehler et al. (2013) found no significant variations of the polarization signals in the weak IN elements with the solar cycle. In our data the average polarization signals appear to be slightly stronger in 2013 than in 2007, but the difference is only marginally significant as compared to the map-to-map variations of the values. This means that our results do not contradict theirs in this point.
Our main new contribution is that we investigated the power of the polarization spatial fluctuations at small scales in IN maps. We found that the polarization fluctuation power at meso-granular, granular, and subgranular scales is independent of the heliocentric angle. This is in favor of statistically isotropic fluctuations of the vertical and horizontal magnetic components at all resolved scales. This agrees with the results obtained by various authors from the inversion of spectropolarimetric observations, for example, in Asensio Ramos & Martínez González (2014).
The linear polarization spectra in IN regions are affected by a high noise level that is higher in 2013. We did not detect any significant difference between our 2007 and 2013 data sets. For the unsigned circular polarization we detected a marginally significant difference between the power spectra in 2013 and 2007, indicating that the power of the fluctuation is weaker in 2013, but that the spectral shape is similar.
The comparison between the unsigned circular polarization reduced spectra (obtained after dividing the polarization map by the average polarization in the map) in the IN also shows similar spectral shapes in 2007 and in 2013 data, but the power of the reduced fluctuations is significantly weaker in 2013 data. We also compared the reduced spectra of the unsigned circular polarization in the IN and in QS maps, which are mainly affected by network elements. We found that the spectral shapes are significantly different, with a stronger decrease of the reduced fluctuations at small scales in the network than in the IN.
This is consistent with previous investigations by Gošić et al. (2014), showing that the IN is the main contributor to network magnetic flux, where the dominant process is the merging of IN elements to form network elements. In this merging process the spectral slope would tend to increase as some small-scale IN elements are lost when they merge to form elements on larger scales in the network.
In our data we also observed an increase of power of the unsigned circular polarization fluctuations at meso-granular scales in the network in 2013 with respect to 2007. We may ascribe this effect to an additional contribution of magnetic flux to the network due to active region remnants that would not affect the IN.
Finally, we remark that the images that we analyzed were obtained from scans of the solar surface, which means that the structures may evolve during the scanning time. In the 2007 observing run, the scanning time for a 10′′ × 10′′ surface was 320 s, whereas it was 640 s in 2013 (the exposure time was multiplied by a factor 2). If some IN elements evolve on timescales shorter than 640 s and longer than 320 s, they may “disappear” from the polarization spectrum in 2013. However, such an effect would likely affect the slope of the spectrum because small IN elements would probably tend to evolve faster than larger ones. This needs to be clarified by using polarization maps obtained from narrow-band filters.
We have detected some variations of the IN magnetic structuring between the maximum and the minimum of the solar cycle. This implies some interactions between the magnetic fields at small scales in the QS and the global dynamo. But if this is the case, the mechanism is not simply the dissipation of active regions, because we found a decrease of the polarization fluctuation power at the solar maximum in the IN. The decrease that we observed could instead be due to some back effect of large-scale magnetic fields on the power of the convective motions in the photosphere and below. In the recent paper by Karak & Brandenburg (2015), three-dimensional dynamo simulations are developed for different parameter regimes. It shows that depending on the dynamo parameters, large-scale and small-scale dynamos may be excited independently. Furthermore, in situations where the large-scale (global) magnetic field is stronger than the equipartition value, an anticorrelation is observed between the small-scale field and the large-scale magnetic cycle.
According to the authors, this anticorrelation can be interpreted as a suppression of the small-scale dynamo at the maximum of the global activity cycle. Our observational results thus indicate that this regime is indeed relevant for the solar dynamo.
However, further studies on larger data sets at various times over the solar cycle are necessary to confirm our results.
Acknowledgments
We thank Bruce Lites for his help in the process of submitting our 2013 observation proposal to the Hinode scientific board and for his comments on the manuscript. We also thank the anonymous referee for useful questions and comments. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway).
References
- Asensio Ramos, A., & Martínez González, M. J. 2014, A&A, 572, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buehler, D., Lagg, A., & Solanki, S. K. 2013, A&A, 555, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010, A&A, 513, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gošić, M., Bellot Rubio, L. R., Orozco Suárez, D., Katsukawa, Y., & del Toro Iniesta, J. C. 2014, ApJ, 797, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, C. L., Wang, J. X., Song, Q., & Zhao, H. 2011, ApJ, 731, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Karak, B. B., & Brandenburg, A. 2015, ApJ, submitted [arXiv:1505.06632] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Akin, D. L., Card, G., et al. 2013, Sol. Phys., 283, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Centeno, R., & McIntosh, S. W. 2014, PASJ, 66, 4 [Google Scholar]
- Martínez Pillet, V. 2013, Space Sci. Rev., 178, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 2 [Google Scholar]
- Sánchez Almeida, J., & Martínez González, M. 2011, in Solar polarization 6, eds. J. R. Kuhn, D. M. Harrington, H. Lin, et al., ASP Conf. Ser., 437, 451 [Google Scholar]
- Solanki, S. K. 2009, in Solar polarization 5: In honor of Jan Stenflo, eds. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 135 [Google Scholar]
- Stein, R. F. 2012, Liv. Rev. Sol. Phys., 9, 4 [Google Scholar]
- Steiner, O., Rezaei, R., Schaffenberger, W., & Wedemeyer-Böhm, S. 2008, ApJ, 680, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 MTF of the SOT/SP instrument. The (u,v) unit is given in pixels. The upper panel shows the data with image sampling of 0.13′′/pixel according to Shannon criteria, in spatial frequency units one pixel is 1/(64 × 0.13) arcsec-1. The lower panel shows the data with undersampling of the images (0.16′′/pixel), the pixel size in spatial frequency units is 1/(64 × 0.16) arcsec-1. |
| In the text | |
 |
Fig. 2 Radial power spectrum of the continuum intensity at disk center in Log-Lin scales. The full line represents the standard averaging method, the dashed line the modified averaging. |
| In the text | |
 |
Fig. 3 The thick full curve represents the standard radial average of the ratio of the continuum intensity power spectra at disk center in 2013 and 2007 data, the thick dashed curve the modified radial average. The thin curves indicate the modified radial average of MTF ratio for various defocus. The dashed line plots the relative phase default of 1.4π, the full line the relative phase default of 1.2π, and the dotted line the relative phase default of π. |
| In the text | |
 |
Fig. 4 Mean value of the polarization in our 98 IN images. Triangles represent 2013 data, black circles the 2007 data. The upper panel shows the unsigned circular polarization, the lower panel the linear polarization after bias correction. |
| In the text | |
 |
Fig. 5 Average power of the unsigned circular polarization fluctuations in the 98 IN images for three spatial frequency bands on a Log scale. Circles represent the 2007 data set, triangles that of 2013. The dashed line indicates the average value in 2007, the dotted lines the average value in 2013. The upper panel shows the meso-granular scales, the middle panel the granular scales, and the lower panel the subgranular scales. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for the linear polarization. |
| In the text | |
 |
Fig. 7 Power spectra of the polarization spatial fluctuations averaged over the 98 IN images in our data sets. The thick full line represents the 2007 data corrected for defocus, the thick dashed linethe 2013 data corrected for defocus, and the dark dotted line the 2007 data without defocus correction. The thin full line indicates the 2007 continuum corrected for defocus, the thin dashed line the 2013 continuum corrected for defocus, and the thin dotted line the 2007 continuum without defocus correction. The upper panel shows the unsigned circular polarization, the lower panel the linear polarization. |
| In the text | |
 |
Fig. 8 Power spectra of the polarization spatial fluctuations in the IN corrected for noise and defocus (see text) shown on log-lin scales. The errors bars show the standard deviations over the 98 IN images in our data sets. The full line represents the 2007 data, the dashed lines the 2013 data. The upper panel shows the unsigned circular polarization, the lower panel the linear polarization. |
| In the text | |
 |
Fig. 9 Comparison of the unsigned circular-polarization-reduced spectra in the IN and in the QS maps. The thick full line represents 2007 IN data, the thick dashed lines the 2013 IN data, the thin full line the 2007 QS maps, and the thin dashed line the 2013 QS maps. The curves are shown on log-lin scales. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


