| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526081 | |
| Published online | 19 October 2015 | |
Making the observational parsimonious richness a working mass proxy
INAF–Osservatorio Astronomico di Brera, via Brera 28,
20121
Milano,
Italy
e-mail:
stefano.andreon@brera.inaf.it
Received: 12 March 2015
Accepted: 5 August 2015
Richness, i.e., the number of bright cluster galaxies, is known to correlate with the cluster mass, however, to exploit it as mass proxy we need a way to estimate the aperture in which galaxies should be counted that minimizes the scatter between mass and richness. In this work, using a sample of 39 clusters with accurate caustic masses at 0.1 <z< 0.22, we first show that the scatter between mass and richness derived from survey data is negligibly small, as small as best mass proxies. The scatter turns out to be smaller than in some previous works and has a 90% upper limit of 0.05 dex in mass. The current sample, adjoining 76 additional clusters analyzed in previous works, establishes an almost scatterless, minimally evolving (if at all), mass-richness scaling in the redshift range 0.03 <z< 0.55. We then exploit this negligible scatter to derive the reference aperture to be used to compute richness and to predict the mass of cluster samples. These predicted masses have a total 0.16 dex scatter with caustic mass, about half of which is not intrinsic to the proxy, but related to the noisiness of the caustic masses used for test proxy performances. These results make richness-based masses of best quality and available for large samples at a low observational cost.
Key words: galaxies: clusters: general / cosmological parameters
© ESO, 2015
1. Introduction
In the next few years, numerous optical and near-infrared surveys, e.g., the Panoramic Survey Telescope and Rapid Response Systems (Kaiser et al. 2010), the Dark Energy Survey (Abbott et al. 2005), Large Synoptic Survey Telescope (Ivezic et al. 2008), Hyper-Suprime Camera (Takada 2010), and Euclid (Laureijs et al. 2011) are expected to generate galaxy catalogs over several thousands of square degrees to sufficient depth to reliably detect galaxy clusters up to z ~ 2. Indeed, the most distant cluster, JKCS 041 at z = 1.803 (Andreon et al. 2009; 2014; Newman et al. 2014) has been discovered on the UKIRT infrared deep sky survey (Lawrence et al. 2007) and Euclid will reach deeper magnitudes over one thousand times wider fields (Laureijs et al. 2011).
One of the main goals of these surveys is to probe the expansion history of the Universe and place tight constraints on cosmological parameters using galaxy clusters. For example, accurate measurements of cluster abundance as a function of cluster mass and redshift can provide important constraints on cosmological parameters such as σ8 and w (see, e.g., Vikhlinin et al. 2009). However, the mass of a galaxy cluster is not directly measurable. These surveys will therefore rely on mass proxies and scaling relations between these observables and mass. Calibration of mass-observable scaling relations is therefore currently a high-priority observational goal because the use of galaxy clusters as cosmological probes is currently limited by our ability to relate observable properties and cluster mass through so-called observable-mass relations. For example, the major source of uncertainty in cosmological estimates by South Pole Telescope clusters is the currently available mass-proxy calibration, not sample size (Reichardt et al. 2013).
For photometric surveys, optical richness is the primary mass proxy, although stellar mass (i.e., the total cluster luminosity) has also been proposed as accurate alternative (Andreon 2012). The former has a scatter of 0.18 dex with mass (Andreon & Hurn 2010, revised downward in Sect. 3.1), the latter has 90% upper limit scatter of 0.06 dex. These performances are however those achieved with knowledge of the radius in which galaxies have to be counted and are expected to degrade when this information is not available, i.e., when richness is used as a mass proxy. Indeed, richness has a 0.29 dex scatter with mass when r200 is inferred from photometric data (Andreon & Hurn 2010, revised downward in Sect. 3.2),which is much worse than if r200 were known. Observables with large scatter are particularly problematic because of the sensitivity of cluster abundance on the uncertainty in the scatter of the mass-observable relation (Lima & Hu 2005), and the latter are expected to increase with scatter. Consequently, a richness estimator that minimizes the scatter in the richness-mass relation is highly desirable to minimize the dilution of the cosmological information.
Therefore, an ideal mass proxy should be characterized by a low intrinsic scatter with cluster mass. It should also satisfy two more requirements. First, the proxy should be observationally parsimonious to obtain: low-scatter mass proxies are of little utility if they are unavailable because they require the acquisition of data challenging to obtain or their measurement is unfeasible. Second, the proxy should be relatively insensitive to the cluster dynamical state: a proxy that heavily relies on hydrostatic or dynamical equilibrium, as some X-ray mass observables, is of low utility for most of the clusters.
Once obtained, mass proxies need to be calibrated. Gravitational lensing offers a way to calibrate the richness-mass relation with the key advantage that the derived cluster mass does not rely on the assumption of hydrostatic or dynamical equilibrium. However, converting the lensing observable (reduced shear) into mass is challenging, as is nicely illustrated in detail by Hoekstra et al. (2015) and also is summarized in Andreon (2015a). Furthermore, the weak-lensing signal is also sensitive to mass in other structures “close” to the cluster (within say 1000 Mpc, because the weak-lensing signal changes little on these scales) such as large-scale-structure. By measuring the total mass projected along a long line of sight, lensing masses have an unavoidable minimal uncertainty of 20 to 50% (Meneghetti et al. 2010; Becker & Kravtsov 2011) because of cluster asphericity and large-scale structure.
Caustics (Diaferio & Geller 1997; Diaferio 1999) are also observationally demanding, because caustics rely on measurements of the escape velocity of galaxies, and are not affected by the cluster non-equilibrium, as weak lensing. Furthermore, and in contrast to the latter, caustics are not affected by the correlated large-scale structures along the line of sight (Diaferio 1999; Serra et al. 2011; Geller et al. 2013) because removing background/foreground at Δv> 3000 km s-1 is straightforward with spectroscopy that is needed anyway for caustics. This is magnificently illustrated by the cluster pair MS0906.5+1110/Abell 750: these clusters are offset by only 3000 km s-1 and are almost on the same line of sight. Caustics easily distinguish the two objects and two entries are found in Rines et al. (2013) mass catalog. Instead, lensing does not distinguish the two clusters and one single entry is found in Hoekstra et al. (2015) catalog, with mass given by the sum of the two clusters.
In this paper, we use an X-ray selected sample of 39 clusters with accurate caustic masses at 0.1 <z< 0.22 to improve upon our past mass-richness calibration (Andreon & Hurn 2010) and we show that the scatter between mass and richness derived from survey data is negligibly small, and indeed smaller than quoted in previous works. Our current analysis benefits of an improved understanding of caustic errors (Serra et al. 2011). We then exploit this negligible scatter to derive the reference aperture to be used to compute richness and to predict the mass of cluster samples, outperforming our (and other people) previous works. Finally, we compare the performances of richness and of a much advertised low-scatter mass proxy, the pseudo-pressure YSZ. The purpose of this work is not to find the optimal overdensity Δ, which minimizes the scatter between predicted and true mass with a variable Δ. Instead, we assumes that MΔ = 200 is the target mass, and look at minimizing the scatter with this mass at this fixed overdensity.
Throughout this paper, we assume ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s-1 Mpc-1. Magnitudes are in the AB system. We use the 2003 version of Bruzual & Charlot (2003, hereafter BC03) stellar population synthesis models with solar metallicity, a Salpeter initial mass function (IMF) and a zf = 3. Results of stochastic computations are given in the form x ± y, where x and y are the posterior mean and standard deviation. The latter also corresponds to 68% intervals because we only summarized posteriors close to Gaussian in this way. All logarithms are in base 10.
2. Samples and data
2.1. The cluster sample
Our starting point is the Hectospec Cluster Survey (HECS, Rines et al. 2013) cluster catalog. Clusters are: a) X-ray flux-selected; b) with 0.1 <z< 0.3 (to allow a good caustic measurement); and c) in the SDSS DR6 footprint. The cluster catalog lists the cluster center, radius r200, and mass within r200, M200, derived by the caustic technique1 (Diaferio & Geller 1997; Diaferio 1999). These masses have, as mentioned, the advantage of not assuming the hydrostatic equilibrium or the relaxed status of the cluster and are computed using, on average, 177 member galaxies per cluster. These masses are three-dimensional (i.e., refer to the mass inside the sphere of radius r200) and are derived assuming a spherical geometry. On the other hand, and similar to other mass estimates, the computation of their uncertainty is challenging (Serra et al. 2011; Gifford et al. 2013). Because of the finite sampling of the velocity field, these masses have a ~20% error (Serra et al. 2011). We adopt this figure, instead of the noisier and suspect (too small) values listed in Rines et al. (2013), and we account for the lack of precise knowledge of the true error, allowing the latter to be 95% of the times within a factor of 2 of the value derived from simulations (20%) and marginalizing over this source of uncertainty (see Andreon & Hurn 2010 concerning how to deal with noisy errors).
From the HECS cluster catalog we only keep clusters whose (passively evolved) limiting magnitude MV,z = 0 = −20 mag is brighter than r = 20 mag, a conservative completeness value of the SDSS (Ivezic et al. 2002). This reduced the sample to clusters with 0.10 <z ≲ 0.22, where the precise upper end depends on the value of the Galactic extinction in the cluster direction. From this sample, we only removed three clusters: a) the cluster pair MS0906.5+1110/Abell 750 because the richness of these clusters cannot be easily derived from photometry alone (see Fig. 11 in Geller et al. 2013) because they are almost on the same line of sight and separated by only 3000 km s-1; and b) the bimodal Abell 2055 cluster because it is formed by two clumps apart by about r200. The spherical symmetry implicit in the caustic method is certainly not satisfied by this cluster, at least at the r200 scale. Table 1 lists the 39 studied clusters, whose distribution in the redshift-mass plane is depicted in Fig. 1.
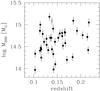 |
Fig. 1 Mass vs. redshift plot of the studied cluster sample. The open point is Abell 1068. |
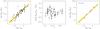 |
Fig. 2 Richness-mass scaling (left-hand and right-hand panels) and residuals (observed minus expected) as a function of redshift (central panel). The solid line marks the mean regression line (of log M200 on log n200) fitted to the individual galaxy data, while the shading indicates the 68% uncertainty (highest posterior density interval). The right-hand panel combines clusters in stacks of eight clusters each, with the exception of the most massive point, composed of just six clusters. Masses are corrected for the negligible best-fit evolution. Points and approximated error bars are derived by adding errors summed in quadrature, as commonly done in the literature. The open point (Abell 1068) is not fitted and is out of scale in the central panel. |
2.2. The data and derivation of cluster richness
Our analysis closely follows previous works, in particular Andreon & Hurn (2010), which uses data from an earlier SDSS data release (for a different cluster sample), and Andreon & Congdon (2014), which extends the analysis to account for evolution of the mass-proxy scaling.
Basically, we aim to count red members within a specified luminosity range and color, and within the r200 radius, as already done for other clusters (Andreon 2006, 2008; Andreon et al. 2008; Andreon & Hurn 2010; Andreon & Bergé 2012). For each cluster, we extracted the galaxy catalogs from the Sloan Digital Sky Survey (SDSS) 12th data release (Alam et al. 2015). Total galaxy magnitudes refer to “cmodel”, while colors are based on “model” magnitude. Colors are corrected for the color–magnitude slope, although this is a minor correction given the small magnitude range explored. We adopt a simple definition of “red”, by only counting galaxies within 0.1 redward and 0.2 blueward in g − r of the color–magnitude relation.
Some of the red galaxies in the cluster line of sight are actually in the cluster fore/background. The contribution from background galaxies is estimated, as usual, from a reference direction (e.g., Zwicky 1957; Oemler 1974; Andreon et al. 2005). The reference direction is formed of three octants, free of contaminating structures (other clusters) and not badly affected by the SDSS imaging masks, of a corona centered on the studied cluster with inner radius 3 Mpc and outer radius 1 degree, therefore fully guaranteeing homogeneous data for cluster and control field. The precise background estimation is however of secondary importance: we found that if a single redshift-dependent value of the background counts per unit arcmin2 were used for all clusters, indistinguishable results would be obtained.
The derived (projected) richness values are listed in Table 1. Since richness is based on galaxy counts, it is computed within a cylinder of radius r200. The mean (log) richness error is 0.06 dex. Richness errors account for Poisson fluctuations in background+cluster counts and the uncertainty in the mean background counts, as detailed in previous works (e.g., Andreon & Congdon 2014; Andreon & Hurn 2010). The derivation of these errors assumes a Gaussian approximation, which is only partially satisfied for these data. For this reason, we also list raw galaxy counts in the cluster and control field directions, and the ratio of the solid angles in which they are computed. These values are used for the mass-richness fit, therefore removing the Gaussian approximation of the listed n200 error.
3. Results
3.1. The mass-richness scaling
Following previous works, we fit the data with a linear relation on log-quantities: 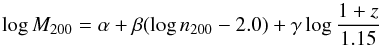 (1)allowing for an intrinsic scatter σintr, noisy mass errors and adopting pivot values of richness and 1 + z close to the sample mean (the values 2.0 and 1.15 in Eq. (1)). We adopt weak priors on parameters (see Andreon & Hurn 2010 for details). To account for the noisiness of mass errors, our baseline analysis uses ν = 6 to quantify that we are 95% confident that quoted mass errors are correct up to a factor of 2 (as mentioned) and we anticipate that results are robust to the choice of ν. Since all clusters in the sample have a measured richness, there is no selection function (at a given mass) to account for (see Andreon & Bergé 2012; Andreon & Congdon 2014). We choose not to account for the data structure (the mass function and the induced Malmquist-Eddington correction in the astronomical parlance, see Andreon & Bergé 2012 for details) because we have a limited aim in this work: we acknowledge that results are derived, and only valid, for clusters drawn from an X-ray selected sample in a given redshift range2.
(1)allowing for an intrinsic scatter σintr, noisy mass errors and adopting pivot values of richness and 1 + z close to the sample mean (the values 2.0 and 1.15 in Eq. (1)). We adopt weak priors on parameters (see Andreon & Hurn 2010 for details). To account for the noisiness of mass errors, our baseline analysis uses ν = 6 to quantify that we are 95% confident that quoted mass errors are correct up to a factor of 2 (as mentioned) and we anticipate that results are robust to the choice of ν. Since all clusters in the sample have a measured richness, there is no selection function (at a given mass) to account for (see Andreon & Bergé 2012; Andreon & Congdon 2014). We choose not to account for the data structure (the mass function and the induced Malmquist-Eddington correction in the astronomical parlance, see Andreon & Bergé 2012 for details) because we have a limited aim in this work: we acknowledge that results are derived, and only valid, for clusters drawn from an X-ray selected sample in a given redshift range2.
 |
Fig. 3 Performances of the richness proxy (i.e., when the true r200 is unknown). Left-hand panel: mass-predicted from richness vs. true (caustic) mass. The solid line is the one-to-one relation (not a fit to the data). The dotted lines show the above line plus or minus the data scatter (0.16 dex). The open point marks the outlier Abell 1068 cluster. Right-hand panel: mass residuals (predicted minus true) with superposed a Gaussian with σ = 0.16 dex. |
The fit to mass, richness, and redshift is shown in Fig. 2. Abell 1068 (the open point in Fig. 2) is an outlier. This cluster is also an outlier of the LX-mass relation (Rines et al. 2013), and we checked that it is also an outlier in the relation between caustic mass and the X-ray mass given in Piffaretti et al. (2011). We therefore removed this cluster from the fitting and analysis, although we show it (with a different symbol) in the figures. For display purposes only, the right-hand panel shows a binned version of the left-hand panel, by combining clusters in bins of eight clusters each, except the most massive one formed by six clusters.
Fitting the individual values, we found that richness scales almost linearly with mass (with slope s = 1.30 ± 0.10), with a negligible redshift-dependent term (slope −0.1 ± 1.0), and with a negligible intrinsic scatter. More precisely, 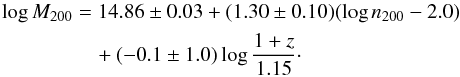 (2)The eqnarray of the richness-mass relation is poorly determined because of the reduced redshift baseline (Δz = 0.1), compared to the more accurate determination in Andreon & Congdon (2014) benefiting from a much larger redshift baseline, 0.15 <z< 0.55, but using richness and mass measured within a fixed metric aperture.
(2)The eqnarray of the richness-mass relation is poorly determined because of the reduced redshift baseline (Δz = 0.1), compared to the more accurate determination in Andreon & Congdon (2014) benefiting from a much larger redshift baseline, 0.15 <z< 0.55, but using richness and mass measured within a fixed metric aperture.
Cluster sample and results of the analysis.
The intrinsic scatter is, as mentioned, negligibly small: the amplitude of the intrinsic scatter is set by the difference of the data scatter and measurement errors. The former is 0.12 dex, the latter are ~0.08 dex on both axis, giving little or no room for an additional intrinsic scatter. In fact, our Bayesian analysis found an intrinsic scatter of σlog M200 | n200< 0.05 dex with 90% probability, consistent and more precise than the value found using weak-lensing masses in Andreon & Congdon (2014). The negligible intrinsic scatter between richness (measured in cylinders) and mass (measured in spheres) indicates a negligible effect of large-scale-structure on the richness proxy, unless it is strongly covariant with cluster elongation along the line of sight. The found tight richness-mass scaling is one of the two main results of this work.
The negligible scatter of the richness-mass scaling (posterior mean: 0.02 dex) scores well compared to those of best survey-based mass proxies: stellar mass (0.08 dex, Andreon 2012, based however on a reduced cluster sample), Ysph (0.09 dex, Marrone et al. 2012), and Planck YSZ (> 0.06 dex, Planck Collaboration XI 2011). The negligible scatter of n200 also fares well compared to proxies that requires follow-up observations, such as gas mass (~0.06 dex, Mahdavi et al. 2013) or pseudo-pressure YX (~0.04 to ~0.10 dex, Arnaud et al. 2007; Mahdavi et al. 2013).
We improve upon our previous work (Andreon & Hurn 2010), based on the CIRS sample of Rines et al. (2006), by reducing the uncertainties of intercept and slope by 30%, and the uncertainty of intrinsic scatter by a > 3 factor as a result of better understood errors and better determined cluster centers (especially important when determining the intrinsic scatter, see also Andreon 2012). Unfortunately, these two samples cannot be easily combined because they adopt slightly different definitions of M200.
To summarize, the 39 clusters studied in this work and the 23 massive clusters at 0.15 <z< 0.55 in Andreon & Congdon (2014) agree in establishing an almost scatterless, minimally evolving (if at all), mass-richness scaling, in broad agreement with the 53 clusters at lower redshift studied in Andreon & Hurn (2010).
 |
Fig. 4 Performances of maxBCG richness (left-hand panel) and of Planck YSZ (right-hand panel) proxies. The plots compare the richness- or YSZ-predicted masses vs. the caustic mass for the very same sample used in Fig. 3. The solid line is the one-to-one relation (not a fit to the data). The dotted lines show the above line plus or minus the claimed mass precision (left-hand panel) or our richness performances (right-hand panel) for comparison with Fig. 3. The (red) ticks on the ordinate of the three panels indicates unmatched clusters. |
3.2. An improved mass proxy estimate
The tightness of the richness-mass scaling makes richness an interesting mass proxy. However, as remarked several times, but not always appreciated, if the observable itself requires knowledge of the cluster mass (because knowledge of r200 is needed) such an observable is not ready to be used as mass proxy until a way to estimate r200 is found. In this section we make richness an effective mass proxy by finding a way to estimate r200 that minimally degrades the performances of the mass proxy.
In Andreon & Hurn (2010) we measured the cluster richness within a fixed aperture, the relation between r200 and this (aperture) richness is calibrated with real data and used to infer the aperture radius, 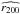 , in which richness should be finally computed (and mass estimated). Because of the inherent scatter in the individual radial profiles of galaxy clusters between aperture radius and
, in which richness should be finally computed (and mass estimated). Because of the inherent scatter in the individual radial profiles of galaxy clusters between aperture radius and 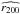 , a large amount of scatter is introduced in the mass-proxy scaling.
, a large amount of scatter is introduced in the mass-proxy scaling.
Kravtsov et al. (2006) proposed a different approach for the YX mass proxy, later also adopted for the YSZ proxy (Planck Collaboration XXVII 2015) and hereafter for richness: r200 and the proxy value (n200 in our case) are estimated at the same time assuming that the proxy-mass relation is scatterless. In practice, an iterative approach is taken: a radius r is taken (1.4 Mpc in our case), n( <r) estimated, then r is updated to the value appropriate for the derived richness if the mass-richness were scatterless (i.e., using Eq. (2), and noting that 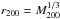 apart from obvious coefficients) and then the process is iterated until convergence. In our case, judging from comparison with results obtained after ten iterations, convergence is achieved at the second or third iteration. We therefore adopt the fifth iteration as the final (but any other iteration would give equivalent results). These values of richness and masses, derived without knowledge of the true r200, are listed in Table 1.
apart from obvious coefficients) and then the process is iterated until convergence. In our case, judging from comparison with results obtained after ten iterations, convergence is achieved at the second or third iteration. We therefore adopt the fifth iteration as the final (but any other iteration would give equivalent results). These values of richness and masses, derived without knowledge of the true r200, are listed in Table 1.
The left-hand panel of Fig. 3 shows the performance of the richness proxy when ready to be used for cluster samples of unknown mass (i.e. without knowledge of the true r200): the richness in the estimated r200, converted in mass using Eq. (2), i.e., the richness-predicted mass, is plotted versus the caustic mass. The scatter between the richness-predicted mass and mass is 0.16 ± 0.02 dex (error computed by bootstrapping), also shown in the right-hand panel of Fig. 3. Of this, 0.08 dex is due to the noisiness of the caustic mass estimate (i.e., caustic errors).
Our quoted error of the richness-based mass is total, in contrast to what is quoted for other mass estimates. For example, it includes the scatter around the relation and errors on the observable. Our choice of quoting all known error terms in the error budgets is not widespread: for example the error quoted by the Planck team for the YSZ-based masses does not include the terms above (Sect. 5.3 of Planck Collaboration XXVII 2015). Finally, and in contrast to some other claims about the error of other proxies, the scatter we derived above is not computed assuming we know the true r200. If we had to follow these works, we should claim a ~0.02 dex error, not the quoted 0.16 dex error.
As mentioned, we removed one single cluster pair (Abell 750/MS0906.5+1110) out of the starting sample (about 40 clusters) because one is projected on the top of the other and with Δv ~ 3000 km s-1, leading to an erreneous richness (and lensing mass). This situation is very rare, no other cluster has been removed from the sample for richness-based reasons, and the other two removed clusters (Abell 1068 and Abell 2055) have unproblematic richnesses but questionable caustic masses. If this sample is representative of clusters in the Universe, we then expect that richness-based masses will be very wrong for only about 2% of the clusters.
The above predicted mass uses accurate cluster centers. Since we also want to exploit richness as mass proxy for clusters without accurate centers, we now check the impact of lacking accurate centers. We therefore implement a way to estimate centers. We iteratively derive the cluster center only using galaxy counts: we consider an aperture of 1.0 Mpc radius, we compute the median right ascension and declination, we consider this the new center, and we iterate ten times. We start the center computation 3 arcmin, about 0.5 Mpc at the median redshift, away from the true cluster center to avoid the advantage of starting from the optimal center. We take the latest computed centers as new cluster centers (but results would be unchanged using, e.g., the fifth iteration), and we solve for radius and mass as before. We found an identical scatter between the richness-predicted mass and mass, as expected because the center error is negligible compared to r200.
Our current richness scores best among all mass proxies based on survey data, as far as we are aware of, as we now illustrate.
First, the left-hand panel of Fig. 4 shows the performance of the maxBCG richness using the mass calibration in Rozo et al. (2009) via plotting the richness-predicted mass vs. caustic mass for the very same HECS sample shown in Fig. 3. While using similar photometry (a previous SDSS release), these authors adopt different recipes for counting the galaxies (notably the adopted aperture) and a different (indirect) approach to mass calibration. Clusters are matched with a 2 arcmin maximum radius and our results are robust to adopted matching aperture. Clusters not found in the maxBCG catalog (about 40%) are shown as ticks on the ordinate. For the remaining 60%, we found a scatter of 0.26 dex (consistent with, but larger than, the advertised value). Our mass proxy performs better, both in terms of scatter and in terms of completeness. Adopting the more recent calibration by Rozo et al. (2014) does not change our results. By taking the richest maxBCG cluster with consistent redshift and within a large matching radius does not change our results either. The improved maxBCG richness by Rykoff et al. (2012) shows a reduced scatter (although larger than advertised) and a large mass bias, the latter anticipated by the authors because of their preliminary calibration. By adopting a direct approach to mass calibration, our richness is not badly affected by systematics. More recent catalogs based on SDSS lack a mass calibration. Considering them would require us to calibrate them first, which is beyond the purpose of this paper.
Second, the right-hand panel of Fig. 4 illustrates the performances of YSZ-based masses, taken from Planck Collaboration XXVII (2015) via plotting the YSZ-predicted mass vs. caustic mass. Clusters are matched with a maximal radius of 3 arcmin (equal to about twice the 68% Planck position error). Unmatched clusters (eight cases) are marked with red tick on the figure ordinate. Some of them are of low mass and are therefore likely absent in the Planck catalog because they are undetected. However, some of them are somewhat massive. The scatter of the remaining 31 YSZ-based masses is comparable to richness-based masses (0.18 vs. 0.16 dex), but perhaps better described by a combination of a slightly narrower distribution (with σ ~ 0.14 dex) plus some (15%) outliers. Enlarging the matching radius does not help to increase the YSZ mass performances because the newly matched objects have large scatter with mass. Decreasing the matching radius is of no help either because it decreases the number of matches without reducing the scatter. By restricting our attention to clusters in the narrow redshift range studied in this work (0.10 <z< 0.22) and by computing the minimal scatter (by allowing a free mass bias), we minimize known redshift- (Andreon 2014) and bias- (von der Linden et al. 2014; Planck Collaboration XXIV 2015) effects of YSZ-based masses. To summarize our comparison with YSZ-based masses, proxy availability and a low intrinsic scatter with mass are essential to evaluate the quality of a mass proxy. The 54 s exposures taken at a 2 m telescope in a mediocre site on Earth (the SDSS) competes well with a satellite at the L2 point from this point of view in the studied redshift range3.
Third, our score of a 0.16 dex scatter is better than all 25 methods considered in the mass reconstruction project (Old et al. 2015), most of which requires spectroscopy, i.e., are observationally more demanding. In particular, in these simulations richness-based masses outperform caustic masses. If the same holds true in our Universe, our work would be measuring the scatter of a precise mass estimate (richness) via comparison to a noisy estimate (caustic masses)! Note however that such a simulation-based analysis should be considered with caution because results depends on the way clusters are populated by galaxies in the simulations, and because nothing guarantee that the best mass proxy in simulations is also best in our Universe.
We recal that a tight mass-proxy scaling is certainly useful, but scalings that involve observationally parsimonious observables are even better, and richness is both parsimonious and display a tight relation with mass. Indeed, richness has already allowed us to derive the mass of three among the most distant clusters and groups known (Strazzullo et al. 2013; Andreon et al. 2014; Webb et al. 2015), which still miss YX- or YSZ-based masses because they are observationally expensive to acquire.
Cluster counts are exponentially sensitive to the properties of dark energy and to the square of the scatter between proxy and mass. Our factor two improvement over Andreon & Hurn (2010) and maxBCG, obtained because the current estimate benefits from a radius measured very close to the true r200 and tailored to each cluster, corresponds to a four times lower dilution of cosmological information contained in number counts. This improvement is our second main result.
4. Conclusions
We studied 39 X-ray selected clusters at 0.1 <z< 0.22 with accurate caustic masses (20% errors) from the HECS catalog. We derived richness within r200 using SDSS photometry and we found an extremely tight, almost scatterless, richness-mass scaling, at least as tight as those derived for other mass proxies, and tighter than quoted in previous works. The current sample, adjoinining 76 more clusters analyzed in previous works, establishes an almost scatterless, minimally evolving (if at all), mass-richness scaling in the redshift range 0.03 <z< 0.55. By assuming that the true relation is scatterless, we rederive cluster richness and r200 at the same time only using SDSS photometry. We found that the newly derived richness is a mass proxy with 0.16 dex scatter, half of which is not intrinsic to the proxy, but related to the noisiness of the caustic masses used for test richness performances.
To summarize, an ideal mass proxy should be characterized by a low intrinsic scatter, be observationally parsimonious to obtain, relatively insensitive to the cluster dynamical state, and easy to compute. Richness seems to be as such. For this reason we are now computing richness-predicted masses of many z< 0.22 clusters in the SDSS footprint, with priorities set by the community input.
Acknowledgments
This work benefits of discussion with caustic specialists, Antonaldo Diaferio, Ana Laura Serra, and Jacob Svensmark, and with Andrea Biviano.
References
- Abbott, T., Abdalla, F. B., Allam, S., et al., 2005, ArXiv e-prints [arXiv:astro-ph/0510346] [Google Scholar]
- Alam, S., Albareti, F. D., Allen de Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2006, MNRAS, 369, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2008, MNRAS, 386, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2012, A&A, 548, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2014, A&A, 570, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2015a, A&A, 575, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2015b, A&A, submitted [Google Scholar]
- Andreon, S., & Bergé, J. 2012, A&A, 547, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Congdon, P. 2014, A&A, 568, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Andreon, S., Punzi, G., & Grado, A. 2005, MNRAS, 360, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Puddu, E., de Propris, R., & Cuillandre, J.-C. 2008, MNRAS, 385, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Maughan, B., Trinchieri, G., & Kurk, J. 2009, A&A, 507, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., Newman, A. B., Trinchieri, G., et al. 2014, A&A, 565, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2007, A&A, 474, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, M. R., & Kravtsov, A. V. 2011, ApJ, 740, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A. 1999, MNRAS, 309, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A., & Geller, M. J. 1997, ApJ, 481, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, M. J., Diaferio, A., Rines, K. J., & Serra, A. L. 2013, ApJ, 764, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Gifford, D., Miller, C., & Kern, N. 2013, ApJ, 773, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Menou, K., Knapp, G. R., et al. 2002, AJ, 124, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., Axelrod, T., Brandt, W. N., et al. 2008, Serb. Astron. J., 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Burgett, W., Chambers, K., et al. 2010, Proc. SPIE, 7733 [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., et al. 2013, ApJ, 767, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Smith, G. P., Okabe, N., et al. 2012, ApJ, 754, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newman, A. B., Ellis, R. S., Andreon, S., et al. 2014, ApJ, 788, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, A., Jr. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Old, L., Wojtak, R., Mamon, G. A., et al. 2015, MNRAS, 449, 1897 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2011, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2015, A&A, submitted [arXiv:1502.01597] [Google Scholar]
- Planck Collaboration XXVII. 2015, A&A, in press, DOI:10.1051/0004-6361/201525823 [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., & Diaferio, A. 2006, AJ, 132, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., & Kurtz, M. J. 2013, ApJ, 767, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Evrard, A., et al. 2009, ApJ, 699, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Bartlett, J. G., Evrard, A. E., & Rykoff, E. S. 2014, MNRAS, 438, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Rykoff, E. S., Koester, B. P., Rozo, E., et al. 2012, ApJ, 746, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, A. L., Diaferio, A., Murante, G., & Borgani, S. 2011, MNRAS, 412, 800 [NASA ADS] [Google Scholar]
- Strazzullo, V., Gobat, R., Daddi, E., et al. 2013, ApJ, 772, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Takada, M. 2010, AIP Conf. Ser., 1279, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, T., Noble, A., DeGroot, A., et al. 2015, ApJ, 809, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F., Herzog, E., Wild, P., Karpowicz, M., & Kowal, C. T. 1961, Catalogue of Galaxies and of Clusters of galaxies, Vol. I (Pasadena: California Institute of Technology, CIT) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Mass vs. redshift plot of the studied cluster sample. The open point is Abell 1068. |
| In the text | |
 |
Fig. 2 Richness-mass scaling (left-hand and right-hand panels) and residuals (observed minus expected) as a function of redshift (central panel). The solid line marks the mean regression line (of log M200 on log n200) fitted to the individual galaxy data, while the shading indicates the 68% uncertainty (highest posterior density interval). The right-hand panel combines clusters in stacks of eight clusters each, with the exception of the most massive point, composed of just six clusters. Masses are corrected for the negligible best-fit evolution. Points and approximated error bars are derived by adding errors summed in quadrature, as commonly done in the literature. The open point (Abell 1068) is not fitted and is out of scale in the central panel. |
| In the text | |
 |
Fig. 3 Performances of the richness proxy (i.e., when the true r200 is unknown). Left-hand panel: mass-predicted from richness vs. true (caustic) mass. The solid line is the one-to-one relation (not a fit to the data). The dotted lines show the above line plus or minus the data scatter (0.16 dex). The open point marks the outlier Abell 1068 cluster. Right-hand panel: mass residuals (predicted minus true) with superposed a Gaussian with σ = 0.16 dex. |
| In the text | |
 |
Fig. 4 Performances of maxBCG richness (left-hand panel) and of Planck YSZ (right-hand panel) proxies. The plots compare the richness- or YSZ-predicted masses vs. the caustic mass for the very same sample used in Fig. 3. The solid line is the one-to-one relation (not a fit to the data). The dotted lines show the above line plus or minus the claimed mass precision (left-hand panel) or our richness performances (right-hand panel) for comparison with Fig. 3. The (red) ticks on the ordinate of the three panels indicates unmatched clusters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


