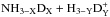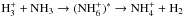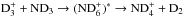| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526468 | |
| Published online | 21 September 2015 | |
Spin-state chemistry of deuterated ammonia⋆
1
Max-Planck-Institute for Extraterrestrial Physics (MPE),
Giessenbachstr. 1,
85748
Garching,
Germany
e-mail:
osipila@mpe.mpg.de
2
Department of Physics, PO Box 64, 00014 University of Helsinki,
Finland
3
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Strasse 77,
50937
Köln,
Germany
Received: 5 May 2015
Accepted: 10 July 2015
Aims. We aim to develop a chemical model that contains a consistent description of spin-state chemistry in reactions involving chemical species with multiple deuterons. We apply the model to the specific case of deuterated ammonia, to derive values for the various spin-state ratios.
Methods. We applied symmetry rules in the context of the complete scrambling assumption to calculate branching ratio tables for reactions between chemical species that include multiple protons and/or deuterons. New reaction sets for both gas-phase and grain-surface chemistry were generated using an automated routine that forms all possible spin-state variants of any given reaction with up to six H/D atoms, using the predetermined branching ratios. Both a single-point and a modified Bonnor-Ebert model were considered to study the density and temperature dependence of ammonia and its isotopologs, and the associated spin-state ratios.
Results. We find that the spin-state ratios of the ammonia isotopologs are, at late times, very different from their statistical values. The ratios are rather insensitive to variations in the density, but present strong temperature dependence. We derive high peak values (~0.1) for the deuterium fraction in ammonia, in agreement with previous (gas-phase) models. The deuterium fractionation is strongest at high density, corresponding to a high degree of depletion, and also presents temperature dependence. We find that in the temperature range 5 K to 20 K, the deuterium fractionation peaks at ~15 K, while most of the ortho/para (and meta/para for ND3) ratios present a minimum at 10 K (ortho/para NH2D has instead a maximum at this temperature).
Conclusions. Owing to the density and temperature dependence found in the abundances and spin-state ratios of ammonia and its isotopologs, it is evident that observations of ammonia and its deuterated forms can provide important constraints on the physical structure of molecular clouds.
Key words: ISM: abundances / ISM: clouds / ISM: molecules / astrochemistry
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The chemical evolution of cold molecular cloud cores is characterized by increasing abundances of the nitrogen-containing species N2H+ and NH3 and by the enhancement of deuterium fractionation (e.g., Tiné et al. 2000; Tafalla et al. 2002). The three isotopologs of deuterated ammonia, NH2D, NHD2, and ND3, therefore look like particularly useful indicators of temporal changes in the chemical composition of starless and prestellar cores. Besides the likelihood that the NH2D/NH3, NHD2/ NH2D, and ND3/ NHD2 abundance ratios increase with time (Flower et al. 2006; Roueff et al. 2015), the ratios of different nuclear spin isomers of these molecules can also vary. The reactions leading to ammonia and its deuterated forms are recapitulated in Rodgers & Charnley (2001). Deuteration occurs primarily in reactions between NH3 and deuterated ions. In dense, cold clouds this mainly means reactions with the deuterated forms of 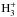 . Through these reactions, the nuclear spin ratios of NH2D, NHD2, and ND3 become dependent on the nuclear spin ratios of H2D+, D2H+, and
. Through these reactions, the nuclear spin ratios of NH2D, NHD2, and ND3 become dependent on the nuclear spin ratios of H2D+, D2H+, and 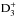 . The latter set of ratios depend on the H2ortho:para ratio, hereafter o/p-H2 (e.g., Walmsley et al. 2004), which also influences the formation rate of ammonia (Le Bourlot 1991; Wirström et al. 2012). The o/p-H2 ratio is predicted to decrease drastically as the core evolves (e.g., Flower & Watt 1984; Pagani et al. 2011; Brünken et al. 2014). While the formation rates of different spin isomers of ammonia probably vary because of competing ion-molecule reactions, grain-surface reactions should produce them in ratios of the nuclear spin statistical weights because H and D atoms are added one by one. However, the accretion of ammonia molecules synthesized in the gas phase leads to gradual changes in the average spin ratios on grains.
. The latter set of ratios depend on the H2ortho:para ratio, hereafter o/p-H2 (e.g., Walmsley et al. 2004), which also influences the formation rate of ammonia (Le Bourlot 1991; Wirström et al. 2012). The o/p-H2 ratio is predicted to decrease drastically as the core evolves (e.g., Flower & Watt 1984; Pagani et al. 2011; Brünken et al. 2014). While the formation rates of different spin isomers of ammonia probably vary because of competing ion-molecule reactions, grain-surface reactions should produce them in ratios of the nuclear spin statistical weights because H and D atoms are added one by one. However, the accretion of ammonia molecules synthesized in the gas phase leads to gradual changes in the average spin ratios on grains.
The ground-state rotational transitions of the ortho and para species of NH2D and NHD2, as well as those of the meta and para species of ND3, are observable with ground-based telescopes (Shah & Wootten 2001; Lis et al. 2002; van der Tak et al. 2002; Roueff et al. 2005; Gerin et al. 2006; Lis et al. 2006)1. In the few sources where these have been determined, the NH2D/NH3 and NHD2/ NH2D column density ratios have been found to lie in the range ~0.1−0.2, whereas the ND3/ NHD2 is somewhat lower, ~0.02−0.1, implying that ND3/ NH3 ~ 10-4−10-3 (Roueff et al. 2005; Gerin et al. 2006; Lis et al. 2006). These numbers signify enormous deuterium enhancements in ammonia with respect to the cosmic D/H abundance ratio. The observed spin ratios are consistent with the nuclear spin statistical weights, if we take observational uncertainties into account. With the increasing sensitivity of (sub)millimeter telescopes, it will be possible to improve the accuracy of these measurements and to extend the investigation to cover larger and more varied samples of dense cores.
A valid description of chemistry in dense cores should be able to explain, for example, the observed abundances of the different deuterated isotopologs and spin isomers of ammonia, which itself belongs to the most useful probes of dense molecular cloud cores. With this goal in mind, we have developed a comprehensive gas-grain chemistry model that includes deuterium and the spin-state chemistry of molecules containing multiple H and/or D nuclei. In an earlier version of this model, the deuterium fractionation and spin selection rules were applied to light molecules (Sipilä et al. 2013). The model has recently been extended to include heavier deuterated molecules and to take the spin selection rules into account for hydrogen in the formation of ammonia and water (Sipilä et al. 2015, hereafter S15). In the present update, we implement the spin selection rules for reactions that involve up to six hydrogen and deuterium nuclei.
As described in Sect. 2 of this paper,including the spin-state chemistry of multiply deuterated species has required a complete revision of the spin separation routine, which is now based on the symmetries of the nuclear spin functions rather than the angular momentum algebra used in the previous versions of the model. In Sect. 3, we predict the abundances of ammonia and its deuterated forms, and the spin ratios of these molecules as functions of time in homogenous models corresponding to dark cloud and dense core conditions. In Sect. 4, we discuss the temperature dependence of the deuteration of ammonia and derive radial abundance profiles in two modified Bonnor-Ebert sphere models. In this section, we also compare our predictions with the gas-phase chemical model of Roueff et al. (2005). Finally, in Sect. 5 we present our conclusions. Appendix A contains a couple of examples of how to calculate the nuclear spin branching ratios using symmetry rules.
2. Model
2.1. Theory
In the present model, the different nuclear spin symmetry states of molecules containing two or more hydrogen and/or deuterium nuclei are treated as separate species. This implies that for the doubly deuterated ammonium ion, 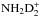 , for example, we keep track of four different forms depending on the two possible spin symmetries, “ortho” (A) and “para” (B), of the pairs of the H and D nuclei. In reactions involving multiple H or D nuclei, the branching ratios between different nuclear spin channels are assumed to be determined by their pure nuclear spin statistical weights, that is, the number of nuclear spin functions belonging to each channel, which are calculated using permutation symmetry algebra (Quack 1977; Park & Light 2007b; Hugo 2009; Hugo et al. 2009). This method uses the assumptions of nuclear spin conservation and full scrambling of nuclei in reactive collisions. The branching ratios are calculated for reactions involving up to six hydrogen or deuterium nuclei.
, for example, we keep track of four different forms depending on the two possible spin symmetries, “ortho” (A) and “para” (B), of the pairs of the H and D nuclei. In reactions involving multiple H or D nuclei, the branching ratios between different nuclear spin channels are assumed to be determined by their pure nuclear spin statistical weights, that is, the number of nuclear spin functions belonging to each channel, which are calculated using permutation symmetry algebra (Quack 1977; Park & Light 2007b; Hugo 2009; Hugo et al. 2009). This method uses the assumptions of nuclear spin conservation and full scrambling of nuclei in reactive collisions. The branching ratios are calculated for reactions involving up to six hydrogen or deuterium nuclei.
In our previous papers (Sipilä et al. 2013; S15), the nuclear spin branching ratios were deduced using the method of Oka (2004) based on angular momentum algebra. The same method was applied to nuclear-spin selection rules of nitrogen hydrides by Rist et al. (2013). For reactions where several deuterium nuclei are involved, Oka’s method is, however, impractical, because species are distinguished by their nuclear spin symmetries, but there is no one-to-one correspondence between angular momentum and symmetry representations for systems with three or more D nuclei (Hugo 2009). A comparison between the total angular momentum and the total symmetry representations of systems containing up to five spin-1/2 and spin-1 particles is presented in Table 2.13 of Hugo (2009). For multiple H nuclei (or any system of spin-1/2 particles), the method using symmetry rules gives the same results as Oka’s method, because for these systems each value of the spin angular momentum is associated with one and only one symmetry representation. Also in the case of multiple D nuclei, the total nuclear spin is conserved when using the symmetry rules. This could be seen from branching ratio tables if the symmetry species were subdivided according to the total nuclear spin (an example of this is given in Hugo 2009; Table 2.1).
For calculating the statistical branching ratios using symmetry rules, one needs to determine the possible symmetry species (i.e., representations) of the reactants (Γi ⊗ Γj; where ⊗ denotes a direct product), the intermediate complex (Γn), and the products (Γk ⊗ Γl, i + j = n = k + l), in appropriate permutation groups (Si ⊗ Sj, Sn, and Sk ⊗ Sl). In addition, one needs to derive the correlation tables between the group of the complex and its subgroups, which represent the reactants and products. This is done by applying the standard methods of group theory. The correlation tables tell us which nuclear spin symmetry species of the reaction complex are feasible given the symmetries of the reactants and which symmetry states of the products are possible when the complex decays (cf. Quack 1977; Eqs. (12)−(15)). In this description, the statistical weight of the product Γk ⊗ Γl is given by f(Γk ⊗ Γl) × dim(Γk) × dim(Γk), where f(Γk ⊗ Γl) is the frequency of Γk ⊗ Γl in the total symmetry representation generated by the nuclear spin functions of the product molecules in Sk ⊗ Sl, and dim(Γ) is the dimension of the representation Γ.
Besides being proportional to the number of nuclear spin functions belonging to each channel, branching ratios calculated in this manner are proportional to the number of rovibronic states occupied by these species in the high temperature limit (Park & Light 2007a, their Appendix A). A couple of examples of the procedure are given in Appendix A. The determination of the symmetries of the nuclear spin wave functions is explained lucidly in Bunker (1979) and in Bunker & Jensen (2006). In this work, where we do not consider the rovibronic states of the molecules, it is sufficient to classify the nuclear spin functions in the complete nuclear spin permutation group, which does not include the inversion operation (see also Crabtree & McCall 2013). Most of the statistical branching ratio tables needed in the present study are available in Tables 3 and 4 of Hugo et al. (2009). To also cover reactions with six identical nuclei, such as 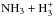 and
and 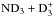 , and to transfer the spin selection rules to the chemical network, we developed an automated routine for producing these tables. The character tables for permutation groups needed in this process were obtained using GAP (2015)2.
, and to transfer the spin selection rules to the chemical network, we developed an automated routine for producing these tables. The character tables for permutation groups needed in this process were obtained using GAP (2015)2.
2.2. Application
We designed a new routine for the spin-state separation of chemical reactions involving multiple protons and/or deuterons, utilizing the group-theoretical approach described above. As opposed to the model described in S15, the new routine produces consistent branching ratios for reactions involving deuterated species, instead of copying the spin-state separation rules from the pure-hydrogen counterpart reactions.
Because hydrogen and deuterium are distinguishable, we can divide each reaction involving both hydrogen and deuterium into two parts. For example, the reaction 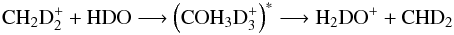 (1)is divided into
(1)is divided into 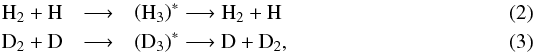 where we have ignored the carbon and oxygen atoms and the charge. The selection rules for hydrogen split reaction (2) into the following branches:
where we have ignored the carbon and oxygen atoms and the charge. The selection rules for hydrogen split reaction (2) into the following branches: 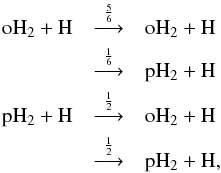 while the selection rules for deuterium split reaction (3) into
while the selection rules for deuterium split reaction (3) into 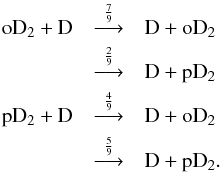 We then combine the hydrogen and deuterium branches by multiplying all possible combinations together, and we end up with 4 × 4 = 16 different branches for reaction (1). As a result,
We then combine the hydrogen and deuterium branches by multiplying all possible combinations together, and we end up with 4 × 4 = 16 different branches for reaction (1). As a result, 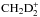 receives a composite spin made up of hydrogen and deuterium spin states, for example,
receives a composite spin made up of hydrogen and deuterium spin states, for example, 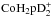 .
.
The spin-state separation routine presented here allows us to explicitly consider the spin states of all species that contain multiple H and/or D atoms. However, we do not track the spin states of all species because this would lead to an enormous reaction network with a total reaction count far into the hundreds of thousands. Instead, we adopt the averaging process described in S15, in which we assume a 1:1 spin-state abundance ratio for those species whose spin states we do not want to keep track of. We have verified that this assumption has a negligible influence on the results presented below. In this paper, we focus on the spin-state chemistry of ammonia and its deuterated forms. We also keep the spin states of the species included in the formation network of water, so that we can compare our new model to the one presented in S15. In reaction (1), the only species for which we retain the spin states is H2DO+, and the averaging process finally results in two branches: 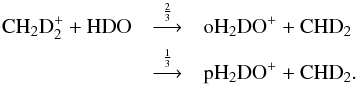 The separation process is fully automated, so any reaction involving multiple protons in our base reaction set (see S15) is automatically deuterated and spin-state-separated according to the selection rules discussed above. The only exception to this is charge transfer reactions, for which we assume that the spin states are conserved in the reaction. The reaction N+ + H2 initiating the ammonia synthesis has been treated in the same manner as in Dislaire et al. (2012) and Roueff et al. (2015), who both use the experimental data from Marquette et al. (1988). In addition to the updates listed in S15, the new reaction set includes the rate coefficients for N+ + HD and N+ + D2 from Marquette et al., taking the slightly different ground-state energies of oD2 and pD2 in the reaction enthalpies into account. For the reactions
The separation process is fully automated, so any reaction involving multiple protons in our base reaction set (see S15) is automatically deuterated and spin-state-separated according to the selection rules discussed above. The only exception to this is charge transfer reactions, for which we assume that the spin states are conserved in the reaction. The reaction N+ + H2 initiating the ammonia synthesis has been treated in the same manner as in Dislaire et al. (2012) and Roueff et al. (2015), who both use the experimental data from Marquette et al. (1988). In addition to the updates listed in S15, the new reaction set includes the rate coefficients for N+ + HD and N+ + D2 from Marquette et al., taking the slightly different ground-state energies of oD2 and pD2 in the reaction enthalpies into account. For the reactions 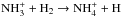 , we adopt the rate coefficients from Le Gal et al. (2014), which correspond to those used in Roueff et al. (2005).
, we adopt the rate coefficients from Le Gal et al. (2014), which correspond to those used in Roueff et al. (2005).
In what follows, we show results calculated with the gas-grain chemical code discussed in S15. In summary, we choose the osu_01_2009 reaction set as the basis set which is deuterated and spin-state separated according to the approaches discussed above. The initial grain-surface chemistry reaction set is adopted from Semenov et al. (2010), and it is similarly deuterated and spin-state-separated. A complete description of the model including adopted model parameters and updates to the (basis) reaction sets is presented in S15.
3. Results
3.1. Comparison to S15
 |
Fig. 1 Spin-state ratios of NH3 (upper panels) and H2O (lower panels) as functions of time at different densities, labeled in the upper left panel. The lefthand panels present results calculated with the (gas-grain) model of S15, while the righthand panels correspond to the present work. |
Because of the isomorphism between the symmetry and angular momentum representations for hydrogenated species, we recover for these the same branching ratios in the present model as with the method of Oka (2004) employed in S15. However, the branching ratios in reactions involving deuterated species are in many cases significantly different between the two models.
 |
Fig. 2 Principal reactions determining the abundances and spin ratios of deuterated ammonia isotopologs at late stages of chemical evolution in cold, dense cores. The reactions |
In Fig. 1, we compare the o/p ratios of ammonia and water predicted by the S15 model and the present model. The temperature is set to T = 10 K, and the other physical parameters are the same as in S15. The addition of spin states for multiply deuterated species generally has little effect on the spin-state ratios of undeuterated species, but some difference is evident, especially for water at high density. Inspection of the reaction rates reveals that the differences between the models seen in both the ammonia and water o/p ratios are mainly caused by the electron recombinations of (o/p) NH3D+ and (o/p) H2DO+. The S15 model contains some pathways for these reactions that are forbidden by the proper selection rules adopted in this work. Nevertheless, the difference between the models is small, and we have checked that this agreement holds for other (undeuterated) species as well.
The results shown in the following sections were calculated with the S15 chemical code, adopting the new reaction sets developed for this paper. As in the test above, the temperature is set to T = 10 K in all calculations, and the other physical parameters are the same as in S15.
3.2. Deuterium fractionation of ammonia
By inspecting the production and destruction rates of deuterated forms of ammonia at various stages of the simulation, one finds that at late times, the deuteration of ammonia proceeds as outlined in the steady-state model of Rodgers & Charnley (2001). The NH3 abundance has already built up when the gas-phase deuteration becomes effective, and deuteron transfer reactions between ammonia and deuterated ions form, e.g., NH3D+, which can recombine with an electron to give NH2D, etc. In the present model, however, H2D+, D2H+, and 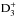 are the most important sources of deuterons at late times. The dominant reactions forming NH2D, NHD2, and ND3 are shown in Fig. 2. This diagram, which is an extension to the schematic NH3 cycle shown in Fig. A.1. of S15, should be compared with Fig. 1 of Rodgers & Charnley (2001). Besides the deuteration pathways, the diagram shows the constant recycling between NH3,
are the most important sources of deuterons at late times. The dominant reactions forming NH2D, NHD2, and ND3 are shown in Fig. 2. This diagram, which is an extension to the schematic NH3 cycle shown in Fig. A.1. of S15, should be compared with Fig. 1 of Rodgers & Charnley (2001). Besides the deuteration pathways, the diagram shows the constant recycling between NH3, 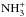 , and
, and 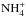 , and similar cyclic processes among their deuterated variants, caused by charge transfer reactions with H+. This recycling tends to reduce the deuterium fractionation, because NH2D+ + H2, for example, also leads to
, and similar cyclic processes among their deuterated variants, caused by charge transfer reactions with H+. This recycling tends to reduce the deuterium fractionation, because NH2D+ + H2, for example, also leads to 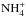 . (We assume a statistical branching ratios, in this case 4:1 in favor of NH3D+.) The reaction N+ + HD → ND+ + H with very low endothermicity (Marquette et al. 1988) speeds up the deuteration of ammonia at early stages, but this pathway has no influence on the abundances at the deuterium peak.
. (We assume a statistical branching ratios, in this case 4:1 in favor of NH3D+.) The reaction N+ + HD → ND+ + H with very low endothermicity (Marquette et al. 1988) speeds up the deuteration of ammonia at early stages, but this pathway has no influence on the abundances at the deuterium peak.
Figure 3 shows the total abundances, i.e., sums over spin states, of ammonia and its deuterated forms. At late times at high density, ammonia starts to deplete from the gas phase (see also S15). For the various forms of deuterated ammonia, an abundance peak is observed that coincides with the initiation of deuterium chemistry due to CO depletion. Like ammonia, its isotopologs also deplete from the gas phase, and do so more strongly than ammonia itself. This is because of the depletion of deuterated molecules (including the ammonia isotopologs) onto grain surfaces, which traps deuterium onto the surfaces; this ultimately results in HD depletion and consequently the overall gas-phase deuteration efficiency decreases (Sipilä et al. 2013; S15).
The abundance ratios of ammonia and its isotopologs are presented in Fig. 4. The deuterium fractionation is highest at high density where depletion is strongest. The relative depletion of the ammonia isotolopogs is fairly uniform, with all abundance ratios ultimately dropping by a factor of 3 to 4 from their peak values. A high degree of fractionation is observed, and the peak values for all of the ratios are ≳0.1. This is further discussed in Sect. 4.3, where we compare our gas-grain modeling results to the gas-phase models of Roueff et al. (2005).
3.3. The spin-state ratios of deuterated ammonia
Spin symmetries of molecules with 2−4 H or D nuclei.
In Fig. 5, we show the spin-state ratios of the deuterated forms of ammonia. All of the ratios show dependence on both time and density. For all of the ammonia isotopologs, the most important formation mechanism is the electron recombination of the (singly or multiply) deuterated ammonium ion. To complement Fig. 5, we show in Fig. 6 the spin-state ratios of selected ions. In the following, we quote the spin symmetries of the various species; these are tabulated in Table 1. The numbers in front of the symmetry labels indicate their frequencies in the total nuclear spin representation of the complex. The values of the possible nuclear spin angular momenta, I, and the nuclear spin statistical weights, gI, are given below each symmetry species, along with their “para”, “ortho”, and “meta” appellations, when applicable.
 |
Fig. 3 Abundances of ammonia and its deuterated forms as functions of time at different densities, labeled in the upper right panel. |
 |
Fig. 4 Abundance ratios of ammonia and its deuterated forms as functions of time at different densities, labeled in the lefthand panel. |
At late times, the ortho:para ratio of NH2D is largely determined by the cycle 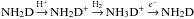 (see Fig. 2). The spin ratio of NH3 was discussed in Appendix A of S15. The electron recombination of NH3D+ yields ortho and para NH2D with the following branching ratios:
(see Fig. 2). The spin ratio of NH3 was discussed in Appendix A of S15. The electron recombination of NH3D+ yields ortho and para NH2D with the following branching ratios: 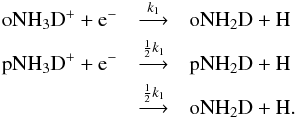 Since the destruction rates of oNH2D and pNH2D (mainly through reactions with H+ and
Since the destruction rates of oNH2D and pNH2D (mainly through reactions with H+ and 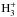 ) are similar, we get o/p-NH2D ~ 1 + 2o/p-NH3D+. Moreover, because the o/p ratio of NH3D+ is ~0.4−0.5 at late times, depending on the density (Fig. 6), o/p-NH2D should obtain the values 2 (low density) or 1.8 (high density), in agreement with Fig. 5.
) are similar, we get o/p-NH2D ~ 1 + 2o/p-NH3D+. Moreover, because the o/p ratio of NH3D+ is ~0.4−0.5 at late times, depending on the density (Fig. 6), o/p-NH2D should obtain the values 2 (low density) or 1.8 (high density), in agreement with Fig. 5.
The o/p ratios of NH2D and NH3D+ are, however, closely coupled because many of the most important destruction pathways of NH2D return NH3D+. This can be seen by inspection of Figs. 5 and 6, which show the results of the full simulation, and from the schematic presentation of the situation at late times in Fig. 2. The spin state is conserved in the charge exchange reaction 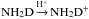 . Assuming total scrambling of nuclei in the reaction NH2D+ + H2, oNH2D+ + pH2 gives rise to the intermediate complex NH4(F1)D+ that dissociates to oNH3D+ and pNH3D+ in ratio 1:2 (the symmetry of H4 is indicated in the brackets, see Table 3 of Hugo et al. 2009). The reaction pNH2D+ + pH2 produces only pNH3D+ through the intermediate complex NH4(E)D+ (only reactions with pH2 are considered because the oH2 abundance is very low at this stage). Using these branching ratios one obtains that the closed cycle
. Assuming total scrambling of nuclei in the reaction NH2D+ + H2, oNH2D+ + pH2 gives rise to the intermediate complex NH4(F1)D+ that dissociates to oNH3D+ and pNH3D+ in ratio 1:2 (the symmetry of H4 is indicated in the brackets, see Table 3 of Hugo et al. 2009). The reaction pNH2D+ + pH2 produces only pNH3D+ through the intermediate complex NH4(E)D+ (only reactions with pH2 are considered because the oH2 abundance is very low at this stage). Using these branching ratios one obtains that the closed cycle 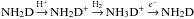 should result in o/p-NH2D ~ 2.3. As discussed above, in the full reaction network this ratio is, however, about 20% lower.
should result in o/p-NH2D ~ 2.3. As discussed above, in the full reaction network this ratio is, however, about 20% lower.
The doubly and triply deuterated forms of ammonia are primarily formed from the electron recombination of 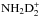 and
and 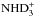 , respectively. (The recombination of the fully deuterated ammonium ion
, respectively. (The recombination of the fully deuterated ammonium ion 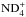 contributes about 10% to ND3.) The cycle
contributes about 10% to ND3.) The cycle 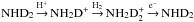 preserves the spin state of D2. The same is true for D3 in the corresponding cycle of ND3.
preserves the spin state of D2. The same is true for D3 in the corresponding cycle of ND3. 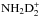 forms mainly from the reaction
forms mainly from the reaction 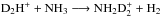 , where the spin state of D2H+ is conserved.
, where the spin state of D2H+ is conserved. 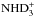 receives contributions from both D2H+ and
receives contributions from both D2H+ and 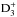 through the reactions
through the reactions 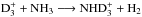 and
and 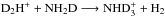 . In the first of these reactions, the spin ratios of
. In the first of these reactions, the spin ratios of 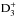 are just copied to NHD
are just copied to NHD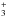 . For the second reaction, the branching ratios can be read from Table 4 of Hugo et al. (2009). For example, taking the most common species, the reaction oD2H+ + oNHD2 forms an intermediate reaction complex
. For the second reaction, the branching ratios can be read from Table 4 of Hugo et al. (2009). For example, taking the most common species, the reaction oD2H+ + oNHD2 forms an intermediate reaction complex 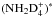 with A1, E, and F1 symmetries of D4 in statistical ratios 15:6:15, and, taking these ratios into account, the complex decay into
with A1, E, and F1 symmetries of D4 in statistical ratios 15:6:15, and, taking these ratios into account, the complex decay into 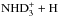 produces A1 (“meta”) and E (“ortho”) symmetries of D3 with probabilities 5/9 and 4/9, respectively (the A2 “para” symmetry is not formed in this reaction because in D4 → D3 + D, A1 → A1, E → E, and F1 → A1 + E, Table 4 of Hugo et al. 2009).
produces A1 (“meta”) and E (“ortho”) symmetries of D3 with probabilities 5/9 and 4/9, respectively (the A2 “para” symmetry is not formed in this reaction because in D4 → D3 + D, A1 → A1, E → E, and F1 → A1 + E, Table 4 of Hugo et al. 2009).
What is said above implies that the spin ratios of NHD2 and ND3 are tied to those of D2H+ and 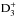 , and this is also evident from Figs. 5 and 6. The o/p ratio of NHD2 increases constantly until very late times, leveling off only after 107 yr in the models shown in Fig. 5 (i.e., outside the range shown here). This depends on the D2H+ o/p ratio, which increases strongly as a function of time (Fig. 6). From Fig. 5 it is observed that para-ND3 is clearly the least abundant of the three spin states of ND3, while the ortho and meta states are equally abundant at late times regardless of the density. This behavior reflects the spin ratios of
, and this is also evident from Figs. 5 and 6. The o/p ratio of NHD2 increases constantly until very late times, leveling off only after 107 yr in the models shown in Fig. 5 (i.e., outside the range shown here). This depends on the D2H+ o/p ratio, which increases strongly as a function of time (Fig. 6). From Fig. 5 it is observed that para-ND3 is clearly the least abundant of the three spin states of ND3, while the ortho and meta states are equally abundant at late times regardless of the density. This behavior reflects the spin ratios of 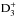 shown in Fig. 6.
shown in Fig. 6.
 |
Fig. 5 Spin-state ratios of the deuterated forms of ammonia as functions of time at different densities, labeled in the lower left panel. |
The statistical values for the spin-state ratios of ortho/para NH2D, ortho/para NHD2 and ortho/meta/para ND3 are 3:1, 2:1, and 16:10:1, respectively. From Fig. 5 it is evident that the various ratios deviate strongly from the statistical values at late times, as already found for ammonia in S15 (see also Fig. 1). The various spin-state ratios are generally fairly insensitive to variations in the density. Some density dependence is usually present between 105 and 106 yr of chemical evolution, but even in this time interval, the difference between the low and high density cases is less than a factor of 2.
Assuming there is nuclear spin conservation and that the same selection rules as used in the gas phase can be applied to the H and D addition reactions on grain surfaces, the different spin isomers of ammonia should form on grains according to their nuclear spin statistical weights indicated above. This is what is seen in the beginning of the simulation. Later on, when the gas-phase ammonia starts to accrete, the spin ratios change on the grains as well, mimicking the ratios in the gas.
Finally, we note that for the lowest density considered (nH = 103 cm-3), many of the plotted spin ratios are increasing even on very long timescales, for example the m/p ratio of ND3 which increases by a factor of ~2 from 106 to 107 yr at this density. We note that this effect is due to the very low density and the spin ratios are expected to stabilize at still longer timescales.
It is well established that deuterium fractionation depends not only on the density, but also on the temperature. In particular, deuteration is expected (in starless cores) to be at its strongest in the temperature range ~10−20 K, because on the one hand, this range lies below the sublimation temperature of CO, allowing the main driver ion of deuterium chemistry, H2D+, to transfer its deuteron to other species, and on the other hand, deuteration efficiency drops toward low temperatures because of the decreasing accretion rates (see below).
We plot in Fig. 7 the abundances of ammonia, its deuterated forms, and the associated abundance ratios at different temperatures. Evidently, the deuterium fractionation is strongest around T = 15 K; both the abundances and the deuterium fractionation peak at this temperature. An analysis of the reaction rates shows that if the temperature is reduced from 15 K to 5 K, the decreased accretion rates lead to relatively high abundances of atomic H and D in the gas phase, which enable efficient conversion of D2H+ to H2D+ through the exchange reaction D2H+ + H− → H2D+ + D. This decreases the ammonia deuterium fractionation because D2H+ is an important part of the production paths of the deuterated forms of ammonia (Fig. 2). On the other hand, as the temperature is increased from 15 K to 20 K, CO starts to desorb efficiently, hindering deuteration in general.
The spin-state ratios of the ammonia isotopologs at different temperatures are shown in Fig. 8. It is observed that the ratios change significantly when the temperature is varied and that the variation is much greater than what is induced by changes in the density. A minimum in the ortho/para (and meta/para for ND3) ratios is observed at T = 10 K, except for the ortho/para ratio of NH2D, which has a maximum at this temperature. These are in contrast to the overall deuteration, which peaks at T = 15 K.
 |
Fig. 6 Spin-state ratios of the deuterated forms of the ammonium ion, as well as D2H+ and |
3.4. Temperature dependence of ammonia D fractionation and spin-state ratios
 |
Fig. 7 Upper panels: abundances of ammonia and its deuterated forms as functions of time at different temperatures, labeled in the lefthand panel. Lower panels: abundance ratios of ammonia and its deuterated forms as functions of time at different temperatures. In all panels, a constant density of nH = 105 cm-3 is adopted. |
As explained in Sect. 3.3, the spin-state ratios of ND3 are determined by those of 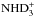 , which are in turn determined by D2H+ and
, which are in turn determined by D2H+ and 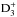 . Moving from 10 K to 20 K, the ortho/para ratio of H2 increases, leading to higher ortho/para D2H+ and meta/ortho (and meta/para)
. Moving from 10 K to 20 K, the ortho/para ratio of H2 increases, leading to higher ortho/para D2H+ and meta/ortho (and meta/para) 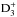 ratios, which ultimately increase the ortho/para and meta/para ratios of ND3 with respect to the values at 10 K. On the other hand, at 5 K, the H2 ortho/para ratio is low, but the abundances of atomic H and D increase owing to decreased accretion rates, and the proton/deuteron exchange reactions with the
ratios, which ultimately increase the ortho/para and meta/para ratios of ND3 with respect to the values at 10 K. On the other hand, at 5 K, the H2 ortho/para ratio is low, but the abundances of atomic H and D increase owing to decreased accretion rates, and the proton/deuteron exchange reactions with the 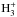 isotopologs (for example,
isotopologs (for example, 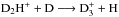 ) increase in importance in determining the various spin-state ratios. The spin-state ratios of NH2D and NHD2 are affected by similar effects with varying temperature.
) increase in importance in determining the various spin-state ratios. The spin-state ratios of NH2D and NHD2 are affected by similar effects with varying temperature.
 |
Fig. 8 Spin-state ratios of the deuterated forms of ammonia as functions of time at different temperatures, labeled in the lower left panel. A constant density of nH = 105 cm-3 is adopted. |
4. Discussion
4.1. Radial profiles for deuterated ammonia
From the above it is clear that both the deuterium fractionation of ammonia and the spin-state ratios depend on time and on the physical parameters (density, temperature). To investigate the implication to observations of deuterated ammonia, we constructed radial abundance profiles for ammonia and its deuterated forms by following the method discussed in Sipilä (2012) and Sipilä et al. (2013), in which chemical calculations are combined with a radiative transfer model to produce self-consistent chemical abundance profiles as functions of density, temperature, and time. For these calculations, we adopt a modified Bonnor-Ebert sphere as the core model (Galli et al. 2002; Keto & Field 2005; Sipilä et al. 2011) of mass M = 1.0 M⊙. We assumed a visual extinction AV = 10 mag at the edge of the core.
 |
Fig. 9 Lefthand panel: gas density (black), gas temperature (red), and dust temperature (blue) as functions of distance from the core center at different time steps (indicated in the middle panel). Middle panel: abundances of NH3 and NH2D as functions of distance from the core center at different time steps. Righthand panel: abundances of NHD2 and ND3 as functions of distance from the core center at different time steps (same legend as in the other panels). The panels correspond to an MBES of mass 1.0 M⊙. |
The density and temperature profiles of the model core are shown in the lefthand panel in Fig. 9. The density and dust temperature profiles hardly change as functions of time. The density is not high enough even in the core center to equalize the dust and gas temperatures. On the other hand, the gas temperature decreases toward the outer areas because of efficient line cooling by (mainly) CO. As the chemical evolution progresses, CO depletes on grain surfaces, reducing the cooling rates, and the gas temperature rises.
The calculated radial abundance profiles are shown in the middle and righthand panels in Fig. 9. The time steps shown in the figure refer to years of chemical evolution with respect to an initially atomic initial state (except for H and D, which are initially in H2 and HD; see S15). The abundances of ammonia and its deuterated isotopologs generally increase as a function of time. Notably, the abundance of ND3 increases by about three orders of magnitude across the core from t = 5 × 104 yr to t = 1 × 106 yr, and the increase in time is stronger for species with more D atoms. The difference in abundance between the core center and edge can be close to two orders of magnitude depending on the species considered and on the time. Depletion slightly decreases the abundances at the core center at the last time step, while the abundances keep increasing at the edge where the density is lower and little depletion is present. An exception to the latter behavior is ammonia, whose abundance has a minimum in the outer core around t = 5 × 105 yr; this kind of behavior is also displayed, for example, in Fig. 7 and discussed in Sect. 4.2.
The results shown here demonstrate, on the one hand, the importance of accurate knowledge of the physical structure, and on the other, the necessity of detailed chemical modeling in ascertaining the chemical age of the object in question. However, quantifying the effect of the varying abundance profiles on observable emission requires calculating the line profiles with a radiative transfer model. This will the subject of a future paper.
4.2. Evolution of the ammonia abundance
Characteristic of the time dependence of the NH3 abundance at high densities and, to a lesser extent, of that of NH2D is a minimum that occurs somewhere between 105 and 106 yr, and a rapid recovery after this minimum. This tendency is most clearly visible in Fig. 7. The behavior is very different from what is observed in the case of CO or CS, for example, but resembles the variation in the abundances of HCN and HNC seen in the models of Loison et al. (2014).
The ammonia production is assumed to start slowly, the widely recognized bottleneck being the slightly endothermic reaction N+ + H2− → NH+ + H, which in practice only works with oH2 in cold clouds (e.g., Dislaire et al. 2012; Roueff et al. 2015). Once NH+ is formed, it is quickly converted to ammonia through 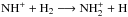 etc. In fact, the flow through the bottleneck is so slow that most of the time the chemical network may find other means of producing NH+. In the present model, NH+ is copiously formed at early times (~104 yr) from the dissociative ionization of HNC by He+, with the bottleneck reaction coming in second. The efficiency of this channel decreases along with the depletion of HNC, and because NH3 accretes onto grains as well, its gas-phase abundance decreases some time before 105 yr or slightly after that, depending on the density.
etc. In fact, the flow through the bottleneck is so slow that most of the time the chemical network may find other means of producing NH+. In the present model, NH+ is copiously formed at early times (~104 yr) from the dissociative ionization of HNC by He+, with the bottleneck reaction coming in second. The efficiency of this channel decreases along with the depletion of HNC, and because NH3 accretes onto grains as well, its gas-phase abundance decreases some time before 105 yr or slightly after that, depending on the density.
A strong increase in the ammonia abundance is seen, however, after the minimum, as an indirect consequence of the depletion of CO and neutrals like HCN and OH, which are ionized in charge transfer reactions with H+. The disappearance of these molecules greatly enhances the abundances of 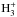 and H+. The
and H+. The 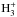 first converts part of N2 to NH through the reaction
first converts part of N2 to NH through the reaction 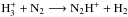 , followed by N2H+ + e−− → N2 + H/NH + N. Although fewer than 10% of the recombinations lead to NH, this channel is important for ammonia, because the increased abundance of H+ directs NH to the ammonia track through the charge transfer reaction H+ + NH− → NH+ + H. Likewise, all the recombination products of
, followed by N2H+ + e−− → N2 + H/NH + N. Although fewer than 10% of the recombinations lead to NH, this channel is important for ammonia, because the increased abundance of H+ directs NH to the ammonia track through the charge transfer reaction H+ + NH− → NH+ + H. Likewise, all the recombination products of 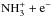 and
and 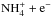 (NH, NH2, NH3) are efficiently returned to the ammonia cycle by H+. In the present model, ammonia passes the cycle
(NH, NH2, NH3) are efficiently returned to the ammonia cycle by H+. In the present model, ammonia passes the cycle 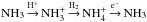 described in Sect. 3.2 several times before colliding with a dust grain. In Fig. 10 we show the fractional abundances of NH3, NH, H+,
described in Sect. 3.2 several times before colliding with a dust grain. In Fig. 10 we show the fractional abundances of NH3, NH, H+, 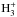 , and HNC as functions of time for a homogeneous model with nH = 105 cm-3, T = 10 K. In this model, NH3 and NH are closely correlated after 105 yr and follow the gradual decrease in the N2 abundance (not shown) at very late times.
, and HNC as functions of time for a homogeneous model with nH = 105 cm-3, T = 10 K. In this model, NH3 and NH are closely correlated after 105 yr and follow the gradual decrease in the N2 abundance (not shown) at very late times.
 |
Fig. 10 Fractional abundances (with respect to nH) of selected species (labeled in the plot) in a homogeneous model with nH = 105 cm-3, T = 10 K. |
4.3. Comparison to Roueff et al. (2005)
Roueff et al. (2005) present observations of NH2D, NHD2, and ND3 toward prestellar cores and discuss the interpretation of the observations in the context of a gas-phase chemical model. Their model is to our knowledge the one that is most directly comparable to our own in terms of the chemistry of deuterated ammonia.
Our model includes time-dependent depletion3, and a chemical steady-state is not reached in the time intervals considered here. However, comparing the values given in Table 9 in Roueff et al. (2005) with our results near the deuterium peak for each density (Fig. 3), we find that the agreement between the models is very good, even though we are using a gas-grain model with different initial abundances and a different value for the cosmic ray ionization rate (here 1.3 × 10-17 s-1; 2 × 10-17 s-1 in Roueff et al. 2005). It should be noted, however, that in our model, depletion also occurs at a density of 104 cm-3, whereas in the Roueff et al. model no depletion is assumed at this density.
 |
Fig. 11 Abundance ratios of ammonia and its deuterated forms (labeled in the plot) as functions of time in a gas-phase chemical model, for different initial values of the H2 ortho/para ratio: 3 (black lines), 10-3 (blue), or 10-5 (green). |
As an additional check, we ran another calculation using a gas-phase model (i.e., no depletion) at n(H2) = 104 cm-3, for three different values of the initial H2 ortho/para ratio. The resulting abundance ratios for ammonia and its deuterated forms are shown in Fig. 11. The gas-phase model predicts a lower deuterium fractionation than the gas-grain model, even for very low initial H2 ortho/para ratios. The main reason for this is that the high abundance of CO hinders the formation of H2D+, D2H+, and 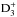 , which in our model are the principal agents in the formation of deuterated ammonia.
, which in our model are the principal agents in the formation of deuterated ammonia.
Roueff et al. (2005) assumed that the release of hydrogen is favored (in a 2:1 ratio) over the release of deuterium in the electron recombinations of the various deuterated ammonium ions, whereas in this work the H/D branching ratios for the recombination reactions are statistical. We tested the effect of assuming a 2:1 ratio for the recombination reactions and found that this has only a marginal effect on the abundances of ammonia and its isotopologs. We note that we adopt the 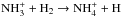 reaction rates from Le Gal et al. (2014), which correspond to the values used by Roueff et al. (2005; see also Roueff et al. 2015). We tested the new coefficients given by Roueff et al. (2015) for these reactions and found that they only have a minor effect on our results.
reaction rates from Le Gal et al. (2014), which correspond to the values used by Roueff et al. (2005; see also Roueff et al. 2015). We tested the new coefficients given by Roueff et al. (2015) for these reactions and found that they only have a minor effect on our results.
The differences between our gas-phase model and that of Roueff et al. (2005) can perhaps be explained by the adoption of different rate coefficients for the 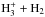 reacting system, since the contribution of the
reacting system, since the contribution of the 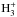 isotopologs to the chemistry of deuterated ammonia is significant as discussed earlier in this paper. Finally we reiterate that the depletion present in our gas-grain model, even at lower densities, enhances deuteration and brings the results close to the gas-phase model of Roueff et al. (2005).
isotopologs to the chemistry of deuterated ammonia is significant as discussed earlier in this paper. Finally we reiterate that the depletion present in our gas-grain model, even at lower densities, enhances deuteration and brings the results close to the gas-phase model of Roueff et al. (2005).
5. Conclusions
We calculated branching ratios for reactions involving multiply deuterated species using group theory. This method produces identical branching ratios for reactions without deuterium, which can be derived with angular momentum algebra (Oka 2004). Our new model allows us to track the spin states of any species that includes multiple protons and/or deuterons. However, in this paper, we concentrated on the spin-state chemistry of deuterated ammonia.
We found that the deuterium fractionation of ammonia is high especially at high density: the NH2D/NH3, NHD2/ NH2D, and ND3/ NHD2 all peak at ~10% for nH = 106 cm-3. The high abundance ratios are in line with the earlier gas-phase models of Roueff et al. (2005). The various spin-state ratios were found to deviate strongly from the statistical values especially at late times, but on the other hand, the ratios appear rather insensitive to variations in the density. We also found that the abundances of ammonia and its isotopologs and the associated spin-state ratios are highly dependent on the temperature; the meta/para ratio of ND3, for example, can vary by a factor of ~5 in the temperature range 5−20 K.
The abundances of NH2D, NHD2, and ND3 and their spin-state ratios in the gas phase are determined by competing ion-molecular reactions, the rates of which depend strongly on the kinetic temperature. The deuterium fractionation is most efficient at 15 K. The temperature dependences of the spin-state ratios are less straightforward: the para species of NHD2 and ND3 reach their abundance maxima at 10 K, whereas para-NH2D has a minimum at this temperature. The reactions leading to deuterated ammonia involve H2D+, D2H+, and 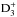 , and benefit from the disappearance of CO, which occurs faster at high densities. Therefore, for objects with density/temperature gradients, such as starless and prestellar cores, significant variations as functions of radius and time can be expected in the abundances and the spin-state ratios of NH2D, NHD2, and ND3. Sensitive observations of these molecules, combined with chemical and radiative transfer modeling, can provide stringent constraints on the physical and chemical structures and on the evolutionary stages of molecular clouds.
, and benefit from the disappearance of CO, which occurs faster at high densities. Therefore, for objects with density/temperature gradients, such as starless and prestellar cores, significant variations as functions of radius and time can be expected in the abundances and the spin-state ratios of NH2D, NHD2, and ND3. Sensitive observations of these molecules, combined with chemical and radiative transfer modeling, can provide stringent constraints on the physical and chemical structures and on the evolutionary stages of molecular clouds.
The present model does not include corrections to the rate coefficients that result from differences in the zero-point energies of deuterated and undeuterated species, except for the 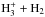 reacting system given by Hugo et al. (2009) and the N+ + H2
reacting system given by Hugo et al. (2009) and the N+ + H2
reaction (Marquette et al. 1988). Moreover, the use of pure nuclear spin statistical weights is based on the implicit assumption that the exothermicity of the reaction is high enough that Pauli-allowed rotational levels of each product species can be populated. For the principal reactions contributing to the interstellar ammonia, this is likely to be true (see also discussion in Rist et al. 2013). However, it is clear that the present model is still incomplete, so an in-depth study of energetics is warranted.
Online material
Appendix A: Calculation of nuclear spin branching ratios using symmetry rules
The method used in deriving the nuclear spin branching ratios is demonstrated by three examples, all dealing with varieties of the reaction 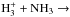
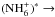
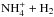 . The method is described in Quack (1977) and in Park & Light (2007b). The collision partners are classified, or labeled, according to the irreducible representations of an appropriate permutation group. These labels tell how the symmetrized nuclear spin functions belonging to this species transform under operations of the group, such as the transposition of two identical nuclei and the permutation of n identical nuclei (e.g., Bunker & Jensen 2006). The branching ratios are obtained from correlations between the group of the intermediate reaction complex and the direct product groups representing the reactants and products (Quack 1977). The statistical weight of each channel corresponds to the number of nuclear spin functions belonging to that symmetry species.
. The method is described in Quack (1977) and in Park & Light (2007b). The collision partners are classified, or labeled, according to the irreducible representations of an appropriate permutation group. These labels tell how the symmetrized nuclear spin functions belonging to this species transform under operations of the group, such as the transposition of two identical nuclei and the permutation of n identical nuclei (e.g., Bunker & Jensen 2006). The branching ratios are obtained from correlations between the group of the intermediate reaction complex and the direct product groups representing the reactants and products (Quack 1977). The statistical weight of each channel corresponds to the number of nuclear spin functions belonging to that symmetry species.
Appendix A.1: Three identical nuclei
As the first example we consider the reaction D2H+ + NH2D →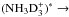
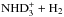 . The H and D symmetries are treated separately. The same result is obtained by considering the mixed system in appropriate direct product groups. From the hydrogen point of view, H2 and H form H3 which dissociates back to H2 + H. On the deuterium side, the reaction forms D3 from D2 + D. In the present model we assume that the branching ratios are equal to the pure nuclear spin symmetry induction and subduction statistical weights, which for these reactions can be read from Tables 3 and 4 of Hugo et al. (2009). We reproduce the appropriate tables in Table A.1.
. The H and D symmetries are treated separately. The same result is obtained by considering the mixed system in appropriate direct product groups. From the hydrogen point of view, H2 and H form H3 which dissociates back to H2 + H. On the deuterium side, the reaction forms D3 from D2 + D. In the present model we assume that the branching ratios are equal to the pure nuclear spin symmetry induction and subduction statistical weights, which for these reactions can be read from Tables 3 and 4 of Hugo et al. (2009). We reproduce the appropriate tables in Table A.1.
Statistical nuclear spin branching ratios for reactions 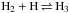 and
and 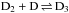 .
.
The numbers in the leftmost columns of Table A.1 are the frequencies of the irreducible representations A1, A2, and E, in the representations of the permutation group S3 generated by the nuclear spin functions of 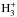 and
and 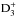 . This means that the symmetry representations of H3 and D3 in S3 can be reduced into the following direct sums (denoted by ⊕):
. This means that the symmetry representations of H3 and D3 in S3 can be reduced into the following direct sums (denoted by ⊕): 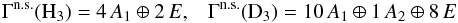 (A.1)(e.g., Bunker & Jensen 2006; Hugo et al. 2009). According to Mulliken’s notation used here, one-dimensional representations are labeled as either A or B, two-dimensional ones are labeled E, three-dimensional F, four-dimensional G, etc. The total nuclear spin statistical weight of each symmetry species can be read from these decompositions by multiplying the frequency by the dimension of the representation, f(Γi) × dim(Γi). The Greek appellations, para, meta, and ortho are used to indicate these statistical weights for the simplest molecules, so that “ortho” has the highest statistical weight. The “para” (E, I = 1/2) and “ortho” (A1, I = 3/2) species of
(A.1)(e.g., Bunker & Jensen 2006; Hugo et al. 2009). According to Mulliken’s notation used here, one-dimensional representations are labeled as either A or B, two-dimensional ones are labeled E, three-dimensional F, four-dimensional G, etc. The total nuclear spin statistical weight of each symmetry species can be read from these decompositions by multiplying the frequency by the dimension of the representation, f(Γi) × dim(Γi). The Greek appellations, para, meta, and ortho are used to indicate these statistical weights for the simplest molecules, so that “ortho” has the highest statistical weight. The “para” (E, I = 1/2) and “ortho” (A1, I = 3/2) species of 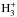 have, however, equal statistical weights.
have, however, equal statistical weights. 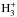 has no nuclear spin functions of species A2, which is antisymmetric with respect to interchange of two nuclei4. H2 and D2 can have the symmetries A or B, and the single nuclei H and D have the A symmetry. The number in the bottom righthand corner of each table gives the total number of linearly independent nuclear spin functions of the molecule, (2I + 1)3, where I = 1/2 for H3 and I = 1 for D3. The branching ratios in Table A.1 are obtained by multiplying the correlation table between S3 and the product group S2 ⊗ S1 by appropriate frequencies. This correlation table is given by
has no nuclear spin functions of species A2, which is antisymmetric with respect to interchange of two nuclei4. H2 and D2 can have the symmetries A or B, and the single nuclei H and D have the A symmetry. The number in the bottom righthand corner of each table gives the total number of linearly independent nuclear spin functions of the molecule, (2I + 1)3, where I = 1/2 for H3 and I = 1 for D3. The branching ratios in Table A.1 are obtained by multiplying the correlation table between S3 and the product group S2 ⊗ S1 by appropriate frequencies. This correlation table is given by
| S 3 | S2 ⊗ S1 | |
| A ⊗ A | B ⊗ A | |
|
|
||
| A 1 | 1 | 0 |
| A 2 | 0 | 1 |
The correlation table S3 ↔ S2 ⊗ S1 presented above is derived using the standard methods of group theory, i.e., by forming the character table of direct product group S2 ⊗ S1, and the character table for the subduced representations of S3 on S2 ⊗ S1, S3 ↓ S2 ⊗ S1. The latter is obtained from that of S3 by stripping it from operations that are unfeasible in the direct product group S2 ⊗ S1, i.e., the class of cyclic permutations of three nuclei, {(123),(132)}. Finally, the orthogonality relation between the characters of irreducible representations is used.
Tables A.1 can be read either from left to right (“subduction”) or top down (“induction”). For example, one can see that the A1 species of H3 and D3 dissociate exclusively to the A symmetry of H2 or D2, whereas the E species dissociate to both A and B symmetries (“ortho” and “para”, respectively) of H2 or D2 with equal probability. In the reaction oD2 + D (A ⊗ A), the A1 (“meta”) and E (“ortho”) species of D3 are formed with the probabilities 10/18 and 8/18, respectively, whereas in the reaction pD2 + D (B ⊗ A), the A2 (“para”) and E (“ortho”) species of D3 are formed with the probabilities 1/9 and 8/9. These branching ratios determine relative abundances of 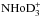 ,
, 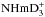 , and
, and 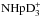 resulting from the reaction D2H+ + NH2D.
resulting from the reaction D2H+ + NH2D.
Appendix A.2: Six identical nuclei
To determine the nuclear spin branching ratios of the reactions 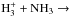
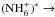
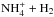 and
and 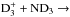
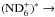
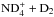 , one needs to determine the nuclear spin symmetry species of H6 and D6 in the permutation group S6. We first calculate the characters, χ(R), of the representations generated by the nuclear spin functions of H6 and D6 under the operations R of S6. Crabtree & McCall (2013) give a convenient formula for this:
, one needs to determine the nuclear spin symmetry species of H6 and D6 in the permutation group S6. We first calculate the characters, χ(R), of the representations generated by the nuclear spin functions of H6 and D6 under the operations R of S6. Crabtree & McCall (2013) give a convenient formula for this: 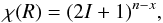 (A.2)where I is the nuclear spin (1/2 for H and 1 for D), n the number of identical nuclei (here 6), and x the number of transpositions or pairwise permutations, which correspond to the operation R. The number of interchanges corresponding to a cyclic permutation of k elements is k − 1, and so x = k − 1. For example, x = 2 for the ternary permutation (123). The character table of S6 is easily obtainable using GAP (2015). By applying the orthogonality relation of the characters of irreducible representations, we derive the following decompositions for the symmetry representations of H6 and D6:
(A.2)where I is the nuclear spin (1/2 for H and 1 for D), n the number of identical nuclei (here 6), and x the number of transpositions or pairwise permutations, which correspond to the operation R. The number of interchanges corresponding to a cyclic permutation of k elements is k − 1, and so x = k − 1. For example, x = 2 for the ternary permutation (123). The character table of S6 is easily obtainable using GAP (2015). By applying the orthogonality relation of the characters of irreducible representations, we derive the following decompositions for the symmetry representations of H6 and D6: 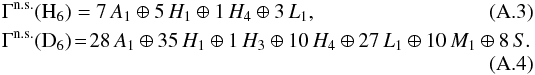 The correlation tables S6 ↔ S3 ⊗ S3 and S6 ↔ S4 ⊗ S2 needed for the induction and subduction statistics are derived as outlined in the previous example. Finally, the branching ratio tables listed in Tables A.2−A.5 are obtained by multiplying the correlation tables by the frequencies of irreducible representations appearing in the decompositions given above. In addition, the columns of the correlation table are multiplied by the dimensions of the subduced representations in order to make the weights correspond to the total number of nuclear spin functions belonging to each representation. In the previous example, all products had one-dimensional representations. The correct normalization of the weights can be checked by inspecting the last rows and columns of the tables. In these tables, species with zero frequencies are not listed.
The correlation tables S6 ↔ S3 ⊗ S3 and S6 ↔ S4 ⊗ S2 needed for the induction and subduction statistics are derived as outlined in the previous example. Finally, the branching ratio tables listed in Tables A.2−A.5 are obtained by multiplying the correlation tables by the frequencies of irreducible representations appearing in the decompositions given above. In addition, the columns of the correlation table are multiplied by the dimensions of the subduced representations in order to make the weights correspond to the total number of nuclear spin functions belonging to each representation. In the previous example, all products had one-dimensional representations. The correct normalization of the weights can be checked by inspecting the last rows and columns of the tables. In these tables, species with zero frequencies are not listed.
Statistical nuclear spin branching ratios of the reaction 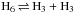 .
.
Statistical nuclear spin branching ratios of the reaction 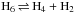 .
.
Statistical nuclear spin branching ratios of the reaction 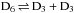 .
.
Statistical nuclear spin branching ratios of the reaction 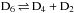 .
.
The use of the branching ratio tables is illustrated in Figs. A.1 and A.2. Figure A.1 gives the outcome of the reaction 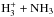 assuming that one of the molecules is of the A1 (“ortho”) symmetry and the other one is E (“para”). The branching probabilities indicated next to the arrows are obtained from Tables A.2 (reading it top down) and from Table A.3 (reading it from left to right). After combining the probabilities of pathways leading to different symmetry species of
assuming that one of the molecules is of the A1 (“ortho”) symmetry and the other one is E (“para”). The branching probabilities indicated next to the arrows are obtained from Tables A.2 (reading it top down) and from Table A.3 (reading it from left to right). After combining the probabilities of pathways leading to different symmetry species of 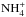 , one finds that the F1, A1, and E species are formed in ratios 15:7:2 in this reaction. Figure A.2 describes the branching of the reaction
, one finds that the F1, A1, and E species are formed in ratios 15:7:2 in this reaction. Figure A.2 describes the branching of the reaction 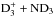 assuming that both species are A1 (“meta”). The branching ratios are obtained from Tables A.4 and A.5. This reaction produces the F1, A1, and E species of
assuming that both species are A1 (“meta”). The branching ratios are obtained from Tables A.4 and A.5. This reaction produces the F1, A1, and E species of 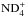 in ratios 9:9:2.
in ratios 9:9:2.
 |
Fig. A.1 Branching ratios of the reaction |
 |
Fig. A.2 Branching ratios of the reaction |
GAP is a system for computational group theory, http://www.gap-system.org
In our model, nitrogen and deuterium deplete as well, unlike in the model of Roueff et al. (2005).
Acknowledgments
We thank the anonymous referee for a careful reading of the manuscript, and Laurent Wiesenfeld for helpful discussions. O.S. and P.C. acknowledge the financial support of the European Research Council (ERC; project PALs 320620)
References
- Brünken, S., Sipilä, O., Chambers, E. T., et al. 2014, Nature, 516, 219 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bunker, P. R. 1979, Molecular Symmetry and Spectroscopy, 1st edn. (New York: Academic Press Inc.), 1, 6 [Google Scholar]
- Bunker, P. R., & Jensen, P. 2006, Molecular Symmetry and Spectroscopy, 2nd edn., Vol. 1 (Ottawa: National Research Council of Canada), ch. 8 [Google Scholar]
- Crabtree, K. N., & McCall, B. J. 2013, J. Phys. Chem. A, 117, 9950 [CrossRef] [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., & Watt, G. D. 1984, MNRAS, 209, 25 [NASA ADS] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GAP 2015, GAP – Groups, Algorithms, and Programming, Version 4.7.7, The GAP Group [Google Scholar]
- Gerin, M., Lis, D. C., Philipp, S., et al. 2006, A&A, 454, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hugo, E. 2009, Ph.D. Thesis, I. Physikalisches Institut, Universität zu Köln, http://kups.ub.uni-koeln.de/2646/ [Google Scholar]
- Hugo, E., Asvany, O., & Schlemmer, S. 2009, J. Chem. Phys., 130, 164302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Keto, E., & Field, G. 2005, ApJ, 635, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J. 1991, A&A, 242, 235 [NASA ADS] [Google Scholar]
- Le Gal, R., Hily-Blant, P., Faure, A., et al. 2014, A&A, 562, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., Roueff, E., Gerin, M., et al. 2002, ApJ, 571, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Gerin, M., Roueff, E., Vastel, C., & Phillips, T. G. 2006, ApJ, 636, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., Wakelam, V., & Hickson, K. M. 2014, MNRAS, 443, 398 [Google Scholar]
- Marquette, J. B., Rebrion, C., & Rowe, B. R. 1988, J. Chem. Phys., 89, 2041 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T. 2004, J. Mol. Spectrosc., 228, 635 [Google Scholar]
- Pagani, L., Roueff, E., & Lesaffre, P. 2011, ApJ, 739, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Park, K., & Light, J. C. 2007a, J. Chem. Phys., 126, 044305 [NASA ADS] [CrossRef] [Google Scholar]
- Park, K., & Light, J. C. 2007b, J. Chem. Phys., 127, 224101 [NASA ADS] [CrossRef] [Google Scholar]
- Quack, M. 1977, Mol. Phys., 34, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Rist, C., Faure, A., Hily-Blant, P., & Le Gal, R. 2013, J. Phys. Chem. A, 117, 9800 [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2001, ApJ, 553, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shah, R. Y., & Wootten, A. 2001, ApJ, 554, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Sipilä, O. 2012, A&A, 543, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Harju, J., & Juvela, M. 2011, A&A, 535, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2013, A&A, 554, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipilä, O., Caselli, P., & Harju, J. 2015, A&A, 578, A55 (S15) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tiné, S., Roueff, E., Falgarone, E., Gerin, M., & Pineau des Forêts, G. 2000, A&A, 356, 1039 [NASA ADS] [Google Scholar]
- van der Tak, F. F. S., Schilke, P., Müller, H. S. P., et al. 2002, A&A, 388, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wirström, E. S., Charnley, S. B., Cordiner, M. A., & Milam, S. N. 2012, ApJ, 757, L11 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spin-state ratios of NH3 (upper panels) and H2O (lower panels) as functions of time at different densities, labeled in the upper left panel. The lefthand panels present results calculated with the (gas-grain) model of S15, while the righthand panels correspond to the present work. |
| In the text | |
 |
Fig. 2 Principal reactions determining the abundances and spin ratios of deuterated ammonia isotopologs at late stages of chemical evolution in cold, dense cores. The reactions |
| In the text | |
 |
Fig. 3 Abundances of ammonia and its deuterated forms as functions of time at different densities, labeled in the upper right panel. |
| In the text | |
 |
Fig. 4 Abundance ratios of ammonia and its deuterated forms as functions of time at different densities, labeled in the lefthand panel. |
| In the text | |
 |
Fig. 5 Spin-state ratios of the deuterated forms of ammonia as functions of time at different densities, labeled in the lower left panel. |
| In the text | |
 |
Fig. 6 Spin-state ratios of the deuterated forms of the ammonium ion, as well as D2H+ and |
| In the text | |
 |
Fig. 7 Upper panels: abundances of ammonia and its deuterated forms as functions of time at different temperatures, labeled in the lefthand panel. Lower panels: abundance ratios of ammonia and its deuterated forms as functions of time at different temperatures. In all panels, a constant density of nH = 105 cm-3 is adopted. |
| In the text | |
 |
Fig. 8 Spin-state ratios of the deuterated forms of ammonia as functions of time at different temperatures, labeled in the lower left panel. A constant density of nH = 105 cm-3 is adopted. |
| In the text | |
 |
Fig. 9 Lefthand panel: gas density (black), gas temperature (red), and dust temperature (blue) as functions of distance from the core center at different time steps (indicated in the middle panel). Middle panel: abundances of NH3 and NH2D as functions of distance from the core center at different time steps. Righthand panel: abundances of NHD2 and ND3 as functions of distance from the core center at different time steps (same legend as in the other panels). The panels correspond to an MBES of mass 1.0 M⊙. |
| In the text | |
 |
Fig. 10 Fractional abundances (with respect to nH) of selected species (labeled in the plot) in a homogeneous model with nH = 105 cm-3, T = 10 K. |
| In the text | |
 |
Fig. 11 Abundance ratios of ammonia and its deuterated forms (labeled in the plot) as functions of time in a gas-phase chemical model, for different initial values of the H2 ortho/para ratio: 3 (black lines), 10-3 (blue), or 10-5 (green). |
| In the text | |
 |
Fig. A.1 Branching ratios of the reaction |
| In the text | |
 |
Fig. A.2 Branching ratios of the reaction |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.