| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201526462 | |
| Published online | 18 September 2015 | |
Calibrating echelle spectrographs with Fabry-Pérot etalons
Institut für Astrophysik (IAG), Georg-August-Universität
Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen,
Germany
e-mail:
fbauer@astro.physik.uni-goettingen.de
Received: 4 May 2015
Accepted: 21 June 2015
Context. Over the past decades hollow-cathode lamps have been calibration standards for spectroscopic measurements. Advancing to cm/s radial velocity precisions with the next generation of instruments requires more suitable calibration sources with more lines and fewer dynamic range problems. Fabry-Pérot interferometers provide a regular and dense grid of lines and homogeneous amplitudes, which makes them good candidates for next-generation calibrators.
Aims. We investigate the usefulness of Fabry-Pérot etalons in wavelength calibration, present an algorithm to incorporate the etalon spectrum in the wavelength solution, and examine potential problems.
Methods. The quasi-periodic pattern of Fabry-Pérot lines was used along with a hollow-cathode lamp to anchor the numerous spectral features on an absolute scale. We tested our method with the HARPS spectrograph and compared our wavelength solution to the one derived from a laser frequency comb.
Results. The combined hollow-cathode lamp/etalon calibration overcomes large distortion (50 m/s) in the wavelength solution of the HARPS data reduction software. The direct comparison to the laser frequency comb shows differences of only 10 m/s at most.
Conclusions. Combining hollow-cathode lamps with Fabry-Pérot interferometers can lead to substantial improvements in the wavelength calibration of echelle spectrographs. Etalons can provide economical alternatives to the laser frequency comb, especially for smaller projects.
Key words: instrumentation: interferometers / instrumentation: spectrographs / methods: data analysis / techniques: radial velocities
© ESO, 2015
1. Introduction
Accurate wavelength calibration is a cornerstone for any measurement with high-resolution spectrographs. It translates the pixel position of the detector into absolute wavelengths and thereby defines the physical scale. As many astronomical research fields benefit from high-precision radial velocity (RV) measurements, the next generation of spectrographs aims for cm/s precisions (D’Odorico & CODEX/ESPRESSO Team 2007). Today, most echelle spectrographs use hollow-cathode lamps (HCLs), for example, thorium-argon or thorium-neon, to perform wavelength calibration, but these lamps are insufficient for the needs of future high-precision instruments.
Hollow-cathode lamps establish collisions between the carrier gas (argon or neon) and the thorium atoms, which thereby are exited (Kerber et al. 2007). When the thorium relaxes into a lower energy state, a photon carries away the energy difference and contributes to an emission line. The laboratory wavelengths of thorium lines can be measured or calculated, as done by Palmer & Engleman (1983), Lovis & Pepe (2007), Kerber et al. (2008), and Redman et al. (2014). The drawback of HCLs is the limited number of reference lines, the wide dynamic range spanned by the lines, and the irregular line distribution. Blending of lines is an additional problem: only 4000–8000 spectral lines in total remain usable in the visual (Lovis & Pepe 2007). In addition to the large intensity differences between thorium lines, the carrier gas often emits strong lines itself. Exposure times have to be well chosen to obtain enough cathode (e.g. thorium) lines for calibration while keeping the number of saturated carrier gas (e.g., argon) lines low. Spectral regions without lines must be interpolated by the wavelength solution, resulting in uncertain wavelengths for these pixels.
To overcome the problems of HCLs, new calibrators are currently under development. Among them are the laser frequency comb (LFC, e.g., Murphy et al. 2007; Wilken et al. 2010, 2012) and the Fabry-Pérot interferometer (FPI, Wildi et al. 2010; Schäfer & Reiners 2012; Reiners et al. 2014; Schwab et al. 2014). LFCs are rather expensive and often cannot be afforded for smaller projects. Here we focus on less expensive FPIs and their use as a calibration source.
A tunable FPI device was already used as dispersing element to develop a high-resolution spectrograph for planet searches at Kitt Peak (McMillan et al. 1988, 1994). The wavelength solution of the spectrograph totally relied on geometrical calibration and accurate tuning of the FPI and demonstrated precisions of 6 m/s. Cochran et al. (1982) used the FPI to superimpose absorption lines of known wavelength in the stellar spectrum. In both works the FPI was used in transmission, which resulted in very low instrument efficiency and led to the development of new techniques such as iodine cells in transmission (Butler et al. 1996) or ultra-stable spectrographs (Mayor et al. 2003). Currently, FPIs are again considered in astronomical spectrographs for nightly drift checks, but not as wavelength calibrators (Wildi et al. 2010).
The advantage of the FPI against HCLs is its ability to produce a dense grid of lines with almost uniform intensity over the entire spectral range. They can be manufactured to match the specifications of most spectrographs as the free spectral range is a function of the cavity width. This solves the problem of empty spectral regions and saturated lines, thereby increasing the robustness of the wavelength solution.
The drawback of FPIs is their weakly constrained absolute wavelength. Line positions are determined by the cavity width of the etalon and the interference order. These are usually not known to the accuracy needed to provide absolute calibration. Furthermore, the group-velocity dispersion limits the predictability of individual peak positions, and the cavity width is very sensitive to temperature and mechanical stress. Hence FPIs are temperature and pressure stabilized to minimize drifts (Wildi et al. 2010; Schäfer & Reiners 2012). Such a stabilized FPI is located at the HARPS spectrograph, and nightly drifts of 10 cm/s were reported (Wildi et al. 2010).
First, we propose in Sect. 2 a method for characterizing the FPI comb pattern with HCLs, using a high-resolution spectrograph. We explain our wavelength calibration concept and model in Sect. 3. In Sect. 4 we combine information from an HCL and an FPI to improve the accuracy and stability of the HARPS wavelength solution as compared to the use of an HCL alone. Furthermore, we investigate the impact of a distorted wavelength solution on RV measurements in Sect. 5
 |
Fig. 1 Spectrum of the CARMENES NIR FPI taken with the Fourier transform spectrometer in Göttingen. |
2. Calibrating the Fabry-Pérot interferometer
2.1. Ideal FPI
The ideal FPI consists of two partly reflective plane-parallel surfaces (Born & Wolf 1999). When light enters the device, it is reflected between the two surfaces and interference takes place between light rays, depending on the phase difference. With a white-light input source, a spectrograph will observe a pattern of transmission peaks that are spaced equidistantly in frequency ν (Fig. 1). The transmission maxima fulfill the interference condition given by the effective FPI cavity width d: 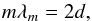 (1)where m is an integer number called interference order, and λm are the transmission maxima wavelengths. The effective cavity width is d = Dn cosθ, with the distance between the two mirrors D, the refraction index n, and the incident ray angle θ.
(1)where m is an integer number called interference order, and λm are the transmission maxima wavelengths. The effective cavity width is d = Dn cosθ, with the distance between the two mirrors D, the refraction index n, and the incident ray angle θ.
Using the FPI as a calibration source requires knowledge of the exact wavelengths for all interference maxima observed by the spectrograph. As the wavelength λm of each FPI interference order depends only on the effective cavity width, d, this parameter must be known with the same accuracy as the wavelength requirement (δd/d = 3 × 10-9 for 1 m/s). For the FPI this means that the spacing d must be known with an accuracy of about 0.15 Å (Reiners et al. 2014). Typically, the mirror distance D is only known to about 1 μm, which is five orders of magnitudes above our requirements. In addition, we do not exactly know the incident ray angle θ. Hence, we need to find a method for calibrating the effective FPI cavity width d. The interference condition of the FPI, Eq. (1), can be used to perform the cavity width measurement. This can be done with any high-resolution spectrograph and its internal calibration sources such as HCLs (Wildi et al. 2010). First, the wavelength solution of the spectrograph must be derived using only HCL lines. Then the line positions of the FPI can be measured on the detector and the HCL wavelength solution can be used to assign the corresponding wavelength to all interference peaks.
Now we need to identify the interference order m for all FPI peaks. From the observed spectra we can only obtain a relative numbering k = m − m1 by simply counting the lines, but the absolute interference order of the first (reddest) peak m1 is not known. To find m1, the fact that the ideal FPI cavity width is a constant number can be used. A guess for m1 and the FPI wavelengths derived from the HCL wavelength solution can be used to obtain the effective cavity width d for each FPI line separately via Eq. (1). If the effective cavity width d is plotted as a function of relative peak number k using the correct m1, the data points are expected to be distributed around a constant value. If the guess for m1 is incorrect, the data points will, however, produce a positive slope for m1 too small or a negative slope for m1 too high. Once the right value for m1 is found, the large number of individual effective cavity width measurements (typically on the order of 104 for high-resolution echelle spectrographs) can be averaged to obtain a good estimate of d.
We now only need this one parameter (the effective cavity width d of the FPI) to globally predict the wavelength of all interference peaks observed. The combined accuracy of all HCL lines anchors the FPI on an absolute wavelength scale. Paired with the high precision of the FPI, local imperfections of the wavelength solution can now be resolved and corrected. The numerous FPI features bridge regions lacking any spectral features of HCLs, and we can now determine whether the wavelength solution model is sufficient or if more detailed models are required.
2.2. Real FPI
In practice, applying the concept of calibrating the effective cavity width using standard calibrators proves to be more difficult for real FPIs. The cavity width is not constant throughout the wavelength range covered by high-resolution echelle spectrographs. FPIs are usually soft coated, allowing photons of different energy to penetrate to different depths of the dielectric surface. Hence, photons of different wavelengths see different cavity widths. As an example, the penetration depth variation over the wavelength range of HARPS easily reaches a few hundred nm (Wildi et al. 2010). If we do not account for this, the computed FPI wavelengths are incorrect by several km s-1. For a full characterization of the FPI spectrum, the task is therefore not only to find the global mean effective cavity width 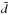 of the FPI, but also to determine the wavelength-dependent function d(λ).
of the FPI, but also to determine the wavelength-dependent function d(λ).
We assumed that the penetration depth is a smooth function of wavelength and therefore also a smooth function of relative interference order k. Because the measured wavelength is uncertain but the relative peak numbering is noise-free, we modeled d as a function of k instead of d as a function of λ. We chose uniform cubic B-splines (de Boor 2001; Dierckx 1995) to fit the function d(k).
The basis of our method is the assumption that the penetration depth variation is smooth. Hence we decided to test this with the CARMENES (Quirrenbach et al. 2011) near-infrared FPI (finesse ~8, Schäfer & Reiners 2012). We obtained 78 spectra with the Bruker IFS 125/HR Fourier transform spectrometer (FTS) with a resolution of R = 500 000 in our optics laboratory. The median signal-to-noise ratio of the coadded spectrum is 350 (Fig. 1). We used the internal wavelength calibration of the FTS as starting guess for all FPI peak wavelengths. This calibration is provided by a He-laser measuring the path length within the spectrometer. With the high resolution of the FTS, the FPI peaks are well resolved in the spectra, and we measured individual line positions by fitting a Lorentz function. The FPI itself was not operated under vacuum conditions, thus water lines contaminated the spectrum. We excluded contaminated peaks from our cavity width measurement. We determined the mean effective cavity width 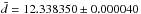 mm, which is consistent with what we expect from the mirror distance given by the manufacturer D = 12.334 mm, the refractive index of air n ~ 1.003, and an incident ray angle of θ = 0 deg.
mm, which is consistent with what we expect from the mirror distance given by the manufacturer D = 12.334 mm, the refractive index of air n ~ 1.003, and an incident ray angle of θ = 0 deg.
The penetration depth variation of the FPI as a function of the relative peak numbering and the measured FTS wavelength is shown in Fig. 2. Fitting a B-spline with 50 nodes results in an rms scatter around the model of 0.326 nm, translating into 8 m/s. We found no discontinuities in d(k) within our measurement precision. Hence our assumption of a smooth penetration depth variation is valid. The rms scatter of 8 m/s is about what we expect from photon noise.
 |
Fig. 2 Upper panel: effective cavity width measurement d(k) for the CARMENES NIR FPI. Lower panel: residuals of the spline fit. We show the data (black dots), clipped lines due to atmosphere absorption features (red crosses), and the spline fit to the data (green line). |
After we determined the model parameters for the effective cavity width d, we searched for the absolute interference number of the first observed FPI peak m1 to compute the wavelength for all interference orders. This is no longer trivial if the effective cavity width d is not a constant.
Reiners et al. (2014) suggested using the mean free spectral range ⟨ Δν ⟩ to calculate the mean effective cavity width and then use Eq. (1) to calculate the absolute order numbering. Wildi et al. (2010) determined the absolute order numbering assuming the effective cavity width d to be exactly the absolute cavity width D specified by the manufacturer and rounding m to the closest integer number they obtained from equation Eq. (1) and the HARPS wavelength solution. Their approach resulted in a penetration depth curve with the least variation.
Other choices of m1 introduce steeper slopes in the effective cavity width d. We show that the choice of m1 influences the overall slope of the function d(k) for the CARMNENES NIR FPI in Fig. 3. Because we do not know enough about the material properties of the coating, the penetration depth variation with wavelength and the alignment of the FPI, we do not know which m1 and which d curve are the true ones. We chose m1 = 13 604 as reference value because it results in the d(k) curve with the least penetration depth variation. We note that this choice is not necessarily the true value of m1
We realized, however, that it is not necessary to know m1 exactly to calibrate the FPI wavelengths. As a result of the degeneracy in Eq. (1) between the absolute peak number m and the effective cavity width d(k), identical peak wavelengths occur for different combinations of m and d(k). Hence, our method for deriving absolute wavelengths for individual FPI peaks is expected to be robust against choosing the wrong value for m1.
To test this, we computed d(k) using two different values for m1 differing by 100 interference orders, m1 = 13 604 and m1 = 13 704. For both cases we obtained the FPI wavelengths using Eq. (1). We calculated the difference of the calibrated FPI wavelengths line by line and show the result as a dashed line in the lower panel of Fig. 3. The largest difference between the calibrated peak wavelengths is 10 cm/s in the region between k = 2000 and k = 10 000. The difference increases up to 5 m/s at the edges because there are fewer data points to constrain the spline fit. Despite the large difference in d(k) (several hundred nm, see upper panel in Fig. 3), the difference between the modeled wavelengths is small (lower panel in Fig. 3).
 |
Fig. 3 Upper panel: effective cavity width d(k) obtained for different absolute interference order numbers m1. The reference curve (m1 = 13 604, black) is shown in Fig. 2. Lower panel: difference in modeled FPI peak wavelength λm using m1 = 13 704 with the reference curve (dashed line). Residuals of the spline fit to the cavity width d(k) obtained with m1 = 13 704 are shown as purple dots. |
3. Wavelength solution model
In this section, we explain our strategy to determine the wavelength solution of a high-resolution echelle spectrograph. First, we introduce our concept for the mapping between wavelength and pixels in the case of a monolithic detector with uniform pixels. We describe our model, the parametrization, and the regression type. Second, we proceed with real detectors and report how we account for uneven pixel sizes in the wavelength solution.
3.1. Mapping wavelengths to detector coordinates
The general idea of wavelength calibration is to feed the spectrograph with a reference spectrum of known wavelengths λl, for example, the known atomic lines of a hollow-cathode lamp, and observe the response at the detector. The positions of the line centers xl in the extracted spectrum are measured by fitting a model of the instrumental profile (e.g., Gaussian functions) to each individual spectral line l. For the set of wavelength-pixels pairs (λl,xl), a relation is established by a fit. Finally, this relation is used to predict the wavelength at the center of every detector pixel.
The wavelengths of standard lines are given by accurate and precise line lists with uncertainties in the range of 10-6−10-7 (~10 m/s) (Redman et al. 2014). On the other hand, the positions of weak lines on the detector exhibit typical measurement errors of 0.1 pixels or about 100 m/s. Hence, in wavelength calibration the standard line wavelength, λl, represents the independent variable (or the cause) and the position on the detector, xl, is the dependent variable (or the spectrograph response).
A common and simple procedure for wavelength calibration is to fit a continuous model for λ(x). From the function λ(x) the wavelength for each pixel can be directly evaluated. In this approach the role between dependent and independent variable is reversed (Isobe et al. 1990), and we call this reverse regression. Reverse regression causes problems when weighting the data.
For this reason, direct regression can be used to fit the detector position of individual lines as a function of wavelength, x(λ). To predict the wavelength for each pixel in this approach, the model x(λ) must be inverted λ(x) = x(λ)-1.
The wavelength solution is usually modeled with polynomials (oλ = poly(x) in case of reverse regression, e.g., Baranne et al. 1996), which can be interpreted as a Taylor expansion of the grating equation ![\begin{equation} o \lambda = n \sigma~[\cos \gamma_1~\sin \alpha_1+\cos \gamma_2~\sin \alpha_2] \label{eq:grating} \end{equation}](/articles/aa/full_html/2015/09/aa26462-15/aa26462-15-eq52.png) (2)in terms of the diffraction angle α2 , which is proportional to the position in the focal plane, x ∝ α2. In Eq. (2), o is the diffraction order, n is the refractive index, σ is the grating constant, α1 and α2 are the angles of the incident and diffracted ray with respect to the grating normal, and γ1 and γ2 are the off-plane angles before and after the grating, respectively (Schroeder 2000).
(2)in terms of the diffraction angle α2 , which is proportional to the position in the focal plane, x ∝ α2. In Eq. (2), o is the diffraction order, n is the refractive index, σ is the grating constant, α1 and α2 are the angles of the incident and diffracted ray with respect to the grating normal, and γ1 and γ2 are the off-plane angles before and after the grating, respectively (Schroeder 2000).
In direct regression with x(λ) = poly(oλ), we basically approximate a re-arranged version of the grating equation ![\begin{equation} \alpha_2 = \arcsin \left( \frac{1}{\cos \gamma_2} \left[\frac{o \lambda}{n \sigma} - \cos \gamma_1~\sin \alpha_1 \right] \right) \ . \label{eq:grating2} \end{equation}](/articles/aa/full_html/2015/09/aa26462-15/aa26462-15-eq62.png) (3)We note that polynomials of higher degree (typically +1) are needed with direct regression for a wavelength solution with similar quality compared to reverse regression. This is because the sine function in Eq. (2) is more amenable to a Taylor expansion than the arcsine function in Eq. (3).
(3)We note that polynomials of higher degree (typically +1) are needed with direct regression for a wavelength solution with similar quality compared to reverse regression. This is because the sine function in Eq. (2) is more amenable to a Taylor expansion than the arcsine function in Eq. (3).
A way of keeping both advantages (lower number of parameters and direct regression) would be to use x = poly(oλ)-1 as forward model, which we might call inverse regression. This requires nonlinear least-squares fitting and thus higher computational effort.
We chose direct regression below. This allows us to correctly weight all data points and to implement unequal pixel sizes in our model (next section). Moreover, instead of simple polynomials for each order, we use 2D polynomials to couple the individual orders. This decreases the number of parameter and increases the robustness of the fit. We also use oλ instead of λ as variable, that is, x(λ,o) = poly(oλ,o). The reparametrization is motivated by Eq. (3). This approach is a direct regression version of the algorithm implemented in the IDL REDUCE package of Piskunov & Valenti (2002).
3.2. Unequal pixel sizes
Standard wavelength calibration procedures usually assume that detector pixels are equally spaced and of the same size. Irregularities in pixel size of CCD detectors are on the order of 10-2 (Wilken et al. 2010), which is becoming a significant limitation for high-precision spectroscopic measurements. For example, Wilken et al. (2010) showed that inhomogeneous pixel sizes lead to discontinuities in the wavelength solution of HARPS on the order of several 10 m/s.
To account for irregular detector pixels, we included the pixel size in our model and distinguished now more strictly between detector coordinates, X (pixel), and focal plane coordinates, x. We denote the size of pixel i by apix,i and assumed that there is no gap space between individual pixels. Thus, the transformation from pixel coordinates to focal plane coordinate is ![\begin{eqnarray} x(X,{\rm a_\mathrm{pix}}) & = & \sum_{i=1}^{[X]} a_{\mathrm{pix},i} + a_{\mathrm{pix},[X]} \cdot \left( X-[X]-\frac{1}{2} \right) \label{eq:coord_transformation} , \end{eqnarray}](/articles/aa/full_html/2015/09/aa26462-15/aa26462-15-eq71.png) (4)where [ X ] is the value of X rounded to the nearest integer (the pixel number). In Eq. (4) we integrate over the width of all preceding pixels (including the current one) and linearly interpolate (backwards) for subpixel position. The zero point of the coordinate system (x = 0) coincides with the left border of the first pixel (X = 0.5). If all pixels have the same size (apix,i = 1), the transformation is simply x = X−0.5. The transformation can also be extended to include virtual pixels for the application to mosaic detectors with gap sizes corresponding to several pixels (apix,i ~ 100 pixels) between the detectors as, for instance, in CARMENES (Quirrenbach et al. 2011) or CRIRES+ (Follert et al. 2014).
(4)where [ X ] is the value of X rounded to the nearest integer (the pixel number). In Eq. (4) we integrate over the width of all preceding pixels (including the current one) and linearly interpolate (backwards) for subpixel position. The zero point of the coordinate system (x = 0) coincides with the left border of the first pixel (X = 0.5). If all pixels have the same size (apix,i = 1), the transformation is simply x = X−0.5. The transformation can also be extended to include virtual pixels for the application to mosaic detectors with gap sizes corresponding to several pixels (apix,i ~ 100 pixels) between the detectors as, for instance, in CARMENES (Quirrenbach et al. 2011) or CRIRES+ (Follert et al. 2014).
Ideally, the sizes of all pixels are known prior to wavelength calibration, but in practice, the individual pixel sizes are not known precisely enough. For future detectors, it might be interesting to determine pixel sizes with a microscope prior to integration in the instrument.
Determining the sizes of all pixels is beyond the scope of ordinary wavelength calibration because the number of free parameters exceeds the number of comb lines, which are separated by a few pixels. But for a few significantly deviating pixels it is indeed possible to simultaneously determine pixel sizes and the wavelength solution if a spectral calibration source with dense line combs (FPI or the LFC) is available.
For example, the HARPS detector exhibits pixel irregularities every 512 pixels (Wilken et al. 2010), and we therefore chose the following pixel size model  (5)where every 512th pixel was allowed to depart from unity, while all others were assumed to be homogeneous and were fixed to unity. The first pixel size irregularity, b = 1, is located in pixel 509, which causes an offset of three pixels in Eq. (5). The number of free parameters can be limited even more by using column sizes instead of individual pixels, as we show in Sect. 4 for HARPS.
(5)where every 512th pixel was allowed to depart from unity, while all others were assumed to be homogeneous and were fixed to unity. The first pixel size irregularity, b = 1, is located in pixel 509, which causes an offset of three pixels in Eq. (5). The number of free parameters can be limited even more by using column sizes instead of individual pixels, as we show in Sect. 4 for HARPS.
To find the pixel sizes wi, we performed a nonlinear least-squares fit by minimizing ![\hbox{$\chi^2 = \sum_{l} \frac{1}{\sigma_l^2}[X_l - X(x(\lambda_l,o_l,{ a_{\mathrm{poly}}}),{a_{\mathrm{pix}}})]^2$}](/articles/aa/full_html/2015/09/aa26462-15/aa26462-15-eq82.png) . To evaluate the χ2 with the observed data Xl, we must invert Eq. (4). The back-transformation of the focal plane coordinates x into the detector coordinates X is
. To evaluate the χ2 with the observed data Xl, we must invert Eq. (4). The back-transformation of the focal plane coordinates x into the detector coordinates X is 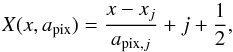 (6)where j is the pixel number into which x falls, which can be found via the condition xj ≤ x<xj + 1 where
(6)where j is the pixel number into which x falls, which can be found via the condition xj ≤ x<xj + 1 where 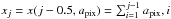 .
.
The best-fitting model and coordinate transformation was then inverted numerically to obtain the wavelength for the center of each pixel. We found that a simple bisection method is appropriate2.
To accelerate the nonlinear least-squares fit, we separated it into a linear and a nonlinear least-squares fit. For a trial set of the nonlinear parameters apix, the position of all calibration lines can be transformed into focal plane coordinates xl(Xl) with Eq. (4). Then a smooth 2D polynomial was fitted with a linear least-squares fit. The smooth model was transformed back into detector coordinates with Eq. (6), and the χ2 with the observed data Xl was computed. Testing different trial sets (e.g., with a downhill simplex; Press 2007), the best-fitting pixel sizes apix were found.
4. Calibrating HARPS using its FPI
4.1. Detector characterization and wavelength solution
To show the potential of Fabry-Pérot interferometers in wavelength calibration procedures for echelle spectrographs, we calibrated the HARPS spectrograph located at the ESO 3.6 m telescope in La Silla Chile (Mayor et al. 2003) with its etalon and our wavelength solution method. HARPS has a resolution of 115 000 (one resolution element is sampled with about 3.2 pixels), covers the wavelength range from 380 to 690 nm, and offers ThAr, FPI, and LFC spectra. The design of the HARPS FPI is described in Wildi et al. (2010). Briefly, the HARPS FPI has a cavity width of about 7.3 mm and a measured finesse of about 4.3. It is fiber coupled and temperature and pressure stabilized inside a vacuum tank.
We analyzed calibration data taken on March 16, 2011, offering both ThAr and FPI exposures. We reduced the calibration spectra using the IDL REDUCE package. The pixel position of the thorium lines were measured by fitting a Gaussian profile to the extracted 1D spectra. The FPI peaks are separated by 8−21 pixels (from blue to red orders). The median FWHM of the FPI lines is about 5 pixels or 1.6 resolution elements, which means that the FPI lines are moderately resolved in the spectra. Hence the line shape of the FPI deviates from the Gaussian-like instrumental profile of HARPS, and we fit a Lorentz function to each peak to obtain the pixel position.
The first step in our calibration procedure is to derive the wavelength solution from the thorium lamp alone using the line list of Palmer & Engleman (1983). Because only few thorium lines are available in single-calibration images, we used a 2D polynomial in the direct regression (seventh degree in dispersion direction and sixth degree in cross dispersion) and uniform pixel sizes. The residuals of the best fit to the thorium lines in block 2 of the blue detector (echelle orders 116 to 135) are plotted in the upper panel of Fig. 4.
This HCL wavelength solution was used as input for the FPI calibration to assign wavelengths to all FPI peaks. We chose m1 = 27526 (λ1 = 5304.24 Å), which resulted in the minimum penetration depth variation. The model for d(k) was a B-spline with 23 nodes in the blue and 13 nodes in the red HARPS regime. The effective cavity width measurement dk = 2 λk (m1 + k) and the according model d(k) are shown in Fig. 5.
 |
Fig. 4 Residuals of Th and FPI positions with respect to a simple polynomial wavelength solution for HARPS orders 116−135 (black dots). The difference in the wavelength solutions between the polynomial model and the model with variable pixel sizes (red lines) shows the captured systematics. |
 |
Fig. 5 Effective cavity width measurement of the HARPS FPI using the thorium wavelength solution. Upper panel: measured effective cavity width (black dots), spline fit to red and blue HARPS CCDs (red and blue line, respectively). Lower panel: residuals of the spline fit. Orders 89−153 are shown here. |
Deviation of column sizes, apix,i from unity in percent for HARPS.
The mean effective cavity width we measured for the HARPS FPI is 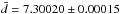 mm. (The spike seen around 430 nm is caused by a CCD defect in the blue detector that systematically influences the line position measurement in this region.)
mm. (The spike seen around 430 nm is caused by a CCD defect in the blue detector that systematically influences the line position measurement in this region.)
From the B-spline model and the peak number we derived the calibrated FPI wavelengths. To check the quality of the thorium wavelength solution, we plot the residuals of the calibrated FPI lines included in block 2 of the blue detector (echelle orders 116 to 135) in the lower panel of Fig. 4. The numerous more lines offered by the FPI now enable us to see systematics that were hidden in the Th residuals simply because of the lack of lines.
These systematics are already known from laser frequency comb calibration and are due to a stitching effect (Wilken et al. 2010). The 4k ×4k HARPS detector consists of two 4k ×2k CCDs; each consists of 8×2 blocks with 512 × 1024 pixels.
To capture the effect caused by the CCD imperfections in our wavelength solution, we applied our pixel size concept (see Sect. 3.2) and modeled the size of every 512th pixel as indicated in Eq. (5). From the HARPS flat fields we see that the first pixel block is three pixels smaller than the rest and ends at pixel 509, while the rest continues in 512 pixel intervals. The edge of the detector is a small block of three pixels, which is not fitted. Furthermore, we assumed that the last pixels in the same column have the same size, which allowed us to limit the number of free pixel parameters to 14 per CCD. We found it necessary to increase the polynomial orders (eighth degree in dispersion direction and seventh degree in cross dispersion). This is possible because of the numerous FPI lines.
We overplot the model difference between the simple polynomial and the full model including inhomogeneous column sizes as solid red lines in the lower panel of Fig. 4. Our new wavelength solution handles most of the systematics that a simple polynomial model cannot account for. Using the FPI along with a wavelength solution that includes unequal pixel or column sizes therefore is a powerful method for characterizing the detector and calibrating the spectrograph at the same time.
Table 1 shows the deviation of column sizes from unity, apix−1. The smallest column we found differs by 5.8% in size, which translates into about 46 m/s for HARPS.
4.2. Comparison to DRS
To check the accuracy of our calibration using the HARPS FPI, we compared our wavelength solution to the standard calibration delivered by the HARPS Data Reduction Software (DRS). The difference between our wavelength solution and the cubic polynomial reverse regression of DRS is shown in the upper panel of Fig. 6. We observe distortions with amplitudes of up to 50 m/s that are repeated in every order. This is very similar to the results found in Wilken et al. (2010) and Molaro et al. (2013) using LFC data. These authors argued that the pattern is caused by DRS not taking into account different sizes of detector pixels. The difference between the LFC solution of Molaro et al. (2013) and the DRS solution yields an rms scatter of 25 m/s. We confirm the distortions in the DRS solution with the use of the HARPS FPI and find an rms scatter between our wavelength solution and the DRS solution of 22 m/s.
4.3. Comparison to LFC
It is also interesting to compare our wavelength solution directly to the LFC solution. Unfortunately, there is no night in the HARPS archive with FPI and LFC spectra. Hence we computed the difference between the LFC wavelength solution of Molaro et al. (2013) for November 24, 2010 and our FPI wavelength solution for March 16, 2011 and corrected for 6 m/s, which is the mean drift between the two thorium solutions. The result is plotted in the lower panel of Fig. 6.
The deviations between our FPI wavelength solution and the LFC solution of Molaro et al. (2013) are smaller, only 8 m/s. Generally, no large amplitude distortions of 50 m/s are visible, as is the case with the ThAr solution.
We comment now on some remaining features. The peak around 477 nm is due to the low flux level of the LFC at this wavelength.
In six-pixel-wide regions at the block borders (marked in cyan and magenta in the lower panel of Fig. 6), the deviations can jump by 50 m/s. This is due to an indexing problem. We realized that the discontinuities (with a 512-pixel period) start at pixel 515 in the LFC solution of Molaro et al. (2013). We chose 509 as the start pixel to match the columns with an anomalous sensitivity in the flat echelle image that is most likely due to their pixel size.
In addition to this deviation, we observe a residual trend across the orders that is not well understood, but we note that four months passed between the two solutions. Differences with amplitudes of about 10 m/s are seen around this trend.
With the current data quality of the HARPS FPI spectra, we cannot completely resolve all the fine structure that is seen with the LFC. Molaro et al. (2013) individually fit a cubic polynomial for each block in each order, that is, their model has more parameters and is capable of handling more small-scale structure. We used a less flexible model because of the problems with the HARPS FPI spectra discussed in detail in Sect. 4.4. If the data quality improves, we might also be able to use more detailed models and to characterize the detector in more detail.
 |
Fig. 6 Upper panel: difference between our FPI wavelength solution and the DRS wavelength solution (solid lines) with an rms of 22 m/s. Difference between FPI wavelengths obtained from the model d(k) and the wavelengths assigned to the FPI from DRS wavelength solution (points). Lower panel: same as above, but using the LFC wavelength solution of Molaro et al. (2013). Orders 116−128 are shown here. |
4.4. Systematic high-frequency noise in the HARPS etalon
When we calibrated the HARPS FPI, the rms scatter around the B-spline model of d(k) was 25 m/s, see Fig. 5. This is about one order of magnitude more than what we expect from photon noise for signal-to-noise ratios of 150 to 300. We found that the residuals are not white but exhibit high frequency variations. The position residuals of lines present in adjacent and overlapping orders are correlated, which indicates a wavelength dependency. Frequency analysis revealed two significant periods. For order 131 we found P1 = 1.5056 ± 0.0017 Å and P2 = 0.6612 ± 0.0005 Å. Furthermore, periodic peak height variations of up to 10% are visible in the 1D extracted FPI spectra. Frequency analysis on the derived FPI amplitudes yields two significant periods that match those found in the position residuals. We assume that an additional low-finess interference signal caused by plane-parallel optical elements in the path of the FPI (e.g. filters or the thickness of the FPI mirrors itself) superimposes on the HARPS FPI (Wildi et al. 2010; Pepe, priv. comm.). The periods would correspond to FPIs with cavity widths on the order of millimeters. Furthermore, we find that the periods decrease towards blue and increase towards red orders, indicating that the effective cavity width of the optical element that causes the additional FPI effect changes with wavelength; this can be caused by a wavelength-dependent refractive index n. We assume that the slopes due to the flux variations shift the photocenter of the FPI lines, which in turn results in systematics in the line position measurement.
Without exact knowledge about the cause of this effect, our attempts to fit and correct the flux variations present in the spectra gave unsatisfying results. Because of this effect the FPI wavelengths are not known precisely enough to resolve the fine structure that is seen in the LFC. Our method involving the FPI in the wavelength calibration for HARPS is thus limited by this systematic high-frequency noise. Our laboratory experiment in Sect. 2.2 is limited by photon noise (8 m/s). With this data quality, we would be able to resolve more details in the wavelength solution systematics of HARPS. For future projects it is advisable to avoid optical elements in the light path of the FPI that might cause additional interference patterns and to characterize the FPI in advance with other instruments.
5. Influence of distortions in the wavelength solution on precise RV measurements
To estimate the influence of distortions in the wavelength solution on precise RV measurements with high-resolution echelle spectrographs, we simulated observations taken over the period of one year. The simulated spectrograph has 70 spectral orders that each cover 57 Å, a delta peak instrumental profile, and a detector with 4096 homogeneous pixels. The observed star is perfectly quiet and has a zero RV signal. Its spectrum consists of randomly distributed delta peaks (100 lines per order). Furthermore, the star lies in the ecliptic, resulting in a 30 000 m/s RV signal from the barycentric motion of Earth. This oversimplified approach allows us to single out the effect of the wavelength solution alone on our observations without additional noise from any other sources.
 |
Fig. 7 Simulation of the RV signal due to a disturbed wavelength solution. RV signal for single orders (gray dots), mean RV of all orders (black squares), and sinusoidal fit to the mean RV (red line). |
In total we simulated 29 observations over one year. We initialized the stellar spectrum by computing random wavelengths such that 100 delta peaks fell on each of the 70 orders of the spectrograph. At time stamp 0 the barycentric motion of Earth toward the star is zero; hence this spectrum represents the rest frame. The spectra for all observation time stamps were computed applying only the Doppler shift corresponding to the barycentric motion of Earth around the Sun (~30 000 m/s). We ignored the effect of Earth’s rotation because it is small compared to the motion of Earth around the Sun (~500 m/s). Spectra were taken every 12.175 days. We used the inverted wavelength solution of the spectrograph to place the stellar lines on the detector and to obtain our simulated observations.
When the true wavelength solution of the simulated spectrograph was used to convert the pixel value back to wavelength and the barycentric motion of Earth was corrected for, we obtained RVs of 0 m/s for all stellar lines within machine precision.
Next we disturbed the wavelength solution of the spectrograph. We wished to test the effect of small systematics in the wavelength solution on precise RV measurements. To do this, the difference between our thorium wavelength solution and our calibrated FPI wavelength solution in HARPS order 118 (Sect. 4.1, red line in Fig. 4) was added to the true wavelength solution of the simulated spectrograph.
Now we used the disturbed wavelength solution, converted the pixel values into wavelengths, corrected for the barycentric motion of Earth, and computed the RVs for all lines. We averaged the RV of single lines to compute the RV order by order for each observation (gray dots in Fig. 7). The RV per time stamp is the mean of the individual order RVs (black squares in Fig. 7).
We observe the following effects in Fig. 7. The RVs derived for individual orders (gray dots) show a scatter of about 1 m/s. This effect is a result of the random distribution of lines on the CCD and the systematics in the wavelength solution.
Depending on the location of a stellar line on the CCD, it will give a different systematically incorrect RV because the systematical error in the wavelength solution is different for different pixels. We can derive the expected RV signal δv resulting from the wavelength solution systematics δλ(x) by inserting the wavelength solution distortion in the Doppler equation: ![\begin{equation} \frac{[\lambda(x_i) + \delta_\lambda(x_i)] - [\lambda(x_0) + \delta_\lambda(x_0)]}{\lambda(x_0) + \delta_\lambda(x_0)}=\frac{v + \delta_v}{c} \label{eq:doppler_dist} , \end{equation}](/articles/aa/full_html/2015/09/aa26462-15/aa26462-15-eq130.png) (7)where x0 and xi correspond to the line positions on the CCD at time stamps t0 = 0 (rest frame) and ti, respectively. The barycentric motion of Earth shifts lines on scales of a few tens of pixels. On this scale, the change in δλ is small and we can approximate the difference δλ(x1) − δλ(x0) with the derivative of the wavelength solution distortion multiplied by the pixel shift dδλ(x) / dx·Δx. The pixel shift Δx depends on the barycentric velocity of Earth RVE and the pixel scale in terms of RV κ. For HARPS one pixel covers approximately 800 m/s/pix. Hence a barycentric velocity of RVE = 30 000 m/s shifts the lines by 37.5 pixels on the detector. Finally, the small term δλ(x0) in the denominator can be neglected, and the velocity signal of a single line δv that is due to the distortion in the wavelength solution δλ(x) can be written as
(7)where x0 and xi correspond to the line positions on the CCD at time stamps t0 = 0 (rest frame) and ti, respectively. The barycentric motion of Earth shifts lines on scales of a few tens of pixels. On this scale, the change in δλ is small and we can approximate the difference δλ(x1) − δλ(x0) with the derivative of the wavelength solution distortion multiplied by the pixel shift dδλ(x) / dx·Δx. The pixel shift Δx depends on the barycentric velocity of Earth RVE and the pixel scale in terms of RV κ. For HARPS one pixel covers approximately 800 m/s/pix. Hence a barycentric velocity of RVE = 30 000 m/s shifts the lines by 37.5 pixels on the detector. Finally, the small term δλ(x0) in the denominator can be neglected, and the velocity signal of a single line δv that is due to the distortion in the wavelength solution δλ(x) can be written as 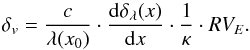 (8)Averaging over all the different δv in one order results in a systematic RV that depends on the random distribution of stellar lines on the CCD. As the distortion is the same for all orders, the simulation results presented in Fig. 7 are equivalent to repeating the test 70 times for one order with different random sets of lines. This means that we observe scatter between the RVs of different orders that is solely caused by the line distribution on the detector. This scatter is mainly caused by lines experiencing different slopes in dδλ(x) / dx and not by single lines moving across the jumps in the wavelength solution.
(8)Averaging over all the different δv in one order results in a systematic RV that depends on the random distribution of stellar lines on the CCD. As the distortion is the same for all orders, the simulation results presented in Fig. 7 are equivalent to repeating the test 70 times for one order with different random sets of lines. This means that we observe scatter between the RVs of different orders that is solely caused by the line distribution on the detector. This scatter is mainly caused by lines experiencing different slopes in dδλ(x) / dx and not by single lines moving across the jumps in the wavelength solution.
The slope dδλ(x) / dx is negative almost everywhere on the CCD, however. Many lines therefore experience systematic RV shifts in the same direction. The mean RV derived from the individual orders accordingly shows a low-amplitude RV signal with a period of one year. The amplitude of this signal is about 0.5 m/s. Advancing to cm/s precision, we cannot afford systematic errors on the order of 0.5 m/s to 1 m/s. This clearly shows that accurate wavelength calibration is critical for reaching the aims with the next generation of instruments.
6. Summary and conclusions
HCLs have been calibration sources for echelle spectrographs for decades, but advancing to cm/s RV precision introduces the need for more suitable standards. In addition to the LFC, FPIs also offer a dense comb pattern of lines that can be used for calibration.
Because the cavity width is not known accurately enough and possibly drifts over time, the peak wavelengths are uncertain and FPIs cannot be used as a stand-alone calibrator. Therefore we developed a method to anchor the dense etalon lines with the absolute HCLs to combine their precision and accuracy. It is central to our method that we modeled the cavity width (including its global wavelength dependency) in the calibration procedure. We exploited the assumption that the wavelength dependency of the cavity width is smooth, which enhances the quality of the wavelength solution on medium to small scales, while the global accuracy is still determined by the HCL. The assumption of smooth cavity width was verified with FTS measurements of the CARMENES FPI.
Along with our model for the FPI, we described our model for the wavelength solution of the spectrograph. Our four main points for the calibration are as follows.
-
We suggest performing direct regression with x(λ) instead of reverse regression λ(x) because the independent quantity is the wavelength λ and not the pixel position x of the spectral line on the detector.
-
We used a 2D polynomial as model in the direct regression. This couples orders, reduces the number of parameters, and enhances the robustness of the fit.
-
Motivated by the grating equation, we parametrized our model as x(λ,o) = poly(oλ,o), which is a better representation of the problem than poly(λ,o).
-
We accounted for inhomogeneous detector pixel sizes apix and transformed the observed pixel positions X to focal plane coordinates x(X,apix) before performing direct regression.
The standard DRS HCL calibration deviates from the LFC solution with an rms scatter of 25 m/s. Direct comparison of our FPI wavelength solution with the LFC yields only small differences of rms = 8 m/s. Hence we showed that the calibrated FPI is a suitable calibration source for high resolution echelle spectrographs.
Finally, we performed simulations to derive the fundamental limits that an imperfect wavelength solution imposes on RV measurements and found that even small distortions in the wavelength solution lead to systematic signals and additional noise, both on the order of 1 m/s. We conclude that wavelength calibrators such as LFCs or FPIs are necessary, which provide a much denser line grid than HCLs do. We suggest that a calibrated FPI can be considered as an economical alternative to LFCs to achieve very high RV precision for current and future instruments.
Acknowledgments
We thank the anonymous referee for careful reading and helpful comments. We thank Sebastian Schäfer, Ulrike Lemke, and Spencer Carmichael for their help in acquiring FTS data of the CARMENES NIR FPI. Florian Franziskus Bauer acknowledges support from the Deutsche Forschungsgemeinschaft under DFG GrK 1351. Mathias Zechmeister acknowledges support by the European Research Council under the FP7 starting Grand agreement number 279347. Ansgar Reiners acknowledges funding through a Heisenberg professorship under DFG RE-1664/9-2.
References
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Born, M., & Wolf, E. 1999, Principles of Optics (New York: Cambridge University Press) [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, W. D., Smith, H. J., & Smith, W. H. 1982, in Instrumentation in Astronomy IV, SPIE Conf. Ser., 331, 315 [Google Scholar]
- de Boor, C. 2001, A Practical Guide to Splines, Applied Mathematical Sciences (New York: Springer) [Google Scholar]
- Dierckx, P. 1995, Curve and Surface Fitting with Splines, Monographs on numerical analysis (Clarendon Press) [Google Scholar]
- D’Odorico, V., & CODEX/ESPRESSO Team 2007, Mem. Soc. Astron. Italiana, 78, 712 [Google Scholar]
- Follert, R., Dorn, R. J., Oliva, E., et al. 2014, SPIE Conf. Ser., 9147, 19 [NASA ADS] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerber, F., Nave, G., Sansonetti, C. J., Bristow, P., & Rosa, M. R. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 461 [Google Scholar]
- Kerber, F., Nave, G., & Sansonetti, C. J. 2008, ApJS, 178, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- McMillan, R. S., Perry, M. L., Smith, P. H., & Merline, W. J. 1988, in Fiber Optics in Astronomy, ed. S. C. Barden, ASP Conf. Ser., 3, 237 [Google Scholar]
- McMillan, R. S., Moore, T. L., Perry, M. L., & Smith, P. H. 1994, Ap&SS, 212, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Esposito, M., Monai, S., et al. 2013, A&A, 560, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, M. T., Udem, T., Holzwarth, R., et al. 2007, MNRAS, 380, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, B. A., & Engleman, R. 1983, Atlas of the thorium spectrum [Google Scholar]
- Piskunov, N. E., & Valenti, J. A. 2002, A&A, 385, 1095 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. 2007, Numerical Recipes, 3rd edn., The Art of Scientific Computing (Cambridge University Press) [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2011, in IAU Symp. 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 545 [Google Scholar]
- Redman, S. L., Nave, G., & Sansonetti, C. J. 2014, ApJS, 211, 4 [Google Scholar]
- Reiners, A., Banyal, R. K., & Ulbrich, R. G. 2014, A&A, 569, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schäfer, S., & Reiners, A. 2012, SPIE Conf. Ser., 8446, 94 [NASA ADS] [Google Scholar]
- Schroeder, D. J. 2000, Astronomical optics (San Diego: Academic Press) [Google Scholar]
- Schwab, C., Stuermer, J., Gurevich, Y. V., et al. 2014, PASP, submitted [arXiv:1404.0004] [Google Scholar]
- Wildi, F., Pepe, F., Chazelas, B., Lo Curto, G., & Lovis, C. 2010, SPIE Conf. Ser., 7735, 4 [Google Scholar]
- Wilken, T., Lovis, C., Manescau, A., et al. 2010, MNRAS, 405, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Wilken, T., Curto, G. L., Probst, R. A., et al. 2012, Nature, 485, 611 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spectrum of the CARMENES NIR FPI taken with the Fourier transform spectrometer in Göttingen. |
| In the text | |
 |
Fig. 2 Upper panel: effective cavity width measurement d(k) for the CARMENES NIR FPI. Lower panel: residuals of the spline fit. We show the data (black dots), clipped lines due to atmosphere absorption features (red crosses), and the spline fit to the data (green line). |
| In the text | |
 |
Fig. 3 Upper panel: effective cavity width d(k) obtained for different absolute interference order numbers m1. The reference curve (m1 = 13 604, black) is shown in Fig. 2. Lower panel: difference in modeled FPI peak wavelength λm using m1 = 13 704 with the reference curve (dashed line). Residuals of the spline fit to the cavity width d(k) obtained with m1 = 13 704 are shown as purple dots. |
| In the text | |
 |
Fig. 4 Residuals of Th and FPI positions with respect to a simple polynomial wavelength solution for HARPS orders 116−135 (black dots). The difference in the wavelength solutions between the polynomial model and the model with variable pixel sizes (red lines) shows the captured systematics. |
| In the text | |
 |
Fig. 5 Effective cavity width measurement of the HARPS FPI using the thorium wavelength solution. Upper panel: measured effective cavity width (black dots), spline fit to red and blue HARPS CCDs (red and blue line, respectively). Lower panel: residuals of the spline fit. Orders 89−153 are shown here. |
| In the text | |
 |
Fig. 6 Upper panel: difference between our FPI wavelength solution and the DRS wavelength solution (solid lines) with an rms of 22 m/s. Difference between FPI wavelengths obtained from the model d(k) and the wavelengths assigned to the FPI from DRS wavelength solution (points). Lower panel: same as above, but using the LFC wavelength solution of Molaro et al. (2013). Orders 116−128 are shown here. |
| In the text | |
 |
Fig. 7 Simulation of the RV signal due to a disturbed wavelength solution. RV signal for single orders (gray dots), mean RV of all orders (black squares), and sinusoidal fit to the mean RV (red line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


