| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526417 | |
| Published online | 21 September 2015 | |
Luminosity-dependent spectral and timing properties of the accreting pulsar GX 304−1 measured with INTEGRAL⋆
Institut für Astronomie und Astrophysik,
Sand 1,
72076
Tübingen,
Germany
e-mail:
malacaria@astro.uni-tuebingen.de
Received: 27 April 2015
Accepted: 1 July 2015
Context. Be/X-ray binaries show outbursts with peak luminosities up to a few times 1037 erg/s, during which they can be observed and studied in detail. Most (if not all) Be/X-ray binaries harbor accreting pulsars, whose X-ray spectra in many cases contain cyclotron resonant scattering features related to the magnetic field of the sources. Spectral variations as a function of luminosity and of the rotational phase of the neutron star are observed in many accreting pulsars.
Aims. We explore X-ray spectral and timing properties of the Be/X-ray binary GX 304-1 during an outburst episode. Specifically, we investigate the behavior of the cyclotron resonant scattering feature, the continuum spectral parameters, the pulse period, and the energy- and luminosity-resolved pulse profiles.
Methods. We analyze the INTEGRAL data from the two JEM-X modules, ISGRI and SPI, covering the 2012 January−February outburst, divided into six observations. We obtain pulse profiles in two energy bands, phase-averaged and phase-resolved spectra for each observation. We combine the luminosity-resolved spectral and timing analysis to probe the accretion geometry and the beaming patterns of the rotating neutron star.
Results. We confirm the positive luminosity dependence of the cyclotron line energy in GX 304-1 and report a dependence of the photon index on luminosity. Using a pulse-phase connection technique, we find a pulse period solution valid for the entire outburst. Our pulse-phase resolved analysis shows that the centroid energy of the cyclotron line varies only slightly with pulse phase, while other spectral parameters show more pronounced variations. Our results are consistent with a scenario in which, as the pulsar rotates, we are exploring only a small portion of its beam pattern.
Key words: X-rays: binaries / stars: neutron / accretion, accretion disks / pulsars: individual: GX 304-1
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
GX 304-1 is a Be/X-ray binary (BeXRB) system discovered as an X-ray source in 1967 during a balloon observation (Lewin et al. 1968a,b). Subsequently, the source was established as an X-ray pulsar with a pulse period of ~ 272 s (McClintock et al. 1977). A study of the recurrent outburst activity revealed a ~ 132.5 d periodicity, probably because of the system’s orbital period (Priedhorsky & Terrell 1983). The optical counterpart of the binary is a B2 Vne star, whose distance has been measured to be 2.4 ± 0.5 kpc (Parkes et al. 1980). Since 1980, the source has entered an X-ray off-state (Pietsch et al. 1986), showing no detectable emission for 28 yr. The quiescence was interrupted in June 2008, when INTEGRAL detected hard X-ray emission from the source (Manousakis et al. 2008). Since then, GX 304-1 has lit up repeatedly, becoming a periodically outbursting X-ray source. The period of the outbursts after 2009 is roughly the same as before 1980 (~ 132.5 d). The peak luminosities are ≲1037erg/s in the 5−100 keV energy band. The origin of the X-ray emission is believed to be accretion of matter from the circumstellar equatorial disk around the optical companion onto a magnetized neutron star. The strong magnetic field of the accretor (~1012G) channels the captured matter toward its magnetic poles where X-ray emission originates in an accretion structure.
A cyclotron resonant scattering feature (CRSF), or cyclotron line, has been detected in the spectrum of GX 304-1 with a centroid energy of ~ 52 keV (Yamamoto et al. 2011). CRSFs are important features in the spectra of accreting pulsars. In a strong magnetic field, electron energies corresponding to their motion perpendicular to the magnetic field lines are quantized at Landau levels, causing resonant scattering of impinging photons. The first such line ever was detected in data from a balloon observation of Her X-1 (Trümper et al. 1978). They have turned out to be fairly common in accreting X-ray pulsars, with ~ 20 objects being confirmed cyclotron line sources and with several objects showing multiple lines (up to four harmonics in 4U 0115+63, Santangelo et al. 1999). Reviews are given by Coburn et al. (2002), Staubert (2003), Heindl et al. (2004), Terada et al. (2007), Wilms (2012), and Caballero & Wilms (2012), among others. The energy of the fundamental line Ecyc is directly proportional to the magnetic field strength at the emission site, Ecyc ~ 11.6 × B12(1 + zg) keV, where B12 is the magnetic field in units of 1012 G, and zg is the gravitational redshift.
More recent observations have shown that the cyclotron line energy in GX 304-1 is positively correlated with the observed luminosity (Klochkov et al. 2012). Such a positive correlation was first observed in Her X-1 by Staubert et al. (2007) and is now observed for GX 304-1 as well, Vela X-1 (Fürst et al. 2014) and recently for A 0535+26 (Sartore et al. 2015).
The opposite correlation, a negative dependence between the cyclotron line energy and the luminosity, was actually detected earlier in high luminosity transient sources (4U 0115+63, Cep X-4, and V 0332+53, Mihara et al. 1991). During the 2004/2005 outburst of V 0332+53, a clear anti-correlation of the line position with X-ray flux was observed (Tsygankov et al. 2006). Similar behavior was observed in outbursts of 4U 0115+63 (Nakajima et al. 2006; Tsygankov et al. 2007). The presence of the correlation in this source, however, is shown to depend on the spectral model used (Müller et al. 2013; Iyer et al. 2015).
It has also been found that the power law spectral index Γ (the absolute value) shows the opposite correlation with flux compared to the cyclotron line energy, on both shorter (Klochkov et al. 2011) and longer (Fürst et al. 2014) time scales.
A model-independent way to probe the correlation of the spectral hardness on flux is through a hardness-intensity diagram as shown by Reig & Nespoli (2013) for BeXRBs, which follow certain patterns in the hardness-intensity diagram and undergo state transitions if they reach a luminosity above a certain critical value. For the physical interpretation of these correlations, which associates sub- and super-Eddington accretion regimes, recent models have been proposed by Becker et al. (2012) and Poutanen et al. (2013).
Recently, GX 304-1 has passed through a new period of quiescence, showing almost no X-ray activity between 2013 and 2015. The data taken during the new active episode allowed Sugizaki et al. (2015) to derive orbital elements for this binary system. Only recently has the source resumed its X-ray activity.
Here we present the results of the timing and spectral studies of GX 304-1, which was observed by INTEGRAL during an outburst in January–February 2012. Our work is primarily focused on the timing analysis, which allowed us to phase-connect the observations throughout the entire outburst, and on the pulse phase-resolved spectroscopy, with the goal of probing the emission geometry of the rotating NS at different viewing angles. The X-ray continuum of the source shows variability with pulse phase, with some features present only at particular pulse-phase intervals. Changes in the spectral parameters with pulse phase are quite common among accreting X-ray pulsars and are generally attributed to a change in the viewing angle of the emitting region (see, e.g., Klochkov et al. 2008a; Vasco et al. 2013). Located relatively nearby and having a prominent cyclotron line feature, GX 304-1 is well suited for such studies. We confirm the results of Klochkov et al. (2012) using the latest version of the INTEGRAL analysis software and calibration. We investigated the continuum variations (photon index and hardness) with luminosity and obtained a pulse period solution that is valid throughout the observed outburst. The measured pulse periods are used to study both pulse profiles in two energy bands and phase-resolved broad band (5−100 keV) spectra.
2. Observations and data
The data used in this work are the same as those used by Klochkov et al. (2012). The observation log is given in Table 1. The analyzed outburst started on the 8 January, 2012 (Yamamoto et al. 2012). The International Gamma-ray Astrophysics Laboratory (INTEGRAL, Winkler et al. 2003) observed the event starting around MJD 55 943.5, when the source flux in the 20−80 keV energy band was ~ 250 mCrab, until MJD ~ 55 965.5, when the flux dropped to ~ 100 mCrab. The peak of the outburst was reached around MJD 55 953 with a flux exceeding 1 Crab. INTEGRAL performed a total of eight observations, one per each satellite orbit (i.e., one every ~ 3 d), with a typical exposure of a few tens of kiloseconds per each observation. The three high energy instruments onboard INTEGRAL allow observations in broad energy ranges: the two Joint European X-ray Monitor units (JEM-X, Lund et al. 2003) are sensitive in the range 3−35 keV; the Imager on Board the INTEGRAL Satellite (IBIS, Ubertini et al. 2003) is sensitive from ~ 20 keV to a few MeV; and the Spectrometer onboard INTEGRAL (SPI, Vedrenne et al. 2003) is sensitive in roughly the same energy range as IBIS. The duration of INTEGRAL observations are shown in Fig. 1, compared to the Swift/BAT light curve of the outburst1. The actual observations are shortened by solar activity, leading to a reduction in the exposure times.
 |
Fig. 1 The Swift/BAT light curve of GX 304-1 during the January−February 2012 outburst. The horizontal bars mark the INTEGRAL observations. The numbers above the bars indicate the last digit “i” of the respective INTEGRAL revolution number – 113i. |
INTEGRAL observations of the GX 304-1 outburst.
For our analysis, we decided to use only data from those observations where all of the three instruments were active, to ensure a broad band coverage and a homogeneous analysis of all observations. Therefore, the revolutions 1133 and 1135 are not taken into account. Of the IBIS instrument, we only used the data from the Integral Soft Gamma-ray Imager detector (ISGRI, Lebrun et al. 2003), which is sensitive in the 20−300 keV energy range. However, according to the recommendation of the instrument team, for the spectral analysis we restricted the duty energy band of each instrument to a safer range that is believed to be free of strong systematics: 5−30 keV for the two JEM-X modules, 22−100 keV for ISGRI and 25−100 keV for SPI. The upper limit of 100 keV for ISGRI and SPI data is due to the reduced photon flux of GX 304-1 above this energy. Data reduction was performed with Version 10 of the Offline Science Analysis (OSA) software2. Following the OSA user manual, we added a systematic error to the final count rates at a level of 1% for ISGRI, 3% for JEM-X, and 0.5% for SPI. In Sect. 4 the previous version of the software (OSA 9) is also used to reduce the same data in order to compare the results and to explore the changes in the calibration, especially in the ISGRI energy scale, between the two versions. Details of the comparison between OSA 9 and OSA 10 are given in Appendix A.
Global timing solution obtained from phase-connection of IBIS/ISGRI (18−80 keV) pulse-profiles and spectral parameters throughout the outburst obtained with OSA 10 plus additional gain correction (see text).
3. Timing analysis
For the timing analysis, we extracted light curves with a time resolution of 3 s from JEM-X1 (in the range 3−20 keV) and IBIS/ISGRI (in the range 18−80 keV). All time stamps were corrected such that they refer to arrival times at the solar system barycenter. For each INTEGRAL observation the pulse period was determined by epoch-folding (Leahy 1987). Using these pulse periods, we generated ISGRI pulse profiles in three energy ranges: 20−40 keV, 40−60 keV, and 18−80 keV. The shapes of the profiles do not vary much within these three energy bands. Thus, to maximize the photon statistics, we chose the 18−80 keV range for further analysis. At the time of preparation, correction for the orbital motion in the binary was not possible since the orbital parameters of the binary system were unknown. Meanwhile, an orbital solution for GX 304-1 has been furnished by Sugizaki et al. (2015). In our analysis, however, phase connection has been successfully achieved without taking the binary motion into account. To refine the pulse periods needed to obtain the pulse profiles, we applied the phase connection techniques (Deeter et al. 1981) to the 18−80 keV pulse profiles, as described in the following.
 |
Fig. 2 IBIS/ISGRI (18−80 keV) normalized pulse profiles obtained with the timing solution resulting from our phase-connection analysis. Each panel represents, from top to bottom, the successive INTEGRAL observations (from Rev# 1131 to 1138, shown in the top left corner). In the top right corner, the luminosity of the source (3−80 keV) in units of 1037 erg/s is reported. The thin straight line around phase 1.0 at the bottom of each panel (except Rev# 1138) approximately indicates the phase range where the sharp features used to phase-connect the observations are found. |
 |
Fig. 3 JEM-X1 normalized pulse profiles in the 3−20 keV energy range. Panels follow the same Rev# and luminosity stage as in in Fig. 2. |
For each INTEGRAL observation, a pulse profile was constructed and used to determine an absolute reference time (in MJD), the arrival time, of the first pulse in the interval by making use of well defined sharp features in the pulse profiles, such as – see Fig. 2 – the peak near pulse phase zero and the minimum around pulse phase 0.1 or the time at the flux level centered at a point midway between the maximum and the minimum.
 |
Fig. 4 Pulse period as a function of time obtained by phase connection. The dashed line represents a linear fit to the data points, yielding a pulse period derivative of Ṗ = (−2.04 ± 0.01) × 10-7. The period error bars are smaller than the symbols. |
If only the first derivative Ṗ of the pulse period P is taken into account, the expected arrival time tn of the nth pulse is 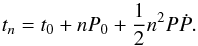 (1)Here, P0 is the pulse period at the reference time t0, n the pulse sequence number, and Ṗ the first period derivative. The pulse period at the time t can be determined as
(1)Here, P0 is the pulse period at the reference time t0, n the pulse sequence number, and Ṗ the first period derivative. The pulse period at the time t can be determined as 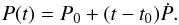 (2)A consistent determination of pulse arrival times is formally only possible if the pulse shape does not change with time.
(2)A consistent determination of pulse arrival times is formally only possible if the pulse shape does not change with time.
In our observations, however, the pulse shape varies substantially between the intervals, and yet the main features of the pulse profile can be recognized clearly in all observations. The uncertainty of the corresponding pulse arrival times is given by the available statistics in the profile for the given shape and sharpness of the feature and, in our case, corresponds to about 0.01 in phase. Using the determined pulse arrival times, the phase connection between the observations can be established. The pulse period solution (t0,P0,Ṗ) is found from the fit of the measured pulse arrival times by formula (1). The uncertainties of P0 and Ṗ are calculated from the χ2 contours at 1σ c.l. This method allows the pulse period evolution to be measured with substantially higher precision compared to epoch folding.
 |
Fig. 5 Cyclotron line centroid energy Ecyc as a function of the logarithm of flux in the 3−80 keV range. The dotted line is the result of a linear fit to the Ecyc − log 10(Flux) data. The error bars indicate 1σ-uncertainties. (The flux uncertainties are smaller than the symbol size.) The top x-axis shows the corresponding isotropic source luminosity assuming a distance of 2.4 kpc. |
The obtained pulse period solution is presented in Table 2 and visualized in Fig. 4. A decrease in the observed pulse period through the outburst is seen. The initial pulse period is P0 = 274.9817 ± 0.0001 at MJD 55 952.4592 and the period derivative is Ṗ = (−2.04 ± 0.01) × 10-7 (constant over the time of observation). This solution turns out to be inconsistent with what found by Sugizaki et al. (2015). However, such a difference is expected from their different approach, which also takes the orbital doppler effects into account. With the final timing solution, we folded the ISGRI light curves to produce a refined set of pulse profiles shown in Fig. 2. We note that there is still a slight phase shift between the pulse profiles, up to Δφ ~ 0.1, as can be determined, for example, by the phase of the sharp minimum after the highest peak. This is probably due to variations in the pulse profile shape, which is most evident in the last observation (see Figs. 2 and 3). The same timing solution has been used to fold JEM-X1 light curves between 3−20 keV and to generate the JEM-X pulse profiles for each of the six observations as shown in Fig. 3.
4. Spectral analysis
For the following spectral analysis, we used version 12.7.1 of the XSPEC software (Arnaud 1996). Following Klochkov et al. (2012), we fit the spectrum of GX 304-1 during the observed outburst with a high energy exponential rolloff model (the cutoffpl component in XSPEC): ![\begin{equation} \label{cutoffpl2} F(E)\propto E^{-\Gamma}\exp[E/E_{\rm fold}] \end{equation}](/articles/aa/full_html/2015/09/aa26417-15/aa26417-15-eq111.png) (3)(where E is the photon energy, Γ the photon index, and Efold the e-folding energy of exponential rolloff in keV) and a multiplicative Gaussian absorption line (the gabs component in XSPEC) to account for the CRSF:
(3)(where E is the photon energy, Γ the photon index, and Efold the e-folding energy of exponential rolloff in keV) and a multiplicative Gaussian absorption line (the gabs component in XSPEC) to account for the CRSF: 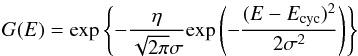 (4)where Ecyc is the cyclotron line centroid energy, η and σ are the line depth (while the optical depth at line center is
(4)where Ecyc is the cyclotron line centroid energy, η and σ are the line depth (while the optical depth at line center is 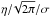 ), and the width of the line, respectively. The 6.4 keV Fe Kα emission line is modeled with an additive Gaussian, even if it does not significantly improve the fit. The photo-electric absorption at low energies is modeled with the wabs component in XSPEC. Using data from both JEM-X modules, ISGRI and SPI, we extracted pulse-phase-averaged spectra for each observation and explored the behavior of the best-fit parameters over the outburst. The results are reported in Table 2, and they confirm the positive correlation of Ecyc with flux in GX 304-1. The obtained values of the cyclotron line energy show, however, a systematic offset with respect to those reported in Klochkov et al. (2012), which in turn is reflected in a higher slope of the fitted line, i.e., 6.51 ± 1.21 keV/log10 (erg/cm2/s). The offset results from the new ISGRI calibration implemented in OSA 10. For technical details about this offset we refer the reader to Appendix A. The variation in Ecyc with flux is shown in Fig. 5.
), and the width of the line, respectively. The 6.4 keV Fe Kα emission line is modeled with an additive Gaussian, even if it does not significantly improve the fit. The photo-electric absorption at low energies is modeled with the wabs component in XSPEC. Using data from both JEM-X modules, ISGRI and SPI, we extracted pulse-phase-averaged spectra for each observation and explored the behavior of the best-fit parameters over the outburst. The results are reported in Table 2, and they confirm the positive correlation of Ecyc with flux in GX 304-1. The obtained values of the cyclotron line energy show, however, a systematic offset with respect to those reported in Klochkov et al. (2012), which in turn is reflected in a higher slope of the fitted line, i.e., 6.51 ± 1.21 keV/log10 (erg/cm2/s). The offset results from the new ISGRI calibration implemented in OSA 10. For technical details about this offset we refer the reader to Appendix A. The variation in Ecyc with flux is shown in Fig. 5.
As mentioned in the Introduction, in addition to the Ecyc–flux correlation, some X-ray pulsars exhibit a correlation between the spectral continuum hardness and flux. Using the power law index Γ (which describes the spectral hardness below the folding energy), an anti-correlation with flux is observed; i.e., the absolute value of the index decreases (the spectra become harder) with increasing flux. This is also true for GX 304-1, for which we find a negative correlation between the photon index and the flux as shown in Fig. 6. A selection of spectra is also shown in Fig. 7, where the spectral variation with luminosity is clear.
For both correlations, Ecyc/ log 10(flux) and Γ/log 10(flux), we determined the Pearson’s correlation coefficients ρ and the corresponding one-sided probabilities p of obtaining the correlations by chance: ρcyc = 0.92, pcyc ~ 0.01, and ρΓ = −0.95, pΓ ~ 0.004, respectively.
The folding energy Efold also shows a negative correlation with the observed flux, similar to that of the observed photon index. To verify whether the anti-correlation between the folding energy and the photon index is artificial (model-driven), we produced contour plots of the two parameters. The correlation between the folding energy and the photon index can be seen in Fig. 8. Altough the contours indicate some intrinsic coupling between Efold and Γ, the confidence regions corresponding to different observations are well detached. Therefore, there must be a physical correlation between the two parameters. In this plot, χ2-contours for four observations are also indicated at different luminosities, showing an anti-correlation between the folding energy and the observed luminosity.
 |
Fig. 6 Variation in the photon index Γ versus the observed flux. The dashed line represents the linear fit to the data points. The luminosity scale on the top x-axis is as in Fig. 5. |
 |
Fig. 7 Phase-averaged spectra of four observations (labelled above each spectrum), from top to bottom, with decreasing luminosity. JEM-X1 (black) and ISGRI (red) data and folded model are shown. Spectra have been scaled for better visualization. Both the Ecyc–flux and the Γ–flux correlations are clearly visible. |
Best-fit parameters of the pulse-phase resolved spectra.
 |
Fig. 8 χ2-contour plots of the folding energy Efold and the photon index Γ for four INTEGRAL observations. The contours correspond to χ2 + 1.0 (the projections of this contour to the parameter axes correspond to the 68% uncertainty for one parameter of interest), and χ2 + 2.3 (68% uncertainty for two parameters of interest). The respective luminosity (3−80 keV) in units of 1037erg s-1 is indicated. |
5. Phase-resolved spectral analysis
As the neutron star rotates, we observe the emitting regions of the neutron star at a certain viewing angle at each time (or phase). To explore the corresponding spectral variability with pulse phase, we extracted the X-ray spectra of GX 304-1 in five equally spaced pulse-phase intervals. Aa finer binning would lead to larger uncertainties.) For this, we filtered the INTEGRAL data with the good time intervals (GTIs) that correspond to our phase bins.
To obtain the phase-resolved spectra, we used the data from both JEM-X modules, ISGRI and SPI. To fit the phase-resolved spectra, we used the spectral model described in Sect. 4. The model provides an acceptable fit (the reduced chi-squared values 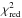 are between 0.8 and 1.2) to the spectra from all but one phase bin (see Table 3). The spectra of the 0.0–0.2 phase bins of all revolutions, except the one from Rev# 1138, however, show large residuals with
are between 0.8 and 1.2) to the spectra from all but one phase bin (see Table 3). The spectra of the 0.0–0.2 phase bins of all revolutions, except the one from Rev# 1138, however, show large residuals with 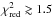 . Strong positive residuals appear around 35 keV.
. Strong positive residuals appear around 35 keV.
These spectra can be modeled with an additional Gaussian emission component (see Fig. 9). However, to enable a meaningful comparison of the spectral parameters in all phase bins, we report the results of the phase-resolved analysis obtained using the same model as in Sect. 4 in Table 3. (that is, without the additional Gaussian emission component to model the residuals around 35 keV). A comparison of the models with and without the inclusion of the additional Gaussian line is shown in Table 4. Alternatively, instead of the Gaussian emission line to model the bump, a Gaussian absorption line at lower energies can be used to fit the residuals around 35 keV, resulting in an equally good fit. In this case, the line centroid energy is about 20 keV.
Best-fit parameters of the first phase-bin spectra using a model with and without additional Gaussian emission line.
As it can be seen in Table 3, the shape of the continuum changes over the pulse phase. At the same time, the cyclotron line energy Ecyc shows only slight variation with pulse phase. However, the results in Table 3 show large uncertainties and the variation in many parameters with the pulse phase cannot be firmly established. Indeed, even if the nominal value of a given parameter shows some variation, it is generally consistent with a constant value. For a deeper investigation of the spectrum variability with pulse phase, we tried to improve the quality of the phase-resolved spectra by stacking the observations together at different fluxes. We therefore extracted X-ray spectra in 12 pulse-phase intervals. The number of phase bins was chosen to ensure adequate statistics in each interval, while the width of the bin was kept equal to 0.075. In two cases, larger bin sizes were used to obtain a meaningful fit. By using this approach we lost information on the luminosity dependence of the spectra and possibly introduced some systematic effects due to the stacking of observations with different spectral shapes. This does, however, improve statistics, and allows us to study the flux-averaged dependence of the spectrum on pulse phase.
 |
Fig. 9 Top: spectrum of the phase bin 0.0–0.2 from revolution 1132 fit with a power-law/rolloff model including the cyclotron line and an additional Gaussian component to account for a bump around 35 keV (see text). JEM-X (red and green), ISGRI (black), and SPI (blue) data are used. Middle: residuals for a fit with the model without the additional Gaussian component. Large residuals appear around the cut-off energy. Bottom: residuals after including the Gaussian emission component to model the bump. |
In this analysis we excluded the data of Rev# 1138, which suffers from much lower photon statistics. The model used for spectral fitting is the same as described in Sect. 4, which provides a good fit (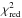 between 0.9 and 1.2) for all phase bins except three: 0–0.075, 0.075–0.225 and 0.675–0.75. Similar to the 0.0–0.2 phase-bin spectra of the individual observations, these phase bins require an additional component to get an acceptable χ2, which can be modeled by a Gaussian emission line around 35 keV. Here also, the residuals in these three phase bins can instead be modeled by a Gaussian absorption line at lower energies, i.e., around 17 keV. Owing to the presence of a very similar feature in the phase-resolved spectra of individual observations, we consider it to be unlikely that such a feature is a result of systematic effects. However, to ensure a meaningful comparison of the results, we used the same model for all phase bins, i.e., the model without the additional Gaussian component. To compare the phase-resolved results with the pulse profile we also produced average pulse profiles in the ISGRI and JEM-X energy bands (18−80 and 3−20 keV, respectively), excluding the data from Rev# 1138. In Fig. 10 we show the best-fit results of the stacked phase-resolved spectroscopy, together with the ISGRI and JEM-X average pulse profiles. The Ecyc does not show significant variation with pulse phase (except for the phase bin 0.525–0.6), while the photon index Γ and the Efold confirm a variation that, however, is less than a factor of ~ 2.
between 0.9 and 1.2) for all phase bins except three: 0–0.075, 0.075–0.225 and 0.675–0.75. Similar to the 0.0–0.2 phase-bin spectra of the individual observations, these phase bins require an additional component to get an acceptable χ2, which can be modeled by a Gaussian emission line around 35 keV. Here also, the residuals in these three phase bins can instead be modeled by a Gaussian absorption line at lower energies, i.e., around 17 keV. Owing to the presence of a very similar feature in the phase-resolved spectra of individual observations, we consider it to be unlikely that such a feature is a result of systematic effects. However, to ensure a meaningful comparison of the results, we used the same model for all phase bins, i.e., the model without the additional Gaussian component. To compare the phase-resolved results with the pulse profile we also produced average pulse profiles in the ISGRI and JEM-X energy bands (18−80 and 3−20 keV, respectively), excluding the data from Rev# 1138. In Fig. 10 we show the best-fit results of the stacked phase-resolved spectroscopy, together with the ISGRI and JEM-X average pulse profiles. The Ecyc does not show significant variation with pulse phase (except for the phase bin 0.525–0.6), while the photon index Γ and the Efold confirm a variation that, however, is less than a factor of ~ 2.
 |
Fig. 10 Best fit parameters of the phase-resolved spectra using the five stacked INTEGRAL observations. The vertical dashed lines indicate the phase-bins. The solid blue curve is the JEM-X average pulse profile, while the green curve is the ISGRI average pulse profile. The vertical error bars are 1σ uncertainties, while the horizontal bars represent the phase bin width. |
6. Discussion
6.1. Timing results
We have explored the behavior of the pulse period in GX 304-1 during its January–February 2012 outburst using a pulse-phase connection technique. The measured period is used to construct pulse profiles in two energy bands, 3−20 keV (JEM-X) and 18−80 keV (ISGRI), as shown in Figs. 2 and 3. An apparent decrease in the pulse period over the outburst is clearly seen. The measured period derivative is Ṗ = (−2.04 ± 0.01) × 10-7 (Fig. 4 and Table 2). This trend is most probably due to a combination of the Doppler effect caused by the orbital motion of the neutron star and an intrinsic spin-up caused by the transfer of angular momentum from the accretion disk to the neutron star.
Considering the JEM-X (3−20 keV) and the ISGRI (18−80 keV) energy bands, the pulse profiles of GX 304-1 are very energy dependent (except in the very end of the outburst, i.e., Rev# 1138), similar to the majority of accreting pulsars. Thereafter, these two bands will only be considered for comparing our pulse profiles results. The ISGRI pulse profiles presented in Fig. 2 show two sharp peaks and a hint of a third peak in between (around phase 0.5) which is not present in all observations. In the JEM-X pulse profiles, however, all three peaks are clearly visible in all observations, with the exception of Rev# 1138. When comparing the pulse profiles in the two energy bands, it appears that the most prominent of the peak in the JEM-X pulse profiles (peaking around phase 0.5 in the top panel of Fig. 3) tends to disappear at higher energies.
While there is no commonly accepted interpretation of the pulse profile dependence on energy and luminosity, we note that similar behavior is observed in Her X-1 (Klochkov et al. 2008b), 4U 0115+63, and V 0332+63 (Tsygankov et al. 2007). A qualitative interpretation of the pulse profile energy-dependence (based on the results of Mowlavi et al. 2006) has been proposed by Tsygankov et al. (2007) to explain the variation in V 0332+63 pulse profiles in a purely geometric fashion: if the axis of the magnetic dipole is at an angle to the rotation axis (a necessary condition to observe pulsation), the neutron star itself can eclipse some of the lower parts of the accretion columns, which are thought to primarily emit the harder photons. Thus, compared to the pulse profile at softer energies, the harder one lacks (at least) one peak. In contrast, the softer photons are primarily from regions higher up in the accretion column, hence visible during most of the spin period.
On the other hand, gravitational light deflection also plays a crucial role in shaping the observed pulse profile. Indeed, depending on to the geometry of the emitting region and the observer’s line of sight, this effect could make the accretion columns visible from all directions (Kraus 2001; Kraus et al. 2003), thus affecting the pulse profile in a significant way. In addition, the pulse profiles luminosity dependence probably reflects a change in the physical condition of the accretion column. For subcritical sources, the height of the accretion column is anti-correlated with the accretion rate, and this could be at least partially responsible for the luminosity dependence of the pulse profiles. However, this is only a qualitative scenario to account for the observed pulse profile changes.
More accurate descriptions of the pulse profiles dependences need more complicated models in order to account for the magnetic field configuration, the scattering cross section along the accretion column, the shape of the emission beam and its dependence on luminosity and energy, and other parameters. On the other hand, other accreting X-ray pulsars show the opposite behavior, where the low-energy pulse-profiles are absorbed, and the extra peak only appears at higher energies (see, e.g., Kreykenbohm et al. 2004, for the case of GX 301-2).
Although the overall morphology of the profile remains the same in all observations (which permits phase connection of the observations, see Sect. 6.3), the relative intensities of the peaks vary slightly with luminosity. Furthermore, in the last stage of the outburst (Rev# 1138), the pulse profile resembles a single broad peak and a weak energy dependence. A similar flux and energy dependence of the pulse profile is also observed by Devasia et al. (2011) during a GX 304-1 outburst in August 2010, when the source reached a peak flux of ~ 700 mCrab (that is, ~ 30% less than the outburst analyzed in this work). However, the different pulse profiles of Rev# 1138 very likely indicate a possible change in the beaming pattern from an almost purely pencil beam at lowest luminosities, to a mixed pencil-fan beam as the luminosity increases (see Becker et al. 2012, and references therein).
The pulsed fraction is only ~ 20% in both energy bands, and it shows only slight variation along the outburst, uncorrelated with the flux. This is contrary to many other X-ray pulsars, where a pulsed fraction >50% is observed, correlated with energy and flux (Lutovinov & Tsygankov 2008). This again may be understood in a qualitative manner following a geometrical interpretation: it is possible that, as the star rotates, we are exploring only a small area of the beam pattern (i.e., the observed flux from one emission region as a function of the direction to the observer), which in turn leads to an observed low pulsed fraction. This scenario is supported by the results discussed in Sect. 6.3.
6.2. Phase-averaged spectral results
With the new INTEGRAL calibration (Caballero et al. 2013) and analysis software (OSA 10), we confirm the luminosity dependence of the cyclotron line energy Ecyc in GX 304-1 reported in Klochkov et al. (2012), with a more precise restriction of the spectral parameters. The observed Ecyc shows a systematic shift of ~ 5% with respect to the energies reported in the previous work. As a consequence, the correlation found in this work has a slightly higher slope than that found by Klochkov et al. (2012). As mentioned in Sect. 1, this dependency has already been found in several cyclotron line sources. The Ecyc–flux correlation is positive in Her X-1 (Staubert et al. 2007), Vela X-1 (Fürst et al. 2014), A 0535+26 (Sartore et al. 2015), and as some indications suggest, also in GX 301-2 (La Barbera et al. 2005). Pulsars with a confirmed negative Ecyc–flux correlation are V 0332+63 (Tsygankov et al. 2006), and 4U 0115+63 where the negative correlation was found using the NPEX model (Nakajima et al. 2006), but not when using a cutoff-power-law model (Müller et al. 2013), or when the fundamental is modeled by two independent sets of CRSF lines at ~ 11 keV and ~ 15 keV (Iyer et al. 2015). Thus, GX 304-1 enlarges the group of sources further, showing the positive correlation.
Klochkov et al. (2012) interpret this correlation according to the model described by Staubert et al. (2007) and Becker et al. (2012). In these models, a critical luminosity Lc distinguishes between two accretion regimes: one in which the height of the emitting column is governed by the ram pressure of the infalling material (for L<Lc, i.e., “subcritical sources”), and the other where a radiation-pressure-dominated emitting column is formed (for L>Lc, i.e., “supercritical sources”). As the luminosity L varies, the X-ray emitting height also moves within the accretion column, so the local magnetic field changes, leading to a variable cyclotron line energy with luminosity. The critical luminosity below which a positive Ecyc-luminosity correlation is expected, has been calculated by Becker et al. (2012) as a function of the magnetic field and other physical parameters of the NS. For typical neutron star parameters, it results in 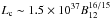 erg s-1. For GX 304-1, this leads to ~ 8 × 1037erg s-1. During the analyzed outburst, the source luminosity clearly remains below this value (see Figs. 5 and 6). Thus, the observed positive Ecyc–flux correlation is consistent with the expected behavior for a subcritical source according to the physical picture outlined in Becker et al. (2012). More recently, a new calculation of the Lc function has been proposed by Mushtukov et al. (2015), where a more detailed accretion scenario is taken into account. The observed positive Ecyc–flux relation in GX 304-1 is consistent with their model as well.
erg s-1. For GX 304-1, this leads to ~ 8 × 1037erg s-1. During the analyzed outburst, the source luminosity clearly remains below this value (see Figs. 5 and 6). Thus, the observed positive Ecyc–flux correlation is consistent with the expected behavior for a subcritical source according to the physical picture outlined in Becker et al. (2012). More recently, a new calculation of the Lc function has been proposed by Mushtukov et al. (2015), where a more detailed accretion scenario is taken into account. The observed positive Ecyc–flux relation in GX 304-1 is consistent with their model as well.
We also investigated the correlation between the spectral photon index Γ and luminosity. In many accreting X-ray pulsars, Γ is luminosity dependent. It had been found that in accreting pulsars showing a positive Ecyc–flux correlation, the correlation between Γ and the flux is negative and vice versa (Klochkov et al. 2011). The exact mechanism of the continuum/flux dependence is not yet clear, especially for supercritical pulsars (with L>Lc). In subcritical sources, including GX 304-1, the observed hardening of the spectrum with flux (Fig. 6) can be qualitatively understood when assuming that the pressure and electron density inside the emitting structure increase with increasing mass accretion rate and luminosity. Indeed, such an increase should lead to a higher optical depth τ, thus to a larger Comptonization parameter y = τkTe/ (mec2). The spectrum formed by Comptonization of the seed photons from the base of the column would then become harder.
Finally, we investigated the dependence of the folding energy Efold on the photon index Γ and, at the same time, on luminosity. These correlations can be seen in the contour plot in Fig. 8. The plot shows that Efold is positively correlated with Γ, and negatively correlated with flux (Efold increases at lower luminosities). Similar behavior is reported for two other accreting pulsars: A 0535+26 (Müller et al. 2013) and RX J0440.9+4431 (Ferrigno et al. 2013). These correlations can be qualitatively understood as follows. It is generally accepted that the power-law–cutoff spectrum of accreting pulsars is a result of Comptonization, i.e., scattering of soft photons off hot electrons supplied by the infalling plasma. As the luminosity increases toward Lc, the radiation field begins to affect the accretion flow and Compton cooling becomes more efficient. This might lead to the observed shift of Efold, thus reflecting the electron temperature Te toward lower energies, while at the same time, the Comptonization process makes the spectrum harder.
The dependence of the spectral hardness on flux has recently been investigated for a number of accreting pulsars in BeXRBs by Reig & Nespoli (2013). They find that the X-ray emission of the sources follows certain patterns in the hardness/intensity diagram. At lower fluxes, the emission first becomes harder with increasing flux. At a certain flux a “turn-over” occurs, so that at higher fluxes the emission again becomes softer (Fig. 6 in Reig & Nespoli 2013). The luminosities corresponding to the fluxes of the turnover are in all cases close to the critical luminosity Lc discussed above. Thus, the turnovers in the hardness/flux dependences may reflect a transition between the aforementioned sub- and super-critical regimes characterized by the opposite Ecyc–flux correlations. To compare our results with those presented in Reig & Nespoli (2013), we constructed a hardness/intensity diagram for GX 304-1 (Fig. 11). We used the same definitions of the soft-color (SC) – the ratio between the fluxes in the 7−10 keV and 4−7 keV ranges. As expected in a subcritical source, the luminosity corresponding to the turnover is not reached in GX 304-1 and the diagram shows only the part where the hardness increases with luminosity, i.e., the “horizontal branch” according to the terminology used in Reig & Nespoli (2013).
 |
Fig. 11 Hardness/intensity diagram for GX 304-1 during the analyzed outburst. The soft color definition is given in the text. The errors are 1σ uncertainties. The errors on the ISGRI rates are smaller than the symbol size. The dashed red curve corresponds to the rising part of the outburst, the dotted blue one – to the decay. |
6.3. Phase-resolved spectral analysis
We modeled the phase-resolved spectra with a rolloff power-law model and a multiplicative Gaussian absorption line to account for the CRSF. The maximum value of the line energy, Ecyc ~ 62 keV, is reached at the peak of the outburst, Rev# 1134, in the pulse phase bin 0.4–0.6 (see Table 3). Using a value of zg = 0.3 for the gravitational redshift (assuming canonical neutron star parameters), this corresponds to a magnetic field strength of 6.9 × 1012Gauss. This is among the strongest observed magnetic fields in an accreting X-ray pulsar.
The centroid energy of the cyclotron line shows only slight variations with pulse phase, which do not exceed ~ 16% (with respect to 0.2 wide phase bins). This is contrary to some other X-ray pulsars (see, e.g., the cases of Cen X-3, Burderi et al. 2000; GX 301-2, Kreykenbohm et al. 2004; and Her X-1, Klochkov et al. 2008a; Vasco et al. 2011), where the energy of the cyclotron line shows up to 30% variation with pulse phase. GX 304-1 , however, is not the only accreting X-ray pulsar where the cyclotron line energy varies only by <20% with pulse phase: see, e.g., the case of 4U 1538-52 (Coburn et al. 2002).
We find that the standard rolloff/power-law model does not lead to good spectral fits for the 0.0–0.2 phase bins. These spectra need an additional component to obtain an acceptable fit. We modeled this component with a Gaussian emission line around 35 keV. Further analysis with more physically motivated models are needed to investigate the feature in more detail, and to understand its origin. The extra component is reminiscent of the “10 keV feature” observed in the spectra of many accreting X-ray pulsars (Coburn et al. 2002; Klochkov et al. 2008a; Müller et al. 2013), for which no accepted explanation of its physical origin exists. However, the centroid energy of the feature in GX 304-1 is at a much higher energy, ~ 35 keV. Interpreted within this context, the feature is likely due to the inadequacy of the underlying phenomenological model. Alternatively, we found that the same feature can be fit by a Gaussian absorption line at lower energies, instead of an emission line. In this case, the absorption line centroid energy is between 12 keV (with σ = 14 keV, η = 37), and 25 keV (with σ = 9 keV, η = 8). To explore the possibility of the feature being the fundamental cyclotron line, we calculated the harmonic ratio between the confirmed cylotron line at ~ 55 keV, assumed to be the first harmonic, and the centroid energy of the absorption feature, and found that it significantly deviates from the canonical ratio of 2. For the feature at 12 keV, the ratio results in an anomalously high value of ~ 4.6, while for the feature at 25 keV the ratio is halved to a value of ~ 2.3. Relatively high deviations from an integer value of the harmonic ratios are also observed in other sources, for example, Vela X-1 (Fürst et al. 2014, and references therein), where the ratio between the confirmed harmonic and fundamental line energies spans the range 2.1–2.7. Those authors invoke photon spawning caused by the harmonic lines as responsible for influencing the shape of the fundamental line, thereby shifting its measured centroid energy from its real value. However, values of the harmonic ratio as high as 4.6 have never been observed for the first harmonic line, and they seem to exclude the possibility that the absorption feature is the fundamental cyclotron line.
Thanks to the successful phase connection (see Sect. 3), we have been able to identify phase bins at different stages of the outburst and, therefore, to perform phase-resolved spectroscopy in order to explore the spectral variability with pulse phase. In particular, we have been able to perform phase-resolved spectroscopy by stacking together all observations (with the exception of Rev# 1138), in order to improve the statistics and investigate the pulse phase variability of spectral parameters with better precision (12 phase bins). The results are shown in Fig. 10 for three parameters of interest: the cyclotron line centroid energy, the photon index and the folding energy. To compare the phase-resolved parameters of the stacked analysis, with the pulse profiles, we produced averaged JEM-X and ISGRI pulse profiles, which are also shown in Fig. 10. The value of Ecyc is constant at ~ 56 keV (with one phase bin showing a ~ 10% higher, although not statistically significant value) The photon index Γ and the folding energy Efold show more prominent variations with pulse phase, but less than a factor of ~ 2. A similar variation in the continuum parameters is also observed in other accreting pulsars (see, e.g., Her X-1, Vasco et al. 2013; GX 301-2, Suchy et al. 2012; Vela X-1, Maitra & Paul 2013), but a consistent theoretical scenario that supports such variations is still missing.
Similar to the phase-resolved analysis of the separated observations, a few phase bins of the stacked phase-resolved spectra need an additional component to give an acceptable χ2. We modeled this component by a Gaussian emission line around 35 keV. An equally good fit is obtained with an absorption Gaussian line at lower energies, i.e., between 16 keV (with σ = 9 keV, η = 17), and 21 keV (with σ = 13 keV, η = 24).
Since our timing analysis shows a low pulsed fraction that is flux- and energy-independent, and the stacked phase-resolved analysis shows a remarkably stable Ecyc, we are tempted to explain these results within the context of the same scenario. Indeed, the steadiness of the cyclotron line energy along the pulse phase can be understood as follows. According to model calculations, the cyclotron line parameters should strongly depend on the viewing angle, hence on the pulse phase (see Schönherr et al. 2007, and references therein). However, if the geometrical configuration is such that we are exploring only a small portion of the beam pattern, then the parameters are mostly insensitive to the pulsar rotation. Therefore, the viewing angle with which we observe the accretion column does not vary appreciably with the NS rotation, and as a consequence, the Ecyc almost turns out to be independent of the rotational phase.
7. Summary and conclusions
In this work, we have presented the results from spectral and timing analysis of INTEGRAL data of the accreting pulsar GX 304-1 observed during an outburst in January−February 2012.
We studied the behavior of the source spectrum as a function of the luminosity by analyzing the pulse phase-averaged and phase-resolved spectral parameters. Our results confirm the positive Ecyc–flux correlation in GX 304-1 with the new INTEGRAL calibration and show a negative correlation between the photon index and the luminosity. The positive Ecyc–flux correlation is also observed in other accreting pulsars whose luminosity is below Lc, such as Her X-1 and Vela X-1, while the negative photon index-luminosity correlation has also been observed in the pulse-to-pulse analysis of Her X-1 and A 0535+26. Then, GX 304-1 is one of the few subcritical sources with a confirmed photon index-luminosity negative correlation. To test the behavior of GX 304-1 below Lc in a model-independent way, we constructed a hardness/intensity diagram and verified that the turnover point, which reflects the critical luminosity, is never reached, and the diagram only shows the so-called horizontal branch. Furthermore, a correlation between the folding energy and the photon index has been found with a relative anti-correlation between the folding energy and the observed luminosity. These correlations seem to fit well in the context of an emergent spectrum shaped by both bulk and thermal Comptonization of blackbody seed photons radiating from the accretion mound (where thermal Comptonization becomes important when the luminosity increases toward Lc). In this context, the observed spectral changes are a consequence of the increasing Compton cooling efficiency at higher luminosity.
Thanks to the pulse profiles main features and to their clear identification in all observations (except the last one), we have been able to phase-connect the pulse profiles, which allowed us to obtain a pulse period solution that is valid over the entire outburst with remarkable precision and to identify phase bins at different stages of the outburst. We measured a period derivative seen over the full outburst, which is probably a combination of the Doppler shift due to the orbital motion of the neutron star and an intrinsic spin-up due to the angular momentum transfer by the accreted material.
The observed pulse profiles compared in the JEM-X (3−20 keV) and ISGRI (18−80 keV) energy bands show a strong energy and luminosity dependence during the outburst, except at the end of the outburst (Rev# 1138), where the pulse profiles are similar in the two energy bands and where they show a much less complex morphology. While the energy-dependent pulse profiles can be justified by a geometrical effect of the rotation of the neutron star, the luminosity dependence probably reflects changes in the physical details of the accretion process in the subcritical regime. Moreover, we observed only a low pulsed fraction, independent of energy and luminosity.
The phase-resolved analysis shows that the cyclotron line is detectable at all rotational phase bins of the neutron star. The maximum reached centroid energy (~ 62 keV) enabled us to infer one of the strongest magnetic field strength on an accreting X-ray pulsar (while the highest belongs to GRO J1008-57 with a cyclotron line energy of ~ 80 keV, Bellm et al. 2014).
Furthermore, we observed no significant variations in the centroid energy with the pulse phase. On the other hand, the depth and the width of the line show more pronounced variations with pulse phase, up to a factor of ~ 3, with no correlation with the pulse profile. In the stacked phase-resolved analysis we were able to show how the cyclotron line energy is essentially constant along the pulse phase.
All these considerations led us to a possible qualitative scenario where the geometrical configuration of the observed NS is such that we are able to explore only a small part of the beam pattern.
We found that, contrary to the phase-averaged spectra, a few phase-resolved spectra lead to large residuals when fit by a standard rolloff/power-law model. They need an additive component that we modeled by a Gaussian emission line around ~ 35 keV, but that can be equally modeled by an absorption line at ~ 20 keV. The additional Gaussian emission line heavily modifies the resulting best-fit parameters, often leading to unphysical values, which most likely indicate that the feature is due to the inadequacy of the underlying phenomenological model.
Online material
Appendix A: The OSA 10 data reduction
Our spectral analysis was performed with the OSA 10 software, which at the time of writing, is the latest version of the INTEGRAL analysis software. OSA 10 is supplied with a new energy calibration of the ISGRI detector, with respect to the previous version (OSA 9). As a result, a more reliable photon energy reconstruction is ensured. The details about the new energy reconstruction are reported in Caballero et al. (2013).
To investigate the difference in energy calibration between OSA 9 and OSA 10, we extracted the data set used in this work with both the software versions. Following Klochkov et al. (2012), after the OSA 9 data reduction, we performed an additional gain correction based on the background spectral line complex of tungsten (W, nominally at 58.8297 keV). After the OSA 10 data reduction, which includes a more accurate gain correction, a small deviation in the inferred energy from the nominal Tungsten line was still noticeable. The deviation amounted up to + 0.5 keV in the Science Windows (ScWs, i.e., INTEGRAL pointings) at the beginning of each INTEGRAL revolution. According to the ISGRI instrument team (priv. comm.), the deviation can be attributed to possible orbital drifts in the detector response, which are responsible for systematic scatter when revolutions start. However, even if orbital variations are not currently corrected, they are mitigated when averaged over a number of revolutions. Nonetheless, to eliminate this deviation, we performed an additional gain correction to ensure the stability of the Tungsten reference line. After the correction, the inferred Tungsten line energy in all ScWs is found to be consistent with its nominal value within 3σ.
To illustrate the effects of the different energy calibrations, we plotted the Ecyc–flux relation for the spectra obtained with the two software versions (Fig. A.1). We note that the energy range indicated in Klochkov et al. (2012) for calculating the flux is erroneously reported as 4−80 keV, while the correct range is 13−80 keV (where the lower limit is constrained by the response matrix energy range of the ISGRI instrument). The two different sets of results clearly show a systematic shift of the
cyclotron line centroid energy, with a deviation (proportional to the measured energy) up to ~ 2 keV. This is the result of the new energy calibration implemented in OSA 10 plus a minor contribution due to the additional gain correction performed after the OSA 10 data reduction. In our scientific analysis, we used the data reduced with OSA 10 with the additional gain correction. This ensures the most accurate measurements of the cyclotron line centroid energy.
 |
Fig. A.1 Cyclotron line centroid energy Ecyc as a function of the logarithm of flux in the 13−80 keV range. The black dots are the results of Klochkov et al. (2012), obtained with OSA 9 and corrected for the ISGRI energy gain drift. The red triangles are the results of this work, obtained with OSA 10 and then gain-corrected. The dashed and dotted lines are the results of linear fits to the Ecyc − log 10 (Flux) data for the two sets resulting from OSA 9 and OSA 10 data reduction, respectively. The error bars indicate 1σ-uncertainties (the statistical flux uncertainties are smaller than the symbol size). The top x-axis shows the corresponding isotropic source luminosity assuming a distance of 2.4 kpc. |
Acknowledgments
We gratefully acknowledge the anonymous referee for numerous comments that greatly improved the manuscript. This research is based on observations with INTEGRAL, an ESA project with the instruments and science data center funded by ESA member states especially the PI countries: Denmark, France, Germany, Italy, Switzerland, Spain, Czech Republic and Poland, and with the participation of Russia and the USA. This work is supported by the Bundesministerium für Wirtschaft und Technologie through the Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR) under the grant number FKZ 50 OR 1204. C.M. thanks the MAXI team (RIKEN, Japan) for the support during our collaboration.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Becker, P. A., Klochkov, D., Schönherr, G., et al. 2012, A&A, 544, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellm, E. C., Fürst, F., Pottschmidt, K., et al. 2014, ApJ, 792, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Robba, N. R., La Barbera, A., & Guainazzi, M. 2000, ApJ, 530, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, I., & Wilms, J. 2012, Mem. Soc. Astron. Italiana, 83, 230 [Google Scholar]
- Caballero, I., Zurita Heras, J. A., Mattana, F., et al. 2013, ArXiv e-prints [arXiv:1304.1349] [Google Scholar]
- Coburn, W., Heindl, W. A., Rothschild, R. E., et al. 2002, ApJ, 580, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Deeter, J. E., Boynton, P. E., & Pravdo, S. H. 1981, ApJ, 247, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Devasia, J., James, M., Paul, B., & Indulekha, K. 2011, MNRAS, 417, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrigno, C., Farinelli, R., Bozzo, E., et al. 2013, A&A, 553, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fürst, F., Pottschmidt, K., Wilms, J., et al. 2014, ApJ, 780, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Heindl, W. A., Rothschild, R. E., Coburn, W., et al. 2004, in X-ray Timing 2003: Rossi and Beyond, eds. P. Kaaret, F. K. Lamb, & J. H. Swank, AIP Conf. Ser., 714, 323 [Google Scholar]
- Iyer, N., Mukherjee, D., Dewangan, G. C., Bhattacharya, D., & Seetha, S. 2015, MNRAS, submitted [arXiv:1506.03376] [Google Scholar]
- Klochkov, D., Santangelo, A., Staubert, R., & Ferrigno, C. 2008a, A&A, 491, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Staubert, R., Postnov, K., et al. 2008b, A&A, 482, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Staubert, R., Santangelo, A., Rothschild, R. E., & Ferrigno, C. 2011, A&A, 532, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Doroshenko, V., Santangelo, A., et al. 2012, A&A, 542, L28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, U. 2001, ApJ, 563, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Zahn, C., Weth, C., & Ruder, H. 2003, ApJ, 590, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Coburn, W., et al. 2004, A&A, 427, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Barbera, A., Segreto, A., Santangelo, A., Kreykenbohm, I., & Orlandini, M. 2005, A&A, 438, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, D. A. 1987, A&A, 180, 275 [NASA ADS] [Google Scholar]
- Lebrun, F., Leray, J. P., Lavocat, P., et al. 2003, A&A, 411, L141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewin, W. H. G., Clark, G. W., & Smith, W. B. 1968a, Nature, 219, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., Clark, G. W., & Smith, W. B. 1968b, ApJ, 152, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutovinov, A., & Tsygankov, S. 2008, in AIP Conf. Ser. 1054, ed. M. Axelsson, 191 [Google Scholar]
- Maitra, C., & Paul, B. 2013, ApJ, 763, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A., Beckmann, V., Bianchin, V., et al. 2008, ATel, 1613, 1 [NASA ADS] [Google Scholar]
- McClintock, J. E., Nugent, J. J., Li, F. K., & Rappaport, S. A. 1977, ApJ, 216, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Mihara, T., Ohashi, T., Makishima, K., et al. 1991, PASJ, 43, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Mowlavi, N., Kreykenbohm, I., Shaw, S. E., et al. 2006, A&A, 451, 187 [Google Scholar]
- Müller, D., Klochkov, D., Caballero, I., & Santangelo, A. 2013, A&A, 552, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, S., Ferrigno, C., Kühnel, M., et al. 2013, A&A, 551, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Poutanen, J. 2015, MNRAS, 447, 1847 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, M., Mihara, T., Makishima, K., & Niko, H. 2006, ApJ, 646, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Parkes, G. E., Murdin, P. G., & Mason, K. O. 1980, MNRAS, 190, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Pietsch, W., Oegelman, H., Kahabka, P., Collmar, W., & Gottwald, M. 1986, A&A, 163, 93 [NASA ADS] [Google Scholar]
- Poutanen, J., Mushtukov, A. A., Suleimanov, V. F., et al. 2013, ApJ, 777, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Priedhorsky, W. C., & Terrell, J. 1983, ApJ, 273, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., & Nespoli, E. 2013, A&A, 551, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santangelo, A., Segreto, A., Giarrusso, S., et al. 1999, ApJ, 523, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Sartore, N., Jourdain, E., & Roques, J.-P. 2015, ApJ, 806, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Schönherr, G., Wilms, J., Kretschmar, P., et al. 2007, A&A, 472, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staubert, R. 2003, ChJA&A, 3, 270 [Google Scholar]
- Staubert, R., Shakura, N. I., Postnov, K., et al. 2007, A&A, 465, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suchy, S., Fürst, F., Pottschmidt, K., et al. 2012, ApJ, 745, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Sugizaki, M., Yamamoto, T., Mihara, T., Nakajima, M., & Makishima, K. 2015, PASJ, accepted [arXiv:1504.04895] [Google Scholar]
- Terada, Y., Mihara, T., Nagase, F., et al. 2007, Adv. Space Res., 40, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J., Pietsch, W., Reppin, C., et al. 1978, ApJ, 219, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Tsygankov, S. S., Lutovinov, A. A., Churazov, E. M., & Sunyaev, R. A. 2006, MNRAS, 371, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Tsygankov, S. S., Lutovinov, A. A., Churazov, E. M., & Sunyaev, R. A. 2007, Astron. Lett., 33, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasco, D., Klochkov, D., & Staubert, R. 2011, A&A, 532, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasco, D., Staubert, R., Klochkov, D., et al. 2013, A&A, 550, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vedrenne, G., Roques, J.-P., Schönfelder, V., et al. 2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilms, J. 2012, in Proceed. 39th COSPAR Sci. Assembly, 14−22 July 2012, Mysore, India, 39, 2159 [Google Scholar]
- Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yamamoto, T., Sugizaki, M., Mihara, T., et al. 2011, PASJ, 63, 751 [Google Scholar]
- Yamamoto, T., Tomida, H., Mihara, T., et al. 2012, ATel, 3856, 1 [NASA ADS] [Google Scholar]
All Tables
Global timing solution obtained from phase-connection of IBIS/ISGRI (18−80 keV) pulse-profiles and spectral parameters throughout the outburst obtained with OSA 10 plus additional gain correction (see text).
Best-fit parameters of the first phase-bin spectra using a model with and without additional Gaussian emission line.
All Figures
 |
Fig. 1 The Swift/BAT light curve of GX 304-1 during the January−February 2012 outburst. The horizontal bars mark the INTEGRAL observations. The numbers above the bars indicate the last digit “i” of the respective INTEGRAL revolution number – 113i. |
| In the text | |
 |
Fig. 2 IBIS/ISGRI (18−80 keV) normalized pulse profiles obtained with the timing solution resulting from our phase-connection analysis. Each panel represents, from top to bottom, the successive INTEGRAL observations (from Rev# 1131 to 1138, shown in the top left corner). In the top right corner, the luminosity of the source (3−80 keV) in units of 1037 erg/s is reported. The thin straight line around phase 1.0 at the bottom of each panel (except Rev# 1138) approximately indicates the phase range where the sharp features used to phase-connect the observations are found. |
| In the text | |
 |
Fig. 3 JEM-X1 normalized pulse profiles in the 3−20 keV energy range. Panels follow the same Rev# and luminosity stage as in in Fig. 2. |
| In the text | |
 |
Fig. 4 Pulse period as a function of time obtained by phase connection. The dashed line represents a linear fit to the data points, yielding a pulse period derivative of Ṗ = (−2.04 ± 0.01) × 10-7. The period error bars are smaller than the symbols. |
| In the text | |
 |
Fig. 5 Cyclotron line centroid energy Ecyc as a function of the logarithm of flux in the 3−80 keV range. The dotted line is the result of a linear fit to the Ecyc − log 10(Flux) data. The error bars indicate 1σ-uncertainties. (The flux uncertainties are smaller than the symbol size.) The top x-axis shows the corresponding isotropic source luminosity assuming a distance of 2.4 kpc. |
| In the text | |
 |
Fig. 6 Variation in the photon index Γ versus the observed flux. The dashed line represents the linear fit to the data points. The luminosity scale on the top x-axis is as in Fig. 5. |
| In the text | |
 |
Fig. 7 Phase-averaged spectra of four observations (labelled above each spectrum), from top to bottom, with decreasing luminosity. JEM-X1 (black) and ISGRI (red) data and folded model are shown. Spectra have been scaled for better visualization. Both the Ecyc–flux and the Γ–flux correlations are clearly visible. |
| In the text | |
 |
Fig. 8 χ2-contour plots of the folding energy Efold and the photon index Γ for four INTEGRAL observations. The contours correspond to χ2 + 1.0 (the projections of this contour to the parameter axes correspond to the 68% uncertainty for one parameter of interest), and χ2 + 2.3 (68% uncertainty for two parameters of interest). The respective luminosity (3−80 keV) in units of 1037erg s-1 is indicated. |
| In the text | |
 |
Fig. 9 Top: spectrum of the phase bin 0.0–0.2 from revolution 1132 fit with a power-law/rolloff model including the cyclotron line and an additional Gaussian component to account for a bump around 35 keV (see text). JEM-X (red and green), ISGRI (black), and SPI (blue) data are used. Middle: residuals for a fit with the model without the additional Gaussian component. Large residuals appear around the cut-off energy. Bottom: residuals after including the Gaussian emission component to model the bump. |
| In the text | |
 |
Fig. 10 Best fit parameters of the phase-resolved spectra using the five stacked INTEGRAL observations. The vertical dashed lines indicate the phase-bins. The solid blue curve is the JEM-X average pulse profile, while the green curve is the ISGRI average pulse profile. The vertical error bars are 1σ uncertainties, while the horizontal bars represent the phase bin width. |
| In the text | |
 |
Fig. 11 Hardness/intensity diagram for GX 304-1 during the analyzed outburst. The soft color definition is given in the text. The errors are 1σ uncertainties. The errors on the ISGRI rates are smaller than the symbol size. The dashed red curve corresponds to the rising part of the outburst, the dotted blue one – to the decay. |
| In the text | |
 |
Fig. A.1 Cyclotron line centroid energy Ecyc as a function of the logarithm of flux in the 13−80 keV range. The black dots are the results of Klochkov et al. (2012), obtained with OSA 9 and corrected for the ISGRI energy gain drift. The red triangles are the results of this work, obtained with OSA 10 and then gain-corrected. The dashed and dotted lines are the results of linear fits to the Ecyc − log 10 (Flux) data for the two sets resulting from OSA 9 and OSA 10 data reduction, respectively. The error bars indicate 1σ-uncertainties (the statistical flux uncertainties are smaller than the symbol size). The top x-axis shows the corresponding isotropic source luminosity assuming a distance of 2.4 kpc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


