| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201526391 | |
| Published online | 26 August 2015 | |
A time-domain deconvolution technique for meteor photometry applied to double-station CCD image data
1 Armagh Observatory, College Hill, Armagh BT61 9DG, UK
e-mail: aac@arm.ac.uk
2 Technische Universität Berlin, Strasse des 17. Juni 135, 10623 Berlin, Germany
e-mail: Anastasios.Margonis@tu-berlin.de
3 German Aerospace Centre (DLR), Rutherfordstrasse 2, 12489 Berlin, Germany
e-mail: Juergen.Oberst@dlr.de
4 Moscow State University for Geodesy and Cartography (MIIGAiK), Gorokhovsky pereulok 4, 105064 Moscow, Russian Federation
Received: 23 April 2015
Accepted: 13 July 2015
Aims. We describe a new algorithm for extracting photometric information from meteor images.
Methods. The time history of a moving point source of variable brightness is explicitly deconvolved from the spatial distribution of the meteor signal on the image. The method can be applied to time-integrated meteor images if kinematic information is independently available or, alternatively, assumed. Formal uncertainty estimation and reporting is included.
Results. We test the algorithm on synthetic meteor images and meteors recorded during a recent double-station meteor observing campaign in Greece. In the first case, we find that both the synthetic signal and the a priori time variation of the flux are faithfully reproduced. In the second, the fluxes obtained from the two stations agree to ∼20%.
Key words: methods: data analysis / methods: numerical / techniques: photometric / meteorites, meteors, meteoroids
© ESO, 2015
1. Introduction
The light emitted from fast-moving meteors in the Earth’s atmosphere contains information on the size, physical structure and chemical composition of interplanetary meteoroids (Campbell-Brown 2005,and references therein). In particular, meteor light curves − point-by-point measurements of a meteor’s changing brightness with time − inform models of the physical structure of the ablating body (Campbell et al. 1999; Pecina & Koten 2009; Koschny et al. 2011, and references therein).
Due to the unpredictable nature of the phenomenon and its unique characteristics (lifetime of order seconds, brightness variation of order of magnitude and rate of sky motion of order tens of degrees per sec), measuring meteor light requires customised instrumentation and techniques, distinct from those used in other areas of astronomy (Hawkes et al. 2001; Campbell-Brown 2005). Indeed, meteor photometry remains one of the few areas of astronomy that still utilises visual observations (e.g. Campbell-Brown 2005).
Advances in detector technology (Hawkes 1990; Molau et al. 1997) had led to the proliferation of multi-station meteor observing networks around the world equipped with inexpensive, light-sensitive, video cameras (Molau 2001; Trigo-Rodriguez et al. 2007; Weryk et al. 2008; SonotaCo 2009; Brown et al. 2010; Gural 2011; Stewart et al. 2013; Campbell-Burns & Kacerek 2014). This has led to the development of several software packages for the analysis of video meteor data, most of which include modules for photometric data reduction (see Molau & Gural 2005, for a review). This process is ongoing and new packages are being produced to handle the ever-increasing volume and quality of data from new and existing facilities (Madiedo et al. 2011; Peterson 2014).
A meteor image contains a fundamental degeneracy: the brightness history of the meteor cannot be uniquely determined from the accumulated signal on each pixel of the image but depends on the rate of meteor motion. Simply put, a bright, fast-moving meteor will generate the same signal on each detector pixel as a slower, fainter one. The degeneracy is lifted when independent information on either the apparent rate of motion or the spatial velocity of the meteoroid is available. In practice, the issue is implicitly resolved during data acquisition. One simply accepts the time resolution inherent in the observational setup, be it video recordings (Hawkes et al. 1993, 2001; Koten 1999) or still images obtained with either a rotating (Ceplecha 1987; Spurný et al. 2007), electronic (Atreya et al. 2012) or liquid crystal (Bettonvil 2011; Towner et al. 2015) shutter.
 |
Fig. 1 Geometric representation of the flux variation within an image pixel over time due to meteor motion. See main text for notation. The concentric ellipses around the meteor position represent loci of constant flux. |
This means, however, that the data is not utilised in the fullest extent possible as useful information is thrown away. For instance, some meteor networks generate still, unshuttered, CCD images concurrently with time-resolved data (Trigo-Rodriguez et al. 2005, and references therein); these can provide an additional, independent record of meteor brightness as a function of time to help constrain the true − as opposed to the formal − brightness1 uncertainties. Moreover, the individual segments of interrupted meteor trails in shuttered images (Spurný et al. 2007; Atreya et al. 2012) or, equivalently, the elongated segments of fast meteors in video frames may contain significant brightness variations (e.g. flares; Spurný & Shrbený et al. 2008). Extracting this information from the data would effectively increase the resolution of the light curve beyond the limit imposed by the frame rate or shutter speed.
Here we present a new method of obtaining a meteor light curve from an image. Through a direct transformation from the spatial (i.e. image coordinates) to the time domain, our algorithm deconvolves the time history of the meteor’s changing brightness from the spatial distribution of its signal on the image. This results in a series of least-squares estimates of the flux over time that can be converted to stellar magnitudes by comparison with field stars. Formal uncertainties for the flux estimates are calculated from the photometric measurement uncertainties as a by-product of the least-squares process. The main strength of the method lies in its ability to extract the brightness of the moving source at multiple points along its trajectory − or, equivalently, multiple times during a single exposure − from the image if the meteor kinematics are known. The resolution of the extracted time series is user-selectable and ultimately depends on the amount of available signal. To our knowledge, the method described in this paper has not been previously used to retrieve the meteor flux history from image data.
The algorithm is intended for application on a large dataset of double station meteors obtained with the Smart Panoramic Optical Sensor Head (SPOSH) CCD camera, designed to detect meteors while looking down on the Earth’s atmosphere from an orbital platform (Oberst et al. 2011). Camera breadboards have been employed in a programme of annual test campaigns, operating in pairs as part of a double station network in the Peloponesian province of Greece. During those campaigns, one of the cameras is fitted with a rotating shutter to introduce breaks into the meteor image every 0.06 s. The meteor velocity in space is obtained by considering both the interrupted (i.e. obtained with the rotating shutter) and uninterrupted images of the same meteor.
This work focuses on presenting the photometric extraction algorithm and on demonstrating its applicability on both simulated (hereafter referred to as “synthetic”) and actual meteor images. Other aspects of the reduction pipeline as well as the results of the full astrometric and photometric reduction of that dataset will be reported in a forthcoming paper. The effects of airglow and persistent trains which are prominent for bright meteor events are also not considered here.
Finally, for the purposes of this paper it has been assumed that the motion of the meteor source is uniform on the image plane. In general, this is not the case; although the three-dimensional or spatial velocity of all but the slowest meteors is approximately constant, its projection on the image plane is not since both the viewing direction and the distance from the observer to the meteor are continuously changing. Future implementation of the algorithm will lift this assumption by making use of a full kinematic model for the source.
The paper is organised as follows: in the next section, we describe the mathematical model relating the meteor signal on the image to the flux of the moving point source and its variation over time. In Sect. 3 we present a series of tests of the algorithm using both synthetic (Sect. 3.1) and real (interrupted and uninterrupted; Sect. 3.2) meteor images. In Sect. 4 we present our conclusions and identify potential future applications of the algorithm. For the reader’s convenience, we summarise in the Appendix some key results from least-squares estimation theory that we have utilised in computing the formal statistical uncertainties of the extracted light curves.
2. Model
The trajectory of the moving source (i.e. the centre of the PSF) on the image plane can be represented by the position vector 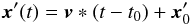 (A.1)where v is the projection of the meteor’s cartesian velocity vector on this plane and
(A.1)where v is the projection of the meteor’s cartesian velocity vector on this plane and 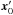 the image projection of its position at time t0. Assuming square pixels, the flux at image coordinates x and at time t due to the point spread function (PSF: here assumed Gaussian with standard deviation σPSF) is
the image projection of its position at time t0. Assuming square pixels, the flux at image coordinates x and at time t due to the point spread function (PSF: here assumed Gaussian with standard deviation σPSF) is 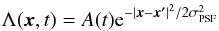 (A.2)and the signal accumulated within a single image pixel for an exposure duration T is the double integral of this function over time and over the area spanned by that pixel.
(A.2)and the signal accumulated within a single image pixel for an exposure duration T is the double integral of this function over time and over the area spanned by that pixel.
 |
Fig. 2 Left panel: synthetic image of a moving source of increasing flux. The red dots denote the pixel locations of the measurements. Middle panel: the initial choice for the source flux over time (black squares) and the estimates from the least-squares fit (red squares). Right panel: the synthetic signal along the central pixel row of the meteor (black curve) and the reconstructed values from the Ak estimates (red diamonds). The value of the goodness-of-fit quantity is indicated in the upper left while the grey error bars represent 1σ formal uncertainties. |
The flux over the solid angle subtended by a square, unit-width pixel at position xj can be represented by the function Λ(x,t) evaluated at xj (Fig. 1). The temporally integrated signal within that pixel for an exposure duration T is then 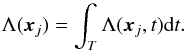 (A.3)We can discretise Eq. (A.3)by partitioning T into n intervals Δt0,Δt1,...,Δtn − 1 where Δtk = tk + 1 − tk. This gives us the m equations of condition:
(A.3)We can discretise Eq. (A.3)by partitioning T into n intervals Δt0,Δt1,...,Δtn − 1 where Δtk = tk + 1 − tk. This gives us the m equations of condition: 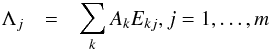 (A.4)where
(A.4)where 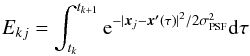 (A.5)and
(A.5)and 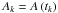 . For Δtk small, the integral in Eq. (A.5)can be approximated by the product
. For Δtk small, the integral in Eq. (A.5)can be approximated by the product ![\hbox{$ \exp\left[{- {| \vec{x}_{j} -\vec{x^{\prime}}(t_{k}) |}^{2}/2 \sigma^{2}_{\rm PSF}}\right] \times \Delta t_{k}$}](/articles/aa/full_html/2015/09/aa26391-15/aa26391-15-eq26.png) . In the next section we compare the performance of this approximation against more elaborate numerical methods of evaluating the integral.
. In the next section we compare the performance of this approximation against more elaborate numerical methods of evaluating the integral.
The problem is now in an appropriate form for a linear regression fit to estimate the parameters Ak that describe the source flux variation over time by minimising 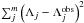 . Measurement errors are assumed Poissonian i.e.
. Measurement errors are assumed Poissonian i.e. 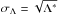 where Λ∗ is the total signal before calibration (meteor+sky+dark). For example, if the meteor signal (data number; DN) is 50, sky signal is 100 and thermal (dark) signal is 50 then the error is
where Λ∗ is the total signal before calibration (meteor+sky+dark). For example, if the meteor signal (data number; DN) is 50, sky signal is 100 and thermal (dark) signal is 50 then the error is 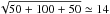 DN, not
DN, not 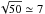 DN. These are used to estimate the uncertainties in the Ak (see Appendix) but may also act as weights for the least-squares procedure. Each of the m pixels contributes an equation of condition. The time resolution n should then be such that m>n i.e. the system is overdetermined.
DN. These are used to estimate the uncertainties in the Ak (see Appendix) but may also act as weights for the least-squares procedure. Each of the m pixels contributes an equation of condition. The time resolution n should then be such that m>n i.e. the system is overdetermined.
We note that the rate of image motion of the meteor enters our model as an independent parameter. The dependence between this parameter and the obtained meteor flux estimates will be illustrated in the following section by way of an example.
 |
Fig. 4 Results of fitting the model on the synthetic meteor in Fig. 2 using only the row of pixel measurements along the meteor trajectory (top) and an additional ten rows on either side (bottom). Left: synthetic measurements (black line) and their model estimates (red diamonds). Right: flux estimates (red squares) plotted against a priori values (black squares). |
3. Tests of algorithm performance
3.1. Synthetic meteor images
To test our model we have generated a series of synthetic meteor images, starting from an initial choice for the Ak values and calculating the signal in each image pixel from Eq. (A.4). We then add Poisson noise to the synthetic measurements and apply the algorithm to recover the flux history Ak through a least-squares process. The results of all our tests for the source brightness are in the form of the rate of accumulation of signal (data numbers per sec or DN/s for short) under the − assumed Gaussian − PSF (Eq. (2)) in each case. The reconstructed signal from the fit is given in terms of the DN. We remind the reader at this point that n refers to the time resolution we wish to achieve for a given exposure duration while m refers to the number of measurements (pixel DNs) used in the fit. Through Eq. (A.1), each of the tk correspond to particular locations − say 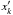 − of the meteor on the image. These should not be confused with xj, the pixel locations corresponding to the m measurements.
− of the meteor on the image. These should not be confused with xj, the pixel locations corresponding to the m measurements.
We show here the results for two cases, one where the source brightness increases linearly with a slope of 250 DN s-1 (Fig. 2) and a second where the meteor brightens from both ends, peaking in the middle of its trajectory (Fig. 3). In both cases, v = 30 pixels s-1 for an exposure duration of 2 s and σPSF = 3. The photon flux was estimated at eight equally-spaced time instants along the trajectory in the first case (i.e. n = 8) and nine on the second (n = 9). Also plotted (grey error bars) are the formal uncertainties calculated from the least-squares fit. However, they are similar in size to the symbols (red squares) representing the flux estimates themselves and difficult to discern.
Next, we have performed a series of fits where the number l of considered pixel rows parallel to the meteor’s trajectory gradually increases from l = 0 (i.e. only the central row) to l = 10 (21 rows in total). In Fig. 4 we show results for l = 0 and l = 10. The goodness-of-fit parameter (R2) is ≳90% in both cases. Considering more rows in the fit typically results in a higher value of R2 as well as lower formal uncertainties for the estimated flux and the reconstructed signal.
 |
Fig. 5 Fits to the image row segment of 110 pixels along the synthetic meteor in Fig. 2 for the model that evaluates formally the integrals in Eq. (A.5)(top) and for the approximation using function-time products (bottom). The flux of the meteor point source was sampled with n = 8 (left), n = 4 (middle) and n = 2 (right). Notation in this and the following figure is as in Fig. 4. |
 |
Fig. 7 Model fit for the double-flaring synthetic meteor described in the text. The chosen time resolution (i.e. value of n) increases from left to right. Top: synthetic meteor images showing the locations, along the meteor path, corresponding to the times tk when the flux is estimated. Middle: best-fit flux profile (red curve) compared to the a priori profile (black curve) used to calculate the signal. Bottom: model fit (red curve) to the synthetic signal (black curve). |
 |
Fig. 8 Illustration of the dependence of the flux estimation process on the assumed velocity: 20 (left panels), 30 (middle panels) and 40 pixels s-1 (right panels). Notation is as in Fig. 4. |
 |
Fig. 9 SPOSH image crops of double-station meteor used in Sect. 3.2. Meteor motion is from top right to bottom left. Left: uninterrupted image. The bright area immediately to the left of the meteor corresponds to a portion of the Milky Way. Right: image interrupted by the rotating shutter. |
 |
Fig. 10 Analysis results of meteor shown in Fig. 9. Top left: difference image (see text) showing the measurements (red line bracketed by the two red diamonds) used to run the model on. Top right: model fit (red diamonds) to the measurements (black line). Bottom left: difference image indicating the positions (or, equivalently, the times) along the meteor trajectory when the flux was estimated. Bottom right: estimated flux as a function of time, from the moment the meteor reached the beginning of the measurement vector. |
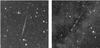 |
Fig. 11 Crops of SPOSH images of a meteor observed from Mainalon (left) and Parnon (right) at 21:34:17 UT. |
We have also investigated the effect of replacing the integration over each time interval Δtk = [tk,tk + 1] in Eq. (A.5)with the products ![\hbox{$ \exp\left[{- {| \vec{x}_{j} -\vec{x^{\prime}}(t_{k}) |}^{2}/2 \sigma^{2}_{\rm PSF}}\right] \times \Delta t_{k}$}](/articles/aa/full_html/2015/09/aa26391-15/aa26391-15-eq26.png) (see Sect. 2). This has been done for the cases n = 8, 6, 4 and 2 and the results are shown in Figs. 5 and 6 for the data fits and the flux estimates respectively. In the fits with the approximate form of the model we observe a modulation of the reconstructed light curve which increases in amplitude as n decreases. At the same time, the flux parameters Ak are somewhat underestimated in the case n = 4 and more significantly so for n = 2. This is because the value of the exponential in Eq. (A.5), rather than remaining approximately constant, varies considerably over Δtk for the high angular rates of image plane motion that are typical of meteors. In comparison, the model that evaluates the integral in Eq. (A.5)uses a numerical implementation of the trapezoidal rule and faithfully reconstructs the meteor light curve for n = 8, 6 and 4. The stepwise appearance of the reconstructed meteor for n = 2− hinted at in the plot for n = 4− is due to how the spatial integral of the meteor flux is evaluated across the image area of a pixel (Sect. 2). Even in this case however, the main features of the light curve (slope and peak flux) are successfully recovered from the fit.
(see Sect. 2). This has been done for the cases n = 8, 6, 4 and 2 and the results are shown in Figs. 5 and 6 for the data fits and the flux estimates respectively. In the fits with the approximate form of the model we observe a modulation of the reconstructed light curve which increases in amplitude as n decreases. At the same time, the flux parameters Ak are somewhat underestimated in the case n = 4 and more significantly so for n = 2. This is because the value of the exponential in Eq. (A.5), rather than remaining approximately constant, varies considerably over Δtk for the high angular rates of image plane motion that are typical of meteors. In comparison, the model that evaluates the integral in Eq. (A.5)uses a numerical implementation of the trapezoidal rule and faithfully reconstructs the meteor light curve for n = 8, 6 and 4. The stepwise appearance of the reconstructed meteor for n = 2− hinted at in the plot for n = 4− is due to how the spatial integral of the meteor flux is evaluated across the image area of a pixel (Sect. 2). Even in this case however, the main features of the light curve (slope and peak flux) are successfully recovered from the fit.
An important feature of the algorithm is that the time resolution of the flux is user-selectable and can, in principle, be chosen to resolve rapid variations of the source. To demonstrate this, we have created a synthetic constant-flux meteor of 0.3 s duration to which we superimposed two sudden increases (“flares”) separated in time by 0.0217 s, shorter than the time resolution of video footage (0.033 s). In Fig. 7 we show the result of applying our algorithm with n = 10, 20 and 30, equivalent to time resolutions of Δt = 0.033, 0.016 and 0.010 s respectively. In the fit with the coarsest time resolution (left column), the algorithm finds only one peak − as it happens, the earlier and least intense of the two − in the flux profile (middle panel) and reconstructs the signal accordingly (bottom panel). Doubling the time resolution (centre column) allows the algorithm to locate the true maximum in the meteor flux (middle panel), yet the two flares are still unresolved. When the time resolution is increased further to n = 30 (right column), the algorithm reproduces the original two-flare profile (middle panel). Note that the goodness-of-fit for the signal is essentially identical between these last two cases (compare bottom centre and bottom right panels), therefore choosing a high time resolution is essential in reproducing the true flux history of the meteor. However, increasing the time resolution also results in higher formal uncertainties for the flux estimates Ak (compare error bars from left to right in middle row). This can be understood in terms of ever smaller portions of the available signal used to estimate each of the parameters. In practice, therefore, one would impose a priori the desired signal-to-noise ratio for the estimates and trade signal with time resolution in order to achieve it.
In the final example of this section, we illustrate the degeneracy that exists in the determination of the meteor flux from the signal due to its direct dependence on the assumed rate of motion. We use the model to reconstruct the flux history from the synthetic meteor shown in Fig. 2 for three different values of v: 20, 30 and 40 pixels s-1. The reader is reminded that the signal was calculated from the a priori known flux history A(t) using v = 30 pixels s-1. The result is shown in Fig. 8 for the reconstructed signal and flux estimates (top and bottom panels respectively). The middle column of panels show the result of applying the model with the correct value for the rate of motion. Assuming a lower (left column) or higher (right column) value results in too low (bottom left) or too high (bottom right) fluxes respectively.
 |
Fig. 12 Analysis results of meteor shown in Fig 11. Top left: estimated flux over time for the uninterrupted image. Top middle: meteor signal (continuous line) along the measurement vector compared to the signal estimates from the fit (red diamonds). Top right: comparison of instrumental magnitude estimates from the uninterrupted (continuous line) and interrupted (dashed line) images. Bottom left: as top left panel, but for the interrupted image. Bottom middle: as top middle panel, but for the interrupted image. Bottom right: as top right panel, but for the flux. |
3.2. Images of real meteors
To demonstrate the applicability of the algorithm on real meteors, we have applied it to a meteor observed from one of the SPOSH stations at 20:30 UT on 09 Aug. 2013 (Fig. 9). This meteor was chosen for its location near the zenith as seen from both stations to ensure that the angular velocity of the source is approximately constant. For the same reason, we chose a meteor with a relatively short luminous path, ∼160 SPOSH pixels or 18° in length. In this test, we apply our algorithm to the uninterrupted image only. We first subtract the previous CCD frame in the sequence (taken 2 s before) to remove the images of stars and the Milky Way, then estimate the angular velocity of the meteor across the sky. Formally, the correct procedure is to solve the two-station problem for the spatial velocity vector and then project that vector on the image plane. However, here we are specifically interested in the stability of the algorithm when applied to real images rather than its precision. So, instead we have manually measured the segments in the shutter-interrupted image to obtain a rough estimate of the angular velocity from one station and assume the same value for the image from the other. Again, this is not formally correct but, given the ∼50 km baseline of our two station observations and that the meteor appears near the local zenith as seen from both stations, our estimate will not be far from the truth.
The estimated angular velocity is found to be 242 pixels s-1 while the estimated value of σPSF was ∼1.0 (in pixel size units). Our measurement vector corresponds to 160 pixels taken from the central portion of the meteor, and shown in the top left panel of Fig. 10. We chose to discretise the model with n = 20 corresponding to a time resolution of Δtk ≃ 0.033 s. The result of the fit is shown in the top right panel of this figure. In the bottom left panel we show the locations, along the meteor trajectory, corresponding to the discrete times at which we evaluated the meteor flux function, with the flux estimates themselves shown on the bottom right panel.
Next we consider a meteor observed from both stations at 21:34 UT on the same night. We apply the algorithm to both the interrupted and uninterrupted images (Fig. 11) and compare the results. Here, the data from the interrupted image serves as an independent check of the flux estimates from our model application to the uninterrupted image.
Proceeding as before, we estimate the angular velocity to be 179 pixels s-1 (i.e. a meteor duration of 0.54 s) from the interrupted image. Our measurement vector for the uninterrupted and interrupted frames consists of the pixel values for the three lines parallel and nearest to the meteor image from each frame, 97 pixels long in both cases. We discretised the model with n = 20 for the uninterrupted image but chose a higher time resolution (n = 50 or Δtk ≃ 0.0108 s) for the interrupted image in order to follow the dimming of the meteor due to the periodic passage of the shutter blade in front of the camera. Given the length of the shutter opening (∼0.06 s), this corresponds to five flux estimates per segment in the interrupted image. The value of σPSF used in the fit was estimated from measuring stellar sources on images taken 10 min earlier. It was found to be 0.95 for the interrupted and 0.66 for the uninterrupted image. We attribute the difference to be due to slightly different seeing conditions at the two sites. The fit results for the uninterrupted and interrupted images are shown in the top and bottom rows of Fig. 12 respectively. The left panels show the best-fit flux parameters Ak while the middle panels show the reconstructed signal. The meteor light curve, in terms of both the instrumental magnitude (top) and the flux (bottom), are shown on the right panels. Despite the apparently good fit to the data, we note the moderate value of the goodness-of-fit coefficient R2 (middle panels). We attribute it to the model smoothing over the signal fluctuations at the higher values and due to the 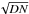 (data number) dependence of the noise. The right panels show the meteor light curves derived from the uninterrupted (continuous line) and interrupted (dashed line) frames. Here, the light curve from the interrupted image (bottom left panel) has been resampled to match the (lower) time resolution from the uninterrupted image. Again, good agreement is observed; the relative difference is ≲20% during the brightest part of the light curve (0.1 s <t< 0.5 s). Note that, even in the resampled light curve, the flux is estimated at two different times during a shutter opening. In this sense, each segment of the meteor in the interrupted image (Fig. 11, right panel) contributes two, rather than just one, flux estimates to the light curve (Fig. 12, right panels). In the case of the interrupted image, brightness values that correspond to the times when the meteor was behind the shutter are estimated by linear interpolation. They are included in the figure to facilitate the visual comparison of the light curves.
(data number) dependence of the noise. The right panels show the meteor light curves derived from the uninterrupted (continuous line) and interrupted (dashed line) frames. Here, the light curve from the interrupted image (bottom left panel) has been resampled to match the (lower) time resolution from the uninterrupted image. Again, good agreement is observed; the relative difference is ≲20% during the brightest part of the light curve (0.1 s <t< 0.5 s). Note that, even in the resampled light curve, the flux is estimated at two different times during a shutter opening. In this sense, each segment of the meteor in the interrupted image (Fig. 11, right panel) contributes two, rather than just one, flux estimates to the light curve (Fig. 12, right panels). In the case of the interrupted image, brightness values that correspond to the times when the meteor was behind the shutter are estimated by linear interpolation. They are included in the figure to facilitate the visual comparison of the light curves.
4. Conclusions and future work
We have described a method for extracting the time history of a meteor’s flux from images given independent knowledge of its motion in space. It is different from methods previously applied to the extraction of photometric information from meteor images in that it utilises an explicit time-domain deconvolution of the signal. This deconvolution may be applied directly on the 2D image and with a PSF that is either Gaussian, as assumed here, or of a different functional form e.g. if the source is faint (Howell 2006). The algorithm was first applied to synthetic meteor images where it accurately reproduced the pixel-by-pixel synthetic signal as well as the a priori meteor brightness. Then, it was applied to all-sky CCD observations of one single-station and one double-station meteor obtained with the SPOSH system (Oberst et al. 2011). The flux profiles retrieved from both the interrupted and uninterrupted images of the double-station meteor closely agree.
The algorithm is currently being integrated into a data reduction pipeline intended for processing the large volume of available SPOSH data. An important outcome of this exercise will be a more complete characterisation of the performance of the algorithm and its software implementation. In addition, it will be instructive to compare the algorithm with other photometric extraction methods currently in use by the community to gain insight on their relative merits and limitations.
Beyond the specific application to the SPOSH data, we have shown that our algorithm can improve the effective time resolution of CCD or video meteor light curves to benefit studies of rapidly-varying phenomena in general. For example, it may be of use in the precise velocity determination for bright meteors (Shrbený & Spurný 2013). As the time resolution achieved by this new technique depends on the available amount of signal, the use of high-sensitivity detectors is advisable. Finally, ensemble properties of meteor showers (e.g. the population index) from single-station observations may be determined by assuming that the meteors’ spatial velocity vector is the same as that of the shower. These and other potential applications of the method to the analysis of meteor images will be investigated in future work.
Acknowledgments
J. Oberst greatly acknowledges being hosted by MIIGAiK and supported by Russian Science Foundation, project # 14-22-00197. Astronomical Research at the Armagh Observatory is funded by the Northern Ireland Department of Culture, Arts and Leisure.
References
- Atreya, P.,Vaubaillon, J.,Colas, F., &Gaillard, B. 2012, MNRAS, 423, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Bettonvil, F. 2011, in Proc. Meteoroids 2010 Conf., eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, NASA CP 2011-216469, 363 [Google Scholar]
- Brown, P.,Weryk, R. J.,Kohut, S.,Edwards, W. N., &Krzeminski, Z. 2010, WGN, J. Int. Meteor Org., 38, 25 [NASA ADS] [Google Scholar]
- Campbell, M., Hawkes, R., & Babcock, D. 1999, in Proc. Meteoroids 1998 Conf., eds. W. J. Baggaley, & V. V. Porubcan (Astronomical Institute of the Slovak Academy of Sciences), 363 [Google Scholar]
- Campbell-Brown, M. D. 2005, Earth Moon Planets, 95, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell-Burns, P., &Kacerek, R. 2014, WGN, J. Int. Meteor Org., 42, 139 [NASA ADS] [Google Scholar]
- Ceplecha, Z. 1987, Bull. Astron. Inst. Czech., 38, 222 [Google Scholar]
- Gural, P. 2011, in Proc. Int. Meteor Conf. 2010 (International Meteor Organisation), 28 [Google Scholar]
- Hawkes, R. L. 1990, WGN, J. Int. Meteor Org., 18, 145 [NASA ADS] [Google Scholar]
- Hawkes, R. L., Mason, K. I., Fleming, D. E. B., & Stultz, C. T. 1993, in Proc. Int. Meteor Conf. 1992, eds. D. Ocenas, & P. Zimnikoval (International Meteor Organisation), 28 [Google Scholar]
- Hawkes, R. L.,Bussey, J. E.,MacPhee, S. L.,Pollock, C. S., &Taggart, L. W. 2001, in Proc. Meteoroids 2001 Conf., ed. B. Warmbein, ESA SP, 495, 281 [NASA ADS] [Google Scholar]
- Howell, S. B. 2006, Handbook of CCD astronomy, Second Edition, Cambridge Observing Handbooks for Research Astronomers (Cambridge University Press) [Google Scholar]
- Koschny, D., Gritsevich, M., & Barentsen, G. 2011, in Proc. Meteoroids 2010 Conf., eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, NASA CP 2011-216469, 156 [Google Scholar]
- Koten, P. 1999, in Proc. Meteoroids 1998 Conf., eds. W. J. Baggaley & V. V. Porubcan (Astronomical Institute of the Slovak Academy of Sciences), 149 [Google Scholar]
- Madiedo, J. M., Trigo-Rodriguez, J. M., & Lyytinen, E. 2011, in Proc. Meteoroids 2010 Conf., eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, NASA CP 2011-216469, 330 [Google Scholar]
- Molau, S. 2001, in Proc. Meteoroids Conf., ed. B. Warmbein, 495, ESA SP, 315 [Google Scholar]
- Molau, S., &Gural, P. S. 2005, WGN, J. Int. Meteor Org., 33, 15 [NASA ADS] [Google Scholar]
- Molau, S.,Nitschke, M., de Lignie, M.,Hawkes, R. L., &Rendtel, J. 1997, WGN, J. Int. Meteor Org., 25, 15 [NASA ADS] [Google Scholar]
- Oberst, J.,Flohrer, J.,Elgner, S., et al. 2011, Planet. Space Sci., 59, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Pecina, P., &Koten, P. 2009, A&A, 499, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, C. 2014, in Proc. Meteoroids 2013 Conf., eds. T. Jopek, F. J. M. Rietmejier, J. Watanabe, & I. P. Williams (A. M. University Press), 319 [Google Scholar]
- Shrbený, L., &Spurný, P. 2013, A&A, 550, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- SonotaCo 2009, WGN, J. Int. Meteor Org., 37, 55 [Google Scholar]
- Spurný, P., &Shrbený, L. 2008, Earth Moon Planets, 102, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Spurný, P., Borovička, J., & Shrbený, L. 2007, in Proc. IAU Symp. 236, eds. G. B. Valsecchi, D. Vokrouhlický, & A. Milani, 121 [Google Scholar]
- Stewart, W.,Pratt, A. R., &Entwistle, L. 2013, WGN, J. Int. Meteor Org., 41, 84 [NASA ADS] [Google Scholar]
- Towner, M. C., Bland, P. A., Cupak, M. C., et al. 2015, in Lunar Planet. Sci. Conf. XLVI, 1693 [Google Scholar]
- Trigo-Rodriguez, J. M.,Castro-Tirado, A. J., et al. 2005, Earth Moon Planets, 102, 553 [NASA ADS] [Google Scholar]
- Trigo-Rodriguez, J. M.,Madiedo, J. M., et al. 2007, WGN, J. Int. Meteor Org., 35, 13 [Google Scholar]
- Weryk, R. J.,Brown, P. G.,Domokos, A., et al. 2008, Earth Moon Planets, 102, 241 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Appendix: Linear least-squares estimators and their statistical properties
In matrix form, the problem may be formulated as 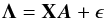 (A.1)where X is the m × n design matrix, Λ the m-fold measurement vector and A the n-fold vector containing the parameters we wish to estimate. The m-fold vector ϵ contains the measurement errors which are assumed Gaussian with a zero mean and a (diagonal) m × m covariance of
(A.1)where X is the m × n design matrix, Λ the m-fold measurement vector and A the n-fold vector containing the parameters we wish to estimate. The m-fold vector ϵ contains the measurement errors which are assumed Gaussian with a zero mean and a (diagonal) m × m covariance of 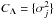 , j = 1,...,m.
, j = 1,...,m.
The least-squares estimate of A, obtained by minimising ϵ′ϵ, is given by 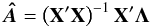 (A.2)where the prime “ ′ ” denotes the transpose of a matrix. The residuals are calculated as
(A.2)where the prime “ ′ ” denotes the transpose of a matrix. The residuals are calculated as 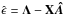 . A quantity used to determine the goodness of fit is the so-called coefficient of determination
. A quantity used to determine the goodness of fit is the so-called coefficient of determination 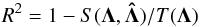 (A.3)where S is the residual sum of squares
(A.3)where S is the residual sum of squares 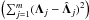 and T the total sum of squares
and T the total sum of squares 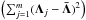 , the bar “ ” indicating the mean value and
, the bar “ ” indicating the mean value and 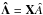 . Values close to 1 indicate a “good” fit − the observations can be predicted by the model − while values close to zero suggest that the particular model cannot provide information on the parameters given the measurements.
. Values close to 1 indicate a “good” fit − the observations can be predicted by the model − while values close to zero suggest that the particular model cannot provide information on the parameters given the measurements.
The covariance matrix CÂ of the parameter estimates is given by 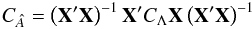 (A.4)while for the covariance of the measurement estimates
(A.4)while for the covariance of the measurement estimates 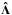 we have
we have 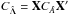 . If the measurements are uncorrelated − in other words, the off-diagonal elements of CΛ are zero − and
. If the measurements are uncorrelated − in other words, the off-diagonal elements of CΛ are zero − and 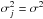 for all j then CÂ = (X′X)-1σ2 and the quantity S/(m − n) is an unbiased estimator of σ2.
for all j then CÂ = (X′X)-1σ2 and the quantity S/(m − n) is an unbiased estimator of σ2.
All Figures
 |
Fig. 1 Geometric representation of the flux variation within an image pixel over time due to meteor motion. See main text for notation. The concentric ellipses around the meteor position represent loci of constant flux. |
| In the text | |
 |
Fig. 2 Left panel: synthetic image of a moving source of increasing flux. The red dots denote the pixel locations of the measurements. Middle panel: the initial choice for the source flux over time (black squares) and the estimates from the least-squares fit (red squares). Right panel: the synthetic signal along the central pixel row of the meteor (black curve) and the reconstructed values from the Ak estimates (red diamonds). The value of the goodness-of-fit quantity is indicated in the upper left while the grey error bars represent 1σ formal uncertainties. |
| In the text | |
 |
Fig. 3 As Fig. 2 but for a moving source peaking in flux at the middle of the trajectory. |
| In the text | |
 |
Fig. 4 Results of fitting the model on the synthetic meteor in Fig. 2 using only the row of pixel measurements along the meteor trajectory (top) and an additional ten rows on either side (bottom). Left: synthetic measurements (black line) and their model estimates (red diamonds). Right: flux estimates (red squares) plotted against a priori values (black squares). |
| In the text | |
 |
Fig. 5 Fits to the image row segment of 110 pixels along the synthetic meteor in Fig. 2 for the model that evaluates formally the integrals in Eq. (A.5)(top) and for the approximation using function-time products (bottom). The flux of the meteor point source was sampled with n = 8 (left), n = 4 (middle) and n = 2 (right). Notation in this and the following figure is as in Fig. 4. |
| In the text | |
 |
Fig. 6 As Fig. 5 but for the time evolution of the flux. |
| In the text | |
 |
Fig. 7 Model fit for the double-flaring synthetic meteor described in the text. The chosen time resolution (i.e. value of n) increases from left to right. Top: synthetic meteor images showing the locations, along the meteor path, corresponding to the times tk when the flux is estimated. Middle: best-fit flux profile (red curve) compared to the a priori profile (black curve) used to calculate the signal. Bottom: model fit (red curve) to the synthetic signal (black curve). |
| In the text | |
 |
Fig. 8 Illustration of the dependence of the flux estimation process on the assumed velocity: 20 (left panels), 30 (middle panels) and 40 pixels s-1 (right panels). Notation is as in Fig. 4. |
| In the text | |
 |
Fig. 9 SPOSH image crops of double-station meteor used in Sect. 3.2. Meteor motion is from top right to bottom left. Left: uninterrupted image. The bright area immediately to the left of the meteor corresponds to a portion of the Milky Way. Right: image interrupted by the rotating shutter. |
| In the text | |
 |
Fig. 10 Analysis results of meteor shown in Fig. 9. Top left: difference image (see text) showing the measurements (red line bracketed by the two red diamonds) used to run the model on. Top right: model fit (red diamonds) to the measurements (black line). Bottom left: difference image indicating the positions (or, equivalently, the times) along the meteor trajectory when the flux was estimated. Bottom right: estimated flux as a function of time, from the moment the meteor reached the beginning of the measurement vector. |
| In the text | |
 |
Fig. 11 Crops of SPOSH images of a meteor observed from Mainalon (left) and Parnon (right) at 21:34:17 UT. |
| In the text | |
 |
Fig. 12 Analysis results of meteor shown in Fig 11. Top left: estimated flux over time for the uninterrupted image. Top middle: meteor signal (continuous line) along the measurement vector compared to the signal estimates from the fit (red diamonds). Top right: comparison of instrumental magnitude estimates from the uninterrupted (continuous line) and interrupted (dashed line) images. Bottom left: as top left panel, but for the interrupted image. Bottom middle: as top middle panel, but for the interrupted image. Bottom right: as top right panel, but for the flux. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


