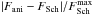| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525928 | |
| Published online | 24 September 2015 | |
Secular diffusion in discrete self-gravitating tepid discs
I. Analytic solution in the tightly wound limit⋆
1 Institut d’Astrophysique de Paris and UPMC, CNRS (UMR 7095), 98bis boulevard Arago, 75014 Paris, France
e-mail: fouvry@iap.fr; pichon@iap.fr
2 Institute of Astronomy & KICC, University of Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
3 Laboratoire de Physique Théorique (IRSAMC), CNRS and UPS, Univ. de Toulouse, 31062 Toulouse, France
e-mail: chavanis@irsamc.ups-tlse.fr
Received: 19 February 2015
Accepted: 2 May 2015
The secular evolution of an infinitely thin tepid isolated galactic disc made of a finite number of particles is described using the inhomogeneous Balescu-Lenard equation. Assuming that only tightly wound transient spirals are present in the disc, a WKB approximation provides a simple and tractable quadrature for the corresponding drift and diffusion coefficients. It provides insight into the physical processes at work during the secular diffusion of a self-gravitating discrete disc and makes quantitative predictions on the initial variations of the distribution function in action space. When applied to the secular evolution of an isolated stationary self-gravitating Mestel disc, this formalism predicts the initial importance of the corotation resonance in the inner regions of the disc leading to a regime involving radial migration and heating. It predicts in particular the formation of a ridge-like feature in action space, in agreement with simulations, but over-estimates the timescale involved in its appearance. Swing amplification is likely needed to resolve this discrepancy. In astrophysics, the inhomogeneous Balescu-Lenard equation and its WKB limit may also describe the secular diffusion of giant molecular clouds in galactic discs, the secular migration and segregation of planetesimals in proto-planetary discs, or even the long-term evolution of population of stars within the Galactic centre.
Key words: galaxies: evolution / galaxies: kinematics and dynamics / galaxies: spiral / diffusion / gravitation
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Understanding the dynamical evolution of galactic discs over cosmic times is a long-standing endeavour. Self-gravitating discs are cold dynamical systems, for which rotation represents an important reservoir of free energy. Fluctuations in the potential induced by discrete (possibly distant) encounters may be strongly amplified, while resonances tend to confine and localise their dissipation: such small stimuli can lead to the spontaneous evolution of discs to distinct equilibria. Quantifying the relative importance of this intrinsically driven evolution with respect to that driven by the environment is of renewed interest now that their cosmological environment is firmly established in the context of the ΛCDM paradigm. The effect of intrinsic susceptibility on secular timescales can be addressed in the context of kinetic theory, which takes explicitly into account such interactions.
The kinetic theory of stellar systems is an old, yet fundamental, topic in astrophysics1. It was initiated by Jeans (1929) and Chandrasekhar (1942) in the context of 3D stellar systems such as elliptical galaxies and globular clusters. The kinetic theory of Coulombian plasmas was developed in parallel by Landau (1936) and Vlasov (1938). When encounters between the particles (stars or electric charges) are neglected, one gets a purely mean field equation (Jeans 1915; Vlasov 1938) called the collisionless Boltzmann equation, or the Vlasov equation. When encounters are taken into account, one gets a kinetic equation that includes a collision term. In early works, the collision term was obtained by assuming that a particle experiences a succession of independent two-body encounters with the other particles. The corresponding kinetic equation can be derived either from the Boltzmann equation by considering a limit of weak deflections (Landau 1936), or directly from the general form of the Fokker-Planck equation by evaluating the diffusion and drift coefficients in a binary collisions approximation (Chandrasekhar 1949; Rosenbluth et al. 1957). In the case of neutral plasmas, the system is spatially homogeneous, so the distribution function depends only on the velocity, hence the name kinetic theory. By contrast, stellar systems are spatially inhomogeneous, so the distribution function depends on position and velocity. In early works on stellar dynamics, spatial inhomogeneity was taken into account in the advection term (Vlasov), but the collisional term was calculated by making a local approximation as if the system were homogeneous. In 3D, the collisional term displays a logarithmic divergence at large scales (Jeans 1929; Landau 1936; Chandrasekhar 1942). In the case of plasmas, this divergence is due to the neglect of collective effects that are responsible for Debye shielding. Landau (1936) phenomenologically introduced a cut-off at the Debye length to regularize the divergence.
Later on, Balescu (1960) and Lenard (1960) developed a rigorous kinetic theory of plasmas, taking collective effects into account, and obtained a kinetic equation, the so-called Balescu-Lenard equation, that does not present any divergence at large scales. The Debye shielding is taken naturally into account in their treatment through the dielectric function (which is absent from the Landau equation). In the case of stellar systems, the divergence at large scales is solved by the spatial inhomogeneity of the system and its finite extent. One can phenomenologically introduce a cut-off at the Jeans scale (Weinberg 1993), i.e. at the system’s size, which would correspond to the analogue of the Debye length in plasma physics, but this ad hoc treatment is not fully satisfactory. Furthermore, it cannot be applied to cold (centrifugally supported) stellar discs where spatial inhomogeneity is more crucial than in 3D.
A more fruitful procedure is to write the kinetic equation with angle-action variables that are the appropriate variables to describe spatially inhomogeneous multi-periodic systems. When collective effects are neglected, one obtains the inhomogeneous Landau equation (Chavanis 2007, 2013b). When collective effects are accounted for, one gets the inhomogeneous Balescu-Lenard equation (Heyvaerts 2010; Chavanis 2012a). The collision term in these equations describes the effect of (possibly distant) encounters between stars. For self-gravitating systems, where the interaction is attractive (instead of being repulsive as in Coulombian plasmas), collective effects are responsible for an anti-shielding which tends to increase the effective mass of the stars, hence reducing the relaxation time. The Balescu-Lenard equation is valid at the order 1 /N in an expansion of the dynamics in terms of this small parameter, where N ≫ 1 is the number of stars. Therefore, it takes finite-N effects (encounters between stars) into account and describes the evolution of the system on a timescale of the order NtD, where tD is the dynamical time. For times t ≪ NtD, or for N → + ∞, it reduces to the Vlasov equation which ignores encounters between stars. Although the kinetic theory was initially developed for 3D stellar systems, the final form of the inhomogeneous Balescu-Lenard equation also applies to stellar discs such as those considered in this paper.
The Balescu-Lenard non-linear equation accounts for self-driven orbital secular diffusion of a self-gravitating system induced by the intrinsic shot noise due to its discreteness and the corresponding long range correlations. Even though this kinetic equation was first written down more than fifty years ago, it has hardly ever been applied in its prime context, but only in various limits where it reduces to simpler kinetic equations, as discussed above.
In this paper, we will focus on solving explicitly such an equation describing the self-gravitating response of a tepid thin disc to its own stochastic fluctuating potential induced by its finite number of components. In this cool regime, the self-gravity of the disc can be tracked via a local WKB-like response, which in turn allows us to simplify the a priori 2D formalism to an effective (non-degenerate) 1D formalism. We will compare the prediction of the WKB limit to a numerical experiment presented in the literature, and discuss its diagnosis power and possible limitations.
The paper is organised as follows. Section 2 briefly presents the content of the inhomogeneous Balescu-Lenard equation. Section 3 focuses on razor thin axisymmetric galactic discs within the WKB approximation. Section 4 investigates the formation of a narrow resonant ridge in an isolated self-gravitating Mestel disc. Finally, Sect. 5 wraps up. Appendix A provides a short sketch of the derivation of the Balescu-Lenard equation. Appendix B considers the inhomogeneous Balescu-Lenard equation without collective effects. Appendix D compares it to other similar kinetic equations, and in particular its Fokker-Planck limit.
2. The inhomogeneous Balescu-Lenard equation
We consider a system made of N particles. We suppose that the gravitational background, associated with the Hamiltonian H0, is stationary and integrable, so that we may always remap the physical phase-space coordinates (x,v) to the angle-action coordinates (θ,J) (Goldstein 1950; Born 1960; Binney & Tremaine 2008). We also introduce the intrisinc frequencies of the system Ω defined as 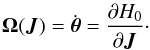 (1)Along the unperturbed trajectories, the angles θ are 2π-periodic evolving with the frequency Ω, whereas the actions J are conserved. To describe the long-term evolution of such a system, one assumes that there are two decoupled timescales: a short dynamical timescale and a secular timescale of collisional evolution. We assume that the system is always in a virialized stable state (i.e. is a stable stationary solution of the Vlasov equation), so that the distribution function can be written as a quasi-stationary distribution F = F(J,t), which satisfies the normalization constraint
(1)Along the unperturbed trajectories, the angles θ are 2π-periodic evolving with the frequency Ω, whereas the actions J are conserved. To describe the long-term evolution of such a system, one assumes that there are two decoupled timescales: a short dynamical timescale and a secular timescale of collisional evolution. We assume that the system is always in a virialized stable state (i.e. is a stable stationary solution of the Vlasov equation), so that the distribution function can be written as a quasi-stationary distribution F = F(J,t), which satisfies the normalization constraint 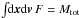 , where Mtot is the total mass of the system. This is a function of the actions only that slowly evolves in time due to stellar encounters (finite-N effects)2. From Heyvaerts (2010) and Chavanis (2012a; see also Appendix A for a short sketch of the derivation), the secular evolution, induced by collisional finite-N effects, of such a quasi-stationary distribution function F(J,t) is given by the inhomogeneous Balescu-Lenard equation which reads
, where Mtot is the total mass of the system. This is a function of the actions only that slowly evolves in time due to stellar encounters (finite-N effects)2. From Heyvaerts (2010) and Chavanis (2012a; see also Appendix A for a short sketch of the derivation), the secular evolution, induced by collisional finite-N effects, of such a quasi-stationary distribution function F(J,t) is given by the inhomogeneous Balescu-Lenard equation which reads ![\begin{eqnarray} \frac{\partial F}{\partial t} &=& \pi (2 \pi)^{d} \mu \frac{\partial }{\partial {\vec J}_{1}} \cdot \Bigg[ \! \sum_{{\vec m}_{1}, {\vec m}_{2}} \! \!{\vec m}_{1} \!\! \int \!\! \mathrm{d} {\vec J}_{2} \, \frac{ \delta_{\rm D} ({\vec m}_{1} \cdot {\vec \Omega}_{1} - {\vec m}_{2} \cdot {\vec \Omega}_{2})}{| \mathcal{D}_{{\vec m}_{1} , {\vec m}_{2}} ({\vec J}_{1} , {\vec J}_{2} , {\vec m}_{1} \cdot {\vec \Omega}_{1}) |^{2}} \nonumber \\ \hskip -0.25cm && \times \left( {\vec m}_{1} \cdot \frac{\partial }{\partial {\vec J}_{1}} - {\vec m}_{2} \cdot \frac{\partial }{\partial {\vec J}_{2}} \right) F ({\vec J}_{1} , t) \, F ({\vec J}_{2} , t) \Bigg] , \label{initial_BL} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq21.png) (2)where d is the dimension of the physical space, μ = Mtot/N is the mass of the individual particles, and where we used the shortened notation Ωi = Ω(Ji). The r.h.s. of Eq. (2)is the Balescu-Lenard operator which encompasses the secular diffusion due to collisional effects, see Fig. 1. Because it is the divergence of a flux, this writing ensures that the total number of stars is exactly conserved during the secular diffusion. The Dirac delta δD(m1·Ω1 − m2·Ω2) is the sharp resonance condition. One must remark that this condition allows us to describe non-trivial gravitational interactions. Indeed, it can cause non-local resonances by coupling different regions of action-space J1 and J2.
(2)where d is the dimension of the physical space, μ = Mtot/N is the mass of the individual particles, and where we used the shortened notation Ωi = Ω(Ji). The r.h.s. of Eq. (2)is the Balescu-Lenard operator which encompasses the secular diffusion due to collisional effects, see Fig. 1. Because it is the divergence of a flux, this writing ensures that the total number of stars is exactly conserved during the secular diffusion. The Dirac delta δD(m1·Ω1 − m2·Ω2) is the sharp resonance condition. One must remark that this condition allows us to describe non-trivial gravitational interactions. Indeed, it can cause non-local resonances by coupling different regions of action-space J1 and J2.
 |
Fig. 1 Top: a) a set of two resonant orbits in the inertial frame; b) in the rotating frame in which they are resonant – here through ILR-COR coupling. Bottom: c) fluctuations in the distribution function in action-space caused by finite-N effects showing overdensities for the blue and red orbits. The dashed lines correspond to 3 contour levels of the intrinsic frequency ω = m·Ω respectively associated with the resonance vector m1 (gray lines) and m2 (black lines). The two sets of orbits satisfy the resonant condition m1·Ω1 = m2·Ω2, and therefore lead to a secular diffusion of the orbital structure of the disc according to Eq. (2). One should emphasize that the resonant orbits need not be caught in the same resonance (m1 ≠ m2), be close in position space, nor in action space. |
Even for local resonances (i.e. J1 = J2), it can allow for non-trivial coupling of oscillations, as soon as m1 and m2 have non-zero components. The coefficients 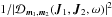 represent the dressed susceptibilities of the system, for which collective effects have been taken into account3. To deal with the resolution of the non-local Poisson equation, following Kalnajs’ matrix method (Kalnajs 1976), one has to introduce a complete biorthonormal basis of potentials and densities ψ(p)(x) and ρ(p)(x) such that
represent the dressed susceptibilities of the system, for which collective effects have been taken into account3. To deal with the resolution of the non-local Poisson equation, following Kalnajs’ matrix method (Kalnajs 1976), one has to introduce a complete biorthonormal basis of potentials and densities ψ(p)(x) and ρ(p)(x) such that ![\begin{eqnarray} \Delta \psi^{(p)} \!= 4 \pi G \rho^{(p)} , \quad \int \!\! \mathrm{d} {\vec x} \, [ \psi^{(p)} ({\vec x}) ]^{*} \, \rho^{(q)} ({\vec x}) = - \, \delta_{p}^{q} . \label{definition_basis} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq37.png) (3)Thanks to this basis, the susceptibility coefficients are given by
(3)Thanks to this basis, the susceptibility coefficients are given by ![\begin{eqnarray} \frac{1}{\mathcal{D}_{{\vec m}_{1}, {\vec m}_{2}} ({\vec J}_{1} , {\vec J}_{2} , \omega)} = \sum_{p , q} \psi_{{\vec m}_{1}}^{(p)} \!({\vec J}_{1}) \, \left[ \mathbf{I} - \widehat{\mathbf{M}} (\omega) \right]^{-1}_{p q} \, \left[ \psi_{{\vec m}_{2}}^{(q)} \!({\vec J}_{2}) \right]^{*}, \label{definition_1/D} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq38.png) (4)where I is the identity matrix and
(4)where I is the identity matrix and  is the response matrix given by
is the response matrix given by ![\begin{eqnarray} \widehat{\mathbf{M}}_{pq} (\omega) = (2 \pi)^{d} \! \sum_{{\vec m}} \!\! \int \!\! \mathrm{d} {\vec J} \, \frac{{\vec m} \cdot \partial F / \partial {\vec J} }{\omega - {\vec m} \cdot {\vec \Omega}} \left[\psi_{{\vec m}}^{(p)} \!({\vec J})\right]^{*} \psi_{{\vec m}}^{(q)} \!({\vec J}) . \label{Fourier_M} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq41.png) (5)In this expression,
(5)In this expression, 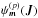 corresponds to the Fourier transform in angles of the basis elements ψ(p)(x), where we used the convention that the Fourier transform of a function X(θ,J) is given by
corresponds to the Fourier transform in angles of the basis elements ψ(p)(x), where we used the convention that the Fourier transform of a function X(θ,J) is given by ![\begin{eqnarray} \begin{cases} \displaystyle X ({\vec \theta} , {\vec J}) = \sum_{{\vec m} \,\in\, \mathbb{Z}^{d}} X_{{\vec m}} ({\vec J}) \, {\rm e}^{{\rm i} {\vec m} \cdot {\vec \theta}},\\[5mm] \displaystyle {X}_{\vec m} ({\vec J}) = \frac{1}{(2 \pi)^{d}} \, \int \, \mathrm{d} {\vec \theta} \, X ({\vec \theta} , {\vec J}) \, {\rm e}^{- {\rm i} {\vec m} \cdot {\vec \theta}} . \end{cases} \label{definition_Fourier_angles} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq44.png) (6)One should note that Eq. (2)is therefore a non-linear function of F, both explicitly via the products of F on the r.h.s., describing the effects of the binary collisions (as in the Boltzmann or Landau equations), but also implicitly via Eq. (5), which encompasses the collective effects and is specific to the Balescu-Lenard equation. We also importantly note that – in contrast to its counterpart in plasma physics – Eq. (2)does not assume that local encounters drive secular evolution; resonant interactions of correlated possibly distant dressed orbits are sourcing long term orbital distortions.
(6)One should note that Eq. (2)is therefore a non-linear function of F, both explicitly via the products of F on the r.h.s., describing the effects of the binary collisions (as in the Boltzmann or Landau equations), but also implicitly via Eq. (5), which encompasses the collective effects and is specific to the Balescu-Lenard equation. We also importantly note that – in contrast to its counterpart in plasma physics – Eq. (2)does not assume that local encounters drive secular evolution; resonant interactions of correlated possibly distant dressed orbits are sourcing long term orbital distortions.
2.1. Content of the diffusion equation
One may also rewrite the Balescu-Lenard Eq. (2)as an anisotropic Fokker-Planck equation introducing the associated drift and diffusion coefficients. It then reads ![\begin{eqnarray} \frac{\partial F}{\partial t} = \sum_{{\vec m}_{1}} \frac{\partial }{\partial {\vec J}_{1}} \cdot \left[ {\vec m}_{1} \left( A_{{\vec m}_{1}} ( {\vec J}_{1} ) \, F ( {\vec J}_{1} ) + D_{{\vec m}_{1}} ( {\vec J}_{1} ) \, {\vec m}_{1} \cdot \frac{\partial F}{\partial {\vec J}_{1}} \right) \right] , \label{initial_BL_rewrite} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq46.png) (7)where Am1(J1) and Dm1(J1) are respectively the anisotropic drift and diffusion coefficients associated with a given resonance m1, i.e. with a given Fourier mode m1 in angles. They both secularly depend on the distribution function F, but this dependence has not been explicitly written out to shorten the notations. The drift coefficients are given by
(7)where Am1(J1) and Dm1(J1) are respectively the anisotropic drift and diffusion coefficients associated with a given resonance m1, i.e. with a given Fourier mode m1 in angles. They both secularly depend on the distribution function F, but this dependence has not been explicitly written out to shorten the notations. The drift coefficients are given by 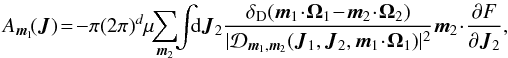 (8)while the diffusion coefficients are given by
(8)while the diffusion coefficients are given by 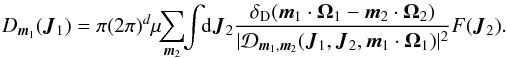 (9)The rewriting from Eq. (7)allows us to discuss some important properties of such anisotropic diffusion equation. We introduce the total flux, ℱtot, associated with this diffusion, which reads
(9)The rewriting from Eq. (7)allows us to discuss some important properties of such anisotropic diffusion equation. We introduce the total flux, ℱtot, associated with this diffusion, which reads 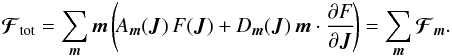 (10)As a consequence, the Balescu-Lenard diffusion equation given by the expressions (2)and (7)takes the shortened form
(10)As a consequence, the Balescu-Lenard diffusion equation given by the expressions (2)and (7)takes the shortened form 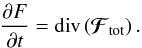 (11)We then define as M(t) the mass contained in a volume
(11)We then define as M(t) the mass contained in a volume 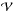 of the action-space at time t, so that we have
of the action-space at time t, so that we have 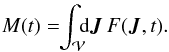 (12)Thanks to the divergence theorem, the variation of mass in
(12)Thanks to the divergence theorem, the variation of mass in 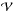 due to secular diffusion corresponds to the flux of particles through the boundary
due to secular diffusion corresponds to the flux of particles through the boundary 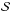 of this volume so that
of this volume so that ![\begin{eqnarray} \frac{\mathrm{d} M}{\mathrm{d} t} \!= \!\! \int_{\mathcal{S}} \!\! {\vec{\mathcal F}}_{\!\rm tot} \!\cdot \!\mathrm{d} {\vec S} \! = \! \sum_{{\vec m}} \!\! \int_{\mathcal{S}} \!\!\! \mathrm{d} S ({\vec m}\! \cdot \! {\vec n}) \left[\! A_{{\vec m}} (\!{\vec J}) F (\!{\vec J}) \!+\! D_{{\vec m}} (\!{\vec J}) \, \!{\vec m} \!\cdot \! \frac{\partial F}{\partial {\vec J}} \!\right]\! ,~~ \label{flux_through_S} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq59.png) (13)where n is the exterior pointing normal vector. One can note in Eq. (13)that the contribution from a given resonance m takes the form of a preferential diffusion in the direction m. This diffusion is therefore anisotropic because it is maximum for n ∝ m and equal to 0 for n·m = 0. To emphasize the anisotropy of the diffusion, one may use the formalism of the slow and fast actions (Lynden-Bell 1979; Earn & Lynden-Bell 1996). For simplicity, we consider the 2D case. For a given resonance m = (m1,m2), we consider the change of coordinates
(13)where n is the exterior pointing normal vector. One can note in Eq. (13)that the contribution from a given resonance m takes the form of a preferential diffusion in the direction m. This diffusion is therefore anisotropic because it is maximum for n ∝ m and equal to 0 for n·m = 0. To emphasize the anisotropy of the diffusion, one may use the formalism of the slow and fast actions (Lynden-Bell 1979; Earn & Lynden-Bell 1996). For simplicity, we consider the 2D case. For a given resonance m = (m1,m2), we consider the change of coordinates 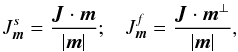 (14)where
(14)where 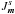 and
and 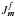 are respectively the slow and fast actions associated with the resonance m. Here m⊥ corresponds to the direction perpendicular to the resonance so that m⊥ = (m2, − m1), and
are respectively the slow and fast actions associated with the resonance m. Here m⊥ corresponds to the direction perpendicular to the resonance so that m⊥ = (m2, − m1), and 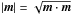 . Thanks to the chain rule, for any function X(J), one has
. Thanks to the chain rule, for any function X(J), one has 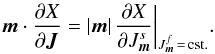 (15)Introducing the natural vector basis elements
(15)Introducing the natural vector basis elements 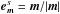 and
and 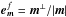 associated with this change of coordinates, the diffusion flux ℱm associated with a resonance m and defined in Eq. (10)takes the form
associated with this change of coordinates, the diffusion flux ℱm associated with a resonance m and defined in Eq. (10)takes the form ![\begin{eqnarray} {\vec{\mathcal F}}_{{\vec m}} (J_{{\vec m}}^{s} , J_{{\vec m}}^{f}) = |{\vec m}| \left[ A_{{\vec m}}({\vec J}) F ({\vec J}) \!+\! |{\vec m}| D_{{\vec m}} ({\vec J}) \frac{\partial F}{\partial J_{{\vec m}}^{s}} \right] {\vec e}_{{\vec m}}^{s} . \label{Flux_m_fast_slow} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq77.png) (16)Such a rewriting illustrates the fact that as soon as only one resonance m dominates the secular evolution, the diffusion flux will be aligned with this resonance. Hence one will observe a narrow mono-dimensional diffusion in the preferential
(16)Such a rewriting illustrates the fact that as soon as only one resonance m dominates the secular evolution, the diffusion flux will be aligned with this resonance. Hence one will observe a narrow mono-dimensional diffusion in the preferential 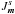 -direction. During this diffusion, particles will conserve their fast action
-direction. During this diffusion, particles will conserve their fast action 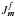 , which can therefore be seen as an adiabatic invariant, whereas their slow action
, which can therefore be seen as an adiabatic invariant, whereas their slow action 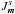 gets to change. This strong anistropy in the diffusion is an essential property of the Balescu-Lenard Eq. (7).
gets to change. This strong anistropy in the diffusion is an essential property of the Balescu-Lenard Eq. (7).
3. Thin tepid discs and their WKB limit
When implementing the inhomogeneous Balescu-Lenard equation, one encounters two main difficulties. The first one is the explicit construction of a mapping (x,v) → (θ,J) since the Balescu-Lenard drift and diffusion coefficients must be computed using angle-action coordinates. Assuming the disc to be tepid, one may rely on the epicylic approximation to construct such a mapping. The second difficulty arises from the non-locality of Poisson’s equation which requires us to introduce potential basis elements ψ(p) as in Eq. (3). One can then compute the response matrix from Eq. (5), which must subsequently be inverted. The following step is to compute the drift and diffusion coefficients from Eqs. (8)and (9)which requires us to explicitly deal with the resonance constraint m1·Ω1 − m2·Ω2 = 0. In the case of a 2D axisymmetric disc, one may implement a WKB approximation (Liouville 1837; Toomre 1964; Kalnajs 1965; Lin & Shu 1966; Palmer et al. 1989) which assumes that the diffusion of the system is made through tightly wound spirals. Such an assumption has two main consequences. First of all, Poisson’s equation becomes local, resulting in a diagonal response matrix. Moreover, it also entails that all the resonances becomes exactly local, allowing an explicit calculation of the resonant constraint δD(m1·Ω1 − m2·Ω2). We now detail these two elements: epicyclic approximation and WKB assumption.
3.1. Epicyclic approximation
For a sufficiently cold disc (i.e. a disc where the radial excursions of the stars are small), one can explicitly build up a mapping (x,v) → (θ,J) thanks to the epicyclic approximation. We introduce the polar coordinates (R,φ) to describe the infinitely thin galactic disc, and introduce their associated momenta (pR,pφ). As the disc at equilibrium is axisymmetric, the stationary Hamiltonian of the system reads ![\begin{eqnarray} H_{0} (R,\phi,p_{R},p_{\phi}) = \frac{1}{2} \!\left[ p_{R}^{2} \!+\! \frac{p_{\phi}^{2}}{ R^{2} }\right] \!+ \psi_{0}(R) , \label{definition_Hamiltonian_disc} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq87.png) (17)where ψ0 is the stationary background potential within the disc. Because ψ0 is axisymmetric, it does not depend on φ, so that pφ is a conserved quantity. We may then define the first action of the system, the angular momentum Jφ, as
(17)where ψ0 is the stationary background potential within the disc. Because ψ0 is axisymmetric, it does not depend on φ, so that pφ is a conserved quantity. We may then define the first action of the system, the angular momentum Jφ, as 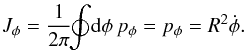 (18)For a given value of Jφ, the equation of evolution of R is then given by
(18)For a given value of Jφ, the equation of evolution of R is then given by 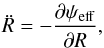 (19)where ψeff is an effective potential defined as
(19)where ψeff is an effective potential defined as 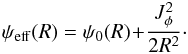 (20)The heart of the epicyclic approximation is to assume that small radial excursions can be approximated as harmonic librations. For a given value of Jφ, we implicitly introduce the guiding radius Rg as
(20)The heart of the epicyclic approximation is to assume that small radial excursions can be approximated as harmonic librations. For a given value of Jφ, we implicitly introduce the guiding radius Rg as 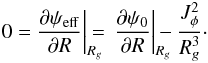 (21)Here Rg(Jφ) is the radius for which stars with an angular momentum of Jφ are on exactly circular orbits. It is important to note that the mapping between Rg and Jφ is bijective and unambiguous (up to the sign of Jφ). We may then define the two frequencies of evolution: Ωφ(Rg) the azimuthal frequency and κ(Rg) the epicyclic frequency as follows
(21)Here Rg(Jφ) is the radius for which stars with an angular momentum of Jφ are on exactly circular orbits. It is important to note that the mapping between Rg and Jφ is bijective and unambiguous (up to the sign of Jφ). We may then define the two frequencies of evolution: Ωφ(Rg) the azimuthal frequency and κ(Rg) the epicyclic frequency as follows 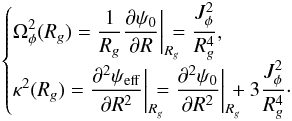 (22)As the radial oscillations are supposed to be small, one may perform a Taylor expansion at first order of the evolution Eq. (19)in the neighbourhood of the minimum R = Rg so that R satisfies the differential equation
(22)As the radial oscillations are supposed to be small, one may perform a Taylor expansion at first order of the evolution Eq. (19)in the neighbourhood of the minimum R = Rg so that R satisfies the differential equation 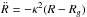 . Hence one can notice that in this limit the evolution of the radius of a star is the one of a harmonic oscillator centred on Rg. Up to an initial phase, one has therefore R(t) = Rg + Acos(κt), where A is the amplitude of the radial oscillations. The associated radial action Jr is then given by
. Hence one can notice that in this limit the evolution of the radius of a star is the one of a harmonic oscillator centred on Rg. Up to an initial phase, one has therefore R(t) = Rg + Acos(κt), where A is the amplitude of the radial oscillations. The associated radial action Jr is then given by 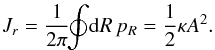 (23)For Jr = 0, the orbit is circular. Within the epicyclic approximation, the frequencies of motion along the action-torii, introduced in Eq. (1)are given by Ω(J) = (Ωφ(Jφ),κ(Jφ)). An important dynamical consequence of this approximation is that these two frequencies are only function of Jφ and do not depend on Jr, so that the resonance constraint m1·Ω1 − m2·Ω2 = 0 becomes simpler. Finally, one can explicitly construct the mapping between (R,φ,pR,pφ) and (θR,θφ,Jr,Jφ) (Lynden-Bell & Kalnajs 1972; Palmer 1994; Binney & Tremaine 2008), which takes at first order the form
(23)For Jr = 0, the orbit is circular. Within the epicyclic approximation, the frequencies of motion along the action-torii, introduced in Eq. (1)are given by Ω(J) = (Ωφ(Jφ),κ(Jφ)). An important dynamical consequence of this approximation is that these two frequencies are only function of Jφ and do not depend on Jr, so that the resonance constraint m1·Ω1 − m2·Ω2 = 0 becomes simpler. Finally, one can explicitly construct the mapping between (R,φ,pR,pφ) and (θR,θφ,Jr,Jφ) (Lynden-Bell & Kalnajs 1972; Palmer 1994; Binney & Tremaine 2008), which takes at first order the form 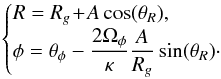 (24)Thanks to this mapping and the definitions of the actions from Eqs. (18)and (23), the epicyclic approximation allows us to build up an explicit mapping between the physical phase-space coordinates and the angle-action ones.
(24)Thanks to this mapping and the definitions of the actions from Eqs. (18)and (23), the epicyclic approximation allows us to build up an explicit mapping between the physical phase-space coordinates and the angle-action ones.
Finally, throughout our calculation, we will assume that the stationary distribution function of the disc is a Schwarzschild distribution function (or locally isothermal DF) given by ![\begin{eqnarray} F (R_{g} , J_{r}) = \frac{\Omega_{\phi} (R_{g}) \, \Sigma (R_{g})}{\pi \, \kappa (R_{g}) \, \sigma_{r}^{2} (R_{g})} \exp \!\left[\! - \frac{\kappa (R_{g}) \, J_{r}}{\sigma_{r}^{2} (R_{g})} \!\right] , \label{definition_DF_Schwarzschild} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq114.png) (25)where Σ(Rg) is the surface density of the disc and
(25)where Σ(Rg) is the surface density of the disc and 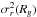 , which varies within the disc, represents the radial velocity dispersion of the stars at a given radius. Increasing values of
, which varies within the disc, represents the radial velocity dispersion of the stars at a given radius. Increasing values of 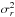 correspond to hotter discs that are therefore more stable.
correspond to hotter discs that are therefore more stable.
3.2. The WKB basis
As we are considering a 2D case, the potential basis elements ψ(p) introduced in Eq. (3)must be written as ψ(p)(R,φ) in the disc polar coordinates and must be orthonormal to the associated surface density Σ(p)(R,φ). Using a WKB approximation amounts to building up local basis elements thanks to which the response matrix will become diagonal.
3.2.1. Definition of the basis elements
We introduce the basis elements ![\begin{eqnarray} \psi^{[k_{\phi} , k_{r} , R_{0}]} (R , \phi) = \mathcal{A} \, {\rm e}^{{\rm i} (k_{\phi} \phi + k_{r} R)} \, \mathcal{B}_{R_{0}} (R), \label{definition_WKB_basis} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq120.png) (26)where the window function ℬR0(R) is defined as
(26)where the window function ℬR0(R) is defined as ![\begin{eqnarray} \mathcal{B}_{R_{0}} (R) = \frac{1}{(\pi \sigma^{2})^{1\!/\!4}} \, \exp \!\left[\! - \frac{(R - R_{0})^{2}}{2 \sigma^{2}} \!\right] \cdot \label{definition_window_B} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq122.png) (27)The basis elements are indexed by three numbers: kφ is an azimuthal number which parametrizes the angular component of the basis elements, R0 is the radius position in the disc around which the Gaussian window ℬR0 is centred, and kr is the radial frequency of the basis element. We also introduced an additional parameter σ of scale-separation, which will ensure the biorthogonality of the basis elements, as detailed later on. Finally,
(27)The basis elements are indexed by three numbers: kφ is an azimuthal number which parametrizes the angular component of the basis elements, R0 is the radius position in the disc around which the Gaussian window ℬR0 is centred, and kr is the radial frequency of the basis element. We also introduced an additional parameter σ of scale-separation, which will ensure the biorthogonality of the basis elements, as detailed later on. Finally, 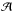 is an amplitude which will be tuned in order to normalize correctly the basis elements. Thanks to a somewhat unsual normalization of ℬR0, we will ensure that
is an amplitude which will be tuned in order to normalize correctly the basis elements. Thanks to a somewhat unsual normalization of ℬR0, we will ensure that 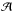 is independent of σ. Figure 2 illustrates the radial dependence of the basis elements.
is independent of σ. Figure 2 illustrates the radial dependence of the basis elements.
 |
Fig. 2 Two WKB basis elements. Each Gaussian is centred around a radius R0. The typical extension of the Gaussian is given by the decoupling scale σ, and they are modulated at the radial frequency kr. |
Figure 3 illustrates the shape of these basis elements in the polar (R,φ)-plane. The next steps will be to ensure that these WKB basis elements have all the properties required to allow for the computation of the dressed susceptibility coefficients introduced in Eq. (4). Therefore, we will successively compute the associated surface density elements Σ[ kφ,kr,R0 ], ensure the biorthogonality of the basis elements and their correct normalization, and finally compute the Fourier transform in angles of the basis elements.
 |
Fig. 3 Two WKB basis elements in the polar (R,φ)-plane. Each basis element is located around a central radius R0, on a region of size σ. The winding of the spirals is governed by the radial frequency kr. The number of azimuthal patterns is given by the index kφ, e.g. kφ = 1 for the interior dark gray element, whereas kφ = 2 for the exterior light gray one. |
3.2.2. Associated surface densities
In order to ensure the biorthogonality of the basis, we will first build up the surface densities associated with the potential elements introduced in Eq. (26). We extend the WKB potential in the z-direction using the Ansatz ![\begin{eqnarray} \psi^{[k_{\phi} , k_{r} , R_{0}]} (R , \phi ,z) = \mathcal{A} \, {\rm e}^{{\rm i} (k_{\phi} \phi + k_{r} R)} \mathcal{B}_{R_{0}} (R) \, Z (z) . \label{ansatz_WKB_potential} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq135.png) (28)Poisson’s equation in vacuum Δψ[ kφ,kr,R0 ] = 0 leads to
(28)Poisson’s equation in vacuum Δψ[ kφ,kr,R0 ] = 0 leads to ![\begin{eqnarray} \frac{Z''}{Z} &=& k_{r}^{2} \Bigg[ 1 - \frac{\rm i}{k_{r} R} + 2 {\rm i} \frac{R - R_{0}}{\sigma^{2}} \frac{1}{k_{r}} + \frac{R - R_{0}}{R} \frac{1}{(\sigma k_{r})^{2}} \nonumber\\ &&+ \frac{1}{(\sigma k_{r})^{2}} + \frac{k_{\phi}^{2}}{(k_{r} R)^{2}} - \Bigg[ \frac{R - R_{0}}{\sigma^{2}}\frac{1}{k_{r}} \Bigg]^{2} \Bigg] \cdot \label{Poisson_psi_vacuum} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq137.png) (29)We now explicitly introduce our WKB assumptions. We assume that the spirals are tightly wound so that
(29)We now explicitly introduce our WKB assumptions. We assume that the spirals are tightly wound so that 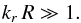 (30)Introducing the typical size of the system Rsys, we also additionally suppose that we have
(30)Introducing the typical size of the system Rsys, we also additionally suppose that we have 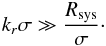 (31)Assuming that kφ is of the order of unity, Eq. (29)becomes
(31)Assuming that kφ is of the order of unity, Eq. (29)becomes 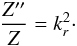 (32)Hence within the WKB limit, the extended potential from Eq. (28)takes the form
(32)Hence within the WKB limit, the extended potential from Eq. (28)takes the form ![\begin{eqnarray} \psi^{[k_{\phi} , k_{r} , R_{0}]} (R , \phi , z) = \psi^{[k_{\phi} , k_{r} , R_{0}]} (R , \phi) \, {\rm e}^{- |k_{r}| z}, \label{ansatz_WKB_potential_final} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq142.png) (33)where we ensured that for z → ± ∞ the potential tends to 0, therefore introducing a discontinuity for ∂ψ/∂z in z = 0. Thanks to Gauss theorem, the associated surface density satisfies
(33)where we ensured that for z → ± ∞ the potential tends to 0, therefore introducing a discontinuity for ∂ψ/∂z in z = 0. Thanks to Gauss theorem, the associated surface density satisfies ![\begin{eqnarray} \Sigma (R , \phi) = \frac{1}{4 \pi G} \left[\lim\limits_{z \to 0^{+}} \frac{\partial \psi}{\partial z} \, - \lim\limits_{z \to 0^{-}} \frac{\partial \psi}{\partial z} \right] , \label{Poisson_equation_2D} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq146.png) (34)so that we have
(34)so that we have ![\begin{eqnarray} \Sigma^{[k_{\phi} , k_{r} , R_{0}]} (R , \phi) = - \frac{|k_{r}|}{2 \pi G} \, \psi^{[k_{\phi} , k_{r} , R_{0}]} (R , \phi) . \label{WKB_surface_density} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq147.png) (35)
(35)
3.2.3. Biorthogonality condition and normalization
One must now ensure that the basis elements introduced in Eqs. (26)and (35)form a biorthogonal basis as assumed in Eq. (3). Indeed, it has to satisfy the property ![\begin{eqnarray} \delta_{k_{\phi}^{p}}^{k_{\phi}^{q}} \delta_{k_{r}^{p}}^{k_{r}^{q}} \delta_{R_{0}^{p}}^{R_{0}^{q}} = - \!\! \int \!\! \mathrm{d} R \, R \, \mathrm{d} \phi \, \!\left[\! \psi^{[k_{\phi}^{p} , k_{r}^{p} , R_{0}^{p}]} \!\right]^{*} \, \Sigma^{[k_{\phi}^{q} , k_{r}^{q} , R_{0}^{q}]} . \label{biorthogonality_condition} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq148.png) (36)The r.h.s. of this expression takes the form
(36)The r.h.s. of this expression takes the form ![\begin{eqnarray} \frac{|k_{r}^{q}|}{2 \pi G} && \mathcal{A}_{p} \mathcal{A}_{q} \frac{1}{\sqrt{\pi \sigma^{2}}} \!\! \int \!\! \mathrm{d} \phi \, {\rm e}^{{\rm i} (k_{\phi}^{p} - k_{\phi}^{q}) \phi}\nonumber \\ && \times \!\! \int \!\! \mathrm{d} R \, R \, {\rm e}^{{\rm i} (k_{r}^{p} - k_{r}^{q}) R} \exp \!\left[\! - \frac{(R - R_{0}^{p})^{2}}{2 \sigma^{2}} \!\right] \, \exp \!\left[\! - \frac{(R - R_{0}^{q})^{2}}{2 \sigma^{2}} \!\right] \cdot \label{calculation_biorthogonality_I} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq149.png) (37)The integration on φ is straightforward and is equal to
(37)The integration on φ is straightforward and is equal to 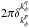 . In order to perform the integration on R, we have to introduce additional assumptions to ensure the biorthogonality of the basis. The peaks of the Gaussians in Eq. (37)can be considered as separated if
. In order to perform the integration on R, we have to introduce additional assumptions to ensure the biorthogonality of the basis. The peaks of the Gaussians in Eq. (37)can be considered as separated if 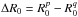 satisfies the condition
satisfies the condition 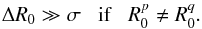 (38)Under this assumption4, the term from Eq. (37)can be assumed to be non-zero only for
(38)Under this assumption4, the term from Eq. (37)can be assumed to be non-zero only for 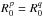 . The r.h.s. of Eq. (36)then takes the form
. The r.h.s. of Eq. (36)then takes the form ![\begin{eqnarray} \delta_{k_{\phi}^{p}}^{k_{\phi}^{q}} \delta_{R_{0}^{p}}^{R_{0}^{q}} \frac{|k_{r}^{q}|}{G} \mathcal{A}_{p} \mathcal{A}_{q} \frac{1}{\sqrt{\pi \sigma^{2}}} \!\! \int \!\! \mathrm{d} R \, R \, {\rm e}^{{\rm i} (k_{r}^{p} - k_{r}^{q}) R} \exp \!\left[\! - \frac{(R - R_{0}^{p})^{2}}{\sigma^{2}} \!\right] \cdot \label{calculation_biorthogonality_II} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq154.png) (39)The integration on R takes the form of a radial Fourier transform of a Gaussian of spread σ at the frequency
(39)The integration on R takes the form of a radial Fourier transform of a Gaussian of spread σ at the frequency 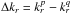 . It is therefore proportional to exp [ − (Δkr)2/ (4 /σ)2 ]. Hence we will suppose that the frequency spread Δkr satisfies
. It is therefore proportional to exp [ − (Δkr)2/ (4 /σ)2 ]. Hence we will suppose that the frequency spread Δkr satisfies 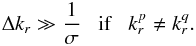 (40)Under this assumption, the term from Eq. (39)is non-zero only for
(40)Under this assumption, the term from Eq. (39)is non-zero only for 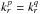 . In order to have a biorthogonal basis, one must therefore consider a spread σ, central radii R0, and radial frequencies kr such that
. In order to have a biorthogonal basis, one must therefore consider a spread σ, central radii R0, and radial frequencies kr such that 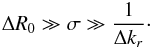 (41)With these constraints, one must necessarily have
(41)With these constraints, one must necessarily have 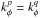 ,
, 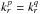 and
and 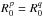 in order to have a non-negligible term in Eq. (36). It then only remains to explicitly estimate the amplitude
in order to have a non-negligible term in Eq. (36). It then only remains to explicitly estimate the amplitude 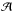 of the basis elements. Equation (36)gives
of the basis elements. Equation (36)gives ![\begin{eqnarray} \mathcal{A}^{2} \frac{|k_{r}|}{G} \frac{1}{\sqrt{\pi \sigma^{2}}} \!\! \int \!\! \mathrm{d} R \, R \, \exp \!\left[\! - \frac{(R - R_{0})^{2}}{\sigma^{2}} \!\right] = 1 . \label{calculation_normalization} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq163.png) (42)Thanks to the WKB assumption from Eq. (41), the integration can be straightforwardly computed and leads to
(42)Thanks to the WKB assumption from Eq. (41), the integration can be straightforwardly computed and leads to 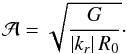 (43)
(43)
3.2.4. Fourier transform in angles
In order to estimate the susceptibility coefficients and the response matrix from Eqs. (4)and (5), one has to be able to calculate 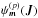 for the WKB basis elements. Thanks to the explicit mapping from Eq. (24), we have to compute
for the WKB basis elements. Thanks to the explicit mapping from Eq. (24), we have to compute ![\begin{eqnarray} \psi_{{\vec m}}^{[k_{\phi} , k_{r} , R_{0}]} ({\vec J}) = \frac{\mathcal{A} \, {\rm e}^{{\rm i} k_{r} R_{g}}}{(2 \pi)^{2}} \!\! \int \!\! \mathrm{d} \theta_{\phi} \!\! \int \!\! \mathrm{d} \theta_{R} \, {\rm e}^{- {\rm i} m_{\phi} \theta_{\phi}} {\rm e}^{- {\rm i} m_{r} \theta_{R}} {\rm e}^{{\rm i} k_{\phi} \theta_{\phi}} \nonumber\\ \times\,\, {\rm e}^{{\rm i} [ k_{r} A \cos (\theta_{R}) - k_{\phi} \!\frac{2 \Omega_{\phi}}{\kappa} \frac{A}{R_{g}} \sin (\theta_{R}) ] } \mathcal{B}_{R_{0}} \!(R_{g} \!+\! A \cos (\theta_{R})) . \label{calculation_psi_m} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq165.png) (44)The integration on θφ is straighforward and equal to
(44)The integration on θφ is straighforward and equal to 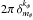 . Regarding the dependence on θR in the complex exponential, we may write
. Regarding the dependence on θR in the complex exponential, we may write 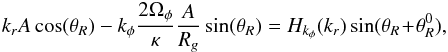 (45)where the amplitude Hkφ(kr) and the phase shift
(45)where the amplitude Hkφ(kr) and the phase shift 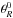 are given by
are given by ![\begin{eqnarray} H_{k_{\phi}} (k_{r}) = A \, | k_{r}| \sqrt{1 \!+\! \left[ \frac{\Omega_{\phi}}{\kappa} \frac{2 k_{\phi}}{k_{r} R_{g}} \right]^{2}}; ~~~\theta_{R}^{0} = \tan^{-1} \left[\! - \frac{\kappa}{\Omega_{\phi}} \frac{k_{r} R_{g}}{2 k_{\phi}} \!\right] \cdot \label{expression_H_theta0} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq172.png) (46)For typical galaxies, we have 1 / 2 ≤ Ωφ/κ ≤ 1 (Binney & Tremaine 2008). Assuming that the azimuthal number kφ is of the order of unity, one can use the WKB hypothesis introduced in Eq. (30), so that Eqs. (46)can be approximated as
(46)For typical galaxies, we have 1 / 2 ≤ Ωφ/κ ≤ 1 (Binney & Tremaine 2008). Assuming that the azimuthal number kφ is of the order of unity, one can use the WKB hypothesis introduced in Eq. (30), so that Eqs. (46)can be approximated as 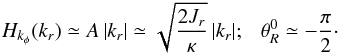 (47)Because we have assumed that the disc is tepid, the radial oscillations are small so that A ≪ Rg. We may then get rid of the dependences on A in ℬR0(Rg + Acos(θR)) by replacing it with ℬR0(Rg), so that the only remaining dependence on A will be in the complex exponentials. To be able to explicitly perform the remaining integration on θR in Eq. (44), we introduce the Bessel functions
(47)Because we have assumed that the disc is tepid, the radial oscillations are small so that A ≪ Rg. We may then get rid of the dependences on A in ℬR0(Rg + Acos(θR)) by replacing it with ℬR0(Rg), so that the only remaining dependence on A will be in the complex exponentials. To be able to explicitly perform the remaining integration on θR in Eq. (44), we introduce the Bessel functions 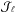 of the first kind which satisfy the relation
of the first kind which satisfy the relation ![\begin{eqnarray} {\rm e}^{{\rm i} z \sin (\theta)} = \sum_{\ell \,\in\, \mathbb{Z}} \mathcal{J}_{\ell} [z] \, {\rm e}^{{\rm i} \ell \theta} . \label{summation_property_Bessel} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq179.png) (48)We then finally obtain the expression of the Fourier transform in angles of the WKB basis elements which reads
(48)We then finally obtain the expression of the Fourier transform in angles of the WKB basis elements which reads ![\begin{eqnarray} \psi_{{\vec m}}^{[k_{\phi} , k_{r} , R_{0}]} ({\vec J}) = \delta_{m_{\phi}}^{k_{\phi}} {\rm e}^{{\rm i} k_{r} R_{g}} {\rm e}^{{\rm i} m_{r} \theta_{R}^{0}} \mathcal{A} \, \mathcal{J}_{m_{r}} [H_{m_{\phi}} (k_{r})] \, \mathcal{B}_{R_{0}} (R_{g}) . \label{Fourier_WKB} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq180.png) (49)
(49)
3.3. Estimation of the response matrix
Thanks to the WKB basis introduced in Eq. (26), one can now explicitly compute the response matrix from Eq. (5). Indeed, we use the expression (49)of the Fourier transform of the basis elements, and after simplification of the phase-shift terms thanks to the approximation from Eq. (47), one has to evaluate ![\begin{eqnarray} &&\widehat{\mathbf{M}}_{[k_{\phi}^{p} , k_{r}^{p} , R_{0}^{p}] , [k_{\phi}^{q} , k_{r}^{q} , R_{0}^{q}]} (\omega) = \nonumber \\ && \;\;\;\;\;\;\;\;\;\; (2 \pi)^{2} \sum_{{\vec m}} \!\! \int \!\! \mathrm{d} {\vec J} \, \frac{{\vec m} \cdot \partial F / \partial {\vec J}}{\omega - {\vec m} \cdot {\vec \Omega}} \delta_{m_{\phi}}^{k_{\phi}^{p}} \delta_{m_{\phi}}^{k_{\phi}^{q}} {\rm e}^{{\rm i} (k_{r}^{q} - k_{r}^{p}) R_{g}} \mathcal{A}_{p} \mathcal{A}_{q} \nonumber \\ && \;\;\;\;\;\;\;\;\;\; \times\, \mathcal{J}_{m_{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}}{\kappa}} k_{r}^{p} \!\right] \mathcal{J}_{m_{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}}{\kappa}} k_{r}^{q} \!\right] \, \mathcal{B}_{R_{0}^{p}} (R_{g}) \, \mathcal{B}_{R_{0}^{q}} (R_{g}) \cdot \label{calculation_M_I} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq181.png) (50)The first step of the calculation is to show that in the WKB limit, the response matrix becomes diagonal. One should note that the previous expression (50)is similar to Eq. (37), where we discussed the biorthogonality of the WKB basis. In Eq. (50), the azimuthal Kronecker symbols ensure that
(50)The first step of the calculation is to show that in the WKB limit, the response matrix becomes diagonal. One should note that the previous expression (50)is similar to Eq. (37), where we discussed the biorthogonality of the WKB basis. In Eq. (50), the azimuthal Kronecker symbols ensure that 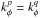 . Moreover, because of our WKB assumptions from Eq. (41)on the step distances of the basis elements, the product of the two radial Gaussians in Rg imposes that
. Moreover, because of our WKB assumptions from Eq. (41)on the step distances of the basis elements, the product of the two radial Gaussians in Rg imposes that 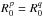 in order to have a non-zero contribution. In order to shorten the notations, we temporarily introduce the function h(Rg) defined as
in order to have a non-zero contribution. In order to shorten the notations, we temporarily introduce the function h(Rg) defined as ![\begin{eqnarray} h(R_{g}) = \left| \frac{\mathrm{d} J_{\phi}}{\mathrm{d} R_{g}} \right| \frac{{\vec m} \cdot \partial F / \partial {\vec J}}{\omega - {\vec m} \cdot {\vec \Omega}} \mathcal{A}_{p} \mathcal{A}_{q} \mathcal{J}_{m_{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}}{\kappa}} k_{r}^{p} \!\right] \mathcal{J}_{m_{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}}{\kappa}} k_{r}^{q} \!\right] , \label{definition_h} \nonumber \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq183.png) which encompasses all the additional radial dependences appearing in Eq. (50). Thanks to the change of variables Jφ → Rg, the integral on Jφ which has to be evaluated in Eq. (50), when estimated for
which encompasses all the additional radial dependences appearing in Eq. (50). Thanks to the change of variables Jφ → Rg, the integral on Jφ which has to be evaluated in Eq. (50), when estimated for 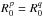 , is qualitatively of the form
, is qualitatively of the form ![\begin{eqnarray} \int \!\! \mathrm{d} R_{g} \, h (R_{g}) \, {\rm e}^{{\rm i} R_{g} (k_{r}^{q} - k_{r}^{p})} \exp \!\left[\! - \frac{(R_{g} - R_{0}^{p})^{2}}{\sigma^{2}} \!\right] \cdot \label{shape_integration_h_I} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq185.png) (51)This expression corresponds to a radial Fourier transform ℱ at the frequency Δkr. It can be rewritten as a convolution of two radial Fourier transforms so that it becomes
(51)This expression corresponds to a radial Fourier transform ℱ at the frequency Δkr. It can be rewritten as a convolution of two radial Fourier transforms so that it becomes ![\begin{eqnarray} \eqref{shape_integration_h_I} \propto \int \!\! \mathrm{d} k' \, \mathcal{F} [h] (k') \, \exp \!\left[\! - \frac{(\Delta k_{r} - k')^{2}}{4 / \sigma^{2}} \!\right] , \label{shape_integration_h_II} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq187.png) (52)where
(52)where 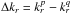 . We now rely on the WKB assumption from Eq. (40). If one has Δkr ≠ 0, because of the Gaussian from Eq. (52), the contribution from ℱ [ h ] will come from the region k′ ~ Δkr ≫ 1 /σ. We assume that the function h is such that its Fourier Transform is limited to the frequency region | k′ | ≲ 1 /σ. This is consistent with assuming that the properties of the disc are radially slowly varying, and this implies that non-zero contributions to the response matrix can only be obtained when
. We now rely on the WKB assumption from Eq. (40). If one has Δkr ≠ 0, because of the Gaussian from Eq. (52), the contribution from ℱ [ h ] will come from the region k′ ~ Δkr ≫ 1 /σ. We assume that the function h is such that its Fourier Transform is limited to the frequency region | k′ | ≲ 1 /σ. This is consistent with assuming that the properties of the disc are radially slowly varying, and this implies that non-zero contributions to the response matrix can only be obtained when 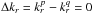 . Therefore, we have shown that within our WKB formalism, the response matrix from Eq. (5)is diagonal.
. Therefore, we have shown that within our WKB formalism, the response matrix from Eq. (5)is diagonal.
In order to shorten the notations, we will denote the matrix eigenvalues as ![\begin{eqnarray} \lambda_{[k_{\phi} , k_{r} , R_{0}]} (\omega) = \widehat{\mathbf{M}}_{[k_{\phi} , k_{r} , R_{0}] , [k_{\phi} , k_{r} , R_{0}]} (\omega) . \label{definition_lambda_short} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq194.png) (53)For these diagonal coefficients, the last step is to explicitly compute the integrals over Jφ and Jr in Eq. (50)to obtain the expression of the response matrix eigenvalues. We now detail this calculation. Thanks to our scale-decoupling approach, we may replace the radial Gaussian from Eq. (51)by a Dirac delta
(53)For these diagonal coefficients, the last step is to explicitly compute the integrals over Jφ and Jr in Eq. (50)to obtain the expression of the response matrix eigenvalues. We now detail this calculation. Thanks to our scale-decoupling approach, we may replace the radial Gaussian from Eq. (51)by a Dirac delta 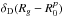 while paying a careful attention to the correct normalization of the Gaussian. Hence we have to evaluate
while paying a careful attention to the correct normalization of the Gaussian. Hence we have to evaluate ![\begin{eqnarray} && \lambda_{[k_{\phi} , k_{r} , R_{0}]} (\omega) = \nonumber \\ && (2 \pi)^{2} \mathcal{A}^{2} \! \left| \frac{\mathrm{d} J_{\phi}}{\mathrm{d} R_{g}} \right|_{R_{0}} \!\! \sum_{{\vec m}} \delta_{k_{\phi}}^{m_{\phi}} \!\!\! \int \!\!\! \mathrm{d} J_{r} \frac{{\vec m} \cdot \partial F / \partial {\vec J}}{\omega - m_{\phi} \Omega_{\phi} - m_{r} \kappa} \mathcal{J}_{m_{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}}{\kappa}} k_{r} \!\right] . \label{calculation_M_II} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq196.png) (54)Because of the presence of the azimuthal Kronecker symbol, we may drop the sum on mφ. The intrinsic frequencies from Eqs. (22)allow us to compute
(54)Because of the presence of the azimuthal Kronecker symbol, we may drop the sum on mφ. The intrinsic frequencies from Eqs. (22)allow us to compute 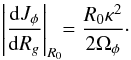 (55)Moreover, we assume that the galactic disc is tepid so that | ∂F/∂Jφ | ≪ | ∂F/∂Jr |. We may then only keep the term corresponding to a gradient with respect to the radial action Jr. Thanks to the expression of the Schwarzschild distribution function from Eq. (25)and the expression of the basis ampitude from Eq. (43), Eq. (54)becomes after some simple algebra
(55)Moreover, we assume that the galactic disc is tepid so that | ∂F/∂Jφ | ≪ | ∂F/∂Jr |. We may then only keep the term corresponding to a gradient with respect to the radial action Jr. Thanks to the expression of the Schwarzschild distribution function from Eq. (25)and the expression of the basis ampitude from Eq. (43), Eq. (54)becomes after some simple algebra ![\begin{eqnarray} \lambda_{[k_{\phi} , k_{r} , R_{0}]} (\omega) & =& \frac{2 \pi G \Sigma |k_{r}|}{\kappa^{2}} \frac{\kappa^{4}}{k_{r}^{2} \sigma_{r}^{4}} \nonumber\\ && \times \, \sum_{m_{r}} \!\! \int \!\! \mathrm{d} J_{r} \, \frac{- m_{r} \exp [ - \kappa J_{r} / \sigma_{r}^{2} ]}{\omega - k_{\phi} \Omega_{\phi} - m_{r} \kappa} \mathcal{J}_{m_{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}}{\kappa}} k_{r} \!\right] . \label{calculation_M_III} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq200.png) (56)We may now use the following integration formula (see formula (6.615) from Gradshteyn & Ryzhik 2007)
(56)We may now use the following integration formula (see formula (6.615) from Gradshteyn & Ryzhik 2007) ![\begin{eqnarray} \int_{0}^{+ \infty} \!\!\!\!\!\!\! \mathrm{d} J_{r} \, {\rm e}^{- \alpha J_{r}} \mathcal{J}_{m_{r}}^{2} \!\left[ \beta \sqrt{J_{r}} \right] = \frac{{\rm e}^{- \beta^{2} / 2 \alpha}}{\alpha} \mathcal{I}_{m_{r}} \!\left[\! \frac{\beta^{2}}{2 \alpha} \!\right] , \label{integration_formula_Bessel} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq201.png) (57)where α> 0, β> 0, mr ∈Z and ℐmr are the modified Bessel functions of the first kind. We apply this formula with
(57)where α> 0, β> 0, mr ∈Z and ℐmr are the modified Bessel functions of the first kind. We apply this formula with 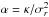 and
and 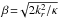 . We also introduce the notation
. We also introduce the notation 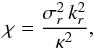 (58)so that Eq. (56)becomes
(58)so that Eq. (56)becomes ![\begin{eqnarray} \lambda_{[k_{\phi} , k_{r} , R_{0}]} (\omega) = \frac{2 \pi G \Sigma |k_{r}|}{\kappa^{2}} \frac{\kappa}{\chi} \sum_{m_{r}} \frac{- m_{r} \, {\rm e}^{- \chi} \, \mathcal{I}_{m_{r}} [\chi] }{\omega - k_{\phi} \Omega_{\phi} - m_{r} \kappa} \cdot \label{calculation_M_IV} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq209.png) (59)We now define the dimensionless shifted frequency s as
(59)We now define the dimensionless shifted frequency s as 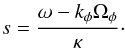 (60)Because we have ℐ− mr [ χ ] = ℐmr [ χ ], we may rewrite Eq. (59)using the reduction factor (Kalnajs 1965; Lin & Shu 1966) defined as
(60)Because we have ℐ− mr [ χ ] = ℐmr [ χ ], we may rewrite Eq. (59)using the reduction factor (Kalnajs 1965; Lin & Shu 1966) defined as ![\begin{eqnarray} \mathcal{F} (s , \chi) = 2 \, (1 - s^{2}) \frac{{\rm e}^{-\chi}}{\chi} \!\! \sum_{m_{r} = 1}^{+ \infty} \! \frac{\mathcal{I}_{m_{r}} [\chi]}{1 - [s / m_{r}]^{2}} \cdot \label{definition_reduction_F} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq213.png) (61)As a conclusion, we obtain that within our WKB formalism the response matrix
(61)As a conclusion, we obtain that within our WKB formalism the response matrix  becomes diagonal and in the limit of tepid discs reads
becomes diagonal and in the limit of tepid discs reads ![\begin{eqnarray} \widehat{\mathbf{M}}_{[k_{\phi}^{p} , k_{r}^{p} , R_{0}^{p}] , [k_{\phi}^{q} , k_{r}^{q} , R_{0}^{q}]} = \delta_{k_{\phi}^{p}}^{k_{\phi}^{q}} \delta_{k_{r}^{p}}^{k_{r}^{q}} \delta_{R_{0}^{p}}^{R_{0}^{q}} \frac{2 \pi G \Sigma |k_{r}| }{\kappa^{2} (1 - s^{2})} \mathcal{F} (s ,\chi) . \label{diagonal_M_tepid} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq215.png) (62)This eigenvalue recovered using the WKB basis introduced in Eq. (26)is in full agreement with the seminal results from Kalnajs (1965) and Lin & Shu (1966). In order to handle the singularity of the eigenvalue appearing for s = n ∈Z, one adds a small imaginary part to the frequency of evaluation, so that s = n + iη. Indeed, as long as η is small compared to the imaginary part of the least damped mode of the disc, adding this complex part makes a negligible contribution to the expression of Re(λ).
(62)This eigenvalue recovered using the WKB basis introduced in Eq. (26)is in full agreement with the seminal results from Kalnajs (1965) and Lin & Shu (1966). In order to handle the singularity of the eigenvalue appearing for s = n ∈Z, one adds a small imaginary part to the frequency of evaluation, so that s = n + iη. Indeed, as long as η is small compared to the imaginary part of the least damped mode of the disc, adding this complex part makes a negligible contribution to the expression of Re(λ).
3.4. Estimation of the susceptibility coefficients
One can now estimate the dressed susceptibility coefficients from Eq. (4). In order to shorten the notations, we will write the WKB basis elements introduced in Eq. (26)as ![\begin{eqnarray} \psi^{(p)} = \psi^{[k_{\phi}^{p} , k_{r}^{p} , R_{0}^{p}]} . \label{short_notation_WKB_basis} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq220.png) (63)We have shown previously in Eq. (62)that within our WKB basis, the response matrix
(63)We have shown previously in Eq. (62)that within our WKB basis, the response matrix  is diagonal. Its eigenvalues will be noted as λp so that we have
is diagonal. Its eigenvalues will be noted as λp so that we have 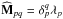 . Hence the expression (4)of the susceptibility coefficients takes the form
. Hence the expression (4)of the susceptibility coefficients takes the form ![\begin{eqnarray} \frac{1}{\mathcal{D}_{\vec{m}_{1} , {\vec m}_{2}} ({\vec J}_{1} , {\vec J}_{2} , \omega)} = \sum_{p} \psi_{{\vec m}_{1}}^{(p)} \!({\vec J}_{1}) \, \!\left[\! \frac{1}{1 - \lambda_{p} (\omega)} \!\right]\! \, \psi_{{\vec m}_{2}}^{(p) *} \!({\vec J}_{2}) . \label{initial_1/D_WKB} \nonumber \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq223.png) Using the expression of the Fourier transformed basis elements obtained in Eq. (49), we obtain
Using the expression of the Fourier transformed basis elements obtained in Eq. (49), we obtain ![\begin{eqnarray} && \frac{1}{ \mathcal{D}_{{\vec m}_{1} , {\vec m}_{2}} ({\vec J}_{1} , {\vec J}_{2} , \omega)} = \!\!\!\! \sum_{k_{\phi}^{p} , k_{r}^{p} , R_{0}^{p}} \!\!\!\! \delta_{m_{1}^{\phi}}^{k_{\phi}^{p}} \delta_{m_{2}^{\phi}}^{k_{\phi}^{p}} \frac{G}{k_{r}^{p} R_{0}^{p}} \frac{1}{1 - \lambda_{p}} \nonumber \\[1.5mm] && \;\;\;\;\;\;\; \times \, \mathcal{J}_{m_{1}^{r}} \!\!\left[\!\! \sqrt{\!\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{r}^{p} \!\right] \mathcal{J}_{m_{2}^{r}} \!\!\left[\!\! \sqrt{\!\tfrac{2 J_{r}^{2}}{\kappa_{2}}} k_{r}^{p}\!\right] {\rm e}^{{\rm i} k_{r}^{p} (R_{1} - R_{2})} {\rm e}^{{\rm i} \theta_{R}^{0 p } (m_{1}^{r} - m_{2}^{r})} \nonumber \\[1.5mm] && \;\;\;\;\;\;\; \times \, \frac{1}{\sqrt{\pi \sigma^{2}}} \exp \!\left[\! - \frac{(R_{1} - R_{0}^{p})^{2}}{2 \sigma^{2}} \!\right] \exp \!\left[\! - \frac{(R_{2} - R_{0}^{p})^{2}}{2 \sigma^{2}} \!\right] ,\label{calculation_1/D_I} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq224.png) (64)where we used the shortened notations κi = κ(Ji), and Ri = Rg(Ji). We also used the approximation introduced in Eq. (47)for the values at which the Bessel functions have to be evaluated. Thanks to the Kronecker symbols in mφ and
(64)where we used the shortened notations κi = κ(Ji), and Ri = Rg(Ji). We also used the approximation introduced in Eq. (47)for the values at which the Bessel functions have to be evaluated. Thanks to the Kronecker symbols in mφ and 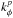 , we necessarily have
, we necessarily have 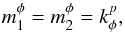 (65)so that the sum on
(65)so that the sum on 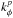 can be dropped.
can be dropped.
3.5. Restriction on the loci of resonance
Before proceeding with the evaluation of the susceptibility coefficients obtained in Eq. (64), one may first emphasize a crucial consequence of the WKB basis from Eq. (26), which is the restriction to only exactly local resonances. Indeed, one can note that the expressions (8)and (9)of the drift and diffusion coefficients all involve an integration over the mute variable J2. For a given value of J1, m1 and m2, this integration should be seen as a scan of the entire action-space, searching for resonant regions where the constraint m1·Ω1 − m2·Ω2 = 0 is satisfied. We first recall the rule for the composition of a Dirac delta and a function which reads 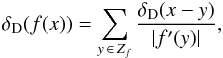 (66)where Zf = { y | f(y) = 0 }, and we have supposed that all the poles of f are simple. As noted in Eq. (22), within the epicyclic approximation, the intrinsic frequencies Ω = (Ωφ,κ) only depend on Rg = Rg(Jφ) and are independent of Jr. Hence, the resonance condition m1·Ω1 − m2·Ω2 = 0 only depends on
(66)where Zf = { y | f(y) = 0 }, and we have supposed that all the poles of f are simple. As noted in Eq. (22), within the epicyclic approximation, the intrinsic frequencies Ω = (Ωφ,κ) only depend on Rg = Rg(Jφ) and are independent of Jr. Hence, the resonance condition m1·Ω1 − m2·Ω2 = 0 only depends on 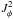 and is independent of
and is independent of 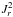 . Hence if we consider fixed J1, m1 and m2, the resonant Dirac delta which has to be studied takes the form
. Hence if we consider fixed J1, m1 and m2, the resonant Dirac delta which has to be studied takes the form ![\begin{eqnarray} \delta_{\rm D} ({\vec m}_{1} \cdot {\vec \Omega}_{1} - {\vec m}_{2} \cdot {\vec \Omega}_{2}) = \!\!\! \sum_{R_{2}^{r} \,|\, f (R_{2}^{r}) \,=\, 0} \frac{\delta_{\rm D} (R_{2} - R_{2}^{r})}{\left| \frac{\partial }{\partial R} [{\vec m}_{2} \cdot {\vec \Omega}] \right|_{R_{2}^{r}}} , \label{rewriting_Dirac_delta} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq236.png) (67)where the resonance condition
(67)where the resonance condition 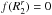 is given by
is given by 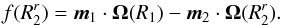 (68)The radii
(68)The radii 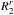 therefore correspond to the resonant radii for which the resonance condition is satisfied. When writing Eq. (67), we assumed that the zeros of the resonance function are simple, which corresponds to the assumption that for any resonant radius
therefore correspond to the resonant radii for which the resonance condition is satisfied. When writing Eq. (67), we assumed that the zeros of the resonance function are simple, which corresponds to the assumption that for any resonant radius 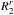 , we have
, we have 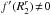 . Assuming that
. Assuming that 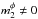 , this condition can be rewritten as
, this condition can be rewritten as 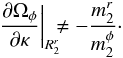 (69)Resonance poles are therefore simple as long as the rates of change of the two intrinsic frequencies are not in a rational ratio. One can note that the Keplerian case for which κ = Ωφ and the harmonic case for which κ = 2Ωφ are in this sense degenerate. They can lead to resonant poles of higher multiplicity and would therefore require a more involved evaluation of the Balescu-Lenard collision operator. In what follows we assume that the potential is non-degenerate.
(69)Resonance poles are therefore simple as long as the rates of change of the two intrinsic frequencies are not in a rational ratio. One can note that the Keplerian case for which κ = Ωφ and the harmonic case for which κ = 2Ωφ are in this sense degenerate. They can lead to resonant poles of higher multiplicity and would therefore require a more involved evaluation of the Balescu-Lenard collision operator. In what follows we assume that the potential is non-degenerate.
One can now use the properties of the WKB basis to restrict the range of resonant radii,  . The expression (64)of the susceptibility coefficients, thanks to the two Gaussians, imposes that the relevant resonant radius
. The expression (64)of the susceptibility coefficients, thanks to the two Gaussians, imposes that the relevant resonant radius  must necessarily be close to R1. As noted in Eq. (65), in order to have a non-zero susceptibility, one also has to satisfy the constraint
must necessarily be close to R1. As noted in Eq. (65), in order to have a non-zero susceptibility, one also has to satisfy the constraint 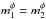 . The resonant condition which has to be satisfied is therefore given by
. The resonant condition which has to be satisfied is therefore given by 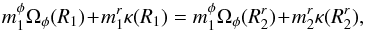 (70)where the distance
(70)where the distance 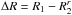 is such that | ΔR | ≤ (few) σ. Because the scale-decoupling parameter σ is supposed to be small compared to the size of the system, we may approximate the previous resonant condition as
is such that | ΔR | ≤ (few) σ. Because the scale-decoupling parameter σ is supposed to be small compared to the size of the system, we may approximate the previous resonant condition as ![\begin{eqnarray} \bigg[ m_{2}^{\phi} \frac{\partial \Omega_{\phi}}{\partial R} \!+\! m_{2}^{r} \frac{\partial \kappa}{\partial R} \bigg] \, \Delta R = \bigg[ m_{1}^{r} - m_{2}^{r} \bigg] \, \kappa (R_{1}) . \label{approximate_resonance_condition} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq250.png) (71)On the l.h.s. of Eq. (71), the term within bracket is non-zero because we assumed in Eq. (69)that the resonant poles are simple. Moreover, ΔR is small because of our scale-decoupling approach. The r.h.s. of Eq. (71)is discrete: it is either zero or at least of the order of κ(R1). Because the l.h.s. is necessarily small, we must have
(71)On the l.h.s. of Eq. (71), the term within bracket is non-zero because we assumed in Eq. (69)that the resonant poles are simple. Moreover, ΔR is small because of our scale-decoupling approach. The r.h.s. of Eq. (71)is discrete: it is either zero or at least of the order of κ(R1). Because the l.h.s. is necessarily small, we must have 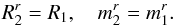 (72)This result is a crucial consequence of our WKB tightly wound spiral assumption because it implies that only local resonances are allowed. In particular this implies that the WKB limit does not allow for distant orbits to resonate (through e.g. propagation of swing amplified wave packets, see below). Then the sum
(72)This result is a crucial consequence of our WKB tightly wound spiral assumption because it implies that only local resonances are allowed. In particular this implies that the WKB limit does not allow for distant orbits to resonate (through e.g. propagation of swing amplified wave packets, see below). Then the sum 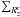 from Eq. (67)can be limited to the evaluation in
from Eq. (67)can be limited to the evaluation in 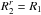 . Hence within this WKB limit, the susceptibility coefficients from Eq. (64)have to be evaluated only for m2 = m1 and R2 = R1, so that we have to deal with the expression
. Hence within this WKB limit, the susceptibility coefficients from Eq. (64)have to be evaluated only for m2 = m1 and R2 = R1, so that we have to deal with the expression ![\begin{eqnarray} &&\frac{1}{\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (R_{1} , J_{r}^{1} , R_{1} , J_{r}^{2} , \omega)} = \!\! \sum_{k_{r}^{p} , R_{0}^{p}} \! \frac{G}{k_{r}^{p} R_{0}^{p}} \frac{1}{1 - \lambda_{p}} \nonumber \\ && \;\; \times \, \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{r}^{p} \!\right] \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{r}^{p} \!\right] \frac{1}{\sqrt{\pi \sigma^{2}}} \exp \!\left[\! - \frac{(R_{1} - R_{0}^{p})^{2}}{\sigma^{2}} \!\right] \cdot \label{calculation_1/D_II} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq258.png) (73)
(73)
3.6. Asymptotic continuous limit
One can note that in Eq. (73)the susceptibility coefficients are still expressed as a discrete sum on the basis index 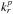 and
and 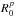 . Our next step is to replace these sums by continuous integrals. The discrete basis elements are separated by the step distances ΔR0 and Δkr, which must satisfy the WKB hypothesis detailed in Eq. (41). We use the Riemann sum formula
. Our next step is to replace these sums by continuous integrals. The discrete basis elements are separated by the step distances ΔR0 and Δkr, which must satisfy the WKB hypothesis detailed in Eq. (41). We use the Riemann sum formula 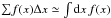 , where Δx controls the distance between the basis elements. This transformation is a subtle stage of the calculation because one has to consider step distances ΔR0 and Δkr, which have to simultaneously be large to comply with the WKB assumption from Eq. (41)and small to allow the use of the Riemann sum formula. As we are going to transform both the sums on
, where Δx controls the distance between the basis elements. This transformation is a subtle stage of the calculation because one has to consider step distances ΔR0 and Δkr, which have to simultaneously be large to comply with the WKB assumption from Eq. (41)and small to allow the use of the Riemann sum formula. As we are going to transform both the sums on 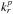 and
and 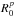 , the exact value of the susceptibility coefficients will depend on our choice for ΔR0 Δkr. One has to consider the case
, the exact value of the susceptibility coefficients will depend on our choice for ΔR0 Δkr. One has to consider the case 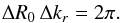 (74)This sampling corresponds to a critical sampling condition (Gabor 1946; Daubechies 1990; see also Fouvry et al. 2015b). Equation (73)then takes the form
(74)This sampling corresponds to a critical sampling condition (Gabor 1946; Daubechies 1990; see also Fouvry et al. 2015b). Equation (73)then takes the form ![\begin{eqnarray} && \frac{1}{\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (R_{1} , J_{r}^{1} , R_{1} , J_{r}^{2} , \omega) } = \frac{G}{2 \pi} \!\! \int \!\! \mathrm{d} k_{r} \, \mathrm{d} R_{0} \, \frac{1}{k_{r} R_{0}} \frac{1}{1 - \lambda_{k_{r}} (R_{0} , \omega)} \nonumber \\ && \;\;\;\;\; \times \, \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{r} \!\right] \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{r} \!\right] \frac{1}{\sqrt{\pi \sigma^{2}}} \exp \!\left[\! - \frac{(R_{1} - R_{0})^{2}}{\sigma^{2}} \!\right] \cdot \label{calculation_1/D_II_bis} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq267.png) (75)One can now assume that the radial Gaussian present in Eq. (75)is sufficiently peaked. Because it is correctly normalized, we may in this limit replace it by δD(R1 − R0). The integration on R0 can then be immediately performed to give
(75)One can now assume that the radial Gaussian present in Eq. (75)is sufficiently peaked. Because it is correctly normalized, we may in this limit replace it by δD(R1 − R0). The integration on R0 can then be immediately performed to give ![\begin{eqnarray} && \frac{1}{\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (R_{1} , J_{r}^{1} , R_{1} , J_{r}^{2} , \omega)} = \frac{1}{2 \pi} \frac{G}{R_{1}} \nonumber \\ && \;\;\;\;\; \times \, \int \!\! \mathrm{d} k_{r} \, \frac{1}{k_{r}} \frac{1}{1 - \lambda_{k_{r}} (R_{1} , \omega)} \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{r} \!\right] \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{r} \!\right] , \label{calculation_1/D_III} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq270.png) (76)where only λkr depends on the frequency of evaluation ω. One may note that in Eq. (76), all the dependencies in σ have disappeared, so that the value of the susceptibility coefficients is independent of the precise choice of the WKB basis. The square of the susceptibility coefficients which is required to estimate the drift and diffusion coefficients from Eqs. (8)and (9)is therefore given by
(76)where only λkr depends on the frequency of evaluation ω. One may note that in Eq. (76), all the dependencies in σ have disappeared, so that the value of the susceptibility coefficients is independent of the precise choice of the WKB basis. The square of the susceptibility coefficients which is required to estimate the drift and diffusion coefficients from Eqs. (8)and (9)is therefore given by ![\begin{eqnarray} &&\left| \frac{1}{\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (R_{1} , J_{r}^{1} , R_{1} , J_{r}^{2} , \omega)} \right|^{2} = \frac{1}{4 \pi^{2}} \frac{G^{2}}{R_{1}^{2}} \nonumber \\ && \;\;\;\;\; \times \, \left\{ \!\! \int_{1\!/\!\sigma_{k}}^{+ \infty} \!\!\!\!\!\!\!\! \mathrm{d} k_{r} \, \frac{1}{k_{r}} \frac{1}{1 - \lambda_{k_{r}} (R_{1} , \omega)} \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{r} \!\right] \! \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{r} \!\right] \right\}^{2}, \label{calculation_1/D^2_I} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq273.png) (77)
(77)
where we introduced a cut-off at 1 /σk for the integration on kr. This bound is justified by the WKB constraint from Eq. (41), which imposes that the probed radial frequency region is bounded from below. It is also important to note that these susceptibility coefficients should be evaluated at R2 = R1, since we proved in Eq. (72)that, consistently with our WKB approximation, exactly local resonances are the only ones which have to be considered.
At this stage, there is an arbitration to make between two possible behaviours depending on the physical properties of the underlying disc. First of all, if the amplification function kr → 1 / (1 − λkr) is asymptotically a sharp function reaching a maximum value λmax for kr = kmax, one can assume that the susceptibility coefficients are dominated by the contribution from the peak in λkr. In this situation, we can perform an approximation of the small denominators. The second possible behaviour arises if the function kr → 1 / (1 − λkr) is asymptotically flat, so that there is no characteristic scale of blow-up of the amplification eigenvalues. In such a situation, the susceptibility coefficients are mostly dominated by the behaviour at the boundaries of integration from Eq. (77)where kr → 1 /σk. The detailed response structure of the self-gravitating disc then does not play a significant role.
We place ourselves within the approximation of the small denominators, assuming that the biggest contribution to the susceptibility coefficients comes from waves which yield the largest λkr. Therefore, one has to suppose that the function kr → 1 / (1 − λkr) is a sharp function reaching a maximum value λmax(R1,ω), for kr = kmax(R1,ω), with a characteristic spread Δkλ(R1,ω). The expression (77)then becomes ![\begin{eqnarray} && \left| \frac{1}{\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (R_{1} , J_{r}^{1} , R_{1} , J_{r}^{2} , \omega) } \right|^{2} = \frac{1}{4 \pi^{2}} \frac{G^{2}}{R_{1}^{2}} \frac{(\Delta k_{\lambda})^{2}}{k_{\rm max}^{2}} \nonumber \\[1.5mm] && \;\;\;\;\;\;\;\;\;\; \times \, \left[ \frac{1}{1 - \lambda_{\rm max} } \right]^{2} \mathcal{J}_{m_{1}^{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{\rm max} \!\right] \mathcal{J}_{m_{1}^{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{\rm max} \!\right] . \label{expression_1/D^2_ASD} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq286.png) (78)While still focusing on the contribution to the susceptibility coefficients due to the waves with the largest amplification λ(kr), one can improve the approximation of the small denominators from Eq. (78). Indeed, starting from Eq. (77), one can instead perform the kr-integration for kr ∈ [ kinf; ksup ], where these bounds are given by λ(kinf / sup) = λmax/ 2. This approach is numerically more demanding but does not alter the principal conclusions drawn in this paper, while allowing a more precise determination of the secular flux structure. All the calculations presented in Sect. 4 were performed with this improved approximation. Finally, in Appendix B, we detail how this same WKB formalism may be applied to the inhomogeneous Balescu-Lenard equation without collective effects (Chavanis 2013b).
(78)While still focusing on the contribution to the susceptibility coefficients due to the waves with the largest amplification λ(kr), one can improve the approximation of the small denominators from Eq. (78). Indeed, starting from Eq. (77), one can instead perform the kr-integration for kr ∈ [ kinf; ksup ], where these bounds are given by λ(kinf / sup) = λmax/ 2. This approach is numerically more demanding but does not alter the principal conclusions drawn in this paper, while allowing a more precise determination of the secular flux structure. All the calculations presented in Sect. 4 were performed with this improved approximation. Finally, in Appendix B, we detail how this same WKB formalism may be applied to the inhomogeneous Balescu-Lenard equation without collective effects (Chavanis 2013b).
3.7. Estimation of the drift and diffusion coefficients
The drift and diffusion coefficients are given by Eqs. (8)and (9). Within the WKB approximation, we have shown in Eqs. (65)and (72)that the susceptibility coefficients have to be evaluated only for m1 = m2, so that the sum on m2 in the expressions of the drift and diffusion coefficients may be dropped. As the resonances are exactly local, using the formula from Eq. (67)adds a prefactor of the form 1 / | ∂(m1·Ω) /∂Jφ |, so that the drift coefficients from Eq. (8)become ![\begin{eqnarray} A_{{\vec m}_{1}} ({\vec J}_{1}) &= & - \frac{4 \pi^{3} \mu}{\left| \frac{\partial }{\partial J_{\phi}} [{\vec m}_{1} \cdot {\vec \Omega}_{1}] \right|_{J_{\phi}^{1}}} \nonumber \\ && \times \, \!\! \int \!\! \mathrm{d} J_{r}^{2} \, \frac{{\vec m}_{1} \cdot \partial F / \partial {\vec J} (J_{\phi}^{1} , J_{r}^{2}) }{|\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (J_{\phi}^{1} , J_{r}^{1} , J_{\phi}^{1} , J_{r}^{2} , {\vec m}_{1} \cdot {\vec \Omega}_{1}) |^{2}} \cdot \label{WKB_drift} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq292.png) (79)Similarly, the diffusion coefficients are given by
(79)Similarly, the diffusion coefficients are given by ![\begin{eqnarray} D_{{\vec m}_{1}} ({\vec J}_{1}) &= & \frac{4 \pi^{3} \mu}{\left| \frac{\partial }{\partial J_{\phi}} [{\vec m}_{1} \cdot {\vec \Omega}_{1}] \right|_{J_{\phi}^{1}}} \nonumber \\ & &\times \, \!\! \int \!\! \mathrm{d} J_{r}^{2} \, \frac{F (J_{\phi}^{1} , J_{r}^{2})}{|\mathcal{D}_{{\vec m}_{1} , {\vec m}_{1}} (J_{\phi}^{1} , J_{r}^{1} , J_{\phi}^{1} , J_{r}^{2} , {\vec m}_{1} \cdot {\vec \Omega}_{1}) |^{2}} \cdot \label{WKB_diff} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq293.png) (80)In both Eqs. (79)and (80), the susceptibility coefficients are given by Eq. (77)or, within the approximation of the small denominators, by Eq. (78).
(80)In both Eqs. (79)and (80), the susceptibility coefficients are given by Eq. (77)or, within the approximation of the small denominators, by Eq. (78).
Such simple expressions of the drift and diffusion coefficients along with the required expression of the susceptibility coefficients constitute a main result of this paper. One should also note that this WKB formalism is self contained and is obtained without any ad hoc assumptions or fittings. Except for the explicit recovery of the amplification eigenvalues from Eq. (62), the calculations presented previously are not limited to the Schwarzschild distribution function from Eq. (25). Indeed, the drift and diffusion coefficients from Eqs. (79)and (80)are valid for any tepid disc, as long as the epicyclic angles-actions mapping from Eq. (24)may be used. In Appendix C, we show how the drift and diffusion coefficients from Eqs. (79)and (80)can be explicitly computed, when one considers a Schwarzschild distribution function as in Eq. (25)and when the susceptibility coefficients are estimated thanks to the approximation of the small denominators from Eq. (78). Finally, in Appendix D, we compare this 2D WKB Balescu-Lenard equation with other similar kinetic equations.
4. Application
We may now illustrate how this WKB approximation of the inhomogeneous Balescu-Lenard equation can be implemented to recover some results obtained via well-crafted numerical simulations. Indeed, Sellwood (2012; hereafter S12) using careful numerical simulations studied the long-term evolution of an isolated stable and stationary Mestel disc (Mestel 1963) sampled by pointwise particles. When evolved for hundreds of dynamical times, such a disc would secularly diffuse in action-space through the spontaneous generation of transient spiral structures. Figure 7 of S12 shows for instance the late time formation of resonant ridges along very specific resonant directions. Such features are possible signatures of secular evolution, which results in a long-term aperiodic evolution of a self-gravitating system, during which small resonant and cumulative effects can add up in a coherent way. These small effects, which are then amplified through the self-gravity of the system originate from finite-N effects. Indeed, the distribution function of the system is made of a finite number N of pointwise particles. Even with a perfect numerical integrator, the system would necessarily undergo encounters during which orbits feel the discreteness of the joint DF through its two point correlation. One should remark that these interactions need not be local but assume that the potential fluctuations are resonant so as to build up a secular evolution of the system. This effect, which is still present even in the absence of any numerical noise, is the effect captured by the Balescu-Lenard equation (see Fig. 1).
4.1. The disc model
The disc considered by S12 is an infinitely thin Mestel disc, for which the circular speed vφ is a constant V0 independent of the radius. Such a model represents fairly well the observed rotation curve of real galaxies. The stationary background potential ψM of such a disc and its associated surface density ΣM are given by ![\begin{eqnarray} \psi_{\rm M} (R) = V_{0}^{2} \ln \!\left[\! \frac{R}{R_{i}} \!\right] ; \;\;\; \Sigma_{\rm M} (R) = \frac{V_{0}^{2}}{2 \pi G R} , \label{potential_Sigma_Mestel} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq298.png) (81)where Ri is a scale parameter. Because of this scale invariance, the relationship between the angular momentum Jφ and the guiding radius Rg is straightforwardly given by
(81)where Ri is a scale parameter. Because of this scale invariance, the relationship between the angular momentum Jφ and the guiding radius Rg is straightforwardly given by 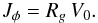 (82)Within the epicyclic approximation, the intrinsic frequencies Ωφ and κ can be computed thanks to Eqs. (22)and read
(82)Within the epicyclic approximation, the intrinsic frequencies Ωφ and κ can be computed thanks to Eqs. (22)and read 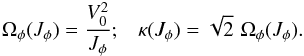 (83)We note that
(83)We note that 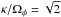 , so that the Mestel disc could be seen as an intermediate case between the Keplerian case for which κ/ Ωφ = 1 and the harmonic case for which κ/ Ωφ = 2. The ratio of the intrinsic frequencies is a important parameter for the system since it will determine the location of the resonances and a constant ratio may introduce dynamical degeneracies. This is the case for the Keplerian and harmonic discs for which κ/ Ωφ is a rational number, as discussed below Eq. (69). By contrast, for the Mestel disc, the non-rational ratio
, so that the Mestel disc could be seen as an intermediate case between the Keplerian case for which κ/ Ωφ = 1 and the harmonic case for which κ/ Ωφ = 2. The ratio of the intrinsic frequencies is a important parameter for the system since it will determine the location of the resonances and a constant ratio may introduce dynamical degeneracies. This is the case for the Keplerian and harmonic discs for which κ/ Ωφ is a rational number, as discussed below Eq. (69). By contrast, for the Mestel disc, the non-rational ratio 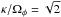 ensures that the potential is non-degenerate. Using the epicyclic approximation, the DF considered by S12 takes, as in Eq. (25), the form of a Schwarzschild DF, where the intrinsic frequencies are given by Eq. (83), the velocity dispersion σr is constant throughout the entire disc, and the surface density is given by Σt, i.e. the active surface density of the disc. Indeed, in order to accommodate the central singularity and the infinite extent of the Mestel disc, one introduces tapering functions Tinner and Touter to damp out the inner and outer regions, which read
ensures that the potential is non-degenerate. Using the epicyclic approximation, the DF considered by S12 takes, as in Eq. (25), the form of a Schwarzschild DF, where the intrinsic frequencies are given by Eq. (83), the velocity dispersion σr is constant throughout the entire disc, and the surface density is given by Σt, i.e. the active surface density of the disc. Indeed, in order to accommodate the central singularity and the infinite extent of the Mestel disc, one introduces tapering functions Tinner and Touter to damp out the inner and outer regions, which read ![\begin{eqnarray} \begin{cases} \displaystyle T_{\rm inner} (J_{\phi}) = \frac{J_{\phi}^{\nu_{\rm t}}}{(R_{i} V_{0})^{\nu_{\rm t}} \!+\! J_{\phi}^{\nu_{\rm t}}} , \\ \displaystyle T_{\rm outer} (J_{\phi}) = \bigg[ 1 \!+\! \bigg[ \frac{J_{\phi}}{R_{0} V_{0}} \bigg]^{\mu_{\rm t}} \bigg]^{-1} , \end{cases} \label{definition_tapering_functions} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq313.png) (84)where νt and μt control the sharpness of the two tapers and R0 is an additional scale parameter. The two tapers are physically motivated by the presence of a bulge and an outer truncation for the disc. Moreover, in order to reduce the susceptibility of the disc, we also suppose that only a fraction ξ of the disc is self-gravitating, with 0 ≤ ξ ≤ 1, so that the rest of the gravitational field is provided by the static halo. As a conclusion, the active surface density Σt is given by
(84)where νt and μt control the sharpness of the two tapers and R0 is an additional scale parameter. The two tapers are physically motivated by the presence of a bulge and an outer truncation for the disc. Moreover, in order to reduce the susceptibility of the disc, we also suppose that only a fraction ξ of the disc is self-gravitating, with 0 ≤ ξ ≤ 1, so that the rest of the gravitational field is provided by the static halo. As a conclusion, the active surface density Σt is given by 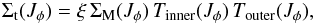 (85)where ΣM is the surface density of the Mestel disc from Eq. (81). We place ourselves in the same units system as in S12, so that we have V0 = G = Ri = 1. The other numerical factors are given by σr = 0.284, νt = 4, μt = 5, ξ = 0.5 and R0 = 11.5. The shape of the active surface density is illustrated in Fig. 4. The initial contours of the Schwarzschild DF from Eq. (25)are shown in Fig. 5. One can also straightforwardly estimate the total active mass of such a disc, given by Mtot ≃ 5.4. For such an almost scale invariant disc, the local Toomre parameter, Q (Toomre 1964)
(85)where ΣM is the surface density of the Mestel disc from Eq. (81). We place ourselves in the same units system as in S12, so that we have V0 = G = Ri = 1. The other numerical factors are given by σr = 0.284, νt = 4, μt = 5, ξ = 0.5 and R0 = 11.5. The shape of the active surface density is illustrated in Fig. 4. The initial contours of the Schwarzschild DF from Eq. (25)are shown in Fig. 5. One can also straightforwardly estimate the total active mass of such a disc, given by Mtot ≃ 5.4. For such an almost scale invariant disc, the local Toomre parameter, Q (Toomre 1964) 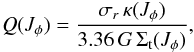 (86)which for Q> 1 ensures the stability of the disc with respect to local axisymmetric disturbances, becomes almost independent of the radius, especially in the intermediate regions of the disc. As illustrated in Fig. 6, Q ≃ 1.5 between the tapers and increases strongly in the tapered regions.
(86)which for Q> 1 ensures the stability of the disc with respect to local axisymmetric disturbances, becomes almost independent of the radius, especially in the intermediate regions of the disc. As illustrated in Fig. 6, Q ≃ 1.5 between the tapers and increases strongly in the tapered regions.
 |
Fig. 4 Surface density Σt of the tapered Mestel disc. The unit system has been chosen so that V0 = G = Ri = 1. Because of the tapering functions, the self-gravity of the disc is turned off in the inner and outer regions. |
 |
Fig. 5 Contours of the initial distribution function in action-space (Jφ,Jr), within the epicyclic approximation. The contours are spaced linearly between 95% and 5% of the distribution function maximum. |
The expression (10)of the secular diffusion flux requires summing on all the resonances m. S12 restricted pertubations forces to mφ = 2, so that we may impose this same restriction on the considered azimuthal number mφ. Throughout our numerical calculations, we will restrict ourselves to only three different resonances which are: the inner Lindblad resonance (ILR) corresponding to 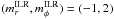 , the outer Lindblad resonance (OLR) given by
, the outer Lindblad resonance (OLR) given by 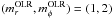 and the corotation resonance (COR) for which
and the corotation resonance (COR) for which 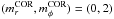 . Moreover, all the calculations in the upcoming sections have also been performed while taking into account the contributions from the resonances with mr = ± 2, which were checked to be subdominant. Being able to perform such a restriction to the relevant resonances appearing in the secular flux ℱtot from Eq. (10)is an important step of the calculation.
. Moreover, all the calculations in the upcoming sections have also been performed while taking into account the contributions from the resonances with mr = ± 2, which were checked to be subdominant. Being able to perform such a restriction to the relevant resonances appearing in the secular flux ℱtot from Eq. (10)is an important step of the calculation.
Returning to the fast and slow coordinates from Eq. (14), one can note that the diffusion associated with the COR resonance amounts to diffusion along the Jφ-axis. Such diffusion brings stars from one quasi-circular orbit to another of a different radius and is called radial migration. Conversely, the diffusion associated with the ILR and OLR resonances exhibits a non-zero diffusion component in the Jr-direction. It therefore increases the velocity dispersion within the disc so as to heat it, while either decreasing (ILR) or increasing (OLR) star’s angular momentum.
4.2. Disc amplification
One may now study the behaviour of the amplification eigenvalues λkr given by Eq. (62), thanks to which one can perform the improved approximation of the small denominators. For a given resonance m and angular momentum Jφ, the amplification function kr → λkr is presented in Fig. 7.
 |
Fig. 6 Dependence of the local Q Toomre parameter with the angular momentum. It is scale invariant except in the inner/outer regions because of the presence of the tapering functions Tinner and Touter. The unit system has been chosen so that V0 = G = Ri = 1. |
 |
Fig. 7 Variations of the response matrix eigenvalues λ with the WKB-frequency kr, for m = mCOR and two values of Jφ. The curve that peaks at large kr is for the smaller value of Jφ. |
As Eq. (62)only depend on s2, the ILR and OLR resonances always have the same response matrix eigenvalues. One can also note that the eigenvalues λ(kr) are maximum for a frequency kmax(Jφ), where λ(kmax) = λmax, in a region whose size is given by the width at half maximum Δkλ. Because of the scale-invariance property of the Mestel disc, it is straighforward to show that Δkλ ∝ 1 /Jφ, kmax ∝ 1 /Jφ and kinf / sup ∝ 1 /Jφ. One can then consider the behaviour of the amplification factor 1 / (1 − λmax), which encodes the strength of the self-gravitating amplification, as shown in Fig. 8.
 |
Fig. 8 Dependence of the amplification factor 1 / (1 − λmax) with the position Jφ in the disc. The amplification associated with the COR is always larger than the one associated with the ILR and OLR. |
We note that the COR resonance is always more amplified than the ILR and OLR resonances, but the maximum amplification (~3 for the COR and ~1.5 for the ILR and OLR) remains sufficiently small, so that the susceptibility coefficients from Eq. (4)are not dominated only by the self-gravitating amplification.
 |
Fig. 9 Map of N div(ℱtot), where the total flux ℱtot has been summed over the three resonances (ILR, COR and OLR). Red contours, for which N div(ℱtot) < 0, correspond to regions from which the orbits will be depleted, whereas blue contours, for which N div(ℱtot) > 0, correspond to regions where secular diffusion will tend to increase the value of the DF. The net fluxes involve simultaneously radial migration near (Jφ,Jr) ~ (1.8,0), and heating near (Jφ,Jr) ~ (1,0.1). |
4.3. Computing the diffusion flux
Given the knowledge of the eigenvalues, it is now straightforward to compute the susceptibility coefficients within the improved approximation of the small denominators thanks to Eq. (77), where the integration on kr is performed for kr ∈ [ kinf ; ksup ]. One can then compute the associated drift and diffusion coefficients respectively given by Eqs. (79)and (80). The diffusion flux ℱtot defined in Eq. (10)immediately follows, where the sum on m is restricted only to the three resonances ILR, COR and OLR. In Appendices E and F, we discuss two specific properties of such a truncated Mestel disc, namely the cancellation between the radial components of the diffusion and drift elements (the Schwarzshild conspiracy, Appendix E) and the natural and intrinsic presence of a temporal frequency bias (Appendix F), both of which enlighten the subtle arbitrations between the different resonances.
 |
Fig. 10 Overlay of the WKB predictions for the divergence of the diffusion flux N div(ℱtot) and the differences between the initial and the evolved DF in S12’s simulation. The opaque contours correspond to the differences in the action-space for the DF in S12 between the time tS12 = 1000 and tS12 = 0 (see the upper panel of S12’s Fig. 10). The red opaque contours correspond to negative differences, so that these regions are emptied from their orbits, whereas blue opaque contours correspond to positive differences, i.e. regions where the DF has increased through diffusion. The transparent contours correspond to the predicted values of N div(ℱtot) using the same conventions as in Fig. 9. We note the overlap of the predicted transparent red and blue contours with the measured solid ones. |
 |
Fig. 11 Overlay of the WKB predictions for the divergence of the diffusion flux N div(ℱtot) on top of the contours of the DF in action-space measured in the S12 simulation. The black background contours are the levels contours of the DF at time tS12 = 1400 (see the lower panel of Fig. 7 of S12). These contours are spaced linearly between 95% and 5% of the DF maximum and exhibit clearly the appearance of a resonant ridge. The coloured transparent contours correspond to the predicted values of N div(ℱtot) using the same conventions as in Fig. 9. We note that the developed late time ridge is consistent with the predicted depletion (red) and enrichment (blue) of orbits. |
Finally, we may compute the divergence of this flux, div(ℱtot) given by Eq. (11)in order to compare quantitatively the WKB predictions with the results from S12’s simulations. Because the mass of the individual particles is given by μ = Mtot/N, we will consider the quantity N div(ℱtot), which is independent of N. Figure 9 represents the contours of N div(ℱtot). Comparisons of our WKB predictions with the results from S12’s simulation are illustrated in Figs. 10 and 11. In Fig. 9, red contours correspond to regions for which N div(ℱtot) < 0, so that thanks to Eq. (11)they are associated with action-space regions where the WKB Balescu-Lenard equation predicts a decrement of the DF during secular evolution. In contrast, blue contours are associated with regions for which N div(ℱtot) > 0, so that the DF will increase there. The overall picture involves two competing processes: i) the beginning of a ridge forming towards (Jφ,Jr) ~ (1,0.1); and ii) the formation of an over density near (Jφ,Jr) ~ (1.8,0). Point i) is in fact consistent with both the early time measurement of S12 as shown in Fig. 10 and the late time measurement of S12 as shown in Fig. 11. These qualitative agreements are in fact surprisingly good, given that the WKB theory is approximate and was only estimated for t = 0+. Interestingly, the early time measurement from Fig. 10 also displays a hint of an over-density on the Jr = 0 axis, in agreement with point ii), while the late time measurement suggests that the over density has split, with a hint of a second ridge forming. The time evolution of Eq. (2) is likely to explain why this over density on the axis seems to split, and why the ridge gets amplified.
In Fig. 9, we explicitly computed N div(ℱtot), so that we may now study the typical timescale of collisional relaxation predicted by the WKB Balescu-Lenard equation. This is the purpose of the next section.
4.4. Physical timescales
Given estimates of the diffusion flux, one can explicitly compute the collisional timescale, i.e. the timescale for which the finite-N effects become significant. Indeed, the larger the number N of particles, the later these effects will come into play. One should remark that our writing of the Balescu-Lenard Eq. (2)depends on N only through the mass of the individual particles given by μ = Mtot/N. Indeed, one can rewrite this kinetic equation under the form ![\begin{eqnarray} \frac{\partial F}{\partial t} + L [F] = \frac{1}{N} \, C_{\rm BL} [F] , \label{BL_with_N} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq373.png) (87)where L is the operator of pure advection, and CBL = N div(ℱtot) is the N-independent Balescu-Lenard collisional operator, i.e. the r.h.s. of Eq. (2)multiplied by N = Mtot/μ. Equation (87)underlines the fact that the collisional term is associated with a kinetic Taylor expansion in the parameter ε = 1 /N ≪ 1. Within the angle-action coordinates, the advection operator is immediately given by
(87)where L is the operator of pure advection, and CBL = N div(ℱtot) is the N-independent Balescu-Lenard collisional operator, i.e. the r.h.s. of Eq. (2)multiplied by N = Mtot/μ. Equation (87)underlines the fact that the collisional term is associated with a kinetic Taylor expansion in the parameter ε = 1 /N ≪ 1. Within the angle-action coordinates, the advection operator is immediately given by 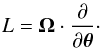 (88)Because we have assumed that F is always quasi-stationary, so that F = F(J,t) (adiabatic approximation), one has L [ F ] = 0. We now introduce the rescaled time
(88)Because we have assumed that F is always quasi-stationary, so that F = F(J,t) (adiabatic approximation), one has L [ F ] = 0. We now introduce the rescaled time 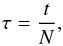 (89)so that Eq. (87)immediately becomes
(89)so that Eq. (87)immediately becomes ![\begin{eqnarray} \frac{\partial F}{\partial \tau} = C_{\rm BL} [F] \cdot \label{BL_with_mu} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq381.png) (90)Equation (90)corresponds to a rewriting of the Balescu-Lenard equation, where N is not present anymore. This will allow us to quantitatively compare the time during which the S12 simulation was run to the diffusion time predicted by our WKB Balescu-Lenard formalism. In order to ease this comparison, we place ourselves in the same units system as the one used by S12. Figure 7 of S12 for which the ridge was observed was obtained with the parameters N = 50 × 106 and ΔtS12 = 1400. Using the rescaled time introduced in Eq. (89), one obtains that S12 observed the resonant ridge after a time ΔτS12 = ΔtS12/N ≃ 3 × 10-5. One can then compare this time with the typical time required to obtain a resonant ridge within our WKB formalism. Given the map of N div(ℱtot) described in Sect. 4.3, one can estimate the typical time for which this flux could lead to the features observed in S12. The contours presented in the Fig. 7 of S12 are separated by a value of
(90)Equation (90)corresponds to a rewriting of the Balescu-Lenard equation, where N is not present anymore. This will allow us to quantitatively compare the time during which the S12 simulation was run to the diffusion time predicted by our WKB Balescu-Lenard formalism. In order to ease this comparison, we place ourselves in the same units system as the one used by S12. Figure 7 of S12 for which the ridge was observed was obtained with the parameters N = 50 × 106 and ΔtS12 = 1400. Using the rescaled time introduced in Eq. (89), one obtains that S12 observed the resonant ridge after a time ΔτS12 = ΔtS12/N ≃ 3 × 10-5. One can then compare this time with the typical time required to obtain a resonant ridge within our WKB formalism. Given the map of N div(ℱtot) described in Sect. 4.3, one can estimate the typical time for which this flux could lead to the features observed in S12. The contours presented in the Fig. 7 of S12 are separated by a value of 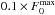 , where
, where 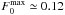 corresponds to the maximum of the normalized DF from Eq. (25). As a consequence, to observe the resonant ridge, the DF should typically change by a value of the order of
corresponds to the maximum of the normalized DF from Eq. (25). As a consequence, to observe the resonant ridge, the DF should typically change by a value of the order of 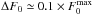 . From Fig. 9, one can note that the maximum value of the divergence of the flux is given by | N div(ℱtot) | ≃ 0.4. Finally, thanks to Eq. (11), one may write the relation ΔF0 ≃ ΔτWKB | N div(ℱtot) |, where ΔτWKB is the minimal time during which the WKB Balescu-Lenard equation has to be considered in order to develop a ridge. Thanks to the previous typical numerical values, one obtains that ΔτWKB ≃ 3 × 10-2. When comparing these two typical times, ΔτS12 the duration during which S12 simulation was performed and ΔτWKB the duration required to observe secular diffusion in the WKB Balescu-Lenard formalism, one obtains the order of magnitude
. From Fig. 9, one can note that the maximum value of the divergence of the flux is given by | N div(ℱtot) | ≃ 0.4. Finally, thanks to Eq. (11), one may write the relation ΔF0 ≃ ΔτWKB | N div(ℱtot) |, where ΔτWKB is the minimal time during which the WKB Balescu-Lenard equation has to be considered in order to develop a ridge. Thanks to the previous typical numerical values, one obtains that ΔτWKB ≃ 3 × 10-2. When comparing these two typical times, ΔτS12 the duration during which S12 simulation was performed and ΔτWKB the duration required to observe secular diffusion in the WKB Balescu-Lenard formalism, one obtains the order of magnitude 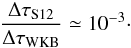 (91)Hence the direct application of the WKB-limited Balescu-Lenard equation does not allow us to predict the observed timescale for the diffusion features in simulations. Indeed, the timescale of collisional diffusion predicted by this WKB formalism seems much larger than the time during which the numerical simulation was performed. This discrepancy is also strengthened by the use of a softening length in numerical simulations, which induces an effective thickening of the disc, so as to slow down the collisional relaxation. A possible explanation for this timescale discrepancy is discussed in the next section.
(91)Hence the direct application of the WKB-limited Balescu-Lenard equation does not allow us to predict the observed timescale for the diffusion features in simulations. Indeed, the timescale of collisional diffusion predicted by this WKB formalism seems much larger than the time during which the numerical simulation was performed. This discrepancy is also strengthened by the use of a softening length in numerical simulations, which induces an effective thickening of the disc, so as to slow down the collisional relaxation. A possible explanation for this timescale discrepancy is discussed in the next section.
4.5. Interpretation
In order to interpret S12’s simulation under the light of a collisional secular diffusion equation, such as the Balescu-Lenard equation and its WKB limit, one should first note the undisputed presence of collisional effects in S12’s simulation. Indeed, Fig. 2 of S12 shows that when the number of particles of the simulation is increased, the strength of the density fluctuations is delayed, which in turn is likely to be related to the amplitude of the secular features. The larger the number of particles, the later the effect of secular diffusion. Such dependence illustrates the fact that discreteness effects do play a role in the secular diffusion observed in S12.
Sellwood & Kahn (1991) have argued that a sequence of causally connected swing amplified transients could occur subject to a (possibly non-local) resonant condition between successive spiral waves. The Balescu-Lenard formalism captures precisely such sequences – in as much as it integrates over dressed correlated potential fluctuations subject to relative resonant conditions, but does not preserve causality nor resolve them on dynamical timescales. The exact initial phases are not relevant in the Balescu-Lenard formalism: see Appendix A for a sketch of a full derivation which makes this point clear.
The timescale discrepancy observed in Eq. (91)might be driven by the incompleteness of the WKB basis. Indeed, Eq. (26)’s basis – thanks to which the susceptibility coefficients were evaluated in Eq. (77)– does not form a complete set, as it can only represent correctly tightly wound spirals. It also enforces local resonances, and does not allow for remote orbits to resonate, or wave packets to propagate between such non-local resonances. The seminal works from Goldreich & Lynden-Bell (1965), Julian & Toomre (1966), Toomre (1981) showed that any leading spiral wave during its unwinding to a trailing wave undergoes a significant amplification, coined swing amplification. Because it involves open spirals this mechanism is not captured by the WKB formalism. This additional amplification is expected to increase the susceptibility of the disc and therefore accelerate secular diffusion (both drift and diffusion), so that the timescales discrepancy from Eq. (91)will become less restrictive. Following the notations from Toomre (1981), the truncated Mestel disc considered in the S12 simulation corresponds to Q ≃ 1.5 and X = 2, so that Fig. 7 from Toomre (1981) shows that significant swing amplification (of order 10) may be expected. It has also been claimed (Toomre & Kalnajs 1991) that swing amplified shot noise in the shearing sheet approximation would behave like significantly heavier macro-particles. Such an amplification would keep a dependence of the secular response with the total number N of particles, but would reduce significantly the effective number of particles.
The Balescu-Lenard WKB limit seems to capture qualitatively the main features of the initial diffusion process in action space (as discussed in Sect. 4.3), but falls short in predicting the relevant timescale. The remaining questions are therefore: what is the exact impact of swing amplification? Can it explain the timescale discrepancy?
5. Conclusion
We implemented the inhomogeneous Balescu-Lenard Eq. (2)for an infinitely thin galactic disc using two main approximations. We first assumed the disc to be tepid. We could then use the epicyclic approximation which allowed for an explicit mapping between the physical coordinates (x,v) and the angle-action coordinates (θ,J) via Eq. (24). Our second approximation relied on the introduction of the tightly wound basis elements from Eq. (26). Because of the corresponding WKB approximation, we obtained in Eq. (62)a diagonal response matrix, so that gravity is effectively treated locally. The associated scale-decoupling hypothesis yields a crucial restriction to only local resonances, as shown in Eq. (72). We then derived in Eq. (77)a simple quadrature for the susceptibility coefficients, given by Eqs. (B.7)and (B.8)for the bare ones. Thanks to this restriction to local resonances, we were also able to write the drift and diffusion coefficients as simple quadratures in Eqs. (79)and (80).
These simple expressions derived within the WKB formalism yield, to our knowledge, a first non-trivial explicit expression for the Balescu-Lenard diffusion and drift coefficients. They are certainly useful to provide insight into the physical processes at work during the secular diffusion of a self-gravitating discrete disc. Moreover, modulo the restriction to the three physically motivated resonances ILR, COR and OLR, our WKB formalism can be used for quantitative comparisons to numerical experiments such as the one presented in Sellwood (2012). It considered a stable isolated Mestel disc sampled by pointwise particles, whose secular evolution is induced by finite-N effects ideally captured by the Balescu-Lenard equation.
The straightforward calculation in the WKB limit of the divergence of the full diffusion flux, N div(ℱtot), illustrated in Figs. 9–11, recovered most of the secular features observed in S12. This qualitative agreement is impressive given the level of approximation involved in the WKB limit. The hints for the formation of a ridge – depletion and enrichment of orbits along a preferred direction – is qualitatively consistent with the findings of S12 and Fouvry & Pichon (2015), Fouvry et al. (2015a), without postulating additional assumptions about the source of fluctuations5.
The comparison of the collisional time predicted in the WKB limit (Eq. (91)) to the diffusion time of S12 simulation, highlights nonetheless a significant quantitative overestimation. We provided a possible explanation which relies on the intrinsic limitations of the WKB formalism, as it cannot account for swing amplification, during which unwinding transient spirals are strongly amplified. This additional amplification, which involves explicitly non-local wave absorption and emission, may be the missing contribution required to reconcile quantitatively our predictions and the simulation. One venue will be to compute numerically exactly Eqs. (8)and (9)in action space – without assuming tightly wound spirals or epicyclic orbits – with a complete basis6. This is the topic of an upcoming numerical investigation in Fouvry et al. (2015c).
Should this complementary investigation explain the timescale mismatch, one would be in a stronger position to validate the accuracy of N-body schemes to correctly capture secular evolution of discrete self-gravitating cold discs over very long timescales. This would clearly be a worthy assessment of such schemes relying on the Balescu-Lenard theory. Once the above described conundrum is resolved, we will also be able to evolve over secular times the Balescu-Lenard equation and predict the full cosmic time evolution of such discrete discs. This may also contribute to solving the timescale discrepancy.
In closing, beyond the application presented in Sect. 4, the above developed tightly wound Balescu-Lenard formalism may for instance describe the secular diffusion of giant molecular clouds in galactic discs (which in turn could play a role in migration driven metallicity gradients and disc thickening), the secular migration of planetesimals in partially self-gravitating proto-planetary discs, or even the long-term evolution of population of stars, gas blobs and debris near the Galactic centre. Such topics will be subject to further investigations.
Online material
Appendix A: Sketch of Balescu-Lenard derivation
Two derivations of the inhomogeneous Balescu-Lenard equation have been presented in the literature. The first one (Heyvaerts 2010) is based on the appropriate truncation at the order 1 /N of the BBGKY hierarchy. The second (Chavanis 2012a) relies on the Klimontovich equation, using a quasilinear approximation. We now briefly sketch the derivation presented in Chavanis (2012a). We consider an isolated system of N particles in interaction, of mass μ, in a physical space of dimension d. Their dynamics is entirely described by Hamilton’s equations 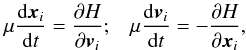 (A.1)where the Hamiltonian of the system is given by
(A.1)where the Hamiltonian of the system is given by 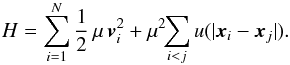 (A.2)Here u( | xi − xj |) is the binary potential of interaction. In the gravitational case, it satisfies u(x) = − G/ | x |. One can now introduce the discrete distribution function Fd(x,v,t) defined as
(A.2)Here u( | xi − xj |) is the binary potential of interaction. In the gravitational case, it satisfies u(x) = − G/ | x |. One can now introduce the discrete distribution function Fd(x,v,t) defined as  (A.3)along with the corresponding potential
(A.3)along with the corresponding potential  (A.4)One can show that Fd satisfies the Klimontovich equation (Klimontovich 1967)
(A.4)One can show that Fd satisfies the Klimontovich equation (Klimontovich 1967) 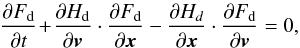 (A.5)where we have defined the Hamiltonian Hd as
(A.5)where we have defined the Hamiltonian Hd as 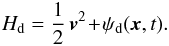 (A.6)At this stage, it is important to note that the Klimontovich Eq. (A.5)contains exactly the same information as Hamilton’s Eqs. (A.1). We now introduce the smooth distribution function F(x,v,t) = ⟨ Fd(x,v,t) ⟩, corresponding to an average of Fd over a large number of initial conditions. One can then write Fd = F + δF, where δF denotes fluctuations around the smooth distribution. In a similar way, we introduce ψ(x,v,t) = ⟨ ψd(x,v,t) ⟩, so that ψd = ψ + δψ. We have therefore decomposed the discrete distribution function Fd into a smooth component F that evolves slowly with time, whereas the fluctuating component δF evolves more rapidly. As a consequence, when considering the evolution of the fluctuations, one can assume the smooth distribution to be frozen. Using this timescale-decoupling approach, one can use the angle-action coordinates (θ1,J1) associated with the quasi-stationary smooth potential ψ to describe the fast evolution of the fluctuations. Using these decompositions and this change of coordinates, Eq. (A.5)takes the form of two evolution equations
(A.6)At this stage, it is important to note that the Klimontovich Eq. (A.5)contains exactly the same information as Hamilton’s Eqs. (A.1). We now introduce the smooth distribution function F(x,v,t) = ⟨ Fd(x,v,t) ⟩, corresponding to an average of Fd over a large number of initial conditions. One can then write Fd = F + δF, where δF denotes fluctuations around the smooth distribution. In a similar way, we introduce ψ(x,v,t) = ⟨ ψd(x,v,t) ⟩, so that ψd = ψ + δψ. We have therefore decomposed the discrete distribution function Fd into a smooth component F that evolves slowly with time, whereas the fluctuating component δF evolves more rapidly. As a consequence, when considering the evolution of the fluctuations, one can assume the smooth distribution to be frozen. Using this timescale-decoupling approach, one can use the angle-action coordinates (θ1,J1) associated with the quasi-stationary smooth potential ψ to describe the fast evolution of the fluctuations. Using these decompositions and this change of coordinates, Eq. (A.5)takes the form of two evolution equations 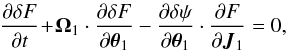 (A.7)and
(A.7)and 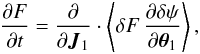 (A.8)where we have introduced the intrinsic frequencies of the system Ω1 = Ω(J1), as in Eq. (1), and where ⟨ . ⟩ denotes an angle average. Because of our timescale-decoupling approach, we may neglect the time variation of F(J1,t) in the calculation of the collision term (adiabatic approximation). It implies that F may be treated as a constant in Eq. (A.7)because F evolves on a (relaxation) timescale much larger than the (dynamical) time corresponding to the evolution of δF. In order to be valid, this approximation requires that N ≫ 1. Finally, we also assume that the distribution F remains Vlasov stable, so that its evolution is only governed by correlations and not by dynamical instabilities.
(A.8)where we have introduced the intrinsic frequencies of the system Ω1 = Ω(J1), as in Eq. (1), and where ⟨ . ⟩ denotes an angle average. Because of our timescale-decoupling approach, we may neglect the time variation of F(J1,t) in the calculation of the collision term (adiabatic approximation). It implies that F may be treated as a constant in Eq. (A.7)because F evolves on a (relaxation) timescale much larger than the (dynamical) time corresponding to the evolution of δF. In order to be valid, this approximation requires that N ≫ 1. Finally, we also assume that the distribution F remains Vlasov stable, so that its evolution is only governed by correlations and not by dynamical instabilities.
The first step of the derivation of the Balescu-Lenard equation is then to study the short timescale evolution Eq. (A.7). One defines the Fourier-Laplace transform of the fluctuation δF as 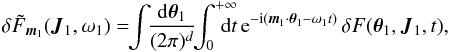 (A.9)valid for Im(ω1) sufficiently large. Similarly to Eq. (6), one also defines the spatial Fourier tranform of the initial value as
(A.9)valid for Im(ω1) sufficiently large. Similarly to Eq. (6), one also defines the spatial Fourier tranform of the initial value as 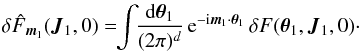 (A.10)Thanks to these transformations, Eq. (A.7)may be rewritten under the form
(A.10)Thanks to these transformations, Eq. (A.7)may be rewritten under the form 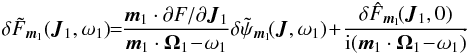 (A.11)We now use the basis elements introduced in Eq. (3), so that we may decompose the potential fluctuations under the form
(A.11)We now use the basis elements introduced in Eq. (3), so that we may decompose the potential fluctuations under the form 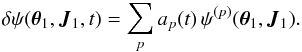 (A.12)We introduce the Laplace transform of ap(t) as
(A.12)We introduce the Laplace transform of ap(t) as 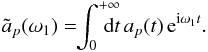 (A.13)One can then take the inverse Fourier transform of Eq. (A.11), multiply by
(A.13)One can then take the inverse Fourier transform of Eq. (A.11), multiply by 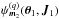 and integrate over θ1 and J1 (using the property that dxdv = dθ1dJ1). One gets
and integrate over θ1 and J1 (using the property that dxdv = dθ1dJ1). One gets ![\appendix \setcounter{section}{1} \begin{eqnarray} \tilde{a}_{p} (\omega_{1}) &=&- (2 \pi)^{d} \sum_{q} \left[ \mathbf{I} - \widehat{\mathbf{M}} (\omega_{1}) \right]_{pq}^{-1} \! \nonumber\\ &&\times \sum_{{\vec m}_{2}} \int \mathrm{d} {\vec J}_{2} \frac{\delta \hat{F}_{{\vec m}_{2}} ({\vec J}_{2} , 0)}{{\rm i} ({\vec m}_{2} \cdot {\vec \Omega}_{2} - \omega_{1} \!)} \, \psi^{(q) *}_{{\vec m}_{2}} ({\vec J}_{2}) , \label{calculation_evolution_fast_II_derivation} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq435.png) (A.14)where the response matrix
(A.14)where the response matrix  is given by Eq. (5). Equation (A.14)can be rewritten under the form
is given by Eq. (5). Equation (A.14)can be rewritten under the form 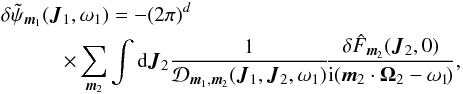 (A.15)where the susceptibility coefficients have been introduced in Eq. (4). One can now compute the collision term appearing in the r.h.s. of Eq. (A.8). It requires us to evaluate
(A.15)where the susceptibility coefficients have been introduced in Eq. (4). One can now compute the collision term appearing in the r.h.s. of Eq. (A.8). It requires us to evaluate 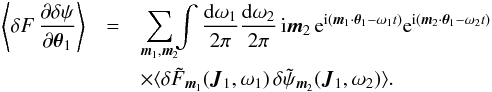 (A.16)Using Eq. (A.11), one immediately obtains that
(A.16)Using Eq. (A.11), one immediately obtains that 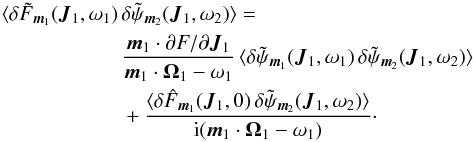 (A.17)In Eq. (A.17), the first term corresponds to the self-correlation of the potential whereas the second term corresponds to the correlations between the potential fluctuations and the distribution function at time t = 0. Each of these terms must then be considered one at a time. Assuming that there is no correlation in the initial phases, one can show (see Appendix C from Chavanis 2012a) that
(A.17)In Eq. (A.17), the first term corresponds to the self-correlation of the potential whereas the second term corresponds to the correlations between the potential fluctuations and the distribution function at time t = 0. Each of these terms must then be considered one at a time. Assuming that there is no correlation in the initial phases, one can show (see Appendix C from Chavanis 2012a) that 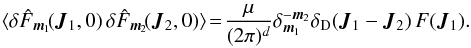 (A.18)Hence, given Eq. (A.15), one can rewrite the first term of Eq. (A.17)under the form
(A.18)Hence, given Eq. (A.15), one can rewrite the first term of Eq. (A.17)under the form 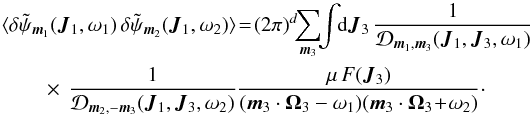 (A.19)If we consider only the contributions that do not decay in time, one can perform the substitution
(A.19)If we consider only the contributions that do not decay in time, one can perform the substitution
Starting from Eq. (A.19), thanks to the previous substitution and using the fact that 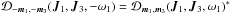 , one can show that the first contribution from Eq. (A.16)takes the form
, one can show that the first contribution from Eq. (A.16)takes the form 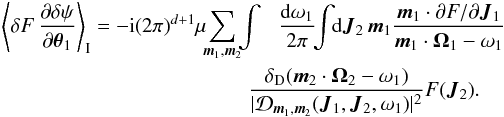 (A.20)The last step of the calculation is to use the Landau prescription ω → ω + i0+ along with Plemelj formula
(A.20)The last step of the calculation is to use the Landau prescription ω → ω + i0+ along with Plemelj formula 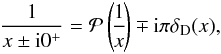 (A.21)where
(A.21)where 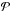 is the principal value. One can then rewrite Eq. (A.20)under the form
is the principal value. One can then rewrite Eq. (A.20)under the form  (A.22)Similarly, one can rewrite the second term of Eq. (A.17)under the form
(A.22)Similarly, one can rewrite the second term of Eq. (A.17)under the form 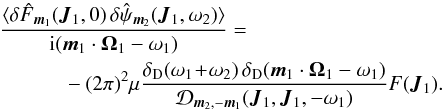 (A.23)Using symmetries of the matrix
(A.23)Using symmetries of the matrix ![\hbox{${ [\mathbf{I} - \widehat{\mathbf{M}}]^{-1} }$}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq450.png) , starting from Eq. (A.23), one can show that the second contribution from Eq. (A.16)finally takes the form
, starting from Eq. (A.23), one can show that the second contribution from Eq. (A.16)finally takes the form 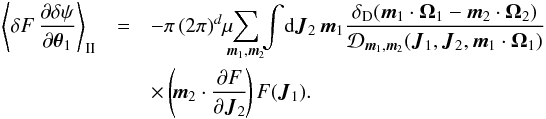 (A.24)Combining the two contributions obtained in Eqs. (A.22)and (A.24), one can rewrite Eq. (A.16)under the form
(A.24)Combining the two contributions obtained in Eqs. (A.22)and (A.24), one can rewrite Eq. (A.16)under the form 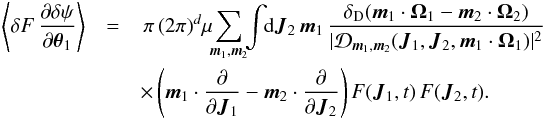 (A.25)Hence, using the slow evolution Eq. (A.8), we recover the Balescu-Lenard equation introduced in Eq. (2). As a final remark, one may notice that on the short dynamical timescale, the evolution is governed by Eq. (A.7), which involves the fluctuating components δF and δψ of the distribution function and the potential. In contrast, on the long secular timescale, the evolution is governed by Eq. (A.8), which after an angle-average only involves the mean distribution function F. Indeed, thanks to the ensemble average, all the cross-correlations between the fluctuations δF and δψ, as in Eqs. (A.18), (A.19)and (A.23)can be expressed in terms of the underlying smooth distribution function F only, so that the fluctuating components are absent from the secular Balescu-Lenard collision operator from Eq. (A.25).
(A.25)Hence, using the slow evolution Eq. (A.8), we recover the Balescu-Lenard equation introduced in Eq. (2). As a final remark, one may notice that on the short dynamical timescale, the evolution is governed by Eq. (A.7), which involves the fluctuating components δF and δψ of the distribution function and the potential. In contrast, on the long secular timescale, the evolution is governed by Eq. (A.8), which after an angle-average only involves the mean distribution function F. Indeed, thanks to the ensemble average, all the cross-correlations between the fluctuations δF and δψ, as in Eqs. (A.18), (A.19)and (A.23)can be expressed in terms of the underlying smooth distribution function F only, so that the fluctuating components are absent from the secular Balescu-Lenard collision operator from Eq. (A.25).
Appendix B: Turning off collective effects
The reference Chavanis (2013b; see also Appendix A of Chavanis 2012a) considers the inhomogeneous Balescu-Lenard equation without collective effects. This collisional kinetic equation is the equivalent of the Landau equation for inhomogeneous systems. It can be straightforwardly obtained as an approximation of the Balescu-Lenard Eq. (2). Indeed, one has to make the substitution from the dressed susceptibility coefficients 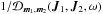 to the bare ones given by Am1,m2(J1,J2), so that the inhomogeneous Balescu-Lenard equation without collective effects (i.e. the inhomogeneous Landau equation) is given by
to the bare ones given by Am1,m2(J1,J2), so that the inhomogeneous Balescu-Lenard equation without collective effects (i.e. the inhomogeneous Landau equation) is given by ![\appendix \setcounter{section}{2} \begin{eqnarray} && \frac{\partial F}{\partial t} = \pi (2 \pi)^{d} \mu \frac{\partial }{\partial {\vec J}_{1}} \cdot \Bigg[ \sum_{{\vec m}_{1} , {\vec m}_{2}} \!\! {\vec m}_{1} \!\! \int \!\! \mathrm{d} {\vec J}_{2} \, \delta_{\rm D} ({\vec m}_{1} \cdot {\vec \Omega}_{1} - {\vec m}_{2} \cdot {\vec \Omega}_{2}) \nonumber \\ && \times \! | A_{{\vec m}_{1} , {\vec m}_{2}} ({\vec J}_{1} , {\vec J}_{2}) |^{2} \!\left( {\vec m}_{1} \! \cdot\! \frac{\partial }{\partial {\vec J}_{1}} \!- \! {\vec m}_{2} \!\cdot\! \frac{\partial }{\partial {\vec J}_{2}} \right) F ({\vec J}_{1} , t) F ({\vec J}_{2} , t) \!\Bigg] , \label{initial_BL_bare} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq456.png) (B.1)where the coefficients Am1,m2 are associated with the Fourier transform in angles of the interaction potential (Pichon 1994; Chavanis 2013b) and read
(B.1)where the coefficients Am1,m2 are associated with the Fourier transform in angles of the interaction potential (Pichon 1994; Chavanis 2013b) and read 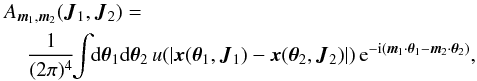 (B.2)where u(x) is the binary potential of interaction given by u(x) = − G/ | x | in the gravitational case. A key remark at this stage is that the expression (B.2)does not require the introduction of biorthogonal basis elements as in Eq. (3), whereas in order to estimate the dressed susceptibility coefficients from Eq. (4), one must necessarily rely on Kalnajs’ matrix method (Kalnajs 1976). It is however possible to express Am1,m2 using the potential basis. Indeed, for a fixed value of x2, we consider the function x1 → u(x1 − x2). One can then decompose this function on the basis elements ψ(p)(x1), so that we may write
(B.2)where u(x) is the binary potential of interaction given by u(x) = − G/ | x | in the gravitational case. A key remark at this stage is that the expression (B.2)does not require the introduction of biorthogonal basis elements as in Eq. (3), whereas in order to estimate the dressed susceptibility coefficients from Eq. (4), one must necessarily rely on Kalnajs’ matrix method (Kalnajs 1976). It is however possible to express Am1,m2 using the potential basis. Indeed, for a fixed value of x2, we consider the function x1 → u(x1 − x2). One can then decompose this function on the basis elements ψ(p)(x1), so that we may write 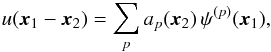 (B.3)where it is important to note that the basis coefficients ap(x2) are functions of x2. Thanks to the biorthogonality property of the basis detailed in Eq. (3), one can obtain the expression of the coefficients ap(x2) which reads
(B.3)where it is important to note that the basis coefficients ap(x2) are functions of x2. Thanks to the biorthogonality property of the basis detailed in Eq. (3), one can obtain the expression of the coefficients ap(x2) which reads ![\appendix \setcounter{section}{2} \begin{eqnarray} a_{p} ({\vec x}_{2}) & =& - \!\! \int \!\! \mathrm{d} {\vec x}_{1} \, u ({\vec x}_{1} - {\vec x}_{2}) \, \rho^{(p) *} ({\vec x}_{1}) \nonumber \\ & =& - \left[ \int \!\! \mathrm{d} {\vec x}_{1} \, u ({\vec x}_{1} - {\vec x}_{2}) \, \rho^{(p)} ({\vec x}_{1}) \right]^{*} \nonumber \\ & = &- \psi^{(p) *} ({\vec r}_{2}) , \label{expression_ap_x2} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq466.png) (B.4)where we used the fact that u is a real function. Hence we finally obtain
(B.4)where we used the fact that u is a real function. Hence we finally obtain 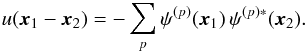 (B.5)Taking appropriately a Fourier transform with respect to the angles as in Eq. (B.2), we obtain
(B.5)Taking appropriately a Fourier transform with respect to the angles as in Eq. (B.2), we obtain 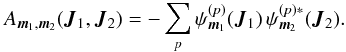 (B.6)This fairly simple relation allows us to express the bare susceptibility coefficients Am1,m2 using the potential basis. One does not need anymore to perform a Fourier transform in angles of the interaction potential because the resolution of Poisson’s equation has been implicitly hidden in the effective construction of the basis elements7. Neglecting the collective effects in the expression (4)of the dressed susceptibility coefficients amounts to taking
(B.6)This fairly simple relation allows us to express the bare susceptibility coefficients Am1,m2 using the potential basis. One does not need anymore to perform a Fourier transform in angles of the interaction potential because the resolution of Poisson’s equation has been implicitly hidden in the effective construction of the basis elements7. Neglecting the collective effects in the expression (4)of the dressed susceptibility coefficients amounts to taking 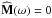 , so that we obtain
, so that we obtain 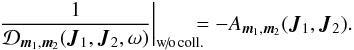 (B.7)The negative sign in Eq. (B.7)plays no significant role in the kinetic equations since one has to make the substitution of the square modulus
(B.7)The negative sign in Eq. (B.7)plays no significant role in the kinetic equations since one has to make the substitution of the square modulus  in the Balescu-Lenard Eq. (2)to obtain the inhomogeneous Landau Eq. (B.1). Using our WKB basis, one can proceed similarly as in the dressed case, by limiting oneself only to local resonances. Equation (76)therefore becomes in the bare case
in the Balescu-Lenard Eq. (2)to obtain the inhomogeneous Landau Eq. (B.1). Using our WKB basis, one can proceed similarly as in the dressed case, by limiting oneself only to local resonances. Equation (76)therefore becomes in the bare case ![\appendix \setcounter{section}{2} \begin{eqnarray} A_{{\vec m}_{1} , {\vec m}_{1}} && (R_{1} , J_{r}^{1} , R_{1} , J_{r}^{2}) = - \frac{1}{2 \pi} \frac{G}{R_{1}} \nonumber \\ && \qquad \qquad\times \, \int_{1\!/\! \sigma_{k}}^{\infty} \!\!\!\!\! \mathrm{d} k_{r} \, \frac{1}{k_{r}} \, \mathcal{J}_{m_{1}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{r} \!\right] \, \mathcal{J}_{m_{2}^{r}} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{r} \!\right] . \label{expression_Am1_m2_WKB} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq473.png) (B.8)This expression of the bare susceptibility coefficients can be straightforwardly obtained from the dressed ones by imposing λ = 0. One should note that because of the absence of the amplification term 1 / (1 − λkr), the approximation of the small denominators cannot be used. Hence a physically motivated evaluation of the expression (B.8)becomes more subtle to perform, especially because of the possibly important role that the Coulomb logarithm 1 /kr might play. Finally, one obtains that even for exactly local resonances, i.e. m1 = m2 and R1 = R2, the use of our WKB formalism allowed us to obtain non-diverging bare susceptibility coefficients. On the other hand, one could try to estimate the bare susceptibility coefficients starting from Eq. (B.2), i.e. without using any potential basis. Using the polar coordinates (R,φ), one has to compute
(B.8)This expression of the bare susceptibility coefficients can be straightforwardly obtained from the dressed ones by imposing λ = 0. One should note that because of the absence of the amplification term 1 / (1 − λkr), the approximation of the small denominators cannot be used. Hence a physically motivated evaluation of the expression (B.8)becomes more subtle to perform, especially because of the possibly important role that the Coulomb logarithm 1 /kr might play. Finally, one obtains that even for exactly local resonances, i.e. m1 = m2 and R1 = R2, the use of our WKB formalism allowed us to obtain non-diverging bare susceptibility coefficients. On the other hand, one could try to estimate the bare susceptibility coefficients starting from Eq. (B.2), i.e. without using any potential basis. Using the polar coordinates (R,φ), one has to compute 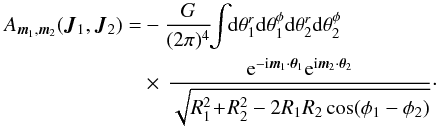 (B.9)By azimuthal symmetry, it is straightforward to show (Pichon & Cannon 1997) that
(B.9)By azimuthal symmetry, it is straightforward to show (Pichon & Cannon 1997) that 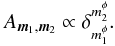 (B.10)Hence the different mφ-modes of the Am1,m2 coefficients are independent. This result is identical to what was obtained in Eq. (65)for the dressed case. In order to illustrate the regularizing role of the WKB basis from Eq. (26), we will place ourselves in the context of an extremely tepid disc, and therefore assume
(B.10)Hence the different mφ-modes of the Am1,m2 coefficients are independent. This result is identical to what was obtained in Eq. (65)for the dressed case. In order to illustrate the regularizing role of the WKB basis from Eq. (26), we will place ourselves in the context of an extremely tepid disc, and therefore assume 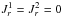 . Thanks to the epicyclic mapping from Eq. (24), one can drop all the dependences on θR appearing in R and φ. Equation (B.9)then immediately implies that
. Thanks to the epicyclic mapping from Eq. (24), one can drop all the dependences on θR appearing in R and φ. Equation (B.9)then immediately implies that 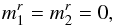 (B.11)and the bare susceptibility coefficients are given by
(B.11)and the bare susceptibility coefficients are given by 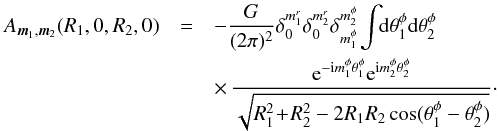 (B.12)In this illustrative limit, we have by construction no contributions from the ILR and OLR resonances for which mr ≠ 0. After an immediate change of variables, using
(B.12)In this illustrative limit, we have by construction no contributions from the ILR and OLR resonances for which mr ≠ 0. After an immediate change of variables, using 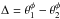 , it becomes
, it becomes 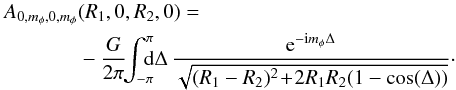 (B.13)The resonance condition from Eq. (68)takes the form mφΩφ(R1) = mφΩφ(R2) because we restricted ourselves in Eq. (B.11)to the case mr = 0. Hence assuming that the function Rg → Ωφ(Rg) is a monotonic function, one has to satisfy the constraint R1 = R2, so that we are restricting ourselves only to local resonances as in Eq. (72). For such resonances, Eq. (B.13)becomes
(B.13)The resonance condition from Eq. (68)takes the form mφΩφ(R1) = mφΩφ(R2) because we restricted ourselves in Eq. (B.11)to the case mr = 0. Hence assuming that the function Rg → Ωφ(Rg) is a monotonic function, one has to satisfy the constraint R1 = R2, so that we are restricting ourselves only to local resonances as in Eq. (72). For such resonances, Eq. (B.13)becomes 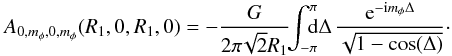 (B.14)At this stage, one must note that this integral is divergent. Indeed, for Δ → 0, one has
(B.14)At this stage, one must note that this integral is divergent. Indeed, for Δ → 0, one has 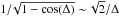 . Hence the expression of the bare susceptibility coefficients derived from the Fourier transform of the interaction potential as in Eq. (B.2), when restricted to exactly local resonances becomes logarithmically divergent. This divergence, which is observed in the case of local resonances, is induced by the interaction of singular orbits. It is important to remark that this divergence was not present in Eq. (B.8)when computing the bare susceptibility coefficients using the WKB basis from Eq. (26). This implies that the WKB basis is not complete. For a complete biorthogonal basis, the expression (B.6)of the Am1,m2 coefficients is an exact expression. However, our calculation shows that the scale-decoupled WKB basis we used, possesses a subtle regularizing incompleteness which gets rid of the diverging contributions to the coefficients Am1,m2 in the limit of exactly local resonances.
. Hence the expression of the bare susceptibility coefficients derived from the Fourier transform of the interaction potential as in Eq. (B.2), when restricted to exactly local resonances becomes logarithmically divergent. This divergence, which is observed in the case of local resonances, is induced by the interaction of singular orbits. It is important to remark that this divergence was not present in Eq. (B.8)when computing the bare susceptibility coefficients using the WKB basis from Eq. (26). This implies that the WKB basis is not complete. For a complete biorthogonal basis, the expression (B.6)of the Am1,m2 coefficients is an exact expression. However, our calculation shows that the scale-decoupled WKB basis we used, possesses a subtle regularizing incompleteness which gets rid of the diverging contributions to the coefficients Am1,m2 in the limit of exactly local resonances.
Appendix C: The Schwarzschild DF case
When considering a Schwarzschild distribution function as in Eq. (25), while relying on the approximation of the small denominators from Eq. (78), one can explicitly perform the remaining integration on the radial action 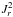 in the expressions (79)and (80)of the drift and diffusion coefficients. We now detail this explicit calculation. For such a Schwarzschild distribution function, it is straightforward to check that the gradients of the distribution function with respect to the actions are given by
in the expressions (79)and (80)of the drift and diffusion coefficients. We now detail this explicit calculation. For such a Schwarzschild distribution function, it is straightforward to check that the gradients of the distribution function with respect to the actions are given by ![\appendix \setcounter{section}{3} \begin{eqnarray} \frac{\partial F}{\partial J_{r}} = - \frac{\kappa}{\sigma_{r}^{2}} F ; \;\;\; \frac{\partial F}{\partial J_{\phi}} = F \frac{\partial }{\partial J_{\phi}} \!\left[ \ln \!\left(\! \frac{\Omega \Sigma}{\pi \kappa \sigma_{r}^{2}} \!\right) - \frac{\kappa J_{r}}{\sigma_{r}^{2}} \!\right] \cdot \label{explicit_gradients_DF} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq493.png) (C.1)Using the expression of the susceptibility coefficients from Eq. (78), after some simple algebra, one can rewrite the drift coefficients from Eq. (79)under the form
(C.1)Using the expression of the susceptibility coefficients from Eq. (78), after some simple algebra, one can rewrite the drift coefficients from Eq. (79)under the form ![\appendix \setcounter{section}{3} \begin{eqnarray} A_{{\vec m}_{1}} ({\vec J}_{1}) &=& - g_{{\vec m}_{1}} (J_{\phi}^{1} , J_{r}^{1}) \!\! \int \!\! \mathrm{d} J_{r}^{2} \, \exp \!\left[\! - \frac{\kappa}{\sigma_{r}^{2}} J_{r}^{2} \!\right] \mathcal{J}_{m_{1}^{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{\rm max} \!\right] \, \nonumber \\ &&\, \times \, \left[ m_{1}^{\phi} \!\left\{ \frac{\partial }{\partial J_{\phi}} \!\left[ \ln \!\left(\! \frac{\Omega \Sigma}{\pi \kappa \sigma_{r}^{2}} \!\right) \right] - J_{r}^{2} \frac{\partial }{\partial J_{\phi}} \!\left[\! \frac{\kappa}{\sigma_{r}^{2}} \!\right] \right\} - m_{1}^{r} \frac{\kappa}{\sigma_{r}^{2}} \right] \cdot \label{explicit_WKB_drift} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq494.png) (C.2)Similarly, the diffusion coefficients from Eq. (80)take the form
(C.2)Similarly, the diffusion coefficients from Eq. (80)take the form ![\appendix \setcounter{section}{3} \begin{eqnarray} D_{{\vec m}_{1}} ({\vec J}_{1}) = g_{{\vec m}_{1}} (J_{\phi}^{1} , J_{r}^{1}) \!\!\! \int \!\!\! \mathrm{d} J_{r}^{2} \, \exp \!\left[\! - \frac{\kappa}{\sigma_{r}^{2}} J_{r}^{2} \!\right] \mathcal{J}_{m_{1}^{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{2}}{\kappa_{1}}} k_{\rm max} \!\right] . \label{explicit_WKB_diff} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq495.png) (C.3)In Eqs. (C.2)and (C.3), in order to shorten the notations, we introduced the function
(C.3)In Eqs. (C.2)and (C.3), in order to shorten the notations, we introduced the function 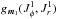 defined as
defined as ![\appendix \setcounter{section}{3} \begin{eqnarray*} g_{{\vec m}_{1}} (J_{\phi}^{1} , J_{r}^{1}) &= \displaystyle \frac{\mu}{({\vec m}_{1} \cdot {\vec \Omega}_{1})'} \frac{G^{2}}{R_{1}^{2}} \frac{\Omega\Sigma}{\kappa \sigma_{r}^{2}} \frac{(\Delta k_{\lambda})^{2}}{k_{\rm max}^{2}} \left[ \frac{1}{1 - \lambda_{\rm max}} \right]^{2} \\ &\quad \times\, \displaystyle \mathcal{J}_{m_{1}^{r}}^{2} \left[ \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{\rm max} \right] , \nonumber \end{eqnarray*}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq497.png) where we used the shortened notation
where we used the shortened notation ![\appendix \setcounter{section}{3} \begin{eqnarray} \frac{1}{({\vec m}_{1} \cdot {\vec \Omega}_{1})'} = \frac{1}{ \left| \frac{\partial }{\partial J_{\phi}} [{\vec m}_{1} \cdot {\vec \Omega}_{1}] \right|_{J_{\phi}^{1}}} \, \label{short_resonance_factor} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq498.png) (C.4)for the term appearing as a prefactor in the expressions (79)and (80)of the drift and diffusion coefficients. In addition to the integration formula (57), we may also rely on the additional identity
(C.4)for the term appearing as a prefactor in the expressions (79)and (80)of the drift and diffusion coefficients. In addition to the integration formula (57), we may also rely on the additional identity ![\appendix \setcounter{section}{3} \begin{eqnarray} \!\! \int_{0}^{+ \infty} \!\!\!\!\!\!\! \mathrm{d} J_{r} \, & J_{r}& \, {\rm e}^{- \alpha J_{r}} \mathcal{J}_{m_{r}}^{2} \!\left[ \beta \sqrt{J_{r}} \right] = \nonumber \\ && \!\!\! \frac{{\rm e}^{- \beta^{2} / 2 \alpha}}{\alpha^{2}} \!\left\{ \left[ - \frac{\beta^{2}}{2 \alpha} \!+\! 1 \!+\! |m_{r}| \right] \mathcal{I}_{m_{r}} \!\left[\! \frac{\beta^{2}}{2 \alpha} \!\right] \!+\! \frac{\beta^{2}}{2 \alpha} \mathcal{I}_{|m_{r}| \!+\! 1} \!\left[\! \frac{\beta^{2}}{2 \alpha} \!\right] \right\} , \label{integration_formula_Bessel_complex} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq499.png) (C.5)where α> 0, β> 0, and mr ∈Z. In analogy with the definition from Eq. (58), we also introduce χmax as
(C.5)where α> 0, β> 0, and mr ∈Z. In analogy with the definition from Eq. (58), we also introduce χmax as 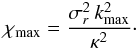 (C.6)One can then immediately perform the integration on
(C.6)One can then immediately perform the integration on 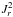 from Eq. (C.3), so that the diffusion coefficients are given by
from Eq. (C.3), so that the diffusion coefficients are given by ![\appendix \setcounter{section}{3} \begin{eqnarray} D_{{\vec m}_{1}} ({\vec J}_{1}) = h_{{\vec m}_{1}}^{D} (J_{\phi}^{1}) \, \mathcal{J}_{m_{1}^{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{\rm max} \!\right] , \label{explicit_WKB_diff_II} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq505.png) (C.7)where the function
(C.7)where the function 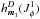 is defined as
is defined as ![\appendix \setcounter{section}{3} \begin{eqnarray} h_{{\vec m}_{1}}^{D} (J_{\phi}^{1}) = \frac{\mu}{({\vec m}_{1} \cdot {\vec \Omega}_{1})'} \frac{G^{2}}{R_{1}^{2}} \frac{\Omega \Sigma}{\kappa^{2}} \frac{(\Delta k_{\lambda})^{2}}{k_{\rm max}^{2}} \!\left[\! \frac{1}{1 - \lambda_{\rm max}} \!\right]^{2} \! {\rm e}^{- \chi_{\rm max}} \mathcal{I}_{m_{1}^{r}} [ \chi_{\rm max} ] . \label{explicit_definition_h_D} \nonumber \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq507.png) After some algebra, the drift coefficients from Eq. (C.2)are given by
After some algebra, the drift coefficients from Eq. (C.2)are given by ![\appendix \setcounter{section}{3} \begin{eqnarray} A_{{\vec m}_{1}} ({\vec J}_{1}) = -\, h_{{\vec m}_{1}}^{A} (J_{\phi}^{1}) \, \mathcal{J}_{m_{1}^{r}}^{2} \!\left[\!\! \sqrt{\tfrac{2 J_{r}^{1}}{\kappa_{1}}} k_{\rm max} \!\right] , \label{explicit_WKB_drift_II} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq508.png) (C.8)where the function
(C.8)where the function 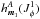 is defined as
is defined as ![\appendix \setcounter{section}{3} \begin{eqnarray} h_{{\vec m}_{1}}^{A} (J_{\phi}^{1}) &=& h_{{\vec m}_{1}}^{D} (J_{\phi}^{1}) \, \Bigg\{ - m_{1}^{r} \frac{\kappa}{\sigma_{r}^{2}} + m_{1}^{\phi} \frac{\partial }{\partial J_{\phi}} \Bigg[\! \ln \Bigg(\frac{\Omega \Sigma}{\pi \kappa \sigma_{r}^{2}} \Bigg) \bigg] \nonumber\\ & &+ m_{1}^{\phi} \frac{\kappa}{\sigma_{r}^{2}}\! \frac{\partial}{\partial J_{\phi}} \!\Bigg[\! \frac{\sigma_{r}^{2}}{\kappa} \bigg] \bigg[ 1 \!+\! |m_{1}^{r}| \!- \! \chi_{\rm max} \!+\! \frac{\mathcal{I}_{|m_{1}^{r}|\! +\! 1} [\chi_{\rm max}] }{\mathcal{I}_{m_{1}^{r}} [\chi_{\rm max}]} \Bigg] \Bigg\} \cdot \label{explicit_definition_h_A} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq510.png) (C.9)These explicit expressions of the diffusion and drift coefficients obtained in Eqs. (C.7)and (C.8)allow us to estimate in a simple way the secular flux in the entire action space J = (Jφ,Jr), once we assume that the distribution function is a Schwarzschild DF given by Eq. (25)and that the susceptibility coefficients can be approximated by Eq. (78).
(C.9)These explicit expressions of the diffusion and drift coefficients obtained in Eqs. (C.7)and (C.8)allow us to estimate in a simple way the secular flux in the entire action space J = (Jφ,Jr), once we assume that the distribution function is a Schwarzschild DF given by Eq. (25)and that the susceptibility coefficients can be approximated by Eq. (78).
Appendix D: Relation to other kinetic equations
The kinetic equation governing the collisional evolution of a system of N stars at the order 1/N is the inhomogeneous Balescu-Lenard Eq. (2). This equation conserves the total number of stars and the energy, and monotonically increases the Boltzmann entropy (H-Theorem). We note that the collisional evolution of the system is due to a condition of resonance encapsulated in the term δD(m1·Ω1 − m2·Ω2). In general, this condition can allow for local and non-local resonances. In the case of tepid discs considered in the present paper, assuming that only tightly wound spirals are sustained by the disc, we justified in Eq. (72)the fact that the resonances are purely local, so that m1 = m2 and 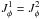 . Furthermore, because of the epicyclic approximation, the intrinsic frequencies of the system, given by Eq. (22), depend only on Jφ, so that Ω = Ω(Jφ). Under these conditions, the Balescu-Lenard equation giving the collisional evolution of F = F(Jφ,Jr,t) may be rewritten as
. Furthermore, because of the epicyclic approximation, the intrinsic frequencies of the system, given by Eq. (22), depend only on Jφ, so that Ω = Ω(Jφ). Under these conditions, the Balescu-Lenard equation giving the collisional evolution of F = F(Jφ,Jr,t) may be rewritten as ![\appendix \setcounter{section}{4} \begin{eqnarray} \frac{\partial F}{\partial t}&=& \, 4\pi^{3} \mu \, \frac{\partial}{\partial {\vec J}} \cdot \Biggl\lbrace \sum_{{\vec m}}{\vec m}\frac{1}{\left| \frac{\partial }{\partial J_{\phi}} [{\vec m} \cdot {\vec \Omega}] \right|_{J_{\phi}}} \!\! \int \!\! \mathrm{d} J_{r}' \mathrm{d}J_{\phi}' \nonumber \\ & & \,\times \frac{\delta_{\rm D} (J_{\phi} - J_{\phi}')}{|\mathcal{D}_{{\vec m}, {\vec m}} (J_{\phi}, J_{r}, J_{\phi}', J_{r}', {\vec m} \cdot {\vec \Omega}) |^{2}}\nonumber\\ &&\!\!\!\!\!\!\!\!\!\!\!\!\! \times {\vec m} \cdot \! \Biggl\lbrack \! F (J_{\phi}' , J_{r}',t) \frac{\partial F}{\partial {\vec J}} (J_{\phi}, J_{r},t) \! - \! F (J_{\phi} , J_{r},t) \frac{\partial F}{\partial {\vec J}} (J_{\phi}', J_{r}',t)\!\Biggr\rbrack\Biggr\rbrace . \label{comp1} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq515.png) (D.1)The integration on
(D.1)The integration on 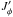 is straightforward because of the δD-function (local resonance), and we are left with
is straightforward because of the δD-function (local resonance), and we are left with ![\appendix \setcounter{section}{4} \begin{eqnarray} \frac{\partial F}{\partial t}&= & \, 4\pi^3 \mu \, \frac{\partial}{\partial {\vec J}} \cdot \Biggl\lbrace \sum_{{\vec m}}{\vec m} \frac{1}{\left| \frac{\partial }{\partial J_{\phi}} [{\vec m} \cdot {\vec \Omega}] \right|_{J_{\phi}}} \!\! \int \!\! \mathrm{d} J_{r}' \nonumber \\ & &\times \frac{1}{|\mathcal{D}_{{\vec m}, {\vec m}} (J_{\phi}, J_{r}, J_{\phi}, J_{r}', {\vec m} \cdot {\vec \Omega}) |^{2}} \nonumber \\ &&\!\!\!\!\!\!\!\!\!\! \!\!\!\!\!\times {\vec m} \cdot \! \Biggl\lbrack \! F (J_{\phi}, J_{r}',t) \frac{\partial F}{\partial {\vec J}} (J_{\phi}, J_{r},t) \! -\! F (J_{\phi} , J_{r},t) \frac{\partial F}{\partial {\vec J}} (J_{\phi}, J_{r}',t)\Biggr\rbrack\Biggr\rbrace , \label{comp2} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq518.png) (D.2)where the susceptibility coefficients are generally given by Eq. (77).
(D.2)where the susceptibility coefficients are generally given by Eq. (77).
The kinetic Eq. (D.2)is an integro-differential equation that governs the evolution of the system as a whole. It describes the effects of encounters between any test particle characterized by the angle-action coordinates (Jφ,Jr) and the field particles characterized by the (running) angle-action coordinates 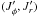 . Actually, there is no distinction between test and field particles, so that they are characterized by the same distribution function F(·,t) that evolves in a self-consistent manner, hence the integro-differential character of the kinetic equation. This is a characteristic of the Balescu-Lenard equation describing the evolution of the system as a whole.
. Actually, there is no distinction between test and field particles, so that they are characterized by the same distribution function F(·,t) that evolves in a self-consistent manner, hence the integro-differential character of the kinetic equation. This is a characteristic of the Balescu-Lenard equation describing the evolution of the system as a whole.
Appendix D.1: Fokker-Planck limit
We can also use this formalism to directly obtain the Fokker-Planck equation governing the relaxation of a test star in a bath of field stars, assumed to be in a steady state with a distribution function 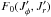 . Proceeding as in Chavanis (2012a), we just have to replace in Eq. (D.2)the distribution function of the field particles
. Proceeding as in Chavanis (2012a), we just have to replace in Eq. (D.2)the distribution function of the field particles 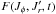 by the static distribution
by the static distribution 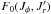 , while the time evolving distribution function of the test particle is rewritten as P(Jφ,Jr,t) for clarity. This heuristic procedure is justified in Chavanis (2012a) by an explicit calculation of the diffusion and drift coefficients of the Fokker-Planck equation. It transforms the integro-differential Eq. (D.2)into a differential equation
, while the time evolving distribution function of the test particle is rewritten as P(Jφ,Jr,t) for clarity. This heuristic procedure is justified in Chavanis (2012a) by an explicit calculation of the diffusion and drift coefficients of the Fokker-Planck equation. It transforms the integro-differential Eq. (D.2)into a differential equation ![\appendix \setcounter{section}{4} \begin{eqnarray} \frac{\partial P}{\partial t}&= & \, 4\pi^3 \mu \, \frac{\partial}{\partial {\vec J}} \cdot \Biggl\lbrace \sum_{{\vec m}}{\vec m} \frac{1}{\left| \frac{\partial }{\partial J_{\phi}} [{\vec m} \cdot {\vec \Omega}] \right|_{J_{\phi}}} \!\! \int \!\! \mathrm{d} J_{r}' \, \nonumber \\ && \times \frac{1}{|\mathcal{D}_{{\vec m}, {\vec m}} (J_{\phi}, J_{r}, J_{\phi}, J_{r}', {\vec m} \cdot {\vec \Omega}) |^{2}} \nonumber \\ &&\!\!\!\!\!\!\!\!\!\!\!\!\! \!\! \times {\vec m} \cdot \Biggl\lbrack F_0 (J_{\phi}, J_{r}') \frac{\partial P}{\partial {\vec J}} (J_{\phi}, J_{r},t) - P (J_{\phi} , J_{r},t) \frac{\partial F_0}{\partial {\vec J}} (J_{\phi}, J_{r}')\Biggr\rbrack\Biggr\rbrace , \label{comp3} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq526.png) (D.3)which can be interpreted as a Fokker-Planck equation. If we assume that the field particles are at statistical equilibrium (thermal bath), described by the Boltzmann distribution
(D.3)which can be interpreted as a Fokker-Planck equation. If we assume that the field particles are at statistical equilibrium (thermal bath), described by the Boltzmann distribution 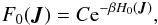 (D.4)then, using the relation ∂F0/∂J = − βF0Ω (see the definition of Ω in Eq. (1)), we can reduce the Fokker-Planck Eq. (D.3)to the form
(D.4)then, using the relation ∂F0/∂J = − βF0Ω (see the definition of Ω in Eq. (1)), we can reduce the Fokker-Planck Eq. (D.3)to the form 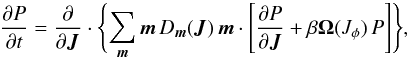 (D.5)with the diffusion coefficient
(D.5)with the diffusion coefficient ![\appendix \setcounter{section}{4} \begin{eqnarray} D_{{\vec m}}({\vec J})\!=\!\frac{4\pi^3 \mu }{\left| \frac{\partial }{\partial J_{\phi}} [{\vec m} \cdot {\vec \Omega}] \right|_{J_{\phi}}} \!\!\int \!\! \mathrm{d} J_{r}' \, \frac{F_0 (J_{\phi}, J_{r}')}{|\mathcal{D}_{{\vec m}, {\vec m}} (J_{\phi}, J_{r}, J_{\phi}, J_{r}', {\vec m} \cdot {\vec \Omega}) |^{2}} \cdot \label{comp6} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq530.png) (D.6)We note that the friction term in the Fokker-Planck Eq. (D.5)is proportional and opposite to the intrinsic frequency Ω, and that the friction coefficient ξ satisfies a (generalized) Einstein relation ξ = Dβ (for each resonance) (Chavanis 2012a).
(D.6)We note that the friction term in the Fokker-Planck Eq. (D.5)is proportional and opposite to the intrinsic frequency Ω, and that the friction coefficient ξ satisfies a (generalized) Einstein relation ξ = Dβ (for each resonance) (Chavanis 2012a).
This Fokker-Planck formalism may have other applications. For example, if we consider a system with two species of particles (e.g. characterized by different masses mA and mB), and if species B has reached an equilibrium state with a distribution  , we can use Eq. (D.3)to describe the relaxation of particles of species A due to the encounters with particles of species B (but neglecting the encounters between particles of species A). This approach is further discussed in Appendix F of Chavanis (2013b). On the other hand, for a single species system, we may describe the early dynamics of the system as a whole with a good approximation by replacing
, we can use Eq. (D.3)to describe the relaxation of particles of species A due to the encounters with particles of species B (but neglecting the encounters between particles of species A). This approach is further discussed in Appendix F of Chavanis (2013b). On the other hand, for a single species system, we may describe the early dynamics of the system as a whole with a good approximation by replacing  in the Balescu-Lenard Eq. (D.2)by the initial distribution function
in the Balescu-Lenard Eq. (D.2)by the initial distribution function 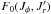 , leading again to an equation of the form (D.3).
, leading again to an equation of the form (D.3).
Appendix D.2: Other kinetic equations
We now compare the previous results to other related kinetic equations. For spatially homogeneous systems with long-range interactions, the Balescu-Lenard equation reads (see Chavanis 2012c): ![\appendix \setcounter{section}{4} \begin{eqnarray} \frac{\partial F}{\partial t}&= & \, \pi (2\pi)^d \mu \frac{\partial}{\partial {\vec v}} \cdot \Biggl\lbrace \! \int \!\! \mathrm{d} {\vec k} \mathrm{d}{\vec v}' \, {\vec k} \frac{\hat{u}({\vec k})^2}{\left| \epsilon({\vec k},{\vec k} \cdot {\vec v})\right|^2} \, \delta_{\rm D} [{\vec k} \cdot ({\vec v} - {\vec v}')] \nonumber \\ && \times {\vec k} \cdot \Biggl\lbrack F ({\vec v}',t) \frac{\partial F}{\partial {\vec v}} ({\vec v},t) - F ({\vec v},t) \frac{\partial F}{\partial {\vec v}} ({\vec v}'\!,t)\Biggr\rbrack\Biggr\rbrace , \label{comp7} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq535.png) (D.7)where
(D.7)where 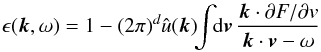 (D.8)is the dielectric function. For one-dimensional systems, it reduces to the trivial form
(D.8)is the dielectric function. For one-dimensional systems, it reduces to the trivial form 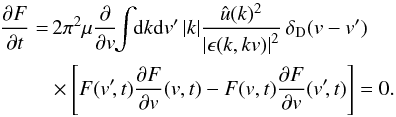 (D.9)In d> 1, there are always resonances between particles with different velocities, implying that the Balescu-Lenard equation relaxes towards the Boltzmann distribution on a timescale of the order NtD, where tD is the dynamical time. By contrast, in d = 1, the resonances become local (in velocity space) and since the term in brackets is anti-symmetric with respect to the interchange of v and v′, the Balescu-Lenard diffusion current vanishes exactly. This implies that the relaxation time is larger than NtD, presumably of the order N2tD, corresponding to the next order term in the expansion of the dynamics in powers of 1 /N. The Fokker-Planck equation describing the evolution of a test particle in a bath of field particles is discussed in Chavanis (2012c, 2013a).
(D.9)In d> 1, there are always resonances between particles with different velocities, implying that the Balescu-Lenard equation relaxes towards the Boltzmann distribution on a timescale of the order NtD, where tD is the dynamical time. By contrast, in d = 1, the resonances become local (in velocity space) and since the term in brackets is anti-symmetric with respect to the interchange of v and v′, the Balescu-Lenard diffusion current vanishes exactly. This implies that the relaxation time is larger than NtD, presumably of the order N2tD, corresponding to the next order term in the expansion of the dynamics in powers of 1 /N. The Fokker-Planck equation describing the evolution of a test particle in a bath of field particles is discussed in Chavanis (2012c, 2013a).
The kinetic equation governing the collisional evolution of a system of N point vortices in two-dimensional hydrodynamics at the order 1 /N can be written, in the axisymmetric case, as (see Chavanis 2012b): ![\appendix \setcounter{section}{4} \begin{eqnarray} \frac{\partial \omega}{\partial t}&= & \, 2\pi^2 \gamma\frac{1}{r} \frac{\partial}{\partial {r}} \!\! \int_0^{+\infty} \!\!\!\!\!\! \mathrm{d}{r}' \, {r}' \chi({r},{r}'\!,\Omega(r,t)) \, \delta_{\rm D} [\Omega(r,t) - \Omega(r'\!,t)] \nonumber \\ && \times \Biggl\lbrack \omega ({r}'\!,t) \frac{1}{r}\frac{\partial \omega}{\partial {r}} ({r},t) - \omega({r},t) \frac{1}{r'}\frac{\partial \omega}{\partial {r}} ({r}'\!,t)\Biggr\rbrack , \label{comp10} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq543.png) (D.10)where ω(r,t) is the profile of vorticity, Ω(r,t) the profile of angular velocity, and χ(r,r′,Ω(r,t)) is related to the dressed potential of interaction between the point vortices (see Chavanis 2012b for more details). This equation conserves the total number of point vortices and the energy, and monotonically increases the Boltzmann entropy (H-theorem). If the profile of angular velocity is monotonic, the kinetic equation reduces to the form
(D.10)where ω(r,t) is the profile of vorticity, Ω(r,t) the profile of angular velocity, and χ(r,r′,Ω(r,t)) is related to the dressed potential of interaction between the point vortices (see Chavanis 2012b for more details). This equation conserves the total number of point vortices and the energy, and monotonically increases the Boltzmann entropy (H-theorem). If the profile of angular velocity is monotonic, the kinetic equation reduces to the form 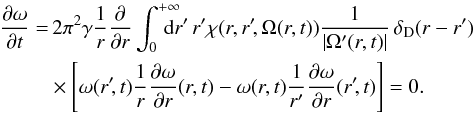 (D.11)For non-monotonic profile of angular velocity, one can have non-local resonances (i.e. distant collisions between point vortices), as studied in Chavanis & Lemou (2007). This produces a diffusion current. If the profile of angular velocity is, or becomes, monotonic, the resonances are purely local and, since the term in brackets is anti-symmetric with respect to the interchange of r and r′, the diffusion current also vanishes. This implies that the relaxation time is larger than NtD as discussed above. The Fokker-Planck equation describing the evolution of a test vortex in a sea of field vortices is discussed in Chavanis (2012b).
(D.11)For non-monotonic profile of angular velocity, one can have non-local resonances (i.e. distant collisions between point vortices), as studied in Chavanis & Lemou (2007). This produces a diffusion current. If the profile of angular velocity is, or becomes, monotonic, the resonances are purely local and, since the term in brackets is anti-symmetric with respect to the interchange of r and r′, the diffusion current also vanishes. This implies that the relaxation time is larger than NtD as discussed above. The Fokker-Planck equation describing the evolution of a test vortex in a sea of field vortices is discussed in Chavanis (2012b).
If we focus on purely local resonances, we note that the inhomogeneous Balescu-Lenard Eq. (D.1)is different from Eqs. (D.9)and (D.11)because it is two-dimensional in Jr and Jφ, and the resonances act only on Jφ. Therefore, purely local resonances do not yield a zero flux, contrary to Eqs. (D.9)and (D.11). This really is an effect of the two-dimensionality of the system. Indeed, for local resonances, the 1D inhomogeneous equation also yields a zero flux: 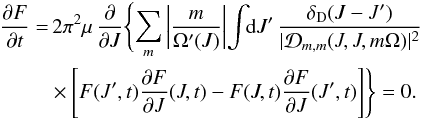 (D.12)
(D.12)
Appendix E: The Schwarzschild conspiracy
The Schwarzschild distribution function introduced in Eq. (25)and considered in S12 simulation has the specificity to be exponential in the Jr-direction, so that F is Boltzmannian with respect to the Jr variable. It is known (e.g. Chavanis 2012a) that the (complete) Boltzmann distribution is the steady state of the Balescu-Lenard Eq. (2). Therefore, we can expect that the (partial) exponential behaviour of the Schwarzschild distribution will induce simplifications that we now detail. In analogy with Eq. (10), the flux associated with a given resonance m is defined as ![\appendix \setcounter{section}{5} \begin{eqnarray} {\vec{\mathcal F}}_{{\vec m}} = {\vec m} \left[ A_{{\vec m}} ({\vec J}) \, F ({\vec J}) + D_{{\vec m}} ({\vec J}) \, {\vec m} \cdot \frac{\partial F}{\partial {\vec J}} \right] \equiv {\vec m} \, \mathcal{F}_{{\vec m}} , \label{definition_Flux_m} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq553.png) (E.1)where the non-bold ℱm is a scalar. Using shortened notations and forgetting numerical prefactors, we may rewrite the drift and diffusion coefficients from Eqs. (79)and (80)under the form
(E.1)where the non-bold ℱm is a scalar. Using shortened notations and forgetting numerical prefactors, we may rewrite the drift and diffusion coefficients from Eqs. (79)and (80)under the form 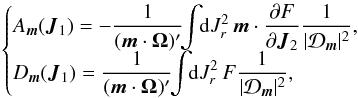 (E.2)where we used the same shortened notation for the resonant factor 1 / (m·Ω)′ as in Eq. (C.4). The flux can then be decomposed as
(E.2)where we used the same shortened notation for the resonant factor 1 / (m·Ω)′ as in Eq. (C.4). The flux can then be decomposed as 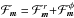 with
with ![\appendix \setcounter{section}{5} \begin{eqnarray} \mathcal{F}_{{\vec m}}^{r}= \frac{m_{r}}{({\vec m} \cdot {\vec \Omega})'} \int \mathrm{d} J_{r}^{2} \frac{1}{|\mathcal{D}_{{\vec m}}|^{2}} \nonumber \\ \times\left[ F \left(J_{r}^{2}\right) \, \frac{\partial F}{\partial J_{r}} \left(J_{r}^{1}\right) - F (J_{r}^{1}) \, \frac{\partial F}{\partial J_{r}} \left(J_{r}^{2}\right) \right], \label{expression_Fm_0} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq558.png) (E.3)and
(E.3)and ![\appendix \setcounter{section}{5} \begin{eqnarray} \mathcal{F}_{{\vec m}}^{\phi}= \frac{m_{\phi}}{({\vec m} \cdot {\vec \Omega})'} \int \mathrm{d} J_{r}^{2} \frac{1}{|\mathcal{D}_{{\vec m}}|^{2}} \nonumber \\ \times\left [ F \left(J_{r}^{2}\right) \, \frac{\partial F}{\partial J_{\phi}} \left(J_{r}^{1}\right) - F \left(J_{r}^{1}\right) \, \frac{\partial F}{\partial J_{\phi}} \left(J_{r}^{2}\right) \right]. \label{expression_Fm} \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq559.png) (E.4)We are interested in the value of the flux at the initial time, where the distribution function is given by the Schwarzschild distribution. Because of the exponential dependence in Jr of the Schwarzschild distribution function, one has
(E.4)We are interested in the value of the flux at the initial time, where the distribution function is given by the Schwarzschild distribution. Because of the exponential dependence in Jr of the Schwarzschild distribution function, one has 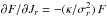 . As a result, the radial component (E.3)of the flux cancels out and the flux is simply given by Eq. (E.4). This coincidence could be called the Schwarzschild conspiracy and has important consequences on the properties of the collisional diffusion. Indeed, for a tepid disc, one has | ∂F/∂Jr | ≫ | ∂F/∂Jφ |. Hence one would expect the gradients with respect to Jr to be the major contributors to the diffusion. When considering independently the drift and diffusion coefficients, the gradients in ∂F/∂Jr dominate the diffusion current. Thus for mr ≠ 0, the diffusion-only flux can be approximated by
. As a result, the radial component (E.3)of the flux cancels out and the flux is simply given by Eq. (E.4). This coincidence could be called the Schwarzschild conspiracy and has important consequences on the properties of the collisional diffusion. Indeed, for a tepid disc, one has | ∂F/∂Jr | ≫ | ∂F/∂Jφ |. Hence one would expect the gradients with respect to Jr to be the major contributors to the diffusion. When considering independently the drift and diffusion coefficients, the gradients in ∂F/∂Jr dominate the diffusion current. Thus for mr ≠ 0, the diffusion-only flux can be approximated by 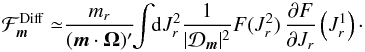 (E.5)As the ILR and the OLR have a non-zero mr compared to the COR, these resonances should dominate independently the drift and diffusion components. However, when considering the full flux made of the contributions from the drift and diffusion coefficients, because of the Schwarzschild conspiracy, there is a simplification of the dominant terms in ∂F/∂Jr, so that one recovers as in Eq. (E.4)that only the smaller gradients ∂F/∂Jφ remain present. The Schwarzschild conspiracy between drift and diffusion will therefore tend to slightly reduce the magnitude of the full diffusion flux, so as to moderately slow down the collisional relaxation. More importantly, the Schwarzschild conspiracy will favour the COR resonance (radial migration) over the ILR resonance (Jr-heating). One should note that the DF which is effectively sampled in S12 is of the form
(E.5)As the ILR and the OLR have a non-zero mr compared to the COR, these resonances should dominate independently the drift and diffusion components. However, when considering the full flux made of the contributions from the drift and diffusion coefficients, because of the Schwarzschild conspiracy, there is a simplification of the dominant terms in ∂F/∂Jr, so that one recovers as in Eq. (E.4)that only the smaller gradients ∂F/∂Jφ remain present. The Schwarzschild conspiracy between drift and diffusion will therefore tend to slightly reduce the magnitude of the full diffusion flux, so as to moderately slow down the collisional relaxation. More importantly, the Schwarzschild conspiracy will favour the COR resonance (radial migration) over the ILR resonance (Jr-heating). One should note that the DF which is effectively sampled in S12 is of the form ![\hbox{${ F = F (E,J_{\phi}) \!\propto\! J_{\phi}^{q} \exp [- E / \sigma_{r}^{2}] }$}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq567.png) , with
, with 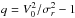 (Toomre 1977; Binney & Tremaine 2008). It is only within the epicyclic approximation that this DF takes the form of the Schwarzschild DF from Eq. (25). As a consequence, in S12 simulation, the Schwarzschild conspiracy is not exactly satisfied as observed in Eq. (E.3), but the residual difference driving the secular diffusion is likely to be subdominant, as illustrated in Fig. E.1.
(Toomre 1977; Binney & Tremaine 2008). It is only within the epicyclic approximation that this DF takes the form of the Schwarzschild DF from Eq. (25). As a consequence, in S12 simulation, the Schwarzschild conspiracy is not exactly satisfied as observed in Eq. (E.3), but the residual difference driving the secular diffusion is likely to be subdominant, as illustrated in Fig. E.1.
 |
Fig. E.1 Contours in action-space (Jφ,Jr) of the difference between the sampled anisotropic DF of S12 simulation |
Appendix F: Temporal frequency selection
An important feature of the diffusion Eq. (7)is that the diffusion takes place along specific resonance directions associated with the vectors m as discussed in Eq. (16). Hence being able to determine the dominant resonance is crucial in order to estimate the direction of the secular diffusion in action space. The temporal frequency associated with a given resonance m in a location J of action-space is given by ω = m·Ω. Thanks to the expression (83), one immediately obtains that for a Mestel disc, one has  (F.1)In Fouvry & Pichon (2015), Fouvry et al. (2015a), we studied the same S12 simulation using the WKB limit of the secular diffusion equation, which intends to describe the secular forcing of a collisionless self-gravitating system perturbed by an external source. An essential assumption of this approach was to consider the external perturbation as originating from numerical Poisson shot noise, and therefore assume it to be proportional to the local active surface density. The autocorrelation of the external perturbation ψext was taken to be equal to
(F.1)In Fouvry & Pichon (2015), Fouvry et al. (2015a), we studied the same S12 simulation using the WKB limit of the secular diffusion equation, which intends to describe the secular forcing of a collisionless self-gravitating system perturbed by an external source. An essential assumption of this approach was to consider the external perturbation as originating from numerical Poisson shot noise, and therefore assume it to be proportional to the local active surface density. The autocorrelation of the external perturbation ψext was taken to be equal to 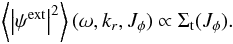 (F.2)One can remark that this crude assumption on the noise properties has no ω dependence, so that all resonances are equally favoured by the Poisson shot noise and are perturbed similarly whatever their associated intrinsic frequencies ω = m·Ω. This ad hoc and simple noise approximation is one of the limitations of the formalism presented in Fouvry & Pichon (2015), Fouvry et al. (2015a). In contrast, in the WKB Balescu-Lenard equation described in this paper, this preferential selection of the resonances based on their intrinsic frequency is naturally present. Indeed, one can note in the expression (E.4)of the flux associated with a resonance m, the presence of the prefactor 1 / (m·Ω)′
(F.2)One can remark that this crude assumption on the noise properties has no ω dependence, so that all resonances are equally favoured by the Poisson shot noise and are perturbed similarly whatever their associated intrinsic frequencies ω = m·Ω. This ad hoc and simple noise approximation is one of the limitations of the formalism presented in Fouvry & Pichon (2015), Fouvry et al. (2015a). In contrast, in the WKB Balescu-Lenard equation described in this paper, this preferential selection of the resonances based on their intrinsic frequency is naturally present. Indeed, one can note in the expression (E.4)of the flux associated with a resonance m, the presence of the prefactor 1 / (m·Ω)′
which arose in Eq. (67)when handling the resonance condition. For the Mestel disc, whose intrinsic frequencies are given by Eq. (83), this term can be straightforwardly computed and reads 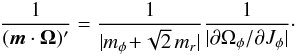 (F.3)Comparing the ILR resonance to the OLR and COR, one immediately obtains that
(F.3)Comparing the ILR resonance to the OLR and COR, one immediately obtains that 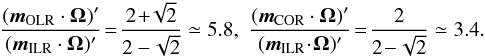 (F.4)Hence because the ILR resonance is associated with lower intrinsic temporal frequency ω = m·Ω, the resonant factor 1 / (m·Ω)′ naturally tends to favour the ILR resonance with respect to the OLR and COR, and therefore performs natively a temporal frequency biasing which was absent from the ad hoc assumption of Eq. (F.2)describing the external forcing considered in Fouvry & Pichon (2015), Fouvry et al. (2015a).
(F.4)Hence because the ILR resonance is associated with lower intrinsic temporal frequency ω = m·Ω, the resonant factor 1 / (m·Ω)′ naturally tends to favour the ILR resonance with respect to the OLR and COR, and therefore performs natively a temporal frequency biasing which was absent from the ad hoc assumption of Eq. (F.2)describing the external forcing considered in Fouvry & Pichon (2015), Fouvry et al. (2015a).
One can even be more specific when comparing the ILR and OLR resonances. The only difference between these two resonances is the sign of mr. The expression (62)of the amplification eigenvalues shows that its value only depends on s2, so that λILR = λOLR. The expression of the susceptibility coefficients from Eq. (77)is also independent of the sign of mr so that 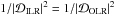 . Hence, when considering the flux ℱm given by Eq. (E.4), one notes that between the ILR and OLR resonances, ℱm only changes through the factor 1 / (m·Ω)′. Thanks to Eq. (F.4), one immediately obtains
. Hence, when considering the flux ℱm given by Eq. (E.4), one notes that between the ILR and OLR resonances, ℱm only changes through the factor 1 / (m·Ω)′. Thanks to Eq. (F.4), one immediately obtains 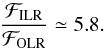 (F.5)The secular diffusion flux associated with the OLR resonance is therefore always much smaller than the one associated with the ILR resonance because of this effect of temporal frequency biasing.
(F.5)The secular diffusion flux associated with the OLR resonance is therefore always much smaller than the one associated with the ILR resonance because of this effect of temporal frequency biasing.
As a conclusion, the temporal frequency selection effect described in Eq. (F.4)will tend to favour the ILR resonance because it is associated with a smaller intrinsic frequency. However, one can observe in Fig. 8 that the COR resonance is always more amplified than the ILR resonance. Finally, the crucial remark is to note that the susceptibility coefficients from Eq. (77)involve Bessel functions  , which are such that
, which are such that  if mr = 0, or = 0 otherwise. As a consequence, close to the Jr = 0 axis, the COR resonance will always tend to become the dominant resonance. There is therefore a non-trivial arbitration between these opposite effects when considering the respective contributions of the various resonances to the full secular diffusion flux.
if mr = 0, or = 0 otherwise. As a consequence, close to the Jr = 0 axis, the COR resonance will always tend to become the dominant resonance. There is therefore a non-trivial arbitration between these opposite effects when considering the respective contributions of the various resonances to the full secular diffusion flux.
For a historical account of the development of kinetic theories in astrophysics, plasma physics, and for systems with long-range interactions, see the Introduction in Chavanis (2013a,b).
In this paper, we are not interested in the initial complex mechanism of violent relaxation (Lynden-Bell 1967), during which the system gets virialized, since we intend to describe the long-term evolution of an already and continuously virialized system.
In the secular timescale limit, the amplification through the propagation of waves between resonances is assumed to be instantaneous, see Appendix A.
In contrast, the formalism of secular forcing presented in Fouvry & Pichon (2015), Fouvry et al. (2015a) postulated a partially ad hoc shape of the perturbation power spectrum, see Eq. (F.2).
An alternative middle ground would be to account for non-local interferences of the WKB wave packets, given by Eq. (26), which in turn would allow for non-local resonances to come into play.
This also explains why the factorization assumption Am1,m2(J1,J2) = Am1(J1) Am2(J2) used in Chavanis (2007) does not hold.
Acknowledgments
J.B.F. thanks the Institute of Astronomy, Cambridge, for hospitality while this investigation was completed. J.B.F. and C.P. also thank the theoretical physics sub-department, Oxford, for hospitality and the CNRS-Oxford exchange program for funding. We thank Donald Lynden-Bell, James Binney, Simon Prunet, Walter Dehnen, John Magorrian and Mir Abbas Jalali for their feedback. This work is partially supported by the Spin(e) grants ANR-13-BS05-0005 of the French Agence Nationale de la Recherche (http://cosmicorigin.org) and by the LABEX Institut Lagrange de Paris (under reference ANR-10-LABX-63) which is funded by ANR-11-IDEX-0004-02.
References
- Balescu, R. 1960, Phys. Fluids, 3, 52 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: (second Edition), Princeton Series in Astrophysics (Princeton University Press) [Google Scholar]
- Born, M. 1960, The Mechanics of the Atom (F. Ungar Pub. Co.) [Google Scholar]
- Chandrasekhar, S. 1942, Principles of Stellar Dynamics (University of Chicago Press) [Google Scholar]
- Chandrasekhar, S. 1949, Rev. Mod. Phys., 21, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H. 2007, Physica A, 377, 469 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chavanis, P.-H. 2012a, Physica A, 391, 3680 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H. 2012b, Physica A, 391, 3657 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chavanis, P.-H. 2012c, Eur. Phys. J. Plus, 127, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chavanis, P.-H. 2013a, Eur. Phys. J. Plus, 128, 126 [CrossRef] [EDP Sciences] [Google Scholar]
- Chavanis, P.-H. 2013b, A&A, 556, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chavanis, P.-H., & Lemou, M. 2007, Eur. Phys. J. B, 59, 217 [Google Scholar]
- Daubechies, I. 1990, Information Theory, IEEE Transactions on, 36, 961 [Google Scholar]
- Earn, D. J. D., & Lynden-Bell, D. 1996, MNRAS, 278, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J.-B., & Pichon, C. 2015, MNRAS, 449, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J.-B., Binney, J., & Pichon, C. 2015a, ApJ, 806, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J.-B., Pichon, C., & Prunet, S. 2015b, MNRAS, 449, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Fouvry, J. B., Pichon, C., Magorrian, J., & Chavanis, P.-H. 2015c, A&A, accepted [arXiv:1507.06887] [Google Scholar]
- Gabor, D. 1946, Electrical Engineers – Part III: Radio and Communication Engineering, 93, 429 [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H. 1950, Classical mechanics (Addison-Wesley) [Google Scholar]
- Gradshteyn, I. S., & Ryzhik, I. M. 2007, Table of integrals, series, and products (Amsterdam: Elsevier/Academic Press) [Google Scholar]
- Heyvaerts, J. 2010, MNRAS, 407, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. 1915, MNRAS, 76, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. 1929, Astronomy and Cosmogony (Cambridge Univ. Press) [Google Scholar]
- Julian, W. H., & Toomre, A. 1966, ApJ, 146, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Kalnajs, A. J. 1965, Ph.D. Thesis (Harvard University) [Google Scholar]
- Kalnajs, A. J. 1976, ApJ, 205, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Klimontovich, I. 1967, The statistical theory of non-equilibrium processes in a plasma (M.I.T. Press) [Google Scholar]
- Landau, L. 1936, Phys. Z. Sowj. Union, 10, 154 [Google Scholar]
- Lenard, A. 1960, Ann. Phys., 10, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. C., & Shu, F. H. 1966, Proc. National Academy of Science, 55, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Liouville, J. 1837, J. Math. Pures Appl., 1, 16 [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1979, MNRAS, 187, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Kalnajs, A. J. 1972, MNRAS, 157, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1963, MNRAS, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, P. 1994, Stability of Collisionless Stellar Systems: Mechanisms for the Dynamical Structure of Galaxies, Astrophys. Space Sci. Lib. (Netherlands: Springer) [Google Scholar]
- Palmer, P. L., Papaloizou, J., & Allen, A. J. 1989, MNRAS, 238, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Pichon, C. 1994, Ph.D. Thesis (University of Cambridge) [Google Scholar]
- Pichon, C., & Cannon, R. C. 1997, MNRAS, 291, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbluth, M., MacDonald, W., & Judd, D. 1957, Phys. Rev., 107, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sellwood, J. A. 2012, ApJ, 751, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Kahn, F. D. 1991, MNRAS, 250, 278 [NASA ADS] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1977, ARA&A, 15, 437 [CrossRef] [Google Scholar]
- Toomre, A. 1981, in Structure and Evolution of Normal Galaxies, eds. S. M. Fall, & D. Lynden-Bell, 111 [Google Scholar]
- Toomre, A., & Kalnajs, A. J. 1991, in Dynamics of Disc Galaxies, ed. B. Sundelius, 341 [Google Scholar]
- Vlasov, A. 1938, Zh. Eksp. i Teor Fiz., 8, 291 [Google Scholar]
- Weinberg, M. D. 1993, ApJ, 410, 543 [Google Scholar]
All Figures
 |
Fig. 1 Top: a) a set of two resonant orbits in the inertial frame; b) in the rotating frame in which they are resonant – here through ILR-COR coupling. Bottom: c) fluctuations in the distribution function in action-space caused by finite-N effects showing overdensities for the blue and red orbits. The dashed lines correspond to 3 contour levels of the intrinsic frequency ω = m·Ω respectively associated with the resonance vector m1 (gray lines) and m2 (black lines). The two sets of orbits satisfy the resonant condition m1·Ω1 = m2·Ω2, and therefore lead to a secular diffusion of the orbital structure of the disc according to Eq. (2). One should emphasize that the resonant orbits need not be caught in the same resonance (m1 ≠ m2), be close in position space, nor in action space. |
| In the text | |
 |
Fig. 2 Two WKB basis elements. Each Gaussian is centred around a radius R0. The typical extension of the Gaussian is given by the decoupling scale σ, and they are modulated at the radial frequency kr. |
| In the text | |
 |
Fig. 3 Two WKB basis elements in the polar (R,φ)-plane. Each basis element is located around a central radius R0, on a region of size σ. The winding of the spirals is governed by the radial frequency kr. The number of azimuthal patterns is given by the index kφ, e.g. kφ = 1 for the interior dark gray element, whereas kφ = 2 for the exterior light gray one. |
| In the text | |
 |
Fig. 4 Surface density Σt of the tapered Mestel disc. The unit system has been chosen so that V0 = G = Ri = 1. Because of the tapering functions, the self-gravity of the disc is turned off in the inner and outer regions. |
| In the text | |
 |
Fig. 5 Contours of the initial distribution function in action-space (Jφ,Jr), within the epicyclic approximation. The contours are spaced linearly between 95% and 5% of the distribution function maximum. |
| In the text | |
 |
Fig. 6 Dependence of the local Q Toomre parameter with the angular momentum. It is scale invariant except in the inner/outer regions because of the presence of the tapering functions Tinner and Touter. The unit system has been chosen so that V0 = G = Ri = 1. |
| In the text | |
 |
Fig. 7 Variations of the response matrix eigenvalues λ with the WKB-frequency kr, for m = mCOR and two values of Jφ. The curve that peaks at large kr is for the smaller value of Jφ. |
| In the text | |
 |
Fig. 8 Dependence of the amplification factor 1 / (1 − λmax) with the position Jφ in the disc. The amplification associated with the COR is always larger than the one associated with the ILR and OLR. |
| In the text | |
 |
Fig. 9 Map of N div(ℱtot), where the total flux ℱtot has been summed over the three resonances (ILR, COR and OLR). Red contours, for which N div(ℱtot) < 0, correspond to regions from which the orbits will be depleted, whereas blue contours, for which N div(ℱtot) > 0, correspond to regions where secular diffusion will tend to increase the value of the DF. The net fluxes involve simultaneously radial migration near (Jφ,Jr) ~ (1.8,0), and heating near (Jφ,Jr) ~ (1,0.1). |
| In the text | |
 |
Fig. 10 Overlay of the WKB predictions for the divergence of the diffusion flux N div(ℱtot) and the differences between the initial and the evolved DF in S12’s simulation. The opaque contours correspond to the differences in the action-space for the DF in S12 between the time tS12 = 1000 and tS12 = 0 (see the upper panel of S12’s Fig. 10). The red opaque contours correspond to negative differences, so that these regions are emptied from their orbits, whereas blue opaque contours correspond to positive differences, i.e. regions where the DF has increased through diffusion. The transparent contours correspond to the predicted values of N div(ℱtot) using the same conventions as in Fig. 9. We note the overlap of the predicted transparent red and blue contours with the measured solid ones. |
| In the text | |
 |
Fig. 11 Overlay of the WKB predictions for the divergence of the diffusion flux N div(ℱtot) on top of the contours of the DF in action-space measured in the S12 simulation. The black background contours are the levels contours of the DF at time tS12 = 1400 (see the lower panel of Fig. 7 of S12). These contours are spaced linearly between 95% and 5% of the DF maximum and exhibit clearly the appearance of a resonant ridge. The coloured transparent contours correspond to the predicted values of N div(ℱtot) using the same conventions as in Fig. 9. We note that the developed late time ridge is consistent with the predicted depletion (red) and enrichment (blue) of orbits. |
| In the text | |
 |
Fig. E.1 Contours in action-space (Jφ,Jr) of the difference between the sampled anisotropic DF of S12 simulation |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\appendix \setcounter{section}{1} \begin{eqnarray} &\dfrac{1}{({\vec m}_{3} \cdot {\vec \Omega}_{3} - \omega_{1}) ({\vec m}_{3} \cdot {\vec \Omega}_{3} + \omega_{2})} \to ~~~~~~~~~~~~~~~~~~~~~~ \nonumber\\[1.5mm] & ~~~~~~~~~~~~~~~~~~~~~~(2 \pi)^{2} \delta_{\rm D} (\omega_{1} \!+\! \omega_{2}) \, \delta_{\rm D} ({\vec m}_{3} \cdot {\vec \Omega}_{3} - \omega_{1}) . \label{substitution_Landau_derivation} \nonumber \end{eqnarray}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq442.png)
![\hbox{${ F_{\rm ani} \!\propto\! J_{\phi}^{q} \exp [- E / \sigma_{r}^{2}]}$}](/articles/aa/full_html/2015/09/aa25928-15/aa25928-15-eq570.png)