| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201425524 | |
| Published online | 21 August 2015 | |
Re-evaluation of the central velocity-dispersion profile in NGC 6388
1
ESA, Space Science Department, Keplerlaan 1, 2200 AG Noordwijk The
Netherlands
e-mail:
nluetzge@rssd.esa.int
2
Department of Astronomy, University of Texas at
Austin, Austin,
TX
78712,
USA
3
School of Mathematics and Physics, University of
Queensland, Brisbane,
QLD
4072,
Australia
4
Max-Planck-Institute for Astronomy, Königstuhl 17, 69117
Heidelberg,
Germany
5
Gemini Observatory, Northern Operations Center, 670 N. A’ohoku
Place Hilo, Hawaii
96720,
USA
6
European Southern Observatory (ESO), Karl-Schwarzschild-Strasse 2, 85748
Garching,
Germany
7
Sterrewacht Leiden, Leiden University,
Postbus 9513, 2300 RA
Leiden, The
Netherlands
Received: 16 December 2014
Accepted: 8 July 2015
Context. The globular cluster NGC 6388 is one of the most massive clusters in our Milky Way and has been the subject of many studies. Recently, two independent groups found very different results when measuring its central velocity-dispersion profile with different methods. While we found a rising profile and a high central velocity dispersion (23.3 km s-1), measurements obtained by Lanzoni et al. (2013, ApJ, 769, 107) showed a value lower by 40%. The value of the central velocity dispersion has a serious effect on the mass and possible presence of an intermediate-mass black hole at the center of NGC 6388.
Aims. The goal of this paper is to quantify the biases arising from measuring velocity dispersions from individual extracted stellar velocities versus the line broadening measurements of the integrated light using new tools to simulate realistic observations made with integral field units (IFU).
Methods. We used a photometric catalog of NGC 6388 to extract the positions and magnitudes from the brightest stars in the central three arcseconds of NGC 6388 and created a simulated SINFONI and ARGUS dataset. The IFU data cube was constructed with different observing conditions (i.e., Strehl ratios and seeing) reproducing the conditions reported for the original observations as closely as possible. In addition, we produced an N-body realization of a ~106 M⊙ stellar cluster with the same photometric properties as NGC 6388 to account for unresolved stars.
Results. We find that the individual radial velocities, that is, the measurements from the simulated SINFONI data, are systematically biased towards lower velocity dispersions. The reason is that the velocities become biased toward the mean cluster velocity as a result of the wings in the point spread function of adaptive optics (AO) corrected data sets. This study shows that even with AO supported observations, individual radial velocities in crowded fields do not reproduce the true velocity distribution. The ARGUS observations do not show this kind of bias, but they were found to have larger uncertainties than previously obtained. We find a bias toward higher velocity dispersions in the ARGUS pointing when fixing the extreme velocities of the three brightest stars, but these variations are within the determined uncertainties. We reran Jeans models and fit them to the kinematic profile with the new uncertainties. This yielded a black-hole mass of M• = (2.8 ± 0.4) × 104 M⊙ and M/L ratio M/L = (1.6 ± 0.1) M⊙/L⊙, consistent with our previous results.
Key words: stars: kinematics and dynamics / methods: numerical / black hole physics
© ESO, 2015
1. Introduction
The measuring of the central velocity-dispersion profiles in Galactic globular clusters aims at detecting the crucial rise that would reveal the presence of an intermediate-mass black hole (IMBH) in the center. In the past years, several techniques have been established to derive the central velocity-dispersion profile in globular clusters. Starting with long-slit observations (e.g., Peterson et al. 1989) employed to measure individual velocities and integrated light, integral field units (IFUs) soon became a valuable tool for measuring the central kinematics. Dubath et al. (1994) performed extensive numerical simulations of the velocity-dispersion determination from integrated light for the globular cluster M15. They found that integrated light measurements over small areas (~1 arsec2) suffer from large statistical errors that are due to shot noise of a few massive stars, but that a larger coverage of the region of interest reproduces the underlying velocity distribution well. In addition to using the integrated spectra of an IFU to determine the velocity dispersion, it is also possible to obtain individual velocities of the stars in the field of view. This has been done using adaptive optics (AO) supported observations and extracting the spectra from the central spaxel of each star (e.g., Lanzoni et al. 2015) or by extracting individual spectra using a sophisticated deconvolution technique developed by Kamann et al. (2013).
The first detection of an IMBH in a globular cluster using IFU spectroscopy was reported by Noyola et al. (2008), who studied the central region of the globular cluster ω Centauri and found the velocity dispersion to be rising toward the center. This detection, however, was challenged by van der Marel & Anderson (2010), who did not observe such a rise in their velocity-dispersion profile when using proper motions and a different photometric center. After this, many IFU observations of globular clusters followed (Lützgendorf et al. 2011, 2013; Feldmeier et al. 2013), which showed signatures of an IMBH in the center in some Galactic globular clusters. However, contradictory results using individual radial velocities instead of IFUs (Lanzoni et al. 2015) or proper motions (McNamara et al. 2012) kept the discussions going on whether or not IMBHs in the centers of globular clusters exist. Furthermore, X-ray and radio observations of the central regions of globular clusters result in no detection and low upper limits on the black-hole mass (e.g., Maccarone et al. 2005; Strader et al. 2012). To date, there is no evidence of accreting IMBHs in globular clusters. The upper limits on black-hole masses from these observations are, however, very dependent on the knowledge of gas densities and accretion variability.
The source NGC 6388 is an excellent example of contradicting measurements with different techniques. Noyola & Gebhardt (2006) found a shallow cusp in the central region of the surface brightness profile of NGC 6388. N-body simulations showed that this is expected for a cluster hosting an intermediate-mass black hole (Baumgardt et al. 2005; Noyola & Baumgardt 2011). However, Vesperini & Trenti (2010) argued that shallow cusps can also be produced by clusters that are in the process of core collapse and do not exhibit IMBHs, and the interpretation of the cusp is therefore still divided. Lanzoni et al. (2007) investigated the projected density profile and the central surface brightness profile with a combination of HST high-resolution and ground-based wide-field observations. They found that the observed profiles are well reproduced by a multimass, isotropic, spherical King (1966) model, with an added central black hole with a mass of ~5.7 × 103 M⊙. Our group presented the first central kinematic measurements of NGC 6388 in Lützgendorf et al. (2011) and found the velocity dispersion profile rising in the center by up to 23.3 km s-1, indicating the presence of an IMBH with a mass of ~104 M⊙. However, Lanzoni et al. (2015) recently claimed the velocity dispersion in the center of NGC 6388 to be lower by 40%. Using individual radial velocities extracted from the AO supported IFU of the SINFONI instrument, they found the velocity dispersion to be 13.2 km s-1 using 52 individual velocities instead of 23.3 km s-1 from the ARGUS measurements. This high discrepancy is worrisome, as it affects the measurement on the existence and mass of a possible intermediate-mass black hole in the center.
Our group has therefore set out to investigate the effect on the velocity dispersion measurement when using individual velocities and integrated light. In Sect. 2 we introduce the two different observations and data sets. Section 3 describes the simulations we conducted to reconstruct the two different IFU observations, and Sect. 4 presents the extraction of the kinematics. The results of the Monte Carlo simulations and a summary are given in Sects. 5 and 6, respectively.
2. Data sets
Two independent data sets provide central velocity dispersions for NGC 6388. The first one was observed with the GIRAFFE spectrograph of the Fiber Large Array Multi Element Spectrograph (FLAMES) instrument at the Very Large Telescope (VLT) using the ARGUS mode (Large Integral Field Unit, Pasquini et al. 2002). The second observation covered a smaller area in the center using the high spatial resolution capabilities of SINFONI (Eisenhauer et al. 2003; Bonnet et al. 2004), a near-IR (1.1–2.45 μm) integral field spectrograph fed by an AO module also mounted on the VLT. In this section we briefly describe the two observations and their conditions.
The ARGUS observations were performed during two nights (2009-06-14/15, ESO proposal ID: 083.D-0444; PI: Noyola) with an average seeing of 0.8′′ (FWHM). The IFU unit was set to the 1:1 magnification scale (pixel size: 0.3′′, 14 × 22 pixel array) with the LR8 filter (820–940 nm,R = 10 400) and pointed to three different positions to cover the central area of NGC 6388. The kinematics were obtained from the analysis of the calcium triplet (~850 nm), which is a strong absorption feature in the spectra. To compute the velocity dispersion profile, we divided the pointing into six independent angular bins. In each bin, all spectra of all exposures were combined with a sigma-clipping algorithm to remove any remaining cosmic rays. Velocity and velocity-dispersion profiles were computed using the penalized pixel-fitting (pPXF) program developed by Cappellari & Emsellem (2004).
The SINFONI observations were carried out between 2008 April and June (ESO proposal ID: 381.D-0329(A); PI: Lanzoni) under an average seeing of ~0.8′′ (FWHM). The instrument was set to the 100 mas plate scale (pixel size: 0.05′′, 3.2′′ × 3.2′′ field of view) using the K-band grating (1.95–2.45 μm, R = 4000). The AO were performed using an R = 12 mag star located ~9′′ away from the cluster center. This resulted in a Strehl ratio (the amount of light contained in the diffraction-limited core of the point spread function (PSF), with respect to the total flux) of ~30%. Velocities were extracted individually for each star by matching the SINFONI pointing with high-resolution HST observations, obtaining an accuracy of better than 0.2 spaxel. The spectra for the individual stars were extracted from the centroid positions of each star. The radial velocities were measured from the CO band-heads using a Fourier cross-correlation method (Tonry & Davis 1979) as implemented in the fxcor IRAF task. The velocity dispersion for the central region was then determined using these 52 individual velocities and using the maximum likelihood method described in Walker et al. (2006).
Figure 11 in Lanzoni et al. (2015) clearly shows the large discrepancy between the two results from the different data sets. In their study they found a central velocity dispersion of σp = 13.2 ± 1.3 km s-1, which is 40% lower than the result of the ARGUS observations (23.3 ± 3.1 km s-1). Both measurements seem to agree with the outer kinematics obtained from Lanzoni et al. (2015) and Lapenna et al. (2015) using GIRAFFE/FLAMES data, however.
A concern is that the individual velocities as measured in Lanzoni et al. (2015) may be biased toward the cluster mean, which would result in a lower velocity dispersion. We addressed this by measuring the velocity dispersion in magnitude bins from their published data. There should be no difference in the velocity dispersion in these magnitude bins since the covered mass range is insignificant. If there is contamination from unresolved cluster light and light from the wings of nearby stars, we expect the effect to be larger for fainter stars, resulting in a lower dispersion value. Figure 1 plots the velocity dispersion measured in three magnitude bins from their published data. It is clear that there is a trend to lower dispersion with magnitude, which signifies a potential bias. It is likely that even the brightest magnitude bin is also biased. By running a Spearman correlation test, using the IDL routine r_correlate, on the absolute values of the individual velocities vs. magnitude, we find a Spearman coefficient of R = −0.29 ± 0.04, which indicates a slight anticorrelation with a two-sided significance of 2.1σ. Thus, it appears that the central velocity dispersion of Lanzoni et al. (2015) is biased low. This trend raises a concern, but is no proof for a bias. For this reason, we set out to test for a possible bias in both datasets in detail. Contamination from neighboring and unresolved stars has been studied in detail in Dubath et al. (1994). We employed a similar analysis to understand this bias, specified to NGC 6388.
3. Simulated IFU observations
We created a tool for simulating IFU observations for arbitrary weather conditions, instrument setups, and objects. A detailed description and verification of the code can be found in Lützgendorf et al. (in prep.). Here we describe the concept of the code and its specific application to NGC 6388 and the two observing techniques.
Before creating the IFU dataset, a suitable star catalog is needed. To stay as close to NGC 6388 as possible, we used the information on the brightest stars from a photometric catalog obtained in Lützgendorf et al. (2011) from an image taken with the Advanced Camera for Surveys (ACS) on the Hubble Space Telescope (HST). We used an N-body realization to add the influence of faint, unresolved stars to the catalog of NGC 6388. The model was set up by fitting an isochrone to the photometric catalog of NGC 6388. The best agreement is found with an age of 12 Gyr and a metallicity of z = 0.002 (Bressan et al. 2012; Chen et al. 2014). The isochrone was used to create an evolved mass function and to obtain the stellar luminosity of individual stars. Using an isotropic King (1966) model, the distribution function with a central potential of W0 = 7 (values taken from McLaughlin et al. 2012) was integrated to retrieve the density profile ρ(r), the enclosed mass M( <r), and the potential φ(r). The stars were distributed in space using ρ(r) and a half-mass radius of rh = 1.5 pc (Harris 1996). As a final step, the distribution function and the potential were used to assign velocities to the individual stars in a way that the cluster fulfills virial equilibrium (see Hilker et al. 2007). We adjusted the number of stars in the simulated cluster such that we obtained the same number of bright stars in the central pointing as measured in the observations, to ensure that we did not overestimate the number of the fainter stars. The final cluster mass is 6.8 × 105 M⊙, slightly lower than stated in the literature (~106, McLaughlin & van der Marel 2005; Lützgendorf et al. 2011). To add the observed stars to the catalog, we interpolated their positions to the isochrone to obtain temperatures, surface gravities, and K magnitudes. We also removed all stars from the catalog that were brighter than the faintest star from the SINFONI sample. In each step we assigned new velocities to the stars by drawing randomly from a velocity distribution centered around 0 km s-1 with a given velocity dispersion that we varied.
 |
Fig. 1 Velocity dispersion as a function of magnitude for the sample of Lanzoni et al. (2015). The sample shows a trend of decreasing velocity dispersion with increasing magnitude, which cannot be explained by mass segregation. |
 |
Fig. 2 Observed (left) and simulated (right) 3.2′′ × 3.2′′ field of view of the SINFONI IFU. The Strehl ratio of the simulated data cube is chosen to be the same as the observed one, 30%. Red crosses in the left panel mark the stars that were detected in the SINFONI observations, while green circles depict the stars that were not used in the final analysis of Lanzoni et al. (2015) because of their low signal-to-noise ratio. |
To construct a realistic data cube from the simulated data, we used a set of synthetic spectra from the high-resolution synthetic stellar library (Coelho et al. 2005) obtained from the VIZIER archive1 for the ARGUS observations and synthetic spectra from Husser et al. (2013) for the infrared observations with SINFONI. These libraries include spectra that cover the calcium triplet region that is used for the ARGUS observations and the CO band heads to simulate SINFONI spectra. The spectra were first convolved with the spectral resolution of the respective instrument (ARGUS: R = 10 400, SINFONI: R = 4000) and were then resampled to the wavelength range to match a number of spectral elements of a typical observed spectrum from each instrument. With this grid of parameters each star in the cluster was assigned a spectrum with a spectral shift according to its radial velocity. As mentioned in Lanzoni et al. (2015), the unresolved background is in general featureless because of the weakening of the CO band-heads with lower temperatures. This effect is also visible in our data, since the stars were assigned a spectrum according to their temperature and surface gravity. However, for completeness, we decided to keep the unresolved background even if it will not have a strong effect on the measurements.
The IFU construction was done by a C program that efficiently parallelizes the tasks of taking each star, finding a spectral match for it, taking its position and flux to construct a Moffat PSF ![\begin{eqnarray} f(x,y; \alpha,\beta)=\left(\beta-1\right)\left(\pi\alpha^2\right)^{-1}\left[1+\left(\frac{x^2+y^2}{\alpha^2}\right)\right]^{-\beta}, \end{eqnarray}](/articles/aa/full_html/2015/09/aa25524-14/aa25524-14-eq41.png) (1)with β = 2.5 and
(1)with β = 2.5 and 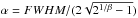 on the IFU grid and combines the spectra of all stars in each spaxel weighted by their luminosity.
on the IFU grid and combines the spectra of all stars in each spaxel weighted by their luminosity.
For the AO observations we used the combination of two Moffat functions, one with an intrinsic FWHM of 0.15′′ and one with the native seeing (i.e., the observed seeing, 0.8′′) weighted by the measured Strehl ratio. The construction of the final PSF for AO observations therefore follows the equation 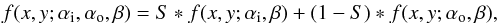 (2)where S is the Strehl ratio and αi and αo are derived from the inner (intrinsic) and outer (native) FWHM. Furthermore, the routine applies noise to each spaxel. We requested a minimum S/N of 10 for the faintest spaxel and applied noise to the remaining spaxels accordingly. Figure 3 compares the central pointing of the SINFONI observations with the simulated data cube. The visual similarity of the two data sets gives confidence in the performance of the IFU simulation routine. The value for the intrinsic FWHM agrees well with the values found in Rusli et al. (2013). In addition, we selected the 11 brightest isolated stars from the SINFONI cube and analyzed their PSF. For each star we extracted a 1D PSF profile and fit a two-component Moffat function. The free parameters are the FWHM of the inner component (FWHMi), the FWHM of the outer component (FWHMo), the Strehl ratio (i.e., the ratio of these two components), and the scale. The fits show that the intrinsic FWHM does vary between 0.13′′ and 0.15′′. The Strehl ratios range from 0.1 to 0.5, with the very brightest stars having the highest values. In general, this shows that the parameters that we used are a good representation of the observed data. Furthermore, we directly compared the 1D profiles of our simulated SINFONI data cube and the observed one and found that they agree very well with the chosen values.
(2)where S is the Strehl ratio and αi and αo are derived from the inner (intrinsic) and outer (native) FWHM. Furthermore, the routine applies noise to each spaxel. We requested a minimum S/N of 10 for the faintest spaxel and applied noise to the remaining spaxels accordingly. Figure 3 compares the central pointing of the SINFONI observations with the simulated data cube. The visual similarity of the two data sets gives confidence in the performance of the IFU simulation routine. The value for the intrinsic FWHM agrees well with the values found in Rusli et al. (2013). In addition, we selected the 11 brightest isolated stars from the SINFONI cube and analyzed their PSF. For each star we extracted a 1D PSF profile and fit a two-component Moffat function. The free parameters are the FWHM of the inner component (FWHMi), the FWHM of the outer component (FWHMo), the Strehl ratio (i.e., the ratio of these two components), and the scale. The fits show that the intrinsic FWHM does vary between 0.13′′ and 0.15′′. The Strehl ratios range from 0.1 to 0.5, with the very brightest stars having the highest values. In general, this shows that the parameters that we used are a good representation of the observed data. Furthermore, we directly compared the 1D profiles of our simulated SINFONI data cube and the observed one and found that they agree very well with the chosen values.
The simulated PSFs assume two simplifications: spherical symmetry and no variability across the field of view. The ellipticity that is observed in the measured datacube is difficult to reproduce in the simulations and would introduce even more free parameters. We concluded, however, that the effect of the elliptic shape of the PSF will be weak on the overall analysis. The ellipticity will cause some of the stars (that are aligned with the minor axis of the ellipse) to be less contaminated by bright stars, while other stars (aligned with the major axis) will be more contaminated. This would have an effect if we were to make a star-by-star analysis. However, since we compute the velocity dispersion of the system, these effects will cancel each other out. The same argument holds for possible variability of the PSF across the field of view. The 1D fits of the PSF show that our models are compatible with the observations and that the fitted PSF parameters scatter around the parameters that we used for the final simulations.
 |
Fig. 3 Observed (left) and simulated (right) 7.2′′ × 8.1′′ field of view of the combined ARGUS IFU. The seeing of the simulated data cube is chosen to fit the observed data cube, 1.10′′. |
 |
Fig. 4 IFU simulations for SINFONI and ARGUS (central bin) with different input velocity dispersions as a function of Strehl ratio and seeing. The input velocity dispersions are shown as dashed lines, the measured velocity dispersions as dots in the corresponding color. |
 |
Fig. 5 Same as Fig. 4 while fixing the velocities of the three brightest stars to their measured velocities and different input velocity dispersions as a function of Strehl ratio and seeing. |
4. Extraction of kinematics
We extracted the kinematics in a similar way as with the observed data. For SINFONI we used the star position from the catalog to extract the spectrum of the central spaxel of each star from the IFU. We note that by skipping the process of cross correlating with an independent catalog we neglected the errors that might arise from mismatches with the catalogs, but we consider them to be marginal since the IFU data cube is constructed using the same catalog. From the extracted spectra we then measured the velocities of each star using fxcor from the IRAF package and a list of templates with the same stellar parameters as the stars. We assumed that the internal parameters of the stars are perfectly known and that we used the perfect template for each star. The final velocity dispersion was then computed by using the maximum likelihood method introduced by Pryor & Meylan (1993) to account for the individual uncertainties on the velocity measurements. We repeated this measurement for IFU simulations with different Strehl ratios ranging from 10% to 100%. The results are discussed in the following section.
For the simulated ARGUS observations we adopted the position of the center and the radial bins from Lützgendorf et al. (2011). We then combined all spectra in each bin by applying an iterative sigma-clipping scheme. The velocity dispersion was derived by performing fits with pPXF on the combined spectrum, but this time not measuring the centroid (i.e., the velocity), but directly the velocity dispersion from the broadening of the lines. For both SINFONI and ARGUS simulations we repeated the procedure described above for 100 iterations in which we assigned new velocities to all the stars in each step. This was performed for four different input velocity dispersions (10, 15, 20, and 25 km s-1) and ten different values for seeing and Strehl ratios. The final values and their uncertainties were taken from the mean and the standard deviation of all iterations.
5. Results
5.1. Velocity measurements
Figure 4 shows the result of the two IFU simulations. For the SINFONI observations we show the obtained velocity dispersion as a function of Strehl ratio and for different input velocity dispersions. For the ARGUS observations the same is shown, but for different seeing values of. The figure shows that despite large uncertainties, the ARGUS measurements closely resemble the input velocity dispersions (dashed lines of the same color). The SINFONI observations, however, are strongly biased toward lower velocity dispersions. This can be explained by individual and especially faint stars being contaminated by the wings of their neighboring stars. This pushes the measured velocities closer to the mean velocity of the cluster and therefore lowers the velocity dispersion. As shown in Fig. 4, this effect is especially severe for low Strehl ratios, but the bias persists even with a perfect Strehl ratio of 100%. We find that a measured velocity dispersion of about 13 km s-1 (as measured in Lanzoni et al. 2015 with a Strehl ratio of 30%) requires an input velocity dispersion of ~25 km s-1. This excellently agrees with the measurements obtained in Lützgendorf et al. (2011) and would explain the discrepancy between the two measurements.
5.2. Discussion of the bias
The bias toward a lower velocity dispersion in the SINFONI dataset raises concerns. To investigate this in more detail, we plotted the measured velocities versus the input velocities of the SINFONI stars for a set of ten Monte Carlo runs. We also color coded the stars by their magnitudes. Figure 6 shows the measured velocities. It is obvious that the bias depends on the magnitude of each star and that for the very bright stars (dark red – red) the velocities are measured well, while for the faint stars (blue) the bias is always directed to a lower velocity.
 |
Fig. 6 Measured velocities versus input velocities for 100 Monte Carlo runs on the SINFONI dataset. The stars are color coded according to their magnitudes. |
The reason for this bias cannot be explained by the unresolved background, since, as discussed in the previous sections, this is featureless. However, the influence of the neighboring stars and the contamination of the faint stars by the wings of the bright stars must not be underestimated. To quantify this effect, we computed a contamination map for each spaxel in the SINFONI pointing. Figure 7 shows the maximum contribution to each spaxel by any star in the left panel. From this map we created the contamination map in the right panel, where we examined the spaxel of the measured stars in the SINFONI pointing and determined to which level these spaxel (that were used to derive the velocity) are contaminated. To give an example, we selected two stars close to the brightest star (A) with different magnitudes and stated their contamination. While star B is already moderately contaminated (30%) by the bright star and other stars around it, star C is highly contaminated by the wing of the very bright star A by a value of ~60%, which means that it contributes less than half of the light to this spaxel. This shows the importance of the PSF wings even in AO observations and the contaminating effect of the bright stars. For a Gaussian velocity distribution, the contamination from the neighboring stars will bias the velocities of the faint stars to the mean velocity. We note that we also reran the simulations using a lower value for the outer FWHM (FWHMo = 0.5′′) to test the effect of the native PSF. We find the bias reduced by 10–15%, but still present, and argue that a seeing of 0.5′′ is not representative of average VLT observations and much lower than the observed seeing of 0.8′′.
 |
Fig. 7 Contamination map for the SINFONI pointing. Left panel shows the maximum contribution of a single star to each spaxel. From this map the right panel is constructed, which shows for each star that is measured in the SINFONI pointing the percentage of contamination by other stars. All stars above the dark blue region are contaminated by more than 20%. |
Compared to the SINFONI data set, the simulated ARGUS data in the right panel of Fig. 4 do not show such a bias. However, the simulations of the innermost bin result in a very large scatter and an uncertainty of more than 20%. Similar results have also been reported by Bianchini et al. (2015). The highest values for σ also show a slight trend toward lower values, but are still consistent with the input velocity dispersion when taking the large uncertainties into account. These lower values most probably arise because the innermost bin is dominated by one or two single stars with narrow absorption lines. We do not show in Fig. 4 the results for the five other bins of the ARGUS IFU that were also included in the simulations. The resulting uncertainties are smaller than for the central bin and are shown in Fig. 8.
To follow the argument by Lanzoni et al. (2015) that the brightest stars might bias the velocity dispersion toward higher values for this specific case of velocity distributions, we ran the same simulations as before, but this time fixed the velocities of the three brightest stars to the measured velocities of v1 = −23.2 km s-1, v2 = 18.4 km s-1 (measured by Lanzoni et al. 2015, the two brightest stars in the sample) and v3 = −46.6 km s-1 (measured from the ARGUS pointing and absent in the dataset used by Lanzoni et al. 2015). The velocities of the remaining stars were again drawn from a velocity distribution with different input velocity dispersion. Figure 5 shows the result of these runs. While the SINFONI dataset is only slightly affected (compared to Fig. 4), the impact of the three bright stars that have opposite velocities is visible in the ARGUS simulation. For low-velocity dispersions the three stars drive the velocity dispersion up to 20 km s-1, but for high-velocity dispersions there is barely a difference (while the bias in the SINFONI data is visible for all velocity dispersions). The reason for this directed bias lies in the fact that adding two very fast stars on top of a velocity distribution with a low-velocity dispersion for all simulation runs is an incorrect representation of this distribution. Furthermore, we stress that a velocity dispersion as low as 18 km s-1 is still allowed by the uncertainties. As a last point, it is worth mentioning that only the central point is heavily affected by this specific constellation of stars, but not the bins farther out. As we show in the next section, only the bins farther out have an effect on the black-hole mass in the Jeans modeling because of the large error bars on the central point.
We therefore conclude that even excluding the central region where the bright stars are, there still is a rise in the dispersion at larger radii where these bright stars have no influence. The observed rise in the dispersion is therefore not dependent on the bright stars. Second, one cannot remove the stars from the sample unless there are reasons for them not to be in dynamical equilibrium. Our simulations are designed to measure the uncertainties on the dispersion, including the brightness of the stars. We must include them when measuring the dispersion, and then we determine the uncertainty from the simulations. Their velocity distribution is irrelevant for the simulations. Furthermore, the possible rotation signature in the center of NGC 6388 is most likely not due to three bright stars, but to a group of stars, as already stated in Lützgendorf et al. (2011). The reason why this is not seen in the dataset of Lanzoni et al. (2015) is probably the bias of the fainter stars towards the mean velocity, which leads to a weakening of the rotation amplitude. While any possible rotation is interesting for the cluster kinematics, it must be included in a dynamical analysis for the enclosed mass. The second moment we measure from the integrated light naturally includes both the ordered and hot components of the stellar kinematics.
5.3. New dynamical models
As mentioned in the previous paragraph, we simulated the remaining five bins of the ARGUS observations in the same way as described above and found that the uncertainties in Lützgendorf et al. (2011) are underestimated (see Fig. 8). The difference might arise from the more advanced IFU modeling compared to the method used in Lützgendorf et al. (2011) where, for example, only one spectral type of star was used. We therefore reran our Jeans models as described in Lützgendorf et al. (2011) and Cappellari (2008), using the same, but slightly smoothed surface brightness profile in addition to an M/L profile obtained from N-body simulations shown in Fig. 9. The M/L profile was obtained by fitting a grid of N-body models to the photometric and kinematic data of NGC 6388 and computing the M/L for the best-fit model. The models were computed with 10% stellar-mass black holes and neutron star retention fraction and an initial Kroupa (2001) mass function. More details about the N-body models are presented in McNamara et al. (2012).
For completeness we also added the most recently published outer datapoints from Lanzoni et al. (2015) and Lapenna et al. (2015, squares) and the corrected datapoint from Lanzoni et al. (2015, triangle, correction is indicated with the dashed arrow, not included in the fit). Figure 8 shows Jeans models with different black-holes masses, the projected M/L profile and its Multi-Gaussian Expansion parametrization, and the χ2 values for each model are shown in Fig. 9. We note that our Jeans models differ from those of Lanzoni et al. (2015) by the M/L profile and result in a higher model central velocity dispersion even without a black hole. Furthermore, models used by Lanzoni et al. (2015) are the results of parametric multimass King (1966) and Wilson (1975) models, while our models only take the measured and smoothed surface brightness profile and a M/L profile as input. Furthermore, it should be stated that the innermost datapoint does not influence the black-hole measurement because of its large uncertainty. However, the bins farther out still show the clear rise and cannot be the result of contamination by the innermost bright stars. The models result in a black-hole mass of M• = (2.8 ± 0.4) × 104 M⊙ and a total M/L = (1.6 ± 0.1) M⊙/L⊙. We note that the uncertainties on the black-hole mass might be underestimated in this case since we did not perform Monte Carlo simulations on the surface brightness profile as in Lützgendorf et al. (2011). Both the black-hole mass and the M/L agree well within their uncertainties with the results from Lützgendorf et al. (2011) (M• = (1.7 ± 0.9) × 104 M⊙,M/L = (1.6 ± 0.3) M⊙/L⊙).
 |
Fig. 8 Jeans models for the velocity dispersion profile of NGC 6388 using the profile obtained in Lützgendorf et al. (2011, dots), the uncertainties on these measurements obtained in this work, the corrected value from Lanzoni et al. (2015, triangle), and the outer points obtained by Lanzoni et al. (2015) and Lapenna et al. (2015, squares). |
We note that we used simplified models to obtain the black-hole mass. By using isotropic Jeans models, we neglected the fact that a globular cluster most likely shows anisotropy in its outer regions. In Lützgendorf et al. (2011) we demonstrated that in the central regions of a globular cluster anisotropy quickly disappears due to relaxation processes. By fitting the entire cluster profile, however, we include regions that can be affected by anisotropy (Zocchi et al. 2015). This can affect the overall shape of the model velocity dispersion. More sophisticated models such as fν (e.g., Zocchi et al. 2012, 2015) or Schwarzschild models (e.g., van den Bosch et al. 2006; Jardel & Gebhardt 2013) would therefore be a better representation of such a complex system, but are beyond the scope of this paper.
6. Summary
We performed IFU simulations of observations with two different IFUs for the particular case of the globular cluster NGC 6388. Using a combination of synthetic spectra, N-body realizations, and observational data, we reproduced observations of the central region of NGC 6388 as close to reality as possible. The kinematics were extracted in similar ways as was done for the observed data. This allowed a direct comparison of the biases associated with the technique of measuring individual velocities and line broadening of integrated light. The results were evaluated for different observing conditions and input velocity dispersions.
We showed that both measurements feature large uncertainties, but only the SINFONI datasets are clearly biased toward lower velocity dispersions depending on the Strehl ratio of the observations. The bias toward lower velocities can be explained by the contamination of neighboring stars, which shifts the velocities of the individual stars closer to the mean velocity. For a measured velocity dispersion of about 13 km s-1, an input velocity dispersion of about 25 km s-1 is required. This agrees well with our measurements presented in Lützgendorf et al. (2011). In the integrated light method, on the other hand, stars and background light are both valuable signals that are used to derive the velocity dispersion. However, we noted a bias toward higher velocity dispersions using integrated light when fixing the extreme velocities of the three brightest stars regardless of the input velocity dispersion. The bias is included in the large uncertainties of the innermost datapoint and disappears for high-velocity dispersions. We ran Jeans models on the whole kinematic dataset including the outer points derived in Lanzoni et al. (2015) and Lapenna et al. (2015), and including the newly derived uncertainties for our points measured with the ARGUS IFU. The fits result in a black-hole mass of M• = (2.8 ± 0.4) × 104 M⊙ and M/L ratio M/L = (1.6 ± 0.1) M⊙/L⊙, which agrees well with the previous results on this data set.
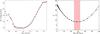 |
Fig. 9 Input M/L profile obtained from N-body simulations (left) and χ2 for the different Jeans models from Fig. 8 (right) with a best-fit black-hole mass of M• = (2.4 ± 0.4) × 104 M⊙. While the rise in the M/L in the central region is due to stellar remnants, the rise at larger radii originates from low-mass stars. |
This analysis is specific for NGC 6388, for which there are many observations and photometric data to compare with. However, biases for measurements with individual velocities are most likely present in all of the data sets that have been obtained so far. NGC 6388 belongs to the densest globular clusters in our Milky Way. Therefore it is understandable that blending effects are severe in this environment. However, even with sparse clusters, one has to be careful when taking individual velocities, and tests for their reliability are always needed. For core-collapsed clusters with densities even higher than NGC 3688, we do not recommend to use this technique at all. One solution to the problem might arise from a new deconvolution technique developed by Kamann et al. (2013). The precise extraction method reduces the overblended effects of neighboring and background stars to a minimum and allows analyzing data with much lower spectral resolution than the integrated method.
For NGC 6388 and other nearby clusters, there are other methods available to measure the velocity dispersion. Proper motions for a large sample of Galactic globular clusters have been obtained in the frame of the ACS survey of Galactic globular clusters (Sarajedini et al. 2007). Using proper motions together with discrete Jeans modeling (e.g., Watkins et al. 2013) brings a vast advantage to globular cluster modeling. By including M/L profiles and anisotropy, these models do not just apply the physics needed to the models, but also do not need to make assumptions for binning. Watkins et al. (2015) published the kinematic profiles of a large set of globular clusters including NGC 6388. Unfortunately, their profile does not extend farther inside than 1 arcsec and therefore does not cover the critical region that was discussed here. When there are enough usable data points on the central parts of NGC 6388 measured in the future, proper motions might help to solve the discrepancies in radial velocity measurements.
A detailed and more general study on the influence of IFU measurements for semi-resolved objects such as globular clusters as a function of cluster properties and observing conditions is crucial to produce reliable results. In terms of non-AO supported observations similar to the ARGUS data set and the deconvolution extraction technique by Kamann et al. (2013), we have performed detailed studies on the reliability of velocity dispersion measurements with IFUs and their effect on the determination of the total mass and the black hole mass in the center, if present. The results of this study will soon be published in Lützgendorf et al. (in prep.). This provides a valuable tool for future and present observations and a key for calibrating measurements performed with IFU instruments.
Available at: http://vizier.cfa.harvard.edu/viz-bin/VizieR?-source=VI/120
References
- Baumgardt, H., Makino, J., & Hut, P. 2005, ApJ, 620, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchini, P., Norris, M. A., van de Ven, G., & Schinnerer, E. 2015, MNRAS, 453, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnet, H., Conzelmann, R., Delabre, B., et al. 2004, in Advancements in Adaptive Optics, eds. D. Bonaccini Calia, B. L. Ellerbroek, & R. Ragazzoni, SPIE Conf. Ser., 5490, 130 [Google Scholar]
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubath, P., Meylan, G., & Mayor, M. 1994, ApJ, 426, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1548 [Google Scholar]
- Feldmeier, A., Lützgendorf, N., Neumayer, N., et al. 2013, A&A, 554, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hilker, M., Baumgardt, H., Infante, L., et al. 2007, A&A, 463, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jardel, J. R., & Gebhardt, K. 2013, ApJ, 775, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Kamann, S., Wisotzki, L., & Roth, M. M. 2013, A&A, 549, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, I. R. 1966, AJ, 71, 64 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzoni, B., Dalessandro, E., Ferraro, F. R., et al. 2007, ApJ, 668, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzoni, B., Mucciarelli, A., Origlia, L., et al. 2015, ApJ, 769, 107 [Google Scholar]
- Lapenna, E., Origlia, L., Mucciarelli, A., et al. 2015, ApJ, 798, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Noyola, E., et al. 2011, A&A, 533, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Gebhardt, K., et al. 2013, A&A, 552, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maccarone, T. J., Fender, R. P., & Tzioumis, A. K. 2005, MNRAS, 356, L17 [NASA ADS] [Google Scholar]
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. J., Harrison, T. E., Baumgardt, H., & Khalaj, P. 2012, ApJ, 745, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., & Baumgardt, H. 2011, ApJ, 743, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., & Gebhardt, K. 2006, AJ, 132, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., Gebhardt, K., & Bergmann, M. 2008, ApJ, 676, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Peterson, R. C., Seitzer, P., & Cudworth, K. M. 1989, ApJ, 347, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski & G. Meylan, ASP Conf. Ser., 50, 357 [Google Scholar]
- Rusli, S. P., Erwin, P., Saglia, R. P., et al. 2013, AJ, 146, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Strader, J., Chomiuk, L., Maccarone, T. J., et al. 2012, ApJ, 750, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, R., de Zeeuw, T., Gebhardt, K., Noyola, E., & van de Ven, G. 2006, ApJ, 641, 852 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Anderson, J. 2010, ApJ, 710, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., & Trenti, M. 2010, ApJ, 720, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2006, AJ, 131, 2114 [NASA ADS] [CrossRef] [Google Scholar]
- Watkins, L. L., van de Ven, G., den Brok, M., & van den Bosch, R. C. E. 2013, MNRAS, 436, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Watkins, L. L., van der Marel, R. P., Bellini, A., & Anderson, J. 2015, ApJ, 803, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. P. 1975, AJ, 80, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Zocchi, A., Bertin, G., & Varri, A. L. 2012, A&A, 539, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zocchi, A., Gieles, M., & Hénault-Brunet, V. 2015, IAU Symp. 312, in press [arXiv:1501.05262] [Google Scholar]
All Figures
 |
Fig. 1 Velocity dispersion as a function of magnitude for the sample of Lanzoni et al. (2015). The sample shows a trend of decreasing velocity dispersion with increasing magnitude, which cannot be explained by mass segregation. |
| In the text | |
 |
Fig. 2 Observed (left) and simulated (right) 3.2′′ × 3.2′′ field of view of the SINFONI IFU. The Strehl ratio of the simulated data cube is chosen to be the same as the observed one, 30%. Red crosses in the left panel mark the stars that were detected in the SINFONI observations, while green circles depict the stars that were not used in the final analysis of Lanzoni et al. (2015) because of their low signal-to-noise ratio. |
| In the text | |
 |
Fig. 3 Observed (left) and simulated (right) 7.2′′ × 8.1′′ field of view of the combined ARGUS IFU. The seeing of the simulated data cube is chosen to fit the observed data cube, 1.10′′. |
| In the text | |
 |
Fig. 4 IFU simulations for SINFONI and ARGUS (central bin) with different input velocity dispersions as a function of Strehl ratio and seeing. The input velocity dispersions are shown as dashed lines, the measured velocity dispersions as dots in the corresponding color. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 while fixing the velocities of the three brightest stars to their measured velocities and different input velocity dispersions as a function of Strehl ratio and seeing. |
| In the text | |
 |
Fig. 6 Measured velocities versus input velocities for 100 Monte Carlo runs on the SINFONI dataset. The stars are color coded according to their magnitudes. |
| In the text | |
 |
Fig. 7 Contamination map for the SINFONI pointing. Left panel shows the maximum contribution of a single star to each spaxel. From this map the right panel is constructed, which shows for each star that is measured in the SINFONI pointing the percentage of contamination by other stars. All stars above the dark blue region are contaminated by more than 20%. |
| In the text | |
 |
Fig. 8 Jeans models for the velocity dispersion profile of NGC 6388 using the profile obtained in Lützgendorf et al. (2011, dots), the uncertainties on these measurements obtained in this work, the corrected value from Lanzoni et al. (2015, triangle), and the outer points obtained by Lanzoni et al. (2015) and Lapenna et al. (2015, squares). |
| In the text | |
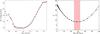 |
Fig. 9 Input M/L profile obtained from N-body simulations (left) and χ2 for the different Jeans models from Fig. 8 (right) with a best-fit black-hole mass of M• = (2.4 ± 0.4) × 104 M⊙. While the rise in the M/L in the central region is due to stellar remnants, the rise at larger radii originates from low-mass stars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


