| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525773 | |
| Published online | 17 July 2015 | |
The outer regions of the giant Virgo galaxy M 87 Kinematic separation of stellar halo and intracluster light ⋆
1
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstrasse,
85741
Garching,
Germany
e-mail: alongobardi@mpe.mpg.de; gerhard@mpe.mpg.de
2
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748
Garching,
Germany
e-mail: marnabol@eso.org; rhanusch@eso.org
Received: 30 January 2015
Accepted: 11 May 2015
Aims. We present a spectroscopic study of a sample of 287 planetary nebulas (PNs) around the brightest cluster galaxy (BCG) M 87 in Virgo A, of which 211 are located between 40 kpc and 150 kpc from the galaxy centre. With these data we can distinguish the stellar halo from the co-spatial intracluster light (ICL) and study both components separately.
Methods. We obtained PN velocities with a high resolution FLAMES/VLT survey targeting eight fields in a total area of ~0.4 deg2. We identified PNs from their narrow and symmetric redshifted λ5007 Å [OIII] emission line, the presence of the second λ4959 Å [OIII] emission line, and the absence of significant continuum. We implement a robust technique to measure the halo velocity dispersion from the projected phase-space to identify PNs associated with the M 87 halo and ICL. Using photometric magnitudes, we construct PN luminosity functions (PNLFs), which are complete down to m5007 = 28.8.
Results. The velocity distribution of the spectroscopically confirmed PNs is bimodal, containing a narrow component centred on the systemic velocity of the BCG and an off-centred broader component, which we identify as halo and ICL, respectively. We find that 243 PNs are part of the velocity distribution of the M 87 halo, while the remaining subsample of 44 PNs are intracluster PNs (ICPNs). Halo and ICPNs have different spatial distributions: the number density of halo PNs follow the galaxy’s surface brightness profile, whereas the ICPNs are characterised by a shallower power-law profile, IICL ∝ Rγ with γ in the range [−0.34, −0.04 ]. No evidence is found for an asymmetry in the halo and ICPN density distributions when the NW and SE fields are studied separately. A study of the composite PN number density profile confirms the superposition of different PN populations associated with the M 87 halo and the ICL, characterised by different PN specific numbers α. We derive αhalo = 1.06 × 10-8NPN L⊙,bol-1 and αICL = 2.72 × 10-8NPN L⊙,bol-1, respectively. The M 87 halo PNLF has fewer bright PNs and a steeper slope towards faint magnitudes than the ICPNLF, and both are steeper than the standard PNLF for the M 31 bulge. Moreover, the ICPNLF has a dip at ~1−1.5 mag fainter than the bright cut-off, reminiscent of the PNLFs of systems with extended star formation history, such as M 33 or the Magellanic clouds.
Conclusions. The BCG halo of M 87 and the Virgo ICL are dynamically distinct components with different density profiles and velocity distributions. Moreover, the different α-parameter values and PNLF shapes of the halo and ICL indicate distinct parent stellar populations, consistent with the existence of a gradient towards bluer colours at large radii. These results reflect the hierarchical build-up of the Virgo cluster.
Key words: galaxies: clusters: general / galaxies: clusters: individual: Virgo cluster / galaxies: halos / galaxies: individual: M 87 / planetary nebulae: general
© ESO, 2015
1. Introduction
Galaxy halos are faint stellar components made of stars gravitationally bound to the individual galaxies. In galaxy clusters these halos may be surrounded by intracluster stars. The existence of a diffuse population of intergalactic stars was first proposed by Zwicky (1937, 1952). As a consequence of its low surface brightness, it was only with the advent of CCD photometry that this diffuse stellar component could be studied in a quantitative way, thus becoming a topic of interest for observational and theoretical studies.
The formation of intracluster light (ICL) and of the extended halos around the brightest cluster galaxies (BCG) is closely related to the morphological transformation of galaxies in clusters. Two of the main physical processes describing the gravitational interaction between galaxies during cluster formation and evolution are dynamical friction (Ostriker & Tremaine 1975; Merritt 1985; Taffoni et al. 2003; Boylan-Kolchin et al. 2008; De Lucia et al. 2012) and tidal stripping (Gallagher & Ostriker 1972; Moore et al. 1996; Gregg & West 1998; Willman et al. 2004; Read et al. 2006). Depending on its mass, central distance, and orbit, these processes determine the fate of a cluster galaxy. Dynamical friction is the primary mechanism dragging a massive satellite towards the host halos centre, where it merges with the BCG. On the other hand, tidal forces strip stars from satellite galaxies which end up orbiting the cluster as unbound ICL (Gnedin 2003; Murante et al. 2004, 2007; Mihos 2004; Rudick et al. 2006). In the ICL and the outer regions of BCGs where the dynamical timescales are long, fossil records of accretion events can be preserved over extended periods (Willman et al. 2004; Rudick et al. 2009; Cooper et al. 2015). Hence, the study of the luminosity, distribution, and kinematics of galaxy halos and ICL may provide information on the evolution of galaxies and their host clusters.
In the last ten years, the analysis of simulated galaxy clusters has shed light upon the nature and origin of the diffuse stellar component and its connection with the BCG (Napolitano et al. 2003; Murante et al. 2004, 2007; Willman et al. 2004; Rudick et al. 2006, 2009; Puchwein et al. 2010; Laporte et al. 2013; Contini et al. 2014). In the framework of cosmological hydrodynamical simulations, Dolag et al. (2010) and Cui et al. (2014) separated stars bound to the cluster potential from those bound to the BCG by adopting a dynamical definition of the main galaxy halo and the diffuse light. Tagging particles as galaxy or intracluster component based on their different velocity distributions, they identified two distinct stellar populations in terms of kinematics, spatial distribution, and physical properties like age and metallicity. Other studies do not adopt this kind of dynamical definition of the two components and treat the BCG and ICL as a single system at the centre of the cluster, consisting of all stars that are not bound to any satellite subhalos in the cluster (e.g. Murante et al. 2004; Cooper et al. 2015).
Galaxy halos, diffuse ICL, and their connection with galaxy evolution in clusters are the subject of many observational studies. Deep imaging of individual objects (Bernstein et al. 1995; Gonzalez et al. 2000; Feldmeier et al. 2004; Mihos et al. 2005; Krick & Bernstein 2007; Rudick et al. 2010) shows that the faint ICL around BCGs often has irregular morphology, consistent with predictions from simulations. From stacking images for a large number of objects (Zibetti et al. 2005; D’Souza et al. 2014), average photometric properties were obtained, showing that the ICL extends to many 100 s of kpcs from the cluster centre. In the Virgo cluster, Kormendy et al. (2009) analysed a sample of ellipticals and spheroidal galaxies and studied their halos through the light profiles. Comparing their results with the earliest simulations of van Albada (1982), they argued that light profiles with a large Sersic index (n > 4) are common in many giant ellipticals whose origin can be associated with merger processes.
Kinematics and stellar population parameters have only been measured in a small number of BCG halos, such as (i) NGC 4889 in the Coma cluster (Coccato et al. 2010), which shows a change of stellar population at large radii; (ii) the central galaxy NGC 3311 in Hydra I (Ventimiglia et al. 2010; Arnaboldi et al. 2012), where the kinematics as well as the morphology of the outer halo signal on-going accretion events; and (iii) NGC 6166 in Abell 2199 (Kelson et al. 2002; Bender et al. 2015), whose velocity dispersion profile blends smoothly into the cluster. In the Coma cluster, the ICL kinematics suggest an on-going merger of two cluster cores (Gerhard et al. 2007). All these studies aimed to understand the role of tidal disruption and merger events as the main processes involved in the formation and evolution of central cluster galaxies and the ICL.
In the nearest clusters, single stars can be used to study the stellar populations associated with the outer halos and the diffuse stellar component (Ferguson et al. 1998; Durrell et al. 2002; Williams et al. 2007; Yan et al. 2008). Globular clusters (GCs) have been used to obtain kinematic information in the outer regions of nearby early-type galaxies (Côté et al. 2001; Schuberth et al. 2010; Strader et al. 2011; Romanowsky et al. 2012; Pota et al. 2013). Planetary nebulas (PNs) have been targeted in several surveys aimed to trace the light and motions in galactic halos (Hui et al. 1993; Méndez et al. 2001; Peng et al. 2004; Coccato et al. 2009; McNeil et al. 2010; McNeil-Moylan et al. 2012; Cortesi et al. 2013), the Virgo cluster IC component (Arnaboldi et al. 1996, 2003, 2004; Aguerri et al. 2005; Doherty et al. 2009; Castro-Rodríguez et al. 2009; Longobardi et al. 2013), and the Hydra I and Coma clusters, out to 50−100 Mpc distance (Ventimiglia et al. 2010, 2011; Gerhard et al. 2005). It was found that the observed properties of the PN population, such as the α parameter that quantifies the stellar luminosity associated with a detected PN, and the PN luminosity function (PNLF) correlate with the age, colour, and metallicity of the parent stellar population (Hui et al. 1993; Ciardullo et al. 2004; Ciardullo 2010; Buzzoni et al. 2006; Longobardi et al. 2013). Thus PNs can be used to trace these physical quantities of their parent stellar populations at surface brightnesses too faint for other techniques.
The giant elliptical galaxy M 87 has one of the oldest stellar populations in the local Universe (Liu et al. 2005), and a stellar halo containing 70% of the galaxy light down to μV = 27.0 mag arcsec-2 (Kormendy et al. 2009). It is close to the centre of sub-cluster A in the Virgo cluster (Binggeli et al. 1987), the nearest galaxy cluster, and it is expected to have transformed over larger timescales because of galaxy mergers (De Lucia & Blaizot 2007). Deep imaging (Mihos et al. 2005; Janowiecki et al. 2010) has revealed a complex network of faint, extended tidal features around M 87, suggesting that it is not completely in equilibrium. Thus, M 87 and the surrounding Virgo cluster core are prime targets to address the formation and evolution of galaxy clusters, ICL, and BCGs. Indeed, M 87 is the subject of many dynamical studies with X-ray measurements (Nulsen & Bohringer 1995; Churazov et al. 2010), integrated stellar kinematics (Murphy et al. 2011, 2014), GC kinematics (Côté et al. 2001; Strader et al. 2011; Romanowsky et al. 2012; Zhu et al. 2014), and PN kinematics (Arnaboldi et al. 2004; Doherty et al. 2009), to estimate its mass and derive the dark matter distribution. Using PN kinematics, Doherty et al. (2009) identified M 87 halo and IC PNs and showed the coexistence, at radii >60 kpc, of a stellar halo bound to the galaxy potential and a surrounding unbound Virgo ICL.
In this work, we report the results of a wide and high resolution spectroscopic survey covering the outer regions of M 87 out to a distance of 150 kpc from the galaxy centre. The aim of this project is to investigate the halo-ICL dichotomy, making use of a large spectroscopic sample of PNs (approximately 15 times larger than the previous sample of Doherty et al. 2009). The paper is structured as follows: in Sect. 2 we describe the spectroscopic survey together with the data reduction procedures and the classification of PN spectra. In Sect. 3 we study the PN phase-space distribution and dynamically separate the halo and IC populations. Spatial density distributions are derived in Sect. 4, and in Sect. 5 we present the properties of the halo and IC PN populations in terms of their α-parameters and the morphology of their PNLFs. Finally, we discuss our results in Sect. 6 and give our conclusions in Sect. 7.
We adopt a distance modulus of 30.8 for M 87 (Ciardullo et al. 2002; Longobardi et al. 2013), implying a physical scale of 73 pc arcsec-1.
2. The FLAMES M 87 PN survey
2.1. Photometric sample
The photometric candidates targeted by our spectroscopic survey come from an earlier imaging survey (Longobardi et al. 2013), covering a 0.43 deg2 region centred on M 87. Images were taken through a narrowband filter centred on the redshifted [OIII]λ5007 Å emission line at the Virgo cluster distance (on-band image), and through a broadband V-filter (off-band image). Because of their bright [OIII]λ5007 Å emission, extragalactic PNs can be identified as unresolved emission sources with positive flux on the on-band [OIII] image and no detection on the off-band image.
We obtained spectra in two observing campaigns. For the first spectroscopic campaign, we selected emission line candidates as objects with positive flux on the colour [OIII]-V band image1 (hereafter difference method, see Feldmeier et al. (2003) for more details). The visual catalogue extracted on the basis of the difference method consisted of 1074 objects, which covered a magnitude range 23 ≤ m5007 ≤ 29.8, and is statistically complete down to m5007 ≃ 28.82.
For the second spectroscopic campaign, we carried out a more stringent selection procedure described in Longobardi et al. (2013). In this procedure, the PN candidates were selected using automatic selection criteria, based on the distribution of the detected sources in the colour-magnitude (CM) diagram and the properties of their point-spread function (PSF; for more details see Arnaboldi et al. 2002; Longobardi et al. 2013). This automatic catalogue is complete within the magnitude range 26.3 ≤ m5007 ≤ 28.4.
The combined total input sample for the spectroscopic survey (visual catalogue plus automatic catalogue) consisted of 1484 emission line candidates.
2.2. Observations and data reduction
 |
Fig. 1 Top panel: core of the Virgo cluster (Mihos et al. 2005) with the positions of the FLAMES fields studied in this work (cyan circles) and in previous surveys (dotted black circles) by Arnaboldi et al. (2004) and Doherty et al. (2009). Black squares represent the Suprime-Cam survey fields used for the extraction of the photometric PN candidates (Longobardi et al. 2013). Bottom panel: schematic zoom-in of the surveyed area (black rectangles). FLAMES pointings (cyan circles) and PN candidates from the photometric survey (black asterisks; Longobardi et al. 2013) are plotted over the isophotes of the M 87 halo surface brightness (Kormendy et al. 2009). The green cross depicts M 87’s centre. North is up, East is to the left. |
Flames configuration and exposure times.
The spectra were acquired in service mode with the FLAMES spectrograph on the VLT-UT2 telescope, in the GIRAFFE+MEDUSA mode. This observing mode allows for up to 132 separate fibres that can be allocated to targets in one plate configuration, covering a circular area of 20′ diameter. The total emission line sample was observed in two observing runs (24h, 088.B-0288(A); 11h, 093.B-0066(A); PI: M. Arnaboldi), which were characterised by clear conditions and seeing better than 0.9″. We used the high resolution grism HR08, covering a wavelength range of ~250 Å centred on 5048 Å with a spectral resolution of R = 22 500. With this setup, the instrumental broadening of the arc lines has a FWHM of 17 km s-1 and the statistical error on the wavelength measurements is 150 m s-1 (see Royer et al. 2002). We refer to Sect. 2.5 for discussion of the velocity accuracy estimated from repeat observations of the same emission line candidates.
Because the [OIII] emission lines from PNs are only a few km s-1 wide, high resolution spectra are also desirable to reduce the sky contamination, making the FLAMES spectrograph the ideal instrument for LOS velocity measurements of extragalactic PNs.
For our first spectroscopic campaign, the visual catalogue was divided into a bright (m5007 < 27.2) and a normal (m5007 > 27.2) sample. The FLAMES plate configurations and exposure times were then optimised to reach the maximum number of fibres allocated, as well as optimal signal-to-noise ratio (S/N) for both samples. Based on the FLAMES/GIRAFFE/HR08 configuration, for a 104 s exposure, the monochromatic [OIII]λ5007 Å emission of a PN with [OIII] flux of F5007 = 1.0 × 10-17 erg cm-2 s-1 (m5007 = 28.8) is detected with S/N = 10 per resolution element (0.29 Å).
In total, we defined 12 FLAMES plate configurations, labelled as M87SUB1 Bright F01-F03, M87SUB1 Norm F01-F03 and M87SUB2 Bright F01-F03, M87SUB2 Norm F01-F03 for the NW (SUB1) and SE (SUB2) Suprime-Cam fields, respectively. The layout of the FLAMES pointings on the sky, together with the coverage of the photometric Suprime-Cam survey, is shown in Fig. 1.
In the second spectroscopic campaign, we added two FLAMES plate configurations covering the very central region of M 87 and the NW edge of the Suprime-Cam imaging survey, in addition to completing the observations of the 12 FLAMES configurations from the first campaign. These two additional FLAMES configurations are shown in Fig. 1 with the labels FCEN and FEDGE, respectively. Table 1 provides an overview of the FLAMES field configurations and the total exposure times.
We reduced the spectroscopic data using the GIRAFFE pipeline3. The reduction procedure included bias subtraction, flat-fielding, identification of the fibre locations on the CCD, geometric distortion correction, wavelength calibration and extraction of the one-dimensional spectra. The calibrated one-dimensional spectra were then corrected to the heliocentric velocity using the IRAF4 task dopcor. Finally, we combined spectra from single exposures using the IRAF task scombine to get the targeted S/N for each spectrum (see above).
2.3. Spectroscopic success rates
We define the nominal success rate as the ratio between the number of spectra with a detected emission line and the number of fibres allocated for a given FLAMES plate configuration. For our observations, it varies from field to field, in a range of values between ~20% and ~60%. These values are similar to those obtained in the spectroscopic follow-up of GCs in the outer halo of M 87 (see Sect. 3 in Strader et al. 2011)5. The low success rates for some of the fields (mostly M87SUB2 fields) are caused by guide star proper motions, which were not correctly accounted for in the FLAMES astrometry input file for the fibre allocation. We were also able to estimate the fraction of fibre-object misalignments, from the repeat observations of the emission objects in common between adjacent FLAMES plate configurations. From this we determined the spectroscopic completeness Cspec,fb. The success rates are affected by the spectroscopic completeness as well as by the presence of stars in the catalogue of candidates to which the fibres are allocated. In Table 2, we report the total number of allocated fibres together with the nominal success rate, the number of spectroscopically confirmed PNs, and the spectroscopic completeness Cspec,fb for all of the FLAMES fields.
Because success rates are also dependent on the absence of stars in the submitted catalogue, candidates from the more stringent automatic sample have higher success rates than candidates from the visual catalogue, reaching >70% in M87SUB1 BrightF03 and M87SUB2 BrightF01 (see Table 2). On the other hand, about 30% of the confirmed spectra come from targets in the visual catalogue: this is consistent with the results of the simulations by Longobardi et al. (2013) for the fraction of missed true line emission sources with automatic selection criteria.
Summary of the total number of allocated fibres, nominal success rate, detected number of PNs, and spectroscopic completeness in all fields.
2.4. Classification of the extracted spectra
The colour selection criteria are based on the strong [OIII] λ5007 Å emission of a PN, with faint or no continuum. Nonetheless, background galaxies like Lyα emitters at z ~ 3.1 and [OII] λ3727.26 Å emitters at z ~ 0.34 have relatively strong lines that fall within the bandpass of the narrowband filter. Thus, we classify the extracted spectra on the basis of the shape of the line profile of the strongest emission. The extracted spectra fall into these categories:
-
PN spectra: the [OIII]λ5007 Å emission of a PN is characterised by a narrow and symmetric line shape and very low continuum. In high S/N spectra, we detected the redshifted [OIII] λ4959/5007 Å doublet. Typical S/Ns for the spectroscopically confirmed PN [OIII]]λ5007 Å cover a range of 2.5 ≤ S/N ≤ 8.5 per resolution element. In Fig. 2 we show examples of single PN spectra with different VLOS.
-
Lyα spectra: the emission line of a Lyα emitter has a broader and more asymmetric line profile, characterised by a steep drop-off at bluer wavelengths. This kind of signature comes from the forest absorption bluewards of Lyα: the symmetric emission line is truncated below the object redshift by Lyα scattering in the intergalactic medium. Figure 3 shows an example of an extracted FLAMES spectrum for a Lyα emitter.
-
[OII] spectra: the [OII]λ3727 Å emitters are characterised by the redshifted, resolved, and broad emission lines of the oxygen doublet at λ3726−3729 Å. Figure 3 shows an example of an extracted FLAMES spectrum for an [OII] line emitting galaxy.
The final sample of emission line objects consists of 380 sources, of which 287 were classified as PNs and the remaining as background emission line galaxies, either as Lyα or as [OII] emitters. This is the largest sample of spectroscopically confirmed PNs around M 87 thus far, which is about a factor 15 larger than the sample of Doherty et al. (2009).
 |
Fig. 2 Spectra of single confirmed PNs. The top panel shows the spectrum for a PN dynamically bound to the halo component. The middle and bottom panels show spectra for PNs dynamically unbound to the halo (see Sect. 3), with higher (middle panel) and lower (bottom panel) velocity than the M 87 systemic velocity. Red vertical lines mark the positions of the two oxygen lines at their redshifted wavelengths. We smoothed the spectra to 0.015 nm per pixel. |
 |
Fig. 3 Spectra for background emission line galaxies: Lyα emitter at z ~ 3.1 (top panel) and [OII] emitter at z ~ 0.34 (bottom panel). Red vertical lines mark the positions of the two components of the λ3726+3729 Å emission. We smoothed the spectra to 0.015 nm per pixel. |
The fraction of background emitters is consistent within one σ with the estimate in the photometric study of Longobardi et al. (2013). They estimated that ~25% of the total imaging sample would be background emission galaxies. Here we find that the same fraction of the automatic catalogue is in fact Lα or [OII] emitters.
2.5. Accuracy of the velocity measurements
From the repeat observations of the same candidates in areas where different FLAMES plate configurations overlap (see Fig. 1), we obtained independent velocity measurements for a subsample of PNs. The median deviation of these measurements is 4.2 km s-1 and the whole distribution covers a range of 0.6 ≤ ΔVLOS ≤ 16.2 km s-1. The largest errors occur when a cosmic ray falls near the wavelength of the [OIII]λ5007 Å emission in one of the exposures.
3. Halo and IC PN components
When studying the outer regions of M 87 out to a distance of ~150 kpc from the galaxy centre, we are tracing the light in the radial range where the M 87 halo blends into the ICL. Arnaboldi et al. (2004) showed that the M 87 stellar halo and the Virgo core ICL coexist for distances >60 kpc from the galaxy centre, and Doherty et al. (2009) showed that the two components overlap out to 150 kpc. Longobardi et al. (2013) showed that the observed slope of the PN number density profile is consistent with the superposition of two PN populations associated with the M 87 halo and ICL, respectively.
In the following subsections, we show that the distribution of LOS velocities obtained from the FLAMES spectra shows evidence for two dynamically distinct PN populations at large radii, confirming this interpretation.
3.1. Projected PN phase-space diagram
 |
Fig. 4 Projected phase-space diagram showing VLOS vs. major axis distance R from the centre of M 87, for all spectroscopically confirmed PNs (black asterisks). The major axis distance is given both in arcsec (bottom axis), and in kpc (top axis), where 73 pc = 1″. The dotted horizontal line shows M 87’s systemic velocity Vsys = 1275 km s-1 from Sect. 3.2. The shaded area represents the region of the projected phase-space where the blue-shifted [OIII] 4959 Å emission line would fall below the wavelength of the blue edge of the FLAMES sort ordering filter HR08. |
For each confirmed PN spectrum, we measured VLOS and computed the major axis distance via the formula 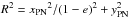 , where e is the isophote’s ellipticity from Kormendy et al. (2009) and xPN,yPN are the PN coordinates measured in a reference frame centred on M 87, where the y axis is aligned with the major axis of the outer elliptical isophotes at PA = −25.6 (Kormendy et al. 2009). In Fig. 4, we show the projected phase-space diagram VLOS,PN vs. R for the spectroscopically confirmed PNs in the M 87 survey (black asterisks).
, where e is the isophote’s ellipticity from Kormendy et al. (2009) and xPN,yPN are the PN coordinates measured in a reference frame centred on M 87, where the y axis is aligned with the major axis of the outer elliptical isophotes at PA = −25.6 (Kormendy et al. 2009). In Fig. 4, we show the projected phase-space diagram VLOS,PN vs. R for the spectroscopically confirmed PNs in the M 87 survey (black asterisks).
In this projected phase-space, PN velocities show a concentration around the systemic velocity of M 87 (Vsys = 1275 km s-1; see Sect. 3.2), in addition to a scattered distribution at higher and lower velocities. In Fig. 5, we show the histogram of the velocities for the entire sample. It has two very strong and quite asymmetric wings around the main peak. The wing (or tail) at low velocities is more extended than the tail at high velocities with respect to the peak. These extended tails are very different from those measured in the LOS velocity distributions (LOSVDs) of isolated early-type galaxies, which are well described by single Gaussian distributions to within ~1% (e.g., Gerhard 1993; Bender et al. 1994). The total velocity distribution is well fitted by a double Gaussian, while a single Gaussian is a poor fit to the observed LOSVD. The reduced χ2 of a double Gaussian fit is 1.1, while for a single Gaussian it is 2.0. Therefore, we fit the LOSVD in Fig. 5 with the sum of two Gaussians. The fit to the data returns a narrow component centred on VLOS,n = 1270.4 km s-1 with velocity dispersion of σn = 298.4 km s-1, and a broad component, centred on VLOS,b = 999.5 km s-1 with a larger velocity dispersion σb = 881.0 km s-1.
The broad component is shifted from the M 87 systemic LOS velocity: both VLOS,b and σb are consistent with those values determined for the LOSVD of galaxies in the main sub-cluster region A of the Virgo cluster (Binggeli et al. 1993; Conselice et al. 2001). The LOSVD around M 87 is thus bimodal, containing a narrow component associated with the systemic velocity of the galaxy plus a broader component associated with the ICL.
 |
Fig. 5 Histogram of the line-of-sight velocities of the spectroscopically confirmed PNs (black histogram) fitted with a double Gaussian (black curve). Red and blue lines represent the two Gaussians associated with the M 87 halo and the IC components. |
Different LOSVDs for the halo and ICL are predicted by cosmological analysis of structure formation. Using hydrodynamical cosmological simulations, Dolag et al. (2010), Cui et al. (2014) study the LOSVD of star particles at the centre of their clusters. These authors find that this LOSVD is well described by the sum of two Gaussians, with similar average velocities but different σ. One component is gravitationally bound to the galaxy and more spatially concentrated; the other is more diffuse and its high-velocity dispersion reflects the satellites’ orbital distribution in the cluster gravitational potential. It is plausible that the halo stars are spatially confined as a consequence of merging processes that led to the formation of the BCG (Murante et al. 2007; Contini et al. 2014).
 |
Fig. 6 Projected phase-space diagram, VLOS vs. major axis distance from the centre of M 87, for all spectroscopically confirmed PNs from this work and Doherty et al. (2009).The major axis distance is given both in arcsec (bottom axis), and in kpc (top axis), where 73 pc = 1″. The PNs are classified as M 87 halo PNs (red asterisks) and ICPNs (blue asterisks), respectively; see text. Black squares identify spectroscopically confirmed PNs from Doherty et al. (2009). The smoothed 1, 2, and 2.5σ thresholds are represented by the dashed, dotted, and dot-dashed lines, respectively. The dashed horizontal line shows the M 87 systemic velocity Vsys = 1275 km s-1 as computed in Sect. 3.2, while the continuous green line shows the effective radius Re = 703.914″ determined by Kormendy et al. (2009). At VLOS = −220 km s-1, we plot the M 86 systemic velocity (long dashed line). |
3.2. Robust separation of the M 87 halo and ICL
The overall LOSVD of the PNs in M 87 is characterised by a narrow component associated with the M 87 halo, superposed on a broad IC component with a shifted mean velocity and much larger velocity width. We are now interested in separating halo and IC PNs based on their different LOSVDs. In this analysis, we combine our PN sample with that of Doherty et al. (2009). We concentrate on those PNs that have a major axis distance R ≤ 190 kpc to study the transition between the M 87 halo and the Virgo ICL. The combined total sample consists of 299 PNs with measured positions and velocities within R ≤ 190 kpc; the PNs from Doherty et al. (2009) further out are classified as ICPNs and are not discussed further.
To separate halo and IC components, we use a sigma clipping algorithm in elliptical radial bins, corresponding to vertical strips in the projected phase-space diagram in Fig. 6. The idea is to separate the velocities in the narrower Gaussian (see Fig. 5) from those in the high- and low-velocity wings of the distribution. By tagging our sources depending on whether their VLOS belongs to the narrower or wider Gaussian, we assign PNs to either the M 87 halo or the ICL.
The velocity dispersion profile of the M 87 halo: a robust sigma estimate – we binned the PN velocity sample in elliptical annuli and, for each bin, we determined the standard deviation of the LOSVD for the PNs in this bin. We applied a 2σ limit with respect to the systemic velocity of M 87 6, Vsys = 1275 ± 24 km s-1, and calculated the dispersion for all PNs with | VLOS − Vsys | < 2σ km s-1. We then scaled this dispersion by a numerical factor determined from Monte Carlo simulations to correct to the dispersion of a complete Gaussian distribution (see McNeil et al. 2010). Since we expect the initial estimate for the 2σ to be influenced by the ICPNs, we repeat this process until the dispersion value stabilises.
Separating M 87 halo and IC PNs: sigma clipping – we now identify the two components using a sigma clipping algorithm. We begin by classifying as ICPNs all velocity outliers that deviate from the M 87 systemic velocity Vsys = 1275 km s-1 by more than 2σ. To obtain the required σ value at the radius of each PN, we took the robust estimates of the velocity dispersions in the elliptical radial bins, and fitted these data with a fourth-order polynomial. This takes radial gradients into account and, at the same time, reduces the effects of binning and scatter in the dispersion profile on the separation of the components. Using the 2σ threshold from the interpolated polynomial, we identify 243 objects as M 87 halo PNs.
Two further steps are still needed. Firstly, the 2σ criterion accounts for ~95.5% of a complete Gaussian distribution; hence we expect it to have missed 11 halo PN candidates. To include these, we considered all outliers within 3σ from the M 87 Vsys and, from those, selected the 11 with the smallest | VLOS − Vsys | /σ ratios. This leads to a final sample of 254 M 87 halo PNs and 45 ICPNs. In this final sample, 11 halo PNs and 1 ICPN came from Doherty et al. (2009).
Secondly, as can be seen in Fig. 5 the ICL and halo velocity distributions overlap, and as result, when using the sigma-clipping algorithm, the ICPNs at low velocities relative to Vsys ~ 1275 km s-1 are considered to be part of the halo component. To statistically quantify this effect, we compared the halo and IC velocity distributions in each radial bin (or slice in the phase-space). We approximated the halo distribution in the bin as a Gaussian centred on the systemic velocity of M 87 with a dispersion equal to the average value for that bin, and for the IC component we used the same Gaussian in all radial bins using the same parameters as in Fig. 5. We then calculated the fraction of ICPNs that lie inside the halo distribution as the area of overlap between the two curves. With this analysis we obtain a statistical estimate of the number of ICPNs contained in the halo velocity distribution in each bin. For all bins combined, we find that a further ~17% of the halo sample, i.e., ~44 PNs, are to be associated with the IC component.
In Fig. 6, we show the projected phase-space distribution of our PNs as in Fig. 4, with velocities colour-coded to show the membership to the halo (red) and ICL (blue). Since we only know statistically, but not individually, which PNs in the halo velocity range are ICPNs, these are also shown with the red halo colour.
In Fig. 6 we also show 1/2/2.5σ limit contours for the halo PNs, obtained by fitting a polynomial to the σ values from the robust estimation. The velocity dispersion profile increases from 250″ to 1200″, and then decreases, showing a colder component at radii R > 1200″. A more detailed analysis of the dispersion profile will be provided in a separate paper (Longobardi et al., in prep.).
We now enquire whether any ICPNs could be associated with other galaxies in the cluster. The first to consider is M 86, because it is bright, has the most extended halo, and is relatively close to M 87 (~1.2° away). Extrapolating the Sersic fit from Janowiecki et al. (2010), we compute the total luminosity associated with the M 86 halo in our surveyed area to be LV,bol ~ 8.0 × 108 L⊙ ,bol. We adopt a similar PN specific number as for M 87, α2.5 = 1.01 × 10-8PN/ L⊙ ,bol (see Sect. 5.1), but we correct for the fact that we can only sample the brightest 2.3 mag of the PNLF because of the larger distance to M 86 (Mei et al. 2007). This leads to a predicted number of 7 M 86 PNs that could be counted as IC component, i.e., only ~2.5% of the completeness-corrected ICPN sample (see Sect. 5.1), or 2 out of a total of 88 ICPNs.
Other fainter galaxies have less extended halos and contribute less to the sampled ICPNs around M 87 unless they are very near or in the survey area. Moreover, from the shape of the ICPNLF (see Sect. 5.2) the majority of ICPNs is likely to have been stripped from low-luminosity star-forming galaxies, such as M 33 and the LMC. Any ICPNs still bound to dwarf galaxies would be correlated with their position and velocity. Only three PNs with velocity V ~ 350 km s-1 out of the ICPN sample seem correlated with the position and systemic velocity of a dwarf galaxy, IC3549, which has VLOS = 375 km s-1 (Adelman-McCarthy & et al. 2009). Hence, we can state that the contribution from other nearby galaxies to the ICPN sample is negligibile and does not affect any of the results we present.
Finally, a few ICPNs are characterised by extraordinary blue shifts relative to M 87 (VLOS < −1000 km s-1). These (hyper-) velocities of | VLOS − Vsys | > 2300 km s-1 relative to M 87, corresponding to several σVirgo, could be because of infall from the outskirts of the Virgo cluster, perhaps associated with the infall of the M 86 group, or they could be tracers of three-body interactions, as previously hypothesised for the extreme GC observed at a projected distance of ~80 kpc from M 87 with a velocity of VLOS < −1025 km s-1 (Caldwell et al. 2014).
3.3. Spectroscopic validation of the PN subsample
In Sect. 2.4 we classified 287 spectra as PNs on the basis of the line profile of the strongest emission. We now strengthen this earlier classification based on the detection of the weaker 4959 Å line of the [OIII] doublet in the PN spectra.
In 114 out of the 287 spectra, nearly 40% of the sample, we are able to detect the Doppler-shifted [OIII]λ4959 Å line with the expected 1:3 ratio of the [OIII]λ4959/5007 Å line fluxes. In the rest of the sample, the single spectra do not have the required S/N (S/N >3) for the main [OIII]λ5007 Å emission line to allow the detection of the weaker 4959 Å line. However, following Arnaboldi et al. (2003) we can achieve the required S/N by stacking these spectra, after shifting their [OIII]λ5007 Å emission to a common reference wavelength. By measuring the [OIII]λ5007/4959 Å line ratio of the coadded spectrum, we can statistically constrain the fraction of misclassified PN spectra: if the stacked spectrum contains misclassified PN candidates, the ratio [OIII]λ5007/4959 Å is larger than three.
The 287 spectra are further grouped in three classes: M 87 halo spectra, IC high-velocity, and IC low-velocity spectra. We have 254, 13, and 31 PN in each category, respectively. Three sources in the IC low-velocity class are not included because their Doppler shifted [OIII]λ4959 Å emission fall at a shorter wavelength than the blue edge of the FLAMES HR08 filter (see Fig. 4). The spectra are shifted so that the main [OIII]λ5007 Å emission falls at the same nominal wavelength for all spectra of a given class. For the halo and IC high-velocity class, we adopt the nominal wavelength of 5029 Å for [OIII]λ5007 Å, i.e. the redshifted wavelength at the systemic velocity of M 87. For the IC low-velocity class, the adopted nominal wavelength is 5000 Å. We shifted the single spectra for each class, and obtained three coadded spectra. These are plotted in Fig. 7. The [OIII] doublet is visible in all spectra, with the [OIII]λ4959 Å line visible at the correspondent shifted wavelength. In all three spectra, the FWHM of [OIII]λ5007 Å is FWHM = 0.6 Å (Table 3), somewhat smaller than the typical FWHM of single spectra, FWHM = 0.8 Å. Because of filter edge effects, together with the shifting and alignment of the spectra with reference to the stronger line, the weaker [OIII]λ4959 Å emission is broader in the IC low-velocity spectrum than in the single PN spectra.
 |
Fig. 7 Combined spectra for the spectroscopically confirmed sub-samples of PNs belonging to the halo (upper panel), IC high-velocity (central panel) and IC low-velocity (bottom panel) classes. As expected from atomic physics, the [OIII]λ4959/5007 Å doublet is detected with a flux ratio 1:3 confirming that the large majority of our candidates are true PNs (see text for more details). |
Fluxes, FWHMs, and line ratios of the [OIII] λ5007/4959 Å doublet for halo, high-velocity, and low-velocity IC PNs subsamples.
The fluxes and FWHMs of the [OIII]λ4959/5007 Å emissions in the coadded spectra are measured via a Gaussian fit to the lines with the IRAF task splot. The errors on the line fluxes were calculated using the relation (Pérez-Montero & Díaz 2003) ![\begin{equation} \sigma_1=\sigma_{\rm c}N^{1/2}[1+EW/(N\Delta)]^{1/2}, \label{flux_err} \end{equation}](/articles/aa/full_html/2015/07/aa25773-15/aa25773-15-eq86.png) (1)where σ1 is the error in the line flux, σc is the standard deviation in a box near the measured line and represents the error in the definition of the continuum, N is the number of pixels used to measure the line flux, EW is the equivalent width of the line, and Δ is the wavelength dispersion in Å pixel-1. In Table 3 we give a summary of the observed properties of the [OIII] doublet of the coadded spectra.
(1)where σ1 is the error in the line flux, σc is the standard deviation in a box near the measured line and represents the error in the definition of the continuum, N is the number of pixels used to measure the line flux, EW is the equivalent width of the line, and Δ is the wavelength dispersion in Å pixel-1. In Table 3 we give a summary of the observed properties of the [OIII] doublet of the coadded spectra.
The [OIII] doublet is visible in the three spectra from the different classes, with approximate flux ratio of 3:1, as expected from atomic physics. Given the uncertainties on the measured fluxes, the spectral validation shows that at 1σ > 99% of the halo and >90% of the IC high-velocity spectra are true PNs. This implies that only two halo PNs and one high-velocity ICPN could be misclassified. For the IC low-velocity PNs, the line ratio of the [OIII]5007/4959 Å is 3.1 ± 0.3 from Table 3. Hence up to 13% of the spectra could be misclassified, i.e. four ICPNs. On the total sample of 287 spectroscopically confirmed PNs, at most seven candidates might have been misclassified, i.e. only 2% of the whole sample.
4. Halo and IC density profiles
By tagging PNs according to their VLOS, we differentiated between halo and IC PNs in the last section. We are now interested in recovering the spatial distribution of these two components and in studying their number density profiles separately.
In Fig. 8 we show the sky positions of the spectroscopically confirmed halo and IC PNs. If the halo and ICL are characterised by different evolutionary histories, their radial distributions may be different. If so, this can be seen in the PN density profile. Because PNs follow light, the presence of a single parent stellar population would be reflected in a PN number density distribution proportional to the surface brightness profile at each radius. Deviations of the PN number density from the light profile would trace the presence of more than one stellar population in the surveyed region (Longobardi et al. 2013).
 |
Fig. 8 Sky positions of the spectroscopically confirmed halo (red crosses) and IC PNs (blue crosses). The green plus sign indicates the centre of M 87. The ellipses (dotted lines) trace the M 87 isophotes between photometric major axis radii |
4.1. Completeness corrections
To construct a PN density profile, we require a spatially complete sample hence we must correct the detected PN number using a completeness function, Ctot(xPN,yPN), which accounts for the selection function of the sampled PNs over the surveyed area. Our PN sample is affected by four different kinds of incompleteness, which are related to the photometric identification of the candidates and the selection effects in the spectroscopic observations. These are:
-
Photometric incompleteness, characterised by:
-
i)
Cphot,sp(R) – spatial incompleteness due to the high galaxy background and foreground stars that affect the detection of PN candidates in the images. This was estimated in Longobardi et al. (2013) by adding a simulated PN population to the scientific images and determining the fraction of simulated objects recovered by SExtractor in the different elliptical annuli shown in Fig. 8.
-
ii)
Cphot,col – colour incompleteness due to the colour criteria adopted for the automatic selection of PN candidates. This colour incompleteness was computed by analysing the properties of the recovered simulated PN population in the colour–magnitude diagram (see Longobardi et al. 2013, for more detail). This incompleteness affects only the M87SUB FCEN and M87SUB FEDGE fields, where the photometric candidates were selected through colour criteria (see Sect. 2), and is magnitude-dependent. For constructing the density profile, however, we use an average value, computed for the whole sample down to 2.5 mag below the bright cut-off, which amounts to 0.7.
-
i)
-
Spectroscopic incompleteness, characterised by:
-
iii)
Cspec,sp(R) – spatial incompleteness due to the limited number of fibres (up to 132) that can be allocated for each FLAMES field. This was estimated by computing the ratio between the number of allocated fibres and the total number of photometric candidates in each elliptical annulus shown in Fig. 8.
-
iv)
Cspec,fb(xPN,yPN) – incompleteness due to fiber-target misalignment. This incompleteness was estimated from the detection statistics of objects in common between overlapping FLAMES plate configurations, whose [OIII] emission was detected in spectra taken with either one or two of the two-plate configurations (see Sect. 2.3).
-
iii)
-
Our spectra are sufficiently deep that we found no dependence of the spectroscopic incompleteness on the magnitude of the PN candidates.
The total completeness function, Ctot(xPN,yPN), is the product of the photometric and spectroscopic incompleteness: 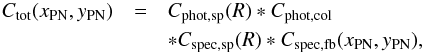 (2)with
(2)with 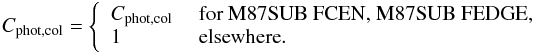 The completeness-corrected number of PNs in each bin of major axis distance R is then
The completeness-corrected number of PNs in each bin of major axis distance R is then 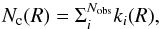 (3)where the sum extends over all PNs of the halo or IC component in the bin, respectively, and ki(R) = 1 /Ctot(xPNi,yPNi) is the completeness-corrected specific weight of each observed PN at its position.
(3)where the sum extends over all PNs of the halo or IC component in the bin, respectively, and ki(R) = 1 /Ctot(xPNi,yPNi) is the completeness-corrected specific weight of each observed PN at its position.
4.2. Density profiles of halo and IC component
To construct the PN number density profile and compare it to the galaxy’s surface brightness profile, we bin our PN sample in elliptical annuli. The radial range of the elliptical annuli is chosen such that they include the major axis distance of the innermost and outermost PN candidates in the photometric sample of Longobardi et al. (2013). Their P.A.s and ellipticities are taken from Kormendy et al. (2009). The sizes of the annuli are determined separately for the halo and IC components, such that for each component all bins contain at least ten spectroscopically confirmed PNs. In each annulus and for each component, we compute the completeness-corrected PN number density as the ratio of the completeness-corrected number of PN (Eq. (3)) and the area of the portion of the annulus intersecting our FOV7, 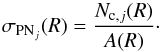 (4)Here we consider all the spectroscopically confirmed PNs whose magnitudes are within 2.5 mag below the bright cut-off. The subscript j indicates the two different PN components, halo and ICL. The major axis distances R in Eq. (4) are determined by computing the average major axis distance of all PNs falling within each elliptical annulus.
(4)Here we consider all the spectroscopically confirmed PNs whose magnitudes are within 2.5 mag below the bright cut-off. The subscript j indicates the two different PN components, halo and ICL. The major axis distances R in Eq. (4) are determined by computing the average major axis distance of all PNs falling within each elliptical annulus.
 |
Fig. 9 Logarithmic PN number density profiles for the M 87 halo (red triangles) and the IC PNs (blue diamonds), corrected for incompleteness. The error bars include counting statistics and completeness correction. The halo PN profile compares well with the surface brightness profile from Kormendy et al. (2009, plus signs). The continuous black line shows their Sersic fit with n = 11.8. The ICPN number density decreases towards larger radii as IICL ∝ Rγ with γ in the range [−0.34; −0.04 ] (full and dashed-dotted blue lines). Black squares show the combined halo and IC PN number density profile, which is well modelled by the two-component photometric model (dot-dashed black line, see Sect. 5). |
In Fig. 9 we show the comparison between the V-band M 87 surface brightness profile μK09 from Kormendy et al. (2009), with the logarithmic PN density profiles for the halo (red triangles) and IC (blue diamonds) PNs, defined as 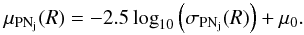 (5)The value μ0 is a constant to be added so that the PN number density profile matches the μK09 surface brightness profile. As described in Sect. 3.2, the kinematic decomposition of the halo and IC components does not identify ICPNs in the velocity range of the halo, and their contribution must be evaluated statistically for each bin. Averaged over the bins, ~10% of the halo PN sample is thus estimated to be associated with the ICL, in addition to the ICPNs identified from their large velocities. For each of the radial bins, we subtract the estimated contribution from the halo component and add it to the IC component. In Fig. 9, the PN number densities for halo and ICL account for this effect. Furthermore, the profiles shown in Fig. 9 are computed using all PNs whose magnitudes are within 2.5 mag from the bright cut-off. However, the halo and IC number density profiles do not change significantly when the fainter spectroscopically confirmed PN are also included.
(5)The value μ0 is a constant to be added so that the PN number density profile matches the μK09 surface brightness profile. As described in Sect. 3.2, the kinematic decomposition of the halo and IC components does not identify ICPNs in the velocity range of the halo, and their contribution must be evaluated statistically for each bin. Averaged over the bins, ~10% of the halo PN sample is thus estimated to be associated with the ICL, in addition to the ICPNs identified from their large velocities. For each of the radial bins, we subtract the estimated contribution from the halo component and add it to the IC component. In Fig. 9, the PN number densities for halo and ICL account for this effect. Furthermore, the profiles shown in Fig. 9 are computed using all PNs whose magnitudes are within 2.5 mag from the bright cut-off. However, the halo and IC number density profiles do not change significantly when the fainter spectroscopically confirmed PN are also included.
We find that the μPNhalo agrees well with the surface photometry: the halo PN logarithmic number density profile follows the surface brightness profile. The ICPN logarithmic number density, as the halo profile, is centrally concentrated towards M 87. However, it has a flatter profile that decreases towards larger radii as IICL ∝ Rγ with γ in the range [−0.34; −0.04 ], depending on the choice of binning. These results are consistent with predictions from hydro-dynamical simulations, where the radial density profile of the bound component, i.e. the halo, is observed to be much steeper than that of the diffuse IC component (Murante et al. 2004; Dolag et al. 2010).
Finally, we compute density profiles for the PNs for the NW and SE sides of M 87 independently, to search for a NW-SE asymmetry in the spatial distribution. For this test, we now use the total sample of PNs, including very faint PNs, to increase the statistics in each half annulus (this also changes the binning). Figure 10 shows the four number density profiles; each pair of profiles are consistent with each other and the halo profiles are consistent with the galaxy surface brightness profile. Thus within the statistical uncertainties, the stellar halo density is NW-SE symmetric and the PN number density follows the light on both sides. The ICPN density profile pair are flatter than the halo again, and consistent with the previous surface brightness profile IICL ∝ Rγ with γ = [ −0.34; −0.04 ]; no asymmetry is evident. In Fig. 10 we also plot the differences between the NW and SE logarithmic densities as function of radius (bottom panel). For both the halo (red filled circles) and the ICL (blue filled circles), these differences are consistent with zero within the uncertainties (see further discussion in Sect. 6).
 |
Fig. 10 Top panel: same as in Fig. 9, but here the halo and IC number density profiles are computed separately for the NW (filled symbols) and SE (open symbols) sides of M 87. Bottom panel: difference between the logarithmic PN number density profiles of the halo (red dots) and IC (blue dots) PNs in the NW and SE M 87 regions. A value of zero indicates no difference in the number of sources on opposite sides at a given major axis distance. |
5. Halo and IC populations
5.1. The α parameter
The total number of PNs, NPN, is proportional to the total bolometric luminosity of the parent stellar population through the luminosity-specific PN density, or α-parameter for short, such that NPN = αLbol. The α-parameter determined for this PN sample is an estimate of the total number of PNs within 2.5 mag of the bright cut-off of the PNLF, because of the magnitude limit of this survey at m5007 = 28.8 and the bright cut-off at 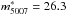 (see Sect. 5.2). The measured value of α is derived from the scaling factor required to match the PN number density profile to the surface brightness profile in the V band and then taking the appropriate bolometric correction into account.
(see Sect. 5.2). The measured value of α is derived from the scaling factor required to match the PN number density profile to the surface brightness profile in the V band and then taking the appropriate bolometric correction into account.
In Fig. 9, we showed the total PN number density profile for the spectroscopically confirmed PNs sample within 2.5 mag from the bright cut-off, together with the halo and IC PN number densities. The total PN number density profile flattens at large radii compared to the V-band surface brightness profile. As already shown in Longobardi et al. (2013), this effect is due to a superposition of stellar populations with different PN specific frequencies. The flattening for the spectroscopocally confirmed PN number density profile provides independent support for these results. Following Longobardi et al. (2013), we can model it by two components such that ![\begin{eqnarray} \label{mod_sigma} \tilde{\sigma}(R) &=& \left[\alpha_{\mathrm{halo}} I(R)_{\mathrm{halo,bol}} +\alpha_{\mathrm{ICL}}I(R)_{\mathrm{ICL,bol}}\right] \\ \label{mod_sigma_ratio} &=& \alpha_{\mathrm{halo}} \left[I(R)_{\mathrm{K09,bol}} +\left(\frac{\alpha_{\mathrm{ICL}}}{\alpha_{\mathrm{halo}}}-1\right)I(R)_{\mathrm{ICL,bol}}\right], \end{eqnarray}](/articles/aa/full_html/2015/07/aa25773-15/aa25773-15-eq118.png) where
where 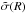 represents the predicted total PN surface density in units of NPN pc-2; I(R)halo and I(R)ICL, with and without subscript bol, are the bolometric and V-band surface brightnesses for the halo and the IC components, in L⊙ pc-2, respectively; IK09 is the M 87 luminosity profile in the V band in L⊙ pc-2, from Kormendy et al. (2009). The surface brightnesses I(R)halo and I(R)ICL are given by the Sersic fit to the observed M 87 surface brightness data (n = 11.8, Kormendy et al. 2009), and by the scaled power-law fit to the IC surface density data from Sect. 4, respectively. They satisfy the relation IK09 = I(R)halo + I(R)ICL, which determines the normalisation of the IC surface brightness profile. In the surveyed area over a radial range 7 kpc <R < 150 kpc, these profiles give total V-band luminosities Lhalo = 4.41 × 1010 L⊙ and LICL = 0.53 × 1010 L⊙, and after the bolometric correction (see below), total bolometric luminosities for the sampled halo and ICL of Lhalo,bol = 9.05 × 1010L⊙ ,bol and LICL,bol = 1.1 × 1010L⊙ ,bol.
represents the predicted total PN surface density in units of NPN pc-2; I(R)halo and I(R)ICL, with and without subscript bol, are the bolometric and V-band surface brightnesses for the halo and the IC components, in L⊙ pc-2, respectively; IK09 is the M 87 luminosity profile in the V band in L⊙ pc-2, from Kormendy et al. (2009). The surface brightnesses I(R)halo and I(R)ICL are given by the Sersic fit to the observed M 87 surface brightness data (n = 11.8, Kormendy et al. 2009), and by the scaled power-law fit to the IC surface density data from Sect. 4, respectively. They satisfy the relation IK09 = I(R)halo + I(R)ICL, which determines the normalisation of the IC surface brightness profile. In the surveyed area over a radial range 7 kpc <R < 150 kpc, these profiles give total V-band luminosities Lhalo = 4.41 × 1010 L⊙ and LICL = 0.53 × 1010 L⊙, and after the bolometric correction (see below), total bolometric luminosities for the sampled halo and ICL of Lhalo,bol = 9.05 × 1010L⊙ ,bol and LICL,bol = 1.1 × 1010L⊙ ,bol.
The surface luminosity 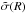 can be related to the bolometric surface brightness through the formula
can be related to the bolometric surface brightness through the formula 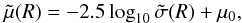 (8)where μ0 is given by the analytical function
(8)where μ0 is given by the analytical function 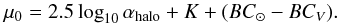 (9)In Eq. (9), αhalo is the specific PN number for the halo, K = 26.4 mag arcsec-2 is the V-band conversion factor from mag arcsec-2 to physical units L⊙ pc-2, BC⊙ = −0.07 is the V-band bolometric correction for the Sun, and BCV = −0.85 is the bolometric correction for the V-band (Buzzoni et al. 2006). According to their simple stellar population (SSP) models for irregular, late, and early-type galaxies, this value can be used with 10% accuracy.
(9)In Eq. (9), αhalo is the specific PN number for the halo, K = 26.4 mag arcsec-2 is the V-band conversion factor from mag arcsec-2 to physical units L⊙ pc-2, BC⊙ = −0.07 is the V-band bolometric correction for the Sun, and BCV = −0.85 is the bolometric correction for the V-band (Buzzoni et al. 2006). According to their simple stellar population (SSP) models for irregular, late, and early-type galaxies, this value can be used with 10% accuracy.
From the offset value μ0 = 16.56 ± 0.08 mag arcsec-2 determined from the density profile in Fig. 9, we compute αhalo = (1.06 ± 0.12) × 10-8 PN 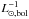 . From Eqs. (6) and (7), the derived value for αICL is then (2.72 ± 0.72) × 10-8 PN
. From Eqs. (6) and (7), the derived value for αICL is then (2.72 ± 0.72) × 10-8 PN 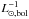 , using the steeper slope − 0.34 for the ICL, but the difference for the shallower slope is only 5%. The difference in α-parameters is then ~2.3σ.
, using the steeper slope − 0.34 for the ICL, but the difference for the shallower slope is only 5%. The difference in α-parameters is then ~2.3σ.
These luminosity specific PN α values are consistent with those obtained by Longobardi et al. (2013) from the photometric sample, and are now independently validated on the basis of the spectroscopically confirmed PNs. Moreover, they also agree within the uncertainties with the preoviously determined values by Durrell et al. (2002), Doherty et al. (2009), see Longobardi et al. (2013). The consistency of the spectroscopic and photometric values confirms the accuracy of the estimated contamination by Lyα background objects in the photometric sample.
We can now compare our αhalo and αICL values with the known α values for PN populations in nearby galaxies. Galaxies with integrated (B − V) colours smaller than 0.8 are empirically characterised by similar values of the α parameter, 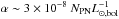 , with a scatter of a factor of two. For redder galaxies with (B − V) > 0.8, the spread of the measured values increases, spanning a range from α ~ 10-9NPN/L⊙ ,bol to ~6 × 10-8NPN/L⊙ ,bol. For these redder galaxies, there is an empirical inverse correlation of the α values with the FUV − V integrated colours of the parent stellar population, such that smaller α values are associated with galaxies with larger FUV − V excess. Hence, observationally, the α values are linked to the metallicity and star formation history of the parent stellar population of the PNs (Peimbert 1990; Hui et al. 1993; Buzzoni et al. 2006; Longobardi et al. 2013).
, with a scatter of a factor of two. For redder galaxies with (B − V) > 0.8, the spread of the measured values increases, spanning a range from α ~ 10-9NPN/L⊙ ,bol to ~6 × 10-8NPN/L⊙ ,bol. For these redder galaxies, there is an empirical inverse correlation of the α values with the FUV − V integrated colours of the parent stellar population, such that smaller α values are associated with galaxies with larger FUV − V excess. Hence, observationally, the α values are linked to the metallicity and star formation history of the parent stellar population of the PNs (Peimbert 1990; Hui et al. 1993; Buzzoni et al. 2006; Longobardi et al. 2013).
Our result that the IC component contributes more PNs per unit bolometric luminosity than the M 87 halo light therefore signals a change in the stellar populations from halo to ICL, consistent with the existence of a gradient towards bluer colours of the M 87 stellar light at large radii (Liu et al. 2005; Rudick et al. 2010). We interpret this gradient as the result of the gradual transition from the redder halo light to the bluer ICL with decreasing surface brightness.
5.2. The halo and ICL PNLFs
The PNLF of [OIII]λ5007 Å emission line fluxes is often empirically described via the truncated exponential formula (Ciardullo et al. 1989) 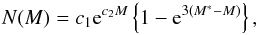 (10)where c1 is a normalisation constant, c2 = 0.307, and M∗(5007) = −4.51 mag is the absolute magnitude of the PNLF bright cut-off. This analytical formula is designed: (i) to reproduce the high-mass cut-off observed for the PN central stars in nearby galaxies; and ii) to model PNs as uniformly expanding homogeneous spheres ionised by a non-evolving central star (Henize & Westerlund 1963).
(10)where c1 is a normalisation constant, c2 = 0.307, and M∗(5007) = −4.51 mag is the absolute magnitude of the PNLF bright cut-off. This analytical formula is designed: (i) to reproduce the high-mass cut-off observed for the PN central stars in nearby galaxies; and ii) to model PNs as uniformly expanding homogeneous spheres ionised by a non-evolving central star (Henize & Westerlund 1963).
Our deep and extended imaging survey of PNs in the outer regions of M 87 shows that the PNLF for this galaxy has significant deviations from Eq. (10) in the faint magnitude bins (Longobardi et al. 2013): its slope ~1−2 mag below the bright cut-off is steeper than expected from the Ciardullo et al. (1989) formula. This is also true for the spectroscopically confirmed PN sample, as we show in Fig. 11 in which we compare the total PNLF with the analytical formula for a distance modulus of 30.8.
 |
Fig. 11 Luminosity function of all spectroscopically confirmed PNs corrected for incompleteness (full dots). The dashed green line represents the Ciardullo et al. (1989) formula for a distance modulus of 30.8, convolved with photometric errors and normalised to the data at the bright end. The spectroscopically confirmed PNLF shows an excess of fainter PNs with respect to the analytical formula, similar to the photometric PNLF (Longobardi et al. 2013). Open circles represent magnitude bins where the sample is not completeness-corrected. The error bars show the uncertainties from counting statistics and completeness correction. |
 |
Fig. 12 Top panel: luminosity function of the spectroscopically confirmed halo PNs, corrected for incompleteness (red circles). The red line shows the fit of the generalised analytical formula (Eq. (10)) to the halo PNLF, with c2 = 0.72 and bright cut-off at 26.3 mag, corresponding to a distance modulus m − M = 30.8. Central panel: completeness-corrected PNLF for the ICPNs (blue circles). The blue line shows the fit of the generalised analytical formula (Eq. (10)) to the ICPNLF, with c2 = 0.66. The ICPNLF shows a dip 1−1.5 mag fainter than the bright cut-off. Bottom panel: PNLFs in absolute magnitude for the spectroscopically confirmed Virgo ICPNs (blue circles) and for the outer disk of M 33 (Ciardullo et al. 2004, cyan triangles) matched at the first bin. For this comparison, the data are corrected for line-of-sight reddening (see text). Absolute magnitudes are determined using a distance modulus of 30.8 for the ICL and 24.86 for M 33 (Ciardullo et al. 2004). |
Our data allow us to analyse separately and compare the PNLFs of the two spectroscopically confirmed PN samples for the M 87 halo and ICL, from the bright cut-off down to 2.5 mag below. In the upper panel of Fig. 12, we show the PNLF for the spectroscopically confirmed sample of halo PNs, corrected for detection incompleteness as a function of magnitude. The data points trace a smooth function, and the fit of the generalised analytical formula (Eq. (10)) to the observed PNLF within the 2.5 mag limit results in c2 = 0.72 and a bright cut-off at 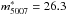 (overplotted on the data). With M∗ = −4.51, this corresponds to a distance modulus (m − M) = 30.8.
(overplotted on the data). With M∗ = −4.51, this corresponds to a distance modulus (m − M) = 30.8.
In the central panel of Fig. 12, we present the ICPNLF (full blue circles), corrected for incompleteness. As for the M 87 halo PNLF, the ICPNLF is consistent with the same distance modulus as for M 87. However, it shows an overall shallower gradient than the M 87 halo PNLF: the best fit of Eq. (10) to the empirical PNLF returns c2 = 0.66.
In addition to the shallower gradient at fainter magnitudes, the ICPNLF shows a clear dip at 1−1.5 mag fainter than 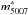 . This feature is statistically significant: the difference between the number of PNs in these bins with respect to the magnitude bins before and after the dip is > 3σdip on both sides, where σdip is the uncertainty from Poisson statistics in the magnitude bins where the dip occurs.
. This feature is statistically significant: the difference between the number of PNs in these bins with respect to the magnitude bins before and after the dip is > 3σdip on both sides, where σdip is the uncertainty from Poisson statistics in the magnitude bins where the dip occurs.
Dips in the PNLF are observed for PN populations detected in star-forming galaxies (irregulars/disks), and are absent in the PNLFs of bulges or early-type galaxies. The magnitude below the bright cut-off at which the dip occurs varies between different PN populations, from ~2 to ~4 mag below M∗ (Jacoby & De Marco 2002; Ciardullo et al. 2004; Hernández-Martínez & Peña 2009; Reid & Parker 2010). We discuss this issue further in Sect. 6.1. In the bottom panel of Fig. 12, we compare the PNLFs for the Virgo ICPNs and for the spectroscopically confirmed sample of PNs for the outer disk of M 33 (Ciardullo et al. 2004). Both LFs are corrected for foreground Galactic extinction, adopting reddening values of E(B − V)ICL = 0.02 (Ciardullo et al. 1998), and E(B − V)M 33 = 0.04 (Ciardullo et al. 2004) for the Virgo ICL and M 33, respectively8. Absolute magnitudes are determined using a distance modulus of 30.8 for the ICL and 24.86 for M 33 (Ciardullo et al. 2004). Both PNLFs show dips relative to the smooth luminosity function: the ICL at 1−1.5 mag fainter than M∗, the outer disk of M 33 at ~2.5 mag fainter than the bright cut-off.
Finally, we recall that about 17% of the PNs contained in the M 87 halo PNLF shown in Fig. 12 are ICPNs whose velocities fall in the same velocity range of the M 87 halo PNs, and can therefore not be individually identified. The hint of a slight dip in the halo PNLF at ~1 mag below the bright cut-off may be due to these ICPNs.
To summarise, the observed properties of the M 87 halo and Virgo ICPN populations i.e. their α-parameters and PNLFs, show significant differences. Because these quantities depend on the physical properties of the parent stellar populations, these differences imply that the M 87 halo and ICL consist of different populations of stars. To understand this better, more work is clearly required for a better theoretical understanding of how metallicity, age, and different star formation histories affect the post-AGB phases of stellar evolution and the resulting PN populations.
6. Discussion
6.1. Distinct halo and IC populations around M 87
In Sect. 3 we presented the projected phase-space distribution of the spectroscopically confirmed PNs in our M 87 fields (Fig. 6). With a robust procedure we showed that the PN velocity distribution splits into two kinematically very different components: the M 87 halo (with mean velocity VLOS,n = 1275 km s-1 and velocity dispersion σn ≃ 300 km s-1) and the ICL (with VLOS,b ≃ 1000 km s-1 and σb ≃ 900 km s-1). Furthermore, in Sect. 5, we found that the halo and IC components were characterised by specific PN numbers (α parameters) that differed by a factor of three, and by different shapes of their PNLFs.
These results demonstrate the coexistence of two distinct PN progenitor stellar populations in this region of the Virgo cluster core: the M 87 halo and the ICL. These two populations have very different surface density distributions, the M 87 halo is described by an n = 11.8 Sersic law, while the ICL follows a shallow power law ∝ Rγ with γ in the range [−0.34, −0.04 ]. We also have external information on the metallicities and ages of both components. At R ~ 35 kpc, the mean metallicity of the M 87 halo obtained with population synthesis models from multi-colour photometry is ~0.7 solar, with a shallow outward gradient, and the mean age is ~10 Gyr (Liu et al. 2005; Montes et al. 2014). On the other hand, the metallicity and age distributions of ICL red giants in a field at R ~ 190 kpc from HST ACS star photometry are dominated by metal-poor ([M/H] ≲ −1), ≳10 Gyr old stars (Williams et al. 2007). Because of the large velocities and shallow surface density profile of the IC stars, these IC population parameters are likely to be similar in the radial range probed by our observations, R ~ 50−140 kpc, whereas the M 87 halo stars might reach ~0.5 solar in the outer regions if the outward gradient continues, as inferred by Liu et al. (2005).
Currently there is no good theoretical understanding of how the properties of a PN population are related to the metallicity and age of a stellar population. Observationally, star-forming and bulge populations have α numbers such as those we find for the ICL, while only the most massive early-type galaxies have α numbers as low as we find for the M 87 halo (Buzzoni et al. 2006; Cortesi et al. 2013). The primary driver is believed to be increased mass loss at high metallicities. The PNLFs are empirically found to steepen from star-forming to old metal-rich populations (Ciardullo et al. 2004; Longobardi et al. 2013). The PNLFs of Local Group star-forming galaxies, such as the SMC (Jacoby & De Marco 2002), LMC (Reid & Parker 2010), M 33 (Ciardullo et al. 2004), and NGC 6822 (Hernández-Martínez & Peña 2009), furthermore show a “dip” 2−2.5 mag down from the PNLF cut-off for the LMC, M 33, and NGC 6822, and 4 mag down from the cut-off for the SMC. A tentative model for this feature is the superposition of a faint PN population with a brighter population of more massive cores from a younger stellar population (Rodríguez-González et al. 2015). We can speculate that as the brighter population fades in older and/or more metal-rich populations, the dip might move towards brighter magnitudes. This could explain why in the Virgo IC population we find the dip 1−1.5 mag down from the cut-off. No other PN population with this PNLF is known; however, PNLFs as deep as for M 87 have only been obtained in the Local Group so far. Clearly, more observational and theoretical work on the nature and location of the dip in the PNLF is needed.
6.2. ICL in Virgo: nature and number of its progenitor galaxies
The combined properties of the Virgo ICPN population, which include the fairly small inferred bolometric luminosity, the relatively large α parameter, and the dip in the PNLF as well as the low mean metallicity from Williams et al. (2007), appear to be most readily explained if this population derives from a faded population of low-luminosity, low-metallicity, star-forming or irregular galaxies, such as M 33 or the LMC, which are very different from M 87 itself.
In Sect. 5.1, we determined the total V-band and bolometric luminosities of the IC component sampled by our survey fields: LICL = 0.53 × 1010 L⊙, and LICL,bol = 1.1 × 1010L⊙ ,bol. Using the total V-band luminosities for M 33 and the LMC listed in NED, LM 33 = 3.65 × 109 L⊙ and LLMC = 1.26 × 109 L⊙, we find that the IC stars sampled in our survey fields correspond to ~1.5 M 33-like galaxies or ~4 LMC-like galaxies9.
We can now also check whether the Virgo ICL associated with the ICPN population could be related to the blue GC population that is found around M 87, that has a shallower and more extended surface density profile than the red GCs, which trace the stellar halo light (Côté et al. 2001; Tamura et al. 2006; Strader et al. 2011; Forte et al. 2012; Durrell et al. 2014). To do this, we need to estimate the total number of GCs associated with M 33 and LMC-like systems. Harris et al. (2013) studied GC populations in a large sample of galaxies and analysed the correlation of the total number of GCs, NGC, with global galaxy properties and type. They find that NGC increases roughly in direct proportion to host galaxy luminosity, with a scatter of a factor of ~2.5. For an LMC-like system with luminosity LLMC = 1.3 × 109 L⊙ the expected mean number of GCs is NGC ~ 20, while for an M 33-like galaxy with LM 33 = 3.7 × 109 L⊙ the expected mean number of GCs is NGC ~ 60. This leads to an estimated number of blue GCs associated with the sampled ICL of NGC,ICL ~ 80−90, with a scatter of a factor ~2.5. If a fraction of the ICL is due to the accretion of even lower luminosity galaxies, the estimated number of GCs would increase (Harris et al. 2013; Coccato et al. 2013).
The recent survey of the GC population in the Virgo cluster around M 87 by Durrell et al. (2014) showed the presence of an ICGC population, mostly associated with blue GCs (see further discussion in Sect. 6.3). This intracluster component has a density equal to 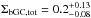 arcmin-2. In our surveyed region, this would lead to a total number of 100−430 ICGCs. This is larger than but consistent within the uncertainties with the value estimated above, suggesting that a substantial fraction of the blue GC population around M 87 could have been accreted with the galaxies that we now see in the ICL.
arcmin-2. In our surveyed region, this would lead to a total number of 100−430 ICGCs. This is larger than but consistent within the uncertainties with the value estimated above, suggesting that a substantial fraction of the blue GC population around M 87 could have been accreted with the galaxies that we now see in the ICL.
6.3. Is there an intracluster component of GCs around M 87?
There has been some controversy in the recent literature about the existence of intracluster GCs in the halo of M 87. The most extensive photometric study of the distribution of GCs in the Virgo cluster so far was carried out by Durrell et al. (2014) as part of the NGVS. They studied density maps of the GC population, selected using colour criteria, and statistically accounted for the contamination to the GC sample by subtracting a modelled map for the expected background, from both Milky Way stars and background galaxies10. The blue GCs in their map have a shallower and more extended profile than the red GCs. Durrell et al. (2014) also found that the total GC (blue plus red) density profile is in good agreement with the number density profile of photometrically selected PNs from Longobardi et al. (2013), including a change of slope and a flatter profile at large radii. They suggested that their blue GCs at distances >215 kpc are part of the intracluster component of Virgo. Cosmological simulations (Dolag et al. 2010; Cui et al. 2014; Cooper et al. 2015) predict that the density of this component would then increase inwards.
Durrell et al. (2014) also found evidence for a spatial asymmetry of GCs surrounding M 87 for major axis distances larger than 20′, with an excess of tracers in the NW region (mostly the blue population). In Sect. 4 we studied the distribution of M 87 halo and IC PNs separately for the NW and SE. We find no clear evidence of asymmetry in either the halo and ICL within major axis distance ~20′ (Fig. 10). Inside this radius, both PN and GC number density profiles are consistent with a symmetric halo and IC distribution. For the halo component, this result is significant, given the number of tracers and radial extent, and indicates, that if the halo was subject to accretion events, these were not recent. For the ICL, we may expect asymmetries, given the longer timescales involved in IC accretion events, but we may not have a large enough sample of ICPNs to see them.
Strader et al. (2011) carried out a spectroscopic study of the GCs around M 87, using colour criteria to select their candidates. In the same colour and magnitude range populated by GCs, 0.55 ≤ (g′ − i′) ≤ 1.15 and 20 ≤ g′ ≤ 24, there is however a large contribution from foreground Milky Way halo stars. To mitigate this effect, Strader et al. (2011) used a combination of photometry, radial velocity, and HST imaging information. However, they considered all objects with velocity VLOS < 150 km s-1 to be stars. In the most ambiguous range, i.e. 150 km s-1 < VLOS < 350 km s-1, they classified all uncertain objects, for which a clean separation between contaminants and GCs could not have been done, as stars. Based on the remaining sample, they reported that the number density profile of the spectroscopically confirmed GCs showed no evidence for a transition between a halo and IC component, either as a sharp truncation of the halo, or a flattening of the GC number density profile at large radii. From the sample kinematics, they observed that their GCs around M 87 have velocity dispersion in the range 300 ≤ σ ≤ 500 km s-1 out to 190 kpc, with ~500 km s-1 for the GCs population at 190 kpc significantly smaller than the velocity dispersion of Virgo cluster galaxies (Binggeli et al. 1993; Conselice et al. 2001). However, from the PN phase-space distribution (VLOS,PN,RPN) in Fig. 6, we see that a large fraction of IC stars near M 87 have velocities VLOS < 350 km s-1. This suggests that the lack of evidence for the IC component reported by Strader et al. (2011) could be caused by the velocity threshold Vmin = 350 km s-1 imposed on the GC sample, which is needed to prevent the contamination from Milky Way halo stars, but may also remove many of the ICGCs from their analysis.
6.4. Relation between BCG and ICL
When studying central galaxies in clusters, one of the main question is to establish where the ICL begins and where the associated BCG ends, or whether any distinction is to be made at all.
For M 87, the differences in the density profiles and velocity distributions of the halo and ICPN populations, as well as in their α-parameters and PNLFs, are sufficient to argue that the two components must be considered to be separate stellar populations, with different metallicities and star formation histories, and not as a continuum. As discussed above, published stellar population data suggest that the halo stars are older and more metal-rich than the ICL (see Sects. 5, 6.1 for more details).
In more distant BCGs where a kinematic decomposition between BCG halo and ICL is not available, the presence of an additional dynamical component in BCGs is usually inferred from a change of slope at large radii in the SB profile (Zibetti et al. 2005; Gonzalez et al. 2007; D’Souza et al. 2014). Photometric properties or colours are obtained by treating the two components as a continuum because no differentiation between the underlying stellar populations is normally possible.
Using a particle tagging method to analyse galaxy clusters in ΛCDM simulations, Cooper et al. (2015) consider the BCG and ICL as a single entity consisting of all stars, which are not bound to any cluster subhalos. They then split the BCG stars into accreted stars and in situ stars, and find that the large majority of BCG stars are accreted stars. They find double-Sèrsic surface density profiles in their simulated BCGs, where the inner component (R < 200 kpc) is dominated by “relaxed” accreted components, and the outer component by “unrelaxed” accreted components. Cooper et al. (2015) argue that the accreted/in situ separation is physically meaningful and that the ICL should naturaly be considered as a continuation of the BCG to low surface brightness because both components are formed by similar mechanisms.
In contrast, a dynamical approach based on the velocity distributions of diffuse light particles in hydrodynamic cosmological simulations (Dolag et al. 2010; Cui et al. 2014) is found to separate these stars into two components: one bound to the cluster potential and the other bound to the BCG. The resulting BCG and diffuse ICL are formed on different timescales, and the simulated stars associated with the two components are different in terms of spatial distribution, ages, and metallicities. Cui et al. (2014) showed that it is possible to dynamically differentiate between halo and IC particles using the particles’ binding energies. Stars with high binding energy, which end up belonging to the BCG, were subjected to relaxation and merging processes such that the gravitational potential changed so quickly that these stars lost memory of the kinematics of their progenitors (Murante et al. 2007; Dolag et al. 2010). On the other hand, stars with lower binding energy, that belong to the diffuse component, still reflect the dynamics of the satellite galaxies. Both Dolag et al. (2010) and Cui et al. (2014) also observed that the slope of the surface brightness profile associated with the two components change, with the halo profile being steeper than the ICL profile.
It is likely that the distinct BCG and IC components found in the hydrodynamical simulations are related to the relaxed and unrelaxed accreted components in the particle tagging analysis, but the inclusion of baryonic processes in the former may accentuate the differences found between BCG and ICL. If we associate the BCG and ICL of Dolag et al. (2010), Cui et al. (2014) with the relaxed and unrelaxed accreted components of Cooper et al. (2015), the progenitors of the stars in the steeper Sèrsic (relaxed) component would be accreted from more massive systems at higher redshifts, while the stars in the shallower and more extended ICL (unrelaxed) component would come from the accretion of less massive systems at lower redshifts. More massive progenitors dominate the diffuse light in simulated clusters close to the centre (Murante et al. 2007; Puchwein et al. 2010) because they move further inwards by dynamical friction. They cause stronger relaxation of the gravitational potential, and if accreted early, they have more time to relax.
To summarise, recent simulations show that a distinction can be made between stars that trace the cluster potential and stars bound to the BCG, based on the physical properties and binding energies of the accreted progenitors. From the study of the PN population around M 87, we have shown the coexistence of two discrete components in the Virgo cluster core, tracing different stellar populations, in agreement with these predictions. While the PN population for the IC component around M 87 indicates low-mass dwarf and star-forming galaxy progenitors, the stellar halo has higher metallicity, ~0.7 solar, indicating more massive progenitors. This bimodality in the progenitors may be the root of the bimodality in the kinematics and density profiles of the M 87 halo and the ICL.
However, we note that this kind of bimodality need not occur in every cluster of galaxies. For example, it is plausible that, for a more continuous distribution of progenitor masses and a more uniform distribution of binding energies of the debris stars, the final BCG plus ICL system would show continuous radial gradients in kinematics and stellar population properties, rather than appear as the sum of several discrete components. It is possible that NGC 6166 in the Abell 2199 cluster is closer to this situation: the velocity dispersion in the high surface brightness halo of this BCG was recently measured to increase up to the cluster velocity dispersion of ~800 km s-1 at 100′′ from the galaxy centre (Bender et al. 2015; see also Kelson et al. 2002).
7. Summary and conclusions
We obtained spectra for 287 PNs in the outer regions of the nearby elliptical galaxy M 87, of which 211 are located between distances 40 kpc to 150 kpc from the galaxy centre. Spectra were acquired with the FLAMES spectrograph in the GIRAFFE+MEDUSA configuration, with spectral resolution of R = 22 500. We observed 14 different FLAMES plate configurations, using candidates from the catalogue described in Longobardi et al. (2013). The spectroscopic survey aimed at measuring the LOS velocities of PNs in the transition region between the galaxy’s stellar halo and the ICL. We identified PNs through their narrow and symmetric, redshifted [OIII]λ5007 Å emission line, with no or negligible continuum, and verified with the second [OIII]λ4959 Å emission line. Spectra were measured for PNs in the magnitude range from m5007 = 26.3 down to 28.8. This is the largest spectroscopic sample of PNs at such galactic radii for a central galaxy, in the number of tracers and magnitude depth.
The area covered by the survey allowed us to trace the transition between the M 87 halo and ICL in the Virgo cluster core. The coexistence of these two components is shown by the bimodality of the LOSVD, whose strong asymmetric wings make it deviate from the near-Gaussian LOSVD typical of early-type galaxies. We separated halo and ICPNs by studying the projected phase-space distribution. We implemented a robust technique to measure the velocity dispersion of the M 87 halo, separating its velocity distribution from the broader component, the ICL. We identified 243 PNs for the M 87 halo and 44 ICPNs. We found that the logarithmic number density profile for the halo PNs follows the V-band SB profile from Kormendy et al. (2009), while the IC number density profile decreases towards large radii as a power-law IICL ∝ Rγ with γ in the range [−0.34, −0.04 ].
The total PN surface density profile at large radii is flatter than the surface brightness profile because of the presence of the IC component (see also Longobardi et al. 2013), which contributes ~3 times more PNs per unit luminosity than the halo population. We find luminosity-specific PN numbers 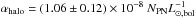 and
and 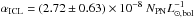 for the M 87 halo and IC PN population, respectively. This is consistent with the known existence of a gradient towards bluer colours at large radii because of the increased contribution of ICL at large distances and its lower metallicity compared to the halo population.
for the M 87 halo and IC PN population, respectively. This is consistent with the known existence of a gradient towards bluer colours at large radii because of the increased contribution of ICL at large distances and its lower metallicity compared to the halo population.
The spectroscopically confirmed PNLFs for both the halo and IC PNs have a steeper slope towards faint magnitudes than is predicted by the analytical formula of Ciardullo et al. (1989), confirming the result from the photometric sample (Longobardi et al. 2013). This steepening is consistent with an old stellar population dominated by PNs with low-mass cores. The PNLF of the ICPN population has a slightly shallower gradient than the M 87 halo PNLF, and in addition shows dip at about ~1−1.5 mag from the bright cut-off. This dip is an evolutionary feature observed in star-forming systems, such as M 33 and the Magellanic clouds, and may be related to rapidly evolving PNs with massive central cores. The presence of the dip in the ICPNLF, but not in the M 87 halo PNLF, provides additional evidence for intrinsic differences between the halo and IC parent stellar populations.
Using PNs as tracers we showed that the stellar halo of the BCG galaxy M 87 is distinct from the surrounding ICL in its kinematics, density profile, and parent stellar population, consistent with the halo of M 87 being redder and more metal-rich than the ICL. We note that the ICL in our surveyed fields corresponds to about four times the luminosity of the LMC, spread out over a region of ~100 kpc diameter. It is remarkable that population properties can be observed for such a diffuse component.
In the Virgo cluster, BCG halo and ICL cannot be considered as components with a gradual transition in their kinematics. This supports results from analysis of galaxy cluster simulations, which suggest that the IC component in Virgo consists of unrelaxed accreted stars bound to the cluster potential, while the stellar halo of M 87 appears to be described as a relaxed accreted component bound to the galaxy itself. Based on its PN population properties, we propose that the progenitors of the Virgo ICL were low-mass, star-forming galaxies, which may also have brought with them a significant fraction of the blue GC population seen in the outer regions of M 87.
The transformation between the AB and 5007 magnitudes for the photometric narrowband filter is given by m5007 = mAB + 2.49 (Longobardi et al. 2013).
In Strader et al. (2011) the “nominal” success rate is defined as the ratio between number of slit/fibres allocated to candidates and the number of identified GCs.
The systemic velocity of M 87 is taken as the median value of the entire sample of velocities within two sigma of the original median. Our value 1275 ± 24 km s-1 is consistent with those obtained by Binggeli et al. (1987) (Vsys = 1258 ± 10 km s-1), and Cappellari et al. (2011) (Vsys = 1284 ± 5 km s-1).
We used the relation of Cardelli et al. (1989) with RV = 3.1 to go from reddening to extinction at 5007 Å.
Acknowledgments
We thank Ken Freeman, John Kormendy, and Sadanori Okamura for discussions and helpful suggestions, and the ESO user support department and the La Silla – Paranal science operation staff for the support of our service mode observations. A.L. is grateful to J. Elliott, and B. Agarwal for helpful discussions. This work made use of the NASA/IPAC extragalactic database (NED) operated by the Jet Propulsion Laboratory and the California Institute of Technology.
References
- Adelman-McCarthy, J. K., et al. 2009, VizieR Online Data Catalog: II/294 [Google Scholar]
- Aguerri, J. A. L., Gerhard, O. E., Arnaboldi, M., et al. 2005, AJ, 129, 2585 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Mendez, R. H., et al. 1996, ApJ, 472, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Aguerri, J. A. L., Napolitano, N. R., et al. 2002, AJ, 123, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Freeman, K. C., Okamura, S., et al. 2003, AJ, 125, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Gerhard, O., Aguerri, J. A. L., et al. 2004, ApJ, 614, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Ventimiglia, G., Iodice, E., Gerhard, O., & Coccato, L. 2012, A&A, 545, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bender, R., Saglia, R. P., & Gerhard, O. E. 1994, MNRAS, 269, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., Kormendy, J., Cornell, M. E., & Fisher, D. B. 2015, ApJ, 807, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G. M., Nichol, R. C., Tyson, J. A., Ulmer, M. P., & Wittman, D. 1995, AJ, 110, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Tammann, G. A., & Sandage, A. 1987, AJ, 94, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Popescu, C. C., & Tammann, G. A. 1993, A&AS, 98, 275 [NASA ADS] [Google Scholar]
- Boylan-Kolchin, M., Ma, C.-P., & Quataert, E. 2008, MNRAS, 383, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Buzzoni, A., Arnaboldi, M., & Corradi, R. L. M. 2006, MNRAS, 368, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, N., Strader, J., Romanowsky, A. J., et al. 2014, ApJ, 787, L11 [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnovi’c, D., et al. 2011, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Castro-Rodríguez, N., Arnaboldi, M., Aguerri, J. A. L., et al. 2009, A&A, 507, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churazov, E., Tremaine, S., Forman, W., et al. 2010, MNRAS, 404, 1165 [NASA ADS] [Google Scholar]
- Ciardullo, R. 2010, PASA, 27, 149 [NASA ADS] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Ford, H. C., & Neill, J. D. 1989, ApJ, 339, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., Feldmeier, J. J., & Bartlett, R. E. 1998, ApJ, 492, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Durrell, P. R., Laychak, M. B., et al. 2004, ApJ, 614, 167 [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., & Arnaboldi, M. 2010, MNRAS, 407, L26 [NASA ADS] [Google Scholar]
- Coccato, L., Arnaboldi, M., & Gerhard, O. 2013, MNRAS, 436, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Gallagher, III, J. S., & Wyse, R. F. G. 2001, ApJ, 559, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, E., De Lucia, G., Villalobos, Á., & Borgani, S. 2014, MNRAS, 437, 3787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooper, A. P., Gao, L., Guo, Q., et al. 2015, MNRAS, 451, 2703 [NASA ADS] [CrossRef] [Google Scholar]
- Cortesi, A., Arnaboldi, M., Coccato, L., et al. 2013, A&A, 549, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Côté, P., McLaughlin, D. E., Hanes, D. A., et al. 2001, ApJ, 559, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W., Murante, G., Monaco, P., et al. 2014, MNRAS, 437, 816 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Weinmann, S., Poggianti, B. M., Aragón-Salamanca, A., & Zaritsky, D. 2012, MNRAS, 423, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Doherty, M., Arnaboldi, M., Das, P., et al. 2009, A&A, 502, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolag, K., Murante, G., & Borgani, S. 2010, MNRAS, 405, 1544 [NASA ADS] [Google Scholar]
- D’Souza, R., Kauffman, G., Wang, J., & Vegetti, S. 2014, MNRAS, 443, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Durrell, P. R., Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., & Sigurdsson, S. 2002, ApJ, 570, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Durrell, P. R., Côté, P., Peng, E. W., et al. 2014, ApJ, 794, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, J. J., Ciardullo, R., Jacoby, G. H., & Durrell, P. R. 2003, ApJS, 145, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, J. J., Mihos, J. C., Morrison, H. L., et al. 2004, ApJ, 609, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C., Tanvir, N. R., & von Hippel, T. 1998, Nature, 391, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Forte, J. C., Vega, E. I., & Faifer, F. 2012, MNRAS, 421, 635 [NASA ADS] [Google Scholar]
- Gallagher, III, J. S., & Ostriker, J. P. 1972, AJ, 77, 288 [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., Arnaboldi, M., Freeman, K. C., et al. 2005, ApJ, 621, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., Arnaboldi, M., Freeman, K. C., et al. 2007, A&A, 468, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gnedin, O. Y. 2003, ApJ, 589, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Zabludoff, A. I., Zaritsky, D., & Dalcanton, J. J. 2000, ApJ, 536, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Zaritsky, D., & Zabludoff, A. I. 2007, ApJ, 666, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Gregg, M. D., & West, M. J. 1998, Nature, 396, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E., Harris, G. L. H., & Alessi, M. 2013, ApJ, 772, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Henize, K. G., & Westerlund, B. E. 1963, ApJ, 137, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Martínez, L., & Peña, M. 2009, A&A, 495, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hui, X., Ford, H. C., Ciardullo, R., & Jacoby, G. H. 1993, ApJ, 414, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., & De Marco, O. 2002, AJ, 123, 269 [Google Scholar]
- Janowiecki, S., Mihos, J. C., Harding, P., et al. 2010, ApJ, 715, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Zabludoff, A. I., Williams, K. A., et al. 2002, ApJ, 576, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Krick, J. E., & Bernstein, R. A. 2007, AJ, 134, 466 [Google Scholar]
- Laporte, C. F. P., White, S. D. M., Naab, T., & Gao, L. 2013, MNRAS, 435, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Zhou, X., Ma, J., et al. 2005, AJ, 129, 2628 [NASA ADS] [CrossRef] [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., et al. 2013, A&A, 558, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McNeil, E. K., Arnaboldi, M., Freeman, K. C., et al. 2010, A&A, 518, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McNeil-Moylan, E. K., Freeman, K. C., Arnaboldi, M., & Gerhard, O. E. 2012, A&A, 539, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mei, S., Blakeslee, J. P., Côté, P., et al. 2007, ApJ, 655, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Riffeser, A., Kudritzki, R.-P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 1985, ApJ, 289, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C. 2004, in Recycling Intergalactic and Interstellar Matter, eds. P.-A. Duc, J. Braine, & E. Brinks, IAU Symp., 217, 390 [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, M., Trujillo, I., Prieto, M. A., & Acosta-Pulido, J. A. 2014, MNRAS, 439, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Murante, G., Arnaboldi, M., Gerhard, O., et al. 2004, ApJ, 607, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Murante, G., Giovalli, M., Gerhard, O., et al. 2007, MNRAS, 377, 2 [Google Scholar]
- Murphy, J. D., Gebhardt, K., & Adams, J. J. 2011, ApJ, 729, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, J. D., Gebhardt, K., & Cradit, M. 2014, ApJ, 785, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Pannella, M., Arnaboldi, M., et al. 2003, ApJ, 594, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Nulsen, P. E. J., & Bohringer, H. 1995, MNRAS, 274, 1093 [NASA ADS] [Google Scholar]
- Ostriker, J. P., & Tremaine, S. D. 1975, ApJ, 202, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M. 1990, Rev. Mex. Astron. Astrofis., 20, 119 [NASA ADS] [Google Scholar]
- Peng, E. W., Ford, H. C., & Freeman, K. C. 2004, ApJ, 602, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Montero, E., & Díaz, A. I. 2003, MNRAS, 346, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Pota, V., Forbes, D. A., Romanowsky, A. J., et al. 2013, MNRAS, 428, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Puchwein, E., Springel, V., Sijacki, D., & Dolag, K. 2010, MNRAS, 406, 936 [NASA ADS] [Google Scholar]
- Read, J. I., Wilkinson, M. I., Evans, N. W., Gilmore, G., & Kleyna, J. T. 2006, MNRAS, 366, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, W. A., & Parker, Q. A. 2010, MNRAS, 405, 1349 [NASA ADS] [Google Scholar]
- Rodríguez-González, A., Hernández-Martínez, L., Esquivel, A., et al. 2015, A&A, 575, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanowsky, A. J., Strader, J., Brodie, J. P., et al. 2012, ApJ, 748, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Royer, F., Blecha, A., North, P., et al. 2002, in Astronomical Data Analysis II, eds. J.-L. Starck, & F. D. Murtagh, SPIE Conf. Ser., 4847, 184 [Google Scholar]
- Rudick, C. S., Mihos, J. C., & McBride, C. 2006, ApJ, 648, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Rudick, C. S., Mihos, J. C., Frey, L. H., & McBride, C. K. 2009, ApJ, 699, 1518 [Google Scholar]
- Rudick, C. S., Mihos, J. C., Harding, P., et al. 2010, ApJ, 720, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strader, J., Romanowsky, A. J., Brodie, J. P., et al. 2011, ApJS, 197, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taffoni, G., Mayer, L., Colpi, M., & Governato, F. 2003, MNRAS, 341, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Tamura, N., Sharples, R. M., Arimoto, N., et al. 2006, MNRAS, 373, 601 [NASA ADS] [CrossRef] [Google Scholar]
- van Albada, T. S. 1982, MNRAS, 201, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Ventimiglia, G., Gerhard, O., Arnaboldi, M., & Coccato, L. 2010, A&A, 520, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventimiglia, G., Arnaboldi, M., & Gerhard, O. 2011, A&A, 528, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willman, B., Governato, F., Wadsley, J., & Quinn, T. 2004, MNRAS, 355, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Ciardullo, R., Durrell, P. R., et al. 2007, ApJ, 656, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., Hathi, N. P., & Windhorst, R. A. 2008, ApJ, 675, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, L., Long, R. J., Mao, S., et al. 2014, ApJ, 792, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., White, S. D. M., Schneider, D. P., & Brinkmann, J. 2005, MNRAS, 358, 949 [Google Scholar]
- Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1952, PASP, 64, 242 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of the total number of allocated fibres, nominal success rate, detected number of PNs, and spectroscopic completeness in all fields.
Fluxes, FWHMs, and line ratios of the [OIII] λ5007/4959 Å doublet for halo, high-velocity, and low-velocity IC PNs subsamples.
All Figures
 |
Fig. 1 Top panel: core of the Virgo cluster (Mihos et al. 2005) with the positions of the FLAMES fields studied in this work (cyan circles) and in previous surveys (dotted black circles) by Arnaboldi et al. (2004) and Doherty et al. (2009). Black squares represent the Suprime-Cam survey fields used for the extraction of the photometric PN candidates (Longobardi et al. 2013). Bottom panel: schematic zoom-in of the surveyed area (black rectangles). FLAMES pointings (cyan circles) and PN candidates from the photometric survey (black asterisks; Longobardi et al. 2013) are plotted over the isophotes of the M 87 halo surface brightness (Kormendy et al. 2009). The green cross depicts M 87’s centre. North is up, East is to the left. |
| In the text | |
 |
Fig. 2 Spectra of single confirmed PNs. The top panel shows the spectrum for a PN dynamically bound to the halo component. The middle and bottom panels show spectra for PNs dynamically unbound to the halo (see Sect. 3), with higher (middle panel) and lower (bottom panel) velocity than the M 87 systemic velocity. Red vertical lines mark the positions of the two oxygen lines at their redshifted wavelengths. We smoothed the spectra to 0.015 nm per pixel. |
| In the text | |
 |
Fig. 3 Spectra for background emission line galaxies: Lyα emitter at z ~ 3.1 (top panel) and [OII] emitter at z ~ 0.34 (bottom panel). Red vertical lines mark the positions of the two components of the λ3726+3729 Å emission. We smoothed the spectra to 0.015 nm per pixel. |
| In the text | |
 |
Fig. 4 Projected phase-space diagram showing VLOS vs. major axis distance R from the centre of M 87, for all spectroscopically confirmed PNs (black asterisks). The major axis distance is given both in arcsec (bottom axis), and in kpc (top axis), where 73 pc = 1″. The dotted horizontal line shows M 87’s systemic velocity Vsys = 1275 km s-1 from Sect. 3.2. The shaded area represents the region of the projected phase-space where the blue-shifted [OIII] 4959 Å emission line would fall below the wavelength of the blue edge of the FLAMES sort ordering filter HR08. |
| In the text | |
 |
Fig. 5 Histogram of the line-of-sight velocities of the spectroscopically confirmed PNs (black histogram) fitted with a double Gaussian (black curve). Red and blue lines represent the two Gaussians associated with the M 87 halo and the IC components. |
| In the text | |
 |
Fig. 6 Projected phase-space diagram, VLOS vs. major axis distance from the centre of M 87, for all spectroscopically confirmed PNs from this work and Doherty et al. (2009).The major axis distance is given both in arcsec (bottom axis), and in kpc (top axis), where 73 pc = 1″. The PNs are classified as M 87 halo PNs (red asterisks) and ICPNs (blue asterisks), respectively; see text. Black squares identify spectroscopically confirmed PNs from Doherty et al. (2009). The smoothed 1, 2, and 2.5σ thresholds are represented by the dashed, dotted, and dot-dashed lines, respectively. The dashed horizontal line shows the M 87 systemic velocity Vsys = 1275 km s-1 as computed in Sect. 3.2, while the continuous green line shows the effective radius Re = 703.914″ determined by Kormendy et al. (2009). At VLOS = −220 km s-1, we plot the M 86 systemic velocity (long dashed line). |
| In the text | |
 |
Fig. 7 Combined spectra for the spectroscopically confirmed sub-samples of PNs belonging to the halo (upper panel), IC high-velocity (central panel) and IC low-velocity (bottom panel) classes. As expected from atomic physics, the [OIII]λ4959/5007 Å doublet is detected with a flux ratio 1:3 confirming that the large majority of our candidates are true PNs (see text for more details). |
| In the text | |
 |
Fig. 8 Sky positions of the spectroscopically confirmed halo (red crosses) and IC PNs (blue crosses). The green plus sign indicates the centre of M 87. The ellipses (dotted lines) trace the M 87 isophotes between photometric major axis radii |
| In the text | |
 |
Fig. 9 Logarithmic PN number density profiles for the M 87 halo (red triangles) and the IC PNs (blue diamonds), corrected for incompleteness. The error bars include counting statistics and completeness correction. The halo PN profile compares well with the surface brightness profile from Kormendy et al. (2009, plus signs). The continuous black line shows their Sersic fit with n = 11.8. The ICPN number density decreases towards larger radii as IICL ∝ Rγ with γ in the range [−0.34; −0.04 ] (full and dashed-dotted blue lines). Black squares show the combined halo and IC PN number density profile, which is well modelled by the two-component photometric model (dot-dashed black line, see Sect. 5). |
| In the text | |
 |
Fig. 10 Top panel: same as in Fig. 9, but here the halo and IC number density profiles are computed separately for the NW (filled symbols) and SE (open symbols) sides of M 87. Bottom panel: difference between the logarithmic PN number density profiles of the halo (red dots) and IC (blue dots) PNs in the NW and SE M 87 regions. A value of zero indicates no difference in the number of sources on opposite sides at a given major axis distance. |
| In the text | |
 |
Fig. 11 Luminosity function of all spectroscopically confirmed PNs corrected for incompleteness (full dots). The dashed green line represents the Ciardullo et al. (1989) formula for a distance modulus of 30.8, convolved with photometric errors and normalised to the data at the bright end. The spectroscopically confirmed PNLF shows an excess of fainter PNs with respect to the analytical formula, similar to the photometric PNLF (Longobardi et al. 2013). Open circles represent magnitude bins where the sample is not completeness-corrected. The error bars show the uncertainties from counting statistics and completeness correction. |
| In the text | |
 |
Fig. 12 Top panel: luminosity function of the spectroscopically confirmed halo PNs, corrected for incompleteness (red circles). The red line shows the fit of the generalised analytical formula (Eq. (10)) to the halo PNLF, with c2 = 0.72 and bright cut-off at 26.3 mag, corresponding to a distance modulus m − M = 30.8. Central panel: completeness-corrected PNLF for the ICPNs (blue circles). The blue line shows the fit of the generalised analytical formula (Eq. (10)) to the ICPNLF, with c2 = 0.66. The ICPNLF shows a dip 1−1.5 mag fainter than the bright cut-off. Bottom panel: PNLFs in absolute magnitude for the spectroscopically confirmed Virgo ICPNs (blue circles) and for the outer disk of M 33 (Ciardullo et al. 2004, cyan triangles) matched at the first bin. For this comparison, the data are corrected for line-of-sight reddening (see text). Absolute magnitudes are determined using a distance modulus of 30.8 for the ICL and 24.86 for M 33 (Ciardullo et al. 2004). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.