| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201425350 | |
| Published online | 10 July 2015 | |
Large Binocular Telescope view of the atmosphere of GJ1214b⋆,⋆⋆
1 INAF – Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
2 Dipartimento di Fisica e Astronomia, Università degli Studi di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: valerio.nascimbeni@unipd.it
3 Leibniz-Institut for Astrophysics, An der Sternwarte 16, 14482 Potsdam, Germany
4 INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
5 INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento, 90134 Palermo, Italy
6 INAF – Osservatorio Astrofisico di Arcetri, largo E. Fermi 5, 50125 Firenze, Italy
7 INAF – Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monte Porzio Catone (RM), Italy
Received: 17 November 2014
Accepted: 6 May 2015
The atmospheric composition and vertical structure of the super-Earth GJ1214b has been a subject of debate since its discovery in 2009. Recent studies have indicated that high-altitude clouds might mask the lower layers. However, some data points that were gathered at different times and facilities do not fit this picture, probably because of a combination of stellar activity and systematic errors. We observed two transits of GJ1214b with the Large Binocular Camera, the dual-channel camera at the Large Binocular Telescope. For the first time, we simultaneously measured the relative planetary radius k = Rp/R⋆ at blue and red optical wavelengths (B + R), thus constraining the Rayleigh scattering on GJ1214b after correcting for stellar activity effects. To the same purpose, a long-term photometric follow-up of the host star was carried out with WiFSIP at STELLA, revealing a rotational period that is significantly longer than previously reported. Our new unbiased estimates of k yield a flat transmission spectrum extending to shorter wavelengths, thus confirming the cloudy atmosphere scenario for GJ1214b.
Key words: techniques: photometric / planetary systems / stars: individual: GJ1214
Based on data acquired using the Large Binocular Telescope (LBT). The LBT is an international collaboration among institutions in the United States, Italy, and Germany. LBT Corporation partners are the University of Arizona on behalf of the Arizona university system; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, the Astrophysical Institute Potsdam, and Heidelberg University; the Ohio State University; and the Research Corporation, on behalf of the University of Notre Dame, University of Minnesota and University of Virginia. Partly based on STELLA WiFSIP data (Strassmeier et al. 2004).
The data of the light curves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/579/A113
© ESO, 2015
1. Introduction
The observational study of exoplanetary atmospheres is a very young field of research that started in 2002 with the space-based detection of sodium around a gaseous giant (Charbonneau et al. 2002) and was followed a few years later by the first such detection from the ground (Redfield et al. 2008). In this context, transiting exoplanets offer a great opportunity to characterize their atmospheres. During a transit the amount of stellar light absorbed or scattered by the planetary limb (and therefore the “effective” planetary radius) is wavelength-dependent and can be interpreted through models of different chemical composition and physical structure (Seager & Deming 2010). While sharp atomic absorption lines such as neutral Na and K are investigated by means of high-resolution spectroscopy, low-resolution spectra and broad-band photometry can be exploited to search for wide molecular bands in the near-infrared (NIR), or for processes affecting the continuum such as Rayleigh scattering (Sing et al. 2011). The latter is more efficient in the ultraviolet (UV) and blue optical regions due to its λ-4 dependence. The positive or null detection of Rayleigh scattering can greatly help in distinguishing between families of atmospheric models that otherwise would be strongly degenerate, as shown by Howe & Burrows (2012). With the advent of more sophisticated instruments, astronomers are focusing on characterizing smaller and smaller targets, now reaching a class of planets with masses between 2 and 10 M⊕. These planets, dubbed super-Earths, lack any analog within our solar system, and their possible composition is still a matter of debate. The missing parameters include the mean molecular weight μ of their atmospheres, a key quantity that also constrains the inner structure of these planets (Valencia et al. 2013).
The first discovered member of the super-Earth class was GJ1214b (Charbonneau et al. 2009), a 2.8 R⊕, 6.3 M⊕ low-density planet hosted by a M4.5V red dwarf (Anglada-Escudé et al. 2013). The atmosphere of GJ1214b has been investigated with different techniques and instruments by many authors (among them, Désert et al. 2011 and Bean et al. 2011), sometimes presenting contradictory results. The lack of consistency can be explained with a combination of 1) an incomplete treatment of correlated noise, also called red noise (Pont et al. 2007); 2) inhomogeneous assumptions (for example, on orbital inclination: Southworth 2008); and 3) a high level of stellar activity of the host GJ1214, which has been known for a long time to be a spotted and flaring star (Berta et al. 2011). More recent works agree on detecting a flat and featureless transmission spectrum, which rules out a cloudless, low-μ atmosphere as for a solar-composition atmosphere (Berta et al. 2012; Fraine et al. 2013; Kreidberg et al. 2014). Flat spectra can be due both to high-altitude clouds masking the lower layers, or to a high-μ atmosphere consisting, for instance, of methane or water vapor. The two model families are very difficult to distinguish by standard techniques, although recently there is some consensus about models based on clouds (Morley et al. 2013; Barstow et al. 2013; Kreidberg et al. 2014). Most of these works were based on NIR spectrophotometry.
Probing Rayleigh scattering could be useful to constrain μ in a complementary way, as was done in our previous work about the hot Uranus GJ3470b (Nascimbeni et al. 2013b). At the same time, it would distinguish between whole classes of models that are based on mixtures of clouds and hazes, as seen for instance in Fig. 21 from Howe & Burrows (2012). The best optical spectral region in which to carry out such a search is that encompassing the Johnson U and B bands, where the Rayleigh signal is at its strongest. Unfortunately, the blue flux of GJ1214, an extremely red star with B = 16.4, is too weak to allow high-precision photometry with medium-sized telescopes. The only previous works that investigated this spectral region (de Mooij et al. 2012, 2013; Narita et al. 2013) delivered relatively low-S/N light curves and large error bars on the transmission spectrum. On the other hand, all those measurements were not simultaneous, which gave rise to some doubts that activity effects (which are both wavelength- and time-dependent) might have biased the results. As our knowledge on stellar activity progresses, it is becoming clearer and clearer that simultaneous multiwavelength transit observations, to be carried out with differential photometry or spectrophotometry, are much more informative than sparse samplings because at least the time-dependent systematic component is zeroed (Ballerini et al. 2012; Oshagh et al. 2013).
In this work, we present for the first time a simultaneous high-S/N measurement of the relative radius k = Rp/R⋆ of GJ1214b in the B and R bands, obtained through Large Binocular Camera (LBC) dual-band photometry. Stellar activity and rotation was monitored during the same season by a long-term photometric follow-up with WiFSIP at STELLA. This paper is organized as follows. In Sect. 2 we describe how the observations were performed and how the light curves were extracted. In Sect. 3 we estimate the period and amplitude of the rotational modulation of GJ1214b, exploiting this information to correct our planetary radii derived from the LBC for activity effects. In Sect. 4, we finally compare our results with the literature by constructing and interpreting a revised transmission spectrum.
2. Observations and data reduction
2.1. LBC dual-channel photometry
We observed two complete transits of GJ1214b during the nights of March 29 and May 17, 2012 with the LBC camera mounted at the double 8.4m Large Binocular Telescope (LBT). We refer to these two events as T1 and T2 hereafter. The LBC is a wide-field, prime-focus imager consisting of two independent channels that are optimized for the optical UV/blue and red region, respectively (Giallongo et al. 2008). In particular, the extremely high blue efficiency of this instrument, combined with its simultaneous dual-channel capability, makes it unrivaled among other 8-10m class facilities. The sky was clear and photometric on both nights. We mounted a Bessel B and Bessel R filter on the blue and red channel, respectively. Exposure times were set to 30 s on both channels during the first transit; during the second one, the exposure time on the blue camera (where the flux of GJ1214 is much fainter) was increased to 60 s to reduce overheads and increase the duty cycle. Hard defocusing was applied to both cameras (up to 2′′ and 6′′ FWHM on the B and R images, respectively) to avoid saturation and minimize pixel-to-pixel systematic errors. Only a 5′ × 7′ CCD window from a single chip of the LBC mosaics was read out to improve speed. Nevertheless, the imaged field of view (FOV) included about fifteen reference stars with a S/N of the same order of our target.
The raw images were corrected for bias and sky flat-field using standard procedures. Stars drifted by about 50 pixels throughout the series. This caused the target to cross a CCD row that is larger than the average pixel size; this is a result of a well-known manufacturing defect first described by Anderson & King (1999). This defect required a special backward correction that was applied as prescribed by the same paper. The light curves of GJ1214b were then extracted by running the STARSKY pipeline, a code optimized to deliver high-precision differential photometry over defocused images, originally developed for the TASTE project (Nascimbeni et al. 2011, 2013a). We refer to our previous work on GJ3470b for further details on how STARSKY has been fine-tuned on the LBC (Nascimbeni et al. 2013b). The four final light curves, hereafter referred to as T1/B, T1/R, T2/B, and T2/R, are shown in the left panel of Fig. 1. Their reduced χ2, evaluated1 on the off-transit part ranges between  and 1.5, meaning that our noise budget is dominated by white-noise sources. The dominant sources of noise are expected to be mostly photon noise in the B light curves and photon noise plus scintillation in the R light curves (Howell 2006). A closer inspection of the effect of correlated noise within the overall noise budget is presented in Sect. 3.3. The average photometric error of the T1/R series is only 0.5 mmag over a 30 s time scale, which makes it one of the most accurate light curves of GJ1214b ever taken from a ground-based facility.
and 1.5, meaning that our noise budget is dominated by white-noise sources. The dominant sources of noise are expected to be mostly photon noise in the B light curves and photon noise plus scintillation in the R light curves (Howell 2006). A closer inspection of the effect of correlated noise within the overall noise budget is presented in Sect. 3.3. The average photometric error of the T1/R series is only 0.5 mmag over a 30 s time scale, which makes it one of the most accurate light curves of GJ1214b ever taken from a ground-based facility.
 |
Fig. 1 Left panel: light curves of GJ1214b gathered through the blue channel of LBC in the Bessel B band (blue points), and through the red channel in Bessel R (red points). Data points are plotted with the original sampling cadence. The black line corresponds to the best-fit model adopting the parameters listed in Table 2. Right panel: same as above, but showing the residuals from the best-fit model. The bump-like feature at phase 0.070 ≲ φ ≲ 0.092 appeared during the second transit and is interpreted as a starspot crossing; it is marked with an arrow in both channels. |
2.2. STELLA photometric follow-up
We monitored the host star GJ1214 in the observing seasons 2012 and 2013 to use its photometric variability as an indicator for the spot coverage on the visible hemisphere at the time of the transit observations. The program was performed with the 1.2m robotic twin telescope STELLA, located in the Observatorio del Teide at Tenerife, Canary Islands, and operated by the Leibniz-Institute for Astrophysics Potsdam (AIP; Strassmeier et al. 2004). We used the wide-field imager WiFSIP, which consists of a 4 k × 4 k back-illuminated CCD with a plate scale of 0.322′′/pixel and four read-out amplifiers. It offers a field of view of 22′ × 22′ on the sky (Weber et al. 2012). Between March 21 and October 10, 2012 we obtained data on 110 nights; and between March 24 and October 4, 2013 we observed on 81 nights. In 2012, we scheduled STELLA to observe GJ1214 with blocks of five exposures through a Johnson V filter and an exposure time of 150 s, followed by five exposures through a Cousins I filter with 60 s of integration time. To monitor the host star activity at wavelengths more sensitive to starspot modulation, in 2013 we switched to filters Johnson B (three exposures per block, 300 s of exposure time each) and Johnson V (three exposures, 150 s). In total, we gathered 197 images in B, 955 images in V, and 739 in I.
Bias and flat-field correction was applied by the STELLA data reduction pipeline (for details see Granzer et al., in prep.). The I-band data showed fringe patterns whose shape varied mainly with the CCD temperature. In addition to changes in the sky OH emission lines and the sky continuum background, a second-order effect in the fringe amplitude is due to a change of opacity in the CCD coating when the detector temperature changed due to low vacuum, for example. We split all our I-band measurements into bins of different CCD temperatures and created a master fringe map for each bin as the average of the individual images after they were filtered from point-like sources and smoothed. The master fringe map of the proper temperature was then scaled to match the fringe amplitude of each individual science frame and subtracted from it. This resulted in a suppression of the fringe features to about 20% of their original value.
Aperture photometry was performed with Source Extractor2 (Bertin & Arnouts 1996). We measured stellar fluxes with the Source Extractor parameter MAG_AUTO, which computes an elliptical aperture according to the second-order moments of the object’s light distribution. This option provides the flexibility to account for very different shapes of the PSF caused by different observing conditions over the length of our follow-up program. We applied stringent selection criteria by rejecting data points above a certain threshold in airmass (X = 1.7), sky background (2000 ADUs), object FWHM and elongation. Furthermore, we rejected images where the target falls onto the edge between different read-out amplifiers. The final sample consisted of 128/436/425 images in B/V/I, respectively. To perform differential photometry, we constructed an artificial comparison star by summing the flux of several stable reference stars. We tested several selection criteria and found that a combination of four nearby stars within 3′ from GJ1214, imaged on the same read-out amplifier, minimized the scatter in the final light curve. The same comparison stars were employed for all three data sets B, V, and I.
 |
Fig. 2 Upper panel: STELLA/WiFSIP differential light curve of GJ1214b, gathered through a Bessel V filter during the 2012 and 2013 observing seasons. Unbinned points are shown in gray, daily averages are plotted with green points. Epochs corresponding to the two transits observed by LBC (T1 and T2) are marked with vertical lines. Middle panel: same as above, but through a Bessel I filter in 2012 (red points) and Bessel B in 2013 (blue points). Lower panels: GLS periodograms of the light curves, plotted with matching colors. The V periodogram has been evaluated on both the whole 2012/2013 data set (solid line) and only on the 2012 season (dashed line). The best-fit period, or the lower limit to it, is reported for each periodogram. |
The final light curves are shown in the two upper panels of Fig. 2 in their original cadence (gray dots). Light curves were also binned by averaging all three or five points within a single block, to obtain measurements that are much more robust against outliers (green, red, and blue circles in Fig. 2 for the V, I, and B data, respectively). From here on, our analysis refers to the binned light curves.
3. Data analysis
3.1. Starspot crossing event
After a few preliminary fits of the LBC data, it became obvious that a bump-like feature (marked with an arrow in the bottom right panel of Fig. 1) is clearly detectable in the residuals of both channels, just before the egress of the second transit (T2/B, T2/R). We fitted each residual light curve (i.e., after the transit model had been subtracted) with a Gaussian function by leaving five free parameters: its height over the transit model δ, its width σ, its center t0, and the coefficients Δ0, Δ1 of a linear baseline Δ0 + Δ1t. The best-fit results, tabulated on Table 1 and plotted in the left panel of Fig. 3, were obtained through a nonlinear least-squares algorithm, while the uncertainties were estimated though 10 000 iterations of a Monte Carlo bootstrap.
Within the error bars, the duration and phase of the bump is consistent in both light curves, while the maximum amplitude is about 40% larger in the B band. This feature can be easily interpreted as the crossing of an active region on the stellar surface. Indeed, the contrast between the unperturbed photosphere and a colder starspot is higher at shorter wavelengths, giving rise to this typical color signature. We emphasize that the two LBC cameras are fully independent, and so are the optical paths of the two LBT telescopes when observing at the prime foci. Furthermore, no similar feature has been detected in either channel among field stars with a red color and similar magnitude to GJ1214 (Fig. 3, left panel, lowest three curves). We can therefore reject the hypothesis of an instrumental or telluric origin of the bump.
A few authors already reported tentative detections of starspots occulted by GJ1214b (Berta et al. 2011; Carter et al. 2011; Kundurthy et al. 2011; Narita et al. 2013), but this is the first firm detection based on multichannel photometry. The size of this active region is probably of the same order as GJ1214b: the approximate timescale of the crossing is 5.8 ± 0.5 min, which is compatible with the time the planet takes to cross a point-like feature on its host star (6.2 min). We caution that since the crossing took place very close (∼2 min before) to the third contact of the transit, where the angle between the normal to the stellar surface and the line of sight is θ ≃ 65°, the amount of photosphere covered by the occulted spot could be up to about twice the disk area of GJ1214b (∼2%), which is a lower limit for the overall spot coverage.
The more obvious effect of a starspot-crossing event on the derived transit parameters is to decrease the best-fit value of k, as well as perturbing the other parameters in unpredictable ways (Oshagh et al. 2013). To avoid this, in the following analysis we masked the bump from the T2/B and T2/R light curves by assigning zero weight to the affected points, at orbital phase 0.070 ≲ φ ≲ 0.092.
 |
Fig. 3 Left panel: modeling of the T2/R (left plots) and T2/B (right plots) light-curve bumps. From the top: residual light curves with the best-fit Gaussian model overplotted (black line; Table 1), residuals from the Gaussian fit, and light curves of three reference stars with a red color and magnitude similar to GJ1214. Within the errors, the bump-like feature is not seen in any other light curve. Right panel: correlated noise diagrams (photometric RMS of the binned time series as a function of bin size) for the GJ1214b LBC residual light curves after the best-fit transit model has been subtracted. The lower sequence in the T2/B, T2/R plots is evaluated after the starspot feature has been masked out. The green lines follow a Poisson-like |
By assuming that the size of the spot is the same as the projected planetary disk, we can obtain a crude estimate of the temperature difference ΔT between the spot and the unspotted photosphere. If one compares the heights δ of the B and R bumps (Table 1) with the depth of the underlying transit model at the central instant of the spot (14.0 mmag under the out-of-transit level), it is straightforward to derive the spot color relative to the average stellar color: (B−R)spot−(B−R)⋆ ≃ 0.17 mag. By assuming 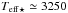 K (Anglada-Escudé et al. 2013) and modeling both fluxes as black-body radiation, we obtain ΔT ≃ 110 K. This agrees with previous observational studies that measured ΔT ≲ 500 K on early-to-mid M dwarf stars (Berdyugina 2005; Barnes et al. 2011; Jackson & Jeffries 2013). Our ΔT guess is of course a lower limit to the true ΔT, as in principle the spot could be smaller than the occulting planetary disk, and as a consequence, Tspot could be cooler than our estimate.
K (Anglada-Escudé et al. 2013) and modeling both fluxes as black-body radiation, we obtain ΔT ≃ 110 K. This agrees with previous observational studies that measured ΔT ≲ 500 K on early-to-mid M dwarf stars (Berdyugina 2005; Barnes et al. 2011; Jackson & Jeffries 2013). Our ΔT guess is of course a lower limit to the true ΔT, as in principle the spot could be smaller than the occulting planetary disk, and as a consequence, Tspot could be cooler than our estimate.
3.2. Transit parameter extraction
The LBC light curves have to be fitted with a transit model to extract the parameters of interest, above all the relative radius k = Rp/R⋆ , which is the wavelength-dependent quantity needed to construct the transmission spectrum. We used the JKTEBOP code3 version 34 (Southworth et al. 2004) to perform this task, adopting a quadratic law to model the stellar limb darkening (LD; Claret 2004). In principle, the free parameters of the fit are the central transit time T0, the orbital period P, the fractional stellar and planetary radii R⋆/a and Rp/a, the orbital inclination i, the Δ0, Δ1 coefficients of a linear baseline Δ0 + Δ1t, and the linear and quadratic LD terms u1, u2. Within this model, k is a derived parameter obtained by dividing Rp/a by R⋆/a.
We did not fit for both LD terms, following a common practice to improve the robustness of the fit (Southworth 2008). Instead, u2 was fixed on all light curves at its theoretical value for the corresponding photometric band by interpolating the LD tables by Claret et al. (2012) computed for cool stars (1500 <Teff< 4800 K). We adopted for GJ1214 the most recent values of Teff, log g and [M / H] estimated by Anglada-Escudé et al. (2013). We investigated the effect on our fit of the linear term u1 by setting it as a free parameter, or by keeping it fixed at its theoretical value over independent JKTEBOP runs. GJ1214b does not show any transit time variation (TTV) within about 10 s (Harpsøe et al. 2013), therefore we fixed both T0 and P at their most recent and accurate values (Kreidberg et al. 2014). Furthermore, the orbital inclination i is well known to be strongly correlated with k (Southworth et al. 2005). To avoid biases when comparing our results with the literature, we fixed the inclination and scaled semi-axis at their best-fit value 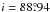 , a/R⋆ = 14.97 found by Bean et al. (2010), following what has been done by most other authors (including Bean et al. 2011; Désert et al. 2011; Croll et al. 2011; de Mooij et al. 2012; Murgas et al. 2012; Teske et al. 2013; Narita et al. 2013; Fraine et al. 2013; de Mooij et al. 2013).
, a/R⋆ = 14.97 found by Bean et al. (2010), following what has been done by most other authors (including Bean et al. 2011; Désert et al. 2011; Croll et al. 2011; de Mooij et al. 2012; Murgas et al. 2012; Teske et al. 2013; Narita et al. 2013; Fraine et al. 2013; de Mooij et al. 2013).
After these considerations, we had only three or four fitted parameters for each light curve: k, Δ0, Δ1 and, when left free, u1. The other parameters were injected into the fit as Gaussian priors, as done in Nascimbeni et al. (2013b); their dispersions were set to the published errors for P, T0 and i by Kreidberg et al. (2014) and Bean et al. (2010), and as the errors propagated on u1 and u2 by assuming the published uncertainties on Teff, log g and [M / H] by Anglada-Escudé et al. (2013). We chose to derive the uncertainties over the best-fit parameters with a Monte Carlo bootstrap algorithm (JKTEBOP task 7; Southworth et al. 2005) because formal errors are known to be underestimated due to correlations between parameters and residual systematic errors (the so-called red noise; Pont et al. 2007; a detailed analysis of it follows in the next subsection). The results are plotted in Table 2, the four individual and the two combined light curves; in the latter case, each pair of transits observed through the same filter was fitted simultaneously.
We note that when leaving u1 free, the best-fit value of the first epoch is consistent with the theoretical prediction. The best-fit values of k are also consistent with those obtained by fitting the light curves of the second transit in the matching filter. For this reason, and because the masking of the bump-like feature does not appear to bias the k measurement, the simultaneous fitting of both transits appears justifiable.
Summary of the best-fit transit parameters of GJ1214b from LBC photometry.
3.3. Correlated noise analysis
After the transits were properly modeled, we investigated whether and to which extent the residual light curve (i.e., after the transit best-fit model has been subtracted) is affected by correlated noise. To this purpose, a commonly used tool is the so-called correlated noise diagram (CND), where the input data are binned on different timescales and the resulting photometric RMS of the binned time series is plotted as a function of bin size (Pont et al. 2007; Carter & Winn 2009). We plotted CNDs for all our four light curves (T1/B, T1/R, T2/B, and T2/R) in the right panel of Fig. 3. For the T2/B and T2/R transits, we separately plotted the CNDs for the full light curve (upper sequence) and after masking the starspot feature (lower sequence). The CNDs have to be compared with a Poissonian 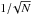 scaling law (where N is the number of points within each time bin), which is expected to predict the RMS after the averaging process in the ideal case when only white noise contributes (dashed-dotted green line on Fig. 3). More realistically, where correlated noise is not negligible, we expect to see an increase of the RMS toward the longest timescales. This is clearly visible in our case. For the T1/R and T1/B light curves, the RMS increase is always within ∼20% of the overall budget even at the longest available timescales (bin size ∼20 min, i.e., the maximum allowed by our requirement of having a set of at least ten bins to evaluate a meaningful RMS). This proves that the effect of red noise on the first transit is marginal. On the other hand, the T2/R and T2/B light curves show more red noise, which boosts the binned RMS by ∼50% even if the starspot bump is not taken into account. This is also confirmed by the best-fit linear slopes, which are steeper for the first transit: , , with respect to the second one: , (the latter values are calculated after masking the spot).
scaling law (where N is the number of points within each time bin), which is expected to predict the RMS after the averaging process in the ideal case when only white noise contributes (dashed-dotted green line on Fig. 3). More realistically, where correlated noise is not negligible, we expect to see an increase of the RMS toward the longest timescales. This is clearly visible in our case. For the T1/R and T1/B light curves, the RMS increase is always within ∼20% of the overall budget even at the longest available timescales (bin size ∼20 min, i.e., the maximum allowed by our requirement of having a set of at least ten bins to evaluate a meaningful RMS). This proves that the effect of red noise on the first transit is marginal. On the other hand, the T2/R and T2/B light curves show more red noise, which boosts the binned RMS by ∼50% even if the starspot bump is not taken into account. This is also confirmed by the best-fit linear slopes, which are steeper for the first transit: , , with respect to the second one: , (the latter values are calculated after masking the spot).
Although the T2 light curve is still dominated by photon noise at the 10−15 min timescale, the question is whether this additional noise is of instrumental, atmospheric, or astrophysical origin. A closer inspection of the T2/R vs. T2/B residual curves (lower right panel of Fig. 1) reveals some correlation between the two channels, but only during the transit. To support this hypothesis, we selected three subsets of data points covering the off-transit part, the in-transit (spot excluded), and the spot feature itself (Fig. 4, upper panel). Points were then paired by matching mid-exposure times that differ by less than 30 s between the two channels. By comparing the B and R residuals of the spot and in-transit series, a strong positive correlation is found (Spearman rank correlation coefficient: ϱ = 0.833 and 0.721, respectively), while the off-transit points are essentially uncorrelated (ϱ = 0.023). Interestingly, if we fit a straight line to the first two subsets (Fig. 4, lower panels), even the slope of the correlation is similar (0.58 vs. 0.46; i.e., the B amplitude in on average about twice the R one). As a similar behavior is not seen in any reference star, we conclude that most of the measured red noise is due to the crossing of additional inhomogeneities on the GJ1214 spotted surface, which was caught here in a relatively active phase. Additional evidence of such an increase of activity is exposed in the next subsection.
 |
Fig. 4 Statistical correlation between the blue (T2/B) and red (T2/R) LBC light curve of the second transit. Upper panel: observed minus calculated (O−C) residuals from the best-fit transit model as a function of orbital phase for the T2/B (square points) and the T2/R (round points) time series. Data are color-coded according to whether they are labeled as off-transit, in-transit (the spot feature being excluded) and spot only. Only points whose mid-exposure time can be matched within 30 s to a frame of the other channel are considered here. Lower panels: correlation plots between residuals from T2/B and T2/R light curves for the three samples defined above. The best-fit straight line calculated by ordinary least-squares is overplotted. The Spearman rank correlation coefficient is tabulated for each subset, along with the blue and red RMS. |
To check whether and to which extent the correlated noise content of our data might bias our derived transit parameters (Table 2), we performed an additional error analysis based on a residual-permutation (RP) or prayer bead algorithm, which is based on the cyclic permutation of the residuals (Southworth 2008). This approach preserves the temporal structure of the correlated noise and propagates it through the whole light curve, leading to more realistic error estimates. We ran the algorithm on our combined data sets, setting JKTEBOP with the same input parameters described in the previous subsection. The resulting best-fit values are k = 0.1176 ± 0.0009 (B) and k = 0.1175 ± 0.0004 (R), which are fully consistent with the previous ones but with a slightly larger error bar. Following a conservative choice, we adopted the RP best-fit values to build the transmission spectrum of GJ1214b.
3.4. Stellar activity and rotation
All our three B, V, I STELLA light curves of GJ1214 (Fig. 2) show clear signs of periodic variability at similar timescales. The phase of that signal is coherent among different filters (V vs. I in 2012 observing season, B vs. V in 2013), while the amplitude is larger at shorter wavelengths. This signature is easily interpreted as rotational modulation, meaning that it is the result of an unevenly spotted photosphere on a rotating star. The photometric variability and flaring behavior of GJ1214 is expected for a M4.5V dwarf and was already known before our study (Kundurthy et al. 2011), but the rotational period Prot is not firmly constrained so far. Berta et al. (2011) tentatively detected a signal with an amplitude of Arot = 3.5 ± 0.7 mmag and Prot ≃ 53 days from their MEarth (i + z)-band light curves gathered in 2010, but the authors themselves cautioned that their other data sets (Mearth 2008, 2009 seasons and FLWO 2010 V-band photometry) are not able to confirm that signal. A more recent multicolor follow-up by Narita et al. (2013) carried out at the MITSuME 50 cm telescope in 2012 found Prot = 44.3 ± 1.2 d, with Arot = 21 ± 4, 5.6 ± 0.8, and 3.2 ± 0.4 mmag on the g′, Rc, and Ic bands, respectively. In this case, the authors cautioned that the g′-band detection is weak because of low S/N and that the limited baseline of their observations prevented them from probing longer periods. More in general, it is possible that the true Prot of a star is an integer multiple (2:1 or 3:1) of the detected photometric period because there are multiple groups of active regions at different stellar longitudes (Walkowicz et al. 2013).
We analyzed our B, V, and I light curves, binned over each observing block of three or five repeated exposures, through a generalized Lomb-Scargle periodogram (GLS; Zechmeister & Kürster 2009). The error bar of each binned point was estimated as the root mean square (RMS) of the single measurements. For the V series, which spans two observing seasons, we analyzed both the whole series and each season separately. This is useful because typical active regions are expected to evolve over timescales ranging from weeks to months, which means that the phase coherence could be broken or attenuated when folding very long time series. The resulting periodograms are plotted in the lower panel of Fig. 2 and the corresponding best-fit GLS solutions in Table 3. We emphasize that the overall shape of the light curves and the resulting periodograms are not influenced by a particular choice of reference stars, as confirmed by further checks.
Most significant photometric periodicities of GJ1214 detected in STELLA/WiFSIP light curves by the GLS periodogram.
All three light curves show long-term (∼80 d) periodicities detected at high confidence. The V whole-series periodogram shows an excess of power between 60 and 100 d (with maximum power at P ≃ 83 d), which turns into a single prominent peak at P ≃ 69 d when only the 2012 season is taken into account (i.e., that with the longest coverage). The formal false-alarm probability (FAP) is 10-13 and 8 × 10-13, respectively. The I series reveals a signal at P ≃ 79 d with an even higher level of confidence (FAP: 7 × 10-16). Through both V and I filters, the pseudo-sinusoidal shape of the signals and their phase coherence are clearly visible in the light curves. A curvature perfectly consistent with the V light curve gathered in the same season is noticeable for the B series. As the smaller baseline of the B data (∼100 d, although only ∼60 d are densely sampled) prevents us from detecting signals at P ≳ 70 d, we assumed P ≃ 70 as a lower limit. All STELLA data therefore converge toward a rotational period of Prot ≃ 80 d, or an integer multiple of it. Interestingly, Berta et al. (2011) reported Prot = 81 d as the most significant period in their MEarth 2008 data, which matches our results very well, with an FAP of 10-4. On the other hand, the 44-d period reported by Narita et al. (2013) could be interpreted as a 2:1 harmonic of our peak, caused by two groups of active regions present at that time.
The V, I photometric amplitudes measured by our group during the 2012 campaign (i.e., when the LBC transits were gathered) are typically two to three times larger than those reported by Berta et al. (2011) and Narita et al. (2013). This suggests a phase of stronger activity undergone by GJ1214 in 2012. This hypothesis is also supported by the occulted starspots in our T2 transit, and in the August 12, 2012 light curve published by Narita et al. (2013). Berdyugina (2005) and Strassmeier (2009) indicated that for an M4 star the typical temperature contrast and filling factor of starspots are ΔT ≲ 500 K and ≲ 20%, respectively. This agrees with our estimate of ΔT ≳ 110 K based on the B−R color of the starspot occulted during the T2 transit, as shown in Sect. 3.1. Using the BT-Settl atmospheric model (Allard et al. 2011) to simulate such an M4 spotted photosphere under the above assumptions for ΔT and filling factor, we can indeed consistently recover the variability amplitude of the STELLA photometric series.
3.5. Correction for unocculted starspots
To construct a transmission spectrum of GJ1214b, the key quantity to derive from our LBC transit light curves is the radius ratio k = Rp/R⋆. This quantity is directly related with the transit depth and can be affected by stellar activity in two complementary ways. The first, most obvious one is by occulted starspots, which give rise to bumps in the light curve that force the fitting procedure to underestimate k. Provided that the S/N of the timeseries is high enough, these bumps are easily identified and masked by assigning them zero weight, as we did on our T2 transit.
A second, subtler way to add a bias on k is due to unocculted spots, because they decrease the mean surface brightness of the visible photosphere, therefore leading to overestimating k. This effect is color-dependent (being stronger at shorter wavelengths, where the contrast between the unspotted photosphere and the cooler spots is increased) and requires a correction that takes into account the spot coverage of the star at the time of observation. We followed the approach of Ballerini et al. (2012) to compute that correction and refer to our previous work on GJ3470b for further details (Nascimbeni et al. 2013b). We neglected the contribution from faculae, as no typical signatures of facular occultations by GJ1214b are recorded either in our data or in the literature light curves. Below, we focus on investigating the impact of activity on k during the first LBC epoch (T1), where we can reasonably assume that there are no occulted starspots (case 2 above). The starspot-crossing event on T2 and the possible presence of additional minor active regions (see Sect. 3.3) instead complicate the modeling, because a mixed scenario with both occulted and unocculted starspots cannot be approximated by either of the simplified cases above.
At the time of T1 transit, the star appeared ΔV ≃ ΔI ≃ 0.023 mag fainter than the maximum luminosity as it is modeled on the V/2012 and I/2012 light curves by the best-fit sinusoids plotted in Fig. 2. Assuming that the net observed stellar flux is the sum of the quiet and spotted photosphere, weighted by the corresponding coverage factor over the visible hemisphere (Afram & Berdyugina 2015; Scandariato & Micela 2014), this translates into an estimated spot coverage of ∼0.020 at the epoch of observation. Following Ballerini et al. (2012), adopting ΔT = 500 K and estimating A = 1−Fspot/F⋆ by means of BT-Settl atmospheric models (Allard et al. 2011), the maximum correction4 we compute is 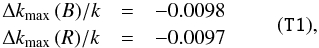 (1)that is, in absolute terms, Δkmax (B) = −0.00115 and Δkmax (R) = −0.00114.
(1)that is, in absolute terms, Δkmax (B) = −0.00115 and Δkmax (R) = −0.00114.
These corrections can then be applied to the apparent B and R radius ratios k(B), k(R) to obtain lower limits for them, named k′(B), k′(R) and reported in the last column of Table 2. These corrections might appear rather significant, as they change k by about 1%. Nevertheless, the color signature introduced by stellar activity is tiny, because the differential correction Δkmax (B)−Δkmax (R) < 0.0001 is well within the measurement error bars σ(k,B) = 0.0009 and σ(k,R) = 0.0004, respectively. We emphasize that Δkmax represents a maximal correction and that the true values probably lie somewhere between k and k′.
By comparing k′(B) = 0.1165 ± 0.009 and k′(R) = 0.1164 ± 0.0004, it is straightforward to conclude that the radius of GJ1214b is not dependent on wavelength within the error bars, even after the effect of unocculted starspots has been accounted for. In other words, based on our LBC data alone, where both the time- and wavelength-dependent activity effects are corrected for, the continuum of the transmission spectrum is flat within ≲1% between B and R. In the next section, we complement our measurements with others published in the literature through several bandpasses. As for the latter, only the apparent values of k are available because most authors of previous studies did not apply any correction for stellar activity. For consistency, we are forced to adopt our uncorrected k values throughout the comparison. However, we demonstrated above that the color effect given by the maximal correction (computed on the bluest and most affected band of the whole set: LBC B) is negligible with respect to the measurement errors, even during a phase of high stellar activity (2012). We are therefore confident that such a correction – even if it were available – would change the mean level of the transmission spectrum, but not the slope, leaving the main scientific result unchanged.
It is worth noting that the corrections computed above neglect the contribution from the fraction of spots that are always visible during a rotation cycle (because they are located in a polar region) or those that are uniformly distributed over the surface. The latter case is the most likely scenario, as fully convective stars at M⋆ ≲ 0.35 M⊙, such as GJ1214, are expected to drive activity in a turbulent dynamo regime rather than with a classic αΩ dynamo (Barnes et al. 2011 and references therein). It is easy to check what would happen if the filling factor due to the component of homogeneously distributed spots is the maximum allowed by previous studies for an M4V star (∼0.20; Berdyugina 2005). Models predict that the correction would scale approximately as a linear function of the filling factor, that is, it would be about ten times larger:  (2)that is, in absolute terms, Δkmax (B) = −0.01378 and Δkmax (R) = −0.01351. We conclude that even after applying such a maximal correction Δkmax (B)−Δkmax (R) ≃ 0.0003, the resulting k′(B) and k′(R) would be consistent with each other within the error bars, leaving the main scientific result unchanged.
(2)that is, in absolute terms, Δkmax (B) = −0.01378 and Δkmax (R) = −0.01351. We conclude that even after applying such a maximal correction Δkmax (B)−Δkmax (R) ≃ 0.0003, the resulting k′(B) and k′(R) would be consistent with each other within the error bars, leaving the main scientific result unchanged.
4. Discussion
 |
Fig. 5 Transmission spectrum of GJ1214b reconstructed by merging results from the present work (magenta circles) with all the published data that assumed the same prior as we did on i and a/R⋆ (see the legend on the right). Theoretical models with different compositions calculated for GJ1214b by Howe & Burrows (2012) are plotted with solid lines. Upper panel: low μ, cloud-free atmosphere with solar composition (red line). Middle panel: high μ, cloud-free atmosphere composed by pure water (blue line). Lower panel: featureless (constant) spectrum simulating a high-altitude layer of opaque clouds (green line). The corresponding χ2 values are reported for each case. |
We reconstructed a transmission spectrum of GJ1214b by merging the two values of k derived in this work (magenta circles on Fig. 5) with all the published data points that assumed the same prior as we did on orbital inclination and scaled semi-axis (centered on 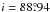 and a/R⋆ = 14.97, first adopted by Bean et al. 2010). As explained in Sect. 3.2, this is to avoid a systematic bias on k, because k and i (and, to a much lesser extent, a/R⋆) are known to be strongly correlated fit parameters. Unfortunately, this choice excludes some very high S/N data sets (including Berta et al. 2012, and Kreidberg et al. 2014, who fixed i at
and a/R⋆ = 14.97, first adopted by Bean et al. 2010). As explained in Sect. 3.2, this is to avoid a systematic bias on k, because k and i (and, to a much lesser extent, a/R⋆) are known to be strongly correlated fit parameters. Unfortunately, this choice excludes some very high S/N data sets (including Berta et al. 2012, and Kreidberg et al. 2014, who fixed i at 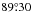 and
and 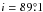 , respectively), but a full homogeneous reanalysis of these data is beyond the scope of this paper. The literature data we gathered include the following light curves, which resulted in 40 data points after combining measurements gathered through the same instrument and setup:
, respectively), but a full homogeneous reanalysis of these data is beyond the scope of this paper. The literature data we gathered include the following light curves, which resulted in 40 data points after combining measurements gathered through the same instrument and setup:
-
one transit from FORS2 at the VLT (spectrophotometry780−1000 nm; SP) by Beanet al. (2010), as later reanalyzed byBean et al. (2011);
-
three transits from FORS2 at the VLT (610–850 nm SP), MMIRS at the Magellan (H + K SP) and HAWKI at the VLT (narrow filter NB2090) by Bean et al. (2011);
-
two transits from IRAC at the Spitzer (IRAC 3.6 μm and 4.6 μm bands) by Désert et al. (2011);
-
four transits from WIRCam at the CFHT (each light curve was gathered by alternatively switching between pair of filters chosen among J, Ks, and a narrow CH4On), by Croll et al. (2011);
-
two transits from WFC at the INT (Sloan r and I), one transit from NOTCam at the NOT (Ks), one transit from LIRIS at the WHT (Kc), and one transit simultaneously observed through four filters (Sloan g, r, i, z) from GROND at the MPI-2.2m, by de Mooij et al. (2012);
-
seventeen transits from IRAC at the Spitzer (fourteen at 4.5 μm and three at 3.6 μm) and seven ground-based transits from TRAPPIST (through a wide band encompassing I + z′) by Fraine et al. (2013);
-
three transits from ACAM at the WHT (Sloan g), FORS2 at the VLT (Bessel B) and WFC at the INT (Sloan g) respectively, by de Mooij et al. (2013);
-
four transits from Mont4k at the Kuiper-1.55 m (two through Harris V and two through Harris R) and five transits from WiFSIP at STELLA (Sloan g′), by Teske et al. (2013);
-
two transits from SuprimeCam at the Subaru and FOCAS at the S ubaru (both in Bessel B), and one transit simultaneously observed through J, H, K from SIRIUS at the IRSF, by Narita et al. (2013).
Theoretical models of different chemical and physical compositions, calculated for GJ1214b by Howe & Burrows (2012), are plotted with solid lines of different colors in Fig. 5, along with the mentioned data. We focus on three representative cases: 1) a low μ, cloud-free atmosphere with solar composition, that is, dominated by hydrogen and helium (red line); 2) a high μ, cloud-free atmosphere composed of pure water vapor (H2O; blue line); 3) a featureless (constant) spectrum simulating a high-altitude layer of opaque clouds (green line), which mask every spectral feature behind that layer. We integrated the model spectrum over the photometric passband of each data point to calculate the residuals between model and observation, then we performed a statistical analysis. The corresponding χ2 values per degree of freedom are reported for each case in the corresponding diagram of Fig. 5.
The solar-abundance model is clearly ruled out at high confidence, the resulting χ2 being 7041. A similar conclusion was already drawn by Bean et al. (2010, 2011) and Désert et al. (2011), was debated by Croll et al. (2011), and later confirmed by most recent studies. The steep increase of absorption at the blue end of this particular model spectrum, which is a signature of Rayleigh scattering by molecular hydrogen H2, is ruled out at 3σ even by the LBC data alone, which makes ours an independent confirmation.
The water-based model returns a better fit, although with a rather high value of χ2 = 319, while the simpler featureless spectrum yields χ2 = 200. Based on this comparison, we selected the latter as the model that best explains the observations. We emphasize that no other model atmosphere among those computed by Howe & Burrows (2012) returns a smaller χ2, while the best-fit 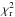 found above implies error bars underestimated by a factor of ∼2, under the hypothesis of an underlying Gaussian distribution. This is frequently observed when comparing results originating from different studies (Southworth 2011, among others, is a rich source of such examples). Possible reasons include the use of poorly suited numerical algorithms to estimate the uncertainties over the parameters, which cannot be calculated without taking into account the presence of highly correlated fit variables. A second explanation is stellar variability, which can alter most transit parameters (including k, the most relevant one to our purposes) as a function of both time and wavelength. For GJ1214b, we expect variability to be the dominant source of scatter in its optical transmission spectrum, following the discussion made in Sect. 3.5, where we estimated that the peak-to-valley relative variation of k owing to stellar activity could reach a few percent under reasonable assumptions.
found above implies error bars underestimated by a factor of ∼2, under the hypothesis of an underlying Gaussian distribution. This is frequently observed when comparing results originating from different studies (Southworth 2011, among others, is a rich source of such examples). Possible reasons include the use of poorly suited numerical algorithms to estimate the uncertainties over the parameters, which cannot be calculated without taking into account the presence of highly correlated fit variables. A second explanation is stellar variability, which can alter most transit parameters (including k, the most relevant one to our purposes) as a function of both time and wavelength. For GJ1214b, we expect variability to be the dominant source of scatter in its optical transmission spectrum, following the discussion made in Sect. 3.5, where we estimated that the peak-to-valley relative variation of k owing to stellar activity could reach a few percent under reasonable assumptions.
It is more challenging, however, to explain why the apparent radius of GJ1214b changes so much when measured at different epochs in the NIR, where spot contrast is expected to be lower and the corresponding effect on the apparent k weaker. This is most strikingly noticeable in the K band, where different authors found radii discrepant by more than 4σ (Narita et al. 2013). On one hand, little is known about the detailed magnetic behavior of stars close to the M5V transition where GJ1214 lies, and the Teff vs. Tspot relation reported by Berdyugina (2005) stops at Teff = 3300 K. It has been hypothesized that much colder spots could begin to appear at those spectral types (Barnes et al. 2011). That would explain why many surveys of mid- and late-M stars measured a photometric jitter that is similar to that usually reported in the optical region (Plavchan et al. 2008, among others).
On the other hand, another plausible interpretation for these cases is the presence of residual red noise, which is known to plague NIR data, often in subtle ways (Swain et al. 2013).
5. Conclusions
We demonstrated that the dual-channel capabilities of the LBC prime-focus camera and its unrivaled efficiency (especially on the blue side of the spectrum) are extremely effective in delivering high-precision photometric time series of faint, red, and active targets such as GJ1214b. Indeed, the Bessel B and R light curves presented in this work are the most precise ever published in their respective spectral regions. Not less important, they are truly simultaneous measurements, which enabled us to remove the time-dependent component of stellar activity. We exploited a smaller, robotic facility (WiFSIP at STELLA) to monitor the photometric variability of GJ1214 over a larger time scale to determine the wavelength-dependent contribution. This resulted in a new, robust estimate of the stellar rotational period at Prot ≃ 80 d. By comparing the WiFSIP light curves with those reported in the literature, we also noted that the activity level of GJ1214 was significantly higher than the average throughout the 2012 observing season. The detection of a large bump in the second transit (T2; 2012/05/17), induced by the crossing of a starspot, appears to support that finding. The nature of this bump is unambiguously confirmed by its B−R signature. The latter allowed us to derive a lower limit to the temperature contrast between the photosphere and the spot (ΔT ≃ 110 K), again highlighting the advantages of multicolor photometry.
The relative radii of GJ1214b through the B and R filter from the LBC data alone, once corrected for the presence of unocculted spots, are perfectly consistent with each other within ∼ 1%. This finding suggests a flat transmission spectrum in the optical region and rules out at 5σ the tentative detection of Rayleigh scattering by H2 that has been claimed by some previous works (de Mooij et al. 2012; Fraine et al. 2013). After combining our points with other optical and NIR measurements, we rule out cloud-free atmospheric models dominated by H/He and by heavier compositions such as pure water vapor. We conclude that a flat transmission spectrum, such as that resulting from an atmosphere with a thick cloud layer at high altitude, is still the model that best explains the available data. Our conclusion is consistent with other recent independent works (most notably, Kreidberg et al. 2014) that also ruled out cloud-free, high-μ models in favor of a featureless spectrum. We have to await the commissioning of future space-based instruments (such as the James Webb Space Telescope) to further investigate the atmosphere of GJ1214 and confirm the cloudy scenario (Belu et al. 2011).
I.e., when no starspots are occulted during the transit: case with focc = 0 (Ballerini et al. 2012).
Acknowledgments
We acknowledge the support from the LBT-Italian Coordination Facility for the execution of observations, data distribution and reduction. V. N. and G. P. acknowledge partial support by the Università di Padova through the “progetto di Ateneo #CPDA103591”. V. N. acknowledges partial support from INAF-OAPd through the grant “Analysis of HARPS-N data in the framework of GAPS project” (#19/2013) and “Studio preparatorio per le osservazioni della missione ESA/CHEOPS” (#42/2013). We thank Thomas Granzer for his extensive technical support with the STELLA monitoring campaign. Some tasks of our data analysis have been carried out with the VARTOOLS (Hartman et al. 2008) and Astrometry.net codes (Lang et al. 2010). This research has made use of the International Variable Star Index (VSX) database, operated at AAVSO, Cambridge, Massachusetts, USA. VN dedicates this paper to the memory of Renzo Nascimbeni (1942–2014).
References
- Afram, N., &Berdyugina, S. V. 2015, A&A, 576, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Anderson, J., &King, I. R. 1999, PASP, 111, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G.,Rojas-Ayala, B.,Boss, A. P.,Weinberger, A. J., &Lloyd, J. P. 2013, A&A, 551, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballerini, P.,Micela, G.,Lanza, A. F., &Pagano, I. 2012, A&A, 539, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, J. R.,Jeffers, S. V., &Jones, H. R. A. 2011, MNRAS, 412, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Barstow, J. K.,Aigrain, S.,Irwin, P. G. J.,Fletcher, L. N., &Lee, J.-M. 2013, MNRAS, 434, 2616 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Miller-Ricci Kempton, E., &Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bean, J. L.,Désert, J.-M.,Kabath, P., et al. 2011, ApJ, 743, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Belu, A. R.,Selsis, F.,Morales, J.-C., et al. 2011, A&A, 525, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Berta, Z. K.,Charbonneau, D.,Bean, J., et al. 2011, ApJ, 736, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, Z. K.,Charbonneau, D.,Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., &Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, J. A., &Winn, J. N. 2009, ApJ, 704, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, J. A.,Winn, J. N.,Holman, M. J., et al. 2011, ApJ, 730, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D.,Brown, T. M.,Noyes, R. W., &Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D.,Berta, Z. K.,Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A.,Hauschildt, P. H., &Witte, S. 2012, A&A, 546, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croll, B.,Albert, L.,Jayawardhana, R., et al. 2011, ApJ, 736, 78 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W.,Brogi, M., de Kok, R. J., et al. 2012, A&A, 538, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mooij, E. J. W.,Brogi, M., de Kok, R. J., et al. 2013, ApJ, 771, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Bean, J., Miller-Ricci Kempton, E., et al. 2011, ApJ, 731, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Fraine, J. D.,Deming, D.,Gillon, M., et al. 2013, ApJ, 765, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E.,Ragazzoni, R.,Grazian, A., et al. 2008, A&A, 482, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harpsøe, K. B. W.,Hardis, S.,Hinse, T. C., et al. 2013, A&A, 549, A10 [Google Scholar]
- Hartman, J. D.,Gaudi, B. S.,Holman, M. J., et al. 2008, ApJ, 675, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, A. R., &Burrows, A. S. 2012, ApJ, 756, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B. 2006, Handbook of CCD astronomy, eds. R. Ellis, J. Huchra, S. Kahn, G. Rieke, & P. B. Stetson [Google Scholar]
- Jackson, R. J., &Jeffries, R. D. 2013, MNRAS, 431, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 407, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L.,Bean, J. L.,Désert, J.-M., et al. 2014, Nature, 505, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kundurthy, P.,Agol, E.,Becker, A. C., et al. 2011, ApJ, 731, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, D.,Hogg, D. W.,Mierle, K.,Blanton, M., &Roweis, S. 2010, AJ, 139, 1782 [Google Scholar]
- Morley, C. V.,Fortney, J. J.,Kempton, E. M.-R., et al. 2013, ApJ, 775, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Murgas, F.,Pallé, E.,Cabrera-Lavers, A., et al. 2012, A&A, 544, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narita, N.,Fukui, A.,Ikoma, M., et al. 2013, ApJ, 773, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Nascimbeni, V.,Piotto, G.,Bedin, L. R., &Damasso, M. 2011, A&A, 527, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nascimbeni, V.,Cunial, A.,Murabito, S., et al. 2013a, A&A, 549, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nascimbeni, V.,Piotto, G.,Pagano, I., et al. 2013b, A&A, 559, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oshagh, M.,Santos, N. C.,Boisse, I., et al. 2013, A&A, 556, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plavchan, P.,Jura, M.,Kirkpatrick, J. D.,Cutri, R. M., &Gallagher, S. C. 2008, ApJS, 175, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F.,Gilliland, R. L.,Moutou, C., et al. 2007, A&A, 476, 1347 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Redfield, S.,Endl, M.,Cochran, W. D., &Koesterke, L. 2008, ApJ, 673, L87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Scandariato, G., & Micela, G. 2014, Exper. Astron. DOI: 10.1007/s10686-014-9390-5 [Google Scholar]
- Seager, S., &Deming, D. 2010, ARA&A, 48, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K.,Pont, F.,Aigrain, S., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J.,Maxted, P. F. L., &Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J.,Smalley, B.,Maxted, P. F. L.,Claret, A., &Etzel, P. B. 2005, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G.,Granzer, T.,Weber, M., et al. 2004, Astron. Nachr., 325, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Swain, M. R., Deroo, P., & Wagstaff, K. L. 2013, ArXiv e-prints [arXiv:1311.3934] [Google Scholar]
- Teske, J. K.,Turner, J. D.,Mueller, M., &Griffith, C. A. 2013, MNRAS, 431, 1669 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D.,Guillot, T.,Parmentier, V., &Freedman, R. S. 2013, ApJ, 775, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Walkowicz, L. M.,Basri, G., &Valenti, J. A. 2013, ApJS, 205, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., Granzer, T., & Strassmeier, K. G. 2012, SPIE Conf. Ser., 8451 [Google Scholar]
- Zechmeister, M., &Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Most significant photometric periodicities of GJ1214 detected in STELLA/WiFSIP light curves by the GLS periodogram.
All Figures
 |
Fig. 1 Left panel: light curves of GJ1214b gathered through the blue channel of LBC in the Bessel B band (blue points), and through the red channel in Bessel R (red points). Data points are plotted with the original sampling cadence. The black line corresponds to the best-fit model adopting the parameters listed in Table 2. Right panel: same as above, but showing the residuals from the best-fit model. The bump-like feature at phase 0.070 ≲ φ ≲ 0.092 appeared during the second transit and is interpreted as a starspot crossing; it is marked with an arrow in both channels. |
| In the text | |
 |
Fig. 2 Upper panel: STELLA/WiFSIP differential light curve of GJ1214b, gathered through a Bessel V filter during the 2012 and 2013 observing seasons. Unbinned points are shown in gray, daily averages are plotted with green points. Epochs corresponding to the two transits observed by LBC (T1 and T2) are marked with vertical lines. Middle panel: same as above, but through a Bessel I filter in 2012 (red points) and Bessel B in 2013 (blue points). Lower panels: GLS periodograms of the light curves, plotted with matching colors. The V periodogram has been evaluated on both the whole 2012/2013 data set (solid line) and only on the 2012 season (dashed line). The best-fit period, or the lower limit to it, is reported for each periodogram. |
| In the text | |
 |
Fig. 3 Left panel: modeling of the T2/R (left plots) and T2/B (right plots) light-curve bumps. From the top: residual light curves with the best-fit Gaussian model overplotted (black line; Table 1), residuals from the Gaussian fit, and light curves of three reference stars with a red color and magnitude similar to GJ1214. Within the errors, the bump-like feature is not seen in any other light curve. Right panel: correlated noise diagrams (photometric RMS of the binned time series as a function of bin size) for the GJ1214b LBC residual light curves after the best-fit transit model has been subtracted. The lower sequence in the T2/B, T2/R plots is evaluated after the starspot feature has been masked out. The green lines follow a Poisson-like |
| In the text | |
 |
Fig. 4 Statistical correlation between the blue (T2/B) and red (T2/R) LBC light curve of the second transit. Upper panel: observed minus calculated (O−C) residuals from the best-fit transit model as a function of orbital phase for the T2/B (square points) and the T2/R (round points) time series. Data are color-coded according to whether they are labeled as off-transit, in-transit (the spot feature being excluded) and spot only. Only points whose mid-exposure time can be matched within 30 s to a frame of the other channel are considered here. Lower panels: correlation plots between residuals from T2/B and T2/R light curves for the three samples defined above. The best-fit straight line calculated by ordinary least-squares is overplotted. The Spearman rank correlation coefficient is tabulated for each subset, along with the blue and red RMS. |
| In the text | |
 |
Fig. 5 Transmission spectrum of GJ1214b reconstructed by merging results from the present work (magenta circles) with all the published data that assumed the same prior as we did on i and a/R⋆ (see the legend on the right). Theoretical models with different compositions calculated for GJ1214b by Howe & Burrows (2012) are plotted with solid lines. Upper panel: low μ, cloud-free atmosphere with solar composition (red line). Middle panel: high μ, cloud-free atmosphere composed by pure water (blue line). Lower panel: featureless (constant) spectrum simulating a high-altitude layer of opaque clouds (green line). The corresponding χ2 values are reported for each case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


