| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323165 | |
| Published online | 30 June 2015 | |
H2 formation on PAHs in photodissociation regions: a high-temperature pathway to molecular hydrogen⋆
1 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: boschman@astro.rug.nl
2 Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands
Received: 2 December 2013
Accepted: 20 April 2015
Aims. Molecular hydrogen is the most abundant molecule in the Universe. It is thought that a large portion of H2 forms by association of hydrogen atoms to polycyclic aromatic hydrocarbons (PAHs). We model the influence of PAHs on total H2 formation rates in photodissociation regions (PDRs) and assess the effect of these formation rates on the total cloud structure.
Methods. We set up a chemical kinetic model at steady state in a PDR environment and included radiative transfer to calculate the chemistry at different depths in the PDR. This model includes known dust grain chemistry for the formation of H2 and a H2 formation mechanism on PAHs. Since H2 formation on PAHs is impeded by thermal barriers, this pathway is only efficient at higher temperatures (T> 200 K). At these temperatures the conventional route of H2 formation via H atoms physisorbed on dust grains is no longer feasible, so the PAH mechanism enlarges the region where H2 formation is possible.
Results. We find that PAHs have a significant influence on the structure of PDRs. The extinction at which the transition from atomic to molecular hydrogen occurs strongly depends on the presence of PAHs, especially for PDRs with a strong external radiation field. A sharp spatial transition between fully dehydrogenated PAHs on the outside of the cloud and normally hydrogenated PAHs on the inside is found. As a proof of concept, we use coronene to show that H2 forms very efficiently on PAHs, and that this process can reproduce the high H2 formation rates derived in several PDRs.
Key words: ISM: molecules / photon-dominated region (PDR) / astrochemistry
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Molecular hydrogen is the most abundant molecule in the Universe (Shull & Beckwith 1982; Black & van Dishoeck 1987; Draine & Bertoldi 1996) and the main constituent of regions where stars are forming. Many ion-molecule and neutral-neutral reactions are driven by the presence of H2. Specifically, H2 facilitates the formation of molecules such as CO, OH, H2O, HCO+, HCN, and H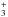 (Oppenheimer & Dalgarno 1974; van Dishoeck & Black 1986; Tielens & Hollenbach 1985). These species, as H2 itself, can be important coolants and provide useful diagnostics of (irradiated) interstellar clouds and shocks (Neufeld & Kaufman 1993; Neufeld et al. 1995; Le Bourlot et al. 1999). As such, it is crucial to understand the formation of H2 from low (~ 10 K) to high (~ 103 K) temperatures.
(Oppenheimer & Dalgarno 1974; van Dishoeck & Black 1986; Tielens & Hollenbach 1985). These species, as H2 itself, can be important coolants and provide useful diagnostics of (irradiated) interstellar clouds and shocks (Neufeld & Kaufman 1993; Neufeld et al. 1995; Le Bourlot et al. 1999). As such, it is crucial to understand the formation of H2 from low (~ 10 K) to high (~ 103 K) temperatures.
Since gas phase routes to form H2 were found to be inefficient, dust grains are recognized as the favoured habitat for H2 formation (Oort & van de Hulst 1946; Gould & Salpeter 1963). These dust grains can adsorb hydrogen atoms on their surface with either a Van der Waals bond (physisorption, Pirronello et al. 1997, 1999; Perry & Price 2003) or a covalent chemical bond (chemisorption, Zecho et al. 2002; Hornekær et al. 2006; Mennella 2006). The typical physisorption energy of a hydrogen atom is 700–800 K (60–70 meV), depending on the dust composition, whereas the typical chemisorption energy is 7000–25 000 K (0.60–2.15 eV) (Duley & Williams 1993; Cazaux & Spaans 2009). Because of their lower binding energies, physisorbed H atoms can easily migrate to another site (physisorbed or chemisorbed), or can evaporate back into the gas phase. If a migrating atom encounters another adsorbed H atom, these two atoms can react to form H2, the Langmuir-Hinshelwood mechanism (LH). H2 can also be formed when a gas phase atom adsorbs onto an already occupied site (Eley-Rideal mechanism, ER).
For both the LH and the ER mechanism to work, hydrogen atoms must be able to adsorb and stick to the surface of the dust grain. As the grain temperature rises, physisorbed H atoms start to evaporate and only chemisorbed H atoms are left on the grain surface. This decreases the H2 formation rate, since the LH mechanism becomes inefficient and H2 formation relies on the ER mechanism involving chemisorbed H atoms. The temperature at which the change of efficiency occurs depends on the physisorption energy, which depends on the composition of the dust grain. Typically, physisorbed H atoms desorb at grain temperatures of 10–20 K (Hollenbach & Salpeter 1971; Cuppen & Herbst 2005; Cazaux & Spaans 2009).
However, high H2 formation rates have been observed in PDRs with high dust and gas temperatures, such that the observed rates cannot be explained by dust grains alone (Habart et al. 2004; Allers et al. 2005). Allers et al. (2005) modelled the structure of the Orion Bar PDR and matched it with observations of different H2 rovibrational lines. Their best-fit model requires an H2 formation rate on dust grains of 3.8 × 10-17 cm3 s-1 at a temperature of 1000 K, which significantly exceeds the standard values for H2 formation on dust grains at 1000 K. Furthermore, the dust grain far-UV extinction cross section must be reduced by a factor of ~ 3 while the photoelectric heating rate in the atomic zone requires an increase of a factor of ~ 3 with respect to the a priori estimates.
Habart et al. (2004) resolved these deviations from the canonical H2 formation rate coefficient (Jura 1974) by including H2 formation on very small grains and polycyclic aromatic hydrocarbons (PAHs), and adjusting the barriers for H2 formation on dust grains. Their model does not fully reproduce the observed H2 formation rates in warm, high-UV environments, such as ρ Oph W and the Orion Bar, where rate coefficients as high as 10-16 cm3 s-1 have been observed.
PAHs make up the low-mass end of the grain size distribution (Weingartner & Draine 2001a). The bulk infrared emission features of PAHs have been detected in interstellar spectra (Allamandola et al. 1989), but it is still impossible to identify individual molecules (Pilleri et al. 2009). Although PAHs are much smaller than the rest of the dust grains, they account for approximately half of the total dust grain surface area available for chemistry (Weingartner & Draine 2001b). In the past decades a plethora of studies has been performed to understand how these PAHs can catalyze the formation of molecular hydrogen.
One of the most widely used mechanisms to form H2 on PAHs consists of two different reactions, in which a gas phase hydrogen atom forms a covalent bond with a PAH and a second step where a different H atom abstracts a hydrogen atom from the PAH to form molecular hydrogen (Bauschlicher 1998). Both reactions have been studied theoretically as well as experimentally with systems as large as coronene (C24H12). Mennella et al. (2012) and Thrower et al. (2012) exposed coronene films to atomic hydrogen and deuterium to derive cross sections for both the addition to and abstraction from coronene. Density functional theory (DFT) calculations by Rauls & Hornekær (2008) indicated the presence of barriers when hydrogenating a PAH, which were later experimentally observed by Boschman et al. (2012). These thermal barriers, which have a typical height of a few 100 K (a few times 10 meV), significantly restrict the formation of H2 on PAHs at low temperatures (T ≲ 200 K).
Alternatively, PAH molecules may lose an H2 molecule after being excited by a UV photon. This photodesorption mechanism has been studied both theoretically and in the laboratory (Allain et al. 1996; Jochims et al. 1994; Le Page et al. 2001). These studies find that loss of an H atom is the most dominant loss process. However, H2 loss is only a few times smaller than H loss, which could make the former process an important candidate for H2 formation on PAHs, on the condition that H atoms also hydrogenate the PAH molecules. It should be noted that the relative importance of these processes probably depends on the size of the PAH molecule.
Several theoretical models have been developed to quantify the formation of H2 on PAHs in astrophysical environments. These models account for the formation of H2 on PAHs in different ways. The Meudon PDR code by Le Petit et al. (2006) considers PAHs as a small-sized extension of the dust grain size distribution, where PAHs are treated as dust grains with a radius between 1 and 50 Å. A model by Le Page et al. (2009) does treat the chemical reactions between H atoms and PAHs explicitly. However, these reactions are limited to the normal hydrogenation state and a singly dehydrogenated state for both neutral and singly ionized molecules. Additionally, it considers a singly superhydrogenated state for PAH cations. Montillaud et al. (2013) presented a model that studies the hydrogenation and charge states of PAHs in PDRs using the Meudon PDR code, where the possible hydrogenation states range from fully dehydrogenated up to the singly superhydrogenated state. These hydrogenation states are available as either a neutral molecule or a singly ionized cation. Although the PAH chemistry is different in Montillaud et al. (2013) and Le Page et al. (2009), they both find that PAHs only exist in either the highest or the lowest possible hydrogenation state, depending on the column density. Intermediate PAHs are rarely observed.
In this study we model the chemistry of PAHs in photodissociation regions (PDRs) to investigate their ability to form H2. We combine H2 formation through LH and ER on dust grains and through abstraction and photodesorption on PAHs to establish total H2 formation rates at different depths in a PDR. We vary the number density of the cloud and the intensity of the external radiation field of the PDR. This allows us to study the effect of the radiation field on the PAH chemistry.
We use a time-dependent rate equation model and report the results obtained at steady state. Since addition barriers have only been derived for coronene, we use this molecule as our generic PAH. The transferability of these results is discussed in Sect. 4.2. We also incorporate the barriers determined in Boschman et al. (2012) for the addition and abstraction of H atoms to coronene, which prohibits the chemical hydrogenation or abstraction cycle for H2 formation on PAHs at gas temperatures below 200 K. In this manner, we find a high-temperature pathway for the formation of H2.
In Sect. 2 we describe the details of the physics and chemistry of our model. The results of the model are shown in Sect. 3. The uncertainties of the model are discussed in Sect. 4, where we also compare our results and previous studies.
2. Model
We describe a cloud by a one-dimensional PDR model with constant density nH. The cloud is irradiated from one side by a star with a UV intensity field G0, denoting the strength of the radiation field between 6 <hν< 13.6 eV in Habing units (1 G0 = 1.6 × 10-3 erg cm-2 s-1, Habing 1968). The cloud is divided into equally sized parcels of gas, which are consecutively brought into chemical equilibrium. The photoprocesses that are included are photoionization of PAHs and carbon atoms, photodissociation of H2, and photodesorption of H and H2 from PAHs. All photoprocesses are mitigated by dust extinction at increasing column densities, and for H2 photodissociation we also include H2 self-shielding. Ionization processes are counteracted by electron recombination, for which we use rates from Ruiterkamp et al. (2005) and the online database KIDA1 (Wakelam et al. 2012). The formation of H2 on interstellar dust grains (silicates and amorphous carbon) as well as on PAHs is considered in our model.
After a parcel has reached chemical equilibrium, we correct the radiation field for dust absorption and H2 self-shielding for the next parcel. The process is then repeated until the entire cloud is in chemical equilibrium. Dust grain and coronene abundances scale linearly with the number density. The parameters defining the cloud are summarized in Table 1.
Model parameters.
The processes involving PAHs that we consider are detailed in the following subsections. In Sect. 2.1.1 we describe the processes of hydrogenation and abstraction of H atoms on PAHs.
In Sect. 2.1.2 we discuss the interactions of PAHs with the impinging radiation field, where we describe the process of photoionization and electron recombination. We also describe the process of photodesorption, where a hydrogen atom or an H2 molecule is removed from the PAH upon absorption of a photon.
The influence of dust grains on the PDR is described in Sect. 2.2, and we treat the photodissociation of H2 in Sect. 2.3. In Sect. 2.4 we discuss the model calculations themselves.
2.1. PAHs
The abundance of PAHs in the interstellar medium (ISM) is very uncertain, and we refer to Weingartner & Draine (2001a) for a comparison between different values in several environments. We assume a total carbon abundance of 2.5 × 10-4, of which a third is locked in PAHs. This is similar to studies by Joblin et al. (1992) and Li & Draine (2001), who find the fraction of carbon atoms locked in PAHs relative to hydrogen to be 6 × 10-5.
We define PAHs as being smaller than 100 Å, and we use coronene (C24H12) as our prototypical PAH of the ISM. This is motivated by the fact that coronene is a well-studied molecule, both theoretically and experimentally. The barriers for single H addition and abstraction, which are instrumental for this study, have been determined only recently. In this sense, we use coronene as a molecule representative of all the PAHs in the PDRs studied in this work. It should be noted that this is a rough assumption, since it is widely believed that small PAHs (NC ≲ 40) cannot survive in strong radiation fields, which would exclude the existence of the coronene molecule in PDR environments (Allain et al. 1996), and that compact PAHs are more stable than extended molecules (Jochims et al. 1994; Ekern et al. 1997). However, other studies show that small PAHs can survive strong radiation fields, but in a very dehydrogenated state (Montillaud et al. 2013). Therefore a more realistic PDR model should consider a distribution of PAHs with different sizes, where larger PAHs with fewer H-bearing outer edge carbon atoms would be present. This implies that these PAHs would be slightly less efficient in forming H2, with an efficiency depending on the number of inner carbon atoms compared to outer edge carbon atoms. Although this would not affect the results drawn in this work, in future work a size distribution of PAHs would further increase the reliability of our model. In Sect. 4.2 we discuss the expected results when coronene is replaced with such a size distribution.
2.1.1. Hydrogenation and abstraction
Hydrogen addition and subsequent abstraction constitute a two-step catalytic cycle for the formation of H2. First, a coronene molecule reacts with a hydrogen atom to form a singly superhydrogenated coronene molecule (C24H13). In the second reaction, another hydrogen atom reacts with this singly superhydrogenated coronene molecule, yielding molecular hydrogen and the coronene molecule (Bauschlicher 1998).
This process is not limited to fully aromatic coronene (C24H12), but can also occur for coronene in other hydrogenation states, with up to 24 additional hydrogen atoms attached to the coronene (C24H36).
A (hydrogenated) coronene molecule can be either neutral or positively or negatively charged, which significantly changes the chemistry. We do not consider the PAH anions since their contributions are mostly important in strongly shielded environments, but concentrate on the barely shielded edges of the PDRs. The system of chemical reactions between coronene and hydrogen is summarized in Eqs. (1) and (2) and is detailed in Table A.1.  These reactions take place at a rate r, which is calculated as
These reactions take place at a rate r, which is calculated as  (3)Here,
(3)Here, 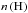 and
and 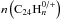 represent the number densities of atomic hydrogen and coronene molecules or cations containing n H atoms, respectively. σ represents the cross section for the specific reaction and vth is the average thermal velocity of atomic hydrogen. We use a cross section of 1.1 Å2 per reactive carbon atom for hydrogenation and 0.06 Å2 per reactive carbon atom for abstraction (Mennella et al. 2012).
represent the number densities of atomic hydrogen and coronene molecules or cations containing n H atoms, respectively. σ represents the cross section for the specific reaction and vth is the average thermal velocity of atomic hydrogen. We use a cross section of 1.1 Å2 per reactive carbon atom for hydrogenation and 0.06 Å2 per reactive carbon atom for abstraction (Mennella et al. 2012).
Since coronene is much more massive than hydrogen, its velocity is negligible compared to that of the gas phase hydrogen atoms. vth is therefore the thermal velocity of hydrogen atoms, which is calculated as 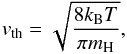 (4)where kB is the Boltzmann constant, T is the gas temperature and mH is the mass of the hydrogen atom.
(4)where kB is the Boltzmann constant, T is the gas temperature and mH is the mass of the hydrogen atom.
The hydrogenation and abstraction of coronene is subject to barriers (Ea), depending on hydrogenation and charge state. The presence of these barriers was predicted for neutral coronene by Rauls & Hornekær (2008) and first experimentally determined for coronene cations by Boschman et al. (2012). The latter study shows an alternating behaviour for the existence of barriers, meaning that the first hydrogenation of the coronene cation is barrierless. The second hydrogenation then has a barrier, while the third does not, etc. More recent experiments in conjuntion with theoretical calculations (Boschman et al., in prep.) show that this alternating behaviour continues until the coronene cation is fully hydrogenated. The hydrogenation barriers are summarized in Table A.1.
Abstraction barriers are only present for abstraction from those hydrogenation states for which adding a hydrogen atom would also have a barrier. In this manner, a distinction is made between chemically stable and chemically unstable hydrogenation states, where the unstable ones have a radical atom. The barrier against abstraction is set at 10 meV, equal to the value calculated by Rauls & Hornekær (2008) for abstracting an outer edge H atom from the doubly hydrogenated coronene molecule (C24H14). The influence of the uncertainties of these barrier heights on the obtained results is discussed in Sect. 4.
With the mechanism for H2 formation catalyzed by PAHs as described in Eqs. (1)and (2), the total H2 formation rate due to abstraction from PAHs is calculated as 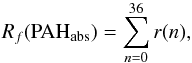 (5)where r(n) is the H2 formation rate as shown in Eq. (3).
(5)where r(n) is the H2 formation rate as shown in Eq. (3).
2.1.2. Photodesorption
In a PDR, PAHs experience a strong interaction with the photons from the impinging radiation field, which can either ionize the PAH or excite it into a higher state. We use Eq. (6)from Le Page et al. (2001) to calculate the total photoionization rate: 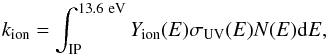 (6)with IP the ionization potential of the molecule and Yion the ionization yield taken from Le Page et al. (2001). σUV(E) is the photoabsorption cross section (Malloci et al. 2007) and N(E) is the intensity of the Habing interstellar radiation field in photons cm-2 s-1 eV-1 (Draine 1978).
(6)with IP the ionization potential of the molecule and Yion the ionization yield taken from Le Page et al. (2001). σUV(E) is the photoabsorption cross section (Malloci et al. 2007) and N(E) is the intensity of the Habing interstellar radiation field in photons cm-2 s-1 eV-1 (Draine 1978).
If the molecule is not ionized but excited, it can dissipate the excitation energy by either IR emission, loss of an H atom, or loss of an H2 molecule (Allain et al. 1996). To calculate the rates for these processes, we use the RRKM method as described in Le Page et al. (2001), which gives the rate of bond dissociation as a function of excitation energy, bond energy and vibrational degrees of freedom in the molecule. The competition between processes is accounted for by dividing the rate of one process by the sum of the rates of all possible processes. In this way, the branching ratio for each dissociation pathway upon excitation is obtained. Multiplying this dissociation probability with the coronene photoabsorption cross section σUV(E) of Malloci et al. (2007) and integrating over the Habing interstellar radiation field N(E) below the Lyman limit gives the total photodissociation rate per G0, as shown in Eqs. (7)and (8): 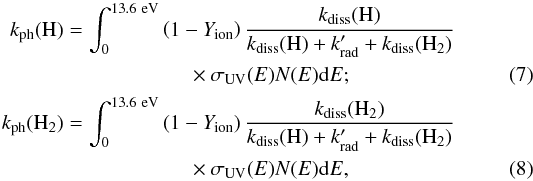 where
where 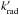 is the rate of IR stabilization.
is the rate of IR stabilization.
We use binding energies from Le Page et al. (2001) and Paris et al. (2014) to calculate the photodissociation rates for both the neutral coronene and the coronene cation in their dehydrogenated, superhydrogenated, and normally hydrogenated states. These photodissociation rates cover both loss of a single H atom and the loss of H2 and are summarized in Table A.2.
In addition to PAH ionization, we also include the photoionization of unbound carbon atoms as a source of free electrons. Recombination reactions are included in our chemical network, which ensures an ionization balance. The rates for recombination reactions on PAH cations are given by 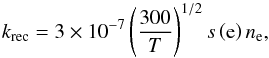 (9)with T the temperature,
(9)with T the temperature, 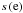 the electron sticking coefficient and ne the number density of free electrons (Ruiterkamp et al. 2005). From Ruiterkamp et al. (2005) we adopt an electron sticking coefficient of
the electron sticking coefficient and ne the number density of free electrons (Ruiterkamp et al. 2005). From Ruiterkamp et al. (2005) we adopt an electron sticking coefficient of 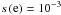 for coronene.
for coronene.
We only use carbon atoms as a source of free electrons, because other metals with an ionization energy comparable to carbon have abundances that are at least one order of magnitude lower. Since the ionization balance is driven by radiation, other metals are not considered.
2.2. H2 formation on dust grains
Dust grains have a significant influence on the chemistry taking place in the PDR because of their catalyzing properties, which strongly depend on the chemical composition of the dust grain, for example, silicates or amorphous carbon.
In our model, we limit the dust grain chemistry to the catalysis of H2 formation, and for this we assume the first H atom to be either physisorbed or chemisorbed. There are then two mechanisms for this H atom to react with another H atom and to form H2. In the first process, an H atom from the gas phase interacts with an adsorbed H atom (Eley-Rideal). In the second process, a different physisorbed H atom travelling around the surface interacts with the adsorbed H atom (Langmuir-Hinshelwood).
For both mechanisms to occur, a hydrogen atom must first adsorb onto the surface of the dust grain and become either chemisorbed or physisorbed. This adsorption process is incorporated into rate equations with a temperature-dependent sticking coefficient (Burke & Hollenbach 1983). Once an H atom is adsorbed onto the surface, it has a certain probability to form H2. This probability ϵ strongly depends on the binding energies of the adsorbed atoms and the gas and dust temperatures. The resulting H2 formation rate equation is given by 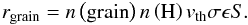 (10)Here n(grain) is the number density of dust grains,
(10)Here n(grain) is the number density of dust grains, 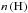 is the number density of atomic hydrogen, and vth is the average thermal velocity in the gas phase. σ is the average cross section of a dust grain, and values for n(grain)σ are taken from Cazaux & Spaans (2009). For the values of formation efficiency ϵ and sticking coefficient S, we use the expressions of Cazaux & Spaans (2009) and the dust grain size distribution derived by Weingartner & Draine (2001a). The sticking coefficient is calculated as
is the number density of atomic hydrogen, and vth is the average thermal velocity in the gas phase. σ is the average cross section of a dust grain, and values for n(grain)σ are taken from Cazaux & Spaans (2009). For the values of formation efficiency ϵ and sticking coefficient S, we use the expressions of Cazaux & Spaans (2009) and the dust grain size distribution derived by Weingartner & Draine (2001a). The sticking coefficient is calculated as 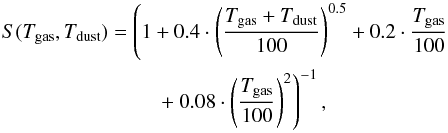 (11)which gives a numerical value for S typically between 0.4 and 0.9. The formation efficiency strongly depends on the surface composition and has a typical value between 0.4 and 1 for amorphous carbon; it lies between 0.01 and 1 for silicates (Cazaux & Spaans 2009).
(11)which gives a numerical value for S typically between 0.4 and 0.9. The formation efficiency strongly depends on the surface composition and has a typical value between 0.4 and 1 for amorphous carbon; it lies between 0.01 and 1 for silicates (Cazaux & Spaans 2009).
Cazaux & Spaans (2009) considered H2 formation on the surfaces of silicates, amorphous carbon and PAHs. We avoid a redundancy by only taking into account H2 formation on silicates and amorphous carbon and defining this as H2 formation on dust. The H2 formation on dust is calculated by using the surface area of silicates (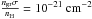 ) and amorphous carbon (
) and amorphous carbon ( ), so as to not count the contribution of PAHs twice.
), so as to not count the contribution of PAHs twice.
2.3. H2 photodissociation
The destruction mechanism for molecular hydrogen in the presence of UV photons is dissociation subsequent to the photo-excitation into a higher electronic state. Approximately 10% of these excited H2 molecules undergo fluorescence into the vibrational continuum of the electronic ground state, giving rise to dissociation of the molecule. The H2 photodissociation rate is given by Black & van Dishoeck (1987) and Draine & Bertoldi (1996): ![\begin{equation} \label{eq:h2diss} k_{\mathrm{diss}} = 3.4 \times 10^{-11} f( N( \mathrm{H_{2}} ) ) G_{0} \exp \left[-2.6 A_{\rm V} \right] \mathrm{s^{-1}}. \end{equation}](/articles/aa/full_html/2015/07/aa23165-13/aa23165-13-eq72.png) (12)In this equation the exponential factor expresses the dust extinction. The factor f(N(H2)) accounts for H2 self-shielding against photodissociation. This self-shielding factor f(N(H2)) has been computed as a function of H2 column density by Draine & Bertoldi (1996),
(12)In this equation the exponential factor expresses the dust extinction. The factor f(N(H2)) accounts for H2 self-shielding against photodissociation. This self-shielding factor f(N(H2)) has been computed as a function of H2 column density by Draine & Bertoldi (1996), ![\begin{eqnarray} \label{eq:h2shield} f( N( \mathrm{H_{2}} ) ) = \frac{0.965}{\left( 1 + x/b_{5} \right)^{2}}+ \frac{0.035}{\sqrt{1 + x}} \times \exp \left[-8.5 \times 10^{-4} \sqrt{1 + x} \right], \end{eqnarray}](/articles/aa/full_html/2015/07/aa23165-13/aa23165-13-eq74.png) (13)where x = N(H2)/5 × 1014 cm-2 is the H2 column density and b5 is the line width of H2 absorption lines expressed in 105 cm s-1, which was set to unity for our calculations.
(13)where x = N(H2)/5 × 1014 cm-2 is the H2 column density and b5 is the line width of H2 absorption lines expressed in 105 cm s-1, which was set to unity for our calculations.
2.4. Computations
In our calculations, we use a one-dimensional plane-parallel slab of gas that is irradiated from one side. This slab is divided into 103 equally sized cells of gas, which all have the same number density and abundances. Initially, there is no molecular hydrogen present, and the only PAH is the normally hydrogenated coronene molecule (C24H12).
Every single reaction in the list of reactions gives rise to a rate equation, and from this the rate for every reaction is calculated at t = 0. We perform a numerical Euler integration until the system reaches convergence, which is defined as the moment when the fractional difference between two time steps is smaller than 10-3 for every chemical species. For the species with abundances higher than 10-9, this condition is met in less than 103 yr. For species with lower abundances it is increasingly difficult to converge, and timescales ranging between 105 and 108 yr are required to reach equilibrium for the entire system. Time-dependent environmental effects may play a role, but this will be a topic of future study. After convergence is reached in a parcel of gas, the calculation starts for the next parcel of gas, including a modification of the radiation field to account for dust extinction and H2 self-shielding.
Temperatures in a PDR are strongly dependent on the external radiation field through various mechanisms. In regions where dust grains are exposed to UV radiation, the gas is indirectly heated via photoionization of dust grains and PAHs. At low densities (nH ≲ 3 × 104 cm-3), the thermal coupling between dust grains and the gas phase does not occur, which leads to gas temperatures significantly different from the dust temperatures. At higher densities (nH ≳ 3 × 104 cm-3) thermal coupling between gas and dust grains has to be taken into account. We extract gas and dust grain temperatures from models of PDRs (Meijerink & Spaans 2005 and refined by Hocuk & Spaans 20112). These models derive gas and dust grain temperatures from the different heating and cooling processes, leading to temperatures for a given combination of radiation field, number density, and column density. We use the outcomes of these models in tabular form, from which we extract the temperatures for our simulations. Temperature fluctuations of dust grains are not considered in this model, because Bron et al. (2014) showed that their effect on the H2 formation rate is limited.
The external radiation field has a significant influence on the structure of the cloud through photoreactions and heating of the gas. At high total column densities (NH ≈ 1021 cm-2) and at solar metallicity, the intensity of the radiation field diminishes due to dust absorption and scattering. The radiation field is therefore a function of column density, as shown in Eq. (14). ![\begin{equation} \label{eq:dustabs} G_{0} (A_{\mathrm{V}}) = G_{0} (0) \exp \left[- \beta \ A_{\mathrm{V}} \right] . \end{equation}](/articles/aa/full_html/2015/07/aa23165-13/aa23165-13-eq88.png) (14)In this expression, β is the process-dependent extinction factor, which has a typical value of 2.5, and AV is the visual extinction calculated by AV = (N(H) + 2N(H2))/2.2 × 1021 cm-2 (Güver & Özel 2009).
(14)In this expression, β is the process-dependent extinction factor, which has a typical value of 2.5, and AV is the visual extinction calculated by AV = (N(H) + 2N(H2))/2.2 × 1021 cm-2 (Güver & Özel 2009).
3. Results
From our model we obtain number densities for all coronene charge and hydrogenation states, as well as the H2 formation rate associated with each of these species. We also obtain the H2 formation rates on dust grains and the number densities of atomic and molecular hydrogen. Together with the gas and dust grain temperatures, this gives us a clear view of the chemistry and physics inside the PDR. We present the spatial distribution of coronene hydrogenation states in Sect. 3.1. In Sect. 3.2 we show the H2 formation rates throughout the PDR, and in Sect. 3.3 we show how the formation of H2 on coronene impacts the PDR structure.
To study the hydrogen-coronene chemistry, the spatial distribution of coronene hydrogenation states is tracked. A region with low hydrogenation states (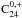 and C24H0, + dominate) indicates that photodesorption occurs at a rate significantly higher than that of hydrogen addition. Conversely, in a region with normal and high hydrogenation states (
and C24H0, + dominate) indicates that photodesorption occurs at a rate significantly higher than that of hydrogen addition. Conversely, in a region with normal and high hydrogenation states (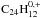 and higher dominate), hydrogenation dominates H-loss processes. Since H2 formation is possible through both photodissociation of coronene and chemical abstraction on coronene, the spatial distribution of the hydrogenation states of coronene can tell us which of these processes is more important for H2 formation. Furthermore, in Sect. 3.2 we compare the formation of H2 on coronene with the formation on dust grains, and report our results.
and higher dominate), hydrogenation dominates H-loss processes. Since H2 formation is possible through both photodissociation of coronene and chemical abstraction on coronene, the spatial distribution of the hydrogenation states of coronene can tell us which of these processes is more important for H2 formation. Furthermore, in Sect. 3.2 we compare the formation of H2 on coronene with the formation on dust grains, and report our results.
3.1. Spatial distribution of coronene
The spatial distribution of coronene states is due to the temperature and radiation profiles of the cloud. At the boundaries of the cloud, the radiation field is very strong and the gas temperature is high (Tgas> 200 K), as is shown in Fig. 1. At these high gas temperatures coronene hydrogenation is very efficient because the H atoms can then easily overcome the barriers against hydrogenation. However, this is easily offset by the intense radiation field that completely dehydrogenates coronene down to the carbon skeleton. Deeper inside the cloud the radiation field is decreased, causing a decrease in the photoionization rate and a subsequent gradual transition from fully dehydrogenated coronene cations to their neutral counterparts is expected. At even higher column densities, the radiation field is too weak for photodissociation to dominate. As a result, a transition to the neutral, normally hydrogenated coronene molecule should occur.
A typical spatial distribution of hydrogenated coronene is presented in Fig. 2. In the outskirts of the cloud coronene is fully dehydrogenated and exists as cations. Deeper inside the cloud, the dominant form of coronene is the fully dehydrogenated neutral molecule, which is subsequently overturned by the normally hydrogenated neutral coronene molecule.
Clearly absent in our results are the highly superhydrogenated species, although coronene with a few extra hydrogen atoms can be abundant at high extinctions. This can be explained by the correlation between the UV intensity and the gas temperature. A high gas temperature is necessary to overcome the energy barriers in the hydrogenation process. These gas temperatures are only reached in regions where the impinging radiation field is strong enough to heat the gas to such temperatures. At the same time, this radiation field is strong enough to photodissociate all the coronene molecules. This is consistent with previous PDR models, such as those of Montillaud et al. (2013), who modelled the north-west PDR of NGC 7023. They reported that at every depth there is one dominant hydrogenation state, which is either the one with the most H atoms removed or the highest possible hydrogenation state. Their hydrogenation states range from full dehydrogenation to one superhydrogenation. Montillaud et al. (2013) concluded that coronene is fully dehydrogenated throughout the entire cloud (AV ≤ 3 mag). This is consistent with our findings, where we report that coronene is dehydrogenated at the edge of the cloud, but normally hydrogenated at extinctions of more than a few mag.
The results shown here are also consistent with a recent study that interpreted Spitzer and ISOCAM observations of NGC 7023 (Joblin et al. 2010). Using the method developed by Pilleri et al. (2012) to identify PAH cations and neutral PAHs, Joblin et al. (2010) showed that there is a sharp transition between PAH cations at the edge of the PDR and neutral PAH molecules deeper into the cloud.
 |
Fig. 1 Distribution of dust and gas temperatures throughout a gas cloud with G0 = 103.5 and nH = 105.5 cm-3. The dotted lines show the distribution of H and H2. |
 |
Fig. 2 Distribution of coronene charge and hydrogenation state for three different values of G0 and nH. Coronene cations are plotted with dashed lines, and neutral coronene molecules have solid lines. Only the most abundant hydrogenation states are shown. The top graph has G0 = 102.5 and nH = 103.5 cm-3, the middle graph G0 = 103.0 and nH = 103.5 cm-3, and the bottom graph corresponds to G0 = 102.5 and nH = 104.5 cm-3. The vertical line marks the location of the H/H2 transition, where n(H) = 2·n(H2). |
The radiation field has a very clear impact on the coronene distribution through two different mechanisms, as shown in Fig. 2. First, an increased radiation field leads to a higher H2 photodissociation rate, pushing the H/H2 front to higher column densities. Second, a higher G0 leads to a higher rate of photoionization of PAHs, changing the transition from cations to neutrals to higher column densities. Furthermore, a stronger radiation field drives the transition from dehydrogenated to normally hydrogenated PAHs to higher column densities.
An increase in the number density of the cloud has the opposite effect of increasing the radiation field. Hence, the hydrogenated/dehydrogenated front is shifted towards lower column densities, as shown in Fig. 2.
3.2. H2 formation rates
The H2 formation rates on coronene and dust grains are strongly dependent on the radiation field and the dust temperature, respectively. For H2 formation on dust, the dust must be cold enough to prevent physisorbed H atoms from desorbing into the gas phase. When Tdust rises above 15–20 K, H2 formation is only possible with chemisorbed H atoms and is less efficient.
For coronene, however, there are two possible pathways for H2 formation, as described in Sects. 2.1.1 and 2.1.2. The dominant H2 formation process is the photodesorption of H2 from coronene with at least two hydrogen atoms. Although the occurence of these molecules is low in PDRs, this process occurs very fast because of the intense radiation. This results in a fast catalytic cycle where the bare carbon skeleton of the coronene molecule consecutively adsorbs two H atoms, which are subsequently photodesorbed as an H2 molecule. The H2 formation rates for this mechanism can be as high as a few times 10-16 cm3 s-1, which is similar to H2 formation rates in PDRs found by Habart et al. (2004).
The formation of H2 through chemical abstraction on coronene is not a dominant process in PDR environments, although the temperatures are high enough to easily cross the thermal barriers associated with this process. For the latter process hydrogen atoms must be adsorbed to the coronene molecule, but the high-radiation field photodesorbs almost all H atoms from the coronene molecule. This leaves most coronene molecules without H atoms, and a small fraction has only one or two hydrogen atoms, rendering the chemical abstraction process negligible.
To compare H2 formation on coronene with H2 formation on dust grains, we present the H2 formation rate coefficients as a function of column density in Figs. 3 and 4. In the same figures the number densities of atomic and molecular hydrogen are reported. To study the effect of the radiation field and the total hydrogen number density, the simulations presented in the three panels of Fig. 3 differ in radiation field or number density nH.
At low column densities, the gas and dust are heated by the impinging radiation field, making coronene the dominant source of H2 formation. At increasing column densities, the temperatures start to decline, and dust grains take over as the dominant H2 formation agent.
 |
Fig. 3 H2 formation rate coefficients on cationic and neutral coronene and dust (solid, dashed-dotted, and dashed lines, left y-axis) and distributions of H and H2 (dotted lines, right y-axis). The top graph has G0 = 102.5 and nH = 103.5 cm-3, the middle graph G0 = 103.0 and nH = 103.5 cm-3, and the bottom graph corresponds to G0 = 102.5 and nH = 104.5 cm-3. The vertical line marks the location of the H/H2 transition, where n(H) = 2·n(H2). |
Increasing the radiation field heats the gas and the dust grains, making the transition from PAHs to dust grains occur at higher column densities, which is shown in the middle panel in Fig. 3. Increasing the density has the opposite effect of increasing the radiation field, causing a decrease of the column density for the PAH/dust grain transition, as illustrated in the bottom panel of Fig. 3.
3.3. Impact of H2 formation on coronene on the PDR structure
H2 formation on coronene can significantly change the structure of a cloud. This influence manifests itself in the column density of the H/H2 transition in the cloud. We consider the H/H2 transition to occur at a column density where 2n(H2) = n(H). This column density is lowered by the presence of PAHs in the PDR.
An example is presented in Fig. 4, where we show the number density profiles of atomic and molecular hydrogen. In the top panel of Fig. 4, H2 can be formed by reactions on coronene and dust grains, and in the bottom panel only H2 formation on dust grains is considered. Comparing these figures, we see that the column density of the H/H2 transition is lowered by a factor of 4 due to the formation of H2 on coronene. The influence of coronene can be quantified by the ratio of the column densities of the transition with and without considering the formation of H2 on coronene. We define the influence parameter IPAH as 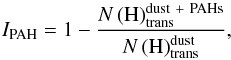 (15)which ranges between 0 and 1. In the case of a value of 0, coronene has no influence on the column density of the H/H2 transition. When IPAH = 1, coronene shifts the H/H2 transition completely to the edge of the cloud. The highest value of IPAH present in our results is approximately 0.8. At this value, the rate of H2 formation on coronene is 200 times higher than H2 formation on dust grains at the column density of the H/H2 transition, while these rates are approximately equal for the lowest values of the influence parameter. This influence parameter is shown as a function of cloud number density and external radiation field in Fig. 5. The influence parameter increases with both increasing number density and external radiation field.
(15)which ranges between 0 and 1. In the case of a value of 0, coronene has no influence on the column density of the H/H2 transition. When IPAH = 1, coronene shifts the H/H2 transition completely to the edge of the cloud. The highest value of IPAH present in our results is approximately 0.8. At this value, the rate of H2 formation on coronene is 200 times higher than H2 formation on dust grains at the column density of the H/H2 transition, while these rates are approximately equal for the lowest values of the influence parameter. This influence parameter is shown as a function of cloud number density and external radiation field in Fig. 5. The influence parameter increases with both increasing number density and external radiation field.
 |
Fig. 4 Comparison between two identical clouds, with (top panel) and without (bottom panel) H2 formation on coronene. H2 formation rate coefficients on ionized (solid) and neutral (dashed-dotted) coronene and dust grains (dashed lines) are represented on the left y-axis. Number densities of H and H2 (dotted lines) are represented on the right y-axis. The thick vertical green line indicates the location where n(H) = 2·n(H2). G0 = 103.5 and nH = 105 cm-3. |
An increased number density increases the rate of reactions between coronene and H atoms, resulting in a higher abundance of PAHs with one or more hydrogen atoms. At a similar radiation field, this yields a higher H2 formation rate, pushing the H/H2 transition to lower column densities. A similar argument applies to the dependence on the radiation field. With an increasing radiation field, all photodissociation rates increase, including those of the H2 forming processes. However, the effect is more subtle because a stronger radiation field changes the population distribution of the hydrogenation states towards a lower fraction of coronene with two or more H atoms. This makes fewer coronene molecules eligible for the release of H2 upon photoabsorption. This effect leads to an optimal radiation intensity for every number density for maximal coronene influence. If the radiation field has a higher intensity, the influence of coronene on the position of the H/H2 front decreases again, as is shown in Fig. 5.
 |
Fig. 5 PAH influence parameter plotted as a function of number density and external radiation field. The influence of PAHs on the cloud structure increases with increasing number density and radiation field. White regions indicate that no data are available. |
Strong radiation fields also correlate with high dust grain temperatures, which inhibit H2 formation. Figure 6 shows the H2 formation rate of dust grains (solid lines) and coronene (dashed lines) as a function of gas temperature for different values of G0 and nH. For each datapoint, the color of the marker indicates the dust temperature. Additionally, observational H2 formation rates derived by Habart et al. (2004) for different PDRs are reported in this figure. It is clear that H2 formation on PAHs is necessary to reproduce the observed H2 formation rates.
From this plot it is also clear that dust grains and PAHs contribute to H2 formation in different temperature regimes. Since the temperature decreases with increasing column density, PAHs have their strongest H2 formation activity at the edges of PDRs, while dust grains dominate this process deeper inside the cloud. PAHs change the cloud structure the most when the conversion from H to H2 occurs at lower extinction than the one at which dust grains start to dominate H2 formation. We can see from Fig. 6 that this is the case when the transition occurs in a region where Tgas ≳ 200 K.
Combining high number densities and radiation fields, H2 formation on PAHs builds up a sufficiently high H2 column density at a relatively low total column density, such that H2 is already self-shielded against photodissociation. At these low total column densities, dust temperatures are still too high for the formation of H2 on dust grains to have any effect (Tdust> 40 K). The column density of the H/H2 transition is in that case entirely due to H2 formation on PAHs.
4. Discussion
4.1. Impact of uncertainties
We find that PAHs, with coronene as a prototypical PAH, affect the structure of a PDR. The formation of H2 on coronene is primarily important on the outskirts of the PDR. In these regions the temperature is sufficiently high that the exact height of the barriers for addition and abstraction does not matter. Deeper inside the cloud the barrier height does matter, but the transition to molecular hydrogen is then already complete, so H2 formation on PAHs is not significant in these regions.
Furthermore, most of the H2 formation on PAHs takes place via photodesorption. These processes occur at low column densities, where the radiation field suffers almost no extinction. At these column densities, photodesorption processes dominate and have a strong influence on the depth of the H/H2 transition. To understand the dependence of the H/H2 transition on these photorates, we vary the binding energies of either H atoms or H2 molecules with 0.2 eV ceteris paribus and recalculate the photorates. With these photorates the simulations are re-evaluated and show only a weak influence on the position of the H/H2 front.
Increasing the H2 or decreasing the H photodissociation energy (E0 in Table A.2) with 0.2 eV results in H2 formation rates reduced by a factor 3. Conversely, the H2 formation rates locally increase by a factor 3 with a similar decrease in the photodissociation energy for H2 loss, or an increase in the photodissociation energy for H loss. However, this does not significantly change the position of the H/H2 front. Furthermore, we see in our simulations that in the clouds where PAHs have a strong influence on the cloud structure, their H2 formation rate is typically one order of magnitude higher than the dust grain H2 formation rate.
 |
Fig. 6 H2 formation rates on for different values of G0 and nH as a function of Tgas. Solid lines indicate H2 formation by PAHs and dashed lines represent dust grain H2 formation. For each datapoint, the color of the marker corresponds to the dust temperature of that datapoint. Both the gas and dust temperatures have been derived from the models in Hocuk & Spaans (2011). The black markers indicate the H2 formation rates reported by Habart et al. (2004) for different PDRs. These formation rates have been estimated using H2 line intensity ratios from the H2 fluorescent lines. |
Another parameter that is subject of discussion is the cross sections used for the hydrogenation and abstraction reactions. The reaction rate scales linearly with the cross section, and the values used in this paper are an average value derived from irradiating coronene films with H atoms (Mennella et al. 2012). Mennella et al. (2012) argued that because coronene molecules only weakly interact, and since the H atoms interact directly with the coronene molecules, without diffusion or absorption, their values are representative for the gas phase molecules as well. In our model abstraction plays a minor role in H2 formation, but this changes for larger PAHs (Sect. 4.2). In the cases where abstraction is the dominant mechanism for H2 formation, the formation rate linearly depends on both the abstraction cross section and the number of H atoms adsorbed onto PAHs. The latter in turn depends on the cross section for the addition of an H atom. We therefore expect that the rate of H2 formation through abstraction linearly depends on both the cross section for addition and abstraction. To make more reliable H2 formation models for larger PAHs than this proof-of-concept approach, both these cross sections have to be established for larger PAHs.
4.2. Expectations for a population of large PAHs
We have used coronene as the only active PAH, where in reality there are many more PAHs of different sizes present in the ISM. For PDR environments, PAHs with more than 40 carbon atoms and a compact structure are favoured because of their photostability. Allain et al. (1996) showed that both H loss and H2 loss significantly decrease with increasing number of carbon atoms. This makes H2 photodesorption a less likely process for H2 formation, but the decreasing rate of H loss will leave more H atoms on the PAH molecule, making H2 formation through abstraction a more dominant process. This also changes the distribution of hydrogenation states throughout the PDR and increases the abundance of higher hydrogenation states. These changes in both the dominant H2 formation mechanism on PAHs and the hydrogenation state distribution are observed in a test run of our model where coronene is substituted by a generic 50C PAH. Since the chemistry between PAHs and hydrogen atoms is less well understood for larger PAHs, we did not include these molecules in our simulations.
Larger molecules like circumcircumcoronene (C96H24) are found to be in the highest hydrogenation state throughout the entire cloud (Montillaud et al. 2013). However, the photo-stability of hydrogenated PAHs is quite unknown, and preliminary experimental results suggest that the addition of hydrogen on PAHs changes their photostability (Reitsma et al. 2014). This implies that the dissociation rates of hydrogenated coronene molecules could be lower than previously assumed. As a result, the formation of H2 through photodesorption will decrease as well. The photodesorption H2 formation rates presented in this paper are therefore an upper limit to possible H2 formation rates through this mechanism. Simultaneously, H2 formation through abstraction will become more dominant on larger PAHs, since the decreased photodesorption rate leaves more H atoms on the PAH molecule. However, to understand to which order abstraction can replace photodesorption as an H2 forming mechanism, a more comprehensive understanding of PAH (photo)chemistry is necessary.
Furthermore, there are other processes for H2 formation on PAHs, such as dissociative recombination between a superhydrogenated PAH cation and an electron (Le Page et al. 2009). This process is found to be effective for superhydrogenated PAHs with up to 200 carbon atoms. In the environments we study the rate for this process is at least an order of magnitude lower than the dominant H2 formation processes. To conclude about H2 formation on PAHs, it is necessary to fully understand every contributing process, since different processes appear to be the dominating mechanism for different PAH sizes and hydrogenation states.
5. Conclusions
The model we presented clearly shows that PAHs play a vital part in the location of the H/H2 transition in PDRs, especially at high gas temperatures (T> 200 K). For high UV fields (G0> 103), PAH (photo)chemistry should therefore be taken into account when modelling the structure of a PDR.
We presented the first chemical model that accounts for more than one superhydrogenation of a PAH molecule and that incorporates thermal barriers into the PAH chemistry taking place. This model also considers photodesorption as a mechanism for H2 formation on PAHs. We showed that the barriers introduce a strong temperature dependence for the H2 formation route on PAHs, and that this formation pathway is the high-temperature complement to the classical H2 formation mechanism on dust grains. Further research into PAHs should be directed at a better understanding of dehydrogenated PAHs and the chemical and photoprocesses that are associated with them. Ideally, this is also directed towards larger PAHs, which are more representative of the ISM.
We conclude that photodesorption of H2 from PAHs can be an important pathway for the formation of H2 in PDR environments. The barriers present in PAH hydrogenation limit the
H2 formation process on PAHs to high gas temperatures. These barriers therefore ensure that H2 formation on PAHs is the high-temperature complement to dust grain H2 formation.
Online material
Appendix A: Chemical reactions
Chemical reactions with different hydrogenation and charge states of coronene, as shown in the first column.
Integrated photodissociation rates for the different hydrogenation and ionization states of the coronene molecule.
Available at http://www.mpe.mpg.de/~seyit/Tgas/
Acknowledgments
L.B. and S.C. are supported by the Netherlands Organization for Scientific Research (NWO). The authors would like to thank Seyit Hocuk for providing gas temperature models of PDRs. The authors would also like to thank the anonymous referee for his or her helpful suggestions.
References
- Allain, T., Leach, S., & Sedlmayr, E. 1996, A&A, 305, 602 [NASA ADS] [Google Scholar]
- Allamandola, L. J., Tielens, A. G. G. M., & Barker, J. R. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Allers, K. N., Jaffe, D. T., Lacy, J. H., Draine, B. T., & Richter, M. J. 2005, ApJ, 630, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, Jr., C. W. 1998, ApJ, 509, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Boschman, L., Reitsma, G., Cazaux, S., et al. 2012, ApJ, 761, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Bron, E., Le Bourlot, J., & Le Petit, F. 2014, A&A, 569, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Spaans, M. 2009, A&A, 496, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2005, MNRAS, 361, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duley, W. W., & Williams, D. A. 1993, MNRAS, 260, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Ekern, S. P., Marshall, A. G., Szczepanski, J., & Vala, M. 1997, ApJ, 488, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, R. J., & Salpeter, E. E. 1963, ApJ, 138, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., Walmsley, C. M., & Pineau des Forêts, G. 2004, A&A, 414, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Hocuk, S., & Spaans, M. 2011, A&A, 536, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Hornekær, L., Šljivančanin, Ž., Xu, W., et al. 2006, Phys. Rev. Lett., 96, 156104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joblin, C., Leger, A., & Martin, P. 1992, ApJ, 393, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Joblin, C., Pilleri, P., Montillaud, J., et al. 2010, A&A, 521, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgartel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jura, M. 1974, ApJ, 191, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., & Flower, D. R. 1999, MNRAS, 305, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2001, ApJS, 132, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2009, ApJ, 704, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Malloci, G., Joblin, C., & Mulas, G. 2007, Chem. Phys., 332, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, V. 2006, ApJ, 647, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Hornekær, L., Thrower, J., & Accolla, M. 2012, ApJ, 745, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Montillaud, J., Joblin, C., & Toublanc, D. 2013, A&A, 552, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., & Kaufman, M. J. 1993, ApJ, 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Lepp, S., & Melnick, G. J. 1995, ApJS, 100, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Oort, J. H., & van de Hulst, H. C. 1946, Bull. Astron. Inst. Netherlands, 10, 187 [NASA ADS] [Google Scholar]
- Oppenheimer, M., & Dalgarno, A. 1974, ApJ, 192, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Paris, C., Alcamí, M., Martín, F., & Díaz-Tendero, S. 2014, J. Chem. Phys., 140, 204307 [NASA ADS] [CrossRef] [Google Scholar]
- Perry, J. S. A., & Price, S. D. 2003, Ap&SS, 285, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Pilleri, P., Herberth, D., Giesen, T. F., et al. 2009, MNRAS, 397, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Pilleri, P., Montillaud, J., Berné, O., & Joblin, C. 2012, A&A, 542, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pirronello, V., Biham, O., Liu, C., Shen, L., & Vidali, G. 1997, ApJ, 483, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Pirronello, V., Liu, C., Roser, J. E., & Vidali, G. 1999, A&A, 344, 681 [NASA ADS] [Google Scholar]
- Rauls, E., & Hornekær, L. 2008, ApJ, 679, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Reitsma, G., Boschman, L., Deuzeman, M., et al. 2014, Phys. Rev. Lett., 113, 053002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ruiterkamp, R., Cox, N. L. J., Spaans, M., et al. 2005, A&A, 432, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shull, J. M., & Beckwith, S. 1982, ARA&A, 20, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Thrower, J. D., Jørgensen, B., Friis, E. E., et al. 2012, ApJ, 752, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1986, ApJS, 62, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001a, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001b, ApJS, 134, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Zecho, T., Guttler, A., Sha, X., Jackson, B., & Kuppers, J. 2002, J. Chem. Phys., 117, 8486 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Chemical reactions with different hydrogenation and charge states of coronene, as shown in the first column.
Integrated photodissociation rates for the different hydrogenation and ionization states of the coronene molecule.
All Figures
 |
Fig. 1 Distribution of dust and gas temperatures throughout a gas cloud with G0 = 103.5 and nH = 105.5 cm-3. The dotted lines show the distribution of H and H2. |
| In the text | |
 |
Fig. 2 Distribution of coronene charge and hydrogenation state for three different values of G0 and nH. Coronene cations are plotted with dashed lines, and neutral coronene molecules have solid lines. Only the most abundant hydrogenation states are shown. The top graph has G0 = 102.5 and nH = 103.5 cm-3, the middle graph G0 = 103.0 and nH = 103.5 cm-3, and the bottom graph corresponds to G0 = 102.5 and nH = 104.5 cm-3. The vertical line marks the location of the H/H2 transition, where n(H) = 2·n(H2). |
| In the text | |
 |
Fig. 3 H2 formation rate coefficients on cationic and neutral coronene and dust (solid, dashed-dotted, and dashed lines, left y-axis) and distributions of H and H2 (dotted lines, right y-axis). The top graph has G0 = 102.5 and nH = 103.5 cm-3, the middle graph G0 = 103.0 and nH = 103.5 cm-3, and the bottom graph corresponds to G0 = 102.5 and nH = 104.5 cm-3. The vertical line marks the location of the H/H2 transition, where n(H) = 2·n(H2). |
| In the text | |
 |
Fig. 4 Comparison between two identical clouds, with (top panel) and without (bottom panel) H2 formation on coronene. H2 formation rate coefficients on ionized (solid) and neutral (dashed-dotted) coronene and dust grains (dashed lines) are represented on the left y-axis. Number densities of H and H2 (dotted lines) are represented on the right y-axis. The thick vertical green line indicates the location where n(H) = 2·n(H2). G0 = 103.5 and nH = 105 cm-3. |
| In the text | |
 |
Fig. 5 PAH influence parameter plotted as a function of number density and external radiation field. The influence of PAHs on the cloud structure increases with increasing number density and radiation field. White regions indicate that no data are available. |
| In the text | |
 |
Fig. 6 H2 formation rates on for different values of G0 and nH as a function of Tgas. Solid lines indicate H2 formation by PAHs and dashed lines represent dust grain H2 formation. For each datapoint, the color of the marker corresponds to the dust temperature of that datapoint. Both the gas and dust temperatures have been derived from the models in Hocuk & Spaans (2011). The black markers indicate the H2 formation rates reported by Habart et al. (2004) for different PDRs. These formation rates have been estimated using H2 line intensity ratios from the H2 fluorescent lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


