| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425249 | |
| Published online | 29 May 2015 | |
High-energy gamma-ray and neutrino backgrounds from clusters of galaxies and radio constraints
1
GRAPPA Institute, University of Amsterdam, Science Park 904, 1098 XH
Amsterdam, The
Netherlands
e-mail: f.zandanel@uva.nl
2
APC, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire
de Paris, Sorbonne Paris
Cité, 75014
Paris,
France
Received:
31
October
2014
Accepted:
10
March
2015
Cosmic-ray protons accumulate for cosmological times in clusters of galaxies because their typical radiative and diffusive escape times are longer than the Hubble time. Their hadronic interactions with protons of the intra-cluster medium generate secondary electrons, gamma rays, and neutrinos. In light of the high-energy neutrino events recently discovered by the IceCube neutrino observatory, for which galaxy clusters have been suggested as possible sources, and the forthcoming results from the Fermi gamma-ray survey, we here estimate the contribution from galaxy clusters to the diffuse gamma-ray and neutrino backgrounds. We modelled the cluster population by means of their mass function, using a phenomenological luminosity-mass relation applied to all clusters, as well as a detailed semi-analytical model. In the latter model, we divide clusters into cool-core/non-cool-core, and loud/quiet subsamples, as suggested by observations, and model the cosmic-ray proton population according to state-of-the-art hydrodynamic numerical simulations. Additionally, we consider observationally-motivated values for the cluster magnetic field. This is a crucial parameter since the observed radio counts of clusters need to be respected owing to synchrotron emission by secondary electrons. For a choice of parameters respecting current constraints from radio to gamma rays, and assuming a proton spectral index of −2, we find that hadronic interactions in clusters contribute less than 10% to the IceCube flux and much less to the total extragalactic gamma-ray background observed by Fermi. They account for less than 1% for spectral indices ≤–2. The high-energy neutrino flux observed by IceCube can be reproduced without violating radio constraints only if a very hard (and speculative) spectral index >–2 is adopted. However, this scenario is in tension with the high-energy IceCube data, which seems to suggest a spectral energy distribution of the neutrino flux that decreases with the particle energy. We prove that IceCube should be able to test our most optimistic scenarios for spectral indices ≥–2.2 by stacking a few nearby massive galaxy clusters. In the case of proton-photon interactions in clusters, we find that very likely protons do not reach sufficiently high energies to produce neutrinos in these environments. We argue that our results are optimistic because of our assumptions and that clusters of galaxies cannot make any relevant contribution to the extragalactic gamma-ray and neutrino backgrounds in any realistic scenario. Finally, we find that the cluster contribution to the angular fluctuations in the gamma-ray background is subdominant, less than 10% on sub-degree scales.
Key words: galaxies: clusters: general / gamma rays: diffuse background / gamma rays: galaxies: clusters / neutrinos
© ESO, 2015
1. Introduction
The extragalactic gamma-ray background (EGB) is the measured radiation that remains after subtracting all known sources from the observed gamma-ray sky. The EGB was measured by the SAS-2 satellite for the first time (Fichtel et al. 1977) then by EGRET (Sreekumar et al. 1998; Strong et al. 2004) and the Fermi-Large Area Telescope (LAT; Fermi LAT Collaboration 2010b, 2015a) most recently. The EGB is likely due to the sum of contributions from different unresolved sources, such as active galactic nuclei (AGN), star-forming galaxies, pulsars, gamma-ray bursts, and intergalactic shocks produced by structure formation (see, e.g., Dermer 2007; Abdo et al. 2010; Stecker & Venters 2011; Siegal-Gaskins et al. 2011; Ackermann et al. 2012; Fornasa et al. 2013; Di Mauro et al. 2014a,b; Tamborra et al. 2014; Ajello et al. 2015; Di Mauro & Donato 2015, and references therein).
Recently, the IceCube neutrino observatory at the South Pole has reported evidence of extraterrestrial neutrinos (Aartsen et al. 2013, 2014a). The four-year IceCube dataset consists of 37 events that exceed the atmospheric background with a significance of more than 5σ (Aartsen et al. 2014a). The neutrino data are compatible with a flux isotropically distributed in the sky, with astrophysical origin and with a possible cutoff at a few PeV. The origin of these events is unknown (see Waxman 2013; and Anchordoqui et al. 2014a, for recent reviews; see also Winter 2014). However, the isotropic distribution in the sky of the observed events suggests that they might come from various extragalactic ~100 PeV cosmic-ray (CR) accelerators, such as gamma-ray bursts, especially untriggered ones (Waxman & Bahcall 1997; Hümmer et al. 2012; Murase & Ioka 2013; Liu & Wang 2013); AGN (Waxman & Bahcall 1999; Halzen & Hooper 2005; Stecker 2013; Winter 2013; Murase et al. 2014; Becker Tjus et al. 2014); star-forming galaxies including starbursts, galaxy mergers, and AGN (Loeb & Waxman 2006; Tamborra et al. 2014; Lacki et al. 2011; Murase et al. 2013; He et al. 2013; Liu et al. 2014; Katz et al. 2013; Kashiyama & Meszaros 2014; Anchordoqui et al. 2014c; Chang & Wang 2014; Tavecchio & Ghisellini 2014); intergalactic shocks and active galaxies embedded in structured regions (Murase et al. 2013); and hypernovae and supernova remnants (Chakraborty & Izaguirre 2015; Senno et al. 2015). A galactic origin for the neutrinos has also been proposed (Ahlers & Murase 2014; Fox et al. 2013; Joshi et al. 2014; Taylor et al. 2014; Anchordoqui et al. 2014b), as well as mixed scenarios of galactic and extragalactic neutrino sources (Ahlers & Murase 2014; Razzaque 2013; Fox et al. 2013; Joshi et al. 2014; Murase et al. 2014; Padovani & Resconi 2014). Exotic models including PeV dark matter decay scenarios have been discussed, too (Feldstein et al. 2013; Esmaili & Serpico 2013; Esmaili et al. 2014).
As shown in Murase et al. (2013), a multi-messenger connection between the measured neutrino fluxes and their photon counterparts could be crucial for unveiling the origin of the high-energy neutrinos, regardless of the physics of their sources. In the following, we assume that the IceCube high-energy neutrinos have an extragalactic origin and are produced in proton-proton collisions. In such a scenario we would expect sources to also emit gamma rays at a flux comparable to that of neutrinos (see, e.g., Kelner et al. 2006); however, the neutrinos could also be produced in proton-photon interactions (see, e.g., Kelner & Aharonian 2008).
Clusters of galaxies are the latest and largest structures to form in the Universe. During their assembly, energies of the same order of magnitude as the gravitational binding energy, 1061 − 1063 erg, should be dissipated through structure-formation shocks and turbulence (Voit 2005). Therefore, even if only a small part of this energy goes into particle acceleration, clusters should host significant non-thermal emission from radio to gamma rays (see, e.g., Brunetti & Jones 2014).
The contribution of clusters of galaxies to the EGB has been discussed by several authors (Loeb & Waxman 2000; Keshet et al. 2003; Gabici & Blasi 2003; Ando & Nagai 2008; Zandanel & Ando 2014). It has been argued that CR hadronic interactions in galaxy clusters could be responsible for a neutrino flux that is comparable to the one recently observed by IceCube (Murase et al. 2008, 2013; Kotera et al. 2009; Murase & Beacom 2013). However, such hadronic interactions could have a dramatic impact on the radio frequencies since secondary electrons are also produced in proton-proton interactions and radiate synchrotron emission when interacting with the magnetic fields in clusters of galaxies. The radio emission from secondary electrons needs to respect radio counts of galaxy clusters (Giovannini et al. 1999; Venturi et al. 2007, 2008; Kale et al. 2013), since the cluster diffuse synchrotron radio emission has been observed (see, e.g., Feretti et al. 2012).
In this work, we estimate the possible contribution to the extragalactic gamma-ray and neutrino backgrounds from galaxy clusters assuming that gamma rays and neutrinos mainly originate in proton-proton interactions, while for the first time taking the consequences in the radio regime into account. We compare our model estimates to the isotropic diffuse gamma-ray background measured by Fermi (Fermi LAT Collaboration 2015a) and to the neutrino flux measured by IceCube (Aartsen et al. 2014a). We also discuss the small-scale anisotropies in EGB recently detected with Fermi (Fermi LAT Collaboration 2012) and compare the measurements with cluster models.
This paper is organised as follows. In Sect. 2, we briefly discuss proton-proton interactions in galaxy clusters and explain how we calculate the emission from secondary electrons, photons, and neutrinos. We then introduce the mass function of galaxy clusters and a phenomenological luminosity-mass relation in Sect. 3. In Sect. 4, we refine our approach by using a detailed semi-analytical model based on state-of-the-art numerical simulations of CRs in clusters and test the robustness of our results with respect to the adopted parameters. We compare our results with stacking upper limits by the IceCube telescope and discuss future detection prospects in Sect. 5. We briefly discuss the neutrino contribution from proton-photon interactions in clusters in Sect. 6 and the angular power spectrum of the EGB in Sect. 7. Finally, in Sect. 8, we summarise our findings.
2. Secondaries from proton-proton interactions
The CR protons accumulate in galaxy clusters for cosmological times (Völk et al. 1996; Berezinsky et al. 1997) and interact with the thermal protons of the intra-cluster medium (ICM) generating secondary particles: electrons, neutrinos, and high-energy photons (Dennison 1980; Blasi & Colafrancesco 1999; Miniati et al. 2001; Pfrommer & Enßlin 2004; Blasi et al. 2007; Pfrommer et al. 2008; Kushnir & Waxman 2009; Kotera et al. 2009; Pinzke & Pfrommer 2010). While the ICM density is typically well known from X-ray measurements of its bremsstrahlung emission, the CR proton spectral and spatial distributions in galaxy clusters are unknown. In fact, whereas the diffuse radio emission observed in several clusters proves the presence of relativistic electrons, direct proof of proton acceleration has yet to be found.
Gamma-ray observations of the possible hadronic-induced emission started to put tight constraints on the proton content of clusters (H.E.S.S. Collaboration 2009a,b; MAGIC Collaboration 2010, 2012; Fermi LAT Collaboration 2010a, 2014; VERITAS Collaboration 2012; Ando & Nagai 2012; Huber et al. 2013; Vazza & Brüggen 2014; Zandanel & Ando 2014; Prokhorov & Churazov 2014; Griffin et al. 2014). Gamma-ray limits also suggest that secondary electrons cannot be uniquely responsible for the observed radio emission in galaxy clusters, at least in the case of the so-called giant radio haloes found in merging clusters like Coma (Brunetti et al. 2012; Zandanel et al. 2014b). As we discuss in the following, an important implication for our purposes is that the observed radio counts represent an optimistic upper limit for the radio emission from secondary electrons since only a fraction of it can have a hadronic origin.
Assuming a power law in momentum for the spectral distribution of CR protons in clusters,
f(p)dp =
ρCRp−
αpdp, the radio
synchrotron luminosity of secondary electrons at a frequency f can be expressed as
(adapted from Pfrommer et al. 2008) 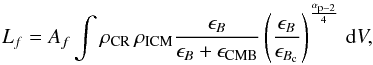 (1)where ρCR and
ρICM are the CR proton and ICM density
distributions, respectively, while ϵB =
B2/ 8π
and ϵCMB are the energy densities of the cluster
magnetic fields and the cosmic microwave background (CMB)1. The parameter ϵBc is the
magnetic energy density corresponding to a characteristic magnetic field Bc =
31(ν/ GHz)μG for the synchrotron
mechanism, and Af encloses the
spectral information (Pfrommer et al. 2008). The
gamma-ray luminosity of secondary photons at an energy E is defined as
(1)where ρCR and
ρICM are the CR proton and ICM density
distributions, respectively, while ϵB =
B2/ 8π
and ϵCMB are the energy densities of the cluster
magnetic fields and the cosmic microwave background (CMB)1. The parameter ϵBc is the
magnetic energy density corresponding to a characteristic magnetic field Bc =
31(ν/ GHz)μG for the synchrotron
mechanism, and Af encloses the
spectral information (Pfrommer et al. 2008). The
gamma-ray luminosity of secondary photons at an energy E is defined as 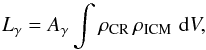 (2)with Aγ enclosing the spectral
information (Pfrommer et al. 2008).
(2)with Aγ enclosing the spectral
information (Pfrommer et al. 2008).
In the following, we make use of Eqs. (1) and (2) to calculate the hadronic-induced emission in galaxy clusters at radio and gamma-ray frequencies. The spectral multipliers Af and Aγ were obtained in Pfrommer & Enßlin (2004) as analytical approximations of full proton-proton interaction simulations. The analytical expressions for Af and Aγ reproduce the results of numerical simulations from energies around the pion bump (~100 MeV) up to a few hundred GeV. A more precise formalism has been derived by Kelner et al. (2006) for the TeV–PeV energy range, relevant to calculating the neutrino fluxes. Therefore, we correct the gamma-ray spectra obtained by adopting the analytical approximations with the recipe in Kelner et al. (2006) for energies above ~0.1–1 TeV. The transition energy between the two approximations depends on αp, and it was chosen as the energy at which the two models coincide.
We compute the corresponding neutrino spectra as prescribed in Kelner et al. (2006). When assuming that proton-proton interactions are the main interactions producing neutrinos and gamma rays, the neutrino intensity for all flavours could also be approximately obtained as a function of the gamma-ray flux (Ahlers & Murase 2014; Anchordoqui et al. 2004): Lν(Eν) ≈ 6 Lγ(Eγ), with Eν ≈ Eγ/ 2, where we ignored the absorption during the propagation of gamma rays for simplicity. From this approximation, one finds that, at a given energy, Lν/Lγ ~ 1.5 for αp = 2. However, detailed calculations by Berezinsky et al. (1997) and Kelner et al. (2006) show that this ratio is slightly smaller for spectral indices αp> 2 and slightly higher for αp < 2.
We do not assume any CR spectral cut-off at high energies or any spectral steepening due to the high-energy protons that are no longer confined to the cluster (Völk et al. 1996; Berezinsky et al. 1997; Pinzke & Pfrommer 2010), and thus, as discussed in the following, our results should be considered as conservative. While this is not relevant when comparing with the Fermi data, it might be relevant for the high-energy neutrino flux.
Since the larger contribution to the total diffuse intensity comes from nearby galaxy clusters (see Fig. 5 and comments therein), we additionally omit the absorption of high-energy gamma rays owing to interactions with the extragalactic background light because this becomes relevant only at high redshifts (see, e.g., Domínguez et al. 2011). We note that our conclusions do not change even when relaxing any of the above approximations.
3. Phenomenological luminosity-mass relation
In this section, we estimate the maximum possible contribution to the extragalactic gamma-ray and neutrino backgrounds from hadronic interactions in galaxy clusters using a simplified phenomenological approach for the luminosity-mass relation.
3.1. Modelling the diffuse gamma-ray intensity
The total gamma-ray intensity from all galaxy clusters in the Universe at a given energy
(dN/dA dt dE) is 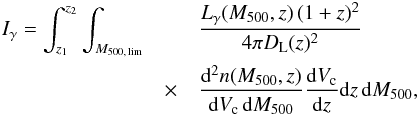 (3)where
the cluster mass MΔ is defined with respect to a density
that is Δ = 500 times the
critical density of the Universe at redshift z. Here, Vc is the comoving volume,
DL(z) the luminosity
distance, and d2n(M500,z)
/dVc
dM500 is the cluster mass function for
which we make use of the Tinker et al. (2008)
formalism and the Murray et al. (2013) on-line
application. The lower limit of the mass integration has been chosen to be M500, lim =
1013.8h-1M⊙, to account
for large galaxy groups. The redshift integration goes from z1 = 0.01, where
the closest galaxy clusters are located, up to z2 = 2. Where not otherwise specified,
we assume Ωm =
0.27, ΩΛ =
0.73, and the Hubble parameter H0 = 100
h70 km s-1 Mpc-1 with h70 = 0.7. Where
we explicitly use h in the units, as for M500,
lim, we assume H0 = 100 h km
s-1
Mpc-1 with
h = 1. As
shown in Fig. 1 (and discussed in Sects. 3.3 and 4.3), our
conclusions are not affected by the specific choice of z2 and
M500,
lim.
(3)where
the cluster mass MΔ is defined with respect to a density
that is Δ = 500 times the
critical density of the Universe at redshift z. Here, Vc is the comoving volume,
DL(z) the luminosity
distance, and d2n(M500,z)
/dVc
dM500 is the cluster mass function for
which we make use of the Tinker et al. (2008)
formalism and the Murray et al. (2013) on-line
application. The lower limit of the mass integration has been chosen to be M500, lim =
1013.8h-1M⊙, to account
for large galaxy groups. The redshift integration goes from z1 = 0.01, where
the closest galaxy clusters are located, up to z2 = 2. Where not otherwise specified,
we assume Ωm =
0.27, ΩΛ =
0.73, and the Hubble parameter H0 = 100
h70 km s-1 Mpc-1 with h70 = 0.7. Where
we explicitly use h in the units, as for M500,
lim, we assume H0 = 100 h km
s-1
Mpc-1 with
h = 1. As
shown in Fig. 1 (and discussed in Sects. 3.3 and 4.3), our
conclusions are not affected by the specific choice of z2 and
M500,
lim.
 |
Fig. 1 Total number density of galaxy clusters for masses above M500, lim = 1013.8h-1 M⊙ as a function of redshift. We show the number density obtained assuming the WMAP (Komatsu et al. 2011), our standard choice if not otherwise specified, and the Planck (Planck Collaboration XVI 2014) cosmological data. At redshift z = 2, the number density is already negligible with respect to the lowest redshift. |
We calculate the total number of detectable galaxy clusters at f = 1.4 GHz, above the flux
Fmin, as 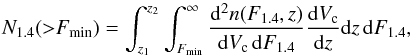 (4)where F1.4 =
L1.4(1 + z) /
4πDL(z)2,
and we compare it with the radio counts from the National Radio Astronomy Observatory Very
Large Array sky survey (NVSS) of Giovannini et al.
(1999)2 . The flux Fmin is defined
as in Eq. (9) of Cassano et al. (2012) by adopting
a noise-level multiplier ξ1 = 1, which is appropriate, while
slightly optimistic, for the low redshifts of the NVSS survey (0.44 ≤ z ≤ 0.2), and a
typical radio half-light radius of R500/ 4 (Zandanel et al. 2014b).
(4)where F1.4 =
L1.4(1 + z) /
4πDL(z)2,
and we compare it with the radio counts from the National Radio Astronomy Observatory Very
Large Array sky survey (NVSS) of Giovannini et al.
(1999)2 . The flux Fmin is defined
as in Eq. (9) of Cassano et al. (2012) by adopting
a noise-level multiplier ξ1 = 1, which is appropriate, while
slightly optimistic, for the low redshifts of the NVSS survey (0.44 ≤ z ≤ 0.2), and a
typical radio half-light radius of R500/ 4 (Zandanel et al. 2014b).
The function d2n(F1.4,z)
/dVc
dF1.4 is obtained numerically from
d2n(M500,z)
/dVc
dM500 by calculating L1.4(M500)
from Lγ(M500)
as explained in the following. We introduce a phenomenologically-driven gamma-ray
luminosity-mass relation: ![\begin{equation} \rmn{log}_{10} \left[\frac{L_{\gamma} (100\,\rmn{MeV})}{\mathrm{s^{-1}\,GeV^{-1}}}\right] = P_{1} + P_{2} \, \rmn{log}_{10} \left(\frac{M_{500}}{{M}_\odot}\right) , \label{eq:LM} \end{equation}](/articles/aa/full_html/2015/06/aa25249-14/aa25249-14-eq67.png) (5)where we omit the
possible redshift-dependence for simplicity3. The
radio luminosity can be obtained from the gamma-ray one by Eqs. (1) and (2).
(5)where we omit the
possible redshift-dependence for simplicity3. The
radio luminosity can be obtained from the gamma-ray one by Eqs. (1) and (2).
Tested parameters and total gamma-ray and neutrino fluxes for the phenomenological luminosity-mass relation.
In this section we assume that the magnetic field is independent of the radius in the
radio-emitting region. Therefore, the relation between radio and gamma-ray luminosities
becomes 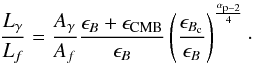 (6)A special limit can be
obtained for B ≫
BCMB in all the radio-emitting region. In
this case, under the hypothesis that electrons lose all their energy through synchrotron
emission and αp ≈
2, the relation between radio and gamma-ray luminosities becomes (Pfrommer 2008):
(6)A special limit can be
obtained for B ≫
BCMB in all the radio-emitting region. In
this case, under the hypothesis that electrons lose all their energy through synchrotron
emission and αp ≈
2, the relation between radio and gamma-ray luminosities becomes (Pfrommer 2008): 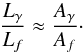 (7)Concerning the
choice of the parameters in Eq. (5), we
need to consider that P1, P2,
αp, B, and the fraction of loud
clusters are degenerate when one tries to find the maximum allowed hadronic-induced
emission. The concept of loud fraction comes from the fact that, even if clusters have the
same X-ray luminosity and therefore the same mass, some of them host radio emission, but
others do not show any sign of it with upper limits about an order of magnitude below the
loud state. This is known as the radio–X-ray bimodality (Brunetti et al. 2009; Cassano et al.
2013). The most recent estimates suggest that the radio-loud percentage is about
20−30% (Kale et al. 2013). The subdivision of the cluster
population into radio-loud and radio-quiet clusters is also reflected in the corresponding
gamma-ray and neutrino fluxes. Therefore, from now on we refer to the two populations as
“loud” and “quiet.”
(7)Concerning the
choice of the parameters in Eq. (5), we
need to consider that P1, P2,
αp, B, and the fraction of loud
clusters are degenerate when one tries to find the maximum allowed hadronic-induced
emission. The concept of loud fraction comes from the fact that, even if clusters have the
same X-ray luminosity and therefore the same mass, some of them host radio emission, but
others do not show any sign of it with upper limits about an order of magnitude below the
loud state. This is known as the radio–X-ray bimodality (Brunetti et al. 2009; Cassano et al.
2013). The most recent estimates suggest that the radio-loud percentage is about
20−30% (Kale et al. 2013). The subdivision of the cluster
population into radio-loud and radio-quiet clusters is also reflected in the corresponding
gamma-ray and neutrino fluxes. Therefore, from now on we refer to the two populations as
“loud” and “quiet.”
In this section we mainly consider the overly optimistic case where all the clusters are loud (100% loud), while we show the case of 30% loud clusters for only one choice of αp. In the following, to reduce the number of free parameters, we fix P2 = 5/3 ≃ 1.67; i.e., we assume that the hadronic-induced luminosity scales as the cluster thermal energy Eth ∝ M2/Rvir ∝ M5/3 (see also Sect. 3.3), where Rvir is the virial radius. The chosen P2 parameter roughly corresponds to what is found using the Zandanel et al. (2014a) multi-frequency mock cluster catalogue (MultiDark database; Riebe et al. 2013) for Lγ(100 MeV)–M500, which typically lies in the range ~1.5−1.65 for different redshifts and different cluster populations (loud, quiet, cool-core, non-cool-core). The parameter P1 is set free to vary under the constraint that it should respect the radio counts from the NVSS survey and current gamma-ray upper limits. We note that, once the thermal content of a cluster is known, the parameter P1 could be seen as the efficiency of how much energy goes into CR acceleration.
We considered the Coma and Perseus cases for comparison with current gamma-ray upper
limits on individual galaxy clusters. We took the Coma upper limit obtained from five
years of Fermi data by Zandanel
& Ando (2014) as reference. We adopted their result for the disk model, a
uniform filling of the cluster up to R200, which is FUL(>
100 MeV) = 2.9 × 10-9 cm-2 s-1, obtained for a spectral index
of 2. For Perseus, we assumed
the upper limit obtained by the MAGIC Collaboration
(2012) for the inner region of 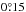 as reference, which is
FUL(> 1 TeV) = 1.4 × 10-13
cm-2
s-1, obtained for
a spectral index of 2.2. We
refer the reader to, for example, Table 1 of Huber et al.
(2013) and Table 2 of MAGIC Collaboration
(2010) for hints to how much the gamma-ray upper limits change when modifying the
spectral index. Such a change is quantifiable within a factor of about two, which does not
affect our conclusions, as we discuss later.
as reference, which is
FUL(> 1 TeV) = 1.4 × 10-13
cm-2
s-1, obtained for
a spectral index of 2.2. We
refer the reader to, for example, Table 1 of Huber et al.
(2013) and Table 2 of MAGIC Collaboration
(2010) for hints to how much the gamma-ray upper limits change when modifying the
spectral index. Such a change is quantifiable within a factor of about two, which does not
affect our conclusions, as we discuss later.
3.2. Results: gamma-ray and neutrino backgrounds
We assume the spectral index αp = 2, 2.2, 2.4 and, as extreme case, αp = 1.5. As for the magnetic field B ≫ BCMB (see Eq. (7)), B = 1μG, and 0.5μG (see Eq. (6)). The first choice of the magnetic field can be regarded as conservative considering that, for example, the volume-averaged magnetic field of Coma, the best-studied cluster for Faraday rotation measurements, is about 2 μG (Bonafede et al. 2010); the latter should be considered optimistic with respect to current estimates. To clarify the meaning of the terms conservative/optimistic, note that the higher the magnetic field, the less room there is for protons, because the radio counts have to be respected, hence the lower the gamma-ray and neutrino fluxes.
For each αp and value of the magnetic field, the corresponding P1 parameter is chosen in such a way that the computed N1.4(>Fmin) does not overshoot the NVSS radio counts, and they are reported in Table 1. To make certain that our models respect current gamma-ray upper limits, the corresponding Coma-like and Perseus-like gamma-ray fluxes above 100 MeV and 1 TeV, respectively, are also shown in Table 1, after assuming M500 as in Reiprich & Böhringer (2002), together with the total gamma-ray and neutrino flux at 100 MeV and 250 TeV, respectively, for all the galaxy clusters in the Universe. All the reported values refer to 100% loud clusters, while the 30% case is studied only for αp = 2. (In the latter case, the remaining fraction of 70% quiet clusters are assumed to have an Lγ(100 MeV) that is one order of magnitude lower than the loud ones.)
In the last column of Table 1 and for αp ≥ 2, we denote the cases that do not respect the gamma-ray upper limits on either Coma or Perseus by “G”. For these cases, we recomputed P1 so as to respect the Coma upper limit, our reference choice (see values in parenthesis in Table 1). However, our recomputed values for αp = 2 still overshoot the current Perseus gamma-ray upper limit. We nevertheless adopt the Coma upper limit as reference because it was calculated for αp = 2 and for a larger spatial extension, up to R200. For αp = 1.5, the cases indicated by “N” in Table 1 exceed the IceCube neutrino data. Also in this case we recalculated P1 to match the IceCube results after averaging over the corresponding energy range.
Figure 2 shows both the comparison of our models to
the radio counts (on the left) and the computed gamma-ray (in black) and neutrino
intensities (in red) as functions of the energy (on the right), for the chosen values of
αp and B assuming 100% loud
clusters. For comparison, we plot the Fermi data (Fermi LAT Collaboration 2015a) and the IceCube 1σ error band as in Aartsen et al. (2014a). The latter refers to the
four-year IceCube data sample. However, more recently a new fit has been provided, using
two-year statistics but including low energy events down to 1 TeV. The best fit of the neutrino spectrum
obtained in this case scales as 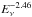 (Aartsen et al. 2015).
(Aartsen et al. 2015).
For αp> 2, both the gamma-ray and the neutrino diffuse backgrounds are well below the Fermi and the IceCube data in all cases. For αp = 2, while the gamma-ray flux is always lower than the Fermi measurements, the neutrino diffuse background could represent a significant fraction of the flux measured by IceCube for B = 1μG and 0.5 μG.
As known from radio observations, the case of 100% loud clusters is not realistic. Therefore, in Fig. 3, we show the same as in Fig. 2 for αp = 2, together with the more realistic case of 30% loud clusters. In the latter, galaxy clusters could make up at most about 10% (20%) of the neutrino flux measured by Ice Cube for B = 1μG (0.5 μG). This gives an estimation of how much our results for other spectral indices would change when moving from 100% loud clusters to the more realistic case of 30% loud clusters: Iγ,ν,30% ≈ Iγ,ν,100%/ 2 (see also Table 1 for comparison).
In the extreme case of αp = 1.5, we could explain the IceCube data by averaging over the corresponding energies for all cases, while respecting all other constraints from radio to gamma rays. However, we note that such a hard spectral index contradicts the most recent IceCube results, thus suggesting a softer spectral index (Aartsen et al. 2015).
Estimates of magnetic fields in clusters from Faraday rotation measurements range from ~μG for merging clusters up to 10 μG for cool-core clusters (Carilli & Taylor 2002; Clarke 2004; Vogt & Enßlin 2005; Bonafede et al. 2010, 2013). The case of B = 0.5μG should therefore be considered illustrative and optimistic because it contradicts current knowledge.
We conclude that, amongst all the cases we studied that respect both radio counts and current gamma-ray upper limits, hadronic interactions in galaxy clusters can realistically contribute at most up to 10% of the total extragalactic neutrino background, while contributing less than a few percentage points to the total extragalactic gamma-ray background. Moreover, the simplified requirement of not overshooting the NVSS radio counts on clusters leads to optimistic results. In fact, as explained in Sect. 2, not all the observed radio emission in clusters has a hadronic origin (Brunetti et al. 2012; Zandanel et al. 2014b). The open question is the exact contribution of protons to the non-thermal content of clusters, the corresponding contribution to the observed radio emission, and therefore, the possible gamma-ray emission (see Zandanel & Ando 2014 for a discussion). This implies that even our results, which respect both NVSS counts and gamma-ray limits, should still be considered rather optimistic.
Finally, we note that, owing to our simplified approach using a gamma-ray luminosity-mass relation, the conclusions of this section can be generalised to any source of CR protons where these mix and hadronically interact with the ICM of galaxy clusters, such as those injected by structure formation shocks and AGNs. For any considered source of protons, the resulting secondary emission must respect both radio and gamma-ray constraints.
 |
Fig. 2 Total gamma-ray and neutrino intensities (right) due to hadronic interactions in galaxy clusters, for 100% loud clusters, and the corresponding radio counts due to synchrotron emission from secondary electrons (left). From top to bottom, we plot the cases with B ≫ BCMB, B = 1μG and 0.5μG, respectively. For comparison, the Fermi (Fermi LAT Collaboration 2015a) and IceCube (Aartsen et al. 2014a) data are shown in the panels on the right. The neutrino intensity is meant for all flavours. All the plotted intensities respect NVSS radio counts and the gamma-ray upper limits on individual clusters. For B = 1μG and αp = 2.4, B = 0.5μG and αp = 2.2,2.4, and for αp = 1.5, the radio counts respecting the gamma-ray and neutrino limits, respectively, are below the y-scale range adopted for the panels on the left. |
 |
Fig. 3 Same as Fig. 3, together with the case of 30% loud clusters for αp = 2. The remaining percentage of 70% quiet clusters has been assumed to have Lγ(100 MeV) one order of magnitude lower than for the loud clusters. The 100% loud case is shown with lighter colours (i.e., in grey and orange). |
3.3. Results: testing our standard assumptions
To make our conclusions more robust, we comment in this section on two of our assumptions and on their effect on our final results: the redshift evolution and the value of the parameter P2 in the luminosity-mass relation.
The redshift dependence has been omitted in Eq. (5). For the sake of completeness, we tested the effect of introducing a redshift dependence in the gamma-ray luminosity-mass relation by adopting Lγ ∝ Ωm (1 + z)3 + ΩΛ, for αp = 2.2, 100% loud clusters and B ≫ BCMB, roughly corresponding to the scaling observed in the Zandanel et al. (2014a) multi-frequency mock-cluster catalogue for Lγ(100 MeV)–M500. We found that omitting the redshift evolution causes both the radio counts and the high-energy fluxes to be only about 20% lower than the redshift-evolution case. Our results would scale accordingly, as would the P1 parameter, and the maximum allowed contribution to the total extragalactic gamma-ray and neutrino fluxes would remain approximately the same. The case of radio counts is not as intuitive, but can be understood if noting that redshift evolution will boost the luminosity of higher redshift objects, pushing them into a regime where they would be detectable and boosting the corresponding estimation of the radio counts, therefore requiring lower P1 with respect to no-redshift evolution.
In Sect. 3.1, we fix the slope of the luminosity-mass relation to P2 = 5/3, assuming that the hadronic-induced luminosity scales as the cluster thermal energy. In the conclusions of Sect. 3.2, we mentioned that our phenomenological approach can be generalised to any source of CR protons in clusters if these mix and hadronically interact with the ICM. However, while our standard choice for the P2 parameter is appropriate for CR protons injected by structure formation shocks, it could be different for other CR sources. Clearly, a steeper slope would assign larger fluxes to high-mass objects that would easily overshoot radio counts. As a consequence, a lower value for P1 would be allowed, and considering that low-mass clusters would have lower luminosities, we estimate that the total gamma-ray and neutrino fluxes would be lower than in the case of P2 = 5 /3, or at most, at the same level owing to the sum of a few very powerful, massive nearby sources.
To assess the changes obtained by assuming a flatter slope in the luminosity-mass relation, we tested the extreme value P2 = 1 for 30% loud clusters, αp = 2 and B = 1μG, our most optimistic, still realistic, case. We underline, however, that a luminosity-mass function with such a flat slope strongly contradicts current knowledge of the diffuse radio emission in galaxy clusters (Brunetti et al. 2009; Cassano et al. 2013). Either way, we found that, to respect radio counts, the maximum allowed contribution to the total extragalactic neutrino flux is about 15%. This behaviour can be understood when noting again that such a flat slope implies that higher luminosities are assigned to lower mass clusters, pushing them into a regime where they would be detectable, hence boosting the corresponding radio counts. For the sake of completeness, we also added a redshift evolution of the luminosity as (1 + z)3 (as, e.g., for AGNs; Barger et al. 2005) to this extreme model that should eventually boost the neutrino production. We found that the maximum allowed contribution to the total extragalactic neutrino flux is 30% of the IceCube flux. We conclude that in all cases, the contribution to the total extragalactic gamma-ray flux is still negligible.
The estimation of a flux that is 30% of the IceCube one is the maximum that can be obtained under realistic conditions (30% loud clusters, B = 1μG) for the extreme value P2 = 1 with αp = 2. The only way to additionally boost the total neutrino flux without changing the radio counts would be to integrate down to lower masses, as we also discuss in Sect. 4.34. We note, however, that our standard lower mass bound is M500, lim = 6.3 × 1013h-1 M⊙ = 9 × 1013 M⊙, roughly corresponding to M200, lim = 1.4 × 1014 M⊙, and it already includes groups of galaxies. Extending the mass integration of the above case down to M500, lim = 1013h-1 M⊙ = 1.4 × 1013 M⊙, the 30% contribution to the total neutrino flux would become about 160%, overshooting the IceCube measurement. One could, of course, fine-tune this mass limit to match the IceCube flux, but we think that such a combination of extreme parameters is highly unlikely. At any rate, the E-2 spectrum is the only one for which such fine-tuning would give a significant total neutrino flux, and it disagrees with the latest IceCube results, suggesting a softer spectral index (Aartsen et al. 2015).
We conclude that the results of the phenomenological approach presented in Sect. 3.2 are robust against our assumptions and that they provide realistic estimates of the maximum allowed contribution of galaxy clusters to the total extragalactic gamma-ray and neutrino fluxes.
4. Semi-analytical model for the cosmic-ray and intra-cluster-medium distributions
In this section, we adopt a more sophisticated approach to modelling the CR and ICM distributions in galaxy clusters, as well as their magnetic field spatial distribution.
 |
Fig. 4 Radio counts due to synchrotron emission of secondary electrons as from the semi-analytical model of Zandanel et al. (2014b, ZPP in the plots) on the left, and total gamma-ray and neutrino intensities on the right. For comparison, we plot the Fermi (Fermi LAT Collaboration 2015a) and IceCube data (Aartsen et al. 2014a) in the panels on the right. The neutrino intensity is meant for all flavours. We show the cases of the model applied to a mass function for 20% and 40% loud clusters, and additionally for 10% loud clusters with parameters as in the Pinzke & Pfrommer (2010) model with a maximum CR proton acceleration efficiency of 15% (PP in the plots). According to this semi-analytical model, galaxy clusters contribute <1% to the diffuse gamma-ray and neutrino backgrounds. |
4.1. Semi-analytical modelling
For the ICM density distribution, we adopt the phenomenological model of Zandanel et al. (2014a), which is based on gas profiles obtained in X-rays (Croston et al. 2008) and on an observational correlation between gas fraction and mass of the clusters (Sun et al. 2009). This method allows a gas density to be assigned to any galaxy cluster using its mass alone, in such a way that the observed X-ray and Sunyaev-Zel’dovich scaling relations are correctly reproduced.
For the CR spatial and spectral distribution, we adopt the hadronic model proposed in Zandanel et al. (2014b), which extends the semi-analytical model of Pinzke & Pfrommer (2010). The latter provides a scaling of the CR distribution with the cluster mass, while Zandanel et al. (2014b) introduced an effective parameterisation on the CR spatial distribution ρCR to account for CR transport phenomena. In all the models analysed in this section, we assume the proton spectral shape as in Pinzke & Pfrommer (2010) where a universal CR spectrum is found amongst the simulated galaxy clusters. We rely on Eqs. (3) and (4) with Lγ(M500,z) and L1.4(M500,z) calculated by using Eqs. (2) and (1), with ρICM and ρCR from the Zandanel et al. (2014a,b) models, including redshift evolution.
The cluster population is divided into 50% cool-core and 50% non-cool-core clusters (as from observations; see, e.g., Chen et al. 2007) with different parameterisation of the ICM and CR profiles. Cool-core clusters are relaxed objects, so CRs could stream out of the core, creating flat CR profiles. Non-cool-core clusters are more turbulent objects that should cause CRs to advect with the gas and create centrally peaked CR profiles. The difference between cool-core and non-cool-core clusters is modelled through the parameter γtu = τst/τtu, i.e., the ratio between the characteristic time scale of streaming and that of turbulence. This parameter ranges from 100 for highly turbulent cluster and centrally peaked CR distributions to 1 for relaxed clusters and flat distributions as CRs move towards the outskirts (Zandanel et al. 2014b). Here, we assume γtu = 3 and 1 for loud and quiet cool-core clusters, and γtu = 60 and 1 for loud and quiet non-cool-core clusters, respectively.
The magnetic field is assumed to radially scale as the gas density: 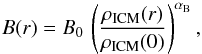 (8)where
B0 is the central magnetic field, and
αB =
0.5 describes the declining rate of the magnetic field strength towards
the cluster outskirts (Dubois & Teyssier
2008; Bonafede et al. 2010; Kuchar & Enßlin 2011, and references therein).
In particular, for quiet clusters, we adopt a central magnetic field B0 of 4
μG (7.5
μG) for
non-cool-core (cool-core) clusters, while we choose 6 μG (10 μG), to account for the
potential turbulent dynamo in loud objects.
(8)where
B0 is the central magnetic field, and
αB =
0.5 describes the declining rate of the magnetic field strength towards
the cluster outskirts (Dubois & Teyssier
2008; Bonafede et al. 2010; Kuchar & Enßlin 2011, and references therein).
In particular, for quiet clusters, we adopt a central magnetic field B0 of 4
μG (7.5
μG) for
non-cool-core (cool-core) clusters, while we choose 6 μG (10 μG), to account for the
potential turbulent dynamo in loud objects.
4.2. Results: gamma-ray and neutrino backgrounds
The model in Zandanel et al. (2014b, ZPP in tables and figures) reproduces the observed radio-to-X-ray and radio-to-Sunyaev-Zel’dovich scaling relations of galaxy clusters and respects current gamma-ray upper limits5. In the left-hand panel of Fig. 4, we show the resulting radio counts for a fraction of 20% and 40% loud clusters. We find that the latter case should be considered extreme because hadronic interactions are known not to be uniquely responsible for the observed radio emission in clusters. Table 2 shows the corresponding total gamma-ray and neutrino fluxes.
Total gamma-ray and neutrino fluxes for the semi-analytical model.
 |
Fig. 5 Same as in the left panel of Fig. 4 for 20% loud clusters. The left panel shows the comparison with the previous model with one obtained adopting z2 = 0.6, and one with a lower mass integration limit, of 1013h-1M⊙. The right panel shows the comparison with the model in Fig. 4 and one obtained using the Planck cosmological data. |
Figure 4 (left panel) also shows the radio counts obtained by adopting 10% loud clusters with parameters corresponding to the model in Pinzke & Pfrommer (2010, PP in tables and figures) with a maximum CR proton acceleration efficiency scaled down to 15% with respect to the originally assumed 50% in order to obey current gamma-ray constraints (Zandanel & Ando 2014; Fermi LAT Collaboration 2014). For the remaining 90% quiet fraction, the parameters of the previous model are assumed. The right-hand panel of Fig. 4 shows the corresponding total gamma-ray and neutrino intensities compared with the data from Fermi and IceCube. We conclude that galaxy clusters contribute less than 1% to the diffuse gamma-ray and neutrino backgrounds.
The results reported in this section are more realistic than the ones shown in Sect. 3. However, we underline as the semi-analytical model adopted here is based on the hypothesis that CRs are accelerated at structure formation shocks, while no assumption on the CR sources is made in the phenomenological approach of Sect. 3.
4.3. Results: dependence on cosmology and lower mass bound
To test the robustness of our results, we computed the gamma-ray and neutrino backgrounds in the case of 20% loud clusters, first extending the integration down to lower masses (M500, lim = 1013h-1 M⊙) and then adopting the most recent Planck results for the cosmological parameters.
The left-hand panel of Fig. 5 shows the gamma-ray and neutrino backgrounds for the same case as shown in Fig. 4 for 20% loud clusters with M500, lim = 1013.8h-1 M⊙ and for M500, lim = 1013h-1 M⊙. In the latter case, the gamma-ray and neutrino diffuse fluxes are significantly higher, while still representing less than 1% of the observational data. At the same time, the radio counts are exactly the same as in Fig. 4 since these are due to the higher mass objects. We additionally show the case with M500, lim = 1013.8h-1 M⊙ integrated up to z2 = 0.6. As anticipated in Sect. 2, low-redshift objects represent the dominant contribution to the diffuse fluxes, because by adopting z2 = 0.6, we obtain 82% of the total flux.
Maximum allowed neutrino flux from nearby clusters at 250 TeV.
The right-hand panel of Fig. 5 shows gamma-ray and neutrino backgrounds for the same case as shown in Fig. 4 for 20% loud clusters and obtained by adopting the cosmological parameters determined by the Planck satellite (Planck Collaboration XVI 2014), i.e., H0 = 67.3 km s-1 Mpc-1, Ωm = 0.32, ΩΛ = 0.68, and the corresponding mass function. The Planck cosmology results in an overall larger number of structures, as is clear in Fig. 1, therefore increasing both the total radio counts (not shown, but still below the 40% loud case of Fig. 4) and the total gamma-ray and neutrino fluxes. As shown in Fig. 5, the contribution to the extragalactic gamma-ray and neutrino background is at any rate lower than 1%.
We note that the changes in M500, lim and in the cosmological parameters would affect the gamma-ray and neutrino diffuse fluxes obtained with the phenomenological approach in Sect. 3.2 approximately in the same way; i.e., they would increase by a factor of around 2, as can be seen from Table 2.
5. Comparison with stacking limits by IceCube and future detection prospects
Recently, Aartsen et al. (2014b) have presented an all-sky point- and extended-source search with one-year IceCube data. In particular, they provide upper limits on a stacked sample of nearby galaxy clusters, namely Virgo, Centaurus, Perseus, Coma, and Ophiuchus, following predictions provided by Murase et al. (2008). Here, we focus on comparing with their “model B”, where CR protons are supposed to be uniformly distributed within the cluster virial radius, and with their “isobaric model”, where CRs are assumed to be distributed like the ICM in the clusters.
Following Abbasi et al. (2011), we estimate the summed output of the five aforementioned clusters to be Iν(250 TeV) = 1.1 × 10-20 and 1.6 × 10-20 cm-2 s-1 GeV-1 for Model B and the isobaric model, respectively. The latest results by Aartsen et al. (2014b) provide the following upper limits Iν, UL(250 TeV) = 6.9 × 10-20 for Model B and 7.7 × 10-20 cm-2 s-1 GeV-1 for the isobaric model.
In Table 3, we provide the maximum allowed neutrino flux for the same five clusters by adopting the phenomenological luminosity-mass relations obtained in Sect. 3. We use the same mass of these clusters as from the literature6 in order to apply our Lγ(100 MeV)–M500 relation, and they should therefore be considered indicative numbers, as in Sect. 3 for Coma and Perseus. We use αp = 2,2.2, and 2.4, omitting the extreme case of 1.5, and always refer to the case with B = 1μG. For αp = 2, we adopt the P1 value for 30% loud clusters. See Table 1 for more details.
The upper limits Iν, UL(250 TeV) for this stacked sample of clusters by Aartsen et al. (2014b) are obtained by assuming a spectral index of ≈2.15, so we can compare with our results for αp = 2.2. From Table 3, we can see that the corresponding IceCube upper limits are just a factor of 1.3−1.5 above the maximum allowed flux for the stacked sample. When αp = 2.4, the maximum allowed flux for the stacked sample is one order of magnitude lower, while for αp = 2 it is one order of magnitude higher, with respect to αp = 2.2. We can conclude that, while special care should be used in considering the profile and extension of the possible signal, IceCube should be able to put constraints on our most optimistic case with αp = 2 and on the αp = 2.2 case in the very near future, while the case with αp = 2.4 is much harder to achieve.
We underline that the fluxes presented in this section for Virgo, Centaurus, Perseus, Coma, and Ophiuchus are quite optimistic for representing the maximum allowed by our phenomenological approach. For example, we know that the fluxes of Virgo, Centaurus, and Ophiuchus should lie significantly below the loud part of the luminosity-mass relation owing to the lack of diffuse radio emission in Virgo and Centaurus, and to the very low surface-brightness radio emission observed in Ophiuchus (see, e.g., Zandanel et al. 2014b), pushing also the possible hadronic-induced gamma-ray and neutrino fluxes to lower levels. Any realistic modelling of these objects should consider this evidence carefully. In fact, the stacked signal from the five nearby clusters presented in this section already significantly overshoots the total signal obtained with the more realistic modelling of the CR proton population in clusters performed in Sect. 4 with our semi-analytical approach.
6. Proton-photon interactions in galaxy clusters
Besides interacting with the ICM, relativistic protons in clusters of galaxies can also interact with the ambient photon fields. The two main interaction processes are electron-positron pair production (p + γ → p + e+ + e−) and photomeson production. (Close to the threshold, the dominant contribution comes from the resonant channel: p + γ → Δ+ → p + π0 or n + π−.) Both photons and neutrinos are expected in photomeson production owing to the decay of neutral and charged pions, respectively (Kelner & Aharonian 2008). Thus, this is another channel to be investigated for assessing the contribution of clusters of galaxies to the diffuse neutrino flux observed by IceCube.
The process of photomeson production has a kinematic threshold and takes place when the
energy of the photon in the rest frame of the proton exceeds Ethr ≃ 145 MeV
(see, e.g., Kelner & Aharonian 2008). The
most prominent radiation field in clusters of galaxies is the CMB (e.g., Pinzke et al. 2011), whose photons have a typical energy
of ECMB ≈ 7 ×
10-4 eV. The threshold energy for a proton to produce a
meson is 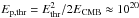 eV, but in fact
protons with slightly smaller energy can also interact with the high-energy tail of the
black body radiation (Greisen 1966; Zatsepin & Kuz’min 1966). Thus, one can conclude
that proton-photon interactions in clusters of galaxies can contribute to the high-energy
neutrino background only if protons with energy in excess of several 1019 eV are present in the ICM.
eV, but in fact
protons with slightly smaller energy can also interact with the high-energy tail of the
black body radiation (Greisen 1966; Zatsepin & Kuz’min 1966). Thus, one can conclude
that proton-photon interactions in clusters of galaxies can contribute to the high-energy
neutrino background only if protons with energy in excess of several 1019 eV are present in the ICM.
Accretion shocks around clusters of galaxies have been proposed as the sites of the acceleration of ultrahigh-energy CRs, the main reason being that their very large size (Mpc scale) would allow the acceleration and confinement of protons of ultrahigh energies (e.g., Norman et al. 1995). An estimate of the maximum energy achievable by protons at cluster accretion shocks can be obtained by equating the acceleration time, computed in the framework of diffusive shock acceleration, to the energy loss time due to proton-photon interactions. Accurate calculations have shown that the maximum energy of protons is determined by the energy losses due to electron-positron pair production and that for the most optimistic assumptions it ranges from a few 1018 eV to a few 1019 eV (Vannoni et al. 2011). Because they are cooled mainly by pair production, protons are thus not expected to produce any appreciable flux of neutrinos through the proton-photon interaction channel. Heavy nuclei, such as iron, can be accelerated up to ≈1020 eV at cluster accretion shocks (e.g., Allard & Protheroe 2009; Vannoni et al. 2011). However, iron cools mainly by photodisintegration in a soft photon field, and in this case the neutrino yield is very suppressed compared to the case of photomeson production (Kotera et al. 2009).
Another possible scenario for the production of neutrinos in the ICM would be to assume that clusters contain sources of ultrahigh-energy CRs. This would lead to two advantages. First of all, the infrared photon background in the cluster core would be enhanced with respect to the cosmological one thanks to the contribution from the galaxies in the cluster (Lagache et al. 2005; Pinzke et al. 2011). Second, the turbulent magnetic field present within the ICM would partially confine ultrahigh-energy protons, enhancing the probability of interaction. These two facts would increase the expected neutrino flux from proton-photon interactions (e.g., de Marco et al. 2006; Kotera et al. 2009). However, the source of ultrahigh-energy CRs will have to be located in the centre of the cluster, where the infrared photon background is enhanced and the confinement of protons is more effective (thanks to a larger magnetic field). As pointed out in Kotera et al. (2009), the high gas density in the core of clusters would also enhance the probability of proton-proton interactions, which would dominate the neutrino production below energies of ≈1018 eV.
Finally, it has to be noticed that the expected spectrum of neutrinos from photopion production interactions is significantly harder than E-2 below the energy threshold, which is at odds with the evidence for a spectral index softer than two revealed by IceCube (Murase et al. 2013; Becker Tjus et al. 2014). This implies that proton-photon interactions make a negligible contribution to the neutrino flux in the energy domain of the IceCube neutrinos.
7. Contribution to the small-scale anisotropies of the gamma-ray background
Recently, Fermi LAT Collaboration (2012) has analysed the anisotropies in the EGB and found an excess in its angular power spectrum over what is expected with a completely diffuse source distribution on multipole ranges 155 ≤ ℓ ≤ 504 (corresponding to ≲2° angular scales). For the first time, this has shown that a major fraction of the EGB is made by discrete sources, and, in fact, Cuoco et al. (2012) point out that the measured level of anisotropies is consistent with predictions for gamma-ray blazars (Ando et al. 2007). They also obtained the upper limit on the angular power spectrum as Cℓ < 3.3 × 10-18 (cm-2 s-1 sr-1)2 sr for 155 ≤ ℓ ≤ 504 and E = 1−10 GeV on other source components, after subtracting the main blazar contribution. Even though clusters are not the dominant contributors to the isotropic component of the diffuse gamma-ray and neutrino backgrounds (as shown in the previous sections), they may make substantial contributions to the EGB anisotropies. In particular, since there are relatively fewer than other astrophysical sources, such as star-forming galaxies, the cluster component in the EGB should be more anisotropic. To this end, we estimate the cluster contribution to the EGB anisotropies in this section and compare it to the Fermi data at sub-degree angular scales.
The angular power spectrum coming from proton-proton interactions in galaxy clusters can be
calculated as follows (e.g., Ando et al. 2007):
![\begin{equation} C_{\ell} = \int \frac{\rmn{d}\chi}{\chi^2} \, W_{\gamma}^2(E\,[1+z],z)\,P_{\rm{C}}\left( k=\frac{\ell}{\chi},\chi \right) , \label{eq:PS} \end{equation}](/articles/aa/full_html/2015/06/aa25249-14/aa25249-14-eq255.png) (9)where χ is the comoving distance
(we use the same redshift range as in previous sections), Wγ = (1 +
z)3Aγ(E
[ 1 + z ] )/4π is
the so-called window function, and PC(k,χ) is the power
spectrum for the cluster gamma-ray emission. The last can be divided into one- and two-halo
terms,
(9)where χ is the comoving distance
(we use the same redshift range as in previous sections), Wγ = (1 +
z)3Aγ(E
[ 1 + z ] )/4π is
the so-called window function, and PC(k,χ) is the power
spectrum for the cluster gamma-ray emission. The last can be divided into one- and two-halo
terms, 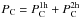 , which
we express as (e.g., Komatsu & Seljak 2002;
Ando et al. 2007)
, which
we express as (e.g., Komatsu & Seljak 2002;
Ando et al. 2007)
![\begin{eqnarray} P_{\rmn{C}}^{\rm{1h}} & = & \int \rmn{d}M \frac{\rmn{d}n}{\rmn{d}M} \left[ \int 4\pi r^2 \rmn{d}r \rho_\rmn{CR}(r) \rho_\rmn{gas}(r) \frac{\sin(kr)}{kr} \right]^2 , \\ P_{\rmn{C}}^{\rm{2h}} & = & \left[ \int \rmn{d}M \frac{\rmn{d}n}{\rmn{d}M} \, b(M,z ) \int 4\pi r^2 \rmn{d}r \rho_\rmn{CR}(r) \rho_\rmn{gas}(r) \frac{\sin(kr)}{kr} \right]^2 \nonumber \\ & & \times \, P_{\rmn{lin}} (k,\chi) , \end{eqnarray}](/articles/aa/full_html/2015/06/aa25249-14/aa25249-14-eq260.png) respectively,
where the radial integration goes up to R500. In the two-halo term, we assume that
the linear matter power spectrum Plin(k,χ) is related to
the cluster power spectrum via the linear bias b(M,z) (Tinker et al. 2010). We find that the one-halo term dominates the
two-halo term at all multipoles ℓ.
respectively,
where the radial integration goes up to R500. In the two-halo term, we assume that
the linear matter power spectrum Plin(k,χ) is related to
the cluster power spectrum via the linear bias b(M,z) (Tinker et al. 2010). We find that the one-halo term dominates the
two-halo term at all multipoles ℓ.
In Fig. 6, we show the angular power spectrum for the
semi-analytical models of Sect. 4 for 20% and 40% loud
clusters integrated in the energy bin from 1 to 10 GeV. We compare with the measurement on
the EGB by Fermi (Fermi LAT Collaboration
2012) and upper limits by Cuoco et al.
(2012). We compare 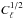 instead of Cℓ. This is because
Cℓ is a variance, so if
each cluster is twice as bright, then Cℓ becomes larger by a
factor of 4. Therefore, taking the square-root will reflect the correct scaling with respect
to the cluster contribution. Our prediction is about one order of magnitude less than the
Fermi upper limit. This means that in scenarios where the total galaxy
cluster intensity is much higher than in the models of Sect. 4, as is potentially realised for some of the simple phenomenological models
discussed in Sect. 3, the angular power spectrum could
be a powerful discriminator, as powerful as radio counts. Additionally, there are other
contributions to the EGB anisotropies that would further increase the gamma-ray angular
power spectrum, such as, but not only, dark matter annihilation (e.g., Ando & Komatsu 2006, 2013;
Fornasa et al. 2013; Fermi LAT Collaboration 2015b), further exacerbating the possible tension
with the upper limits by Cuoco et al. (2012).
instead of Cℓ. This is because
Cℓ is a variance, so if
each cluster is twice as bright, then Cℓ becomes larger by a
factor of 4. Therefore, taking the square-root will reflect the correct scaling with respect
to the cluster contribution. Our prediction is about one order of magnitude less than the
Fermi upper limit. This means that in scenarios where the total galaxy
cluster intensity is much higher than in the models of Sect. 4, as is potentially realised for some of the simple phenomenological models
discussed in Sect. 3, the angular power spectrum could
be a powerful discriminator, as powerful as radio counts. Additionally, there are other
contributions to the EGB anisotropies that would further increase the gamma-ray angular
power spectrum, such as, but not only, dark matter annihilation (e.g., Ando & Komatsu 2006, 2013;
Fornasa et al. 2013; Fermi LAT Collaboration 2015b), further exacerbating the possible tension
with the upper limits by Cuoco et al. (2012).
 |
Fig. 6 Gamma-ray angular power spectrum for emission resulting from proton-proton interactions in galaxy clusters in the energy range 1−10 GeV. We show the result for the semi-analytical model of Sect. 4 for 20% and 40% loud clusters. We plot the EGB anisotropy measured by Fermi (Fermi LAT Collaboration 2012) for comparison, which is explained by unresolved blazars, and the upper limits obtained once the blazar component is subtracted (Cuoco et al. 2012). We plot the square root of ℓ(ℓ + 1)Cℓ/ 2π, which implies that the shown quantity is directly proportional to an increase in intensity. |
8. Discussion and conclusions
In this work we estimated the contribution from hadronic proton-proton interactions in galaxy clusters to the total extragalactic gamma-ray and neutrino fluxes, while including radio constraints for the first time. We modelled the cluster population by means of their mass function. Our approach makes use of a phenomenological luminosity-mass relation applied to all clusters, constructed by requiring radio counts to be respected. We adopted four different proton spectral indices αp = 1.5,2,2.2, and 2.4, and three different magnetic field values B ≫ BCMB, B = 1μG, and B = 0.5μG. The last is meant to only be an illustrative case, because it contrasts with current estimates of magnetic fields in clusters.
Radio observations reveal that not all galaxy clusters host diffuse synchrotron radio emission, with upper limits about an order of magnitude below the loud state (Brunetti et al. 2009; Cassano et al. 2013). For the sake of simplicity, we adopted 100% loud clusters, leading to an optimistic estimation. However, we also discussed the case with 30% loud clusters for αp = 2, corresponding to our most optimistic case, according to recent estimates of the loud fraction. In our phenomenological model, the slope of the luminosity-mass relation is fixed to 5/3, assuming that the hadronic-induced luminosity scales as the cluster thermal energy, and the redshift evolution was omitted for simplicity. We showed that our assumptions are robust, and we estimated that ignoring the redshift evolution results in only about a 20% underestimation of the radio counts and total high-energy fluxes.
By requiring all the current constraints to be respected from radio counts to gamma-ray upper limits on individual clusters, we showed that galaxy clusters can contribute at most up to 10% of the total neutrino background for αp = 2, while contributing much less to the EGB. For αp> 2, the gamma-ray and neutrino backgrounds in all considered cases are <1% of the gamma-ray and neutrino fluxes measured by Fermi (Fermi LAT Collaboration 2010b, 2015a) and IceCube (Aartsen et al. 2014a), respectively. Only for the extreme case with αp = 1.5 is the neutrino flux of the same order of magnitude as the IceCube data; however, such a hard spectral shape contrasts with the most recent IceCube spectral fit of neutrino flux (Aartsen et al. 2015).
We also adopted a more refined approach that employs a semi-analytical model where the ICM density is constructed from X-ray observations, and the CR spatial and spectral distribution is based on state-of-art hydrodynamic simulations (Zandanel et al. 2014b). In this case, we divided the cluster population into cool-core/non-cool-core and loud/quiet subsamples, as suggested by observations, where the transition from the loud to the quiet state is achieved through a change in the CR propagation properties. We find that galaxy clusters contribute to <1% to the EGB and to the neutrino flux measured by IceCube. While this semi-analytical model is more realistic than the simplified phenomenological model discussed above, we assume in this case that CRs are accelerated at structure formation shocks, while no assumption on the CR sources was made in the phenomenological approach.
We then compared the flux of five nearby clusters − Virgo, Centaurus, Perseus, Coma and Ophiuchus − to recent results by IceCube (Aartsen et al. 2014b). The IceCube upper limits are just a factor 1.5 above our maximum allowed (stacked) flux for these objects for the case of αp = 2.2, which compares well to what is used in Aartsen et al. (2014b). We showed that, despite the small contribution to the total neutrino flux, IceCube should be able to put constraints on our most optimistic case with αp = 2, and very soon in the case with αp = 2.2, using the stacked sample of nearby massive clusters.
We briefly also discussed the case of proton-photon interactions in galaxy cluster. We found that this channel gives a negligible contribution to the expected neutrino flux in the multi TeV–PeV energy domain.
While galaxy clusters represent a sub-dominant contribution to the EGB, they could
substantially contribute to its anisotropy because they are fewer in number than other
astrophysical sources and, therefore, are expected to be more anisotropic. For this reason,
we computed the angular power spectrum for the considered semi-analytical models and showed
that the amplitude of the angular fluctuations, represented by
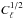 ,
is about one order of magnitude below the Fermi upper limits.
,
is about one order of magnitude below the Fermi upper limits.
We conclude that there is no realistic scenario in which galaxy clusters can contribute substantially to either the EGB or the extragalactic neutrino flux, since the maximum contribution is at most 10% in the simple phenomenological modelling, while it is less than 1% in most cases and in the more realistic semi-analytical modelling. We also proved that our conclusions are not significantly affected by our assumptions. Our results therefore put earlier works into prospective, which turned out to be overly optimistic in estimating the galaxy cluster contribution (e.g., Loeb & Waxman 2000; Murase et al. 2013).
We would like to conclude with a few additional comments on our assumptions. In our calculations, we omitted both a possible cut-off in the CR spectrum at high energies caused by protons that are no longer confined to the cluster and the absorption of high-energy gamma rays due to interactions with the extragalactic background light. The former implies larger high-energy neutrino fluxes, while the latter implies slightly optimistic gamma-ray fluxes. Additionally, we stress once more how requiring the synchrotron emission from secondary electrons not to overshoot radio counts also results in rather optimistic gamma-ray and neutrino fluxes. This is because so-called giant radio haloes hosted in merging, non-cool-core clusters cannot be explained solely by hadronic emission (Brunetti et al. 2012; Zandanel et al. 2014b). Therefore, the secondary emission seems to represent only a fraction of the total observed radio emission.
As a final note on the semi-analytical modelling, we underline that the transition from the loud to the quiet state in the galaxy cluster population is not achieved in the classical hadronic model, meaning that it predicts that all clusters should have the same level of secondary emission. This clearly contradicts observations and represents one of the problems with the hadronic scenario (see Enßlin et al. 2011 for a discussion). The only mechanism that has been proposed so far to solve this problem is to vary CR propagation properties (see, e.g., Wiener et al. 2013), which was also adopted in our semi-analytical approach through the Zandanel et al. (2014b) model. We note, however, that it is still being debated whether the conditions for CR diffusion can be reached in the ICM. In the worst-case scenario, the secondary electrons produced in proton-proton collisions in clusters would only be seed electrons for subsequent turbulent re-acceleration (see, e.g., Brunetti & Lazarian 2011; Brunetti et al. 2012). This would imply a much lower secondary emission only at the level of the quiet state. If this turns out to be the case, the total gamma-ray and neutrino fluxes from galaxy clusters should be even lower than what we have estimated here.
The total energy density of photons should also include the contribution from star light: ϵph = ϵstars + ϵCMB. However, ϵstars is subdominant in the cluster volume (see, e.g., Fig. 5 of Pinzke et al. 2011), therefore ϵph ≈ ϵCMB.
We use the cumulative number density function as in Cassano et al. (2010). Cassano et al. (2010) do not use the fluxes of Giovannini et al. (1999), but rather the ones from follow-up observations of the same sample of galaxy clusters, which are higher than the NVSS ones (Cassano, priv. comm.).
Because the larger contribution to both the number of detectable clusters in radio (Zandanel et al. 2014b) and the total gamma-ray and neutrino fluxes is dominated by nearby clusters, the high-redshift dependence is negligible for our purposes (see Sects. 3.3 and 4.3 for more details).
In Sect. 4.3 we also estimate the changes obtained by adopting the most recent Planck results for the cosmological parameters (Planck Collaboration XVI 2014). While for the semi-analytical model of the next section, the radio counts, total gamma-ray, and neutrino fluxes are enhanced by a factor of only about 1.7, in the phenomenological model with P2 = 1, this would significantly boost the radio counts requiring the corresponding P1 value to be lowered.
The parameters for the corresponding Lγ(100 MeV)–M500 scaling relation at z = 0 are P1 = 21.68 and P2 = 1.62 for non-cool-core clusters, and P1 = 22.41 and P2 = 1.57 for cool-core clusters. This translates in Coma-like and Perseus-like fluxes, for αp = 2.2, of F(> 100 MeV) = 1.6 × 10-9 and F(> 1 TeV) = 7.6 × 10-14 cm-2 s-1, respectively, below the current upper limits.
The mass M500 for Centaurus, Perseus, Coma, and Ophiuchus is taken from Reiprich & Böhringer (2002), while for Virgo it is derived from Pinzke et al. (2011).
Acknowledgments
We thank the anonymous referee for useful comments. We thank Denis Allard, Rossella Cassano, and Kohta Murase for useful discussions. This work was supported by the Netherlands Organisation for Scientific Research (NWO) through a Vidi grant (S.A., I.T., and F.Z.) and a PHC Van Gogh grant (S.G.).
References
- Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013, Phys. Rev. Lett., 111, 021103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2014a, Phys. Rev. Lett., 113, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2014b, ApJ, 796, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2015, Phys. Rev. D, 91, 022001 [NASA ADS] [CrossRef] [Google Scholar]
- Abbasi, R., Abdou, Y., Abu-Zayyad, T., et al. 2011, ApJ, 732, 18 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 720, 435 [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2012, ApJ, 755, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Ahlers, M., & Murase, K. 2014, Phys. Rev. D, 90, 023010 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Gasparrini, D., Sanchez-Conde, M., et al. 2015, ApJ, 800, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, D., & Protheroe, R. J. 2009, A&A, 502, 803 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anchordoqui, L. A., Goldberg, H., Halzen, F., & Weiler, T. J. 2004, Phys. Lett., 600, 202 [CrossRef] [Google Scholar]
- Anchordoqui, L. A., Barger, V., Cholis, I., et al. 2014a, J. High Energy Astrophys., 1, 1 [Google Scholar]
- Anchordoqui, L. A., Goldberg, H., Paul, T. C., da Silva, L. H. M., & Vlcek, B. J. 2014b, Phys. Rev. D, 90, 123010 [NASA ADS] [CrossRef] [Google Scholar]
- Anchordoqui, L. A., Paul, T. C., da Silva, L. H. M., Torres, D. F., & Vlcek, B. J. 2014c, Phys. Rev. D, 89, 127304 [NASA ADS] [CrossRef] [Google Scholar]
- Ando, S., & Komatsu, E. 2006, Phys. Rev. D, 73, 023521 [NASA ADS] [CrossRef] [Google Scholar]
- Ando, S., & Komatsu, E. 2013, Phys. Rev. D, 87, 123539 [NASA ADS] [CrossRef] [Google Scholar]
- Ando, S., & Nagai, D. 2008, MNRAS, 385, 2243 [NASA ADS] [CrossRef] [Google Scholar]
- Ando, S., & Nagai, D. 2012, J. Cosmol. Astro-Part. Phys., 7, 17 [Google Scholar]
- Ando, S., Komatsu, E., Narumoto, T., & Totani, T. 2007, Phys. Rev. D, 75, 063519 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J., Cowie, L. L., Mushotzky, R. F., et al. 2005, ApJ, 129, 578 [Google Scholar]
- Becker Tjus, J., Eichmann, B., Halzen, F., Kheirandish, A., & Saba, S. M. 2014, Phys. Rev. D, 89, 123005 [NASA ADS] [CrossRef] [Google Scholar]
- Berezinsky, V. S., Blasi, P., & Ptuskin, V. S. 1997, ApJ, 487, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., & Colafrancesco, S. 1999, Astropart. Phys., 12, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Gabici, S., & Brunetti, G. 2007, Int. J. Mod. Phys. A, 22, 681 [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Vazza, F., Brüggen, M., et al. 2013, MNRAS, 433, 3208 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 30007 [Google Scholar]
- Brunetti, G., & Lazarian, A. 2011, MNRAS, 410, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Cassano, R., Dolag, K., & Setti, G. 2009, A&A, 507, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetti, G., Blasi, P., Reimer, O., et al. 2012, MNRAS, 426, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Cassano, R., Brunetti, G., Röttgering, H. J. A., & Brüggen, M. 2010, A&A, 509, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassano, R., Brunetti, G., Norris, R. P., et al. 2012, A&A, 548, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassano, R., Ettori, S., Brunetti, G., et al. 2013, ApJ, 777, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborty, S., & Izaguirre, I. 2015, Phys. Lett. B, 745, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, X.-C., & Wang, X.-Y. 2014, ApJ, 793, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y.-Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarke, T. E. 2004, J. Kor. Astron. Soc., 37, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Pratt, G. W., Böhringer, H., et al. 2008, A&A, 487, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuoco, A., Komatsu, E., & Siegal-Gaskins, J. M. 2012, Phys. Rev. D, 86, 063004 [NASA ADS] [CrossRef] [Google Scholar]
- de Marco, D., Hansen, P., Stanev, T., & Blasi, P. 2006, Phys. Rev. D, 73, 043004 [NASA ADS] [CrossRef] [Google Scholar]
- Dennison, B. 1980, ApJ, 239, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D. 2007, AIP Conf. Proc., 921, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Di Mauro, M., & Donato, F. 2015, Phys. Rev. D, submitted [arXiv:1501.05316] [Google Scholar]
- Di Mauro, M., Calore, F., Donato, F., Ajello, M., & Latronico, L. 2014a, ApJ, 780, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Di Mauro, M., Donato, F., Lamanna, G., Sanchez, D. A., & Serpico, P. D. 2014b, ApJ, 786, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2008, A&A, 482, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T., Pfrommer, C., Miniati, F., & Subramanian, K. 2011, A&A, 527, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esmaili, A., & Serpico, P. D. 2013, J. Cosmol. Astro-Part. Phys., 1311, 054 [Google Scholar]
- Esmaili, A., Kang, S. K., & Serpico, P. D. 2014, J. Cosmol. Astro-Part. Phys., 12, 054 [Google Scholar]
- Feldstein, B., Kusenko, A., Matsumoto, S., & Yanagida, T. T. 2013, Phys. Rev. D, 88, 015004 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Fermi LAT Collaboration 2010a, ApJ, 717, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi LAT Collaboration 2010b, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fermi LAT Collaboration 2012, Phys. Rev. D, 85, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi LAT Collaboration 2014, ApJ, 787, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi LAT Collaboration 2015a, ApJ, 799, A86 [Google Scholar]
- Fermi LAT Collaboration 2015b, J. Cosmol. Astro-Part. Phys., submitted, [arXiv:1501.05464] [Google Scholar]
- Fichtel, C. E., Hartman, R. C., Kniffen, D. A., et al. 1977, ApJ, 217, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasa, M., Zavala, J., Sánchez-Conde, M. A., et al. 2013, MNRAS, 429, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, D., Kashiyama, K., & Meszaros, P. 2013, ApJ, 774, 74 [Google Scholar]
- Gabici, S., & Blasi, P. 2003, Astropart. Phys., 19, 679 [Google Scholar]
- Giovannini, G., Tordi, M., & Feretti, L. 1999, New Astron., 4, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Greisen, K. 1966, Phys. Rev. Lett., 16, 748 [Google Scholar]
- Griffin, R. D., Dai, X., & Kochanek, C. S. 2014, ApJ, 795, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Halzen, F., & Hooper, D. 2005, Astropart. Phys., 23, 537 [NASA ADS] [CrossRef] [Google Scholar]
- He, H.-N., Wang, T., Fan, Y.-Z., Liu, S.-M., & Wei, D.-M. 2013, Phys. Rev. D, 87, 063011 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration. 2009a, A&A, 502, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration. 2009b, A&A, 495, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huber, B., Tchernin, C., Eckert, D., et al. 2013, A&A, 560, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hümmer, S., Baerwald, P., & Winter, W. 2012, Phys. Rev. Lett., 108, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joshi, J. C., Winter, W., & Gupta, N. 2014, MNRAS, 439, 3414 [NASA ADS] [CrossRef] [Google Scholar]
- Kale, R., Venturi, T., Giacintucci, S., et al. 2013, A&A, 557, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashiyama, K., & Meszaros, P. 2014, ApJ, 790, L14 [Google Scholar]
- Katz, B., Waxman, E., Thompson, T., & Loeb, A. 2013, arXiv e-prints [arXiv:1311.0287] [Google Scholar]
- Kelner, S. R., & Aharonian, F. A. 2008, Phys. Rev. D, 78, 034013 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Keshet, U., Waxman, E., Loeb, A., Springel, V., & Hernquist, L. 2003, ApJ, 585, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., & Seljak, U. 2002, MNRAS, 336, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kotera, K., Allard, D., Murase, K., et al. 2009, ApJ, 707, 370 [Google Scholar]
- Kuchar, P., & Enßlin, T. A. 2011, A&A, 529, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kushnir, D., & Waxman, E. 2009, J. Cosmol. Astro-Part. Phys., 8, 2 [Google Scholar]
- Lacki, B. C., Thompson, T. A., Quataert, E., Loeb, A., & Waxman, E. 2011, ApJ, 734, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R.-Y., & Wang, X.-Y. 2013, ApJ, 766, 73 [Google Scholar]
- Liu, R.-Y., Wang, X.-Y., Inoue, S., Crocker, R., & Aharonian, F. 2014, Phys. Rev. D, 89, 083004 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., & Waxman, E. 2000, Nature, 405, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., & Waxman, E. 2006, J. Cosmol. Astro-Part. Phys., 0605, 003 [Google Scholar]
- MAGIC Collaboration. 2010, ApJ, 710, 634 [NASA ADS] [CrossRef] [Google Scholar]
- MAGIC Collaboration. 2012, A&A, 541, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miniati, F., Ryu, D., Kang, H., & Jones, T. W. 2001, ApJ, 559, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., & Beacom, J. F. 2013, J. Cosmol. Astro-Part. Phys., 2, 28 [Google Scholar]
- Murase, K., & Ioka, K. 2013, Phys. Rev. Lett., 111, 121102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Murase, K., Inoue, S., & Nagataki, S. 2008, ApJ, 689, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Ahlers, M., & Lacki, B. C. 2013, Phys. Rev. D, 88, 121301 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Inoue, Y., & Dermer, C. D. 2014, Phys. Rev. D, 90, 023007 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, S. G., Power, C., & Robotham, A. S. G. 2013, Astron. Comput., 3, 23 [CrossRef] [Google Scholar]
- Norman, C. A., Melrose, D. B., & Achterberg, A. 1995, ApJ, 454, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., & Resconi, E. 2014, MNRAS, 443, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C. 2008, MNRAS, 385, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Pfrommer, C., & Enßlin, T. A. 2004, A&A, 413, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfrommer, C., Enßlin, T. A., & Springel, V. 2008, MNRAS, 385, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., & Pfrommer, C. 2010, MNRAS, 409, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Pinzke, A., Pfrommer, C., & Bergström, L. 2011, Phys. Rev. D, 84, 123509 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prokhorov, D. A., & Churazov, E. M. 2014, A&A, 567, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Razzaque, S. 2013, Phys. Rev. D, 88, 081302 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Riebe, K., Partl, A. M., Enke, H., et al. 2013, Astron. Nachr., 334, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Senno, N., Mészáros, P., Murase, K., Baerwald, P., & Rees, M. J. 2015, ApJ, in press [arXiv:1501.04934] [Google Scholar]
- Siegal-Gaskins, J. M., Reesman, R., Pavlidou, V., Profumo, S., & Walker, T. P. 2011, MNRAS, 415, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Sreekumar, P., Bertsch, D. L., Dingus, B. L., et al. 1998, ApJ, 494, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W. 2013, Phys. Rev. D, 88, 047301 [NASA ADS] [CrossRef] [Google Scholar]
- Stecker, F. W., & Venters, T. M. 2011, ApJ, 736, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Reimer, O. 2004, ApJ, 613, 956 [Google Scholar]
- Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Tamborra, I., Ando, S., & Murase, K. 2014, J. Cosmol. Astro-Part. Phys., 9, 43 [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2014, MNRAS, submitted [arXiv:1411.2783] [Google Scholar]
- Taylor, A. M., Gabici, S., & Aharonian, F. 2014, Phys. Rev. D, 89, 103003 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Vannoni, G., Aharonian, F. A., Gabici, S., Kelner, S. R., & Prosekin, A. 2011, A&A, 536, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., & Brüggen, M. 2014, MNRAS, 437, 2291 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Dallacasa, D., et al. 2008, A&A, 484, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VERITAS Collaboration. 2012, ApJ, 757, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2005, A&A, 434, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., Aharonian, F. A., & Breitschwerdt, D. 1996, Space Sci. Rev., 75, 279 [Google Scholar]
- Waxman, E. 2013, Proc. 9th Rencontres du Vietnam: Windows on the universe, Aug. 11−17, Quy Nhon, Binh Dinh, Vietnam [arXiv:1312.0558] [Google Scholar]
- Waxman, E., & Bahcall, J. 1997, Phys. Rev. Lett., 78, 2292 [CrossRef] [Google Scholar]
- Waxman, E., & Bahcall, J. 1999, Phys. Rev. D, 59, 023002 [Google Scholar]
- Wiener, J., Oh, S. P., & Guo, F. 2013, MNRAS, 434, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, W. 2013, Phys. Rev. D, 88, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, W. 2014, Phys. Rev. D, 90, 103003 [NASA ADS] [CrossRef] [Google Scholar]
- Zandanel, F., & Ando, S. 2014, MNRAS, 440, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Zandanel, F., Pfrommer, C., & Prada, F. 2014a, MNRAS, 438, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Zandanel, F., Pfrommer, C., & Prada, F. 2014b, MNRAS, 438, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Zatsepin, G. T., & Kuz’min, V. A. 1966, Sov. J. Exp. Theoret. Phys. Lett., 4, 78 [Google Scholar]
All Tables
Tested parameters and total gamma-ray and neutrino fluxes for the phenomenological luminosity-mass relation.
All Figures
 |
Fig. 1 Total number density of galaxy clusters for masses above M500, lim = 1013.8h-1 M⊙ as a function of redshift. We show the number density obtained assuming the WMAP (Komatsu et al. 2011), our standard choice if not otherwise specified, and the Planck (Planck Collaboration XVI 2014) cosmological data. At redshift z = 2, the number density is already negligible with respect to the lowest redshift. |
| In the text | |
 |
Fig. 2 Total gamma-ray and neutrino intensities (right) due to hadronic interactions in galaxy clusters, for 100% loud clusters, and the corresponding radio counts due to synchrotron emission from secondary electrons (left). From top to bottom, we plot the cases with B ≫ BCMB, B = 1μG and 0.5μG, respectively. For comparison, the Fermi (Fermi LAT Collaboration 2015a) and IceCube (Aartsen et al. 2014a) data are shown in the panels on the right. The neutrino intensity is meant for all flavours. All the plotted intensities respect NVSS radio counts and the gamma-ray upper limits on individual clusters. For B = 1μG and αp = 2.4, B = 0.5μG and αp = 2.2,2.4, and for αp = 1.5, the radio counts respecting the gamma-ray and neutrino limits, respectively, are below the y-scale range adopted for the panels on the left. |
| In the text | |
 |
Fig. 3 Same as Fig. 3, together with the case of 30% loud clusters for αp = 2. The remaining percentage of 70% quiet clusters has been assumed to have Lγ(100 MeV) one order of magnitude lower than for the loud clusters. The 100% loud case is shown with lighter colours (i.e., in grey and orange). |
| In the text | |
 |
Fig. 4 Radio counts due to synchrotron emission of secondary electrons as from the semi-analytical model of Zandanel et al. (2014b, ZPP in the plots) on the left, and total gamma-ray and neutrino intensities on the right. For comparison, we plot the Fermi (Fermi LAT Collaboration 2015a) and IceCube data (Aartsen et al. 2014a) in the panels on the right. The neutrino intensity is meant for all flavours. We show the cases of the model applied to a mass function for 20% and 40% loud clusters, and additionally for 10% loud clusters with parameters as in the Pinzke & Pfrommer (2010) model with a maximum CR proton acceleration efficiency of 15% (PP in the plots). According to this semi-analytical model, galaxy clusters contribute <1% to the diffuse gamma-ray and neutrino backgrounds. |
| In the text | |
 |
Fig. 5 Same as in the left panel of Fig. 4 for 20% loud clusters. The left panel shows the comparison with the previous model with one obtained adopting z2 = 0.6, and one with a lower mass integration limit, of 1013h-1M⊙. The right panel shows the comparison with the model in Fig. 4 and one obtained using the Planck cosmological data. |
| In the text | |
 |
Fig. 6 Gamma-ray angular power spectrum for emission resulting from proton-proton interactions in galaxy clusters in the energy range 1−10 GeV. We show the result for the semi-analytical model of Sect. 4 for 20% and 40% loud clusters. We plot the EGB anisotropy measured by Fermi (Fermi LAT Collaboration 2012) for comparison, which is explained by unresolved blazars, and the upper limits obtained once the blazar component is subtracted (Cuoco et al. 2012). We plot the square root of ℓ(ℓ + 1)Cℓ/ 2π, which implies that the shown quantity is directly proportional to an increase in intensity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


