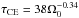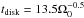| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526146 | |
| Published online | 13 May 2015 | |
The extreme ultraviolet and X-ray Sun in Time: High-energy evolutionary tracks of a solar-like star
1
Department of AstrophysicsUniversity of Vienna,
Türkenschanzstrasse 17,
1180
Vienna,
Austria
e-mail: lin.tu@univie.ac.at; colin.johnstone@univie.ac.at; manuel.guedel@univie.ac.at
2
Space Research Institute, Austrian Academy of
Sciences, Schmiedlstrasse
6, 8042
Graz,
Austria
e-mail:
helmut.lammer@oeaw.ac.at
Received: 20 March 2015
Accepted: 17 April 2015
Aims. We aim to describe the pre-main-sequence and main-sequence evolution of X-ray and extreme-ultaviolet radiation of a solar-mass star based on its rotational evolution starting with a realistic range of initial rotation rates.
Methods. We derive evolutionary tracks of X-ray radiation based on a rotational evolution model for solar-mass stars and the rotation-activity relation. We compare these tracks to X-ray luminosity distributions of stars in clusters with different ages.
Results. We find agreement between the evolutionary tracks derived from rotation and the X-ray luminosity distributions from observations. Depending on the initial rotation rate, a star might remain at the X-ray saturation level for very different time periods, from ≈10 Myr to ≈300 Myr for slow and fast rotators, respectively.
Conclusions. Rotational evolution with a spread of initial conditions leads to a particularly wide distribution of possible X-ray luminosities in the age range of 20–500 Myr, before rotational convergence and therefore X-ray luminosity convergence sets in. This age range is crucial for the evolution of young planetary atmospheres and may thus lead to very different planetary evolution histories.
Key words: Sun: evolution / stars: rotation / stars: activity / stars: solar-type / planets and satellites: atmospheres
© ESO, 2015
1. Introduction
High-energy radiation from solar-like main-sequence (MS) stars decays over time as a result of stellar spin-down. The early Sun’s X-ray (≈1−100 Å) and extreme-ultraviolet (EUV; ≈100−900 Å) emissions could thus have exceeded the present-day Sun’s level by orders of magnitude (Ribas et al. 2005). By driving atmospheric erosion, such extreme radiation levels were critically important for both the primordial hydrogen atmospheres (e.g. Lammer et al. 2014) and the secondary nitrogen atmospheres (Lichtenegger et al. 2010) of solar system planets. As a consequence of higher solar activity levels, stronger winds would have added to atmospheric mass loss through non-thermal processes such as ion pick-up (Kislyakova et al. 2013, 2014).
Magnetic activity is strongly linked to rotation via a stellar dynamo such that the total X-ray luminosity decays with increasing rotation period, P, as LX ∝ P-3 to ∝P-2; for small P, LX saturates at LX ≈ 10-3Lbol (Lbol being the stellar bolometric luminosity; see Wright et al. 2011, hereafter W11). Since older (>1 Gyr) stars spin down in time approximately as P ∝ t0.5 (Skumanich 1972), LX decays as LX ∝ t-1.5 (Güdel et al. 1997). This evolutionary trend has commonly been formulated using regression fits to LX of stars with known ages, typically starting at the saturation level close to the zero age main sequence (ZAMS; see e.g. Güdel et al. 1997; Ribas et al. 2005).
However, stars in young stellar clusters have a wide range of rotation rates, Ω, in particular at ages younger than 500 Myr before they converge to a unique mass-dependent value (Soderblom et al. 1993). As a consequence, LX values also scatter over a wide range among such stars (e.g. Stauffer et al. 1994), and the age at which stars fall out of saturation depends on the star’s initial Ω. Given the importance of high-energy radiation in this age range for planetary atmosphere evolution, a unique description with a single radiation decay law is problematic and needs to be replaced by a description of the LX distribution and its long-term evolution (Penz et al. 2008; Johnstone et al. 2015), spanning a wide range of possible evolutionary tracks for stars with different initial Ω.
In this Letter we use a rotational evolution model to predict such luminosity distributions as a function of age, based on a range of initial Ω, and we show that these predictions agree with the observed time-dependent scatter of LX. We derive a radiative evolution model based on the full range of rotation histories for a solar-mass star, and thus find a description of the possible past histories of our own Sun, which is useful to model the corresponding evolution of solar-system planetary atmospheres. This Letter is an extension of Johnstone et al. (2015), who similarly estimated evolutionary tracks for wind properties. In this Letter, we concentrate mostly on 1 M⊙ stars, and will extend this to other stellar masses in future work.
 |
Fig. 1 Comparisons between observed and predicted distributions of LX at ages of 150 Myr (left) and 620 Myr (right). The grey symbols show predicted distributions calculated using Eq. (1) and the distributions of rotation rates derived by Johnstone et al. (2015). The red circles and green triangles show detections and upper limits for stars in the Pleiades (left) and Hyades (right). The horizontal blue lines show detection thresholds. The upper line of stars in the theoretical distributions is caused by the stars whose rotation rates lie above the mass dependent saturation threshold. |
2. Rotation and radiation models
As in previous studies (e.g. Gallet & Bouvier 2013), we constrain our rotation models by assuming that the percentiles of the rotational distributions for star clusters with different ages can be combined to estimate the time evolution of a star’s rotation rate. We consider only stars in the mass range 0.9 M⊙ to 1.1 M⊙. Johnstone et al. (2015) collected measured rotation periods of over 2000 stars in clusters of ages 150, 550, and 1000 Myr on the MS, giving observational constraints on the percentiles at these ages (with 230, 134, and 36 stars, respectively at the considered ages). We use additional constraints for pre-main-sequence (PMS) rotation from the ≈2 Myr cluster NGC 6530 (28 stars; Henderson & Stassun 2012) and the ≈12 Myr cluster h Per (117 stars; Moraux et al. 2013). For NGC 6530, the 10th, 50th, and 90th percentiles are at 2.7Ω⊙, 6.2Ω⊙, and 35.1Ω⊙, respectively (assuming Ω⊙ = 2.9 × 10-6 rad s-1), and for h Per, they are at 3.4Ω⊙, 8.4Ω⊙, and 76.0Ω⊙, respectively.
We use an extension of the rotational evolution model of Johnstone et al. (2015). For the wind torque, we use the formula derived by Matt et al. (2012) which relates the wind torque to stellar parameters, the star’s dipole field strength, Bdip, and the wind mass loss rate, Ṁ⋆. We assume that both Bdip and Ṁ⋆ saturate at a Rossby number of Ro = 0.13, as suggested by the saturation of X-ray emission (W11), where Ro = Prot/τ⋆ and τ⋆ is the convective turnover time. For Ṁ⋆, we use the scaling law derived by Johnstone et al. (2015), which is derived by fitting the rotational evolution model to observational constraints. We modify the scaling law by relating Ṁ⋆ to Ro; this allows us to take into account the change in τ⋆ on the PMS. Since we only consider solar-mass stars, the scaling relation derived by Johnstone et al. (2015) can be rewritten as 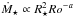 . We find a = 2 provides a good fit to the observational constraints (which is larger than the value of a = 1.33 found by Johnstone et al. 2015). For Bdip, we use the scaling law derived by Vidotto et al. (2014) of Bdip ∝ Ro-1.32.
. We find a = 2 provides a good fit to the observational constraints (which is larger than the value of a = 1.33 found by Johnstone et al. 2015). For Bdip, we use the scaling law derived by Vidotto et al. (2014) of Bdip ∝ Ro-1.32.
To reproduce the spin-up on the PMS due to the decrease in the stellar moment of inertia, previous studies have found that core-envelope decoupling must be included (Krishnamurthi et al. 1997). We use the core-envelope decoupling model described by Gallet & Bouvier (2015) and adopt coupling timescales of 30 Myr, 20 Myr, and 10 Myr for the 10th, 50th and 90th percentile tracks, respectively, which we find give us good agreement between the rotational evolution model and the observations. Finally, we assume that during the first few million years, the stellar rotation rates do not evolve with time due to “disk-locking”, i.e. magnetic interactions with the circumstellar disk. We assume disk-locking timescales of 10 Myr, 5 Myr, and 2 Myr for the 10th, 50th, and 90th percentile tracks, respectively.
To predict LX along the rotation tracks, we use the relation derived from MS stars by W11, 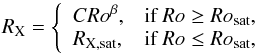 (1)where Rosat = 0.13 is the saturation Rossby number, RX = LX/Lbol, and RX,sat = 10-3.13 is the saturation RX value. We use β = −2.7 (W11). We assume that this relation can be used on the PMS if the evolution of Lbol and τ⋆ are treated correctly. Sanz-Forcada et al. (2011) derived a power law to convert LX (5−100 Å) into EUV luminosity, LEUV (100−920 Å), of log LEUV = 4.8 + 0.86log LX, where LX and LEUV are in erg s-1.
(1)where Rosat = 0.13 is the saturation Rossby number, RX = LX/Lbol, and RX,sat = 10-3.13 is the saturation RX value. We use β = −2.7 (W11). We assume that this relation can be used on the PMS if the evolution of Lbol and τ⋆ are treated correctly. Sanz-Forcada et al. (2011) derived a power law to convert LX (5−100 Å) into EUV luminosity, LEUV (100−920 Å), of log LEUV = 4.8 + 0.86log LX, where LX and LEUV are in erg s-1.
To calculate the evolution of the stellar radius, Lbol, the moment of inertia, and τ⋆, we use the stellar evolution models of Spada et al. (2013). However, their τ⋆ values are approximately a factor of two above those of W11 for 1 M⊙ stars; we therefore normalise τ⋆ at all ages such that the MS value is consistent with Eq. (1).
 |
Fig. 2 Left: predicted rotational evolution tracks for stars at the 10th (red), 50th (green), and 90th (blue) percentiles of the rotational distribution. The solid and dotted lines show the envelope and core rotational evolution, respectively, and the horizontal solid lines show the observational constraints on the percentiles. The dashed black line shows the time dependent saturation threshold for Ṁ, Bdip, and LX calculated assuming a constant saturation Ro and the τ⋆ values of Spada et al. (2013). Right: predicted LX along each of our rotation tracks and comparisons to observed LX values of single stars in several clusters with upper limits shown by ▽ symbols. The solid horizontal lines show the 10th, 50th, and 90th percentiles of the observed distributions of LX at each age calculated by counting upper limits as detections. The two solar symbols at 4.5 Gyr show the range of LX for the Sun over the course of the solar cycle. The scale on the right y-axis shows the associated LEUV. |
3. X-ray observations
To test our predictions for X-ray distributions at each age, we collect LX values of single stars from ROSAT, XMM-Newton, and Chandra of open clusters with ages from 30 Myr to 620 Myr. The clusters are NGC 2547 (30 Myr; Jeffries et al. 2006), α Persei (50 Myr; Prosser et al. 1998), NGC 2451 (50 Myr; Hünsch et al. 2003), Blanco I (50 Myr; Pillitteri et al. 2003), Pleiades (100 Myr; Micela et al. 1999; Stauffer et al. 1994), NGC 2516 (110 Myr; Pillitteri et al. 2006; Jeffries et al. 1997), NGC 6475 (300 Myr; Prosser et al. 1995), and Hyades (620 Myr; Stern et al. 1995). For NGC 6475, since no optical catalogue was available, Prosser et al. (1995) did not report upper limits for the non-detected stars and therefore the percentiles for the distribution of LX should be considered upper limits. For all MS clusters, except Blanco I where masses were given, we derive masses by converting from (B − V)0 using a relation derived from the An et al. (2007) stellar evolution models. For the PMS cluster NGC 2547, we calculated masses using the Siess et al. (2000) models. Since we use these X-ray observations only to compare them to (or: only for comparison with) our predictions from rotation, we do not attempt to homogenise the M⋆ and LX determinations for each cluster. Our quantitative determinations of the LX tracks are based on the relation from W11 where this homogenisation was done.
4. Results
Johnstone et al. (2015) combined rotation period measurements of four young clusters with ages of ~150 Myr and used a rotational evolution model to predict the evolution of the resulting distribution of Ω on the MS. The sample contains 1556 stars in the 0.4−1.1 M⊙ mass range. In Fig. 1, we show predictions for the distributions of LX based on these Ω distributions at ages of 150 Myr and 620 Myr comparing them with observed values in the Pleiades and Hyades. There is good overall agreement, although intrinsic X-ray variability (typically factors of 2−3) introduces some additional scatter such as is visible for stars exceeding the saturation threshold.
To predict the range of possible LX evolution tracks, we calculate rotation models for solar-mass stars at the 10th, 50th, and 90th percentiles of the Ω distributions, shown in Fig. 2a. Our models fit well the observational constraints on the percentiles, except for a slight underestimation of the 10th percentile track in the first 20 Myr. This might cause us to underestimate the age by a few Myr when stars on the 10th percentile track come out of saturation. Figure 2b shows predicted tracks for LX and LEUV together with observed LX for stars in the 0.9−1.1 M⊙ range for each cluster listed in Sect. 3. Because of the low number of observations in NGC 2547 (30 Myr), we extend the mass range to 0.8−1.2 M⊙. The tracks correspond very well to the observed percentiles in the individual clusters given the somewhat limited observational samples. The solar LX (6 × 1026−5 × 1027 erg s-1, Ayres 1997; Peres et al. 2000; Judge et al. 2003) has been included as well and fits our models excellently.
Stars on our rotation tracks drop out of saturation at ≈6 Myr (10th percentile, red), ≈20 Myr (50th, green), and ≈300 Myr (90th, blue), i.e. either as young PMS stars, as near-ZAMS stars, or as slightly evolved MS stars. The spread in LX amounts to as much as 1.5 orders of magnitude for several 100 Myr.
Figure 3 gives the age when a star falls out of saturation, tsat, as a function of initial Ω, derived from our rotation model. This saturation time can be approximated by 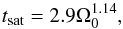 (2)where tsat is in Myr and Ω0 is the rotation rate at 1 Myr in units of the solar rotation rate. Assuming that the saturation level, LX,sat ≈ 10-3.13 Lbol, ⊙, is constant in time, which is approximately true, we obtain log LX,sat = 30.46. If we approximate LX by a power law after tsat (see Fig. 2b), for a given Ω0 we obtain
(2)where tsat is in Myr and Ω0 is the rotation rate at 1 Myr in units of the solar rotation rate. Assuming that the saturation level, LX,sat ≈ 10-3.13 Lbol, ⊙, is constant in time, which is approximately true, we obtain log LX,sat = 30.46. If we approximate LX by a power law after tsat (see Fig. 2b), for a given Ω0 we obtain ![\begin{equation} L_{\rm X} = \left\{ \begin{array}{l l} L_{\rm X, sat}, & \quad \text{if}\ t\le t_{\rm sat},\\[0.2cm] a t^b, & \quad \text{if}\ t \ge t_{\rm sat}.\\ \end{array} \right. \end{equation}](/articles/aa/full_html/2015/05/aa26146-15/aa26146-15-eq54.png) (3)We require that the power law also fits the Sun with LX, ⊙ = 1027.2 erg s-1 at an age of t⊙ = 4570 Myr. We thus find
(3)We require that the power law also fits the Sun with LX, ⊙ = 1027.2 erg s-1 at an age of t⊙ = 4570 Myr. We thus find 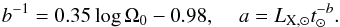 (4)For the 10th, 50th, and 90th percentiles in Ω0, corresponding to Ω0 ≈ 1.8Ω⊙, 6.2Ω⊙, and 45.6 Ω⊙ with tsat ≈ 5.7 Myr, 23 Myr, and 226 Myr, respectively, we find
(4)For the 10th, 50th, and 90th percentiles in Ω0, corresponding to Ω0 ≈ 1.8Ω⊙, 6.2Ω⊙, and 45.6 Ω⊙ with tsat ≈ 5.7 Myr, 23 Myr, and 226 Myr, respectively, we find ![\begin{equation} L_{\rm X} = \left\{ \begin{array}{l} 2.0\times 10^{31} t^{-1.12} \\[0.15cm] 2.6\times 10^{32} t^{-1.42} \\[0.15cm] 2.3\times 10^{36} t^{-2.50} \\[0.15cm] \end{array} \right. L_{\rm EUV} = \left\{ \begin{array}{l l} 7.4\times 10^{31} t^{-0.96} & \quad \text{10th}\\[0.15cm] 4.8\times 10^{32} t^{-1.22} & \quad \text{50th}\\[0.15cm] 1.2\times 10^{36} t^{-2.15} & \quad \text{90th}\\[0.15cm] \end{array} \right. \nonumber \end{equation}](/articles/aa/full_html/2015/05/aa26146-15/aa26146-15-eq61.png) where the luminosities are in erg s-1. The slope of the median LX track, b = −1.42, is very close to the values reported from linear regression to the Sun in Time sample (Güdel et al. 1997; Ribas et al. 2005). These power-law fits, valid for t>tsat, thus describe the range of possible evolutionary tracks for LX and LEUV.
where the luminosities are in erg s-1. The slope of the median LX track, b = −1.42, is very close to the values reported from linear regression to the Sun in Time sample (Güdel et al. 1997; Ribas et al. 2005). These power-law fits, valid for t>tsat, thus describe the range of possible evolutionary tracks for LX and LEUV.
 |
Fig. 3 Saturation time as a function of initial rotation rate Ω0. To calculate each rotation track, we fit power laws to the core-envelope coupling timescale and disk-locking timescales for our 10th, 50th, and 90th percentile models of |
5. Discussion
The large differences in the evolutionary tracks, and therefore LX and LEUV values, make it necessary to reconsider critically the atmospheric erosion of planets by high-energy radiation. To a first approximation, the thermal mass loss rate from a simple hydrogen dominated planetary atmosphere, Ṁpl, can be estimated using the energy limited approach (Watson et al. 1981; Lammer et al. 2009), where Ṁpl is proportional to the incident stellar EUV flux for a given set of planetary parameters. We therefore assume that Ṁpl ∝ FEUV, where FEUV is the EUV flux at the planetary orbit. As an example, we consider the case of a 0.5 MEarth planet at 1 AU around a 1 M⊙ star with an initial hydrogen atmosphere of 5 × 10-3MEarth. For this case, Lammer et al. (2014) calculated Ṁpl from the atmosphere of 3.5 × 1032mH s-1 with FEUV = 100 erg s-1 cm-2, where mH is the mass of a hydrogen atom (see the fifth case in their Table 4). We therefore assume that Ṁpl = 5.9 × 106FEUV, where FEUV is in erg s-1 cm-2 and Ṁ is in g s-1.
We show in Fig. 4 the evolution of the planetary atmospheric mass between 10 Myr and 5 Gyr assuming that the central star follows the LEUV tracks shown in Fig. 2. In all three cases the planet at 10 Myr has identical atmospheric masses; however, by 5 Gyr the atmospheric hydrogen contents are very different. Orbiting the slowly rotating star, the planet retains 45% of its initial atmosphere; orbiting the rapidly rotating star, the planet loses its entire atmosphere within 100 Myr; orbiting the 50th percentile rotator, the planet also loses its atmosphere, but this instead takes almost a Gyr. Although this is a simple calculation of a single example atmosphere, it is sufficient to show that the star’s initial rotation rate – and the subsequent rotational evolution – is an important aspect that needs to be properly considered when studying the evolution of the atmospheres of terrestrial planets.
 |
Fig. 4 Evolution of the planetary atmospheric mass of a 0.5 MEarth planet orbiting a 1 M⊙ star at 1 AU with an initial mass of 5 × 10-3MEarth. The tracks correspond to planets orbiting stars that are in the 10th (red), 50th (green), and 90th (blue) percentiles of the rotational distributions. The vertical lines show the stellar saturation times. |
Acknowledgments
The authors thank the referee, Nicholas Wright, for valuable comments. L.T. was supported by an “Emerging Fields” grant of the University of Vienna through the Faculty of Earth Sciences, Geography and Astronomy. C.P.J., M.G., and H.L. acknowledge the support of the FWF NFN project S11601-N16 “Pathways to Habitability: From Disks to Active Stars, Planets and Life”, and the related FWF NFN subprojects S11604-N16 “Radiation & Wind Evolution from T Tauri Phase to ZAMS and Beyond” and S11607-N16 “Particle/Radiative Interactions with Upper Atmospheres of Planetary Bodies Under Extreme Stellar Conditions”. This publication is supported by the Austrian Science Fund (FWF).
References
- An, D., Terndrup, D. M., & Pinsonneault, M. H. 2007, ApJ, 671, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R. 1997, J. Geophys. Res., 102, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Guinan, E. F., & Skinner, S. L. 1997, ApJ, 483, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, C. B., & Stassun, K. G. 2012, ApJ, 747, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Hünsch, M., Weidner, C., & Schmitt, J. H. M. M. 2003, A&A, 402, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffries, R. D., Thurston, M. R., & Pye, J. P. 1997, MNRAS, 287, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Evans, P. A., Pye, J. P., & Briggs, K. R. 2006, MNRAS, 367, 781 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johnstone, C. P., Güdel, M., Brott, I., & Lüftinger, T. 2015, A&A, 577, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Judge, P. G., Solomon, S. C., & Ayres, T. R. 2003, ApJ, 593, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K., Lammer, H., Holmström, M., et al. 2013, Astrobiology, 13, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Kislyakova, K. G., Johnstone, C. P., Odert, P., et al. 2014, A&A, 562, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Odert, P., Leitzinger, M., et al. 2009, A&A, 506, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lammer, H., Stökl, A., Erkaev, N. V., et al. 2014, MNRAS, 439, 3225 [NASA ADS] [CrossRef] [Google Scholar]
- Lichtenegger, H., Lammer, H., Grießmeier, J., et al. 2010, Icarus, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012, ApJ, 754, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Micela, G., Sciortino, S., Harnden, Jr., F. R., et al. 1999, A&A, 341, 751 [NASA ADS] [Google Scholar]
- Moraux, E., Artemenko, S., Bouvier, J., et al. 2013, A&A, 560, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penz, T., Micela, G., & Lammer, H. 2008, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peres, G., Orlando, S., Reale, F., Rosner, R., & Hudson, H. 2000, ApJ, 528, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Pillitteri, I., Micela, G., Sciortino, S., & Favata, F. 2003, A&A, 399, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillitteri, I., Micela, G., Damiani, F., & Sciortino, S. 2006, A&A, 450, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prosser, C. F., Stauffer, J. R., Caillault, J.-P., et al. 1995, AJ, 110, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Prosser, C. P., Randich, S., & Simon, T. 1998, Astron. Nachr., 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Guinan, E. F., Güdel, M., & Audard, M. 2005, ApJ, 622, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D., Stauffer, J., MacGregor, K., & Jones, B. 1993, ApJ, 409, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., Demarque, P., Kim, Y.-C., & Sills, A. 2013, ApJ, 776, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Caillault, J.-P., Gagne, M., Prosser, C. F., & Hartmann, L. W. 1994, ApJS, 91, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, R. A., Schmitt, J. H. M. M., & Kahabka, P. T. 1995, ApJ, 448, 683 [Google Scholar]
- Vidotto, A. A., Gregory, S. G., Jardine, M., et al. 2014, MNRAS, 441, 2361 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N., Drake, J., Mamajek, E., & Henry, G. 2011, ApJ, 743, 48 (W11) [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Comparisons between observed and predicted distributions of LX at ages of 150 Myr (left) and 620 Myr (right). The grey symbols show predicted distributions calculated using Eq. (1) and the distributions of rotation rates derived by Johnstone et al. (2015). The red circles and green triangles show detections and upper limits for stars in the Pleiades (left) and Hyades (right). The horizontal blue lines show detection thresholds. The upper line of stars in the theoretical distributions is caused by the stars whose rotation rates lie above the mass dependent saturation threshold. |
| In the text | |
 |
Fig. 2 Left: predicted rotational evolution tracks for stars at the 10th (red), 50th (green), and 90th (blue) percentiles of the rotational distribution. The solid and dotted lines show the envelope and core rotational evolution, respectively, and the horizontal solid lines show the observational constraints on the percentiles. The dashed black line shows the time dependent saturation threshold for Ṁ, Bdip, and LX calculated assuming a constant saturation Ro and the τ⋆ values of Spada et al. (2013). Right: predicted LX along each of our rotation tracks and comparisons to observed LX values of single stars in several clusters with upper limits shown by ▽ symbols. The solid horizontal lines show the 10th, 50th, and 90th percentiles of the observed distributions of LX at each age calculated by counting upper limits as detections. The two solar symbols at 4.5 Gyr show the range of LX for the Sun over the course of the solar cycle. The scale on the right y-axis shows the associated LEUV. |
| In the text | |
 |
Fig. 3 Saturation time as a function of initial rotation rate Ω0. To calculate each rotation track, we fit power laws to the core-envelope coupling timescale and disk-locking timescales for our 10th, 50th, and 90th percentile models of |
| In the text | |
 |
Fig. 4 Evolution of the planetary atmospheric mass of a 0.5 MEarth planet orbiting a 1 M⊙ star at 1 AU with an initial mass of 5 × 10-3MEarth. The tracks correspond to planets orbiting stars that are in the 10th (red), 50th (green), and 90th (blue) percentiles of the rotational distributions. The vertical lines show the stellar saturation times. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.