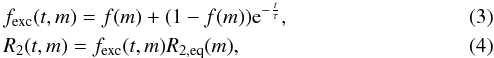| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201323018 | |
| Published online | 20 May 2015 | |
White dwarf masses in cataclysmic variables
1
Instituto de Física y Astronomía, Facultad de Ciencias, Universidad de
Valparaíso,
Valparaíso,
Chile
2
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
e-mail:
thomas.wijnen@astro.ru.nl
3
ICM nucleus on protoplanetary disks, Universidad de
Valparaíso, Av. Gran Bretaña
1111, Valparaíso,
Chile
Received: 8 November 2013
Accepted: 8 March 2015
Context. The white dwarf (WD) mass distribution of cataclysmic variables (CVs) has recently been found to dramatically disagree with the predictions of the standard CV formation model. The high mean WD mass among CVs is not imprinted in the currently observed sample of CV progenitors and cannot be attributed to selection effects. Two possibilities have been put forward to solve this issue: either the WD grows in mass during CV evolution, or in a significant fraction of cases, CV formation is preceded by a (short) phase of thermal time-scale mass transfer (TTMT) in which the WD gains a sufficient amount of mass.
Aims. Here we investigate if and under which conditions a phase of TTMT before CV formation or mass growth in CVs can bring theoretical predictions and observations into agreement.
Methods. We employed binary population synthesis models using the binary_c/nucsyn code to simulate the present intrinsic CV population. To that end we incorporated aspects specific to CV evolution such as an appropriate mass-radius relation of the donor star and a more detailed prescription for the critical mass ratio for dynamically unstable mass transfer. We have also implemented a previously suggested wind from the surface of the WD during TTMT and tested the idea of WD mass growth during the CV phase by arbitrarily changing the accretion efficiency. We compare the model predictions of the TTMT and the mass growth model with the characteristics of CVs derived from observed samples.
Results. We find that mass growth of the WDs in CVs fails to reproduce the observed WD mass distribution. In the case of TTMT, we are able to produce a large number of massive WDs if we assume significant mass loss from the surface of the WD during the TTMT phase. However, the model still produces too many CVs with helium WDs. Moreover, the donor stars are evolved in many of these post-TTMT CVs, which contradicts the observations.
Conclusions. We conclude that in our current framework of CV evolution neither TTMT nor WD mass growth can fully explain either the observed WD mass or the period distribution in CVs.
Key words: accretion, accretion disks / instabilities / novae, cataclysmic variables / binaries: close
© ESO, 2015
1. Introduction
The class of compact binary stars comprises a great diversity of stellar objects and phenomena in the galactic zoo. They are very important probes of our comprehension of stellar evolution in general and mass transfer in particular. Cataclysmic variables (CVs) are compact binaries consisting of a white dwarf (WD) and a low-mass main sequence (MS) star that transfers mass to the WD by Roche-lobe overflow. CVs have been investigated for several decades, but their formation and evolution is still not fully understood. It is generally accepted that CVs result from wide binaries evolving into a common envelope (CE) structure, from which the core of the giant, that is, the primary, remains as a WD and in which the separation decreases significantly by means of drag forces within the envelope (Paczyński 1976). After the envelope is expelled, the orbit of the detached post-common-envelope binary (PCEB) is further reduced through the loss of orbital angular momentum by gravitational radiation (GR) and magnetic breaking (MB). When the orbit is sufficiently close, the accompanying MS star fills its Roche lobe, and if the resulting mass transfer is stable, a CV is born.
According to this CV formation scenario, WDs in the newly formed CVs should have a mass distribution that is similar to the mass distribution of single WDs, if not shifted towards lower masses by an early expulsion of the envelope, which prematurely terminates the mass growth of the giant’s core. This naive expectation of on average low WD masses has been confirmed by binary population models of CVs, Politano (1996) for instance predicted a mean WD mass of 0.49 M⊙ for the primaries of CVs. However, measurements of WD masses in CVs have been in the range of [0.8−1.2] M⊙ (e.g., Warner 1973, 1976; Ritter 1976; Robinson 1976), which is significantly higher than predicted. This discrepancy between the observed and expected mean WD mass in CVs has been successfully interpreted as a selection effect by Ritter & Burkert (1986). Simply speaking, the idea is that the higher the WD mass, the more energy is released per accreted unit mass and the more extended is the accretion disk around the WD. Thus, CVs with massive WDs are (on average) significantly brighter and much easier to be discovered. However, Zorotovic et al. (2011) recently showed that this previous explanation does no longer hold. They showed that the observed WD mass distribution of faint CVs (dominated by the emission from the WD instead of by that from the accretion disk) should be biased towards low-mass WDs, while, as shown by Littlefair et al. (2008) and Savoury et al. (2011), the measured mean WD mass for these systems still remains at ~0.8 M⊙.
Thus the standard model of CV evolution might miss an important ingredient. Zorotovic et al. (2011) suggested two possibilities. First, WDs in CVs may gain mass through accretion of transferred matter over a nova cycle if less mass is expelled during the eruptions than is accreted between them. This contradicts standard theories for nova outbursts (Prialnik 1986; Prialnik & Kovetz 1995; Yaron et al. 2005). WD masses can only grow in CVs if no mixing of core matter with accreted matter is assumed (Williams 2013; Starrfield 2015), which is unrealistic. However, given the large discrepancy between the observed and predicted WD mass distributions, we need to investigate all possible scenarios. Therefore, we here present binary population models that include different mass accretion efficiencies in CVs.
The second possible explanation put forward by Zorotovic et al. (2011) is that a large number of CVs descend from binaries with initially more massive secondary stars. This implies a preliminary phase of thermal time-scale mass transfer (TTMT) in which the mass of the WD grows through stable hydrogen burning on its surface (Schenker et al. 2002). At that stage, the system might be observed as a super-soft X-ray source (Kahabka & van den Heuvel 1997). A small sample of UV observations has shown that 10−15% of CVs accrete CNO processed material, indicating that the companion has been stripped of its external layers by a previous phase of TTMT (Schenker & King 2002; Gänsicke et al. 2003). These companions therefore appear to be more evolved than a single MS star of the same mass. While binary population models of new-born CVs with evolved donor stars have been applied in the past (e.g. de Kool 1992; Baraffe & Kolb 2000; Podsiadlowski et al. 2003; Kolb & Willems 2005), a systematic study of the impact of TTMT on the WD mass distribution of CVs is missing. Here we fill this gap by using updated binary population models and investigate whether a large number of CVs descending from a phase of TTMT might explain the large masses of CV primaries.
2. Code
We simulated the evolution of a large number of binaries and selected those systems that evolve into a CV within the age of the Galaxy. Then we quantitatively investigated their characteristics and the evolutionary channel by which they have formed. We used the population nucleosynthesis code binary_c/nucsyn of Izzard et al. (2004, 2006, 2009) based on the binary star evolution code of Hurley et al. (2002).
To simulate CVs, some specific aspects of their evolution have to be taken into account. In particular, the implementation and treatment of the stability of mass transfer, the mass-radius relation of the donor star, and the fate of the transferred matter have to be considered carefully. We address these issues in detail below.
2.1. Mass transfer
 |
Fig. 1 Different regimes of stability against mass transfer for MS donor stars, depending on the mass ratio and the mass of the donor. The hatched region corresponds to the critical mass ratios for which, according to Politano (1996), the mass transfer becomes dynamically unstable as a function of the donor’s mass. The dotted line indicates the shape of this regions if one uses the condition that is originally in the code (see text). The solid curve represents the critical mass ratio for zero-age MS stars of solar composition above which mass transfer occurs on the thermal time-scale. This mass ratio is derived from the thermal mass-radius exponent by using the zero-age MS mass-radius relation implemented in the code (Tout et al. 1996) and assuming that mass transfer is conservative. |
The stability of mass transfer is determined by the change of the radius with respect to the Roche lobe. If the adiabatic response of the donor is unable to retain the star within its Roche lobe, mass transfer will occur in a dynamically unstable way and will probably lead to a CE. However, if the star is able to restore hydrostatic equilibrium, mass transfer is determined by the thermal readjustments of the star. If the new thermal equilibrium radius exceeds the Roche lobe radius, mass transfer is driven by readjustments of the star on the thermal time-scale. Otherwise, the binary is stable against mass transfer and mass transfer is driven by angular momentum loss or nuclear evolution.
The adiabatic mass-radius exponent for low-mass MS donors is very sensitive to the depth of their convective envelope. For low-mass MS stars (≲0.7 M⊙) the envelope is deeply convective and the donor star is no longer able to restore hydrostatic equilibrium in response to mass loss, except for very low mass ratios. Therefore, the adiabatic mass-radius exponent and corresponding critical mass ratio decrease steeply around 0.7 M⊙. Figure 1 shows an analytic fit from Politano (1996) to the critical mass ratio for dynamically unstable mass transfer (hatched region): 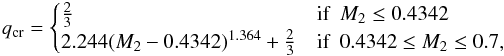 (1)where M2 represents the mass of the donor star in solar masses and the mass ratio is defined as
(1)where M2 represents the mass of the donor star in solar masses and the mass ratio is defined as 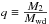 . This fit is based on the adiabatic mass-radius exponent as determined by detailed model calculations of Hjellming (1989) and is valid for conservative mass transfer. We used this more accurate prescription instead of the standard prescription in binary_c/nucsyn, that is, a constant qcr of 0.695 for M2 ≲ 0.7 M⊙ (which is also shown in Fig. 1 for comparison). For masses above 0.7 M⊙, mass transfer is assumed to be dynamically stable if q< 1.6 in our simulations (de Mink et al. 2007). This line is not shown in Fig. 1.
. This fit is based on the adiabatic mass-radius exponent as determined by detailed model calculations of Hjellming (1989) and is valid for conservative mass transfer. We used this more accurate prescription instead of the standard prescription in binary_c/nucsyn, that is, a constant qcr of 0.695 for M2 ≲ 0.7 M⊙ (which is also shown in Fig. 1 for comparison). For masses above 0.7 M⊙, mass transfer is assumed to be dynamically stable if q< 1.6 in our simulations (de Mink et al. 2007). This line is not shown in Fig. 1.
Since binary_c/nucsyn does not follow the thermal mass-radius exponent of the donor (Hurley et al. 2002, Sect. 2.6.3) and mass transfer might not be conservative during TTMT, we used the mass-transfer rate to distinguish between the CV phase and a phase of TTMT. We identify a binary as a system with TTMT if the primary is a WD, consisting of either helium (He), carbon-oxygen (C/O), or oxygen-neon (O/Ne), the donor is a MS star and the mass-transfer rate is higher than the limit for stable hydrogen burning, as described in Meng et al. (2009). Furthermore, the mass of the WD has to increase by at least 0.01 M⊙ during the TTMT phase, otherwise we do not define the emerging CV as a post TTMT system. Likewise, if the mass-transfer rate is below the limit for stable hydrogen burning, the primary is a WD, and the donor is a MS star, we identify the system as a CV. This definition of CVs may include some long orbital period systems with massive secondaries (≳0.7 M⊙) and lower mass WDs that just started thermally unstable mass transfer but did not yet reach the limit for stable hydrogen burning. We count these systems as CVs keeping in mind that they are apparently different from typically observed CVs.
2.2. Mass-radius relation for CV donors
Mass transfer can force the donor star out of thermal equilibrium when the time-scale of mass transfer is shorter than the thermal time-scale of the donor. In the case of low-mass donors, the mass transfer is driven by the loss of angular momentum due to MB and/or GR. We subtracted the angular momentum loss due to MB directly from the orbit, assuming the orbit and spin are coupled. We used the prescription of Hurley et al. (2002) for MB. MB is assumed to be active until the donor star becomes fully convective (Rappaport et al. 1983). For single zero-age MS (ZAMS) stars and in detached binaries, this occurs when the mass is ~0.35 M⊙ and MB is probably reduced significantly in an abrupt manner (Schreiber et al. 2010). This disrupted MB scenario can explain the observed gap between ~2 and 3 h in the orbital period distribution of CVs (e.g. Spruit & Ritter 1983). In semi-detached binaries that contain a secondary with a radiative core, the strong angular momentum loss and the resulting high mass transfer rates due to MB drive the MS donor out of thermal equilibrium, which causes the radius of the donor star to exceed its thermal equilibrium radius. As a result of this bloating and readjustments of the donor on relatively long thermal time-scales, the stellar structure of the donor corresponds to the stellar structure of a more massive single star on the MS (Howell et al. 2001; Knigge 2006). In other words, the mass of the donor is lower than that of a MS star with the same radius and stellar structure. Therefore the mass-transferring donor in a CV becomes fully convective at a lower mass than its MS counterparts in detached binaries or single stars. As a result, the dynamo mechanism responsible for MB remains active for donor masses ≳[ 0.2−0.26 ] M⊙ (McDermott & Taam 1989; Howell et al. 2001; Patterson et al. 2005). When MB becomes inefficient at an orbital period of ~3 h, the donor has time to relax its radius to its equilibrium value, which is lower than the value of the Roche-lobe radius. The binary, having become a detached system, evolves towards shorter orbital periods driven by GR alone. At an orbital period of ~2 h, mass transfer starts again, but at a much lower rate. In other words, the standard scenario for CV evolution explains the deficit of CVs in the period gap by predicting that CVs pass the gap as detached systems.
Because of this standard theory of CV evolution, the mass-radius relation of the donor star is of crucial importance for properly simulating the standard model of CV evolution, as the disrupted MB scenario only works if secondaries above the gap have a larger radius than their MS radius. Not assuming an increased radius above the gap would not allow simulating the orbital period gap seen in the observed distribution of CVs. Consequently, we would not be able to separate systems below and above the gap, which, as we show below, might be imperative for understanding the WD mass distribution in CVs. To account for the larger radius when the donor is out of thermal equilibrium, we implemented the mass-radius relation for low-mass MS donors in CVs, as deduced by Knigge et al. (2011). To establish a smooth transition between the equilibrium radius (R2,eq) given by binary_c/nucsyn and the increased radius for CV donor stars (R2,CV), we define the factor by which the radius is increased with respect to its thermal equilibrium value, as a function of the current mass of the donor star m, 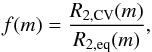 (2)and let the radius grow exponentially with time towards the fully inflated value (i.e. R2,CV) given by Knigge et al. (2011). The equilibrium radius excess (fexc) and current radius (R2) as a function of time and mass are thus given by
(2)and let the radius grow exponentially with time towards the fully inflated value (i.e. R2,CV) given by Knigge et al. (2011). The equilibrium radius excess (fexc) and current radius (R2) as a function of time and mass are thus given by
where t is the time since the donor filled its Roche lobe and τ is the time scale for angular momentum loss in CVs, typically 107 yr (Davis et al. 2008). In accordance with the value for Mconv from Knigge et al. (2011), we assume MB is disrupted at 0.20 M⊙ for CVs. When MB becomes inefficient, the donor has time to relax its radius to its equilibrium value. In this case, we use Eqs. (2) and (4), replace R2,CV with the radius the star had just before it detached and R2,eq with the radius as described in Knigge et al. (2011) for donors below the period gap. This radius decrease is implemented in the code in a similar fashion as the increase (Eq. (3)), that is, decreasing the radius exponentially, where now 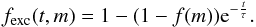 (5)We assume that donor stars whose initial mass is lower than 0.35 M⊙ do not experience efficient MB, analogous to single ZAMS stars. Therefore, we did not inflate the radius for these donors, but only used the radius for CV donors below the gap. As pointed out by Knigge et al. (2011), the power-law approximation for the mass-radius relation of MS donors breaks down for masses ≤0.05 M⊙. We therefore only considered CVs with a secondary more massive than 0.05 M⊙.
(5)We assume that donor stars whose initial mass is lower than 0.35 M⊙ do not experience efficient MB, analogous to single ZAMS stars. Therefore, we did not inflate the radius for these donors, but only used the radius for CV donors below the gap. As pointed out by Knigge et al. (2011), the power-law approximation for the mass-radius relation of MS donors breaks down for masses ≤0.05 M⊙. We therefore only considered CVs with a secondary more massive than 0.05 M⊙.
2.3. CVs with evolved donor stars
While the assumed mass radius relation of CVs is reasonable for CVs with MS donor stars, we have to take into account that CVs from binaries with more massive secondaries, such as those that passed through a phase of TTMT, may have significantly evolved donor stars.
As has been shown by Podsiadlowski et al. (2003), the orbital period evolution of CVs with donor stars that have a central hydrogen fraction below 0.4 significantly differs from those with less evolved secondary stars. In particular, CVs with evolved donors do not become fully convective at an orbital period of ~3 h as “normal” CVs do, but at possibly much shorter periods (Baraffe & Kolb 2000; Podsiadlowski et al. 2003). In fact, they may even bounce back and evolve to longer periods before becoming fully convective. As a consequence, CVs with evolved donors pass the period gap as accreting systems with a bloated donor star that is significantly hotter than a typical CV donor at the same period. Such systems have indeed been found (Thorstensen et al. 2002; Littlefair et al. 2006; Thorstensen 2013; Rebassa-Mansergas et al. 2014). Thus, if many of them are produced in our simulations, then the predicted orbital period distribution could be significantly affected. Incorporating evolutionary tracks for CVs with evolved secondaries in our simulations is beyond the scope of this paper. Instead, we simply keep track of the central hydrogen fraction of the CV donors, derived from their initial mass and current age, and determine the fraction of systems in our simulation that contain evolved donors as defined by Podsiadlowski et al. (2003), that is, with donor stars that have a central hydrogen fraction below 0.4.
To evaluate whether a given predicted fraction of evolved systems would disagree with the observations, we derived an upper limit from the observed period distribution. Assuming that all observed CVs in the gap are CVs with evolved donors (this is a strict upper limit as some CVs with un-evolved donors are born in the gap) and taking into account that the number of CVs at the lower edge of the gap in the observed distribution increases roughly by a factor of 3−5 (Gänsicke et al. 2009; Knigge et al. 2011), we estimate an upper limit for the fraction of CVs with evolved donors (that evolve through the gap as accreting systems) of ~20−30 per cent. If this fraction is exceeded, one would expect more CVs in the gap and a smaller increase of the number of CVs at the lower edge of the gap than is observed.
2.4. Modelling the mass-transfer rate
Binary_c/nucsyn is a parametrized stellar evolution code and does not calculate the various mass-radius exponents that are discussed in Sect. 2.1. Instead the calculation of the rate at which mass is transferred to the accretor, Ṁtr, contains a numerical factor to ensure that the mass-transfer rate is (numerically) steady (see Eq. (59) from Hurley et al. 2002). However, this factor is too small to let the star follow its Roche lobe within a few per cent during stable mass transfer when the radius is inflated. In other words: when the system is a CV, the mass-transfer rate is too low to be self-regulating. Furthermore, this parametrization of the mass transfer rate does not correctly model mass transfer on the thermal time-scale of the donor. We therefore adapted this factor for both cases separately as described below.
2.4.1. Stable CV mass transfer
To prevent the star from overfilling its Roche lobe by more than a few per cent, we made the mass transfer prescription more sensitive to changes in the donor radius by multiplying Eq. (59) from Hurley et al. (2002) with a factor of 1000 for stable mass transfer when the binary is a CV.
For a numerically smooth transition, we increased the factor from 1 to 1000 on the same time-scale that we inflated the radius of the donor star. This allows the mass-transfer rate to be self-regulating during the CV phase and prevents numerical instabilities in calculating the mass-transfer rate.
2.4.2. Thermal time-scale mass transfer
In the case of TTMT, the original prescription of Hurley et al. (2002) underestimates the mass transfer rate. We therefore included the same factor as derived by Claeys et al. (2014), who have tested the resulting calculation of the mass transfer rate against a detailed binary stellar evolution code (STARS, Eggleton 1971; Pols et al. 1995; Glebbeek et al. 2008). This provides a better description of TTMT, although the mass transfer rate may be a factor of three higher than the maximum from the detailed STARS code, in which case the duration of TTMT is correspondingly shorter (see their Sect. 2.2.4).
2.5. Response of the primary to mass transfer
In the previous sections we have described the consequences of mass transfer for the mass-losing star. An equally crucial and precarious question is how the primary star reacts to accretion, in particular, if the mass transfer is conservative. In what follows, we describe our approach for both TTMT and mass transfer driven by angular momentum loss.
2.5.1. Thermal time-scale mass transfer
When the mass-transfer rate is within the limits of stable hydrogen burning, all transferred hydrogen-rich matter is processed into helium and accreted onto the WD. If the mass-transfer rate exceeds this limit, hydrogen will be accreted faster than it can be processed into helium. Two scenarios for this situation have been proposed in the literature. The first is that the redundant hydrogen-rich matter accumulates onto the surface of the WD and forms a red-giant-like envelope (Nomoto et al. 1979). Consequently, the system will probably evolve into a second CE instead of becoming a CV. The other scenario is that the burning of hydrogen may cause a very strong wind (Hachisu et al. 1996). This wind ejects part of the accreted matter and tends to stabilize the mass accretion onto the WD, thus preventing the formation of a new giant-like envelope. A certain amount of matter will still be accreted onto the surface of the WD, at a rate Ṁacc, depending on the mass accumulation efficiency of hydrogen burning, ηH, and the mass accumulation efficiency for helium-shell flashes, ηHe. This rate can be expressed as 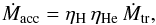 (6)where Ṁtr is the rate at which mass is transferred from the donor to the WD. The efficiency parameters ηH and ηHe depend on Ṁtr (Meng et al. 2009). We refer to this wind as the Hachisu wind.
(6)where Ṁtr is the rate at which mass is transferred from the donor to the WD. The efficiency parameters ηH and ηHe depend on Ṁtr (Meng et al. 2009). We refer to this wind as the Hachisu wind.
A second problem concerning the response of the WD to mass accretion occurs if the WD is made of helium. The accretion of helium can occur either directly or through stable hydrogen burning on the surface of the WD. Models from Woosley et al. (1986) have shown that a detonation due to the accretion of helium at a rate of 2 × 10-8M⊙ yr-1 can occur when the star reaches 0.66 M⊙, while previous models by Nomoto & Sugimoto (1977) found a limit of 0.78 M⊙ for the accretion of hydrogen at the same rate. Based on these predictions, the maximum mass of a helium WD (He WD) was set to 0.7 M⊙ in binary_c/nucsyn (Hurley et al. 2002). However, Shen & Bildsten (2009) showed that all of the pre-1991 results are calculated with an erroneously high value of the conductive opacity and the resulting ignition masses are a factor of 2 too low. Furthermore, Saio & Nomoto (1998) found that the accretion of helium onto a 0.4 M⊙ WD at a rate of 10-7M⊙ yr-1 and 10-6M⊙ yr-1, that is, the rate of TTMT, induces a stably burning helium star. This implies that a phase of TTMT can eventually turn a low-mass He WD into a high-mass carbon-oxygen WD (C/O WD). Since there is currently no clear stringent limit on the mass of He WDs, if there is any, we did not assume a mass-limit for accreting He WDs.
2.5.2. Mass transfer driven by angular momentum loss
When the mass transfer rate is below the limit of stable hydrogen burning, the accreted hydrogen is compressed onto the surface of the WD and is subsequently ignited under highly degenerate conditions. This leads to unstable hydrogen-shell burning and flashes, that is, to nova eruptions. As mass transfer can be assumed to be stable and conservative in between two (virtually) instantaneous nova eruptions, the critical mass ratio given by Eq. (1) can be used to distinguish CVs from systems that are unstable against dynamical mass transfer, and might evolve into a second CE. However, it has been subject of debate for several decades how much mass is lost during outbursts. The long-standing paradigm has been that nova eruptions in CVs expel most of the mass that has been accreted before the nova outbursts and probably even more (Prialnik 1986; Prialnik & Kovetz 1995; Townsley & Bildsten 2004; Yaron et al. 2005). We used macc and mej from Table 2 in Yaron et al. (2005) to construct an interpolation table with efficiencies for mass “accretion” during nova cycles, which we implemented in binary_c/nucsyn. The amount of mass loss, or in other words, the “accretion” efficiency, depends on the mass of the WD, the mass-transfer rate, and the core temperature of the WD. We derived the core temperature of the WD from its mass and luminosity (Mestel 1952).
As outlined in the introduction, the immense discrepancy between observed and predicted WD mass distributions in CVs motivated us to investigate the implications of WD mass growth during nova cycles in a separate model. In these models we arbitrarily increased the mass accretion efficiency during a nova cycle from 10 to 100%.
3. Binary population synthesis
We generated a three-dimensional grid with M1, M2 and the separation as free initial parameters. Our resolution was 150 for each parameter, thus for each model we simulated ~3 × 106 binary systems. We let the initial mass of the primary, M1, range from 1 to 9 M⊙, to let the primary evolve into a WD within the Hubble time. The initial mass function (IMF) of the primary is given by Kroupa et al. (1993). For M2 we assumed an initial mass-ratio distribution that is flat in mass ratio q (Sana et al. 2009). The initial mass of M2 ranged from 0.08 to 3.5 M⊙. Both M1 and M2 were picked from their initial mass distribution with a logarithmic spacing. The initial orbital separation a was assumed to be flat in log a (Popova et al. 1982; Kouwenhoven et al. 2007) and ranged from 3 to 104R⊙ to cover the whole space of binaries that will interact within the Hubble time. Each binary in the grid was given an individual formation probability, depending on the assumed distribution of the initial parameters and taking into account the logarithmic spacing in mass. We furthermore assumed circular orbits and solar metallicity for all binaries. We set the CE efficiency parameter, αce, equal to 0.25, in accordance with the range of values determined by Zorotovic et al. (2010). For details of the CE prescription we used, see Hurley et al. (2002) and Zorotovic et al. (2010). The binaries were formed with a constant star formation rate by randomly assigning them a lifetime between 0 and 13.5 Gyr, our assumed age of the Galaxy (Pasquini et al. 2004).
The motivation for this work is the disagreement between observed and predicted WD mass distributions of CVs. Zorotovic et al. (2011) suggested two possible solutions for the high WD masses in the observed sample, and we calculated three models to test both ideas against the standard scenario of CV evolution. In the first model, we assumed that a giant-like envelope is formed when the mass transfer rate exceeds the limit for stable hydrogen burning, which should produce relatively few post-TTMT CVs. This model, which we refer to as the reference model, contains the most common assumptions of CV formation and evolution as discussed in the previous sections. In our second model, we added the stabilizing Hachisu wind during TTMT as this is known to be fundamental to produce large numbers of post-TTMT CVs, which potentially contain massive WDs. In a third model, we incorporated net mass growth during nova cycles into our reference model instead of the “accretion” efficiencies derived from Yaron et al. (2005).
The three main models can thus be summarized as follows:
-
1.
Our reference model based on typical assumptions for CV evolution.
-
2.
Our reference model, including a wind from the accreting WD that stabilizes mass transfer and prevents the formation of a giant-like envelope (Sect. 2.5.1).
-
3.
Our reference model, but assuming different efficiencies of mass accretion onto the WD.
4. Results
We first describe the results of our reference model for CV evolution. Subsequently, we address the effects of including the Hachisu wind, and then the mass growth.
4.1. Reference model
 |
Fig. 2 Centre: two-dimensional histogram of the orbital period and WD mass distributions in CVs for our reference model. The colour intensity represents the sum of the formation probabilities of all CVs residing in that two-dimensional bin. The vertical dashed lines mark the upper (3.18 h) and lower edge (2.15 h) of the observed period gap (Knigge 2006). The hatched region indicates the parameter space in which mass transfer will become dynamically unstable, assuming qcr is given as in Eq. (1). The dotted line marks the shape of the dynamically unstable region if one assumes a constant qcr of 0.695 for M2 ≲ 0.7 M⊙. These regions are depicted in the same way as their corresponding regions in Fig. 1. The dashed-dotted line marks the region where mass transfer becomes dynamically unstable if one assumes the ZAMS mass-radius from Tout et al. (1996). Bottom panel: orbital period distribution of the CVs in our reference model. Left panel: WD mass distribution of the CVs in our reference model. |
Figure 2 shows the binaries that are identified as a CV at the present epoch (according to our definition of a CV, see Sect. 2.1). The distribution of both the orbital period (bottom) and WD mass (left) are shown, as well as their combined probability distribution in the two-dimensional plane. The vertical dashed lines mark the upper (3.18 h) and lower edge (2.15 h) of the observed period gap (Knigge 2006). The hatched region indicates the parameter space in which mass transfer will become dynamically unstable, assuming qcr as given as in Eq. (1). The dotted line marks the shape of the dynamically unstable region if one assumes a constant qcr of 0.695 for M2 ≲ 0.7 M⊙. These regions are depicted in the same way as their corresponding regions in Fig. 1 and were calculated by equating the radius of the donor star, as given by Knigge et al. (2011), with its Roche-lobe radius and solving for the orbit with Kepler’s third law using the corresponding critical mass ratio. The right border of this region corresponds to a donor mass of 0.7 M⊙, the curved left border corresponds to the critical mass ratio. Some CVs are located in the region for dynamically unstable mass transfer. To explain this, we have also shown the right border for this region if one assumes the mass-radius relation that is originally in the code (Tout et al. 1996), indicated by the dashed-dotted line. Since virtually all of the CVs in the hatched region are located on the stable side of the dashed-dotted border, it illustrates that these CVs have formed recently and their radius is still inflating towards the value given by Knigge et al. (2011). The mass of the CV donors in this region is higher than 0.7 M⊙ and the system is currently still stable against mass transfer. These CVs, however, will experience dynamically unstable mass transfer when the donor star becomes deeply convective at a donor mass of ~0.7 M⊙.
The orbital period distribution shows a clear spike at the period minimum, corresponding to very low-mass secondaries (Msec ≲ 0.08 M⊙). Most CVs in our standard model are currently below the period gap, but only 33.6% of the current CV population was born in or below the gap. This is a well-known prediction of binary population models of CVs (e.g. Kolb 1993): because angular momentum loss is assumed to be much lower below the gap than above the gap, the evolutionary time-scale is shorter above the gap than below by one to two orders of magnitude.
The absence of CVs with low-mass WDs in the ~3−4 h orbital period range, that is, in the hatched region in Fig. 2, has been predicted by previous models (de Kool 1992) and can be explained as follows: mass transfer becomes dynamically unstable for CVs whose mass ratio exceeds the critical value given by Eq. (1). This will occur within the region marked by the solid line in Fig. 2. CVs are thus not able to evolve towards shorter periods through this region without experiencing dynamically unstable mass transfer and merging. This means CVs with a WD ≲ 0.7 M⊙ and  have to be born there or must have descended from higher WD masses.
have to be born there or must have descended from higher WD masses.
 |
Fig. 3 Same as in Fig. 2, but for model 2, in which a wind from the WD that stabilizes mass transfer is included (Sect. 2.5.1). This wind allows more binaries that experience TTMT to evolve into CVs. The prescription for qcr is crucial for the subsequent CV evolution. |
The WD mass distribution shows three peaks. The first peak at 0.4 M⊙ consists of He WDs that evolved into a CE when the primary was on the first giant branch (FGB). The second peak at 0.55 M⊙ corresponds to binaries for which the mass growth of their core was terminated when they were on the asymptotic giant branch (AGB). These are C/O WDs with a lower mass than expected for single WDs as a result of the earlier expulsion of the envelope. The steep decline after the peak for C/O WDs agrees with the observed mass distribution of single WDs (Kepler et al. 2007). The third peak predicted at 0.75 M⊙ is atypical for the mass distribution of single WDs. This peak contains a significant fraction (32.5%) of CVs that have experienced TTMT and thus originates from CVs that initially resided at longer orbital periods and that had more massive secondaries. It is a direct consequence of using Eq. (1) for the critical mass ratio at which mass transfer becomes dynamically unstable instead of a constant value for qcr, as is assumed by default in binary_c/nucsyn. The region in which mass transfer becomes dynamically unstable for a constant qcr of 0.695 for M2 ≲ 0.7 M⊙ extends towards high-mass WDs as indicated by the dotted line in Fig. 2. Thus, in this case, all CVs with a WD ≲ 1 M⊙ and  would merge eventually. The occurrence of this third peak has been previously predicted by CV population models, using the same prescription for the critical mass ratio (see Politano 1996,his Fig. 4). If this prescription had not been used, the predicted WD mass distribution would be similar to the one derived by de Kool (1992).
would merge eventually. The occurrence of this third peak has been previously predicted by CV population models, using the same prescription for the critical mass ratio (see Politano 1996,his Fig. 4). If this prescription had not been used, the predicted WD mass distribution would be similar to the one derived by de Kool (1992).
Our reference model predicts that 15% of the CVs have undergone TTMT before evolving into a CV, which is consistent with the results from UV observations from Gänsicke et al. (2003). The relatively small fraction of such post TTMT CVs is caused by the formation of a giant-like envelope if the mass-transfer rate of hydrogen-rich matter exceeds the limit for stable hydrogen burning. Consequently, He WD primaries evolve into FGB stars and C/O or O/Ne WDs primaries into AGB stars. Therefore, the binaries do not evolve into CVs, but eventually evolve into a second CE and merge. In other words, the limits for the mass-transfer rate, between which hydrogen burning on the surface of the WD is stable, define a range that is very narrow. Mass-transfer rates are thus typically either too high, causing the CVs to merge, or too low to allow the WD to gain a sufficient amount of mass. This limits the impact of post TTMT CVs on the WD mass distribution of CVs in our reference model.
4.2. CV populations including the Hachisu wind
In our second model the implementation of the Hachisu wind (see Sect. 2.5.1) prevents the WDs from forming a new giant-like envelope in the case of TTMT. This wind thus serves as a tool for investigating the consequences of extending the narrow range for stable hydrogen burning to higher mass-transfer rates, that is to say, extending the parameter space for TTMT systems that may evolve into CVs. The resulting WD mass (left) and orbital period (bottom) distributions are shown in Fig. 3. As in Fig. 2, the vertical dashed lines indicate the location of the observed orbital period gap, while the solid and dashed lines in the main grey-scale plot represent the region in which mass transfer becomes dynamically unstable according to the two prescriptions for qcr discussed previously. The dashed-dotted line marks the dynamically unstable region, assuming the mass-radius relation from Tout et al. (1996).
The WD mass distribution for Mwd ≲ 0.7 M⊙ is practically the same as the distribution predicted by the reference model shown in Fig. 2, and so are their evolutionary paths. Assuming a wider range of mass-transfer rates that allow stable hydrogen burning without the formation of a new giant-like envelope, however, leads to the prediction of a much larger number of CVs with massive WDs (≳0.7 M⊙), which in the reference model evolved into a giant-like star. This increases the total number of predicted CVs by 50% with respect to the reference model and now almost half of all CVs, 46%, have undergone TTMT. The mean WD mass of post-TTMT CVs increased significantly during TTMT: from 0.56 M⊙ before the phase of TTMT, to 0.86 M⊙ afterwards. When only the CVs with a WD ≳ 0.7 M⊙ are considered, 74.8% experienced TTMT.
The impact of the description used for qcr on the predicted distributions is even stronger than in the reference model. Most WDs with masses between 0.7 M⊙ and 1 M⊙ would not evolve into CVs if one assumes a constant qcr of 0.695, because they would experience dynamically unstable mass transfer when they evolve towards the region bordered by the dotted line (see Fig. 3). In that case, the only possibility to form WDs in CVs with a mass around 0.8 M⊙ below the gap are initial primary masses ≳3 M⊙, which have a very low formation probability compared to less massive stars.
The predicted WD mass distribution is fairly broad above the gap and more strongly peaked below, while the mean WD mass is comparable for both distributions (0.76 and 0.70 M⊙). This is caused by two effects. First, as most CVs with high-mass WDs below the gap descend from CVs above the gap (meaning that they are not born below the gap), the assumed mass loss during nova cycles as described in Sect. 2.5.2 slightly erodes these massive WDs (0.8−1.2 M⊙) on their way from long (~9.5 h, i.e. 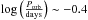 ) to short orbital periods. Second, CVs containing low-mass WDs (0.4−0.6 M⊙) above the gap cannot avoid dynamically unstable mass transfer when evolving towards shorter periods, that is, they enter the hatched region in Figs. 1 and 3 when the secondary develops a deep convective envelope (at a secondary mass of ~0.7 M⊙) and merge during a second CE. Consequently, the distribution of WD masses above the gap shows a wider spread than the distribution of WD masses below the gap.
) to short orbital periods. Second, CVs containing low-mass WDs (0.4−0.6 M⊙) above the gap cannot avoid dynamically unstable mass transfer when evolving towards shorter periods, that is, they enter the hatched region in Figs. 1 and 3 when the secondary develops a deep convective envelope (at a secondary mass of ~0.7 M⊙) and merge during a second CE. Consequently, the distribution of WD masses above the gap shows a wider spread than the distribution of WD masses below the gap.
4.3. Mass growth during nova cycles
 |
Fig. 4 WD mass distributions for different fractions of mass growth during nova cycles, i.e. assuming that more mass is accreted between two nova outbursts than is expelled during the eruption. The fractions are normalized to the total formation probability of all the CVs in each model. A higher accretion efficiency shifts the peak at 0.8 M⊙ to higher masses. |
In the third model, we investigate the other possibility to produce many CVs containing high-mass WDs mentioned by Zorotovic et al. (2011): we tested whether net mass growth of the WD in a CV evolving through a nova cycle can shift the low-mass WDs towards higher masses. We used the same assumptions as in our reference model, but instead of the standard assumption of slow erosion of the WD, we here tested four different accretion efficiencies. Figure 4 shows the WD mass distributions assuming that 10, 20, 50, or 100% (from top to bottom) of the transferred mass is accreted, which means that it remains on the WD after a nova outburst. These WD mass distributions are normalized by the sum of the formation probabilities of all CVs in each model. Assuming an accretion efficiency of only 10% has little consequences for the predicted WD masses. The mean mass increases slightly, but the overall shape of the distribution with its three peaks remains the same (the peak at 0.55M⊙ is smoothed out because of the bin size). This is simply because the low-mass WDs with relatively high-mass secondaries still evolve into the dynamically unstable mass transfer region and those with low-mass secondaries gain very little mass. The situation remains relatively similar for an accretion efficiency of 20%, but changes significantly if 50% of the transferred mass is assumed to contribute to mass growth of the WD. In the latter case, many CVs with low-mass WDs and initially massive secondaries can circumnavigate the dynamically unstable region and evolve into CVs below the gap. In addition, many WDs gain a significant amount of mass. As a consequence, the peak located at 0.75 M⊙ in the distribution predicted by the reference model largely dominates the distribution and is moved towards higher masses (~1.0 M⊙). This effect becomes stronger if all the transferred mass is assumed to be accreted by the WD. In this case, many CVs evolve into SN Ia candidates with WD masses ≳1.2 M⊙. The latter model is, of course, not a realistic one (because a significant fraction of mass is obviously expelled during nova eruptions), but it serves to illustrate the potential effect of mass growth on the WD mass distribution in CVs.
5. Discussion
Table 1 shows the statistics for our different simulations. Our results can be summarized as follows: the reference model predicts the WD mass distribution to be dominated by low-mass WDs and a third peak at ~0.75 M⊙ where most post-TTMT CVs reside. The fraction of CVs that experienced a previous phase of TTMT increased by a factor of three when we incorporated the Hachisu wind, which makes the peak at ~0.75 M⊙ more prominent. Finally, the models in which we allowed for mass growth during the CV phase predict relatively small changes for low accretion efficiencies, that is, a slight increase of the number of systems containing high-mass WDs. High fractions of mass growth predict CV populations dominated by systems containing very massive WDs (≳1.0 M⊙).
Statistics of our different models.
Below we first address to what extend our results depend on the assumptions and simplifications we made on our modelling approach, before we compare our model predictions with the observations.
5.1. Model uncertainties
The model predictions are sensitive to several assumptions, for instance to the critical mass ratio for dynamically unstable mass transfer, the Hachisu wind, the calculation of the TTMT rate, the mass limit for He WDs, the initial mass-ratio distribution, the strength of MB, and the efficiency of CE evolution.
5.1.1. Critical mass ratio
We demonstrated that the simulation of CV evolution is extremely sensitive to the analytic fit for qcr from Politano (1996). This analytic fit allows a significant number of CVs with a massive WD to evolve towards shorter periods, while they would have been regarded as dynamically unstable if one would have used a constant qcr for all low-mass MS stars, that is, a rough cut-off at ~0.7 M⊙. The critical mass ratio, and the corresponding region in which mass transfer becomes dynamically unstable, functions as a kind of “road block” that prevents CVs with low-mass WDs to evolve towards shorter orbital periods. Instead, dynamically unstable mass transfer leads most likely to a second CE and the stars probably merge. The value of qcr therefore has a huge influence on the formation of ~0.8 M⊙ WDs. Even fine-tuning all other parameters towards producing many post TTMT CVs, such as the Hachisu wind, would predict few WDs around 0.8 M⊙ if qcr were constant. It is therefore of crucial importance to use an accurate value of qcr instead of a crude approximation.
Since the critical mass ratio depends on the adiabatic mass-radius exponent, it is mainly determined by the stellar structure of the donor star and whether mass transfer is conservative or not. To our knowledge, the prescription we use for qcr is the most accurate currently available, but it is still based on two assumptions that might be critical for the formation of CVs, that is, a MS structure of the donor and conservative mass transfer.
First, the detailed structure of the secondary stars evolving from TTMT, especially the mass at which a convective envelope develops, is quite uncertain because these systems were initially more massive. These donors are probably driven out of thermal equilibrium by mass transfer at a high rate and their structure might thus to some degree correspond to that of a more massive star. If this is the case, the mass at which a deep convective envelope develops, that is, where the adiabatic mass-radius exponent increases steeply, could be lower than the canonical value of 0.7 M⊙. Thus, for a given WD mass, the mass ratio of a system evolving from long orbital periods to shorter orbital periods could be lower when facing the dynamically unstable boundary. Therefore more CVs with less massive WDs (≲0.75 M⊙) would evolve towards shorter periods without merging because the left-shifted boundary provides a higher qcr for a given secondary mass. This would concern CVs born at long orbital periods and post-TTMT systems. The peak of the WD mass distribution at 0.75 M⊙ in the reference model (and in the model including the Hachisu wind) would probably be shifted towards slightly lower masses. The impact of shifting the mass limit at which the donor stars develop a deep convective envelope towards lower masses on the resulting WD mass distribution would be even stronger when the masses of the WDs are assumed to grow during the CV phase, which would allow low-mass WDs at long orbital periods to circumnavigate dynamically unstable mass transfer if they accrete a sufficient amount of mass.
Second, we assumed that stable mass transfer (driven by angular momentum loss) during the CV phase is conservative. However, CVs experience nova eruptions during which both mass and angular momentum is lost. If the angular momentum taken away by the mass expelled during a nova outburst significantly exceeds the specific angular momentum of WD material, the critical mass ratio would be lower for a given value of the mass-radius exponent than it would be in the case of conservative mass transfer. This would cause stable mass transfer to occur only in systems with low mass ratios and may solve the problem of the large number of predicted CVs with low-mass WD. We will discuss this possibility in a follow-up paper.
This reasoning and the sensitivity of the results to the critical mass ratio imply that we may underestimate the relative number of massive WDs in our models. The adiabatic mass-radius exponent as shown in Fig. 1 is currently being scrutinized (Nelemans & Webbink, priv. comm.). A more accurate value for mass-transferring stars based on detailed stellar models would drastically reduce the uncertainties in our model predictions.
5.1.2. Hachisu wind
Since there is a consensus on the regime in which the mass-transfer rate enables stable hydrogen burning (Nomoto et al. 2007; Williams 2013), the only option to increase the number of CVs that descend from TTMT is to assume non-conservative mass transfer. The most popular mechanism for mass loss during TTMT is a strong wind that reduces the mass accretion rate and allows more systems to maintain stable hydrogen burning on the surface of the WD (Hachisu et al. 1996). In the framework of this wind model, the mass accumulation efficiency for hydrogen burning, ηH, and in particular the mass accumulation efficiency for helium shell flashes, ηHe, during the wind determine how much the WD is growing and thus how fast the mass ratio changes as the mass of the secondary decreases. These efficiencies therefore define the evolutionary course along which a system evolves towards lower secondary masses, that is, to the left in Fig. 1. Higher efficiencies would imply a steeper decline of the mass ratio and more CVs with a phase of TTMT could circumnavigate dynamically unstable mass transfer. In contrast, lower efficiencies imply that CVs with a phase of TTMT are more likely to run into dynamically unstable mass transfer. Thus, the relative number of post-TTMT CVs, and consequently also the resulting WD mass distribution, depend sensitively on the mass accumulation efficiencies during TTMT.
5.1.3. Calculating the thermal time-scale mass transfer rate
The calculation of the mass transfer rate in binary_c/nucsyn does not depend on the mass-radius exponent. In the case of TTMT the prescription from Claeys et al. (2014) may overestimate the mass transfer rate. We therefore also ran our simulations with the original prescription, which underestimates the mass transfer rate. The outcomes differ in which binaries actually become a CV after TTMT, but the overall distributions of both the WD mass and the orbital period look the same. We therefore argue that using a method that models TTMT more adequately (see e.g. Chen et al. 2014) would not (significantly) change the WD mass distribution. The period distribution, on the other hand, may look different since we have a large number of evolved donor stars in our CV population. We address this question below (see also Sect. 2.3).
5.1.4. Accretion onto He WDs
An important uncertainty that has not been tested by our model calculations is the maximum mass of He WDs that accrete hydrogen rich material (that might be fused into He on the surface of the WD). According to the literature, this value is highly uncertain, as outlined in Sect. 2.5.1. If He WDs can be more massive than 0.7 M⊙, they provide a serious contribution to the observed peak at 0.8 M⊙ and simultaneously reduce the relative number of WDs ≲0.5 M⊙. In the model including the Hachisu wind (see Fig. 3) the contribution of He WDs that accreted a significant amount of mass during TTMT to the peak at ~0.8 M⊙ reaches 24.9%. Thus, if there exists a mass limit for accreting He WDs, the predicted peak in the WD mass distribution will be significantly less pronounced.
5.1.5. Initial mass-ratio distribution
One of the most important and critical ingredients of binary population models is the initial mass-ratio distribution. We assumed that all initial mass ratios are equally probable. Although both early (Popova et al. 1982) as well as more recent observational works (Raghavan et al. 2010) seem to support a mass-ratio distribution favouring equal-mass binaries, the general consensus is that the initial mass ratio distribution is flat, even for massive stars that appear to be most biased towards equal masses (Sana et al. 2009, 2012). An initial mass-ratio that is flat in q does not favour the formation of nearly equal-mass binaries, which is essential to produce large fractions of post-TTMT CVs. An initial mass-ratio distribution that is proportional to q would thus significantly increase the fraction of CVs containing high-mass WDs in the resulting distributions. This would cause the peak at 0.75 M⊙ to dominate the peaks at 0.55 and 0.4 M⊙ more strongly, as is observed.
5.1.6. MB and CE efficiency
We have assumed MB to be inefficient for fully convective secondary stars. This, so named, disrupted MB scenario has been well established during the past decade both in single stars (see e.g. Reiners & Mohanty 2012, and references therein) and in close compact binary stars (Schreiber et al. 2010). However, the strength of MB when the secondary star contains a radiative core is not well known. Current prescriptions differ by several orders of magnitude (Schreiber & Gänsicke 2003; Knigge et al. 2011). Reducing the strength of MB, for instance by considering the normalization factor implemented by Davis et al. (2008), would increase the evolutionary time-scale of detached PCEBs with secondary stars in the mass range ~0.35−0.7 M⊙ and slows CV evolution towards shorter periods for systems with donor star masses in the range ~0.2−0.7 M⊙. This implies that CVs with high-mass WDs, that is, those systems that form the peak at ~0.8 M⊙ in the model including the Hachisu wind, would dominate the systems that become CVs below the period gap less strongly at shorter periods. Furthermore, owing to the slower evolution towards shorter orbital periods of CVs above the gap, our models would predict more systems in this period range for decreased MB.
Equally uncertain as the strength of MB, but perhaps even more important for close compact binary evolution, is the efficiency of CE evolution. It seems that, at least for low-mass secondary stars (~0.1−0.5 M⊙), a relatively low value of the CE efficiency (~0.25) agrees best with the observations (Zorotovic et al. 2010) and numerical simulations (Ricker & Taam 2012). However, CE evolution is extremely uncertain mostly because of three reasons. First, we have currently no idea if this low value also holds for higher secondary masses, second, we do not know if perhaps a post-CE circumbinary disk efficiently extracts angular momentum from the binary orbit of the emerging detached PCEB (Kashi & Soker 2011), and finally, it also remains an open discussion if perhaps the internal energy stored in the envelope such as the recombination energy contributes to the envelope ejection process (Webbink 2008; Rebassa-Mansergas et al. 2012).
However, the main effect that the CE efficiency would have on the predicted WD mass distributions is that higher values lead to the prediction of more CVs containing He WDs. This is simply because a significantly larger fraction of initially close binaries that start mass transfer when the primary star is on the first giant branch can survive CE evolution. This has recently been confirmed by Zorotovic et al. (2014), who showed that increasing αce from 0.25 to 1 results in an increasing fraction of PCEBs with He WDs and an extension of the WD mass distribution towards lower masses that cannot be obtained with lower efficiencies. Therefore, using a higher value of αce would increase the disagreement between our simulations and observations.
5.2. Comparison with observations
The model uncertainties presented in the previous section imply that performing binary population models of CVs has to be based on several assumptions, and changing these assumptions affects the predicted distributions. We have shown that mass growth during the CV phase can shift large fractions to higher masses but struggles to predict a broad distribution with the mean value around 0.8 M⊙. We have also shown that the latter can naturally be obtained if a large fraction of CVs are assumed to descend from TTMT, but a large population of CVs with He WDs remains in all our models compared to the observations. Below we compare in detail the model predictions with the observations of CVs and their progenitors. Because the orbital period is an observable that is much easier to measure than the stellar masses, we first inspect whether the orbital period distributions predicted by our models agree with the observations before we take a detailed look at the predicted WD mass distributions.
5.2.1. Orbital period distribution
In general, our simulations predict orbital period distributions that resemble those of previous models (Kolb 1993; Howell et al. 2001) and agree well with the main features of the observed distribution. The predicted period minimum, the accumulation of systems at the period minimum, the orbital period gap, and the prediction of most CVs residing below the gap all agree with the largest homogeneous sample of observed CVs currently available (Gänsicke et al. 2009). This agreement is expected as the predicted period minimum and period gap are a direct consequence of the mass-radius relation we used for CV donor stars (Knigge et al. 2011), which has been designed to reproduce the period gap and the period minimum.
However, our models disagree with the observed distributions with respect to some details. For example, we predict a deficit of CVs between 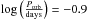 and − 0.7 but a number of CVs at longer orbital periods, while the opposite seems to be observed (Gänsicke et al. 2009). Furthermore, the accumulation of systems at the orbital period minimum seems to be more pronounced in our simulations than in the observed sample. These disagreements are caused by both model uncertainties as described in the previous section and, probably more important, observational biases and selection effects. For instance, while the predicted relative number of CVs above the gap sensitively depends on the strength of MB and the CE efficiency, the disagreement between the predicted number of these systems and the observations is most likely dominated by observational biases. CVs at the upper edge of the period gap are particularly bright (high mass-transfer rates) while systems at the period minimum are particularly faint (low mass-transfer rates). Both the larger number of systems at the upper edge of the gap and the less pronounced peak at the orbital period minimum are therefore probably caused by the fact that bright systems are more likely to be observed. This becomes clear when comparing the orbital period distribution of the complete sample of CVs with the most homogeneous sample identified so far (see Gänsicke et al. 2009,their Fig. 2). Similar results are obtained if observational biases are taken into account. In fact, Pretorius et al. (2007) have shown that observational biases impose a large discrepancy between the predicted and observed period distribution of CVs. Their predicted period distribution looks very similar to the period distribution of our models (see their Fig. 11).
and − 0.7 but a number of CVs at longer orbital periods, while the opposite seems to be observed (Gänsicke et al. 2009). Furthermore, the accumulation of systems at the orbital period minimum seems to be more pronounced in our simulations than in the observed sample. These disagreements are caused by both model uncertainties as described in the previous section and, probably more important, observational biases and selection effects. For instance, while the predicted relative number of CVs above the gap sensitively depends on the strength of MB and the CE efficiency, the disagreement between the predicted number of these systems and the observations is most likely dominated by observational biases. CVs at the upper edge of the period gap are particularly bright (high mass-transfer rates) while systems at the period minimum are particularly faint (low mass-transfer rates). Both the larger number of systems at the upper edge of the gap and the less pronounced peak at the orbital period minimum are therefore probably caused by the fact that bright systems are more likely to be observed. This becomes clear when comparing the orbital period distribution of the complete sample of CVs with the most homogeneous sample identified so far (see Gänsicke et al. 2009,their Fig. 2). Similar results are obtained if observational biases are taken into account. In fact, Pretorius et al. (2007) have shown that observational biases impose a large discrepancy between the predicted and observed period distribution of CVs. Their predicted period distribution looks very similar to the period distribution of our models (see their Fig. 11).
5.2.2. WD mass distributions of PCEBs
 |
Fig. 5 Mass distribution of WDs in PCEBs. From top to bottom: observed sample used in Zorotovic et al. (2011), distribution predicted by our reference model, distribution derived from the reference model including a strong wind during TTMT, distribution predicted if it is assumed that 20% of the transferred mass during a nova cycle remains on the WD. The fractions are normalized to the total formation probability of all PCEBs in each model. The predicted PCEB distributions are identical (because mass growth during TTMT or during nova cycles does not affect the WD masses of the progenitors) and agree reasonably well with the observations. |
As shown by Zorotovic et al. (2011), the high WD masses in CVs are not imprinted on the observed sample of PCEBs containing low-mass (M-dwarf) secondary stars. This led the authors to the conclusion that either the currently known pre-CV sample is not representative for CV progenitors or the masses of the WDs in CVs grow during nova cycles. In this paper we tested both possibilities. Before we directly compare the predicted WD mass distributions for CVs, we first test whether the PCEB WD mass distributions of our models agree with the observed one. The corresponding distributions are shown in Fig. 5, where we define a binary as a PCEB if it had a CE, currently does not have Roche-lobe overflow, and consists of a WD (He, C/O, O/Ne) and a MS star. We used relatively large bins because the uncertainties in the masses derived from observations are significant. As expected, the WD mass distribution of PCEBs does not depend on our assumptions because both mass growth during nova cycles or during a phase of TTMT occur after the detached PCEB phase. Furthermore, the simulated WD mass distribution of PCEBs looks similar to the distribution of the PCEB sample from Zorotovic et al. (2011). Both distributions have the same tendency to peak at 0.5 M⊙ and show similar scatter around their mean value. However, our models fail to reproduce the extremely high-mass WDs (≳0.8 M⊙) that seem to be present in the observed distributions. This is probably due to uncertainties in the masses derived from observations. The WD masses shown in the top panel of Fig. 5 have been measured using the spectral decomposition/fitting method described in Rebassa-Mansergas et al. (2007). We recently learned that more robust measurements of the WD mass using eclipse light curves indicate a much lower mass for those systems were the spectra indicate massive WDs (see Parsons et al. 2013,for one example). Therefore, the disagreement between prediction and observation concerning the massive WDs in PCEBs is most likely caused by limitations of the spectral decomposition/fitting method. We also conclude from Fig. 5 that, according to all three types of models, either virtually all CVs with a WD more massive than ~0.8 M⊙ have grown in mass due to mass transfer instead of being born this massive, or the whole population of PCEBs is not representative of CV progenitors and only a small fraction of them (those with more massive WDs) may evolve into CVs.
5.2.3. CV WD mass distribution
Figure 6 shows the observed WD mass distribution and the distributions predicted by the different calculations that we performed, which are normalized by the sum of the formation probabilities of all CVs in each model. We used a larger bin size than in Figs. 2 and 3 to facilitate comparison with the observed distribution. Our reference model, which is mostly based on the current hypotheses of CV evolution, drastically disagrees with the observed distribution (second and first panel from the top, respectively). While a small peak at 0.8 M⊙ is predicted, the distribution still contains far too many low-mass WDs and therefore also peaks at 0.4 M⊙, which is not observed. The mean WD mass predicted by the reference model, that is, 0.62 M⊙, clearly is too low when compared to the value derived from observations: ⟨ MWD ⟩ = 0.83 ± 0.02 (Zorotovic et al. 2011). As shown by Zorotovic et al. (2011), the high WD masses derived from observations cannot be explained by observational biases, and therefore it seems that an important ingredient of CV formation and/or evolution is missing in the standard model.
One of the possibilities proposed by Zorotovic et al. (2011) is to assume that a large number of CVs descend from TTMT. Indeed, as shown in the third panel from the top in Fig. 6, the mean WD mass increases to ⟨ MWD ⟩ = 0.71 M⊙ if a strong wind that extends the range of mass-transfer rates leading to stable hydrogen burning is assumed during TTMT. However, the distribution is still not in accordance with the mean mass derived from observations by Zorotovic et al. (2011) i.e. ⟨ MWD ⟩ = 0.83 ± 0.02. Most importantly, there is still a significant contribution (20.9%) of low-mass WDs, in particular He WDs, to the WD mass distribution, which is not observed (Zorotovic et al. 2011).
The second option outlined by Zorotovic et al. (2011) is mass growth during the CV phase, that is, assuming that during a nova cycle the WDs gain mass instead of slowly being eroded as predicted by the standard model. However, while this does allow increasing the mean WD mass, none of the distributions calculated for different fractions of mass growth is similar to the observed one. In Fig. 6 (bottom panel) we show the distribution assuming that 20% of the transferred mass is not lost during a nova eruption. This shows that it is in principle possible to obtain a WD mass distribution of CVs that is dominated by massive WDs assuming mass growth during nova cycles, but the predicted distribution still disagrees with the observed one. The peak at 0.8 M⊙ is less dominant and less broad than in the observed distribution, and the predicted distribution also shows a peak for He WDs at 0.4 M⊙, which is not observed.
 |
Fig. 6 Mass distribution of WDs in CVs for the different models described in this work and the distribution derived from observations. From top to bottom: observed sample used in Zorotovic et al. (2011) with the black histogram representing a sub-sample for which the mass determination is presumably more reliable, distribution predicted by our reference model, distribution derived from the reference model including a strong wind during TTMT, distribution predicted if it is assumed that 20% of the transferred mass during a nova cycle remains on the WD. The fractions are normalized to the total formation probability of all CVs in each model. |
Based on Fig. 6, none of the two options that we tested seems to be the definitive answer for the WD mass distribution in CVs, especially regarding the lack of systems with He WDs observed. However, we did not perform any fine-tuning but just used standard assumptions plus the wind proposed by Hachisu during TTMT or allowed for mass growth of the WD mass during the CV phase. As discussed in Sect. 5.1.6, one could further reduce the He WD fraction for example by reducing the CE efficiency or the critical mass ratio for stable mass transfer in CVs. The latter option will be discussed in a second paper.
5.2.4. WD masses as a function of period
 |
Fig. 7 WD mass distribution used by Zorotovic et al. (2011; left) of our model with the Hachisu wind (middle) and of our model including 20 per cent mass growth of the WD during a nova cycle (right) separated into the distribution of CVs in or below the gap (top panels) and CVs above the gap (bottom panels). The black histograms in the left figure represent a sub-sample of which the mass determination is presumably more reliable. The fractions in the middle and right panel are normalized to the total formation probability of all CVs in our models. The observations show a dispersion of WD masses above the gap, while the WD masses below the gap are more concentrated around 0.8 M⊙. Both features can also be seen in the model that includes the Hachisu wind (middle), but not in the 20 per cent mass growth model (right). |
Zorotovic et al. (2011) not only showed the general WD mass distribution of CVs derived from observations, but also the WD mass distributions of CVs above and below the gap. This division shows that the dispersion of WD masses above the gap is larger than of WD masses below the gap, which strongly peaks at 0.8 M⊙, while the mean masses of both sub-samples are nearly identical (see Fig. 7, left).
The best model assuming mass growth disagrees with both observed properties, the predicted mean mass increases towards shorter orbital periods and both distributions are equally peaked (see Fig. 7, right). In contrast, our model incorporating the Hachisu wind that produces a large fraction of CVs descending from TTMT and which best reproduces the overall observed WD mass distribution, also shows a wide spread of WD masses above the gap and a concentration around 0.8 M⊙ below the gap (see Fig. 7, middle). This could indicate that a significant fraction of post-TTMT CVs might be the missing ingredient in our current understanding of CV evolution. However, as mentioned in the last section, the latter model still produces far too many CVs containing He-core WDs.
5.2.5. Fraction of CVs with evolved donors
Schenker et al. (2002) were the first to predict that the secondary stars of CVs that went through a phase of TTMT can look different from the secondaries of CVs that did not. First, the secondaries of post-TTMT CVs descend from relatively massive stars and might therefore be significantly more evolved than genuine low-mass stars. This should cause them to have later spectral types above the gap and earlier spectral types below the gap (Kolb & Baraffe 1999). The first is apparently the case for two famous long orbital period CVs, AE Aqr and V1309 Ori. The latter has become the standard explanation for some CVs below the period gap with very early spectral types (Thorstensen et al. 2002; Littlefair et al. 2006; Thorstensen 2013). Recently, such a system has been found well inside the period gap (Rebassa-Mansergas et al. 2014), in agreement with the predictions of Kolb & Baraffe (1999) that CVs with evolved donors should enter the period gap at shorter orbital periods or not at all.
As a second possibility for identifying post-TTMT CVs, Schenker et al. (2002) predicted unusually high N/C UV line ratios for low-mass secondaries if CNO processed material is brought to the surface by convection. Shortly after this prediction had been made, an HST/STIS snapshot program of 31 CVs with strong emission lines revealed that indeed four systems had extremely enhanced N/C UV line ratios (Gänsicke et al. 2003).
Thus, there is clear observational evidence for the existence of post-TTMT CVs. However, the fraction of systems with extremely enhanced N/C UV line flux ratios seems to be significantly smaller than the fraction of post-TTMT CVs suggested by the model including the Hachisu wind. Thus the model represents a viable explanation if only a fraction of post-TTMT CVs shows enhanced N/C UV line ratios.
A second problem for the Hachisu model is that the predicted fraction of CVs containing evolved donor stars increases with the increasing number of post-TTMT CVs (see Table 1). This number would further increase if for instance a lower CE efficiency was used to reduce the number of CVs with He-core WDs (which currently is too large compared with the observations). In Sect. 2.3 we estimated that the fraction of CVs with evolved donors (that evolve through the gap as accreting systems) should not exceed ~20−30 per cent because otherwise the period gap would be less pronounced than is observed. Our simulated CV population assuming the Hachisu wind predicts almost 40 per cent of CVs with evolved donors, which exceeds this limit. We therefore conclude that assuming a large number of CVs descending from TTMT can at least partly explain the high WD masses in CVs but – unfortunately – generates problems with the classical explanation of the orbital period gap.
6. Conclusion
We have performed binary population models of CVs with special emphasis on the predicted WD mass distributions with the aim to evaluate possible solutions for the problem of the high-mass WDs in CVs identified by Zorotovic et al. (2011). We investigated the possibilities of WD mass growth during a preceding phase of thermal time-scale mass transfer and assuming net mass growth of WDs in CVs during nova cycles. In the latter case the predicted WD mass distributions drastically disagree with the observed one. In the first case, we find the best resemblance to the observed WD mass distribution by assuming a strong wind that increases the range of mass transfer rates, leading to stable hydrogen burning (as is frequently assumed in the single degenerate scenario for SN Ia, Hachisu et al. 1996). This model also explains the observation that the dispersion of WD masses is larger above than below the orbital period gap. However, this model still predicts a large population of CVs with He WD primaries and evolved donor stars, which clearly contradicts the observations. We therefore conclude that WD mass growth during nova cycles or during a preceding phase of thermal time-scale mass transfer cannot solve the discrepancy between the observed and predicted WD masses in CVs.
Acknowledgments
We are grateful to Joke Claeys, Onno Pols and Rob Izzard for valuable discussions, comments and advice. M.Z. acknowledges support from CONICYT/FONDECYT/POSTDOCTORADO/3130559. M.R.S. thanks FONDECYT (project 1141269) and the Millennium Nucleus RC130007 (Chilean Ministry of Economy).
References
- Baraffe, I., & Kolb, U. 2000, MNRAS, 318, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-L., Woods, T. E., Yungelson, L. R., Gilfanov, M., & Han, Z., 2014, MNRAS, 445, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, P. J., Kolb, U., Willems, B., & Gänsicke, B. T. 2008, MNRAS, 389, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- de Kool, M. 1992, A&A, 261, 188 [NASA ADS] [Google Scholar]
- de Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Gänsicke, B. T., Szkody, P., de Martino, D., et al. 2003, ApJ, 594, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Gänsicke, B. T., Dillon, M., Southworth, J., et al. 2009, MNRAS, 397, 2170 [NASA ADS] [CrossRef] [Google Scholar]
- Glebbeek, E., Pols, O. R., & Hurley, J. R. 2008, A&A, 488, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S. 1989, Ph.D. Thesis, AA (Illinois Univ. at Urbana-Champaign, Savoy) [Google Scholar]
- Howell, S. B., Nelson, L. A., & Rappaport, S. 2001, ApJ, 550, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dray, L. M., Karakas, A. I., Lugaro, M., & Tout, C. A. 2006, A&A, 460, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kahabka, P., & van den Heuvel, E. P. J. 1997, ARA&A, 35, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O., Kleinman, S. J., Nitta, A., et al. 2007, MNRAS, 375, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C. 2006, MNRAS, 373, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kolb, U. 1993, A&A, 271, 149 [NASA ADS] [Google Scholar]
- Kolb, U., & Baraffe, I. 1999, MNRAS, 309, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Kolb, U., & Willems, B. 2005, in The Astrophysics of Cataclysmic Variables and Related Objects, eds. J.-M. Hameury, & J.-P. Lasota, ASP Conf. Ser., 330, 17 [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Dhillon, V. S., Marsh, T. R., & Gänsicke, B. T. 2006, MNRAS, 371, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Dhillon, V. S., Marsh, T. R., et al. 2008, MNRAS, 388, 1582 [NASA ADS] [CrossRef] [Google Scholar]
- McDermott, P. N., & Taam, R. E. 1989, ApJ, 342, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 2103 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1952, MNRAS, 112, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., & Sugimoto, D. 1977, PASJ, 29, 765 [NASA ADS] [Google Scholar]
- Nomoto, K., Nariai, K., & Sugimoto, D. 1979, PASJ, 31, 287 [NASA ADS] [Google Scholar]
- Nomoto, K., Saio, H., Kato, M., & Hachisu, I. 2007, ApJ, 663, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1976, in Structure and Evolution of Close Binary Systems, IAU Symp., 73, 75 [Google Scholar]
- Parsons, S. G., Gänsicke, B. T., Marsh, T. R., et al. 2013, MNRAS, 429, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Bonifacio, P., Randich, S., Galli, D., & Gratton, R. G. 2004, A&A, 426, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patterson, J., Kemp, J., Harvey, D. A., et al. 2005, PASP, 117, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Han, Z., & Rappaport, S. 2003, MNRAS, 340, 1214 [NASA ADS] [CrossRef] [Google Scholar]
- Politano, M. 1996, ApJ, 465, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Popova, E. I., Tutukov, A. V., & Yungelson, L. R. 1982, Ap&SS, 88, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Pretorius, M. L., Knigge, C., & Kolb, U. 2007, MNRAS, 374, 1495 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D. 1986, ApJ, 310, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., & Kovetz, A. 1995, ApJ, 445, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rappaport, S., Joss, P. C., & Verbunt, F. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Rebassa-Mansergas, A., Gänsicke, B. T., Rodríguez-Gil, P., Schreiber, M. R., & Koester, D. 2007, MNRAS, 382, 1377 [NASA ADS] [CrossRef] [Google Scholar]
- Rebassa-Mansergas, A., Zorotovic, M., Schreiber, M. R., et al. 2012, MNRAS, 423, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Rebassa-Mansergas, A., Parsons, S. G., Copperwheat, C. M., et al. 2014, ApJ, 790, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H. 1976, MNRAS, 175, 279 [NASA ADS] [Google Scholar]
- Ritter, H., & Burkert, A. 1986, A&A, 158, 161 [NASA ADS] [Google Scholar]
- Robinson, E. L. 1976, ApJ, 203, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Nomoto, K. 1998, ApJ, 500, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Gosset, E., & Evans, C. J. 2009, MNRAS, 400, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Savoury, C. D. J., Littlefair, S. P., Dhillon, V. S., et al. 2011, MNRAS, 415, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Schenker, K., & King, A. R. 2002, in The Physics of Cataclysmic Variables and Related Objects, eds. B. T. Gänsicke, K. Beuermann, & K. Reinsch, ASP Conf. Ser. 261, 242 [Google Scholar]
- Schenker, K., King, A. R., Kolb, U., Wynn, G. A., & Zhang, Z. 2002, MNRAS, 337, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, M. R., & Gänsicke, B. T. 2003, A&A, 406, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, M. R., Gänsicke, B. T., Rebassa-Mansergas, A., et al. 2010, A&A, 513, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2009, ApJ, 699, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., & Ritter, H. 1983, A&A, 124, 267 [NASA ADS] [Google Scholar]
- Starrfield, S. 2015, AiP Adv., 4, 041007 [Google Scholar]
- Thorstensen, J. R. 2013, PASP, 125, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Thorstensen, J. R., Fenton, W. H., Patterson, J. O., et al. 2002, ApJ, 567, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A., Pols, O. R., Eggleton, P. P., & Han, Z. 1996, MNRAS, 281, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, D. M., & Bildsten, L. 2004, ApJ, 600, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1973, MNRAS, 162, 189 [NASA ADS] [Google Scholar]
- Warner, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 85 [Google Scholar]
- Webbink, R. F. 2008, in Ap&SS Lib. 352, eds. E. F. Milone, D. A. Leahy, & D. W. Hobill, 233 [Google Scholar]
- Williams, R. 2013, in IAU Symp., 281, 88 [Google Scholar]
- Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., Prialnik, D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & NebotGómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., & Gänsicke, B. T. 2011, A&A, 536, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., García-Berro, E., et al. 2014, A&A, 568, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Different regimes of stability against mass transfer for MS donor stars, depending on the mass ratio and the mass of the donor. The hatched region corresponds to the critical mass ratios for which, according to Politano (1996), the mass transfer becomes dynamically unstable as a function of the donor’s mass. The dotted line indicates the shape of this regions if one uses the condition that is originally in the code (see text). The solid curve represents the critical mass ratio for zero-age MS stars of solar composition above which mass transfer occurs on the thermal time-scale. This mass ratio is derived from the thermal mass-radius exponent by using the zero-age MS mass-radius relation implemented in the code (Tout et al. 1996) and assuming that mass transfer is conservative. |
| In the text | |
 |
Fig. 2 Centre: two-dimensional histogram of the orbital period and WD mass distributions in CVs for our reference model. The colour intensity represents the sum of the formation probabilities of all CVs residing in that two-dimensional bin. The vertical dashed lines mark the upper (3.18 h) and lower edge (2.15 h) of the observed period gap (Knigge 2006). The hatched region indicates the parameter space in which mass transfer will become dynamically unstable, assuming qcr is given as in Eq. (1). The dotted line marks the shape of the dynamically unstable region if one assumes a constant qcr of 0.695 for M2 ≲ 0.7 M⊙. These regions are depicted in the same way as their corresponding regions in Fig. 1. The dashed-dotted line marks the region where mass transfer becomes dynamically unstable if one assumes the ZAMS mass-radius from Tout et al. (1996). Bottom panel: orbital period distribution of the CVs in our reference model. Left panel: WD mass distribution of the CVs in our reference model. |
| In the text | |
 |
Fig. 3 Same as in Fig. 2, but for model 2, in which a wind from the WD that stabilizes mass transfer is included (Sect. 2.5.1). This wind allows more binaries that experience TTMT to evolve into CVs. The prescription for qcr is crucial for the subsequent CV evolution. |
| In the text | |
 |
Fig. 4 WD mass distributions for different fractions of mass growth during nova cycles, i.e. assuming that more mass is accreted between two nova outbursts than is expelled during the eruption. The fractions are normalized to the total formation probability of all the CVs in each model. A higher accretion efficiency shifts the peak at 0.8 M⊙ to higher masses. |
| In the text | |
 |
Fig. 5 Mass distribution of WDs in PCEBs. From top to bottom: observed sample used in Zorotovic et al. (2011), distribution predicted by our reference model, distribution derived from the reference model including a strong wind during TTMT, distribution predicted if it is assumed that 20% of the transferred mass during a nova cycle remains on the WD. The fractions are normalized to the total formation probability of all PCEBs in each model. The predicted PCEB distributions are identical (because mass growth during TTMT or during nova cycles does not affect the WD masses of the progenitors) and agree reasonably well with the observations. |
| In the text | |
 |
Fig. 6 Mass distribution of WDs in CVs for the different models described in this work and the distribution derived from observations. From top to bottom: observed sample used in Zorotovic et al. (2011) with the black histogram representing a sub-sample for which the mass determination is presumably more reliable, distribution predicted by our reference model, distribution derived from the reference model including a strong wind during TTMT, distribution predicted if it is assumed that 20% of the transferred mass during a nova cycle remains on the WD. The fractions are normalized to the total formation probability of all CVs in each model. |
| In the text | |
 |
Fig. 7 WD mass distribution used by Zorotovic et al. (2011; left) of our model with the Hachisu wind (middle) and of our model including 20 per cent mass growth of the WD during a nova cycle (right) separated into the distribution of CVs in or below the gap (top panels) and CVs above the gap (bottom panels). The black histograms in the left figure represent a sub-sample of which the mass determination is presumably more reliable. The fractions in the middle and right panel are normalized to the total formation probability of all CVs in our models. The observations show a dispersion of WD masses above the gap, while the WD masses below the gap are more concentrated around 0.8 M⊙. Both features can also be seen in the model that includes the Hachisu wind (middle), but not in the 20 per cent mass growth model (right). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.