| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425155 | |
| Published online | 09 April 2015 | |
The environment of radio sources in the VLA-COSMOS survey field⋆
1
University of Bologna, Department of Physics and Astronomy
(DIFA), v.le Berti Pichat
6/2, 40127
Bologna,
Italy
e-mail:
nicola.malavasi@unibo.it
2
INAF–Osservatorio Astronomico di Bologna, via Ranzani
1, 40127
Bologna,
Italy
3
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille), UMR 7326, 13388
Marseille,
France
Received: 13 October 2014
Accepted: 24 December 2014
Context. Several problems with the process of galaxy formation are still open. One of them is the role played by active galactic nuclei (AGNs) phenomena in galaxy build-up and, in particular, in quenching star formation (SF). On the other hand, the theory of AGN formation predicts that these phenomena are correlated with the host-galaxy environment, therefore opening links among SF quenching, environment and AGN phenomena in galaxy formation, and the evolution paradigm.
Aims. This work focuses on the correlations among environmental density, radio AGN presence and the probability that a galaxy hosts a radio AGN.
Methods. Using data from the photometric COSMOS survey and its radio 1.4 GHz follow-up (VLA-COSMOS), a sample of radio AGNs has been defined. The environment was studied using the richness distributions inside a parallelepiped with base side of 1 Mpc and height proportional to the photometric redshift precision. Richness distributions were compared as a function of both the redshift and the relative evolution of the stellar masses of galaxies and AGN hosts up to z = 2.
Results. Radio AGNs are always located in environments that are significantly richer and denser than those around galaxies in which radio emission is absent, so the environment seems to enhance the probability of a galaxy hosting a radio AGN. Moreover, a distinction between high-power and low-power radio AGNs leads to the conclusion that the significance of the environmental effect is only maintained for low-power radio sources. By studying the evolution of stellar masses, it is possible to conclude that radio AGN presence is a phenomenon related to quiescent galaxies up to z = 2, with a significant increase in the fraction of quiescent galaxies hosting a radio AGN with decreasing redshift. Hints of an environmental effect are present as well.
Conclusions. The results found with this work lead to concluding that denser environments play a significant role in enhancing the probability that a galaxy hosts a radio AGN and, in particular, low-power ones.
Key words: galaxies: active / galaxies: evolution / galaxies: formation / galaxies: clusters: general / galaxies: star formation / galaxies: luminosity function, mass function
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
It is well known that the morphology of galaxies is related to the local density in clusters 25. Moreover, luminosity functions 52, colours 21 and stellar masses 10 show dependencies up to redshift z ∼ 1 with the density field. Nevertheless, the mechanism that transforms star-forming galaxies into quiescent ones in dense environments has not yet been understood well. Recently, Peng et al. 43 have suggested a model where the star formation (SF) quenching is separable in a mechanism that depends on the galaxy mass and density; the first mechanism acts principally on massive objects at the centre of haloes, while the second is concerned with satellite galaxies.
The mass quenching can be related to the so-called feedback. This term simply indicates an energy input that causes an early stop in the star formation in a galaxy. This energy input was first introduced to reconcile cosmological simulations with observations see for example 28; 20 and since then it has been associated naturally with the activity of an active galactic nucleus (AGN).
By noting that X-ray and radio AGNs have different clustering properties, Hickox et al. 31 suggest that the central AGN co-evolves with the host galaxy: while the host galaxy transforms from a star-forming to a quiescent one, the AGN passes from a quasar, X-ray emitter phase to a radio-galaxy one. These transformations happen at earlier epochs for haloes of higher mass. This evolution of AGN type with galaxy transformation could be the reason behind the estimate that radio AGNs constitute ∼10% of the whole AGN population see for example 31, although projection effects and the limiting flux of current radio surveys may also play a role. The reason for such a small fraction of radio-to-total AGNs has still not been fully understood. Since the analysis conducted in this work focuses on radio AGN samples, in later work we will explicitly refer to this kind of source.
In the scenario developed by Hickox et al. 31 and Peng et al. 43, the environment is still related to the SF quenching of massive galaxies in an indirect way, in the sense that massive galaxies (where the mass quenching is effective) reside primarily in high-density environments, where early-type galaxies dominate at low redshifts 44; 17. Moreover, it was already known that many radio AGNs reside in early-type galaxies 37 and that the probability that a galaxy hosts an AGN is increasing with stellar mass 2. Also, on the basis of the zCOSMOS 10k sample 38; 39, Bardelli et al. 3 show that the fraction of radio active early-type galaxies is an increasing function of local density.
However, what is not clear is what is meant when environment is considered, since its definition is related to the spatial scale studied. In fact, environments estimated with nearest-neighbour methods consider different scales at different redshifts in a non trivial way. For example, Best 7 claims that the larger scale (i.e. the scale typical of groups and clusters) is more important than the smaller scale (typical of galaxy pairs or companions) for determining the AGN radio emission, at least at low redshifts.
In this work the environment of radio sources of the VLA-COSMOS survey 45, cross-identified with the COSMOS photometric redshift sample 32, is explored. With respect to Bardelli et al. 2, this sample allows an increase in both redshift range and statistics, but at the price of greater error in the redshifts (photometric versus spectroscopic redshifts), which excludes the possibility of a small spatial-scale definition for the environment. The scale of the environment is fixed at 1 Mpc, in order not to depend on the scale-redshift relation.
The data and the method used to define the radio AGN sample are described in Sects. 2 and 3 respectively. In Sect. 4 the method of comparing the overdensity richness distributions is presented and in Sects. 5 and 6 the results for various sub-samples are discussed. In Sect. 7 a correlation with known clusters and groups catalogues is attempted and in Sect. 8 the integrated mass functions of radio AGNs and normal galaxies are presented and analysed. Conclusions are drawn in Sect. 9. Throughout the text, masses are expressed in units of solar masses, while radio luminosities are expressed in SI units. The assumed cosmology is ΩΛ = 0.7, Ωm = 0.3, and H0 = 70 km s-1 Mpc-1. For the SED fitting procedure, in order to derive stellar masses and SF rates, Ilbert et al. 33 used SED templates produced with a Chabrier 15 IMF.
2. Data
Two main datasets have been used here. Optical data (with photometry in 30 bands from UV to mid-IR) were used to estimate photometric redshifts for all the sources, to determine the environment around every object in every sample, and to extract Control samples as explained later in the text.
Radio data at 1.4 GHz, instead, were used to create the radio source and AGN samples around which the environment has been studied.
2.1. Optical data
The data at optical wavelengths are constituted of the photometric sample of Capak et al. 12, used in the construction of the version 1.8 of the photometric redshift catalogue of Ilbert et al. 32. This sample is a compilation of photometric data taken from the COSMOS survey 47, which covers a field with an area of about 1.4° × 1.4° that is centred at RA (J2000.0) = 10h00m28.6s and Dec (J2000.0) = + 02°12′21.0″.
Size of every sample and redshift range of every bin used in the data analysis.
In Ilbert et al. 32, photometric redshifts have been calculated through a spectral energy distribution (SED) fitting procedure, using 30 broad-, intermediate-, and narrow-band filters from UV to mid-IR frequencies (see their Table 1). The fit was performed with a χ2 minimization algorithm on a template library using the Le Phare code (S. Arnouts & O. Ilbert). The redshifts obtained with the described procedure have been compared with those obtained using the zCOSMOS spectroscopic survey 38. The accuracy of the photometric redshifts (zp) is estimated to be 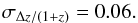 (1)This value will be assumed throughout this work. The error has been conservatively selected as the maximum value of those obtained as a function of both magnitude and redshift in Ilbert et al. 32, see their Fig. 9, taking the depth of the optical catalogue used for the analysis into account. To check the consistency of such a choice, the effect of degrading the value to σΔz/ (1 + z) = 0.1 ÷ 0.2 for high-redshift sources has been tested. As explained later, it was found that it does not change the results of this work significantly.
(1)This value will be assumed throughout this work. The error has been conservatively selected as the maximum value of those obtained as a function of both magnitude and redshift in Ilbert et al. 32, see their Fig. 9, taking the depth of the optical catalogue used for the analysis into account. To check the consistency of such a choice, the effect of degrading the value to σΔz/ (1 + z) = 0.1 ÷ 0.2 for high-redshift sources has been tested. As explained later, it was found that it does not change the results of this work significantly.
Other sources of uncertainties in the photometric redshifts determination that must be kept in mind are the so-called catastrophic errors. The definition of catastrophic errors is applied to those sources for which the redshift calculation fails in the form of 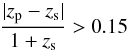 (2)where zs is the spectroscopic redshift. It is estimated that the fraction η of catastrophic errors rises from 1% to 20% going from i+< 22.5 to i+ ∼ 24.
(2)where zs is the spectroscopic redshift. It is estimated that the fraction η of catastrophic errors rises from 1% to 20% going from i+< 22.5 to i+ ∼ 24.
Only those objects are considered that are not in masked areas and that have magnitude i+< 26.5. This magnitude limit corresponds approximately to the point where the magnitude-number-count histogram stops increasing. At this limit the average number of filters used for the photometric redshift determination is 18. Although the effect of such a deep cut in limiting magnitude is to increase the uncertainties in the physical quantities derived from the optical photometry, it also has the advantage of greatly increasing the statistics for the environment estimate. For this reason, this cut will be assumed for all samples in this work. As explained extensively in Sect. 4, tests were performed by introducing brighter magnitude cuts from i+< 25.5 to i+< 24 to check the problematics related to also including in the analysis very faint objects. These tests showed that the magnitude cut has no major effect on the results found with this work.
From the optical catalogue, a sample of 823 939 sources with optical data and measured photometric redshift has been extracted (hereafter “O sample”). Star formation rates (SFRs) and stellar masses (M∗) are both derived through SED fitting with population synthesis models see 33, together with other physical parameters.
Samples definition.
2.2. Radio data
The radio data are taken from the VLA-COSMOS Large Project version 2.0 catalogue 45; 46, whose observations were carried out with the Very Large Array in its A configuration. This grants a resolution of about 1.5″ at full width half maximum (FWHM) in the observation wavelength of 1.4 GHz. A total of 23 pointings was necessary to cover the full COSMOS field, for 240 h of observation, performed between 2004 and 2005. The observations reached a sensitivity of about 11 μJy rms and the 5σ detection limit catalogue contains 2417 radio sources, 78 of which have been classified as multi-component radio sources.
The search for the optical counterparts used the photometric redshift sample (version 1.8) by Ilbert et al. 32, with no limitation on the optical magnitude, while for the radio catalogue, the VLA-COSMOS Large Project version 2.0 was used, but without the 78 multi-component radio sources (2339 radio sources).
The optical identification used the likelihood ratio method, described in Sutherland & Saunders 50, Ciliegi et al. 18, and Brusa et al. 11. For the likelihood ratio analysis a Q value was adopted (the probability that the optical counterpart of the radio sources is brighter than the magnitude limit of the optical catalogue) of 0.9 and a likelihood ratio cut-off of 0.1 (1−Q). Using a likelihood ratio cut-off equal to 1−Q ensures that all the optical counterparts of the radio sources with only one identification and a likelihood ratio greater than the cut-off value have a reliability greater than 0.5. With these thresholds 2069 radio sources with an optical counterpart have been found, ∼26 of which (∼1.3%) could be spurious positional coincidences. Applying the same cuts as used to define the O sample (objects not in masked areas and with magnitude i+< 26.5) to the 2069 identified radio sources, a sample of 1806 optically identified radio souces was created (hereafter “R sample”). The data analysis has, nevertheless, been performed only out to z ≤ 2.0, i.e. on a selection from the R sample of 1427 objects. The sizes of the various samples can be found in Table 1, while a summary of the sample definitions can be found in Table 2.
In Fig. 1 the redshift distributions for the O, R, MR and AGN samples (the last two are introduced later in the text) are compared. It can be seen that the distributions referring to radio galaxies peak at lower redshift, while the distribution for the optical galaxies is wider in a more extended redshift range.
 |
Fig. 1 Redshift distributions. The black solid line refers to the O sample, the red dashed one to the R sample, the cyan dot-dashed line refers to the MR sample and the green triple dot-dashed one refers to the AGN sample. |
The greatest difference in the samples is highlighted in Fig. 2, which shows the stellar mass distributions for the same samples as in the previous plot. It can be easily seen that the galaxies showing radio emission (R, MR, and AGN samples) are found almost only in high-mass galaxies (peak around log (M∗) ∼ 11), while objects from the O sample span a much wider range of masses, with a peak at log (M∗) ∼ 9.
 |
Fig. 2 Stellar mass distributions. The black solid line refers to the O sample, the red dashed one to the R sample, the cyan dot-dashed line refers to the MR sample and the green triple dot-dashed one refers to the AGN sample. |
This could be due both to an evolutionary effect, which sees the onset of radio emission mainly in high-mass galaxies, or to the limiting flux of the VLA-COSMOS, which could limit the kind of galaxy detected to only the most massive and luminous ones. Aside from the physical process responsible for the shape of the stellar mass distributions, that the radio galaxy samples are located at higher masses with respect to normal galaxies must be considered, in order not to introduce a bias in the conclusions drawn from these samples. For this reason a cut in stellar mass has been introduced by selecting only the most massive radio sources. When considering only radio sources at log (M∗) ≥ 10, the sample size becomes of 1448 objects, (“MR sample”). Again, the data analysis has only been conducted on a selection of 1218 with z ≤ 2.0. The cut to log (M∗) ≥ 10 also accounts for the possibility that the radio sources without optical identification are faint galaxies with low stellar mass. Therefore selecting only high-mass radio sources should avoid the insurgence of any bias in the results from missing optical identifications of radio sources.
3. The AGN sample
It is well known that radio emission could be due both to SF and to AGN phenomena. Several methods have been suggested for dividing the two populations where each of the two phenomena is dominant. There are several recipes for segregating the radio population into sources with emission from an AGN or from star formation (see e.g. 49; 2; 8, and references therein). In this work two ways that share a common hypothesis have been adopted.
The first way of defining a sample of radio AGNs is through a cut in specific SFR (SSFR). For each object, the SSFR is defined as the ratio of the SFR and the stellar mass, with both quantities derived from the SED fitting procedure. Quiescent galaxies are selected, and it is assumed that for this kind of sources all the radio flux comes from AGN activity. For this purpose, the SSFR vs. stellar mass (SSFR–M∗) plane is analysed (Fig. 3). From this plot, the locus of star-forming galaxies is clearly visible as a horizontal region within a narrow range of SSFR (−11 ≤ log (SSFR/ yr-1) ≤ −7). To the right of the figure, a vertical band located at 10 ≤ log (M∗) ≤ 12 represents the galaxies that are switching their SF off (“the dead line”). As AGN sample it has been chosen to select radio sources with log (M∗) ≥ 10 and log (SSFR/ yr-1) ≤ −11. With these cuts, a sample of 276 radio AGNs has been defined (272 at z ≤ 2).
 |
Fig. 3 SSFR–M∗ plane. The black crosses refer to the R sample, the red triangles to the AGN sample defined through the SSFR cut and the cyan squares to the AGN sample defined through SFR comparison. The green lines correspond to the cuts in stellar mass and SSFR described in text. In yellow, the O sample is reported for comparison. |
Although efficient, this method adopts an extreme hypothesis, since it assumes that all radio flux is coming from radio AGN activity in quiescent galaxies. The cuts applied to the sample may actually result inaccurate as more reliable methods of distinguishing radio activity from AGN phenomena and from star formation can be developed.
One of these is described in Bardelli et al. 3. It consists in the comparison between SFRs as resulted from the SED fitting of Ilbert et al. 33 and as estimated from the radio power as done in Bell 4. The hypothesis is that all radio flux exceeding that given by the SFRSED is due to AGN activity.
The SFRRadio has been computed using the Bell 4 formula (which is derived for a Salpeter IMF), with a correction of ∼2 in the normalization introduced to be consistent with Herschel-PEP data (Bardelli et al., in prep.). This normalization correction also considers the difference between IMFs used in the SFR derivation from optical SED fitting and in the formula from Bell 4. In this particular work, the normalization is less important, since only the identification of the locus of star-forming galaxies matters. The comparison between the two SFRs is reported in Fig. 4. In this figure it is clearly visible an elongated region due to the star-forming galaxies with a slight zero point shift and tilt. To fit this relation, only those objects that have log (SFRRadio) ≤ log (SFRSED) + 2 have been considered. The linear fit resulted in log (SFRRadio) = 1.176×log (SFRSED) + 0.685. The distribution of the distances from the best-fit line was then fitted with a Gaussian distribution, obtaining a dispersion of 1.40. To be very conservative, all the objects that lie at a distance greater than 3σ from the fit line are defined as AGNs. With this method, 164 sources are selected (154 at z ≤ 2).
 |
Fig. 4 AGN sample definition. The black crosses represent the R sample, the red triangles represent the AGNs selected through the cut in SSFR, while the cyan squares represent the AGN sample defined through SFR comparison. The dashed green line represents the linear fit relation described in text, while the solid blue line shows the SFRRadio = SFRSED relation. |
It has to be noted that this second method is more conservative, since the assumptions are less extreme: it is now possible for every galaxy, even for the quiescent ones, that part of the radio emission could be due to residual SF. The discrimination is set to decide which of the two phenomena (radio AGN activity or the formation of stars) prevails on the other. With this method, the probability of correctly selecting a radio AGN source (purity) is increased, in spite of completeness, since some radio AGN sources may not be individuated by the selection criteria. Figures 3 and 4 both show that the radio AGN samples derived with the two methods overlap.
Since the infrared emission is a better tracer of the SFR, a more rigorous approach would be to apply the method described above using the SFR derived from IR data, rather than from optical ones. For this reason the R sample has also been matched to the DR1 catalogue of the Herschel PACS Evolutionary Probe1 (Herschel-PEP). A description of the survey, observational strategies, and data reduction techniques may be found in Lutz et al. 40, while SFR and physical quantities were obtained through a SED fitting procedure performed with a modified version of the MAGPHYS code see 5; 23, and references therein for a detailed description. A total of 923 sources have been found by matching the R sample, 45 of which are in the AGN sample and are all situated at lower SFR values compared with other Herschel sources.
A sample of 83 AGNs was created from comparing the SFRRadio with the SFR from the IR data, which was derived through a procedure of SED fitting that allows for correction of the AGN contribution to galaxy emission (SFRIR). This method is equal to the one applied in previous paragraphs: the SFRRadio and SFRIR are compared and the bulk of the relation is linearly fitted to isolate sources with an excess of SFRRadio with respect to SFRIR. The distribution of the distances of each object from the best-fit line is fitted with a Gaussian distribution and only sources residing farther from the best-fit line than 3σ are defined as AGNs.
The environmental analysis was performed on these sources in the same way as for the other AGN samples. The environmental segregation effect is recovered, but unfortunately the sample is too small to make the results significant.
Extensive tests were performed to check whether the various methods of defining AGNs yield differences in the results found in this work. No significant discrepancies emerge from the tests. The AGN sample defined through the cuts in SSFR and stellar mass were used since it permits slightly more complete statistics, but all the conclusions derived in the following also remain valid if the radio AGNs are selected through the SFRRadio and SFRSED (or SFRIR) comparison.
4. Method
The aim of this work has been to investigate the presence and properties of galaxy overdensities in the COSMOS Survey field, especially at high redshift. First of all, a definition of overdensity is needed, since many different ways of defining this quantity can be found in the literature 48; 36; 22 and new ways are still being developed e.g. 13. Here we chose simplest approach by counting objects in a parallelepiped with a base side of 1 Mpc (comoving), centred on the considered source, and height twice Δz = 3 × σΔz/ (1 + z) × (1 + zp). It is useful to define three kinds of samples, as referred to in the following.
-
Starting sample. This kind of sample is composed of the objectsaround which the environment is to be estimated and which areplaced at the centre of each parallelepiped. Starting samples arethe R, MR, and AGN samples.
-
Target sample. These objects are those that are counted inside each parallelepiped and that are used to estimate the environment around every galaxy of each Starting sample. The O sample is used as Target sample.
-
Control sample. The absolute values and richness distributions of overdensities do not have any direct meaning if not compared with those obtained with a Control sample. To create it, the redshift has been maintained for each galaxy of a Starting sample, but coordinates have been randomly extracted. The way this is achieved is different for each sample and is explained thoroughly in Sect. 4.1. The environment was then estimated again for each Control sample using the same Target sample as for the corresponding real ones. The richness distributions between each sample and its corresponding Control one have been compared with a Kolmogorov-Smirnov test. To not be influenced by only one extraction, this process was repeated 100 times.
As already mentioned in previous sections, several tests have been performed to check whether the choice of the photometric redshift error and of the magnitude cut performed on the sample do in fact affect the results of this work. In particular, the environmental analysis was performed by also using a cut on the O sample at brighter magnitudes: i+< 25.5, i+< 25 and i+< 24. Only the magnitude cut on the O sample has been changed, since no AGN sources have 25 <i+< 26.5. In this way, while the magnitude distribution for the AGN sample is maintained, that of the Control samples and of the sources used to trace the environment have been changed. In the first two magnitude cuts, the assumption of the photometric redshift error has also been degraded to σΔz/ (1 + z) = 0.1 ÷ 0.2 in the third redshift bin (z ∈ [ 1.0−2.0 ]). The significance of the results is maintained for all the combinations, except for the AGNs in the highest redshift bin when using a magnitude cut for the O sample of i+< 24. This is not unexpected, though, since tracing the environment using only the most luminous sources and comparing AGNs with luminous control galaxies has the effect of comparing objects residing (especially at high redshift) in similar environments, therefore reducing the significance of the signal of environmental segregation. It is therefore possible to conclude that neither the magnitude cut used nor the value of the photometric redshift error assumed have a systematic effect on the results of this work.
Number of extractions of the various Control samples that are below the significance threshold of 0.05.
4.1. Control sample definition
As briefly explained above, the Control samples for the R, MR, and AGN sub-samples were created with optical data. For every galaxy in the R, MR, and AGN samples, coordinates have been randomly extracted from the O sample in the same redshift bin for every Starting sample. In addition, the following prescriptions were used separately for each sub-sample.
-
R Sample. The Control sample RO was extracted from O, so as tohave the same number of sources as the R sample in every redshiftbin.
-
MR Sample. The Control sample MO has been extracted from O, so as to have the same number of sources as the MR sample in every redshift bin. Moreover, every galaxy of the Control sample has been extracted among those having stellar mass in an interval of ± 0.5 dex from the mass of each galaxy composing the MR sample. In this way, the MO sample was extracted with the same stellar mass distribution as the MR one.
-
AGN Sample. The Control sample QO has been extracted from O, so to have the same number of sources as the AGN sample in every redshift bin. It has also been extracted having the same stellar mass distribution as the AGN sample, with the same method as used to extract the MO Control sample. Also, the galaxies used as a pool for the QO sample extraction were selected to be quiescent (log (SSFR/ yr-1) ≤ −11), therefore the QO sample is located in the same lower right-hand region of Fig. 3 as the AGN sample.
5. Results
In this section the results of the analysis of the environment performed on the various Starting samples are analysed. As explained above, to make the differences in the environment around radio sources and around galaxies with no radio emission (represented by the extracted Control samples) more apparent, the overdensity richness distributions were compared using a Kolmogorov-Smirnov test, repeated with 100 independent extractions of the various Control samples. When applied, the KS test gives the probability that two distributions come from the same parent population. To quantify the difference in the environments recovered, only richness distributions that have a KS probability value lower than 0.05 of being extracted from the same parent population will be considered as significant. In Table 3 the number of Control sample extractions (out of 100) that are below the significance threshold of 0.05 are reported, together with the median values of the KS probability value distributions (in brackets).
5.1. R Sample
At first, the environment is estimated around sources from Starting samples R and RO. It has to be kept in mind that the R sample is the whole radio catalogue. This sample does not distinguish whether the radio emission comes from star formation or AGN activity. The Target sample used is represented by the whole O sample. Results of the KS test between R and the 100 RO extractions are listed in the first line of Table 3. From these values it can already be seen that the environment around radio sources is significantly different from the environment around sources with no sign of radio emission, in every redshift bin. The total of the Control sample extractions is always below the significance threshold with very low median values. The way in which these environments differ is exemplified by Fig. 5.
 |
Fig. 5 Galaxy overdensity richness distributions, R and RO samples. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The red solid line refers to the R sample, and the grey lines correspond to the 100 extractions of the RO Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
In this figure, the overdensity richness distributions are shown for the R sample and for all the 100 extractions of the RO Control sample. The richness distribution of the Control sample extraction that corresponds to the median of the KS probability value distribution is in evidence. It can be seen that in every redshift bin the radio sources are systematically distributed at higher overdensity richness than normal galaxies.
Although important, this result could be due to other effects, such as the different mass distributions or evolutionary status of R and RO galaxies. A deeper investigation of the phenomenon is thus needed.
5.2. M Sample
It has been shown (see Fig. 2) that optical galaxies and radio sources have different mass distributions. In particular, radio sources are primarily found in high-mass galaxies, which in turn are known to reside primarily in high-density environments. This could be the actual reason behind the difference in environmental density found between sources from the R and RO samples described in the previous section.
The sample MR and its corresponding Control sample MO have been created to rule out this effect. These samples are designed to include only massive galaxies (log (M∗) ≥ 10) and to have the same stellar mass distribution. In this way, because the MR sample is composed of radio sources and its corresponding Control sample MO of optical galaxies, any difference in the environment between the two can be ascribed to the actual presence of radio emission.
The second line of Table 3 confirms the trend already found for the R and RO sample. The environment around radio sources and the environment around normal galaxies are significantly different, as demonstrated by the fact that all 100 extractions of the MO Control sample are below the significance threshold, with very low median values. Again a visual inspection of the overdensity richness distributions, such as those reported in Fig. 6 for the MR sample and all of the 100 extractions of the MO Control sample, confirms that overdensities found around massive radio sources are distributed at higher richness values than those around massive galaxies without radio emission.
 |
Fig. 6 Galaxy overdensity richness distributions, samples MR and MO. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The solid red line refers to the MR sample, the grey lines correspond to the 100 extractions of the MO Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
It is therefore possible to exclude a stellar mass effect behind the differences in the environment around normal galaxies and radio-emitting ones. Instead these differences are to be ascribed to the physical process behind the radio emission and its correlation with environmental density.
6. The environment of radio AGNs
The main focus of this study is the environment around radio AGN sources in the VLA-COSMOS Survey field. This task has also been performed in a similar way in other works for example 6; 30. In this work a general approach is adopted and the results are in good agreement with the literature.
The radio AGN sample for environment definition has been extracted from the whole population of radio sources in the way described in Sect. 3. By using a cut in SSFR, only those sources whose radio emission is due to AGN activity were selected and their environment determined using the O sample as Target sample.
Nevertheless, the method used to isolate radio AGNs has the effect of also selecting radio sources hosted by massive and quiescent galaxies. These two kinds of objects are both naturally found in high-density environments, therefore leading to a possible bias in the conclusions drawn. In fact, any difference in the environment around radio AGNs compared to optical galaxies could actually be due to quiescent galaxies usually being found inside overdensities or to massive galaxies being more clustered. To not be affected by these problems, the QO Control sample has been selected carefully to avoid this bias. Galaxies in the QO sample were extracted in the same SSFR range and with the same stellar mass distribution of the AGN sample. In this way, every difference in the environmental properties can be ascribed to the presence of radio AGN phenomena.
The results of the comparison of the overdensity richness distributions are shown in the third line of Table 3. It can be seen that the environment around radio AGN sources is significantly different from the environment around normal galaxies, with the vast majority of the extractions of the QO sample being under the significance threshold. Also the median values confirm this trend, since they are always under 5%. This is the most important result of this work by showing a definite correlation between environment and the presence of radio AGN phenomena.
Figure 7 shows the overdensity richness distributions for the AGN sample and for the 100 extractions of the QO Control sample. It can be clearly seen that overdensities around radio AGNs are distributed at higher richness values than those around normal galaxies. It is therefore possible to conclude that the environment around radio AGNs is significantly richer than around normal galaxies, with this effect being due to radio AGN presence rather than to radio AGNs being found primarily in massive or quiescent galaxies (see for example 31; 37). In other words, galaxies in denser environments show an enhanced probability of hosting a radio AGN than galaxies in less dense environments.
 |
Fig. 7 Galaxy overdensity richness distributions, samples AGN and QO. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The solid red line refers to the AGN sample, the grey lines correspond to the 100 extractions of the QO Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
As a check on the results, the environment around a sample of radio-emitting star-forming galaxies was also estimated, as selected in the upper right-hand quadrant of Fig. 3. These sources, characterized by log (M∗) ≥ 10 and log (SSFR/ yr-1) ≥ −11, were compared with a Control sample extracted in the same SSFR region and with the same stellar mass distribution. An environmental effect has been found in this sample, too, at all redshifts, with star-forming radio sources in higher density environments. The median values of the KS probability value distribution, though, are higher by an order of magnitude than those in the last line of Table 3, except in the highest redshift bin, even if the sample of star-forming radio sources is ∼10 times greater than the AGN one (450 SF sources against 53 AGNs). Although the great inequality in statistics between radio AGNs and star-forming sources surely plays a major role in determining the significance of the environmental effect for the latter kind of objects, the cause of this is also probably residual differences in the SFR between the star-forming radio sources and the Control sample ones. This is proven by the fact that, although they are situated in the same SFR range, the star-forming radio sources are detected by the VLA instrument while the Control sample galaxies are not. Therefore the SFR is higher in the radio-detected sample compared to the Control one, or there could still be some residual contamination from AGN emission, which induces the environmental effect on these sources.
6.1. High-power and low-power radio sources
It has been suggested see 42; 16 that low-power radio AGNs are often found in high-density regions see also 14; 2; 24. In fact, low-power radio AGNs are used to detect protoclusters at high redshifts e.g. 19; 51. In this section we explore whether the environmental density actually depends on the radio power. To do this, each sample was divided between a high-power sub-sample (log (L1.4 GHz) ≥ 24.5) and a low-power one (24 ≤ log (L1.4 GHz) < 24.5). The reason for the lower limit at log (L1.4 GHz) = 24 is to avoid the effect of the flux limit of the VLA-COSMOS Survey. Such an effect is visible in Fig. 8, which shows the dependence on the redshift of the radio luminosity for the R sample.
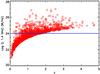 |
Fig. 8 Redshift dependence of radio luminosity. Only the R sample is represented. |
It can be seen that only the most luminous sources will be detected at high redshifts, owing to the survey limiting flux (effect known as the Malmquist Bias). This could lead to a bias in the results based on the sample, since more luminous objects could represent a different population of radio sources than do less luminous ones. This problem can be solved by considering only those sources that are more luminous than log (L1.4 GHz) = 24. In this way, a complete sample of radio sources up to z = 2 can be created.
It is worth noting that the limit at log (L1.4 GHz) = 24.5, set to divide the high-power and low-power radio sub-samples, roughly corresponds to the canonical division between FRI and FRII objects 26.
Therefore the samples AGNH and QOH (where H in the sample name stands for high power) and the samples AGNL and QOL (where L stands for low power) have been created. The number of galaxies in each sample is shown in Table 4.
Number of galaxies in each sample for every redshift bin.
The results of the analysis of the environment in relation to the distinction in radio power are now discussed. In particular, in Table 5 the number of Control sample extractions below the significativity level of 0.05 are reported, together with the median values of the KS probability value distribution.
Number of extractions of the various Control samples that are below the significance threshold of 0.05.
It is possible to see that the high-power and low-power samples have different KS probabilities: the environmental effect remains present only for low-power radio sources. In fact, in Table 5 it can be seen that the number of extractions below the significance level is fairly low for the-high power radio AGNs, never reaching even 50% of the total, and the median KS probability value is always greater than 0.05. On the other hand, for low-power radio AGNs the number of extractions below the significance threshold is close to 100%. Only in the highest redshift bin is the value very low (37%), but it is nevertheless higher than the corresponding value in the same redshift bin for the high-power AGNs. In Fig. 9 overdensity richness distributions are shown for the case of the AGNL sample and for the extractions of the corresponding QOL Control sample. That the distributions of the AGNL sample are systematically shifted towards higher richness values confirms the trend.
 |
Fig. 9 Galaxy overdensity richness distributions, samples AGNL and QOL. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The solid red line refers to the AGNL sample, the grey lines correspond to the 100 extractions of the QOL Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
This is another important result of this work: when considering the environment of radio sources, low-power AGNs are usually found in high-density environments. Therefore, higher overdensity richness values enhance the probability that a galaxy hosts a low-power radio AGN. This result is not unexpected. In fact, it could arise as a direct consequence of different accretion modes for low-power and high-power AGNs. In particular, theory predicts that low-power radio AGNs are fuelled by hot gas (such as the one found at the centre of clusters where cooling flows are present), whereas high-power AGNs are fuelled by cold gas see for example 29, and references therein. If this were true, then low-power AGNs (fuelled by hot gas) would be expected to reside at the centre of rich overdensities, such as clusters and groups (where hot gas is present). On the other hand, high-power AGNs would not be found in high-density environments, both for the lack of cold gas necessary for accretion and for the inefficiency of wet mergers (due to the high velocity dispersions of galaxies at the centre of clusters and rich overdensities), which are the trigger mechanism that has been proposed for the ignition of high-power radio AGNs. The results of this work seem to support this view of AGN and galaxy formation.
7. Correlation with known cluster and group catalogues
In the previous sections it has been found that radio AGNs live in environments that are on average denser than those of normal galaxies. We therefore explored whether these overdensities are related to virialized or bound objects. Two compilations of clusters and groups from the literature have been used: that of Finoguenov et al. 27, found in the COSMOS field analysing deep Chandra and XMM observations (see references in the paper), and the zCOSMOS group catalogue 35. For this comparison, only the two most distant redshift bins of the AGN sample have been considered (z ∈ [ 0.7−1.0 [ and z ∈ [ 1.0−2.0 ]). At those redshifts, a 0.5 Mpc value corresponds approximately to 71 (z = 0.7), 63 (z = 1.0) and 61 (z = 2.0) arcsec. However, the largest source of uncertainties comes from the large error in the photometric redshifts.
To be conservative, all objects that are within a radius of ∼60 arcsec and | Δz | < 0.12 for 0.7 ≤ z< 1.0 and ∼60 arcsec and | Δz | < 0.2 for 1.0 ≤ z ≤ 2.0 of the cluster locations reported in the two catalogues have been considered, in order to take the varying error in the photometric redshifts estimate into account.
In Table A.1, the 26 associations with the Finoguenov et al. 27 sample are listed, while in Table A.2 those with the zCOSMOS group catalogue of Knobel et al. 35 are reported. It has been found that ∼10–20% of the AGN sample is in groups and clusters. Furthermore, no significant difference between the radio power distributions of the radio AGNs in clusters and groups and of the radio sources of this work is detected. The only noticeable source is the one with log (L1.4 GHz) = 26.86 in a cluster in the most distant redshift bin, which is also the brightest object in the AGN sample.
For the X-ray luminosities, there is a slight tendency of clusters hosting a radio AGN at z ∈ [ 0.7−1.0 [ to be brighter, with a KS probability of being extracted by the same population of ∼0.09. However the statistics is not sufficient to say anything for the highest redshift bin.
In the case of zCOSMOS groups, the richness distributions are significantly different, with groups hosting a radio AGN being richer (KS probability of ∼10-3). This also holds when considering only groups with more than three elements.
8. Mass functions
We now investigate whether there is a relative evolution of the mass functions of radio AGNs and those of normal galaxies. To perform this task, stellar masses as determined in the UltraVISTA Survey 41; 34 are used. A limiting magnitude for the UltraVISTA Survey of KS = 24 is assumed in the data. Moreover, the radio power limit of log (L1.4 GHz) ≥ 24 previously introduced has also been applied to the AGN sample (leading to a total of 88 sources), since lack of completeness in the radio data could bias the estimate of the redshift evolution of the mass functions.
Stellar mass functions are computed with the non-parametric 1 /Vmax estimator (1; see also 9, and references therein for further information). For radio objects, the Vmax is calculated by taking the different radio and KS limiting magnitudes of the surveys into account. In particular, the minimum between the Vmax set by radio and optical data was used. Mass functions were calculated for all UltraVISTA galaxies, a sub-sample of quiescent ones (selected through a cut to log (SSFR/ yr-1) ≤ −11) and the AGN sample. The size of the AGN sample is too small to draw conclusions as a function of mass, therefore only the integral of the stellar mass functions for galaxies more massive than log (M∗) = 11 is considered. (This new cut further reduces the sample to 71 sources.) These results are shown in Fig. 10. Error bars were computed by simply summing all the 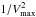 terms due to Poisson statistics, as explained in Bolzonella et al. 9.
terms due to Poisson statistics, as explained in Bolzonella et al. 9.
 |
Fig. 10 Redshift evolution of the integrated mass functions. Upper panel: value of the integrated mass functions. The curves refer to all UltraVISTA galaxies (green diamonds) and to a selection of only the quiescent ones (red triangles) and the radio AGN sample (cyan squares). Lower panel: ratio of the integrated mass function values for AGN hosting and quiescent galaxies. Points have been placed at values of redshift corresponding to the mean redshift of each redshift bin. |
Although the integrated mass function for all galaxies varies, within a factor ∼2, between the redshift bins [ 1.0−2.0 ] and [ 0.7−1.0 [ the corresponding variation for the integrated mass function of quiescent and radio AGNs is even stronger (a factor ∼5 and almost an order of magnitude for the two samples respectively). In these same redshift bins the ratio of radio AGN hosting to quiescent galaxies increases from ∼0.02 to ∼0.04. This increase could confirm that the presence of a radio AGN is a phenomenon that evolves with quiescent galaxies, but at a different rate.
To explore whether the ratio of radio AGNs to quiescent galaxies also evolves as a function of the local density, all samples have been divided in two, considering objects above and below the median of the overdensity richness distributions of all galaxies as obtained with our method. With these cuts, the number of objects in the AGN sample in the high/low density regions are, respectively, 13/3, 33/11,17/10 for the low, middle, and high redshift bins. For the quiescent sample, the statistics are, instead, always in the 2000–3000 range in every redshift bin.
As expected, the objects from the AGN sample are systematically more numerous above the median value than below. This could indicate the effect previously discovered in a more significant way of radio AGNs being found in higher density environments. The effect of the environment on the integrated mass functions and on the ratio of AGN-hosting to quiescent galaxies is shown in Fig. 11.
 |
Fig. 11 Environment effect on the integrated mass functions. All samples have been split in two, as stated by the legend, with the terms “Over”and “Under”referring to high-density environments (over the median value) and low-density ones (under the median value). Upper panel: red and purple triangles refer to quiescent UltraVISTA galaxies, cyan and blue squares to the AGN sample. Lower panel: black and grey curves represent the ratio of AGN hosting to quiescent galaxies. Solid lines are for high-density environments, dashed lines for the low-density ones. Points have been placed at values of redshift corresponding to the mean redshift of each redshift bin. |
The ratio of AGN-hosting galaxies to quiescent ones shows that the environmental segregation is present. In particular the ratio is higher in high-density environments than in low-density ones at z ≤ 0.7. In the first redshift bin there is a factor ∼4 difference between high- and low-density environments. This seems to indicate that the environmental segregation is somewhat more important for radio AGNs. Also, while the evolution is similar, both the integrated mass function of the AGN sample and the ratio of AGN to quiescent galaxies show an enhanced probability that a galaxy hosts a radio AGN in high-density environments in the lowest redshift bin. This result is in very good agreement with what has been found in previous sections with other methods.
9. Conclusions and summary
The aim of this work was to investigate the role of the environment in determining the presence and the properties of radio AGN phenomena. These phenomena are predicted and needed by the theory of galaxy formation, therefore understanding the way environment influences their development could lead to a better comprehension of the processes through which galaxies are formed. The deep photometric redshift sample extracted from the COSMOS survey 32 was used, together with the VLA-COSMOS survey 45 for the radio data.
From these surveys, various samples were extracted, with particular focus on AGN samples. Results may be summarized as follows:
-
1.
Analysing the R sample and the RO Control sample, it wasfound that the environment where radio sources reside issignificantly denser than the environment around galaxieswithout radio emission.
-
2.
These results are not due to radio sources being hosted by high-mass galaxies (which in turn are known to reside in denser environments). In fact, by repeating the environment estimate on samples designed to have the same stellar mass distributions (MR and MO samples) the effect of radio sources residing in systematically and significantly denser environments still holds.
-
3.
A sample of radio AGNs was extracted from the whole catalogue of radio sources. The environment around radio AGNs is significantly denser than the environment around normal galaxies in the same stellar mass and specific SFR range (QO sample). This shows that the environmental segregation that was found is actually due to an enhanced probability that galaxies host a radio AGN in denser environments. This led to concluding that environment plays a role in determining the onset of AGN phenomena in galaxies and that these phenomena are important in the process of galaxy formation.
-
4.
The environmental effect in enhancing the probability of a galaxy hosting a radio AGN is dominated by low-power radio AGNs. In fact, the difference in the environment between low-power radio AGNs and normal galaxies is significant, while for high-power radio AGNs it is not. This was found by splitting all the previously analysed samples according to a cut in their radio luminosity. This effect of low-power radio AGNs showing the only signal of environmental segregation could be related to the thermodynamic properties of the gas fuelled to the AGN see for example 29.
-
5.
After analysing the integrated mass functions, calculated for the whole population of the UltraVISTA galaxies and sub-samples of only quiescent and radio AGN-hosting ones, hints of a redshift evolution can be found. This can be seen both in the decrease in the value of the integrated mass functions with redshift for the samples of quiescent galaxies and radio AGNs, as well as in the same decrease with redshift in their ratio.
-
6.
Exploring the dependence from the environment of the integrated mass functions, it is found that the fraction of radio AGNs is always enhanced in high-density environments, in agreement with the stronger results found using richness distributions. Moreover, radio AGNs are also the population with the greatest difference in the values of integrated mass functions between high- and low-density environments.
The picture that emerges from this work is that a high-density environment is indeed related to the presence and the properties of radio AGNs. This is in good agreement with the current theory of galaxy formation, which predicts that galaxies in high-density environments undergo SF quenching faster and in a more efficient way. Future studies and the increase in the statistics for the mass functions could open the way to more thorough analysis of the existing correlations.
Online material
Appendix A: Tables of host X-ray clusters and galaxy groups
In this Appendix the complete tables of candidate associations between radio AGNs found in this work and known clusters and groups catalogues are reported.
Candidate associations of radio AGNs and X-ray clusters from the catalogue of Finoguenov et al. 27.
Candidate associations between radio AGN and groups from the catalogue of Knobel et al. 35.
Acknowledgments
Part of this work is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO programme ID 179.A-2005 and on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium. We thank the anonymous referee for the helpful comments.
References
- Avni, Y., &Bahcall, J. N. 1980, ApJ, 235, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Bardelli, S.,Zucca, E.,Bolzonella, M., et al. 2009, A&A, 495, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardelli, S.,Schinnerer, E.,Smolčic, V., et al. 2010, A&A, 511, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F. 2003, ApJ, 586, 794 [Google Scholar]
- Berta, S.,Lutz, D.,Santini, P., et al. 2013, A&A, 551, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Best, P. N. 2000, MNRAS, 317, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N. 2004, MNRAS, 351, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N.,Kauffmann, G.,Heckman, T. M., &Ivezić, Ž. 2005, MNRAS, 362, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M.,Pelló, R., &Maccagni, D. 2002, A&A, 395, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolzonella, M.,Kovač, K.,Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brusa, M.,Zamorani, G.,Comastri, A., et al. 2007, ApJS, 172, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P.,Aussel, H.,Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Castignani, G.,Chiaberge, M.,Celotti, A., &Norman, C. 2014, ApJ, 792, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Castignani, G.,Chiaberge, M.,Celotti, A.,Norman, C., & De Zotti, G. 2014, ApJ, 792, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M.,Capetti, A.,Macchetto, F. D., et al. 2010, ApJ, 710, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Chuter, R. W.,Almaini, O.,Hartley, W. G., et al. 2011, MNRAS, 413, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Ciliegi, P.,Zamorani, G.,Bondi, M., et al. 2005, A&A, 441, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooke, R.,Pettini, M., &Murphy, M. T. 2012, MNRAS, 425, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J.,Springel, V.,White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O.,Iovino, A.,Kovač, K., et al. 2010, A&A, 524, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O.,Marinoni, C.,Iovino, A., et al. 2010, A&A, 520, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I.,Gruppioni, C.,Pozzi, F., et al. 2014, MNRAS, 439, 2736 [NASA ADS] [CrossRef] [Google Scholar]
- Donoso, E.,Li, C.,Kauffmann, G.,Best, P. N., &Heckman, T. M. 2010, MNRAS, 407, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., &Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A.,Guzzo, L.,Hasinger, G., et al. 2007, ApJS, 172, 182 [Google Scholar]
- Granato, G. L., De Zotti, G.,Silva, L.,Bressan, A., &Danese, L. 2004, ApJ, 600, 580 [Google Scholar]
- Hardcastle, M. J.,Evans, D. A., &Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Hatch, N. A.,Wylezalek, D.,Kurk, J. D., et al. 2014, MNRAS, 445, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Hickox, R. C.,Jones, C.,Forman, W. R., et al. 2009, ApJ, 696, 891 [Google Scholar]
- Ilbert, O.,Capak, P.,Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knobel, C.,Lilly, S. J.,Iovino, A., et al. 2012, ApJ, 753, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K.,Lilly, S. J.,Cucciati, O., et al. 2010, ApJ, 708, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Ledlow, M. J., &Owen, F. N. 1996, AJ, 112, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O.,Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V.,Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lutz, D.,Poglitsch, A.,Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCracken, H. J.,Milvang-Jensen, B.,Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miley, G., & De Breuck, C. 2008, A&ARv, 15, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J.,Lilly, S. J.,Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Quadri, R. F.,Williams, R. J.,Franx, M., &Hildebrandt, H. 2012, ApJ, 744, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E.,Smolčić, V.,Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E.,Sargent, M. T.,Bondi, M., et al. 2010, ApJS, 188, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N.,Aussel, H.,Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N.,Arnouts, S.,Aussel, H., et al. 2013, ApJS, 206, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V.,Schinnerer, E.,Scodeggio, M., et al. 2008, ApJS, 177, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, W., &Saunders, W. 1992, MNRAS, 259, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Wylezalek, D.,Galametz, A.,Stern, D., et al. 2013, ApJ, 769, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E.,Bardelli, S.,Bolzonella, M., et al. 2009, A&A, 508, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Number of extractions of the various Control samples that are below the significance threshold of 0.05.
Number of extractions of the various Control samples that are below the significance threshold of 0.05.
Candidate associations of radio AGNs and X-ray clusters from the catalogue of Finoguenov et al. 27.
Candidate associations between radio AGN and groups from the catalogue of Knobel et al. 35.
All Figures
 |
Fig. 1 Redshift distributions. The black solid line refers to the O sample, the red dashed one to the R sample, the cyan dot-dashed line refers to the MR sample and the green triple dot-dashed one refers to the AGN sample. |
| In the text | |
 |
Fig. 2 Stellar mass distributions. The black solid line refers to the O sample, the red dashed one to the R sample, the cyan dot-dashed line refers to the MR sample and the green triple dot-dashed one refers to the AGN sample. |
| In the text | |
 |
Fig. 3 SSFR–M∗ plane. The black crosses refer to the R sample, the red triangles to the AGN sample defined through the SSFR cut and the cyan squares to the AGN sample defined through SFR comparison. The green lines correspond to the cuts in stellar mass and SSFR described in text. In yellow, the O sample is reported for comparison. |
| In the text | |
 |
Fig. 4 AGN sample definition. The black crosses represent the R sample, the red triangles represent the AGNs selected through the cut in SSFR, while the cyan squares represent the AGN sample defined through SFR comparison. The dashed green line represents the linear fit relation described in text, while the solid blue line shows the SFRRadio = SFRSED relation. |
| In the text | |
 |
Fig. 5 Galaxy overdensity richness distributions, R and RO samples. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The red solid line refers to the R sample, and the grey lines correspond to the 100 extractions of the RO Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
| In the text | |
 |
Fig. 6 Galaxy overdensity richness distributions, samples MR and MO. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The solid red line refers to the MR sample, the grey lines correspond to the 100 extractions of the MO Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
| In the text | |
 |
Fig. 7 Galaxy overdensity richness distributions, samples AGN and QO. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The solid red line refers to the AGN sample, the grey lines correspond to the 100 extractions of the QO Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
| In the text | |
 |
Fig. 8 Redshift dependence of radio luminosity. Only the R sample is represented. |
| In the text | |
 |
Fig. 9 Galaxy overdensity richness distributions, samples AGNL and QOL. The top panel refers to 0 ≤ z< 0.7, the middle panel to 0.7 ≤ z< 1, and the bottom panel to 1 ≤ z ≤ 2. The solid red line refers to the AGNL sample, the grey lines correspond to the 100 extractions of the QOL Control sample. The dashed black line is the richness distribution of the Control sample extraction corresponding to the median value of the KS probability value distribution. |
| In the text | |
 |
Fig. 10 Redshift evolution of the integrated mass functions. Upper panel: value of the integrated mass functions. The curves refer to all UltraVISTA galaxies (green diamonds) and to a selection of only the quiescent ones (red triangles) and the radio AGN sample (cyan squares). Lower panel: ratio of the integrated mass function values for AGN hosting and quiescent galaxies. Points have been placed at values of redshift corresponding to the mean redshift of each redshift bin. |
| In the text | |
 |
Fig. 11 Environment effect on the integrated mass functions. All samples have been split in two, as stated by the legend, with the terms “Over”and “Under”referring to high-density environments (over the median value) and low-density ones (under the median value). Upper panel: red and purple triangles refer to quiescent UltraVISTA galaxies, cyan and blue squares to the AGN sample. Lower panel: black and grey curves represent the ratio of AGN hosting to quiescent galaxies. Solid lines are for high-density environments, dashed lines for the low-density ones. Points have been placed at values of redshift corresponding to the mean redshift of each redshift bin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


