| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 21 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201424759 | |
| Published online | 02 April 2015 | |
Gaia-ESO Survey: Analysis of pre-main sequence stellar spectra
1 Università di Catania, Dipartimento di Fisica e Astronomia, Sezione Astrofisica, via S. Sofia 78, 95123 Catania, Italy
e-mail: Alessandro.Lanzafame@oact.inaf.it
2 INAF–Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
3 INAF–Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
4 INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
5 Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
6 Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
7 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
8 Universidad Complutense de Madrid, Departamento de Astrofísica, 28040 Madrid, Spain
9 Università di Palermo, Dipartimento di Fisica e Chimica, Viale delle Scienze, Ed. 17, 90128 Palermo, Italy
10 INAF–Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
11 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
12 Astrophysics Group, Research Institute for the Environment, Physical Sciences and Applied Mathematics, Keele University, Keele, Staffordshire ST5 5BG, UK
13 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
14 Research School of Astronomy & Astrophysics, Australian National University, Cotter Road, Weston Creek, ACT 2611, Australia
15 Rudolf Peierls Centre for Theoretical Physics, Keble Road, Oxford, OX1 3NP, UK
16 GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
17 Centre for Astrophysics Research, STRI, University of Hertfordshire, College Lane Campus, Hatfield AL10 9AB, UK
18 Lund Observatory, Department of Astronomy and Theoretical Physics, Box 43, 221 00 Lund, Sweden
19 Institute of Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
20 Departamento de Física, Ingeniería de Sistemas y Teoría de la Señal, Universidad de Alicante, Apdo. 99, 03080 Alicante, Spain
21 ESA, ESTEC, Keplerlaan 1, Po Box 299 2200 AG Noordwijk, The Netherlands
22 Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
23 INAF–Padova Observatory, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
24 Instituto de Astrofísica de Andalucía-CSIC, Apdo. 3004, 18080 Granada, Spain
25 Universidad de La Laguna, Dept. Astrofísica, 38206 La Laguna, Tenerife, Spain
26 Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
27 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
28 Moscow MV Lomonosov State University,Sternberg Astronomical Institute, 119992 Moscow, Russia
29 Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
30 Laboratoire Lagrange (UMR 7293), Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, CS 34229, 06304 Nice Cedex 4, France
31 Department for Astrophysics, Nicolaus Copernicus Astronomical Center, ul. Rabiańska 8, 87–100 Toruń, Poland
32 Institut d’Astronomie et d’Astrophysique, Université libre de Brussels, Boulevard du Triomphe, 1050 Brussels, Belgium
33 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
34 Instituto de Física y Astronomiía, Universidad de Valparaiíso, 951 Blanco, Chile
35 European Southern Observatory, Alonso de Cordova 3107 Vitacura, Santiago de Chile, Chile
Received: 5 August 2014
Accepted: 14 January 2015
Context. The Gaia-ESO Public Spectroscopic Survey is obtaining high-quality spectroscopy of some 100 000 Milky Way stars using the FLAMES spectrograph at the VLT, down to V = 19 mag, systematically covering all the main components of the Milky Way and providing the first homogeneous overview of the distributions of kinematics and chemical element abundances in the Galaxy. Observations of young open clusters, in particular, are giving new insights into their initial structure, kinematics, and their subsequent evolution.
Aims. This paper describes the analysis of UVES and GIRAFFE spectra acquired in the fields of young clusters whose population includes pre-main sequence (PMS) stars. The analysis is applied to all stars in such fields, regardless of any prior information on membership, and provides fundamental stellar atmospheric parameters, elemental abundances, and PMS-specific parameters such as veiling, accretion, and chromospheric activity.
Methods. When feasible, different methods were used to derive raw parameters (e.g. line equivalent widths) fundamental atmospheric parameters and derived parameters (e.g. abundances). To derive some of these parameters, we used methods that have been extensively used in the past and new ones developed in the context of the Gaia-ESO survey enterprise. The internal precision of these quantities was estimated by inter-comparing the results obtained by these different methods, while the accuracy was estimated by comparison with independent external data, such as effective temperature and surface gravity derived from angular diameter measurements, on a sample of benchmarks stars. A validation procedure based on these comparisons was applied to discard spurious or doubtful results and produce recommended parameters. Specific strategies were implemented to resolve problems of fast rotation, accretion signatures, chromospheric activity, and veiling.
Results. The analysis carried out on spectra acquired in young cluster fields during the first 18 months of observations, up to June 2013, is presented in preparation of the first release of advanced data products. These include targets in the fields of the ρ Oph, Cha I, NGC 2264, γ Vel, and NGC 2547 clusters. Stellar parameters obtained with the higher resolution and larger wavelength coverage from UVES are reproduced with comparable accuracy and precision using the smaller wavelength range and lower resolution of the GIRAFFE setup adopted for young stars, which allows us to provide stellar parameters with confidence for the much larger GIRAFFE sample. Precisions are estimated to be ≈120 K rms in Teff, ≈0.3 dex rms in log g, and ≈0.15 dex rms in [Fe/H] for the UVES and GIRAFFE setups.
Key words: open clusters and associations: general / surveys / methods: data analysis / stars: pre-main sequence / stars: fundamental parameters
© ESO, 2015
1. Introduction
Spectrum analyses of pre-main sequence (PMS) stars require special techniques to resolve the peculiarities of cool, low-mass members of young clusters. Optical spectra of such stars may include veiling, large broadening due to fast rotation, emission lines due to accretion and/or chromospheric activity, and molecular bands. Subtracting inhomogeneous and variable nebular emission may also be problematic, and some residual features can remain in spectra of some young cluster members after removing the sky-background.
One of the main objectives of the Gaia-ESO Survey is to provide radial velocities (RV) with a precision ≈0.2−0.25 km s-1 for stars in young open clusters to complement Gaia proper motions with comparable accuracy for a statistically significant sample (Gilmore et al. 2012; Randich et al. 2013) that also reaches fainter targets. In addition, this survey complements Gaia by deriving metallicity and detailed abundances for several elements, including lithium, which is particularly relevant to study the evolution of low-mass stars and determine cluster ages. This requires deriving all fundamental parameters (effective temperatures Teff, metallicity [Fe/H], surface gravity log g, and projected rotational velocity vsini) independently of the Gaia results.
The Hα profile of these young low-mass stars bears information on their chromospheric activity, accretion rate, and mass loss. Because of their common origin, strong accretion is expected to be correlated with veiling; this can be used to verify our results because no correlation would be indicative of large uncertainties, and to explore the extent and details of such a correlation. Chromospheric activity is known to depend on stellar rotation, and both evolve in time; Gaia-ESO is also going to provide the possibility of exploring the activity-rotation relation and their evolution on a large sample of young stars.
The Gaia-ESO target selection aims at producing unbiased catalogues of stars in open clusters. Selection criteria based mainly on photometry, supported, when possible, by kinematic memberships, have been adopted for this purpose, although this implies that a large number of non-members are also observed, which are identified a posteriori from the radial velocity measurements (Bragaglia et al., in prep.). In our case, the GIRAFFE targets are late-type (F to early-M) stars in the magnitude range 12 ≤ V ≤ 19 mag in the PMS or main sequence (MS) phase. Based on available information, the selection of UVES targets tries to include only slowly rotating (vsini< 15 km s-1) single G–K stars in the magnitude range 9 <V< 15 without or with weak accretion (Ṁacc< 10-10 M⊙ yr-1). To optimise the throughput of the survey, observations of cool stars in the fields of young open clusters are only carried out in the GIRAFFE/HR15N setup (R = 17 000, λ from 6470 to 6790 Å) and the Red 580 UVES setup (R = 47 000 centred at λ = 5800 Å with a spectral band of 2000 Å). The Medusa mode of the fibre-fed system is used throughout the survey, allowing the simultaneous allocation of 132 and 8 fibres feeding GIRAFFE and UVES, respectively, with about 20 (GIRAFFE) and 1 (UVES) fibres used to observe the sky background spectrum.
The GIRAFFE/HR15N setup covers the Hα and Li (6707.84 Å) lines and is therefore particularly useful to study young stars. However, Teff, log g, and [Fe/H] diagnostics in this wavelength range are poorer than in other settings and still not satisfactorily reproduced by theoretical models. For example, the paucity of Fe lines in the HR15N spectral range makes it difficult to derive log g and [Fe/H] in G-type stars from the analysis of the equivalent widths of the Fe i and Fe ii lines.
This paper presents the analysis of the Gaia-ESO spectra in the fields of young open clusters (age <100 Myr) and is one of a series describing the Gaia-ESO survey in preparation of its first release of advanced data products. Other papers in this series will discuss the Gaia-ESO scientific goals, observations strategies, team organisation, target selection strategy, data release schedule, data reduction, analysis of OBA-type and FGK-type stars not in the fields of young open clusters, non-standard objects and outliers, external calibration, and the survey-wide homogenisation process.
The paper is organised as follows: in Sect. 2 we present the data analysed in the first two Gaia-ESO internal data releases. In Sect. 3 we outline the principles and general strategies of the Gaia-ESO PMS analysis. Methods and validation for the initial raw measurements, fundamental parameters (Teff,log g, [Fe/H], micro-turbulence velocity, veiling, and vsini), and derived parameters (chromospheric activity, accretion rate, and elemental abundances) are presented in Sects. 4−6. We conclude in Sect. 7.
2. Data
Young open clusters (age <100 Myr) observed by the Gaia-ESO survey in the first 18 months of observations, whose analysis is discussed in this paper.
The survey analysis is performed in cycles, following the data reduction of newly observed spectra. Each new analysis cycle improves upon the last one with updated input data (e.g. atomic and molecular data), improved analysis methods, and improved criteria to define the final recommended parameters. At the end of each cycle an internal data release (iDR) is produced and made available within the Gaia-ESO consortium for scientific validation. We here describe the methods and recommended parameter criteria applied to the analysis of the first two years of observations, which will form the basis of the first release of advanced data products to ESO. The validation procedures presented in this paper consider the first 18 months of observations (iDR1 and iDR2).
The young open clusters observed in the first 18 months of observations are listed in Table 1, along with the total number of observed stars for each cluster and the number of stars identified as T Tauri from the properties of Hα emission, spectral type, and Li absorption (see Sect. 4.1). A total of 813 and 45 T Tauri stars have been identified in the GIRAFFE and UVES spectra, respectively. The memberships of these young clusters, including stars not clearly showing the T Tauri distinctive features, will be discussed in other Gaia-ESO science verification papers (e.g. Jeffries et al. 2014). The 200 Myr cluster NGC 6705 (M11) has been observed in different setups (see e.g. Cantat-Gaudin et al. 2014b) to allow inter-comparison and validation of the analysis methods across the survey and, for this purpose, is included in our analysis.
3. General analysis strategy
The Gaia-ESO consortium is set up in several working groups (WGs). The analysis of PMS stars is carried out by WG12, to which six nodes contributed: INAF–Osservatorio Astrofisico di Arcetri, Centro de Astrofisica de Universidade do Porto (CAUP), Università di Catania and INAF–Osservatorio Astrofisico di Catania (OACT), INAF–Osservatorio Astronomico di Palermo (OAPA), Universidad Complutense de Madrid (UCM), and the Eidgenössische Technische Hochschule Zürich (ETH).
The main input to the Gaia-ESO PMS spectrum analysis consists of UVES and GIRAFFE spectra of cool stars in the field of young open clusters. The preliminary selection criteria are briefly outlined in Sect. 1 and will be detailed in one of the papers of this series (Bragaglia et al., in prep.).
Gaia-ESO PMS analysis output parameters.
The data reduction is performed as described in Sacco et al. (2014) for the UVES spectra and in Lewis et al. (in prep.) for the GIRAFFE spectra. These are wavelength calibrated and shifted to a barycentric reference frame. Sky-background subtraction, as well as a normalisation to the continuum, is also performed in the data reduction process. Multi-epoch spectra of the same source are combined in the co-added spectrum. Quality information is provided, including variance spectra, signal-to-noise ratio (S/N), non-usable pixels, etc. Additional inputs are the radial and rotational velocities, as described in Gilmore et al. (in prep.) and Sacco et al. (2014), and photometric data. Cluster distances and reddening are also considered as input to the spectrum analysis validation.
Double-lined spectroscopic binaries (SB2) and multiple systems are identified by examining the shape of the cross-correlation function. These stars are excluded from the current analysis, and a multiplicity flag is reported in the final database.
To ensure the highest homogeneity possible in the quantities derived, all the different Gaia-ESO spectrum analysis methods adopt the same atomic and molecular data (Heiter et al., in prep.) and the same set of model atmospheres (MARCS, Gustafsson et al. 2008).
The output parameters of the Gaia-ESO PMS spectrum analysis are listed in Table 2. To apply a detailed quality control on the output parameters and optimise the analysis according to the stellar characteristics, these are divided into three groups: raw, fundamental, and derived. Raw parameters are the Hα emission and Li equivalent widths (W(Hα) and W(Li)), and the Hα width at 10% of the line peak (Hα 10%, see, e.g., Natta et al. 2004). These are directly measured on the input spectra and do not require any prior information. They are measured before any other procedure to identify PMS stars, and their values are used to optimise the evaluation of the fundamental parameters in one of the methods used (see Sect. 5). In addition to Teff, log g, and [Fe/H]1, the fundamental parameters derived include also micro-turbulence velocity (ξ), projected rotational velocity (vsini), veiling (r, see, e.g., Hartigan et al. 1988), and a gravity-sensitive spectral index (γ, see Damiani et al. 2014). Finally, the derived parameters are those whose derivation requires prior knowledge of the fundamental parameters, that is, elemental abundances (log ϵ(X)2), mass accretion rate (Ṁacc), chromospheric activity indices (ΔW(Hα)chr and ΔW(Hβ)chr), and chromospheric line fluxes (F(Hα)chr and F(Hβ)chr).
Most parameters listed in Table 2 are derived from either UVES or GIRAFFE spectra, with the exception of ξ, ΔW(Hβ)chr, F(Hβ)chr, and log ϵ(X), which are derived from UVES spectra only, and the gravity-sensitive spectral index γ, which is derived from GIRAFFE spectra only (see Sect. 5).
In general, whenever possible, the same parameter is derived by different methods; this allows thoroughly checking the derived parameters by inter-comparing the results and flagging discrepant results, which are then used to outline possible weaknesses of the methods and discard unreliable results. In the absence of significant biases, the results from different methods are combined by taking a σ-clipped average to obtain the recommended parameters. If significant biases are present, all results obtained with a method that can give rise to inaccurate or unreliable results in some ranges of parameters are rejected before combining the results as above. These general criteria, whose application is discussed in detail in Sects. 4–6, are first applied on the raw parameters, then on the fundamental parameters, and finally on the derived parameters. The fundamental parameters are also validated by comparing the results of the analysis methods applied to our spectra against fundamental parameters from angular diameter and parallax measurements (Sect. 5.6). A comparison with Teff derived from photometry for objects that are not affected by photometric excesses is reported in Appendix C. The recommended raw and fundamental parameters are then used to produce the recommended derived parameters. When satisfactory comparisons cannot be achieved, recommended parameters are not provided and only results from individual nodes are made available. Recommended parameter uncertainties are estimated as both node-to-node dispersion and as average of individual node uncertainties. The final results minimise – as much as possible – biases that can affect individual methods, and the associated uncertainties take differences into account that may arise from the use of different methods and algorithms.
Final results are further validated by a general analysis of the output log g−Teff diagram, consistency of the parameters, and overview of the results based on the comparison of different clusters.
4. Raw measurements
Measuring the raw parameters before carrying out any other analyses allows us to (a) identify stars with strong accretion whose spectra may be affected by veiling; (b) perform a quality control on the raw parameters before they are used in the subsequent analysis; and (c) apply the appropriate masks to the spectra to determine fundamental parameters.
To derive raw parameters from a large dataset of spectra it is convenient to use procedures that are as automatic as possible. In the case of PMS sources extending to M spectral type, however, such procedures must also be capable to handle large rotational broadening and molecular bands. Here different methods are used, with different levels of automatism, which allows examining biases, eliminate systematic discrepancies, and combine the results with a σ-clipping to disregard casual mistakes and outliers.
In the following we briefly describe the methods used to derive the raw parameters.
4.1. Hα equivalent width and Hα width at 10% of the line peak
Spectra with Hα in emission are examined to identify stars with strong accretion that are therefore probably affected by veiling. To do this, we used their W(Hα) and Hα 10% measurements.
The Arcetri node measures W(Hα) and Hα 10% on the continuum-normalised co-added spectra of all stars that clearly show Hα emission with a semi-automatic procedure. After manually defining the wavelength range and level of continuum, W(Hα) is calculated by a direct integration of the flux above the continuum, while Hα 10% is derived by considering the level corresponding to 10% of the maximum flux above the continuum in the selected wavelength range. All measurements are visually checked and repeated in case of miscalculation (e.g. caused by multiple peaks). Uncertainties are estimated using multi-epoch observations of stars belonging to the first two young clusters that have been observed (i.e. γ Vel and Cha I). Specifically, W(Hα) and Hα 10% are first measured on each spectrum before co-adding, then the relative uncertainty for each star is estimated as , where W1 and W2 are two measurements for the same star from spectra observed at different epochs. A similar formula is used for ΔHα 10%. Finally, the medians of ΔW(Hα) and ΔHα 10% are assumed as the relative uncertainties for all stars3.
The CAUP node makes use of an automatic IDL4 procedure to first select stars with Hα in emission and then measure Hα 10% and W(Hα) on the normalised spectra. Measurement uncertainty is evaluated from the spectrum S/N.
The OACT node pre-selects spectra with Hα in emission by visual inspection. Then, W(Hα) and Hα 10% are measured using an IDL procedure. W(Hα) is measured by a direct integration of the Hα emission profile, and its uncertainty is evaluated by multiplying the integration range by the mean error in two spectral regions close to the Hα line. The Hα 10% uncertainty is evaluated by assuming an error of 10% in the position of the continuum level.
The OAPA node employed two methods, one based on DAOSPEC (Stetson & Pancino 2008) and an IDL procedure, the other on a combination of IRAF and IDL tools. In the first method, DAOSPEC is used to perform a continuum fit of the spectral region around Hα. The Hα profile in the unnormalised input spectrum is masked by giving a variable FWHM as input to DAOSPEC that takes the rotational and instrumental profiles into account. The fitted continuum is then used to normalise the input spectrum. This continuum-normalised spectrum is used to measure Hα 10% with an automatic IDL procedure. Since the uncertainties are assumed to be dominated by the fitting of the continuum, this is repeated four times using different orders (10, 15, 20, and 25) of the polynomial fitting in DAOSPEC. The resulting Hα 10% values are then averaged to produce the final result. In the second method the normalisation is performed through IRAF with three different orders of the polynomial fitting (2, 5, and 10), then W(Hα) and Hα 10% are measured with an automatic IDL routine and uncertainties derived as above. A final visual inspection is performed to verify the results and identify broad emission and P Cygni-like profiles. For the first data release both methods where used, while in the second data release only the second method was used.
The final spectra of NGC 2264 are affected by some residual nebular emission, and a good subtraction of this contribution from the Hα emission line cannot be achieved because the nebular emission is concentrated in the region near the Hα line peak and is spatially variable (see a detailed description of this topic for the analogous case of the cluster NGC 6611 in Bonito et al. 2013). In this case, additional visual inspection of the spectra was necessary to ensure that the narrow nebular emission did not significantly affect the measurements.
 |
Fig. 1 W(Hα) vs. Hα 10% for all young open clusters observed in the first 18 months of observations. Filled symbols are used for stars classified as CTTS, open symbols for stars classified as WTTS. |
In the node-to-node comparison of the W(Hα) results, average differences and dispersions ~5 Å were found in the analysis of both UVES and GIRAFFE spectra, with only a few outliers. Average differences in Hα 10% in the node-to-node comparison was ~10 km s-1, with a dispersion ~50 km s-1.
Only a 1σ-clipping was therefore applied before computing the average W(Hα) and Hα 10% as recommended values. The recommended uncertainty was given, conservatively, as the largest amongst the average of individual uncertainties and the standard deviation of the mean.
The recommended Hα 10% is used, together with the recommended W(Li) (Sect. 4.2), in our WTTS/CTTS classification. If the Hα is in emission and W(Li)> 100 mÅ, the star is identified as a T Tauri. Following White & Basri (2003), the T Tauri star is then classified as CTTS if Hα 10%≥ 270 km s-1.
A comparison of W(Hα) vs. Hα 10% for all young open clusters observed in the first 18 months of observations is shown in Fig. 1. Note that the correlation of the two parameters is as expected from other works (e.g., White & Basri 2003) and the fraction of CTTS consistently decreases with the age of the cluster.
4.2. Li equivalent width
 |
Fig. 2 Illustrative node-to-node W(Li) comparison for γ Vel. Left panel: comparison between OAPA (DAOSPEC, iDR1) and Arcetri (iDR2) for GIRAFFE spectra. Right panel: comparison between Arcetri code and OACT (IRAF) for UVES spectra. Arrows indicate upper limits. |
At young ages, the Li doublet line is often in the saturation regime, and the rotational broadening frequently dominates. As a consequence, in general, a direct profile integration of the Li line is to be preferred to a Gaussian or a Voigt profile fitting in deriving W(Li). Furthermore, due to rotational broadening, the integration wavelength interval is very different from one spectrum to another. The Li doublet is also superimposed to molecular bands in spectra of M-type stars, which makes the placement of the continuum difficult, particularly when using automatic procedures. In such cases, interactive procedures like those available in IRAF remain one of the best options for measuring W(Li), at least for comparison purposes, even though these procedures are slow and prone to human error and subjective choices. Weak Li lines in slowly rotating stars, on the other hand, can reliably be fitted with a Gaussian or a Voigt profile and integrated analytically; this method can be easily implemented in automatic procedures and is more accurate than low-order numerical integration at low S/N.
The Gaia-ESO PMS analysis makes use of three independent methods to derive W(Li) from the GIRAFFE spectra: the direct profile integration available in the IRAF-splot procedure (OACT node), DAOSPEC (Stetson & Pancino 2008, OAPA node), and a semi-automatic IDL procedure specifically developed for the Gaia-ESO by the Arcetri node.
The IRAF-splot task was applied by the OACT node to the unnormalised spectra to make use of the built-in Poisson statistics model of the data. These measurements are only performed when the Li line and nearby continuum are clearly identifiable, which implies that, in general, small W(Li) (≲10 mÅ), low S/N (≲20), and spectra with very high vsini (≳200 km s-1) are not considered.
The DAOSPEC (OAPA) measurements were applied to all iDR1 spectra with S/N> 20 and to spectra with S/N< 20 showing a strong lithium line. The spectra were re-normalised before the equivalent width was determined using high-order Legendre polynomial fitting, which allows following the shape of molecular bands in M-type stars and still maintain a good agreement with the continuum of earlier type stars. The typical width of absorption lines in each spectrum was estimated by convolving the instrumental and rotational profile using vsini from the data reduction pipeline. Relative internal uncertainties are always better than 5% for high equivalent widths (>200 mÅ) and degrade up to ~50% for very low equivalent widths (~10 mÅ).
The semi-automatic IDL procedure developed by the Arcetri node performs a spline fitting of the continuum over a region of ± 20 Å around the Li line using an iterative σ-clipping and masking both the Li line and the nearby Ca i line at 6717.7 Å. When the automatic continuum fitting is not satisfactory (generally for poor S/N spectra or M-type stars), the fit is repeated by setting the continuum level manually. The W(Li) is then computed by direct integration of the line within a given interval, which depends on the stellar rotation and was determined by measuring the line widths on a series of rotationally broadened synthetic spectra. Errors are derived using the formula of Cayrel (1988), when no Li line (including blends) is visible, the upper limit is set as three times the error.
The contribution of lines blended with Li in the GIRAFFE spectra was estimated after determining the fundamental parameters (Sect. 5) by a spectral synthesis using Spectroscopy Made Easy (SME, Valenti & Piskunov 1996) with MARCS model atmospheres as input, taking the stellar Teff, log g, and [Fe/H] into account. For solar metallicity dwarfs above 4000 K the estimated blends agree with the relation reported by Soderblom et al. (1993).
Four nodes (Arcetri, CAUP, OACT, and UCM) calculated W(Li) in the UVES spectra. At the UVES resolution, when the star rotates slowly (vsini≲ 25 km s-1) and the S/N is sufficiently high (S/N ≳ 60), it is possible to de-blend the Li line from the nearby features.
Both the CAUP and UCM nodes employed the splot task in IRAF on the unnormalised UVES spectra. When the Li line and the nearby blends, mainly with Fe lines, are distinguishable, these are de-blended, in which case a Gaussian fitting to the line profile is adopted. In contrast, when the lines are indistinguishable, the blend contribution is estimated using the ewfind driver within MOOG code (Sneden 1973), and a direct integration of the line is adopted.
The Arcetri node adopted the same method as was used for GIRAFFE (see above), except when it was possible to de-blend the line using IRAF, as done by the CAUP and UCM nodes. When this was not possible, the blends were estimated using SME.
For iDR1, the OACT node employed IRAF as for the GIRAFFE spectra, using SME to estimate the blends. For iDR2, W(Li) was derived by subtracting the spectra with the template with the closest fundamental parameters but no (or negligible) Li absorption. In this latter case the blends are removed by the spectra subtraction itself.
We emphasise that the PMS analysis output includes blend-corrected and -uncorrected W(Li). When a node does not provide blend-corrected W(Li), this is estimated using SME and the node’s fundamental parameters if available. In analysing GIRAFFE spectra, blends are estimated using SME in all cases; the recommended blend-corrected W(Li) are calculated from the recommended blend-uncorrected W(Li) using the recommended fundamental parameters. Conversely, in the analysis of UVES spectra, the recommended blend-corrected W(Li) are derived by averaging the node values, as discussed below.
The blend-uncorrected W(Li) obtained by the three different methods from GIRAFFE spectra were first compared to check for systematic differences before combining them to produce the final results (see Fig. 2 for an illustrative comparison). After discarding results of one node that were inconsistent with the other two, no significant bias remained and the relative standard deviation of the W difference was at 20% level. Moreover, no trend of the node-to-node differences with respect to S/N nor vsini was present in the selected results. As a conservative uncertainty estimate on the recommended W(Li) we adopted the larger of the standard deviations and the mean of the individual method uncertainties. In iDR1, 90% of the W(Li) measurements have relative uncertainties better than 14% and 28% in γ Vel and Cha I, respectively, the differences being due to the higher fraction of stars of low Teff and spectra with lower S/N in Cha I with respect to γ Vel. About 90% of all the iDR2-GIRAFFE W(Li) measurements have an uncertainty better than 16 mÅ.
In the W(Li) UVES measurements no systematic deviation nor trends of the node-to-node differences with S/N nor vsini were found from the node-to-node comparison (see Fig. 2 for an illustrative comparison), and the recommended values were derived by taking the mean with a 1σ-clipping. In iDR1 the median uncertainties are 3 mÅ (4%) and 10 mÅ (3%) for γ Vel and Cha I, respectively5. About 90% of all the iDR2-UVES W(Li) measurements have an uncertainty better than 22 mÅ.
When all W(Li) measurements for a given star are flagged as upper limits, the recommended W(Li) is also flagged as an upper limit and the lowest measurement is adopted. Conversely, when at least one W(Li) measurement for a given star is not flagged as upper limit, all upper limit estimates for that star are disregarded, and the recommended value is derived as above.
 |
Fig. 3 Blend-corrected W(Li) vs. Teff for all young open clusters observed in the first 18 months. For comparison, the lower and upper envelope in the Pleiades are shown as solid lines, while dashes and dotted lines are the upper envelopes of IC 2602 and the Hyades, respectively. Dots are used for nonmembers. Upper limits are not included for clarity. |
Recommended blend-corrected W(Li) vs. Teff are shown in Fig. 3, compared with the Pleiades upper and lower envelope and the upper envelopes of IC 2602 (30 Myr) and the Hyades (Sestito & Randich 2005, and references therein). Note the increasing Li depletion with age at Teff≳ 3500 K and the lack of depletion at lower Teff as expected. A comparison with theoretical models can be found in Jeffries et al. (2014) for γ Vel. The NGC 2547 Li depletion pattern is found in remarkable agreement with Jeffries & Oliveira (2005).
5. Fundamental parameters
Two nodes (OACT and OAPA) provide fundamental parameters from the analysis of GIRAFFE spectra, and four nodes (Arcetri, CAUP, OACT, and UCM) from the analysis of UVES spectra. With the exception of OACT, the nodes analysing UVES spectra use similar, classical procedures, that is, measurements of equivalent widths and MOOG (Sneden 1973), enforcing the usual equilibrium relations. However, different strategies are adopted to select the lines to be used and in the automatisation of the procedures, as described in Sects. 5.3−5.5.
As anticipated in Sect. 3, the validation of fundamental parameters is carried out internally by a node-to-node comparison (Sect. 5.7) and externally by comparisons with Teff and log g derived from angular diameter measurements on a sample of stars taken as benchmark (Sect. 5.6)
5.1. OACT
The code ROTFIT (e.g., Frasca et al. 2006) has been extensively used to determine fundamental parameters in PMS stars. It compares the target spectrum with a set of template spectra from ELODIE observations of slowly rotating non-active stars (Prugniel & Soubiran 2001) that are artificially rotation-broadened and veiled at varying vsini and r. Below we briefly summarise the method implemented by ROTFIT, together with some adaptations to the case at hand.
In ROTFIT, the template spectra that most closely reproduce the target spectrum when broadened and veiled are selected and their weighted average Teff, log g, and [Fe/H] assigned to the target star. As a figure of merit, the χ2 calculated on the target spectrum and the rotational-broadened and veiled template spectrum is adopted. The weight used in the average is proportional to χ-2. We discuss the ROTFIT templates together with the homogenisation with the Gaia-ESO spectrum analysis in Appendix A. The ROTFIT analysis requires different wavelength masks for different types of objects. The masking criteria to apply this to the Gaia-ESO survey are reported in Appendix B.
For the GIRAFFE/HR15N spectra the whole spectral range from 6445 to 6680 Å and the ten best templates (i.e. with the lowest χ2) are considered. The UVES 580 spectra are independently analysed on segments of 100 Å each (excluding the parts that contain strong telluric lines and the core of Balmer lines), by considering only the five best templates for each segment. The final parameters Teff, log g, [Fe/H], and vsini are obtained by taking the weighted averages of the mean values for each segment, with the weight being proportional to χ-2 and to the amount of information contained in the segment, quantified by the total line absorption fi = ∫ (Fλ/FC − 1)dλ (where Fλ/FC is the continuum normalised flux).
The Teff, log g, [Fe/H], and vsini uncertainties are given as the standard errors of the weighted means, to which the average uncertainties of the templates’ stellar parameters are added quadratically. These are estimated to be ±50 K, ±0.1 dex, ±0.1 dex, and ±0.5 km s-1 for Teff, log g, [Fe/H], and vsini, respectively. The target spectral type corresponds to that of the best template.
The code also provides an estimate of the veiling by searching for the r value that gives the lowest χ2. The determination of the fundamental parameters for a star with veiling is more uncertain than in the non-veiled case because (a) the depths of the lines and molecular bands are lower in veiled spectra; and (b) the determination of the veiling parameter r implies introducing an additional degree of freedom in the parameter fitting, degrading the overall accuracy with respect to the non-veiled stars. However, stars with mass accretion whose spectra are expected to be affected by veiling can be preliminarily identified based on the values of Hα 10% or W(Hα) (White & Basri 2003; Natta et al. 2004). It is therefore possible to restrict the veiling calculation to presumably accreting stars alone, thus preserving the accuracy for stars for which no veiling is expected. Following White & Basri (2003), we assume that stars with Hα 10%> 270 km s-1 can be optically veiled, with an additional margin to take uncertainties into account (see Sect. 4.1).
Within the Gaia-ESO analysis, vsini is also provided by WG8 for GIRAFFE spectra (Koposov et al., in prep.), together with radial velocities and a first estimate of fundamental parameters, using a conceptually similar approach but with a different fitting strategy and different templates. The comparison between the results of these two methods was useful in identifying WG8 unsuccessful fitting for some stars with strong veiling and emission lines. An illustrative comparison of the results of these two methods for γ Vel can be found in Frasca et al. (2015), who found a mean difference of ≈2.88 km s-1 and σ ≈ 6.27 for stars in the field of γ Vel. An investigation on the lower limit imposed by the resolution of the instruments by means of Monte-Carlo simulations is also reported in Frasca et al. (2015), according to which the lower vsini limit has been set to 7 km s-1 in GIRAFFE spectra and 3 km s-1 in UVES spectra.
5.2. OAPA
An alternative approach for GIRAFFE/HR15N spectra, proposed by Damiani et al. (2014), is based on spectral indices in different wavelength ranges of the spectrum. The derived spectral indices are calibrated against stars with known parameters, yielding quantitative estimates of Teff, log g, and [Fe/H]. This type of approach is usually applied to spectra with lower resolution than GIRAFFE. These narrow-band indices are affected by fast rotation: Teff becomes unreliable for vsini> 90 km s-1, [Fe/H] above 70 km s-1, and log g above 30 km s-1. Therefore, depending on the vsini of the star, not all parameters can be provided. Using an appropriate combination of flux ratios, this method is also capable of producing an independent estimate of the veiling parameter r (see, Damiani et al. 2014, for details).
5.3. Arcetri
The Arcetri node adopted DOOp (DAOSPEC Option Optimiser pipeline, Cantat-Gaudin et al. 2014a) to measure line equivalent widths and FAMA (Magrini et al. 2013) to determine the fundamental parameters. Line equivalent widths are measured using Gaussian fitting after a re-normalisation of the continuum; W in the range between 20–120 mÅ, for the Fe i and Fe ii lines, and in the range between 5–120 mÅ, for the other elements, were used. The code FAMA makes use of the Fe i and Fe ii equivalent widths to derive the fundamental stellar parameters. The stellar parameters are obtained by searching iteratively for the three equilibria (excitation, ionisation, and trend between log n(Fe i) and log (W/λ)), that is, with a series of recursive steps starting from a set of initial atmospheric parameters and arriving at a final set of atmospheric parameters that fulfils the three equilibrium conditions. The convergence criterion is set using the information on the quality of the W measurements, meaning that the minimum reachable slopes are linked to the quality of the spectra, as expressed by the dispersion around the average ⟨ log n(Fe i)⟩. This is correct in the approximation that the main contribution to the dispersion is due to the error in the W measurement and not to inaccuracy in atomic parameters, as is the case for example for the oscillator strengths (log gf).
5.4. CAUP
The fundamental parameters are automatically determined with a method used in previous works (e.g. Sousa et al. 2008, 2011) now adapted to the Gaia-ESO survey. The method is based on the excitation and ionisation balance of iron lines using [Fe/H] as a proxy for the metallicity. The iron lines constraining the parameters were selected from the Gaia-ESO line list using a new procedure detailed in Sousa et al. (2014). The equivalent widths are automatically measured using the ARES6 code (Sousa et al. 2007) following the approach of Sousa et al. (2008, 2011) that takes the S/N of each spectrum into account. The stellar parameters are computed assuming LTE using the 2002 version of MOOG (Sneden 1973) and the MARCS grid of atmospheric models. For this purpose, the interpolation code provided with the MARCS grid was modified to produce an output model readable by MOOG. Moreover, a wrapper program was implemented into the interpolation code to automatise the method. The atmospheric parameters are inferred from the previously selected Fe i–Fe ii line list. The downhill simplex (Press et al. 1992) minimisation algorithm is used to find the best parameters. To identify outliers caused by incorrect W values, a 3σ-clipping of the Fe i and Fe ii lines is performed after a first determination of the stellar parameters. After this clipping, the procedure is repeated without the rejected lines. The uncertainties in the stellar parameters are determined as in previous works (Sousa et al. 2008, 2011).
5.5. UCM
The UCM node employed the code StePar (Tabernero et al. 2012, 2013), which was modified to operate with the spherical and non-spherical MARCS models. For iDR1 the W measurements were carried out with the code ARES (Sousa et al. 2007)7. For iDR2 the UCM node adopted the code TAME (Kang & Lee 2012)8 The manual mode has an interface that allows the user control over the W measurements to verify problematic spectra when needed. We adopted the approach of Kang & Lee (2012) to adjust the TAME continuum σ rejection parameter according to the S/N of each spectrum. The code StePar computes the stellar atmospheric parameters using MOOG (Sneden 1973). The 2002 and 2013 versions of MOOG were used in iDR1 and iDR2, respectively. Five line lists were built for different regimes: metal-rich dwarfs, metal-poor dwarfs, metal-rich giants, metal-poor giants, and extremely metal-poor stars. The code iterates until it reaches the excitation and ionisation equilibrium and minimises trends of abundance vs. log (W/λ). The downhill simplex method (Press et al. 1992) was employed to minimise a quadratic form composed of the excitation and ionisation equilibrium conditions. The code performs a new simplex optimisation until the metallicity of the model and the iron abundance are the same. Uncertainties for the stellar parameters are derived as described in Tabernero et al. (2012, 2013). In addition, a 3σ rejection of the Fe i and Fe ii lines is performed after a first determination of the stellar parameters; StePar is then re-run without the rejected lines.
5.6. Comparison with benchmark stars
 |
Fig. 4 GIRAFFE benchmark comparison. Black for [Fe/H] < 0.1, blue for [Fe/H] > 0.1. Size is inversely proportional to log g in the Teff plot, proportional to Teff in the log g and [Fe/H] plot. |
The precision of the fundamental parameters can be assessed by comparison with results from accurate independent methods such as interferometric angular diameter measurements (e.g. Boyajian et al. 2012a,b), which, in combination with the Hipparcos parallax and measurements of the stellar bolometric flux, allow computing absolute luminosities, linear radii, and effective temperatures. As part of the Gaia-ESO activities, and also in support of the Gaia mission, a list of stars with accurate fundamental parameters derived from such independent methods is being compiled (Jofré et al. 2014; Heiter et al., in prep.) and included in the Gaia-ESO target list. For the range of parameters of interest to the PMS analysis, however, only very few benchmark stellar spectra are available in iDR1 and iDR2.
A comparison of the iDR2-GIRAFFE fundamental parameters of benchmark stars with those compiled from the literature is shown in Fig. 4 and Table 3 for the range of interest. In this case, the Teff deviations are mostly within ≈200 K. There is a systematic strong deviation of OACT values above 6000 K. At lower temperatures, deviations stronger than ≈200 K are found in OAPA results for HD 10700. Therefore, although the sample analysed is limited, good results are found for both nodes, except for OACT above 6000 K. Excluding the OACT values above this limit, the standard deviation is ≈120 K for both datasets. The OACT Teff upper limit for the GIRAFFE analysis was further lowered to 5500 K based on comparison with Teff from photometry (Appendix C; see also Sect. 5.7).
Deviations as strong as almost 0.7 dex in log g are found in the comparison with the benchmarks, with the standard deviation ≈0.3 dex for both datasets. From the comparison with benchmarks alone it is not possible to identify a range in which one method performs better than the other. The node-to-node comparisons for each cluster outlined a rather complex situation that led to the parameter selection described in Sect. 5.7.
In the parameters range of interest (i.e. excluding very metal-poor stars), [Fe/H] is approximately reproduced with a maximum deviation of 0.3 dex and a standard deviation of ≈0.15 dex.
 |
Fig. 5 UVES benchmarks comparison. Black for [Fe/H] < 0.1, blue for [Fe/H] > 0.1. Size inversely proportional to log g in the Teff and ξ plot, proportional to Teff in the log g and [Fe/H] plot. Reference ξ from Bergemann et al. (in prep.; see also Smiljanic et al. 2014). |
The comparison of the UVES fundamental parameters of benchmarks with those compiled from the literature is shown in Fig. 5 and Table 3. The results for the solar spectrum are outlined in Table 4.
In general, Teff deviations from benchmarks are all within 300 K (maximum) with a few outliers. Amongst these, UCM Teff for 61 Cyg A differs by about 800 K, but this strong deviation does not point to particular problems in some parameter ranges, as verified by the node-to-node comparison.
The OACT systematic discrepancies in Teff above 6500 K, on the other hand, indicate a Teff upper limit for the validity of ROTFIT UVES analysis as well. This discrepancy is also seen in the node-to-node comparison, from which we estimate an upper limit of 6200 K for the validity of the OACT results.
Excluding these outliers, the standard deviation is ≈100 K for the Arcetri, CAUP, and UCM nodes, and ≈120 K for the OACT node, with an average difference of 34 K for CAUP, 38 K for OACT, and 55 K for Arcetri and UCM.
Within the UVES dataset of young open clusters, very few sources have Teff< 4000 K. In this range, recommended data are based on OACT results alone because the molecular bands prevent an analysis based on MOOG.
UVES results on the solar spectrum.
The agreement in log g is approximately at the same level for all nodes. The benchmark log g is generally reproduced within a maximum deviation of ≈0.7 dex and a standard deviation of ≈0.3, only one Arcetri value deviates by more than that.
[Fe/H] is generally reproduced within a maximum deviation of ≈0.3 dex, except for one and two measurements by the Arcetri and OACT nodes, respectively, with deviations of ≈0.5 dex. The standard deviation is ≲0.1 dex for the CAUP and UCM nodes, ≈0.2 dex for the Arcetri node, and ≈0.3 for the OACT node. The OACT node tends to overestimate (underestimate) the metallicity below (above) [Fe/H] = 0. However, this does not lead to significant systematic differences in individual clusters, and the OACT results are therefore maintained. The node-to-node comparisons for individual clusters show that the Arcetri node systematically overestimates [Fe/H], which is not evident in the comparison with the benchmarks possibly because of the large and coarse parameter distributions of the latter. To overcome this systematic behaviour, in iDR2 the value obtained by the Arcetri node for the solar spectrum ([Fe/H] = 0.09, see Table 4) is subtracted in all measurements before computing the recommended [Fe/H]. The recommended [Fe/H] agrees with the benchmarks within 0.15 dex rms.
Solutions with large uncertainties or large ξ (≳2 km s-1) are disregarded by the nodes. Differences in ξ with respect to the values tabulated for the benchmarks are generally below 1 km s-1.
The recommended fundamental parameters are therefore computed taking the average of the node results with a 1σ-clipping when at least three values are provided. As discussed above, below 4000 K, only the OACT values are given as recommended values. In iDR2 we disregarded the OACT UVES values for Teff> 6200 K.
Despite the large difference in resolution and spectral range, the comparison with benchmarks shows that the UVES Teff accuracy is only marginally better than that of GIRAFFE, while log g and [Fe/H] results from the two setups are of similar accuracy. Our recommended values include Teff and [Fe/H] for 11 stars and log g for 3 stars (see Sect. 5.7) from both the UVES and GIRAFFE setups. The comparison of our results for the same stars in the two setups shows that the Teff ratio (GIRAFFE/UVES) has a mean of 0.99 and a median of 1.00. The differences in [Fe/H] (GIRAFFE-UVES) have a mean of 0.13 dex and a median of 0.16 dex. Among the three benchmark stars for which we give recommended log g from both GIRAFFE and UVES setups according to the criteria described in Sect. 5.7, two are in the range of interest (log g≈ 4.0), and the largest difference with the benchmark value is −0.09 dex.
5.7. Internal comparison
The node-to-node comparison for the UVES individual cluster results before data selection and calibration (see Sect. 5.6) gives systematic differences in the ranges 80−160 K in Teff, 0.1−0.3 dex in log g, and 0.06−0.17 dex in [Fe/H], while dispersions are in the ranges 160−260 K in Teff, 0.1−0.3 dex in log g, and 0.13−0.45 dex in [Fe/H]. The application of the data selection and calibration discussed in Sect. 5.6 reduces systematic differences below 100 K in Teff, and below 0.15 dex in [Fe/H]. The final node-to-node mean dispersion in the recommended data is 110 K in Teff, 0.21 dex in log g, and 0.10 dex in [Fe/H]. These values are very close to the median dispersion: 106 K in Teff, 0.17 dex in log g, and 0.11 dex in [Fe/H]. Biases in the recommended data are therefore successfully reduced.
For the GIRAFFE results, systematic differences before data selection are in the ranges 110−200 K in Teff, 0.4−0.8 dex in log g, and 0.01−0.03 in [Fe/H], while dispersions are in the ranges 210−330 K in Teff, 0.65−1.00 dex in log g, and 0.17−0.26 dex in [Fe/H]. The situation here is more complex than in the UVES case. The problems to address are the following:
-
(1)
The OACT (ROTFIT) log g for PMS stars tend to betoo high, clustering essentially on the MS9.
-
(2)
The OAPA log g for PMS stars tends to be too low, often lower than suggested by models10.
-
(3)
The PMS domain is contaminated by nonmembers with spurious log g in both log g−Teff diagrams.
-
(4)
The RGB in the OACT log g−Teff diagram follows the calibrated relation taken from Cox (2000), while in the OAPA diagram it does not.
-
(5)
The OAPA log g−Teff diagram outside the MS, PMS, and RGB domains is sparsely populated, with some very low as well as some very high values, which are indicative of possible presence of some large errors.
-
(6)
The OAPA Teff, log g, and [Fe/H] are valid for vsini< 90, 30, and 70 km s-1, respectively.
-
(7)
Because of a continuum normalisation problem on the Hα wings, in iDR1 and iDR2 the OACT parameters need to be discarded for Teff> 5500 K.
To reduce biases as much as possible and provide reliable recommended results, we adopted the following solution:
-
1.
The OAPA Teff are only considered for vsini< 90 km s-1. The OACT Teff are only considered below 5500 K. If both the OACT and OAPA Teff are available, they are averaged. In all other cases, the remaining value, if any, is adopted as recommended Teff.
-
2.
The OAPA [Fe/H] are only considered for vsini< 70 km s-1. The OACT [Fe/H] are considered only below 5500 K. If both the OACT and OAPA [Fe/H] are available these are averaged. In all other cases the remaining value, if any, is adopted as recommended [Fe/H].
-
3.
The OAPA log g are only considered for vsini< 30 km s-1. The OACT log g are only considered for Teff< 5500 K. If both the OACT and OAPA log g are available, they are averaged if they differ by less than 0.3 dex. When they differ by more than 0.3 dex, if the OACT log g> 4.2 and the OAPA log g> 5, the OACT log g is given as recommended value. In all other cases we do not give recommended log g.
-
4.
The OAPA gravity–sensitive γ index (Damiani et al. 2014) is given as a recommended parameter for vsini< 30 km s-1.
The application of such criteria leads to a final node-to-node mean dispersion in the recommended data of 98 K in Teff, 0.23 dex in log g, and 0.14 dex in [Fe/H]. These values are very close to the median dispersion: 95 K in Teff, 0.22 dex in log g, and 0.14 dex in [Fe/H]. Biases in the recommended data are therefore successfully reduced in the GIRAFFE case as well.
When a recommended log g is not given, it may be still possible to identify an approximate evolutionary status based on the OACT and OAPA results. Stars for which a trustworthy log g cannot be recommended are therefore flagged, when possible, as PMS, MS, or post-MS stars according to the criteria listed in Table 5.
Criteria for the evolutionary status.
 |
Fig. 6 OAPA gravity-sensitive γ index vs. Teff for all clusters analysed in iDR1 and iDR2. The group of younger clusters (ρ Oph, Cha I, and NGC 2264) are clearly distinguishable from the group of older clusters (γ Vel and NGC 2547). |
The gravity-sensitive spectral index γ obtained by the Damiani et al. (2014) approach can provide a rank order in age of the clusters. This is shown in Fig. 6 for the clusters analysed to date, where values for the group of younger clusters (ρ Oph, Cha I, and NGC 2264) are clearly separated from those of the group of older clusters (γ Vel and NGC 2547). The scatter in γ and the small age differences between clusters in the younger or older group still prevent a clear separation in age, however.
5.8. Overview in the log g–Teff plane
As a final check on our recommended fundamental parameters, we examine the log g–Teff diagram obtained with our data (Fig. 7) and compare it with the calibration of MK spectral classes reported in Cox (2000) and the theoretical PMS isochrones from Allard et al. (2011). We note the clustering of field stars on the MS and the RGB, as expected, while for the PMS cluster members a residual bias towards the MS and the RGB remains. In fewer than half of the cases, log g values for PMS stars are located approximately where the models predicted, although with large uncertainties.
 |
Fig. 7 log g–Teff diagram for all targets. Grey filled circles are used for cluster nonmembers and stars not classified as CTTS nor WTTS. The red dashed lines are the dwarf and giant sequences from Cox (2000). The blue dotted-dashed lines are the isochrones at 1, 5, 10, and 20 Myr from Allard et al. (2011). |
5.9. Comparison between fundamental parameters derived from GIRAFFE and UVES
Several stars in the γ Vel field have been observed with both UVES and GIRAFFE. For iDR2, our analysis produced Teff and [Fe/H] values for 31 stars and log g for 16 stars in this common sample. The fewer log g values arise because we applied the criteria described in Sect. 5.7, which were applied to iDR2 but not to iDR1. The comparison of the recommended values for this sample is satisfactory (see Fig. 8 for iDR2) and supports the validity of our approach both in determining the parameters and in deriving the recommended values. A similar comparison is reported in Spina et al. (2014b) for iDR1. That we can reproduce the parameters obtained with the higher resolution and larger wavelength coverage from UVES using a much smaller wavelength range and a lower resolution than in GIRAFFE is a remarkable achievement and increases our confidence in our parameter determination from the much larger GIRAFFE sample.
5.10. Veiling vs. Hα emission
For iDR1, the ROTFIT veiling parameter was adopted as the recommended one. In iDR2, however, it was recognised that some residual nebular emission remained after sky subtraction, particularly in NGC 2264, which was not sufficiently masked in the ROTFIT calculations. As a consequence, the ROTFIT veiling parameter for NGC 2264 was clearly overestimated and the OAPA solution was adopted as recommended in iDR2. This does not invalidate the results of iDR1 because γ Vel and Cha I spectra are unaffected by residual sky emission in the reduced spectra.
Frasca et al. (2015) found a positive correlation between Hα flux and r in the iDR1 data for Cha I objects with r ≥ 0.25, for which the Spearman rank analysis yielded a coefficient ρ = 0.58 with a significance of σ = 0.003. The same analysis for all clusters in iDR2 gives a coefficient ρ = 0.39 with a significance of σ = 0.004. No correlation between r and Hα 10% or W(Hα) is detected in the iDR2 data (see Fig. 9), however, where we do see an increase of the upper envelope with either Hα 10% or W(Hα), but the large scatter makes the correlation insignificant. This is at variance with expectations from previous work (e.g., White & Basri 2003) and therefore it outlines possible limitations in our veiling determination. A more detailed validation based on a comparison with different methods is deferred to future work.
 |
Fig. 8 Comparison between fundamental parameters derived from GIRAFFE and UVES spectra in the γ Vel field (iDR2). |
6. Derived parameters
6.1. Li abundance
In the whole GIRAFFE analysis, Li abundances, log ϵ(Li), were computed from the fundamental parameters (Sect. 5) and the W(Li) measurements (Sect. 4.2) using the curve of growth (COG) from Soderblom et al. (1993) and Palla et al. (2007) above and below 4000 K, respectively, with a linear interpolation between the tabulated values. The recommended log ϵ(Li) was derived using the recommended fundamental parameters and recommended W(Li) as input. Uncertainties were obtained by propagating the Teff and W(Li) uncertainties.
The approach adopted in the GIRAFFE case has the advantage of allowing us to focus on the accuracy of the fundamental parameters and W(Li), relying then on the best COG available to derive node-specific and recommended log ϵ(Li). The two COGs adopted do not join smoothly at 4000 K, but the interpolation scheme ensures a smooth transition between the two regimes. We plan to derive a self-consistent COG in the whole Teff range as a future improvement. The node-to-node dispersion for GIRAFFE data (see Fig. 10 for the whole iDR2) then only propagates from the W(Li) measurements and shows a fairly random distribution with a median of 0.17 dex.
In the UVES analysis, the OACT and Arcetri log ϵ(Li) were derived in the same way as for GIRAFFE. The CAUP and UCM nodes, on the other hand, derived log ϵ(Li) by a standard LTE analysis using the driver abfind in the revised version of the spectral synthesis code MOOG (Sneden 1973; see also Sects. 5 and 6.2). CAUP used the 2010 version of MOOG, while UCM used the 2002 and 2013 versions for iDR1 and iDR2, respectively. Uncertainties were estimated by varying each atmospheric parameter within its uncertainty range to derive the propagated uncertainty in log ϵ(Li). The propagated uncertainties where then combined quadratically. In this case, the recommended value is given as the average of all available node estimates with a σ-clipping when at least three measurements are available. Figure 10 shows that here the node-to-node dispersion is also fairly randomly distributed, with a median uncertainty of 0.12 dex.
Possible 6Li contribution was neglected throughout.
6.2. Other elemental abundances
Elemental abundances were computed by three nodes (Arcetri, CAUP, and UCM) when good-quality UVES spectra were available in stars that were unaffected by veiling and/or large vsini.
The Arcetri node computed abundances using FAMA. We refer to Magrini et al. (2013) for a description of the method and the way in which lines are selected for the abundance analysis.
The CAUP node derived individual abundances using the driver abfind in the 2010 version of MOOG (see Neves et al. 2009; Adibekyan et al. 2012, for details) and equivalent widths measured with the code ARES. The line list for elements other than Fe (with atomic number A ≤ 28) was selected by cross-matching between the line list used by Adibekyan et al. (2012) and the line list provided by Gaia-ESO. For elements with A> 28, lines that were suitable for W measurements (as tested by the Gaia-ESO line-list working group) were first selected, and from these, those that ARES was able to measure were used. The atomic data from the Gaia-ESO Survey were adopted. CAUP considered hyperfine splitting in the analysis of Cu, Ba, Nd, Sm and Eu abundances, that is, for all the elements affected with A> 28 (using the driver blends in MOOG). The errors of the abundances are given as the line-to-line scatter (when more than one line is measured).
 |
Fig. 9 Veiling parameter r vs. Hα 10% (top panel) and vs. W(Hα) (bottom panel) for iDR2. |
 |
Fig. 10 Li abundance uncertainty histogram for all sources in iDR2. For the GIRAFFE spectra the log ϵ(Li) uncertainty is propagated from the uncertainty in Teff and W(Li). For the UVES spectra the node-to-node dispersion is considered. A solid line is used for the cumulative probability (right ordinate axis). See text for details. |
The UCM node adopted an approach similar to CAUP. For iDR1, two line-lists were prepared: one for dwarfs (log g ≥ 4.0) and one for giants (log g ≤ 4.0). For iDR2 five line lists were used, as was done for the stellar parameters (see Sect. 5). A total of 13 elements were analysed: Fe, the α-elements (Mg, Si, Ca, and Ti), the Fe-peak elements (Cr, Mn, Co, and Ni), and the odd-Z elements (Na, Al, Sc, and V). To obtain individual abundances, the equivalent widths were fed into MOOG, and then a 3σ-clipping for each chemical element was applied.
The elements for which at least two nodes derived abundances for at least one star, which were considered in the recommended results, are Na, Mg, Al, Si, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Zn, Zr, Mo, and Ce. Only one node result was considered for Cu, Y, Ba, La, Pr, Nd, Sm, and Eu. Abundances were taken from the neutral species, except for Ba, La, Ce, Pr, Nd, Sm, and Eu, for which they were taken from the ionised species.
 |
Fig. 11 iDR2 node-to-node dispersion of elemental abundances. |
The node-to-node dispersions of elemental abundances in iDR2 is shown in Fig. 11. In general, ≈90% of the results for each elements have dispersions below ≈0.2 dex. The tail of the distributions extends to higher values in more difficult cases for which differences that arise from the different W measurements (see Smiljanic et al. 2014) and line selection strategies play a role, however. The dispersion also tends to be higher for abundances of ions such as Ti ii and Cr ii. Poor agreement is found for Zn i and Zr ii. Note that abundances for elements that require hyperfine splitting were only provided by the CAUP node.
The internal precision is comparable with that of the UVES spectra of FGK-type analysis (excluding stars in the field of young open clusters; Smiljanic et al. 2014). Note that Smiljanic et al. (2014) used the median of the absolute deviations from the median of the data (MAD) to quantify the node-to-node dispersion, but this cannot be used here because too few nodes provide abundances. The dispersion from the mean used here probably overestimates the node-to-node dispersion with respect to the MAD, although this is mitigated by the applied σ-clipping. In summary, all this indicates that our internal precision for elemental abundances is roughly at the same level as that of Smiljanic et al. (2014).
A survey inter-comparison with results of Smiljanic et al. (2014) on the common calibration open cluster NGC 6705 was carried out for all elements except for Ce, La, Pr, and Sm, for which results did not pass the quality control criteria of Smiljanic et al. (2014). The inter-comparison was satisfactory and confirmed that our precision is similar to that of the results of Smiljanic et al. (2014).
6.3. Mass accretion rate
 |
Fig. 12 Mass accretion rates vs. mass for all clusters in iDR2. Symbols and colours are the same as in Fig. 1. The dashed line represents the relationship Ṁ ∝ M2. |
Mass accretion rates are estimated from the Hα 10% using Eq. (1) of Natta et al. (2004). The use of alternative methods, for example, using the W(Hα), is discussed in Frasca et al. (2015) and will be implemented in the Gaia-ESO PMS analysis in future data releases.
Using the relationship reported by Natta et al. (2004) undoubtedly has the advantage of allowing a simple estimate of Ṁacc from only the Hα 10%. The accuracy and validity of this empirical relationship has, however, been debated (see, e.g., Costigan et al. 2012, and references therein), especially in cases when only single-epoch observations are available.
Recently, Alcalá et al. (2014) have computed the accretion rate by modelling the excess emission from the UV to the near-IR and provided empirical relationships between accretion luminosity and the luminosity of 39 emission lines from X-Shooter spectra. In particular, they have shown that the comparison between Ṁacc derived through primary diagnostics (like the UV-excess) and that obtained with the Natta et al. (2004) relationship has a large scatter, with this latter tending to underestimate Ṁacc for Hα 10%< 400 km s-1 and to overestimate Ṁacc for Hα 10%> 400 km s-1.
A comparison of the iDR1 Ṁacc of γ Vel and Cha I with mass accretion rates derived from line luminosity and the relationship of Hartmann (1998) has been presented in Frasca et al. (2015). They found discrepancies of ~0.8 dex for Cha I and ~0.7 dex for γ Vel on average. Frasca et al. (2015) also compared the results obtained for Cha I with literature values, finding a fair agreement, with differences that can be ascribed to variability, different methodologies, and the use of different evolutionary models.
Mass accretion rates derived for all clusters in the first 18 months of observations vs. stellar mass are shown in Fig. 12. Stellar mass is estimated from the recommended Teff and the age of the cluster using the Baraffe et al. (1998) models11. The expectations are that Ṁ ∝ Mα with α ~ 2 (e.g., Muzerolle et al. 2005; Herczeg & Hillenbrand 2008; Alcalá et al. 2014). As for the γ Vel and Cha I cases discussed in Frasca et al. (2015), however, the large scatter in Ṁ prevents us from meaningfully comparing our results with this relationship. The Spearman rank correlation analysis for Cha I for iDR2 yields ρ = 0.43 and σ = 0.005, which is a higher significance than found by Frasca et al. (2015) for iDR1 (ρ = 0.26,σ = 0.16 for Ṁ derived from Hα 10%), which indicates a better accuracy of our recommended iDR2 Hα 10% parameter. Amongst the younger clusters in our sample, we find ρ = 0.47 and σ = 0.14 for ρ Oph, while the correlation is rather poor for NGC 2264 (ρ = 0.19, σ = 0.022), possibly because of the larger uncertainties due to the residual nebular emission in the spectra of this cluster. The scatter in Fig. 12 is dominated by NGC 2264. Ignoring this cluster, the scatter is consistent with what was found by Alcalá et al. (2014) in their validation of the relationship of Natta et al. (2004). Interestingly, for the older clusters in our sample we find an insignificant correlation in γ Vel (ρ = 0.29, σ = 0.247), but a well-defined correlation in NGC 2547 (ρ = 0.89, σ = 0.018). In these two cases, two kinematically distinct populations with different ages have been discovered (Jeffries et al. 2014; Sacco et al. 2015), whose possible effects on the relationship Ṁ vs. M still need to be explored.
6.4. Chromospheric Hα and Hβ flux
After the ROTFIT determination of the fundamental parameters, a best-matching template within the library of slowly rotating inactive stars is identified. The chromospheric excesses ΔW(Hα)chr and ΔW(Hβ)chr are derived using a spectral subtraction method (see, e.g., Barden 1985; Frasca & Catalano 1994; Montes et al. 1995, and references therein), which has been extensively used in the past. The photospheric flux is removed by subtracting the spectrum of an inactive template star with very close fundamental parameters, rotationally broadened at the target vsini, over the line wavelength range. Such chromospheric W excesses, ΔW(Hα)chr and ΔW(Hβ)chr, are then converted to flux, F(Hα)chr and F(Hβ)chr, by multiplying it by the theoretical continuum flux at the line wavelength (see, e.g., Frasca et al. 2015, and references therein). It may be argued that even the templates may have some chromospheric basal flux (see, e.g., Judge & Carpenter 1998, and references therein), also variable in time following the stellar cycles (see, e.g., Schröder et al. 2012), which a detailed semi-empirical NLTE chromospheric modelling (e.g., Houdebine & Panagi 1990; Lanzafame 1995) could take into account. This latter is, however, unpractical for applications to large datasets like the Gaia-ESO dataset. Furthermore, the chromospheric flux in young stars is much higher than the basal flux, so that this latter can be safely neglected.
 |
Fig. 13 Chromospheric Hα flux vs. Teff for all young clusters observed in the first 18 months of observations. Symbols and colours are the same as in Fig. 1, with filled (open) symbols used for CTTS (WTTS). The dashed line represents the chromospheric activity – accretion dividing line of Frasca et al. (2015). |
Results for γ Vel and Cha I (iDR1) are discussed in Frasca et al. (2015), who were able to distinguish between chromospheric-dominated and accretion-dominated Hα flux. ΔW(Hα)chr vs. Teff for all clusters observed in the first 18 months of observations (iDR2) is shown in Fig. 13. We note that the chromospheric activity – accretion dividing line proposed by Frasca et al. (2015; log FHα = 6.35 + 0.00049(Teff − 3000)) delimits quite neatly the two regimes in this larger sample as well, with some larger uncertainties for NGC 2264 that are likely due to residual nebular emission. This dividing line was also found by Frasca et al. (2015) to agree remarkably well with the saturation limit that was adopted by Barrado y Navascués & Martín (2003) to separate CTTS and WTTS.
 |
Fig. 14 Chromospheric Hα equivalent width excess vs. vsini for all young clusters observed in the first 18 months of observations. Colour coding is used for Teff. |
Finally, in Fig. 14 we show ΔW(Hα)chr vs. vsini for all young clusters observed in the first 18 months of observations. While a full discussion on the activity-rotation relationship is deferred to future work, we note that our data display a Teff-dependent activity-rotation correlation regime at low vsini, followed by a Teff-dependent saturation regime at high vsini, as expected. The behaviour at different Teff is quite neatly distinguishable, which further confirms the overall consistency of our results.
7. Summary and conclusions
The Gaia-ESO PMS spectrum analysis provides an extensive list of stellar parameters from spectra acquired in the FLAMES/GIRAFFE/HR15N and FLAMES/UVES/580 setups in the field of young open clusters. These include raw parameters that are directly measured on the input spectra (W(Hα), Hα 10%, and W(Li)), fundamental parameters (Teff, log g, [Fe/H], ξ, vsini, and r), and derived parameters (log ϵ(Li), log ϵ(X)), Ṁacc, ΔW(Hα)chr, ΔW(Hβ)chr, F(Hα)chr, and F(Hβ)chr) that require prior knowledge of the former. Our analysis strategy is devised to solve problems posed by peculiarities of PMS stars and young stars in general such as veiling, large broadening due to fast-rotation, emission lines due to accretion and/or chromospheric activity, and molecular bands. The analysis is also made robust against residual sky-background or foreground features that cannot be completely removed, for instance, for inhomogeneous nebular emission.
The availability of different methods for deriving stellar parameters increases our confidence in the output of our analysis. It allows us to efficiently identify and discard outliers such as those from failed fits or problems in the input spectra, as well as to derive realistic uncertainties from the internal dispersion of the data. For Teff and log g the external precision is estimated by comparison with results from interferometric angular diameter measurements. These are estimated to be ≈120 K rms in Teff and ≈0.3 dex rms in log g for both the UVES and GIRAFFE setups. The comparison with Teff derived from photometry for a selected group of stars in γ Vel with the same foreground extinction and free from accretion signatures yields an agreement of ≈260 K rms. Our recommended [Fe/H] results agree with assessed literature values for such a set of benchmark stars within ≈0.15 dex rms. A comparison with a previous [Fe/H] determination for Cha I is discussed in Spina et al. (2014a). Weaknesses or limitations of the methods used were identified by the node-to-node comparisons and by comparison with benchmark stars.
The observation strategy poses significant challenges to the analysis, because to optimise the observation time, most of the relevant observations are only carried out in the FLAMES/GIRAFFE/HR15N setup. For our purposes, the wavelength range of this setup is the best available in the optical because it contains very important diagnostics for young stars, such as the Hα and Li line. At the same time, surface gravity diagnostics in the HR15N setup are poorer than in other wavelength ranges and are still not modelled with sufficient accuracy. A Teff determination for spectral types earlier than early-G is also challenging since it is mostly based on the Hα wings. For this wavelength range, two methods based on the comparison with spectra or spectral indices of template stars have proved effective in providing fundamental parameters. A satisfactory self-consistency of the results has been achieved, at the expense of discarding log g values when a sufficient agreement between the two methods cannot be reached.In these cases, however, it is still possible to provide an evolutionary flag because it can be established with confidence whether the star is in a PMS, an MS or a post-MS stage. An uncalibrated gravity-sensitive spectral index is also provided, which is useful for a rank order in age.
The reproducibility of the parameters obtained with the higher resolution and larger wavelength coverage from UVES using a much smaller wavelength range and a lower resolution than in the GIRAFFE/HR15N setup, together with the similar accuracy and precision achieved in the two setups, is a remarkable achievement of this work. This allows us to confidently provide parameters for the much larger GIRAFFE sample.
The Gaia-ESO is an ongoing project, and this paper describes the PMS spectrum analysis carried out on the first two data releases. Work is ongoing to improve our analysis even more for the next releases. The tables with the public-release results will be available through the ESO data archive12 and through the Gaia-ESO Survey science archive13, which is hosted by the Wide Field Astronomy Unit (WFAU) of the Institute for Astronomy, Royal Observatory, Edinburgh, UK.
The solar Fe abundance of Grevesse et al. (2007), log ϵ(Fe)⊙ = 7.45, is adopted.
ARES is available for download at http://www.astro.up.pt/~sousasag/ares/
The approach of Sousa et al. (2008) to adjust the ARES parameters according to the S/N of each spectrum was followed.
Acknowledgments
Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’ Istruzione, dell’ Università e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012” and the grant “The Chemical and Dynamical Evolution of the Milky Way and Local Group Galaxies” (prot. 2010LY5N2T). The results presented here benefit from discussions held during the Gaia-ESO workshops and conferences supported by the ESF (European Science Foundation) through the GREAT Research Network Programme. H.M.T. acknowledges the financial support from BES-2009-012182 and the ESF and GREAT for an exchange grant 4158. H.M.T. and D.M. acknowledges the financial support from the Spanish Ministerio de Economía y Competitividad (MINECO) under grant AYA2011-30147-C03-02. J.I.G.H. acknowledges financial support from the MINECO under grants AYA2011-29060, and 2011 Severo Ochoa Program SEV-2011-0187. S.G.S, E.D.M., and V.Zh.A. acknowledge support from the Fundação para a Ciência e Tecnologia (Portugal) in the form of grants SFRH/BPD/47611/2008, SFRH/BPD/76606/2011, SFRH/BPD/70574/2010, respectively. T.B. was funded by grant No. 621-2009-3911 from The Swedish Research Council.
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Natta, A., Manara, C. F., et al. 2014, A&A, 561, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Barden, S. C. 1985, ApJ, 295, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Barrado y Navascués, D., & Martín, E. L. 2003, AJ, 126, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2012, MNRAS, 424, 3178 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bonito, R., Prisinzano, L., Guarcello, M. G., & Micela, G. 2013, A&A, 556, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012a, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012b, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., Donati, P., Pancino, E., et al. 2014a, A&A, 562, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Vallenari, A., Zaggia, S., et al. 2014b, A&A, 569, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [Google Scholar]
- Costigan, G., Scholz, A., Stelzer, B., et al. 2012, MNRAS, 427, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, Allen’s astrophysical quantities (New York: AIP Press; Springer) [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/2246 [Google Scholar]
- Damiani, F., Prisinzano, L., Micela, G., et al. 2014, A&A, 566, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., & Catalano, S. 1994, A&A, 284, 883 [NASA ADS] [Google Scholar]
- Frasca, A., Guillout, P., Marilli, E., et al. 2006, A&A, 454, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Biazzo, K., Lanzafame, A. C., et al. 2015, A&A, 575, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartigan, P., Hartmann, L., Kenyon, S., Hewett, R., & Stauffer, J. 1988, in BAAS, 20, 1092 [Google Scholar]
- Hartmann, L. 1998, Accretion Processes in Star Formation (Cambridge: University Press), 160, 53 [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2008, ApJ, 681, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Hartmann, L., Calvet, N., et al. 2008, ApJ, 686, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, unpublished [arXiv:1008.4686] [Google Scholar]
- Houdebine, E. R., & Panagi, P. M. 1990, A&A, 231, 459 [NASA ADS] [Google Scholar]
- Jeffries, R. D., & Oliveira, J. M. 2005, MNRAS, 358, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Naylor, T., Walter, F. M., Pozzo, M. P., & Devey, C. R. 2009, MNRAS, 393, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Cottaar, M., et al. 2014, A&A, 563, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Judge, P. G., & Carpenter, K. G. 1998, ApJ, 494, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, W., & Lee, S.-G. 2012, MNRAS, 425, 3162 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzafame, A. C. 1995, A&A, 302, 839 [NASA ADS] [Google Scholar]
- Magrini, L., Randich, S., Friel, E., et al. 2013, A&A, 558, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montes, D., de Castro, E., Fernandez-Figueroa, M. J., & Cornide, M. 1995, A&AS, 114, 287 [NASA ADS] [Google Scholar]
- Muzerolle, J., Luhman, K. L., Briceño, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., Muzerolle, J., et al. 2004, A&A, 424, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
- Neves, V., Santos, N. C., Sousa, S. G., Correia, A. C. M., & Israelian, G. 2009, A&A, 497, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palla, F., Randich, S., Pavlenko, Y. V., Flaccomio, E., & Pallavicini, R. 2007, ApJ, 659, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzo, M., Jeffries, R. D., Naylor, T., et al. 2000, MNRAS, 313, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in C. The art of scientific computing, 2nd edn. (Cambridge: University Press) [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium. 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sacco, G. G., Morbidelli, L., Franciosini, E., et al. 2014, A&A, 565, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sacco, G. G., Jeffries, R. D., Randich, S., et al. 2015, A&A, 574, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, K.-P., Mittag, M., Pérez Martínez, M. I., Cuntz, M., & Schmitt, J. H. M. M. 2012, A&A, 540, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, The University of Texas [Google Scholar]
- Soderblom, D. R., Jones, B. F., Balachandran, S., et al. 1993, AJ, 106, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., et al. 2011, A&A, 526, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Adibekyan, V., et al. 2014, A&A, 561, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014a, A&A, 568, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014b, A&A, 567, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stauffer, J. R., Hartmann, L. W., Fazio, G. G., et al. 2007, ApJS, 172, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Tabernero, H. M., Montes, D., & González Hernández, J. I. 2012, A&A, 547, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabernero, H. M., González Hernández, J. I., & Montes, D. 2013, in Highlights of Spanish Astrophysics VII Comp. Ref., 673 [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. J., & Basri, G. 2003, ApJ, 582, 1109 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: ROTFIT templates
 |
Fig. A.1 Parameters of the whole set of ROTFIT templates adopted for the Gaia-ESO analysis. |
 |
Fig. A.2 Comparison between PASTEL and FAMA fundamental parameters of the ELODIE templates used by ROTFIT. See text for details. |
The method implemented in ROTFIT relies on existing determinations of fundamental parameters for the template stars and, in the past, the PASTEL catalogue (Soubiran et al. 2010) has been used as input. To ensure homogeneity amongst the Gaia-ESO spectrum analysis, however, the template parameters have been re-determined using the fast automatic MOOG analysis (FAMA, Magrini et al. 2013), adopting the Gaia-ESO-recommended model atmospheres and atomic parameters. The template parameters were updated for most of the stars in the range from mid-F to late K, while for the M dwarf, we adopted the parameters recently determined by Rojas-Ayala et al. (2012) and Boyajian et al. (2012b). The parameters of the whole set of ROTFIT templates adopted for the Gaia-ESO analysis are illustrated in Fig. A.1. In Fig. A.2 we show the comparison between the PASTEL and FAMA parameters. Average differences are 30 K, 0.10 dex, and 0.04 dex for Teff, log g, and [Fe/H], respectively. Standard deviations are 123 K, 0.27 dex, and 0.11 dex for Teff, log g, and [Fe/H], respectively. A table with the ROTFIT template parameters used for the Gaia-ESO analysis is reported in Frasca et al. (2015).
Appendix B: ROTFIT masks
Spectra of accreting stars or of stars that are embedded in a dense cloud require wavelength masks to exclude the residual nebular emission features that still remain after the data reduction process. The Hα profile in non-accreting young stars is nonetheless affected by significant chromospheric contribution, which also varies in time. The Hα core must therefore be masked out to avoid considering the non-photospheric contribution to the line profile. On the other hand, the Hα wings are essential fundamental parameter diagnostics, especially in GIRAFFE/HR15N spectra of F- and G-type stars, for which the rest of the passband offers very poor constraints. In some cases (e.g., old and inactive stars in the field), the whole of the Hα profile can be used. Because of the Li depletion that occurs in the stellar interior, W(Li) decreases rapidly with age in PMS stars of later spectral type and can be very different in stars with similar fundamental parameters; therefore this line must also be masked out. The Hα and Li (6707.84 Å) lines must be masked in the spectra of accreting stars as well, but in such cases, the Hα mask must be wide enough to include the wings of the lines, which can be very broad.
Therefore, the measurement of the raw parameters as a first step in the analysis process allows us to divide the spectra into three classes:
-
NHL. Spectra with negligible Li absorption andno Hα emission for which only a narrow Hα-core mask(± 2 Å) is required and no r evaluation is carried out.
-
HL. Spectra with significant Li absorption, Hα core emission, or both, for which accretion, and therefore r evaluation, can be excluded, but require a slightly larger Hα-core mask (± 5 Å).
-
HLV. Spectra with accretion signatures, which require a mask for the entire Hα profile (± 20 Å), plus the evaluation of r.
For HL and HLV classes, a mask of ± 3 Å is applied around the Li line core.
Appendix C: Comparison with Teff from photometry
A more extensive comparison can be made, at this stage, with Teff derived from photometry for cluster members that have all the same foreground extinction and are not significantly affected by colour excesses due to circumstellar material. Fortunately, this was feasible for γ Vel because the extinction is fairly uniform, and many probable members are free from large colour excess.
BVI photometry of γ Vel was presented in Pozzo et al. (2000) and in Jeffries et al. (2009). The photometry was taken in the Harris B, V and Kron-Cousins I filters and was converted into the standard Johnsons-Cousins photometric system by Jeffries et al. (2009). This data have been supplemented with 2MASS (Cutri et al. 2003) and Spitzer data (Hernández et al. 2008) where available.
We used two different methods to derive Teff from photometry, one based on the (V − I) vs. (B − V) colour−colour diagram (TCC), the other one based on the simultaneous fit of all available magnitudes, from the optical to the Spitzer bands (TSED).
 |
Fig. C.1 V − I versus B − V colour−colour diagram for probable members of γ Vel. Stars with radial velocities higher than 9 km s-1 from the mean velocity of γ Vel are crossed out. The empirical main-sequence locus relationship from Kenyon & Hartmann (1995) is over-plotted in green, the theoretical main-sequence locus from BT-Settl (Allard et al. 2011) in cyan, the theoretical pre-main sequence locus for an age of 7 Myr from BT-Settl in purple, and finally the locus obtained from Eq. (C.1) in red. All the colour loci plotted as lines have been shifted assuming an extinction of E(B − V) = 0.038 (Jeffries et al. 2009) and E(V − I) /E(B − V) = 1.6 (Rieke & Lebofsky 1985). |
The (V − I) vs. (B − V) colour-colour diagram for probable members of γ Vel, corrected for the foreground extinction as estimated by Jeffries et al. (2009), is shown in Fig. C.1. The membership is based on Li and radial velocity and about 85% of the stars in Fig. C.1 are expected to be actual cluster members (see Jeffries et al. 2014). The narrowness of this locus indicates that there is little differential extinction or veiling in γ Vel. When excluding stars with radial velocities higher than 9 km s-1 from the mean velocity of γ Vel, this locus is even narrower. As Fig. C.1 shows, neither the empirical Teff-to-colour conversion for the ZAMS (Kenyon & Hartmann 1995, hereafter KH95) nor the theoretical BT-Settl ZAMS and 7 Myr PMS isochrones (Allard et al. 2011) overlap with the observed locus in the colour-colour diagram.
 |
Fig. C.2 Top left panel: comparison of TSED and TCC for all GIRAFFE spectra in the γ Vel field for which |
The theoretically computed colours from BT-Settl do not reproduce the stellar magnitudes accurately, possibly the opacity is still incompletely described. However, we can use them to define a new locus based on the assumption that the models correctly predict the colour difference due to gravity effects. If this assumption holds, we can add the colour shift between the theoretical ZAMS and PMS isochrones to the empirical ZAMS colours to derive the actual PMS intrinsic colours; this procedure is conceptually similar to that used by Bell et al. (2013). For every effective temperature, a new colour has been calculated using  (C.1)with a similar equation for (V − I). This new locus clearly describes the observed locus in γ Vel much better than the alternatives (see Fig. C.1). The fit can probably be improved further by varying the age and extinction within the ranges given by Jeffries et al. (2009), but we did not explore that here.
(C.1)with a similar equation for (V − I). This new locus clearly describes the observed locus in γ Vel much better than the alternatives (see Fig. C.1). The fit can probably be improved further by varying the age and extinction within the ranges given by Jeffries et al. (2009), but we did not explore that here.
Assuming a constant extinction of E(B − V) = 0.038 (Jeffries et al. 2009) and zero veiling, which is probably approximately true for most stars that lie on the observed narrow locus, we can fit TCC to the observed colours through a least-square minimisation, which has been generalised for two dimensions with correlated uncertainties (Hogg et al. 2010), 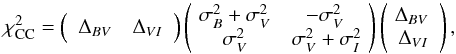 (C.2)where ΔBV ≡ Δ(B − V) and ΔVI ≡ Δ(V − I) give the difference between the observed colours and those predicted from our new locus as a function of the stellar temperature. These colour differences are multiplied with the inverse of the covariance matrix, which is given here as a function of the photometric uncertainties σB, σV, and σI. The temperatures computed in this way are based on the KH95 colour-temperature conversion of ZAMS stars with the colours adjusted for the lower surface gravity of PMS stars.
(C.2)where ΔBV ≡ Δ(B − V) and ΔVI ≡ Δ(V − I) give the difference between the observed colours and those predicted from our new locus as a function of the stellar temperature. These colour differences are multiplied with the inverse of the covariance matrix, which is given here as a function of the photometric uncertainties σB, σV, and σI. The temperatures computed in this way are based on the KH95 colour-temperature conversion of ZAMS stars with the colours adjusted for the lower surface gravity of PMS stars.
In Fig. C.2 (top right panel) we compare the recommended Teff with TCC for probable γ Vel members. An additional selection has been applied by considering TCC with 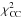 < 7 (i.e., consistent with being drawn by chance at the 99% level) to avoid considering stars that may be significantly affected by colour excess due to circumstellar material. The formal uncertainties of TCC were excessively small as a result of the definition of the locus in the (V − I, B − V) plane and the insensitivity of TCC to B − V at low temperatures. The comparison shows that the agreement is mostly within the estimated uncertainties, although the spectroscopic Teff is systematically higher than TCC above ≈3600 K, with an average difference of ≈180 K and a standard deviation of σ ≈ 250 K.
< 7 (i.e., consistent with being drawn by chance at the 99% level) to avoid considering stars that may be significantly affected by colour excess due to circumstellar material. The formal uncertainties of TCC were excessively small as a result of the definition of the locus in the (V − I, B − V) plane and the insensitivity of TCC to B − V at low temperatures. The comparison shows that the agreement is mostly within the estimated uncertainties, although the spectroscopic Teff is systematically higher than TCC above ≈3600 K, with an average difference of ≈180 K and a standard deviation of σ ≈ 250 K.
As an alternative approach, Teff from photometry was also derived by taking all photometry available from optical, 2MASS, and Spitzer into account. In this case, we fitted TSED by a downhill simplex multidimensional minimisation (Nelder & Mead 1965) of  (C.3)where xi ≡ (V − Mλ) is the observed colour derived from the V-band magnitude and each of the photometric magnitudes available (Mλ), σi is its uncertainty, and wi = wi(Teff,log g, [Fe/H]) is the theoretical colour from the BT-Settl models (Allard et al. 2011) that are interpolated in Teff and log g with [Fe/H] fixed at the solar value. We estimated the standard deviation using Monte-Carlo simulations with 1000 random synthetic realisations for each star. This method is, effectively, a fit of the stellar spectral energy distribution (SED) and has the advantage of considering colours more sensitive to Teff than only (V − I) and (B − V) in the temperature range of interest. The weakness of this method lies mostly in the theoretical model that, although it is amongst the most advanced available to date, yet does not accurately reproduce the observed PMS colour (see, e.g., Bell et al. 2012; Stauffer et al. 2007).
(C.3)where xi ≡ (V − Mλ) is the observed colour derived from the V-band magnitude and each of the photometric magnitudes available (Mλ), σi is its uncertainty, and wi = wi(Teff,log g, [Fe/H]) is the theoretical colour from the BT-Settl models (Allard et al. 2011) that are interpolated in Teff and log g with [Fe/H] fixed at the solar value. We estimated the standard deviation using Monte-Carlo simulations with 1000 random synthetic realisations for each star. This method is, effectively, a fit of the stellar spectral energy distribution (SED) and has the advantage of considering colours more sensitive to Teff than only (V − I) and (B − V) in the temperature range of interest. The weakness of this method lies mostly in the theoretical model that, although it is amongst the most advanced available to date, yet does not accurately reproduce the observed PMS colour (see, e.g., Bell et al. 2012; Stauffer et al. 2007).
Figure C.2 (top left panel) shows the comparison between TSED and TCC for all GIRAFFE spectra in the γ Vel field for which  (no significant IR-excess), irrespective of Li- and RV-membership. Although some systematic deviations in some temperature ranges are present (viz., TCC< 3800 K), mainly due to the way in which TCC is derived, the two models agree within the error bars, the mean difference is ≃−40 K, and the standard deviation σ ≃ 150 K. The comparison of the recommended Teff and TSED for GIRAFFE is shown in the bottom left panel of Fig. C.2. The two sets generally agree within the error bars, the mean difference is ≃180 K and σ ≃ 240 K. Finally, the comparison of the UVES-recommended Teff with TSED for γ Vel radial velocity members (as in Spina et al. 2014b) is shown in the bottom right panel of Fig. C.2.
(no significant IR-excess), irrespective of Li- and RV-membership. Although some systematic deviations in some temperature ranges are present (viz., TCC< 3800 K), mainly due to the way in which TCC is derived, the two models agree within the error bars, the mean difference is ≃−40 K, and the standard deviation σ ≃ 150 K. The comparison of the recommended Teff and TSED for GIRAFFE is shown in the bottom left panel of Fig. C.2. The two sets generally agree within the error bars, the mean difference is ≃180 K and σ ≃ 240 K. Finally, the comparison of the UVES-recommended Teff with TSED for γ Vel radial velocity members (as in Spina et al. 2014b) is shown in the bottom right panel of Fig. C.2.
Note, finally, that the intrinsic variability of the targets together with the asynchronicity of the spectroscopic and photometric observations must also play a role in the comparisons presented here. If we also consider the uncertainties and the probable spread in age, which are not reliably estimated as yet, the comparison with photometry can be considered quite satisfactory.
All Tables
Young open clusters (age <100 Myr) observed by the Gaia-ESO survey in the first 18 months of observations, whose analysis is discussed in this paper.
All Figures
 |
Fig. 1 W(Hα) vs. Hα 10% for all young open clusters observed in the first 18 months of observations. Filled symbols are used for stars classified as CTTS, open symbols for stars classified as WTTS. |
| In the text | |
 |
Fig. 2 Illustrative node-to-node W(Li) comparison for γ Vel. Left panel: comparison between OAPA (DAOSPEC, iDR1) and Arcetri (iDR2) for GIRAFFE spectra. Right panel: comparison between Arcetri code and OACT (IRAF) for UVES spectra. Arrows indicate upper limits. |
| In the text | |
 |
Fig. 3 Blend-corrected W(Li) vs. Teff for all young open clusters observed in the first 18 months. For comparison, the lower and upper envelope in the Pleiades are shown as solid lines, while dashes and dotted lines are the upper envelopes of IC 2602 and the Hyades, respectively. Dots are used for nonmembers. Upper limits are not included for clarity. |
| In the text | |
 |
Fig. 4 GIRAFFE benchmark comparison. Black for [Fe/H] < 0.1, blue for [Fe/H] > 0.1. Size is inversely proportional to log g in the Teff plot, proportional to Teff in the log g and [Fe/H] plot. |
| In the text | |
 |
Fig. 5 UVES benchmarks comparison. Black for [Fe/H] < 0.1, blue for [Fe/H] > 0.1. Size inversely proportional to log g in the Teff and ξ plot, proportional to Teff in the log g and [Fe/H] plot. Reference ξ from Bergemann et al. (in prep.; see also Smiljanic et al. 2014). |
| In the text | |
 |
Fig. 6 OAPA gravity-sensitive γ index vs. Teff for all clusters analysed in iDR1 and iDR2. The group of younger clusters (ρ Oph, Cha I, and NGC 2264) are clearly distinguishable from the group of older clusters (γ Vel and NGC 2547). |
| In the text | |
 |
Fig. 7 log g–Teff diagram for all targets. Grey filled circles are used for cluster nonmembers and stars not classified as CTTS nor WTTS. The red dashed lines are the dwarf and giant sequences from Cox (2000). The blue dotted-dashed lines are the isochrones at 1, 5, 10, and 20 Myr from Allard et al. (2011). |
| In the text | |
 |
Fig. 8 Comparison between fundamental parameters derived from GIRAFFE and UVES spectra in the γ Vel field (iDR2). |
| In the text | |
 |
Fig. 9 Veiling parameter r vs. Hα 10% (top panel) and vs. W(Hα) (bottom panel) for iDR2. |
| In the text | |
 |
Fig. 10 Li abundance uncertainty histogram for all sources in iDR2. For the GIRAFFE spectra the log ϵ(Li) uncertainty is propagated from the uncertainty in Teff and W(Li). For the UVES spectra the node-to-node dispersion is considered. A solid line is used for the cumulative probability (right ordinate axis). See text for details. |
| In the text | |
 |
Fig. 11 iDR2 node-to-node dispersion of elemental abundances. |
| In the text | |
 |
Fig. 12 Mass accretion rates vs. mass for all clusters in iDR2. Symbols and colours are the same as in Fig. 1. The dashed line represents the relationship Ṁ ∝ M2. |
| In the text | |
 |
Fig. 13 Chromospheric Hα flux vs. Teff for all young clusters observed in the first 18 months of observations. Symbols and colours are the same as in Fig. 1, with filled (open) symbols used for CTTS (WTTS). The dashed line represents the chromospheric activity – accretion dividing line of Frasca et al. (2015). |
| In the text | |
 |
Fig. 14 Chromospheric Hα equivalent width excess vs. vsini for all young clusters observed in the first 18 months of observations. Colour coding is used for Teff. |
| In the text | |
 |
Fig. A.1 Parameters of the whole set of ROTFIT templates adopted for the Gaia-ESO analysis. |
| In the text | |
 |
Fig. A.2 Comparison between PASTEL and FAMA fundamental parameters of the ELODIE templates used by ROTFIT. See text for details. |
| In the text | |
 |
Fig. C.1 V − I versus B − V colour−colour diagram for probable members of γ Vel. Stars with radial velocities higher than 9 km s-1 from the mean velocity of γ Vel are crossed out. The empirical main-sequence locus relationship from Kenyon & Hartmann (1995) is over-plotted in green, the theoretical main-sequence locus from BT-Settl (Allard et al. 2011) in cyan, the theoretical pre-main sequence locus for an age of 7 Myr from BT-Settl in purple, and finally the locus obtained from Eq. (C.1) in red. All the colour loci plotted as lines have been shifted assuming an extinction of E(B − V) = 0.038 (Jeffries et al. 2009) and E(V − I) /E(B − V) = 1.6 (Rieke & Lebofsky 1985). |
| In the text | |
 |
Fig. C.2 Top left panel: comparison of TSED and TCC for all GIRAFFE spectra in the γ Vel field for which |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


