| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 27 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424819 | |
| Published online | 23 January 2015 | |
A 1.3 cm line survey toward IRC +10216⋆,⋆⋆
1
Purple Mountain Observatory & Key Laboratory for Radio Astronomy,
Chinese Academy of Sciences, 2 West
Beijing Road, 210008, Nanjing,
PR China
e-mail: ygong@pmo.ac.cn
2
Max-Planck Institute für Radioastronomy,
Auf dem Hügel 69, 53121
Bonn,
Germany
3
University of Chinese Academy of Sciences,
No. 19A Yuquan Road, 100049
Beijing, PR
China
4
Astronomy Department, King Abdulaziz University,
PO Box 80203, 21589
Jeddah, Saudi
Arabia
5
I. Physikalisches Institut, Universität zu Köln,
50937
Köln,
Germany
6
University of Applied Sciences Bonn-Rhein-Sieg,
Grantham-Allee 20, 53757
Sankt Augustin,
Germany
Received: 15 August 2014
Accepted: 19 November 2014
Context. IRC +10216 is the prototypical carbon star exhibiting an extended molecular circumstellar envelope. Its spectral properties are therefore the template for an entire class of objects.
Aims. The main goal is to systematically study the λ ~ 1.3 cm spectral line characteristics of IRC +10216.
Methods. We carried out a spectral line survey with the Effelsberg-100 m telescope toward IRC +10216. It covers the frequency range between 17.8 GHz and 26.3 GHz (K-band).
Results. In the circumstellar shell of IRC +10216, we find 78 spectral lines, among which 12 remain unidentified. The identified lines are assigned to 18 different molecules and radicals. A total of 23 lines from species known to exist in this envelope are detected for the first time outside the solar system and there are additional 20 lines first detected in IRC +10216. The potential orgin of “U” lines is also discussed. Assuming local thermodynamic equilibrium (LTE), we then determine rotational temperatures and column densities of 17 detected molecules. Molecular abundances relative to H2 are also estimated. A non-LTE analysis of NH3 shows that the bulk of its emission arises from the inner envelope with a kinetic temperature of 70 ± 20 K. Evidence for NH3 emitting gas with higher kinetic temperature is also obtained, and potential abundance differences between various 13C-bearing isotopologues of HC5N are evaluated. Overall, the isotopic 12C/13C ratio is estimated to be 49 ± 9. Finally, a comparison of detected molecules in the λ ~ 1.3 cm range with the dark cloud TMC-1 indicates that silicate-bearing molecules are more predominant in IRC +10216.
Key words: astrochemistry / ISM: molecules / stars: individual: IRC +10216 / radio lines: stars
Appendices are available in electronic form at http://www.aanda.org
Spectra as FITS files are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/574/A56
© ESO, 2015
Existing line surveys of IRC +10216.
1. Introduction
Molecular line surveys are a powerful tool for analyzing both physical and chemical parameters of astronomical objects. In fact, they are the only means of obtaining a complete, unbiased view of the molecular inventory of a given source. However, despite the long history of powerful large radio telescopes, few unbiased frequency surveys have been conducted in the cm-wave regime. A 4.4 GHz bandwidth survey from 17.6 to 22.0 GHz toward the massive star-forming region W51 has been reported by Bell et al. (1993b) showing many previously unidentified lines. The dark cloud TMC-1 has been observed in selected bands from 4−6 and 8−10 GHz (Kalenskii et al. 2004), as well as at 9−50 GHz (Kaifu et al. 2004). More recently, some systematic observations toward the galactic center have also been reported by Remijan et al. (2008) in the course of their GBT PRIMOS project1.
Spectroscopic features that are expected at long wavelengths (i.e. in the cm-wave regime) include recombination lines from HI, HeI, and CI, which can be assigned in a straightforward manner. In addition, complex molecules have small rotational constants so that their lowest-energy transitions arise at cm-wavelenths. In this way, emission or absorption features from long carbon-chain molecules can be observed (e.g. HC3N, HC5N, HC7N, HC9N). Since systematic and highly sensitive surveys at these (low) frequencies that cover different sources have rarely been carried out, one can only speculate as to what else may be observed. The enormous potential of cm-wave astronomy for detecting new molecules in space has been highlighted in the recent past through GBT detections of complex organic molecules such as CH2CHCHO (propenal), CH3CH2CHO (propanal), and CNCHO (cyanoformaldehyde; Hollis et al. 2004; Remijan et al. 2008).
For this paper, we performed a 1.3 cm line survey toward IRC +10216, which is also known as CW Leonis. It is found to be the brightest object outside the solar system at 5 μm (Becklin et al. 1969). It is a well-studied asymptotic giant branch (AGB) carbon star with a high mass loss rate (2.0 × 10-5M⊙ yr-1) at a distance of ~130 pc (Crosas & Menten 1997; Menten et al. 2012), which results in a dense circumstellar envelope (CSE). The CSE is the ideal target for studying gas-phase chemistry in a peculiar, namely carbon-rich environment. Existing surveys, summarized in Table 1, cover parts of the frequency range from 4 GHz to 636.5 GHz for IRC +10216. These efforts have resulted in the discovery of over 70 species toward this object, including unusual carbon-chain molecules, metal cyanides such as MgNC, NaCN, and AlNC (Cernicharo et al. 2000; Ziurys et al. 2002), and even metal halides: NaCl, AlCl, KCl, and AlF (Cernicharo & Guelin 1987). However, the frequency range between 18 and 26 GHz is still largely unexplored. Here, we therefore systematically study the characteristics of IRC +10216 in the important λ ~ 1.3 cm (K-band) spectral range, which is known to contain a number of lines from prominent molecules like H2O, NH3, and the cyanopolyynes.
 |
Fig. 1 Overview of the 1.3 cm line survey toward IRC +10216 with strong lines marked. |
2. Observations and data reduction
The observations were carried out in a position-switching mode with the primary focus λ = 1.3 cm K-band receiver of the 100 m telescope at Effelsberg/Germany2, during 2012 in January, April, and 2013 in January, March, and May. On- and off-source integration times were two minutes per scan. The newly installed Fast Fourier Transform Spectrometer (FFTS) was used as backend. Each spectrometer, covering one of the two orthogonal linear polarizations with a bandwidth of 2 GHz provides 32 768 channels, resulting in a channel spacing of 61 kHz, equivalent to 0.7 km s-1 at 26 GHz. The actual frequency and velocity resolutions are coarser by a factor of 1.16 (Klein et al. 2012). Several frequency setups were tuned to cover the entire frequency range from 17.8 GHz to 26.3 GHz with an overlap of at least 100 MHz between two adjacent frequency setups. Across the whole frequency range, the beamsize is 35′′–50′′ (~40′′ at 23 GHz). The survey encompasses a total of ~130 observing hours. The focus was checked every few hours, in particular after sunrise and sunset. Pointing was obtained every hour toward the quasar PG 0851+202 (OJ +287) and was found to be accurate to about 5′′. Strong continuum sources (mostly 3C 286) were also used to calibrate the spectral line flux according to their standard flux densities (Ott et al. 1994). The typical rms noise is about 1−3 mJy in ~0.7 km s-1 wide channels. In view of the width of the IRC +10216 spectra, ~30 km s-1, smoothed spectra typically reach rms noise levels of about 1 mJy. The conversion factor from Jy on a flux density scale (Sν) to K on a main beam brightness temperature scale (Tmb) is Tmb/Sν ~ 1.5 K/Jy at 22 GHz.
For the data reduction, the GILDAS3 software package including CLASS and GREG was employed. During the data reduction, some inevitable defects occured at the edges of the spectra. Therefore 100 channels at each edge were excluded. Fourth- to tenth-order baselines were subtracted from each spectrum with 2000 to 3000 channels to avoid lines being truncated at the edge of subspectra, and then these subspectra were stitched together to resconstruct the complete spectrum. Since some of the subspectra suffer contamination from time variable radio frequency interference (RFI), the channels showing RFI signals have been “flagged”, i.e. discarded from further analysis, resulting in some limited gaps in the averaged spectra. Furthermore, there were a few individual bad channels, which have also been eliminated.
3. Results
3.1. Line identifications
The line identification was performed on the basis of the JPL4, CDMS5, and splatalogue6 databases as well as on the online Lovas line list7 for astronomical spectroscopy (Müller et al. 2005; Pickett et al. 1998; Lovas & Dragoset 2004). A line is identified as real if it is characterized by a signal-to-noise ratio of at least five. Figure 1 presents an overview of our λ ~ 1.3 cm line survey toward IRC +10216. We find 78 spectral lines, among which 12 remain unidentified. The identified lines are assigned to 18 different molecules. Except for SiS and NH3, they are all C-bearing molecules. Twenty-three lines from already known species are detected for the first time outside the solar system and there are additional 20 lines first detected in IRC +10216. Details are described in Sect. 3.2.
The spectrum is dominated by the strong profiles from six species: SiS, HC3N, and HC5N with Sν> 100 mJy; HC7N, c-C3H2, and SiC2 with Sν> 20 mJy. Figure B.1 shows the observed spectrum in more detail. Each panel covers ~500 MHz of the spectrum. Furthermore, there is a 10 MHz overlap between adjacent panels so that lines truncated in one panel will not be truncated in the other panel. In addition, Fig. B.2 shows zoom-in plots of all detected transitions.
We used the SHELL fitting routine in CLASS to derive the line parameters including peak intensity, integrated intensity, and expansion velocity, which is defined as the half-width at zero power. For the lines with hyperfine structure (hfs, like HC3N, NH3, etc.), only their main components are fitted with the routine to obtain their expansion velocities. For the lines that are blended or weak, the parameters are estimated directly by integrating the line profiles. The observed properties of the lines are displayed in Table 3. The fitted lines reveal an expansion velocity of around 14.0 km s-1, which is consistent with previous studies (e.g., Cernicharo et al. 2000; He et al. 2008). There are some previously reported narrow lines with expansion velocities of <10 km s-1 that are mainly from high-J transitions in the ground vibrational state or from transitions in vibrationally excited states (Patel et al. 2009; He et al. 2008), originating in the innermost, not yet fully accelerated shell. Lines with expansion velocities <10 km s-1 are not seen in our study.
3.2. Newly detected lines
In the following, we briefly describe most of the 23 newly detected lines (denoted by an “N” in the last column of Table 3) and most of the other 20 lines newly detected in IRC +10216 (“NS”), together with related, already detected transitions from the same species. These transitions belong to HC5N, HC7N, HC9N, SiC4, NH3, MgNC, l-C5H, C6H, C6H−, and C8H. The 13C-bearing isotopologues of HC5N are also briefly addressed (see also Sect. 4.4).
HC5N. – There are three transitions of cyanobutadiyne (HC5N) in our observed frequency range. All of them have been detected, and the HC5N line intensities rise with increasing frequency. HC5N (9–8) has been reported by Winnewisser & Walmsley (1978), but their peak intensity is almost twice the peak intensity measured by us even though their data were also obtained at Effelsberg. Significant variations in line intensities measured at submm and far-infrared wavelengths have recently been reported by Cernicharo et al. (2014). However, unpublished HC5N and HC7N monitoring observations at Effelsberg about 25 yr ago (Henkel, priv. comm.) did not reveal time variability in excess of 20%. Furthermore, the λ ~ 3 mm data of Cernicharo et al. (2014) also show no strong variability. This, as well as other discrepancies outlined below, are therefore very likely caused by narrower bandwidths, lower quality baselines, and noise diodes with a more frequency-dependent output, thus resulting in a less accurate calibration than we have obtained here.
13C-bearing HC5N isotopologues. – We have detected 11 transitions from the 13C-bearing isotopologues of HC5N. Seven of them are first detected outside the solar system, while four other transitions have already been studied with the NRAO-43 m telescope (Bell & Feldman 1991).
HC7N. – Eight transitions of HC7N from J = 16−15 to J = 23−22 fall in our band and are all detected. From Fig. A.1, their line intensities rise with increasing frequency. Furthermore, we find that higher J transitions have deeper dips than lower J transitions in the center of line profiles. This is because the higher angular resolution of the higher J transitions ends up lowering the contribution of emission from the CSE’s outer regions to the line profiles. Apparently, the possible decrease in source size owing to higher excitation requirements of higher J lines is less pronounced than effects caused by the decreasing beam size. HC7N (21–20) has been reported before (Winnewisser & Walmsley 1978), but the peak intensity also obtained for it with the 100 m telescope is almost twice the peak intensity measured by us.
HC9N. – There are 14 transitions of HC9N in our band. Five of them have been reported before (Bell et al. 1992; Truong-Bach et al. 1993). The intensity of HC9N (43–42) measured by us is roughly twice the intensity reported, also from Effelsberg, by Truong-Bach et al. (1993).
SiC4. – There are three lines of SiC4 in this band and two of them are detected. They have lower upper level energies than previously reported transitions that span a frequency range from ~30 to ~100 GHz (Kawaguchi et al. 1995; Mauersberger et al. 2004). Although SiC4 (6–5) falls into our frequency range as well, it is apparently too weak and remained undetected. This is consistent with the fact that the J = 7–6 line is found to be significantly weaker than the J = 8–7 line.
NH3. – We measured the five metastable inversion transitions (J,K) = (1, 1),(2, 2),(3, 3),(4, 4),(6, 6) of ammonia (NH3). The (5, 5) line, also inside the measured band, is not seen (the non-detection of NH3 (5, 5) is discussed in Sect. 4.3). NH3 (1, 1) and NH3 (2, 2) have been reported by Nguyen-Q-Rieu et al. (1984) with the 100 m telescope, and their peak intensities are similar to ours. Inspecting Fig. A.1 and Table 3, we find that the metastable inversion lines become slightly narrower with increasing J. Furthermore, we do not find clear evidence for hfs components in the NH3 lines. For example, the (1, 1) transition has one main and four satellite groups of hfs components, the centroid velocities of the groups of hfs components are symmetrically spaced by ≈±7.6 km s-1 and ±19.4 km s-1 from the main group (Kukolich 1967). Had the satellite groups appreciable optical depths this would lead to a significant (and symmetrical) broadening of this line. Assuming that all components of NH3 (1, 1) have the same excitation temperature, the limits on integrated intensity ratios (>8) between the main component and the hyperfine structure components indicate that the optical depth of NH3 (1, 1) is very low and might even depart from local thermodynamic equilibrium (LTE ratios on the order of 4). Meanwhile, there are no non-metastable NH3 lines (J>K) detected. Non-metastable NH3 lines require extreme densities (spontaneous radiative decay for rotational lines is ~105 times faster than for pure inversion transitions) or radiation fields to get excited and thus should only originate in the innermost shell. Any emission from this region would suffer from significant beam dilution effects.
MgNC. – The radical’s higher J transitions have already been studied before (Kawaguchi et al. 1995; Guelin et al. 1993). This confirms our assignment about the N = 2−1, J = 5/2−3/2 transition of MgNC at 23 875.0 MHz while the N = 2−1, J = 3/2−1/2 transition, also located within our frequency range, remains undetected. This is expected, since its integrated intensity may be ~90 mJy km s-1 (corresponding to a peak intensity of 3 mJy assuming an expansion velocity of 14 km s-1 and a flat-topped line profile) according to the expected intensity ratio between N = 2−1, J = 5/2−3/2 and N = 2−1, J = 3/2−1/2 lines under conditions of LTE and optically thin emission (see Sect. 4) and there are large uncertainties related to weak transitions.
l-C5H. – Five
lines are detected in this survey, and they are from both the
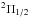 and
and
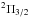 ladders. Transitions of l-C5H at higher frequencies have
already been reported from IRC +10216 (Kawaguchi et al.
1995; Cernicharo et al. 1986).
ladders. Transitions of l-C5H at higher frequencies have
already been reported from IRC +10216 (Kawaguchi et al.
1995; Cernicharo et al. 1986).
C6H. – The first
identification of the C6H radical toward IRC +10216 has been reported by Guelin et al. (1987). Six lines of C6H are observed here, stemming
from both the 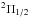 and the
and the
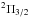 ladders.
ladders.
C6H−. – C6H− was the first detected interstellar anion, and its identification has been confirmed by observations toward IRC +10216 and TMC-1 (McCarthy et al. 2006). Three transitions of C6H− fall into our band, and two of them are detected. C6H− (7–6) is also inside the frequency range covered by this survey, but is expected to be weaker than C6H− (8–7).
C8H. –
C8H is the
longest C2nH molecule detected so far. It was first
discovered toward IRC +10216 by Cernicharo & Guelin
(1996). Four lines of C8H are detected in this survey, all from the
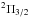 ladder. Their hfs is not resolved.
C8H
J =
39/2−37/2 has been detected in IRC +10216 by Remijan et al. (2007), and the intensity agrees well with our
measurement.
ladder. Their hfs is not resolved.
C8H
J =
39/2−37/2 has been detected in IRC +10216 by Remijan et al. (2007), and the intensity agrees well with our
measurement.
3.3. Unidentified lines
We do not see the 22.2 GHz line of water vapor (see Melnick et al. 2001; Cherchneff 2011; Neufeld et al. 2011, 2013, for detections of higher frequency transitions). This may be due to a coherent gain path of insufficient length or incorrect density-temperature combinations. For the 22.2 GHz line to mase, Tkin ~ 400 K and 108 cm-3<n< 109 cm-3 may be required (e.g., Kylafis & Norman 1991). This could be met in the inner envelope. If the density were too high in the T ~ 400 K region, the maser action would be quenched. However, in that case, thermal emission would be expected. Assuming optically thick emission at Tkin = 600 K for the 22.2 GHz line and an emitting region of ten stellar radii or 0.8′′ (roughly consistent with the Tkin-radius profile in Fig. 5 of Crosas & Menten 1997), we get in our 43′′ beam (Sect. 2) Tmb = 600 × 103 × (1.6/43)2 mK, which gives an approximate Tmb ~ 800 mK. We clearly do not see this at a 5σ noise level of Tmb ~ 10 mK and conclude that the assumption of optically thick emission must be incorrect. This is consistent (Gonzalez-Alfonson, priv. comm.) with the model that reproduces the H2O data from Herschel, published by Neufeld et al. (2011). The C5S lines are also not seen in our K-band spectral range (see Agúndez et al. 2014, for a report about the discovery of C5S in IRC +10216) while Bell et al. (1993a) claimed detecting one C5S line at 23 990.2 MHz with a peak flux density of almost 20 mJy. With expected rotational temperatures of 18−44 K and expected column densities of (2−14) × 1012 cm-2 (Agúndez et al. 2014), we can estimate the peak intensity of the C5S 23 990.2 MHz line by assuming a low opacity, a flat-topped line profile, an expansion velocity of 14 km s-1, a source size of 30′′ and a beamsize of 40′′. The derived peak intensity is estimated to be 0.3−4 mJy, corresponding to an integrated intensity of 8.4–112 mJy km s-1, where its electric dipole moment is taken to be 5.12 D (Botschwina 2003). Thus, our non-detection of the C5S lines is expected and the detection reported by Bell et al. (1993a) remains unconfirmed.
When referring to detected spectral features, we find 12 unidentified lines in this
survey that cannot be assigned to any transitions in the spectroscopic catalogs available
to us. Their high percentage (~15% of the total number of lines) is probably due to the high
sensitivity of the survey since their peak intensities are all less than 10 mJy. All of
them show U-shaped or flat-topped profiles so they may represent isotopologues of
well-known molecules or vibrationally excited lines or new species, and are marked with
“U” in Table 3. The frequencies of unidentified
lines are determined by eye assuming a source velocity of Vlsr = −26.0
km s-1. The
accuracy of the frequencies of the U lines is estimated to lie within ~180 kHz which is equivalent to three
raw channels. The “U” line at 24 901.4 MHz is close to C4H
(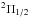 ) (ν7 = 1,
J =
5/2−3/2, l =
e), and their frequency difference is 454 kHz,
corresponding to ~5.5
km s-1. Another
“U” line at 25 111.8 MHz is close to CH2CHCN (101,9–101,10) with a rest frequency at 25 111.4 MHz, but this
line as observed would not be expected from this molecule because its fitted expansion
velocity is about 19 km s-1, if we use a single component to fit it. This is higher
than the typical expansion velocity deduced from other detected transitions of
CH2CHCN in
IRC +10216 (Agúndez et al. 2008). Furthermore, the
integrated intensity of CH2CHCN (101,9–101,10) is expected to be around 0.3 mJy
km s-1 under the
LTE assumption and assuming the column density and rotational temperature determined by
Agúndez et al. (2008) , which is much less than
that of this “U” line.
) (ν7 = 1,
J =
5/2−3/2, l =
e), and their frequency difference is 454 kHz,
corresponding to ~5.5
km s-1. Another
“U” line at 25 111.8 MHz is close to CH2CHCN (101,9–101,10) with a rest frequency at 25 111.4 MHz, but this
line as observed would not be expected from this molecule because its fitted expansion
velocity is about 19 km s-1, if we use a single component to fit it. This is higher
than the typical expansion velocity deduced from other detected transitions of
CH2CHCN in
IRC +10216 (Agúndez et al. 2008). Furthermore, the
integrated intensity of CH2CHCN (101,9–101,10) is expected to be around 0.3 mJy
km s-1 under the
LTE assumption and assuming the column density and rotational temperature determined by
Agúndez et al. (2008) , which is much less than
that of this “U” line.
Among the “U” lines, we find that there are three doublets, at 22 304.854 MHz and
22 323.3 MHz (pair-1, 18.5 MHz apart), at 25 094.3 MHz and 25 111.8 MHz (pair-2, 17.5 MHz
apart), and at 25 976.2 MHz and 25 992.8 MHz (pair-3, 16.6 MHz apart). Their separations
(16 MHz to 19 MHz) could be caused by hfs or different 13C substitutions. Estimates of
their carrier’s rotational constant (B) and centrifugal stretching constant
(D) can
help to make guesses about their identity. Assuming that two or three of them are from the
same linear molecule, B and D can be derived via the formula (Wilson et al. 2009) 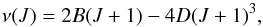 (1)where ν is the rest frequency of
the J –
(J − 1)
transition. We follow two steps to fit the parameters B and D. First, we obtain the
number of J
with D = 0.
J has to be
an integer. Secondly, B and D can be derived with J fixed. We find that the
three doublets cannot be attributed to one species. If they belonged to one species, the
three doublets would have to be assigned to the J, J + 3, and J + 4 levels but the
J + 1 and
J + 2
levels are not detected in our band. Furthermore, the fitted D would be negative. Thus,
we assume that two of them belong to the J and J + 1 levels of one species to derive the
parameters J,
B, and
D. Since
D is
usually a very small number, results are dismissed when the derived D is larger than 0.5 MHz.
The results are given in Table 2.
(1)where ν is the rest frequency of
the J –
(J − 1)
transition. We follow two steps to fit the parameters B and D. First, we obtain the
number of J
with D = 0.
J has to be
an integer. Secondly, B and D can be derived with J fixed. We find that the
three doublets cannot be attributed to one species. If they belonged to one species, the
three doublets would have to be assigned to the J, J + 3, and J + 4 levels but the
J + 1 and
J + 2
levels are not detected in our band. Furthermore, the fitted D would be negative. Thus,
we assume that two of them belong to the J and J + 1 levels of one species to derive the
parameters J,
B, and
D. Since
D is
usually a very small number, results are dismissed when the derived D is larger than 0.5 MHz.
The results are given in Table 2.
Fitted results for the “U” line doublets.
We find that the derived rotational constants are very small, which indicates a heavy molecule. When we assume that pair-1 and pair-2 come from the same species, the derived rotational constants are similar to that (1391.2 MHz) of C6H. We note, however, that these rotational constants allow us to predict additional lower J lines within our surveyed frequency range, which are not seen. It is probably because the lower J level transitions are weaker than higher ones and cannot be detected by this survey.
Lines detected in the survey of IRC+10216.
4. Discussion
4.1. Rotational temperatures and column densities
Line shapes can be used to evaluate the optical depth of individual transitions in
IRC +10216. Parabolic lines arise from optically thick emission like that of CO (1–0),
while flat-topped and U-shaped lines arise from optically thin spatially unresolved and
resolved emission, respectively (Olofsson et al.
1982; Kahane et al. 1988). We find no
lines that show parabolic profiles among the identified spectral features in this survey.
Also, lines with hfs should allow for estimates of their optical depth, if the hfs
components are sufficiently displaced from each other (see the case of NH3 discussed above). For such
lines in our survey (NH3, HC3N, C3N, etc.), we find low opacities. Thus, it is reasonable
to assume optically thin emission for all the lines detected in this work. Assuming LTE,
we use rotational diagrams to roughly estimate rotational temperatures and column
densities. The standard formula used here is 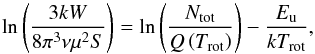 (2)where k is the Boltzmann
constant, W
the integrated intensity, S the transition’s intrinsic strength,
μ the
permanent dipole moment, Ntot the total column density,
Trot the rotational temperature,
Q the
partition function, and Eu the upper level energy of the
transition. The values of Q and μ are taken from the CDMS and JPL catalogs.
(2)where k is the Boltzmann
constant, W
the integrated intensity, S the transition’s intrinsic strength,
μ the
permanent dipole moment, Ntot the total column density,
Trot the rotational temperature,
Q the
partition function, and Eu the upper level energy of the
transition. The values of Q and μ are taken from the CDMS and JPL catalogs.
Column densities and rotational temperatures of the molecules in IRC +10216.
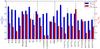 |
Fig. 2 Comparison of the column densities and rotational temperatures of different molecules. The labels for column densities are blue on the left side, while those for rotational temperatures are red on the right side. Here, a Trot of 39.1 K has been taken for para and ortho NH3 (see Sect. 4.1 and Table 4). |
 |
Fig. 3 RADEX non-LTE modeling for NH3. a) the integrated intensity ratio
|
At least two transitions of the same molecule with significant energy differences are required to determine rotational temperatures with this method. For those molecules with only one transition detected or without a wide dynamic range in upper level energies, we make use of the 28 GHz to 50 GHz data from Kawaguchi et al. (1995), the C8H data from Remijan et al. (2007), and the C3N data from He et al. (2008), because those data have nearly the same resolution (~40′′) as our observations. The intensities of blended lines have large uncertainties, so are not included. SiS is also excluded, since SiS (1–0) is a maser in IRC +10216 (Grasshoff et al. 1981; Henkel et al. 1983) and the populations must deviate from LTE.
To derive the physical parameters, the intensities should be corrected for beam dilution
by dividing by 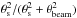 , where θs is the source
size, and θbeam is the beam size. Based on previous
high resolution mapping of different molecules toward IRC +10216, we take the same source
sizes as those listed in Table 4. For species
without high resolution mapping, their sizes are taken to be the same as chemically
related species (details are described in the notes of Table 4). We also used different source sizes θs =
15″,18″,30″,50″ to study the influence on the derived rotational
temperatures and column densities of these molecules. It turns out that the uncertainties
of the total column densities vary within a factor of four while the rotational
temperatures nearly remain the same.
, where θs is the source
size, and θbeam is the beam size. Based on previous
high resolution mapping of different molecules toward IRC +10216, we take the same source
sizes as those listed in Table 4. For species
without high resolution mapping, their sizes are taken to be the same as chemically
related species (details are described in the notes of Table 4). We also used different source sizes θs =
15″,18″,30″,50″ to study the influence on the derived rotational
temperatures and column densities of these molecules. It turns out that the uncertainties
of the total column densities vary within a factor of four while the rotational
temperatures nearly remain the same.
We carried out linear least-square fits to the rotational diagrams of 17 species and four
13C isotopologues
of HC5N, which are
shown in Fig. A.2. For these fits, only data with
signal-to-noise ratios higher than five are taken. The figures show that a few lines from
the literature are outliers. In particular, SiC4 (16–15) at Eu/k = 20.0 K is much
weaker than expected, and the data of C6H (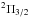 ) from Kawaguchi et al. (1995) show significant scatter. This is due to weak lines with
signal-to-noise ratios less than five, which, as mentioned above, have not been included
in the fits. Therefore, only data points with higher signal-to-noise ratios than five are
taken into account if there are enough points for the fits. Otherwise, data points with
lower signal-to-noise ratios are also included and the fit to the data is represented not
by a dashed but by a dash-dotted line. For example, those data points with signal-to-noise
ratios less than five are used for the fits of 13C isotopologues of HC5N and C8H. The quality of the
calibration of our observations is indicated by the fact that the data points for the
HC7N transitions
show very little scatter about the fitted line in Fig. A.2, while their frequencies cover nearly the entire frequency range surveyed by
us. For l-C5H
(
) from Kawaguchi et al. (1995) show significant scatter. This is due to weak lines with
signal-to-noise ratios less than five, which, as mentioned above, have not been included
in the fits. Therefore, only data points with higher signal-to-noise ratios than five are
taken into account if there are enough points for the fits. Otherwise, data points with
lower signal-to-noise ratios are also included and the fit to the data is represented not
by a dashed but by a dash-dotted line. For example, those data points with signal-to-noise
ratios less than five are used for the fits of 13C isotopologues of HC5N and C8H. The quality of the
calibration of our observations is indicated by the fact that the data points for the
HC7N transitions
show very little scatter about the fitted line in Fig. A.2, while their frequencies cover nearly the entire frequency range surveyed by
us. For l-C5H
(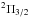 ), we only detect one line that cannot be
fitted with the data from Kawaguchi et al. (1995),
because this would result in a negative excitation temperature. We therefore use the
rotational temperature derived from their data and our measured transition to obtain its
column density (see the lower dashed line in the respective panel of Fig. A.2; the upper dashed line refers solely to the data of
Kawaguchi et al. 1995).
), we only detect one line that cannot be
fitted with the data from Kawaguchi et al. (1995),
because this would result in a negative excitation temperature. We therefore use the
rotational temperature derived from their data and our measured transition to obtain its
column density (see the lower dashed line in the respective panel of Fig. A.2; the upper dashed line refers solely to the data of
Kawaguchi et al. 1995).
HC9N shows large
scatter, which may result from uncertainties related to its low line intensities. The
HC9N transitions
from Kawaguchi et al. (1995) are not included since
they show an even larger scatter. For NH3 and c-C3H2, we fit their para and ortho states individually. If we
only take NH3
(1, 1), (2, 2), and (3, 3) into account, the ortho/para ratio of NH3 is estimated to be
1.3 ± 0.6 in IRC +10216,
which roughly agrees with the fact that the ortho/para abundance ratio approaches the
statistical ratio of unity if NH3 was formed in a medium with a kinetic temperature higher
than ~40 K (Takano et al. 2002). Including the NH3 (4, 4) and NH3 (6, 6) lines yields a higher
rotational temperature and a lower ortho column density (see Table 4). The ortho/para abundance ratio then becomes 0.6 ± 0.2. The derived ortho/para ratio of
c-C3H2 is about 1.4 ± 0.3, which is much less than the expected theoretical value of 3. We
only have two points to fit the rotational temperature, and para and ortho Trot values are
assumed to be the same. We also fit the 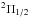 and
and
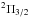 states, separately, for l-C5H and C6H. However, the fits for
l-C5H
(
states, separately, for l-C5H and C6H. However, the fits for
l-C5H
(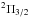 ) shown in Fig. A.2 are tentative and should have large uncertainties because the data
used here have an energy range (ΔE/k) less than 10 K.
) shown in Fig. A.2 are tentative and should have large uncertainties because the data
used here have an energy range (ΔE/k) less than 10 K.
The derived rotational temperatures (Trot) and column densities
(N),
together with results from the literature, are listed in Table 4. MgNC and C2S show the largest uncertainties in the rotational
temperature, which is due to the narrow energy ranges covered. From Table 4, we find that the derived column densities agree
roughly with previous studies. From Fig. 2, taking
Trot = 39.1 ±
10.5 K for the bulk of the para and ortho NH3, we find rotational
temperatures ranging from 5.5 to 47.2 K and molecular column densities ranging from
5.2 × 1012 to
2.4 × 1015
cm-2.
C6H
(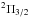 ) has the highest rotational temperature,
while c-C3H2 has the lowest rotational temperatures indicating that
they should be present in the cold outer molecular envelope. C4H, SiC2 and HC3N are found to be the most
abundant carbon-bearing molecules in our survey while C6H−, C8H, and the 13C substitutions of
HC5N have the
lowest column densities (see Table 4). The column
densities of all these species are spread over two orders of magnitude, and more complex
molecules tend to be less abundant.
) has the highest rotational temperature,
while c-C3H2 has the lowest rotational temperatures indicating that
they should be present in the cold outer molecular envelope. C4H, SiC2 and HC3N are found to be the most
abundant carbon-bearing molecules in our survey while C6H−, C8H, and the 13C substitutions of
HC5N have the
lowest column densities (see Table 4). The column
densities of all these species are spread over two orders of magnitude, and more complex
molecules tend to be less abundant.
4.2. Fractional abundances relative to H2
To obtain molecular abundances relative to H2, one has to know the H2 column density. Kendall et al. (2002) employed optical absorption
spectroscopy toward background stars lying behind the envelope and found that the
H+2H2 column
density at an offset of 37′′
from IRC +10216 is ~2 ×
1021 cm-2. Based on the optically thin lines of 13CO (1–0), (2–1), and (3–2),
Groesbeck et al. (1994) determined a
beam-averaged (~20′′) CO column density of ~2 × 1018 cm-2 toward IRC +10216 by taking 12C/13C to be 44. Previous studies
have shown the fractional abundance CO/H2 to be 6 ×
10-4 in IRC +10216 (Kwan
& Linke 1982; Huggins et al. 1988),
resulting in an H2
column density of 3.3 ×
1021 cm-2. Furthermore, the average H2 column density can also be
calculated from the mass loss rate via the formula 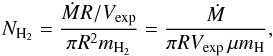 (3)where Ṁ is the mass loss rate
which is believed to be 2.0 ×
10-5M⊙ yr-1 (Crosas & Menten 1997); R is the radius; Vexp is the
expansion velocity of the CSE which is equal to 14 km s-1; μ is the mean molecular
weight, which we assume to be equal to 2.8; and mH is the mass of a hydrogen atom. Of
course, reference H2 column densities to be used for abundance calculations
depend on the location of their emission region in the CSE (see Formula 3). For example, if we take R as the CO radius
(100′′; Fong et al. 2006) and the HC3N radius of 15′′ (Table 4), the H2 average column densities inside these radii are
3.2 × 1020
cm-2 and
2.1 × 1021
cm-2,
respectively. While each line has a different distribution and therefore an individual
NH2, the choice of a specific
NH2 for all molecules is needed
for a meaningful comparison with other studies. Thus, we use the H2 average column density
(2.1 × 1021
cm-2) within a
typical radius of 15′′ to
calculate molecular fractional abundances relative to H2. The uncertainty of the average
H2 column density
is within a factor of two since most detected molecules have a characteristic radius
ranging from 7.5′′ to
30′′ in IRC +10216. The
results are given in the fourth column of Table 4.
We find the fractional abundances relative to H2 range for K-band detected species from 2.5 × 10-9 to 1.1 × 10-6 in IRC +10216.
(3)where Ṁ is the mass loss rate
which is believed to be 2.0 ×
10-5M⊙ yr-1 (Crosas & Menten 1997); R is the radius; Vexp is the
expansion velocity of the CSE which is equal to 14 km s-1; μ is the mean molecular
weight, which we assume to be equal to 2.8; and mH is the mass of a hydrogen atom. Of
course, reference H2 column densities to be used for abundance calculations
depend on the location of their emission region in the CSE (see Formula 3). For example, if we take R as the CO radius
(100′′; Fong et al. 2006) and the HC3N radius of 15′′ (Table 4), the H2 average column densities inside these radii are
3.2 × 1020
cm-2 and
2.1 × 1021
cm-2,
respectively. While each line has a different distribution and therefore an individual
NH2, the choice of a specific
NH2 for all molecules is needed
for a meaningful comparison with other studies. Thus, we use the H2 average column density
(2.1 × 1021
cm-2) within a
typical radius of 15′′ to
calculate molecular fractional abundances relative to H2. The uncertainty of the average
H2 column density
is within a factor of two since most detected molecules have a characteristic radius
ranging from 7.5′′ to
30′′ in IRC +10216. The
results are given in the fourth column of Table 4.
We find the fractional abundances relative to H2 range for K-band detected species from 2.5 × 10-9 to 1.1 × 10-6 in IRC +10216.
4.3. The RADEX non-LTE modeling for NH3: the kinetic temperature
Here we present a non-LTE analysis of NH3 to determine the envelope’s kinetic temperature using the RADEX expanding sphere code for IRC +10216 (van der Tak et al. 2007). NH3 is well suited to temperature determinations even with the limited frequency range covered by our survey, since its transitions arise from a wide range of energies above the ground state. Moreover, the metastable inversion lines are widely used as a galactic and extragalactic molecular temperature tracer (e.g., Walmsley & Ungerechts 1983; Ho & Townes 1983; Mauersberger et al. 2003).
Assuming that NH3
has a typical expanding velocity of 14 km s-1 and a size of 18′′ (see Sect. 4.1), we obtain a velocity gradient of about 2468 km s-1 pc-1. Adopting a fixed
para-NH3
abundance of 1.1 ×
10-7 (see Table 4
and, for chemical considerations, Menten et al.
2010) and a velocity gradient of 2500 km s-1 pc-1, we arrive at a
para-NH3
abundance per velocity gradient [
X ] /(dv/ dr) of
4.4 ×
10-11 pc (km s-1)-1. The modeled kinetic temperatures range from 10 to 300
K with a step size of 5 K. The H2 number density log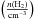 varies from 2.0 to 7.0 with a step size of
0.1. For an adopted size of the NH3 region of 18′′, the density is around 105 cm-3 according to the density profile toward IRC +10216
(Groenewegen et al. 1997). We modeled the
integrated intensity ratios
varies from 2.0 to 7.0 with a step size of
0.1. For an adopted size of the NH3 region of 18′′, the density is around 105 cm-3 according to the density profile toward IRC +10216
(Groenewegen et al. 1997). We modeled the
integrated intensity ratios 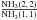 in this study, which are shown in Fig.
3a, because (a) the ratio between NH3 (1, 1) and NH3 (2, 2) is not affected by an
ortho-to-para abundance ratio, because (b) NH3 rotation temperatures provide lower limits to the
kinetic temperature (e.g., Walmsley & Ungerechts
1983) with the (J,K)
= (1, 1), (2, 2), and (3, 3) transitions revealing the lowest
Trot values, and because (c) beam-filling
factors (the (1, 1) and (2, 2) frequencies are less than 30 MHz apart) should not play a
role. Assuming that both lines arise from the same source, we obtain a kinetic temperature
of 70 ± 20 K for
NH3 in the
density range from 104.5 to 105.5 cm-3 with an integrated intensity ratio
in this study, which are shown in Fig.
3a, because (a) the ratio between NH3 (1, 1) and NH3 (2, 2) is not affected by an
ortho-to-para abundance ratio, because (b) NH3 rotation temperatures provide lower limits to the
kinetic temperature (e.g., Walmsley & Ungerechts
1983) with the (J,K)
= (1, 1), (2, 2), and (3, 3) transitions revealing the lowest
Trot values, and because (c) beam-filling
factors (the (1, 1) and (2, 2) frequencies are less than 30 MHz apart) should not play a
role. Assuming that both lines arise from the same source, we obtain a kinetic temperature
of 70 ± 20 K for
NH3 in the
density range from 104.5 to 105.5 cm-3 with an integrated intensity ratio
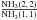 of 0.73 ± 0.1 (see Fig. 3a).
of 0.73 ± 0.1 (see Fig. 3a).
The value of the para-NH3 abundance per velocity gradient [ X ] /(dv/
dr), which was given at the start of the previous
paragraph, may have a large uncertainty, potentially also leading to a significant error
bar in our Tkin estimate. Thus, we carried out a
non-LTE analysis with a fixed density of 105 cm-3 (see previous paragraph) and the
para-NH3
abundance per velocity gradient [
X ] /(dv/ dr)
ranging from 1.0 ×
10-13 to 1.0 ×
10-9 pc (km s-1)-1. The result is shown in Fig. 3b. We find that the kinetic temperature does not depend on the
para-NH3
abundance per velocity gradient [
X ] /(dv/ dr) in
the range of 10-13
to 10-9 pc (km s-1)-1, because the lines are optically thin. Therefore, the
kinetic temperature of 70 ± 20
K derived from the integrated intensity ratio 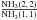 is reasonable for the NH3 environment in IRC +10216.
is reasonable for the NH3 environment in IRC +10216.
At the same time, we also modeled the integrated intensity ratios
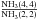 and
and
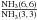 (see Figs. 3c and d). While modeling the integrated intensity ratios
(see Figs. 3c and d). While modeling the integrated intensity ratios
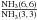 , an ortho-NH3 abundance per velocity gradient
[ X ] /(dv/
dr) of 5.6 × 10-11 pc (km s-1)-1 is used with the same velocity
gradient as for para-NH3. With the observed integrated intensity ratio
, an ortho-NH3 abundance per velocity gradient
[ X ] /(dv/
dr) of 5.6 × 10-11 pc (km s-1)-1 is used with the same velocity
gradient as for para-NH3. With the observed integrated intensity ratio
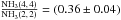 and the assumption that NH3 (2, 2) and (4, 4) arise from
the same region, we obtain a kinetic temperature of
120
and the assumption that NH3 (2, 2) and (4, 4) arise from
the same region, we obtain a kinetic temperature of
120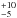 K in the density range from
104.5 to
105.5
cm-3. We note
that NH3 (4, 4)
might be blended (see Fig. B.2) by a feature of
unknown origin, in which case the derived kinetic temperature would be slightly
overestimated. In any case, the derived kinetic temperature is higher than obtained from
the observed integrated intensity ratio
K in the density range from
104.5 to
105.5
cm-3. We note
that NH3 (4, 4)
might be blended (see Fig. B.2) by a feature of
unknown origin, in which case the derived kinetic temperature would be slightly
overestimated. In any case, the derived kinetic temperature is higher than obtained from
the observed integrated intensity ratio 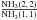 , which indicates a kinetic temperature
gradient with NH3
(4, 4) originating in a warmer region.
, which indicates a kinetic temperature
gradient with NH3
(4, 4) originating in a warmer region.
For ortho-NH3, the
observed line ratio 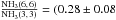 ) is beyond the modeled range, which
indicates that NH3
(6, 6) may arise from a very hot region with a kinetic temperature larger than 300 K.
Alternatively, the (6, 6) emission may be affected by population inversion and an optical
depth not far below unity. Such NH3 (6, 6) masers have already been found in NGC 6334I (Beuther et al. 2007), W51–IRS2 (Henkel et al. 2013), and perhaps even in the nearby galaxy IC 342
(Lebrón et al. 2011), all of which are sources
where a strong infrared radiation field may significantly contribute to the molecule’s
excitation. The inner parts of IRC +10216’s envelope also possess this strong a radiation
field. On the other hand, NH3 (5, 5) is not detected in this survey. Adopting
Trot =
62.3 K from a fit to the (1, 1), (2, 2), and (4, 4)
para-NH3 lines,
the integrated intensity of NH3 (5, 5) is predicted to be 35 mJy km s-1 which is too weak to be
detected. The non-detection of the (5, 5) and (7, 7) lines does not provide evidence for
NH3 formation
pumping, which has recently been suggested for a variety of molecules in star-forming
regions (Lis et al. 2014; see also Wilson et al. 2006 for a particularly compelling
observational candidate).
) is beyond the modeled range, which
indicates that NH3
(6, 6) may arise from a very hot region with a kinetic temperature larger than 300 K.
Alternatively, the (6, 6) emission may be affected by population inversion and an optical
depth not far below unity. Such NH3 (6, 6) masers have already been found in NGC 6334I (Beuther et al. 2007), W51–IRS2 (Henkel et al. 2013), and perhaps even in the nearby galaxy IC 342
(Lebrón et al. 2011), all of which are sources
where a strong infrared radiation field may significantly contribute to the molecule’s
excitation. The inner parts of IRC +10216’s envelope also possess this strong a radiation
field. On the other hand, NH3 (5, 5) is not detected in this survey. Adopting
Trot =
62.3 K from a fit to the (1, 1), (2, 2), and (4, 4)
para-NH3 lines,
the integrated intensity of NH3 (5, 5) is predicted to be 35 mJy km s-1 which is too weak to be
detected. The non-detection of the (5, 5) and (7, 7) lines does not provide evidence for
NH3 formation
pumping, which has recently been suggested for a variety of molecules in star-forming
regions (Lis et al. 2014; see also Wilson et al. 2006 for a particularly compelling
observational candidate).
4.4. Abundance differences among 13C isotopologues of HC5N and the 12C/13C ratio in IRC +10216
Chemical fractionation of 13C-bearing species has been observed toward low-temperature regions. Takano et al. (1998) reported chemical fractionation between the 13C isotopologues of HC3N toward TMC-1. Sakai et al. (2007) report a C13CS/13CCS ratio of 4.2 ± 2.3 (3σ) in TMC-1. Sakai et al. (2010) also find the C13CH/13CCH abundance ratios to be 1.6 ± 0.4 (3σ) and 1.6 ± 0.1 (3σ) for TMC-1 and L1527. Finally, Sakai et al. (2013) find abundance differences among 13C isotopologues of C3S and C4H in TMC-1, which are believed to be caused by different formation processes or 13C isotope exchange reactions. However, in IRC +10216, 13C isotope fractionation is still not very well studied.
In our band, the 13C isotopologues of HC3N, HC5N, C2S, C3S, and C4H can be used to address this issue. However, H13CCCN (2–1) at 17 633.7 MHz lies outside of our frequency range. The bands related to the (2–1) transition of HC13CCN and HCC13CN at 18 120.8 MHz and 18 119.0 MHz are flagged. Meanwhile, the 13C isotopologues of C2S, C3S, and C4H are too weak to be detected in this survey. However, many of the 13C-bearing isotopologues of HC5N have been measured (see Sect. 3.2) and are thus used to investigate potential abundance differences among the 13C species toward IRC +10216. The J = 9−8 transitions of the 13C-bearing isotopologues are the strongest in our band, so we compare their integrated intensities, except for HC13CCCCN (9−8), which is blended with C6H at 23 719.4 MHz. With the four other J = 9−8 transitions, the integrated line intensity ratios, applying a factor ν2 correction between H13CCCCCN, HCC13CCCN, HCCC13CCN, and HCCCC13CN, are estimated to be 1.00:(1.07 ± 0.08):(1.28 ± 0.09):(1.02 ± 0.07). The errors represent 1σ. Therefore, the results suggest that the abundances of the 13C isotopologues of HC5N may not be all the same in IRC +10216. He et al. (2008) may also have found an abundance differentiation among the 13C isotopologues of HC3N in IRC +10216 by obtaining the integrated line intensity ratios H13CCCN:HC13CCN:HCC13CN = 1.00:(1.19 ± 0.14):(1.31 ± 0.15), applying mm-wave spectroscopy. Thus, we suggest that abundance differences possibly exist between the 13C isotopologues of HC5N, but this has to be further checked by deeper integrations.
The 12C/13C ratio is an important tool for tracing processes of
stellar nucleosynthesis (Wilson & Rood 1994).
Here the carbon isotope ratio is based on the ratios between the same J transitions from
HC5N and its
13C
isotopologues. (The blended lines are not included.) The transitions of HC5N and its 13C substitutions are optically
thin as mentioned in Sect. 4.1. Thus, the isotopic
ratio can be directly obtained from their integrated intensity ratio. Figure 4 shows the 12C/13C ratios determined with eight pairs of unblended
transitions from HC5N and its 13C isotopologues. The derived 12C/13C ratios are 35 ± 6 from J = 7−6, 56 ± 9, 56 ± 9, and 38 ± 3 from J = 8−7, and
55 ± 3, 51 ± 3, 43 ± 2, and 54 ± 3 from J = 9−8. The unweighted
average 12C/13C ratio is 49 ± 9, where the error is the standard deviation of the mean. This is
greater than was derived from [SiCC]/[Si13CC] (34.7 ±
4.3) by He et al. (2008) and
less than the 71 obtained from [12CO]/[13CO] by Ramstedt &
Olofsson (2014), but these results may suffer from opacity effects. Our value
agrees well with the 47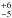 of Kahane
et al. (1988) derived from HC3N, CS, HNC, CCH, SiCC, and their isotopologues.
Therefore, we confirm that the 12C/13C ratio in IRC +10216 is much smaller than the
terrestrial ratio (89) and is also smaller than the value found for the local interstellar
medium (~70) (Wilson & Rood 1994).
of Kahane
et al. (1988) derived from HC3N, CS, HNC, CCH, SiCC, and their isotopologues.
Therefore, we confirm that the 12C/13C ratio in IRC +10216 is much smaller than the
terrestrial ratio (89) and is also smaller than the value found for the local interstellar
medium (~70) (Wilson & Rood 1994).
 |
Fig. 4 12C/13C isotopic abundance ratios from HC5N. The ratios are based on the integrated intensity of the transitions of HC5N and its 13C isotopologues. The ratios derived from the J = 7−6, J = 8−7, and J = 9−8 transitions are denoted with filled squares, pentagrams, and circles, respectively. The dashed line denotes the unweighted average 12C/13C value. |
4.5. Comparison of the IRC +10216 and TMC-1 chemistry
IRC +10216 and TMC-1, the dark cloud in the Taurus region, are the two prototypical sources for detailed studies of carbon chain molecules in outer space. Seen at distances of D ~ 130 pc (Sect. 1) and 140 pc (e.g., Pratap et al. 1997), respectively, they can be studied with similar linear resolution and sensitivity. Kaifu et al. (2004) carried out a line survey toward the cyanopolyyne peak of the dark cloud TMC-1 that includes the frequency range (17.8−26.3 GHz) discussed in this work. This allows us to compare chemical compositions between two physically different, prototypical astronomical environments characterized by large amounts of carbon chain molecules. We note that such a comparison may be biased by (1) the use of different telescopes; (2) by different source morphologies; and (3) by differences in line shapes, which all will affect relative sensitivities. While the TMC-1 study, carried out with the Nobeyama 45-m telescope, is characterized by a larger beam size, emission from TMC-1 is more extended than from IRC +10216, so that our Effelsberg 100 m data may actually suffer from smaller beam-filling factors. On the other hand, lines from IRC +10216, affected by an expansion velocity of ~14 km s-1, are much broader than those from TMC-1, thus allowing us to smooth contiguous channels and to compensate for this disadvantage. This implies that sensitivities match each other by a factor of a few. Below, we constrain ourselves mainly to K-band data, but referring also to lines from other spectral ranges if needed.
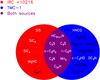 |
Fig. 5 Schematic diagram of detected molecules in the same λ ~ 1.3 cm spectral range toward IRC +10216 and TMC-1. Molecules in the red, blue, and purple regions indicate that they are detected in IRC +10216, TMC-1, and both sources, respectively. The molecules in black indicate that they have been seen in both sources but are not detected toward the other source in the λ ~ 1.3 cm spectral range (see Sect. 4.5). |
Comparing the detected molecules in the same λ ~ 1.3 cm spectral range (see Fig. 5), we find that five molecules are only detected in
IRC +10216, nine molecules are only detected in TMC-1, and 13 molecules are detected in
both sources. The five K-band molecules only detected in IRC +10216 are SiS,
SiC2,
SiC4, MgNC, and
C6H−. While C6H− is not detected in the Nobeyama survey (Kaifu et al. 2004) toward TMC-1, it has been reported
in later studies (e.g. McCarthy et al. 2006; Brünken et al. 2007). In contrast, MgCN could not be
detected in a more recent sensitive study with the Green Bank 100 m telescope (Turner et al. 2005). This also holds for Si-bearing
molecules (Ziurys et al. 1989). The nine
K-band
molecules only detected in TMC-1 are HNCO, HNCCC, CH3CN, CH2CHCN, c-C3HD, HCCNC, CH2CN, H2CCC, and DC3N. While HNCCC,
CH3CN,
CH2CHCN, HCCNC,
CH2CN, and
H2CCC are not
detected in our survey, they have been reported by other studies (e.g., Gensheimer 1997; Agúndez
et al. 2008; Cernicharo et al. 2000). The
other K-band
molecules, HC2n+1N
(n =
1,2,3,4), C2nH (n = 2,3,4), c-C3H2, l-C5H, C3N, C2S, C3S, and NH3, are detected in both sources
which indicates, as already mentioned, that the two targets are both effective in forming
long carbon-chain molecules. The ratio 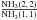 is less than 0.1 in TMC-1, indicating that
the NH3 emitting
region in TMC-1 is much colder (~10 K) than in IRC +10216, consistent with its more pronounced
deuteration of molecules. The cyanopolyyne abundance ratios are estimated to be
HC5N:HC7N:HC9N = (18.4 ± 10.3):(14.8 ± 8.4):1 in IRC +10216 while they are
HC5N:HC7N:HC9N = 13.1:4.8:1 in TMC-1 (Sakai et al. 2008). The difference is probably related to different physical
conditions or time scales for the formation and destruction of the cyanopolyynes in
IRC +10216 and TMC-1. Meanwhile, there is no trend of the rotational temperatures of the
cyanopolyynes increasing with the C-chain length that is found in TMC-1 (Bell et al. 1998). This indicates that the
cyanopolyynes are probably emitting line photons from nearly the same region in
IRC +10216. In IRC +10216, our C6H−/C6H ratio is estimated to be (3.6 ± 0.8)%. (The C6H column density is the sum of
the column densities of the
is less than 0.1 in TMC-1, indicating that
the NH3 emitting
region in TMC-1 is much colder (~10 K) than in IRC +10216, consistent with its more pronounced
deuteration of molecules. The cyanopolyyne abundance ratios are estimated to be
HC5N:HC7N:HC9N = (18.4 ± 10.3):(14.8 ± 8.4):1 in IRC +10216 while they are
HC5N:HC7N:HC9N = 13.1:4.8:1 in TMC-1 (Sakai et al. 2008). The difference is probably related to different physical
conditions or time scales for the formation and destruction of the cyanopolyynes in
IRC +10216 and TMC-1. Meanwhile, there is no trend of the rotational temperatures of the
cyanopolyynes increasing with the C-chain length that is found in TMC-1 (Bell et al. 1998). This indicates that the
cyanopolyynes are probably emitting line photons from nearly the same region in
IRC +10216. In IRC +10216, our C6H−/C6H ratio is estimated to be (3.6 ± 0.8)%. (The C6H column density is the sum of
the column densities of the 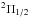 and the
and the
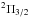 states.) The value is lower than the 8.6%
derived in a previous study of IRC +10216 (Kasai et al.
2007), because they obtained a higher rotational temperature (33 K) for
C6H, resulting in
a lower column density. To summarize, both C6H−/C6H ratios in IRC +10216 are at least as high as the value
(2.5%) reported for TMC-1 (McCarthy et al. 2006).
states.) The value is lower than the 8.6%
derived in a previous study of IRC +10216 (Kasai et al.
2007), because they obtained a higher rotational temperature (33 K) for
C6H, resulting in
a lower column density. To summarize, both C6H−/C6H ratios in IRC +10216 are at least as high as the value
(2.5%) reported for TMC-1 (McCarthy et al. 2006).
5. Summary and conclusions
We performed a 1.3 cm line survey toward IRC +10216 using the 100 m telescope at Effelsberg. In total, 78 spectral lines were detected, among which 12 remain unidentified. The identified lines are assigned to 18 different molecules and radicals. No new species was found, but 23 lines from already known species were detected for the first time outside the solar system and there are an additional 20 lines first detected in IRC +10216. We also discuss the origin of the “U” lines.
Assuming LTE, we derived rotational temperatures and column densities of 17 detected molecules. Their rotational temperatures range from 5.5 to 39.1 K, and molecular column densities range from 5.2 × 1012 to 2.4 × 1015 cm-2. Molecular abundances relative to H2 range between 2.5 × 10-9 and 1.1 × 10-6. A non-LTE analysis of NH3 shows that its (1, 1) and (2, 2) emission arises from the inner envelope with a kinetic temperature of 70 ± 20 K, but there may be warmer gas as is indicated by the detected (4, 4) line. The (6, 6) inversion line shows surprisingly strong emission and might indicate inverted populations and an optical depth not far below unity. Comparing transitions from the 13C isotopologues of HC5N, we find there might be abundance differences between them. The isotopic 12C/13C ratio is estimated to be 49 ± 9 from the integrated intensity ratios of transitions from HC5N and its 13C isotopologues. Finally, we compare the chemical compositions of IRC +10216 and TMC-1 in the λ ~ 1.3 cm spectral range. Apparently, Si-bearing molecules are favored in IRC +10216.
Online material
Appendix A: Observed lines in this survey
 |
Fig. A.1 Detected spectra of HC7N and NH3 with transitions marked in the upper right of each panel. The NH3 (4, 4) and (6, 6) lines have been smoothed to have a channel width of ~3.3 km s-1, while the channel width of other lines is ~0.8 km s-1. In the NH3 (1, 1) panel, the positions of the satellites are indicated by red solid lines. The blue dashed line traces the systemic LSR velocity (−26.0 km s-1) of IRC +10216. |
 |
Fig. A.2 Rotational diagrams for the observed molecules in IRC +10216. For lines with hfs,
all observed components have been taken into account. The circles with error bars
are from our Effelsberg-100 m observations, where in addition to uncertainties in
the fit to the integrated line intensities, a calibration error of 20% has also
been included. Filled and open symbols indicate signal-to-noise ratios that are
larger than or less than five, respectively. The triangles without error bars are
obtained from Kawaguchi et al. (1995). The
pentagrams with error bars for C8H are obtained from Remijan et al. (2007), and the squares for C3N are from He et al. (2008). Their values have been
corrected for beam dilution. The molecules and their corresponding rotational
temperatures, obtained from unweighted linear fits, are given in the upper right
corner of each panel. Black dashed lines represent linear least-squares fit to the
rotational diagram accounting for data presented by filled symbols, and the black
dot-dashed lines represent the fit when the open circles are included. The red and
blue dashed lines represent fits for the para and ortho states of
NH3 and
c-C3H2 and the |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
Appendix B: Zoom-in plots of observed spectra
 |
Fig. B.1 Observed spectrum of IRC +10 216 from 17.8 to 26.3 GHz. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.2 Zoom in all detected and tentative lines. The rest frequency in MHz and the assigned molecule of each line are shown in the upper right of each panel. Weak lines have been smoothed to have a channel width of ~3.3 km s-1, and they are marked with “smoothed” in the upper left of the corresponding panels. Otherwise, the channel width is ~0.8 km s-1 (see Sect. 3.1). The blue dashed line traces the systemic LSR velocity (−26.0 km s-1) of IRC +10216. In the C6H 23 565.2 MHz panel, the other blue dashed line near −50 km s-1 refers to the C6H’s hfs component at 23567.2 MHz. |
 |
Fig. B.2 continued. |
 |
Fig. B.2 continued. |
 |
Fig. B.2 continued. |
Acknowledgments
We would like to thank the anonymous referee for a helpful report that led to improvements in the paper. We greatly thank Denise Keller for providing source size information from her new JVLA observations. We also wish to thank J. Kauffmann, T. Pillai, and E. Gonzalez-Alfonso for discussions or an exchange of emails and appreciate the assistance of the Effelsberg 100-m operators during the observations. Y. Gong acknowledges support by the MPG-CAS Joint Doctoral Promotion Program (DPP), and NSFC Grants 11127903, 11233007, and 10973040. S. Thorwirth gratefully acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG) through grant TH 1301/3-2.
References
- Agúndez, M., Fonfría, J. P., Cernicharo, J., Pardo, J. R., & Guélin, M. 2008, A&A, 479, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2014, A&A, 570, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araya, E., Hofner, P., Goldsmith, P., Slysh, S., & Takano, S. 2003, ApJ, 596, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Avery, L. W., Amano, T., Bell, M. B., et al. 1992, ApJS, 83, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Becklin, E. E., Frogel, J. A., Hyland, A. R., Kristian, J., & Neugebauer, G. 1969, ApJ, 158, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, M. B., & Feldman, P. A. 1991, ApJ, 367, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, M. B., Avery, L. W., MacLeod, J. M., & Matthews, H. E. 1992, ApJ, 400, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, M. B., Avery, L. W., & Feldman, P. A. 1993a, ApJ, 417, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, M. B., Avery, L. W., & Watson, J. K. G. 1993b, ApJS, 86, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, M. B., Watson, J. K. G., Feldman, P. A., & Travers, M. J. 1998, ApJ, 508, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Walsh, A. J., Thorwirth, S., et al. 2007, A&A, 466, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bieging, J. H., & Tafalla, M. 1993, AJ, 105, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Botschwina, P. 2003, Phys. Chem. Chem. Phys., 5, 3337 [Google Scholar]
- Brünken, S., Gupta, H., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2007, ApJ, 664, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., & Guelin, M. 1987, A&A, 183, L10 [NASA ADS] [Google Scholar]
- Cernicharo, J., & Guelin, M. 1996, A&A, 309, L27 [NASA ADS] [Google Scholar]
- Cernicharo, J., Kahane, C., Gomez-Gonzalez, J., & Guelin, M. 1986, A&A, 167, L5 [NASA ADS] [Google Scholar]
- Cernicharo, J., Kahane, C., Guelin, M., & Hein, H. 1987, A&A, 181, L9 [NASA ADS] [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Waters, L. B. F. M., Decin, L., et al. 2010, A&A, 521, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Teyssier, D., Quintana-Lacaci, G., et al. 2014, ApJ, 795, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I. 2011, A&A, 526, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordiner, M. A., & Millar, T. J. 2009, ApJ, 697, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Crosas, M., & Menten, K. M. 1997, ApJ, 483, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, D., Meixner, M., Sutton, E. C., Zalucha, A., & Welch, W. J. 2006, ApJ, 652, 1626 [NASA ADS] [CrossRef] [Google Scholar]
- Gensheimer, P. D. 1997, Ap&SS, 251, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Grasshoff, M., Tiemann, E., & Henkel, C. 1981, A&A, 101, 238 [NASA ADS] [Google Scholar]
- Groenewegen, M. A. T., van der Veen, W. E. C. J., Lefloch, B., & Omont, A. 1997, A&A, 322, L21 [NASA ADS] [Google Scholar]
- Groesbeck, T. D., Phillips, T. G., & Blake, G. A. 1994, ApJS, 94, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Guelin, M., Cernicharo, J., Kahane, C., Gomez-Gonzalez, J., & Walmsley, C. M. 1987, A&A, 175, L5 [NASA ADS] [Google Scholar]
- Guelin, M., Lucas, R., & Cernicharo, J. 1993, A&A, 280, L19 [Google Scholar]
- He, J. H., Dinh-V-Trung, Kwok, S., et al. 2008, ApJS, 177, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Henkel, C., Matthews, H. E., & Morris, M. 1983, ApJ, 267, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Henkel, C., Wilson, T. L., Asiri, H., & Mauersberger, R. 2013, A&A, 549, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Møllendal, H. 2004, ApJ, 610, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Huggins, P. J., Olofsson, H., & Johansson, L. E. B. 1988, ApJ, 332, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, L. E. B., Andersson, C., Ellder, J., et al. 1984, A&A, 130, 227 [NASA ADS] [PubMed] [Google Scholar]
- Johansson, L. E. B., Andersson, C., Elder, J., et al. 1985, A&AS, 60, 135 [NASA ADS] [Google Scholar]
- Kahane, C., Gomez-Gonzalez, J., Cernicharo, J., & Guelin, M. 1988, A&A, 190, 167 [NASA ADS] [Google Scholar]
- Kaifu, N., Ohishi, M., Kawaguchi, K., et al. 2004, PASJ, 56, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kalenskii, S. V., Slysh, V. I., Goldsmith, P. F., & Johansson, L. E. B. 2004, ApJ, 610, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kasai, Y., Kagi, E., & Kawaguchi, K. 2007, ApJ, 661, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., Kasai, Y., Ishikawa, S.-I., & Kaifu, N. 1995, PASJ, 47, 853 [Google Scholar]
- Kendall, T. R., Mauron, N., McCombie, J., & Sarre, P. J. 2002, A&A, 387, 624 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, B., Hochgürtel, S., Krämer, I., et al. 2012, A&A, 542, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kukolich, S. G. 1967, Phys. Rev., 156, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kwan, J., & Linke, R. A. 1982, ApJ, 254, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Kylafis, N. D., & Norman, C. A. 1991, ApJ, 373, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Lebrón, M., Mangum, J. G., Mauersberger, R., et al. 2011, A&A, 534, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., Schilke, P., Bergin, E. A., et al. 2014, ApJ, 785, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Lovas, F. J., & Dragoset, R. A. 2004, J. Phys. Chem. Ref. Data, 33, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., Guélin, M., Kahane, C., Audinos, P., & Cernicharo, J. 1995, Ap&SS, 224, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Mauersberger, R., Henkel, C., Weiß, A., Peck, A. B., & Hagiwara, Y. 2003, A&A, 403, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauersberger, R., Ott, U., Henkel, C., Cernicharo, J., & Gallino, R. 2004, A&A, 426, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCarthy, M. C., Gottlieb, C. A., Gupta, H., & Thaddeus, P. 2006, ApJ, 652, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, G. J., Neufeld, D. A., Ford, K. E. S., Hollenbach, D. J., & Ashby, M. L. N. 2001, Nature, 412, 160 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Menten, K. M., Wyrowski, F., Alcolea, J., et al. 2010, A&A, 521, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menten, K. M., Reid, M. J., Kamiński, T., & Claussen, M. J. 2012, A&A, 543, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., González-Alfonso, E., Melnick, G., et al. 2011, ApJ, 727, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Tolls, V., Agúndez, M., et al. 2013, ApJ, 767, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen-Q-Rieu, Graham, D., & Bujarrabal, V. 1984, A&A, 138, L5 [NASA ADS] [Google Scholar]
- Ohishi, M., Kaifu, N., Kawaguchi, K., et al. 1989, ApJ, 345, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H., Johansson, L. E. B., Hjalmarson, A., & Nguyen-Quang-Rieu. 1982, A&A, 107, 128 [NASA ADS] [Google Scholar]
- Ott, M., Witzel, A., Quirrenbach, A., et al. 1994, A&A, 284, 331 [NASA ADS] [Google Scholar]
- Patel, N. A., Young, K. H., Brünken, S., et al. 2009, ApJ, 692, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, N. A., Young, K. H., Gottlieb, C. A., et al. 2011, ApJS, 193, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Pratap, P., Dickens, J. E., Snell, R. L., et al. 1997, ApJ, 486, 862 [Google Scholar]
- Ramstedt, S., & Olofsson, H. 2014, A&A, 566, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2007, ApJ, 664, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Ikeda, M., Morita, M., et al. 2007, ApJ, 663, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Saruwatari, O., Sakai, T., Takano, S., & Yamamoto, S. 2010, A&A, 512, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakai, N., Takano, S., Sakai, T., et al. 2013, J. Phys. Chem. A, 117, 9831 [CrossRef] [Google Scholar]
- Takano, S., Masuda, A., Hirahara, Y., et al. 1998, A&A, 329, 1156 [NASA ADS] [Google Scholar]
- Takano, S., Nakai, N., & Kawaguchi, K. 2002, PASJ, 54, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, E. D., Dodd, J. L., Milam, S. N., Woolf, N. J., & Ziurys, L. M. 2010, ApJS, 190, 348 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Truong-Bach, Graham, D., & Nguyen-Q-Rieu. 1993, A&A, 277, 133 [NASA ADS] [Google Scholar]
- Turner, B. E., Petrie, S., Dunbar, R. C., & Langston, G. 2005, ApJ, 621, 817 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walmsley, C. M., & Ungerechts, H. 1983, A&A, 122, 164 [NASA ADS] [Google Scholar]
- Wilson, T. L., Henkel, C., & Hüttemeister, S. 2006, A&A, 460, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2009, Tools of Radio Astronomy (Springer-Verlag) [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Winnewisser, G., & Walmsley, C. M. 1978, A&A, 70, L37 [NASA ADS] [Google Scholar]
- Ziurys, L. M., Friberg, P., & Irvine, W. M. 1989, ApJ, 343, 201 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ziurys, L. M., Savage, C., Highberger, J. L., et al. 2002, ApJ, 564, L45 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Overview of the 1.3 cm line survey toward IRC +10216 with strong lines marked. |
| In the text | |
 |
Fig. 2 Comparison of the column densities and rotational temperatures of different molecules. The labels for column densities are blue on the left side, while those for rotational temperatures are red on the right side. Here, a Trot of 39.1 K has been taken for para and ortho NH3 (see Sect. 4.1 and Table 4). |
| In the text | |
 |
Fig. 3 RADEX non-LTE modeling for NH3. a) the integrated intensity ratio
|
| In the text | |
 |
Fig. 4 12C/13C isotopic abundance ratios from HC5N. The ratios are based on the integrated intensity of the transitions of HC5N and its 13C isotopologues. The ratios derived from the J = 7−6, J = 8−7, and J = 9−8 transitions are denoted with filled squares, pentagrams, and circles, respectively. The dashed line denotes the unweighted average 12C/13C value. |
| In the text | |
 |
Fig. 5 Schematic diagram of detected molecules in the same λ ~ 1.3 cm spectral range toward IRC +10216 and TMC-1. Molecules in the red, blue, and purple regions indicate that they are detected in IRC +10216, TMC-1, and both sources, respectively. The molecules in black indicate that they have been seen in both sources but are not detected toward the other source in the λ ~ 1.3 cm spectral range (see Sect. 4.5). |
| In the text | |
 |
Fig. A.1 Detected spectra of HC7N and NH3 with transitions marked in the upper right of each panel. The NH3 (4, 4) and (6, 6) lines have been smoothed to have a channel width of ~3.3 km s-1, while the channel width of other lines is ~0.8 km s-1. In the NH3 (1, 1) panel, the positions of the satellites are indicated by red solid lines. The blue dashed line traces the systemic LSR velocity (−26.0 km s-1) of IRC +10216. |
| In the text | |
 |
Fig. A.2 Rotational diagrams for the observed molecules in IRC +10216. For lines with hfs,
all observed components have been taken into account. The circles with error bars
are from our Effelsberg-100 m observations, where in addition to uncertainties in
the fit to the integrated line intensities, a calibration error of 20% has also
been included. Filled and open symbols indicate signal-to-noise ratios that are
larger than or less than five, respectively. The triangles without error bars are
obtained from Kawaguchi et al. (1995). The
pentagrams with error bars for C8H are obtained from Remijan et al. (2007), and the squares for C3N are from He et al. (2008). Their values have been
corrected for beam dilution. The molecules and their corresponding rotational
temperatures, obtained from unweighted linear fits, are given in the upper right
corner of each panel. Black dashed lines represent linear least-squares fit to the
rotational diagram accounting for data presented by filled symbols, and the black
dot-dashed lines represent the fit when the open circles are included. The red and
blue dashed lines represent fits for the para and ortho states of
NH3 and
c-C3H2 and the |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. B.1 Observed spectrum of IRC +10 216 from 17.8 to 26.3 GHz. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.2 Zoom in all detected and tentative lines. The rest frequency in MHz and the assigned molecule of each line are shown in the upper right of each panel. Weak lines have been smoothed to have a channel width of ~3.3 km s-1, and they are marked with “smoothed” in the upper left of the corresponding panels. Otherwise, the channel width is ~0.8 km s-1 (see Sect. 3.1). The blue dashed line traces the systemic LSR velocity (−26.0 km s-1) of IRC +10216. In the C6H 23 565.2 MHz panel, the other blue dashed line near −50 km s-1 refers to the C6H’s hfs component at 23567.2 MHz. |
| In the text | |
 |
Fig. B.2 continued. |
| In the text | |
 |
Fig. B.2 continued. |
| In the text | |
 |
Fig. B.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


