| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423987 | |
| Published online | 29 January 2015 | |
High resolution observations of HCN and HCO+J = 3–2 in the disk and outflow of Mrk 231
Detection of vibrationally excited HCN in the warped nucleus⋆,⋆⋆
1
Department of Earth and Space SciencesChalmers University of Technology,
Onsala Observatory,
439 94
Onsala,
Sweden
e-mail:
saalto@chalmers.se
2
Observatorio Astronómico Nacional (OAN)–Observatorio de
Madrid, Alfonso XII
3, 28014
Madrid,
Spain
3
Institut de Radio Astronomie Millimétrique (IRAM), 300 rue de la
Piscine, Domaine Universitaire de Grenoble, 38406St. Martin d′Hères, France
4
Universidad de Alcalá de Henares, Departamento de Física y
Matemáticas, Campus Universitario, 28871 Alcalá de Henares, Madrid, Spain
5
Leiden Observatory, Leiden University,
2300 RA
Leiden, The
Netherlands
6
Instituto de Astrofísica de Andalucía,
Glorieta de la Astronomía, s/n,
18008
Granada,
Spain
7
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
8
Astronomy Department, King Abdulaziz University,
PO Box 80203, 21589
Jeddah, Saudi
Arabia
Received: 14 April 2014
Accepted: 3 November 2014
Aims. Our goal is to study molecular gas properties in nuclei and large scale outflows/winds from active galactic nuclei (AGNs) and starburst galaxies.
Methods. We obtained high resolution (0.̋25 to 0.̋90) observations of HCN and HCO+J = 3 → 2 of the ultraluminous QSO galaxy Mrk 231 with the IRAM Plateau de Bure Interferometer (PdBI).
Results. We find luminous HCN and HCO+J = 3 → 2 emission in the main disk and we detect compact (r ≲ 0''̣1 (90 pc)) vibrationally excited HCN J = 3 → 2ν2 = 1f emission centred on the nucleus. The velocity field of the vibrationally excited HCN is strongly inclined (position angle PA = 155°) compared to the east-west rotation of the main disk. The nuclear (r ≲ 0.̋1) molecular mass is estimated to 8 × 108 M⊙ with an average N(H2) of 1.2 × 1024 cm-2. Prominent, spatially extended (≳350 pc) line wings are found for HCN J = 3 → 2 with velocities up to ± 750 km s-1. Line ratios indicate that the emission is emerging in dense gas n = 104−5 × 105 cm-3 of elevated HCN abundance X(HCN) = 10-8−10-6. The highest X(HCN) also allows for the emission to originate in gas of more moderate density. We tentatively detect nuclear emission from the reactive ion HOC+ with HCO+/HOC+ = 10−20.
Conclusions. The HCN ν2 = 1f line emission is consistent with the notion of a hot, dusty, warped inner disk of Mrk 231 where the ν2 = 1f line is excited by bright mid-IR 14 μm continuum. We estimate the vibrational temperature Tvib to 200−400 K. Based on relative source sizes we propose that 50% of the main HCN emission may have its excitation affected by the radiation field through IR pumping of the vibrational ground state. The HCN emission in the line wings, however, is more extended and thus likely not strongly affected by IR pumping. Our results reveal that dense clouds survive (and/or are formed) in the AGN outflow on scales of at least several hundred pc before evaporating or collapsing. The elevated HCN abundance in the outflow is consistent with warm chemistry possibly related to shocks and/or X-ray irradiated gas. An upper limit to the mass and momentum flux is 4 × 108 M⊙ and 12LAGN/c, respectively, and we discuss possible driving mechanisms for the dense outflow.
Key words: galaxies: evolution / galaxies: individual: Mrk 231 / galaxies: active / ISM: molecules / ISM: jets and outflows / quasars: general
Based on observations carried out with the IRAM Plateau de Bure Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
The reduced data cubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/574/A85
© ESO, 2015
1. Introduction
The ultraluminous infrared galaxy (ULIRG, log(LIR) = 12.37) Mrk 231 is often referred to as the closest IR quasar (QSO). It has been identified as a major merger, and it hosts powerful active galactic nucleus (AGN) activity as well as a young, dusty starburst with an extreme star formation rate of ≈200 M⊙ yr-1 (Taylor et al. 1999; Gallagher et al. 2002; Lípari et al. 2009). Large amounts of molecular gas are located in an almost face-on east-west rotating disk (Bryant & Scoville 1996; Downes & Solomon 1998). Mrk 231 shows evidence of various types of mechanical feedback from the nuclear activity including radio jets (from pc to kpc scales) (Carilli et al. 1998; Lonsdale et al. 2003) and optical absorption lines tracing starburst driven winds and the jet acceleration of ionized and atomic gas to high velocities (≈1400 km s-1) (Rupke & Veilleux 2011). Mrk 231 also has a powerful molecular outflow manifested by broad (750 km s-1) CO wings (Feruglio et al. 2010; Cicone et al. 2012) and in OH-absorption by Fischer et al. (2010) and recently at very high velocities (1500 km s-1) in highly excited OH (González-Alfonso et al. 2014). Feruglio et al. (2010) estimate the outflow of molecular gas as 700 M⊙ yr-1, emptying the reservoir of cold gas within 10 Myr.
The high mass outflow rates seem to support the notion that the bulk of the gas is driven out by the AGN (e.g. Feruglio et al. 2010; Rupke & Veilleux 2011). However, little is known about the properties of the molecular gas in the outflow. Reliable estimates of molecular masses will rely on determining the physical conditions of the molecular gas in the outflow. The properties of the gas and dust within the inner few hundred pc of Mrk 231 are still poorly constrained, including how they relate to the nuclear activity and the molecular gas in the outflow.
Recently, we have found that in the Mrk 231 outflow the HCN/CO J = 1 → 0 line ratio is very high with a ratio 0.3−1 (Aalto et al. 2012). This is even higher than in the line core where the HCN luminosity is already elevated (Solomon et al. 1992). The HCN emission covers the same velocity width (±750 km s-1) as the one seen in CO 1−0 by (Feruglio et al. 2010). We suggested that the high brightness of HCN 1−0 is a result of the molecular mass in the outflow residing mostly in dense (n ≳ 104 cm-3) gas. However, the possibility that the luminous HCN emission was due to mid-IR pumping via the 14 μm bending modes could not be entirely dismissed. In particular, the CO emission seems to be subthermally excited in the outflow (Cicone et al. 2012), indicating low to moderate densities. Recently, rotational transitions of HCN within the vibrationally excited state ν2 = 1 have been detected towards the LIRG NGC 4418 (Sakamoto et al. 2010) and towards the ULIRG IRAS 20551-4250 (Imanishi & Nakanishi 2013). Radiative excitation may populate the ν2 = 1 ladder and may in turn also pump the ν = 0 vibrational ground state levels affecting the excitation of the whole molecule. It is therefore fundamental to investigate the excitation of molecular emission towards luminous IR galaxies so that the molecular properties in both nuclei and outflows may be understood.
In the paper we present IRAM Plateau de Bure A- and B-array HCN, HCO+J = 3 → 2 high resolution data of the disk and outflow of Mrk 231. We also detected the J = 3 → 2ν2 = 1f vibrational line and use it to further understand the properties and kinematics of the very nuclear gas. From now on we refer to the HCN and HCO+J = 3 → 2 lines in the vibrational ground state (ν = 0) as HCN and HCO+ 3−2 (apart from Sect. 4.1.1 where we use ν2 = 1/ν = 0 for the line ratio between HCN J = 3 → 2ν2 = 1f and ν = 0). The HCN J = 3 → 2 ν2 = 1f vibrational line will be referred to as HCN 3−2 ν2 = 1f.
2. Observations
The 1 mm observations were carried out with the six-element IRAM Plateau de Bure array in February 2012 in A-array and in February 2013 in B-array. The phase centre was set to α = 12:56:14.232 and δ = 56:52:25.207 (J2000). Mrk 231 was observed for hour angles 2 to 8 and the radio seeing ranged between 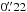 and
and 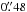 . The receivers were tuned to a frequency of 255.88 GHz, the centre between the two red-shifted line frequencies for HCN (ν = 255.13 GHz) and HCO+ (ν = 256.73 GHz). We used the WideX correlator providing a broad frequency range of 3.6 GHz.
. The receivers were tuned to a frequency of 255.88 GHz, the centre between the two red-shifted line frequencies for HCN (ν = 255.13 GHz) and HCO+ (ν = 256.73 GHz). We used the WideX correlator providing a broad frequency range of 3.6 GHz.
The bandpass of the individual antennas was derived from the bright quasar 3C 273. The flux calibration was set on 3C 273. The quasars close to Mrk 231 J1150 + 497 (~2 Jy at 1 mm) and J1418 + 546 (~0.55 Jy) were observed regularly for complex gain calibration every 25 minutes.
Line flux densities.
After calibration within the GILDAS reduction package, the visibility set was converted into FITS format, and imported into the GILDAS/MAPPING and AIPS packages for further imaging. We merged the A and B array data sets, rebinning to 40 MHz (47 km s-1) cleaned with a natural weighting resulting in a beam size of 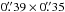 (100 mJy = 14 K) and position angle PA = 0° (rms noise is 0.8 mJy channel-1). By default it is this combined dataset that we use when we discuss the results in this paper. However, we also use the A- and B-array datasets individually where the A-array data were cleaned with a robust weighting of − 2, resulting in a beam size of
(100 mJy = 14 K) and position angle PA = 0° (rms noise is 0.8 mJy channel-1). By default it is this combined dataset that we use when we discuss the results in this paper. However, we also use the A- and B-array datasets individually where the A-array data were cleaned with a robust weighting of − 2, resulting in a beam size of 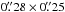 (100 mJy = 25 K) and position angle PA = 59° (rms noise is 1.6 mJy channel-1). The B-array data were tapered and cleaned with a natural weighting resulting in a beam size of
(100 mJy = 25 K) and position angle PA = 59° (rms noise is 1.6 mJy channel-1). The B-array data were tapered and cleaned with a natural weighting resulting in a beam size of 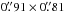 (100 mJy = 2.4 K) and position angle PA = 83° (rms noise is 1.5 mJy channel-1).
(100 mJy = 2.4 K) and position angle PA = 83° (rms noise is 1.5 mJy channel-1).
Zero velocity refers to the redshift z = 0.042170 (Carilli et al. 1998) throughout the paper, resulting in a spatial scale of 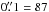 pc.
pc.
 |
Fig. 1 Separate A- and B-array spectra towards the central beam. Spectra have been Gaussian smoothed (over two channels). We show the spectra for the A- and B-array separately to emphasize that identified features appear in both separate datasets. The central spectrum for the combined A+B dataset is shown in Fig. 6. Left: B-array spectrum of HCN J = 3−2, HCO+J = 3−2, HCN J = 3−2ν2 = 1, and a tentative detection of HOC+J = 3−2. Right: a-array spectrum of the same lines. The green velocity scale is for HCO+. |
3. Results
Line fluxes, source size fits (FWHM), line widths (ΔV) and emission position angles (PA), including fits to the line wing emission, are presented in Table 1.
3.1. HCN 3–2
3.1.1. Integrated intensities
The HCN 3−2 emission consists of luminous emission from the line core (± 250 km s-1) and higher velocity, fainter line wing emission (Fig. 1). We divide the presentation of the HCN 3−2 integrated intensities into two sections – one where we discuss the line core emission emerging from the main disk and one where we discuss the line wing emission:
Main disk: the HCN 3−2 emission is distributed in a bright nuclear component surrounded by extended disk emission (Fig. 2). The lower-surface brightness emission extends out to a radius of at least 0.̋8 (700 pc). Downes & Solomon (1998) use CO 2−1 position-velocity (pV) maps to estimate the disk size along the line of nodes indicating a 0.̋6 radius inner disk and a 1.̋5 outer disk – where the line of nodes has a PA = 90°. The HCN 3−2 emission thus appears to be residing in the inner part of the CO disk.
Tongues of fainter emission extend at least 1′′ (870 pc) from the nucleus of Mrk 231 and they connect to the south-west in what appears like a ring-like feature. It is possible that this structure is the result of a remnant side-lobe (and then would not be real). However, side-lobes should be symmetric and there is no evidence of a similar feature on the other side of the nucleus. The feature is also brighter than the expected side-lobe response. Furthermore, Mrk 231 shows evidence of distinct optical circular shell like features at a whole range of radii – resulting from a complicated pattern of outflows and winds (Lípari et al. 2005). Our HCN 3−2 ring-like feature coincides with their shell feature S3.
Line wings: HCN 3−2 line wings are detected out to velocities of at least 750 km s-1 (Fig. 1), similar to those found in HCN 1−0 by Aalto et al. (2012). We integrated the line wings over velocities V = 350−990 km s-1 to be safely away from the rotation (Vrot ± 150 km s-1) of the main disk of Mrk 231 and to be consistent with the fits to the HCN 1−0 line wings.
The line wings are faint and spatially extended. In the A+B combined and naturally weighted integrated intensity map (with 3σ cut-off) we recover only 50% of the flux in the wings compared to the tapered (0.̋91 × 0.̋81) B-array data. This is despite the lower sensitivity in the B-array only data. Even when we taper the combined A+B array data to 0.̋9 resolution we still miss 20% of the flux recovered in the B-array data. Therefore, we use the B-array data to study the extent and total flux of the HCN 3−2 line wings. A two-dimensional Gaussian fit to the integrated intensity maps results in FWHM sizes of 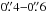 (350−520 pc) (see Fig. 3). The spatial shift between the red- and blue wings is smaller than the beam: the blue wing is shifted 0.̋15 to the west of the nucleus and the red wing 0.̋1 to the north.
(350−520 pc) (see Fig. 3). The spatial shift between the red- and blue wings is smaller than the beam: the blue wing is shifted 0.̋15 to the west of the nucleus and the red wing 0.̋1 to the north.
Since the line wings are broad and relatively faint, the determination of their positions depends on a reliable continuum subtraction. We subtracted the continuum in the uv plane and tried both a fit to the line-free spectral channels of order 0 and order 1 (linear fit allowing a slope). We then compared the results of the two methods and conclude that there is no measurable difference between them.
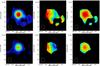 |
Fig. 2 Top panels: combined A+B moment maps of the HCN 3−2 line emission from the main disk (as defined in the text). Left panel: integrated intensity with contour levels 0.5 × (1,2,4,8,16,32) Jy beam-1 km s-1 and grey (colour) scale ranging from 0 to 15 Jy beam-1 km s-1 (peak integrated flux is 22 Jy beam-1 km s-1). Centre: velocity field with contour levels starting at − 56 km s-1 and then increasing by steps of 18.8 km s-1 until +38 km s-1. The grey (colour) scale ranges from − 65 to 50 km s-1. Right: dispersion map where contours start at 30 km s-1 and then increase by steps of 30 km s-1. Greyscale ranges from 0 to 115 km s-1 and peak dispersion is 130 km s-1. The cross marks the position of the peak HCN 3−2 integrated intensity. Lower panels: combined A+B moment maps of the HCO+ 3−2 line. Left panel: integrated intensity with contour levels 0.5 × (1,2,4,8,16,32) Jy beam-1 km s-1 and grey (colour) scale ranging from 0 to 15 Jy beam-1 km s-1 (peak integrated flux is 12 Jy beam-1 km s-1). Centre: velocity field with contour levels starting at − 56 km s-1 and then increasing by steps of 18.8 km s-1 until +38 km s-1. The grey (colour) scale ranges from − 65 to 50 km s-1. Right: dispersion map where contours start at 30 km s-1 and then increase by steps of 30 km s-1. Greyscale ranges from 0 to 115 km s-1 and peak dispersion is 98 km s-1. The cross marks the position of the peak HCN 3−2 integrated intensity. (In the online version of this figure the greyscale is replaced with a rainbow color scale ranging from dark blue to red.) |
 |
Fig. 3 Left: moment 0 maps (integrated intensity) of the HCN 3−2 line wings in tapered B array. Contour levels are 0.2 × (1,3,5,7,9) Jy beam-1 km s-1 and greyscale ranges from 0 to 2 Jy beam-1 km s-1. The cross marks the position of the peak HCN 3−2 integrated intensity. Right: pV diagrams of the tapered B array map. Upper: east-west cut along the line of nodes of the main disk rotation. Lower: north-south cut along the minor axis of the main disk rotation. Greyscale ranges from 0 to 120 mJy beam-1, contours are 3 × (1, 2, 4, 8, 16, 32) mJy beam-1. First contour is 2σ. |
3.1.2. Velocity field, channel map and pV diagrams
The HCN 3−2 velocity field and dispersion map are presented in Fig. 2. The velocity field indicates rotation with the line of nodes at PA = 90° tracing the east-west rotation of the main disk- just as the CO 2−1 (Downes & Solomon 1998). However, the channel map in Fig. 4 suggests a more complex velocity structure and the isovelocity contours in the velocity field clearly twist away from a simple spider diagram of orderly east-west rotation. The dispersion map peaks on the nucleus – but there is also a suggestion that the dispersion is tracing extentions to the south, north and west.
Position-velocity (pV) diagrams HCN 3−2 pV diagrams are presented in Fig. 5. We have cut along the east-west axis (along the line of nodes of the main disk rotation) and the north-south axis. In the east-west cut the dominant rotation of the main disk is evident. Emission close to systemic velocity is found 1.̋5 (1.3 kpc) to the south and 2.̋5 (2.2 kpc) to the west of the emission peak. These features are found also in the HCN 1−0 map (Aalto et al. 2012). The western feature is found at forbidden velocities, redder than V = 0 by 50−100 km s-1, which means that they do not represent a simple extension of the rotating main disk.
In Fig. 3 we present the tapered B-array data pV diagrams to better show the emission from the line wings. Their extended nature is evident as is the fact that the spatial shift between the red and blue wings is smaller than their extent.
3.2. Vibrational HCN 3–2 ν2 = 1f
For the first time the HCN J = 3−2 ν2 = 1f line is detected in Mrk 231 (see Fig. 1 for A and B-array spectra, Fig. 6 for A+B combined array spectrum). The integrated intensity shows a compact unresolved structure centred on the nucleus (Fig. 7). The velocity field of the HCN 3−2 ν2 = 1f line (Fig. 7) has a different position angle than that of the HCN 3−2 main line (Fig. 2). Its line of nodes are oriented with a PA of 150° ± 20°. A Gaussian fit to the HCN and HCO+ lines in the combined A+B spectra (see Fig. 6) suggest a line width (FWHM) of 257 km s-1 (±10 km s-1) for the HCN 3−2 ν2 = 1f line. Note that the HCN J = 3−2 ν2 = 1f line is located 400 km s-1 to the red side of the HCO+ 3−2 line which may cause some line blending when lines are broad.
3.2.1. Potential alternative interpretations
There are two possible alternative interpretations of the emission feature that we identify as the vibrational HCN 3−2 ν2 = 1f line. One is that it is a wing to the HCO+ 3−2 line and the other is that it is the SO 43−34 line. Below we discuss these possibilities and why we dismiss them.
Why is this not a wing of the HCO+ line? The HCN 3−2 ν2 = 1f line is expected to have its maximum intensity 400 km s-1 to the red side of the HCO+ line which is where we find it. Furthermore, the HCN 3−2 ν2 = 1f line emission is compact and the source size fit is ≲0.̋2 compared to >0.̋4 for the HCN line wings. In addition, the HCN 3−2 ν2 = 1f line has a distinct kinematic pattern (see above) that is different from that of the HCN wind in the vibrational ground state.
Could this instead be an SO line?It is important to consider the possibility that the feature identified as the HCN 3−2 ν2 = 1f line could instead be the SO 43−34 line. Since we have both 2 mm and 3 mm interferometric data of Mrk 231 we can test for this possibility through searching for other SO lines. We ran RADEX non-LTE radiative transport models (van der Tak et al. 2007) for a range of physical conditions (Tk = 20−200 K; n = 103−106 cm-3) and we find that the 2 mm 178 GHz 45−34 SO line is always two orders of magnitude brighter than the 43−34 line. Fortunately the 178 GHz SO line falls into the band of our HCN 2−1 PdBI data (Lindberg et al., in prep.). We do not see any signs of this line and put a very conservative upper limit to its brightness of 4 mJy. The corresponding 43−34 line would not be detectable in our data. Thus we conclude that we have correctly identified the feature 400 km s-1 redwise of HCO+ 3−2 as the HCN 3−2 ν2 = 1f line.
3.3. HCO+ 3–2
For HCO+ 3−2 we detect only the line core emission – no line wings. The emission feature 400 km s-1 redshifted from HCO+ 3−2 is identified as the HCN 3−2 ν2 = 1f vibrational line (see previous section).
The HCO+ 3−2 integrated intensity map of the total line emission is presented in Fig. 2. The size and structure of the map is similar to that of the HCN 3−2 even if the total flux is lower by a factor of 1.5−2. The HCO+ 3−2 emission has a slightly larger source size than HCN 3–2 due to the absence of strongly peaked nuclear emission. Part of the intensity difference between HCN and HCO+ is also due to the broader HCN line.
The velocity field and dispersion map are presented in Fig. 2. The velocity dispersion is clearly lower than that of HCN 3–2 and the difference in line FWHM is more than 70 km s-1 (see also Table 2) The velocity field is dominated by the east-west rotation already seen in the HCN 3–2 map.
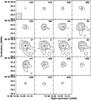 |
Fig. 4 Channel map of the HCN 3−2 emission towards Mrk 231, as obtained from the combination of the A and B configuration data. Contours are logarithmic: 3.6 × (1, 2, 4, 8, 16) mJy beam-1 where the first contour is at 4.5σ. The synthesized beam of |
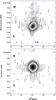 |
Fig. 5 HCN 3−2 position-velocity (pV) diagrams of the A+B combined data: Top: east-west cut along the line of nodes of the main disk rotation. Lower: north-south cut along the minor axis of the main disk rotation. Greyscale ranges from 0 to 40 mJy beam-1, contours are 1.4 × (1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 20, 25, 30) mJy beam-1. First contour is 2σ (1″ = 870 pc). Green dashed line outline the stellar velocity curve from Davies et al. (2004). |
3.4. HOC+J = 3–2
At the edge of the band (Fig. 1) we tentatively detect the HOC+J = 3–2 line (ν = 268.451 GHz and redshifted to 257.588 GHz). We do not pick up the complete HCO+ line so we can only estimate the HCO+/HOC+ 3–2 line ratio to 10–20 based on the peak emission. For comparison the HCO+/HOC+ 1–0 ratio for the nearby Seyfert galaxy NGC 1068 is 80 (integrated, 40–50 peak temperature ratio; Usero et al. 2004) implying that the HOC+ line emission is relatively brighter in Mrk 231. The HOC+ line emission will be discussed further in Lindberg et al. (in prep.).
3.5. Continuum
Gaussian fits to the continuum in the A-array and A+B-array observations are presented in Table 2. If we consider the A and B- array dataset separately we find that in the B-array data the integrated flux density is 44.9 ± 1.5 mJy, while in the A-array data the flux is a factor of 1.9 lower. From uv fitting we concluded (before merging the datasets) that this difference is caused by the shorter baselines of the B-array data and that a significant fraction of the 1 mm continuum is extended beyond the compact nucleus and emerges from the main disk.
 |
Fig. 6 Gaussian fits to the A+B combined data central spectrum. Fits are peak flux and line width: HCN ν = 0 line centre (63 mJy/beam, 250 km s-1), line wings (7 mJy/beam, 840 km s-1); HCN ν2 = 1f (6 mJy/beam, 260 km s-1); HCO+ (45 mJy/beam, 227 km s-1). Since the A- and B-array data had a slight shift in centre frequency the edges of the band have been cut, leaving out the HOC+ detection at the blue end of the spectrum. |
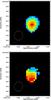 |
Fig. 7 Top panel: integrated intensity of the HCN J = 3−2ν2 = 1f line emission where the contour levels are 0.14 × (1,3,5,7,9) Jy beam-1 km s-1. The peak flux is 1.5 Jy beam-1 km s-1 and the cross marks the position of the peak HCN 3–2 integrated intensity. Lower panel: velocity field with contour levels starting at − 60 km s-1 and then increasing by steps of 15 km s-1 until +30 km s-1. The grey (colour) scale ranges from − 60 to 40 km s-1. (In the online version of this figure the greyscale is replaced with a rainbow color scale ranging from dark blue to red.) |
 |
Fig. 8 Integrated intensity of the 256 GHz continuum with contour levels 2 × (1,2,4,8) mJy beam-1 km s-1 and grey scale ranging from − 2.6 to 25 mJy beam-1 km s-1 (peak integrated flux is 25 mJy beam-1 km s-1). |
4. Discussion
4.1. Vibrationally excited HCN in the QSO nucleus
The J = 3–2 v2 = 1, l = 1f line is a rotational transition within a vibrationally excited state. The first excited bending state of HCN is doubly degenerate, so that each rotational level ν2 = 1J is split into a closely spaced pair of levels (f and e). The ν2 = 1e 3–2 line is blended with the HCN 3–2 line in the vibrational ground state (ν = 0) and cannot be studied for extragalactic sources while the ν2 = 1f line has rest frequency ν = 267.1993 GHz, shifted by 358 MHz (+400 km s-1) from the HCO+ 3–2 line. (The HCN ν2 = 1l = 1e line is right on top of the main ν = 0 line and will not affect the interpretation of the line shape of the main line. It may be absorbed by the ν = 0 line or may boost the line centre emission by a similar intensity as the HCN ν2 = 1f line.) The energy above ground of the ν2 = 1 state is TE/k = 1050 K and intense TB(IR) > 100 K mid-IR emission is required to excite these states. The critical density of the line is large enough that collisional excitation is unlikely (Ziurys & Turner 1986; Mills et al. 2013). HCN vibrational lines therefore directly probe the size, structure and dynamics of optically thick mid-IR dust cores.
The fits to the source size suggest that the emission is located within 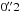 (r< 90 pc) of the AGN (Table 1, Fig. 7). This is consistent with mid-IR imaging of Mrk 231 which reveal a compact (≲0.̋13) source of TB(IR) > 141 K (Soifer et al. 2000) and with the dust model for Mrk 231 by González-Alfonso et al. (2010) where the mid-IR is dominated by a hot component with Td = 150−400 K emerging from the inner 40−50 pc. Furthermore, the 14 μm absorption line (ν2 = 0−1) of HCN has been detected towards Mrk 231 with the Spitzer Telescope (Lahuis et al. 2007). This shows that HCN in Mrk 231 absorbs mid-IR continuum which can populate the vibrational ν2 = 1 ladder.
(r< 90 pc) of the AGN (Table 1, Fig. 7). This is consistent with mid-IR imaging of Mrk 231 which reveal a compact (≲0.̋13) source of TB(IR) > 141 K (Soifer et al. 2000) and with the dust model for Mrk 231 by González-Alfonso et al. (2010) where the mid-IR is dominated by a hot component with Td = 150−400 K emerging from the inner 40−50 pc. Furthermore, the 14 μm absorption line (ν2 = 0−1) of HCN has been detected towards Mrk 231 with the Spitzer Telescope (Lahuis et al. 2007). This shows that HCN in Mrk 231 absorbs mid-IR continuum which can populate the vibrational ν2 = 1 ladder.
4.1.1. The vibrational temperature Tvib
We can estimate a Tvib through comparing the intensities of the ν2 = 1f and vibrational ground state (ν = 0) lines. We use the peak brightness ratio (=10) from the A-array data since the ν2 = 1f line is nuclear and compact. Assuming optically thin emission for both lines, and that the lines are co-spatial, we estimate Tvib to 400 K.
If the lines are optically thick: we know from the low HCN/H13CN 1−0 ratio of 7 (Costagliola et al. 2011) that HCN is unlikely to be optically thin. If we adopt an optical depth for the HCN main line τ(HCN 3–2) of 10 (assuming the ν2 = 1f line remains thin) Tvib is reduced to 210 K, for τ(HCN 3–2) = 20 Tvib = 185 K. We know that a firm lower limit to Tvib must be 100 K since at lower IR brightness temperatures the ν2 = 1f line is not excited. However, the ν2 = 1/ν = 0 brightness ratio drops quickly with temperature so at our sensitivity we would not detect TB(vib) much below 200 K.
If lines are not co-spatial: the ν2 = 1f emission region seems to be smaller than that of the ν = 0 line even in the A-array beam. This causes us to underestimate Tvib for the HCN ν2 = 1f emitting region since the real ν2 = 1/ν = 0 ratio will be higher.
To resolve both issues we must observe lines of multiple transitions at even higher resolution, but we can conclude that Tvib ≳ 200 K and may exceed 400 K.
4.1.2. Is the vibrational HCN tracing a warped disk?
The velocity field of the HCN J = 3–2 ν2 = 1f line is tilted with respect to the east-west rotation of the almost face-on main disk. From stellar absorption line studies Davies et al. (2004) propose that the inner 0″2−0″3 (170−250 pc) of Mrk 231 is warped out of its original disk plane. They present a model of the warp where they tilt the disk slightly (10°) within 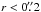 and then let it decline uniformly to zero at
and then let it decline uniformly to zero at 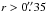 . The result is a major axis of the inner part of the disk of PA = −25°. High resolution OH megamaser observations by (Klöckner et al. 2003; Richards et al. 2005) suggest an even stronger effect of warping in the centre of Mrk 231 with a dusty disk or torus inclined by 56°. Interestingly the OH velocity field of Klöckner et al. (2003) is similar to the one we find for the HCN J = 3–2 v2 = 1, l = 1f line (see Fig. 7).
. The result is a major axis of the inner part of the disk of PA = −25°. High resolution OH megamaser observations by (Klöckner et al. 2003; Richards et al. 2005) suggest an even stronger effect of warping in the centre of Mrk 231 with a dusty disk or torus inclined by 56°. Interestingly the OH velocity field of Klöckner et al. (2003) is similar to the one we find for the HCN J = 3–2 v2 = 1, l = 1f line (see Fig. 7).
Davies et al. (2004) comment that it is difficult to warp a stellar disk but point out that the stars in the disk of Mrk 231 are young and that the warp likely occured first in a gaseous disk and that the young stars then were formed in situ.
The question is then why we do not see evidence of this warp in the inner part of the HCN 3–2 velocity structure. An inspection of the velocity field (Fig. 2) reveals a complex structure and the velocities to the south-west of the nucleus are bluer than expected from an east-west rotating disk while the velocities to the north-east are too red. One possible explanation to this is that the nuclear inclined dusty structure drives an HCN 3–2 outflow with blueshifted emission south-west of the nucleus and redshifted emission to the north-east. This will become superposed on the underlying east-west rotation creating a convoluted velocity field. If the molecular outflow of Mrk 231 is driven by several sources (jet, disk, warped nuclear disk) the resulting outflow pattern is indeed expected to be complex. However, there are also other potential explanations and higher resolution observations paired with modelling of the velocity structure is necessary to effectively address these issues.
4.1.3. The nuclear gas mass and inclination
The map of integrated intensities with the highest resolution (A-array map with 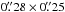 resolution) has a peak HCN 3–2 integrated flux of 19 Jy km s-1 which translates to 4750 K km s-1. We could now apply an HCN to dense gas mass conversion factor to estimate the Mdense in the centre of Mrk 231. Gao & Solomon (2004) were to our knowledge the first to suggest a global relation between the HCN 1–0 luminosity and the mass of dense gas Mdense = 10 × L(HCN 1–0). Just as is the case for the CO-to-H2 conversion factor this rests on the assumption on the HCN emission emerging from a standard cloud similar to dense cores in the Milky Way. However, García-Burillo et al. (2012) suggest that the L(HCN 1−0) to H2 conversion factor should be lower for ULIRGs and other HCN overluminous objects (where L(HCN)/L(CO) ≳ 0.1) by a factor of 1/3.2. For the nucleus of Mrk 231, the HCN excitation is affected by IR and not all of its nuclear emission is emerging from the inferred warped disk (see discussion in the section above). Instead, we can use the HCO+ 3–2 emission as a proxy for an HCN emission uncontaminated by radiative excitation. The HCN conversion factor has been calibrated for the 1−0 transition so we will also assume a 3−2/1−0 lineratio of 0.5. Using the more conservative conversion factor of García-Burillo et al. (2012; see also Sect. 4.3.2) we obtain a mass Mdense ≈ 3.1 × L(HCN 1−0) ≈3.1 × L(HCO+ 3−2) of 8 × 108 M⊙ in the inner r = 0.̋13 and a average N(H2) of 1.2 × 1024 cm-2.
resolution) has a peak HCN 3–2 integrated flux of 19 Jy km s-1 which translates to 4750 K km s-1. We could now apply an HCN to dense gas mass conversion factor to estimate the Mdense in the centre of Mrk 231. Gao & Solomon (2004) were to our knowledge the first to suggest a global relation between the HCN 1–0 luminosity and the mass of dense gas Mdense = 10 × L(HCN 1–0). Just as is the case for the CO-to-H2 conversion factor this rests on the assumption on the HCN emission emerging from a standard cloud similar to dense cores in the Milky Way. However, García-Burillo et al. (2012) suggest that the L(HCN 1−0) to H2 conversion factor should be lower for ULIRGs and other HCN overluminous objects (where L(HCN)/L(CO) ≳ 0.1) by a factor of 1/3.2. For the nucleus of Mrk 231, the HCN excitation is affected by IR and not all of its nuclear emission is emerging from the inferred warped disk (see discussion in the section above). Instead, we can use the HCO+ 3–2 emission as a proxy for an HCN emission uncontaminated by radiative excitation. The HCN conversion factor has been calibrated for the 1−0 transition so we will also assume a 3−2/1−0 lineratio of 0.5. Using the more conservative conversion factor of García-Burillo et al. (2012; see also Sect. 4.3.2) we obtain a mass Mdense ≈ 3.1 × L(HCN 1−0) ≈3.1 × L(HCO+ 3−2) of 8 × 108 M⊙ in the inner r = 0.̋13 and a average N(H2) of 1.2 × 1024 cm-2.
Interestingly, this simple estimate of the nuclear gas mass is similar to the H2 mass (2.5−5 × 108 M⊙) calculation of the core (quiescent, QC) component of Mrk 231 by González-Alfonso et al. (2014) from their Herschel OH observations. We do not know the inclination of the nuclear warped disk, but if we constrain it to have a lower limit to its dynamical mass of 5 × 108 M⊙ (the maximum H2 mass from González-Alfonso et al. 2014) at a radius of 0.̋13 and we use the FWHM of the HCN ν2 = 1f line to indicate that its projected rotational velocity is 130 km s-1, then its inclination must be 60° or lower – which fits both the Davies et al. (2004) and Klöckner et al. (2003) models.
4.1.4. Comparison to HC3N and HNC
The detection of vibrationally excited HCN is also interesting in the context of our recent detection of 3 mm HC3N 10–9 in Mrk 231 (Aalto et al. 2012). Models by Harada et al. (2013) find that HC3N abundances may be enhanced substantially in warm (>200 K) regions in the midplane of dense disks around AGNs. Lindberg et al. (2011) find a strong correlation between OH megamaser activity and HC3N emission implying that the regions may be co-spatial. We therefore suggest that the HC3N and HCN vibrational line emission are both centred on the dusty central region of Mrk 231.
We have also previously found that the velocity field of the HNC 1−0 emission in Mrk 231 is inclined with respect to the main east-west rotation. The PA of the HNC rotation is 130° indicating that at least part of the emission seems to be associated with the proposed warped dusty structure (Aalto et al. 2012). Costagliola et al. (2011) find a correlation between the HC3N and HNC luminosities which is not immediately obvious from a chemical perspective. However, both molecules can be IR pumped at mid-IR wavelengths and a possibility is that both are tracers of dust environments – just like vibrationally excited HCN.
4.2. IR pumping of HCN?
The luminous HCN emission towards many LIRGs (and in particular ULIRGs) have been used to argue that the relative dense n ≳ 104 cm-3 gas content is higher in LIRGs than in normal galaxies. The relation between CO/HCN 1–0 line ratio and IR luminosity has also been used as grounds to suggest that the IR luminosity is largely driven by star formation – rather than AGN activity (e.g. Gao & Solomon 2004). Elevated HCN/HCO+ 1–0 line intensity ratios (>1) in the nuclei of Seyfert galaxies (e.g. Kohno 2003; Usero et al. 2004) and in ULIRGs (e.g. Graciá-Carpio et al. 2006) are suggested to be due to abundance enhancements of HCN for example due to X-ray dominated chemistry near an AGN (e.g. Maloney et al. 1996; Kohno 2003) or due to high temperatures (e.g. Harada et al. 2013; Kazandjian et al. 2012).
The above arguments are based on the assumption that HCN is collisionally excited. However, it is possible that the IR pumping that leads to the detection of the ν2 = 1 lines also may affect the excitation of the ground state lines. HCN has degenerate bending modes in the IR. The molecule absorbs IR-photons to the bending mode (its first vibrational state) and then it decays back to the ground state via its P or R branch. In this way, a vibrational excitation may produce a change in the rotational state in the ground level and can be treated (effectively) as a collisional excitation in the statistical equations. Thus, IR pumping excites the molecule to the higher rotational level by a selection rule ΔJ = 2. For a molecular medium consisting of dense clumps surrounded by lower density gas the net effect of IR pumping may be that the HCN emission from the dense clumps gets added to by IR-pumped HCN emission from the low density gas (for a discussion of this scenario see e.g. Aalto et al. 2007) resulting in a boosted total HCN luminosity. How large this effect is depends on the balance between dense and low density gas, the size and intensity of the IR field, and the HCN abundance.
We can make a rough estimate of the fraction of the HCN 3−2 emission in Mrk 231 that could be influenced by IR-pumping through comparing source sizes and fluxes of the HCN and ν2 = 1f emission. We (conservatively) assume that IR-pumping of HCN is only important where we detect the ν2 = 1f line (inside 0.̋2). About half of the HCN 3–2 flux is found inside the A-array central beam – thus 50% of the HCN 3−2 line emission is likely affected by IR pumping.
4.3. The molecular outflow
4.3.1. HCN excitation – dense gas in the outflow
The HCN 3–2 line wings extend out to ±750 km s-1 and has a spatial extent of at least 0.̋4 (350 pc). The actual extent may be larger and the data allows for a total extent of 0.̋9. We can compare the flux of the 3–2 line to that of the previously published (Aalto et al. 2012) 1–0 line to determine the excitation assuming that they emerge from the same region and that the line ratio is constant through the outflow. The flux in the 1–0 line wing is 0.8 (red) and 0.6 (blue) Jy km s-1. We find HCN 3–2 line wing fluxes of 2.5 (red) and 1.9 (blue) Jy km/s. The flux line ratio is then 3 for both line wings and in brightness temperature scale TB(3–2)/TB(1–0) this corresponds to ≈0.35. This value is uncertain since we have different uv-coverage and sensitivity in the 3−2 and 1−0 data, but the ratio suggests that the emission is subthermally excited.
In the above section (Sect. 4.2) we concluded that IR pumping is affecting the HCN emission in the inner 0.̋2 of Mrk 231. The line wings are more extended suggesting that they are unlikely to be significantly impacted by the nuclear IR source (apart from in the very inner part of the outflow) and that the HCN wing emission is therefore dominated by collisions. The J = 3–2 transition of HCN has a critical density of ≈107 cm-3 and significant HCN 3–2 emission may start to emerge at densities of 105 cm-3. Hence, when collisionally excited, HCN 3−2 is tracing dense gas and a 3–2/1–0 line ratio of ≈0.35 suggests that the number density range for the HCN-emitting gas is n = 104−5 × 105 cm-3 (for kinetic temperatures Tk = 30−100 K) and HCN abundances X(HCN) of 109−108 (see next section).
The outflow may consist of a two-phase molecular medium where the bulk of the HCN-emitting molecular mass resides in dense clouds and lower density, diffuse molecular gas is traced by low-J CO. This scenario is consistent with the apparent subthermal excitation of CO (Cicone et al. 2012).
4.3.2. Estimating the mass of dense gas in the outflow
The extremely bright HCN emission of the outflowing gas shows that the gas properties are very different from those where the conversion factor from CO luminosity to H2 mass was calibrated – giant molecular clouds (GMCs) in the disk of the Milky Way. The molecular mass is difficult to determine in an environment where the physical conditions, structure and stability of the clouds are poorly known. However, we can attempt to estimate the mass of dense gas through applying an L(HCN) to H2 conversion factor. We adopt the same factor (determined for HCN luminous sources García-Burillo et al. 2012) that we applied to the nuclear emission in Sect. 4.1.3. Aalto et al. (2012) do not give a L(HCN 1–0) for the outflow, but we can estimate it here through dividing L(HCN 3–2) (from Table 1) with 0.35 (the estimated HCN 3–2/1–0 line intensity ratio from the previous section) resulting in L(HCN 1–0) ≈1.2 × 108 K km s-1 pc2 for both the red and blue wings and the resulting Mdense ≈ 4 × 108 M⊙. (Note that the L(HCN 3–2) in Table 1 is a lower limit to the real L(HCN 3−2) since we only include flux above a 4σ cutoff in the integrated intensity from which L(HCN 3–2) is derived. Hence the inferred L(HCN 1–0) is also a lower limit.)
We can also investigate masses obtained assuming that the HCN emission is emerging from a population of dense cloud cores which we first consider to be self-gravitating and then we allow the line width per cloud to increase so that the clouds are no longer bound. We consider clouds of typical cloud core mass of 10 M⊙ and warm temperature of Tk = 50 K (Goldsmith 1987).
A. Self-gravitating clouds: we use the RADEX non-LTE code to investigate the effect of varying HCN abundances (X(HCN) ranging from 10-8 to 10-6) on the brightness temperatures, luminosities and line ratios for three model clouds of densities n = 3 × 103, 104 and 105 cm-3 (where n = 3 × 103 is the lowest density for which a solution could be found for the given range of X(HCN)). In Table 3 we present a few examples of model clouds that fulfil the observed line ratios (within the errors) keeping in mind that they are illustrations of possible solutions. To get the total mass of dense gas from the ensemble of model clouds we divided the observed L(HCN 3–2) by the luminosity per model cloud. For high abundances (X(HCN) = 10-6) we can find solutions to fit the observed line ratios for the lower density model clouds and total dense gas masses are Mdense = 4.4 × 108 and 3.5 × 108 M⊙. When we lower the HCN abundances to more normal values of 10-8 we find solutions only for the high density model cloud. The luminosity per cloud is lower due to the smaller radius and Mdense = 1.7 × 109 M⊙.
We can conclude that an ensemble of self-gravitating clouds with a high HCN abundance reproduces the mass of dense gas we obtain quite well when adopting the L(HCN) to Mdense conversion factor at the beginning of the section. This is not surprising since inherent in the conversion factor lies an assumption of self-gravitating clouds. In addition the modified L(HCN) conversion factor for luminous HCN sources (see Sect. 4.1.3) attempts to scale down the masses obtained for extremely luminous (relative to CO) HCN sources. In our RADEX model we achieve this through adopting a large HCN abundance for self-gravitating clouds. For lower HCN abundances we require denser clouds to fit the line ratios and the resulting total mass goes up since the luminosity per cloud goes down. It is also generally true that if we increase the kinetic temperature the luminosity per cloud increases reducing the total molecular mass.
Model HCN 3–2 luminosities – self-gravitating cloud.
B. Non self-gravitating clouds: we can simulate an ensemble of unbound clouds through increasing the line width ΔV per cloud. Now the clouds will be “overluminous” with respect to their mass compared to self-gravitating clouds. We can test this scenario through taking the first model cloud (1) in Table 3 and increase the linewidth by a factor of twenty – keeping all other parameters intact. The increase in ΔV results in a drop in HCN 3–2 brightness temperature by a factor of 13, so the net increase in luminosity per cloud is 1.5. Now, however, the HCN 3−2/1−0 line ratio becomes too low and the HCN 1–0 emission too faint compared to CO 1−0 (see Aalto et al. 2012). We can compensate for this through increasing the HCN abundance further to > 10-5 (which is a very high abundance). As a consequence, low density (n ≲ 104 cm-3) solutions need extreme HCN abundances to compensate for the loss in optical depth and excitation caused by the increased line width. It is easier to maintain a high HCN brightness in denser clouds since the excitation is less subthermal. For example, increasing ΔV by a factor of 10 and X(HCN) to 10-6 for model cloud 3. in Table 3 will result in a factor of 23 more HCN 3–2 luminosity per cloud reducing Mdense to ≈ 7 × 107.
To summarize, for a medium consisting of self-gravitating dense clouds we find a mass of dense gas Mdense ≈ 4 × 108 M⊙ – which will accomodate most reasonable RADEX solutions as well as the mass when applying the HCN to H2 conversion factor at the beginning of this section. An ensemble consisting of non-self-gravitating clouds may have lower molecular masses by up to an order of magnitude for the same HCN luminosity, but it requires X(HCN) ≳10-6 to maintain the large HCN brightness in relation to CO. Abundances of X(HCN) ≈10-8 would be considered rather typical for Galactic GMCs and larger scale star forming regions (Irvine et al. 1987). Enhanced abundances of HCN are found in warm, dense regions, for example in hot cores or shocks Jørgensen et al. (2004); Tafalla et al. (2010) where HCN may be enhanced by factors 10−100 over HCO+. Harada et al. (2013) also suggest that HCN is enhanced in X-ray dominated/illuminated regions (XDRs) in AGNs where the HCN-enhancement is caused by the high temperatures in the XDRs. Possible HCN abundance enhancements in the outflow of Mrk 231 would likely stem from shocks potentially originating from the radio jet interacting with the outflowing gas and/or multiple phases of the outflow colliding.
Finally, the distribution of the dense clouds is unlikely to be smooth within the outflow and even viewing them as individual clouds could be wrong since they may (for example) consitute dense condensations along filaments or along walls of bipolar structures. As is already evident in the pV diagrams (see Fig. 3) the wing emission is clumpy in velocity space showing that the gas is not smoothly distributed. We will discuss this further in a subsequent paper (Lindberg et al., in prep.). We adopt the mass of self-gravitating clouds (and the modified conversion factor) Mdense ≈ 4 × 108 M⊙ as an upper limit to the dense molecular gas mass in the outflow.
4.3.3. Can dense clouds survive in the outflow?
Results from recent simulations by Gabor & Bournaud (2014) of the physical conditions of thermal AGN outflows imply that the outflow consists mostly of hot (107 K) gas of low density. Dense clumps may be entrained by these hot flows but they are warmer and less dense than the disk gas. Gabor & Bournaud (2014) also find that only a small mass fraction of the outflow consists of molecular gas and that the AGN feedback does not strongly affect the surrounding disk since it only impacts the diffuse gas. Models by Zubovas & King (2014) instead imply that the outflows can not remain in a hot-gas phase, but forms a two-phase medium where cold clumps are mixed in with the tenuous gas and most of the mass is in the dense clumps. The authors suggest that cooling should lead to star formation in the outflow where the star formation efficiency (SFE) is high and quickly removes dense gas from the outflow. We also note that there is observational evidence that molecules may reform in fast outflows as seen in the supernova remnant Cas A where dense CO clumps are detected in the region of the reverse shock (Wallström et al. 2013).
We note that the low-J CO emission seems to extend out to twice the radial distance than the HCN outflow (Feruglio et al. 2010; Cicone et al. 2012) which suggests that the dense gas is either more difficult to drive to large distances. Alternatively the dense gas evaporates or is turned into stars. Our results therefore seem to (tentatively) support the models of Zubovas & King (2014) over those of Gabor & Bournaud (2014) – or that the outflow of Mrk 231 is atypical for AGN outflows. The latter seems unlikely since luminous Wallström et al. (2013) HCN 4−3 emission is detected in the AGN-driven outflow of NGC 1068 (García-Burillo et al. 2014) together with bright CO 6−5 emission indicating the presence of dense clouds. The outflow is likely powered by the AGN jets and also for Mrk231 it is possible that the dense gas is not primarily being driven out by a thermal wind from the AGN, but by the radio jet or by radiation pressure from the hot dusty warped disk.
4.3.4. What is powering the dense outflow?
The mechanical luminosity of the outflowing dense gas is challenging to determine since we have significant error bars on its mass. We can take the upper limit of 4 × 108 M⊙ (Sect. 4.3.2) and let it move at a (constant) velocity of 750 km s-1. Let the total kinetic energy be Ekin = Ebulk + Eturbulent (Veilleux et al. 2001) where 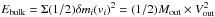 is then ≈ 2.4 × 1057 erg. We cannot measure a reliable limit of the turbulence of the gas, but assume that the contribution is significantly smaller than that of the bulk movement. We do not know the radial extent of the outflow, but a lower limit is 350 pc which results in an upper limit to the mechanical luminosity of Lmech = 1.5 × 1044 erg s-1 or 4 × 1010L⊙. The outflow rate Ṁout = 800 M⊙ yr-1 and the momentum flux Ṗ = Ṁ × v = 4 × 1036 g cm s-2. This is about 12LAGN/c (for LAGN = 2.8 × 1012L⊙). However, if the dense clouds in the outflow are not self-gravitating (or near self-gravitating) the mass of dense gas in the outflow may be one order of magnitude lower with a corresponding reduction in kinetic energy and momentum flux. Furthermore, if the outflow is decelerating so that a portion of the gas has lower velocities then estimates will come down further.
is then ≈ 2.4 × 1057 erg. We cannot measure a reliable limit of the turbulence of the gas, but assume that the contribution is significantly smaller than that of the bulk movement. We do not know the radial extent of the outflow, but a lower limit is 350 pc which results in an upper limit to the mechanical luminosity of Lmech = 1.5 × 1044 erg s-1 or 4 × 1010L⊙. The outflow rate Ṁout = 800 M⊙ yr-1 and the momentum flux Ṗ = Ṁ × v = 4 × 1036 g cm s-2. This is about 12LAGN/c (for LAGN = 2.8 × 1012L⊙). However, if the dense clouds in the outflow are not self-gravitating (or near self-gravitating) the mass of dense gas in the outflow may be one order of magnitude lower with a corresponding reduction in kinetic energy and momentum flux. Furthermore, if the outflow is decelerating so that a portion of the gas has lower velocities then estimates will come down further.
From the dust models of González-Alfonso et al. (2010) the luminosity of the hot (150−400 K) compact (r = 23 pc) dust component) and the warm (95 K) component (r = 120 pc) is estimated to be Ldust = Lhot + Lwarm = 7.5 × 1011 + 1.9 × 1012 = 2.65 × 1012L⊙. Simulations of clumpy outflows by Roth et al. (2012) suggest that momentum driven outflows may exceed L/c, but only by factors of up to 5 (although this seems to be dependent on the scale height of their model disk). Thus for the maximum mass estimate of the dense outflow radiation pressure will not play a major role in driving out the gas – instead winds from the AGN and/or boosting from the jets are the main candidates for the powering of the outflow. However, if the Ṗ is instead 1.2LAGN/c (for the lower mass (and/or lower velocity) estimate) then radiation pressure may well be the main power source.
4.3.5. Comparing to the OH outflow
Herschel observations of IR OH towards Mrk 231 reveal two outflowing components: one low excitation feature with velocities 200−800 km s-1 (LEC component) and one high excitation feature (HVC component) with velocities up to ≈1500 km s-1 (González-Alfonso et al. 2014). The dense HCN 3–2 outflow studied here has velocities similar to the OH LEC component. Our estimated mechanical luminosities agree within a factor of 2−3. The gas densities required to excite the HCN 3–2 line in the outflow, however, are much higher than the averaged values derived from OH and CO, strongly pointing towards a clumpy structure in the HCN outflow.
We see no sign of the high ≈1500 km s-1 velocities seen in the highly excited OH absorption. This component seems to be nuclear and radiatively excited and González-Alfonso et al. (2014) suggest that it may probe an interclump medium of the torus itself that is flowing past the dense clumps and hence would move faster than the dense gas. It is suggested that interaction with the dense clumps would decelerate the outflowing gas with increasing radius. The OH HVC component is radiatively excited but would not be seen as a radiatively excited HCN component in emission due to too low column density – and too small spatial extent. While absorption measurements of high lying lines towards very warm continuum sources are primarily sensitive to the rates (Ṁ, Ṗ, Lmech), emission measurements are more sensitive to integral values (Mgas, Ekin; González-Alfonso et al. 2014).
4.4. Mrk 231 as a dust-obscured QSO
The detection of the HCN J = 3–2 ν2 = 1, l = 1f vibrational line shows that the HCN molecule is abundant even in extreme, hot nuclear environments. Since the HCN vibrational line is excited by intense IR dust emission it also suggests that the QSO has not yet shed itself of its nuclear shroud and this dusty, warm region may represent the final stage of the obscured, X-ray absorbed (Page et al. 2004) accretion phase of the QSO. The lack of mid-IR AGN signatures may indicate that the coronal region around the AGN is blocked from our line of sight (Armus et al. 2007). Interestingly, the far-ultraviolet spectrum shows a lack of absorption signatures (Veilleux et al. 2013) and recent X-ray studies by Teng et al. (2014) suggest that the AGN is being viewed through a patchy and Compton-thin (N(H2) ≈ 1023 cm-2) column. The authors propose that the AGN is intrinsically X-ray faint thus explaining the lack of mid-IR signatures.
The ν2 = 1f HCN line is excited by mid-IR dust emission, and its optical depth will peak at the location of the dust source. The position of the QSO core agrees (within the errors) with the peak of the host dust, which is consistent with the notion that there is an inner radius of the torus/disk is close (20 pc) to the AGN (Klöckner et al. 2003; Richards et al. 2005). Our estimated N(H2) in the inner diameter of 0.̋13 of 1.2 × 1024 cm-2 is an average value that is consistent with the scenario where the QSO has blown a hole in the central gas and dust distribution, creating a torus-like structure inside the warped nuclear disk.
Further observations may reveal to what degree the warped dusty disk is collimating the outflowing dense gas. The inclination of the nuclear structure is not constrained and the structure of the dense outflow seems complex, meaning that even higher spatial resolution is needed to disentangle the nuclear and outflow dynamics. In addition, more studies will also reveal whether there is a massive inflow of gas to replenish the central region feeding the powerful molecular outflow. If so, Mrk 231 may continue to be a dust-obscured QSO until all gas reservoirs have been exhausted, or until the inflow process is halted. If there is no significant inflow and if the molecular outflow indeed originates in the inner region near the AGN, the available bulk of gas of ≈ 5 × 108 M⊙ will be emptied within the extremely short time of 0.5 Myr, assuming a steady flow and adopting the upper limit on the mass estimate from Sect. 4.3.2.
5. Conclusions
We detected luminous emission from HCN and HCO+J = 3–2 in the main disk of Mrk 231. The HCN 3–2 emission is concentrated towards the inner region (FWHM r = 0.̋17 (150 pc)) but disk emission for both HCN and HCO+ extends out to at least 600 pc – with southern and western emission features of 1 kpc. Line wings are detected for HCN where velocities are found to be similar to those found for CO and HCN J = 1–0 (± 750 km s-1). No line wings are found for HCO+ 3–2. We find that both the blue- and redshifted HCN J = 3−2 line wings are spatially extended >0.̋4 (≳350 pc) centred on the nucleus. 256 GHz continuum is detected at 46 mJy – more than half of it is extended on the scales of the main disk. Emission from the reactive ion HOC+ is tentatively detected with a HCO+/HOC+J = 3–2 line intensity ratio of 10−20.
We detected the HCN J = 3–2 ν2 = 1f vibrational line for the first time in Mrk 231. The HCN ν2 = 1f line emission is compact (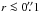 (90 pc)) and centred on the nucleus where it is excited by bright mid-IR 14 μm continuum to a vibrational temperature Tvib = 200−400 K (assuming co-spatial HCN ν = 0 and ν2 = 1f). The HCN ν2 = 1f velocity field line of nodes are oriented with a PA of 155° ± 10° – strongly inclined to the rotation of the main disk. We suggest that the HCN J = 3–2 ν2 = 1f line is emerging from the inner dusty region of a warped disk, as seen also in stellar absorption lines and in OH megamaser emission. The nuclear (
(90 pc)) and centred on the nucleus where it is excited by bright mid-IR 14 μm continuum to a vibrational temperature Tvib = 200−400 K (assuming co-spatial HCN ν = 0 and ν2 = 1f). The HCN ν2 = 1f velocity field line of nodes are oriented with a PA of 155° ± 10° – strongly inclined to the rotation of the main disk. We suggest that the HCN J = 3–2 ν2 = 1f line is emerging from the inner dusty region of a warped disk, as seen also in stellar absorption lines and in OH megamaser emission. The nuclear (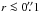 ) molecular mass is estimated to 8 × 108 M⊙ and the average column density N(H2) = 1.2 × 1024 cm-2. The detection of the HCN J = 3–2 ν2 = 1f vibrational line is consistent with the notion of Mrk 231 as a QSO in the final stages of its dust-obscured phase.
) molecular mass is estimated to 8 × 108 M⊙ and the average column density N(H2) = 1.2 × 1024 cm-2. The detection of the HCN J = 3–2 ν2 = 1f vibrational line is consistent with the notion of Mrk 231 as a QSO in the final stages of its dust-obscured phase.
The HCN J = 3–2 ν2 = 1f vibrational line also reveals that the HCN excitation is affected by IR radiative excitation and that IR pumping may also affect the rotational levels of the vibrational ground state, hence the excitation of the whole molecule. A vibrational excitation may produce a change in the rotational state in the ground level and can be treated (effectively) as a collisional excitation in the statistical equations. We estimate that 50% of the HCN 3–2 emission in the main disk may be influenced by radiative excitation.
The HCN emission from the line wings is extended, so we concluded that IR pumping does not strongly influence the excitation (apart from possibly in the inner part). Instead, we propose that most of the HCN emission in the outflow is collisionally excited. Line ratios indicate that the emission is emerging in dense gas n = 104−5 × 105 cm-3, but elevated HCN abundances may also allow for emission originating from more moderate densities. The HCN abundance in the outflow seems high and X(HCN) may be 10-6. Elevated HCN abundances are found in warm, dense gas in star-forming and shocked regions in the Galaxy. Models also indicate that HCN may be very abundant in X-ray irradiated warm gas in AGN disks. We estimated an upper limit to the dense mass of 4 × 108 M⊙ with an outflow rate Ṁout = 800 M⊙ yr-1 and a momentum flux Ṗ ≲ 12 LAGN. If the dense gas clouds are not self-gravitating, the mass and momentum flux will be lower.
Acknowledgments
We thank the IRAM PdBI staff for excellent support. We are grateful to A. Richards and E. Varenius for discussions of the positional accuracy of radio and mm interferometric data. S.A. thanks the Swedish National Science Council for grant (Dnr. 621-2011-4143) support.
References
- Aalto, S., Spaans, M., Wiedner, M. C., & Hüttemeister, S. 2007, A&A, 464, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armus, L., Charmandaris, V., Bernard-Salas, J., et al. 2007, ApJ, 656, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Bryant, P. M., & Scoville, N. Z. 1996, ApJ, 457, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., Wrobel, J. M., & Ulvestad, J. S. 1998, AJ, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Feruglio, C., Maiolino, R., et al. 2012, A&A, 543, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costagliola, F., Aalto, S., Rodriguez, M. I., et al. 2011, A&A, 528, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R. I., Tacconi, L. J., & Genzel, R. 2004, ApJ, 613, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J., Sturm, E., González-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabor, J. M., & Bournaud, F. 2014, MNRAS, 441, 1615 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Brandt, W. N., Chartas, G., Garmire, G. P., & Sambruna, R. M. 2002, ApJ, 569, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- García-Burillo, S., Usero, A., Alonso-Herrero, A., et al. 2012, A&A, 539, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F. 1987, in Interstellar Processes, eds. D. J. Hollenbach, & H. A. Thronson, Jr., Astrophys. Space Sci. Lib., 134, 51 [Google Scholar]
- González-Alfonso, E., Fischer, J., Isaak, K., et al. 2010, A&A, 518, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2014, A&A, 561, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graciá-Carpio, J., García-Burillo, S., Planesas, P., & Colina, L. 2006, ApJ, 640, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Harada, N., Thompson, T. A., & Herbst, E. 2013, ApJ, 765, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., & Nakanishi, K. 2013, AJ, 146, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., Goldsmith, P. F., & Hjalmarson, A. 1987, in Interstellar Processes, eds. D. J. Hollenbach, & H. A. Thronson, Jr., Astrophys. Space Sci. Lib., 134, 561 [Google Scholar]
- Jørgensen, J. K., Hogerheijde, M. R., Blake, G. A., et al. 2004, A&A, 415, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kazandjian, M. V., Meijerink, R., Pelupessy, I., Israel, F. P., & Spaans, M. 2012, A&A, 542, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klöckner, H.-R., Baan, W. A., & Garrett, M. A. 2003, Nature, 421, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Kohno, K. 2003, in The Proceedings of the IAU 8th Asian-Pacific Regional Meeting, Vol. 1, eds. S. Ikeuchi, J. Hearnshaw, & T. Hanawa, ASP Conf. Ser., 289, 349 [Google Scholar]
- Lahuis, F., Spoon, H. W. W., Tielens, A. G. G. M., et al. 2007, ApJ, 659, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Lindberg, J. E., Aalto, S., Costagliola, F., et al. 2011, A&A, 527, A150 [Google Scholar]
- Lípari, S., Terlevich, R., Zheng, W., et al. 2005, MNRAS, 360, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Lipari, S., Sanchez, S. F., Bergmann, M., et al. 2009, MNRAS, 392, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Lonsdale, C. J., Smith, H. E., & Diamond, P. J. 2003, ApJ, 592, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, E. A. C., Güsten, R., Requena-Torres, M. A., & Morris, M. R. 2013, ApJ, 779, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., Stevens, J. A., Ivison, R. J., & Carrera, F. J. 2004, ApJ, 611, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Patnaik, A. R., Browne, I. W. A., Wilkinson, P. N., & Wrobel, J. M. 1992, MNRAS, 254, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, A. M. S., Knapen, J. H., Yates, J. A., et al. 2005, MNRAS, 364, 353 [NASA ADS] [Google Scholar]
- Roth, N., Kasen, D., Hopkins, P. F., & Quataert, E. 2012, ApJ, 759, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., & Veilleux, S. 2011, ApJ, 729, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Aalto, S., Evans, A. S., Wiedner, M. C., & Wilner, D. J. 2010, ApJ, 725, L228 [NASA ADS] [CrossRef] [Google Scholar]
- Soifer, B. T., Neugebauer, G., Matthews, K., et al. 2000, AJ, 119, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Downes, D., & Radford, S. J. E. 1992, ApJ, 387, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Santiago-García, J., Hacar, A., & Bachiller, R. 2010, A&A, 522, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, G. B., Silver, C. S., Ulvestad, J. S., & Carilli, C. L. 1999, ApJ, 519, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Teng, S. H., Brandt, W. N., Harrison, F. A., et al. 2014, ApJ, 785, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S., Wrobel, J. M., Roy, A. L., et al. 1999, ApJ, 517, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Usero, A., García-Burillo, S., Fuente, A., Martín-Pintado, J., & Rodríguez-Fernández, N. J. 2004, A&A, 419, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Shopbell, P. L., & Miller, S. T. 2001, AJ, 121, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Trippe, M., Hamann, F., et al. 2013, ApJ, 764, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Wallström, S. H. J., Biscaro, C., Salgado, F., et al. 2013, A&A, 558, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ziurys, L. M., & Turner, B. E. 1986, ApJ, 300, L19 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zubovas, K., & King, A. R. 2014, MNRAS, 439, 400 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Separate A- and B-array spectra towards the central beam. Spectra have been Gaussian smoothed (over two channels). We show the spectra for the A- and B-array separately to emphasize that identified features appear in both separate datasets. The central spectrum for the combined A+B dataset is shown in Fig. 6. Left: B-array spectrum of HCN J = 3−2, HCO+J = 3−2, HCN J = 3−2ν2 = 1, and a tentative detection of HOC+J = 3−2. Right: a-array spectrum of the same lines. The green velocity scale is for HCO+. |
| In the text | |
 |
Fig. 2 Top panels: combined A+B moment maps of the HCN 3−2 line emission from the main disk (as defined in the text). Left panel: integrated intensity with contour levels 0.5 × (1,2,4,8,16,32) Jy beam-1 km s-1 and grey (colour) scale ranging from 0 to 15 Jy beam-1 km s-1 (peak integrated flux is 22 Jy beam-1 km s-1). Centre: velocity field with contour levels starting at − 56 km s-1 and then increasing by steps of 18.8 km s-1 until +38 km s-1. The grey (colour) scale ranges from − 65 to 50 km s-1. Right: dispersion map where contours start at 30 km s-1 and then increase by steps of 30 km s-1. Greyscale ranges from 0 to 115 km s-1 and peak dispersion is 130 km s-1. The cross marks the position of the peak HCN 3−2 integrated intensity. Lower panels: combined A+B moment maps of the HCO+ 3−2 line. Left panel: integrated intensity with contour levels 0.5 × (1,2,4,8,16,32) Jy beam-1 km s-1 and grey (colour) scale ranging from 0 to 15 Jy beam-1 km s-1 (peak integrated flux is 12 Jy beam-1 km s-1). Centre: velocity field with contour levels starting at − 56 km s-1 and then increasing by steps of 18.8 km s-1 until +38 km s-1. The grey (colour) scale ranges from − 65 to 50 km s-1. Right: dispersion map where contours start at 30 km s-1 and then increase by steps of 30 km s-1. Greyscale ranges from 0 to 115 km s-1 and peak dispersion is 98 km s-1. The cross marks the position of the peak HCN 3−2 integrated intensity. (In the online version of this figure the greyscale is replaced with a rainbow color scale ranging from dark blue to red.) |
| In the text | |
 |
Fig. 3 Left: moment 0 maps (integrated intensity) of the HCN 3−2 line wings in tapered B array. Contour levels are 0.2 × (1,3,5,7,9) Jy beam-1 km s-1 and greyscale ranges from 0 to 2 Jy beam-1 km s-1. The cross marks the position of the peak HCN 3−2 integrated intensity. Right: pV diagrams of the tapered B array map. Upper: east-west cut along the line of nodes of the main disk rotation. Lower: north-south cut along the minor axis of the main disk rotation. Greyscale ranges from 0 to 120 mJy beam-1, contours are 3 × (1, 2, 4, 8, 16, 32) mJy beam-1. First contour is 2σ. |
| In the text | |
 |
Fig. 4 Channel map of the HCN 3−2 emission towards Mrk 231, as obtained from the combination of the A and B configuration data. Contours are logarithmic: 3.6 × (1, 2, 4, 8, 16) mJy beam-1 where the first contour is at 4.5σ. The synthesized beam of |
| In the text | |
 |
Fig. 5 HCN 3−2 position-velocity (pV) diagrams of the A+B combined data: Top: east-west cut along the line of nodes of the main disk rotation. Lower: north-south cut along the minor axis of the main disk rotation. Greyscale ranges from 0 to 40 mJy beam-1, contours are 1.4 × (1, 2, 3, 4, 5, 6, 7, 8, 9, 15, 20, 25, 30) mJy beam-1. First contour is 2σ (1″ = 870 pc). Green dashed line outline the stellar velocity curve from Davies et al. (2004). |
| In the text | |
 |
Fig. 6 Gaussian fits to the A+B combined data central spectrum. Fits are peak flux and line width: HCN ν = 0 line centre (63 mJy/beam, 250 km s-1), line wings (7 mJy/beam, 840 km s-1); HCN ν2 = 1f (6 mJy/beam, 260 km s-1); HCO+ (45 mJy/beam, 227 km s-1). Since the A- and B-array data had a slight shift in centre frequency the edges of the band have been cut, leaving out the HOC+ detection at the blue end of the spectrum. |
| In the text | |
 |
Fig. 7 Top panel: integrated intensity of the HCN J = 3−2ν2 = 1f line emission where the contour levels are 0.14 × (1,3,5,7,9) Jy beam-1 km s-1. The peak flux is 1.5 Jy beam-1 km s-1 and the cross marks the position of the peak HCN 3–2 integrated intensity. Lower panel: velocity field with contour levels starting at − 60 km s-1 and then increasing by steps of 15 km s-1 until +30 km s-1. The grey (colour) scale ranges from − 60 to 40 km s-1. (In the online version of this figure the greyscale is replaced with a rainbow color scale ranging from dark blue to red.) |
| In the text | |
 |
Fig. 8 Integrated intensity of the 256 GHz continuum with contour levels 2 × (1,2,4,8) mJy beam-1 km s-1 and grey scale ranging from − 2.6 to 25 mJy beam-1 km s-1 (peak integrated flux is 25 mJy beam-1 km s-1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


