| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424138 | |
| Published online | 06 January 2015 | |
Antisolar differential rotation of the K1-giant σ Geminorum revisited
1 Konkoly Observatory of the Hungarian Academy of Sciences, Konkoly Thege út 15-17, 1121 Budapest, Hungary
e-mail: kovari@konkoly.hu
2 Leibniz-Institute for Astrophysics (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
Received: 5 May 2014
Accepted: 3 November 2014
Context. Surface differential rotation and other global surface flows on magnetically active stars are among the observable manifestations of the underlying stellar dynamo. Therefore, these types of observations are important for stellar dynamo theory and useful constraints for solar dynamo studies as well.
Aims. We revisit the active K1-giant component of the long-period RS CVn-type binary system σ Gem and its global surface flow pattern.
Methods. We refine the differential rotation law from recovering the spot migration pattern. We apply a detailed cross-correlation technique to a unique set of 34 time-series Doppler images recovered using data from 1996−97. By increasing the number of the available cross-correlation function maps, we expect a more robust determination of the differential surface rotation law. In addition, we present a new time-series Doppler imaging study of σ Gem using our advanced surface reconstruction code iMap for a data set collected in 2006−07.
Results. Results from the reprocessed cross-correlation study confirm that the star performs antisolar-type differential rotation with a surface shear α of − 0.04 ± 0.01, i.e., almost a factor of two larger compared to the previously claimed value. We also confirm the evidence of a global poleward spot migration, with an average velocity of 0.21 ± 0.03 km s-1, in accordance with theoretical predictions. From the new observations, we obtain three subsequent Doppler images. The time evolution of these images confirms the antisolar-type differential rotation of the same amount.
Key words: stars: activity / stars: imaging / stars: late-type / starspots / stars: individual: σGeminorum
© ESO, 2015
1. Introduction
Differential rotation (DR) on stars with convective envelopes carries important information on the dynamo process beneath the surface. The combined effects of the Coriolis force and stratification lead to a Reynolds stress and a horizontal component in the convective heat flux that result in a deviation from the cylinder-shaped velocity pattern and thus in DR (Kitchatinov & Rüdiger 1995; Käpylä et al. 2011; Warnecke et al. 2013). The rotation pattern predicted is predominantly solar-type, even for K giants, and the total surface shear varies to a high degree with the effective temperature and to a low degree with the rotation rate (Küker & Rüdiger 2011, 2012). However, antisolar DR can be maintained by strong meridional circulation, as suggested by Kitchatinov & Rüdiger (2004). Theoretical support for the existence of antisolar-type DR in cool single stars was recently reinforced by Gastine et al. (2014) who found that stars with large Rossby numbers maintain the initial antisolar pattern. Note that antisolar DR was reported mostly for giants in close binary systems, where tidal forces could have a strong influence.
It is understood that in close binaries, such as the RS CVn-systems, tidal effects help maintain the fast rotation and thus higher levels of magnetic activity. Furthermore, tidal coupling between the star with a differentially rotating envelope and its companion star is thought to play a significant role (cf. Scharlemann 1981, 1982; Schrijver & Zwaan 1991; Holzwarth & Schüssler 2002, 2003). Retrieving the right connection between characteristic parameters of magnetic activity on binary stars and the exact physical parameters of the binary system will bring us closer to understanding activity in star-hot Jupiter systems as well.
Gaining deeper observational insight into magnetic dynamos in active stars, and enabling comparison with that in the Sun, yields important experimental input for dynamo theory. Still, it is not fully understood how stellar dynamos work. Therefore, theoretical development needs continuous feedback from observations of a sample of stars of different types.
We have learned from solar studies that sunspot groups tend to move together with the solar plasma, i.e., tracking sunspots can reveal DR and other surface flow fields like meridional circulation (e.g., Wöhl 2002; Wöhl et al. 2010). If time-resolved surface maps are available for spotted stars, starspots are also suitable for tracking stellar surface velocity fields. Korhonen & Elstner (2011) found in their mean-field simulations that the large-scale dynamo field does not trace the differential rotation, while the small-scale fields trace the DR very well. Time-series Doppler imaging is a powerful tomographic inversion technique to recover the time evolution of the surface patterns on spotted stars (Strassmeier & Bartus 2000; Marsden et al. 2007). Surface flows on stars have already been detected by analyzing such “Doppler-movies” frame-by-frame (see, e.g., Kővári et al. 2004, 2007a, 2009).
We revisit the rapidly-rotating K1-giant σ Geminorum (75 Gem, HR 2973, HD 62044) by performing a new time-series Doppler imaging analysis. Our target is a long-period RS CVn-type system (Prot = 19.6 days) with a K1III primary star and an unseen companion star. A summary of its astrophysical parameters was given in Kővári et al. (2001, hereafter Paper I). A 70-night long observing run with the 1.5 m McMath-Pierce telescope at Kitt Peak National Solar Observatory (NSO) in 1996−97 allowed us to collect long-term data on σ Gem. The data were used to prepare six time-series Doppler maps (see Paper I), which revealed cool spots at low to mid-latitudes. We found that none of the maps recovered a polar spot. Simultaneous photometric data showed a temporal evolution of the light curve during the full 3.6 rotation cycles. This was reconfirmed by a comparative analysis of the consecutive Doppler maps. However, in spite of this spot evolution, no conclusive DR pattern from a simple cross-correlation of consecutive maps was found, which was attributed to the masking effect of short-term spot changes. Those six time-series Doppler maps were reanalyzed by Kővári et al. (2007b, hereafter Paper II, but see also 2007c) using a more sophisticated cross-correlation technique, developed for time-series Doppler-maps. This more detailed analysis yielded antisolar-type differential rotation with a surface shear of α ≈ − 0.022. Evidence of a poleward migration trend of spots was also found with an average velocity of ≈0.3 km s-1.
In Sect. 2 we present a new time-series of Doppler images, including 34 frames for two independent mapping lines. This Doppler-movie is used to perform an even more detailed study (see Sect. 2.4) to confirm or confute our former findings. In Sect. 3 an additional Doppler surface image reconstruction is performed using a set of high-resolution spectra obtained with the 1.2 m STELLA-I telescope (Tenerife, Spain) in 2006–07. In Sect. 4 the results from old and new data are compared with each other and discussed. The revealed DR law for σ Gem is set against other detections for RS CVn-type binaries to reach a better understanding how differential rotation could be affected by tidal forces in RS CVn-type close binaries.
2. Doppler images of σ Gem for 1996-97
2.1. The NSO time series
The data that enabled a new time-series Doppler-imaging analysis consist of 52 high-resolution optical spectra, taken at NSO/McMath during a 70-night long observing run in 1996−97. The spectral range included two mapping lines, namely Fe i at 6430 Å and Ca i at 6439 Å, which are used for the imaging process. From these 52 time-series spectra, 34 data subsets are formed in such a way that every subset holds 18 consecutive spectra, i.e., the first subset consists of the first 18 observations, the second subset is formed from spectra of serial numbers between 2 and 19, and so on, while the last (34th) subset consists of the last 18 spectra. Subsets cover approximately one rotation period, and thus are suitable for recovering a total of 34 “Doppler-frames” simultaneously for the two mapping lines. For the surface inversion we used our Doppler imaging code TempMap (Rice et al. 1989; Rice & Strassmeier 2000).
2.2. Is σ Gem elliptical?
Kővári et al. (2007a) demonstrated that neglecting a possible ellipsoidal distortion, i.e., the tidally induced Roche-geometry of the evolved component in a close binary system such as σ Gem, can introduce systematic errors into the Doppler reconstruction. Ellipsoidal variation of σ Gem might be indicated by the double wave that emerged from long-term photometric data over ≈13 years (see Fig. 1), which, on the other hand, could also be explained by two preferred active longitudes where starspots or starspot groups tend to appear (Oláh et al. 1988). Since previously (Papers I and II) spherical geometry was assumed for this target, at this point we switch to using TempMapε, a sub-version of our inversion code developed specifically for imaging ellipsoidally distorted stars in order to scan the significance of a possible ellipsoidal shape on the Doppler reconstruction (for the definition of the stellar distortion parameter ε and for a description of TempMapε see Kővári et al. 2007a). The Doppler imaging procedure allows us to fine-tune some stellar parameters by searching for the minimum of the goodness-of-fit of the Doppler reconstruction (Unruh 1996), therefore we fine-tuned the distortion parameter ε over a reasonable range of the parameter space. The resulting O−C map suggested ignorable distortion (most likely ε ≈ 0), thus, we kept the spherical assumption, as concluded also by Duemmler et al. 1997.
 |
Fig. 1 Photometric V observations of σ Gem over ≈13 years are phased with the orbital period after removing long-term trends. The double wave can be caused by either ellipticity or starspots that appear stably at preferred active longitudes. |
2.3. The Doppler-movies
The 34 finalized Doppler images for the combined (Fe i-6430 + Ca i-6439) line reconstructions in time order make up the motion picture of the time evolution of the stellar surface in the course of 3.6 consecutive stellar rotations. The respective maps for the two different mapping lines agree well, and confirm our former result that spots are found mostly at low to mid-latitudes, but no spots appear near the pole. Figure 2 shows three surface maps as examples from the entire set, namely the 1st, the 17th, and the 34th, corresponding to mean Heliocentric Julian Date (hereafter HJD) values of 2 450 400.41, 2 450 423.58, and 2 450 444.02, respectively, i.e., the three maps follow each other by approximately one rotation period.
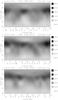 |
Fig. 2 Snapshots from the NSO time-series Doppler images of σ Gem. As examples, the 1st (top), the 17th (middle), and the last (bottom) combined (Fe+Ca) maps are shown. Arrows below the maps mark the phases of the observations. Time lags between the consecutive maps are 23.17 days (from 1st to 17th) and 20.44 days (from 17th to 34th). |
2.4. Antisolar-type differential rotation
Surface differential rotation can be detected from cross-correlating in longitudinal direction the consecutive but contiguous Doppler image pairs, i.e., successive maps with the least possible time gaps. This way the blurring effect of the rapid spot evolution can be reduced, since the time lag is minimized. By averaging all the 17 available cross-correlation maps, the differential rotation pattern can be amplified. For this method, called ACCORD (average cross-correlation of Doppler-images) see e.g., Kővári et al. (2004, 2007a, Paper II, 2009, 2012). For further processing, the Fe i-6430 and Ca i-6439 image reconstructions were combined. The resulting average cross-correlation function (CCF) map is shown in Fig. 3. On the CCF map we fit the correlation peak for each latitudinal stripe of 5°-bin with a Gaussian profile. Gaussian peaks (with their FWHMs as error bars) are then fitted with a quadratic DR law of the form 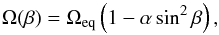 (1)where Ω(β) is the angular velocity at latitude β, while the surface shear parameter α is defined as (Ωeq − Ωpole)/Ωeq where Ωeq and Ωpole are the angular velocities at the equator and the pole, respectively. By applying this simple 2nd degree solar model, we can estimate the order of the surface shear and determine whether the DR pattern is of solar or antisolar type, yet, without overrating the content of the data. In practice, we expect the DR curve to be more complicated, especially since tidal forces may induce nonaxisymmetric structures in the DR pattern. The resulting correlation pattern in Fig. 3 indicates antisolar-type differential rotation, in agreement with Paper II. Indeed, the average correlation pattern became more significant, according to the standard deviations of the values in the average CCF map. The fitted parameters of the revised rotation law are Ωeq = 18.26 ± 0.07 [°/day] and α = −0.04 ± 0.01, with a lap time of ≈500 days, i.e., the redetermined surface shear is found to be almost two times stronger compared to the result in Paper II, where only six Doppler maps, hence, only four CCF maps were available. Nevertheless, this result is still in good agreement with the previous finding, considering the limitations of Doppler imaging and the cross-correlation method as well as the estimated error bars.
(1)where Ω(β) is the angular velocity at latitude β, while the surface shear parameter α is defined as (Ωeq − Ωpole)/Ωeq where Ωeq and Ωpole are the angular velocities at the equator and the pole, respectively. By applying this simple 2nd degree solar model, we can estimate the order of the surface shear and determine whether the DR pattern is of solar or antisolar type, yet, without overrating the content of the data. In practice, we expect the DR curve to be more complicated, especially since tidal forces may induce nonaxisymmetric structures in the DR pattern. The resulting correlation pattern in Fig. 3 indicates antisolar-type differential rotation, in agreement with Paper II. Indeed, the average correlation pattern became more significant, according to the standard deviations of the values in the average CCF map. The fitted parameters of the revised rotation law are Ωeq = 18.26 ± 0.07 [°/day] and α = −0.04 ± 0.01, with a lap time of ≈500 days, i.e., the redetermined surface shear is found to be almost two times stronger compared to the result in Paper II, where only six Doppler maps, hence, only four CCF maps were available. Nevertheless, this result is still in good agreement with the previous finding, considering the limitations of Doppler imaging and the cross-correlation method as well as the estimated error bars.
 |
Fig. 3 Average cross-correlation function map of σ Gem from the NSO 1996−97 data set. The resulting differential rotation pattern for the combined (Fe+Ca) time-series Doppler images gives evidence of antisolar-type differential rotation. The background shade scales the strength of the correlation (white: no correlation, dark: strong correlation). The dots are the correlation peaks per 5°-latitude bin. Their error bars are defined as the FWHMs of the corresponding Gaussians. Assuming a quadratic DR law, the derived surface shear parameter α is − 0.04 ± 0.01. |
2.5. Poleward drift of spots
Latitudinal shifts of spots can also be measured from the time-series Doppler images by applying the average cross-correlation technique along latitudinal columns, i.e., perpendicular to rotation (Weber & Strassmeier 2001; Kővári et al. 2007a; Paper II). First, we apply this method for the available Doppler image pairs (i.e., 17 latitudinal ccf maps). The averaged latitudinal ccf map (see Fig. 4) indicates a joint poleward spot migration, such as in Paper II, yielding ≈4° per rotation period. However, despite the conspicuous correlation pattern of a joint positive shift, the method of latitudinal cross-correlation suffers from an incompleteness due to the singularity rising toward the pole. To avoid this imperfection, we carried out another study, as follows.
For a more reliable measure of the poleward drift (and for better visualization as well) we cut our Mercator-maps longitudinally into 72 meridional slices of 5° width each. For a given longitude value l, the corresponding meridional stripe is normalized for the maximum temperature offset (i.e., the temperature minima) and finally these stripes are ranked in time order. Resulting plots (see examples in Fig. 5 top) indicate the meridional replacement of the temperature minima over the 34 time-series Doppler images for the given longitude l. Figure 5 clearly suggests a poleward drift of the most prominent features. To quantify this drift we fitted the trace of the temperature minima with straight lines. The resulting fits with their mean (plotted in Fig. 5 bottom) estimate an average poleward flow of 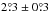 per rotation period (the error is the standard deviation of the weighted mean). With the stellar parameters from Paper I, this value would correspond to 203 ± 27 m s-1 velocity on the stellar surface. This result is slightly smaller than the velocity derived from the average latitudinal cross-correlation study, but the two results are still in accordance with each other. Note, e.g., that the steepest slope from the top four panels in Fig. 5 corresponds to l = 115°, which is just the longitude of the maximum latitude shift in Fig. 4.
per rotation period (the error is the standard deviation of the weighted mean). With the stellar parameters from Paper I, this value would correspond to 203 ± 27 m s-1 velocity on the stellar surface. This result is slightly smaller than the velocity derived from the average latitudinal cross-correlation study, but the two results are still in accordance with each other. Note, e.g., that the steepest slope from the top four panels in Fig. 5 corresponds to l = 115°, which is just the longitude of the maximum latitude shift in Fig. 4.
 |
Fig. 4 Average latitudinal cross-correlation map from time-series Doppler images. For the combined (Fe+Ca) reconstructions 17 image pairs are averaged. Best correlating latitudinal shifts are marked with dots (Gaussian peaks); the corresponding error bars are proportional to the Gaussian FWHMs. The joint positive shift suggests poleward spot migration at an average velocity of ≈4° per rotation period. |
 |
Fig. 5 Top: examples of meridional spot redistributions during the covered timespan of about 43.5 days at arbitrarily chosen quadrant longitudes of 25°, 115°, 205°, and 295° (top: left, right, below: left, right, respectively). In each case, the replacements of the maximum temperature offsets (dots) are fitted with a 1st degree function. Bottom: all the 72 available line fits. Red (thick) line indicates their average slope, suggesting a common poleward flow of |
3. Doppler images for 2006-07
3.1. The STELLA time series
We collected a spectroscopic data set with a total of 71 observations over ≈5 rotation cycles between 30th September 2006 and 7th January 2007 with the 1.2 m STELLA-I telescope (Tenerife, Spain), equipped with STELLA Echelle Spectrograph (SES) (Weber et al. 2008; Strassmeier et al. 2010). All spectra covered the wavelength range between 3900–8800 Å. The resolving power was R = 55 000, corresponding to a spectral resolution of 0.12 Å at 6500 Å. Further details of the performance of the system were reported by Weber et al. (2012) and Granzer et al. (2010).
Unfortunately, the data set included a few large gaps that compromised the phase coverage, thus, a detailed time-series analysis, similar to that described in Sect. 2 could not be possible. After some exploration and consideration of the data distribution, we formed three subsets. To further improve phase coverage, however, we tried to fill in the largest phase gaps, which involved only a few neighboring observations, while keeping the consistency of the data. We note that such phase exchange had no significant impact on the reconstruction, thus, we finally kept the three subsets listed in Table 1, which have acceptable phase distributions and are independent from each other, and therefore suitable for cross-correlation study.
The observing log in Table 1 lists the HJDs with corresponding observing dates and phases, and signal-to-noise values for three data subsets (S1, S2, S3). All spectra are phased using the same ephemeris as in Papers I−II: 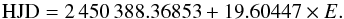 (2)
(2)
Observing log of STELLA-I SES spectra from 2006−07.
 |
Fig. 6 Doppler images of σ Gem for three subsequent data sets S1, S2, and S3 (from top to bottom, respectively) in 2006−07. The corresponding mid-HJDs are 2 454 018.16, 2 454 061.38, and 2 454 092.50, respectively. Maps are shown in spherical projection in four quadrants with colorbars for the given temperature scale. |
3.2. The image reconstruction code iMap
Here we give a very brief description of the DI and ZDI code iMap we have used in this work (see Carroll et al. 2012, for further details). In its latest version, the code performs a new multiline inversion to use the information of a large number of photospheric line profiles simultaneously. The line profiles are calculated by solving the full (polarized) radiative transfer (Carroll et al. 2008). Individual atomic line parameters are taken from the VALD line database (Kupka et al. 1999). The code uses Kurucz model atmospheres (Castelli & Kurucz 2004), which are interpolated for each occurrent temperature, gravity, and metallicity value through the inversion.
The typical ill-posed nature of the problem is tackled with an iterative regularization based on a Landweber algorithm (Carroll et al. 2012). This has the advantage that no additional constraints are imposed in the image domain. The surface segmentation for the current problem is set to a 5° × 5° equal-degree partition. For each surface segment, the full radiative transfer of all involved line profiles are calculated according to the current effective temperature and atmospheric model. The line profile discrepancy is reduced by adjusting the surface temperature of each segment according to the local (temperature) gradient information until the O−C minimum is reached.
3.3. Doppler image reconstructions
A big advantage of the inversion code iMap compared to the original TempMap code is the fact, that during the inversion process several (typically 20−30) spectral lines are taken into account simultaneously. This way the signal-to-noise ratio is increased by a factor of ≈5, which improves the resolving power of distortions in a line profile caused by surface spots. Furthermore, the surface reconstruction benefits from a large number of lines, as different absorption lines form in different photospheric depths. In the case of σ Gem, 20 suitable absorption lines were chosen, including 16 Fe i and 4 Ca i lines in the range between 5000–6500 Å. These lines were selected for their depth of formation, blends, continuum, and temperature sensitivity. The two mapping lines often used for TempMap inversions, i.e., Fe i at 6430 Å and Ca i at 6439 Å, are included as well. The astrophysical parameters were taken from Paper I.
Resulting Doppler images are plotted in Fig. 6. The corresponding line profile fits for the combined spectra are plotted in Fig. 7. All reconstructed spots are located between approximately 30° and 70° latitudes with a minimum spot temperature of ≈3800 K.
We note that the surface maps resemble those of the previous Doppler study in Paper I, i.e., having dominant cool regions at mid-latitudes and practically no polar spottedness. Concerning the short-term surface evolution, some redistribution of the spotted surface is clearly seen from one data set to the next, despite the moderate time resolution of the maps.
3.4. Differential rotation
In analogy to our data set from 1996−97, we derived the surface shear for the 2006−07 images with our cross-correlation technique ACCORD (cf. Sect. 2.4). Because of the disadvantageous phase coverage we could prepare only three data subsets for Doppler mapping, thus only three CCF maps were obtained for the three possible correlation pairs (i.e., S1-S2, S2-S3, and S1-S3).
The average CCF map is shown in Fig. 8 and indicates antisolar-type DR with a surface shear of α = −0.04 ± 0.01. The shear parameter derived for the 2006−07 images is pretty much the same as the value presented in Sect. 2.4. We note, however, that because of the applied regularization we have limited information from a latitude belt below ≈30°, providing only six points in the CCF map to be fitted. The reliability of such a fit alone would be questionable. On the other hand, the antisolar nature and the order of the fitted rotation law are in agreement with the result derived from the NSO data.
 |
Fig. 8 Average cross-correlation function map of σ Gem from the STELLA 2006−07 data set. The background shade scales the strength of the correlation (white: no correlation, dark: strong correlation). The dots are the correlation peaks per 5°-latitude bin. Their error bars are defined as the FWHMs of the corresponding Gaussians. Assuming a quadratic DR law, the derived surface shear parameter α is − 0.04 ± 0.01. |
4. Discussion and conclusions
Antisolar-type differential rotation has been detected in a growing number of late-type giants (e.g., Strassmeier et al. 2003; Oláh et al. 2003; Weber et al. 2005; Vida et al. 2007; etc.). Theoretically, this kind of feature can be explained by considering a fast meridional flow (Kitchatinov & Rüdiger 2004). Sufficiently strong meridional flow can be maintained by either large-scale surface inhomogeneities or tidal effects in binaries. On the other hand, there are examples among RS CVn-type binaries that fulfill both criteria, yet perform solar-type DR (increasing angular velocity toward the equator): e.g., ζ And (Kővári et al. 2007a, 2012); EI Eri (Kővári et al. 2009), V711 Tau (Petit et al. 2004), IL Hya (Kővári et al. 2014a), etc. It seems to be evident that the strength and even the orientation of the DR are influenced by close companions, although it is not clear how. In many cases, peculiar spot distributions (quadrature positions, spots facing towards or away from the companion) i.e., spots fixed in the orbital frame, indicate coupling magnetic fields between the binary components. It is not understood, however, what kind of general relationship exists in close binaries between the characteristics of the DR and other astrophysical parameters (cf., e.g., Dunstone et al. 2008; Holzwarth & Schüssler 2003; but see also Gastine et al. 2014).
According to the mechanism introduced by Scharlemann (1981, 1982), in an RS CVn-type binary, after the synchronization reaches its terminal phase due to tidal dissipation, the surface of the star with a convective envelope will have parts that rotate more slowly than the orbital period, while other parts will rotate faster. The two regions are separated by the so-called corotation latitude, which can be determined from stellar and system parameters, thus they can be compared directly with observations. Applying Scharlemann’s (1981, 1982) theory for σ Gem, this separator latitude is estimated to be around 22°, i.e., essentially the same as we derived from our time-series Doppler study. This could also be a sign that in σ Gem tidal coupling either is near to or has already reached its relaxed phase.
 |
Fig. 9 The Fourier amplitude spectrum of σ Gem using V-band photometry over ≈13 years. Top: power spectrum showing the strongest peak (Prot), with the orbital period (Porb) aside, and their overtones. Middle: amplitude spectrum around the orbital period with marking the equatorial and polar rotation periods (Peq, Ppole) from the differential rotation law in Sect. 2.4. Bottom: window function of the signal. |
Unfortunately, Doppler imaging provides only a limited sample of stars to be mapped, because of the known restrictions (e.g., inclination angle being far from extremes, large enough rotational broadening, good quality homogeneous data providing sufficient phase coverage, etc.). On the other hand, long-term photometric observations exist for a much wider sample of spotted stars in binary systems (e.g., Strassmeier et al. 1997, 2011; Oláh & Strassmeier 2002; Oláh et al. 2003, 2013; Lindborg et al. 2013, etc.), which can also be used for investigating the role of binarity in the formation of magnetic activity. Fourier analysis for the available V-band observations over ≈13 years is shown in Fig. 9. Usually the strongest period signal is expected from the largest and coolest spots. According to the available time-series Doppler maps, during the covered time interval the coolest regions appeared mostly between ≈30–70° latitudes. This is in agreement with the results of the first Doppler imaging study of σ Gem (Hatzes 1993), as well as with our finding in Fig. 9, where the location of the strongest amplitude peak corresponds to a mid-latitude belt that is rotating faster than the orbit (cf. that the corotation latitude is at ≈22°). Indeed, this feature seems to be stable for much longer term than the range of our Doppler observations, affirming that tidal effects may organize preferred longitudes, as well as latitudes of activity in close binaries (cf. Kajatkari et al. 2014 and see also the summary by Oláh 2007).
We conclude that from our cross-correlation technique ACCORD for 34 time-series Doppler images of the active K1-giant σ Gem, a clear sign of antisolar-type surface DR was derived with a shear of − 0.04 ± 0.01 and a lap time of ≈490 days. This result is almost a factor of two stronger than reported in Paper II, where only six time-series Doppler images were available. We note that artefacts related to imperfect Doppler reconstruction (e.g., due to sparse phase coverage or mirroring of a high latitude feature, etc.) have no significant impact on the retrieved DR pattern, when using ACCORD (see Kővári et al. 2014b and Appendix A). Furthermore, three additional Doppler surface reconstructions from a more recent data set (see Sect. 3) enabled us to arrive at a similar result, despite the unfavorable time resolution compared to the NSO 1996−97 data.
Also, reprocessing the latitudinal cross-correlation study for the 34 time-series Doppler images resulted in a common poleward meridional migration of the spots. This detection, if attributed to the surface pattern of meridional circulation, would mean an average poleward velocity field of 203 ± 27 m s-1, supporting theoretical expectations (cf. Kitchatinov & Rüdiger 2004). Recently, Cole et al. (2014) reinforced the findings from mean-field theory that there is a nonaxisymmetric dynamo mode in convective shell dynamos. Their direct 3D numerical simulations even showed a retrograde mode (wave). Its pattern speed does not reflect the speed of the DR at any depth and could be an alternative explanation for the latitude drift of spots and could even compete against or amplify the DR pattern.
Acknowledgments
The authors appreciate the referee’s comments, which helped to improve the paper. The authors from Konkoly Observatory are grateful to the Hungarian Scientific Research Fund (OTKA) for support through grant no. K-109276. This work is supported by the “Lendület-2009” and “Lendület-2012” Young Researchers’ Program of the Hungarian Academy of Sciences. The authors acknowledge the support of the German Deutsche Forschungsgemeinschaft, DFG through projects KO 2320/1 and STR645/1. K.G.S. acknowledges the generous allotment of telescope time at NSO.
References
- Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, T. A., Strassmeier, K. G., Rice, J. B., & Künstler, A. 2012, A&A, 548, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
- Cole, E., Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2014, ApJ, 780, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Duemmler, R., Ilyin, I. V., & Tuominen, I. 1997, A&AS, 123, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunstone, N. J., Hussain, G. A. J., Collier Cameron, A., et al. 2008, MNRAS, 387, 1525 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Yadav, R. K., Morin, J., Reiners, A., & Wicht, J. 2014, MNRAS, 438, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, T., Weber, M., & Strassmeier, K. G. 2010, Adv. Astron., 2010, 79 [Google Scholar]
- Hatzes, A. 1993, ApJ, 410, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2002, Astron. Nachr., 323, 399 [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2003, A&A, 405, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kajatkari, P., Hackman, T., Jetsu, L., Lehtinen, J., & Henry, G. W. 2014, A&A, 562, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Mantere, M. J., Guerrero, G., Brandenburg, A., & Chatterjee, P. 2011, A&A, 531, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1995, A&A, 299, 446 [NASA ADS] [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 2004, Astron. Nachr., 325, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Korhonen, H., & Elstner, D. 2011, A&A, 532, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Strassmeier, K. G., Bartus, J., et al. 2001, A&A, 373, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Strassmeier, K. G., Granzer, T., et al. 2004, A&A, 417, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Bartus, J., Strassmeier, K. G., et al. 2007a, A&A, 463, 1071 [Google Scholar]
- Kővári, Zs., Bartus, J., Strassmeier, K. G., et al. 2007b, A&A, 474, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Bartus, J., Svanda, M., et al. 2007c, Astron. Nachr., 328, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Kővári, Zs., A., Washuettl, A., Foing, B. H., et al. 2009, in: 15th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, 21−25 July, 2008, St Andrews, Scotland, ed. E. Stempels, AIP Conf. Proc., 1094, 676 [Google Scholar]
- Kővári, Zs., Korhonen, H., Kriskovics, L., et al. 2012, A&A, 539, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., Kriskovics, L., Oláh, K., et al. 2014a, in Magnetic Fields Throughout the Stellar Evolution, 26−30 August, 2013, Biarritz, France, eds. M. Jardine, P. Petit, & H. Spruit, Proc. IAU Symp. (Cambridge: Cambridge University Press), 302, 379 [Google Scholar]
- Kővári, Zs., Bartus, J., Kriskovics, L., Vida, K., & Oláh, K. 2014b, in Magnetic Fields Throughout the Stellar Evolution, 26−30 August, 2013, Biarritz, France, eds. M. Jardine, P. Petit, & H. Spruit, Proc. IAU Symp. (Cambridge: Cambridge University Press), 302, 198 [Google Scholar]
- Küker, M., & Rüdiger, G. 2011, Astron. Nachr., 332, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Küker, M., & Rüdiger, G. 2012, Astron. Nachr., 333, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Lindborg, M., Mantere, M. J., Olspert, N., et al. 2013, A&A, 559, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K. 2007, in Binary Stars as Critical Tools & Tests in Contemporary Astrophysics, 22−25 August, 2006, Prague, Czech Republic, eds. W. I. Hartkopf, E. F. Guinan, & P. Harmanec, Proc. IAU Symp. (Cambridge: Cambridge University Press), 240, 442 [Google Scholar]
- Oláh, K., & Strassmeier, K. G. 2002, Astron. Nachr., 323, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Jurcsik, J., & Strassmeier, K. G. 2003, A&A, 410, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Panov, K. P., Pettersen, B. R., Valtaoja, E., & Valtaoja, L. 1988, A&A, 218, 192 [Google Scholar]
- Oláh, K., Moór, A., Strassmeier, K. G., Borkovits, T., & Granzer, T. 2013, Astron. Nachr., 334, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, S. C., Berdyugina, S. V., Donati, J.-F., Eaton, J. A., & Williamson, M. H. 2007, Astron. Nachr., 328, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Donati, J.-F., Wade, G. A., et al. 2004, MNRAS, 348, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, J. B., & Strassmeier, K. G. 2000, A&AS, 147, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, J. B., Wehlau, W. H., & Khokhlova, V. L. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]
- Scharlemann, E. T. 1981, ApJ, 246, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Scharlemann, E. T. 1982, ApJ, 253, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 1991, A&A, 251, 183 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., & Bartus, J. 2000, A&A, 354, 537 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Kratzwald, L., & Weber, M. 2003, A&A, 408, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Carroll, T. A., Weber, M., et al. 2011, A&A, 535, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unruh, Y. C. 1996, in Stellar Surface Structure, eds. K. G. Strassmeier, & J. L. Linsky, IAU Symp., 176, 35 [Google Scholar]
- Vida, K., Kővári, Zs., Švanda, M., et al. 2007, Astron. Nachr., 328, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 1998, A&A, 330, 1029 [NASA ADS] [Google Scholar]
- Weber, M., & Strassmeier, K. G. 2001, A&A, 373, 974 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weber, M., Strassmeier, K. G., & Washuettl, A. 2005, Astron. Nachr., 326, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, Proc. SPIE, 7019 [Google Scholar]
- Weber, M. Granzer, T., & Strassmeier, K. G. 2012, Proc. SPIE, 8451 [Google Scholar]
- Warnecke, J., Käpylä, P. J., Mantere, M. J., & Brandenburg, A. 2013, ApJ, 778, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Wöhl, H. 2002, Astron. Nachr., 323, 329 [Google Scholar]
- Wöhl, H., Brajša, R., Hanslmeier, A., & Gissot, S. F. 2010, A&A, 520, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Testing the effect of imperfect Doppler reconstruction on the DR pattern retrieved by ACCORD
 |
Fig. A.1 Top: two examples from a time series of 28 artificial surface temperature maps as snapshots of a differentially rotating test star applying α = 0.006 surface shear. Below, in the second, third, and forth rows plotted are the corresponding recoveries assuming no data noise, S/N = 200, and S/N = 100, respectively. Phases of the artificial observations are indicated by arrows underneath. In the righthand column, the retrieved DR functions are plotted as best fits (continuous lines) for the correlation patterns of the average cross-correlation function maps. The respective shear parameters are α = 0.0058 ± 0.0002 (no noise, right top), α = 0.0067 ± 0.0006 (S/N = 200, right middle), α = 0.0069 ± 0.0012 (S/N = 100, right bottom). |
Doppler reconstruction is often biased by imperfections. It is understood that either sparse phase coverage or low signal-to-noise ratio (S/N) can result in artificial shadows of dominant high latitude features. These shadows and appendages at lower latitudes can interfere when retrieving the latitudinal rotation law through spot tracking. We demonstrate that in our test artefacts related to imperfect Doppler reconstruction due to low S/N and sparse phase coverage have no significant impact on the retrieved DR pattern, when using our average cross-correlation method called ACCORD. Details of the test can be found in Kővári et al. (2014b).
In Fig. A.1 top, we show two original test images, which were arbitrarily chosen as examples from a series of 28 artificial surface temperature maps. These maps were prepared as time-series snapshots of a differentially rotating test star. A weak solar-type surface DR law was incorporated with α = 0.006 shear parameter. Below the originals are the recoveries with different S/N values and phase coverages. It is clear that imperfections emanate from sparse phase coverage, even when no data noise is assumed (note that only eight spectra were taken for each map only). Low latitude shadows and these kinds of imperfections become stronger when S/N decreases. Still, the retrieved correlation patterns and their fits (see the righthand panels of Fig. A.1) imply that these artefacts have no significant impact on either the sign or magnitude of the resulting surface shear. In the test case, the phase coverages were more unfavorable, the S/N values were lower, and the surface shear was much weaker compared to the case of σ Gem in Sect. 2 of this paper.
All Tables
All Figures
 |
Fig. 1 Photometric V observations of σ Gem over ≈13 years are phased with the orbital period after removing long-term trends. The double wave can be caused by either ellipticity or starspots that appear stably at preferred active longitudes. |
| In the text | |
 |
Fig. 2 Snapshots from the NSO time-series Doppler images of σ Gem. As examples, the 1st (top), the 17th (middle), and the last (bottom) combined (Fe+Ca) maps are shown. Arrows below the maps mark the phases of the observations. Time lags between the consecutive maps are 23.17 days (from 1st to 17th) and 20.44 days (from 17th to 34th). |
| In the text | |
 |
Fig. 3 Average cross-correlation function map of σ Gem from the NSO 1996−97 data set. The resulting differential rotation pattern for the combined (Fe+Ca) time-series Doppler images gives evidence of antisolar-type differential rotation. The background shade scales the strength of the correlation (white: no correlation, dark: strong correlation). The dots are the correlation peaks per 5°-latitude bin. Their error bars are defined as the FWHMs of the corresponding Gaussians. Assuming a quadratic DR law, the derived surface shear parameter α is − 0.04 ± 0.01. |
| In the text | |
 |
Fig. 4 Average latitudinal cross-correlation map from time-series Doppler images. For the combined (Fe+Ca) reconstructions 17 image pairs are averaged. Best correlating latitudinal shifts are marked with dots (Gaussian peaks); the corresponding error bars are proportional to the Gaussian FWHMs. The joint positive shift suggests poleward spot migration at an average velocity of ≈4° per rotation period. |
| In the text | |
 |
Fig. 5 Top: examples of meridional spot redistributions during the covered timespan of about 43.5 days at arbitrarily chosen quadrant longitudes of 25°, 115°, 205°, and 295° (top: left, right, below: left, right, respectively). In each case, the replacements of the maximum temperature offsets (dots) are fitted with a 1st degree function. Bottom: all the 72 available line fits. Red (thick) line indicates their average slope, suggesting a common poleward flow of |
| In the text | |
 |
Fig. 6 Doppler images of σ Gem for three subsequent data sets S1, S2, and S3 (from top to bottom, respectively) in 2006−07. The corresponding mid-HJDs are 2 454 018.16, 2 454 061.38, and 2 454 092.50, respectively. Maps are shown in spherical projection in four quadrants with colorbars for the given temperature scale. |
| In the text | |
 |
Fig. 7 Line profile fits of the three Doppler reconstructions in Fig. 6. |
| In the text | |
 |
Fig. 8 Average cross-correlation function map of σ Gem from the STELLA 2006−07 data set. The background shade scales the strength of the correlation (white: no correlation, dark: strong correlation). The dots are the correlation peaks per 5°-latitude bin. Their error bars are defined as the FWHMs of the corresponding Gaussians. Assuming a quadratic DR law, the derived surface shear parameter α is − 0.04 ± 0.01. |
| In the text | |
 |
Fig. 9 The Fourier amplitude spectrum of σ Gem using V-band photometry over ≈13 years. Top: power spectrum showing the strongest peak (Prot), with the orbital period (Porb) aside, and their overtones. Middle: amplitude spectrum around the orbital period with marking the equatorial and polar rotation periods (Peq, Ppole) from the differential rotation law in Sect. 2.4. Bottom: window function of the signal. |
| In the text | |
 |
Fig. A.1 Top: two examples from a time series of 28 artificial surface temperature maps as snapshots of a differentially rotating test star applying α = 0.006 surface shear. Below, in the second, third, and forth rows plotted are the corresponding recoveries assuming no data noise, S/N = 200, and S/N = 100, respectively. Phases of the artificial observations are indicated by arrows underneath. In the righthand column, the retrieved DR functions are plotted as best fits (continuous lines) for the correlation patterns of the average cross-correlation function maps. The respective shear parameters are α = 0.0058 ± 0.0002 (no noise, right top), α = 0.0067 ± 0.0006 (S/N = 200, right middle), α = 0.0069 ± 0.0012 (S/N = 100, right bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.