| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 10 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201423790 | |
| Published online | 06 August 2014 | |
Flux calibration of medium-resolution spectra from 300 nm to 2500 nm: Model reference spectra and telluric correction⋆
1
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching,
Germany
e-mail: smoehler@eso.org; amodigli@eso.org; wfreudli@eso.org; jvinther@eso.org
2
Département de Physique, Université de Montréal,
CP. 6128, Succursale Centre-Ville,
Montréal, QC
H3C 3J7,
Canada
e-mail:
noemi@astro.umontreal.ca
3
Homer L. Dodge Department of Physics and Astronomy, University of
Oklahoma, 440 W. Brooks
St., Norman,
OK, 73019, USA
e-mail:
alexg@nhn.ou.edu
4
Observatoire astronomique de Strasbourg, Université de Strasbourg,
CNRS, UMR 7550, 11 rue de l’Université, 67000
Strasbourg,
France
e-mail: anais.gonneau@astro.unistra.fr; ariane.lancon@astro.unistra.fr
5
Institut für Astro- und Teilchenphysik, Universität Innsbruck,
Technikerstr. 25/8,
6020
Innsbruck,
Austria
e-mail: Wolfgang.Kausch@uibk.ac.at; Stefan.Noll@uibk.ac.at
6
Institute for Astronomy and Astrophysics, Kepler Center for Astro
and Particle Physics, Eberhard Karls University, Sand 1, 72076
Tübingen,
Germany
e-mail:
rauch@astro.uni-tuebingen.de
Received: 10 March 2014
Accepted: 7 April 2014
Context. While the near-infrared wavelength regime is becoming more and more important for astrophysics there is a marked lack of spectrophotometric standard star data that would allow the flux calibration of such data. Furthermore, flux calibrating medium- to high-resolution échelle spectroscopy data is challenging even in the optical wavelength range, because the available flux standard data are often too coarsely sampled.
Aims. We will provide standard star reference data that allow users to derive response curves from 300 nm to 2500 nm for spectroscopic data of medium to high resolution, including those taken with échelle spectrographs. In addition we describe a method to correct for moderate telluric absorption without the need of observing telluric standard stars.
Methods. As reference data for the flux standard stars we use theoretical spectra derived from stellar model atmospheres. We verify that they provide an appropriate description of the observed standard star spectra by checking for residuals in line cores and line overlap regions in the ratios of observed (X-shooter) spectra to model spectra. The finally selected model spectra are then corrected for remaining mismatches and photometrically calibrated using independent observations. The correction of telluric absorption is performed with the help of telluric model spectra.
Results. We provide new, finely sampled reference spectra without telluric absorption for six southern flux standard stars that allow the users to flux calibrate their data from 300 nm to 2500 nm, and a method to correct for telluric absorption using atmospheric models.
Key words: standards / techniques: spectroscopic
The reference model spectra described here are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/568/A9
© ESO, 2014
1. Introduction
Accurate flux calibration of astronomical spectra remains a significant challenge. Spectral flux calibration requires flux calibrators with known absolute fluxes that are accessible with the same spectrograph that also takes the spectra of the science targets. With the arrival of new generations of spectrographs that cover wide wavelength ranges and produce relatively high-resolution spectra, known and well-tested spectrophotometric standard star catalogues as listed by Oke (1990) and Hamuy et al. (1992, 1994) are no longer adequate for spectral flux calibration because they do not extend to the near-infrared (NIR) and/or are too coarsely sampled to permit the flux calibration of high-resolution spectra. For example, the European Southern Observatory’s (ESO) X-shooter instrument covers, in a single exposure, the spectral range from 300 nm to 2500 nm and operates at intermediate spectral resolution (R ≈ 4000–17 000, depending on wavelength and slit width) with fixed échelle spectral format in three optimized arms (UVB: 300 nm–550 nm, VIS: 550 nm–1000 nm, NIR: 1000 nm–2500 nm; see Vernet et al. 2011 for more details).
In this paper we present a new set of calibrated model spectra for flux standard stars covering the wavelength range from 300 nm to 2500 nm. These spectra are useful for deriving consistent instrumental response curves over this wide range of wavelengths with a spectral resolving power of up to 40 000 and possibly more. We also describe in detail how to use the spectra in this manner.
Our approach to obtain fully calibrated model spectra was as follows. First, we selected a set of flux standard stars observable from the southern hemisphere that cover the full right ascension range, whose spectra can be modelled accurately, and for which X-shooter spectra exist (Sects. 2.1–2.3). We then used X-shooter observations of these stars to compute the ratio of the observed spectra to the model spectra, i.e. the instrumental response (see Sect. 2.4). If the model spectra perfectly described the spectra of all stars, response curves derived from different stars observed with the same instrumental setup should only differ by signatures imposed by the atmosphere (e.g. telluric absorption, varying atmospheric transmission). However, due to small deficiencies in the model spectra, for most of the stars such ratios show star-specific features in regions dominated by overlapping lines (see Fig. 2). To be able to identify and fit such deficiencies we observed a star that does not show any lines within the X-shooter spectral range and whose spectrum can be modelled accurately. We used the ratio between model and observations of that star together with the observed spectra of all our stars to derive corrections to their model spectra (Sect. 2.5). Finally, we use the available (spectro-)photometric data for the stars to compute the absolute flux scale of the corrected model spectra (see Sect. 2.6). The result is a self-consistent new set of fully flux calibrated spectrophotometric standards for the southern hemisphere.
In order to compute response curves for an instrument from observed spectra and the models, the effect of the Earth’s atmosphere must be removed from the observed spectra. In Sect. 3, we describe a method for such a correction that we used for X-shooter spectra. This includes a fast and efficient removal of the telluric absorption feature, that is sufficiently accurate for the intended purpose of deriving response curves and can be adapted for any other instrument providing spectra of sufficient resolution between 600 nm and 2500 nm. Finally, in Sect. 4, we describe in detail the full procedure of our approach to compute response curves for the X-shooter instrument, i.e. medium-resolution échelle spectra covering a very wide wavelength range.
2. Reference spectra
2.1. Sample selection
Spectral flux calibration utilizes as reference either well-calibrated observations or a spectral model of a standard star. The advantage of using a model is that it is noiseless, and does not include features imposed by the terrestrial atmosphere. The process of flux calibration requires computing the ratio of an observed spectrum with the model, and such a ratio is less sensitive to errors in the wavelength scale if the spectrum is smooth and featureless. Therefore, the ideal star to be used as a spectral flux standard has a smooth and featureless spectrum that can be accurately modelled with a minimum number of parameters. Since spectral models in most cases cannot predict the absolute scaling of the spectrum, the model must be accompanied by accurate absolutely calibrated (spectro-)photometric observations at some wavelengths within the wavelength range covered by the spectrum. Unfortunately, only few available standards satisfy all criteria simultaneously. However, it should be noted that the model of a star can be used to derive the shape of the response curve of an instrument even if no absolute spectral calibration is available. Such a spectrum can therefore be used to test and improve the model spectra of other stars.
For the current work, we searched for stars with the following criteria. In order to be able to model the spectra, we limited our search to hot white dwarfs and hot subdwarfs. As a first step, we limited our search to stars in the southern hemisphere, and to stars with available flux information from Hamuy et al. (1992, 1994) or the Hubble Space Telescope1 and X-shooter spectra in the ESO archive. This selection resulted in six standard stars, namely EG 274, GD 71, GD 153, LTT 3218, LTT 7987 (all hot DA white dwarfs), and Feige 110 (a hot subdwarf). We then extended our search to include at least one star in the southern hemisphere that has a spectrum free of absorption lines between 300 nm and 2500 nm, regardless of whether X-shooter observations existed, and found L97-3 (a white dwarf with a featureless spectrum in the X-shooter wavelength range).
2.2. Data
The six standard stars are routinely observed with X-shooter as part of its regular calibration plan. We selected X-shooter spectra of these flux standard stars observed in NODDING2 mode between June 1, 2011 and July 5, 2012 (always referring to the beginning of the night), which resulted in 203 spectra per arm, observed on 185 nights. We used data from nights of any photometric quality as we are interested in the shape of the response curves and not in their absolute level.
Figure 1 shows example X-shooter spectra of the flux standard star LTT 7987, that clearly show the deep and wide stellar lines (marked in red) in the blue (top), which may extend across more than one échelle order, and the telluric absorption (marked in green) in the redder part of the wavelength range (middle and bottom).
The DC white dwarf L97-3 was observed on the nights October 1, 2012, October 20, 2012, and December 21, 2012, in the same way as the flux standard stars listed above, i.e. with a slit width of 5′′ and in NODDING mode, with total exposure times between 1200 s and 1360 s.
2.3. Modelling of hot white dwarfs
 |
Fig. 1 Observed X-shooter spectra of LTT 7987, corrected for gain, exposure time, and extinction. The stellar lines (marked in red) are most pronounced in the UVB arm, while the NIR arm and the red part of the VIS arm are strongly affected by telluric absorption (marked in green). All wavelength ranges also show some evidence of instrumental features (marked in blue). |
The spectra of our standard stars include hydrogen lines (in the case of Feige 110 also helium lines) of varying strength (see Fig. 1 for an example) that need to be properly modelled if one wants to sample the response of an instrument on scales of some nanometres.
For the past 20 years the physical parameters of hot white dwarfs and other hot, high-gravity stars have been determined by fitting the profiles of the hydrogen (and/or helium) absorption lines in their optical spectra (Bergeron et al. 1992; see Gianninas et al. 2011 and Giammichele et al. 2012 for more recent examples and Koester et al. 2001 for work with high-resolution échelle spectra).
The difficulty of modeling these spectra is illustrated in Fig. 2. The left panel shows an example of a parametric fit by Giammichele et al. (2012). The method of fitting the Balmer lines profiles has the advantage that it is sensitive to changes in temperature and surface gravity at high effective temperature, when optical and near-infrared photometry become insensitive to changes in these parameters. Consequently, this means that model spectra with a wrong effective temperature or surface gravity will not correctly describe the strong hydrogen and/or helium absorption lines in the spectra of these stars. Such a mismatch is most severe at the blue end of the wavelength range studied in this paper, namely between 380 nm and 420 nm, where the lines may overlap with each other, causing a lack of continuum. An example of such a mismatch can be seen in the right plot in Fig. 2, which shows the ratio of the observed spectrum to the fitted model spectrum for LTT 3218. The bump between 400 nm and 410 nm is caused by an imperfect description of the line overlap region between the Balmer lines Hδ and Hϵ. Compared to the line depths of about 50% the effects are small (at about 2%), but sufficient to introduce artefacts in the resulting response curves. To ensure that no such mismatches exist in the finally selected reference spectra, however, one has to know the true response of the instrument with which the spectra, that are used for the analysis, are observed.
By contrast, the featureless spectra of L97−3 can easily be modelled at the same wavelengths, which was our primary motivation for including it in our sample. This is illustrated in Fig. 3, which shows the ratio of model spectrum to observed spectrum from the observed spectra of L97-3 for the regions containing strong lines in the spectra of the flux standard stars discussed here. We used as reference data a stellar model spectrum calculated by Koester (2010) for the parameters reported by Giammichele et al. (2012) for this star. This model spectrum was adjusted to the photometry of the star reported in Simbad34 using the pseudo-magnitudes described in Sect. 2.6. The curves in Fig. 3 are rather smooth without significant structure on nanometer scales (as opposed to Fig. 2). This suggests that the spectrum has been sucessfully modelled, and the structure in the ratio of observed and modelled spectra reflects the true response curve of the instruments.
 |
Fig. 2 Model fit for LTT 3218 (individual lines only) from Giammichele et al. (2012, and the ratio between their observation and model spectrum (right). The ratio plot on the right clearly shows residuals in the line cores and also some bumps between the lines. |
2.4. Selection of model spectra
We used the X-shooter observations described in Sect. 2.2 to verify the quality of the various model spectra available for our standard stars by comparing instrumental response curves from different standard stars. We concentrated first on the wavelength range 380 nm to 420 nm for the reasons discussed above. Once an acceptable description of the blue range has been achieved we will verify its suitability for the redder wavelength ranges as well.
For our analysis we used one-dimensional extracted and merged X-shooter spectra of the flux standard stars processed with the reflex workflow5 (Freudling et al. 2013) of X-shooter. These spectra were then corrected for atmospheric extinction using the Paranal extinction curve from Patat et al. (2011, see also Sect. 3.1 and normalized by exposure time.
We shifted the model spectrum for a given star to the same radial velocity as the observed spectrum to avoid the introduction of pseudo-P Cygni profiles when the observed spectrum is divided by the model spectrum. We resample the noise-free model spectra instead of the observed spectra because this can be done without loss of information. The radial velocity was obtained from the positions of the line cores of Hδ (UVB), Hα (VIS), and Paγ (NIR). Each observed standard star spectrum was divided by the shifted reference star spectrum. Finally the ratios were averaged per star to achieve a better signal-to-noise ratio. This provided us with raw, i.e. unsmoothed, response curves that allowed us to look for systematic discrepancies between the observed and the model spectra. A response curve is instrument specific and therefore expected to be stable for a long time. Any feature in these ratios that appears only for a particular standard star points strongly towards deficiencies in the reference spectra of these standard stars. Instrumental effects should not depend on which standard star is used. We selected as best description of the UVB spectrum those model spectra that showed the smallest star-specific bumps in the averaged ratio spectra. Section 2.5 describes how we adjusted the selected model spectra empirically to remove the remaining small discrepancies.
2.4.1. White dwarfs
For the purpose of this work, we considered the models of EG 274, LTT 3218, and LTT 7987 presented by Giammichele et al. (2012) and the models of GD 71 and GD 153 by Gianninas et al. (2011), hereafter referred to as Montréal spectra, and the model spectra calculated by Koester (2010, in the following referred to as Kiel spectra) for the parameters from Giammichele et al. (2012) and Gianninas et al. (2011).
These model spectra provided good fits to all white dwarfs, but bumps like the one seen in Fig. 2 can be seen in the ratios of observed to stellar model spectra, pointing to remaining mismatches. Residuals of this kind (of the order of 2–3%) are not unexpected for stars with such strong (flux in line core about 40% of continuum level) and overlapping lines (line widths up to 20 nm as can be seen in Fig. 2, left plot).
For EG 274, GD 71, and LTT 3218 the Montréal model spectra showed the smallest star-specific bumps in the averaged ratio spectra, while the Kiel model spectra for the Montréal parameters provided the best description for GD 153 and LTT 7987. The parameters are listed in Table 1.
 |
Fig. 3 Average ratios of observed standard spectrum and shifted reference spectrum for UVB and VIS data of L97-3 for the same wavelength ranges as in Fig. 7. The two narrow windows on the right share the same range along the y-axis. None of the residuals seen in Fig. 7 is visible here. |
2.4.2. Feige 110
For Feige 110, we fit FORS26 and X-shooter UVB spectra (flux-calibrated with a response curve obtained from GD 71 observations) with TMAP (Tübingen NLTE Model-Atmosphere Package7) model spectra (Rauch & Deetjen 2003; Werner et al. 2003) to obtain an appropriate reference spectrum.
Parameters for the flux standard star reference spectra.
2.5. Correction of model spectra at short wavelengths
In order to correct the mismatches between model and observed spectra that cause the bumps we reprocessed all flux standard stars observed in NODDING in 2012 with the new model spectra as reference spectra. We first divided each (extinction-corrected) one-dimensional spectrum by the radial-velocity shifted reference spectrum and then by the smoothed response curve derived from L97-3. The products of this procedure are expected to be equal to 1 in an ideal case, but differences in atmospheric conditions result in residual slopes. The parking of the Atmospheric Dispersion Compensators8 since August 2012 might also play a role here, as the UVB spectra observed at higher airmass are no longer at a constant position along the slit at all wavelengths, but show instead some curvature at shorter wavelengths, which may in turn affect the extraction. In addition, remaining mismatches between model spectra and observations cause narrow spikes and bumps that we want to correct (see Fig. 4, top). For every star we fitted the shape of this ratio spectrum by a low-order polynomial fit to remove the large-scale variations. Then we smoothed the result and fit the remaining bumpy regions (see Fig. 4, middle, for an example). Applying the fit to the model spectrum we obtained the red curve shown in Fig. 4 (bottom).
 |
Fig. 4 Top: average raw response (extinction-corrected observation)/(radial-velocity shifted model), divided by the smoothed response for L97-3, for EG 274. The narrow spikes are due to mismatches in the line cores, while the broad bumps at 405 nm and 420 nm are due to imperfect line broadening, which underestimates the flux between the lines in the model spectra. Middle: raw response from the top plot, with large scale variations removed by a low-order polynomial fit and smoothed (black). The black curve was fit with a spline (red) after masking the regions of the line cores (masked regions in cyan). Bottom: model spectrum before correction (black) and corrected with the fit (red). |
The bump corrections were smallest for GD 71, GD 153, and Feige 110, while EG 274, LTT 7987, and LTT 3218 had significant corrections (increasing in this order). This is expected as the last three stars have the strongest and widest lines and thus present the biggest challenge when it comes to the correct treatment of overlapping lines. Since the mismatches in the line cores were not corrected (as they vary with spectral resolution) some masking is still required when fitting a response (see Sect. 4). We also verified that in the spectral range 550 nm to 2500 nm the only residuals seen are those in the line cores of hydrogen and/or helium lines.
2.6. Absolute flux calibration
We have now defined a set of model spectra which adequately reproduce the observed X-shooter spectra of the six flux standard stars, with residuals (outside line cores, that are affected by resolution effects) well below 2%. To allow a proper flux calibration we have to verify that the overall flux distribution of these model spectra reproduces the independently observed (spectro-)photometric data. To do so we convolved the model spectra to a resolution of 1.6 nm for the UVB/VIS spectral range and then binned them to 5 nm steps to reproduce the Hamuy et al. (1992, 1994)data9. These reference data are based on absolutely flux calibrated low-resolution spectra, that are tied to the Vega calibration of Hayes (1985) via a recalibration of the secondary standard stars from Taylor (1984). For the NIR range we convolved the data to a resolving power of 2000 (J band) and 1500 (H + K band) and integrated them over the wavelength ranges given in Vernet et al. (2008) for EG 274, Feige 110, LTT 3218, and LTT 7987. These flux values were then converted to pseudo-magnitudes 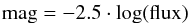 (1)and aligned to the respective Hamuy and SINFONI (Spectrograph for Integral Field Observations in the Near Infra-red at the ESO VLT; Eisenhauer et al. 2003) data by a constant factor across the full wavelength range. Figure 5 shows the results for EG 274.
(1)and aligned to the respective Hamuy and SINFONI (Spectrograph for Integral Field Observations in the Near Infra-red at the ESO VLT; Eisenhauer et al. 2003) data by a constant factor across the full wavelength range. Figure 5 shows the results for EG 274.
 |
Fig. 5 Model spectrum for EG 274 (black), aligned to the data from Hamuy et al. (1992, 1994, blue), Vernet et al. (2008, green), and broadband photometry from the SIMBAD database (red). |
 |
Fig. 6 Aligned model spectrum for Feige 110 (black) compared to the data from Hamuy et al. (1992, 1994, blue) and from HST (red). |
For GD 71 and GD 153 our new model spectra could also be aligned by a constant factor to the HST model spectra, which are tied to the Vega scale by HST STIS and NICMOS observations (Bohlin et al. 2001). In Fig. 6 we compare our aligned model spectrum for Feige 110 to the data from Hamuy and from HST.
Figure 7 shows the average ratio of observed and reference spectra for the new model spectra.
3. Correction of atmospheric effects
We have now defined reference spectra that describe the flux standard stars very well. In order to derive a response curve the effects of the Earth’s atmosphere have to be removed from the observed spectra. Otherwise the response curve will contain a mixture of instrumental effects and atmospheric effects. The atmospheric effects consist of two major parts: atmospheric extinction (small variation with time in the case of Paranal due to the low aerosol content, which governs the extinction variability) and telluric absorption lines (strong variation with time in the case of water vapour). The first affects principally the wavelength range 300 nm to 1 000 nm, while the second is important for data above 680 nm (X-shooter NIR arm and the redder part of the VIS arm; see Fig. 1, middle and bottom plot).
3.1. Correcting the atmospheric extinction down to 300 nm
Patat et al. (2011) provide an extinction curve for Paranal that is based on FORS2 observations and therefore covers only wavelengths longer than 320 nm. X-shooter data, however, extend down to 300 nm. In order to cover a larger wavelength range we obtained from F. Patat a Line-By-Line Radiative Transfer Model (LBLRTM10, Clough et al. 2005) spectrum for Paranal, that describes the continuous and line absorption caused by the Earth’s atmosphere. As the spectrum was calculated without aerosol contributions, we added the aereosol contribution defined as kaer = 0.014·(λ [ μm ] )-1.38 (see Patat et al. 2011 for more details). The LBLRTM model spectrum was calculated for the wavelength range 300 nm–1099.4 nm and also contains absorption by telluric lines, which vary rapidly with time and can therefore not be corrected by a static extinction curve (see Sect. 3.2 for the correction of telluric lines). To exclude the telluric lines from the extinction curve we interpolated across the regions of strong telluric absorption in the VIS range (585.5 nm–599.2 nm, 626.1 nm–634.9 nm, 643.8 nm–660.0 nm, 682.1 nm–709.4 nm, 712.7 nm–743.4 nm, 756.2 nm–773.1 nm, 780.1 nm–861.3 nm, 879.8 nm–1033.8 nm, >1050 nm). Figure 8 shows the model and our interpolation in comparison to the FORS2 measurements.
 |
Fig. 7 Average ratios of observed standard star spectrum (corrected for atmospheric extinction) and shifted reference spectrum for UVB and VIS data for the regions containing Balmer lines, using the bump-corrected model spectra. The curves have been normalized at the red end of the respective plot windows, which show the Balmer lines Hα (right), Hβ (middle), and Hγ to H9 (left). The two narrow windows on the right share the same range along the y-axis. |
3.2. Telluric absorption
If one does not correct at least those parts of the spectrum that contain low to medium telluric absorption, one has to interpolate the response across very wide wavelength ranges, which results in large systematic uncertainties for the resulting flux calibration. Traditionally such corrections use so-called telluric standard stars, i.e. stars with either no features or extremely well-known features in the regions of telluric absorption, that allow the user to determine the telluric absorption spectrum (see for instance Vacca et al. 2003; Maiolino et al. 1996). This method relies on the assumption that the conditions governing the telluric absorption have not changed between the observation of the science target and the observation of the standard star. Since this assumption is often not fulfilled, we decided instead to use a catalogue of telluric model spectra (Noll et al. 2012; Jones et al. 2013) to correct the telluric absorption lines. Alternatively, a large number of telluric standard star observations can be used to extract the principal components of the telluric transmission (Chen et al. 2014).
The high-resolution transmission spectra (R = 60 000) were calculated for the wavelength range from 300 nm to 30 μm using the LBLRTM radiative transfer code, the HITRAN molecular line database (see Rothman et al. 2009), and different average atmospheric profiles (pressure, temperature, and molecular abundances) for Cerro Paranal. The atmospheric profiles were derived from the MIPAS equatorial standard profile (Remedios 2001; see Seifahrt et al. 2010), profiles for pressure, temperature, and relative humidity from the Global Data Assimilation System (GDAS)11, provided on a 3 h basis for a 1° × 1° global grid up to an altitude of 26 km, and data from the Cerro Paranal meteorological station. The spectra we used cover the airmass values 1.0, 1.5, and 2.0 at six different bimonthly periods (plus an annual mean) and three night-time periods (plus a nocturnal mean). We will refer to this telluric library as the time-dependent library.
 |
Fig. 8 LBLRTM model for Paranal (black line) compared to the FORS2 data points from Patat et al. (2011, red crosses) and the interpolated curve (green line). |
To identify the best telluric model spectrum to correct a given observation, the telluric model spectra first have to be aligned to the observed spectrum in both resolution and wavelength. Then the telluric model spectrum that leaves the smallest residuals after applying it to the observation has to be identified. We used the following step-by-step procedure:
-
1.
Convert the wavelength scale (in nm) of the model and observedspectra to natural logarithm.
-
2.
Extract appropriate ranges for cross correlation (NIR: 7.0 ≤ lnλnm ≤ 7.1, H2O feature; VIS: 6.828 ≤ lnλnm ≤ 6.894, H2O feature).
-
3.
Cross correlate the extracted telluric model and observed spectra with a maximum shift of 500 sampling units (each of size 10-5) in natural logarithmic space.
-
4.
Fit a Gaussian profile within ±0.001 in ln(λ) around the cross correlation peak.
-
5.
Shift the logarithmic model wavelength scale by the fitted peak position of the cross-correlation curve.
-
6.
Create a Gaussian with the measured FWHM.
-
7.
Convolve the model spectrum with the Gaussian in ln(λ) space (X-shooter has a constant resolving power R of 4350/7450/5300 for an 1.̋0/0.̋9/0.̋9 slit in the UVB/VIS/NIR arm, respectively)12.
-
8.
Convert the shifted and convolved model spectrum to linear wavelength space.
-
9.
Divide the observed spectrum by the convolved and shifted telluric model spectrum (whereby we avoid resampling the observed spectrum).
-
10.
Use predefined continuum points (avoiding regions of strong telluric absorption as well as known lines of the observed star, see Sect. 2.3) and fit a cubic spline to the telluric corrected spectrum.
-
11.
Divide the telluric corrected spectrum by the fit of the continuum.
-
12.
Determine mean and rms for regions of moderate telluric absorption in the normalized corrected spectrum.
Then, we choose as best fitting model the one for which the average residuals computed over regions of moderate telluric absorption is minimal. The telluric corrected spectrum of the flux standard star is then compared to the stellar model spectrum (see Sect. 2.3 for details) to determine the response. Figure 9 shows examples for a good telluric correction (bottom) and for undercorrection (top).
 |
Fig. 9 Results of the telluric correction (red) for a bad (top) and a good (bottom) case. The grey areas mark regions of extremely high telluric absorption and thus high noise in the corrected data. The lines at 1093.5 nm and 1281.4 nm are stellar lines and the variable peak at about 2100 nm is caused by variations in the flux level and spectral energy distribution of the NIR flat field lamp. |
The absorption in the wavelength regions 1985 nm–2030 nm and 2037 nm–2089 nm is caused mainly by CO2 features, whose abundance is not varied in the telluric model spectra for a given airmass. These regions were therefore ignored when looking for the best fit. We do not restrict the search for the best telluric model spectrum in airmass, as we found that in some cases a telluric model spectrum for an airmass quite different from the observed one can still provide a good fit in the regions that we analyse.
The telluric model spectra discussed so far do not cover high precipitable water vapour (PWV) conditions, which result in stronger telluric absorption lines, and therefore spectra taken during such conditions are undercorrected (see Fig. 9, top, for an example). This problem is more pronounced in the NIR than in the VIS arm. Therefore we investigated another set of model spectra, which extends to higher PWV conditions (PWV = 0...20 mm) and higher airmass values (PWV-dependent library). Tests with these models showed good corrections for NIR data taken under high PWV conditions (which could not be corrected with the time-dependent grid), but were less successful for data taken during intermediate and low PWV conditions. For the VIS arm the PWV-dependent telluric model catalogue provided good corrections for all of the about 100 flux standard spectra that we tested.
Users who want to employ the telluric model spectra to correct their data can find information about the Cerro Paranal sky model (see Noll et al. 2012) at http://www.eso.org/sci/software/pipelines/skytools/ together with the following pre-calculated libraries13:
-
1.
PWV-dependent library with 45 spectra at airmasses 1.0, 1.5,2.0, 2.5, 3.0, and PWV (in mm) of 0.5, 1.0, 1.5, 2.5, 3.5, 5.0, 7.5,10.0, and 20.0.
-
2.
Latest version of time-dependent library with 35 spectra at airmasses 1.0, 1.5, 2.0, 2.5, 3.0, and bi-monthly average PWV values (1 = December/January ...6 = October/November) as well as a yearly average PWV content (labelled 0). Compared to the time-dependent library used in this paper the airmass coverage has been increased, the night-time periods have been dropped, and the CO2 content has been updated.
The spectra are provided with resolutions of 60 000 and 300 000 and do not include Rayleigh scattering. The SkyCalc web application14 can always be used to produce sky radiance and transmission spectra with more specific parameters, including Rayleigh scattering.
The quality of the telluric correction has to be kept in mind when fitting a response to the ratio of such a corrected spectrum to the corresponding stellar model spectrum, as regions with remaining absorption or overcorrected features may distort the fit. For this reason we finally decided to mask the following regions when fitting a response curve to avoid potential telluric residuals: 634 nm–642 nm, 684 nm–696 nm, 714.7 nm–732.3 nm, 757.5 nm–770.5 nm, 813 nm–836.5 nm, 893.9 nm–924 nm, 928 nm–983 nm, 1081 nm–1171 nm, 1267 nm–1271 nm, 1300 nm–1503 nm, 1735 nm–1981 nm, 1995 nm–2035 nm, 2048 nm–2082 nm. We note that this masking rejects far less of the spectrum than would be necessary if no telluric correction had been applied.
4. Pipeline implementation
The procedures described in the previous sections have been implemented in ESO’s pipeline15 for the reduction of X-shooter data. Below we provide some more details on the algorithms and reference data used in the pipeline.
4.1. Radial velocity correction
As described in Sect. 2.4 the model spectra need to be shifted to the same radial velocity as the observed spectra to avoid the generation of pseudo-P Cygni profiles in the response curve. The pipeline uses a robust polynomial fit to the line core to determine the radial velocity. The fit accuracy is limited to 1 pixel (0.02 nm for UVB and VIS, 0.06 nm for NIR). Because of the limited accuracy of the radial velocity correction pseudo-P Cygni profiles are sometimes created when dividing the shifted reference spectrum by the observed one. This effect is taken into account when defining the fit regions for the response curve (see Sect. 4.2).
4.2. New fitting routine for response determination
The ratio of the shifted reference spectrum to the observed spectrum (telluric corrected for VIS and NIR) shows residuals at the line cores (see Figs. 7 and 10). At the same time both UVB and VIS spectra show variations on intermediate scales that need to be fit by the response curve because they are instrumental features (see Fig. 1; features at 365 nm and 560–620 nm). Therefore, we created for each flux standard star and arm a list of wavelength points at which the response is fit with a cubic spline fit. The pipeline determines at each point the median of the ratio over a predefined range (±0.04 nm for UVB, ±1 nm for VIS, and ±5 nm for NIR). The points are selected so that the wavelength ranges used for the median do not overlap and regions of strong telluric absorption (e.g. between J and H and between H and K) are excluded (see Sect. 3.2 for details). Figure 10 shows the response curves derived for EG 274 with the pipeline. This new routine has been implemented in the X-shooter pipeline since version 2.2.0.
 |
Fig. 10 X-shooter response curves derived for EG 274. The red dots mark the fit points described in Sect. 4.2 and the green line marks the fit through these points. |
 |
Fig. 11 Spectrum of LTT 7987, corrected for telluric absorption and flux-calibrated with a response curve derived from observations of EG 274. The red curve is the reference spectrum for LTT 7987. Regions of very high telluric absorption are marked in grey. |
4.3. New reference data
The newly derived reference spectra for the flux standard stars described in Sect. 2.3 have been delivered with the X-shooter pipeline since version 2.2.0.
The adjusted LBLRTM model is used to correct the atmospheric extinction of X-shooter UVB and VIS spectra in pipeline version 2.3.0 and higher. For the NIR arm there is no extinction correction.
Since the PWV-dependent grid provides good corrections for NIR data taken during high PWV conditions (which could not be corrected with the time-dependent telluric library), but is less successful for intermediate and low PWV conditions, we decided to use the time-dependent telluric library described in paragraph 2 of Sect. 3.2 as pipeline default for the NIR arm and provide the PWV-dependent library as possible alternative. For the VIS arm the PWV-dependent telluric library is used. The telluric correction and the corresponding catalogues have been part of the X-shooter pipeline since version 2.2.0.
5. Summary
In this paper we have presented flux-calibrated model spectra of southern sky spectral photometric standards in the wavelength range from 300 nm to 2500 nm. The calibrated model spectra are available at the CDS. The consistency of the set of models were verified using X-Shooter observations, and the region of strong line overlap between 380 nm and 450 nm in the model spectra was adjusted taking advantage of X-shooter observations of the featureless spectrum of L97–3. Our analysis shows that the use of stellar model spectra as reference data for flux standard has significant advantages when it comes to calibrating medium-resolution data as they are available on a finely sampled grid. Another significant advantage is the fact that model spectra are not affected by telluric absorption.
Our models are useful to determine the response curve of spectrographs, and the resulting response curve can in turn be used to flux-calibrate spectra of other targets. We have discussed in detail a methodology to carry out such a flux calibration. Beyond the proper choice of stellar model spectra, an appropriate correction of telluric absorption features is essential to flux calibrate data with wavelengths above 680 nm. Our method includes the use of telluric model spectra to correct spectral regions with low to moderate telluric absorption.
To illustrate the quality that can be achieved with the methods and model spectra described in this paper, we show in Fig. 11 an example of a standard star (LTT 7987). The spectrum was flux-calibrated with the response curve determined from a different star observed on the same night, namely EG 274. The response curve used for this calibration is shown in Fig. 10.
While our set of standards is adequate to flux calibrate spectra in the whole southern hemisphere, additional standards would be useful both to enlarge the number of potential calibrators in the south, and to provide a similar set of standards in the northern hemisphere. Our methodology can be used to derive such a set of model spectra. Necessary ingredients for such an endeavour are accurate model spectra16, availability of flux information (e.g. Hamuy et al. 1994), and observed uncalibrated spectra for both the new calibrators and at least one of the standard stars discussed here to correct for instrumental features.
Original data from Hauck & Mermilliod (1998, uvby; Subasavage et al. (2007, RI; Skrutskie et al. (2006, 2MASS point source catalogue, JHK.
For hot (pre-) white dwarfs like the flux standard stars discussed here and many others, a good starting point for model spectra would be the TMAP spectral energy distributions at the registered VO service TheoSSA provided by the German Astrophysical Virtual Observatory.
Acknowledgments
This research has made use of NASA’s Astrophysics Data System Bibliographic Services and of the SIMBAD database, operated at CDS, Strasbourg, France. It has been partly carried out in the framework of the Austrian ESO In-kind project funded by the Austrian Federal Ministry for Science and Research BM:wf under contracts BMWF-10.490/0009- II/10/2009 and BMWF-10.490/0008-II/3/2011. We thank D. Koester for making his model spectra available to us. We appreciate J. Pritchard’s comments that improved the readability of this paper. We are grateful to J. Vernet, V. Mainieri, and F. Kerber for sharing their SINFONI results with us. We thank F. Patat, R. Lallement and W. Reis for their help with the improvements of the X-shooter response. T.R. is supported by the German Aerospace Center (DLR, grant 05 OR 1301). We thank an anonymous referee for helpful suggestions that improved this paper.
References
- Bergeron, P., Saffer, R. A., & Liebert, J. 1992, ApJ, 394, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Dickinson, M. E., & Calzetti, D. 2001, AJ, 122, 2118 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-P., Trager, S. C., Peletier, R. F., et al. 2014, A&A, 565, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clough, S. A., Shephard, M. W., Mlawer, E. J., et al. 2005, J. Quant. Spectr. Rad. Transf., 91, 233 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1548 [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giammichele, N., Bergeron, P., & Dufour, P. 2012, ApJS, 199, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Gianninas, A., Bergeron, P., & Ruiz, M. T. 2011, ApJ, 743, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Walker, A. R., Suntzeff, N. B., et al. 1992, PASP, 104, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Suntzeff, N. B., Heathcote, S. R., et al. 1994, PASP, 106, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayes, D. S. 1985, in Calibration of Fundamental Stellar Quantities, eds. D. S. Hayes, L. E. Pasinetti, & A. G. D. Philip, IAU Symp., 111, 225 [Google Scholar]
- Jones, A., Noll, S., Kausch, W., Szyszka, C., & Kimeswenger, S. 2013, A&A, 560, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koester, D. 2010, Mem. Soc. Astron. Italiana, 81, 921 [Google Scholar]
- Koester, D., Napiwotzki, R., Christlieb, N., et al. 2001, A&A, 378, 556 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Rieke, G. H., & Rieke, M. J. 1996, AJ, 111, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oke, J. B. 1990, AJ, 99, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Moehler, S., O’Brien, K., et al. 2011, A&A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T. & Deetjen, J. L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 103 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spectr. Rad. Transf., 110, 533 [Google Scholar]
- Seifahrt, A., Käufl, H. U., Zängl, G., et al. 2010, A&A, 524, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Subasavage, J. P., Henry, T. J., Bergeron, P., et al. 2007, AJ, 134, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, B. J. 1984, ApJS, 54, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2003, PASP, 115, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Kerber, F., Saitta, F., et al. 2008, in SPIE Conf. Ser., 7016, 9 [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, K., Deetjen, J. L., Dreizler, S., et al. 2003, in Stellar Atmosphere Modeling Astronomical, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 31 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Observed X-shooter spectra of LTT 7987, corrected for gain, exposure time, and extinction. The stellar lines (marked in red) are most pronounced in the UVB arm, while the NIR arm and the red part of the VIS arm are strongly affected by telluric absorption (marked in green). All wavelength ranges also show some evidence of instrumental features (marked in blue). |
| In the text | |
 |
Fig. 2 Model fit for LTT 3218 (individual lines only) from Giammichele et al. (2012, and the ratio between their observation and model spectrum (right). The ratio plot on the right clearly shows residuals in the line cores and also some bumps between the lines. |
| In the text | |
 |
Fig. 3 Average ratios of observed standard spectrum and shifted reference spectrum for UVB and VIS data of L97-3 for the same wavelength ranges as in Fig. 7. The two narrow windows on the right share the same range along the y-axis. None of the residuals seen in Fig. 7 is visible here. |
| In the text | |
 |
Fig. 4 Top: average raw response (extinction-corrected observation)/(radial-velocity shifted model), divided by the smoothed response for L97-3, for EG 274. The narrow spikes are due to mismatches in the line cores, while the broad bumps at 405 nm and 420 nm are due to imperfect line broadening, which underestimates the flux between the lines in the model spectra. Middle: raw response from the top plot, with large scale variations removed by a low-order polynomial fit and smoothed (black). The black curve was fit with a spline (red) after masking the regions of the line cores (masked regions in cyan). Bottom: model spectrum before correction (black) and corrected with the fit (red). |
| In the text | |
 |
Fig. 5 Model spectrum for EG 274 (black), aligned to the data from Hamuy et al. (1992, 1994, blue), Vernet et al. (2008, green), and broadband photometry from the SIMBAD database (red). |
| In the text | |
 |
Fig. 6 Aligned model spectrum for Feige 110 (black) compared to the data from Hamuy et al. (1992, 1994, blue) and from HST (red). |
| In the text | |
 |
Fig. 7 Average ratios of observed standard star spectrum (corrected for atmospheric extinction) and shifted reference spectrum for UVB and VIS data for the regions containing Balmer lines, using the bump-corrected model spectra. The curves have been normalized at the red end of the respective plot windows, which show the Balmer lines Hα (right), Hβ (middle), and Hγ to H9 (left). The two narrow windows on the right share the same range along the y-axis. |
| In the text | |
 |
Fig. 8 LBLRTM model for Paranal (black line) compared to the FORS2 data points from Patat et al. (2011, red crosses) and the interpolated curve (green line). |
| In the text | |
 |
Fig. 9 Results of the telluric correction (red) for a bad (top) and a good (bottom) case. The grey areas mark regions of extremely high telluric absorption and thus high noise in the corrected data. The lines at 1093.5 nm and 1281.4 nm are stellar lines and the variable peak at about 2100 nm is caused by variations in the flux level and spectral energy distribution of the NIR flat field lamp. |
| In the text | |
 |
Fig. 10 X-shooter response curves derived for EG 274. The red dots mark the fit points described in Sect. 4.2 and the green line marks the fit through these points. |
| In the text | |
 |
Fig. 11 Spectrum of LTT 7987, corrected for telluric absorption and flux-calibrated with a response curve derived from observations of EG 274. The red curve is the reference spectrum for LTT 7987. Regions of very high telluric absorption are marked in grey. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


