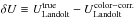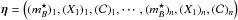| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 32 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201423413 | |
| Published online | 08 August 2014 | |
Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples⋆,⋆⋆
1 LPNHE, CNRS/IN2P3, Université Pierre et Marie Curie Paris 6, Université Denis Diderot Paris 7, 4 place Jussieu, 75252 Paris Cedex 05, France ;
e-mail: marc.betoule@lpnhe.in2p3.fr
2 Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago IL 60637, USA
3 Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue Chicago IL 60637, USA
4 LBNL, 1 Cyclotron Rd, Berkeley CA 94720, USA
5 Department of Physics and Astronomy, University of Pennsylvania, 209 South 33rd Street, Philadelphia PA 19104, USA
6 Argonne National Laboratory, 9700 South Cass Avenue, Lemont IL 60439, USA
7 Center for Particle Astrophysics, Fermi National Accelerator Laboratory, PO Box 500, Batavia IL 60510, USA
8 African Institute for Mathematical Sciences, 6-8 Melrose Road, Muizenberg, Cape Town, South Africa
9 South African Astronomical Observatory, Observatory, Cape Town, South Africa
10 Department of Maths and Applied Maths, University of Cape Town, 7701 Rondebosch, South Africa
11 George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, and Department of Physics and Astronomy, Texas A & M University, College Station TX 77843-4242, USA
12 Institute of Astronomy, Madingley Road, Cambridge CB4 0HA, UK
13 Institute of Cosmology & Gravitation, University of Portsmouth, Portsmouth PO1 3FX, UK
14 Department of Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto ON M5S 3H4, Canada
15 Department of Physics and Astronomy, Wayne State University, Detroit MI 48202, USA
16 Center for Astrophysics andSpace Astronomy 389-UCB, University of Colorado, Boulder CO 80309, USA
17 Institute of Astronomy, Graduate Shool of Science, The Univ. of Tokyo, 2-21-1 Osawa, 181-0015 Mitaka, Japan
18 Research center for the early universe, Graduate School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, 113-0033 Tokyo, Japan
19 Kavli Institute for the Physics and Mathematics of the Universe, 5-1-5 Kashiwanoha, 277-8583 Kashiwa, Japan
20 Department of Astrophysics, California Institute of Technology, MS 249-17, Pasadena CA 91125, USA
21 Department of Physics and Astronomy, University of Victoria, PO Box 3055 STN CSC, Victoria BC V8T 1M8, Canada
22 University of California, Berkeley CA 94720, USA
23 Astronomy Department, University of Illinois at Urbana-Champaign, 1002 W. Green Street, Urbana IL 61801, USA
24 Department of Physics, University of Illinois Urbana-Champaign, 1110 W. Green Street, Urbana IL 61801, USA
25 CPPM, Aix-Marseille Universit, CNRS/IN2P3, Marseille, France
26 Institut de Física d’Altes Energies, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain
27 Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
28 The Oskar Klein Centre, Department of Physics, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
29 McDonald Observatory, University of Texas at Austin, 2515 Speedway, Stop C1402, Austin TX 78712-1206, USA
30 Department of Astrophysical Sciences, Princeton University Peyton Hall, 4 Ivy Lane, Princeton NJ 08544, USA
31 Department of Physics (Astrophysics), University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
32 INAF – Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monteporzio (RM), Italy
33 Las Cumbres Observatory Global Telescope Network, 6740 Cortona Dr., Suite 102, Goleta CA 93117, USA
34 Department of Physics, University of California, Santa Barbara, Broida Hall, Mail Code 9530, Santa Barbara CA 93106-9530, USA
35 Department of Physics and Astronomy, Rutgers, The State University of New Jersey, Piscataway NJ 08854, USA
36 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
37 Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia
38 CEA, Centre de Saclay, Irfu/SPP, 91191 Gif-sur-Yvette, France
39 CENTRA – Centro Multidisciplinar de Astrofísica and Dep. Física, Instituto Superior Técnico, Universidade de Lisboa, Portugal
40 Department of Physics and Astronomy, University of Utah, Salt Lake City UT 84112, USA
41 School of Physics and Astronomy, Rochester Institute of Technology, Rochester NY 14623, USA
42 Department of Physics and Astronomy, Johns Hopkins University, Baltimore MD 21218, USA
43 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore MD 21218, USA
44 Department of Astronomy and Astrophysics and the Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park PA 16802, USA
45 Department of Physics, University of the Western Cape, 7535 Cape Town, South Africa
46 The Oskar Klein Centre, Department of Astronomy, AlbaNova, 106 91 Stockholm, Sweden
47 School of Physics and Astronomy, University of Southampton, Southampton, SO17 1BJ, UK
48 Department of Astronomy, University of Texas at Austin, Austin TX 78712, USA
Received: 13 January 2014
Accepted: 9 April 2014
Aims. We present cosmological constraints from a joint analysis of type Ia supernova (SN Ia) observations obtained by the SDSS-II and SNLS collaborations. The dataset includes several low-redshift samples (z< 0.1), all three seasons from the SDSS-II (0.05 <z< 0.4), and three years from SNLS (0.2 <z< 1), and it totals 740 spectroscopically confirmed type Ia supernovae with high-quality light curves.
Methods. We followed the methods and assumptions of the SNLS three-year data analysis except for the following important improvements: 1) the addition of the full SDSS-II spectroscopically-confirmed SN Ia sample in both the training of the SALT2 light-curve model and in the Hubble diagram analysis (374 SNe); 2) intercalibration of the SNLS and SDSS surveys and reduced systematic uncertainties in the photometric calibration, performed blindly with respect to the cosmology analysis; and 3) a thorough investigation of systematic errors associated with the SALT2 modeling of SN Ia light curves.
Results. We produce recalibrated SN Ia light curves and associated distances for the SDSS-II and SNLS samples. The large SDSS-II sample provides an effective, independent, low-z anchor for the Hubble diagram and reduces the systematic error from calibration systematics in the low-z SN sample. For a flat ΛCDM cosmology, we find Ωm =0.295 ± 0.034 (stat+sys), a value consistent with the most recent cosmic microwave background (CMB) measurement from the Planck and WMAP experiments. Our result is 1.8σ (stat+sys) different than the previously published result of SNLS three-year data. The change is due primarily to improvements in the SNLS photometric calibration. When combined with CMB constraints, we measure a constant dark-energy equation of state parameter w =−1.018 ± 0.057 (stat+sys) for a flat universe. Adding baryon acoustic oscillation distance measurements gives similar constraints: w =−1.027 ± 0.055. Our supernova measurements provide the most stringent constraints to date on the nature of dark energy.
Key words: cosmology: observations / distance scale / dark energy
Appendices are available in electronic form at http://www.aanda.org
Full Table F.3 and covariance matrix are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/568/A22
© ESO, 2014
1. Introduction
The accelerating expansion of the universe was discovered fifteen years ago by measuring accurate distances to distant type Ia supernovae (Riess et al. 1998; Perlmutter et al. 1999). The reason for the acceleration remains unknown, and the term “dark energy” is used to describe the phenomenon. Understanding the nature of dark energy is currently one of the major goals of fundamental physics, and this drives a large experimental effort in observational cosmology. While a cosmological constant may be the simplest explanation for the accelerating expansion, alternatives such as dynamical dark energy or modified gravity (see, e.g., Amendola et al. 2013, for a recent review) can be tested through their effects in either the late-time expansion history or the growth of structures in the universe. By precisely mapping the distance-redshift relation up to redshift z ≈ 1, type Ia supernovae remain, at this stage, the most sensitive probe of the late-time expansion history of the universe.
This goal motivated large-scale systematic searches for SNe Ia in the past decade. High-redshift (up to z ~ 1) programs include the Supernova Legacy Survey (SNLS, Astier et al. 2006; Sullivan et al. 2011), the ESSENCE project (Wood-Vasey et al. 2007), and the Pan-STARRS survey (Tonry et al. 2012; Scolnic et al. 2013; Rest et al. 2013). Intermediate redshifts (0.05 <z< 0.4) were targeted by the SDSS-II supernovae survey (Frieman et al. 2008; Kessler et al. 2009a; Sollerman et al. 2009; Lampeitl et al. 2010a; Campbell et al. 2013). Nearby (z< 0.1) programs include the Harvard-Smithsonian Center for Astrophysics survey (CfA, Hicken et al. 2009), the Carnegie Supernova Project (CSP, Contreras et al. 2010; Folatelli et al. 2010; Stritzinger et al. 2011), the Lick Observatory Supernova Search (LOSS, Ganeshalingam et al. 2013), and the Nearby Supernova Factory (SNF, Aldering et al. 2002). At z> 1, supernova discovery and follow-up have been carried out with the Hubble Space Telescope (HST) by several groups (Riess et al. 2007; Suzuki et al. 2012). With a total of about one thousand SNe Ia discovered and spectroscopically confirmed, these second-generation surveys provide a measurement of luminosity-distance ratios with a high statistical precision between z ≈ 0.01 and z ≈ 0.7.
As noted in the recent studies (Conley et al. 2011; Suzuki et al. 2012; Scolnic et al. 2013), the accuracy of cosmological constraints is currently limited by systematic measurement uncertainties, particularly the uncertainty in the band-to-band and survey-to-survey relative flux calibration. Since relative flux measurements are the heart of this technique, this situation is not surprising, especially if one considers the large number of surveys and instruments involved. Significant efforts have been undertaken to overcome this limitation (Ivezić et al. 2007; Regnault et al. 2009; Tonry et al. 2012). In addition, several other sources of systematic uncertainty have been identified in SN Ia analyses. The most important concerns are potential biases related to model assumptions in light-curve fitting techniques (Conley et al. 2007; Kessler et al. 2009a, 2013; Scolnic et al. 2014), and variation in the average luminosity of SNe Ia with the properties of their host galaxies (Sullivan et al. 2010; Kelly et al. 2010; Lampeitl et al. 2010b; Gupta et al. 2011; Johansson et al. 2013b). Comprehensive discussions of the various effects associated with the SN Ia Hubble diagram can be found in Kessler et al. (2009a) and Conley et al. (2011, hereafter C11).
This paper is part of an SNLS-SDSS collaborative effort called the joint light-curve analysis (hereafter JLA). The JLA was initiated in 2010 to address the most important limitations identified in previous analyses. More specifically, the effort was primarily directed at 1) improving the accuracy of the photometric calibration of both surveys; 2) more rigorously determining uncertainties in the SN Ia light-curve models; and 3) including the full SDSS-II SNe Ia spectroscopic sample in both the light-curve training and cosmology analysis1. The SDSS-II spectroscopic sample is part of the final release of the SDSS-II supernova survey (Sako et al. 2014). The resulting improvements in the SDSS and SNLS photometric calibration accuracy are described in Betoule et al. (2013, hereafter B13). Improvements in the SALT2 model and its uncertainties are described here and in Mosher et al. (2014, hereafter M14). These improvements were made without regard to their affect on the derivation of cosmological parameters from our data. In particular, the recalibration was completed in October 2012, before its impact on cosmology was determined.
The main goal of the present paper is to provide stronger cosmological constraints from a new analysis of the nearby, SDSS-II and SNLS three-year samples using the full SDSS-II sample and the reductions in systematic uncertainties that resulted from the JLA analyses. Otherwise, we follow closely the approach described in the analysis of the first three years of SNLS (Guy et al. 2010; Conley et al. 2011; Sullivan et al. 2011). Improvements in calibration understanding apply only to the SDSS-II and SNLS SNe. Therefore, focusing on the control of systematics, we restrict ourselves to adding only the last two seasons of the SDSS-II to the SN data samples that were used in the C11 analysis.
The outline of the paper is as follows. The data samples are briefly presented in Sect. 2. We describe the joint recalibration of the SNLS and SDSS photometry in Sect. 3. We summarize improvements in the systematic uncertainties and validation of the distance estimates based on the SALT2 model in Sect. 4. We detail the construction of a low-systematic-error joint Hubble diagram in Sect. 5. A determination of Ωm for a flat ΛCDM universe from supernovae alone is described in Sect. 6. We explain, in this section, the relative impact of each change relative to the C11 analysis. We also compare our measurement with the independent measurement provided by the Planck CMB experiment. Section 7 uses additional astrophysical probes in combination with SNe Ia to break degeneracies and constrain dark energy in more generic models. In particular, we include precise measurements of the cosmic microwave background (CMB) and baryon acoustic oscillations (BAO). We summarize the main results and discuss prospects for improvement in Sect. 8.
2. Data samples
In this paper, we present a new compilation of SN Ia light curves including data from the full three years of the SDSS survey. The rest of our sample is taken from the compilation assembled in Conley et al. (2011), hereafter referred to as the “C11 compilation”, comprising SNe from SNLS, HST and several nearby experiments. This extended sample of 740 SNe Ia is referred to as the JLA sample.
2.1. The SDSS-II SN Ia sample
The data release of the SDSS-II supernova survey (Sako et al. 2014) delivers light curves for 10 258 variable and transient sources, as well as host galaxy identification for thousands of transients, photometric classifications for the candidates with good multicolor light curves, dedicated spectroscopic observations for a subset of 889 transients, and host galaxy redshifts obtained using spectra from the original SDSS spectrograph, the SDSS-III BOSS spectrograph, and the telescopes used to obtain SDSS SN spectra. These observations resulted in the largest sample of supernova candidates ever compiled with 4607 likely supernovae, 500 of which have been confirmed as SNe Ia by the spectroscopic follow-up. Our JLA sample includes a selection of 374 SNe Ia from this spectroscopic sample. Here we give a brief summary of the survey, photometry and calibration.
The SDSS-II Supernova Survey used the SDSS camera (Gunn et al. 1998) on the SDSS 2.5 m telescope (York et al. 2000; Gunn et al. 2006) at the Apache Point Observatory (APO) to search for SNe in the northern fall seasons (September 1 through November 30) of 2005 to 2007. This survey scanned a region centered on the celestial equator in the southern Galactic hemisphere (designated stripe 82) that is 2.5° wide and spans right ascensions of 20h to 4h, covering a total area of 300 deg2 with a typical cadence of observations of once every four nights. Images were taken in five broad passbands, ugriz (Fukugita et al. 1996; Doi et al. 2010), with 55 s exposures and processed through the PHOTO photometric pipeline (Lupton et al. 2001). Within 24 h of collecting the data, a dedicated computing cluster at APO was used to search the images for SN candidates. Spectra of selected SN candidates were observed in a program involving about a dozen telescopes: the Hobby-Eberly Telescope (HET), the Apache Point Observatory 3.5 m Telescope (APO), the Subaru Telescope, the 2.4-m Hiltner Telescope at the Michigan-Dartmouth-MIT Observatory (MDM), the European Southern Observatory (ESO) New Technology Telescope (NTT), the Nordic Optical Telescope (NOT), the Southern African Large Telescope (SALT), the William Herschel Telescope (WHT), the Telescopio Nazionale Galileo (TNG), the Keck I Telescope, and the Magellan Telescope. Details of the SDSS-II SN Survey are given in Frieman et al. (2008) and Sako et al. (2008), and the procedures for spectroscopic identification and redshift determinations are described in Zheng et al. (2008). Some subsamples of the spectra have been subjected to more detailed analyzes (Östman et al. 2011; Konishi et al. 2011b; Foley et al. 2012). The determination of host galaxy redshifts for the BOSS data is described in Olmstead et al. (2014).
The SN photometry for SDSS-II is based on scene model photometry (SMP) described in Holtzman et al. (2008). The basic approach of SMP is to simultaneously model the ensemble of survey images covering an SN candidate location as a time-varying point source (the SN) and sky background plus a time-independent galaxy background and nearby calibration stars, all convolved with a time-varying point-spread function (PSF). The fitted parameters are SN position, SN flux for each epoch and passband, and the host-galaxy intensity distribution in each passband. The galaxy model for each passband is a 20 × 20 grid of CCD pixels (approximately 8″ × 8″), and each of the 15 × 15(pixels) × 5(passbands) = 1125 galaxy intensities is an independent fit parameter. As there is no pixel resampling or convolution of the observed images, the procedure yields reliable statistical error estimates.
The calibration is based on the catalog in Ivezić et al. (2007), and the resulting SN fluxes returned by SMP are in the native SDSS system. Here we use true AB magnitudes obtained by applying the small AB offsets in Table 23 of B13. As part of this JLA effort, a declination-dependent calibration adjustment has been applied as described in B13 and Sect. 3.3.2 below.
2.2. The C11 compilation
The C11 compilation includes 242 spectroscopically confirmed SNe Ia from the first three seasons of the five-year SNLS survey. The survey covered four 1 deg2 fields using the MegaCam imager on the 3.6 m Canada-France-Hawaii Telescope (CFHT). Images were taken in four passbands similar to those used by the SDSS: gM,rM,iM,zM, where the subscript M denotes the MegaCam system. Each field and passband was repeatedly imaged four or five times per lunation, with exposure times of ~1 h (see Sullivan et al. 2006 for details) in order to discover SNe at redshifts up to z ~ 1. The SNLS images were rapidly processed to discover live transients. About 1000 supernovae were discovered in the redshift range 0.2 <z< 1, and 420 of them have been confirmed as a type Ia by massive spectroscopic follow-up programs (Howell et al. 2005; Bronder et al. 2008; Ellis et al. 2008; Balland et al. 2009; Walker et al. 2011).
The rest of the compilation is dominated by low-z (z< 0.08) SNe from the third release (Hicken et al. 2009) of photometric data acquired at the Whipple Observatory of the Harvard-Smithsonian Center for Astrophysics (CfA3). The data were acquired between 2001 and 2008 using three different CCD cameras (Keplercam, Minicam and 4Shooter2) and photometry in the natural systems (UBVRI or UBVri) is provided. We also include high quality photometric data from the first release (Contreras et al. 2010) of the Carnegie Supernova Project (CSP). Those data were acquired by the SWOPE instrument at the Las Campanas Observatory. We make use of the photometry available in the natural SWOPE system (ugriBV). The low-z part of the compilation is complemented with older data from various origins (mostly Altavilla et al. 2004; Hamuy et al. 1996; Jha et al. 2006; Riess et al. 1999). Those data are calibrated against the Landolt (1992) photometric standards and color corrected to the Landolt UBVRI system. This last step introduces additional uncertainties in the photometry that needs to be taken into account (see Appendix B.2).
Finally, the C11 compilation includes photometry of 14 very high redshift (0.7 <z< 1.4) SNe Ia from space-based observations with the HST (Riess et al. 2007). The observations were obtained with the Advanced Camera for Surveys (ACS in wide-field mode) and camera 2 of the NICMOS instrument.
3. Joint photometric calibration of the SNLS and the SDSS-II surveys
3.1. The SDSS-II and SNLS supernova surveys
The SDSS-II and SNLS experiments provide a large fraction of the currently available SNe Ia sample (613 out of 740 SNe Ia in our sample). Both experiments were part of large photometric and spectroscopic surveys, with the photometric component conducted in rolling-search mode using a single, well-characterized photometric instrument.
The similarity (in design) and complementarity (in redshift) of the two surveys motivated the attempt to combine efforts for a joint analysis of the data. While B13 gives a detailed description of the recalibration of the SDSS-II and SNLS surveys, a brief summary is given below along with the details of the calibration transfer to the photometry of supernovae. We then describe consistent estimates of calibration uncertainties for the full sample.
3.2. Calibration of photometric measurements
Many of the stars surrounding supernovae in the science fields are non-variable at the mmag level and can be used as flux references. The photometry of supernovae is made relative to those stars, referred to as “tertiary standards”.
The photometry for the SDSS and SNLS samples was performed completely independently but with methods that were similar. The description of the SN differential photometry technique applied to the SNLS data is given in Astier et al. (2013, Sect. 5, hereafter A13).The algorithm has been validated using semi-artificial sources introduced in real images and has demonstrated to accurately recover the supernovae flux relative to surrounding stars with a systematic uncertainty about 1.5 mmag. The SDSS photometry is described in Holtzman et al. (2008) and has also been tested with artificial sources and null sources using pre-explosion epochs of real SN.
The photometry methods deliver instrumental fluxes of supernovae and tertiary standards in consistent but arbitrary units. The interpretation of those “instrumental” fluxes φ then relies on the following model: 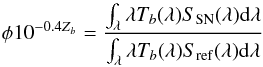 (1)where SSN(λ) is the supernova spectral energy distribution (SED) as a function of wavelength, Tb(λ) is the effective instrument transmission in photometric band b, Sref(λ) is the SED reference which defines the magnitude system, and
(1)where SSN(λ) is the supernova spectral energy distribution (SED) as a function of wavelength, Tb(λ) is the effective instrument transmission in photometric band b, Sref(λ) is the SED reference which defines the magnitude system, and 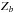 is the calibration constant (zero-point) which anchors the magnitude system to physical units. The precise determination of
is the calibration constant (zero-point) which anchors the magnitude system to physical units. The precise determination of 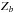 and Tb is the purpose of survey calibration.
and Tb is the purpose of survey calibration.
Currently, our model for Tb(λ) is built from laboratory or in situ transmission measurements of the CCD and filter passbands, combined with on site measurements of the mean atmospheric absorption. The determination of 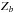 relies on observations of flux standards. This role is currently played by spectrophotometric standard stars. SN Ia studies rely on the most accurate set of standards available, which were established using the HST STIS instrument, and are obtained from the CALSPEC database (Bohlin & Gilliland 2004; Bohlin 2010).
relies on observations of flux standards. This role is currently played by spectrophotometric standard stars. SN Ia studies rely on the most accurate set of standards available, which were established using the HST STIS instrument, and are obtained from the CALSPEC database (Bohlin & Gilliland 2004; Bohlin 2010).
SDSS-II and SNLS had independent calibration strategies, both relying on observations obtained with intermediate instruments. SNLS calibration relied on observations of the BD +17 4708 primary standard in the Landolt photometric system (Landolt & Uomoto 2007), while in SDSS, the tertiary stars were compared to the HST solar analog standard stars using a dedicated monitor telescope (Tucker et al. 2006). The joint calibration analysis of the SNLS and SDSS surveys (B13) resulted in improvements in our understanding of survey instruments and calibration accuracy. Detailed comparisons of the two instrument responses led to two revisions:
-
1.
The effective transmission curves Tr(λ) and Ti(λ) of MegaCam in r and i bands were revised. This revision resulted in a 3 nm shift of the central wavelength toward the red, which is larger than the previously estimated uncertainty in the MegaCam passbands (about 1 nm).
-
2.
A 2% non-uniformity of the SDSS monitor telescope photometric response has been corrected. This non-uniformity had virtually no impact on the calibration transfer; however, the uniformity of the SN survey was affected.
3.3. Recalibration of SDSS-II and SNLS supernova light curves
The joint calibration resulted the large set of calibrated tertiary standard stars (published in B13) for the SDSS-II and SNLS science fields. We now turn to the transfer of this calibration to the supernovae photometry.
3.3.1. SNLS
We rely on the SNLS3 photometry of supernovae published in Guy et al. (2010, hereafter G10). The SNLS3 photometry used the PSF “resampled photometry” method (RSP) described in A13. Here we improve the calibration transfer from tertiary stars to supernovae that accounts for the differences between aperture photometry (used for the standards stars2) and PSF photometry (for SNe). According to the analysis of A13, Sect. 8, we implement two corrections to address the following issues:
- 1.
The actual shape of the PSF varies with wavelength. This variation is not taken into account by the PSF photometry method. As a consequence, the effective throughput of the photometry varies with wavelength (see, e.g., G10, Sect. 3.2). In practice, natural PSF and aperture magnitudes correspond to slightly different photometric systems.
- 2.
Individual measurements with aperture photometry are contaminated by local background structure (B13, Sect. 4.3.4).
Taking the two effects into account, the calibration equation for the PSF zero-points reads: 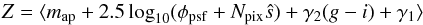 (2)where map are the aperture magnitudes published in B13, φpsf are the instrumental PSF fluxes, Npixŝ accounts for the effective contamination of apertures of size Npix (about 800 pixels) by background residual levels ŝ (estimated for each star along with PSF fluxes), g − i are the AB colors of tertiary stars, and γ1 and γ2 are the coefficients of a linear color transformation between the aperture and PSF systems. The γ1 and γ2 coefficients are given in Table 1.
(2)where map are the aperture magnitudes published in B13, φpsf are the instrumental PSF fluxes, Npixŝ accounts for the effective contamination of apertures of size Npix (about 800 pixels) by background residual levels ŝ (estimated for each star along with PSF fluxes), g − i are the AB colors of tertiary stars, and γ1 and γ2 are the coefficients of a linear color transformation between the aperture and PSF systems. The γ1 and γ2 coefficients are given in Table 1.
Coefficient of synthetic color transformation between aperture and PSF MegaCam magnitudes.
Selection of SNLS tertiary stars entering the determination of zero-points.
The weighted ensemble average of all the tertiary stars in a given band, field, and CCD is used to compute the zero-point. A few quality cuts are applied to the tertiary stars prior to the fit, and are summarized in Table 2. In particular we select stars in a magnitude range where the aperture catalog is not affected by selection bias (B13, Fig. 12) and in a color range where the aperture to PSF transformations are accurate. We discard potentially variable stars by applying a cut on the χ2 of repeated measurements. Outliers are rejected iteratively at 2.5σ. Residuals for the zero-point fit are displayed as a function of magnitude in Fig. 1 and show that the non-linearities noted in G10, Fig. 5 are now corrected at the mmag level by the aperture contamination correction. The cuts leave about 25 stars, on average, per CCD and field for the determination of each zero-point. The typical statistical uncertainty on the zero-point determination is about 1 mmag, which is small compared to the systematic uncertainties. The systematic uncertainty associated with the color transformation and aperture corrections amounts to 0.1, 0.8, 1.0, 0.9 mmag in griz, respectively. In addition, A13 quotes a 1.5 mmag systematic accounting for potential bias in the RSP photometry method.
With respect to the previous release of SNLS light curves (G10), the griz zero-points are shifted on average by −12.9, −0.9, 1.3 and −17.9 mmag. The main contribution to this change is the recalibration of the tertiary standard catalog, the new transfer procedure described above contributing only noticeably in g and i. The changes in the calibration of the SNLS tertiaries involved the correction of a sign error (described in B13, Sect. 10.4) in addition to the revision of MegaCam r and i transmission curves and the new calibration data described above (Sect. 3.2). Note that the new calibration relies on the observations of 5 HST standards (three observed directly) rather than just a single one3 as in C11. The change in g zero-point is the most significant (3σ), as the various contributions act in the same direction in this band. The other zero-point changes are well within the previously quoted uncertainties.
 |
Fig. 1 Difference between aperture and PSF photometry as a function of the SNLS tertiary standard star magnitude. The aperture photometry from B13 has been corrected for residual contamination using an estimate of the local background level obtained with PSF photometry. The magnitude range used in the zero-point fit (vertical dashed lines) is chosen so that the aperture catalog is expected to be free from selection bias (B13, Fig. 12). |
3.3.2. SDSS
The photometry of SDSS-II supernovae and their calibration is described in Holtzman et al. (2008). The differential supernova photometry is based on a comparison of the PSF magnitude of the supernova and the PSF magnitudes of nearby tertiary standard stars and is insensitive to errors in the PSF. Chromatic effects in the SDSS PSF are expected to be negligible. The joint calibration study (B13) calibrates directly the PSF magnitudes of SDSS tertiary stars. Direct measurements of HST standard stars by the monitor telescope and by MegaCam, transformed to the SDSS survey telescope, allow a computation of the zero-points for each SDSS filter. The HST solar analog standard stars are used to minimize any possible error in color terms in the transformation from the monitor to the survey telescope. The zero-points thus obtained are slightly different than the nominal SDSS zero-points, resulting in small corrections to the reported magnitudes. Since the SDSS photometry is obtained as a difference between the SN and stellar magnitudes, the correction of the PSF catalogs described in B13 can be readily applied to SN photometry. The correction takes the following form: 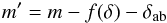 (3)where f is the uniformity correction that is a function of declination δ as given in B13, Fig. 23, and δab is the average offset of corrected SDSS magnitudes to the AB system given in B13, Table 23. Recalibration of SDSS-II light curves is carried out by applying Eq. (3) to the natural SN magnitudes. Once this correction is applied, the average calibration of SDSS-II SNe is shifted by −31, −4, 0, 0 and −6 mmag in u, g, r, i and z. The gri changes are well within expected uncertainties (about 6 mmag). The u and z band photometry were not used in previous analyses of the SDSS SN spectroscopic sample (Kessler et al. 2009b; Conley et al. 2011). A full description of the recalibrated light curves can be found in Sako et al. (2014).
(3)where f is the uniformity correction that is a function of declination δ as given in B13, Fig. 23, and δab is the average offset of corrected SDSS magnitudes to the AB system given in B13, Table 23. Recalibration of SDSS-II light curves is carried out by applying Eq. (3) to the natural SN magnitudes. Once this correction is applied, the average calibration of SDSS-II SNe is shifted by −31, −4, 0, 0 and −6 mmag in u, g, r, i and z. The gri changes are well within expected uncertainties (about 6 mmag). The u and z band photometry were not used in previous analyses of the SDSS SN spectroscopic sample (Kessler et al. 2009b; Conley et al. 2011). A full description of the recalibrated light curves can be found in Sako et al. (2014).
Number of STIS visits for the observed CALSPEC standards.
Internal calibration uncertainties for the low-z samples split by photometric systems.
3.4. Uncertainties in the photometric calibration of light curves
The interpretation of supernova measurements is affected by uncertainties on the Tb(λ) and 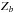 terms of Eq. (1). We parameterize the uncertainty on Tb by a single parameter: the shift of the mean wavelength
terms of Eq. (1). We parameterize the uncertainty on Tb by a single parameter: the shift of the mean wavelength 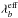 (interpreted as a global shift of the transmission function). The vector of calibration parameters is thus
(interpreted as a global shift of the transmission function). The vector of calibration parameters is thus 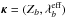 with b running over all the photometric bands of all the instruments. We summarize the uncertainties affecting those parameters in a single covariance matrix assembled as follows.
with b running over all the photometric bands of all the instruments. We summarize the uncertainties affecting those parameters in a single covariance matrix assembled as follows.
In all cases, our primary flux calibration reference is the HST system as defined in the CALSPEC 2011 release. We thus consider the following sources of uncertainty:
-
1.
The uncertainty on the color of the primary flux reference, i.e.,the definition of the HST system itself.
-
2.
The STIS measurement error affecting the transfer of the primary HST calibrators to the CALSPEC secondary standards.
-
3.
The error in the ground-based photometric measurements of the CALSPEC standards.
-
4.
The error in the calibration transfer from the CALSPEC standards to the tertiary standards.
-
5.
Extra sources of systematic uncertainties introduced by the SN photometry method.
-
6.
Uncertainties in the instrument response curves.
Items 1–2 constitute an external source of uncertainty (affecting the CALSPEC spectra) which is common to all surveys. Items 3–5 affect the accuracy of the calibration transfer from the primary CALSPEC standards to the supernova measurements. Item 3 is thought to be well estimated and understood in all cases. Items 4 and 5 are survey specific. In the case of SNLS and SDSS they are thought to be well controlled (B13). The control of Item 6 also varies from one survey to another; however, its importance in the calibration is typically of second order.
Note that we do not consider uncertainties on the absolute flux scale of the primary flux reference as such uncertainties would only affect the overall normalization, which is marginalized away in our Hubble diagram analysis.
3.4.1. Global uncertainties on the flux standards
We follow the assumptions made in B13 for modeling the uncertainty on CALSPEC spectra. Namely, we assume a global 0.5% slope uncertainty (1σ) over the range 3000–10 000Å for the uncertainty in the white-dwarf system color4.
In addition, we consider the STIS measurement error for individual spectra, which is accurately measured from the repeated observations of the monitoring star AGK +81 266. We assume that the measurement uncertainty on composite spectra decreases as the square root of the number of STIS visits. When the number of visits is not the same for the two grisms considered, we conservatively use the smaller number of visits. The number of visits per star for CALSPEC spectra version 003 is given in Table 3.
3.4.2. Uncertainties in the SNLS and SDSS calibration
Uncertainties affecting the calibration transfer from HST standard to the SNLS and SDSS tertiary stars are taken from B13, Table 22. We account for correlations between bands introduced by the cross-calibration of the two surveys, for the correlation between filter wavelength shifts 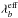 , and the definition of the AB zero-point
, and the definition of the AB zero-point 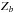 . For SNLS only, we add in quadrature the systematic uncertainty associated with the calibration transfer from tertiary standards to supernova light curves discussed above (Sect. 3.3).
. For SNLS only, we add in quadrature the systematic uncertainty associated with the calibration transfer from tertiary standards to supernova light curves discussed above (Sect. 3.3).
3.4.3. Uncertainties in the calibration of the low-z sample
All low-z experiments are calibrated against secondary photometric standards: either the Smith (Smith et al. 2002) or Landolt (Landolt 1992) equatorial standards. In both cases, photometry in the secondary system for the F-subdwarf BD +17 4708 CALPSEC spectrophotometric standard is available (Smith et al. 2002; Landolt & Uomoto 2007), and can be used to anchor the photometry to the HST flux scale. We must account for measurement uncertainties of BD +17 4708 in both systems as a correlated source of uncertainties for all low-z samples.
A complete review of internal calibration uncertainties was made in C11. We follow their prescriptions except for uncertainties in the CSP and CfAIII samples that are revised according to Stritzinger et al. (2011), Mosher et al. (2012), and a comparison study described in Appendix B.1. We also revisit the U band calibration uncertainty in the low-z sample as described in Appendix B.2. Table 4 summarizes internal calibration uncertainties attributed to the low-z sample.
3.4.4. Uncertainties in the calibration of HST supernovae
We use the interpretation of Riess et al. (2007) HST SN calibration described in C11, Sect. 2.4. Given the small statistical weight of the HST sample included in this analysis, it was not necessary to propagate recent improvements in the treatment of the NICMOS non-linearity (Suzuki et al. 2012).
3.4.5. Full covariance matrix of calibration uncertainties
We summarize the calibration uncertainties, accounting for correlated effects between bands and surveys, into a covariance matrix of the calibration parameter vector κ. The full covariance matrix is released with the data (see Appendix F). The square roots of the diagonal elements of the covariance matrix are given in Table 5. For the SDSS-II and SNLS surveys that dominate our sample, the accuracy of the average calibration is at the 5 mmag level, primarily due to the uncertainty in the CALPSEC flux standards.
Uncertainties in calibration parameters.
4. Joint training of the light-curve model
4.1. Supernova models and distance estimates
Distance estimation with SNe Ia is based on the empirical observation that these events form a homogeneous class whose remaining variability is reasonably well captured by two parameters (see, e.g., Tripp 1998). One parameter describes the time stretching of the light-curve (X1 in what follows), and the other describes the supernova color at maximum brightness (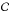 in what follows).
in what follows).
Specifically, the distance estimator used in this analysis (and in most similar cosmological analyses) assumes that supernovae with identical color, shape and galactic environment have on average the same intrinsic luminosity for all redshifts. This hypothesis is quantified by a linear model, yielding a standardized distance modulus μ = 5log 10(dL/ 10 pc):  (4)where
(4)where 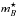 corresponds to the observed peak magnitude in rest-frame B band and α, β and MB are nuisance parameters in the distance estimate. Both the absolute magnitude MB and β parameter were found to depend on host galaxy properties (Sullivan et al. 2011; Johansson et al. 2013b) although the mechanism is not fully understood. We use the C11 procedure to approximately correct for these effects assuming that the absolute magnitude is related to the host stellar mass (Mstellar) by a simple step function5:
corresponds to the observed peak magnitude in rest-frame B band and α, β and MB are nuisance parameters in the distance estimate. Both the absolute magnitude MB and β parameter were found to depend on host galaxy properties (Sullivan et al. 2011; Johansson et al. 2013b) although the mechanism is not fully understood. We use the C11 procedure to approximately correct for these effects assuming that the absolute magnitude is related to the host stellar mass (Mstellar) by a simple step function5: 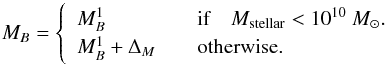 (5)The light-curve parameters
(5)The light-curve parameters 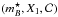 result from the fit of a model of the SN Ia spectral sequence to the photometric data. Light-curve fitting techniques have a long history, and the potential biases introduced by specific model choices have raised some concerns (see, e.g., Kessler et al. 2009a). The estimate of model systematics in the C11 analysis was based on the comparison of light-curve parameters reconstructed from the same data by two different models (SALT2 and SiFTO, Conley et al. 2008). Such a scheme is only moderately satisfying as both methods could share similar biases, leading to underestimated errors, or one model could have substantially larger errors than the other.
result from the fit of a model of the SN Ia spectral sequence to the photometric data. Light-curve fitting techniques have a long history, and the potential biases introduced by specific model choices have raised some concerns (see, e.g., Kessler et al. 2009a). The estimate of model systematics in the C11 analysis was based on the comparison of light-curve parameters reconstructed from the same data by two different models (SALT2 and SiFTO, Conley et al. 2008). Such a scheme is only moderately satisfying as both methods could share similar biases, leading to underestimated errors, or one model could have substantially larger errors than the other.
By using extensive Monte Carlo simulations, the analysis from M14 provides a significant improvement in the determination of light-curve model biases. Varying the underlying supernova model in the range currently allowed by data, it demonstrates that the data-driven SALT2 method, trained on samples comparable to the G10 sample, recovers the input distances without introducing a significant bias between low and high-redshift distances (see Sect. 4.4). Therefore, we adopt the SALT2 method for the present analysis, and base our systematic estimate on the M14 results.
4.2. The SALT2 model
The SALT2 model is a first order description of the time-spectral sequence of SNe Ia, multiplied by a time independent color-law. At phase p and wavelength λ, the flux density model for a given supernova is: 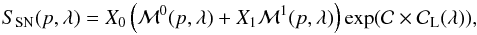 (6)where the normalization, shape and color parameters X0, X1 and
(6)where the normalization, shape and color parameters X0, X1 and 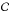 , respectively, are evaluated for each SN6. The mean spectral sequence ℳ0, the first order deviation around the mean sequence ℳ1 and the phase-independent color-law
, respectively, are evaluated for each SN6. The mean spectral sequence ℳ0, the first order deviation around the mean sequence ℳ1 and the phase-independent color-law 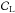 are trained on a photometric and spectroscopic sample of spectroscopically identified SNe Ia (see below Sect. 4.3).
are trained on a photometric and spectroscopic sample of spectroscopically identified SNe Ia (see below Sect. 4.3).
The model does not capture all the variability of observed supernovae. The remaining deviations to the model, sometimes referred to as the “intrinsic scatter”, have to be accounted for in some way. In SALT2, the remaining scatter db,p affecting a measurement point at phase p in band b is modeled as: 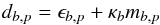 (7)where mb,p is the magnitude prediction from Eq. (6) and ϵb,p and κb are assumed to be independent, centered Gaussian random variables. The term ϵb,p describes phase dependent variations in the magnitude around the predicted light-curve in band b. The set of the ϵb,p are referred to as the “error snake”. The term κb describes variations in the relative amplitude of the multiband light curves around the predicted color-law. The κb are referred to as the “k-correction error”. The variances of ϵb,p and κb are functions fitted as part of the training process, so that the final model describes the observed variability.
(7)where mb,p is the magnitude prediction from Eq. (6) and ϵb,p and κb are assumed to be independent, centered Gaussian random variables. The term ϵb,p describes phase dependent variations in the magnitude around the predicted light-curve in band b. The set of the ϵb,p are referred to as the “error snake”. The term κb describes variations in the relative amplitude of the multiband light curves around the predicted color-law. The κb are referred to as the “k-correction error”. The variances of ϵb,p and κb are functions fitted as part of the training process, so that the final model describes the observed variability.
The training of ℳ0, ℳ1, 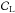 and the associated error model are done iteratively. A detailed description of the model and training procedure is given in M14.
and the associated error model are done iteratively. A detailed description of the model and training procedure is given in M14.
4.3. Training SALT2 on the JLA sample
The previous public release of the SALT2 model (v2.2) was described in G10. It has been trained on photometric and spectroscopic data from the literature (e.g., Schmidt et al. 1994; Patat et al. 1996; Hamuy et al. 2002; Benetti et al. 2004; Matheson et al. 2008) and high-z supernovae data from the SNLS (Ellis et al. 2008; Balland et al. 2009). The training sample also includes high quality data from nearby SNe Ia that are not in the Hubble flow. Biasing of the model could occur due to contamination by peculiar events, use of poorly sampled light curves with ill-defined maximum date, or biased selection of brightest events. To prevent such biases, cuts in redshift and quality were applied to form the G10 sample.
Here we add SDSS-II photometric data to the G10 training sample, and we refer to this extended G10+SDSS-II sample as the “JLA” training sample. Our selection of SDSS-II data follows the procedure of G10. We use only the spectroscopically identified sample, and we estimate the initial fit parameters from a fit with the G10 SALT2 model. As selection biases become significant in the SDSS-II sample at z> 0.25, we discard SNe above this limit. We evaluated the dependence of the cosmology on the redshift cut by using alternative cuts at z = 0.2 and z = 0.3 and found that the dependence was weak enough to be ignored. We require the date of maximum t0 and the light-curve shape parameter X1 to be well constrained, which efficiently selects light curves with good sampling. We discard SNe whose fitted color and shape parameters lie well outside the range of model validity. Finally, we select SNe with limited extinction by dust in the Milky-Way. The cuts are listed in Table 6 along with the number of supernovae discarded at each step. The remaining supernova light curves were visually inspected, as detailed in Appendix A. A total of 24 problematic light curves were discarded, mostly because of apparent problems in the sampling or photometry.
Number of supernovae discarded by the successive cuts applied to the SDSS-II sample before inclusion in the training sample.
 |
Fig. 2 Comparison of ℳ0 templates between the previous release of the SALT2 model (G10) and the present release trained on the JLA sample. Left: the present model is shown as a black dashed line at three different phases: early (−10 days), close to maximum (0 day), and late (+15 days). The G10 model is shown as the red solid line. Right: relative differences in the two models (JLA/G10 − 1) at the three selected phases. |
The resulting sample of 207 new SDSS-II SNe was added to the G10 training sample. A single SN in the original sample was removed: SNLS 03D4gl, which does not have post-max data. We retrained SALT2 on this extended and recalibrated training sample. The resulting model functions are compared to those of the G10 model in Figs. 2 and 3. The larger changes occur in the UV and infrared region where the model is now better constrained by the newly added data. The recalibrated and retrained version of the SALT2 model can be obtained from the SALT2 web page (see Appendix F).
4.4. Light-curve model uncertainties
The SALT2 training procedure described above was evaluated with Monte Carlo (MC) simulations in M14. The basic principle of this analysis is to perform an end-to-end SALT2 analysis on realistic simulations, where the analysis starts with training and ends with fitting for w. For a given reference supernova model, realistic SALT2 training sets including light curves and spectra are generated using the SNANA package (Kessler et al. 2009b). They have the same cadence, wavelength coverage and noise as the SALT2 training sample used in the present study; in that sense, they are realistic. For each of those training samples, the SALT2 model is trained, and then used to fit the light curves of a statistically independent sample of supernovae generated using the same reference model. The light-curve parameters of those test supernovae are used to estimate distances μ (Eq. (4)). The distances are corrected for selection effects using a dedicated simulation, similar to the one described in Sect. 5.3. Finally, the set of corrected distance moduli, μcorr, are compared to the input cosmology to test for potential biases.
4.4.1. Regularization in the training of SALT2
The current training sample lacks reliable spectroscopic data at early phases in the UV. Constrained only by photometric data, the training of the spectroscopic sequences in these regions is an unstable deconvolution process that requires some amount of regularization. A high level of regularization, however, distorts the spectral model by smoothing spectral features. The simulation tests in M14 have shown that our choice of regularization results in a small bias in the distance modulus of about 0.005 mag in the redshift range 0.2 <z< 1.
 |
Fig. 3 Top: comparison of the reconstructed color law CL for two trainings of the SALT2 model (see Eq. (6)): the present release trained on the JLA sample (back dashed line) and the previous release of the SALT2 model from G10 (red solid line). We display −0.1 log CL, which is approximately the rms magnitude variation from color variation. Bottom: difference in the two color laws. |
4.4.2. Limitations in the parameterization
For extreme values of the shape parameter, the first order expansion from Eq. (6) cannot describe the actual shape of SN Ia light curves at early and late phases. To test this limitation, we evaluated the bias from input models based on the time stretching of the spectral sequence established by Hsiao et al. (2007), which cannot be fully reproduced by SALT2. The simulations in M14 indicate that the distance modulus bias from this limitation of the SALT2 model are less than 3 mmag.
4.4.3. Residual scatter model
The current SALT2 model compresses the multiwavelength information available on SNe Ia into the two parameters 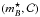 . This compression is trained to describe the mean behavior of the SN Ia population, but does not encompass all their diversity as already explained in Sect. 4.2. Whatever the physical phenomenon causing the remaining scatter (differences between extrinsic and intrinsic extinction, unmodeled variability of spectral features ...), it is treated as noise independent from one broad-band to another. Modeling the scatter restores the capacity to predict distances when the SN Ia population is biased from selection effects (see the discussion on selection biases in Sect. 5.3) and enables proper error propagation to distances. However, the accuracy of bias corrections depends on the accuracy of the underlying assumptions about the scatter model. Thus, the exact impact on cosmology depends on subtle interplay between the SN model training, the light-curve fitting to determine distances, and the bias corrections.
. This compression is trained to describe the mean behavior of the SN Ia population, but does not encompass all their diversity as already explained in Sect. 4.2. Whatever the physical phenomenon causing the remaining scatter (differences between extrinsic and intrinsic extinction, unmodeled variability of spectral features ...), it is treated as noise independent from one broad-band to another. Modeling the scatter restores the capacity to predict distances when the SN Ia population is biased from selection effects (see the discussion on selection biases in Sect. 5.3) and enables proper error propagation to distances. However, the accuracy of bias corrections depends on the accuracy of the underlying assumptions about the scatter model. Thus, the exact impact on cosmology depends on subtle interplay between the SN model training, the light-curve fitting to determine distances, and the bias corrections.
The SALT2 model assumes there is no correlation of the scatter between different photometric bands. As part of the JLA analysis, the impact of this assumption was tested recently in Kessler et al. (2013, hereafter K13), on simulated samples drawn from models with correlations. In particular, models of the intrinsic scatter were built from measurements of spectral scatter in SNFactory data (Chotard et al. 2011). This analysis, however, did not include training the SALT2 model on the simulated sample. Based on the same models of intrinsic scatter, M14 is the first analysis to evaluate the effect using the entire analysis chain, including the training of the SALT2 model and the bias correction. The M14 results, therefore, supersede those in K13. They show that, in the most adverse case, the bias on reconstructed distance moduli is less than 0.03 mag at very high redshifts that are most sensitive to the rest-frame UV region.
M14 does not test explicitly for variations of spectral features, in particular the strong variations of Calcium features in the near UV. However, by introducing broadband magnitude scatter trained on measured spectral scatter as given in Chotard et al. (2011), the simulation implicitly includes the impact of spectral features on broadband magnitudes.
As noted recently by Scolnic et al. (2014, hereafter S14), the intrinsic scatter models from K13 that are used in M14 do not vary the assumptions regarding the distribution of extrinsic color. S14 propose an alternative model where extinction is attributed entirely to interstellar dust with properties similar to dust in the Milky Way (i.e., β ≈ 4.1). This reddening is then smeared by intrinsic color variations uncorrelated with brightness, explaining both the observed color distribution and the low recovered β value. This model is similar to the model labeled “H-C11”7 in M14. The differences are the value of β, set to 4.1 in S14 instead of 3.1 in M14, and the underlying distribution of extrinsic color, which in the S14 model is strongly asymmetric with c> − 0.1, instead of only slightly asymmetric in M14. Biasing of distances arises if the simulated bias corrections are based on an incorrect model of intrinsic scatter. As the assumptions about intrinsic dispersion remain the same in both cases, the changes proposed in S14 are not expected to significantly alter the conclusion from M14. We check this expectation by modifying the simulations from K13 to use the S14 model. After applying the full cosmology analysis, including bias corrections based on the G10 intrinsic scatter model, the distance-modulus bias as a function of redshift is shown in Fig. 4. The resulting bias is contained within 0.02 mag and is compatible with the bias obtained in M14 for the H-C11 model.
 |
Fig. 4 Bias in reconstructed distance modulus as a function of redshift. Simulations follow the color variation model described in Scolnic et al. (2014, Sect. 3.1). The simulated sample includes low-z, SDSS-II and SNLS SNe Ia and is representative of our JLA sample described in Sect. 5.1. The analysis of the simulated sample includes the bias correction described in Sect. 5.3 (computed under the baseline SALT2 assumptions). The SALT2 model was not retrained on the simulated sample, similarly to what is done in Kessler et al. (2013). |
4.4.4. SALT2 model uncertainties
The Hubble diagram biases for realistic simulated samples (mimicking the JLA sample) and plausible assumptions about the SN Ia dispersion are given in M14, Fig. 16. They are shown to be within 0.03 mag in all cases over the entire redshift range.
As part of the systematic uncertainty in the cosmology analysis, we adopt a light-curve model uncertainty based on these results. We consider the input model in M14 that leads to the largest Hubble diagram bias (labeled G10′-C11 in M14, Table 7). We conservatively use the recovered bias as our model uncertainty. In addition, statistical uncertainties from the finite training sample size are propagated to distances using the approximate error propagation described in G10, Appendix A.
5. The JLA Hubble diagram
In this section, we present distance estimates (and associated uncertainties) for our JLA SN Ia compilation. Those distance estimates are based on light-curve parameters fitted with the retrained SALT2 light-curve model from Sect. 4. The distance estimates also depend on other ingredients; in particular, we rely on models for the:
-
instrument responses (see Sect. 3);
-
relation between the SN Ia luminosity and the host environment properties (in our case the host stellar mass-luminosity relation from Eq. (5));
-
survey selection biases;
-
peculiar velocities of nearby supernovae;
-
extinction by dust in the Milky Way;
-
contamination of the sample by mis-classified non-Ia events.
While the parameters of these models are held fixed when fitting for light-curve parameters and distances, we propagate the uncertainties associated with these parameters to the cosmological fit, resulting in correlations between the distances of individual SN.
Number of SDSS-II supernovae discarded by the successive cuts applied before inclusion in the cosmology sample.
We built upon the C11 analysis that modeled each item listed above and quantified the associated systematic uncertainty. We revised only what was necessary to use the extended dataset and the JLA work on the dominant systematics (B13; M14). With respect to the C11 analysis, we made the following changes:
-
1.
The SDSS-II and SNLS light curves have been recalibrated.
-
2.
We use only the SALT2 light-curve fitting method, validated by simulation results from M14. The amount of regularization applied in the training has been validated on the simulations, and we include a model uncertainty derived from M14 results.
-
3.
SALT2 was retrained with SDSS-II SN Ia light curves added to the G10 sample as discussed above, to maximize the benefit of the improved calibration and extended photometric coverage in both wavelength and epoch.
-
4.
A selection of photometric data from the full SDSS-II spectroscopic sample has been added to the cosmology sample.
-
5.
The impact of calibration uncertainties on the light-curve model and parameters has been recomputed.
-
6.
We gathered self-consistent host mass estimates for the full cosmology sample including SDSS-II SNe. We also revised some of the host mass estimates for the supernovae in the C11 compilation.
-
7.
We recomputed selection bias corrections and associated uncertainties accounting for refined models of the intrinsic dispersion of SNe Ia (K13).
-
8.
We doubled the systematic uncertainty in the Milky Way dust extinction correction described in C11, Sect. 5.6, to encompass concerns raised by Schlafly & Finkbeiner (2011) on the accuracy of the Schlegel et al. (1998) extinction map.
-
9.
We used observer frame UV photometry from the low-z and SDSS surveys. We determined a consistent calibration uncertainty for those as described in Appendix B.
-
10.
Based on considerations described in Appendix B, we revise uncertainties for low-z measurements that were not reported in the natural photometric system of their instrument.
The peculiar velocity model for low-z supernovae, the correction for Milky Way dust extinction and the estimated contamination of the sample by non-Ia events are left unchanged with respect to the C11 analysis. We refer the reader to C11 for a description of these components and the estimate of the associated uncertainties. Items 1 and 2 have been extensively treated in Sects. 3 and 4 respectively. In the rest of this section, we describe the selection of SDSS-II events for the JLA cosmology sample (item 4). We then detail items 5, 6, and 7 and discuss corresponding uncertainties. Items 9 and 10 are detailed in Appendix B.
A substantial effort has been conducted by several authors over the last few years to investigate potential redshift-dependent biases of the supernova distances inferred from the simple stretch and color corrections to supernova magnitudes. Of concern are i) a correlation of the intrinsic supernova color (especially UV) with metallicity (a non exhaustive list of recent works: Foley 2012; Foley et al. 2012; Wang et al. 2012; Foley & Kirshner 2013; Walker et al. 2012; Maguire et al. 2012); ii) the existence of several subclasses of SNe Ia with different intrinsic colors as identified by their correlation with spectral indicators (Wang et al. 2009, 2013; Nordin et al. 2011; Foley et al. 2011); iii) a potential evolution of the effective dust extinction law due to a mixture of intrinsic color variation, circumstellar dust, and extinction in the interstellar medium of the SNe host galaxies (Amanullah & Goobar 2011; Silverman et al. 2013; Maguire et al. 2013; Johansson et al. 2013a; Phillips et al. 2013). In the context of the present study, because the data do not allow reliable identification of SN subclasses, we consider a single SN Ia population and work with the assumption that any redshift evolution of SN properties (change of demographics, metallicity, dust properties) should be also be imprinted in the properties of their host galaxies.
Within this hypothesis, redshift evolution is corrected for, on average, when host galaxy properties are taken into account in the distance estimate (see Sect. 5.2). We have not found evidence of any residual redshift-dependent evolution. For instance, the average SN color as a function of redshift is well described by selection effects, and we do not see a significant evolution of the color–magnitude relation with redshift (more details can be found in M14).
Diffuse intergalactic dust extinction could, however, be undetected in our analysis and lead to biased distances. Ménard et al. (2010) have quantified the bias on w to be as large 0.03 when combining supernovae, CMB and BAO. Their study is based on a diffuse intergalactic extinction model constrained by an observed correlation between the color of distant quasars and the positions of foreground galaxies. The impact of this potential systematic error has been re-evaluated in Amanullah et al. (2010), who have obtained a much smaller systematic uncertainty on w of 0.012. In a recent study, Johansson & Mörtsell (2012) have further constrained the intergalactic dust models using both quasar colors and the soft X-ray background. Because it has a minor contribution, we have not propagated this source of systematic uncertainty to our JLA analysis, limiting the differences between our analysis and C11 analysis to the more crucial points.
As in C11, our estimates of systematic uncertainties are summarized into contributions to the covariance matrix of the light-curve parameters. At the end of this section we describe the statistical and systematic contributions of the full distance modulus covariance matrix to be used in the cosmological fits.
5.1. The JLA cosmology sample
We add SDSS-II SNe to the cosmology sample with cuts similar to those imposed for the C11 compilation. The cosmology sample requires SNe in the Hubble flow (z> 0.01) but can accommodate less stringent selection criteria than the training sample. In particular, we do not impose an upper redshift cut to the sample, since selection bias can be corrected for as described in Sect. 5.3. We require the fitted color and shape parameters to lie in the range of validity of the SALT2 model, and we discard supernovae affected by strong Milky Way extinction. The cuts on the uncertainty on t0 and X1, discarding poorly sampled light curves, are loosened since the resulting uncertainty is accurately propagated to the cosmology fits. In addition, 25 SNe have been discarded because they are either known to be peculiar events, or because they have apparent problems in the light-curve sampling or photometry. The detailed list of SNe is given in Appendix A. The selection requirements are summarized in Table 7, and result in 374 spectroscopically confirmed SDSS-II SNe Ia included in the JLA cosmology sample.
For the rest of the sample, including low-z, SNLS and HST SNe, we started from the original C11 selection, which was typically slightly stricter. We did not allow for any SNe to reenter this part of the sample, however we discarded a few problematic SNe: three SNLS SNe, 03D4gl which does not have post-max data, 03D1bk and 04D3cp which are extremely blue; 1 CfAIII SN the fast declining SN 2001da; and the 5 HST SNe named Borg, Ferguson, Greenberg, Sasquatch and Strolger, whose sampling is not sufficient to give a proper constraint on the date of maximum.
The resulting cosmology sample includes 740 SNe Ia whose best-fit light-curve parameters according to the retrained SALT2 model are given in Table F.3. The contributions of the different surveys to the final sample is summarized in Table 8. The corresponding Hubble diagram is shown in Fig. 8.
Contribution of the different surveys to the cosmology sample.
5.2. Host mass estimates for the extended sample
Kelly et al. (2010), Lampeitl et al. (2010b) and Sullivan et al. (2010) have found, in independent samples, a correlation between the shape and color corrected luminosities of type Ia supernovae and the stellar mass of their host galaxies (respectively for low-z, SDSS-II, and SNLS SNe). The corrected luminosities are brighter for supernovae in massive host galaxies: the average difference of Hubble residuals between SNe with host stellar masses that are lower and larger than 1010 M⊙ is found to be 0.08 ± 0.02 mag (from Sullivan et al. 2010, Table 5). We use this value as a reference for error propagation in the following, with the label 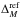 . This correlation, known as the “mass step”, could be a consequence of a correlation of both the SN luminosities and the host masses with the metallicity of the host galaxy (e.g., Kasen et al. 2009) or with the age of its stellar population (e.g., Krueger et al. 2010).
. This correlation, known as the “mass step”, could be a consequence of a correlation of both the SN luminosities and the host masses with the metallicity of the host galaxy (e.g., Kasen et al. 2009) or with the age of its stellar population (e.g., Krueger et al. 2010).
Gupta et al. (2011) improve the stellar mass estimate of the SDSS-II sample using UV and near-IR photometry in addition to the SDSS visible photometry, and they confirm the SN-luminosity correlation with host mass. D’Andrea et al. (2011, see also Konishi et al. 2011a use host-galaxy spectra of star-forming galaxies to obtain gas-phase metallicities and star-formation rates. They find that Hubble residuals are correlated with both quantities, consistent with the correlations of stellar mass to those same quantities. Childress et al. (2013) and Pan et al. (2014) find similar results at low-z from analyses of the Nearby Supernova Factory and Palomar Transient Factory data samples. They also find a correlation between SN Ia intrinsic color and host metallicity. Using the same data and local measurements of the Hα emission in the SN neighborhood, Rigault et al. (2013) recently reported a 3.1σ difference in shape and color-corrected luminosity between SNe Ia from Hα emitting regions (SNe Iaα) and SNe Ia from neutral environments (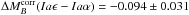 mag). They show that invoking a subclass of SNe Ia specific to passive environments (as traced by the absence of local Hα emission) and intrinsically brighter by about 0.2 mag, could explain both the observed difference and the mass step.
mag). They show that invoking a subclass of SNe Ia specific to passive environments (as traced by the absence of local Hα emission) and intrinsically brighter by about 0.2 mag, could explain both the observed difference and the mass step.
Those correlations indicate that the distance estimator of Eq. (4), which is based on SN light-curve width and color corrections to the luminosity, does not capture an important remaining source of variation in luminosity. Understanding the variation and optimizing the technique to correct for the variation using broad-band light curves or spectroscopic data (or both) is currently a subject of active research. In this paper we use the approach in C11 and fit for two different absolute magnitude parameters depending on the SN host stellar mass, with a split at 1010 M⊙. This method corrects for the induced redshift-dependent bias on distance moduli, at least approximately. We discuss an alternative model in Sect. 6.3.
We use the host stellar mass estimates of C11 for all SNe except for those in the SDSS-II sample. For the latter, we use a similar (but independent) estimate of the masses, also based on the PEGASE spectral synthesis code (Fioc & Rocca-Volmerange 1997). The SDSS-II host galaxy masses, computed according to the technique of Smith et al. (2012), are listed in Sako et al. (2014). We obtain good agreement with the host masses of the ~100 SDSS-II SNe that were in the C11 sample, with a dispersion of 0.2 dex, no significant offset (0.03 ± 0.03), and few outliers8.
The C11 compilation is missing estimates of the host galaxy mass for 61 nearby SNe (mostly because of missing photometry for the host), 36 SDSS-II supernovae and 16 SNLS supernovae for which a host galaxy has not been clearly identified. These SNe were assigned to the high mass bin in the C11 analysis but were also assigned a large magnitude error to account for a potentially incorrect assignment. In our analysis, we recover estimates for 57 of the 61 missing galaxy mass values, as described in Appendix C. According to those new estimates 14 of the 61 SNe-Ia were reassigned to the low-mass bin. The SDSS-II and SNLS SNe without identified host masses are assigned to the low mass bin, with an uncertainty on distance moduli of 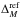 added in quadrature to the other sources of uncertainty.
added in quadrature to the other sources of uncertainty.
In the cosmology fit, we use as free parameters 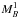 , the absolute magnitude of supernovae in hosts with Mstellar< 1010 M⊙ (following the notation of Sullivan et al. 2011), and ΔM, the magnitude offset of supernovae in more massive hosts (see Eq. (5)). The results obtained with this parameterization are further discussed in Sect. 6.3. As in C11, we also consider the systematic uncertainty of this correction. Because the stellar mass is only a proxy for an uncertain environmental property that alters supernova luminosities, the value of the mass cut is quite arbitrary. We therefore consider the effects of choosing cuts at 109 and 1011 M⊙. We assign correlated uncertainties of
, the absolute magnitude of supernovae in hosts with Mstellar< 1010 M⊙ (following the notation of Sullivan et al. 2011), and ΔM, the magnitude offset of supernovae in more massive hosts (see Eq. (5)). The results obtained with this parameterization are further discussed in Sect. 6.3. As in C11, we also consider the systematic uncertainty of this correction. Because the stellar mass is only a proxy for an uncertain environmental property that alters supernova luminosities, the value of the mass cut is quite arbitrary. We therefore consider the effects of choosing cuts at 109 and 1011 M⊙. We assign correlated uncertainties of 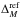 to those supernovae that change from the low to high mass range by adding a term to the covariance of the peak brightness:
to those supernovae that change from the low to high mass range by adding a term to the covariance of the peak brightness: 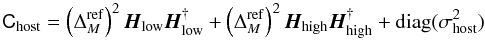 (8)where, † denotes the matrix transposition, and for a supernova i,
(8)where, † denotes the matrix transposition, and for a supernova i, 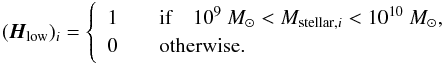
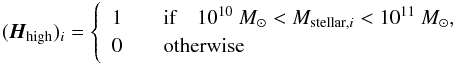 and
and 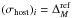 if, given the uncertainty on the host mass, the supernova i may be assigned to one mass bin or the other. If not, (σhost)i = 0.
if, given the uncertainty on the host mass, the supernova i may be assigned to one mass bin or the other. If not, (σhost)i = 0.
5.3. Bias correction
Flux-limited surveys are affected by selection biases which impact the reconstructed distance moduli μ in a rather complex manner. A detailed discussion of the biasing mechanisms can be found in M14, Sect. 6.2. We determine a correction for μ in our analysis from simulations using the SNANA simulation package (Kessler et al. 2009b). The bias is computed in redshift bins as follows: 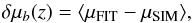 (9)where μSIM is the input distance modulus in the simulation and μFIT is the distance modulus reconstructed using the SALT2 fit parameters along with α and β determined from a combined fit to the low-z+SDSS+SNLS simulated sample. It is argued in C11 (Sect. 2.7.2) that the HST sample included in our analysis is essentially free from selection bias. In addition, given the smallness of the sample, its relative weight in the analysis is small. For these reasons, we exclude the HST sample from the simulations.
(9)where μSIM is the input distance modulus in the simulation and μFIT is the distance modulus reconstructed using the SALT2 fit parameters along with α and β determined from a combined fit to the low-z+SDSS+SNLS simulated sample. It is argued in C11 (Sect. 2.7.2) that the HST sample included in our analysis is essentially free from selection bias. In addition, given the smallness of the sample, its relative weight in the analysis is small. For these reasons, we exclude the HST sample from the simulations.
The uncertainty of the reconstructed bias is relatively large for two reasons. First, the effective selection function of each survey is the result of a combination of effects that are difficult to model accurately (see Dilday et al. 2008; Perrett et al. 2010 for evaluations of the SDSS and SNLS selection functions). The selection of spectroscopic targets, in particular, involves human decisions influenced by complex operational factors that cannot be simulated from first principles. The uncertainty in the selection function is the primary uncertainty in determining the bias. Second, the relation between the selection function and the distance modulus bias depends on the details of the underlying SNe Ia model, which are themselves uncertain.
For the spectroscopic selection function, we computed the data/MC ratio as a function of peak magnitude after all known selection requirements are applied (see Kessler et al. 2013, for details). The cuts are applied to the SDSS and SNLS9 samples, for both data and MC. For the nearby sample the analysis cuts are rather complicated for the various subsamples and we therefore define the spectroscopic selection function to include both the analysis and survey selections. The SNLS spectroscopic selection function is evaluated as a function of peak i band magnitude. Modeling of the SDSS spectroscopic selection requires a function of the peak g − r color in addition to r band peak magnitudes, as noted in Kessler et al. (2013, Sect. 3). A possible explanation for this color dependence is that the selection of SDSS spectroscopic targets favored intrinsically bluer events. Given the finite number of SNe in each sample, the parameters of the selection functions are subject to statistical uncertainty, which was estimated by applying our procedure to 20 simulated random data samples.
The selection functions of the low-z samples are more uncertain. Most of the low-z sample comes from galaxy targeted searches where the discovery is not expected to be magnitude limited. However, the color distribution of the low-z sample slightly trends to the blue when the redshift increases, indicating that our sample likely suffer from a slight selection bias. We thus consider two extreme cases 1) the search is free from selection bias and 2) the search is entirely magnitude limited so that the selection function can be determined from data/MC comparisons can be determined from data/MC comparisons of the peak B band magnitude. We use 2) as the most realistic case as it is better at reproducing observed distributions. We use the difference between 2) and 1) as a conservative estimate of the uncertainty on our choice. This is an acceptable solution given the limited impact of low-z selection bias on cosmological parameters. In a ΛCDM fit, using one or the other solution shifts the recovered value of Ωm by only 0.004 which is one order of magnitude smaller than the global uncertainty on this parameter.
The baseline bias correction is shown in Fig. 5. The simulated statistics are about 400 times greater than the data statistics, leading to a small statistical uncertainty in the MC. The dominant statistical uncertainty is in the determination of the selection functions. The Monte Carlo results for the low-z, SDSS-II and SNLS samples are fit with smooth polynomial functions, shown as solid lines in Fig. 5. The apparent brightness parameter  of each SN Ia is corrected for the value taken by the corresponding function at the redshift of the supernova.
of each SN Ia is corrected for the value taken by the corresponding function at the redshift of the supernova.
The mu-bias from the nearby and SNLS subsamples decreases with redshift as expected from a selection bias giving brighter SNe Ia with increasing redshift. The SDSS-II sample, however, has a mu-bias that is essentially flat with redshift. This flat (or slightly positive) bias at the high-redshift end of the SDSS-II sample occurs when intrinsic color scatter is considered. It arises from a compensation of the selection of positive brightness fluctuations by the selection of blue color fluctuations. The correction itself is strongly uncertain (in particular above z> 0.3) because the color dependency of the SDSS selection function is itself uncertain. The relatively flat bias correction for the SDSS data is a feature of the spectroscopic selection efficiency; the photometric selection used in Campbell et al. (2013) results in a significant increase in bias with redshift.
The uncertainty in the bias correction is computed by propagating the statistical uncertainty in the polynominal coefficients to the uncertainty on  , forming an additional covariance matrix Cbias. We also estimate systematic uncertainties on the bias correction by varying uncertain parameters in the simulation, such as the intrinsic brightness of SNe Ia, the evolution of SN Ia rate and the underlying cosmology, over the ranges allowed by current data. In each case, we derive error estimates from the difference between the baseline analysis and the alternative, and add them to the Cbias matrix. We do not consider the uncertainty on the intrinsic scatter model as a source of systematic error here because it is already accounted for as part of the light-curve model uncertainty (Sect. 4.4).
, forming an additional covariance matrix Cbias. We also estimate systematic uncertainties on the bias correction by varying uncertain parameters in the simulation, such as the intrinsic brightness of SNe Ia, the evolution of SN Ia rate and the underlying cosmology, over the ranges allowed by current data. In each case, we derive error estimates from the difference between the baseline analysis and the alternative, and add them to the Cbias matrix. We do not consider the uncertainty on the intrinsic scatter model as a source of systematic error here because it is already accounted for as part of the light-curve model uncertainty (Sect. 4.4).
 |
Fig. 5 Bias corrections computed from Monte Carlo simulations of the cosmological analysis (see Eq. (9)). Error bars show the statistical uncertainty of the correction due to MC noise and uncertainty in the selection function. The smallest error bars show the contribution from Monte Carlo noise alone. |
5.4. Propagation of the photometric calibration uncertainties
The systematic uncertainty induced by calibration uncertainties on light-curve parameters is described by the covariance matrix: 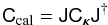 (10)where Cκ is the covariance matrix of κ described in Sect. 3.4 and J is the Jacobian matrix of light-curve parameters with respect to the calibration uncertainties. Defining the vector of light-curve parameters
(10)where Cκ is the covariance matrix of κ described in Sect. 3.4 and J is the Jacobian matrix of light-curve parameters with respect to the calibration uncertainties. Defining the vector of light-curve parameters 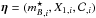 where i runs over all the SNe Ia in the sample, the matrix J can be written as J = (∂η/∂κ).
where i runs over all the SNe Ia in the sample, the matrix J can be written as J = (∂η/∂κ).
We set up a pipeline to compute J numerically. The derivatives are obtained by shifting each calibration quantity by a small amount from its fiducial value (0.01 mag for zero-points and 1 nm for central wavelengths) and determining both η and the SALT2 model spectral surfaces again. Thus, each partial derivative computation involves a full retraining of the SALT2 model. Neglecting the impact of the calibration uncertainties on the SALT2 training would result in a significant underestimate of their effect on the cosmology. To limit numerical and statistical noise arising in the computation, the derivatives are smoothed as a function of redshift10. Figure 6 illustrates the derivatives of light-curve parameters with respect to a zero-point shift in the MegaCam g filter. All SNe in the sample (not only the SNLS SNe) are affected by shifts of the SNLS calibration because any change to the training sample changes the SALT2 model, which affects all the SNe.
 |
Fig. 6 Effect of changing the zero-point in the g MegaCam filter by 10 mmag on light-curve parameters and distance modulus as a function of redshift for SNe in the low-z (blue crosses), SDSS (green squares), SNLS (orange circles) and HST (red ×) samples. The effect on the distance modulus is computed using the fiducial values α = 0.14 and β = 3.15. The dots show the numerical values of the derivatives (including numerical noise) before smoothing. |
5.5. The Hubble diagram covariance matrix
Following the prescription of the previous sections, we assemble a 3NSN × 3NSN = 2220 × 2220 covariance matrix for the light-curve parameters including statistical and systematic uncertainties. 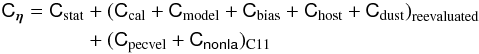 (11)Cstat is obtained from error propagation of light-curve fit uncertainties as described in G10, Appendix B. We consider a total of 7 sources of systematic uncertainty. The computation of the systematic uncertainty matrices associated with the calibration Ccal, the light-curve model uncertainty Cmodel, the bias correction uncertainty Cbias, and the mass step uncertainty Chost were described above in Sects. 5.4, 4.4, 5.3 and 5.2, respectively. The model for systematic uncertainties in the peculiar velocity corrections and the contamination of the Hubble diagram by non-Ia are directly taken from C11. As done in C11, we include Milky-Way extinction as part of the light-curve fitting model. However, we consider a correlated systematic uncertainty twice as large (20%) in the E(B − V) values, to encompass the systematic deviations found in Schlafly & Finkbeiner (2011). The net effect of this increased uncertainty is to decrease the weight of extinguished SNe Ia in the cosmology fit, which reduces the sensitivity of our analysis to incorrect determinations for Milky Way dust extinction.
(11)Cstat is obtained from error propagation of light-curve fit uncertainties as described in G10, Appendix B. We consider a total of 7 sources of systematic uncertainty. The computation of the systematic uncertainty matrices associated with the calibration Ccal, the light-curve model uncertainty Cmodel, the bias correction uncertainty Cbias, and the mass step uncertainty Chost were described above in Sects. 5.4, 4.4, 5.3 and 5.2, respectively. The model for systematic uncertainties in the peculiar velocity corrections and the contamination of the Hubble diagram by non-Ia are directly taken from C11. As done in C11, we include Milky-Way extinction as part of the light-curve fitting model. However, we consider a correlated systematic uncertainty twice as large (20%) in the E(B − V) values, to encompass the systematic deviations found in Schlafly & Finkbeiner (2011). The net effect of this increased uncertainty is to decrease the weight of extinguished SNe Ia in the cosmology fit, which reduces the sensitivity of our analysis to incorrect determinations for Milky Way dust extinction.
The distance estimate of Eq. (4) can be rewritten with matrix notation by forming a matrix11A such that: 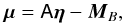 (12)with the components of the intrinsic luminosity vector MB given by Eq. (5). The covariance matrix of the vector of distance modulus estimates μ is
(12)with the components of the intrinsic luminosity vector MB given by Eq. (5). The covariance matrix of the vector of distance modulus estimates μ is 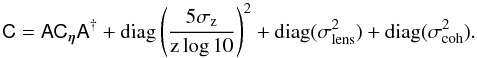 (13)The last three terms account for the uncertainty in cosmological redshift due to peculiar velocities, the variation of magnitudes caused by gravitational lensing, and the intrinsic variation in SN magnitude not described by the other terms. Our approximation of redshift uncertainties by magnitude uncertainties is a good approximation only at low redshift, but this term is negligible at higher redshifts. We follow C11 in using cσz = 150km s-1, as well as σlens = 0.055 × z as suggested in Jönsson et al. (2010). We now discuss further the estimate of σcoh.
(13)The last three terms account for the uncertainty in cosmological redshift due to peculiar velocities, the variation of magnitudes caused by gravitational lensing, and the intrinsic variation in SN magnitude not described by the other terms. Our approximation of redshift uncertainties by magnitude uncertainties is a good approximation only at low redshift, but this term is negligible at higher redshifts. We follow C11 in using cσz = 150km s-1, as well as σlens = 0.055 × z as suggested in Jönsson et al. (2010). We now discuss further the estimate of σcoh.
In the analysis of C11 (their Sect. 3.4), an intrinsic variation term, σint in that paper, was determined for each supernova sample, requiring that the best fit χ2 per degree of freedom in a specific cosmological fit with Ωm and w as free parameters be equal to 1. It has been mentioned by several authors, including C11, that this procedure precludes statistical tests of the adequacy of the cosmological model to describe the data.
One possibility to circumvent this problem is to introduce additional degrees of freedom in the fit of the Hubble diagram so that the best fit χ2 value is dominated by the scatter of the Hubble residuals at similar redshifts and is insensitive to the choice of the fiducial cosmological model. A simple implementation splits the SNe into several redshift bins and fits an arbitrary average offset for each of bin when determining the best fit χ2.
The restricted log-likelihood (the REML method, see, e.g., Harville 1977) 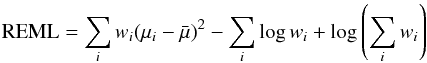 (14)is defined for each bin and is minimized to determine the offset
(14)is defined for each bin and is minimized to determine the offset  and σcoh for that bin. The
and σcoh for that bin. The  are the inverses of the diagonal elements of C, which contains the
are the inverses of the diagonal elements of C, which contains the  terms (Eq. (13)). The minimum of the REML provides an unbiased estimate of
terms (Eq. (13)). The minimum of the REML provides an unbiased estimate of 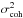 .
.
We compute σcoh for only seven subsamples in order to have sufficient statistical precision: two bins for the low-z sample split at the average redshift of z = 0.03, two bins for SDSS-II SNe split at z = 0.2, two bins for SNLS split at z = 0.5, and a single bin for the few HST supernovae. The results are shown in Fig. 7. The error bars represent 68% confidence levels based on the values of the REML. This likelihood is almost Gaussian for the subsamples considered here (except for the small HST sample).
The values of σcoh are compatible with a constant value of 0.106 ± 0.006 (with χ2 = 7.2 for six degrees of freedom) despite an apparent trend with redshift12. However, other factors may affect our results including survey-dependent errors in estimating the measurement uncertainty, survey dependent errors in calibration, and a redshift dependent tension in the SALT2 model which might arise because different redshifts sample different wavelength ranges of the model. In addition, the fit value of σcoh in the first redshift bin depends on the assumed value of the peculiar velocity dispersion (here 150 km s-1) which is somewhat uncertain.
We follow the approach of C11 which is to use one value of σcoh per survey. We consider the weighted mean per survey of the values shown in Fig. 7. Those values are listed in Table 9 and are consistent with previous analysis based on the SALT2 method (Conley et al. 2011; Campbell et al. 2013).
 |
Fig. 7 Values of σcoh determined for seven subsamples of the Hubble residuals: low-zz< 0.03 and z> 0.03 (blue), SDSS z< 0.2 and z> 0.2 (green), SNLS z< 0.5 and z> 0.5 (orange), and HST (red). |
6. ΛCDM constraints from SNe Ia alone
The SN Ia sample presented in this paper covers the redshift range 0.01 <z< 1.2. This lever-arm is sufficient to provide a stringent constraint on a single parameter driving the evolution of the expansion rate. In particular, in a flat universe with a cosmological constant (hereafter ΛCDM), SNe Ia alone provide an accurate measurement of the reduced matter density Ωm. However, SNe alone can only measure ratios of distances, which are independent of the value of the Hubble constant today (H0 = 100 h km s-1 Mpc-1). In this section we discuss ΛCDM parameter constraints from SNe Ia alone. We also detail the relative influence of each incremental change relative to the C11 analysis.
Values of σcoh used in the cosmological fits.
6.1. ΛCDM fit of the Hubble diagram
Using the distance estimator given in Eq. (4), we fit a ΛCDM cosmology to supernovae measurements by minimizing the following function: 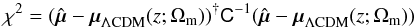 (15)with C the covariance matrix of
(15)with C the covariance matrix of 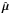 described in Sect. 5.5 and computed for a fixed fiducial value13 of H0 = 70km s-1 Mpc-1, assuming an unperturbed Friedmann-Lematre-Robertson-Walker geometry, which is an acceptable approximation (Ben-Dayan et al. 2013). The free parameters in the fit are Ωm and the four nuisance parameters α, β,
described in Sect. 5.5 and computed for a fixed fiducial value13 of H0 = 70km s-1 Mpc-1, assuming an unperturbed Friedmann-Lematre-Robertson-Walker geometry, which is an acceptable approximation (Ben-Dayan et al. 2013). The free parameters in the fit are Ωm and the four nuisance parameters α, β, 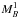 and ΔM from Eq. (4). The Hubble diagram for the JLA sample and the ΛCDM fit are shown in Fig. 8. We find a best fit value for Ωm of 0.295 ± 0.034. The fit parameters are given in the first row of Table 10.
and ΔM from Eq. (4). The Hubble diagram for the JLA sample and the ΛCDM fit are shown in Fig. 8. We find a best fit value for Ωm of 0.295 ± 0.034. The fit parameters are given in the first row of Table 10.
For consistency checks, we fit our full sample excluding systematic uncertainties and we fit subsamples labeled according to the data included: SDSS+SNLS, lowz+SDSS and lowz+SNLS. Confidence contours for Ωm and the nuisance parameters α, β and ΔM are given in Fig. 9 for the JLA and the lowz+SNLS sample fits. The correlation between Ωm and any of the nuisance parameters is less than 10% for the JLA sample.
 |
Fig. 8 Top: Hubble diagram of the combined sample. The distance modulus redshift relation of the best-fit ΛCDM cosmology for a fixed H0 = 70 km s-1 Mpc-1 is shown as the black line. Bottom: residuals from the best-fit ΛCDM cosmology as a function of redshift. The weighted average of the residuals in logarithmic redshift bins of width Δz/z ~ 0.24 are shown as black dots. |
Best-fit ΛCDM parameters for SNe Ia alone.
 |
Fig. 9 68% and 95% confidence contours for the ΛCDM fit parameters. Filled gray contours result from the fit of the full JLA sample; red dashed contours from the fit of a subsample excluding SDSS-II data (lowz+SNLS). |
The ΛCDM model is already well constrained by the SNLS and low-z data thanks to their large redshift lever-arm. However, the addition of the numerous and well-calibrated SDSS-II data to the C11 sample is interesting in several respects. Most importantly, cross-calibrated accurately with the SNLS, the SDSS-II data provide an alternative low-z anchor to the Hubble diagram, with better understood systematic uncertainties. This redundant anchor adds some weight in the global ΛCDM fit, thanks to high statistics, and helps in the determination of Ωm with a 25% reduction in the total uncertainty.
The complete redshift coverage makes it possible to assess the overall consistency of the SN data with the ΛCDM model. Residuals from the ΛCDM fit can be seen for the entire redshift range in the bottom panel of Fig. 8. The consistency is better assessed when residuals are binned by survey as in Fig. 10. A notable feature of this plot is the high statistical precision of the SDSS data, constraining the mean relative distance at z ~ 0.16 with an accuracy of 0.007 mag (statistical error only).
 |
Fig. 10 Residuals from the ΛCDM fit of the JLA Hubble diagram by survey. The weighted bin average and error bars are computed without systematic uncertainties. We further distinguish the different low-z surveys, the four non-contiguous SNLS fields, and the nothern and southern part of the SDSS stripe. |
The large number of SNe from the SDSS-II also improves constraints on the nuisance parameters as can be seen in Fig. 9. In particular, the mass step parameter is measured more accurately with SDSS-II data (Table 10, row 3 vs. 5).
Finally, the region of overlap between the SDSS-II and SNLS in the redshift range 0.2 <z< 0.4 provides an opportunity to assess the accuracy of the bias corrections (Sect. 5.3). In this redshift range, we can compare distance estimates from the complete SNLS sample to the distance estimates from the incomplete SDSS-II sample. The upper panel in Fig. 11 presents the evolution with redshift of the mean color of the SNLS and SDSS-II samples. The residuals from the Hubble diagram are shown on the lower panel in the same plot. The shift in mean color induced by selection bias becomes about −0.08 mag at z ~ 0.35 for the SDSS-II sample (a value comparable to the bias in the SNLS sample at z ~ 0.9). Nevertheless, distances measured from the SDSS-II and SNLS SNe at z ~ 0.35 are in good agreement, giving confidence in the bias corrections. For example, a β value error of −1 would appear in this plot as a bias of ~−0.08 in SDSS-II distances at z ~ 0.35, a possibility which is excluded by the data.
 |
Fig. 11 Top: average color of the samples in redshift bins. The low-z (blue crosses), the SDSS-II (green squares) and the SNLS (orange circles) samples are binned separately. The plot provides a visual assessment of the selection bias affecting each survey. Bottom: residuals from the ΛCDM fit of the JLA Hubble diagram as a function of redshift. The different surveys are shown separately. |
6.2. The relative importance of the sources of uncertainty
Section 5.5 presents our composite model (Eq. (11)) of the measurement error. To gain insight into the relative importance of each component, we decompose the variance V of the fit parameter Ωm. Close to the likelihood maximum, the fit parameters θ are determined from the measurements by: 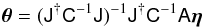 (16)where J is the Jacobian matrix at the maximum likelihood. Defining W = (J†C-1J)-1J†C-1A, we evaluate the contribution Vx of each component x from Eq. (11) using
(16)where J is the Jacobian matrix at the maximum likelihood. Defining W = (J†C-1J)-1J†C-1A, we evaluate the contribution Vx of each component x from Eq. (11) using  (17)We report the diagonal entries of Vx for the Ωm parameter (denoted
(17)We report the diagonal entries of Vx for the Ωm parameter (denoted 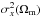 ) in Table 11. As an aid to interpretation, we also report in Table 11
) in Table 11. As an aid to interpretation, we also report in Table 11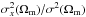 as a percentage of the total variance. These values are not the result of a proper sensitivity analysis because the weights are held fixed, but they provide a useful, qualitative overview of the relative importance of the uncertainties.
as a percentage of the total variance. These values are not the result of a proper sensitivity analysis because the weights are held fixed, but they provide a useful, qualitative overview of the relative importance of the uncertainties.
Contribution of various source of measurement uncertainties to the uncertainty in Ωm.
Calibration uncertainties still stand out as the dominant systematic, but the improvement in the accuracy of the calibration, made possible by the joint calibration analysis, results in an uncertainty that is smaller than the statistical uncertainty. And fitting our sample using the calibration uncertainties from C11 would have produced a 15% increase in the uncertainty, with the contribution from calibration uncertainty dominating all the other sources. On the other hand, in spite of a conservative estimate, the uncertainty on the bias correction does not significantly affect the overall accuracy of the Ωm estimate.
Uncertainties associated with the SALT2 model and host relation are still subdominant assuming that the standardization model of Eq. (4) holds and, in particular, that the host-mass-luminosity relation of Eq. (5) captures the full effect of the environmental dependence. As already mentioned, the subject is an open question, and we discuss it further below.
6.3. Assessment of the mass step correction
Recent analyses of large samples of type Ia supernovae have produced evidence for a remaining environmental dependence of the SN Ia shape and color-corrected luminosities. Correlations were found (see Sect. 5.2) between the Hubble residuals and several characteristics of host galaxies (stellar mass, star formation rate, inferred stellar age, metallicity) which evolve with redshift and are therefore likely to cause a bias if not corrected. Unfortunately, no correction for these effects based on measured SN Ia light-curve properties is known.
The most significant empirical correlation is with the host mass. Therefore, a correction for this effect was adopted in the C11 analysis, which we also use in the present analysis. It takes the form given in Eq. (5), namely a step function of the host mass, which is the functional form suggested by current data (see, e.g., Childress et al. 2013; Johansson et al. 2013b).
We confirm the measurement of a non-zero mass dependent step in Hubble residuals at 5σ in our sample. In the framework of ΛCDM, we determine ΔM =−0.061 ± 0.012 for the full JLA sample, including all systematic uncertainties except the uncertainty from the mass step correction itself (Eq. (8)). The Hubble residuals of the JLA sample as a function of the host galaxy stellar mass are shown in Fig. 12.
 |
Fig. 12 Residuals from the ΛCDM fit of the JLA Hubble diagram as a function of the host galaxy mass. The fit does not include the mass step correction. Binned residuals are shown as black squares. The red line shows the mass step correction for a step at Mstellar = 1010 M⊙. |
Drift in the parameters with respect to the C11 analysis.
Since there is no clear understanding of the underlying phenomena, it is important to explore possible models for this apparent mass step effect. Rigault et al. (2013, Sect. 6.1.2) propose an alternative explanation for the mass step origin that involves a subclass of SNe Ia, peculiar to passive environments, that are about 0.26 mag brighter than the bulk of the population after standardization. In this model, the mean intrinsic magnitude of SNe Ia in passive and active environment differs by a quantity denoted Δα due to this subclass. The subclass is also subdominant in low-mass host galaxies, explaining the observed mass step. Assuming that the proportion of SNe Ia from active environments follows the specific star formation rate, this model predicts that an evolution of the induced mass step with redshift is possible, in which case a redshift-independent mass step correction is incorrect.
In this model, the predicted bias on cosmology can be computed and is directly related to the evolution of the mass step. Fig. 13 shows the mass steps measured as a function of redshifts for the JLA sample. Our data does not show any significant evolution of the mass step with redshift and therefore allowing for an evolution of the mass step in the cosmology fit has little effect on the result, shifting Ωm by only −0.002 for example. Further splitting Hubble residuals between globally passive and globally star-forming hosts in the SNLS and SDSS subsamples does not show measurable difference after correcting for the mass-step. A significant remaining environmental bias unrelated to the mass effect is therefore unlikely.
 |
Fig. 13 Measurements of the mass step in four redshift bins: z< 0.18, 0.18 ≤ z< 0.31, 0.31 ≤ z< 0.6, z> 0.6. The dashed line shows the measured value for a redshift-independent mass step. |
Alternatively, Shafer & Huterer (2014) address the issue of environmental dependence by introducing three independent pairs of M parameters in three redshift bins. This approach suppresses the cosmological information on SN distance ratios across those bins. In our sample, it is roughly equivalent to fitting only the low redshift slice (z< 0.5) which is the one with the largest weight. Again the shift in cosmological parameter is small (ΔΩm = 0.007) and compatible with the statistical fluctuation expected from the change in the model14. The recovered M parameters are also compatible across the three bins.
Overall, our sample does not provide evidence for a significant evolution of the mass step in the covered redshift range15. Because the evidence for this model is weak and the uncertainty of our baseline model is already consistent with the results from alternative models, we have not increased the systematic error associated with variations in the SN environment, leaving our analysis of this effect the same as that of C11.
6.4. Comparison with the C11 analysis
Our best fit value for Ωm differs from the value published in C11 (Ωm =0.228 ± 0.038 ) by 1.8σ (stat+sys). This discrepancy is not simply a statistical fluctuation because a large part of the data sample remains the same. The C11 value was dependent on the light-curve model and we discuss that difference below.
6.4.1. SALT2/SiFTO differences in the C11 analysis
The upper part of Table 12 provides the best-fit ΛCDM parameters for the C11 sample. The “C11 combined” analysis combines light-curve parameters derived from the SALT2 and SiFTO light-curve models. We also report separately the results obtained from the two models.
As previously noted in Planck Collaboration XVI (2014, Sect. 5.4) the light-curve parameters and covariance matrices obtained for the SiFTO light-curve model lead to an Ωm value significantly lower than that obtained from the SALT2 analysis. Interestingly, the comparison of the SiFTO and SALT2 analyses obtained when the systematic uncertainties are not taken into account (“stat” rows in Table 12) produces a difference with the opposite sign, with the SiFTO value increasing by 0.047 (>2σ stat). Applying SiFTO systematic uncertainties to the SALT2 Hubble diagram results in a smaller but still significant shift (0.027 in Ωm).
The inclusion of systematic uncertainties in the fit, particularly calibration uncertainties, alters the relative weight of each survey in the global fit. The shift in Ωm when the weighting is changed is evidence of tensions between the C11 Hubble diagram and the ΛCDM model. The present analysis does not exhibit the same behavior. The best-fit parameters do not change significantly when including systematic uncertainties in the fit, as witnessed by the two first rows in Table 1016. In particular the difference in Ωm is only 0.006.
We conclude that the SiFTO/SALT2 differences observed in the C11 analysis are related to tensions between the C11 datasets (before the recalibration of the present study) and the ΛCDM model, and that the tensions are reduced by the recalibration. Those tensions result in differences between SALT2 and SiFTO analyses because of different weights assigned to SNe on the Hubble diagram rather than differences in the models.
6.4.2. Differences with the C11 SALT2 analysis
To further understand the relative impact of the changes introduced by the present analysis, we decompose the list of changes given at the beginning of Sect. 5, taking C11 SALT2 (stat) as a starting point. For the purposes of this discussion we will distinguish three steps. For the first step, we employ the changes in analysis relative to C11, namely the changes in the SALT2 training procedure (item 2), the revision of host-mass estimates (item 6), the change in the computation of bias corrections (item 7) and the revision of low-z measurement uncertainties (items 9 and 10). Together, these changes constitute a fully consistent reanalysis of the C11 sample that we label “C11-reanalyzed”. In a second step we apply the B13 recalibration to the SNLS and first-year SDSS light curves (item 1). This constitutes the recalibrated-reanalysis of the C11 sample that we label “C11-recalibrated”. Finally, we include the full, recalibrated, SDSS-II spectroscopic dataset in both the training and the cosmology sample (items 3 and 4), which is the final JLA result.
We performed a ΛCDM fit for each of these three steps; the results are reported in the bottom part of Table 12. We consider only the statistical uncertainties in these fits, so that changes in parameters cannot be attributed to different interpretations of systematic uncertainties. The full reanalysis of the C11 sample (C11-reanalyzed) is consistent with the C11 SALT2 results. The recalibration is the most important effect, shifting Ωm by 0.06 (i.e., 3σ of the statistical uncertainty). The most important calibration changes are the revision of the MegaCam zero-points in the g band (by 0.012 or ~3σ) and z band (by 0.018 or ~1σ), and the corrections to the MegaCam r and i filter bandpasses (~3 nm on the central wavelength). The revision of SNLS zero-points included the correction of a sign error (described in B13, Sect. 10.4) and the addition of more calibration data, including SDSS calibration data and direct observations of HST standards (see Sect. 3). We note that, after recalibration, the ΛCDM model is a better fit to the data with a χ2 decrease of ~20. Adding the full SDSS-II sample to both the training and cosmology sample leaves the Ωm value virtually unchanged but further reduces the uncertainty.
The β values in Table 12 vary by as much as 0.6, much larger than the ~0.1 uncertainty. As discussed in M14, the color definition, training procedure, and selection biases can introduce a bias on beta that is comparable to the variations seen in Table 12. Since β is a nuissance parameter, we do not attempt to report bias-corrected values. However, its impact on the cosmology analysis has been included in M14 and in the systematic uncertainties reported here.
6.5. Differences with the SDSS first year data analysis
The first-season SDSS-II analysis (Kessler et al. 2009a) reported two different sets of distances17 computed using the SALT2 model and the MLCS2k2 model (Jha et al. 2007). Fitting the ΛCDM model to the nearby+SDSS sample gives respectively Ωm = 0.340 ± 0.083stat for the SALT2 model, and Ωm = 0.278 ± 0.084stat for the MLCS2k2 model18. The difference in these two results was traced to the difference between light-curve models, particularly in the rest-frame ultraviolet region, and to the contribution of the observed SN color to the standardized SN magnitude. In addition to the obvious improvements in sample size and calibration uncertainty, this JLA result substantially reduces the uncertainties in the earlier SDSS-II analysis.
The SALT2 model has been retrained with the full SDSS-II sample, which, like the lower redshift SN data, contains significant data in the observer-frame ultraviolet wavelength range. In addition, we have examined the accuracy and consistency of the other low redshift data as described in detail in Appendix B. These studies have resulted in an improved SALT2 model and model errors that are consistent with the data. We did not attempt to retrain MLCS2k2, partly because of the significant effort that would be required, but primarily because we favor use of SALT2, which models details of the SN Ia spectrum.
Another result of the Kessler et al. (2009a) SALT2 analysis was evidence for a variation in the effective value of the standardized magnitude–color correlation parameter β with redshift. This potential systematic was addressed in G10 and found to be an artifact of poorly determined model uncertainties. Here we perform extensive end-to-end simulations including the interrelated problems of intrinsic scatter, correlations between color and standardized magnitude, and selection effects (particularly Malmquist bias). The basic technique is to measure the sensitivity to different spectral variations that are consistent with the SALT2 light-curve residuals. These simulations were not available in previous analyses. The studies of intrinsic scatter (K13) and systematic uncertainties from the SALT2 method (M14) show that the SN light-curve data are consistent with a redshift independent value of β.
 |
Fig. 14 Comparison of various measurements of Ωm for a ΛCDM cosmology. |
6.6. Comparison with other measurements of Ωm
The comparison of our ΛCDM constraints with other analyses and datasets is summarized in Fig. 14. Our value is in good agreement with the CMB value from Planck (Planck Collaboration XVI 2014), eliminating the previously noted ~2σ discrepancy between Planck and C11. As discussed in Sect. 6.4.2, this change is primarily a result of the recalibration of the SDSS-II and SNLS light curves. The recalibration analysis elucidated and corrected an unanticipated systematic effect (the aging of MegaCam r and i band filters, see Sect. 3.2), and is further bolstered by more precise and redundant calibration observations. We conclude, therefore, that the previously found discrepancy should be attributed to systematic errors in the supernova measurements and that, with our new analysis, the two probes yield consistent measurements of Ωm in the ΛCDM model. Our value is also compatible with the Ωm ΛCDM measurement from WMAP9 (Hinshaw et al. 2013). The CMB measurement of Ωm with Planck and our SN measurement would have comparable precision, if systematic uncertainties in the SN analysis were neglected, showing that, despite notable improvements, systematic measurement uncertainties remain a crucial issue.
Our measurement is also in agreement with the SN Ia measurement from the Union 2.1 sample (Suzuki et al. 2012). This is not, however, a fully independent confirmation as both analyses share part of the dataset and methodology. There are nonetheless notable differences between the two SN samples: the second and third years of the SDSS-II and SNLS surveys, which constitute the large majority of our sample, are not part of Suzuki et al. (2012) while the ESSENCE survey (Miknaitis et al. 2007), most of the high-z HST supernovae, as well as some older samples are included in the Union 2.1 sample.
7. Dark energy constraints from the combination of supernovae and complementary probes
The redshift lever arm of our SN Ia sample is insufficient to constrain all the parameters in more general dark energy models. In this section we combine SNe Ia with other probes to test extensions of the ΛCDM model. We do not seek to be comprehensive, but restrict our study to combining our SNe constraints with the most recent measurements of the CMB fluctuations and of the BAO scale.
7.1. Complementary data
7.1.1. Power spectrum of the cosmic microwave background fluctuations
The most recent measurement of the CMB temperature fluctuations has been provided by the 2013 release of the Planck experiment results (Planck Collaboration I 2014). This release is based on data gathered in the first 15.5 months of satellite operation. It delivered maps of temperature fluctuations over the entire sky in nine frequency bands (30−857 GHz). The analysis of Planck data exploits the multiwavelength coverage to determine the CMB temperature fluctuation power spectrum after removing the foreground emissions (Planck Collaboration XII 2014; Planck collaboration XV 2014). Their results are summarized by a likelihood function for the CMB spectrum given the Planck data (Planck collaboration XV 2014).
The CMB temperature power spectrum is directly sensitive to matter densities and measures precisely the angular diameter distance at the last-scattering surface (z ≈ 1090). This precise measurement of the early universe complements very well the SN Ia distance measurements in the late Universe. The combination produces constraints on dark-energy models that cannot be obtained from the CMB alone because of the geometric degeneracy.
For this analysis, we use the Planck measurement of the CMB temperature fluctuations and the WMAP measurement of the large-scale fluctuations of the CMB polarization (Bennett et al. 2013). This combination of CMB data is denoted “Planck+WP” to follow the nomenclature used by Planck Collaboration XVI (2014). We summarize the geometrical constraints inferred from those measurements by a Gaussian prior on the value of the baryon density today ωb = Ωbh2, the cold dark matter density today ωc = Ωch2, and θMC the CosmoMC approximation of the sound horizon angular size computed from the Hu & Sugiyama (1996) fitting formulae. This combination of parameters is well constrained by the temperature power spectrum and is independent of any assumptions about dark energy (for the range of models considered in this paper). The WMAP polarization information slightly improves the Planck constraints by reducing degeneracies, which involve the damping of small scale fluctuations by reionization and are unresolved by the temperature spectrum alone. Our prior has the form19: 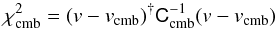 (18)where:
(18)where: 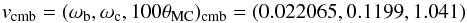 (19)and Ccmb is the best fit covariance matrix for v (marginalized over all other parameters):
(19)and Ccmb is the best fit covariance matrix for v (marginalized over all other parameters): 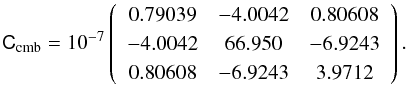 (20)The use of a distance prior is only an approximate summary of CMB constraints for dark energy. In particular, the sensitivity of the CMB to the late-time growth of structure is neglected. However, these effects are small, and our approximation is known to adequately represent more sensitive combinations such as CMB+SNe Ia and CMB+BAO (see, e.g., the discussions in Komatsu et al. 2011, Sect. 5.5 and references therein). Our approach has the advantage of being purely geometrical and easy to calculate. We provide a comparison of our results with the full Planck likelihood (Planck collaboration XV 2014) in Appendix D: in the case of a flat universe model with a constant equation of state, the difference in best fit values for w is less than 0.3σ and the uncertainties are the same. We provide the tools to use our data in investigations of more general dark energy models in which the above approximation is not valid (see Appendix F).
(20)The use of a distance prior is only an approximate summary of CMB constraints for dark energy. In particular, the sensitivity of the CMB to the late-time growth of structure is neglected. However, these effects are small, and our approximation is known to adequately represent more sensitive combinations such as CMB+SNe Ia and CMB+BAO (see, e.g., the discussions in Komatsu et al. 2011, Sect. 5.5 and references therein). Our approach has the advantage of being purely geometrical and easy to calculate. We provide a comparison of our results with the full Planck likelihood (Planck collaboration XV 2014) in Appendix D: in the case of a flat universe model with a constant equation of state, the difference in best fit values for w is less than 0.3σ and the uncertainties are the same. We provide the tools to use our data in investigations of more general dark energy models in which the above approximation is not valid (see Appendix F).
Best fit parameters for the o-ΛCDM cosmological model.
Best fit parameters for the flat w-CDM cosmological model.
Best fit parameters for the flat wz-CDM cosmological model. The point (w0,wa) = ( − 1,0) corresponds to the cosmological constant hypothesis.
Planck also provides a reconstruction of the CMB weak-lensing potential (Planck Collaboration XVII 2014) that breaks part of the geometric degeneracy that arises from the CMB temperature spectrum alone. Better constraints on the foreground contamination of the temperature spectrum can also be obtained from higher resolution experiments, such as the Atacama Cosmology Telescope (Das et al. 2014) and the South Pole Telescope (Reichardt et al. 2012). Exhaustive investigations of constraints provided by the various combinations of CMB data are conducted in Planck Collaboration XVI (2014). These results suggest little difference from the additional lensing and high-ℓ likelihoods in dark energy studies when used in combination with later distance measurements such as SNe Ia and BAOs. Therefore, we do not consider their use in the present study.
We also present constraints obtained in combination with WMAP for comparison (labeled WMAP9). For this purpose, we use the distance prior given in Hinshaw et al. (2013, Sect. 4.6.1).
7.1.2. Baryon acoustic oscillations
The detection of the characteristic scale of the BAO in the correlation function of different matter distribution tracers provides a powerful standard ruler to probe the angular-diameter-distance versus redshift relation and Hubble parameter evolution. The BAO scale has now been detected in the correlation function of various galaxy surveys (Eisenstein et al. 2005; Beutler et al. 2011; Blake et al. 2011; Anderson et al. 2012), as well as in the Lyα forest of distant quasars (Busca et al. 2013; Slosar et al. 2013). Large-scale surveys also probe the horizon size at matter-radiation equality. However, this latter measurement appears to be more affected by systematic uncertainties than the robust BAO scale measurement.
BAO analyses usually perform a spherical average of their scale measurement constraining a combination of the angular scale and redshift separation: 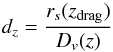 (21)with:
(21)with: 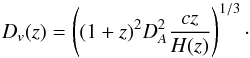 (22)For this work, we follow Planck Collaboration XVI (2014) in using the measurement of the BAO scale at z = 0.106,0.35, and 0.57 from Beutler et al. (2011); Padmanabhan et al. (2012); Anderson et al. (2012), respectively. We consider a BAO prior of the form:
(22)For this work, we follow Planck Collaboration XVI (2014) in using the measurement of the BAO scale at z = 0.106,0.35, and 0.57 from Beutler et al. (2011); Padmanabhan et al. (2012); Anderson et al. (2012), respectively. We consider a BAO prior of the form: 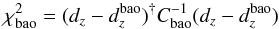 (23)with zdrag computed from the Eisenstein & Hu (1998) fitting formulae,
(23)with zdrag computed from the Eisenstein & Hu (1998) fitting formulae, 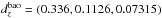 and
and 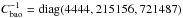 .
.
7.2. Constraints on cosmological parameters for various dark energy models
We consider three alternatives to the base ΛCDM model:
-
The one-parameter extension allowing for non-zero spatial curvature Ωk, labeled o-ΛCDM.
-
The one-parameter extension allowing for dark energy in a spatially flat universe with an arbitrary constant equation of state parameter w, labeled w-CDM.
-
The two-parameter extension allowing for dark energy in a spatially flat universe with a time varying equation of state parameter parameterized as w(a) = w0 + wa(1 − a) with a = 1/(1 + z) (Linder 2003) and labeled wz-CDM.
We follow the assumptions of Planck Collaboration XVI (2014) to achieve consistency with our prior. In particular we assume massive neutrinos can be approximated as a single massive eigenstate with mν = 0.06 eV and an effective energy density when relativistic: 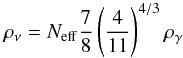 (24)with ργ the radiation energy density and Neff = 3.046. We use Tcmb = 2.7255 K for the CMB temperature today.
(24)with ργ the radiation energy density and Neff = 3.046. We use Tcmb = 2.7255 K for the CMB temperature today.
Best-fit parameters for different probe combinations are given in Tables 13–15. Errors quoted in the tables are 1σ Cramér-Rao lower bounds from the approximate Fisher Information Matrix. Confidence contours corresponding to Δχ2 = 2.28 (68%) and Δχ2 = 6 (95%) are shown in Figs. 15−17. For all studies involving SNe Ia, we used likelihood functions similar to Eq. (15), with both statistical and systematic uncertainties included in the computation of C. We also performed fits involving the SNLS+SDSS subsample and the C11 “SALT2” sample for comparison (see Sect. 6).
 |
Fig. 15 68% and 95% confidence contours (including systematic uncertainty) for the Ωm and ΩΛ cosmological parameters for the o-ΛCDM model. Labels for the various datasets correspond to the present SN Ia compilation (JLA), the Conley et al. (2011) SN Ia compilation (C11), the combination of Planck temperature and WMAP polarization measurements of the CMB fluctuation (Planck+WP), and a combination of measurements of the BAO scale (BAO). See Sect. 7.1 for details. The black dashed line corresponds to a flat universe. |
 |
Fig. 16 Confidence contours at 68% and 95% (including systematic uncertainty) for the Ωm and w cosmological parameters for the flat w-ΛCDM model. The black dashed line corresponds to the cosmological constant hypothesis. |
In all cases the combination of our supernova sample with the two other probes is compatible with the cosmological constant solution in a flat universe, which could have been anticipated from the agreement between CMB and SN Ia measurements of ΛCDM parameters (see Sect. 6.6). This concordance is the main result of the present paper. We note that this conclusion still holds if we use the WMAP CMB temperature measurement in place of the Planck measurement (see Table 14).
For the w-CDM model, in combination with Planck, we measure w =−1.018 ± 0.057. This represents a substantial improvement in uncertainty (30%) over the combination Planck+WP+C11 (w =−1.093 ± 0.078 ). The ~1σ (stat+sys) change in w is caused primarily by the recalibration of the SNLS sample as discussed in detail in Sect. 6. The improvement in errors is due to the inclusion of the full SDSS-II spectroscopic sample and to the reduction in systematic errors due to the joint recalibration of the SDSS-II and SNLS surveys. As an illustration of the relative influence of those two changes, using the C11 calibration uncertainties would increase the uncertainty of w to 6.5%.
Interestingly, the CMB+SNLS+SDSS combination delivers a competitive measurement of w with an accuracy of 6.9%, despite the absence of the low-z SNe Ia. This measurement is expected to be robust since the dominant systematic uncertainty (photometric calibration error) was the subject of careful review in the joint analysis of the SDSS-II and SNLS surveys. This subsample is also likely to be less sensitive to errors in the environmental dependence of the SN Ia luminosity as the distribution of SNLS and SDSS host properties are closer than are the distribution of SNLS and low-z surveys. As an illustration, fitting the w-CDM model to the CMB+SNLS+SDSS data, and imposing ΔM = 0, provides w =−0.996 ± 0.069, a small shift (δw< 0.003) with respect to the value reported for the same sample and ΔM = −0.070 ± 0.023 in Table 14.
Combined with CMB and BAO, SNe Ia yields a 5.4% measurement of w which represents significantly tighter constraint than what can be obtained from CMB and BAO alone (11.0%). The combination of CMB, BAO and SNe Ia constrains models with a varying equation of state w =−0.957 ± 0.124 and wa =−0.336 ± 0.552 (see Table 15), yielding a figure of merit as defined by the dark energy task force (DETF; Albrecht et al. 2006) of 31.3. This is a factor 2 improvement in the FoM with respect to the C11+DR7+WMAP7 combination considered in Sullivan et al. (2011). This gain is attributable, for roughly equal parts, to our improvement in SN measurements and to the improvement in CMB and BAO external constraints.
 |
Fig. 17 Confidence contours at 68% and 95% (including systematic uncertainty) for the w and wa cosmological parameters for the flat w-ΛCDM model. |
Finally, the combination of CMB, BAO and SN Ia data constrains the value of the Hubble parameter H0 at better than 2% even in generic dark energy models. Our result, H0 =68.50 ± 1.27km s-1 Mpc-1, is slightly lower (1.9σ) than the direct measurement of H0 = 73.8 ± 2.4km s-1 Mpc-1 given in Riess et al. (2011). A recalibration of the absolute distance of NGC 4258, one of the three distance anchors involved in this direct measurement, is given in Humphreys et al. (2013). They report a slightly smaller value determined from this anchor H0 = 72.0 ± 3.0km s-1 Mpc-1. In addition, Efstathiou (2014) suggests that possible biases were introduced in the Cepheid period-luminosity relation by subluminous low metallicity Cepheids and shows some sensitivity of the results to outlier rejections. He finds, using a revised outlier rejection algorithm, H0 = 70.6 ± 3.3km s-1 Mpc-1, using only the recalibrated NGC 4258 distance anchor and H0 = 72.5 ± 2.5km s-1 Mpc-1 combining the three anchors. In conclusion, the recalibrated direct measurement of H0 improves agreement (1.4σ) with our indirect determination.
8. Summary and perspectives
We have reported improved cosmological constraints from the Hubble diagram of type Ia supernovae, based on a joint analysis of the SNLS and SDSS-II SN Ia samples. These results are based on combining the SN Ia compilation assembled in Conley et al. (2011) by SNLS with the full SDSS-II three-year SN Ia sample (Sako et al. 2014). We have explicitly chosen not to include all newly available SN Ia data, and instead focus on the control of systematic uncertainties.
The results obtained here benefit from joint SNLS/SDSS analyses addressing dominant systematic issues. The effects of the systematic studies on the cosmological parameters were unknown until the systematic studies were completed; in this sense, our analysis is a “blind” analysis. The largest systematic error has been reduced by the notable improvement in the accuracy of the SNLS and SDSS photometric calibration that resulted from a joint analysis of the calibration data of both surveys (Betoule et al. 2013). The other major improvement was the result of detailed investigations of systematic uncertainties and biases associated with the model of the type-Ia supernovae spectral evolution (Kessler et al. 2013; Mosher et al. 2014). In particular, Mosher et al. (2014) performs a thorough analysis of the SALT2 light-curve model (Guy et al. 2007) used in the present analysis. Thanks to these analyses we are able to derive distances for 740SNe Ia with improved and well-understood measurement systematics. The data release is succinctly described in Appendix F.
In the ΛCDM model, the JLA sample provides a measurement of the reduced matter density parameter Ωm =0.295 ± 0.034, independent of the CMB measurement. Our result is in good agreement with the recent measurement from the Planck satellite. We show that the ~2σ disagreement previously observed with Conley et al. (2011) is largely eliminated when using the joint recalibration results reported in Betoule et al. (2013). Combining our sample with the Planck CMB measurement, we find no evidence for dynamical dark energy. Assuming a flat universe, we measure a constant dark-energy equation of state parameter of w =−1.018 ± 0.057, where both statistical and systematic uncertainties are included. In all the cases we considered, our results are compatible with the cosmological constant hypothesis.
About half of the gain in precision obtained with respect to the Conley et al. (2011) result arises from the improvement in the calibration accuracy. This demonstrates that substantial gain was obtained by working on improving calibration systematics. In spite of these improvements, the accuracy of the photometric calibration remains (by far) the limiting systematic uncertainty. However, there is no known reason why this situation cannot be improved in future surveys. Our result is based on a photometric calibration which is limited at the ~0.5% level by the accuracy of the primary stellar calibration standards. Further improvements, either in the accuracy of stellar spectrophotometric standards, or in the delivery of laboratory-made calibration sources, should make it possible to approach the current systematic limit of ~1 mmag with CCD-based photometric measurements (Astier et al. 2013). The use of CCD detectors with enhanced sensitivity in the near infrared will make it possible to observe low and high-redshift supernovae in more nearly similar rest-frame bands. Better wavelength coverage would alleviate the partial degeneracy between the cosmology, the calibration and the SNe Ia model, the degeneracy that is responsible for a large part of the sensitivity of cosmology to calibration uncertainties. In particular, the Dark Energy Survey (DES) experiment, which has just begun its high-redshift SNe survey (Bernstein et al. 2012), will exploit improved sensitivity in the infrared to reduce the model-calibration-cosmology degeneracy. Also DES, unlike SNLS, has a shallow survey (24 deg2) that will provide both high and medium redshift SN in the same experiment. DES will also have a continual, in situ, modeling of the filter transmission. All three features should ease the calibration problem. LSST should be even better than DES in both these respects. However, neither DES nor LSST will be able to spectroscopically identify a large fraction of their candidates because the required spectroscopic time would be prohibitive. Each survey will hence have to contend with the problem of contamination in their SN Ia samples. Several analyses have already addressed this issue (e.g., in SNLS and SDSS, Bazin et al. 2011; Campbell et al. 2013) and showed that good control of the contamination (<4%) can be reached.
According to our estimates, issues related to the environmental dependence of SNe Ia standardized luminosity contribute a subdominant part of the error budget. However, this conclusion is less robust than our understanding of other uncertainties because the phenomena are, at best, only partially understood. This topic is currently the subject of active research and there is hope that firm conclusions can be reached with increased statistics, complementary data (e.g., local properties of the SN environment, Stanishev et al. 2012) and possibly improved theoretical modeling. Increased statistics are already available: about 150 additional spectroscopically confirmed SNe Ia from the 5 year SNLS sample; extended samples from several low-z experiments (Stritzinger et al. 2011; Hicken et al. 2012); and numerous spectral data samples (Blondin et al. 2012; Silverman et al. 2012; Maguire et al. 2012; Pereira et al. 2013), which should provide better constraints on the SNe Ia model.
Online material
Appendix A: Visual inspection
In addition to the software cuts, we performed a visual inspection of the SN light-curve fits. We discarded the following SNe Ia, for which the SALT2 fits were particularly poor20:
-
1.
Fit probability <0.01 due to apparent problems in the photometry: SDSS739⋆, SDSS1316⋆, SDSS3256 (2005hn), SDSS6773 (2005iu), SDSS12780, SDSS12907, SDSS13327⋆, SDSS16287, SDSS16578⋆, SDSS16637⋆, SDSS17176⋆, SDSS18456, SDSS18643, SDSS19381 (2007nk), SDSS20376⋆, SDSS20528 (2007qr), SDSS21810⋆.
-
2.
Poor fit, probable 1986G-like: SDSS17886 (sn2007jh) (Stritzinger et al. 2011).
-
3.
Poor fit, 2002cx-like: SDSS20208 (sn2007qd) (McClelland et al. 2010; Foley et al. 2013).
-
4.
Pathological sampling leading to unstable fit results: SDSS17500⋆, SDSS16692⋆.
We also discarded the following four events that are >3σ outliers on the Hubble diagram:
-
1.
Over-luminous: SDSS14782 (2006jp), SDSS15369 (2006ln).
-
2.
Subluminous: SDSS15459 (2006la), SDSS17568 (2007kb).
Last, a proper and stable determination of the date of maximum is necessary for SNe Ia entering in the training sample, because the date of maximum is held fixed in the training. We looked for remaining poorly sampled light curves in the training sample, and discarded the following nine SNe (only from the training sample):
-
1.
Too few observations after the epoch of peak brightness(despite a reported uncertainty on t0 passing the cuts): SDSS10434, SDSS19899, SDSS20470, SDSS21510.
-
2.
Too few observations before the epoch of peak brightness: SDSS6780, SDSS12781, SDSS12853 (2006ey), SDSS13072, SDSS18768.
Appendix B: Details on calibration systematics
Appendix B.1: Consistency of the CfAIII and CSP photometric calibration
A few low-z SNe Ia have been observed contemporaneously with several telescopes which provides a way to assess their relative calibration. Mosher et al. (2012) studied nine spectroscopically confirmed Type Ia supernova observed by both the CSP and the SDSS-II surveys. The study provides us with stringent constraints on possible differences between the CSP calibration and the SDSS/SNLS calibration of B13. The Mosher et al. (2012) results are reproduced in Table B.1.
Calibration offsets.
Spectroscopically confirmed SNe Ia in common between CSP and CFA.
We performed a similar study on SNe Ia observed by both the CfAIII and CSP surveys. To increase the statistics available for this comparison, we consider SNe Ia from both the first (Contreras et al. 2010) and second (Stritzinger et al. 2011) CSP data release. The list of all SNe Ia in common is given in Table B.2.
We use SALT2 to interpolate between measurements (in phase and wavelength) as follows: for each SN Ia, we perform an initial fit using all available data to determine its shape, color, and date of maximum. Holding these parameters fixed, we redetermine the amplitude parameter x0 for each band independently. In a given band, comparing the values of obtained for two different instruments gives an estimate of the calibration difference between them. This method is similar to the S-correction and spline interpolation applied in Mosher et al. (2012). However, instead of transforming the CfA data to bring them to the CSP native system, both sets data are transformed in the same manner. Applied to the same sample, the two methods deliver very similar results.
We exclude peculiar type-Ia supernovae from the comparison. Light curves with aberrant photometric points were rejected: SN2005M U and r band light curves, SN2005ir, SN2006ev and SN2005mc r band. Finally, B, V and r′ band data for 2006hb are too long after maximum brightness to be reliably compared to CSP measurements. The results are given in the second part of Table B.1. Our analysis shows an excellent agreement in the B, V and i′ bands. The offset measured in r′ appears statistically significant, justifying the upward adjustment of the r′ calibration uncertainty quoted in C11. The U band also shows surprisingly good consistency considering the fact that CfAIII U band measurements are color-corrected to the Landolt system using a color transformation determined using ordinary stars. However, given the small number of SNe Ia in the U-band comparison, we are concerned that the agreement may be fortuitous and do not revise the 0.07 mag uncertainty used by Hicken et al. (2009). This choice of a relatively large U-band uncertainty is justified in Sect. B.2 where a SN U-band color-correction error is evaluated.
Appendix B.2: Errors induced by the color-transformation of nearby supernova measurements
A substantial fraction of our low-z sample is composed of SNe Ia with photometry reported in the Landolt system, which means that flux measurements in the natural system have been transformed to the Landolt system using color transformations determined by ordinary stars. This procedure introduces errors because SNe Ia have spectral properties different from those of main sequence stars (see, e.g., the discussion in Jha et al. 2006, Sect. 2.4, hereafter J06). Here we seek quantitative estimates for these errors.
J06 provides effective filter transmissions for several combinations of UBVRI filter sets and CCD cameras used for the SN observations. Using these transmissions, along with an effective model of Landolt filters21, we can compute synthetic magnitudes of stars in both the natural and the Landolt system. We use the stellar libraries of Gunn & Stryker (1983) and Pickles (1998), selecting stars in a range of U − B and B − V colors matching that of the SN calibration stars. For SNe, we use the SALT2 average spectral sequence (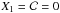 ).
).
Using those synthetic magnitudes, we compare the “true” (synthetic) Landolt magnitude to the Landolt magnitude estimated with a color transformation of the (synthetic) natural magnitudes. For these color transformations, we use the color terms given in Table 3 of J06, and define 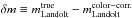 to be the difference between those two values. The calibration bias for SNe is given by the difference of δm for SNe and main sequence stars. Indeed the latter value sets the normalization of SN magnitudes through the assignement of a zero-point to the images. We label this difference Δm ≡ δm(SN) − δm(stars).
to be the difference between those two values. The calibration bias for SNe is given by the difference of δm for SNe and main sequence stars. Indeed the latter value sets the normalization of SN magnitudes through the assignement of a zero-point to the images. We label this difference Δm ≡ δm(SN) − δm(stars).
An uncertainty on the quantity Δm can be estimated by varying the SN model, the spectral library, or the filter transmissions. In practice, the uncertainty on the filter transmissions is dominant. Figure B.1 shows that δm is a function of the star color, which means that the filter model is inadequate. By construction, δm is color-independent for real observations. One can adjust wavelength shifts of the filter transmissions in order to obtain a color-independent value of δm for stars. This approach also results in a change of Δm that we can subsequently use as an estimate of the uncertainty due to approximate filter transmissions.
For the AndyCam CCD camera (CfA) with the Harris filter set (Harris et al. 1981), we have found ΔB = 0 ± 0.015 mag, ΔV = 0.03 ± 0.01 mag, and ΔR = 0.03 ± 0.03 mag. In other words, the color-correction does not significantly bias the measurements for the BVR bands. The situation for the U-band is, however, different. We have found a value as large as 0.1 for the 4Shooter camera (CfA), chip 1, with SAO filters. The values of δm for SNe and stars are represented in Fig. B.1 for this latter instrumental setup. One can also see on the figure that the residual color term is quite important. A U-band shift of ~3 nm is needed to obtain a flat distribution of δm, and in that case one finds an even larger value of ΔU = 0.15.
 |
Fig. B.1 Synthetic values of |
A primary motivation for this study is the existence of significant calibration offsets between observer-frame UV observations from different instruments (see, e.g., Krisciunas et al. 2013, for a longer discussion of this effect) and with rest-frame UV observations at higher redshift. Kessler et al. (2009a) found that this latter discrepancy was responsible for a large part of the difference between the SALT2 and MLCS2k2 (Jha et al. 2007) models, MLCS2k2 being trained solely on low-z SNe. This U-band offset introduced by the application of a color-correction to SNe data could explain some of the discrepancy. However, the U-band filter transmissions are too uncertain to secure a good interpretation of natural magnitudes. For this reason, we adopt the magnitudes that are color-transformed to the Landolt system for the low-z samples (except for the CSP data and the CfA-III BVri light curves where we use the natural magnitudes and measured filter response functions), but assign a coherent systematic uncertainty of 0.1 mag to the amplitude of U-band light curves.
In all bands, the (phase dependent) error introduced by color transformations is not included, so measurement errors are typically underestimated. As a consequence, the uncertainties in the fit light-curve parameters are underestimated. The training of SALT2 is also affected by this problem. At present, we cannot afford discarding the color-transformed low-z and must deal with this issue. We estimate the measurement errors again for color transformed measurements in the low-z sample as follows. Since the SDSS-II and SNLS measurement errors are reliable, we trained a version of SALT2 as described in Sect. 4, but considering only the SNLS and SDSS-II measurements in the computation of the “error-snake”. We then use this version with reliable modeling of the intrinsic dispersion to fit all the color transformed low-z light curves. For each light-curve, we fit an ad-hoc two parameter (γ2 and γ3) correction of the measurement errors σi affecting the measurement di by minimizing the following residual likelihood: 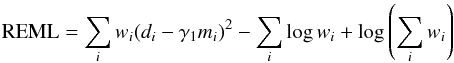 (B.1)with
(B.1)with 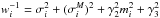 , where mi is the flux predicted by the best fit light-curve model and
, where mi is the flux predicted by the best fit light-curve model and 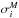 the model value of the intrinsic dispersion. We simultaneously fit for γ1, γ2 and γ3. When the light-curve contains less than five points, we fix the value of γ3 to zero. We then alter the errors in the light-curve accordingly to the fit values of γ2 and γ3. We found a mean value of 0.007 mag for γ2.
the model value of the intrinsic dispersion. We simultaneously fit for γ1, γ2 and γ3. When the light-curve contains less than five points, we fix the value of γ3 to zero. We then alter the errors in the light-curve accordingly to the fit values of γ2 and γ3. We found a mean value of 0.007 mag for γ2.
Appendix C: Estimates of missing host stellar masses in the C11 sample
The C11 compilation is missing estimates of the galaxy host mass for 61 nearby SNe (mostly because of missing photometry for the host). We describe estimates obtained for 57 of the 61 missing galaxy mass values.
For 49 of the nearby SN host galaxies, we derived an estimate based on Ks photometry (Bell & de Jong 2001; Bell et al. 2003) from the 2003 2MASS All-Sky Data Release of the Two Micron All Sky Survey (Skrutskie et al. 2006). The photometric data are extracted from the NASA/IPAC Extragalactic Database (NED) database. A linear model is fit between the mass and the Ks absolute magnitude on 51 objects with stellar mass estimates from C11. This linear model yields a residual of 0.15 dex and is used to provide galaxy mass estimates. For 8 galaxies without 2MASS Ks magnitudes, we rely on less precise models based on the total B band RC3 magnitude (de Vaucouleurs et al. 1991, three objects), the r C-Model magnitude (1 object from the SDSS DR6, Adelman-McCarthy et al. 2008), the B magnitude (three objects published in Hamuy et al. 2000), and the B magnitude in Strolger et al. (2002) for the low-luminosity host of SN 1999aw. The four remaining supernovae have no identified host and were assigned to the low-mass bin with an uncertainty on distance moduli of 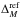 added in quadrature to the other sources of uncertainty.
added in quadrature to the other sources of uncertainty.
Appendix D: Accuracy of the CMB distance prior
In Sect. 7, we summarized the dark energy constraints from the CMB in the form of a distance prior. A computationally intensive, but more general, approach is to directly compare the CMB data to theoretical predictions for the fluctuation power spectra computed from a Boltzmann code. In this appendix, we briefly compare the results from both approaches for a fit of the w-CDM model to the combination of our SNe Ia JLA sample with CMB constraints.
The Planck collaboration (Planck collaboration XV 2014) has released code to compute the likelihood of theoretical models given Planck data22. This enables the marginalization of several sources of systematic uncertainty in the CMB spectra, such as errors in the instrumental beams and contamination by astrophysical foregrounds. In our comparison we make use of the full Planck temperature likelihood complemented with the WMAP measurement of the large scale CMB polarization (Bennett et al. 2013). We use the CAMB Boltzmann code (Lewis et al. 2000, March 2013) for our computation of CMB spectra. We follow assumptions from Planck Collaboration XVI (2014), fitting for the baryon density today ωb = Ωbh2, the cold dark matter density today ωc = Ωch2, θMC, the CosmoMC approximation of the sound horizon angular size computed from the Hu & Sugiyam (1996) fitting formulae, τ, the Thomson scattering optical depth due to reionization, ln(1010As), the log power of the primordial curvature perturbations at the pivot scale k0 = 0.05 Mpc-1, ns, the primordial spectrum index, and w, the dark energy equation of state parameter.
 |
Fig. D.1 Comparison of two derivations of the 68 and 95% confidence contours in the Ωm and w parameters for a flat w-CDM cosmology. In one case, constraints are derived from the exploration of the full Planck+WP+JLA likelihood (blue). In the other case CMB constraints are summarized by the geometric distance prior described in Sect. 7.1 (dashed red). |
Best-fit parameters of the w-CDM fit for the full Planck+WP+JLA likelihood, and for the distance prior (DP+JLA).
We explored the Planck+WP+JLA likelihood with Markov chain Monte Carlo (MCMC) simulations of the posterior distribution assuming flat priors for parameters as given in Planck Collaboration XVI (2014, Table 1). Eight sample chains were drawn using CosmoMC (Lewis & Bridle 2002; Lewis 2013). Convergence of the simulation is monitored using the Gelman & Rubin (1992)R statistic23.
The mean value of the posterior distribution and 68% limits for the fit parameters to the Planck+WP+JLA likelihood are given in Table D.1. Best-fit parameters obtained using the distance prior in Sect. 7.2 are shown for comparison. The 68% and 95% contours from these simulations are drawn in Fig. D.1. Overplotted is the Planck+WP+JLA contour from Fig. 16. The differences are small as expected from the fact that the supplementary constraints brought by the complete CMB power spectrum are weak compared to the supernova constraints.
Appendix E: Compressed form of the JLA likelihood
Figure 9 shows that the correlation between the nuisance parameters (α, β, ΔM) and the cosmological parameter Ωm is small as a result of the high density of SNe in this Hubble diagram (especially in the SDSS sample at intermediate redshifts). This suggests that, for a limited class of models (those predicting isotropic luminosity distances evolving smoothly with redshifts), the estimate of distances can be made reasonably independent of the estimate of cosmological parameters. In this appendix, we seek to provide the cosmological information of the JLA Hubble diagram in a compressed form that is faster and easier to evaluate and still remains accurate for the most common cases. Studies investigating alternate cosmology or alternate standardization hypotheses for SNe-Ia should continue to rely on the complete form.
Appendix E.1: Binned distance estimates
The distance modulus is typically well approximated by a piece-wise linear function of log (z), defined on each segment zb ≤ z<zb + 1 as: 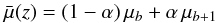 (E.1)with α = log (z/zb)/log (zb + 1/zb) and μb the distance modulus at zb. As an example, for 31 log-spaced control points zb in the redshift range 0.01 <z< 1.3, the difference between the Λ-CDM distance modulus and its linear interpolant is everywhere smaller than 1 mmag.
(E.1)with α = log (z/zb)/log (zb + 1/zb) and μb the distance modulus at zb. As an example, for 31 log-spaced control points zb in the redshift range 0.01 <z< 1.3, the difference between the Λ-CDM distance modulus and its linear interpolant is everywhere smaller than 1 mmag.
Such an interpolant can be fit to our measured Hubble diagram by minimizing a likelihood function similar to the one proposed in Eq. (15): 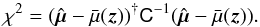 (E.2)The free parameters of the fit are α, β, ΔM and μb at the chosen control points. We use a fixed fiducial value of
(E.2)The free parameters of the fit are α, β, ΔM and μb at the chosen control points. We use a fixed fiducial value of 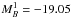 to provide uniquely determined μb. Results are compared to the best fit Λ-CDM cosmology in Fig. E.1. The structure of the correlation matrix of the best-fit μb is shown in Fig. E.2. It displays significant large scale correlation mostly due to systematic uncertainties. The tri-diagonal structure arises from the linear interpolation.
to provide uniquely determined μb. Results are compared to the best fit Λ-CDM cosmology in Fig. E.1. The structure of the correlation matrix of the best-fit μb is shown in Fig. E.2. It displays significant large scale correlation mostly due to systematic uncertainties. The tri-diagonal structure arises from the linear interpolation.
 |
Fig. E.1 Binned version of the JLA Hubble diagram presented in Fig. 8. The binned points are solid circles. There are significant correlations between bins. The error bars are the square root of the diagonal of the covariance matrix given in Table F.2. |
 |
Fig. E.2 Correlation matrix of the binned distance modulus μb. |
 |
Fig. E.3 Comparison of the cosmological constraints obtained from the full JLA likelihood (filled contour) with approximate version derived by binning the JLA supernovae measurements in 20 bins (dashed blue contour) and 30 bins (continuous red contour). |
Appendix E.2: Cosmology fit to the binned distances
Cosmological models predicting isotropic luminosity distances evolving smoothly with redshifts can be fitted directly to the binned distance estimates. We denote DL(z;θ) the luminosity distance predicted by a model dependent of a set of cosmological parameters θ. A good approximation of the full JLA likelihood is generally given by the following likelihood function: 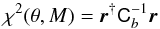 (E.3)with:
(E.3)with: 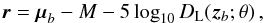 (E.4)M a free normalization parameter, and Cb the covariance matrix of μb (see Table F.2). As an illustration, a comparison of the cosmological constraints obtained from the approximate and full version of the JLA likelihood for the w-CDM model is shown in Fig. E.3. For the models evaluated in Sect. 7 in combination with CMB and BAO constraints, the difference in best-fit estimates between the approximate and full version is at most 0.018σ and reported uncertainties differ by less than 0.3%.
(E.4)M a free normalization parameter, and Cb the covariance matrix of μb (see Table F.2). As an illustration, a comparison of the cosmological constraints obtained from the approximate and full version of the JLA likelihood for the w-CDM model is shown in Fig. E.3. For the models evaluated in Sect. 7 in combination with CMB and BAO constraints, the difference in best-fit estimates between the approximate and full version is at most 0.018σ and reported uncertainties differ by less than 0.3%.
We warn that the normalization parameter M must be left free in the fit and marginalized over when deriving uncertainties. Not doing so would be equivalent to introducing artificial constraints on the H0 parameter and would result in underestimated errors.
Appendix F: Data release
The light-curve fit parameters for the JLA sample are given in Table F.3. We provide the covariance matrices, described in Sect. 5.5, of statistical and systematic uncertainties in light-curve parameters. These two products contain all the information required to compute the likelihood function from Eq. (15) in a cosmological fit. We provide the necessary computer code in two forms: a CosmoMC plugin and an independent C++ code.
Alternatively, we deliver estimates of binned distance modulus μb obtained, as described in appendix E, for 31 control points
(30 bins) in Table F.1 and the associated covariance matrix in Table F.2. These values can be used to evaluate the approximate version of the JLA likelihood function proposed in Eq. (E.3).
In addition, we provide the retrained SALT2 model, the covariance matrix of calibration parameters, and the SNLS recalibrated light curves. The SDSS-II light curves can be obtained from the SDSS SN data release (Sako et al. 2014)24.
Binned distance modulus fitted to the JLA sample.
Covariance matrix of the binned distance modulus.
Parameters for the type Ia supernovae in the joint JLA cosmology sample.
BD +17 4708, which is somewhat peculiar, as discussed in Regnault et al. (2009, Sect. 11).
The white dwarf system was recently redefined by a change in the modeling of the white dwarf fluxes (see http://www.stsci.edu/hst/observatory/crds/calspec.html). The change induced in color (about 0.003 in g − z color) is consistent with our estimate of the uncertainty.
H-C11 definition: H refers to the Hsiao et al. (2007) spectral sequence that is modified with time stretching and the G10 color law; C11 refers to the intrinsic scatter model based on Chotard et al. (2011), and it includes much more color variation compared to the G10 scatter model.
This agreement is better than what is obtained for the host stellar mass estimates from Gupta et al. (2011). For consistency, we thus use the Smith et al. (2012) estimates. However the agreement does not exclude possible differences in mass estimates obtained from different photometry, and a fully consistent analysis of the host galaxy is desirable.
For the SNLS sample, some of the Conley et al. (2011) analysis cuts were left out of the MC analysis, resulting in 8% too many simulated SNe; we ran additional simulations using these different cuts and found that the change in the best fit value of Ωm is negligible (5 × 10-4).
Within each survey, a smoothing spline sk(z) is fit to the derivatives. The smoothness of the spline is adjusted so that ∑ n(Jik − s(zi))2 = Nσ2 where σ is an estimate of the SN to SN dispersion computed in redshift bins of ten SNe. We also checked that the cosmology result was stable when varying the spline smoothness parameter.
This statement continues to be true even when we artificially vary the weights. As an illustration, we can fit ΛCDM to the subsample of the JLA supernovae that are part of the “C11 SiFTO” sample, but using the weights resulting from the systematics of the C11 SiFTO analysis. We then recover an Ωm value that differs by only 0.013 (~0.5σ) from the stat-only value.
Those numbers correspond to the best-fit parameters and covariance for the exploration of the Planck temperature and WMAP polarization likelihood (Planck+WP in Planck Collaboration XVI (2014) terminology) to a flat w-CDM cosmology as retrieved from the Planck Legacy Archive http://pla.esac.esa.int/pla/aio/planckProducts.html
Landolt filters from Bessell (1990), with wavelength shifts of −31, + 8, + 3, + 22, and +11Å for the UBVRI bands respectively; see the Appendix A of C11 for a detailed discussion.
We use the publicly available clik code to compute the high and low-ℓPlanck and WMAP low-ℓ polarization likelihood functions. Both the Planck likelihood code v1.0 and corresponding data (CAMSPEC v6.2TN_2013_02_26, commander v4.1_lm49 and lowlike v222) are available from the Planck Legacy archive http://pla.esac.esa.int/pla/aio/planckResults.jsp?
All data and software can be retrieved from http://supernovae.in2p3.fr/sdss_snls_jla/ReadMe.html
Acknowledgments
Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, Cambridge University, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. The Hobby-Eberly Telescope (HET) is a joint project of the University of Texas at Austin, the Pennsylvania State University, Stanford University, Ludwig-Maximillians-Universität München, and Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly. The Marcario Low-Resolution Spectrograph is named for Mike Marcario of High Lonesome Optics, who fabricated several optics for the instrument but died before its completion; it is a joint project of the Hobby-Eberly Telescope partnership and the Instituto de Astronomía de la Universidad Nacional Autónoma de México. The Apache Point Observatory 3.5-m telescope is owned and operated by the Astrophysical Research Consortium. We thank the observatory director, Suzanne Hawley, and site manager, Bruce Gillespie, for their support of this project. The Subaru Telescope is operated by the National Astronomical Observatory of Japan. The William Herschel Telescope is operated by the Isaac Newton Group, and the Nordic Optical Telescope is operated jointly by Denmark, Finland, Iceland, Norway, and Sweden, both on the island of La Palma in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. Observations at the ESO New Technology Telescope at La Silla Observatory were made under programme IDs 77.A-0437, 78.A-0325, and 79.A-0715. Kitt Peak National Observatory, National Optical Astronomy Observatory, is operated by the Association of Universities for Research in Astronomy, Inc. (AURA) under cooperative agreement with the National Science Foundation. The WIYN Observatory is a joint facility of the University of Wisconsin-Madison, Indiana University, Yale University, and the National Optical Astronomy Observatories. The W. M. Keck Observatory is operated as a scientific partnership among the California Institute of Technology, the University of California, and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. The South African Large Telescope of the South African Astronomical Observatory is operated by a partnership between the National Research Foundation of South Africa, Nicolaus Copernicus Astronomical Center of the Polish Academy of Sciences, the Hobby-Eberly Telescope Board, Rutgers University, Georg-August-Universität Göttingen, University of Wisconsin-Madison, University of Canterbury, University of North Carolina-Chapel Hill, Dartmough College, Carnegie Mellon University, and the United Kingdom SALT consortium. The Telescopio Nazionale Galileo (TNG) is operated by the Fundación Galileo Galilei of the Italian INAF (Istituo Nazionale di Astrofisica) on the island of La Palma in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. This paper is based in part onobservations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/IRFU, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. Part of the results are derived from observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. We also makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. We acknowledge the use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This work was completed in part with resources provided by the University of Chicago Research Computing Center. The French authors acknowledge support from CNRS/IN2P3, CNRS/INSU and CEA. G.L. is supported by the Swedish Research Council through grant No. 623-2011-7117. DARK is funded by DNRF. J.F. and R.K. are grateful for the support of National Science Foundation grant 1009457, a grant from France and Chicago Collaborating in the Sciences (FACCTS), and support from the Kavli Institute for Cosmological Physics at the University of Chicago. A.V.F. has received generous financial assistance from the Christopher R. Redlich Fund, the TABASGO Foundation, and NSF grant AST-1211916. MSu acknowledges support from the Royal Society.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006 [arXiv:astro-ph/0609591] [Google Scholar]
- Aldering, G., Adam, G., Antilogus, P., et al. 2002, in Survey and Other Telescope Technologies and Discoveries, eds. J. A. Tyson, & S. Wolff, SPIE Conf. Ser., 4836, 61 [Google Scholar]
- Amanullah, R., & Goobar, A. 2011, ApJ, 735, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Amanullah, R., Lidman, C., Rubin, D., et al. 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Amendola, L., Appleby, S., Bacon, D., et al. 2013, Liv. Rev. Relativity, 16, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astier, P., El Hage, P., Guy, J., et al. 2013, A&A, 557, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balland, C., Baumont, S., Basa, S., et al. 2009, A&A, 507, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bazin, G., Ruhlmann-Kleider, V., Palanque-Delabrouille, N., et al. 2011, A&A, 534, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Ben-Dayan, I., Gasperini, M., Marozzi, G., Nugier, F., & Veneziano, G. 2013, J. Cosmol. Astropart. Phys., 6, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, S., Meikle, P., Stehle, M., et al. 2004, MNRAS, 348, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Bernstein, J. P., Kessler, R., Kuhlmann, S., et al. 2012, ApJ, 753, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Betoule, M., Marriner, J., Regnault, N., et al. 2013, A&A, 552, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Kazin, E. A., Beutler, F., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Blondin, S., Matheson, T., Kirshner, R. P., et al. 2012, AJ, 143, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C. 2010, AJ, 139, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004, AJ, 128, 3053 [NASA ADS] [CrossRef] [Google Scholar]
- Bronder, T. J., Hook, I. M., Astier, P., et al. 2008, A&A, 477, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busca, N. G., Delubac, T., Rich, J., et al. 2013, A&A, 552, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, H., D’Andrea, C. B., Nichol, R. C., et al. 2013, ApJ, 763, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Childress, M., Aldering, G., Antilogus, P., et al. 2013, ApJ, 770, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Chotard, N., Gangler, E., Aldering, G., et al. 2011, A&A, 529, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conley, A., Carlberg, R. G., Guy, J., et al. 2007, ApJ, 664, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Sullivan, M., Hsiao, E. Y., et al. 2008, ApJ, 681, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2011, ApJS, 192, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contreras, C., Hamuy, M., Phillips, M. M., et al. 2010, AJ, 139, 519 [NASA ADS] [CrossRef] [Google Scholar]
- D’Andrea, C. B., Gupta, R. R., Sako, M., et al. 2011, ApJ, 743, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Das, S., Louis, T., Nolta, M. R., et al. 2014, J. Cosmol. Astropart. Phys., 4, 14 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr., H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies, Vol. I: Explanations and references, Vol. II: Data for galaxies between 0h and 12h. Vol. III: Data for galaxies between 12h and 24h [Google Scholar]
- Dilday, B., Kessler, R., Frieman, J. A., et al. 2008, ApJ, 682, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G. 2014, MNRAS, 440, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, R. S., Sullivan, M., Nugent, P. E., et al. 2008, ApJ, 674, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Folatelli, G., Phillips, M. M., Burns, C. R., et al. 2010, AJ, 139, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J. 2012, ApJ, 748, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., & Kirshner, R. P. 2013, ApJ, 769, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Narayan, G., Challis, P. J., et al. 2010, ApJ, 708, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Sanders, N. E., & Kirshner, R. P. 2011, ApJ, 742, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Filippenko, A. V., Kessler, R., et al. 2012, AJ, 143, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Challis, P. J., Chornock, R., et al. 2013, ApJ, 767, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Frieman, J. A., Bassett, B., Becker, A., et al. 2008, AJ, 135, 338 [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Ganeshalingam, M., Li, W., & Filippenko, A. V. 2013, MNRAS, 433, 2240 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gunn, J. E., & Stryker, L. L. 1983, ApJS, 52, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, R. R., D’Andrea, C. B., Sako, M., et al. 2011, ApJ, 740, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamuy, M., Trager, S. C., Pinto, P. A., et al. 2000, AJ, 120, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Maza, J., Pinto, P. A., et al. 2002, AJ, 124, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E., Fitzgerald, M. P., & Reed, B. C. 1981, PASP, 93, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Harville, D. A. 1977, J. Am. Stat. Assoc., 358, 320 [CrossRef] [Google Scholar]
- Hicken, M., Challis, P., Jha, S., et al. 2009, ApJ, 700, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Challis, P., Kirshner, R. P., et al. 2012, ApJS, 200, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Marriner, J., Kessler, R., et al. 2008, AJ, 136, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Perrett, K., et al. 2005, ApJ, 634, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Sugiyama, N. 1996, ApJ, 471, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, L., Reid, M., Moran, J., Greenhill, L., & Argon, A. 2013, ApJ, submitted [arXiv:1307.6031] [Google Scholar]
- Ivezić, Ž., Smith, J. A., Miknaitis, G., et al. 2007, AJ, 134, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, J., & Mörtsell, E. 2012, MNRAS, 426, 3360 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, J., Amanullah, R., & Goobar, A. 2013a, MNRAS, 431, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, J., Thomas, D., Pforr, J., et al. 2013b, MNRAS, 435, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Jönsson, J., Sullivan, M., Hook, I., et al. 2010, MNRAS, 405, 535 [NASA ADS] [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, P. L., Hicken, M., Burke, D. L., Mandel, K. S., & Kirshner, R. P. 2010, ApJ, 715, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Becker, A. C., Cinabro, D., et al. 2009a, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Bernstein, J. P., Cinabro, D., et al. 2009b, PASP, 121, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Guy, J., Marriner, J., et al. 2013, ApJ, 764, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Konishi, K., Cinabro, D., Garnavich, P. M., et al. 2011a, ApJ, submitted [arXiv:1101.4269] [Google Scholar]
- Konishi, K., Yasuda, N., Tokita, K., et al. 2011b, AJ, submitted [arXiv:1101.1565] [Google Scholar]
- Krisciunas, K., Bastola, D., Espinoza, J., et al. 2013, AJ, 145, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Krueger, B. K., Jackson, A. P., Townsley, D. M., et al. 2010, ApJ, 719, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Lampeitl, H., Nichol, R. C., Seo, H.-J., et al. 2010a, MNRAS, 401, 2331 [NASA ADS] [CrossRef] [Google Scholar]
- Lampeitl, H., Smith, M., Nichol, R. C., et al. 2010b, ApJ, 722, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U., & Uomoto, A. K. 2007, AJ, 133, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A. 2013, Phys. Rev. D, 87, 103529 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, E. V. 2003, Phys. Rev. Lett., 90, 091301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lupton, R., Gunn, J. E., Ivezić, Z., Knapp, G. R., & Kent, S. 2001, in Astronomical Data Analysis Software and Systems X, eds. F. R. Harnden, Jr., F. A. Primini, & H. E. Payne, ASP Conf. Ser., 238, 269 [Google Scholar]
- Maguire, K., Sullivan, M., Ellis, R. S., et al. 2012, MNRAS, 426, 2359 [NASA ADS] [CrossRef] [Google Scholar]
- Maguire, K., Sullivan, M., Patat, F., et al. 2013, MNRAS, 436, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Matheson, T., Kirshner, R. P., Challis, P., et al. 2008, AJ, 135, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- McClelland, C. M., Garnavich, P. M., Galbany, L., et al. 2010, ApJ, 720, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Ménard, B., Kilbinger, M., & Scranton, R. 2010, MNRAS, 406, 1815 [NASA ADS] [Google Scholar]
- Miknaitis, G., Pignata, G., Rest, A., et al. 2007, ApJ, 666, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Mosher, J., Sako, M., Corlies, L., et al. 2012, AJ, 144, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Mosher, J., Guy, J., Kessler, R., et al. 2014, ApJ, submitted [arXiv:1401.4065] [Google Scholar]
- Nordin, J., Östman, L., Goobar, A., et al. 2011, ApJ, 734, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Olmstead, M. D., Brown, P. J., Sako, M., et al. 2014, AJ, 147, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Östman, L., Nordin, J., Goobar, A., et al. 2011, A&A, 526, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padmanabhan, N., Xu, X., Eisenstein, D. J., et al. 2012, MNRAS, 427, 2132 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pan, Y.-C., Sullivan, M., Maguire, K., et al. 2014, MNRAS, 438, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Benetti, S., Cappellaro, E., et al. 1996, MNRAS, 278, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, R., Thomas, R. C., Aldering, G., et al. 2013, A&A, 554, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K., Balam, D., Sullivan, M., et al. 2010, AJ, 140, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Simon, J. D., Morrell, N., et al. 2013, ApJ, 779, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Planck Collaboration I. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321529 [Google Scholar]
- Planck Collaboration XII. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321580 [Google Scholar]
- Planck collaboration XV. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321573 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321591 [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321543 [Google Scholar]
- Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, C. L., Shaw, L., Zahn, O., et al. 2012, ApJ, 755, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Rest, A., Scolnic, D., Foley, R. J., et al. 2013, ApJ, submitted [arXiv:1310.3828] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 730, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Rigault, M., Copin, Y., Aldering, G., et al. 2013, A&A, 560, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sako, M., Bassett, B., Becker, A., et al. 2008, AJ, 135, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, M., Bassett, B., Becker, A. C., et al. 2014, ApJS, submitted [arXiv:1401.3317] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. P., Kirshner, R. P., Leibundgut, B., et al. 1994, ApJ, 434, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D., Rest, A., Riess, A., et al. 2013, ApJ, submitted [arXiv:1310.3824] [Google Scholar]
- Scolnic, D. M., Riess, A. G., Foley, R. J., et al. 2014, ApJ, 780, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Shafer, D. L., & Huterer, D. 2014, Phys. Rev. D, 89, 063510 [CrossRef] [Google Scholar]
- Silverman, J. M., Foley, R. J., Filippenko, A. V., et al. 2012, MNRAS, 425, 1789 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. M., Nugent, P. E., Gal-Yam, A., et al. 2013, ApJS, 207, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Slosar, A., Iršič, V., Kirkby, D., et al. 2013, J. Cosmol. Astropart. Phys., 4, 26 [Google Scholar]
- Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [Google Scholar]
- Smith, M., Nichol, R. C., Dilday, B., et al. 2012, ApJ, 755, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sollerman, J., Mörtsell, E., Davis, T. M., et al. 2009, ApJ, 703, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Stanishev, V., Rodrigues, M., Mourão, A., & Flores, H. 2012, A&A, 545, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stritzinger, M. D., Phillips, M. M., Boldt, L. N., et al. 2011, AJ, 142, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Strolger, L.-G., Smith, R. C., Suntzeff, N. B., et al. 2002, AJ, 124, 2905 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Howell, D. A., Perrett, K., et al. 2006, AJ, 131, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Conley, A., Howell, D. A., et al. 2010, MNRAS, 406, 782 [NASA ADS] [Google Scholar]
- Sullivan, M., Guy, J., Conley, A., et al. 2011, ApJ, 737, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, N., Rubin, D., Lidman, C., et al. 2012, ApJ, 746, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Tripp, R. 1998, A&A, 331, 815 [NASA ADS] [Google Scholar]
- Tucker, D. L., Kent, S., Richmond, M. W., et al. 2006, Astron. Nachr., 327, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, E. S., Hook, I. M., Sullivan, M., et al. 2011, MNRAS, 410, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, E. S., Hachinger, S., Mazzali, P. A., et al. 2012, MNRAS, 427, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Filippenko, A. V., Ganeshalingam, M., et al. 2009, ApJ, 699, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Wang, L., Filippenko, A. V., et al. 2012, ApJ, 749, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Wang, L., Filippenko, A. V., Zhang, T., & Zhao, X. 2013, Science, 340, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Wood-Vasey, W. M., Miknaitis, G., Stubbs, C. W., et al. 2007, ApJ, 666, 694 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zheng, C., Romani, R. W., Sako, M., et al. 2008, AJ, 135, 1766 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Coefficient of synthetic color transformation between aperture and PSF MegaCam magnitudes.
Internal calibration uncertainties for the low-z samples split by photometric systems.
Number of supernovae discarded by the successive cuts applied to the SDSS-II sample before inclusion in the training sample.
Number of SDSS-II supernovae discarded by the successive cuts applied before inclusion in the cosmology sample.
Contribution of various source of measurement uncertainties to the uncertainty in Ωm.
Best fit parameters for the flat wz-CDM cosmological model. The point (w0,wa) = ( − 1,0) corresponds to the cosmological constant hypothesis.
Best-fit parameters of the w-CDM fit for the full Planck+WP+JLA likelihood, and for the distance prior (DP+JLA).
All Figures
 |
Fig. 1 Difference between aperture and PSF photometry as a function of the SNLS tertiary standard star magnitude. The aperture photometry from B13 has been corrected for residual contamination using an estimate of the local background level obtained with PSF photometry. The magnitude range used in the zero-point fit (vertical dashed lines) is chosen so that the aperture catalog is expected to be free from selection bias (B13, Fig. 12). |
| In the text | |
 |
Fig. 2 Comparison of ℳ0 templates between the previous release of the SALT2 model (G10) and the present release trained on the JLA sample. Left: the present model is shown as a black dashed line at three different phases: early (−10 days), close to maximum (0 day), and late (+15 days). The G10 model is shown as the red solid line. Right: relative differences in the two models (JLA/G10 − 1) at the three selected phases. |
| In the text | |
 |
Fig. 3 Top: comparison of the reconstructed color law CL for two trainings of the SALT2 model (see Eq. (6)): the present release trained on the JLA sample (back dashed line) and the previous release of the SALT2 model from G10 (red solid line). We display −0.1 log CL, which is approximately the rms magnitude variation from color variation. Bottom: difference in the two color laws. |
| In the text | |
 |
Fig. 4 Bias in reconstructed distance modulus as a function of redshift. Simulations follow the color variation model described in Scolnic et al. (2014, Sect. 3.1). The simulated sample includes low-z, SDSS-II and SNLS SNe Ia and is representative of our JLA sample described in Sect. 5.1. The analysis of the simulated sample includes the bias correction described in Sect. 5.3 (computed under the baseline SALT2 assumptions). The SALT2 model was not retrained on the simulated sample, similarly to what is done in Kessler et al. (2013). |
| In the text | |
 |
Fig. 5 Bias corrections computed from Monte Carlo simulations of the cosmological analysis (see Eq. (9)). Error bars show the statistical uncertainty of the correction due to MC noise and uncertainty in the selection function. The smallest error bars show the contribution from Monte Carlo noise alone. |
| In the text | |
 |
Fig. 6 Effect of changing the zero-point in the g MegaCam filter by 10 mmag on light-curve parameters and distance modulus as a function of redshift for SNe in the low-z (blue crosses), SDSS (green squares), SNLS (orange circles) and HST (red ×) samples. The effect on the distance modulus is computed using the fiducial values α = 0.14 and β = 3.15. The dots show the numerical values of the derivatives (including numerical noise) before smoothing. |
| In the text | |
 |
Fig. 7 Values of σcoh determined for seven subsamples of the Hubble residuals: low-zz< 0.03 and z> 0.03 (blue), SDSS z< 0.2 and z> 0.2 (green), SNLS z< 0.5 and z> 0.5 (orange), and HST (red). |
| In the text | |
 |
Fig. 8 Top: Hubble diagram of the combined sample. The distance modulus redshift relation of the best-fit ΛCDM cosmology for a fixed H0 = 70 km s-1 Mpc-1 is shown as the black line. Bottom: residuals from the best-fit ΛCDM cosmology as a function of redshift. The weighted average of the residuals in logarithmic redshift bins of width Δz/z ~ 0.24 are shown as black dots. |
| In the text | |
 |
Fig. 9 68% and 95% confidence contours for the ΛCDM fit parameters. Filled gray contours result from the fit of the full JLA sample; red dashed contours from the fit of a subsample excluding SDSS-II data (lowz+SNLS). |
| In the text | |
 |
Fig. 10 Residuals from the ΛCDM fit of the JLA Hubble diagram by survey. The weighted bin average and error bars are computed without systematic uncertainties. We further distinguish the different low-z surveys, the four non-contiguous SNLS fields, and the nothern and southern part of the SDSS stripe. |
| In the text | |
 |
Fig. 11 Top: average color of the samples in redshift bins. The low-z (blue crosses), the SDSS-II (green squares) and the SNLS (orange circles) samples are binned separately. The plot provides a visual assessment of the selection bias affecting each survey. Bottom: residuals from the ΛCDM fit of the JLA Hubble diagram as a function of redshift. The different surveys are shown separately. |
| In the text | |
 |
Fig. 12 Residuals from the ΛCDM fit of the JLA Hubble diagram as a function of the host galaxy mass. The fit does not include the mass step correction. Binned residuals are shown as black squares. The red line shows the mass step correction for a step at Mstellar = 1010 M⊙. |
| In the text | |
 |
Fig. 13 Measurements of the mass step in four redshift bins: z< 0.18, 0.18 ≤ z< 0.31, 0.31 ≤ z< 0.6, z> 0.6. The dashed line shows the measured value for a redshift-independent mass step. |
| In the text | |
 |
Fig. 14 Comparison of various measurements of Ωm for a ΛCDM cosmology. |
| In the text | |
 |
Fig. 15 68% and 95% confidence contours (including systematic uncertainty) for the Ωm and ΩΛ cosmological parameters for the o-ΛCDM model. Labels for the various datasets correspond to the present SN Ia compilation (JLA), the Conley et al. (2011) SN Ia compilation (C11), the combination of Planck temperature and WMAP polarization measurements of the CMB fluctuation (Planck+WP), and a combination of measurements of the BAO scale (BAO). See Sect. 7.1 for details. The black dashed line corresponds to a flat universe. |
| In the text | |
 |
Fig. 16 Confidence contours at 68% and 95% (including systematic uncertainty) for the Ωm and w cosmological parameters for the flat w-ΛCDM model. The black dashed line corresponds to the cosmological constant hypothesis. |
| In the text | |
 |
Fig. 17 Confidence contours at 68% and 95% (including systematic uncertainty) for the w and wa cosmological parameters for the flat w-ΛCDM model. |
| In the text | |
 |
Fig. B.1 Synthetic values of |
| In the text | |
 |
Fig. D.1 Comparison of two derivations of the 68 and 95% confidence contours in the Ωm and w parameters for a flat w-CDM cosmology. In one case, constraints are derived from the exploration of the full Planck+WP+JLA likelihood (blue). In the other case CMB constraints are summarized by the geometric distance prior described in Sect. 7.1 (dashed red). |
| In the text | |
 |
Fig. E.1 Binned version of the JLA Hubble diagram presented in Fig. 8. The binned points are solid circles. There are significant correlations between bins. The error bars are the square root of the diagonal of the covariance matrix given in Table F.2. |
| In the text | |
 |
Fig. E.2 Correlation matrix of the binned distance modulus μb. |
| In the text | |
 |
Fig. E.3 Comparison of the cosmological constraints obtained from the full JLA likelihood (filled contour) with approximate version derived by binning the JLA supernovae measurements in 20 bins (dashed blue contour) and 30 bins (continuous red contour). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.