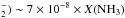| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201423748 | |
| Published online | 29 July 2014 | |
Upper limits to interstellar NH+ and para-NH2− abundances
Herschel-HIFI observations towards Sgr B2 (M) and G10.6−0.4 (W31C)⋆,⋆⋆
1
Chalmers University of TechnologyDepartment of Earth and Space Sciences,
Onsala Space Observatory,
439 92
Onsala,
Sweden
e-mail:
carina.persson@chalmers.se
2
Department of Physics & Astronomy,
Siena College, Loudonville, NY
12211,
USA
3
Department of Chemistry, University of Virginia,
McCormick Road, Charlottesville, VA
22904,
USA
4
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937
Köln,
Germany
5
Centro de Astrobiologìa, CSIC-INTA, 28850
Madrid,
Spain
6
California Institute of Technology, Cahill Center for Astronomy and Astrophysics
301-17, Pasadena,
CA
91125,
USA
7
Radboud University Nijmegen, IMM – Faculty of
Science, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
8
LERMA-LRA, UMR 8112 du CNRS, Observatoire de Paris, École Normale Supérieure, UPMC & UCP,
24 rue Lhomond, 75231
Paris Cedex 05,
France
9
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
Received:
3
March
2014
Accepted:
21
May
2014
The understanding of interstellar nitrogen chemistry has improved significantly with recent results from the Herschel Space Observatory. To set even better constraints, we report here on deep searches for the NH+ ground state rotational transition J = 1.5−0.5 of the 2Π1/2 lower spin ladder, with fine-structure transitions at 1013 and 1019 GHz, and the para-NH2− 11,1−00,0 rotational transition at 934 GHz towards Sgr B2 (M) and G10.6−0.4 (W31C) using the Herschel Heterodyne Instrument for the Far-Infrared (HIFI). No clear detections of NH+ are made and the derived upper limits relative to the total number of hydrogen nuclei are ≲2 × 10-12 and ≲7 × 10-13 in the Sgr B2 (M) molecular envelope and in the G10.6−0.4 molecular cloud, respectively. The searches are, however, complicated by the fact that the 1 013 GHz transition lies only −2.5 km s-1 from a CH2NH line, which is seen in absorption in Sgr B2 (M), and that the hyperfine structure components in the 1019 GHz transition are spread over 134 km s-1. Searches for the so far undetected NH2− anion turned out to be unfruitful towards G10.6−0.4, while the para-NH2− 11,1−00,0 transition was tentatively detected towards Sgr B2 (M) at a velocity of 19 km s-1. Assuming that the absorption occurs at the nominal source velocity of +64 km s-1, the rest frequency would be 933.996 GHz, offset by 141 MHz from our estimated value. Using this feature as an upper limit, we found N(p-NH2−) ≲4 × 1011 cm-2, which implies an abundance of ≲8 × 10-13 in the Sgr B2 (M) molecular envelope. The upper limits for both species in the diffuse line-of-sight gas are less than 0.1 to 2% of the values found for NH, NH2, and NH3 towards both sources, and the abundance limits are ≲2−4 × 10-11. An updated pseudo time-dependent chemical model with constant physical conditions, including both gas-phase and surface chemistry, predicts an NH+ abundance a few times lower than our present upper limits in diffuse gas and under typical Sgr B2 (M) envelope conditions. The NH2− abundance is predicted to be several orders of magnitudes lower than our observed limits, hence not supporting our tentative detection. Thus, while NH2− may be very difficult to detect in interstellar space, it could, on the other hand, be possible to detect NH+ in regions where theionisation rates of H2 and N are greatly enhanced.
Key words: ISM: abundances / ISM: molecules / line: formation / submillimeter: ISM / astrochemistry / molecular processes
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
An important species in the nitrogen chemistry, NH+, has for a long time been
awaiting its first discovery. Besides its key chemical role in the reaction chain leading to
more complex nitrogen-bearing species, NH+ has also been identified as a potential candidate for
probing variations in the fine-structure constant, α, and electron-to-proton
mass ratio, μ
(Beloy et al. 2011). Another undetected but
interesting species in the nitrogen chemistry is the anion
NH .
.
Searches for NH+ and
NH are, however, difficult not only because of their expected very low abundances, but also
since their strongest transitions lie at frequencies that are generally inaccessible to
ground-based telescopes. With the launch of Herschel (Pilbratt et al. 2010; Roelfsema et al.
2012) and its sensitive Heterodyne Instrument for the Far-Infrared (HIFI), which
was designed to perform high-resolution observations at frequencies 480−1250 and 1410−1910 GHz, searches for the fundamental
rotational transitions of NH+ and NH
are, however, difficult not only because of their expected very low abundances, but also
since their strongest transitions lie at frequencies that are generally inaccessible to
ground-based telescopes. With the launch of Herschel (Pilbratt et al. 2010; Roelfsema et al.
2012) and its sensitive Heterodyne Instrument for the Far-Infrared (HIFI), which
was designed to perform high-resolution observations at frequencies 480−1250 and 1410−1910 GHz, searches for the fundamental
rotational transitions of NH+ and NH became possible.
became possible.
Previous searches for NH+ using Herschel-HIFI in the diffuse line-of-sight gas towards the high-mass star-forming regions G10.6−0.4 and W49N, resulted in average upper limits of the NH+ abundance relative to molecular hydrogen ≲ 4× 10-10, and N(NH+)/N(NH) ≲ 4−7% (Persson et al. 2012).
Observed NH+
and para-NH transitions.
transitions.
In this paper we present the results of new, deeper searches for NH+, and for the first time also for
NH ,
towards G10.6−0.4 and
Sgr B2 (M). Both sources are very well-known star-forming regions and extremely luminous
sub-millimetre and infrared continuum sources. The ultra-compact H ii region
G10.6−0.4 in the star-forming
complex W31 is located in the Galactic 30 km s-1 arm at a distance of 4.95 kpc (Sanna et al. 2014), and the Sgr B2 (M) region is one of the chemically
rich sources close to the Galactic centre at a distance of 8.5 kpc (e.g. Nummelin et al. 2000; Bergin et al. 2010). We also model the abundances of NH+ and
NH
,
towards G10.6−0.4 and
Sgr B2 (M). Both sources are very well-known star-forming regions and extremely luminous
sub-millimetre and infrared continuum sources. The ultra-compact H ii region
G10.6−0.4 in the star-forming
complex W31 is located in the Galactic 30 km s-1 arm at a distance of 4.95 kpc (Sanna et al. 2014), and the Sgr B2 (M) region is one of the chemically
rich sources close to the Galactic centre at a distance of 8.5 kpc (e.g. Nummelin et al. 2000; Bergin et al. 2010). We also model the abundances of NH+ and
NH under four different interstellar conditions with a pseudo time-dependent chemical model,
and explore how the surface chemistry, cosmic ionisation rate, and assumed initial metal
abundances influence the derived abundances.
under four different interstellar conditions with a pseudo time-dependent chemical model,
and explore how the surface chemistry, cosmic ionisation rate, and assumed initial metal
abundances influence the derived abundances.
2. Spectroscopy, observations, and data reduction
The observed transitions are listed in Table 1.
Measurements of the two fine-structure transitions in the lowest N = 1−1,J = 1.5−0.5 rotational transition of NH+ in its 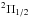 lower spin
ladder were performed by Verhoeve et al. (1986) and
included resolved hyperfine structure (hfs). An energy-level diagram can be found in Hübers et al. (2009, their Fig. 1). The Einstein
A values
(Tables D.1−D.2) were derived by one of us
(HSPM) from these data, using the experimental ground-state electric dipole moment of 1.988
(28) D (Mount et al. 2012), and taking additional
parameters from Hübers et al. (2009) into account.
The frequency of the
lower spin
ladder were performed by Verhoeve et al. (1986) and
included resolved hyperfine structure (hfs). An energy-level diagram can be found in Hübers et al. (2009, their Fig. 1). The Einstein
A values
(Tables D.1−D.2) were derived by one of us
(HSPM) from these data, using the experimental ground-state electric dipole moment of 1.988
(28) D (Mount et al. 2012), and taking additional
parameters from Hübers et al. (2009) into account.
The frequency of the 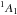 ,
JKa,Kc
= 11,1−00,0
NH
,
JKa,Kc
= 11,1−00,0
NH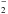 transition was taken from the Madrid molecular spectroscopy excitation (MADEX) database
(Cernicharo 2011, Table D.3). It was calculated from the spectroscopic parameters reported by
Tack et al. (1986). The uncertainties of the
infrared transition frequencies are of the order of 100 MHz. While statistics may improve
the prediction of transition frequencies, correlation among the spectroscopic parameters or
vibration-rotation interaction may lead to significantly increased uncertainties. Botschwina et al. (1993) calculated a ground-state dipole
moment of 1.311 D with an estimated uncertainty of 0.01 D.
transition was taken from the Madrid molecular spectroscopy excitation (MADEX) database
(Cernicharo 2011, Table D.3). It was calculated from the spectroscopic parameters reported by
Tack et al. (1986). The uncertainties of the
infrared transition frequencies are of the order of 100 MHz. While statistics may improve
the prediction of transition frequencies, correlation among the spectroscopic parameters or
vibration-rotation interaction may lead to significantly increased uncertainties. Botschwina et al. (1993) calculated a ground-state dipole
moment of 1.311 D with an estimated uncertainty of 0.01 D.
Emission or absorption features of other species were assigned by consulting the Cologne Database for Molecular Spectroscopy (CDMS) (Müller et al. 2001, 2005), Jet Propulsion Laboratory (JPL) (Pickett et al. 1998), or MADEX catalogues. Specifically, the NH2 (Gendriesch et al. 2001), CH2NH (Dore et al. 2012), and SO2 (Müller & Brünken 2005) entries were taken from the CDMS catalogue while the methanol entry (Xu et al. 2008) was taken from the JPL catalogue.
The observations, which took place in April and September 2012, are summarised in Table 1 and the observational identifications are found in the on-line Table D.4. We used the dual beam switch mode and the wideband spectrometer (WBS) with a bandwidth of 4×1 GHz and an effective spectral resolution of 1.1 MHz (Δv = 0.3 km s-1). Two orthogonal polarisations were used in all the observations. All lines towards G10.6−0.4 were observed with three different overlapping frequency settings of the local oscillator (LO) to determine the sideband origin of the lines since HIFI uses double sideband (DSB) receivers. Towards Sgr B2 (M) we used the spectral scan mode and eight different overlapping LO settings because of its extreme density of emission lines.
The pointings were centred at α
= 17h47m20  6, δ = −28°23′03.2″
(J2000) for
Sgr B2 (M), and α =
18h10m28
6, δ = −28°23′03.2″
(J2000) for
Sgr B2 (M), and α =
18h10m28 7, δ = −19°55′50.0″
(J2000) for
G10.6−0.4. The source systemic
velocities are 58–69 and −3 km
s-1 for Sgr B2 (M)
and G10.6−0.4, respectively.
Absorptions in the source molecular clouds are centred at +64 and −0.5 km s-1, and the foreground gas along
the respective sight-line is detected in absorption from −140 to 27, and 10 to 55 km s-1.
7, δ = −19°55′50.0″
(J2000) for
G10.6−0.4. The source systemic
velocities are 58–69 and −3 km
s-1 for Sgr B2 (M)
and G10.6−0.4, respectively.
Absorptions in the source molecular clouds are centred at +64 and −0.5 km s-1, and the foreground gas along
the respective sight-line is detected in absorption from −140 to 27, and 10 to 55 km s-1.
The data were reprocessed using the hifiPipeline task in HIPE version 9.0, up to level 2
providing fully calibrated DSB spectra for G10.6−0.4 on the 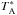 antenna
temperature intensity scale where the lines are calibrated to single sideband (SSB) and the
continuum to DSB. For the Sgr B2 (M) observations, we used in addition the doDeconvolution
task up to level 2.5 to provide fully calibrated SSB spectra. The FitHifiFringe task was
then used to fit and remove residual ripples in the spectra, except for the
NH+ 1 019 GHz data
towards Sgr B2 (M) since this spectrum had too many spectral features. The
G10.6−0.4 data quality is
excellent with very low intensity ripples, with good agreement between the three LO-tunings,
and without any visible contamination from the image sidebands.
antenna
temperature intensity scale where the lines are calibrated to single sideband (SSB) and the
continuum to DSB. For the Sgr B2 (M) observations, we used in addition the doDeconvolution
task up to level 2.5 to provide fully calibrated SSB spectra. The FitHifiFringe task was
then used to fit and remove residual ripples in the spectra, except for the
NH+ 1 019 GHz data
towards Sgr B2 (M) since this spectrum had too many spectral features. The
G10.6−0.4 data quality is
excellent with very low intensity ripples, with good agreement between the three LO-tunings,
and without any visible contamination from the image sidebands.
The FITS files were exported to the spectral line software package
xs1, which was used in the
subsequent data reduction. All tunings and both polarisations were included in the averaged
noise-weighted spectra for all transitions, which were convolved to a channel width of 1
km s-1. Baselines
of order five were removed from the G10.6−0.4 spectra, and of order three and seven from the Sgr B2 (M)
NH and NH+ 1013 GHz
spectra (average TC added afterwards). No baseline was
removed from the Sgr B2 (M) NH+ 1019 GHz spectrum.
and NH+ 1013 GHz
spectra (average TC added afterwards). No baseline was
removed from the Sgr B2 (M) NH+ 1019 GHz spectrum.
3. Results
Figures 1–2 show
the averaged WBS spectra of all observed transitions as a function of the local standard of
rest velocity, VLSR. The continuum and rms are given in
Table 1. We performed an unbiased search for emission
and absorption lines from NH+ and para-NH in the source molecular clouds, and absorption from diffuse or translucent gas along the
lines-of-sight. Despite the low noise levels, no detections are found in the
G10.6−0.4 data (Fig. 1). Column densities are therefore 3σ upper limits, estimated
with a typical line width (4 km s-1) and the total line-of-sight velocity range. The emission
line visible in the NH+ 1013 GHz band (upper panel) at +21 km s-1 is identified as
ortho-NH242,2−41,3.
in the source molecular clouds, and absorption from diffuse or translucent gas along the
lines-of-sight. Despite the low noise levels, no detections are found in the
G10.6−0.4 data (Fig. 1). Column densities are therefore 3σ upper limits, estimated
with a typical line width (4 km s-1) and the total line-of-sight velocity range. The emission
line visible in the NH+ 1013 GHz band (upper panel) at +21 km s-1 is identified as
ortho-NH242,2−41,3.
Towards Sgr B2 (M), we find two absorption features at VLSR ≈ 60 km
s-1 in both
NH+ spectra (upper
and middle panels in Fig. 2). It is to be noted that
the 1013 and 1019 GHz lines are expected to show very different line profiles since they
both have 14 hfs components and are spread over velocity ranges of 26 and 134 km
s-1, respectively.
To check whether the observed line profiles fit the respective NH+ hfs, we model the absorption of
both lines using Gaussian optical depth profiles generated for each hfs component. These
profiles are made to fit the observations under the condition that the VLSR and line
width are the same for both transitions (cf. Method I in Persson et al. 2012). Assuming a sideband gain ratio of unity, we calculate the
line opacities as , where
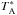 is the SSB
antenna temperature. As seen in Fig. A.1 (on-line
material) the fit to the 1013 GHz line shows a very good agreement with the observed line
profile, whereas the 1019 GHz fit suggests either that the detection is not real, or that a
considerable part of the absorption comes from other species, or that it is (partly) caused
by remaining ripples which we were not able to remove.
is the SSB
antenna temperature. As seen in Fig. A.1 (on-line
material) the fit to the 1013 GHz line shows a very good agreement with the observed line
profile, whereas the 1019 GHz fit suggests either that the detection is not real, or that a
considerable part of the absorption comes from other species, or that it is (partly) caused
by remaining ripples which we were not able to remove.
 |
Fig. 1 G10.6−0.4: searches for
NH+ and
p-NH |
 |
Fig. 2 Sgr B2 (M): searches for NH+ and p-NH |
Resulting NH+
and NH column densities, N, column density ratios with related species,
and abundances, X, with respect to the total amount of hydrogen
towards Sgr B2 (M) and G10.6−0.6.
column densities, N, column density ratios with related species,
and abundances, X, with respect to the total amount of hydrogen
towards Sgr B2 (M) and G10.6−0.6.
Despite the agreement of the fits, we ascribe the largest part of the feature in the 1013 GHz spectrum to CH2NH. This species has two transitions with similar line strengths close to NH+ at 1013 GHz: 33,1−22,0 (with El = 41 K) only +8.5 MHz (−2.5 km s-1) from the NH+ line, and 33,0−22,1 seen as a narrow absorption at 21 km s-1 in Fig. 2 (upper panel). This line, however, blends with the SO2415,37−404,36 (1 012.673 GHz) emission and is therefore easily missed. Our identification is also supported by previous observations of CH2NH in both absorption (11,1−00,0) and emission towards Sgr B2 (M) (Nummelin et al. 2000). We modelled the SO2 emission, both CH2NH absorptions, and the o-NH242,2−41,3 emission line wing (seen at ~70 km s-1 in Fig. 2, upper panel) in order to subtract these lines in the search for any remaining weak NH+ absorption. More details of the modelling are found in on-line Sect. A, and all modelled lines are shown in Fig. A.2. After subtraction of the modelled lines, we find a weak remaining absorption feature at VLSR = 69 km s-1 with an integrated opacity of 0.08 km s-1. This feature is considered as an upper limit of NH+ in the SgrB2 (M) molecular envelope. An unidentified remaining absorption feature is also seen at 45.5 km s-1 with an integrated opacity of 0.19 km s-1. Both these features are, however, very weak and may well be remaining artefacts from our modelling or ripples in the baseline.
In the 934 GHz band we find an unidentified absorption feature at VLSR ≈ + 18.5 km
s-1 towards
Sgr B2 (M) with a line width of ≈9 km s-1 and an integrated opacity of 0.09 km s-1 (lower panel in Fig. 2). This feature is used as an upper limit to the
para-NH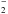 11,1−00,0 line. If the absorption is caused by
para-NH
11,1−00,0 line. If the absorption is caused by
para-NH ,
it implies a rest frequency of 933.973–934.009 GHz for this transition, which is 118–154 MHz
higher than our estimated frequency assuming that the nominal source velocity is between 56
and 68 km s-1.
Results of quantum chemical calculations on NH
,
it implies a rest frequency of 933.973–934.009 GHz for this transition, which is 118–154 MHz
higher than our estimated frequency assuming that the nominal source velocity is between 56
and 68 km s-1.
Results of quantum chemical calculations on NH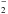 were recently reported employing high level coupled cluster calculations with additional
correction and large basis sets with extrapolation to infinite basis set size (Huang & Lee 2009). Using their best spectroscopic
parameters, a frequency of 932.726 GHz is derived for the J = 11,1−00,0 transition. The level of agreement
with the value derived from the experimental spectroscopic parameters corresponds to the one
expected under favourable conditions and does not permit exclusion of the Sgr B2 (M)
absorption feature as being potentially due to NH
were recently reported employing high level coupled cluster calculations with additional
correction and large basis sets with extrapolation to infinite basis set size (Huang & Lee 2009). Using their best spectroscopic
parameters, a frequency of 932.726 GHz is derived for the J = 11,1−00,0 transition. The level of agreement
with the value derived from the experimental spectroscopic parameters corresponds to the one
expected under favourable conditions and does not permit exclusion of the Sgr B2 (M)
absorption feature as being potentially due to NH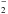 .
.
We convert the upper limits of NH+ opacities to column densities with the non-equilibrium homogeneous radiative transfer code RADEX2 (van der Tak et al. 2007) to correct for possible population of molecules in unobserved excited levels. We use n(H2) = 70 cm-3 and a kinetic temperature TK = 100 K for the diffuse line-of-sight conditions, and n(H2) = 102−104 cm-3 and TK = 20−40 K for the denser envelopes of the source molecular clouds. The results are not very sensitive to changes in density because of the high critical density of the nitrogen hydrides (ncrit ~ 108 cm-3). For the line-of-sight, we use the average Galactic background radiation in the solar neighbourhood plus the cosmic microwave background radiation as background radiation field. In addition, for the source molecular clouds we include their respective observed spectral energy distribution.
Since no collisional coefficients are available for
NH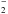 ,
we estimate the column density of molecules in the ground-state using
,
we estimate the column density of molecules in the ground-state using
![\begin{equation} N_l\left(\mathrm{p-NH}_2^-\right) = 8\pi \frac{\nu^3}{c^3} \frac{g_{\rm l}}{g_{\rm u}\,A_{\rm ul}} \! \int \!\tau \mathrm{d}V = 4.7 \times 10^{12} \!\int\! \tau \mathrm{d}V \, \, \left[\mathrm{cm}^{-2}\right] . \end{equation}](/articles/aa/full_html/2014/07/aa23748-14/aa23748-14-eq112.png) (1)The resulting upper
limits for the column density and abundance with respect to the total column of hydrogen are
found in Table 2. Here we also present limiting
abundance ratios, relative to the chemically related species NH, NH2, and NH3 along the line-of-sight gas
towards both sources. Column densities towards G10.6−0.4 (averaged over VLSR = 10−55 km
s-1) are taken from
Persson et al. (2012). A full spectral scan of
Sgr B2 (M) using Herschel-HIFI has been performed by the HEXOS Key
Programme (Bergin et al. 2010). From these data,
spectra of the ground-state rotational transitions of NH, NH2, and NH3 were extracted and compared to
our data. Resulting ratios are consistent with the findings in Persson et al. (2010), and N(NH3) is in agreement with Wirström et al. (2010). We reduced these data in a manner
similar to that described in Sect. 2 for our Sgr B2 (M)
data, and fitted Gaussian optical depth profiles to the absorption lines to estimate the
column densities.
(1)The resulting upper
limits for the column density and abundance with respect to the total column of hydrogen are
found in Table 2. Here we also present limiting
abundance ratios, relative to the chemically related species NH, NH2, and NH3 along the line-of-sight gas
towards both sources. Column densities towards G10.6−0.4 (averaged over VLSR = 10−55 km
s-1) are taken from
Persson et al. (2012). A full spectral scan of
Sgr B2 (M) using Herschel-HIFI has been performed by the HEXOS Key
Programme (Bergin et al. 2010). From these data,
spectra of the ground-state rotational transitions of NH, NH2, and NH3 were extracted and compared to
our data. Resulting ratios are consistent with the findings in Persson et al. (2010), and N(NH3) is in agreement with Wirström et al. (2010). We reduced these data in a manner
similar to that described in Sect. 2 for our Sgr B2 (M)
data, and fitted Gaussian optical depth profiles to the absorption lines to estimate the
column densities.
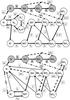 |
Fig. 3 Major formation paths of nitrogen hydrides at t = 106 years for translucent gas conditions (upper panel) and diffuse gas conditions (lower panel). Gas phase species appear in white and grain surface species in grey. Solid lines indicate gas phase reactions, dashed lines photo-dissociation, dotted lines dissociative recombination, electronic radiative recombination and attachment processes, and dot-dashed lines non-thermal desorption from the grain surfaces. |
4. Chemical modelling
In Persson et al. (2010) we modelled abundances of the nitrogen hydrides with a pseudo time-dependent chemical model with constant physical conditions, taking both the gas-phase and grain surface chemistry into account, using the Ohio State University (OSU) gas-grain code (Hasegawa et al. 1992). The predicted NH+ abundance was at most ~10-13−10-14 in translucent clouds with AV = 2−3.
In this paper, we have updated the chemical models to include the formation and destruction
of NH .
The expanded reaction network also includes high temperature reactions (Harada et al. 2010; Hassel et al. 2011) and presently considers 7176 reactions involving a total of
669 gaseous and surface species.
.
The expanded reaction network also includes high temperature reactions (Harada et al. 2010; Hassel et al. 2011) and presently considers 7176 reactions involving a total of
669 gaseous and surface species.
Figure 3 shows two chemical networks outlining the
major reaction pathways involving nitrogen hydrides at t = 106 years,
under translucent and diffuse gas conditions. In both cases, the production of
NH+ purely by
gas-phase processes largely depends on a sufficient source of N+, which can be formed by cosmic
ray ionisation of N or by reactions of He+ with N2 or CN. It should be noted that
H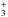 does not react rapidly with N, hence the latter route is the most important one in denser
gas, while the former dominates in diffuse gas. In standard gas-phase ion-molecule
chemistry, NH+ then
initiates the production of nitrogen hydrides (NH, NH2, and NH3) via subsequent reactions with
H2 and electron
recombination. This is, however, not effective in diffuse gas where hydrogen exists mostly
in atomic form. Included in the chemical networks of Fig. 3 is also the surface reaction pathway for the formation of nitrogen hydrides, in
which H atoms are added to N, and NH3 is in turn destroyed by photo-dissociation. The species
NH2 and
NH3 can then be
liberated into the gas phase through non-thermal desorption via the Rice-Ramsperger-Kassel
(RRK) mechanism (Garrod et al. 2006, 2007), where the species desorb as a result of exothermic
surface reactions with an efficiency governed by the parameter aRRK, which is
typically set to 0.01. We have also considered the addition of photodesorption of
NH3 with an assumed
yield of YPD =
10-3 molecules/UV photon in the absence of a measured yield,
based on the formulation of Öberg et al. (2007) for
desorption of CO by both the direct interstellar radiation field and the field caused by
cosmic rays. The direct photodesorption process is of secondary importance to the RRK
mechanism for the formation of NH3(gas) in the translucent gas models and of even lesser
importance in the diffuse gas models. In the diffuse model, the major form of nitrogen is
predominantly elemental N at 106 yrs, while in the the translucent model, elemental N,
NH3(ice), and
N2(gas) are the
major forms. In addition to the processes shown here, there are some minor processes, such
as O + CN → CO + N,
C + NO → N + CO, and
NO+ + e− → N +
O, that return some elemental N to the gas phase from less abundant
forms, but these are omitted from Fig. 3.
does not react rapidly with N, hence the latter route is the most important one in denser
gas, while the former dominates in diffuse gas. In standard gas-phase ion-molecule
chemistry, NH+ then
initiates the production of nitrogen hydrides (NH, NH2, and NH3) via subsequent reactions with
H2 and electron
recombination. This is, however, not effective in diffuse gas where hydrogen exists mostly
in atomic form. Included in the chemical networks of Fig. 3 is also the surface reaction pathway for the formation of nitrogen hydrides, in
which H atoms are added to N, and NH3 is in turn destroyed by photo-dissociation. The species
NH2 and
NH3 can then be
liberated into the gas phase through non-thermal desorption via the Rice-Ramsperger-Kassel
(RRK) mechanism (Garrod et al. 2006, 2007), where the species desorb as a result of exothermic
surface reactions with an efficiency governed by the parameter aRRK, which is
typically set to 0.01. We have also considered the addition of photodesorption of
NH3 with an assumed
yield of YPD =
10-3 molecules/UV photon in the absence of a measured yield,
based on the formulation of Öberg et al. (2007) for
desorption of CO by both the direct interstellar radiation field and the field caused by
cosmic rays. The direct photodesorption process is of secondary importance to the RRK
mechanism for the formation of NH3(gas) in the translucent gas models and of even lesser
importance in the diffuse gas models. In the diffuse model, the major form of nitrogen is
predominantly elemental N at 106 yrs, while in the the translucent model, elemental N,
NH3(ice), and
N2(gas) are the
major forms. In addition to the processes shown here, there are some minor processes, such
as O + CN → CO + N,
C + NO → N + CO, and
NO+ + e− → N +
O, that return some elemental N to the gas phase from less abundant
forms, but these are omitted from Fig. 3.
The abundance of NH+ thus directly depends on a N+ source and the cosmic ionisation rate ζ(H2). Radiative recombination of N+ is a slow process; therefore, in the presence of just a small H2 fraction, N+ is removed mainly by N+ + H2 → NH+ + H , which is the source reaction of NH+. Thus almost every cosmic ray ionisation of N will produce NH+. Reactions with H2 and with electrons removes NH+, but the reactions with H2 dominate as long as e−/H2 ≲ 0.001. Within this limit, independent of density and temperature, the NH+ fractional abundance is of the order of 10-12 at n(H2) ≈ 100 cm-3 and X(N) ≈ 10-4.
The NH anion can form via the dissociative attachment process through electron-impact on
NH3
anion can form via the dissociative attachment process through electron-impact on
NH3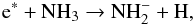 (2)where e∗ represents an
energetic electron. The energetic threshold for this process is ε = 3.857 eV. The possible
destruction processes of NH
(2)where e∗ represents an
energetic electron. The energetic threshold for this process is ε = 3.857 eV. The possible
destruction processes of NH include photo-detachment, reactions with H2, and mutual neutralisation in reactions with the most
abundant positive ions. If the reaction with H2 is the dominant loss process, then the density of
NH
include photo-detachment, reactions with H2, and mutual neutralisation in reactions with the most
abundant positive ions. If the reaction with H2 is the dominant loss process, then the density of
NH at T = 50−100
K will be of the order of
at T = 50−100
K will be of the order of ![\begin{equation} n(\mathrm{NH}_2^-) \sim 7\times 10^{-8}\,\frac{n(\mathrm{NH}_3)}{n(\mathrm{H}_2)}\ \ \mathrm{[cm^{-3}]} , \end{equation}](/articles/aa/full_html/2014/07/aa23748-14/aa23748-14-eq136.png) (3)which immediately
suggests a very low NH
(3)which immediately
suggests a very low NH abundance. A second formation route of NH
abundance. A second formation route of NH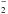 is via slow radiative attachment of electrons to NH2
is via slow radiative attachment of electrons to NH2 (4)Finally, if the anion
is formed in a local region rich in atomic rather than molecular hydrogen, it can be
destroyed by associative attachment with atomic hydrogen,
(4)Finally, if the anion
is formed in a local region rich in atomic rather than molecular hydrogen, it can be
destroyed by associative attachment with atomic hydrogen,
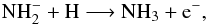 (5)or competitively via
photo-detachment. Details about the different formation and destruction routes of
NH
(5)or competitively via
photo-detachment. Details about the different formation and destruction routes of
NH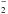 are found in Appendix B.
are found in Appendix B.
 |
Fig. 4 Temporal evolution of the NH+ (left) and
NH |
Chemical models.
Figure 4 shows the resulting temporal evolution of the
NH+ and
NH abundances using the updated chemical network and a typical active non-thermal desorption
efficiency aRRK =
0.01. We have modelled both species under four different physical
conditions: typical dense gas, translucent gas, diffuse gas, and a special model for the
Sgr B2 (M) molecular envelope. All model parameters are found in Table 3.
abundances using the updated chemical network and a typical active non-thermal desorption
efficiency aRRK =
0.01. We have modelled both species under four different physical
conditions: typical dense gas, translucent gas, diffuse gas, and a special model for the
Sgr B2 (M) molecular envelope. All model parameters are found in Table 3.
The choice of initial elemental abundance values vary for the different models. For the translucent and dense models, we adopt “low metal” initial abundances, whereas we adopt a set of “high metal” initial abundances for the diffuse and Sgr B2 (M) models. The “low metal” values account for the incorporation of elements into refractory grains on the basis of observations of ζ Oph (Graedel et al. 1982; Garrod et al. 2007), and the “high metal” values were developed to estimate the abundances if all of this material initially existed in the gas phase (Wakelam & Herbst 2008; Garrod & Herbst 2006). The different values are listed in Table D.5, and the effects of the adoption on abundance of NH+ is explored in Fig. C.1, where the choice of high metal abundances can be seen to increase the abundance of NH+ towards the observational upper limit for the diffuse model. The same trend is found for the Sgr B2 (M) and dense models, however, not for the translucent model.
The dense models are representative of the massive sources themselves, the translucent cloud conditions are traced by, for example, the NH, NH2, and NH3 absorptions along the sight-lines (Persson et al. 2012), and the diffuse cloud conditions are representative of the line-of-sight clouds, from where we believe NH+ originates. The Sgr B2 (M) model reflects the very special conditions found in this source. In Fig. C.2 we show the four models again, but this time with the addition of NH, NH2, and NH3 for comparative purposes. We note that the above results for the translucent model are very similar to the models from Persson et al. (2010).
To check how the surface chemistry affects the resulting abundances we also show (i) gas
and surface chemistry and inactive non-thermal desorption efficiency aRRK = 0; (ii) gas
and surface chemistry with two different aRRK desorption efficiencies; and (iii)
pure gas phase chemistry for the translucent model in Fig. C.3 (on-line material). This figure, as well as Fig. 3, illustrates that the surface chemistry with reactive desorption is a key factor
in the formation of NH2 and NH3, followed in importance by the addition of electrons to
NH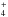 .
We find, however, that our models are not very sensitive to the exact value of the
desorption probability, since the model with aRRK = 0.1 gives very similar results to
the model using aRRK
= 0.01.
.
We find, however, that our models are not very sensitive to the exact value of the
desorption probability, since the model with aRRK = 0.1 gives very similar results to
the model using aRRK
= 0.01.
Since a high cosmic ray ionisation rate is crucial for the production of NH+, our results are sensitive to its assumed value. In the on-line Fig. C.4 we show, therefore, how the NH+ abundance varies in the diffuse model using seven different values of ζ(H2). The NH+ abundance increases by more than an order of magnitude and reaches the observational limit when ζ(H2) increases from 10-17 to 10-14 s-1. The other models also show similar trends.
The rotational transitions of NH+ observed by us provide a sensitive way to search for this
ion in absorption. There are also other kinds of transitions suitable, however, for
interstellar absorption studies as pointed out by de Almeida
& Singh (1982). For example, the ground-state Λ-doubling transition at 13.6 GHz is
observable from Earth and now has well determined hfs frequencies (Hübers et al. 2009). If we neglect hfs in both the lowest pure-rotational
and Λ-doubling transitions and
consider a column density of N(NH+) ~ 1012 cm-2, then the integrated optical
depths in the 1013 and 1019 GHz lines are ∫τdv ~ 0.15 km
s-1 while the
corresponding integrated optical depth at 13.6 GHz is ~0.005 km s-1. The electronic transitions at blue and ultraviolet
wavelengths are slightly more sensitive than the 13.6 GHz transition. Based on the
oscillator strengths tabulated by de Almeida & Singh
(1982), the corresponding values of ∫τdv are 0.009, 0.01, and
0.007 km s-1 in the A
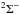 – X
– X
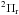 (0, 0), (1, 0),
and (2, 0) bands near 464, 434, and 410 nm wavelength, respectively. The ultraviolet band C
(0, 0), (1, 0),
and (2, 0) bands near 464, 434, and 410 nm wavelength, respectively. The ultraviolet band C
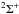 – X
– X
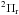 (0, 0) near 289
nm will yield ∫τdv ~ 0.009 km
s-1 under the same
conditions. The existing upper limits on visible and UV lines of NH+ (Snow 1976, 1980; Jenkins et al. 1973) were not very sensitive compared to the submm-wave
results presented here. As far as we are aware, no limits have been derived from more modern
optical data. Possible archival spectra of stars behind diffuse molecular clouds in which
equivalent widths of Wλ ≲ 1 mÅ could easily
be measured in the 434 nm band corresponding to a column density ≲6
× 1011 cm-2, slightly better than the best limit in Table 2.
(0, 0) near 289
nm will yield ∫τdv ~ 0.009 km
s-1 under the same
conditions. The existing upper limits on visible and UV lines of NH+ (Snow 1976, 1980; Jenkins et al. 1973) were not very sensitive compared to the submm-wave
results presented here. As far as we are aware, no limits have been derived from more modern
optical data. Possible archival spectra of stars behind diffuse molecular clouds in which
equivalent widths of Wλ ≲ 1 mÅ could easily
be measured in the 434 nm band corresponding to a column density ≲6
× 1011 cm-2, slightly better than the best limit in Table 2.
5. Conclusions
Our derived NH+ upper limits are an order of magnitude lower than previous estimates (Persson et al. 2012). On the other hand, our chemical modelling suggests that the NH+ abundance may still be a few times lower than our present limits in diffuse gas and under typical Sgr B2 (M) molecular envelope conditions, and several orders of magnitude lower in translucent and dense gas. Since a high ionisation rate is crucial for high NH+ abundances, future searches should focus on regions with greatly enhanced ionisation rates (cf. Indriolo et al. 2012). Searches for NH+ are, however, complicated by the fact that one of its lowest rotational transitions at 1 013 GHz lies only −2.5 km s-1 from the 33,1−22,0 CH2NH line seen in absorption in Sgr B2 (M).
In contrast to NH+,
the NH anion has very low abundances in all models, not supporting our tentative detection in
Sgr B2 (M). This suggests that this species will be very difficult to detect in interstellar
space.
anion has very low abundances in all models, not supporting our tentative detection in
Sgr B2 (M). This suggests that this species will be very difficult to detect in interstellar
space.
Online material
Appendix A: Modelling the CH2NH absorption lines
CH2NH has two transitions with similar line strengths close to NH+ at 1013 GHz: 33,1−22,0 (1012.531 GHz) with El = 41 K only +8.5 MHz (−2.5 km s-1) from NH+, and 33,0−22,1 (1012.661 GHz) seen as a narrow absorption at 21 km s-1. It should be noted that this line blends with the SO2415,37−404,36 (1012.673 GHz) emission. We model the SO2 emission, both CH2NH absorptions, and the o-NH242,2−41,3 emission line wing (seen at ~70 km s-1) in order to subtract these lines in the search for any remaining weak NH+ absorption. All modelled lines are shown in Fig. A.2 together with the original data in black and the resulting spectra after subtraction of the above described lines is shown in red.
 |
Fig. A.1 Sgr B2 (M). Gaussian fits of NH+ 1013 and 1019 GHz line profiles, including all hfs components, to the observations. The arrows mark the velocity range in which the fit was made. |
 |
Fig. A.2 Sgr B2 (M). Observed NH+ 1 013 GHz search spectrum (black) along with models of the two absorbing CH2NH transitions (green and cyan), the expected SO2 (blue) and NH2 (pink) emissions, and the remaining spectrum after removal of their expected contributions (red; more details in Sect. 3). |
The numerous SO2 lines observed in our band (e.g. 395,35−384,34 and 435,39−424,38), as well as in the HEXOS spectral line survey, are used to reconstruct the SO2 1012.673 GHz line. The true CH2NH absorption is then found by comparing the reconstructed SO2 emission with the observed line profile. Finally, the modelled CH2NH absorption is used as a template for the CH2NH absorption at 1012.531 GHz since their line strengths are similar. We use RADEX to check our modelled CH2NH lines together with the 225 GHz (11,1−00,0) line observed in absorption by Nummelin et al. (2000). The integrated opacities of these three lines are matched using a density of n(H2) ~ 105 cm-3, a kinetic temperature of ~100 K, a column density N(CH2NH) ~ 1 × 1015 cm-2, and a line width of ~15 km s-1 which supports the above modelling and results. After subtracting all modelled lines, we find a weak remaining absorption feature at VLSR = 69 km s-1 with an integrated opacity of 0.08 km s-1, which is used as an upper limit to NH+.
 |
Fig. A.3 Absorption feature found at a velocity of +18.5 km s-1 is tentatively
identified as p-NH |
Appendix B: NH chemistry
chemistry
The NH anion can form via the dissociative attachment process through electron-impact on
NH3
anion can form via the dissociative attachment process through electron-impact on
NH3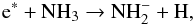 (B.1)where
e∗ represents an energetic electron. The
energetic threshold for this process is ε = 3.857 eV, potentially leading to an unusually
high production rate. At kinetic temperatures of the order of 100 K or less, the thermal
electrons have a characteristic energy less than 9 meV. Therefore, the hot electrons
required to form the anion are extremely superthermal. A self-consistent treatment of
the electron speed distribution in the weakly ionised interstellar medium is currently
being investigated (Black, in prep.). The crucial energy range for reaction (B.3) is 3.8 to 8.5 eV. In photon-dominated
regions, including diffuse molecular clouds, such electrons are produced mainly by the
same photoelectric effect involving dust and large molecules that dominates the heating
of the gas. Energetic electrons are thermalised primarily by collisions with neutrals (H
and H2), rather
than by elastic collisions with thermal electrons, as long as the fractional ionisation
is less than 10-3. The cross-section, σDA, for the
dissociative attachment process has a peak value of 1.6 Mb near ε = 5.8 eV, with
vanishing values at ε< 4.2 and at
ε>
8.5 eV (Sharp & Dowell
1969; Rawat et al. 2008). The number
density of electrons integrated over the interval 3.857 to 8.5 eV is 9.9 × 10-8 cm-3. We find a production rate
for NH
(B.1)where
e∗ represents an energetic electron. The
energetic threshold for this process is ε = 3.857 eV, potentially leading to an unusually
high production rate. At kinetic temperatures of the order of 100 K or less, the thermal
electrons have a characteristic energy less than 9 meV. Therefore, the hot electrons
required to form the anion are extremely superthermal. A self-consistent treatment of
the electron speed distribution in the weakly ionised interstellar medium is currently
being investigated (Black, in prep.). The crucial energy range for reaction (B.3) is 3.8 to 8.5 eV. In photon-dominated
regions, including diffuse molecular clouds, such electrons are produced mainly by the
same photoelectric effect involving dust and large molecules that dominates the heating
of the gas. Energetic electrons are thermalised primarily by collisions with neutrals (H
and H2), rather
than by elastic collisions with thermal electrons, as long as the fractional ionisation
is less than 10-3. The cross-section, σDA, for the
dissociative attachment process has a peak value of 1.6 Mb near ε = 5.8 eV, with
vanishing values at ε< 4.2 and at
ε>
8.5 eV (Sharp & Dowell
1969; Rawat et al. 2008). The number
density of electrons integrated over the interval 3.857 to 8.5 eV is 9.9 × 10-8 cm-3. We find a production rate
for NH by reaction (B.3) of
by reaction (B.3) of
![\appendix \setcounter{section}{2} \begin{equation} \int n_\mathrm{e}(\varepsilon)\,\sigma_\mathrm{DA}(\varepsilon)\,\upsilon\,\mathrm{d}\varepsilon = 7.0\times10^{-18}\ \ \mathrm{[s^{-1}\ per\ NH_3}] . \end{equation}](/articles/aa/full_html/2014/07/aa23748-14/aa23748-14-eq190.png) (B.2)The possible
destruction processes of NH
(B.2)The possible
destruction processes of NH include photo-detachment, reactions with H2, and mutual neutralisation in reactions with the most
abundant positive ions. The reaction with H2,
include photo-detachment, reactions with H2, and mutual neutralisation in reactions with the most
abundant positive ions. The reaction with H2, 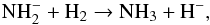 (B.3)is known to be
rapid at low temperatures around 20 K but to decrease with increasing temperature (Otto et al. 2008). If the reaction with
H2 is the
dominant loss process, then the density of NH
(B.3)is known to be
rapid at low temperatures around 20 K but to decrease with increasing temperature (Otto et al. 2008). If the reaction with
H2 is the
dominant loss process, then the density of NH at T = 50−100 K will be of the order of
at T = 50−100 K will be of the order of
![\appendix \setcounter{section}{2} \begin{equation} n(\mathrm{NH}_2^-) \sim 7\times 10^{-8}\,\frac{n(\mathrm{NH}_3)}{n(\mathrm{H}_2)}\ \ \mathrm{[cm^{-3}]}, \end{equation}](/articles/aa/full_html/2014/07/aa23748-14/aa23748-14-eq192.png) (B.4)which immediately
suggests a very low NH
(B.4)which immediately
suggests a very low NH abundance.
abundance.
A second formation route of NH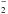 is via slow radiative attachment of electrons to NH2
is via slow radiative attachment of electrons to NH2 (B.5)Radiative
attachment via emission from excited vibrational states has been calculated to be an
efficient process to produce negative molecular ions with large electron affinities
(3−4 eV) and at least four
atoms (Herbst & Osamura 2008). The
NH
(B.5)Radiative
attachment via emission from excited vibrational states has been calculated to be an
efficient process to produce negative molecular ions with large electron affinities
(3−4 eV) and at least four
atoms (Herbst & Osamura 2008). The
NH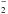 anion is smaller than this limit and has only a moderate electron affinity of 0.771 eV
(Wickham-Jones et al. 1989). Using Eq. (11)
anion is smaller than this limit and has only a moderate electron affinity of 0.771 eV
(Wickham-Jones et al. 1989). Using Eq. (11)
in Herbst & Osamura (2008), we estimate
the rate coefficient for radiative attachment via the vibrational mechanism to be only
1 ×
10-17(T/ 300 K)−1
/ 2 cm3 s-1. The process is at most
competitive with dissociative attachment of NH3 via non-thermal electrons, and does not change the
conclusion that the NH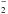 anion has a low abundance. Finally, if the anion is formed in a local region rich in
atomic rather than molecular hydrogen, it can be destroyed by associative attachment
with atomic hydrogen,
anion has a low abundance. Finally, if the anion is formed in a local region rich in
atomic rather than molecular hydrogen, it can be destroyed by associative attachment
with atomic hydrogen, 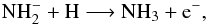 (B.6)or
competitively via photo-detachment.
(B.6)or
competitively via photo-detachment.
Appendix C: Chemical models
 |
Fig. C.1 Temporal evolution of the NH+ abundance for all four models (Table 3) where each model is plotted with a high metal abundance (dashed lines) and with a low metal abundance (solid lines). The translucent and dense models are plotted for TK = 30 K alone. The observed upper limits are indicated with dashed horizontal lines following the respective model colour code. |
 |
Fig. C.2 Temporal evolution of the nitrogen hydride abundances. Upper
left: dense gas; upper right: translucent gas;
lower left: diffuse gas; lower right:
Sgr B2 (M) envelope model (see Table 3).
The dot-dashed and dotted lines for NH |
 |
Fig. C.3 Translucent gas conditions in all models (see Table 3). Upper left: pure gas phase chemistry.
Upper right: gas and surface chemistry and inactive non-thermal
desorption efficiency aRRK = 0. Lower
left: gas and surface chemistry and active non-thermal desorption with
the typical efficiency aRRK = 0.01. Lower
right: gas and surface chemistry and high active non-thermal desorption
(aRRK =
0.1). The observed abundances and upper limits are indicated
with solid and dashed horizontal lines, respectively, following the respective
species colour code. The dot-dashed and dotted lines for
NH |
 |
Fig. C.4 Temporal evolution of the NH+ abundance for different cosmic ray ionisation rates for diffuse gas conditions (Table 3). The dashed black line represents the observed upper NH+ limit in the diffuse gas. |
Appendix D: Tables
Hyperfine structure components of NH+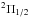 N = 1−1,J =
1.5−−0.5+.
N = 1−1,J =
1.5−−0.5+.
Hyperfine structure components of NH+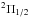 N = 1−1,J =
1.5+−0.5−.
N = 1−1,J =
1.5+−0.5−.
Para-NH
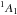 ,
JKa,Kc
= 11,1−00,0. Spectroscopic data from Tack et al. (1986). See Sect. 2 for more details.
,
JKa,Kc
= 11,1−00,0. Spectroscopic data from Tack et al. (1986). See Sect. 2 for more details.
Herschel OBSID’s of the observed transitions analysed in this paper.
Initial elemental abundances.
Acknowledgments
HIFI has been designed and built by a consortium of institutes and university departments from across Europe, Canada, and the United States under the leadership of SRON, Netherlands Institute for Space Research, Groningen, The Netherlands and with major contributions from Germany, France, and the US. Consortium members are: Canada: CSA, U. Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronómico Nacional (IGN), Centro de Astrobiología (CSIC-INTA). Sweden: Chalmers University of Technology – MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University – Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHSC. C.P., J.H.B., and E.S.W. acknowledge generous support from the Swedish National Space Board. E.H. acknowledges the support of NASA for research related to the Herschel HIFI programme. H.S.P.M. is very grateful to the Bundesministerium für Bildung und Forschung (BMBF) for financial support aimed at maintaining the Cologne Database for Molecular Spectroscopy, CDMS. H.M.C. acknowledges the European Research Council (ERC-2010-StG, Grant Agreement No. 259510-KISMOL) for financial support. Support for this work was provided by NASA through an award issued by JPL/Caltech.
References
- Beloy, K., Kozlov, M. G., Borschevsky, A., et al. 2011, Phys. Rev. A, 83, 062514 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botschwina, P., Seeger, S., & Flügge, J. 1993, J. Chem. Phys., 99, 8349 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 2011, EAS Publ. Ser. 58, Proc. the European Conference on Laboratory Astrophysics, 58, 251 [Google Scholar]
- de Almeida, A. A., & Singh, P. D. 1982, A&A, 113, 199 [NASA ADS] [Google Scholar]
- Dore, L., Bizzocchi, L., & Degli Esposti, C. 2012, A&A, 544, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dulieu, F., Congiu, E., Noble, J., et al. 2013, Nature Sci. Rep., 3, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Lada, C. J., Kleinmann, D. E., et al. 1978, ApJ, 221, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Faraday Discuss., 133, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garwood, R. W., & Dickey, J. M. 1989, ApJ, 338, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Gendriesch, R., Lewen, F., Winnewisser, G., & Müller, S. P. 2001, J. Mol. Struct., 599, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, B., Falgarone, E., Gerin, M., et al. 2012, A&A, 540, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graedel, T. E., Langer, W. D., & Frerking, M. A. 1982, ApJS, 48, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Harada, N., Herbst, E., & Wakelam, V. 2010, ApJ, 721, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Hassel, G. E., Harada, N., & Herbst, E. 2011, ApJ, 743, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & Osamura, Y. 2008, ApJ, 679, 1670 [Google Scholar]
- Huang, X., & Lee, T. J. 2009, J. Chem. Phys., 131, 104301 [NASA ADS] [CrossRef] [Google Scholar]
- Hübers, H., Evenson, K. M., Hill, C., & Brown, J. M. 2009, J. Chem. Phys., 131, 034311 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2012, ApJ, 758, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B., Drake, J. F., Morton, D. C., et al. 1973, ApJ, 181, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., & Goldsmith, P. F. 1989, ApJ, 337, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Monje, R. R., Emprechtinger, M., Phillips, T. G., et al. 2011, ApJ, 734, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Mount, B. J., Redshaw, M., & Myers, E. G. 2012, Phys. Rev. A, 85, 012519 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., & Brünken, S. 2005, J. Mol. Spectr., 232, 213 [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 2000, ApJS, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Fuchs, G. W., Awad, Z., et al. 2007, ApJ, 662, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, J., Weiß, A., Staveley-Smith, L., Henkel, C., & Meier, D. S. 2014, ApJ, 785, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Otto, R., Mikosch, J., Trippel, S., Weidemüller, M., & Wester, R. 2008, Phys. Rev. Lett., 101, 063201 [NASA ADS] [CrossRef] [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, C. M., De Luca, M., Mookerjea, B., et al. 2012, A&A, 543, A145 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, I. R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transfer, 60, 883 [Google Scholar]
- Pilbratt, G., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Rawat, P., Prabhudesai, V. S., Rahman, M. A., Ram, N. B., & Krishnakumar, E. 2008, Int. J. Mass Spectrom., 277, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Reid, M. J., Menten, K. M., et al. 2014, ApJ, 781, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, T. E., & Dowell, J. T. 1969, J. Chem. Phys., 50, 3024 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, Jr., T. P. 1976, ApJ, 204, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, Jr., T. P. 1980, in Interstellar Molecules, ed. B. H. Andrew, IAU Symp., 87, 247 [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Tack, L. M., Rosenbaum, N. H., Owrutsky, J. C., & Saykally, R. J. 1986, J. Chem. Phys., 85, 4222 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Belloche, A., Schilke, P., et al. 2006, A&A, 454, L99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhoeve, P., Ter Meulen, J. J., Meerts, W. L., & Dyamanus, A. 1986, Chem. Phys. Lett., 132, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., & Herbst, E. 2008, ApJ, 680, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Wickham-Jones, C. T., Ervin, K. M., Ellison, G. B., & Lineberger, W. C. 1989, J. Chem. Phys., 91, 2762 [NASA ADS] [CrossRef] [Google Scholar]
- Wirström, E. S., Bergman, P., Black, J. H., et al. 2010, A&A, 522, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, L.-H., Fisher, J., Lees, R. M., et al. 2008, J. Mol. Spectr., 251, 305 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Resulting NH+
and NH column densities, N, column density ratios with related species,
and abundances, X, with respect to the total amount of hydrogen
towards Sgr B2 (M) and G10.6−0.6.
column densities, N, column density ratios with related species,
and abundances, X, with respect to the total amount of hydrogen
towards Sgr B2 (M) and G10.6−0.6.
Para-NH
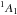 ,
JKa,Kc
= 11,1−00,0. Spectroscopic data from Tack et al. (1986). See Sect. 2 for more details.
,
JKa,Kc
= 11,1−00,0. Spectroscopic data from Tack et al. (1986). See Sect. 2 for more details.
All Figures
 |
Fig. 1 G10.6−0.4: searches for
NH+ and
p-NH |
| In the text | |
 |
Fig. 2 Sgr B2 (M): searches for NH+ and p-NH |
| In the text | |
 |
Fig. 3 Major formation paths of nitrogen hydrides at t = 106 years for translucent gas conditions (upper panel) and diffuse gas conditions (lower panel). Gas phase species appear in white and grain surface species in grey. Solid lines indicate gas phase reactions, dashed lines photo-dissociation, dotted lines dissociative recombination, electronic radiative recombination and attachment processes, and dot-dashed lines non-thermal desorption from the grain surfaces. |
| In the text | |
 |
Fig. 4 Temporal evolution of the NH+ (left) and
NH |
| In the text | |
 |
Fig. A.1 Sgr B2 (M). Gaussian fits of NH+ 1013 and 1019 GHz line profiles, including all hfs components, to the observations. The arrows mark the velocity range in which the fit was made. |
| In the text | |
 |
Fig. A.2 Sgr B2 (M). Observed NH+ 1 013 GHz search spectrum (black) along with models of the two absorbing CH2NH transitions (green and cyan), the expected SO2 (blue) and NH2 (pink) emissions, and the remaining spectrum after removal of their expected contributions (red; more details in Sect. 3). |
| In the text | |
 |
Fig. A.3 Absorption feature found at a velocity of +18.5 km s-1 is tentatively
identified as p-NH |
| In the text | |
 |
Fig. C.1 Temporal evolution of the NH+ abundance for all four models (Table 3) where each model is plotted with a high metal abundance (dashed lines) and with a low metal abundance (solid lines). The translucent and dense models are plotted for TK = 30 K alone. The observed upper limits are indicated with dashed horizontal lines following the respective model colour code. |
| In the text | |
 |
Fig. C.2 Temporal evolution of the nitrogen hydride abundances. Upper
left: dense gas; upper right: translucent gas;
lower left: diffuse gas; lower right:
Sgr B2 (M) envelope model (see Table 3).
The dot-dashed and dotted lines for NH |
| In the text | |
 |
Fig. C.3 Translucent gas conditions in all models (see Table 3). Upper left: pure gas phase chemistry.
Upper right: gas and surface chemistry and inactive non-thermal
desorption efficiency aRRK = 0. Lower
left: gas and surface chemistry and active non-thermal desorption with
the typical efficiency aRRK = 0.01. Lower
right: gas and surface chemistry and high active non-thermal desorption
(aRRK =
0.1). The observed abundances and upper limits are indicated
with solid and dashed horizontal lines, respectively, following the respective
species colour code. The dot-dashed and dotted lines for
NH |
| In the text | |
 |
Fig. C.4 Temporal evolution of the NH+ abundance for different cosmic ray ionisation rates for diffuse gas conditions (Table 3). The dashed black line represents the observed upper NH+ limit in the diffuse gas. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.