| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424027 | |
| Published online | 25 June 2014 | |
Period and amplitude variations in post-common-envelope eclipsing binaries observed with SuperWASP⋆
1 Department of Physical Sciences, The Open University, Walton Hall, Milton Keynes MK7 6AA, UK
e-mail: Marcus.Lohr@open.ac.uk
2 Astrophysics Group, Keele University, Staffordshire ST5 5BG, UK
3 SUPA, School of Physics & Astronomy, University of St. Andrews, North Haugh, Fife KY16 9SS, UK
4 Department of Physics, University of Warwick, Coventry CV4 7AL, UK
5 Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, UK
6 Isaac Newton Group of Telescopes, Apartado de Correos 321, 38700 Santa Cruz de la Palma, Tenerife, Spain
Received: 17 April 2014
Accepted: 16 May 2014
Period or amplitude variations in eclipsing binaries may reveal the presence of additional massive bodies in the system, such as circumbinary planets. Here, we have studied twelve previously-known eclipsing post-common-envelope binaries for evidence of such light curve variations, on the basis of multi-year observations in the SuperWASP archive. The results for HW Vir provided strong evidence for period changes consistent with those measured by previous studies, and help support a two-planet model for the system. ASAS J102322−3737.0 exhibited plausible evidence for a period increase not previously suggested; while NY Vir, QS Vir and NSVS 14256825 afforded less significant support for period change, providing some confirmation to earlier claims. In other cases, period change was not convincingly observed; for AA Dor and NSVS 07826147, previous findings of constant period were confirmed. This study allows us to present hundreds of new primary eclipse timings for these systems, and further demonstrates the value of wide-field high-cadence surveys like SuperWASP for the investigation of variable stars.
Key words: stars: variables: general / binaries: close / binaries: eclipsing
Appendix A is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/566/A128
© ESO, 2014
1. Introduction
Since the discovery of planetary-mass objects around millisecond pulsar PSR B1257+12 (Wolszczan & Frail 1992), exoplanets have been detected in a range of surprising environments. Numerous hot Jupiters present a challenge to planetary system formation models (e.g. Mayor & Queloz 1995); planets have been found orbiting single members of binary and higher-order multiple star systems (e.g. Butler et al. 1997; Anglada-Escudé et al. 2012); and recently a number of circumbinary planets have been observed (e.g. Doyle et al. 2011). In the last few years, claims of planets in post-common-envelope binaries (PCEBs) have proved especially controversial, and in this paper we aim to add to the evidence needed to evaluate models for such systems, using archival survey data.
A notable class of binary star systems have passed through a phase of common envelope evolution (Paczynski 1976). The details of the process and its various possible outcomes are not yet fully understood (for a recent review see Ivanova et al. 2013); however, one observed outcome is the formation of a PCEB consisting of a hot subdwarf B (sdB) or OB stellar core (Heber 2009) or white dwarf (WD) primary, and a low-mass main sequence star or brown dwarf companion, in a close but detached orbital configuration. Eclipsing PCEBs of these types are especially valuable for understanding common envelope evolution and subsequent system behaviours, since their parameters can be determined with high precision. Their photometric light curves are also highly distinctive, often exhibiting well-defined very deep primary eclipses and strong reflection effects (e.g. HW Vir in Fig. 1). Together with their short orbital periods (usually a few hours), these features facilitate accurate measurement of timings of minimum light, and thereby the construction of observed minus calculated (O−C) diagrams to reveal any changes in orbital period over time.
 |
Fig. 1 SuperWASP light curves for 12 eclipsing PCEBs phase-folded at periods given in Table 1, with binned mean curves overplotted in red (online only). The x axes indicate phase; the y axes SuperWASP flux in arbitrary units (pseudo-V magnitudes are given by 15 − 2.5log (flux). A typical point’s uncertainty is shown in the bottom right of each panel. |
PCEBs observable in SuperWASP archive.
Zorotovic & Schreiber (2013) compiled a list of currently known eclipsing PCEBs, including 13 with an sdB primary and 43 with a WD primary, and noted that for five sdB systems and four WD systems apparent period changes had been observed: a surprisingly high proportion of those which have been well-studied over long time bases. Many researchers have seen these period changes as evidence for the presence of additional massive bodies in the system: circumbinary giant planets1 or brown dwarfs e.g. Lee et al. (2009); Beuermann et al. (2010). The reality of such PCEB planets is somewhat controversial. Where multiple circumbinary planets have been proposed in a single system, the long-term dynamical stability of their orbits has often been questioned e.g. Horner et al. (2013); Wittenmyer et al. (2013), though the dynamical stability analyses used have also been criticized on methodological grounds (Marsh et al. 2014). Zorotovic & Schreiber (2013) carried out binary population syntheses which suggested that giant planets should be rare in the progenitors of PCEBs, leaving secondary planet formation (Völschow et al. 2014) or a non-planetary cause such as the Applegate mechanism (Applegate 1992) as the most likely explanations for the observed period changes.
Distinguishing between different proposed architectures for circumbinary planetary systems, and indeed determining whether planets are plausible in PCEBs at all, relies largely upon the quality of the eclipse timing observations: ideally, we would have a large number of precise measurements of light curve minima, evenly covering a long time-base. In practice, many systems for which period changes indicative of circumbinary planets have been claimed, fall far short of this ideal. Therefore, here we search the archive of the SuperWASP (Wide Angle Search for Planets) project (Pollacco et al. 2006) for evidence of period changes in those PCEBs from Zorotovic & Schreiber’s Table 1 which have been observed by SuperWASP. The archive contains high-cadence photometric light curves for bright sources (V ~ 8–15 mag) over almost the whole sky, stretching back to 2004 in many cases, and so should be capable of filling in gaps or extending the coverage of O−C diagrams for many of these systems. We have previously observed and measured period changes in short-period main sequence eclipsing binary candidates using SuperWASP data (Lohr et al. 2012, 2013); here, we develop our analytical method to improve the precision and robustness of its period change measurements, and to search for variations in light curve amplitude as well. It is hoped that the results may shed light on future investigations of this intriguing group of eclipsing binary systems.
2. Method
The SuperWASP archive was first searched for objects within 1 arcmin of the coordinates of known bright eclipsing PCEB systems. Matching light curves were extracted, and checked visually for evidence of the expected variability. In marginal cases, and where sources neighbouring each other on the sky exhibited a similar pattern of variability, the custom IDL code described below was used to determine objectively whether the eclipsing signal was detectable in the data, or to select the source with the strongest signal amongst near neighbours. Once the set of usable SuperWASP eclipsing PCEBs had been established, their Sys-Rem-corrected fluxes (Tamuz et al. 2005; Mazeh et al. 2006), from a 3.5 pixel-radius aperture, formed the basis of further analysis.
2.1. Orbital period and mean light curve determination
Extreme outliers can often complicate the analysis of SuperWASP light curves; here, a first pass stripped out physically-impossible data points, and then an envelope enclosing a plausibly-relevant range of fluxes was determined from the flux frequency distribution.
Reference orbital periods were found using a form of phase dispersion minimization (Lafler & Kinman 1965; Stellingwerf 1978), by folding each light curve on a range of trial periods (initially separated by 1 s), binning the folded curves by pseudo-phase, and summing the standard deviations of fluxes in each bin to give a total dispersion measure per trial period. The lowest dispersion should correspond to the best folding, where the data points have minimal scatter about the mean light curve shape. The period could then be refined further by repeating the search with smaller time steps between trial periods. Slightly different final periods are found if different numbers of phase bins are used to calculate dispersions; therefore, by repeating the whole period-determination procedure with a range of binnings, a mean reference period and an indication of its uncertainty were determined for each object, and these values were used for the remainder of our analysis (P in Table 1).
A third stage of outlier-removal was then applied, iteratively cleaning out points lying 4.5 standard deviations from the binned mean flux values. This allowed a smoother light curve template shape to be determined for each object; the number of points used for each template also affected its out-of-eclipse smoothness and the sharpness of its eclipses, and this was optimized by visual inspection.
As yet the folded curves had arbitrary pseudo-phases associated with their minima, so each deeper (primary) minimum was aligned with phase zero in a two-step process. First, an approximate zero-phase was found from the bin with the lowest mean flux (this would give inaccurate results if each bin covered a significant fraction of the orbital period, or if the primary eclipses were flat-bottomed). Then, folded data points within 0.1 phases of the approximate zero point were used to define the true zero, by mirror-folding about a number of trial zeroes, and applying phase dispersion minimization again. This method has the advantage of using all the data near eclipse, rather than just the binned means, and so is able to benefit from the long time-base and extensive cycle-coverage of a modern time-domain automated survey like SuperWASP. However, it does rely on the assumption of basically symmetric primary eclipses, like the method of Kwee & van Woerden (1956), which is still used widely with high-quality photometric light curves covering a small number of nights. Where eclipses are clearly asymmetric, a minimum-flux approach to finding the zero phase would probably be more meaningful; in these PCEBs, however, primary eclipses were indeed highly symmetric, and so a method allowing direct comparison between SuperWASP eclipse timings and those measured by others using Kwee & van Woerden’s approach was preferred here.
2.2. Period and amplitude variation measurement
Expected primary eclipse times (on the assumption of constant periods) were then calculated for every cycle within the time-base covered by SuperWASP data. The first of these reference minima, converted to barycentric Julian date (BJD-TDB), is given for each object in the final column of Table 1; in combination with the given periods, this provides SuperWASP linear ephemerides. Using these, each night of observed data was compared with a fitting template covering appropriate phases, derived from the binned mean light curve template generated earlier, interpolated by a spline curve as necessary to match the exact times of observation. The template could be adjusted using three parameters: x-axis position (time), y-axis position (flux), and scaling in the y-direction (amplitude of curve). At each fitting step, the observed curve was compared with 125 synthetic curves generated from the template by varying the three parameters simultaneously according to a cubic grid of possible values, and the minimum χ2 value was chosen as indicating the best fit. The first step had the expected x-y location and scale of the template as the centre of the parameter “cube”; subsequent steps recentred the cube on the parameter combination with the lowest χ2 value at the previous step. If a fitting attempt repeatedly moved the centre to the edge of the previous cube, it was deemed not to be converging, and was abandoned. If the cube’s centre did not move between steps, the separation between grid points was reduced, and the fitting step was repeated. This continued until the difference between adjacent steps’ minimum χ2 values fell below a critical threshold (0.001).
In this way, an optimum fit between the light curve template found for the whole data set folded at its mean (reference) period, and each night of observed data, could be determined. This best fit provided an x-axis offset from the expected value, which corresponded to an O−C value for the night as a whole, but which could also be combined with the nearest time of calculated minimum to produce a BJD (TBD) for that eclipse, allowing direct comparison with other published times of minima for the same source. Our approach here, fitting an adjustable template light curve to the whole of a night’s data (which could cover several orbital cycles in the case of some short-period PCEBs), aimed to take full advantage of the SuperWASP project’s strengths: long-term, numerous, fairly high-cadence observations, without being hampered by its relatively low signal-to-noise photometry in comparison with larger telescopes. On many occasions, a useful time of primary eclipse could be obtained even when the eclipse itself was not captured by the night’s observations, since the reflection effect and shape of secondary minimum provided sufficient information for an excellent fit (see Fig. 2 for an example single-night fit).
Changes in light curve amplitude could also be measured, using the y-scaling parameter adjustment for the best fit. The remaining fixed-scale y-shifting parameter would track any changes in flux level for the whole night’s curve, relative to the full light curve’s out-of-eclipse mean flux; such changes might be expected to result from varying air mass or Moon proximity on different nights, or from instrumental noise. Approximate starting uncertainties for each of the three parameter values were obtained from the curvature of the χ2 volume in the final cubic grid.
 |
Fig. 2 First night of SuperWASP observations of HW Vir, with best fit overplotted (final uncertainty in timing <2 s). |
 |
Fig. 3 O−C diagrams for six PCEBs potentially indicating period change, constructed using SuperWASP data only. The x axes indicate night count since the start of observation (since whole nights are fitted with template curves); the y axes give O−C measurements in seconds. Automatically-excluded outliers are in black and selected good minimum timings in red (colour online only); a small number of more extreme outliers lie outside the bounds of some plots. Best linear (red solid line) and quadratic (blue dashed line) fits to the selected data points are overplotted. |
2.3. Outlier removal and method testing
After all nights had been processed, convergent results could be plotted on three diagrams corresponding to the different fitting parameters. Outliers in the O−C diagram in particular (e.g. HW Vir in Fig. 3) tended to complicate the determination of period change. Night-by-night visual checks of the fitted data did not suggest any underlying physical cause for short-term variations such as spots or additional eclipses. We may note that similar visual checks of apparent contact eclipsing binary 1SWASP J093010.78+533859.5, occasioned by its erratic O−C diagram, revealed a second eclipsing binary (Lohr et al. 2013); the outlying values here present a far more chaotic appearance, and are most probably produced by a range of atmospheric and instrumental complicating factors, like the outliers in SuperWASP light curves in general.
To some extent, these O−C outliers could be excluded by the size of their uncertainties: some nights of data contained only a handful of apparently erratic observations, and the resulting poor fits had large uncertainties for their parameter values. However, some nights resulted in well-constrained good fits despite being obvious outliers relative to the local O−C trend, so this criterion was not sufficient. Excluding nights with small numbers of observations would also have removed many perfectly good values from the O−C diagram (where those observations were spaced closely around the primary minimum, for example). Removing points on the basis that they lay several standard deviations from the mean O−C value would also have been unhelpful, since it would have removed valid points if the underlying shape of the data set was parabolic. It was of course not known in advance whether a linear or quadratic fit would be appropriate for each O−C diagram, and the presence of outliers could easily change which function gave a better fit to the data set.
Therefore, an automated iterative procedure was carried out (without any prior preference for either function) attempting linear and quadratic fits alternately to each O−C diagram, and removing points lying >3 standard deviations from the better fit or with uncertainties >3 standard deviations larger than the mean uncertainty size. Sinusoidal fits were not attempted, since this would introduce too many degrees of freedom, and since the time-base covered appeared short enough that sinusoidal variation would show up as approximately quadratic in any case. The plot of amplitude variation was also used to exclude extreme outliers in that dimension; however, the absolute flux variation plot was not used, since sudden and substantial variations in that dimension appeared entirely physically plausible. If the χ2 value of the better fit ever fell below 1, the uncertainties of the remaining points were rescaled accordingly. The process halted when no further points needed to be removed2.
Following this procedure, period change was either supported, if a quadratic function gave a better fit to the remaining data points in the O−C diagram, or unsupported, if a linear function gave a better fit. (A linear fit with slope significantly different from zero would also arise if the period used were too long or too short, though irregular or sparse coverage of the time base could also produce a non-zero gradient even with an accurate period.) However, some cases of apparent period change were only marginally supported, in that the best linear fit produced a (modified) χ2 value only slightly higher than the best quadratic fit. Since the points’ uncertainties had been adjusted during the process of outlier removal, it was not clear how large a difference in χ2 values would be required to indicate e.g. a 95% confidence level in a measurement of period change. In particular, there seemed no reason to believe that the same level would be valid in all cases.
Therefore, tests using synthetic light curves were carried out to determine the reliability of the program. Each object’s mean (template) light curve was used as the basis for generating a large number of “background” synthetic curves, and the time sampling and point uncertainties of the original light curve were applied to each synthetic curve. Each flux value was then perturbed randomly according to a normal distribution with standard deviation equal to the corresponding original data point’s uncertainty. Correlations between observations made on the same night in SuperWASP light curves were accounted for by determining the mean residual flux of each night’s observations relative to the template, and adding one of these values, chosen at random, to each night’s fluxes in the synthetic curve. Histograms of the final synthetic curves’ residual fluxes, relative to their mean curves, followed approximately Gaussian distributions (like the original objects), but with slightly greater widths i.e. the synthetic curves had slightly larger uncertainties than the real light curves. No period change was included in the synthetic curves. They were then processed by our code in exactly the same way as the real light curves, to see what proportion of them produced false positives, and how large the difference between best linear and quadratic fit χ2 values was. This allowed us to distinguish between statistically significant and non-significant period changes.
A similar approach was used to check the sensitivity of the program to genuine period change. Synthetic curves were generated as before, with the characteristics of the test objects; here, however, steady period change was included, with a known sign and magnitude. Our code was then run on the synthetic curves, to determine lower limits of detectability for each system i.e. how rapid a period change would need to be in order to be reliably detected and accurately measured using SuperWASP archive data.
3. Results
Of Zorotovic & Schreiber’s collected eclipsing PCEBs, twelve were bright enough to have usable observations in the SuperWASP archive, of which nine were HW Vir-type systems (sdB or sdOB primary with an M dwarf or brown dwarf companion), and three contained a WD with a low-mass main sequence companion (Table 1). In the case of QS Vir, two nearby sources fell within the SuperWASP aperture, resulting in a pair of very similar archive light curves containing the eclipsing signal of the same system. One curve was slightly brighter and had a larger amplitude, and was selected for further analysis here.
Orbital periods were determined for the twelve objects by the method described in Sect. 2, accurate to between 7 and 9 significant figures (see Table 1, which also gives the date ranges during which they were observed by SuperWASP). Their light curves, phase-folded using these periods, are shown in Fig. 1. All exhibit a strong reflection effect; in ASAS 10232 and 2M 1938+4603 this dominates the light curve shape. The other systems all show deep, well-defined primary eclipses, which are flat-bottomed in the cases of the WD systems and AA Dor. V471 Tau exhibited extreme short-term variability in light curve shape and amplitude, which prevented further analysis of possible period changes since no typical template curve could be determined for it. It therefore plays no further part in this study, though an individual customized analysis of its SuperWASP archive data might yield useful results in future.
The remaining eleven objects were searched for evidence of period change, and a selection of their O−C diagrams are given in Fig. 3. In six cases, the best fit to the data following outlier removal was quadratic (ASAS 10232, EC 10246−2707, HW Vir, NSVS 14256825, NY Vir and QS Vir), so the significance of the period change implied was tested for these objects. HW Vir exhibited highly significant period increase over the observed time base (p-value of 0.002 i.e. 0.2% of “background” tests provided equally strong or stronger evidence for period change, purely by chance). ASAS 10232 and NY Vir showed very plausible evidence for period change (p-values of 0.02 and 0.06, respectively). Even considering that 11 trials were run, we would expect to find three or more results with p ≤ 0.06 by accident only ~2.5% of the time. QS Vir, NSVS 14256825 and EC 10246−2707 provided increasingly weak and non-significant support for period change (p-values of 0.22, 0.28 and 0.36, respectively); however, we note that the direction and approximate magnitude of the changes suggested for QS Vir and NSVS 14256825 accord with the findings of other researchers (see Sects. 4.11 and 4.8 below). The other five objects did not show evidence of period change over the time bases considered.
The full set of SuperWASP light curves had widely-varying sensitivities to genuine change: for DE CVn changes of up to 0.03 s yr-1 would not have been detectable, while for NSVS 07826147, any changes would have to be slower than 0.0003 s yr-1 to be missed. Table 1 gives the measured period changes (Ṗ) and the limits of expected period change detectability (Ṗ limit). Tables A.1–A.22 (available at the CDS) give the times of minima for the eleven objects, in BJD (BDT).
No clear evidence of change in light curve amplitudes was observed, though there was a possible suggestion of curvature in ASAS 10232’s amplitude-time diagram which might repay further investigation.
4. Discussion
For easier comparison with others’ findings, previously-published eclipse timings were collected for each object, and converted to BJD (TDB) where necessary3. O−C diagrams were then compiled relative to a recent or widely-used ephemeris, and the new SuperWASP values were included after seasonal binning to improve the clarity of the trends they indicate (Fig. 4). Objects are discussed individually.
 |
Fig. 4 O−C diagrams for eleven PCEBs according to ephemerides given in text, including previously published eclipse timings (black squares) and new binned SuperWASP timings (red crosses). The x axes indicate cycle count; the y axes O−C values in seconds. For HW Vir, the region containing new SuperWASP values is surrounded by a red rectangle for clarity. For HS 2231+2441, larger black squares indicate the approximate locations of the unpublished observations of Qian et al. (2010b), with their fitted curve overplotted as a solid line. |
4.1. AA Dor
AA Dor was discovered, identified as an eclipsing sdB binary, and given an initial solution in a series of papers by Kilkenny et al. (1978, 1979, 1981), and eclipse timings have been published for it covering the period 1977–2010 (Kilkenny 1986, 2011; Kilkenny et al. 1991, 2000). The ephemeris used here is from Kilkenny (2011): 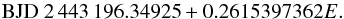 (1)They conclude that a linear ephemeris is sufficient to explain the observations to date, and the addition of our partially-overlapping timings, extending coverage to March 2011, does not contradict this. They suggest that any change greater than about 3 × 10-7 s yr-1 would be ruled out. AA Dor is notable within the set of objects because, as Zorotovic & Schreiber point out, “it is so far the only PCEB with continuous high-precision eclipse time measurements that does not show any signs of apparent period variations”.
(1)They conclude that a linear ephemeris is sufficient to explain the observations to date, and the addition of our partially-overlapping timings, extending coverage to March 2011, does not contradict this. They suggest that any change greater than about 3 × 10-7 s yr-1 would be ruled out. AA Dor is notable within the set of objects because, as Zorotovic & Schreiber point out, “it is so far the only PCEB with continuous high-precision eclipse time measurements that does not show any signs of apparent period variations”.
4.2. ASAS 10232
The discovery paper for ASAS 10232 as an eclipsing sdB binary is Schaffenroth et al. (2013), which also provides an orbital solution, but only a single time of minimum obtained from Carnes Hill Observatory BVI light curves from March 2008: HJD 2 454 538.99689±0.00042 (or possibly 0.000042). They determine a period from the first three years of SuperWASP archived observations, covering May 2006–January 2009; since our data points used here form a superset of their data, extending coverage to June 2011, we prefer our period (Table 1) with their cycle zero to form the ephemeris: 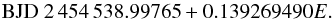 (2)Schaffenroth et al. also measured individual eclipse times from their SuperWASP data, by a similar method to that used here (fitting a mean light curve to night-by-night data), to produce an O−C diagram (their Fig. 7), to which they fit a downward-opening parabola. On the basis of this they suggest a possible period decrease in the system, but note that it requires more observations to confirm. The fitting method used here is able to benefit from a longer time-base and hence a better-defined mean light curve; thus we have apparently been able to measure the times of eclipse more precisely from the same source of data. Although their point uncertainties are not shown, the majority of their O−C values seem to fall within ~400 s of the fitted curve; ours (Fig. 3) fall mostly within ~100 s of the preferred quadratic fit. After binning every two weeks’ O−C values together (Fig. 4) the trend is even more clearly indicated: over six years, the system appears to be increasing, rather than decreasing in period. Of course, the variation may be more complex e.g. sinusoidal, on a still longer timescale, and further independent observations are needed to help clarify the behaviour of this system.
(2)Schaffenroth et al. also measured individual eclipse times from their SuperWASP data, by a similar method to that used here (fitting a mean light curve to night-by-night data), to produce an O−C diagram (their Fig. 7), to which they fit a downward-opening parabola. On the basis of this they suggest a possible period decrease in the system, but note that it requires more observations to confirm. The fitting method used here is able to benefit from a longer time-base and hence a better-defined mean light curve; thus we have apparently been able to measure the times of eclipse more precisely from the same source of data. Although their point uncertainties are not shown, the majority of their O−C values seem to fall within ~400 s of the fitted curve; ours (Fig. 3) fall mostly within ~100 s of the preferred quadratic fit. After binning every two weeks’ O−C values together (Fig. 4) the trend is even more clearly indicated: over six years, the system appears to be increasing, rather than decreasing in period. Of course, the variation may be more complex e.g. sinusoidal, on a still longer timescale, and further independent observations are needed to help clarify the behaviour of this system.
4.3. EC 10246−2707
Although previously known to contain an sdB star, EC 10246−2707 was not described as an eclipsing binary until Barlow et al. (2013), which also estimates the system parameters and provides eclipse timings between February 1997 and June 2012. We use their ephemeris: 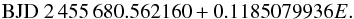 (3)They find no evidence for period change on the basis of their data, and determine a limit on detectability of change of 0.0003 s yr-1. Our results here support this non-detection of change, and help to fill a gap in their coverage of the system’s behaviour during 2006–2008.
(3)They find no evidence for period change on the basis of their data, and determine a limit on detectability of change of 0.0003 s yr-1. Our results here support this non-detection of change, and help to fill a gap in their coverage of the system’s behaviour during 2006–2008.
4.4. HS 2231+2441
The discovery paper for HS 2231+2441 is Østensen et al. (2007), who determine system parameters and provide the ephemeris: 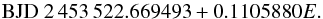 (4)Qian et al. (2010b) describe observations of the system between 2005 and 2009, and provide an O−C diagram (their Fig. 4), which they fit with a function including both a quadratic and a sinusoidal term. Therefore, they suggest the presence of a secular decrease in orbital period, associated with magnetic braking, and a tertiary companion responsible for the sinusoidal variation. Since their times of minima do not appear to have been published yet, we compare our SuperWASP eclipse timings with their fitted curve, and estimate the cycle numbers of their observations from their O−C diagram; their data values are placed on the fitted curve despite exhibiting some scatter about it (Fig. 4). Although fairly close to their fit during 2006 and 2007, our observations do not strongly support it outside their original data range i.e. during 2004 and 2012, and a linear function might provide a better fit to the full data set. A straight-line fit with negative slope would be expected in an O−C diagram if the period used to construct it were too long; we note that Østensen et al.’s period, based on just three nights of observations during June and September 2005, is fractionally longer than ours (0.11058784 d), and quoted to lower precision, and this may be a cause for the apparent long-term downward trend seen here.
(4)Qian et al. (2010b) describe observations of the system between 2005 and 2009, and provide an O−C diagram (their Fig. 4), which they fit with a function including both a quadratic and a sinusoidal term. Therefore, they suggest the presence of a secular decrease in orbital period, associated with magnetic braking, and a tertiary companion responsible for the sinusoidal variation. Since their times of minima do not appear to have been published yet, we compare our SuperWASP eclipse timings with their fitted curve, and estimate the cycle numbers of their observations from their O−C diagram; their data values are placed on the fitted curve despite exhibiting some scatter about it (Fig. 4). Although fairly close to their fit during 2006 and 2007, our observations do not strongly support it outside their original data range i.e. during 2004 and 2012, and a linear function might provide a better fit to the full data set. A straight-line fit with negative slope would be expected in an O−C diagram if the period used to construct it were too long; we note that Østensen et al.’s period, based on just three nights of observations during June and September 2005, is fractionally longer than ours (0.11058784 d), and quoted to lower precision, and this may be a cause for the apparent long-term downward trend seen here.
4.5. HW Vir
The prototype for eclipsing sdB binaries, HW Vir was discovered by Menzies & Marang (1986), and its times of minima were documented between 1984 and 2002 by a group at the South African Astronomical Observatory (Marang & Kilkenny 1989; Kilkenny et al. 1991, 1994, 2000, 2003), who also studied AA Dor and NY Vir over many years. Following Beuermann et al. (2012b), we include their eclipse timings in Fig. 4 along with others having a quoted error ≤0.0001 d (Wood et al. 1993; Lee et al. 2009; Brát et al. 2011), and Beuermann et al.’s own results, up to February 2012. For clearer comparison of our results with the recent models of Lee et al. and Beuermann et al., we use their ephemeris: 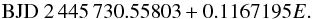 (5)Lee et al. interpreted the O−C diagram up to 2009 (epoch ~76 000; their Fig. 5 top panel) as the sum of a downward-opening parabola (secular period decrease caused by magnetic braking) and two sinusoidal terms (LITE associated with two substellar circumbinary companions). However, Beuermann et al. pointed out that the proposed companions’ orbits crossed, indicating a probable near-encounter or collision within 2000 y; moreover, the O−C values after 2009 diverge substantially from Lee et al.’s fit, curving upwards rather than following the proposed quadratic decline. They argue for an alternative model without the long-term period decrease, and involving two circumbinary low-mass objects in orbits which they found to be stable for more than 108 y. We note that our new SuperWASP eclipse timings, covering July 2006 to March 2011, strongly support Beuermann et al.’s model over that of Lee et al., in that a significant period increase is clear, and several previously undocumented parts of the general trend during this time are now well covered. HW Vir is also the system in which the contribution of SuperWASP archival data is most readily apparent: some 180 primary eclipse timings could be measured with uncertainties below 0.00006 d, covering about six years.
(5)Lee et al. interpreted the O−C diagram up to 2009 (epoch ~76 000; their Fig. 5 top panel) as the sum of a downward-opening parabola (secular period decrease caused by magnetic braking) and two sinusoidal terms (LITE associated with two substellar circumbinary companions). However, Beuermann et al. pointed out that the proposed companions’ orbits crossed, indicating a probable near-encounter or collision within 2000 y; moreover, the O−C values after 2009 diverge substantially from Lee et al.’s fit, curving upwards rather than following the proposed quadratic decline. They argue for an alternative model without the long-term period decrease, and involving two circumbinary low-mass objects in orbits which they found to be stable for more than 108 y. We note that our new SuperWASP eclipse timings, covering July 2006 to March 2011, strongly support Beuermann et al.’s model over that of Lee et al., in that a significant period increase is clear, and several previously undocumented parts of the general trend during this time are now well covered. HW Vir is also the system in which the contribution of SuperWASP archival data is most readily apparent: some 180 primary eclipse timings could be measured with uncertainties below 0.00006 d, covering about six years.
4.6. 2M 1938+4603
2M 1938+4603, a Kepler-field object (Borucki et al. 2010) known to contain an sdB star, was observed to possess shallow primary and secondary eclipses, in addition to its substantial reflection effect, by Østensen et al. (2010) (who also discovered HS 2231+2441). On the basis of 13 supplementary ground-based timings covering June 2008–May 2010, they provide the ephemeris 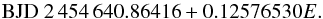 (6)Our SuperWASP timings extend coverage back to May 2004, and although they are individually not very precise, when binned together they suggest a long-term negative linear trend. As with HS 2231+2441, we suspect Østensen et al.’s period is fractionally too long (ours is 0.12576522 d), creating a downward slope in the O−C diagram (their timing uncertainties may also be underestimated, given the scatter of their observations about the mean). Allowing for this, our data set does not seem to suggest any period change in this system. It is interesting to note that Østensen et al. also provide 77 extremely precise consecutive eclipse timings from Kepler observations (around epoch 2500); when the full continuous space-based light curve for this object is made available, it should be possible to determine whether 2M 1938+4603 is undergoing period variations with unprecedented confidence and precision.
(6)Our SuperWASP timings extend coverage back to May 2004, and although they are individually not very precise, when binned together they suggest a long-term negative linear trend. As with HS 2231+2441, we suspect Østensen et al.’s period is fractionally too long (ours is 0.12576522 d), creating a downward slope in the O−C diagram (their timing uncertainties may also be underestimated, given the scatter of their observations about the mean). Allowing for this, our data set does not seem to suggest any period change in this system. It is interesting to note that Østensen et al. also provide 77 extremely precise consecutive eclipse timings from Kepler observations (around epoch 2500); when the full continuous space-based light curve for this object is made available, it should be possible to determine whether 2M 1938+4603 is undergoing period variations with unprecedented confidence and precision.
4.7. NSVS 07826147
NSVS 07826147 was discovered by Kelley & Shaw (2007), and primary eclipse timings have been published for it by For et al. (2010); Liying & Shengbang (2010); Backhaus et al. (2012). We use Backhaus et al.’s ephemeris to construct our O−C diagram: 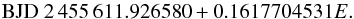 (7)No period change has been claimed yet for this system, though the previously-published timings only covered February 2008–October 2011; the addition of our SuperWASP timings extends the coverage back to May 2004, and provides stronger support for a constant orbital period. Indeed, our results suggest an upper limit on any period variation of about 0.0003 s yr-1.
(7)No period change has been claimed yet for this system, though the previously-published timings only covered February 2008–October 2011; the addition of our SuperWASP timings extends the coverage back to May 2004, and provides stronger support for a constant orbital period. Indeed, our results suggest an upper limit on any period variation of about 0.0003 s yr-1.
4.8. NSVS 14256825
NSVS 14256825 was identified as an eclipsing sdB binary by Wils et al. (2007), who published some eclipse timings; others have been provided by Kilkenny & Koen (2012); Beuermann et al. (2012a); Almeida et al. (2013). Qian et al. (2010b) report observations of the system since 2006, and claim evidence for a cyclic variation, but have not yet published supporting timing measurements. Here, we use the ephemeris of the most recent analysis of the system, Hinse et al. (2014): 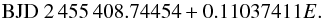 (8)On the basis of very similar O−C variations, Beuermann et al. (2012a) argue for a single circumbinary low-mass companion in an elliptical orbit, while Almeida et al. (2013) prefer a two-planet model. Hinse et al. (2014), however, find that the data are insufficient to constrain any particular one-planet model, and provide no convincing evidence for a second circumbinary companion. Unfortunately, while our new timings are quite consistent with previous measurements, and independently support period increase over June 2006–August 2011, they do not add much to the coverage or clarify the longer-term trends of period variation for this particular system.
(8)On the basis of very similar O−C variations, Beuermann et al. (2012a) argue for a single circumbinary low-mass companion in an elliptical orbit, while Almeida et al. (2013) prefer a two-planet model. Hinse et al. (2014), however, find that the data are insufficient to constrain any particular one-planet model, and provide no convincing evidence for a second circumbinary companion. Unfortunately, while our new timings are quite consistent with previous measurements, and independently support period increase over June 2006–August 2011, they do not add much to the coverage or clarify the longer-term trends of period variation for this particular system.
4.9. NY Vir
Kilkenny et al. (1998) published the discovery paper for NY Vir, and provided eclipse timings and an ephemeris for it between 1996 and 2010 (Kilkenny et al. 2000; Kilkenny 2011). Additional times are given in Çamurdan et al. (2012) and Qian et al. (2012); the latter also provides the revised ephemeris: 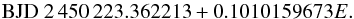 (9)A steady period decrease was observed in the O−C diagram by Kilkenny (2011); Çamurdan et al. (2012); Qian et al. (2012), and is independently supported by our new SuperWASP timings. Qian et al. argue that this is unlikely to be caused by the Applegate mechanism, gravitational radiation or magnetic braking, due to its magnitude and the fully convective nature of the stars, and suggest instead that it is part of a long-term (>15 y) cyclic variation associated with a circumbinary planet; furthermore, they claim that the O−C diagram provides evidence for a shorter-period fourth body in the system.
(9)A steady period decrease was observed in the O−C diagram by Kilkenny (2011); Çamurdan et al. (2012); Qian et al. (2012), and is independently supported by our new SuperWASP timings. Qian et al. argue that this is unlikely to be caused by the Applegate mechanism, gravitational radiation or magnetic braking, due to its magnitude and the fully convective nature of the stars, and suggest instead that it is part of a long-term (>15 y) cyclic variation associated with a circumbinary planet; furthermore, they claim that the O−C diagram provides evidence for a shorter-period fourth body in the system.
4.10. DE CVn
DE CVn was identified as an X-ray source in the ROSAT catalogue (Voges et al. 1999), and as an eclipsing binary containing a WD by Robb & Greimel (1997), who also published several times of minima. Other timings are provided by van den Besselaar et al. (2007); Tas et al. (2004); Parsons et al. (2010), and Parsons et al. also give the ephemeris we use in Fig. 4: 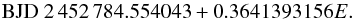 (10)Although the previously-published eclipse timings of DE CVn cover 1997–2006, Parsons et al. feel that most are too uncertain to allow any claims regarding period change to be made. Our new timings extend coverage to March 2011, and although they also have large uncertainties, we may note at least that the whole O−C diagram is fully consistent with a constant period for this system, over about 14 years.
(10)Although the previously-published eclipse timings of DE CVn cover 1997–2006, Parsons et al. feel that most are too uncertain to allow any claims regarding period change to be made. Our new timings extend coverage to March 2011, and although they also have large uncertainties, we may note at least that the whole O−C diagram is fully consistent with a constant period for this system, over about 14 years.
4.11. QS Vir
QS Vir was discovered and later identified as an eclipsing WD binary by Kilkenny et al. (1997); O’Donoghue et al. (2003). They and Kawka et al. (2002); Qian et al. (2010a); Parsons et al. (2010) provide eclipse timings for it, and here we use the ephemeris of Parsons et al.: 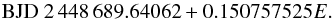 (11)(Almeida & Jablonski 2011 also refer to new timings for the system, but have not yet published them.) The substantial period changes evident in Fig. 4 are demonstrated by Parsons et al. to be an order of magnitude too large to be caused by the Applegate mechanism; however, they are also doubtful about the plausibility of a third body in the system, while noting that it “remains the only mechanism able to produce such a large period variation”. The data set available to them covered April 1992–February 2010; Almeida & Jablonski (2011) add a few more points extending it to August 2010, and argue on this basis for a system containing two circumstellar low-mass bodies. Our partly-overlapping new timings extend the time base to March 2011, and provide independent, if weak, support for a recent increase in QS Vir’s orbital period.
(11)(Almeida & Jablonski 2011 also refer to new timings for the system, but have not yet published them.) The substantial period changes evident in Fig. 4 are demonstrated by Parsons et al. to be an order of magnitude too large to be caused by the Applegate mechanism; however, they are also doubtful about the plausibility of a third body in the system, while noting that it “remains the only mechanism able to produce such a large period variation”. The data set available to them covered April 1992–February 2010; Almeida & Jablonski (2011) add a few more points extending it to August 2010, and argue on this basis for a system containing two circumstellar low-mass bodies. Our partly-overlapping new timings extend the time base to March 2011, and provide independent, if weak, support for a recent increase in QS Vir’s orbital period.
5. Conclusions
Twelve PCEBs with observations covering between three and seven years in the SuperWASP archive were analysed here for evidence of period and/or light curve amplitude change, potentially indicating the presence of circumbinary planets. Their periods were found to high precision, agreeing very closely with those found in previous studies. Hundreds of primary eclipse timings were also determined for the objects, in many cases for previously unobserved epochs, and are made available in the electronic version of this article, for future study of these systems’ period variations.
Period changes found in much previous work were strongly confirmed here for HW Vir, as was the stability of the periods of AA Dor and NSVS 07826147. New eclipse timings of NSVS 14256825, NY Vir and QS Vir, previously suggested as hosts for third bodies, provided some support for period change, while claims of period variations for HS 2231+2441 were not supported by our data. V471 Tau could not be analysed for period variations due to its dramatic and apparently irregular amplitude changes. For 2M 1938+4603 and DE CVn, previously published eclipse timings had not been sufficient to make strong claims; we found no plausible evidence for period changes in these systems. However, for ASAS 10232, our data provided fairly strong evidence for period increase between May 2006 and June 2011, and perhaps for systematic amplitude changes as well, which might suggest this system as a further candidate for containing a circumbinary third body.
Planets might also in principle be detected through sinusoidal variations of an sdB star’s pulsation period, as suggested for isolated pulsator V391 Peg (Silvotti et al. 2007).
Acknowledgments
The WASP project is currently funded and operated by Warwick University and Keele University, and was originally set up by Queen’s University Belfast, the Universities of Keele, St. Andrews and Leicester, the Open University, the Isaac Newton Group, the Instituto de Astrofisica de Canarias, the South African Astronomical Observatory and by STFC. This work was supported by the Science and Technology Funding Council and the Open University.
References
- Almeida, L. A., & Jablonski, F. 2011, in The Astrophysics of Planetary Systems: Formation, Structure, and Dynamical Evolution, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss (CUP), IAU Symp., 276, 495 [Google Scholar]
- Almeida, L. A., Jablonski, F., & Rodrigues, C. V. 2013, ApJ, 766, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Backhaus, U., Bauer, S., Beuermann, K., et al. 2012, A&A, 538, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barlow, B. N., Kilkenny, D., Drechsel, H., et al. 2013, MNRAS, 430, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Dreizler, S., et al. 2010, A&A, 521, L60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Breitenstein, P., Debski, B., et al. 2012a, A&A, 540, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Dreizler, S., Hessman, F. V., & Deller, J. 2012b, A&A, 543, 138 [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brát, L., Trnka, J., Šmelcer, L., et al. 2011, Open European Journal on Variable Stars, 137, 1 [NASA ADS] [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., Hauser, H., & Shirts, P. 1997, ApJ, 474, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Çamurdan, C. M., Çamurdan, D. Z., & İbanoǧlu, C. 2012, New Astron., 17, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- For, B. Q., Green, E. M., Fontaine, G., et al. 2010, ApJ, 708, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Hinse, T. C., Lee, J. W., Goździewski, K., Horner, J., & Wittenmyer, R. A. 2014, MNRAS, 438, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Wittenmyer, R. A., Tinney, C. G., et al. 2013, in Proc. of the 12th Australian Space Science Conference, eds. W. Short, & I. Cairns (National Space Society of Australia), 103 [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&AR, 21, 59 [Google Scholar]
- Kawka, A., Vennes, S., Koch, R., & Williams, A. 2002, AJ, 124, 2853 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, N., & Shaw, J. S. 2007, J. Southeastern Association Res. Astron., 1, 13 [Google Scholar]
- Kilkenny, D. 1986, Observatory, 106, 160 [NASA ADS] [Google Scholar]
- Kilkenny, D. 2011, MNRAS, 412, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., & Koen, C. 2012, MNRAS, 421, 3238 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1978, MNRAS, 183, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1979, MNRAS, 187, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Hill, P. W., & Penfold, J. E. 1981, MNRAS, 194, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Harrop-Allin, M., & Marang, F. 1991, Inform. Bull. Variable Stars, 3569, 1 [NASA ADS] [Google Scholar]
- Kilkenny, D., Marang, F., & Menzies, J. W. 1994, MNRAS, 267, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., O’Donoghue, D., Koen, C., Stobie, R. S., & Chen, A. 1997, MNRAS, 287, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., O’Donoghue, D., Koen, C., Lynas-Gray, A. E., & van Wyk, F. 1998, MNRAS, 296, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Keuris, S., Marang, F., et al. 2000, Observatory, 120, 48 [Google Scholar]
- Kilkenny, D., van Wyk, F., & Marang, F. 2003, Observatory, 123, 31 [Google Scholar]
- Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Netherlands, 12, 327 [Google Scholar]
- Lafler, J., & Kinman, T. D. 1965, ApJS, 11, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. W., Kim, S.-L., Kim, C.-H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Liying, Z., & Shengbang, Q. 2010, Ap&SS, 329, 107 [Google Scholar]
- Lohr, M. E., Norton, A. J., Kolb, U. C., et al. 2012, A&A, 542, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lohr, M. E., Norton, A. J., Kolb, U. C., et al. 2013, A&A, 549, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marang, F., & Kilkenny, D. 1989, Inform. Bull. Variable Stars, 3390, 1 [NASA ADS] [Google Scholar]
- Marsh, T. R., Parsons, S. G., Bours, M. C. P., et al. 2014, MNRAS, 437, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Tamuz, O., Zucker, S., Udalski, A., & the Wasp Consortium. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, eds. L. Arnold, F. Bouchy, & C. Moutou (Frontier Group), 165 [Google Scholar]
- Menzies, J. W., & Marang, F. 1986, in Instrumentation and Research Programmes for Small Telescopes, eds. J. B. Hearnshaw, & P. L. Cottrell (D. Reidel), IAU Symp., 118, 305 [Google Scholar]
- O’Donoghue, D., Koen, C., Kilkenny, D., et al. 2003, MNRAS, 345, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R., Oreiro, R., Drechsel, H., et al. 2007, in 15th European Workshop on White Dwarfs, eds. R. Napiwotzki, & M. R. Burleigh (San Francisco: ASP), ASP Conf. Ser., 372, 483 [Google Scholar]
- Østensen, R. H., Green, E. M., Bloemen, S., et al. 2010, MNRAS, 408, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. B. Paczynski, P. Eggleton, S. Mitton, & J. Whelan (D. Reidel), IAU Symp., 73, 75 [Google Scholar]
- Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010, MNRAS, 407, 2362 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Cameron, A. C., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S. B., Liao, W. P., Zhu, L. Y., et al. 2010a, MNRAS, 401, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S. B., Zhu, L. Y., Liu, L., et al. 2010b, Ap&SS, 329, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S. B., Zhu, L. Y., Dai, Z. B., et al. 2012, ApJ, 745, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Robb, R. M., & Greimel, R. 1997, Inform. Bull. Variable Stars, 4486, 1 [Google Scholar]
- Schaffenroth, V., Geier, S., Drechsel, H., et al. 2013, A&A, 553, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silvotti, R., Schuh, S., Janulis, R., et al. 2007, Nature, 449, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Tas, G., Sipahi, E., Dal, H. A., et al. 2004, Inform. Bull. Variable Stars, 5548, 1 [Google Scholar]
- van den Besselaar, E. J. M., Greimel, R., Morales-Rueda, L., et al. 2007, A&A, 466, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Völschow, M., Banerjee, R., & Hessman, F. V. 2014, A&A, 562, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wils, P., di Scala, G., & Otero, S. A. 2007, Inform. Bull. Variable Stars, 5800, 1 [Google Scholar]
- Wittenmyer, R. A., Horner, J., & Marshall, J. P. 2013, MNRAS, 431, 2150 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, J. H., Zhang, E.-H., & Robinson, E. L. 1993, MNRAS, 261, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., & Schreiber, M. R. 2013, A&A, 549, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SuperWASP light curves for 12 eclipsing PCEBs phase-folded at periods given in Table 1, with binned mean curves overplotted in red (online only). The x axes indicate phase; the y axes SuperWASP flux in arbitrary units (pseudo-V magnitudes are given by 15 − 2.5log (flux). A typical point’s uncertainty is shown in the bottom right of each panel. |
| In the text | |
 |
Fig. 2 First night of SuperWASP observations of HW Vir, with best fit overplotted (final uncertainty in timing <2 s). |
| In the text | |
 |
Fig. 3 O−C diagrams for six PCEBs potentially indicating period change, constructed using SuperWASP data only. The x axes indicate night count since the start of observation (since whole nights are fitted with template curves); the y axes give O−C measurements in seconds. Automatically-excluded outliers are in black and selected good minimum timings in red (colour online only); a small number of more extreme outliers lie outside the bounds of some plots. Best linear (red solid line) and quadratic (blue dashed line) fits to the selected data points are overplotted. |
| In the text | |
 |
Fig. 4 O−C diagrams for eleven PCEBs according to ephemerides given in text, including previously published eclipse timings (black squares) and new binned SuperWASP timings (red crosses). The x axes indicate cycle count; the y axes O−C values in seconds. For HW Vir, the region containing new SuperWASP values is surrounded by a red rectangle for clarity. For HS 2231+2441, larger black squares indicate the approximate locations of the unpublished observations of Qian et al. (2010b), with their fitted curve overplotted as a solid line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


