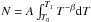| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423430 | |
| Published online | 11 June 2014 | |
Warm molecular gas temperature distribution in six local infrared bright Seyfert galaxies⋆
1 Istituto di Astrofisica e Planetologia Spaziali, INAF, via Fosso del Cavaliere 100, 00133 Roma, Italy
e-mail: miguel.pereira@iaps.inaf.it
2 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
3 Centro de Astrobiología (INTA-CSIC), Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid, Spain
Received: 15 January 2014
Accepted: 8 April 2014
We simultaneously analyze the spectral line energy distributions (SLEDs) of CO and H2 of six local luminous infrared (IR) Seyfert galaxies. For the CO SLEDs, we used new Herschel/SPIRE FTS data (from J = 4–3 to J = 13–12) and ground-based observations for the lower-J CO transitions. The H2 SLEDs were constructed using archival mid-IR Spitzer/IRS and near-IR VLT/SINFONI data for the rotational and ro-vibrational H2 transitions, respectively. In total, the SLEDs contain 26 transitions with upper level energies between 5 and 15 000 K. A single, constant density, model (nH2 ~ 104.5−6 cm-3) with a broken power-law temperature distribution reproduces well both the CO and H2 SLEDs. The power-law indices are β1 ~ 1–3 for warm molecular gas (20 K<T< 100 K) and β2 ~ 4–5 for hot molecular gas (T> 100 K). We show that the steeper temperature distribution (higher β) for hot molecular gas can be explained by shocks and photodissociation region (PDR) models; however, the exact β values are not reproduced by PDR or shock models alone and a combination of both is needed. We find that the three major mergers among our targets have shallower temperature distributions for warm molecular gas than the other three spiral galaxies. This can be explained by a higher relative contribution of shock excitation, with respect to PDR excitation, for the warm molecular gas in these mergers. For only one of the mergers, IRASF 05189–2524, the shallower H2 temperature distribution differs from that of the spiral galaxies. The presence of a bright active galactic nucleus in this source might explain the warmer molecular gas observed.
Key words: galaxies: active / galaxies: ISM / galaxies: nuclei / galaxies: starburst
© ESO, 2014
1. Introduction
Molecular gas is an important phase of the interstellar medium (ISM). This phase contains a significant fraction of the total mass, and stars form in it. But the study of molecular gas presents some complications. First, the lower energy levels of H2, the main component of the ISM phase, have energies >500 K, thus in cold molecular gas (T< 100 K) most of the H2 is in the fundamental state and no H2 emission lines are produced. And second, only the near infrared (IR) ro-vibrational H2 transitions, with Eup> 6000 K, are observable from ground telescopes, so only very high-temperature (T> 1500 K) molecular gas can be detected.
Sample of IR bright Seyfert galaxies observed with Herschel/SPIRE FTS.
To overcome the first caveat, other abundant molecules with observable transitions in the millimeter range (like CO, HCN, etc.) are used as tracers of molecular gas. In particular, the lowest rotational transitions of CO, the second most abundant molecule, are commonly used to study the molecular gas content of galaxies. However, these low-J CO transitions mainly originate in the coldest molecular gas. Thus, ground observations are limited to the study of either the warmest or the coldest molecular gas.
Just recently, thanks to IR and sub-millimeter space observatories like the Infrared Space Observatory (ISO; Kessler et al. 1996), the Spitzer Space Telescope (Werner et al. 2004), and the Herschel Space Observatory (Pilbratt et al. 2010), the rotational H2 transitions as well as the intermediate-J CO transitions became accessible for a large number of local galaxies (e.g., Rigopoulou et al. 2002; Roussel et al. 2007; van der Werf et al. 2010; Pereira-Santaella et al. 2013). Therefore, now for the first time, it is possible to obtain a complete snapshot of molecular gas emission and study its physical properties (temperature, density, column density, etc.) and the excitation mechanisms (ultraviolet (UV) radiation, shocks, and X-ray and cosmic rays).
In this work, we present new data obtained by the Fourier transform spectrometer (FTS) module of the Spectral and Photometric Imaging Receiver (SPIRE) instrument on-board Herschel (Griffin et al. 2010; Naylor et al. 2010; Swinyard et al. 2010) for six local active luminous IR galaxies. These SPIRE/FTS data cover the 210–670 μm (450–1440 GHz) spectral range, so the mid-J CO lines (J = 4–3 to J = 13 − 12) are observed. We completed the CO spectral line energy distributions (SLEDs) with ground-based observations of the three lowest J CO transitions.
In addition, we complemented the CO SLEDs with the H2 SLEDs obtained from near- and mid-IR observations of these galaxies. We used the available mid-IR spectroscopy obtained by the Spitzer IR spectrograph (IRS; Houck et al. 2004) to measure the lowest rotational H2 transitions (e.g., Wu et al. 2009; Pereira-Santaella et al. 2010), and near-IR integral field spectroscopy obtained by the Spectrograph for INtegral Field Observations in the Near-Infrared (SINFONI; Eisenhauer et al. 2003) on the Very Large Telescope (VLT) for the ro-vibrational H2 transitions. For the first time, we have performed a radiation transfer analysis of the whole set of molecular lines together (i.e., CO rotational and H2 rotational and ro-vibrational) in local IR bright galaxies. In total, the compiled CO and H2 SLEDs contain information for 26 transitions with upper level energies between 5 and 15 000 K, thus the emission from most of the molecular gas is included.
The paper is organized as follows. In Sect. 2, we present the sample and the data reduction. Sections 3 and 4 describe the radiative transfer models used, and the fitting of the SLEDs. The cold-to-warm molecular gas ratio and the heating mechanisms are discussed in Sects. 5 and 6, respectively. We summarize the main results in Sect. 7.
2. Observations and data reduction
2.1. Sample
Our sample contains six local (50–180 Mpc) IR bright Seyfert galaxies observed by SPIRE/FTS through two programs (PIs: P. van der Werf and L. Spinoglio). Their log LIR/L⊙ ranges between 11.4 and 12.2 (see Table 1). All of them host an active nucleus (AGN), although the AGN dominates the energy output of the galaxy only for IRASF 05189–2524. For the remaining galaxies, the AGN contributes between 2 and 35% of the total luminosity. Three of the galaxies (NGC 34, IRASF 05189–2524, and UGC 05101) are advanced major mergers. The other three galaxies (NGC 5135, NGC 7130, and NGC 7469) are spirals, although NGC 7130 and NGC 7469 have peculiar morphologies suggesting recent minor interactions (Genzel et al. 1995; Bellocchi et al. 2012).
2.2. Herschel SPIRE/FTS spectroscopy
We obtained SPIRE/FTS high-resolution (1.45 GHz) spectroscopic observations of six nearby Seyfert luminous IR galaxies. Integration times varied between 5 and 34 ks corresponding to a 3σ line detection limit ~0.5–1 × 10-15 erg cm-2 s-1.
The SPIRE/FTS consists of two bolometer arrays, the spectrometer short wavelength (SSW; 925–1545 GHz) and the spectrometer long wavelength (SLW; 446–948 GHz). They sparsely cover a field of view (FoV) of ~2′ with the central bolometer centered at the nuclei of the galaxies. The full width at half maximum (FWHM) of the SSW beam is 18′′ almost constant with frequency. For the SLW bolometers the beam FWHM varies between ~30 and ~42′′ with a complicated dependence on frequency (Swinyard et al. 2010). The SSW beams size correspond to 5–15 kpc at the distance of our galaxies, therefore these galaxies are almost point like sources for both the SSW and SLW bolometers (see also Fig. 1 of Pereira-Santaella et al. 2013).
The data was reduced as described by Pereira-Santaella et al. (2013), but using the more recent Herschel interactive pipeline environment software (HIPE) version 11 (Ott 2010). In brief, the pipeline first creates the interferograms from the bolometer timelines. After the interferogram phase errors are corrected and the baselines removed a Fourier transform is applied to obtain the spectra. These are dominated by the thermal emission of the telescope that is later removed. Residual background emission is subtracted by averaging the off-source bolometers. Finally, the point-source calibration is applied to the spectra extracted from the central bolometers (SLWC3 and SSWD4). The final spectra are plotted in Fig. 1.
To measure the line fluxes, we fitted a sinc function to the line profiles1. The local continuum was estimated using a linear fit around the line frequency. When two lines were close in frequency we fitted them simultaneously. The fluxes of the 12CO, HF, H2O, and fine structure atomic transitions are listed in Table 2. Transitions of CH+, H2O+, and OH+ detected in some galaxies are reported in Table 3.
The SPIRE/FTS data of two of these galaxies, UGC 05101 and NGC 7130, were already presented by Pereira-Santaella et al. (2013). To take advantage of the newest pipeline and calibration they were reprocessed with the rest of the sample. For these two galaxies, the line fluxes in Tables 2 and 3 agree with those in Pereira-Santaella et al. (2013) within the 1σ uncertainties.
 |
Fig. 1 Observed SPIRE/FTS spectra of our sample. The black and gray lines are the SSW and SLW spectra, respectively. Notice the overlap between the two spectra in the 960 and 990 GHz spectral range. The dashed red lines mark the position of the detected lines. The error bars indicate the median 1σ uncertainty of each spectrum. |
 |
Fig. 1 continued. |
SPIRE/FTS line fluxes.
SPIRE/FTS CH+, HF, o-H2O+, and OH+ fluxes.
2.3. Spitzer/IRS spectroscopy
Mid-IR Spitzer/IRS spectroscopic observations of these galaxies were available on the Spitzer data archive. Most of the data is already published in several papers (e.g., Armus et al. 2004; Wu et al. 2009; Pereira-Santaella et al. 2010; Tommasin et al. 2010; Esquej et al. 2012), but the fluxes (and upper limits) of the H2 transitions are not always reported. For this reason, we retrieved the data from the archive and reprocessed it in a uniform way.
These observations include low- and high-resolution spectroscopy (R ~ 60–120 and 600, respectively) covering the spectral range 5.5–14 μm (short-low resolution modules) and 10–36 μm(short- and long-high-resolution modules).
The observations obtained in the staring mode were processed using the standard pipeline version S18.18 included in the Spitzer IRS Custom Extraction software (SPICE). We assumed the point source flux calibration for these galaxies. To process the spectral mapping observations, we used CUBISM (Smith et al. 2007a). This software combines the individual slit observations to create the spectral data cubes. From the cubes, we extracted the spectra using a 15′′ × 15′′ square aperture and then we applied an aperture correction (see Alonso-Herrero et al. 2012). The spectra are shown in Fig. 2.
We measured the fluxes of the H2 rotational transitions S(0), S(1), and S(2) in the high-resolution spectra2 fitting a Gaussian profile and a linear function for the local continuum (Table 4). The H2 S(3) and S(5) transitions were measured in low-resolution spectra. Because of the large number of spectral features in the mid-IR range, it is not trivial to determine the continuum for the low-resolution spectra. Therefore, we used PAHFIT (Smith et al. 2007b) to fit the complete spectrum and estimate the continuum and line fluxes. It is not possible to obtain a reliable measurement of the H2 S(4) transition at 8.03 μm because it is blended with the 7.7 μm PAH broad feature. Similarly, the H2 S(5) transition at 6.91 μm is blended with the [Ar iii]6.99 μm line, which in our galaxies is always stronger than the H2 line. Therefore, the H2 S(5) fluxes should be considered with caution.
The strength of the silicate feature at 9.7 μm (SSi) was measured in the low-resolution spectra as described by Pereira-Santaella et al. (2010). It is defined as SSi = ln(fobs/fcont), thus negative SSi implies that the feature is seen in absorption (Table 5). We used the strength of the silicate feature to estimate extinction in our galaxies (see Sect. 2.6).
 |
Fig. 2 Rest-frame Spitzer/IRS spectra. The short-low (5.5–14 μm), short-high (10–19 μm), and long-high (19–36 μm) spectra are plotted for each galaxy. For clarity, the spectra are multiplied by the following factors 1, 2.5, 14, 100, 220, and 2000, from bottom to top. The wavelengths of the H2 rotational transitions are indicated. |
2.4. SINFONI integral field spectroscopy
We made use of K-band (1.95–2.45 μm) seeing-limited and adaptive optics assisted near-IR SINFONI observations for several objects of the sample. The observations where carried out during different periods, i.e., 60A (NGC 7469), 77B (NGC 5135 and NGC 7130), 80B (IRASF 05189–2524), and 82B (NGC 34), with a spectral resolution of R ~ 4000, using different plate scales that yield different FoVs. For further details of the NGC 7469 data, see Hicks et al. (2009), and for NGC 5135 and NGC 7130, please refer to Piqueras López et al. (2012).
We made use of archive data for IRASF 05189–2524 and NGC 34, observed on December 2007 and October 2008, respectively. The observations were made using the 0.̋05 × 0.̋10 pixel-1 setup, which yields a FoV of ~3′′ × 3′′, and split into individual exposures of 900 s following a jittering O-S-O pattern for sky and on-source frames. The total on-source integration times for each galaxy were 5400 s for IRASF 05189–2524 and 1800 s for NGC 34. To perform the flux calibration and to correct for the instrument response and atmospheric absorption, we used three spectrophotometric standard stars, Hip032193 and Hip052202 for IRASF 05189–2524, and Hip001115 for NGC 34, which were observed with their respective sky frames.
The reduction and calibration of the raw data were performed following the same procedure outlined in Piqueras López et al. (2012), i.e., we used the standard ESO pipeline ESOREX (version 2.0.5) to perform the standard corrections of dark subtraction, flat fielding, detector linearity, geometrical distortion, and wavelength calibration. After these corrections were applied to each frame, the sky emission was subtracted from each individual on-source exposure. We constructed individual cubes from each sky-corrected frame that were then flux-calibrated separately, and combined into a single final cube taking the relative shifts in the jittering pattern into account. The absolute flux calibration to translate the counts into physical units is based on the K-band magnitudes from the 2MASS catalog (Skrutskie et al. 2006).
To obtain the integrated K-band spectra, first we fitted the brightest H2 line (1–0 S(1) at 2.12 μm) in every spaxel to produce the intensity and velocity map of the H2 emission. Then we combined the spectra of all the spaxels with signal to noise ratio >3 in the 1–0 S(1) line, correcting for the relative velocity of each spaxel. The integrated spectra are shown in Fig. 3. Finally, we measured the line fluxes and upper limits of the H2 transitions in the integrated spectra by fitting a Gaussian profile with fixed FWHM and position that were first determined from the 1–0 S(1) fit. Fluxes and upper limits are presented in Table 4.
H2 rotational and ro-vibrational fluxes.
2.5. Aperture matching
We combined data from instruments with different FoVs and angular resolutions. The SPIRE/FTS beam size varies between 20 and 40′′, which correspond to 5–35 kpc at the distance of our galaxies, so they appear as point-like sources at this resolution. By contrast, the Spitzer/IRS slit width varies between 3.6 and 11.1′′ (1–10 kpc), depending on the IRS module. For the most distant galaxies in our sample, IRASF 05189-2524 and UGC 05101, these apertures encompass their mid-IR emission. Likewise, most of the mid-IR emission of NGC 34 and NGC 7469 is produced in the compact nuclear region (few kpc, Esquej et al. 2012; Díaz-Santos et al. 2010), thus no aperture matching corrections are needed. For the more nearby NGC 5135 and NGC 7130, Spitzer/IRS spectral mapping observations are available and it is possible to extract their mid-IR spectra from a 15 × 15′′ aperture (5 × 5 kpc) comparable to the SPIRE/FTS beam size and large enough to include most of their bright nuclear mid-IR emission.
The SINFONI FoV for the IRASF 05189-2524 observations is 3 × 3′′ (2.5 × 2.5 kpc). This source is unresolved in the SINFONI data (FWHM ~ 0.3′′), and therefore we expect that most of the flux is included in our measurements. For NGC 7469, the FoV of SINFONI data is 0.8 × 0.8′′ (0.2 × 0.2 kpc), so only the nuclear emission is included. NGC 7469 has a kpc scale star-forming ring, thus to account for the missing near-IR H2 emission we added the emission measured in the star-forming ring by Díaz-Santos et al. (2007) to the nuclear fluxes (Table 4). This correction increases the fluxes by a factor of ~2.
Finally, the SINFONI FoVs are 8 × 8′′ and 8 × 16′′, respectively, for NGC 5135 and NGC 7130. This corresponds to 2.5–5 kpc which is similar to the source sizes (Arribas et al. 2012), so no correction is applied to the measured integrated SINFONI fluxes.
2.6. Extinction correction
Near- and mid-IR emission in luminous and ultra-luminous IR galaxies (LIRGs and ULIRGs) is affected by extinction due to the large amount of dust present in these galaxies. To estimate the extinction, we measured the SSi (see Sect. 2.3), SSi and AK are related according to the extinction law. In particular, using the Chiar & Tielens (2006) local ISM extinction law we obtained that AK/SSi = −2.20. The SSi values in our galaxies range from −1.50 to −0.13 (Table 5), which correspond to AK between 0.3 and 3.3 mag.
Regions producing H2 and ~10 μm continuum emissions (where the SSi is measured) may have different extinction levels. We cannot use the near-IR lines to test if we can use the estimated AK values to correct for the obscuration effects in the H2 transitions because the differential extinction between the different transitions is small (Aλ/AK = 0.93–1.16, see Table 4). On the contrary, the H2 0–0 S(3) transition at 9.67 μm lies close to the peak of the silicate absorption, so its flux is more affected by extinction than the rest of the mid-IR H2 lines. This is clear for UGC 05101, whose 0–0 S(1)/0–0 S(3) ratios are 2.3 ± 0.4 and 0.8 ± 0.1 before and after the extinction correction. Actually, all the galaxies (except NGC 34, see below) have very similar 0−0 S(1)/0–0 S(3) ratios, 0.76 ± 0.06, after the extinction correction based on SSi.
NGC 34 has a strong silicate absorption (SSi = −1.10) and an observed 0–0 S(1)/0–0 S(3) = 0.77 ± 0.07, which is compatible with the average extinction corrected ratio of the other galaxies. Therefore, it is possible that the regions producing the H2 and ~10 μm continuum emissions in NGC 34 suffer from very different extinction levels. Moreover, the NGC 34 uncorrected H2 SLED does not have any indication of attenuation of the 0–0 S(3) transition (see Fig. 5). This is at odds with the UGC 05101 (SSi = −1.50) SLED that shows a clear deficit of 0–0 S(3) emission. As a consequence, we do not apply any correction to NGC 34 since we do not have an accurate measurement of extinction toward the H2 emitting regions.
3. Radiative transfer models
Previous works have analyzed the Herschel mid-J CO SLEDs of galaxies by fitting non-LTE radiative transfer models (e.g., Rangwala et al. 2011; Spinoglio et al. 2012; Pereira-Santaella et al. 2013; Rigopoulou et al. 2013). In general, a model with two components at different temperatures is used. In these models, the “cold” component (usually Tkin< 100 K) reproduces the lowest J CO lines, whereas the “warm” component (Tkin several hundred K) accounts for the higher J emission.
Similarly, when the mid-IR rotational H2 transitions are analyzed, models with two components are used (e.g., Rigopoulou et al. 2002; Roussel et al. 2007). In these studies, the derived Tkin are always higher than ~100 K since at lower temperatures the rotational H2 emission is negligible. In addition, it is assumed that H2 is in LTE because the critical density of these lines is low (nH2< 104 cm-3, see Fig. 3 of Roussel et al. 2007).
For the near-IR ro-vibrational H2 lines, the molecular gas is usually assumed LTE too, although the critical densities of these transitions are higher (ncrit> 107 cm-3). The derived temperatures from these lines are around 2000 K. In general, it is concluded that they are collisionally excited and UV excitation has relatively low importance for the excitation of the H2ν = 1–0 transitions (e.g., Davies et al. 2003; Bedregal et al. 2009).
In this work, we analyze the SLED of low- and mid-J CO transitions as well as pure rotational and ro-vibrational H2 transitions. Therefore, to explain the emission of all these lines, our model would need at least four components with different temperatures ranging from ~50 K to 2000 K. Instead, we use an alternative approach assuming a continuous distribution of temperatures. This is advantageous since we avoid using a somewhat arbitrary number of model components to fit the data.
It is common to find that the observed SLEDs have a positive curvature, that is, the rotational temperature derived from a pair of consecutive transitions increases with the energy of their upper levels (e.g., Neufeld 2012). Therefore, emission could come from gas with a continuous distribution of temperatures instead of several discrete temperatures. To model this distribution of temperatures we assumed that the column density follows a power-law (dN ~ T− βdT). A similar method has been used to model the ro-vibrational and rotational H2 emission in shocked gas (e.g., Brand et al. 1988; Neufeld & Yuan 2008; Shinn et al. 2009), or the CO emission (e.g., Goicoechea et al. 2013).
In the following, we describe our model in detail. First, we explain how the models for single temperature and density are obtained, and then how they are combined to reproduce a power-law temperature distribution.
Extinction.
 |
Fig. 3 Rest-frame SINFONI integrated spectra. For clarity the spectra are shifted by the following factors 0, 0, 3.5, 4.0, and 4.0 × 10-11 erg cm-2 s-1 from bottom to top. The wavelengths of the H and H2 transitions are indicated. |
Ground-based CO data.
3.1. Single temperature non-LTE model
To solve the radiative transfer equations for the molecular emission we used the code RADEX (van der Tak et al. 2007). This code uses the escape probability approximation to obtain the molecular level populations and the intensities of the emission lines.
We constructed two sets of models, one for CO and other for H2, covering a wide range of kinetic temperature (Tkin = 10–2800 K) and H2 density (nH2 = 102−109 cm-3). For the H2 grid, we also consider collisions with atomic H with nH/nH2 ratios between 1 and 10-5. In these grids, we assume the LTE H2 ortho-to-para ratio, which varies between 0 for low temperatures and 3 for Tkin> 200 K (see Fig. 4 of Burton et al. 1992).
The H2 transitions are optically thin for NH2/ Δv lower than ~1024 cm-2 (km s-1)-1, thus in our models we assume optically thin H2 emission3. Similarly, we assume optically thin mid-J CO emission, this condition is fulfilled when NCO/ Δv is lower than ~1015 cm-2 (km s-1)-1. In general, this is the case for the mid-J CO observations of galaxies (e.g., Kamenetzky et al. 2012; Pereira-Santaella et al. 2013).
For the CO grid, we used the collisional rate coefficients of Yang et al. (2010) expanded by Neufeld (2012) for high-J levels (J = 41 to 80). This is important for the high temperature models as a non negligible fraction of the CO molecules are in energy levels with J> 40 that otherwise are ignored.
We created two sub-grids of H2 models. One for high-temperature (Tkin> 100 K) and another for low temperature. For the high-temperature sub-grid we used the H2-H2 collisional rate coefficients of Le Bourlot et al. (1999) and the H2-H coefficients of Wrathmall et al. (2007) that cover kinetic temperatures between 100 and 6000 K. For the lower temperature sub-grid (Tkin< 100 K) we used the H2-H2 collisional coefficients of Lee et al. (2008). They only include the lowest nine rotational energy levels of H2 (Eupper< 5900 K), but at Tkin< 100 K, no molecules are expected at higher rotational energy levels. Collisions with atomic H are mostly important for vibrational excited H2 levels, so they are neglected for the low-temperature sub-grid. The grids for ortho-H2 and para-H2 were constructed separately, although they were later combined assuming the LTE H2 ortho-to-para ratio.
3.2. Power-law temperature distribution
We want to obtain the level populations for gas following a power-law temperature distribution, dN ~ T− βdT. From the grids described in Sect. 3.1, we can obtain the fractional population of the molecular level i, ni(T,nH2), for a given kinetic temperature and H2 density. Therefore, the total column density of molecules in the energy level i for a kinetic temperature distribution following a power-law between T0 and T1 is 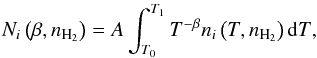 (1)where
(1)where 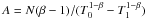 is a normalization constant and N is total molecular gas column density4. In our models, we use T0 = 20 K and T1 = 3500 K. This temperature range is required to model the lower-J CO and the near-IR H2 transitions, respectively.
is a normalization constant and N is total molecular gas column density4. In our models, we use T0 = 20 K and T1 = 3500 K. This temperature range is required to model the lower-J CO and the near-IR H2 transitions, respectively.
In Sect. 4, we show that it is not possible to fit simultaneously the SLEDs of both CO and H2 using a single power-law temperature distribution. We find that the temperature distribution is much steeper for H2 (β ~ 5) than for CO (β ~ 3). Therefore, for the SLED fitting we used a broken power-law model with two exponents (β1 and β2). This can be modeled with the following equation: 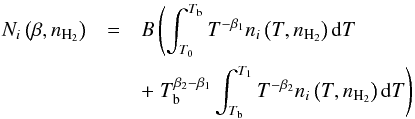 (2)where Tb is the break temperature, and
(2)where Tb is the break temperature, and 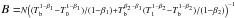 .
.
4. CO and H2 SLED fitting
To fit the SLEDs, we converted the observed fluxes into beam averaged column densities using the following relation 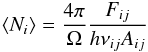 (3)where Fij is the flux of the transition between levels i and j, νij and Aij are its frequency and Einstein coefficient, respectively, h is the Planck constant, and Ω is the beam solid angle. Since our sources are barely resolved by Herschel we assume a beam FWHM of 18′′, which is the SSW beam size. This beam size is also used for the rest of measurements as they should include most of the emission in this area (see Sect. 2.5 for details). Using this relation, we assume that the emission is optically thin, which is reasonable for the H2 transitions as well as for the mid-J CO lines (see Sect. 3).
(3)where Fij is the flux of the transition between levels i and j, νij and Aij are its frequency and Einstein coefficient, respectively, h is the Planck constant, and Ω is the beam solid angle. Since our sources are barely resolved by Herschel we assume a beam FWHM of 18′′, which is the SSW beam size. This beam size is also used for the rest of measurements as they should include most of the emission in this area (see Sect. 2.5 for details). Using this relation, we assume that the emission is optically thin, which is reasonable for the H2 transitions as well as for the mid-J CO lines (see Sect. 3).
First, we attempted to fit the SLEDs using a power-law temperature distribution. The free parameters of this model are the CO and H2 column densities, nH2 and nH densities, and β. However, it was not possible to obtain a good fit to both the CO and H2 emissions. Nevertheless, the CO and H2 SLEDs individually are well reproduced by a power-law model, although each SLED has different β values.
In these models, there is a strong degeneracy between β and nH2, β decreases for decreasing nH2 when densities are below the critical density of the transitions (nH2< 106 cm-3 for CO and nH2< 104 cm-3 for H2). This is because changes in nH2 and β produce similar variations in the SLED shape when the gas is not thermalized. In Fig. 4, we plot the χ2 values for one of the galaxies where this degeneracy is evident. In addition, it is clear that the CO and H2 SLEDs are not simultaneously reproduced by any pair of β and nH2 parameters. For our galaxies, we find that β is always higher for H2 (steeper temperature distribution) for any given nH2. The β values range between 2.5 and 3.5 for CO and between 4.5 and 5.5 for H2 for nH2 higher than the critical densities of the transitions.
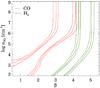 |
Fig. 4 χ2 values for the power-law temperature distribution model as a function of β and nH2 for NGC 7130. The red (green) contours are the 1, 2, and 3σ confidence levels for the CO (H2) SLED. |
As anticipated in Sect. 3.2, to account for the difference on the β values for the CO and H2 SLEDs, we used an alternative model consisting of a broken power-law, which has two exponent values, β1 and β2, for temperatures below and above the threshold temperature Tb, respectively. With this model, it is possible to fit all the available CO and H2 transitions for our galaxies, with the exception of the CO transition, which is always underpredicted by the model. The later can be caused by the presence of low temperature molecular gas that would not follow the power-law distribution. Consequently, we included a cold gas component at 15 K assuming optically thin emission for the CO transition. In general, CO emission is not optically thin, so the obtained column densities are lower limits.
Best-fit parameters of the CO and H2 SLEDs.
The value of the breaking temperature (Tb) is not well constrained because the upper level energies of the CO and H2 transitions do not overlap. When Tb is left as a free parameter it varies between 100 and 500 K with 1σ uncertainties ~100 K, and its variation affects the β values slightly. The average Tb is 200 ± 130 K. It is not possible to accurately determine Tb with our data, therefore, we fixed it to the average value.
As discussed above, β1 and nH2 are strongly correlated, specially for CO, when nH2 is below the critical densities. The CO column density (NCO) is relatively constant when β1 and nH2 vary. But, on the contrary, the H2 column density variation is large. This is because we only measure the warm H2 column density directly, which represents a small fraction of the total H2, and the total H2 column density is extrapolated using the β1 exponent. Therefore, in our model, lower nH2 also implies lower H2 column densities (and higher CO abundances) because of the smaller value of β1.
We used this to estimate a lower limit for nH2 given that the CO abundance should be lower or equal to that of C. Assuming the solar atomic C abundance (2.4 × 10-4; Lodders 2003), the lower limit for nH2 is ~104.0±0.5 cm-3, depending on the galaxy. In the case of sub-solar abundances in these galaxies, the nH2 upper limit would be slightly higher. Similarly, we can obtain a lower limit for the CO abundance by setting nH2 to a value above the CO critical density (e.g., 106 cm-3). The minimum CO abundance ranges between 10-5 and 10-6. In Table 7, we list the best-fit parameters for nH2 = 104.5 cm-3 and nH2 = 106 cm-3. We plot the best-fit models in Fig. 5.
The nH value depends mostly on the ratio between the intensities of the rotational and near-IR ro-vibrational H2 lines. For our galaxies we obtain nH values between 103–104 cm-3. The critical densities for collisions with H of the near-IR H2 transitions are nH ~ 104 − 105 cm-3 at 1500 K, much lower than the critical densities for collisions with H2. Therefore, a relatively small abundance of atomic H can enhance the luminosity of the near-IR transitions. For the assumed nH2 = 104.5 and 106 cm-3 the ro-vibrational near-IR emission would be one or two orders of magnitude lower than the observed if we did not include collisions with H in our model.
 |
Fig. 5 CO and H2 rotational diagrams. The red (blue) line is the best-fit model for the warm (cold) component. The number close to the data points is the J quantum number of the level. For H2, circles correspond to the vibrational level ν = 0, diamonds to ν = 1, and squares to ν = 2. |
5. Cold-to-warm molecular gas ratio
To estimate the cold molecular gas mass, we used the CO to H2 conversion factor from Leroy et al. (2011), Nc(H2)(cm-2) = 2 × 1020ICOJ = 1 − 0 (K km s-1). We compare this cold molecular gas column density with the warm molecular gas column density obtained from the fit of the CO and H2 SLEDs (Table 7). The warm molecular gas fraction ranges between 1 and 20% for the models with nH2 = 104.5 cm-3 and between 15 and >100% for the models with nH2 = 106 cm-3. This suggests that for the two galaxies where the warm column density exceeds the cold column density (UGC 05101 and NGC 5135) the model with nH2 = 106 cm-3 overestimates the Nw(H2). Thus, in the following we use the nH2 = 104.5 cm-3 model for these two galaxies. Moreover, these are the only two sources where the χ2 is lower for the nH2 = 104.5 cm-3 model.
For our sample of IR bright galaxies it might be adequate to use the lower CO to H2 conversion factor NH2 (cm-2) = 0.5 × 1020ICOJ = 1 − 0 (K km s-1) measured by Downes & Solomon (1998) in active galaxies. Therefore, the cold-to-warm ratio could be lower by a factor of 4.
6. Molecular gas heating
In the previous sections, we showed that the CO and H2 SLEDs are compatible with a broken power-law temperature distribution, however, we did not discuss how the molecular gas is heated. Three main mechanisms are invoked to explain the heating of the molecular gas: UV radiation, shocks, and X-ray and cosmic rays. In this section, we compare the molecular gas temperature distribution expected in photodissociation region (PDRs; UV radiation) and shocks regions with the observed temperature distribution.
X-ray and cosmic ray heating can be important for AGNs, however, in this work we analyze active galaxies with strong star-formation (see Table 1). The AGN contribution to the mid-J CO emission seems to be small compared to that of SF (e.g., Pereira-Santaella et al. 2013). Likewise, SF dominates the H2 emission in LIRGs (e.g., Roussel et al. 2007; Pereira-Santaella et al. 2010). For these reasons, we consider that X-ray heating should not contribute significantly in the integrated spectra of these galaxies.
 |
Fig. 6 Left panel: chemical structure and temperature of a PDR with G0 = 104 and nH = 104 cm-3. The thick black line is the gas temperature (left axis). The other lines represent the abundances (left axis) of H (black), H2 (orange), C+ (blue), C i (violet), and CO (green). Right panel: H2 (orange) and CO (green) column densities as a function of the temperature. The dashed lines are the best power-law fits to the distribution (see Sect. 6.1). |
6.1. UV radiation: PDRs
We used the radiative transfer code Cloudy version 13.02 (Ferland et al. 2013) to estimate the gas temperature distribution of PDRs. We used a constant density slab model illuminated by the interstellar radiation field of Black (1987). We created a grid of models with nH between 104 and 106 cm-3 and radiation field intensity between 101 and 104G0, where G0 = 1.6×10-3 erg cm-2 s-1 is the intensity integrated between 6 and 13.6 eV. Since we are interested only in the PDR region we extinguished the input spectra to remove the ionizing radiation.
We extracted the CO and H2 abundances and kinetic temperatures as a function of the column density from the output of the models, which we used to compute the temperature distribution of CO and H2. Then we fitted these distributions with a power-law function. In the fit we only included gas with T> 20 K and T> 150 K, for CO and H2, respectively, because lower temperature gas does not produce significant emission of the observed transitions.
In Fig. 6, we show an example Cloudy PDR model and the fit to the temperature distribution. We find that, in general, H2 distributions are steeper than those of CO. The power-law index5 for CO is ~3–10 for nH2 = 104.5 cm-3, and ~5–7 for nH2 = 106 cm-3, and for H2β ranges between ~10 and 15. That is, these β values are higher than the values derived from our fits to the observed SLEDs (Sect. 4).
6.2. Shocks
To calculate the molecular gas temperature distribution in shocks we used a simple model. We assumed that molecular gas is heated at a constant rate up to a certain temperature, which depends on the shock velocity and is high enough to produce H2 emission, and after that it is cooled radiatively by the dominant cooling molecule.
The main coolant of warm molecular gas is H2, CO, or H2O depending on the density and temperature of the gas (Neufeld & Kaufman 1993). For our galaxies, the H2O transitions are weaker than the CO transitions for those with similar Eup values. That is, H2O cooling does not seem to dominate the cooling for the average conditions in these galaxies, and therefore, we do not consider H2O in our model.
First, we calculated the non-LTE cooling functions of CO and H2 as a function of the gas density and kinetic temperature using the grid of models described in Sect. 3.1. For the H2 cooling function we do not include the effect of collisional excitation by H since it would only affect the cooling of high-temperature gas through ro-vibrational emission of H2.
The temperature dependence of these cooling functions can be approximated with a power-law (e.g., Draine & McKee 1993). Thus we fitted the calculated cooling functions using a power-law in the temperature range between 30 and 150 K for CO, and 150 and 1000 K for H2. These are the temperature ranges where CO and H2 dominate the gas cooling (Neufeld & Kaufman 1993).
 |
Fig. 7 Power-law indices of the temperature dependence of the CO (top) and H2 (bottom) non-LTE cooling functions (solid line; see Sect. 6.2). The fits are valid for a temperature range between 30 and 150 K for CO and 150 and 1000 K for H2. The fitted β values form the models with nH2 = 104.5 cm-3 and nH2 = 106 cm-3 are also plotted for each galaxy. For visualization the abscissa of the data points are slightly offset. |
Then, assuming that the molecular gas cools radiatively after being heated according to these fitted cooling functions (i.e., dU/ dt ~ − Tγ, where U = 5/2 kT is the internal kinetic energy), the observed temperature distribution of the molecular gas is dN/ dT ~ T− γ. That is, the β we fitted for the SLEDs should be compared with γ. The power-law indices, γ, for CO and H2 as a function of the density are shown in Fig. 7.
6.3. Comparison with the observations
In our fits, we obtained that the power-law index varies between 1.2 and 3.5 for CO and between 4.3 and 4.9 for H2. In general, these values are lower than those expected in PDR, but higher than those expected from shocks (see Table 7 and Fig. 7). Therefore, the combination of PDRs and shocks are needed to explain the intermediate power-law indices.
The CO emission is compatible with that predicted by shock models only for NGC 51356, whose best-fit model has nH2 = 104.5 cm-3. This result, however, strongly depends on the adopted density. For instance, for the model with nH2 = 106 cm-3, which provides only a slightly worse fit to the CO SLED of NGC 5135, the CO emission would need a PDR component.
If we combine these PDR and shock models, the PDR SLEDs would dominate the lower-J CO transitions because of their steeper power-law index, while the contribution from shocks would be dominant for higher-J CO transitions. Moreover, only gas with T> 100 K produces H2 emission so, depending on the G0 values of the PDRs and the shock velocities, the contributions of PDRs and shocks may differ in the CO and H2 SLEDs.
Our sample includes three spiral galaxies (NGC 5135, NGC 7130, and NGC 7469) and three major mergers (NGC 34, IRASF 05189–2524, and UGC 05101). The latter have lower β1 values for their CO SLEDs (Fig. 7) suggesting that the relative contribution from shocks to the CO emission in these mergers is larger than in the spirals. For the H2 emission only IRASF 05189–2524 has a β2 value lower than the rest of galaxies, so in this source, shocks able to heat the molecular gas up to T> 100 K could be important. Also, this galaxy is the most luminous in our sample and the galaxy with the higher AGN contribution (Table 1), so the bright AGN might affect its CO and H2 emissions.
6.4. Comparison with two-component models
The CO SLEDs of two of our galaxies (UGC 05101 and NGC 7130) were presented by Pereira-Santaella et al. (2013). In that paper, a model consisting of two components was used to fit the data: a cold component that contributed mainly to the CO emission, and a warm component with variable H2 density and kinetic temperature.
Once corrected for the different beam sizes used, the beam-averaged CO column densities derived by both methods agree within the uncertainties, although, this could be a particular case due to the specific SLEDs of these two galaxies.
The interpretation of the nH2 and Tkin of the two-component model (TCM) is not so straightforward. The high kinetic temperature needed by the TCM reveals the presence of warm molecular gas, but the exact temperature value is not necessarily a representative temperature of the molecular gas. The obtained nH2 and Tkin are biased toward the conditions in the most luminous regions. Actually, the luminosity of each CO transition, for a given molecular mass, depends on nH2 and Tkin. So, the derived nH2 and Tkin will depend on the unknown distribution of densities and temperatures of the molecular gas. This problem is partially solved assuming a functional form for the dN/ dT, as we adopted in our models.
In addition, nH2 and Tkin are correlated (lower nH2 and higher Tkin, and higher nH2 and lower Tkin produce similar CO SLEDs) and this adds an extra uncertainty to the derived values. This is equivalent to the uncertainty due to the β-nH2 correlation for our models (see Sect. 4).
Although the TCM provides useful information, when the analyzed molecular transitions comprise a wide range of excitation temperatures, the need for additional components for the SLED fitting can make the modeling contrived. Instead, the power-law models used here could better represent the integrated temperature distribution of the molecular gas in a galaxy.
7. Conclusions
We have studied the integrated CO and H2 emission of six local IR bright galaxies using non-LTE models. Assuming a broken power-law distribution for the molecular gas temperatures, our model reproduces both the CO SLED (from Jup = 1 to Jup = 13) and the H2 SLED (Jup ≤ 7 for the lowest three vibrational levels) in our sample of galaxies.
The main findings of this work are summarized in the following:
-
1.
With a single power-law temperature distribution it is notpossible to fit simultaneously the CO andH2 SLEDs. The H2 SLEDs have amuch steeper power-law index(β2 ~ 4–5) than the CO SLED (β1 ~ 1–3). This is the expected behavior for the temperature distributions in PDRs and shocks.
-
2.
We found that for most of the galaxies, the models with nH2 = 106 cm-3 provide the best fit to the observed data, thus the majority of the transitions are close to LTE. The minimum acceptable density for the warm gas is ~nH2 = 104 ± 0.5 cm-3, lower densities would imply CO abundances higher than the atomic C abundance. Likewise, we obtained that the minimum CO abundance in the warm gas is xCO ~ 10-6 − 10-5 assuming LTE conditions.
-
3.
The column densities of the warm molecular gas (T> 20 K) represents between 10 and 100% of the molecular gas traced by the CO transition.
-
4.
We used PDR and shock models to determine the excitation mechanism of the molecular gas. Our models show that the temperature distributions are steeper for PDRs than for shocks. We also found that the temperature distribution of the warmest gas (T> 100 K) emitting in H2 is steeper than that of coldest gas (T> 30 K), which produces the mid-J CO emission for both PDR and shocks models. This is because of the different main coolant of the warm and cold molecular gas (H2, and CO, respectively).
-
5.
Neither PDR nor shocks alone can explain the derived temperature distributions. A combination of both is needed to reproduce the observed SLEDs. In this case, the lower-J CO transitions would be dominated by PDR emission, whereas the higher-J CO transitions would be dominated by shocks.
-
6.
The three major mergers among our targets (NGC 34, IRASF 05189–2524, and UGC 05101) have shallower temperature distributions for CO than the other three spirals. This suggests that the relative contribution of shocks to the heating of warm molecular gas (T< 100 K) in these major mergers is higher than in the other three spirals.
-
7.
For only one of the mergers, IRASF 05189–2524, the shallower H2 temperature distribution (hot molecular gas) suggests that the relative importance of shocks is high. This galaxy also has a bright AGN that dominates the bolometric luminosity, which can contribute to the molecular gas heating. For the other two mergers, the H2 temperature distribution is similar to that of the spiral galaxies. Therefore the shocks producing the extra contribution to the CO emission in these mergers are not able to heat the molecular gas to temperatures higher than 100 K, which would be necessary to see the H2 emission.
Acknowledgments
We thank anonymous referee for comments that improved the paper. This work was funded by the Agenzia Spaziale Italiana (ASI) under contract I/005/11/0. J.P.L. acknowledge support from the Spanish Plan Nacional de Astronomía y Astrofísica AYA2010-21161-C02-01 and AYA2012-32295. SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including: Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Albrecht, M., Krügel, E., & Chini, R. 2007, A&A, 462, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., García-Marín, M., Monreal-Ibero, A., et al. 2009, A&A, 506, 1541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., Rieke, G. H., & Rigopoulou, D. 2012, ApJ, 744, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Armus, L., Charmandaris, V., Spoon, H. W. W., et al. 2004, ApJS, 154, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Colina, L., Alonso-Herrero, A., et al. 2012, A&A, 541, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedregal, A. G., Colina, L., Alonso-Herrero, A., & Arribas, S. 2009, ApJ, 698, 1852 [NASA ADS] [CrossRef] [Google Scholar]
- Bellocchi, E., Arribas, S., & Colina, L. 2012, A&A, 542, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H. 1987, in Interstellar Processes, eds. D. J. Hollenbach & H. A. Thronson, Jr., Astrophys. Space Sci. Lib., 134, 731 [Google Scholar]
- Brand, P. W. J. L., Moorhouse, A., Burton, M. G., et al. 1988, ApJ, 334, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Hollenbach, D. J., & Tielens, A. G. G. 1992, ApJ, 399, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Chiar, J. E., & Tielens, A. G. G. M. 2006, ApJ, 637, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Sternberg, A., Lehnert, M., & Tacconi-Garman, L. E. 2003, ApJ, 597, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Alonso-Herrero, A., Colina, L., Ryder, S. D., & Knapen, J. H. 2007, ApJ, 661, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Charmandaris, V., Armus, L., et al. 2010, ApJ, 723, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Abuter, R., Bickert, K., et al. 2003, in SPIE Conf. Ser. 4841, Conf. Ser., eds. M. Iye, & A. F. M. Moorwood, 1548 [Google Scholar]
- Esquej, P., Alonso-Herrero, A., Pérez-García, A. M., et al. 2012, MNRAS, 423, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Genzel, R., Weitzel, L., Tacconi-Garman, L. E., et al. 1995, ApJ, 444, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., Etxaluze, M., Cernicharo, J., et al. 2013, ApJ, 769, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Hicks, E. K. S., Davies, R. I., Malkan, M. A., et al. 2009, ApJ, 696, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, F. P. 2009, A&A, 493, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamenetzky, J., Glenn, J., Rangwala, N., et al. 2012, ApJ, 753, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., & Flower, D. R. 1999, MNRAS, 305, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, T.-G., Balakrishnan, N., Forrey, R. C., et al. 2008, ApJ, 689, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, JMoSt, 742, 215 [Google Scholar]
- Naylor, D. A., Baluteau, J.-P., Barlow, M. J., et al. 2010, in SPIE Conf. Ser., 7731, 29 [Google Scholar]
- Neufeld, D. A. 2012, ApJ, 749, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Kaufman, M. J. 1993, ApJ, 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Yuan, Y. 2008, ApJ, 678, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Papadopoulos, P. P., van der Werf, P. P., Xilouris, E. M., et al. 2012, MNRAS, 426, 2601 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Rieke, G. H., et al. 2010, ApJS, 188, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Santos-Lleo, M., et al. 2011, A&A, 535, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Spinoglio, L., Busquet, G., et al. 2013, ApJ, 768, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Piqueras López, J., Colina, L., Arribas, S., Alonso-Herrero, A., & Bedregal, A. G. 2012, A&A, 546, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rangwala, N., Maloney, P. R., Glenn, J., et al. 2011, ApJ, 743, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Rigopoulou, D., Kunze, D., Lutz, D., Genzel, R., & Moorwood, A. F. M. 2002, A&A, 389, 374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigopoulou, D., Hurley, P. D., Swinyard, B. M., et al. 2013, MNRAS, 434, 2051 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H., Helou, G., Hollenbach, D. J., et al. 2007, ApJ, 669, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Shinn, J.-H., Koo, B.-C., Burton, M. G., Lee, H.-G., & Moon, D.-S. 2009, ApJ, 693, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Armus, L., Dale, D. A., et al. 2007a, PASP, 119, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007b, ApJ, 656, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Spinoglio, L., Pereira-Santaella, M., Busquet, G., et al. 2012, ApJ, 758, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010, A&A, 518, L4 [Google Scholar]
- Tommasin, S., Spinoglio, L., Malkan, M. A., & Fazio, G. 2010, ApJ, 709, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Werf, P. P., Isaak, K. G., Meijerink, R., et al. 2010, A&A, 518, L42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veilleux, S., Rupke, D. S. N., Kim, D.-C., et al. 2009, ApJS, 182, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Wilson, C. D., Petitpas, G. R., Iono, D., et al. 2008, ApJS, 178, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Wrathmall, S. A., Gusdorf, A., & Flower, D. R. 2007, MNRAS, 382, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Huang, J., Spinoglio, L., & Tommasin, S. 2009, ApJ, 701, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, T.-T., Kewley, L. J., & Sanders, D. B. 2010, ApJ, 709, 884 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Observed SPIRE/FTS spectra of our sample. The black and gray lines are the SSW and SLW spectra, respectively. Notice the overlap between the two spectra in the 960 and 990 GHz spectral range. The dashed red lines mark the position of the detected lines. The error bars indicate the median 1σ uncertainty of each spectrum. |
| In the text | |
 |
Fig. 1 continued. |
| In the text | |
 |
Fig. 2 Rest-frame Spitzer/IRS spectra. The short-low (5.5–14 μm), short-high (10–19 μm), and long-high (19–36 μm) spectra are plotted for each galaxy. For clarity, the spectra are multiplied by the following factors 1, 2.5, 14, 100, 220, and 2000, from bottom to top. The wavelengths of the H2 rotational transitions are indicated. |
| In the text | |
 |
Fig. 3 Rest-frame SINFONI integrated spectra. For clarity the spectra are shifted by the following factors 0, 0, 3.5, 4.0, and 4.0 × 10-11 erg cm-2 s-1 from bottom to top. The wavelengths of the H and H2 transitions are indicated. |
| In the text | |
 |
Fig. 4 χ2 values for the power-law temperature distribution model as a function of β and nH2 for NGC 7130. The red (green) contours are the 1, 2, and 3σ confidence levels for the CO (H2) SLED. |
| In the text | |
 |
Fig. 5 CO and H2 rotational diagrams. The red (blue) line is the best-fit model for the warm (cold) component. The number close to the data points is the J quantum number of the level. For H2, circles correspond to the vibrational level ν = 0, diamonds to ν = 1, and squares to ν = 2. |
| In the text | |
 |
Fig. 6 Left panel: chemical structure and temperature of a PDR with G0 = 104 and nH = 104 cm-3. The thick black line is the gas temperature (left axis). The other lines represent the abundances (left axis) of H (black), H2 (orange), C+ (blue), C i (violet), and CO (green). Right panel: H2 (orange) and CO (green) column densities as a function of the temperature. The dashed lines are the best power-law fits to the distribution (see Sect. 6.1). |
| In the text | |
 |
Fig. 7 Power-law indices of the temperature dependence of the CO (top) and H2 (bottom) non-LTE cooling functions (solid line; see Sect. 6.2). The fits are valid for a temperature range between 30 and 150 K for CO and 150 and 1000 K for H2. The fitted β values form the models with nH2 = 104.5 cm-3 and nH2 = 106 cm-3 are also plotted for each galaxy. For visualization the abscissa of the data points are slightly offset. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.