| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201323138 | |
| Published online | 05 June 2014 | |
WINGS-SPE
III. Equivalent width measurements, spectral properties, and evolution of local cluster galaxies⋆,⋆⋆,⋆⋆⋆
1
Sterrenkundig Observatorium Vakgroep Fysica en Sterrenkunde Universiteit
Gent,
Krijgslaan 281, S9,
9000
Gent,
Belgium
e-mail:
jacopo.fritz@UGent.be
2
INAF-Osservatorio Astronomico di Padova, vicolo Osservatorio 5,
35122
Padova,
Italy
3
Observatoire de Genève, Université de Genève,
51 Ch. des
Maillettes, 1290
Versoix,
Switzerland
4
Dipartimento di Astronomia, vicolo Osservatorio 2, 35122
Padova,
Italy
5
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza
San Juan 1, planta 2, 44001
Teruel,
Spain
6
Centre for Astrophysics and Supercomputing, Swinburne University
of Technology, Melbourne,
VIC
3122
Howthorn,
Australia
7
Australian Astronomical Observatory, NSW,
2113
Sydney,
Australia
8
Observatories of the Carnegie Institution of Washington,
Pasadena
CA
91101,
USA
9
Niels Bohr Institute, Juliane Maries Vej 30, 2100
Copenhagen,
Denmark
10
Specola Vaticana, 00120
Stato Città del Vaticano,
Italy
Received: 27 November 2013
Accepted: 13 February 2014
Context. Cluster galaxies are the ideal sites to look at when studying the influence of the environment on the various aspects of the evolution of galaxies, such as the changes in their stellar content and morphological transformations. In the framework of wings, the WIde-field Nearby Galaxy-cluster Survey, we have obtained optical spectra for ~6000 galaxies selected in fields centred on 48 local (0.04 < z < 0.07) X-ray selected clusters to tackle these issues.
Aims. By classifying the spectra based on given spectral lines, we investigate the frequency of the various spectral types as a function of both the clusters’ properties and the galaxies’ characteristics. In this way, using the same classification criteria adopted for studies at higher redshift, we can consistently compare the properties of the local cluster population to those of their more distant counterparts.
Methods. We describe a method that we have developed to automatically measure the equivalent width of spectral lines in a robust way, even in spectra with a non optimal signal-to-noise ratio. This way, we can derive a spectral classification reflecting the stellar content, based on the presence and strength of the [Oii] and Hδ lines.
Results. After a quality check, we are able to measure 4381 of the ~6000 originally observed spectra in the fields of 48 clusters, of which 2744 are spectroscopically confirmed cluster members. The spectral classification is then analysed as a function of galaxies’ luminosity, stellar mass, morphology, local density, and host cluster’s global properties and compared to higher redshift samples (MORPHS and EDisCS). The vast majority of galaxies in the local clusters population are passive objects, being also the most luminous and massive. At a magnitude limit of MV < −18, galaxies in a post-starburst phase represent only ~11% of the cluster population, and this fraction is reduced to ~5% at MV < −19.5, which compares to the 18% at the same magnitude limit for high-z clusters. “Normal” star-forming galaxies (e(c)) are proportionally more common in local clusters.
Conclusions. The relative occurrence of post-starbursts suggests a very similar quenching efficiency in clusters at redshifts in the 0 to ~1 range. Furthermore, more important than the global environment, the local density seems to be the main driver of galaxy evolution in local clusters at least with respect to their stellar populations content.
Key words: galaxies: clusters: general / galaxies: evolution / galaxies: stellar content / methods: data analysis
Based on observations taken at the Anglo Australian Telescope (3.9 m- AAT) and at the William Herschel Telescope (4.2 m-WHT).
Full Table A.1 is available in electronic form at both the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/566/A32 and by querying the wings database at http://web.oapd.inaf.it/wings/new/index.html
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
It is now widely accepted that the evolution of the properties of galaxies such as morphology, gas and dust content and stellar population properties, has a very strong dependence on the environment where galaxies are found. Not only are the average characteristics of cluster galaxies different from those that we observe in the field, but also the physical processes driving their evolution are different. By evolution in this context, we mean the transformations that galaxies undergo from both the morphological aspect and with respect to their stellar population content as a function of the cosmic time.
A striking example of this environmental dependency is the paucity of blue, late-type galaxies at the centre of local clusters, which are at odd with what it was found in higher redshift rich clusters where a large population of blue, star-forming galaxies was already discovered more than 3 decades ago (Butcher & Oemler 1978a,b, 1984). This is one of the most clear examples of the consequences of the evolutionary effects observable in galaxies in dense environments, and evidence for it have been gathered during the following years (see, among the others, Couch et al. 1994; Lavery et al. 1992; Margoniner & de Carvalho 2000; De Propris et al. 2003, 2004; Haines et al. 2009).
Since then, galaxy clusters have proved to be a very important place to study galactic evolution and were used to probe an extremely wide range of physical conditions from the dense cores to the outermost, low-density regions. During the past years, this was achieved, from both a morphological perspective (see, e.g., Hausman & Ostriker 1978; Dressler 1980; Buote & Tsai 1995; Dressler et al. 1997; Fasano et al. 2000; van Dokkum & Franx 2001; Goto et al. 2004; Sánchez-Blázquez et al. 2009; Poggianti et al. 2009a) and from the point of view of the stellar populations hosted by these galaxies (e.g., Couch & Sharples 1987; Dressler & Gunn 1983, 1992; Dressler et al. 1999, 2013; Postman et al. 2001; Gladders et al. 2013).
Furthermore, evidence has been already in place for many years that the cluster environment acts not only on a global scale but also locally. For example, Prugniel et al. (1999) demonstrated how the presence of young stellar populations is affected by the local environment, showing that galaxies hosting recent star formation tend to prefer the less dense environment of the field or of poor groups. On the other hand, the emission-line galaxy fraction was found to decrease towards the centre of dense clusters (e.g., Biviano et al. 1997; Dale et al. 2001), proving the importance of the local conditions. Similarly, the projected distance from the cluster’s centre was found to be the main factor driving the differences between passive ellipticals and actively star-forming spirals (see Thomas & Katgert 2006, and references therein), proving the importance of the global environment.
The best approach when trying to understand how blue, actively star-forming galaxies, which are so common in high-redshift galaxy clusters, turn into red and passive systems, is to probably focus on those objects that are experiencing a transition in between the two phases. Among these, there are the so-called E+A galaxies (Dressler & Gunn 1983; Zabludoff et al. 1996), also named k+a and a+k (Dressler et al. 1999) or simply “post-starburst”. Their designation is derived from the characteristics in their spectra, which lack lines in emission and present strong Balmer absorption lines. They are typical of A-class stars (hence the “A” in their names), having a lifetime of some hundreds of Myr, up to about 1 Gyr. For this reason, such a spectral signature is very often used to identify a burst or an episode of enhanced star formation on those time scales.
The presence of strong hydrogen lines in absorption and the concomitant absence of any emission line in the optical can be easily achieved when the duration of the two phenomena producing them is different with emission lines being typically produced from the intense ionizing continuum of very young (i.e. ages less than ~2 × 107 years) stars. Such a combination can appear as the result of a star-bursting episode being observed a few tens of Myr after the star formation has stopped (e.g., Poggianti et al. 1999). Alternatively, a truncation in an otherwise continuous, regularly star-forming pattern, might produce moderately strong Balmer absorption lines as well (e.g., Newberry et al. 1990; Leonardi & Rose 1996).
Hence, in most cases, these are galaxies which have recently experienced a quenching of the star-formation activity, and are on their way to become passively evolving objects. Thus, despite that they are quite rare if compared to the whole galactic population (see Quintero et al. 2004, and references therein), they may be one of the important keys to address galaxy evolution questions.
The E+A galaxies were initially believed to be a prerogative of galaxy clusters, and a number of mechanisms have been proposed to explain their formation, including high speed galaxy-galaxy interactions (e.g., Zabludoff et al. 1996), mergers (Bekki et al. 2001), and gas stripping by ram-pressure from the hot intracluster gas (Tonnesen et al. 2007; Ma et al. 2008). The latter in particular, detected in X-rays, is believed to be one of the main actors in a galaxy’s life, causing the quenching of the star formation in those systems, which are accreting into clusters, through the efficient removal of their gas reservoirs.
Optical spectra contain the information we need for the study of the stellar content of a galaxy. The stellar mass, the ages of stellar populations, their metallicity, and the dust content are all characteristics that can to some degree be derived from this data.
The wings1 project (Fasano et al. 2006) and its spectroscopic follow-up (Cava et al. 2009) is providing the largest set of homogeneous spectroscopic data for galaxies belonging to nearby clusters. Spectral lines are of fundamental importance to characterize the stellar content and properties of a galaxy, providing a quick and simple way to broadly classify them, according to their star-formation history. The reader can refer to Poggianti et al. (1999) for an interpretation from a theoretical point of view of the meaning of the various spectroscopic classes.
In this paper, we describe the details of a method used to automatically measure the equivalent width (EW) of the most prominent spectral lines in the wings optical spectra. The method, as presented in Fritz et al. (2007) for the first time, is able to deal with low S/N spectra and provides a robust estimate of the uncertainty as well. We present and describe the catalogue of the rest-frame EW, providing a spectral classification, and we compare the spectral properties of ~2000 galaxies to other characteristics such as their luminosity, mass, morphology, and the environment where they reside.
The paper outline is as follows: we briefly present the dataset in Sect. 2 and explain and discuss the measurement method in Sect. 3. In Sect. 4 we point out some observational issues and describe the spectroscopic classification criteria, while we describe the properties of galaxies in our sample in Sect. 5, based on their spectroscopic classification in relation with both other galaxies’ properties (such as luminosity, stellar mass, etc.) and with cluster’s properties as well. This is followed by a comparison with high redshift cluster galaxies (Sect. 6) and by a summary of our results (Sect. 7). Details on the EW catalogue with an example are given in Appendix A.
Throughout this paper we have adopted the usual convention of identifying emission lines with negative values of the EWs, and absorption lines with positive ones with all the quantities given at restframe. Whenever stellar masses are used, we always refer to a Salpeter (1955) IMF with masses in the 0.15−120 M⊙ range and stellar mass definition n.2, as discussed in Longhetti & Saracco (2009). Furthermore, we assume a standard Λ cold dark matter (ΛCDM) cosmology with H0 = 70, Ωm = 0.3 and ΩΛ = 0.7.
2. The dataset
Out of the 77 cluster fields imaged by the wings photometric survey (see Varela et al. 2009, for the presentation of the photometric catalogue), 48 were also followed-up spectroscopically. While the reader should refer to Cava et al. (2009) for a complete description of the spectroscopic sample, including data reduction, quality check, and completeness analysis, we briefly summarize here the features that are more relevant for this work’s purposes. The results presented in this paper are based on wings spectra and catalogues discussed in Cava et al. (2009). Our apparent magnitude limit (V ~ 20) is 1.5 to 2.0 mag deeper than the 2dFRS and sdss surveys, respectively, and this, in general, is reflected in a higher mean number of member galaxies detected per cluster.
The target selection was based on the available wings optical B and V photometry (Varela et al. 2009), which adopts a generous red cut well above the cluster red sequence. The aim of the selection strategy was to maximize the chances of observing galaxies at the cluster redshift without biasing the sample.
A good knowledge of the completeness level of the spectroscopic observations is required by the analysis that we present, as this is a factor that must be considered in the derivation of luminosity function, and anytime we want to use the spectroscopic sample to study magnitude-dependent properties (e.g., the different galaxy population fractions inside clusters, see Poggianti et al. 2006). We have computed both magnitude and geometrical (to account for the crowding of the fiber spectroscope near the clusters’ centre) completeness which we describe in more detail in Appendix B.
Medium resolution spectra for ~6000 galaxies were obtained during several runs at the William Herschel Telescope (WHT) and at the Anglo-Australian Telescope (AAT) with multi-fiber spectrographs (WYFFOS and 2dF, respectively), yielding reliable redshift measurements. The fiber apertures were 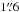 and 2′′, and the spectral resolution ~6 and ~9 Å FWHM for WHT and AAT spectra, respectively. The wavelength coverage ranges from ~3590 to ~6800 Å for the WHT observations, while spectra taken at the AAT cover the ~3600 to ~8000 Å domain.For just one observing run at WHT (during which 3 clusters were observed), note also that due to a different setup, the spectral resolution was ~3 Å FWHM with the spectral coverage ranging from ~3600 to ~6890 Å.
and 2′′, and the spectral resolution ~6 and ~9 Å FWHM for WHT and AAT spectra, respectively. The wavelength coverage ranges from ~3590 to ~6800 Å for the WHT observations, while spectra taken at the AAT cover the ~3600 to ~8000 Å domain.For just one observing run at WHT (during which 3 clusters were observed), note also that due to a different setup, the spectral resolution was ~3 Å FWHM with the spectral coverage ranging from ~3600 to ~6890 Å.
The spectra were observed by adopting two configurations, depending on the galaxies’ flux: bright and faint (see Cava et al. 2009, for further details). In principle, an issue possibly affecting our observations is the presence of saturated emission lines. While this would not be an issue for the spectral classification, it could indeed affect the lines’ flux measurements. However, saturation does not represent a relevant problem for our dataset, as spectra taken in the bright configuration are mostly luminous early-type galaxies with no or at most faint emission lines. Spectra from the faint configuration, on the other hand, belong to galaxies, which are not bright enough to display saturated emission lines.
3. The method
Given the rather large number of spectra in the wings spectroscopic sample, we developed an automatic method capable of yielding accurate measurements of the most important spectral lines. In Table 1 we list the 14 lines that are measured for each spectrum.
List of lines, whose equivalent width was measured, is reported here with their respective theoretical central λ.
Some automatic measurement procedures are already available in the literature (such as ARES, Sousa et al. 2007, DAOSPEC; Stetson & Pancino 2008, PACCE; Riffel & Borges Vale 2011 or; more recently, TAME by Kang & Lee 2012). While they are mainly focused on the measurement of absorption lines and in spectra with a high signal-to-noise (S/N) in general, we would ideally like to be able to use the information from spectra where the lines are still detectable, even though they are somehow affected by the noise. For example, as Goto et al. (2003) noted, an EW value derived by means of a Gaussian fit to the line yields reliable results only in high S/N spectra unless the fit is performed interactively. Furthermore, we are also interested in emission lines and in the “mixed” case, in which absorption and emission profiles overlap.
When measuring an EW in a spectrum, the choice of the continuum turns out to be a critical issue. In general, one would require that the line profile is fully included and that the measurement is made without being affected by other lines in the proximity, or by noisy features, such as spikes, which could dramatically change the continuum level, and hence the EW value. Defining the line profile by adopting a fixed wavelength range, which is centred on the theoretical wavelength characterizing each line, can be an unreliable choice because: 1) the line width can depend on the EW itself (being larger as its value increases) or on the galactic kinematic and 2) on a blind-measure approach, it is not possible to verify whether the noise is dominating both the line and the continuum level. The method we adopted for the lines measurements has already been described in Fritz et al. (2007), where we have preliminarily used it to constrain the lines’ intensity on a theoretical spectral model. Here, we recall the most salient features and go into a more detailed description.
The algorithm measures the equivalent width of a line, no matter if in absorption, in emission, or with both components by choosing the appropriate value of the full width at zero intensity, Δλ, which is symmetric with respect to the nominal (theoretical) line’s centre (see Table 1). As we show in Fig. 1, the edges of this interval are used to define both the spectral continuum (red markers at the extremes of the green-dashed line) and the range over which the line is measured. The spectral continuum is approximated by a green-dashed straight line in Fig. 1, and the EW value is found by summing the dashed areas, divided by the average continuum value.
To find the proper EW value, the line is first measured over a very short interval Δλ, which under samples the real value; then, various values of the EW are computed as a function of Δλ, which is increased at steps of 1 Å, starting from an initial width of 4 to 8 Å, depending on which line is measured, up to ~80 Å. The upper panel of Fig. 2 illustrates this process. Here the red straight lines represent the continuum level defined over increasingly larger values of Δλ, and the dashed regions represent the area, where the spectral line is measured (and whose profile is highlighted with a blue line).
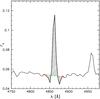 |
Fig. 1 How areas used to compute an equivalent width are defined. In this example we plot an Hβ profile which includes both an absorption and an emission component. The green-dashed line is meant to approximate the spectral continuum while its length, Δλ, is used also to define the wavelength range over which the line itself is measured. |
The correct value of the EW is found, among those measured in this way, by analysing the EW trend curve (see Fig. 2, lower panel). The absolute value of the EW will, in general, monotonically increase as the Δλ increases, since the line profile is increasingly better sampled. The point where the trend curve has its first change in slope (first derivative equal to zero) is generally where the line should ideally be measured for both emission and absorption lines. In spectra with high S/N, or in theoretical SSPs spectra, an asymptotic behaviour of the trend curve is also providing the correct EW value. An important exception is the case of an absorption + emission profile, which can be easily found in lines such as Hβ, Hγ, or in some cases even in the higher order lines. In this case, the first change in the slope of the trend curve happens in correspondence to the change from sampling the emission and the absorption profile. When this is the case, the second change in slope identifies the correct EW value (see Fig. 2, where such an example is given).
 |
Fig. 2 Illustration of how our EW measurement method works on an observed Hβ line: in the upper panel we show how the EW is iteratively measured at increasingly larger Δλ (red, straight line) which are also used to define the continuum level. The dashed regions correspond to the area measured for the EW determination. The analysis of the EW trend curve, plotted on the lower panel, provides the correct observed value, shown by the red cross. In this case, in which both emission and absorption components are present, it corresponds to the second zero of the first derivative of the trend curve itself. |
Hence, to recognise the absorption+emission pattern we first checked whether the EW trend curve starts with negative or positive values for those lines that can be both measured in absorption and emission (hydrogen lines). If small values of Δλ yield negative EW, then we are very likely in the presence of an emission+absorption pattern and the EW determination is treated accordingly.
The Hα line is treated in a different way: due to the close proximity of the two Nitrogen forbidden lines (λ = 6548 and 6584 Å, respectively) when the line is in emission, the trend curve analysis may become too complicated and impossible to treat with this method. This is particularly true in a number of different, various situations, such as when the lines are very bright, or if the gas emitting the lines has multiple velocities components, so that the three lines’ profile can be partially blended. It is also true for medium resolution spectra, as the ones we are dealing with. To properly deal with such an issue, we first measure the line within a small (~15 Å) Δλ interval; in this way, we check whether the line is in absorption or in emission. In the first case, the trend curve analysis method is applied as for the other lines. In the second case, a fixed Δλ ~ 70 Å is adopted, so that this measure will safely include both Hα and the two Nitrogen lines.
We stress here that this method has been tweaked to deal with spectra dominated by an emission component of stellar origin. Of course, we can also properly measure lines in LINERS or type-2 AGN at least for the few ones found in wings (an adjustment to the maximum value of the EW might be needed to deal with the high-luminosity ones). The measurements of (emission) lines in type-1 AGN is instead a much more complicated issue, as in the case where permitted lines can have FWHM of several thousands of km s-1, and they easily end up blending with neighbouring ones (e.g., Hβ+[Oiii]). Our method is currently not capable of properly measuring lines in such spectra, which are anyway extremely rare in our sample, hence not affecting by any means the scientific analysis.
In Table 1 we summarize the rules used for the choice of the most appropriate value of Δλ. In general, when only one of the profiles (i.e., emission or absorption) is present, the first change in the slope of the EW trend curve represents the best guess for the continuum determination. If both the emission and absorption components are instead present, the Δλ corresponding to the second slope change is instead chosen.
We have chosen a sample of spectra of different types, which span from early to late type and with a different S/N. We have measured using the package splot within iraf the equivalent widths of the most significant lines. The comparison between the automatic and the manual methods are shown for a subsample of four lines in Fig. 3 of Fritz et al. (2007), but the results are very similar for the other lines. In summary, we found that our automatic method returns EW values, which agree within the estimated errorbars with those that have been manually measured. Furthermore, the detection of emission lines is reliable for observed spectra with a S/N values down to ~5. Some subjectivity can, of course, affect the choice of the underlying continuum, especially in spectra with the lowest quality, but this is then reflected in a larger errorbar.
3.1. Uncertainties
Giving an estimate of the errorbars associated with an EW measurement is not straightforward. We consider the main source of uncertainty to be the choice of the continuum. As already pointed out, the EW measurement is quite dependent on the fluctuations of the nearby continuum, hence, on the local S/N. To account for this, we measure the equivalent width of the line adjusting Δλ by ± 5 Å than the value found by the automatic tool (this number is defined empirically, by checking the lines’ measurements on observed spectra at different S/N). The semi-difference of these two values is used as the errorbar. By adopting such a definition for the uncertainties on the definition of the spectral continuum, we note that the better the latter is defined, the smaller the measured uncertainty will be. Even though this is the dominant source of uncertainty, we also account for a “Poissonian” error, given by 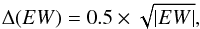 (1)which is added in quadrature to the measurement uncertainty. Errorbars computed in this way are in very good agreement with those formally computed by propagating the measured errors.
(1)which is added in quadrature to the measurement uncertainty. Errorbars computed in this way are in very good agreement with those formally computed by propagating the measured errors.
As a further check, we have used the subsample of sdss galaxies with spectroscopic data which are in common with our survey (see also the comparison performed in Fritz et al. 2011) to compare the EW values and see whether they agree within the uncertainties calculated by the measurement method. Of the 395 objects with spectroscopic data from both surveys we use for this comparison, ~250 that are brighter than MV = −18 (see Sect. 4.2). Before proceeding, an important caveat must be considered: there is a difference in the size of the fibers used in taking wings and sdss’ data, and this means that the physical regions we are observing might include slightly different stellar populations in some cases. Added to this, the location of the fiber might also not be exactly the same and the S/N of some of the spectra can also be very different. All these effects might increase the scatter in the comparison.
Despite this, we find that the EW values measured for the two different datasets, and in particular those of [Oii] and Hδ (which are those upon which our classification scheme is based) very well agree within the given uncertainties. The rms of the relation comparing [Oii] measurements is ~6 Å, which is in fair agreement with the average errorbar of ~4 Å, especially if we take into account the aforementioned caveats on the fiber size and position. In the case of Hδ, the rms is ~0.8, which again is consistent with the average errorbar of ~0.7 Å. This not only makes us more confident that the EW uncertainties are well estimated, but it further strengthens the reliability of the spectral classification.
3.2. Noisy detections and caveats
One of the trickiest issues concerns the detection of lines in spectral regions with low S/N or in the proximity of the telluric absorption bands which are sometimes not properly subtracted from the spectra. First of all, we do not want the measurements, or the analysis of the EW trend curve, to be influenced by the fluctuations produced by noise and, second, we require that noise fluctuations and spikes are not interpreted as real spectral lines. The blue range of a spectrum contains seven relevant lines within a 400 Å range for typical wings spectra and redshifts and, unfortunately, is also the most prone to flux calibration uncertainties and the most affected by noise. To overcome this issue, some empirical criteria are defined to recognise noisy patterns and to distinguish them from real spectral lines:
-
the EW of forbidden lines can only be negative (i.e. in emission); positive values are, hence, interpreted as the line being absent or the spectrum highly noisy in that region;
-
late Balmer lines, such as Hδ or Hϵ, can be measured in emission if and only if other lines, such as [Oii], [Oiii], Hβ, or Hα, which are typically brighter, are also detected in emission;
-
an upper limit is set to the values of both absorption and emission lines: EWs of absorption lines cannot be higher than 16 Å, a value derived from SSP models. When emission lines are taken into account, the maximum (absolute) value that a line can assume is dependent on the line itself and was computed from SSP spectra. Lines having EW outside these ranges are considered as noise.
The shape and, even more in general, the characteristics of the EW trend curve can depend on the spectral resolution. Especially in low S/N and high resolution spectra, the trend curve can assume erratic behaviour, particularly at a local level. Thus, the method had to be slightly tweaked as to take into account for a possible sensitivity to the spectral resolution. This was done by testing and calibrating the algorithm on spectra having the same resolution of those in the wings datasets. Furthermore, as described in Sect. 3.1, we have applied our method to a set of sdss spectra and found that it does not show a strong sensitivity on the resolution, at least as far as datasets with such characteristics are considered.
Finally, we consider as unreliable values above −2 Å for the EW of [Oii] and [Oiii]. These cases are identified with a 0.0 in the catalogues.
4. WINGS spectra
The wings spectroscopic sample was built up from two sets of observations: spectra of galaxies in clusters at negative declinations were taken with the 2dF multi-fiber spectrograph at the Anglo-Australian Telescope and constitute the “south sample”. Spectra in the “north sample” were instead taken at the WHT using the AF2/WYFFOS (see Sect. 2 for more detailed information about the spectra).
Due to both technical issues and bad weather conditions, a number of spectra taken at the WHT turned out to be of very poor quality and had to be discarded as not suitable for our work. In this way, the number of spectra of members for some clusters had been so drastically reduced that we decided not to include these clusters in our analysis. In Appendix C, we provide more details both on the issues and on the adopted rejection/acceptance criteria.
List of the clusters used for this work.
This selection reduces the number of spectra that are used in this work to 4381 out of the ~6000 that were originally observed, of which 2744 are spectroscopically confirmed members, belonging to 29 clusters in both the south and north sample. In Table 2, we report the cluster names, the total number of spectra and the confirmed members, and their redshifts.
4.1. Spectral classification
Adopting the spectral classification defined by Dressler et al. (1999, MORPHS collaboration), which was developed to study distant galaxy clusters, we divide the spectra of our sample into six classes, based on the EW of [Oii] and Hδ, according to the scheme presented in Table 3. Spectra for which none of the two lines was detected are classified as noisy. The broad physical meaning of such a classification is discussed in detail by Poggianti et al. (1999) and Poggianti et al. (2009b); we summarize it briefly in the following:
 |
Fig. 3 Distributions of absolute V magnitude for galaxies in the north and south samples (different colours and lines). Absolute magnitudes are computed as the integral convolution between the rest-frame model spectrum and the V-band transmission curve. All distributions are normalised to their peak number, and both magnitude and geometrical completenesses are taken into account. |
-
e(a) emission-line spectra with strong Hδ in absorption, signature of the presence of A-type stars. They are typical either of dusty starbursts, or of systems where an episode of substantial star formation was abruptly interrupted, and only a residual activity might be currently present;
-
e(b) emission-line spectra with very strong emission lines, typical of star-bursting systems with low to moderate dust extinction;
-
e(c) emission-line spectra with moderate-to-weak emission and moderate-to-weak Hδ in absorption, which is typical of a regular (non-starbursting) star-formation pattern, as those distinctive of “normal” spiral galaxies;
-
k spectra resembling those of K-type stars, lacking emission lines and with weak Hδ in absorption, which is typical of passively evolving galaxies with neither current nor recent star formation activity. Such spectra are normally found in elliptical galaxies;
-
k+a/a+k spectra displaying a combination of signatures typical of both K and A-type stars with strong Hδ in absorption and no emission lines, which are typical of post-starburst/post-starforming galaxies whose star formation was suddenly truncated at some point during the last 0.5−1 Gyr.
Following this broad classification, all emission-line galaxies are those which are undergoing a process of star formation at the very moment of their observation. Another origin of emission lines is also possible and it discussed later on. The other types represent “passive” spectra; the k being dominated by old stars (older than ~2 Gyr) and the k+a and a+k showing evidence for an increasingly important presence of A-class stars, which are commonly recognised as a signature of a relatively recent (<1 Gyr) burst or at least activity of star formation.
Summary of the criteria adopted to classify the spectra based on spectral lines criteria.
In a few cases, to distinguish between the three emission-line classes, we used, if possible, also Hβ and [Oiii]. These two lines were used in these cases, mostly for spectra of the north sample, for which the [Oii] line was either out of the observed range, or it was non-detected (the blue range of the spectra is often quite noisy). The use of Hβ in particular, has been already exploited by Yan et al. (2006) as a means to distinguish and properly classify e(a) and k+a spectra. We searched for a relation between either the EW of [Oiii] (5007 Å), which is easily detected when present, or that of Hβ and the EW of the [Oii]. This relation is intended to be used only to distinguish between the e(b) ([Oii] < −40 Å) and the e(c) ([Oii] ≥ −40 Å) classes, while the classification as an e(a) is made mainly by means of Hδ.
No clear trend is found for either of the two lines, and if we average the EW value of [Oiii] and Hβfor those galaxies where EW([Oii]) ≤ −40, we obtain −12.5 and −32.5 Å for Hβ and [Oiii], respectively. We choose to use Hβ, as a proxy for the [Oii] line, since it has the lower dispersion (even though we are conscious that this is in part because the average value of Hβ EW is lower with respect to that of [Oiii]). Table 3 is meant to summarize the criteria used to assign the spectral classification.
Note that the spectrographs at both telescopes allow us to observe for all wings clusters the spectral region containing the [Oii] line, which is crucial for the classification scheme we have chosen. In the worse case at the cluster’s average redshift, the [Oii] line is observed at ~3880 Å, well above the lower limit of 3600 Å. On the other side, most of the spectra in the north sample do not encompass the Hα line, which is anyway not used for spectral classification purposes, hence not affecting any of the derived quantity we use for the present work.
4.2. Compatibility between south and north sample classification
The V-band absolute magnitude distributions are shown in Fig. 3 for the north and south samples separately, distinguishing the spectroscopically confirmed members. Absolute magnitudes used for this work are those computed based on the best-fit model to the observed spectrum (see Fritz et al. 2011), so that the k-correction is automatically taken into account, and no assumptions need to be made. We note that the north distribution declines at magnitudes brighter than the south sample (MV ≃ −18.5) at the faint end, probably due to the severe incompleteness setting in at brighter magnitudes in the north. Nevertheless, as the north subsample contains less than 10% of the total wings members, this does not alter the significance of our results. For these reasons, we can carry on our analysis of the whole sample using galaxies with MV < −18.
In Fig. 4, we show the distribution of the various classes within the north and south subsamples for member galaxies. Following what was previously discussed, a cut in absolute magnitude at MV = −18 was applied. We choose to show only cluster members, since the non-member population contains a mix of field galaxies and foreground structures, which we are not able to properly distinguish. The percentage of the various classes are computed, which takes into account both magnitude and geometric completeness.
 |
Fig. 4 Spectral types distribution of wings spectroscopically confirmed members. South and north samples are shown separately with different colours and lines for comparison. A cut at absolute magnitude MV = −18 has been applied. |
As described in Appendix C, the EW measurements had to be performed manually for some spectra. This could, at least in principle, make the measures and, hence, the classification, non-homogeneous between the south and north subsample, possibly introducing some bias.
From Fig. 4, we note that the relative number of the various spectral types is similar in the two samples, which means that once completeness corrections are taken into account, and as long as galaxies brighter than MV = −18 are considered, the two samples can be considered as homogeneous and comparable within the statistical uncertainties.
5. The characteristics of the local clusters galaxy population
We now analyse the properties of the galaxies in our sample with a focus on their spectral classification and related characteristics.
5.1. General properties
We were able to successfully classify about 90% of the spectra of our survey (both cluster members and background objects) based on [Oii] and Hδ (or Hβ, when the [Oii] lines was not observed, see Sect. 4.1). Spectra without a classification either have a very low S/N, or the lines were not measured due to strong artifacts affecting their profiles.
With this information, we can now analyse the properties of the cluster population, discussing the characteristics of the various spectral types as a function of their physical properties, such as luminosity, morphology, stellar mass, and position within the cluster. To properly do this, we limit our sample so that it includes only galaxies with a total absolute magnitude equal or brighter than −18 in the V band (see Sect. 4.2). With this cut in magnitude, we are left with 2296 out of the original 2744 in the members’ sample. From now on, we consider only objects in this magnitude limited sample unless otherwise stated. We stress here that the south sample is complete at the ~70% level (see the discussion in Cava et al. 2009) at this magnitude limit.
 |
Fig. 5 Left panel: shaded histograms represent the number of galaxies in the six spectral types as a function of the absolute V magnitude; the green-dashed line marks the magnitude limit of the subsample used in the analysis (for this plot only, we consider no cut in magnitude). Galaxies brighter than MV = −22.5 are included in the brightest bin. Right panel: occurrence of morphological types as a function of the spectral class. The percentages refer to the number of objects with a given morphology with respect to each spectroscopic class. For both plots, data have been weighted by both magnitude and geometric completeness. For the right-hand plot only galaxies with MV < −18 have been considered. |
Table 4 summarizes the number distribution of the three main morphological types. Galaxy morphologies are taken from Fasano et al. (2012) and have been obtained with MORPHOT, an automated tool designed to simulate a visual morphological classification as closely as possible. MORPHOT uses a combination of 21 imaging parameters that complement the classical Concentration/Asymmetry/clumpinesS indicators, which are derived from the V-band wings images and provides a parametrical morphological classification based both on a maximum likelihood technique and on a neural network machine (see Fasano et al. 2012, for details). This piece of information will be used later on (see, Sect. 5.3).
Summary of all the morphological types, identified as cluster members in our magnitude limited sample (corrections for incompleteness are here not taken into account).
Considering the spectral classification as outlined in Sect. 4.1, we found that the galaxy population in local clusters is dominated by the k spectral type, including about 50% of the galaxies in our spectral sample and about 30% by the e(c) class. The post-starburst classes (k+a and a+k) represent about 11% of all the galaxies, while the two other emission-lines classes, e(a) and e(b), contain 7 and 3% of all members, respectively (see Table 3). These fractions have been calculated taking into account completeness corrections.
5.2. The V-band luminosity distribution
On the left panel of Fig. 5, we compare the distributions of the V-band absolute magnitude for the various spectral classes. Note that this magnitude was computed from the best fit model to the observed spectrum (see Fritz et al. 2007, 2011).
The V-band luminosity distributions span a range of 3 to 5 mag, depending on the spectral type, peaking in general at different magnitudes and also displaying a different median luminosity as a function of the spectral class.
It shows no significant differences between the e(a) and the e(b) spectral classes, peaking around MV ~ −18 for both types, having the same median luminosity and very similar range. The luminosity function for the other emission-line type, the e(c) galaxies, substantially differs in that not only it displays a tail towards brighter magnitudes, but it also peaks at higher luminosities (MV ~ −19; note this is above the magnitude limit we consider).
As for the distributions of the two post-starburst classes k+a and a+k, they both peak around MV ~ −18, even though, we are most likely limited by the poor statistics especially in the case of the a+k class. They differ, though, with respect to the range in luminosity which is broader for the k+a class, reaching MV ~ −22. This almost matches the high-luminosity tail seen for the e(c) and k galaxies. The characteristics of the luminosity distribution we find for the k+a class, are very similar to those in the local, massive Coma cluster (see Poggianti et al. 2004), which lacks a significant bright population, and have a similar typical absolute magnitude of ~−18.
The V-band luminosity distribution of galaxies with a k-like spectrum is yet clearly different with respect to all the other classes in basically all of its characteristics: peaking at MV ~ −20.5, they also have the most luminous tail in the distribution, while a significant population of objects with absolute magnitudes lower than MV ~ −19 at the same time are lacking when compared to the other classes. With the e(c) type, this is the only class whose luminosity function decreases before our magnitude limit cut.
5.3. Morphology distribution of the spectral types
An analysis of the morphological mix of the wings galaxy population has already been carried out in Poggianti et al. (2009a). Here, we focus on the relation between morphology and spectral type.
In the right-hand panel of Fig. 5, we show how the spectral classification correlates with the morphology for our magnitude-limited sample. The wings galaxies follow the broad relation between morphology and star formation history in general.
Globally, the dominant morphological type is represented by S0s, accounting for more than 50% of both the passive spectral type k and the post-starburst k+a. They are also the most numerous among every spectral class with the exception of the e(b), which is instead dominated by late-type spirals (Sc). More than 80% of the passive galaxies k are early-types (E+S0), and the same goes for the post-star forming k+a class.
On the other side, the majority of e(a), e(b), and a+k are spirals. While the morphological fractions of e(a) and a+k are similar, the e(b) class clearly stands out being dominated by spiral galaxies with more than the 50% of objects being found among later types than Sb. The e(c) spectral type is almost equally populated by early (E+S0) and late types (Sp).
The presence of the various morphological types among the k and k+a galaxies is very similar: we observe a clear prevalence of ellipticals and S0s, no Sd/Irregular, and a fraction of spirals less than 20% in both classes. Furthermore, this fraction is monotonically decreasing when going from a+k to k+a and finally to k, where the relative occurrence of Spiral galaxies is the lowest, which probably mirrors the transition from a post-star forming phase to a passive evolution pattern.
Finally, there seems to be a significant difference in the morphology distribution between the two so-called post-starburst classes, k+a and a+k, with the latter distribution resembling more that of the spiral types (even though it should be pointed out that the statistic is not optimal for the a+k class). A similar result was found by Dressler et al. (1999) at a higher redshift.
To summarize, while there is indeed a broad correspondence between the morphological and spectral classifications, we find that galaxies in local clusters lack an univocal equivalence between their morphology and their spectral characteristics. This result already well known at high redshift (e.g. Dressler et al. 1999; Couch et al. 2001), meaning that the evolution of these two properties is, at least to some degree, decoupled.
5.4. Emission-line galaxies in local clusters
As already described in Sect. 5.2, the V-band luminosity distribution is very similar for the e(a) and e(b) spectral type but substantially different for the e(c). This somehow reflects the stellar mass distribution (see Fig. 6; mass values are taken from the catalogue presented in Fritz et al. 2011.): e(c) galaxies peak at around 1010.5 M⊙, while the distribution for e(a) and e(b) peaks at stellar mass values 0.5 dex lower with the e(a) population having, in proportion, a slightly higher fraction of massive galaxies with respect to the e(b)’s; otherwise, the distributions of the latter two spectral types are very similar.
 |
Fig. 6 Stellar mass distribution for the six spectral types in the magnitude limited sample and for objects within R500. |
As we noted in Fritz et al. (2007), it should be said that, the more a galaxy has been actively forming stars in a recent past, the more difficult it is to have a robust estimate of the stellar mass of the oldest stars from optical spectra alone, given their high mass-to-light ratios. Thus, in principle, the mass of e(b) galaxies is the one potentially more prone to be underestimated when calculated with data similar to ours. Nevertheless, a comparison with an estimate of the stellar mass calculated using only B and V-band photometry and adopting the Bell & de Jong (2001) recipe, gives fully compatible results (see Fritz et al. 2011). A similar check exploiting K-band photometry from Valentinuzzi et al. (2009), further validates our results.
We now analyse the fraction of star-forming galaxies as a function of the cluster properties, such as its velocity dispersion and X-ray luminosity. As done in several previous works (see Dressler et al. 1999; Poggianti et al. 2006), we use the [Oii] (3727 Å) as a tracer for the star formation activity, so to be able to consistently compare our results with other studies, especially those at higher redshift. Even though this line is prone to reddening issues and its intensity depends on both the gas metallicity and physical conditions, its presence/absence can be reliably used to discriminate between star-forming/passively evolving galaxies.
For each cluster, we calculate the fractions of galaxies, weighted for completeness, displaying the [Oii] line in emission, or having a rest-frame EW < −2 Å. As the data coverage, in terms of projected radial distance, is limited by the characteristics of the spectrographs we have used for the survey and since the clusters span a non-negligible range in redshifts, observing galaxies in clusters at different distances means we are sampling areas at different distances from the cluster’s centre. For this reason, only galaxies within R500 (we use the relation R500 ≃ 0.50 × R200) are considered to not introduce any bias and sample the galaxy population homogeneously.
The results are then plotted against the two main global properties of the clusters, namely their velocity dispersion and X-ray luminosities and displayed in Fig. 7.
 |
Fig. 7 Fraction of emission-line galaxies (i.e., belonging to any of the first three spectral classes defined in Table 3) as a function of the cluster velocity dispersion (left) and total X-ray luminosity (right). Only galaxies within R500 are taken into account (see text for details). |
In Poggianti et al. (2009a), we have already analysed the frequency of morphological types as a function of the cluster velocity dispersion and X-ray luminosity. Here we perform a similar analysis based on the spectral classification, where X-ray luminosity (LX) and the cluster velocity dispersion (σ) are used as a proxy of the total cluster mass.
Similar to what was found in Poggianti et al. (2009a), we note that there is no, or at most a weak correlation, between the fraction of galaxies with emission lines and the velocity dispersion as far as clusters having a velocity dispersion in the ~500 ÷ 1400 km s-1 range are concerned (i.e. the range of wings clusters). This also agrees with the results of Poggianti et al. (2006), who analysed a low-z galaxy cluster sample drawn from the sdss. This result suggests that the global properties of a cluster are not the main physical drivers of the build up of the mixture of spectral types. A similar result is also found for post-starburst galaxies (see Sect. 5.5).
We checked with a Spearman test to see whether there is any significant correlation between the emission-line fraction and the X-ray luminosity. The test yielded a correlation coefficient of 0.26, which indicates that there is none.
The fraction of star-forming galaxies in wings clusters, which are calculated from each single cluster, is ~33 ± 10%, with a large scatter at any given σ and LX. This fraction is larger than the 23% found in Poggianti et al. (2006) but this is likely due to the differences in the magnitude limit in these two studies, being deeper in wings, and the different limit for [Oii]detection (−3 Å for the latter work).
Let us now focus on the characteristics of the e(c) type galaxy population in a deeper detail. As we have already stressed in Sect. 5.1, these galaxies constitute a major component in local clusters and their luminosity distribution is quite distinct with respect to the other emission-lines types: not only does the distribution peak at a brighter value but, most importantly, it contains a substantial population of brighter objects, which is instead completely absent from the other two emission-line classes. If we look at the properties of the most luminous (i.e. MV ≤ −20) tail of e(c) galaxies, we compare them to the less luminous ones and note that
-
they have fainter [Oii]: in most of them the equivalent width of this line is ≥−5 Å;
-
they have older ages (both mass- and luminosity-weighted: values are taken from Fritz et al. 2011);
-
their spectra have redder (B − V) colour (median value of 1.0 against 0.8);
-
they are on average more massive (a median mass of ~4 × 1010 M⊙, compared to a mean value of ~1010 M⊙ for the others).
To check whether this particular subsample is biased by noisy measurements of the [Oii] line which is, for these cases, faint, we visually inspected the spectra and came to the conclusion that the detection is real and the measure is reliable in the vast majority of cases.
It is worth stressing that the detection of the [Oii] line, which is the main feature used for classifying e(c) and distinguishes them from k, is not univocally related to the presence of a star forming activity in galaxies but can instead have a different origin (see Yan et al. 2006). Indeed, when inspected one-by-one, most of the high-mass (M⋆> 1010.5 M⊙) elliptical and S0 galaxies with an e(c) classification display spectral features typical of LINERS or low-activity AGNs. This can include an enhanced [Nii] (6584 Å) emission as compared to Hα. This goes along the line of the findings by Yan et al. (2006), who pointed out that “[Oii]-only” galaxies, or even those with a high [Oii]/Hα ratio, are more common among the reddest in their sdss emission-line sample, which likely indicates the most massive ones. They classified “post-starburst” as galaxies that display a high [Oii]/Hα ratio (or even with a [Oii] detection but no Hα, which are the so-called [Oii]-only galaxies), and these were found to be red in colour, similar to those in our subsample.
While we find ellipticals to represent only about 10% of e(a) and e(b) galaxies, the occurrence of this morphological type among the e(c) is higher than 20%, and it is mainly populated by the most luminous ones.
The occurrence of the [Oii] line and other emission lines in local elliptical galaxies is an already known phenomenon (see e.g. Caldwell 1984; Phillips et al. 1986). These are either passive galaxies that are showing a residual, very low star formation level, or LINERS. A number of mechanisms other than star-formation can be responsible for the production of the ionizing flux needed for the formation of forbidden lines: the presence of blue and evolved stellar populations, such as horizontal branch (HB), post-asymptotic giant branch (post-AGB) stars, energetic gas shock waves or cooling flows. Post-AGB stars, in particular, seem to be one of the most likely sources for such spectral features, as a recent work by Singh et al. (2013) demonstrates, especially for massive galaxies, with very low levels of star formation activity as those in our bright e(c) sample.
This issue, of course, is much easier to deal with for us as far as type-1 AGNs are concerned, as they are easily recognized by our spectral fitting routine. Given their extremely blue continuum and the presence of very broad emission lines, which are not compatible with the typical spectral features of stars, in such cases, it is not possible to obtain an acceptable fit by means of SSP spectra. Because of this, a high χ2 value is returned, so that it is possible to easily recognize these objects with a targeted visual inspection.
Type-2 AGNs and LINERS have instead been identified in our spectra by fitting the underlying stellar continuum and investigating line-ratio diagnostic diagrams, as described in detail in Marziani et al. (in prep.). However, only 0.8% of the galaxies in our cluster sample turn out to be AGNs (either Seyfert-1 or Seyfert-2); therefore, they are a negligible component of our spectroscopic sample.
In view of these considerations, we argue that part of the e(c)-classified objects might very likely be constituted by galaxies with characteristics very similar to the passive class k (see Sect. 5.6) but either host some very low-energy LINER activity or are influenced by one or more gas ionizing mechanisms as outlined above.
The location of a galaxy with respect to its companions and neighbours in a cluster, the so-called local density, plays an important role in shaping and defining some of its characteristics. The values of the projected local density that we use are calculated from a circular area enclosing the first 10 most nearby galaxies, which also accounts for background counts as expected from Berta et al. (2006) and is corrected for border effect (see Vulcani et al. 2012, for details). The local density is expressed as the logarithm of the number of galaxies with MV ≤ −19.5 per Mpc-2.
In Fig. 8, we show the fraction of galaxies of the different spectral types, grouped into the three broad classes of passive (k), emission-line [e(a), e(b), and e(c)] and post-starburst (k+a and a+k) at different values of the local density and displayed in bins of 0.25 dex. Emission-line galaxies dominate the regions at the lowest densities, but their relative number monotonically decreases as the local density increases, and they are basically not found at the highest values.
 |
Fig. 8 Percentage of the passive post-starburst and emission-line types as a function of the (projected) local density. |
Keeping the three emission-line classes separate slightly increases the noise in this plot, and the interpretation does not significantly change. The classes e(a) and e(b) share a similar distribution with respect to the local density, and they are both extremely rare at densities above ~60 Mpc-2 (log [ 1.75 ]): no more than 13% of galaxies in these two classes are found beyond those densities. A very similar trend is found for e(c)’s, whose distribution extends towards slightly higher density values and is mainly responsible for the tail at high values observed in Fig. 8. The three emission-line classes are distributed in a very similar manner compared to the two post-starburst classes; all of them display a peak between log (1.25) and log (1.50) Mpc-2 in their distribution.
5.5. The properties of the post-starburst population
The k+a and a+k spectral classes, often referred to as post-starburst or post-star forming, make up about 11% of the local cluster population at magnitudes brighter than −18 (~10% and ~1% for the k+a and a+k, respectively). This number is in strong contrast with the value found from the catalogue of local clusters of Dressler & Shectman (1988) but is broadly consistent with a fraction of ~15% found among lower luminosity galaxies in 5 low-z cluster by Caldwell & Rose (1997). The reason for the striking difference with the sample of Dressler & Shectman (1988) is probably due to the difference in the magnitude limit of the two surveys.
As described in Sect. 5.3, k+a galaxies tend to have morphological characteristics very similar to passive objects, with a slight preference towards later morphological types, when viewed as two separate classes, while a+k are more similar to the emission-line types in this respect. This would fit the picture in which a+k galaxies are the direct descendants of emission-line objects, especially star-bursting ones, such as the e(b) types, that gradually arise some 107 years after the star formation has stopped, when the most massive stars provide the UV radiation necessary for the production of lines in emission, have already died. Furthermore, the observational evidence that no k+a and a+k are classified as Sd/Irregular argues against merging as the main mechanism to produce such spectra and is in the line with the results in clusters at high-z of Dressler et al. (1999): other processes must be the main responsible for the presence of such galaxies in clusters. Ma et al. (2008) reached a similar conclusion by studying a massive cluster at z = 0.55 by analysing the positions and velocities they display in the cluster, and they ruled out mergers as the dominant mechanism driving their creation and evolution in clusters.
Remarkably enough, while not extremely different in the distribution of the morphological types, k+a and k galaxy differ substantially with respect both to their mass and luminosity function (see also Sect. 5.6); this is expected as an effect of downsizing, where the most massive galaxies have already evolved into passive types.
We note that there is a significant difference in the V-band luminosity distribution between the two post-starburst classes (see Fig. 5) with the k+a displaying a tail towards high luminosity, which is completely missing in a+k. This might be an indication that at least part of the k+a types (the high luminosity ones) are not coming from a+k.
As the number of a+k is quite small when compared to all the other classes, we consider these two classes as one in the rest of our analysis, adopting the broad definition of post-starburst for both.
 |
Fig. 9 Fraction of post-starburst galaxies as a function of the two cluster mass tracers, velocity dispersion (left) and LX (right). k+a and a+k are considered as one single class. As done for Fig. 7, only galaxies within R500 are taken into account. Points with different colours refer to different magnitude limits and are used later on for a comparison with high redshifts samples. |
 |
Fig. 10 Left-hand panel: cumulative radial distribution of the three spectral types as defined in the text. Right-hand: average velocity dispersion in bins of radial distance for the three main spectral classes. Void stars represent the high-z data points from Dressler et al. (1999). In all cases, the distances are calculated from the cluster’s BCG and are expressed in terms of R200. |
Similarly to what we find for emission-line galaxies, we do not see any correlation between the fraction of post-starburst and the cluster velocity dispersion or X-ray luminosity (see Fig. 9): the average fraction, calculated over all the clusters, is 8.7 ± 5.4. This is at odds with results in the distant clusters, where the incidence of such galaxies strongly correlates with the cluster velocity dispersion (Poggianti et al. 2009b).
Poggianti et al. (2009b) define “quenching efficiency” as the ratio between the number of post-starburst and the active fraction, where “active” includes both emission-line galaxies, but also the recently star forming classes k+a and a+k. We check whether this fraction, computed from weighted counts, correlates with any of the cluster properties. The value we have calculated by averaging over each cluster in our sample is 20.7 ± 11.7%, and we see no significant dependency on either the X-ray luminosity or the velocity dispersion.
The post-starburst class has, in general, properties, which are in between the passive and the star-forming galaxies. For example, the stellar mass distribution peaks at mass values which are intermediate between the k and the e(a) and e(b) class (see Fig. 6). The projected radial distribution of the spectral types tells a similar story: passive galaxies display the average tendency of gathering towards the cluster centre, while emission-line objects are more frequent in the outskirts and post-starbursts occupy a region somewhere in between. This can be clearly seen in the left-hand panel of Fig. 10, where we plot the cumulative radial distribution of wings spectral type, which is broadly divided in three classes.
On the right-hand panel of the same figure, we show the average velocity dispersion in four bins of projected radial distances. The average velocity dispersions of the post-starburst class have generally intermediate values between the passive and emission-line classes, as if they were in an intermediate state of virialization between the passive and actively star-forming galaxies. The result we get by combining the information provided by the two panels in this figure indicates ram-pressure stripping as the most effective mechanism for the creation of a k+a/a+k spectrum. When a galaxy falls into a cluster, star formation is triggered as it reaches the cluster’s virial radius (e.g., Byrd & Valtonen 1990; Fujita 1998), and it is then abruptly quenched once the galaxy enters deeper into the cluster environment. Its interstellar medium gets very efficiently stripped by the intracluster hot gas (Gunn & Gott 1972; Treu et al. 2003; Ma et al. 2008; Abadi et al. 1999). Because we see post-starburst galaxies in a shell-like radial distribution, it somehow suggests that they define a transition region, which might indeed reflect the result of such a picture.
Finally, when considering the influence of the environment onto a galaxy through the local density (see Fig. 8), post-starbursts follow the trend of emission-line galaxies, which contribute gradually less to the total population, as the local density increases. Already at densities values larger than ~30 Mpc-2, they make up only the 10% of the total galactic population, while being almost as numerous as the emission-line class at the lowest density values.
5.6. Passive galaxies
This class includes all those galaxies whose spectrum do not show any [Oii] emission (see Sect. 4.1 and Table 3) and weak Hδ absorption. By adopting this definition, we can consistently compare the properties of galaxies in our sample to those at higher redshift. Of course, this potentially leaves out other lines such as, for example, the Hα+[Nii], triplet, which could be in principle detected even when no [Oii] emission is measured. We checked the values of the Hα line in the k sample and found that only in ~2% (57) of the spectra our method was able to detect an emission. These 57 objects do not show any preference in the values of the stellar mass or luminosity or other specific common properties.
As already shown, the great majority of k galaxies are early types from a morphological perspective; around the 86% of them are classified as either ellipticals or S0s. This class is also dominated by higher luminosity galaxies and the luminosity distribution, peaking at MV ≃ −20.5, is radically different from that of any of the other classes.
Similarly, the stellar mass distribution is substantially different from that of the other five spectral classes: this class hosts the most massive galaxies, and only 20% of them have a mass lower than 1010 M⊙ in our magnitude limited sample; in clear contrast to all the other classes where most of the galaxies have instead masses below that limit (see Fig. 6), the e(c) galaxies are the only exception.
Following what has been done for the e(c) type, we distinguish passive galaxies in two ranges of V-band luminosity as well, namely brighter and fainter than MV = −21.5. As noted by Biviano et al. (2002) (but see also Beisbart & Kerscher 2000), the brightest early types should display the highest degree of segregation.
This is somehow confirmed for the wings sample as well, as can be seen in the left-hand panel of Fig. 10: the high-luminosity k spectral-type galaxies are proportionally more numerous than all other spectral types (with the exception of the luminous emission-line, which we have already discussed in Sect. 5.4) in the very central regions of clusters, even though the difference is not as evident as the one found by Thomas & Katgert (2006).
As for the distribution of the passive class as a function of the local density, Fig. 8 clearly shows how galaxies in this class are the ones detected in the widest range of projected densities with objects basically found in any kind of local environment. They make up about the 60% of the galaxies at densities larger than ~50 Mpc-2, and they are basically the only ones found in our magnitude-limited sample at Σ10 ≳ 100 Mpc-2.
5.7. Galaxies in local clusters
In this section, we give a summary of the properties, which describe the local population of cluster galaxies, and the picture, which emerges from our analysis. This allows us to more easily compare low and high-z galaxies, as we do in the following section.
About 50% of the galaxies in local clusters have spectra resembling those of passively evolving objects, while almost 40% display emission lines and only about 10% show the signatures typical of objects in a post-starburst/post-starforming phase (see Table 3). Passive galaxies are not only, on average, the most massive ones, but also the most luminous, while the emission-line classes clearly show a deficit of luminous/massive objects (see the left panel of Fig. 5). This picture very well fits the downsizing scenario, in which the most massive galaxies are the first that are formed, and are already evolving in a passive fashion (i.e., following the stellar evolution) since at least z ~ 1 (e.g., De Propris et al. 2007; Andreon 2008; Strazzullo et al. 2010). At progressively lower masses, we find objects with increasingly higher specific star formation rates.
A remarkable exception to this picture is that of the e(c) class, which contains a family of luminous (and more massive than the average) galaxies almost resembling the high luminosity tail of the passive type. When analysed with a closer look, these turn out to have characteristics, which are very similar to those of the k’s. The only difference is in the presence of the [Oii] line, which is on average not very intense, and it is likely produced by physical processes different than star formation.
When comparing the luminosity functions of the spectral types, it is tempting to view them as mirroring an evolutionary sequence, going from the star-forming e(b) and e(a), which contains the least luminous galaxies to the more extreme post starburst class a+k, whose luminosity distribution is similar to that of the e(b) and e(a) classes; containing a higher fraction of luminous object, galaxies in the k+a class are characterized by a luminosity distribution in between the star-forming and the passive types of k, which host, in turn, the most luminous objects. The e(c) are, once again, an exception to this scheme because both their classification might be influenced by the nature of the [Oii] line production and because they probably contain the field galaxies, which are being accreted by the clusters and eventually end up “feeding” the high luminosity tail of the k+a family.
Contrary to the findings of Poggianti et al. (2009a), who have found that the spiral fraction in the wings clusters correlates with the X-ray luminosity, we note how neither the fraction of emission-line galaxies nor that of post-starbursts depends on the global properties of the cluster, more precisely on the clusters’ velocity dispersion or their X-ray luminosity. This can be noted from Figs. 7 and 9. What drives the spectral characteristics is instead the local environment, as the dependence of the spectral type on the projected local density demonstrates (see Fig. 8): galaxies in dense environment tend to have their star formation quenched.
6. A comparison with the high-redshift clusters population
In this section, we attempt a comparison of some of the properties of the local cluster galaxies with those at higher redshift. In this way, we can trace the evolution of these properties as a function of the cosmic time to shed some light on the physical mechanisms that drive the physical and structural changes of galaxies in dense environments.
Two surveys provide samples, which are ideal to perform such a comparison: one was collected by the MORPHS1 collaboration, which observed galaxies in clusters at redshifts in the 0.37−0.56 range; the second was the ESO Distant Cluster Survey2 (EDisCS; White et al. 2005), targeting instead cluster galaxies with redshifts between 0.4 and ~1.
To properly compare the high-z samples and wings, which minimizes the effect of possible biases, the magnitude limits of these surveys must be matched and, furthermore, these must also be corrected to account for evolution effects. That is, the changes occurring in the mass-to-light ratios as the stellar populations in galaxies get progressively older at different cosmic ages, should be taken into account. If we assume that stellar evolution is the only mechanism acting in the luminosity change and if we consider a common redshift of formation, we can exploit stellar populations models to calculate the change in luminosity from redshift 0.55 to redshift 0.04, which represent the most extreme difference between wings and MORPHS. Assuming that the oldest stars are as old as the Universe at a given redshift, we compare the V-band luminosity of simple stellar populations with an age as close as possible to the age of the Universe at z = 0.04 and z = 0.55, which is TU ≃ 12.9 and TU ≃ 8.08 Gyr, respectively. The difference is, assuming a solar metallicity and a Salpeter (1955) IMF, of ~0.3 mag.
In their analysis of EDisCS galaxies, Poggianti et al. (2009b) use a cut in absolute V-band magnitude at MV = −20.1 at z = 0.4, which corresponds to MV = −19.8 for wings, the completeness limit is MV = −19 + 5·log 10h, while in the work by Dressler et al. (1999) using MORPHS data, corresponding to about MV = −19.5 for wings. We use this latter value to compare the high and low redshift galaxies but we have verified that using −19.8 does not change our results.
6.1. Occurrence of the spectral classes
We find that post-starburst galaxies in local clusters are less abundant with respect to their counterpart at high redshift. To our MV < −18 magnitude limit, we have classified about the 11% of the local cluster population as post-starburst (i.e., either a k+a or a a+k). At brighter magnitudes, matching the limits of the two aforementioned high redshift studies, the post-starburst fraction is 18% at high-z (as calculated for MORPHS galaxies by Dressler et al. 1999), while it lowers down to 4.6% in the wings clusters (if we assume a brighter limit, at MV < −19.8 the fraction further reduces to 4.4%). These numbers are spot on those predicted by Poggianti et al. (2009b) for z ≃ 0 clusters under the hypothesis that the star formation quenching efficiency is similar between local and distant clusters. Assuming post-starburst galaxies are formed after star formation is stopped in infalling star-forming system, and adopting the same value of the quenching efficiency, as defined in Sect. 5.5, of 23%, which is calculated at high redshift, and a star forming fraction of 20% for the local clusters (taken from the study of Poggianti et al. 2006, exploiting sdss data), the expected fraction of local post-starburst would be 4.6%.
Indeed, if we calculate the quenching efficiency for galaxies in the wings sample, we find a value of 22.0 ± 0.6%, which reduces to 15.5 ± 1.0 if a magnitude limit of −19.5 is considered. In their work, using both EDisCS and MORPHS data, Poggianti et al. (2009b) found a dependency of the quenching efficiency to the cluster velocity dispersion (see their Fig. 5), which is particularly evident for the highest velocity dispersion values. This dependence is instead absent in wings clusters (see discussion below). Hence, the aforementioned ~15% value is mainly to be intended for clusters with velocity dispersions below ~1000 km s-1 and is, within this limit, in fairly good agreement with the high-z result.
Unlike their higher redshift progenitor, we find a weak dependence of the relative incidence of post-starburst galaxies on total cluster mass as traced by the velocity dispersion and the X-ray luminosity. Looking at Fig. 9, it is especially evident that there is a flat trend in the occurrence of this class as a function of the cluster X-ray luminosity, while it seems that a weak anticorrelation is present when the same quantity is considered as a function of the velocity dispersion. This is compatible with the interpretation that the cluster mass at low-z has little or no effect in producing this particular spectral class, in particular, at low luminosities where we find most of them.
At the high redshift magnitude limit, the wings sample is dominated by the passive k type, which contains 2/3 of the whole population, a significantly higher fraction with respect to the 47% found in Dressler et al. (1999). Meaningful differences are also found for the emission-line galaxies: the fraction of e(a) reduces from 11% to a local value of 2% and, at these bright absolute magnitudes, the e(b) class almost disappears declining from a 16% to less than 1%, which clearly reveals the well known Butcher-Oemler effect. Instead, the continuous star-forming like spectrum e(c) experiences an increase when going from high to low redshifts, moving from a bare 5% to 27% locally. While part of this increase might come from high-ze(b) galaxies and progressively slow down their star-forming activity, this is barely enough to make up the local e(c) fraction. Two effects might explain this high number of local luminous e(c) we measure when compared to high redshift clusters. The first is methodological in nature and might arise from the lower detection limit that we have assumed for the [Oii] lines, EW = −2 Å vs. −5, which discriminates between the e(c) and k type. If this was the reason, we would end up having a even larger fraction of local k galaxies. Indeed, if we assign a k classification to ALL e(c) galaxies with EW([Oii]) > −5 Å, their fraction would considerably reduce, moving to a much lower 14%, while passive k-type galaxies would become the dominant galaxies and contain almost 80% of the objects. Still, this is far from the 5% fraction observed at high-z.
We could observe a second, more phenomenological effect, as the different e(c) fraction might reflect the way star formation proceeds in field galaxies that have been recently captured by the cluster, at a lower and steadier pace at lower redshift, as opposed to a higher and bursty-like activity at high redshift.
Finally, we note a drastic decrease in the incidence of e(a) galaxies (from 11% to 2%) as well. These are unlikely to have turned into the k+a or a+k we observe in wings clusters, as long as passive evolution only is considered (i.e., no merger or gas accretion events). The time scale during which the spectral features typical of A-stars dominate is around ~1 Gyr, which is much shorter than the 5 Gyr period separating the redshift range we are investigating, and after which the Balmer lines become progressively fainter. If star formation has ceased, such galaxies would eventually end up showing a k spectrum.
Another quite striking aspect differentiating wings and MORPHS galaxies concerns the morphological properties. Generally speaking, when compared to the high-z sample, we note the absence of irregular galaxies among the local k, k+a and a+k spectral type, and a much lower incidence of the later morphological classes. In the distant sample, most post-starbursts are classified as late-type with only ~27% of the objects being assigned ellipticals or S0 morphology (see also Tran et al. 2003, for a similar results on a study at comparable redshift). This number compares to a much higher fraction (~70%) of low redshift galaxies, which have instead a morphological early type (E or S0) classification.
6.2. The luminosity distributions
Dressler et al. (1999) compared of the V-band luminosity functions for six spectral types, where each definition matches the one we have adopted for this work. In Fig. 11, we plot these same luminosity distributions, which we have corrected to account for passive luminosity evolution, with the local ones. Having in mind that the high-z sample is to be considered complete for MV ≲ −19.5, we limit the analysis to the brightest galaxies and we can consistently compare the two samples.
 |
Fig. 11 Comparison of the high and low redshift V-band luminosity distribution for the six spectral types. High-z data have been corrected for passive evolution to match the local clusters data (see text for details). The vertical dashed line marks the MV = −19.5 limit. |
Galaxies with the strongest emission lines, e(b), are lacking a significant presence of objects more luminous than MV < −20 throughout all the redshift range here considered. From the uppermost panel of Fig. 11, it is tempting to claim that higher redshift star-bursting galaxies are in general more luminous compared to their most nearby counterparts, even though incompleteness at high redshift might be driving, at least partially, this comparison. Very luminous star-bursting galaxies are anyway not observed in local clusters, but nothing more can be said on their luminosity distribution based on these datasets.
Taking magnitude limits into account, the luminosity of e(c) galaxies turns out to be very similar at these redshifts, while the e(a) types mostly differ due to the presence of a significantly brighter population in the MORPHS sample, which is compatible with the luminosity distribution of the low-redshift k+a class. It seems unlikely that the high redshift e(a) can be considered as the progenitors of the local k+a, as the elapsed time since z ~ 0.5 to now is a factor of 3−4 higher than the life of the A star features, unless they host a significant amount of obscured and prolonged star formation, which will eventually leave its k+a/a+k signature in local clusters.
The luminosity functions of k galaxies at low and high redshift are quite similar. Interestingly, above MV = −22, the local population contains a slightly higher number of brighter objects. This could either be due to a somehow incomplete sampling of the high-redshift population (the MORPHS sample only contains 10 clusters, as opposed to the ~30 in wings), or it could be a real evolution effect, for which these passive galaxies would have undergone dry-merger events, having left their spectral features unchanged, while only increasing their luminosity.
A significant difference can also be observed in the post-starburst class galaxies, whose high-z sample displays a) a slightly more luminous tail; b) a higher number of galaxies with higher luminosities; and c) a significantly different peak magnitude, ~−20.2 vs. ~−18.5 (even though the latter value may be limited by incompleteness) at high and low z, respectively. Once again, this fits a downsizing galaxy evolution scenario, in which the most active galaxies are those at progressively lower mass (luminosity) as one moves from high to the low redshift Universe.
6.3. Spectral properties and the position in the cluster
Finally, we compare the radial distribution of the spectral types for the different surveys. We consider only three main spectroscopic classes: emission-line galaxies, passive galaxies (which include only the spectroscopic type k), and the k+a and a+k post-starburst class.
In the left-hand panel of Fig.10, we plot the cumulative radial distribution of the three spectral types defined above. At low redshift, the k type galaxies (especially the brightest ones, MV ≤ −21.5) are the most centrally concentrated, while emission-line galaxies tend to prefer the clusters’ outskirts. The post-starburst population generally sits at an intermediate region between the two. Of the k galaxies, 50% are found within a projected radial distance of ~0.25 R200, while the same percentage is reached at ~0.40 R200 for the emission-line, showing the tendency to avoid the innermost regions of the clusters, which are dominated by the early-type, passive population.
Although this analysis inevitably suffers from projection effects, it still provides some clue to how the characteristics of the galaxies are, on average, shaped by the environment. These trends are similar to those found in distant clusters by both Dressler et al. (1999) and Poggianti et al. (2009a), even though the differences between the three aforementioned classes seem to be less evident for our sample. If we limit our comparison to the sample matching the distant clusters absolute magnitude at low redshift, the situation does not change for emission-line and passive galaxies, even though the radial distribution for post-starbursts becomes noise-dominated, which is hampered by the very low number of objects at this magnitude limit.
We also compare the radial distribution of the velocity dispersions for the spectral classes, which we have shown in the right panel of Fig. 10 for wings galaxies between the high (MORPHS) and low z clusters. In general, we find that the values measured in wings clusters are up to ~50% lower with respect to the higher redshift counterparts, most likely due to the achievement of a more advanced state of virialization of the local clusters. Apart from this, the average trend, which sees the early types having the lowest velocity dispersion at any radius and the late types displaying a similar trend but at higher velocities, is also seen in local clusters, even though at a much higher dispersion. Furthermore, the decline of the velocity as a function of the projected radius is quite similar for the two samples in all the spectral classes.
What is significantly different in local clusters is the average difference in velocities, between passive and emission-line galaxies, which are clearly distinct at high-z. Overall, the velocity dispersions between the different spectral types at low redshift is much more similar with an average ratio σe/σk = 1.22 ± 0.11, which is only marginally consistent with the 1.40 ± 0.16 ratio of the MORPHS sample.
7. Summary and conclusions
In this paper, we have presented a catalogue of equivalent widths of the most prominent spectral lines in the ~3700 to 6600 Å range, which is automatically measured in medium resolution spectra from the wings spectroscopic survey. We use these measures to classify galaxies based on the intensity and presence/absence of the Hδ and [Oii] lines, and we focus our analysis on those objects which are spectroscopically confirmed cluster members. This classification reflects the stellar content of a galaxy and is widely used as a mean to derive clues on the star formation history both locally and at higher redshifts.
We investigate how the properties of the different spectral types relate to other physical parameters and characteristics such as morphology (Fasano et al. 2012), stellar mass, and absolute magnitude (Fritz et al. 2011), of the wings galaxy sample. In this way, we try to understand how the characteristics of the stellar populations vary as a function of other galactic properties and of both local and global environment in local clusters.
Having used a classification scheme which is adopted by several other studies at higher redshifts, we can then compare the characteristics of local cluster galaxies to their more distant progenitors.
We can summarize our results as follows:
-
1.
The local cluster population at magnitudes MV ≤ − 18 is dominated by the passive k spectral type followed by e(c) galaxies, even though it is possibly contaminated, especially at high luminosity (or stellar mass), by emission lines from non-stellar origin. About 11% of galaxies display a post-starburst spectrum;
-
2.
the k galaxies are not only the most luminous ones, but they also display the broader range of V-band luminosities. The value of e(c) has a similar spread, but a significantly lower (~1.5 mag) peak luminosity;
-
3.
the k galaxies are also the slowest in clusters (see Fig. 10, right-hand panel). This is consistent with early types, which are on average more virialized with respect to late types and with the findings that they were already in place, since z ≃ 0.6 (see Smail et al. 1997);
-
4.
there is a broad correlation between the morphological and the spectroscopical classification: more than 80% of the k and k+a spectra are ellipticals or S0s, while the majority of the recently star-forming galaxies [e(a), e(b) and a+k ] are spirals. The e(c) class is almost equally populated by early (E+S0) and late (Sp) morphological types. Yet most of the spectral types display a full range of morphologies and suggests that the evolution of these two properties is, at least partially, decoupled;
-
5.
no significant correlation is found between the relative number of emission-line galaxies and the cluster general properties, such as their X-ray luminosities or velocity dispersion;
-
6.
the local density, instead, clearly plays a role in the spectral type segregation: a great fraction of passive galaxies is found at the largest values of projected density, while other spectral types are instead more common in less dense environment;
-
7.
there is a fraction of the e(c) population showing substantial differences with respect to the other emission-line classes: they display properties more similar to the passive type. In this particular case, we argue that part of it might be k type galaxies where the [Oii] line is not related to star formation but has instead a different origin;
-
8.
we confirm the lack of local high luminosity post-starbursts, strengthening the idea that these galaxies have undergone a significant evolution. The luminosity function is also significantly different with respect to the one at high redshift;
-
9.
local post-starbursts display the tendency to prefer earlier morphological types, as compared to the high redshift ones (i.e., no irregular k+a and a+k are found in the wings sample);
-
10.
the star-formation quenching efficiency is similar between high and low redshift, as long as clusters with velocity dispersions less than ~1000 km s-1 are considered with some differences possibly due to downsizing effects. This strongly suggests RAM-pressure stripping as the main mechanism for halting star formation in infalling galaxies across the z ~ 0 −1 redshift range.
Finally, we briefly describe the EW catalogue (see an example of the typical quantities and format in Appendix A), which is made publicly available through both the CDS an the Virtual Observatory. More details on this catalogue and on wings in general and its products can be found in Moretti et al. (2014).
Online material
Appendix A: Equivalent widths catalogue
The catalogue presented in this paper contains 14 EW values that are among the most prominent emission and absorption lines in the optical range (see Table 1), as measured in the rest-frame observed spectra. Errorbars on the measures, taking into account both the spectral S/N and the measurement method, are also provided with the details of their calculation being explained in Sect. 3.1. These values, inparticular those of the [Oii] and Hδ, are used to derive a rough spectral classification, which is included in the catalogue in the form of a numerical flag. Emission-line galaxies are labelled with 1, 2, and 3 for e(a), e(b) and e(c), respectively, while the “non-starforming” types are flagged with 4, 5, and 6 (k, k+a, and a+k respectively). Where no classification was possible, we flag the spectrum with a 0. In Fig. A.1, we report the number of spectra in which each line was successfully measured, for the entire sample and distinguish those that were measured in emission (red histograms).
Non-detections and noise-dominated lines are flagged with a 99.00, while the value 999.00 is used to identify those lines that lie outside the observed range. We also measure two classical, widely-used, indices: D(4000) (Bruzual A. 1983) and Dn(4000) (Balogh et al. 1999). As already mentioned, whenever a [Oii] and [Oiii] EW has a value, which is higher than −2 Å, we treat this as a non-reliable detection, which is flagged by a 0.000 value. In the catalogue we are also reporting the values of the magnitude and radial completeness (C(m) and C(r)). Table A.1 shows an example of how the catalogue looks like. Column 1 reports the wings name, based on the galaxy’s coordinate; Cols. 2 to 15 report the equivalent width values expressed in Å; Cols. 16 to 29 report the uncertainties, following the same order as the EW values; Cols. 30 and 31 contain the spectral indexes D4000 and Dn4000, respectively; in Col. 32, we give the spectral class flag and in Cols. 33 and 34, we provide the photometric and geometrical completeness, respectively.
Since the measurements of lines shortwards of ~4300 Å is not reliable in most of them for [Oii], Hδ, and the two calcium lines (Cak and Cah+Hϵ), for the spectra of the north sample we
give the values that were manually measured, while values for the other lines that are longwards of 4300 Å are taken from the automatic measurement.
The presence of sky lines, which are not always properly subtracted from observed spectra, might also influence both the detection and the lines’ measurement. If we consider the most prominent of such lines, or those at 5577, 5894, 6300, and 7246 Å, we find that only the Mg and the Na lines might fall close to these sky features, as far as wings cluster members are concerned especially in the higher redshift clusters. None of the other lines are instead affected, but we strongly suggest a visual check before using the values for these two lines. Similarly, a visual check should be performed in the spectra of higher redshift, foreground galaxies in our samples. For example, spectra of galaxies at z ~ 0.108, have both Hα and the [Oiii] lines critically close to such sky lines.
 |
Fig. A.1 Statistics on the line measurement. The histograms show the number of spectra for which a given line was properly measured. Red, dashed-line histograms refer to lines in emission (EW < 0). |
Example of the catalogue as it is made publicly available.
Appendix B: Notes on the completeness
The parent catalogue from which spectroscopic targets were selected has been generated by adopting the following selection criteria:
-
1.
Vtot < 20
-
2.
Vfib < 21.5
-
3.
(B − V)5 kpc ≲ 1.4
where Vfib is the V-band magnitude in an aperture matching that of the spectroscopic fiber, Vtot is the total V magnitude, and (B − V)5 kpc is the colour computed from a 5 kpc aperture.
The exact cut in the colour–magnitude diagram varied slightly from cluster to cluster due to the small differences in cluster redshift and to minimise the level of contamination from the background. In a few cases, the cut has purposely included with a secondary red sequence, such as for Abell 151, to be able to study also background clusters. To optimize the observational setup in a few cases, galaxies at fainter magnitudes or larger colours have been observed. These loose selection limits were applied to avoid any bias in the observed galaxy type, as is the case of a selection based on the colour-magnitude relation only (which selects only red, early type galaxies).
We computed magnitude and geometrical completeness from which we define a specific weight for each galaxy in the catalogue defined as  (B.1)where C(m)i and C(r)i are the magnitude and geometrical completeness in the opportune radial and V-band magnitude bin.
(B.1)where C(m)i and C(r)i are the magnitude and geometrical completeness in the opportune radial and V-band magnitude bin.
The completeness as a function of magnitude is defined as 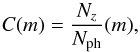 (B.2)where Nz is the number of galaxies with measured redshifts and Nph is the number of galaxies in the parent photometric catalogue. Completeness is usually a decreasing function of the magnitude because priority was given to brighter objects in observations.
(B.2)where Nz is the number of galaxies with measured redshifts and Nph is the number of galaxies in the parent photometric catalogue. Completeness is usually a decreasing function of the magnitude because priority was given to brighter objects in observations.
The success rate, which is the fraction of galaxies with redshift determination with respect to the total number of observed galaxies, is similarly defined as  (B.3)where Nz is defined as in Eq. (B.2) and Ntg is the number of target galaxies we actually observed. Besides that, we also computed the radial completeness for our sample. It is known that fiber collision problems can lead to a variable density of observed sources at different radii, given that it is more difficult to allocate many fibers near the crowded cluster centre. On the other hand, central parts of the clusters are usually privileged due
(B.3)where Nz is defined as in Eq. (B.2) and Ntg is the number of target galaxies we actually observed. Besides that, we also computed the radial completeness for our sample. It is known that fiber collision problems can lead to a variable density of observed sources at different radii, given that it is more difficult to allocate many fibers near the crowded cluster centre. On the other hand, central parts of the clusters are usually privileged due
to the higher density of galaxies, and observers tend to allocate as many fibers as possible there. Having several fibre configurations for a given cluster, as in our case, helps mitigating the fibre collision problem even further. The net result in our case is pretty flat behaviour of the defined radial completeness function defined, which is analogous to the magnitude completeness: 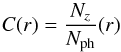 (B.4)with Nz and Nph defined as in Eq. (B.2) but for radial bins.
(B.4)with Nz and Nph defined as in Eq. (B.2) but for radial bins.
Appendix C: Rejection of spectra
Due to the absence of calibration lines in the UV, several spectra taken at WHT (the “north sample”) suffer from a wavelength calibration issue affecting the wavelength range shortwards of ~4300 Å. Hence, it is often not possible to automatically recognize and properly measure a spectral line in this wavelength range due to a displacement, which can in few extreme cases reach some tens of Å in the case of the [Oii] line (which is the bluest line that we measure). Since this displacement is not only wavelength dependent but it may also vary from spectrum to spectrum, it is not possible to automatically correct for this effect in a straightforward way. It is not always possible to properly measure some of the lines that typically characterize the stellar populations. This makes the automatic spectral fitting, that was the main reason for having a reliable EW measure (Fritz et al. 2007, 2011), meaningless in some cases.
To recover as much information as possible and use as many spectra as we could from the north sample, we proceeded as follows. After running our fitting procedure over the entire north sample, we measured the EW of the four most prominent UV lines, namely [Oii], the two calcium lines (h and k; 3969 and 3934 Å, respectively), and Hδ. This was done manually for each of these four lines and for each spectrum displaying the calibration problem. Due to these issues, care must be taken when judging the quality of a fit by means of the χ2 value only. We recalculate χ2 by only considering spectral features (i.e. lines and continuum emission) longwards of 4300 Å and rejected all the spectra with a 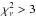 . On the remaining spectra, we checked that the values, which we have manually measured were compatible with those of the best fit model. When this was the case, the fit with the derived physical quantities (e.g. stellar mass, star formation rate, etc.) was considered to be acceptable, and the spectrum considered in the analysis.
. On the remaining spectra, we checked that the values, which we have manually measured were compatible with those of the best fit model. When this was the case, the fit with the derived physical quantities (e.g. stellar mass, star formation rate, etc.) was considered to be acceptable, and the spectrum considered in the analysis.
After the selection procedure described above, some of the clusters from the north sample were very poorly sampled. They only had a few galaxies that were spectroscopically confirmed members (Cava et al. 2009). We decided not to include those clusters with a number of confirmed members less than 20 in all of the statistical studies that will follow in the paper. This leaves us with only seven clusters of the north sample, which still contains more than 50% of the usable spectra from this catalogue.
You can refer to the wings website for a description of the project and updated details on the survey and its products: http://web.oapd.inaf.it/wings/new/index.html
Acknowledgments
This work made use of Virtual Observatory tools, namely TOPCAT (http://www.star.bris.ac.uk/~mbt/topcat/). Facilities: Anglo-Australian Telescope (3.9 m-AAT); William Herschel Telescope (4.2 m- WHT). Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. We are grateful to the anonymous referee, whose comments and remarks helped us to improve the readability of this work.
References
- Abadi, M. G., Moore, B., & Bower, R. G. 1999, MNRAS, 308, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2008, MNRAS, 386, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Beisbart, C., & Kerscher, M. 2000, ApJ, 545, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., Shioya, Y., & Couch, W. J. 2001, ApJ, 547, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, S., Rubele, S., Franceschini, A., et al. 2006, A&A, 451, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Katgert, P., Mazure, A., et al. 1997, A&A, 321, 84 [NASA ADS] [Google Scholar]
- Biviano, A., Katgert, P., Thomas, T., & Adami, C. 2002, A&A, 387, 8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, A. G. 1983, ApJ, 273, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., & Tsai, J. C. 1995, ApJ, 452, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A., Jr. 1978a, ApJ, 219, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A. , Jr 1978b, ApJ, 226, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A., Jr. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Byrd, G., & Valtonen, M. 1990, ApJ, 350, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, N. 1984, PASP, 96, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, N., & Rose, J. A. 1997, AJ, 113, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Cava, A., Bettoni, D., Poggianti, B. M., et al. 2009, A&A, 495, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Couch, W. J., & Sharples, R. M. 1987, MNRAS, 229, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, W. J., Ellis, R. S., Sharples, R. M., & Smail, I. 1994, ApJ, 430, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, W. J., Balogh, M. L., Bower, R. G., et al. 2001, ApJ, 549, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Giovanelli, R., Haynes, M. P., Hardy, E., & Campusano, L. E. 2001, AJ, 121, 1886 [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 2003, ApJ, 598, 20 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Colless, M., Peacock, J. A., et al. 2004, MNRAS, 351, 125 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., Holden, B. P., & Rosati, P. 2007, AJ, 133, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Gunn, J. E. 1983, ApJ, 270, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Gunn, J. E. 1992, ApJS, 78, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Shectman, S. A. 1988, AJ, 95, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, A., Jr., Couch, W. J., et al. 1997, ApJ, 490, 57 [Google Scholar]
- Dressler, A., Smail, I., Poggianti, B. M., et al. 1999, ApJS, 122, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, A., Jr., Poggianti, B. M., et al. 2013, ApJ, 770, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Fasano, G., Poggianti, B. M., Couch, W. J., et al. 2000, ApJ, 542, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Fasano, G., Marmo, C., Varela, J., et al. 2006, A&A, 445, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fasano, G., Vanzella, E., Dressler, A., et al. 2012, MNRAS, 420, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Poggianti, B. M., Bettoni, D., et al. 2007, A&A, 470, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fritz, J., Poggianti, B. M., Cava, A., et al. 2011, A&A, 526, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujita, Y. 1998, ApJ, 509, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., Oemler, A., Dressler, A., et al. 2013, ApJ, 770, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Nichol, R. C., Okamura, S., et al. 2003, PASJ, 55, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Yagi, M., Tanaka, M., & Okamura, S. 2004, MNRAS, 348, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Smith, G. P., Egami, E., et al. 2009, ApJ, 704, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Hausman, M. A., & Ostriker, J. P. 1978, ApJ, 224, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, W., & Lee, S.-G. 2012, MNRAS, 425, 3162 [NASA ADS] [CrossRef] [Google Scholar]
- Lavery, R. J., Pierce, M. J., & McClure, R. D. 1992, AJ, 104, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- Leonardi, A. J., & Rose, J. A. 1996, AJ, 111, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Longhetti, M., & Saracco, P. 2009, MNRAS, 394, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C.-J., Ebeling, H., Donovan, D., & Barrett, E. 2008, ApJ, 684, 160 [Google Scholar]
- Margoniner, V. E., & de Carvalho, R. R. 2000, AJ, 119, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Poggianti, B. M., Fasano, G., et al. 2014, A&A, 564, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newberry, M. V., Boroson, T. A., & Kirshner, R. P. 1990, ApJ, 350, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Jenkins, C. R., Dopita, M. A., Sadler, E. M., & Binette, L. 1986, AJ, 91, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Smail, I., Dressler, A., et al. 1999, ApJ, 518, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Bridges, T. J., Komiyama, Y., et al. 2004, ApJ, 601, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Fasano, G., Bettoni, D., et al. 2009a, ApJ, 697, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Aragón-Salamanca, A., Zaritsky, D., et al. 2009b, ApJ, 693, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Lubin, L. M., & Oke, J. B. 2001, AJ, 122, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., Golev, V., & Maubon, G. 1999, A&A, 346, L25 [NASA ADS] [Google Scholar]
- Quintero, A. D., Hogg, D. W., Blanton, M. R., et al. 2004, ApJ, 602, 190 [Google Scholar]
- Riffel, R., & Borges Vale, T. 2011, Ap&SS, 187 [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sánchez-Blázquez, P., Jablonka, P., Noll, S., et al. 2009, A&A, 499, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, R., van de Ven, G., Jahnke, K., et al. 2013, A&A, 558, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smail, I., Ellis, R. S., Dressler, A., et al. 1997, ApJ, 479, 70 [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Strazzullo, V., Rosati, P., Pannella, M., et al. 2010, A&A, 524, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, T., & Katgert, P. 2006, A&A, 446, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tonnesen, S., Bryan, G. L., & van Gorkom, J. H. 2007, ApJ, 671, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, K.-V. H., Franx, M., Illingworth, G., Kelson, D. D., & van Dokkum, P. 2003, ApJ, 599, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Ellis, R. S., Kneib, J.-P., et al. 2003, ApJ, 591, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Valentinuzzi, T., Woods, D., Fasano, G., et al. 2009, A&A, 501, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dokkum, P. G., & Franx, M. 2001, ApJ, 553, 90 [Google Scholar]
- Varela, J., D’Onofrio, M., Marmo, C., et al. 2009, A&A, 497, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vulcani, B., Poggianti, B. M., Fasano, G., et al. 2012, MNRAS, 420, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Clowe, D. I., Simard, L., et al. 2005, A&A, 444, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, R., Newman, J. A., Faber, S. M., et al. 2006, ApJ, 648, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., Zaritsky, D., Lin, H., et al. 1996, ApJ, 466, 104 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
List of lines, whose equivalent width was measured, is reported here with their respective theoretical central λ.
Summary of the criteria adopted to classify the spectra based on spectral lines criteria.
Summary of all the morphological types, identified as cluster members in our magnitude limited sample (corrections for incompleteness are here not taken into account).
All Figures
 |
Fig. 1 How areas used to compute an equivalent width are defined. In this example we plot an Hβ profile which includes both an absorption and an emission component. The green-dashed line is meant to approximate the spectral continuum while its length, Δλ, is used also to define the wavelength range over which the line itself is measured. |
| In the text | |
 |
Fig. 2 Illustration of how our EW measurement method works on an observed Hβ line: in the upper panel we show how the EW is iteratively measured at increasingly larger Δλ (red, straight line) which are also used to define the continuum level. The dashed regions correspond to the area measured for the EW determination. The analysis of the EW trend curve, plotted on the lower panel, provides the correct observed value, shown by the red cross. In this case, in which both emission and absorption components are present, it corresponds to the second zero of the first derivative of the trend curve itself. |
| In the text | |
 |
Fig. 3 Distributions of absolute V magnitude for galaxies in the north and south samples (different colours and lines). Absolute magnitudes are computed as the integral convolution between the rest-frame model spectrum and the V-band transmission curve. All distributions are normalised to their peak number, and both magnitude and geometrical completenesses are taken into account. |
| In the text | |
 |
Fig. 4 Spectral types distribution of wings spectroscopically confirmed members. South and north samples are shown separately with different colours and lines for comparison. A cut at absolute magnitude MV = −18 has been applied. |
| In the text | |
 |
Fig. 5 Left panel: shaded histograms represent the number of galaxies in the six spectral types as a function of the absolute V magnitude; the green-dashed line marks the magnitude limit of the subsample used in the analysis (for this plot only, we consider no cut in magnitude). Galaxies brighter than MV = −22.5 are included in the brightest bin. Right panel: occurrence of morphological types as a function of the spectral class. The percentages refer to the number of objects with a given morphology with respect to each spectroscopic class. For both plots, data have been weighted by both magnitude and geometric completeness. For the right-hand plot only galaxies with MV < −18 have been considered. |
| In the text | |
 |
Fig. 6 Stellar mass distribution for the six spectral types in the magnitude limited sample and for objects within R500. |
| In the text | |
 |
Fig. 7 Fraction of emission-line galaxies (i.e., belonging to any of the first three spectral classes defined in Table 3) as a function of the cluster velocity dispersion (left) and total X-ray luminosity (right). Only galaxies within R500 are taken into account (see text for details). |
| In the text | |
 |
Fig. 8 Percentage of the passive post-starburst and emission-line types as a function of the (projected) local density. |
| In the text | |
 |
Fig. 9 Fraction of post-starburst galaxies as a function of the two cluster mass tracers, velocity dispersion (left) and LX (right). k+a and a+k are considered as one single class. As done for Fig. 7, only galaxies within R500 are taken into account. Points with different colours refer to different magnitude limits and are used later on for a comparison with high redshifts samples. |
| In the text | |
 |
Fig. 10 Left-hand panel: cumulative radial distribution of the three spectral types as defined in the text. Right-hand: average velocity dispersion in bins of radial distance for the three main spectral classes. Void stars represent the high-z data points from Dressler et al. (1999). In all cases, the distances are calculated from the cluster’s BCG and are expressed in terms of R200. |
| In the text | |
 |
Fig. 11 Comparison of the high and low redshift V-band luminosity distribution for the six spectral types. High-z data have been corrected for passive evolution to match the local clusters data (see text for details). The vertical dashed line marks the MV = −19.5 limit. |
| In the text | |
 |
Fig. A.1 Statistics on the line measurement. The histograms show the number of spectra for which a given line was properly measured. Red, dashed-line histograms refer to lines in emission (EW < 0). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


