| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322517 | |
| Published online | 18 June 2014 | |
HALOGAS observations of NGC 4414: fountains, interaction, and ram pressure
1 Netherlands Institute for Radio Astronomy (ASTRON), Postbus 2, 7990 AA Dwingeloo, The Netherlands
e-mail: blok@astron.nl
2 Astrophysics, Cosmology and Gravity Centre, Department of Astronomy, University of Cape Town, Private Bag X3, 7701 Rondebosch, South Africa
3 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV, Groningen, The Netherlands
4 Department of Astronomy, New Mexico State University, PO Box 30001, MSC 4500, Las Cruces, NM 88003, USA
5 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281, 9000 Gent, Belgium
6 Department of Physics and Astrophysics, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
7 Astronomisches Institut Ruhr-Universität Bochum, Universitätstrasse 150, 44801 Bochum, Germany
8 CSIRO Astronomy and Space Science, Australia Telescope National Facility, PO Box 76, Epping, NSW 1710, Australia
9 Department of Physics and Astronomy, University of New Mexico, 1919 Lomas Blvd NE, Albuquerque, NM 87131-1156, USA
Received: 21 August 2013
Accepted: 29 April 2014
We present deep H i imaging of the nearby spiral galaxy NGC 4414, taken as part of the Westerbork HALOGAS (Hydrogen Accretion in LOcal GAlaxieS) survey. The observations show that NGC 4414 can be characterized by a regularly rotating inner H i disk, and a more disturbed outer disk. Modeling of the kinematics shows that the outer disk is best described by a U-shaped warp. Deep optical imaging also reveals the presence of a low surface brightness stellar shell, indicating a minor interaction with a dwarf galaxy at some stage in the past. Modeling of the inner disk suggests that about 4 percent of the inner H i is in the form of extra-planar gas. Because of the disturbed nature of the outer disk, this number is difficult to constrain for the galaxy as a whole. These new, deep observations of NGC 4414 presented here show that even apparently undisturbed galaxies are interacting with their environment.
Key words: galaxies: halos / galaxies: ISM / galaxies: kinematics and dynamics / galaxies: individual: NGC 4414 / galaxies: structure
© ESO, 2014
1. Introduction
The last decade has seen a large increase in our knowledge of the resolved neutral hydrogen distribution in nearby disk galaxies. This is largely due to the results from surveys such as THINGS (Walter et al. 2008), LVHIS (Koribalski 2010), LITTLE THINGS (Hunter et al. 2012), VLA-ANGST (Ott et al. 2012), FIGGS (Begum et al. 2008), and SHIELD (Cannon et al. 2011). These surveys have all yielded detailed information on the morphology and dynamics of well over a hundred nearby galaxies. An important science goal of many of these surveys is to explore the physical processes that link gas and star formation within the galaxy disks. To probe the relevant size scales (down to those of giant molecular clouds), these surveys usually focus on maximizing spatial resolution.
What happens to the gas during other phases of the gas-star formation cycle is a question these surveys have so far only addressed to a much smaller extent. How much gas is expelled from the disk due to star formation (“galactic fountain”; Shapiro & Field 1976); how much gas stays in the halo and how much eventually falls back on the disk? Is all the cold gas in the halo due to star formation processes? Can we also find gas accreted from intergalactic space (the “cosmic web”)? An overview of these issues is given in Sancisi et al. (2008). However, the opposite processes are also at work. Just as gas can be accreted, it can also be lost again, usually through interactions or stripping due to the environment.
As noted before, many of the current large H i surveys of nearby galaxies are optimized for resolution, and may not always reach the column density sensitivity needed to probe the gas accretion and gas loss at significant levels. The Westerbork HALOGAS (Hydrogen Accretion in LOcal GAlaxieS) survey (Heald et al. 2011) was designed to overcome this problem. It used the Westerbork Synthesis Radio Telescope (WSRT) to observe a sample of ~20 disk galaxies in the local Universe (out to 11 Mpc, as based on the distances given in Tully 1988) for 10 times longer than “typical” H i observations and has produced some of the most sensitive interferometric H i data available. The survey is sensitive to angular scales which are most useful for studying faint, diffuse gas in and around nearby galaxies, and has the primary goal of revealing the global characteristics of low column density gas in and around spiral galaxies in the local universe.
As described in Heald et al. (2011), the HALOGAS sample is selected on the basis of a number of objective criteria, mainly Hubble type, size, distance, and inclination. This leads to a sample containing a great variety of global properties, and, in particular, H i morphologies.
1.1. NGC 4414
Here we present an analysis of NGC 4414. Global properties of NGC 4414 as taken from Heald et al. (2011, 2012) are listed in Table 1. We refer to these papers for more information. The distance of NGC 4414 as determined by the HST Hubble Key Project is 17.8 Mpc (Freedman et al. 2001), and this is also the distance adopted here. This distance is therefore significantly different from the 9.7 Mpc given in Tully (1988) (cf. Table 1 in Heald et al. 2011). The optical appearance of NGC 4414 is characterized by a flocculent spiral structure. It has the highest star formation rate (4.2 M⊙ yr-1) of the galaxies in the HALOGAS sample (Heald et al. 2012; Moustakas & Kennicutt 2006; Sanders et al. 2003). This rate is, however, not extraordinarily high for a spiral galaxy, and NGC 4414 certainly cannot be said to be undergoing a starburst. The galaxy has a prominent, smooth, and regularly rotating molecular gas disk which coincides with the main star forming body (Sakamoto 1996; Braine et al. 1997). Previous H i observations (Braine et al. 1993; Thornley & Mundy 1997) showed a gas disk extending far beyond the optical disk. The inner part of this neutral gas disk was found to be in regular rotation, but the outer parts showed signs of asymmetries. The emphasis in these previous studies was on the link between gas, spiral structure, and star formation. Two other studies concentrated on the mass-to-light ratio of the stellar disk (Vallejo et al. 2002) and the dark matter distribution (Vallejo et al. 2003). These show that the inner disk of NGC 4414 is dominated by the stellar population, with only a small dark matter contribution.
Properties of NGC 4414.
The consensus in these papers is that NGC 4414 has no close companions, has not recently suffered a major interaction, but also that there is some evidence of weak interactions having taken place. The observed asymmetry of the outer H i distribution suggests this, but it is also supported by asymmetries in the magnetic field (Soida et al. 2002).
The galaxy NGC 4414 is part of the Coma I group. Other HALOGAS targets, such as NGC 4062, NGC 4274, NGC 4448, NGC 4565, and NGC 4559 are also found in or near the Coma I group. Together, these observations can be used to study the effects on the outer parts of their H i disks of environment and location within the group, however, in this paper the focus is on NGC 4414.
The paper is organized as follows. In Sect. 2 we describe the H i and optical data. Section 3 contains the kinematical modeling of the H i disk while in Sect. 4 we present an interpretation of the models. In Sect. 5 we give a brief summary.
2. Data
2.1. H II data
As described in Heald et al. (2011), the data were taken using the WSRT. We also refer to that paper for a description of the observational set-up and data reduction. For each galaxy in the HALOGAS sample, two standard data cubes were created. One is created using a robust parameter of 0 for intermediate resolution and sensitivity. To maximize sensitivity to faint extended emission a second data cube is produced using a Gaussian u,v taper corresponding to 30′′ in the image plane. For the WSRT array, this taper gives the best compromise between resolution and column density sensitivity (cf. description in Heald et al. 2011). We will use both data cubes in this paper, but the analysis of the dynamics will lean heavily on the 30′′ tapered cube.
The synthesized beam size of the tapered cube is 39.0′′ × 33.5′′, with a channel spacing of 4.12 km s-1. HALOGAS cubes are Hanning-smoothed, and the channel spacing equals the velocity resolution. The 1σ noise per channel in the tapered cube is 0.23 mJy beam-1, resulting in a 1σ, 1-channel column density sensitivity of 0.8 × 1018 cm-2 or, more typical for an H i profile, a sensitivity of 1.0 × 1019 cm-2 for a 3σ, 16 km s-1 signal.
The robust-weighted cube has a beam size of 25.9′′ × 13.7′′. Its noise per channel is 0.19 mJy beam-1, resulting in a 1σ, 1-channel column density sensitivity of 2.4 × 1018 cm-2 or 2.2 × 1019 cm-2 for a 3σ, 16 km s-1 H i profile.
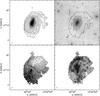 |
Fig. 1 Overview of NGC 4414 derived from the 30′′ tapered data cube. Top-left: integrated H i intensity map (zeroth moment). The contour levels shown are (2,5,10) × 1019 cm-2 (black) and (2,5,10) × 1020 cm-2 (white). Top-right: integrated H i intensity overplotted on a deep KPNO B-band image. The optical image is shown using a logarithmic intensity scale. Contours shown are (2,20) × 1019 cm-2. The two short vertical lines indicate galaxy SDSS J122646.27+311904.8, as discussed in Sect. 4.2. Bottom-left: intensity-weighted mean first-moment velocity field. The thick black countour shows the systemic velocity of 711.5 km s-1. Black contours then decrease in steps of 25 km s-1, white contours increase in steps of 25 km s-1. The dashed white ellipse indicates the division between inner and outer disk as defined in Sect. 3. Bottom-right: second-moment velocity dispersion map. Black contours show values of (5, 10, 20) km s-1 (light-gray to dark-gray background). White contours show (50, 100) km s-1 (dark-gray to black background). The white ellipse indicates the division between inner and outer disk. |
Moment maps were created by first convolving the tapered cube to 60′′, and clipping the resulting smoothed cube at the 2.5σ level. The clipped, smoothed cube was used as a mask for the original resolution cube. The moment maps were created from the masked, original cube, with the added constraint that at each position emission had to be present in a minimum of three consecutive channels in the smoothed cube. Lastly, and only for cosmetic reasons, a few remaining spurious noise peaks were removed. The same mask and procedure was used for the robust cube.
In order to keep uniform noise properties we do not make a correction for the primary beam. The only exception is when measuring total fluxes. However, we found the corrections there to be ~1% and therefore negligible compared to other uncertainties.
 |
Fig. 2 Left: robust-weighted integrated column density map. Contour levels are (1,2,5) × 1020 cm-2 (black) and 1 × 1021 cm-2 (white). The gray box shows the area shown in the right-panel. Right: integrated H i column density based on the robust weighted cube overplotted on a deep KPNO Hα image. Contour levels are the same as in the left panel. The main Hα distribution is encompassed by the 1 × 1021 cm-2 contour, with low-level Hα primarily found within the 5 × 1020 cm-2 contour. Virtually no Hα is found outside these countours. The bright source in the top-left is a residual continuum artifact. |
While the noise in a channel, σchan, and therefore the sensitivity in a channel, is well-defined, the sensitivity in an integrated column density map (zeroth moment) depends on σchan as well as on the number of channels N that are contributing to each spatial position in the map. For a Hanning-smoothed cube with independent channels the zeroth moment map noise σmom is defined as 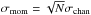 . We created a map of σmom and by comparing this with the integrated H i map itself, determined the signal-to-noise ratio (S/N) in the integrated H i map as a function of position. The average integrated intensity value of all pixels with 4.5 <S/N< 5.5 is 0.015 Jy beam-1 km s-1 for the tapered cube and 0.016 Jy beam-1 km s-1 for the robust cube. Because of the clipping used before we do not expect σmom to have a Gaussian distribution. Nevertheless we can use the number derived here as an estimate for the column density sensitivity, leading to S/N ~ 5 column density values of 5.3 × 1019 cm-2 for the tapered cube and 2.1 × 1020 cm-2 for the robust cube (this is an averaged number derived from all pixels with 4.5 <S/N< 5.5, as described above). These numbers differ from the column density sensitivity given earlier. The latter refer to the sensitivity per channel, whereas in a zeroth-moment map multiple channels contribute to one pixel, increasing the noise in the zeroth-moment map at that position. (The noise increases as
. We created a map of σmom and by comparing this with the integrated H i map itself, determined the signal-to-noise ratio (S/N) in the integrated H i map as a function of position. The average integrated intensity value of all pixels with 4.5 <S/N< 5.5 is 0.015 Jy beam-1 km s-1 for the tapered cube and 0.016 Jy beam-1 km s-1 for the robust cube. Because of the clipping used before we do not expect σmom to have a Gaussian distribution. Nevertheless we can use the number derived here as an estimate for the column density sensitivity, leading to S/N ~ 5 column density values of 5.3 × 1019 cm-2 for the tapered cube and 2.1 × 1020 cm-2 for the robust cube (this is an averaged number derived from all pixels with 4.5 <S/N< 5.5, as described above). These numbers differ from the column density sensitivity given earlier. The latter refer to the sensitivity per channel, whereas in a zeroth-moment map multiple channels contribute to one pixel, increasing the noise in the zeroth-moment map at that position. (The noise increases as 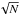 while the signal increases with N; isolating regions with signal thus means an effective
while the signal increases with N; isolating regions with signal thus means an effective 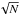 increase in sensitivity in the moment map.)
increase in sensitivity in the moment map.)
The moment maps and velocity field derived from the tapered cube are shown in Fig. 1. We see that the H i distribution of NGC 4414 is lopsided, with the degree of lopsidedness depending on the column density level. At intermediate column densities, the disk extends farther towards the SE. In contrast, at lower column densities the disk column densities drop much faster is towards the SE than to the NW. This NW part of the disk breaks up into what appear to be fragments of arms and clumps. The inner part of the velocity field is clearly dominated by rotation, and symmetrical, despite the disturbed looking H i morphology. The southern part of the disk seems to show regular rotation out to large radii, whereas the northern part looks more disturbed with a large change in kinematical PA. The extreme outer eastern and western edges of the disk also show strong kinks in the velocity contours indicating streaming motions or strong discontinuities in PA or inclination.
The second-moment map (indicative of the velocity dispersion for symmetrical, single Gaussian profiles) shows a significant area with values higher than 20 km s-1. Most of this is, however, is not caused by an intrinsically high velocity dispersion. The central area with high dispersion is due to beamsmearing caused by the steep rotation curve. The curved area with high values to the NE is due to double and asymmetric profiles where a separate H i feature is seen projected onto the main disk (this coincides with the strong kinks in the velocity field contours). Also shown in the figure is an overlay of the H i emission on top of an optical B-band image (described below in Sect. 2.2).
An integrated column density map based on the robust cube is shown in Fig. 2. It is clear that the disk is better resolved but at the cost of lower sensitivity. An overlay of the robust zeroth moment map on top of an Hα image (details below in Sect. 2.2) is shown in the same figure. The high-level star formation is encompassed by the 1 × 1021 cm-2 contour, with lower-level star formation happening within the 5 × 1020 cm-2 contour. No additional massive star formation is detected outside the 2 × 1020 cm-2 contour. The two distinct levels of star formation in the inner and outer disk are consistent with the classification of NGC 4414 as a Type 1 XUV disk (Thilker et al. 2007; Type 1 XUV disks are defined as showing structured UV emission beyond the location of the star formation threshold). In their description of NGC 4414, they mention the XUV clumps “hugging the main disk”, with some of them coinciding with Hα clumps.
Selected channel maps of the 30′′-tapered cube are shown in Fig. 3. Note the sharp twist in position angle between inner and outer disk emission (e.g., at V = 568.9 km s-1). Similar sharp twists remain visible throughout most of the data cube. The inner, higher column density emission does show the signatures of regular rotation.
We also derived a global H i profile using a primary-beam corrected tapered cube. This profile is shown in Fig. 4. The profile is asymmetric with one of the horns more prominent than the other, reflecting the disturbed nature of the outer part of the galaxy. The total flux derived from the profile is 60.4 Jy km s-1, translating into a total H i mass of 4.5 × 109 M⊙. This corresponds well with previous determinations. For example, Braine et al. (1993) find a total flux of 64.9 Jy km s-1 and an H i mass of 4.8 × 109 M⊙ (corrected to our assumed distance). The small difference can almost certainly be attributed to the lower sensitivity of the older observations (1 × 12h instead of 10 × 12h) leading to larger susceptibility to the effects of noise. We measure velocity widths of W20 = 391 km s-1 and W50 = 333 km s-1 (not corrected for channel width).
 |
Fig. 3 Selected channel maps from the 30′′ tapered cube. Only every fourth channel map is shown. Contour levels are (2,5,10,20,50)·σ where σ = 0.23 mJy beam-1 or 0.8 × 1018 cm-2. The beam is indicated in the bottom-left of the top-left panel. The heliocentric velocity in km s-1 is indicated in the top-left of each panel. |
2.2. Optical data
NGC 4414 was observed on March 20, 2012 in B, Hα, and R (for continuum-subtraction) on the Mosaic 1.1 Wide Field Imager instrument on the KPNO 4-m telescope. The weather was clear with moderate wind with typical seeing of ~1.2′′. The Mosaic instrument has eight 1k × 4k CCDs with 15 micron pixels, resulting in a field of view of 36′ on a side and 0.26 arcsec pixel-1. At the distance of NGC 4414 (17.8 Mpc), the Mosaic yields a field of view of 186 kpc on a side with 22.4 pc pixel-1. We used the FillGap dither command to observe, which offsets the telescope with a five-exposure pattern in order to cover the 20-arcsec gaps between CCDs. We observed NGC 4414 for a total of 30 (5 × 6) min in Hα, 90 (15 × 6) min in B, and 10 (5 × 2) min in R. The Hα filter is centered at 6575 Å with a full-width at half maximum (FWHM) of 81 Å, which includes the [NII] emission lines at 6548 Å and 6584 Å. We assume a ratio of [NII]/Hα of 0.4 for Hα flux measurements. Only the B and Hα images are used in this paper.
For the data reduction, we used the MSCRED Mosaic Data Reduction Package within the Image Reduction and Analysis Facility (IRAF). We used CCDPROC for the basic reduction and implemented additional recommended steps including a secondary flat field correction and ghost pupil reflection artifact removal (present in B and Hα, but not R).
We flux-calibrated our images based on observations of spectrophotometric stars and standard star observations over a range of airmasses taken throughout the four night observing run. The B-band image has a zeropoint of 23.33 ± 0.03 mag arcsec-2 and an rms of 0.042 counts/s or 26.78 mag arcsec-2. The final Hα flux-calibrated image has an rms noise of ~3 × 1034 erg s-1 at the distance of NGC 4414. This is deep enough to detect a faint H ii region ionized by a single B0 star.
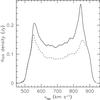 |
Fig. 4 Global H i profile based on the primary-beam corrected 30′′-tapered cube (full line). The dashed line shows the global profile of the inner disk only. |
In addition, NGC 4414 was observed in r′ band in 2010 February 4, at the Isaac Newton Telescope (INT), La Palma, Spain. The observations were conducted as part of the HALOSTARS campaign. The goal of HALOSTARS is to map HALOGAS galaxies with the wide field camera (WFC) of the INT to a sufficient depth to detect faint, extended stellar features that might indicate recent interactions of the target galaxies. Sky flats and bias frames were obtained at the beginning and at the end of the night. A total of 17 exposures of 300 s each were taken to obtain a total of 5100 s on-source integration time under variable weather conditions in presence of the moon. The projected size of NGC 4414 is too large to fit on a single INT WFC chip. We hence used a wide dithering scheme to make a mosaic of the source. To process the raw data, we made use of the wide-field imaging reduction pipeline THELI (Schirmer 2013). After overscan- and bias-correcting the images, the chips were flatfielded using the sky flats in addition to a smoothed averaged night sky calculated from the exposures on NGC 4414 (a “super-flat”). Image errors (hot and cold pixels, cosmics) were automatically masked. Using SCAMP (Bertin 2006), a (relative) photometric calibration was applied, and the images were background-subtracted and co-added, solving for astrometric distortion by making use of the SDSS (DR8) catalog. Also using the SDSS catalog, an absolute calibration was applied. The zeropoint was determined to be 24.67 ± 0.1 mag. The rms noise of 0.027 ADU s-1 implies a 1σ level of 26.2 mag arcsec-1. Both images will be further discussed and presented in Sect. 4.2.
3. Modeling
As noted earlier, in kinematical terms, NGC 4414 can be divided into a symmetrical, regularly rotating inner disk, and a more asymmetrical, somewhat disturbed outer disk. The disturbance of the outer disk can be quantified using a Fourier decomposition of the H i surface density σ as described by Rix & Zaritsky (1995). We use σ(r,φ) = a0(r) + ∑ am(r)cos(mφ − φm(r)), where a0(r) is the mean surface density, φ the azimuthal angle in the plane of the galaxy and am and φm the mth amplitude and phase of the harmonic coefficient. Lopsidedness can be characterized by an m = 1 mode. Here, we calculate the normalized amplitude A1(r) = am(r) /a0(r). Figure 5 shows the variation of A1 with radius. We see a distinct difference between inner and outer disk. The lopsidedness parameter A1 is low (mostly <0.1) in the relatively symmetric and undisturbed inner disk. In the outer disk, it increases rapidly up to 0.5, which is far above the commonly adopted lopsidedness threshold (A1 = 0.1–0.2; see, e.g., Angiras et al. 2006; van Eymeren et al. 2011; Zaritsky et al. 2013).
 |
Fig. 5 Normalized lopsidedness parameter A1 as a function or radius. The different behavior in inner and outer disk (separated by the vertical line at a radius of 240′′) is clear. |
We analyze and model the kinematics of the inner and outer disk separately. Based on the lopsidedness we define the inner disk as the part of the galaxy inside a radius of 240′′. The outer disk consists of the remaining disk outside 240′′. The inner disk contains 3.3 × 109 M⊙ of H i, or 72% of the total H i mass of the system. The global profile of the inner disk is compared with that of the entire disk in Fig. 4. Although not entirely symmetric, it is clear that in the inner disk the difference between approaching and receding sides is smaller than for the entire disk. All modeling described below uses the 30′′ tapered cube. The emphasis in this paper is on the geometry of NGC 4414 and we will not analyse the dark matter content of the system. The outer disk is too asymmetric for such an analysis; for the inner disk we refer to Vallejo et al. (2003).
3.1. The inner disk
3.1.1. Tilted-ring fits
In addition to the moment maps we also created a Hermite velocity field from the 30′′ tapered cube. We fitted third-order Hermite polynomials to the H i velocity profiles, retaining only those profiles where the peak flux was higher than 3σ, the velocity dispersion larger than one channel width, and the velocity of the peak of the profile within the velocity range of the galaxy. The integrated H i map was additionally used as a mask to remove spurious fits outside the galaxy disk. The Hermite velocity field is shown in Fig. 6 alongside the first-moment map. Inspection of the velocity fields shows the different extent of the Hermite field compared to the moment map. This is due to the rejection criteria used for the construction of the Hermite velocity field. The velocity contours are also different, indicating the presence of non-Gaussian profiles in a significant fraction of the disk. This, of course, is the reason we are using the Hermite field: in the presence of asymmetric profiles, it gives a better description of the rotation of the bulk of the gas than an intensity-weighted first-moment map. See de Blok et al. (2008) for an extensive discussion on this.
We first derive a rotation curve in the conventional manner using the Hermite velocity field. We use the GIPSY task ROTCUR for a tilted-ring fit. This task assumes that the gas rotates as a set of concentric rings, each with their own inclination, position angle, and rotation velocity. Parameters of these rings are varied until the model velocity field shows a sufficiently good match with the observed one. Usually the number of free parameters in tilted-ring models is too large for all parameters to be determined simultaneously. In practice, sets of parameters are progressively fixed, and models with an increasingly smaller number of free parameters are used to iterate to the optimum fit. See de Blok et al. (2008) and Gentile et al. (2013) for an extensive description of this procedure.
 |
Fig. 6 Left: hermite velocity field based on the 30′′-tapered cube. The thick black countour shows a systemic velocity of 711.5 km s-1. Black contours then decrease in steps of 25 km s-1, white contours increase in steps of 25 km s-1. The white dashed ellipse with a major axis radius of 240′′ delimits the inner and outer disk. Right: intensity-weighted first-moment map. Contours as in left panel. |
We first run ROTCUR with all parameters free (position of center X,Y, systemic velocity Vsys, position angle PA, inclination i, and rotation velocity Vrot). At this stage we assume the rotation is purely circular, with no radial motions. We choose rings with a width of 30′′ with the largest ring having a radius of 500′′. The resulting values of the tilted ring parameters as a function of radius are shown in Fig. 7 (top three rows). It is immediately obvious from the Figure that most parameters are well-behaved up until a radius between ~250′′ and ~300′′, before starting to show strong trends or large scatter at larger radii. The position of the center is most restrictive in that regard, both the X and Y coordinates start to deviate from a constant value around R ~ 250′′. NGC 4414 does not show a compact central continuum source that would further constrain the position of the center.
The rest of this sub-section deals exclusively with the inner disk. Based on the first model, we determine the mean X and Y position of the center of the inner disk. We find a position (X,Y) of the dynamical center corresponding to (α,δ)(2000.0) = (12h26m27.07s,31°13′23.3′′). The scatter in these parameters is 0.98′′ and 2.76′′ in X and Y, respectively. The position of the dynamical center of the inner disk is therefore unambiguous and well-determined. This is illustrated in the top panels of Fig. 7. This position corresponds closely to the central position of the bulge as determined from archival HST WFPC-2 imaging, namely (α,δ)(2000.0) = (12h26m27.19s,31°13′22.9′′), a difference of only 0.12s or 1.5′′ in right ascension, and 0.4′′ in declination.
 |
Fig. 7 Summary of NGC 4414 models. In all panels the vertical dotted line delimits the inner and outer disk. Top three rows, inner disk: open circles indicate the tilted ring parameters derived from a ROTCUR fit with all fit parameters free as described in Sect. 3.1.1. The thick, full lines indicate the final model chosen for the inner disk. In the third row, right-hand panel, the filled circles indicate the resulting final ROTCUR model for the rotation curve of the inner disk. The long-dashed and dotted curves indicate the receding and approaching side rotation curves of the inner disk, respectively. Top three rows, outer disk: the dashed thick lines in the outer disk part of the plots indicates the values chosen for the final TiRiFiC model. In the left-hand panel of the third row the thick long-dashed line indicates the PA distribution for the approaching side, the short-dashed thick line that of the receding side. The thin long- and short-dashed lines show the PA values of the two sides when a ROTCUR fit is made to the velocity field with only PA and Vrot as free parameters. Bottom row: the left-hand panel shows the H i radial surface density distribution. Open squares indicate the approaching side, filled squares the receding side. The right-hand panel in the bottom row shows the approaching and receding sides rotation curves as open and filled squares, respectively. The horizontal line in the outer disk indicates the flat rotation curve assumed in the TiRiFiC modeling. |
Fixing the position of the dynamical center and an additional ROTCUR run gives a value for the systemic velocity Vsys = 711.5 ± 4.6 km s-1 (second row, left panel in Fig. 7). Fixing Vsys in turn, we find a constant inclination of i = 52.3° ± 1.5° (excluding the innermost points; second row, right panel in Fig. 7). We checked for differences between values for the approaching and receding side, but find almost identical results: i = 52.7 ± 1.3 for the receding side, and i = 52.4 ± 2.5 for the approaching side. So far, the inner disk of NGC 4414 thus seems to be a very well-behaved, regularly rotating disk without any major asymmetries.
The values for PA show some radial variation: the innermost ring gives PA ≃ 155°, which then increases to ~161° at R ~ 125′′, and decreases again to ~155° at R = 240′′ (third row, left panel in Fig. 7). In light of the large apparent differences in the velocity field of the outer disk, we explore whether the trend in PA is the result of differences between the approaching and receding sides of the inner disk. We made ROTCUR models of the approaching and receding sides separately, using the parameters given above, and with PA and Vrot as free parameters. The radial variation of PA for both sides is remarkably similar in the inner disk: we find almost identical trends, with a mean absolute difference between the PA values of only ~0.6°, with the largest difference being 1.4° for the innermost ring (also shown in the third row, left panel in Fig. 7).
We describe the PA behavior in the inner disk with a simple three-line-piece model, and with all parameters except Vrot fixed, we derive the final tilted-ring rotation curve of the inner disk. This is shown in the right-hand panel in the third row in Fig. 7. There is a the striking resemblance with the curve derived with all parameters free. The only significant difference is in the innermost point, where the unconstrained inclination for the all-free curve resulted in a higher rotation velocity. The outer rotation curve remains flat. We will return to this when discussing the outer disk.
Using the final rotation curve we build a model velocity field, and compare this with the observed one in Fig. 8. The overlay on the model velocity field on the Hermite velocity field shows good agreement. Small local deviations exist, but the global properties of the velocity field of the inner disk are captured well. We also show the residual velocity field (derived by subtracting the model from the observations), and find no large-scale systematic deviations there. The average value of the residual velocity field is −0.4 km s-1 with an rms spread of 6.2 km s-1. The median of the absolute value of the residuals is 4.4 km s-1 or just over one channel spacing.
 |
Fig. 8 Left panel: the Hermite velocity field (grayscale with black contours) with the best-fitting model velocity field for the inner disk overlaid. Contours are as in Fig. 6 with a contour spacing of 25 km s-1. Right panel: residual velocity field derived by subtracting the model from the observations. The thick black contour shows the 0 km s-1 level. The thin black contour + 10 km s-1, the thin white contour −10 km s-1. The maximum and minimum values found are + 16 and −16 km s-1, respectively. |
The rotation curves of the approaching and receding sides separately are also shown in Fig. 7 (third row, right-hand panel). They show the same global behavior, namely the sharp rise in the center followed by the gentle decline out to R ~ 240′′. The mean difference between both curves (defined as approaching minus receding) is + 0.1 ± 13.4 km s-1 measured over the inner disk. The mean absolute difference is 10.5 ± 7.3 km s-1. The lack of global residual patterns in Fig. 8, and the good agreement of the model velocity field with the data, suggests that the differences are mainly caused by local velocity deviations, and not by global asymmetries.
 |
Fig. 9 Overlay of the best TiRiFiC model of the inner disk on the major axis pV diagram. The data is shown in gray-scale and light-gray contours. The model in black contours. For both, the lowest contour level shown is 1.5σ. Subsequent contour levels each increase by a factor 2.5. For the data, the dashed contours also show the −1.5σ level. The vertical dashed lines delimit the inner disk. |
3.1.2. TiRiFiC fit
The inner disk of NGC 4414 is well-behaved without major asymmetries and disturbances, and, as shown, can be very well described using a tilted-ring model. We now use this tilted ring model as input for more sophisticated modeling using the Tilted Ring Fitting Code (TiRiFiC; Józsa et al. 2007). TiRiFiC distributes cloud particles through a user-created three-dimensional (right ascension, declination, velocity) data cube, using user-defined geometric and kinematic parameters as distribution functions. Among the parameters that can be defined are the rotation curve, radially varying inclination and position angles, the surface density profile, the vertical distribution and extent of the gas, and the velocity dispersion. By convolving with the beam of the observation, TiRiFiC produces a data cube that can be “observed” and treated like the original observation.
We again limit the modeling to the inner disk and model the approaching and receding sides of the disk separately. We use the tilted ring orientation parameters derived above to derive H i surface density profiles of the approaching and receding sides using the ELLINT task in GIPSY. These profiles are used as additional input for TiRiFiC and are shown in Fig. 7.
We model the galaxy with a single thin disk component. A number of exploratory runs of TiRiFiC confirms the results from the ROTCUR runs: the inclination and position angle values are well-behaved, and for all practical purposes the values of these parameters are equal to the ones derived previously. In subsequent runs we therefore fixed i and PA to the ROTCUR values.
The gas velocity dispersion was determined using TiRiFiC and we find a value of 11 km s-1. This number is not corrected for instrumental velocity resolution (channel spacing), which would bring the number down to 10 km s-1. We assume a vertical sech2 profile and find a vertical scale height of z0 = 0.25 kpc, although this value is uncertain. Scale heights between ~0.1 and ~0.5 kpc give similar results.
The H i surface density profile, which was kept fixed in the fits so far, was then allowed to vary (keeping all other parameters fixed). We tested models where the surface density profile was left completely free, where the profiles were allowed to vary using one single scale factor for the entire profile, and one where corresponding radii from approaching and receding side were allowed to vary in tandem. In the end we found the best solutions for the model with the constant scale factor, with surface densities differing only a few percent from their input values. These are the models presented in the rest of the paper.
The parameters of this best-fitting single disk model are shown in Fig. 7. An overlay of the model on the major axis position-velocity diagram is shown in Fig. 9, while in Fig. 10 we compare selected model channel maps directly with the data.
 |
Fig. 10 Overlay of the best model of the inner disk on selected channel maps. Contour levels for both data and model are (2,5,10,20,50)·σ where σ = 0.23 mJy beam-1 or 0.8 × 1018 cm-2. The dashed ellipse denotes the inner disk. |
The distribution and kinematics of the H i in the inner disk of NGC 4414 are well described by this simple single-disk model. We only see evidence of small amounts of “beard” gas (i.e., gas at velocities lower than the local rotation velocity) that is not captured by this model. Compare for example our observations with those of NGC 3198, presented in (Gentile et al. 2013, their Fig. 4), where the “beard” is much more prominent.
In Fig. 9 one can see that on the receding side the “beard” component is present up to a radius of ~200′′. On the approaching side, we see a small amount of gas associated with the rising part of the rotation curve (“beard”), as well as an additional component between −2.5′ and −4′. We interpret these components as extra-planar gas and determine its mass in several ways.
First, we determine the total flux in the best-fitting model for the inner disk, and compare this with the observed inner disk flux. The model results in an H i mass of 2.9 × 109 M⊙, compared with an observed inner disk H i mass of 3.3 × 109 M⊙. The difference is 4 × 108 M⊙, or 12 per cent of the inner disk mass. A possible disadvantage of this method is that the radially averaged H i surface density has been used as an input for the model, and it is not clear how this affects the comparison with the non-averaged observed surface densities. This value is therefore best regarded as an upper limit.
A second estimate can be derived by noting that in Fig. 9 the extra-planar gas has a predominantly low column density, while the part of the galaxy described by the model mostly has higher column-density values. We can therefore blank all high-column density values in the data cube, and measure the mass of the remaining low-column density gas by blanking in the data cube all pixels in the cylinder describing the inner disk that are brighter than 0.46 mJy beam-1 (the lowest contour of the model plotted, corresponding to a 2σ level in the data). We find an H i mass of 2.1 × 108 M⊙, or 6.5 per cent of the total H i mass of the inner disk. It is possible that this is a slight overestimate, it may still contain emission from faint wings from bright inner disk profiles.
A third way to derive the amount of extra-planar gas is to use the method described in Fraternali et al. (2002) where Gaussian fits are made to velocity profiles in a data cube where in each profile, values less than 30 per cent of the respective peak value have been blanked. These Gaussian fits thus describe the bright cores of the profiles. Subtracting these from the original, non-blanked profiles, results in a data cube containing only the emission from broad, low-level wings, secondary components etc. Using this method on the entire disk, we find that prominent extra-planar gas components are only present in the inner disk. The method does produce some low-level fitting artefacts, so we use several different flux cut-offs to gauge the reliability of the emission. We find the extra-planar gas in the inner disk to be ~2.7 to ~4.0 per cent of the mass of the inner disk, or ~2.0 to ~3.0 per cent of the total disk. These numbers should probably be regarded as a lower limit, as gas which is extra-planar with no corresponding main-disk gas at the same position (such as gas in a warp) will not be accounted for by this method.
Although not the topic of this subsection, this method also allows an estimate of the amount of “extra” gas in the outer disk. We call it “extra”, as it is not clear whether this outer disk gas is strictly speaking “extra-planar” due to the disturbed nature of the outer disk. We find that ~1.0 to ~2.0 per cent of the total H i mass is in the form of “extra” outer disk gas. This gas, in contrast with the inner disk, is distributed at a low level throughout the outer disk, and it is very well possible that this happens at a level below the accuracy allowed by this method.
We explored a fourth method, which uses the Hermite velocity field to shift all H i profiles in velocity so their peaks all align at a common reference velocity. Blanking the velocity channels closest to this reference velocity automatically isolates the high-velocity emission, and would thus indicate the importance of the extra-planar gas. In practice, however, beam smearing broadens the innermost profiles, making the method unusable.
In summary, we find that a single, regularly rotating disk model is a good description of the inner disk of NGC 4414. Depending on the method used we find that 12 (uncertain upper limit) or 6.5 (upper limit) or 2–3 percent (lower limit) of the total H i mass in the inner disk is associated with an extra-planar component. An estimate of around 4 per cent thus seems appropriate. Given the high star-formation rate and location coinciding with the optical disk, it is likely that most, if not all, of the extraplanar gas above the inner disk is associated with star formation processes.
3.2. The outer disk
While the inner disk has a regular morphology and is symmetrical, this is clearly not the case for the outer disk. The H i disk is more extended towards the south and to the northwest. In the northern part of the disk we also find what look like arms or streams. In the eastern part of the disk the column density contours are closer together, suggesting either a sharp edge to the H i distribution, or one that is bending into the line of sight.
The Hermite velocity field shows a similar wealth of structures. In the outer disk the PA values of the approaching and receding sides diverge sharply: the PA of the receding side remains more or less constant at ~155° (but with a large scatter), while that of the approaching side drops sharply to values of ~130° at the outermost radii. This behavior clearly justifies our division in an inner and outer disk. Kinks in the velocity contours towards the edge of the disk indicate either abrupt changes in the geometrical parameters, or the presence of non-circular motions.
Many of these features can be identified in the channel maps as well (Fig. 3). The strong position angle twist is visible between V ~ 550 and ~600 km s-1. The kinks in the velocity contours in the eastern part of the disk show up as low-column density components perpendicular to the main H i structure in the channel maps between V ~ 650 and ~800 km s-1.
The asymmetry in the disk and the presence of localized structures already indicate that it will be more difficult to capture these details in a simple, symmetrical tilted-ring model, than was the case with the inner disk, especially as our goal here is to describe the system without adding a large number of ad hoc local components. We will therefore construct a model that reproduces the large-scale features of the outer disk, but we will not attempt to try and incorporate every small-scale feature in this description. The disturbed nature of the outer disk also means an unambiguous separation between planar and extra-planar gas (even if such a distinction is meaningful for this particular case) will be difficult, if not impossible, to achieve, and we will not attempt to do so here. All modeling is again done with the TiRiFiC program.
 |
Fig. 11 Overlay of the models on selected channel maps. Contour levels for both data and model are (2,10,50)·σ where σ = 0.23 mJy beam-1 or 0.8 × 1018 cm-2. The two dashed ellipses in each panel denotes the outer radii of the inner and outer disk. Details of the models are described in the text. |
As the geometry of the outer disk is much less constrained, we first make a number of assumptions. We assume that the outer disk has a flat rotation curve with a rotation velocity of 184 km s-1, a constant systemic velocity of 711.5 km s-1, and a constant inclination of 52.3°. These last two values are also the values adopted for the inner disk. These assumptions are not unreasonable as Fig. 7 shows. We assume the H i surface density profiles also shown in Fig. 7 (bottom-left panel). We model the approaching and receding sides separately. For the inner disk we retain the model derived in the previous section. We define the outer disk as the part of the galaxy between 240′′<R< 480′′. This covers most of the disk, except for a small number of isolated H i features at larger radii which we do not attempt to capture in the model. The small filling factors of these potential outer rings would make any model be of limited value.
The models presented here were not fitted to the data in a strict sense. The large number of free parameters and asymmetric nature of the disk make this a challenge. Models were therefore mostly adjusted and evaluated by eye, by careful comparisons of overlays on channel maps and position velocity slices along various axes. Here we do not present all models investigated, but only the ones that lead to an acceptable description of NGC 4414.
As a compact way of illustrating features of the different models, we plot selected channel maps where we show the models overlaid on the data. As stated earlier, the actual evaluation of the models was done using a much larger set of overlays and slices.
The first model (“pa”) incorporates the changes of PA with radius mentioned earlier. Approaching and receding sides show a distinctly different behavior: for the receding side we keep the value constant at PA = 156.7°, which is the outermost value found in the inner disk. The approaching side shows a strong PA twist and here we change the PA linearly from 156.7° at the outermost radius of the inner disk to 133° at the outer radius of the outer disk. This is illustrated in Fig. 7.
In the top panel of Fig. 11 we compare the data and model “pa”. The model still has a number of flaws. The emission in the eastern part of the disk extends too far radially and does not have the sharp drop-off observed in the data. This is clearly visible in the channel maps at V = 717.2 and 750.2 km s-1. The model emission in the southern part of the disk is also offset azimuthally clock-wise from the observed emission (visible at at V = 816.1 and 849.1 km s-1). A similar offset is seen in the northern outer part at V = 585.4 km s-1, but here the model emission is offset azimuthally counter-clockwise from the observed emission.
We found that most of these flaws can be rectified by a systematic change in the position of the dynamical center with radius. We incorporate this in the next model (“pa+off”) and change the position of the dynamical center of both sides of the disk linearly as a function of radius from (α,δ)(2000.0) = (12h26m27.07s,31°13′23.3′′) at R = 240′′ to (α,δ)(2000.0) = (12h26m24.46s,31°13′58.8′′) at R = 480′′. This corresponds to a change of −67′′ in right ascension and −24′′ in declination, or a maximum shift of 71′′ towards a position angle of 236°. At the distance of NGC 4414 this shift corresponds to 6.1 kpc (as projected on the sky; further interpretation of this shift is given in Sect. 4). Additional modeling shows that the magnitude of the shift is constrained to about ±10′′. The effect of this shift on the model is a compression of the column density contours towards the east and an extension of the H i distribution towards the west, in better agreement with the data. The model and data are compared in the middle panel of Fig. 11. The emission now extends farther west, is more compressed towards the east, and the azimuthal offsets in the north and south have mostly disappeared.
The model does not yet adequately describe the “trailing” and “leading” H i emission seen at the outer edge of the disk in the channel maps around V = 750 km s-1 (eastern edge) and V = 700 km s-1 (western edge) in Fig. 3. This turns out to be more difficult to model with standard tilted ring parameters, and necessitates the introduction of radial velocities. We introduce a radial velocity term of −20 km s-1 for all rings in the outer disk (model “pa+off+rad”). The model is also shown in Fig. 11. The difference is most clearly seen at V = 750.2 km s-1. The PA of the outer emission at V = 717.2 km s-1 is also better described, as is the slight lengthening of the northern emission “arm” at V = 651.3 and V = 684.3 km s-1 and the slight PA change in the western “arm” in the same channels. If we assume that the spiral arms in NGC 4414 are trailing arms, then the eastern side of the disk is closest to us. In that case a negative radial velocity as modeled here corresponds to an inflow.
As noted before, due to the asymmetries in the disk, not all small-scale features can be captured in a tilted-ring model, nor do we model the outermost western features. The two most important features not modeled are the H i clumps visible on the western side of the disk in the channel maps between 618.4 and 717.2 km s-1. The integrated H i map in Fig. 1 shows that these form an arm or tail that is present at large radius over a limited range in position angle. The second feature not modeled is present between 750.2 and 816.1 km s-1 on the eastern side. This is caused by the difference in PA distribution between the approaching and receding side. The model for the receding side has a constant PA in the outer disk (in order to model the outer disk around 850 km s-1), while the approaching side has a twist in the PA (in order to model the outer H i at 585.4 km s-1). The same twist does also capture the change in PA visible in the outer disk at 717.2 and 750.2 km s-1 in Fig. 11. We would be able to fit the similar features visible in the channels at V = 783.2 and V = 816.1 km s-1 in Fig. 11 by applying the PA twist there. The reason for not doing this is that it would worsen the model fit on the western side if the disk, where no such strong PA variations are seen.
This model still assumes constant inclination. We ran a number of models to check whether this assumption still held, or whether non-constant values could improve the result. With inclination as a free parameter, the average value of i for the approaching side changes by ~1°, with a large scatter. The receding side prefers a somewhat lower value of ~45°, although this does not result in an increase in quality of the models, improving the fit in one channel map, while worsening it in others. No gains are therefore made by changing the inclination, and we keep it fixed at a constant value.
Finally, in the next section, we will interpret our best model as showing the presence of a U-shaped warp. In such a model the systemic velocity could potentially vary with radius. We have tested a number of models where the outer disk has a different systemic velocity than the inner disk. We find that models where the outer systemic velocity is higher than the inner systemic velocity do not perform well. A lower outer systemic velocity is however possible, down to a minimum value of ~695 km s-1. The discriminatory power of the models is not great, however, and we proceed to keep using the constant Vsys model.
In summary, the outer disk can be reasonably modeled by introducing a small shift in the position of the dynamical center, and the addition of small radial motions. All this indicates that the outer disk is probably not in an equilibrium state, and confirms the conclusion derived from the H i morphology that NGC 4414 must have undergone or is undergoing some kind of disturbance.
 |
Fig. 12 Combination of the deep B-band image (grayscale) and a SDSS image (color). The B-band image is smoothed to 2′′ resolution to enhance the shell features. |
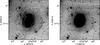 |
Fig. 13 Left: B-band KPNO image in grayscale with H i contours overlaid in white. Contours shown are (2,20) × 1019 cm-2. Right: the HALOSTARS R-band image showing similar features as the KPNO image. |
4. Discussion
4.1. A U-shaped warp
The previous section established that NGC 4414 can be characterized by a symmetrical, very regular inner disk, and a more asymmetric, disturbed outer disk, which, although mostly dominated by rotation, shows evidence of radial motions and systematic shifts in the position of the dynamical center.
This shift in dynamical center position occurs roughly along the minor axis of the galaxy. This can be interpreted as a distortion of the rings in the plane of the galaxy, but also as the projection on the sky of an offset of the outer rings perpendicular to the plane of the inner disk (i.e., in the z-direction). In other words, a U-shaped warp. This could also explain the sharp edge in the eastern part of the disk, with the emission bending into the line of sight. The increased second-moment values (due to the presence of multiple velocity components) towards the NE part of the disk support this (see Fig. 1).
Using the known inclination and a simple geometrical model, we can translate the shift of the center Δr on the sky into the spatial offset of the rings perpendicular to the inner disk Δr′ = Δr/ sini. The maximum shift in the plane of the sky (of the outermost ring) is ~6.1 kpc. This translates into a maximum offset perpendicular to the plane of ~7.6 kpc. This can be compared with the diameter of the inner disk of 41.5 kpc, or the diameter of the outermost ring of 83.0 kpc. The latter value results in a ratio of maximum vertical offset of the outer ring and the outer ring diameter of ~1:11. The warp angle (angle between main disk and a line connecting the center of the galaxy with the outermost warped ring) is ~10°. Comparing this with a study of warps in edge-on disk galaxies by García-Ruiz et al. (2002), we find that NGC 4414 has a slightly higher than average warp angle, but that the value is not exceptional.
One cause of U-shaped warps is thought to be the interaction with the intergalactic (intra-cluster) medium through ram-pressure. Ram pressure effects are usually associated with denser environments, such as clusters, and the question is whether the less dense intra-group medium in Coma I can be responsible for these effects as well. In a study of the H i in NGC 300 in the Sculptor group, Westmeier et al. (2011) evaluate the conditions for ram pressure effects in a group environment, and show that for a velocity with respect to the intra-group medium of >200 km s-1 and a intra-group medium density larger than a few times 10-5 cm-3, the effects of ram pressure should be visible in the outer parts of galaxies in these group environments.
The interaction with the intra-group medium is modeled in Haan & Braun (2014) and used to explain the formation of warps. They model the movement of a disk galaxy with an extended H i disk through the intragroup medium of a galaxy group with a mass of ~1013h-1M⊙, the mass of the most commonly occuring galaxy groups (the Coma I group has an estimated mass of ~5 × 1013 M⊙; Karachentsev et al. 2011). Haan & Braun (2014) show that having a disk galaxy move with respect to the intragroup medium at a velocity corresponding to the three-dimensional velocity dispersion of the group (~260 km s-1) and with a typical intragroup medium density of ~1 × 10-4 cm-3, is enough to rapidly (within two rotational periods of the galaxy) set up a warp-structure which is long-lived (at least 10 rotational periods). With these parameters the gravitational force of the galaxy dominates the ram pressure force, and a warp structure can exist without actual stripping of gas occuring.
Without more accurate estimates for the peculiar velocity of NGC 4414 and the surrounding group medium it is, however, difficult to say anything more quantitative about the ram pressure effects.
Lastly, the morphology of NGC 4414 could be caused by an interaction with a neighboring galaxy. As NGC 4414 is part of a group environment it is likely that (unless it is falling in the first time) it will have undergone some interaction with other group members in the past. The peculiar motions of galaxies in the Coma I region are however complex (Karachentsev et al. 2011) and it is difficult to unambiguously define a candidate galaxy that could have caused the current H i morphology of NGC 4414.
4.2. Optical shells
As described in Sect. 2.2, deep optical imaging has been obtained from two separate observing campaigns, resulting in a B-band image from KPNO and an r′-band image from the La Palma INT telescope. The independent observations allow us to gauge the reality of faint features in the images, and in the following we only discuss features present in both images.
A high-contrast version of the B-band image is shown in Fig. 12 with a SDSS image of the main disk (at the same spatial scale) superimposed. The deep image has been smoothed to 2′′ from its original resolution of ~1.2′′ to enhance the low surface brightness features.
We see that the main stellar disk extends much farther out than the shallow SDSS image suggests. This optical disk is surrounded by a low surface brightness shell, which is most clearly defined towards the west and SW, where we see a sharp and well-defined edge to the shell. A faint condensation in the shell is visible to the NNE of the main disk (at a position angle of ~30°), marking the top of a short “plume” extending radially away from the disk. Stacking of SDSS images, using the technique described in Miskolczi et al. (2011) also reveals the presence of these features (A. Miskoliczi, priv. comm.).
In the 2′′ KPNO image, the surface brightness of the shell has a level of ~3–4 times the RMS of the background, which gives the shell a surface brightness of ~26.4B-mag arcsec-2. There is no clear evidence of the presence of multiple shells.
Figure 13 shows an overlay of the H i on top of the optical image. While the shell and the H i disk largely coincide, we do not see any small-scale agreement between gas and stellar features. The shell and plume typically extend to larger radii than the H i disk.
The presence of the shell suggests NGC 4414 has undergone a minor interaction. Numerical simulations of interactions between a low mass disk galaxy, and a more massive elliptical galaxy showed that the interaction could cause shells to form (Quinn 1984; Hernquist & Quinn 1988). Some of these models also show the presence of a plume, as we observe here, which is a remnant of the interloper galaxy. Later work showed that shells could also form as the result of the interaction of a small disk galaxy with a more massive disk galaxy (Hernquist & Quinn 1989), and shells have indeed been observed around some of them (Schweizer & Seitzer 1988). Recently, Cooper et al. (2011) suggested that the formation of shells around galaxies also occurs naturally as a product of continuous accretion of clumps of dark matter and stars in a cold dark matter universe.
The simulations by Hernquist & Quinn (1988) and Hernquist & Quinn (1989) show that shell formation can occur on timescales of ~108 years and that shells can persist for a few Gyr. These timescales are longer than in the ram pressure scenario discussed above, and it is therefore likely that the shell formation occured in a separate event.
The simulations mentioned above assumed a mass ratio of 1:100 for the interactions, but the much lower velocity dispersions of disk galaxies compared to ellipticals should allow encounters with much larger mass ratios to create shells in disk galaxies as well, as disk galaxies are more easily disturbed than ellipticals (Hernquist & Quinn 1989). A rough comparison of the luminosities of the NGC 4414 shell and extended low-surface brightness halo with that of the main disk gives a luminosity ratio of ~1:(1 − 5) × 104. The asymmetry between the sharp edge of the shell towards the west and the much more diffuse distribution in the other directions suggest an interaction that was not entirely radial (see, e.g., Fig. 4 in Hernquist & Quinn 1989). Beyond this it is difficult to derive much more on the geometry and nature of the interaction.
Even assuming a mass ratio of 1:100 gives the intruding galaxy an H i mass of only ~107 M⊙ (assuming a similar MHI/Mdyn as NGC 4414). It is therefore unlikely that a significant fraction of the gas in NGC 4414 originally belonged to the intruder galaxy. There are no “smoking gun” candidate intruder galaxies in the immediate vicinity of NGC 4414. If the incoming galaxy has not been completely disrupted, then one tentative candidate could be a small galaxy, SDSS J122646.27+311904.8, that lies just beyond the tip of the plume. The galaxy is indicated in the optical image presented in Fig. 1. It distinguishes itself from other (background) galaxies in the vicinity by being the only galaxy that is not centrally concentrated, is more fuzzy, and has a lower surface brightness. Assuming this galaxy is at the same distance as NGC 4414, its luminosity would be ~1200 times fainter than NGC 4414. Unfortunately no redshift is know for this galaxy, and no H i is detected at this position.
The interaction that resulted in the optical shell most likely did not cause the observed H i morphology due to the small mass of the intruder galaxy. The formation of the optical shell and the observed H i morphology therefore are the result of two different processes or events. This shows that even in low-density groups such as Coma I, deep enough observations will show that galaxies are still affected by their environment. As noted before, many of the HALOGAS targets are in the Coma I group and a future paper will contain a fuller discussion of the effects of the group environment.
5. Summary
We have presented deep H i observations of NGC 4414. These show that NGC 4414 can be characterized by a regularly rotating, symmetrical inner disk. An extra-planar gas component is present above the inner disk, representing ~4 per cent of the inner disk H i mass (or about 3 per cent of the total H i mass).
The outer disk is disturbed and needs to be modeled assuming a variable dynamical center position and radial motions. This can be interpreted as a U-shaped warp.
Deep optical imaging shows the presence of an extensive low surface brightness stellar halo containing a clear shell feature surrounding the main galaxy. Simulations indicate that such shells are the result of minor interactions with low mass galaxies.
Finally, the difference between conclusions reached here, of NGC 4414 being a disturbed galaxy, and the previous literature concensus (based on more shallow observations), of NGC 4414 being undisturbed, points at the importance of obtaining deep H i and optical observations in order to properly chararacterise the evolutionary state of a galaxy.
Acknowledgments
We thank the anonymous referee for the constructive comments. W.J.G.d.B. is supported by the European Commission (grant FP7-PEOPLE-2012-CIG #333939). G.G. is a postdoctoral researcher of the FWO-Vlaanderen (Belgium). R.A.M.W. and M.P. acknowledge support from the National Science Foundation through Grant AST-0908126. R.J.R. acknowledges support from the National Science Foundation through Grant AST-0908106. The Isaac Newton Telescope is operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. The Westerbork Synthesis Radio Telescope is operated by the ASTRON (Netherlands Foundation for Research in Astronomy) with support from the Netherlands Foundation for Scientific Research NWO. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Angiras, R. A., Jog, C. J., Omar, A., & Dwarakanath, K. S. 2006, MNRAS, 369, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Begum, A., Chengalur, J. N., Karachentsev, I. D., Sharina, M. E., & Kaisin, S. S. 2008, MNRAS, 386, 1667 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2006, Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Panz, & E. Solano, ASP Conf. Ser., 351, 112 [Google Scholar]
- Braine, J., Combes, F., & van Driel, W. 1993, A&A, 280, 451 [NASA ADS] [Google Scholar]
- Braine, J., Brouillet, N., & Baudry, A. 1997, A&A, 318, 19 [NASA ADS] [Google Scholar]
- Cannon, J. M., Giovanelli, R., Haynes, M. P., et al. 2011, ApJ, 739, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., Martínez-Delgado, D., Helly, J., et al. 2011, ApJ, 743, L21 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
- García-Ruiz, I., Sancisi, R., & Kuijken, K. 2002, A&A, 394, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraternali, F., van Moorsel, G., Sancisi, R., & Oosterloo, T. 2002, AJ, 123, 3124 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Jozsa, G. I. G., Serra, P., et al. 2013, A&A, 554, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haan, S., & Braun, R. 2014, MNRAS, 440, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Józsa, G., Serra, P., et al. 2011, A&A, 526, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heald, G., Józsa, G., Serra, P., et al. 2012, A&A, 544, A1 [Google Scholar]
- Hernquist, L., & Quinn, P. J. 1988, ApJ, 331, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L., & Quinn, P. J. 1989, ApJ, 342, 1 [Google Scholar]
- Hunter, D. A., Ficut-Vicas, D., Ashley, T., et al. 2012, AJ, 144, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Józsa, G. I. G., Kenn, F., Klein, U., & Oosterloo, T. A. 2007, A&A, 468, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Nasonova, O. G., & Courtois, H. M. 2011, ApJ, 743, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Koribalski, B. S. 2010, Galaxies in Isolation: Exploring Nature Versus Nurture, eds. Verdes-Montenegro, A. del Olmo, & J. Sulentic (San Francisco: ASP), 421, 137 [Google Scholar]
- Miskolczi, A., Bomans, D. J., & Dettmar, R.-J. 2011, A&A, 536, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moustakas, J., & Kennicutt, R. C., Jr. 2006, ApJS, 164, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, J., Stilp, A. M., Warren, S. R., et al. 2012, AJ, 144, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, P. J. 1984, ApJ, 279, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., & Zaritsky, D. 1995, ApJ, 447, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K. 1996, ApJ, 471, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&ARv, 15, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Schirmer, M. 2013, ApJS, 209, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Schweizer, F., & Seitzer, P. 1988, ApJ, 328, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, P. R., & Field, G. B. 1976, ApJ, 205, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Soida, M., Beck, R., Urbanik, M., & Braine, J. 2002, A&A, 394, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thilker, D. A., Bianchi, L., Meurer, G., et al. 2007, ApJS, 173, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Thornley, M. D., & Mundy, L. G. 1997, ApJ, 490, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B. 1988, Nearby galaxies catalog (Cambridge: Cambridge University) [Google Scholar]
- Vallejo, O., Braine, J., & Baudry, A. 2002, A&A, 387, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vallejo, O., Braine, J., & Baudry, A. 2003, Ap&SS, 284, 715 [NASA ADS] [CrossRef] [Google Scholar]
- van Eymeren, J., Jütte, E., Jog, C. J., Stein, Y., & Dettmar, R.-J. 2011, A&A, 530, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Westmeier, T., Braun, R., & Koribalski, B. S. 2011, MNRAS, 410, 2217 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Salo, H., Laurikainen, E., et al. 2013, ApJ, 772, 135 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Overview of NGC 4414 derived from the 30′′ tapered data cube. Top-left: integrated H i intensity map (zeroth moment). The contour levels shown are (2,5,10) × 1019 cm-2 (black) and (2,5,10) × 1020 cm-2 (white). Top-right: integrated H i intensity overplotted on a deep KPNO B-band image. The optical image is shown using a logarithmic intensity scale. Contours shown are (2,20) × 1019 cm-2. The two short vertical lines indicate galaxy SDSS J122646.27+311904.8, as discussed in Sect. 4.2. Bottom-left: intensity-weighted mean first-moment velocity field. The thick black countour shows the systemic velocity of 711.5 km s-1. Black contours then decrease in steps of 25 km s-1, white contours increase in steps of 25 km s-1. The dashed white ellipse indicates the division between inner and outer disk as defined in Sect. 3. Bottom-right: second-moment velocity dispersion map. Black contours show values of (5, 10, 20) km s-1 (light-gray to dark-gray background). White contours show (50, 100) km s-1 (dark-gray to black background). The white ellipse indicates the division between inner and outer disk. |
| In the text | |
 |
Fig. 2 Left: robust-weighted integrated column density map. Contour levels are (1,2,5) × 1020 cm-2 (black) and 1 × 1021 cm-2 (white). The gray box shows the area shown in the right-panel. Right: integrated H i column density based on the robust weighted cube overplotted on a deep KPNO Hα image. Contour levels are the same as in the left panel. The main Hα distribution is encompassed by the 1 × 1021 cm-2 contour, with low-level Hα primarily found within the 5 × 1020 cm-2 contour. Virtually no Hα is found outside these countours. The bright source in the top-left is a residual continuum artifact. |
| In the text | |
 |
Fig. 3 Selected channel maps from the 30′′ tapered cube. Only every fourth channel map is shown. Contour levels are (2,5,10,20,50)·σ where σ = 0.23 mJy beam-1 or 0.8 × 1018 cm-2. The beam is indicated in the bottom-left of the top-left panel. The heliocentric velocity in km s-1 is indicated in the top-left of each panel. |
| In the text | |
 |
Fig. 4 Global H i profile based on the primary-beam corrected 30′′-tapered cube (full line). The dashed line shows the global profile of the inner disk only. |
| In the text | |
 |
Fig. 5 Normalized lopsidedness parameter A1 as a function or radius. The different behavior in inner and outer disk (separated by the vertical line at a radius of 240′′) is clear. |
| In the text | |
 |
Fig. 6 Left: hermite velocity field based on the 30′′-tapered cube. The thick black countour shows a systemic velocity of 711.5 km s-1. Black contours then decrease in steps of 25 km s-1, white contours increase in steps of 25 km s-1. The white dashed ellipse with a major axis radius of 240′′ delimits the inner and outer disk. Right: intensity-weighted first-moment map. Contours as in left panel. |
| In the text | |
 |
Fig. 7 Summary of NGC 4414 models. In all panels the vertical dotted line delimits the inner and outer disk. Top three rows, inner disk: open circles indicate the tilted ring parameters derived from a ROTCUR fit with all fit parameters free as described in Sect. 3.1.1. The thick, full lines indicate the final model chosen for the inner disk. In the third row, right-hand panel, the filled circles indicate the resulting final ROTCUR model for the rotation curve of the inner disk. The long-dashed and dotted curves indicate the receding and approaching side rotation curves of the inner disk, respectively. Top three rows, outer disk: the dashed thick lines in the outer disk part of the plots indicates the values chosen for the final TiRiFiC model. In the left-hand panel of the third row the thick long-dashed line indicates the PA distribution for the approaching side, the short-dashed thick line that of the receding side. The thin long- and short-dashed lines show the PA values of the two sides when a ROTCUR fit is made to the velocity field with only PA and Vrot as free parameters. Bottom row: the left-hand panel shows the H i radial surface density distribution. Open squares indicate the approaching side, filled squares the receding side. The right-hand panel in the bottom row shows the approaching and receding sides rotation curves as open and filled squares, respectively. The horizontal line in the outer disk indicates the flat rotation curve assumed in the TiRiFiC modeling. |
| In the text | |
 |
Fig. 8 Left panel: the Hermite velocity field (grayscale with black contours) with the best-fitting model velocity field for the inner disk overlaid. Contours are as in Fig. 6 with a contour spacing of 25 km s-1. Right panel: residual velocity field derived by subtracting the model from the observations. The thick black contour shows the 0 km s-1 level. The thin black contour + 10 km s-1, the thin white contour −10 km s-1. The maximum and minimum values found are + 16 and −16 km s-1, respectively. |
| In the text | |
 |
Fig. 9 Overlay of the best TiRiFiC model of the inner disk on the major axis pV diagram. The data is shown in gray-scale and light-gray contours. The model in black contours. For both, the lowest contour level shown is 1.5σ. Subsequent contour levels each increase by a factor 2.5. For the data, the dashed contours also show the −1.5σ level. The vertical dashed lines delimit the inner disk. |
| In the text | |
 |
Fig. 10 Overlay of the best model of the inner disk on selected channel maps. Contour levels for both data and model are (2,5,10,20,50)·σ where σ = 0.23 mJy beam-1 or 0.8 × 1018 cm-2. The dashed ellipse denotes the inner disk. |
| In the text | |
 |
Fig. 11 Overlay of the models on selected channel maps. Contour levels for both data and model are (2,10,50)·σ where σ = 0.23 mJy beam-1 or 0.8 × 1018 cm-2. The two dashed ellipses in each panel denotes the outer radii of the inner and outer disk. Details of the models are described in the text. |
| In the text | |
 |
Fig. 12 Combination of the deep B-band image (grayscale) and a SDSS image (color). The B-band image is smoothed to 2′′ resolution to enhance the shell features. |
| In the text | |
 |
Fig. 13 Left: B-band KPNO image in grayscale with H i contours overlaid in white. Contours shown are (2,20) × 1019 cm-2. Right: the HALOSTARS R-band image showing similar features as the KPNO image. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


