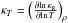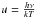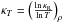| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220507 | |
| Published online | 14 May 2014 | |
Seismic models of O and B stars with Kurucz’s opacity data⋆
Astronomical Institute of the Wroclaw University,
ul. Kopernika 11,
51-622
Wroclaw,
Poland
e-mail: cugier@astro.uni.wroc.pl
Received:
5
October
2012
Accepted:
14
March
2014
Aims. We investigated seismic models of O and B stars calculated with the new Kurucz opacities implemented in the Opacity Project (OP) and Rogers & Iglesias OPAL opacity tables (OPAL).
Methods. We studied the problem using Dziembowski’s computer codes for linear, nonadiabatic, and nonradial oscillations. We considered seismic models of main sequence (MS) stars for different chemical compositions of elements in the mass-range 9 ≤ M ≤ 70 M⊙.
Results. The new opacity bump at lgT ≈ 5.06 that occurs in Kurucz’s data influences evolutionary tracks mainly for M ≥ 30 M⊙ and markedly changes the driving zone for pulsations of stars in the whole mass range studied. We obtained no unstable oscillation modes for models corresponding to the abundance parameter Z ≤ 0.013 and only unstable low-frequency g-modes for 0.013 < Z ≤ 0.021.
Conclusions. The opacity bump at lgT ≈ 5.3 should be significantly larger than the opacity bump at lgT ≈ 5.06 to drive pulsations of B stars in low-degree p-modes. Models with an increased OPAL (or OP) opacity bump at lgT ≈ 5.3 by a factor of about 1.7 have sufficiently large driving zones to excite modes in the β Cephei frequency-domain for 0.003 ≤ Z ≤ 0.021. These values of Z are in a good agreement with those derived spectroscopically for stars in the Galaxy and Magellanic Clouds.
Key words: asteroseismology / atomic data / stars: early-type / pulsars: general
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The opacity and equation of state (EOS) are important ingredients for modeling the structure, evolution, and pulsation of stars. Three sets of data are commonly used, including: Rogers & Inglesias OPAL results (OPAL), the Opacity Project (OP), and Kurucz’s data. The OPAL data are based on an OPAL computing code developed by Rogers, et al. (cf. Rogers et al. 1988; Rogers & Iglesias 1992; Iglesias & Rogers 1996, and the OPAL website1). The OP data were calculated by an international team led by Seaton (OP, cf. Seaton 1987; Seaton et al. 1994; Badnell et al. 2005, and the OP website2). Since 1970 the opacity data and EOS calculated by Kurucz are the basic tools when local thermodynamic equilibrium (LTE) atmosphere models are considered (cf. Kurucz 2005, 2011, and Kurucz’s website3).
The atmosphere and envelope models calculated with the same OP data are reasonably close to each other at the optically thick layers (Cugier 2012). A simple fit of the atmosphere model (with the proper treatment of the transport of radiation energy) and envelope model, which is usually calculated with the diffusion approximation, at τR = 100 is then justified. There are obstacles to this approach when atmosphere models calculated with the Kurucz’s atomic data were fitted to the OPAL or OP internal models of early-type stars. This is explained by the current results of the Kurucz’s (2011) project, which attempts to include all spectral lines of atoms, revealing a large excess of opacity relative to the OPAL and OP data near lgT = 5.06 (Cugier 2012).
The new opacity bump at lgT ≈ 5.06 should be considered, in addition to the already known four opacity maxima. The first two maxima (at lgT ≈ 4.0 and 4.7) are mainly due to hydrogen and helium (Seaton et al. 1994). The other two maxima (at lgT ≈ 5.3 and 6.3) are caused by heavier elements (metals). The maximum at lgT ≈ 5.3 is of particular importance for stellar pulsations of early-type stars and is produced by the iron-group elements, among which Fe dominates. The elements C, N, O, and Ne give an opacity enhancement at lgT ≈ 5.1 and form, with the iron-group elements, the fourth opacity maximum at lgT ≈ 6.3 clearly seen when the solar (X = 0.70 and Z = 0.02) abundance of elements was assumed by Seaton et al. (1994). The remaining elements considered in the OPAL and OP projects yield the largest contributions near lgT ≈ 5.9. As usual, X, Y, and Z parameters describe the mass abundances of hydrogen, helium, and metals, respectively.
In addition to atomic physics, the abundance of metals has an important influence on seismic models, especially for early-type stars, where the hydrogen and helium opacity bumps play a minor (if any) role. In the last two decades, one can observe that the metal abundance parameter Z derived from spectroscopic observations of stars decreased markedly. The present-day solar photospheric elemental abundances Z/X = 0.0181 given by Asplund et al. (2009) lead to X = 0.7381 and Z = 0.0134, assuming a seismic measurement of Y = 0.2485 (Basu & Antia 2004). Previously, the value of Z/X = 0.0245 was accepted following Grevesee & Noels (1993). Recently, Vorontsov et al. (2013) obtained 0.008 < Z < 0.013 and 0.240 < Y < 0.255 from the reanalysis of the solar p-modes measurements. The results depend mainly on a particular version of the EOS used. No unstable low-degree oscillation modes in the p-domain were obtained for models of B stars using Grevesse & Noels (1993) mixture of elements for Z < 0.01 (Pamyatnykh 1999; Miglio et al. 2007). If a small contribution of C, N, O, and Ne to Z as listed in Asplund et al. (2009), then Z ≥ 0.007 is needed for excitation of p-modes in B stars (Salmon et al. 2012), because of the higher contribution of iron-group elements to Z. In this context, variable B stars observed in the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC) are interesting. Compilations of spectroscopic data listed in Brott et al. (2011) and Salmon et al. (2012) indicates that Z = 0.0047−0.0060 and Z = 0.0021−0.0024 for the LMC and SMC, respectively. Several candidates for β Cephei-type stars were, however, found by Pigulski & Kolaczkowski (2002), Kolaczkowski et al. (2004, 2006), Diago et al. (2008a,b), Karoff et al. (2008), and Pigulski & Pojmanski (2008).
The aim of this paper is to investigate the evolutionary and seismic models of stars, which are closely related via Kurucz’s opacity data available for T ≤ 200 kK. In Sect. 2, we briefly review oscillation spectra predicted for O and B type stars using the OPAL and OP data. The new opacity bump at lgT = 5.06 is discussed in Sect. 3 for different abundances of elements. Examples of evolutionary tracks for stellar models calculated with Kurucz’s opacity data are shown in Sect. 4. Seismic models are discussed in Sect. 5 and conclusions are described in Sect. 6.
2. Oscillation spectra of early-type stars
In this section, a few aspects of theoretical oscillation spectra related to observations of O- and B-type stars were briefly pointed out. This is well justified because the pulsational instability mechanism and theoretical oscillation spectra of B stars were already reviewed by Dziembowski & Pamyatnykh (1992), Gautsschy & Saio (1993), Dziembowski et al. (1993), Moskalik (1995), Dupret (2001), and others. More recent investigations (e.g. Pamyatnykh 1999; Saio et al. 2000, Daszynska-Daszkiewicz et al. 2005; Miglio et al. 2007; Daszynska-Daszkiewicz & Walczak 2010; Salmon et al. 2012) lead to quantitatively different results when different abundances of elements were assumed, but the basic results for the chemical composition not far from X ≈ 0.70 and Z ≈ 0.02 are remarkably the same as obtained as early as the 1990 s (Dziembowski 2009).
The radial and some nonradial modes are called p-modes because the restoring force for pulsations is predominantly the gas pressure. Nonradial modes may also be governed by buoyancy acting as restoring force, and these are called g-modes. These two kinds of modes are well separated in the frequency-domain for stellar models near the zero age main sequence (ZAMS). Nonradial modes may have also mixed character for evolved main sequence (MS) stars (Dziembowski & Pamyatnykh 1992; Balona & Dziembowski 1999). Those B stars with predominant variations in frequency domain characteristic of p-modes are called β Cephei-type stars, while those with variations in the frequency domain characteristic of g-modes are called SPB-type stars. A number of β Cephei stars, however, show low-frequency pulsations characteristic of SPB stars. They are known as β Cep/SPB hybrids (e.g. De Cat et al. 2007; Pigulski & Pojmanski 2008; Handler 2009; Balona et al. 2011; Degroote et al. 2012b; Pápics et al. 2012).
In addition, there are also f-modes (for l ≥ 2) (e.g. Cox 1980; Saio & Cox 1980). In the frequency domain they are located between p- and g-modes for models near ZAMS. According to Balona & Dziembowski (1999), some high degree (l ≥ 12) of unstable modes can be regarded as f-modes when models far from ZAMS are considered. Daszynska-Daszkiewicz et al. (2006) suggested that high-frequency modes observed in FG Vir (a δ Scuti star) can be explained by f-modes.
The amplitude limit for ground-based observations are typically a few millimagnitudes. At this level, modes with the spherical harmonic degree l ≤ 2 were usually considered because of large cancelation effects over the stellar disk for higher values of l. The dominant mode of oscillation (the mode with the highest amplitude) may be either the radial or nonradial mode in β Cephei stars (e.g. Cugier et al. 1994). An unprecedented level of precision, a few ppm, was recently achieved from space-based instruments aboard Convection Rotation and Planetary Transits (CoRoT, cf. Auvergne et al. 2009) and Kepler (cf. Gilliland et al. 2010) satellites. Balona et al. (2011) concluded that the frequency spectra are quite different from what is seen from ground-based observations. They suggest that pulsations with values of l as high as 20, or even higher, may be visible in Kepler photometry. Basic properties of such modes were discussed by Balona & Dziembowski (1999) and Dziembowski (2009). There are, however, also stars within the β Cephei and SPB instability strips with no detected variability at the level of a few ppm (Balona et al. 2011).
In the case of O-type stars, the linear, nonadiabatic theory predicts that two or three radial modes and a similar number of nonradial p-models with low l-values are unstable using the OPAL and OP data for X = 0.70 and Z = 0.02 (e.g. Pamyatnykh 1999; Pamyatnykh & Ziomek 2007). The instability strip extends to masses well above 50 M⊙ for l ≤ 2 (e.g. Moskalik 1995). Observations do not show, however, that variability with frequency characteristics for p-modes is a common feature in O stars (e.g. Balona 1992; Pigulski & Kolaczkowski 1998). The β Cephei-type pulsations were, however, found in O-type stars (e.g. Walker et al. 2005; Pigulski & Pojmanski 2008), and oscillations with periods of the order of one day were commonly present, as was first predicted by Vogt & Penrod (1983) from observed variability of line profiles detected by Walker et al. (1979). CoRoT observations show further examples of the variability of O stars and several frequencies in light curves were found, which were not predicted to be unstable modes by the OPAL and OP seismic models (cf. Blomme et al. 2011; Briquet et al. 2011; Degroote et al. 2010; Mahy et al. 2011).
In summary, although the driving κ-mechanism of oscillations has been identified using the OPAL and OP data, there are still unsolved problems related to the identification and selection of oscillation modes for O and B stars. Consequently, our understanding of the observed oscillation spectra of early-type stars is not complete. Therefore, some numerical experiments with opacity in the driving zones for stellar pulsations were also made (e.g. Pamyatnykh et al. 2004; Zdravkov & Pamyatnykh 2008; Salmon et al. 2012). Some critical remarks regarding the atomic physics and accuracy of the OP data were given by Prandhan & Nahar (2009).
3. Kurucz’s opacity data
 |
Fig. 1 Rosseland-mean opacity κR [ cm2 g-1 ] vs. lgT taken from the Castelli & Kurucz (2003) atmosphere models of lgg = 5.0, Teff = 15 000, 20 000, 25 000, 30 000 K (left panel) and Teff = 35 000,40 000,45 000 K (right panel) in comparison with envelope models calculated with the OPAL data. The atmosphere models corresponding to the microturbulent velocity ξ = 0 (taken from the Castelli website) were plotted as lines with pluses. Both the CK and OPAL models were calculated for X = 0.7347 and Z = 0.0169. |
Recently, Castelli & Kurucz (2003) and Meszaros et al. (2012) calculated two extensive grids of atmosphere models and Rosseland-mean opacities. The same Kurucz atom models were used, but data given by Grevesse & Sauval (1998) and Asplund et al. (2005) were assumed to be the solar elemental mixture, respectively. Both Castelli & Kurucz (CK) and Meszaros et al. (M) models (available from Castelli4 and ATLAS-APOGEE5 websites) reveal an excess of opacity at high optical depths in comparison with atmosphere and envelope models calculated with the OPAL and OP data. Examples are plotted in Fig. 1. The atmosphere models (shown as lines with pluses) ended at the Rosseland-mean optical depth equal to 100 and the opacity bump at lgT = 5.06 can therefore be overlooked for lgTeff < 4.7. In the following, we used the Rosseland-mean opacities (CK, M, OPAL and OP) given in a tabular form. Details are provided in Appendix A.
First, we selected the OPAL and OP opacity data for a comparative study. In particular, we calculated the OPAL models (Nos. 1–8 in Table 1) for scaled metal abundances based on Grevesse & Noels (1993) data, while the chemical mixtures listed in Asplund et al. (2009) were used for OP models Nos. 9 and 10. In the last case, we selected the mean values of Y and Z from the best-fit solution (Y = 0.25, Z = 0.008) obtained by Vorontsov et al. (2013) for the SAHA-S3 EOS, using p-modes trapped in the upper half of the solar convective envelope, and (Y = 0.245, Z = 0.010) for p-modes trapped in deeper layers.
Next, we calculated the K-OPAL and K-OP models with hybrid CK/OPAL and M/OP opacity data, viz., for the CK or M opacity at outer stellar layers (up to lgT = 5.2) implemented with the OPAL or OP data for lgT > 5.2. Models calculated using the OPAL and CK/OPAL opacities can be regarded as representative for the aim of this paper because basic characteristics of the M/OP and CK/OP opacities are the same. Names of the K-OPAL models contain information about both sets of the opacity data used (Appendix A). Nuclear reaction rates and EOS were calculated for the initial (at ZAMS) chemical composition X and Z listed in Table 1. The K-OPAL models are divided into three groups explained in Sects. 3.1–3.3.
Opacity data for stellar models analyzed.
 |
Fig. 2 Rosseland-mean opacities κR [ cm2 g-1 ] vs. lgT for lgR = lgρ − 3lgT + 18 = −6.0, −5.0, −4.5, and −4.0. The OPAL (blue lines) and K-OPAL/A (red lines) data were plotted for Z = 0.0266,0.0168 and 0.00542, viz., opacity data Nos. 1, 3, 7, 11, 13, and 16 listed in Table 1 were displayed. The K-OPAL data with α-enhanced elements (m05a in Table A.1) were also plotted as green lines. (A color version of the figure is available online.) |
3.1. The K-OPAL/A opacity data
We built the K-OPAL/A models (Table 1) using the
CK and OPAL opacity data selected for the same abundance parameters of X and Z. In Fig. 2, we plotted examples of these hybrid opacities in
comparison with the pure OPAL data for Z = 0.00542,0.0169, and
0.0266. As one can see, the
CK Rosseland-mean opacities, 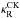 , differ
markedly from the OPAL,
, differ
markedly from the OPAL, 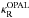 ,
opacities at 4.7 <
lgT < 5.2. The opacity bump
at lgT ≈ 5.06
dominates for lgR =
lgρ − 3lgT + 18 < −5 and its role decreases for higher densities, but is still important
for subphotospheric layers of early-type stars (lgR ≤ −3.5). In this case, we see two opacity
bumps (at lgT =
5.06 and 5.3). The local minimum of the opacity occurs at
lgT ≈ 5.2,
where
,
opacities at 4.7 <
lgT < 5.2. The opacity bump
at lgT ≈ 5.06
dominates for lgR =
lgρ − 3lgT + 18 < −5 and its role decreases for higher densities, but is still important
for subphotospheric layers of early-type stars (lgR ≤ −3.5). In this case, we see two opacity
bumps (at lgT =
5.06 and 5.3). The local minimum of the opacity occurs at
lgT ≈ 5.2,
where 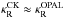 . A deeper
insight into why the local minimum of κR takes place at lgT ≈ 5.2 follows from an
analysis of monochromatic opacities (Appendix A).
. A deeper
insight into why the local minimum of κR takes place at lgT ≈ 5.2 follows from an
analysis of monochromatic opacities (Appendix A).
3.2. The K-OPAL/B opacity data
We considered K-OPAL/B models to study how the relative strength of the opacity bumps at
lgT = 5.06
and 5.3 influences seismic
models of early-type stars. They are basically the OPAL models for Z = 0.0266 and
Z = 0.0169
at all stellar layers, with the exception that 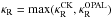 was selected near the opacity
bump at lgT ≈
5.06 (models Nos. 18–24 in Table 1). Further details were provided in Appendix A.
was selected near the opacity
bump at lgT ≈
5.06 (models Nos. 18–24 in Table 1). Further details were provided in Appendix A.
3.3. The K-OPAL/C opacity data
We also searched K-OPAL/C models with enhanced opacities at lgT> 5.2 (opacity data Nos. 25–27 in Table 1) motivated mainly by Pradhan & Nahar (2009) who suggested that the missing opacity in the OP data may lie in an energy range from a few eV to few hundreds of eV, depending on the element and ionization stage. In the case of No. 25, we used EOS and nuclear reaction rates for the initial chemical composition of X = 0.7394, Y = 0.2498, and Z = 0.0108. We assumed the CK opacity data (m02, Z = 0.0108) at lgT < 5.2, but the OPAL data for Z = 0.0266 at lgT> 5.2. The models Nos. 26 and 27 were constructed for Z = 0.00542 and 0.00306 with enhanced opacities (OPAL: Z = 0.0169 and 0.0135) at lgT> 5.2, respectively. The above described approach leads to an increase of the opacity bump at lgT = 5.3 by a factor of about 1.7 for all K-OPAL/C models listed in Table 1. The CK/OP Rosseland-mean opacities calculated from OP monochromatic cross-sections increased by factors of 1–5 at lgT> 5.2 shown with similar results (Cugier 2014).
4. The K-OPAL models of early-type stars
 |
Fig. 3 H-R diagram for OPAL (blue lines) and K-OPAL (black lines) models of M = 70,60,50,40,35,30, and 20 M⊙ calculated with the initial chemical composition X = 0.7347 and Z = 0.0169. No mass loss and no core overshooting were included in the calculations. Lo means the solar luminosity and Mo solar mass. (A color version of the figure is available online.) |
We note first that it is sufficient to consider κR for stellar evolution models, while the derivatives of the opacity over temperature and density are necessary for seismic models of stars discussed in Sect. 5. In some computing codes for stellar evolution, the opacity derivatives are also used, but only in the convergence process. The original OPAL opacity data (Iglesias & Rogers 1996) contain tables of κR(T,ρ,X,Y,Z). In particular, temperature is in the range lgT = 3.75−8.7 with steps of 0.05 dex. (for lgT = 3.75−6.0), and 0.1 dex. (for lgT = 6.0−8.1), and 0.2 dex. (for lgT = 8.1−8.7), while density ρ, expressed by the parameter of lgR, is in the range lgR = −8.0 −1.0 with a step of 0.5 dex, respectively. These data were extended toward lower temperatures using molecular and grain opacities calculated by Alexander & Ferguson (1994).
The above described opacity data are sometimes interpolated for a denser grid of parameters by decreasing steps in lgT and lgR by a factor N. The purpose of this is to allow further linear interpolation in the opacity tables by computing codes for modeling stellar evolution to save computing time. This approach is justified for calculations of evolutionary tracks of stars, but the accuracy of seismic models may be decreased. In particular, we found that this linear interpolation influences the net pulsational energy gain during one cycle of some oscillation modes even for N = 5, and thereby affects their stability properties. A better approach (adopted in this paper) is to use, e.g., N = 2 with a more accurate interpolation procedure in the computing code for modeling stellar structure.
Now we calculate stellar models with the OPAL and CK/OPAL opacity data. Examples are shown in Fig. 3, where we plotted the Hertzsprung-Russel (H-R) diagram for the models of M = 20−70 M⊙, calculated assuming the initial abundance parameters equal to X = 0.7347 and Z = 0.0169 (opacity data Nos. 3 and 13 in Table 1). The evolutionary tracks are shown from ZAMS to the moment when the central temperature reaches the value of lgTc = 8.0, just before helium ignition in the stellar core. We did not assume any mass loss, rotation or core overshooting. This means that the models reveal only differences in the opacity data used. The ZAMS, terminal age main sequence (TAMS), and the end of the MS overall contraction phase are seen for all tracks. Clearly, the K-OPAL/A models show a very broad band of the MS phase of evolution for M> 20 M⊙. This is caused by a high gradient of radiation pressure at optically thick regions, lgT ≈ 5.06, where the CK Rosseland-mean opacities approach maximum (see Sect. 3). Consequently, this leads to an increase in the stellar radius. The deeper layers are almost the same in the both cases, however, because of the same (OPAL) opacities assumed there.
Figures 4–5 show the H-R diagram for OPAL and K-OPAL models of 40 and 12 M⊙ calculated with different chemical compositions. In the case of M = 40 M⊙ (Fig. 4), one can see that the above mentioned effect of the gradient of radiation pressure near lgT = 5.06 is important even for Z = 0.00542, but Z < 0.0108 is sufficient to prevent MS stellar evolution to a very low effective temperature of approximately lgTeff < 4.4. Mass loss is another important reason that can markedly change evolutionary tracks of massive stars. In the models presented here, we took the mixing of elements into account, but only within the range of the convective core with the boundary determined by the Schwarzschild criterion. The effect of the initial chemical composition remains important for M ≤ 20 M⊙ (Fig. 5), but the differences between the OPAL and K-OPAL/A evolutionary tracks are small for a given stellar mass at least up to the moment of helium ignition in the stellar core. The K-OPAL/C models of No. 25 with enhanced opacities at lgT> 5.2 show a bit lower luminosity on the H-R diagram. Here, we also plot models of No. 25 for M = 13 M⊙. This evolutionary track is not far from that calculated for M = 12 M⊙ models of Nos. 5 and 14, shown in Fig. 5, with the exception of higher luminosity by about 0.05 dex.
 |
Fig. 4 H-R diagram for OPAL and K-OPAL models of M = 40 M⊙ calculated with different initial chemical compositions. The evolutionary tracks were numbered according to the opacity data listed in Table 1. (A color version of the figure is available online.) |
 |
Fig. 5 Same as Fig. 4, but for M = 12 M⊙. The evolutionary track for M = 13 M⊙ (only for the opacity data No. 25; violet line) was also plotted. (A color version of the figure is available online.) |
 |
Fig. 6 Frequencies ν [c/d] of unstable modes (l ≤ 10) for the OPAL, OP, and K-OPAL models of M = 12 M⊙ with the central hydrogen content Xc = 0.24. The models were numbered according to the opacity data used (Table 1). Symbols are explained in the right hand panel. (A color version of the figure is available online.) |
5. Seismic models
The basic physical assumptions remain the same as those used in the well-known Dziembowski’s (1977) computing code for linear and nonadiabatic stellar oscillations. Both radial and nonradial oscillations were considered. In this paper, we used a computing code based on the PERIBC and PIGMOD codes elaborated by Dziembowski (2000, priv. comm., cf. also Balona & Dziembowski 1999). In these codes, outer layers were treated in the full nonadiabatic approach, while deeper layers in quasiadiabatic approximation. We refer the readers to Dziembowski (1977), where both approaches were described in detail.
The calculated seismic models were examined with review propagation diagrams, oscillation
energy, E, work
integrals, W,
and eigenfunctions of oscillation modes. All first order perturbed quantities were assumed
to be proportional to 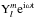 . The
period, Π, and frequency,
ν, of
oscillation is given by
. The
period, Π, and frequency,
ν, of
oscillation is given by 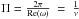 , while
the imaginary part of ω gives the excitation rate. The dimensionless
frequency, σ,
is defined as σ =
ω(4πG ⟨ ρ ⟩ )−1/2, where ⟨ ρ ⟩ is the mean density of
the star and G
is the gravitational constant. The propagation diagrams for the oscillation modes involve
the Brunt-Väisälä (N) and Lamb (Ll) frequencies (e.g. Cox
1980). The g-modes propagate in the
regions where
, while
the imaginary part of ω gives the excitation rate. The dimensionless
frequency, σ,
is defined as σ =
ω(4πG ⟨ ρ ⟩ )−1/2, where ⟨ ρ ⟩ is the mean density of
the star and G
is the gravitational constant. The propagation diagrams for the oscillation modes involve
the Brunt-Väisälä (N) and Lamb (Ll) frequencies (e.g. Cox
1980). The g-modes propagate in the
regions where 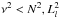 , while the
p-modes
propagate in the regions where
, while the
p-modes
propagate in the regions where 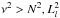 . The remaining
regions are called evanescent zones. The properties of the basic eigenfunctions, kinetic
energy distributions and work integrals for models of B stars were already discussed by
Dziembowski & Pamyatnykh (1992), Dziembowski
et al. (1993), Pamyatnykh (1999), Dziembowski (2009), Dupret (2001), and others. The proper behavior of the Rosseland-mean opacity and
eigenfunctions are necessary, but not sufficient conditions for the κ-mechanism to work. The
other requirement is that the thermal timescale of the driving zone is comparable or longer
than the period of oscillation considered (cf. papers cited above). A mode is unstable when
the cumulative work integral, W, is positive.
. The remaining
regions are called evanescent zones. The properties of the basic eigenfunctions, kinetic
energy distributions and work integrals for models of B stars were already discussed by
Dziembowski & Pamyatnykh (1992), Dziembowski
et al. (1993), Pamyatnykh (1999), Dziembowski (2009), Dupret (2001), and others. The proper behavior of the Rosseland-mean opacity and
eigenfunctions are necessary, but not sufficient conditions for the κ-mechanism to work. The
other requirement is that the thermal timescale of the driving zone is comparable or longer
than the period of oscillation considered (cf. papers cited above). A mode is unstable when
the cumulative work integral, W, is positive.
 |
Fig. 7 Differential work integrals, Rosseland-mean opacities and their derivatives over temperature of l = 1 modes were plotted for the OPAL (opacity data No. 3), K-OPAL/A (No. 13), and K-OPAL/B (No. 20) models of M = 12 M⊙ (Xc ≈ 0.24). For better visibility, κR and κT were multiplied by factors equal to 10 and 8, respectively. The numbers shown on the top of the panels (1,1.92) mean l = 1 and σ = 1.92, etc. (A color version of the figure is available online.) |
 |
Fig. 8 Same as Fig. 7, but for models of M = 40 M⊙ (Xc ≈ 0.26) calculated with the opacity data Nos. 3, 13, and 24, respectively. (A color version of the figure is available online.) |
 |
Fig. 9 Examples of the luminosity f = fR + ifI and radial displacement y = yR + iyI eigenfunctions for unstable modes of seismic models of M = 40 M⊙ (Xc ≈ 0.26) calculated with the opacity data Nos. 3, 13, and 24, respectively. κR and κT were also plotted. (A color version of the figure is available online.) |
In the case of l = 1 p1- and g1-modes, the kinetic energy density have two maxima, one in the region of gravity wave propagation and other one in the region of acoustic wave propagation. For higher overtones, the number of nodes, n, equals to the number of maxima in the kinetic energy distribution.
5.1. The OPAL models
Figure 6 shows frequencies ν [c/d] of unstable modes for stellar models calculated for M = 12 M⊙ at the moment when the central hydrogen content was decreased to Xc = 0.24. The number of a model describes the opacity data used (Table 1). The low-degree modes (l = 0, 1, and 2) were marked individually, while the modes with 3 ≤ l ≤ 10 are shown as small (black) points. The fundamental and first overtone radial, and three l = 1, and three l = 2 nonradial modes were unstable for the OPAL models Nos. 1–3. In addition, a high number of 3 ≤ l ≤ 10 modes were also unstable, especially in the g-mode frequency domain. An increase in the Z-parameter leads to a higher radiation pressure, larger stellar radius and lower frequencies of the modes. Note also that the oscillation spectra have a hybrid character, but g-modes with l ≥ 4 (model No. 1), l ≥ 5 (model No. 2), and l ≥ 6 (model No. 3) were unstable in the low-frequency domain (ν < 3 [c/d]). In the case of model No. 4, only modes with l ≥ 3 are unstable in the whole frequency domain studied in this paper. A lack of data for OPAL models Nos. 5–8 (Z ≤ 0.0108) in Fig. 6 means that (l ≤ 10,0.2 ≤ σ ≤ 6) modes were stable.
Frequencies of all unstable l ≤ 3 modes are shown in the second column of Table 2 for a model of M = 40 M⊙, Xc ≈ 0.25, and Z = 0.0169. They are p- and low-order (n ≤ 4) g-modes of the mixed character.
5.2. The OP models
The OP models Nos. 9 and 10, plotted in Fig. 6, illustrate how Asplund et al. (2009) solar abundances of metals implemented with helioseismic measurements, of Y in Basu & Antia (2004), and Y and Z in Vorontsov et al. (2013), change the oscillation spectra of unstable modes for models of early-type stars. Note that the OPAL models were stable for Z < 0.0108. Now, the evolved MS models with lower abundances of C, N, O, and Ne elements accompanied by higher contribution of iron group elements to Z = 0.009 show unstable modes including low-degree modes in the β Cephei frequency domain. In Table 2, we also show frequencies of all unstable l ≤ 3 modes for the OP models of M = 40 M⊙ and Xc ≈ 0.26.
5.3. The K-OPAL/A models
According to Sect. 4, MS evolutionary tracks for models of M ≤ 20 M⊙ calculated with the OPAL and K-OPAL/A opacity data are almost the same. However, the additional opacity bump at lgT ≈ 5.06, which occurs at the K-OPAL/A models, markedly changes the driving zone for stellar pulsations. Consequently, low-degree oscillation p-modes were stable (Fig. 6) and only g-modes (l ≥ 8) were unstable with the exception of two l = 2 modes at model No. 11. Again, the lack of the models Nos. 14–17 means that (l ≤ 10,0.2 ≤ σ ≤ 5) modes were stable. In inner zones, the propagation diagrams and oscillation energy distributions for the K-OPAL/A models are basically the same as for the OPAL models. The luminosity, f, pressure, p, and radial displacement y-eigenfunctions of unstable modes were similar, but not identical, to those discussed in Cugier et al. (1994). The opacity bump at lgT = 5.06 has a minor influence on these functions for models of B stars.
Figure 7 shows a comparison of the differential work
integrals, 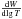 ,
for two modes of l =
1 calculated for the OPAL (with the opacity data No. 3, Fig. 7a) and K-OPAL/A (No. 13, Fig. 7b) models of M = 12 M⊙. The local
κ-driving
is sufficient for the OPAL model, but is much less efficient and cannot overcome the
radiative damping for the K-OPAL/A model. In the case of low-degree (l ≤ 2) g-modes, the driving is too
weak, even for the OPAL model.
,
for two modes of l =
1 calculated for the OPAL (with the opacity data No. 3, Fig. 7a) and K-OPAL/A (No. 13, Fig. 7b) models of M = 12 M⊙. The local
κ-driving
is sufficient for the OPAL model, but is much less efficient and cannot overcome the
radiative damping for the K-OPAL/A model. In the case of low-degree (l ≤ 2) g-modes, the driving is too
weak, even for the OPAL model.
The above discussion concerns a model of M = 12 M⊙ with Xc ≈ 0.25, but the basic results have a more general character. Low-degree p-modes were stable for the K-OPAL/A models with Z ≤ 0.0213 shown in Table 1, as well as for other stellar masses corresponding to β Cephei stars.
The K-OPAL/A model of an M = 40 M⊙ star at the moment when the central hydrogen abundance decreases from X = 0.7347 to Xc ≈ 0.26 shows almost the same value of luminosity as the OPAL model, but markedly lower effective temperature. This reflects the fact that the stellar interior was the same, but stellar radius was larger, as discussed in Sect. 4. Now, unlike the OPAL model, the l ≤ 2 modes were stable (Table 2), but unstable l = 3g7- and g4-modes. Figure 8 shows the differential work integrals of two l = 1 modes for the OPAL (panel a) and K-OPAL/A (panel b) models. The former modes mimic the behavior of unstable modes already discussed for less massive stars. In the case of the K-OPAL/A model, the driving zone was markedly changed by the two-peak structure of κR. The driving corresponding to the opacity bump at lgT = 5.3 was very weak because of the local plateau in κR near lgT ≈ 5.2 (r/R ≈ 0.8). Consequently, l ≤ 2 modes were stable despite an additional driving in outer layers (r/R ≈ 0.92) due to the opacity bump at lgT = 5.06. The driving was more effective for l = 3 (panel b) and three unstable modes were found (Table 2). In Fig. 9, examples of the luminosity f- and radial displacement y-eigenfunctions were plotted for unstable modes. Again, the OPAL modes mimic the behavior of the OPAL modes calculated for less massive stars (cf. Fig. 9a and Cugier et al. 1994), while the K-OPAL/A eigenfunctions are markedly influenced by the opacity bump at lgT = 5.06 (Fig. 9b).
5.4. The K-OPAL/B models
Frequencies of unstable K-OPAL/B modes calculated for seismic models with opacity data Nos. 18–24 were plotted in the right hand panel of Fig. 6. Clearly, the oscillation frequencies are determined by the structure of the stellar interior, while the outer layers control the stability of the modes. No unstable modes were found for ν ≥ 2.6 [c/d] if large opacity took place at lgT = 5.06. In the case of smaller opacity, as in model No. 21, only l ≥ 2 modes were unstable. For a very small opacity bump at lgT = 5.06 (as in model No. 18) we have a seismic model not far from the OPAL model for Z = 0.0266. The models calculated with the opacity data Nos. 22–24 show further evidence that differences between opacity bumps at lgT = 5.06 and 5.3 should be sufficiently large to obtain unstable p-modes. The other condition is that the opacity bump at lgT = 5.3 must be large enough to drive pulsations of β Cephei stars.
Figures 7c and 8c show examples of the differential work integrals of unstable modes for the K-OPAL/B models of M = 12 and 40 M⊙ stars, respectively. Unstable modes were also shown in Table 2 for M = 40 M⊙. The differential work integrals (plotted in Fig. 8c) and the f- and y-eigenfunctions (plotted in Fig. 9c) are quantitatively the same as mentioned above for the K-OPAL/A model No. 13, shown in Figs. 8b and 9b.
5.5. The K-OPAL/C models
 |
Fig. 10 Same as Fig. 6, but opacity data No. 25 (Table 1) were used. Models of M = 9 (No. 25.1), 10 (No. 25.2), 11 (No. 25.3), and 12 M⊙ (No. 25.4) are shown for Xc = 0.70,0.50,0.24, and 0.006. (A color version of the figure is available online.) |
Figure 10 shows the K-OPAL/C models (cf. Sect. 3) for M = 9–12 M⊙. Here, we examined seismic models with the central abundance of hydrogen equal to Xc = 0.70, 0.5, 0.24, and 0.006. The initial chemical composition of elements (X = 0.7394 and Z = 0.0108) and the opacity data No. 25 were selected. As one can see from Fig. 10a, models located very close to ZAMS (Xc = 0.70) show a hybrid character of oscillation spectra. In the high-frequency domain, only f-modes (l ≥ 2,n = 0) were unstable, but the fundamental radial mode (l = 0,σ = 1.886, ν = 11.13 [c/d]) for M = 9 M⊙. Table 3 shows frequencies of all unstable f-modes for M = 9−12 M⊙.
 |
Fig. 11 Differential work integrals, κR and κT were plotted. Panel a) shows unstable f-modes (l = 9n = 0 and l = 10, n = 0) for M = 12 M⊙ and Xc ≈ 0.65 (opacity data No. 25). Panel b) shows unstable l = 1 modes for M = 12 M⊙ and Xc = 0.25 (opacity data No. 25). Panel c) shows unstable l = 3 and l = 4 modes for M = 10 M⊙ and Xc ≈ 0.26 (opacity data No. 27). (A color version of the figure is available online.) |
 |
Fig. 12 Same as Fig. 7, but for models of M = 40 M⊙ and Xc ≈ 0.25 calculated with opacity data Nos. 20 and 25. (A color version of the figure is available online.) |
In more advanced evolutionary models (Xc = 0.50, Fig. 10b), low-degree p-modes (l ≤ 2) were unstable in the high-frequency domain, including the fundamental radial mode. For Xc = 0.25, the radial modes were stable in the model M = 9 M⊙, but unstable for higher masses. Near the end of MS phase of evolution (Xc = 0.006 ) only l ≥ 2 modes remained unstable in the high-frequency domain. In this case, g-modes of l = 2 were also unstable (ν ≈ 0.5 [c/d]) for M = 9 M⊙ (Fig. 10d).
Next, we examined whenever an increase of the OPAL opacity bump at lgT ≈ 5.3 by a factor of 1.7 (cf. Sect. 3.3) was sufficient to drive pulsations of B stars in the Magellanic Clouds. For this purpose we calculated the K-OPAL/C models with the opacity data Nos. 26 and 27. The models of No. 26 show unstable low-degree modes in the p-mode frequency domain. The seismic models of No. 27 (Z ≈ 0.00306) show unstable modes for M ≤ 11 M⊙. In particular, we found unstable modes of l = 3−7 for M = 10 M⊙ in the frequency domain 5.1 ≤ ν ≤ 6.9 [c/d] and l ≥ 8 modes in 2.2 ≤ ν ≤ 3.0 [c/d].
We plotted examples of the differential work integrals for the K-OPAL/C models of M = 10,12, and 40 M⊙ in Figs. 11 and 12. Again, the driving zone of the model of 40 M⊙ has two well separated components, shown in Fig. 12b, for unstable modes of l = 2 (σ = 0.54 and 0.58; cf. Table 2). Note also, that the differential work integrals are almost the same for unstable g8- and g9-modes plotted in Figs. 12a and c. Similar behavior was seen for less massive models (cf. Figs. 7c and 11b). This indicates that the results depend mainly on the opacity data used, but not on EOS for the hybrid K-OPAL (K-OP) models of early-type stars.
6. Conclusions
The present-day results of the Kurucz (2011) opacity project to include all spectral lines of elements are the basic ingredients for the new atmosphere models calculated by Castelli & Kurucz (2003) and Meszaros et al. (2012). According to Kurucz6, much more complete atom models than used so far should increase opacities elsewhere, not only in models of stellar atmospheres. The main motivation for this paper was to investigate seismic models, which are closely related to the new atmosphere models calculated based on the Kurucz’s opacity data.
First, we present further evidence that Kurucz’s more detailed atom models lead to a large excess of opacity at lgT ≈ 5.06 in comparison with the OPAL (and OP) data. This new opacity bump has only a minor counterpart in the OPAL and OP data (Sect. 1).
We calculated the OPAL, OP, K-OPAL, and K-OP models (Sect. 4) for stellar masses M = 9−70 M⊙ from ZAMS to the moment short before helium ignition in the stellar core. We did not assume any mass loss, rotation, or core overshooting. However, we considered different chemical compositions following Castelli & Kurucz (2003) and Meszaros et al. (2012) atmosphere models as well as recent helioseismic measurements of Y and Z made by Vorontsov et al. (2013). The K-OPAL (K-OP) models mean that hybrid CK/OPAL (CK/OP) opacity data were used, viz., the Castelli & Kurucz or Meszaros et al. data at outer layers (up to lgT ≈ 5.2) and the OPAL (OP) data at lgT> 5.2. The evolutionary tracks for the K-OPAL (K-OP) models differ markedly from the OPAL (OP) models for M ≥ 30 M⊙. The effect was caused by the high gradient of radiation pressure near lgT = 5.06. This influences the K-OPAL (K-OP) models of stellar structure at outer layers and thereby stellar radius. Near TAMS, the models M ≥ 50 M⊙ show very low values of lgTeff ≪ 4.4, even for Z ≈ 0.0107. Probably, mass loss at sufficiently high rates is able to end the MS phase of evolution of these stars with higher surface temperature. Note, that TAMS is located near lgTeff ≈ 4.4 for all OPAL (OP) models of massive stars considered. In the case of 9 ≤ M ≤ 20 M⊙, K-OPAL (K-OP) evolutionary tracks are almost the same as for the OPAL (OP) models for a given chemical composition. Now the gradient of radiation pressure at lgT ≈ 5.06 is well below the local gravity acceleration.
Next, we examined (Sect. 5) seismic models considering oscillation modes for the spherical harmonic degree l ≤ 20 and dimensionless frequencies 0.2 ≤ σ ≤ 6. The frequencies of modes are determined by stellar regions where the kinetic energy of the oscillation is high, viz., in the inner layers of early-type stars investigated. This means that the models with the same opacities in these layers show similar frequencies. If the abundance parameter Z ≈ 0.009 is as low as preferred by recent helioseismic measurements (Vorontsov et al. 2013) then the OPAL and OP models of early-type stars were stable for the Grevesse & Noels (1993) mixture. The OP models were, however, unstable in low-degree modes using Asplund et al. (2009) mixture of elements.
We found that the new opacity bump at lgT = 5.06 has important consequences for seismology even for stellar models with almost the same evolutionary tracks as the OPAL (OP) models. In particular, we obtain no unstable high-frequency modes for the K-OPAL/A (K-OP/A) models with masses 10 ≤ M ≤ 20 M⊙ for Z ≤ 0.0213. In the case of O stars, the K-OPAL (K-OP) models show unstable nonradial modes, but only in the low-frequency domain. Such models fit better observed frequencies reported by Blomme et al. (2011) and Mahy et al. (2011). The OPAL and OP models predict unstable modes (Table 3) in the frequency domain not seen in the CoRoT observations of the investigated O stars.
The opacity bump at lgT = 5.3 must be markedly larger than the new opacity bump at lgT = 5.06 to drive pulsations of B stars in p-modes. An increase of the current OPAL (OP) opacities by a factor of about 1.7 at lgT ≈ 5.3 is needed to sufficiently develop large driving zones to excite p-modes at K-OPAL (K-OP) models. The same factor, 1.7, is large enough to obtain unstable modes for Z = 0.0054 and 0.003. These values of Z are not far from the spectroscopic measurements for the Magellanic Clouds.
An increase of the opacity bumps at lgT ≈ 5.3 and 6.3 was already postulated by Pamyatnykh et al. (2004) and Zdravkov & Pamyatnykh (2008) to explain observed oscillation spectra in β Cephei stars. In this paper, we suggest that the opacity bump at lgT ≥ 5.3 may be markedly underestimated as a result of atom models used in the OPAL and OP projects. The diffusion of some elements, because of high radiation pressure near lgT ≈ 5.06, may also be important for asteroseismology of O and B stars. In this context, we note that opacities caused by the α-rich elements (O, Ne, Mg, Na, Si, S, Ar, Ca, and Ti) may play some role. For high abundances of these elements at stellar layers near lgT = 5.06, the κ-mechanism is not expected to be efficient to drive instability in B stars. If a contribution of these elements is smaller (as in Asplund et al. 2009, mixture), then the driving zone for stellar pulsations is more extended. This means that the factor of 1.7 can be regarded as an upper limit.
Finally, we would like to point out that there are several points that were crudely approximated. Some of them result from the present lack of sufficient atomic data (e.g. Pradhan & Nahar 2009). However, the current OPAL and OP opacities, which include the old Kurucz’s atomic data for Fe I–IV (Badnell et al. 2005), could also be upgraded, using the new Kurucz data for metals at higher ionization stages. In addition, the Rosseland-mean opacities are sensitive to pressure-broadening parameters of bound-bound transitions, especially at metallic opacity bumps. Relatively little is known about how this affects seismic models of stars (Appendix A).
Online material
Appendix A: Details about Kurucz’s and K-OPAL opacity data
Examples of Meszaros et al. (2012) opacity data available from ATLAS-APOGEE website.
 |
Fig. A.1 Rosseland-mean opacities lgκR [ cm2 g-1 ] calculated by Castelli & Kurucz for different chemical composition of elements and ξ = 0. The data plotted for the gas pressure, lgPg = 2,4,6, and 8 (in cgs units) were taken from the Castelli website on 2012. Black lines show opacity data Nos. 1–9 listed in Table A.1, while blue lines display opacity data Nos. 10–22. |
 |
Fig. A.2 Same as Fig. A.1, but the Rosseland-mean opacities lgκR [ cm2 g-1 ] calculated by Castelli & Kurucz for enhanced abundances of O, Ne, Mg, Si, S, Ar, Ca, and Ti elements by +0.4 dex, viz., opacity data Nos. 23–35 listed in Table A.1 were plotted. |
 |
Fig. A.3 Examples of the Rosseland-mean opacities lgκR [ cm2 g-1 ] calculated by Meszaros et al. for different chemical composition of elements and ξ = 2km s-1 (Table A.2). The data plotted for the gas pressure, lgPg = 2,4,6, and 8 (in cgs units) were taken from the ATLAS-APOGEE website on 2013. |
 |
Fig. A.4 Derivatives of the Rosseland-mean opacities over density
|
 |
Fig. A.5 Same as Fig. A.4, but for |
 |
Fig. A.6 OP monochromatic cross-sections lgσ (in atomic units) vs.
|
 |
Fig. A.7 Derivatives of the Rosseland-mean opacities over temperature
|
The Rosseland-mean opacities calculated by Castelli & Kurucz are available in tabular form for different metallicities and microturbulent velocities ξ = 0,1,2,4, and 8 km s-1. Following Kurucz, the data (Table A.1) were named using the scheme, which describes abundances of metals relative to the solar abundances listed in Grevesse & Sauval (1998). In particular, p15 corresponds to enhanced abundances of metals by [m/H] = lg(m/H) − lg(m/H)⊙ = +1.5 dex, the solar chemical composition ([m/H] = +0.0) is denoted as p00, and [m/H] = −4.0 as m40. The X, Y, and Z abundance parameters and the mass abundances of oxygen (ZO) and iron (ZFe) were also shown in Table A.1. The opacity data Nos. 1–22 have the same relative abundances of metals taken from Grevesse & Sauval (1998), while data Nos. 23–35 have enhanced abundances of O, Ne, Mg, Si, S, Ar, Ca, and Ti by +0.4 dex. These elements are produced by stellar nucleosyntheses in the α-process. The last two rows in Table A.1 show the abundance parameters listed in Asplund et al. (2005) and Asplund et al. (2009).
The CK Rosseland-mean opacities, 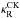 , were
tabulated for 3.3 ≤ lgT ≤
5.3 and −4.0 ≤
lgPg ≤ 8.0, where Pg is the gas
pressure in the cgs units. Figure A.1 shows
, were
tabulated for 3.3 ≤ lgT ≤
5.3 and −4.0 ≤
lgPg ≤ 8.0, where Pg is the gas
pressure in the cgs units. Figure A.1 shows 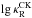 as a
function of lgT for lgPg =
2,4,6, and 8, and ξ = 0. In each panel, the
top line corresponds to X =
0.4786 and Z = 0.3596, while the bottom line to
X =
0.7474 and Z = 1.49 × 10-7 (Table A.1). Clearly, the opacity bump at lgT ≈ 5.06 is caused by
metals and can be explained by much more detailed atom models of the new Kurucz data.
The opacities with enhanced abundances of the α-rich elements (O, Ne, Mg, Si, S, Ar, Ca, and
Ti) by +0.4 dex. were plotted in Fig. A.2. These elements participate in the opacity
bump at lgT ≈
5.06 in addition to other heavy elements (cf. also Fig. 2, where the data of m05 and m05a
were plotted).
as a
function of lgT for lgPg =
2,4,6, and 8, and ξ = 0. In each panel, the
top line corresponds to X =
0.4786 and Z = 0.3596, while the bottom line to
X =
0.7474 and Z = 1.49 × 10-7 (Table A.1). Clearly, the opacity bump at lgT ≈ 5.06 is caused by
metals and can be explained by much more detailed atom models of the new Kurucz data.
The opacities with enhanced abundances of the α-rich elements (O, Ne, Mg, Si, S, Ar, Ca, and
Ti) by +0.4 dex. were plotted in Fig. A.2. These elements participate in the opacity
bump at lgT ≈
5.06 in addition to other heavy elements (cf. also Fig. 2, where the data of m05 and m05a
were plotted).
Recently, an extensive grid of atmosphere models, as well as the Rosseland-mean
opacities, 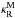 , were
recalculated by Meszaros et al. (2012) for scaled
solar abundances of metals given by Asplund et al. (2005). Examples are shown in Table A.2
and Fig. A.3. The data were named using the Kurucz scheme for the scaled metal
(m)
abundances composed with a standard/nonstandard content of C (c) and O (o).
, were
recalculated by Meszaros et al. (2012) for scaled
solar abundances of metals given by Asplund et al. (2005). Examples are shown in Table A.2
and Fig. A.3. The data were named using the Kurucz scheme for the scaled metal
(m)
abundances composed with a standard/nonstandard content of C (c) and O (o).
We would like to note that Castelli & Kurucz’s mixture of elements has higher values of Z and ZO than those of Asplund et al. (2009), but the same abundance of Fe. The Meszaros et al. data (M) have lower Z- and ZFe-values. In addition, the helium abundance of the CK and M standard (solar) mixtures is not far from the helioseismological value Y = 0.2485 given by Basu & Antia (2004). This helium abundance was adopted by Grevesse & Sauval (1998), Asplund et al. (2005) and Asplund et al. (2009). The CK and M elemental mixtures have Y = 0.1635−0.2526 (Tables A.1 and A.2).
The CK and M atmosphere models are available from Castelli and ATLAS-APOGEE websites (Sect. 3), respectively. The older models, available from Kurucz website, were calculated for older opacity distribution functions (ODF) with about 58 million lines of atoms and molecules in total. Despite this, according to Kurucz (2011), the line opacity was underestimated because not enough lines were included in calculations.
According to Kurucz (2012, priv. comm.), the CK opacities are less reliable for
lgT ≥
5.2. The K-OPAL models were therefore calculated using the CK (or M)
opacities for lgT < 5.2 and the OPAL (or
OP) data for higher temperatures. We adjusted these two kinds of Rosseland-mean
opacities at lgT =
5.2, assuming ![\hbox{$\lg \kappa_{\rm{R}}^{\rm{K-OPAL}~(or ~ \rm{K-OP})}(5.2, P_{\rm{g}}) = [\lg \kappa_{\rm{R}}^{\rm{CK}~ (or~ \rm{M})}(5.175, P_{\rm{g}}) + \lg \kappa_{\rm{R}}^{\rm{OPAL}~ (or ~ \rm{OP})}(5.225, P_{\rm{g}})]/2$}](/articles/aa/full_html/2014/05/aa20507-12/aa20507-12-eq328.png) . The opacity data are
usually included as tables of κR(lgT,lgR)
(the OPAL format) in computing codes for modeling stellar structure, where
lgR = lgρ
− 3lgT + 18. We attempted to achieve good accuracy
in the transformation of κR from (lgT,lgPg) to
(lgT,lgR) variables. First, we
solved the EOS with a Kurucz’s computing code to find out gas densities, ρ, for each pair of
(lgT,
lgPg). Next, we interpolated the opacity
data to (lgT, lgR)-points. In addition to κR, the
derivatives of the Rosseland-mean opacities over temperature and density were calculated
numerically with two methods. In the first method, having already calculated tables of
κR(lgT,lgρ),
we used Kurucz’s (1970) differentiation procedure
to obtain
. The opacity data are
usually included as tables of κR(lgT,lgR)
(the OPAL format) in computing codes for modeling stellar structure, where
lgR = lgρ
− 3lgT + 18. We attempted to achieve good accuracy
in the transformation of κR from (lgT,lgPg) to
(lgT,lgR) variables. First, we
solved the EOS with a Kurucz’s computing code to find out gas densities, ρ, for each pair of
(lgT,
lgPg). Next, we interpolated the opacity
data to (lgT, lgR)-points. In addition to κR, the
derivatives of the Rosseland-mean opacities over temperature and density were calculated
numerically with two methods. In the first method, having already calculated tables of
κR(lgT,lgρ),
we used Kurucz’s (1970) differentiation procedure
to obtain 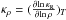 and
and
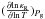 .
Next, we used the thermodynamic identity for
.
Next, we used the thermodynamic identity for
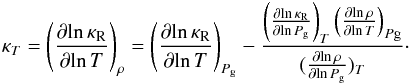 (A.1)Again,
the CK (or M) and OPAL (or OP) derivatives were adjusted at lgT = 5.2. In the second
method, we started from κR(lgT,lgR)
and ran Seaton’s (1993) bicubic interpolation
procedure, which involves 16 neighborhood points as well as the derivatives of
κR over temperature and density. Both
methods yield similar results, although the second method reveals a little bit more
regular behavior of the derivatives because of the higher number of data points involved
in the procedure. In the rest of this paper we used data obtained from the second
method. No additional smoothing procedure was ran.
(A.1)Again,
the CK (or M) and OPAL (or OP) derivatives were adjusted at lgT = 5.2. In the second
method, we started from κR(lgT,lgR)
and ran Seaton’s (1993) bicubic interpolation
procedure, which involves 16 neighborhood points as well as the derivatives of
κR over temperature and density. Both
methods yield similar results, although the second method reveals a little bit more
regular behavior of the derivatives because of the higher number of data points involved
in the procedure. In the rest of this paper we used data obtained from the second
method. No additional smoothing procedure was ran.
The K-OPAL opacity data discussed in Sect. 3 show two opacity bumps at lgT = 5.06 and
5.3. Examples of the
hybrid opacities, κR were plotted in Fig. 2 and their derivatives over density, (κρ)T,
and temperature (κT)ρ,
in Figs. A.4 and A.5, respectively. The local minimum of the opacity at lgT = 5.2 plays a crucial
role in the K-OPAL seismic models of B stars as discussed in Sect. 5. A deeper insight
into the problem follows from an analysis of the OP monochromatic opacities. Figure A.6
shows contributions of different elements to the total opacity (yellow lines) for
lgT =
4.8,5.0, and 5.3, and lgNe = 16. The
black lines display opacity caused by H, He, Fe, and electron scattering
(σe), while cross-sections of Fe are
shown as violet lines. In Fig. A.6, the monochromatic cross-sections, σ(u) are
given in atomic units, where 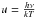 .
The Rosseland-mean opacity per unit mass is then
.
The Rosseland-mean opacity per unit mass is then
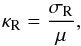 (A.2)where
(A.2)where
![\appendix \setcounter{section}{1} \begin{eqnarray} \frac{1}{\sigma_{\rm{R}}} &=& \int_0^\infty \frac{1}{\sigma(u)} F(u) {\rm d}u, \\ F(u)&=& \frac{15}{\pi^4} u^4 {\rm e}^{-u} /[1-{\rm e}^{-u}]^2 \end{eqnarray}](/articles/aa/full_html/2014/05/aa20507-12/aa20507-12-eq345.png) and
μ is the
mean atomic weight. The smooth red lines in Fig. A.6, corresponding to lgF(u) +
C, display that a spectral region near
u = 3.83
contributes mostly to the Rosseland-mean opacity. The constant C was introduced for
better visibility of the Rosseland-mean weighting function (corrected for stimulated
emission), F(u). In the cases of
lgT = 4.8
and 5.0, the Fe-curtain (violet lines in Fig. A.6) is located well below opacity caused
by H, He, and σe at spectral region near
u ≈ 3.83.
Note that the contribution of metals other than Fe is significant at lgT = 5.0. This is the
reason why the new Kurucz data were able to change the Rosseland-mean opacity mostly
near lgT =
5.06. The Fe-curtain dominates at lgT = 5.3 (Fig. A.6).
Now, the OP (and OPAL) opacity is caused mostly by very many lines due to Fe in electron
configurations of the type 3sx3py3dz and
3sx3py3dznl, (Iglesias et al.
1990; Lynas-Gray et al. 1995; Seaton et al. 1994). As
one can see, the synthetic Fe cross-section is located above the total cross-sections
caused by H, He, and σe (a brown line) near u ≈ 3.83 (and
u ≥ 7).
This changes quickly depending on the temperature. At lgT = 5.2, the Fe-curtain
is also seen, but its maximum is shifted to u ≈ 5. Similarly, the maximum is located at
u ≈ 2.3
for lgT =
5.5. As a result, the OP (and OPAL) opacity bump at lgT = 5.3 is narrow and
the K-OP (and K-OPAL) data have a two-peak structure of κR with the
additional opacity bump at lgT = 5.06.
and
μ is the
mean atomic weight. The smooth red lines in Fig. A.6, corresponding to lgF(u) +
C, display that a spectral region near
u = 3.83
contributes mostly to the Rosseland-mean opacity. The constant C was introduced for
better visibility of the Rosseland-mean weighting function (corrected for stimulated
emission), F(u). In the cases of
lgT = 4.8
and 5.0, the Fe-curtain (violet lines in Fig. A.6) is located well below opacity caused
by H, He, and σe at spectral region near
u ≈ 3.83.
Note that the contribution of metals other than Fe is significant at lgT = 5.0. This is the
reason why the new Kurucz data were able to change the Rosseland-mean opacity mostly
near lgT =
5.06. The Fe-curtain dominates at lgT = 5.3 (Fig. A.6).
Now, the OP (and OPAL) opacity is caused mostly by very many lines due to Fe in electron
configurations of the type 3sx3py3dz and
3sx3py3dznl, (Iglesias et al.
1990; Lynas-Gray et al. 1995; Seaton et al. 1994). As
one can see, the synthetic Fe cross-section is located above the total cross-sections
caused by H, He, and σe (a brown line) near u ≈ 3.83 (and
u ≥ 7).
This changes quickly depending on the temperature. At lgT = 5.2, the Fe-curtain
is also seen, but its maximum is shifted to u ≈ 5. Similarly, the maximum is located at
u ≈ 2.3
for lgT =
5.5. As a result, the OP (and OPAL) opacity bump at lgT = 5.3 is narrow and
the K-OP (and K-OPAL) data have a two-peak structure of κR with the
additional opacity bump at lgT = 5.06.
As mentioned in Sect. 3.2, the K-OPAL/B models were designed to study how the relative
strength of the opacity bumps at lgT = 5.06 and 5.3 influence seismic models of
early-type stars. They are basically the OPAL models for Z = 0.0264 and
Z =
0.0168, but 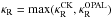 was selected near the opacity
bump at lgT ≈
5.06. The CK opacity data of m075,m05,m04,m02,
and p00
were considered. Figures A.7 show κR and κT for models
of Nos. 18–20 (Table 1) in comparison with the
OPAL (No. 1) and K-OPAL/A data (No. 11).
was selected near the opacity
bump at lgT ≈
5.06. The CK opacity data of m075,m05,m04,m02,
and p00
were considered. Figures A.7 show κR and κT for models
of Nos. 18–20 (Table 1) in comparison with the
OPAL (No. 1) and K-OPAL/A data (No. 11).
Relatively little is known about the sensitivity of the OP and OPAL data to the pressure-broadening parameters for spectral lines. There is little sensitivity at high densities, where the lines become very broad and give a quasicontinuum, or at very low densities, where the profiles are mainly determined by Doppler broadening and radiation damping. At intermediate densities, like lgNe = 15.5 and lgT = 5.2 (lgR = −5.8) discussed by Seaton et al. (1994), an increase of the pressure broadening parameters of Fe lines by a factor of 2 results in an increase in the Rosseland-mean opacity by 33 per cent for the solar mix of elements. The opacity is much lower when only doppler broadening of lines is assumed (Rogers & Iglesias 1992).
In addition, including more electron configurations and many more line transitions, as in Kurucz (2011), would probably also increase opacity at lgT> 5.2. Another potentially important reason why the OP (and OPAL) opacities should be upgraded is related to autoionizing transitions. In the OP project, these transitions were treated as resonances in photoionization cross-sections (Bautista 1997). To make the problem tractable, each LS-term was represented by only one level with its average energy. The splitting of spectroscopic LS terms
into individual levels may be necessary for final calculations of photoionization cross-sections with resonance structures. This is suggested by Kurucz’s treatment of autoionizing transitions (Castelli & Kurucz 2004) and by recent results published by Nahar et al. (2011), which include the fine structure explicitly for Fe XVII. Similarly, the new effective cross-sections with photoexcitation-of-core (PEC) resonances for O III and Fe XXI are much higher, up to two orders of magnitude, than in the OP data (Fig. 1 in Pradhan & Nahar 2009). The missing opacity in the OP data may lie in an energy range from a few eV to few hundreds of eV, depending on the element and ionization stage. Therefore, we also searched K-OPAL/C (and K-OP/C) models (with opacity data Nos. 23–25) with enhanced opacities at lgT> 5.2. In the case of No. 23, EOS and nuclear reaction rates were calculated for the initial (at ZAMS) chemical composition of X = 0.7394, Y = 0.2499, and Z = 0.0107. The CK opacity data corresponding to Z = 0.0107 were assumed at lgT < 5.2, but the OPAL opacities corresponding to Z = 0.0264 at lgT> 5.2. Similarly, models of Nos. 24 and 25, were calculated for Z = 0.00537 and 0.00303 with enhanced opacities at lgT> 5.2 (OPAL: Z = 0.0168 and 0.0134), respectively.
Examples of κR and κT are shown in Figs. 11 and 12 (Sect. 5), where differential work integrals were plotted for the K-OPAL models.
Acknowledgments
The author acknowledges the referee’s helpful comments and language editor’s corrections.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash (San Fransisco, CA: ASP), ASP Conf. Ser. 336, 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A. 1992, MNRAS, 254, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., & Dziembowski, W. A. 1999, MNRAS, 309, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A., Pigulski, A., Cat, P. De, et al. 2011, MNRAS, 413, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Antia, H. M. 2004, ApJ, 606, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. A. 1997, A&AS, 122, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blomme, R., Mahy, L., Catala, C., et al. 2011, A&A, 533, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briquet, M., Aerts, C., Auvergne, M., et al. 2011, A&A, 527, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, IAU Symp., 210, 10 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, A&A, 419, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, J. P. 1980, Theory of Stellar Evolution (Printeton, New Jersey: Princeton University Press) [Google Scholar]
- Cugier, H. 2012, A&A, 547, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cugier, H. 2014, IAU Symp., 301, 401 [NASA ADS] [Google Scholar]
- Cugier, H., Dziembowski, W. A., & Pamyatnykh, A. A. 1994, A&A, 291, 143 [NASA ADS] [Google Scholar]
- Daszynska-Daszkiewicz, J., & Walczak, P. 2010, MNRAS, 403, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Daszynska-Daszkiewicz, J., Dziembowski, W. A., & Pamyatnykh, A. A. 2005, A&A, 441, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daszynska-Daszkiewicz, J., Dziembowski, W. A., & Pamyatnykh, A. A. 2006, Mem. Soc. Astron. It., 77, 113 [Google Scholar]
- De Cat, P., Briquet, M., Aerts, C., et al. 2007, A&A, 463, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degroote, P., Briquet, M., Auvergne, M., et al. 2010, A&A, 519, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Degroote, P., Aerts, C., Michel, E., et al. 2012, A&A, 542, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diago, P. D., Gutierrez-Soto, J., Fabregat, J., & Martayan, C. 2008a, A&A, 480, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diago, P. D., Gutierrez-Soto, J., Fabregat, J., Martayan, C., & Soso, J. 2008b, Comm. Asteroseism., Wroclaw HELAS Workshop, eds. M. Breger, W. Dziembowski, & M. Thompson, 157, 299 [Google Scholar]
- Dziembowski, W. 1997, A&A, 27, 203 [Google Scholar]
- Dziembowski, W. A. 2009, Comm. Asteroseismol., 158, 227 [NASA ADS] [Google Scholar]
- Dziembowski, W. A., & Pamyatnykh, A. A. 1992, MNRAS, 262, 204 [Google Scholar]
- Dziembowski, W. A., Moskalik, P., & Pamyatnykh, A. A. 1993, MNRAS, 265, 588 [NASA ADS] [Google Scholar]
- Dupret, M. A. 2001, A&A, 366, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gautschy, A., & Saio, H. 1993, MNRAS, 262, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Perfectionnement de l’Association Vaudoise de Chercheurs en Physique, AVCP, Lausanne, 205 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Handler, G. 2009, MNRAS, 398, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, A. A., Rogers, F. J., & Wilson, B. G. 1990, ApJ, 360, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C., Arentoft, T., Glowienka, L., et al. 2008, MNRAS, 386, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Kolaczkowski, Z., Pigulski, A., Soszynski, I., et al. 2004, in Variable stars in the Local Group, eds. D. W. Kurtz, & K. R. Pollatd, Astron. Soc. Pac., San Francisco, ASP Conf. Ser., 310, 22 [Google Scholar]
- Kolaczkowski, Z., Pigulski, A., Soszynski, I., et al. 2006, Mem. Soc. Astron. It., 77, 336 [Google Scholar]
- Kurucz, R. 1970, SAOSR, 309 [Google Scholar]
- Kurucz, R. 2005, Mem. Soc. It. Supp., 8, 14 [Google Scholar]
- Kurucz, R. 2011, Can. J. Phys., 89, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lynas-Gray, A. E., Seaton, M. J., & Storey, P. J. 1995, J. Phys. B, 28, 2817 [NASA ADS] [CrossRef] [Google Scholar]
- Mahy, L., Gosset, E., Baudin, F., et al. 2011, A&A, 525, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meszaros, Sz., Allen de Prieto, C., Edvardson, B., et al. 2012, AJ, 144, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Montalban, J., & Dupret, M. A. 2007, MNRAS, 37, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Moskalik, P. 1995, in Proc. IAU Coll. 155, eds. R. S. Stobie, & P. A. Whitelock, ASP Conf. Ser., 83, 44 [Google Scholar]
- Nahar, S. N., Pradhan, A. K., Chen, G.-X., & Eissner, W. 2011, Phys. Rev. A, 83, 053417 [NASA ADS] [CrossRef] [Google Scholar]
- Pamyatnykh, A. A. 1999, A&A, 49, 119 [Google Scholar]
- Pamyatnykh, A. A., Handler, G., & Dziembowski, W. A. 2004, MNRAS, 350, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Pamyatnykh, A. A., & Ziomek, W. 2007, Comm. Asteroseism., 150, 207 [Google Scholar]
- Pápics, P. I., Briquet, M., Baglin, A., et al. 2012, A&A, 542, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pigulski, A., & Kolaczkowski, Z. 1998, in A Half-Centaury of Stellar Pulsation Interpretations, eds. P. A. Bradley, & J. A. Guzik, ASP Conf. Ser., 135, 153 [Google Scholar]
- Pigulski, A., & Kolaczkowski, Z. 2002, A&A, 388, 88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pigulski, A., & Pojmanski, G. 2008, A&A, 477, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pradhan, A. K., & Nahar, S. N. 2009, AIP Conf. Proc., 1171, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Wison, B. G., & Iglesias, C. A. 1988, Phys. Rev. A, 38, 5007 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, S., Montalban, J., Morel, T., et al. 2012, MNRAS, 422, 346 [Google Scholar]
- Saio, H., & Cox, J. P. 1980, ApJ, 236, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Kambe, E., & Lee, U. 2000, ApJ, 543, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1987, J. Phys. B: At. Mol. Phys., 20, 6363 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1993, MNRAS, 256, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J., Yan, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Vogh, S. S., & Penrod, G. D. 1983, ApJ, 275, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Vorontsov, S. V., Baturin, V. A., Ayukov, S. V., & Gryaznov, V. K. 2013, MNRAS, 430, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G. A. H., Yang, S., & Fahlmman, G. G. 1979, ApJ, 233, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G. A. H., Kuschnig, R., Matthews, J. M., et al. 2005, ApJ, 623, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Zdravkov, T., & Pamyatnykh, A. A. 2008, Comm. Asteroseism., 157, 385 [Google Scholar]
All Tables
Examples of Meszaros et al. (2012) opacity data available from ATLAS-APOGEE website.
All Figures
 |
Fig. 1 Rosseland-mean opacity κR [ cm2 g-1 ] vs. lgT taken from the Castelli & Kurucz (2003) atmosphere models of lgg = 5.0, Teff = 15 000, 20 000, 25 000, 30 000 K (left panel) and Teff = 35 000,40 000,45 000 K (right panel) in comparison with envelope models calculated with the OPAL data. The atmosphere models corresponding to the microturbulent velocity ξ = 0 (taken from the Castelli website) were plotted as lines with pluses. Both the CK and OPAL models were calculated for X = 0.7347 and Z = 0.0169. |
| In the text | |
 |
Fig. 2 Rosseland-mean opacities κR [ cm2 g-1 ] vs. lgT for lgR = lgρ − 3lgT + 18 = −6.0, −5.0, −4.5, and −4.0. The OPAL (blue lines) and K-OPAL/A (red lines) data were plotted for Z = 0.0266,0.0168 and 0.00542, viz., opacity data Nos. 1, 3, 7, 11, 13, and 16 listed in Table 1 were displayed. The K-OPAL data with α-enhanced elements (m05a in Table A.1) were also plotted as green lines. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 3 H-R diagram for OPAL (blue lines) and K-OPAL (black lines) models of M = 70,60,50,40,35,30, and 20 M⊙ calculated with the initial chemical composition X = 0.7347 and Z = 0.0169. No mass loss and no core overshooting were included in the calculations. Lo means the solar luminosity and Mo solar mass. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 4 H-R diagram for OPAL and K-OPAL models of M = 40 M⊙ calculated with different initial chemical compositions. The evolutionary tracks were numbered according to the opacity data listed in Table 1. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for M = 12 M⊙. The evolutionary track for M = 13 M⊙ (only for the opacity data No. 25; violet line) was also plotted. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 6 Frequencies ν [c/d] of unstable modes (l ≤ 10) for the OPAL, OP, and K-OPAL models of M = 12 M⊙ with the central hydrogen content Xc = 0.24. The models were numbered according to the opacity data used (Table 1). Symbols are explained in the right hand panel. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 7 Differential work integrals, Rosseland-mean opacities and their derivatives over temperature of l = 1 modes were plotted for the OPAL (opacity data No. 3), K-OPAL/A (No. 13), and K-OPAL/B (No. 20) models of M = 12 M⊙ (Xc ≈ 0.24). For better visibility, κR and κT were multiplied by factors equal to 10 and 8, respectively. The numbers shown on the top of the panels (1,1.92) mean l = 1 and σ = 1.92, etc. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 8 Same as Fig. 7, but for models of M = 40 M⊙ (Xc ≈ 0.26) calculated with the opacity data Nos. 3, 13, and 24, respectively. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 9 Examples of the luminosity f = fR + ifI and radial displacement y = yR + iyI eigenfunctions for unstable modes of seismic models of M = 40 M⊙ (Xc ≈ 0.26) calculated with the opacity data Nos. 3, 13, and 24, respectively. κR and κT were also plotted. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 10 Same as Fig. 6, but opacity data No. 25 (Table 1) were used. Models of M = 9 (No. 25.1), 10 (No. 25.2), 11 (No. 25.3), and 12 M⊙ (No. 25.4) are shown for Xc = 0.70,0.50,0.24, and 0.006. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 11 Differential work integrals, κR and κT were plotted. Panel a) shows unstable f-modes (l = 9n = 0 and l = 10, n = 0) for M = 12 M⊙ and Xc ≈ 0.65 (opacity data No. 25). Panel b) shows unstable l = 1 modes for M = 12 M⊙ and Xc = 0.25 (opacity data No. 25). Panel c) shows unstable l = 3 and l = 4 modes for M = 10 M⊙ and Xc ≈ 0.26 (opacity data No. 27). (A color version of the figure is available online.) |
| In the text | |
 |
Fig. 12 Same as Fig. 7, but for models of M = 40 M⊙ and Xc ≈ 0.25 calculated with opacity data Nos. 20 and 25. (A color version of the figure is available online.) |
| In the text | |
 |
Fig. A.1 Rosseland-mean opacities lgκR [ cm2 g-1 ] calculated by Castelli & Kurucz for different chemical composition of elements and ξ = 0. The data plotted for the gas pressure, lgPg = 2,4,6, and 8 (in cgs units) were taken from the Castelli website on 2012. Black lines show opacity data Nos. 1–9 listed in Table A.1, while blue lines display opacity data Nos. 10–22. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but the Rosseland-mean opacities lgκR [ cm2 g-1 ] calculated by Castelli & Kurucz for enhanced abundances of O, Ne, Mg, Si, S, Ar, Ca, and Ti elements by +0.4 dex, viz., opacity data Nos. 23–35 listed in Table A.1 were plotted. |
| In the text | |
 |
Fig. A.3 Examples of the Rosseland-mean opacities lgκR [ cm2 g-1 ] calculated by Meszaros et al. for different chemical composition of elements and ξ = 2km s-1 (Table A.2). The data plotted for the gas pressure, lgPg = 2,4,6, and 8 (in cgs units) were taken from the ATLAS-APOGEE website on 2013. |
| In the text | |
 |
Fig. A.4 Derivatives of the Rosseland-mean opacities over density
|
| In the text | |
 |
Fig. A.5 Same as Fig. A.4, but for |
| In the text | |
 |
Fig. A.6 OP monochromatic cross-sections lgσ (in atomic units) vs.
|
| In the text | |
 |
Fig. A.7 Derivatives of the Rosseland-mean opacities over temperature
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.