| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201322848 | |
| Published online | 04 April 2014 | |
MHD modeling of coronal loops: the transition region throat ⋆
1
Dipartimento di Fisica & ChimicaUniversità di
Palermo,
Piazza del Parlamento 1,
90134
Palermo,
Italy
e-mail:
m.guarrasi@cineca.it
2
now at: CINECA – Interuniversity consortium, via Magnanelli 6/3,
40033 Casalecchio di Reno, Bologna, Italy
3
INAF-Osservatorio Astronomico di Palermo, Piazza del Parlamento 1,
90134
Palermo,
Italy
4
Dipartimento di Fisica Generale, Università di
Torino, via Pietro Giuria
1, 10125
Torino,
Italy
5
NASA Goddard Space Flight Center, Greenbelt
MD
20771,
USA
Received:
14
October
2013
Accepted:
29
January
2014
Context. The expansion of coronal loops in the transition region may considerably influence the diagnostics of the plasma emission measure. The cross-sectional area of the loops is expected to depend on the temperature and pressure, and might be sensitive to the heating rate.
Aims. The approach here is to study the area response to slow changes in the coronal heating rate, and check the current interpretation in terms of steady heating models.
Methods. We study the area response with a time-dependent 2D magnetohydrodynamic (MHD) loop model, including the description of the expanding magnetic field, coronal heating and losses by thermal conduction, and radiation from optically thin plasma. We run a simulation for a loop 50 Mm long and quasi-statically heated to about 4 MK.
Results. We find that the area can change substantially with the quasi-steady heating rate, e.g., by ~40% at 0.5 MK as the loop temperature varies between 1 MK and 4 MK, and, therefore, affects the interpretation of the differential emission measure vs. temperature (DEM(T)) curves.
Key words: Sun: corona / Sun: magnetic fields / Sun: transition region / magnetohydrodynamics (MHD)
The movie associated to Fig. 4 is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
An important challenge in trying to understand the structure and heating of solar active regions is to explain the relative amounts of material at different temperatures. This is typically expressed in terms of the differential emission measure distribution (DEM(T)). Models that use steady heating and a flux tube geometry that slowly expands with height are unable to reproduce the observed distributions. However, realistic flux tubes are expected to expand very rapidly with height between the chromosphere and corona, where the plasma beta (β = 8πP/B2) changes from being much greater than to much less than unity. The thin transition region where temperatures increase from chromospheric to coronal values occurs somewhere within this rapidly expanding throat. Thus, we expect the cross-sectional area of flux tubes to be a strong function of temperature. If the dependence has the right form, steady heating models may in fact be able to explain the observed DEM(T). This was demonstrated by Warren et al. (2010b) for the core of an active region (the generally hot central part of the active region that connects opposite polarity moss regions, which are the transition region footpoints of the hot loops).
A potential difficulty with this picture has been pointed out by Tripathi et al. (2010). The height of the transition region depends on
the coronal pressure and so moves up and down in response to changes in the coronal heating
rate, either fast or slow. If the heating rate increases, so too does the pressure, and the
transition region is forced downward. If the heating rate decreases, some of the overlying
pressure is relieved, which allows the transition region to move upward. For gradual heating
variations, the amount of vertical displacement is given approximately by 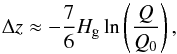 (1)where Hg is the
gravitational scale height of the chromosphere (approximately 500 km), Q is the new heating rate,
and Q0 is the original heating rate. We have
made use of the fact that Q ∝ p7/6
for quasi-static evolution, where p is the pressure. See Klimchuk (2006) for a similar expression appropriate to impulsive
heating. A heating rate increase of a factor of 100, which increases the loop apex
temperature by a factor of 3.7, causes the transition region to be displaced downward by
approximately 2700 km. This is not small compared to the length scale of expansion in the
flux tube throat (Gabriel 1976; Athay 1981). Thus, the cross-sectional area at any given temperature
A(T) could change dramatically. This
would alter DEM(T) so that a model is no longer compatible with
observations. The very sensitive dependence of the A(T)
relationship on the heating rate suggests that too much fine tuning is required for a steady
heating model to have widespread applicability.
(1)where Hg is the
gravitational scale height of the chromosphere (approximately 500 km), Q is the new heating rate,
and Q0 is the original heating rate. We have
made use of the fact that Q ∝ p7/6
for quasi-static evolution, where p is the pressure. See Klimchuk (2006) for a similar expression appropriate to impulsive
heating. A heating rate increase of a factor of 100, which increases the loop apex
temperature by a factor of 3.7, causes the transition region to be displaced downward by
approximately 2700 km. This is not small compared to the length scale of expansion in the
flux tube throat (Gabriel 1976; Athay 1981). Thus, the cross-sectional area at any given temperature
A(T) could change dramatically. This
would alter DEM(T) so that a model is no longer compatible with
observations. The very sensitive dependence of the A(T)
relationship on the heating rate suggests that too much fine tuning is required for a steady
heating model to have widespread applicability.
The last statement involves a big caveat, however. It assumes that flux tubes remain rigid as the heating and pressure change. This is not the case in a real magnetohydrodynamic (MHD) system. With increasing pressure, a flux tube will expand laterally at the same time that the transition region is pushed downward. Hence, the area at a given temperature might remain constant, whereas it would decrease in a rigid tube. It is possible that the A(T) relationship in the transition region could remain largely unchanged. (We note, however, that any lateral expansion would be even more pronounced in the corona, so the emission measure relationship between the transition region and corona would then change.) The purpose of our study is to determine how A(T) varies in response to changes in the coronal heating rate, especially slow changes corresponding to quasi-static evolution. If there is a strong dependence on the heating rate, then the steady heating interpretation of DEM(T) should be reexamined.
In this paper we present a 2D MHD loop model that naturally accounts for loop expansion through the transition region. We have used this model to study the plasma response to the heating into and around the moss regions. At variance with 1D models having a specified expanding cross section (Emslie et al. 1992; Mikić et al. 2013), we use a full MHD description, i.e., the full set of MHD equations is solved together in a 2D spatial domain; this allows us to describe a beta-changing system and to have feedback between plasma and magnetic field in the critical region, i.e., around the transition region. As a consequence, and at variance with previous works, in our model the loop cross-sectional area is also a function of time and changes as the heating changes. Our 2D cylindrical coordinates make the description realistic for a 3D structure with cylindrical symmetry, which is a good approximation of a coronal loop (but see Malanushenko & Schrijver 2013 for deviations from circular loop cross sections). We have focussed on the expansion around the transition region, not in the whole loop (Peter & Bingert 2012). Our numerical experiment is devoted to answering a very specific question on the interaction between the coronal heating and the cross section of the transition region. It is complementary to self-consistent 3D MHD descriptions of coronal boxes (Bingert & Peter 2013).
In Sect. 2 we describe our model, the related equations and numerical code, the initial and boundary conditions, and how we set up the simulation of interest. The simulation and its results are illustrated in Sect. 3 and discussed in Sect. 4.
2. The model
The concept here is to study the reaction and readjustments of a magnetic loop and of the plasma confined therein under the effect of a gradual heating release inside it. We focus on a single loop and its surroundings, and therefore our approach is complementary to large-scale modeling (e.g., Carlsson et al. 2010; Gudiksen et al. 2011; Bingert & Peter 2011; Martínez-Sykora et al. 2011a,b).
We describe a coronal loop as a magnetic flux tube linking two far locations of the solar chromosphere. The footpoints are so far from each other that we can assume that they are rooted in independent chromospheres. For simplicity of modeling, we then describe the loop as straightened into a vertical flux tube linking two chromospheric layers at opposite extremes of the geometric domain (top and bottom boundaries). We keep the gravity proper of a curved flux tube. The geometry of our domain is 2D cylindrical (r − z). The spatial domain is much broader than the cross section of a typical loop. The proper loop corona forms as soon as we put a heating excess in the region around the central axis (r = 0) and not elsewhere. The heating is transported along the magnetic field lines and makes plasma expand from the chromospheres upwards, filling the space between the footpoints in the central region.
Our model considers the time-dependent MHD equations including gravity (for a curved loop), thermal conduction (including the effects of heat flux saturation), a heating function, and radiative losses from optically thin plasma.
The MHD equations are solved in the non-dimensional conservative form, ![\begin{eqnarray} \label{MHD_mass_cons_eq_1} &&\frac{\partial \rho}{\partial t} + {\bf \nabla} \cdot \left( \rho {\vec u} \right) = 0 \\ \label{MHD_mom_cons_eq_1}&& \frac{\partial \rho {\vec u}}{\partial t} + {\bf \nabla} \cdot \left( \rho {\vec u} {\vec u} - {\vec B} {\vec B} + {\vec I} P_{t} \right) = \rho {\vec g} \\ \label{MHD_Ene_cons_eq_1} &&\frac{\partial \rho E}{\partial t} + {\bf \nabla} \cdot \left[ {\vec u} \left( \rho E + P_{t} \right) - {\vec B} \left( {\vec v} \cdot {\vec B} \right) \right] = \nonumber \\ && \rho {\vec u} \cdot {\vec g} - {\bf \nabla} \cdot {\vec F_{\rm c}} - n_{\rm e} n_{\rm H} \Lambda\left( T\right) + H \left( r, z, t \right) \\ \label{MHD_Induct_eq_1} && \frac{\partial {\vec B}}{\partial t} + {\bf \nabla} \cdot \left( {\vec u} {\vec B} - {\vec B} {\vec u}\right) = 0 \\ \label{Maxwell_02} & &{\bf \nabla} \cdot {\vec B} = 0, \end{eqnarray}](/articles/aa/full_html/2014/04/aa22848-13/aa22848-13-eq13.png) where
where
![\begin{eqnarray} \label{MHD_P_t} && P_{t} = p + \frac{{\vec B} \cdot {\vec B}}{2} \\ \label{MHD_Ene_tot} && E = \epsilon + \frac{{\vec u} \cdot {\vec u}}{2} + \frac{{\vec B} \cdot {\vec B}}{2 \rho} \\ \label{TC_flux_pes_summary} && {\vec F_{\rm c}} = \frac{F_{\rm sat}}{F_{\rm sat} + \left| {\vec F_{\rm class}} \right|} {\vec F_{\rm class}} \\ \label{TC_flux_class_summary} && {\vec F_{\rm class}} = k_{||} {\vec {\hat b}} \left( {\vec {\hat b}} \cdot {\bf \nabla} T \right) + k_{\bot} \left[ {\bf \nabla} T - {\vec {\hat b}} \left( {\vec {\hat b}} \cdot {\bf \nabla} T \right) \right] \\ \label{TC_flux_abs_class_summary} && \left| {\vec F_{\rm class}} \right| = \sqrt{\left( {\vec {\hat b}} \cdot {\bf \nabla} T\right)^{2}(k_{||}^{2} - k_{\bot}^{2}) + k_{\bot}^{2} {\bf \nabla} T^{2}} \\ \label{TC_flux_sat_summary} && F_{\rm sat} = 5\phi \rho c_{\rm iso}^3 \end{eqnarray}](/articles/aa/full_html/2014/04/aa22848-13/aa22848-13-eq14.png) are
the total pressure and total energy density (internal energy ϵ, kinetic energy, and
magnetic energy), respectively; t is the time; ρ = μmHnH
is the mass density; μ = 1.265 is the mean atomic mass (assuming metal
abundance of solar values; Anders & Grevesse
1989); mH is the mass of hydrogen atom;
nH
is the hydrogen number density; u is the plasma velocity;
g is the gravity acceleration vector for a
curved loop; I is the identity tensor; T is the temperature;
Fc is the thermal conductive
flux (see Eqs. (9)–(12)), the subscripts | | and ⊥ denote, respectively, the parallel and
normal components to the magnetic field; k| | = K| |T5/2
and k⊥ = K⊥ρ2/(B2T1/2)
are the thermal conduction coefficients along and across the field; K| | and
K⊥
are constants; ciso is the isothermal sound speed;
φ = 1 is a
free parameter and Fsat is the maximum flux magnitude in the
direction of Fc;
are
the total pressure and total energy density (internal energy ϵ, kinetic energy, and
magnetic energy), respectively; t is the time; ρ = μmHnH
is the mass density; μ = 1.265 is the mean atomic mass (assuming metal
abundance of solar values; Anders & Grevesse
1989); mH is the mass of hydrogen atom;
nH
is the hydrogen number density; u is the plasma velocity;
g is the gravity acceleration vector for a
curved loop; I is the identity tensor; T is the temperature;
Fc is the thermal conductive
flux (see Eqs. (9)–(12)), the subscripts | | and ⊥ denote, respectively, the parallel and
normal components to the magnetic field; k| | = K| |T5/2
and k⊥ = K⊥ρ2/(B2T1/2)
are the thermal conduction coefficients along and across the field; K| | and
K⊥
are constants; ciso is the isothermal sound speed;
φ = 1 is a
free parameter and Fsat is the maximum flux magnitude in the
direction of Fc;
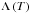 represents the optically thin radiative losses per unit emission measure derived from the
CHIANTI v. 7.0 database (Dere et al. 1997; Young
et al. 2003; Reale & Landi 2012)
assuming coronal metal abundances (Feldman 1992) and
H(s,t)
is a function of space and time describing the phenomenological heating rate (see Sect.
3). We use the ideal gas law, P = (γ − 1)ρϵ. We
assume negligible viscosity and resistivity, except for those intrinsic in the numerical
scheme.
represents the optically thin radiative losses per unit emission measure derived from the
CHIANTI v. 7.0 database (Dere et al. 1997; Young
et al. 2003; Reale & Landi 2012)
assuming coronal metal abundances (Feldman 1992) and
H(s,t)
is a function of space and time describing the phenomenological heating rate (see Sect.
3). We use the ideal gas law, P = (γ − 1)ρϵ. We
assume negligible viscosity and resistivity, except for those intrinsic in the numerical
scheme.
The calculations are performed using the PLUTO code (Mignone et al. 2007, 2012), a modular, Godunov-type code for astrophysical plasmas. The code provides a multiphysics, algorithmic modular environment particularly oriented toward the treatment of astrophysical flows in the presence of discontinuities as in the case treated here. The code is designed to make efficient use of massive parallel computers using the message-passing interface (MPI) library for interprocessor communications. The MHD equations are solved using the MHD module available in PLUTO, configured to compute intercell fluxes with the Harten-Lax-Van Leer approximate Riemann solver, while the second order in time is achieved using a Runge-Kutta scheme. A Van Leer limiter for the primitive variables is used. The evolution of the magnetic field is carried out adopting the constrained transport approach (Balsara & Spicer 1999) that maintains the solenoidal condition (∇·B = 0) at machine accuracy.
The PLUTO code includes optically thin radiative losses in a fractional step formalism (Mignone et al. 2007), which preserves the second-order time accuracy, since the advection and source steps are at least second-order accurate; the radiative loss Λ values are computed at the temperature of interest using a table lookup/interpolation method. The thermal conduction is treated separately from advection terms through operator splitting. In particular, we adopted the super-time-stepping technique (Alexiades et al. 1996) which has been proved to be very effective at speeding up explicit time-stepping schemes for parabolic problems. This approach is crucial when high values of plasma temperature are reached (e.g., during flares), explicit scheme being subject to a rather restrictive stability condition (i.e., Δt ≤ (Δx)2/2η, where η is the maximum diffusion coefficient), because the thermal conduction timescale τcond is shorter than the dynamical one τdyn (e.g., Orlando et al. 2005, 2008).
2.1. The loop setup
We address a typical active region loop, with half length L = 3 × 109 cm and temperature T ~ 3 × 106 K.
We choose as the initial plasma condition a plane-parallel loop atmosphere with the temperature and density profile from a model of a hydrostatic loop (Serio et al. 1981) with an apex temperature about 8 × 105 K. For the chromospheric part of the loop we use a hydrostatic atmosphere with a uniform temperature (i.e., 104 K). The temperature spans from 104 K in the chromosphere to 8 × 105 K in the corona. The density spans from ~1014 cm-3 in the chromosphere to ~108 cm-3 in the corona. This atmosphere is much more tenuous and cool than the subsequently heated one. The corona and the chromosphere are connected through a thin transition region where the temperature jumps from 104 K to 106 K in less than 108 cm.
The computational domain (see Fig. 1) extends from −3.1 × 109 cm to 3.1 × 109 cm in the z-direction (i.e., along the loop axis), and from r = 0 to r = 3.5 × 109 cm in the r-direction (i.e., across the loop). High resolution (dr ~ dz ~ 3 × 106 cm) is needed to describe appropriately the thin transition region from the chromosphere to the corona. The grid that we use is non-uniform but fixed. Figure 1 shows the pixel map in the domain. We have the maximum resolution around the transition region (|z| ≈ 2.4 × 109 cm, i.e., the layers where the colors change abruptly in Fig. 1) in the vertical direction and along the loop axis in the r-direction (r ≈ 0).
 |
Fig. 1 Top: color maps in logarithmic scale of density (left, [cm-3]) and temperature (right, [K]) before the loop heating is switched on. The chromosphere is red in the density map and blue in the temperature map. The magnetic field lines are also marked (white lines). Bottom: pixel map in the computational domain. Each box encloses 10 × 10 grid points. |
A fundamental ingredient of our study is that the loop where we inject the heating expands from the chromosphere to the corona. We want the magnetic field to have this expansion right from the beginning of the heating release. Therefore, our strategy involves two steps. First, we build the magnetic configuration in a tenuous, static and plane parallel atmosphere, i.e., we build an empty loop. Second, we inject the heating in a localized region of the domain to switch the loop on. For the first step, we start with a magnetic field that is in the vertical direction in the entire spatial domain, i.e., the field lines are straight and perpendicular to the two dense independent chromospheres. The magnetic field and the plasma density are more intense around the central axis, i.e., around r = 0. This configuration is not at equilibrium, and a preliminary simulation is devoted to letting the configuration relax to equilibrium. The central initial density is chosen so that at equilibrium it is approximately equal to that of the surroundings.
In the tenuous corona, around the central axis the magnetic field pressure is much higher than the plasma pressure, i.e., the ratio of thermal pressure and magnetic pressure is β ≪ 1. As a result, the magnetic field expands considerably in the corona. The magnetic pressure is instead only a small perturbation in the chromosphere (β ≫ 1) and is left almost unchanged there. We let the whole system evolve freely, keeping a small heating that compensates for radiative and conductive losses. A quasi-steady state is reached after t ~ 4000 s (the Alfven and sound crossing time are ~50 s and ~1000 s, respectively). The result of this preliminary step is a steady and stable loop atmosphere, with the strong expansion of the magnetic field lines from the chromosphere to the corona around the loop central axis, as we supposed (Fig. 1). The magnetic field intensity decreases from a few hundred G in the chromosphere to a few G in the corona (sufficient to confine the loop plasma). As shown in Fig. 1, the area expansion is a factor of 6 from the bottom of the chromosphere to the top of the transition region, another factor of 2 in the first 3000 km above the transition region, and another factor of 2 to the top of the loop (middle of the domain).
The plasma atmosphere also readjusts to a new equilibrium: in Fig. 1 we see that in the magnetically-expanded configuration the atmosphere is no longer strictly plane parallel both in the temperature and in the density, but the inhomogeneities are small and leave the corona very tenuous and much cooler than 1 MK. We also see some ripples in the chromosphere that do not affect the evolution when the loop heating is on. All plasma motions are a few km/s at most.
Many different initial conditions have been tested, finding that the resolution in the transition region is critical for accuracy. We adopt axisymmetric boundary conditions along the symmetry axis (i.e., at r = 0), reflective conditions at the outer boundary (r = 3.5 × 109 cm) and reflective conditions, but with reverse sign, for the magnetic field components at the lower and upper boundary (z = ± 3.1 × 109 cm).
3. The loop simulation
We use the results of the preliminary simulation as the starting point of a new simulation that studies the response of the loop to heating. Our scope is to study what level of variability is expected in the moss at the base of a high-pressure loop. We check, for instance, whether the loop heating drives variations in the loop and in particular of its cross section in the transition region, by considering the situation in which the loop is heated as smoothly as possible (e.g., Winebarger et al. 2011; Warren et al. 2010a,b).
The heating function that we use is divided into two terms: the first is the static term
Hs
that covers the entire corona uniformly, and the second Ht that slowly varies with
time and covers only a part of the loop: 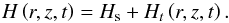 (13)According to the
scaling law (Rosner et al. 1978), the static term is
set to Hs = 4.2 × 10-5 erg
cm-3
s-1, which is
sufficient to sustain a static loop with an apex temperature of about 8 × 105 K (see Sect. 2.1).
(13)According to the
scaling law (Rosner et al. 1978), the static term is
set to Hs = 4.2 × 10-5 erg
cm-3
s-1, which is
sufficient to sustain a static loop with an apex temperature of about 8 × 105 K (see Sect. 2.1).
The second term varies with time and space as 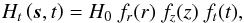 (14)where
(14)where 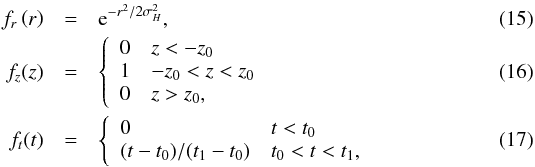 and
where z0 = 2.4 × 109 cm,
t0 = 0, and t1 = 3600 s. The
heating increases linearly in a time much longer than the typical dynamic and cooling times
(Reale 2010). We set the maximum rate
H0 = 2 × 10-3 erg
cm-3
s-1, which can
sustain a loop with an apex temperature about 3 × 106 K according to the scaling laws (Rosner et al. 1978). We have checked that the results do
not change significantly either if we assume a heating function that increases exponentially
with a comparable rising time, or if we consider a magnetic field with half intensity.
and
where z0 = 2.4 × 109 cm,
t0 = 0, and t1 = 3600 s. The
heating increases linearly in a time much longer than the typical dynamic and cooling times
(Reale 2010). We set the maximum rate
H0 = 2 × 10-3 erg
cm-3
s-1, which can
sustain a loop with an apex temperature about 3 × 106 K according to the scaling laws (Rosner et al. 1978). We have checked that the results do
not change significantly either if we assume a heating function that increases exponentially
with a comparable rising time, or if we consider a magnetic field with half intensity.
The radial distribution of the heating has a Gaussian shape centered on the r = 0 axis. The width of the Gaussian is σH = 3 × 108 cm, i.e., 1/10 of the loop’s half-length. The heating distribution is uniform with height (z).
3.1. Results
The heating is released with gradually increasing intensity around the loop’s central axis. Along this axis we expect an evolution very similar to that obtained from a typical loop model. The profiles in Fig. 2 show that this is indeed the case. The temperature gradually increases in the heated region and reaches ~3 MK when the heating reaches its maximum rate, i.e., t ~ 3600 s (red curves in Fig. 2). As is typical of coronal loop models, the density increases gradually because of the very slow growth rate of the heating, while the plasma evaporates from the chromosphere because of the higher pressure driven by the heating. The plasma dynamics is minor at all times. The maximum apex density (at the final time) is ~2 × 109 cm-3. The loop pressure increases uniformly in the corona above 1 dyn/cm2.
Figure 3 shows maps of temperature and density at three different times, i.e., at the beginning, middle, and end of the heating. The heating is conducted only along the magnetic field lines, and the proper coronal loop forms and is clearly visible at the end of the heating (bottom panel), both in the temperature and in the density maps. No local features are visible1. Overall, the evolution can be described as quasi-static.
 |
Fig. 2 Evolution of the density, temperature, and pressure profiles along the loop central axis (r = 0) in logarithmic scale after the time-dependent heating is switched on. Different line colors mark different times, from black (early) to red (late). The profiles are sampled regularly with a cadence of ≈400 s. |
 |
Fig. 3 Density (left, [cm-3]) and temperature (right, [K]) in logarithmic scale at three subsequent times after the loop heating is switched on: beginning (t = 0), half-way (t = 1825 s), and end of the heating (t = 3610 s). The magnetic field lines are also marked (white lines). |
Our attention now turns more specifically to the transition region, and in particular to the loop cross section in the expansion region. Figure 4 shows an enlargement around the region at one loop footpoint at two different times. While at early times, before the heating is switched on, the transition region layer is almost flat with only small ripples, later we see that the transition region of the heated part of the flux tube clearly drifts deeper in the chromosphere where the heating is more intense, and forms a kind of bowl. We now focus on layers at certain fixed temperatures of the transition region, and check whether and to what extent the area of that section changes with time because of this drift.
 |
Fig. 4 Evolution of the moss region and analysis of the transition region drift and area change: enlargement of density/temperature maps (Fig. 3) in the transition region at two times t = 0 and t = 3610 s (see online supplementary movie for an animated version of this evolution). Magnetic field lines are marked (white and black lines). The black lines bound the region where we measure the cross section. We also mark the relevant cross section with a horizontal segment. The bottom panels show plots of the cross-section radius (left) and of the z position of the layer at five linearly increasing temperatures, i.e., 1, 2, 3, 4, 5 × 105 K as a function of time, since the beginning of the time-dependent heating. |
For quantitative analysis, we consider two magnetic field lines on the sides of the heated part of the loop. The field lines are chosen to bound the width of the heated region in the corona (i.e., their distance corresponds to the σH in the corona). These field lines are symmetric and separated from the central axis by 5 × 107 cm at the lower boundary, 108 cm in the transition region, and 4 × 108 cm at the loop apex (Fig. 4). They enclose most of the heated region (σH = 3 × 108 cm in Eq. (15); see Sect. 3). We have checked that the results do not change much by choosing other field lines on both sides. The field lines experience some readjustments during the loop evolution, e.g., they become straighter in the low loop region (Fig. 4). This is because the pressure increase affects the low-beta corona more than the chromosphere or transition region, causing it to expand to a greater degree.
To study the moss visibility we concentrate on layers with fixed temperatures, that will be continuously visible in an EUV narrow-band detector, for instance. We choose to measure the position and width of the layer between the selected field lines at temperatures increasing linearly from 105 K to 5 × 105 K as the simulation progresses. Figure 4 shows that both the width and the height decrease as the heating increases. As mentioned above, the width varies considerably at all selected temperatures by ~40%, more at higher temperature. This occurs because the layers deepen in the chromosphere by a few 108 cm, in good agreement with the estimate from Eq. (1). The layer becomes progressively narrower with time, essentially because the transition region drifts deeper inside the chromosphere as the coronal pressure increases2 in regions where β gets smaller. This variation is faster at the beginning and then slows down near the end of the simulation. The minimum radius of the cross section is ≈0.9 × 108 cm and is nearly the same at all selected temperatures because the transition region gets thinner as the heating rate increases. Overall, since the area variation is a tracer of a variation in the brightness, this result indicates that even slow changes in heating lead to considerable differences in the appearance of the moss.
In both plots at the bottom of Fig. 4, we see
periodic oscillations that modulate the decreasing trend. These are due to the heating
process. The increasing heating drives moderate pressure fronts that hit and overshoot in
the chromosphere. The period is approximately 300 s which is compatible with the traveling
times of a perturbation at the sound speed (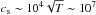 cm/s) along a tube
5 × 109 cm long.
cm/s) along a tube
5 × 109 cm long.
From the model results, we synthesize the Fe IX line emission. In particular, we derive
the emission measure in the j-th domain cell as
em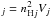 , where
nHj is the hydrogen
number density in the cell and Vj is the cell volume.
From the values of emission measure and temperature in the cell, we synthesize the
corresponding emission in the Fe IX line, using CHIANTI. Figure 5a shows the 2D map of the emission at time t = 0 in the same region as
Fig. 4. From the maps at different times, we first
derive the profiles of the emission along the r-axis at each time t by integrating the
emission along the z-axis. The time-space plot of the emission evolution
is then derived from these profiles, each normalized to its maximum. The result is shown
in Fig. 5b. Looking, for instance, at the edge of the
red color, we can clearly see that the emission shrinks as time progresses and the heating
increases, and is consistent with the results shown in Fig. 4. The oscillations are emphasized because of the dependence on the square of
the density. It can be estimated that the radial size is two times smaller.
, where
nHj is the hydrogen
number density in the cell and Vj is the cell volume.
From the values of emission measure and temperature in the cell, we synthesize the
corresponding emission in the Fe IX line, using CHIANTI. Figure 5a shows the 2D map of the emission at time t = 0 in the same region as
Fig. 4. From the maps at different times, we first
derive the profiles of the emission along the r-axis at each time t by integrating the
emission along the z-axis. The time-space plot of the emission evolution
is then derived from these profiles, each normalized to its maximum. The result is shown
in Fig. 5b. Looking, for instance, at the edge of the
red color, we can clearly see that the emission shrinks as time progresses and the heating
increases, and is consistent with the results shown in Fig. 4. The oscillations are emphasized because of the dependence on the square of
the density. It can be estimated that the radial size is two times smaller.
4. Discussion
We investigated an MHD model of an active region loop, and in particular the variation in the loop cross section in the moss region. To study the low-lying parts of the loops in high detail, the assumption of constant cross section all along the loop cannot hold, because it is known that the loop expands considerably going up from the transition region to the corona (e.g., Gabriel 1976). We could not help including this effect in the modeling, and how it changes in time and with the plasma β, and this required a proper time-dependent magnetohydrodynamic description.
Our model considers the time-dependent MHD equations in a 2D cylindrical geometry including the gravity (for a curved loop), the thermal conduction, the coronal heating, and the radiative losses from optically thin plasma.
We first created the proper loop topology, with an expanding cross section from the chromosphere to the corona, ready for the injection of heating. Then, we heated our loop with a large-scale slowly-changing (quasi-steady) heating (e.g., Winebarger et al. 2011; Warren et al. 2010a,b). We focussed on the structure of the moss in active regions, i.e., the thin loop layers at temperature ranging between about 0.1 MK and 1 MK, that are generally interpreted as the footpoints of hotter loops. We measured the position and size of the moss layers.
From Fig. 4 we have seen that the position and size of the moss region change with time. Consequently, the emission from the moss also varies.
The primary result from our simulations is that the area of the transition region can change substantially if there is a sizable change in the quasi-steady heating rate. For example, the area at 0.5 MK changes by about 40% as the peak temperature in the flux tube varies between 1 MK and 4 MK. The plasma beta at the relevant heights is low enough that the magnetic field is minimally influenced by the enhanced gas pressure. The dominant effect of the pressure is to force the transition region downward to a place where the tube is more highly constricted. This alters the DEM(T) curve, since the shape of the curve, including the ratio of coronal to transition region emission, depends on how the flux tube area varies with temperature. It may not be reasonable to independently specify a particular A(T) dependence when modeling the solar atmosphere. Warren et al. (2010b) found an A(T) that reproduces the observed DEM(T) of an active region core, but it is not obvious that this A(T) is consistent with the assumed steady heating rate.
Our model is simplified in several respects. Our 2D cylindrical description assumes a cylindrical symmetry around the loop’s central axis. Although there are some indications that this might not always be the case (Malanushenko & Schrijver 2013), we do not expect considerable differences in the results for moderate deviations in the shape of the cross section. The structure and energy balance of the chromosphere are also simplified into an isothermal structure with no radiation transport, but our study focusses on layers at much higher temperatures that should not be highly affected by this approximation. Finally, although our model implies a full MHD description, it is still not entirely self-consistent, since the heating is imposed artificially. A fully consistent model is out of the scope of this work, since we focus on the very specific question of the reaction of the low corona to heating.
 |
Fig. 5 a) Synthetic emission in the Fe IX 171 Å line at t = 0, in the same enlargement as in Fig. 4. The emission is normalized to its maximum and the color scale is shown in panel b). b) Time–space plot of the synthetic emission in the Fe IX 171 Å line. We plot the radial profile of the emission in the vertical direction at all times. Each profile is normalized to its maximum. |
Another interesting result is the magnitude of the flux tube area expansion between the transition region and the corona. The area increases by a factor of 2 to 3 over the first 3000 km above
the chromosphere in our model, depending on the peak temperature. This increase is much smaller than in the Gabriel (1976), Athay (1981), Dowdy et al. (1986) and Warren et al. (2010b) models. These models have a throat of rather extreme expansion, which we suggest may not be realistic. The Gabriel and Athay models use a potential field and assume that the flux tube is highly constricted at the top of the chromosphere. They also assume that the flux tube is isolated, with no surrounding field, which is probably a poor assumption, as discussed in Dahlburg et al. (2005). Our β-sensitive MHD model suggests that throats of extreme expansion are unlikely, although convective motions, not included here, may serve to enhance the effect. We note that the dependence of A(T) on heating rate would be even stronger if these throats did exist.
Online material
Movie of Fig. 4 Access here
Acknowledgments
We thank the anonymous referee for constructive comments and suggestions. We acknowledge support from the ItalianMinistero dell’Università e Ricerca and Agenzia Spaziale Italiana (ASI), contract I/023/09/0 and I/015/07/0. PLUTO was developed at the Astronomical Observatory of Turin in collaboration with the Department of Physics at the University of Turin. We acknowledge the CINECA awards no. HP10CWS0PW and no. HP10B54VL7 under the ISCRA initiative, and the HPC facility (SCAN) of the INAF – Osservatorio Astronomico di Palermo, for the availability of high-performance computing resources and support. CHIANTI is a collaborative project involving the NRL (USA), the Universities of Florence (Italy) and Cambridge (UK), and George Mason University (USA). The work of J.A.K. was supported by the NASA Supporting Research and Technology Program. We thank the International Space Science Institute (ISSI) for hosting the International Team of S. Bradshaw and H. Mason: Coronal Heating – Using Observables to Settle the Question of Steady vs. Impulsive Heating.
References
- Alexiades, V., Amiez, G., & Gremaud, P. A. 1996, Commun. Numer. Methods Eng., 12, 31 [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Athay, R. G. 1981, ApJ, 249, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S., & Spicer, D. S. 1999, J. Comput. Phys., 149, 270 [Google Scholar]
- Bingert, S., & Peter, H. 2011, A&A, 530, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bingert, S., & Peter, H. 2013, A&A, 550, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., Hansteen, V. H., & Gudiksen, B. V. 2010, Mem. Soc. Astron. Italiana, 81, 582 [Google Scholar]
- Dahlburg, R. B., Klimchuk, J. A., & Antiochos, S. K. 2005, ApJ, 622, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dowdy, Jr., J. F.,Rabin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., Li, P., & Mariska, J. T. 1992, ApJ, 399, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U. 1992, Phys. Scr., 46, 202 [CrossRef] [Google Scholar]
- Gabriel, A. H. 1976, R. Soc. London Phil., Trans. Ser. A, 281, 339 [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Malanushenko, A., & Schrijver, C. J. 2013, ApJ, 775, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., Testa, P., & Hansteen, V. 2011a, ApJ, 743, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Sykora, J., Hansteen, V., & Moreno-Insertis, F. 2011b, ApJ, 736, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Mikić, Z., Lionello, R., Mok, Y., Linker, J. A., & Winebarger, A. R. 2013, ApJ, 773, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Orlando, S., Peres, G., Reale, F., et al. 2005, A&A, 444, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlando, S., Bocchino, F., Reale, F., Peres, G., & Pagano, P. 2008, ApJ, 678, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H., & Bingert, S. 2012, A&A, 548, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reale, F. 2010, Liv. Rev. Sol. Phys., 7, 5 [Google Scholar]
- Reale, F., & Landi, E. 2012, A&A, 543, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Serio, S., Peres, G., Vaiana, G. S., Golub, L., & Rosner, R. 1981, ApJ, 243, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, D., Mason, H. E., & Klimchuk, J. A. 2010, ApJ, 723, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., Kim, D. M., DeGiorgi, A. M., & Ugarte-Urra, I. 2010a, ApJ, 713, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., Winebarger, A. R., & Brooks, D. H. 2010b, ApJ, 711, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Winebarger, A. R., Schmelz, J. T., Warren, H. P., Saar, S. H., & Kashyap, V. L. 2011, ApJ, 740, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Del Zanna, G., Landi, E., et al. 2003, ApJS, 144, 135 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Top: color maps in logarithmic scale of density (left, [cm-3]) and temperature (right, [K]) before the loop heating is switched on. The chromosphere is red in the density map and blue in the temperature map. The magnetic field lines are also marked (white lines). Bottom: pixel map in the computational domain. Each box encloses 10 × 10 grid points. |
| In the text | |
 |
Fig. 2 Evolution of the density, temperature, and pressure profiles along the loop central axis (r = 0) in logarithmic scale after the time-dependent heating is switched on. Different line colors mark different times, from black (early) to red (late). The profiles are sampled regularly with a cadence of ≈400 s. |
| In the text | |
 |
Fig. 3 Density (left, [cm-3]) and temperature (right, [K]) in logarithmic scale at three subsequent times after the loop heating is switched on: beginning (t = 0), half-way (t = 1825 s), and end of the heating (t = 3610 s). The magnetic field lines are also marked (white lines). |
| In the text | |
 |
Fig. 4 Evolution of the moss region and analysis of the transition region drift and area change: enlargement of density/temperature maps (Fig. 3) in the transition region at two times t = 0 and t = 3610 s (see online supplementary movie for an animated version of this evolution). Magnetic field lines are marked (white and black lines). The black lines bound the region where we measure the cross section. We also mark the relevant cross section with a horizontal segment. The bottom panels show plots of the cross-section radius (left) and of the z position of the layer at five linearly increasing temperatures, i.e., 1, 2, 3, 4, 5 × 105 K as a function of time, since the beginning of the time-dependent heating. |
| In the text | |
 |
Fig. 5 a) Synthetic emission in the Fe IX 171 Å line at t = 0, in the same enlargement as in Fig. 4. The emission is normalized to its maximum and the color scale is shown in panel b). b) Time–space plot of the synthetic emission in the Fe IX 171 Å line. We plot the radial profile of the emission in the vertical direction at all times. Each profile is normalized to its maximum. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


