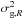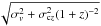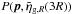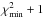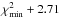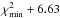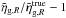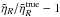| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321942 | |
| Published online | 28 February 2014 | |
The VIMOS Public Extragalactic Redshift Survey (VIPERS)
Ωm0 from the galaxy clustering ratio measured at z ~ 1⋆
1
Aix Marseille Université, CNRS, CPT, UMR 7332,
13288
Marseille,
France
e-mail:
jbel@cpt.univ-mrs.fr
2 Institut Universitaire de France
3
INAF – Osservatorio Astronomico di Brera, via Brera 28, 20122
Milano, via E. Bianchi 46, 23807
Merate,
Italy
4
Dipartimento di Fisica, Università di
Milano-Bicocca, P.zza della Scienza
3, 20126
Milano,
Italy
5
SUPA, Institute for Astronomy, University of Edinburgh, Royal
Observatory, Blackford
Hill, Edinburgh
EH9 3HJ,
UK
6
Dipartimento di Matematica e Fisica, Università degli Studi Roma
Tre, via della Vasca Navale
84, 00146
Roma,
Italy
7
INFN, Sezione di Roma Tre, via della Vasca Navale 84,
00146
Roma,
Italy
8
INAF – Osservatorio Astronomico di Roma,
via Frascati 33, 00040
Monte Porzio Catone ( RM),
Italy
9
INAF – Osservatorio Astronomico di Bologna, via Ranzani 1,
40127,
Bologna,
Italy
10
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Milano,
via Bassini 15, 20133
Milano,
Italy
11
INAF – Osservatorio Astrofisico di Torino,
10025
Pino Torinese,
Italy
12
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
13
Canada-France-Hawaii Telescope, 65–1238 Mamalahoa Highway,
Kamuela,
HI
96743,
USA
14
Laboratoire Lagrange, UMR7293, Université de Nice
Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300
Nice,
France
15
Institute of Astronomy and Astrophysics, Academia Sinica,
PO Box 23-141,
Taipei
10617,
Taiwan
16
Dipartimento di Fisica e Astronomia – Università di Bologna,
viale Berti Pichat
6/2, 40127
Bologna,
Italy
17
INAF – Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11,
34143
Trieste,
Italy
18
Institute of Physics, Jan Kochanowski University,
ul. Swietokrzyska
15, 25-406
Kielce,
Poland
19
Department of Particle and Astrophysical Science, Nagoya
University, Furo-cho,Chikusa-ku,
464-8602
Nagoya,
Japan
20
INFN, Sezione di Bologna, viale Berti Pichat 6/2,
40127
Bologna,
Italy
21
Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre
et Marie Curie, 98 bis Boulevard
Arago, 75014
Paris,
France
22
Astronomical Observatory of the Jagiellonian University,
Orla 171,
30-001
Cracow,
Poland
23
National Centre for Nuclear Research, ul. Hoza 69,
00-681
Warszawa,
Poland
24
Max-Planck-Institut für Extraterrestrische Physik,
84571
Garching b. München,
Germany
25
Universitätssternwarte München, Ludwig-Maximillians Universität,
Scheinerstr. 1,
81679
München,
Germany
26
Institute of Cosmology and Gravitation, Dennis Sciama Building,
University of Portsmouth, Burnaby
Road, Portsmouth,
PO1 3FX,
UK
27
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Bologna,
via Gobetti 101, 40129
Bologna,
Italy
28
INAF – Istituto di Radioastronomia, via Gobetti 101,
40129
Bologna,
Italy
29
Università degli Studi di Milano, via G. Celoria 16, 20130
Milano,
Italy
30
Université de Toulon, CNRS, CPT, UMR 7332,
83957
La Garde,
France
Received:
22
May
2013
Accepted:
20
November
2013
We use a sample of about 22 000 galaxies at 0.65 < z < 1.2 from the VIMOS Public Extragalactic Redshift Survey (VIPERS) Public Data Release 1 (PDR-1) catalogue, to constrain the cosmological model through a measurement of the galaxy clustering ratio ηg,R. This statistic has favourable properties, which is defined as the ratio of two quantities characterizing the smoothed density field in spheres of a given radius R: the value of its correlation function on a multiple of this scale, ξ(nR), and its variance σ2(R). For sufficiently large values of R, this is a universal number, which captures 2-point clustering information independently of the linear bias and linear redshift-space distortions of the specific galaxy tracers. In this paper, we discuss how to extend the application of ηg,R to quasi-linear scales and how to control and remove observational selection effects, which are typical of redshift surveys as VIPERS, in detail. We verify the accuracy and efficiency of these procedures using mock catalogues that match the survey selection process. These results show the robustness of ηg,R to non-linearities and observational effects, which is related to its very definition as a ratio of quantities that are similarly affected. At an effective redshift z = 0.93, we measured the value ηg,R(15) = 0.141 ± 0.013 at R = 5h-1 Mpc. Within a flat ΛCDM cosmology and by including the best available priors on H0, ns and baryon density, we obtain a matter density parameter at the current epoch Ωm,0 = 0.270-0.025+0.029. In addition to the great precision achieved on our estimation of Ωm using VIPERS PDR-1, this result is remarkable because it appears to be in good agreement with a recent estimate at z ≃ 0.3, which was obtained by applying the same technique to the SDSS-LRG catalogue. It, therefore, supports the robustness of the present analysis. Moreover, the combination of these two measurements at z ~ 0.3 and z ~ 0.9 provides us with a very precise estimate of Ωm,0 = 0.274 ± 0.017, which highlights the great consistency between our estimation and other cosmological probes, such as baryonic acoustic oscillations, cosmic microwave background, and supernovae.
Key words: cosmological parameters / dark matter / large-scale structure of Universe
Based on observations collected at the European Southern Observatory, Cerro Paranal, Chile, using the Very Large Telescope under programmes 182.A-0886 and partly 070.A-9007. Also based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The VIPERS web site is http://www.vipers.inaf.it/
© ESO, 2014
1. Introduction
The present-day large-scale structure in cosmological matter distribution is formed by the gravitational amplification of small density perturbations that are a relic of the early Universe. The amplitude of these fluctuations as a function of scale carries unique information about the fundamental cosmological parameters, which describe the dominant constituents of the Universe and their densities with the global expansion history. Since the primordial density field is commonly thought to be a random Gaussian process, the Fourier power spectrum, or, its real-space counterpart, the correlation function provide a complete statistical description. Linear growth of small fluctuations preserves the shape of both, suggesting that observations of the large-scale structure today should still be able to extract pristine cosmological information.
This idealized picture is complicated in practice, as galaxies do not faithfully trace the
distribution of matter but are undoubtedly biased to some extent. The
reason this is inevitable is because galaxies form within dark matter haloes, and the more
massive haloes form at special places within the cosmic density field. This generates a
large-scale linear bias that gives a two-point correlation function, ξ(r), of
galaxies that is related to that of mass by:
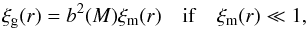 (1)where the bias
parameter, b,
depends on halo mass (Kaiser 1984; Mo & White 1996; Sheth & Tormen 1999).
(1)where the bias
parameter, b,
depends on halo mass (Kaiser 1984; Mo & White 1996; Sheth & Tormen 1999).
On small scales where the correlations are non-linear, the correlation function gains additional contributions, which arise from pairs within haloes that are massive enough to host more than one galaxy. Thus, the galaxy correlation function varies in shape and amplitude for different classes of galaxies because different classes of galaxy occupy different masses of haloes to different extents, and the distribution of galaxies within each halo does not necessary follow that of the mass (this is the basis of the “halo model” – see e.g. Cooray & Sheth 2002). Weak non-linearities in the mapping between the underlying matter density field and the distribution of collapsed objects also develop on quasi-linear scales (Sigad & Tormen 2000; Marinoni et al. 2005), as a consequence of the complex interplay between galaxy formation processes and gravitational dynamics. Additionally, there may be some scatter in the galaxy properties found in a set of haloes of the same mass; these effects are collected under the heading of “stochastic bias” (e.g. Dekel & Lahav 1999; Gao & White 2007) and have been shown to be small but non-zero in the observed galaxy distribution (e.g. Wild et al. 2005).
The non-linear physics responsible for galaxy formation can be mitigated by surveys covering large volumes, which can probe the power spectrum closer to the linear regime, or by focussing on robust features such as baryonic acoustic oscillations (BAO), the relic of the baryon-photon interactions in the pre-recombination plasma. These strategies have motivated the large “low-redshift” surveys of the past decade (e.g SDSS-3 BOSS, Eisenstein et al. 2011; Anderson et al. 2012; WiggleZ, Drinkwater 2010; Blake et al. 2011; 2dFGRS, Colless et al. 2001) and are also a major driver for the next generation of projects from the ground or space (e.g. BigBoss Schlegel et al. 2011; Euclid Laureijs 2011).
The development of multi-object spectrographs on 8-m class telescopes during the 1990s triggered a number of deep redshift surveys with measured distances beyond z ~ 0.5 over areas of 1–2 deg2 (e.g. VVDS, Le Fèvre et al. 2005; DEEP2, Newman et al. 2013 and zCOSMOS, Lilly et al. 2009). Even so, it was not until the wide extension of VVDS was produced (Garilli et al. 2008) that a survey existed with sufficient volume to attempt cosmologically meaningful computations at z ~ 1 (Guzzo et al. 2008). In general, clustering measurements at z ≃ 1 from these samples remained dominated by cosmic variance, as dramatically shown by the discrepancy observed between the VVDS and zCOSMOS correlation functions at z ≃ 0.8 (de la Torre et al. 2010).
The VIMOS Public Extragalactic Redshift Survey (VIPERS) is part of this global attempt to take cosmological measurements at z ~ 1 to a new level in terms of statistical significance. In contrast to the BOSS and WiggleZ surveys, which use large-field-of-view (~1 deg2) fibre optic positioners to probe huge volumes at low sampling density, VIPERS exploits the features of VIMOS at the ESO VLT to yield a dense galaxy sampling over a moderately large field of view (~0.08 deg2). It reaches a volume at 0.5 < z < 1.2, which is comparable to that of the 2dFGRS (Colless et al. 2001) at z ~ 0.1, allowing the cosmological evolution to be tested with small statistical errors.
In parallel to improving the samples, we can try and devise statistical estimators that are capable of probing the density field, while being weakly sensitive to galaxy bias and non-linear evolution (e.g. Zhang et al. 2007; Bel & Marinoni 2012). This is the motivation for a new statistic introduced by Bel & Marinoni (2014; hereafter BM13), who proposed the use of the clustering ratio ηg,R(r), the ratio of the correlation function to the variance of the galaxy over-density field δR smoothed on a scale R. BM13 argue that this statistic has a redshift-space form that is independent of the specific bias of the galaxies used and is essentially only sensitive to the shape of the non-linear real-space matter power spectrum in two relatively narrow bandwidths.
BM13 have used numerical simulations to thoroughly discuss the level of precision reachable through this method on large linear scales. In particular, they showed that the clustering ratio measured from the simulations differs from the theoretical prediction by only 0.1% for some specific choices of the scales R and r that are involved in the smoothing of the auto-correlation of the galaxy density field. They also applied this technique to the SDSS-DR7 Luminous Red Galaxy sample with z < 0.4 by obtaining an estimate of the present matter density (Ωm,0 = 0.283 ± 0.023), which is 20% more precise than the measurement of Percival et al. (2010) from a BAO analysis of the same sample. This demonstrates the sensitivity of relative clustering measurements made on different scales to Ωm,0, which controls the horizon scale at matter-radiation equality and the corresponding turn-over in the growth rate of fluctuations.
The η statistics remains sensitive to non-linearities if we probe small enough scales. Since the statistical errors decline as we add small-scale data, there is a careful balance to be struck in attaining a result that has a small error bar, while lacking significant systematic errors. Non-linearities in themselves are unimportant, since the non-linear evolution of the matter power spectrum is in effect a solved problem at the level of precision we need and can be predicted for any model we wish to test. The non-trivial problem is eventually inadequate for the local bias hypothesis (Fry & Gaztañaga 1993) – i.e., a possible dependence of the bias parameter on the separation scale r (cf. Eq. (1)). We address this issue carefully in the present paper, using realistic simulated galaxy distributions, and show that the likely degree of scale dependence of the biasing relation in Fourier space is small enough that it does not constitute a significant uncertainty in the interpretation of our measurements of η.
In this paper, we measure the ηg,R statistic from the VIPERS Public Data Release 1 (PDR-1) redshift catalogue, by including ~64% of the final number of redshifts expected at completion (see Guzzo et al. 2013, hereafter Paper I, for a detailed description of the survey data set). The paper is organized as follows. In Sect. 2, we introduce the VIPERS survey and the features of the PDR-1 sample. In Sect. 3, we review the basics of the η-test, and we discuss how the galaxy clustering ratio is estimated from VIPERS data. In Sect. 4, we present the formalism that allows us to also predict the amplitude of this new cosmological observable in the non-linear regime, and we assess its overall viability with numerical simulations. This analysis helps us to identify the range of the parameter space where cosmological results can be meaningfully interpreted. In Sect. 5, we discuss the correction schemes adopted to account for the imprint of the specific VIPERS mask and selection effects, testing them with VIPERS mock surveys. Cosmological results are presented in Sect. 6 and conclusions are drawn in Sect. 7.
Throughout this paper, the Hubble constant is parameterized via h = H0/100 km s-1 Mpc-1, and all magnitudes in this paper are in the AB system (Oke & Gunn 1983). We do not give an explicit AB suffix. We do not fix cosmological parameters to a fiducial set of value. For consistency, we reconstruct the galaxy clustering ratio and analyse data in any tested cosmology.
2. Data
As already mentioned in this paper, we use the new data of the VIPERS, which is being built using the VIMOS spectrograph at the ESO VLT. The survey target sample is selected from the Canada-France-Hawaii Telescope Legacy Survey Wide (CFHTLS-Wide) optical photometric catalogues (Mellier et al. 2009). The VIPERS covers ~24 deg2 on the sky divided over two areas within the W1 and W4 CFHTLS fields. Galaxies are selected to a limit of iAB < 22.5, which further applies a simple and robust gri colour pre-selection, as to effectively remove galaxies at z < 0.5. Coupled to an aggressive observing strategy (Scodeggio et al. 2009), this allows us to double the galaxy sampling rate in the redshift range of interest with respect to a pure magnitude-limited sample (~40%). At the same time, the area and depth of the survey result in a fairly large volume, ~5 × 107h-3 Mpc3, analogous to that of the 2dFGRS at z ~ 0.1. Such combination of sampling and depth is quite unique over current redshift surveys at z > 0.5. The VIPERS spectra are collected with the VIMOS multi-object spectrograph (Le Fèvre et al. 2003) at moderate resolution (R = 210), using the LR Red grism, providing a wavelength coverage of 5500–9500Å and a typical redshift error of 141(1 + z) km s-1. The full VIPERS area of ~24 deg2 is covered through a mosaic of 288 VIMOS pointings (192 in the W1 area and 96 in the W4 area). A discussion of the survey data reduction and management infrastructure is presented in Garilli et al. (2012). An early subset of the spectra used here is analysed and classified through a Principal Component Analysis (PCA) in Marchetti et al. (2013).
A quality flag is assigned to each measured redshift based on the quality of the corresponding spectrum. Here and in all parallel VIPERS science analyses, we use only galaxies with flags 2 to 9 inclusive, which correspond to a global redshift confidence level of 98%. The redshift confirmation rate and redshift accuracy have been estimated using repeated spectroscopic observations in the VIPERS fields. A more complete description of the survey construction from the definition of the target sample to the actual spectra and redshift measurements is given in the parallel survey description paper (Paper I).
The data set used in this and the other papers is the VIPERS PDR-1 catalogue, which was made publicly available in September 2013. This includes 55,359 objects which are spread over a global area of 8.6 × 1.0 deg2 and 5.3 × 1.5 deg2, respectively, in W1 and W4. It corresponds to the data frozen in the VIPERS database at the end of the 2011/2012 observing campaign with 64% of the final expected survey yield. For the specific analysis presented here, the sample has been further limited to its higher-redshift part, selecting only galaxies with 0.65 < z < 1.2. The reason for this selection is related to the necessity of covering a minimum physical size in the declination direction, which, given the angular aperture of the survey, cannot be obtained for smaller distances (more details are given at the end of Sect. 3.2). This reduces the usable sample to 13 688 and 12 923 galaxies in W1 and W4, respectively (always with quality flag ≥2, as defined earlier). The corresponding volumes of the two samples are 1.3 and 1.2 × 107h-3 Mpc3 with a spanned largest linear dimension at z = 1.2 of ~400 and 250 h-1 Mpc, respectively.
 |
Fig. 1 Distribution on the sky of the galaxies with measured redshifts in the VIPERS PDR-1
catalogue within the W1 and W4 fields (blue points). The pattern described
by the gaps separating the VIMOS quadrants, as well as the areas not covered by the
PDR-1, are clearly visible. Superimposed to the spectroscopic data, we also plot for
illustrative purposes the projection of a subset of the spherical cells used to
estimate the variance |
3. Method
Here we briefly review the basic features of the clustering ratio cosmological test as proposed by BM13. We then discuss the procedure adopted to estimate it from a redshift survey like VIPERS.
3.1. The clustering ratio
Let δg,R(x)
be the galaxy overdensity field that is smoothed on a scale R at the real-space
position x (In the following, we assume that
smoothing is done by convolving the field with a spherical Top Hat window of radius
R). Its
variance 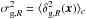 and
2-point correlation function
ξg,R(r) = ⟨ δg,R(x)δg,R(x + r) ⟩ c
(here ⟨ ... ⟩ c indicates
cumulant expectation values) can be combined to define the galaxy clustering ratio
and
2-point correlation function
ξg,R(r) = ⟨ δg,R(x)δg,R(x + r) ⟩ c
(here ⟨ ... ⟩ c indicates
cumulant expectation values) can be combined to define the galaxy clustering ratio
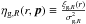 (p emphasis
the dependency regarding to cosmological parameters). This statistic is a measure of the
“slope” of the correlation function, which is smoothed over a particular double kernel
structure (cf. Eq. (14) of Bel & Marinoni 2012). What is interesting about this
statistic is that the galaxy clustering ratio and the mass clustering ratio in real space,
which is defined as
(p emphasis
the dependency regarding to cosmological parameters). This statistic is a measure of the
“slope” of the correlation function, which is smoothed over a particular double kernel
structure (cf. Eq. (14) of Bel & Marinoni 2012). What is interesting about this
statistic is that the galaxy clustering ratio and the mass clustering ratio in real space,
which is defined as 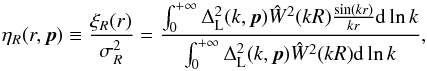 (2)coincide, or
ηg,R(r,p) = ηR(r,p).
This equality follows from the hypothesis that galaxy and mass density fields on a scale
R are
related via a linear local deterministic biasing scheme (Fry & Gaztañaga 1993). Note that, Ŵ is the Fourier transform
of the smoothing window and
(2)coincide, or
ηg,R(r,p) = ηR(r,p).
This equality follows from the hypothesis that galaxy and mass density fields on a scale
R are
related via a linear local deterministic biasing scheme (Fry & Gaztañaga 1993). Note that, Ŵ is the Fourier transform
of the smoothing window and 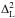 is the
dimensionless linear power spectrum of matter density fluctuations in Eq. (2). Two fundamental observations motivated the
definition of the galaxy clustering ratio. Because it is a ratio between clustering at
different scales, the clustering ratio is effectively insensitive to linear redshift
distortions, which alter the amplitude of clustering in a way that is independent of phase
or frequency (Kaiser 1987). We therefore have that
is the
dimensionless linear power spectrum of matter density fluctuations in Eq. (2). Two fundamental observations motivated the
definition of the galaxy clustering ratio. Because it is a ratio between clustering at
different scales, the clustering ratio is effectively insensitive to linear redshift
distortions, which alter the amplitude of clustering in a way that is independent of phase
or frequency (Kaiser 1987). We therefore have that
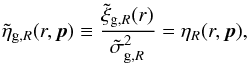 (3)where quantities that are
evaluated in redshift space are labelled with a tilde. Because the amplitude of the galaxy
clustering is not affected by galaxy bias, we use this as the second salient feature of
our definition.
(3)where quantities that are
evaluated in redshift space are labelled with a tilde. Because the amplitude of the galaxy
clustering is not affected by galaxy bias, we use this as the second salient feature of
our definition.
The galaxy clustering ratio depends on the cosmological model through both the linear power spectrum in Eq. (2), which alters the right-hand-side (RHS) of Eq. (3) and the conversion applied to convert redshifts into distances, which alters the left-hand-side (LHS). The equivalence expressed by Eq. (3) holds true if and only if the LHS and RHS are both estimated in the “true” cosmological model. This is the basis of the “Alcock-Paczynski” approach to constraining the cosmological geometry (Alcock & Paczynski 1979; Ballinger et al. 1996; Marinoni & Buzzi 2010).
There are a few difficulties for the application of the clustering ratio test to the VIPERS data. The high density and small volume of the VIPERS survey mean that we can only accurately calculate the η statistic on smaller scales (typically R = 5 h-1 Mpc) when compared to those for which this cosmological indicator was originally conceived. It is therefore necessary to extend the theoretical formalism of the η test to account for the effects of structure formation in the non-linear regimes. Adopting a non-linear power spectrum to predict the amplitude of the clustering ratio on these scales is necessary, but not sufficient. We must also properly incorporate a model for the non-linear redshift space distortion effect induced by the virial motions of galaxies into the theoretical framework, or the so-called Finger-of-God effect. The additional modelling required to extend the linear formalism of BM13 into the quasi-linear regime is presented and tested using simulations of the large scale structure in Sect. 4. Another concern is that results obtained on small scales might be more sensitive to a failure of a fundamental hypothesis on which the η formalism is built, or the locality of the biasing relation. Particular care is thus devoted to demonstrate via the analysis of numerical simulations that even the amplitude of the galaxy clustering ratio is not affected by using VIPERS galaxies as tracers on such small scales as R = 5 h-1 Mpc. That is, it can be safely predicted without requiring the specification of a biasing scheme.
3.2. Estimating 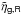 from VIPERS data
from VIPERS data
The estimation of the clustering ratio as a counts-in-cells statistic was presented in
BM13. Here we review the measurement and describe the application to VIPERS data.
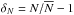 , where
N is the
number of galaxies in spheres of radius R and
, where
N is the
number of galaxies in spheres of radius R and 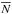 its average value
(we compute its value at the radial position r, corresponding to some look-back
time t by averaging the cell counts within survey slices r ± 10R).
These spheres tessellate the whole VIPERS survey in a regular way; their centres (called
hereafter seeds) being located on a lattice of rectangular symmetry and spacing
R (see Fig.
1). The 1-point, second order moment
its average value
(we compute its value at the radial position r, corresponding to some look-back
time t by averaging the cell counts within survey slices r ± 10R).
These spheres tessellate the whole VIPERS survey in a regular way; their centres (called
hereafter seeds) being located on a lattice of rectangular symmetry and spacing
R (see Fig.
1). The 1-point, second order moment
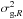 is measured as the variance (corrected for shot noise effects) of δN. The spheres partially
include gaps in the survey due to the spacing of the VIMOS quadrants and to failed
observations. Additionally, the sampling rate of the survey varies with the quadrant, as
described in Paper I. The impact of these effects is investigated in Sect. 5.2.
is measured as the variance (corrected for shot noise effects) of δN. The spheres partially
include gaps in the survey due to the spacing of the VIMOS quadrants and to failed
observations. Additionally, the sampling rate of the survey varies with the quadrant, as
described in Paper I. The impact of these effects is investigated in Sect. 5.2.
To estimate the correlation function of the counts, we add a motif of isotropically distributed spheres around each seed (see right hand side of Fig. 1), and as proper seeds we retain only those for which the spheres of the motifs lie completely within the survey boundaries. The centre j of each new sphere is separated from the proper seed i by the length r = nR (where n is a generic real parameter usually taken without loss of generality to be an integer), and the pattern is designed in such a way as to maximize the number of quasi-non-overlapping spheres at the given distance r (the maximum allowed overlapping between contiguous spheres is 2% in volume). Incidentally, if the galaxy field is correlated on a scale r = 3R = 15 h-1 Mpc, the number of spheres in a motif, or spheres isotropically placed around each proper seed is 26. ξg,R(r) is then estimated as ⟨ δNiδNj ⟩, which is by averaging the counts over any cell i and j. In this last statistical quantity, note that we do not need to correct for shot noise since random sampling errors are uncorrelated. In Sect. 5.2, we discuss residual systematic effects arising from the survey geometry and sampling rate.
Considering cells of R = 5 h-1 Mpc and after removing those cells that fall in bad or masked areas (see Sect. 5.2), the effective number of spheres used to estimate 1-point statistics is 68 667 in W1 and 58 684 in W4. Where 2-point statistics are concerned, the number of proper seeds is 37 814 in W1 and 39 459 in W4. Note that we can place more cells in W1 than in W4, since this last region is characterised by a smaller field of view. On the contrary, the number of proper seeds is larger in W4. This is explained by the angular shape of the field. The shallower extension in declination of W1 limits the number of motifs that we can fit inside the survey area. Since the error budget in the measurement of ηg,R is essentially dominated by the errors of the 2-point statistic, the clustering ratio is thus estimated in W4 with slightly higher precision. In this way, the small aperture of W1 also limits the effective redshift range we can probe. To be able to place an entire motif (see right hand side of top panel of Fig. 1) in W1, we need to restrict the analysis to redshifts above 0.65.
4. The clustering ratio in the non-linear regime
Because of the survey geometry, the galaxy clustering ratio can be precisely estimated from
the VIPERS data only on relatively small scales, R < 8 h-1 Mpc.
It is thus necessary to generalize Eq. (3) to
non-linear regimes and to test the validity of the hypothesis underlying such modelling.
This entails additional assumptions with respect to the simple requirement of a
deterministic biasing relation on a given smoothing scale R. Two distinct distortions
must be modelled: linear theory over predicts the real space amplitude of the galaxy
clustering ratio ηg,R in regimes of
strong gravity, and the redshift-space amplitude of the galaxy clustering ratio
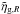 is biased high with respect to ηg,R because of the
Finger-of-God (FoG) effect (Jackson 1972; Tully & Fisher 1978). Concerns about these points
can be addressed by using numerical simulations. We create these from the MultiDark
simulation (Prada et al. 2012), a large flat
ΛCDM simulation containing
20483 particles,
with mass of 8.721 × 108 h-1M⊙
within a cube of side 1 h-1 Gpc. The simulation starts at an
initial redshift zi = 65 with the
following parameters: (Ωm = 0.27,ΩΛ = 0.73,H0 = 70 km s-1 Mpc-1,Ωb = 0.0469,ns = 0.95,σ8 = 0.82).
We match VIPERS against the time snapshot corresponding to z = 1 (although the sense of
our conclusions is unchanged when other time outputs are considered in the analysis). This
box (hereafter labelled Bh) contains nearly 14 millions haloes
with mass M > 1011.5 h-1 M⊙
and is used to check real-space properties of the clustering ratio with high statistical
resolution.
is biased high with respect to ηg,R because of the
Finger-of-God (FoG) effect (Jackson 1972; Tully & Fisher 1978). Concerns about these points
can be addressed by using numerical simulations. We create these from the MultiDark
simulation (Prada et al. 2012), a large flat
ΛCDM simulation containing
20483 particles,
with mass of 8.721 × 108 h-1M⊙
within a cube of side 1 h-1 Gpc. The simulation starts at an
initial redshift zi = 65 with the
following parameters: (Ωm = 0.27,ΩΛ = 0.73,H0 = 70 km s-1 Mpc-1,Ωb = 0.0469,ns = 0.95,σ8 = 0.82).
We match VIPERS against the time snapshot corresponding to z = 1 (although the sense of
our conclusions is unchanged when other time outputs are considered in the analysis). This
box (hereafter labelled Bh) contains nearly 14 millions haloes
with mass M > 1011.5 h-1 M⊙
and is used to check real-space properties of the clustering ratio with high statistical
resolution.
We also consider a suite of 31 nearly independent light-cones, each extends over the
redshift range 0.65 < z < 1.2
and covers a cosmological volume similar to that surveyed by the VIPERS PDR-1 data in the
W4 field.
These light-cones (hereafter indicated as Lh) incorporate redshift distortion
effects, contain a total of ~105 haloes each, and have a constant comoving radial
density of objects, which is ~5
times higher than the mean effective density of galaxies in the VIPERS sample. These samples
allow us to analyse the redshift space properties of the
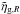 observable with great statistical resolution.
observable with great statistical resolution.
Note that the simulated haloes do not cover the whole range of masses in which the VIPERS galaxies are expected to reside, resulting in a different bias with respect to the real data. This is not expected to affect the realism of the tests performed, given that the η statistic is insensitive to linear galaxy bias. This aspect is discussed in depth in Sect. 4.3.
 |
Fig. 2 Impact of non-linear clustering on the measurement and theoretical modelling of the galaxy clustering ratio η. The latter is measured in real space for the halo catalogues of the Bh simulation and compared to both the linear and non-linear predictions, as described respectively by a simple Eisenstein & Hu (1998) linear power spectrum (dot-dashed lines) and after correction through the non-linear HALOFIT prescription of Smith et al. (2003) (solid lines). The clustering ratio is shown as a function of the smoothing scale R adopted to filter the discrete distribution of haloes and for various correlation lengths (r = nR) with n = { 2,3,4 }. Errors bars are obtained using 64 block-jackknife resampling of the data which excludes a cubic volume of linear size 250 h-1 Mpc each time. |
4.1. Non-linear effects in real space
We first explore whether the assumption of a simple phenomenological prescription for the amplitude and scaling of the matter power spectrum provided by Smith et al. (2003) is accurate enough for an effective implementation of the η-test with VIPERS data. We estimate the galaxy clustering ratio in real space (ηg,R(3R)) using the numerical simulations and compare them against the model given by the RHS of Eq. (2), which is calculated using either the linear power spectrum, or the non-linear model of Smith et al. (2003). Figure 2 shows the failure of the predictions based on a simple linear power spectrum model for the Bh halo box at z = 1. The amplitude of the clustering ratio is systematically over predicted on all R-scales and for all correlation lengths investigated. In contrast, the simple non-linear model of Smith et al. (2003) describes the data with greater accuracy over a wider interval of scales. On a scale as small as R = 5 h-1 Mpc, the typical scale adopted to extract the maximum signal from VIPERS data, or the precision with which the amplitude of ηg,R(3R) is predicted is of order 3.6%,2.5% and 2.8% for the correlation scales n = 2,3, and 4, respectively. On scales R = 8 h-1 Mpc and for the same correlation lengths, the relative discrepancy between theory and data is of order 1%,1.5%, and 2.5%, respectively.
These figures suggest that the remaining systematic error on the real-space model calculated by adopting the Smith et al. (2003) model is essentially negligible compared to the statistical uncertainty associated with current measurements of the clustering ratio ηg,R from VIPERS data (which is, δη/η ~ 10% at best when the field is filtered on the scale R = 5 h-1 Mpc). Considering that the clustering ratio recovered on the correlation scale n = 2 and n = 4 is affected respectively by too large theoretical systematics (non-linearities in the power spectrum), by too large observational uncertainties (due to the shape of VIPERS fields), and in agreement with the analysis of BM13, we focus the rest of our analysis to the specific case, where the smoothed field is correlated on a scale r = 3R. Furthermore, we only consider the non-linear matter power spectrum model of Smith et al. (2003) from now on.
We remark that this analysis confirms the accuracy of the approximate relation (3) (upon implementation of a non-linear power spectrum model) even in regimes where σg,R is large. This is essentially due to the fact that, even on the small R-scales probed by VIPERS the second order coefficient of the bias relation is small with respect to the linear term.
4.2. Non-linear effects in redshift space
An interesting feature of Eq. (2) is that it is effectively insensitive to redshift distortions, and, therefore, independent of their specific modelling in the linear limit. This simplicity is lost when we consider small scales, R ~ 5 h-1 Mpc, which are the typical scales probed by VIPERS, where non-linear motions are expected to contaminate the cosmological signal.
The existence of such effects is shown in Fig. 3,
where we compare measurements of the galaxy clustering ratio for haloes selected in real
space and in redshift space from the Lh simulations (ηg,R and
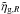 ,
respectively). The discrepancy between measurements is significant with relative
deviations ~14% for
R = 4 h-1 Mpc and
~9% at R = 5 h-1 Mpc. In the
following, we show that theory allows us to account for these distortions in a neat and
effective way.
,
respectively). The discrepancy between measurements is significant with relative
deviations ~14% for
R = 4 h-1 Mpc and
~9% at R = 5 h-1 Mpc. In the
following, we show that theory allows us to account for these distortions in a neat and
effective way.
 |
Fig. 3 Effect of redshift-space distortions on the measurement and modelling of the
clustering ratio. The values estimated in real and redshift space from the
Lh halo catalogues (main panel) are
compared with the theoretical predictions; these have been named
|
A typical assumption is that the non-linear distortion induced on the 2-point correlation function is driven by
random motions and can be described as a convolution of the real-space correlation
function with a Gaussian or Exponential kernel f(v12) that describes
the distribution of pairwise velocities along the line of sight (Davis & Peebles
1983) 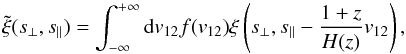 (4)where
s∥ and s⊥ are the
separations along and perpendicular to the observer’s line of sight, H(z) is
the Hubble parameter at redshift z, and
(4)where
s∥ and s⊥ are the
separations along and perpendicular to the observer’s line of sight, H(z) is
the Hubble parameter at redshift z, and 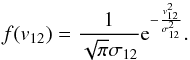 With
this definition note that the 1D Gaussian pairwise velocity dispersion σ12 is
With
this definition note that the 1D Gaussian pairwise velocity dispersion σ12 is
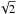 times the dispersion in the pairwise velocity v12 and it induces a dispersion in the
radial comoving distance of amplitude σx = σv(1 + z)/H(z),
where σv = σ12/2
is the dispersion of galaxy peculiar velocities. Interestingly, this kernel has also been
shown to model quasi-linear redshift-space effects (Percival & White 2009). This model can be straightforwardly re-mapped to
Fourier space (Peacock & Dodds 1994), where
the global (linear coherent + non-linear random) redshift-space distortions can be
expressed as
times the dispersion in the pairwise velocity v12 and it induces a dispersion in the
radial comoving distance of amplitude σx = σv(1 + z)/H(z),
where σv = σ12/2
is the dispersion of galaxy peculiar velocities. Interestingly, this kernel has also been
shown to model quasi-linear redshift-space effects (Percival & White 2009). This model can be straightforwardly re-mapped to
Fourier space (Peacock & Dodds 1994), where
the global (linear coherent + non-linear random) redshift-space distortions can be
expressed as 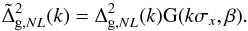 In
this expression,
In
this expression, 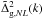 and
and
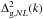 give the (non-linear) power
spectrum in redshift and real space, respectively, and
give the (non-linear) power
spectrum in redshift and real space, respectively, and ![\begin{equation} \begin{array}{rl} G(y,\beta)\equiv & \displaystyle\frac{\sqrt{\pi}}{8} \frac{{\rm erf}(y)}{y^5}\left[ 3\beta^2+4\beta y^2+4 y^4\right] \\ & \displaystyle - \frac{{\rm e}^{-y^2}}{4 y^4}\left[ 3\beta^2+2\beta(2+\beta)y^2\right] \end{array} \label{pred} \end{equation}](/articles/aa/full_html/2014/03/aa21942-13/aa21942-13-eq158.png) (5)with
β = f/b
as the usual redshift space distortion parameter defined as the ratio between the linear
growth rate and the linear bias parameter. Since we are essentially interested on scales,
where y < 1, we can expand Eq.
(5) as
(5)with
β = f/b
as the usual redshift space distortion parameter defined as the ratio between the linear
growth rate and the linear bias parameter. Since we are essentially interested on scales,
where y < 1, we can expand Eq.
(5) as 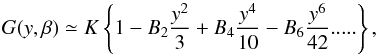 (6)where,
(6)where,
![\begin{eqnarray*} \begin{array}{rl} K & = 1 + \frac{2}{3}\beta+\frac{1}{5}\beta^2 \\[2mm] B_2 & = 1 + \frac{2}{5}K^{-1}(4/3\beta+4/7\beta^2)\\[2mm] B_4 & = 1 + \frac{4}{3}K^{-1}(4/7\beta+4/15\beta^2)\\[2mm] B_6 & = 1 + K^{-1}(8/9\beta+24/55\beta^2). \end{array} \end{eqnarray*}](/articles/aa/full_html/2014/03/aa21942-13/aa21942-13-eq162.png) K is the familiar Kaiser
correction factor, while the even coefficients B2n ~ 1 in the limit
β < 1. Under these
conditions,
K is the familiar Kaiser
correction factor, while the even coefficients B2n ~ 1 in the limit
β < 1. Under these
conditions, 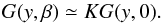 (7)With this
approximation and G computed from Eq. (5), we can predict with sufficient accuracy the non-linear amplitude of
η in
redshift space,
(7)With this
approximation and G computed from Eq. (5), we can predict with sufficient accuracy the non-linear amplitude of
η in
redshift space, 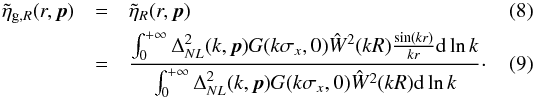 Interestingly,
both the linear bias parameter and the scale-independent Kaiser correction have dropped
out of this expression with the above “derivation” isolating the leading order
contribution in G(y,β) and at the same time,
decoupling the Kaiser model from the random dispersion. For a realistic value of
β
(≃0.5), assuming σv = 175 km s-1
and considering the scale R = 5 h-1 Mpc, the
approximation (8) is 1.6% at z = 1.
Interestingly,
both the linear bias parameter and the scale-independent Kaiser correction have dropped
out of this expression with the above “derivation” isolating the leading order
contribution in G(y,β) and at the same time,
decoupling the Kaiser model from the random dispersion. For a realistic value of
β
(≃0.5), assuming σv = 175 km s-1
and considering the scale R = 5 h-1 Mpc, the
approximation (8) is 1.6% at z = 1.
 |
Fig. 4 Relative difference between the clustering ratio in real (ηg,R) and redshift
( |
Figure 3 shows how well Eq. (8) describes the actual behaviour of haloes in the Lh catalogues. For R = 4 h-1 Mpc the relative discrepancy between theory and data is reduced from 14% to 4%, while for R = 5 h-1 Mpc is as small as 2%. As discussed in Sect. 4.1, this level of systematic error (which is less than the statistical errors to be expected from VIPERS) is expected from the limitations of the adopted phenomenological description of the non-linear power spectrum in Eq. (8) (Smith et al. 2003) or from a possible non-local nature of galaxy bias at small R. The accuracy achieved with this simple model over the wide range of filtering scales R is remarkable, especially because it is not the result of fine-tuning the pairwise dispersion σ12. In Fig. 3, the value was fixed to the value σ12 = 200 km s-1 as measured from a dark matter simulation with similar mass resolution (Bianchi et al. 2012; Marulli et al. 2012). Such a low value for σ12 is expected since haloes do not sample their own inner velocity dispersion. In Sect. 5.3, we discuss the robustness of Eq. (8) in more detail for a wider range of velocity dispersions. Notwithstanding, we show in Fig. 4 how well the simple model given in Eq. (8) accounts for small scale peculiar velocities in more realistic mock catalogues. To this purpose, we consider a galaxy sample obtained by populating haloes according to the halo occupation distribution (HOD) method. In Sect. 5.1 of de la Torre et al. (2013), they describe step by step how they obtained these mock catalogues from the MultiDark simulation (see Prada et al. 2012).
These results motivate our choice of R = 5 h-1 Mpc as a smoothing scale for the analysis of the VIPERS data, since it maximises both the accuracy (minimizing the distance between data and theory, see Fig. 3) and the statistical precision of the estimate of η.
 |
Fig. 5 Testing the sensitivity of η to the bias of the adopted tracers.
Clustering statistics are estimated from two sub sets of the halo simulated
catalogues, known as mid and low sub-samples tant
include haloes with masses limited to M < 1013 h-1 M⊙ and
M < 1012 h-1 M⊙,
respectively. The left and right panels show the relative variation
in the variance |
4.3. Sensitivity to galaxy bias
In the linear regime, Eq. (8) is
independent of galaxy biasing, where the clustering ratio does not depend on the
particular tracer we use to estimate it. This is clearly only an approximation when
non-linear scales are included. Evidence of the inadequacy of the hypothesis of locality,
where a scale-dependence of galaxy bias (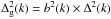 ), emerges naturally on
small scales. Similarly, the approximated redshift-space relation (8) explicitly neglects high order
β
contributions. We now establish the scales where the η statistics remains
independent of the choice of the galaxy tracer.
), emerges naturally on
small scales. Similarly, the approximated redshift-space relation (8) explicitly neglects high order
β
contributions. We now establish the scales where the η statistics remains
independent of the choice of the galaxy tracer.
The effects of scale-dependent bias are mitigated by the very definition of the
η statistic
as a ratio. For example, let’s consider the biasing model
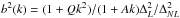 with
parameters A = 1.7 and Q = 9.6 (Cole et al 2005).
The relative variation db2/b2
is as high as 32% in the
interval 0.01 < k(h/Mpc)< 1, but results in
ηR(r)
change by less then 7%.
Indeed, the clustering ratio on scales (R,r) = (5,15) h-1 Mpc
roughly measures the relative strength of the power spectra at kj0 ~ 0.09 h/Mpc
and kW ~ 0.3 h /Mpc,
as shown by BM13 (see Sect. 3 of that paper), and, as a consequence, it is only sensitive
to the variation in the bias between these two scales. Although useful in appreciating the
favourable properties of the η statistic, this simple argument is clearly
insufficient to quantify the impact of scale-dependent bias of VIPERS data on
η.
Analysing galaxy simulations is a more effective way to estimate the amplitude of the
remaining systematic error.
with
parameters A = 1.7 and Q = 9.6 (Cole et al 2005).
The relative variation db2/b2
is as high as 32% in the
interval 0.01 < k(h/Mpc)< 1, but results in
ηR(r)
change by less then 7%.
Indeed, the clustering ratio on scales (R,r) = (5,15) h-1 Mpc
roughly measures the relative strength of the power spectra at kj0 ~ 0.09 h/Mpc
and kW ~ 0.3 h /Mpc,
as shown by BM13 (see Sect. 3 of that paper), and, as a consequence, it is only sensitive
to the variation in the bias between these two scales. Although useful in appreciating the
favourable properties of the η statistic, this simple argument is clearly
insufficient to quantify the impact of scale-dependent bias of VIPERS data on
η.
Analysing galaxy simulations is a more effective way to estimate the amplitude of the
remaining systematic error.
We use the Bh (in real space) and Lh (in redshift space) simulated catalogues at z = 1, which contain haloes with masses up to M = 7 × 1014 h-1 M⊙. From these, we select two sub-samples that, have a lower bias compared to the full parent catalogues, by construction. We call these mid and low samples and include, respectively, only haloes with masses M < 1013 h-1 M⊙ and M < 1012 h-1 M⊙. The variance and 2-point correlation function of the smoothed density contrast δR from these samples are plotted in the upper and middle panels of Fig. 5, as a function of R. These are expressed in terms of their relative difference with respect to the full parent catalogues. The different bias of the two samples is evident on both local and non-local scales, as probed respectively by the two statistics σg,R and ξg,R. As predicted by theory, the lower panel confirms that, both quantities are biased in similar ways, such that the clustering ratio is essentially insensitive to this: systematic errors are limited to less than 1% (3%) in real (redshift) space with this choice of the mass threshold.
A further indication of the limited impact of a scale-dependent bias on the estimate of
ηR from the VIPERS data
is provided by a parallel analysis of the data themselves. Marulli et al. (2013) and de la Torre et al.
(2013) measure the dependence of the galaxy correlation function on galaxy
luminosity. The presence of any differential scale-dependent bias between samples with
different luminosities would make us wary of non-local biasing effects entering in the
clustering ratio as well. To investigate this, we consider the halo occupation
distribution model fits to the measured VIPERS two-point correlations for five samples at
⟨ z ⟩ = 0.8 and luminosity between MB < −22
and −20 (de la Torre et al. 2013, Fig. 12). Figure 6 shows HOD model power spectra
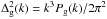 corresponding to the
best-fit HOD parameters for these samples. The plot shows that the shapes of the power
spectra all follow the HALOFIT prescription, and only begin to diverge at k > 1 h /Mpc,
or on scales to which ηR has little
sensitivity. A luminosity-dependent scale-independent bias model therefore provides an
excellent match to the data. The clustering ratio is sensitive to the power spectrum over
two scales probed by the smoothed correlation function and the variance: Ŵ2(kR)j0(nkR)
and Ŵ2(kR). The range of
wavenumbers that affect the ratio is determined by the broader top hat kernel
Ŵ2(kR) with effective
width kmax ~ π/R.
From this argument, we see that the clustering ratio is mainly determined by the power
spectrum at k < 0.6 h Mpc-1
for R = 5,
thus by significantly smaller k’s than indicated by the tests of Fig. 6. This is explicitly shown by the right panel of the
same figure, where ηR(3R)
is computed as a function of R for the VIPERS galaxy samples. At R = 5 h-1 Mpc, the
difference between the Halofit prediction and the values estimated for the VIPERS samples
differ by no more than 2%. Given the ~10% random errors expected on the estimates of η from the current PDR-1
VIPERS sample (Sect. 6), this shows that any systematic effect due to scale dependence of
galaxy bias is expected to be negligible.
corresponding to the
best-fit HOD parameters for these samples. The plot shows that the shapes of the power
spectra all follow the HALOFIT prescription, and only begin to diverge at k > 1 h /Mpc,
or on scales to which ηR has little
sensitivity. A luminosity-dependent scale-independent bias model therefore provides an
excellent match to the data. The clustering ratio is sensitive to the power spectrum over
two scales probed by the smoothed correlation function and the variance: Ŵ2(kR)j0(nkR)
and Ŵ2(kR). The range of
wavenumbers that affect the ratio is determined by the broader top hat kernel
Ŵ2(kR) with effective
width kmax ~ π/R.
From this argument, we see that the clustering ratio is mainly determined by the power
spectrum at k < 0.6 h Mpc-1
for R = 5,
thus by significantly smaller k’s than indicated by the tests of Fig. 6. This is explicitly shown by the right panel of the
same figure, where ηR(3R)
is computed as a function of R for the VIPERS galaxy samples. At R = 5 h-1 Mpc, the
difference between the Halofit prediction and the values estimated for the VIPERS samples
differ by no more than 2%. Given the ~10% random errors expected on the estimates of η from the current PDR-1
VIPERS sample (Sect. 6), this shows that any systematic effect due to scale dependence of
galaxy bias is expected to be negligible.
 |
Fig. 6 Left:best-fitting galaxy power spectra given the halo occupation distribution model fits for VIPERS galaxies in de la Torre et al. (2013). We examine five luminosity thresholded samples from MB < −22.0 to MB < −20 at z = 0.8. The HALOFIT matter power spectrum (black curve) and linear power spectrum (dashed curve) are overplotted. The galaxy power spectra are consistent with a luminosity-dependent constant bias model with respect to HALOFIT up to k = 1 h /Mpc. Right: values for the clustering ratio ηR(3R) are computed for the VIPERS galaxy power spectra. We find an agreement with the HALOFIT prediction at the 2% level at all scales down to R = 4 h-1 Mpc. |
 |
Fig. 7 Left: radial number density of galaxies in the simulated W4 field before (diamonds) and after (triangles) implementing the radial selection function of VIPERS PDR-1. Right: estimations of the variance σg,R (upper), correlation function ξg,R(3R) (centre), and clustering ratio ηg,R(3R) (lower) from the true population of galaxies in the W4 field (diamonds) and from the sub-sample with the same VIPERS radial density profile (triangles) are shown as a function of the filtering scale R. Squares show estimates obtained after correcting the relevant statistical quantities for shot noise, using the local Poisson model (Layser 1956). |
5. The impact of observational effects on η
In this section, we discuss how observational effects have been accounted for in our analysis, and we test the robustness and limitations in producing an unbiased estimate of η from the VIPERS data.
For this, we use simulated galaxy samples that implement the VIPERS selection effects. We construct artificial galaxy light cones (named Lg hereafter) by populating the Lh simulations with a specific Halo Occupation Distribution (HOD) prescription, which are calibrated using VIPERS observations (de la Torre et al. 2013). The next step in obtaining fully realistic VIPERS mocks is to add the detailed survey selection function. The procedure that we follow is the same discussed in de la Torre et al. (2013): we first apply the magnitude cut iAB < 22.5, then compute the observed redshift by incorporating the peculiar velocity contribution and a random component that reproduces the VIPERS redshift error distribution. We then add the effect of the colour selection on the radial distribution of the mocks. The latter is obtained by depleting the mocks at z < 0.6, so as to reproduce the Colour Sampling Rate (CSR, see Paper I). The mock catalogues that we obtain are then similar to the VIPERS parent photometric sample. We next apply the slit-positioning algorithm (SPOC, Bottini et al. 2005) with the same setting as for the data. This allows us to reproduce the VIPERS footprint on the sky; the small-scale angular incompleteness is due to spectra collisions and the variation in Target Sampling Rate across the fields. Finally, we deplete each quadrant to reproduce the effect of the Survey Success Rate (SSR). In this way, we end up with a set of 31 and 26 realistic mock catalogues (named LgV hereafter), which simulate the detailed survey completeness function and observational biases of VIPERS in the W4 and W1 fields, respectively.
It is important to remark that the parent mock galaxy catalogues used here are not precisely the “standard” ones created for VIPERS or those discussed in de la Torre et al. (2013). In the latter, the mass resolution of the original Lh halo catalogues was improved by artificially adding low mass haloes following the prescriptions of de la Torre & Peacock (2013). This method uses the initial halo density field estimated on a regular grid, where the size is set by the mass resolution of the dark matter simulation. For the purpose of extending the halo mass range in the MultiDark simulation and creating VIPERS mock galaxy catalogues, an optimal grid size of 2.5 h-1 Mpc has been chosen. However, as shown in de la Torre & Peacock (2013), the grid size, or reconstruction scale λ, can have some impact on the accuracy with which galaxy two-point correlations are reproduced. In particular, values of λ larger than the typical halo-halo separation, which are about 1 h-1 Mpc, can lead to an underestimation of the two-point correlation function of galaxies that populate the reconstructed haloes. In de la Torre & Peacock (2013), they showed that the two-point correlation function on scales around 1 h-1 Mpc is underestimated by few percents for the faintest galaxies for the adopted reconstruction scale used to create the standard VIPERS mocks. We found that the variance of the smoothed galaxy field measured in the standard mocks is also affected by this effect. For this reason and without loss of generality, we thus decided to use the Lg mock catalogues without the galaxies residing in the reconstructed haloes. Because these galaxies are hosted by haloes, which are systematically more massive than those hosting real VIPERS galaxies, does not affect the amplitude of the clustering ratio, which, as discussed in Sect. 4.3, is independent of the specific mass tracer.
 |
Fig. 8 PDF of the number count overdensities δN within spheres of radius R = 5 h-1 Mpc (histograms) are measured from mock surveys that reproduce the full selection functions of the VIPERS W1 and W4 fields (left and right groups of four panels). This is compared with a reference sample drawn from the Poissonian PDF shown by the dashed lines. The four panels of each VIPERS field correspond to the PDF that one obtains when rejecting an increasingly larger number of cells, which depends on whether the fraction of the cells volume affected by the survey mask is smaller than the threshold wth indicated in the insets. The effect of “corrupted” cells is stronger in the W1 field, where it is necessary to reject all cells for which more than 40% of the volume is affected by the survey mask to recover the correct PDF. Error bars are obtained as the standard deviation over 50 distinct random catalogues. In the inset, we also quote the significance level of the Kolmogorov-Smirnov test on the agreement of the two distributions. |
5.1. Effects related to the radial selection function: shot noise
One effect of the selection function in a flux-limited sample is the increase in the shot noise as a function of distance due to the corresponding decrease of the mean density. One could correct for this by increasing the size of the smoothing window R, but this would remove the ability to compare fluctuations on the same scale at different redshifts. Rather, we assume that the data represents a local Poisson sampling of the underlying continuous density field and correct for this statistically (Layser 1956) and verify the limits of this assumption using our mock samples.
The right panel of Fig. 7 shows the effect of the
shot noise correction on the two-point correlation function, the variance, and the
clustering ratio. While the two-point function is insensitive to shot noise by
construction, the variance does need to be corrected for the increasing Poisson noise,
which is given by the inverse of the average counts in the spherical cells
![\hbox{$\left[\bar{N}^{-1}(z)\right]$}](/articles/aa/full_html/2014/03/aa21942-13/aa21942-13-eq234.png) . When
subtracted from the observed value, the effect is completely removed (square symbols).
. When
subtracted from the observed value, the effect is completely removed (square symbols).
 |
Fig. 9 Testing the effectiveness of our correction for the VIPERS angular selection function on the clustering ratio η. From top to bottom, we show (for a smoothing radius R = 5 h-1 Mpc) the impact on the variance, 2-point correlation function, and clustering ratio ηg,R(3R). In each panel, we plot the mean and scatter over the mock samples of the relative difference δ between the “observed” and “true” quantities (multiplied by 100): triangles are for no correction at all, while squares corresponds to measurements using the correction method discussed in the text. The cyan shaded area correspond to a relative deviation smaller than ± 5%. Left and right panels correspond to W1 and W4, respectively. |
5.2. Effects related to the angular selection function
The VIPERS redshifts are being collected by tiling the selected sky areas with a uniform mosaic of VIMOS fields. The area covered is not contiguous but presents regular gaps due to the specific footprint of the instrument field of view, as well as to intrinsic unobserved areas due to bright stars or defects in the original photometric catalogue. The VIMOS field of view has four rectangular regions of about 8 × 7 square arcminutes each, which are separated by an unobserved cross (Guzzo et al. 2013; de la Torre et al. 2013). This creates a regular pattern of gaps in the angular distribution of the measured galaxies, which is clearly visible in Fig. 1. Additionally, the Target Sampling Rate and the Survey Success Rate vary among the quadrants, and a few of the latter were lost because of mechanical problems within VIMOS (see Paper I for details). Finally, the slit-positioning algorithm, SPOC, also introduces some small-scale angular selection effects with different constraints along the dispersion and spatial directions of the spectra, as thoroughly discussed in de la Torre et al. (2013). Clearly, this combination of angular selection effects has to be taken properly into account when estimating any clustering statistics.
In our specific case, this issue has been addressed as follows. We simulate a random (Poissonian) distribution of galaxies (hereafter called “parent catalogue”) and apply the global VIPERS angular selection function, which results from the combination of the photometric and spectroscopic masks, the TSR and the SSR.
We test whether the distributions of counts within cells of radius R match the expected Poisson distribution in Fig. 8 using the “parent” Lg (dashed line) and “observed” LgV (histograms) mocks discussed earlier on. When the probability distribution function (PDF) is reconstructed using all possible cells that can be accommodated within the rectangular footprint of the W1 and W4 fields, the result is severely biased, which indicates that the sampling of the underlying PDF is not random. It is clear that gaps and holes lead to a broadening of the PDF, which is artificially skewed towards low counts and an overestimate of the power in 1- and 2-point statistics. We have demonstrated (Bel et al., in prep.) that this effect is mainly due to the missing full quadrants with a negligible contribution of the smaller gaps produced by the VIMOS footprint, or of the small-scale biases of the SPOC slit-positioning scheme. We also see that the effects are almost independent of the scale R used to compute the clustering statistics within the range explored here (3–8 h Mpc-1).
Bel et al. (in prep.) introduce a method to correct for such angular selection effects and recover the correct shape of the PDF and the corresponding moments to all orders. Here, we briefly summarize how we obtained a correct estimate of the variance, which we need for building the clustering ratio. As shown by Fig. 8, the size of the VIPERS PDR-1 sample is such that we can simply reject all spherical cells for which more 40% of the volume is affected by the overall survey mask, which corresponds to regions not covered by the survey. With this threshold, we recover the random sampling regime. Accordingly, we shall reject all the “seeds” for which at least one sphere of the surrounding motif does not satisfy the inclusion condition (see Sect. 3.2) in the computation of the two-point function. Once this selection process is applied, the underlying statistical properties of galaxies are properly reconstructed without any additional de-biasing procedure. The net result on the estimated statistics from the mocks is shown in Fig. 9. The three panels show that the variance, two-point correlation function, and clustering ratio for the “observed” LgV mocks converge to the “true” value from the parent Lg. Independent of the correction, it is interesting to remark how, η is fairly insensitive to these effects. This happens because η is defined as the ratio of two quantities that are similarly affected. This is particularly impressive in the case of the W4 field, where η is virtually exact even without the correction. The price paid for this increased accuracy is clearly a larger statistical error on η due to the smaller effective survey volume.
5.3. Impact of redshift errors
 |
Fig. 10 Clustering ratio ηg,R estimated
from Lh haloes in real space (diamonds)
is shown as a function of the filtering radius R and of the
correlation length r = 3R. We also plot the
clustering ratio |
 |
Fig. 11 Impact and handling of the VIPERS redshift measurement errors on the usual
statistical quantities that enter the definition of η, as plotted as a
function of the filtering scale R and tested using the Lg mock
catalogues. Triangles correspond to measurements performed after adding a redshift
error randomly drawn from a Gaussian distribution with standard deviation
σcz = 141(1 + z)
to each galaxy position, which is representative of the errors affecting VIPERS
redshifts (Guzzo et al. 2013). Diamonds give
the reference values and are computed in redshift space without measurement errors.
The dotted and solid lines give the clustering ratio predicted by Eq. (8) when a dispersion σv = 100 km s-1
or |
Using repeated observations of 1215 objects in the the PDR-1 catalogue, the rms measurement error of VIPERS redshifts has been estimated to be σz = 0.00047(1 + z) or σcz = 141(1 + z) km s-1 (see Paper I). At z ~ 1, this translates into an error in the radial comoving distance of ~3 h-1 Mpc, which is expected in principle to have an impact on counts-in-cell statistics, for comparable cell sizes R.
The net effect of redshift errors is to smooth the galaxy distribution in redshift-space
along the radial direction, suppressing the amplitude of 1-point statistics. This is
similar to the effect of small-scale random peculiar velocities (although the latter on
small scales are better described by an exponential distribution rather than a Gaussian).
We therefore model the effect of redshift errors in the expression of η (Eq. (8)) by using an effective dispersion
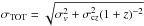 in the Gaussian damping term, or by adding in quadrature the VIPERS rms redshift error to
the peculiar velocity dispersion of galaxies. We test the goodness of this description
using the Lg mock surveys as described earlier, to
which we add a radial displacement drawn from a Gaussian distribution with the appropriate
dispersion. The results of measuring the variance
in the Gaussian damping term, or by adding in quadrature the VIPERS rms redshift error to
the peculiar velocity dispersion of galaxies. We test the goodness of this description
using the Lg mock surveys as described earlier, to
which we add a radial displacement drawn from a Gaussian distribution with the appropriate
dispersion. The results of measuring the variance 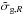 ,
two-point correlation function
,
two-point correlation function 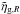 ,
and clustering ratio
,
and clustering ratio 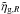 of the smoothed field on the perturbed and unperturbed mocks, as compared to the corrected
and uncorrected model, are shown in Fig. 11. As
expected, the figure shows that, as expected, the amplitude of the effect (an
underestimate of
of the smoothed field on the perturbed and unperturbed mocks, as compared to the corrected
and uncorrected model, are shown in Fig. 11. As
expected, the figure shows that, as expected, the amplitude of the effect (an
underestimate of 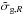 and an overestimate of
and an overestimate of 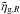 )
increases for a decreasing smoothing scale R, when the latter becomes comparable to the
redshift errors. To test the correction, we have estimated ηg,R in the
Lh light cones of haloes in real space
after having introduced random errors, which are characterised by the dispersion parameter
σu (σcz = σu(1 + z)),
in the cosmological redshift. The outcome of this analysis is presented in Fig. 10 and shows that Eq. (8) allows us to account for either small scale peculiar velocities or
redshift errors.
)
increases for a decreasing smoothing scale R, when the latter becomes comparable to the
redshift errors. To test the correction, we have estimated ηg,R in the
Lh light cones of haloes in real space
after having introduced random errors, which are characterised by the dispersion parameter
σu (σcz = σu(1 + z)),
in the cosmological redshift. The outcome of this analysis is presented in Fig. 10 and shows that Eq. (8) allows us to account for either small scale peculiar velocities or
redshift errors.
5.4. Combined correction of systematic effects
We finally want to compare how well the combination of the different pieces we have developed and implemented into our description to account for non-linear and observational biases is capable of recovering the correct original value of η. This test is performed by comparing the “idealized” Lh mock surveys, which contain a population of dark matter haloes with constant density (no selection function, no mask) within the volume of the VIPERS survey, and the set of LgV mocks, which contain HOD simulated galaxies that are selected according to the VIPERS selection function. We want to test whether the clustering ratio reconstructed from the VIPERS-like samples of galaxies after the correction for all the survey selection functions traces the clustering ratio reconstructed from the Lh samples. In other words, we want to determine if the clustering ratio is in agreement with catalogues characterized by a different set of tracers (haloes) masses (in the range 3 × 1011 < M h-1 M⊙ < 7 × 1014) without any VIPERS observational selection function (except from random redshift errors that we add to the haloes according to the techniques explained in Sect. 5.3).
The results of this analysis, as shown in Fig. 12, confirm the robustness of the clustering ratio. The same figure also shows the separate impact of the different effects and how η is particularly insensitive to some of them, due to its definition, as already shown in the previous sections. Specifically, these are all those biases that affect 1- and 2-point clustering statistics in the same sense.
6. Cosmological constraints from the VIPERS PDR-1 data
Using the methodology developed and tested in the previous sections, we are now in the position to apply the clustering ratio test to the VIPERS survey and study how well we can constrain the values of (at least some) cosmological parameters using the current catalogue.
 |
Fig. 12 Overall impact and treatment of VIPERS selection effects on the estimate of the
galaxy clustering ratio as a function of the smoothing scale R and for a correlation
scale n = 3. The reference values of
|
 |
Fig. 13 Galaxy clustering ratio |
6.1. Likelihood definition
Let us first illustrate the procedure to evaluate P(p | ηg,R), which has the likelihood of the unknown set of parameters p = (Ωm,ΩX,w,H0,Ωbh2,ns,σ8,σ12), given the observed value of ηg,R. The probability distribution function of the clustering ratio is not immediately obvious since this observable is defined via a ratio of two non-independent random variables. By using both simulated and real data, BM13 showed that the PDF of ηg,R is very well described by a Gaussian function, meaning that we can apply a standard χ2 analysis.
In the analysis of the VIPERS sample we have considered two cases:
-
a single redshift bin in the interval 0.65 < z < 1.2 (i.e. N = 1 in Eq. (8));
-
two uncorrelated bins, at 0.65 < z < 0.93 and 0.93 < z < 1.2, i.e. with N = 2 in Eq. (8) (see Fig. 13).
In the following, we shall take their mean redshift as centres of these two bins rather than the median of the galaxy distribution. This choice is justified by the fact that this is approximately the redshift at which the accuracy in the estimate of η, as determined by the tradeoff between a decreasing number of objects and an increasing number of cells, has its peak. Note that this choice has no effect on the cosmological results.
In our analysis, we assume a flat cosmology in which the accelerated expansion is caused by a cosmological constant term in Einstein’s field equations (i.e., we fix the dark energy equation of state parameter to w = −1). As in BM13, we assume Gaussian priors on the baryonic matter density parameter Ωbh2 = 0.0213 ± 0.0010, the Hubble constant H0 = 73.8 ± 2.4 km s-1Mpc-1 and the primordial index ns = 0.96 ± 0.014, as provided respectively by BBN (Pettini et al. 2008), HST (Riess et al. 2011) and WMAP7 (Larson et al. 2011) determinations. Additionally, we assume Gaussian priors on σ8, which is re-parameterized as ΔR(kwmap)2 = (2.208 ± 0.078) × 10-9 with kwmap = 0.027 Mpc-1 (Komatsu et al. 2011) and on the effective pairwise velocity dispersion (σ12 = 2σTOT = 514 ± 24 km s-1), as estimated from the VIPERS data themselves (priv. comm. by de la Torre). Finally, we underline that we do not include the full WMAP likelihood, which would introduce a strong prior on the matter density parameter Ωmh2.
The clustering ratio ηg,R(r,p) is estimated from the data by re-mapping the observed galaxy angular positions and redshifts into comoving distances, which vary the cosmology on a grid in a 6D space (Ωm, H0, Ωbh2, ns, σ8, σ12). A consequence of this is that the posterior ℒ does not vary smoothly among the different models because the number of galaxies counted in any given cell that varies from model to model. However, the computation of the observable ηg,R(3R,p) is rather fast, given the counts-in-cells nature of the method. Therefore, shot noise is the price we have decided to pay in order to avoid fixing cosmological parameters at fiducial values and to obtain an unbiased likelihood hyper-surface.
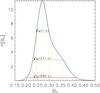 |
Fig. 14 Normalized 1D posterior probability of the density parameter at the current epoch,
Ωm,
estimated from the full VIPERS sample that is centred at z = 0.93. The curve
is obtained by marginalizing the posterior |
6.2. Results
In Fig. 13, we show the values of
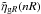 measured from the VIPERS data for (R,n) = (5 h-1 Mpc,3), which splits the
survey in different fashions (points). Note how the scatter between the estimates obtained
by analysing the two fields W1 and W4 separately is compatible with the error bars
that are estimated from the mock samples, suggesting that cosmic variance largely
dominates the error budget. The curves correspond to the model (cf. Eq. (8)), which is computed for the best fit values
of the parameters, as obtained for the whole survey. The solid line corresponds to the
full model, which accounts for all non-linear corrections, whereas the dotted line gives
the expected redshift-independent behaviour if η were measured (with the same derived parameters)
on fully linear scales (for larger R as, for example, in BM13). The short-dashed line
corresponds instead to only correcting for non-linear clustering but not for
redshift-space distortions, while the magenta long-dashed line demonstrates the intrinsic
sensitivity to Ωm,
which is further discussed in the following section (Sect. 6.3).
measured from the VIPERS data for (R,n) = (5 h-1 Mpc,3), which splits the
survey in different fashions (points). Note how the scatter between the estimates obtained
by analysing the two fields W1 and W4 separately is compatible with the error bars
that are estimated from the mock samples, suggesting that cosmic variance largely
dominates the error budget. The curves correspond to the model (cf. Eq. (8)), which is computed for the best fit values
of the parameters, as obtained for the whole survey. The solid line corresponds to the
full model, which accounts for all non-linear corrections, whereas the dotted line gives
the expected redshift-independent behaviour if η were measured (with the same derived parameters)
on fully linear scales (for larger R as, for example, in BM13). The short-dashed line
corresponds instead to only correcting for non-linear clustering but not for
redshift-space distortions, while the magenta long-dashed line demonstrates the intrinsic
sensitivity to Ωm,
which is further discussed in the following section (Sect. 6.3).
The best fit parameters have been first estimated splitting the data into two redshift
bins (0.65 ≤ z < 0.93 and
0.93 < z ≤ 1.2). For these
two volumes, the likelihood analysis yields 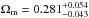 and
and 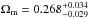 ,
respectively. Noticeably, error bars are smaller in the high redshift bin, despite the
lower number density of galaxies. This is mainly the result of the 30% larger total volume but also of the
smaller fraction of rejected cells in the process of mask correction. When the full
redshift range 0.65 < z ≤ 1.2 is analysed
at once, we obtain
,
respectively. Noticeably, error bars are smaller in the high redshift bin, despite the
lower number density of galaxies. This is mainly the result of the 30% larger total volume but also of the
smaller fraction of rejected cells in the process of mask correction. When the full
redshift range 0.65 < z ≤ 1.2 is analysed
at once, we obtain 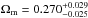 ,
which is the value used to produce the model curves in Fig. 13.
,
which is the value used to produce the model curves in Fig. 13.
Figure 14 shows the 1D normalized posterior probability of Ωm for this case, which is obtained by marginalizing P(p,ηg,R) over the remaining p elements. It is also interesting to note that if each element of the vector p = (Ωm,H0,Ωbh2,ns,σ8,σ12) is perturbed by + 10%, the corresponding variation induced in the amplitude of the clustering ratio is (−8.5%, −14.6%, 2.7%, 12%, 3%, 3%). This shows the specific sensitivity of η to the values of Ωm, h, and ns, as well as its weak dependence on Ωbh2, σ8 and σ12. The latter is particularly relevant, as the last two parameters enter into play here only because η is pushed to non-linear scales. The indication is therefore, once again, that the dependence on these specific parameters is weak. By giving a −40% change to the assumed central value of the Gaussian prior on the peculiar velocity dispersion σv, we change the estimated value of the matter density parameter by only −7%. This however remains as the biggest potential systematic in our analysis.
For comparison, the η-test to LRG galaxies of the SDSS DR7 sample is applied and (but smoothing the field on larger, more linear scales using R = 14 h-1 Mpc), BM13 obtain Ωm = 0.275 ± 0.020. This value is compared to those obtained here in Fig. 15. The roughly comparable uncertainty of the VIPERS and SDSS measurements, despite the smaller volume and number of objects of VIPERS, is explained by the much larger number of cells available to compute the statistic, when the field is smoothed on scales R = 5 h-1 Mpc, as for VIPERS, rather than on 14 h-1 Mpc, as used in the SDSS analysis of BM13. The price to be paid in the former case is that of having to handle and model non-linear scales.
 |
Fig. 15 Value of the matter density parameter Ωm as estimated at different redshifts from the SDSS DR7 (Bel & Marinoni 2014) and VIPERS samples; the full sample (blue square) and two non-overlapping redshift bins (grey filled circles) correspond to 0.65 ≤ z < 0.93 and 0.93 < z ≤ 1.2. Both analyses assume a flat ΛCDM model and the same priors on common parameters. The dotted line shows the best fitting value for Ωm, as obtained combining the SDSS and VIPERS measurements. |
 |
Fig. 16 Left:two-dimensional marginalized constraints on Ωm,0 and H0 obtained by fitting the η measurements from VIPERS data with a flat ΛCDM model. Contours are plotted for ℒ−ℒmin < 2.3,6.17. In this case, Ωb h2, ns, σ8, and σ12 are fixed to the value quoted in the text (i.e. they have a Dirac delta prior). We also draw curves corresponding to degeneracy along the loci Ωm,0h2 = const. (dotted line) and Ωm,0h = const. (dashed line). Right: the same but in the plane [Ωm,0, ns]. |
 |
Fig. 17 Sensitivity of the clustering ratio to the cosmological model, through
left: isocontours of the function
|
The excellent consistency of these measurements over a wide redshift interval (0 < z < 1.2) and from fully independent data sets is remarkable and strongly support the reliability of the measurements made by de la Torre et al. (2013). The combination of SDSS and VIPERS estimates of the matter density parameter gives Ωm,0 = 0.274 ± 0.017, which improves the precision of the WMAP7 determination (Ωm = 0.267 ± 0.029, Larson et al. 2011) by 75%, and by more than a factor of two when it is obtained by the joint analysis of the WMAP3 and SDSS DR5 data (Ωm = 0.259 ± 0.039, Eisenstein et al. 2005). Our precision is comparable to that obtained by Percival et al. (2010; Ωm = 0.278 ± 0.018) from the combination of BAO measurements from SDSS DR7 and 2dFRGS and the full WMAP5 likelihood (Dunkley et al. 2009). We also note that the most recent analyses of the BOSS data give Ωm = 0.298 ± 0.017, when using BAO and WMAP7 (Anderson et al. 2012) and Ωm0 = 0.282 ± 0.015 from the combination of the full correlation function with WMAP7 (Sanchez et al. 2012).
It is important to remark that our estimates of Ωm using the observed values of η were obtained without including the full CMB likelihood, as this would have forced a very strong prior on Ωmh2. We did, however, include priors on the parameters H0 and ns on which the analysis is sensitive, as discussed earlier. The additional degrees of freedom arising when these two priors in the likelihood analysis are relaxed are shown in Fig. 16. At least for the range explored, the degeneracy axis in the (Ωm,h) plane develops along the line Ωmh2 = const. This is different from measurements in the linear regime, where the degeneracy roughly follows an Ωmh = const. locus. In principle, a redshift survey larger than (but as dense as) VIPERS could be able to simultaneously constrain Ωm and h with a single probe by combining measurements of η with small and large smoothing scale R.
We also note that the VIPERS value 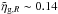 is only ~7% smaller than the value we obtain from
the LgV mock catalogues in
a ΛCDM cosmology. Given that
the best fitting and the simulated cosmological models are extremely close, this agreement
independently confirms that systematic errors are effectively taken care of.
is only ~7% smaller than the value we obtain from
the LgV mock catalogues in
a ΛCDM cosmology. Given that
the best fitting and the simulated cosmological models are extremely close, this agreement
independently confirms that systematic errors are effectively taken care of.
6.3. Discussion: specific sensitivity of η to cosmological parameters
In Fig. 13, we provide an explicit example of how
the η test
works by plotting both the measurements (open squares) and the expectation of the full
non-linear model (long-dashed line) when a different cosmology is adopted. In this case,
Ωm has been set
to 0.4 within the same flat Λ
model. The choice of a slightly wrong cosmology makes the data and the model incompatible.
On one side, the distortion of the cosmological volume of the cell due to the calculation
of distances results in a smaller measured value of
 .
At the same time, the theoretical expectation is even lower due to the different shape of
P(k) implied by the higher
Ωm.
.
At the same time, the theoretical expectation is even lower due to the different shape of
P(k) implied by the higher
Ωm.
In terms of specific cosmological parameters, the right-hand side of Eq. (8) depends on the shape of the matter power spectrum in real space. This means it is directly sensitive to the primordial index ns and to the parameters determining the size of the horizon scale at matter-radiation equality1, or Ωmh2 and Ωbh2. Since we pushed the analysis into the weakly non-linear regimes in this case, two additional parameters appear in the theoretical model (8) with respect to the linear analysis of BM13: the normalization of the power spectrum σ8, which enters the expression of the shape of the quasi-linear power spectrum of Smith et al. (2003) and the galaxy pairwise velocity dispersion σ12, which parameterizes the suppression of small-scale power produced by disordered peculiar velocities. The distance-redshift relation enters the left-hand side of Eq. (8) changing the volume and shape of each sphere and their relative distance in the directions parallel and perpendicular to the observer line’s of sight (Alcock-Paczynski effect). Together, these add some sensitivity to the density parameter, Ωx, and equation of state, w, of dark energy.
It is interesting to discuss the relative contribution of the geometrical and power
spectrum shape, which are shown and compared in Fig. 17. The geometric distortions in ηg,R(r)
(for R = 5 h-1 Mpc and
r = 3R) are equally sensitive to
both the dark matter and the dark energy densities as indicated by the degeneracy axes
(i.e. the isocontours), which are tilted by ~45° in the [Ωm,ΩX] plane. The absolute
amplitude of the distance-redshift translation, however, is weak. The clustering ratio
varies from 10% to
−20% around its true value
(estimated in the true cosmology) when the matter density parameter goes from
0.2 to 0.8 as shown in Fig. 17. The mass clustering ratio is extremely sensitive to the matter
density parameter Ωm. A change by ~0.1(−0.1) of the true value (in this case Ωm = 0.27) induces a change in
ηR of ~−30%(+60%). Note also the extremely
weak dependence of the isocontours on the dark energy parameter. This arises because we
parameterize the local normalization σ8 in terms of the seven-year WMAP
normalization prior 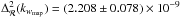 ,
where kwmap = 0.027
Mpc-1 (Komatsu et al. 2011). Mapping the primordial (linear)
curvature perturbations ℛ into
the present day rms of the matter density fluctuations, σ8, causes the
non-linear power spectrum to acquire an extra sensitivity to the dark energy content (and
to the gravitational model) of the universe.
,
where kwmap = 0.027
Mpc-1 (Komatsu et al. 2011). Mapping the primordial (linear)
curvature perturbations ℛ into
the present day rms of the matter density fluctuations, σ8, causes the
non-linear power spectrum to acquire an extra sensitivity to the dark energy content (and
to the gravitational model) of the universe.
In conclusion, we see that the cosmological signal measured by η from the VIPERS data is primarily encoded in the shape of the power spectrum rather than in space geometry. To obtain meaningful limits on Ωv (or, more directly, the degree of matter domination at z ≃ 1), Fig. 17 indicates that it is necessary to measure Ωm to a precision of better than about 5%. This is approximately the precision achieved in the current analysis, so it will be worth revisiting the geometrical aspect of the η test when the final VIPERS dataset is complete.
7. Summary
In this paper, we have applied the galaxy clustering ratio proposed by Bel & Marinoni (2014) to a sub set of the new VIPERS PDR-1 redshift catalogue which includes 26 611 galaxies. A large part of the paper has been dedicated to verifying the robustness of applying this statistics to mildly non-linear scales, where non-linear clustering, redshift-space distortions, and scale-dependence of biasing need to be accounted for.
Ideally, ηg,R(r) should be estimated in the linear regime (large R and r values), where its amplitude is theoretically predicted in a straightforward way. Nonetheless, we have shown that a simple, theoretically motivated modelling of the expected non-linear corrections is sufficient to preserve its value as a powerful cosmological probe also in the mildly non-linear regime in this paper. These corrections include: (a) the effect of random peculiar velocities, or non-linear redshift distortions on small scales: we have also shown that the effect of redshift errors can be incorporated within the same scheme once an effective pairwise dispersion is considered. (b) The scale dependence of bias: we have shown that this effect does not introduce a significant systematic error on the measurements of η for realistic dependences. This is not simply a question of assuming a mild dependence on scale of the bias but that its effect can be minimized by a careful choice of the scales of smoothing (R) and correlation (r) in terms of which η is defined.
Based on these results, we have used η to extract cosmological information from the new
PDR-1 data of the VIPERS survey, which is limited to z > 0.65. We first split the
sample into two redshift slices with a mean redshift z = 0.79 and z = 1.07. This exercise
yielded two independent estimates of the matter density parameter at the current epoch,
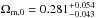 and
and 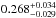 ,
respectively. To obtain these estimates, we included external priors on Ωbh2,h,ns
and
,
respectively. To obtain these estimates, we included external priors on Ωbh2,h,ns
and 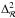 , but not the
strong one on Ωmh2 from WMAP. We also
analysed the full redshift range 0.65 < z < 1.2
as a single sample, obtaining a value
, but not the
strong one on Ωmh2 from WMAP. We also
analysed the full redshift range 0.65 < z < 1.2
as a single sample, obtaining a value 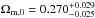 .
.
The two measurements of η from VIPERS with that from the SDSS by BM13 provide us with three independent estimates at three different cosmic epochs based on the same external priors. These allow us to: i) confirm the consistency of the standard ΛCDM cosmological model over a wide redshift baseline, covering almost half the age of the Universe; and ii) obtain a stronger constraint on the local value of Ωm than allowed by the two redshift surveys alone (~7%), corresponding to a transition redshift between the matter and cosmological-constant dominated epochs of zmd = 0.395 ± 0.04.
It is interesting to compare these figures to those we previously obtained using the angular power spectrum of the full CFHTLS parent galaxy sample (sliced using the same VIPERS colour selection criteria), which are coupled to an earlier VIPERS catalogue (Granett et al. 2012). This sample, assuming flatness and letting the matter density as a free fitting parameter (with Dirac priors on all other relevant cosmological quantities), yielded Ωm,0 = 0.30 ± 0.06.
The VIPERS measurement of Ωm,0 is also consistent with the estimate obtained by BM13 using the same technique applied to the SDSS LRG sample at z ~ 0.3, Ωm,0 = 0.275 ± 0.020. The combination of these two estimates of Ωm,0, as obtained from data that cover the large range 0 < z < 1.2, gives a best value of Ωm,0 = 0.274 ± 0.017. For comparison, the recent combination of the Planck TT power spectrum with WMAP polarization gives Ωm,0 = 0.315 ± 0.017. Note that the apparent tension between those measurements is mainly due to the prior on H0 coming from the HST measurements. Indeed, a lower value of H0 would result in a larger matter density.
Acknowledgments
J.B. and C.M. acknowledge useful discussions with F. Bernardeau, E. Gaztañaga, and I. Szapudi. We thank the referee for well-directed comments. We acknowledge the crucial contribution of the ESO staff for the management of service observations. In particular, we are deeply grateful to M. Hilker for his constant help and support of this programme. Italian participation to VIPERS has been funded by INAF through PRIN 2008 and 2010 programmes. L.G. and B.J.G. acknowledges support of the European Research Council through the Darklight ERC Advanced Research Grant (# 291521). O.L.F. acknowledges support of the European Research Council through the EARLY ERC Advanced Research Grant (# 268107). Polish participants have been supported by the Polish Ministry of Science (grant N N203 51 29 38), the Polish-Swiss Astro Project (co-financed by a grant from Switzerland, through the Swiss Contribution to the enlarged European Union), the European Associated Laboratory Astrophysics Poland-France HECOLS and a Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowship for Foreign Researchers (P11802). G.D.L. acknowledges financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 202781. W.J.P. and R.T. acknowledge financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 202686. W.J.P. is also grateful for support from the UK Science and Technology Facilities Council through the grant ST/I001204/1. E.B., F.M. and L.M. acknowledge the support from grants ASI-INAF I/023/12/0 and PRIN MIUR 2010-2011. C.M. is grateful for support from specific project funding of the Institut Universitaire de France and the LABEX OCEVU.
References
- Alcock, C., & Paczynski, B. 1979, Nature, 281, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Amendola, L., Appleby, S., Bacon, D., et al. 2013, Liv. Rev. Relativ., 16, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, E., Bailey, S., et al. 2012, MNRAS, 427, 3435 [Google Scholar]
- Ballinger, W. E., Peacock, J. A., & Heavens, A. F. 1996, MNRAS, 282, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, J., & Marinoni, C. 2012, MNRAS, 424, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, J., & Marinoni, C. 2014, A&A, 563, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, D., Guzzo, L., Branchini, E., et al. 2012, MNRAS, 427, 2420 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, C., Glazebrook, K., Davis, T. M., et al. 2011, MNRAS, 418, 1707 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bottini, D., Garilli, B., Maccagni, D., et al. 2005, PASP, 117, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Percival, W., & Peacock, J., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Lahav, O. 1999, ApJ, 520, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- de la Torre, S., & Peacock, J. 2013, MNRAS, 435, 743 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Guzzo, L., Kovac, K., et al. (the ZCOSMOS collaboration) 2010, MNRAS, 409, 867 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. (VIPERS team) 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drinkwater, M. J., Jurek, R. J., Blake, C., et al. 2010, MNRAS, 401, 1429 [Google Scholar]
- Dunkley, J., Spergel, D. N., Komatsu, E., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Fry, J. N., & Gaztañaga, E. 1993, ApJ, 413, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, L., & White, S. D. M. 2007, MNRAS, 377, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Le Fèvre, O., Guzzo, L., et al. (the VVDS collaboration) 2008, A&A, 486, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garilli, B., Paioro, L., Scodeggio, M., et al. 2012, PASP, 124, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Granett, B. R., Guzzo, L., Coupon, J., et al. 2012, MNRAS, 421, 251 [NASA ADS] [Google Scholar]
- Guzzo, L., Pierleoni, M., Meneux, B., et al. (the VVDS team) 2008, Nature, 451, 541 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. (the VIPERS team) 2013, A&A, submitted [arXiv:1303.2623] [Google Scholar]
- Heitmann, K., White, M., Wagner, C., Habib, S., & Higdon, D. 2010, ApJ, 715, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. C. 1972, MNRAS, 156 [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, 9 [Google Scholar]
- Kaiser, N. 1987, MNRAS, 227, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kovac, K., Porciani, C., Lilly, S. J., et al. 2011, ApJ, 731, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kron, R. C. 1980, ApJ, 241, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. (the EUCLID collaboration) 2011 [arXiv:1110.3193] [Google Scholar]
- Layser, D. 1956, ApJ, 61, 1243 [Google Scholar]
- Le Fèvre, O., Prieto, E., & Posselt, W. 2000, ASPC, 207, 313L [NASA ADS] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, Proc. SPIE, 4841, 1670 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. (the ZCOSMOS collaboration) 2009, ApJS, 184, 218 [Google Scholar]
- Marchetti, A., Granett, B. R., Guzzo, L., et al. (the VIPERS team) 2013, MNRAS, 428, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C. & Buzzi, A. 2010, Nature, 468, 539 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marinoni, C., Le Fèvre, O., Meneux, B., et al. 2005, A&A, 442, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marinoni, C., Bel, J., & Buzzi, A. 2012, JCAP, 10, 36 [Google Scholar]
- Marulli, F., Bianchi, D., Branchini, E., et al. 2012, MNRAS, 426, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bolzonella, M., Branchini, E., et al. (the VIPERS team) 2013, A&A, 557, 17A [Google Scholar]
- Mellier, Y., Bertin, E., Hudelot, P., et al. 2008, The CFHTLS T0005 Release, http://terapix.iap.fr/cplt/oldSite/Descart/CFHTLS-T0005-Release.pdf [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. (the DEEP2 collaboration) 2013, ApJS, 208, 5 [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A. 1992, MNRAS, 258, 581 [NASA ADS] [Google Scholar]
- Peacock, J. A., & Dodds, S. J. 1994, MNRAS, 267, 1020 [NASA ADS] [Google Scholar]
- Peacock, J. A., Cole, S., Norberg, P., et al. 2001, Nature, 410, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Percival, W. J., & White, M. 2009, MNRAS, 393, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Zych, B., Murphy, M. T., Lewis, A., & Steidel, C. C. 2008, MNRAS, 391, 1499 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2011, ApJ, 730, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, A. G., Scoccola, C. G., Ross, A. J., et al. 2012, MNRAS, 425, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D., Abdalla, F., Abraham, T., et al. (the BigBOSS Collaboration) 2011 [arXiv:1106.1706] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2009, The Mesenger, 135, 13 [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Sigad, Y., Branchini, E., & Dekel, A. 2000, ApJ, 540, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, B., & Fisher, J. R. 1978, IAU Symp., 79, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Verde, L., Heavens, A. F., Percival, W. J., et al. 2002, MNRAS, 335, 432 [Google Scholar]
- Wild, V., Peacock, J., Lahav, O., et al. (the 2dFGRS team) 2005, MNRAS, 356, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., Liguori, M., Bean, R., & Dodelson, S. 2007, Phys. Rev. Lett., 99, 141302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Fig. 1 Distribution on the sky of the galaxies with measured redshifts in the VIPERS PDR-1
catalogue within the W1 and W4 fields (blue points). The pattern described
by the gaps separating the VIMOS quadrants, as well as the areas not covered by the
PDR-1, are clearly visible. Superimposed to the spectroscopic data, we also plot for
illustrative purposes the projection of a subset of the spherical cells used to
estimate the variance |
| In the text | |
 |
Fig. 2 Impact of non-linear clustering on the measurement and theoretical modelling of the galaxy clustering ratio η. The latter is measured in real space for the halo catalogues of the Bh simulation and compared to both the linear and non-linear predictions, as described respectively by a simple Eisenstein & Hu (1998) linear power spectrum (dot-dashed lines) and after correction through the non-linear HALOFIT prescription of Smith et al. (2003) (solid lines). The clustering ratio is shown as a function of the smoothing scale R adopted to filter the discrete distribution of haloes and for various correlation lengths (r = nR) with n = { 2,3,4 }. Errors bars are obtained using 64 block-jackknife resampling of the data which excludes a cubic volume of linear size 250 h-1 Mpc each time. |
| In the text | |
 |
Fig. 3 Effect of redshift-space distortions on the measurement and modelling of the
clustering ratio. The values estimated in real and redshift space from the
Lh halo catalogues (main panel) are
compared with the theoretical predictions; these have been named
|
| In the text | |
 |
Fig. 4 Relative difference between the clustering ratio in real (ηg,R) and redshift
( |
| In the text | |
 |
Fig. 5 Testing the sensitivity of η to the bias of the adopted tracers.
Clustering statistics are estimated from two sub sets of the halo simulated
catalogues, known as mid and low sub-samples tant
include haloes with masses limited to M < 1013 h-1 M⊙ and
M < 1012 h-1 M⊙,
respectively. The left and right panels show the relative variation
in the variance |
| In the text | |
 |
Fig. 6 Left:best-fitting galaxy power spectra given the halo occupation distribution model fits for VIPERS galaxies in de la Torre et al. (2013). We examine five luminosity thresholded samples from MB < −22.0 to MB < −20 at z = 0.8. The HALOFIT matter power spectrum (black curve) and linear power spectrum (dashed curve) are overplotted. The galaxy power spectra are consistent with a luminosity-dependent constant bias model with respect to HALOFIT up to k = 1 h /Mpc. Right: values for the clustering ratio ηR(3R) are computed for the VIPERS galaxy power spectra. We find an agreement with the HALOFIT prediction at the 2% level at all scales down to R = 4 h-1 Mpc. |
| In the text | |
 |
Fig. 7 Left: radial number density of galaxies in the simulated W4 field before (diamonds) and after (triangles) implementing the radial selection function of VIPERS PDR-1. Right: estimations of the variance σg,R (upper), correlation function ξg,R(3R) (centre), and clustering ratio ηg,R(3R) (lower) from the true population of galaxies in the W4 field (diamonds) and from the sub-sample with the same VIPERS radial density profile (triangles) are shown as a function of the filtering scale R. Squares show estimates obtained after correcting the relevant statistical quantities for shot noise, using the local Poisson model (Layser 1956). |
| In the text | |
 |
Fig. 8 PDF of the number count overdensities δN within spheres of radius R = 5 h-1 Mpc (histograms) are measured from mock surveys that reproduce the full selection functions of the VIPERS W1 and W4 fields (left and right groups of four panels). This is compared with a reference sample drawn from the Poissonian PDF shown by the dashed lines. The four panels of each VIPERS field correspond to the PDF that one obtains when rejecting an increasingly larger number of cells, which depends on whether the fraction of the cells volume affected by the survey mask is smaller than the threshold wth indicated in the insets. The effect of “corrupted” cells is stronger in the W1 field, where it is necessary to reject all cells for which more than 40% of the volume is affected by the survey mask to recover the correct PDF. Error bars are obtained as the standard deviation over 50 distinct random catalogues. In the inset, we also quote the significance level of the Kolmogorov-Smirnov test on the agreement of the two distributions. |
| In the text | |
 |
Fig. 9 Testing the effectiveness of our correction for the VIPERS angular selection function on the clustering ratio η. From top to bottom, we show (for a smoothing radius R = 5 h-1 Mpc) the impact on the variance, 2-point correlation function, and clustering ratio ηg,R(3R). In each panel, we plot the mean and scatter over the mock samples of the relative difference δ between the “observed” and “true” quantities (multiplied by 100): triangles are for no correction at all, while squares corresponds to measurements using the correction method discussed in the text. The cyan shaded area correspond to a relative deviation smaller than ± 5%. Left and right panels correspond to W1 and W4, respectively. |
| In the text | |
 |
Fig. 10 Clustering ratio ηg,R estimated
from Lh haloes in real space (diamonds)
is shown as a function of the filtering radius R and of the
correlation length r = 3R. We also plot the
clustering ratio |
| In the text | |
 |
Fig. 11 Impact and handling of the VIPERS redshift measurement errors on the usual
statistical quantities that enter the definition of η, as plotted as a
function of the filtering scale R and tested using the Lg mock
catalogues. Triangles correspond to measurements performed after adding a redshift
error randomly drawn from a Gaussian distribution with standard deviation
σcz = 141(1 + z)
to each galaxy position, which is representative of the errors affecting VIPERS
redshifts (Guzzo et al. 2013). Diamonds give
the reference values and are computed in redshift space without measurement errors.
The dotted and solid lines give the clustering ratio predicted by Eq. (8) when a dispersion σv = 100 km s-1
or |
| In the text | |
 |
Fig. 12 Overall impact and treatment of VIPERS selection effects on the estimate of the
galaxy clustering ratio as a function of the smoothing scale R and for a correlation
scale n = 3. The reference values of
|
| In the text | |
 |
Fig. 13 Galaxy clustering ratio |
| In the text | |
 |
Fig. 14 Normalized 1D posterior probability of the density parameter at the current epoch,
Ωm,
estimated from the full VIPERS sample that is centred at z = 0.93. The curve
is obtained by marginalizing the posterior |
| In the text | |
 |
Fig. 15 Value of the matter density parameter Ωm as estimated at different redshifts from the SDSS DR7 (Bel & Marinoni 2014) and VIPERS samples; the full sample (blue square) and two non-overlapping redshift bins (grey filled circles) correspond to 0.65 ≤ z < 0.93 and 0.93 < z ≤ 1.2. Both analyses assume a flat ΛCDM model and the same priors on common parameters. The dotted line shows the best fitting value for Ωm, as obtained combining the SDSS and VIPERS measurements. |
| In the text | |
 |
Fig. 16 Left:two-dimensional marginalized constraints on Ωm,0 and H0 obtained by fitting the η measurements from VIPERS data with a flat ΛCDM model. Contours are plotted for ℒ−ℒmin < 2.3,6.17. In this case, Ωb h2, ns, σ8, and σ12 are fixed to the value quoted in the text (i.e. they have a Dirac delta prior). We also draw curves corresponding to degeneracy along the loci Ωm,0h2 = const. (dotted line) and Ωm,0h = const. (dashed line). Right: the same but in the plane [Ωm,0, ns]. |
| In the text | |
 |
Fig. 17 Sensitivity of the clustering ratio to the cosmological model, through
left: isocontours of the function
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.