| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201322878 | |
| Published online | 06 February 2014 | |
Investigating the hard X-ray emission from the hottest Abell cluster A2163 with Suzaku
1
Department of PhysicsNara Women’s University, Kitauoyanishi-machi, 630-8506
Nara, Japan
e-mail: naomi@cc.nara-wu.ac.jp
2
Institute of Space and Astronautical Science (ISAS), Japan
Aerospace Exploration Agency (JAXA), 3-1-1 Yoshinodai, Sagamihara, 229-8510
Kanagawa,
Japan
3
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS –
Université Paris Diderot, Bât. 709,
CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
4
Toho University, 2-2-1 Miyama, Funabashi, 274-8510
Chiba,
Japan
5
Nobeyama Radio Observatory, Minamimaki, Minamisaku,
, 384-1805
Nagano,
Japan
6
Argelander Institute for Astronomy, Bonn University,
Auf dem Hügel 71, 53121
Bonn,
Germany
Received:
20
October
2013
Accepted:
13
December
2013
Context. We present the results from Suzaku of the hottest Abell galaxy cluster A2163 at z = 0.2.
Aims. To study the physics of gas heating in cluster mergers, we investigated hard X-ray emission from the merging cluster A2163, which hosts the brightest synchrotron radio halo.
Methods. We analyzed hard X-ray emission spectra accumulated from two-pointed Suzaku observations. Non-thermal hard X-ray emission should result from the inverse Compton scattering of relativistic electrons by photons in the cosmic microwave background. To measure this emission, the dominant thermal emission in the hard X-ray band must be modeled in detail. To this end, we analyzed the combined broadband X-ray data of A2163 collected by Suzaku and XMM-Newton, assuming single- and multi-temperature models for thermal emission and the power-law model for non-thermal emission. Comparing the non-thermal hard X-ray flux to radio synchrotron emission, we also estimated the magnetic field in the cluster.
Results. From the Suzaku data, we detected significant hard X-ray emission from A2163 in the 12–60 keV band at the 28σ level (or at the 5.5σ level if a systematic error of the non-X-ray background model is considered). The Suzaku HXD spectrum alone is consistent with the single-temperature thermal model of gas temperature kT = 14 keV. From the XMM-Newton data, we constructed a multi-temperature model including a very hot (kT = 18 keV) component in the north-east region. Incorporating the multi-temperature and the power-law models into a two-component model with a radio-band photon index, where Γ = 2.18, the 12–60 keV energy flux of non-thermal emission is constrained within 5.3 ± 0.9 (±3.8) × 10-12 erg s-1cm-2 (the first and second errors refer to the 1σ statistical and systematic uncertainties, respectively). The 90% upper limit of detected inverse Compton emission is marginal (FNT < 1.2 × 10-11 erg s-1cm-2 in the 12–60 keV band). The estimated magnetic field in A2163 is B > 0.098 μG. While the present results represent a three-fold increase in the accuracy of the broadband (0.3–60 keV) spectral model of A2163, more sensitive hard X-ray observations are needed to decisively test for the presence of hard X-ray emission due to inverse Compton emission.
Key words: galaxies: clusters: individual: A2163 / galaxies: clusters: intracluster medium / X-rays: galaxies: clusters / cosmology: observations
© ESO, 2014
1. Introduction
The most energetic events in the Universe since the Big Bang are cluster mergers, which have kinetic energy on the order 1065 ergs. Cluster collisions release a huge amount of energy; a fraction of which is expected to heat the gas and generate non-thermal particles through shock waves. Hence, shock-heated gas provides important clues for understanding high-energy phenomena and the evolution of galaxy clusters. Synchrotron emission at radio wavelengths extending over scales of megaparsec have been observed in many clusters (Feretti et al. 2012). The existence of extended radio halos suggest the acceleration of relativistic electrons in the intracluster space. In the hard X-ray band, non-thermal emission is predicted to be generated by the inverse Compton (IC) scattering of these electrons by photons in the cosmic microwave background (CMB).
The inverse Compton hard X-ray emissions from nearby clusters have been detected by RXTE and BeppoSAX satellites (for review, see Rephaeli et al. 2008). The Coma cluster is the archetypal case (Rephaeli & Gruber 2002; Fusco-Femiano et al. 2004). On the other hand, no significant non-thermal X-ray emissions have been detected by the Suzaku and Swift satellites (Wik et al. 2009, 2011). This discrepancy might be reconciled by considering different sizes of viewing fields (Fusco-Femiano et al. 2011). Suzaku has searched for non-thermal X-ray emissions in nine bright clusters: the Centaurus cluster (Kitaguchi et al. 2007), the Ophiuchus cluster (Fujita et al. 2008), RX J1347.5–1145 (Ota et al. 2008), A3376 (Kawano et al. 2009), A2319 (Sugawara et al. 2009), A3667 (Nakazawa et al. 2009), the Coma cluster (Wik et al. 2009), the Perseus cluster (Nishino et al. 2010), and A2199 (Kawaharada et al. 2010). The hard X-ray spectra can be explained by thermal emission; adding a non-thermal power-law component does not improve data fitting (Ota 2012, and reference therein). Ajello et al. (2009, 2010) suggested that the hard X-ray emission from clusters (except the Bullet cluster) most likely had a thermal origin on the basis of the Swift observations of 20 clusters. Stacked spectra, which were constructed and analyzed from Fermi data, yielded no significant γ-ray signal from clusters (Huber et al. 2013). Ackermann et al. (2013) searched for cosmic-ray induced γ-ray emission through a combined analysis of 50 clusters to exclude hadronic injection efficiency in simple hadronic models, and also derived limits on the γ-ray flux on individual clusters.
For merging clusters, it is worth noting that the radio synchrotron power P1.4 is correlated with the X-ray luminosity of the thermal emission LX. On the other hand, relaxed clusters with no radio halo lie in a completely separate regime in the P1.4−LX plane (Brunetti et al. 2009; Cassano et al. 2013). This suggests that the generation of high-energy particles is connected to cluster evolution. Massive clusters that emit luminous X-rays contain high-energy particles and an intracluster magnetic field. Thus, we question whether radio-loud clusters similarly produce significant non-thermal X-ray emission? To answer this question, we focus on the hottest Abell cluster A2163, located at the brightest end of the P1.4−LX relationship.
The mean temperature of A2163
(z = 0.203) is 14 keV (Arnaud et al.
1992). This cluster hosts a huge, powerful synchrotron halo of radio power
P1.4 = 155 mJy (Feretti et al.
2004) and also possesses a complex temperature structure (Markevitch & Vikhlinin 2001; Bourdin
et al. 2011). The presence of high-temperature gas in the cluster has been
confirmed by the XMM-Newton and Chandra observations,
indicating that the cluster has undergone recent merging. From weak lensing observations,
Okabe et al. (2011) and Soucail (2012) showed that the mass distribution in A2163 is bimodal, which supports the merging hypothesis.
Hard X-ray observations of A2163 were carried out
by BeppoSAX and RXTE. BeppoSAX yielded the 90% upper limit
of non-thermal IC emission as
FNT(20−80 keV) < 5.6 × 10-12 erg s-1 cm-2
(Feretti et al. 2001). Detection was claimed from
the RXTE data with a long exposure time but was associated with large uncertainty
(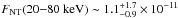 erg s-1 cm-2; Rephaeli et al. 2006).
erg s-1 cm-2; Rephaeli et al. 2006).
To constrain the non-thermal hard X-ray emission from the A2163 cluster, we analyze hard X-ray spectra obtained by the hard X-ray detector (HXD; Takahashi et al. 2007) onboard the Suzaku satellite (Mitsuda et al. 2007). From a joint analysis of the Suzaku and XMM-Newton data, we aim to understand the origin of hard X-ray emission and properties of shock-heated gas.
Throughout this paper, we adopt a cosmological model with standard parameters: matter density ΩM = 0.27, cosmological constant ΩΛ = 0.73, and the Hubble constant H0 = 70 km s-1 Mpc-1. At the cluster redshift (z = 0.203), 1′ corresponds to 201 kpc. Unless otherwise specified, quoted errors indicate the 90% confidence intervals.
2. Observation and data reduction
2.1. Suzaku/HXD
A2163 has been observed in two pointings (Fig. 1): the central region (A2163, PI: T. Reiprich) and the northeast region (A2163_NE, PI: N. Ota). The observational details are listed in Table 1. The HXD-PIN spectral data have a narrow field-of-view (30′ × 30′ (FWHM)) and low background level (Takahashi et al. 2007) enabling the study of hard X-ray emission from A2163 up to several tens of keV. This energy range is ideal for this study.
 |
Fig. 1 XMM-Newton EMOS image of A2163 in the 0.2–10 keV band. The boxes indicate the HXD-PIN field of views during two pointed observations. The white circle delineates the XMM-Newton spectral region of cluster emission (r < 10′). |
The HXD data reduction was performed using HEASOFT version 6.13 and CALDB version 2011-09-13 for HXD. The data were reprocessed and screened in a standard manner using the Suzaku reprocessing tool aepipeline. The screening criteria are as follows: Earth elevation angle >5°, geomagnetic cut-off rigidity >6 GV, and satellite outside the South Atlantic anomaly. The source spectra were extracted by hxdpinxbpi. Figure 2 shows the HXD spectrum for each pointing.
 |
Fig. 2 HXD spectra of A2163 in the 10–60 keV band for the central region a) and the northeast region b). In each panel, observed HXD data denoted as “Data”, the NXB model, the CXB model, and the background-subtracted data, “Data – (NXB+CXB)”, are shown using black crosses, red crosses, green crosses, and black circles, respectively. The point-source contribution estimated from the XMM-Newton observations of the same field is shown using blue crosses. |
The HXD-PIN detector background was subtracted using the non-X-ray background (NXB) files provided by the HXD instrument team. The cosmic X-ray background (CXB) was calculated by a power-law model with an exponential cut-off at 40 keV, which was previously determined from HEAO-1 A2 data (Boldt 1987). In spectral fitting, we used the PIN response function, which is appropriate for the observational epoch but corrected for the off-axis response with hxdarfgen. Here we approximated the surface brightness profile by the β-model and extended it to r = 10′.
The background in the HXD band is dominated by NXB. Following the same method described in Ota et al. (2008), the accuracy of NXB model is estimated to be 2% based on a comparison between the NXB model and data collected during periods of Earth occultation. This estimate agrees with the typical uncertainty reported in Fukazawa et al. (2009). Thus, we assume a 1σ systematic error =2% and propagate this error throughout our spectral analysis of HXD-PIN data.
We also estimated a hard X-ray flux of point sources inside the HXD field-of-view from the XMM-Newton data of the same field (see the next subsection). Assuming the average photon index of 27 detected sources Γ = 1.5, we simulated the HXD spectrum expected for each pointing. Here the HXD angular response function was considered by using hxdarfgen. In Fig. 2, the spectrum of the sum of the detected sources is shown. The contribution from the point sources to the source spectrum is estimated as 6%, which is negligible compared to the uncertainty of the above-mentioned NXB model.
2.2. XMM-Newton
A2163 was observed in a mosaic of five pointings in 2000. This study analyzes only the central pointing, OBSID 0112230601, as obtained in revolution 0132. Observation data files were retrieved from the XMM-Newton archive1 and reprocessed with the XMM-Newton science analysis system (SAS) v10.0 using the standard calibration. The initial data reduction, including solar flare screening, event selection, and vignetting correction, followed the procedure in Pratt et al. (2007). The exposure time after data screening was 10 and 6 ks for EMOS and EPN, respectively. The background data sets were the accumulated blank-sky data of Read & Ponman (2003); these were subjected to the same screening and vignetting correction as the source files and normalized by the count rates in the 10–12 keV band for EMOS and in the 12–14 keV band for EPN. Background subtraction was performed in two steps, as described in Arnaud et al. (2002), using a source-free annulus at the edge of the field of view ().
Single-component fitting to the HXD data.
 |
Fig. 3 HXD spectrum of A2163 in the 12–60 keV band with CXB and NXB subtracted. The HXD spectrum (the crosses in the upper panels) is fitted by the APEC model a) and the power-law model b). Below the spectra (lower panels), the residuals are expressed in number of standard deviations. |
 |
Fig. 4 XMM and HXD spectra of A2163 in the 0.3–60 keV band fitted by a) the APEC model and b) the APEC and power-law model. The EMOS1/EMOS2/EPN data are shown by the black/red/green crosses; the blue crosses denote HXD data. Solid lines indicate the best-fit models for each instrument. In panel b), the power-law component is also indicated by the dotted line. |
3. HXD analysis
Since the spectra extracted from the two data sets are statistically consistent across the HXD-PIN band, both spectra were added, yielding a total exposure time of 154 ks. Figure 3 shows the HXD spectrum of A2163 with the NXB and CXB components removed. The 12–60 keV flux is measured as 1.70 ± 0.06 (± 0.30) × 10-11 erg s-1 cm-2, where the first and second errors are the 1σ statistical and 1σ systematic errors, respectively. The hard X-ray emission is detected at the 28σ confidence level. Considering the systematic error of the NXB, the significance of the detection is 5.5σ. Hence the present data provide the highest-quality X-ray spectra of A2163.
Next, the HXD spectrum in the 12–60 keV band was fitted to two single-component models: (1) the astrophysical plasma emission code (APEC) thin-thermal plasma model (Smith et al. 2001) and (2) the power-law model. The Galactic absorption was fixed at NH = 1.65 × 1021 cm-2. The results are shown in Fig. 3 and Table 2. In Model (1), the metallicity and redshift were fixed at Z = 0.3 solar and z = 0.203, respectively.
To examine the impact of background uncertainty, the NXB intensity was intentionally
altered by ± 2%. We find that both models are statistically acceptable at the 90% level. The
measured temperature 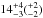 keV and normalization factor
keV and normalization factor
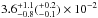 obtained from the model (1) favorably agreed
with those obtained from the XMM-Newton data,
obtained from the model (1) favorably agreed
with those obtained from the XMM-Newton data,
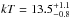 keV, and Norm
=
keV, and Norm
=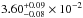 . Thus, the relative normalization factor
between Suzaku HXD and XMM-Newton EMOS1 is 1.00 ± 0.28.
This result is statistically consistent with the cross-calibration between Suzaku
XIS and XMM-Newton (Tsujimoto et
al. 2011), considering the relative normalization factor between Suzaku
XIS and HXD reported by the instrument team2.
On the other hand, the power-law model requires a large photon index of Γ ~ 3 to fit
the data, indicating that the cluster emission spectrum is soft and
predominantly thermal.
. Thus, the relative normalization factor
between Suzaku HXD and XMM-Newton EMOS1 is 1.00 ± 0.28.
This result is statistically consistent with the cross-calibration between Suzaku
XIS and XMM-Newton (Tsujimoto et
al. 2011), considering the relative normalization factor between Suzaku
XIS and HXD reported by the instrument team2.
On the other hand, the power-law model requires a large photon index of Γ ~ 3 to fit
the data, indicating that the cluster emission spectrum is soft and
predominantly thermal.
4. XMM and HXD joint analysis
To more thoroughly investigate the origin of hard X-ray emission, we performed a joint analysis of the XMM and HXD data. Since most of the cluster emission appears to be thermal, the thermal emission must be modeled in detail to constrain the contribution from non-thermal hard X-ray emissions. To this end, we replicate thermal emission by using a single-component APEC model and multi-temperature APEC models and constrain the quantity of non-thermal hard X-ray emission.
4.1. Single-temperature model
Figure 4 and Table 3 show the results of fitting the XMM and HXD broadband spectra of A2163 to the single-temperature APEC model. The 0.3–60 keV spectra were well fitted by a kT ~ 14 keV thermal model, indicating that the observed hard X-ray emission is likely dominated by hot thermal emission. The bolometric luminosity was estimated as 9.0 × 1045 erg s-1.
Incorporating the power-law component into the spectral model, we can derive the upper limit of the non-thermal component. The power-law index assumes a radio-band photon index; i.e., Γ = 2.18 (Feretti et al. 2004). The combined model did not significantly improve the fit relative to the case of APEC model alone; the resulting χ2/d.o.f. = 1238/1179. Thus, we infer the absence of significant non-thermal hard X-ray emission. Summing the statistical and systematic errors in quadrature, we estimate the 90% upper limit on the 12–60 keV energy flux as FNT < 1.2 × 10-12 erg s-1 cm-2.
 |
Fig. 5 Multi-temperature model derived from the XMM-Newton data. a) Definition of spectral regions used to construct the multi-temperature model, b) temperature map obtained from the XMM-Newton spectral analysis, c) and best-fit multi-temperature model. Panel a) shows the central 25 grids (1 grid = 2′ × 2′) and the surrounding region within a circle of r = 10′. In panel b), the color scale indicates the gas temperature in keV, ranging from 5 (navy) to 25 (white). Panel c) shows the total model (solid line) as well as the APEC models for the 26 spectral regions within r < 10′ (the dashed lines). |
Single-temperature analysis of the XMM and HXD data.
4.2. Multi-temperature model
Multi-temperature modeling enables more accurate determination of the hard X-ray property. Because of the complex temperature distribution in A2163, the multi-temperature model was constructed from the spatially-resolved XMM-Newton EMOS spectra. As shown in Fig. 5a, the central 10′ × 10′ square was divided into 2′ × 2′ grids. The XMM-Newton spectra were extracted from the central 25 grids and the surrounding region inside the circle of r = 10′. The 26 spectra, represented by a single-temperature APEC model, were simultaneously fitted under the condition that their sum reproduces the global cluster spectrum (r < 10′), obtained from XMM-Newton EPN. The APEC normalization factor and the temperature were freely selectable within each region but the metal abundance was fixed at its mean value (0.29 solar) for all regions.
Panels b and c of Fig. 5 show the resultant temperature map and the best-fit multi-temperature spectral model, respectively. The observed EPN spectra were well represented by the multi-temperature model. The temperature deduced from this analysis showed that the very hot (kT ~ 18 keV) gas exists in the northeast region (regions 2, 7, and 12 in Fig. 5a), which is consistent with Bourdin et al. (2011). Based on this model, the absorption-corrected energy flux of the very hot gas is estimated as FNE = 5.4 × 10-12 and 2.7 × 10-12 erg s-1cm-2 in the 0.5–10, 12–60 keV bands, respectively. The impact of uncertainty in the hard X-ray flux emitted by the very hot gas is examined later.
Next, the multi-temperature model was extrapolated to the hard X-ray band to investigate whether it properly fits the observed HXD spectrum. Since the APEC normalization factors of the HXD and XMM data are consistent (Sect. 3), the relative normalization was fixed at 1. The reduced χ2 was 3.3, 8.8, and 0.9 for NXB rescaling factors of 1.00, 0.98, and 1.02, respectively. Thus, the fit is sensitive to the amplitude of the NXB model.
 |
Fig. 6 HXD spectra of A2163 in the 12–60 keV band (crosses) fitted by the multi-temperature and power-law model. The solid line is the best-fit model. Spectral components of the multi-temperature and power-law models are shown as black dotted and blue dashed lines, respectively. |
Result of fitting the multi-temperature and power-law model to the HXD data.
To constrain IC emission, the HXD-PIN data was then fitted by a model consisting of thermal and non-thermal power-law models (Fig. 6). The thermal component was fixed to the best-fit multi-temperature model derived above, while the power-law normalization was unrestrained. In the multi-temperature model, the relative normalization factor between HXD and XMM was again fixed to 1.0. In this model, the chi-squared value is 8.0 for 12 degrees of freedom. The estimated 12–60 keV power-law flux is FNT = 5.3 ± 0.9 (± 3.8) × 10-12 erg s-1 cm-2 (where the first and second errors are the 1σ statistical and 1σ NXB systematic error, respectively). The fitting results and power-law fluxes after removing the NXB model (rescaled by factors of 1 and 0.98) are summarized in Table 4.
Another possible source of systematic error is flux uncertainty in the high-temperature
component of the NE region, whose hard X-ray emission contributes to approximately 15% to
the observed HXD spectrum. Fitting the APEC model to the EMOS spectra accumulated from
regions 2, 7, and 12, the 12−60 keV flux and its 1σ error was estimated
to be (2.7 ± 0.5) × 10-12 erg s-1 cm-2. Thus, the
flux uncertainty of the hot component is less than the systematic error in NXB. Adding the
statistical and systematic errors in quadrature, the 12–60 keV power-law flux is obtained
as (5.3 ± 3.9) × 10-12 erg s-1 cm-2. Therefore, IC
emission is only marginally detected (1.3σ); its 90% upper limit is
FNT < 1.2 × 10-11 erg s-1 for
Γ = 2.18. Assuming Γ = 1.5, the non-thermal 12–60 keV flux is
FNT < 1.6 × 10-11 erg s-1,
corresponding to 1.7 × 10-11 erg s-1 in the 20–80 keV. Thus, the
accuracy of our joint analysis is improved threefold from that of previous long RXTE
observations (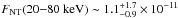 erg s-1 cm-2; Rephaeli et al. 2006), and a stronger limit on
non-thermal emission is imposed.
erg s-1 cm-2; Rephaeli et al. 2006), and a stronger limit on
non-thermal emission is imposed.
A2163 and RX J1347.5–1145 (Ota et al. 2008) represent the sole examples for which strong constraints on non-thermal emission have been derived from a detailed multi-temperature broadband spectral analysis. As demonstrated here, the joint analysis allows us to take advantage of both Suzaku’s high spectral capability in the hard X-ray band and XMM’s spatial resolution, and this is worth applying to other merging clusters to improve the precision of the hard X-ray measurement of the non-thermal property.
5. Discussion and conclusion
Analyzing the long Suzaku HXD observations, we detected significant hard X-ray emission from the hottest Abell cluster A2163 at z = 0.2. In Sect. 5.1, we discuss the origin of this hard X-ray emission and compare the results with previous observations of other clusters. In Sect. 5.2, we estimate the magnetic field in the cluster by comparing the hard X-ray flux with radio synchrotron emission.
5.1. Origin of hard X-ray emission from A2163
Analyzing the high-quality data collected by Suzaku HXD, we find that the hard X-ray emission from A2163 is well approximated by the 14 keV thermal model. Because A2163 has a complex temperature distribution, the multi-temperature model (including the very hot (kT = 18 keV) gas in the northeast region) imposes more accurate constraint on the non-thermal flux. Following a careful assessment of the uncertainty in the NXB, we obtained a 90% upper limit of FNT < 1.2 × 10-11 erg s-1cm-2 due to inverse Compton emission in the 12–60 keV band. Thus the present result, even though it places tighter constraints on the non-thermal flux than previous analyses, still suggests that the emission in this energy band is predominantly of thermal origin.
It is worth noting that the very hot (kT ~ 18 keV) gas in the northeast region contributes non-negligibly to the hard X-ray emission. The very hot gas contributes to 15% of the observed HXD flux. This finding is reminiscent of the hottest (kT ~ 25 keV) gas in the distant merging cluster RX J1347.5–1145 reported by Ota et al. (2008). They suggested that such high-temperature gas is over-pressurized, and therefore disappears over a relatively short time scale (0.5 giga-years). The presence of very hot gas in A2163 supports a recent merger of this cluster, as also suggested from multi-wavelength observations.
Next, we compare the obtained limit on the IC flux in A2163 with that of other clusters. Ota (2012) compiled the IC flux measurements from several observatories with hard X-ray capability, namely, RXTE, BeppoSAX, INTEGRAL, Swift, and Suzaku. Figure 7 shows the fluxes of 12 clusters as a function of gas temperature. As seen in this figure, different measurements yielded different fluxes, although their error bars overlapped for most of the objects. Since IC emission cannot be confirmed from these measurements, independent experiments are required. It should be noted that the IC flux estimation strongly depends on modeling of both thermal component and the power-law index of the non-thermal component. Furthermore, the published results are based on different assumptions. To further explore shock heating and particle acceleration in clusters, a higher sensitivity in the hard X-ray band is needed.
 |
Fig. 7 Non-thermal hard X-ray flux for 12 clusters, as measured by RXTE (magenta), BeppoSAX (black), INTEGRAL (light blue), Swift (blue), and Suzaku (red). RXTE and BeppoSAX results are taken from Rephaeli et al. (2008) and references therein. The INTEGRAL results are taken from Lutovinov et al. (2008), Eckert et al. (2008). The Swift results are taken from Ajello et al. (2009), Ajello et al. (2010), Wik et al. (2011). The Suzaku results are presented in Kitaguchi et al. (2007), Fujita et al. (2008), Ota et al. (2008), Kawano et al. (2009), Sugawara et al. (2009), Nakazawa et al. (2009), Wik et al. (2009), Nishino et al. (2010), Kawaharada et al. (2010). |
5.2. Cluster magnetic field
Blumenthal & Gould (1970) derived equations for
the radio synchrotron emission at the frequency νSyn and the
IC hard X-ray emission at νIC: 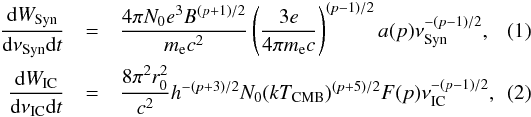 where N0 and
p are the normalization and the power-law index of the electron
distribution,
N(γ) = N0γ−p
(γ is the Lorentz factor of the electron),
r0 is the classical electron radius, h is
the Planck constant, TCMB is CMB temperature, and
TCMB = 2.73(1 + z) K. The functions
a(p) and F(p) are
given by Eqs. (4.60) and (2.66) in Blumenthal & Gould
(1970), respectively. Given that the ratio of observed flux densities of the IC
hard X-ray emission SIC to the radio synchrotron emission
SSyn is equal to
(dWSyn/dνSyndt)/(dWIC/dνICdt),
the magnetic field in the intracluster space B can be directly estimated.
where N0 and
p are the normalization and the power-law index of the electron
distribution,
N(γ) = N0γ−p
(γ is the Lorentz factor of the electron),
r0 is the classical electron radius, h is
the Planck constant, TCMB is CMB temperature, and
TCMB = 2.73(1 + z) K. The functions
a(p) and F(p) are
given by Eqs. (4.60) and (2.66) in Blumenthal & Gould
(1970), respectively. Given that the ratio of observed flux densities of the IC
hard X-ray emission SIC to the radio synchrotron emission
SSyn is equal to
(dWSyn/dνSyndt)/(dWIC/dνICdt),
the magnetic field in the intracluster space B can be directly estimated.
Substituting SIC < 0.25 μJy at 12 keV (derived from the joint analysis with Γ = 2.18 (Sect. 4.2)) and Ssyn = 155 mJy at 1.4 GHz (Feretti et al. 2004), the 90% lower limit on the magnetic field in A2163 is obtained as B > 0.098 μG. When Γ = 1.5, we obtain B > 0.006 μG. The above limits, though weak, are consistent with those of other clusters, B ~ 0.1−1 μG (e.g., Rephaeli et al. 2008; Ajello et al. 2010).
While our results provide important information on the non-thermal nature of ICM, their accuracy is limited by the sensitivity of the hard X-ray instrument. We expect that hard X-ray imaging by NuSTAR (Harrison et al. 2013) and the future ASTRO-H mission (Takahashi et al. 2012) will enable more accurate determination of very hot thermal components that predominate in the hard X-ray band. In addition, these instruments should accurately locate the merger shock, thereby improving the signal-to-noise ratio of the non-thermal component.
Acknowledgments
The authors thank the Suzaku team for the operation and instrumental calibrations. We also thank R. Smith and H. Yamaguchi for providing the plasma code, which covers a broader energy range. This work is supported in part by the Grant-in-Aid by MEXT, KAKENHI Grant Number 22740124 (NO). G.W.P. acknowledges ANR grant ANR-11-BD56-015. T.H.R. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG) through Emmy Noether grant RE 1462/2, Heisenberg grant RE 1462/5 and grant RE 1462/6.
References
- Ackermann, M., et al. (The Fermi-LAT Collaboration) 2013 [arXiv:1308.5654] [Google Scholar]
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2009, ApJ, 690, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2010, ApJ, 725, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Hughes, J. P., Forman, W., et al. 1992, ApJ, 390, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Majerowicz, S., Lumb, D., et al. 2002, A&A, 390, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Boldt, E. 1987, in Observational Cosmology, eds. A. Hewitt, G. Burbidge, & L. Z. Fang, IAU Symp., 124, 611 [Google Scholar]
- Bourdin, H., Arnaud, M., Mazzotta, P., et al. 2011, A&A, 527, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunetti, G., Cassano, R., Dolag, K., & Setti, G. 2009, A&A, 507, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassano, R., Ettori, S., Brunetti, G., et al. 2013, ApJ, 777, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Produit, N., Paltani, S., Neronov, A., & Courvoisier, T. J.-L. 2008, A&A, 479, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Fusco-Femiano, R., Giovannini, G., & Govoni, F. 2001, A&A, 373, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Orrù, E., Brunetti, G., et al. 2004, A&A, 423, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Fujita, Y., Hayashida, K., Nagai, M., et al. 2008, PASJ, 60, 1133 [NASA ADS] [Google Scholar]
- Fukazawa, Y., Mizuno, T., Watanabe, S., et al. 2009, PASJ, 61, 17 [NASA ADS] [Google Scholar]
- Fusco-Femiano, R., Orlandini, M., Brunetti, G., et al. 2004, ApJ, 602, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco-Femiano, R., Orlandini, M., Bonamente, M., & Lapi, A. 2011, ApJ, 732, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, B., Tchernin, C., Eckert, D., et al. 2013, A&A, 560, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawaharada, M., Makishima, K., Kitaguchi, T., et al. 2010, PASJ, 62, 115 [NASA ADS] [Google Scholar]
- Kawano, N., Fukazawa, Y., Nishino, S., et al. 2009, PASJ, 61, 377 [NASA ADS] [Google Scholar]
- Kitaguchi, T., Nakazawa, N., Makishima, K., et al. 2007, in Proc. XMM-Newton: The Next Decade, 28 http://xmm.esac.int/external/xmm_science/workshops/2007_science [Google Scholar]
- Lutovinov, A. A., Vikhlinin, A., Churazov, E. M., Revnivtsev, M. G., & Sunyaev, R. A. 2008, ApJ, 687, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2001, ApJ, 563, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Bautz, M., Inoue, H., et al. 2007, PASJ, 59, 1 [Google Scholar]
- Nakazawa, K., Sarazin, C. L., Kawaharada, M., et al. 2009, PASJ, 61, 339 [NASA ADS] [Google Scholar]
- Nishino, S., Fukazawa, Y., Hayashi, K., Nakazawa, K., & Tanaka, T. 2010, PASJ, 62, 9 [NASA ADS] [Google Scholar]
- Okabe, N., Bourdin, H., Mazzotta, P., & Maurogordato, S. 2011, ApJ, 741, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, N. 2012, Res. Astron. Astrophys., 12, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, N., Murase, K., Kitayama, T., et al. 2008, A&A, 491, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Böhringer, H., Croston, J. H., et al. 2007, A&A, 461, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, A. M., & Ponman, T. J. 2003, A&A, 409, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rephaeli, Y., & Gruber, D. 2002, ApJ, 579, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Gruber, D., & Arieli, Y. 2006, ApJ, 649, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Nevalainen, J., Ohashi, T., & Bykov, A. M. 2008, Space Sci. Rev., 16 [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Soucail, G. 2012, A&A, 540, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sugawara, C., Takizawa, M., & Nakazawa, K. 2009, PASJ, 61, 1293 [NASA ADS] [Google Scholar]
- Takahashi, T., Abe, K., Endo, M., et al. 2007, PASJ, 59, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2012, in Proc. SPIE, 8443, 1Z [Google Scholar]
- Tsujimoto, M., Guainazzi, M., Plucinsky, P. P., et al. 2011, A&A, 525, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wik, D. R., Sarazin, C. L., Finoguenov, A., et al. 2009, ApJ, 696, 1700 [NASA ADS] [CrossRef] [Google Scholar]
- Wik, D. R., Sarazin, C. L., Finoguenov, A., et al. 2011, ApJ, 727, 119 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 XMM-Newton EMOS image of A2163 in the 0.2–10 keV band. The boxes indicate the HXD-PIN field of views during two pointed observations. The white circle delineates the XMM-Newton spectral region of cluster emission (r < 10′). |
| In the text | |
 |
Fig. 2 HXD spectra of A2163 in the 10–60 keV band for the central region a) and the northeast region b). In each panel, observed HXD data denoted as “Data”, the NXB model, the CXB model, and the background-subtracted data, “Data – (NXB+CXB)”, are shown using black crosses, red crosses, green crosses, and black circles, respectively. The point-source contribution estimated from the XMM-Newton observations of the same field is shown using blue crosses. |
| In the text | |
 |
Fig. 3 HXD spectrum of A2163 in the 12–60 keV band with CXB and NXB subtracted. The HXD spectrum (the crosses in the upper panels) is fitted by the APEC model a) and the power-law model b). Below the spectra (lower panels), the residuals are expressed in number of standard deviations. |
| In the text | |
 |
Fig. 4 XMM and HXD spectra of A2163 in the 0.3–60 keV band fitted by a) the APEC model and b) the APEC and power-law model. The EMOS1/EMOS2/EPN data are shown by the black/red/green crosses; the blue crosses denote HXD data. Solid lines indicate the best-fit models for each instrument. In panel b), the power-law component is also indicated by the dotted line. |
| In the text | |
 |
Fig. 5 Multi-temperature model derived from the XMM-Newton data. a) Definition of spectral regions used to construct the multi-temperature model, b) temperature map obtained from the XMM-Newton spectral analysis, c) and best-fit multi-temperature model. Panel a) shows the central 25 grids (1 grid = 2′ × 2′) and the surrounding region within a circle of r = 10′. In panel b), the color scale indicates the gas temperature in keV, ranging from 5 (navy) to 25 (white). Panel c) shows the total model (solid line) as well as the APEC models for the 26 spectral regions within r < 10′ (the dashed lines). |
| In the text | |
 |
Fig. 6 HXD spectra of A2163 in the 12–60 keV band (crosses) fitted by the multi-temperature and power-law model. The solid line is the best-fit model. Spectral components of the multi-temperature and power-law models are shown as black dotted and blue dashed lines, respectively. |
| In the text | |
 |
Fig. 7 Non-thermal hard X-ray flux for 12 clusters, as measured by RXTE (magenta), BeppoSAX (black), INTEGRAL (light blue), Swift (blue), and Suzaku (red). RXTE and BeppoSAX results are taken from Rephaeli et al. (2008) and references therein. The INTEGRAL results are taken from Lutovinov et al. (2008), Eckert et al. (2008). The Swift results are taken from Ajello et al. (2009), Ajello et al. (2010), Wik et al. (2011). The Suzaku results are presented in Kitaguchi et al. (2007), Fujita et al. (2008), Ota et al. (2008), Kawano et al. (2009), Sugawara et al. (2009), Nakazawa et al. (2009), Wik et al. (2009), Nishino et al. (2010), Kawaharada et al. (2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


