© ESO, 2014

1. Introduction

Nitrogen is the fifth most abundance element in the universe and comprises two isotopes with relative populations ¹⁴N/¹⁵N ≃ 400. The dominant reservoir of elemental N is in the form of atoms and N₂, which are essentially unobservable outside of the solar system, the former because its ionic form, N⁺, is readily removed by charge exchange with neutral hydrogen with the latter lacking a rotational emission spectrum because it is homonuclear. The observation of electronic transitions of N₂ is limited to technically-challenging ultraviolet (UV) wavelengths shorter than 1000 Å.

There have been numerous detections of N-derived molecules such as N₂H⁺, CN, HCN, and NH₃ in interstellar space, protostellar envelopes and discs, and extra-galactically, (e.g., van Zadelhoff et al. 2001; Bergin et al. 2002; Gerin et al. 2009; Öberg et al. 2010; Tobin et al. 2012), as well as for their isotopologues (e.g., Wannier et al. 1991; Gerin et al. 2009; Adande & Ziurys 2012; Hily-Blant et al. 2013; Bizzocchi et al. 2013; Daniel et al. 2013). The balance of chemically active N and highly stable N₂ is an important parameter in the chemistry of these more complex amines and nitriles. The primary driver of this balance in environments exposed to an ultraviolet flux is photodissociation of N₂.

The value of ¹⁴N/¹⁵N in observable species constitutes an astronomical puzzle. The solar elemental ratio, 440 (Marty et al. 2010), is considered representative of the local interstellar medium, but differs from the terrestrial value, 270; in the atmospheric of Titan, 180 (Niemann et al. 2005); and in interplanetary dust, meteorites and comets, 68–330 (Floss et al. 2006; Jehin et al. 2009; Aléon 2010; Mumma & Charnley 2011). Observational surveys have been made of galactic star-forming regions (Adande & Ziurys 2012) and dark clouds (Hily-Blant et al. 2013) and also point to a range of values, as well as variations by source and the molecular species observed. Some variation of ¹⁴N/¹⁵N is clearly due to the details of local nuclear synthesis, with an increasing excess of ¹⁵N towards the galactic centre (Wilson 1999; Adande & Ziurys 2012). Another proposed explanation for the observed ratios of C¹⁴N/C¹⁵N, HC¹⁴N/HC¹⁵N and ¹⁴NH₃/¹⁵NH₃ is low-temperature isotopic-exchange chemistry. Models considering this mechanism (e.g., Rodgers & Charnley 2008; Wirström et al. 2012; Le Gal et al. 2014) have been successful in introducing strongly non-elemental abundance ratios under specific conditions. The critical exchange reactions, e.g., $\begin{array}{ccc}\mathrm{H}{\mathrm{C}}^{\mathrm{14}}\mathrm{N}{\mathrm{H}}^{\mathrm{+}}\mathrm{+}{}^{\mathrm{15}}\mathrm{N}\leftrightharpoons \mathrm{H}{\mathrm{C}}^{\mathrm{15}}\mathrm{N}{\mathrm{H}}^{\mathrm{+}}\mathrm{+}{}^{\mathrm{14}}\mathrm{N}\mathrm{+}\mathrm{energy}\mathit{,}& & \end{array}$rely on the lower zero-point energy of the heavier molecular species and are exothermic by ≤30 K (Terzieva & Herbst 2000), limiting their significance to cold environments. This is in contrast to similar reactions affecting the H/D abundance in molecules which may proceed at temperatures as high as 170 K.

An alternative route to the mass fractionation of molecules is isotope selective photodissociation. For the case of N₂ dissociation, self-shielding has been shown to drive the HC¹⁴N/HC¹⁵N ratio in the atmosphere of Titan (Liang et al. 2007). Additionally, there is strong observational evidence that the fractionation of protostellar oxygen isotopes is assisted by the self-shielding of CO, which has very similar molecular structure to N₂ (Sheffer et al. 2002; Lyons & Young 2005; Smith et al. 2009). The investigation of isotope selective N₂ photodissociation in interstellar clouds and protoplanetary environments is then highly warranted.

The importance of photodissociation due to the interstellar radiation field (ISRF) or an ultraviolet emitting star will decrease as the radiation is attenuated below the surface of an interstellar cloud, circumstellar envelope, or protoplanetary disc. Li et al. (2013) made a detailed assessment of the dissociation rate of ¹⁴N₂ and the shielding of ultraviolet radiation by relevant materials (H₂, H, ¹⁴N₂ itself, and dust grains). This work considered in detail the sharply structured absorption spectrum of N₂ and shielding species. This was made possible by means of an accurate and comprehensive quantum-mechanical model of N₂ photoabsorption and dissociation, which was informed by an extensive history of N₂ spectroscopy in the laboratory (e.g., Ajello et al. 1989; Helm et al. 1993; Sprengers et al. 2003, 2004, 2005a; Stark et al. 2008; Lewis et al. 2008b; Heays et al. 2009, 2011) and theoretically (e.g., Spelsberg & Meyer 2001; Lewis et al. 2005b,a, 2008a,c; Haverd et al. 2005; Ndome et al. 2008). This model, detailed in Sect. 2, explicitly accounts for the nuclear masses and so is equally applicable to the case of ¹⁴N 15N. In Sect. 3 of this paper, we describe new calculations of ¹⁴N 15N photodissociation rates in interstellar and blackbody radiation fields.

The interior regions of interstellar clouds and protoplanetary discs may be completely shielded from external sources of ultraviolet photons. However, collisions between high-energy cosmic rays and H₂ produce a weak local UV field that could be important for photodissociation. The cosmic ray induced photoionisation and photodissociation of molecular and atomic species is well established (Gredel et al. 1987, 1989; Dalgarno 2006; Padovani et al. 2009). In Sect. 4 we combine our model of N₂ photoabsorption with a similarly thorough theoretical treatment of the H₂ line emission associated with cosmic rays. This is, to study in detail for the first time the photodissociation of ¹⁴N₂ and ¹⁴N 15N in cloud and disc interiors. We also revisit calculations of the CO dissociation rate due to cosmic rays (Gredel et al. 1987) taking advantage of an updated photodissociation cross section.

In Sect. 5 of this paper we present the results of chemical models of an interstellar cloud and protoplanetary disc. These include linked chemical networks for species containing ¹⁴N and ¹⁵N and the photodissociation rates of Li et al. (2013) and Sects. 3 and 4. Using these models we investigate the consequences of isotope selective photodissociation on the abundances of atomic and molecular nitrogen and other N-bearing species observed in clouds and discs.

2. The model of photoabsorption and photodissociation

The photodissociation of N₂ first requires excitation into bound states that then rapidly predissociate. Thus, the photoabsorption spectrum contains well separated electronic-rovibrational lines and must be treated at high resolution (~10^-3 Å) but over a comparatively large wavelength range (912–1000 Å). Actually, N₂ absorbs strongly at considerably shorter wavelengths but the present application is limited to longwards of the atomic H ionisation threshold at 912 Å. Here, a broadband and detailed spectrum is calculated by means of a quantum mechanical model which solves a coupled Schrödinger equation (CSE) for the vibrational wavefunction of the molecule. Properties of the electronic wavefunction are described by potential-energy curves and state coupling parameters optimised with respect to a large database of laboratory line positions, oscillator strengths, and predissociation rates. These empirical parts of the CSE model formulation are independent of molecular mass, and so are unchanged by isotopic substitution of one or both nuclei. Then, the explicit calculation of vibrational wavefunctions models the quantum mixing of electronic states and its dependence on the nuclear masses. A more detailed description of the method, the important electronic states and potential-energy curves used in the model is given in our previous publication (Li et al. 2013), and the chemical physics literature (Lewis et al. 2005b,a, 2008c; Haverd et al. 2005; Heays 2011) with specific discussion of ¹⁴N 15N given in Vieitez et al. (2008) and Heays et al. (2011).

Electric-dipole-allowed photoabsorption from the ground state occurs for wavelengths shorter than 1000 Å and accesses two valence states and several Rydberg series of ${}^{\mathrm{1}}\mathrm{\Pi }_{\mathit{u}}$ and ${}^{\mathrm{1}}\mathrm{\Sigma }_{\mathit{u}}^{\mathrm{+}}$ symmetry. Potential-energy curves depicting these states are shown in Fig. 1 with the lowest-energy photoabsorbing state, b ¹Π_u, occurring at 12.6 eV. There is strong electronic coupling between valence and Rydberg states of the same symmetry which leads to a very perturbed spectrum, including constructive and destructive interference in the absorption strength and predissociation rates of vibrational bands (Dressler 1969; Spelsberg & Meyer 2001; Lewis et al. 2005b). Additional rotational interactions between ${}^{\mathrm{1}}\mathrm{\Pi }_{\mathit{u}}$ and ${}^{\mathrm{1}}\mathrm{\Sigma }_{\mathit{u}}^{\mathrm{+}}$ states lead to strong rotational dependence of line strengths and predissociation rates (or linewidths) (Stark et al. 2005; Heays et al. 2011).

Fig. 1 Diabatic-basis potential-energy curves of N2 excited states relevant to ultraviolet photoabsorption and photodissociation. The energy scale is referenced to v = 0, J = 0 of the $\mathit{X}\hspace{0.17em}{}^{\mathrm{1}}\mathrm{\Sigma }_{\mathit{g}}^{\mathrm{+}}$ ground state and is related to the wavelength scale assuming transitions from this fundamental level. Also indicated are the excitation states of atomic products arising from dissociation and the absorption limit imposed by the ionisation of atomic H. The potential-energy curves of the ${\mathit{c}}_{\mathit{n}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}$ and ${\mathit{c}}_{\mathit{n}\mathrm{+}\mathrm{1}}^{\mathrm{\prime }}{\mathrm{1}}^{}{\mathrm{\Sigma }}_{\mathit{u}}^{\mathrm{+}}$ states are indistinguishable at the plotted scale. The N2 ionisation potential energy occurs at 15.4 eV in this figure.

Predissociation occurs through spin-orbit coupling of ${}^{\mathrm{1}}\mathrm{\Pi }_{\mathit{u}}$ states with a number of states with ${}^{\mathrm{3}}\mathrm{\Pi }_{\mathit{u}}$ symmetry, including an unbound level, and one state of ${}^{\mathrm{3}}\mathrm{\Sigma }_{\mathit{u}}^{\mathrm{+}}$ symmetry. These are shown in Fig. 1 and lead to dissociation into N atoms in the ⁴S, ²D, or ²P states. The spin-selection rules forbid the appearance of N₂ triplet states in optical spectra although many have been observed in the laboratory regardless, due to their coupling with ${}^{\mathrm{1}}\mathrm{\Pi }_{\mathit{u}}$ levels (Sprengers et al. 2005a; Lewis et al. 2008b). The majority of excited vibrational states predissociate after an absorption event with near certainty, that is, they have a predissociation fraction of ~1. For those states that decay substantially by emission, a reduction of the CSE-calculated photoabsorption cross section, σ^abs, has been made by their less-than-unity predissociation fractions, η^pre, leading to a photodissociation cross section σ^pd, so that ${\mathit{\sigma }}^{\mathrm{pd}}\mathrm{=}{\mathit{\eta }}^{\mathrm{pre}}{\mathit{\sigma }}^{\mathrm{abs}}\mathit{.}$(1)

This provides an example of the utility of the physically-based CSE model. That is, the b ¹Π_u(v = 1) level of ¹⁴N₂ is known to predissociate significantly less rapidly than for ¹⁴N 15N (Sprengers et al. 2004, 2005b; Wu et al. 2012) because of mass-change-induced shifts of the interacting ${}^{\mathrm{1}}\mathrm{\Pi }_{\mathit{u}}$ and ${}^{\mathrm{3}}\mathrm{\Pi }_{\mathit{u}}$ levels. These shifts are evaluated explicitly by the CSE model and calculated predissociation fractions for b ¹Π_u(v = 1) are shown in Fig. 2 for rotational levels with angular momentum quantum number, J ≤ 30.

Fig. 2 An example of isotopically-dependent predissociation. The predissociation fraction, ηpre, of individual rotational levels, J, of b 1Πu(v = 1) calculated by the CSE model for 14N2 and 14N15N.

There is a strong dependence on rotational angular momentum, J, for both isotopologues. At the low temperatures of interstellar space only rotational levels with J < 10 are accessible. Then, photons absorbed by ¹⁴N 15N and leading to excitation of the b ¹Π_u(v = 1) level are nearly twice as likely to lead to a dissociation event than for ¹⁴N₂.

We have calculated ¹⁴N 15N photoabsorption and photodissociation cross sections as Li et al. (2013) did for ¹⁴N₂. A comparison is made in Fig. 3 between transmission functions derived from the two CSE-calculated photoabsorption cross sections. The principal difference is a shift of ¹⁴N 15N absorption bands to longer wavelengths which mostly increases with vibrational excitation, that is, with shortening wavelength. However, there are many further differences between the spectra of different N₂ isotopologues due to the strong coupling between excited states, such as depicted in Fig. 2 with respect to the b ¹Π_u(v = 1) predissociation fraction, and these should not be neglected (e.g., Vieitez et al. 2008; Lewis et al. 2008b; Heays et al. 2011).

Fig. 3 Upper panels: representative transmission functions calculated from theoretical photoabsorption cross sections of important molecular species, with column densities: N(H) = 1022, N(H2) = 1020, and $\mathit{N}\mathrm{\left(}{}^{\mathrm{14}}\mathrm{N}_{\mathrm{2}}\mathrm{\right)}\mathrm{=}\mathit{N}\mathrm{\left(}{}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}\mathrm{\right)}\mathrm{=}\mathit{N}\mathrm{\left(}\mathrm{CO}\mathrm{\right)}\mathrm{=}{\mathrm{10}}^{\mathrm{15}}\hspace{0.17em}{\mathrm{cm}}^{-2}$; and simulating an excitation temperature of 50 K for all molecular absorption. Lower panels: probability per Å of H2 emission following a cosmic-ray induced ionisation event. Spectra are shown assuming two different values for the H2 ortho:para ratio.

The wavelengths of the majority of the modelled rovibrational lines are accurate to within 0.01 Å when compared with laboratory measurements (Heays 2011). The magnitudes of the calculated cross sections are accurate to about 10%, with their principal uncertainty arising from the absolute calibration of the laboratory absorption oscillator strengths used to constrain the model electronic transition moments (Stark et al. 2005, 2008; Heays et al. 2009). The predissociation fractions pertaining to the longest wavelength bands are well known and modelled (Lewis et al. 2005b) but are less certain at shorter wavelengths. For these, a predissociation fraction of 1 is assumed. This is a reliable assumption with respect to ${}^{\mathrm{1}}\mathrm{\Pi }_{\mathit{u}}$ states, many of which are known to exhibit significant predissociation broadening (Stark et al. 2008; Heays et al. 2011). It is less certain that all ${}^{\mathrm{1}}\mathrm{\Sigma }_{\mathit{u}}^{\mathrm{+}}$ levels responsible for absorption at shorter wavelengths are completely predissociative. Further practical details regarding the calculation of N₂ cross sections and dissociation fractions at different temperatures may be found in Li et al. (2013).

Also shown in Fig. 3 are transmission functions representing further line-absorbing species relevant to the following treatment of the shielding of N₂ absorption in astrophysical environments. For these, photoabsorption cross sections for H₂ are synthesised from data obtained from the Meudon PDR code website (Le Petit et al. 2006), and those for CO are taken from the model of Visser et al. (2009).

3. Photodissociation rates and shielding functions

The photodissociation rate, k₀, of N₂ exposed to UV radiation can be calculated according to ${\mathit{k}}_{\mathrm{0}}\mathrm{=}\mathrm{\int }{\mathit{\sigma }}^{\mathrm{pd}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathit{I}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathrm{d}\mathit{\lambda ,}$(2)where σ^pd(λ) is the N₂ photodissociation cross section described in Sect. 2, I is the intensity of the radiation field, and λ the wavelength. The unattenuated interstellar radiation field (ISRF) of Draine (1978), in units of photons cm^-2 s^-1 Å^-1 sr^-1, is used in most of the following calculations and is given by $\begin{array}{ccc}\mathit{F}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{1}}{\mathrm{4}\mathit{\pi }}\mathrm{(}\mathrm{3.2028}\mathrm{\times }{\mathrm{10}}^{\mathrm{15}}{\mathit{\lambda }}^{-3}\mathrm{-}\mathrm{5.1542}\mathrm{\times }{\mathrm{10}}^{\mathrm{18}}{\mathit{\lambda }}^{-4}\\ & & \mathrm{+}\mathrm{2.0546}\mathrm{\times }{\mathrm{10}}^{\mathrm{21}}{\mathit{\lambda }}^{-5}\mathrm{)}\mathit{,}\end{array}$(3)with λ in Å. In the following we employ an angle-integrated intensity, $\mathit{I}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathrm{=}\mathrm{4}\mathit{\pi \chi F}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathit{,}$(4)with an additional scaling factor relative to the Draine field, χ.The integral in Eq. (2) must be computed between 912 and 1000 Å. This range is defined by the long-wavelength onset of the N₂ absorption spectrum and the complete suppression of ultraviolet radiation for wavelengths shorter than the atomic H ionisation limit.

The photodissociation rates of ¹⁴N₂ and ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ calculated from Eq. (2) are given in Table 1 assuming several different radiation fields. In all cases the difference between ¹⁴N₂ and ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ rates is below 5%, and the calculated dependences on the N₂ ground state excitation temperature and the form of the incident field (a Draine ISRF, or blackbody radiation) are similar to those calculated by Li et al. (2013) for ¹⁴N₂.

For N₂ embedded in an externally irradiated cloud or disc, the intervening gaseous and granular material acts as a shield and leads to a reduced photodissociation rate, k < k₀. The precise nature of shielding by H, H₂, ¹⁴N₂, and ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ is influenced by the wavelength dependence of their absorption cross sections, but is more usefully applied as a wavelength-integrated ratio of shielded and unshielded dissociation rates. That is, the shielding function given by $\begin{array}{ccc}\mathit{\theta }& \mathrm{=}& \frac{\mathit{k}}{{\mathit{k}}_{\mathrm{0}}}\\ & \mathrm{=}& \frac{\mathrm{\int }\mathit{I}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\exp \mathrm{[}\mathrm{-}{\sum }_{\mathit{X}}{\mathit{N}}_{\mathit{X}}{\mathit{\sigma }}_{\mathit{X}}^{\mathrm{abs}}\mathrm{(}\mathit{\lambda }{\mathrm{)}}^{\mathrm{]}}\exp \left(\mathrm{-}{\mathit{\gamma }}_{\mathrm{dust}}{\mathit{A}}_{\mathit{V}}\right){\mathit{\sigma }}^{\mathrm{pd}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\hspace{0.17em}\mathrm{d}\mathit{\lambda }}{\mathrm{\int }\mathit{I}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}{\mathit{\sigma }}^{\mathrm{pd}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\hspace{0.17em}\mathrm{d}\mathit{\lambda }}\mathrm{·}\end{array}$(5)Here, ${\mathit{\sigma }}_{\mathit{X}}^{\mathrm{abs}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}$, 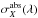is the absorption cross section of shielding species X and N_X its shielding column density.

The term exp(−γ_dustA_V) in Eq. (5) describes shielding of the UV flux by dust grains, where the visual (5500 Å) extinction is assumed proportional to the column density of hydrogen nuclei, N_H, according to A_V = N_H/1.6 × 10²¹ (Savage et al. 1977). In principle, this is a wavelength dependent quantity which depends on the distribution of dust grain sizes, their composition, and their geometries. The use of a simple parameterisation of declining intensity with increasing visual extinction is warranted by the significant uncertainties in these parameters. Radiative transfer calculations considering the destruction and scattering of photons by a realistic distribution of interstellar dust grains were made by Roberge et al. (1981, 1991). The ultraviolet extinction relevant to various molecules was parameterised by van Dishoeck et al. (2006) as a decaying exponential like that in Eq. (5) using the the dust optical properties of Roberge et al. (1991). Their extinction calculated for the wavelength range appropriate to CO is adopted here for N₂, that is with γ_dust = 3.53. Further calculations were made by van Dishoeck et al. (2006) assuming larger dust grains (>1 μm in size) as identified in protoplanetary discs (Li & Lunine 2003b; Jonkheid et al. 2006). For this case γ_dust = 0.6.

Fig. 4 Top left: self-shielding functions for ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ (solid lines) and 14N2 (dotted lines) at various temperatures defining their excitation state and thermal Doppler broadening. Top right: shielding of 14N 15N photodissociation by 14N2 at various excitation and Doppler broadening temperatures. Bottom: shielding of ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ (solid lines) and 14N2 (dotted lines) photodissociation by H and H2 as a function of their column densities.

Detailed shielding functions for ¹⁴N₂ were given in Li et al. (2013) and the associated on-line material. Here, new calculations are made for ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ using Eq. (5), with some representative results plotted in Fig. 4, and full details are available from the Leiden photodissociation database¹. The data in Fig. 4 assume that the lines of shielding H and H₂ are Doppler broadened by b = 1 and 3 km s^-1, respectively. The N₂ lines are assigned thermal Doppler widths according to their excitation temperatures but are also naturally broadened by the predissociation process, in some cases by a few km s^-1.

Unsurprisingly, the similarity of the two isotopologues leads to very similar shielding functions. There is some difference evident in Fig. 4 with respect to shielding by atomic hydrogen. That is, the shielding of ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ by a N(H) = 10²⁰ cm^-2 column is somewhat more effective than for ¹⁴N₂. This is the result of a nearer alignment of the $\mathit{b}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{3}\mathrm{)}\mathrm{\leftarrow }\mathit{X}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime \prime }}\mathrm{=}\mathrm{0}\mathrm{)}$ absorption band of ¹⁴N₂ and the line-centre of the shielding 4p ← 1s transition of atomic hydrogen. The relevant ¹⁴N₂, ¹⁴N 15N, and H features are plotted in Fig. 3 near 972 Å. For a larger H column, like that in Fig. 3, with heavily saturated and broadened H lines, the misalignment of H and ¹⁴N₂ transitions near 972 Å loses its significance.

Also shown in Fig. 4 is the shielding of ¹⁴N 15N photodissociation by ¹⁴N₂. This rivals ¹⁴N 15N self-shielding because of the much greater abundance of ¹⁴N₂. This is particularly true at higher temperatures where the wavelength offset between isotopologues is compensated for by their broader rotational distributions and Doppler widths. A discussion of the relative importance of different species in mixed shielding media is given in Sect. 5 with respect to an example protoplanetary disc.

Shielding functions calculated according to Eq. (5) describe the reduction in photodissociation rate due to the attenuation of unidirectional radiation. A related quantity, θ_iso(N), describes this reduction as a function of column density for an extended medium illuminated isotropically at its surface. The resultant non-perpendicular rays penetrate less deeply and θ_iso(N) is smaller than the shielding function in the unidirectional case, θ(N) (Röllig et al. 2007). For a plane-parallel shielding medium with N defined perpendicular to its surface, the two shielding functions are related geometrically by the formula ${\mathit{\theta }}_{\mathrm{iso}}\mathrm{\left(}\mathit{N}\mathrm{\right)}\mathrm{=}{\mathrm{\int }}_{\mathrm{0}}^{\frac{\mathit{\pi }}{\mathrm{2}}}\mathit{\theta }\left(\frac{\mathit{N}}{\cos \mathit{\phi }}\right)\sin \mathit{\phi }\hspace{0.17em}\mathrm{d}\mathit{\phi }\mathit{.}$(6)

4. Photodissociation due to cosmic-rays

4.1. Cosmic-ray induced emission and photodissociation model

The ionisation of H₂ by cosmic ray collisions leads to the generation of free electrons. These may collisionally excite (or ionise) further H₂ whose radiative relaxation generates an ultraviolet flux (Prasad & Tarafdar 1983; Cecchi-Pestellini & Aiello 1992). Sternberg et al. (1987), Gredel et al. (1987), and Gredel et al. (1989) estimated the photodissociation properties of several small molecules due to ultraviolet photons arising from this process. Similar calculations are made here for the dissociation of N₂ including the detailed effects of line absorption as modelled by the CSE dissociation cross sections.

The H₂ emission flux between 912 and 1000 Å is dominated by line transitions. This emission occurs primarily through the Lyman and Werner bands connecting the ground state with the $\mathit{B}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{u}}^{\mathrm{+}}$ and C ¹Π_u excited states (Sternberg et al. 1987), and with a smaller contribution arising from other excited states (Gredel et al. 1989). Here, we use a model simulating the excitation of 9 electronic states of H₂ by cosmic-ray generated electrons and the resulting emission, developed and expounded in detail by Gredel et al. (1987, 1989). This model includes the effects of cascading from sufficiently high-energy states into $\mathit{B}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{u}}^{\mathrm{+}}$ and competing predissociative decay.

The final result of the H₂ emission model is a spectrum, P(λ), describing the number of photons generated per unit spectral density per H₂ ionisation event. A plot of P(λ) is shown in Fig. 3 and demonstrates a large number of narrow emission lines which actually occupy very little of the wavelength interval shown. The widths of these lines are Doppler limited and assigned full-width half-maxima of 0.005 Å, which is appropriate for a typical dark-cloud non-thermal Doppler broadening of b = 1 km s^-1. This is comparable to the widths of N₂ absorption lines, also shown in Fig. 3, so model spectra of both species are treated at similarly high resolution. Spectra are shown in Fig. 3 assuming limiting high- and low-temperature ratios for the ortho:para H₂ populations, o−H₂:p−H₂ = 3:1 and 0:1, respectively. The difference is quite apparent and is significant in the following calculations of N₂ photodissociation. Despite the 170 K energy separation of o−H₂ and p−H₂ ground-state levels it is not evident that their low-temperature equilibrium populations are always attained in real molecular clouds (Tielens 2013). Thus, we choose to contrast high and low temperature limits in the present study.

The rate of ultraviolet photons generated by cosmic ray collisions per unit spectral density per hydrogen nucleus is given by $\mathit{R}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathrm{=}\mathit{\zeta }{\mathit{x}}_{{\mathrm{H}}_{\mathrm{2}}}\mathit{P}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathit{,}$(7)

where x_H2 = n(H₂)/[n(H) + 2n(H₂)] is the relative abundance of molecular hydrogen with respect to H nuclei and ζ is the cosmic-ray-induced ionisation rate per H₂ molecule. A value of ζ = 10^-16  s^-1 per H₂ is adopted for the following calculations and falls within the broad range of rates estimated from observations of ions in diffuse and translucent clouds (Dalgarno 2006; Padovani et al. 2009; Indriolo & McCall 2012; Rimmer et al. 2012). This collection of observations suggest a rate as high as 10^-15 s^-1 at the edge of an interstellar cloud, which decreases with extinction to ~10^-16 s^-1 for A_V = 10 mag as the lowest-energy cosmic rays are attenuated. Our adopted value is higher than observed in the interiors of the densest clouds with ζ < 10^-17 s^-1 (Hezareh et al. 2008). Theoretical consideration of a range of source and attenuation mechanisms influencing the cosmic ray flux (Padovani et al. 2009; Cleeves et al. 2013) suggest a smaller rate ζ than 10^-16 s^-1 may be expected in circumstellar environments, because of the possible influence of any stellar wind and magnetic field. The photodissociation results presented here may be adapted to ionisation rates other than ζ = 10^-16 s^-1 by a simple scaling.

The cosmic-ray generated photons may be absorbed by dust grains and by abundant line-absorbing species: H₂, H, N₂, and CO. The idea of an absorbing column density is inappropriate because of the local nature of the photon source. Instead, the fraction of ultraviolet radiation absorbed by a particular species, X, and leading to its dissociation is determined from its relative abundance x_X, according to ${\mathit{p}}_{\mathit{X}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\mathrm{=}\frac{{\mathit{x}}_{\mathit{X}}{\mathit{\sigma }}_{\mathit{X}}^{\mathrm{pd}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}}{{\mathit{x}}_{\mathrm{dust}}{\mathit{\sigma }}_{\mathrm{dust}}\mathrm{+}{\sum }_{\mathit{i}}{\mathit{x}}_{\mathit{i}}{\mathit{\sigma }}_{\mathit{i}}^{\mathrm{abs}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}}\mathrm{·}$(8)Here, x_i and ${\mathit{\sigma }}_{\mathit{i}}^{\mathrm{abs}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}$ are the abundances and photoabsorption cross sections of various species, x_dustσ_dust represents dust absorption, and ${\mathit{\sigma }}_{\mathit{X}}^{\mathrm{pd}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}$ is a photodissociation cross section.

An important term in the summation in Eq. (8) arises from H₂. For the cases of X being ¹⁴N₂ or CO, self-shielding is important and must also be included. Self-shielding and shielding by ¹⁴N₂ are both important for the case of ¹⁴N 15N photodissociation. Atomic hydrogen is also a source of UV shielding at the edge of a cloud or disc but is assumed here to have too low abundance (about 10^-4 relative to H₂) to be important in fully shielded regions. Consequently, the common assumption that all radiation shortwards of 912 Å is completely consumed by H ionisation does not apply here. However, the N₂ photodissociation cross section at shorter wavelengths and approaching the photoionisation limit at 800 Å contributes less than 10% to its total photodissociation rate, and is neglected here.

Shielding of a penetrating interstellar radiation field by dust grains was discussed in Sect. 3. The extinction of cosmic-ray induced radiation is treated differently. In this case, all photons are assumed absorbed before traversing a significant fraction of the dark interior of the interstellar cloud or disk where they are generated. Then, the detailed angular scattering of photons by dust grains is inconsequential and only the absorption cross section need be considered. The dust absorption cross section is related to its extinction cross section by ${\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{abs}}\mathrm{=}{\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{ext}}\mathrm{(}\mathrm{1}\mathrm{-}\mathit{\omega }\mathrm{)}\mathit{,}$(9)

where ω is the grain albedo. We adopt a commonly used value derived from observations (Savage et al. 1977; Bohlin et al. 1978) for the dust extinction cross section per hydrogen nucleus of 2 × 10^-21 cm² and assume an albedo of ω = 0.5. Then, ${\mathit{x}}_{\mathrm{dust}}{\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{abs}}\mathrm{=}{\mathrm{10}}^{-21}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$ in Eq. (8).

The assumption of locally-absorbed UV photons is only appropriate for a sufficiently large and homogeneous medium. The mean-free-path of cosmic-ray generated photons in an interstellar cloud of density n_H = 10³ cm^-3 is 30 000 AU, assuming the UV-to-visual extinction factor of 3.53 discussed in Sect. 3. For the larger densities found near the midplane of a protoplanetary disc (Jonkheid et al. 2006) this distance is accordingly reduced, e.g., n_H = 10⁸ cm^-3 and ~1 AU. In principle, the various cosmic-ray induced photodissociation rates calculated below will be overestimated for objects which are not significantly larger than this mean-free-path, due to the escape of some UV photons. However, the significance of cosmic-ray induced photon fluxes is generally limited to regions fully-shielded from external UV radiation, and such regions also necessarily shield the escape of internally-generated photons.

The dust grains in a protoplanetary disc are likely larger than those in interstellar space, which have radii <1  μm (Mathis et al. 1977). Li & Lunine (2003b) deduced properties of the dust grains in one protoplanetary system, HD 4796A, by reference to observed infrared and sub-millimetre wavelength emission. Their modelling required a lower limit of 1 μm on the grain size distribution. The N₂-dissociating cosmic-ray induced UV flux considered here has wavelengths shorter than 1000 Å and will not be as strongly absorbed by grains larger than this. However, a population of polycyclic aromatic hydrocarbons (PAHs) has been inferred in a number of discs (e.g., Li & Lunine 2003a; Geers et al. 2006, 2007; Maaskant et al. 2013) and will absorb extra UV radiation (Siebenmorgen & Krügel 2010). Chaparro Molano & Kamp (2012) assumed a dust distribution with a minimum grain size of 0.1 μm in their study of cosmic-ray induced photodissociation in a model disc. Following from this assumption they deduced a value of ${\mathit{x}}_{\mathrm{dust}}{\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{abs}}\mathrm{=}\mathrm{1.47}\mathrm{\times }{\mathrm{10}}^{-22}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$, significantly below the commonly-adopted interstellar value. Here, we explore an even lower value, ${\mathit{x}}_{\mathrm{dust}}{\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{abs}}\mathrm{=}{\mathrm{10}}^{-23}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$, in order to contrast a more extreme case of grain growth in a protoplanetary disc with interplanetary dust.

Finally, the photodissociation rate of species X (per molecule X) due to cosmic ray induced photons may be calculated according to ${\mathit{k}}_{\mathit{X}}\mathrm{=}\frac{\mathrm{1}}{{\mathit{x}}_{\mathit{X}}}\mathrm{\int }\mathit{R}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}{\mathit{p}}_{\mathit{X}}\mathrm{\left(}\mathit{\lambda }\mathrm{\right)}\hspace{0.17em}\mathrm{d}\mathit{\lambda }\mathit{.}$(10)In some previous descriptions of cosmic-ray induced photodissociation (Gredel et al. 1989; McElroy et al. 2013) an efficiency is defined by factoring the H₂ ionisation rate and dust grain albedo from Eq. (10). In this case, the importance of molecular line absorption in Eq. (8) prevents the factoring of dust properties.

4.2. Cosmic-ray induced photodissociation of N₂

The rate of dissociation of ¹⁴N₂ and ¹⁴N 15N due to cosmic-ray induced ultraviolet radiation has been calculated and listed in Table 2. This rate is dependent on the local physical conditions, and a set of base conditions is chosen which plausibly simulate the interior of a dark interstellar cloud:

• The assumed abundances of ¹⁴N₂ and CO relative to n_H = n(H) + 2n(H₂) are 10^-5 and 7 × 10^-5, respectively, and reflect typical dense cloud abundances (Aikawa et al. 2008).

• A ${}^{\mathrm{14}}\mathrm{N}_{\mathrm{2}}\mathrm{:}{}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ ratio of 225 is chosen, appropriate for the solar elemental ratio of 450 (Marty et al. 2010).

• All molecular species are assumed to have a thermal excitation of T_ex = 20 K and be turbulently broadened with Doppler velocity b = 1 km s^-1.

• Dust grains are assumed to have a scattering cross section per H nucleus of ${\mathit{x}}_{\mathrm{dust}}{\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{abs}}\mathrm{=}{\mathrm{10}}^{-21}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^{\mathrm{2}}$.

• The high temperature limit, 3:1, is assumed for the ortho:para ratio of emitting H₂.

Further calculations listed in Table 2 probe variations on this set of parameters.

For the base set of parameters considered in Table 2, the ¹⁴N₂ photodissociation rate is 14 × 10^-16 s^-1. This is 5 orders of magnitude below the rate calculated for a standard interstellar radiation field in Sect. 3. The cosmic-ray induced photodissociation rates calculated by Gredel et al. (1989) for a large number of other molecular species are generally larger than the N₂ value determined here, in many cases by multiple orders of magnitude. For example, assuming ζ = 10^-16 s^-1 and a grain albedo of ω = 0.5, their photodissociation rates for H₂O and CN are 2.0 × 10^-14 and 1.8 × 10^-13 s^-1, respectively.

The self-shielding of ¹⁴N₂ cannot be neglected because of the resonant nature of its spectrum. For this reason, decreasing the ¹⁴N₂ density rapidly increases the dissociation rate, until the abundance relative to H nuclei, ${\mathit{x}}_{{}^{\mathrm{14}}\mathrm{N}_{\mathrm{2}}}$, falls below about 10^-7, as is evident from the values in Table 2. Line absorption of H₂ also effectively shields N₂ dissociation, reducing its rate by a factor of 2. Dust opacity reduces the ${}^{\mathrm{14}}\mathrm{N}_{\mathrm{2}}$ dissociation rate by a further 35%, and shielding by CO less than 5%.

Fig. 5 Modelled molecular absorption lines for two different excitation temperatures, 20 and 100 K, and cosmic-ray induced H2 emission. Otherwise calculated as for Fig. 3. Left: overlap of an o-H2 emission line with the ${\mathit{c}}_{\mathrm{3}}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime }}\mathrm{=}\mathrm{0}\mathrm{)}\mathrm{\leftarrow }\mathit{X}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime \prime }}\mathrm{=}\mathrm{0}\mathrm{)}$P(4) absorption line of 14N2. Right: overlap of two p-H2 emission lines with absorption by the ${\mathit{o}}_{\mathrm{3}}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{2}\mathrm{)}\mathrm{\leftarrow }{\mathit{X}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{0}\mathrm{)}$ band of 14N 15N, with R and P branches indicated.

The effective dissociation of ¹⁴N₂ arises from relatively few overlaps between its absorption lines and H₂ emission lines. These are indicated by steps in an accumulation of the integrated dissociation rate with wavelength, as shown in Fig. 6. This accumulation is dominated by a line overlap occurring at 960.45 Å, plotted in detail in Fig. 5. This corresponds to the P(4) line of the ${\mathit{c}}_{\mathrm{3}}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime }}\mathrm{=}\mathrm{0}\mathrm{)}\mathrm{\leftarrow }\mathit{X}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime \prime }}\mathrm{=}\mathrm{0}\mathrm{)}$ absorption band of ¹⁴N₂ and the P(3) line of the $\mathit{B}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{u}}^{\mathrm{+}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime }}\mathrm{=}\mathrm{13}\mathrm{)}\mathrm{\to }\mathit{X}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime \prime }}\mathrm{=}\mathrm{0}\mathrm{)}$ H₂ Lyman emission band. The significance of this overlap is dependent on the assumed excitation temperatures of absorbing ¹⁴N₂ and shielding H₂. When T_ex = 20 K, also indicated in Figs. 5 and 6, the fraction of N₂ ground state molecules in the J = 4 rotational level is low and the significance of the 960.45 Å overlap is small. For T_ex = 100 K, the J = 3 level population of ground state H₂ becomes significant and P(3) absorption effectively shields ¹⁴N₂ photodissociation. Thus, the largest ¹⁴N₂ photodissociation rate occurs at intermediate temperature.

Only small increases in the ¹⁴N₂ photodissociation rate occur for increased turbulent broadening, b. Greater sensitivity is found with respect to the assumed o−H₂:p−H₂ ratio. This is limited to 0:1 and 3:1 at high and low temperatures, respectively, given sufficiently high densities for thermal equilibrium to be maintained. The ¹⁴N₂ photodissociation rate is approximately halved when the low temperature limit is adopted, primarily because the H₂ emission at 960.45 Å arises from an excited o−H₂ level.

Table 2 also includes photodissociation rates assuming reduced absorption by dust grains, in order to simulate the interior of a protoplanetary disc. The adopted value of ${\mathit{x}}_{\mathrm{dust}}{\mathit{\sigma }}_{\mathrm{dust}}^{\mathrm{abs}}$ effectively removes dust from the competitive absorption of photons. The N₂ photodissociation rate is then somewhat higher than for an interstellar cloud, but follows the same trends with respect to temperature and the o−H₂:p−H₂ ratio.

Calculations of the cosmic-ray induced photodissociation of ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ are also presented in Table 2. The resultant rate assuming the base conditions designed to represent a typical dark interstellar cloud is 21 × 10^-16 s^-1. This is slightly larger than for ¹⁴N₂ and is the result of a different collection of overlapping N₂ absorption and H₂ emission lines. The ¹⁴N 15N dissociation rate is found to be much larger than for ¹⁴N₂ in the cold-temperature limit o−H₂:p−H₂ = 0:1 and for T ≃ 30 K. This is due to a strong overlap of H₂ emission lines near 913.1 and 913.3 Å with absorption lines corresponding to low rotational levels of the ${\mathit{o}}_{\mathrm{3}}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{2}\mathrm{)}\mathrm{\leftarrow }{\mathit{X}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{0}\mathrm{)}$ transition of ¹⁴N 15N, plotted in Fig. 5. The influence of these overlaps dominate the accumulated dissociation rate shown in Fig. 6. The isotopologue difference between dissociation rates is increased significantly when the reduced dust shielding in a protoplanetary disc is accounted for and approaches a factor of 8. Thus, from Table 2, the most likely candidate for isotopic fractionation and an enhancement of atomic ¹⁵N due to cosmic ray induced photodissociation occurs in disc material around 30 K and with a small o−H₂/p−H₂ ratio. The difference between ¹⁴N₂ and ¹⁴N 15N dissociation rates diminishes for temperatures below 30 K, and is negligible at 10 K when assuming a low-temperature limit for o−H₂/p−H₂.

4.3. Cosmic-ray induced photodissociation of CO

We also combined the high-resolution H₂ cosmic-ray induced emission model with the CO photodissociation cross sections of Visser et al. (2009). There is an example CO transmission spectrum plotted in Fig. 3 which exhibits similar band structure as for N₂. The reduced symmetry of heteronuclear CO allows for greater perturbation of its excited states and leads to more rapid predissociation on average than for N₂. The CO rotational absorption lines are then somewhat broader than for N₂.

The CO photodissociation rates in a cosmic-ray induced UV field assuming various physical parameters are listed in Table 2 and are of a similar magnitude to the N₂ rates. The on-average broader absorption lines of CO overlaps with H₂ emission lines more frequently than for N₂, and the resulting photodissociation is then less sensitive to variations in the assumed excitation temperature and o−H₂:p−H₂ ratio.

The calculated CO photodissociation rate in Table 2 for the base conditions representing an interstellar cloud is 8.1 × 10^-16 s^-1. This is somewhat less than the value calculated by Gredel et al. (1987), 13 × 10^-16 s^-1 (assuming ω = 0.5 and ζ = 10^-16 s^-1), who used a less sophisticated model of CO photodissociation.

5. Chemical models including photodissociation

5.1. Interstellar cloud model

A chemical model simulating an interstellar cloud was studied in order to explore the details of ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ photodissociation due to an interstellar radiation field impinging on its surface and a flux of cosmic rays within its interior. The model is similar to that of Li et al. (2013). Here, we used a modified version of the UMIST 2012 chemical network (McElroy et al. 2013). The network was stripped down to species containing only H, He, C, N and O; and a maximum of two C, N or O atoms. Supra-thermal chemistry was included to enhance the formation of CH⁺ (and thus also CO) at low A_V, following Visser et al. (2009). This boosts the rate of ion-neutral reactions after setting the Alfvén speed to 3.3 km s^-1 for column densities less than 4 × 10²⁰ cm^-2.

Fig. 6 Dissociation rate of N2 due to cosmic-ray induced H2 emission under interstellar cloud conditions, integrated cumulatively with increasing wavelength. Rates for 14N2 are plotted with for several temperatures (solid curves), for and Tex = 20 K (black dotted curve), and a single case is included for 14N 15N (red dotted curve).

Freeze-out and thermal evaporation for all neutral species were added to the gas-phase only UMIST network as well as the grain-surface hydrogenation reactions used by Visser et al. (2011). The latter include H₂ formation and the conversion of C to CH₄, N to NH₃, O to H₂O, and S to H₂S.Photodesorption due to the UV field generated from cosmic-ray ionisation and the attenuated ISRF were included, but direct cosmic-ray desorption was not.

The wavelength dependence of the Draine ISRF was adopted for a unidirectional radiation field perpendicularly incident on the model cloud’s edge. This was scaled by a factor of χ = 2 so that one-sided irradiation of the cloud leads to the same unshielded dissociation rates at its edge as those given in Table 1. The cloud is assumed sufficiently thick that no radiation penetrates from the far side. Self-shielding of CO is computed using the shielding functions of Visser et al. (2009), for ¹⁴N₂ we use those calculated by Li et al. (2013) at 30 K, and the presently calculated shielding functions are used for ¹⁴N ¹⁵N. The scattering of UV radiation out of the incident beam is not included in our model.

The wavelength dependence of the Draine ISRF was designed to simulate an isotropic field generated from a remote stellar population (Draine 1978), and some previous interstellar cloud models also assume isotropic radiation (Röllig et al. 2007). The transition between atomic and molecular H₂ was shown by Röllig et al. (2007) to differ between irradiation geometries, occurring at lower A_V for the isotropic case relative to unidirectional radiation. The transition for N₂ occurring in our unidirectional model would be similarly shifted to shallower depth if the incident radiation were isotropic.

The elemental abundances relative to H are those of Aikawa et al. (2008): 0.0975 for He, 7.86 × 10^-5 for C, 2.47 × 10^-5 for N, and 1.80 × 10^-4 for O. The elemental ¹⁴N:¹⁵N ratio was fixed to the protosolar value, 450:1. The rate of H₂ ionisation due to cosmic rays was set to 5 × 10^-17 s^-1. The abundances of N, N₂ and CO reach steady state after ~1 Myr, regardless of whether the gas starts in atomic or molecular form.

The cloud was assumed to have a constant hydrogen-nuclei density of n_H = n(H) + 2n(H₂) = 10³ cm^-3 and a temperature of 30 K. The turbulent broadening, b, of CO, H₂, and H were set to 0.3, 3, and 5 km s^-1; respectively; and N₂ lines were assigned linewidths equivalent to their thermal Doppler width at 30 K, in an identical fashion to the similar model of Li et al. (2013).

The dust population was assigned a coefficient γ_dust = 3.53 in Eq. (5) to simulate grains with an interstellar size distribution, with radius ~0.1 μm size. A value for the cosmic-ray induced photodissociation rate of N₂ was adopted corresponding to the low temperature o−H₂:p−H₂ ratio, 0:1.

The nitrogen reaction network was augmented so that separate accounting of pure ¹⁴N and single-¹⁵N containing species was possible. For this, all N-containing species and reactions were cloned and a ¹⁴N to ¹⁵N substitution made. Two kinds of isotope-differentiating reactions are included in our model chemical network: photodissociation and low-temperature ion-molecule exchange reactions. The selective effects of photodissociation are encoded in the shielding functions and cosmic-ray induced photodissociation rates presented in Sects. 3 and 4.2. Exchange reactions were added to our network using the rates listed in Table 2 of Terzieva & Herbst (2000). These reactions exothermically favour increased abundances of ¹⁵N in more complex species because of the lower zero-point energy of molecules with heavier nuclei, with typical excess energies of 10 to 30 K.

Fig. 7 Top: abundances relative to H nuclei and left-to-right accumulated column densities of the isotopologues of N and N2 in the modelled interstellar cloud. Bottom: ratios of abundances and column densities of 14N- and 15N-bearing species. Also indicated are the adopted elemental ratios of 14N / 15N and 14N2 / 14N 15N (dashed lines).

Fig. 8 Top: abundances relative to H nuclei and right-to-left accumulated column densities of atomic and molecular nitrogen, and N2 ice in the modelled protoplanetary disc as a function of height above the midplane at a radius of 105 AU. Also shown for species with a single 15N substitution i.e., 15N and 14N 15N (dotted curves). Bottom: ratios of abundances and column densities of 14N- and 15N-bearing species. In some cases the ice and gaseous N2 curves coincide. Also indicated is the elemental ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ ratio (dashed line).

Fig. 9 Shielding functions for 14N2 and ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ calculated for the protoplanetary disc model column densities. Partial shielding functions are shown considering dust grains only and with progressively more line absorption.

Figure 7 shows the calculated abundances of ¹⁴N, ¹⁵N, ¹⁴N₂, and ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ as well as their accumulated column densities, i.e., $\mathrm{Cumulativecolumndensity}\mathrm{=}{\mathrm{\int }}_{\mathrm{0}}^{\mathit{z}\mathrm{\left(}{\mathit{A}}_{\mathit{V}}\mathrm{\right)}}\mathit{n}\mathrm{\left(}\mathit{X}\mathrm{\right)}\hspace{0.17em}\mathrm{d}\mathit{z,}$(11)where n(X) is the absolute abundance of species X and z(A_V) is the distance from the clouds edge for a particular extinction. The trend of these quantities as a function of A_V is qualitatively very similar for either isotopologue. Nitrogen is preserved in atomic form near the edge of the cloud due to the intense photodissociating interstellar radiation field. Increasing shielding with depth into the cloud permits a significant population in molecular form beginning around A_V = 1.5.

The relative abundances of ¹⁴N/¹⁵N and ¹⁴N₂/${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ calculated by the model are shown in Fig. 7. Any fractionation process will alter the isotopic abundances from the assumed elemental ratios ¹⁴N/¹⁵N = 450 and ¹⁴N₂/${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}\mathrm{=}\mathrm{225}$. There is indeed an enhancement of ¹⁵N in atomic form for A_V between 1 and 3 mag, and its concurrent depletion in the form of N₂. This range of extinction corresponds to a column-density of ¹⁴N₂ sufficiently large to significantly self-shield the ISRF and slow its rate of photodissociation. The lower column of ¹⁴N¹⁵N is not as effectively self-shielding and leads to a larger ¹⁴N¹⁵N photodissociation rate and the calculated excess of ¹⁵N atoms.

A modified model was also run neglecting ion-molecule exchange reactions in order to test their contribution to the calculated fractionation. The modelled abundances were not significantly altered by this modification and the fractionation between A_V = 1 and 3 mag is completely dominated by isotope-selective photodissociation due to self-shielding, at least at the adopted temperature of 30 K.In contrast, significant enhancements of ¹⁵N in NH₃ and HCN were produced in the models of Charnley & Rodgers (2002), Rodgers & Charnley (2004), and Wirström et al. (2012) which simulate dense protostellar cores. These models included isotope-exchange reactions similar to those adopted here and neglected isotope-selective photodissociation. They also simulated somewhat colder conditions than ours (10 versus 30 K), enhancing the rate of the fractionating exchange reactions, and assumed significant depletion of CO relative to N₂ by condensation onto grains, slowing the effect of fractionation-reducing reprocessing to N₂. It is then possible that the observed fractionation of N-isotopes may have a combined chemical and photolytic origin.

Fig. 10 Top: abundances relative to H nuclei and right-to-left accumulated column densities of CN, HCN, and their ices in the modelled protoplanetary disc as a function of height above the midplane at a radius of 105 AU. Also shown for species with a single 15N substitution (dotted curves). Bottom: ratios of abundances and column densities of 14N- and 15N-bearing species. Also indicated is the elemental ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ ratio (dashed line).

There is no indication in Fig. 7 for fractionation in the abundance of N₂ or N in the completely shielded interior of the interstellar cloud model (A_V ≳ 3). This is despite the inclusion of isotope-selective ion-molecule exchange reactions and a 40% faster rate of cosmic ray induced photodissociation for ¹⁴N 15N relative to ¹⁴N₂ given the physical parameters selected for this cloud model. Ultimately, cosmic-ray induced photodissociation is rendered irrelevant by faster and isotopologue-independent destruction mechanisms included in our model: ${\mathrm{N}}_{\mathrm{2}} \stackrel{\mathrm{H}{\mathrm{e}}^{\mathrm{+}}}{\mathrm{\to }} {\mathrm{N}}^{\mathrm{+}}\mathrm{+}\mathrm{N}$(12)and ${\mathrm{N}}_{\mathrm{2}} \stackrel{{\mathrm{H}}_{\mathrm{3}}^{\mathrm{+}}}{\mathrm{\to }} {\mathrm{N}}_{\mathrm{2}}{\mathrm{H}}^{\mathrm{+}}\mathit{.}$(13)The combined destruction rate due to these processes exceeds 10^-13 s^-1 and is two orders of magnitude faster than cosmic-ray induced photodissociation.

The total-column fractionation of N and N₂ depends on the assumed depth of the modelled cloud, and is also plotted in Fig. 7 as a function of A_V. For our plane-parallel single-side-illuminated model this is maximal for A_V between 1.5 and 2 mag, but never exceeds a factor of two for atomic or molecular species.

The minor contribution of cosmic-ray induced photodissociation to the nitrogen chemistry in our model does not presuppose a similar conclusion for other molecules, some of which have significantly higher cosmic-ray induced predissociation rates (Gredel et al. 1989).

5.2. Protoplanetary disc model

We have run a second chemical model for a vertical slice through a circumstellar disc using the same network of reactions as in Sect. 5.1. The model setup is identical to that of Visser et al. (2009) and Li et al. (2013). Briefly, we take the disc geometry, dust density and temperature distributions directly from the previous model of D’Alessio et al. (1999) without modification. This simulates a disc of mass of 0.07 M_⊙ and outer radius 400 AU surrounding a T Tauri star of mass 0.5 M_⊙ and radius 2 R_⊙. The simulated vertical slice is located at a radius of 105 AU.

A radiation field with the Draine wavelength dependence is perpendicularly incident on the surface of the slice, 120 AU above the midplane. The use of a scaled Draine field to represent the combined UV flux from the central star and the ISRF has been previously investigated in detail for the same disc geometry employed here (van Zadelhoff et al. 2003; Jonkheid et al. 2004). From these studies, a Draine field with χ = 516 is a satisfactory proxy for a more realistic field including the details of the stellar spectrum at a disc radius of 105 AU. Dust grains of radius 1 μm are assumed to populate the disc which leads to weaker shielding and a greater penetration of ultraviolet radiation than for the interstellar cloud model of Sect. 5.1.

The abundances and cumulative column densities of atomic and molecular nitrogen in the disc model are plotted in Fig. 8. The abundance of N₂ becomes significant about 40 AU above the midplane and a rapid freeze-out of gaseous N₂ onto dust grains occurs 20 AU above the midplane, where the temperature falls below 20 K. The effect of photodissociative fractionation in the intervening 20 to 40 AU region is evident in the abundance ratios plotted in Fig. 8, where the atomic ratio of ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ dips by a factor of 10 below the elemental ratio. However, fractionation of the total atomic N column is negligible because of its low abundance in this region. As for the interstellar cloud model, cosmic-ray induced photodissociation of N₂ is found to be negligible throughout the disc slice, and does not contribute to isotopic fractionation. Similarly, the contribution of ion-molecule exchange reactions to the calculated chemical abundances was found to be negligible following comparison with an alternative model where these are neglected. That is, the ice-phase predominance of nitrogen species in our model for disc heights with sufficiently low-temperature for chemical fractionation to occur suppresses these reactions.

The contribution of different species to the shielding of ¹⁴N₂ and ¹⁴N 15N photodissociation were calculated as a function of height and A_V and are plotted in Fig. 9. These calculations include all shielding species in an integral with the form in Eq. (5) by adopting column densities output from the disc model. From this, it is evident that shielding by 1 μm dust grains (approximated for Fig. 9 by assuming γ_dust = 0.6) and the hydrogen column are comparably effective. The shielding by CO is quite negligible because of the rarity of its overlaps with N₂, evident in Fig. 3. The significance of photodissociation-induced isotopic fractionation of atomic N relies on the relative importance of self-shielding of ¹⁴N₂ and ¹⁴N 15N. For ¹⁴N₂ this becomes important around 40 AU above the midplane and is comparable to dust and hydrogen shielding between 20 and 35 AU. For ¹⁴N 15N, self-shielding never contributes more than 10% of the total shielding and is about equivalent to its shielding by ¹⁴N₂.

The appearance of N and N₂ fractionation between 20 and 40 AU in Fig. 8 has consequences for other nitrogen bearing species. For example, Fig. 10 shows the abundances, column densities, and isotopic ratios of CN, HCN, and their ices; which are formed primarily from atomic N via the reactions $\mathrm{N} \stackrel{\mathrm{CH}}{\mathrm{\to }} \mathrm{CN}\mathit{,}$(14)and $\mathrm{N} \stackrel{\mathrm{C}{\mathrm{H}}_{\mathrm{2}}}{\mathrm{\to }} \mathrm{HCN}\mathit{.}$(15)Additionally, CN and HCN are themselves susceptible to photodissociation and do not survive far from the midplane. Then, their maximum abundances occur within the region of enhanced ¹⁵N atoms and this enhancement is mirrored in their integrated column densities. The isotopic fractionation of HCN gas and ice columns is plotted in Fig. 10 and approaches a factor of 10, whereas the fractionation of gaseous CN is somewhat less because a major portion of its column forms above 40 AU and outside the region of photo-fractionated N.

Fig. 11 Top: abundances relative to H nuclei and right-to-left accumulated column densities of NH3 and NH3 ice in the modelled protoplanetary disc as a function of height above the midplane at a radius of 105 AU. Also shown for species with a single 15N substitution (dotted curves). Bottom: ratios of abundances and column densities of 14N- and 15N-bearinge species. Also indicated is the elemental ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ ratio (dashed line).

A different isotope fractionation pattern is evident in Fig. 11 for NH₃. The majority of the NH₃ population is frozen onto grain surfaces and its abundance has a sharp maximum at the inner edge of the ¹⁵N / ¹⁴N fractionation zone, near 20 AU. We do not compute much difference between the integrated column densities of ¹⁴NH₃ and ¹⁵NH₃ in either gas or ice phases but the local ¹⁵NH₃ abundance is significantly enhanced and depleted in the ranges 20–25 and 25–40 AU, respectively. The pattern of NH₃ photolytic fractionation is more complex than for CN and HCN due to a more complex formation mechanism. There are two pathways leading to NH₃ in our model, the first occurring entirely in the gas phase and initiated from molecular N₂, that is, $\mathrm{N}\mathrm{2} \stackrel{\mathrm{H}{\mathrm{e}}^{\mathrm{+}}}{\mathrm{\to }} \mathrm{N}\mathrm{+}{\mathrm{N}}^{\mathrm{+}} \stackrel{\mathit{n}{\mathrm{H}}_{\mathrm{2}}}{\mathrm{\to }} \mathrm{N}{\mathrm{H}}_{\mathrm{4}}^{\mathrm{+}} \stackrel{{\mathrm{e}}^{\mathrm{-}}}{\mathrm{\to }} \mathrm{N}{\mathrm{H}}_{\mathrm{3}}\mathit{,}$(16)and the second follows from the hydrogenation of atomic N after its condensation onto ice grains, $\mathrm{N} \stackrel{\mathit{T}\lesssim \mathrm{20}\hspace{0.17em}\mathrm{K}}{\mathrm{\to }} \mathrm{N}\hspace{0.17em}\mathrm{ice} \stackrel{\mathit{n}\mathrm{H}}{\mathrm{\to }} \mathrm{N}{\mathrm{H}}_{\mathrm{3}}\mathrm{ice}\mathit{.}$(17)Intermediate species NH and NH₂ in the reaction series summarised by Eq. (17) are also allowed to evaporate in our model and contribute to the gaseous NH₃ beginning with their ionisation by H⁺, e.g., $\mathrm{N}{\mathrm{H}}_{\mathrm{2}} \stackrel{{\mathrm{H}}^{\mathrm{+}}}{\mathrm{\to }} \mathrm{N}{\mathrm{H}}_{\mathrm{2}}^{\mathrm{+}} \stackrel{{\mathrm{H}}_{\mathrm{2}}}{\mathrm{\to }} \mathrm{N}{\mathrm{H}}_{\mathrm{3}}\mathit{.}$(18)The balance between formation routes given in Eqs. (16)–(18) dictates the height-dependent isotopic fractionation of NH₃ in sympathy with the fractionation of their respective precursors, N₂ or N. The occurrence of formation route (16) is limited to approximately 20 to 40 AU above the midplane, where there is an abundance of gaseous N₂. The process in Eq. (17) requires condensed atomic N and is even more restricted. That is, sufficiently low temperatures only occur within 25 AU of the midplane in our model, whereas the necessary source of gaseous N is limited to above 20 AU. Then, the NH₃ fractionation pattern resembles that of atomic N between 20 and 25 AU, and N₂ above this.

Overall, the complexity of photodissociative fractionation of NH₃ deduced here suggests the induced ¹⁴NH₃ / ¹⁵NH₃ column density ratio in a particular environment will depend sensitively on its temperature and density profiles. The photodissociative fractionation of CN and HCN is likely more robust because the formation routes of these molecules are relatively simple. The enhancement of ¹⁵N in CN and HCN within the self-shielding zone of our model disc (10 ×) is actually larger than for observations of cometary CN and HCN (2–3 ×) (Jehin et al. 2009; Mumma & Charnley 2011). This supports the feasibility of photodissociation as a mechanism for cometary fractionation. The greater fractionation of ¹⁵N and HCN relative to NH₃ calculated for our particular protoplanetary disc also suggests that photodissociation may contribute to the explanation of a similar difference observed in the cold prestellar core L1544 (Hily-Blant et al. 2013; Bizzocchi et al. 2013), but not necessarily elsewhere in the galaxy (Daniel et al. 2013).

6. Conclusions

We used a high-resolution theoretical spectroscopic model of ¹⁴N 15N to calculate its dissociation rate in interstellar space due to ultraviolet radiation, as well as the shielding of this radiation by dust grains and gas phase species. We obtain an unshielded rate of 1.73 × 10^-10 s^-1 assuming a Draine ISRF and an excitation temperature of 30 K, which is very near to the rate for ¹⁴N₂ obtained in our previous study (Li et al. 2013). Comprehensive tabulated shielding functions for ¹⁴N₂ and ¹⁴N 15N are available online².

To calculate the rate of photodissociation in regions fully shielded from external radiation, the model of ¹⁴N₂ and ¹⁴N 15N was combined with a detailed theoretical spectrum of H₂ emission arising from cosmic rays. Assuming ζ = 10^-16 s^-1, a variable rate of ~10^-15 s^-1 was found to depend on the assumed details of the local environment, most significantly, the excitation temperature of N₂ and shielding species, the o−H₂:p−H₂ ratio, and the dust opacity at ultraviolet wavelengths. Isotope-dependent cosmic-ray induced photodissociation was also investigated, with the most extreme difference occurring when assuming 30 K, o−H₂:p−H₂ = 0:1, and a low dust absorption cross section appropriate to a protoplanetary disc experiencing grain growth. Then, the dissociation rate of ¹⁴N 15N exceeds that of ¹⁴N₂ by a factor of 8. This large isotopic difference does not occur at a lower excitation temperature of 10 K. We also calculated the rate of CO dissociation by cosmic-ray induced photons previously determined by Gredel et al. (1987) using more accurate photodissociation cross sections, and deduced a ~40 % lower value.

Chemical models were run simulating an interstellar cloud and a protoplanetary disc to test the importance of self-shielding of external radiation and cosmic ray initiated photodissociation to the balance of ¹⁴N- and ¹⁵N-bearing species. An enhancement of atomic ¹⁵N relative to ¹⁴N is found at extinctions with 1 ≲ A_V ≲ 3, and is due to more effective self-shielding of the ISRF by ¹⁴N₂ than by ¹⁴N 15N. This fractionation is larger for our disc model where weaker dust shielding was assumed to simulate the growth and depletion of small dust grains. The photodissociation due to cosmic-ray induced ultraviolet radiation is found to be too slow to significantly influence the chemistry in the dark interiors of our models.

The isotopically-dependent photodissociation of N₂ in our protoplanetary disc model leads to a significant enhancement in the column densities of HC¹⁵N relative to HC¹⁴N. Our model predicts a value of HC¹⁴N/HC¹⁵N ≃ 100, when assuming an elemental nitrogen abundance ratio of ¹⁴N/15_N = 450. This corresponds to an isotopic fractionation in δ-notation of ${}^{\mathrm{15}}\mathit{\delta }_{\mathrm{HCN}}$ ≃ -800 %0. This enhancement mirrors the fractionation of atomic N induced by photodissociation. Our model predicts a lower fractionation ratio for CN, with C¹⁴N/C¹⁵N ≃ 250. This is because the region where CN forms does not coincide as neatly with the peak of N₂ isotope dependent photodissociation. The formation chemistry of NH₃ is more complex and can be initiated from both N₂ and atomic N. This species is then less fractionated in our model.

Many assumptions must be made when modelling the chemistry of complex and remote objects such as protoplanetary discs. However, the calculations underpinning our predictions of photodissociative fractionation are based on reliable laboratory and theoretical spectroscopy and may be resilient to many structural details of astrophysical objects.

Acknowledgments

Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA), by a Spinoza grant and grant 648.000.002 from the Netherlands Organisation for Scientific Research (NWO) via the Dutch Astrochemistry Network, and by the European Community’s Seventh Framework Programme FP7/2007-2013 under grant agreements 291141 (CHEMPLAN) and 238258 (LASSIE). Calculations of the N₂ photodissociation cross sections were supported by the Australian Research Council Discovery Program, through Grant Nos. DP0558962 and DP0773050. We would also like to thank Simon Bruderer and Xiaohu Li for discussions on the optical properties of protoplanetary dust grains and ¹⁴N₂ photodissociation, respectively.

References

All Tables

All Figures

Fig. 1 Diabatic-basis potential-energy curves of N2 excited states relevant to ultraviolet photoabsorption and photodissociation. The energy scale is referenced to v = 0, J = 0 of the $\mathit{X}\hspace{0.17em}{}^{\mathrm{1}}\mathrm{\Sigma }_{\mathit{g}}^{\mathrm{+}}$ ground state and is related to the wavelength scale assuming transitions from this fundamental level. Also indicated are the excitation states of atomic products arising from dissociation and the absorption limit imposed by the ionisation of atomic H. The potential-energy curves of the ${\mathit{c}}_{\mathit{n}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}$ and ${\mathit{c}}_{\mathit{n}\mathrm{+}\mathrm{1}}^{\mathrm{\prime }}{\mathrm{1}}^{}{\mathrm{\Sigma }}_{\mathit{u}}^{\mathrm{+}}$ states are indistinguishable at the plotted scale. The N2 ionisation potential energy occurs at 15.4 eV in this figure.

In the text

	Fig. 2 An example of isotopically-dependent predissociation. The predissociation fraction, ηpre, of individual rotational levels, J, of b 1Πu(v = 1) calculated by the CSE model for 14N2 and 14N15N.
In the text

Fig. 3 Upper panels: representative transmission functions calculated from theoretical photoabsorption cross sections of important molecular species, with column densities: N(H) = 1022, N(H2) = 1020, and $\mathit{N}\mathrm{\left(}{}^{\mathrm{14}}\mathrm{N}_{\mathrm{2}}\mathrm{\right)}\mathrm{=}\mathit{N}\mathrm{\left(}{}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}\mathrm{\right)}\mathrm{=}\mathit{N}\mathrm{\left(}\mathrm{CO}\mathrm{\right)}\mathrm{=}{\mathrm{10}}^{\mathrm{15}}\hspace{0.17em}{\mathrm{cm}}^{-2}$; and simulating an excitation temperature of 50 K for all molecular absorption. Lower panels: probability per Å of H2 emission following a cosmic-ray induced ionisation event. Spectra are shown assuming two different values for the H2 ortho:para ratio.

In the text

Fig. 4 Top left: self-shielding functions for ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ (solid lines) and 14N2 (dotted lines) at various temperatures defining their excitation state and thermal Doppler broadening. Top right: shielding of 14N 15N photodissociation by 14N2 at various excitation and Doppler broadening temperatures. Bottom: shielding of ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ (solid lines) and 14N2 (dotted lines) photodissociation by H and H2 as a function of their column densities.

In the text

Fig. 5 Modelled molecular absorption lines for two different excitation temperatures, 20 and 100 K, and cosmic-ray induced H2 emission. Otherwise calculated as for Fig. 3. Left: overlap of an o-H2 emission line with the ${\mathit{c}}_{\mathrm{3}}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime }}\mathrm{=}\mathrm{0}\mathrm{)}\mathrm{\leftarrow }\mathit{X}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}{\mathit{v}}^{\mathrm{\prime \prime }}\mathrm{=}\mathrm{0}\mathrm{)}$P(4) absorption line of 14N2. Right: overlap of two p-H2 emission lines with absorption by the ${\mathit{o}}_{\mathrm{3}}{\hspace{0.17em}}^{\mathrm{1}}{\mathrm{\Pi }}_{\mathit{u}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{2}\mathrm{)}\mathrm{\leftarrow }{\mathit{X}}^{\mathrm{1}}{\mathrm{\Sigma }}_{\mathit{g}}^{\mathrm{+}}\mathrm{(}\mathit{v}\mathrm{=}\mathrm{0}\mathrm{)}$ band of 14N 15N, with R and P branches indicated.

In the text

	Fig. 6 Dissociation rate of N2 due to cosmic-ray induced H2 emission under interstellar cloud conditions, integrated cumulatively with increasing wavelength. Rates for 14N2 are plotted with for several temperatures (solid curves), for and Tex = 20 K (black dotted curve), and a single case is included for 14N 15N (red dotted curve).
In the text

	Fig. 7 Top: abundances relative to H nuclei and left-to-right accumulated column densities of the isotopologues of N and N2 in the modelled interstellar cloud. Bottom: ratios of abundances and column densities of 14N- and 15N-bearing species. Also indicated are the adopted elemental ratios of 14N / 15N and 14N2 / 14N 15N (dashed lines).
In the text

Fig. 8 Top: abundances relative to H nuclei and right-to-left accumulated column densities of atomic and molecular nitrogen, and N2 ice in the modelled protoplanetary disc as a function of height above the midplane at a radius of 105 AU. Also shown for species with a single 15N substitution i.e., 15N and 14N 15N (dotted curves). Bottom: ratios of abundances and column densities of 14N- and 15N-bearing species. In some cases the ice and gaseous N2 curves coincide. Also indicated is the elemental ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ ratio (dashed line).

In the text

	Fig. 9 Shielding functions for 14N2 and ${}^{\mathrm{14}}\mathrm{N}^{\mathrm{15}}\mathrm{N}$ calculated for the protoplanetary disc model column densities. Partial shielding functions are shown considering dust grains only and with progressively more line absorption.
In the text

Fig. 10 Top: abundances relative to H nuclei and right-to-left accumulated column densities of CN, HCN, and their ices in the modelled protoplanetary disc as a function of height above the midplane at a radius of 105 AU. Also shown for species with a single 15N substitution (dotted curves). Bottom: ratios of abundances and column densities of 14N- and 15N-bearing species. Also indicated is the elemental ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ ratio (dashed line).

In the text

Fig. 11 Top: abundances relative to H nuclei and right-to-left accumulated column densities of NH3 and NH3 ice in the modelled protoplanetary disc as a function of height above the midplane at a radius of 105 AU. Also shown for species with a single 15N substitution (dotted curves). Bottom: ratios of abundances and column densities of 14N- and 15N-bearinge species. Also indicated is the elemental ${\mathrm{14}}^{}\mathrm{N}{\mathit{/}}^{\mathrm{15}}\mathrm{N}$ ratio (dashed line).

In the text