| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322661 | |
| Published online | 05 February 2014 | |
Spectroscopic and physical parameters of Galactic O-type stars
II. Observational constraints on projected rotational and extra broadening velocities as a function of fundamental parameters and stellar evolution⋆
1
Institute of Astronomy with NAO, BAS,
PO Box 136,
4700
Smolyan,
Bulgaria
e-mail:
nmarkova@astro.bas.bg
2
Universitäts-Sternwarte, Scheinerstrasse 1, 81679
München,
Germany
e-mail:
uh101aw@usm.uni-muenchen.de
3
Instituto de Astrofísica de Canarias, 38200, La Laguna, Tenerife, Spain
e-mail: ssimon@iac.es; ahd@iac.es
4
Departamento de Astrofísica, Universidad de La
Laguna, 38205, La
Laguna, Tenerife,
Spain
e-mail:
ahd@iac.es
5
Argelander-Institut für Astronomie, Bonn University,
53121
Bonn,
Germany
e-mail:
nlanger@astro.uni-bonn.de
Received: 13 September 2013
Accepted: 15 October 2013
Context. Rotation is of key importance for the evolution of massive star, including their fate as supernovae or gamma-ray bursts. However, the rotational velocities of OB stars are difficult to determine.
Aims. Based on our own data for 31 Galactic O stars and incorporating similar data for 86 OB supergiants from the literature, we aim at investigating the properties of rotational and extra line-broadening as a function of stellar parameters and at testing model predictions about the evolution of stellar rotation.
Methods. Fundamental stellar parameters were determined by means of the code FASTWIND. Projected rotational and extra broadening velocities, vsini and ΘRT, originate from a combined Fourier transform and the goodness-of-fit method. Model calculations published previously were used to estimate the initial evolutionary masses, Mevolinit.
Results. The sample O stars with Mevolinit ≳ 50 M⊙ rotate with less that 26% of their break-up velocity, and they also lack slow rotators (vsini ≲ 50 km s-1). For the more massive stars (Mevolinit ≥ 35 M⊙) on the hotter side of the bi-stability jump, the observed and predicted rotational rates agree quite well; for those on the cooler side of the jump, the measured velocties are systematically higher than the predicted ones. In general, the derived ΘRT values decrease toward cooler Teff, whilst for later evolutionary phases they appear, at the same vsini, higher for high-mass stars than for low-mass ones. None of the sample stars shows ΘRT ≥ 110 km s-1. For the majority of the more massive stars, extra broadening either dominates or is in strong competition with rotation.
Conclusions. For OB stars of solar metallicity, extra broadening is important and has to be accounted for in the analysis. When appearing at or close to the zero-age main sequence, most of the single and more massive stars rotate slower than previously thought. Model predictions for the evolution of rotation in hot massive stars may need to be updated.
Key words: stars: early-type / stars: fundamental parameters / stars: rotation / stars: evolution
© ESO, 2014
1. Introduction
Rotation has been initially considered as a secondary effect for the evolution of massive stars. This view was challenged later on by a number of significant discrepancies between model predictions and observations (see, e.g., Maeder 1995 and references therein) which, on the contrary, suggest that rotation may have an impact comparable to that of mass loss, a possibility that has been entirely confirmed by the new generation of evolutionary models that account for stellar rotation (Meynet & Maeder 2000a; Brott et al. 2011).
Although of critical importance for constraining evolutionary predictions, the rotational rates of massive OB stars are not clearly determined yet, and one of the major difficulties is related to the additional broadening in the spectrum of these stars (Slettebak 1956; Rozendhal 1970; Conti & Ebbets 1977; Penny 1996; Howarth et al. 1997), which is typically designated as macroturbulence.
Even though the nature and the origin of macroturbulence is still unclear, its presence in the atmospheres of hot massive stars may have important implications for our knowledge of the physics of these objects. In particular, through its effect on the projected rotational rates, macroturbulence may affect the interpretation of stellar evolution calculations, providing a clue for understanding the lack of consistency between model predictions and observations regarding the role of rotational mixing in enriching surface N abundances in massive OB stars (Hunter et al. 2008, 2009; Rivero-Gonzalez et al. 2012). Through its effect on the shape and width of spectral lines, it might also modify stellar properties derived by means of model atmosphere analyses.
While the number of Galactic B-type stars with reliably determined physical properties, including chemical abundances and rotational and extra broadening velocities, has progressively increased during the past decade (e.g., Morel et al. 2006, 2008; Dufton et al. 2006b; Crowther et al. 2006; Hunter et al. 2008, 2009; Markova & Puls 2008; Lefever et al. 2010; Fraser et al. 2010), O-type stars are currently under-represented in the stellar samples investigated so far (e.g., Bouret et al. 2012; Martins et al. 2012a,b).
Motivated by the lack of high-quality observational data, an extensive and detailed spectroscopic survey of O and early-B stars in our Galaxy has been initiated by us and is currently under way. The immediate aim is to obtain reliable and coherent estimates for the photospheric and wind parameters (including nitrogen and helium abundances) and projected rotational rates for a statistically significant number of stars while allowing for the effect of extra broadening. By means of these data and incorporating similar data from the literature, we plan (i) to address the important question on the nature and the origin of extra broadening in the spectra of hot massive stars and (ii) to test model predictions about the evolution of rotation and the role of rotational mixing in surface chemical enrichment during the main-sequence (MS) phase. In this paper, we present the main results from our analysis of 31 O-type stars from the southern hemisphere. Results from the analysis of an even larger sample, observed within the IACOB project (Simón-Díaz et al. 2011), will be presented in a forthcoming study (Simón-Díaz et al., in prep.).
Our paper is structured as follows: in Sect. 2 we describe the observational material and its reduction. In Sect. 3 we outline the procedures used to determine the fundamental stellar parameters and to disentangle and measure the relative contributions of rotational and extra broadening. The main results are outlined and discussed in Sects. 4, and 5 and are summarized in Sect. 6.
2. Stellar sample and observations
Our basic sample consists of 31 O-type stars in the Milky Way (MW), selected by means of the following criteria: (i) to sample the luminosity classes I, III and V, and the spectral subtypes from O3 to O9.7; (ii) to be presumably single1; (iii) to cover a wide range of projected rotational velocities; (iv) to be preferentially members of clusters and associations (i.e., to have known distances); and (v) to be bright enough (V ≤ 10 mag) to allow for good quality spectra to be obtained during relatively short exposure times using medium-class telescopes.
For 24 of the 31 targets we used our own observations, collected with the FEROS spectrograph (Kaufer et al. 1999) at the 2.2 m MPI/ESO telescope at La Silla; for the rest, MPI-FEROS spectra available from the ESO archive, were used. All spectra have a spectral resolving power of 48 000, with a typical signal-to-noise ratio (S/N) of about 200. One-dimensional, wavelength-calibrated spectra were extracted using the FEROS pipeline. Stellar IDs along with some spectral and physical parameters derived in the present study are listed in Table 1.
Derived stellar properties of our basic O-star sample.
3. Spectral analysis
3.1. Spectral classification
Because earlier classifications of O-type stars can be subject to significant uncertainties (see, e.g., Markova et al. 2011 and Sota et al. 2011), we refrained from using these classifications, but proceeded as follows: for the stars in common with Sota et al. (2011) and Sana et al. (in prep.), we adopted the spectral types and luminosity classes as provided in the corresponding studies; for the rest (highlighted by italics in Col. 1 of Table 1) we derived our own classifications, following the premises by Sota et al. (2011) and consulting the atlas of Galactic O-type standards, as compiled by Sana et al. Spectral types and luminosity classes of our sample stars are listed in Col. 2 of Table 1. The accuracy of these data is typically one subtype.
3.2. Measuring the projected rotational and extra broadening velocities
Projected rotational velocities (vsini) of OB stars were estimated by applying various methods, among which the most commonly used are: the full-width-at-half-maximum (FWHM) method (e.g., Abt et al. 2002); the goodness-of-fit (GOF) method (e.g., Conti & Ebbets 1977; Ryans et al. 2002); the cross-correlation (CC) method (e.g., Penny 1996; Howarth et al. 1997), and the Fourier transform (FT) method (viz. Gray 1976, 2005, see also Simón-Díaz & Herrero 2007; Markova & Puls 2008; Fraser et al. 2010). While the CC and the FWHM methods work under the assumption that factors other than rotation do not significantly affect the line widths, the GOF and the FT methods are, in principle, able to separate rotational broadening from other broadening mechanisms.
To separate and measure the relative contributions of rotational and extra broadening in our O-star sample, we considered a newly developed FT+GOF approach and applied it to the O III λ5591 line2. The method consists of a three-step procedure: first, the FT of the line is computed, and from the position of the first zero the corresponding projected rotational velocity (vsini (FT)) is estimated; second, the observed profile is compared with a synthetic one, degraded to the resolving power of the analyzed spectrum, and convolved with broadening functions calculated for an appropriate range of projected rotational and extra broadening rates. From the minimum in the χ2 distribution, optimum values for the two broadening agents (vsini (GOF) and Θ(GOF)), are derived. Third, by a thorough analysis of all estimates thus obtained, the final values of the rotational and extra broadening rates are fixed. For the particular case of our sample, we adopted as final values the vsini derived with the FT method and the GOF solution for extra broadening – obtained by assuming a radial-tangential (RT) distribution of velocities with a radial component being equal to the tangential one (hereafter ΘRT)3.
 |
Fig. 1 Illustration of the quality of the fit to strategic helium and hydrogen lines for a star with a weak wind, HD 93222. |
The projected rotational and extra line-broadening velocities, obtained as described above, are listed in Cols. 4 and 5 of Table 1, respectively. The uncertainties in these estimates range from 10% to 20%, with higher values typical for more rapid rotators. The limit to the lowest vsini, imposed by the resolving power of the spectrograph, equals ~12 km s-1. Since the quality of our spectra is relatively high, while the O III λ5591 line used in this analysis is relatively weak, we do not expect our vsini to be significantly affected by instrumental effects, as described in Simón-Díaz & Herrero (2007). On the other hand, for stars with fast rotation (vrot ≥ 200 km s-1), processes such as differential rotation, limb or gravity darkening may be present, which will alter the profile shape and thus its Fourier transform (see, e.g., Reiners 2003), while for those with slow rotation microturbulence may be a problem (Gray 1973). These possibilities are taken into account when we discuss the outliers (if present).
Finally, we point out here that we are aware that our description of extra broadening in terms of large-scale turbulent motions may be problematic (because of the obtained highly supersonic velocities), and that an explanation in terms of collective effects from numerous high-order, low-amplitude nonradial g-mode pulsations has been suggested by Aerts et al. (2009). Nevertheless, we consider our approach suitable because (i) it allows to compare our results for O-type stars with similar results for B-type stars from the literature (see Sect. 5); and (ii) the pulsation hypothesis, although promising for massive early B-type supergiants (Simón-Díaz et al. 2010), needs to be confirmed in a wider parameter space. On the other hand, if stellar pulsations were responsible for the extra broadening, a risk of underestimating the actual vsini when applying the FT method may be present (Aerts et al. 2009).
3.3. Atmospheric parameters
Stellar and wind parameters of our basic O-star sample were determined from the best fit (estimated by eye) between observed and theoretical profiles of strategic lines. The synthetic profiles were calculated by applying a recently updated version of the FASTWIND code (see Santolaya-Rey et al. 1997 and Puls et al. 2005 for previous versions; and Rivero-Gonzalez et al. 2012 for a brief summary of the latest version), and were broadened using corresponding values of vsini and ΘRT as listed in Cols. 4 and 5 of Table 1. Detailed information about the model atmosphere analysis of our sample stars will be presented in a forthcoming paper (Markova et al., in prep.), while here we note that all models were calculated by adopting a microturbulent velocity of 10 km s-1for both the atmospheric structure calculations and the line profile synthesis. By default, normal helium and nitrogen abundances (YHe = NHe/NH = 0.10 and [N] = log N/H + 12 = 7.7) were used and were adjusted when necessary. An example of a good-quality fit is provided in Fig. 1.
The resulting values for Teff and log g are listed in Cols. 6 and 7 of Table 1, respectively. The error on these data, estimated from the best fit to the strategic lines, is typically ±500 to 1500 K in Teff and ±0.1 dex in log g (but see Sect. 5.1).
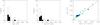 |
Fig. 2 Left and middle panels: distributions of projected rotational velocities for the O-star sample, based on our determinations for vsini (PF) (extra line-broadening neglected) and vsini (FT+GOF) (extra line-broadening taken into account). In both panels, the binsize is 30 km s-1, and the contribution of supergiants is highlighted by the shaded area. Right panel: vsini (FT+GOF) versus vsini (PF). Luminosity class I objects are highlighted in dark blue, II and III objects in light blue, and IV and V objects in green. The one-to-one relation is marked by the solid line. |
4. Results for the ESO O-star sample
4.1. Influence of extra broadening on the projected rotational velocities
To reveal whether and to which extent the spectra of our sample O stars are influenced by effects of extra broadening, we proceeded as follows: first, we created an internally consistent dataset of vsini without accounting for extra broadening (these data are referred to as vsini (PF), see below); second, we analyzed these data for possible selection effects and effects caused by a limited number of objects, and third, we compared the vsini (PF) and the vsini (FT+GOF) values, attributing the corresponding differences to the effect of extra broadening.
Step 1.
For the majority of our sample stars, previous determinations of vsini are available in the literature, mainly from Penny (1996) and Howarth et al. (1997) but also from Uesugi & Fukuda (1982), none of which provide a complete overlap. To avoid possible inconsistencies caused by the use of data from different sources, we decided to perform our own determinations of vsini, which do not take into account extra broadening. To this end, for each sample star we used the best fit FASTWIND model, obtained as described in Sect. 3.3, and optimized the fit between observed and synthetic lines now neglecting the extra broadening. The vsini obtained in this way are listed in Col. 3 of Table 1 and are referred to as vsini (PF), where PF abbreviates profile fitting method. The uncertainty in these data, determined by the quality of the fits estimated by eye, is typically lower than 10 percent.
Step 2.
In their studies of statistically significant samples of Galactic O stars, Penny (1996) and Howarth et al. (1997) found that the derived distributions of vsini (which do not account for extra broadening!) are quite peculiar, showing a low-velocity maximum at about 80 km s-1and a high-velocity tail dominated by MS stars. Supergiants show fewer rapid rotators (vsini ≥ 200 km s-1), and they also lack sharp-lined stars (vsini ≤ 60 km s-1).
An inspection of the data shown in the left panel of Fig. 2 indicates that the vsini (PF) distribution of our basic O-star sample is characterized by features similar to those described by Penny (1996) and Howarth et al. (1997). Comparing this distribution and the one derived for the case when extra broadening is accounted for (middle panel of the same figure), we furthermore note that while in general the stars move to lower velocities, the sample still lacks slowest projected rotators and may also lack fast rotators. Taken at face value, these findings might indicate that either the sample is biased toward objects with only medium high and medium low velocities, or that in the parameter space covered by our targets very fast and very slow rotators are intrinsically rare.
Step 3.
The right panel of Fig. 2 shows the correspondence between vsini (PF) and vsini (FT+GOF). Apparently, for the majority of sample stars the velocities originating from the combined FT+GOF approach are lower than those obtained via the profile-fitting method. The differences are larger than the error budget of the two datasets, and we ascribe them to the effect of extra broadening. In agreement with previous results from Simón-Díaz et al. (2011), we see that not only supergiants but also O-type giants and dwarfs are subject to significant extra broadening. The influence of this broadening on the projected rotational velocities, averaged over the whole sample, is estimated to be −20 ± 15 km s-1, in perfect agreement with similar results from Bouret et al. (2012) regarding supergiants.
 |
Fig. 3 Extra broadening rates (in km s-1) for the O-star sample as a function of vsini (upper panel) and Teff (lower panel). In both panels, luminosity class I stars are colored in dark blue, luminosity class II and III objects in light blue, and luminosity class IV and V objects in green. Intermediate (110 ≤ vsini (FT+GOF) ≤ 200 km s-1) and fast rotating stars (vsini (FT+GOF) > 200 km s-1) are additionally marked by large circles. In the upper panel, the solid line indicates the one-to-one relation. |
4.2. Extra broadening velocities
Figure 3 depicts the ΘRT values as a function of vsini 4 (upper panel) and Teff (lower panel). Different luminosity classes are colored differently. Intermediate and fast rotators5 are additionally marked by large circles.
From the upper panel of this figure, we find that the sample can be divided into two groups: objects in which rotational broadening is stronger than extra broadening, and those in which extra broadening either dominates or is in strong competition with rotation. The majority of stars appears to be members of the second group. Interestingly, and on a general scale as well as within each of the two groups, the ΘRT values tend to increase toward higher vsini, without exceeding a specific value of 110 km s-1, however. Marginal evidence of supergiants with higher extra broadening velocities than dwarfs and giants seems to present as well: the mean values of ΘRT averaged over the subsamples of supergiants, giants, and dwarfs equals 88 ± 17, 77 ± 22 and 76 ± 19 km s-1, respectively.
From the lower panel we furthermore note that while within the total sample no clear indication of a connection between ΘRT and Teff can be seen, within the subgroups of supergiants and dwarfs a tendency for the hotter objects to exhibit higher ΘRT may be present. This possibility has been confirmed by a Spearman rank-correlation test, providing a correlation coefficient and a two-sided significance of its deviations from zero6 (given in brackets) of 0.21 (0.26), 0.80 (0.0003) and 0.52 (0.10) for the total sample, and the subsamples of supergiants and dwarfs, respectively. Our findings are consistent with similar results from Simón-Díaz et al. (2011) who also suggested that the extra broadening rates of hot massive stars most likely increase when moving from early-B to early-O subtypes, with values that are systematically higher for supergiants than for giants and dwarfs.
Interestingly, for the sample giants and bright giants, we were unable to confirm the positive correlation between ΘRT and Teff, as suggested by Simón-Díaz et al. (2011): for this subgroup of stars we basically found no correlation at all (SR correlation coefficient with a two-sided significance of −0.22 (0.60)). The explanation for this inconsistency is currently unclear, but reasons such as a limited number of objects (eight in total), unrecognized binarity, and possible biases toward intermediate and fast rotators – almost half of these stars rotate with vsini ≥ 110 km s-1 – might equally contribute.
Summarizing our results, we conclude that the spectra of O stars (at least those of solar metallicity) are subject to significant extra broadening, whose effect (when expressed as a velocity) most likely scales with effective temperature and luminosity.
5. Extending the sample toward B-supergiants
The spectra of massive B-supergiants have been proven to experience significant extra broadening (e.g., Dufton et al. 2006b; Lefever et al. 2007; Markova & Puls 2008; Fraser et al. 2010; Simón-Díaz & Herrero 2007; Simón-Díaz et al. 2010). To obtain more insight into the properties of this enigmatic phenomenon, we decided to extend our analysis toward lower temperatures and lower surface gravities, incorporating appropriate data for B supergiants from the literature.
There are three Galactic studies (Lefever et al. 2007; Markova & Puls 2008; Fraser et al. 2010) that investigate atmospheric parameters and rotational and extra broadening velocities of massive B-supergiants, applying methodologies similar to ours (but see next section). From these studies we selected 73 targets with non-negligible extra broadening, 46 from Fraser et al. (2010), 19 from Lefever et al. (2007) (their group I stars only), and eight from Markova & Puls (2008). To these, we added five more B-supergiants from the work of Simón-Díaz et al. (2010), for which reliable determinations of Teff and log g were found in the literature (from Searle et al. 2008 and Markova et al. 2008).
Recently, Bouret et al. (2012) have published stellar and wind parameters and projected rotational and extra line-broadening rates for a sample of eight massive O-supergiants in the MW, derived by means of a combined FUV, UV, and optical analysis. Since five of these are intermediate and fast rotators, while the number of such stars in our ESO O-star sample is limited to only two (see Fig. 2), we incorporated these eight objects into our analysis as well. Thus, the total number of objects in our enlarged OB sample amounts to 117, 39 of which are O stars and 78 are massive B-type supergiants.
5.1. Consistency check
Ideally, one would like to perform a consistency check by comparing stars in common between different datasets. Unfortunately, however, the number of such objects among the sample OB stars is too limited to allow for firm conclusions: there is one star in common between our O-star sample and the one studied by Bouret et al. (2012) (HD 66811); three stars between Simón-Díaz et al. (2010) and Markova & Puls (2008) (HD 190603, HD 206165 and HD 191243), and one between Fraser et al. (2010) and Lefever et al. (2007) (HD 148688). Nevertheless, it is encouraging that in all these cases the corresponding estimates agree within the error.
On the other hand, in three of the five studies mentioned above, namely Lefever et al. (2007), Markova & Puls (2008), and Simón-Díaz et al. (2010), a methodology similar to ours has been used to separate and measure the relative contributions of rotation and extra broadening, suggesting that systematic differences between the corresponding datasets are unlikely.
 |
Fig. 4 Distribution of extra broadening velocities for the B-supergiants in the OB sample. The data derived by assuming different models for extra broadening are highlighted in different colors: red denotes an isotropic Gaussian model (Fraser et al. 2010), whilst green refers to a radial-tangential one (Lefever et al. 2007; Markova & Puls 2008; Simón-Díaz et al. 2010). Note the systematic shift along the vertical axes between the green and the red dots (upper panel) and that this shift disappears after the original Fraser et al. (2010) data for extra broadening have been corrected to make them consistent with the rest (lower panel). For dotted lines, see Sect. 5.1. |
While in the investigations by Fraser et al. (2010) and Bouret et al. (2012) the vsini values have been derived by applying the FT method and thus are expected to be consistent with the rest of the OB sample, a somewhat different approach has been adopted to quantify the amount of extra broadening: instead of a radial-tangential model for the turbulent velocity field, they used an isotropic Gaussian one.
From a corresponding analysis of our ESO O-star sample, we derived that the RT model provides broadening velocities that are ~20 km s-1 higher than those originating from an isotropic Gaussian model. The data shown in the upper panel of Fig. 4 suggest that the situation is similar for the B supergiants, since at a given Teff the estimates of Fraser et al. (2010) for extra broadening (red dots) are systematically lower than those obtained by Lefever et al. (2007), Markova & Puls (2008), and Simón-Díaz et al. (2010) (green dots). Indeed, from linear fits to the two datasets (dotted lines), we estimated a mean difference of 19 ± 4 km s-1, in perfect agreement with our estimate for the ESO O-star sample and results from Dufton et al. (2006a) for B supergiants in the SMC. Following these findings, we added a constant value of 19 km s-1 to the extra line-broadening velocities adopted from Fraser et al. (2010) and Bouret et al. (2012), to make them consistent with the rest of the OB sample.
Regarding the Teff and log g values of the stars included in the OB sample, the majority of them have been derived by applying the non-LTE, line-blanketed model atmosphere codes (allowing for spherical extension and stellar winds) FASTWIND (present study, Lefever et al. 2007; Markova & Puls 2008; Markova et al. 2008) or CMFGEN (Bouret et al. 2012; Searle et al. 2008). Only in Fraser et al. (2010), the non-LTE, line-blanketed, plane-parallel model atmosphere and line formation codes TLUSTY and SYNSPEC (see, e.g. Hubeny 1988; Hubeny & Lanz 1995; Lanz & Hubeny 2007) were used instead. While the overall agreement between these codes (within their domains of application) was generally considered as satisfactory (see, e.g., Puls et al. 2005; Crowther et al. 2006; Markova & Puls 2008), in a recent study Massey et al. (2013) noted a systematic difference between O-star surface gravities derived by either FASTWIND or CMFGEN, with the former being smaller by about 0.1 dex. To account for these new results, a possible asymmetric error of +0.2/−0.1 dex in log g was considered for all stars in the OB sample.
5.2. Projected rotational and extra line-broadening velocities as a function of effective temperatures
 |
Fig. 5 Projected rotational (upper panel) and extra line-broadening velocities (lower panel) for the OB sample as a function of Teff. O and B supergiants are highlighted in dark blue and red, respectively, and O giants and dwarfs in light blue. Intermediate- and fast-rotating stars (vsini ≥ 110 km s-1) are additionally marked by large circles (for more information and arrows see Sect. 5.2). |
The upper panel of Fig. 5 displays the run of the vsini values for the OB sample as a function of Teff. On a global scale, a general trend of decreasing projected rotational velocities with decreasing temperatures is observed, where the hotter stars are spread over a wider range of values than the cooler ones. Since massive B supergiants are considered as evolutionary successors of O-type stars, this result may indicate that – in agreement with evolutionary predictions (Meynet & Maeder 2000a; Brott et al. 2011) – the surface equatorial velocities of hot massive stars decrease continuously while crossing the Hertzsprung-Russell diagram (HRD), with a scatter being caused by projection and differences in stellar masses and initial rotational rates.
Additionally, our data reveal that while the hotter stars appear to demonstrate a deficit of very slow rotators – we have only one star with vsini below 40 km s-1 – those at the cooler edge of the B-supergiant domain lack fast rotators7, with a border line between the two subgroups located at log Teff of 4.25–4.30 dex.
The steep drop in massive star rotational rates at Teff of about 22 000 K has been highlighted by Vink et al. (2010) based on the dataset of Howarth et al. (1997) for vsini, which does not account for extra broadening (see their Fig. 2). To explain this feature, the authors suggested two potential scenarios: enhanced mass loss at the predicted location of the bi-stability (BS) jump, or post-MS angular momentum loss.
Regarding the deficit of slowest projected rotators among the hotter stars in the OB sample, we mentioned in Sect. 4.1 that this feature might be due to selection effects (we recall that our vsini were derived accounting for extra broadening). Indeed, a comparison of Fig. 2 from Vink et al. (2010) and the upper panel of our Fig. 5 reveals that while in the sample of Howarth et al. (1997) there are a large number of slowly rotating, low-luminosity O stars, such stars are missing in our case. On the other hand, it is clear that this finding does not apply to supergiants: both samples demonstrate a deficit of narrow-lined objects toward higher Teff. Thus, we may conclude that reasons different from observational selection must be present and contribute to the deficit of slowest projected rotators among the hotter and more luminous stars in the OB sample. This matter is discussed in more detail in the next section.
In the lower panel of Fig. 5, we show the run of ΘRT with Teff. Interestingly, the decline of ΘRT toward cooler Teff established for the supergiants in our basic O-star sample (see Fig. 3) becomes questionable with the inclusion of the targets of Bouret et al. (2012) at intermediate and fast rotation, leading to broadening velocities quite similar to those observed for the hotter B supergiants. While the explanation of this finding is currently unclear, one can see that the ΘRT velocities for the cooler B supergiants are definitely lower that those for the O stars and hotter B supergiants, suggesting that changes in the evolutionary stage of hot massive stars may play a role in determining the properties of extra broadening.
Comparing the upper and lower panels of Fig. 5, the run of ΘRT with Teff is surprisingly similar to that of vsini, even regarding details. This refers for instnce to the spread of O-type dwarfs and giants toward lower vsini; the presence of two targets with peculiarly low vsini for their Teff (HD 159110, log Teff = 4.27, vsini = 9 km s-1and HD 52089, log Teff = 4.3, vsini = 22 km s-1); and the two local depressions in the vsini distribution, marked by vertical arrows. These similarities are quite interesting because they may indicate that the two broadening agents are linked (this question is addressed in more detail in Sect. 5.5).
5.3. Projected rotational velocities as a function of stellar mass and evolution
5.3.1. Dependence on stellar mass
The upper panel of Fig. 6 depicts the distribution of the OB sample in a 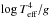 versus log Teff diagram, with symbol sizes proportional to the values of vsini8. Overplotted are the evolutionary tracks from Brott et al. (2011) for Z = 0.02, with initial equatorial rotational velocities (vinit) ranging from 312 km s-1 for the 60 M⊙ model to 329 km s-1 for the 15 M⊙ model, and an initial mass (
versus log Teff diagram, with symbol sizes proportional to the values of vsini8. Overplotted are the evolutionary tracks from Brott et al. (2011) for Z = 0.02, with initial equatorial rotational velocities (vinit) ranging from 312 km s-1 for the 60 M⊙ model to 329 km s-1 for the 15 M⊙ model, and an initial mass ( ) of 15, 20, 30, 40, 50, 60, and 80 M⊙.
) of 15, 20, 30, 40, 50, 60, and 80 M⊙.
From these data we find that all the stars in the OB sample lie in a region between ~15 and ~80 M⊙, with an obvious deficit of MS objects with  ≲ 40 M⊙. Thus, our sample can be considered as representative only for the more massive OB stars.
≲ 40 M⊙. Thus, our sample can be considered as representative only for the more massive OB stars.
Additionally, we see that while objects close to the zero-age main sequence (ZAMS) can have quite different vsini (most likely due to projection), there is, on a general scale, a progressive decline of vsini toward later evolutionary stages. Suggestive evidence for the cooler, less massive B supergiants showing somewhat lower vsini than the most massive ones at the same Teff seems to be present as well. While the former result is qualitatively consistent with evolutionary predictions, the latter is somewhat confusing, because according to the models, the opposite effect is to be expected (see Meynet & Maeder 2000a; Brott et al. 2011).
 |
Fig. 6 Upper panel: values of |
To investigate this problem in more detail, in the lower panel of Fig. 6 we display vsini as a function of  : O-type stars are highlighted in blue and B-supergiants in red. For each individual star,
: O-type stars are highlighted in blue and B-supergiants in red. For each individual star,  is determined by interpolating between the available evolutionary tracks. We are aware that Fraser et al. (2010) and Bouret et al. (2012) provided their own estimates of
is determined by interpolating between the available evolutionary tracks. We are aware that Fraser et al. (2010) and Bouret et al. (2012) provided their own estimates of  for their sample stars. However, since these data were obtained using evolutionary tracks from Meynet & Maeder (2000b), we performed our own determinations of
for their sample stars. However, since these data were obtained using evolutionary tracks from Meynet & Maeder (2000b), we performed our own determinations of  for these objects as well for consistency reasons9. For the stars listed in Table 1,
for these objects as well for consistency reasons9. For the stars listed in Table 1,  are given in Col. 8. The uncertainty in these data reflects the errors on the effective temperatures and surface gravities and is on the order of −37/+25% and −20/+12% for the higher- and the lower-mass end, respectively10.
are given in Col. 8. The uncertainty in these data reflects the errors on the effective temperatures and surface gravities and is on the order of −37/+25% and −20/+12% for the higher- and the lower-mass end, respectively10.
One very conspicuous feature of the distribution, shown in the lower panel of Fig. 6, is the well-defined trend of increasing minimum vsini toward higher masses. Indeed, for the O stars this feature is not clearly manifested due to the limited number of objects with masses below 50 M⊙. However, since a similar trend has been observed by Penny (1996) for a statistically significant sample of O-type stars uniformly distributed over a mass range from ~10 to ~90 M⊙ and by Wolff et al. (2006) for a comparatively limited (55 vs. 200 objects from Penny) sample of O stars with masses between ~20 and ~40 M⊙, and since for a given mass range their estimates agree quantitatively well with ours (see the horizontal lines shown in the lower panel of Fig. 6), we consider the following conclusion as reasonable: the distribution of vsini as a function of  for the OB sample is characterized by a lowest value of vsini that increases toward higher masses, leading to a remarkable deficit of slowest projected rotators among the most massive objects.
for the OB sample is characterized by a lowest value of vsini that increases toward higher masses, leading to a remarkable deficit of slowest projected rotators among the most massive objects.
Because for a given initial mass hot massive stars are predicted to slow down when evolving to cooler temperatures, it follows from the lower panel of Fig. 6 that high-mass stars do not evolve to velocities as low as those reached by low-mass ones. Using the evolutionary calculations of Brott et al. (2011) for vinit ~ 300 km s-1, we investigated the evolutionary status of the stars tracing out the trend, and found that while those with  between 60 and ~80 M⊙ appear to be at the end of the MS phase with ages between 2.8–3.6 Myr, those with
between 60 and ~80 M⊙ appear to be at the end of the MS phase with ages between 2.8–3.6 Myr, those with  between 15 and less than 40 M⊙ might be considered as post-MS objects at the end of the B-supergiant phase, with ages ranging from ~4.5 to ~12 Myr (provided they all are moving to the red supergiant phase, but see below). Since the surface equatorial velocities of less-massive stars after the MS are predicted to drop very fast due to rapid expansion after core hydrogen exhaustion (Meynet & Maeder 2000b; Brott et al. 2011), one may speculate that differences in evolutionary status can provide a clue for understanding the connection between the minimum vsini and
between 15 and less than 40 M⊙ might be considered as post-MS objects at the end of the B-supergiant phase, with ages ranging from ~4.5 to ~12 Myr (provided they all are moving to the red supergiant phase, but see below). Since the surface equatorial velocities of less-massive stars after the MS are predicted to drop very fast due to rapid expansion after core hydrogen exhaustion (Meynet & Maeder 2000b; Brott et al. 2011), one may speculate that differences in evolutionary status can provide a clue for understanding the connection between the minimum vsini and  for the stars from the OB sample.
for the stars from the OB sample.
There are, at least, two problems with this hypothesis: first, the models do not predict the presence of stars with log Teff ≤ 4.25 because of the short lifetimes in these phases (see next section), and second, differences in evolutionary stages cannot account for the complete lack of slowest projected rotators among the most massive stars because such objects are expected to be present in our sample as well as in the studies by Conti & Ebbets (1977), Penny (1996), Howarth et al. (1997), and Wolff et al. (2006), due to projection effects and stars with intrinsically low vinit.
One way to address this puzzling problem is to challenge the conventional view of randomly oriented rotational axes, assuming that those of the most massive OB supergiants are preferentially aligned with the Galactic poles. While this hypothesis may seem speculative and difficult to argue for, we mention that a similar possibility has been discussed in previous investigations regarding unusual vsini distributions observed for supergiants of late spectral types (see Gray 1987 and references therein).
From a different point of view, one may assume that the FT method fails to detect low values of vsini due to an effect that is notable for the more massive objects and negligible for the less massive ones. Since instrumental effects cannot be responsible – note that all data included in our analysis originate from high-quality observations allowing reliable estimates to be obtained down to vsini of 10 to 15 km s-1 – and since extra broadening has been taken into account, we suggest that by introducing additional zeros in the FT, microturbulence might explain the lack of slow rotators among the more massive sample stars (Gray 1973; see also Simón-Díaz & Herrero 2007). The problem with this explanation, at least at present, is that while it requires vmic to increase toward higher masses for the OB sample, no evidence of a mass-dependent microturbulence was found when analyzing the corresponding data. On the other hand, it is worthwhile to note that microturbulent motions that become stronger toward higher masses and lower temperatures could result from subsurface convection caused by the iron opacity peak (Cantiello et al. 2009). Clearly, additional effort is required to understand these observational results and to obtain a coherent picture about the nature and the origin of the deficit of slowest rotators among more massive OB stars11.
Another intriguing feature regarding the vsini properties of hot massive stars is that in our sample as well as in the samples studied by previous investigators (e.g., Conti & Ebbets 1977; Penny 1996; Howarth et al. 1997; Wolff et al. 2006) there are hardly any O stars with vsini in excess of 400 km s-1. For the particular case of stars with masses between 20 and 40 M⊙, located close to the ZAMS, Wolff et al. (2006) argued that the 400 km s-1 limit may be representative for their initial velocities. How this argumentation applies to O stars with masses above 40 M⊙ is currently unknown. However, from the data shown in the lower panel of Fig. 6 and Fig. 5 in Penny (1996), it appears that these stars tend to rotate generally more slowly than the less massive ones, with rapid rotators being extremely rare amongst them (see the horizontal lines shown in the lower panel of Fig. 6). We return to this matter in the next section.
5.3.2. Comparison with evolutionary predictions
In Fig. 7 we show the vsini vs. log Teff distribution for the OB sample against the model tracks from Brott et al. (2011) for five values of  (quoted in the upper left corner of each plot), and three values of vinit: ~100, ~200 and ~300 km s-1. All tracks were scaled by a factor π/4 to account for projection, assuming a random orientation of rotational axes. To facilitate the comparison, all stars were binned into three mass ranges: from 15 to 30 M⊙ (bottom panel), from 31 to 50 M⊙ (middle panel), and from 51 to ~80 M⊙ (top panel). Since for
(quoted in the upper left corner of each plot), and three values of vinit: ~100, ~200 and ~300 km s-1. All tracks were scaled by a factor π/4 to account for projection, assuming a random orientation of rotational axes. To facilitate the comparison, all stars were binned into three mass ranges: from 15 to 30 M⊙ (bottom panel), from 31 to 50 M⊙ (middle panel), and from 51 to ~80 M⊙ (top panel). Since for  ≥ 60 M⊙ no model predictions for the evolution of rotation are available, the sample stars with masses above 70 M⊙ are highlighted with a different symbol in the top panel. The dotted vertical lines mark the position of the bi-stability (BS) region, as predicted by Vink et al. (1999) (but see Sect. 5.4).
≥ 60 M⊙ no model predictions for the evolution of rotation are available, the sample stars with masses above 70 M⊙ are highlighted with a different symbol in the top panel. The dotted vertical lines mark the position of the bi-stability (BS) region, as predicted by Vink et al. (1999) (but see Sect. 5.4).
Before outlining our results, we note that particularly the models of Brott et al. (2011) are interesting to compare with ours, since the overshooting parameter used in these models was calibrated such that the log g value at the terminal age main-sequence of 10...20 M⊙ stars corresponds to the observed log g value at which the LMC B stars’ rotational velocity distribution as a function of log g shows a sudden drop in the mentioned mass range. While this leads to a wider main sequence band than was, for instance found in the Geneva models (Meynet & Maeder 2000b), the evolution of the surface rotational velocity with time is qualitatively similar in both types of models.
 |
Fig. 7 Projected rotation velocities and effective temperatures for the OB supergiants (red) and the O-type giants and dwarfs (blue) from our sample, plotted against evolutionary tracks from Brott et al. (2011). All stars have been binned into three mass ranges: 15 M⊙ ≤ M ≤ 30 M⊙ (bottom panel); 31 M⊙ ≤ M ≤ 50 M⊙ (middle panel), and M ≥ 51 M⊙ (top panel). O-type stars close to the ZAMS with anomalously low vsini are additionally highlighted by asterisks. The large diamond marks HD 93843, which has been recently identified as a magnetic star (Hubrig et al. 2011). In the top panel, the most massive stars ( |
The case of more massive stars.
From the data illustrated in the top and middle panel of Fig. 7, we see that the models with  ≥ 35 M⊙ predict a significant decline in vsini before the BS-region, followed by a second steep decline within this region, and values going to zero after that (the so-called BS braking, see Vink et al. 2010). By confronting model predictions with the observations, we furthermore find that
≥ 35 M⊙ predict a significant decline in vsini before the BS-region, followed by a second steep decline within this region, and values going to zero after that (the so-called BS braking, see Vink et al. 2010). By confronting model predictions with the observations, we furthermore find that
-
i)
before the BS-region (Teff ≥ 4.44 dex), the agreement between theory and observations is quite satisfactory, with the majority of datapoints being located between tracks with vinit of 100 and 200 km s-1, and individual cases clustering around the 300 km s-1model. Since all these stars appear to be relatively young MS objects with ages ranging between one and 4.0 Myr, and since their number seems to be too large to be solely explained by projection effects12, we suggest that a large part of them may have been rotating much slower than critical when appearing at or close to the ZAMS rather than been spun down within the first few Myr of evolution.
-
ii)
after the BS-region (Teff ≤ 4.35 dex), a significant discrepancy between the measured and predicted rotational rates is observed, where the former do not go to zero, as predicted by the models, but display a mild decline toward lower Teff, being at the same time systematically higher than the model values. This result might imply that for more massive stars the ejection of angular momentum during the BS-jump has been overpredicted (due to an overpredicted jump in Ṁ , for example see Markova & Puls 2008), leading to significantly lower rates than observed. Alternatively, and related to our discussion in Sect. 5.3.1, the FT method may have led to an overestimate of vsini for slow rotators, in particular for the cooler and more massive B supergiants.
Comparing the observed values of vsini with critical velocities, vcrit, as calculated by Brott et al. (2011), we find that the most massive stars ( ≳ 50 M⊙) in the OB sample may appear at or close to the ZAMS with velocities that do not exceed 26% of their vcrit; for the majority of them this limit might be even lower, about 17%. Similar findings for stars with masses between 10 and 40 M⊙ indicate an upper limit of ~50%, with most of the stars rotating at less than 30% of the critical rate (Wolff et al. 2006). Taken together, these results suggest (i) that the initial velocity of hot massive stars might be mass-dependent; and (ii) that some unique mechanism must be at work to keep the rotational rates of these stars low at birth. A potential candidate for this role is gravitational torque, which seems to be able to solely prevent the central object from spinning-up to more than half of its break-up velocity (Lin Min-Kai et al. 2011). For high-mass stars, intensive mass loss during the first one Myr – when the stars might be obscured by gas in their parental clouds and thus are inaccessible for observation – might additionally contribute to spin these objects down to even lower velocities.
≳ 50 M⊙) in the OB sample may appear at or close to the ZAMS with velocities that do not exceed 26% of their vcrit; for the majority of them this limit might be even lower, about 17%. Similar findings for stars with masses between 10 and 40 M⊙ indicate an upper limit of ~50%, with most of the stars rotating at less than 30% of the critical rate (Wolff et al. 2006). Taken together, these results suggest (i) that the initial velocity of hot massive stars might be mass-dependent; and (ii) that some unique mechanism must be at work to keep the rotational rates of these stars low at birth. A potential candidate for this role is gravitational torque, which seems to be able to solely prevent the central object from spinning-up to more than half of its break-up velocity (Lin Min-Kai et al. 2011). For high-mass stars, intensive mass loss during the first one Myr – when the stars might be obscured by gas in their parental clouds and thus are inaccessible for observation – might additionally contribute to spin these objects down to even lower velocities.
During the past decade two mechanisms have been proposed to explain the formation of massive stars: via mergers of low-mass protostellar cores (Bally & Zinnecker 2005) or via a single lower-mass core that grows in mass via competitive accretion of surrounding molecular gas (Bonnell et al. 2005). Since in the former model the result of the mergers is predicted to rotate rapidly (Bally & Zinnecker 2005), while in the latter the final product is expected to rotate relatively slowly, at a speed well below the critical velocity (Shu et al. 1994; Lin Min-Kai et al. 2011), the very low rotational velocities reported here and in Wolff et al. (2006) suggest that a single core formation and not a core merger is the likely mechanism for massive stars to form. Studying the rotational rates of a large sample of single O stars in the LMC, Ramírez-Agudelo et al. (2013) came to the same conclusion.
Because significant effects for the evolution of massive single stars, including their potential to develop a long-duration gamma-ray burst (LGRB) at the end of their life, are expected for vinit above 200... 300 km s-1 (Brott et al. 2011; Langer 2012), these results may also suggest that such effects are weaker then previously thought – unless a massive star is spun up later in its life due to close binary interaction.
The case of less massive stars.
From the bottom panel of Fig. 7, one may conclude that while on the hotter side of the BS region no constraints on model predictions can be put due to the lack of less-massive hot stars in the sample, on the cooler side and inside this region the observed vsini agree generally well with the predictions – with the majority of datapoints clustering between the tracks with vinit of ~100 and ~200 km s-1.
However, we note that while Fig. 7 does show how the rotational velocity of the models evolves after the end of core hydrogen burning, a comparison of the corresponding part of the tracks with the observed stars at log Teff ≤ 4.25 is not meaningful, because the evolutionary timescale of the models is very short, and practically no stars are predicted to exist at these temperatures. Note also that this is not a particular feature of the models of Brott et al. (2011). Fraser et al. (2010), for instance, compared their vsini determinations for Galactic B supergiants with models from Meynet & Maeder (2000b). These models also expand rapidly after core-hydrogen exhaustion, and a comparison of their post-main sequence rotational velocities with the observed values – even though performed by Fraser et al. (2010) – is basically meaningless. The interpretation of the rotation rates of B supergiants in the considered mass range has to await stellar evolution models that predict their existence with a frequency similar to that of evolved stars during core-hydrogen burning (cf. Vink et al. 2010).
We conclude this section with comments on the slowly rotating O-stars in the OB sample relatively close to the ZAMS (upper panel of Fig. 6, datapoints colored in blue). These are: HD 64568, HD 91572, HD 91824, CPD −58 2620, HD 97848, and HD 46202. Traditionally, these stars can be explained by projection effects. However, there are recent evolutionary calculations (ud-Doula et al. 2009; Meynet et al. 2011), supported by observational results (Townsend et al. 2010), which show that magnetic fields can effectively reduce the rotation rates of hot massive stars with line-driven winds (the so-called magnetic braking). With this possibility in mind, we searched the literature and found that one of the noted six targets (CPD −58 2620) has been investigated for the presence of magnetic fields, with no detection above the one sigma level, however (Hubrig et al. 2011). For another star, HD 93843, a mean longitudinal magnetic field above the 3σ level has been detected (but see also Bagnulo et al. 2012), which might possibly explain its relatively low vsini (cf. the large diamond in the upper panel of Fig. 7). On the other hand, following Meynet et al. (2011), we find that if our six O-type dwarfs with peculiarly low vsini had masses of 10 M⊙, then a magnetic- field strength of one kG for solid body rotation and of one to three kG for differential rotation would be enough to spin them down to the observed vsini. How these numbers would translate into the case of stars with masses above 40 M⊙ is currently unclear. Thus, and at least at present, it does not seem possible to judge whether or not magnetic braking is responsible for the low rotational rates of our O-type dwarfs relatively close to the ZAMS.
5.3.3. Some insights into the nature of low rotational rates of cooler B supergiants
Vink et al. (2010) highlighted the absence of rapid rotators among B-supergiants with Teff below 22 kK in our Galaxy and in the LMC, discussing two possible explanations: wind-induced braking due to bi-stability, and post-MS angular momentum loss. While within the first scenario the stars on both sides of 22 kK are required to undergo core-hydrogen burning, within the second one the cool B-supergiants would form a population entirely separated from the hotter MS stars.
To test these possibilities, we investigated the evolutionary status of our sample using evolutionary tracks from Brott et al. (2011) with vinit ~ 300 km s-1 and found that all stars with  ≥ 40 M⊙ and log Teff ≳ 4.20 dex appear to be MS objects. These results suggest that changes of the wind properties in the BS region can in principle be responsible for the deficit of rapid rotators among the cooler and more massive B-supergiants in our sample. Indeed, the fact that only one of the more massive stars located inside the BS-region (see top and middle panels of Fig. 7) has a vsini significantly higher than those observed after this region might lead to the conclusion that our data do not give clear evidence of a steep drop in vsini inside the BS-region. This conclusion, however, would be somewhat premature: reasons such as the established deficit of very fast rotators among more massive O-stars as well as the short time-interval needed for a more massive hot star to cross the BS-region (less than ~4 × 105 yr compared to ~2–2.5 × 106 yr for a star with a mass below 30 M⊙, Brott et al. 2011) might equally contribute, leading to the picture described above. Additionally, it is clear that at least for the stars with vinit ≥ 200 km s-1 some kind of additional braking is necessary to spin these objects down to vsini ~ 60 to 50 km s-1 at log Teff ~ 4.35 dex. We note that the rotating models of Meynet & Maeder (2000b) in the mass range 30...50 end their core-hydrogen burning at log Teff< 4.35 and thus predict a very small number of B supergiants with lower effective temperatures.
≥ 40 M⊙ and log Teff ≳ 4.20 dex appear to be MS objects. These results suggest that changes of the wind properties in the BS region can in principle be responsible for the deficit of rapid rotators among the cooler and more massive B-supergiants in our sample. Indeed, the fact that only one of the more massive stars located inside the BS-region (see top and middle panels of Fig. 7) has a vsini significantly higher than those observed after this region might lead to the conclusion that our data do not give clear evidence of a steep drop in vsini inside the BS-region. This conclusion, however, would be somewhat premature: reasons such as the established deficit of very fast rotators among more massive O-stars as well as the short time-interval needed for a more massive hot star to cross the BS-region (less than ~4 × 105 yr compared to ~2–2.5 × 106 yr for a star with a mass below 30 M⊙, Brott et al. 2011) might equally contribute, leading to the picture described above. Additionally, it is clear that at least for the stars with vinit ≥ 200 km s-1 some kind of additional braking is necessary to spin these objects down to vsini ~ 60 to 50 km s-1 at log Teff ~ 4.35 dex. We note that the rotating models of Meynet & Maeder (2000b) in the mass range 30...50 end their core-hydrogen burning at log Teff< 4.35 and thus predict a very small number of B supergiants with lower effective temperatures.
 |
Fig. 8 Same as the lower panel of Fig. 6, but for the extra line-broadening velocities. Intermediate and fast rotators are highlighted by large circles. |
 |
Fig. 9 Extra line-broadening velocities as a function of Teff for the stars from the three mass ranges as defined in Sect. 5.3.2. Intermediate- and fast-rotating stars are additionally marked with large circles. The solid and dotted vertical lines mark the position of the observed and the theoretically predicted BS region, respectively. All other symbols have the same meaning as in Fig. 7. |
5.4. Extra broadening as a function of stellar mass and evolution
Figure 8 shows the ΘRT values for the stars from OB sample as a function of  : again, O-type stars are highlighted in blue, and B-supergiants in red. Taken at face value, these data suggest that on a general scale the extra broadening rates of massive stars may decrease toward lower masses. Interestingly, for the intermediate and fast rotators no indication of a mass-dependent behaviour of ΘRT can be seen. Due to the limited number of such objects in the OB sample, this result must be considered with caution, however.
: again, O-type stars are highlighted in blue, and B-supergiants in red. Taken at face value, these data suggest that on a general scale the extra broadening rates of massive stars may decrease toward lower masses. Interestingly, for the intermediate and fast rotators no indication of a mass-dependent behaviour of ΘRT can be seen. Due to the limited number of such objects in the OB sample, this result must be considered with caution, however.
To investigate the evolution of extra broadening when accounting for its possible dependence on stellar mass, we display in Fig. 9 ΘRT as a function of Teff for the stars from the three mass ranges as defined in the previous section. From the top and middle panels of this figure, one may note that while for log Teff ≥ 4.35 the available data do not give evidence of a systematic change when the stars evolve to cooler temperatures, a progressive decline toward later evolutionary stages is observed for the stars on the cooler side of this temperature limit. Whether these findings apply also to the less-massive stars with  ≤ 35 M⊙ (bottom panel of Fig. 9) cannot be judged at the momement due to the limited number of objects with log Teff ≥ 4.35 and the problem outlined for the cooler B-supergiants in this mass regime (see Sect. 5.3.2).
≤ 35 M⊙ (bottom panel of Fig. 9) cannot be judged at the momement due to the limited number of objects with log Teff ≥ 4.35 and the problem outlined for the cooler B-supergiants in this mass regime (see Sect. 5.3.2).
Based on theoretical considerations, Vink et al. (2000) argued that the mass-loss rates of hot massive stars should increase steeply between log Teff ≈ 4.35...4.45 because of the bi-stability mechanism. Since the predicted jump in mass loss is located at temperatures that are somewhat hotter than the one at which the extra broadening velocities change from higher and relatively constant values to values decreasing toward cooler temperatures (see the two dashed vertical lines in Fig. 9), one might conclude that changes in the wind properties when crossing the BS region cannot be responsible for or contribute to the observed behavior of ΘRT with Teff. However, we recall that there is observational evidence that indicates that the mass-loss rates of hot massive stars may not increase at the BS jump, and that the jump is located at somewhat cooler temperatures than those predicted by Vink et al. (Markova & Puls 2008). In this situation, the results shown in the top and middle panel of Fig. 9 indicate that the BS jump plays a role in determining the properties of extra broadening in massive stars. More investigations are required before one can judge which of the two possibilities is the more likely one.
Finally, we return to our suggestion that the slow rotators relatively close to the ZAMS might be due to projection or magnetic fields (see Sect. 5.3). From Fig. 9 we see that these stars (marked additionally by asterisks) also tend to show the lowest values of ΘRT for the corresponding mass range and temperatures. Interestingly, the same is true for HD 93843 (marked by a diamond) which is the only confirmed magnetic O-type star in our sample. Taken together, this might imply that extra broadening can be subject to projection effects, and that magnetic fields can play a role in determining the properties of this phenomenon. Evidence in support of the latter possibility has recently bee provided by Sundqvist et al. (2013).
5.5. Interplay between rotation and extra broadening
From the analysis of the ESO O-star sample (Sect. 4.2), we found that ΘRT tends to increase with increasing vsini. From the larger dataset displayed in Fig. 10, we see that this result is also valid for the complete OB sample (open circles and asterisks), where the connection is now traced down to significantly lower velocities. However, the relation is obviously not unique: stars with the same or similar vsini can show quite different values of ΘRT, and vice versa. Although a direct influence of vsini on ΘRT cannot be excluded especially for very fast rotators, we find this to indicate that the two broadening mechanisms are tied together through similar dependences on stellar parameters and are not directly linked.
 |
Fig. 10 Extra line-broadening vs. projected rotational velocities for the stars from our OB sample (open circles) and the sample studied by Lefever et al. (2010, filled dots). Stars assumed to be affected by projection are highlighted by asterisks. The large diamond indicates the magnetic star HD 93843. The solid and dashed lines represent the one-to-one correspondence and the 110 km s-1 limit of ΘRT, respectively. |
For most of the sample stars with vsini ≤ 110 km s-1, the extra broadening either dominates or is in strong competition with rotation. Interestingly, among the outliers one can note the objects that are assumed to be influenced by projection effects (asterisks) and the magnetic star HD 93843 (large diamond), which supports our previous suggestion that extra broadening in hot massive stars is subject to projection effects and effects caused by magnetic fields.
In a previous study, Lefever et al. (2010) reported evidence for a positive correlation between ΘRT and vsini for a large sample of low-mass B-stars (2 M⊙ ≤  ≤ 6 M⊙) from the GAUDI database (Ground-based Asteroseismology Database Interface, Solano et al. 2005). Since their estimates have been derived by applying a methodology similar to ours, we overplotted their data onto ours to allow for a direct comparison (filled dots in Fig. 10). Inspection reveals that while the ΘRT for the low-mass B-type stars indeed do increase with increasing vsini, they are generally smaller than those observed for the massive OB stars at the same vsini. Consequently, rotational broadening is stronger than the extra broadening for the majority of the low-mass stars. Interestingly, none of the targets studied by Lefever et al. (2010) shows extra broadening in excess of 110 km s-1.
≤ 6 M⊙) from the GAUDI database (Ground-based Asteroseismology Database Interface, Solano et al. 2005). Since their estimates have been derived by applying a methodology similar to ours, we overplotted their data onto ours to allow for a direct comparison (filled dots in Fig. 10). Inspection reveals that while the ΘRT for the low-mass B-type stars indeed do increase with increasing vsini, they are generally smaller than those observed for the massive OB stars at the same vsini. Consequently, rotational broadening is stronger than the extra broadening for the majority of the low-mass stars. Interestingly, none of the targets studied by Lefever et al. (2010) shows extra broadening in excess of 110 km s-1.
Summarizing, we conclude that (i) extra broadening is most likely a fundamental feature of the spectra of OB stars with masses between ~2 to ~80 M⊙; (ii) rotational broadening is stronger than extra broadening in low-mass hot stars, whilst in high-mass ones it either dominates (for stars with vsini ≥ 110 km s-1) or is of secondary importance (for stars with vsini ≤ 110 km s-1) compared with the extra broadening; (iii) objects with ΘRT in excess of 110 km s-1 are either very rare among OB stars or are not present at all.
6. Summary
Based on our own data for a sample of 31 Galactiy O-type stars and incorporating similar data for 86 O stars and massive B-supergiants from the literature, we investigated the statistical properties of projected rotational and extra line-broadening rates as a function of stellar parameters and derived constraints on model predictions for the evolution of rotation in hot massive stars.
The initial evolutionary masses of our sample stars range from ~15 to ~80 M⊙, but the available data provide a good coverage from close to the ZAMS until the end of the B-supergiant phase only for  ≳ 40 M⊙. Thus, the results summarized below can be considered as representative for the more massive OB stars at solar metallicity only.
≳ 40 M⊙. Thus, the results summarized below can be considered as representative for the more massive OB stars at solar metallicity only.
-
1.
In good correspondence with results from Simón-Díaz et al. (2011), we found that O-type stars, irrespective of their luminosity class, are subject to significant extra broadening. The impact of this broadening on the derived vsini averaged over the whole sample was estimated as −20 ± 15 km s-1, in perfect agreement with similar results from Bouret et al. (2012) regarding O-supergiants alone.
-
2.
Although our derived vsini values were corrected for the effects of extra broadening, we repeated previous findings (e.g. Penny 1996 and Howarth et al. 1997) that O stars and massive B supergiants show a clearly defined trend of increasing minimum vsini with increasing
 , leading to a remarkable deficit of slowest projected rotators among the most massive objects. While differences in evolutionary stage can play a role to explain this puzzling problem, we suggested that either the axes of more massive OB supergiants are preferentially aligned with the Galactic poles, or that at the low-velocity regime there are additional (broadening) effects that influence the Fourier transform, with microturbulence being a potential candidate.
, leading to a remarkable deficit of slowest projected rotators among the most massive objects. While differences in evolutionary stage can play a role to explain this puzzling problem, we suggested that either the axes of more massive OB supergiants are preferentially aligned with the Galactic poles, or that at the low-velocity regime there are additional (broadening) effects that influence the Fourier transform, with microturbulence being a potential candidate. -
3.
We found suggestive evidence that stars with
 ≳ 50 M⊙ rotate relatively slowly when appearing at or close to the ZAMS, with velocities which do not exceed 26% of their critical equatorial velocities; for the majority, this limit might be even lower, about 17%. Similar results have been reported by Wolff et al. (2006) for a sample of 55 Galactic O stars with masses between 10 and 40 M⊙, and by Ramírez-Agudelo et al. (2013) for a sample of 216 presumably single O-type stars in 30 Dor in the Large Magellanic Cloud. The possibility that massive stars can appear close to the ZAMS with velocities significantly lower than the critical speed may have important implications for the formation and evolution of these objects, including their potential to develop LGRB at the end of their lives.
≳ 50 M⊙ rotate relatively slowly when appearing at or close to the ZAMS, with velocities which do not exceed 26% of their critical equatorial velocities; for the majority, this limit might be even lower, about 17%. Similar results have been reported by Wolff et al. (2006) for a sample of 55 Galactic O stars with masses between 10 and 40 M⊙, and by Ramírez-Agudelo et al. (2013) for a sample of 216 presumably single O-type stars in 30 Dor in the Large Magellanic Cloud. The possibility that massive stars can appear close to the ZAMS with velocities significantly lower than the critical speed may have important implications for the formation and evolution of these objects, including their potential to develop LGRB at the end of their lives. -
4.
We confirmed evolutionary predictions from Brott et al. (2011) that stars with
 ≥ 35 M⊙ loose significant amounts of their angular momentum when evolving from the ZAMS throughout the B-supergiant phase, with the BS jump playing an important role, especially for objects with high initial rotation. While for the stars on the hotter side of the BS jump the measured and the predicted rates also agree quantitatively, for those after the jump a significant discrepancy was detected, with the former being systematically higher than the latter. To reconcile theory with observations, we discussed two possibilities: either the observed vsini are overestimated due to problems of the FT method (microturbulence?), and/or the angular momentum loss has been overpredicted, caused by overpredicted mass-loss rates in the BS region. At least at present, we consider the second possibility as the more likely one.
≥ 35 M⊙ loose significant amounts of their angular momentum when evolving from the ZAMS throughout the B-supergiant phase, with the BS jump playing an important role, especially for objects with high initial rotation. While for the stars on the hotter side of the BS jump the measured and the predicted rates also agree quantitatively, for those after the jump a significant discrepancy was detected, with the former being systematically higher than the latter. To reconcile theory with observations, we discussed two possibilities: either the observed vsini are overestimated due to problems of the FT method (microturbulence?), and/or the angular momentum loss has been overpredicted, caused by overpredicted mass-loss rates in the BS region. At least at present, we consider the second possibility as the more likely one. -
5.
For massive B supergiants with Teff ≤ 4.25 dex, our analysis confirms prebious results about the lack of fast rotators. Following Vink et al. (2010) and using evolutionary tracks from Brott et al. (2011), we argued that for masses above ~35 M⊙, BS braking can potentially be responsible for the absence of fast-rotating stars at the cooler edge of the B-supergiant domain.
-
6.
Described in terms of large-scale photospheric turbulence with a radial- tangential distribution, the extra broadening velocities, ΘRT, of our sample stars were found to be highly supersonic, with values ranging from ~35 to ~110 km s-1. The main properties of this broadening, as derived in the present study, can be summarized as follows:
-
a)
The ΘRT values of hot massive stars appear todecline toward cooler temperatures, later evolutionarystages, and lower initial mass. Marginal evidence that thisbroadening is subject to projection and effects caused bymagnetic fields was found. While the latter possibility isconsistent with recent findings from Sundqvistet al. (2013), the former, ifconfirmed by future analyses, would hint at an aspheric originof the extra broadening phenomenon.
-
b)
None of our sample stars shows ΘRT in excess of 110 km s-1. Since the same limit applies to the stars with
 between 2 and 6 M⊙ as studied by Lefever et al. (2010), we suggested that
this is a general feature of the extra broadening phenomenon in OB stars with
non-negligible extra broadening. The explanation of this result remains
unclear so far.
between 2 and 6 M⊙ as studied by Lefever et al. (2010), we suggested that
this is a general feature of the extra broadening phenomenon in OB stars with
non-negligible extra broadening. The explanation of this result remains
unclear so far. -
c)
The extra broadening velocities of massive OB stars and of low-mass B-type stars show a tendency to increase toward higher vsini. Because stars with same or similar vsini can show quite different values of ΘRT, and vice versa, we suggested that this finding most likely reflects similar dependencies of ΘRT and vsini on stellar parameters and is not indicative of a direct relation between them.
-
d)
Although on a general scale the extra broadening rates of more massive stars (
 ≥ 35 M⊙) decrease toward cooler temperatures,
there is suggestive evidence that this decline may depend on
Teff because it is negligible for log
Teff ≳ 4.3, but clearly notable below. Since
the limiting temperatures of these two regimes coincide with the
observed position of the BS jump as determined by Markova & Puls (2008), we
suggested that extra broadening might be sensitive to changes of the wind
properties when crossing the BS region.
≥ 35 M⊙) decrease toward cooler temperatures,
there is suggestive evidence that this decline may depend on
Teff because it is negligible for log
Teff ≳ 4.3, but clearly notable below. Since
the limiting temperatures of these two regimes coincide with the
observed position of the BS jump as determined by Markova & Puls (2008), we
suggested that extra broadening might be sensitive to changes of the wind
properties when crossing the BS region.
-
a)
A detailed description of the FT+GOF method along with a discussion of its applicability and limitations in the case of O and early B-type stars can be found in Simón-Díaz & Herrero (2013).
As in a log g vs. log Teff diagram, the knowledge of the stellar distance is not required to include stars in this diagram. Furthermore, it has the property that for stars with normal helium abundance, 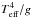 is proportional to their Eddington factor Γe, such that a value of
is proportional to their Eddington factor Γe, such that a value of ![\hbox{$ \left [ \Teffe^{4}/g \right ] \simeq 4.6 $}](/articles/aa/full_html/2014/02/aa22661-13/aa22661-13-eq70.png) corresponds to Γe = 1. Square brackets denote logarithmic values in units of solar ones.
corresponds to Γe = 1. Square brackets denote logarithmic values in units of solar ones.
Interestingly, underestimated gravities lead to overestimated initial masses when derived via the 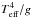 vs. Teff diagram, which basically reflects the impact of the mass-luminosity relation, with an additional uncertainty being related to the accuracy of the model tracks and differences between the actual vinit of the targets and the model value of about 300 km s-1.
vs. Teff diagram, which basically reflects the impact of the mass-luminosity relation, with an additional uncertainty being related to the accuracy of the model tracks and differences between the actual vinit of the targets and the model value of about 300 km s-1.
We refer to Simón-Díaz & Herrero (2013) for an in-depth discussion on the possible explanation of the lack of low vsini stars due to the effects of microturbulent broadening in the case of OB-type stars.
Acknowledgments
We thank the referee, Ian Howarth, for his valuable comments and suggestions. We are also thank Conny Aerts for stimulating discussions about important issues concerning the analysis of extra broadening. N.M. acknowledges travel support from the German DAAD (grant number A/12/01733).
References
- Abt, H., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Puls, J., Godart, M., et al. 2009, A&A, 508, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Fossati, L., & Kochukhov, O. 2012, A&A, 538, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bally, J., & Zinnecker, H. 2005, AJ, 129, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Vine, S. G., & Bate, M. R. 2005, MNRAS, 349, 735 [Google Scholar]
- Bouret, J.-C., Hillier, D. J., Lanz, T., & Fullerton, A. 2012, A&A, 544, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conti, P. S., & Ebets, D. 1977, ApJ, 213, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Crouther, P., Lennon, D., & Walborn, N. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dufton, P. L., Ryans, R. S., Simón-Díaz, S., et al. 2006a, A&A, 451, 603 [Google Scholar]
- Dufton, P. L., Smartt, S. J., Lee, J. K., et al. 2006b, A&A, 457, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Scholler, M., Kharchenko, N. V., et al. 2011, A&A, 528, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howarth, I., Siebert, K., Hussain, G., et al. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1998, Comp. Phys. Comm., 52, 103 [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 514 [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2009, A&A, 504, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraser, M., Dufton, P. L., Hunter, I., et al. 2010, MNRAS, 404, 1306 [NASA ADS] [Google Scholar]
- Gray, D. E. 1973, ApJ, 184, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. E. 1976, The observations and analysis of stellar photosphere, 1st edn. (New York: Wiley) [Google Scholar]
- Gray, D. E. 1987, ApJ, 322, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. E. 2005, The observations and analysis of stellar photosphere, 3rd edn. (Cambridge University Press) [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, Msngr., 95, 8 [Google Scholar]
- Langer, N. 2012, Ann. Rev. Astron. Astroph., 50, 107 [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 63 [Google Scholar]
- Lefever, K., Puls, J., & Aerts, C. 2007, A&A, 463, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lefever, K., Puls, J., Morel, T., et al. 2010, A&A, 515, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, M-KKrumholz, M. R., & Kratter, K. 2011, MNRAS, 416, 580 [NASA ADS] [Google Scholar]
- Maeder, A. 1995, in Astrophysical application of stellar pulsations, eds. R. S. Stobie, & P. A. Whitelock, ASP Conf. Ser., 83, 1 [Google Scholar]
- Markova, N., & Puls, J. 2008, A&A, 478, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markova, N., Prinja, R., Markova, H., et al. 2008, A&A, 487, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markova, N., Puls, J., Scuderi, S., et al. 2011, A&A, 530, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F. Escolano, C. Wde, G. A. et al., 2012a, A&A, 538, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Mahy, L., Hillier, D. J., et al. 2012b, A&A, 538, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, Ph., Neugent, K. F., Hillier, D. J., & Puls, J. 2013, ApJ, 768, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2000a, A&A, 361, 1010 [Google Scholar]
- Meynet, G., & Maeder, A. 2000b, A&A, 411, 543 [Google Scholar]
- Meynet, G. Eggenberger, P. & Maeder, A. 2011, A&A, 525, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Butler, F., Aerts, C., et al. 2006, A&A, 457, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, T., Hubrig, S., & Briquer, M. 2008, A&A, 481, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penny, L. R. 1996, ApJ, 463, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A. 2003, A&A, 408, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivero-Gonzalez, J. G., Puls, J., Najarro, F., & Brott, I. 2012, A&A, 537, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rozendhal, J. 1970, ApJ, 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Ryans, R. S. I., Dufton, P. L., Rolleston, W. R., et al. 2002, MNRAS, 336, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Santolaya-Rey, A. E. uls, J. & Herrero, A. 1997, A&A, 323, 488 [NASA ADS] [Google Scholar]
- Searle, S. C., Prinja, R. K., Massa, D., et al. 2008, A&A, 481, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F., Najita, J., Ostriker, E., et al. 1995, ApJ, 429, 781 [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S. & Herrero, A. 2013, A&A, accepted, DOI: 10.1051/0004-6361/201322758 [Google Scholar]
- Simón-Díaz, S., Herrero, A., Uytterhoeven, C., et al. 2010, ApJ, 720, 174 [Google Scholar]
- Simón-Díaz, S., Castro, N., Garcia, M., et al. 2011, Bull. Soc. Roy. Sci. Liège, 80, 514 [NASA ADS] [Google Scholar]
- Slettebak, A. 1956 ApJ, 124, 153 [Google Scholar]
- Solano, E., Catala, C., Carrido, R., et al. 2005, AJ, 129, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A. Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Petit, V., Owocki, S., et al. 2013, MNRAS, 433, 2497 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D., Oksala, M. E., Cohen, D. H., et al. 2010, ApJ, 714, L318 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., Owocki, S. P., Townsend, R. H. D., et al. 2009, MNRAS, 392, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Uesugi. A., & Fukuda, I. 1982, Revised Catalogue of Stellar Rotational Velocities, VizieR Online Data Catalog, III/226 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. M. L. 1999, A&A, 350, 181 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. M. L. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Vink, J., Brott, I., Grafener, G., Langer, N., et al. 2010, A&A, 512, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walborn, N. R. Sota, A. Maíz Apellániz, J., et al. 2010, ApJ, 711, 143 [Google Scholar]
- Wolff, S. C., Strom, S. E., Drot, D., et al. 2006, AJ, 132, 749 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Illustration of the quality of the fit to strategic helium and hydrogen lines for a star with a weak wind, HD 93222. |
| In the text | |
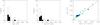 |
Fig. 2 Left and middle panels: distributions of projected rotational velocities for the O-star sample, based on our determinations for vsini (PF) (extra line-broadening neglected) and vsini (FT+GOF) (extra line-broadening taken into account). In both panels, the binsize is 30 km s-1, and the contribution of supergiants is highlighted by the shaded area. Right panel: vsini (FT+GOF) versus vsini (PF). Luminosity class I objects are highlighted in dark blue, II and III objects in light blue, and IV and V objects in green. The one-to-one relation is marked by the solid line. |
| In the text | |
 |
Fig. 3 Extra broadening rates (in km s-1) for the O-star sample as a function of vsini (upper panel) and Teff (lower panel). In both panels, luminosity class I stars are colored in dark blue, luminosity class II and III objects in light blue, and luminosity class IV and V objects in green. Intermediate (110 ≤ vsini (FT+GOF) ≤ 200 km s-1) and fast rotating stars (vsini (FT+GOF) > 200 km s-1) are additionally marked by large circles. In the upper panel, the solid line indicates the one-to-one relation. |
| In the text | |
 |
Fig. 4 Distribution of extra broadening velocities for the B-supergiants in the OB sample. The data derived by assuming different models for extra broadening are highlighted in different colors: red denotes an isotropic Gaussian model (Fraser et al. 2010), whilst green refers to a radial-tangential one (Lefever et al. 2007; Markova & Puls 2008; Simón-Díaz et al. 2010). Note the systematic shift along the vertical axes between the green and the red dots (upper panel) and that this shift disappears after the original Fraser et al. (2010) data for extra broadening have been corrected to make them consistent with the rest (lower panel). For dotted lines, see Sect. 5.1. |
| In the text | |
 |
Fig. 5 Projected rotational (upper panel) and extra line-broadening velocities (lower panel) for the OB sample as a function of Teff. O and B supergiants are highlighted in dark blue and red, respectively, and O giants and dwarfs in light blue. Intermediate- and fast-rotating stars (vsini ≥ 110 km s-1) are additionally marked by large circles (for more information and arrows see Sect. 5.2). |
| In the text | |
 |
Fig. 6 Upper panel: values of |
| In the text | |
 |
Fig. 7 Projected rotation velocities and effective temperatures for the OB supergiants (red) and the O-type giants and dwarfs (blue) from our sample, plotted against evolutionary tracks from Brott et al. (2011). All stars have been binned into three mass ranges: 15 M⊙ ≤ M ≤ 30 M⊙ (bottom panel); 31 M⊙ ≤ M ≤ 50 M⊙ (middle panel), and M ≥ 51 M⊙ (top panel). O-type stars close to the ZAMS with anomalously low vsini are additionally highlighted by asterisks. The large diamond marks HD 93843, which has been recently identified as a magnetic star (Hubrig et al. 2011). In the top panel, the most massive stars ( |
| In the text | |
 |
Fig. 8 Same as the lower panel of Fig. 6, but for the extra line-broadening velocities. Intermediate and fast rotators are highlighted by large circles. |
| In the text | |
 |
Fig. 9 Extra line-broadening velocities as a function of Teff for the stars from the three mass ranges as defined in Sect. 5.3.2. Intermediate- and fast-rotating stars are additionally marked with large circles. The solid and dotted vertical lines mark the position of the observed and the theoretically predicted BS region, respectively. All other symbols have the same meaning as in Fig. 7. |
| In the text | |
 |
Fig. 10 Extra line-broadening vs. projected rotational velocities for the stars from our OB sample (open circles) and the sample studied by Lefever et al. (2010, filled dots). Stars assumed to be affected by projection are highlighted by asterisks. The large diamond indicates the magnetic star HD 93843. The solid and dashed lines represent the one-to-one correspondence and the 110 km s-1 limit of ΘRT, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$ [ \Teffe^{4}/g ] = \log ( \Teffe^{4}/g ) - \log ( \Teffe^{4}/g )_\odot$}](/articles/aa/full_html/2014/02/aa22661-13/aa22661-13-eq44.png)