| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322236 | |
| Published online | 21 February 2014 | |
Reconstructing the density and temperature structure of prestellar cores from Herschel data: A case study for B68 and L1689B⋆
1
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/Service
d’Astrophysique, C.E. Saclay, Orme
des Merisiers, 91191
Gif-sur-Yvette,
France
e-mail: Arabindo.Roy@cea.fr; philippe.andre@cea.fr
2
Institut d’Astrophysique Spatiale, CNRS/Université Paris-Sud 11, 91405
Orsay,
France
3
Université de Bordeaux, Laboratoire d’Astrophysique de Bordeaux,
CNRS/INSU, UMR 5804, BP
89, 33271
Floirac Cedex,
France
4
School of Physics & Astronomy, Cardiff
University, Cardiff
CF29 3AA,
UK
5
Jeremiah Horrocks Institute, University of Central
Lancashire, Preston
PR1 2HE,
UK
6
INAF-Istituto di Astrofisica e Planetologia
Spaziali, via Fosso del Cavaliere
100, 00133
Rome,
Italy
7
Joint ALMA Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
8
Canadian Institute for Theoretical Astrophysics, University of
Toronto, 60 St. George
Street, Toronto,
ON
M5S 3H8,
Canada
9
Université de Toulouse, UPS-OMP, IRAP,
Toulouse,
France
10
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
11
Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre
& Marie Curie, 98 bis
boulevard Arago, 75014
Paris,
France
12
Department of Physics and Astronomy, The Open
University, Walton
Hall, Milton Keynes
MK7 6AA,
UK
13
RAL Space, STFC Rutherford Appleton Laboratory,
Chilton Didcot
OX11 0QX,
UK
Received:
9
July
2013
Accepted:
8
November
2013
Utilizing multiwavelength dust emission maps acquired with Herschel, we reconstruct local volume density and dust temperature profiles for the prestellar cores B68 and L1689B using an inverse-Abel transform-based technique. We present intrinsic radial dust temperature profiles of starless cores directly from dust continuum emission maps disentangling the effect of temperature variations along the line of sight, which were previously limited to the radiative transfer calculations. The reconstructed dust temperature profiles show a significant drop in the core center, a flat inner part, and a rising outward trend until the background cloud temperature is reached. The central beam-averaged dust temperatures obtained for B68 and L1689B are 9.3 ± 0.5 K and 9.8 ± 0.5 K, respectively, which are lower than the temperatures of 11.3 K and 11.6 K obtained from direct SED fitting. The best mass estimates derived by integrating the volume density profiles of B68 and L1689B are 1.6 M⊙ and 11 M⊙, respectively. Comparing our results for B68 with the near-infrared extinction studies, we find that the dust opacity law adopted by the HGBS project, κλ = 0.1 × (λ/300 μm)-2 cm2 g-1 agrees to within 50% with the dust extinction constraints.
Key words: stars: formation / submillimeter: general / ISM: individual objects: B68 / ISM: individual objects: L1689B / dust, extinction
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Recent submillimeter observations with the Herschel Space Observatory (Pilbratt et al. 2010) and particularly the results obtained as part of the Herschel Gould Belt Survey (HGBS; André et al. 2010) have significantly improved our global understanding of the early stages of low-mass star formation. It is now becoming clear that the formation of prestellar cores is intimately related to the ubiquitous filamentary structure present in the cold interstellar medium (ISM; Arzoumanian et al. 2011). On one hand one of the main objectives of the HGBS is to measure the prestellar core mass function (CMF) in nearby cloud complexes and to clarify the relationship between the CMF and the stellar initial mass function (IMF) on the other hand we also look at the link with the structure of the ISM (cf. Könyves et al. 2010; André et al. 2010, for preliminary results).
An accurate determination of the prestellar CMF requires reliable estimates of core masses. In the context of the HGBS project, core masses are derived from dust continuum emission maps obtained with Herschel between 160 μm and 500 μm. Dust emission is almost always optically thin at these wavelengths and can thus act as a surrogate tracer of the total (gas + dust) mass along the line of sight (LOS). This requires an assumption about the dust opacity in the submillimeter regime and reliable estimates of the dust temperature, Td. Herschel multiwavelength data can be used to estimate ⟨Td⟩ LOS through single-temperature greybody fits to the observed spectral energy distributions (SEDs; cf. Könyves et al. 2010). A complication, however, is that such fits only provide the average temperature along the LOS and do not account for temperature gradients within the target sources. This is potentially a very significant problem when studying self-gravitating starless (or protostellar) cores with stratified density structures heated by an external or internal radiation field. The central temperatures of cold, starless cores and sometimes their mass-averaged temperatures can be overestimated due to the relatively strong emission from the screen of warmer dust in the outer layers of the cores which bias core mass estimates to lower values (cf. Malinen et al. 2011). Likewise, temperature variations along the LOS may hamper the derivation of reliable density profiles for prestellar cores (e.g., Kirk et al. 2005; Ysard et al. 2012) using submillimeter emission maps (e.g., Kirk et al. 2005; Ysard et al. 2012). Radiative transfer calculations (e.g., Evans et al. 2001; Stamatellos et al. 2007) have been performed to predict the dust temperature profiles of starless cores whose outer surfaces are exposed to heating by the local interstellar radiation field (ISRF). These calculations generally find a significant drop in Td at the center of starless cores, but the actual magnitude of this temperature drop remained poorly constrained observationally before the advent of Herschel (see Ward-Thompson et al. 2002 for early results with ISO, however).
Here, we use Herschel observations to quantify the dust temperature gradient within two well-studied starless cores, B68 and L1689B. We introduce a simple yet powerful inversion technique based on the Abel integral transform to simultaneously reconstruct the 3D density and dust temperature profiles of dense cores by using the inputs of Herschel maps in four bands between 160 μm and 500 μm (also see Marsh et al. 2014 for an independent approach of solving similar problem). The basic goal of the present paper is to demonstrate the performance of the Abel inversion technique. We apply our algorithm to B68 and L1689B and compare the results with previous infrared extinction/absorption studies, which allow us to validate the dust opacity assumption made in earlier HGBS papers. We also test our technique on synthetic core models with known density and temperature profiles. While the method assumes spherically symmetric cores, we show that it yields satisfactory results for prolate or oblate ellipsoidal cores with realistic aspect ratios that are ≲2.
2. Herschel observations of B68 and L1689B
As part of the HGBS key project, two fields in the Pipe and Ophiuchus molecular cloud complexes containing B68 and L1689B with areas of ~1°̣5 × 1°̣5 and ~3°̣0 × 3°̣5 were observed for an integration time of 2.6 and 10.2 h, respectively. These target fields were mapped1 in two orthogonal scan directions at a scanning speed of 60′′ s-1 in parallel mode, acquiring data simultaneously in five bands with the SPIRE (Griffin et al. 2010) and PACS (Poglitsch et al. 2010) bolometer cameras. The data were reduced using HIPE version 7.0. The SPIRE data were processed with modified pipeline scripts. Observations during the turnaround of the telescope were included, and a destriper module with a zero-order polynomial baseline was applied. The default “naïve” mapper was used to produce the final map. For the PACS data, we applied the standard HIPE data reduction pipeline up to level 1 with improved calibration. Further processing of the data, such as subtraction of (thermal and non-thermal) low-frequency noise and map projection was performed with Scanamorphos v11 (Roussel 2012). Note that the Scanamorphos map-maker avoids any high-pass filtering, which is crucial for preserving extended emission.
3. Description of the Abel inversion method
Consider a spherically symmetric core with radial density profile, ρ(r),
embedded in a uniform background and isotropic ISRF. Assuming optically thin dust emission,
the specific intensity Iν(p)
of the core when observed at impact parameter, p, may be expressed as ![\begin{equation} I_\nu (p) = 2\, \int_{p}^{+\infty}\, \rho (r)\, B_\nu\left[T_{\rm d}(r)\right]\, \kappa_\nu \frac{r\,{\rm d}r}{\sqrt{r^2-p^2}}+ I_{\nu,\rm bg} +I_{\nu, \rm N}, \label{eq:a} \end{equation}](/articles/aa/full_html/2014/02/aa22236-13/aa22236-13-eq21.png) (1)where Iν,bg and Iν,N represent the
background emission and instrumental noise, respectively, Bν [Td(r)]
is the Planck function for the dust temperature Td(r) at radius
r from core
center, and κν is the
frequency-dependent dust opacity2, which is assumed
here to be uniform throughout the core. Given the symmetry of the problem, we can use the
inverse Abel transform (e.g. Bracewell 1986) to
obtain the integrand of Eq. (1) at each
observed frequency ν:
(1)where Iν,bg and Iν,N represent the
background emission and instrumental noise, respectively, Bν [Td(r)]
is the Planck function for the dust temperature Td(r) at radius
r from core
center, and κν is the
frequency-dependent dust opacity2, which is assumed
here to be uniform throughout the core. Given the symmetry of the problem, we can use the
inverse Abel transform (e.g. Bracewell 1986) to
obtain the integrand of Eq. (1) at each
observed frequency ν: ![\begin{equation} \rho (r)\, B_\nu\left[T_{\rm d}(r)\right]\, \kappa_\nu = -\frac{1}{\pi}\, \int_{r}^{+\infty}\, \frac{{\rm d}I_\nu}{{\rm d}p} \frac{{\rm d}p}{\sqrt{p^2-r^2}}\cdot \label{eq:b} \end{equation}](/articles/aa/full_html/2014/02/aa22236-13/aa22236-13-eq29.png) (2)From Eq. (2), we see that the physical parameters of
interest, ρ(r) and Td(r), only depend on the
first derivatives of the radial intensity profiles. With a pre-defined assumption about the
dust opacity law κν, one may thus
estimate Td(r) at each radius
r by fitting
a single-temperature modified blackbody to the SED obtained from evaluating the right-hand
side of Eq. (2) at each observed band between
160 μm and 500
μm (see Sect.
3.1 for further details). The density profile,
ρ(r), can be derived simultaneously
from the normalization of the fit at each radius.
(2)From Eq. (2), we see that the physical parameters of
interest, ρ(r) and Td(r), only depend on the
first derivatives of the radial intensity profiles. With a pre-defined assumption about the
dust opacity law κν, one may thus
estimate Td(r) at each radius
r by fitting
a single-temperature modified blackbody to the SED obtained from evaluating the right-hand
side of Eq. (2) at each observed band between
160 μm and 500
μm (see Sect.
3.1 for further details). The density profile,
ρ(r), can be derived simultaneously
from the normalization of the fit at each radius.
For simplicity, Eq. (1) above neglects the convolution with the telescope beam. However, simulations confirm that beam smearing has little effect in the case of well-resolved cores (see Appendix B). In the case of starless cores, such as B68 and L1689B, with a flat inner density profile inside a radius Rflat, or angular radius θflat, we find that the beam effect can be parameterized by the ratio θflat/HPBW (where HPBW is the half-power beam width), and that the reconstructed column density profile agrees with the intrinsic profile within 20% (in the absence of noise) for θflat/HPBW ≳ 1 as is the case for B68 and L1689B. More generally, simulations indicate that the reconstructed temperature and column density profiles essentially coincide with the corresponding intrinsic profiles convolved to the effective beam resolution (see Appendix B) in the absence of noise. Importantly, our Abel inversion technique does not depend on the subtraction of a flat background level, since the derivative of a constant background3 does not contribute to the integral of Eq. (2). The reconstruction is, however, quite sensitive to noise fluctuations in the outer parts of the core.
 |
Fig. 1 Column density map (left) and LOS dust temperature map (right) of B68, which is derived by fitting modified blackbody SEDs to the Herschel data between 160 μm and 500 μm on a pixel-by-pixel basis (see Sect. 3.1 for details). The column density contours go from 1.6×1021 to 9.6×1022 in steps of 1.6 × 1021 in units of H2 molecules per cm2 (left), and the temperature contours are 16, 15, 14, and 13 K (right). The cross symbol shows the center of the core obtained by fitting a 2D-Gaussian to the column density map. |
Planck offsets in MJy sr-1.
3.1. SED fitting and profile reconstruction
Column density and corresponding LOS-averaged dust temperature maps are shown in Figs.
1 and 3 for
B68 and L1689B, respectively. They were obtained by fitting modified blackbody functions
to the Herschel SEDs longward of 160 μm on a pixel-by-pixel
basis, as seen in earlier HGBS papers (Könyves et al.
2010; see also Hill et al. 2011 for
HOBYS). While fitting the SEDs, we weighted each data point by the corresponding
calibration errors at SPIRE (~10%) and PACS (~15%) wavelengths. Appropriate zero-level offsets were added to each
image (see Table 1), which were obtained by
correlating the Herschel data with the Planck and IRAS
data of the same fields (see Bernard et al. 2010).
The same dust opacity law as in earlier HGBS (see also Motte et al. 2010 for the HOBYS key program) papers is adopted in the present
paper (similar to Hildebrand 1983):
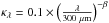 cm2 per g (of gas
+ dust) with a dust
emissivity index of β = 2. Our dust opacity value at the normalizing
wavelength is also close to the Ossenkopf &
Henning (1994) opacity model for dust grains with thin ice mantles. A mean
molecular weight μH2 = 2.8 is assumed4 to express column density in units of H2 molecules per
cm2. Using our
adopted dust opacity law, we find that even the central LOSs for B68 and L1689B with
NH2≤5 × 1022 cm-2 has small optical depths ≲0.08 at 160 μm, confirming that the
core emission is optically thin longward of 160 μm.
cm2 per g (of gas
+ dust) with a dust
emissivity index of β = 2. Our dust opacity value at the normalizing
wavelength is also close to the Ossenkopf &
Henning (1994) opacity model for dust grains with thin ice mantles. A mean
molecular weight μH2 = 2.8 is assumed4 to express column density in units of H2 molecules per
cm2. Using our
adopted dust opacity law, we find that even the central LOSs for B68 and L1689B with
NH2≤5 × 1022 cm-2 has small optical depths ≲0.08 at 160 μm, confirming that the
core emission is optically thin longward of 160 μm.
The same assumptions have been adopted for the modified blackbody fits required at each
radius by the Abel inversion technique. A single-temperature description of the SEDs is
suitable in this case because we are sampling both local density and dust temperature at a
given radius r. Prior to the SED fitting, the Herschel
data are convolved to a common resolution of either
36 3 (i.e., HPBW
resolution of SPIRE at 500 μm) or 24
3 (i.e., HPBW
resolution of SPIRE at 500 μm) or 24 9 (i.e., HPBW
resolution of SPIRE at 350 μm when the 500 μm data are not used). At
each wavelength, a circularly averaged intensity profile about the core center is first
derived from the Herschel data, and the derivative of this average
profile is then numerically evaluated and integrated over the kernel shown in the
right-hand side of Eq. (2). The central
position of the core is obtained from fitting a 2D-Gaussian model to the column density
map (see the cross symbols in Figs. 1 and 3 for B68 and L1689B, respectively). The integration is
performed up to an outer radius corresponding to ~2–2.5 times the FWHM diameter
of the core as estimated from the 2D-Gaussian fit to the column density map. In
practice, the integral on the right-hand side of Eq. (2) converges rapidly and does not depend much on the precise value of
the integration outer radius as long as it encompasses the entire core – see Appendix
A and Fig. A.1.
9 (i.e., HPBW
resolution of SPIRE at 350 μm when the 500 μm data are not used). At
each wavelength, a circularly averaged intensity profile about the core center is first
derived from the Herschel data, and the derivative of this average
profile is then numerically evaluated and integrated over the kernel shown in the
right-hand side of Eq. (2). The central
position of the core is obtained from fitting a 2D-Gaussian model to the column density
map (see the cross symbols in Figs. 1 and 3 for B68 and L1689B, respectively). The integration is
performed up to an outer radius corresponding to ~2–2.5 times the FWHM diameter
of the core as estimated from the 2D-Gaussian fit to the column density map. In
practice, the integral on the right-hand side of Eq. (2) converges rapidly and does not depend much on the precise value of
the integration outer radius as long as it encompasses the entire core – see Appendix
A and Fig. A.1.
 |
Fig. 2 Column density a) and dust temperature b) profiles of B68
obtained at 500 μm resolution by applying the Abel inversion
method to the circularly averaged intensity profiles observed with Herschel
between 160 μm and 500 μm. a)
Comparison between the column density profiles derived from the Abel reconstruction
(solid black line) and LOS-averaged SED fitting (thick dashed line). The red curve
shows the best-fit Bonnor-Ebert model to the Abel-inverted profile (see Table 2 for parameters). The vertical dotted line
represents the half power beam radius of 36 |
 |
Fig. 3 Same as Fig. 1 but for L1689B. The column density contours are 6 × 1021, 1 × 1022, 1.4 × 1022, 1.8 × 1022, and 2.6 × 1022 H2 cm-2 (left), and the temperature contours are 16.5, 15.5, 14.5, and 13.5 K (right). The column density image shows that L1689B is embedded inside a filamentary structure. |
3.2. Assessment of uncertainties
The errors bars on the reconstructed profiles at each radius can be estimated from the
standard deviations of the density and temperature profiles obtained by repeating the Abel
reconstruction along different angular directions around the source (i.e., averaging the
data separately over a series of angular sectors instead of circularly averaging the
data). In the case of the reconstructed profiles of B68 and L1689B as shown in Figs. 2 and 4, sixteen
equally-spaced angular sectors were used to derive the error bars. The errors we report on
the best estimates of the (column) density and temperature at core center correspond to
the standard error in the mean, 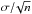 ,
where n is
the number of independently measured sectors.
,
where n is
the number of independently measured sectors.
The uncertainty in the normalization of the dust opacity law directly affects the column density estimates but not the temperature estimates, whereas the uncertainty in the emissivity index β influences both the dust temperature and the column density estimates in an anti-correlated fashion. When β is varied from 2 to 1.5, for instance, the dust temperature increases by ~10% and the column density decreases by ~40%. The uncertainty in the central position of the core also introduces errors on the derived parameters. To assess the magnitude of this effect in the case of B68, we varied the central position within a radius of 6′′ and found that the resulting central dust temperature and central column density had standard deviations of ±0.3 K and ±0.04 × 1022 cm-2, respectively. Additionally, departures from spherical symmetry due to asymmetries in the density distribution (cf. L1689B in Fig. 3) or an anisotropic background radiation field (cf. Nielbock et al. 2012) may break the symmetry of the quantity ρ(r)Bν(T(r)) in Eqs. (1) and (2), introducing additional errors. In principle the latter are included in the error bars estimated from the fluctuations of the radial profiles reconstructed along various angular directions. Moreover, we show in Appendix B that cores with moderate departures from spherical symmetry (such as prolate or oblate ellipsoidal cores with aspect ratios ≲2) can be reconstructed with reasonable accuracy.
For both B68 and L1689B, the net measurement errors in the derived central Td and NH2values are estimated to be ±0.5 K and ±0.1 × 1022 cm-2, respectively, excluding the systematic uncertainties associated with our assumptions on the dust opacity and the calibration errors. In Appendix B.1 we show that the calibration errors lead to an additional uncertainty of ~12% on column density and ~5% on temperature estimates.
4. Detailed results for B68 and L1689B
4.1. B68 core
B68 is a well studied isolated bok globule in the Pipe nebula cloud complex (e.g. Alves et al. 2001; Nielbock et al. 2012). We adopt a distance of 125 pc (de Geus et al. 1989) for the present study. Figure 2 shows the reconstructed column density and temperature profiles obtained from our Herschel observations of B68 with the Abel inversion method described as in Sect. 3.
In Fig. 2b, the Abel-inverted radial dust temperature profile (solid curve) is compared with the LOS-averaged SED temperature profile (dashed curve). While both temperature profiles exhibit similar features with a broad minimum around the core center, a positive gradient outside the flat inner plateau of the column density profile, and similar values (Td~16.5 ± 2 K) at large radii, the minimum Abel-reconstructed temperature at core center is ~2 K lower than the minimum SED temperature observed through the central LOS. Accordingly, the central column density derived with the Abel inversion method (1.3 ± 0.1 × 1022 cm-2) is 30% higher than the LOS-averaged column density of ~1.0 × 1022 cm-2 that is derived from standard SED fitting for the central LOS. The difference between the Abel-reconstructed and the LOS-averaged column density becomes negligible in the outer parts of the core. This is indicative of stronger temperature variations along the central LOS compared to the outer LOSs.
Recently, Nielbock et al. (2012) constrained the
dust temperature and volume density profiles of B68 using an iterative approach based on
3D radiative transfer modeling of multiwavelength dust continuum data. This included
Herschel observations that were obtained as a part of the EPoS (Launhardt et al. 2013) key project. They employed a
3-dimensional grid of Plummer-like (Plummer 1911)
density profiles and obtained initial guesses of the parameters from LOS-averaged SED
fits. Altogether their model was tuned with eight free parameters, yielding a central dust
temperature of Td =
8.2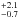 K. The primary reason for the dispersion in the central dust temperature in Nielbock et al. (2012) is the uncertainty of a factor
of ~2 on the dust opacity in
the infrared regime. Although we obtain a higher central dust temperature, Td =
9.3 ± 0.5 K, with our
Abel-inversion method, our results agree with the Nielbock et al. analysis within the
range of the quoted uncertainties.
K. The primary reason for the dispersion in the central dust temperature in Nielbock et al. (2012) is the uncertainty of a factor
of ~2 on the dust opacity in
the infrared regime. Although we obtain a higher central dust temperature, Td =
9.3 ± 0.5 K, with our
Abel-inversion method, our results agree with the Nielbock et al. analysis within the
range of the quoted uncertainties.
Based on extinction measurements (Alves et al.
2001), the column density profile of B68 closely resembles that of a Bonnor-Ebert
(BE; e.g., Bonnor 1956) isothermal sphere with a
flattened inner region. The overplotted red curve in Fig. 2 shows the best-fit BE model to the reconstructed column density profile. The
best-fit BE parameters along with the physical properties that follow directly from the
fit such as the radius of the flat inner plateau, 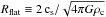 ,
the density contrast, ρc/ρs,
and the external pressure, Pext, are summarized in Table 2. They are consistent with the BE parameters found by
Alves et al. (2001).
,
the density contrast, ρc/ρs,
and the external pressure, Pext, are summarized in Table 2. They are consistent with the BE parameters found by
Alves et al. (2001).
The NH2 column density profile obtained by integrating the Abel-inverted volume density profile is shown in Fig. 2. This can be directly compared with the near-infrared extinction results Alves et al. (2001) because extinction traces material independently of temperature. For this comparison, we adopted a standard conversion factor, NH2/AV of 9.4 × 1020 cm-2 mag-1 (Bohlin et al. 1978), to translate column density to equivalent visual extinction AV at low column densities (i.e., NH2≲6 × 1021 cm-2). For higher column densities, we used the conversion NH2/AV = 6.9 × 1020 cm-2 mag-1 given by Draine (2003) and later adopted by Evans et al. (2009), which is consistent with an extinction curve with a total-to-selective extinction, RV≡AV/E(B − V) = 5.5 that is appropriate in higher density regions.
Best-fit parameters of Bonnor-Ebert core models for B68 and L1689B.
Using the Bohlin conversion factor, we obtain an AV of 3.2 mag at
a radius of 104 AU,
which agrees within ~60% with
the value of 5 mag reported by Alves et al. (2001)
at the same radius. Furthermore, if we correct our estimate for the weak empirical trend
between submillimeter dust opacity and column density, κλ ∝ NH20.28, as inferred by Roy et al. (2013) in the regime of 1 ≲ AV ≲ 10 and
interpreted as evidence of dust grain evolution, then we find a corrected column density
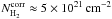 ,
which is equivalent to a corrected
,
which is equivalent to a corrected 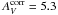 mag.
This is in excellent (10%) agreement with Alves et al.
(2001) at 104 AU.
mag.
This is in excellent (10%) agreement with Alves et al.
(2001) at 104 AU.
Using the Draine conversion factor, we derive an AV of
19 ± 2 mag through the
center of the B68 core as compared to the AV of 30 mag obtained from extinction by
Alves et al. (2001), corresponding to a 60%
agreement. However, the effective angular resolution of the Alves et al. extinction map
was about ~10′′, approximately four times
higher than the beam resolution (36 3) of SPIRE at
500 μm. For
better comparison, we performed a similar Abel reconstruction analysis at the beam
resolution (24
3) of SPIRE at
500 μm. For
better comparison, we performed a similar Abel reconstruction analysis at the beam
resolution (24 9) of the SPIRE
350 μm
observations, ignoring the 500 μm data. In this case, the central
Abel-reconstructed column density corresponds to AV = 20 ± 2 mag, which
agrees within 50% with the results of Alves et al.
(2001). (The central dust temperature derived at 350 μm resolution coincides
within the uncertainties with the 500 μm resolution estimate.)
9) of the SPIRE
350 μm
observations, ignoring the 500 μm data. In this case, the central
Abel-reconstructed column density corresponds to AV = 20 ± 2 mag, which
agrees within 50% with the results of Alves et al.
(2001). (The central dust temperature derived at 350 μm resolution coincides
within the uncertainties with the 500 μm resolution estimate.)
Likewise, the total mass of 1.6±0.07M⊙, which is derived by integrating the Abel-reconstructed density profile of B68 within the outer radius of 1.4 × 104 AU, agrees within 30% with the mass of 2.1 M⊙ as obtained by Alves et al. (2001) from the extinction data. For comparison, the mass derived from fitting a modified blackbody to the integrated flux densities is 1.4 ± 0.05M⊙. The latter does not account for temperature variations along the LOS and thus slightly underestimates the intrinsic total mass of the core. For a moderate density core such as B68, however, we stress that the global SED temperature (12.5 ± 0.1 K here) is close to the mass-averaged dust temperature and the SED mass agrees within ~15% of the Abel-reconstructed mass.
Using the above results on the density and temperature structure, we can check the energy balance of the B68 core. Assuming optically thin submillimeter emission, a total output luminosity of 0.35 ± 0.04L⊙ is obtained by integrating the quantity 4π∫ρ(r)Bν [Td(r)] κνdν over the volume of the core. A very similar output luminosity (0.41 ± 0.05L⊙) is estimated by integrating the observed SED over wavelengths. These output estimates should be compared to the input luminosity of ~0.40 L⊙ provided to the core by the local ISRF (Mathis et al. 1983; with G0 ~ 1), which are calculated from the total ISRF flux density that is absorbed5 by a spherical object with the same density profile and outer radius as B68 using Eq. (4) of Lehtinen et al. (1998). Note that the three luminosity values above agree with one another.
4.2. L1689B
Compared to B68, L1689B is a slightly denser and more centrally condensed core (e.g. André et al. 1996; Bacmann et al. 2000) located in the Ophiuchus complex at a distance of ~140 pc. The Herschel images reveal that it is embedded within a larger-scale filamentary structure (see Fig. 3). Given the elongated morphology that is observed in the plane of the sky and the mean apparent aspect ratio ~1.3 of the core, the hypothesis of spherical symmetry underlying Eq. (1) is not strictly verified.
To assess the validity of our Abel-inversion scheme in this case, we therefore performed test reconstructions for prolate and oblate ellipsoidal model cores with similar aspect ratios. These tests suggest that small departures from spherical symmetry have little impact on the reconstruction results (see Appendix B).
The upper panel of Fig. 4 shows the results of three distinct reconstructions of the column density profile of L1689B, as obtained by applying the Abel inversion method to a) the circularly averaged intensity profiles (thick solid curve); b) the intensity profiles observed in sectors oriented east-west (EW), i.e., approximately along the apparent major axis of the core (blue dash-dotted curve); and c) the intensity profiles observed in sectors oriented north-south (NS), i.e., approximately along the apparent minor axis of the core (green dash-dotted curve). While the three column density profiles agree with each other within the central plateau region, the EW profile lies 30% above the NS profile at large radii ≳104 AU, and the circularly averaged profile is intermediate between the other two. For reference and comparison with B68, a BE model was fitted to each of the three column density profiles and the results of these fits are given in Table 2. (For the sake of clarity, only the model fit to the circularly averaged intensity profiles is shown in Fig. 4, as a red solid curve.) All three fits yield a consistent value for the radius of the flat inner plateau, Rflat ~ 4500 ± 100 AU (corresponding to ~32″). The average reconstructed column density within Rflat is 3.5 ± 0.1 × 1022 cm-2, which agrees well (~30%) with the H2 column density that is averaged over the flat inner part of the core of 4.5–4.7 × 1022 cm-2. This value was found by Bacmann et al. (2000) based on their ISOCAM mid-infrared absorption study (see their Table 2).
 |
Fig. 4 a) Column density profile of L1689B obtained at 500 μm resolution by applying the Abel reconstruction method to the circularly averaged intensity profiles between 160 μm and 500 μm (solid black curve). The dash-dotted blue and green profiles show the column density profiles obtained from reconstructing the intensity profiles observed along EW and NS sectors, respectively. The overplotted solid red line shows the best-fit Bonnor-Ebert model (see Table 2 for parameters). The vertical dotted line is same as in Fig. 2. b) Reconstructed dust temperature profile of L1689B (solid curve) compared with the LOS-averaged temperature profile derived from simple SED fitting (thick dashed curve). |
Our best estimate of the total core mass obtained from Abel reconstructing is 11 ± 2M⊙. The tests we performed for ellipsoidal synthetic cores (cf. Appendix B) indicate that the relative error in this mass introduced by the departure from spherical symmetry is less than 4% for an intrinsic aspect ratio of ~1.3. Our mass estimate is in excellent agreement with the total mass reported by Bacmann et al. (2000). The SED mass derived from fitting a modified blackbody to the integrated flux densities is 7.8 ± 0.2M⊙, which is about 30% lower than our best mass estimate. The corresponding global SED temperature of the core is 12.5 ± 0.2 K.
The central dust temperature obtained for L1689B using the Abel transform technique is 9.8 ± 0.5 K (see lower panel of Fig. 4). This value is higher than the very low central dust temperature of 7.5 K advocated by Evans et al. (2001) which is based on radiative transfer calculations if a standard ISRF (G0 = 1) is assumed. At least part of this discrepancy can be explained by the fact that the effective external radiation field for L1689B is about one order of magnitude stronger than the standard ISRF, due to the presence of early-type stars in the immediate vicinity of the Ophiuchus cloud (cf. Liseau et al. 1999).
5. Conclusions
The results of B68 and L1689B discussed in Sect. 4, along with the tests on model cores presented in Appendix B, demonstrate that the Abel transform technique can successfully produce meaningful radial density and dust temperature profiles for spatially resolved prestellar cores. The most rewarding result is the reconstruction of a radial dust temperature profile that is directly from Herschel dust continuum imaging data and independent of any radiative transfer model. The Abel inversion technique (Sect. 3) is very general: it is insensitive to background subtraction to first order and can perform equally well for externally-heated (isotropically) starless cores or internally-heated protostellar cores. While the technique assumes spherically symmetric cores in principle, tests performed on ellipsoidal cores suggest that satisfactory results are obtained even when the hypothesis of spherical symmetry is not strictly valid (such as in the L1689B case – cf. Fig. 3). A similar Abel-transform scheme may also be employed to reconstruct the intrinsic beam-averaged density and temperature profiles of (approximately) cylindrically symmetric filaments from the observed radial intensity profiles averaged along the filament main axes.
For both B68 and L1689B, we find a characteristic dip in the dust temperature profile with minimum beam-averaged values of 9.3 ± 0.5 K and 9.8 ± 0.5 K at core center, respectively. The temperature profile smoothly merges with the background cloud temperature at the outer core radii.
The Abel transform technique yields central beam-averaged H2 densities of 7.5 ± 0.5 × 104 cm-3 and 2.0 ± 0.1 × 105 cm-3 for B68 and L1689B, respectively, which correspond to central column densities of 1.3 ± 0.1 × 1022 cm-2 and 3.6 ± 0.1 × 1022 cm-2 after integration of the reconstructed volume density profiles along the LOS. These central column density estimates are approximately 15% larger than the values obtained from direct SED fitting. Comparison of our results with the independent near-IR extinction measurement of the B68 column density profile by Alves et al. (2001) suggests that the dust opacity law adopted by the HGBS consortium, with κ300 μm = 0.1 cm2 per g (of gas + dust) at λ = 300μm and β = 2, is more accurate than (and possibly overestimated by) 50% in the 160–500 μm range. This value is for sources of (column) densities that are comparable to B68 and L1689B. Our adopted opacity value is within ~20% of the value6 obtained by Suutarinen et al. (2013) for the dust inside a core of similar column density to the ones considered here. Assuming that the weak trend between submillimeter dust opacity and column density (κλ ∝ NH20.28) found by Roy et al. (2013) at AV ≲ 10 also holds at higher AV, we argue that the HGBS dust opacity law may remain valid to within 50% accuracy in the whole range of H2 column densities between ~3 × 1021 cm-2 and ~1023 cm-2.
Since the Abel transformation technique can help us correct the effect of LOS temperature variations on the derivation of total masses, we conclude that the Herschel data of the HGBS project holds the promise of delivering core masses to accuracy more than factor of 1.5 to 2, at least for spatially-resolved cores.
Online material
Appendix A: Surface brightness profiles and the outer radius of B68
The top panel of Fig. A.1 shows the circularly
averaged intensity profiles of the B68 core at SPIRE and PACS wavelengths, which were
used to construct the column density and temperature profiles shown in Fig. 2. The bottom panel of Fig. A.1 shows the logarithmic slope of the column density profile (black
line), which is defined as s ≡ d ln NH2/d ln r
(dimensionless), as a function of radius. The measured logarithmic slope is
s = 0
near the core center due to flat inner density profile and the finite resolution of the
observations. The logarithmic slope profile reaches a minimum value smin ~ −1.5
at r ~ 104 AU and goes back to
s ~ 0 at
the outer boundary, where the core merges with a slowly-varying background. For
comparison, a spherical core with outer density profile ρ ∝ r-2 would have
s = −1
at large radii. In the same plot, we show the logarithmic slope of the 500
μm
surface brightness profile (blue line), which has a shallower slope due to the
additional effect of the positive outward temperature gradient. Inspection of the
intensity and slope profiles shown in Fig. A.1
allows us to select an appropriate upper integration radius in the right-hand side of
Eq. (2) when the density and temperature
structure of B68 (see Sect. 3) are reconstructed.
Since 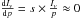 beyond a radius
~25 000 AU, larger radii
do not contribute to the integral of Eq. (2). In practice, we adopt an upper integration radius Rup = 37 500
AU for B68, as shown by the dashed vertical line in Fig. A.1. The reconstruction results, however, are insensitive to the precise
choice of Rup as long as Rup ≳ 25 000
AU. The adjacent dot-dashed vertical line shows the effective radius of ~27 000 AU (or ~200″), as derived by the
getsources source-finding algorithm for the “footprint” of B68. The
getsources algorithm (Men’shchikov et
al. 2012) is the source extraction method used by the HGBS consortium to
produce the first-generation catalogs of dense cores found by Herschel
in the regions covered by the HGBS survey. The footprint of a core corresponds
to the area just outside, of which getsources estimates the local
background emission and over which it integrates the background-subtracted emission to
derive the total flux densities of the core. In the case of B68, the results
automatically derived by getsources are in excellent agreement with
those obtained through a detailed radial profile analysis (cf. Fig. A.1).
beyond a radius
~25 000 AU, larger radii
do not contribute to the integral of Eq. (2). In practice, we adopt an upper integration radius Rup = 37 500
AU for B68, as shown by the dashed vertical line in Fig. A.1. The reconstruction results, however, are insensitive to the precise
choice of Rup as long as Rup ≳ 25 000
AU. The adjacent dot-dashed vertical line shows the effective radius of ~27 000 AU (or ~200″), as derived by the
getsources source-finding algorithm for the “footprint” of B68. The
getsources algorithm (Men’shchikov et
al. 2012) is the source extraction method used by the HGBS consortium to
produce the first-generation catalogs of dense cores found by Herschel
in the regions covered by the HGBS survey. The footprint of a core corresponds
to the area just outside, of which getsources estimates the local
background emission and over which it integrates the background-subtracted emission to
derive the total flux densities of the core. In the case of B68, the results
automatically derived by getsources are in excellent agreement with
those obtained through a detailed radial profile analysis (cf. Fig. A.1).
 |
Fig. A.1 a) Circularly averaged radial surface brightness profiles of B68 at 70, 160, 250, 350, 500 μm derived from Herschel/SPIRE and PACS data (after adding Planck offsets). b) Logarithmic slopes of the circularly averaged column density profile (solid black curve) and 500 μm intensity profile (solid blue curve) of B68 as a function of radius. The horizontal dotted line is the logarithmic slope s = −1 expected for the column density profile of a core with a ρ ∝ r-2 density profile. The vertical dashed line marks the integration upper bound adopted when integrating the right-hand side of Eq. (2) to perform the Abel reconstruction of the density and temperature profiles (see Sect. 3). The vertical dot-dashed line shows the radius of the footprint automatically derived for B68 by the getsources source-finding algorithm. |
Appendix B: Tests of the Abel inversion method using simple models
Appendix B.1: Spherically symmetric core model
To test the performance level of our Abel inversion scheme and quantify the
robustness of the reconstruction, we applied the algorithm as described in Sect. 3 to synthetic images corresponding to model starless
cores of known density and temperature distributions. First, we considered a
spherically-symmetric core model with a Plummer-type density distribution for
r ≤ Rout,
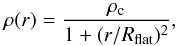 (B.1)which is
parameterized by physical parameters that are approximately similar to the derived
properties of B68 (see Sect. 4.1): central
H2 number
density nc ≡ ρc/μH2mH = 8 × 104
cm-3, flat
inner radius Rflat= 5 × 103 AU, and outer
radius Rout = 1.5 × 104 AU. The
surface density profile of such a model core has an analytical form of
(B.1)which is
parameterized by physical parameters that are approximately similar to the derived
properties of B68 (see Sect. 4.1): central
H2 number
density nc ≡ ρc/μH2mH = 8 × 104
cm-3, flat
inner radius Rflat= 5 × 103 AU, and outer
radius Rout = 1.5 × 104 AU. The
surface density profile of such a model core has an analytical form of
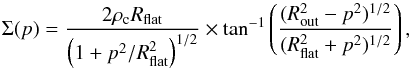 (B.2)where p represents the impact
parameter from core center in the plane of the sky and NH2(p) = Σ(p)/μH2mH
is the H2
column density profile. The intrinsic density profile of the model is shown as a black
solid curve in Fig. B.1a and the corresponding
column density profile as a black solid curve in Fig. B.1b. The synthetic dust temperature profile is shown as a black solid curve
in Fig. B.1c and was obtained for a
solar-neighborhood ISRF (G0 = 1) using an analytic
approximation formula that reproduces a grid of spherically symmetric models performed
with the dust radiative transfer code MODUST (Bouwman et al., in prep.; see Bouwman et al. 2001; and André et al. 2003).
(B.2)where p represents the impact
parameter from core center in the plane of the sky and NH2(p) = Σ(p)/μH2mH
is the H2
column density profile. The intrinsic density profile of the model is shown as a black
solid curve in Fig. B.1a and the corresponding
column density profile as a black solid curve in Fig. B.1b. The synthetic dust temperature profile is shown as a black solid curve
in Fig. B.1c and was obtained for a
solar-neighborhood ISRF (G0 = 1) using an analytic
approximation formula that reproduces a grid of spherically symmetric models performed
with the dust radiative transfer code MODUST (Bouwman et al., in prep.; see Bouwman et al. 2001; and André et al. 2003).
 |
Fig. B.1 Comparison between intrinsic (black curves) and reconstructed (red and blue
curves) volume density a), column density b), and dust
temperature c) profiles for a spherically symmetric core model with
a Plummer-like density distribution (see Eq. (B.1) and text for model parameters). The cross symbols show
the results obtained by applying the Abel reconstruction scheme on the synthetic
160–500 μm intensity profiles with “infinite”
resolution. The red and blue curves show the reconstruction results obtained
from synthetic emission maps smoothed to HPBW resolutions of
36 |
A set of synthetic emission maps was created by line-of-sight integration of this
model core at all Herschel wavelengths, assuming optically thin
dust emission (see Eq. (1)) and the
same dust opacity law as given in Sect. 3.1. The
density and temperature profiles of the model core were then reconstructed as
described in Sect. 3 from the circularly averaged
radial intensity profiles of the model emission. The cross symbols overlaid on the
model density, column density, and temperature profiles in Fig. B.1a–c show the Abel-reconstructed profiles that would be obtained
with “infinite” angular resolution (and in the absence of noise). It can be seen in
Fig. B.1 that, the reconstruction is perfect in
this case, demonstrating the validity of our Abel-inversion code. The overplotted red
curves in Fig. B.1a–c show the reconstructed
volume density, column density, and temperature profiles that result from the
Abel-inversion method after convolution of the model images to a common resolution of
36 3. This
corresponds to the Herschel resolution at 500 μm. Likewise, the
overplotted blue curves in Fig. B.1a–c show the
results obtained at a resolution of 24
3. This
corresponds to the Herschel resolution at 500 μm. Likewise, the
overplotted blue curves in Fig. B.1a–c show the
results obtained at a resolution of 24 9 using the
synthetic data convolved to the Herschel resolution at 350
μm and
ignoring the 500 μm data. It can be seen that the profiles
reconstructed at the Herschel resolution remain in excellent (1%)
agreement with the intrinsic profiles in the outer part of the core. Although the
reconstruction becomes somewhat inaccurate below the Herschel
resolution limit (marked by vertical dotted lines in Fig. B.1), the reconstructed column density and
temperature profiles still agree with the corresponding intrinsic profiles to within
20% and 9%, respectively, at 500 μm resolution. The accuracy of the results at
small radii improves to 11% and 5% when the reconstruction is performed at 350
μm
resolution. (Although in the presence of noise with real data, the statistical
measurement uncertainties are somewhat larger at 350 μm resolution.) At both
resolutions, the Abel-reconstructed temperature and column density profiles coincide
within 1% with the corresponding intrinsic profiles that are convolved
with the effective beam resolution. The reconstructed central temperature and
column density thus provide excellent estimates of the beam-averaged central
temperature and column density in the model. The total mass that is estimated by
integrating the reconstructed column density profile agrees with the model mass more
accurate than 0.1% even at 500 μm resolution.
9 using the
synthetic data convolved to the Herschel resolution at 350
μm and
ignoring the 500 μm data. It can be seen that the profiles
reconstructed at the Herschel resolution remain in excellent (1%)
agreement with the intrinsic profiles in the outer part of the core. Although the
reconstruction becomes somewhat inaccurate below the Herschel
resolution limit (marked by vertical dotted lines in Fig. B.1), the reconstructed column density and
temperature profiles still agree with the corresponding intrinsic profiles to within
20% and 9%, respectively, at 500 μm resolution. The accuracy of the results at
small radii improves to 11% and 5% when the reconstruction is performed at 350
μm
resolution. (Although in the presence of noise with real data, the statistical
measurement uncertainties are somewhat larger at 350 μm resolution.) At both
resolutions, the Abel-reconstructed temperature and column density profiles coincide
within 1% with the corresponding intrinsic profiles that are convolved
with the effective beam resolution. The reconstructed central temperature and
column density thus provide excellent estimates of the beam-averaged central
temperature and column density in the model. The total mass that is estimated by
integrating the reconstructed column density profile agrees with the model mass more
accurate than 0.1% even at 500 μm resolution.
 |
Fig. B.2 a) Synthetic column density image of a prolate ellipsoidal core
model with an aspect ratio of 1.3 and a Plummer-like density distribution (see
Eq. (B.4) and the text for model
parameters). The horizontal dotted line shows the axis of symmetry in the plane
of sky, and the contour levels are the same as in Fig. 3. b) Comparison between the intrinsic (solid
curves) and the reconstructed (crosses) column density profiles of the model.
c) Comparison between the intrinsic (solid curves) and the
reconstructed (crosses) dust temperature profiles of the model. The blue and red
curves represent the intrinsic radial profiles along and perpendicular to the
axis of symmetry, respectively. The green curves represent the intrinsic
circularly averaged radial profiles. The blue and red crosses display the
results of the Abel-inversion method applied to the synthetic 160–500
μm intensity profiles of the model, which are
convolved to 36 |
We also assessed the contribution of background fluctuations and calibration errors
to the uncertainties in the derived parameters (NH2and Td). To do
so, we considered 500 realizations of synthetic skies, which included a random
Gaussian noise component7, σν, and a random
multiplicative calibration factor, (1 + g):
, \end{equation}](/articles/aa/full_html/2014/02/aa22236-13/aa22236-13-eq149.png) (B.3)where
g is a
Gaussian random number with a mean zero and standard deviation of 10% and 15% at SPIRE
and PACS wavelengths, respectively. (We assumed 100% correlated calibration errors at
SPIRE wavelengths and an independent calibration error in the PACS 160 μm band.) The net
uncertainties in nH2, NH2, and Td were
estimated to be 15%, 12%, and 5%, respectively. The resulting 1σ errors in the derived
parameters are displayed in Fig. B.1.
(B.3)where
g is a
Gaussian random number with a mean zero and standard deviation of 10% and 15% at SPIRE
and PACS wavelengths, respectively. (We assumed 100% correlated calibration errors at
SPIRE wavelengths and an independent calibration error in the PACS 160 μm band.) The net
uncertainties in nH2, NH2, and Td were
estimated to be 15%, 12%, and 5%, respectively. The resulting 1σ errors in the derived
parameters are displayed in Fig. B.1.
Appendix B.2: Ellipsoidal core model
As real cores, such as L1689B, are often elongated and thus not strictly spherically
symmetric (see Sect. 4.2), we also tested the
reliability of our Abel inversion scheme using a simple non-spherical model with an
ellipsoidal Plummer-like density distribution for r ≤ Rout and
z ≤ Zout with
cylindrical symmetry about the z axis (assumed to lie in the plane of the
sky): 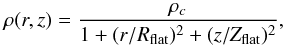 (B.4)where Rflat and
Zflat are the radii of the flat inner
core region perpendicular and parallel to the z axis of symmetry (see
Fig. B.2a), respectively. We considered both the
prolate (Zflat > Rflat)
and the oblate (Zflat<Rflat)
configuration but are primarily describing the prolate case here, as it is more likely
for cores embedded within filaments such as L1689B (see Fig. 3). The synthetic temperature distribution was also assumed to be
cylindrically symmetric about the z axis and was constructed using the same grid
of MODUST radiative transfer models as in Appendix B.1. The synthetic temperature profiles along both the z axis and the radial
(r)
direction are shown in Fig. B.2. For direct
comparison
(B.4)where Rflat and
Zflat are the radii of the flat inner
core region perpendicular and parallel to the z axis of symmetry (see
Fig. B.2a), respectively. We considered both the
prolate (Zflat > Rflat)
and the oblate (Zflat<Rflat)
configuration but are primarily describing the prolate case here, as it is more likely
for cores embedded within filaments such as L1689B (see Fig. 3). The synthetic temperature distribution was also assumed to be
cylindrically symmetric about the z axis and was constructed using the same grid
of MODUST radiative transfer models as in Appendix B.1. The synthetic temperature profiles along both the z axis and the radial
(r)
direction are shown in Fig. B.2. For direct
comparison
with L1689B (see Figs. 3 and B.2a), we adopted physical parameters approximately consistent with the observed characteristics of the L1689B core (see Sect. 4.2): central H2 number density nc = 2 × 105 cm-3; aspect ratio Zflat/Rflat = Zout/Rout = 1.3; flat inner radius along the minor axis Rflat = 4000 AU; and outer radius along the minor axis Rout = 6.7 × Rflat = 26 800 AU.
Because of the lack of spherical symmetry, we applied our Abel reconstruction scheme to three sets of intensity profiles: 1) the profiles measured along the major axis of the model (intrinsic profiles shown as blue curves and results as blue crosses in Fig. B.2); 2) the profiles measured along the minor axis of the model (intrinsic profiles shown as red curves and results as red crosses in Fig. B.2); and 3) circularly averaged intensity profiles (intrinsic profiles shown as green curves and results as green crosses in Fig. B.2). Here, again, it can be seen that the reconstruction results are very satisfactory (2% agreement) beyond the beam radius (marked by the vertical dotted line in Fig. B.2). The reconstruction performed perpendicular to the axis of symmetry, i.e., along the minor axis for a prolate core, is more accurate (1%) than the reconstruction performed along the axis of symmetry (4%). In particular, the best estimate of the central dust temperature is obtained from the reconstruction performed along the minor axis. The reconstruction along the major axis nevertheless provides better estimates of the column density and temperature at large radii along the major axis. The central column density reconstructed at 500 μm resolution slightly underestimates but still agrees to within 20% with the true column density at core center. The best estimate of the total core mass, as obtained by using the results of the reconstruction performed on the circularly averaged intensity profiles, agrees more accurate than 4% with the model core mass. Even for a more elongated core model with an aspect ratio of 2 (instead of 1.3), the reconstructed core mass still agrees with the model mass to within 5%.
We also performed similar simulations for an oblate core model observed edge-on. The accuracy of the reconstruction results was found to be essentially the same as for the prolate case. Again, the reconstruction performed perpendicular to the axis of symmetry, i.e., along the major axis in this case, was found to be more accurate than the reconstruction performed along the axis of symmetry. The best estimate of the total core mass was again obtained from reconstructing the circularly averaged intensity profiles.
A more detailed description about the observations and data reductions are available on the HGBS archives webpage: http://gouldbelt-herschel.cea.fr/archives. The reduced SPIRE/PACS maps for B68 and L1689B as well as the column density and temperature maps can also be retrieved from the same website.
Note the dust-to-gas fraction of 1% is implicitly included in our definition of the dust opacity (see also Sect. 3.1) so that ρ(r) represents the radial gas density of the object.
Note that this differs from the first HGBS papers (e.g. André et al. 2010; Könyves et al. 2010; Arzoumanian et al. 2011), where μ = 2.33 was assumed and column density was expressed in units of mean free particles per cm2.
The ISRF energy is mostly absorbed at short wavelengths (0.095 μm to 100 μm). In calculating the absorbed energy we adopted the dust absorption model of Draine (2003) with RV = 3.1.
Suutarinen et al. 2013 quote κ250 μm = 0.08 cm2 g-1 with β = 2 and argue that this value is underestimated by 40% inside the core due to temperature variations along the LOS.
Acknowledgments
This work has benefited from the support of the CNES and the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013 – ERC Grant Agreement no. 291294). P.P. acknowledges funding by the Fundação para a Ciência e a Tecnologia (Portugal). SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC (UK); and NASA (USA). PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KUL, CSL, IMEC (Belgium); CEA, OAMP (France); MPIA (Germany); IFSI, OAP/AOT, OAA/CAISMI, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI (Italy), and CICT/MCT (Spain).
References
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- André, P., Ward-Thompson, D., & Motte, F. 1996, A&A, 314, 625 [NASA ADS] [Google Scholar]
- André, P., Bouwman, J., Belloche, A., & Hennebelle, P. 2003, in Proc. SFChem 2002: Chemistry as a Diagnostic of Star Formation, eds. C. L. Curry, & M. Fich (Ottawa: NRC Press), 127 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bracewell, R. N. 1986, The Fourier Transform and its applications, 2nd edn. (New York: McGraw-Hill) [Google Scholar]
- de Geus, E. J., de Zeeuw, P. T., & Lub, J. 1989, A&A, 216, 44 [NASA ADS] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, J. M., Ward-Thompson, D., & André, P. 2005, MNRAS, 360, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehtinen, K., Lemke, D., Mattila, K., & Haikala, L. K. 1998, A&A, 333, 702 [NASA ADS] [Google Scholar]
- Liseau, R., White, G. J., Larsson, B., et al. 1999, A&A, 344, 342 [NASA ADS] [Google Scholar]
- Malinen, J., Juvela, M., Collins, D. C., Lunttila, T., & Padoan, P. 2011, A&A, 530, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, K. A., Griffin, M. J., André, P., et al. 2014, MNRAS, submitted [arXiv:1401.7871] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2012, A&A, 542, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nielbock, M., Launhardt, R., Steinacker, J., et al. 2012, A&A, 547, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H. 2012, PASP, 125, 1126 [Google Scholar]
- Roy, A., Martin, P. G., Polychroni, D., et al. 2013, ApJ, 763, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., Whitworth, A. P., & Ward-Thompson, D. 2007, MNRAS, 379, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Suutarinen, A., Haikala, L. K., Harju, J., et al. 2013, A&A, 555, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward-Thompson, D., André, P., & Kirk, J. M. 2002, MNRAS, 329, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Ysard, N., Juvela, M., Demyk, K., et al. 2012, A&A, 542, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Column density map (left) and LOS dust temperature map (right) of B68, which is derived by fitting modified blackbody SEDs to the Herschel data between 160 μm and 500 μm on a pixel-by-pixel basis (see Sect. 3.1 for details). The column density contours go from 1.6×1021 to 9.6×1022 in steps of 1.6 × 1021 in units of H2 molecules per cm2 (left), and the temperature contours are 16, 15, 14, and 13 K (right). The cross symbol shows the center of the core obtained by fitting a 2D-Gaussian to the column density map. |
| In the text | |
 |
Fig. 2 Column density a) and dust temperature b) profiles of B68
obtained at 500 μm resolution by applying the Abel inversion
method to the circularly averaged intensity profiles observed with Herschel
between 160 μm and 500 μm. a)
Comparison between the column density profiles derived from the Abel reconstruction
(solid black line) and LOS-averaged SED fitting (thick dashed line). The red curve
shows the best-fit Bonnor-Ebert model to the Abel-inverted profile (see Table 2 for parameters). The vertical dotted line
represents the half power beam radius of 36 |
| In the text | |
 |
Fig. 3 Same as Fig. 1 but for L1689B. The column density contours are 6 × 1021, 1 × 1022, 1.4 × 1022, 1.8 × 1022, and 2.6 × 1022 H2 cm-2 (left), and the temperature contours are 16.5, 15.5, 14.5, and 13.5 K (right). The column density image shows that L1689B is embedded inside a filamentary structure. |
| In the text | |
 |
Fig. 4 a) Column density profile of L1689B obtained at 500 μm resolution by applying the Abel reconstruction method to the circularly averaged intensity profiles between 160 μm and 500 μm (solid black curve). The dash-dotted blue and green profiles show the column density profiles obtained from reconstructing the intensity profiles observed along EW and NS sectors, respectively. The overplotted solid red line shows the best-fit Bonnor-Ebert model (see Table 2 for parameters). The vertical dotted line is same as in Fig. 2. b) Reconstructed dust temperature profile of L1689B (solid curve) compared with the LOS-averaged temperature profile derived from simple SED fitting (thick dashed curve). |
| In the text | |
 |
Fig. A.1 a) Circularly averaged radial surface brightness profiles of B68 at 70, 160, 250, 350, 500 μm derived from Herschel/SPIRE and PACS data (after adding Planck offsets). b) Logarithmic slopes of the circularly averaged column density profile (solid black curve) and 500 μm intensity profile (solid blue curve) of B68 as a function of radius. The horizontal dotted line is the logarithmic slope s = −1 expected for the column density profile of a core with a ρ ∝ r-2 density profile. The vertical dashed line marks the integration upper bound adopted when integrating the right-hand side of Eq. (2) to perform the Abel reconstruction of the density and temperature profiles (see Sect. 3). The vertical dot-dashed line shows the radius of the footprint automatically derived for B68 by the getsources source-finding algorithm. |
| In the text | |
 |
Fig. B.1 Comparison between intrinsic (black curves) and reconstructed (red and blue
curves) volume density a), column density b), and dust
temperature c) profiles for a spherically symmetric core model with
a Plummer-like density distribution (see Eq. (B.1) and text for model parameters). The cross symbols show
the results obtained by applying the Abel reconstruction scheme on the synthetic
160–500 μm intensity profiles with “infinite”
resolution. The red and blue curves show the reconstruction results obtained
from synthetic emission maps smoothed to HPBW resolutions of
36 |
| In the text | |
 |
Fig. B.2 a) Synthetic column density image of a prolate ellipsoidal core
model with an aspect ratio of 1.3 and a Plummer-like density distribution (see
Eq. (B.4) and the text for model
parameters). The horizontal dotted line shows the axis of symmetry in the plane
of sky, and the contour levels are the same as in Fig. 3. b) Comparison between the intrinsic (solid
curves) and the reconstructed (crosses) column density profiles of the model.
c) Comparison between the intrinsic (solid curves) and the
reconstructed (crosses) dust temperature profiles of the model. The blue and red
curves represent the intrinsic radial profiles along and perpendicular to the
axis of symmetry, respectively. The green curves represent the intrinsic
circularly averaged radial profiles. The blue and red crosses display the
results of the Abel-inversion method applied to the synthetic 160–500
μm intensity profiles of the model, which are
convolved to 36 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.