| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322236 | |
| Published online | 21 February 2014 | |
Online material
Appendix A: Surface brightness profiles and the outer radius of B68
The top panel of Fig. A.1 shows the circularly
averaged intensity profiles of the B68 core at SPIRE and PACS wavelengths, which were
used to construct the column density and temperature profiles shown in Fig. 2. The bottom panel of Fig. A.1 shows the logarithmic slope of the column density profile (black
line), which is defined as s ≡ d ln NH2/d ln r
(dimensionless), as a function of radius. The measured logarithmic slope is
s = 0
near the core center due to flat inner density profile and the finite resolution of the
observations. The logarithmic slope profile reaches a minimum value smin ~ −1.5
at r ~ 104 AU and goes back to
s ~ 0 at
the outer boundary, where the core merges with a slowly-varying background. For
comparison, a spherical core with outer density profile ρ ∝ r-2 would have
s = −1
at large radii. In the same plot, we show the logarithmic slope of the 500
μm
surface brightness profile (blue line), which has a shallower slope due to the
additional effect of the positive outward temperature gradient. Inspection of the
intensity and slope profiles shown in Fig. A.1
allows us to select an appropriate upper integration radius in the right-hand side of
Eq. (2) when the density and temperature
structure of B68 (see Sect. 3) are reconstructed.
Since 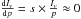 beyond a radius
~25 000 AU, larger radii
do not contribute to the integral of Eq. (2). In practice, we adopt an upper integration radius Rup = 37 500
AU for B68, as shown by the dashed vertical line in Fig. A.1. The reconstruction results, however, are insensitive to the precise
choice of Rup as long as Rup ≳ 25 000
AU. The adjacent dot-dashed vertical line shows the effective radius of ~27 000 AU (or ~200″), as derived by the
getsources source-finding algorithm for the “footprint” of B68. The
getsources algorithm (Men’shchikov et
al. 2012) is the source extraction method used by the HGBS consortium to
produce the first-generation catalogs of dense cores found by Herschel
in the regions covered by the HGBS survey. The footprint of a core corresponds
to the area just outside, of which getsources estimates the local
background emission and over which it integrates the background-subtracted emission to
derive the total flux densities of the core. In the case of B68, the results
automatically derived by getsources are in excellent agreement with
those obtained through a detailed radial profile analysis (cf. Fig. A.1).
beyond a radius
~25 000 AU, larger radii
do not contribute to the integral of Eq. (2). In practice, we adopt an upper integration radius Rup = 37 500
AU for B68, as shown by the dashed vertical line in Fig. A.1. The reconstruction results, however, are insensitive to the precise
choice of Rup as long as Rup ≳ 25 000
AU. The adjacent dot-dashed vertical line shows the effective radius of ~27 000 AU (or ~200″), as derived by the
getsources source-finding algorithm for the “footprint” of B68. The
getsources algorithm (Men’shchikov et
al. 2012) is the source extraction method used by the HGBS consortium to
produce the first-generation catalogs of dense cores found by Herschel
in the regions covered by the HGBS survey. The footprint of a core corresponds
to the area just outside, of which getsources estimates the local
background emission and over which it integrates the background-subtracted emission to
derive the total flux densities of the core. In the case of B68, the results
automatically derived by getsources are in excellent agreement with
those obtained through a detailed radial profile analysis (cf. Fig. A.1).
 |
Fig. A.1
a) Circularly averaged radial surface brightness profiles of B68 at 70, 160, 250, 350, 500 μm derived from Herschel/SPIRE and PACS data (after adding Planck offsets). b) Logarithmic slopes of the circularly averaged column density profile (solid black curve) and 500 μm intensity profile (solid blue curve) of B68 as a function of radius. The horizontal dotted line is the logarithmic slope s = −1 expected for the column density profile of a core with a ρ ∝ r-2 density profile. The vertical dashed line marks the integration upper bound adopted when integrating the right-hand side of Eq. (2) to perform the Abel reconstruction of the density and temperature profiles (see Sect. 3). The vertical dot-dashed line shows the radius of the footprint automatically derived for B68 by the getsources source-finding algorithm. |
| Open with DEXTER | |
Appendix B: Tests of the Abel inversion method using simple models
Appendix B.1: Spherically symmetric core model
To test the performance level of our Abel inversion scheme and quantify the
robustness of the reconstruction, we applied the algorithm as described in Sect. 3 to synthetic images corresponding to model starless
cores of known density and temperature distributions. First, we considered a
spherically-symmetric core model with a Plummer-type density distribution for
r ≤ Rout,
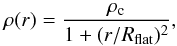 (B.1)which is
parameterized by physical parameters that are approximately similar to the derived
properties of B68 (see Sect. 4.1): central
H2 number
density nc ≡ ρc/μH2mH = 8 × 104
cm-3, flat
inner radius Rflat= 5 × 103 AU, and outer
radius Rout = 1.5 × 104 AU. The
surface density profile of such a model core has an analytical form of
(B.1)which is
parameterized by physical parameters that are approximately similar to the derived
properties of B68 (see Sect. 4.1): central
H2 number
density nc ≡ ρc/μH2mH = 8 × 104
cm-3, flat
inner radius Rflat= 5 × 103 AU, and outer
radius Rout = 1.5 × 104 AU. The
surface density profile of such a model core has an analytical form of
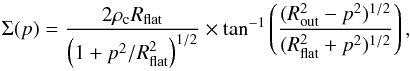 (B.2)where p represents the impact
parameter from core center in the plane of the sky and NH2(p) = Σ(p)/μH2mH
is the H2
column density profile. The intrinsic density profile of the model is shown as a black
solid curve in Fig. B.1a and the corresponding
column density profile as a black solid curve in Fig. B.1b. The synthetic dust temperature profile is shown as a black solid curve
in Fig. B.1c and was obtained for a
solar-neighborhood ISRF (G0 = 1) using an analytic
approximation formula that reproduces a grid of spherically symmetric models performed
with the dust radiative transfer code MODUST (Bouwman et al., in prep.; see Bouwman et al. 2001; and André et al. 2003).
(B.2)where p represents the impact
parameter from core center in the plane of the sky and NH2(p) = Σ(p)/μH2mH
is the H2
column density profile. The intrinsic density profile of the model is shown as a black
solid curve in Fig. B.1a and the corresponding
column density profile as a black solid curve in Fig. B.1b. The synthetic dust temperature profile is shown as a black solid curve
in Fig. B.1c and was obtained for a
solar-neighborhood ISRF (G0 = 1) using an analytic
approximation formula that reproduces a grid of spherically symmetric models performed
with the dust radiative transfer code MODUST (Bouwman et al., in prep.; see Bouwman et al. 2001; and André et al. 2003).
 |
Fig. B.1
Comparison between intrinsic (black curves) and reconstructed (red and blue
curves) volume density a), column density b), and dust
temperature c) profiles for a spherically symmetric core model with
a Plummer-like density distribution (see Eq. (B.1) and text for model parameters). The cross symbols show
the results obtained by applying the Abel reconstruction scheme on the synthetic
160–500 μm intensity profiles with “infinite”
resolution. The red and blue curves show the reconstruction results obtained
from synthetic emission maps smoothed to HPBW resolutions of
36 |
| Open with DEXTER | |
A set of synthetic emission maps was created by line-of-sight integration of this
model core at all Herschel wavelengths, assuming optically thin
dust emission (see Eq. (1)) and the
same dust opacity law as given in Sect. 3.1. The
density and temperature profiles of the model core were then reconstructed as
described in Sect. 3 from the circularly averaged
radial intensity profiles of the model emission. The cross symbols overlaid on the
model density, column density, and temperature profiles in Fig. B.1a–c show the Abel-reconstructed profiles that would be obtained
with “infinite” angular resolution (and in the absence of noise). It can be seen in
Fig. B.1 that, the reconstruction is perfect in
this case, demonstrating the validity of our Abel-inversion code. The overplotted red
curves in Fig. B.1a–c show the reconstructed
volume density, column density, and temperature profiles that result from the
Abel-inversion method after convolution of the model images to a common resolution of
36 3. This
corresponds to the Herschel resolution at 500 μm. Likewise, the
overplotted blue curves in Fig. B.1a–c show the
results obtained at a resolution of 24
3. This
corresponds to the Herschel resolution at 500 μm. Likewise, the
overplotted blue curves in Fig. B.1a–c show the
results obtained at a resolution of 24 9 using the
synthetic data convolved to the Herschel resolution at 350
μm and
ignoring the 500 μm data. It can be seen that the profiles
reconstructed at the Herschel resolution remain in excellent (1%)
agreement with the intrinsic profiles in the outer part of the core. Although the
reconstruction becomes somewhat inaccurate below the Herschel
resolution limit (marked by vertical dotted lines in Fig. B.1), the reconstructed column density and
temperature profiles still agree with the corresponding intrinsic profiles to within
20% and 9%, respectively, at 500 μm resolution. The accuracy of the results at
small radii improves to 11% and 5% when the reconstruction is performed at 350
μm
resolution. (Although in the presence of noise with real data, the statistical
measurement uncertainties are somewhat larger at 350 μm resolution.) At both
resolutions, the Abel-reconstructed temperature and column density profiles coincide
within 1% with the corresponding intrinsic profiles that are convolved
with the effective beam resolution. The reconstructed central temperature and
column density thus provide excellent estimates of the beam-averaged central
temperature and column density in the model. The total mass that is estimated by
integrating the reconstructed column density profile agrees with the model mass more
accurate than 0.1% even at 500 μm resolution.
9 using the
synthetic data convolved to the Herschel resolution at 350
μm and
ignoring the 500 μm data. It can be seen that the profiles
reconstructed at the Herschel resolution remain in excellent (1%)
agreement with the intrinsic profiles in the outer part of the core. Although the
reconstruction becomes somewhat inaccurate below the Herschel
resolution limit (marked by vertical dotted lines in Fig. B.1), the reconstructed column density and
temperature profiles still agree with the corresponding intrinsic profiles to within
20% and 9%, respectively, at 500 μm resolution. The accuracy of the results at
small radii improves to 11% and 5% when the reconstruction is performed at 350
μm
resolution. (Although in the presence of noise with real data, the statistical
measurement uncertainties are somewhat larger at 350 μm resolution.) At both
resolutions, the Abel-reconstructed temperature and column density profiles coincide
within 1% with the corresponding intrinsic profiles that are convolved
with the effective beam resolution. The reconstructed central temperature and
column density thus provide excellent estimates of the beam-averaged central
temperature and column density in the model. The total mass that is estimated by
integrating the reconstructed column density profile agrees with the model mass more
accurate than 0.1% even at 500 μm resolution.
 |
Fig. B.2
a) Synthetic column density image of a prolate ellipsoidal core
model with an aspect ratio of 1.3 and a Plummer-like density distribution (see
Eq. (B.4) and the text for model
parameters). The horizontal dotted line shows the axis of symmetry in the plane
of sky, and the contour levels are the same as in Fig. 3. b) Comparison between the intrinsic (solid
curves) and the reconstructed (crosses) column density profiles of the model.
c) Comparison between the intrinsic (solid curves) and the
reconstructed (crosses) dust temperature profiles of the model. The blue and red
curves represent the intrinsic radial profiles along and perpendicular to the
axis of symmetry, respectively. The green curves represent the intrinsic
circularly averaged radial profiles. The blue and red crosses display the
results of the Abel-inversion method applied to the synthetic 160–500
μm intensity profiles of the model, which are
convolved to 36 |
| Open with DEXTER | |
We also assessed the contribution of background fluctuations and calibration errors
to the uncertainties in the derived parameters (NH2and Td). To do
so, we considered 500 realizations of synthetic skies, which included a random
Gaussian noise component7, σν, and a random
multiplicative calibration factor, (1 + g):
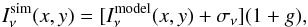 (B.3)where
g is a
Gaussian random number with a mean zero and standard deviation of 10% and 15% at SPIRE
and PACS wavelengths, respectively. (We assumed 100% correlated calibration errors at
SPIRE wavelengths and an independent calibration error in the PACS 160 μm band.) The net
uncertainties in nH2, NH2, and Td were
estimated to be 15%, 12%, and 5%, respectively. The resulting 1σ errors in the derived
parameters are displayed in Fig. B.1.
(B.3)where
g is a
Gaussian random number with a mean zero and standard deviation of 10% and 15% at SPIRE
and PACS wavelengths, respectively. (We assumed 100% correlated calibration errors at
SPIRE wavelengths and an independent calibration error in the PACS 160 μm band.) The net
uncertainties in nH2, NH2, and Td were
estimated to be 15%, 12%, and 5%, respectively. The resulting 1σ errors in the derived
parameters are displayed in Fig. B.1.
Appendix B.2: Ellipsoidal core model
As real cores, such as L1689B, are often elongated and thus not strictly spherically
symmetric (see Sect. 4.2), we also tested the
reliability of our Abel inversion scheme using a simple non-spherical model with an
ellipsoidal Plummer-like density distribution for r ≤ Rout and
z ≤ Zout with
cylindrical symmetry about the z axis (assumed to lie in the plane of the
sky): 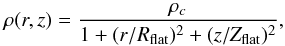 (B.4)where Rflat and
Zflat are the radii of the flat inner
core region perpendicular and parallel to the z axis of symmetry (see
Fig. B.2a), respectively. We considered both the
prolate (Zflat > Rflat)
and the oblate (Zflat<Rflat)
configuration but are primarily describing the prolate case here, as it is more likely
for cores embedded within filaments such as L1689B (see Fig. 3). The synthetic temperature distribution was also assumed to be
cylindrically symmetric about the z axis and was constructed using the same grid
of MODUST radiative transfer models as in Appendix B.1. The synthetic temperature profiles along both the z axis and the radial
(r)
direction are shown in Fig. B.2. For direct
comparison
(B.4)where Rflat and
Zflat are the radii of the flat inner
core region perpendicular and parallel to the z axis of symmetry (see
Fig. B.2a), respectively. We considered both the
prolate (Zflat > Rflat)
and the oblate (Zflat<Rflat)
configuration but are primarily describing the prolate case here, as it is more likely
for cores embedded within filaments such as L1689B (see Fig. 3). The synthetic temperature distribution was also assumed to be
cylindrically symmetric about the z axis and was constructed using the same grid
of MODUST radiative transfer models as in Appendix B.1. The synthetic temperature profiles along both the z axis and the radial
(r)
direction are shown in Fig. B.2. For direct
comparison
with L1689B (see Figs. 3 and B.2a), we adopted physical parameters approximately consistent with the observed characteristics of the L1689B core (see Sect. 4.2): central H2 number density nc = 2 × 105 cm-3; aspect ratio Zflat/Rflat = Zout/Rout = 1.3; flat inner radius along the minor axis Rflat = 4000 AU; and outer radius along the minor axis Rout = 6.7 × Rflat = 26 800 AU.
Because of the lack of spherical symmetry, we applied our Abel reconstruction scheme to three sets of intensity profiles: 1) the profiles measured along the major axis of the model (intrinsic profiles shown as blue curves and results as blue crosses in Fig. B.2); 2) the profiles measured along the minor axis of the model (intrinsic profiles shown as red curves and results as red crosses in Fig. B.2); and 3) circularly averaged intensity profiles (intrinsic profiles shown as green curves and results as green crosses in Fig. B.2). Here, again, it can be seen that the reconstruction results are very satisfactory (2% agreement) beyond the beam radius (marked by the vertical dotted line in Fig. B.2). The reconstruction performed perpendicular to the axis of symmetry, i.e., along the minor axis for a prolate core, is more accurate (1%) than the reconstruction performed along the axis of symmetry (4%). In particular, the best estimate of the central dust temperature is obtained from the reconstruction performed along the minor axis. The reconstruction along the major axis nevertheless provides better estimates of the column density and temperature at large radii along the major axis. The central column density reconstructed at 500 μm resolution slightly underestimates but still agrees to within 20% with the true column density at core center. The best estimate of the total core mass, as obtained by using the results of the reconstruction performed on the circularly averaged intensity profiles, agrees more accurate than 4% with the model core mass. Even for a more elongated core model with an aspect ratio of 2 (instead of 1.3), the reconstructed core mass still agrees with the model mass to within 5%.
We also performed similar simulations for an oblate core model observed edge-on. The accuracy of the reconstruction results was found to be essentially the same as for the prolate case. Again, the reconstruction performed perpendicular to the axis of symmetry, i.e., along the major axis in this case, was found to be more accurate than the reconstruction performed along the axis of symmetry. The best estimate of the total core mass was again obtained from reconstructing the circularly averaged intensity profiles.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


