| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322229 | |
| Published online | 23 December 2013 | |
An independent determination of Fomalhaut b’s orbit and the dynamical effects on the outer dust belt
1 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
e-mail: Herve.Beust@obs.ujf-grenoble.fr
2 Observatoire de Paris, Section de Meudon, 92195 Meudon Principal Cedex, France
3 Department of Astronomy, University of California at Berkeley, Berkeley CA 94720, USA
Received: 8 July 2013
Accepted: 13 November 2013
Context. The nearby star Fomalhaut harbors a cold, moderately eccentric (e ~ 0.1) dust belt with a sharp inner edge near 133 au. A low-mass, common proper motion companion, Fomalhaut b (Fom b), was discovered near the inner edge and was identified as a planet candidate that could account for the belt morphology. However, the most recent orbit determination based on four epochs of astrometry over eight years reveals a highly eccentric orbit (e = 0.8 ± 0.1) that appears to cross the belt in the sky plane projection.
Aims. We perform here a full orbital determination based on the available astrometric data to independently validate the orbit estimates previously presented. Adopting our values for the orbital elements and their associated uncertainties, we then study the dynamical interaction between the planet and the dust ring, to check whether the proposed disk sculpting scenario by Fom b is plausible.
Methods. We used a dedicated MCMC code to derive the statistical distributions of the orbital elements of Fom b. Then we used symplectic N-body integration to investigate the dynamics of the dust belt, as perturbed by a single planet. Different attempts were made assuming different masses for Fom b. We also performed a semi-analytical study to explain our results.
Results. Our results are in good agreement with others regarding the orbit of Fom b. We find that the orbit is highly eccentric, is close to apsidally aligned with the belt, and has a mutual inclination relative to the belt plane of <29° (67% confidence). If coplanar, this orbit crosses the disk. Our dynamical study then reveals that the observed planet could sculpt a transient belt configuration with a similar eccentricity to what is observed, but it would not be simultaneously apsidally aligned with the planet. This transient configuration only occurs a short time after the planet is placed on such an orbit (assuming an initially circular disk), a time that is inversely proportional to the planet’s mass, and that is in any case much less than the 440 Myr age of the star.
Conclusions. We constrain how long the observed dust belt could have survived with Fom b on its current orbit, as a function of its possible mass. This analysis leads us to conclude that Fom b is likely to have low mass, that it is unlikely to be responsible for the sculpting of the belt, and that it supports the hypothesis of a more massive, less eccentric planet companion Fomalhaut c.
Key words: planetary systems / stars: individual: Fomalhaut / methods: numerical / celestial mechanics / planets and satellites: dynamical evolution and stability / planet-disk interactions
© ESO, 2013
1. Introduction
The presence of circumstellar dust orbiting the nearby (d = 7.7 pc; Mamajek 2012; van Leeuwen 2007) A3V star Fomalhaut (αPsa, HD 216956, HIP 113368) has been known for a long time through its thermal emission (Aumann 1985). The spatial structure of its debris disk was furthermore specified by direct imaging (Holland et al. 2003; Kalas et al. 2005). Hubble Space Telescope (HST) coronographic images by Kalas et al. (2005) have revealed a large dust belt in optical scattered light, extending between 133 au and 158 au and modeled as a moderately eccentric ring (e = 0.11 ± 0.1) with a 13.4 ± 1.0 au offset between its center and the star. The investigators suggest that an undetected planet could account for these features, as supported by numerical (Deller & Maddison 2005) and semi-analytic studies (Quillen 2006).
Kalas et al. (2008) then reported the detection of a planet candidate (subsequently termed Fomalhaut b, hereafter Fom b) orbiting the star at 119 au, only 18 au inside the dust belt, thus strongly supporting its putative shepherding role for the inner edge of the belt. The optical detections of Fom b with HST/ACS were confirmed by two independent analyses of the data (Currie et al. 2012; Galicher et al. 2013). Since Fom b was not detected at infrared wavelengths (Kalas et al. 2008; Marengo et al. 2009; Janson et al. 2012), it has been suggested that Fom b could represent starlight reflected from dust grains, possibly bound to a planet in the form of a large planetary ring (Kalas et al. 2008) or a cloud due to the collisional erosion of irregular planetary satellites (Kennedy & Wyatt 2011).
The mass and orbit of Fom b continues to require better constraints. An accurate knowledge of these parameters would clearly help define its interaction with the dust ring orbiting Fomalhaut. It is not possible to constrain Fom b’s mass (hereafter m) from photometry because the emission detected is likely dominated by the circumplanetary dust scattering. Dynamical modeling of its interaction with its environment is therefore a valuable way to derive constraints. Kalas et al. (2008) give a conservative upper limit m < 3 Jupiter masses (hereafter MJup), while Chiang et al. (2009) reduce it to possibly 0.5 MJup, under the assumption that the planet is responsible for the sculpting of the dust ring. Based on photometric estimates, Currie et al. (2012) claim m < 2 MJup, but other recent studies (dynamical or photometric) suggest a possibly much lower mass in the super-Earth regime (Janson et al. 2012; Kennedy & Wyatt 2011; Galicher et al. 2013). According to Janson et al. (2012), the recent non-detection of Fom b at λ = 4.5 μm in thermal infrared excludes any Jovian-sized planet, and is rather compatible with a ~10 M⊕ object.
Based on the first two epochs of HST detections in 2004 and 2006, separated by only 1.7 years, Fom b’s orbit was initially thought to be nearly circular or moderately eccentric (e = 0.11−0.13 Chiang et al. 2009) and coplanar with the outer dust belt, as its orbital motion was detected nearly parallel to its inner edge. This constraint was deduced assuming that Fom b is responsible for the belt’s inner edge sculpting. This assumption was nevertheless recently questioned by Boley et al. (2012) who suggest the presence of other shepherding planets, in particular outside the outer edge of the ring. Fom b was recovered at a third (2010) and fourth (2012) epoch using HST/STIS coronagraphy (Kalas et al. 2013), allowing accurate measurements of its sky-plane motion when all four epochs of astrometry are combined. These investigators independently developed a Markov chain Monte Carlo (MCMC) code to estimate the orbital elements (Graham et al. 2013), producing a surprising result that the orbit of Fomalhaut b is highly eccentric, and will appear to cross the dust belt in the sky plane projection.
The purpose of this paper is first to perform an independent analysis of the available astrometric data of Fom b to derive refined orbital constraints using a MCMC method that was developed by one of us (H. Beust) and already used to fit βPic b’s orbit (Chauvin et al. 2012). This independent analysis confirms the eccentric nature of the orbit, and that it is very probably coplanar with the disk and apsidally aligned (Sect. 2). In Sect. 3 we numerically investigate the dynamics of the Fomalhaut system including Fom b and the dust belt. We present in Sect. 4 a semi-analytical study to explain the numerical result we derive. Our conclusions are presented in Sect. 5.
Summary of compiled astrometric data of Fom b relative to Fomalhaut.
2. Orbital fitting
2.1. Astrometric data
Fom b was observed with HST/ACS/HRC and HST/STIS at four epochs in 2004, 2006, 2010 and 2012. A detailed analysis and the corresponding astrometric data are given in Kalas et al. (2013). Galicher et al. (2013) also give independently derived astrometric measurement for all epochs before 2012. All these data are summarised in Table 1. While both sets of data are mutually compatible within their respective error bars, we note a slight difference between data from Kalas et al. (2013) and those from Galicher et al. (2013). To check the sensitivity of our orbital determination, we chose then to perform our orbital analysis with two independent sets of data: a first one with all data from Kalas et al. (2013), and a second one with the Galicher et al. (2013) data for the 2004, 2006 and 2010 data points, and the 2012 measurement from Kalas et al. (2013).
2.2. Orbital fit
The detected orbital motion with four epochs is in principle sufficient to try a first orbital determination. This is nevertheless not a straightforward task. Given the long expected orbital period of Fom b (hundreds of years), our four astrometric epochs cover only a tiny part of the orbit. We thus expect any orbital determination to come with large error bars. In this context, a standard least-square fitting procedure like Levenberg-Marquardt (Press et al. 1992) may produce meaningless results with huge error bars, as the χ2 surface is probably very chaotic with many local minima. This was confirmed by our first attempts. Therefore we moved to a more robust statistical approach using the MCMC Bayesian analysis technique (Ford 2005, 2006). This technique applied to astrometric orbits was already successfully used to constrain the orbit of the giant planet βPic b (Chauvin et al. 2012). We use here the same code for Fom b. We assume d = 7.7 pc and M = 1.92 M⊙ for the distance and the mass of Fomalhaut (van Leeuwen 2007; Mamajek 2012).
 |
Fig. 1 Resulting MCMC distribution of the orbital elements of Fom b’s orbit. In all plots, the black curves correspond to the first run using the full Kalas et al. (2013) data, and the red one to the second run using Galicher et al. (2013) data before 2012. Upper row, from left to right: semi-major axis (a), orbital period (P), eccentricity (e); second row, id: periastron (q), inclination (i), longitude of ascending node (Ω); third row, id: argument of periastron (ω), time for periastron passage (tp), and inclination relative to the disk plane (irel). |
 |
Fig. 2 Resulting 2D MCMC distribution of Fom b’s orbital elements for two couples of parameters, for the run with the full Kalas et al. (2013) data: semi-major axis (a)–eccentricity (e) (left); longitude of ascending node (Ω)–inclination (i) (right). The color scale represents the joint 2D density of solutions for the considered set of parameters. In the right plot, the star indicates the corresponding location of the mid-plane of the dust disk (Kalas et al. 2005). The same plot using Galicher et al. (2013) data is almost identical. |
Summary of various statistical parameters resulting from the MCMC distribution of Fom b’s orbital solutions (run with Kalas et al. 2013 data).
After convergence of the Markov chains (10 simultaneously), a sample of 500 000 orbits (out of ~107) is picked up randomly in the chains of orbital solutions. This sample is assumed to represent the probability (posterior) distribution of Fom b’s orbit. This distribution is presented in Figs. 1 and 2.
Figure 1 shows histograms of the distribution of individual orbital elements. In each plot we show two histograms. The black one corresponds to the first MCMC run (using Kalas et al. 2013 data), and the red one corresponds to the second run (using Galicher et al. 2013, data for epochs before 2012). The reference frame OXYZ with respect to which the orbit is referred to is chosen as usual in such a way that the OZ axis points towards the Earth (hence the OXY plane corresponds to the plane of the sky); the OX axis points towards North. In the framework of this formalism, the astrometric position of the planet relative to the central star reads: 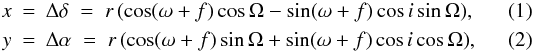 where Ω is the longitude of the ascending node (measured counterclockwise from North), ω is the argument of periastron, i is the inclination, f is the true anomaly, and r = a(1 − e2)/(1 + ecosf), where a stands for the semi-major axis and e for the eccentricity. With this convention, an i = 0 inclination would correspond to a prograde pole-on orbit, i = 90° to a edge-on viewed orbit (like βPictoris b), and i = 180° to a pole-on retrograde orbit.
where Ω is the longitude of the ascending node (measured counterclockwise from North), ω is the argument of periastron, i is the inclination, f is the true anomaly, and r = a(1 − e2)/(1 + ecosf), where a stands for the semi-major axis and e for the eccentricity. With this convention, an i = 0 inclination would correspond to a prograde pole-on orbit, i = 90° to a edge-on viewed orbit (like βPictoris b), and i = 180° to a pole-on retrograde orbit.
In Fig. 1, the distributions of Ω and ω appear twofold, with two distinct peaks separated by 180°. This is due to a degeneracy in the Keplerian formalism. It can be seen from Eqs. (1) and (2) that changing simultaneously Ω and ω to Ω + π and ω + π leads to the same orbital model. Consequently these orbital parameters are only determined with a ± 180° degeneracy. However, their sum Ω + ω and difference Ω − ω are unambiguously determined. It is easy to rewrite Eqs. (1) and (2) as a function of Ω + ω and Ω − ω instead of ω and Ω: 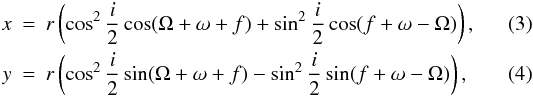 We used those formulas in our MCMC code, which in fact fits Ω + ω and Ω − ω. This avoids erratic changes in the solution between degenerate solutions, and subsequently ensures convergence of the chains. So, each time an orbital solution is taken in the chains with fitted values for Ω + ω and Ω − ω, it results in two solutions with similar orbital parameters but different (Ω,ω) sets. This is why we have dual peaks distributions for Ω and ω.
We used those formulas in our MCMC code, which in fact fits Ω + ω and Ω − ω. This avoids erratic changes in the solution between degenerate solutions, and subsequently ensures convergence of the chains. So, each time an orbital solution is taken in the chains with fitted values for Ω + ω and Ω − ω, it results in two solutions with similar orbital parameters but different (Ω,ω) sets. This is why we have dual peaks distributions for Ω and ω.
The only way to eliminate the degeneracy is to obtain information regarding the OZ axis. This can be radial velocity data points, or information about which side of the orbit in foreground in the images. In the case of βPictoris, information about the Keplerian gas disk help to fix the ambiguity. But here no such information is available for Fomalhaut, so we keep all possible solutions.
Figure 1 shows orbital distributions with well identified peaks, although this could appear surprising given the paucity of the data points. Detailed statistical parameters such as peak values and confidence intervals for various parameters are given in Table 2. The semi-major axis appears to peak at ~110−120 au, a value comparable to the present day location of Fom b with respect to the star, but surprisingly, the eccentricity is very high. The peak of the eccentricity distribution is ~0.92−0.94 (depending on the data set taken), virtually all solutions have e ≳ 0.5−0.6, and even e ≳ 0.8 with a 70% confidence level. It must be noted that the eccentricity distribution never extends up to e = 1. No solution with e ≥ 0.98 is derived in the distribution. Thus we are confident in the fact that Fom b is actually bound to Fomalhaut, although it may be on a very eccentric orbit. As a consequence of this high eccentricity, the periastron value of the orbit is small with a peak value of 7 − 8 au, and subsequently the apoastron is ≳ 200 au with a high confidence level. Figure 2 (left) shows a 2D joint probability map for a and e, for the first run only. We clearly see a peak of solutions around (a = 120 au, e = 0.94). A similar plot built with the data from the second run would appear nearly identical with a peak around (a = 110 au, e = 0.92).
There are indeed very few differences between the histograms derived from the two independent runs. The semi-major axis distribution appears slightly shifted towards shorter values in the second run (red curves, use of Galicher et al. 2013 data), with a peak appearing at a = 110 au instead of a = 120 au. Similarly, the eccentricity peaks at e = 0.92 in the second run instead of e = 0.94. These are the only noticeable differences between the two resulting distributions, all remaining differences barely reaching the level of the noise in the histograms. The differences are in all cases far below the bulk uncertainty on the corresponding parameters and therefore not very significant. We may therefore consider our orbital determination as robust. In the following, the dynamical study are performed with a Fom b orbit with a = 120 au and e = 0.94, i.e. corresponding to the peak values in the first run. The use of a = 110 au and e = 0.92 (the peak values for the second run) appears not to change anything noticeable to the dynamical behavior we describe below.
The inclination distribution in Fig. 1 shows that all solutions are with i < 90°, confirming a prograde orbit. The inclination peaks at 66.7°, a value very close to the disk inclination quoted by Kalas et al. (2005). The longitude of ascending node exhibits (due to the quoted degeneracy) two peaks separated by 180° at −27.8° and 152.2°. This is again very close to the PA = 156° of the belt ellipse quoted by Kalas et al. (2005). As our longitudes of nodes are counted counterclockwise from North like PAs, these similarities of values are a strong indication in favor of a coplanarity, or near coplanarity between the dust belt and Fom b’s orbit. We therefore plot in Fig. 1 the statistical distribution of the mutual inclination iirel between Fom b’s orbit and the dust disk, assuming the inclination and PA values given by Kalas et al. (2005). We see a sharp peak at 6.3°, which clearly suggests quasi-coplanarity. The fact that the peak is not at irel = 0 does not necessarily indicate a non-coplanarity. Due to the error bars on the disk orbit parameters, strict coplanarity (irel = 0) is just less probable than a few degrees offset. If the direction vector perpendicular to Fom b’s orbit was drawn randomly on a sphere, the natural statistical distribution for irel = 0 would be ∝ sinirel. This is equivalent to saying that the coplanar configuration would be the least probable one if the orientation of Fom b’s orbital plane was distributed randomly. Now, if we consider that error bars on the determination on the dust ring orbital plane and on our determination of Fom b’s orbital plane lead to an uncertainty of ~ 10° on the determination of irel, this means that we add a stochastic component to our measurement of irel, which should follow the ∝ sinirel distribution, at least up to ~10°. This is enough to create a peak in the MCMC distribution of irel that appears offset from the pure coplanar configuration by a few degrees.
Note also that when computing irel, due to the Keplerian degeneracy, two mutual inclinations could be deduced for each solution. We systematically chose the lower one. This shows also up in Fig. 2 (right), which shows a 2D joint probability map for Ω and i, for the first run (full Kalas et al. 2013 data). We clearly identify the two peaks. The star indicates now the corresponding values for the dust disk taken from Kalas et al. (2005), which fall very close to the peaks of the distribution. This unambiguously suggests coplanarity or quasi-coplanarity.
The argument of periastron ω peaks at −148.3 or 31.7. Kalas et al. (2005) report that the periastron of the elliptic dust belt is at PA = 170°. Taking into account the PA of the disk and its inclination, we derive an argument of periastron ωdisk = −148.9°, which is extremely close to our peak value of ω. While this could be considered a strong indication for Fom b’s orbit to be apsidally aligned with the elliptic dust belt, the real alignment may not be this perfect given the uncertainties of ω and ωdisk. The uncertainty on ωdisk is roughly ± 25°, and that on our ω determination is comparable. A a result the agreement within less than 1° between both values could be a pure coincidence. All we can stress looking at the whole ω distribution is that we have apsidal alignment within less than ±30−40° with a good level of confidence (~70%).
The conclusions is that we confirm the orbital determination of Fom b independently inferred by Kalas et al. (2013). The inclination distributions are compatible (within a sign convention in Kalas et al. 2013), as well as the Ω and ω distribution, although only single peak distributions are given in Kalas et al. (2013). The shapes of the semi-major axis and eccentricity distributions are noticeably similar. The eccentricity and semi-major axis intervals are very similar, except the that our semi-major axis distribution extends a bit lower and our eccentricity distribution a bit higher (Table 2). We also confirm that Fom b’s orbit is very probably nearly coplanar and apsidally aligned within a few tens of degrees with the dust belt.
3. Numerical study assuming coplanarity
3.1. Pericenter glow for low eccentricity orbits
We thus conclude like Kalas et al. (2013) that a dust belt crossing orbit for Fom b is consistent with the data. This automatically raises the question of the long-term stability of this configuration. Thus we move now to a dynamical study to address this issue. fomb’s orbit turns out to be nearly coplanar and apsidally aligned with the elliptic dust ring. This is a strong indication for a pericenter glow phenomenon.
Pericenter glow occurs when a disk of planetesimals orbiting a star is secularly perturbed by a planet moving on an eccentric orbit. We briefly recall here the theory, which is described in detail in Wyatt et al. (1999) and Wyatt (2005). We consider the motion of a planetesimal perturbed by the planet. We use Laplace-Lagrange theory, based on an expansion of the disturbing function in ascending powers of eccentricities and inclinations and a truncation to second order, assuming that eccentricities and inclinations remain low (Murray & Dermott 1999). This causes the secular system to become linear. The analytical solution for the planetesimal eccentricity can be described for the eccentricity variables as 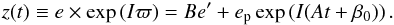 (5)Here z(t) is the complex eccentricity and I2 = −1; e is the planetesimal’s eccentricity while e′ is that of the planet; ϖ = ω + Ω is the longitude of periastron with respect to the direction of the planet’s periastron. B and A are coefficients that depend on the orbital configuration of the two bodies via Laplace coefficients (see Wyatt 2005, for details). The first term in Eq. (5) is a fixed forced eccentricity due to the eccentricity of the perturbing planet. The second term is a proper oscillating term with additional parameters ep and β0 that depend on the initial conditions.
(5)Here z(t) is the complex eccentricity and I2 = −1; e is the planetesimal’s eccentricity while e′ is that of the planet; ϖ = ω + Ω is the longitude of periastron with respect to the direction of the planet’s periastron. B and A are coefficients that depend on the orbital configuration of the two bodies via Laplace coefficients (see Wyatt 2005, for details). The first term in Eq. (5) is a fixed forced eccentricity due to the eccentricity of the perturbing planet. The second term is a proper oscillating term with additional parameters ep and β0 that depend on the initial conditions.
Consider now that we start with an initially cold disk, i.e., planetesimals on circular orbits (z(0) = 0). This could be the case at the end of the protoplanetary phase, because before the disappearance of the gas, the eccentricity of all solid particles tend to be damped by gas drag. Then obviously β0 = π and ep = Be′, so that the full solution now reads 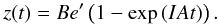 (6)The complex eccentricity z(t) describes a circle path in complex plane with radius Be′, centered on the point (Be′,0). It results from Eq. (6) that the maximum eccentricity emax = 2Be′ is reached for At ≡ π [2π] , when ϖ = 0. This means that the maximum eccentricity in the secular evolution is reached when the planetesimal is apsidally aligned with the planet.
(6)The complex eccentricity z(t) describes a circle path in complex plane with radius Be′, centered on the point (Be′,0). It results from Eq. (6) that the maximum eccentricity emax = 2Be′ is reached for At ≡ π [2π] , when ϖ = 0. This means that the maximum eccentricity in the secular evolution is reached when the planetesimal is apsidally aligned with the planet.
When e′ ≠ 0, Wyatt (2005) showed that a steady-state regime is reached after a transient phase characterized by spiral structures. In the steady-state regime all planetesimals are at various phases on their secular eccentricity cycle, but those which are close to their peak eccentricity are approximately apsidally aligned with the planet. The global result is an elliptic dust ring apsidally aligned with the planet.
From an observational point of view, the pericenter side of the ring appears more luminous, thanks to a more efficient scattering of stellar light by the dust particles produced by the planetesimals. The same applies also to thermal emission, as grains are hotter near pericenter. This phenomenon termed pericenter glow was invoked to explain many observed asymmetric global structures in debris disks, such as HR 4796 (Wyatt et al. 1999; Moerchen et al. 2011), HD 141569 (Wyatt 2005) or more recently ζ2 Reticuli (Faramaz et al., in prep.). Concerning Fomalhaut, the dynamical study by Chiang et al. (2009), based on a moderately eccentric orbit of Fom b shepherding the dust ring were made in this framework.
Fomalhaut’s dust ring and Fom b’s orbit share many characteristics that are typical of pericenter glow: an eccentric ring with an offset center, coplanar and apsidally aligned with Fom b. It is therefore tempting to invoke it here. But the linear theory outlined above holds for moderately eccentric orbits that do not cross each other. Here with e = 0.94, we are far from any linear regime. It is then important to characterize what happens in the high eccentricity regime. This must be done numerically.
 |
Fig. 3 Result of the N-body integration with a perturbing planet with m = 1 MJup. We display here upper views of the planetesimal disk together with the planet’s orbit (top) and semi-major axis–eccentricity diagrams of the disk (bottom), at three epochs: beginning of the simulation (t = 0, left), at t = 5 Myr (middle) and t = 100 Myr (right). The color scale is proportional to the projected densities of particles (top plots) and of orbits in (a,e) space (bottom plots). The red circles represent the location of the star and of the planet. The planet’s orbit is sketched as a black ellipse. |
3.2. Pericenter glow phenomenon with highly eccentric perturbers
We present now a numerical study of the Fomalhaut system, to properly address the case of high eccentricity orbits. We take an initial ring of 105 massless particles (i.e., planetesimals) between 110 au and 170 au, i.e., extending wider than the observed ring, and we add a planet orbiting on an orbit corresponding to our best fit: a = 120 au and e = 0.94. The initial eccentricities of the particles are randomly sorted between 0 and 0.05, while their inclinations with respect to the planet’s orbital plane are chosen between 0 and 3°. The dynamics of this system is integrated using the symplectic N-body code Swift_rmvs (Levison & Duncan 1994) which takes into account close encounters between the planet and the disk particles. The integration is extended up to 500 Myr, i.e, a bit longer than the estimated age of Fomalhaut (440 Myr; Mamajek 2012).
Taking into account close encounters is indeed important here. As the planet’s orbit crosses the disk we expect to have many encounters. The perturbing action of the planet onto the disk particles is twofold: all particles crossing the planet’s path within a few Hill radii undergo a close encounter that most of the time scatters them out of the disk; but as long as the particles do not encounter the planet, they are subject to a secular evolution more or less comparable to the one described in the previous section. We expect any global shaping of the disk to be due to secular perturbations rather than close encounters, as close encounters rather have a destructive effect on the disk.
The balance between the two effects (secular and close encounters) depends actually on the mass of Fom b, which we will consider to be a free parameter.
3.2.1. Massive planet
We first present a run with a massive planet, i.e., m = 1 MJup, but still fitting the observational constraints (Janson et al. 2012). The result is shown in Fig. 3. We represent here upper views of the particle disk and semi-major axis versus eccentricity plots, at the beginning of the simulation and at two subsequent epochs: t = 5 Myr and t = 100 Myr. As early as t = 5 Myr, the disk appears extremely perturbed and actually no longer assumes a disk shape. Many particles have already had a close encounter with the planet and have been scattered. Interestingly, a few disk particles have been trapped in co-orbiting orbits (or 1:1 resonance) with the planet. At t = 100 Myr, i.e., well below the age of Fomalhaut, these are no longer present. The disk now contains fewer particles. Many of them have been lost in close encounters with the planet. To illustrate this, we plot in Fig. 4 the number of remaining disk particles (i.e., those particles which have not been ejected yet) as a function of time. Starting from 105, we see that it is reduced to 4000 at t = 100 Myr and to 400 at t = 500 Myr. We can then safely claim that this situation does not match the observation, unless the planet was very recently scattered ( ≲ 10 Myr; see Fig. 4) onto its present orbit. Over any longer time-scale, the disk is virtually destroyed by close encounters, which are just too efficient here with such a massive planet. In fact, even a few Myrs is already too long. The disk particles reach high eccentricities much earlier than that. An average eccentricity of 0.1 for the disk particles, which we should consider as matching the observations, is reached only ~ 3 × 104 yr after the beginning of the simulations. As a result any subsequent configuration must be considered as incompatible with the observation.
 |
Fig. 4 Evolution of the number of active disk particles as a function of time in the simulations described in Figs. 3 (black), 5 (red) and 6 (green). All missing particles have been ejected by close encounters. This phenomenon mainly concerns the m = 1 MJup case. |
 |
Fig. 5 Result of the N-body integration with a perturbing planet with m = 0.02 MJup. The conventions are the same as in Fig. 3. Three epochs are represented: t = 5 Myr (left), t = 20 Myr (middle) and t = 440 Myr (right). |
3.2.2. Super-Earth planet
We come now to a similar simulation, but with a lower mass for Fom b. Figure 5 presents a simulation with a mass m = 0.02 MJup = 6.28 M⊕ (Super-Earth regime). The disk is represented at three epochs: t = 5 Myr, t = 20 Myr and t = 440 Myr, i.e., the estimated age of Fomalhaut. We do not show the initial disk, as it is identical to that in Fig. 3. At t = 5 Myr, we note a drastic difference with the previous simulation. The disk now still assumes a disk shape with a moderate (e ~ 0.2) eccentricity. This disk configuration actually roughly matches the observed disk, but the elliptic disk is not apsidally aligned with the planet’s orbit. It instead appears rotated by ~70°. This contradicts both our orbital determination, which suggests apsidal alignment, and the predictions of the standard pericenter glow theory. This is actually due to the high eccentricity of Fom b; see explanation in Sect. 4.
At t = 20 Myr, the disk still assumes this elliptic shape with a similar angular tilt with respect to the planet’s apsidal line. But now the disk particles have reached much higher eccentricities (~0.6− ~ 1), causing the disk to no longer resemble the observed one. In fact, the bulk eccentricity of the disk increases continuously with time. At t = 5 Myr it is ~0.2, while at t = 20 Myr it is ≳ 0.6. An average disk eccentricity of 0.1, considered as a good match to the observations, is reached earlier than t = 5 Myr, in fact at t = 2 Myr (plot not shown here). But even in that case, the disk appears tilted the same way as at t = 5 Myr.
At t = 440 Myr, the particles’ eccentricities have spread over all possible values. The disk no longer assumes a ring shape. This indeed appears to be the case much earlier in the simulation. After t = 20 Myr, the particles’ eccentricity keep increasing up to high values, and the disk structure is already lost at t = ~80 Myr. In fact the situation at t = 440 Myr with m = 0.02 MJup is comparable to that at t = 5 Myr with m = 1 MJup, except that less particles have been lost in close encounters.
3.2.3. Sub-Earth regime
 |
Fig. 6 Result of the N-body integration with a perturbing planet with m = 0.002 MJup. The conventions are the same as in Fig. 3. Three epochs are represented: t = 40 Myr (left), t = 200 Myr (middle) and t = 440 Myr (right). |
Figure 6 presents now a simulation with a mass m = 0.002 MJup = 0.628 M ⊕ (Earth or sub-Earth regime). The epochs represented are now t = 40 Myr, t = 200 Myr and t = 440 Myr. The main difference is that at all 3 epochs, the disk still assumes an elliptic disk shape. But as with m = 0.02 MJup, the global disk eccentricity increases to reach high values. This is of course due to the increase of the eccentricity of the disk particles which keep being apsidally tilted by ~70° with respect to the planet’s orbit. In fact, the situation at t = 40 Myr with m = 0.002 MJup is somewhat comparable to that at t = 5 Myr with m = 0.02 MJup, and the situation at t = 200 Myr with m = 0.002 MJup also compares with that at t = 20 Myr with m = 0.02 MJup. An average disk eccentricity of 0.1 is reached at ~20 Myr.
It must be specified that this last simulation may be less realistic than the others, in the sense that the planet’s mass is now lower than the mass of the dust disk. According to Wyatt & Dent (2002) and Chiang et al. (2009), a mass of planetesimals ranging between 3 M⊕ and 20 M⊕ is required to sustain the dust disk over the age of the star. This issue is investigated further in Sect. 4.3.
3.2.4. Discussion
The three simulations described above with different masses for Fom b present similarities and differences. The comparison between the various outputs reveals comparable sequences: the disk is first perturbed to assume an elliptic shape. This is due to an increase of the eccentricities of the particles, while their longitudes of periastron remain more or less constrained to ~70° with respect to the apsidal line of the planet. Then the global eccentricity increases to reach very high values. Afterwards, the particles spread in eccentricities and the structure of the disk is lost. The main difference resides in the time-scale of this process. At t = 5 Myr with m = 1 MJup the particles have already very high eccentricities, and the structure of the disk is already getting lost. At t = 440 Myr with m = 0.002 MJup we are barely reaching this stage after the disk particles have seen their eccentricities increase. Comparing the three runs, the time-scale of the process turns out to be roughly inversely proportional to the planet’s mass. This is characteristic for a secular process, as the secular disturbing function due to the planet is proportional to its mass while the topology of the Hamiltonian depends only weakly on the planet’s mass (see next section).
Another difference between the three simulations resides in the loss of particles. Obviously the higher the mass, the more efficiently particles are lost. Particle loss is due to scattering by close encounters. As expected, more massive planets are more efficient at scattering particles. With m = 1 MJup, particle scattering actually dominates the dynamics after ~5 Myr, so that there is virtually no particle left at the age of the star. This is conversely not the case for low mass planets. Figure 4 shows that the loss of particles, although it is present, is not significant over a time-scale of Fomalhaut’s age. Thus we may stress that for low mass planets, the dynamics is essentially secular, and that close encounters are negligible. Note that this does not necessarily mean that there are no close encounters. There are inevitably encounters, but they are less numerous, thanks to a shorter Hill sphere. However, as the Hill radius scales as m1/3, the effect should not be so drastic. The other reason is that for a low mass planet, it would take many subsequent encounters to actually eject a particle.
We also tried to vary the orbital configuration, in particular to add a few degrees inclination (5°) to the planet with respect to the disk mid-plane. This appeared not to produce significant changes in the global results describe here, so that our conclusion still hold and may be regarded as robust.
It turns out that with the orbit we deduced from our fitting procedure, assuming a low mass for Fom b is enough to prevent the destruction of the disk by scattering close encounters over a time-scale corresponding to the age of the star, even if the planet crosses the disk. The secular perturbations by the planet succeed in rendering the disk eccentric, but they inevitably drive the particles towards very high eccentricities that do not match the observation. Depending on the mass assumed for Fom b an average disk eccentricity of 0.1 is reached between a few 106 to a few 107 yr after the beginning of the simulations, which is still far below the age of the system. Moreover, even when its global eccentricity matches the observation, the disk appears not apsidally aligned with the planet’s orbit, which does not match the conclusion of our orbital fit (Sect. 2). This is also in contradiction with the pericenter glow dynamics, where the particles get their maximum eccentricities when they are apsidally aligned with the planet, causing the global disk figure to be aligned similarly. The linear pericenter glow analysis obviously does no longer apply here. This is a consequence of the very high eccentricity assumed for the planet, as we detail below.
 |
Fig. 7 Phase portraits of secular averaged Hamiltonian |
4. Semi-analytical study
4.1. Theoretical background
We consider a massless disk particle moving in the gravitational field of the star Fomalhaut with mass M and the planet Fom b with mass m. The motion of the particle is thus described in the framework of the restricted three body system. The Hamiltonian of the particle’s motion then reads in stellocentric reference frame 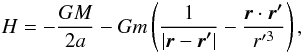 (7)where G is the gravitational constant, a is the particle’s semi-major axis in stellocentric referential frame, and r and r′ are the position vectors of the particle and the planet in the same referential frame. We shall restrict ourselves to the planar problem, where all three bodies move in the same plane. With this assumption, the Hamiltonian H reduces to two degrees of freedom.
(7)where G is the gravitational constant, a is the particle’s semi-major axis in stellocentric referential frame, and r and r′ are the position vectors of the particle and the planet in the same referential frame. We shall restrict ourselves to the planar problem, where all three bodies move in the same plane. With this assumption, the Hamiltonian H reduces to two degrees of freedom.
The secular dynamics of the particle is then studied taking the time average of H over both orbits 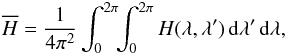 (8)where λ and λ′ are the mean longitudes of the particle and of the planet respectively. This averaged Hamiltonian describes accurately the secular motion of the particle as long as i) there is no close encounter between the particle and the planet; ii) the two bodies are not locked in a mean-motion resonance. We will assume that both conditions are fulfilled, even when both orbits cross each other. The numerical study showed indeed that as long as we do not take too high a mass for Fom b, scattering by close encounters remains a minor phenomenon (Fig. 4). Similarly, most planetesimals in our simulation are very probably not in resonance with Fom b, as mean-motion resonances usually cover small areas in semi-major axis. In fact, to enhance resonance structures, additional mechanisms such as planet migration are required (Reche et al. 2008; Wyatt 2003).
(8)where λ and λ′ are the mean longitudes of the particle and of the planet respectively. This averaged Hamiltonian describes accurately the secular motion of the particle as long as i) there is no close encounter between the particle and the planet; ii) the two bodies are not locked in a mean-motion resonance. We will assume that both conditions are fulfilled, even when both orbits cross each other. The numerical study showed indeed that as long as we do not take too high a mass for Fom b, scattering by close encounters remains a minor phenomenon (Fig. 4). Similarly, most planetesimals in our simulation are very probably not in resonance with Fom b, as mean-motion resonances usually cover small areas in semi-major axis. In fact, to enhance resonance structures, additional mechanisms such as planet migration are required (Reche et al. 2008; Wyatt 2003).
The averaged Hamiltonian 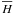 cannot in general be expressed in closed form. A full analytical treatment requires first to perform an expansion of H before averaging. There are two ways to do this. The first is to assume that both orbits have very different sizes. Then H can be written in ascending powers of r/r′ (or r′/r depending on which orbit is the wider) using Legendre polynomials. The final averaging is then written in ascending powers of a′/a (or a/a′), where a and a′ are the semi-major axes. The second way to average is to consider that both orbits may be of comparable sizes, but that the eccentricities and inclinations are and will remain low. H is then expanded in ascending powers of eccentricities and inclinations using Laplace coefficients and then averaged over both orbital motions. This second technique, once truncated to second order in eccentricities and inclinations, leads to describing the pericenter glow phenomenon.
cannot in general be expressed in closed form. A full analytical treatment requires first to perform an expansion of H before averaging. There are two ways to do this. The first is to assume that both orbits have very different sizes. Then H can be written in ascending powers of r/r′ (or r′/r depending on which orbit is the wider) using Legendre polynomials. The final averaging is then written in ascending powers of a′/a (or a/a′), where a and a′ are the semi-major axes. The second way to average is to consider that both orbits may be of comparable sizes, but that the eccentricities and inclinations are and will remain low. H is then expanded in ascending powers of eccentricities and inclinations using Laplace coefficients and then averaged over both orbital motions. This second technique, once truncated to second order in eccentricities and inclinations, leads to describing the pericenter glow phenomenon.
We stress that none of these techniques can be applied here. As Fom b’s orbit crosses the disk, the disk particles’ orbits cannot be considered as significantly wider or smaller than Fom b’s, and the very high eccentricity we determine for Fom b prevents from using any technique based on an expansion in ascending powers of eccentricity. A semi-analytical study is nevertheless possible. As we consider the planar problem, the Hamiltonian H has two degrees of freedom. But the averaged Hamiltonian 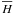 has only one, as thanks to the averaging process, the semi-major axis is a secular invariant. Considering then that a is a secular invariant,
has only one, as thanks to the averaging process, the semi-major axis is a secular invariant. Considering then that a is a secular invariant, 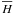 is basically a function of only two dependant variables, namely the eccentricity e and the longitude of periastron ϖ. It is even more relevant to describe it as a function of e and of ν = ϖ′ − ϖ, where ϖ′ is the longitude of periastron of the planet. It is then possible, for a given semi-major axis value a, to compute numerically the value of
is basically a function of only two dependant variables, namely the eccentricity e and the longitude of periastron ϖ. It is even more relevant to describe it as a function of e and of ν = ϖ′ − ϖ, where ϖ′ is the longitude of periastron of the planet. It is then possible, for a given semi-major axis value a, to compute numerically the value of 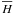 for various sets of variables (ν, e), and to draw level curves of
for various sets of variables (ν, e), and to draw level curves of 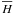 in (ν, e) space. As
in (ν, e) space. As 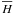 is itself a secular invariant, any secular evolution must be done following one of these level curves. This technique of phase portrait drawing has already proved efficiency to describe non-linear dynamics, such as in resonant configurations in the βPictoris case (Beust & Morbidelli 1996; Beust & Valiron 2007).
is itself a secular invariant, any secular evolution must be done following one of these level curves. This technique of phase portrait drawing has already proved efficiency to describe non-linear dynamics, such as in resonant configurations in the βPictoris case (Beust & Morbidelli 1996; Beust & Valiron 2007).
4.2. Application to a test particle perturbed by Fom b
The result in the case of a disk test particle perturbed by Fom b is shown in Fig. 7 for three planet eccentricity values (from left to right): e = 0.1, e = 0.5, e = 0.94. Of course, given our orbital determination, the latter value is more relevant for Fom b. The semi-major axis ratio was fixed to a/a′ = 1.2, as typical of the situation under study. Assuming indeed a′ = 120 au for Fom b, a/a′ = 1.2 leads to a = 144 au, i.e., a typical particle in the middle of the dust belt (Kalas et al. 2005). We also checked nearby a/a′ values also representative for various belt particles. We do not show the corresponding phase portraits here. The Hamiltonian topology described in Fig. 7 turns out indeed to be only slightly affected by the fixed a/a′ value, so that the conclusions we derive here with a/a′ = 1.2 still hold. Similarly, the mass ratio between the planet and the star was fixed to m/M = 10-6 to build the phase portraits, i.e., an Earth-sized planet. Changing m/M appears not to change anything noticeable to the shape of the Hamiltonian level curves, so that we do not show corresponding phase portraits which are virtually identical to those displayed here. This can be understood easily. The variable part of H, which is responsible for the topology, is just proportional to m. Therefore changing m only scales that variable part accordingly but does not affect the global topology.
In the phase portraits of Fig. 7, the red curve separates regions where both orbits not only overlap in distance, but actually cross each other (assuming they are coplanar) from regions where they do not. We first describe the e′ = 0.1 case (left plot). We note an island of ν-libration around ν = 0 surrounded by smooth ν-circulating curves. We stress that this phase portrait actually faithfully describes the pericenter glow phenomenon. Any particle moving along a ν-circulating curve will be subject to a precession of ν (i.e., of the longitude of periastron ϖ) coupled with an eccentricity modulation, and the maximum eccentricity will be reached for ν = 0, i.e., when both orbits are apsidally aligned. This is characteristic for pericenter glow, and this secular evolution exactly matches the circular path of z(t) in complex plane described above. The same applies to particles moving in the ν-libration island around ν = 0. This corresponds to cases where the circular z(t) path does not encompass the zero point. This situation can be viewed as a secular resonance where ϖ no longer circulates.
 |
Fig. 8 Views of the simulations of Figs. 6 and 5 in (ν,e) space like in Fig. 7. The three upper plots refer to Fig. 6 (m = 0.002 MJup) at t = 40 Myr, t = 100 Myr, t = 200 Myr, while the lower left plot corresponds to t = 440 Myr. The lower middle plot refers to Fig. 5 (m = 0.02 MJup) at t = 200 Myr. |
The situations with e′ = 0.5 and e′ = 0.94 are different. With e′ = 0.5, the island of ν-libration around ν = 0 is still present, but it reaches now much higher eccentricities. It actually encircles a small region in (ν,e) space where both orbits do not cross. But the main difference concerns the circulating curves. They all reach very high eccentricities, virtually e = 1. This means that any particle starting at low eccentricity is about to evolve to this very high eccentricity regime, unless it is subject to a close encounter before. Contrary to what could be suggested from the phase portrait, these particles do not pass beyond e = 1, i.e., they are not ejected by the secular process. Our numerical simulations show that they pass through a very high eccentricity maximum before going down in the diagram (see below). This does not show up in Fig. 7, but can be understood in terms of orbital energy. As the semi-major axis a is a secular invariant, so is the orbital energy − GM/2a (the fixed part of Hamiltonian H). It thus remains negative, hence the particle remains bound to the star. The only way to eject a particle here is to have a close encounter which has the ability to affect the orbital energy.Strictly speaking, ν does not circulate in this regime, but rather librates around ν = 180°. Such ν = 180°-librating curves are in fact already present in the e′ = 0.1 case, but only in the very high eccentricity regime (top of the diagram). With e′ = 0.5, this regime extends down to low eccentricities and the ν-circulating regime has disappeared.
The situation at e′ = 0.94 is similar to that with e′ = 0.5, except that it is even more drastic. The island of ν-libration is now confined to a tiny region close to ν = 0 at high eccentricity. As a consequence, nearly all particles initially at low eccentricity in the disk must evolve to the very high eccentricity regime. We claim that this phase portrait exactly describes the dynamics observed in Figs. 5 and 6. We must specify here that the level curves of Fig. 7 are explored in a fixed sense that is imposed by Hamiltonian dynamics. For e′ = 0.94, basically the left part of the diagram ν < 180° corresponds to growing eccentricities, while the right part ν > 180° corresponds to decreasing eccentricities. Now, consider a disk of particles initially at low eccentricities and random ν values. Following the 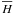 level curves, all particles will see their eccentricity grow when they reach 60° ≲ ν ≲ 90°. Irrespective of their initial ν value, they will all have similar longitudes of periastron during their eccentricity growth phase up to e ≃ 1. This is the exact origin of the eccentric disk tilted by ~70° we observe in Figs. 5 and 6. Remember that in these simulations we had chosen the perturbing planet in such a way that ϖ′ = 0, so that ν = ϖ.
level curves, all particles will see their eccentricity grow when they reach 60° ≲ ν ≲ 90°. Irrespective of their initial ν value, they will all have similar longitudes of periastron during their eccentricity growth phase up to e ≃ 1. This is the exact origin of the eccentric disk tilted by ~70° we observe in Figs. 5 and 6. Remember that in these simulations we had chosen the perturbing planet in such a way that ϖ′ = 0, so that ν = ϖ.
To illustrate this, we plot in Fig. 8 snapshots of the simulations described in Figs. 5 and 6, but in (ν,e) space to better compare with Fig. 7. The first four plots (upper plots and lower left one) show the evolution with m = 0.002 MJup (Fig. 6) at various epochs. The correspondence with the phase portrait in Fig. 7 is striking. We clearly see the eccentricity growth phase of the particles with constrained ν. A discrepancy can nevertheless be noted in the lower left plot (at t = 440 Myr) with respect to the corresponding plot in Fig. 6, where we note that the global orientation of the disk leads to suggest that most particles have 0° < ν < 180°, while in Fig. 8, it turns out that at the same time, they mostly have 180° < ν < 360°. As explained in Sect. 5, this apparent discrepancy is due to an inclination effect. At this time, most particles have indeed moved to retrograde orbits, which does not show up in the projected upper view of Fig. 6.
We also see that once the particles reach high eccentricities, they start to diffuse in the upper part of the diagram, before starting to get down to lower eccentricities in the right part of the diagram. But at this level the cloud of particles is much less concentrated in (ν,e) space, resulting in a less sharp eccentric disk. This diffusion is due to the difference in secular evolution time-scales for the individual particles. All particles do not rigorously evolve at the same speed in (ν,e) space, so that they inevitably diffuse after a few cycles. This is illustrated in the fifth plot of Fig. 8 (lower middle), which corresponds now to m = 0.02 MJup (Fig. 5) at t = 200 Myr. As pointed out above, the dynamical evolutions in both cases are almost identical, but with m = 0.02 MJup it is just achieved faster, actually in a manner proportional to m, as the variable part of H is ∝ m. The situation at t = 200 Myr with m = 0.02 MJup can therefore also be regarded as virtually corresponding to t = 2 Gyr with m = 0.002 MJup, as long as close encounters can be neglected. At this stage, we see that the cloud of particles has diffused in all parts of the diagram. A kind of steady-state regime has been achieved where individual particles are at random phases of their evolution tracks. They still gather around ν ≃ 70° and ν ≃ 290° when their eccentricities grow or decrease, but the disk no longer achieves an eccentric ring shape (Fig. 5). This picture does not change drastically if we adopt different orbital parameters for the perturbing planet. Assuming different eccentricity and semi-major axis values, the gathering points at ν ≃ 70° and ν ≃ 290° appear to move by no more than ~20°.
It could been argued looking at the left plot of Fig. 7 that a disk of particles starting at zero eccentricity and perturbed by a planet with e′ = 0.1 may start start to gather around ν ≃ 70° before filling all the available phase space and generate the pericenter glow phenomenon. This corresponds indeed to the transient spiral structures noted by Wyatt (2005). But this transient phase lasts at most a few Myr (Wyatt 2005), which is very short. The steady-state regime, characterized by diffusion of particles into the phase space and subsequent apsidal alignment, sets on more quickly.
4.3. Disk self-gravity and very low mass regime for Fom b
As pointed out above, the simulations involving a very low mass Fom b might be unrealistic because of the neglected disk mass. In our simulations indeed, the disk is made of massless particles which do not influence Fom b’s orbit nor perturb each other. This approximation remains justified as long as Fom b’s mass remains higher than the disk mass. According to Wyatt & Dent (2002) and Chiang et al. (2009), a mass of planetesimals ranging between ~3 M ⊕ and ~20 M ⊕ is required to sustain the dust production in the debris disk over the age of the star. It is of course hard to derive a more accurate estimate, but obviously, when we consider a 6 M⊕ Fom b, its mass is comparable to that of the disk, and with m = 0.6 M⊕ it is clearly below. Consequently the reality of some of our simulations may appear questionable.
Strictly speaking, addressing this issue would require to perform simulations with a self-gravitating disk over the age of the star, which would be extremely computing time consuming. It is nevertheless possible to derive the effect of the disk mass using our semi-analytical approach. As long as close encounters and mean-motion resonances are not considered, which is the case here, the secular effect of an elliptic disk is basically identical to that of a planet with the same mass and orbiting on the same orbit. In fact, the averaging process described in Eq. (8) is virtually equivalent to replacing both bodies with massive rings spread over their orbits. Terquem & Ajmia (2010) showed for instance directly that a planet perturbed by a massive inclined disk is subject to Kozai effect exactly as if it was perturbed by another planet.
 |
Fig. 9 A phase portrait equivalent to the left plot of Fig. 7, but with a/a′ = 0.8. This situation mimics the dynamics of Fom b as perturbed by a massive disk (see text). |
The first thing we need to investigate is the secular effect of a massive ring on the orbit of Fom b. This situation can be modeled treating Fom b as a test particle initially at a = 120 au and e = 0.94, perturbed by a planet orbiting at a′ = 140 − 150 au and e′ = 0.1. This is in fact very close to the situation depicted in the left plot of Fig. 7, except that the semi-major axis ratio should be now taken as a/a′ ≃ 0.8 instead of 1.2. The result is shown in Fig. 9, which appears indeed very similar to the left plot of Fig. 7. The initial configuration of Fom b (e = 0.94 and ν ≃ 0) corresponds to the top curves of the phase diagram. Following any of these curves, we see that due to the disk perturbation, the periastron of Fom b is subject to precession, but that in any case, its eccentricity will never get below ~0.6. Figure 7 shows then that the dynamics of disk particles perturbed by a e = 0.6 Fom b is very similar to that with a e = 0.94 Fom b. We are thus confident in the fact that even if its orbit is secularly perturbed by the disk, this does not prevent Fom b from perturbing the disk particles as described above.
 |
Fig. 10 Phase portraits similar to those of Fig. 7 but to which we have added a second perturbing planet (representing the disk) apsidally aligned with the first one (Fom b). The second planet is assumed to orbit at the same semi-major axis as the disk particle. The important parameter is the mass ratio ρ between the two planets. Left plot: ρ = 0.1, i.e., a disk 10 times less massive than Fom b; Middle plot: ρ = 1, disk and Fom b have equal masses; Right plot: ρ = 10, i.e., a disk 10 times more massive than Fom b. |
The second potential effect is the self-gravity of the disk, i.e., the perturbation the massive disk can rise on disk particles. This can be investigated adding a second perturbing planet to the situation depicted in Fig. 7 and averaging the resulting Hamiltonian over all orbits. This is illustrated in Fig. 10. Fom b’eccentricity is taken equal to 0.94. The planets are taken apsidally aligned to mimic the alignment between Fom b and the disk, and the second planet’s semi-major axis is taken equal to that of the test particle, i.e., 1.2 times that of Fom b. The important parameter here is the mass ratio ρ between the perturbing planets, i.e., between the disk and Fom b. In Fig. 10 we show phase diagrams for ρ = 0.1 (left plot, disk less massive than Fom b), ρ = 1 (middle plot, equal masses), ρ = 10, (right plot, disk more massive than Fom b). With ρ = 0.1, the situation is very close to that of Fig. 7 with e = 0.94, which is not surprising as Fom b dominates the dynamics. With ρ = 1 (middle plot) the situation is now somewhat changed. An island of libration appears now at low eccentricity around ν = 0. This island corresponds to a secular resonance pericenter glow region controlled by the second planet. But not all disk particles moving at low eccentricity are concerned by this behavior. Contrary to a pure pericenter glow configuration (left plot of Fig. 7), those which are not trapped in the libration island actually follow a route that drives them to high eccentricity almost exactly as if the second planet was not there. Those particles are stilled controlled by the highly eccentric Fom b. Given the limited size of the libration island around ν, the latter class of particles is potentially more crowded that the former. As a result we may claim that a disk perturbed by an equal mass Fom b would still see a significant part of its particles evolve towards high eccentricities and yield a disk figure that does not match the present day observation.
With ρ = 10 (right plot), now the bottom part of the phase diagram closely looks like that of the left plot of Fig. 7. Only the particles initially moving at high eccentricity actually feel a noticeable perturbation by Fom b. Conversely, all particles moving at low eccentricity follow a route entirely controlled by the disk treated as a second planet. This does not explain the eccentricity of the disk, as the second planet was initially given the suitable eccentricity. All we stress here is that we expect here the disk to be no longer affected by Fom b, which is not surprising as it is now 10 times less massive than the disk.
We also checked intermediate values of ρ (not shown here). When increasing ρ from 1 to 10, the island of libration at low eccentricity around ν = 0 gets higher. The transition between the regime where a significant part of the low eccentricity particles are still perturbed towards high eccentricity and that where all particles remain at low eccentricity occurs around ρ ≃ 3.5. As a result, even if Fom b is 3 times less massive than the disk, it can still perturb it in such a way that many particles are driven towards high eccentricities. Given the disk mass estimates by Wyatt & Dent (2002) and Chiang et al. (2009), we conclude that a super-Earth sized Fom b (like in the simulation of Fig. 5) is very probably capable of efficiently perturb the disk, while this is certainly no longer the case for a sub-Earth sized Fom b. Our corresponding simulation (Fig. 6) can therefore be considered as unrealistic given the probable mass of the disk. We nevertheless presented it here to illustrate the mechanism we describe and how its time-scale scales with the planet’s mass.
We may thus distinguish two regimes: for a ~super-Earth sized Fom b and above, the dynamics outlined in the previous section holds, while for lower masses, the secular effect of Fom b is overridden by the self-gravity of the disk so that its influence of the disk is very small.
5. Vertical structures
 |
Fig. 11 Same simulation as presented in Fig. 6, but in inclination–eccentricity space (i,e), at the same corresponding times: t = 40 Myr (left), t = 200 Myr (middle), t = 440 Myr (right). |
As of yet, we only cared about planar structures, Fom b and the disk were assumed to be coplanar. This choice was indeed guided by the result of the orbital determination. However, in all simulations presented above, the disk of particles was not initially strictly planar. While Fom b was assumed to lie in the mid-plane of the disk, a random inclination between 0 and 3° was given to the particles at the beginning, as to mimic a realistic inclination dispersion within a real disk. Figures 3–6 present in fact projected upper views of the disk. We come now to discussing vertical structures in the disk and their consequences. All the results presented below concern the simulation with the m = 0.002 MJup Fom b, as it is the slowest evolving one, keeping in mind that this simulation is probably unrealistic if we consider the self-gravity of the disk. But the secular evolution we present here holds for any mass regime. For higher masses, the evolution is the same except that it occurs faster.
Figure 11 shows the same simulation as presented in Fig. 6, but in inclination–eccentricity space. We see that at the beginning of the simulation (t = 40 Myr), all particles are as expected still at low inclination while the eccentricities have started to grow; at t = 200 Myr, the eccentricities are high, but the inclinations are still moderate, although the peak inclination value of the distribution is now ~ 30°. Recalling that all inclinations were initially below 3°, this shows that the inclinations have grown significantly; at t = 440 Myr, the particles have now passed their peak eccentricity phase (see Fig. 8), but most inclinations have now jumped close to 180°, meaning they have evolved to retrograde orbits.
Basically, the typical inclination evolution of a disk particle is the following: as long as the eccentricity grows, the inclination keeps increasing while remaining moderate. When the eccentricity nearly reaches 1, the inclination rapidly jumps close to 180° and keeps evolving retrograde afterwards.
This behavior was of course already present in Figs. 3 − 6, but somewhat hidden by the upper view projections. As noted above, at t = 440 Myr in Fig. 6, most particles seem to have 0° < ν < 180°, while in Fig. 8, they obviously have 180° < ν < 360°. This discrepancy is indeed due to the inclination. At this time, most particles already have retrograde orbits, so that once projected onto the OXY plane, the apparent longitude of periastron Ω + ωcosi rather corresponds to Ω − ω than to Ω + ω. To explain this behavior, we must get back to our semi-analytical study. The main difficulty here is that contrary to the planar problem, the averaged Hamiltonian of the particle has now two degrees of freedom. The averaged Hamiltonian is usually described by the classical canonically conjugate Delaunay variables: ![\begin{equation} \begin{array}{lcl} \dy \omega ,& & G=\sqrt{a(1-e^2)}\\[\jot]\dy \Omega ,& & G\cos i\end{array}, \end{equation}](/articles/aa/full_html/2014/01/aa22229-13/aa22229-13-eq221.png) (9)or similarly, introducing ϖ = ω + Ω:
(9)or similarly, introducing ϖ = ω + Ω: ![\begin{equation} \begin{array}{lcl} \dy \varpi ,& & P=\sqrt{a}\,\left(1-\sqrt{1-e^2}\right)\\[\jot] \dy \Omega ,& & G\cos i \end{array} , \end{equation}](/articles/aa/full_html/2014/01/aa22229-13/aa22229-13-eq222.png) (10)where i is the inclination. As long as the eccentricity does not reach 1, the fact that the inclination remains moderate actually validates the planar motion which is described by the canonically conjugate variables (ϖ,P), or equivalently (ν,P). Now, Fig. 7 shows that with e′ = 0.94, a particle starting at low eccentricity will evolve towards high eccentricity with ~ constant ϖ (ν ≃ 70°). As ϖ and P are canonically conjugate, a ~ constant ϖ means
(10)where i is the inclination. As long as the eccentricity does not reach 1, the fact that the inclination remains moderate actually validates the planar motion which is described by the canonically conjugate variables (ϖ,P), or equivalently (ν,P). Now, Fig. 7 shows that with e′ = 0.94, a particle starting at low eccentricity will evolve towards high eccentricity with ~ constant ϖ (ν ≃ 70°). As ϖ and P are canonically conjugate, a ~ constant ϖ means 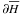 /∂P ≃ 0, which is equivalent to
/∂P ≃ 0, which is equivalent to 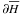 /∂e ≃ 0. We may thus expect the Hamiltonian to weakly depend on the eccentricity during this phase. The dynamics of the particle during the eccentricity increase will then be approximately well described drawing level curves of Hamiltonian in (Ω,Gcosi) space, or equivalently in (Ω,i) space for a fixed ν ≃ 70° and a fixed arbitrary e value.
/∂e ≃ 0. We may thus expect the Hamiltonian to weakly depend on the eccentricity during this phase. The dynamics of the particle during the eccentricity increase will then be approximately well described drawing level curves of Hamiltonian in (Ω,Gcosi) space, or equivalently in (Ω,i) space for a fixed ν ≃ 70° and a fixed arbitrary e value.
 |
Fig. 12 A phase portrait in (Ω,i) space of the averaged spatial Hamiltonian of a massless particle perturbed by Fom b in the same conditions as in Fig. 7, computed with constant ν = 65° and e = 0.8. This approximately describes the secular inclination evolution of the particle during its eccentricity growth. |
 |
Fig. 13 Views of the simulation of Fig. 6 and in (Ω,i) space like in Fig. 12 at t = 250 Myr and t = 440 Myr. |
Figure 12 shows the result of this computation, performed with fixed ν = 65° and e = 0.8. We see two major libration islands that inevitably drive any particle starting at low inclination towards high inclination. The Hamiltonian curves are here again explored clockwise. We checked that other choices of ν and e along the separatrix of the right plot in Fig. 7 lead to similar diagrams. Following the Hamiltonian level curves, we clearly see how the particles move towards retrograde orbits.
To check the reality of this analysis, we plot snapshots of our simulation with m = 0.002 MJup (Figs. 6 and 11) in (Ω,i) space like in Fig. 12. This is done in Fig. 13 at t = 250 Myr and t = 440 Myr. At the beginning of the simulation (not shown here), all inclinations are below 3° while the Ω values are drawn randomly. All particles appear thus in the bottom of the diagram in (Ω,i) space. This remains true for a long time as long as the inclinations remain low. At t = 250 Myr (at this time most particles have already e > 0.8, hence our choice of e in Fig. 12), the inclinations have started to grow with Ω value concentrated around 20° and 200°. Obviously, the particles follow a route in (Ω,i) space that is very close to the level curves of Fig. 13. At t = 440 Myr, all particles have moved in the upper part of the diagram following this route and become retrograde. Afterwards, the particles get back to low inclinations and cycle around the two island of libration in (Ω,i) space.
 |
Fig. 14 Same simulation as presented in Fig. 6, at the same corresponding times (left: t = 40 Myr, middle: t = 200 Myr, right: t = 440 Myr) but the disk is now viewed with a 67° with respect to pole-on, as to mimic the viewing conditions of Fomalhaut’s disk from Earth. |
For higher Fom b masses like in Fig. 5 (m = 0.02 MJup), the same dynamics is observed but it occurs proportionally faster. At the end of the simulation, we have at each time approximately as many prograde particles as retrograde ones. The initial disk of particles now assumes a cloud shape rather than a disk shape. This is illustrated in Fig. 14, which shows the disk of particles, here again for the m = 0.002 MJup case and at the same epochs as in Fig. 6, but viewed with a 67° inclination with respect to pole-on. This mimics the viewing conditions of Fom b’s disk from the Earth. At t = 20 Myr, the disk still appears as a clearly eccentric disk with moderate eccentricities. This is marginally the case at t = 200 Myr and obviously no longer applies at t = 440 Myr. At this stage (and even earlier) the simulated disk no longer matches the observed one.
The simulations presented here assumed that the orbital plane of the perturbing Fom b is coplanar with the mid-plane of the disk. As the coplanarity is not strictly established observationally due to the uncertainties, we checked other configuration with disks inclined up to 20° with respect to the orbital plane of the planet. In all cases, the behavior reported in the previous sections remains almost unchanged. All particles evolve towards high eccentricities and become retrograde with respect to the planet’s orbital plane when reaching very high eccentricities, so that our conclusions are unchanged: the disk inevitably gets a too high eccentricity to match the observations. Moreover, due to the evolution of the inclinations of the particles, the disk no longer assumes a disk shape.
6. Discussion
6.1. Disk shaping by Fom b: an unlikely scenario?
Our numerical and semi-analytical study shows that if the perturber is massive enough to efficiently affect the disk, the pericenter glow dynamics that applies in the low eccentricity regime cannot be transposed to the case where the perturber is very eccentric. In that case, we have a completely different dynamics where the disk particles reach very high eccentricities and high inclinations. In a first transient phase, the disk actually achieves an eccentric disk shape with growing eccentricity, but afterwards the particles diffuse in phase space and the steady-state regime does no longer correspond to an eccentric disk figure. A moderate eccentricity approximately matching the observed one is in all cases reached shortly after the beginning of the secular process. The desired time roughly scales as 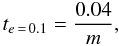 (11)where m is given in Jupiter masses and te = 0.1 in Myrs. Reaching this stage at t = 440 Myr would indicate an extremely low planetary mass (~2.3 Lunar masses). As described in the previous section, such a low mass perturber is unlikely to be able to perturb the dust ring, given its probable mass. In this regime, the dynamics of the disk is virtually unaffected by Fom b.
(11)where m is given in Jupiter masses and te = 0.1 in Myrs. Reaching this stage at t = 440 Myr would indicate an extremely low planetary mass (~2.3 Lunar masses). As described in the previous section, such a low mass perturber is unlikely to be able to perturb the dust ring, given its probable mass. In this regime, the dynamics of the disk is virtually unaffected by Fom b.
Alternatively, the perturbation of the disk might be recent rather than primordial. According to that scenario, Fom b’s mass should be closely linked with the date of this event by Eq. (11) to generate a disk with the suitable bulk eccentricity today. This situation is nevertheless a transient phase, as the bulk disk eccentricity is supposed to keep growing. The disk can only survive in its observed configuration for a short time period comparable to te = 0.1. As a consequence, the higher Fom b’s mass, the less probable this picture is.
In all cases however, the transient elliptic disk is not apsidally aligned with the perturbing planet, which does not match our orbital determination for Fom b. However, it is difficult to derive a firm conclusion on this sole basis, as the determination of the orbital alignment is only accurate within a few tens of degrees. It must nevertheless be noted that a ~ 70° misalignment would only be marginally compatible with the data.
Consequently, we come to a contradiction. If we forget its high eccentricity, the compared orientations of Fom b’s orbit and the dust ring share all characteristics of a pericenter glow phenomenon. But our analysis revealed that pericenter glow no longer applies at the eccentricity of Fom b. Even if we consider the lowest possible eccentricity according to our MCMC distribution (e′ ≃ 0.6, Fig. 1), Fig. 7 shows that the topology of the Hamiltonian map is already very different from that leading to pericenter glow.
 |
Fig. 15 Sketch of the two scenarios for Fom b and Fom c interaction. Left: Scenario 1, with non-crossing orbits for Fom b and Fom c, locked in apsidal resonance; Right: Scenario 2, with Fom b recently scattered from an inner orbit onto its present day one by a moderately eccentric Fom c. The latter orbital configuration of Fom b is supposed to be metastable. |
We thus have two conclusions. First, Fom b is very likely to be a low mass planet (~Earth or super-Earth sized). On a ~10 Myr time-scale, a massive planet would destroy the dust ring (Fig. 3). Before that, its secular action would inevitably drive the disk particles towards high eccentricities incompatible with the observations. According to Eq. (11), this occurs within ~ 105 yr, which is very short. This would require Fom b to have been put on its present day orbit more recently than that. Given the age of the star, this seems rather unlikely. We must however note that this is only an order-of-magnitude estimate. Equation (11) is actually an empirical fit that hides some unknown dependencies on the semi-major axis and the eccentricity of Fom b. Putting a lower mass limit on Fom b is less straightforward. We have seen that below ~ Earth-sized, the planet has virtually no secular effect on the disk, but this is not incompatible with the observations. It would just mean that something else than Fom b is responsible for the disk shaping. In fact, a very low mass Fom b would hardly retain enough dust around it to be detected directly. This was earlier suggested by Kennedy & Wyatt (2011) and more recently by the numerical experiments in Kalas et al. (2013). Kalas et al. (2013) propose a lower limit to the mass between Ceres and Pluto, under the assumption that the more likely models are the most long lived, and this requires a cloud of dust to be bound to a central object and have sufficient size to explain the optical luminosity. Alternatively, Fom b could also just be short lived cloud of dust with no planet mass inside, such as might be created when planetesimal in the 10 − 100 km size range collide with each other (Kalas et al. 2008; Galicher et al. 2013).
Our second conclusion is that Fom b can hardly be responsible for the shaping of the dust ring into a moderately eccentric ring on its own. This is actually independent of its mass. If we assume that Fom b is ~sub-Earth sized, then it is just not massive enough to efficiently influence the ring. According to our semi-analytical study, this regime holds up to ~Earth-sized planets. If Fom b is more massive, then it has a secular action on the dust ring and inevitably drives particles towards high eccentricity. This occurs in any case before the age of the star. Typically, with a super-Earth sized Fom b, the present-day disk eccentricity is obtained ~10−20 Myr after the beginning of the simulation. This would imply Fom b to have been put on its orbit that time ago. Here again, given the age of the star, this seems unlikely, but less unrealistic than the 105 yr required for a massive planet. Therefore we cannot rule out this possibility. But if Fom b was put on its present-day orbit a few 107 yr ago by some scattering event, necessarily this event was caused by another, more massive planet (see below) which very probably controls the dynamics of the ring more efficiently than Fom b itself. So, irrespective of its mass, Fom b is very probably not responsible for the sculpting of the observed dust ring.
6.2. Another planet
If Fom b cannot be responsible for the disk sculpting, a subsequent conclusion is that there must be another, more massive planet shepherding the dust ring. Kalas et al. (2013) came to the same conclusion and their numerical experiments assume that a Jupiter mass planet exists with a ~ 120 au, e ~ 0.1 and serves to dynamically maintain the inner edge of the belt. Chiang et al. (2009) actually already invoked the hypothesis of another planet accounting at least partly for the forced eccentricity of the belt, concluding that given the residual proper acceleration of Fomalhaut measured by the Hipparcos satellite, a ~30 MJup brown dwarf could be orbiting Fomalhaut at ~5 au. This possibility was nevertheless ruled out by Kenworthy et al. (2013), who compiled their own observations with other direct searches for additional companions to Fomalhaut (Absil et al. 2011; Kenworthy et al. 2009). They conclude that no companion more massive than ~20 MJup is to be expected from 4 au to 10 au and than ~30 MJup closer. Less massive companions (Jovian-sized?) are nevertheless not excluded. The main problem in this context is to combine the shepherding of the disk and the survival of Fom b. Basically, to confine the inner edge of the dust belt at 133 au as it is observed, a moderately eccentric Jovian-sized planet must orbit the star between ~90 au and ~120 au, depending on its mass (see detailed calculations by Chiang et al. 2009). But given its high eccentricity, Fom b’s orbit will inevitably cross the orbit of that additional planet (let us name it Fom c hereafter), which raises the issue of its dynamical stability. Figure 1 shows indeed that Fom b’s periastron is most probably as low as ~8 au.
There are two ways to possibly solve this paradox (see Fig. 15). The first scenario to suppose that Fom b is locked in a secular (apsidal) resonance with Fom c that prevents the orbits to cross each other. This occurs for instance inside the loops around ν = 0 delimited by the red curves in the e′ = 0.5 and e′ = 0.94 cases in Fig. 7. Inside these loops, the particle is subject to a secular resonance where it remains apsidally aligned with the perturbing planet, while it never crosses its path. Here the particle would be Fom b itself, while Fom c would be the perturber. This kind of locking in secular resonance has already been observed in some extrasolar systems like υAndromedae (Chiang & Murray 2002). Although the eccentricity regime is higher here, this cannot be excluded. It would have the advantage that it would explain the apsidal alignment of Fom b with the dust ring, as both would be apsidally aligned with Fom c (the belt being apsidally aligned with Fom c thanks to pericenter glow). Figure 7 nevertheless shows that locking in secular resonance at very high eccentricity, as it is the case for Fom b, requires a high eccentricity perturber (Fom c). As Fom c is assumed to control the dynamics of the belt instead of Fom b, one needs to explain now how the disk remains at low eccentricity, in other words, why a regular pericenter glow dynamics seems to apply to the disk with respect to Fom c despite its high eccentricity. This is in contradiction with our previous analysis, but could possibly be due to a wider separation between Fom c and the disk. Although we cannot firmly rule it out, we nevertheless consider this scenario as less probable. Obviously a dedicated parametric study is required to determine in which conditions it could eventually be possible.
The second scenario assumes that Fom b is presently on a metastable orbit (Fig. 15). In this context, Fom b would have resided initially closer to the star, and it would have been put more or less recently on its present orbit by a scattering event, possibly originating from Fom c. We are then back to the hypothesis of a transient configuration with a more or less recent scattering event. This scenario would quite naturally explain the very high eccentricity of Fom b and its puzzling belt-crossing orbital configuration. We could also possibly explain the presence of solid material around this planet, which actually renders it observable. This material could actually be captured from the dust belt each time Fom b crosses it. The plausibility of this scenario is basically a matter of time-scales compared to the masses of both planets. Figure 4 shows that after ~ 100 Myr, a particle crossing the orbit of a Jovian-sized planet has only a few percent chances not to have been ejected earlier by a close encounter. It can be argued that this time-scale is not that short compared to the age of the star. This depends however on the mass of the perturber, here Fom c. Assuming a more massive Fom c would inevitably drastically shorten the ejection time-scale and render the present day observation of Fom b on its metastable orbit very unlikely. Conversely, a less massive (Saturn-sized?) Fom c would make it more plausible, but it should remain massive enough to be able to efficiently sculpt the dust belt. Another difficulty with this scenario is that it does not provide a natural explanation for the apsidal alignment between Fom b and the dust belt. As a result of pericenter glow dynamics, the dust belt would be apsidally aligned with Fom c. It would then be necessary to explain how Fom b would have been put on an apsidally aligned orbit by the scattering action of Fom c. We must however keep in mind that the observed apsidal alignment of Fom b with the disk is not accurately constrained, so that a fortuitous near-alignment within a few tens of degrees is still possible. In that scenario, the mass of Fom b is less constrained, as its perturbing action on the disk is recent. We stress however that a massive Fom b (~Jovian) is rather unlikely, for two reasons. First, scattering a Jovian-sized planet onto a high eccentricity metastable orbit would require a very massive Fom c, which could not fit the observational limits. Second, given the efficiency of close encounters with a massive Fom b, the scattering event should have occurred very recently. Given the age of the star, we would then be very lucky to witness this event today. For these reasons, we think that a low-mass Fom b is still more likely even in this second scenario. If Fom b is less massive than the Earth, then its influence on the disk is damped by the self-gravity of the disk so that no constraint can be derived anymore this way. The only limitation is then the survival of Fom b versus close encounters with Fom c.
Both scenarios turn out to present advantages and disadvantages. The first one is a steady-state configuration where the dynamical stability of Fom b as perturbed by Fom c is not ensured, and where the sculpting of the disk in its present-day shape by a very eccentric Fom c is questionable, but that would more naturally explain the apsidal alignment between the ring and Fom b; the second one points towards transient configuration with a more or less recent scattering event that placed Fom b on its current orbit. The likelihood of the former depends on the hypothetical dynamical stability of Fom b as perturbed by Fom c and on the hypothetical existence of configurations allowing the disk to remain at low eccentricity despite Fom c’s high eccentricity, while that of latter is related to the evolution and survival timescales of the transient configuration, as compared to Fomalhaut’s age. We nevertheless consider that scenario as more likely than the first one.
An alternative scenario would be that the dust confinement in Fomalhaut’s disk is due to its interaction with gas without any Fom c, such as suggested recently by Lyra & Kuchner (2013). As of yet this cannot be confirmed nor ruled out. As pointed out by Lyra & Kuchner (2013), the key point is the hypothetical presence of gas in Fomalhaut’s disk, moreover at such a long orbital distance. We know that younger debris disks like βPictoris actually contain gas (Brandeker et al. 2004; Lagrange et al. 1996), but for an older system like Fomalhaut, it is less obvious. Only upper limits are available (Liseau 1999).
Both scenarios imply the presence of planets with very short periastron values. Fom b itself has a probable periastron in the 7–8 au range. If scenario 1 holds, then Fom c has an even shorter periastron than that. Lebreton et al. (2013) attributed the near- and mid-infrared interferometric excesses of Fomalhaut (see also Mennesson et al. 2013; Absil et al. 2009) to an asteroid belt at about 2 au producing a mid-infrared excess, which subsequently produces even hotter dust detected in the near-infrared. To produce the observed amount of dust, Lebreton et al. (2013) argue that the inner belt had to be somehow excited. The presence of planets with such short periastron values could actually provide the suspected source of excitation, or, more generally, may be related to the process that placed Fom b on its peculiar. In scenario 1, Fom c would have a periastron in the 2 − 3 au range, which would be enough to excite a belt at 2 au. The dynamical stability of this belt would even be questionable and render this scenario unlikely. In scenario 2, the scattering event that more or less recently put Fom b on its present-day orbit causes it to suddenly approach the inner belt thanks to its low periastron. This could explain the excitation of the inner belt and the enhanced dust production.
In all cases, our main conclusions are that Fom b is very probably a low mass planet, possibly orbiting on a metastable orbit, and that another, more massive planet (Fom c) is required to control the disk dynamics and to be possibly responsible for the transient orbital configuration of Fom b. The interplay between both planets is still an open issue. Further work that continues to investigate and quantify the masses and orbits of the planets are clearly required. This will be the purpose of forthcoming work.
Acknowledgments
All computations presented in this paper were performed at the Service Commun de Calcul Intensif de l’Observatoire de Grenoble (SCCI) on the super-computer funded by the Agence Nationale pour la Recherche under contracts ANR-07-BLAN-0221, ANR-2010-JCJC-0504-01 and ANR-2010-JCJC-0501-01. We gratefully acknowledge financial support from the French Programme National de Planétologie (PNP) of the CNRS/INSU, and from the ANR through contract ANR-2010-BLAN-0505-01 (Exozodi). P. Kalas and J. R. Graham acknowledge support from NSF AST-0909188 and NASA Origins NNX11AD21G.
References
- Absil, O., Mennesson, B., & Le Bouquin, J.-B. 2009, ApJ, 704, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Absil, O., Le Bouquin, J.-B., Berger, J.-P., et al. 2011, A&A, 535, A68 [Google Scholar]
- Augereau, J.-C., & Papaloizou, J. C. B. 2004, A&A, 414, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumann, H. H. 1985, PASP, 97, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., & Morbidelli, A. 1996, Icarus, 120, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., & Valiron, P. 2007, A&A, 466, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boley, A. C., Payne, M. J., Corder, S., et al. 2012, ApJ, 750, L21 [Google Scholar]
- Brandeker, A., Liseau, R., Olofsson, G., & Fridlund, M. 2004, A&A, 413, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Beust, H., et al. 2012, A&A, 542, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, E. I., & Murray, N. 2002, ApJ, 576, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., Kite, E., Kalas, P., Graham, J. R., & Clampin, M. 2009, ApJ, 693, 734 [Google Scholar]
- Currie, T., Debes, J., & Rodigas, T. J. 2012, ApJ, 760, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., & Maddison, S. T. 2005, ApJ, 625, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B. 2005, AJ, 129, 1706 [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Galicher, R., Marois, C., Zuckerman, B., & Macintosh, B. 2013, ApJ, 769, 42 [Google Scholar]
- Graham, J. R., Fitzgerald, M. P., Kalas, P., & Clampin, M. 2013, AAS, 221, 324.03 [Google Scholar]
- Holland, W. S., Greaves, J. S., Dent, W. R. F., et al. 2003, ApJ, 582, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Carson, J. C., Lafrenière, D., et al. 2012, ApJ, 747, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kalas, P., Graham, J. R., Fitzgerald, M. P., & Clampin, M. 2013, ApJ, 775, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., & Wyatt, M. C. 2011, MNRAS, 412, 2137 [NASA ADS] [CrossRef] [Google Scholar]
- Kenworthy, M. A., Mamajek, E. E., Hinz, P. M., et al. 2009, ApJ, 697, 1928 [NASA ADS] [CrossRef] [Google Scholar]
- Kenworthy, M. A., Meshkat, T., Quanz, S. P., et al. 2013, ApJ, 764, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, A.-M., Plazy, F., Beust, H., et al. 1996, A&A, 310, 547 [NASA ADS] [Google Scholar]
- Lebreton, J., van Lieshout, R., Augereau, J.-C., et al. 2013, A&A, 555, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Liseau, R. 1999, A&A, 348, 133 [NASA ADS] [Google Scholar]
- Lyra, W., & Kuchner, M. 2013, Nature, 499, 18 [Google Scholar]
- Mamajek, E. E. 2012, ApJ, 754, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Marengo, M., Stapelfeldt, K., Werner, M. W., et al. 2009, ApJ, 700, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Mennesson, B., Absil, O., Lebreton, J., et al. 2013, ApJ, 763, 199 [Google Scholar]
- Moerchen, M. M., Churcher, L. J., & Telesco, C. M. 2011, A&A, 526, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar system dynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Quillen, A. C. 2006, MNRAS, 372, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Reche, R., Beust, H., Augereau, J.-C., & Absil, O. 2008, A&A, 480, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terquem, C., & Ajmia, A. 2010, MNRAS, 404, 409 [NASA ADS] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the new reduction of the raw data, Astrophys. Space Sci. Lib., 350 [Google Scholar]
- Wyatt, M. C. 2003, ApJ, 598, 1321 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wyatt, M. C. 2005, A&A, 440, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C., & Dent, W. R. F. 2002, MNRAS, 334, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Dermott, S. F., Telesco, C. M., et al. 1999, ApJ, 527, 918 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of various statistical parameters resulting from the MCMC distribution of Fom b’s orbital solutions (run with Kalas et al. 2013 data).
All Figures
 |
Fig. 1 Resulting MCMC distribution of the orbital elements of Fom b’s orbit. In all plots, the black curves correspond to the first run using the full Kalas et al. (2013) data, and the red one to the second run using Galicher et al. (2013) data before 2012. Upper row, from left to right: semi-major axis (a), orbital period (P), eccentricity (e); second row, id: periastron (q), inclination (i), longitude of ascending node (Ω); third row, id: argument of periastron (ω), time for periastron passage (tp), and inclination relative to the disk plane (irel). |
| In the text | |
 |
Fig. 2 Resulting 2D MCMC distribution of Fom b’s orbital elements for two couples of parameters, for the run with the full Kalas et al. (2013) data: semi-major axis (a)–eccentricity (e) (left); longitude of ascending node (Ω)–inclination (i) (right). The color scale represents the joint 2D density of solutions for the considered set of parameters. In the right plot, the star indicates the corresponding location of the mid-plane of the dust disk (Kalas et al. 2005). The same plot using Galicher et al. (2013) data is almost identical. |
| In the text | |
 |
Fig. 3 Result of the N-body integration with a perturbing planet with m = 1 MJup. We display here upper views of the planetesimal disk together with the planet’s orbit (top) and semi-major axis–eccentricity diagrams of the disk (bottom), at three epochs: beginning of the simulation (t = 0, left), at t = 5 Myr (middle) and t = 100 Myr (right). The color scale is proportional to the projected densities of particles (top plots) and of orbits in (a,e) space (bottom plots). The red circles represent the location of the star and of the planet. The planet’s orbit is sketched as a black ellipse. |
| In the text | |
 |
Fig. 4 Evolution of the number of active disk particles as a function of time in the simulations described in Figs. 3 (black), 5 (red) and 6 (green). All missing particles have been ejected by close encounters. This phenomenon mainly concerns the m = 1 MJup case. |
| In the text | |
 |
Fig. 5 Result of the N-body integration with a perturbing planet with m = 0.02 MJup. The conventions are the same as in Fig. 3. Three epochs are represented: t = 5 Myr (left), t = 20 Myr (middle) and t = 440 Myr (right). |
| In the text | |
 |
Fig. 6 Result of the N-body integration with a perturbing planet with m = 0.002 MJup. The conventions are the same as in Fig. 3. Three epochs are represented: t = 40 Myr (left), t = 200 Myr (middle) and t = 440 Myr (right). |
| In the text | |
 |
Fig. 7 Phase portraits of secular averaged Hamiltonian |
| In the text | |
 |
Fig. 8 Views of the simulations of Figs. 6 and 5 in (ν,e) space like in Fig. 7. The three upper plots refer to Fig. 6 (m = 0.002 MJup) at t = 40 Myr, t = 100 Myr, t = 200 Myr, while the lower left plot corresponds to t = 440 Myr. The lower middle plot refers to Fig. 5 (m = 0.02 MJup) at t = 200 Myr. |
| In the text | |
 |
Fig. 9 A phase portrait equivalent to the left plot of Fig. 7, but with a/a′ = 0.8. This situation mimics the dynamics of Fom b as perturbed by a massive disk (see text). |
| In the text | |
 |
Fig. 10 Phase portraits similar to those of Fig. 7 but to which we have added a second perturbing planet (representing the disk) apsidally aligned with the first one (Fom b). The second planet is assumed to orbit at the same semi-major axis as the disk particle. The important parameter is the mass ratio ρ between the two planets. Left plot: ρ = 0.1, i.e., a disk 10 times less massive than Fom b; Middle plot: ρ = 1, disk and Fom b have equal masses; Right plot: ρ = 10, i.e., a disk 10 times more massive than Fom b. |
| In the text | |
 |
Fig. 11 Same simulation as presented in Fig. 6, but in inclination–eccentricity space (i,e), at the same corresponding times: t = 40 Myr (left), t = 200 Myr (middle), t = 440 Myr (right). |
| In the text | |
 |
Fig. 12 A phase portrait in (Ω,i) space of the averaged spatial Hamiltonian of a massless particle perturbed by Fom b in the same conditions as in Fig. 7, computed with constant ν = 65° and e = 0.8. This approximately describes the secular inclination evolution of the particle during its eccentricity growth. |
| In the text | |
 |
Fig. 13 Views of the simulation of Fig. 6 and in (Ω,i) space like in Fig. 12 at t = 250 Myr and t = 440 Myr. |
| In the text | |
 |
Fig. 14 Same simulation as presented in Fig. 6, at the same corresponding times (left: t = 40 Myr, middle: t = 200 Myr, right: t = 440 Myr) but the disk is now viewed with a 67° with respect to pole-on, as to mimic the viewing conditions of Fomalhaut’s disk from Earth. |
| In the text | |
 |
Fig. 15 Sketch of the two scenarios for Fom b and Fom c interaction. Left: Scenario 1, with non-crossing orbits for Fom b and Fom c, locked in apsidal resonance; Right: Scenario 2, with Fom b recently scattered from an inner orbit onto its present day one by a moderately eccentric Fom c. The latter orbital configuration of Fom b is supposed to be metastable. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


