| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322032 | |
| Published online | 09 January 2014 | |
3D maps of the local ISM from inversion of individual color excess measurements⋆
1 GEPI Observatoire de Paris, CNRS, Université Paris Diderot, Place Jules Janssen, 92190 Meudon, France
e-mail: rosine.lallement@obspm.fr; lucky.puspitarini@obspm.fr
2 ACRI-ST, 260 route du Pin Montard, 06904 Sophia Antipolis, France
e-mail: jeanluc.vergely@latmos.ipsl.fr
3 Institut des Sciences de la Terre, IRD: UR219, Université de Savoie, CNRS: UMR 5275 LGIT-Savoie, 73376 Le-Bourget-du-Lac, France
4 Observatoire de Genève, Université de Genève, Chemin des Maillettes 51, 1290 Sauverny, Switzerland
5 Research School of Astronomy & Astrophysics, Mount Stromlo Observatory, The Australian National University, ACT 2611 Weston Creek, Australia
Received: 6 June 2013
Accepted: 24 September 2013
Aims. Three-dimensional (3D) maps of the Galactic interstellar matter (ISM) are a potential tool of wide use, but accurate and detailed maps are still lacking. One of the ways to construct the maps is to invert individual distance-limited ISM measurements, a method we have applied here to measurements of stellar color excess in the optical.
Methods. We assembled color excess data together with the associated parallax or photometric distances to constitute a catalog of ≃23 000 sightlines for stars within 2.5 kpc. The photometric data are taken from Strömgren catalogs, the Geneva photometric database, and the Geneva-Copenhagen survey. We also included extinctions derived towards open clusters. We applied an inversion method based on a regularized Bayesian approach to this color excess dataset, a method previously used for mapping at closer distances.
Results. We show the dust spatial distribution resulting from the inversion by means of planar cuts through the differential opacity 3D distribution, and by means of 2D maps of the integrated opacity from the Sun up to various distances. The mapping assigns locations to the nearby dense clouds and represents their distribution at the spatial resolution that is allowed by the dataset properties, i.e. ≃10 pc close to the Sun and increasing to ≃100 pc beyond 1 kpc. Biases toward nearby and/or weakly extincted stars make this dataset particularly appropriate to mapping the local and neighboring cavities and to locating faint, extended nearby clouds, which are both goals that are difficult or impossible with other mapping methods. The new maps reveal a ≃1 kpc wide empty region in the third quadrant in the continuation of the so-called CMa tunnel of the Local Cavity, a cavity that we identify as the Superbubble GSH238+00+09 detected in radio emission maps and that is found to be bounded by the Orion and Vela clouds. The maps also show an extended narrower tunnel in the opposite direction (l ≃ 70°) that also extends the Local Bubble further and together with it forms a conspicuous cavity bounded by the main Lup, Sco, Oph, Aql, Lac, Cep, and Tau clouds and OB associations. This chain of cavities and surrounding dense regions constitute the first computed representation of the well known Gould belt/Lindblad ring structures. Finally, almost all off-plane faint features that appear in 2D dust maps have a counterpart in the 3D maps, providing the dust distribution in nearby tenuous clouds.
Key words: local insterstellar matter / dust, extinction / ISM: bubbles / ISM: clouds
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
While emission surveys at various wavelengths are providing increasingly detailed maps of interstellar matter (ISM) in the Galaxy, they lack precise information on the distance to the emitting clouds. In particular, distance assignment based on their radial velocities and a mean Galactic rotation curve leads to a poor 3D description of the ISM in the Sun’s vicinity, while most of the medium and high-latitude emissions originate in this vicinity.
Other ways to obtain realistic 3D distributions of the ISM is to gather absorption data toward target stars located at known and widely distributed distances and to invert those line of sight data in some way. Absorption data may be gaseous lines that provide absorbing columns of gaseous species or color excess measurements that provide extinctions and dust columns. In the case of reddening data, they can be derived in a statistical way from stellar photometric surveys by means of color–color/ color–magnitudes diagrams or stellar population synthesis and Galactic models (in particular the Galactic model of Robin et al. 2003), or they can be based on individual stellar reddening values, themselves based on photometric or spectrophotometric measurements and appropriate calibrations (see Marshall et al. 2006, 2009; Sale & Drew 2010; Gontcharov 2012; Chen et al. 2013; Knude 2010; Cambrésy et al. 2011; Reis et al. 2011; Knude & Lindstrøm 2012, for details on various data and methods). In the absence of parallax measurements, photometric distances are derived along with the reddening in a consistent way, or distances are estimated by comparing the density of foreground stars with models (as in Lombardi et al. 2010). Those methods based on large surveys have the strong advantage of being based on a huge amount of targets, however the achievable spatial resolution is limited due to the required statistics and most of those techniques are not appropriate for mapping at small distance due to the need for zero reddening references. Those methods that are based on individual sightlines can potentially produce a higher radial spatial resolution (in principle only limited by the mean radial distance between two target stars) and are appropriate for the solar neighborhood. However, there is not much data available today, and those maps are still restricted to the Sun’s vicinity. This situation will hopefully change in future thanks to data from high-resolution multiplex spectrographs and from the ESA astrometric mission Gaia, and for this reason it is useful to investigate inversion techniques and their application to individual reddening data of increasing number, which is the focus of the present work.
The first attempt to compute a 3D distribution of the ISM by inverting individual line-of-sight data was made by Vergely et al. (2001), who used compiled data on neutral interstellar (IS) absorbers (NaI and HI), as well as the corresponding Hipparcos parallaxes, and inverted those individual data using a robust tomographic method (Tarantola & Valette 1982). Lallement et al. (2003) gathered data for the specific purpose of mapping the so-called Local Bubble or Local Cavity, a 100–200 pc-wide cavity around the Sun, and applied the same method to a larger NaI dataset (around 1000 sightlines) with Hipparcos distances. It confirmed the view that there is a cavity that is deficient in cold and neutral interstellar gas and that the closest dense and cold gas is at ≃80 pc (Cox & Reynolds 1987). The inverted map also revealed interstellar tunnels that connect the Local Bubble to surrounding cavities. High-latitude sightlines with the smallest absorption are found in chimneys, whose directions are perpendicular to the Gould belt plane. The maps show that the Local Bubble is squeezed by surrounding shells in a complicated pattern. Welsh et al. (2010) presented 600 pc wide NaI and CaII maps using a catalog of absorptions towards 1857 early-type stars located within 800 pc of the Sun. While NaI traces dense and neutral IS, CaII traces both dense neutral and ionized gas. The CaII exhibit strong spatial similarities to those of their equivalent NaI absorption maps, since the dominant features are the dense cloud associations. More recently, Vergely et al. (2010) has developed the inversion method further, and updated the sodium maps and inverted ≃6000 extinction measurements based on stellar Strömgren photometry and stars possessing Hipparcos parallaxes. The similarity between the locations of the major dust clouds deduced from the extinction inversion and the gas clouds deduced from NaI within 250 pc has been a first test of the inversion method. Most features, the main opaque regions, the Local Cavity boundaries, and the tunnels to surrounding cavities were also derived by Reis et al. (2011) from Strömgren photometry measurements and reddening-distance relationships. See also Reis et al. (2011) for a general review of solar neighborhood mapping, by means of any method.
Here we extend the inversion and the mapping to greater distances by making use of more distant stars and by merging target stars possessing Hipparcos parallaxes and targets with photometric distances. Section 2 describes the data used for the inversion. In Sect. 3, we briefly describe the improved inversion method and discuss its parameters. In Sect. 4, we present the resulting 3D distributions by means of separate planar cuts. In Sect. 5 we show distance-limited 2D reddening maps based on the inverted 3D distribution and integration up to spheres of various radii. We discuss the results in Sect. 6.
2. Color excess data and distances
We started with the Vergely et al. (2010)E(b − y) dataset, i.e., color excesses derived from Strömgren photometry for nearby stars possessing Hipparcos parallax measurements. We used parallax values here and associated errors from the most recent analysis of van Leeuwen (2007). The types were distributed between B0 to G2, with 60% of F-G types.
We added to this list reddening and photometric distances derived self-consistently from Geneva photometric measurements for a large dataset of B stars (Cramer 1999; Burki & Cramer, priv. comm., see the Geneva photometric database). The catalog is composed of early-type stars, O, and a large majority of B-type stars. There are 614 targets in common with the Strömgren-based dataset, and they were used to establish the relationship between the Strömgren E(b − y) and the Geneva E(B − V) color excess values. This relationship, already described in Raimond et al. (2012) was found to be E(B − V) (Geneva) = (1.585 ± 0.0129) E(b − y) + (0.0221 ± 0.0007). Thus, we converted the Geneva E(B − V)s into E(b − y)s following this relationship, then converted all E(b − y)s into Johnson E(B − V)s following the relationship E(B − V)J = 1.335 E(b − y). In the case of repeating stars, we chose to use the Strömgren and Hipparcos distances.
We then added the catalog of color excess and distances derived for the target stars from the latest revision of the Geneva-Copenhagen Survey (Nordström et al. 2004; Casagrande et al. 2011). The catalog is composed of late-type stars, mainly F and G stars. The reddening estimates are based on the intrinsic color calibration of Olsen (1988), which has a stated accuracy of ≃0.01 mag. Similar to the former catalogs, such observational errors might lead to negative values of reddening for nearby stars that have zero or very weak reddening. We removed stars already contained in the two other catalogs. Finally, we used color excess measurements towards a series of stellar clusters, as well as the best estimates of the cluster distances, all from the recent new catalog of Dias et al. (2012).
All extinction measurements were scaled to the Johnson system. For the last three sources, we used the photometric distances, even for stars possessing a Hipparcos parallax, since they were derived self-consistently along with the extinction. All those datasets were filtered for known binaries in cases of potentially affected extinction and distance derivations. For all datasets we kept the negative values of the color excess, in order to avoid any statistical bias at a short distance. We then retained from this merged list only those stars fulfilling the following conditions: estimated distance below 2500 pc, estimated distance to the plane smaller than 300 pc, E(B − V)J ≥ − 0.02 (see below), and relative uncertainties on the distances smaller than 35% for both Hipparcos and photometric distances). The limitation in distances is guided by experience. Keeping a few isolated, very distant stars with uncertain distance provides weak additional constraints resulting in elongated structures of poor interest (see the map descriptions). On the other hand, using a threshold on the relative uncertainty allows maintaining moderately distant targets that have a particularly good accuracy and to exclude those nearby stars that have very large uncertainties. The limitation in height above the plane results in a limited distance for the inversion that is a function of the latitude, more precisely dlimit = 300/sin(b). We come back to this point in Sect. 4. Our final list contains 22 883 remaining targets: 5106, 12 120, 4830, and 827 targets are from the four sources.
3. The inversion method applied to extinction data
The present inversion is based on the pioneering work of Tarantola & Valette (1982) who derived general formalisms for nonlinear, least squares inverse problems. We use here their specific formalism adapted to the solution for functions of continuous variables. In our context the differential reddening (or, equivalently, differential opacity) is a continuous function of the 3D interstellar space. Given our datasets of distance-limited data, reconstructing such a 3D map is by far underconstrained. However, the inversion can be regularized and performed by requiring that the solution is smooth and by using a Bayesian formulation; i.e., the solution is based not only on the color excess data but also on prior knowledge of the opacity distribution (see Vergely et al. 2010). These two information sources complement each other: where the constraints from the data are insufficient, the inversion restores the prior density; in the opposite case, it favors the information contained in the data. For more details on the inversion technique applied to IS line-of-sight data, see Vergely et al. (2010). We mention hereafter the specific changes from this previous work.
3.1. Data and associated errors
The data are the color excess measurements toward the target stars and the target distances. It is important to determine their biases and standard deviations. The color excess is assumed to be proportional to the dust opacity toward the target. At variance with the previous inversion, we make use of independent color excess datasets that are not based on the same wavelength intervals, while still using a unique differential color excess as a variable. More specifically, during the computation, it is defined as the Johnson E(B − V)J color excess per parsec (in units of mag pc-1). Because a color excess is a combination of both the dust volume density and of the dust properties, i.e. of the local reddening law, having merged the data after a simple scaling and using a unique variable is equivalent to implicitly assuming that spatial variabilities in the reddening law do not change the ratios significantly between the various color excess quantities. However, because the wavelength ranges are very close, this is a reasonable assumption.
3.1.1. Color excess data
For all data we carefully kept all meaningful negative values to avoid biases at low reddening. We also proceeded in the following conservative way for errors. The standard deviation of the color excess data comes essentially from the uncertainty on the photometric measurements and uncertainties linked to the calibration or intrinsic dispersion in the color-magnitude diagrams. Uncertainties on the color excess measurements introduced in the inversion code are as follows. i) For the Strömgren dataset, uncertainties on the E(b − y)s were taken from Table 2 of Vergely et al. (2010) and correspond to combined errors on the diagram dispersion and on photometry. The errors on E(b − y) were converted to errors on E(B − V) according to the relationship quoted above. ii) The Geneva database provides a precise determination of the photometric error, which is small and well below the error linked to the use of calibration laws. We used here a conservative value of 0.014 mag for the uncertainty on E(B − V). iii) In the case of the Geneva-Copenhagen data, we estimated the uncertainties conservatively, which are taken here to be very similarly on the order of 0.016. iv) For the uncertainties on the cluster data, they were taken from the Dias et al. (2012) catalog that are also conservatively estimated. An additional error σcal = 0.01 is introduced (see also below) to represent uncertainties linked to the use of different photometric systems and calibration methods. The choice of this value is somewhat arbitrary and is a compromise between the offset of 0.02 found at the origin of the linear relationship between the Strömgren and Geneva values (the most different systems here) and zero. This offset is corrected for, but we do not have any comparison between the cluster data and the other systems, and there are potential departures from linearity that remain hidden within the intrinsic uncertainties for all systems. Also, we deliberately wanted the total error estimate to be conservative.
3.1.2. Distances
Uncertainties on the distances are crucial for the inversion process. Relative errors on the distances are either the Hipparcos errors in the case of parallax measurements, or arbitrarily taken to be 20% for all photometric determinations, except for the cluster distances for which Dias et al. (2012) provided conservative estimates. It is important that in case of Hipparcos or cluster data, as mentioned above, we removed all targets for which the relative error exceeds 35%. This is important for Hipparcos parallaxes, since it is well known that the accuracy may drop strongly for distant stars (≳300 pc). Also, errors on photometric distances to the clusters are not independent, which may introduce stronger discrepancies than in groups of independent stars in the same region.
3.1.3. Propagated errors
During the inversion, quantities that are computed and adjusted are integrated quantities along pathlengths, and as a consequence, errors on those integrals arise from both extinction and distance uncertainties. For this reason they are not treated independently during the inversion (see Vergely et al. 2010). In the present work, the total errors σtot on the integrated opacities toward the targets have been taken to be the quadratic sum of three terms:
 where
where
-
i)
σphot is the extinction measurement error quoted above;
-
ii)
σcal is an additional error equal to 0.01 to represent uncertainties linked to the use of different photometric systems and calibration methods (see above); and
-
iii)
σEd is the error on the distance d propagated to the extinction E(B − V), estimated to be
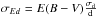 under the assumption of a constant opacity along the LOS. We also assume that
under the assumption of a constant opacity along the LOS. We also assume that 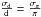 for Hipparcos parallaxes π.
for Hipparcos parallaxes π.
About the assumption that 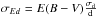 , it may appear highly questionable to assume a constant opacity given the strong clumpiness of the ISM. However, the combined errors are used in the model computation, in the frame where IS matter is much more smoothly distributed than in the actual medium. This makes the assumption significantly more realistic. Moreover, as d increases,
, it may appear highly questionable to assume a constant opacity given the strong clumpiness of the ISM. However, the combined errors are used in the model computation, in the frame where IS matter is much more smoothly distributed than in the actual medium. This makes the assumption significantly more realistic. Moreover, as d increases, 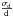 increases but the assumption generally does not become more invalid, since the smoothness and structure size also increase with distance as a result of the target scarcity. Finally, if there are strong incompatibilities between some data due to this assumption, uncertainties are accordingly increased during the iteration process (see the Appendix).
increases but the assumption generally does not become more invalid, since the smoothness and structure size also increase with distance as a result of the target scarcity. Finally, if there are strong incompatibilities between some data due to this assumption, uncertainties are accordingly increased during the iteration process (see the Appendix).
 |
Fig. 1 Inverted differential opacity distribution in the Galactic plane. The Sun is at coordinates (x,y) = (0,0) and the Galactic center direction to the right. The opacity increases from red to violet (scale to the right). Note the 1000 pc long cavity centered on l ≃ + 225° that we identified as the major super-bubble GSH238+00+09 detected in radio by Heiles (1998). We call Cygnus cavities the empty regions at l ≃ + 70°. Several well known opaque regions are indicated on the maps, and their identification is based on the literature. The gradient axis for interstellar helium ionization points to the center of the GSH238+00+09. |
3.2. Prior information on the model and associated variances
Here the model parameters are functions. We define the correlation kernel ψ(x,x′) as the correlation of the opacity between two points in space x and x′. It is fundamental since it controls the spatial variability of the model, the shape of allowed structures, and the smoothing length. Evidently the smoothing length cannot be shorter than the average distance between the targets, here varying between a few pc to ≃100 pc depending on the distance from the Sun and the location, otherwise the problem is too under-constrained.
Making use of a simple Gaussian kernel, 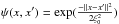 , where ξ0 is the smoothing length, yields a poor fit that we interpret as the consequence of the ISM clearly showing different characteristic lengths. It is thus well-advised to use multiscale kernels (Serban & Jacobsen 2001; Vergely et al. 2010). Vergely et al. (2010) used two exponential kernels, the first one characterizing the warm diffuse matter and the second one the more compact clouds. However, the smallest structures (pc and sub-pc scale) cannot be represented because the spatial fluctuations that are smaller than the smoothing length are not detected.
, where ξ0 is the smoothing length, yields a poor fit that we interpret as the consequence of the ISM clearly showing different characteristic lengths. It is thus well-advised to use multiscale kernels (Serban & Jacobsen 2001; Vergely et al. 2010). Vergely et al. (2010) used two exponential kernels, the first one characterizing the warm diffuse matter and the second one the more compact clouds. However, the smallest structures (pc and sub-pc scale) cannot be represented because the spatial fluctuations that are smaller than the smoothing length are not detected.
After a number of tests, we chose the following two kernels as best representing the different scales that can be detected given the dataset. They have two different functional forms to produce both an exponential wing and a Gaussian core. The exponential law is appropriate in the case of multiscale structures, and it allows the intercloud phase and large scales to be reproduced. On the other hand the Gaussian kernel allows to reach denser structures, while introducing a threshold in their sizes to avoid too much power in unrealistic, very small, and dense structures. The final choice was finally based on the quality of the adjustments. The kernel is expressed as 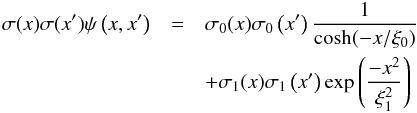 (1)where
(1)where 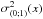 represents the model variance at point x that controls the departures from the prior distribution, and ξ(0;1) are the characteristic scales allowed in the model. Parameters are given in Appendix A.
represents the model variance at point x that controls the departures from the prior distribution, and ξ(0;1) are the characteristic scales allowed in the model. Parameters are given in Appendix A.
In addition, the density of IS matter decreases strongly with the distance to the Galactic plane. The prior model is therefore characterized by an exponential decrease with the distance to the plane 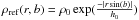 . Following Vergely et al. (2010), we chose to use h0 = 200 pc for the opacity scale height, a value deliberately above the average measurement (Chen et al. 1998) to avoid the loss of the tenuous high-latitude structures during the inversion, which may happen when the prior density is too low. Finally, the computed variable is the logarithm of the opacity per distance α (i.e. ρ(x) = exp(α(x))) to ensure the positivity of the solution.
. Following Vergely et al. (2010), we chose to use h0 = 200 pc for the opacity scale height, a value deliberately above the average measurement (Chen et al. 1998) to avoid the loss of the tenuous high-latitude structures during the inversion, which may happen when the prior density is too low. Finally, the computed variable is the logarithm of the opacity per distance α (i.e. ρ(x) = exp(α(x))) to ensure the positivity of the solution.
4. Results
The line of sight data are inverted to produce a tridimensional differential opacity distribution in a Sun-centered volume whose total dimensions are 4 × 4 × 0.6 kpc3, with 0.6 kpc the vertical extent, i.e. 300 pc above and below the horizontal plane containing the Sun (for simplicity we call Galactic plane this horizontal plane, despite the non-zero distance of the Sun to the actual plane). However, only for about half of this volume is the model significantly constrained, since the target stars are too sparse at a large distance where the opacity distribution remains equal or very close to the prior model, and for this reason the results presented below are restricted to the central regions. To better illustrate the limits of the inversion a b = 0° planar cut in the full inverted volume is shown in the appendix (Fig. A.1). We also illustrate in an appendix the distribution of stars that are close to the plane and that constrain the distribution. The reason for maintaining targets as distant as 2500 pc during the inversion is that they may contribute to the constraints at closer distance, e.g. in the case of very low reddening, and they may reveal some trends. The inverted quantity is the smoothed reddening per distance, here E(B − V) in magnitude per pc (color scale in Fig. 1). The map can be used to estimate the total reddening toward a target contained in the represented plane, by using the color scale and the Sun-target trace on the map. For clarity in the maps, we have added a few annotations. We recall that (mainly distant) regions where the distribution looks fully homogeneous and varies as a function of only Z are those for which the prior distribution has been unchanged, owing to the lack of constraining targets. We use the Galactic plane map to discuss the uncertainties associated to the inversion method.
 |
Fig. 2 Comparison between the extended map and the 500 pc wide map from Vergely et al. (2010). The black line is an iso-contour at dE(B − V)/dr = 0.0002 mag per pc drawn from the previous 3D distribution and delimiting the Local Cavity. Hatched areas correspond to the closest dense regions revealed in those previous maps. Depending on locations, the new maps reveal the full extent of those opaque regions at larger radial distances, or their division into distinct groups of clouds that the poorer resolution did not allow distinguishing earlier. |
4.1. Extinction in the Galactic plane
Figure 1 shows the color-coded differential opacity distribution in the plane. We have added iso-differential opacity contours in order to enhance the characteristics of the distribution. We warn the reader again about the impact of the correlation kernel on the actual values of the differential opacity: high numbers, that would correspond to the densest structures and cloud cores, are not reached anywhere, but instead the inverted quantity corresponds to an average over regions of size on the order of 15 or 30 pc. Still, the color-coded map allows the reddening to be estimated up to a given distance.
It is informative to compare this updated map with the former map of Vergely et al. (2010) based on about a quarter of the present dataset, and we present such a comparison for the Galactic plane. This is illustrated in Fig. 2 where we have superimposed on the new map an iso-differential opacity contour computed from the 500 pc wide former map. The differential opacity value that has been chosen for this iso-contour, namely dE(B − V)/dr = 0.0002 mag per pc corresponds to the marked transition between the Local Cavity and its boundaries. It can be seen that this contour is quite similar to the new Local Cavity boundary now found in the inner part of the new map. The new boundary is traced by the first new contour (thin red line) that has been drawn for dE(B − V)/dr = 0.00016 mag per pc. Hatched areas show the locations of the dense clouds that came out from the previous inversion. It can be seen that, while those areas still correspond to dense regions in the new, more extended maps, the clouds now often extend to greater distances. The reason is that regions beyond the first opaque clouds were simply not showing up previously due to the lack of constraining target stars, because those stars were too extinguished, hence absent from the dataset. Instead the prior distribution was kept in those external regions. These limitations still exist for the new maps, albeit now pushed away at larger distances. This is why we call attention on the fact that dense structures at large distance and located exactly beyond other, closer dense clouds may be underestimated or even missing in the maps.
 |
Fig. 3 Achievable resolution in the Galactic plane resulting from the target distribution. |
 |
Fig. 4 Opacity distribution in vertical planes containing the Sun, equally spaced by 15°. The north pole direction b = + 90° is at the top and longitudes of intersections with the Galactic plane are indicated. Some iso-differential opacity contours have been superimposed to help visualize the low- and high-opacity regions. OB associations from De Zeeuw (1999), as well as CO and HI clouds listed by Perrot & Grenier (2003) have been displayed when they are within 25 pc of this vertical plane. We also add the molecular cloud locations derived by Knude (2010). The tenuous cloud close to the north pole direction. |
To quantify the limitations from the limited number of distant targets, we show in Fig. 3 the achievable resolution at each location in the plane resulting from the target distributions. There are strong asymmetries between the quadrants that reflect the mentioned biases and the predominance of empty or dense areas. We also display in Fig. B.1 (resp. B.2) of the appendix those stars that are within 10 (resp 150) pc from the Galactic plane and are the main contributors to the opacity pattern, superimposed on the Galactic plane map itself. This comparison allows us to figure out at which distance and in which direction constraints are getting too loose and the prior solution is preferred. It is also a way to figure out the minimum size of the structures that can be reconstructed during the inversion from the distance between the targets. It can be seen that the minimum size increases from ≃10 pc close to the Sun (see Fig. B.1) up to ≃150 pc at 1 kpc (see Fig. B2). Errors on the locations of the clouds depend on the target distribution and evidently distance uncertainties, but are difficult to quantify. If a structure is defined by a statistically significant number of targets, errors on the distances average out and the center of the structure is correctly defined. The extent of the clouds, however, increases as a result of all distance uncertainties. In case only a few targets define a structure, there may be very different errors among the various situations. If the targets are angularly close but have different distances, the model produces radially elongated structures that are easily identified, and the radial size of those structures allow inferring the error on the cloud location. If targets are both scarce and irregularly located towards a structure, e.g., if they are missing towards the densest area, then individual errors on distances may have their strongest impact; i.e., the error on the cloud location may reach the mean error on the target distances. Fortunately, this is not the case for most of the clouds.
 |
Fig. 5 Same as Fig. 4 for the next three vertical planes. In the l = 45° and l = 60° half planes (top and middle), the HI Hercules shell is indicated at the 60–150 pc distance derived by Lilienthal et al. (1992) for its low-velocity component. Such a location is in good agreement with the elongated feature at b ≃ 40°. The second component at 250 pc may correspond to the fainter distant feature in the l = 60° half plane. |
The map reveals the top or bottom parts of the series of dense structures that bound the so-called Local Cavity, the ≃100 pc wide empty region around the Sun: the Aquila, Ophiuchus, Scorpius, Lupus, Crux, and Centurus dense clouds in the first and fourth quadrants; the Cassiopeia, Lacerta, Perseus, Taurus, and Orion clouds in the anti-center area. It is beyond the scope of this article to discuss those clouds in details; instead, we only superimpose the major cloud complexes and OB associations on the series of vertical maps presented in the next section. The distribution in Fig. 1 shows a conspicuous, huge empty cavity in the third quadrant. This cavity is in the continuation of the so-called CMa tunnel, the rarefied region that extends up to 130–150 pc in the direction of the star ϵCMa. A dense region located at ≃180 pc marks a partial limit between the two cavities, but it is angularly limited. As shown in other planar cuts, this huge cavity is not limited to the plane but extends both above and below to large distances. We note that the existence of this cavity has been inferred by Heiles (1998) based on radio maps and other emission data. The schematic representation of GSH238+00+09 by Heiles (1998) corresponds quite well to the geometry that is coming out from the inversion. As already noted in this work, this super-bubble is bounded by the Orion clouds at lower longitude, and by Vela clouds at ≃260–270°.
4.2. Extinction in vertical planes
We show in Figs. 4 to 7 the opacity distributions in a series of 12 vertical planes containing the Sun, with two consecutive planes separated by 15° in longitude. For each plane we superimpose – when they happen to be located within 25 pc from it – the locations of the central parts of the nearby OB associations as they have been estimated by de Zeeuw et al. (1999), as well as the HI and CO clouds listed by Perrot & Grenier (2003) and whose distances have been estimated by de Geus et al. (1990), Grenier et al. (1989), Maddalena et al. (1986), Murphy & Myers (1985), Murphy et al. (1986) and Ungerechts & Thaddeus (1987). This allows checking that those structures have their counterpart in the form of a dense region (for the clouds) or a cavity closely bounded by a dense region (for the OB associations) in the inverted maps. We did not include Collinder 121 whose distance has been the object of several discussions (e.g., Kaltcheva & Makarov 2007; Burningham et al. 2003) and maybe much larger than 500 pc. The new Hipparcos determinations of van Leeuwen (2007) indeed show that there are various distance ranges for the members. Interestingly, our maps do not reveal any cloud at ≃500 pc in the direction of Col121 (l,b = 236, –10). We also indicate the distances to the main nearby molecular clouds (or cloud complexes) derived by Knude (2010) based on Hipparcos and 2MASS.
One of the main advantages of the present method and of the dataset is the large number of nearby stars for which very low extinctions have been measured. This allows locating nearby tenuous clouds. Indeed, all vertical planes reveal low-density structures above the plane that are isolated or linked to denser structures, and whose shapes do appear quite complex. Because these structures are faint and the target star density decreases with the distance to the plane, they appear blurred sometimes, but the comparison between their locations in the maps and the coordinates of the medium and high-latitude clouds that show up in the 2D dust maps of (Schlegel et al. 1998, hereafter SFD) leaves no doubt about their reality. To allow the reader to make those comparisons we have superimposed on the SFD dust map the traces of the vertical planes of Figs. 4 to 7. This is shown in Fig. 8. We use a logarithmic scale for E(B − V) in order to identify the faint medium and high latitude clouds more easily. Interestingly, almost all features seen in Fig. 8 along those meridian lines have a counterpart under the form of an enhanced opacity in the corresponding vertical plane.
 |
Fig. 8 The Schlegel et al. (1998) dust map is reproduced, along with the traces of the vertical planes of Figs. 4 to 7 superimposed. The color–coded quantity is the logarithm of E(B − V). The six contours are for log (E(B − V)) = 0 (thin pink), –0.5 (thin violet), –1 (thick violet), –1.2 (thick pink), –1.4 (yellow), and –1.6 (black). Counterparts to the tenuous clouds at mid or high latitudes that appear in this SFD map can be searched for in Figs. 4 to 7, using the l,b grid. |
As a first example we consider the l = 105 − 285° vertical plane (Fig. 6 middle).
-
i)
The l = 105° half plane north: in the SFD map (Fig. 8) there is a northern extension of the dust (yellow contour up to b = + 45°) and many very small features (seen in yellow) at higher latitudes up to b = + 60; +80°. In Fig. 6 (middle), just above the main concentrations extending from the plane up to b = + 30; +40° (and colored violet, green, yellow), is a fainter feature apparently linked to the bulk but extending further up to +45° (faint yellow-orange) and located at ≃200 pc. We believe this is the counterpart of the cloud seen in the 2D map. In addition, there is a faint dust cloud located much closer (≤50 pc), that must produce small absorptions up to +80° latitude and probably explains the very faint, high latitude features in the 2D map.
-
ii)
The l = 285° half plane north: in Fig. 8 it can be seen that compared to the previous half plane the opacity is stronger at high latitude. More quantitatively, the E(B − V) = 0.063 (thick pink) contour extends up to b = +35°, instead of +20°. The E(B − V) = 0.04 (yellow) contour extends up to +55°, disappears above, then a more opaque area reappears at b = +55°. A look at Fig. 6 (middle) indeed shows nearby dust (green) up to b ≃ +55° and faint extensions visible almost up to the pole.
-
iii)
The l = 105° half plane south: in Fig. 8 the E(B − V) = 0.063 (thick pink) contour extends down to b = −55°, which corresponds to the cloud seen at ≃170 pc in Fig. 6 (pale green and yellow). On the other hand, the 80 pc distant feature at lower latitude (b = −65°) in Fig. 6 may be the counterpart to the b = −70° small cloud seen in Fig. 8.
-
iv)
The l = 285° half plane south: in Fig. 8 the E(B − V) = 0.063 (thick pink) contour extends down to b = −45; −50°, which corresponds to the cloud seen at 150 pc in Fig. 6 (dark blue, green, yellow). The –60; –50° small extension seen in Fig. 8 has no clear counterpart but may be simply the southern extension of the previous feature (faint yellow). Alternatively, it may be more distant than 350 pc, or missing due to the lack of constraining targets.
Comparing in the same way all half planes shows that most of the high-latitude features in Fig. 8 are found in the maps. As a second example we consider the l = 15−195° vertical plane in Fig. 4 (middle). At l = 15°, the inverted map shows clearly in the north dense high-latitude clouds up to b = + 60°, with a small extension at even higher latitude (around +70°) that is seen up to 150 pc (in the same direction there is also a very faint cloud much closer to the Sun). This is similarly found in Fig. 8 along the northern part of the l = +15 meridian. In the south, Fig. 4 (middle) reveals a dense cloud at b ≃ −25; −30° and at d ≃ 150 pc, whose emission is clearly marked in the Fig. 8 (green color). At l = 195° there is a strong contrast between the northern latitudes, where an appreciable opacity is reached as low as b ≲ +20° (transition between yellow and orange), and the south where dust extends down to b = −55; –60°. The l = 195° meridian in Fig. 8 indeed shows clearly this low-latitude cloud extension (pink contour) while the same level of dust emission does not go beyond +20° in the north. We note, however, a discrepancy between the total absence of opacities detected in the north in the inverted maps above b ≃ +30° (at this latitude there is a small feature at +450 pc) and the SFD map that shows E(B − V) = 0.04 up to +42°. This discrepancy seems to exist for the whole interval l = 180 − 230°. This dust may be much more distant than 1 kpc or missing in the maps due the lack of constraining targets. Apart from this region, agreements exist for all directions, and it is possible to assign a distance to the Fig. 8 high-latitude emission features by using the appropriate maps. This suggests that our limitation of Z = 300 pc for the target stars had no significant influence on the results.
 |
Fig. 9 Same as Fig. 4 for the l = 82−262° plane. The Vela SNR and the Wolf-Rayet system γ2Vel are shown. The locations of the Iras Vela shell (IVS) and Gum Nebula contours are drawn according to the scenario of Sushch et al. (2011). |
 |
Fig. 10 Same as Fig. 4 for the l = 160–340° plane. Here are shown the locations of the Lupus molecular clouds derived by Knude (2010). |
 |
Fig. 11 Opacity E(B − V) from the Sun to the distance Dlim = 100, 150, 250, and 400 pc, respectively (top to bottom), on a logarithmic scale. The maps are in Aitoff projections, with meridian traces for l = 45, 90, 135, 225, 270, and 315° and parallel traces for b = −60, –30, +30, and +60° shown as dashed and long-dashed lines, resp. The color scale is identical in the four maps. |
 |
Fig. 12 Same as Fig. 11, but for Dlim = 500, 750, 1000, and 2000 pc and a different (and still unique) color scale. Superimposed on the first and last maps is the E(B − V) = 0.1 iso-contour from the SFD map. E(B − V) = 0.1 corresponds the white-to-green transition in the distance-limited opacity maps. |
 |
Fig. 13 Distance from the Sun at which the integrated opacity, computed from the inverted differential opacity distribution, is reaching E(B − V) = 0.02 mag. Directions corresponding to distances above 300 pc correspond to the purple color. The minimum value (darkest green) is ≃80 pc. |
 |
Fig. 14 Same as Fig. 13 for E(B − V) = 0.06 mag. The minimum value (darkest green) for the distance is ≃90 pc. |
Given the limited number of faint stars, the mapping performs in some case less well for the very dense structures, in the sense that dense clouds may be underestimated due to the lack of strongly reddened targets, or their densest areas appearing slightly displaced with respect to the actual cloud centers. This is the case for the Orion structures for example in the l = 210° half plane (Fig. 4 bottom) that are centered at b = −15°, while the CO clouds are located a few degrees below. Also, their extent is not as wide as in the 2D maps and they do not appear as opaque as the dust maps predict. Such biases due to the target star distribution and the inversion should disappear by increasing the extinction databases.
Several planes are particularly interesting since they contain well-studied regions and in some case the maps shed some light on their distances; for example the l = 30° half plane crosses the Aquila rift (Fig. 4, bottom). We find a cloud complex at low latitude (b = 5°) that starts at ≃190 pc and centered at d ≃ 220 pc. It corresponds to the Serpens cloud and its recent distance assignment by Knude (2011) (193 pc) and Straižys et al. (2003) (225 pc). We note that there is a second cloud complex at ≃420 pc that appears at a lower latitude on our map. Its distance is in perfect agreement with the 420 pc distance determination of the star EC95 by Dzib et al. (2010), which is also believed to be part of the Serpens cloud. We consider the alignment of the two different clouds as a potential explanation for the discrepancy between the two measurements: the 420 pc cloud may extend at slightly higher latitudes than in our inverted maps, where its northern part is not part of the maps due to the absence of targets stars located beyond the Serpens cloud. Those stars are too extincted. EC95 could be part of it and seen in projection against the Serpens clouds.
There is another potentially interesting feature, this time in the opposite half plane l = 210°. We have drawn in Fig. 4 (bottom) the two directions that mark the limits of thenorthern and southern parts of the Barnard’s Loop crescent. Interestingly, they correspond to two elongated parts of a cloud located at ≃170 pc, while the Loop is believed to be associated to the extended Orion region at 440 pc, also visible in the map beyond the 170 pc cloud. We believe that this coincidence deserves further studies of the distance to the Barnard’s Loop.
We have also displayed in Fig. 9 the l = 82 − 262° plane. This specific plane is particular interesting due to the presence of the several objects that gave rise to many discussions and analyses: the Vela supernova remnant (SNR), the Wolf-Rayet system γ2Vel, the Iras Vela shell (IVS), and the Gum Nebula. In particular, the four were modeled as part of a global scenario by Sushch et al. (2011). The locations of the clouds derived by inversion agree well with this recently devised scenario.
Similarly the l = 160 − 340° plane drawn in Fig. 10 is particularly rich in clouds. We note here very good agreements between the maps and the cloud distances derived by Knude (2010) for the series of Lupus clouds and LDN1459. The more distant Aur-California dark cloud does not correspond to a very dense region in the map; however, this may be due to the screening effect of Taurus clouds and the lack of targets beyond them.
 |
Fig. 15 Interactive 3D iso-opacity surface for 0.0004 mag pc-1. The Sun is represented by a cube. (See PDF file to display the interactive image in 3D) |
5. Distance-limited 2D reddening maps
To facilitate the comparison of the inverted 3D distribution with 2D maps based on emission data, we have computed the integral of the differential opacity up to various, selected distances Dlim and for one degree steps in longitude and latitude to cover the whole sky. The resulting maps are shown in Figs. 11 and 12. The series of maps at increasing distances from Dlim = 100 pc to Dlim = 2 kpc allows us to infer at which distances the most conspicuous clouds start to get visible in the 2D maps. In the first and last maps of Fig. 12, which were computed for a radius of 500 pc and 2 kpc resp. We have superimposed the E(B − V) = 0.1 iso-contour of the SFD map. It can be compared with the log (E(B − V)) = −1 iso-contour in the 500 pc and 2 kpc integrated maps (not drawn but easily seen thanks to the white-green transition). Although the inverted maps lack details, the similarities between the two E(B − V) = 0.1 contours in the 2 kpc map show that in all directions that define this contour most of the extinction measured by SFD is actually generated closer than 2 kpc and retrieved through the inversion. At variance with the Dlim = 2 kpc map, the two contours are significantly different in the Dlim = 500 pc map, especially at 90 and 270°. In those directions the extinction is generated beyond 500 pc.
It is important to note that many of the weak features at mid and high latitudes that appear in the vertical planes in Figs. 4 to 7 are not seen in the integrated extinction maps for Dlim beyond ≃200–300 pc. This is mainly due to the high differential opacity value chosen for the prior distribution. As a matter of fact, we used a large height scale h0 = 200 pc, which results in a small decrease of the differential opacity with increasing distance from the plane. This high prior opacity makes the integrated opacity of the tenuous clouds weak or negligible in comparison with the full integrals. However, as we explained above, in practice this large scale height facilitates the detection of the nearby weak features. A typical example of this effect is the case of the North Celestial Pole Loop. The arch that extends from l ≃ 120° to l ≃ 170° and culminates at b ≃ = 40° is clearly seen in the SFD or Planck maps. It appears as a broad extension at high latitude in the Dlim = 250 pc map (it is located at ≃200 pc) but does not appear in any of the 2D maps for Dlim ≥ 500 pc. As a conclusion, the search for the distances to the high latitude thin clouds should be essentially performed in the planar cuts in the 3D distribution.
We show in Fig. 13 (resp. Fig. 14) 2D maps of the distance at which the integrated opacity, computed from the inverted differential opacity distribution, reaches the limiting value E(B − V) = 0.02 (resp. 0.06) mag. It allows to visualize where the Local Cavity boundaries are the closest. The closest part of the Aquila Rift and the upper Scorpius and Centaurus regions appear conspicuously. The comparison of those maps as well as Figs. 11 and 12 with the results in distance bins of Reis et al. (2011) show many similarities. More maps of this kind will be presented in a future paper analyzing soft X-ray background data in conjunction with the 3D maps.
6. 3D visualization
The last figure of this article is interactive and represents an iso-differential opacity surface corresponding to 0.0004 mag pc-1, which was made with the YT software (Turk et al. 2011). It allows the global distribution of the main cloud complexes to be visualized. Such a representation, on the other hand, does not allow visualizing details within those surfaces nor visualizing cavity contours. Two additional interactive 3D images showing transparent surfaces and more structures can be seen at http://mygepi.obspm.fr/~rlallement/ism3d.html and http://mygepi.obspm.fr/~rlallement/ism3dcrevace.html. However, faint features must be searched for in the slices presented above.
7. Discussion
We have presented new differential opacity maps of the local ISM based on the merging of several photometric catalogs and associated color excess measurements. The data are inverted using a Bayesian code based on the Tarantola & Valette (1982) theoretical work and developed by Vergely et al. (2001, 2010). New spatial correlation kernels were introduced in order to reproduce the ISM structure in a better way, and the quantitative parameters were chosen in a very conservative way to avoid unrealistic condensations. The maps extend the earlier results of Vergely et al. (2010) to distances of 800–1000 pc at low latitudes and 300 pc below and above the plane.
Our main findings are the following:
-
The comparison with the former maps shows good agreementdespite using a different reddening database, and differentcorrelation kernels. In particular, the addition of a large number ofearly-type stars did not affect the Local Cavity boundarymapping. The main clouds are located in 3D spacein a way that is coherent with other independent determinationsand with 2D dust maps. This demonstrates that thepresent inversion method gives satisfying results providedparameters are carefully and conservatively chosen inaccordance with the number of sightlines entered in the inversionprocess.
-
The combination of the inversion technique and the dataset characteristics is particularly appropriate for revealing nearby interstellar cavities. The geometry and distribution in sizes of those various cavities are available for comparisons with 3D hydrodynamical models of the ISM and bubble evolutions under the repetitive action of stellar winds and supernovae (de Avillez & Breitschwerdt 2009). In particular, the maps reveal a huge cavity that we identify as the superbubble GSH238+00+09 (Heiles 1998) and an elongated cavity in the opposite direction. By giving a global perspective on the distribution of the main clouds and cavities, the new maps may also help shed light on the formation of the Gould belt/Lindblad ring structure, e.g., the scenario devised by Olano (2001) that attributes the formation of the Local arm and the Gould belt to a supercloud having entered a spiral arm 100 Myr ago (see also the recent work of Perrot & Grenier 2003). Indeed, the majority of the cloud complexes seem to surround the chain of cavities formed by GSH238+00+09, the Local Bubble and the l = 70° cavity, and this clearly points to a special role of this 60(70)°–240(250)° direction in the local ISM history. We note that this direction is identical to the one of the interstellar helium ionization gradient axis found by Wolff et al. (1999), a potential additional consequence of the event that gave rise to the whole structure.
-
The inversion technique and the dataset are also particular appropriate to locating the faint structures that lie above or below the plane (E(B − V) ≤ 0.1) and are apparent in the emission maps (Schlegel et al. 1998). Such faint and angularly extended clouds cannot be mapped using statistical techniques. The majority of these features are located in 3D and found to be close, at less than ≃150 pc. While there is definitely an inclined cavity fully devoid of dust (linking the local chimneys to the halo), around this cavity the dust pattern is quite complex. Most faint clouds like the Northern Loop1 arches and the North Celestial Pole Loop are located between 100 and 200 pc.
-
The maps can be used to potentially disentangle coincidental similarities in directions for unrelated clouds at different distances. We discussed two particular cases.
We must caution that, in addition to the limitations in spatial resolution, which are linked to the use of a smoothing length, the present dataset is not appropriate for a detailed mapping of the dense clouds. As a matter of fact, there is a limitation in the brightness of the target stars, and the subsequent lack of strongly reddened stars results. This results in a poor representation of regions beyond opaque clouds, because they are badly sampled. There is for the same reasons a bias towards low opacities and some of the opaque clouds are under-represented. Hopefully in future, additional data toward weaker targets will allow those biases to be eliminated, and the decrease in the mean distance between targets will allow using shorter smoothing lengths, leading to better spatial resolution. This is especially mandatory for the dense atomic and molecular phase. This should help for understanding the complex kinematical structure of the whole Sco-Cen area recently derived by Pöppel et al. (2010) based on HI 21 cm data from the Leiden-Dwingeloo Survey and its link with the Gould belt formation. Present or future surveys and especially the Gaia mission should help improving the mapping.
The use of the kinematics that are available from gas emission or absorption data should also help for disentangling the structures and lead to better maps.
Online material
Appendix A: Convergence and treatment of oscillations
For most of the choices of parameters, the inversion takes about three to four iteration steps for convergence. We have checked that allowing for more steps does not modify significantly the distribution. The results here were obtained after ten iterations. A number of values for the four main parameters, ξ0,ξ1,σ0,σ1 were tested. We show here the results for one favored set of parameters. It corresponds to ξ0 = 30 pc, σ0 = 0.6, ξ1 = 15 pc, and σ1 = 0.8. Our criteria for this choice of parameters are guided by a balance between the quality of the adjustments to the data and a conservative choice of the smoothing lengths. We are also helped by the distribution pattern itself and, in particular, the appearance of elongated radial structures where there are not enough target stars with regard to the used kernel. However, we cannot avoid such radial structures at large distances where targets are missing if we want to keep a kernel appropriate to the nearby regions and uncover the nearby structures. This is illustrated in the Appendix.
Apart from the introduction of new kernels, the updated code now includes a new stage of convergence control. Indeed, in some areas (the problem arose around l = 80° and b = 0°, a direction that corresponds to strong changes in the cloud properties with increasing longitude) the correlation length is large compared to the distances, thus the model has difficulties by fitting strong extinctions which are mixed with weak extinctions at distances much shorter than the correlation length. Under these conditions, the model oscillates from one iteration to the other
between the presence of a strong structure of extinction and the absence of extinction: two solutions are then possible for the model. To avoid these oscillations, at the end of the third iteration, one detects the extinction data, which are farther than three sigma from the model. In fact, the model practically converged in the majority of the areas of the Galaxy, except in the significant areas where the gradients in extinction are particularly important. The data that are farther from the model show the areas where the model cannot reach the data. In this case, one increases the variance of the data by a factor of 2; this allows putting less weight on the data that deviate too much from the model. One starts again this filtering with each new iteration. From a practical point of view, about 300 sightlines are thus filtered in third iteration, from the total of 23 000. This number decreases from one iteration to the next and vanishes at the end of the sixth iteration. After convergence, the estimated model privileges smoothed solutions with low extinction values.
Appendix B: Distribution at large distances: constraint limitations
While the inversion was performed in a 4000 × 4000 × 600 pc3, the scarcity of distant stars results in very low or in null constraints beyond ≃800 pc. In this case the prior distribution is kept unchanged. We show in Fig. B.1 the computed inverted distribution in the Galactic plane up to + or –2 kpc, in order to illustrate the limits of the area that is actually constrained.
 |
Fig. B.1 Galactic plane cut in the 4000 pc 3D distribution of inverted opacity. This map clearly shows the limits between the prior distribution (homogeneous color) and areas where the model has been constrained by the dataset. The elongated radial structures correspond to directions where cavities over dense areas are detected but the number of target stars is too small to constrain their location, hence the spread over a large distance. |
Appendix C: Target distribution
The distribution of the target stars gives the constraints for the inversion. We show in Fig. C.1 those target stars that are located within 10 pc from the plane and have mainly contributed to the computed distribution in this plane, superimposed on the inner part of the computed map. It allows to infer the spatial resolution that can be achieved in a given location. Figure C.2 shows those target stars that are located within 150 pc from the plane and allows to figure out the achievable spatial resolution at larger distance.
 |
Fig. C.1 The Galactic plane cut in the 3D distribution of inverted opacity with stars within 10 pc from the plane superimposed (plus signs). The distribution shows the regions that are well constrained by the data, and how, given the present limited dataset, nearby cavities are better represented than cloud complexes. The distribution also allows the limiting size for the structures to be figured out from the distance between neighboring targets, on the order of 10 pc in the Sun vicinity. |
 |
Fig. C.2 Same as Fig. C.1, but extending up to 800 pc and displaying stars within 150 pc from the plane. The limiting size for the inverted structures varies from 40 to 200 pc at 800 pc depending on the regions. |
Acknowledgments
J.L.V, R.L., and L.P. acknowledge funding by the French Research Agency in the framework of the STILISM project. We thank I. Grenier and J.M. Casandjian for useful discussions, and Matthew Turk from the YT project for helping us with the 3D figure.
References
- Burningham, B., Naylor, T., Jeffries, R. D., & Devey, C. R. 2003, MNRAS, 346, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L., Rho, J., Marshall, D. J., & Reach, W. T. 2011, A&A, 527, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Schoenrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, B., Vergely, J. L., Valette, B., & Carraro, G. 1998, A&A, 336, 137 [NASA ADS] [Google Scholar]
- Chen, B. Q., Schultheis, M., Jiang, B. W., et al. 2013, A&A, 550, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, D. P., & Reynolds, R. J. 1987, ARA&A, 25, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Breitschwerdt, D. 2009, ApJ, 697, L158 [NASA ADS] [CrossRef] [Google Scholar]
- de Geus, E. J., Bronfman, L., & Thaddeus, P. 1990, A&A, 231, 137 [NASA ADS] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lepine, J. R. D. 2012, VizieR Online Data Catalog, II/22 [Google Scholar]
- Dzib, S., Loinard, L., Mioduszewski, A. J., et al. 2010, ApJ, 718, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Cramer, N. 1999, New Astron. Rev., 43, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Gontcharov, G. A. 2012, Astron. Lett., 38, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, I. A., Lebrun, F., Arnaud, M., Dame, T. M., & Thaddeus, P. 1989, ApJ, 347, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1998, ApJ, 498, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, E. H. 1988, A&A, 189, 173 [NASA ADS] [Google Scholar]
- Kaltcheva, N., & Makarov, V. 2007, ApJ, 667, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Knude, J. 2010 [arXiv:1006.3676] [Google Scholar]
- Knude, J. 2011 [arXiv:1103.0455] [Google Scholar]
- Knude, J., & Lindstrøm, H. E. P. 2012 [arXiv:1202.3600] [Google Scholar]
- Lallement, R., Welsh, B. Y., Vergely, J. L., Crifo, F., & Sfeir, D. 2003, A&A, 411, 447 [EDP Sciences] [Google Scholar]
- Lilienthal, D., Hirth, W., Mebold, U., & de Boer, K. S. 1992, A&A, 255, 323 [NASA ADS] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2010, A&A, 512, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maddalena, R. J., Morris, M., Moscowitz, J., & Thaddeus, P. 1986, ApJ, 303, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, D. J., Joncas, G., & Jones, A. P. 2009, ApJ, 706, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, D. C., & Myers, P. C. 1985, ApJ, 298, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, D. C., Cohen, R., & May, J. 1986, A&A, 167, 234 [NASA ADS] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olano, C. A. 2001, AJ, 121, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Perrot, C. A., & Grenier, I. A. 2003, A&A, 404, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pöppel, W. G. L., Bajaja, E., Arnal, E. M., & Morras, R. 2010, A&A, 512, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raimond, S., Lallement, R., Vergely, J.-L., Babusiaux, C., & Eyer, L. 2012 [arXiv:1207.6092] [Google Scholar]
- Reis, W., Corradi, W., de Avillez, M. A., & Santos, F. P. 2011, ApJ, 734, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sale, S. E., & Drew, J. E. 2010, Highlights of Astronomy (Berlin: Springer-Verlag), 15, 785 [NASA ADS] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 (SFD) [NASA ADS] [CrossRef] [Google Scholar]
- Serban, D. Z., & Jacobsen, B. H. 2001, Geophys. J. Int., 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūtė, S. 2003, A&A, 405, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sushch, I., Hnatyk, B., & Neronov, A. 2011, A&A, 525, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tarantola, A., & Valette, B. 1982, Rev. Geophys. Space Phys., 20, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Ungerechts, H., & Thaddeus, P. 1987, ApJS, 63, 645 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergely, J.-L., Freire Ferrero, R., Siebert, A., & Valette, B. 2001, A&A, 366, 1016 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergely, J.-L., Valette, B., Lallement, R., & Raimond, S. 2010, A&A, 518, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., Lallement, R., Vergely, J.-L., & Raimond, S. 2010, A&A, 510, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolff, B., Koester, D., & Lallement, R. 1999, A&A, 346, 969 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Inverted differential opacity distribution in the Galactic plane. The Sun is at coordinates (x,y) = (0,0) and the Galactic center direction to the right. The opacity increases from red to violet (scale to the right). Note the 1000 pc long cavity centered on l ≃ + 225° that we identified as the major super-bubble GSH238+00+09 detected in radio by Heiles (1998). We call Cygnus cavities the empty regions at l ≃ + 70°. Several well known opaque regions are indicated on the maps, and their identification is based on the literature. The gradient axis for interstellar helium ionization points to the center of the GSH238+00+09. |
| In the text | |
 |
Fig. 2 Comparison between the extended map and the 500 pc wide map from Vergely et al. (2010). The black line is an iso-contour at dE(B − V)/dr = 0.0002 mag per pc drawn from the previous 3D distribution and delimiting the Local Cavity. Hatched areas correspond to the closest dense regions revealed in those previous maps. Depending on locations, the new maps reveal the full extent of those opaque regions at larger radial distances, or their division into distinct groups of clouds that the poorer resolution did not allow distinguishing earlier. |
| In the text | |
 |
Fig. 3 Achievable resolution in the Galactic plane resulting from the target distribution. |
| In the text | |
 |
Fig. 4 Opacity distribution in vertical planes containing the Sun, equally spaced by 15°. The north pole direction b = + 90° is at the top and longitudes of intersections with the Galactic plane are indicated. Some iso-differential opacity contours have been superimposed to help visualize the low- and high-opacity regions. OB associations from De Zeeuw (1999), as well as CO and HI clouds listed by Perrot & Grenier (2003) have been displayed when they are within 25 pc of this vertical plane. We also add the molecular cloud locations derived by Knude (2010). The tenuous cloud close to the north pole direction. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 for the next three vertical planes. In the l = 45° and l = 60° half planes (top and middle), the HI Hercules shell is indicated at the 60–150 pc distance derived by Lilienthal et al. (1992) for its low-velocity component. Such a location is in good agreement with the elongated feature at b ≃ 40°. The second component at 250 pc may correspond to the fainter distant feature in the l = 60° half plane. |
| In the text | |
 |
Fig. 6 Same as Fig. 4 for the next three vertical planes. |
| In the text | |
 |
Fig. 7 Same as Fig. 4 for the next three vertical planes. |
| In the text | |
 |
Fig. 8 The Schlegel et al. (1998) dust map is reproduced, along with the traces of the vertical planes of Figs. 4 to 7 superimposed. The color–coded quantity is the logarithm of E(B − V). The six contours are for log (E(B − V)) = 0 (thin pink), –0.5 (thin violet), –1 (thick violet), –1.2 (thick pink), –1.4 (yellow), and –1.6 (black). Counterparts to the tenuous clouds at mid or high latitudes that appear in this SFD map can be searched for in Figs. 4 to 7, using the l,b grid. |
| In the text | |
 |
Fig. 9 Same as Fig. 4 for the l = 82−262° plane. The Vela SNR and the Wolf-Rayet system γ2Vel are shown. The locations of the Iras Vela shell (IVS) and Gum Nebula contours are drawn according to the scenario of Sushch et al. (2011). |
| In the text | |
 |
Fig. 10 Same as Fig. 4 for the l = 160–340° plane. Here are shown the locations of the Lupus molecular clouds derived by Knude (2010). |
| In the text | |
 |
Fig. 11 Opacity E(B − V) from the Sun to the distance Dlim = 100, 150, 250, and 400 pc, respectively (top to bottom), on a logarithmic scale. The maps are in Aitoff projections, with meridian traces for l = 45, 90, 135, 225, 270, and 315° and parallel traces for b = −60, –30, +30, and +60° shown as dashed and long-dashed lines, resp. The color scale is identical in the four maps. |
| In the text | |
 |
Fig. 12 Same as Fig. 11, but for Dlim = 500, 750, 1000, and 2000 pc and a different (and still unique) color scale. Superimposed on the first and last maps is the E(B − V) = 0.1 iso-contour from the SFD map. E(B − V) = 0.1 corresponds the white-to-green transition in the distance-limited opacity maps. |
| In the text | |
 |
Fig. 13 Distance from the Sun at which the integrated opacity, computed from the inverted differential opacity distribution, is reaching E(B − V) = 0.02 mag. Directions corresponding to distances above 300 pc correspond to the purple color. The minimum value (darkest green) is ≃80 pc. |
| In the text | |
 |
Fig. 14 Same as Fig. 13 for E(B − V) = 0.06 mag. The minimum value (darkest green) for the distance is ≃90 pc. |
| In the text | |
 |
Fig. 15 Interactive 3D iso-opacity surface for 0.0004 mag pc-1. The Sun is represented by a cube. (See PDF file to display the interactive image in 3D) |
| In the text | |
 |
Fig. B.1 Galactic plane cut in the 4000 pc 3D distribution of inverted opacity. This map clearly shows the limits between the prior distribution (homogeneous color) and areas where the model has been constrained by the dataset. The elongated radial structures correspond to directions where cavities over dense areas are detected but the number of target stars is too small to constrain their location, hence the spread over a large distance. |
| In the text | |
 |
Fig. C.1 The Galactic plane cut in the 3D distribution of inverted opacity with stars within 10 pc from the plane superimposed (plus signs). The distribution shows the regions that are well constrained by the data, and how, given the present limited dataset, nearby cavities are better represented than cloud complexes. The distribution also allows the limiting size for the structures to be figured out from the distance between neighboring targets, on the order of 10 pc in the Sun vicinity. |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1, but extending up to 800 pc and displaying stars within 150 pc from the plane. The limiting size for the inverted structures varies from 40 to 200 pc at 800 pc depending on the regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


