| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322429 | |
| Published online | 13 December 2013 | |
Small vs. large dust grains in transitional disks: do different cavity sizes indicate a planet?
SAO 206462 (HD 135344B) in polarized light with VLT/NACO ⋆,⋆⋆
1 Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
e-mail: antonio.garufi@phys.ethz.ch
2 Department of Astronomy and Steward Observatory, University of Arizona, Tucson, AZ 85721, USA
3 Max-Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
4 Sterrenkundig Instituut Anton Pannekoek, Science Park 904, 1098 XH Amsterdam, The Netherlands
5 Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
6 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
7 University of Kiel, Institute of Theoretical Physics and Astrophysics, Leibnizstrasse 15, 24098 Kiel, Germany
Received: 2 August 2013
Accepted: 13 November 2013
Context. Transitional disks represent a short stage of the evolution of circumstellar material. Studies of dust grains in these objects can provide pivotal information on the mechanisms of planet formation. Dissimilarities in the spatial distribution of small (μm−size) and large (mm−size) dust grains have recently been pointed out.
Aims. Constraints on the small dust grains can be obtained by imaging the distribution of scattered light at near-infrared wavelengths. We aim at resolving structures in the surface layer of transitional disks (with particular emphasis on the inner 10−50 AU), thus increasing the scarce sample of high-resolution images of these objects.
Methods. We obtained VLT/NACO near-IR high-resolution polarimetric differential imaging observations of SAO 206462 (HD 135344B). This technique allows one to image the polarized scattered light from the disk without any occulting mask and to reach an inner working angle of ~0.1″.
Results. A face-on disk is detected in H and Ks bands between 0.1″ and 0.9″. No significant differences are seen between the H and Ks images. In addition to the spiral arms, these new data allow us to resolve for the first time an inner disk cavity for small dust grains. The cavity size (≃28 AU) is much smaller than what is inferred for large dust grains from (sub-)mm observations (39 to 50 AU). This discrepancy cannot be ascribed to any resolution effect.
Conclusions. The interaction between the disk and potential orbiting companion(s) can explain both the spiral arm structure and the discrepant cavity sizes for small and large dust grains. One planet may be carving out the gas (and, thus, the small grains) at 28 AU, and generating a pressure bump at larger radii (39 AU), which holds back the large grains. We analytically estimate that, in this scenario, a single giant planet (with a mass between 5 and 15 MJ) at 17 to 20 AU from the star is consistent with the observed cavity sizes.
Key words: stars: pre-main sequence / protoplanetary disks / ISM: individual objects: SAO 206462 / techniques: polarimetric
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere, Chile, under program number 089.C-0611(A).
Reduced data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/560/A105
© ESO, 2013
1. Introduction
To enhance our understanding of planet formation, a study of circumstellar material at different evolutionary stages is necessary. Most young stars (with ages up to a few Myr) harbor circumstellar disks which are thought to be the birthplaces of planets. A small sample of disks, the so-called transitional disks, shows a peculiar dip in the infrared spectral energy distribution (SED) indicating a depletion of warm dust near the central star (Strom et al. 1989; Skrutskie et al. 1990). Since this type of disks represents only a few percent of the total, the process of dispersal of disk material must occur rapidly (less than 1 Myr, Muzerolle et al. 2010). Mechanisms responsible for such a fast dissipation are still under debate. Gravitational interaction with an orbiting companion (e.g. Rice et al. 2003; Ireland & Kraus 2008), photoevaporation (Alexander & Armitage 2007), and particle growth (Dullemond & Dominik 2005) have been proposed as clearing processes and innumerable attempts are made to predict the rapidly increasing observational evidence.
One of the proposed mechanisms of planet formation is dust coagulation in the inner few tens of au (e.g. Dullemond & Dominik 2004). Direct imaging of those regions is therefore essential. Polarimetric differential imaging (PDI) is a high-contrast technique allowing imaging of near-IR scattered light from circumstellar disks with unprecedented inner working angle (e.g. Apai et al. 2004; Quanz et al. 2011, 2012, 2013; Hashimoto et al. 2012). This technique takes advantage of the fact that direct stellar light is essentially unpolarized whereas scattered light from dust grains from the disk surface is polarized. PDI allows direct imaging of regions as close as 0.1″ to the central star.
Basic properties of SAO 206462.
The study of different dust components in and around the central cavity of transitional disks provides insights into the mechanisms of planet formation. Direct detections of these cavities have been provided, among others, by the Submillimeter Array (SMA) interferometer (e.g. Andrews et al. 2009, 2011) at sub-millimeter wavelengths, and by VLT/NACO (e.g. Quanz et al. 2011, 2013) and Subaru/HiCiao (e.g. Mayama et al. 2012; Hashimoto et al. 2012) in near-IR polarized light. Sub-millimeter and near-IR data probe different dust grain sizes (and, thus, different disk layers). Intriguingly, in some cases they are suggesting unexpected differences in the small and large dust grain distribution. Dong et al. (2012) highlighted that the polarized near-IR images from Subaru/HiCiao do not always show the inner cavities observed at millimeter wavelengths with SMA as close as the inner working angle (0.1″ − 0.2″). Their model suggests a decoupled spatial distribution of the big and small dust particles inside the cavity.
In this paper, we present PDI observations of the transitional disk around SAO 206462 (HD135344B) obtained with VLT/NACO. SAO 206462 is an extensively studied, rapidly-rotating (Müller et al. 2011) F4Ve star (Dunkin et al. 1997) hosting a transitional disk. It is located in the Sco OB2-3 star-forming region (d = 140 ± 42 pc, van Boekel et al. 2005). The angular separation from HD 135344A is 21″ (Mason et al. 2001), which translates into a physical separation >2900 AU. The proper motions of the two stars are comparable (Høg et al. 2000). Thus, in a scenario where the stars have highly eccentric orbits, a gravitational interaction between them cannot be ruled out. Spatially resolved imaging in the near-IR (Vicente et al. 2011) ruled out the presence of stars more massive than 0.22 M⊙ at 0.1″, and of any brown dwarf at separations larger than 0.27″. Table 1 shows the stellar parameters of SAO 206462.
The properties of the disk around SAO 206462 have been constrained via imaging (e.g. Grady et al. 2009; Muto et al. 2012), spectroscopy (e.g. Dent et al. 2005; Brown et al. 2007), and interferometry (e.g. Fedele et al. 2008; Andrews et al. 2011). A large inner dust cavity (R < 40−50 AU) has been predicted by SED fitting (Brown et al. 2007) and successively imaged at sub- and millimeter wavelengths (Brown et al. 2009; Lyo et al. 2011). Grady et al. (2009) and Muto et al. (2012) both resolved the disk in scattered light but no evidence of the inner hole was found down to ~42 AU and ~28 AU respectively. In particular, the Subaru/HiCiao observations by Muto et al. (2012) revealed two small-scale spiral structures, with the brightest portion of the spirals roughly coinciding with the thermal emission peak at 12 μm (Mariñas et al. 2011). An enhanced emission to SE side and a deficit to north are observed in all sub- and millimeter images and in the 1.1 μm HST/NICMOS data (Grady et al. 2009). The presence of gas in the inner cavity has been inferred by Pontoppidan et al. (2008) by means of CO rovibrational lines, and van der Plas et al. (2008) by means of [OI] 6300 Å line. The presence of a narrow (sub-au scale) inner dust disk has been inferred by SED modeling (Brown et al. 2007; Grady et al. 2009) and interferometric N-band observations (Fedele et al. 2008). A variable mass accretion rate of a few 10-8 M⊙/yr has been derived by Sitko et al. (2012) from emission lines. The disk inclination is consistently estimated to be 11−14° by Dent et al. (2005), Pontoppidan et al. (2008), Andrews et al. (2011), and Lyo et al. (2011). Periodic variations of the photospheric emission indicates a stellar inclination of ~11° (Müller et al. 2011), suggesting aligned star-disk angular momentum. However, Fedele et al. (2008) estimated the inclination of the inner dust disk to be ~60°. Ellipse fitting of mid-IR imaging suggests a larger inclination also for the outer disk (i = 40−50°, Doucet et al. 2006; Mariñas et al. 2011).
The paper is organized as follows. Firstly, in Sect. 2 we describe the observations and the data reduction. Secondly, in Sect. 3 we present the results from the PDI images and, finally, in Sect. 4 we discuss a possible scenario for the origin of the structures in the dusty disk of the source.
2. Observations and data reduction
The observations were performed on 2012 July 24 with the high-resolution near-IR NAOS/CONICA (NACO, Lenzen et al. 2003; Rousset et al. 2003) instrument, mounted on UT4 at the Very Large Telescope (VLT). We used the SL27 camera (pixel scale =27 mas pixel-1) in HighDynamic mode and readout in Double RdRstRd mode. SAO 206462 was observed in the context of a small survey of Herbig Ae/Be disks performed with VLT/NACO in PDI mode on three consecutive nights. The sample contains, among others, HD169142 (Quanz et al. 2013) and HD142527 (Avenhaus et al. 2013). We obtained images of SAO 206462 in H,NB 1.64,Ks, and NB 2.17 filters. The use of narrow band filters is due to the complementary need for exposures with the central star unsaturated, which is unachievable with broad band filters. The total integration times were 3240 and ~3232.9 s in H and Ks filters respectively and 270 s in each narrow band filter. No photometric standard was observed. Instead, we use the central star itself for photometric calibration. Observing conditions were photometric, with an excellent seeing (varying from 0.58″ to 1.01″), a good coherence time (from 28 to 46 ms), and an average airmass of 1.1. The angular resolution of the final images in H and Ks band (≃ 0.09″) is determined from the FWHM of the stellar unsaturated profile in the respective narrow band filter. Observing settings and conditions are summarized in Table 2.
Summary of observations.
The basic principle of the PDI observing mode is the simultaneous imaging of the linear polarization of the source along two orthogonal directions. With NACO, this is provided by a Wollaston prism which splits the incoming light into ordinary and extraordinary beams, offset by 3.5″ along the vertical direction of the detector. A polarimetric mask prevents the overlap of the two beams by alternating open and opaque stripes. A rotatable half-wave plate (HWP) allows an observing strategy with beam switch for the correction of pixel-to-pixel efficiency variations. The polarization measurements at half-wave position angle of 0.0° and − 45° yield the Stokes Q parameter, those at angle of −22.5° and −67.5° the U parameter.
The detailed data reduction procedure and correction for instrumental polarization are described by Avenhaus et al. (2013). Shortly, we correct the exposures for dark current and flat field and then perform a row-by-row subtraction of each exposure because of a non-static read-out noise pattern along the rows. Bad pixels are substituted by the mean of the surrounding pixels. The center of the stellar profile in ordinary and extraordinary beams is determined at sub-pixel accuracy by fitting a two-dimensional gaussian to the point spread function (PSF) halo. For this procedure, values above the linearity regime of the sensor are dismissed. After that, both beams are extracted and all images are upscaled by a factor 3 and aligned on top of each other.
NACO suffers from instrumental polarization and crosstalk effects (see Witzel et al. 2010; Quanz et al. 2011). To correct for the former, we assume the stellar PSF to be largely unpolarized, and we impose the count ratio in ordinary/extraordinary beams to be unity. The latter is corrected by scaling the damped signal in Stokes U by a factor defined from the data (see Avenhaus et al. 2013).
The final products of the data reduction are the tangential and radial Stokes parameters P⊥ and P∥, computed as: 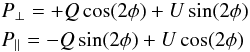 (1)with
(1)with 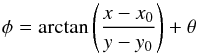 (2)where Q and U are the Stokes parameters with respect to the sky coordinates (N over E, see Schmid et al. 2006), φ the polar angle of a given position (x,y) of the detector with respect to the position of the central star, denoted as (x0,y0), and θ = −3.7° an offset due to polarization cross-talk effects and a possible misalignment of the HWP rotation within the NACO instrument. By construction, P⊥ and P∥ describe the polarization in the tangential direction and ± 45° with respect to that, respectively. In systems with tangential polarization only, P⊥ is equivalent to
(2)where Q and U are the Stokes parameters with respect to the sky coordinates (N over E, see Schmid et al. 2006), φ the polar angle of a given position (x,y) of the detector with respect to the position of the central star, denoted as (x0,y0), and θ = −3.7° an offset due to polarization cross-talk effects and a possible misalignment of the HWP rotation within the NACO instrument. By construction, P⊥ and P∥ describe the polarization in the tangential direction and ± 45° with respect to that, respectively. In systems with tangential polarization only, P⊥ is equivalent to 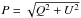 , which denotes the polarized flux, while P∥ is not expected to contain a signal and can be used to estimate the error on P⊥. We use this technique because, unlike the P parameter, their computation does not involve the squares of Q and U parameters.
, which denotes the polarized flux, while P∥ is not expected to contain a signal and can be used to estimate the error on P⊥. We use this technique because, unlike the P parameter, their computation does not involve the squares of Q and U parameters.
The photometric calibration of the images is performed with the approach described by Quanz et al. (2011). We estimate the total count rates of the source in H and Ks bands (for which the images show a saturated stellar profile) by means of the average of all images in NB 1.64 and NB 2.17 filters respectively, taking the different exposure time of the observations and transmission curve of the filters into account. Then, we convert the count rate in each pixel to surface brightness using the 2MASS magnitudes in H and Ks bands (see Table 1). This approach intrinsically assumes that the source has the same magnitude in H and Ks bands as in their respective narrow bands. However, the presence of a strong Brγ line from the star (Sitko et al. 2012) may introduce a bias in the calibration of the Ks band. Furthermore, the substantial near-IR variability of the source (30% in the K band, Sitko et al. 2012) is not taken into account. We estimate that this technique provides an absolute flux calibration only good to 50%.
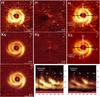 |
Fig. 1 Reflection nebulosity around SAO 206462. First two rows, from left to right: P⊥ image, P∥ image, and P⊥ image with blue and pink stripes indicating the position of the major and minor axis, respectively. The first row is H band, the second is Ks band. Third row, from left to right: comparison between the P⊥ image in Ks band and continuum emission from sub-mm observations by Brown et al. (2009), polar mapping of H and Ks band with angles measured with respect to north. Images are upscaled by a factor 3 to minimize smoothing effects throughout the sub-pixel data shifting and are scaled with r2 to compensate for stellar light dilution. The color scale is linear and arbitrary. The red central region indicates the area on the detector with non-linear pixels. Continuum contours are drawn at 3σ intervals starting from 3σ. |
 |
Fig. 2 Radial profile of the polarized surface brightness. Top: along the major axis in NE (right half) and in SW (left half) direction for H (red) and Ks band (blue). Bottom: along the minor axis in NW (right half) and in SE (left half) direction, namely the far and near disk side, respectively. The grey box indicates the region that our data resolved for the first time. In all profiles (except the H band NW minor axis), the depletion inside this region is evident. Errors are 3σ noise calculated from the P∥ images (see Sect. 2) and do not include systematic uncertainties in the photometric calibration. |
3. Results
Figure 1 shows the final P⊥ and P∥ images in H and Ks band. A nebulosity is clearly detected in both P⊥ images but not in the P∥ images. According to the construction of these parameters (see Sect. 2), this is indicative of light which is scattered in a tangentially-symmetric way.
The images in Ks band are higher-quality because of a better AO correction. Both P∥ images reveal partially uncorrected diffraction spikes and read-out noise pattern (see Sect. 2). These artifacts are also present in the P⊥ images.
The P⊥ images reveal the nebulosity from ~0.1″ to ~0.9″ (~14−130 AU) in both H and Ks band. They show three main peculiarities: (i) an inner region (inside 0.15″−0.18″) with scattered light depleted down to a few percent of a theoretical continuous distribution (the cavity); (ii) a bright quasi-circular rim at ~0.2″ (the ring); (iii) two elongated non-axisymmetric spiral arms extending from the ring to ~0.5″ and covering an azimuthal angle of ~180° each (S1 being that in the W and S2 that in the E, following Muto et al. 2012). The total intensity of polarized light integrated between 0.1″ and 0.9″ is 11.7 mJy ±50% in H band and 4.3 mJy ± 50% in Ks band.
In the following, we analyze the polarized brightness distribution of the images, starting from the disk outside the ring and then moving to the inner 0.2″, namely the region that our images resolved in scattered light for the first time.
3.1. The brightness distribution: r > 0.2′′
The radial polarized brightness is complex and azimuth-dependent because of the presence of spiral arms. Figure 2 shows the radial profile obtained with 3-pixel wide cuts along the major axis (PA = 56°, Lyo et al. 2011) and the minor axis (see blue and pink stripes in Fig. 1). The relative errors are obtained from the noise estimated from the P∥ images (see Sect. 2) but do not consider any systematic uncertainty from the absolute flux calibration. No significant difference in the brightness profile is found between H and Ks band (apart from the polarized flux being a factor 2.5−3 higher in the former than that in the latter).
We average the radial profiles over all angular directions neglecting any geometrical effect due to the disk inclination. Since the disk is known to be almost face-on (11°, Andrews et al. 2011), we assume that this approach does not introduce large systematic errors. The azimuthally-averaged profile of both bands is fitted by a power-law with β = −2.9 ± 0.1. However, we find that a spatially separate fit with a broken power-law provides a better match. A slope of −1.9 ± 0.1 is found for the range 0.2″−0.4″ (~28−56 AU) and a slope of −5.7 ± 0.1 (H band) and −6.3 ± 0.1 (Ks band) for the range 0.4″−0.8″ (~56−114 AU) (see Fig. 3).
The two spirals are starting from axisymmetric locations on the rim. The contrast of the spiral with the surrounding disk varies from 1.5 to 3.0. S1 appears as the most prominent arm. It covers an angle of ~ 240° and shows an enhancement to the SW (almost twice as luminous in surface brightness as the contiguous part of the arm). S2 covers a smaller angle (~160°) but also shows a “knot” (to the SE, factor 1.5 brighter in surface brightness than the contiguous part of the arm).
From our images, we resolve a narrow dip in the emission along the radial direction at a position angle of 340°. This feature is very clear on the ring but can be traced out to 0.5″ in both bands (see polar mapping of Fig. 1). A slight deficit can be observed on a larger scale (~90°) in the NW. A diffuse enhanced emission is also visible in Fig. 1 to the east side. This feature can be traced in both bands from the outer edge of S2 to ~ 0.7″, covering an angle of ~ 30°.
The inclination of the nebulosity is not strongly constrained by our observations. However, by measuring the nebulosity size along the major and the minor axis and assuming overall circular shape, we can rule out values of inclination higher than 25°.
3.2. The brightness distribution: r < 0.2′′
As shown in Fig. 2, the polarized flux decreases inward of 0.15″ − 0.18″ in both bands. At 0.12″ from the star, the surface brightness is 6% of a continuous flux distribution (as extrapolated from the power-law fit) in H band and 14% in Ks band, decreasing to 2% in the innermost region traced by our observations (0.10″). These depletion factors are by far larger than the 3σ error, as shown in the azimuthally-averaged radial profile of Fig. 3, and therefore significant.
At the outer edge of the cavity, a quasi-circular ring-like structure is present in both bands. The width of the ring (~ 0.09″) is comparable with the angular resolution of the observations, suggesting that the structure is not resolved. The radial location of the brightest part of the ring varies with the azimuthal angle from 0.19″ to 0.21″. This amount of ellipticity is what is expected from the geometrical projection on the sky (considering i ~ 10° − 20°). Therefore, we do not infer any intrinsic eccentricity for the ring.
In Fig. 4 we show the azimuthal profile of the ring in Ks band, obtained averaging concentric annuli from 0.17″ to 0.21″. Besides the azimuthal dip ubiquitous along the far minor axis, we identify two features (bumps at PA ~ 220° and ~135°). The former is directly associated to S1, since it overlaps with the starting-point of the arm.
 |
Fig. 3 Azimuthally-averaged radial profiles in H (red) and Ks (blue) bands and power-law best fits for 0.2″ < r < 0.4″ (dashed lines) and for 0.4″ < r < 0.8″ (dotted lines). Errors are the same as in Fig. 2. |
4. Discussion
Since the P⊥ parameter traces, by construction, the light which is scattered in a tangentially-symmetric way, we interpret the reflection nebulosity revealed in the P⊥ images as stellar radiation scattered by the circumstellar disk.
In this section, we interpret the results presented in Sect. 3. In particular, in Sect. 4.1 we interpret the features observed in the outer part of the disk and compare them with previous works. In Sect. 4.2, we focus on the inner cavity and, in Sect. 4.3, discuss a possible scenario for the origin of the observed features. Finally, in Sect. 4.4 we speculate on the mechanisms responsible for the inner cavity and the spiral arms and, in Sect. 4.5, estimate mass and location of the companion potentially sculpting the inner disk.
4.1. The outer disk
SAO 206462 was detected in scattered light with HST/NICMOS at 1.1 and 1.6 μm by Grady et al. (2009) and, later, in polarized light with Subaru/HiCIAO in H band by Muto et al. (2012). The latter were the first to resolve the spiral structure. The outer extent inferred by our observations (0.9″) is in good agreement with their estimate. The azimuthally averaged radial profile fitting our observations (power-law with β = −2.9) is in the range of typically observed values for Herbig stars, both in scattered light (e.g. Grady et al. 2007) and polarized light (e.g. Quanz et al. 2011). The value is in agreement with what was inferred for SAO 206462 by Muto et al. (2012, r-3. The total polarized light intensity measured in the H band (11.7 mJy) is a factor 1.15 higher than the measurement by Muto et al. (2012) but the results agree within the error bars. Furthermore, a small part (~ 10%) of the total intensity is from the inner region (<0.2″) that is masked in the images by Muto et al. (2012), reinforcing the agreement. Finally, the total polarized light intensity in Ks band (4.3 mJy) was never measured before.
 |
Fig. 4 Azimuthal profile of the polarized surface brightness along the ring in Ks band, averaged over the 0.17″ − 0.21″ radii. Two main bumps are visible. One is associated to the starting point of S1. Errors are the same as in Fig. 2, averaged over 0.17″ − 0.21″ radii. |
The spiral arms are by far the most tantalizing feature of the disk. Spiral arms have been observed in a few other protoplanetary disks. Among them, we point out AB Aur (Hashimoto et al. 2011), HD 100546 (Grady et al. 2001), HD142527 (Avenhaus et al. 2013; Casassus et al. 2012), and MWC 758 (Grady et al. 2013). Since only very recent techniques are capable of resolving these structures, it is difficult to infer how common spiral arms are among protoplanetary disks. Because PDI observations trace the stellar radiation which is scattered by a thin surface layer of the disk, the spiral arms detected with this technique can either constitute intrinsic changes of the disk grain properties or small local variations of the disk geometry, which modify the incidence angle of the photons. In particular, small ripples in the disk scale height may be sufficient to explain the light contrast shown by the spirals around SAO 206462 with the contiguous disk (a factor 1.5 to 3.0). Disks with this configuration might not show spiral structures in their thermal images.
The brightness deficit in the NW was also observed by Muto et al. (2012). The same deficit was observed in scattered light by Grady et al. (2009) at 1.1 μm. Curiously, they did not resolve it at 1.6 μm, whereas our H band image (of polarized light) does. Lyo et al. (2011) inferred from CO observations that the SW side is receding. Spirals are typically trailing and, thus, as remarked by Muto et al. (2012), the region of the deficit may represent the far side of the disk. In particular, the dip in polarized light at 340° is roughly coincident with the minor axis (326°). Given this, the narrow dip and the general deficit can be ascribed to depolarization. Since the degree of linear polarization is maximized at ~90° scattering angle (e.g. Draine 2003; Min et al. 2012), polarized images of inclined disks are indeed expected to show minima along the near and far side of the disk (see case of MWC480, Kusakabe et al. 2012). However, no deficit is observed on the near side. This might indicate that dust grains preferentially forward-scatter the radiation, thus compensating for the depolarization effect.
The horseshoe structure revealed from thermal images by Brown et al. (2009) and Lyo et al. (2011) has a possible connection with the polarized light (see comparison in Fig. 1). The bright part of the horseshoe is in the south, where also the luminous part of the disk in scattered light is located. Interestingly, the peak of the thermal emission, in the SE, seems to lie in a darker region of the PDI images, namely between the tail of S1 and the enhanced feature in the east. However, the nature of this enhanced feature is unclear. The spread deficit in polarized light, in the north, is also resolved in the thermal images, suggesting that the lack of polarized light can be (partially) ascribed to some geometrical properties of the local dust, such as a diminished scale height.
4.2. The cavity and the ring
The inner region (r < 0.2″) of the disk was never resolved before in scattered light. Therefore, we dedicate the rest of the section to the features identified therein. We interpret the drop in surface brightness inside 0.15″ − 0.18″ as a real depletion of small dust grains. In the following, we refer to the region showing this depletion as the cavity. This definition is meant to indicate a region showing an abrupt discontinuity in the dust radial profile but does not imply that this region is completely void of dust. The ring revealed at the outer edge of the cavity represents the most luminous region of the disk and we interpret it as the inner wall of the outer disk which is directly illuminated by the central star. Thus, we infer the outer edge of the cavity from the (unresolved) ring radial profile along the major axis. We find that the cavity extends from the instrumental inner working angle (~14 AU) to 28 ± 6 AU. This cavity edge is in good agreement with what was recently inferred for this source by Maaskant et al. (2013) with Q-band (24.5 μm) imaging (30 AU).
Interestingly, the outer edge of the observed cavity considerably differs from that predicted by SED fitting (R = 45 AU, Brown et al. 2007) and that imaged at sub-millimeter (R = 39 AU and 46 AU, Brown et al. 2009; Andrews et al. 2011) and millimeter wavelengths (R = 50 AU, Lyo et al. 2011). Even though the angular resolution of (sub-)millimeter observations is coarser than that of our PDI images, this discrepancy cannot be explained by observational effects. In fact, downgrading the resolution of our images acts to fill in the gap, thus raising the difference between the datasets. Discrepancies between thermal and polarized light were already noticed by Muto et al. (2012). However, they found no evidence of discontinuity at radii as small as 28 AU.
The inner (sub-au scale) 60°-inclined dust belt inferred by Fedele et al. (2008) should cast a shadow on the outer disk wall, presumably on two distinct axisymmetric points of the ring. However, we do not infer the presence of shadow cones, neither on the ring nor on the external part of the disk. This might not appear as a contradiction, since Espaillat et al. (2010) showed that, for typical pre-transitional disks, significant portions of the cavity wall might be out of the shadow casted by the inner wall.
Azimuthal asymmetry in transitional disks are now intensively studied because of the recent discovery of highly azimuthal-asymmetric disks (e.g. Brown et al. 2009; van der Marel et al. 2013). Lin & Papaloizou (2011) have shown that the gas accumulated at the outer edge of a cavity carved out by a planet may become unstable and, thus, generate vortices. In the assumption that small dust grains at the cavity edge are perfectly coupled to the gas, dust accumulation in rings might be detected from PDI observations and could possibly be a signpost of the presence of a planet in the cavity. The bump in the azimuthal profile of Fig. 4 at PA ~ 220° is associated with the starting-point of S1. Curiously, the position of this bump is consistent with that of the azimuthal asymmetry shown by CO lines in the inner 25 AU (at PA ~ 240°, Pontoppidan et al. 2008). The other bump (at PA ~ 135°) is not in evident relation with other features of our images and should be considered as possible location for small dust grain concentration in the rim. Finally, the azimuthal dip at PA ~ 340° can be explained by the depolarization effect, as described in Sect. 4.1.
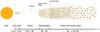 |
Fig. 5 Illustrative sketch showing the dust radial distribution in the disk around SAO 206462, as proposed in this work according to data from this paper, Fedele et al. (2008), and Brown et al. (2009). No speculation on the vertical structure is contained in the sketch. |
4.3. Small and large dust grains at the cavity edge
The size of the cavity of many transitional disks has been inferred from sub-millimeter observations (see e.g. Andrews et al. 2011). However, the presence of small dust grains well inside millimeter-grains cavities has been inferred by means of PDI observations (e.g. UX Tau A; SR21, Tanii et al. 2012; Follette et al. 2013) and modeling of multi-wavelength observations (e.g. HH 30, Madlener et al. 2012). On the other hand, some objects (e.g. GM Aur, Gräfe et al. 2011) do not show any dissimilarity in the cavity size for different grain sizes. Since PDI and thermal images trace different components of the dust (μm-sized grains in the scattered light images, mm-sized grains in the thermal images), this discrepancy can provide important information on the dust distribution in the inner regions.
Rice et al. (2006) have shown that, at the outer edge of a disk gap cleared by a planet, a local pressure bump can act as a filter, allowing small (≲10 μm-sized) particles to drift inward but holding back larger grains. In order for the SED to show the near- to mid-IR dip typical of transitional disks, the region inside the cavity must contain optically thin dust. However, Zhu et al. (2012) argued that dust filtration alone cannot explain the observed spectral deficit (invoking additional processes such as dust growth). Dong et al. (2012) put the three observational evidence together (spectral deficit, cavity in sub-mm images, and continuous radial distribution of polarized light) and proposed a model with dust filtration and flat or inward-decreasing surface density profile inside the cavity (consistent with dust growth).
Nevertheless, our observations replace, for the particular case of SAO 206462, one element: the small dust grains are not continuously distributed down to the sublimation radius but show an abrupt discontinuity. Since the location of the observed discontinuity (0.15″) is comparable with the typical inner working angles of PDI (0.1″ − 0.2″), we argue that the case of SAO 206462 may not be unique. The presence of a depletion for small dust grains represents a direct, qualitative explanation for the spectral deficit, without necessarily invoking simultaneous dust growth inside the cavity. Disk cavities were already detected in PDI in a number of other objects (e.g. HD 100546 and HD 169142, Quanz et al. 2011, 2013). Additional PDI observations (with inner working angle of 0.1″ or lower) of a sample of transitional disks are needed to speculate whether two families of geometries (abrupt and continuous radial dust profiles) may exist.
Dust filtration permits the presence of small grains inside the edge observed at millimeter wavelengths but cannot explain why these grains are held back at a different, inner location. A possible explanation invokes the gas distribution inside the cavity. Pinilla et al. (2012) have shown that the outer edge of the gaseous halo carved out by a planet may not coincide with the location of the pressure bump generated by the same planet. They show how the pile-up of the dust occurs, depending on the planet mass, at radii 1.4 to 2.0 times farther from the planet than the gap outer edge in the gas. Only particles larger than a certain minimum size (typically at sub- to millimeter scale at distances of 20−50 AU) are perfectly trapped in the pressure maximum. We expect that the small (μm-size) particles at R ~ 40 AU are perfectly coupled to the gas and can, thus, be dragged along with it. To show this, we calculate the Stokes number St, defined as: 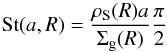 (3)(Birnstiel et al. 2010) where a is the particle size, ρS the solid density of dust particles, and Σg the gas column density. We calculate St for μm-size particles located at R = 40 AU using a typical ρS = 1 g/cm3 and Σg as constrained for this disk by Andrews et al. (2011):
(3)(Birnstiel et al. 2010) where a is the particle size, ρS the solid density of dust particles, and Σg the gas column density. We calculate St for μm-size particles located at R = 40 AU using a typical ρS = 1 g/cm3 and Σg as constrained for this disk by Andrews et al. (2011): 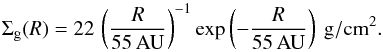 (4)We find that St(a = 1 μm, R = 40 AU) ≃ 10-5. Since strong interplay with the gas is expected for particles with St ≪1, this result suggests that μm-size dust grains at the cavity edge of mm-size grains are very well coupled to the gas.
(4)We find that St(a = 1 μm, R = 40 AU) ≃ 10-5. Since strong interplay with the gas is expected for particles with St ≪1, this result suggests that μm-size dust grains at the cavity edge of mm-size grains are very well coupled to the gas.
In a scenario where a planet is carving out the disk (see Sect. 4.4), the observed inner cavity of μm-size dust grains at 28 AU might coincide with the outer edge of the gaseous cavity, whereas the mm-size particles are piled-up at the pressure bump located at 39 AU. However, the inner region is not void of gas, as inferred from the presence of CO ro-vibrational lines as far as 25 AU (considering d = 142 pc, Pontoppidan et al. 2008; Carmona et al., in prep.). This may not appear as a contradiction of the proposed scenario if we assume that the gas is carved out in a narrow ring (consistently with the presence of a single planet) because CO line profile fitting may not reveal such a fine structure. The observed depletion (one order of magnitude) of CO gas in the central region of the disk (Lyo et al. 2011) might also support a scenario where the gas is partially cleared. In fact, the tidal action of a planet is also expected to significantly deplete material in the region inside the location of the planet (Tatulli et al. 2011). Furthermore, the presence of gas and small dust grains inside the cavity is required to explain the inner dust belt and the substantial accretion rate of the source. In Fig. 5, we depict the suggested dust radial distribution around SAO 206462.
4.4. What can cause cavity and spiral arms?
Spiral arms and large inner cavities are among the most intriguing features observed in protoplanetary disks. These two features (both shown by the dusty disk around SAO 206462) can provide insight into the dynamical processes occurring in the disk.
Inner cavity. One possible process responsible for the clearing of a large inner region of disks is the interaction with orbiting companion(s) (e.g. Rice et al. 2003). Dodson-Robinson & Salyk (2011) have shown with hydrodynamical simulations that a multiple planets system is required to open holes as large as the millimeter observations suggest. However, Pinilla et al. (2012) also considered modeling of dust evolution demonstrating that the gap carved out by a single planet can be much larger than expected by means of pure gas hydrodynamical simulations. Photoevaporation can also generate disk inner holes. Alexander & Armitage (2007) argued that UV photoevaporation can induce holes only in systems with accretion rates ≲10-10 M⊙ yr-1. Thus, the substantial accretion rate shown by SAO 206462 (a few 10-8 M⊙/yr, Sitko et al. 2012) rules out this possibility. Dust grain growth has also been proposed to explain the observed cavities (Dullemond & Dominik 2005). However, this process is expected to produce smooth radial profiles, inconsistent with our PDI observations. Furthermore, the growth of μm-size particles should give rise to a family of mm-size grains, which is not observed at (sub-)mm wavelengths (Brown et al. 2009; Lyo et al. 2011). Birnstiel et al. (2012) showed indeed that large cavities cannot be caused by grain growth alone. Finally, the role of magnetorotational instability (MRI) in disk clearing has been discussed by Chiang & Murray-Clay (2007). However, Dominik & Dullemond (2011) argued that the dust grains cannot be held back by radiation pressure alone. In addition, the presence of a thick dust belt close to the star (Fedele et al. 2008) rules out any mechanism operating with inside-outside modality (namely, the photoevaporation and the MRI instability).
Spirals. Disk-planet interaction can result in spiral density waves (e.g. Tanaka et al. 2002) and possibly generate both a disk gap and a spiral arm structure (Crida et al. 2006). Alternatively, gravitational instability has been proposed as mechanism of spiral wave excitation in disks (e.g. Durisen et al. 2007). Disks are considered gravitationally unstable at a certain radius r if the Toomre parameter Q(r) ≲ 1. To speculate about the stability of the disk around SAO 206462, we use a global Q as calculated by Kamp et al. (2011): 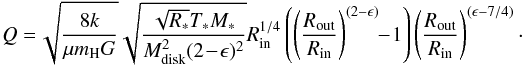 (5)We use the stellar radius R∗, temperature T∗, and mass M∗ assumed by Müller et al. (2011), a disk mass Mdisk of 0.026 M⊙ (Andrews et al. 2011), disk outer radius Rout of 220 AU (Lyo et al. 2011), and inner radius Rin from this dataset. We vary the column density power-law ϵ over a range of realistic values (0.5 to 1.5, Kamp et al. 2011). We find that Q always exceeds 25, meaning that the disk is (globally) highly stable. To enter the unstable regime, the disk would have to be more than twenty times more massive. However, the degree of instability necessary to generate small wiggles on the disk surface (see Sect. 4.1) may be lower than what is usually assumed as an edge of the two regimes. Finally, formation of spiral arms is expected in disks around binary stars because of strong tidal forces (e.g. Boss 2006). The physical separation between SAO 206462 and its visual companion HD 135344A is at least 2900 AU. In the case of highly eccentric orbits (e = 0.9) and face-on orbital plane, the semi-minor axis of this potential binary system can be as small as ~150 AU. Duchêne (2010) showed that binaries wider than 100 AU are indistinguishable from single stars in terms of their circumstellar disks and planetary systems. Nevertheless, we cannot rule out a marginal gravitational interaction between the two stars. This study is beyond the scope of the current work.
(5)We use the stellar radius R∗, temperature T∗, and mass M∗ assumed by Müller et al. (2011), a disk mass Mdisk of 0.026 M⊙ (Andrews et al. 2011), disk outer radius Rout of 220 AU (Lyo et al. 2011), and inner radius Rin from this dataset. We vary the column density power-law ϵ over a range of realistic values (0.5 to 1.5, Kamp et al. 2011). We find that Q always exceeds 25, meaning that the disk is (globally) highly stable. To enter the unstable regime, the disk would have to be more than twenty times more massive. However, the degree of instability necessary to generate small wiggles on the disk surface (see Sect. 4.1) may be lower than what is usually assumed as an edge of the two regimes. Finally, formation of spiral arms is expected in disks around binary stars because of strong tidal forces (e.g. Boss 2006). The physical separation between SAO 206462 and its visual companion HD 135344A is at least 2900 AU. In the case of highly eccentric orbits (e = 0.9) and face-on orbital plane, the semi-minor axis of this potential binary system can be as small as ~150 AU. Duchêne (2010) showed that binaries wider than 100 AU are indistinguishable from single stars in terms of their circumstellar disks and planetary systems. Nevertheless, we cannot rule out a marginal gravitational interaction between the two stars. This study is beyond the scope of the current work.
It turns out that the interaction with an orbiting companion is the only process capable of explaining both the inner disk clearing and the spiral arms structure. Any other known mechanism cannot account for at least one observational evidence. However, we cannot claim that a potential companion responsible for the inner clearing is also responsible for the spiral excitation. In fact, Muto et al. (2012) and Grady et al. (2013) estimated the location of the possible planet exciting spiral arms (of SAO 206462 and MWC 758, respectively) to be outside of the spirals themselves. Grady et al. (2013) argued that such a planet could not account for the cavity observed around MWC 758.
In the following section, we focus on the possible companion responsible for clearing. The scenario for which the spiral arms are excited by the same (or by another) companion is not further discussed in this paper.
4.5. An orbiting companion?
In the intriguing prospect that a single object is responsible for the observed large inner hole, we constrain the location and the mass that such a companion should have. We use the results by Dodson-Robinson & Salyk (2011) and Pinilla et al. (2012) to determine a testable range of realistic locations for that object and, then, infer its mass.
The gap width in the disk is regulated by the tidal radius, or Hill radius, of the companion, defined as: 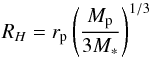 (6)being rp and Mp the planet location and mass and M∗ the stellar mass. Dodson-Robinson & Salyk (2011) showed that tidal interactions with planets are very fast at scattering disk particles within ~ 3 RH (≲104 yr) while the scattering timescale for particles at ~5 RH approaches 1 Myr. These results argue against the single planet carving out the gap, because of the inability of reproducing the hole sizes observed at millimeter wavelengths. However, Pinilla et al. (2012) predicted that the accumulation of large dust grains can occur at radii 1.4 to 2.0 larger than the outer edge of the gaseous gap (i.e. ~7 to ~10 RH).
(6)being rp and Mp the planet location and mass and M∗ the stellar mass. Dodson-Robinson & Salyk (2011) showed that tidal interactions with planets are very fast at scattering disk particles within ~ 3 RH (≲104 yr) while the scattering timescale for particles at ~5 RH approaches 1 Myr. These results argue against the single planet carving out the gap, because of the inability of reproducing the hole sizes observed at millimeter wavelengths. However, Pinilla et al. (2012) predicted that the accumulation of large dust grains can occur at radii 1.4 to 2.0 larger than the outer edge of the gaseous gap (i.e. ~7 to ~10 RH).
Inspired by this statement, we use the speculated outer edge of the gas cavity (R = 28 AU, as inferred from our observations of small dust grains, see Sect. 4.2), and impose it to be the outer edge of a gap with size (i.e. distance planet-edge) of κgas = 3 to 5 times RH. Moreover, we use the observed cavity dimension for mm-size dust particles (R = 39 AU, from Brown et al. 2009) and impose it to be the outer edge of a gap of κdust = 7 to 10 RH (depending, in turn, on the mass planet, see Pinilla et al. 2012). By varying κgas and κdust over a discrete range of values, we find a family of solutions (see Fig. 6). A potential companion responsible for the observed geometry should be located at a radius spanning from 17 to 20 AU with a mass between 5 and 15 MJ, being, thus, a giant planet. These companion masses are not in contradiction with the upper mass limit inferred by Vicente et al. (2011) with VLT/NACO narrow-band imaging (~230 MJ at 14 AU).
In a scenario with a 5 to 15 MJ giant planet, the gravitational torque is much larger than the viscous torque and, thus, the radial location of the trapping is not significantly affected by the disk viscosity (considering typical α parameters of 10-4−10-2, Pinilla et al. 2012).
Finally, we argue that the estimate of this section is valid only on the assumption that a single planet is capable of clearing the observed cavity. We did not explore the scenario of multiple planets. However, such a system seems in contradiction with the presence of diffuse gas inside the cavity (see Sect. 4.3).
 |
Fig. 6 Locations and masses of a potential single companion responsible for the observed inner cavity in the disk (see Sect. 4.5, for details). Errors are obtained from the uncertainties in the location of the observed cavity edges (from this work and Brown et al. 2009). |
5. Summary and conclusions
Transitional disks are considered a key-stage of the process of planet formation. These objects show a large region of highly-depleted dust surrounded by a dust rim that can act as a filter, holding back large dust grains but allowing small particles to move inward. Since the particles trapped at the cavity edge can evolve on longer timescales, this scenario has been proposed as a solution to the radial drift barrier. A deeper comprehension of the processes occurring at these cavity edges is, thus, needed. In particular, since small and large grains are expected to behave differently, comparisons of near-IR and millimeter images are an excellent vehicle of investigation. PDI observations of the scattered light from circumstellar disks (e.g. Hashimoto et al. 2012; Quanz et al. 2013) are providing unprecedented high-contrast near-IR images, whereas SMA (Andrews et al. 2009) and ALMA are allowing one to study the thermal emission from an ever growing number of objects.
The F4 young star SAO 206462 (HD 135344B) is known to host a transitional disk that shows a narrow dust inner belt (Fedele et al. 2008), a large dust cavity at millimeter wavelengths (~39 AU, Brown et al. 2009), and a prominent spiral arms structure (Muto et al. 2012). No cavity was revealed at near-IR wavelengths down to ~ 28 AU (Muto et al. 2012). This discrepancy was highlighted for a number of other objects (e.g. Tanii et al. 2012; Follette et al. 2013). To explain both this property and the observed spectral deficit at near-IR wavelengths, a scenario with dust filtration and grain growth inside the cavity was proposed (Dong et al. 2012).
In this paper, we have shown new PDI observations of SAO 206462 obtained with VLT/NACO and tracing the polarized light from the disk as down as 0.1″. The main results from our PDI observations are summarized as follows:
-
The disk is detected in polarized light out to ~130 AU in both H and Ks band. No particular difference is found between the two bands. The azimuthally-averaged polarized brightness profile is fitted by a power-law with β = −2.9. However, a broken power-law (β = −1.9 fitting the inner ~ 60 AU, β = −6.0 fitting outside) provides a better fit.
-
The images reveal the double spiral arms resolved by Muto et al. (2012), a general dip along the axis at θ = 325° (due to depolarization), and a diffuse enhancement of unclear origin to the east side.
-
We resolve an inner cavity (brightness down to 2% of a continuous distribution) surrounded by a non-resolved bright rim located at 28 ± 6 AU. The rim does not show signs of eccentricity but the azimuthal brightness profile reveals two small bumps, one of which is associated to a spiral arm.
The scenario with planet(s) carving out the cavity also provides an explanation for the observed diversity of small and large grain distribution. Pinilla et al. (2012) suggested that the pressure bump induced by an orbiting planet (and trapping large particles only) can be located at radii much larger than the outer edge of the gaseous cavity opened by the same planet. Inspired by this model, we propose a scenario where one giant planet is responsible for holding millimeter-size particles at 39 AU but permits μm-size grains, perfectly coupled to the gas, to move inward down to 28 AU, where the gas itself is retained by the planet. The presence of gas inside the cavity (Pontoppidan et al. 2008) seems to suggest that this is carved out in a narrow ring, rather than in the entire cavity. In any case, the suggested scenario implies a depletion of gas in the inner few tens of AU, in agreement with the observations by Lyo et al. (2011). In particular, we analytically calculate that all observations are consistent with a potential planet located at 17−20 AU with mass 5−15 MJ carving out the cavity. A multiple-planet system is not ruled out by our observations but appears as a contradiction to the presence of diffuse gas inside the cavity.
To fully comprehend the dynamics of dust in the exciting inner regions (~ 10 − 50 AU) of transitional disks, complementary observations tracing the distribution of small and large grains are necessary. In the upcoming era of ALMA and VLT/SPHERE, a large sample of high-resolution images of these disks will be available, both at (sub-)millimeter and optical/near-IR wavelengths. PDI remains one of the best techniques to image circumstellar disks in the near-IR as close as 0.1″ from the star. Therefore, further PDI investigations of Herbig Ae/Be and T Tauri stars and consequent comparisons with millimeter images are crucial. Finally, L′ band images in angular differential imaging mode of SAO 206462 are needed to test the speculated existence of the giant planet sculpting the disk.
Acknowledgments
The authors acknowledge the staff at VLT for their excellent support during the observations. We also thank the anonymous referee, A. Carmona, and J. Pineda for valuable comments on the paper, J. Brown for sharing the SMA data, as well as I. Kamp and K. Pontoppidan for useful discussions. This work is supported by the Swiss National Science Foundation. F.M. is supported by the ETH Zurich Postdoctoral Fellowship Program as well as by the Marie Curie Actions for People COFUND program. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Alexander, R. D., & Armitage, P. J. 2007, MNRAS, 375, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Apai, D., Pascucci, I., Brandner, W., et al. 2004, A&A, 415, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Schmid, H. M., et al. 2013, ApJ, submitted [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Andrews, S. M., & Ercolano, B. 2012, A&A, 544, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 2006, ApJ, 641, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Perez, M. S., Jordán, A., et al. 2012, ApJ, 754, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E., & Murray-Clay, R. 2007, Nature Physics, 3, 604 [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources. [Google Scholar]
- Dent, W. R. F., Greaves, J. S., & Coulson, I. M. 2005, MNRAS, 359, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
- Dominik, C., & Dullemond, C. P. 2011, A&A, 531, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, R., Rafikov, R., Zhu, Z., et al. 2012, ApJ, 750, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Doucet, C., Pantin, E., Lagage, P. O., & Dullemond, C. P. 2006, A&A, 460, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G. 2010, ApJ, 709, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, in Extrasolar Planets: Today and Tomorrow, eds. J. Beaulieu, A. Lecavelier Des Etangs, & C. Terquem, ASP Conf. Ser., 321, 361 [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunkin, S. K., Barlow, M. J., & Ryan, S. G. 1997, MNRAS, 290, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Durisen, R. H., Boss, A. P., Mayer, L., et al. 2007, in Protostars and Planets V (Tucson: Univ. of Arizona Press), 607 [Google Scholar]
- Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Fedele, D., van den Ancker, M. E., Acke, B., et al. 2008, A&A, 491, 809 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Follette, K. B., Tamura, M., Hashimoto, J., et al. 2013, ApJ, 767, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Polomski, E. F., Henning, T., et al. 2001, AJ, 122, 3396 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Schneider, G., Hamaguchi, K., et al. 2007, ApJ, 665, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Schneider, G., Sitko, M. L., et al. 2009, ApJ, 699, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Muto, T., Hashimoto, J., et al. 2013, ApJ, 762, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfe, C., Wolf, S., Roccatagliata, V., Sauter, J., & Ertel, S. 2011, A&A, 533, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hashimoto, J., Tamura, M., Muto, T., et al. 2011, ApJ, 729, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, J., Dong, R., Kudo, T., et al. 2012, ApJ, 758, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Hog, E., Kuzmin, A., Bastian, U., et al. 1998, A&A, 335, L65 [NASA ADS] [Google Scholar]
- Ireland, M. J., & Kraus, A. L. 2008, ApJ, 678, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Kamp, I., Woitke, P., Pinte, C., et al. 2011, A&A, 532, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kusakabe, N., Grady, C. A., Sitko, M. L., et al. 2012, ApJ, 753, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 944 [Google Scholar]
- Lin, M.-K., & Papaloizou, J. C. B. 2011, MNRAS, 415, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Lyo, A.-R., Ohashi, N., Qi, C., Wilner, D. J., & Su, Y.-N. 2011, AJ, 142, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Maaskant, K. M., Honda, M., Waters, L. B. F. M., et al. 2013, A&A, 555, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madlener, D., Wolf, S., Dutrey, A., & Guilloteau, S. 2012, A&A, 543, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mariñas, N., Telesco, C. M., Fisher, R. S., & Packham, C. 2011, ApJ, 737, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayama, S., Hashimoto, J., Muto, T., et al. 2012, ApJ, 760, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M., Canovas, H., Mulders, G. D., & Keller, C. U. 2012, A&A, 537, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, A., van den Ancker, M. E., Launhardt, R., et al. 2011, A&A, 530, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Allen, L. E., Megeath, S. T., Hernández, J., & Gutermuth, R. A. 2010, ApJ, 708, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., van Dishoeck, E. F., et al. 2008, ApJ, 684, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Schmid, H. M., Geissler, K., et al. 2011, ApJ, 738, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Birkmann, S. M., Apai, D., Wolf, S., & Henning, T. 2012, A&A, 538, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quanz, S. P., Avenhaus, H., Buenzli, E., et al. 2013, ApJ, 766, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Wood, K., Armitage, P. J., Whitney, B. A., & Bjorkman, J. E. 2003, MNRAS, 342, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Armitage, P. J., Wood, K., & Lodato, G. 2006, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in SPIE Conf. Ser. 4839, eds. P. L. Wizinowich, & D. Bonaccini, 140 [Google Scholar]
- Schmid, H. M., Joos, F., & Tschan, D. 2006, A&A, 452, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sitko, M. L., Day, A. N., Kimes, R. L., et al. 2012, ApJ, 745, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Dutkevitch, D., Strom, S. E., et al. 1990, AJ, 99, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, K. M., Strom, S. E., Edwards, S., Cabrit, S., & Skrutskie, M. F. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Tanii, R., Itoh, Y., Kudo, T., et al. 2012, PASJ, 64, 124 [NASA ADS] [Google Scholar]
- Tatulli, E., Benisty, M., Ménard, F., et al. 2011, A&A, 531, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Boekel, R., Dullemond, C. P., & Dominik, C. 2005, A&A, 441, 563 [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Plas, G., van den Ancker, M. E., Fedele, D., et al. 2008, A&A, 485, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vicente, S., Merín, B., Hartung, M., et al. 2011, A&A, 533, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witzel, G., Eckart, A., Lenzen, R., & Straubmeier, C. 2010, The Messenger, 142, 5 [NASA ADS] [Google Scholar]
- Zhu, Z., Nelson, R. P., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Reflection nebulosity around SAO 206462. First two rows, from left to right: P⊥ image, P∥ image, and P⊥ image with blue and pink stripes indicating the position of the major and minor axis, respectively. The first row is H band, the second is Ks band. Third row, from left to right: comparison between the P⊥ image in Ks band and continuum emission from sub-mm observations by Brown et al. (2009), polar mapping of H and Ks band with angles measured with respect to north. Images are upscaled by a factor 3 to minimize smoothing effects throughout the sub-pixel data shifting and are scaled with r2 to compensate for stellar light dilution. The color scale is linear and arbitrary. The red central region indicates the area on the detector with non-linear pixels. Continuum contours are drawn at 3σ intervals starting from 3σ. |
| In the text | |
 |
Fig. 2 Radial profile of the polarized surface brightness. Top: along the major axis in NE (right half) and in SW (left half) direction for H (red) and Ks band (blue). Bottom: along the minor axis in NW (right half) and in SE (left half) direction, namely the far and near disk side, respectively. The grey box indicates the region that our data resolved for the first time. In all profiles (except the H band NW minor axis), the depletion inside this region is evident. Errors are 3σ noise calculated from the P∥ images (see Sect. 2) and do not include systematic uncertainties in the photometric calibration. |
| In the text | |
 |
Fig. 3 Azimuthally-averaged radial profiles in H (red) and Ks (blue) bands and power-law best fits for 0.2″ < r < 0.4″ (dashed lines) and for 0.4″ < r < 0.8″ (dotted lines). Errors are the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Azimuthal profile of the polarized surface brightness along the ring in Ks band, averaged over the 0.17″ − 0.21″ radii. Two main bumps are visible. One is associated to the starting point of S1. Errors are the same as in Fig. 2, averaged over 0.17″ − 0.21″ radii. |
| In the text | |
 |
Fig. 5 Illustrative sketch showing the dust radial distribution in the disk around SAO 206462, as proposed in this work according to data from this paper, Fedele et al. (2008), and Brown et al. (2009). No speculation on the vertical structure is contained in the sketch. |
| In the text | |
 |
Fig. 6 Locations and masses of a potential single companion responsible for the observed inner cavity in the disk (see Sect. 4.5, for details). Errors are obtained from the uncertainties in the location of the observed cavity edges (from this work and Brown et al. 2009). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


