| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219257 | |
| Published online | 02 December 2013 | |
Improving three-dimensional mass mapping with weak gravitational lensing using galaxy clustering
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: psimon@astro.uni-bonn.de
Received: 21 March 2012
Accepted: 3 September 2013
Context. The weak gravitational lensing distortion of distant galaxy images (defined as sources) probes the projected large-scale matter distribution in the Universe. The availability of redshift information in galaxy surveys also allows us to recover the radial matter distribution to a certain degree.
Aims. To improve quality in the mass mapping, we combine the lensing information with the spatial clustering of a population of galaxies (defined as tracers) that trace the matter density with a known galaxy bias.
Methods. We construct a minimum-variance estimator for the 3D matter density that incorporates the angular distribution of galaxy tracers, which are coarsely binned in redshift. Merely the second-order bias of the tracers has to be known, which can in principle be self-consistently constrained in the data by lensing techniques. This synergy introduces a new noise component because of the stochasticity in the matter-tracer density relation. We give a description of the stochasticity noise in the Gaussian regime, and we investigate the estimator characteristics analytically. We apply the estimator to a mock survey based on the Millennium Simulation.
Results. The estimator linearly mixes the individual lensing mass and tracer number density maps into a combined smoothed mass map. The weighting in the mix depends on the signal-to-noise ratio (S/N) of the individual maps and the correlation, R, between the matter and galaxy density. The weight of the tracers can be reduced by hand. For moderate mixing, the S/N in the mass map improves by a factor ~2–3 for R ≳ 0.4. Importantly, the systematic offset between a true and apparent mass peak distance (defined as z-shift bias) in a lensing-only map is eliminated, even for weak correlations of R ~ 0.4.
Conclusions. If the second-order bias of tracer galaxies can be determined, the synergy technique potentially provides an option to improve redshift accuracy and completeness of the lensing 3D mass map. Herein, the aim is to visualise the spatial distribution of cluster-sized mass peaks. Our noise description of the estimator is accurate in the linear, Gaussian regime. However, its performance on sub-degree scales depends on the details in the galaxy bias mechanism and, hence, on the choice of the tracer population. Nonetheless, we expect that the mapping technique yields qualitatively reasonable results even for arcmin smoothing scales, as observed when this technique is applied to the mock survey with two different tracer populations.
Key words: gravitational lensing: weak / large-scale structure of Universe / dark matter / methods: data analysis
© ESO, 2013
1. Introduction
The weak gravitational lensing effect is a well-established tool to infer properties of the projected large-scale matter distribution (e.g. Munshi et al. 2008; Schneider 2006a,b). These therein exploited coherent shear distortions of distant galaxy images (defined as sources) result from the continuous deflection of light bundles by the intervening fluctuations in the large-scale gravitational field, which are most prominent and detectable around galaxy clusters. The lensing distortions probe the total matter content in the Universe, which makes them an excellent tool for studying the dark matter component, an essential ingredient of the standard cosmological model of cold dark matter with a cosmological constant (ΛCDM, e.g., Dodelson 2003).
The shear distortion pattern can be translated into a map of projected matter fluctuations. Early non-parametric mapping algorithms, which were refined later to obtain optimised methods for finite fields, achieved this only on the basis of a catalogue of source angular positions and ellipticities (e.g. Kaiser & Squires 1993; Seitz & Schneider 2001). With the advent of distance indicators of galaxies in wide field galaxy surveys, the purely geometric relation between shear magnitude and source (and lens) distance was incorporated into a new three-dimensional (3D) lensing algorithm to also recover information on the radial distribution of matter (Hu & Keeton 2002; Bacon & Taylor 2003; Simon et al. 2009; VanderPlas et al. 2011; Leonard et al. 2012). The best studied methodologies so far utilise linear inversion techniques, such as Wiener filtering or a radial matter-density eigenmode decomposition with a suppression of low signal-to-noise (S/N) modes. Owing to the relatively sparse and noisy sampling of the survey area with background sources, however, the resulting maps are usually very noisy, and significant detections are basically restricted to mass peaks of a galaxy cluster scale that has only moderate redshift accuracy. Moreover, the linear inversion utilises a radial smoothing with a broad smoothing kernel that (a) smears out localised peaks in a radial direction and (b) biases the peak distances (known as z-shift bias; Simon et al. 2009), which potentially renders the resulting maps hard to interpret. To attain more realistic 3D maps, the radial elongation of peaks inside the map can be mended by regularising the inversion (Leonard et al. 2012), or by finding the maximum likelihood positions of one or a few individual mass peaks along the line-of-sight (LOS) given the radial smoothing kernel and radial density profile in the map (Simon et al. 2012). However, this does not alleviate the principle problem of noisy maps and inaccurate peak distances. It merely provides more realistic estimators for the 3D mass map. Moreover, the noise properties of the maps are likely to be complex in regularised, non-linear methods.
On the other hand, galaxy positions themselves are also tracers of the 3D matter density field and could therefore be employed to add extra information to the matter density maps that are obtained from 3D lensing. However, there are two complications here: (i) galaxies trace the matter density field only up to a systematic mismatch, which is generally dubbed galaxy bias; and (ii) a sampling by galaxy positions is affected by shot-noise (e.g. Dekel & Lahav 1999; Martínez & Saar 2002). The strategy of this paper is to refine the minimum-variance estimator in Simon et al. (2009, STH09 hereafter) for the 3D matter density by adding the galaxy clustering information to the map making process. Since the minimum-variance estimators (Zaroubi et al. 1995) require second-order statistics of the input data to be specified, only the second-order bias parameters of the galaxy tracers have to be known (Gaussian bias or linear stochastic bias; Dekel & Lahav 1999). The galaxy bias as a function of scale and redshift could in principle be acquired in a self-consistent approach from the data by using lensing techniques (Schneider 1998; van Waerbeke 1998; Pen et al. 2003; Fan 2003; Jullo et al. 2012; Simon 2012), or with lesser certainty from simulations (Yoshikawa et al. 2001; Somerville et al. 2001; Weinberg et al. 2004). We therefore assume that it is basically known. The galaxy noise covariance within the minimum-variance estimator takes care of the galaxy sampling shot-noise. The outline of this paper is as follows. Sections 2 and 3 present the details of the algorithm and a formalism to quantify its noise properties. We discuss the algorithm in the context of an idealised survey and then apply it to simulated data. In Sect. 4, we give details of the fiducial survey and the mock data. The results on the expected performance of the algorithm are presented in Sect. 5 and discussed in final Sect. 6.
2. Independent reconstructions
We first consider the reconstruction of the matter density field and galaxy-number density field separately. The next section combines both into one 3D mass map.
2.1. Matter density on lens planes
We briefly summarise here the formalism already presented in STH09. We adopt the exact notation that is employed therein. For more details, we refer the reader to this paper.
We split the source catalogue into i = 1...Nz sub-samples where a redshift probability distribution (p.d.f.) is known. The complex ellipticities (Bartelmann & Schneider 2001) of the sources belonging to the ith sub-sample are binned on a 2D grid that covers the field-of-view of the survey area. This ellipticity grid is denoted by vector ϵ(i), whose elements are the sorted pixel values of the grid. Every sub-sample uses the same grid geometry. The paper assumes that the weak lensing approximation is accurate enough for the lensing catalogue on the whole. That is, for the given source redshift and in the LOS direction θi, the complex ellipticity, ϵs, is an unbiased estimator of the shear distortion, γ = γ1 + iγ2, 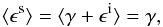 (1)where ϵi denotes the intrinsic (unlensed) complex ellipticity of a source image. Moreover, we assume a flat sky with a Cartesian coordinate frame.
(1)where ϵi denotes the intrinsic (unlensed) complex ellipticity of a source image. Moreover, we assume a flat sky with a Cartesian coordinate frame.
We slice the light-cone volume, where the matter distribution is reconstructed, into Nlp slices. Within the slices we approximate the matter density contrast as constant along the line-of-sight. Every grid pixel defines a solid angle associated with a LOS direction θ. Thus, the fluctuations of the matter density field inside a slice are fully described by the angular distribution of mean density contrasts on a plane (lens plane) and the width of the slice. The matter density contrast on a lens plane, 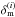 , is binned with the same angular grid as the source ellipticities. We represent the grids, ϵ(i) and
, is binned with the same angular grid as the source ellipticities. We represent the grids, ϵ(i) and 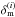 , as vectors of equally ordered pixel values. We refer to a particular pixel by
, as vectors of equally ordered pixel values. We refer to a particular pixel by 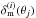 , where θj is the position of the pixel on the sky. Therefore, our algorithm represents the 3D-matter density contrast as an approximation by a discrete set of lens planes, which numerically limits the radial resolution, and a discrete set of pixels on the sky, limiting the angular resolution. The complete sets of ellipticity planes and lens planes are combined inside vectors of grids:
, where θj is the position of the pixel on the sky. Therefore, our algorithm represents the 3D-matter density contrast as an approximation by a discrete set of lens planes, which numerically limits the radial resolution, and a discrete set of pixels on the sky, limiting the angular resolution. The complete sets of ellipticity planes and lens planes are combined inside vectors of grids:
![\begin{eqnarray} && \vec{\epsilon}=\left[\vec{\epsilon}^{(1)},\ldots,\vec{\epsilon}^{(N_{\rm z})}\right],\\ && \vec{\delta}_{\rm m}=\left[\vec{\delta}_{\rm m}^{(1)},\ldots,\vec{\delta}_{\rm m}^{(N_{\rm lp})}\right], \end{eqnarray}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq20.png) respectively. The brackets, which group together the vector arguments, should be understood as big vectors that are obtained by piling up all embraced vectors on top of each other.
respectively. The brackets, which group together the vector arguments, should be understood as big vectors that are obtained by piling up all embraced vectors on top of each other.
In the weak lensing regime, the (pixelised) lensing convergence κ(i)(θj) in the lowest-order Born approximation is the weighted projection of the density contrast on the lens planes: ![\begin{equation} \vec{\kappa}= \left[ \sum_{i\,=\,1}^{N_{\rm lp}}Q_{1i}\vec{\delta}_{\rm m}^{(i)},\ldots, \sum_{i\,=\,1}^{N_{\rm lp}}Q_{N_{\rm z}i}\vec{\delta}_{\rm m}^{(i)} \right]=: \mat{Q}\vec{\delta}_{\rm m}, \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq22.png) (4)where the coefficients Qij express the response of the ith convergence plane κ(i) to the density contrast in the jth lens plane. Namely,
(4)where the coefficients Qij express the response of the ith convergence plane κ(i) to the density contrast in the jth lens plane. Namely, 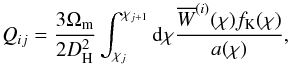 (5)where
(5)where 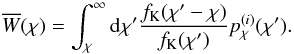 (6)The function
(6)The function 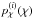 denotes the p.d.f. of sources in comoving distance χ of the ith source sub-sample, and [ χj,χj + 1 [ sets the comoving radial boundaries of the jth matter slice. We use DH: = c/H0 for the Hubble radius and fK(χ) for the (comoving) angular diameter distance. The projection from a grid vector in δm-space to a grid vector in κ-space is hence denoted by the operator Q that is acting on δm.
denotes the p.d.f. of sources in comoving distance χ of the ith source sub-sample, and [ χj,χj + 1 [ sets the comoving radial boundaries of the jth matter slice. We use DH: = c/H0 for the Hubble radius and fK(χ) for the (comoving) angular diameter distance. The projection from a grid vector in δm-space to a grid vector in κ-space is hence denoted by the operator Q that is acting on δm.
The next step connects the convergence planes κ to the shear planes by a convolution of the lensing convergence on the grid ![\begin{equation} \vec{\gamma}= \left[ \mat{P}_{\gamma\kappa}\vec{\kappa}^{(1)},\ldots, \mat{P}_{\gamma\kappa}\vec{\kappa}^{(N_{\rm z})} \right]=: \mat{P}_{\gamma\kappa}\vec{\kappa}, \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq36.png) (7)which introduces the operator Pγκ to map κ(i) to the corresponding shear plane γ(i) (Hu & Keeton 2002). In this sense, Pγκ performs a linear transformation from κ- to γ-space.
(7)which introduces the operator Pγκ to map κ(i) to the corresponding shear plane γ(i) (Hu & Keeton 2002). In this sense, Pγκ performs a linear transformation from κ- to γ-space.
Using this compact notation, we express the linear relation between the matter density (contrast) on the lens planes and the observed, binned ellipticity planes as: 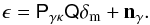 (8)Here, an additional vector nγ denotes the binned intrinsic ellipticties of the sources of all source sub-samples. In the language of lensing, we consider this the noise term that dilutes the shear signal PγκQδm.
(8)Here, an additional vector nγ denotes the binned intrinsic ellipticties of the sources of all source sub-samples. In the language of lensing, we consider this the noise term that dilutes the shear signal PγκQδm.
For the scope of this paper, possible correlations between shear and intrinsic shapes are ignored (Hirata & Seljak 2004). According to STH09, minimum-variance estimator of δm in Eq. (8) is then 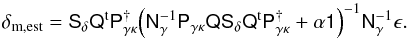 (9)As the only input, the minimum-variance filter requires the signal covariance
(9)As the only input, the minimum-variance filter requires the signal covariance 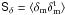 , which specifies the presumed two-point correlation between pixel values of
, which specifies the presumed two-point correlation between pixel values of 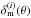 on the lens plane(s) and the noise covariance
on the lens plane(s) and the noise covariance 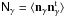 , which quantifies the shear pixel noise variance and the correlation of noise between different pixels. Pixels that contain no sources have infinite noise. For the signal covariance, correlations between pixels that belong to different lens planes are set to zero. We note here that the signal covariance does not need to be the true signal covariance in the data, although the reconstruction may be sub-optimal as to map noise when it is not.
, which quantifies the shear pixel noise variance and the correlation of noise between different pixels. Pixels that contain no sources have infinite noise. For the signal covariance, correlations between pixels that belong to different lens planes are set to zero. We note here that the signal covariance does not need to be the true signal covariance in the data, although the reconstruction may be sub-optimal as to map noise when it is not.
The signal covariance determines the degree of smoothing in the 3D map. The smoothing is uniquely defined by the linear transformation 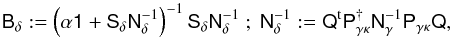 (10)and can be utilised for a comparison of the map δm,est to a theoretical matter distribution δm,th by Bδδm,th (Simon et al. 2012). The radial smoothing is characterised by a radial point-spread function (PSF) of the filter (STH09). After smoothing with the radial PSF, a peak in the true matter distribution δm,th does not necessarily peak at the same distance on average as in the smoothed map, which gives rise to the so-called redshift bias or z-bias. Inside the filter, the constant α ∈ [ 0,1 ] tunes the level of smoothing by rescaling the noise covariance.
(10)and can be utilised for a comparison of the map δm,est to a theoretical matter distribution δm,th by Bδδm,th (Simon et al. 2012). The radial smoothing is characterised by a radial point-spread function (PSF) of the filter (STH09). After smoothing with the radial PSF, a peak in the true matter distribution δm,th does not necessarily peak at the same distance on average as in the smoothed map, which gives rise to the so-called redshift bias or z-bias. Inside the filter, the constant α ∈ [ 0,1 ] tunes the level of smoothing by rescaling the noise covariance.
From a practical point of view, the Wiener filter consists of a series of linear operators that is applied step-by-step from the right to the left on the grids (Appendix B of STH09). Within this process, the signal covariance, Sδ, is a convolution or, equivalently, a multiplication in Fourier space of Fourier modes,  , of the ith lens plane with the angular signal power spectrum,
, of the ith lens plane with the angular signal power spectrum,  , which is implicitly defined by
, which is implicitly defined by 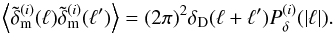 (11)We approximate the power spectrum by using Limber’s equation in Fourier space:
(11)We approximate the power spectrum by using Limber’s equation in Fourier space: ![\begin{equation} \label{eq:pdelta} P_\delta^{(i)}(\ell)= \frac{|\tilde{F}(\ell)|^2}{(\Delta \chi_i)^2} \int_{\chi_i}^{\chi_{i+1}} \!\!\!\frac{\d\chi}{[f_{\rm K}(\chi)]^2}P_{\rm 3d}\left(\frac{\ell}{f_{\rm K}(\chi)},\chi\right), \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq56.png) (12)where Δχi: = χi + 1 − χi,
(12)where Δχi: = χi + 1 − χi, 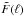 is the Fourier transform of the pixel window function, P3d(k,χ) is the 3D matter-density power spectrum at radial distance χ for wave-number k, and δD(x) is Dirac’s delta function (Kaiser 1992). We denote the Fourier transforms of flat fields, f(θ), on the sky by
is the Fourier transform of the pixel window function, P3d(k,χ) is the 3D matter-density power spectrum at radial distance χ for wave-number k, and δD(x) is Dirac’s delta function (Kaiser 1992). We denote the Fourier transforms of flat fields, f(θ), on the sky by 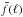 , which is defined by
, which is defined by 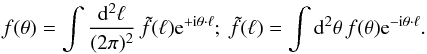 (13)
(13)
2.2. Galaxy numbers densities on lens planes
To improve the information in the 3D matter map and to possibly alleviate the z-shift bias, we add the information gained from galaxy positions, which also probe the matter distribution (they are defined as tracers).
In this section, however, we first visit the problem of mapping the spatial galaxy number densities. For this purpose, we estimate the number density of galaxies projected onto the previously defined lens planes. Hence, we slice the full true 3D galaxy distribution into Nlp distance slices with distance limits [ χi,χi + 1 [. The galaxies are counted within each slice and angular grid pixel of the solid angle Aω. Thereby, we receive the galaxy number density 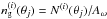 in the LOS direction θj of the ith slice, where N(i)(θj) is the number of counted galaxies. We compile the galaxy-number density values inside a grid vector
in the LOS direction θj of the ith slice, where N(i)(θj) is the number of counted galaxies. We compile the galaxy-number density values inside a grid vector 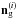 , and we then arrange all grids inside a vector of grids:
, and we then arrange all grids inside a vector of grids: ![\begin{equation} \vec{n}_{\rm g}= \left[\vec{n}_{\rm g}^{(1)},\ldots,\vec{n}_{\rm g}^{(N_{\rm lp})}\right]. \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq69.png) (14)This number density distribution of galaxies is what the following scheme seeks to recover from a galaxy sample with inaccurate distance information. Towards this goal, we split the observed galaxy sample utilising their redshift estimators, zest ∈ [ z(χi),z(χi + 1) [, into Nlp sub-samples with known radial p.d.f.
(14)This number density distribution of galaxies is what the following scheme seeks to recover from a galaxy sample with inaccurate distance information. Towards this goal, we split the observed galaxy sample utilising their redshift estimators, zest ∈ [ z(χi),z(χi + 1) [, into Nlp sub-samples with known radial p.d.f. 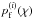 ; z(χ) denotes the redshift corresponding to χ. By projecting the ith sample onto a 2D grid on the sky, one obtains the observed number density distribution
; z(χ) denotes the redshift corresponding to χ. By projecting the ith sample onto a 2D grid on the sky, one obtains the observed number density distribution 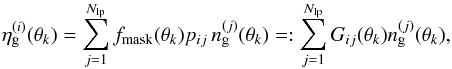 (15)where fmask ∈ { 0,1 } flags mask pixels (= 0 for mask), and
(15)where fmask ∈ { 0,1 } flags mask pixels (= 0 for mask), and 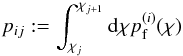 (16)is the probability that a galaxy inside
(16)is the probability that a galaxy inside 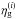 belongs to slice j. Owing to the redshift errors and masking, the observed distribution on the lens planes,
belongs to slice j. Owing to the redshift errors and masking, the observed distribution on the lens planes, 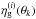 , does not exactly match the true distribution
, does not exactly match the true distribution 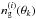 . Therefore, 0 ≤ Gij(θk) ≤ 1 denotes the expected fraction of galaxies on the jth lens plane that is mapped onto the grid
. Therefore, 0 ≤ Gij(θk) ≤ 1 denotes the expected fraction of galaxies on the jth lens plane that is mapped onto the grid 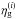 . Because of masking, the total number of galaxies is not necessarily conserved; that is
. Because of masking, the total number of galaxies is not necessarily conserved; that is 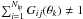 . By a proper arrangement of the elements Gij(θk) inside a matrix G, the effect of Gij(θk) on the entire 3D grid ng can be written as
. By a proper arrangement of the elements Gij(θk) inside a matrix G, the effect of Gij(θk) on the entire 3D grid ng can be written as 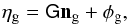 (17)where
(17)where ![\begin{equation} \vec{\eta}_{\rm g}= \left[\vec{\eta}_{\rm g}^{(1)},\ldots,\vec{\eta}_{\rm g}^{(N_{\rm lp})}\right]. \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq86.png) (18)We presume that galaxies sample an underlying smooth galaxy number density by a discrete Poisson process (e.g., Martínez & Saar 2002). Therefore, the observable galaxy counts sample the underlying galaxy number density ng up to shot-noise, which is here formally expressed by the noise component φg.
(18)We presume that galaxies sample an underlying smooth galaxy number density by a discrete Poisson process (e.g., Martínez & Saar 2002). Therefore, the observable galaxy counts sample the underlying galaxy number density ng up to shot-noise, which is here formally expressed by the noise component φg.
By analogy with the matter density δm, we can find an minimum-variance filter to estimate the true distribution of galaxies on the lens planes; namely 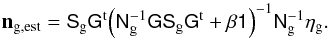 (19)As before,
(19)As before, 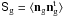 is the signal covariance, which is the angular clustering two-point correlation function of the galaxies on the lens planes, and
is the signal covariance, which is the angular clustering two-point correlation function of the galaxies on the lens planes, and 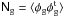 denotes the shot-noise covariance. The degree of smoothing by the Wiener filter is tunable by using β ∈ [ 0,1 ], which does not need to equal parameter α in Eq. (9). For the Poisson shot-noise covariance, we adopt a diagonal noise covariance, [ Ng ] ij = 0 for i ≠ j, with
denotes the shot-noise covariance. The degree of smoothing by the Wiener filter is tunable by using β ∈ [ 0,1 ], which does not need to equal parameter α in Eq. (9). For the Poisson shot-noise covariance, we adopt a diagonal noise covariance, [ Ng ] ij = 0 for i ≠ j, with ![\hbox{$[\mat{N}_{\rm g}]_{ii}=\bar{\eta}_{\rm g}^{(k)}(\vec{\theta}_l)$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq95.png) for unmasked grid pixels θl, and infinite noise otherwise. The Wiener filter in the given form requires the inverse noise covariance, such that elements with infinite noise on the diagonal are zero. By
for unmasked grid pixels θl, and infinite noise otherwise. The Wiener filter in the given form requires the inverse noise covariance, such that elements with infinite noise on the diagonal are zero. By 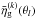 , we denote the estimated mean number density of galaxies in pixel θl of the kth sub-sample (see next section).
, we denote the estimated mean number density of galaxies in pixel θl of the kth sub-sample (see next section).
As for the matter density Wiener filter, a practical implementation of the Wiener filter in Eq. (19) consists of a series of linear operations applied to ηg. The effect of Sg is to multiply every angular mode 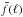 of the ith lens plane with the prior galaxy power spectrum
of the ith lens plane with the prior galaxy power spectrum 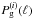 , which we define relative to the matter power spectrum using the galaxy bias factor b(i)(ℓ) ≥ 0 (e.g., Tegmark & Peebles 1998):
, which we define relative to the matter power spectrum using the galaxy bias factor b(i)(ℓ) ≥ 0 (e.g., Tegmark & Peebles 1998): ![\begin{equation} \label{eq:galaxybias} \Ave{\tilde{n}^{(i)}_{\rm g}(\vec{\ell})\tilde{n}^{(i)}_{\rm g}(\vec{\ell}^\prime)}= (2\pi)^2\delta_{\rm D}(\vec{\ell}+\vec{\ell}^\prime)\, \underbrace{\left[\bar{n}_{\rm g}^{(i)}b^{(i)}(|\vec{\ell}|)\right]^2 P_\delta^{(i)}(|\vec{\ell}|)}_{P_{\rm g}^{(i)}(\ell)}, \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq102.png) (20)where
(20)where 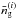 denotes the true mean number density of galaxies on the ith lens plane. For this definition of the bias factor, the shot-noise contribution to the galaxy power spectrum is excluded as it is already accounted for in φg.
denotes the true mean number density of galaxies on the ith lens plane. For this definition of the bias factor, the shot-noise contribution to the galaxy power spectrum is excluded as it is already accounted for in φg.
The angular bias factor b(i)(ℓ) is related to the 3D bias factor b(k,χ), where k is the comoving 3D wave-number, by a projection that is approximated by Limber’s equation: ![\begin{eqnarray} {[b^{(i)}(\ell)]^2P_\delta^{(i)}(\ell)}&=&\frac{|\tilde{F}(\ell)|^2}{[\Delta\chi_i]^2}\int_{\chi_i}^{\chi_{i+1}}\frac{\d\chi}{[f_{\rm K}(\chi)]^2}\nonumber\\ &&\times~ b^2\left(\frac{\ell}{f_{\rm K}(\chi)},\chi\right) P_{\rm 3d}\left(\frac{\ell}{f_{\rm K}(\chi)},\chi\right); \end{eqnarray}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq106.png) (21)
(21)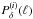 is given by Eq. (12). For this approximation, we assume that the number density of galaxies stays constant as function of χ inside the slice.
is given by Eq. (12). For this approximation, we assume that the number density of galaxies stays constant as function of χ inside the slice.
2.3. True mean galaxy numbers
The true galaxy number densities 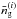 in Eq. (20) have to be derived from the data itself. For an estimator of
in Eq. (20) have to be derived from the data itself. For an estimator of 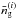 , we go back to Eq. (17), which relates the observed number of galaxies, ηg, to the true number on the lens planes, ng. For an ensemble average of this relation, we expect
, we go back to Eq. (17), which relates the observed number of galaxies, ηg, to the true number on the lens planes, ng. For an ensemble average of this relation, we expect 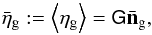 (22)wherein all elements
(22)wherein all elements 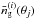 equal the same number
equal the same number 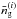 owing to the statistical homogeneity of the galaxy-number density fields, hence
owing to the statistical homogeneity of the galaxy-number density fields, hence 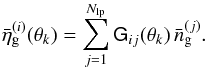 (23)Summing over all pixels with Np in total of the ith tracer sample yields
(23)Summing over all pixels with Np in total of the ith tracer sample yields 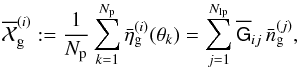 (24)where
(24)where 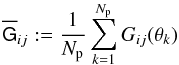 (25)averages Gij over the area of the grid. Inverting the former equation, gives
(25)averages Gij over the area of the grid. Inverting the former equation, gives ![\begin{equation} \label{eq:nbarest1} \bar{n}_{\rm g}^{(i)}= \sum_{j=1}^{N_{\rm lp}}\left[\bar{\mat{G}}^{-1}\right]_{ij}\, \overline{\cal X}_{\rm g}^{(j)};~~ \overline{\cal X}_{\rm g}^{(i)}\approx \frac{1}{N_{\rm p}}\sum_{k=1}^{N_{\rm p}}\eta^{(i)}_{\rm g}(\vec{\theta}_k). \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq115.png) (26)For an unbiased estimator of
(26)For an unbiased estimator of 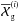 on the right hand side, we insert the observed galaxy number densities, which is
on the right hand side, we insert the observed galaxy number densities, which is 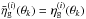 . The value of
. The value of 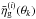 , which is utilised for the noise covariance Ng in the foregoing section, is computed from Eq. (23) and the estimated
, which is utilised for the noise covariance Ng in the foregoing section, is computed from Eq. (23) and the estimated 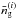 .
.
In the simple case of negligible redshift errors, we find 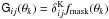 , where
, where 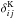 denotes the Kronecker symbol. In this case, we consequently find
denotes the Kronecker symbol. In this case, we consequently find ![\begin{equation} [\bar{\mat{G}}^{-1}]_{ij}=\delta^{\rm K}_{ij}\frac{N_{\rm p}}{N}\; \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq122.png) (27)for the number N of unmasked pixels. Moreover, we find
(27)for the number N of unmasked pixels. Moreover, we find 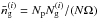 for a number
for a number 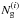 of galaxies within the ith sub-sample and a survey area Ω. Thus, the galaxy number density
of galaxies within the ith sub-sample and a survey area Ω. Thus, the galaxy number density 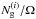 is scaled up by Np/N to account for the mask.
is scaled up by Np/N to account for the mask.
However, the estimator in Eq. (26) has one caveat, since 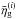 is basically a convolution of
is basically a convolution of 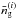 with the redshift error of galaxies. A deconvolution through
with the redshift error of galaxies. A deconvolution through 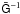 possibly results in oscillating and negative values for
possibly results in oscillating and negative values for 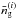 . We therefore regularise Eq. (26) by a constrained solution of
. We therefore regularise Eq. (26) by a constrained solution of 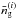 that maximises the likelihood:
that maximises the likelihood: 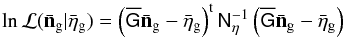 (28)under the condition that
(28)under the condition that 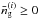 for all i. We determine this solution numerically. The additional covariance Nη can be used to give different weights to the observed
for all i. We determine this solution numerically. The additional covariance Nη can be used to give different weights to the observed 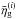 values, such as by weighting the number of galaxies in each galaxy sample in order to account for the galaxy shot-noise. For equal weights, we simply set Nη = 1.
values, such as by weighting the number of galaxies in each galaxy sample in order to account for the galaxy shot-noise. For equal weights, we simply set Nη = 1.
3. Combined reconstruction
In this section, we combine the information on the 3D matter density in the lensing data and the galaxy distribution.
3.1. Minimum-variance estimator
Up to now, we have considered the galaxy number density and matter density fields separately. However, ηg contains information about δm and vice versa, as galaxies trace the matter distribution to a certain degree. On a statistical level, this relation is reflected by a non-vanishing cross-correlation, 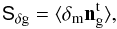 (29)for pairs of pixels on the same lens plane, which has not entered our formalism thus far. Slices are thought to be wide enough, such that correlations between pixels belonging to different lens plane are negligible.
(29)for pairs of pixels on the same lens plane, which has not entered our formalism thus far. Slices are thought to be wide enough, such that correlations between pixels belonging to different lens plane are negligible.
We combine the δm- and ng-grids inside one new vector, ![\begin{equation} \label{eq:eq30} \vec{s}:=\left[\vec{\delta}_{\rm m},\vec{n}_{\rm g}\right]. \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq136.png) (30)Equations (8) and (17) relate s to the observed shear and the tracer number density grids,
(30)Equations (8) and (17) relate s to the observed shear and the tracer number density grids, ![\begin{equation} \vec{d}:=\left[\vec{\gamma},\vec{\eta}_{\rm g}\right], \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq138.png) (31)according to
(31)according to ![\begin{equation} \vec{d}= \Big[\mat{P}_{\gamma\kappa}\mat{Q}\vec{\delta}_{\rm m},\mat{G}\vec{n}_{\rm g}\Big]+\vec{n} =:\mat{R}\vec{s}+\vec{n}, \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq139.png) (32)where the combined noise vector is
(32)where the combined noise vector is ![\begin{equation} \vec{n}:=\left[\vec{n}_\gamma,\vec{\phi}_{\rm g}\right]. \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq140.png) (33)In this compact notation, the action of a matrix
(33)In this compact notation, the action of a matrix 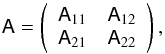 (34)on a product vector v = [ v1,v2 ] is defined as
(34)on a product vector v = [ v1,v2 ] is defined as ![\begin{equation} \mat{A}\vec{v}:= \big[ \mat{A}_{11}\vec{v}_1+\mat{A}_{12}\vec{v}_2, \mat{A}_{21}\vec{v}_1+\mat{A}_{22}\vec{v}_2 \big]. \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq143.png) (35)In this sense, the projection matrix R is
(35)In this sense, the projection matrix R is 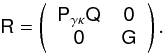 (36)Following the usual assumptions of a minimum-variance filter, the optimal filter for estimating s from d in this combined problem is
(36)Following the usual assumptions of a minimum-variance filter, the optimal filter for estimating s from d in this combined problem is 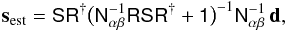 (37)which uses the short-hand notations,
(37)which uses the short-hand notations, 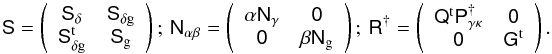 (38)The galaxy shot-noise φg and the intrinsic ellipticities of the sources, which are comprised in nγ, are assumed to be uncorrelated. By choosing different tuning parameters α ≠ β, the impact of the Wiener smoothing can be adjusted independently for the matter and galaxy map.
(38)The galaxy shot-noise φg and the intrinsic ellipticities of the sources, which are comprised in nγ, are assumed to be uncorrelated. By choosing different tuning parameters α ≠ β, the impact of the Wiener smoothing can be adjusted independently for the matter and galaxy map.
The novelty of the combined reconstruction is that tracer number and matter density maps exchange information, if the cross-correlation matrix Sδg is non-vanishing. In a practical implementation of the filter (37), we apply step by step linear operations to the grids stored inside d as before. As with the previous operators Sδ and Sg, the application of Sδg amounts to a multiplication of angular grid modes with the cross-correlation power spectrum, 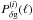 , determined by
, determined by 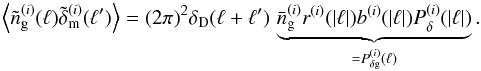 (39)(See the next section for details on the implementation.) We define
(39)(See the next section for details on the implementation.) We define 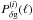 with respect to the matter power spectrum
with respect to the matter power spectrum 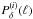 by employing the galaxy-matter cross-correlation factor r(i)(ℓ) (Tegmark & Peebles 1998). The angular function r(i)(ℓ) is approximately related to the 3D correlation factor r(k,χ) according to
by employing the galaxy-matter cross-correlation factor r(i)(ℓ) (Tegmark & Peebles 1998). The angular function r(i)(ℓ) is approximately related to the 3D correlation factor r(k,χ) according to ![\begin{eqnarray} {r^{(i)}(\ell)b^{(i)}(\ell)P_\delta^{(i)}(\ell)} &=& \frac{|\tilde{F}(\ell)|^2}{[\Delta\chi_i]^2}\nonumber\\ &&\hspace*{-1cm}\times~ \int_{\chi_i}^{\chi_{i+1}} \!\!\!\!\frac{\d\chi}{[f_{\rm K}(\chi)]^2} \,r\left(k_\ell,\chi\right) b\left(k_\ell,\chi\right) P_{\rm 3d}\left(k_\ell,\chi\right), \end{eqnarray}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq156.png) (40)where kℓ: = ℓ/fK(χ).
(40)where kℓ: = ℓ/fK(χ).
To understand the mode of operation of the minimum-variance filter in Eq. (37), it is instructive to recast it into the mathematically equivalent form: 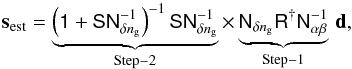 (41)where
(41)where 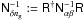 . Step-1 involves no Wiener smoothing to construct the maps; no matrix S is involved in this step. As this is usually too noisy, we apply an additional smoothing to these maps by virtue of the Wiener filter in Step-2. This filter linearly combines and averages pixel values in the maps based upon the expected S/N in the unbiased maps. It is Step-2, the analogue of the matrix Bδ in Sect. 2.1, that introduces biases into the maps, especially through a radial smoothing. Moreover, only Step-2 formally mixes pixels from the mass map and the tracer number density map by means of the off-diagonal matrix Sδg. Therefore, Step-1 makes independent mass and tracer maps that are only later combined in Step-2, according to our prior knowledge of their correlation. Setting α = β = 0 results in a unity matrix for Step-2 or no smoothing.
. Step-1 involves no Wiener smoothing to construct the maps; no matrix S is involved in this step. As this is usually too noisy, we apply an additional smoothing to these maps by virtue of the Wiener filter in Step-2. This filter linearly combines and averages pixel values in the maps based upon the expected S/N in the unbiased maps. It is Step-2, the analogue of the matrix Bδ in Sect. 2.1, that introduces biases into the maps, especially through a radial smoothing. Moreover, only Step-2 formally mixes pixels from the mass map and the tracer number density map by means of the off-diagonal matrix Sδg. Therefore, Step-1 makes independent mass and tracer maps that are only later combined in Step-2, according to our prior knowledge of their correlation. Setting α = β = 0 results in a unity matrix for Step-2 or no smoothing.
Analogous to a lensing-only reconstruction, the Wiener filter thus applies a radial and transverse smoothing to the map to increase the S/N. The smoothing makes the maps biased estimators of the matter and galaxy-number density fields. The smoothing is, however, uniquely defined by 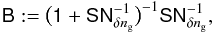 (42)which and can be applied to theoretical maps of the matter and galaxy number density for a quantitative comparison to the data.
(42)which and can be applied to theoretical maps of the matter and galaxy number density for a quantitative comparison to the data.
3.2. Fourier space representation
For shear and galaxy number noise homogeneous over infinite grids with no gaps, the estimator in Eq. (37) takes a simple form in Fourier space. Under these idealistic conditions, the angular modes of all lens planes combine to ![\begin{equation} \tilde{\vec{s}}(\vec{\ell})= \left[\vec{\tilde{\delta}}_{\rm m}(\vec{\ell}),\vec{\tilde{n}}_{\rm g}(\vec{\ell})\right], \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq164.png) (43)which are only linear functions of the ηg- and γ-modes of the same ℓ; there is no mixing between modes of different ℓ. Therefore, a reconstruction is then done most easily in Fourier space by
(43)which are only linear functions of the ηg- and γ-modes of the same ℓ; there is no mixing between modes of different ℓ. Therefore, a reconstruction is then done most easily in Fourier space by 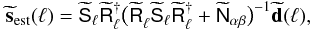 (44)where
(44)where ![\hbox{$\wtilde{\vec{d}}(\vec{\ell})= \left[\wtilde{\vec{\gamma}}(\vec{\ell}),\wtilde{\vec{\eta}}_{\rm g}(\vec{\ell})\right]$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq170.png) are the observable input grids. The tuned covariance matrix of the (homogeneous) noise is
are the observable input grids. The tuned covariance matrix of the (homogeneous) noise is 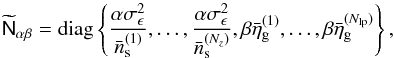 (45)where
(45)where 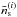 is the mean source number density of the ith source sample (out of in total Nz);
is the mean source number density of the ith source sample (out of in total Nz); ![\hbox{$\sigma^2_\epsilon=\ave{\epsilon^{\rm i}[\epsilon^{\rm i}]^\ast}$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq174.png) is their intrinsic shape noise variance, and
is their intrinsic shape noise variance, and 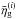 is the Poisson shot-noise power (white noise). Possible noise contributions owing to intrinsic alignments of sources are ignored here, hence
is the Poisson shot-noise power (white noise). Possible noise contributions owing to intrinsic alignments of sources are ignored here, hence 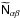 has no off-diagonal elements. Furthermore, one has
has no off-diagonal elements. Furthermore, one has 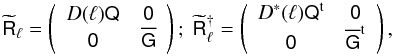 (46)where D(ℓ) = ℓ/ℓ∗ (Kaiser & Squires 1993). For ℓ = 0, we set D(ℓ) = 0. Here, G does not depend on θk. The signal covariance is
(46)where D(ℓ) = ℓ/ℓ∗ (Kaiser & Squires 1993). For ℓ = 0, we set D(ℓ) = 0. Here, G does not depend on θk. The signal covariance is 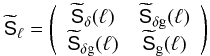 (47)with
(47)with
![\begin{eqnarray} && \wtilde{\mat{S}}_\delta(\ell)= {\rm diag}\left\{P_\delta^{(1)}(\ell),\ldots, P_\delta^{(i)}(\ell),\ldots,P_\delta^{(N_{\rm lp})}(\ell)\right\},\\ && \wtilde{\mat{S}}_{\delta\rm g}(\ell)= {\rm diag}\left\{ \ldots,\bar{n}^{(i)}_{\rm g}r^{(i)}(\ell)b^{(i)}(\ell)P_\delta^{(i)}(\ell),\ldots\right\},\\ && \wtilde{\mat{S}}_{\rm g}(\ell)= {\rm diag}\left\{ \ldots, [\bar{n}^{(i)}_{\rm g}b^{(i)}(\ell)]^2 P_\delta^{(i)}(\ell),\ldots\right\}. \end{eqnarray}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq182.png) Because of the diagonal structure of the last three matrices, the matrix
Because of the diagonal structure of the last three matrices, the matrix  acting on a vector
acting on a vector  actually only mixes the matter and tracer density modes from the same lens plane and of the same wave vector ℓ. Thus, rearranging the modes inside
actually only mixes the matter and tracer density modes from the same lens plane and of the same wave vector ℓ. Thus, rearranging the modes inside 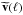 and pairing together matter and tracer density modes of the same lens plane render
and pairing together matter and tracer density modes of the same lens plane render 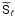 a diagonal block matrix, such that
a diagonal block matrix, such that 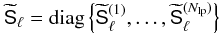 (51)with 2 × 2-blocks
(51)with 2 × 2-blocks ![\begin{equation} \wtilde{\mat{S}}^{(i)}_{\ell}=\left( \begin{array}{cc} 1 & \bar{n}_{\rm g}^{(i)}r^{(i)}(\ell)b^{(i)}(\ell) \\ \bar{n}_{\rm g}^{(i)}r^{(i)}(\ell)b^{(i)}(\ell) & [\bar{n}_{\rm g}^{(i)}b^{(i)}(\ell)]^2 \end{array}\right)\times P_\delta^{(i)}(\ell) \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq188.png) (52)on the diagonal. This structure is useful when implementing the action of S in (37) in practise. Clearly, modes will not affect each other when r(i)(ℓ) = 0 with no improvement by the synergy of lensing and galaxy tracers.
(52)on the diagonal. This structure is useful when implementing the action of S in (37) in practise. Clearly, modes will not affect each other when r(i)(ℓ) = 0 with no improvement by the synergy of lensing and galaxy tracers.
3.3. Radial point spread function
The radial PSF is the average sight-line profile of a single mass peak in the smoothed matter map. Ideally, the PSF spikes at the true mass peak redshift (no z-shift bias). In reality, however, a z-shift bias is one of the main nuisances in Wiener reconstructions with 3D lensing data. We assume a homogeneous survey, where the choice of the LOS direction θ is irrelevant. We hence arbitrarily pick θ = 0 as a reference direction and omit the pixel index θ in the following.
We consider a singular test peak with a profile of 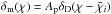 in the un-smoothed map; Ap is the peak amplitude. It is located at the distance
in the un-smoothed map; Ap is the peak amplitude. It is located at the distance 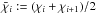 of the ith lens plane. For circular pixels with angular radius Θs, the pixel value of this peak is in the un-smoothed map
of the ith lens plane. For circular pixels with angular radius Θs, the pixel value of this peak is in the un-smoothed map 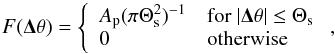 (53)or in the Fourier space,
(53)or in the Fourier space, 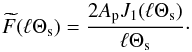 (54)By Jn(x), we denote the spherical Bessel functions of the first kind. Because of the linearity of the reconstruction algorithm, the peak amplitude is unimportant for the shape of the radial PSF We therefore simply set Ap = 1. Unlike the discussion in STH09 for calculating the radial PSF, we also have to factor in the tracer number density on the ith lens plane here (and same direction θ). As this is a random variable for r(ℓ) ≠ 1, we define the PSF as the radial density profile in the smoothed map given a matter peak
(54)By Jn(x), we denote the spherical Bessel functions of the first kind. Because of the linearity of the reconstruction algorithm, the peak amplitude is unimportant for the shape of the radial PSF We therefore simply set Ap = 1. Unlike the discussion in STH09 for calculating the radial PSF, we also have to factor in the tracer number density on the ith lens plane here (and same direction θ). As this is a random variable for r(ℓ) ≠ 1, we define the PSF as the radial density profile in the smoothed map given a matter peak 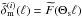 on the ith lens plane that is marginalised over the tracer density
on the ith lens plane that is marginalised over the tracer density 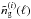 . This is associated with the mass peak. This conditional mean tracer number density is given by
. This is associated with the mass peak. This conditional mean tracer number density is given by 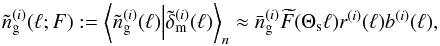 (55)where the conditional ensemble average
(55)where the conditional ensemble average 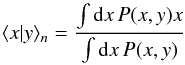 (56)is taken over all realisations of the tracer density field and P(x,y) denotes the bivariate p.d.f. of the tracer number density x and the matter density y. The expression on the r.h.s. in the Eq. (55) is exact only for Gaussian statistics, which is assumed here as lowest-order approximation (Appendix A). For differing statistics, such as a log-normal tracer density field (Coles & Jones 1991), we have to expect deviations from this expression. Evidently, the conditional average will vanish if the correlation factor is r(i)(ℓ) = 0. The average tracer number density about a mass peak vanishes in this case.
(56)is taken over all realisations of the tracer density field and P(x,y) denotes the bivariate p.d.f. of the tracer number density x and the matter density y. The expression on the r.h.s. in the Eq. (55) is exact only for Gaussian statistics, which is assumed here as lowest-order approximation (Appendix A). For differing statistics, such as a log-normal tracer density field (Coles & Jones 1991), we have to expect deviations from this expression. Evidently, the conditional average will vanish if the correlation factor is r(i)(ℓ) = 0. The average tracer number density about a mass peak vanishes in this case.
According to this definition, the radial PSF equals the average sight-line density profile (analogous to Eq. (77) of STH09): ![\begin{equation} \label{eq:radialpsf} \left[\bar{\vec{\delta}}_{\rm m}(\Theta_{\rm s}),\bar{\vec{n}}_{\rm g}(\Theta_{\rm s})\right]= \int_0^\infty\frac{\d\ell\ell}{2\pi}\, \wtilde{F}(\ell\Theta_{\rm s}) \,\wtilde{\mat{W}}_{\ell} \left[\vec{\tilde{\delta}}_{\rm m}(\ell),\vec{\tilde{n}}_{\rm g}(\ell)\right], \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq207.png) (57)where the Wiener filter
(57)where the Wiener filter 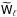 is given in Eq. (60) and the vectors
is given in Eq. (60) and the vectors 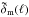 and
and 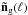 (Nlp elements) vanish everywhere except in their ith element that equals 1 and
(Nlp elements) vanish everywhere except in their ith element that equals 1 and 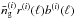 , respectively. The elements of the vector
, respectively. The elements of the vector 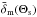 encapsulate the radial PSF of the matter map, and the radial PSF of the tracer number density map in the case of
encapsulate the radial PSF of the matter map, and the radial PSF of the tracer number density map in the case of 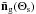 . The former is the focus in the following.
. The former is the focus in the following.
3.4. Map signal-to-noise
With the estimator (44) at hand, we forecast the S/N of the matter and tracer number density modes as a function of angular wave-number ℓ. To this end, we compare the cosmic average power spectrum, 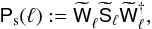 (58)of the reconstructed matter and galaxy-number density modes on the lens planes to noise in the reconstruction from shape noise and tracer sampling noise, which is
(58)of the reconstructed matter and galaxy-number density modes on the lens planes to noise in the reconstruction from shape noise and tracer sampling noise, which is 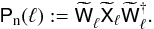 (59)Here we use the definitions
(59)Here we use the definitions 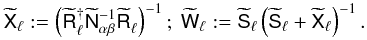 (60)In this reconstruction, the Wiener filter
(60)In this reconstruction, the Wiener filter 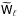 uses the true signal power
uses the true signal power 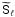 present in the data. As pointed out earlier, this is not a necessity but is required for an optimal minimum-variance filter. For α = β = 0 (neither smoothing nor mixing), the noise covariance is
present in the data. As pointed out earlier, this is not a necessity but is required for an optimal minimum-variance filter. For α = β = 0 (neither smoothing nor mixing), the noise covariance is 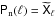 .
.
3.5. Galaxy-stochasticity noise
The noise covariance Pn(ℓ) contains only a part of the statistical uncertainty in a combined reconstruction; namely, this is the noise originating from the unknown intrinsic source galaxy shapes and galaxy sampling noise. In the presence of stochasticity between matter and tracer density, however, there is a random scatter in the sample-noise-free tracer density for a given matter density field that gives rise to the additional noise covariance Pgsn, 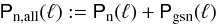 (61)(called random biasing field in Dekel & Lahav 1999). Contrary to Poisson shot-noise, this galaxy-stochasticity noise (GSN) is also present, if the number of tracer galaxies were infinite. This is a new feature compared to reconstruction techniques relying only on the 3D lensing signal. Possible realisations of a galaxy-number density field for a given matter density field on the lens planes depend on the details of the physics behind the galaxy bias. Consequently, a precise estimate of the GSN level can only be provided if the galaxy bias scheme is known.
(61)(called random biasing field in Dekel & Lahav 1999). Contrary to Poisson shot-noise, this galaxy-stochasticity noise (GSN) is also present, if the number of tracer galaxies were infinite. This is a new feature compared to reconstruction techniques relying only on the 3D lensing signal. Possible realisations of a galaxy-number density field for a given matter density field on the lens planes depend on the details of the physics behind the galaxy bias. Consequently, a precise estimate of the GSN level can only be provided if the galaxy bias scheme is known.
For a first-order estimate of GSN, we assume Gaussian fluctuations in the galaxy number and matter density on every lens plane. In this Gaussian approximation, the bivariate p.d.f. of modes of the matter density contrast, 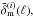 and a galaxy number density,
and a galaxy number density, 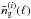 , are fully determined by the variance
, are fully determined by the variance 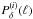 of
of 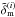 , the variance
, the variance ![\hbox{$[\bar{n}_{\rm g}^{(i)}b^{(i)}(\ell)]^2P^{(i)}_\delta(\ell)$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq227.png) of
of 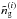 , and the cross-correlation coefficient r(i)(ℓ) of both. From this the variance of a galaxy tracer mode about a fixed matter density mode follows:
, and the cross-correlation coefficient r(i)(ℓ) of both. From this the variance of a galaxy tracer mode about a fixed matter density mode follows: ![\begin{equation} \label{eq:Pgcn} P_{\rm gsn}^{(i)}(\ell)= \left[\bar{n}_{\rm g}^{(i)}b^{(i)}(\ell)\right]^2 \left(1-[r^{(i)}(\ell)]^2\right)P^{(i)}_\delta(\ell). \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq229.png) (62)See Appendix A for details. The random biasing field is an independent Gaussian realisation with power spectrum
(62)See Appendix A for details. The random biasing field is an independent Gaussian realisation with power spectrum 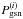 . The essential parameter for this random scatter is r(ℓ), which vanishes for | r(ℓ) | = 1, but reaches a maximum in amplitude for r(ℓ) = 0. On the other hand, a smaller r(ℓ) also results in a reduction of the mixing of matter and tracer density modes by the minimum-variance filter. On the extreme end for r(ℓ) = 0, the filter does not make use of any tracer information at all for the matter density map. The total noise power per angular mode in the mass map can hence then be approximated by
. The essential parameter for this random scatter is r(ℓ), which vanishes for | r(ℓ) | = 1, but reaches a maximum in amplitude for r(ℓ) = 0. On the other hand, a smaller r(ℓ) also results in a reduction of the mixing of matter and tracer density modes by the minimum-variance filter. On the extreme end for r(ℓ) = 0, the filter does not make use of any tracer information at all for the matter density map. The total noise power per angular mode in the mass map can hence then be approximated by 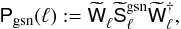 (63)where
(63)where 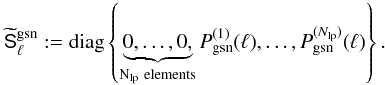 (64)For each lens plane, we translate these ℓ-dependent GSN levels to the noise variance on the map pixel scale by virtue of the integral (STH09)
(64)For each lens plane, we translate these ℓ-dependent GSN levels to the noise variance on the map pixel scale by virtue of the integral (STH09) ![\begin{equation} \label{eq:pixelvar} \Ave{[\delta^{(i)}_{\rm gsn}(\Theta_{\rm s})]^2}= \int_0^\infty\frac{\d\ell\ell}{2\pi} |\wtilde{F}(\ell\Theta_{\rm s})|^2 [\mat{P}_{\rm gsn}(\ell)]_{ii}, \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq236.png) (65)and likewise to compute
(65)and likewise to compute ![\hbox{$\ave{[\delta^{(i)}_{\rm m}(\Theta_{\rm s})]^2}$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq237.png) for the signal power [ Ps(ℓ) ] ii in Eq. (58). The resulting ratios of GSN and signal power are
for the signal power [ Ps(ℓ) ] ii in Eq. (58). The resulting ratios of GSN and signal power are ![\begin{equation} f^{(i)}_{\rm gsn}= \sqrt{\frac{\ave{[\delta^{(i)}_{\rm gsn}(\Theta_{\rm s})]^2}}{\ave{[\delta^{(i)}_{\rm m}(\Theta_{\rm s})]^2}}}:= \frac{\sigma^{(i)}_{\rm gsn}}{\sigma^{(i)}_{\rm s}} \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq239.png) (66)for pixels in our fiducial mass map. For this estimate of
(66)for pixels in our fiducial mass map. For this estimate of 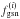 , we take the cosmic average
, we take the cosmic average 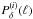 . This certainly underestimates the matter fluctuations in galaxy cluster regions. On the other hand, the GSN scales, at least for Gaussian random fields, linearly with the amplitude of the actual matter density fluctuations, as in Eq. (62), such that the ratio
. This certainly underestimates the matter fluctuations in galaxy cluster regions. On the other hand, the GSN scales, at least for Gaussian random fields, linearly with the amplitude of the actual matter density fluctuations, as in Eq. (62), such that the ratio 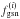 should be a robust approximation for Gaussian fields with more matter clustering.
should be a robust approximation for Gaussian fields with more matter clustering.
3.6. Correction for galaxy-stochasticity noise
In practise, we estimate the S/N of the synergy reconstructions by dividing pixel values δm,est(θ) in the map by the pixel variance in noise realisations of the map. We obtain the noise realisations by randomising the source ellipticities and the tracer positions in accordance with their completeness and redshift errors G. However, the noise realisations do not include the GSN but only contributions of σshot from galaxy shape- and tracer sampling noise. In this section, we propose a GSN correction factor that is applied to this S/N map. The correction factor is based on the foregoing 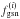 and the variance σshot in the noise realisations.
and the variance σshot in the noise realisations.
For each lens plane of the map the pixel variance 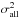 has three independent components,
has three independent components, 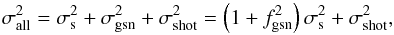 (67)where σs is the variance in the matter density signal, σgsn is the GSN variance, and σshot is the source shape- and tracer shot-noise variance. On the right hand side, we have substituted the GSN variance by the signal variance and fgsn. A S/N map that accounts for both σshot and σgsn is
(67)where σs is the variance in the matter density signal, σgsn is the GSN variance, and σshot is the source shape- and tracer shot-noise variance. On the right hand side, we have substituted the GSN variance by the signal variance and fgsn. A S/N map that accounts for both σshot and σgsn is 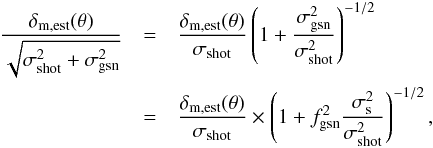 (68)where δm,est(θ)/σshot on the right hand side is the S/N invoking shot-noise only, as produced by randomising the catalogues. For the correction factor inside the brackets, the signal variance σs can be estimated by employing Eq. (65) with an appropriate Wiener-filtered signal power spectrum. In addition, the shot-noise variance, σshot, is determined by Eq. (65) with the Wiener filter noise power spectrum Pn(ℓ) inside the integral. For a signal variance σs ≪ σshot, the correction factor is roughly unity, which is always the case for a cosmic average matter density power spectrum and our fiducial survey. As we are mainly targeting galaxy cluster regions with lensing cartography, however, a fiducial value of σs with higher variance than a cosmic average is likely. To obtain a more realistic fiducial value, we construct an alternative signal power spectrum for σs, assuming (i) Gaussian fluctuations, (ii) randomly scattered haloes with an average number density
(68)where δm,est(θ)/σshot on the right hand side is the S/N invoking shot-noise only, as produced by randomising the catalogues. For the correction factor inside the brackets, the signal variance σs can be estimated by employing Eq. (65) with an appropriate Wiener-filtered signal power spectrum. In addition, the shot-noise variance, σshot, is determined by Eq. (65) with the Wiener filter noise power spectrum Pn(ℓ) inside the integral. For a signal variance σs ≪ σshot, the correction factor is roughly unity, which is always the case for a cosmic average matter density power spectrum and our fiducial survey. As we are mainly targeting galaxy cluster regions with lensing cartography, however, a fiducial value of σs with higher variance than a cosmic average is likely. To obtain a more realistic fiducial value, we construct an alternative signal power spectrum for σs, assuming (i) Gaussian fluctuations, (ii) randomly scattered haloes with an average number density 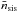 and (iii) haloes with an average singular isothermal sphere (SIS) matter density profile (STH09):
and (iii) haloes with an average singular isothermal sphere (SIS) matter density profile (STH09): ![\begin{equation} \label{eq:sismodel} \tilde{\delta}^{(i)}_{\rm sis}(\ell)= \frac{8\pi^2}{3\Omega_{\rm m}[1+z(\bar{\chi}_i)]} \left(\frac{\sigma_{\rm v}}{c}\right)^2 \frac{D_{\rm H}^2}{f_{\rm K}(\bar{\chi}_i)\Delta\chi_i} \frac{1}{\ell}\; \end{equation}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq252.png) (69)in Fourier space and SIS velocity σv. Therefore, the matter power spectrum for the ith lens plane is described by
(69)in Fourier space and SIS velocity σv. Therefore, the matter power spectrum for the ith lens plane is described by 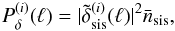 (70)which we insert into Eq. (58) and Eq. (65) to calculate the pixel signal-variance σs (Appendix B).
(70)which we insert into Eq. (58) and Eq. (65) to calculate the pixel signal-variance σs (Appendix B).
3.7. Cluster signal-to-noise
We now consider the significance with which a single mass peak at a given radial distance can be detected in a synergy reconstruction. For a fiducial mass peak, we adopt a SIS-like matter over-density 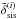 that is fully contained inside the ith lens plane, as in Eq. (69). The associated average number density of tracers is on the level of a Gaussian approximation
that is fully contained inside the ith lens plane, as in Eq. (69). The associated average number density of tracers is on the level of a Gaussian approximation 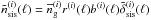 , which is analogous to the rationale in Sect. 3.3, and vanishes for all other lens planes j ≠ i. When we combine this peaked mass model
, which is analogous to the rationale in Sect. 3.3, and vanishes for all other lens planes j ≠ i. When we combine this peaked mass model 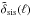 and the tracer density model,
and the tracer density model, 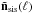 , in
, in ![\hbox{$[\tilde{\vec{\delta}}_{\rm sis}(\ell),\tilde{\vec{n}}_{\rm sis}(\ell)]$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq260.png) , we acquire the average map response
, we acquire the average map response ![\hbox{$[\overline{\vec{\delta}}_{\rm sis}(\Theta_{\rm s}),\overline{\vec{n}}_{\rm sis}(\Theta_{\rm s})]$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq261.png) in a smoothed map by Eq. (57), where Θs is the transverse smoothing kernel size. The vector
in a smoothed map by Eq. (57), where Θs is the transverse smoothing kernel size. The vector 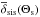 exhibits the expected mass map response to the central pixel of a SIS peak in the map.
exhibits the expected mass map response to the central pixel of a SIS peak in the map.
This signal is compared to the expected noise level inside a pixel. Relevant contributions to noise are (i) sample and shot noise, 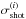 , (ii) the GSN variance
, (ii) the GSN variance 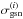 , and (iii) interference
, and (iii) interference 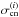 by intervening matter density fluctuations on lens planes that do not host the fiducial SIS peak. The sources of noise (i) and (ii) are detailed in the Sect. 3.4 and 3.5. For (ii), we additionally assume that the interfering matter density power on all lens planes j ≠ i, which do not host the SIS, is given by the cosmic average
by intervening matter density fluctuations on lens planes that do not host the fiducial SIS peak. The sources of noise (i) and (ii) are detailed in the Sect. 3.4 and 3.5. For (ii), we additionally assume that the interfering matter density power on all lens planes j ≠ i, which do not host the SIS, is given by the cosmic average 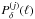 in Eq. (62), whereas we have Eq. (70) as a GSN model for the ith plane . We determine the pixel variance
in Eq. (62), whereas we have Eq. (70) as a GSN model for the ith plane . We determine the pixel variance 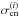 in (iii) by the signal covariance Ps(ℓ), as noted in Eq. (58), whose diagonals [ Ps(ℓ) ] ii are inserted into Eq. (65). Finally, the radial S/N profile of the SIS peak in the map is
in (iii) by the signal covariance Ps(ℓ), as noted in Eq. (58), whose diagonals [ Ps(ℓ) ] ii are inserted into Eq. (65). Finally, the radial S/N profile of the SIS peak in the map is ![\hbox{$\delta_{\rm sis}^{(i)}(\Theta_{\rm s})/\sqrt{[\sigma^{(i)}_{\rm s}]^2+[\sigma^{(i)}_{\rm gsn}]^2+[\sigma^{(i)}_{\rm cn}]^2}$}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq269.png) . As a theoretical S/N of the detection, we pick the lens plane index i at maximum S/N, which may not correspond to the true distance of the SIS peak due to the z-shift bias.
. As a theoretical S/N of the detection, we pick the lens plane index i at maximum S/N, which may not correspond to the true distance of the SIS peak due to the z-shift bias.
4. Survey parameters
We consider an idealised survey with homogeneous noise and a G that is independent of the pixel position to discuss the impact of a joint reconstruction in the following sections. This section defines the fiducial cosmology and binning details of the idealised survey. Moreover, we generate mock data to which the reconstruction algorithm is applied. The mocks utilise a N-body simulation of the large-scale dark matter density field populated with semi-analytical galaxies.
4.1. Fiducial parameters of the idealised survey
As fiducial cosmology, we use a standard flat ΛCDM model with the matter-density parameter Ωm = 0.27, where baryons are Ωb = 0.046 and a shape parameter of Γ = 0.19. The normalisation of the matter fluctuations within a sphere of radius 8 h-1 Mpc at a redshift of zero is σ8 = 0.8. For the spectral index of the primordial matter power spectrum, we use ns = 0.96. With these parameters, we construct a fiducial 3D matter power spectrum according to Smith et al. (2003) which is then used to model the signal covariance 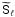 .
.
For the fiducial survey, we split the source galaxy catalogue into Nz = 20 equally sized redshift slices of width Δz = 0.1, which span the redshift range of z = 0...2. For the sources, we neglect the effect of redshift errors greater than the width of the redshift slices, such that the true p.d.f. 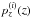 of sources of the ith slice is well-described within z ∈ [ zi,zi + 1 ] by the p.d.f. of redshift estimates of the full sample,
of sources of the ith slice is well-described within z ∈ [ zi,zi + 1 ] by the p.d.f. of redshift estimates of the full sample, 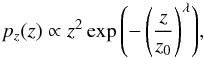 (71)where z0 = 0.57, λ = 1.5, and zi = (i − 1)Δz. We represent the reconstruction volume by Nlp = 10 lens planes between z = 0 and z = 2 that are centred within slices of moderate width Δzlp = 0.2. The total number density of sources on the sky is
(71)where z0 = 0.57, λ = 1.5, and zi = (i − 1)Δz. We represent the reconstruction volume by Nlp = 10 lens planes between z = 0 and z = 2 that are centred within slices of moderate width Δzlp = 0.2. The total number density of sources on the sky is 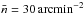 with an intrinsic shape noise of σϵ = 0.3.
with an intrinsic shape noise of σϵ = 0.3.
To support the matter density reconstruction, we include fiducial galaxy tracers with known galaxy bias. For simplicity, their p.d.f. of redshift estimates is identical to pz(z). Contrary to the sources, however, we now also emulate the effect of redshift errors by adopting a root-mean-square (rms) accuracy of σz(z) = 0.04(1 + z) (Gaussian errors), which is built into G in Eq. (15). The slicing scheme for the tracers is equivalent to the scheme of the sources. From this, we compute the average number density of tracers 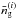 and
and 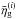 from Eq. (23) for each redshift slice, and the observed redshift distributions
from Eq. (23) for each redshift slice, and the observed redshift distributions 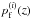 by piecewise convolving the p.d.f. pz(z) with a Gaussian kernel of the r.m.s. σz(z). For low redshifts, we have
by piecewise convolving the p.d.f. pz(z) with a Gaussian kernel of the r.m.s. σz(z). For low redshifts, we have 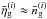 , but we find differences at higher redshifts where Δzlp ≈ σz. For the fiducial survey, we reduce the total number of tracers to 10 percent of the sources,
, but we find differences at higher redshifts where Δzlp ≈ σz. For the fiducial survey, we reduce the total number of tracers to 10 percent of the sources, 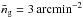 , since a reconstruction realistically requires a specifically selected tracer population for an accurately known bias. Here, the tracers are clustered as matter with b(ℓ) = 1 for all redshifts, but, more relevantly, we assume a slight stochasticity on all scales, namely, r(ℓ) = 0.8. A high correlation, r ≳ 0.5, for various galaxy populations is expected from theoretical models (e.g., Guzik & Seljak 2001) and observed for some cases (Hoekstra et al. 2002; Simon et al. 2007; Jullo et al. 2012).
, since a reconstruction realistically requires a specifically selected tracer population for an accurately known bias. Here, the tracers are clustered as matter with b(ℓ) = 1 for all redshifts, but, more relevantly, we assume a slight stochasticity on all scales, namely, r(ℓ) = 0.8. A high correlation, r ≳ 0.5, for various galaxy populations is expected from theoretical models (e.g., Guzik & Seljak 2001) and observed for some cases (Hoekstra et al. 2002; Simon et al. 2007; Jullo et al. 2012).
4.2. N-body mock data
For a realistic application of the methodology we employ the Millennium Simulation data set, a state-of-the-art N-body cold dark matter simulation with fiducial parameters of Ωm = 0.25, ΩΛ = 0.75, Γ = 0.21, ns = 1, and σ8 = 0.9 (Springel 2005; Springel et al. 2005). In the simulation, haloes of dark matter were populated with galaxies according to a semi-analytic recipe, as described in Guo et al. (2011)1. We select galaxies with SDSS magnitudes of mr < 25 as a set of observable galaxies with known redshifts; Fig. 1 displays the redshift distributions of all magnitude limited galaxy samples. For the simulated survey, we use galaxies from a 1 × 1 deg2 field and galaxies down to a redshift of z = 2, yielding an average density of ~25 sources per square arcmin. The mean redshift of the sources is 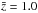 . Each source galaxy is equipped with a shear signal corresponding to its angular position and redshift. The shear signal is estimated by ray-tracing through a series of simulation snapshots in the direction of a source (Hilbert et al. 2009). For the intrinsic shape noise we adopt a variance of the ellipticity of σϵ = 0.3. We further subdivide the total galaxy sample into red (mu − mr > 2.2) and blue galaxies (mu − mr ≤ 2.2) to be used as galaxy tracers for the reconstruction technique of the mass map. We use only tracers below or equal z = 1 to aid the reconstruction, which provides a density of ~10 blue and ~5 red tracers per square arcmin. For the mapping, all galaxy samples are split into redshift slices of width Δz = 0.1 within the regime 0 ≤ z < 1, and a width of Δz = 0.2 within 1 ≤ z < 2 for the sources. Similar to the idealised fiducial survey we add Gaussian errors to the tracer redshifts with σz(z) = 0.04(1 + z).
. Each source galaxy is equipped with a shear signal corresponding to its angular position and redshift. The shear signal is estimated by ray-tracing through a series of simulation snapshots in the direction of a source (Hilbert et al. 2009). For the intrinsic shape noise we adopt a variance of the ellipticity of σϵ = 0.3. We further subdivide the total galaxy sample into red (mu − mr > 2.2) and blue galaxies (mu − mr ≤ 2.2) to be used as galaxy tracers for the reconstruction technique of the mass map. We use only tracers below or equal z = 1 to aid the reconstruction, which provides a density of ~10 blue and ~5 red tracers per square arcmin. For the mapping, all galaxy samples are split into redshift slices of width Δz = 0.1 within the regime 0 ≤ z < 1, and a width of Δz = 0.2 within 1 ≤ z < 2 for the sources. Similar to the idealised fiducial survey we add Gaussian errors to the tracer redshifts with σz(z) = 0.04(1 + z).
The mapping methodology requires the specification of second-order galaxy bias parameters { b(ℓ),r(ℓ) } of the tracer samples as a function of the angular scale ℓ and redshift. We acquire estimators of the angular galaxy bias parameters by applying the methodology of Schneider (1998) and van Waerbeke (1998) to our simulated galaxy catalogues separately for each tracer redshift slice. We average the results thereof over all simulated 128 one-square-degree fields. Herein, we set the intrinsic shape noise to zero, as we do not attempt to account for uncertainties in bias parameters here. This lensing technique has already successfully been applied to real lensing data, as seen in Simon et al. (2007). We refer the reader to the latter article for the method details, which are irrelevant here. Figure 2 summarises the galaxy bias results of our tracer samples, including errorbars due to cosmic variance and sampling variance. In the following, we take the mean of all fields. To determine these measurements, we employed, as in Simon et al. (2007), a polynomial filter for the aperture statistics. These statistics probe the angular second-order galaxy bias averaged over a ℓ-band centred on ℓcen ≈ 4.25/θap, where θap is the aperture radius in radians. The top x-axes values in the figure denote the values of θap that correspond to ℓcen (bottom x-axes). The red tracers are more strongly clustered than matter, where b(ℓ) > 1, and highly correlated with the matter density field of r(ℓ) ≈ 1 on scales larger than a few arcmin. Blue tracers, on the other hand, are less clustered and less well correlated in both cases.
 |
Fig. 1 Distribution dN/dz in units of galaxies per arcmin2 of three simulated galaxy samples in our N-body data. The data adopt a maximum depth of mr < 25 for all galaxies. The total galaxy sample used for the lensing analysis (sources) is further subdivided into red (mu − mr > 2.2) and blue galaxies (mu − mr ≤ 2.2). |
 |
Fig. 2 Galaxy bias parameters b(ℓ) and r(ℓ) in the Millennium Simulation data set as a function of angular scale ℓ (x-axis) and galaxy redshift (curves; see key for mean redshifts). The top numbers denote the corresponding aperture radius (arcmin) of the aperture statistics that were utilised to infer the galaxy bias from angular correlation functions (polynomial filter). The left panels correspond to red galaxies with mr < 25 and mu − mr > 2.2 and the right panels to blue galaxies with mr < 25 and mu − mr ≤ 2.2. The error bars denote the remaining standard error based on 128 simulated survey fields with one square degree each. |
The correlation factor r(ℓ) can exceed values of | r(ℓ) | = 1, because it is defined here and in the aforementioned references in terms of the tracer power spectrum 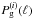 from which the Poisson shot-noise
from which the Poisson shot-noise 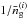 has been subtracted. In the framework of a halo model and on scales dominated by haloes that are populated on average by ⟨ N ⟩ < 1 galaxies, the shot-noise subtraction may lead naturally to r(ℓ) > 1, because galaxies can trace the matter distribution inside haloes by a sub-Poisson sampling process with a variance ⟨ N(N − 1) ⟩ 1/2 < ⟨ N ⟩ (Guzik & Seljak 2001; Seljak 2000). The presence of central galaxies has a similar impact. We clearly observe this effect here for small angular scales in the simulation. The Wiener filters in Eq. (37) or Eq. (44) diverge for | r(ℓ) | > 1, because the signal matrix S becomes singular. This indicates that our minimum-variance Ansatz, presuming sampling by a Poisson process, breaks down where the sub-Poisson effects become significant. To avoid this problem specific to small angular scales, we use more smoothing of Θs = 2 arcmin and clip correlation factors at r(ℓ) = 0.9. The latter affects the filter artificially by reducing the mixing for clipped modes and adding less information from the tracer clustering to the mass map. Note that we can always reduce the mixing inside the Wiener filter by adopting a lower correlation factor than in the data.
has been subtracted. In the framework of a halo model and on scales dominated by haloes that are populated on average by ⟨ N ⟩ < 1 galaxies, the shot-noise subtraction may lead naturally to r(ℓ) > 1, because galaxies can trace the matter distribution inside haloes by a sub-Poisson sampling process with a variance ⟨ N(N − 1) ⟩ 1/2 < ⟨ N ⟩ (Guzik & Seljak 2001; Seljak 2000). The presence of central galaxies has a similar impact. We clearly observe this effect here for small angular scales in the simulation. The Wiener filters in Eq. (37) or Eq. (44) diverge for | r(ℓ) | > 1, because the signal matrix S becomes singular. This indicates that our minimum-variance Ansatz, presuming sampling by a Poisson process, breaks down where the sub-Poisson effects become significant. To avoid this problem specific to small angular scales, we use more smoothing of Θs = 2 arcmin and clip correlation factors at r(ℓ) = 0.9. The latter affects the filter artificially by reducing the mixing for clipped modes and adding less information from the tracer clustering to the mass map. Note that we can always reduce the mixing inside the Wiener filter by adopting a lower correlation factor than in the data.
 |
Fig. 3 Radial PSF in the smoothed mass maps for the case r(ℓ) = 0.8 (right panel) and no mixing of lensing and galaxy clustering (r(ℓ) = 0; left panel). The details of the fiducial survey are found in Sect. 4.1. Both panels adopt α = 0.01 and β = 0.1. The redshifts of the density peaks in the un-smoothed maps are the small number labels, which are only shown up to z = 1.3. The map pixel size is Θs = 1 arcmin. |
5. Results
In this section, we present our results for the S/N and radial PSF in the idealised survey, and demonstrate the methodology for mock data based on a N-body simulation as blueprint for a realistic survey.
For the idealised survey, we set α = 0.01 to be consistent with Fig. 11 of STH09 for a lensing-only reconstruction with a transverse filter. Generally, the parameter α must not be too close to unity, as this results in too much radial smoothing, which moves basically all mass peaks to the middle of the reconstruction volume (no radial information). Adjusting the tuning parameters below unity means that we scale the noise covariance towards less noise in the Wiener filter. Note that this does not mean that we obtain less noise in the reconstruction. In contrast, the Wiener filter applies less smoothing, which yields more noise in the map, but less bias. For the synergy reconstruction, we adopt β = 0.1. A parameter β greater than α is a means to down-weight the impact of the tracers in the joint reconstruction, which is desirable if the details of the galaxy bias are not accurately known.
5.1. Radial point spread function
The resulting PSF of the idealised fiducial survey and a pixel size of Θs = 1 arcmin is depicted in Fig. 3 for the cases r(ℓ) = 0,0.8. Owing to the Wiener smoothing, the mass peaks are generally radially smeared, and their amplitude is suppressed, especially for very small and high redshifts. Compared to the lensing-only technique (r(ℓ) = 0), however, adding tracers with r ≠ 0 to the map-making process clearly improves the PSF: The radial profiles are narrowed and more pronounced; the amplitudes are less suppressed. The peak maximum of the PSF (apparent redshift) for given mass peak redshift (true redshift) determines the z-bias. The bias as a function of tracer correlation coefficient r(ℓ) is explored by Fig. 4. We essentially find no z-shift bias for r(ℓ) ≥ 0.4.
 |
Fig. 4 Peak redshifts of the profiles of smeared mass peaks (ordinate) compared to the true peak redshifts (abscissa) for different correlation factors: r(ℓ) = 0 (solid), r(ℓ) = 0.2 (dashed), r(ℓ) = 0.4 (dash-dotted), and r(ℓ) = 0.6,0.8 (indistinguishable diagonal lines). |
5.2. Signal-to-noise of map
For the idealised survey, Fig. 5 depicts the S/N of the lens plane density modes as a function of angular scale and lens plane redshift. In the left panel, we have the matter density modes; the right panel shows the tracer number density modes. Different line styles correspond to different lens planes with the thin lines to reconstructions with mode mixing switched off, or r(ℓ) = 0, and the thick lines to the joint reconstruction. In addition, the black thin lines in the left panel depict the S/N in a map with no radial smoothing (α = 0) and no mixing. Clearly, a lensing-only map absolutely requires some radial smoothing, which is seen here by comparing the low S/N of the thin black lines to the boosted S/N in the red lines. The impact of mixing on the S/N of the tracer number density maps (right panel) is small, which is most prominently on the small angular scales. This changes slightly if we choose an even larger tuning parameter β (that is not shown): a larger β scales with the shot-noise matrix of the tracers inside the Wiener filter, which attributes even more weight to the lensing data in the joint reconstruction. As the S/N of the tracers in the data is actually higher than that of the shear, this will result in a decreased S/N for the galaxy-number density maps in comparison to a reconstruction with no mixing; the joint reconstruction is not optimal as to the map noise.
5.3. Galaxy-stochasticity noise
Figure 6 shows the estimated ratios fgsn of the pixel GSN-variance and pixel signal-variance for lens planes of increasing redshift. The map smoothing scale is Θs = 1 arcmin. We find the GSN on a pixel scale to be most prominent for r(ℓ) ~ 0.8, which declines for correlations greater or weaker than that; between r(ℓ) = 0.6 − 0.8, there is only little change, and in the absence of stochasticity, where r(ℓ) = 1, fgsn vanishes. The dependence on lens plane redshift is marginal; most of the change occurs below z ≲ 0.4. The GSN increases with the bias factor b(ℓ) of the tracers. Overall, typical figures for 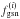 are below 30%, but can be above this level for strongly clustered tracers.
are below 30%, but can be above this level for strongly clustered tracers.
5.4. Cluster signal-to-noise
In Fig. 7 we plot the S/N detection of a SIS mass peak as a function of peak redshift. The peak has the mass of a large galaxy cluster with M200 = 6.6 × 1014 M⊙ h-1, or σv = 103 km s-1, at z = 0. Until redshift value z ~ 0.6 this peak is visible above a 3σ limit when only 3D lensing information and a tuning of α = 0.01 are used; see the black solid line with r = 0. The S/N scales with 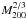 as discussed in STH09. The S/N detection improves when we combine the lensing information with the galaxy tracer information, adopting β = 0.1; see lines with r > 0. The S/N improvement is greater for higher correlation factors r(ℓ) or more clustering b(ℓ) of the tracers. Unless we have extreme cases of high correlations, where r ~ 0.9, and strong clustering, where b ~ 3, the S/N enhancement is only moderate between the factors of 2 − 3. The GSN model adopts a Gaussian approximation with
as discussed in STH09. The S/N detection improves when we combine the lensing information with the galaxy tracer information, adopting β = 0.1; see lines with r > 0. The S/N improvement is greater for higher correlation factors r(ℓ) or more clustering b(ℓ) of the tracers. Unless we have extreme cases of high correlations, where r ~ 0.9, and strong clustering, where b ~ 3, the S/N enhancement is only moderate between the factors of 2 − 3. The GSN model adopts a Gaussian approximation with 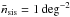 . For this approximation, shape noise and sampling noise are still the dominating source of pixel noise, such that a scaling of the S/N detection
. For this approximation, shape noise and sampling noise are still the dominating source of pixel noise, such that a scaling of the S/N detection  is also found for the synergy technique within ~10% accuracy. We verified this within the mass range 5 × 1013 M⊙ h-1 ≤ M200 ≤ 1015 M⊙ h-1.
is also found for the synergy technique within ~10% accuracy. We verified this within the mass range 5 × 1013 M⊙ h-1 ≤ M200 ≤ 1015 M⊙ h-1.
When we consider both r = 0.8 and b = 1 for the GSN correction factor, we find that the S/N levels in a randomised map have to be reduced to ~75% at z = 0.15, 90% at z = 0.25, and ≳93% at all other values (Sect. 3.6). These figures are typical values for r(ℓ) ∈ [ 0,1 ] and b(ℓ) ∈ [ 0,3 ]. Therefore, the GSN is a small effect in the Gaussian regime and mostly relevant at redshifts z ≲ 0.3.
5.5. N-body mock data
 |
Fig. 5 S/N of density modes for the matter density maps (left panel) and galaxy tracer density maps (right panel). The lines assume cosmic-average fluctuations in the density fields and b(ℓ) = 1 for the tracers. Different line styles correspond to different lens plane redshifts: z = 0.1 (solid), z = 0.3 (dashed), z = 0.5 (dash-dotted), z = 0.7 (dotted), and z = 0.9 (dot-dot-dashed). The black thin lines do not employ any smoothing, while red thins lines use smoothing. Both use no mixing of lensing and galaxy clustering information. In the right panel, red and black thin lines coincide. Thick lines depict values in a Wiener smoothed map (α = 0.01, β = 0.1) and a mixing with r(ℓ) = 0.8 for all redshifts. The S/N does not include GSN. |
In Fig. 8, we show the simulated mass mapping of one N-body simulated field in different versions. The field has been randomly selected from the set of 128 one square degree fields. The top left panel displays transparent matter density contrast iso-surfaces of the data without source galaxy shape noise and without synergy. This ideal map has subsequently been transversely smoothed with a Gaussian kernel of 2 arcmin r.m.s. size. All maps in this figures are subject to the same angular smoothing. The top right panel corresponds to a map based on the lensing catalogue only but now with shape-noise of variance σϵ = 0.3 and α = 0.05. This map and the following other two depict iso-surfaces of S/N based on 500 noise realisations that do not include GSN. The two bottom panels are the mass maps that include both the noisy lensing data and the information from galaxy tracers, which are either red galaxies with mu − mr > 2.2 or blue galaxies with mu − mr ≤ 2.2. The galaxy catalogues are flux-limited with mr ≤ 25.0. In these maps, we set the tuning parameters to α = 0.05 and β = 0.5. Mass peaks of more than ~3σ in the lensing-only map are designated by numbers between 1 and 6. Mass peaks along the same line-of-sight and that are closest in redshift obtain the same number in the noise-free map. The distribution of mass peaks in the noise-free map was confusing and needed to be viewed on a computer display from different view angles to identify possible matches, especially at higher redshifts where a redshift slice of the light cone contains more volume. The complex 5 comprises a series of peaks that are connected by lines to guide the eye. Significant mass peaks in the combined reconstruction that are not visible in the lensing-only map are given capital letters between A and F. Their possible matches are also indicated in the noise-free map. The question mark in 1? indicates that the match to 1 in the noise-free map is uncertain. By 5/B, we mean that the peak is located between the peaks 5 and B, which are both along the same LOS but at different redshifts. All maps recover the prominent structures 2 and 3 at low redshifts but fail to significantly recover C and X, which both appear prominent in the noise-free map. The benefit from adding tracer information is mostly visible at higher redshifts, at z ≳ 0.5, where more individual structures are lifted above the 3σ threshold; peaks are less elongated in this regime as well. In particular, B and 5 are resolved when using red tracers, whereas the lensing-only map merges both together at an intermediate redshift. The blue tracers do not recover 5 but at least B at lower redshift. When using red tracers overall the S/N in the map is higher because red galaxies are more strongly clustered than blue galaxies and stronger correlated with the matter density field. The blue tracers render the original lensing-only map modestly in comparison by shifting the lensing signal in 5/B to B, correcting 6, weighting down 7, and adding a couple of new features of A, D, and E that are insignificant in the lensing-only map. The redshift offset of peaks can be as high as Δz ≈ 0.2, as for seen for 1? (blue), or F (red).
6. Discussion
A synergy of 3D lensing data and galaxy clustering information can potentially alleviate the notorious z-shift bias in 3D lensing mass maps, provided the distribution of the tracers is statistically correlated with the underlying mass-density field. This can be seen in Fig. 3, which compares the radial PSF for uncorrelated tracers to the PSF in a synergy reconstruction with highly correlated tracers. The synergy produces a mass map in which the PSF now peaks on average at the redshift of the original mass peaks and in which mass peaks are less smeared out in radial direction (width of PSF). Moreover, the z-shift bias is already fixed for relatively loosely correlated tracers with r(ℓ) > 0.4, as Fig. 4 shows. Mixing the tracer and lensing information therefore promises to be an effective technique to address the z-shift bias.
 |
Fig. 6 GSN variance fgsn on a pixel scale of Θs = 1 arcmin radius relative to the signal variance in the fiducial survey as function of lens plane redshift. The lines differ in their assumed r(ℓ). Except for one line, the bias factor of the tracers is b(ℓ) = 1. This figure uses α = 0.01 and β = 0.1. |
The 3D mass mapping with gravitational lensing is essentially a tool for the visualisation of the spatial distribution of mass peaks on a galaxy-cluster mass scale; a moderate synergy with tracers improves the accuracy of the distance estimates and the detection rate at greater distances. Figure 7 displays the change in S/N of cluster-sized mass peaks in a synergy map with moderate mixing (α/β = 0.1). In the case of r ≳ 0.4, we expect a S/N enhancement by a factor 2 − 3. Strongly clustered tracers with a bias of b ~ 3 are an exception here as they yield even more enhancement. They, however, should not be utilised in a reconstruction, because large density fluctuations clearly cannot obey a Gaussian statistics, which is the underlying assumption of the GSN treatment in the figure; Gaussian density fluctuations, δ, require a symmetric distribution about δ = 0, whereas large fluctuations ⟨ δ ⟩ 2 ≫ 1 are bound to have a skewed distribution due to the constraint δ ≥ − 1. The S/N improvement at larger distances is underlined by Fig. 8. An increase in the S/N and less radial smearing, which is visible in Fig. 3, at the same time results in a higher redshift accuracy of the mass peaks, because radial profiles of mass peaks are distinguishable more easily (Simon et al. 2012). Therefore, the benefit from our new algorithm is also a higher redshift accuracy instead of a more complete visualisation of the spatial distribution of cluster-sized masses. Based on this, the search for lensing mass peaks can be supported by galaxy tracers, and lensing mass models of clusters can be refined by accounting for possible alignments of peaks close to a single LOS.
 |
Fig. 7 Trends in the S/N for the detection of a SIS-like mass peak as function of the peak redshift (α = 0.01 and β = 0.1); the pixel scale is Θs = 1 arcmin. The mass of the peak corresponds to M200 = 6.6 × 1014 M⊙ h-1. The S/N values scale roughly with |
 |
Fig. 8 Simulated reconstructions of the original N-body data in the top left panel (density contrast iso-surfaces). The lens planes covering one square degree have sizes of 128 × 128 pixel2 on the x- and y-axes. All maps are subject to smoothing (Gaussian kernel with two arcmin r.m.s. width). Top right: reconstruction using only the lensing information (α = 0.05). Bottom left: reconstruction adding information from red galaxy tracers with mu − mr ≥ 2.2 (α = 0.05, β = 0.5). Bottom right: reconstruction including information from blue galaxies tracers with mu − mr > 2.2 (α = 0.05, β = 0.5). The number and capital letter labels indicate mass peak matches across different maps. The simulated reconstructions display S/N iso-surfaces. The combined maps do not account for GSN. |
Our synergy technique is linear and for this reason has limited applicability on sub-degree scales due to a potentially non-linear galaxy bias. The red thin lines in the left panel of Fig. 5 display the S/N of matter density modes in the 3D mass map before synergy. Compare this to the thin red lines in the right panel, which exhibit the S/N of the tracer number density modes that is roughly ten times higher. This basically quantifies the information on the matter density field as encoded in the tracer distribution, if there is no stochastic galaxy bias and if the exact mapping between tracer and matter density is known (deterministic galaxy bias; e.g., Mann et al. 1998). This seems to favour a large weight for the galaxy tracers in a synergy reconstruction, and this would result in a S/N boost compared to a lensing mass map. In reality, however, galaxy bias is stochastic, non-linear and possibly even non-local (e.g., Tegmark & Bromley 1999; Yoshikawa et al. 2001; Hoekstra et al. 2002; Dekel & Lahav 1999; Matsubara 1999), which is not properly accounted for in a linear filter: our filter assumes by construction a linear relation between tracer and matter density, which is a Gaussian bias, and a Poisson process by which tracers sample the matter density field. The former can be seen by the fact that only a linear mixing of both fields is possible within the filter. Gaussianity is a valid assumption on (smoothing) scales, where density fluctuations are small, ⟨ δ2 ⟩ ≪ 1, or on large scales beyond ~10 Mpc. Hence it is a fair assumption on angular scales larger than ~45 arcmin (15 arcmin) at z ~ 0.2(0.8) but, on the other hand, is prone to bias the mass maps on smaller angular scales. Moreover, sub-Poisson sampling processes become relevant on small angular scales, as indicated by the shot-noise corrected correlation factor of r(ℓ) > 1 in Fig. 2. To reduce bias on these scales we weight down the tracer information by adopting small values of α/β ≲ 0.1 at the expense of map S/N, and we smooth the map with a kernel of several arcmin size. To further relax this problem, it is also conceivable to exclude tracer information by setting r(ℓ) = 0 at low redshifts of z ≲ 0.3 where the lensing information is highest, as seen in Fig. 7. Despite these issues, we conclude that a moderate mixing and smoothing yields qualitatively sensible results from the reconstructions in Fig. 8 with two different tracer samples. Nevertheless, giving less weight to the tracers adds less information to the mass map, so that realistically only a modest S/N improvement is feasible with the synergy method on non-linear scales. In addition, there remains an uncertainty in the GSN due to non-linear stochastic galaxy bias that can only be quantified by more accurate modelling.
In contrast to red galaxy tracers, blue galaxy tracers lead to modest but presumably more reliable improvements in 3D mapping. We draw this conclusion from Fig. 8 that shows the combined reconstructions with red and blue galaxies in comparison. Clearly, including red galaxy clustering information adds more S/N to the map than blue galaxies. This can be explained by Fig. 7 by considering that red galaxies are both more clustered and more strongly correlated with the matter density field in terms of r(ℓ) as seen Fig. 2. On the other hand, the assumption of a Gaussian bias model is less appropriate for red galaxies than for blue galaxies because of their greater density fluctuations ⟨ δ2 ⟩. Typical blue galaxies exhibit density fluctuations smaller by a factor of ~5 on arcmin scales, which in theory is even less than matter (b < 1), and their number density is higher, which reduces the shot-noise error. Furthermore, blue galaxies are frequently field galaxies so that they also map out the large-scale matter distribution outside of clusters unlike red galaxies, which are preferentially found in galaxy clusters (Postman & Geller 1984; Zehavi et al. 2011). Considering the unknowns of the galaxy bias scheme, a blue tracer population is hence presumably the more favourable choice.
The galaxy properties have been obtained through the Millennium Simulation databases (Lemson & Virgo Consortium 2006).
Acknowledgments
I thank Stefan Hilbert and Jan Hartlap for providing simulated galaxy and shear catalogues, based on the Millennium Simulation, which were utilised to demonstrate the reconstruction algorithm. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory. I also acknowlegde the useful comments by Stefan Hilbert and the anonymous referee on the paper. The work in this was supported by the European DUEL Research-Training Network (MRTN-CT-2006-036133) and the Deutsche Forschungsgemeinschaft in the framework of the Collaborative Research Center TR33 “The Dark Universe”.
References
- Bacon, D. J., & Taylor, A. N. 2003, MNRAS, 344, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, P., & Jones, B. 1991, MNRAS, 248, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Lahav, O. 1999, ApJ, 520, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dodelson, S. 2003, Modern cosmology (Amsterdam: University Press) [Google Scholar]
- Fan, Z. 2003, ApJ, 594, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Guzik, J., & Seljak, U. 2001, MNRAS, 321, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., Hartlap, J., White, S. D. M., & Schneider, P. 2009, A&A, 499, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirata, C. M., & Seljak, U. 2004, Phys. Rev. D, 70, 063526 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., van Waerbeke, L., & Gladders, M. D. E. 2002, ApJ, 577, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Keeton, C. R. 2002, Phys. Rev. D, 66, 063506 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., Rhodes, J., Kiessling, A., et al. 2012, ApJ, 750, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1992, ApJ, 388, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., & Squires, G. 1993, ApJ, 404, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lemson, G., & Virgo Consortium, T. 2006 [arXiv:astro-ph/0608019] [Google Scholar]
- Leonard, A., Dupé, F.-X., & Starck, J.-L. 2012, A&A, 539, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mann, R. G., Peacock, J. A., & Heavens, A. F. 1998, MNRAS, 293, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez, V. J., & Saar, E. 2002, Statistics of the Galaxy Distribution (Chapman and Hall/CRC) [Google Scholar]
- Matsubara, T. 1999, ApJ, 525, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., Valageas, P., van Waerbeke, L., & Heavens, A. 2008, Phys. Rep., 462, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Pen, U.-L., Lu, T., van Waerbeke, L., & Mellier, Y. 2003, MNRAS, 346, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., & Geller, M. J. 1984, ApJ, 281, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P. 1998, ApJ, 498, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P. 2006a, in Saas-Fee Advanced Course 33: Gravitational lensing: strong, weak and micro, eds. G. Meylan, P. Jetzer, et al. (Berlin: Springer), 1 [Google Scholar]
- Schneider, P. 2006b, in Saas-Fee Advanced Course 33: Gravitational lensing: strong, weak and micro, eds. G. Meylan, P. Jetzer, et al. (Berlin: Springer), 269 [Google Scholar]
- Seitz, S., & Schneider, P. 2001, A&A, 374, 740 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seljak, U. 2000, MNRAS, 318, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, P. 2012, A&A, 543, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, P., Hetterscheidt, M., Schirmer, M., et al. 2007, A&A, 461, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, P., Taylor, A. N., & Hartlap, J. 2009, MNRAS, 399, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, P., Heymans, C., & Schrabback, E. 2012, MNRAS, 419, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Lemson, G., Sigad, Y., et al. 2001, MNRAS, 320, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tegmark, M., & Bromley, B. C. 1999, ApJ, 518, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., & Peebles, P. J. E. 1998, ApJ, 500, 79 [Google Scholar]
- van Waerbeke, L. 1998, A&A, 334, 1 [NASA ADS] [Google Scholar]
- VanderPlas, J. T., Connolly, A. J., Jain, B., & Jarvis, M. 2011, ApJ, 727, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, D. H., Davé, R., & Katz, N. E. 2004, ApJ, 601, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshikawa, K., Taruya, A., & Jing, Y. P. E. 2001, ApJ, 558, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Zaroubi, S., Hoffman, Y., & Fisher, K. B. E. 1995, ApJ, 449, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Gaussian galaxy bias
Let 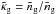 and
and 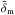 be the real part of the Fourier coefficients of the galaxy tracer number density contrast and matter density fluctuations, respectively, on a given lens plane and for a given angular mode ℓ. In the Gaussian regime the bivariate p.d.f. of both is given by
be the real part of the Fourier coefficients of the galaxy tracer number density contrast and matter density fluctuations, respectively, on a given lens plane and for a given angular mode ℓ. In the Gaussian regime the bivariate p.d.f. of both is given by 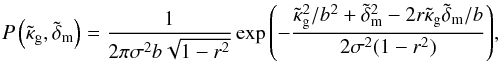 (A.1)where the matter variance is
(A.1)where the matter variance is 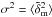 , { b,r } are the Gaussian bias parameters, and all means
, { b,r } are the Gaussian bias parameters, and all means 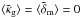 vanish. The same relation holds for the imaginary parts of the Fourier coefficients; the real and imaginary parts are independent. The conditional p.d.f.
vanish. The same relation holds for the imaginary parts of the Fourier coefficients; the real and imaginary parts are independent. The conditional p.d.f. 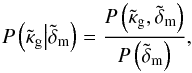 (A.2)is therefore also a Gaussian, namely with a mean of
(A.2)is therefore also a Gaussian, namely with a mean of 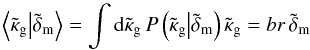 (A.3)and variance of
(A.3)and variance of 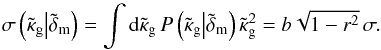 (A.4)The variance in
(A.4)The variance in  is given by the matter power spectrum Pδ(ℓ) for the lens plane, the solid angle Afov of the plane, and
is given by the matter power spectrum Pδ(ℓ) for the lens plane, the solid angle Afov of the plane, and 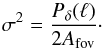 (A.5)Therefore, we expect an average tracer number density of
(A.5)Therefore, we expect an average tracer number density of 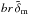 with r.m.s. variance
with r.m.s. variance 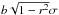 for a fixed matter density mode
for a fixed matter density mode 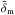 . The latter gives rise to the GSN in the Gaussian case (Dekel & Lahav 1999).
. The latter gives rise to the GSN in the Gaussian case (Dekel & Lahav 1999).
Appendix B: SIS power spectrum
A set of Nh haloes with positions θj on the ith lens plane and an average, axial-symmetric matter density contrast, δsis( | θ |), produces the combined density contrast 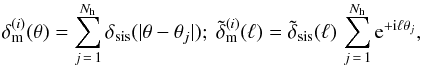 (B.1)where the second equation on the right hand side is the Fourier transform of
(B.1)where the second equation on the right hand side is the Fourier transform of 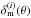 . Averaging the two-point correlator of the density in Fourier space over all halo positions results in
. Averaging the two-point correlator of the density in Fourier space over all halo positions results in ![\appendix \setcounter{section}{2} \begin{eqnarray} \lefteqn{\Ave{\tilde{\delta}_{\rm m}^{(i)}(\vec{\ell}_1)\tilde{\delta}_{\rm m}^{(i)}(\vec{\ell}_2)}=}\\ &&\nonumber \tilde{\delta}_{\rm sis}(\ell_1)\tilde{\delta}_{\rm sis}(\ell_2) \left[\sum_{j\,=\,1}^{N_{\rm h}}\Ave{{\rm e}^{+{\rm i}(\vec{\ell}_1+\vec{\ell}_2)\vec{\theta}_j}} + \sum_{j\,\ne k\,=\,1}^{N_{\rm h}} \Ave{{\rm e}^{+{\rm i}\vec{\ell}_1\vec{\theta}_j} {\rm e}^{+{\rm i}\vec{\ell}_2\vec{\theta}_k}} \right]. \end{eqnarray}](/articles/aa/full_html/2013/12/aa19257-12/aa19257-12-eq414.png) (B.2)We ignore the clustering of the haloes over the field-of-view Afov, so that the two-halo term in the second sum vanishes, and
(B.2)We ignore the clustering of the haloes over the field-of-view Afov, so that the two-halo term in the second sum vanishes, and 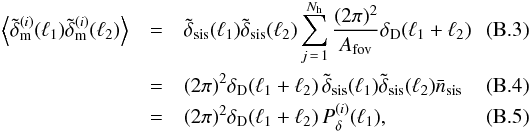 where
where 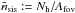 expresses the mean number density of haloes. Therefore, we obtain in this scenario
expresses the mean number density of haloes. Therefore, we obtain in this scenario 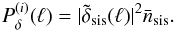 (B.6)
(B.6)
All Figures
 |
Fig. 1 Distribution dN/dz in units of galaxies per arcmin2 of three simulated galaxy samples in our N-body data. The data adopt a maximum depth of mr < 25 for all galaxies. The total galaxy sample used for the lensing analysis (sources) is further subdivided into red (mu − mr > 2.2) and blue galaxies (mu − mr ≤ 2.2). |
| In the text | |
 |
Fig. 2 Galaxy bias parameters b(ℓ) and r(ℓ) in the Millennium Simulation data set as a function of angular scale ℓ (x-axis) and galaxy redshift (curves; see key for mean redshifts). The top numbers denote the corresponding aperture radius (arcmin) of the aperture statistics that were utilised to infer the galaxy bias from angular correlation functions (polynomial filter). The left panels correspond to red galaxies with mr < 25 and mu − mr > 2.2 and the right panels to blue galaxies with mr < 25 and mu − mr ≤ 2.2. The error bars denote the remaining standard error based on 128 simulated survey fields with one square degree each. |
| In the text | |
 |
Fig. 3 Radial PSF in the smoothed mass maps for the case r(ℓ) = 0.8 (right panel) and no mixing of lensing and galaxy clustering (r(ℓ) = 0; left panel). The details of the fiducial survey are found in Sect. 4.1. Both panels adopt α = 0.01 and β = 0.1. The redshifts of the density peaks in the un-smoothed maps are the small number labels, which are only shown up to z = 1.3. The map pixel size is Θs = 1 arcmin. |
| In the text | |
 |
Fig. 4 Peak redshifts of the profiles of smeared mass peaks (ordinate) compared to the true peak redshifts (abscissa) for different correlation factors: r(ℓ) = 0 (solid), r(ℓ) = 0.2 (dashed), r(ℓ) = 0.4 (dash-dotted), and r(ℓ) = 0.6,0.8 (indistinguishable diagonal lines). |
| In the text | |
 |
Fig. 5 S/N of density modes for the matter density maps (left panel) and galaxy tracer density maps (right panel). The lines assume cosmic-average fluctuations in the density fields and b(ℓ) = 1 for the tracers. Different line styles correspond to different lens plane redshifts: z = 0.1 (solid), z = 0.3 (dashed), z = 0.5 (dash-dotted), z = 0.7 (dotted), and z = 0.9 (dot-dot-dashed). The black thin lines do not employ any smoothing, while red thins lines use smoothing. Both use no mixing of lensing and galaxy clustering information. In the right panel, red and black thin lines coincide. Thick lines depict values in a Wiener smoothed map (α = 0.01, β = 0.1) and a mixing with r(ℓ) = 0.8 for all redshifts. The S/N does not include GSN. |
| In the text | |
 |
Fig. 6 GSN variance fgsn on a pixel scale of Θs = 1 arcmin radius relative to the signal variance in the fiducial survey as function of lens plane redshift. The lines differ in their assumed r(ℓ). Except for one line, the bias factor of the tracers is b(ℓ) = 1. This figure uses α = 0.01 and β = 0.1. |
| In the text | |
 |
Fig. 7 Trends in the S/N for the detection of a SIS-like mass peak as function of the peak redshift (α = 0.01 and β = 0.1); the pixel scale is Θs = 1 arcmin. The mass of the peak corresponds to M200 = 6.6 × 1014 M⊙ h-1. The S/N values scale roughly with |
| In the text | |
 |
Fig. 8 Simulated reconstructions of the original N-body data in the top left panel (density contrast iso-surfaces). The lens planes covering one square degree have sizes of 128 × 128 pixel2 on the x- and y-axes. All maps are subject to smoothing (Gaussian kernel with two arcmin r.m.s. width). Top right: reconstruction using only the lensing information (α = 0.05). Bottom left: reconstruction adding information from red galaxy tracers with mu − mr ≥ 2.2 (α = 0.05, β = 0.5). Bottom right: reconstruction including information from blue galaxies tracers with mu − mr > 2.2 (α = 0.05, β = 0.5). The number and capital letter labels indicate mass peak matches across different maps. The simulated reconstructions display S/N iso-surfaces. The combined maps do not account for GSN. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


