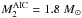| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 25 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321662 | |
| Published online | 01 October 2013 | |
Evolution towards and beyond accretion-induced collapse of massive white dwarfs and formation of millisecond pulsars
1 Argelander-Insitut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: tauris@astro.uni-bonn.de
2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3 Department of Physical Sciences, IISER Kolkata, Mohanpur, 741252, Nadia, West Bengal, India
4 Department of Physics & Astronomy, Seoul National University, Gwanak-gu, Gwanak-ro 1, 151-742 Seoul, Korea
Received: 8 April 2013
Accepted: 27 July 2013
Context. Millisecond pulsars (MSPs) are generally believed to be old neutron stars (NSs), formed via type Ib/c core-collapse supernovae (SNe), which have been spun up to high rotation rates via accretion from a companion star in a low-mass X-ray binary (LMXB). In an alternative formation channel, NSs are produced via the accretion-induced collapse (AIC) of a massive white dwarf (WD) in a close binary.
Aims. Here we investigate binary evolution leading to AIC and examine if NSs formed in this way can subsequently be recycled to form MSPs and, if so, how they can observationally be distinguished from pulsars formed via the standard core-collapse SN channel in terms of their masses, spins, orbital periods and space velocities.
Methods. Numerical calculations with a detailed stellar evolution code were used for the first time to study the combined pre- and post-AIC evolution of close binaries. We investigated the mass transfer onto a massive WD (treated as a point mass) in 240 systems with three different types of non-degenerate donor stars: main-sequence stars, red giants, and helium stars. When the WD is able to accrete sufficient mass (depending on the mass-transfer rate and the duration of the accretion phase) we assumed it collapses to form a NS and we studied the dynamical effects of this implosion on the binary orbit. Subsequently, we followed the mass-transfer epoch which resumes once the donor star refills its Roche lobe and calculated the continued LMXB evolution until the end.
Results. We show that recycled pulsars may form via AIC from all three types of progenitor systems investigated and find that the final properties of the resulting MSPs are, in general, remarkably similar to those of MSPs formed via the standard core-collapse SN channel. However, as a consequence of the fine-tuned mass-transfer rate necessary to make the WD grow in mass, the resultant MSPs created via the AIC channel preferentially form in certain orbital period intervals. In addition, their predicted small space velocities can also be used to identify them observationally. The production time of NSs formed via AIC can exceed 10 Gyr which can therefore explain the existence of relatively young NSs in globular clusters. Our calculations are also applicable to progenitor binaries of SNe Ia under certain conditions.
Key words: binaries: close / accretion, accretion disks / white dwarfs / supernovae: general / stars: neutron / X-rays: binaries
© ESO, 2013
1. Introduction
The final outcome of close binary stellar evolution is a pair of compact objects if the system avoids disruption following a supernova (SN) explosion or a merger event in a common envelope (CE). The nature of the compact objects formed can be either black holes, neutron stars (NSs), or white dwarfs (WDs), depending primarily on the initial stellar masses and orbital period of the zero-age main-sequence (ZAMS) binary. Systems in which the primary star is not massive enough to end its life as a NS may leave behind an oxygen-neon-magnesium white dwarf (ONeMg WD) of mass MWD ≃ 1.1 − 1.3 M⊙, which may stem from primaries with initial masses in the interval of MZAMS ≃ 6 − 16 M⊙, depending on the mass of the secondary star and, in particular, on the orbital period which affects both the important carbon/oxygen-ratio at the depletion of core helium burning and the occurrence of a second dredge-up phase at the beginning of the asymptotic giant branch (see e.g. Wellstein & Langer 1999; Podsiadlowski et al. 2004). In systems where an ONeMg WD forms, the WD may later accrete sufficient material, when the secondary star subsequently evolves and fills its Roche lobe, such that it reaches the Chandrasekhar-mass limit and implodes via an accretion-induced collapse (AIC) to form a NS (e.g. Nomoto et al. 1979a; Taam & van den Heuvel 1986; Michel 1987; Canal et al. 1990; Nomoto & Kondo 1991). The donor star in these systems can either be a main-sequence star, a low-mass giant, or a helium star. The first aim of this paper is to investigate in which binaries AIC can occur.
Millisecond pulsars (MSPs) are traditionally believed to be old NSs which have been spun up to high rotation rates via accretion of mass and angular momentum from a companion star in a low-mass X-ray binary, LMXB (e.g. Bhattacharya & van den Heuvel 1991; Tauris & van den Heuvel 2006, and references therein). It is important to investigate whether or not this standard recycling scenario is the sole formation channel of MSPs. Three key questions arise in the context of AIC:
-
1.
Could the implosion of the ONeMg WD leaddirectly to the formation of an MSP?
-
2.
When an additional accretion phase is necessary for NSs formed via AIC in order to explain the observed rapid spins and low B-fields of MSPs, is it possible at all to form MSPs via post-AIC accretion from the same donor star?
-
3.
If so, can MSPs produced this way be distinguished observationally from MSPs that formed via the standard core-collapse SN channel?
In the context of direct and indirect formation of MSPs via AIC (i.e. prompt or after additional accretion, respectively), we point out that the origin of pulsar B-fields is not well understood. In direct MSP formation, B-fields could be created from conservation of magnetic flux of the collapsing core, as originally hypothesized for NSs by Woltjer (1964), or as suggested by theoretical work on thermomagnetic effects during or shortly after the NS is formed (Reisenegger 2003; Spruit 2008). In principle, a Chandrasekhar mass WD with an equatorial radius of about 3000 km and a B-field of 103G could, assuming flux conservation, undergo AIC and directly produce an MSP with B ≃ 108G and a spin period of a few ms, equivalent to typical values of observed recycled radio MSPs (Tauris & van den Heuvel 2006) and accreting X-ray MSPs (Patruno & Watts 2012) near the spin-up line in the PṖ-diagram. Producing the spin of the MSP via AIC is not a problem if just a small fraction of the spin angular momentum of the WD is conserved during the collapse (Dessart et al. 2006).
Until recently, it was thought that the distribution of WD B-fields is strongly bimodal, with a large majority of WDs being non-magnetic and a smaller fraction (~15%, primarily in binaries) having larger fields of typically ~107G (Wickramasinghe & Ferrario 2000; Liebert et al. 2003). However, by using more sensitive instruments it has been demonstrated that some 15 − 20% of WDs could have weak B-fields of the order of 103G (e.g. Jordan et al. 2007). Hence, AIC may lead to the formation of NSs with a potential large range of possible B-field values, if flux conservation is at work. One the other hand, regardless of its formation mechanism any newborn NS is extremely hot and liquid, and therefore differentially rotating, which may amplify any seed magnetic field such that the B-fields of NSs formed via AIC could be similar to those formed via an iron-core collapse. In this respect, it is important that none of the more than 40 known young NSs associated with SN remnants are observed with the characteristic properties of MSPs: low B-fields and fast spin. The B-fields of MSPs (107 − 9 G) are typically lower than that of young, normal pulsars (1012 − 14 G) by five orders of magnitude. It is therefore questionable if an MSP would form directly from any type of collapse: iron-core collapse, electron capture SN, or AIC1. For the rest of this work, we therefore focus our attention exclusively on the possibility of indirect formation of MSPs via AIC, i.e. following the scenario where an AIC leads to the formation of a normal NS which then subsequently accretes matter, resulting in a weaker B-field and a faster spin.
The AIC route of forming MSPs has three main advantages: 1) it can explain the low space velocities of many recycled pulsars and the large fraction of NSs retained in globular clusters (Bailyn & Grindlay 1990) due to both the small amount of mass lost and the small momentum kick expected to be associated with the implosion (for details of simulations of the implosion, see e.g. Kitaura et al. 2006; Dessart et al. 2006); 2) it can explain the existence of apparently young NSs in globular clusters (Lyne et al. 1996; Boyles et al. 2011); and finally 3) it may explain the presence of a number of peculiar high B-field and slowly spinning Galactic disk NSs in close binaries with (semi)degenerate companions (e.g. Yungelson et al. 2002). In addition, direct formation of MSPs via AIC could possibly help explain the postulated birthrate problem (Kulkarni & Narayan 1988) between the small number of LMXB progenitor systems and the large observed number of MSPs.
A recent, detailed population synthesis study by Hurley et al. (2010) concluded that one cannot ignore the AIC route to MSP formation and that some binary MSPs in wide orbits are best explained by an AIC scenario (see also Ivanova et al. 2008, for a specialized study on NS formation in globular clusters). There are, however, many uncertainties involved in even the best population synthesis studies and in particular in the applied physical conditions for making the ONeMg WD mass grow sufficiently.
The weaknesses of the AIC formation channel are that it lacks direct observational evidence of the AIC event itself and, as already mentioned, the difficulty in predicting the spin rate and the surface B-field associated with a newborn NS formed via AIC (e.g. Kitaura et al. 2006; Dessart et al. 2006, 2007). It is not clear whether or not the AIC would be an observable transient event. According to Dessart et al. (2006), during the AIC only a few 0.001 M⊙ of material is ejected (of which ~25% is 56Ni, decaying into 56Fe via 56CO) which quickly becomes optically thin. Hence, AIC events are most likely underluminous and very short-lived. The studies by Kitaura et al. (2006), Metzger et al. (2009), Darbha et al. (2010) also yield somewhat small amounts (<0.015 M⊙) of 56Ni ejected in the AIC process, possibly synthesized in a disk, which may result in a radioactively powered SN-like transient that peaks after ≤1day with a bolometric luminosity ≃1041ergs-1. It is also possible that a transient radio source may appear, lasting for a few months, following the AIC event (Piro & Kulkarni 2013). In any case, these amounts are small enough to justify our assumption that the whole WD mass gets converted into the mass of the newborn NS (see Sect. 3).
Another issue is that any NS formed via AIC may shortly afterwards begin to accrete additional material from its companion star, once this donor star re-fills its Roche lobe when recovering from the dynamical effects of the implosion (partly caused by the released gravitational binding energy in the transition from a WD to a more compact NS). Therefore, regardless of its initial properties, any NS formed via AIC could in principle subsequently be spun up to become an MSP, as suggested by Helfand et al. (1983). The problem is, as pointed out by Hurley et al. (2010), that this post-AIC accretion phase should then resemble the conditions under which normal, old NSs are spun up to become MSPs via the conventional channel and, consequently, one cannot easily distinguish the outcome of this formation path from the standard scenario.
In this work, we therefore concentrate on answering the second and the third questions raised above, i.e. if MSPs can be produced via AIC events which are immediately followed by subsequent mass transfer and, if so, how they can be distinguished observationally from those MSPs formed via the standard SN channel. We aim at investigating which progenitor binaries lead to AIC in the first place and we present detailed modelling of both pre- and post-AIC evolution to predict the properties of MSPs formed via the indirect AIC channel. The structure of our paper is as follows: in Sect. 2 we review the suggested observational evidence for NS production via AIC. The computer code and our assumptions governing the pre- and post-AIC mass-transfer processes are given in Sect. 3. In Sects. 4, 5, and 6 we present those of our calculated systems which successfully lead to AIC with main-sequence star, giant star, and helium star donors, respectively, and review the properties of the binary pulsars formed. We discuss our results in a broader context in Sect. 7 and summarize our conclusions in Sect. 8.
2. Observational evidence for AIC
The question of the origin of NSs is closely related to many of their observable parameters: spin, B-field, age, space velocity, and the nature of their companion star. As already pointed out, the observational evidence suggested in the literature for NSs formed via AIC can be categorized into three groups. We now review this evidence in more detail.
2.1. The role of NS kicks
It has been well established from observations of radio pulsar velocities that most NSs receive a momentum kick at birth (Lyne & Lorimer 1994; Hobbs et al. 2005). These kicks are possibly associated with SN explosion asymmetries and may arise from non-radial hydrodynamic instabilities (neutrino-driven convection and the standing accretion-shock instability) in the collapsing stellar core. These instabilities lead to large-scale anisotropies of the innermost SN ejecta, which interact gravitationally with the proto-NS and accelerate the nascent NS on a timescale of several seconds (e.g. Janka 2012; Wongwathanarat et al. 2013). For the entire population of NSs, the range of required kick velocity magnitudes extends basically from a few 10km s-1 to more than 1000km s-1, in order to explain both the existence of NSs residing inside globular clusters (which have small escape velocities, vesc < 50km s-1) as well as bow shocks and SN remnants associated with high-velocity pulsars. However, when considering only young NSs in the Galactic disk the study by Hobbs et al. (2005) is interesting; it revealed that the velocities of young (<3Myr) radio pulsars are well described by a single Maxwellian distribution with a three-dimensional mean speed of ~400km s-1. Furthermore, there are no detections of any low-velocity (v⊥ < 60kms-1) single radio pulsars with a characteristic age, τ < 1Myr. These facts indicate that NSs which formed recently in young stellar environments (the Galactic disk) received large kicks and that iron core-collapse SNe of type II and type Ib/c therefore, in general, result in these large kicks.
On the other hand, about half of the approximately 300 known MSPs are detected in globular clusters (Ransom et al. 2005; Freire et al. 2008). Obviously, pulsars retained in globular clusters (GCs) cannot have formed with large kicks since these clusters have small escape velocities, except in a few rare cases where an isolated low-velocity pulsar could form in a disrupted binary involving a large kick with a finetuned direction (cf. Fig. 5 in Tauris & Takens 1998). It is therefore tempting to believe that many of these MSPs in GCs were not formed by iron core-collapse SNe.
2.1.1. Electron capture SNe
It seems clear that the lowest mass SN progenitors may not evolve all the way to form iron cores (see Langer 2012, for a recent review on pre-SN evolution of massive single and binary stars). The final fate of these stars with ONeMg cores is an electron-capture SN (EC SN), i.e. a collapse triggered by loss of pressure support owing to the sudden capture of electrons by neon and/or magnesium nuclei (e.g. Nomoto 1984; Wheeler et al. 1998). Work by Poelarends et al. (2008) shows that the initial mass range for EC SNe is quite narrow, only about 0.25 M⊙ wide, which would imply that some 4% of all single-star SNe would be of this type. However, it has been suggested by Podsiadlowski et al. (2004) that EC SNe could occur in close binaries for stars with masses between 8 − 11 M⊙ since these stars lose their envelopes via mass transfer before entering the AGB phase and thus avoid the dredge-up and the consequent erosion of the CO core by this process. Therefore, these stars undergo EC SNe rather than becoming ONeMg WDs, the likely outcome of most single stars of the same mass. Furthermore, these authors argue that EC SNe lead to prompt explosions (rather than slow, delayed neutrino-driven explosions) that naturally produce NSs with low-velocity kicks (see also van den Heuvel 2004, who proposed similar ideas). The idea of different NS kick magnitudes comes from the discovery of two classes of Be/X-ray binaries with significantly different orbital eccentricities (Pfahl et al. 2002). Furthermore, the low eccentricities and the low masses (~1.25 M⊙) of second-born NSs in double NS systems supports this picture (Schwab et al. 2010, and references therein).
2.2. The role of young NSs in GCs
In Table 1 we list a number of apparently young NSs (characterized by slow spin and relatively high B-fields) that are found in GCs. The lifetime as an observable radio source is of the order of 100 Myr for a young (i.e. non-recycled) pulsar. Therefore, if these NSs had formed via iron core-collapse SNe their existence in GCs would not only be unlikely for kinematic reasons (as explained above), it would simply be impossible given that the stellar progenitor lifetimes of SNe II and SNe Ib/c are less than a few 10 Myr, much shorter than the age of the many Gyr old stellar populations in GCs. Similarly, the nuclear evolution timescales of stars undergoing EC SNe is of the order of 20 − 50Myr, which is still short compared to the age of GCs, and for this reason also EC SNe cannot explain the existence of young NSs in GCs today. It is therefore clear that these NSs in GCs, if they are truly young2, are formed via a different channel.
2.2.1. A strong link to AIC – first piece of evidence
An AIC event is not very different from an EC SN and it is therefore expected that also NSs formed via AIC will receive a small kick (if any significant kick at all). For this reason formation via AIC could explain the many NSs in GCs and, more importantly, also the young ages of some of these NSs. As we shall demonstrate in this work, pre-AIC binaries may, in some cases, reach ages exceeding 10 Gyr before a low-mass giant companion star initiates Roche-lobe overflow (RLO) leading to the AIC event. Therefore, we would expect ongoing AIC events, and thus formation of newborn NSs, in GCs even today.
2.2.2. NS formation via the merger of two massive WDs?
For the sake of completeness, we also mention that the merger of two massive WDs may also produce a pulsar (Saio & Nomoto 1985, 2004). This could be an alternative way of producing young pulsars in an old stellar population like a GC. Even binary pulsars may be produced this way in a GC, since in a dense environment a single produced NS can capture a companion star later on (Ransom et al. 2005). It is more difficult for this scenario to produce MSPs in binaries in the Galactic disk. This scenario would not only require an initial triple system origin, which is somewhat rare in the Galactic disk (although recent work by Rappaport et al. (2013) suggests that at least 20% of all close binaries have tertiary companions), it would also require the remaining binary orbit to survive the dynamical effects of the merger event. However, it should be noted that the merging double CO WD event is also a key scenario (the so-called double-degenerate scenario) suggested as a progenitor of SNe Ia (cf. Webbink 1984; Iben & Tutukov 1984; Yoon et al. 2007; van Kerkwijk et al. 2010; Pakmor et al. 2012).
Neutron stars that are candidates for being formed via AIC in a globular cluster (a–d) or in the Galactic disk (e–h), respectively.
2.3. AIC candidates in the Galactic disk
The evidence for AIC is found not only in GCs. In Table 1 we list a number of Galactic disk binary NS systems which are postulated candidates for having formed via AIC. A common feature of these NSs is a slow spin and a relatively high B-field and an ultra-light (≤0.10 M⊙) companion star in a close orbit. The idea that the origin of some high B-field, slow spinning NSs (e.g. 4U 1626−67, Her X−1, and PSR B0820+08) is associated with AIC was originally suggested by Taam & van den Heuvel (1986). Although it was believed at that time that B-fields decay spontaneously on a timescale of only 50 Myr (and therefore these NSs could not have much larger ages), many of these sources remain good candidates for AIC today even though it has been demonstrated that pulsar B-fields can remain high on much longer timescales (Kulkarni 1986; Bhattacharya et al. 1992). One reason why these NS systems remain good AIC candidates is the very small masses of their companion stars which indicate that a significant amount of material (0.5 − 1.0 M⊙) was transfered towards the compact object3. The paradox is therefore that these NSs still have high B-fields and slow spins even though a significant mass transfer has occurred (see below).
2.3.1. The role of accretion-induced B-field decay in NSs
There is solid observational evidence that the surface B-field strengths of NSs decrease with accretion (Taam & van den Heuvel 1986; Shibazaki et al. 1989; van den Heuvel & Bitzaraki 1994, 1995). The exact mechanism for this process is still unknown. It may be related to decay of crustal fields by ohmic dissipation and diffusion from heating via nuclear processing of accreted material (Romani 1990; Geppert & Urpin 1994; Konar & Bhattacharya 1997), burial (screening) of the field (Zhang 1998; Cumming et al. 2001; Payne & Melatos 2007), or decay of core fields due to flux tube expulsion from the superfluid interior induced by rotational slow-down in the initial phases of mass accretion (Srinivasan et al. 1990); see also review by Bhattacharya (2002). Even a small amount of material accreted may lead to significant B-field decay, contradicting the observational evidence that these binary NSs have accreted large amounts of material.
2.3.2. A strong link to AIC – second piece of evidence
A possible solution to the above-mentioned paradox of observing close binaries with ultra-light companions orbiting high B-field NSs, would be if these NSs were formed recently via AIC during the very final stages of the mass-transfer process in a binary.
The associated required finetuning of the AIC event to occur near the termination of the mass-transfer phase is important for preventing accretion of significant amounts of matter after the formation of the NS (resulting in low B-fields and fast spin). This finetuning problem will be investigated further in this paper. We note that the slow spins are expected from efficient loss of rotational energy due to the emission of magnetodipole waves from these high B-field NSs.
In Sect. 7.5.1 we return to additional discussions of observational evidence for AIC in view of our theoretical calculations, and also comment on a handful of recycled radio pulsars in the Galactic disk with puzzling characteristics.
3. Numerical methods and physical assumptions of AIC
The numerical models presented in this work are divided into two parts: 1) evolution prior to AIC and 2) post-AIC LMXB evolution. Both parts are computed with a binary stellar evolution code originally developed by Braun (1997) on the basis of a single-star code (Langer 1998, and references therein). It is a one-dimensional implicit Lagrangian code which solves the hydrodynamic form of the stellar structure and evolution equations (Kippenhahn & Weigert 1990). The evolution of the donor star, the mass-transfer rate, and the orbital separation are computed simultaneously through an implicit coupling scheme (see also Wellstein & Langer 1999) using the Roche-approximation in the formulation of Eggleton (1983). To compute the mass-transfer rate, we use the prescription of Ritter (1988). In Sect. 5.3 we discuss the limitations of this description in wide-orbit LMXBs with giant donor stars. We employ the radiative opacities of Iglesias & Rogers (1996), which we interpolated in tables as function of density, temperature, and chemical element mass fractions, including carbon and oxygen. For the electron conduction opacity, we follow Hubbard & Lampe (1969) in the non-relativistic case, and Canuto (1970) in the relativistic case. The stellar models are computed using extended nuclear networks including the PP I, II, and III chains and the four CNO-cycles. In our default models we assumed a mixing-length parameter of α = l/Hp = 1.5 (Langer 1991) and a core convective overshooting parameter of δov = 0.10. We tested several models using α = l/Hp = 2.0 which resulted in only slightly larger final WD masses (~1%) orbiting recycled pulsars in somewhat larger orbits (up to ~3% increase in Porb).
If the accreting ONeMg WD reached the limiting Chandrasekhar mass for a rigidly rotating WD (i.e. MChan = 1.48 M⊙, e.g. Yoon & Langer 2005) we assumed it collapsed to form a NS. Differential rotation can persist if the timescale of angular momentum transport is smaller than the accretion timescale in accreting WDs, and leads to a critical mass that is significantly higher than the canonical Chandrasekhar mass (e.g. Yoon & Langer 2004). However, magnetic torques resulting from the Spruit-Tayler dynamo may enforce nearly rigid rotation in accreting WDs with the considered accretion rates in this study. Further research is needed to verify this.
The WD collapse was modelled both with and without a momentum kick imparted to the newborn NS. Although AIC is generally believed to result in no kick, or possibly a small kick, we applied three different kick values (w = 0,50,450 km s-1) to the newborn NS. Given that the physics behind the kick mechanism is still unclear, we have included a few extra models with a large kick of 450km s-1 to probe the extreme boundary conditions of our calculations. We solved for the combined effects of sudden mass loss and imparted momentum kick on the orbital dynamics following Hills (1983). In all cases we assumed the mass equivalent of 0.20 M⊙ was lost as released gravitational binding energy yielding a post-AIC NS gravitational mass of 1.28 M⊙. The post-AIC LMXB evolution was followed using the same computer code (see also Tauris et al. 2011, 2012, for additional details). For a more general discussion of MSP formation from LMXBs we refer to e.g. Ergma et al. (1998), Tauris & Savonije (1999), Podsiadlowski et al. (2002), Deloye (2008).
3.1. Accretion onto a white dwarf
The mass-transfer process and the physics of accretion onto a WD has been described in a large number of papers, e.g. Whelan & Iben (1973), Nomoto & Sugimoto (1977), Nomoto (1982), Prialnik & Kovetz (1995), Iben & Tutukov (1996), Li & van den Heuvel (1997), Hachisu et al. (1999), Langer et al. (2000), Livio (2000), Han & Podsiadlowski (2004), Yoon & Langer (2003, 2004), Nomoto et al. (2007), and more recently in Hachisu et al. (2012), Wheeler (2012), Idan et al. (2012), Starrfield et al. (2012), Newsham et al. (2013), Denissenkov et al. (2013), Ma et al. (2013). Most of these papers aim at investigating progenitors of type Ia supernovae (SN Ia) which are important for cosmology studies of the accelerating Universe (e.g. Riess et al. 1998; Perlmutter et al. 1999). In these progenitor systems an accreting CO WD reaches the Chandrasekhar limit and explodes. Observationally, these systems manifest themselves as cataclysmic variables (Hellier 2001), symbiotic systems (Kenyon 1986), and supersoft X-ray sources (van den Heuvel et al. 1992; Kahabka & van den Heuvel 1997), depending on the companion star mass, its evolutionary status, and the mass-transfer rate. It should be noted that the classification scheme overlaps somewhat on certain aspects. The cataclysmic variables (CVs) can be further subdivided into several classes: (classical) novae, recurrent novae, dwarf novae, polars, AM CNn stars etc., again depending on the nature of the companion star, the orbital separation, as well as the magnetic field strength of the accreting WD and accretion disk morphology.
The classical novae have only been reported to erupt once whereas the recurrent novae usually erupt every one or two decades. The symbiotic variable star binaries have low-mass red giant donors which transfer mass at a fairly low rate via (beginning atmospheric) RLO. They undergo nova-like outbursts which last for a few decades before decaying back to their original luminosity. The luminous persistent supersoft X-ray sources, on the other hand, display luminosities between 1036−1039 erg s-1 revealing high mass-transfer rates of the order of 10-7 M⊙ yr-1. These systems often have a more massive main-sequence donor star undergoing thermal timescale mass transfer.
It is generally believed that the accreting WDs in supersoft X-ray sources can grow in mass by accretion since the thermonuclear fusion of accreted hydrogen can be fairly stable with these high accretion rates, in contrast to the case of nova systems where nova explosions (caused by a violent ignition in a thin shell of degenerate hydrogen) may erode the WDs (Wiescher et al. 1986; Patterson et al. 2013). The supersoft X-ray sources are therefore believed to represent progenitors of SNe Ia, because many of these systems may produce a Chandrasekhar mass CO WD. However, existing multicycle computations of hydrogen accretion onto massive WDs at a high rate are still somewhat controversial. In a recent study Idan et al. (2012) showed that the accumulated helium is completely lost in strong helium flashes, thereby making SN Ia and AIC impossible, whereas another study by Newsham et al. (2013) concluded that WDs continue to grow toward the Chandrasekhar limit.
A number of numerical simulations show that when a CO WD approaches the Chandrasekhar limit with accretion rates of the order of ṀWD ≃ 10-7 − 10-6 M⊙ yr-1, a thermonuclear-runaway caused by carbon burning can occur at central densities of about ρc = 2 − 5 × 109g cm-3 (e.g. Nomoto et al. 1984; Yoon & Langer 2003; Lesaffre et al. 2006), which may result in a SN Ia explosion. In case an ONeMg WD mass grows to the Chandrasekhar limit, electron-captures onto 24Mg and 20Ne make the central density increase to about 1010 g cm-3 before oxygen ignites at the center (Miyaji et al. 1980; Miyaji & Nomoto 1987; Nomoto 1987). The consequent oxygen deflagration with this high density cannot lead to a thermonuclear explosion because of very rapid electron-captures onto heavy elements produced by the oxygen burning (Miyaji et al. 1980; Timmes & Woosley 1992). Therefore, a NS is the most likely outcome in the case of the collapse of an ONeMg WD.
Although it is generally believed that accreting CO WDs reaching the Chandrasekhar mass limit lead to a SNe Ia, and that accreting ONeMg WDs reaching this limit undergo AIC and produce NSs, the outcome could in some cases be the opposite – see Sect. 7.2 for further discussion.
 |
Fig. 1 Accretion window of the WD, the corresponding critical mass-transfer rates, and our assumed mass-accumulation fractions, ηH, here calculated with a hydrogen abundance of X = 0.70 of the accreted matter (see text). |
3.1.1. Dependence on mass-transfer rates
The response of the WD to mass transfer from the donor star depends on the mass-transfer rate, |Ṁ2|. In this work we assume that the WD receives (but does not necessarily accrete) mass at the same rate as it is lost from the donor star, |Ṁ2|. White dwarfs which accrete faster than the rate at which their cores can grow (Ṁup) will puff up their envelope to giant star dimensions (see below). If the WD envelope does expand to such huge radii it will engulf the donor star and the system is likely to evolve through a common envelope (CE) and spiral-in phase (Paczyński 1976; Iben & Livio 1993). The relevant critical mass-transfer rates for our work are (see Fig. 1):
 where we have adopted the following ad hoc condition:
where we have adopted the following ad hoc condition: 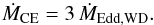 (1)The Eddington accretion limit is found by equating the outward radiation pressure to the gravitational force per unit area acting on the nucleons of the accreted plasma. The radiation pressure (from photons that scatter on plasma electrons) is generated from both nuclear burning at the WD surface and from the release of gravitational binding energy of the accreted material. The total energy production is given by: L = (ϵnuc + ϵacc) ṀWD, where ṀWD is the accretion rate of the WD and ϵnuc and ϵacc denote the specific energy production from nuclear burning at the WD surface and release of gravitational binding energy, respectively. Hence, the Eddington accretion limit depends on the chemical composition of the accreted material and on the mass of the WD and is roughly given by:
(1)The Eddington accretion limit is found by equating the outward radiation pressure to the gravitational force per unit area acting on the nucleons of the accreted plasma. The radiation pressure (from photons that scatter on plasma electrons) is generated from both nuclear burning at the WD surface and from the release of gravitational binding energy of the accreted material. The total energy production is given by: L = (ϵnuc + ϵacc) ṀWD, where ṀWD is the accretion rate of the WD and ϵnuc and ϵacc denote the specific energy production from nuclear burning at the WD surface and release of gravitational binding energy, respectively. Hence, the Eddington accretion limit depends on the chemical composition of the accreted material and on the mass of the WD and is roughly given by: 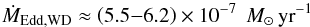 (2)for the WDs studied in this work.
(2)for the WDs studied in this work.
The value of ṀCE is probably the largest uncertainty in our modelling. The rationale of even considering an accretion rate |Ṁ2| > ṀEdd,WD is that the WD may drive a strong wind in a bipolar outflow which may prevent the WD envelope from otherwise expanding into giant star dimensions (Nomoto et al. 1979b). Many previous studies of accreting WDs have adapted the optically thick wind model of Kato & Iben (1992) and Kato & Hachisu (1994), without any restrictions on |Ṁ2| (see Cassisi et al. 1998; Langer et al. 2000, for a critique of this assumption). Given the uncertainties regarding the validity of this model, we adopt a maximum allowed mass-transfer rate limit of |Ṁ2| = ṀCE = 3 ṀEdd,WD. For most of our models we stopped the calculations if |Ṁ2| > ṀCE (assuming the system evolved into a CE and merged). To test the dependence of this limit we also computed some models by allowing ṀCE = 10 ṀEdd,WD for comparison. As we shall see, the role of adapting the optically thick wind model or not has important consequences for the progenitor parameter space leading to AIC. Constraints of the wind mass loss from an accreting WD can be determined directly from radio observations of SN Ia remnants (Chomiuk et al. 2012). Hence, there is some hope that future observations can clarify the situation.
If a wind is driven from the WD (when |Ṁ2| > Ṁup) we calculate its mass-accumulation fraction using: ηH = Ṁup/ |Ṁ2| to restrict the accretion rate to a maximum of Ṁup. This value represents the upper limit for steady shell hydrogen burning of a WD and can be estimated from the growth rate of the degenerate core in red giant stars undergoing hydrogen shell burning by applying the relation between core mass and luminosity (Iben & Tutukov 1989). As an example, Hachisu & Kato (2001) found:  (3)which is valid for a hydrogen mass fraction X ≥ 0.10. There is a variety of similar expressions for this critical limit in the literature (e.g. Nomoto 1982; Hachisu et al. 1996, 1999; Nomoto et al. 2007). However, they do not differ by much and our results are stable against these minor variations. (We note that Ṁup ≃ ṀEdd,WD).
(3)which is valid for a hydrogen mass fraction X ≥ 0.10. There is a variety of similar expressions for this critical limit in the literature (e.g. Nomoto 1982; Hachisu et al. 1996, 1999; Nomoto et al. 2007). However, they do not differ by much and our results are stable against these minor variations. (We note that Ṁup ≃ ṀEdd,WD).
The minimum value for steady hydrogen shell burning is given by Nomoto (1982): 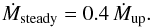 (4)Although the hydrogen burning is not steady below this limit, the shell flashes are found to be weak for accretion rates just slightly below the limit. Following Hachisu et al. (1999) we therefore assume ηH = 1 in the entire interval: Ṁaccu < |Ṁ2| < Ṁup, where
(4)Although the hydrogen burning is not steady below this limit, the shell flashes are found to be weak for accretion rates just slightly below the limit. Following Hachisu et al. (1999) we therefore assume ηH = 1 in the entire interval: Ṁaccu < |Ṁ2| < Ṁup, where 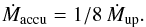 (5)If the mass-accretion rate is below Ṁaccu violent shell flashes and nova outbursts cannot be avoided and thus the WD is prevented from increasing its mass (i.e. ηH = 0), or may even erode.
(5)If the mass-accretion rate is below Ṁaccu violent shell flashes and nova outbursts cannot be avoided and thus the WD is prevented from increasing its mass (i.e. ηH = 0), or may even erode.
Following hydrogen burning the helium is processed into carbon and oxygen. The mass accumulation efficiency in helium shell flashes was studied in detail by Kato & Hachisu (2004). We have adapted their mass accumulation efficiencies for helium burning, ηHe into our code. The long-term effective mass-accretion rate of the WD is therefore given by: 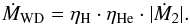 (6)For accretion of pure helium we used ṀWD = ηHe· |Ṁ2| and
(6)For accretion of pure helium we used ṀWD = ηHe· |Ṁ2| and 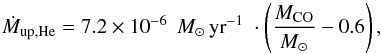 (7)where MCO is the mass of the CO core of the helium donor star (Nomoto 1982). According to Jose et al. (1993), ηHe might be somewhat smaller for direct accretion of helium, which leads to stronger shell flashes, compared to the case where helium is accumulated via multiple cycles of hydrogen burning (i.e. double shell burning).
(7)where MCO is the mass of the CO core of the helium donor star (Nomoto 1982). According to Jose et al. (1993), ηHe might be somewhat smaller for direct accretion of helium, which leads to stronger shell flashes, compared to the case where helium is accumulated via multiple cycles of hydrogen burning (i.e. double shell burning).
For recent discussions on the WD growth rate and the dependence on the WD mass and the mixing of the accreted material, see e.g. Denissenkov et al. (2013) and Newsham et al. (2013).
3.2. Orbital dynamics
We consider close interacting binary systems which consist of a non-degenerate (evolved) donor star and a compact object, in our case initially a massive WD and later on, in the case of an AIC event, a NS. When the donor star fills its Roche lobe, any exchange and loss of mass from such an X-ray binary will also lead to alterations of the orbital dynamics, via modifications in the orbital angular momentum, and hence changes in the size of the critical Roche-lobe radius of the donor star. The stability of the mass-transfer process therefore depends on how these two radii evolve (i.e. the radius of the star and its Roche-lobe radius). The various possible modes of mass exchange and mass loss include, for example, fast wind mass loss (Jeans mode), Roche-lobe overflow (with or without isotropic re-emission), and common envelope evolution (e.g. van den Heuvel 1994; Soberman et al. 1997, and references therein). The RLO mass transfer can be initiated while the donor star is still on the main sequence (Case A RLO), during hydrogen shell burning (Case B RLO), or during helium shell burning (Case C RLO). The corresponding evolutionary timescales for these different cases will in general proceed on a nuclear, thermal, or dynamical timescale, respectively, or a combination thereof. This timescale is important for the amount of mass that can be accreted and for the extent to which the NS produced in the AIC can be recycled after its formation.
The dynamical evolution of a binary system can be found by solving for the changes in the orbital separation, a. The orbital angular momentum of a circular binary system is given by: Jorb = μ Ω a2, where μ is the reduced mass and the orbital angular velocity is: 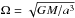 . A simple logarithmic differentiation of the orbital angular momentum equation yields the rate of change in orbital separation:
. A simple logarithmic differentiation of the orbital angular momentum equation yields the rate of change in orbital separation: 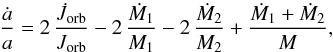 (8)where the two stellar masses are given by M1 and M2, the total mass is M = M1 + M2, and the total change in orbital angular momentum per unit time is given by:
(8)where the two stellar masses are given by M1 and M2, the total mass is M = M1 + M2, and the total change in orbital angular momentum per unit time is given by: 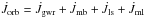 . These four terms represent gravitational wave radiation, magnetic braking, other spin-orbit couplings, and mass loss, respectively (e.g. Tauris & van den Heuvel 2006, and references therein).
. These four terms represent gravitational wave radiation, magnetic braking, other spin-orbit couplings, and mass loss, respectively (e.g. Tauris & van den Heuvel 2006, and references therein).
In this work we adopt the so-called isotropic re-emission mode4 for modelling the mass-transfer and the mass loss from the binary (e.g. Bhattacharya & van den Heuvel 1991; Soberman et al. 1997). We let the mass ratio between the donor star (M2) and the accretor (M1) be denoted by q = M2/M1. Assuming that the direct wind mass loss of the donor star is negligible compared to the RLO mass-transfer rate from the donor star, |Ṁ2|, and ignoring mass stored in a circumbinary torus, one can show that a binary system always widens (ȧ > 0) as a result of mass transfer if q < 1. Similarly, a binary always decreases (ȧ < 0) if 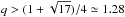 , irrespective of the amount of mass ejected from the vicinity of the accretor (e.g. see Sect. 16.4.3 in Tauris & van den Heuvel 2006). This fact is worth remembering when we analyse our results.
, irrespective of the amount of mass ejected from the vicinity of the accretor (e.g. see Sect. 16.4.3 in Tauris & van den Heuvel 2006). This fact is worth remembering when we analyse our results.
In our calculations we have ignored any changes in Jorb due to magnetic braking or any other tidal spin-orbit interactions. Magnetic braking is only known to operate efficiently in low-mass stars (≲1.5 M⊙) which have convective envelopes. As we shall see, our calculations show that only main-sequence donor stars with masses in the range 1.4 − 2.6 M⊙ (depending on metallicity) transfer mass at the rates needed for AIC events to take place. Therefore, to be consistent with all our calculations, we have not included magnetic braking in the very few borderline cases. (These low-mass donors all have low-metallicities resulting in some stability against convective envelopes.) Our code includes gravitational wave radiation by calculating  and correcting for it. However, for these AIC progenitor systems the RLO mass-transfer timescales are always significantly shorter than the timescales on which gravitational wave radiation is important.
and correcting for it. However, for these AIC progenitor systems the RLO mass-transfer timescales are always significantly shorter than the timescales on which gravitational wave radiation is important.
In all our calculations we assumed an initial (ONeMg) WD mass of MWD = 1.20 M⊙ prior to accretion. As mentioned earlier, for these calculations the WD is simply treated as a point mass.
 |
Fig. 2 Evolutionary tracks in the (Porb,M2)-plane. The initial system configurations are: M2 = 2.6 M⊙, Porb = 1.0 days (red tracks) and M2 = 2.2 M⊙, Porb = 2.5 days (blue tracks). The ONeMg WD has an initial mass of 1.20 M⊙ and grows to 1.48 M⊙ when the AIC occurs. After the AIC three tracks were computed for each system depending on the kick velocity applied in the AIC. Here we applied w = 0, w = 50kms-1 (φ = θ = 0°), and w = 450kms-1 (φ = 107° and θ = 90°) resulting in different values of Porb for the post-AIC system. In two post-AIC cases presented here, and in general if the donor star is quite evolved by the time it refills its Roche lobe (i.e. because the post-AIC Porb is large) and if the donor star is significantly more massive than the newborn NS (1.28 M⊙), the RLO becomes dynamically unstable and the system evolves through a common envelope (marked by CE). |
3.2.1. The dynamical effect of the AIC on the orbit
If the WD mass reached 1.48 M⊙ we assumed that the WD was subject to instantaneous AIC. The effect of sudden mass loss in a binary has been studied in detail by Hills (1983) for bound systems, and by Tauris & Takens (1998) for disrupted systems. Assuming a circular pre-AIC orbit we here follow Hills (1983) to find the changes of the binary orbital parameters. The change of the binary semi-major axis, as a result of an asymmetric AIC, is given by: ![\begin{equation} \frac{a}{a_0}=\left[ \frac{1-(\Delta M/M_0)}{1-2(\Delta M/M_0)-(w/v_{\rm c})^2-2\cos\theta\;(w/v_{\rm c})} \right] , \label{eq:kick} \end{equation}](/articles/aa/full_html/2013/10/aa21662-13/aa21662-13-eq138.png) (9)where a0 is the pre-AIC semi-major axis (radius), a the post-AIC semi-major axis, ΔM = 0.20 M⊙ the effective mass loss during the AIC when the 1.48 M⊙ WD is compressed to a NS with a gravitational mass of 1.28 M⊙ (Zeldovich & Novikov 1971), M0 = MWD + M2 the pre-AIC total mass,
(9)where a0 is the pre-AIC semi-major axis (radius), a the post-AIC semi-major axis, ΔM = 0.20 M⊙ the effective mass loss during the AIC when the 1.48 M⊙ WD is compressed to a NS with a gravitational mass of 1.28 M⊙ (Zeldovich & Novikov 1971), M0 = MWD + M2 the pre-AIC total mass, 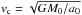 the pre-AIC orbital velocity of the collapsing WD in a reference fixed on the companions star, w the magnitude of the kick velocity, and θ the angle between the kick velocity vector, w and the pre-AIC orbital velocity vector, vc. The post-AIC eccentricity is given by:
the pre-AIC orbital velocity of the collapsing WD in a reference fixed on the companions star, w the magnitude of the kick velocity, and θ the angle between the kick velocity vector, w and the pre-AIC orbital velocity vector, vc. The post-AIC eccentricity is given by: 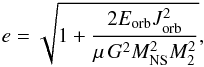 (10)where the post-AIC orbital energy of the system is given by: Eorb = − GMNSM2/2a, and the orbital angular momentum is given by:
(10)where the post-AIC orbital energy of the system is given by: Eorb = − GMNSM2/2a, and the orbital angular momentum is given by: 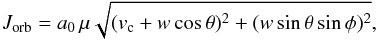 (11)where μ is the post-AIC reduced mass and φ is the angle between the projection of the kick velocity vector onto a plane perpendicular to the pre-AIC velocity vector of the WD and the pre-AIC orbital plane. We neglected any shell impact effects on the companion star since the amount of material ejected in an AIC event is expected to be negligible. Even for SN Ib/c where a significant shell is ejected, the impact effect on the orbital dynamics is small if the pre-SN separation is larger than a few R⊙ (Tauris & Takens 1998).
(11)where μ is the post-AIC reduced mass and φ is the angle between the projection of the kick velocity vector onto a plane perpendicular to the pre-AIC velocity vector of the WD and the pre-AIC orbital plane. We neglected any shell impact effects on the companion star since the amount of material ejected in an AIC event is expected to be negligible. Even for SN Ib/c where a significant shell is ejected, the impact effect on the orbital dynamics is small if the pre-SN separation is larger than a few R⊙ (Tauris & Takens 1998).
Following the AIC we checked if the post-AIC periastron separation, a(1 − e) is smaller than the radius of the companion star, R2. In that case we assumed that the system merges. The post-AIC orbit is expected to be circularized with time and we therefore assumed that the tidal interactions reduced the semi-major axis by a factor of (1 − e2) in order to conserve Jorb. When no momentum kick was added (w = 0) to the newborn NS, the relation between post-AIC orbital separation (including the subsequent effect of tidal circularization), acirc and the pre-AIC orbital radius, a0 is simply given by (Verbunt et al. 1990; Bhattacharya & van den Heuvel 1991): 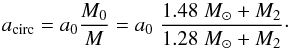 (12)Since post-AIC evolution calculations also require a significant amount of computational time, and each AIC event can lead to a large set of possible parameter outcomes for (w,θ,φ), we have restricted ourselves to those cases which best probe the extreme cases for the post-AIC evolution with respect to orbital periods and systemic recoil velocities resulting from the AIC event.
(12)Since post-AIC evolution calculations also require a significant amount of computational time, and each AIC event can lead to a large set of possible parameter outcomes for (w,θ,φ), we have restricted ourselves to those cases which best probe the extreme cases for the post-AIC evolution with respect to orbital periods and systemic recoil velocities resulting from the AIC event.
3.3. Post-AIC LMXB evolution
The evolution of post-AIC binaries is, in principle, similar to normal LMXB evolution (i.e. a donor star which transfers matter and angular momentum to an accreting NS). For this recycling process we follow Tauris & Savonije (1999) and Tauris et al. (2012) for tracking the evolution of the LMXB (see also Sect. 3.2 below). The accretion rate onto the NS is assumed to be Eddington limited and is given by: ![\begin{equation} \dot{M}_{\rm NS} = \left( |\dot{M}_2| -\max \left[|\dot{M}_2|-\dot{M}_{\rm Edd}\;,0\right] \right)\cdot e_{\rm acc}\cdot k_{\rm def} , \label{MdotNS} \end{equation}](/articles/aa/full_html/2013/10/aa21662-13/aa21662-13-eq159.png) (13)where eacc is the fraction of matter transfered to the NS which actually ends up being accreted and remains on the NS, and kdef is a factor that expresses the ratio of gravitational mass to rest mass of the accreted matter (depending on the equation-of-state of supranuclear matter kdef ≃ 0.85 − 0.90; e.g. Lattimer & Prakash 2007). Here we assumed eacc·kdef = 0.30. Our motivation for this value is the increasing evidence of inefficient accretion in LMXBs, even in close systems where the mass-transfer rate is expected to be sub-Eddington (|Ṁ2| < ṀEdd) at all times (e.g. Jacoby et al. 2005; Antoniadis et al. 2012). Possible mechanisms for inefficient accretion include propeller effects, accretion disc instabilities, and direct irradiation of the donor’s atmosphere from the pulsar (Illarionov & Sunyaev 1975; van Paradijs 1996; Dubus et al. 1999). For the post-AIC NS, we calculated the Eddington mass-accretion rate using:
(13)where eacc is the fraction of matter transfered to the NS which actually ends up being accreted and remains on the NS, and kdef is a factor that expresses the ratio of gravitational mass to rest mass of the accreted matter (depending on the equation-of-state of supranuclear matter kdef ≃ 0.85 − 0.90; e.g. Lattimer & Prakash 2007). Here we assumed eacc·kdef = 0.30. Our motivation for this value is the increasing evidence of inefficient accretion in LMXBs, even in close systems where the mass-transfer rate is expected to be sub-Eddington (|Ṁ2| < ṀEdd) at all times (e.g. Jacoby et al. 2005; Antoniadis et al. 2012). Possible mechanisms for inefficient accretion include propeller effects, accretion disc instabilities, and direct irradiation of the donor’s atmosphere from the pulsar (Illarionov & Sunyaev 1975; van Paradijs 1996; Dubus et al. 1999). For the post-AIC NS, we calculated the Eddington mass-accretion rate using: 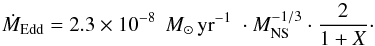 (14)In Sect. 4.3.3 we specify a relation between the amount of mass accreted and the final pulsar spin period.
(14)In Sect. 4.3.3 we specify a relation between the amount of mass accreted and the final pulsar spin period.
3.4. Complete evolution in the (Porb,M2)-plane
To demonstrate the orbital evolution: 1) during pre-AIC mass transfer, followed by 2) post-AIC mass transfer in an LMXB, and to show the effect of possible kicks associated with the AIC, we have plotted complete evolutionary tracks in the (Porb,M2)-plane in Fig. 2. The two donor stars in these examples (M2 = 2.6 M⊙ and M2 = 2.2 M⊙) are both more massive than the accreting ONeMg WD (initially with mass ratio, q ~ 2.) This explains why both systems decrease in Porb prior to the AIC event. At the moment of the AIC the orbits widen instantaneously as a consequence of the sudden mass loss (cf. Sect. 3.2.1). The larger the kick, w, the larger the post-AIC Porb becomes at which the donor star refills its Roche lobe and continues mass transfer to the newborn NS in the LMXB source. The final products are binary MSPs with He WDs. During the LMXB phase the orbit changes from a converging system to a diverging system when the mass ratio inverses (the exact value depends on the mass-transfer rate, cf. Sect. 3.2).
It is interesting that for the original 2.2 M⊙ donor star, the post-AIC mass transfer is not dynamically stable if the AIC was asymmetric (i.e. if w = 50 km s-1 or w = 450km s-1). In this case the post-AIC binary becomes wide enough that the donor star develops a deep convective envelope before refilling its Roche lobe. The result is that the subsequent mass-transfer stage leads to excessive mass-transfer rates and thus to the formation of a CE. We did not follow the evolution of these systems further, although it is possible, in principle, that some of the donor star envelopes would be loosely enough bound to allow for ejection during spiral-in and thereby leave behind a mildly recycled pulsar orbiting a WD in a tight orbit. We return to this possibility in Sect. 7.5.
4. AIC in systems with main-sequence star donors
In the following three sections we present our results of AIC calculations in systems with main-sequence, giant, and helium star donors, respectively. We evolved a total of 240 binary systems. Key parameters from 36 examples of complete calculations (i.e. both pre-AIC and post-AIC LMXB computations leading to a recycled binary pulsar) are given in Table 2. Model names beginning with MS and MZ refer to main-sequence donor stars at solar metallicity (Z = 0.02) and Z = 0.001, respectively; giant donor star models are denoted by GS (or GSZ for Z = 0.001), and helium donor star models are denoted by He. The given parameters for each model are the following: 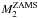 and
and 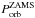 refer to initial donor star mass and orbital period; tRLO is the age of the donor star when it initiates RLO; and Xc is its central hydrogen content at that time; ΔtCV is the duration of the mass-transfer phase until the AIC event; and
refer to initial donor star mass and orbital period; tRLO is the age of the donor star when it initiates RLO; and Xc is its central hydrogen content at that time; ΔtCV is the duration of the mass-transfer phase until the AIC event; and 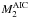 and
and 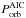 are the donor star mass and the orbital period at the moment of the AIC. When a momentum kick (w > 0) is added to the newborn NS, its magnitude and direction are given. The resulting systemic recoil velocity of each post-AIC system is given by vsys. As a result of the AIC the system temporarily detaches. The time it takes until the donor star refills its Roche lobe is denoted by Δtdetach, and
are the donor star mass and the orbital period at the moment of the AIC. When a momentum kick (w > 0) is added to the newborn NS, its magnitude and direction are given. The resulting systemic recoil velocity of each post-AIC system is given by vsys. As a result of the AIC the system temporarily detaches. The time it takes until the donor star refills its Roche lobe is denoted by Δtdetach, and 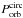 is the orbital period at that time (after circularization). The duration of the subsequent post-AIC LMXB phase is given by ΔtLMXB. Finally, the parameters MWD,
is the orbital period at that time (after circularization). The duration of the subsequent post-AIC LMXB phase is given by ΔtLMXB. Finally, the parameters MWD, 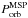 , MNS, ΔMNS, Pspin, and ttotal denote the WD mass, the orbital period, the NS mass, the amount of mass accreted by the NS during the post-AIC mass transfer, the final spin period of the recycled pulsar, and the total age of the binary system at this end point.
, MNS, ΔMNS, Pspin, and ttotal denote the WD mass, the orbital period, the NS mass, the amount of mass accreted by the NS during the post-AIC mass transfer, the final spin period of the recycled pulsar, and the total age of the binary system at this end point.
Summary of selected systems which evolved successfully to AIC and later produced recycled pulsars.
For hydrogen-rich donors we have initiated our calculations assuming a ZAMS star orbiting an ONeMg WD. The error in placing the companion star on the ZAMS, and neglecting the evolution of this star while the ONeMg WD forms, is not very significant. As we shall see in a moment, our main-sequence companions have maximum masses of M2 = 2.6 M⊙, and even these stars evolve on a much longer timescale (at least by a factor of ~10) compared to the typical 6 − 8 M⊙ progenitor stars of ONeMg WDs.
 |
Fig. 3 Grid of investigated initial orbital periods and masses for main-sequence donor stars with a metallicity of Z = 0.02 (upper panel) and Z = 0.001 (lower panel). The grey shaded region in each panel corresponds to systems which successfully evolve to the AIC stage (green circles). The blue triangles and purple asterisks correspond to cases where the mass-transfer rate was too high or too low, respectively, to allow for the WD to reach a critical mass of 1.48 M⊙. The red squares indicate orbits which are too narrow to initially accommodate the ZAMS donor star. The blue triangles inside green circles in the upper panel are systems leading successfully to AIC assuming ṀCE = 10 ṀEdd,WD. Details of the mass-transfer process of the binaries inside the marked cross in the upper panel are represented in Figs. 4 and 5. |
 |
Fig. 4 Mass-transfer rates of the four pre-AIC binaries shown in the horizontal part of the cross in the upper panel of Fig. 3. The mass-transfer-rate from the donor star in the system with Porb = 1.5d is too low (see Fig. 1) to cause the accreting WD to grow sufficiently in mass and trigger an AIC event. For the donors in the other systems, on the other hand, the mass-transfer rate is too high to result in stable mass gain of the accretor. Hence, none of these models resulted in a successful AIC. The differences in these mass-transfer rates can be understood in terms of different thicknesses of convective envelopes (see text and Fig. 6). |
4.1. Pre-AIC evolution with main-sequence donors
In Fig. 3 we have plotted a grid of the initial orbital periods and donor star masses of our investigated systems with main-sequence donor stars (i.e. supersoft X-ray sources). The upper and lower panels are for different donor star metallicities. The type of symbol in each grid point represents the outcome of the computations, which we discuss in more detail below. We note that the term main-sequence donor star is slightly misleading here since many of these stars have passed the termination age of the main sequence (TAMS) by the time they fill their Roche lobes and become donors. Hence, many of these systems evolve via early Case B RLO from Hertzsprung-gap subgiant donors. The systems which successfully evolve to the AIC event stage have initial orbital periods between 0.5−4 days and initial donor star masses between 2.0−2.6 M⊙ for a metallicity of Z = 0.02 and between 1.4−2.2 M⊙ for Z = 0.001.
The shift in parameters in Fig. 3 is interesting, in particular in allowed donor star masses, which lead to AIC depending on the chemical composition of the donor star. The shift to lower donor star masses for lower metallicity can be understood from the smaller radii of these stars (due to their lower opacities) compared to stars with higher metallicity. Therefore, these stars become more evolved when eventually initiating their RLO, leading to higher values of |Ṁ2| (see also Langer et al. 2000).
At first it may seem peculiar that neighbouring grid points can lead to a mass-transfer rate that is too low/too high for the WD to grow sufficiently in mass (see e.g. M2 = 1.8 M⊙, Porb = 1.5d − 2.8d, and Z = 0.02 along the horizontal part of the cross marked in the upper panel of Fig. 3). However, this behaviour can be understood from the required finetuning of the WD accretion rate. In Fig. 4 we see that while the donor star in an orbit with an initial Porb = 1.5d delivers an insufficient mass-transfer rate, the same system with Porb = 2.0d is seen to produce an excessive mass-transfer rate. The reason for this strong dependence on Porb is due to the corresponding rapid increase in the depth of the convective envelope with increasing radius of these shell hydrogen burning donor stars (Paczyński & Sienkiewicz 1972). This is demonstrated in the Kippenhahn plot shown in Fig. 6. The negative mass-radius exponents (ζ = ∂lnR/∂lnM) of convective envelopes cause these stars to expand in response to mass loss and thereby result in excessive mass-transfer rates. Only in the first case for Porb = 1.5d (upper-left panel of Fig. 6) will the mass transfer remain stable since here the mass ratio is inverted (causing the binary to widen) by the time the envelope has developed a deep convection zone. Similarly, in Fig. 5 we have shown the results of our mass-transfer calculations along four vertical, neighbouring points in the cross marked in the upper panel of Fig. 3. These points correspond to 1.6 ≤ M2/ M⊙ ≤ 2.2, and in all cases Porb = 2.0d. Again the explanation for the different outcomes is the differences in the depth of the convective envelopes. The donor stars with M2 ≲ 1.9 M⊙ require a more advanced evolution to fill their Roche lobes and therefore they develop deep convective envelopes before, or during, the RLO which leads to |Ṁ2| being too large. Hence, of those systems with Porb = 2.0d and Z = 0.02, only those binaries with initial donor star masses of 2.0 ≤ M2/ M⊙ ≤ 2.5 make it to the AIC event.
 |
Fig. 5 Mass-transfer rates of the pre-AIC binaries shown in the vertical part of the cross in the upper panel of Fig. 3. The four donor stars have masses of 1.6 − 2.2 M⊙ and Porb = 2.0d. The arrows mark the collapse of the accreting ONeMg WD (AIC) for the two most massive stars. Donor stars with initial masses M2 ≥ 2.6 M⊙ result in excessive mass-transfer rates and thus do not produce AIC events (see text). |
In general, for all initial Porb, donor stars with M2 ≥ 2.6 M⊙ result in |Ṁ2| being too large (unless the criteria in Eq. (1) is relaxed to allow for ṀCE = 10 ṀEdd,WD in which case we get AIC solutions up to M2 ≈ 3.0 M⊙). The reason is that in these systems the mass ratio, q > 2, and therefore their orbits become significantly tighter with RLO, resulting in a large value of |Ṁ2| (see Sect. 3.2).
 |
Fig. 6 Kippenhahn diagram of four 1.8 M⊙ donor stars undergoing early Case B RLO in X-ray binaries with an accreting WD and orbital periods of 1.5, 2.0, 2.5, and 2.8 days, respectively. The plots show cross-sections of the stars in mass-coordinates from the centre to the surface of the star, along the y-axis, as a function of stellar age on the x-axis. The green hatched areas denote zones with convection (according to the Ledoux criterion) initially in the core and later in the envelope of the donor stars. The intensity of the blue/purple color indicates the net energy-production rate; the hydrogen burning shell is clearly seen in all panels at m/ M⊙ ≃ 0.2. In the top-left panel, the donor star decreases its mass from 1.8 M⊙ until it finally detaches from the Roche lobe and forms a 0.28 M⊙ He WD. In the top-right panel, our calculation stops when the donor star reached 1.62 M⊙ since the mass-transfer rate became too high when the donor star refilled its Roche lobe, following an initial phase of stable RLO with a lower value of |Ṁ2|. In the two lower panels the mass-transfer rate went immediately up to the critical value at the onset of the RLO. The response of a donor star to mass loss depends strongly on the depth of its convective envelope and thus, as seen here, it depends on Porb. See Fig. 4 and text for a discussion. |
 |
Fig. 7 Left panel: mass-transfer rates of four 2.5 M⊙ donor stars in pre-AIC binaries with initial orbital periods between 1.0 − 3.0 days leading to the post-AIC LMXB systems shown in the right panel. The arrows mark the collapse of the accreting WD (AIC) and the evolution from this point onwards can be ignored since it is now followed in the post-AIC LMXB systems shown in the right panel. The dashed line is the adopted upper limit for stable mass transfer (see Sect. 3.1.1). It is seen how the pre-AIC mass-transfer rates were quite close to our accepted upper limit. A slightly more massive donor star would lead to excessive mass-transfer rates and thus not result in an AIC event (see also the systematic effect of an increasing donor mass in Fig. 5). The open circles indicate hypothetical super-Chandrasekhar WD masses of 2.0 M⊙. Right panel: mass-transfer rates of the post-AIC LMXBs plotted as a function of time since the AIC event. The reason for the difference in time intervals between the AIC event and the donor stars refilling their Roche lobe (see initial interceptions of the four graphs with the x-axis) is mainly due to different expansions of the orbit due to the AIC event, caused by different Porb at the moment of the WD collapse. The vertical text at the lower left side of each graph yields the mass of the donor star at the moment of the AIC, the mass of the final WD following the LMXB and the amount of mass accreted by the NS, ΔMNS. The dashed line is the Eddington accretion limit for a NS. Only the systems with initial pre-AIC orbital periods of 1.0 days (red curve) and 1.5 days (green curve) experienced a long phase (>100Myr) of post-AIC mass-transfer driven by hydrogen shell burning. This phase leads to significant accretion onto the NS (and effective recycling) since |Ṁ2| < ṀEdd. Hence, the NSs in these systems were able to accrete more mass which results in faster spinning MSPs (partly due to their smaller magnetospheres). |
4.2. Post-AIC LMXB evolution with main-sequence donors
The post-AIC binary mass transfer resembles that of normal LMXB evolution with an accreting NS. The only difference is that the donor star has already lost some of its mass during the pre-AIC evolution. To model these LMXB systems we proceeded as explained in Sect. 3.3. An example of the results of this modelling is shown in the right panel of Fig. 7 (the left panel shows the evolution of the pre-AIC binaries leading to these systems). An interesting feature becomes clear when comparing the four evolutionary tracks. Whereas the two donor stars in the widest orbits (initial Porb = 2.5d−3.0d) are already undergoing shell hydrogen burning (Case AB RLO) at the time of the AIC, the two donors in the shortest period systems (initial Porb = 1.0d − 1.5d) are still undergoing Case A RLO (core hydrogen burning) at the moment of the AIC. Hence, these latter systems remain LMXB (post-AIC) sources on much longer timescales (250Myr − 1Gyr), initially via Case A RLO, and later via Case AB RLO once the hydrogen shell is ignited.
As a consequence of the AIC event the binaries detach for 3000 − 100 000yr before the donor stars refill their Roche lobes on a thermal timescale. (During pre-AIC mass loss the donor stars become smaller than their thermal equilibrium sizes. After the AIC they expand to recover thermal equilibrium.) This is a very short (thermal) time interval compared to the typical lifetime of a young pulsar (about 50 − 100Myr) and therefore the possibility of detecting a system right at this epoch between the two long-lasting X-ray phases is quite small. Indeed, none of the 6 known radio pulsars with a main-sequence companion are candidates for being post-AIC systems: in all cases they have Porb > 50d and their companions are largely underfilling their Roche lobes.
Next to each coloured graph in the right panel of Fig. 7 is listed the mass of the donor star at the moment of the AIC, 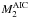 , the final mass of the WD remnant orbiting the recycled pulsar, MWD, and the amount of mass accreted by the pulsar, ΔMNS (assuming an accretion efficiency of 30% at sub-Eddington mass-transfer rates, see Sect. 3.3). The differences between the two main mass-transfer histories mentioned above (post-AIC Case A RLO vs Case AB RLO) is reflected in both ΔMNS and MWD. The consequences for the final MSPs systems will be discussed below.
, the final mass of the WD remnant orbiting the recycled pulsar, MWD, and the amount of mass accreted by the pulsar, ΔMNS (assuming an accretion efficiency of 30% at sub-Eddington mass-transfer rates, see Sect. 3.3). The differences between the two main mass-transfer histories mentioned above (post-AIC Case A RLO vs Case AB RLO) is reflected in both ΔMNS and MWD. The consequences for the final MSPs systems will be discussed below.
4.3. Resulting MSPs
4.3.1. Final orbital periods
 |
Fig. 8 Final orbital period of the MSP binaries formed via AIC as a function of WD mass, evolving from main-sequence donor stars with a metallicity of Z = 0.02 (upper panel) and Z = 0.001 (lower panel). The different symbols refer to different kicks during the AIC. The filled green circles correspond to w = 0 (no kick), the open pink stars to w = 50km s-1, and the filled red stars are for w = 450km s-1. The symbols connected with a black line are for the same pre-AIC binaries but different values of the kick, w. The dotted line is the (MWD,Porb)-relation taken from Tauris & Savonije (1999) and applies solely to low-mass donors with degenerate He cores. The blue triangles in green circles are explained in Fig. 3. See text for further details and discussions. |
In Fig. 8 we have plotted our resulting binary MSPs in the final (MWD, Porb)-plane. The upper panel shows the resulting MSPs using a donor star metallicity of Z = 0.02. The lower panel is for Z = 0.001. For clarity we have not included all systems shown in Fig. 3 which successfully evolved to the AIC, but we have included most systems and made sure to display those that yield the more extreme values of MWD and Porb. All the green filled circles were calculated assuming a symmetric AIC (i.e. w = 0). The pink open stars represent AIC with a small kick magnitude of 50km s-1 and in all cases kick angles of θ = 0° and φ = 0°. The red filled stars represent systems surviving AIC with a large kick w = 450km s-1. In these cases the kick angles were always chosen to yield the widest possible post-AIC orbits from a systematic trial procedure. See Table 2 for examples. The black lines connecting three symbols show the final results of three different kick values applied to the same AIC system. One should keep in mind that AICs are most likely not accompanied with a kick (see Sect. 1). However, we include the option here for the sake of completeness.
From the lower panel of Fig. 8 we note that for donor stars with low metallicity (Z = 0.001) all of the final MSP systems fall approximately on the well-known (MWD,Porb)-relation (e.g. Savonije 1987; Tauris & Savonije 1999), shown as a dashed line. This relation follows from the relation between the radius of a giant star and the mass of its degenerate He-core (Refsdal & Weigert 1971). However, the more massive donors (M2 > 2.3 M⊙) with non-degenerate cores do not obey this relation. This explains why many of the systems in the upper panel (Z = 0.02) deviate from the (MWD,Porb)-relation. Most of these donor stars leave behind relatively massive (hybrid) CO WD remnants, see Sect. 4.3.2.
An interesting outcome of these calculations is that the binary MSPs only form within a limited interval of Porb. We conclude that the final orbital periods of MSPs, formed via AIC with main-sequence donor stars, are in the interval: 10d < Porb < 60d. Only in the unlikely case where large AIC kicks were applied is it possible to form binary MSPs with Porb up to 120 days.
4.3.2. Nature of the final WD orbiting the MSP
To illustrate which donors leave He WDs and which leave CO WDs, we have plotted in Fig. 9 evolutionary tracks in the (ρc,Tc)-plane of WD progenitor stars with different masses and different values of Porb. It is seen that the donors with lower masses and/or shorter initial orbital periods are more exposed to a high pressure of degenerate electrons and a lower core temperature than the more massive donors. Hence, these lighter donors leave He WDs while the latter systems reach higher core temperatures and ignite helium to produce CO WDs. We find that the minimum threshold mass for efficient helium burning and production of a CO WD is about 0.33 M⊙, in agreement with previous work by e.g. Kippenhahn & Weigert (1990), Tauris et al. (2000), Podsiadlowski et al. (2002). A more correct description of these low-mass CO WDs in Fig. 9 of masses 0.335 M⊙, 0.391 M⊙, and 0.411 M⊙ is hybrid WDs, since they have a composite composition of a CO core surrounded by a thick helium mantle (e.g. Iben & Tutukov 1985; Iben et al. 1997). In these stars, the temperature was never high enough to cause helium burning throughout the outer layers and thus the growth of the CO core was stalled when it reached a mass fraction of 50−75%. Each of these WDs has a tiny hydrogen envelope of mass 1.2 − 3.7 × 10-4 M⊙ and evolved via one or more final hydrogen shell flashes due to unstable CNO burning in a thin hydrogen layer near their surfaces before they settled on the WD cooling track (e.g. Althaus et al. 2001; Nelson et al. 2004). As an example, our 0.335 M⊙ hybrid CO-He WD underwent one last, vigorous hydrogen shell flash lasting only 15 yr, which caused it to fill its Roche lobe and transfer 5 × 10-5 M⊙ towards the NS with a maximum rate of 1.1 × 10-5 M⊙ yr-1 (almost ~103ṀEdd).
4.3.3. MSP spin periods
Given our calculated amounts of mass accreted by the NSs (ΔMNS), we can constrain the possible pulsar spin periods after spin-up by using the formula (see Tauris et al. 2012, for details): 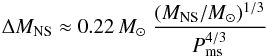 (15)or
(15)or 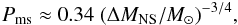 (16)where Pms is the final equilibrium spin period in milliseconds, and MNS is the initial NS mass (here, always 1.28 M⊙ following the AIC). Obviously, it is not possible to spin up a NS to faster rotation than its break-up spin period at ~0.6 ms, and our values do not include the circumstance of being limited by either gravitational wave radiation or a relatively large magnetospheric radius of the pulsar. Similarly, we discard the potential possibility of initially preventing post-AIC accretion onto the young energetic pulsar as a consequence of the so-called radio ejection mechanism (i.e. ejection of material from the system caused by the outward magnetodipole radiation pressure exceeding the inward ram pressure of material at the first Lagrangian point; Burderi et al. 2001). In Table 2 we list ΔMNS and Pms for our calculated post-AIC LMXB systems. It is seen that in almost all systems with main-sequence donor stars we obtain ΔMNS > 0.1 M⊙ and therefore we find that these MSPs will be fully recycled.
(16)where Pms is the final equilibrium spin period in milliseconds, and MNS is the initial NS mass (here, always 1.28 M⊙ following the AIC). Obviously, it is not possible to spin up a NS to faster rotation than its break-up spin period at ~0.6 ms, and our values do not include the circumstance of being limited by either gravitational wave radiation or a relatively large magnetospheric radius of the pulsar. Similarly, we discard the potential possibility of initially preventing post-AIC accretion onto the young energetic pulsar as a consequence of the so-called radio ejection mechanism (i.e. ejection of material from the system caused by the outward magnetodipole radiation pressure exceeding the inward ram pressure of material at the first Lagrangian point; Burderi et al. 2001). In Table 2 we list ΔMNS and Pms for our calculated post-AIC LMXB systems. It is seen that in almost all systems with main-sequence donor stars we obtain ΔMNS > 0.1 M⊙ and therefore we find that these MSPs will be fully recycled.
 |
Fig. 9 Evolutionary tracks in the core density-core temperature (ρc,Tc)-plane. For each graph the initial (ZAMS) values of the donor star mass, M2, the orbital period, Porb, and in parenthesis the main chemical composition and the mass of the final WD are listed. The dotted line separates regions where the stellar pressure is dominated by the gas pressure (left) and the degenerate electron pressure (right). On each track the symbols represent: the termination of core hydrogen burning (filled squares), the end of the RLO (filled circles), the onset of the 3α-process (open circles) and the onset of efficient helium burning (i.e. when the luminosity generated by the 3α–process exceeds the energy loss rate by neutrinos, open triangles). The calculations were followed to the WD cooling track, except for two cases causing numerical instabilities during hydrogen shell flashes. |
We conclude that in all our models where MSPs formed via AIC, the predicted equilibrium spin periods of a few ms are identical to those expected for MSPs formed via the conventional recycling channel where the NS was formed in a SN Ib/c.
4.3.4. MSP systemic space velocities
We kept track of the post-AIC systemic velocities relative to the centre-of-mass rest frame of the pre-AIC binaries. The systems receive a recoil due to the sudden mass loss, possibly combined with a smaller kick, during the AIC. From conservation of momentum we obtain (e.g. following Tauris & Bailes 1996): 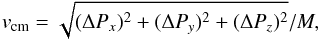 (17)where the change in momentum is given by (cf. Sect. 3.2.1):
(17)where the change in momentum is given by (cf. Sect. 3.2.1): 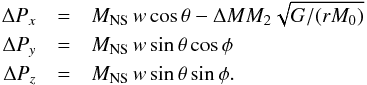 (18)In Table 2 we also list the calculated systemic velocities of post-AIC binaries. If large kicks (e.g. w = 450 km s-1) were associated with AIC then the MSPs formed via this channel would reach velocities of up to 200km s-1, similar to the calculated systemic velocities of MSPs where the NS formed via a core collapse SN (Tauris & Bailes 1996). However, for w = 0 − 50 km s-1 we find that the expected velocities of the resultant MPS formed via AIC will be quite small and of the order of 10−30 km s-1 at maximum5.
(18)In Table 2 we also list the calculated systemic velocities of post-AIC binaries. If large kicks (e.g. w = 450 km s-1) were associated with AIC then the MSPs formed via this channel would reach velocities of up to 200km s-1, similar to the calculated systemic velocities of MSPs where the NS formed via a core collapse SN (Tauris & Bailes 1996). However, for w = 0 − 50 km s-1 we find that the expected velocities of the resultant MPS formed via AIC will be quite small and of the order of 10−30 km s-1 at maximum5.
5. AIC in systems with giant star donors
In Fig. 10 we have plotted a grid of the initial orbital periods and donor star masses of our investigated systems with giant star donors. These systems could potentially be detected as novae-like, symbiotic X-ray sources while the WD accretes material. The giant star donors which successfully lead to AIC have masses between 0.9 − 1.1 M⊙. The upper limit is set by the mass-transfer rate (which is too high for larger values of M2), and the lower limit is set by the age of our Universe (0.9 M⊙ donors only evolve into giant stars within a Hubble-timescale of 13.7 Gyr if the metallicity is low enough). The initial parameter space dependence on metallicity is in general much weaker for these giant stars compared to the case of main-sequence donor stars shown in Fig. 3. The orbital periods, Porb at the onset of the RLO must be at least 60 − 80days. If Porb is smaller than this value the mass-transfer rate is too weak for the WD to grow efficiently in mass. The reason for different outcomes of 1.1 M⊙ donor star models (Z = 0.02) with Porb = 150d − 190d is that Ṁ2 is very close to, and fluctuating near, our hard threshold limit, ṀCE.
5.1. Mass-transfer from giant star donors
The mass-transfer modelling with giant star donors is difficult to calculate for two reasons. First, giant stars have low surface gravities and thus extended atmospheres which make it non-trivial to estimate the turn-on of the RLO mass-transfer process. In some cases (see full discussion in Sect. 5.3) there is a significant amount of mass transfer through the inner Lagrangian point while the donor star is still underfilling its Roche lobe (the so-called optically thin mass transfer). Hence, for donor stars in the widest pre-AIC orbits (Porb ≥ 400d) our code runs into problems, in particular for low-metallicity giant donors. Second, even low-mass giant stars have substantial wind mass loss (Reimers 1975) which causes the orbits to widen prior to the RLO. In some cases Porb may increase by 20% prior to the RLO while the donor star loses up to 30% of its mass. In our modelling, we have neglected the wind mass loss of the giant prior to RLO in order to isolate and better investigate the above-mentioned effect of optically thin mass transfer from these donor stars with extended atmospheres.
As can be seen in Fig. 10 for giant star donors, the transition from low values of |Ṁ2| to donors which result in excessive values of |Ṁ2| is very narrow for donor star masses, M2 > 1.1 M⊙. Again the explanation is the sudden set-in of rapid growth of the thickness of the convective envelope. Including the effect of stellar winds is expected to shift the green points (successful AIC) in Fig. 10 slightly to the left and upward.
5.2. Resulting MSPs
The binary pulsars formed via AIC from giant star donors all end up in wide systems with Porb > 500d. The WD companions are either 0.40−0.46 M⊙ He WDs, or CO WDs more massive than 0.46 M⊙. The pulsars are, in general, expected to be only mildly recycled with estimated spin periods of 10 − 500ms due to the short mass-transfer phase, lasting ΔtLMXB ≃ 104 − 106yr, following the AIC. Given this short phase of post-AIC mass transfer, combined with the effects of a young energetic pulsar (Sect. 4.3.3), the final spin periods are expected to be somewhat slower than indicated above and in Table 2. More notably, the systemic velocities of these binaries will be very small, vsys ~ 1km s-1, given the general assumption that AICs are not accompanied by a momentum kick. Hence, these will be at rest with respect to the local stellar population.
By the time the low-mass giant star donors initiate mass transfer towards the WD, they have already reached ages of the order of 10 Gyr (see Table 2). Therefore, we expect ongoing formation of NSs via the AIC channel in GCs today. In order for the giant star donors to deliver high enough mass-transfer rates to make the accreting WD grow sufficiently in mass, the initial Porb must be large. Hence, the orbital period at the moment of the AIC and the subsequent post-AIC LMXB orbit are also quite large. Such wide binaries enhance the likelihood of disruption by stellar encounters in a GC (e.g., Verbunt & Freire 2013) and thus result in a number of isolated, young NSs in GCs as observed (or young NSs in close orbits formed after a three body exchange event), see Table 1.
We conclude that AIC is an attractive model to explain the small space velocities of some NSs and, in particular, the retention of NSs in GCs. Furthermore, the AIC channel can explain the existence of relatively young NSs in GCs.
 |
Fig. 10 Grid of investigated initial orbital periods and masses for giant star donors with a metallicity of Z = 0.02 (top) and Z = 0.001 (bottom). The meaning of the various symbols is equivalent to those in Fig. 3. The grey shaded region in each panel corresponds to systems which successfully evolve to the AIC stage. Only giant donors with masses 0.9 ≤ M2/ M⊙ ≤ 1.1 are able to produce MSPs via the AIC channel. The hatched regions indicate donor stars which evolve on a timescale longer than the Hubble-timescale. The cross-hatched region corresponds to giant donors which have so large atmospheric, hydrogen pressure scale-heights that our adopted mass-transfer scheme breaks down – see text. |
5.3. Break-down of the applied mass-transfer scheme for giant donors
According to the canonical criterion for mass-transfer (Kippenhahn & Weigert 1967) one simply has to ask whether the donor star radius, R2 is larger or smaller than its Roche-lobe radius, RL. Hence, one makes the implicit assumption that the edge of the star is infinitely sharp and therefore that the mass transfer starts/ends abruptly rather than following a gradual transition. Ritter (1988) improved this criterion by taking the finite scale height of the stellar atmosphere properly into account. The mass loss from the donor star was modelled as a stationary isothermal, subsonic flow of gas which reaches sound velocity near the nozzle at the first Lagrangian point, L1. The accompanying mass-transfer rate is given by: 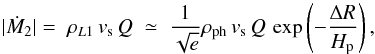 (19)where ρph is the gas density at the donors’ photosphere,
(19)where ρph is the gas density at the donors’ photosphere, 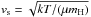 the isothermal sound speed, Q the effective cross section of the flow at L1 (see Meyer & Meyer-Hofmeister 1983), and ΔR ≡ RL − R2. The last parameter,
the isothermal sound speed, Q the effective cross section of the flow at L1 (see Meyer & Meyer-Hofmeister 1983), and ΔR ≡ RL − R2. The last parameter, 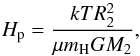 (20)is the pressure scale-height of the stellar atmosphere (μ is the mean molecular weight). This scheme was developed to study the turn-on (turn-off) of mass transfer in nearly semi-detached systems, the so-called optically thin mass transfer for which R2 < RL (see also D’Antona et al. 1989; Kolb & Ritter 1990)6. However, this mass-transfer algorithm was derived for low-mass main-sequence donor stars in CV binaries for which Hp ≪ R2, and therefore mass transfer was only assumed to occur for ΔR ≪ R2.
(20)is the pressure scale-height of the stellar atmosphere (μ is the mean molecular weight). This scheme was developed to study the turn-on (turn-off) of mass transfer in nearly semi-detached systems, the so-called optically thin mass transfer for which R2 < RL (see also D’Antona et al. 1989; Kolb & Ritter 1990)6. However, this mass-transfer algorithm was derived for low-mass main-sequence donor stars in CV binaries for which Hp ≪ R2, and therefore mass transfer was only assumed to occur for ΔR ≪ R2.
For giant stars this picture has to change (Pastetter & Ritter 1989). These stars with low surface gravities often have Hp/R2 ≃ 0.04 and as a result we find that they can in some cases cause mass-transfer rates above 10-7 M⊙ yr-1 even for ΔR = 0.3 R2 (i.e. while the donor star is still underfilling its Roche lobe by 23% in radius). Hence, for giant star donors the assumptions behind the original Ritter scheme breaks down. As a consequence, we did not allow for mass transfer with ΔR > 0.3 R2 and our calculations were abandoned if this limit was reached (see cross-hatched region in Fig. 10).
As mentioned previously, we did not include wind mass loss in our models. This effect would cause the binaries to widen further and thereby stabilize the systems against dynamical unstable mass transfer (Pastetter & Ritter 1989). Another uncertainty is the effect of irradiation feedback on the long-term evolution of a compact binary (e.g. Büning & Ritter 2004). However, the impact and the modelling of this effect, leading to cyclic accretion, is still unclear and is not included in our study. Recent work by Benvenuto et al. (2012) on the evolution of ultra-compact X-ray binaries suggests that the inclusion of irradiation feedback is not very significant for the final properties of these systems. Furthermore, for the wide-orbit LMXBs with giant donors Ritter (2008) argued that irradiation-driven mass-transfer cycles cannot occur since these systems are transient because of disc instabilities.
 |
Fig. 11 Grid of investigated initial orbital periods and masses for helium star donors with Y = 0.98 and a metallicity of Z = 0.02. The meaning of the various symbols is explained in Fig 3. The grey shaded region corresponds to systems that have successfully evolved to the AIC stage. See text for further discussions. |
 |
Fig. 12 Evolutionary tracks in the HR–diagram for three 1.1 M⊙ helium stars: two in binaries with a 1.2 M⊙ WD and one evolving as a single star. The loops in the upper-left corner of the two binary helium star tracks are caused by the ignition of shell helium burning. |
6. AIC in systems with helium star donors
6.1. Mass transfer from helium star donors
Binary stars evolving from the ZAMS may lead to the formation of a tight binary with a massive WD, i.e. the remnant of the former primary star, and a helium star, i.e. the core of the secondary star that lost its envelope via CE evolution (e.g. Liu et al. 2010). These systems will thereafter proceed their post-CE evolution as described below, once the helium star fills its Roche-lobe (via so-called Case BB RLO).
We constructed helium star donors with Z = 0.02 (1.5% 14N, 0.2% 20Ne, and 0.3% isotopes of mainly Mg, Si, C, and O). As seen in Fig. 11, the WDs that successfully accreted mass up to the AIC limit (1.48 M⊙) had helium star donors with masses between 1.1 − 1.5 M⊙ and initial Porb between 1 h(0.04days) and 1.2days, see Table 2 for details of 8 models. The mass-transfer rates become higher than the critical limit (ṀCE) for helium stars in relatively wide orbits. However, for the lightest helium stars (≤1.1 M⊙) this is not the case. Even in the widest orbits the mass-transfer rates become too low to yield significant WD accretion because the orbits expand further in response to mass-transfer, given that q < 1 at all times.
In the HR-diagram in Fig. 12 we compare the evolution of two 1.1 M⊙ helium stars in binaries, with initial Porb = 0.3d and 1.3d, respectively, with the evolution of an isolated helium star of the same mass. Whereas the single helium star evolves to a radius above 40 R⊙ during shell helium burning, the binary helium stars which suffer from mass loss (and restriction in size due to their Roche lobes) only evolve up to a radius of maximum ~2.6 R⊙ (for an initial Porb = 1.3d) before they evolve towards the WD cooling track as 0.80 − 0.82 M⊙ CO WDs.
We note that our models are computed with OPAL opacities which include carbon and oxygen abundances (cf. Sect. 3). Models computed with OPAL opacities (Iglesias et al. 1992) that do not account for high C/O abundances (not shown here) resulted in final CO WD masses that were 4−9% larger than those in the models presented here.
6.2. Resulting MSPs
It can be seen in Table 2 that the post-AIC LMXB phase, ΔtLMXB lasts for less than about 1 Myr (typically only 105yr), except for one model (He1) where the RLO was initiated early on the helium star main sequence, resulting in ΔtLMXB = 7.96Myr. Given the short lasting LMXB phase for these systems the final pulsar masses are all close to their original post-AIC mass of 1.28 M⊙. For the same reason, these pulsars are only mildly recycled with minimum initial spin periods between 20 − 100ms and we expect their B-fields to be larger than those of the fully recycled MSPs. (We note that the spin periods could be slower than stated in Table 2 for the reasons given in Sect. 4.3.3.)
The pulsar companions are all CO WDs with masses between 0.6 − 0.9 M⊙ and Porb ≃ 2h − 2days, see Fig. 13. If a hypothetical large kick (w > 450km s-1) is applied the final Porb may reach 3 days. However, such large kicks are not expected for AIC (cf. Sect. 2).
The tight binaries with initial helium star companions cause the post-AIC systemic velocities to reach about 20 − 30km s-1 (in models with no kicks) which is substantially faster than the recoil velocities imparted to the wider systems with main-sequence or giant star companions, although much smaller than the velocities calculated for systems evolving via the standard SN channel.
 |
Fig. 13 Final orbital periods of recycled radio pulsars as a function of their CO WD companion masses for systems evolving from helium star donors with a metallicity of Z = 0.02. Data points connected with a green line were calculated from the same initial helium star mass (1.2 M⊙ and 1.4 M⊙, respectively). Data points with black dots were all calculated from a binary with an initial orbital period of 0.1 days. The solid red star and the open purple star, connected with a black line to the green data points, indicate similar calculations including an applied hypothetical kick velocity of 50km s-1 and 450km s-1, yielding the widest possible orbit. The less massive the initial helium star donor, and the more narrow the orbit, the more material the NS accretes and the faster spin it obtains. The dashed lines indicate roughly where the pulsar is spun up to 15 ms and 80 ms, respectively. See text for discussions. |
 |
Fig. 14 Grid showing all successful AIC systems, starting from an accreting 1.2 M⊙ (ONeMg) WD orbiting a main-sequence star (green), a giant star (red), or a helium star (blue) with a metallicity of Z = 0.02. Hatched areas are calculated for Z = 0.001. The initial parameter space shown here is equivalent to that for progenitor binaries of SN Ia with an accreting 1.2 M⊙ (CO) WD (see text). |
7. Discussion
Using a detailed stellar evolution code to probe the combined pre- and post-AIC evolution, we have demonstrated that it is possible to form MSPs indirectly via the AIC channel. In Fig. 14 we show the initial parameter space of all binaries which successfully evolve to AIC according to our calculations. In this section, we discuss our findings in more detail in relation to the predicted physical properties of the resultant NS binaries and compare them with observations. We also discuss the connection between AIC and SNe Ia progenitors and compare our work to other recent studies.
7.1. Fully recycled MSPs or young NSs?
A general problem with postulating that a given observed high B-field NS was formed via AIC is that (as pointed out by Wijers 1997, and also demonstrated by Sutantyo & Li 2000) it requires quite some finetuning to have the AIC occurring at the very final phases of the mass transfer in order to explain the high B-field of the NS. If the WD collapses earlier, the B-field of the newly formed NS (and its spin period, depending on Ṁ2) should decrease significantly when the donor star refills its Roche lobe following the AIC, thereby evolving through a relatively long lasting (107−109yr) post-AIC LMXB phase. In that case, all traces of its origin will be erased and the final NS cannot be distinguished from those recycled pulsars formed via the standard SN channel. Even accretion of a few 0.01 M⊙ is enough to decrease the B-field significantly according to some models (e.g. Wijers 1997; Zhang & Kojima 2006, and references therein). In all our model calculations the newborn NS undergoes post-AIC accretion, although in some extreme cases less than 10-3 M⊙ is accreted.
 |
Fig. 15 Corbet diagram for 55 MSPs (or mildly recycled pulsars) produced via AIC formation and subsequent accretion, including those listed in Table 2. The three different donor star progenitor classes (green, red, and blue) are clearly distinguished, corresponding to main-sequence, giant star, and helium star donors, respectively. Open circles are MSPs with He WD companions, solid diamonds indicate MSPs with (hybrid) CO WD companions. Symbols with a superimposed open black star correspond to AIC models where a kick was applied. For a few systems with giant star donors only upper limits are given for Porb (and P) because of computational difficulties, cf. Sect. 5.3. |
7.1.1. The AIC Corbet diagram
In Fig. 15 we have plotted the Corbet diagram for a sample of our modelled NS systems which formed via the AIC channel (including the models listed in Table 2). For systems with main-sequence donor stars, the resultant NSs eventually become fully recycled MSPs (i.e. with spin periods of a few ms and most likely weak B-fields). Their orbital periods are confined to the interval: 10d < Porb < 60d (up to 120 days when kicks are applied, cf. Sect. 4.3.1). In Sect. 7.5.1 we compare with the observed distribution of binary pulsars with He WD companions. For systems with either giant star or helium star donors, the spread in predicted final spin periods is much broader: from 4 ms to 0.5 s. However, the orbital periods are constrained to values of Porb > 500d and Porb ≤ 2d, respectively.
The predictions with respect to the values of the final spin periods are uncertain for systems with either giant star or helium star donors, since in both of these cases the post-AIC LMXB phase is short-lived. On the one hand, if the NS in these systems only accretes 10-3 − 10-2 M⊙ after its formation, we would expect it to form a mildly recycled pulsar with P ≃ 4 − 500ms as shown in Fig. 15. On the other hand, in case the AIC produces (initially) very rapidly spinning and strong B-field pulsars, we cannot rule out that the radio ejection (Sect. 4.3.3) or the propeller mechanism will prevent these NSs from accreting matter during the short (105 − 106yr) post-AIC LMXB phase. In that case, for these particular systems (red and blue symbols), the amount of material accreted by the post-AIC NS, ΔMNS could be substantially smaller (and the resulting spin periods longer) than modelled here (see Fig. 16 for our modelled values for ΔMNS). Therefore, it might be possible to produce NSs via the AIC channel which retain relatively high B-fields and which therefore also appear young (similar to what is observed, cf. Table 1). To fully answer this question, one needs to model the accretion disk-magnetosphere interactions in greater detail combined with a decisive model for the decay of the NS B-field.
Nevertheless, if the AIC formation channel is significant in terms of numbers (Hurley et al. 2010, conclude that the AIC route is just as important as the standard SN route), then one may expect to observe a few cases where the AIC happened near the very end of the mass-transfer epoch, resulting in a young, high B-field pulsar.
 |
Fig. 16 Amount of mass accreted by the NSs during the post-AIC LMXB phase, ΔMNS as a function of the duration of the post-AIC LMXB phase, ΔtLMXB. The symbols correspond to those in Fig. 15. Our calculations assumed an accretion efficiency of 30%. The deviation from a straight line is caused by the lower mass-transfer rates |Ṁ2| ≪ ṀEdd in systems with long mass-transfer timescales. The more mass a NS accretes, the faster is the final spin rate of the resultant MSP (see text). |
The orbital period distribution in Fig. 15 is interesting. The resultant MSPs created via the AIC channel preferentially form in certain orbital period intervals. The fully recycled MSPs mainly form with 10d < Porb < 60d (from systems with main-sequence donor stars), whereas mildly recycled pulsars form in either very wide orbit systems with Porb > 500d (from systems with giant star donors) or end up in close binaries with Porb < 2.0d (all with massive CO WD companions, left behind by helium stars donors). The tightest of these latter systems will merge within 1 Gyr. Hence, according to our modelling there is a gap in orbital periods roughly between 60d < Porb < 500d where MSPs from AIC systems should not form (unless a kick is applied, in which case the lower limit increases to 100d). The reason why larger values of Porb are not possible for systems with main-sequence star donors is that the mass-transfer rate becomes too high for systems which could potentially widen to such large orbital periods. Only systems with low-mass giant star donors may produce MSPs in wider systems. However, the final values of Porb for these systems exceed 500 days. In Sect. 7.5 we compare this modelled Porb distribution with observed NS binaries.
7.1.2. Production of young NSs in GCs
In GCs, the possibilities are more favourable for producing young NSs which (initially) avoid recycling. The reason is that some post-AIC binaries in GCs may become disrupted by an encounter event before the newborn NS experiences much accretion. We note that for these systems the duration of the post-AIC detachment phase is comparable to the duration of the subsequent LMXB phase (compare Δtdetach and ΔtLMXB in Table 2). Considering that GCs have an old stellar population, young NSs can only be produced from AIC with a giant star companion, since all possible main-sequence and helium star donors leading to AIC have nuclear evolution timescales much shorter than the age of the GCs (and thus these stars would already have evolved a long time ago). Therefore, AIC events in GCs only occur in wide binaries which also enhances the probability of disruption before the post-AIC RLO has terminated, thereby strengthening the case for observing a young NS in a GC.
On a much longer timescale it is, of course, quite likely that these isolated NSs may capture a companion star and become recycled. The LMXB IGR J17480−2446 in Terzan 5 might be an example of a NS formed via AIC that has captured a new companion star and is now undergoing recycling, as suggested by Patruno et al. (2012).
7.2. AIC vs. SN Ia: implosion or explosion
All calculations in this work assumed an initial binary configuration with an accreting 1.2 M⊙ WD, treated as a point mass. We implicitly assumed that when the (ONeMg) WD reaches the Chandrasekhar mass at 1.48 M⊙ (the maximum mass of a rigidly rotating WD; e.g. Yoon & Langer 2005) it collapses and forms a NS. However, predicting the final fate of accreting massive WDs is not trivial (e.g. Nomoto & Kondo 1991). Accreting ONeMg WDs reaching the Chandrasekhar limit may not always lead to an implosion that leaves behind a NS. The outcome depends on whether or not the effects of electron captures dominate over nuclear burning (oxygen deflagration) and hence it is sensitive to the central density where explosive nuclear burning is ignited (Nomoto et al. 1979a). If the central density is too low, the timescale of electron captures is too long compared to that of the nuclear energy release and the result may be explosive oxygen ignition and a SN Ia.
Similarly, it may not always be the case that accreting CO WDs explode in SNe Ia when reaching the Chandrasekhar limit. This requires that the interior temperature (affected by heat inflow from surface layers) is high enough to ignite carbon at a relatively low density. Therefore, the outcome depends on the duration of accretion phase and thus on the initial mass of the CO WD. If the initial CO WD mass is relatively high (≥1.2 M⊙), then the accretion phase leading to the Chandrasekhar limit is short and thus it may not result in a temperature high enough for such a (high-density) WD to explode in a SN Ia (Nomoto & Kondo 1991).
Nonetheless, using our stellar evolution code we find that WDs formed with an initial mass of 1.2 M⊙ in close binaries are more likely to be ONeMg WDs (or at least hybrid WDs with ONeMg cores embedded in a thick CO mantle) compared to CO WDs.
7.2.1. SN Ia progenitor calculations and shell impact
Assuming instead that our point mass WD is a CO WD leading to a SN Ia (despite the uncertainties mentioned above), we have probed the progenitor parameter space for the single degenerate scenario with the results presented in this work (see Fig. 14 and the discussion in Sect. 7.3). In addition, we have a library of many donor star structures, of different nature and at various evolutionary epochs, at the moment of the SN Ia events (cf. Table 2 for examples of stars for which we have detailed structures). These models can be used in future work to study the impact of the SN Ia explosion on the donor star and thus help predict the expected properties of former companions stars when searching for these in SN Ia remnants (see e.g. Marietta et al. 2000; Di Stefano & Kilic 2012; Liu et al. 2012; Pan et al. 2010, 2012, 2013). These authors demonstrated that whereas helium star donors may only lose about 5% of their mass, and main-sequence star donors lose some 10–20%, giant star donors may lose most of their envelope because of the SN impact. Since much less material is ejected in an AIC event, compared to a SN Ia, the impact effect will be less severe. However, even if there were somewhat less donor material to recycle the post-AIC pulsars, the main findings in this work would remain intact.
7.2.2. Super-Chandrasekhar mass WDs
Recent observations of exceptionally luminous SNe Ia (e.g. Howell et al. 2006; Scalzo et al. 2010) suggest that their WD progenitors had a super-Chandrasekhar mass (~2.0 − 2.5 M⊙). The possibility of super-Chandrasekhar mass WDs has been investigated theoretically for differentially rotating WDs (e.g. Yoon & Langer 2005), WDs with extreme magnetic fields (e.g. Das & Mukhopadhyay 2013) and merging WDs (e.g. Iben & Tutukov 1984).
Our binary calculations are able to produce such massive WDs, but only in systems with main-sequence star donors. In the left panel of Fig. 7, we show how WDs up to about 2.1 M⊙ (if they exist in nature) can be produced in these systems (the open circles indicate when the WDs reach a mass of 2.0 M⊙). The potential formation of these massive accreting WDs was also found in Langer et al. (2000). It is obvious that the initial parameter space for producing SNe Ia, or AIC events, is much more limited for such super-Chandrasekhar mass WDs.
7.3. Comparison to previous work
To explain the existence of high B-field NSs in old stellar populations, or in close binaries in the Galactic disk, it has been suggested in the literature that: 1) these NSs are formed via the AIC formation channel (cf. Sect. 2), and 2) post-AIC accretion, in general, does not affect these newborn NS significantly and therefore they remain to appear as young pulsars or, at most, mildly recycled pulsars (e.g. Ivanova et al. 2008). Our calculations partly disagree with the second hypothesis. We find that the majority of pulsars formed via AIC would have accreted significant amounts of matter following the AIC event, leading to the low B-fields of recycled pulsars (in particular, this is the most likely outcome if the donor is a main-sequence star). A similar conclusion was also found by Sutantyo & Li (2000) who argue that it is difficult to reproduce high B-field pulsars in close orbits (e.g. PSR B1831−00) via the AIC formation scenario. However, as pointed out in Sect. 7.1, in a few cases one would indeed expect to find pulsars that are not recycled, or are only very mildly recycled, as a consequence of late AIC towards the end of the mass-transfer process, disruption of the post-AIC binary by an encounter in a GC, or hampering of post-AIC accretion due to the propeller and/or the radio ejection mechanism for systems with giant star or helium star donors. A population synthesis investigation might help to study the probabilities of these events happening.
7.3.1. Initial (Porb, M2)-parameter space
In Fig. 14 we summarize our results in terms of the initial parameter space of AIC progenitors in a (Porb, M2)-diagram. Langer et al. (2000) studied in detail the binary evolution of main-sequence star donors with 0.7 − 1.0 M⊙ WD accretors, somewhat less massive than the initial WD mass of 1.2 M⊙ assumed here. Three examples of studies which did have a 1.2 M⊙ WD accretor include Li & van den Heuvel (1997) and Wang et al. (2010), who studied the progenitors of SN Ia for main-sequence and giant star donors, and Han & Podsiadlowski (2004) who studied the SN Ia progenitors for main-sequence stars. One can compare Figs. 2 or 3 in these three papers to our Fig. 14. For giant stars, our results are generally in agreement, except for Wang et al. who did not reach the Chandrasekhar limit for giant stars in systems with Porb > 25d, possibly as a consequence of their inclusion of accretion disk instabilities. For the main-sequence donors, however, a key difference is that we are not able to produce systems leading to WD collapse for 3 M⊙ donor stars. In our work, as discussed in Sect. 3.1.1, we did not allow for the optically thick wind model (Kato & Iben 1992; Kato & Hachisu 1994) to operate for high values of |Ṁ2|. With our assumptions, when the mass-transfer rate becomes very high for these massive donors, the fate of the system is a merger. Therefore, our maximum main-sequence donor star mass is ~2.7 ± 0.1 M⊙. Only if we let ṀCE = 10 ṀEdd,WD are we able to produce AIC events with 3 M⊙ donor stars.
Whereas Li & van den Heuvel (1997) and Han & Podsiadlowski (2004) found that SN Ia could result from systems having main-sequence donor stars with masses up to ~3.5 M⊙, Hachisu et al. (2008) propose solutions with main-sequence donor stars up to ~7 M⊙ by introducing an efficient stripping of the donor star via impact of a strong wind from the accreting WD. By assuming a stripping rate up to a factor of 10 larger than the wind mass-loss rate of the WD (Ṁstrip ≲ 10 Ṁwind) the systems can remain dynamically stable and avoid evolving into a CE. We find this scenario questionable, both with respect to its realization and its stability, although attractive if the main goal is to match the observed SN Ia rates with theoretical modelling based solely on the single-degenerate scenario. In a recent paper Bours et al. (2013) demonstrated the strong dependence on the predicted SN Ia rates on the wind-stripping effect and on the mass accumulation (retention) efficiency of the accreting WD.
Wang & Han (2010) and Liu et al. (2010) studied the helium star donor channel for SNe Ia. From their Figs. 2 and 4, respectively, we can directly compare their results to ours shown in Fig. 11. The discrepancy is quite large. According to their work, systems with massive helium star donors (up to ~3 M⊙) lead to a Chandrasekhar-mass WD, and Wang & Han (2010) even find that SNe Ia occur for low-mass helium star donors in very wide systems (up to 100 days). We find that only systems with initial helium star donor masses M2 ≤ 1.5 M⊙ (and Porb ≤ 1.2d) are able to produce WDs undergoing AIC (or SN Ia). Again, the main reason for this difference is their use of the optically thick wind model, as discussed above.
To investigate this question of wind dynamical instability for helium stars donors, we performed two test runs without restrictions from obtained values of |Ṁ2|. We considered a 2.0 M⊙ and a 2.6 M⊙ helium star in a binary with a 1.2 M⊙ WD and Porb = 0.10d. Although the orbital size shrinks by up to 30%, the systems remain dynamically stable in both cases. However, the mass-transfer rates become quite super-Eddington. For the 2.6 M⊙ helium star, |Ṁ2| ≃ 1.0 × 10-4 M⊙ yr-1 (corresponding to |Ṁ2| > 100 ṀEdd,WD). Whether or not the optically thick wind model remains valid in this regime is questionable and more research is needed to clarify this important question.
Another factor that determines the parameter space of systems evolving successfully to a critical WD mass (and therefore affects the Galactic SN Ia birthrate) is the assumed Chandrasekhar mass. Whereas we applied a threshold mass of 1.48 M⊙ (to include the effect of rotation), a smaller limit of ~1.38 M⊙ was applied by Han & Podsiadlowski (2004), Wang & Han (2010), and Wang et al. (2010), which facilitates reaching the critical WD mass point.
7.3.2. Population synthesis studies of MSP formation via AIC
Hurley et al. (2010) performed a population synthesis study of binary MSPs formed via the AIC channel. A few interesting points become clear when comparing our results to their Figs. 1d, 2d, and 3d. They produce a large number of very wide systems with CO WDs and Porb = 103 − 106days. Although, it is expected that some systems widen significantly at the moment of the AIC when a small kick is applied, the numbers of these very wide systems is surprising to us. The donor stars in these systems are giants which later settle as CO WDs. However, given that these giants have initial masses 0.9 ≤ M2/ M⊙ ≤ 1.1, their maximum radii reach just a few 102 R⊙ and therefore they are unlikely to serve as donor stars in binaries expanding much beyond 1400 days. Hence, recycled pulsars are not expected in systems with Porb > 1400days (cf. our models GS1−4 and GSZ1). Similarly, we cannot reproduce the distribution of massive (~0.8 M⊙) CO WDs in a wide range of systems with Porb ≃ 0.1 − 100days. The progenitors of these systems are binaries with an accreting WD and a helium star donor. We find that for these systems the expected final orbital periods are Porb ≃ 0.05 − 2.0days. (Even applying large kicks will not change this picture much.) The reason for these apparent discrepancies is not clear to us and cannot simply be explained by using different limits for the WD accretion window, although we apply a different prescription for the mass accumulation of helium-rich material. It is also possible that the BSE code used by Hurley et al. (2010) fails to trace the mass-transfer process with sufficient accuracy.
There are, however, also similarities in our results. Most notably, Hurley et al. (2010) find that the minimum orbital period of MSPs with He WD companions, produced via AIC, is about 5 days (we find a minimum Porb ≃ 10days) and that there is a gap in the orbital period distribution between ~50 − 200days (depending on their chosen model), where we find the gap is roughly between 60 − 500days (cf. Table 2 for models with no AIC kick, w = 0). Ideally, our work in this paper would be used as a basis for a new population synthesis study for comparison with the work of Hurley et al. (2010), for example.
 |
Fig. 17 Systemic recoil velocities of MSPs formed indirectly via AIC. The two upper panels show sample calculations of the recoil velocities, vsys obtained for a fixed kick of w = 50km s-1 and kick angles θ = 0 − 180° (upper panel), or a fixed value of θ = 36° and kicks w = 0 − 100km s-1 (central panel), in both cases as a function of the pre-AIC orbital separation, a0. The lower panel shows vsys as a function of kick velocities, w for fixed values of a0 and variable values of θ = 0 − 180°. In all cases we assumed a companion star mass of |
7.4. Space velocities: distinguishing AIC from SNe Ib/c
In Fig. 17 (partly adapted from Tauris & Bailes 1996) we show examples of systemic recoil velocities expected for MSPs which formed indirectly via AIC. For systems with main-sequence donors, the pre-AIC orbital separations are typically 5 − 10 R⊙ and the resulting velocities are vsys ≤ 50km s-1, even when applying hypothetical kicks up to w = 100km s-1. For NSs formed via AIC with helium star donors the expected values of vsys are somewhat larger because of their narrower orbits. Neutron stars formed via AIC with giant star donors only survive in binaries if the associated kicks are very small (w ≪ 50km s-1) as a result of their large pre-AIC orbital separations, a0 > 200 R⊙.
To summarize, we expect binary pulsars formed via AIC to have small systemic velocities relative to their local stellar environment; as opposed to what is expected for systems where the NS was formed via standard SN Ib/c SNe (Tauris & Bailes 1996).
In the histogram in Fig. 18 we have plotted the distribution of all 39 measured transverse velocities, v⊥ (derived from proper motions) of binary radio pulsars with a WD companion. The average transverse velocity is ⟨ v⊥ ⟩ = 120km s-1 and the median value is 89km s-1. These values correspond to 3D systemic space velocities which, in average for random orientation of their velocity vectors with respect to the line-of-sight, are larger by a factor of 4/π, i.e. ⟨ vsys ⟩ ≈ 160km s-1. (Here we assume that these space velocities correspond to typical peculiar velocities of the systems with respect to the local standard of rest at their birth locations in the Galactic plane.) It is seen that the vast majority of the observed systems have much larger vsys than the expected 10 − 30km s-1 for NS binaries that were formed via the AIC channel. Based on this alone, one could be tempted to conclude that the fraction of binary pulsars formed via AIC must be rather small (at least less than 20%), if AICs are symmetric or even accompanied by a small kick, w < 50km s-1. However, one must keep in mind the selection effects at work given that it is much easier to determine the proper motions of fast moving objects. In the future when the number of measured velocities has increased significantly it may be possible to identify structured peaks in the velocity distribution, reflecting NS origins from AIC (or EC SNe) and SN Ib/c.
 |
Fig. 18 All measured transverse velocities of binary radio pulsars with a WD companion. Data taken from the ATNF Pulsar Catalogue in March 2013 (Manchester et al. 2005 http://www.atnf.csiro.au/research/pulsar/psrcat). AIC is expected to form binary pulsars with v⊥ < 30km s-1. However, the observed binary pulsars with such small velocities could also have formed by EC SNe. |
7.5. Formation of high B-field NSs in close Galactic binaries
In this work, we have presented the suggested observational evidence for pulsars formed via AIC in GCs. Considering orbital parameters of binary pulsars, however, sources located in GCs are generally not suitable as tracers of their binary evolution history because of the frequent encounters and exchanges of companion stars in the dense environments (Sigurdsson & Phinney 1993; Heggie et al. 1996; Ransom et al. 2005). We therefore proceed to discuss only binary parameters of NSs in the Galactic disk.
In Table 1 we presented four NS binaries in the Galactic disk with unusual properties (i.e. relatively slow spins and high B-fields, despite being in close binaries with an ultra low-mass companion star), see Sect. 2.3. The interesting question now is if we can reproduce these systems with our AIC modelling. The answer is no. Whereas the slow spin periods and the large B-fields may be accounted for in some post-AIC binaries with similar orbital periods less than a few days (see Sect. 7.1.1), all our calculated close-orbit post-AIC systems have massive CO WD companions with masses 0.65 < MWD/ M⊙ < 0.85. This is in clear contrast to the four binaries in Table 1 which all have companion stars with masses ≤0.10 M⊙. One way to reconcile this companion mass discrepancy is if the newborn NSs have evaporated their companion stars very efficiently after the AIC event. Although the available spin-down luminosity of these slow NSs is relatively small (Ė ∝ P-3) at the present epoch, these NSs could have been much more energetic in the past. An evaporation scenario could possibly also apply to post-AIC systems that evolved into (and survived) a CE, in case of main-sequence star donors (cf. Fig. 2 and Sect. 3.4). The ultra-compact X-ray binary 4U 1626−67 exhibits UV and X-ray emission lines of C, O, and Ne which suggests an evolved helium star or even a WD donor (Nelemans et al. 2010). For further discussions on 4U 1626−67 and PSR J1744−3922, see Yungelson et al. (2002) and Breton et al. (2007), respectively. The formation of these four abnormal NS binaries is one of the biggest challenges to our understanding of close binary evolution.
 |
Fig. 19 Distribution of 115 Galactic binary radio pulsars in the PṖ–diagram. The error bars are much smaller than the size of each symbol. The caption to the right explains the nature of the companion stars. Pulsars with a He WD companion marked by a circle are discussed in Sect. 7.5.1. The B-fields (dashed lines) and the spin-up lines (grey lines) were calculated following Tauris et al. (2012) and assuming MNS = 1.4 M⊙ and sinα = φ = ωc = 1. Data taken from the ATNF Pulsar Catalogue in March 2013. All observed Ṗ values were corrected for kinematic effects. The grey-shaded areas mark empty regions that cannot be populated according to current recycling scenarios. |
7.5.1. Puzzling radio pulsars in the Corbet diagram
Besides the four systems discussed above, one may ask if there are additional potential AIC candidates among the binary radio pulsars in the Galactic disk. Figure 19 shows the location of the known Galactic binary pulsars in the PṖ-diagram. The mildly recycled MSPs (10 ms < P < 100 ms) are dominated by systems with CO/ONeMg WD and NS companions. As shown in Tauris et al. (2012), their relatively slow spin rates are expected from an evolutionary point of view as a consequence of the rapid mass-transfer phase from a relatively massive donor star.
As seen in Fig. 19 there is also a group of pulsars that have similarly slow spin periods, and relatively large B-fields, but with He WD companions. These pulsars (marked with a large open circle) may also have had a limited recycling phase which could hint at a possible alternative origin. Their puzzling nature is clearer when plotting all binary radio pulsars with He WDs in the Corbet diagram. As shown in Fig. 20, an interesting pattern is revealed and we now briefly discuss four regions in this diagram.
 |
Fig. 20 Corbet diagram for the observed distribution of the 64 binary radio pulsars with a He WD companion. The plot reveals four regions, labelled by I, II, III, and IV, that may be understood from an evolutionary point of view (see text). The pulsars in region II are also marked by a circle in the PṖ–diagram in Fig. 19 and their potential link to an AIC origin is discussed in the text (figure updated after Tauris 2011). |
Region I shows that MSPs can be fully recycled over a spread of 3 orders of magnitude in final orbital period. If the Porb ≳ 200d the pulsars are only partially recycled, as noticed from their slow spin periods (region III). This could be related to the relatively short mass-transfer phase in wide-orbit LMXBs where the donor star is highly evolved by the time it fills its Roche lobe (Tauris & Savonije 1999). In region II, one sees the small sub-population of puzzling systems (marked by circles and discussed above) with 1d < Porb < 200d, all of which are only mildly recycled MSPs with spin periods between 20 and 100 ms. Where do these systems come from? And why do they have much slower spin periods than the pulsars in region I with similar orbital periods? (In this group of marked pulsars in region II we exclude PSR J0348+0432 at Porb = 0.1024days and P = 39ms, since this system can probably be explained by standard evolution of a converging LMXB system; Antoniadis et al. 2013).
Given their slow spins these six pulsars might originate from progenitor systems where the amount of mass accreted was limited. Whereas the populations in regions I and III are thought to be produced from standard LMXBs with different initial orbital periods following a core-collapse SNe, the situation might be different for pulsars in region II. Could these systems then perhaps (as suggested in Tauris 2011) originate from AICs where the subsequent spin up of the newborn NS only resulted in a mild spin-up? The rationale is that if a limited amount of material remains in the donor star envelope by the time the ONeMg WD undergoes AIC, then only a limited amount of material is available to spin up the pulsar later on. Furthermore, the narrow range of orbital periods for these pulsars could then reflect the finetuned interval of allowed mass-transfer rates needed for the progenitor ONeMg WDs to accrete and grow in mass to the Chandrasekhar limit before their implosion. This is a tempting hypothesis but, as we argue below, we find that this cannot be the case.
In this paper we have demonstrated that MSPs with He WD companions and Porb < 10d do not form via AIC for the following reason: main sequence donor stars must have masses above at least 1.6 M⊙ to ensure sufficiently high mass-transfer rates for the WD mass to grow to the AIC limit, and therefore magnetic braking is not expected to operate in these systems since such massive main-sequence stars do not have convective envelopes. As a consequence of this, the systems leading to AIC avoid significant loss of orbital angular momentum and their final orbital periods will always exceed 10 days. Given that three out of the six puzzling pulsars have Porb < 10days we conclude that the AIC channel cannot explain the origin of their characteristics. Last but not least, two of these six binary pulsars have measured transverse velocities and their values are extraordinarily large: v⊥ = 269km s-1 for PSR J1745−0952 and v⊥ = 326km s-1 for PSR J1810−2005, according to the ATNF Pulsar Catalogue, based on measurements by Janssen et al. (2010). Such large transverse velocities are clearly in contradiction with the expectations of an AIC origin.
7.5.2. Observed pulsars with CO WDs in the Corbet diagram
For the observed distribution of recycled binary pulsars with CO WDs in the Corbet diagram, we refer to Fig. 3 in Tauris et al. (2012). We note that some of our modelled systems with an AIC origin, plotted in Fig. 15, share properties of a subpopulation of the observed systems. These are systems with helium star donors which leave behind recycled pulsars with 4 ms < P < 200 ms and Porb < 2d. The very wide orbit radio pulsars with CO WDs, which result from our AIC channel modelling in systems with giant star donors (e.g. model GS3), also resemble an observed system: PSR B0820+02. This pulsar is in a 1232 day orbit, has a spin period of 0.86 s, and a CO WD companion of mass >0.52 M⊙ (Koester & Reimers 2000). Hence, it is indeed possible that some of the observed radio pulsars with CO WDs could have an AIC origin. If this is the case, then these pulsars should all have a mass close to 1.28 M⊙ since they do not accrete much in the post-AIC LMXB phase. This is in contrast to the binary pulsars with He WDs, which may accrete ~0.4 M⊙ following the AIC event. One observed pulsar with a CO WD and a low-mass NS is PSR J1802−2124 which has MNS = 1.24 ± 0.11 M⊙, P = 12.6ms, Porb = 0.70d, and a 0.78 ± 0.04 M⊙ CO WD (Ferdman et al. 2010). This pulsar shares some properties of our AIC models He3 and He4 (cf. Table 2). However, binary pulsars with CO WDs formed via the standard SN Ib/c channel are not expected to have accreted much either (since here too the mass-transfer phase is short lived, either in intermediate-mass X-ray binaries with relatively close orbits or LMXBs with very wide orbits and giant star donors). However, these NSs could have formed in SN Ib/c with birth masses substantially larger than 1.28 M⊙ and hence their measured masses could be much larger too.
7.6. Optimal evidence for NSs formed via AIC?
One may ask what observational evidence would be needed to firmly prove the AIC formation channel of NSs? This is a difficult question to answer since we do not know the exact NS properties expected from AIC. However, we could point to a few hypothetical cases of NSs which are not expected to exist from current knowledge of pulsar recycling. For example, it would be interesting if future observational surveys discover either a very slowly spinning (~100ms) radio pulsar associated with a very low B-field (~108G), or a close binary MSP with a very rapid spin (<5ms) and a high B-field (>1010G), orbiting a companion star which has experienced mass loss (see grey-shaded areas in Fig. 19). None of these pulsars is expected to form according to present recycling and spin-up theory (e.g. Tauris et al. 2012). However, even if the second kind of pulsar existed it would be very unlikely to be detected given that its strong magnetic dipole radiation would slow down its rapid spin rate within a few 100kyr. In our view, the best evidence for AIC is the apparently young NSs detected in GCs.
8. Conclusions
We have demonstrated, using a detailed stellar evolution code modelling both the pre- and the post-AIC binary evolution (to our knowledge, for the first time), that MSPs can be formed indirectly via the AIC formation channel. In this scenario, a normal NS is formed in an AIC event and which subsequently undergoes recycling by accretion (from the same donor star, now in a post-AIC LMXB) leading to the formation of an MSP. This scenario is possible for systems with donor stars that are either main-sequence stars, giants stars, or helium stars. The first type of donor stars lead to fully recycled MSPs with He WD companions, whereas the other two types of donors lead to more mildly recycled pulsars with mainly CO WD companions. The parameter space of the successful progenitor systems is restricted to three limited areas in the initial (Porb,M2)-plane.
Millisecond pulsars formed via AIC are difficult to distinguish from MSPs formed via the standard SN Ib/c channel with respect to their masses, B-fields, spin periods, and WD companions. The reason for this is that the donor stars in most cases transfer more than 0.1 M⊙ of material to the NS after the AIC event, in a process which mimics the standard recycling scenario.
Nevertheless, we identify two parameters which can, at least in some cases, be used to differentiate the two formation channels. First, MSPs formed via AIC and which have He WD companions have Porb between 10 and 60 days (or Porb > 500d for giant star donors). Second, the velocities of pulsars formed via AIC are predicted to be less than 30km s-1, which agrees well with the hypothesis of AIC being the origin of some pulsars retained in GCs. In contrast, MSPs formed via the standard SN Ib/c channel and which have He WD companions may obtain Porb in a continuous wide range between a few hours and up to ~1000days, and their space velocities typically exceed 100km s-1.
In a few cases where the post-AIC LMXB phase is short-lived, and particularly in GCs where the probability of disruption of a wide binary by an encounter event is large, pulsars formed via AIC will be largely unaffected by, or will avoid, subsequent accretion from the donor star. This could, for example, be the explanation for the existence of some GC pulsars which appear to be young.
More research is needed on optically thick wind modelling, and direct observations of SN Ia remnants to constrain pre-SN Ia wind mass loss, as well as modelling of the prescription for calculating the mass-transfer rates from giant star donors with small surface gravities and extended atmospheres. As demonstrated in this paper, the application of the optically thick wind model is very important for the estimated event rate of both AIC and SNe Ia.
A small companion-star mass suggests that the previous (or ongoing) mass-transfer episode was (is) dynamically stable (Tauris & Savonije 1999; Podsiadlowski et al. 2002). However, even observed radio pulsars which are thought to have evolved via a CE phase have B < 5 × 109G (Tauris et al. 2012), in general much smaller that the B-fields of the NSs listed in Table 1.
Although at present there is not much observational evidence behind this model (not surprising given that systems with extremely high mass-transfer rates are short lived) there is some evidence of excess mass loss in the case of Cyg X-2, as demonstrated by King & Ritter (1999) and Podsiadlowski & Rappaport (2000). This mass loss could have been be caused in the past by a relativistic jet (as observed in SS433) or by coronal winds from the outer parts of the accretion disk (Blandford & Begelman 1999).
In Table 2 we always chose θ = 0° for applied kicks of w = 50km s-1 which resulted in the largest possible post-SN values of Porb, but also in the smallest values of vsys. For θ = 180° we obtain typical values of vsys ≈ 30km s-1, for w = 50km s-1.
We note that ΔR and the mass ratio, q are defined differently in Ritter (1988) and Kolb & Ritter (1990). The first paper has a typo in the last term in Eq. (A8), which should be 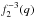 .
.
Acknowledgments
It is a pleasure to thank Ed van den Heuvel for very helpful references and comments on the manuscript. T.M.T. gratefully acknowledges support and hospitality from the Argelander-Insitut für Astronomie, Universität Bonn and the Max-Planck-Institut für Radioastronomie.
References
- Althaus, L. G., Serenelli, A. M., & Benvenuto, O. G. 2001, MNRAS, 324, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniadis, J., van Kerkwijk, M. H., Koester, D., et al. 2012, MNRAS, 423, 3316 [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
- Bailyn, C. D., & Grindlay, J. E. 1990, ApJ, 353, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., De Vito, M. A., & Horvath, J. E. 2012, ApJ, 753, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, D. 2002, JA&A, 23, 67 [NASA ADS] [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, D., Wijers, R. A. M. J., Hartman, J. W., & Verbunt, F. 1992, A&A, 254, 198 [NASA ADS] [Google Scholar]
- Biggs, J. D., Bailes, M., Lyne, A. G., Goss, W. M., & Fruchter, A. S. 1994, MNRAS, 267, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Begelman, M. C. 1999, MNRAS, 303, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bours, M. C. P., Toonen, S., & Nelemans, G. 2013, A&A, 552, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyles, J., Lorimer, D. R., Turk, P. J., et al. 2011, ApJ, 742, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, H. 1997, Ph.D. Thesis, Ludwig-Maximilians-Univ. München [Google Scholar]
- Breton, R. P., Roberts, M. S. E., Ransom, S. M., et al. 2007, ApJ, 661, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Büning, A., & Ritter, H. 2004, A&A, 423, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burderi, L., Possenti, A., D’Antona, F., et al. 2001, ApJ, 560, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Canal, R., Isern, J., & Labay, J. 1990, ARA&A, 28, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. 1970, ApJ, 159, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Iben, Jr., I., & Tornambe, A. 1998, ApJ, 496, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., Soderberg, A. M., Moe, M., et al. 2012, ApJ, 750, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Zweibel, E., & Bildsten, L. 2001, ApJ, 557, 958 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Mazzitelli, I., & Ritter, H. 1989, A&A, 225, 391 [NASA ADS] [Google Scholar]
- Darbha, S., Metzger, B. D., Quataert, E., et al. 2010, MNRAS, 409, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Das, U., & Mukhopadhyay, B. 2013, Phys. Rev. Lett., 110, 071102 [NASA ADS] [CrossRef] [Google Scholar]
- Deloye, C. J. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 501 [Google Scholar]
- Denissenkov, P. A., Herwig, F., Bildsten, L., & Paxton, B. 2013, ApJ, 762, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Burrows, A., Ott, C. D., et al. 2006, ApJ, 644, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Burrows, A., Livne, E., & Ott, C. D. 2007, ApJ, 669, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Di Stefano, R., & Kilic, M. 2012, ApJ, 759, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G., Lasota, J.-P., Hameury, J.-M., & Charles, P. 1999, MNRAS, 303, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Ergma, E., Sarna, M. J., & Antipova, J. 1998, MNRAS, 300, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Ferdman, R. D., Stairs, I. H., Kramer, M., et al. 2010, ApJ, 711, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Ransom, S. M., Bégin, S., et al. 2008, ApJ, 675, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, U., & Urpin, V. 1994, MNRAS, 271, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1999, ApJ, 522, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 2008, ApJ, 679, 1390 [Google Scholar]
- Hachisu, I., Kato, M., Saio, H., & Nomoto, K. 2012, ApJ, 744, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, P. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C., Hut, P., & McMillan, S. L. W. 1996, ApJ, 467, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Helfand, D. J., Ruderman, M. A., & Shaham, J. 1983, Nature, 304, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C. 2001, Cataclysmic Variable Stars (Springer) [Google Scholar]
- Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Nugent, P. E., et al. 2006, Nature, 443, 308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hubbard, W. B., & Lampe, M. 1969, ApJS, 18, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., Wickramasinghe, D. T., Ferrario, L., & Kiel, P. D. 2010, MNRAS, 402, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373 [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1985, ApJS, 58, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1989, ApJ, 342, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1996, ApJS, 105, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., Tutukov, A. V., & Yungelson, L. R. 1997, ApJ, 475, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Idan, I., Shaviv, N. J., & Shaviv, G. 2012, J. Phys. Conf. Ser., 337, 012051 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1992, ApJ, 397, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Ivanova, N., Heinke, C. O., Rasio, F. A., Belczynski, K., & Fregeau, J. M. 2008, MNRAS, 386, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, B. A., Hotan, A., Bailes, M., Ord, S., & Kulkarni, S. R. 2005, ApJ, 629, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Janka, H.-T. 2012, Ann. Rev. Nucl. Part. Sci., 62, 407 [Google Scholar]
- Janssen, G. H., Stappers, B. W., Bassa, C. G., et al. 2010, A&A, 514, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jordan, S., Aznar Cuadrado, R., Napiwotzki, R., Schmid, H. M., & Solanki, S. K. 2007, A&A, 462, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jose, J., Hernanz, M., & Isern, J. 1993, A&A, 269, 291 [NASA ADS] [Google Scholar]
- Kahabka, P., & van den Heuvel, E. P. J. 1997, ARA&A, 35, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Iben, Jr., I. 1992, ApJ, 394, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 1994, ApJ, 437, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J. 1986, The symbiotic stars (Cambridge University Press) [Google Scholar]
- King, A. R., & Ritter, H. 1999, MNRAS, 309, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1967, ZAp, 65, 251 [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin: Springer) [Google Scholar]
- Kitaura, F. S., Janka, H.-T., & Hillebrandt, W. 2006, A&A, 450, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koester, D., & Reimers, D. 2000, A&A, 364, L66 [NASA ADS] [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Konar, S., & Bhattacharya, D. 1997, MNRAS, 284, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. R. 1986, ApJ, 306, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S. R., & Narayan, R. 1988, ApJ, 335, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Langer, N. 2012, ARA&A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lesaffre, P., Han, Z., Tout, C. A., Podsiadlowski, P., & Martin, R. G. 2006, MNRAS, 368, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
- Liebert, J., Bergeron, P., & Holberg, J. B. 2003, AJ, 125, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W.-M., Chen, W.-C., Wang, B., & Han, Z. W. 2010, A&A, 523, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Z. W., Pakmor, R., Röpke, F. K., et al. 2012, A&A, 548, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Livio, M. 2000, in Type Ia Supernovae, Theory and Cosmology, eds. J. C. Niemeyer, & J. W. Truran, 33 [Google Scholar]
- Lyne, A. G., & Lorimer, D. R. 1994, Nature, 369, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Biggs, J. D., Harrison, P. A., & Bailes, M. 1993, Nature, 361, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Manchester, R. N., & D’Amico, N. 1996, ApJ, 460, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, X., Chen, X., Chen, H., Denissenkov, P. A., & Han, Z. 2013, ApJL, submitted [arXiv:1307.7730] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Piro, A. L., & Quataert, E. 2009, MNRAS, 396, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1983, A&A, 121, 29 [NASA ADS] [Google Scholar]
- Michel, F. C. 1987, Nature, 329, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, S., & Nomoto, K. 1987, ApJ, 318, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, S., Nomoto, K., Yokoi, K., & Sugimoto, D. 1980, PASJ, 32, 303 [Google Scholar]
- Nelemans, G., Yungelson, L. R., van der Sluys, M. V., & Tout, C. A. 2010, MNRAS, 401, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, L. A., Dubeau, E., & MacCannell, K. A. 2004, ApJ, 616, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Newsham, G., Starrfield, S., & Timmes, F. 2013 [arXiv:1303.3642] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1987, ApJ, 322, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., & Kondo, Y. 1991, ApJ, 367, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., & Sugimoto, D. 1977, PASJ, 29, 765 [NASA ADS] [Google Scholar]
- Nomoto, K., Miyaji, S., Sugimoto, D., & Yokoi, K. 1979a, in White Dwarfs and Variable Degenerate Stars, eds. H. M. van Horn, & V. Weidemann, IAU Coll., 53, 56 [Google Scholar]
- Nomoto, K., Nariai, K., & Sugimoto, D. 1979b, PASJ, 31, 287 [NASA ADS] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Nomoto, K., Saio, H., Kato, M., & Hachisu, I. 2007, ApJ, 663, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan (Dordrecht, Holland), IAU Symp., 73, 75 [Google Scholar]
- Paczyński, B., & Sienkiewicz, R. 1972, Acta Astron., 22, 73 [NASA ADS] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2010, ApJ, 715, 78 [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012, ApJ, 750, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2013, ApJ, 773, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Pastetter, L., & Ritter, H. 1989, A&A, 214, 186 [NASA ADS] [Google Scholar]
- Patruno, A., & Watts, A. L. 2012, in Timing Neutron Stars: Pulsations, Oscillations and Explosions, eds. T. Belloni, M. Mendez, Astrophys. Space Sci. (Springer) [Google Scholar]
- Patruno, A., Alpar, M. A., van der Klis, M., & van den Heuvel, E. P. J. 2012, ApJ, 752, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Oksanen, A., Monard, B., et al. 2013 [arXiv:1303.0736] [Google Scholar]
- Payne, D. J. B., & Melatos, A. 2007, MNRAS, 376, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pfahl, E., Rappaport, S., Podsiadlowski, P., & Spruit, H. 2002, ApJ, 574, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Kulkarni, S. R. 2013, ApJ, 762, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., & Rappaport, S. 2000, ApJ, 529, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Poelarends, A. J. T., Herwig, F., Langer, N., & Heger, A. 2008, ApJ, 675, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., & Kovetz, A. 1995, ApJ, 445, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Ransom, S. M., Hessels, J. W. T., Stairs, I. H., et al. 2005, Science, 307, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rappaport, S., Deck, K., Levine, A., et al. 2013, ApJ, 768, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, S., & Weigert, A. 1971, A&A, 13, 367 [NASA ADS] [Google Scholar]
- Reimers, D. 1975, in Circumstellar envelopes and mass loss of red giant stars (New York: Springer-Verlag), 229 [Google Scholar]
- Reisenegger, A. 2003 [arXiv:astro-ph/0307133] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Ritter, H. 2008, New A Rev., 51, 869 [Google Scholar]
- Romani, R. W. 1990, Nature, 347, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Nomoto, K. 1985, A&A, 150, L21 [NASA ADS] [Google Scholar]
- Saio, H., & Nomoto, K. 2004, ApJ, 615, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Savonije, G. J. 1987, Nature, 325, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Scalzo, R. A., Aldering, G., Antilogus, P., et al. 2010, ApJ, 713, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Schwab, J., Podsiadlowski, P., & Rappaport, S. 2010, ApJ, 719, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Shibazaki, N., Murakami, T., Shaham, J., & Nomoto, K. 1989, Nature, 342, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Phinney, E. S. 1993, ApJ, 415, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 391 [Google Scholar]
- Srinivasan, G., Bhattacharya, D., Muslimov, A. G., & Tsygan, A. J. 1990, Current Science, 59, 31 [NASA ADS] [Google Scholar]
- Starrfield, S., Timmes, F. X., Iliadis, C., et al. 2012, Baltic Astron., 21, 76 [NASA ADS] [Google Scholar]
- Sutantyo, W., & Li, X.-D. 2000, A&A, 360, 633 [NASA ADS] [Google Scholar]
- Taam, R. E., & van den Heuvel, E. P. J. 1986, ApJ, 305, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M. 2011, in Evolution of Compact Binaries, eds. L. Schmidtobreick, M. R. Schreiber, & C. Tappert, ASP Conf. Ser., 447, 285 [Google Scholar]
- Tauris, T. M., & Bailes, M. 1996, A&A, 315, 432 [NASA ADS] [Google Scholar]
- Tauris, T. M., & Savonije, G. J. 1999, A&A, 350, 928 [NASA ADS] [Google Scholar]
- Tauris, T. M., & Takens, R. J. 1998, A&A, 330, 1047 [NASA ADS] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2006, in Formation and evolution of compact stellar X-ray sources (Cambridge University Press), 623 [Google Scholar]
- Tauris, T. M., van den Heuvel, E. P. J., & Savonije, G. J. 2000, ApJ, 530, L93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2011, MNRAS, 416, 2130 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2012, MNRAS, 425, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Woosley, S. E. 1992, ApJ, 396, 649 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 1994, in Interacting Binaries, eds. H. Nussbaumer, & A. Orr (Berlin: Springer), 263 [Google Scholar]
- van den Heuvel, E. P. J. 2004, in 5th INTEGRAL Workshop on the INTEGRAL Universe, eds. V. Schoenfelder, G. Lichti, & C. Winkler, ESA SP, 552, 185 [Google Scholar]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1994, Mem. Soc. Astron. Italiana, 65, 237 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J., & Bitzaraki, O. 1995, A&A, 297, L41 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J., Bhattacharya, D., Nomoto, K., & Rappaport, S. A. 1992, A&A, 262, 97 [NASA ADS] [Google Scholar]
- van Kerkwijk, M. H., Chang, P., & Justham, S. 2010, ApJ, 722, L157 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J. 1996, ApJ, 464, L139 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J., van den Heuvel, E. P. J., Kouveliotou, C., et al. 1997, A&A, 317, L9 [NASA ADS] [Google Scholar]
- Verbunt, F., Wijers, R. A. M. J., & Burm, H. M. G. 1990, A&A, 234, 195 [NASA ADS] [Google Scholar]
- Wang, B., & Han, Z. 2010, A&A, 515, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., Li, X.-D., & Han, Z.-W. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Wellstein, S., & Langer, N. 1999, A&A, 350, 148 [NASA ADS] [Google Scholar]
- Wheeler, J. C. 2012, ApJ, 758, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, Jr., I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C., Cowan, J. J., & Hillebrandt, W. 1998, ApJ, 493, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Wickramasinghe, D. T., & Ferrario, L. 2000, PASP, 112, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Wiescher, M., Gorres, J., Thielemann, F.-K., & Ritter, H. 1986, A&A, 160, 56 [NASA ADS] [Google Scholar]
- Wijers, R. A. M. J. 1997, MNRAS, 287, 607 [NASA ADS] [Google Scholar]
- Woltjer, L. 1964, ApJ, 140, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Wongwathanarat, A., Janka, H.-T., & Müller, E. 2013, A&A, 552, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2003, A&A, 412, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Podsiadlowski, P., & Rosswog, S. 2007, MNRAS, 380, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Yungelson, L. R., Nelemans, G., & van den Heuvel, E. P. J. 2002, A&A, 388, 546 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Y. B., & Novikov, I. D. 1971, Relativistic Astrophysics: Stars and Relativity (Chicago: University of Chicago Press) [Google Scholar]
- Zhang, C. M. 1998, A&A, 330, 195 [NASA ADS] [Google Scholar]
- Zhang, C. M., & Kojima, Y. 2006, MNRAS, 366, 137 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Neutron stars that are candidates for being formed via AIC in a globular cluster (a–d) or in the Galactic disk (e–h), respectively.
Summary of selected systems which evolved successfully to AIC and later produced recycled pulsars.
All Figures
 |
Fig. 1 Accretion window of the WD, the corresponding critical mass-transfer rates, and our assumed mass-accumulation fractions, ηH, here calculated with a hydrogen abundance of X = 0.70 of the accreted matter (see text). |
| In the text | |
 |
Fig. 2 Evolutionary tracks in the (Porb,M2)-plane. The initial system configurations are: M2 = 2.6 M⊙, Porb = 1.0 days (red tracks) and M2 = 2.2 M⊙, Porb = 2.5 days (blue tracks). The ONeMg WD has an initial mass of 1.20 M⊙ and grows to 1.48 M⊙ when the AIC occurs. After the AIC three tracks were computed for each system depending on the kick velocity applied in the AIC. Here we applied w = 0, w = 50kms-1 (φ = θ = 0°), and w = 450kms-1 (φ = 107° and θ = 90°) resulting in different values of Porb for the post-AIC system. In two post-AIC cases presented here, and in general if the donor star is quite evolved by the time it refills its Roche lobe (i.e. because the post-AIC Porb is large) and if the donor star is significantly more massive than the newborn NS (1.28 M⊙), the RLO becomes dynamically unstable and the system evolves through a common envelope (marked by CE). |
| In the text | |
 |
Fig. 3 Grid of investigated initial orbital periods and masses for main-sequence donor stars with a metallicity of Z = 0.02 (upper panel) and Z = 0.001 (lower panel). The grey shaded region in each panel corresponds to systems which successfully evolve to the AIC stage (green circles). The blue triangles and purple asterisks correspond to cases where the mass-transfer rate was too high or too low, respectively, to allow for the WD to reach a critical mass of 1.48 M⊙. The red squares indicate orbits which are too narrow to initially accommodate the ZAMS donor star. The blue triangles inside green circles in the upper panel are systems leading successfully to AIC assuming ṀCE = 10 ṀEdd,WD. Details of the mass-transfer process of the binaries inside the marked cross in the upper panel are represented in Figs. 4 and 5. |
| In the text | |
 |
Fig. 4 Mass-transfer rates of the four pre-AIC binaries shown in the horizontal part of the cross in the upper panel of Fig. 3. The mass-transfer-rate from the donor star in the system with Porb = 1.5d is too low (see Fig. 1) to cause the accreting WD to grow sufficiently in mass and trigger an AIC event. For the donors in the other systems, on the other hand, the mass-transfer rate is too high to result in stable mass gain of the accretor. Hence, none of these models resulted in a successful AIC. The differences in these mass-transfer rates can be understood in terms of different thicknesses of convective envelopes (see text and Fig. 6). |
| In the text | |
 |
Fig. 5 Mass-transfer rates of the pre-AIC binaries shown in the vertical part of the cross in the upper panel of Fig. 3. The four donor stars have masses of 1.6 − 2.2 M⊙ and Porb = 2.0d. The arrows mark the collapse of the accreting ONeMg WD (AIC) for the two most massive stars. Donor stars with initial masses M2 ≥ 2.6 M⊙ result in excessive mass-transfer rates and thus do not produce AIC events (see text). |
| In the text | |
 |
Fig. 6 Kippenhahn diagram of four 1.8 M⊙ donor stars undergoing early Case B RLO in X-ray binaries with an accreting WD and orbital periods of 1.5, 2.0, 2.5, and 2.8 days, respectively. The plots show cross-sections of the stars in mass-coordinates from the centre to the surface of the star, along the y-axis, as a function of stellar age on the x-axis. The green hatched areas denote zones with convection (according to the Ledoux criterion) initially in the core and later in the envelope of the donor stars. The intensity of the blue/purple color indicates the net energy-production rate; the hydrogen burning shell is clearly seen in all panels at m/ M⊙ ≃ 0.2. In the top-left panel, the donor star decreases its mass from 1.8 M⊙ until it finally detaches from the Roche lobe and forms a 0.28 M⊙ He WD. In the top-right panel, our calculation stops when the donor star reached 1.62 M⊙ since the mass-transfer rate became too high when the donor star refilled its Roche lobe, following an initial phase of stable RLO with a lower value of |Ṁ2|. In the two lower panels the mass-transfer rate went immediately up to the critical value at the onset of the RLO. The response of a donor star to mass loss depends strongly on the depth of its convective envelope and thus, as seen here, it depends on Porb. See Fig. 4 and text for a discussion. |
| In the text | |
 |
Fig. 7 Left panel: mass-transfer rates of four 2.5 M⊙ donor stars in pre-AIC binaries with initial orbital periods between 1.0 − 3.0 days leading to the post-AIC LMXB systems shown in the right panel. The arrows mark the collapse of the accreting WD (AIC) and the evolution from this point onwards can be ignored since it is now followed in the post-AIC LMXB systems shown in the right panel. The dashed line is the adopted upper limit for stable mass transfer (see Sect. 3.1.1). It is seen how the pre-AIC mass-transfer rates were quite close to our accepted upper limit. A slightly more massive donor star would lead to excessive mass-transfer rates and thus not result in an AIC event (see also the systematic effect of an increasing donor mass in Fig. 5). The open circles indicate hypothetical super-Chandrasekhar WD masses of 2.0 M⊙. Right panel: mass-transfer rates of the post-AIC LMXBs plotted as a function of time since the AIC event. The reason for the difference in time intervals between the AIC event and the donor stars refilling their Roche lobe (see initial interceptions of the four graphs with the x-axis) is mainly due to different expansions of the orbit due to the AIC event, caused by different Porb at the moment of the WD collapse. The vertical text at the lower left side of each graph yields the mass of the donor star at the moment of the AIC, the mass of the final WD following the LMXB and the amount of mass accreted by the NS, ΔMNS. The dashed line is the Eddington accretion limit for a NS. Only the systems with initial pre-AIC orbital periods of 1.0 days (red curve) and 1.5 days (green curve) experienced a long phase (>100Myr) of post-AIC mass-transfer driven by hydrogen shell burning. This phase leads to significant accretion onto the NS (and effective recycling) since |Ṁ2| < ṀEdd. Hence, the NSs in these systems were able to accrete more mass which results in faster spinning MSPs (partly due to their smaller magnetospheres). |
| In the text | |
 |
Fig. 8 Final orbital period of the MSP binaries formed via AIC as a function of WD mass, evolving from main-sequence donor stars with a metallicity of Z = 0.02 (upper panel) and Z = 0.001 (lower panel). The different symbols refer to different kicks during the AIC. The filled green circles correspond to w = 0 (no kick), the open pink stars to w = 50km s-1, and the filled red stars are for w = 450km s-1. The symbols connected with a black line are for the same pre-AIC binaries but different values of the kick, w. The dotted line is the (MWD,Porb)-relation taken from Tauris & Savonije (1999) and applies solely to low-mass donors with degenerate He cores. The blue triangles in green circles are explained in Fig. 3. See text for further details and discussions. |
| In the text | |
 |
Fig. 9 Evolutionary tracks in the core density-core temperature (ρc,Tc)-plane. For each graph the initial (ZAMS) values of the donor star mass, M2, the orbital period, Porb, and in parenthesis the main chemical composition and the mass of the final WD are listed. The dotted line separates regions where the stellar pressure is dominated by the gas pressure (left) and the degenerate electron pressure (right). On each track the symbols represent: the termination of core hydrogen burning (filled squares), the end of the RLO (filled circles), the onset of the 3α-process (open circles) and the onset of efficient helium burning (i.e. when the luminosity generated by the 3α–process exceeds the energy loss rate by neutrinos, open triangles). The calculations were followed to the WD cooling track, except for two cases causing numerical instabilities during hydrogen shell flashes. |
| In the text | |
 |
Fig. 10 Grid of investigated initial orbital periods and masses for giant star donors with a metallicity of Z = 0.02 (top) and Z = 0.001 (bottom). The meaning of the various symbols is equivalent to those in Fig. 3. The grey shaded region in each panel corresponds to systems which successfully evolve to the AIC stage. Only giant donors with masses 0.9 ≤ M2/ M⊙ ≤ 1.1 are able to produce MSPs via the AIC channel. The hatched regions indicate donor stars which evolve on a timescale longer than the Hubble-timescale. The cross-hatched region corresponds to giant donors which have so large atmospheric, hydrogen pressure scale-heights that our adopted mass-transfer scheme breaks down – see text. |
| In the text | |
 |
Fig. 11 Grid of investigated initial orbital periods and masses for helium star donors with Y = 0.98 and a metallicity of Z = 0.02. The meaning of the various symbols is explained in Fig 3. The grey shaded region corresponds to systems that have successfully evolved to the AIC stage. See text for further discussions. |
| In the text | |
 |
Fig. 12 Evolutionary tracks in the HR–diagram for three 1.1 M⊙ helium stars: two in binaries with a 1.2 M⊙ WD and one evolving as a single star. The loops in the upper-left corner of the two binary helium star tracks are caused by the ignition of shell helium burning. |
| In the text | |
 |
Fig. 13 Final orbital periods of recycled radio pulsars as a function of their CO WD companion masses for systems evolving from helium star donors with a metallicity of Z = 0.02. Data points connected with a green line were calculated from the same initial helium star mass (1.2 M⊙ and 1.4 M⊙, respectively). Data points with black dots were all calculated from a binary with an initial orbital period of 0.1 days. The solid red star and the open purple star, connected with a black line to the green data points, indicate similar calculations including an applied hypothetical kick velocity of 50km s-1 and 450km s-1, yielding the widest possible orbit. The less massive the initial helium star donor, and the more narrow the orbit, the more material the NS accretes and the faster spin it obtains. The dashed lines indicate roughly where the pulsar is spun up to 15 ms and 80 ms, respectively. See text for discussions. |
| In the text | |
 |
Fig. 14 Grid showing all successful AIC systems, starting from an accreting 1.2 M⊙ (ONeMg) WD orbiting a main-sequence star (green), a giant star (red), or a helium star (blue) with a metallicity of Z = 0.02. Hatched areas are calculated for Z = 0.001. The initial parameter space shown here is equivalent to that for progenitor binaries of SN Ia with an accreting 1.2 M⊙ (CO) WD (see text). |
| In the text | |
 |
Fig. 15 Corbet diagram for 55 MSPs (or mildly recycled pulsars) produced via AIC formation and subsequent accretion, including those listed in Table 2. The three different donor star progenitor classes (green, red, and blue) are clearly distinguished, corresponding to main-sequence, giant star, and helium star donors, respectively. Open circles are MSPs with He WD companions, solid diamonds indicate MSPs with (hybrid) CO WD companions. Symbols with a superimposed open black star correspond to AIC models where a kick was applied. For a few systems with giant star donors only upper limits are given for Porb (and P) because of computational difficulties, cf. Sect. 5.3. |
| In the text | |
 |
Fig. 16 Amount of mass accreted by the NSs during the post-AIC LMXB phase, ΔMNS as a function of the duration of the post-AIC LMXB phase, ΔtLMXB. The symbols correspond to those in Fig. 15. Our calculations assumed an accretion efficiency of 30%. The deviation from a straight line is caused by the lower mass-transfer rates |Ṁ2| ≪ ṀEdd in systems with long mass-transfer timescales. The more mass a NS accretes, the faster is the final spin rate of the resultant MSP (see text). |
| In the text | |
 |
Fig. 17 Systemic recoil velocities of MSPs formed indirectly via AIC. The two upper panels show sample calculations of the recoil velocities, vsys obtained for a fixed kick of w = 50km s-1 and kick angles θ = 0 − 180° (upper panel), or a fixed value of θ = 36° and kicks w = 0 − 100km s-1 (central panel), in both cases as a function of the pre-AIC orbital separation, a0. The lower panel shows vsys as a function of kick velocities, w for fixed values of a0 and variable values of θ = 0 − 180°. In all cases we assumed a companion star mass of |
| In the text | |
 |
Fig. 18 All measured transverse velocities of binary radio pulsars with a WD companion. Data taken from the ATNF Pulsar Catalogue in March 2013 (Manchester et al. 2005 http://www.atnf.csiro.au/research/pulsar/psrcat). AIC is expected to form binary pulsars with v⊥ < 30km s-1. However, the observed binary pulsars with such small velocities could also have formed by EC SNe. |
| In the text | |
 |
Fig. 19 Distribution of 115 Galactic binary radio pulsars in the PṖ–diagram. The error bars are much smaller than the size of each symbol. The caption to the right explains the nature of the companion stars. Pulsars with a He WD companion marked by a circle are discussed in Sect. 7.5.1. The B-fields (dashed lines) and the spin-up lines (grey lines) were calculated following Tauris et al. (2012) and assuming MNS = 1.4 M⊙ and sinα = φ = ωc = 1. Data taken from the ATNF Pulsar Catalogue in March 2013. All observed Ṗ values were corrected for kinematic effects. The grey-shaded areas mark empty regions that cannot be populated according to current recycling scenarios. |
| In the text | |
 |
Fig. 20 Corbet diagram for the observed distribution of the 64 binary radio pulsars with a He WD companion. The plot reveals four regions, labelled by I, II, III, and IV, that may be understood from an evolutionary point of view (see text). The pulsars in region II are also marked by a circle in the PṖ–diagram in Fig. 19 and their potential link to an AIC origin is discussed in the text (figure updated after Tauris 2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.