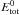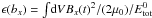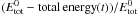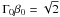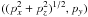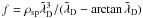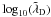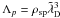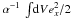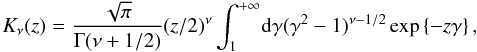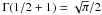| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 24 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321557 | |
| Published online | 18 October 2013 | |
Apar-T: code, validation, and physical interpretation of particle-in-cell results
1 École Normale Supérieure, CRAL, UMR CNRS 5574, Université de Lyon, Lyon, France
e-mail: mickael.melzani@ens-lyon.fr
2 CSCS Lugano, Switzerland
3 NVIDIA Switzerland, Technoparkstr 1, 8005 Zürich, Switzerland
Received: 23 March 2013
Accepted: 25 July 2013
We present the parallel particle-in-cell (PIC) code Apar-T and, more importantly, address the fundamental question of the relations between the PIC model, the Vlasov-Maxwell theory, and real plasmas. First, we present four validation tests: spectra from simulations of thermal plasmas, linear growth rates of the relativistic tearing instability and of the filamentation instability, and nonlinear filamentation merging phase. For the filamentation instability we show that the effective growth rates measured on the total energy can differ by more than 50% from the linear cold predictions and from the fastest modes of the simulation. We link these discrepancies to the superparticle number per cell and to the level of field fluctuations. Second, we detail a new method for initial loading of Maxwell-Jüttner particle distributions with relativistic bulk velocity and relativistic temperature, and explain why the traditional method with individual particle boosting fails. The formulation of the relativistic Harris equilibrium is generalized to arbitrary temperature and mass ratios. Both are required for the tearing instability setup. Third, we turn to the key point of this paper and scrutinize the question of what description of (weakly coupled) physical plasmas is obtained by PIC models. These models rely on two building blocks: coarse-graining, i.e., grouping of the order of p ~ 1010 real particles into a single computer superparticle, and field storage on a grid with its subsequent finite superparticle size. We introduce the notion of coarse-graining dependent quantities, i.e., quantities depending on p. They derive from the PIC plasma parameter ΛPIC, which we show to behave as ΛPIC ∝ 1/p. We explore two important implications. One is that PIC collision- and fluctuation-induced thermalization times are expected to scale with the number of superparticles per grid cell, and thus to be a factor p ~ 1010 smaller than in real plasmas, a fact that we confirm with simulations. The other is that the level of electric field fluctuations scales as 1/ΛPIC ∝ p. We provide a corresponding exact expression, taking into account the finite superparticle size. We confirm both expectations with simulations. Fourth, we compare the Vlasov-Maxwell theory, often used for code benchmarking, to the PIC model. The former describes a phase-space fluid with Λ = + ∞ and no correlations, while the PIC plasma features a small Λ and a high level of correlations when compared to a real plasma. These differences have to be kept in mind when interpreting and validating PIC results against the Vlasov-Maxwell theory and when modeling real physical plasmas.
Key words: plasmas / methods: numerical / relativistic processes / instabilities / magnetic reconnection
© ESO, 2013
1. Introduction
Full particle codes are now used by a large number of groups worldwide to study plasmas out of equilibrium in a large variety of environments, including electronic devices, inertial fusion (Dieckmann et al. 2006; Bret et al. 2010), tokamaks, Earth and solar magnetospheres (Hesse et al. 2001; Daughton et al. 2006; Drake et al. 2006; Klimas et al. 2008; Markidis et al. 2012; Baumann & Nordlund 2012), or high-energy astrophysics (Silva et al. 2003; Pétri & Lyubarsky 2007; Zenitani & Hoshino 2008; Cerutti et al. 2012; Jaroschek et al. 2005; Nishikawa et al. 2008; Sironi & Spitkovsky 2011).
Particle simulations actually appeared along with the first computers at universities and in industry around 1950. They first concerned electron beams in vacuum tubes, a device extensively used in the computers themselves. The beams were cold (Hartree 1950) or later hot (Tien & Moshman 1956), and consisted of roughly 300 electron slabs moving in one dimension.
The step to plasma simulations was taken by Buneman (1959). He simulated an electrostatic plasma of 512 ions and electrons in one dimension, and showed that particle codes could be used to study the linear, nonlinear, and saturation phases of instabilities. At the time, the relevance of simulations with so few particles per Debye sphere was not clear and in 1962 Dawson (1962) and Eldridge & Feix (1962) made an important contribution by showing that correct thermal behavior was produced.
All these algorithms used particle-particle interactions, and the first particle-mesh codes to introduce a grid appeared only later (Burger 1965; Hockney 1966; Yu et al. 1965). A great deal of literature on the drawbacks and benefits of the grid then appeared, and is now mostly concentrated in the two reference books of Birsdall & Langdon (1985) and Hockney & Eastwood (1988). Refinements of the algorithms quickly appeared (higher order grid interpolation, quiet codes, etc.), as well as code optimizations, at a time when programs were written in assembly language and depended heavily on machine architecture. Fully electromagnetic, relativistic, and 3D codes appeared with the studies of laser induced fusion (Buneman 1976), and closely resemble today’s codes.
In 1967, it was possible for Birdsall (1967) to list the papers concerning simulations, and he noticed that they had grown exponentially since 1956. In 1956, “many particles” meant 300; in 1985, 106; in 2008, 109; and in 2012, 1012. For more historical details on PIC simulations, one may consult Birdsall (1967, 1999), Hockney & Eastwood (1988, Sect. 9.1), or the introduction of Birsdall & Langdon (1985).
Today, the latest generation of PIC algorithms consists of large versatile codes, featuring high order integration schemes and efficient parallelization. We can quote codes such as TRISTAN-MP (Spitkovsky 2005), OSIRIS (Fonseca et al. 2002, 2008), VORPAL (Nieter & Cary 2004), WARP (Grote et al. 2005), ALaDyn (Benedetti et al. 2008), iPIC3D (Markidis et al. 2010), Photon-Plasma (Haugboelle et al. 2013), or Zeltron (Cerutti et al. 2013). They employ various simulation methods. The equations solved can differ: electrostatic codes, electromagnetic codes, Darwin approximation (Huang & Ma 2008). The integration scheme can also vary: integration directly on the fields staggered on a grid, either with a charge conserving scheme or via solution of Poisson equation (Cerutti et al. 2012); or integration of the potential and correction of the discrepancies to charge conservation (Daughton et al. 2006). The time integration can be explicit or implicit (Markidis et al. 2012). Special parts of the numerical scheme can also differ; for example, the order of the field integration or the use of Fourier transforms. The interpolation of particle quantities to grid points and reciprocally can be done by a nearest grid point method (NGP), by a linear weighting (cloud in cell (CIC), or the PIC algorithm in the old terminology), or by a smoother shape (spline interpolation, Esirkepov 2001).
This article documents a new PIC code, Apar-T. Its first version, Tristan, was written by O. Buneman in 1990 (Matsumoto & Omura 1993). It was then made parallel by Messmer (2001), and used in Messmer (2002) or Paesold et al. (2005). Given the large quantity of simulation methods, it is useful to first detail our algorithm. This is done in Sect. 2 and Appendix A.
In Sect. 3, we present a set of test problems and the results obtained with Apar-T. The first test is the study of the fluctuation spectra of a thermal plasma. The second and third tests explore the linear and nonlinear stages of the filamentation instability. A last test is the computation of the linear growth rates of the relativistic tearing instability, for which we give the general equilibrium relations for the relativistic Harris configuration with arbitrary temperature and mass ratio between the two species (Appendix C). In Sect. 4 we describe a method for loading a Maxwell-Jüttner momentum distribution with an arbitrary bulk velocity and temperature. The naive method, which initializes the comobile distribution and then boosts particles individually, is shown to be incorrect, mainly because space contraction is absent from the PIC code.
In Sect. 5, motivated by the above tests, we explore the physical implications of two main differences between PIC plasmas and real plasmas: coarse-graining, i.e., a reduction in the number of particles by a factor reaching p ~ 1010, and the representation of the fields on a grid. We introduce the notion of coarse-graining dependent quantities, i.e., physical parameters depending on the number of real particles represented by a single computer superparticle. The prototype of these quantities is the plasma parameter Λ, which scales for a PIC plasma as 1/p. The dependence on coarse-graining has important consequences for key physical quantities such as the thermalization time, the collision time, or the level of field fluctuations.
We point out more generally that a PIC code simulates a microstate constituted by a restricted number of finite-sized particles each representing up to 1010 real plasma particles, while the Vlasov-Maxwell system models a plasma macrostate described by a continuous fluid in six-dimensional phase-space. These two descriptions are not equivalent and in particular PIC systems, with their small numbers of particles per Debye sphere, suffer from abnormally high noise levels and include to an unknown degree particle correlations absent from Vlasov-Maxwell equations.
We conclude in Sect. 6, stressing that validation and interpretation of PIC simulations requires detailed knowledge of the code as presented here as well as awareness of the above differences between the PIC model, the Vlasov-Maxwell model, and a real plasma.
2. Physical model and numerical implementation
This section presents the numerical scheme used in Apar-T. Broadly speaking, Apar-T is a parallel electromagnetic relativistic 3D PIC code with a staggered grid, where the fields are integrated via Faraday and Maxwell-Ampère equations, currents are computed by charge conserving volume weighting (CIC), and fields are interpolated with the same CIC volume weighting method.
2.1. The PIC plasma
The code simulates the time-evolution of charged particles under the action of the electromagnetic fields that they generate, and the evolution of these fields.
Plasmas in nature contain millions to tens of billions of particles per Debye sphere, and relevant microphysical phenomena spread over numerous Debye lengths. It is impossible to track these particles one by one. Rather, the numerical particles represent numerous real particles, and are consequently called superparticles.
A superparticle represents either p real ions (having then a rest mass msp = p × mi and a charge qsp = p × qi), or p real electrons (having then a rest mass msp = p × me and a charge qsp = p × qe). The ratio of ion to electron charge is always qi/qe = −1, while that of their rest masses mi/me can be freely specified. Pair plasmas can thus be simulated. In Apar-T the number of real particles per superparticles p is the same for all superparticles at all times, but other codes can introduce superparticle splitting (Fujimoto & Machida 2006; Haugboelle et al. 2013; Cerutti et al. 2013).
We denote the physical size of a grid cell by X0, a reference number of superparticles per cell by 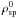 (including both ion superparticles and electron superparticles), and its associated number density of electrons by
(including both ion superparticles and electron superparticles), and its associated number density of electrons by 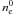 . Initially, the plasma is assumed to be quasi-neutral, in the sense that we load the same number of ion superparticles and electron superparticles in each cell. We have the relation
. Initially, the plasma is assumed to be quasi-neutral, in the sense that we load the same number of ion superparticles and electron superparticles in each cell. We have the relation 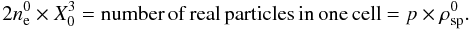 (1)The equations governing the superparticle plasma are the equation of motion with the Lorentz force for each superparticle, and Maxwell equations coupled to the superparticle motions by the current:
(1)The equations governing the superparticle plasma are the equation of motion with the Lorentz force for each superparticle, and Maxwell equations coupled to the superparticle motions by the current:  Here, c is the speed of light, e the electric field, b = cB is c times the magnetic field; qsp, msp, γsp, vsp, and xsp are the charge, mass, Lorentz factor, velocity, and position of the superparticle number sp. The fields are stored on a grid, and a consequence is that the superparticles are seen by the grid as having a finite shape S, linked to the interpolation scheme used in the code.
Here, c is the speed of light, e the electric field, b = cB is c times the magnetic field; qsp, msp, γsp, vsp, and xsp are the charge, mass, Lorentz factor, velocity, and position of the superparticle number sp. The fields are stored on a grid, and a consequence is that the superparticles are seen by the grid as having a finite shape S, linked to the interpolation scheme used in the code.
In Apar-T we do not integrate the two other Maxwell equations because if they hold initially, then fulfilling the equation of conservation of charge and Eqs. (2c) and (2d) at all times insures that they remain correct to round-off errors. That the current is indeed computed in a charge conserving way is detailed in Appendix A.1. Initially, the fields and the charge density are correctly built by setting a magnetic field satisfying ∇ ∧ b = μ0j, a null electric field, and by placing the superparticles by pairs with one ion superparticle and one electron superparticle on top of each other so that the charge density is zero.
2.2. Numerical implementation of Apar-T
The code is based on the PIC program Tristan written by Buneman (Matsumoto & Omura 1993), parallelized by Messmer (2001). We largely modified its structure, that now uses Fortran modules and allows for more flexibility, including the possibility of switching between different initial conditions or boundaries by changing entries in a configuration textfile.
The need for a deep understanding of simulation methods to interpret their results, as is the case for the test problems of Sect. 3, motivated a detailed description of Apar-T. This section presents important points. More details (numerical scheme and parallelization efficiency) can be found in Appendix A.
Briefly, the global integration scheme of Eqs. (2a) − (2e) is a time-centered and time-reversible leap-frog scheme, and is second-order accurate in time and space. The electric and magnetic fields are stored on a staggered Yee lattice, which allows for a simple integration explicit in time of Eqs. (2c) and (2d) (without the current). The current is computed with the volume change of the superparticles in the grid cells, and added in a time explicit way to the integration of the electric field (Eq. (2d)).
2.2.1. Temporal and spatial discretization, normalization
The spatial discretization of the code is 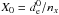 , a fraction nx of the electron skin depth
, a fraction nx of the electron skin depth 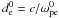 , where the electron plasma pulsation is
, where the electron plasma pulsation is 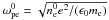 , with − e and me the electron charge and rest mass. The timestep Δt is a fraction nt of the electron plasma period:
, with − e and me the electron charge and rest mass. The timestep Δt is a fraction nt of the electron plasma period: 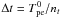 , with
, with 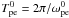 . We stress that the superscript
. We stress that the superscript  is used for quantities based on the reference density
is used for quantities based on the reference density 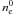 .
.
Spatial quantities are normalized by the cell length X0, and normalized quantities are then denoted with a tilde. For example, the electron Debye length 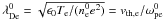 (with
(with 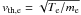 ) has for normalized counterpart
) has for normalized counterpart 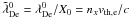 .
.
2.2.2. Superparticle volume
The use of a grid for PIC algorithms implies that the fields are known at grid nodes, and that information relative to the superparticles (charge and current) need to be interpolated on the grid. This interpolation is equivalent to considering the superparticles as clouds of charge of finite extension (Langdon 1970). The shape of the cloud then determines the interpolation formula.
In our case, a superparticle is assumed to be a cube of volume 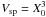 , and the current it produces is calculated by the change of the volume of the superparticle in the cell containing its center. This interpolation scheme is equivalent to linear weighting (CIC) and is exactly charge conserving. Details of the numerical implementation of the current computation can be found in Appendix A; in Sect. 5 the implications of the superparticle finite sizes are discussed.
, and the current it produces is calculated by the change of the volume of the superparticle in the cell containing its center. This interpolation scheme is equivalent to linear weighting (CIC) and is exactly charge conserving. Details of the numerical implementation of the current computation can be found in Appendix A; in Sect. 5 the implications of the superparticle finite sizes are discussed.
2.2.3. Particle initialization in momentum space
Several momentum distributions can be loaded: Maxwell-Boltzmann distribution with anisotropic temperature, boosted Maxwell-Boltzmann distribution, waterbag distribution, or Maxwell-Jüttner distribution. We have not found in the literature a method for initializing the Maxwell-Jüttner distribution when both the bulk velocity and the temperature are relativistic, so we present one in Sect. 4.
2.2.4. Input, output, and data analysis
Data output and data analysis can be very time consuming for large scale simulations. To reduce data storage and writing time, we implemented parallel output in HDF5 format1. Files are written according to the .h5part format, and can be read by the advanced visualization and data-analysis software VisIt (Childs et al. 2012), which is fully parallel, but also by a reader in Python. The .h5part files can either contain the whole simulation data, and then be used to restart the simulation, or be lighter with only a fraction of the particles. These lighter files then include cell-averaged quantities related to the particles, such as the mean particle velocity or number, temperature, highest energy, etc.
We implemented the VisIt Libsim in situ library (Whitlock et al. 2011) into Apar-T. In this way, VisIt is able to connect to the simulation while it is running and to access the solver’s data at the current timestep. It can then perform data visualization and data analysis without the need to write data on the hard drive. This feature is fully parallelized, by exploiting the data-distribution model of the code, and as such is not restricted to the current parallelization model. It allows the data-IO from memory to hard drive – which is a major reason for slow-down of simulations using big data-sets – to be significantly reduced. For example, a volume-rendering of 3D data performed in situ takes less time than dumping 10 GB of data to the disk. VisIt in situ is also well suited to monitor ongoing simulations and to single-step through the execution and is, in this way, of great help for debugging.
Finally, a set of test problems has been implemented. Based on a Python script, these problems can be automatically run to check code sanity after modifications.
3. Examples and code validation
3.1. Cold plasma modes
A first test is to simulate a thermal plasma at rest and to observe its modes of oscillation. It is an easy test if we focus on the pulsations for modes of zero wavevector, k = 0. To do so, we compute at each timestep tj the sum of the momentum of the particles along a given direction, for example the x-direction, ∑ spγsp(tj) vsp,x(tj), where the summation runs over all the electron superparticles in the simulation (of Lorentz factor γsp and velocity vsp). This sum is equivalent to the volume integral of the momentum, and is thus equal to the k = 0 Fourier mode of the electron momentum, with a spectral resolution of 2π/ [box size in units of electron skin depth] . We then perform a Fourier transform in time to extract the pulsations of oscillation, 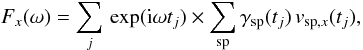 (3)and similarly along y and z.
(3)and similarly along y and z.
For all the simulations of this section, the initial state consists of a homogeneous plasma at rest, with superparticles loaded according to a classical Maxwell-Boltzmann distribution. A uniform background magnetic field along z is set up for the magnetized plasma case. Periodic boundaries are used.
When the background magnetic field B0 is strong (electron cyclotron pulsation larger than electron plasma pulsation, ωce ≫ ωpe), the particle trajectories are Larmor gyrations in B0, unperturbed by collective effects such as Langmuir oscillations. This example then probes the accuracy of the particle motion integrator. When the background magnetic field is weaker (ωce ≲ ωpe), the dynamics is set by Langmuir oscillations possibly modified by B0. These oscillations involve the creation of electric fields by local charge imbalance. The fields set the particles into motion, and the particles then oscillate because of their finite inertia. Several parts of the algorithm are thus involved: electric field production and propagation, as well as particle motion.
3.1.1. No background magnetic field
With no background magnetic field, the only cold modes are the electromagnetic transverse wave of dispersion relation ![\hbox{$\omega_{\rm Tr}^2 = \omega_{\rm P}^2 [1 + (kc/\omega_{\rm P})^2]$}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq66.png) and the electrostatic Langmuir oscillation at the plasma frequency ωP = ωpe(1 + me/mi)1/2. The latter is modified by thermal effects to a wave of dispersion relation
and the electrostatic Langmuir oscillation at the plasma frequency ωP = ωpe(1 + me/mi)1/2. The latter is modified by thermal effects to a wave of dispersion relation 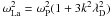 . Consequently, we expect Fa(ω) to peak at ωLa(k = 0) = ωTr(k = 0) = ωP.
. Consequently, we expect Fa(ω) to peak at ωLa(k = 0) = ωTr(k = 0) = ωP.
Our simulations span a large range of parameters: nx and nt (spatial and temporal resolution, see Sect. 2.2.1) vary between 5 and 50 and between 300 and 2000, respectively; ρsp (the number of superparticles per cell) varies between 4 and 32; and the thermal velocity 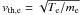 of the electrons between 0.04c and 0.1c (the ions have the same temperature as the electrons). This results in Debye lengths between 0.2 and 2 cells. We checked that the simulation box size, comprised between 10 and 30 Debye lengths, does not influence the results.
of the electrons between 0.04c and 0.1c (the ions have the same temperature as the electrons). This results in Debye lengths between 0.2 and 2 cells. We checked that the simulation box size, comprised between 10 and 30 Debye lengths, does not influence the results.
We use a mass ratio mi/me = 49, which results in ωP = 1.010 ωpe. Our simulations last 100 Tpe, so that the frequency resolution is Δω = 2π/(100Tpe) = 0.01ωpe.
For all these parameters, we find that the position and width of the frequency peak are always the same as in Fig. 1. It coincides with the theoretical plasma pulsation, which is expected because our temporal spectra are for the wavenumber k = 0, and because ω(k = 0) = ωP for the two modes present in this situation.
This is the case even for simulations where the Debye length is not resolved. However, an under-resolved Debye length leads to more numerical heating and can trigger instabilities in situations less trivial than a thermal plasma at rest (see Appendix B), so that we have not pushed our investigations too far in this direction.
The main difference between the simulations is that less resolved ones present noisier spectra, and thus more fluctuations. The increase of fluctuation level with decreasing resolution is a universal feature of PIC simulations and is explored in more detail in Sect. 5.
 |
Fig. 1 Power spectra of the total momentum of the electrons | Fa | 2 (Eq. (3)) with a = x, y, or z in the unmagnetized case. The inset is a zoom around the peak. Here nx = 25, nt = 500, ρsp = 16, vth,e = 0.04c, Ti = Te, box size of 25 × 25 × 25 cells, duration of 100 Tpe. |
Theoretical versus experimental pulsations for a magnetized cold plasma.
3.1.2. With a background magnetic field
In a uniform and cold magnetized plasma, the plasma modes depend solely on the ratio of the electron cyclotron pulsation ωce = eB/me to the electron plasma pulsation ωpe (for a fixed mi/me). This ratio sets the relative importance of individual particle motion (ωce) against collective effects (ωpe). In addition, the background magnetic field favors a direction, thus making the mode spectrum anisotropic (however, the mode pulsations for k = 0 remain independent of the direction of the wavevector).
For wavevectors parallel to the magnetic field, the Langmuir oscillation remains unchanged because the oscillations of the particles are longitudinal, and thus along B0 and unaffected by the magnetic field. On the other hand, the electromagnetic wave with k along B0 separates into two branches, one starting at ![\hbox{$\omega_{\vec{k}=0}=\omega_{\rm L} = 0.5[(\omega_{\rm ce}^2+4\omega_{\rm pe}^2)^{1/2}-\omega_{\rm ce}]$}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq122.png) and the other at
and the other at ![\hbox{$\omega_{\vec{k}=0} = \omega_{\rm R} = 0.5[(\omega_{\rm ce}^2+4\omega_{\rm pe}^2)^{1/2}+\omega_{\rm ce}]$}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq123.png) (see, e.g., Fitzpatrick 2011, chap. 4), in both cases with particles oscillating in the transverse plane, i.e., perpendicular to B0. Two other branches appear, but they start at ωk = 0 = 0 and will thus not appear in Fa(ω).
(see, e.g., Fitzpatrick 2011, chap. 4), in both cases with particles oscillating in the transverse plane, i.e., perpendicular to B0. Two other branches appear, but they start at ωk = 0 = 0 and will thus not appear in Fa(ω).
For wavevectors perpendicular to the magnetic field, the presence of the background magnetic field deforms the Langmuir oscillation ω(k) = ωP into a branch starting from ωk = 0 = ωL, with particle oscillations in the plane perpendicular to B0. The transverse electromagnetic wave still exists with particle oscillations along B0, unaffected by the magnetic field. Another branch appears, which is a deformation of the transverse electromagnetic wave for particle oscillations not along B0, and starts at ωk = 0 = ωR with oscillations in the plane perpendicular to B0. Another branch appears, starting at ωk = 0 = 0.
All in all, we expect to find a peak at ω = ωP for the component of the momentum parallel to B0, and two peaks at ω = ωL and ωR for the component of the momentum perpendicular to B0. We ran the set of simulations described in Table 1, with a ratio ωce/ωpe ranging from 0.5 to 4, nx from 16 to 128, nt from 1000 to 4000, and ρsp from 4 to 16, and we did find the required pulsation peaks for Fa(ω) (see Fig. 2 for a sample spectrum). The positions and widths of these three peaks are almost constant within our parameter range.
 |
Fig. 2 Power spectra of the total momentum of the electrons | Fa | 2 (Eq. (3)) with a = x, y, or z in the magnetized case. Parameters are given in Table 1 (case labeled Fig. 2). The purple lines are the pulsations |
We note that the peak positions and widths are not changed even for cases where the thermal Larmor radius 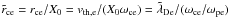 is not resolved. It is expected that the resolution of the Larmor radius by the grid is of no importance to describe particle trajectories in constant fields, because the interpolation of these fields from grid points to superparticle position gives the same result regardless of the grid size if the fields are constant. The relevant constraint is instead that rce should be resolved along the trajectory, vspΔt < rce, with vsp the superparticle velocity. This relation is equivalent to
is not resolved. It is expected that the resolution of the Larmor radius by the grid is of no importance to describe particle trajectories in constant fields, because the interpolation of these fields from grid points to superparticle position gives the same result regardless of the grid size if the fields are constant. The relevant constraint is instead that rce should be resolved along the trajectory, vspΔt < rce, with vsp the superparticle velocity. This relation is equivalent to 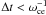 .
.
However, for simulations with under-resolved Larmor radii the electric field energy starts to behave abnormally after some tens of plasma pulsations, and energy conservation curves present an exponential heating (see Sect. 3.1.3) that can lead to dramatic consequences. This parameter range must be avoided.
3.1.3. Energy conservation
Independent of the strength of the background magnetic field, we observe a linear increase of the total energy with time that is due to interactions of particles with the grid (see Appendix B.2). The growth rate is independent of the size of the timestep (from nt = 2000 down to Courant condition Δt ~ X0/c, equivalent to nt = 2πnx). Its dependence on the number of superparticles per cell is quite precisely given by 1/ρsp. However, its dependence on the spatial resolution nx and thermal spread vth,e is less clear. In particular, it does not depend only on the product 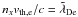 . The rate increases with increasing vth,e, and decreases with increasing nx. Some examples are given for reference in Table 2.
. The rate increases with increasing vth,e, and decreases with increasing nx. Some examples are given for reference in Table 2.
Energy conservation for simulations of a thermal plasma with no background magnetic field.
Simulations with under-resolved Larmor radii 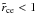 show an exponential (instead of linear) increase of the total energy starting after roughly 40 Tpe. This numerical instability is believed to arise because field perturbation at wavelength λ = 2rce and their aliases ( ± λ + n × 2π/X0, with n an integer and X0 the grid size) are allowed to couple when 2X0 > λ (see Appendix B.2). An inspection of the energy curves shows that the energy gain is for the kinetic energy. We note that it did not disturbed the spectra of Sect. 3.1.2 because they were computed before the heating reached a significant level. It is interesting to note that this numerical instability is develops slowly, so that particles with under-resolved Larmor radii in constant fields can be included in simulations if they spend a small amount of time before being heated or before reaching areas with smaller magnetic fields.
show an exponential (instead of linear) increase of the total energy starting after roughly 40 Tpe. This numerical instability is believed to arise because field perturbation at wavelength λ = 2rce and their aliases ( ± λ + n × 2π/X0, with n an integer and X0 the grid size) are allowed to couple when 2X0 > λ (see Appendix B.2). An inspection of the energy curves shows that the energy gain is for the kinetic energy. We note that it did not disturbed the spectra of Sect. 3.1.2 because they were computed before the heating reached a significant level. It is interesting to note that this numerical instability is develops slowly, so that particles with under-resolved Larmor radii in constant fields can be included in simulations if they spend a small amount of time before being heated or before reaching areas with smaller magnetic fields.
3.2. Linear growth rates of the counter-streaming instability
Another standard test is to study the linear phase of the counter-streaming instability. We use relativistic streaming velocities to validate the behavior of the algorithm for relativistic particle motions. Moreover, since magnetic fields are generated for this range of parameters, this test also probes the integration of b.
The initial setup consists of two unmagnetized and cold counter-streaming electron-positron beams, with velocity 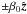 and associated Lorentz factor Γ0. There is no background magnetic field, and the particles are loaded according to a drifting Maxwell-Boltzmann distribution. This situation is unstable, and the kinetic energy of the beam is converted into particle thermal kinetic energy and electromagnetic field energy, the initial perturbation coming from fluctuations due to the finite superparticle number. The linear instability spectrum is described by a branch comprising an electrostatic longitudinal two-stream mode and a transverse electromagnetic filamentation mode, the general case being an oblique mixed mode (Bret et al. 2010).
and associated Lorentz factor Γ0. There is no background magnetic field, and the particles are loaded according to a drifting Maxwell-Boltzmann distribution. This situation is unstable, and the kinetic energy of the beam is converted into particle thermal kinetic energy and electromagnetic field energy, the initial perturbation coming from fluctuations due to the finite superparticle number. The linear instability spectrum is described by a branch comprising an electrostatic longitudinal two-stream mode and a transverse electromagnetic filamentation mode, the general case being an oblique mixed mode (Bret et al. 2010).
3.2.1. Theoretical model
We take the growth rates derived analytically by Michno & Schlickeiser (2010) on the basis of a cold two-fluid model and denote this result as theoretical. Our thermal velocity vth, identical for both species, is low enough to insure that thermal effects are negligible (Bret et al. 2010, Eq. (28)), but high enough to have a resolved Debye length and to avoid numerical instabilities (Appendix B). Our parameters are chosen such that the transverse filamentation mode always dominates. The fastest growing modes are those at large wavenumbers perpendicular to the beams, i.e., 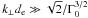 (with de = c/ωpe), and that grow according to
(with de = c/ωpe), and that grow according to 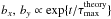 with
with 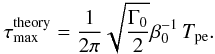 (4)The k ⊥ -dependance of the growth rate is plotted in Fig. 3. We see that all modes above a few
(4)The k ⊥ -dependance of the growth rate is plotted in Fig. 3. We see that all modes above a few 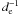 quickly reach the maximum growth rate
quickly reach the maximum growth rate  .
.
 |
Fig. 3 Wavenumber dependance of the growth rate τtheory(k ⊥ ), represented here as the deviation |
 |
Fig. 4 Top: energy curves for the filamentation instability (case labeled Fig. 4 in Table 3). They are normalized by the total initial energy |
 |
Fig. 5 Top: growth of individual Fourier modes for bx (for the run labeled Fig. 4 in Table 3). The modes shown are those for i = 0,1,2, and j = 0,1,...,25, and one mode every 100 modes for the remaining. We note that the graphic has been cut and that the weak modes actually fill a continuum down to an energy of 10-7. The sum of all 320 × 90 modes is shown in orange. We recall that mode (i,j) corresponds to (kzde,kxde) = 2π × 20(i/640,j/180). Bottom: growth map of the Fourier modes, in units of Tpe. |
3.2.2. Method of measurement
We measure the growth rates of the magnetic fields bx and by with two methods. The first is a direct measure on the total energy curve, e.g., 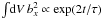 (see Fig. 4, top, for an illustration). It gives an effective growth rate that we denote by
(see Fig. 4, top, for an illustration). It gives an effective growth rate that we denote by 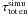 , equal to 0.48Tpe in this case.
, equal to 0.48Tpe in this case.
The second consists in following the time evolution of the Fourier modes of the fields. At a fixed time t0, we compute the 2D Fourier transform of the fields in a plane (x,z) with a fixed y, that we denote by FTy = y0(t0,kx,kz). We then average the power spectrum over all the planes y = cst to obtain the power spectrum PS(t0,kx,kz) = ∑ y0 | FTy = y0(t0,kx,kz) | 2. We then repeat this procedure for several t0. The discrete mode spectrum is sampled with (kzde,kxde) = 2πnx(i/Nz,j/Nx), where Nz and Nx are the total number of cells in the z and x directions, and i = 0...Nz/2, j = 0..Nx/2. The spectral resolution in the direction perpendicular to the beam is thus Δk ⊥ de = 2πnx/Nx = 2π/(box width in de). The squares in Fig. 3 represent this spectral resolution for the different box sizes that we use.
3.2.3. Results
Figure 5 is an example of the temporal evolution of the modes of bx for the same simulation as in Fig. 4. The sum of all modes grows at the same effective growth rate as the total energy in bx (to within ± 1%), 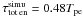 . However, the fastest growing modes are those for kz = 0 and 0 ≤ kxde ≤ 5, with
. However, the fastest growing modes are those for kz = 0 and 0 ≤ kxde ≤ 5, with 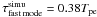 , which is close to the cold-fluid result
, which is close to the cold-fluid result 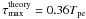 . It is seen from Fig. 5 that the large difference between the effective growth rate
. It is seen from Fig. 5 that the large difference between the effective growth rate 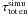 and the growth rate of the fastest modes
and the growth rate of the fastest modes 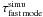 is due to a significant contribution of all the modes during the whole linear phase. The fastest mode thus never dominates the total energy in the linear phase. We suspect that this is due to the large noise level present in PIC simulations.
is due to a significant contribution of all the modes during the whole linear phase. The fastest mode thus never dominates the total energy in the linear phase. We suspect that this is due to the large noise level present in PIC simulations.
 |
Fig. 6 Difference between the growth rate measured on the total energy curve |
These results hold for all the test simulations that we conducted, which are summarized in Table 3. The effective growth rates 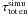 measured on the total energy present various levels of discrepancies with
measured on the total energy present various levels of discrepancies with 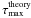 , between 14% and 67%. Figure 6 shows the dependance of these discrepancies. There is a small sensitivity with respect to the timestep (nt) and the box size, and an important influence of the spatial resolution (nx). There is a systematic decrease in the difference when the superparticle number per cell ρsp is increased (all other parameters are kept constant). Since the fluctuation level in the PIC plasma decreases with increasing ρsp, this indicates that the high fluctuation level excites all the modes and prevents the fastest ones from dominating the energy.
, between 14% and 67%. Figure 6 shows the dependance of these discrepancies. There is a small sensitivity with respect to the timestep (nt) and the box size, and an important influence of the spatial resolution (nx). There is a systematic decrease in the difference when the superparticle number per cell ρsp is increased (all other parameters are kept constant). Since the fluctuation level in the PIC plasma decreases with increasing ρsp, this indicates that the high fluctuation level excites all the modes and prevents the fastest ones from dominating the energy.
 |
Fig. 7 Three snapshots of the filamentation instability, at times 2.5, 4, and 5.5Tpe (from left to right) for the simulation of Fig. 4. Colors represent the current magnitude per cell (units are number of superparticles per cell times their mean velocity), while arrows are the magnetic field. Lengths are in cell number. |
Theoretical versus experimental values of the filamentation growth rate τ.
Theoretical versus experimental values of the tearing growth rate τ.
On the other hand, the growth rates 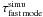 measured on the fastest modes differ from
measured on the fastest modes differ from 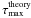 by a more systematic factor, 14% for β0 = 0.95, 7 ± 1% for β0 = 0.995, and 6% for β0 = 0.999. These systematic differences can be explained by looking at the mode spectrum. In all the simulations, the fastest modes are for kz = 0 and 0 ≤ kxde ≤ 5 − 15 (see, e.g., Fig. 5, bottom). Given the spectral resolution Δk ⊥ de = 2π/(box length in de), these modes actually cover a portion of k ⊥ de where the curves τtheory(k ⊥ ) of Fig. 3 vary significantly and do not yet reach
by a more systematic factor, 14% for β0 = 0.95, 7 ± 1% for β0 = 0.995, and 6% for β0 = 0.999. These systematic differences can be explained by looking at the mode spectrum. In all the simulations, the fastest modes are for kz = 0 and 0 ≤ kxde ≤ 5 − 15 (see, e.g., Fig. 5, bottom). Given the spectral resolution Δk ⊥ de = 2π/(box length in de), these modes actually cover a portion of k ⊥ de where the curves τtheory(k ⊥ ) of Fig. 3 vary significantly and do not yet reach 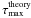 . It explains the sign and order of magnitude of the difference
. It explains the sign and order of magnitude of the difference 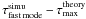 . It also explains the increasingly better agreement when β0 increases.
. It also explains the increasingly better agreement when β0 increases.
We note that e and bz are zero in the linear two-fluid theory, and the fact that they are not zero in our simulation (see Fig. 4) reflects an early nonlinear evolution or the effects of fluctuations and correlations absent from the linear model but present in PIC simulations. These differences are discussed further in Sect. 5.
3.3. Nonlinear evolution of the filamentation instability: filament merging
We now consider the nonlinear phase of the filamentation instability. We study the same counter-streaming configuration as in Sect. 3.2, with the setup labeled by Fig. 4 in Table 3. The energy curves are shown in Fig. 4.
As a diagnostic, we focus on the filament growing and merging processes. The linear phase of the filamentation instability produces current filaments. Since they are threaded by parallel currents, they attract each other and, starting from the end of the linear phase, start to merge to produce larger and larger filaments (Medvedev et al. 2005). This is clearly visible in Fig. 7.
We measure the size of the filaments by computing the two-dimensional autocorrelation function, in the x − y plane, of the z-averaged current amplitude (z is the direction of the beams). This autocorrelation function is azimuthally averaged to obtain a radial function corr(r). We normalize corr(0) to 1. The scale of the filaments is then taken to be five times the radius where corr(r) = 0.8 (taking this scale as the radius at which corr(r) first vanishes yields the same results).
The results are shown in Fig. 4 (bottom). We clearly see two regimes: one during the linear growth of the filamentation instability (from t = 2.2 to 3.6Tpe) where the filament correlation length is set by the wavelength of the fastest growing mode and remains constant, and one in the nonlinear regime (after t = 3.6Tpe) where the filaments merge and thus quickly increase their size. In the second case, the growth is roughly linear with time, which agrees with the PIC simulation results of Dieckmann (2009) for a similar setup. After t = 6.5Tpe, the filament growth stops. However, we suspect that the periodic boundaries start influencing the dynamics at this point.
3.4. Linear growth rates of the relativistic tearing instability
We also study the linear phase of the tearing mode for a relativistic Harris sheet in a pair plasma. Contrary to the preceding case, this example provides a test of the algorithm in a situation where thermal effects are essential.
The equilibrium consists of a magnetic field 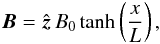 (5)sustained by a population of electrons and positrons of density ∝ 1/cosh2(x/L) flowing with opposite bulk velocities Ue = −Ui in the ± y directions. We denote the associated Lorentz factor by Γe, and the temperature of the two species by Θ = T/(mec2). The exact relations between the different parameters to satisfy the equilibrium are given in Appendix C. In particular, one should be careful to distinguish between quantities in the frame moving with one species (denoted with a prime) and quantities in the simulation frame. For example, contraction of the electron density leads to
(5)sustained by a population of electrons and positrons of density ∝ 1/cosh2(x/L) flowing with opposite bulk velocities Ue = −Ui in the ± y directions. We denote the associated Lorentz factor by Γe, and the temperature of the two species by Θ = T/(mec2). The exact relations between the different parameters to satisfy the equilibrium are given in Appendix C. In particular, one should be careful to distinguish between quantities in the frame moving with one species (denoted with a prime) and quantities in the simulation frame. For example, contraction of the electron density leads to 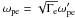 .
.
The superparticles are loaded according to a drifting Maxwell-Jüttner distribution with the method described in Sect. 4. There is no initial perturbation, and the instability grows out of the fluctuations produced by the finite number of superparticles.
As can be seen in Table 4, the bulk velocities and the temperatures of electrons and positrons are relativistic. Loading these distributions in a PIC code is a non-trivial task, and we have developed a special method for this. It is presented in Sect. 4.
The simulation domain is periodic along z and y. Reflecting boundaries for particles and fields are present along the x direction. There are no background particles, only that of the current sheet.
An example of the energy evolution is presented in Fig. 8. After some time, the system becomes unstable and the magnetic field starts reconnecting. As expected, bz dwindles while bx rises, which corresponds to the formation of magnetic islands. We measure the linear growth rate on bx as 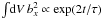 . For comparison, we use the linear growth rates derived by Pétri & Kirk (2007) by linearizing the Vlasov-Maxwell system around the drifting Maxwell-Jüttner distribution C.1 and the magnetic field of Eq. (5).
. For comparison, we use the linear growth rates derived by Pétri & Kirk (2007) by linearizing the Vlasov-Maxwell system around the drifting Maxwell-Jüttner distribution C.1 and the magnetic field of Eq. (5).
The results are summarized in Table 4. Discrepancies with Pétri & Kirk (2007) range between 5% and 8%. These growth rates vary by less than 3% when the numerical resolution is doubled (i.e., when ρsp, nx, and nt are doubled all together). We restrict our analysis to total energy curves because contrary to the case of the filamentation instability, the linear growth of the field energy spans several orders of magnitude and the fastest modes have enough time to dominate the total energy.
 |
Fig. 8 Energy curves for the tearing instability (labeled Fig. 8 in Table 4). Shown are the energy curves, for example ∫dVBx(t)2/(2μ0). They are normalized by the total initial energy |
We note that when the simulation is launched, an electromagnetic wave is seen to propagate from the sheet in the ± x directions. This wave is a necessary consequence of the fact that at t = 0 we load the superparticles by pairs of electron-positron at the same location, and we set a zero electric field everywhere (see Sect. 2.1). The system then has to relax from this very peculiar state: in less than one plasma period, charge screening is established and an electric field appears. It is this field that partly propagates outside of the sheet. It is then reflected on the ± x boundaries and propagates back to the sheet, causing the oscillations in ey seen in Fig. 8. We have checked that their incidence does not influence the linear growth by using different domain sizes.
It is more puzzling that the sheet contracts slightly just after the beginning of the simulation and the current magnitude at its center rises by ≲ 10%. This may be related to the fact that our algorithm does not solve the Vlasov-Maxwell system in a strict sense (see also Sects. 5 and 6.3).
4. Loading a relativistic particle distribution
This section deals with the general problem of loading particles with momenta that reproduce a given distribution function.
Very common cases are waterbag and Maxwell-Boltzmann distributions with a mean bulk velocity U0. A simple method is then to load the particles in the frame comoving with the plasma, which is fairly easy because in this frame the distributions are isotropic, and then to add to every particle the velocity U0 or, if U0 is close to c, to boost every particle with the Lorentz boost corresponding to U0. We will see, however, that this method is no longer correct when both U0 and the rest frame distribution are relativistic, mainly because boosting particles in a PIC code does not boost space. We present here another method, correct in all cases2.
4.1. Transformation of the distribution function
We start by explaining how the particle distribution changes from one frame to another (see e.g. Mihalas & Mihalas 1984; Pomraning 1973).
We consider a frame ℛ where the plasma has a mean velocity U0 and follows the distribution f(x,p). In the comoving frame or plasma rest frame ℛ0, the plasma mean velocity is zero and follows the distribution f0(x,p). We follow a group of particles. Seen from ℛ, they are in a volume d3x around x and have momentum p with a scatter d3p; seen from ℛ0 these quantities change respectively to d3x0, x0, p0, and d3p0. The number of particles in our group is 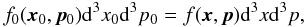 (6)so that to find the link between f and f0 we have to find a relation between d3x0d3p0 and d3xd3p.
(6)so that to find the link between f and f0 we have to find a relation between d3x0d3p0 and d3xd3p.
We start with the momentum. In the rest frame, our group of particles have momenta spanning a range d3p0. Seen in the boosted frame, their momenta transform according to the Lorentz transformation, and span a new range d3p. These two volumes are thus linked by the Jacobian of the Lorentz transformation, and it can be shown that 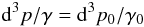 (7)where γ and γ0 are the Lorentz factors associated to p and p0.
(7)where γ and γ0 are the Lorentz factors associated to p and p0.
We now consider the space volumes. Because of space contraction/dilatation, the group of particles will occupy a different volume in different frames. We consider the frame ℛ′ comoving with the group of particles. This is possible because the particles all move at nearly the same velocity v0 = p0/γ0. We denote by a prime all quantities seen from this frame. In ℛ′, the particles occupy a volume d3x′. Since only one direction is contracted, and since ℛ′ moves relative to ℛ0 with Lorentz factor 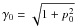 , we have the relation d3x0 = d3x′/γ0. Similarly, ℛ′ moves relative to ℛ with Lorentz factor
, we have the relation d3x0 = d3x′/γ0. Similarly, ℛ′ moves relative to ℛ with Lorentz factor 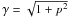 , and we have d3x = d3x′/γ. All in all:
, and we have d3x = d3x′/γ. All in all: 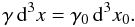 (8)From this, we deduce that
(8)From this, we deduce that 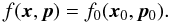 (9)
(9)
4.2. Why boosting particles from the rest frame is incorrect for relativistic distributions
We now come back to PIC simulations. We assume that we load particles uniformly in space, with momenta following f0(x0,p0), and that we boost each particle with a velocity U0. The momentum volume elements are then transformed according to Eq. (7), but positions are not changed. Equation (8) does not hold, and we obtain a particle distribution 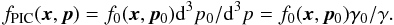 (10)The volume contraction/dilatation is not performed, and the factor γ0/γ does not cancel.
(10)The volume contraction/dilatation is not performed, and the factor γ0/γ does not cancel.
Consequently, boosting each particle from the rest frame leads to the expected distribution only if γ0/γ is independent of the particle. We can write this ratio as 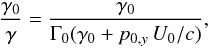 (11)with p0,y the y component of p0 and
(11)with p0,y the y component of p0 and 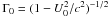 , so that this is the case only if p0,y ≪ 1 (or if the boost is non-relativistic, U0 ≪ c). If p0,y ≪ 1, then γ0/γ ~ 1/Γ0 and when it is inserted back into Eq. (10), we find the usual result of density contraction.
, so that this is the case only if p0,y ≪ 1 (or if the boost is non-relativistic, U0 ≪ c). If p0,y ≪ 1, then γ0/γ ~ 1/Γ0 and when it is inserted back into Eq. (10), we find the usual result of density contraction.
However, when the particle distribution is relativistic in the rest frame of the plasma, γ0/γ is not a constant factor and Eq. (10) does not have the expected dependence on momentum p.
4.3. Loading a drifting Maxwell-Jüttner distribution with arbitrary temperature and drift speed
We now present a method for loading the superparticle momenta directly in the frame where the distribution has a bulk velocity.
In the literature, there is some agreement around the fact that the particle distribution of a relativistic plasma in thermodynamic equilibrium is given by the Maxwell-Jüttner distribution (Jüttner 1911; Cubero et al. 2007; Chacón-Acosta et al. 2010; Dunkel & Hänggi 2009) and, even if some alternatives are also debated (Treumann et al. 2011), this is the distribution used in PIC simulations (e.g., Pétri & Lyubarsky 2007; Zenitani & Hoshino 2008; Jaroschek & Hoshino 2009).
In the plasma rest frame, the Maxwell-Jüttner distribution is given by 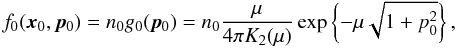 (12)with n0 the uniform particle number density and g0 the momentum distribution, both in the restframe, μ = mc2/T, p = γv/c, and K2 the modified Bessel function of the second kind. If we now denote by f the distribution in the frame where the plasma moves with a bulk velocity cβ0 (and associated Lorentz factor Γ0), by n the particle density, and by g the momentum distribution, both in this same frame, we have f(x,p) = ng(p). Equation (9) then gives g(p) = g0(p0) × n0/n. Now using n = Γ0n0, we arrive at
(12)with n0 the uniform particle number density and g0 the momentum distribution, both in the restframe, μ = mc2/T, p = γv/c, and K2 the modified Bessel function of the second kind. If we now denote by f the distribution in the frame where the plasma moves with a bulk velocity cβ0 (and associated Lorentz factor Γ0), by n the particle density, and by g the momentum distribution, both in this same frame, we have f(x,p) = ng(p). Equation (9) then gives g(p) = g0(p0) × n0/n. Now using n = Γ0n0, we arrive at 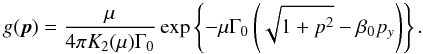 (13)This distribution is normalized to unity:
(13)This distribution is normalized to unity: 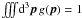 .
.
 |
Fig. 9 Maxwell-Jüttner distribution for T = mc2 and |
The main difficulty with Eq. (13) is that the variables px, py, and pz are coupled and cannot be chosen independently. The solution is to compute the marginal distribution for the variable py. With this, one can choose the y-component of p independently of the others, and then use the distribution g(p ⊥ ,py) knowing py to choose the component normal to y. Details are presented in Appendix D, where we provide the expressions for the marginal distribution and the conditional probability, as well as a method for generating the velocity by using the cumulative distributions.
Figure 9 shows an example of the distribution generated with this method for T = mc2 and Γ0β0 = 1.41, and compares it to the theoretical expectation and to the distribution obtained by boosting individually the superparticles from the restframe. We clearly see the accuracy of our algorithm, and the mismatch between the simpler boosting method and the expected result. We note that this mismatch can have significant consequences. For example, when used for the tearing instability of Sect. 3.4 it leads to large adjustments in the initial conditions, and for the most extreme temperatures to a complete disruption of the current sheet.
We also provide in Table 5 the analytical expressions of various quantities averaged over the Maxwell-Jüttner distribution, for example, the mean Lorentz factor, mean momentum, or the enthalpy. The method used to derive these expressions is presented in Appendix E. Besides being of general interest, these expressions served to further validate our generated distributions by comparing the analytical results of Table 5 with averages performed over particles generated with our method.
5. Real, PIC, and Vlasov-Maxwell plasmas
Particle-in-cell simulations have brought tremendous new insights into astrophysical plasmas, for example through studies of kinetic instabilities in their nonlinear phase, kinetic turbulence, particle acceleration via the Fermi-process, or 3D magnetic reconnection and the associated particle acceleration. However, as we will detail in this section, there remain a number of questions with respect to the degree to which PIC models are able to completely mirror real plasmas.
The modeling of a real plasma by a PIC plasma implies two steps (see the right branch of Fig. 12): the grouping of many real particles into a single superparticle, known as coarse-graining, and the discretization of the equations with the presence of a grid. Each of these steps raises questions:
-
1.
Coarse-graining: Is plasma behavior still expected with so fewsuperparticles per Debye sphere? Is the noise level too large?With this, do nonlinearities appear sooner than in real plasmas?Does the PIC plasma remain collisionless? And what are welosing when we gather the particles into the superparticles?
-
2.
Discretization and grid: At least for explicit schemes, they bring with them numerical stability problems, reviewed in Appendix B. Moreover, the interpolation of superparticle quantities to grid points implies a finite volume for the superparticles, which in turn implies a vanishing two-point force at short distances and thus reduces drastically the influence of collisions; it helps the PIC plasma to be collisionless, but is it enough? And what are the consequences of having superparticles whose sizes reach a significant fraction of the Debye length?
We discuss some of these questions in Sects. 5.1 to 5.3.
The distinguishing feature of the Vlasov-Maxwell description of a plasma is the absence of collisions and of correlations between particles. Given the two preceding points, we can wonder if a PIC plasma can be described by the Vlasov-Maxwell system, or if it has too few superparticles per cell and thus correlation levels that are too high for this description to be accurate. The differences between PIC and Vlasov-Maxwell descriptions are examined in Sect. 5.4.
5.1. The plasma parameter Λ: a coarse-graining dependent quantity
As said earlier and expressed in Eq. (1), a real plasma is represented in the computer by grouping many particles into superparticles. This is what is called coarse-graining. Unlike fluid equations3, Eqs. (2a) − (2e) are not invariant under coarse-graining (because of the definition of the current, Eq. (2e)). The prototype of p-dependent quantities is the plasma parameter4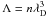 , which is close to the number of particles per Debye sphere (we recall that p is the number of particles per superparticles, λD the Debye length and n the real particle number density).
, which is close to the number of particles per Debye sphere (we recall that p is the number of particles per superparticles, λD the Debye length and n the real particle number density).
The plasma parameter Λ also expresses the ratio of the particles’ kinetic energy to their electrostatic potential energy of interaction and, as such, varies as 1/p because kinetic energy is proportional to the superparticles’ mass msp ∝ p while charge interaction energy involves their charge 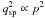 . This can be seen directly by writing
. This can be seen directly by writing 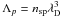 for the superparticle plasma, with nsp the number density of superparticles. The Debye length, being derived from fluid theory, is invariant under coarse-graining, and since n = p × nsp, one has that
for the superparticle plasma, with nsp the number density of superparticles. The Debye length, being derived from fluid theory, is invariant under coarse-graining, and since n = p × nsp, one has that 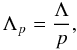 (14)with Λ = Λp = 1 the real plasma parameter.
(14)with Λ = Λp = 1 the real plasma parameter.
In a real plasma Λ ranges from 104 to 1020 (for example Λ ~ 106 in solar coronal loops; 1012 in the magnetotail, magnetopause, or in typical Crab flares; 1017 in AGN jets), while in computer experiments where we have to simulate thousands to millions of Debye spheres, Λ reaches hardly a few tens (for a discussion see, e.g., Bykov & Treumann 2011, Sect. 4). The corresponding number of particles per superparticles then reaches p ~ 103 to 1019. The question of the relevance of PIC simulations for describing collisionless plasmas has thus been asked from the beginning, and concerns both terms, collisionless and plasma, that we now discuss.
5.1.1. Plasma behavior
A weakly coupled plasma is characterized by the predominance of collective effects over individual effects. The ratio of these effects is contained in the plasma parameter Λp, which can be seen as the ratio of collective behavior (the interaction of one particle with the electromagnetic fields collectively generated by all others, which is coarse-graining independent) to binary effects (which are proportional to 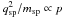 ).
).
Since plasma behavior, with Debye screening and local charge neutrality, requires a high plasma parameter, it is wise to ask how large it should be in a PIC plasma. Birsdall & Langdon (1985, chap. 1) and Hockney & Eastwood (1988) have shown that it is not necessary for this ratio to be as high as in real plasmas, and that a Λp of about a few suffices for correct plasma behavior.
5.1.2. Collisionless behavior
A plasma behaves collisionlessly if the time and length scales of interest are negligible toward the collision time and the mean-free path, respectively. Since the collision time scales as Λp times the plasma period, it is not clear whether a PIC computer plasma with a plasma parameter on the order of unity will be collisionless.
Particle-in-cell plasmas are helped by the superparticle finite sizes, which imply that the two-point force decreases to zero for separations smaller than this size. This fact, albeit degrading the accuracy of single particle dynamics, greatly reduces the relative importance of binary collisions so that in order to correctly simulate a collisionless plasma for scales accessible in simulations, one has to insure that (Birsdall & Langdon 1985; Hockney & Eastwood 1988, chap. 1) 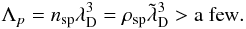 (15)(Here,
(15)(Here, 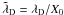 is the normalized Debye length. It can be expressed as
is the normalized Debye length. It can be expressed as 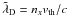 with
with 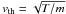 .)
.)
This is all the more true if rc < X0, where X0 is the grid size and rc is the effective collision radius for Coulomb encounters, expressed by equating the kinetic energy of the meeting particles to their potential energy of interaction: 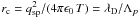 (rc is also p-dependent). The Debye length must be resolved for reasons of numerical stability (Sect. 3.1 and Appendix B), so that we arrive at an optimal ordering rc < X0 < λD, which is allowed only if, again, λD/rc = Λp > 1.
(rc is also p-dependent). The Debye length must be resolved for reasons of numerical stability (Sect. 3.1 and Appendix B), so that we arrive at an optimal ordering rc < X0 < λD, which is allowed only if, again, λD/rc = Λp > 1.
However, because the PIC model is a description of a plasma of cloud charges, grazing collisions will still be present and will lead to thermalization (Birsdall & Langdon 1985, Chap. 1; Hockney & Eastwood 1988, Chaps. 1 and 9), a point discussed in the next section.
5.2. Thermalization time: a coarse-graining dependent quantity
In a PIC plasma, the behavior of plasma quantities depending on Λ can be guessed by replacing Λ by Λp. This is the case for the thermalization time of a plasma by grazing Coulomb collisions (Spitzer 1965) or by electric field fluctuations (Birsdall & Langdon 1985, p. 282), which is on the order of tth ~ TP × Λ (with TP the plasma period). This has two important consequences:
-
We expect tth to depend on resolution and coarse-graining, roughly as
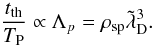 (16)
(16) -
Since Λp = Λ/p is several orders of magnitude smaller than the real plasma parameter Λ, we expect the thermalization by grazing collisions and fluctuations to be vastly more efficient in PIC codes than in reality.
This can have important consequences in simulations where thermalization plays a key role. For example in real collisionless shocks, the mean free path for collisions lmean free path is far larger than the shock thickness Δshock and the thermalization processes are collisionless kinetic instabilities. Since the mean free path 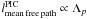 in a PIC plasma is smaller by a factor of p ~ 1010 than in a real plasma, it is not obvious that the ordering
in a PIC plasma is smaller by a factor of p ~ 1010 than in a real plasma, it is not obvious that the ordering 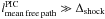 still holds. To truly describe a collisionless shock with a PIC algorithm, one has to be careful that the unphysically fast thermalization by collisions or fluctuations remains slower than thermalization by kinetic instabilities.
still holds. To truly describe a collisionless shock with a PIC algorithm, one has to be careful that the unphysically fast thermalization by collisions or fluctuations remains slower than thermalization by kinetic instabilities.
 |
Fig. 10 Top: electron temperatures for the hot (2) and cold (1) plasmas, from four simulations with different ρsp. The curves for ion temperatures are similar, except for an overall time dilatation by a factor ~ (mi/me)1/2 = 5. In this figure we use T∞(t) = (T1(t) + T2(t))/2. Except for ρsp = 4 where there is significant numerical heating, T∞(t) is constant in time. Bottom: half-thermalization time for ions and electrons, versus number of superparticles per cell. For ions, we have plotted tth/(mi/me)1/2. The times reported are measured as the initial slope of the temperature curves in a log-lin plot, and thus correspond to tth/2. We see the scaling tth ∝ ρsp. |
To illustrate the dependance of the collision and fluctuation induced thermalization time, we present simulations that initially have two thermal ion-electron plasmas. The first is cold, with a temperature T1,e(0) = T1,i(0) = 1.6 × 10-3mec2 for its electrons and ions, while the second is hot, with T2,e(0) = T2,i(0) = 1.8 × 10-2mec2. The mass ratio is mi/me = 25. The four species interact via collisions and correlations (no sign of plasma kinetic instabilities were found) and tend to reach the same final temperature 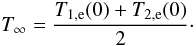 (17)Particle-in-cell results are shown in Fig. 10 (top) for the electrons, for four simulations with a number of superparticles per cell (including all species) ρsp = 4, 16, 64, or 128. The other parameters are kept fixed: nx = 25, nt = 500, and box size of 253 cells. It results in
(17)Particle-in-cell results are shown in Fig. 10 (top) for the electrons, for four simulations with a number of superparticles per cell (including all species) ρsp = 4, 16, 64, or 128. The other parameters are kept fixed: nx = 25, nt = 500, and box size of 253 cells. It results in 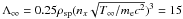 , 61, 243, or 485. The temperatures are measured with
, 61, 243, or 485. The temperatures are measured with 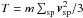 , where the sum runs over all the superparticles of a given species. In Fig. 10 (top) we clearly see a slower thermalization as ρsp increases.
, where the sum runs over all the superparticles of a given species. In Fig. 10 (top) we clearly see a slower thermalization as ρsp increases.
To evaluate the thermalization times, we use the result of Spitzer (1965): for two species at temperature T1 and T2, thermalization occurs according to 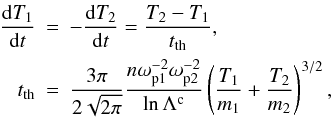 (18)with n = n1 = n2 the particle number density,
(18)with n = n1 = n2 the particle number density, 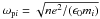 , and lnΛc the Coulomb logarithm, or the logarithm of the ratio of the largest to closest distances used in the collision integral. In a PIC code, lnΛc = lnλD/X0. Clearly, (T1(t) + T2(t))/2 is constant and equal to T∞. It follows that if mass m1 and m2 are equal, the thermalization time is also constant and can be written
, and lnΛc the Coulomb logarithm, or the logarithm of the ratio of the largest to closest distances used in the collision integral. In a PIC code, lnΛc = lnλD/X0. Clearly, (T1(t) + T2(t))/2 is constant and equal to T∞. It follows that if mass m1 and m2 are equal, the thermalization time is also constant and can be written 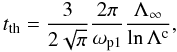 (19)with Λ∞ = n [ϵ0T∞/(ne2)] 3/2 the plasma parameter based on the temperature T∞. It also follows that the temperatures vary exponentially as T1 = T∞ − 0.5 [T2(0) − T1(0)] exp { − 2t/tth } , and similarly for T2.
(19)with Λ∞ = n [ϵ0T∞/(ne2)] 3/2 the plasma parameter based on the temperature T∞. It also follows that the temperatures vary exponentially as T1 = T∞ − 0.5 [T2(0) − T1(0)] exp { − 2t/tth } , and similarly for T2.
Here we do not find the temperature curves to be strictly exponential, mainly because there are four species. The cold electrons interact with the hot electrons on a timescale t0, but also with the hot ions on a timescale mi/met0 = 25t0. The cold ions are heated by interactions with the hot ions on a timescale (mi/me)1/2t0 = 5t0, and by interactions with the hot electrons on a timescale mi/met0 = 25t0. Since the cold ions are heated more slowly than the cold electrons, a temperature difference between these two components appears and they also start heating or cooling each other. Nevertheless, given the separation of scales we expect a measure of the slope around t = 0 to reflect the electron-electron or ion-electron thermalization times when measured on the electron or ion temperature curves, respectively.
Results are shown in Fig. 10 (bottom). We see that the relation tth ∝ ρsp is roughly correct for both electrons and ions. We also underline the difference with a real plasma, where tth/Tpe ~ Λ reaches 1010 or more, while it is on the order of Λp ≤ 104 in PIC simulations.
5.3. Field fluctuation level dependence: coarse-graining and finite superparticle size
The previous section showed that the behavior of PIC plasma quantities can be guessed by the substitution Λ → Λp. While it is true for orders of magnitude estimates, this recipe is, however, not exact, and coarse-graining dependent quantities generally follow other relations than their real counterparts with respect to physical parameters (temperature, Debye length, plasma parameter, etc.). The main reason for this is that the finite volume of the superparticles implies a cutoff of the physical processes at smaller scales, an effect that becomes even more important when the superparticle size is close to the Debye length: 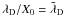 typically ranges between one (or less) and ten in simulations.
typically ranges between one (or less) and ten in simulations.
This section illustrates this double dependence (Λ → Λp and superparticle size) with a detailed study of the level of electric field fluctuations ε in a PIC thermal plasma.
In a real plasma in thermal equilibrium, it is given by (Callen 2006, Sect. 1.1) 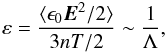 (20)where the symbol ⟨ · ⟩ denotes an average over space.
(20)where the symbol ⟨ · ⟩ denotes an average over space.
Dieckmann et al. (2004) studied the spectrum of thermal fluctuations in a PIC plasma, but without investigating their levels. Hockney (1971, see also Hockney & Eastwood 1988 measured ratios like ε in a series of 2D simulations of thermal plasmas, and found a good agreement with the empirical formula 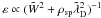 , where
, where 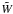 is the superparticle geometrical size in number of cells. Its algorithm was two dimensional, electrostatic, and based on the integration of the Poisson equation.
is the superparticle geometrical size in number of cells. Its algorithm was two dimensional, electrostatic, and based on the integration of the Poisson equation.
We perform these simulations with our 3D electromagnetic code and measure the level of energy in the electric field. We use thermal velocities from 0.04c to 0.10c, ρsp from 2 to 500, and nx from 10 to 128. It results in 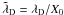 from 0.4 to 12.8, and in
from 0.4 to 12.8, and in 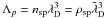 from 0.1 to 75 000. The fluctuation levels do not depend on the timestep (which varies from nt = 2000 down to close to the Courant limit Δt ~ X0/c) nor on box size (which is always bigger than nx). We use a pair plasma, but increasing the mass of the ions would only multiply the fluctuation levels by a constant factor.
from 0.1 to 75 000. The fluctuation levels do not depend on the timestep (which varies from nt = 2000 down to close to the Courant limit Δt ~ X0/c) nor on box size (which is always bigger than nx). We use a pair plasma, but increasing the mass of the ions would only multiply the fluctuation levels by a constant factor.
The results are summarized in Fig. 11: ε is found to be proportional to 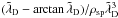 , and not exactly to 1/Λp. To explain this, we generalize the computation of Hockney to three dimensions.
, and not exactly to 1/Λp. To explain this, we generalize the computation of Hockney to three dimensions.
For a plasma in thermal equilibrium, the energy in the electric field at location (x,t) can be evaluated by adding the electric field produced at x by charges at location x0 and having a velocity v0, Ex0,v0(x,t), 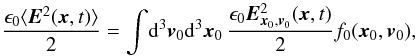 (21)where ⟨ · ⟩ means an ensemble average (which coincides with a spatial average); Ex0,v0(x,t) is a generalization of the Debye electric field for moving particles (Nicholson 1983, Chap. 9); and Eq. (21) can be evaluated for a plasma of finite-sized particles as (Hockney 1971; Birsdall & Langdon 1985)
(21)where ⟨ · ⟩ means an ensemble average (which coincides with a spatial average); Ex0,v0(x,t) is a generalization of the Debye electric field for moving particles (Nicholson 1983, Chap. 9); and Eq. (21) can be evaluated for a plasma of finite-sized particles as (Hockney 1971; Birsdall & Langdon 1985) 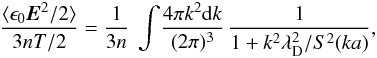 (22)where S(ka) is the Fourier transform of the shape of the superparticles and a the characteristic size of the superparticles (in our case a ~ X0); S(ka) tends to 1 as k-1 ≫ a.
(22)where S(ka) is the Fourier transform of the shape of the superparticles and a the characteristic size of the superparticles (in our case a ~ X0); S(ka) tends to 1 as k-1 ≫ a.
 |
Fig. 11 Top: field energy levels as a function of |
Equation (22) cannot be used as such for a real plasma of point particles (S(ka) = 1) because it includes the electric field at arbitrarily small distances from the charge, which has an infinite energy. It leads to Eq. (20) only if a truncation at small distances is performed, for example k < (αλD)-1 with α any constant: ⟨ ϵ0E2/2 ⟩ in Eq. (20) is then the energy in the electric field for wavelengths larger than αλD. Alternatively and to avoid a cutting procedure, we note that the electric field in Eq. (20) can be taken as the total field produced by the particles to maintain the screening Debye clouds (the polarization electric field; see Callen 2006, Sect. 1.1).
In the case of a PIC plasma all processes at scales below the grid size a = X0 are ignored, so that the upper bound of the integral is kmax = a-1 and there is no small scale divergence. Since S(ka) ~ 1 for k ≪ a-1, and given that the integration stops at k = a-1, we will assume that S(ka) = 1.
Changing to spherical coordinates, using u = λDk and 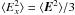 , we arrive at
, we arrive at 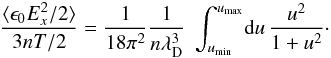 (23)A primitive of the integral is u − arctan(u). We use kmax = 1/X0 or
(23)A primitive of the integral is u − arctan(u). We use kmax = 1/X0 or 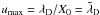 , while the largest wavelength is given by the simulation domain size and verifies umin ≪ umax. Consequently, we obtain
, while the largest wavelength is given by the simulation domain size and verifies umin ≪ umax. Consequently, we obtain 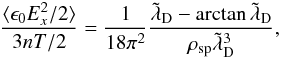 (24)in good agreement with the simulations (Fig. 11, top panel), except for the constant factors 18π2 ~ 178 (which can be attributed to an approximate choice of umax).
(24)in good agreement with the simulations (Fig. 11, top panel), except for the constant factors 18π2 ~ 178 (which can be attributed to an approximate choice of umax).
The two limits are interesting. For a very high resolution, 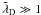 , the field energy decreases as
, the field energy decreases as 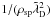 , which is non-trivial and different from what is expected in a real plasma where it decreases as
, which is non-trivial and different from what is expected in a real plasma where it decreases as 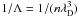 . The empirical formula of Hockney (1971), generalized to 3D, would also predict
. The empirical formula of Hockney (1971), generalized to 3D, would also predict 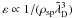 in the high resolution limit. However, our experiments clearly preclude this dependence, and are compatible with Eq. (24) (see Fig. 11). The presence of a finite superparticle volume and of the grid is retained in our calculation only in the upper bound of the integral: physically speaking, physical processes with k-1 < X0 are smoothed out. This explains the difference between Eq. (24) and that of a real plasma.
in the high resolution limit. However, our experiments clearly preclude this dependence, and are compatible with Eq. (24) (see Fig. 11). The presence of a finite superparticle volume and of the grid is retained in our calculation only in the upper bound of the integral: physically speaking, physical processes with k-1 < X0 are smoothed out. This explains the difference between Eq. (24) and that of a real plasma.
For low resolutions, 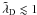 , an expansion of the arctangent shows that the field energy behaves as 1/(54π ρsp), which is finite and independent of
, an expansion of the arctangent shows that the field energy behaves as 1/(54π ρsp), which is finite and independent of 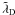 . In a real plasma, ε would go to zero as the screening distance vanishes. That this is not the case here indicates that the screening distance does not vanish, because the finite size of the superparticles also plays the role of the screening mechanism.
. In a real plasma, ε would go to zero as the screening distance vanishes. That this is not the case here indicates that the screening distance does not vanish, because the finite size of the superparticles also plays the role of the screening mechanism.
5.4. Comparing the PIC and Vlasov-Maxwell models
We now highlight some differences between PIC models and kinetic models based on Liouville or Klimontovich equations. To do so, we recall how the Vlasov-Maxwell system is derived from these formalisms.
A plasma is constituted of many charged particles in mutual electromagnetic interaction. Under relativistic conditions, a plasma microstate is fully characterized by the positions and velocities of the N particles and by the value of the fields at all space points (the fields must be treated as independent from the particles because of retarded interactions), plus the necessary boundary conditions. Within the frame of classical electrodynamics, the time evolution of a microstate is described by Maxwell equations and by the equations of motion for the particles under the action of the Lorentz force:  (25)\arraycolsep1.75ptHere, c is the speed of light, em the microscopic electric field; bm = cBm is c times the microscopic magnetic field, qj, mj, γj, vj, and xj the charge, mass, Lorentz factor, velocity, and position of the particle number j. We also define its momentum pj = mjγjvj.
(25)\arraycolsep1.75ptHere, c is the speed of light, em the microscopic electric field; bm = cBm is c times the microscopic magnetic field, qj, mj, γj, vj, and xj the charge, mass, Lorentz factor, velocity, and position of the particle number j. We also define its momentum pj = mjγjvj.
At a given time t, a microstate is represented by a point  in the 6N-dimensional phase-space, and by the fields. One can then consider the collection of microstates having the same macroscopic properties (which can depend on what one is looking for), place them as points in the 6N-dimensional phase-space, and define the N-particle distribution function
in the 6N-dimensional phase-space, and by the fields. One can then consider the collection of microstates having the same macroscopic properties (which can depend on what one is looking for), place them as points in the 6N-dimensional phase-space, and define the N-particle distribution function 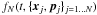 as the number density, at a given time, of these microstates in the 6N-dimensional phase-space. Given that the number of microstates in phase-space is chosen as a continuum, fN is a smooth function (Klimontovich 1982; Nicholson 1983). It defines a macrostate, i.e., an ensemble average of a collection of compatible microstates. The dynamic evolution is then obtained by the Liouville equation, which states that the number of microstates is conserved
as the number density, at a given time, of these microstates in the 6N-dimensional phase-space. Given that the number of microstates in phase-space is chosen as a continuum, fN is a smooth function (Klimontovich 1982; Nicholson 1983). It defines a macrostate, i.e., an ensemble average of a collection of compatible microstates. The dynamic evolution is then obtained by the Liouville equation, which states that the number of microstates is conserved 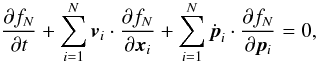 (26)supplemented by Maxwell equations for the microscopic fields em and bmwith for sources the particles of the corresponding microstate.
(26)supplemented by Maxwell equations for the microscopic fields em and bmwith for sources the particles of the corresponding microstate.
When there is no background magnetic field, and when the particles are non-relativistic, the magnetic field remains negligible toward the electric field which can be computed directly from the particle positions at time t with the use of the electrostatic potential V(r) = q2/(4πϵ0r) (the Coulomb model). The Liouville equation can then be transformed to the infinite BBGKY hierarchy. The first BBGKY level involves the one-particle distribution function f1(t,w) (with w = (x,p)) and the two-point distribution function f2 via the correlation function g2(t,w1,w2) = f2(t,w1,w2) − f1(t,w1)f1(t,w2): ![% subequation 6977 0 \begin{eqnarray} &&\frac{\partial f_1}{\partial t} + \vec{v}_1\cdot\frac{\partial f_1}{\partial {\vec{x}}} - \frac{\partial}{\partial {\vec{x}_1}}\overline{V}_{t,\vec{x}_1}[f_1]\cdot\frac{\partial f_1}{\partial \vec{p}} = C[g_2], \label{equ:Vlasov_NR} \\ &&\overline{V}_{t,\vec{x}_1}[f_1] = \int\!\dif^6\vec{w}_2 V(|\vec{x}_1-\vec{x}_2|) f_1(t,\vec{w}_2). \end{eqnarray}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq520.png) Here C is an integral operator, vanishing with g2. The quantity
Here C is an integral operator, vanishing with g2. The quantity ![\hbox{$\overline{V}_{t,\vec{x}_1}[f_1]$}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq523.png) is the mean potential due to the particle distribution f1. Since f1(w) is the probability of finding a particle near w independently of the positions of all others, this potential does not include short-range correlations, but only long-range collective effects. It is a macroscopic quantity, just as the fields entering into the Vlasov-Maxwell system (Eq. (28)).
is the mean potential due to the particle distribution f1. Since f1(w) is the probability of finding a particle near w independently of the positions of all others, this potential does not include short-range correlations, but only long-range collective effects. It is a macroscopic quantity, just as the fields entering into the Vlasov-Maxwell system (Eq. (28)).
Approximations can then be made to truncate the BBGKY hierarchy. Evaluations of the right-hand side of Eq. (27a) can lead, depending on the hypothesis made, to Boltzmann, Landau, Lenard-Balescu, or more refined kinetic equations. For a fully ionized plasma, the relevant approximation parameter is the number of particles per Debye sphere, or plasma parameter Λ. For large Λ, collisions and correlations between small numbers of particles are negligible toward interactions of particles with the fields collectively generated by all others. Keeping only these collective interactions is equivalent to a truncation of BBGKY hierarchy at its lowest level, i.e., g2 = 0, and leads to the Vlasov-Maxwell system. Generalized to relativistic plasmas5 and to two species, it reads 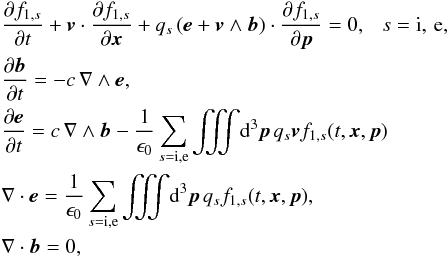 (28)\arraycolsep1.75ptwith f1,s(t,x,p) the one-particle distribution function, for electrons (s = e) or ions (s = i), defined from fN. It is also a smooth function, and the Vlasov-Maxwell system describes the evolution of a continuous fluid in the six-dimensional phase-space, where information on the individual nature of the particles has been smoothed out. In particular within this description, the plasma parameter Λ is infinite, the fluctuation- and collision-induced thermalization time is infinite, and the level of electric field fluctuations ε is zero. We note that these are analytical properties. Numerical solutions of the Vlasov-Maxwell-system will also not strictly recover the collisionless behavior of the plasma. For instance, numerical diffusion arising necessarily from the discretization of Eq. (28) will also lead to a finite thermalization time. We are, however, not aware of a comprehensive study of such effects for algorithms solving the discretized Vlasov-Maxwell system.
(28)\arraycolsep1.75ptwith f1,s(t,x,p) the one-particle distribution function, for electrons (s = e) or ions (s = i), defined from fN. It is also a smooth function, and the Vlasov-Maxwell system describes the evolution of a continuous fluid in the six-dimensional phase-space, where information on the individual nature of the particles has been smoothed out. In particular within this description, the plasma parameter Λ is infinite, the fluctuation- and collision-induced thermalization time is infinite, and the level of electric field fluctuations ε is zero. We note that these are analytical properties. Numerical solutions of the Vlasov-Maxwell-system will also not strictly recover the collisionless behavior of the plasma. For instance, numerical diffusion arising necessarily from the discretization of Eq. (28) will also lead to a finite thermalization time. We are, however, not aware of a comprehensive study of such effects for algorithms solving the discretized Vlasov-Maxwell system.
In contrast, the models underlying PIC simulations follow a different path, illustrated in Fig. 12. It consists in following the time evolution of the microstate constituted by N/p superparticles and the fields, Eqs. (2a) − (2e), with p reaching 1010 or more. One of the consequences is that the PIC plasma has a plasma parameter Λp = Λ/p (from Eq. (14)) far smaller than that of the real plasma, so that it includes relatively large correlation and noise levels.
 |
Fig. 12 Different plasma models. Dashed arrows are transitions showing non-trivial effects. Coarse-graining and discretization are discussed in Sects. 5.1 to 5.3. |
5.5. Higher-order effects of coarse-graining
We have highlighted that the coarse-graining step, the description of a real plasma of N particles by a PIC plasma of N/p superparticles, each containing p real particles, involves a reduction of the plasma parameter Λ by a factor p. This is the main effect of coarse-graining. Higher-order effects arise because after coarse-graining, the model ignores the internal dynamics and correlations of the particles contained within a superparticle.
This can be seen by writing explicitly the grouping: we label the particles either by wn, n = 1...N (with w = (x,p)), or by wij with i = 1...N/p representing the group number, and j = 1...p the particle number within this group. We denote by  the position and velocity of the center-of-mass of the group number i. The N-particle distribution function fN of the real plasma can then be written formally as
the position and velocity of the center-of-mass of the group number i. The N-particle distribution function fN of the real plasma can then be written formally as ![\begin{eqnarray} \label{equ:decomp_fn_PIC} f_N&(t,w_1,...,w_N) = g_{\rm corr}(t,w_1,...,w_N)\notag \\[-1mm] &+ f_{N\!/\!p}(t,\overline{w}_{\mathrm{sp},1},...,\overline{w}_{\mathrm{sp},N\!/\!p}) \times \prod_{i=1}^{N\!/\!p}f_{\mathrm{sp},i}(t,w_{i1},...,w_{ip}). \end{eqnarray}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq541.png) (29)This equation introduces
(29)This equation introduces 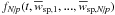 , the analog of fN but for the center-of-mass of the particle groups (i.e., of the superparticles); fsp,i(t,wi1,...,wip), the distribution function of the particles contained within a group, which represents the dynamics and correlations between particles of the same group; and gcorr(t,w1,...,wN), the correlations ignored by writing fN = fN/p × fsp,1...fsp,N/p, i.e., the correlations between particles of different groups. The PIC approximation then consists in setting gcorr = 0 and fsp,i(t,wi1,...,wip) = const.
, the analog of fN but for the center-of-mass of the particle groups (i.e., of the superparticles); fsp,i(t,wi1,...,wip), the distribution function of the particles contained within a group, which represents the dynamics and correlations between particles of the same group; and gcorr(t,w1,...,wN), the correlations ignored by writing fN = fN/p × fsp,1...fsp,N/p, i.e., the correlations between particles of different groups. The PIC approximation then consists in setting gcorr = 0 and fsp,i(t,wi1,...,wip) = const.
A complete understanding of these approximations would require developing a BBGKY hierarchy from Eq. (29) and making explicit the electric and magnetic field contributions from the particle groups. This is a complex task. We can, however, stress important consequences of the assumption fsp,i(t,wi1,...,wip) = const.:
-
The superparticles are assumed incompressible. Thecompressibility due to particle motion within a particle group isthus absent from the coarse-grained plasma.
-
The velocity dispersion of the particles within a group is ignored in the coarse-grained plasma. The kinetic pressure resulting from this dispersion is thus also absent.
-
The electric fields present in the PIC plasma are computed from the superparticles. This is equivalent to saying that they are computed by taking into account only the monopole distribution of charge created by the internal arrangement of the particles within a group, with higher-order multipole terms neglected. The same holds for the magnetic field.
6. Discussion and conclusion
6.1. Code validation
We have presented our particle-in-cell code Apar-T (Sect. 2 and Appendix A), and studied several validation tests.
Computation of the spectra from a magnetized or unmagnetized thermal plasma at rest (Sect. 3.1) has proven very accurate, with the plasma pulsation and the right and left cutoff pulsations precisely recovered (Figs. 1 and 2), even in cases where the Debye length and the Larmor radius are not resolved. This proves that the description of individual particle motions in a constant magnetic field and of collective particle dynamics is accurate, and robust with respect to numerical resolution. In particular we showed that Larmor orbits in a constant magnetic field are well described provided that the cyclotron pulsation is well resolved, independently of the grid size. We found, however, a numerical instability with abnormal behavior in the energy curves and high noise levels for under-resolved Debye length or under-resolved Larmor radius, so that this parameter range should be avoided.
Simulations of the filamentation instability (Sect. 3.2) showed a good agreement with linear cold theories, provided that the growth rates are computed from the temporal evolution of the Fourier modes. Discrepancies with theory then range from 5% to 13%, and can be explained by the wavenumber dependence of the growth rates. On the other hand, the linear growth rates derived from the total energy curves, or equivalently from the sum of all Fourier modes, present larger discrepancies with linear theory, ranging between 12% to 61%. This is explained by the high level of fluctuations in PIC codes that prevent the fastest growing modes to dominate the total energy before the end of the linear phase of the instability.
Simulations of the tearing instability in a relativistic pair plasma gave linear growth rates within 8% of those found by Pétri & Kirk (2007) with an analytical linear Vlasov-Maxwell solution, a result not varying significantly when changing the numerical resolution (Sect. 3.4, Fig. 8, and Table 4). This example, where the shape of the velocity distribution is a key feature, is thus in agreement with the Vlasov-Maxwell description. It also validates the new method used to load the relativistic (in both temperature and bulk velocity) Maxwell-Jüttner distribution that we present in Sect. 4 and Appendix D, as well as the general relations used for the relativistic Harris equilibrium (Appendix C). We note that in this case the total energy curves can be used for evaluation of the linear growth rates because the linear phase spans several orders of magnitude in field intensity, so that the fastest growing modes have enough time to dominate the energy.
All in all, these tests show that our code Apar-T is a sound basis for future explorations. They also serve as a base to explore important questions regarding the nature of a PIC plasma, that we summarize in the next section.
6.2. PIC and real plasmas
The widespread use of PIC codes for studying plasmas out of equilibrium calls for a deep understanding of the PIC model, and of its relation with a real plasma and with the Vlasov-Maxwell description. Section 5 attempted to provide some explanations.
We have seen that the PIC model lies on two building blocks. The first stems from the capability of computers to handle only up to ~ 1010 particles, while real plasmas contain from 104 to 1020 particles per Debye sphere. This means that a coarse-graining step must be used, whereby of the order of p ~ 1010 real particles are represented by a single computer superparticle. The second step is field storage on a grid with its subsequent finite superparticle size.
We have introduced the notion of coarse-graining dependent quantities, i.e., physical quantities depending on p. The prototype of such quantities is the plasma parameter Λ, that behaves as Λp ∝ 1/p. This vast reduction of Λ induces higher noise levels and correlations, but we have again seen that it does not threaten plasma and collisionless behavior as long as Λp remains above unity. All coarse-graining dependent quantities can be expressed as the product of a fluid quantity (which is coarse-graining independent) and a parameter expressing a number of particles per fluid volume. Examples of such parameters include 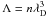 , n(c/ωpe)3, n(c/ωpi)3, ... Their behavior in the PIC plasma can be guessed by taking into account the reduction by a factor p of the number of particles, leading for example to the substitution Λ → Λp = Λ/p in the relevant analytical expressions. We checked this for the collision and fluctuation induced thermalization time (Sect. 5.2), which is indeed proportional to the number of computer superparticles per cell; the lower the number the shorter the thermalization time. Bret et al. (2013) similarly reduce the parameter n(c/ωpe)3 by a factor p when applying their theory for the magnetic fluctuation level in a drifting plasma to their PIC simulations. However, the substitution Λ → Λp is strictly valid only for point-size particles, and the large finite size of the superparticles, which reaches a fraction of a Debye length, suppresses interactions and fluctuations at shorter wavelengths and modifies these scalings. We have detailed how this works for the electric field fluctuation level in a thermal plasma in Sect. 5.3.
, n(c/ωpe)3, n(c/ωpi)3, ... Their behavior in the PIC plasma can be guessed by taking into account the reduction by a factor p of the number of particles, leading for example to the substitution Λ → Λp = Λ/p in the relevant analytical expressions. We checked this for the collision and fluctuation induced thermalization time (Sect. 5.2), which is indeed proportional to the number of computer superparticles per cell; the lower the number the shorter the thermalization time. Bret et al. (2013) similarly reduce the parameter n(c/ωpe)3 by a factor p when applying their theory for the magnetic fluctuation level in a drifting plasma to their PIC simulations. However, the substitution Λ → Λp is strictly valid only for point-size particles, and the large finite size of the superparticles, which reaches a fraction of a Debye length, suppresses interactions and fluctuations at shorter wavelengths and modifies these scalings. We have detailed how this works for the electric field fluctuation level in a thermal plasma in Sect. 5.3.
We stress that the reduction of the collision and fluctuation induced thermalization time and of other related timescales (e.g., the slowing-down time of fast particles), by 10 or more orders of magnitude, can have important consequences for the relevance of simulations: one has to insure that collisionless kinetic processes remain more efficient than the artificially enhanced collisional and fluctuation induced PIC effects. Similarly, we have seen in Sect 3.2 that the high level of fluctuations alter the linear spectrum of instabilities by preventing the fastest growing modes to dominate the total energy.
A more subtle effect of coarse-graining is due to the loss of the dynamics of the p particles represented by each superparticle. We intuitively expect that it will lead to the overall loss of compressibility due to superparticle incompressibility, of the contribution to kinetic pressure of the particle velocity spreading within a superparticle, and of the multipole contribution to the electric and magnetic fields created by the distribution of particles within a superparticle (see Sect. 5.5). The relevance of these missing effects remains unclear.
6.3. PIC and Vlasov-Maxwell plasmas
We have highlighted in Sect. 5.4 that a PIC algorithm simulates a plasma of finite-sized charges in their self-fields, and does not strictly solve the Vlasov-Maxwell system. Using the Vlasov equation assumes that the plasma is represented in phase space by a continuous fluid. In this limit of an infinite number of particles, the plasma parameter Λ and the thermalization time are infinite, and the collision frequency and the thermal field fluctuation levels are zero. Using a PIC algorithm amounts to dividing the continuous phase space fluid into discrete elements, and to following their orbits. In this sense, one can say that we integrate the characteristics of the Vlasov equation. However, the newly introduced graininess (which is far higher than that of the original plasma) implies the presence of binary collisions and of correlations between superparticles that is not easy to evaluate, in part because they are reduced by the finite size of the superparticles and the subsequent vanishing of the two-point force at short distances (see Sect. 5.1). The intricate dependence of Eq. (24) is a hint to this complexity. We note that Birsdall & Langdon (1985, Chap. 12) have derived a generalization of the Balescu-Guernsey-Lenard kinetic equation that includes the use of a grid (and thus of finite sized superparticles), and of the discretization in space and time of the equations. The correlations just mentioned are partly present in this equation, but difficult to extract.
These differences between PIC and Vlasov-Maxwell plasmas are especially enhanced in the linear phase of instabilities. We see two main points. The first is that nonlinear effects absent from the linear theory, and possibly enhanced by the high noise level of the simulation (Sect. 5.3), may have visible consequences (Birsdall & Langdon 1985, Sect. 13.6; Dieckmann et al. 2006). This example is reported by Daughton (2002) in the context of the drift kink instability of a current sheet: the instability is found to grow faster than predicted by the linear Vlasov theory because the early development of another instability quickly produces nonlinear effects. Bret et al. (2010, Fig. 23) also report significant early nonlinear behavior in counter-streaming situations. We have also reported the presence of field components due to nonlinear effects in Fig. 4.
The second point is that the high level of fluctuations delays the dominance of the fastest growing Fourier modes over the sum of other modes. The consequence is that effective linear growth rates measured from total energy curves appear slower than the growth rates of the fastest modes. This is even more important in instabilities where the linear phase is short, and explains the differences between the effective growth rates and the linear cold theory of the counter-streaming instability measured in Sect. 3.2, with discrepancies reaching 60% or more. It may also explain the differences between theory and measured growth rates of Cottrill et al. (2008), Dieckmann et al. (2006), Haugboelle et al. (2013) for the counter-streaming instability. On the other hand, the differences can be small if the linear phase lasts long enough for the fastest mode to dominate the energy, as is the case for the relativistic tearing instability in Sect. 3.4 or for the Weibel instability of Markidis et al. (2010).
6.4. Modeling astrophysical plasmas
In the light of what has been said so far one may wonder what this all implies for the modeling of astrophysical plasmas. We attempt to give some answers in the following. We have shown that the PIC description of an astrophysical plasma bears some risk because the plasma parameter Λ is always underestimated, leading to systematic errors in the evaluation of important parameters of the plasma such as the collision and fluctuation induced thermalization time. We stress that this does not lessen the important role of PIC algorithms for deepening our understanding of plasma physics. In particular they also have their virtues, for instance the consideration of certain correlations and of direct particle encounters (with the restrictions discussed in Sect. 5). They provide an accurate description of collisionless kinetic processes such as instabilities, and of the induced turbulence and eventual associated thermalization relevant to collisionless environments.
The Vlasov-Maxwell equations perfectly describe a plasma free of collisions and fluctuations. However, their discretization will again introduce different plasma characteristics. A thorough discussion of these effects is still missing. On the other hand, a collisionless description of astrophysical plasmas is not always correct. On larger spatial and temporal scales, the description of flows and the propagation of non-thermal particles must include collisions to a certain degree. In this regime other models, and in particular Fokker-Planck models, have been shown to give a good description of the plasma and have provided significant results. However, Fokker-Planck models have their own drawbacks, notably that they are local and use dragging and diffusion coefficients not self-consistently derived.
These discrepancies between real, PIC, and Vlasov-Maxwell plasmas are complex, and it needs to be discussed in further detail under what circumstances which model and which numerical realization comes closest to a real plasma. In the long term, it may be justified to use models including correlations in a more systematic way, for example the Landau or the Lenard-Balescu equation on the theoretical side, and P3M algorithms on the numerical side (that include short-range particle-particle interactions Hockney & Eastwood 1988). Both approaches should then be faced with results from well-controlled collisionless plasma experiments, which are presently in their infancy (see, e.g., Grosskopf et al. 2013).
We note that after the submission of our article, Swisdak (2013) published a similar method.
The relativistic Vlasov-Maxwell system is usually derived by using the Klimontovich formalism, not the Liouville formalism (see, e.g., Nicholson 1983; Klimontovich 1982).
Acknowledgments
We would like to thank Jérôme Pétri for information and discussions about linear growth rates. We also thank the anonymous referee for comments that allowed to significantly improve the manuscript. We acknowledge support from the French Stellar Astrophysics Program PNPS. Some of the simulations have been performed at pôle scientifique de modélisation numérique, PSMN, at ENS-Lyon, whose staff we thank for their steady technical support. Larger simulations were performed using HPC ressources from GENCI (Grand Équipement National de Calcul Intensif) at CINES and CCRT, under the allocation x2012046960.
References
- Baumann, G., & Nordlund, Å. 2012, ApJ, 759, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Benedetti, C., Sgattoni, A., Turchetti, G., & Londrillo, P. 2008, IEEE Trans. Plasma Sci., 36, 1790 [NASA ADS] [CrossRef] [Google Scholar]
- Birdsall, C. K. 1967, NASA Special Publ., 153, 375 [NASA ADS] [Google Scholar]
- Birdsall, C. K. 1999, in Dynamical Systems, Plasmas and Gravitation, eds. P. G. L. Leach, S. E. Bouquet, J.-L. Rouet, & E. Fijalkow, Lect. Notes Phys. (Berlin: Springer Verlag), 518, 383 [Google Scholar]
- Birsdall, C., & Langdon, A. 1985, Plasma Physics via Computer Simulation (New-York: McGraw-Hill) [Google Scholar]
- Bret, A., Gremillet, L., & Dieckmann, M. E. 2010, Phys. Plasmas, 17, 120501 [NASA ADS] [CrossRef] [Google Scholar]
- Bret, A., Stockem, A., Fiuza, F., et al. 2013, Phys. Plasmas, 20, 042102 [NASA ADS] [CrossRef] [Google Scholar]
- Buneman, O. 1959, Phys. Rev., 115, 503 [Google Scholar]
- Buneman, O. 1976, Comp. Phys. Comm., 12, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Burger, P. 1965, J. Appl. Phys., 36, 1938 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., & Treumann, R. A. 2011, A&ARv, 19, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Callen, J. 2006, Fundamentals of Plasma Physics (Madison: University of Wisconsin) [Google Scholar]
- Cerutti, B., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2012, ApJ, 754, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Cerutti, B., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2013, ApJ, 770, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Chacón-Acosta, G., Dagdug, L., & Morales-Técotl, H. A. 2010, Phys. Rev. E, 81, 021126 [NASA ADS] [CrossRef] [Google Scholar]
- Childs, H., Brugger, E., Whitlock, B., et al. 2012, in High Performance Visualization-Enabling Extreme-Scale Scientific Insight, 357 [Google Scholar]
- Cottrill, L. A., Langdon, A. B., Lasinski, B. F., et al. 2008, Phys. Plasmas, 15, 082108 [NASA ADS] [CrossRef] [Google Scholar]
- Cubero, D., Casado-Pascual, J., Dunkel, J., Talkner, P., & Hänggi, P. 2007, Phys. Rev. Lett., 99, 170601 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Daughton, W. 2002, Phys. Plasmas, 9, 3668 [NASA ADS] [CrossRef] [Google Scholar]
- Daughton, W., Scudder, J., & Karimabadi, H. 2006, Phys. Plasmas, 13, 072101 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, J. 1962, Phys. Fluids, 5, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Dieckmann, M. E. 2009, Plasma Phys. Control. Fusion, 51, 124042 [NASA ADS] [CrossRef] [Google Scholar]
- Dieckmann, M. E., Ynnerman, A., Chapman, S. C., Rowlands, G., & Andersson, N. 2004, Phys. Scr., 69, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Dieckmann, M. E., Frederiksen, J. T., Bret, A., & Shukla, P. K. 2006, Phys. Plasmas, 13, 112110 [NASA ADS] [CrossRef] [Google Scholar]
- DLMF 2013, NIST Digital Library of Mathematical Functions, http://dlmf.nist.gov/, Release 1.0.6 of 2013-05-06 [Google Scholar]
- Drake, J. F., Swisdak, M., Che, H., & Shay, M. A. 2006, Nature, 443, 553 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dunkel, J., & Hänggi, P. 2009, Phys. Rep., 471, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eldridge, O. C., & Feix, M. 1962, Phys. Fluids, 5, 1076 [Google Scholar]
- Esirkepov, T. Z. 2001, Comput. Phys. Comm., 135, 144 [Google Scholar]
- Fitzpatrick, R. 2011, The Phys. Plasmas [Google Scholar]
- Fonseca, R. A., Silva, L. O., Tsung, F. S., et al. 2002, Lect. Notes Comput. Sci., 2331, 342 [CrossRef] [Google Scholar]
- Fonseca, R. A., Martins, S. F., Silva, L. O., et al. 2008, Plasma Phys. Control. Fusion, 50, 124034 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, K., & Machida, S. 2006, J. Comput. Phys., 214, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, A. D., Cartwright, K. L., Luginsland, J. W., & Baca, E. A. 2004, provided by the SAO/NASA Astrophysics Data System, J. Comput. Phys., 201, 665, [NASA ADS] [CrossRef] [Google Scholar]
- Grosskopf, M., Drake, R., Kuranz, C., et al. 2013, High Energy Density Physics, 9, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Grote, D. P., Friedman, A., Vay, J.-L., & Haber, I. 2005, in Electron Cyclotron Resonance Ion Sources, ed. M. Leitner, Am. Ins. Phys. Conf. Ser., 749, 55 [Google Scholar]
- Hartree, D. R. 1950, Appl. Sci. Res., 1, 379 [CrossRef] [Google Scholar]
- Haugboelle, T., Fredriksen, J. T., & Nordlund, A. 2013, Phys. Plasmas, 20, 062904-062904-24 [NASA ADS] [CrossRef] [Google Scholar]
- Hededal, C. 2005, Ph.D. Thesis, Niels Bohr Institute [Google Scholar]
- Hesse, M., Kuznetsova, M., & Birn, J. 2001, J. Geophys. Res., 106, 29831 [NASA ADS] [CrossRef] [Google Scholar]
- Hockney, R. W. 1966, Phys. Fluids, 9, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Hockney, R. W. 1971, J. Comput. Phys., 8, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hockney, R. W., & Eastwood, J. W. 1988, Computer simulation using particles (Institute of Physics Publishing) [Google Scholar]
- Hoh, F. C. 1966, Phys. Fluids, 9, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J., & Ma, Z.-W. 2008, Chin. Phys. Lett., 25, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Jaroschek, C. H., & Hoshino, M. 2009, Phys. Rev. Lett., 103, 075002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jaroschek, C. H., Lesch, H., & Treumann, R. A. 2005, ApJ, 618, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Jüttner, F. 1911, Ann. Phys., 339, 856 [Google Scholar]
- Kirk, J. G., & Skjæraasen, O. 2003, ApJ, 591, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Klimas, A., Hesse, M., & Zenitani, S. 2008, Phys. Plasmas, 15, 082102 [NASA ADS] [CrossRef] [Google Scholar]
- Klimontovich, I. L. 1982, Oxford Pergamon Press International Series on Natural Philosophy, 105 [Google Scholar]
- Langdon, A. B. 1970, J. Comput. Phys., 6, 247 [Google Scholar]
- Markidis, S., Lapenta, G., & Rizwan-uddin 2010, Math. Comput. Simul., 80, 1509 [CrossRef] [Google Scholar]
- Markidis, S., Henri, P., Lapenta, G., et al. 2012, Nonlinear Processes in Geophysics, 19, 145 [Google Scholar]
- Matsumoto, H., & Omura, Y. 1993, Computer Space Plasma Physics: Simulation Techniques and Software [Google Scholar]
- Medvedev, M. V., Fiore, M., Fonseca, R. A., Silva, L. O., & Mori, W. B. 2005, ApJ, 618, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Messmer, P. 2001, Ph.D. Thesis, Institute of Astronomy, ETH Zürich, Switzerland, No. 14412 [Google Scholar]
- Messmer, P. 2002, A&A, 382, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michno, M. J., & Schlickeiser, R. 2010, ApJ, 714, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Nicholson, D. R. 1983, Introduction to Plasma Theory, eds. John Wiley & Sons [Google Scholar]
- Nieter, C., & Cary, J. R. 2004, J. Comput. Phys., 196, 448 [Google Scholar]
- Nishikawa, K.-I., Mizuno, Y., Fishman, G. J., & Hardee, P. 2008, Int. J. Mod. Phys. D, 17, 1761 [Google Scholar]
- Nishikawa, K.-I., Niemiec, J., Medvedev, M., et al. 2011, in AIP Conf. Ser. 1366, eds. V. Florinski, J. Heerikhuisen, G. P. Zank, & D. L. Gallagher, 163 [Google Scholar]
- Paesold, G., Blackman, E. G., & Messmer, P. 2005, Plasma Phys. Control. Fusion, 47, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J., & Kirk, J. G. 2007, Plasma Phys. Control. Fusion, 49, 1885 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J., & Lyubarsky, Y. 2007, A&A, 473, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pomraning, G. C. 1973, The equations of radiation hydrodynamics (Pergamon Press) [Google Scholar]
- Silva, L. O., Fonseca, R. A., Tonge, J. W., et al. 2003, ApJ, 596, L121 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2011, ApJ, 726, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Spitkovsky, A. 2005, in Astrophysical Sources of High Energy Particles and Radiation, eds. T. Bulik, B. Rudak, & G. Madejski, Am. Inst. Phys. Conf. Ser., 801, 345 [Google Scholar]
- Spitzer, L. 1965, Physics of fully ionized gases (New York: Interscience Publication) [Google Scholar]
- Swisdak, M. 2013, Phys. Plasmas, 20, 062110-062110-4 [NASA ADS] [CrossRef] [Google Scholar]
- Tien, P. K., & Moshman, J. 1956, J. Appl. Phys., 27, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Treumann, R. A., Nakamura, R., & Baumjohann, W. 2011, Ann. Geophys., 29, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Trier Frederiksen, J., Haugbølle, T., Medvedev, M. V., & Nordlund, Å. 2010, ApJ, 722, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Vay, J.-L. 2008, Phys. Plasmas, 15, 056701 [NASA ADS] [CrossRef] [Google Scholar]
- Whitlock, B., Favre, J. M., & Meredith, J. 2011, In Proc. of the 11th Eurographics Symposium on Parallel Graphics and Visualization (EGPGV’11), 101 [Google Scholar]
- Yu, S. P., Kooyers, G. P., & Buneman, O. 1965, J. Appl. Phys., 36, 2550 [NASA ADS] [CrossRef] [Google Scholar]
- Zenitani, S., & Hoshino, M. 2008, ApJ, 677, 530 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Numerical implementation
This Appendix is the direct continuation of Sect. 2.
A.1. Computation of the current
Before going through the normalization of Eqs. (2a) − (2e), we have to understand how the current is computed. As said in Sect. 2.2.2, interpolation of particle quantities to grid nodes is done by attributing to the superparticles a finite volume 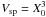 . We consider a superparticle, and the cell that contains its center. At time t, the superparticle occupies a volume Vt of the cell. The charge in the cell is given by Qcell(t) = qsp × (Vt/Vsp). The charge continuity equation then gives
. We consider a superparticle, and the cell that contains its center. At time t, the superparticle occupies a volume Vt of the cell. The charge in the cell is given by Qcell(t) = qsp × (Vt/Vsp). The charge continuity equation then gives 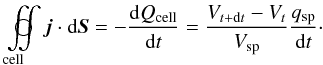 (A.1)The superparticle volume necessarily intersects three faces of the cell that contains its center: one of perpendicular along x, one along y, and one along z. Consequently, the motion of this superparticle will create a current through these three faces, and we can write
(A.1)The superparticle volume necessarily intersects three faces of the cell that contains its center: one of perpendicular along x, one along y, and one along z. Consequently, the motion of this superparticle will create a current through these three faces, and we can write 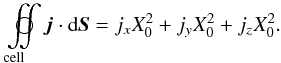 (A.2)We have to know which part of the volume variation Vt + dt − Vt is attributed to each part of the current. The displacement of the superparticle between t and t + dt is denoted (Δx,Δy,Δz). The volume variation depends on this displacement, and the part of it proportional to Δx is attributed to jx, and similarly for the y and z components. More specifically, we can write Vt + dt − Vt = AxΔx + AyΔy + AzΔz. The areas Ai can be evaluated with some geometry (see Sect. A.3.4). Then (and similarly for y and z):
(A.2)We have to know which part of the volume variation Vt + dt − Vt is attributed to each part of the current. The displacement of the superparticle between t and t + dt is denoted (Δx,Δy,Δz). The volume variation depends on this displacement, and the part of it proportional to Δx is attributed to jx, and similarly for the y and z components. More specifically, we can write Vt + dt − Vt = AxΔx + AyΔy + AzΔz. The areas Ai can be evaluated with some geometry (see Sect. A.3.4). Then (and similarly for y and z): 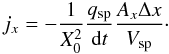 (A.3)This way of computing the current ensures that the discrete charge conservation equation is fulfilled, and justifies the advection of the divergence of the fields.
(A.3)This way of computing the current ensures that the discrete charge conservation equation is fulfilled, and justifies the advection of the divergence of the fields.
A.2. Normalization
The problem is formulated with as many equations as variables (Eqs. (2a) − (2e), variables e, b, j, xsp, and vsp for each superparticle), and it is possible to normalize the equations in a way independent of any physical quantity. We denote normalized quantities with a tilde.
We choose to normalize lengths by X0. Consequently, the normalized step-size is unity. Times are normalized by T0 = X0/c, and velocities are then naturally normalized to X0/T0 = c. For the fields E and B, we use e = E and b = cB. These last two quantities are normalized by e0 = b0 = mec2/(eX0). With this, Eqs. (2a), (2b), and (2c) transform into ![\appendix \setcounter{section}{1} % subequation 7931 0 \begin{eqnarray} &&\dfrac{\dif\tilde{\vec{x}}}{\dif\tilde{t}} = \tilde{\vec{v}}, \label{equ:dyn1norm}\\ &&\dfrac{\dif\gamma \tilde{\vec{v}}}{\dif\tilde{t}} = \left[\dfrac{m_\lec}{m_s} \dfrac{q_s}{e}\right] (\tilde{\vec{e}} + \tilde{\vec{v}}\wedge \tilde{\vec{b}}), \label{equ:dyn2norm}\\ &&\dfrac{\partial\tilde{\vec{b}}}{\partial\tilde{t}} = -\tilde{\nabla}\wedge\tilde{\vec{e}}, \end{eqnarray}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq575.png) \arraycolsep1.75ptwith ms = me or mi and qs = −e or e (e is positive).
\arraycolsep1.75ptwith ms = me or mi and qs = −e or e (e is positive).
For the current j, the algorithm computes the quantity AxΔx/Vsp. Writing for example the x component of Eq. (2d) gives ![\appendix \setcounter{section}{1} \begin{equation} \label{equ:max2bis} \dfrac{\partial\tilde{e_x}}{\partial \tilde{t}} = (\tilde{\nabla}\wedge\tilde{\vec{b}})_x + \underbrace{\left[\dfrac{1}{\epsilon_0} \dfrac{e^2}{m_\lec c^2X_0}p \dfrac{q_s}{e}\right]}_{\alpha}\,\left[\dfrac{\tilde{A}_x\Delta \tilde{x}}{\tilde{V}_{\rm sp}} \right]\dfrac{1}{\widetilde{{\rm d}t}}. \end{equation}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq580.png) (A.5)Using Eq. (1), we can write
(A.5)Using Eq. (1), we can write 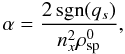 (A.6)where sgn is the sign of the charge.
(A.6)where sgn is the sign of the charge.
With this, all the equations are completely independent of any physical quantity related to the simulated problem, and depend only on space discretization (nx) and particle coarse-graining ( ). Time discretization (nt) will play a role in time integration.
). Time discretization (nt) will play a role in time integration.
As a final comment, we note that 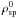 is a priori unrelated to the actual number of superparticles per cell during the simulation. One should, however, make these two values not too far apart, because the size and timesteps are a fraction nx and nt of the skin depth and plasma period of a
is a priori unrelated to the actual number of superparticles per cell during the simulation. One should, however, make these two values not too far apart, because the size and timesteps are a fraction nx and nt of the skin depth and plasma period of a 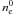 -density plasma. If, for example, the superparticle density in the simulation is twice
-density plasma. If, for example, the superparticle density in the simulation is twice 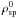 , then nx cells will now represent two skin depths of the
, then nx cells will now represent two skin depths of the 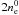 -density plasma, and the resolution will decrease. This must be kept in mind in simulations where high density contrasts appear.
-density plasma, and the resolution will decrease. This must be kept in mind in simulations where high density contrasts appear.
A.3. Discrete version of the equations
In this section we drop the tilde over normalized quantities. We denote the time at which they are considered by a superscript and their spatial location on the grid by a subscript.
A.3.1. The main loop
The strategy is to use a leap-frog scheme. It has the advantages of being time centered and reversible, and second order in time and space.
Before the loop, b and v are known at time t − dt/2, and e and x are known at time t. This should also be true for the initial conditions, so that initially we integrate backward the velocities and the b-field by − dt/2. Injected particles (if any) should also be correctly staggered.
The structure of the main loop is the following:
-
1.
Half advance ofbt − dt/2 with ∇ ∧ et; b is now at time t.
-
2.
Update of vt − dt/2 with bt and et; v is now at time t + dt/2.
-
3.
Update of xt with vt + dt/2; x is now at time t + dt.
-
4.
Half advance of bt with ∇ ∧ et; b is now at time t + dt/2.
-
5.
Boundary for b.
-
6.
Full advance of et with ∇ ∧ bt + dt/2; e is now at time t + dt.
-
7.
Boundary for e.
-
8.
Boundary for particles.
-
9.
Computation of the currents from vt + dt and xt + dt/2.
-
10.
Filtering of the currents.
-
11.
Boundary for the currents.
-
12.
Add currents to et + dt.
A.3.2. Integration of the fields
The fields are stored on the grid in a staggered way, with e at the center of the grid edges and b at the center of the grid faces (Fig. A.1). This is the so-called Yee lattice. It allows an easy integration of the fields, and is second-order accurate in time and space (Birsdall & Langdon 1985, Sect. 15), 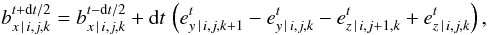 (A.7)and similarly for the other components of b and for e.
(A.7)and similarly for the other components of b and for e.
To reduce the effects of Čerenkov emission (see Appendix B.1), we have also implemented a fourth order solver (Greenwood et al. 2004).
 |
Fig. A.1 Grid and fields locations. |
A.3.3. Moving the particles
Integration of the equation of motion for the superparticles is done with the algorithm described by Birsdall & Langdon (1985, Sect. 15.4). It is a relativistic generalization of the leap-frog scheme, time centered, time reversible, and second order accurate. We note however that, as pointed out by Vay (2008), it can have shortcomings for ultrarelativistic particles. In short, Eqs. (A.4a) and (A.4b) are discretized as 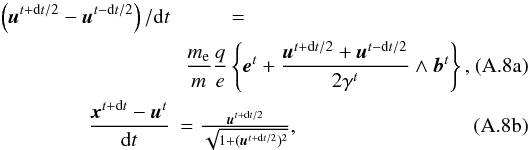 with u = γv and γ the Lorentz factor. Defining u − = ut − dt/2 + qme/(em)etdt/2 and u + = ut + dt/2 − qme/(em)etdt/2 and substituting into (A.8a) leads to
with u = γv and γ the Lorentz factor. Defining u − = ut − dt/2 + qme/(em)etdt/2 and u + = ut + dt/2 − qme/(em)etdt/2 and substituting into (A.8a) leads to 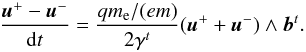 (A.9)This equation is the classical rotation around a b field (Birsdall & Langdon 1985, Sect. 4.4; Hockney & Eastwood 1988, Sect. 4.7.1), and is solved via
(A.9)This equation is the classical rotation around a b field (Birsdall & Langdon 1985, Sect. 4.4; Hockney & Eastwood 1988, Sect. 4.7.1), and is solved via 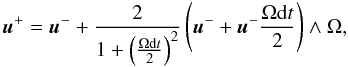 (A.10)with the rotation vector Ω = qme/(2emγt)bt. Finally, we use
(A.10)with the rotation vector Ω = qme/(2emγt)bt. Finally, we use 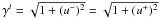 . In Eq. (A.8a), the fields have to be known at time t. It explains the need for the half advances of b in the general scheme.
. In Eq. (A.8a), the fields have to be known at time t. It explains the need for the half advances of b in the general scheme.
The interpolation of the fields at particle positions is done via a trilinear interpolation. We denote by (i,j,k) the nodes of the main grid A (Fig. A.1), and we introduce a second grid B whose cell centers are on (i,j,k). Consider a superparticle at position x = i + δx, y = j + δy, z = k + δz. The superparticle is actually a charge cloud of volume equal to a cell, and this volume intersects the cell of the second grid with center (i,j,k) in a volume Vi,j,k = (1 − δx)(1 − δy)(1 − δz), the cell of the second grid with center (i + 1,j,k) in a volume Vi + 1,j,k = δx(1 − δy)(1 − δz), and so on. For a quantity f defined at grid points (i,j,k), the weight associated to fi,j,k is Vi,j,k, the one associated to fi + 1,j,k is Vi + 1,j,k, and so on for a total of 8 points.
However, neither e nor b are defined at grid points (i,j,k) (Fig. A.1), and they must be first interpolated at grid points before applying the above procedure. This is done for example with fi,j,k = 0.5(ex,i − 1,j,k + ex,i,j,k) or fi,j,k = 0.25(bz,i,j,k + bz,i − 1,j,k + bz,i − 1,j − 1,k + bz,i,j − 1,k). Details can be found in Matsumoto & Omura (1993); Messmer (2001).
We note that the superparticle shape used for interpolation of fields to particle position and for interpolation of the current to grid nodes is the same. This is required to avoid the existence of a self-force on the superparticles and to conserve the total momentum (Birsdall & Langdon 1985, Sect. 8.6).
A.3.4. Computation of the current
The current ji,j,k is defined at the same locations as ei,j,k. For current deposition, we again consider the volumes occupied by the superparticle in the grid B cells. As the superparticle moves, these volumes vary. We denote by (i + δx,j + δy,k + δz) the position of the superparticle at t − dt, and we assume that it moves from (Δx,Δy,Δz) between t − dt and t.
Consider, for example, the volume of the superparticle in the cell of center (i,j,k). Its variation is given by dV = (1 − δx − Δx)(1 − δy − Δy)(1 − δz − Δz) − (1 − δx)(1 − δy)(1 − δz). Defining dx = δx + Δx/2, cx = 1 − dx, and similarly for y and z, one finds ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{equ:current_dep} dV &=& ~\Delta x \left[ -c_yc_z - \Delta y \Delta z /12 \right] ~~~\rightarrow j_{x|i,j,k}\nonumber \\ &&+ \Delta y \left[ -c_zc_x - \Delta z \Delta x /12 \right] ~~~\rightarrow j_{y|i,j,k}\nonumber \\ &&+ \Delta z \left[ -c_xc_y - \Delta x \Delta y /12 \right] ~~~\rightarrow j_{z|i,j,k}. \end{eqnarray}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq631.png) (A.11)As explained in Appendix A.1, the part of (A.11) proportional to the displacement along x is attributed to jx | i,j,k, and so on.
(A.11)As explained in Appendix A.1, the part of (A.11) proportional to the displacement along x is attributed to jx | i,j,k, and so on.
A similar treatment is done with the cells that intersect the superparticle volume. These are cells centered in (i + ϵ,j + η,k + ξ), with ϵ, η and ξ equal either to 0 or 1 (8 cells). For each of these cells, only the faces intersecting the superparticle volume are concerned, so that in total there are only 12 currents to update.
Currents can be smoothed before being added to e. This has the effect of reducing electromagnetic noise (see Appendix B.2). This is done in the following way for the current of cell (i,j,k): attribute a weight of 1 to cell (i,j,k); of 0.5 to cells (i ± 1,j,k), (i,j ± 1,k), and (i,j,k ± 1); of 0.25 to cells (i ± 1,j ± 1,k), (i ± 1,j,k ± 1), and (i,j ± 1,k ± 1); of 0.125 to cells (i ± 1,j ± 1,k ± 1); and normalize the sum of the weights to 1.
 |
Fig. A.2 Simulation time duration versus number of cores, the spatial domain extending in proportion to the number of cores. The standard deviation corresponds to 4% of the mean value. |
A.4. Boundaries
Periodic and reflective boundaries are available. The latter simulate a perfect conductor at the domain boundary by imposing the correct values for the electric and magnetic fields (b = e = 0 inside the conductor, bnormal = etangential = 0 at the conductor surface), and by reflecting the particles.
A.5. Parallel efficiency
The code parallelization was performed and tested by Messmer (2001, Chap. 4). It uses Fortran 90 and MPI. The simulation domain is decomposed in sub-domains of equal length along the z direction, and all the cells and particles of each sub-domain are assigned to a processor. To minimize communications between processors, ghost cells for the fields are added to each sub-domain. Communication between neighboring processors occurs at each step involving the boundaries: for particles leaving or entering the domain, for the fields, and for the currents.
The domain is currently decomposed along one direction only. This is relevant for simulations of collisionless shocks where the domain is elongated along the flow direction, or for 2D magnetic reconnection simulations where the presence of the over-dense current sheet at the domain center would lead to load balancing issues if a 2D domain decomposition were used.
We have tested the efficiency of this implementation with simulations using 16 superparticles per cell and a domain size of 60 × 60 × (16nproc), where the number of cores varied from nproc = 16 to 256. The corresponding (weak) scaling results, shown in Fig. A.2, are satisfactory. Simulation times scatter with a standard deviation of 4% around a constant value. The scatter is probably due to the uncontrolled node geometry.
Appendix B: Numerical effects
We have said in Sect. 5 that passing from a real plasma to a PIC model implies a discretization of the equations. This step comes with numerical issues that have been largely studied by Birsdall & Langdon (1985) and Hockney & Eastwood (1988). We highlight part of their work here.
B.1. Local numerical effects
-
Stability of the electric part of the superparti-cle motion integrator used here requires thatΩΔt < 2, with Ω the pulsation of oscillation of the superparticles (usually the plasma pulsation). The magnetic part is unconditionally stable.
-
Courant condition for the stability of the field integrator in vacuum is
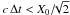 .
. -
The dispersion relation of electromagnetic waves in vacuum is modified by the grid. This modification depends on the angle of propagation with respect to the grid, and waves can have a phase velocity smaller than c (Greenwood et al. 2004). If superparticles with velocity close to c are present, they can overtake light waves and emit Čerenkov radiation. This results in the production of non-physical fields. The situation can be improved with a higher order interpolation scheme for the fields.
B.2. Global numerical effects
By considering the algorithm as a whole, Birsdall and Langdon were able to identify numerical effects not predicted by the consideration of subparts alone.
For example, the discrete space representation of the continuous quantities introduces a periodicity in Fourier space of period k0 = 2π/X0 (with X0 the grid spacing). A physical mode of wavenumber k = 2π/λ will then have, in the numerical plasma, aliases of wavenumbers k + nk0, and − k + nk0, with n an integer. Instabilities can arise if the physical mode couples resonantly with one of the aliases. This coupling cannot occur if k < − k + k0, i.e., if λ > 2X0 (we note that it is Nyquist-Shannon criterion to avoid spectral aliasing). Just as in signal processing, the strength of the aliases can be reduced by low-pass filtering the time-series, and this is what is done by attributing a cloud shape to the superparticles. Aliases are even more reduced when the superparticle shapes have a fast decaying Fourier transform, that is, when they are smoother.
We mention in particular the following effects due to grid aliasing:
-
A cold beam of velocity vbeam becomes unstable if the Doppler shifted frequency of Langmuir oscillations is near the grid-crossing frequency kgrid vbeam. The beam is then heated. It is not the case if λD/X0 > 0.046.
-
λD/X0 > 1/π is needed to avoid an artificial numerical heating of a Maxwellian plasma. Otherwise, the plasma is heated up to the point where λD reaches X0/π.
-
The rate of passage of the superparticles through the cell faces produces a high-frequency noise; the rougher the superparticle shapes, the more important is the noise.
Similarly to grid effects, a finite timestep implies that harmonics differing from a multiple of 2π/Δt are not differentiated by the algorithm, and there are time aliases as well.
-
This implies no other instabilities in the case of a non-magnetizedMaxwellian plasma.
-
In a magnetized plasma, artificial coupling of cyclotron harmonics can lead to instabilities.
A last point is that the effects of the grid, as well as other errors, act as a random force F(t) on the superparticles. Consequently, the velocity of a superparticle undergoes a random walk, dv/dt ∝ F(t), and the kinetic energy ⟨ v2 ⟩ increases linearly with time. Hockney & Eastwood (1988, Sect. 9.2) shows that this is indeed the cause of plasma self-heating in superparticle simulations. This is also what we find in our thermal simulations (see Sect. 3.1.3).
B.3. Qualitative constraints on timestep and sizestep
-
The step-size X0 of the grid (which is also roughly the superparticle size), and the time-step Δt, must be smaller than the scales of the phenomena studied. This scale can be an instability wavelength or growth rate, the cyclotron radius or pulsation, gradient scales, etc.
-
The same is true for the mean distance between superparticles:
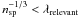 . This is equivalent to having a high enough number of superparticles per volume
. This is equivalent to having a high enough number of superparticles per volume 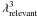 . The case λrelevant = λD applies to the description of plasma behavior.
. The case λrelevant = λD applies to the description of plasma behavior. -
If thermal effects are important, then one should insure that the distribution function g(p) is well represented on scales where these effects are important. It requires a high enough number of superparticles per relevant volume. Birsdall & Langdon (1985, Sect. 15.19) mention that it is sufficient to have a good representation of the relevant projections of g.
-
The plasma should remain collisionless: the collision time should be greater than relevant timescales (instability growth rates, etc.).
B.4. Limitations for the computation of photon spectra
-
The highest frequency represented is2πc/X0 = 2πnxωpe, so that high energy radiation is absent from the code and must be computed separately to extract photon spectra. This is done for example by Hededal (2005), Trier Frederiksen et al. (2010), Nishikawa et al. (2011), and Cerutti et al. (2012) from superparticle motions, with the inclusion of radiative energy losses. However, even in these cases, effects such as plasma frequency cutoff, Raizin effect, or transition radiation are not described because they are due to the back-reaction of the plasma particles on the electromagnetic waves, waves that are absent from the PIC code and are only computed afterward.
Appendix C: Relativistic Harris current sheet
Harris configuration is one of the rare fully consistent solutions of the Vlasov-Maxwell system in a non-homogeneous case. Its generalization to the relativistic case is not difficult, and was partly done by Hoh (1966) for a Maxwell-Jüttner distribution and non-relativistic current speeds. The fully relativistic case appeared later for pair plasmas with the same temperature for both species, for example in Kirk & Skjæraasen (2003) or Pétri & Kirk (2007). Here, we propose a formulation for the relativistic case with an arbitrary temperature and mass ratio for ions (singly ionized) and electrons.
We define a frame ℛ0, where the magnetic field is assumed to have the dependence given by Eq. (5), and the particles sustaining this field are assumed to have a Maxwell-Jüttner distribution function given in ℛ0 by 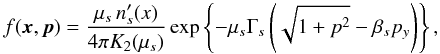 (C.1)with s = i for ions or e for electrons, μs = 1/Θs = msc2/Ts, p = γv/c, and K2 the modified Bessel function of the second kind; Us is the bulk velocity of species s, and Γs the associated Lorentz factor. We note that fs is normalized with respect to p to
(C.1)with s = i for ions or e for electrons, μs = 1/Θs = msc2/Ts, p = γv/c, and K2 the modified Bessel function of the second kind; Us is the bulk velocity of species s, and Γs the associated Lorentz factor. We note that fs is normalized with respect to p to 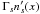 , so that
, so that 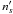 is the density of species s in its comobile frame (noted with a prime), and
is the density of species s in its comobile frame (noted with a prime), and 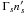 its density in ℛ0.
its density in ℛ0.
Inserting Eq. (C.1) into the Vlasov equation expressed in ℛ0, 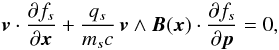 (C.2)leads to the relation for the comobile number density
(C.2)leads to the relation for the comobile number density 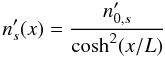 (C.3)with
(C.3)with 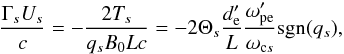 (C.4)with sgn(qs) the sign of the charge, ωcs = | qs | B0/ms,
(C.4)with sgn(qs) the sign of the charge, ωcs = | qs | B0/ms, 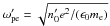 , and
, and 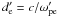 .
.
We note that the absence of electric field in Eq. (C.2) implicitly assumes that the plasma is quasi neutral in ℛ0, which is true only if the overall charge density in this frame vanishes: 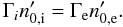 (C.5)We now use the Maxwell-Ampère equation in ℛ0:
(C.5)We now use the Maxwell-Ampère equation in ℛ0: ![\hbox{$\nabla\wedge\vec{B} = \mu_0 e [\Gamma_\ionperso n'_\ionperso(x) U_\ionperso - \Gamma_\lec n'_\lec(x) U_\lec]$}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq692.png) . Insertion of n′(x) and B(x) leads, not surprisingly, to a pressure balance between the unmagnetized center of the sheet and the magnetically dominated outer domain:
. Insertion of n′(x) and B(x) leads, not surprisingly, to a pressure balance between the unmagnetized center of the sheet and the magnetically dominated outer domain: 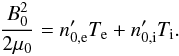 (C.6)Manipulating Eq. (C.6) and defining χ = (1 + Ti/Te)/2 we obtain
(C.6)Manipulating Eq. (C.6) and defining χ = (1 + Ti/Te)/2 we obtain 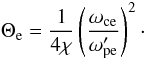 (C.7)Given a temperature ratio χ, the four variables
(C.7)Given a temperature ratio χ, the four variables 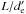 , Θe,
, Θe, 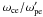 and ΓeUe/c are constrained by the two Eqs. (C.4) (for s = e) and (C.7). Consequently, one needs to specify two of them. Then, the ion velocity and temperature are easily deduced with Eq. (C.4) for s = i and with χ; L and ωce expressed in units of de and ωpe, that are useful for a setup in a simulation, are then deduced with Γe. A special case is when the temperatures are equal: then ΓiUi = −ΓeUe,
and ΓeUe/c are constrained by the two Eqs. (C.4) (for s = e) and (C.7). Consequently, one needs to specify two of them. Then, the ion velocity and temperature are easily deduced with Eq. (C.4) for s = i and with χ; L and ωce expressed in units of de and ωpe, that are useful for a setup in a simulation, are then deduced with Γe. A special case is when the temperatures are equal: then ΓiUi = −ΓeUe, 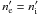 , and
, and 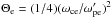 .
.
Appendix D: A method for loading a drifting Maxwell-Jüttner distribution
This Appendix directly follows the notations of Sect. 4, and presents a concrete way to load a drifting Maxwell-Jüttner distribution in a PIC code.
Starting from the distribution in Eq. (13), we make a first change of variables (px,py,pz) → (x,y,z) = (px/γy,py,pz/γy), where 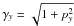 , and we then change to cylindrical coordinates (r,θ,y) with the axis along y. We integrate along θ. Finally, a last change of variables
, and we then change to cylindrical coordinates (r,θ,y) with the axis along y. We integrate along θ. Finally, a last change of variables 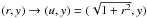 leads to the distribution for the random variables (U,Y) ∈ [1, + ∞ [ × ]−∞, + ∞ [ :
leads to the distribution for the random variables (U,Y) ∈ [1, + ∞ [ × ]−∞, + ∞ [ : 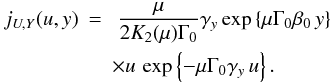 (D.1)It is then easy to obtain the marginal distribution for Y:
(D.1)It is then easy to obtain the marginal distribution for Y: 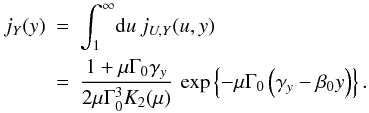 (D.2)From this, we deduce the conditional probability distribution of U given the value y of Y:
(D.2)From this, we deduce the conditional probability distribution of U given the value y of Y: 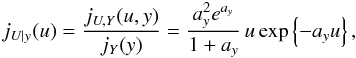 (D.3)with
(D.3)with 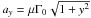 .
.
Then, for each particle, one has to generate y = py according to distribution D.2, compute ay, and generate u according to distribution D.3.
For the first step, we use the method of the inversion of the cumulative distribution. This method is based on the fact that if W is a uniform random variable on [0,1] , if 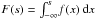 is the cumulative distribution of the distribution f and F-1 its inverse, then F-1(W) follows the distribution f. In practice, one has to choose random numbers wi in [0,1] , and the yi = F-1(wi) will be distributed according to f.
is the cumulative distribution of the distribution f and F-1 its inverse, then F-1(W) follows the distribution f. In practice, one has to choose random numbers wi in [0,1] , and the yi = F-1(wi) will be distributed according to f.
There is, however, no analytic expression for the cumulative distribution 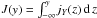 . We compute numerically J-1(t) on a grid of points ti = i/N, i = 1...(N − 1). For each index i, we want to find yi such that
. We compute numerically J-1(t) on a grid of points ti = i/N, i = 1...(N − 1). For each index i, we want to find yi such that 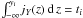 . We thus compute numerically the integral
. We thus compute numerically the integral 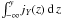 up to the point where it reaches ti, and then attribute the value of y to yi. We use the following algorithm:
up to the point where it reaches ti, and then attribute the value of y to yi. We use the following algorithm:
-
1.
Choose a maximal integration step δymax, and set δy = δymax. Choose a tolerance tol.
-
2.
Start from a low enough value y0 such that jY(y0) ≪ 1, and set y = y0. Also set i = 1.
-
3.
Set J = 0, or if possible
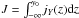 .
. -
4.
Compute J = J + δy jY(y).
-
J is now an estimation of
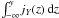 . If | J − ti | < tol, then the desired yi = J-1(ti) is y. Set i = i + 1, and go back to step 4. If J < ti, set y = y + δy, and go back to step 4. If J > ti, set δy = δy/2 and go back to step 4.
. If | J − ti | < tol, then the desired yi = J-1(ti) is y. Set i = i + 1, and go back to step 4. If J < ti, set y = y + δy, and go back to step 4. If J > ti, set δy = δy/2 and go back to step 4.
We run this algorithm once for the needed μ and Γ0β0 and store the yi in a file. Then, during the particle initialization, we choose random integers i between 1 and N − 1 and set py = yi.
Once y is known, we have to pick a u according to Eq. (D.3). Since ay can be anything between μΓ0 and + ∞, we cannot generate a file before the program run, and we have to invert F on the flight. It turns out that we can integrate jU | y. After some basic manipulations, we arrive at 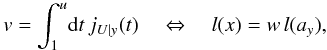 (D.4)where x = ayu, l(x) = (1 + x)exp( − x), and v and w are two random numbers between 0 and 1. Inversion of the right side of Eq. (D.4) is easily done with a Newton method because of the smoothness of the function l. Starting from x = ay is a good idea, and one must enforce a minimum number of iterations.
(D.4)where x = ayu, l(x) = (1 + x)exp( − x), and v and w are two random numbers between 0 and 1. Inversion of the right side of Eq. (D.4) is easily done with a Newton method because of the smoothness of the function l. Starting from x = ay is a good idea, and one must enforce a minimum number of iterations.
In Fig. 9, we show that the method is accurate.
Appendix E: Analytical expressions for quantities averaged over a Maxwell-Jüttner distribution
This Appendix details a method used to obtain the analytical expressions of Table 5 for the averaged quantities weighted by a Maxwell-Jüttner distribution. The notations are those in Sect. 4.
E.1. In the comoving frame
We start with averages over the distribution with zero drift velocity (i.e., the distribution in the frame comoving with the plasma). The calculations are easier when the distribution function is expressed in terms of Lorentz factors γ0: 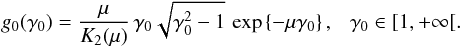 (E.1)We introduce two relations6:
(E.1)We introduce two relations6:
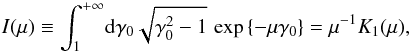 (E.3)and (DLMF 2013, Eq. (10.29.4))
(E.3)and (DLMF 2013, Eq. (10.29.4)) ![\appendix \setcounter{section}{5} \begin{equation} \label{equ:calc_of_der_of_Kmu} \frac{\dif}{\dif \mu}\left[\mu^{-\nu}K_\nu(\mu)\right] = -\mu^{-\nu}K_{\nu+1}(\mu). \end{equation}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq775.png) (E.4)The method is then to derive Eq. (E.3) as many times as needed with respect to μ, with the help of Eq. (E.4). For example the integral of g0 is easily deduced from dI/dμ.
(E.4)The method is then to derive Eq. (E.3) as many times as needed with respect to μ, with the help of Eq. (E.4). For example the integral of g0 is easily deduced from dI/dμ.
E.2. Drifting distribution
We now consider the distribution with a drift velocity 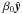 . We assume that we want the average of a quantity M,
. We assume that we want the average of a quantity M, 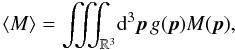 (E.5)with g given by Eq. (13). We use the change of variables p0,x = px,
(E.5)with g given by Eq. (13). We use the change of variables p0,x = px, 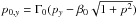 , p0,z = pz, which amounts to passing back into the comoving frame. Using d3p/γ = d3p0/γ0, we arrive at
, p0,z = pz, which amounts to passing back into the comoving frame. Using d3p/γ = d3p0/γ0, we arrive at 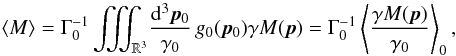 (E.6)where ⟨ · ⟩ 0 means that the average is taken with g0, and where γ and p are to be expressed with comoving quantities (subscript 0). With this last formula, one is left with averages in the comoving frame and can use the previous method.
(E.6)where ⟨ · ⟩ 0 means that the average is taken with g0, and where γ and p are to be expressed with comoving quantities (subscript 0). With this last formula, one is left with averages in the comoving frame and can use the previous method.
All Tables
Energy conservation for simulations of a thermal plasma with no background magnetic field.
All Figures
 |
Fig. 1 Power spectra of the total momentum of the electrons | Fa | 2 (Eq. (3)) with a = x, y, or z in the unmagnetized case. The inset is a zoom around the peak. Here nx = 25, nt = 500, ρsp = 16, vth,e = 0.04c, Ti = Te, box size of 25 × 25 × 25 cells, duration of 100 Tpe. |
| In the text | |
 |
Fig. 2 Power spectra of the total momentum of the electrons | Fa | 2 (Eq. (3)) with a = x, y, or z in the magnetized case. Parameters are given in Table 1 (case labeled Fig. 2). The purple lines are the pulsations |
| In the text | |
 |
Fig. 3 Wavenumber dependance of the growth rate τtheory(k ⊥ ), represented here as the deviation |
| In the text | |
 |
Fig. 4 Top: energy curves for the filamentation instability (case labeled Fig. 4 in Table 3). They are normalized by the total initial energy |
| In the text | |
 |
Fig. 5 Top: growth of individual Fourier modes for bx (for the run labeled Fig. 4 in Table 3). The modes shown are those for i = 0,1,2, and j = 0,1,...,25, and one mode every 100 modes for the remaining. We note that the graphic has been cut and that the weak modes actually fill a continuum down to an energy of 10-7. The sum of all 320 × 90 modes is shown in orange. We recall that mode (i,j) corresponds to (kzde,kxde) = 2π × 20(i/640,j/180). Bottom: growth map of the Fourier modes, in units of Tpe. |
| In the text | |
 |
Fig. 6 Difference between the growth rate measured on the total energy curve |
| In the text | |
 |
Fig. 7 Three snapshots of the filamentation instability, at times 2.5, 4, and 5.5Tpe (from left to right) for the simulation of Fig. 4. Colors represent the current magnitude per cell (units are number of superparticles per cell times their mean velocity), while arrows are the magnetic field. Lengths are in cell number. |
| In the text | |
 |
Fig. 8 Energy curves for the tearing instability (labeled Fig. 8 in Table 4). Shown are the energy curves, for example ∫dVBx(t)2/(2μ0). They are normalized by the total initial energy |
| In the text | |
 |
Fig. 9 Maxwell-Jüttner distribution for T = mc2 and |
| In the text | |
 |
Fig. 10 Top: electron temperatures for the hot (2) and cold (1) plasmas, from four simulations with different ρsp. The curves for ion temperatures are similar, except for an overall time dilatation by a factor ~ (mi/me)1/2 = 5. In this figure we use T∞(t) = (T1(t) + T2(t))/2. Except for ρsp = 4 where there is significant numerical heating, T∞(t) is constant in time. Bottom: half-thermalization time for ions and electrons, versus number of superparticles per cell. For ions, we have plotted tth/(mi/me)1/2. The times reported are measured as the initial slope of the temperature curves in a log-lin plot, and thus correspond to tth/2. We see the scaling tth ∝ ρsp. |
| In the text | |
 |
Fig. 11 Top: field energy levels as a function of |
| In the text | |
 |
Fig. 12 Different plasma models. Dashed arrows are transitions showing non-trivial effects. Coarse-graining and discretization are discussed in Sects. 5.1 to 5.3. |
| In the text | |
 |
Fig. A.1 Grid and fields locations. |
| In the text | |
 |
Fig. A.2 Simulation time duration versus number of cores, the spatial domain extending in proportion to the number of cores. The standard deviation corresponds to 4% of the mean value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



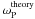
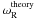
![\hbox{$[\tau^\mathrm{theory}(k_\perp)-\tau^\mathrm{theory}_{\rm max}]/\tau^\mathrm{theory}_{\rm max}$}](/articles/aa/full_html/2013/10/aa21557-13/aa21557-13-eq168.png)