Table 5
Useful averages for the Maxwell-Jüttner distribution f(x,p) = ng(p) (Eq. (13)) of temperature Θ = 1/μ = T/(mc2).
| Without drift velocity: U0 = 0 | |||
| Parameter | Value | NR | UR |
|
|
|||
| ⟨ γ ⟩ | κ32(μ) − μ-1 | 1 + 3Θ/2 | 3Θ |
| ⟨ (γβ)2 ⟩ | 3Θκ32(μ) | 3Θ | 12Θ2 |
| ⟨ β2 ⟩ | 3Θκ12(μ) | 3Θ | 3/2 |
| ⟨ γβ2 ⟩ | 3Θ | ||
| Larmor radius |
|
||
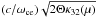
| Pressure P | nT | ||
| Enthalpy h | κ32(μ) | 1 + 5Θ/2 | 4Θ |
| Adiabatic | |||
exponent  |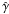
1 + (μκ32(μ) − μ − 1)-1 | 5/3 | 4/3 |
With a drift velocity  |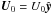
|||
| Parameter | Value | NR | UR |
|
|
|||
| ⟨ v ⟩ | U 0 | ||
| ⟨ γv ⟩ | κ32(μ)Γ0U0 | Γ0U0 | 4ΘΓ0U0 |
| ⟨ γ ⟩ |
|
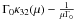
Γ0 |
|
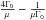
| ⟨ pxvx ⟩ = ⟨ pzvz ⟩ | Θ/Γ0 | ||
| ⟨ pyvy ⟩ |
|
||
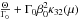
| ⟨(pi − ⟨ pi ⟩ )(vj − ⟨ vj ⟩ )⟩ | δij Θ/Γ0 | ||
Notes. We define κij(μ) = Ki(μ)/Kj(μ), with Kn the modified Bessel function of the nth kind. The Larmor radius is defined by ⟨ rce ⟩ = ⟨ (γv ⊥ )2 ⟩ 1/2/ωce, the pressure by P = (1/3)n ⟨ v·(γmv) ⟩ , the enthalpy by h = (n ⟨ γmc2 ⟩ + P)/(nmc2), and the adiabatic exponent by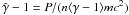 
. NR means non-relativistic limit (Θ → 0, κ32(μ) ~ 1 + 5Θ/2), and UR ultra-relativistic limit (Θ → + ∞, κ32(μ) ~ 4Θ), with in both cases no constraints on Γ0.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.