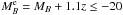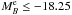| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321411 | |
| Published online | 21 October 2013 | |
The VIMOS VLT Deep Survey⋆
The different assembly history of passive and star-forming LB ≳ LBB galaxies in the group environment at z < 1
1 Aix Marseille Université, CNRS, LAM
(Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
e-mail: clsj@cefca.es
2 Centro de Estudios de Física del
Cosmos de Aragón, Plaza San Juan 1, planta 2, 44001
Teruel,
Spain
3 INAF-Osservatorio Astronomico di
Bologna, via Ranzani 1, 40127
Bologna,
Italy
4 Institut de Recherche en
Astrophysique et Planétologie (IRAP), CNRS, 14 avenue Édouard Belin, 31400
Toulouse,
France
5 IRAP, Université de Toulouse,
UPS-OMP,
31400
Toulouse,
France
Received:
5
March
2013
Accepted:
15
August
2013
Aims. Understanding the role of environment in galaxy evolution is an important but still open issue. In the present work we study the close environment of red and blue LB ≳ LB* galaxies hosted by VVDS-Deep groups.
Methods. We use the VIMOS VLT Deep Survey to study the close environment of galaxies in groups at 0.2 ≤ z < 0.95. Close neighbours of LB ≳ LB* galaxies (MBe = MB + 1.1z ≤ -20) are identified with MBe ≤ −18.25 and within a relative distance 5 h-1 kpc ≤ rp ≤ 100 h-1 kpc and relative velocity Δv ≤ 500 km s-1. The richness 𝒩 of a group is defined as the number of MBe ≤ −18.25 galaxies belonging to that group. We split our principal sample into red, passive galaxies with NUV − r ≥ 4.25 and blue, star-forming galaxies with NUV − r < 4.25. We study how the number of close neighbours per LB ≳ LB* galaxy depends on 𝒩, colour, and redshift.
Results. Blue galaxies with a close neighbour are primarily located in poor groups, while the red ones are in rich groups. The number of close neighbours per red galaxy increases with 𝒩, ‾nred ∝ 0.11𝒩, while that of blue galaxies does not depend on 𝒩 and is roughly constant. In addition, these trends are found to be independent of redshift, and only the average ‾nblue evolves, decreasing with cosmic time.
Conclusions. Our results support the following assembly history of LB ≳ LB* galaxies in the group environment: red, massive (M⋆ ~ 1010.8 M⊙) galaxies were formed in/accreted by the dark matter halo of the group at early times (z ≳ 1), therefore their number of neighbours provides a fossil record of the stellar mass assembly of groups, traced by their richness 𝒩. On the other hand, blue, less massive (M⋆ ~ 1010.2 M⊙) galaxies have recently been accreted by the group potential and are still in their parent dark matter halo, having the same number of neighbours irrespective of 𝒩. As time goes by, these blue galaxies settle in the group potential and turn red and/or fainter, thus becoming satellite galaxies in the group. With a toy quenching model, we estimate an infall rate of field galaxies into the group environment of ℜinfall = 0.9−1.5 × 10-4 Mpc-3 Gyr-1 at z ~ 0.7.
Key words: galaxies: groups: general / galaxies: evolution
Based on data obtained with the European Southern Observatory Very Large Telescope, Paranal, Chile, under Large Programmes 070.A-9007 and 177.A-0837. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
© ESO, 2013
1. Introduction
Since the discovery of the morphology – density relation by Dressler (1980), a number of investigations have aimed at a better understanding of the role of environment in the evolution of galaxies. Several works at 0.2 < z < 1.0 studied how different galaxy properties depend on density and redshift. Some of these properties are the red, passive, and early-type fraction (e.g., Cucciati et al. 2006; Gerke et al. 2007; Cooper et al. 2007; Cucciati et al. 2010a; Tasca et al. 2009; Iovino et al. 2010; Vulcani et al. 2011; Grützbauch et al. 2011), the luminosity and mass function (e.g., Ilbert et al. 2005; Bolzonella et al. 2010; Pozzetti et al. 2010), or the merger fraction (Lin et al. 2010; de Ravel et al. 2009, 2011; Kampczyk et al. 2013). One of the most important results is that stellar mass seems to be driving most of the observed properties, most notably the higher fraction of red and early-type galaxies as mass increases. It is equally evident that environment is playing a significant role, particularly in participating in the transformation of blue galaxies with M⋆ ≲ 1010.7 M⊙ into red ones (Cucciati et al. 2010a; Peng et al. 2010).
The density contrast, which is defined as the ratio of the local density excess around a galaxy with respect to the cosmological mean density at its redshift, is a continuous density tracer of the local environment from voids to the highest density peaks, which allows studying the dependence of galaxy properties on environment. However, the scale length on which environment affects galaxy properties the most is still a matter of debate. Previous works have suggested that the observed effects of large-scale environment on galaxy properties are the mirror of the trends observed on much smaller scales (e.g., Kauffmann et al. 2004; Blanton et al. 2006; Cucciati et al. 2010a; and see also Wilman et al. 2010). Nevertheless, it has not yet been verified that the large-scale environment does not play any role in shaping galaxy properties, and many times the explored small scales are not as small as desired, but simply the smallest allowed by the survey characteristics. Finding the scale on which environment affects the most galaxy properties would help, for instance, in disentangling the role of the different physical processes taking places on different scale lengths.
Another way to trace the effect of environment is to study the properties of galaxies residing in groups and clusters. Galaxy populations can be studied as a function of the distance from the group and cluster centre or of the group and cluster richness or mass, or can be compared with field galaxies. The advantage of this analysis is that groups and clusters can be directly related to the underlying dark matter (DM) structures, placing the analysis in a broader context.
In the present paper we use close neighbours to provide an indication of the density field on small scales (less than 0.1 h-1 Mpc) of those galaxies hosted by groups of richness  . This novel approach is physically motivated, since both close neighbours and richness are related to the underlying DM distribution. On the one hand, the number of close neighbours with a projected separation
. This novel approach is physically motivated, since both close neighbours and richness are related to the underlying DM distribution. On the one hand, the number of close neighbours with a projected separation 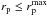 in the sky plane, noted
in the sky plane, noted 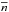 , is a proxy for the integral of the correlation function up to
, is a proxy for the integral of the correlation function up to 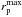 (Bell et al. 2006; Lin et al. 2008; de Ravel et al. 2009; Robaina et al. 2010). The correlation function is a powerful tool for understanding the relation between galaxies and their host DM haloes. In this framework, halo occupation models have provided this connection in a phenomenological way (e.g., Cooray & Sheth 2002; Zheng et al. 2005; Abbas et al. 2010; Coupon et al. 2012). In these models, the so-called one-halo component governs the behaviour of the galaxy correlation function on scales smaller than ≲2 h-1 Mpc, while at larger separations galaxy correlations are dominated by the gravitational clustering of virialised DM haloes (the two-halo component). As a result, the number of close neighbours encodes information about the mass of the DM halo in which galaxies reside (e.g., More et al. 2011). On the other hand, group richness
(Bell et al. 2006; Lin et al. 2008; de Ravel et al. 2009; Robaina et al. 2010). The correlation function is a powerful tool for understanding the relation between galaxies and their host DM haloes. In this framework, halo occupation models have provided this connection in a phenomenological way (e.g., Cooray & Sheth 2002; Zheng et al. 2005; Abbas et al. 2010; Coupon et al. 2012). In these models, the so-called one-halo component governs the behaviour of the galaxy correlation function on scales smaller than ≲2 h-1 Mpc, while at larger separations galaxy correlations are dominated by the gravitational clustering of virialised DM haloes (the two-halo component). As a result, the number of close neighbours encodes information about the mass of the DM halo in which galaxies reside (e.g., More et al. 2011). On the other hand, group richness  is tightly correlated with the DM halo mass of the groups (dispersion of the relation σ ~ 0.2−0.3 dex, Rozo et al. 2009a,b; Andreon & Hurn 2010). A positive correlation between
is tightly correlated with the DM halo mass of the groups (dispersion of the relation σ ~ 0.2−0.3 dex, Rozo et al. 2009a,b; Andreon & Hurn 2010). A positive correlation between 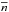 and
and  for a given population therefore implies that this population is located in the DM halo of the group, while a lack of correlation suggests that the population is hosted by sub-haloes inside the more massive halo of the group. In the present paper we study the
for a given population therefore implies that this population is located in the DM halo of the group, while a lack of correlation suggests that the population is hosted by sub-haloes inside the more massive halo of the group. In the present paper we study the 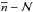 relation for red and blue
relation for red and blue 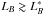 galaxies at 0.2 ≤ z < 0.95 by using the close neighbour candidates from López-Sanjuan et al. (2011) and the group catalogue from Cucciati et al. (2010b), both obtained in the deep part of the VIMOS-VLT Deep Survey1 (VVDS, Le Fèvre et al. 2005, 2013).
galaxies at 0.2 ≤ z < 0.95 by using the close neighbour candidates from López-Sanjuan et al. (2011) and the group catalogue from Cucciati et al. (2010b), both obtained in the deep part of the VIMOS-VLT Deep Survey1 (VVDS, Le Fèvre et al. 2005, 2013).
This paper is organised as follows. In Sect. 2 we summarise the VVDS-Deep data set, and in Sect. 3 we describe the methodology for obtaining the richness of groups and the list of group members. In Sect. 4 we estimate the number of close neighbours as a function of group richness, galaxy colour, and redshift, and we discuss the implications of our results in Sect. 5. Finally, we present our conclusions in Sect. 6. We use H0 = 100 h km s-1 Mpc-1, h = 0.7, Ωm = 0.3, and ΩΛ = 0.7 throughout. All magnitudes refer to the AB photometric system (Oke & Gunn 1983). We assumed a Chabrier (2003) initial mass function (IMF).
2. The VVDS-Deep data set
The VVDS-Deep sample (Le Fèvre et al. 2005, 2013) is magnitude-selected with 17.5 ≤ IAB ≤ 24. This spectroscopic survey has been conducted on the 0224-04 field with the VIMOS multi-slit spectrograph on the VLT (Le Fèvre et al. 2003), with 4.5 h integration using the LRRED grism at a spectral resolution R ~ 230. The multi-slit data processing has been performed using the VIPGI package (Scodeggio et al. 2005). Redshift measurement has followed a strict approach, with initial guesses based on cross-correlation with reference templates at the same redshift, followed by careful, independent eye-checking by two team members before comparing their results. The final redshifts and quality flags follow a statistically well-defined behaviour, leading to a survey for which at least 80% of the sample has a secure spectroscopic redshift (zspec). This comprises sources with quality flag = 4 (100% secure), 3 (98% secure), 2 (84% secure), and 9 (those with only a single secure spectral feature in emission in their spectrum, 72% secure). The accuracy in the redshift measurement is 202 km s-1 (Le Fèvre et al. 2013).
Deep photometry is available in this field from a first campaign with the CFH12K camera in BVRI (Le Fèvre et al. 2004; and McCracken et al. 2003), followed by very deep observations with the CFHTLS survey in the u∗g′r′i′z′ bands (Goranova et al. 2009) and with the WIRDS survey in JHKs bands (Bielby et al. 2012). Using photometric redshifts, computed as in Ilbert et al. (2006), we show that for the galaxies making up the 20% incompleteness, about half have a tentative (quality flag = 1) spectroscopic redshift that is 48% secure, and the other half have unknown spectroscopic redshifts (quality flag = 0), but we use photometric redshift estimates to fully understand the survey completeness as a function of magnitude and redshift.
Several first-epoch VVDS-Deep galaxies with flag = 1 and 2 have been re-observed in the VVDS-Ultradeep (IAB ≤ 24.75, Le Fèvre et al. 2013), providing a robust measurement of their redshift. This offers the opportunity to correct the redshift distribution of VVDS-Deep flag = 1 and 2 sources, bringing the final VVDS-Deep data set to the equivalent of 96% completeness.
A total of 6445 galaxies with 0.2 ≤ zspec < 0.95 and 17.5 ≤ IAB ≤ 24 (primary objects with flags = 1, 2, 3, 4, 9; and secondary objects, those that lie by chance in the slits, with flags = 21, 22, 23, 24, 29) from first- and second-epoch VVDS-Deep data (Le Fèvre et al. 2013) have been used in this paper (Fig. 1). We used flag = 1 sources, which are 48% secure, when we search for kinematical close neighbours (Sect. 2.1), thanks to the improved weighting scheme in VVDS-Deep (see Sect. 2.3, and also Cucciati et al. 2012; and Le Fèvre et al. 2013, for more details). On the other hand, we used flag ≥ 2 sources to identify galaxy groups (Sect. 2.2).
We derived the intrinsic luminosities and star formation rates (SFR) as fully described in Cucciati et al. (2012). In summary, we used the full photometric information that is available to perform a fit of the spectral energy distribution (SED) with an updated version of the code Le Phare2. The adopted method minimises the dependency on the template chosen for the SED fitting. The template library is from Bruzual & Charlot (2003). Dust extinction was applied to the templates using the Calzetti et al. (2000) law. We derived stellar masses from the same SED fitting: the best fit template is normalised at one solar mass, and the stellar mass is the factor needed to rescale the template to the intrinsic luminosities.
 |
Fig. 1 Rest-frame B-band absolute magnitude as a function of zspec (dots) in the VVDS-Deep. Solid and dashed lines mark the principal ( |
2.1. Kinematical close neighbours in the VVDS-Deep
The distance between two sources can be measured as a function of their projected separation in the sky plane, rp, and of their rest-frame relative velocity along the line of sight, Δv = c | zj − zi | /(1 + zi), where zi and zj are the redshift of the principal galaxy (the brightest galaxy in the pair) and of the companion galaxy, respectively. Two galaxies are defined as a close pair if 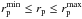 and Δv ≤ Δvmax. In our case we use
and Δv ≤ Δvmax. In our case we use 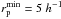 kpc,
kpc, 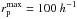 kpc, and Δvmax = 500 km s-1. The lower limit in rp is imposed to avoid spatial resolution limitations due to the size of the observed point spread function. The previous definition of “close pair” is widely used in merger fraction studies (e.g., Patton et al. 2002; Lin et al. 2004, 2008; De Propris et al. 2007; de Ravel et al. 2009, 2011; López-Sanjuan et al. 2010) since 50% to 70% of the selected close pairs will finally merge (Patton et al. 2000; Patton & Atfield 2008; Bell et al. 2006). The close pair condition above selects close bound systems even when they are located in dense environments, such as the groups in the present work, but in these environments the probability of finding unbound close pairs increases (e.g., Lin et al. 2010; Jian et al. 2012; Kampczyk et al. 2013), providing information about the DM halo of the groups. Thus, in the present work we are interested in neither the merger fraction nor the merger rate, but instead in the total number of close neighbours around bright galaxies even if they will not merge with their principal galaxy. To avoid any confusion with merger studies, in the following we speak about close neighbours instead of close pairs.
kpc, and Δvmax = 500 km s-1. The lower limit in rp is imposed to avoid spatial resolution limitations due to the size of the observed point spread function. The previous definition of “close pair” is widely used in merger fraction studies (e.g., Patton et al. 2002; Lin et al. 2004, 2008; De Propris et al. 2007; de Ravel et al. 2009, 2011; López-Sanjuan et al. 2010) since 50% to 70% of the selected close pairs will finally merge (Patton et al. 2000; Patton & Atfield 2008; Bell et al. 2006). The close pair condition above selects close bound systems even when they are located in dense environments, such as the groups in the present work, but in these environments the probability of finding unbound close pairs increases (e.g., Lin et al. 2010; Jian et al. 2012; Kampczyk et al. 2013), providing information about the DM halo of the groups. Thus, in the present work we are interested in neither the merger fraction nor the merger rate, but instead in the total number of close neighbours around bright galaxies even if they will not merge with their principal galaxy. To avoid any confusion with merger studies, in the following we speak about close neighbours instead of close pairs.
We select principal galaxies as those with an evolving rest-frame B-band absolute magnitude 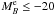 , where
, where 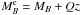 and the constant Q = 1.1 takes the evolution of the luminosity function in the VVDS-Deep into account (Ilbert et al. 2005). These principal galaxies are more luminous than
and the constant Q = 1.1 takes the evolution of the luminosity function in the VVDS-Deep into account (Ilbert et al. 2005). These principal galaxies are more luminous than 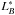 at each redshift, since
at each redshift, since 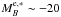 (Ilbert et al. 2005). To define close neighbours, we looked for those galaxies in the named companion sample that fulfils the close neighbour criterion for each galaxy of the principal sample. If one principal galaxy has more than one close neighbour, we took each possible pair separately (i.e., if the companion galaxies B and C are close to the principal galaxy A, we study the pairs A-B and A-C as independent). We also imposed a difference in the rest-frame B-band luminosity between the pair members of LB,2/LB,1 ≥ 1/5, which is an absolute B-band difference of MB,2 − MB,1 ≤ 1.75. The companion sample therefore comprises galaxies with
(Ilbert et al. 2005). To define close neighbours, we looked for those galaxies in the named companion sample that fulfils the close neighbour criterion for each galaxy of the principal sample. If one principal galaxy has more than one close neighbour, we took each possible pair separately (i.e., if the companion galaxies B and C are close to the principal galaxy A, we study the pairs A-B and A-C as independent). We also imposed a difference in the rest-frame B-band luminosity between the pair members of LB,2/LB,1 ≥ 1/5, which is an absolute B-band difference of MB,2 − MB,1 ≤ 1.75. The companion sample therefore comprises galaxies with 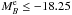 . This ensures that our samples are complete in the redshift range under study, 0.2 ≤ z < 0.95 (Fig. 1). There are 895 galaxies in the principal sample satisfying the
. This ensures that our samples are complete in the redshift range under study, 0.2 ≤ z < 0.95 (Fig. 1). There are 895 galaxies in the principal sample satisfying the 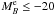 selection, and 4156 galaxies with
selection, and 4156 galaxies with 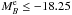 in which the neighbours of the principal galaxies have been searched for. In addition, in the following we refer to blue and red galaxies as those with rest-frame colour NUV − r < 4.25 and NUV − r ≥ 4.25, respectively (see Arnouts et al. 2007; and López-Sanjuan et al. 2011, for details about this selection). This colour is an excellent indicator of the present over past star formation activity. In Fig. 2 we show the cumulative histogram of both red and blue principal galaxies as a function of their SFR. On the one hand, 95% of the red principals have SFR ≤ 1 M⊙ yr-1 and 92% have a specific star formation rate sSFR = SFR/M⋆ ≤ 10-11 yr-1. On the other hand, 16% of the blue principals have SFR ≤ 1 M⊙ yr-1 and 6% have sSFR ≤ 10-11 yr-1. With this sSFR limit, we can assume that red galaxies are passive and blue galaxies are star-forming (Schiminovich et al. 2007).
in which the neighbours of the principal galaxies have been searched for. In addition, in the following we refer to blue and red galaxies as those with rest-frame colour NUV − r < 4.25 and NUV − r ≥ 4.25, respectively (see Arnouts et al. 2007; and López-Sanjuan et al. 2011, for details about this selection). This colour is an excellent indicator of the present over past star formation activity. In Fig. 2 we show the cumulative histogram of both red and blue principal galaxies as a function of their SFR. On the one hand, 95% of the red principals have SFR ≤ 1 M⊙ yr-1 and 92% have a specific star formation rate sSFR = SFR/M⋆ ≤ 10-11 yr-1. On the other hand, 16% of the blue principals have SFR ≤ 1 M⊙ yr-1 and 6% have sSFR ≤ 10-11 yr-1. With this sSFR limit, we can assume that red galaxies are passive and blue galaxies are star-forming (Schiminovich et al. 2007).
Following the previous definitions, we find 64 close neighbours in the ~0.5 deg2 VVDS-Deep area3, of which 24 have a red principal galaxy and 40 have a blue principal galaxy. We did not impose any colour selection to the neighbours.
 |
Fig. 2 Cumulative histogram of red (thick line) and blue (thin line) principal galaxies as a function of their star formation rate. The definition of red and blue galaxy is labelled in the figure. The vertical dashed line marks SFR = 1 M⊙ yr-1. |
2.2. The VVDS-Deep group catalogue
All the details about the methodology used to define reliable groups from spectroscopic surveys are in Cucciati et al. (2010b), so we only recall the main steps here.
The adopted group-finding algorithm is based on the Voronoi-Delaunay method (Marinoni et al. 2002). In brief, a polyhedron is assigned to each galaxy, with a volume inversely proportional to the 3D density of galaxies in that given region (the higher the density, the smaller the polyhedron volume). Then, a three-phase group detection begins. In Phase I, group seeds are detected, when we searching for galaxies in a cylindrical window centred on the galaxies with the smallest Voronoi volumes. During Phase II, a larger cylindrical window is used to add members to the seeds, with the aim of recovering the central richness of the groups. Finally, Phase III consists in assigning the total number of members to the groups, when searching for galaxies residing in a cylindrical window with dimensions that scale with the central richness found in Phase II.
The algorithm has been fine-tuned using simulated mock galaxy catalogues taken from the MILLENNIUM Simulation (Springel et al. 2005), where the semi-analytical prescription of De Lucia & Blaizot (2007) were applied. These mock catalogues were prepared to reproduce the same VVDS observational strategy (flux limits, sampling rate, field geometry, etc.). The fine-tuning had the aim of maximising the completeness and the purity of the resulting group catalogue, and to minimise possible selection effects. In particular, the number density distribution as a function of both redshift, n(z), and velocity dispersion, n(σ), of the VVDS groups are in qualitative agreement with the corresponding n(z) and n(σ) recovered from the mock catalogues. The final VVDS group catalogue is characterised by an overall completeness of ~60% and a purity (fraction of detected groups that actually are a bound structure) of ~50%.
The group catalogue has been produced using the most secure redshifts (flag = 2, 3, 4, and 9 for primary galaxies, and flag = 22, 23, 24, and 29 for secondary galaxies) without any luminosity or mass selection. In this case we used neither flag = 1 nor 21 galaxies. Although the VVDS selection function described in the next section is well suited to recovering the total number of galaxies in the sample, we used the most accurate redshifts to obtain a reliable group catalogue.
2.3. Weighting scheme in the VVDS-Deep
The final VVDS selection function is fully detailed in Le Fèvre et al. (2013), and described in Cucciati et al. (2012). Here we only make a short summary.
Since ~25% of the total number of potential targets in the VVDS-Deep field have been spectroscopically observed and since the redshifts are not measured with 100% accuracy, we have to correct the number of galaxies in the VVDS-Deep sample using the target sampling rate (TSR) and the spectroscopic success rate (SSR). They have been computed as a function of redshift, source magnitude, and source size (x). The SSR is independent of the galaxy type, as demonstrated up to z ~ 1 in Zucca et al. (2006). Because several first-epoch VVDS-Deep galaxies with flag = 1 and 2 have been observed again in the VVDS-Ultradeep survey (IAB ≤ 24.75), providing a robust measurement of their redshift, this offers the opportunity to estimate the correct n(z) of VVDS-Deep flag = 1 and 2 sources, and we defined a weight w129 to take this into account. We also defined the weight w129 for flag = 9 sources by comparison with the latest photometric redshifts in the VVDS-Deep field (see Cucciati et al. 2012, for details about the latest photometric data set in this field). By definition, w129 = 1 for flag = 3 and 4 sources. We derived the spectroscopic completeness weight for each galaxy i in the catalogue as 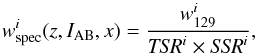 (1)and also defined a weight
(1)and also defined a weight 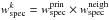 for each close neighbour, where
for each close neighbour, where 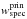 and
and 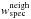 are the spectroscopic completeness weights of the principal and the neighbouring galaxy, respectively.
are the spectroscopic completeness weights of the principal and the neighbouring galaxy, respectively.
Since the observations were performed under a typical ground-based seeing of 1′′, we need to correct for the increasing incompleteness in targeting both components of close pairs because the separation between them is getting smaller. Assuming a clustered distribution of galaxies, the number of galaxy pairs should be a monotonically decreasing function of the pair separation (e.g., Bell et al. 2006; Lin et al. 2008; de Ravel et al. 2009). However, pairs start to be under-counted for separations θ ≤ 2′′ because of seeing effects. We apply a weight 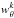 on each close neighbour using the ratio
on each close neighbour using the ratio 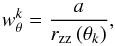 (2)where a is the probability of randomly selecting a pair, obtained at large separations, and rzz (θk) is the ratio between the observed pair count with separation θk in the spectroscopic catalogue (Nzz) over the observed pair count at the same separation in the photometric one (Npp). For large separations (θ > 50′′), rzz ~ a, but at small separations rzz < a because of the artificial decrease in pairs due to seeing effects (see de Ravel et al. 2009; López-Sanjuan et al. 2011, for further details). This weight also accounts for other geometrical biases in the survey, e.g., those related to the minimum separation between spectral slits.
(2)where a is the probability of randomly selecting a pair, obtained at large separations, and rzz (θk) is the ratio between the observed pair count with separation θk in the spectroscopic catalogue (Nzz) over the observed pair count at the same separation in the photometric one (Npp). For large separations (θ > 50′′), rzz ~ a, but at small separations rzz < a because of the artificial decrease in pairs due to seeing effects (see de Ravel et al. 2009; López-Sanjuan et al. 2011, for further details). This weight also accounts for other geometrical biases in the survey, e.g., those related to the minimum separation between spectral slits.
3. Connecting close neighbours and group environment
3.1. Measuring the group richness
In this section we describe how we estimated the richness  of the VVDS-Deep groups and the number of principal galaxies belonging to these groups. We assigned to each group those galaxies in the companion sample that lie within the group’s volume Vg, where Vg is defined as the cylinder used in the Phase III of the group finding algorithm. To obtain the total number of galaxies in the group, i.e., their richness
of the VVDS-Deep groups and the number of principal galaxies belonging to these groups. We assigned to each group those galaxies in the companion sample that lie within the group’s volume Vg, where Vg is defined as the cylinder used in the Phase III of the group finding algorithm. To obtain the total number of galaxies in the group, i.e., their richness  , we summed the weights of the group members:
, we summed the weights of the group members: 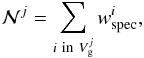 (3)where the index i spans the galaxies in the companion sample4 and the index j spans the VVDS-Deep groups. If we assigned fewer than two companion galaxies to a given group, we set
(3)where the index i spans the galaxies in the companion sample4 and the index j spans the VVDS-Deep groups. If we assigned fewer than two companion galaxies to a given group, we set 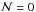 . This happened to 114 (30%) of the groups, leaving 260 groups in VVDS-Deep with
. This happened to 114 (30%) of the groups, leaving 260 groups in VVDS-Deep with 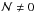 at 0.2 ≤ z < 0.95. In Fig. 3 we show the redshift distribution of those groups with
at 0.2 ≤ z < 0.95. In Fig. 3 we show the redshift distribution of those groups with 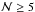 ,
, 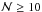 and
and 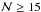 . The typical DM halo mass of our groups is Mh ~ 1013−13.5 M⊙. We estimated this DM halo mass using the relation between the richness of bright galaxies (
. The typical DM halo mass of our groups is Mh ~ 1013−13.5 M⊙. We estimated this DM halo mass using the relation between the richness of bright galaxies (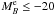 ) and Mh derived by Knobel et al. (2009) in the zCOSMOS5 (Lilly et al. 2007) survey.
) and Mh derived by Knobel et al. (2009) in the zCOSMOS5 (Lilly et al. 2007) survey.
 |
Fig. 3 Redshift distribution of the VVDS-Deep groups with richness |
 |
Fig. 4 Cumulative histogram of red (thick line) and blue (thin line) principal galaxies as a function of the richness |
 |
Fig. 5 Fraction of red, passive galaxies, fred, as a function of group richness |
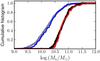 |
Fig. 6 Cumulative histogram of red and blue principal galaxies as a function of the stellar mass. The blue or red (thin) lines are for blue or red principal galaxies hosting by groups, while the grey or black (thick) lines are for red or blue principals outside groups. |
Red, passive fraction, fred, of principal and companion galaxies as a function of group richness  .
.
We followed the procedure described above to assign the 895 galaxies in the principal sample to each group, both red and blue, 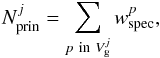 (4)where the index p spans the red or blue galaxies in the principal sample. We find 197 (22%) of the principal galaxies in groups, while 176 of those (91%) are in
(4)where the index p spans the red or blue galaxies in the principal sample. We find 197 (22%) of the principal galaxies in groups, while 176 of those (91%) are in 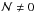 groups. In Fig. 4 we show the cumulative histogram of red (61) and blue (115) principal galaxies as a function of the group richness
groups. In Fig. 4 we show the cumulative histogram of red (61) and blue (115) principal galaxies as a function of the group richness  . The blue principals are more numerous in poor groups, while red principals are mainly in rich ones. This translates to an increase in the red, passive fraction (fred) of principal galaxies with
. The blue principals are more numerous in poor groups, while red principals are mainly in rich ones. This translates to an increase in the red, passive fraction (fred) of principal galaxies with  , see Fig. 5 and Table 1. This has already been shown by Cucciati et al. (2010b) with first-epoch VVDS-Deep data. In addition, Fig. 5 shows that the red fraction of principal galaxies outside groups is lower than in groups (e.g., Gerke et al. 2007; Balogh et al. 2009; Iovino et al. 2010; Cucciati et al. 2010b; Presotto et al. 2012). These trends are also present in the companion sample, but fred is a factor of two lower than for principal galaxies (Fig. 5). This luminosity dependence is consistent with Iovino et al. (2010) results.
, see Fig. 5 and Table 1. This has already been shown by Cucciati et al. (2010b) with first-epoch VVDS-Deep data. In addition, Fig. 5 shows that the red fraction of principal galaxies outside groups is lower than in groups (e.g., Gerke et al. 2007; Balogh et al. 2009; Iovino et al. 2010; Cucciati et al. 2010b; Presotto et al. 2012). These trends are also present in the companion sample, but fred is a factor of two lower than for principal galaxies (Fig. 5). This luminosity dependence is consistent with Iovino et al. (2010) results.
Finally, we studied the stellar mass of red and blue galaxies. The distribution of the stellar mass of both red and blue principal galaxies hosting by groups and outside groups is similar (Fig. 6). In both colour cases, the mass distribution of principals in groups is described well in logarithmic space by a Gaussian function with median μred = 10.76 and dispersion σred = 0.25 for red galaxies, and median μblue = 10.23 and dispersion σblue = 0.43 for blue galaxies.
3.2. Assigning close neighbours to groups
We counted how many neighbours of red or blue principal galaxies belong to each group j with the following equation, 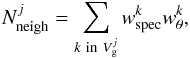 (5)where the index k spans the close neighbours of the red or blue principals. We find 20 of the 24 neighbours of red galaxies in groups with
(5)where the index k spans the close neighbours of the red or blue principals. We find 20 of the 24 neighbours of red galaxies in groups with 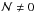 (83%), and 34 of the 40 neighbours of the blue ones (85%). However, we expected that all our close neighbours belong to groups with at least two members. We checked that in three of the ten orphan neighbours the companion galaxy has flag = 1, which were not used in group determination. The remaining seven neighbours not linked to groups are explained by the performance of the group-finding algorithm, which leads to a completeness in group detection of ~60% (see Cucciati et al. 2010b, for details). Taking this into account, the identification of ~90% of the neighbours in groups supports the reliability of the group-finding algorithm. This detection rate is similar to that in the DEEP2 spectroscopic survey (see Lin et al. 2010, for details).
(83%), and 34 of the 40 neighbours of the blue ones (85%). However, we expected that all our close neighbours belong to groups with at least two members. We checked that in three of the ten orphan neighbours the companion galaxy has flag = 1, which were not used in group determination. The remaining seven neighbours not linked to groups are explained by the performance of the group-finding algorithm, which leads to a completeness in group detection of ~60% (see Cucciati et al. 2010b, for details). Taking this into account, the identification of ~90% of the neighbours in groups supports the reliability of the group-finding algorithm. This detection rate is similar to that in the DEEP2 spectroscopic survey (see Lin et al. 2010, for details).
We find that blue principals with a close neighbour are mainly located in poor groups, while red principals with a close neighbour appear in the richer ones (Fig. 7). This has already been noted by Lin et al. (2010). In the next section we study in detail how the number of neighbours per red and blue principal galaxy depends on  .
.
 |
Fig. 7 Cumulative histogram of red (thick line) and blue (thin line) principal galaxies with a close neighbour as a function of group richness |
4. Number of neighbours per red and blue principal galaxy as a function of 
In this section we estimate the dependence of the number of neighbours on  and on the colour of the principal galaxy. We define the number of neighbours per principal galaxy in the richness range
and on the colour of the principal galaxy. We define the number of neighbours per principal galaxy in the richness range 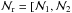 ) as
) as 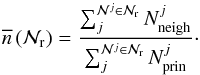 (6)Because each principal galaxy can have more than one close neighbour (see Sect. 2.1) and of the weighting scheme described in Sect. 2.3,
(6)Because each principal galaxy can have more than one close neighbour (see Sect. 2.1) and of the weighting scheme described in Sect. 2.3, 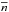 can be higher than one and should not be confused with a (close pair) merger fraction. We estimated the uncertainty in
can be higher than one and should not be confused with a (close pair) merger fraction. We estimated the uncertainty in 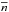 by applying the Bayesian approach described in Cameron (2011).
by applying the Bayesian approach described in Cameron (2011).
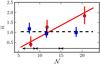 |
Fig. 8 Number of close neighbours per principal galaxy as a function of group richness |
Number of close neighbours (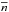 ) per red, passive and blue, star-forming principal galaxy as a function of group richness
) per red, passive and blue, star-forming principal galaxy as a function of group richness  .
.
We measured 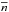 in three richness ranges,
in three richness ranges, 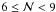 ,
, 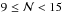 , and
, and 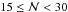 . These ranges provide a similar number of red and blue principal galaxies in each bin and ensure good statistics. Because red principal galaxies are primarily found in richer groups (Fig. 5), we estimated the average richness of the groups that host red or blue principal galaxies in the range
. These ranges provide a similar number of red and blue principal galaxies in each bin and ensure good statistics. Because red principal galaxies are primarily found in richer groups (Fig. 5), we estimated the average richness of the groups that host red or blue principal galaxies in the range 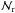 with the following equation:
with the following equation: 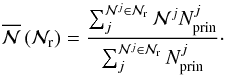 (7)We summarise our results in Table 2 and show them in Fig. 8. We find that
(7)We summarise our results in Table 2 and show them in Fig. 8. We find that
-
the number of neighbours per red, passive galaxy increases with
 . The error-weighted least-squares fit of the function
. The error-weighted least-squares fit of the function 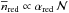 to the data yields αred = 0.11±0.04. We checked that this positive trend remains significant (~2σ) when different richness bins are used.
to the data yields αred = 0.11±0.04. We checked that this positive trend remains significant (~2σ) when different richness bins are used. -
The number of neighbours per blue, star-forming galaxy is roughly constant with
 ,
, 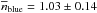 . In this case the slope from the linear fit is consistent with zero, αblue = −0.01 ± 0.03. As in the previous case, the use of different richness bins does not change this result.
. In this case the slope from the linear fit is consistent with zero, αblue = −0.01 ± 0.03. As in the previous case, the use of different richness bins does not change this result.
That the trends in the number of neighbours for red and blue galaxies are different is the main result of the present paper, and in the next sections we estimate the redshift evolution of these relations.
 |
Fig. 9 Number of neighbours per principal galaxy as a function of group richness |
4.1. The redshift evolution of 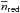 in groups
in groups
To estimate the evolution of the 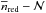 relation with redshift, we defined two redshift bins that comprise ten neighbours of red principals each, zr,1 = [ 0.2,0.65) and zr,2 = [ 0.65,0.95). We find that the slope αred is constant with redshift, with αred = 0.11±0.06 at zr,1 and αred = 0.11±0.05 at zr,2 (Table 3 and Fig. 9, top panel). In addition, the normalisation of the relation is consistent with a non-evolving value. This fact suggests that red galaxies move along the
relation with redshift, we defined two redshift bins that comprise ten neighbours of red principals each, zr,1 = [ 0.2,0.65) and zr,2 = [ 0.65,0.95). We find that the slope αred is constant with redshift, with αred = 0.11±0.06 at zr,1 and αred = 0.11±0.05 at zr,2 (Table 3 and Fig. 9, top panel). In addition, the normalisation of the relation is consistent with a non-evolving value. This fact suggests that red galaxies move along the 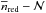 relation with cosmic time, i.e., that their number of neighbours increases with the accretion of new members by their hosting group.
relation with cosmic time, i.e., that their number of neighbours increases with the accretion of new members by their hosting group.
A non-evolving 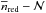 relation is expected by cosmological models. In their work, McGee et al. (2009) study the assembly history of clusters and groups in the semi-analytic model of Font et al. (2008). They find that two DM haloes with the same mass but observed at different redshifts have a similar accretion history. The only difference between these two DM haloes is the time scale of the accretion process, which is faster for high redshift clusters and groups (i.e., the available cosmic time to reach a given mass is shorter at high z). That is, the accretion histories of two groups with the same richness at different redshifts should be similar, so also a similar number of close neighbours at a given
relation is expected by cosmological models. In their work, McGee et al. (2009) study the assembly history of clusters and groups in the semi-analytic model of Font et al. (2008). They find that two DM haloes with the same mass but observed at different redshifts have a similar accretion history. The only difference between these two DM haloes is the time scale of the accretion process, which is faster for high redshift clusters and groups (i.e., the available cosmic time to reach a given mass is shorter at high z). That is, the accretion histories of two groups with the same richness at different redshifts should be similar, so also a similar number of close neighbours at a given  is expected for red galaxies irrespective of z, as we observe.
is expected for red galaxies irrespective of z, as we observe.
In summary, the observed 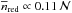 relation does not evolve with redshift, as expected from the semi-analytic model of Font et al. (2008). This suggests that red, passive galaxies move along the relation as groups and clusters grow.
relation does not evolve with redshift, as expected from the semi-analytic model of Font et al. (2008). This suggests that red, passive galaxies move along the relation as groups and clusters grow.
Number of close neighbours per red, passive principal galaxy (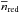 ) as a function of group richness
) as a function of group richness  and redshift.
and redshift.
Number of close neighbours per blue, star-forming principal galaxy ( ) as a function of group richness
) as a function of group richness  and redshift.
and redshift.
4.2. The redshift evolution of  in groups
in groups
We split our groups into two redshift bins, zr,3 = [ 0.2,0.81) and zr,4 = [ 0.81,0.95). We chose this binning to have a similar number of close neighbours of blue galaxies in both bins. We find that the slope of the 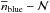 relation is consistent with zero in both redshift ranges: αblue = −0.02±0.03 at
relation is consistent with zero in both redshift ranges: αblue = −0.02±0.03 at 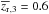 and αblue = 0.03 ± 0.06 at
and αblue = 0.03 ± 0.06 at 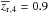 . In addition, the average number of neighbours increases with redshift from
. In addition, the average number of neighbours increases with redshift from 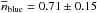 at zr,3 to
at zr,3 to 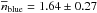 at zr,4 (Table 4 and Fig. 9, bottom panel), a factor of two difference that reflects the fast evolution in the close pair fraction of blue, star-forming galaxies (e.g., Lin et al. 2008; de Ravel et al. 2009; Chou et al. 2011; López-Sanjuan et al. 2011, 2013). We explore the possible physical explanations of the observed trends and their redshift evolution in Sect. 5.
at zr,4 (Table 4 and Fig. 9, bottom panel), a factor of two difference that reflects the fast evolution in the close pair fraction of blue, star-forming galaxies (e.g., Lin et al. 2008; de Ravel et al. 2009; Chou et al. 2011; López-Sanjuan et al. 2011, 2013). We explore the possible physical explanations of the observed trends and their redshift evolution in Sect. 5.
5. The assembly of passive and star-forming 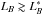 galaxies in the group environment
galaxies in the group environment
As we show in Sect. 1, a positive correlation between 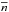 and
and  for a given population implies that this population is located in the DM halo of the group, while a lack of correlation suggests that the population is hosted by DM sub-haloes inside the more massive halo of the group. Based on this fact, our results suggest the picture below for the assembly of passive and star-forming bright galaxies in the group environment.
for a given population implies that this population is located in the DM halo of the group, while a lack of correlation suggests that the population is hosted by DM sub-haloes inside the more massive halo of the group. Based on this fact, our results suggest the picture below for the assembly of passive and star-forming bright galaxies in the group environment.
We find that the number of neighbours of the red, passive principal galaxies, which have a stellar mass 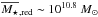 , increases with the richness of the group and that this relation is redshift independent. This seems to indicate that red galaxies “know” about the full potential of their hosting group and its assembly history (the larger the number of accreted galaxies, the richer the group and the higher the number of close neighbours of the red galaxies), suggesting that they have been residing in the main DM haloes of the groups for a long time (z ≳ 1). In their study of the group and cluster assembly in a cosmological contest, McGee et al. (2009) find that a Mh ~ 1013.6 M⊙ DM halo (groups with
, increases with the richness of the group and that this relation is redshift independent. This seems to indicate that red galaxies “know” about the full potential of their hosting group and its assembly history (the larger the number of accreted galaxies, the richer the group and the higher the number of close neighbours of the red galaxies), suggesting that they have been residing in the main DM haloes of the groups for a long time (z ≳ 1). In their study of the group and cluster assembly in a cosmological contest, McGee et al. (2009) find that a Mh ~ 1013.6 M⊙ DM halo (groups with 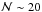 ) at z = 1 (z = 0.5) has more than 50% of its mass in Mh ≥ 1013 M⊙ DM haloes (groups with
) at z = 1 (z = 0.5) has more than 50% of its mass in Mh ≥ 1013 M⊙ DM haloes (groups with 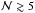 ) since z ~ 1.7 (z ~ 1.2). This is consistent with our picture and supports the idea that massive galaxies were born in or accreted by the group and cluster DM haloes at early times, with a massive red sequence starting building-up in these structures at z ~ 2 (i.e., Kodama et al. 2007; Bielby et al. 2010; Strazzullo et al. 2010; Andreon & Huertas-Company 2011; Tanaka et al. 2013). As time goes by, DM haloes hosting the groups are accreting new members from the field, increasing the richness of the groups. Because red galaxies were in place early in the potential well of the groups, their number of neighbours provides a fossil record of matter accretion in the group and leads to the observed correlation between
) since z ~ 1.7 (z ~ 1.2). This is consistent with our picture and supports the idea that massive galaxies were born in or accreted by the group and cluster DM haloes at early times, with a massive red sequence starting building-up in these structures at z ~ 2 (i.e., Kodama et al. 2007; Bielby et al. 2010; Strazzullo et al. 2010; Andreon & Huertas-Company 2011; Tanaka et al. 2013). As time goes by, DM haloes hosting the groups are accreting new members from the field, increasing the richness of the groups. Because red galaxies were in place early in the potential well of the groups, their number of neighbours provides a fossil record of matter accretion in the group and leads to the observed correlation between 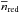 and
and  . In this picture, some of these newly accreted members are our blue, star-forming principal galaxies. These blue galaxies have the same number of neighbours irrespective of the group richness, suggesting that this is a recently infalling population from the field. This may also indicate that the parent lower-mass DM haloes in which these blue galaxies reside have become sub-haloes of the larger group structure in which they have fallen.
. In this picture, some of these newly accreted members are our blue, star-forming principal galaxies. These blue galaxies have the same number of neighbours irrespective of the group richness, suggesting that this is a recently infalling population from the field. This may also indicate that the parent lower-mass DM haloes in which these blue galaxies reside have become sub-haloes of the larger group structure in which they have fallen.
The time evolution is important in our picture. For example, some time after their infall, blue principal galaxies will finally settle in the group potential, and then might present a positive trend with  as the red galaxies do; that is, their number of neighbours would increase with the group richness. Instead, a constant number of neighbours with
as the red galaxies do; that is, their number of neighbours would increase with the group richness. Instead, a constant number of neighbours with  is observed at the redshifts we have investigated. This fact, added to the increase on the average
is observed at the redshifts we have investigated. This fact, added to the increase on the average  with z, can be explained either by (i) the population of infalling blue galaxies increases with cosmic time, statistically diluting the expected positive trend and the past higher number of companions at lower redshift; or by (ii) the high-redshift blue population disappears because galaxies become red, so only the recently infalling population is visible at low z. As the fraction of blue galaxies in groups and clusters decreases with cosmic time, the so-called Butcher-Oemler effect (Butcher & Oemler 1984; De Propris et al. 2003; Cucciati et al. 2010b; Iovino et al. 2010), the second scenario seems to be the more likely one: because of some process, the star formation in blue galaxies is quenched, and they become fainter and/or red, hence no longer observed as the brightest galaxy (our principal sample) but as a companion. In addition, 85% of our blue principals have M⋆ ≤ 1010.7 M⊙, the mass regime in which environment is expected to notably affect the properties of blue galaxies (Sect. 1). The quenching process could be harassment (the combined effect of multiple high-speed galaxy-galaxy encounters and the interaction with the potential of the group or the cluster, e.g., Moore et al. 1996, 1999), starvation (the removal of warm and hot gas from the galaxy halo, which cuts off the gas supply, e.g., Larson et al. 1980; Kawata & Mulchaey 2008), or ram pressure stripping by the intergroup medium (e.g., Rasmussen et al. 2006, 2012). We explore further this scenario in the next section.
with z, can be explained either by (i) the population of infalling blue galaxies increases with cosmic time, statistically diluting the expected positive trend and the past higher number of companions at lower redshift; or by (ii) the high-redshift blue population disappears because galaxies become red, so only the recently infalling population is visible at low z. As the fraction of blue galaxies in groups and clusters decreases with cosmic time, the so-called Butcher-Oemler effect (Butcher & Oemler 1984; De Propris et al. 2003; Cucciati et al. 2010b; Iovino et al. 2010), the second scenario seems to be the more likely one: because of some process, the star formation in blue galaxies is quenched, and they become fainter and/or red, hence no longer observed as the brightest galaxy (our principal sample) but as a companion. In addition, 85% of our blue principals have M⋆ ≤ 1010.7 M⊙, the mass regime in which environment is expected to notably affect the properties of blue galaxies (Sect. 1). The quenching process could be harassment (the combined effect of multiple high-speed galaxy-galaxy encounters and the interaction with the potential of the group or the cluster, e.g., Moore et al. 1996, 1999), starvation (the removal of warm and hot gas from the galaxy halo, which cuts off the gas supply, e.g., Larson et al. 1980; Kawata & Mulchaey 2008), or ram pressure stripping by the intergroup medium (e.g., Rasmussen et al. 2006, 2012). We explore further this scenario in the next section.
We have been studying relatively small groups (Mh ~ 1013−13.5 M⊙), so they should accrete even smaller structures from the field, such as pairs or single galaxies. In turn, groups such as those in our sample are accreted by larger groups and clusters. The role of environment in shaping galaxy properties in such small groups, before accretion into clusters, is very important. This is known as pre-processing (see, e.g., Boselli & Gavazzi 2006, and references therein). Some physical processes affecting galaxy properties are more efficient in galaxy groups than in clusters, such as galaxy mergers, thanks to the lower velocity dispersion in groups. The study of galaxy properties within groups is thus strongly related to the understanding of galaxy pre-processing.
5.1. Infall rate of field galaxies into groups at z ~ 0.7
Motivated by the previous results, and following Peng et al. (2010), we develop in this section a simple quenching model in the group environment to estimate the infall rate of field galaxies into groups. We started our model at 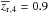 by extracting 1000 random sources i with
by extracting 1000 random sources i with 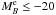 drawn from a Schechter function, obtaining the initial magnitudes MB,i (z = 0.9). We used the Schechter function parameters for spectroscopic type 2, 3, and 4 (i.e., star-forming) galaxies in the VVDS-Deep from Zucca et al. (2006). We checked that our conclusions are the same if the parameters for blue galaxies in Faber et al. (2007) are used. Then, we added our sources into the group environment, as an “infall”, starting the quenching process (e.g., Presotto et al. 2012). Quenched galaxies become less luminous in the B-band and eventually reach the red sequence after a quenching time TQ. We assumed that in this quenching process the blue star-forming galaxy i fades by one magnitude after TQ, MB,i (t) = MB,i (z = 0.9) + t/TQ,i6, where t is the cosmological time since z = 0.9. The main hypothesis in our model is the quenching time. As shown by Tinker & Wetzel (2010), the quenching time due to environmental processes decreases with redshift as TQ ∝ (1 + z)-1.5, and we took TQ(z = 0.9) = 1.8±0.4 Gyr from their estimations. That is, we assigned a TQ,i to each random source drawn from a Gaussian with mean 1.8 Gyr and standard deviation 0.4 Gyr. Finally, we estimated at which redshift our galaxies in groups leave the blue principal sample, zsat, by becoming either red at TQ,i (i.e., we assumed an instantaneous transition in the colour) or less luminous than the
drawn from a Schechter function, obtaining the initial magnitudes MB,i (z = 0.9). We used the Schechter function parameters for spectroscopic type 2, 3, and 4 (i.e., star-forming) galaxies in the VVDS-Deep from Zucca et al. (2006). We checked that our conclusions are the same if the parameters for blue galaxies in Faber et al. (2007) are used. Then, we added our sources into the group environment, as an “infall”, starting the quenching process (e.g., Presotto et al. 2012). Quenched galaxies become less luminous in the B-band and eventually reach the red sequence after a quenching time TQ. We assumed that in this quenching process the blue star-forming galaxy i fades by one magnitude after TQ, MB,i (t) = MB,i (z = 0.9) + t/TQ,i6, where t is the cosmological time since z = 0.9. The main hypothesis in our model is the quenching time. As shown by Tinker & Wetzel (2010), the quenching time due to environmental processes decreases with redshift as TQ ∝ (1 + z)-1.5, and we took TQ(z = 0.9) = 1.8±0.4 Gyr from their estimations. That is, we assigned a TQ,i to each random source drawn from a Gaussian with mean 1.8 Gyr and standard deviation 0.4 Gyr. Finally, we estimated at which redshift our galaxies in groups leave the blue principal sample, zsat, by becoming either red at TQ,i (i.e., we assumed an instantaneous transition in the colour) or less luminous than the 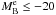 selection.
selection.
We show in Fig. 10 the probability distribution of zsat from our fiducial model. The probability of leaving the principal sample is nearly constant in the range z ∈ (0.6−0.9), has its maximum at z ~ 0.6, and then starts to decline to z ~ 0.4. The maximum is located TQ = 1.8 Gyr after the beginning of the model, reflecting the imposed transition to the red sequence. The constant regime is dominated by those galaxies that are still blue but have become too faint to be selected as principals. We estimate that half of the initial sources at z = 0.9 have left the principal sample at z ~ 0.65, whilst only ~30−35% remain at 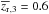 . Since the number density of blue principals increases from z = 0.9 to z = 0.6, as we show in Fig. 11, the fading sources must be replaced by new principals infalling from the field. This implies that (i) at z = 0.6 the blue principals are dominated by galaxies accreted at z < 0.9, in agreement with the observed evolution in the normalisation of the
. Since the number density of blue principals increases from z = 0.9 to z = 0.6, as we show in Fig. 11, the fading sources must be replaced by new principals infalling from the field. This implies that (i) at z = 0.6 the blue principals are dominated by galaxies accreted at z < 0.9, in agreement with the observed evolution in the normalisation of the 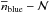 relation (Sect. 4.2), and (ii) an infall rate of ℜinfall ~ 1.1 × 10-4 Mpc-3 Gyr-1 is needed to explain the observed number density of principals at z = 0.7. We estimate this infall rate as
relation (Sect. 4.2), and (ii) an infall rate of ℜinfall ~ 1.1 × 10-4 Mpc-3 Gyr-1 is needed to explain the observed number density of principals at z = 0.7. We estimate this infall rate as ![\begin{equation} \frac{\Re_{\rm infall}}{{\rm Mpc}^{-3}\ {\rm Gyr}^{-1}} = \frac{f_{\rm group}}{T} [\,\rho_{\rm blue}\,(0.7) - (1 - f_{\rm sat})\,\rho_{\rm blue}\,(0.9) ], \end{equation}](/articles/aa/full_html/2013/10/aa21411-13/aa21411-13-eq223.png) (8)where ρblue (z) is the number density of blue principal galaxies at redshift z, fgroup is the fraction of blue principal galaxies in groups with respect to the total population of blue principals, T is the cosmological time spanned between z = 0.9 and z = 0.7 in Gyr, and fsat is the fraction of blue principal galaxies at z = 0.9 that have become a satellite at z = 0.7. We measured fgroup = 0.18 from our data, while our model yields fsat = 0.41. To estimate ρblue (z), we performed a linear fit to the number density evolution of blue principal galaxies from Zucca et al. (2006) in the range 0.2 < z < 1.5. The obtained fit is ρblue (z) = (18.7−7.7z) × 10-4 Mpc-3 (Fig. 11).
(8)where ρblue (z) is the number density of blue principal galaxies at redshift z, fgroup is the fraction of blue principal galaxies in groups with respect to the total population of blue principals, T is the cosmological time spanned between z = 0.9 and z = 0.7 in Gyr, and fsat is the fraction of blue principal galaxies at z = 0.9 that have become a satellite at z = 0.7. We measured fgroup = 0.18 from our data, while our model yields fsat = 0.41. To estimate ρblue (z), we performed a linear fit to the number density evolution of blue principal galaxies from Zucca et al. (2006) in the range 0.2 < z < 1.5. The obtained fit is ρblue (z) = (18.7−7.7z) × 10-4 Mpc-3 (Fig. 11).
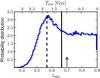 |
Fig. 10 Probability distribution of zsat, the redshift at which a blue principal galaxy at z = 0.9 becomes a satellite. The upper x-axis shows the cosmological time spanned since z = 0.9. The solid vertical line shows the redshift at which half of the initial sources have become a satellite. The dashed line marks TQ = 1.8 Gyr after z = 0.9. The arrow marks the redshift at which we estimate the infall rate. |
The main hypothesis in our toy model is the quenching time, so it is also our main uncertainty. We repeated the previous analysis with TQ = 1.4 and 2.2 Gyr, keeping the dispersion of 0.4 Gyr. In the latter case, the peak in zsat distribution is delayed, and ~50% of the initial sources have left the principal sample by z = 0.6. In the former case, only ~15% of the initial sources survive by z = 0.6, and a higher infall rate is needed. From these two extreme models, our best estimation of the infall rate is ℜinfall = 0.9−1.5 × 10-4 Mpc-3 Gyr-1.
In their work, Kovač et al. (2010) estimate that the fraction of M⋆ ~ 1010.3 M⊙ galaxies in groups increase with cosmic time with a rate of finfall ~ 7−8% Gyr-1 because of the infall of field galaxies into the group environment. We also estimate this infall fraction from our model. Assuming that our blue principal galaxies are representative of the M⋆ ~ 1010.3 M⊙ population, we estimate an infall fraction of finfall ~ 7−10% Gyr-1, in agreement with Kovač et al. (2010). Because of the simplicity of our model, this agreement is remarkable and supports our infall scenario of blue principal galaxies.
 |
Fig. 11 Number density of blue principal galaxies in the VVDS-Deep as a function of redshift. The solid line is the best least-squares linear fit to the data. |
Our toy model has several limitations. For example, infall is a continuous process, so we do not expect peaks in the principal–to–satellite transition, which our toy model produces. In the limiting case of the same TQ for all the galaxies, all the principals reach the red sequence at the same time, and only those that have crossed the selection boundary contribute to the infall rate. Using TQ = 1.8 Gyr, we obtain ℜinfall = 1.1 × 10-4 Mpc-3 Gyr-1, similar to our fiducial value. On the other hand, if we increase the dispersion in TQ up to 1 Gyr to spread the peak, we find a probability distribution that decreases with cosmic time. Now several galaxies have low TQ,i values (even close to zero) and leave the principal sample faster than before. In this case we estimate ℜinfall = 1.3 × 10-4 Mpc-3 Gyr-1, inside our confidence range. Another limitation in our model is that those galaxies that have infalled at z < 0.9 also fade and turn red, thus implying a higher infall rate than estimated from our fiducial model. To deal with this limitation, we reduced the redshift range in which we estimated the infall rate. If we use z = 0.87 (~0.15 Gyr since the beginning of the model) instead of z = 0.7 to measure the infall rate, we obtain ℜinfall = 1.3 × 10-4 Mpc-3 Gyr-1, which is consistent with our confidence range.
In summary, the infall rate from our toy model is mainly determined by the assumed quenching time, and our best estimation is ℜinfall = 0.9−1.5 × 10-4 Mpc-3 Gyr-1. More complex quenching models (i.e., Wetzel et al. 2013) are needed to fully explore our suggested picture.
6. Conclusions
We have studied the small-scale environment of 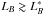 galaxies hosted by VVDS-Deep groups. We traced the small-scale environment with the number of close neighbours
galaxies hosted by VVDS-Deep groups. We traced the small-scale environment with the number of close neighbours 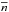 , defined as those
, defined as those 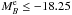 galaxies with a relative distance 5 h-1 kpc ≤ rp ≤ 100 h-1 kpc and a relative velocity Δv ≤ 500 km s-1 with respect to our principal galaxies (
galaxies with a relative distance 5 h-1 kpc ≤ rp ≤ 100 h-1 kpc and a relative velocity Δv ≤ 500 km s-1 with respect to our principal galaxies (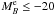 ). We characterised each group by its richness
). We characterised each group by its richness  , defined as the number of
, defined as the number of 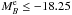 galaxies belonging to each group. We split our principal galaxies within 0.2 ≤ z < 0.95 by their rest-frame NUV − r colour into red, passive (NUV − r ≥ 4.25) and blue, star-forming (NUV − r < 4.25).
galaxies belonging to each group. We split our principal galaxies within 0.2 ≤ z < 0.95 by their rest-frame NUV − r colour into red, passive (NUV − r ≥ 4.25) and blue, star-forming (NUV − r < 4.25).
We find that, on the one hand, the distributions of red and blue principal galaxies in groups as a function of  are different, showing an increase in the red, passive fraction with
are different, showing an increase in the red, passive fraction with  . On the other hand, blue principals with a close neighbour are primarily located in poor groups, while red ones are in rich groups. Combining both results we find that the number of close neighbours per red galaxy increases with
. On the other hand, blue principals with a close neighbour are primarily located in poor groups, while red ones are in rich groups. Combining both results we find that the number of close neighbours per red galaxy increases with  ,
, 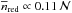 , while that per blue galaxy is roughly constant with
, while that per blue galaxy is roughly constant with  . In addition, these trends are independent of redshift, and only the average
. In addition, these trends are independent of redshift, and only the average  evolves, decreasing with cosmic time.
evolves, decreasing with cosmic time.
Our results support the following assembly history in the group environment: red, massive (M⋆ ~ 1010.8 M⊙) galaxies were either formed or accreted early (z ≳ 1) in the DM haloes of the groups. Because they are already settled in the group potential at z ≲ 1, the number of neighbours of red, passive galaxies is a record of the accretion history of the group, traced by its richness  . On the other hand, blue, less massive (M⋆ ~ 1010.3 M⊙) galaxies are an infalling population from the field. They have been accreted by the group potential recently and are still located in their parent DM sub-halo, having the same number of neighbours irrespective of
. On the other hand, blue, less massive (M⋆ ~ 1010.3 M⊙) galaxies are an infalling population from the field. They have been accreted by the group potential recently and are still located in their parent DM sub-halo, having the same number of neighbours irrespective of  . As time goes by, these blue star-forming galaxies settle in the group potential and turn fainter and/or red, thus becoming satellite galaxies. Thanks to a simple quenching model, we estimate an infall rate of field galaxies into the group environment of ℜinfall = 0.9−1.5 × 10-4 Mpc-3 Gyr-1 at z ~ 0.7.
. As time goes by, these blue star-forming galaxies settle in the group potential and turn fainter and/or red, thus becoming satellite galaxies. Thanks to a simple quenching model, we estimate an infall rate of field galaxies into the group environment of ℜinfall = 0.9−1.5 × 10-4 Mpc-3 Gyr-1 at z ~ 0.7.
This proposed picture makes some specific predictions that have to be explored in the future. First, the 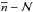 relation should be present, for both red and blue galaxies, in low-redshift groups. Second, a constant
relation should be present, for both red and blue galaxies, in low-redshift groups. Second, a constant  as a function of the normalised distance to the centre of the group might be expected, whilst an increase in
as a function of the normalised distance to the centre of the group might be expected, whilst an increase in 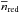 towards the group potential centre should be observed. This could be tested using the lower redshift GAMA7 (Galaxy and Mass Assembly, Driver et al. 2011; z ~ 0.1) survey or the low-redshift end of zCOSMOS (0.2 ≤ z ≤ 0.5). Finally, the study of the
towards the group potential centre should be observed. This could be tested using the lower redshift GAMA7 (Galaxy and Mass Assembly, Driver et al. 2011; z ~ 0.1) survey or the low-redshift end of zCOSMOS (0.2 ≤ z ≤ 0.5). Finally, the study of the 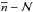 relation in mass-selected samples is needed to better understand the quenching mechanism that operates in the group environment.
relation in mass-selected samples is needed to better understand the quenching mechanism that operates in the group environment.
An extra red neighbour+neighbour pair is not included because we are interested in principal+neighbour statistics. That is, we find a triplet of principal red galaxies and discard the pair between the two fainter ones. We checked that our results are the same if this neighbour+neighbour pair is included.
Acknowledgments
We dedicate this paper to the memory of our six IAC colleagues and friends who met with a fatal accident in Piedra de los Cochinos, Tenerife, in February 2007, with special thanks to Maurizio Panniello, whose teachings of python were so important for this paper. We thank the anonymous referee for the comments and suggestions. This work is supported by funding from ANR-07-BLAN-0228 and ERC-2010-AdG-268107-EARLY.
References
- Abbas, U., de La Torre, S., LeFèvre, O., et al. 2010, MNRAS, 406, 1306 [NASA ADS] [Google Scholar]
- Andreon, S., & Huertas-Company, M. 2011, A&A, 526, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balogh, M. L., McGee, S. L., Wilman, D., et al. 2009, MNRAS, 398, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Phleps, S., Somerville, R. S., et al. 2006, ApJ, 652, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Bielby, R. M., Finoguenov, A., Tanaka, M., et al. 2010, A&A, 523, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bielby, R., Hudelot, P., McCracken, H. J., et al. 2012, A&A, 545, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., & Zehavi, I. 2006, ApJ, 645, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Kovač, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, Jr., A., 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E. 2011, PASA, 28, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, R. C. Y., Bridge, C. R., & Abraham, R. G. 2011, AJ, 141, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Coil, A. L., et al. 2007, MNRAS, 376, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Kilbinger, M., McCracken, H. J., et al. 2012, A&A, 542, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Iovino, A., Kovač, K., et al. 2010a, A&A, 524, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Marinoni, C., Iovino, A., et al. 2010b, A&A, 520, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 2003, ApJ, 598, 20 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Conselice, C. J., Liske, J., et al. 2007, ApJ, 666, 212 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Fèvre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ravel, L., Kampczyk, P., Le Fèvre, O., et al. 2011, A&A, submitted [arXiv:1104.5470] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., Bower, R. G., McCarthy, I. G., et al. 2008, MNRAS, 389, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Faber, S. M., et al. 2007, MNRAS, 376, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Goranova, Y., Hudelot, P., Magnard, F., et al. 2009, the CFHTLS T0006 Release [Google Scholar]
- Grützbauch, R., Conselice, C. J., Varela, J., et al. 2011, MNRAS, 411, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iovino, A., Cucciati, O., Scodeggio, M., et al. 2010, A&A, 509, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jian, H.-Y., Lin, L., & Chiueh, T. 2012, ApJ, 754, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kampczyk, P., Lilly, S. J., de Ravel, L., et al. 2013, ApJ, 762, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kawata, D., & Mulchaey, J. S. 2008, ApJ, 672, L103 [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., Tanaka, I., Kajisawa, M., et al. 2007, MNRAS, 377, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Cucciati, O., et al. 2010, ApJ, 708, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 1670 [Google Scholar]
- Le Fèvre, O., Mellier, Y., McCracken, H. J., et al. 2004, A&A, 417, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, in press DOI: 10.1051/0004-6361/201322179 [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Koo, D. C., Willmer, C. N. A., et al. 2004, ApJ, 617, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Cooper, M. C., Jian, H., et al. 2010, ApJ, 718, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pérez-González, P. G., et al. 2010, A&A, 518, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., de Ravel, L., et al. 2011, A&A, 530, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Tasca, L. A. M., et al. 2013, A&A, 553, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marinoni, C., Davis, M., Newman, J. A., & Coil, A. L. 2002, ApJ, 580, 122 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Radovich, M., Bertin, E., et al. 2003, A&A, 410, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGee, S. L., Balogh, M. L., Bower, R. G., Font, A. S., & McCarthy, I. G. 2009, MNRAS, 400, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Lake, G., Quinn, T., & Stadel, J. 1999, MNRAS, 304, 465 [NASA ADS] [CrossRef] [Google Scholar]
- More, S., van den Bosch, F. C., Cacciato, M., et al. 2011, MNRAS, 410, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., & Atfield, J. E. 2008, ApJ, 685, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Pritchet, C. J., Carlberg, R. G., et al. 2002, ApJ, 565, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Presotto, V., Iovino, A., Scodeggio, M., et al. 2012, A&A, 539, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasmussen, J., Ponman, T. J., & Mulchaey, J. S. 2006, MNRAS, 370, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, J., Bai, X.-N., Mulchaey, J. S., et al. 2012, ApJ, 747, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Robaina, A. R., Bell, E. F., van der Wel, A., et al. 2010, ApJ, 719, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Evrard, A., et al. 2009a, ApJ, 699, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Koester, B. P., et al. 2009b, ApJ, 703, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Schiminovich, D., Wyder, T. K., Martin, D. C., et al. 2007, ApJS, 173, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strazzullo, V., Rosati, P., Pannella, M., et al. 2010, A&A, 524, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, M., Finoguenov, A., Mirkazemi, M., et al. 2013, PASJ, 65, 17 [NASA ADS] [Google Scholar]
- Tasca, L. A. M., Kneib, J.-P., Iovino, A., et al. 2009, A&A, 503, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinker, J. L., & Wetzel, A. R. 2010, ApJ, 719, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Vulcani, B., Poggianti, B. M., Aragón-Salamanca, A., et al. 2011, MNRAS, 412, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Tinker, J. L., Conroy, C., & van den Bosch, F. C. 2013, MNRAS, 432, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, D. J., Zibetti, S., & Budavári, T. 2010, MNRAS, 406, 1701 [NASA ADS] [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Red, passive fraction, fred, of principal and companion galaxies as a function of group richness  .
.
Number of close neighbours (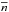 ) per red, passive and blue, star-forming principal galaxy as a function of group richness
) per red, passive and blue, star-forming principal galaxy as a function of group richness  .
.
Number of close neighbours per red, passive principal galaxy (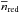 ) as a function of group richness
) as a function of group richness  and redshift.
and redshift.
Number of close neighbours per blue, star-forming principal galaxy ( ) as a function of group richness
) as a function of group richness  and redshift.
and redshift.
All Figures
 |
Fig. 1 Rest-frame B-band absolute magnitude as a function of zspec (dots) in the VVDS-Deep. Solid and dashed lines mark the principal ( |
| In the text | |
 |
Fig. 2 Cumulative histogram of red (thick line) and blue (thin line) principal galaxies as a function of their star formation rate. The definition of red and blue galaxy is labelled in the figure. The vertical dashed line marks SFR = 1 M⊙ yr-1. |
| In the text | |
 |
Fig. 3 Redshift distribution of the VVDS-Deep groups with richness |
| In the text | |
 |
Fig. 4 Cumulative histogram of red (thick line) and blue (thin line) principal galaxies as a function of the richness |
| In the text | |
 |
Fig. 5 Fraction of red, passive galaxies, fred, as a function of group richness |
| In the text | |
 |
Fig. 6 Cumulative histogram of red and blue principal galaxies as a function of the stellar mass. The blue or red (thin) lines are for blue or red principal galaxies hosting by groups, while the grey or black (thick) lines are for red or blue principals outside groups. |
| In the text | |
 |
Fig. 7 Cumulative histogram of red (thick line) and blue (thin line) principal galaxies with a close neighbour as a function of group richness |
| In the text | |
 |
Fig. 8 Number of close neighbours per principal galaxy as a function of group richness |
| In the text | |
 |
Fig. 9 Number of neighbours per principal galaxy as a function of group richness |
| In the text | |
 |
Fig. 10 Probability distribution of zsat, the redshift at which a blue principal galaxy at z = 0.9 becomes a satellite. The upper x-axis shows the cosmological time spanned since z = 0.9. The solid vertical line shows the redshift at which half of the initial sources have become a satellite. The dashed line marks TQ = 1.8 Gyr after z = 0.9. The arrow marks the redshift at which we estimate the infall rate. |
| In the text | |
 |
Fig. 11 Number density of blue principal galaxies in the VVDS-Deep as a function of redshift. The solid line is the best least-squares linear fit to the data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.