EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A100 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A100
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201321528
Published online 10 September 2013

© ESO, 2013

1. Introduction

Gamma-ray bursts (GRBs) are powerful cosmic explosions that are visible up to high redshifts (z > 5; Lamb & Reichart 2000; Boër et al. 2006; Bloom et al. 2009; Vedrenne & Atteia 2009). GRBs have two phases: a very bright flash of high-energy radiation usually lasting several seconds (sometimes also seen in visible light), called the prompt emission, followed by a long-lasting decaying afterglow, visible at longer wavelengths during several hours to months. This behavior is understood as the manifestation of a transient relativistic jet pointing towards the Earth, with the prompt emission being released inside the jet and the afterglow resulting from the interaction of the jet with the surrounding medium. The prompt emission is usually recorded with wide-field gamma-ray imagers or spectrometers and the afterglow with follow-up telescopes in space and on the ground. One essential element of GRB observations is the measurement of their redshift, which is done with visible or near infrared spectrographs on large ground-based telescopes. Most often, this measurement relies on the identification of absorption lines from the host galaxy in the spectrum of the afterglow, while it is bright enough. After measuring the redshift of a GRB one can correct from cosmological effects and infer its intrinsic properties.

A surprising result obtained by Amati et al. (2002) was the discovery of a strong correlation between Epi, the peak energy of the νFν spectrum of the prompt emission at the source, and Eiso, the energy released by a GRB assuming isotropic emission. This correlation was first observed on a sample of ten GRBs with a redshift and well measured spectral parameters (Amati et al. 2002). After this discovery, the validity of this Epi – Eiso relation (often called Amati relation) has been widely discussed, with conflicting results (e.g. Band & Preece 2005; Ghirlanda et al. 2005; Nakar & Piran 2005; Sakamoto et al. 2006; Butler et al. 2007; Cabrera et al. 2007; Schaefer & Collazzi 2007; Butler et al. 2009; Firmani et al. 2009; Krimm et al. 2009; Butler et al. 2010; Shahmoradi & Nemiroff 2011; Collazzi et al. 2012; Kocevski 2012; Goldstein 2012). Despite these discussions, the Epi – Eiso relation was quickly proposed as a tool to infer GRB redshifts (Atteia 2003), to constrain the physics of the prompt emission (Eichler & Levinson 2004; Rees & Mészáros 2005) and the geometry of GRB jets (Lamb et al. 2005; Toma et al. 2005), and to standardize GRBs, in much the same way as the Phillips relation was used to standardize SNe Ia (Phillips 1993). This last approach aims at constructing standard candles with GRBs and at using them to constrain the cosmological parameters (e.g. Dai et al. 2004; Friedman & Bloom 2005; Ghirlanda et al. 2006).

One difficulty of the study of the Epi – Eiso relation is the need to measure both the peak energy of the νFν spectrum (called Epo in the observer’s frame, and Epi in the source frame) and the redshift. The simultaneous operation of Swift and Fermi since July 2008 (Gehrels et al. 2004; Atwood et al. 2009; Meegan et al. 2009) has provided a new sample of bursts whose parameters are available, allowing exploring the Epi – Eiso relation over a larger parameter space than it was previously possible (see also Amati 2010). This paper discusses the distribution in the plane Epi – Eiso of 43 GRBs with a redshift and 243 GRBs without a redshift, all events having Epo measured with Fermi/GBM. The GRB samples are presented in Sect. 2. The distribution in the plane Epi – Eiso is discussed in Sect. 3. The impact of selection effects on this distribution is addressed in Sects. 4 and 5, this last section addressing more specifically the selection effects associated with the measurement of redshift. The main results of our study and their interpretation are summarized in Sect. 6.

In all this paper we use a flat ΛCDM cosmology with H0 = 70 km s-1 Mpc-1 and ΩΛ = 0.7, since these values allow the direct comparison of our results with those of Nava et al. (2012). Calculations of luminosity distances are done using the analytical approximation of Wickramasinghe & Ukwatta (2010) that has an accuracy better than 0.3% in the redshift range used in this paper.

2. GRB sample

We select events with well measured spectral parameters from the Fermi GRB spectral catalog of Goldstein et al. (2012; see also Paciesas et al. 2012) that provides the spectral parameters of 482 GRBs between GRB 080714086 and GRB 100709602 (about two years of data). We parametrize GRB spectra with the Band function (Band et al. 1993) that consists of two smoothly connected power laws. Following standard naming, we call α the photon spectral index of the low-energy power law (α > −2), and β the photon spectral index of the high-energy power law (β < −2). The νFν spectrum peaks at the energy Epeak, near the junction of the two power laws. The selection is made with the application of the following cuts:

  • First, we make a selection on the duration. We consider GRBswith T90 between 2 and 1000 s. This criterion excludes short GRBs (T90 < 2 s), and very long GRBs that are superimposed on a varying background and whose Epeak is difficult to measure accurately.

  • Second, we require accurate spectral parameters. We exclude GRBs with one or more spectral parameters missing. We exclude GRBs with an error on alpha (the low-energy index of the Band function) larger than 0.4. We exclude a few GRBs with α < −2.0, and GRBs with β > α because such values suggest a confusion between fitting parameters. We exclude GRBs with large errors on Epo, defined by a ratio of the 90% upper limit to the 90% lower limit larger than 3. We have less stringent constraints on beta (the high-energy index of the Band function) since we have checked that the position of GRBs in the Epi – Eiso plane changes very little with beta. When the error on β in the catalog is lacking or larger than 1.0, we assign to β the classical value of –2.3 and we give no error. In a few cases, the high energy spectral index in the Fermi catalog is >−2, and the catalog gives the energy of a spectral break that is not Epo. In these cases we look for Epo in the GCN Circulars, and if we cannot find it, we simply remove the burst from the sample. This procedure suppresses one GRB with a redshift and ten GRBs without a redshift.

267 bursts pass the cuts, 24 with a measured redshift. This is a small number, so we extend the sample of GRBs with a redshift with the addition of 19 Fermi GRBs found in GCN circulars that respect the same selection criteria. In the end, we have two samples: 43 GRBs with a redshift, and 243 GRBs without one. GRBs in each sample are listed in Tables A.1 and A.2. The redshifts span the range [0.34–4.35], with a median value z˜ = 1.71, smaller than the median redshift of Swift GRBs (z˜ = 2.14), measured by Jakobsson et al. (2012).

thumbnail Fig. 1

Fermi GRBs in the plane Epi –Eiso. The black symbols show 43 GRBs with a redshift and the black solid lines show the corresponding best fit Epi – Eiso relation with its two sigma limits. Black circles are 34 GRBs detected simultaneously by Fermi/GBM and Swift/BAT. Black triangles are nine GRBs detected simultaneously by Fermi/GBM and another positioning instrument (usually Fermi/LAT). The purple circles indicate GRBs whose redshift has been measured with the emission lines of the host galaxy. The green and red lines show the possible positions of GRBs without a redshift when they are placed at distances ranging from z = 0.34 (leftmost point) to z = 4.35 (rightmost point). Red lines indicate GRBs that are beyond the two sigma limit of the Epi – Eiso relation at any redshift. The dotted blue lines show the best fit Epi – Eiso relation of Nava et al. (2012) with its two sigma limits. The dashed blue lines show the best fit Epi – Eiso relation of Amati (2006) with its two sigma limits.

3. The Epi – Eiso relation of Fermi GRBs

3.1. GRBs with a redshift

Figure 1 shows with black symbols the locations of 43 Fermi GRBs with a redshift in the Epi – Eiso plane. These bursts show a clear correlation between Epi and Eiso, as for the previous missions. The coefficient of correlation is 0.70, and the best fit correlation is 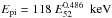, where E52 is the GRB isotropic energy in units of 1052 ergs (the best fit correlation is obtained by weighting each point quadratically by its error on Epi). This will be the definition of the Epi – Eiso relation in the rest of this paper.

This relation is close to the one found by Gruber et al. (2012) from a sample of Fermi GRBs (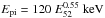), and by Nava et al. (2012) for a larger sample including GRBs from Fermi and other missions (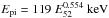). If we freeze the slope to its best-fit value (0.486), we can compute the vertical standard deviation of data points around the fit: sigma = 0.34 (if we measure the standard deviation perpendicular to the best fit line, we get sigma = 0.21). The two-sigma limits are shown in Fig. 1, they are defined by 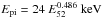for the lower limit, and 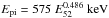, for the upper limit. Figure 1 evidences a broadening of the two sigma confidence region with respect to the relation of Amati (2006) for pre-Fermi GRBs that had a vertical sigma = 0.21. This broadening was already noted by Nava et al. (2012) and by Gruber et al. (2012), who measure sigma = 0.34 along the vertical axis, equivalent to the value found here.

3.2. GRBs without a redshift

The green and red dashed lines in Fig. 1 represent the possible locations of GRBs without a redshift in the Epi – Eiso plane, considering that their redshift may vary between 0.34 and 4.35, the extreme values measured for GRBs with a redshift. We plot in green GRBs lying within the two sigma limits of the Epi – Eiso relation for some redshifts, and in red the bursts that remain outside these boundaries at any redshift.

For most of the redshift range [0.34–4.35], the green and red lines are nearly parallel to the Epi – Eiso relation, allowing assessing the position of GRBs without redshifts with respect to this relation. First, we note a clear asymmetry between GRBs above and below the best fit Epi – Eiso relation. While GRBs with a redshift are more or less symmetric with respect to the best fit Epi – Eiso relation (22 above and 21 below), the situation is markedly different for GRBs without a redshift. 72% of them lie entirely above the best fit Epi – Eiso relation, 22% cross it, and 6% only lie entirely below it. This asymmetry is accompanied by a lack of events in the lower right corner of the plot. Since GRBs in this region have large Eiso and low Epi, they should have plenty of photons and we cannot attribute their deficit to selection effects. We conclude that GRBs with a large Eiso and a low Epi are intrinsically rare.

We finally note that 29 GRBs are located outside the two sigma limits of the Epi – Eiso relation at all redshifts, all of them lie above the two sigma upper limit of the Epi – Eiso relation. This is larger than the number of six GRBs expected on a purely statistical basis (assuming a gaussian shape of the distribution around the Epi – Eiso relation ). It is difficult to infer the exact significance of this excess, because our definition of the two-sigma limits is rather arbitrary and the uncertainties on Epeak make difficult evaluating the true number of outliers. Despite these uncertainties, it is not possible to move more than a few outliers within the two-sigma limits, and we conclude safely that Fermi GRBs without a redshift include a significant fraction of outliers to the Epi – Eiso relation.

At this point we are facing two results: on one hand GRBs with a redshift seem to follow a broad Epi – Eiso relation, while on the other hand the overall GRB population shows a fraction of outliers of 12% in a region of the plane where GRBs are difficult to detect, suggesting a much broader distribution in the Epi – Eiso plane. The following sections discuss how the observed Epi – Eiso distribution is affected by selection effects. In Sect. 4 we discuss selection effects on GRB detection, while in Sect. 5 we discuss selection effects on the measurement of the redshift.

thumbnail Fig. 2

Distribution of three classes of GRBs (see Fig. 1) in a photon fluence – peak photon flux plane. Several outliers to the Epi – Eiso relation (in red) are GRBs at the limit of detection, with low photon fluence and peak photon flux.

4. Study of the outliers

In the rest of this paper, we call outliers GRBs located above the two-sigma limit of the Epi – Eiso relation. There are 33 outliers, four GRBs with a redshift, and 29 GRBs without a redshift, they are shown in boldface in Tables A.1 and A.2. In this section we compare the properties of the 33 outliers, with those of the remaining 253 GRBs, in order to understand whether they are affected by significant selection effects. Table 1 shows the results of Kolmogorov-Smirnov (KS) tests comparing the duration T90, spectral parameters, and brightness between the two classes. Outliers differ from GRBs that follow the Epi – Eiso relation by their Epo and their brightness: on average, outliers a have larger Epo (a median Epo of 715 keV vs. 151 keV) and a smaller fluence (a median fluence of 28 × 10-7 erg cm-2 vs. 74 × 10-7 erg cm-2). These differences are clearly visible in Fig. 3 that shows the cumulative distribution functions (CDF) of these parameters: on average outliers have an observed Epeak four times larger and a photon fluence five times smaller than other GRBs.

Table 1

Comparison of the observed properties of 33 GRBs incompatible with Epi – Eiso relation at all redshifts (outliers) with 253 GRBs that are within two sigma of the Epi – Eiso relation (others).

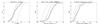thumbnail Fig. 3

Cumulative distribution function (CDF) of 3 GRB parameters: Epo, photon fluence, and peak photon flux for the three classes of Fermi GRBs defined in Fig. 1. Black solid line: 43 GRBs with a redshift; green dashed line: 253 GRBs with or without a redshift that may be compatible with the Epi – Eiso relation at some redshift; red dash-dotted line: 29 GRBs without a redshift that are incompatible with the Epi – Eiso relation at any redshift (outliers). This figure emphasizes the larger Epo and smaller photon fluence of outliers.

The main consequence is that outliers are much more difficult to detect (see Band 2003, for a discussion of GRB sensitivity of different detectors). In fact, it is difficult to assess the true extension of the GRB population above the Epi – Eiso relation because GRBs in this region have fewer photons as the direct consequence of their large Epo. The fraction of outliers found here is thus a lower limit of the true fraction of outliers. We conclude that, above the Epi – Eiso relation, the observed GRB distribution is currently limited by the sensitivity of gamma-ray detectors.

Similar conclusions were reached by Nakar & Piran (2005), Goldstein et al. (2010), and Shahmoradi & Nemiroff (2011) based on BATSE GRBs, by Butler et al. (2007) based on Swift GRBs and by Collazzi et al. (2012) based on various GRB samples from pre-Fermi missions, and by Kocevski (2012) based on a synthetic GRB population. Other authors have stressed the role of selection effects, however they consider that they have little impact on the Epi – Eiso relation. Ghirlanda et al. (2008) show that the existence of an Epo – fluence correlation could impact the Epi – Eiso relation of Swift GRBs and that pre-Swift GRBs also could be affected by unknown selection effects, and Nava et al. (2008) states that, although selection effects are present, they do not determine the spectral-energy correlations. In order to clarify this debate, we now compare the distribution of GRBs with a redshift and GRBs without a redshift in the Epi – Eiso plane.

5. GRBs with a redshift

In order to compare GRBs with a redshift and GRBs without a redshift, we discuss the differences between the two classes in terms of their observed properties in Sect. 5.1, and in terms of their intrinsic properties in Sect. 5.2. We limit the sample of GRBs with a redshift to the bursts that have the same selection criteria as GRBs without a redshift, that is to a sample of 34 GRBs detected simultaneously by Fermi/GBM (for the spectral parameters) and Swift/BAT (for the localization). This excludes nine GRBs detected and localized by Fermi/LAT, IPN, or INTEGRAL that were outside the field-of-view of Swift/BAT at the time of the burst. Including these events in the sample of GRBs with a redshift would artificially increase the fraction of very bright GRBs, biasing the comparison between Fermi GRBs with and without a redshift, as explained in Sect. 5.3 below.

5.1. Observed properties

Table 2 compares the properties of GRBs with a redshift with the population of GRBs with no redshift. GRBs with a redshift differ from the general population by their larger brightness (fluence and peak flux). This is not surprising since GRBs that are brighter in gamma-rays are also expected to be brighter in visible (e.g. Wanderman & Piran 2010). The larger average fluence and peak flux of GRBs with a redshift is explained in part by a smaller distance (the median redshift of our sample is z˜ = 1.71, compared z˜ = 2.14 for Swift GRBs.) and in part by a greater ease to measure the redshift of brighter GRBs. This effect however cannot create the Epi – Eiso relation that is an intrinsic property of GRBs. It is thus necessary to check whether the measurement of the redshift biases the intrinsic properties of GRBs, and more specifically their distribution in the Epi – Eiso plane.

Table 2

Comparison of the observed properties of 34 GRBs with a redshift and 243 GRBs without a redshift.

thumbnail Fig. 4

Comparison of simulated GRB populations. Left panel. Epi as a function of Eiso. Right panel. Slope of the Epi – Eiso relation as a function of Eiso. Green: Fermi GRBs with no redshift not localized by Swift/BAT; purple: Fermi GRBs with no redshift localized by Swift/BAT; blue: Fermi GRBs with a redshift localized by Swift/BAT; black: Fermi GRBs with a redshift, irrespective of the satellite used for the localization. The crosses show the median values and the corresponding error, measured from 1000 simulated samples. The point symbols show the values measured for two actual samples: in blue 34 GRBs studied in Sect. 5.2, and in black the full sample of 43 GRBs with a redshift.

5.2. Intrinsic properties

In order to check whether the measurement of the redshift impacts the distribution of GRBs in the Epi – Eiso plane, we use the following procedure: from the sample of 243 GRBs without a redshift, we randomly select 34 GRBs, we assign them the redshifts of the 34 GRBs with measured redshifts, and we compute their Epi, Eiso, and the slope of the best fit Epi – Eiso relation. We repeat this procedure 1000 times and we compare the median values of Epi, Eiso, and the slope of the Epi – Eiso relation with those of GRBs with redshifts. We apply the same procedure to the subsample of 34 GRBs with a redshift, in order to understand how the redshift redistribution impacts the results. For sake of completeness, we study two additional distributions: 25 Fermi GRBs localized by Swift without a redshift, and the full sample of 43 GRBs with a redshift. The results are summarized in Fig. 4. The crosses show the median Eiso, Epi, the median slope of the Epi – Eiso relation and the one-sigma error on these values, for the four simulated GRBs samples. The blue and black symbols show the values measured for GRBs with a redshift (excluding or not the GRBs detected by Fermi/LAT).

These simulations bring the following results:

  • The compatibility (within errors) of the green and purple crossesshows that the localization with Swift/BAT does not bias thedistribution of Epi or Eiso.

  • The comparison of the blue and green crosses shows that GRBs with a redshift have slightly larger Eiso (median =9.2 × 1052 erg vs. 4.8 × 1052 erg), similar Epi (median = 345 keV vs. 440 keV), and slopes of the Epi – Eiso relation that are compatible (~0.3). The measurement of the redshift thus favors GRBs that are more energetic, with large Eiso.

  • The comparison of the simulated populations (blue and black crosses) with the actual GRBs (blue and black symbols) shows that the redshift redistribution builds simulated populations that have more or less the same Eiso and Epi as the original population, but a significantly smaller slope of the Epi – Eiso relation. This difference can be attributed to the fact that, unlike real GRBs, simulated GRBs can occupy the empty region in the lower right corner of the Epi – Eiso plane, decreasing the slope of the correlation.

The differences pointed here between GRBs with a redshift and GRBs without a redshift concern average values of the parameters. They provide no information on the joint distribution in the plane Epi – Eiso for the two groups. A look at Fig. 1 suggests different distributions of the two groups, with GRBs with a redshift gathered closer to the Epi – Eiso boundary. To verify this hypothesis, we have divided our GRB sample (34 GRBs with a redshift plus 243 GRBs without a redshift) into four subsamples according to their distance to the Epi – Eiso boundary (for GRBs with a redshift) or to their smallest distance to this line (for GRBs without a redshift). Since we have excluded the nine GRBs with a redshift detected by Fermi/LAT, each subsample includes eight or nine GRBs with a redshift. We have computed the fraction of GRBs with a redshift in each subsample, obtaining the following numbers with increasing distance from the boundary: 9/44 = 0.20; 9/42 = 0.21; 8/68 = 0.12; and 8/123 = 0.065. These numbers clearly show that GRBs with a redshift do not follow the general GRB distribution in the plane Epi – Eiso, being more concentrated near the Epi – Eiso boundary. This is illustrated in Fig. 5 that shows with different colors the groups of GRBs at different distances from the Epi – Eiso boundary.

With this observation, we finally get a coherent picture of the origin of Epi – Eiso relation. This correlation can be attributed to the combination of two effects: a physical boundary in the plane Epi – Eiso, and biases favoring the detection and the measurement of redshift of GRBs located along this boundary. We have evidenced two biases acting in the same direction. First, for a given Eiso, GRBs far from the Epi – Eiso boundary have fewer gamma-ray photons, making their detection and localization with gamma-ray detectors more difficult. This is confirmed with the computation of V/Vmax as a proxy for the signal-to-noise ratio1. We find that the median V/Vmax increases with the distance from the Epi – Eiso boundary, with median (V/Vmax) = 0.28−0.35−0.51−0.75 for the 4 groups of GRBs with a redshift defined in the previous paragraph. These numbers only concern a small fraction of GRBs but they clearly show that GRBs close to the Epi – Eiso boundary have larger signal-to-noise and are more easily detected.

thumbnail Fig. 5

GRBs classification in 4 groups according to their distance to the Epi – Eiso boundary. The parameter used to separate the 4 groups is their vertical distance (for GRBs with a redshift) or their smallest vertical distance (for GRBs without a redshift) to the black line. The black line has a slope = 0.486, assumed to be the slope of the Epi – Eiso boundary. The position of the black line is arbitrary, it does not impact the groups as long as it stays below the GRB sample.

The second bias is connected with the measurement of the redshift: we have found that the fraction of GRBs with a redshift increses close to the Epi – Eiso boundary. This suggests the existence of a bias that makes easier the measurement of the redshift when a GRB is close to the Epi – Eiso boundary. Since the capability to measure the redshift is closely linked with the optical brightness of the afterglow, we infer that there are factors enhancing the optical luminosity of GRBs close to the Epi – Eiso boundary. The verification of this hypothesis requires a systematic study of the optical luminosity of GRB afterglows, which is beyond the scope of this paper. This bias contributes to further reduce the width of the distribution of GRBs with a redshift. As a consequence of these two biases, GRBs with a redshift appear preferentially along a narrow band above the Epi – Eiso boundary, giving rise to correlation found by Amati et al. (2002).

5.3. Bright GRBs detected with LAT and IPN

Figure 1 shows that the 9 GRBs that were not localized by Swift (the black triangles) concentrate in the upper right of the Epi – Eiso relation, increasing the significance of the correlation. In our interpretation, these very bright GRBs cannot have low Epi because of the Epi – Eiso boundary. Since they brightness facilitates the measurement of their redshift, they play an important role in shaping the Epi – Eiso relation.

This is also the case of GRB 130427A (the rightmost point in Figs. 2 and 5) that is one of the few nearby energetic GRBs (like GRB 030329 detected by Hete-2 at z = 0.17, Vanderspek et al. 2004). GRB 130427A is at redshift z = 0.34, the value of V/Vmax for this GRB, V/Vmax = 0.003, indicates that there is a 10% chance observing this GRB so close among 30 similar bursts at higher redshift. Considering that Fermi has detected more than 1100 GRBs from its launch to the end of April 2013, the detection of a nearby energetic GRB like GRB 130427A is not unexpected. Interestingly, GRB 130427A lies perfectly along the Amati relation (Amati et al. 2013). This is compatible with our interpretation that highly energetic bursts cannot have low Epi because of the Epi – Eiso boundary.

6. Discussion

The results presented in this paper are based on the distribution of GRBs in the plane Epi – Eiso. We discuss below some selection effects that may affect this distribution. First, it is not possible to measure Epo outside the energy range of the detector. This restricts the range of measured Epo to [30–1300] keV. These bounds prevent us to include X-Ray Flashes (soft GRBs with Epeak < 30 keV) in our analysis but they do not bias the distribution of GRBs in the Epi – Eiso plane and the conclusions of our analysis. Second, we have studied the impact of the errors on Epo and on the energy fluence Sγ given in Table A.2. If we systematically replace Epo with Epo−σEpo for all GRBs without a redshift, the number of outliers decreases from 29 to 18. Similarly, if we change the fluence Sγ with Sγ−σSγ for all GRBs without a redshift, the number of outliers decreases from 29 to 28. Thus, we cannot get rid of the outliers, even with this rather drastic method.

Two additional effects, acting in opposite directions, can affect the observed distribution in the Epi – Eiso plane. First, GRBs in the upper left part of the plot are more difficult to detect because they have intrinsically fewer photons than GRBs closer to the Amati relation. Since this bias acts against the detection of outliers, it leads to underestimate the true fraction of outliers, as explained in Sect. 4. On the other hand, it is possible to “create” outliers from GRBs following the Amati relation if the measurements of Epi or Eiso are strongly biased. One possibility is the “duration bias” discussed by Kocevski & Petrosian (2013). This bias results from the inability of count-limited instruments to detect the parts of GRBs with low count rates, artificially reducing T90 and Eiso of faint GRBs. The duration bias may also affect the measurement of Epeak since the brightest parts of faint GRBs are often those with the largest Epeak. Since Table 1 shows that outliers have essentially the same duration distribution as the rest of GRBs, there is no hint in the data of a strong duration bias that could significantly alter our analysis. We have also checked the possible biases on Epeak with the measurement of the ratio RE = Epeak (at peak)/Epeak (average) for outliers and for other GRBs. We find that RE is broadly distributed with median(RE) = 0.74 ± 0.30 for outliers, median(RE) = 1.14   ±   0.28 for other GRBs, and median(RE) = 1.06 ± 0.28 for GRBs with a redshift. These numbers show that outliers are only marginally affected by selection effects that could modify their Epeak. Overall, we found no bias capable of “creating” the observed outliers from GRBs that follow the Epi – Eiso relation.

The main conclusion of this paper is that the Epi – Eiso relation is due to the combination of two effects: a physical limit that prevents the existence of GRBs with a large Eiso and a low Epi (creating an Epi – Eiso boundary ), and the sensitivity of gamma-ray and optical imagers that strongly favor the detection and localization of GRBs located close to the Epi – Eiso boundary (see also Shahmoradi & Nemiroff 2011). The combination of these two effects creates a band in the Epi – Eiso plane where GRBs are more easily detected, and a thinner band where their redshift can be measured. We believe that this interpretation explains the apparently contradictory results obtained by people who have checked the validity of Epi – Eiso relation either using large samples of GRBs without a redshift or only using GRBs with a redshift. The first have consistently found large fractions of outliers dismissing the relation (e.g. Band & Preece 2005; Nakar & Piran 2005; Butler et al. 2007, 2010; Shahmoradi & Nemiroff 2011; Collazzi et al. 2012), while the second usually confirmed its validity (e.g. Ghirlanda et al. 2005; Sakamoto et al. 2006; Krimm et al. 2009; Nava et al. 2012). The horizontal extent of the Epi – Eiso relation depends on the GRB luminosity function, on the evolution of the GRB rate with redshift, and on the volume of detection for each type of GRB. We have checked that the leftmost part of the Epi – Eiso relation contains mainly faint GRBs with low Epi detected at low redshift (z < 1), while the rightmost part is made of luminous GRBs with large Epi that can only be found in large volumes of observation (except GRB 130427A discussed in Sect. 5.3). Finally, we note that similar studies could be performed with other relations, like the Epi – Liso relation (Yonetoku et al. 2004) or the Epi – Eγ relation (Ghirlanda et al. 2004), to check their nature and their validity.

A discussion of the origin of the Epi – Eiso boundary is beyond the scope of this paper. If it is a consequence of the dominant radiation mechanism at work in GRBs, as we expect, theoretical studies may help understanding the nature and the true location of this boundary (see for instance Eichler & Levinson 2004; Yamazaki et al. 2004; Rees & Mészáros 2005; Thompson et al. 2007; Giannios 2012; Mochkovitch et al. 2012; Beniamini & Piran 2013; Shahmoradi 2013, for explanations within the framework of different theoretical or phenomelogical models). The observation of an Epi – Eiso relation in time-resolved spectra (e.g. Ghirlanda et al. 2010; Frontera et al. 2012; Basak & Rao 2012; Lu et al. 2012) may also provide insights into the origin of the Epi – Eiso boundary. Finally, Since the Epi – Eiso relation is not an intrinsic property of GRBs, it may be difficult to use it to standardize GRBs (Ghirlanda et al. 2006; Mészáros & Gehrels 2012). This might nevertheless be possible if one finds a way of identifying GRBs close to the Epi – Eiso boundary, thanks to their temporal properties (e.g. spectral lags) or to the characteristics of their afterglows.

Online material

Appendix A: Data tables

The following tables provide the names and the spectral properties of the 286 GRBs used in this study, extracted from the Fermi GRB catalog of Goldstein et al. (2012).

Table A.1

43 GRBs with a redshift.

Table A.2

243 GRBs without a redshift.

Table A.2

continued.

Table A.2

continued.

Table A.2

continued.

1

V/Vmax is a number between 0 and 1 that represents the position of a GRB within its “volume of detectability”. GRBs with a low signal-to-noise ratio that are close to the detection limit have V/Vmax ≲ 1; in contrast GRBs with a large signal-to-noise ratio have V/Vmax ≈ 0.

Acknowledgments

The authors gratefully acknowledge the use of the online Fermi GRB catalog2, the use of the GRB table compiled by J. Greiner (http://www.mpe.mpg.de/~jcg/grbgen.html), and the use of the table of GRB redshifts compiled by Páll Jakobsson3. Y.Z. welcomes financial support from IRAP (UMR5277/CNRS/UPS).

References

  1. Amati, L. 2006, MNRAS, 372, 233 [NASA ADS] [CrossRef] [Google Scholar]
  2. Amati, L. 2010 [arXiv:1002.2232] [Google Scholar]
  3. Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Amati, L., Dichiara, S., Frontera, F., & Guidorzi, C. 2013, GRB Coordinates Network, 14503, 1 [Google Scholar]
  5. Atteia, J.-L. 2003, A&A, 407, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  7. Band, D. L. 2003, ApJ, 588, 945 [NASA ADS] [CrossRef] [Google Scholar]
  8. Band, D. L., & Preece, R. D. 2005, ApJ, 627, 319 [NASA ADS] [CrossRef] [Google Scholar]
  9. Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
  10. Basak, R., & Rao, A. R. 2012, ApJ, 749, 132 [NASA ADS] [CrossRef] [Google Scholar]
  11. Beniamini, P., & Piran, T. 2013, ApJ, 769, 69 [NASA ADS] [CrossRef] [Google Scholar]
  12. Berger, E., & Rauch, M. 2008, GRB Coordinates Network, 8542, 1 [NASA ADS] [Google Scholar]
  13. Bissaldi, E., McBreen, S., Wilson-Hodge, C. A., & von Kienlin, A. 2008, GRB Coordinates Network, 8263, 1 [NASA ADS] [Google Scholar]
  14. Bloom, J. S., Perley, D. A., Li, W., et al. 2009, ApJ, 691, 723 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Boër, M., Atteia, J. L., Damerdji, Y., et al. 2006, ApJ, 638, L71 [NASA ADS] [CrossRef] [Google Scholar]
  16. Briggs, M. S., & Younes, G. 2011, GRB Coordinates Network, 12744, 1 [Google Scholar]
  17. Burenin, R., Khamitov, I., Galeev, A., et al. 2008, GRB Coordinates Network, 8088, 1 [NASA ADS] [Google Scholar]
  18. Butler, N. R., Kocevski, D., Bloom, J. S., & Curtis, J. L. 2007, ApJ, 671, 656 [NASA ADS] [CrossRef] [Google Scholar]
  19. Butler, N. R., Kocevski, D., & Bloom, J. S. 2009, ApJ, 694, 76 [NASA ADS] [CrossRef] [Google Scholar]
  20. Butler, N. R., Bloom, J. S., & Poznanski, D. 2010, ApJ, 711, 495 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cabrera, J. I., Firmani, C., Avila-Reese, V., et al. 2007, MNRAS, 382, 342 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cenko, S. B., Bloom, J. S., Morgan, A. N., & Perley, D. A. 2009a, GRB Coordinates Network, 9053, 1 [NASA ADS] [Google Scholar]
  23. Cenko, S. B., Perley, D. A., Junkkarinen, V., et al. 2009b, GRB Coordinates Network, 9518, 1 [NASA ADS] [Google Scholar]
  24. Chaplin, V. 2012, GRB Coordinates Network, 13737, 1 [Google Scholar]
  25. Chornock, R., & Berger, E. 2011, GRB Coordinates Network, 11544, 1 [Google Scholar]
  26. Chornock, R., Perley, D. A., Cenko, S. B., & Bloom, J. S. 2009, GRB Coordinates Network, 9028, 1 [NASA ADS] [Google Scholar]
  27. Collazzi, A. C. 2012, GRB Coordinates Network, 13145, 1 [Google Scholar]
  28. Collazzi, A. C., Schaefer, B. E., Goldstein, A., & Preece, R. D. 2012, ApJ, 747, 39 [NASA ADS] [CrossRef] [Google Scholar]
  29. Cucchiara, A., & Fox, D. B. 2009, GRB Coordinates Network, 8774, 1 [NASA ADS] [Google Scholar]
  30. Cucchiara, A., & Fox, D. B. 2010, GRB Coordinates Network, 10606, 1 [Google Scholar]
  31. Cucchiara, A., & Fumagalli, M. 2013, GRB Coordinates Network, 14207, 1 [Google Scholar]
  32. Cucchiara, A., & Levan, A. J. 2011, GRB Coordinates Network, 12761, 1 [Google Scholar]
  33. Cucchiara, A., & Prochaska, J. X. 2012, GRB Coordinates Network, 12865, 1 [Google Scholar]
  34. Cucchiara, A., Fox, D. B., Cenko, S. B., & Berger, E. 2008a, GRB Coordinates Network, 8346, 1 [NASA ADS] [Google Scholar]
  35. Cucchiara, A., Fox, D. B., Cenko, S. B., & Berger, E. 2008b, GRB Coordinates Network, 8713, 1 [NASA ADS] [Google Scholar]
  36. Cucchiara, A., Fox, D. B., Cenko, S. B., & Berger, E. 2008c, GRB Coordinates Network, 8065, 1 [NASA ADS] [Google Scholar]
  37. Cucchiara, A., Fox, D., Levan, A., & Tanvir, N. 2009a, GRB Coordinates Network, 10202, 1 [NASA ADS] [Google Scholar]
  38. Cucchiara, A., Fox, D. B., Cenko, S. B., Tanvir, N., & Berger, E. 2009b, GRB Coordinates Network, 10031, 1 [NASA ADS] [Google Scholar]
  39. Cucchiara, A., Fox, D. B., Tanvir, N., & Berger, E. 2009c, GRB Coordinates Network, 9873, 1 [NASA ADS] [Google Scholar]
  40. Dai, Z. G., Liang, E. W., & Xu, D. 2004, ApJ, 612, L101 [NASA ADS] [CrossRef] [Google Scholar]
  41. D’Avanzo, P., D’ Elia, V., & Covino, S. 2008, GRB Coordinates Network, 8350, 1 [NASA ADS] [Google Scholar]
  42. de Ugarte Postigo, A., Thoene, C. C., Fynbo, J. P. U., et al. 2008, GRB Coordinates Network, 8089, 1 [NASA ADS] [Google Scholar]
  43. de Ugarte Postigo, A., Gorosabel, J., Malesani, D., Fynbo, J. P. U., & Levan, A. J. 2009a, GRB Coordinates Network, 9383, 1 [NASA ADS] [Google Scholar]
  44. de Ugarte Postigo, A., Jakobsson, P., Malesani, D., et al. 2009b, GRB Coordinates Network, 8766, 1 [NASA ADS] [Google Scholar]
  45. de Ugarte Postigo, A., Goldoni, P., Milvang-Jensen, B., et al. 2011, GRB Coordinates Network, 11579, 1 [Google Scholar]
  46. de Ugarte Postigo, A., Tanvir, N., Sanchez-Ramirez, R., et al. 2013, GRB Coordinates Network, 14437, 1 [Google Scholar]
  47. D’Elia, V., Goldoni, P., Xu, D., et al. 2012, GRB Coordinates Network, 13494, 1 [Google Scholar]
  48. Dittmann, J., Laskar, T., & Berger, E. 2011, GRB Coordinates Network, 12759, 1 [Google Scholar]
  49. Eichler, D., & Levinson, A. 2004, ApJ, 614, L13 [NASA ADS] [CrossRef] [Google Scholar]
  50. Fatkhullin, T., Moskvitin, A., Castro-Tirado, A. J., & de Ugarte Postigo, A. 2009, GRB Coordinates Network, 9542, 1 [NASA ADS] [Google Scholar]
  51. Firmani, C., Cabrera, J. I., Avila-Reese, V., et al. 2009, MNRAS, 393, 1209 [Google Scholar]
  52. Flores, H., Fynbo, J. P. U., de Ugarte Postigo, A., et al. 2010, GRB Coordinates Network, 11317, 1 [Google Scholar]
  53. Foley, S., & Briggs, M. 2010, GRB Coordinates Network, 10851, 1 [Google Scholar]
  54. Friedman, A. S., & Bloom, J. S. 2005, ApJ, 627, 1 [NASA ADS] [CrossRef] [Google Scholar]
  55. Frontera, F., Amati, L., Guidorzi, C., Landi, R., & in’t Zand, J. 2012, ApJ, 754, 138 [NASA ADS] [CrossRef] [Google Scholar]
  56. Fynbo, J. P. U., Malesani, D., Hjorth, J., Sollerman, J., & Thoene, C. C. 2008, GRB Coordinates Network, 8254, 1 [NASA ADS] [Google Scholar]
  57. Fynbo, J. P. U., Malesani, D., Jakobsson, P., & D’Elia, V. 2009, GRB Coordinates Network, 9947, 1 [NASA ADS] [Google Scholar]
  58. Fynbo, J. P. U., Xu, D., Jakobsson, P., Armstrong, D., & Cardenes, R. 2012, GRB Coordinates Network, 13632, 1 [Google Scholar]
  59. Garnavich, P. 2013, GRB Coordinates Network, 14605, 1 [Google Scholar]
  60. Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
  61. Ghirlanda, G., Ghisellini, G., & Lazzati, D. 2004, ApJ, 616, 331 [NASA ADS] [CrossRef] [Google Scholar]
  62. Ghirlanda, G., Ghisellini, G., & Firmani, C. 2005, MNRAS, 361, L10 [NASA ADS] [Google Scholar]
  63. Ghirlanda, G., Ghisellini, G., & Firmani, C. 2006, New J. Phys., 8, 123 [NASA ADS] [CrossRef] [Google Scholar]
  64. Ghirlanda, G., Nava, L., Ghisellini, G., Firmani, C., & Cabrera, J. I. 2008, MNRAS, 387, 319 [NASA ADS] [CrossRef] [Google Scholar]
  65. Ghirlanda, G., Nava, L., & Ghisellini, G. 2010, A&A, 511, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Giannios, D. 2012, MNRAS, 422, 3092 [NASA ADS] [CrossRef] [Google Scholar]
  67. Goldstein, A. 2012, in Gamma-Ray Bursts Conference (GRB 2012) [Google Scholar]
  68. Goldstein, A., Preece, R. D., & Briggs, M. S. 2010, ApJ, 721, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  69. Goldstein, A., Burgess, J. M., Preece, R. D., et al. 2012, ApJS, 199, 19 [NASA ADS] [CrossRef] [Google Scholar]
  70. Graham, J. F., Tanvir, N. R., Fruchter, A. S., Wiersema, K., & Levan, A. J. 2008, GRB Coordinates Network, 8718, 1 [NASA ADS] [Google Scholar]
  71. Greiner, J., Clemens, C., Krühler, T., et al. 2009, A&A, 498, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Greiner, J., Rau, A., Schady, P., Saviane, I., & Cenko, B. 2012, GRB Coordinates Network, 13493, 1 [Google Scholar]
  73. Gruber, D. 2010a, GRB Coordinates Network, 11248, 1 [Google Scholar]
  74. Gruber, D. 2010b, GRB Coordinates Network, 11454, 1 [Google Scholar]
  75. Gruber, D. 2011, GRB Coordinates Network, 12221, 1 [Google Scholar]
  76. Gruber, D. 2012, GRB Coordinates Network, 12874, 1 [Google Scholar]
  77. Gruber, D., & Goldstein, A. 2012, GRB Coordinates Network, 13498, 1 [Google Scholar]
  78. Gruber, D., & Pelassa, V. 2012, GRB Coordinates Network, 13437, 1 [Google Scholar]
  79. Gruber, D., et al. 2012 [arXiv:1207.4620] [Google Scholar]
  80. Hartoog, O. E., Malesani, D., Wiersema, K., et al. 2012, GRB Coordinates Network, 13730, 1 [Google Scholar]
  81. Jakobsson, P., Hjorth, J., Malesani, D., et al. 2012, ApJ, 752, 62 [NASA ADS] [CrossRef] [Google Scholar]
  82. Kocevski, D. 2012, ApJ, 747, 146 [NASA ADS] [CrossRef] [Google Scholar]
  83. Kocevski, D., & Petrosian, V. 2013, ApJ, 765, 116 [NASA ADS] [CrossRef] [Google Scholar]
  84. Krimm, H. A., Yamaoka, K., Sugita, S., et al. 2009, ApJ, 704, 1405 [NASA ADS] [CrossRef] [Google Scholar]
  85. Kruehler, T., Greiner, J., & Kann, D. 2013a, GRB Coordinates Network, 14500, 1 [Google Scholar]
  86. Kruehler, T., Malesani, D., Xu, D., et al. 2013b, GRB Coordinates Network, 14264, 1 [Google Scholar]
  87. Lamb, D. Q., & Reichart, D. E. 2000, ApJ, 536, 1 [Google Scholar]
  88. Lamb, D. Q., Donaghy, T. Q., & Graziani, C. 2005, ApJ, 620, 355 [NASA ADS] [CrossRef] [Google Scholar]
  89. Levan, A. J., Cenko, S. B., Perley, D. A., & Tanvir, N. R. 2013, GRB Coordinates Network, 14455, 1 [Google Scholar]
  90. Lu, R.-J., Wei, J.-J., Liang, E.-W., et al. 2012, ApJ, 756, 112 [NASA ADS] [CrossRef] [Google Scholar]
  91. Malesani, D., Goldoni, P., Fynbo, J. P. U., et al. 2009, GRB Coordinates Network, 9942, 1 [NASA ADS] [Google Scholar]
  92. McBreen, S. 2009a, GRB Coordinates Network, 9535, 1 [NASA ADS] [Google Scholar]
  93. McBreen, S. 2009b, GRB Coordinates Network, 10266, 1 [NASA ADS] [Google Scholar]
  94. McGlynn, S. 2012, GRB Coordinates Network, 14012, 1 [Google Scholar]
  95. Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
  96. Mészáros, P., & Gehrels, N. 2012, RA&A, 12, 1139 [Google Scholar]
  97. Milisavljevic, D., Drout, M., & Berger, E. 2012, GRB Coordinates Network, 12867, 1 [Google Scholar]
  98. Mochkovitch, R., Hascoët, R., Daigne, F., et al. 2012, in Gamma-Ray Bursts 2012 Conference (GRB 2012) [Google Scholar]
  99. Nakar, E., & Piran, T. 2005, MNRAS, 360, L73 [NASA ADS] [CrossRef] [Google Scholar]
  100. Nava, L., Ghirlanda, G., Ghisellini, G., & Firmani, C. 2008, MNRAS, 391, 639 [NASA ADS] [CrossRef] [Google Scholar]
  101. Nava, L., Salvaterra, R., Ghirlanda, G., et al. 2012, MNRAS, 421, 1256 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  102. OMeara, J., Chen, H.-W., & Prochaska, J. X. 2010, GRB Coordinates Network, 11089, 1 [Google Scholar]
  103. Paciesas, W. S., Meegan, C. A., von Kienlin, A., et al. 2012, ApJS, 199, 18 [NASA ADS] [CrossRef] [Google Scholar]
  104. Palazzi, E., Fugazza, D., & Piranomonte, S. 2011, GRB Coordinates Network, 12763, 1 [Google Scholar]
  105. Pancoast, A., Rosen, R., Bennert, V., Cucchiara, A., & Prochaska, J. X. 2012, GRB Coordinates Network, 12866, 1 [Google Scholar]
  106. Perley, D. A., Prochaska, J. X., Kalas, P., et al. 2009, GRB Coordinates Network, 10272, 1 [NASA ADS] [Google Scholar]
  107. Perley, D. A., Prochaska, J. X., & Morgan, A. N. 2012, GRB Coordinates Network, 14059, 1 [Google Scholar]
  108. Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
  109. Prochaska, J. X., Perley, D., Howard, A., et al. 2008, GRB Coordinates Network, 8083, 1 [NASA ADS] [Google Scholar]
  110. Rau, A. 2009, GRB Coordinates Network, 9556, 1 [NASA ADS] [Google Scholar]
  111. Rees, M. J., & Mészáros, P. 2005, ApJ, 628, 847 [NASA ADS] [CrossRef] [Google Scholar]
  112. Rossi, A., Afonso, P., & Greiner, J. 2009, GRB Coordinates Network, 9382, 1 [NASA ADS] [Google Scholar]
  113. Sakamoto, T., Barbier, L., Barthelmy, S. D., et al. 2006, ApJ, 636, L73 [NASA ADS] [CrossRef] [Google Scholar]
  114. Salvaterra, R., Campana, S., Vergani, S. D., et al. 2012, ApJ, 749, 68 [NASA ADS] [CrossRef] [Google Scholar]
  115. Sanchez-Ramirez, R., Gorosabel, J., de Ugarte Postigo, A., & GonzalezPerez, J. M. 2012, GRB Coordinates Network, 13723, 1 [Google Scholar]
  116. Schaefer, B. E., & Collazzi, A. C. 2007, ApJ, 656, L53 [NASA ADS] [CrossRef] [Google Scholar]
  117. Schulze, S., Covino, S., Flores, H., et al. 2011, GRB Coordinates Network, 12770, 1 [Google Scholar]
  118. Shahmoradi, A. 2013, ApJ, 766, 111 [NASA ADS] [CrossRef] [Google Scholar]
  119. Shahmoradi, A., & Nemiroff, R. J. 2011, MNRAS, 411, 1843 [NASA ADS] [CrossRef] [Google Scholar]
  120. Sparre, M., Sollerman, J., Fynbo, J. P. U., et al. 2011, ApJ, 735, L24 [NASA ADS] [CrossRef] [Google Scholar]
  121. Tanvir, N. R., Wiersema, K., & Levan, A. J. 2010, GRB Coordinates Network, 11230, 1 [Google Scholar]
  122. Tanvir, N. R., Wiersema, K., Levan, A. J., Cenko, S. B., & Geballe, T. 2011, GRB Coordinates Network, 12225, 1 [Google Scholar]
  123. Tanvir, N. R., Levan, A. J., & Matulonis, T. 2012a, GRB Coordinates Network, 14009, 1 [Google Scholar]
  124. Tanvir, N. R., Wiersema, K., Levan, A. J., et al. 2012b, GRB Coordinates Network, 13441, 1 [Google Scholar]
  125. Tello, J. C., Sanchez-Ramirez, R., Gorosabel, J., et al. 2012, GRB Coordinates Network, 13118, 1 [Google Scholar]
  126. Thoene, C. C., de Ugarte Postigo, A., Vreeswijk, P. M., Malesani, D., & Jakobsson, P. 2008, GRB Coordinates Network, 8058, 1 [NASA ADS] [Google Scholar]
  127. Thoene, C. C., Goldoni, P., Covino, S., et al. 2009, GRB Coordinates Network, 10233, 1 [NASA ADS] [Google Scholar]
  128. Thoene, C. C., de Ugarte Postigo, A., Gorosabel, J., et al. 2012, GRB Coordinates Network, 13628, 1 [Google Scholar]
  129. Thompson, C., Mészáros, P., & Rees, M. J. 2007, ApJ, 666, 1012 [NASA ADS] [CrossRef] [Google Scholar]
  130. Toma, K., Yamazaki, R., & Nakamura, T. 2005, ApJ, 635, 481 [Google Scholar]
  131. van der Horst, A. J. 2009, GRB Coordinates Network, 8805, 1 [NASA ADS] [Google Scholar]
  132. van der Horst, A. J. 2010, GRB Coordinates Network, 11477, 1 [Google Scholar]
  133. Vanderspek, R., Sakamoto, T., Barraud, C., et al. 2004, ApJ, 617, 1251 [NASA ADS] [CrossRef] [Google Scholar]
  134. Vedrenne, G., & Atteia, J.-L. 2009, Gamma-Ray Bursts (Springer Praxis Books) [Google Scholar]
  135. von Kienlin, A. 2008, GRB Coordinates Network, 8640, 1 [NASA ADS] [Google Scholar]
  136. von Kienlin, A. 2009a, GRB Coordinates Network, 8877, 1 [NASA ADS] [Google Scholar]
  137. von Kienlin, A. 2009b, GRB Coordinates Network, 8912, 1 [NASA ADS] [Google Scholar]
  138. von Kienlin, A. 2009c, GRB Coordinates Network, 9271, 1 [NASA ADS] [Google Scholar]
  139. von Kienlin, A. 2009d, GRB Coordinates Network, 9579, 1 [NASA ADS] [Google Scholar]
  140. von Kienlin, A. 2010a, GRB Coordinates Network, 11006, 1 [Google Scholar]
  141. von Kienlin, A. 2010b, GRB Coordinates Network, 11015, 1 [Google Scholar]
  142. von Kienlin, A. 2010c, GRB Coordinates Network, 11099, 1 [Google Scholar]
  143. von Kienlin, A. 2013, GRB Coordinates Network, 14473, 1 [Google Scholar]
  144. Vreeswijk, P. M., Fynbo, J. P. U., Malesani, D., Hjorth, J., & de Ugarte Postigo, A. 2008, GRB Coordinates Network, 8191, 1 [NASA ADS] [Google Scholar]
  145. Wanderman, D., & Piran, T. 2010, MNRAS, 406, 1944 [NASA ADS] [Google Scholar]
  146. Wickramasinghe, T., & Ukwatta, T. N. 2010, MNRAS, 406, 548 [NASA ADS] [CrossRef] [Google Scholar]
  147. Wiersema, K., de Ugarte Postigo, A., & Levan, A. 2009a, GRB Coordinates Network, 9250, 1 [NASA ADS] [Google Scholar]
  148. Wiersema, K., Tanvir, N. R., Cucchiara, A., Levan, A. J., & Fox, D. 2009b, GRB Coordinates Network, 10263, 1 [NASA ADS] [Google Scholar]
  149. Wilson-Hodge, C. A. 2009, GRB Coordinates Network, 9849, 1 [NASA ADS] [Google Scholar]
  150. Xiong, S., & Meegan, C. 2012, GRB Coordinates Network, 13644, 1 [Google Scholar]
  151. Xiong, S., & Rau, A. 2013, GRB Coordinates Network, 14429, 1 [Google Scholar]
  152. Xu, D., Fynbo, J. P. U., Tanvir, N. R., et al. 2009, GRB Coordinates Network, 10053, 1 [NASA ADS] [Google Scholar]
  153. Xu, D., Fynbo, J. P. U., McCormac, J., & Jakobsson, P. 2011, GRB Coordinates Network, 12764, 1 [Google Scholar]
  154. Xu, D., de Ugarte Postigo, A., Schulze, S., et al. 2013, GRB Coordinates Network, 14478, 1 [Google Scholar]
  155. Yamazaki, R., Ioka, K., & Nakamura, T. 2004, ApJ, 606, L33 [NASA ADS] [CrossRef] [Google Scholar]
  156. Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [NASA ADS] [CrossRef] [Google Scholar]
  157. Younes, G., & Barthelmy, S. D. 2012, GRB Coordinates Network, 13721, 1 [Google Scholar]
  158. Yu, D. 2012, GRB Coordinates Network, 14078, 1 [Google Scholar]

All Tables

Table 1

Comparison of the observed properties of 33 GRBs incompatible with Epi – Eiso relation at all redshifts (outliers) with 253 GRBs that are within two sigma of the Epi – Eiso relation (others).

In the text
Table 2

Comparison of the observed properties of 34 GRBs with a redshift and 243 GRBs without a redshift.

In the text
Table A.1

43 GRBs with a redshift.

In the text
Table A.2

243 GRBs without a redshift.

In the text
Table A.2

continued.

In the text
Table A.2

continued.

In the text
Table A.2

continued.

In the text

All Figures

thumbnail Fig. 1

Fermi GRBs in the plane Epi –Eiso. The black symbols show 43 GRBs with a redshift and the black solid lines show the corresponding best fit Epi – Eiso relation with its two sigma limits. Black circles are 34 GRBs detected simultaneously by Fermi/GBM and Swift/BAT. Black triangles are nine GRBs detected simultaneously by Fermi/GBM and another positioning instrument (usually Fermi/LAT). The purple circles indicate GRBs whose redshift has been measured with the emission lines of the host galaxy. The green and red lines show the possible positions of GRBs without a redshift when they are placed at distances ranging from z = 0.34 (leftmost point) to z = 4.35 (rightmost point). Red lines indicate GRBs that are beyond the two sigma limit of the Epi – Eiso relation at any redshift. The dotted blue lines show the best fit Epi – Eiso relation of Nava et al. (2012) with its two sigma limits. The dashed blue lines show the best fit Epi – Eiso relation of Amati (2006) with its two sigma limits.
In the text
thumbnail Fig. 2

Distribution of three classes of GRBs (see Fig. 1) in a photon fluence – peak photon flux plane. Several outliers to the Epi – Eiso relation (in red) are GRBs at the limit of detection, with low photon fluence and peak photon flux.
In the text
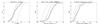thumbnail Fig. 3

Cumulative distribution function (CDF) of 3 GRB parameters: Epo, photon fluence, and peak photon flux for the three classes of Fermi GRBs defined in Fig. 1. Black solid line: 43 GRBs with a redshift; green dashed line: 253 GRBs with or without a redshift that may be compatible with the Epi – Eiso relation at some redshift; red dash-dotted line: 29 GRBs without a redshift that are incompatible with the Epi – Eiso relation at any redshift (outliers). This figure emphasizes the larger Epo and smaller photon fluence of outliers.
In the text
thumbnail Fig. 4

Comparison of simulated GRB populations. Left panel. Epi as a function of Eiso. Right panel. Slope of the Epi – Eiso relation as a function of Eiso. Green: Fermi GRBs with no redshift not localized by Swift/BAT; purple: Fermi GRBs with no redshift localized by Swift/BAT; blue: Fermi GRBs with a redshift localized by Swift/BAT; black: Fermi GRBs with a redshift, irrespective of the satellite used for the localization. The crosses show the median values and the corresponding error, measured from 1000 simulated samples. The point symbols show the values measured for two actual samples: in blue 34 GRBs studied in Sect. 5.2, and in black the full sample of 43 GRBs with a redshift.
In the text
thumbnail Fig. 5

GRBs classification in 4 groups according to their distance to the Epi – Eiso boundary. The parameter used to separate the 4 groups is their vertical distance (for GRBs with a redshift) or their smallest vertical distance (for GRBs without a redshift) to the black line. The black line has a slope = 0.486, assumed to be the slope of the Epi – Eiso boundary. The position of the black line is arbitrary, it does not impact the groups as long as it stays below the GRB sample.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.