| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321440 | |
| Published online | 02 September 2013 | |
Constraining the location of rapid gamma-ray flares in the flat spectrum radio quasar 3C 273
1
Max-Planck-Institut für
Radioastronomie (MPIfR),
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: brani@mpifr-bonn.mpg.de
2
Université Bordeaux 1, CNRS/IN2p3, Centre d’Études Nucléaires de Bordeaux
Gradignan, 33175
Gradignan,
France
Received:
8
March
2013
Accepted:
2
July
2013
We present a γ-ray photon flux and spectral variability study of the flat-spectrum radio quasar 3C 273 over a rapid flaring activity period between September 2009 to April 2010. Five major flares were observed in the source during this period. The most rapid flare observed in the source has a flux doubling time of 1.1 hr. The rapid γ-ray flares allow us to constrain the location and size of the γ-ray emission region in the source. The γγ-opacity constrains the Doppler factor δγ ≥ 10 for the highest energy (15 GeV) photon observed by the Fermi-Large Area Telescope (LAT). Causality arguments constrain the size of the emission region to 1.6 × 1015 cm. The γ-ray spectra measured over this period show clear deviations from a simple power law with a break in the 1−2 GeV energy range. We discuss possible explanations for the origin of the γ-ray spectral breaks. Our study suggests that the γ-ray emission region in 3C 273 is located within the broad line region (< 1.6 pc). The spectral behavior and temporal characteristics of the individual flares indicate the presence of multiple shock scenarios at the base of the jet.
Key words: gamma rays: galaxies / galaxies: active / quasars: individual: 3C 273
© ESO, 2013
1. Introduction
The γ-ray bright blazar 3C 273 is classified as a flat spectrum radio quasar (FSRQ) at a redshift z = 0.158 (Strauss et al. 1992). It was the first discovered quasar (Schmidt 1963), and the first extragalactic source detected in γ-ray band, by COS-B (Swanenburg et al. 1978). The source is categorized as a low synchrotron peaked blazar (LSP) by Abdo et al. (2010a). The broadband spectrum, the correlation among multi-frequency flares, and the VLBI jet kinematics of the source were extensively studied in the past (e.g., Krichbaum et al. 2001; Rani et al. 2010, 2011; Soldi et al. 2008; Savolainen et al. 2010; Abdo et al. 2010e,and references therein).
After the first detection in γ-rays by COS-B, 3C 273 was also observed by EGRET in 1999 (3EG J1229+0210 in Hartman et al. 1999) with an average flux of F(E > 100 MeV) = 0.18 × 10-6 ph cm-2 s-1. Krichbaum et al. (2001) noticed a correlation between jet component ejection and EGRET γ-ray flux variations, which constrained the location of the γ-ray emission region to ~2000 Schwarzschild radii (< 0.2 pc) from the central black hole (BH). The Fermi-Large Area Telescope (LAT) detected the source in the γ-ray band from the beginning of observations in 2008 (Abdo et al. 2010a). The source was observed in a bright outburst phase at the beginning of July 2009. The first flaring event lasted for ~10 days in August 2009 (Bastieri 2009). The source exhibited another γ-ray outburst in September 2009 with two bright flares from September 15 to 19, 2009 and from September 20 to 23, 2009. Abdo et al. (2010e) discussed the flare characteristics and spectral behavior during this outburst period. Before the brightest γ-ray flare was observed in 3C 454.3 in December 2009 (Escande & Tanaka 2009; Abdo et al. 2011), 3C 273 was the brightest extragalactic non γ-ray burst source observed by Fermi-LAT. Although the γ-ray spectrum of 3C 273 integrated over the first six months of LAT observations showed a significant break around 1.5 GeV (Abdo et al. 2010d), the spectra integrated over shorter periods of time in September 2009 did not provide indication for such curvature (Abdo et al. 2010e).
The second flare during September 20 to 30, 2009 displayed a first short peak and was followed by a period of high-activity indicating either a series of substructures or a long decay tail (Abdo et al. 2010e). The source continued the rapid flaring activity until April 2010 and later was observed in a quiescent state, which is still continuing. We refer to the flaring interval between August 2009 to April 2010 as the high-activity period. Thanks to the high flux during August 2009 to April 2010, we are able to obtain light curves with good statistics using a time binning of only 3 h, allowing us to investigate the evolution of these outbursts. The focus of this study is to probe the location and size of the γ-ray emission region in 3C 273 by investigating its intra-day variability and associated spectral changes in the γ-ray band.
This paper is structured as follows. Section 2 provides a brief description of observations and data reduction. In Sect. 3, we report our results. We discuss our results in Sect. 4. Conclusions are given in Sect. 5.
2. Observations and data reduction
The γ-ray flux and spectral variations of the source were investigated using the Fermi-LAT data. The γ-ray data employed here were collected during a time period between JD = 2 454 683 (August 04, 2008) to 2 455 889 (November 23, 2011) in survey mode by Fermi-LAT. We analyzed the LAT data using the standard ScienceTools (software version v9.23.1) and instrument response functions P7V61. Photons in the Source event class were selected for this analysis. We selected γ-ray photons with zenith angles less than 100° to greatly reduce contamination from γ-rays produced by cosmic-ray interactions in the upper atmosphere. The diffuse emission from our Galaxy was modeled using a spatial model (gal_2yearp7v6_v0.fits) that was refined by the Fermi-LAT data taken during the first two years of operation. The extragalactic diffuse and residual instrumental backgrounds were modeled as an isotropic component (isotropic_p7v6source.txt), and were provided with the data analysis tools. We analyzed a region of interest of 10° in radius, centered at the position of the γ-ray source associated with 3C 273 using a maximum-likelihood algorithm2 (Mattox et al. 1996). In the model for the γ-ray emission from the region, we included all the 30 sources within 10° with their model parameters fixed to their catalog values except for 3C 279 and MG1 J123931+0443. The other sources are reported as being not significantly variable in the 2FGL catalog (see Nolan et al. 2012). For 3C 279 and MG1 J123931+0443, we set all model parameters free.
We investigated the source variability by producing light curves by likelihood analysis with different time binnings (3 h, 6 h, 12 h, 1 day, and 1 week) and over different energy ranges (E > 100 MeV, E < 1 GeV, and E > 1 GeV). The light curves were produced by modeling the spectra for each time bin and energy range by a simple power law that was sufficient for the relatively short time ranges considered here. Also, the statistical uncertainties on the power law (PL) indices were smaller than those obtained from broken power law (BPL) fits.
We also computed photon flux light curves above the de-correlation energy E0 (Lott et al. 2012) that minimizes the correlations between integrated photon flux and photon index (Γ). Over the course of ~3 years of observations, we find E0 = 167 MeV. We generated the constant uncertainty (15%) light curve above E0 through the adaptive binning method following Lott et al. (2012). The estimated systematic uncertainty on the flux is 10% at 100 MeV, 5% at 500 MeV, and 20% at 10 GeV (Ackermann et al. 2012).
We performed the spectral analysis by fitting the γ-ray spectra with multiple models over the whole energy range covered by Fermi-LAT above 100 MeV. The different spectral forms are simple power law [PL, N(E) = N0(E)−Γ, N0: prefactor, and Γ: power law index], smoothed broken power law [SBPL, N(E) = N0E−Γ1(1 + (E/Ebreak)−(Γ1−Γ2)/b)−b, Γ1, Γ2: the two power law indices, and EBreak: break energy, b: smoothing parameters set to 0.1], and a log-parabola function [logP, N(E) = N0(E/EP)−(α + β log (E/EP), α: power law index, β: index parameter that characterizes the spectral curvature, and EP: the peak energy fixed at 1 GeV]. We also examined the spectral behavior over the whole energy range with a simple PL model that we fitted over equally spaced logarithmic energy bins, with Γ kept constant and equal to the value obtained by fitting over the whole energy range.
 |
Fig. 1 a) Weekly (blue circles) and monthly (red open symbols) averaged flux (E > 100 MeV) light curves of 3C 273 measured by Fermi-LAT since its launch. The green histogram represents the arrival time distribution of E > 10 GeV photons associated with 3C 273. The yellow box represents the high γ-ray flux activity period. b) One-day averaged light curve of the source over the high-activity period within the box shown at the top of the figure. |
3. Analysis and results
3.1. Temporal characteristics
3.1.1. Light curves
The source was exhibiting significant flux variability throughout the whole Fermi mission (Abdo et al. 2010b). Figure 1a displays the weekly averaged flux F100 (F [E > 100 MeV] in units of 10-6 ph cm-2 s-1) light curve of the source. A sequence of flares is observed in the source between JD′3 = 1042 to 1320 (August 2009 to April 2010) and no substantial flux variability has been observed since then. The source seems to have been in a quiescent state since April 2010, which is still continuing. The high-activity period can be seen in the box in Fig. 1. Figure 1b shows the one-day averaged F100 light curve over this period. Five major flares labeled A to E were observed in the source during this period (see Fig. 1b). Interestingly, the major flares were separated from each other by roughly 50 days. The high flux level during the flaring periods allowed us to investigate the evolution of outbursts with a temporal resolution as fine as 3 h (corresponding to one sky scan of the LAT).
Figure 1a shows the arrival time distribution of γ-ray photons with energies greater than 10 GeV. During the ~3 years of observations, the highest energy photon associated with 3C 273 was detected at JD′ = 1151 with an energy of 15.4 GeV. This photon is converted in the front section of the LAT tracker, where the angular resolution is best (Ackermann et al. 2012). The reconstructed arrival direction of the photon is 0.07° away from 3C 273. Based on our model fit of the epoch which contains the highest-energy photon, we find the probability that the photon was associated with 3C 273 (as opposed to all other sources in the model including the diffuse emission and nearby point sources) is 99.98%, or > 3σ. Interestingly, the highest energy photon was observed during the flaring period.
Flare A had a duration of ~12 days with a peak flux of ~5.1 × 10-6 ph cm-2 s-1. Flare B consisted of two main sub-flares, each one having a total duration of ~2 days and a peak flux of ~12 × 10-6 ph cm-2 s-1. The first sub-flare showed a nice smooth time profile, suggesting that it is well resolved; the second sub-flare, after a first short peak, shows a series of high spikes that indicate substructures in a long decay tail. A detailed study of flux and spectral variations of these two outbursts is given in Abdo et al. (2010e). Flare C was recorded ~50 days later than flare B, and was followed by an extremely rapid flare D, and a number of sub-flares as flare E.
We also investigated the evolution of these flares with finer time resolution depending
upon the γ-ray brightness of the source. The light curves for
F100, with 3 h and 12 h time binning for the individual
flares, are shown in Fig. 2. A fit consisting of a
slowly varying background and rapid sub-flaring components is performed for each
individual flare. The slowly varying background is roughly approximated by a flux
value = 0.42 × 10-6 ph cm-2 s-1. Each component is
fitted by a function of the form ![\begin{equation} F(t) = 2~F_0 \big [ {\rm e}^{(t_0 - t)/T_{\rm r}} + {\rm e}^{(t - t_0)/T_{\rm f}} \big ]^{-1}, \end{equation}](/articles/aa/full_html/2013/09/aa21440-13/aa21440-13-eq47.png) (1)where
Tr and
Tf are the rise and decay times,
respectively, and F0 is the flux at
t0 representing approximately the flare amplitude. The
solid curves in Fig. 2 represent the fitted flare
components and the fitted parameters for each sub-component are given in Table 1. The doubling times of the individual flares is
given in the last column of Table 1. We note that
the flares have similar halving times because of comparable rise and decay timescales.
(1)where
Tr and
Tf are the rise and decay times,
respectively, and F0 is the flux at
t0 representing approximately the flare amplitude. The
solid curves in Fig. 2 represent the fitted flare
components and the fitted parameters for each sub-component are given in Table 1. The doubling times of the individual flares is
given in the last column of Table 1. We note that
the flares have similar halving times because of comparable rise and decay timescales.
The short duration of flare D, with timescales similar to the orbital period of Fermi (~96 min), makes the standard analysis, where the photons are binned in time, inappropriate for a detailed temporal characterization of the flare. A different, unbinned (in the time domain) method taking into account the strongly varying rate of accumulation of exposure associated with the survey mode was employed instead for this purpose. In this method, based on the same log-likelihood approach as described in Lott et al. (2012), a time-dependent function f(t,E) = F(t) × N(E) where F(t) is given in Eq. (1) and N(E) is a power law distribution (neglecting any spectral changes during the flare), was fitted to the unbinned data. The results are plotted in Fig. 3, showing from top to bottom the exposure rate, the comparison between the predicted source-photon detection rate and that estimated from the data, and the flux light curve. The parameters for F(t) are given in Table 1.
During the first component of flare D the source brightens to F100 ~ 12 with a flux doubling time of 1.1 h. The second component of flare D has a peak flux value F100 ~ 7 with a flux doubling time of 1.5 h. During flare D, the Moon was close to the region of interest of 3C 273. We therefore checked for the possible contribution from the Moon. We found that the Moon was closest to the source on January 07, 2010 with an angular distance of 11°, which is larger than the region of interest of the source, and therefore unlikely to cause any significant contamination in the observed rapid flux variations.
 |
Fig. 2 Light curves of 3C 273 above 100 MeV with time binning of 12 h (flare C and E) and 3 h (flare D). The lines are the fitted sub-flaring components (see Table 1). |
 |
Fig. 3 Top: exposure rate during flare D. Middle: predicted (red) and observed (blue) source photon detection rates. Bottom: photon flux light curve of flare D. The red curve shows the results of the time-domain-unbinned analysis, and the blue (15%) and green (25%) symbols represent the adaptive-binning analysis results. |
Fitted parameters of flares.
Flare A shows essentially equal rise (~1.81 day) and decay timescales (~1.79 day), which implies that flare A has a symmetric temporal profile. In contrast to flare A, the components of flare B are characterized by decay times (~2.50 day) longer than the rise time (~0.50 day; Abdo et al. 2010e). For flare C, the components have a symmetric profile except the middle sub-component (see Table 1). Both the components of flare D have relatively symmetric evolution. All the components of flare E are characterized by symmetric temporal profiles. Therefore, most of the flares have symmetric profiles except flare B.
3.1.2. Flux variations at different energy bands
The flux variations below and above 1 GeV energy during the high-activity period are shown in Fig. 4. The flux variations below 1 GeV seem to be more pronounced, but we note that the characteristic decay timescales of the individual flares are similar for the FE < 1 GeV and FE > 1 GeV light curves using 12 h time binning. Even with a finer temporal resolution of 6 h for the brightest flare B (component 1 and 2), we find that the decay timescales for the FE < 1 GeV and FE > 1 GeV light curves are not statistically different. The rise and decay timescales, the peak flux value and the respective time of peak of the flare for the 6 h binned light curves of these flares at different energy scales are given in Table 2.
To search for a possible time lag and to quantify the correlation among the γ-ray flux variations below and above 1 GeV, we compute the discrete cross-correlation function (DCF) of the two light curves (E below and above 1 GeV) following the method described by Edelson & Krolik (1988). The 12 h binned DCF analysis curve (Fig. 5) shows a peak (DCF = 0.82 ± 0.21) at a time lag of 0.00 ± 0.25 days. This confirms the existence of a significant correlation between the flux variations below and above 1 GeV with zero time delay. Because of limited statistics for the more finely binned light curves, we cannot claim any time delay shorter than our binning interval of 12 h.
 |
Fig. 4 One-day averaged γ-ray light curve of the source below (bottom) and above (top) 1 GeV during the high-activity period. |
Fitted parameters of the bright flares at different energy scales.
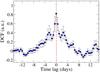 |
Fig. 5 DCF curve of the 12 h binned γ-ray light curves below and above 1 GeV. The dotted line marks a possible time lag of 0 ± 0.25 day. |
3.1.3. Photon index variations
We investigated the flux variations above the de-correlation energy (E0) that minimizes the correlations between integrated photon flux and photon index. We generated the constant uncertainty (15%) light curve above E0 using the adaptive binning method (Lott et al. 2012). Figure 6 shows the photon flux and index variations during the high-activity period between JD′ = 1050 to 1320 at E > E0. The different flaring activity periods of the source are separated by vertical columns. We note substantial variations in photon spectral index during different modes of flux activity. As we see in Fig. 6, for each flare Γ drops from a value of ~(2.9−2.7) at the beginning of the flare to ~(2.3−2.1) close to the peak of the flare, and then at the end of the flare the spectrum softens to a photon index value ~(3.0−2.8). Therefore, a strong evolution of Γ during the different activity states is observed in the source.
An alternative way to investigate the spectral evolution during different γ-ray flares is to plot variations in Γ as a function of flux variations. A counter-clockwise loop is observed during flare A while during flare B, the spectral index, and flux changes follow a clockwise path (Abdo et al. 2010e). In Fig. 6 (bottom), we also plot the photon indices as a function of the γ-ray fluxes during flares C, D, and E. As shown, flares C and E suggest a clockwise loop, while flare D follows a counter-clockwise loop. A clockwise loop indicates that the flux started to increase at low energy and then propagates to high energy; the reverse would produce a counter-clockwise path. This may reflect the alternating dominance of acceleration and cooling processes. We note that the subsequent flares loop in opposite directions, starting with a counter-clockwise loop for flare A.
 |
Fig. 6 Top panel: the constant uncertainty (15%) light curve of 3C 273 above E0 obtained with the adaptive binning method over the high-activity period (see text for details). The lower panel shows the variations in Γ during this period. The vertical columns separate the different flaring periods. Bottom: Γ vs. flux above E0 for flare C, D, and E. |
3.2. The gamma-ray spectrum
We constructed the γ-ray spectrum using data for the entire flaring period (JD′ = 1042−1294) and for the quiescent state (JD′ = 1300−1720). Figure 7a shows the γ-ray spectrum of the source over the high-activity period and the quiescent state. The observed spectrum shows a clear deviation from a simple power law. The spectral analysis using a broken power law model returns a break energy of 1.5 ± 0.1 GeV with a likelihood test statistic relative to the power law LRT = −2Δ(ln L) = 35.1 (L is the value of the likelihood function) that corresponds to a significance of ~5.58σ. The significance is estimated using Wilks’ theorem, i.e., the LRT follows a chi-square distribution with Δn degrees of freedom (Δn is difference of number of degrees of freedom of the two spectral models). However, the spectrum does not exhibit a sharp break; rather, the spectrum shows curvature near the break frequency. We therefore added a smoothing parameter b to the broken power law model (see Sect. 2) , which is fixed to 0.14 while fitting.
We also investigated the spectral shape using the log-parabola (logP) model. For the high-activity period, the LRT value of SBPL with respect to logP is 5.3, which corresponds to a significance of ~2.3σ with one degree of freedom. This implies that the SBPL model provides a marginally better fit compared to the logP model. The curves in Fig. 7a represent the fitted power laws, i.e., PL, logP, and SBPL in an energy range between 100 MeV and 300 GeV using the maximum likelihood method. The fitted model parameters over the energy range between 100 MeV to 300 GeV are summarized in Table 3. The difference of the logarithm of likelihood −2ΔL of SBPL and logP with respect to SPL is given in Col. 9 of Table 3 along with the corresponding significance by which SBPL and logP are favored compared to the PL model. We therefore conclude that both smoothed broken power law and log-parabola models better describe the γ-ray spectral shape than the simple PL model with a break energy Ebreak = 1.2 ± 0.2 GeV. A similar indication of break at ~1.5 GeV in the spectrum of 3C 273 integrated over the first six months of LAT observations has been also reported in Abdo et al. (2010d).
 |
Fig. 7 Gamma-ray spectral energy distributions of 3C 273 during different activity states along with the fitted PL (dashed curve), logP (dotted-dashed curve), and SBPL (solid curve) spectral models. |
The high-activity period (JD′ = 1042−1294) consists of five rapid flares (A, B, C, D, E). It is very likely that the physical conditions within the emission region change during different flares. We therefore investigated the γ-ray spectra for the individual flares. Figure 7(b)-(f) show the γ-ray spectra of the source for the individual flares. For each flare we found that the spectrum shows a smooth rather than sharp break between 1 to 2 GeV. As discussed in Sect. 3.1.1, the bright flares (A to E) are further composed of a number of sub-flares. Because of low photon statistics, the curvature in the spectra of the sub-flares cannot be studied. Similarly, the absence of curvature was also noticed by Abdo et al. (2010e) during the two bright γ-ray sub-flares (sub-components of Flare B).
The variation of break energy (calculated using SBPL) with the photon flux variations is displayed in Fig. 8a. As we see here, no strong variation in break energy with respect to the flux variation is found in the source. This is similar to other bright Fermi blazars (Abdo et al. 2011; Ackermann et al. 2010; Rani et al. 2013b). The break energy Ebreak varies within a factor of 2, while, the flux varies by a factor of ≈ 16. Figure 8b displays the variation of ΔΓ = Γ2−Γ1 (see Sect. 2) with the break energy (Ebreak). Again, the break energy remains nearly constant for a significant variation in ΔΓ.
Parameters of fitted power laws.
 |
Fig. 8 a) Break energy plotted as a function of flux for the different activity periods. b) Change of the spectral slope ΔΓ as a function of break energy. In both plots, the squares represent the high-activity period, the diamonds the low-activity period, and the circles are the individual flares during the high-activity period. |
3.3. Gamma-ray Doppler factor
The minimum Doppler factor δγ can be
evaluated using the fact that the high-energy γ-ray photons can collide
with the softer radiation to produce e ± pairs. The
cross-section of this process is maximized
~σT/5 (Svensson 1987), where σT is the Thompson scattering
cross-section. This leads to a lower limit on δ with the requirement that
the optical depth
τγγ(ν) < 1
(Dondi & Ghisellini 1995; Finke et al. 2008),
![\begin{equation} \delta_{\gamma} > \left[ \frac{2^{a-1} (1+z)^{2-2a} \sigma_{\rm T} d_L^2}{m_{\rm e} c^4 t_{\rm var}} \epsilon f_{\epsilon^{-1}}^{\rm syn} \right]^\frac{1}{6 - 2a}, \end{equation}](/articles/aa/full_html/2013/09/aa21440-13/aa21440-13-eq96.png) (2)where a
is the power law index of synchrotron flux, i.e.,
(2)where a
is the power law index of synchrotron flux, i.e., 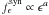 ,
me is the electron mass, and
ϵ = E/(mec2)
is the dimensionless energy of the γ-ray photon with energy
E for which the optical depth of the emitting region
τ = 1. The luminosity distance
dL corresponding to
z = 0.158 (Strauss et al. 1992) is
dL = 0.749 Gpc5 for a ΛCDM cosmology with Ωm = 0.27,
Ωλ = 0.73, and
H0 = 71 km s-1 Mpc-1 (Spergel et al. 2003). For the highest energy γ-ray (15.4 GeV)
photon observed in the source, we obtain
ϵ = 15.4 GeV/(5.11 × 10-4 GeV) = 3 × 104 and
ϵ-1 = 3.3 × 10-5. Using
,
me is the electron mass, and
ϵ = E/(mec2)
is the dimensionless energy of the γ-ray photon with energy
E for which the optical depth of the emitting region
τ = 1. The luminosity distance
dL corresponding to
z = 0.158 (Strauss et al. 1992) is
dL = 0.749 Gpc5 for a ΛCDM cosmology with Ωm = 0.27,
Ωλ = 0.73, and
H0 = 71 km s-1 Mpc-1 (Spergel et al. 2003). For the highest energy γ-ray (15.4 GeV)
photon observed in the source, we obtain
ϵ = 15.4 GeV/(5.11 × 10-4 GeV) = 3 × 104 and
ϵ-1 = 3.3 × 10-5. Using
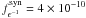 erg cm-2 s-1,
observed by Swift/UVOT from January 10 to 13, 2010 (Giommi et al. 2012) and tvar = 0.07 days
(taken as the rising time of the most rapid flare D), we obtain
δγ ≥ 10.4. The estimated
δγ value is comparable to
δVLBI = 5−12 found by Savolainen et al. (2006) and Jorstad
et al. (2005) using kinematics of the parsec scale VLBI jet derived at radio wavelength.
erg cm-2 s-1,
observed by Swift/UVOT from January 10 to 13, 2010 (Giommi et al. 2012) and tvar = 0.07 days
(taken as the rising time of the most rapid flare D), we obtain
δγ ≥ 10.4. The estimated
δγ value is comparable to
δVLBI = 5−12 found by Savolainen et al. (2006) and Jorstad
et al. (2005) using kinematics of the parsec scale VLBI jet derived at radio wavelength.
3.4. Size of the emission region
One can also obtain an estimate of the size of the emission region (R) using the the calculated Doppler factor and variability time scale (tvar), i.e., R ≤ c tvar δγ/(1 + z) (Rani et al. 2013a). Using tvar = 0.07 days, we obtain R ≤ 1.6 × 1014 δγ cm. A lower limit of the estimated Doppler factor δγ ≥ 10.4 gives R ≅ 1.6 × 1015 cm.
The angular size of the emission region is calculated using the equation (Rani et al. 2013a) 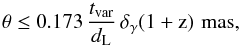 (3)where
dL is is the luminosity distance in Gpc.
Using tvar = 0.07 days,
dL = 0.749 Gpc,
δγ ≥ 10.4, we obtain
θ ≅ 0.52 μas which is much smaller than the size of
the core region θcore = (70 ± 10) μas
estimated using VLBA observations (Savolainen et al.
2008). It is worth pointing out that the R and
θ values found in this section could be smaller, since the variability
timescale only gives upper limits, or larger, since the Doppler factor used is a lower
limit.
(3)where
dL is is the luminosity distance in Gpc.
Using tvar = 0.07 days,
dL = 0.749 Gpc,
δγ ≥ 10.4, we obtain
θ ≅ 0.52 μas which is much smaller than the size of
the core region θcore = (70 ± 10) μas
estimated using VLBA observations (Savolainen et al.
2008). It is worth pointing out that the R and
θ values found in this section could be smaller, since the variability
timescale only gives upper limits, or larger, since the Doppler factor used is a lower
limit.
4. Discussion
4.1. Rapid gamma-ray flares
A prominent flaring activity was observed in the source between August 2009 and April 2010. The high-activity period of the source was later followed by a quiescent state which is still continuing. The fastest γ-ray flare observed in the source had a flux doubling timescale of 1.1 h. Gamma-ray flares on similar time scales are also observed in many other bright Fermi-blazars (Abdo et al. 2010c; Foschini et al. 2011, 2013; Saito et al. 2013; Nalewajko 2013; Abdo et al. 2011). Flux doubling times in the GeV band have been reported in PKS1510−089 to be less than 3 h (Brown 2013; Saito et al. 2013) or as short as 20 min (Foschini et al. 2013). Although these analyses did not properly take into account the discontinuous LAT exposure pattern as our method did, we conclude that the fastest flare observed in 3C 273 is comparable to the most rapid flares seen in other Fermi-LAT detected blazars.
Compared to the asymmetric profile of the very strong events of September 2009 (flare B), flares A, C, D, and E are characterized by symmetric profiles. The asymmetric profile can be explored in terms of a fast injection of accelerated particles and a slower radiative cooling and/or escape from the active region (Sikora et al. 2001). The result of the superposition and blending of several episodes of short duration could provide symmetric flare shapes (Valtaoja et al. 1999). Although the authors only consider external Comptonization in their model, it is worth pointing out that synchrotron self-Comptonization is also possible. Nalewajko (2013) argued that different Doppler boosting for different shells of the emission region could also be responsible for the asymmetry of γ-ray flares.
4.2. Origin of spectral breaks
Our analysis shows that the γ-ray spectrum of the source clearly deviates from a simple power law and is better described by a smooth break at ~1.2 GeV. For the individual bright flares the break energy lies between 1−2 GeV. During the individual flares, the change in spectral slope above and below the break energy, ΔΓ, varies between 0.47 to 1.36.
The observed spectral breaks in many bright Fermi blazars mostly lie within 2−10 GeVs (Poutanen & Stern 2010; Tanaka et al. 2011). Among the proposed scenarios, the absorption of γ-rays via photon-photon pair production on He II Lyman recombination continuum and lines within the broad-line region (BLR; e.g., Poutanen & Stern 2010; Tanaka et al. 2011, and references therein) can be responsible for the observed breaks. The γ-ray emitting region must be located within the BLR for this model to work. Alternatively, the γ-ray spectral breaks could also be explained by a combination of two Compton-scattered components, i.e., Compton scattering of the disk and BLR radiation as proposed by Finke & Dermer (2010). Dermer et al. (in prep.) proposes a three-parameter log-parabola model for the electron energy distribution, which naturally produces a GeV spectral cutoff by scattering Ly-α and BLR radiation. Another explanation refers to an intrinsic origin of the spectral breaks. A change in spectral index below and above the break of order ~0.5 can be interpreted as a typical cooling break associated with radiative losses (Abdo et al. 2009). The observed softening may instead be due to an intrinsic decline or break in the particle distribution also.
For 3C 273, the change in spectral slope (ΔΓ) above and below the break energy varies between 0.47 to 1.36. The estimated ΔΓ values for flare E with ΔΓ ~ 1.36 do not favor the standard radiative cooling models that predict a spectral break of 0.5 units. Although for flare A to D, ΔΓ is close to 0.5, but it is difficult to reconcile the constancy of the break energy with respect to the photon flux variations within the cooling break scenario. This does not argue in favor of the intrinsic origin of the observed spectral breaks in 3C 273 associated with the radiative cooling.
If the spectral breaks are due to γγ absorption, then one can estimate the frequency of the most efficiently interacting target photons with γ-rays. For head-on collisions, we have ν ≈ 6 × 1014(E/100 GeV)-1 Hz. A spectral break at Ebreak = 1−2 GeV in the observer frame corresponds to 0.86−1.73 GeV (Ebreak/(1 + z)) in the source frame. Therefore, for the spectral break within 0.86−1.73 GeV, the target photons fall within (3.4−6.9) × 1016 Hz, i.e., are extreme ultra-violet photons. This implies that the target photon energy is higher than the He II and H I recombination continuum. Moreover, spectral breaks close to 1 GeV are not very likely to be observed within this scenario because of low opacity at these energies (Poutanen & Stern 2010).
The optical-UV spectrum of the FSRQ 3C 273 shows a prominent excess of emission, which is mainly interpreted as a contribution of the accretion disk emission (see Ulrich 1981; Soldi et al. 2008, and references therein) or the presence of a hot corona particularly in the UV-Xray regime (Haardt et al. 1994). The excess optical-UV emission can be approximated by a black body with a temperature of ~21 000−26 000 K with a characteristic dimension of 1016 cm (Ulrich 1981; Pian et al. 1999). Consequently, Compton processes of a thermal plasma in the disk or in the corona can contribute efficiently to the high-energy radiation. The optical-UV spectrum of 3C 273 also shows strong emission lines, i.e., Ly-α, CIV, OVI, CIII, NIII, and SVI (e.g., Appenzeller et al. 1998; Paltani & Türler 2003, and references therein). Therefore it might not be surprising to find a contribution of inverse-Compton scattered radiation from both the disk and the BLR.
4.3. Location of the gamma-ray emission region
Assuming a conical geometry, the observed variability timescale of the source can also be used to put an upper limit on the distance of the emission region (rγ) from the central engine (Tavecchio et al. 2010) using rγ < (tvar c δ)/(θjet (1 + z)), where θjet is the opening angle of the jet. Moreover, as we are using a lower limit of Doppler factor δγ, the estimated value of rγ is supposed to be close to the actual value. Using the rising time of flare D, tvar = 0.07 day, δγ = 10, and θjet ~ 1.4° (Jorstad et al. 2005), we obtain rγ ~ 0.03 pc. However we stress that this is a very rough assumption as the jet may not be conical (Hada et al. 2012; Krichbaum et al. 2006). Moreover, the γ-ray emitting region of the jet could be much closer to the black hole (with a different Doppler factor) compared to the portion of the jet resolved by the VLBI (Rani et al. 2013a).
The energy dependence of the cooling timescale can also be used as an alternative approach to constrain the location of the γ-ray emission region (Dotson et al. 2012). For 3C 273, we found that the cooling timescales of the bright γ-ray flares are similar for E < 1 GeV and E > 1 GeV light curves with a possible minimum temporal resolution of 6 h. This implies that the allowed difference for FE < 1 GeV and FE > 1 GeV decay timescale is shorter than 6 h. An upper limit for the distance of the γ-ray emission region from the central engine is given by rγ < 2.3 × 1019 Γbulk [Δtmax,hr LMT,45/(1 + z)1/2]1/2 cm, where LMT,45 is the molecular torus luminosity in units of 1045 erg s-1 and Γbulk is the bulk Lorentz factor (Dotson et al. 2012). The molecular torus luminosity can be considered as a 0.1−0.5 fraction of the accretion disk luminosity (LAD). For 3C 273, we have LAD ~ 1.6 × 1046 erg s-1 (Kriss et al. 1999; Soldi et al. 2008; Giommi et al. 2012). Using LMT,45 ~ 1.6, Γbulk,10 = 10.6 ± 2.8 (Jorstad et al. 2005) and Δtmax < 6 h, we obtain rγ < 1.6 pc.
Finke & Dermer (2010) argue that a region
where the Compton-scattered disk and BLR emissions are approximately equal can explain the
Fermi-LAT emission in 3C 454.3. Their analysis implies that the
location of γ-ray emission region
(rγ) is
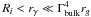 , where
Ri is the inner radius of BLR,
Γbulk is the bulk Lorentz factor, and
rg is Schwarzschild radius of the central
black hole. They also propose a robust solution where the external field energy density
from disk and BLR radiation decays as ~r-3. In this
scenario, a comparison of BLR and disk radiation gives
τBLR = (Ri/rg)-1
(τBLR is the Thomson depth of the BLR) for the emission
regions formed in the BLR. For 3C 273,
M9 = MBH/(109 M⊙) ≈ 0.9−2.4
(Paltani & Türler 2005; Peterson et al. 2004), where
MBH is the black hole mass. Using
τBLR = 0.01 to 0.1 (Boettcher & Dermer 1998), and Γbulk = 10.6 ± 2.8 (Jorstad et al. 2005), we obtain
0.005 pc < rγ < 1.4 pc.
The achromatic cooling of flares constrains
rγ within 1.6 pc. Therefore, the allowed
range of rγ using the two methods is
0.005 pc < rγ < 1.6 pc.
, where
Ri is the inner radius of BLR,
Γbulk is the bulk Lorentz factor, and
rg is Schwarzschild radius of the central
black hole. They also propose a robust solution where the external field energy density
from disk and BLR radiation decays as ~r-3. In this
scenario, a comparison of BLR and disk radiation gives
τBLR = (Ri/rg)-1
(τBLR is the Thomson depth of the BLR) for the emission
regions formed in the BLR. For 3C 273,
M9 = MBH/(109 M⊙) ≈ 0.9−2.4
(Paltani & Türler 2005; Peterson et al. 2004), where
MBH is the black hole mass. Using
τBLR = 0.01 to 0.1 (Boettcher & Dermer 1998), and Γbulk = 10.6 ± 2.8 (Jorstad et al. 2005), we obtain
0.005 pc < rγ < 1.4 pc.
The achromatic cooling of flares constrains
rγ within 1.6 pc. Therefore, the allowed
range of rγ using the two methods is
0.005 pc < rγ < 1.6 pc.
Our analysis suggests that the location of the γ-ray flaring activity observed in 3C 273 lies within 1.6 pc distance from the central engine. The achromatic cooling of the γ-ray flares below and above 1 GeV is consistent with the γ-ray emission region being located within the BLR. Also, the observed spectral breaks (at ~1−2 GeV) can be well described by γ-ray absorption within the BLR. Moreover, as a result of γγ pair production, the BLR of FSRQs is opaque to γ-rays above ~20 GeV, while the MT region is not (Donea & Protheroe 2003). As we saw in Sect. 3.1, the highest energy γ-ray photon observed for 3C 273 has energy of 15.4 GeV, and provided the fact that the source has not been detected at TeV energies so far; therefore, our results are consistent with the γ-ray emission site being located within the BLR.
4.4. The orphan flare E
We found that the ΔΓ for flare E (~1.5) is significantly different from that for flares A to D (~0.5). We note that flare E is the last flare observed during the high-activity period. Also, the break energy of flare E (Ebreak ~ 2 GeV) is higher than for the rest of the flares. Moreover, the doubling time scales of flare E are comparatively longer than those for flares A to D. We also notice that in the monthly averaged light curves (Fig. 1), flares A to D are the sub-components of a single flaring event, while flare E seems to be an independent flaring event.
The impact of the geometry of the BLR on the expected absorption, through the γγ process was recently discussed by Tavecchio & Ghisellini (2012). They argued that if the BLR has a full covering factor, the break energy does not change as long as the emission occurs within the BLR, but ΔΓ decreases as the emission region moves away from the central engine. A correlated ΔΓ – Ebreak variation is expected for the partially covered BLR. For flare A to D, the nearly constant values of ΔΓ and Ebreak suggest an approximately fixed location of the emission region from the black hole. The higher ΔΓ value for flare E implies a closer location to the central engine compared to flare A to D. However, the longer variability timescale for flare E could argue for an emitting region larger and farther out (if the jet is not stratified), contrary to the result from the larger ΔΓ.
With the recent jet kinematics study of 3C 273 at 7 mm wavelength, Jorstad et al. (2012) reported an ejection of four components during the high γ-ray activity period between mid-2009 to mid-2010. The authors identified two components during the high γ-ray activity period. The ejection of the fastest knot was associated with the most prominent γ-ray peak (flare B), while the brightest component had maximum flux coinciding with flare E. This suggests that the flares A-D and E are independent flaring events. Multiple shock scenarios and/or shock-shock interactions are among the feasible mechanisms for these flaring events (Sokolov & Marscher 2004; Fromm et al. 2012). It could also be possible that flare E is located at a similar distance from the central engine to flares A-D, but is in a different layer or sheath in the jet. This scenario is expected within the multi-zone emission model of Marscher (2013), which describes a stratified jet.
5. Conclusions
The continuous monitoring in the high-energy γ-ray band by the Fermi-LAT allows us to investigate the γ-ray flux and spectral variability of the FSRQ 3C 273. The source displays prominent flaring activity from August 2009 to April 2010. Five rapid flares are observed in the source during the interval. The rapid flares recur roughly at 50 day intervals. Each individual flare is also composed of sub-flaring components with characteristic rise and decay timescales as fast as few hours. The fastest γ-ray flare observed in the source has a characteristic flux doubling time scale of 1.1 h and is compatible with the fast γ-ray flares observed in other Fermi blazars. The 3 h peak flux of the flare above 100 MeV is (12.3 ± 2) × 10-6 ph cm-2 s-1, corresponding to an apparent isotropic γ-ray luminosity of 2.6 × 1046 erg s-1. The source exhibits a strong evolution of spectral index (Γ) during the different activity states.
The highest energy γ-ray photon (15.4 GeV) observed for the source arrives during this high-activity period. The minimum γ-ray Doppler factor δγ derived using γγ-opacity constraints for the highest energy γ-ray photon is 10, which is comparable to δVLBI ~ 5−11 obtained using jet kinematics (Savolainen et al. 2006; Jorstad et al. 2005). Causality arguments constrain the size of the emission region to 1.6 × 1015 cm.
The γ-ray spectra measured over this period show clear deviation from a simple power law with a break in the 1−2 GeV energy range. During different flaring epochs, no strong evolution of Ebreak is found. We have discussed possible explanations for the origin of γ-ray spectral breaks. The different possible scenarios allow us to constrain the location of γ-ray emission region(s) within the BLR (< 1.6 pc). We argue that the observed γ-ray emission in 3C 273 is unlikely to have a contribution of the molecular torus photons in external Comptonization. We found that the spectral parameters (Ebreak and ΔΓ) of flare E are not comparable to the spectral parameters of flares A to D. A comparison of the γ-ray flares with the jet kinematics (Jorstad et al. 2012) suggests that flare E has a different physical origin. A detailed discussion of physical mechanisms, along with results of the study focused on broadband flux variability and spectral modeling of the source will shed more light on this, and will be given in a separate paper (Rani et al., in prep.).
The results are not sensitive to dL = 0.784 Gpc for the recent Planck measurements of cosmology parameters (Planck Collaboration et al. 2013).
Acknowledgments
The Fermi-LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat á l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK), and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council, and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. We would like to thank Stefano Ciprini, the internal referee for the Fermi-LAT Collaboration, Stefanie Komossa, Seth Digel, Marco Ajello, and Justin Finke for their useful suggestions and comments. We thank the referee for constructive comments that have helped us to improve the paper. B.R. gratefully acknowledges the travel support the COSPAR Capacity-Building Workshop fellowship program.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJS, 183, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010a, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 722, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 710, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 710, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010e, ApJ, 714, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 733, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2010, ApJ, 721, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Krautter, J., Mandel, H., et al. 1998, ApJ, 500, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Bastieri, D. 2009, The Astronomer’s Telegram, 2168, 1 [NASA ADS] [Google Scholar]
- Boettcher, M., & Dermer, C. D. 1998, ApJ, 501, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. M. 2013, MNRAS, 431, 824 [Google Scholar]
- Dondi, L., & Ghisellini, G. 1995, MNRAS, 273, 583 [NASA ADS] [Google Scholar]
- Donea, A.-C., & Protheroe, R. J. 2003, Astropart. Phys., 18, 377 [Google Scholar]
- Dotson, A., Georganopoulos, M., Kazanas, D., & Perlman, E. S. 2012, ApJ, 758, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Escande, L., & Tanaka, Y. T. 2009, The Astronomer’s Telegram, 2328, 1 [NASA ADS] [Google Scholar]
- Finke, J. D., & Dermer, C. D. 2010, ApJ, 714, L303 [NASA ADS] [CrossRef] [Google Scholar]
- Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, ApJ, 686, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Ghisellini, G., Tavecchio, F., Bonnoli, G., & Stamerra, A. 2011, A&A, 530, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foschini, L., Bonnoli, G., Ghisellini, G., et al. 2013, A&A, 555, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromm, C. M., Perucho, M., Ros, E., et al. 2012, Int. J. Mod. Phys. Conf. Ser., 8, 323 [CrossRef] [Google Scholar]
- Giommi, P., Polenta, G., Lähteenmäki, A., et al. 2012, A&A, 541, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Kino, M., Nagai, H., et al. 2012, ApJ, 760, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S., Marscher, A., Smith, P., et al. 2012, Int. J. Mod. Phys. Conf. Ser., 8, 356 [CrossRef] [Google Scholar]
- Krichbaum, T. P., Graham, D. A., Witzel, A., et al. 2001, in Particles and Fields in Radio Galaxies Conference, eds. R. A. Laing, & K. M. Blundell, ASP Conf. Ser., 250, 184 [Google Scholar]
- Krichbaum, T. P., Graham, D. A., Bremer, M., et al. 2006, J. Phys. Conf. Ser., 54, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Kriss, G. A., Davidsen, A. F., Zheng, W., & Lee, G. 1999, ApJ, 527, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Lott, B., Escande, L., Larsson, S., & Ballet, J. 2012, A&A, 544, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marscher, A. P. 2013 [arXiv:1304.2064] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K. 2013, MNRAS, 430, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Paltani, S., & Türler, M. 2003, ApJ, 583, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Paltani, S., & Türler, M. 2005, A&A, 435, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pian, E., Urry, C. M., Maraschi, L., et al. 1999, ApJ, 521, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2013, A&A, submitted [arXiv:1303.5076] [Google Scholar]
- Poutanen, J., & Stern, B. 2010, ApJ, 717, L118 [Google Scholar]
- Rani, B., Gupta, A. C., Strigachev, A., et al. 2010, MNRAS, 404, 1992 [NASA ADS] [Google Scholar]
- Rani, B., Gupta, A. C., Joshi, U. C., Ganesh, S., & Wiita, P. J. 2011, MNRAS, 413, 2157 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, B., Krichbaum, T. P., Fuhrmann, L., et al. 2013a, A&A, 552, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Krichbaum, T. P., Lott, B., Fuhrmann, L., & Zensus, J. A. 2013b, Adv. Space Res., 51, 2358 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, S., Stawarz, Ł., Tanaka, Y. T., et al. 2013, ApJ, 766, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., & Tornikoski, M. 2006, A&A, 446, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., & Tornikoski, M. 2008, in Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, eds. T. A. Rector, & D. S. De Young, ASP Conf. Ser., 386, 451 [Google Scholar]
- Savolainen, T., Homan, D. C., Hovatta, T., et al. 2010, A&A, 512, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, M. 1963, Nature, 197, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Błażejowski, M., Begelman, M. C., & Moderski, R. 2001, ApJ, 554, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sokolov, A., & Marscher, A. P. 2004, in X-ray Timing 2003: Rossi and Beyond, eds. P. Kaaret, F. K. Lamb, & J. H. Swank, AIP Conf. Ser., 714, 198 [Google Scholar]
- Soldi, S., Türler, M., Paltani, S., et al. 2008, A&A, 486, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Huchra, J. P., Davis, M., et al. 1992, ApJS, 83, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Svensson, R. 1987, MNRAS, 227, 403 [NASA ADS] [Google Scholar]
- Swanenburg, B. N., Hermsen, W., Bennett, K., et al. 1978, Nature, 275, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y. T., Stawarz, Ł., Thompson, D. J., et al. 2011, ApJ, 733, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2012, MNRAS, submitted [arXiv:1209.2291] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Ghirlanda, G. 2010, MNRAS, 405, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, M.-H. 1981, Space Sci. Rev., 28, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Valtaoja, E., Lähteenmäki, A., Teräsranta, H., & Lainela, M. 1999, ApJS, 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) Weekly (blue circles) and monthly (red open symbols) averaged flux (E > 100 MeV) light curves of 3C 273 measured by Fermi-LAT since its launch. The green histogram represents the arrival time distribution of E > 10 GeV photons associated with 3C 273. The yellow box represents the high γ-ray flux activity period. b) One-day averaged light curve of the source over the high-activity period within the box shown at the top of the figure. |
| In the text | |
 |
Fig. 2 Light curves of 3C 273 above 100 MeV with time binning of 12 h (flare C and E) and 3 h (flare D). The lines are the fitted sub-flaring components (see Table 1). |
| In the text | |
 |
Fig. 3 Top: exposure rate during flare D. Middle: predicted (red) and observed (blue) source photon detection rates. Bottom: photon flux light curve of flare D. The red curve shows the results of the time-domain-unbinned analysis, and the blue (15%) and green (25%) symbols represent the adaptive-binning analysis results. |
| In the text | |
 |
Fig. 4 One-day averaged γ-ray light curve of the source below (bottom) and above (top) 1 GeV during the high-activity period. |
| In the text | |
 |
Fig. 5 DCF curve of the 12 h binned γ-ray light curves below and above 1 GeV. The dotted line marks a possible time lag of 0 ± 0.25 day. |
| In the text | |
 |
Fig. 6 Top panel: the constant uncertainty (15%) light curve of 3C 273 above E0 obtained with the adaptive binning method over the high-activity period (see text for details). The lower panel shows the variations in Γ during this period. The vertical columns separate the different flaring periods. Bottom: Γ vs. flux above E0 for flare C, D, and E. |
| In the text | |
 |
Fig. 7 Gamma-ray spectral energy distributions of 3C 273 during different activity states along with the fitted PL (dashed curve), logP (dotted-dashed curve), and SBPL (solid curve) spectral models. |
| In the text | |
 |
Fig. 8 a) Break energy plotted as a function of flux for the different activity periods. b) Change of the spectral slope ΔΓ as a function of break energy. In both plots, the squares represent the high-activity period, the diamonds the low-activity period, and the circles are the individual flares during the high-activity period. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


